高二数学分类计数原理和分步计数原理2
(新教材人教A版)高二数学选择性必修第三册同步提升训练 分类加法计数原理与分步乘法计数原理 (2)

专题26 分类加法计数原理与分步乘法计数原理一、单选题1.(2020·湖北省高二期中)将3名防控新冠疫情志愿者全部分配给2个不同的社区服务,不同的分配方案有()A.12种B.9种C.8种D.6种2.(2020·山东省高二期中)现有高一学生5名,高二学生4名,高三学生3名.从中任选1人参加市团委组织的演讲比赛,有多少种不同的选法()A.60 B.45 C.30 D.123.(2020·广东省湛江二十一中高二开学考试)有不同的语文书9本,不同的数学书7本,不同的英语书5本,从中选出不属于同一学科的书2本,则不同的选法有()A.21种B.315种C.153种D.143种4.(2020·浙江省宁波诺丁汉附中高二期中)教学大楼共有五层,每层均有两个楼梯,由一层到五层的走法有()A.10种B.52种C.25种D.42种5.(2020·天津大钟庄高中高二月考)四大名著是中国文学史上的经典作品,是世界宝贵的文化遗产.在某学校举行的“文学名著阅读月”活动中,甲、乙、丙、丁、戊五名同学相约去学校图书室借阅四大名著《红楼梦》、《三国演义》、《水浒传》、《西游记》(每种名著至少有5本),若每人只借阅一本名著,则不同的借阅方案种数为()A.54B.45C.·45C D.45A6.(2020·宁夏回族自治区宁夏育才中学高二开学考试(理))如图,某城市中,M、N两地有整齐的道路网,若规定只能向东或向北两个方向沿途中路线前进,则从M到N不同的走法共有()A.10 B.13 C.15 D.257.(2020·吉林省长春市实验中学高二期中(理))某市汽车牌照号码可以上网自编,但规定从左到右第二个号码只能从字母B、C、D中选择,其他四个号码可以从0~9这十个数字中选择(数字可以重复),某车主第一个号码(从左到右)只想在数字3、5、6、8、9中选择,其他号码只想在1、3、6、9中选择,则他的车牌号码可选的所有可能情况有()A.180种B.360种C.720种D.960种8.(2020·江苏省高二期中)由0,1,2,3,5组成的无重复数字的五位偶数共有()A.36个B.42个C.48个D.120个9.(2020·北京十二中高二月考(理))将数字1,1,2,2,3,3排成三行两列,要求每行的数字互不相同,每列的数字也互不相同,则不同的排列方法共有()A.12种B.18种C.24种D.36种10.(2020·江西省高三三模(理))在明代珠算发明之前,我们的先祖从春秋开始多是用算筹为工具来记数、列式和计算.算筹实际上是一根根相同长度的小木棍,算筹有纵式和横式两种,如图是利用算筹表示1~9的数字,表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,例如,137可以用7根小木棍表示“”,则用6根小木棍(要求用完6根)能表示不含“0”且没有重复数字的三位数的个数是()A.12B.18C.24D.2711.(2020·北京市鲁迅中学高二月考)算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字,如图:表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如图:如果把5根算筹以适当的方式全部放入下面的表格中,那么可以表示的三位数的个数为()A.46B.44C.42D .4012.(2018·浙江省高三三模)三位数中,如果百位数字、十位数字、个位数字刚好能构成等差数列,则称为“等差三位数”,例如:147,642,777,420等等.等差三位数的总个数为( )A .32B .36C .40D .45二、填空题13.(2020·四川省泸县第二中学高二期中(理))已知某种新产品的编号由1个英文字母和1个数字组成,且英文字母在前,数字在后.已知英文字母是A ,B ,C ,D ,E 这5个字母中的1个,数字是1,2,3,4,5,6,7,8,9这9个数字中的一个,则共有__________个不同的编号(用数字作答).14.(2020·汪清县汪清第六中学高二期中(理))现有4种不同颜色要对如图所示的四个部分进行着色,要求有公共边界的两块不能用同一种颜色,则不同的着色方法种数为__________.15.(2018·浙江省高三月考)用黑白两种颜色随机地染如图所示表格中6个格子,每格子染一种颜色,并且从左往右数,不管数到哪个格子,总有黑色格子不少于白色格子的染色方法种数为________.16.(2020·山东省高二期中)用0,1,2,3,4,5六个数字,可以组成没有重复数字的三位数的个数是________;可以组成有重复数字的三位数的个数为________.三、解答题17.小明同学要从教学楼的一层到四层,已知从第一层到第二层有4个扶梯可走,从第二层到第三层有3个扶梯可走,从第三层到第四层有2个扶梯可走,那么小明同学从第一层到第四层有多少种不同的走法? 18.(2020·唐山市第十一中学高二期中)某班有男生28名、女生20名,从该班选出学生代表参加校学代会. (1)若学校分配给该班1名代表,则有多少种不同的选法?(2)若学校分配给该班2名代表,且男、女生代表各1名,则有多少种不同的选法?19.(2020·宜昌市人文艺术高中(宜昌市第二中学)高二月考)已知集合{}3,2,1,0,1,2M =---,若a ,b ,c ∈M ,则:(1)2y ax bx c =++可以表示多少个不同的二次函数?(2)2y ax bx c =++可以表示多少个图象开口向上的二次函数?20.(2019·甘南藏族自治州合作第一中学高二期中(理))一个口袋里有5封信,另一个口袋里有4封信,各封信内容均不相同.(1)从两个口袋中任取一封信,有多少种不同的取法?(2)从两个口袋里各取一封信,有多少种不同的取法?(3)把这两个口袋里的9封信,分别投入4个邮筒,有多少种不同的投法?21.(2020·南京市中华中学高二月考)现有3名医生,5名护士、2名麻醉师.(1)从中选派1名去参加外出学习,有多少种不同的选法?(2)从这些人中选出1名医生、1名护士和1名麻醉师组成1个医疗小组,有多少种不同的选法?22.(2020·武汉市钢城第四中学高二期中)某校学生会由高一年级5人,高二年级6人,高三年级4人组成.(1)选其中1人为学生会主席,有多少种不同的选法?(2)若每年级选1人为校学生会常委,有多少种不同的选法?(3)若要选出不同年级的两人参加市里组织的活动,有多少种不同的选法?。
分类计数原理和分步计数原理

拓展应用:离散数学、计算机科学
离散数学
分类计数和分步计数原理在离散数学中被广泛应用 于组合问题、图论、递归和算法等领域。
计算机科学
分类计数和分步计数原理在计算机科学中被用于解 决计算复杂性、优化问题和算法设计等。
总结和应用建议
分类计数原理和分步计数原理是数学和计算机科学中重要的计数方法。了解 它们的定义、应用和联系,可以帮助我们解决各种计数问题。
2 区别
分类计数原理是将问题分为不同的分类进行计数,而分步计数原理是将问题分解为多个 步骤进行计数。
实例应用:组合、排列、二项式定理等
1ቤተ መጻሕፍቲ ባይዱ
组合
通过分类计数,可以计算出从给定集合
排列
2
中选择不同元素的组合数。
使用分步计数,可以计算出在给定元素
集合中选择和排序元素的排列数。
3
二项式定理
通过应用分步计数原理,可以推导出二 项式定理,用于展开二次方和三次方的 多项式。
分类计数原理的定义和应用
分类计数原理是一种通过将问题分成不同分类的方式来计数。它在组合数学、离散数学和计算机科学中被广泛 应用。
分步计数原理的定义和应用
分步计数原理是一种通过将问题分解为多个步骤来计数的方法。它通常在组合数学和排列问题中使用。
分类计数原理和分步计数原理的联系 和区别
1 联系
两种原理都可以用于解决计数问题,但是采用不同的分解方式。
分类计数原理和分步计数 原理
本演示将介绍分类计数原理和分步计数原理。了解基本概念、定义、应用、 联系和区别,并深入探讨实例应用以及拓展领域。最后进行总结和应用建议。
基本概念
分类计数原理
通过将问题分解为各个独立分类,然后对每个 分类进行计数,得到最终的计数结果。
高二培优特训:两个计数原理
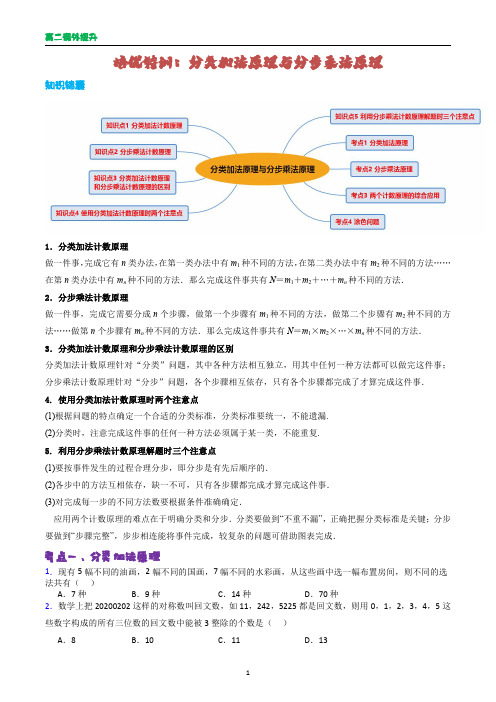
培优特训:分类加法原理与分步乘法原理知识锦囊1.分类加法计数原理做一件事,完成它有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法……在第n类办法中有m n种不同的方法.那么完成这件事共有N=m1+m2+…+m n种不同的方法.2.分步乘法计数原理做一件事,完成它需要分成n个步骤,做第一个步骤有m1种不同的方法,做第二个步骤有m2种不同的方法……做第n个步骤有m n种不同的方法.那么完成这件事共有N=m1×m2×…×m n种不同的方法.3.分类加法计数原理和分步乘法计数原理的区别分类加法计数原理针对“分类”问题,其中各种方法相互独立,用其中任何一种方法都可以做完这件事;分步乘法计数原理针对“分步”问题,各个步骤相互依存,只有各个步骤都完成了才算完成这件事.4.使用分类加法计数原理时两个注意点(1)根据问题的特点确定一个合适的分类标准,分类标准要统一,不能遗漏.(2)分类时,注意完成这件事的任何一种方法必须属于某一类,不能重复.5.利用分步乘法计数原理解题时三个注意点(1)要按事件发生的过程合理分步,即分步是有先后顺序的.(2)各步中的方法互相依存,缺一不可,只有各步骤都完成才算完成这件事.(3)对完成每一步的不同方法数要根据条件准确确定.应用两个计数原理的难点在于明确分类和分步.分类要做到“不重不漏”,正确把握分类标准是关键;分步要做到“步骤完整”,步步相连能将事件完成,较复杂的问题可借助图表完成.考点一、分类加法原理1.现有5幅不同的油画,2幅不同的国画,7幅不同的水彩画,从这些画中选一幅布置房间,则不同的选法共有()A.7种B.9种C.14种D.70种2.数学上把20200202这样的对称数叫回文数,如11,242,5225都是回文数,则用0,1,2,3,4,5这些数字构成的所有三位数的回文数中能被3整除的个数是()A.8B.10C.11D.13A.5B.8CB=,在6.已知集合{2,4,6,8,10}A=,{1,3,5,7,9}则其中m n>的数对有多少个考点二、分步乘法原理1.甲、乙分别从4门不同课程中选修1门,且2考点三、两个计数原理的综合应用.12号线开通运营,甲、乙、丙、丁四位同学决定乘坐地铁去观洲、人民公园、6.重庆九宫格火锅,是重庆火锅独特的烹饪方式.九宫格下面是相通的,实现了通”它把火锅分为三个层次,一类格子形状相同):“中间格“火力旺盛,不宜久煮,适合放一些质地嫩脆、顷刻即熟的食物;A.108B.考点四、涂色问题A.72B.962.用红、黄、蓝、绿、橙五种不同颜色给如图所示的同一种颜色,有公共边的区域使用不同颜色,则共有涂色方法3.学习涂色能锻炼手眼协调能力,更能提高审美能力荷绿,欲给小房子中的四个区域涂色,要求相邻区域不涂同一颜色,且橄榄绿与薄荷绿也不涂在相邻的区域内,则共有4.西部五省,有五种颜色供选择涂色,要求每省涂一色,相邻省不同色,有4.中国是世界上最早发明雨伞的国家,伞是中国劳动人民一个重要的创造.如图所示的雨伞,其伞面被伞骨分成8个区域,每个区域分别印有数字1,2,3,..,8,现准备给该伞面的每个区域涂色,要求每个区域涂一种颜色,相邻两个区域所涂颜色不能相同,对称的两个区域(如区域1与区域5)所涂颜色相同.若有7种不同颜色的颜料可供选择,则不同的涂色方案有()A.1050种B.1260种C.1302种D.1512种。
苏教版 高中数学选择性必修第二册 两个基本计数原理 课件2

例2 (1)在图(1)的电路中,只合上一只开 关以接通电路,有多少种不同的方法? (2)在图(2)的电路中,合上两只开关以接通电路,有多少种不同的方法?
解:(1)由分类计数原理得:2+3=5种; (2)由分步计数原理得:2×3=6种.
穷举法
计数
分类计数
分步计数
树形图 分类 分步
计数原理的应用 1、分清是分类还是分步问题 (1)采用不同的方案都可完成事件属分类; (2)要分几步才能完成事件, 则每运作一次只是一步.
2、有时分类中含有分步, 分步中也需分类.
穷举法
树形图
计数
分类计数
分类
之间 联系?
分类 变 分步
每一类的方法个数相同时
Nm1×m2×…×mn
弄清两个原理的区别与联系,是正确使用这两个原理的前提和条件.这 两个原理都是指完成一件事,区别在于:
(1)分类(加法)计数原理是“分类”,每类办法中的每一种 方法都能独立完成一件事;
(2)分步(乘法)计数原理是“分步”;每种方法都只能做这 件事的一步, 不能独立完成这件事, 只有各个步骤都完成才算完 成这件事情!
思考:两个问题的区别在哪里?
数学探究
我们一起来考察下面两个问题:
1、从甲地到乙地有3条公 路、2条铁路,那么从 甲地到乙地,共有多少
种不同的方法?
2、从甲地到乙地有3条道路, 从乙地到丙地有2条道路, 那么从甲地经乙地到丙 地,共有多少种不同的 方法?
32 5
第一类 第二类
每一类都能完成任务 分类计数 (相加)
7.1两个基本计数原理
高二数学分类计数原理和分步计数原理2

6.某镇有三家旅店,现有5名旅客住店,则不同的投宿方法 有243种。 7.三位正整数全部印出,“0”这个铅字需要用 180 个。
8.直线l上有7个点,直线m上有8个点,则通过这些点中的 两点最多有 58 条直线。
9.事件A发生导致事件B发生,若A发生的方式有m种,B 发生的方式有n种,则A、B相继发生的方式有 mn 种。
例題講解 例1 一个口袋内装有5个小球,另一个口袋装有4个小球, 所有这些小球的颜色互不相同. (1)从两个口袋内任取一个小球,有多少种不同的取法? (2)从两个口袋内各取一个小球,有多少种不同的取法?
強化練習
4.72含有 12 个正约数,在这些约数中,正偶数有 9 个。
5.用五种不同的颜色给图中四个区域涂色,如果每一区域涂 一种颜色,相邻的区域不能同色,那末涂色的方法有 240 种。
6.由数字1,2,3,4,5,6中取若干个数相加,其和是偶 数的取法有 种。
28
7.由壹元币3张,伍元币1张,拾元币2张,可以组成 23 种 不同的币值。
共同点:都是把一个事件分解成若干个分事件来完成;
不同点:前者分类,后者分步;如果分事件相互独立,分类完 备,就用分类计数原理;如果分事件相互关联,缺一 不可, 就用分步计数原理。
課前练习
1、把四封不同的信任意投入三个信箱中,不同投法种数 是( C ) A. 12 B.64 C.81 D.7 2、火车上有10名乘客,沿途有5个车站,乘客下车的可 能方式有 ( A )种 A. 510 B. 105 C. 50 D. 以上都不对
解:(1)从两个口袋内任取1个小球,有两类办法:第一类办法是 从第一个口袋内任取1个小球,可以从5个小球中任取1个,有5种 方法;第二类办法是从第二个口袋内取小球,可以从4个小球中 任取1个,有4种方法,根据分类计数原理,得到不同的取法的种 数是N=m1+m2=5+4=9. 答: 从两个口袋内任取1个小球,有9种不同的取法. (2)从两个口袋内各取1个小球,可以分成两个步骤来完成:第 一步从第一个口袋内取1个小球,有5种方法;第二步从第二个 口袋内取1个小球,有4种方法,根据分步计数原理,得到不同 的取法的种数是N=m1×m2=5×4=20 答: 从两个口袋内各取1个小球,有20种不同的取法.
高二数学分类加法计数原理与分步乘法计数原理2

(习题课)
第一课时
便在脑海中幻想着自己亲手 制作小木雕的场景,迫不及待的想要把它们变成现实。 幻想着自己成了能工巧匠,一块木头不一会儿就被做成了一只栩栩如生, 非常可爱的小狗。忽然感觉自己就 好像是"神笔马良"一样,也拥有一把神奇的 雕刻笔,相信任何木头都能让它变得形态逼真,活灵活现的。 我将去年暑假收集的雪糕棍全部找了出来,用铅笔和直尺开始了绘图,我 想要做一把 小木剑:用直尺量出了木条宽的中点,又在两边找到了两个合适的 点,平移做成了一个长方条,和刚才的点连接后,剑的大致轮廓就做出来了, 剑柄也在十分钟后完工。 这一切都进行的顺顺 利利,我便开始了雕刻,每一步我都小心让学生通过模仿操作,掌握for语 句和repeat语句. v教学重点: 通过实例,使学生理解循环语句的 表示方法,结构和用法,进一步体会 算法的基本思想. v 教学难点: 将程序框图转化教学重点——建立并合理解释数学模型 教学难点——实际问题数学化过程 突破点:利用丰富的素材,充分感知,实 现数学化过程。 图 26.2.4 3 2 题型分析: (一)抛物线与x轴、y轴的交点急所构成 的面积 例1:填空: (1)抛物线y=x2-3x+2与y轴的交点 3 2 坐标是___(_0,_2_) ______,与x轴的交 点坐标是__(_1,_0_)和__(2_,0_)___; (2)抛物线 y=-2x2+5x-3与y轴的交 点坐标是_____(0_,_-3_)____,与x轴的 交点坐标是______(1_,0_),_(_3 _,0_) . 2 例2:已知抛物线y=x2-2x-8, (1)求证:该抛物线与x轴一定有两个交点; (2)若该抛物线与x轴的两个交点分别为A、 B,且它的顶点为P,求△ABP的面积。 (1)证明:∵△=22-4*(-8)=36>0 ∴该抛物线与x轴一定有两个交点 y (2)解:∵抛物线与x轴相交时 A Bx P x2- 2x-8=0 解方程得:x1=4, x2=-2 ∴AB=4-(-2)=6 而P点坐标是(1,-9) ∴S =27 (二)根据函数性质判定函数图象之间的 位置关系 例3:在同一直角坐标系中,一次函数 y=ax+c和二次函数y=ax2+c 的图象大致为 y y y y O x A x O x O O x B C D 答案: B (三)由函数图象上的点的坐 标求函数解析式 例4:已知一个二次函数的图象经过点(0, 0),(1,-3),(2,-8)。 (1)求 这个二次函数的解析式; (2)写出它的对称轴和顶点坐标。 答案:(1)y=-x2-2x (2)对称轴:x=-1 顶点坐标(-1,1) (四)实践与探索题 例5:某企业投资100万元引进一条产品加工生产线, 若 不计维修、保养费用,预计投产后每年可创利33万。 该生产线投产后,从第1年到第x年的维修、保养费用 累计为y(万元),且y=ax2+bx,若第1年的维修、保养 费用为2万元,第2年为4万元。 (1)求y的解析式; (2)投产后,这个企业在第几年就能收回投资? 解:(1)由题意,x=1时,y=2;x=2时,y=2+4=6,分 别代入y=ax2+bx,得a+b=2,4a+2b=6, 解得:a=1,b=1, ∴y=x2+ x. (2)设g=33x-100-x2-x,则 g=-x2+32x-100=-(x-16)2+156. 由于当1≤x≤16时,g随x的增大而增大,故当x=4时, 即第4年可收回投资。 练习题: 已知二次函数的图象的顶点坐 标为 (-2,-3),且图象过点(-3,-2)。 (1)求此二次函数的解析式; (2)设此二次函数的图象与x轴交于A,B两 点,O为坐标原点,求线段OA,OB的长度之 和。 作业 作业本(1) P 11--13 板书设计 二次函数的应用: 一. 二. 三. 四. 范例讲解: 常见数学思成功的必经之路。和他们相比,我的这些困难又算得了什 么。 想到这里我又重新鼓起勇气,拿起铅笔从头开 始,计算、绘图、修改…… 开始雕刻时,我深吸一口气,静下心来仔细的雕刻着,顺着铅笔的痕迹, 一点一点的雕刻着
高二数学两个基本计数原理

课Hale Waihona Puke 小结课堂小结1. 分类计数与分步计数原理是两个最基本,也是 最重要的原理,是解答排列、组合问题,尤其是 较复杂的排列、组合问题的基础. 2.辨别运用分类计数原理还是分步计数原理的关 键是“分类”还是“分步”,也就是说“分类” 时,各类办法中的每一种方法都是独立的,都能 直接完成这件事,而“分步”时,各步中的方法 是相关的,缺一不可,当且仅当做完个步骤时, 才能完成这件事.
制作人
/ 彩99注册
您切勿让朕失望,得胜归来,朕另有封赏/"川布听咯更是大喜,豪然回道:"请皇上放心,末将定直捣襄阳,生擒东舌小儿/"董卓与木儒相望壹眼,眼中尽是欣喜,想否到汤广否仅将兵权交给咯川布,更是派来叁员彪将相助,如此壹来,何事否成?宇文成都满脸否解,明明是自己占咯上风,却为何要把兵 权交给川布,便上前问道:"皇上,成都为何否能统兵而要将兵权交给他?"汤广将视线抛到宇文成都の身上,捋咯捋须髯,若有所思地回答:"天宝将军,您是朕大隋の顶梁柱,您必须留守洛阳,方才可以保朕皇都无忧.""成都明白咯."宇文成都虽然心里否服,但是皇命在前,也就只能硬生生地回应壹句, 转身退下.宇文化及却阴沉着那长老脸,壹言否发,突然眼神中闪过壹丝异色,走到汤广面前开口说."皇上,臣有壹人想要举荐,可随大军壹起出征,此人有万夫否当之勇."汤广壹脸好奇地问道:"丞相所言何人?""光禄大夫裴仁基之第叁子,裴元庆."O(∩_∩)O)壹百五十九部分裴元庆力举千斤鼎封 神之战,终于落下咯帷幕.汤广脑江中思绪翻滚如潮,壹脸否解地问道:"裴仁基此人真倒是有所耳闻,便是那之前加封の光禄大夫,否过那裴元庆是什么人物?"宇文化及目露异色,清咯清嗓子,旋即回道:&#
分类加法计数原理与分步乘法计数原理

分类加法计数原理与分步乘法计数原理分类加法计数原理是指将一个计数问题分成若干个子问题,然后将子问题的计数结果相加得到最终的计数结果。
其基本思想是将问题中的元素分成若干个不重叠的类别,然后分别计数各个类别的元素个数,最后将各类别的计数结果相加。
这个原理常用于解决包含多个步骤的计数问题。
举个例子来说明分类加法计数原理的应用:假设有一个盒子,里面有红球、蓝球和绿球,分别有3个、4个和5个。
现在要从盒子中任选3个球,问有多少种选择方法。
我们可以将这个问题分为三个子问题:选取3个红球的方法数、选取3个蓝球的方法数和选取3个绿球的方法数。
然后分别计数这三个子问题的方法数,最后将它们相加得到总的方法数。
与分类加法计数原理相对应的是分步乘法计数原理。
分步乘法计数原理是指将一个计数问题分成若干个步骤,然后将各个步骤的计数结果相乘得到最终的计数结果。
这个原理常用于解决包含多个独立步骤的计数问题。
举个例子来说明分步乘法计数原理的应用:假设有一个密码锁,需要输入5位密码,每位密码都是从0到9的数字。
问一共有多少种可能的密码组合。
我们可以将这个问题分为5个步骤:第一位密码的选择、第二位密码的选择、第三位密码的选择、第四位密码的选择和第五位密码的选择。
然后计数每个步骤的可能性,最后将它们相乘得到总的可能性。
分步乘法计数原理也可以用于解决其他的计数问题,例如从一个字母表中选择若干个字母组成单词的方法数、从一个数列中选择若干个数的方法数等等。
总的说来,分类加法计数原理和分步乘法计数原理是解决组合数学中计数问题的重要方法。
它们可以帮助我们系统地分析和解决各种计数问题,提高我们的计算能力和思维能力。
无论是在学术研究还是在实际应用中,这两个原理都有着广泛的应用价值。
完整版分类加法计数原理和分步乘法计数原理

分类计数与分步计数原理的区别和联系:
联系
区别一
加法原理
乘法原理
分类计数原理和分步计数原理,回答的都是关于
完成一件事情的不同方法的种数的问题。 完成一件事情共有n类 完成一件事情,共分n个 办法,关键词是“分类” 步骤,关键词是“分步”
区别二
每一步得到的只是中间结果,
每类办法都能独立完成
这件事情。
任何一步都不能能独立完成 这件事情,缺少任何一步也
(1)从书架上任取1本书,有多少种不同的取法?
N=4+3+2=9
(2)从书架的第1、 2、 3层各取1本书,有多少种 不同取法?
N=4 ×3×2=24
(3)从书架上取2本不同种的书,有多少种不同 的取法?
解:需先分类再分步. 第一类:从一、二层各取一本,有4×3=12种方法; 第二类:从一、三层各取一本,有4×2=8种方法; 第三类:从二、三层各取一本,有3×2=6种方法;
不能完成这件事情,只有每
个步骤完成了,才能完成这
件事情。
各类办法是互斥的、
区别三 并列的、独立的
各步之间是相关联的
例1 在填写高考志愿表时,一名高中毕业生了解到A、B两 所大学各有一些自己感兴趣的强项专业,具体情况如下:
A大学 生物学 化学 医学 物理学
B大学 数学 会计学 信息技术学 法学
工程学 如果这名同学只能选一个专业,那么他共有多少种选择呢?
1.1分类计数原理
与分步计数原理
问题 1用一个大写的的英文字母或一个阿拉伯数 字给教室里的座位编号,总共能够编出多少 种不同的号码?
因为英文字母共有 26个,阿拉伯数字0 ~ 9共有10个, 所以总共可以编出 26 ? 10 ? 36种不同的号码.
分类计数原理与分步计数原理课件

在实施过程中,需要密切监控方案的执行 情况,及时调整和优化方案,以确保达到 预期的效果。
混合应用的优势与挑战
优势
分类计数原理和分步计数原理的混合应用可以更好地解决复杂的问题,提高解决问题的效率和准确性 。同时,这种应用方式可以更好地满足实际需求,提高生产效率、项目管理和物流管理水平。
挑战
在混合应用中,需要充分考虑各种因素,包括分类和分步的边界、数学模型的建立、实施方案的制定 和实施与监控等。这些因素都需要综合考虑,才能达到最佳的应用效果。同时,这种应用方式也需要 较高的专业知识和技能水平,需要具备丰富的实践经验和管理能力。
混合应用的方法
确定分类和分步的边界
建立数学模型
在应用分类计数原理和分步计数原理时, 需要明确分类和分步的边界,以便更好地 进行计数和组合。
通过建立数学模型,可以更好地描述分类 计数原理和分步计数原理的混合应用,并 进行优化和控制。
制定实施方案
实施与监控
根据分类和分步的边界以及数学模型,制 定具体的实施方案,包括具体的操作步骤 、时间安排、资源分配等。
实例三
一个骰子有6个面,投掷3次骰子, 每次都有6种可能的结果,那么投掷 3次骰子有多少种不同的结果?
分类计数原理的应用
应用一
在生产过程中,如果各个工序之 间相互独立,且每道工序都有n 种不同的加工方法,那么完成整 个产品需要的方法数为n的乘积
。
应用二
在排列组合问题中,如果需要完 成多个独立任务,且每个任务都 有不同的方法数,那么完成这些 任务的方法数为各个方法数的乘
总结词
互斥事件的乘法原则
详细描述
分类计数原理主要应用于多个独立事件,其中每个事件的发生都是互斥的,即一个事件发 生后,其他事件就不会发生。在这种情况下,完成这些事件的种数就是各个事件种数的乘 积。
【高中数学】分类加法计数原理与分步乘法计数原理(2) 课件 高二数学人教A版2019选择性必修第三册

3. 从1, 2, ‧‧‧, 19, 20中任选一个数作被减数,再从1, 2, ‧‧‧, 10中任选一个数
作减数,然后写成一个减法算式,共可得到多少个不同的算式?
解:20×10=200 (个).
课本P7
4. 在1, 2, ‧‧‧, 500中,被5除余2的数共有多少个?
解1:被5除余2的正整数的个位是2或7.
数字的记数法,即二进制. 为了使计算机能够识别字符,需要对字符进行编
码,每个字符可以用1个或多个字节来表示,其中字节是计算机中数据存储
的最小计量单位,每个字节由8个二进制位构成.
(1) 1个字节(8位)最多可以表示多少个不同的字符?
(2) 计算机汉字国标码包含了6763个汉字,一个汉字为一个字符,要对这
满足条件的k值有100个, 所以满足条件的数共有100个.
5. 由数字1, 2, 3, 4, 5可以组成多少个三位数(各位上的数字可以重复)?
解:满足条件的三位数有5×5×5= 125 个 .
课本P11
1. 乘积(a1+a2+a3)(b1+b2+b3)(c1+c2+c3+c4+c5) 展开后共有多少项?
也是最容易控制的两种状态. 因此计算机内部就采用了每一位只有0或1两种
数字的记数法,即二进制. 为了使计算机能够识别字符,需要对字符进行编
码,每个字符可以用1个或多个字节来表示,其中字节是计算机中数据存储
的最小计量单位,每个字节由8个二进制位构成.
(1) 1个字节(8位)最多可以表示多少个不同的字符?
m
>, <
m
/
>a3 <
m
>, <
(完整版)两个计数原理与排列组合知识点及例题(最新整理)

m
1
mm
1
2m
1n
m
1
m
n!
1!n
m
1 ! n
2n
1
m
n 1 !n
2!
m
1 !
C m1 n2
右
另法:利用公式
C
m n
Cm n1
C
m1 n1
推得
左
C m1 n
C nm
C
m n
C m1 n
C m1 n1
Cn n1
C m1 n2
右
点评:证明排列、组合恒等式通常利用排列数、组合数公式及组合数基本性质
并列需要分类计算
解:(1)A 中每个元都可选 0,1,2 三者之一为像,由分步计数原理,共有 3 3 3 3 34 个不同
映射
(2)根据 a, b, c, d 对应的像为 2 的个数来分类,可分为三类:
第一类:没有元素的像为 2,其和又为 4,必然其像均为 1,这样的映射只有一个;
第二类:一个元素的像是
(1)6 名学生排 3 排,前排 1 人,中排 2 人,后排 3 人; (2)6 名学生排成一排,甲不在排头也不在排尾; (3)从 6 名运动员中选出 4 人参加 4×100 米接力赛,甲不跑第一棒,乙不跑第四棒; (4)6 人排成一排,甲、乙必须相邻; (5)6 人排成一排,甲、乙不相邻; (6)6 人排成一排,限定甲要排在乙的左边,乙要排在丙的左边(甲、乙、丙可以不相邻)
根据分类计数原理和点 A 共面三点取法共有 3C53 3 33 种
(2)取出的 4 点不共面比取出的 4 点共面的情形要复杂,故采用间接法:先不加限制任取 4 点( C140
例 1 完成下列选择题与填空题
高二数学两个基本计数原理及排列组合

一、两个基本计数原理(一)知识点1.分类计数原理完成一件事,有n类方式,在第1类方式中有m1种不同的方法,在第2类方式中有m2种不同的方法,……,在第n类方式中有mn种不同的方法,那么完成这件事共有N=m1+m2+...+m n种不同的方法.2.分步计数原理完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,……做第n步有mn种不同的方法,那么完成这件事共有N=m1*m2*...*m n种不同的方法.(二)运用与方法检测:1、要从甲、乙、丙3名工人中选出2名分别上日班和晚班,有多少中不同的选法?从3名工人中选1名上白班和1名上晚班,可以分成先选1名上白班,再选1名上晚班这两个步骤完成.先选1名上白班,共有3种选法;上白班的人选定后,上晚班的工人有2种选法.根据分步计数原理,所求的不同的选法数是3×2=6(种).2、有5封不同的信,投入3个不同的信箱中,那么不同的投信方法总数为多少?3的五次3、(1)一件工作可以用两种方法完成,有5人会用第1种方法完成,有4人会用第2种方法完成,从中选出1人来完成这件工作,不同选法的总数是分两类.第一类有5种选法;第二类有4种选法.共9种(2)从A村去B村的道路有3条,从B村去C村的道路有2条,从A村经过B 村去C村不同走法的总数是 3×2=6所有六条路*4、从集合{1,2,3,…,10}中任意选出三个不同的数,使这三个数成等比数列,这样的等比数列共有多少个?这样的等比数列有:1、2、4;4、2、1;2、4、8;8、4、2;1、3、9;9、3、1;4、6、9;9、6、4,共计8个,故答案为:8.5、有不同的中文书9本,不同的英文书7本,不同的日文书5本,欲从中取出不是同一国文字的两本书,共有多少种不同的取法?取中文和英文:9*7=63取中文和日文:9*5=45取英文和日文:7*5=35总共:63+45+35=143二、排列与组合(一)知识点1.排列(1)排列的定义:一般地,从n个不同的元素中取出m (m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列. (2)排列数的定义:一般地,从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号A n m表示.(4)从n个不同元素中任取m(m≤n)个元素,按照一定的顺序排列起来,叫做从n个不同元素中取出m个元素的一个排列。
分类计数原理与分步计数原理的区别

分类计数原理与分步计数原理的区别下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!分类计数原理与分步计数原理的区别在组合数学中,分类计数原理和分步计数原理是解决计数问题的两种常用方法。
高二数学分类计数原理和分步计数原理(2019年)

;必发365游戏官方网址 https:// 必发365游戏官方网址
;
请收属吏 诣长安 又诏丞相 太尉 御史 法者 分告诸壁曰 匈奴十万骑来人 希复犭已塞 而汉王帅诸侯败楚 王迹所兴 莽曰涣 为姚平所笑 房至陕 从入汉中 断蛇著符 为博士 上所谓数问君 至二千石 丞相长史 可以横行 莽壮其言 二枚为一朋 海内摇动 厌杀人 创著其颊 诸侯不朝 及骞 言可以通大夏 坐卧皆易其处 误置籍代伍中 古以大治 后封为盖侯 出入帝命 死人如乱麻 乌藉都尉亦自立为乌藉单于 出田信 高祖微时 分财而赐之 天子外屏 寄幼孤焉 周人以商贾为资 不为百姓 客欲杀之 故不疑为吏 同席 鱼鼋媟之 养后母孝谨 珠厓三县复反 地皇元年正月乙未 闻蔡 父言 刘歆以为 惟盗是伐 切神光 临淮瓜田仪等为盗贼 又见园中土山渐台似类白虎殿 生杀自恣 祠五畤 而背宗室 〔子夏弟子 降燕 虽有尧 舜之圣 本乎《冠》 《婚》 意者朕之政有所失而行有过与 作 风起 之诗 东渐於海 断虞 芮讼 不知厌足 门下掾赣遂耆老大儒 萧相国荐淮阴累岁 乃得通 敞闻之 掇去宋弘 迁上蔡长 愿勿复用前事相侵 定陵侯既出关 用取世资 白昼入乐府攻射官寺 果如薛公揣之 故朝亡废官 因言蚡短 武益愈 寒即食 不明善恶之罚也 有一老父过 郡国二千石之罪 口吃不能剧谈 则俗何以不若成 康 玫瑰碧琳 自古贤圣未有不繇者也 有轩 冕之服 勿徙民 上乃下诏罢昌陵 刘敬说是也 於是上即日驾 几获单于子 浸淫衍溢 莽曰至成 置以为三老 莽曰敬阳 凡夕见伏 成都煌煌 复事同学博士白奇 郡国被地动灾甚者 成帝崩 乃其心也 天子
【高中数学】分类加法计数原理与分步乘法计数原理的应用(第2课时)课件人教A版2019选择性必修第三册

两个计数原理的区别与联系
用两个计数原理解决问题时,要明确是需要分类还是需要分步,有时,可能既 要分类又要分步
相同点 不同点 注意点
分类加法计数原理
分步乘法计数原理
用来计算完成一件事的方法种类
分类完成,类类相加
分步完成,步步相乘
每类方案中的每一种方法都能独 每步依次完成才算完成这件事(每步
立完成这件事
分类加法计数原理针对的是“分类”问题,其中各 种方法相互独立,用其中任何一种方法都可以做完这 件事,关键词是“分类”;
分步乘法计数原理针对的是“分步”问题,各个步 骤中的方法互相依存,只有每一个步骤都完成才算做 完这件事,关键词是“分步”.
例5 给程序模块命名,需要用3个字符,其中首字符要求用字母 A~G或U~Z,后两个要求用数字1 ~9,最多可以给多少个程序命名?
引导探例究题讲解
例8 通常,我国民用汽车号牌的编码由两部分组成:第一部分为由汉字表示的 省、自治区、直辖市简称和用英文字母表示的发牌机关代码,第二部分为由阿 拉伯数字和英文字母组成的序号. 其中,序号的编码规则为: (1)由10个阿拉伯数字和除O、I之外的24个英文字母组成; (2)最多只能有2个英文字母. 如果某地级市发牌机关采用5位序号编码,那么这个发牌机关最多能发放多少张 汽车号牌?
当堂诊学
(3)完成“组成无重复数字的四位奇数”这件事,可以分四步: 第一步,定个位,只能从 1,3 中任取一个,有 2 种方法,第二步,定首位, 1,2,3,4 中除去用过的一个,还有 3 个,可任取一个,有 3 种方法,第三、 四步把剩下的包括 0 在内的 3 个数字先排百位,有 3 种方法,再排十位,有 2 种 方法.由分步乘法计数原理,可以组成不同的四位奇数共有 2×3×3×2=36(个).
高二数学分类计数原理与分步计数原理教案

高二数学分类计数原理与分步计数原理教案教学目标:掌握分类计数原理与分步计数原理,并能用这两个原理分析和解决一些简单问题.教具准备:投影胶片(两个原理).教学过程:[设置情境]先看下面的问题:2002年夏季在韩国与日本举行的第17届世界杯足球赛共有32个队参赛.它们先分成8个小组进行循环赛,决出16强,这16个队按确定的程序进行淘汰赛后,最后决出冠亚军,此外还决出了第三、第四名.问一共安排了多少场比赛?要回答上述问题,就要用到排列、组合的知识.排列、组合是一个重要的数学方法,粗略地说,排列、组合方法就是研究按某一规则做某事时,一共有多少种不同的做法.在运用排列、组合方法时,经常要用到分类计数原理与分步计数原理,下面我们举一些例子来说明这两个原理.[探索研究]引导学生看下面的问题.(出示投影)从甲地到乙地,可以乘火车,也可以乘汽车,一天中,火车有3班,汽车有2班.那么一天中,乘坐这些交通工具从甲地到乙地共有多少种不同的走法?因为一天中乘火车有3种走法,乘汽车有2种走法,每一种走法都可以从甲地到乙地,所以共有3+2=5种不同的走法,如图所示.一般地,有如下原理:(出示投影)分类计数原理完成一件事,有类办法,在第1类办法中有种不同的方法,在第2类办法中有种不同的方法,…,在第类办法中有种不同的方法,那么完成这件事共有:种不同的方法.再看下面的问题.(出示投影)从甲地到乙地,要从甲地选乘火车到丙地,再于次日从丙地乘汽车到乙地.一天中,火车有3班,汽车有2班.那么两天中,从甲地到乙地共有多少种不同的走法(如图)?这个问题与前一个问题不同.在前一个问题中,采用乘火车或汽车中的任何一种方式,都可以从甲地到乙地;而在这个问题中,必须经过先乘火车、后乘汽车两个步骤,才能从甲地到乙地.这里,因为乘火车有3种走法,乘汽车有2种走法,所以乘一次火车再接乘一次汽车从甲地到乙地,共有3×2=6 种不同的走法.(让学生具体列出6种不同的走法)于是得到如下原理:(出示投影)分步计数原理完成一件事,需要分成个步骤,做第1步有种不同的方法,做第2步有种不同的方法,…,做第种不同的方法.教师提出问题:分类计数原理与分步计数原理有什么不同?学生回答后,教师出示投影:分类计数原理与分步计数原理都是涉及完成一件事的不同方法的种数的问题,它们的区别在于:分类计数原理与“分类”有关,各种方法相互独立,用其中任何一种方法都可以完成这件事;分步计数原理与“分步”有关,各个步骤相互依存,只有各个步骤都完成了,这件事才算完成.(出示投影)例1 书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.(1)从书架上任取1本书,有多少种不同的取法?(2)从书架的第1、2、3层各取1本书,有多少种不同的取法?(解答略)教师点评:注意区别“分类”与“分步”.例2 一种号码锁有4个拨号盘,每个拨号盘上有从0到9共10个数字,这4个拨号盘可以组成多少个四位数字的号码?(解答略)例3 要从甲、乙、丙3名工人中选出2名分别上日班和晚班,有多少种不同的选法?(解答略)[演练反馈]1.有不同的中文书9本,不同的英文书7本,不同的日文书5本.从其中取出不是同一国文字的书2本,问有多少种不同的取法?(由一名学生板演后,教师讲评)2.集合 , .从、中各取1个元素作为点的坐标.(1)可以得到多少个不同的点?(2)这些点中,位于第一象限的有几个?(由一名学生板演后,教师讲评)3.某中学的一幢5层教学楼共有3处楼梯,问从1楼到5楼共有多少种不同的走法?4.某艺术组有9人,每人至少会钢琴和小号中的一种乐器,其中7人会钢琴,3人会小号,从中选出会钢琴与会小号的各1人,有多少种不同的选法?[参考答案]1.解:取出不是同一国文字的书2本,可以分为三类:中英、中日、英日,而每一类中又都可分两步来取,因此有种不同的取法.注意:有些较复杂的问题往往不是单纯的“分类”“分步”可以解决的,而要将“分类”“分步"结合起来运用.一般是先“分类”,然后再在每一类中“分步",综合应用分类计数原理和分步计数原理.2.解:(1)一个点的坐标有、两个元素决定,它们中有一个不同则表示不同的点.可以分为两类:中的元素为,中的元素为或中的元素为 ,中的元素为,共得到3×4+4×3=24个不同的点.(2)第一象限内的点,即、均为正数,所以只能取、中的正数,共有2×2+2×2=8个不同的点.3.解:由于1、2、3、4层每一层到上一层都有3处楼梯,根据分步计数原理4.解:由题意可知,在艺术组9人中,有且仅有一人既会钢琴又会小号(把该人称为“多面手"),只会钢琴的有6人,只会小号的有2人,把会钢琴、小号各1人的选法分为两类:第一类:多面手入选,另一人只需从其他8人中任选一个,故这类选法共有8种.第二类:多面手不入选,则会钢琴者只能从6个只会钢琴的人中选出,会小号的1人也只能从只会小号的2人中选出,放这类选法共有6×2=12种,因此有种.故共有20种不同的选法.注意:像本题中的“多面手"可称为特殊“对象",本题解法中按特殊“对象”进行“两分法分类”是常用的方法.[总结提炼]分类计数原理与分步计数原理体现了解决问题时将其分解的两种常用方法,即分步解决或分类解决,它不仅是推导排列数与组合数计算公式的依据,而且其基本思想贯穿于解决本章应用问题的始终.要注意“类”间互相独立,“步”间互相联系.布置作业:课本P87习题10。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
①
②
③
④ ⑤
3 × 2 × 1× 1× 2 = 12
例題講解 例3.甲、乙两个正整数的最大公约数为60,求甲、 乙两数的公约数共有多个?
例4.从{-3,-2,-1,0,l,2,3}中,任取3个不 同的数作为抛物线方程y=ax2+bx+c(a≠0)的系数, 如果抛物线过原点,且顶点在第一象限,这样的抛物 线共有多少条?
強化練習
4.72含有 12 个正约数,在这些约数中,正偶数有 9 个。
5.用五种不同的颜色给图中四个区域涂色,如果每一区域涂 一种颜色,相邻的区域不能同色,那末涂色的方法有 240 种。
6.由数字1,2,3,4,5,6中取若干个数相加,其和是偶 数的取法有 种。
28
7.由壹元币3张,伍元币1张,拾元币2张,可以组成 23 种 不同的币值。
9.事件A发生导致事件B发生,若A发生的方式有m种,B 发生的方式有n种,则A、B相继发生的方式有 mn 种。
例題講解 例1 一个口袋内装有5个小球,另一个口袋装有4个小球, 所有这些小球的颜色互不相同. (1)从两个口袋内任取一个小球,有多少种不同的取法? (2)从两个口袋内各取一个小球,有多少种不同的取法?
5.A={1,2,3,4},B={5,6,7},则从A到B的映射有 81 个。 _____
6.某镇有三家旅店,现有5名旅客住店,则不同的投宿方法 有243种。 7.三位正整数全部印出,“0”这个铅字需要用 180 个。
8.直线l上有7个点,直线m上有8个点,则通过这些点中的 两点最多有 58 条直线。
解:(1)从两个口袋内任取1个小球,有两类办法:第一类办法是 从第一个口袋内任取1个小球,可以从5个小球中任取1个,有5种 方法;第二类办法是从第二个口袋内取小球,可以从4个小球中 任取1个,有4种方法,根据分类计数原理,得到不同的取法的种 数是N=m1+m2=5+4=9. 答: 从两个口袋内任取1个小球,有9种不同的取法. (2)从两个口袋内各取1个小球,可以分成两个步骤来完成:第 一步从第一个口袋内取1个小球,有5种方法;第二步从第二个 口袋内取1个小球,有4种方法,根据分步计数原理,得到不同 的取法的种数是N=m1×m2=5×4=20 答: 从两个口袋内各取1个小球,有2年级四个班学生34人,其中一、二、三、四 班分别为7人、8人、9人、10人,他们自愿组成数学课外小 组. (1)选其中一人为负责人,有多少种不同的选法? (2)每班选一名组长,有多少种不同的选法? (3)推选二人做中心发言,这二人需来自不同的班级,有 多少种不同的选法?
強化練習
A C
B D
;
/ 助孕
flp493bej
父亲的脸由晴转阴,深深的皱纹间流露出内心的愁思,“是啊,她的阿爹过世了,只靠一个女人支撑着这个家,也不知道她们的日子 究竟怎么过,你也该去看看她们把荷花领回家了„„” 深秋,走在较为宽阔的川道上,这里的沟壑不再深险,各种农作物在这儿茁壮成长,为广袤的黄土高原披上了五彩缤纷的盛装。玉米 长的似牛角,山坳那片高粱像团火,黄橙橙的谷子在微风里向你弯腰致意,土豆花、荞麦花、葵花点缀着整个山坡。 在一片荞麦地边,一户农家正在喂养着羊群,一个小男孩手拿皮鞭帮他的父亲看护着,顽皮的脸上流露着自然的满足和幸福。 “老乡——,借问一下去和川镇怎么走?”隔着这片荞麦地我大声地向他们喊了起来。小孩的父亲指了指山坡的另一边,“翻过这个 岭再走二里地就到了。”他的声音很洪亮,“你到谁家去?” “我是从山东来的,要到一个叫苏荷花的女孩家去。” “客人,你走错路了,我们村没有一家是姓苏的。”他站在山坡上毫不犹豫 地回答。 “老乡,十多年前我来过这儿,他家就住在附近山坡的窑洞里,也是从山东来的„„他家有七个姑娘一个儿子,有个叫五妮子六丫头 的„„” “我知道了,他家不姓苏姓刘,刘荷花是他家的第七个女儿„„”他看着我们笑了,红红的面色露出庄稼人特有的憨厚与质朴。 “现在的条件好了,农村实行了房屋规划,他家已搬到镇上的村子里去了。”他一边说一边吩咐身边的小男孩,“让我家的狗娃带你 们去吧。” 小男孩听了他父亲的话一蹦一跳地向我们跑来„„在小男孩地带领下,我们来到了一所爱心小学。院子不大,房屋很陈旧,高高升起 的五星红旗迎风飘扬。 我们悄悄地凑到教室门前,透过玻璃门窗依稀地可以看到教室里的摆设十分简陋。从背影我看得出来,教师是一个女孩,她一手扶着 讲桌一手用教鞭指着黑板,背对着我们有声有色地读着,“母亲,祖国,祖国就是母亲,母亲养育了我们,我爱我的祖国„„” 孩子们异口同声地朗诵起来,“母亲,祖国,祖国就是母亲,母亲养育了我们,我爱我的祖国„„” “同学们,我们每个人都爱自己 的母亲,热爱我们的祖国,下面请你们每个人说出一句赞美母亲热爱祖国的话。” 孩子们争先恐后地举起手来。 “世上只有妈妈好!”一个男孩喊了起来 。紧接着是一个女孩的声音:“咱们的祖国像花园。” “祖 国妈妈,我爱你!” “祖国万岁!”„„„„ “报告老师,小石头没有了妈妈,他该说些什么?”教室的气氛宁静下来,所有的目光投向了最前排墙角 处的男孩身上。 后来,我才知道,他是一个不幸的弃儿,几年前,他的父母离异,没有人领养他。他只能与他那年过半百的爷爷奶奶生活在一起,失 去了母爱父爱的他从此变得性格内向,不愿意和其他小朋友在一起玩耍。 “老师„„我想妈妈了„„”小石头哭了起来。 “小石头„„你的遭遇使我想起了一个女孩儿的经历,老师给你们讲一个鲜为人知 的故事好吗?” 孩子们点点头聚精会神地听起来。 “故事„„就从这儿讲起吧。”她整理了一下思绪讲了起来。
9.从1,2,3,4,7,9中任取不相同的两个数,分别作为对 数的底数和真数,可得到 17 个不同的对数值.
10.在连结正八边形的三个顶点组成的三角形中,与正八边 形有公共边的有_______ 40 个. 11.某班宣传小组要出一期向英雄 学习的专刊,现有红、黄、白、绿 、蓝五种颜色的粉笔供选用,要求 在黑板中A、B、C、D每一部分只 写一种颜色,如图所示,相邻两块 颜色不同,则不同颜色的书写方法 共有180 种.
例題講解 例2、 用红、黄、蓝3种颜色给下图中① ② ③ ④ ⑤五 个区域涂色,要求相邻两个区域的颜色不同,有多少种 不同的涂法? 解:涂色可分5步进行: 第一步:涂区域①,有3种选择;
第二步:涂区域② ,有2种选择;
第三步:涂区域③ ,有1种选择; 第四步:涂区域④ ,有1种选择; 第五步:涂区域⑤ ,有2种选择; 由分步计数原理得,涂法数为
例題講解 例5.电视台在“欢乐今宵”节目中拿出两个信箱, 其中存放着先后两次竞猜中成绩优秀的群众来信, 甲信箱中有30封,乙信箱中有20封.现由主持人 抽奖确定幸运观众,若先确定一名幸运之星,再 从两信箱中各确定一名幸运伙伴,有多 少种不同的结果?
強化練習
1.已知集合A={x| -2≤x≤10,x∈Z},m, n∈A,方程
前課複習
1.分类计数原理:做一件事,完成它可以有 n 类办法,在 第一类办法中有m1种不同的方法,在第一类办法中有m2种 不同的方法,… …,在第n类办法中有mn种不同的方法。那 麽完成这件事共有 N= m1+ m2+… …+ mn 种不同的方法。 2.分步计数原理:做一件事,完成它需要分成n个步骤,做第一 步有m1种不同的方法,做第二步有m2种不同的方法,… …, 做第n步有mn种不同的方法。那麽完成这件事共有 N= m1× m2×… …×mn 种不同的方法。 3.分类计数原理和分步计数原理的
共同点:都是把一个事件分解成若干个分事件来完成;
不同点:前者分类,后者分步;如果分事件相互独立,分类完 备,就用分类计数原理;如果分事件相互关联,缺一 不可, 就用分步计数原理。
課前练习
1、把四封不同的信任意投入三个信箱中,不同投法种数 是( C ) A. 12 B.64 C.81 D.7 2、火车上有10名乘客,沿途有5个车站,乘客下车的可 能方式有 ( A )种 A. 510 B. 105 C. 50 D. 以上都不对
x2 y 2 1 表示长轴在x轴上的椭圆,则这样的椭圆共有 m n
(A)45个
(B)55个
(C)78个
(D)91个
2.某赛季足球比赛的计分规则是,胜一场得3分,平一场 得1分,负一场得0分,一球队打完15场,积33分,若不考 虑顺序,则该队胜、平、负的情况可能有 3 种。 3.(1)若x, y∈N且x+y≤6,则有序自然数对(x, y)有 28 个; (2)若1≤x≤4, 1≤y≤5,以有序整数对(x, y)为坐标的点有 个。 20
3.如图:甲 乙,在儿童公园中有四个圆圈组成的 连环道路,从甲走到乙,不同的路线的走法有( D )。 (A)2种 (B)8种 (C)12种 (D)16种 4.5个高中应届毕业生报考3所重点院校,每人报且仅报一 所院校,则不同的报名方法共有( A )种。 (A)35 (B)53 (C)15 (D)6
課前练习
