18-19 章末综合测评1 算法初步
18-19 章末综合测评1

章末综合测评(一)(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下面对程序框图中的图形符号的说法错误的是( ) A .起、止框是任何流程不可少的,表明程序开始和结束 B .输入、输出可用在算法中任何需要输入、输出的位置 C .算法中间要处理数据或计算,可分别写在不同的注释框内D .当算法要求对两个不同的结果进行判断时,判断条件要写在判断框内 C [算法中间要处理数据或计算,可分别写在不同的处理框内.]2.阅读如图1的程序框图:若输出结果为0,则①处的执行框内应填的是( )图1A .x =-1B .b =0C .x =1D .a =32A [先确定执行框内是给x 赋值然后倒着推,b =0时,2a -3=0,解得a =32,a=32时,2x +1=32,解得x =-1.]3.如图2是一个算法的程序框图,该算法所输出的结果是( )图2A.12B.23C.34D.45C [运行第一次的结果为n =0+11×2=12;第二次n =12+12×3=23;第三次n =23+13×4=34.此时i =4,程序终止,即输出n =34.]4.用更相减损术求得420和84的最大公约数为( ) A .84 B .12 C .168 D .252A [(420,84)→(336,84)→(252,84)→(168,84)→(84,84),所以420和84的最大公约数为84.]5.下面的程序语句输出的结果S 为( )A .17B .19C .21D .23C [当i 为7的时候i <8,执行循环体后i =9,S =21.] 6.如图3所示,当x 1=6,x 2=9,p =8.5时,x 3等于( )图3A .7B .8C .10D .11B [由程序框图知,p =8.5≠6+92,∴p =x 2+x 32=8.5,∴x 3=8.5×2-9=8.] 7.阅读如图4所示的程序框图,则循环体执行的次数为()图4A .50B .49C .100D .99B [∵i =i +2,∴当2+2n ≥100时循环结束,此时n ≥49,故选B .] 8.下面的程序运行后,输出的结果是( ) a =1;b =3;a =a +b ;b =a -b ;print (%io (2),b ,a );A .1,3B .4,1C .0,0D .6,0B [该程序运行过程中a ,b 的值变化如下:a =1;b =3;a =4,b =4-3=1,故选B .]9.阅读如图5所示的程序框图,运行相应的程序.若输入x 的值为1,则输出S 的值为()图5A .64B .73C .512D .585B [第1次运行:S =0+13=1<50,第2次运行:x =2,S =1+23=9<50, 第3次运行:x =4,S =9+43=73>50,∴输出S =73,选B.] 10.运行如下的程序,输出的结果为( ) (提示:1+3+5+…+(2n -1)=n 2) S =0;i =1;while S<=1000S =S +i ;i =i +2;endi =i -2print (%io (2),i );A .32B .33C .61D .63D [本程序实现的是:求满足1+3+5+…+n >1 000的最小的整数n . 当n =31时,1+3+…+61=312=961<1 000,当n =32时,1+3+…+63=322=1 024>1 000,此时i =63+2=65, 结束循环,i =65-2=63.]11.执行如图6所示的程序框图后,输出的值为4,则P 的取值范围是( )图6A .78<P ≤1516B .P >1516 C .34<P ≤78D .78≤P <1516C [∵S <P 时,执行循环体,S ≥P 时输出n =4,∴S 加上最后一项为123=18,此时S =12+14+18=78,∴78≥P ,结合输出n =4知,34<P ≤78.]12.根据如图7所示的程序框图,要使得输出的结果在区间[-1,0]上,则输入的x 的取值范围是( )图7A .⎣⎢⎡⎦⎥⎤2,52B .[0,2]C .[-1,0]D .⎣⎢⎡⎦⎥⎤0,52A [由程序框图可得输出y =⎩⎪⎨⎪⎧x 2,x <0,4-2x ,x ≥0,若y ∈[-1,0],则⎩⎪⎨⎪⎧ -1≤x 2≤0,x <0,或⎩⎪⎨⎪⎧-1≤4-2x ≤0,x ≥0,解得2≤x ≤52.] 二、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中的横线上) 13.如图8程序框图,若输入的数满足b >c >a ,则输出________.图8b [此框图表示的是找出a 、b 、c 三个数中的最大数,故输出b .] 14.给出一个算法:根据以上算法,可求得f(-1)+f(2)=________. 0 [f (x )=⎩⎪⎨⎪⎧ 4x ,2x ,x ≤0,x >0,∴f (-1)+f (2)=-4+22=0.]15.如图9是求12+22+32+…+1002的值的程序框图,则正整数n =________.图9100 [因为第一次判断执行后,s =12,i =2,第二次判断执行后,s =12+22,i =3,而题目要求计算12+22+32+…+1002,故n =100.]16.执行如图10所示的程序框图,若输入x =4,则输出y 的值为________.图10-54[当输入x =4时,计算y =12x -1,得y =1.不满足|y -x |<1,于是得x =1,此时y =12-1=-12,不满足|y -x |<1,此时x =-12,得y =-54.这样|y -x |=⎪⎪⎪⎪⎪⎪-54+12=34<1,执行“是”,所以输出的是-54.]三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)用更相减损之术求282与470的最大公约数.[解]∵(470,282)→(188,282)→(188,94)→(94,94),∴470与282的最大公约数为94.18.(本小题满分12分)某公司为激励广大员工的积极性,规定:若推销产品价值在10 000元之内的年终提成5%;若推销产品价值在10 000元以上(包括10 000元),则年终提成10%,设计一个求公司员工年终提成f(x)的算法的程序框图.[解]程序框图如下图所示:19.(本小题满分12分)用秦九韶算法求多项式f(x)=7x7+6x6+5x5+4x4+3x3+2x2+x,当x=3时的值.[解]f(x)=((((((7x+6)x+5)x+4)x+3)x+2)x+1)x,v0=7,v1=7×3+6=27,v2=27×3+5=86,v3=86×3+4=262,v4=262×3+3=789,v5=789×3+2=2 369,v6=2 369×3+1=7 108,v7=7 108×3=21 324,∴f(3)=21 324.20.(本小题满分12分)画出求函数y =⎩⎪⎨⎪⎧12x +5(x >0),0(x =0),x 2-3(x <0)的值的程序框图,并写出程序. [解] 程序框图为程序为21.(本小题满分12分)下列是某个问题的算法程序,将其改为程序语言,并画出框图. 算法:S1 令i =1,S =0.S2 若i ≤999成立,则执行S3. 否则,输出S ,结束算法. S3 S =S +1i .S4 i =i +2,返回S2. [解] 程序和框图如下:S=0;i =1;while i<=999 S =S +1/i ;i =i +2;endprint (%io (2),S );22.(本小题满分12分)如果我国工业年产值每年以9%的增长率增长,那么几年后我国工业年产值翻一番?画出程序框图,并写出算法程序. [解] 程序框图如图所示:程序如下所示:p=1;R=0.09;n=0;while p<2p=p*(1+R);n=n+1;endprint(%io(2),n);11。
第一章算法初步综合素质检测

第一章 算法初步综合检测试题一、选择题1.算法共有三种逻辑结构,即顺序结构、条件结构和循环结构.下列说法中,正确的是( ) A .一个算法只能含有一种逻辑结果 B .一个算法最多可以包含两种逻辑结构C .一个算法必须含有上述三种逻辑结构D .一个算法可以含有上述三种逻辑结构的任意组合 2.下列赋值语句错误的是( ) A .i =i -1 B .m =m 2+1 C .k =-1kD .x*y =a3.计算机执行下面的程序段后,输出的结果是( )A .1,3B .4,1C .0,0D .6,0 a =1b =3a =a +b b =a -bPRINT a ,b4.用秦九韶算法求多项式f (x )=4x 5-x 2+2当x =3时的值时,需要________次乘法运算和________次加法(或减法)运算.( )A .4,2B .5,3C .5,2D .6,25.利用秦九韶算法计算f (x )=x 5+2x 4+3x 3+4x 2+5x +6在x =5时的值为( )A .4881B .220C .975D .48186.(2014全国高考重庆卷)执行如图所示的程序框图,若输出k 的值为6,则判断框内可填入的条件是( )A .s >12B .s >75C .s >710D .s >457.执行下图的程序框图,若输入的a ,b ,k 分别为1,2,3,则输出的M =( )A.203 B.165 C.72D .1588.下列各进位制数中,最大的数是( ) A .11111(2) B .1221(3) C .312(4)D .56(8)9.(2013~2014·山东淄博一模)某程序框图如图所示,现输入如下四个函数:f (x )=x 2,f (x )=1x,f (x )=e x ,f (x )=x 3,则可以输出的函数是( )A .f (x )=x 2B .f (x )=1xC .f (x )=e xD .f (x )=x 310.为了在运行下面的程序之后得到输出16,键盘输入x 应该是( ) INPUT xIF x<0 THENy=(x+1)*(x+1) ELSEy=(x-1)*(x-1)END IFPRINT y ENDA . 3或-3B . -5C .5或-3D .5或-511.计算机常用的十六进制是适十六进一,采用数字0~9和字母A ~F 共16个计算符号,这些符号与十进制数的对应关系如下表:A .6EB .72C .5FD .5B12.(2013·江西)阅读图所示的程序框图,如果输出i =5,那么在空白矩形框中应填入的语句为( )A .S =2*i -2B .S =2*i -1C .S =2*iD .S =2*i +4二、填空题13.217与155的最大公约数是________.14.用秦九韶算法计算多项式f (x )=x 6-12x 5+60x 4-160x 3+240x 2-192x +64当x =2时的值时,v 4的值为________.15.(2014·全国高考湖北卷)阅读如图所示的程序框图,运行相应的程序,若输入n 的值为9,则输出S 的值为________.三、解答题16.已知一个正三角形的周长为a ,求这个正三角形的面积,设计一个算法解决这个问题.17. (1)用辗转相除法求567与405的最大公约数. (2)用更相减损术求2 004与4 509的最大公约数.19.求函数y =⎩⎪⎨⎪⎧x 2-2x ,x ≥2,-2,x <2的值的程序框图如图所示.(1)指出程序框图中的错误,并写出算法;(2)重新绘制解决该问题的程序框图,并回答下面提出的问题. ①要使输出的值为正数,输入的x 的值应满足什么条件? ②要使输出的值为8,输入的x 值应是多少? ③要使输出的y 值最小,输入的x 值应是多少?第一章 算法初步综合检测试题参考答案一、1、[答案] D2.[答案] D [解析] 执行i =i -1后,i 的值比原来小1,则A 正确;执行m =m 2+1后,m 的值等于原来m 的平方再加1,则B 正确;执行k =-1k后,k 的值是原来的负倒数,则C 正确;赋值号的左边只能是一个变量,则D 错误.3.[答案] B[解析] 把1赋给变量a ,把3赋给变量b ,由语句“a =a +b ”得a =4,即把4赋给定量a ,由语句“b =a -b ”得b =1,即把1赋给变量b ,输出a ,b ,即输出4,1.4.[答案] C [解析] f (x )=4x 5-x 2+2=(((4x )x )x -1)x )x +2,所以需要5次乘法程算和2次加法(或减法)运算.5.[答案] A[解析] 依据秦九韶算法,把多项式改写为f (x )=((((x +2)x +3)x +4)x +5)x +6.按照从内到外的顺序,依次计算x =5时的值: v 0=1; v 1=1×5+2=7; v 2=7×5+3=38;v 3=38×5+4=194; v 4=194×5+5=975; v 5=975×5+6=4881. 故f (5)=4881.6.[答案] C [解析] ∵s =1·910·89·78=710,7.[答案] D [解析] 输入a =1,b =2,k =3,n =1时,M =1+12=32,a =2,b =32;n =2时;M =2+23=83,a =32,b =83;n =3时;M =32+38=158,a =83,b =158;n =4时;输出M =1588.[答案] C [解析] 11111(2)=1×24+1×23+1×22+1×21+1=31,1221(3)=1×33+2×32+2×3+1=52,312(4)=3×42+1×4+2=54,56(8)=5×8+6=46,9.[答案] D [解析] 由程序框图知,输出的函数应该即是奇函数,又存在零点. 10.[答案] D11.[答案] A [解析] 本题考查进位制间的相互转化.用十进制表示A ×B =10×11=110,而110=6×16+14=6E (16),故选A.12.[答案] C [解析] 题中框图依次执行如下循环:第一次:i =1,S =0,i =1+1=2,i 是奇数不成立,S =2*2+1=5,继续循环; 第二次:i =2+1=3,i 是奇数成立,继续循环;第三次:i =3+1=4,i 是奇数不成立,S =2*4+1=9,继续循环;第四次:i =4+1=5,i 是奇数成立,由题意知此时应跳出循环,输出i =5,即S <10不成立. 故应填S =2*i (此时S =10<10不成立).若填S =2*i +4,则在第二次循环中就跳出循环.故选C. 二、填空题 13. [答案] 31[解析] 217=155×1+62,155=62×2+31,62=31×2,所以217与155的最大公约数为31.14. [答案] 80 [解析] v 0=1,v 1=v 0x +a 5=1×2-12=-10,v 2=v 1x +a 4=-10×2+60=40,v 3=v 2x +a 3=40×2-160=-80,v 4=v 3x +a 2=-80×2+240=80.15.[答案] 1067 [解析] S =0+(21+1)+(22+2)+…+(29+9)=(21+22+…+29)+(1+2+3+…+9)=2 1-291-2+ 1+9 ×92=1067.三、解答题16. [解析] 算法步骤如下: 第一步,输入a 的值.第二步,计算l =a 3的值. 第三步,计算S =34l 2的值. 第四步,输出S 的值.17.[解析] (1)∵567=405×1+162,405=162×2+81,162=81×2.∴567与405的最大公约数为81. (2)∵4 509-2 004=2 505,2 505-2 004=501,2 004-501=1 503,1 503-501=1 002,1 002-501=501.∴2 004与4 509的最大公约数为501.18.[解析] (1)题中程序框图上的一段流程线缺少表达程序执行顺序的箭头;再者由于是求分段函数的函数值,输出的函数值的计算方法取决于输入的x 值所在的范围,所以必须引入判断框,应用条件结构.正确的算法步骤如下:第一步,输入x .第二步,如果x <2,那么y =-2;否则,y =x 2-2x . 第三步,输出y .(2)根据以上算法步骤,可以画出如图所示的程序框图.①要使输出的值为正数,则x 2-2x >0,∴x >2或x <0(舍去).故当输入的x >2时,输出的函数值为正数.②要使输出的值为8,则x 2-2x =8,∴x =4或x =-2(舍去).故输入x 的值应为4.③当x ≥2时,y =x 2-2x ≥0,当x <2时,y =-2,又-2<0,故要使输出的y 值最小,只要输入的x 满足x <2即可.。
人教b版数学必修三:第1章《算法初步》章末检测(含答案)

第一章 章末检测(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分) 1.下列关于算法的叙述不正确的是( )A .在任何数值计算或非数值计算的过程中所采取的方法和步骤,都可称之为算法B .解决一类问题的方法和步骤C .算法并不给出问题的精确的解,只是说明怎样才能得到解D .算法中执行的步骤可以是无限次的,能无休止地执行下去 2.下列给出的赋值语句中正确的是( ) A .4=M B .M =-M C .B =A =3 D .x +y =03.下列问题的算法适合用条件分支结构表示的是( ) A .求点P (-1,3)到直线l :3x -2y +1=0的距离 B .由直角三角形的两条直角边求斜边 C .解不等式ax +b >0(a ≠0) D .计算100个数的平均数4.循环语句for x =3:3:99循环的次数是( ) A .99 B .34 C .33 D .305.下面的四个问题中必须用条件分支结构才能实现的个数是( ) ①已知:梯形上、下两底为a 、b ,高为h ,求梯形面积; ②求方程ax 2+bx +c =0 (a 、b 、c 为常数)的根; ③求三个实数a 、b 、c 中的最小者;④计算函数f (x )=⎩⎪⎨⎪⎧x 2 (x >0)2x -7 (x ≤0)的函数值.A .4个B .3个C .2个D .1个 6.下列算法中,最后输出的x 、y 的值是( )A .4 011,2 006B .4 011,-1C .4 011,2 005D .4 011,17.下面的程序框图表示的算法是( )A .求1+2+3+…+100的值B.求12+22+32+…+1002的值C.求1+3+5+…+99的值D.求12+32+52+…+992的值8.在如图所示的程序中输入-2和2,则输出的结果分别是()A.2和6 B.0和6 C.3和6 D.3和29.下面程序表示求________的值.()A.3×10 B.39C.310D.1×2×3×…×1010.下列程序执行的目的是()A.求2×6×10×…×68的值B.求1×2×3×…×68的值C.求2×4×6×…×68的值D.求2×4×6×…×66的值11.用秦九韶算法计算多项式f(x)=2x7+x6+3x3+2x+1,当x=2时的函数值时,需要做加法和乘法的次数分别为()A.7,4 B.4,7 C.7,7 D.4,412.如果执行下边的程序框图,输入x=-2,h=0.5,那么输出的各个数的和等于()A.3 B.3.5 C.4 D.4.5二、填空题(本大题共4小题,每小题5分,共20分)13.三个数72,120,168的最大公约数是________.14.有如下程序框图:则该程序框图表示的算法的功能是_____________________________________________.15.下面是一个算法程序,回答下列问题:当输入的值为3时,输出的结果为________.16.下面是一个算法程序,按这个程序写出的程序在计算机上执行,其算法功能是求__________________________的值.三、解答题(本大题共6小题,共70分)17.(10分)求两底半径分别为2和4,且高为4的圆台的表面积及体积,写出该问题的算法.18.(12分)设计一个算法,求表达式12+22+32+…+102的值,画出程序框图.19.(12分)用秦九韶算法求多项式f(x)=3x5+8x4-3x3+5x2+12x-6当x=2时的值.20.(12分)计算:102+202+302+…+1002,写出解决该问题的算法程序,并画出相应的算法程序框图.21.(12分)有一只猴子第1天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个,第2天早上又将剩下的桃子吃了一半,又多吃了一个,以后每天早上都吃了前一天剩下的一半多一个,到第10天早上想再吃时,只剩下一个桃子,求第1天共摘了多少桃子?并设计程序.22.(12分)用100元钱购买100只鸡,其中公鸡每只5元,母鸡每只3元,小鸡3只1元,问能买多少只公鸡?多少只母鸡?多少只小鸡?写出程序解决这个问题.第一章 章末检测1.D [本题主要考查算法的基本概念和特点:算法就是解决问题的方法,可以是数值或者非数值操作,它必须是有限的步骤,不能无休止地执行下去,必须“有始有终”.]2.B 3.C 4.C5.B [只有②③④必须用条件分支结构.]6.C [x =2 005+2 006=4 011,y =2 005+2 006-2 006=2 005.] 7.D8.C [该算法是求y =⎩⎪⎨⎪⎧3, x ≤0x +4, x>0的值.∴当x =-2时,y =3;当x =2时,y =2+4=6.] 9.C10.C [i 的初始值为2,依次加2,相乘直到68.] 11.B12.B [输入x =-2时,y =0,执行x =x +0.5后x =-1.5. 当x =-1.5时,y =0,执行x =x +0.5后x =-1. 当x =-1时,y =0,执行x =x +0.5后x =-0.5. 当x =-0.5时,y =0,执行x =x +0.5后x =0. 当x =0时,y =0,执行x =x +0.5后x =0.5. 当x =0.5时,y =0.5,执行x =x +0.5后x =1. 当x =1时,y =1,执行x =x +0.5后x =1.5. 当x =1.5时,y =1,执行x =1.5+0.5后x =2. 当x =2时,y =1,此时2≥2,因此结束循环. 故输出各数之和为0.5+1+1+1=3.5.] 13.2414.求使1×3×5×…×n>10 000成立的最小正整数n 的值 15.26解析 计算函数y =⎩⎪⎨⎪⎧x 3-1 x<52x 2+2 x ≥5,解当x =3时,∴y =33-1=26.16.1+33+53+…+9993 17.解 算法:第一步,取r 1=2,r 2=4,h =4. 第二步,计算l =(r 2-r 1)2+h 2.第三步,计算S =πr 21+πr 22+π(r 1+r 2)l 与V =1π(r21+r22+r1r2)h.3第四步,输出S,V.18.解算法:第一步,令S=0,i=1.第二步,判断i是否小于或等于10,若是,则执行第三步;若否,则输出S.第三步,令S=S+i2,并令i=i+1,然后返回第二步.程序框图:19.解根据秦九韶算法,把多项式改写成如下形式:f(x)=((((3x+8)x-3)x+5)x+12)x-6,按照从内到外的顺序,依次计算一次多项式当x=2时的值.v0=3,v1=v0×2+8=3×2+8=14,v2=v1×2-3=14×2-3=25,v3=v2×2+5=25×2+5=55,v4=v3×2+12=55×2+12=122,v5=v4×2-6=122×2-6=238,∴当x=2时,多项式的值为238.20.解程序:相应程序框图如右图所示.21.解第10天为S10=1第9天为S9=(1+1)×2=4,第8天为S8=(S9+1)×2=10,…,第1天为S 1=(1+S 2)×2,从而可得递推式S n =2(1+S n +1),S 10=1,n =1,2, (9)故第一天共摘了S 1=1 534个桃子. 程序如下:22.解 设公鸡、母鸡、小鸡各有x 、y 、z 只,首先可以大致确定x ,y ,z 的范围;若100元钱全买公鸡,则最多可买20只,所以x 的范围是0~20,同理y 的范围是0~33;当x ,y 确定后,小鸡的只数也就确定了.事实上,本题就是求不定方程组:⎩⎪⎨⎪⎧x +y +z =100,5x +3y +z3=100的正整数解.程序如下:。
算法初步高考综合试题(含答案)
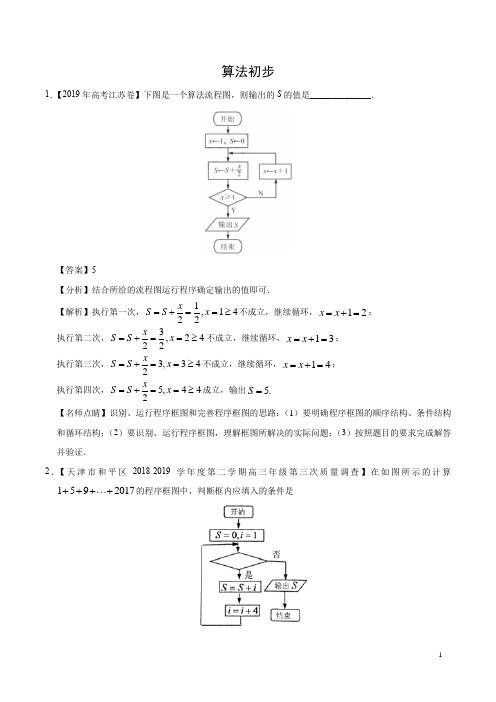
算法初步1.【2019年高考江苏卷】下图是一个算法流程图,则输出的S 的值是______________.【答案】5【分析】结合所给的流程图运行程序确定输出的值即可. 【解析】执行第一次,1,1422x S S x =+==≥不成立,继续循环,12x x =+=; 执行第二次,3,2422x S S x =+==≥不成立,继续循环,13x x =+=; 执行第三次,3,342xS S x =+==≥不成立,继续循环,14x x =+=;执行第四次,5,442xS S x =+==≥成立,输出 5.S =【名师点睛】识别、运行程序框图和完善程序框图的思路:(1)要明确程序框图的顺序结构、条件结构和循环结构;(2)要识别、运行程序框图,理解框图所解决的实际问题;(3)按照题目的要求完成解答并验证.2.【天津市和平区2018-2019学年度第二学期高三年级第三次质量调查】在如图所示的计算1592017++++的程序框图中,判断框内应填入的条件是A .2017?i ≤B .2017?i <C .2013?i <D .2021?i ≤【答案】A【解析】由题意结合流程图可知当2017i =时,程序应执行S S i =+,42021i i =+=, 再次进入判断框时应该跳出循环,输出S 的值;结合所给的选项可知判断框内应填入的条件是2017?i ≤.故选A .3.【吉林省长春市北京师范大学长春市附属中学2019届高三第四次模拟考试】根据如图所示的程序框图,当输入的x 值为3时,输出的y 值等于A .1B .eC .1e -D .2e -【答案】C【解析】由题3x =,231x x =-=-,此时0x >,继续运行,1210x =-=-<,程序运行结束,得1e y -=,故选C .4.【西南名校联盟重庆市第八中学2019届高三5月高考适应性月考卷(六)】执行如图所示的程序框图,则输出的值为C .6D .7【答案】C【解析】由题可得3,27,315,431,563,6S i S i S i S i S i ==→==→==→==→==, 此时结束循环,输出6i =,故选C .5.【山东省济宁市2019届高三二模】阅读如图所示的程序框图,运行相应的程序,输出的S 的值等于A .30B .31C .62D .63【答案】B【解析】由流程图可知该算法的功能为计算123412222S =++++的值,即输出的值为512341(12)122223112S ⨯-=++++==-.故选B .6.【辽宁省大连市2019届高三第二次模拟考试】执行如图所示的程序框图,若输出结果为1,则可输入的实数x 值的个数为C .3D .4【答案】B【分析】根据程序框图的含义,得到分段函数221,2log ,2x x y x x ⎧-≤⎪=⎨>⎪⎩,分段解出关于x 的方程,即可得到可输入的实数x 值的个数.【解析】根据题意,该框图的含义是:当2x ≤时,得到函数21y x =-;当2x >时,得到函数2log y x =, 因此,若输出的结果为1时,若2x ≤,得到211x -=,解得x = 若2x >,得到2log 1x =,无解,因此,可输入的实数x的值可能为,共有2个.故选B . 7.【江西省新八校2019届高三第二次联考】如图所示的程序框图所实现的功能是A .输入a 的值,计算2021(1)31a -⨯+的值B .输入a 的值,计算2020(1)31a -⨯+的值C .输入a 的值,计算2019(1)31a -⨯+的值D .输入a 的值,计算2018(1)31a -⨯+的值【答案】B【解析】由程序框图,可知1a a =,132n n a a +=-,由i 的初值为1,末值为2019, 可知,此递推公式共执行了201912020+=次,又由132n n a a +=-,得113(1)n n a a +-=-,得11(1)3n n a a --=-⨯即1(1)31n n a a -=-⨯+,故2021120202021(1)31(1)31a a a -=-⨯+=-⨯+,故选B .8.【山西省2019届高三考前适应性训练(二模)】执行如图所示的程序框图,则输出x 的值为A .2-B .13-C .12D .3【答案】A【分析】根据程序框图进行模拟运算得到x 的值具备周期性,利用周期性的性质进行求解即可.【解析】∵12x =,∴当1i =时,13x =-;2i =时,2x =-; 3i =时,3x =,4i =时,12x =,即x 的值周期性出现,周期数为4, ∵201850442=⨯+,则输出x 的值为2-,故选A .【名师点睛】本题主要考查程序框图的识别和判断,结合条件判断x 的值具备周期性是解决本题的关键,属于中档题.9.【青海省西宁市第四高级中学、第五中学、第十四中学三校2019届高三4月联考】若某程序框图如图所示,则该程序运行后输出的值是A .5B .4C .3D .2【答案】B【分析】模拟执行循环结构的程序得到n 与i 的值,计算得到2n =时满足判断框的条件,退出循环,输出结果,即可得到答案.【解析】模拟执行循环结构的程序框图, 可得:6,1n i ==, 第1次循环:3,2n i ==; 第2次循环:4,3n i ==; 第3次循环:2,4n i ==,此时满足判断框的条件,输出4i =.故选B .【名师点睛】本题主要考查了循环结构的程序框图的应用,其中解答中根据给定的程序框图,根据判断框的条件推出循环,逐项准确计算输出结果是解答的关键,着重考查了考生的运算与求解能力,属于基础题.10.【江苏省七市(南通、泰州、扬州、徐州、淮安、宿迁、连云港)2019届高三第三次调研】下图是一个算法流程图.若输出y 的值为4,则输入x 的值为______________.【答案】1-【解析】当1x ≤时,由流程图得3y x =-, 令34y x =-=,解得1x =-,满足题意. 当1x >时,由流程图得3y x =+, 令34y x =+=,解得1x =,不满足题意. 故输入x 的值为1-.11.【北京市人大附中2019届高三高考信息卷(三)】执行如图所示的程序框图,若输入x 值满足24x -<≤,则输出y 值的取值范围是______________.【答案】[3,2]-【解析】根据输入x 值满足24x -<≤,利用函数的定义域,分成两部分:即22x <<﹣和24x ≤≤,当22x <<﹣时,执行23y x =- 的关系式,故31y -≤<, 当24x ≤≤时,执行2log y x =的关系式,故12y ≤≤. 综上所述:[3,2]y ∈-,故输出y 值的取值范围是[3,2]-.。
高中数学算法初步综合检测考试试题含答案解析A

算法初步本章达标测评(总分:150分;时间:120分钟)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下面对算法的描述正确的一项是( )A.算法只能用自然语言来描述B.算法只能用图形语言来表示C.同一问题可以有不同的算法D.同一问题的算法不同,结果必然不同2.执行如图所示的框图,输入N=5,则输出S的值为( )A.54B.45C.65D.563.下面一段程序执行后的结果是( )A.6B.4C.8D.104.算式1 010(2)+10(2)的值是( )A.1 011(2)B.1 100(2)C.1 101(2)D.1 000(2)5.执行如图所示的程序框图,当输入的值为3时,输出的结果是( )A.3B.8C.12D.206.若如图所示的程序框图的功能是计算1×12×13×14×15的结果,则在空白的执行框中应该填入( )A.T=T·(i+1)B.T=T·iC.T=T·1i+1D.T=T·1i7.已知7 163=209×34+57,209=57×3+38,57=38×1+19,38=19×2.根据上述一系列等式,可确定7 163和209的最大公约数是( )A.57B.3C.19D.348.已知44(k)=36,则把67(k)转化成十进制数为( )A.8B.55C.56D.629.执行如图所示的程序框图,若输出的k=5,则输入的整数p的最大值为( )A.7B.15C.31D.6310.用秦九韶算法求多项式f(x)=12+35x-8x2+79x3+6x4+5x5+3x6在x=-4时的值时,其中v4的值为( )A.-57B.124C.-845D.22011.某程序框图如图所示,若该程序运行后输出的值是9,则( )5A.a=4B.a=5C.a=6D.a=712.执行如图所示的程序框图,则输出的n的值是( )A.29B.31C.61D.63二、填空题(本大题共4小题,每小题4分,共16分,把正确答案填在题中横线上)13.输入8,则下列程序运行后输出的结果是.化成十进制数,结果为,再将该结果化成七进制数,结14.将二进制数110 101(2)果为.15.执行如图所示的程序框图,则输出结果S= .16.阅读下面程序,当输入x的值为3时,输出y的值为.(其中e为自然对数的底数)三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)17.(12分)下面给出一个用循环语句编写的程序:(1)指出程序所用的是何种循环语句,并指出该程序的算法功能;(2)请用另一种循环语句的形式把该程序写出来.18.(12分)输入10个数,找出其中最大的数并输出,画出程序框图,并写出程序.19.(12分)如图所示,在边长为4的正方形ABCD的边上有一点P,沿着折线BCDA由点B(起点)向点A(终点)运动(不与A、B重合).设点P运动的路程为x,△APB的面积为y,求y与x之间的函数关系式,画出程序框图,写出程序.20.(12分)把区间[0,1]10等分,求函数y=√2x+1+|x-2|在各分点(包括区间端点)的函数值,写出程序.21.(12分)设计一个程序求11×4+13×6+15×8+…+199×102的值.22.(14分)“角谷猜想”是由日本学者角谷静夫首先提出的,所以称为“角谷猜想”.猜想的内容是:对于任意一个大于1的整数n,如果n 为偶数就除以2,如果n 是奇数,就将其乘3再加1,然后将得到的结果再进行以上处理,则最后结果总是1.试设计一个算法的程序框图,对任意输入的整数n(n≥2)进行检验,要求输出每一步的结果,直到结果为1时结束.附加题1.(2015河北石家庄一模,★★☆)执行下面的程序框图,如果输入的依次是1,2,4,8,则输出的S 为( )A.2B.2√2C.4D.62.(2015山西四校联考三,★★☆)执行如图的程序框图,则输出S 的值为( )D.-1 A.2 016 B.2 C.12一、选择题1.C 算法可以用自然语言、图形语言和程序语言来描述;同一个问题可以有不同的算法,但算法的结果相同.2.D 第一次循环,S=0+11×2=12,k=2;第二次循环,S=12+12×3=23,k=3;第三次循环,S=23+13×4=34,k=4;第四次循环,S=34+14×5=45,k=5;第五次循环,S=45+15×6=56,此时k=5不满足判断框内的条件,跳出循环,输出S=56,选D.3.A 由程序知a=2,2×2=4,4+2=6,故最后输出a 的值为6,故选A.4.B 1 010(2)+10(2)=(1×23+0×22+1×21+0×20)+(1×21+0×20)=12=1 100(2).5.B 3<5,执行y=x 2-1,所以输出结果为8.故选B.6.C 程序框图的功能是计算1×12×13×14×15的结果,依次验证选项可得选项C 正确. 7.C 由辗转相除法的思想可得结果. 8.B 由题意得,36=4×k 1+4×k 0,所以k=8. 则67(k)=67(8)=6×81+7×80=55.9.B 由程序框图可知:①S=0,k=1;②S=1,k=2;③S=3,k=3;④S=7,k=4;⑤S=15,k=5,输出k,此时S=15≥p,则p 的最大值为15,故选B. 10.D由已知,得a 0=12,a 1=35,a 2=-8,a 3=79,a 4=6,a 5=5,a 6=3,所以v 0=3,v 1=3×(-4)+5=-7,v 2=(-7)×(-4)+6=34,v 3=34×(-4)+79=-57,v 4=(-57)×(-4)-8=220.11.A 此程序框图的作用是计算S=1+11×2+12×3+…+1a (a+1)的值,由已知得S=95,即S=1+1-12+12-13+…+1a -1a+1=2-1a+1=95,解得a=4.12.D 开始:p=5,n=1;p=9,n=3;p=15,n=7;p=23,n=15;p=31,n=31;p=31,n=63,此时log 3163>1,结束循环,输出n=63. 二、填空题 13.答案 0.7解析 这是一个用条件语句编写的程序,由于输入的数据为8,8<-4不成立,所以c=0.2+0.1×(8-3)=0.7. 14.答案 53;104(7)解析 110 101(2)=1×25+1×24+0×23+1×22+0×21+1×20=53,然后用除7取余法得53=104.(7)15.答案 1 007解析根据程序框图知,S=(-1+2)+(-3+4)+…+(-2 013+2 014)=1 007,故输出的S的值为1 007.16.答案 1.5解析当输入x=3时,由于3>e,故执行y=0.5x,即y=0.5×3=1.5.三、解答题17.解析(1)本程序所用的循环语句是WHILE循环语句,其功能是计算12+22+32+…+92的值.(2)用UNTIL语句改写程序如下:18.解析程序框图如图.程序:19.解析 函数关系式为 y={2x (0<x ≤4),8(4<x ≤8),2(12-x )(8<x <12).程序框图如图所示:程序:20.解析把区间[0,1]10等分,故步长为0.1,∴用“x=x+0.1”表达,y=√2x+1+|x-2|,用“y=SQR(2*x+1)+ABS(x-2)”表达,循环控制条件x≤1.程序如下:21.解析程序:22.解析程序框图如图:附加题1.B 由程序框图可知,S=1,i=1;S=1,i=2;S=√2,i=3;S=2,i=4;S=2√2,i=5,此时跳出循环,输出S=2√2.故选B.2.B 循环前S=2,k=0,第一次循环,得S=11-2=-1,k=1;第二次循环,得S=11-(-1)=12,k=2;第三次循环,得S=11-12=2,k=3;……,由此可知S 的值的变化周期为3,又2 016=672×3,所以输出S 的值为2,故选B.。
高中数学 第一章 算法初步章末测试 新人教A版必修3

高中数学 第一章 算法初步章末测试 新人教A 版必修3(时间:90分钟 满分:100分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列程序框中表示处理框的是( )2.下列关于算法的描述正确的是( ) A .只有解决数学问题才有算法B .算法过程要一步一步执行,每一步的操作都是明确的C .有的算法可能无结果D .算法的三种基本逻辑结构是模块结构、条件结构、循环结构3.已知函数y =⎩⎪⎨⎪⎧lg(x +1),x ≥0,x +1,x <0,输入自变量x 的值,输出对应的函数值.设计程序框图时,需用到的基本逻辑结构是( )A .顺序结构B .条件结构C .顺序结构、条件结构D .顺序结构、循环结构4.编写程序,计算1×2×3×…×n (n ∈N *)的值时,需用到的基本算法语句是( ) A .输入语句、输出语句、赋值语句 B .赋值语句、条件语句、输出语句 C .输出语句、循环语句、赋值语句D .输入语句、输出语句、赋值语句、条件语句、循环语句 5.执行下面的程序后,输出的结果是( )A .1,3B .6,06.用秦九韶算法求当x =1.032时多项式f (x )=3x 2+2x +3的值时,需要乘法运算和加法运算的次数分别为( )A.3 2 B.4 3 C.2 2 D.2 37.根据下面的算法,可知输出的结果S为( )第一步,i=1.第二步,判断i<10是否成立,若成立,则i=i+2,S=2i+3,重复第二步,否则执行下一步.第三步,输出S.A.19 B.21 C.25 D.278.如图是求x1,x2,…,x10的乘积S的程序框图,图中空白框中应填入的内容为( )A.S=S×(n+1) B.S=S×x n+1C.S=S×n D.S=S×x n9.执行如图所示的程序框图,若输出x的值为23,则输入的x值为( )A.0 B.1 C.2 D.1110.某店一个月的收入和支出分别记录为a1,a2,…,a N,其中收入记为正数A,支出记为负数T.该店用如图所示的程序框图计算月总收入S和月净盈利V,那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的( )A.A>0,V=S-T B.A<0,V=S-TC.A>0,V=S+T D.A<0,V=S+T二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上)11.用辗转相除法求两个正整数a,b(a>b)的最大公约数时,得到表达式a=nb+r(n∈N),这里r的取值范围是________.12.459与357的最大公约数是________.13.将258化成四进制数是__________.14.如图是求12+22+32+…+1002的值的程序框图,则正整数n=__________.15.某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中4位居民的月均用水量分别为x1,…,x4(单位:吨).根据如图所示的程序框图,若x1,x2,x3,x4分别为1,1.5,1.5,2,则输出的结果s为__________.三、解答题(本大题共2小题,共25分.解答时应写出文字说明、证明过程或演算步骤)16.(本小题满分10分)如图所示的程序框图.(1)试写出该程序框图的功能;(2)若输出的值为3,求输入x的值.17.(本小题满分15分)有如下算法:第一步,使x=3,S=0.第二步,使x=x+2.第三步,使S=S+x.第四步,若S≥2 008,则执行第五步;否则,返回第二步继续执行.第五步,打印x,算法结束.那么由第五步打印出的数值是多少?并画出程序框图.参考答案一、1.A2.B3.C4.D5.解析:执行过程是:A=1,B=3,A=1+3=4,B=4-3=1,输出4,1.答案:B6.解析:f(x)=(3x+2)x+3,则需2次乘法,2次加法运算.答案:C7.解析:该算法的运行过程是:i=1i=1<10成立i=1+2=3S=2×3+3=9i=3<10成立i=3+2=5S=2×5+3=13i=5<10成立i=5+2=7S=2×7+3=17i=7<10成立i=7+2=9S=2×9+3=21i=9<10成立i=9+2=11S=2×11+3=25i=11<10不成立输出S=25.答案:C8.解析:由于是求输入的10个数的积,所以题图中空白框中应填入的内容为S=S×x n. 答案:D9.解析:设输入x的值为m,该程序框图的运行过程是:x=m,n=1n=1≤3成立x=2m+1n=1+1=2n=2≤3成立x=2(2m+1)+1=4m+3n=2+1=3n=3≤3成立x=2(4m+3)+1=8m+7n=3+1=4n=4≤3不成立输出x=8m+7,则有8m+7=23,解得m=2,即输入的x值为2.答案:C10.解析:由条件结构及已知可得A>0,由已知总收入S和盈利V的值知:V=S+T,故C项正确.答案:C二、11.[0,b)12.解析:459=357×1+102357=102×3+51102=51×2所以459与357的最大公约数是51.答案:5113.解析:利用除4取余法.则258=10 002(4).答案:10 002(4)14.解析:当i=1时,s=12;当i=2时,s=12+22;……当i =99时,s =12+22+…+992; 当i =100时,s =12+22+…+992+1002. 答案:10015.解析:4位居民的月均用水量分别为1,1.5,1.5,2,该程序框图的运行过程是:x 1=1,x 2=1.5,x 3=1.5,x 4=2 s 1=0,i =1 i =1≤4成立 s 1=0+1=1 s =11×1=1 i =1+1=2 i =2≤4成立 s 1=1+1.5=52s =12×52=54i =2+1=3 i =3≤4成立 s 1=52+1.5=4 s =13×4=43i =3+1=4 i =4≤4成立 s 1=4+2=6 s =14×6=32i =4+1=5 i =5≤4不成立输出s =32答案:32三、16.答案:解:(1)该程序框图的功能是输入自变量x 的值,输出函数y =⎩⎪⎨⎪⎧2x 2-5,x <0,x -1,x ≥0对应的函数值.(2)若输出的值为3,当x<0时,2x2-5=3,解得x=2(舍去),或x=-2;当x≥0时,x-1=3,解得x=4.综上所得x=-2或x=4.17.答案:解:由第五步打印出的数值是89.程序框图如图所示.。
2019_2020学年高中数学第一章算法初步章末综合检测(一)课件新人教B版必修3

第一章 算法初步
12.执行如图所示的程序框图,如果输入的 N 是 6,那么输出的 p 是( )
A.120 C.1 440
B.720 D.5 040
第一章 算法初步
解析:选 B.当输入的 N 是 6 时,由于 k=1,p=1,因此 p=p·k =1.此时 k=1,满足 k<6,故 k=k+1=2. 当 k=2 时,p=1×2,此时满足 k<6,故 k=k+1=3. 当 k=3 时,p=1×2×3,此时满足 k<6,故 k=k+1=4. 当 k=4 时,p=1×2×3×4,此时满足 k<6,故 k=k+1=5. 当 k=5 时,p=1×2×3×4×5,此时满足 k<6,故 k=k+1 =6. 当 k=6 时,p=1×2×3×4×5×6=720, 此时 k<6 不再成立,因此输出 p=720.
第一章 算法初步
章末综合检测(一)
第一章 算法初步
一、选择题:本题共 12 小题,每小题 5 分,在每小题给出的 四个选项中,只有一项是符合题目要求的. 1.下列赋值语句中,正确的是( ) A.m=n=3 B.x+y=sqrt(5) C.N=-N^2 D.9=T 解析:选 C.赋值语句不能给表达式赋值,不能给常数赋值,故 A、B、D 均错.
第一章 算法初步
6.运行下面程序后,输出数的个数为( )
i=1 while i<10
i=i+1; print i;
end
A.1
B.10
C.9
D.11
解析:选 C.由于输出语句 print i 在循环体内,故每循环一次
输出一个数,又条件 i<10,当 i=10 即停止循环不再输出,
所以共输出 9 个数.
=-2 时 v2 的值为( )
人教新课标版数学高一B版必修3综合检测 第一章 算法初步

综合检测(一) 第一章 算法初步(时间:90分钟 满分:120分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.算法共有三种逻辑结构,即顺序结构、条件分支结构、循环结构,下列说法正确的是( )A .一个算法只能含有一种逻辑结构B .一个算法最多可以包含两种逻辑结构C .一个算法必须含有上述三种逻辑结构D .一个算法可以含有上述三种逻辑结构的任意组合【解析】 任何一个算法都是由上述三种逻辑结构组成的,它可以含有三种结构中的一种,也可以是两种或三种.【答案】 D2.给出以下四个问题.①输入一个数x ,输出它的相反数;②求体积为6的正方体的棱长;③求三个数a ,b ,c 中的最小数;④求函数f (x )=⎩⎨⎧x -1,x ≥0x +2,x <0的函数值.其中不需要用条件语句来描述其算法的有( ) A .1个 B .2个 C .3个D .4个【解析】 仅②不需要分情况讨论,即不需要用条件语句. 【答案】 A3.用更相减损之术求186和98的最大公约数为( ) A .2 B .4 C .6D .8【解析】由更相减损之术可知:(186,98)→(98,88)→(88,10)→(78,10)→(68,10)→(58,10)→(48,10)→(38,10)→(28,10)→(18,10)→(8,10)→(8,2)→(6,2)→(4,2 )→(2,2).【答案】 A图14.(2013·天津高考)阅读如图1所示的程序框图,运行相应的程序,则输出n的值为()A.7B.6C.5D.4【解析】n=1,S=0.第一次:S=0+(-1)1×1=-1,-1<2,n=1+1=2,第二次:S=-1+(-1)2×2=1,1<2,n=2+1=3,第三次:S=1+(-1)3×3=-2,-2<2,n=3+1=4,第四次:S=-2+(-1)4×4=2,2=2,满足S≥2,跳出循环,输出n=4.【答案】 D5.下面程序输入x=π时的运算结果是()A .-2B .1C .πD .2【解析】 该程序的功能是求分段函数 y =⎩⎪⎨⎪⎧-2 (x >0),0 (x =0),2 (x <0)的函数值,由于π>0,∴y =-2.【答案】 A6.给出如图2程序框图图2循环体执行的次数是( ) A .50 B .49 C .100D .99【解析】 2+2×49=100,∴执行次数为49. 【答案】 B7.(2013·北京高考)图3执行如图3所示的程序框图,输出的S值为()A.1 B.2 3C.1321 D.610987【解析】当i=0,S=1时,执行S=S2+12S+1后得S=23,i=i+1=1;当i=1,S=23时,执行S=S2+12S+1后得S=1321,i=i+1=2.由于此时i≥2是成立的,因此输出S=1321.【答案】 C图48.(2012·安徽高考)如图4所示,程序框图(算法流程图)的输出结果是() A.3 B.4C.5 D.8【解析】当x=1,y=1时,满足x≤4,则x=2,y=2;当x=2,y=2时,满足x≤4,则x=2×2=4,y=2+1=3;当x=4,y=3时,满足x≤4,则x=2×4=8,y=3+1=4;当x=8,y=4时,不满足x≤4,则输出y=4.【答案】 B9.以下程序运行的输出结果是()A.17 B.19C.15 D.13【解析】S=2×(5+2)+1=15.【答案】C10.以下给出的是计算12+14+16+…+120的值的一个程序框图(如图5所示),其中判断框内应填入的条件是()图5 A.i>10 B.i<10C.i>20 D.i<20【解析】这是一个循环结构,其中变量i是计数变量,它应使循环执行10次,因此条件应是i>10.【答案】 A二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)11.若输入8,则下列程序执行后输出的结果是________.【解析】这是一个用条件语句编写的程序,由于输入8时,t≤4不成立,故应有c=0.2+0.1×(8-3)=0.7.【答案】0.712.(2012·湖南高考)如果执行如图6所示的程序框图,输入x=-1,n=3,则输出的数S=________.图6【解析】 当n =3时,i =3-1=2,满足i ≥0, 故S =6×(-1)+2+1=-3.执行i =i -1后i 的值为1,满足i ≥0, 故S =(-3)×(-1)+1+1=5.再执行i =i -1后i 的值为0,满足i ≥0, 故S =5×(-1)+0+1=-4.继续执行i =i -1后i 的值为-1,不满足i ≥0,故输出S =-4. 【答案】 -413.已知函数y =⎩⎨⎧log 2x , x ≥2,2-x , x<2.如图7表示的是给定x 的值,求其对应的函数值y 的程序框图,①处应填写________;②处应填写________.图7【解析】 根据分段函数解析式及程序框图知,当满足x<2时,执行y =2-x ,故判断框中条件为x<2,不满足条件x<2,即x ≥2时,y =log 2x ,故②中为y =log 2x.【答案】x<2y=log2x14.如图8是求12+22+32+…+1002的值的程序框图,则正整数n=________.图8【解析】因为第一次判断执行后,s=12,i=2,第二次判断执行后,s=12+22,i=3,而题目要求计算12+22+32+…+1002,故n=100.【答案】100三、解答题(本大题共4小题,共50分,解答应写出文字说明,证明过程或演算步骤)15.(本题满分12分)画程序框图,求使1+2+22+…+2n<1 000成立的最大整数n.【解】16.(本小题满分12分)用秦九韶算法求多项式f(x)=8x7+5x6+3x4+2x+1当x=2时的值.【解】本题中有几项不存在.在计算时,我们应该将这些项加上,比如x3这一项可看做0·x3.f(x)=8x7+5x6+0·x5+3·x4+0·x3+0·x2+2x+1=((((((8x+5)x+0)x+3)x+0)x+0)x+2)x+1.v0=8;v1=8×2+5=21;v2=21×2+0=42;v3=42×2+3=87;v4=87×2+0=174;v5=174×2+0=348;v6=348×2+2=698;v7=698×2+1=1 397;∴当x=2时,多项式的值为1 397.17.(本小题满分13分)有一列数1,2,5,26,…,你能找出它的规律吗?如图9的程序框图是输出这列数的前10项,并求和的算法,试将框图补充完整,并写出相应的程序.图9【解】这列数的规律是从第2项起每个数是前一个数的平方加1.设变量为m,用m=m2+1实现递推.故①处填m=m2+1;②处填i=i+1.程序如下:18.(本小题满分13分)意大利数学家菲波那契在1202年出版的一书里提出了这样的一个问题:一对兔子饲养到第二个月进入成年,第三个月生一对小兔,以后每个月生一对小兔,所生小兔能全部存活并且也是第二个月成年,第三个月生一对小兔,以后每月生一对小兔.则这样下去到年底应有多少对兔子?试画出解决此问题的程序框图,并编写相应的程序.【解】程序框图如图所示.程序如下.。
18-19 章末综合测评1 算法初步

章末综合测评(一) 算法初步(满分:150分 时间:120分钟)一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下面对算法的描述正确的一项是( )A.算法只能用自然语言来描述B.算法只能用图形语言来表示C.同一问题可以有不同的算法D.同一问题的算法不同,结果必然不同C 2.如图1所示的程序框图,下列说法正确的是( )【导学号:49672133】图1A.该框图只含有顺序结构、条件结构B.该框图只含有顺序结构、循环结构C.该框图只含有条件结构、循环结构D.该框图包含顺序结构、条件结构、循环结构D [由框图知,三种逻辑结构均含有.]3.下列程序语句正确的是( )A.输出语句PRINT A=4B.输入语句INPUT x=3C.赋值语句A=A*A+A-3D.赋值语句55=aC [输入语句、输出语句中输入、输出的是变量或数值,而不是等式.A、B均错;赋值语句格式是“变量=表达式”,D错;C对.] 4.用辗转相除法,计算56和264的最大公约数时,需要做的除法次数是( )【导学号:49672134】A.3 B.4C.6 D.7B [由辗转相除法264=56×4+40,56=40×1+16,40=16×2+8,16=8×2,即最大公约数为8,做4次除法.]5.下列各进制数中,最小的是( )A.1 002(3) B.210(6)C.1 000(4)D.111 111(2)A [1 002(3)=29,210(6)=78,1 000(4)=64,111 111(2)=63,故1 002(3)最小.]6.对于程序:【导学号:49672135】试问,若输入m=-4,则输出的数为( )A.9 B.-7C.5或-7 D.5D [由程序,先输入m,判断m>-4是否成立,因为m=-4,所以不成立,则执行m=1-m,最后输出结果为5.]7.如图2是求x1,x2,…,x10的乘积S的程序框图,图中空白框中应填入的内容为( )图2A.S=S*(n+1) B.S=S*x n+1C.S=S*n D.S=S*x nD [由于求x1,x2,…,x10的乘积,故空白处应为“S=S*x n”.]8.阅读下面的程序:【导学号:49672136】上述程序的功能是( )A.计算3×10的值B.计算39的值C.计算310的值D.计算1×2×3×…×10的值C [该程序使用了循环语句,在i不超过10的条件下,反复执行循环体,依次得到S的值为3,32,33,…,310,所以循环结束时,输出结果为310.] 9.用秦九韶算法求多项式f(x)=4x5-x2+2当x=3时的值时,需要做乘法运算和加法(或减法)运算的次数分别为( )A.4,2 B.5,3C.5,2 D.6,2C [f(x)=4x5-x2+2=((((4x)x)x-1)x)x+2,所以需要做5次乘法运算和2次加(减)法运算.]10.考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图3所示的程序框图,运行相应程序,输出的结果i=( )图3A.4 B.5C.6 D.7D [模拟算法:开始:a=10,i=1,a=1不成立;a是奇数,不成立,a=5,i=2,a=1不成立;a是奇数,不成立,a=16,i=3,a=1不成立;a是奇数,不成立,a=8,i=4,a=1不成立;a是奇数,不成立,a=4,i=5,a=1不成立;a是奇数,不成立,a=2,i=6,a=1不成立;a是奇数,不成立,a=1,i=7,a=1成立;输出i=7,结束算法.]11.阅读如图4所示的程序框图,运行相应的程序,若输出的结果是4,则程序框图中的处理框“①”处应填写的是( )【导学号:49672137】图4A.n=n-1 B.n=n-2C.n=n+1 D.n=n+2C [因为起始n=1,输出的n=4,所以排除A、B.若“①”处填n=n+1.则S==-1,n=2,判断-1≠2,继续循环;S==,n=3,判断≠2,继续循环;S==2,n=4,判断2=2,则输出n的值为4,故选C.]12.对于任意函数f(x),x∈D,可按如图5构造一个数字发生器,其工作原理如下:图5①输入数据x0∈D,经过数字发生器,输出x1=f(x0);②若x1∉D,则数字发生器结束工作;若x1∈D,则将x1反馈回输入端,再输出x2=f(x1),并依此规律继续下去.现定义f(x)=2x+1,D=(0,1 000).若输入x0=0,当发生器结束工作时,输出数据的总个数为( )A.8 B.9C.10 D.11C [依题中规律,当输入x0=0时,可依次输出1,3,7,15,31,63,127,255,511,1 023,共10个数据.]二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题纸的横线上)13.若运行下面的程序,输出的结果为5,则横线处应填写的内容为________.【导学号:49672138】2或-2 [程序的功能是求所输入的两个数的平方和,由题意得12+y2=5,y =±2.]14.执行下面的程序后输出的第3个数是________.2 [第一次输出的数是1,第二次输出的数是x=1+=,第三次输出的数是x =+=2.]15.运行如图6所示的程序框图,若输出的y值的范围是[0,10],则输入的x的取值范围是________.图6[-7,9] [本题中的程序框图是计算分段函数y=的函数值.当0≤3-x≤10时,-7≤x<-1;当0≤x2≤10时,-1≤x≤1;当0≤x+1≤10时,1<x≤9.故输入的x的取值范围是[-7,9].]16.张老师给学生出了一道题:试画一个程序框图,计算S=1++++.同学们有如下四种画法,其中错误的程序框图是________(填相应的序号).【导学号:49672139】图7③ [③中,当i=7时,执行最后一次循环,此时S=S+,与题意不符;①②④均正确.]三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)下面给出了一个问题的算法:第一步,输入x.第二步,若x≥4,则y=2x-1;否则,y=x2-2x+3.第三步,输出y.问题:(1)这个算法解决的问题是什么?(2)当输入的x值为多少时,输出的y值最小?[解] (1)这个算法解决的问题是求分段函数y=的函数值.(2)当x≥4时,y=2x-1≥7;当x<4时,y=x2-2x+3=(x-1)2+2≥2,所以y min =2,此时x=1.即当输入的x值为1时,输出的y值最小.18.(本小题满分12分)分别用辗转相除法和更相减损术求282和470的最大公约数.【导学号:49672140】[解] 辗转相除法:470=1×282+188,282=1×188+94,188=2×94,∴282与470的最大公约数为94.更相减损术:470与282分别除以2得235和141.∴235-141=94,141-94=47,94-47=47.∴470与282的最大公约数为47×2=94.]19.(本小题满分12分)下面给出一个用循环语句编写的程序:(1)指出程序所用的是何种循环语句,并指出该程序的算法功能;(2)请用另一种循环语句的形式把该程序写出来.[解] (1)本程序所用的循环语句是WHILE循环语句,其功能是计算12+22+32+…+92的值.(2)用UNTIL语句改写程序如下:20.(本小题满分12分)到某银行办理个人异地汇款业务时,银行要收取一定的手续费,汇款不超过100元时,收取1元的手续费;超过100元时,按汇款的1%收取手续费,但最高收取50元的手续费.请你按照银行的规定,设计一个算法,要求输入汇款额x(元)时,输出银行收取的手续费y(元),并画出程序框图.【导学号:49672141】[解] 算法步骤如下:第一步,输入x.第二步,如果x≤100,那么y=1;否则,执行第三步.第三步,如果x≤5 000,那么y=0.01x;否则,y=50.第四步,输出y.程序框图如图.21.(本小题满分12分)如图8(1),在边长为4的正方形ABCD的边上有一点P 沿着折线BCDA由点B(起点)向点A(终点)运动.设点P运动的路程为x,△APB的面积为y,且y与x之间的函数关系式用如图8(2)所示的程序框图给出.图8(1)写出框图中①,②,③处应填写的式子;(2)若输出的面积y值为6,则程序输入x的值为多少?并指出此时点P在正方形的什么位置上?[解] (1)框图中①,②,③处应填写的式子分别为y=2x,y=8,y=24-2x.(2)若输出的面积y值为6,则2x=6或24-2x=6,解得x=3或x=9.当x=3时,此时点P在正方形的边BC上,且BP=3;当x=9时,此时点P在正方形的边DA上,且AP=3.22.(本小题满分12分)某商场第一年销售计算机6 000台,如果以后每年销售比上一年增加12%,那么从第一年起,大约经过几年可使总销量达到150 000台?画出解决此问题的程序框图,并写出程序.【导学号:49672142】[解] 程序框图如图所示:程序如下:。
2018-2019学年高中数学第1章算法初步1.1算法的含义课件苏教版必修

3.下面是求 1+11+21+31+41 的值的一个算法,请将其补充完整. 第一步 计算 1+11,得 12; 第二步 将第一步中的运算结果 12 与 21 相加,得到 33; 第三步 将第二步中的运算结果 33 与 31 相加,得到 64; 第四步 ______________________________________,即为最后结果.
将第三步中的运算结果 64 与 41 相加,得到 105 [本题是一个连续相加 的问题,可以按逐一相加的方法解决.]
4.有人对命题“任何大于4的偶数都能写成两个奇质数之和”设计了如 下操作步骤: 第一步 检验6=3+3. 第二步 检验8=3+5. 第三步 检验10=5+5. … 利用计算机一直进行下去! 请问:利用这种步骤能够证明猜想的正确性吗?这是一个算法吗? 【导学号:20132001】
算法 2: 第一步 取 n=7; 第二步 计算 n2; 第三步 输出运算结果. 算ቤተ መጻሕፍቲ ባይዱ 3: 第一步 使 p=1; 第二步 使 i=3;
第三步 使 p+i 的和仍放在变量 p 中,可表示为 p=p+i; 第四步 使 i 的值加 2,即 i=i+2; 第五步 若 i≤13, 返回第三步, 重新执行第三步及之后的第四、 第五步, 否则,算法结束,最后得到的 p 的值就是 1+3+5+7+9+11+13 的值.
算法在实际生活中的应用
一位商人有 9 枚银元,其中有 1 枚略轻的是假银元,你能用天 平(不用砝码)将假银元找出来吗?写出解决这一问题的一种算法. 【导学号:20132004】
[解析] 可以两枚两枚地称,直到称出假银元为止,也可以先分组再 称.
[解] 法一: 第一步 任取 2 枚银元分别放在天平的两边,如果天平左右不平衡,则 轻的一枚就是假银元,如果天平平衡,则进行第二步; 第二步 取下右边的银元,放在一边,然后把剩余的 7 枚银元依次放在 右边进行称量,直到天平不平衡,偏轻的那一枚就是假银元.
第一章算法初步章末综合检测(人教A版必修3)

(时间:100 分钟,满分:120 分) 一、 选择题(本大题共 10 小题. 在每小题给出的四个选项中, 只有一项是符合题目要求的) 1.下面对算法描述正确的一项是( ) A.算法只能用自然语言来描述 B.算法只能用图形方式来表示 C.同一个问题可以有不同的算法 D.同一问题的算法不同,结果必然不同 解析:选 C.算法可以用自然语言、程序框图、程序语句等来描述,同一个问题可以有不 同的算法,但结果是相同的. 2.算法共有三种逻辑结构,即顺序结构、条件结构和循环结构,下列说法正确的是( ) A.一个算法只含有一种逻辑结构 B.一个算法最多可以包含两种逻辑结构 C.一个算法必须含有上述三种逻辑结构 D.一个算法可以含有上述三种逻辑结构 解析:选 D.一个算法中具体含有哪种结构,主要看如何解决问题或解决怎样的问题,以 上三种逻辑结构在一个算法中都有可能体现,故选 D. 3.(2014· 日照高一检测)如果执行如图所示的程序框图,输入正整数 N(N≥2)和实数 a1, a2,„,aN,输出 A,B,则( )
x2-3 (x≥0), 18.(本小题满分 10 分)已知函数 y= 2 画出程序框图,对每输入的一个 2x -6 (x<0),
x 值,都得到相应的函数值. 解:程序框图如图所示:
19.(本小题满分 12 分)以下是某次数学考试中某班 15 名同学的成绩(单位:分):72,91, 58,63,84,88,90,55,61,73,64,77,82,94,60.要求用程序框图将这 15 名同学中成 绩高于 80 分的同学的平均分数求出来. 解:程序框图如图所示:
20.(本小题满分 12 分)已知某算法的程序框图如图所示,若将输出的(x,y) 值依次记为(x1,y1),(x2,y2),„,(xn,yn),„ (1)若程序运行中输出的一个数组是(9,t),求 t 的值; (2)程序结束时,共输出(x,y)的组数为多少; (3)写出程序框图的程序语句. 解:(1)开始时,x=1 时,y=0;接着 x=3,y=-2;然后 x=9,y=-4, 所以 t=-4; (2)当 n=1 时,输出一对,当 n=3 时,又输出一对,„,当 n=2 013 时, 输出最后一对,共输出(x,y)的组数为 1 007; (3)程序框图的程序语句如下:
高三数学 章末综合测试题19算法初步与框图 试题

2021届高三数学章末综合测试题〔19〕算法初步与框图一、选择题:本大题一一共12小题,每一小题5分,一共60分.1.算法一共有三种逻辑构造,即顺序构造,条件构造和循环构造,以下说法正确的选项是( )A.一个算法必定含有条件构造B.一个算法必定含有循环构造C.一个算法必定含有上述三种构造D.一个算法可以是顺序构造和其他两个构造的有机组合解析:一个算法必定含有顺序构造,其他两个构造根据需要可有可无.答案:D2.对算法的理解不.正确的选项是( )A.一个算法包含的步骤是有限的B.一个算法中每一步都是明解可操作的,而不是模棱两可的C.算法在执行后,结果应是明解的D.一个问题只可以有一个算法解析:对于同一个问题,它的算法不唯一,故D错.答案:D3.成员、老师、后勤人员、理科老师、文科老师的构造图正确的选项是( )解析:成员包含老师和后勤人员,而老师又包含理科老师和文科老师.答案:A4.以下程序中,输出时A的值是输入时A的值的( )A.1倍B.2倍C.3倍D.4倍解析:由所给的程序可知输入A后进展了两次赋值,每次的计算都是2倍运算. 答案:D5.以下几个不同进制数最大的是( )A.3(10)B.11(2)C.3(8)D.11(3)解析:都化成十进制为3(10)=3,11(2)=1×21+1×20=3,3(8)=3×80=3, 11(3)=1×31+1×30=4. 答案:D6.给出以下四个问题:①输入一个数x ,输出它的绝对值;②求函数f (x )=⎩⎪⎨⎪⎧x 2-1 (x ≥1),3x (x <0),的函数值;③求面积为6的正方形的周长; ④求三个数a 、b 、c 中的最大数.其中不需要用条件语句来描绘其算法的有( ) A .1个 B .2个 C .3个D .4个解析:计算①、②、④都需要做出判断,都需要用条件语句.计算③只需顺序构造就够了.答案:A7.用辗转相除法求得111与1 850的最大公约数是( ) A .3 B .11 C .37D .111解析:利用辗转相除法得1 850=16×111+74 111=1×74+37 74=2×37 ∴111与1 850的最大公约数是37. 答案:C8.如以下图所示的程序的输出结果为S =132,那么判断框中应填( )A.i≥10? B.i≥11?C.i≤11? D.i≥12?解析:i的初值为12,S的初值为1,第一次运算S=1×12=12,第二次运算S=12×11=132,所以循环了两次,∴应填i≥11?.答案:B9.在以下图的程序框图中,假设输入的x的值是5,那么输出的结果是( )A.x是方程2x2-3x-2=0的根B.x不是方程2x2-3x-2=0的根C.y≠0D.不输出任何结果解析:当x=5时,y=2×52-3×5-2=33≠0,应选B.答案:B10.执行以下图的程序框图,输出的S和n的值分别是( )A .9,3B .9,4C .11,3D .11,4解析:执行程序框图.S =0,T =0,n =1.又∵T ≤S ,∴S =S +3=0+3=3,T =1,n =2. 又∵T ≤S ,∴S =6,T =4,n =3. 又∵T ≤S ,∴S =9,T =11,n =4. ∵T >S ,∴输出S =9,n =4. 答案:B11.程序框图计算的数学式是( )A .1+2+3+…+nB .1!+2!+3!+…+n!C .1!+12!+13!+…+1n !D .1+12+13+…+1n解析:不妨设n =3,循环体一共循环3次, 输出S =1+12!+13!,由此可知选C.答案:C12.为解决四个村庄用电问题,政府HY 在建电厂与这四个村庄之间架设输电线路,现这四个村庄及电厂之间的间隔 如下图(间隔 单位:千米),那么能把电力输送到这四个村庄的输电线路的最短总长度应该是( )A .19.5B .20.5C .21.5解析:要使电厂与四个村庄相连,至少需四条线路,仔细观察所给的图,发现电厂离A 村最近,A 村离D 村最近,D 村离C 村最近,A 村到B 村最近,故如图架线总路程最短,最短总长为5+4+5.5+6=20.5.答案:B二、填空题:本大题一一共4个小题,每一小题5分,一共20分.13.如下图,这是计算12+14+16+…+120的值的一个程序框图,其中判断框内应填入的i 的条件是__________.解析:这是一道数列求和题,n从2开场到20完毕,那么i从1开场到10完毕,所以判断框内应填入i≤10?答案:i≤1014.执行以下图所示的程序,假设P=0.9,那么输出的n值是__________.解析:当n=1时,S=0<0.9;答案:515.阅读下面的程序框图,答复以下问题:假设a=5,b5,c=log5,那么输出的数是__________.解析:此框图的功能是输出a、b、c中最大的数,∵a=50.6>1,0<b=0.65<1,c=log0.55<0.∴输出的数是50.6.答案:16.以下图是某个函数求值的程序框图,那么满足该程序的函数解析式为__________.解析:由程序框图可知:当x<0时,f(x)=2x-3,当x≥0时,f(x)=5-4x.答案:三、解答题:本大题一一共6小题,一共70分.17.(10分)某一完全寄宿,设有幼儿部、小学部、初中部、高中部,幼儿部下设托儿所、学前班,小学部下设一、二、三、四、五、六一共六个年级,初中部下设初一、初二、初三一共三个年级,高中部下设文科和理科两部,文理两部都分别下设高一、高二、高三一共三个年级.试画出该设置的组织构造图.解析:18.(12分)设计算法求:11×2+12×3+13×4+…+199×100的值,要求画出程序框图.解析:这是一个累加求和问题,一共99项相加,可设计一个计数变量,一个累加变量,用循环构造实现这一算法,程序框图如下图.19.(12分)有甲、乙、丙三种溶液分别重147 g 、343 g 、133 g ,现要将它们分别全部装入小瓶中,每个小瓶装入液体的质量一样,问每瓶最多装多少?解析:由题意,每个小瓶装的溶液的质量应是三种溶液质量的最大公约数.先求147与343的最大公约数.343-147=196, 196-147=49, 147-49=48, 98-49=49.所以147与343的最大公约数是49.再求49与133的最大公约数:133-49=84,84-49=35,49-35=14,35-14=21,21-14=7,14-7=7.所以147,343,133的最大公约数是7.所以,每瓶最多装7 g.20.(12分)根据下面的程序写出相应的算法功能,并画出相应的程序框图.解析:其程序的算法功能是求和,12+32+52+ (9992)其程序框图如下.21.(12分)以下算法:①初始值x=3,S=0;②x=x+2;③S=S+x;④如S ≥2 003,那么进展⑤,否那么从②继续进展;⑤输出x ;⑥完毕算法.试求第⑤步输出的数值.解析:循环执行语句②,③,第一次可以得到x 1=5,S 1=5;第二次得到x 2=7,S 2=12;依次可以得到x 3=9,S 3=21;x 4=11,S 4=32;…,显然{x n }是以5为首项,2为公差的等差数列,∴x n =5+2(n -1)=2n +3.由算法得:S n +1=S n +x n +1,∴S n -S n -1=2n +3,…,S 2-S 1=7,以上n -1个等式相加得S n =5+(2n +3)2×n =n 2+4n , 由n 2+4n ≥2 003及n ∈N *,得n ≥43,那么x 43=2×43+3=89,因此语句⑤输出的数值为89.22.(12分)有一个数据运算装置,如下图,输入数据x 通过这个运算装置就输出一个数据y ,输入一组数据,那么会输出另一组数据.要使输入的数据介于20~100之间(含20和100,且一个都不能少),输出后的另一组数据满足以下要求:①新数据在10~40之间(含10和40,也一个都不能少);②新数据的大小关系与原数据的大小关系相反,即原数据较大的对应的新数据较小.(1)假设该装置的运算规那么是一次函数,求出这种关系;(2)假设该装置的运算规那么是y =a (x -h )2(a >0),求出这种关系.解析:(1)假设该运算装置的运算规那么是一次函数,设y =kx +b (k ≠0),根据题意,那么⎩⎪⎨⎪⎧ 40=20k +b ,10=100k +b ,解得⎩⎪⎨⎪⎧ b =-38,b =952,∴y =-38x +952. (2)要使规那么y =a (x -h )2(a >0)满足以上条件,那么必须有函数y =a (x -h )2(a >0)的定义域为[20,100],值域为[10,40].且该函数在[20,100]上单调递减. 故a ,h 应满足条件⎩⎪⎨⎪⎧ 40=a (20-h )2,10=a (100-h )2,h ≥100,a >0,解得⎩⎪⎨⎪⎧ a =1640,h =180,所以y =1640(x -180)2.励志赠言经典语录精选句;挥动**,放飞梦想。
全国通用版2018_2019高中数学第一章算法初步检测A新人教B版必修3201811133113

第一章算法初步检测(A)(时间:90分钟满分:120分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1下列关于算法的叙述不正确的是()A.在任何数值计算或非数值计算的过程中所采取的方法和步骤,都可称之为算法B.计算机解决问题的方法和步骤,就是计算机的算法C.算法并不给出问题的精确的解,只是说明怎样才能得到解D.算法中执行的步骤可以是无限次数的,能无休止地执行下去解析本题主要考查算法的基本概念和特点.算法就是解决问题的步骤,可以是数值或者非数值操作,它必须是有限的步骤,不能无休止地执行下去,必须“有始有终”.答案D2“x=4+5”,“x=x-1”是某一程序中先后相邻的两个语句,那么下列说法正确的是()①x=4+5的意思是x=4+5=9,此式与算术中的式子是一样的;②x=4+5是将数值9赋给x;③x=4+5可以写成4+5=x;④x=x-1语句在执行时,“=”右边x的值是9,执行后左边x的值是8.A.①③B.②④C.①④D.②③解析在x=4+5中,是先计算4+5,再用其结果9代替左边的x,由于赋值号“=”左边与右边的含义不一样,因而x=4+5不能写成4+5=x.答案B3下列程序运行的结果是()a=1;b=2;c=3;a=b;b=c;c=a;abcA.1,2,3B.2,3,1C.2,3,2D.3,2,1解析由已知得a=1,b=2,c=3⇒a=2⇒b=3⇒c=2,故a,b,c的值分别是2,3,2.答案C4对于下列算法,a=input(“a=”);if a>5b=4;elseif a<3b=5;elseb=9;endendprint(%io(2),a);print(%io(2),b);如果在运行时,输入2,那么输出的结果是()A.2,5B.2,4C.2,3D.2,9解析本题主要考查条件语句的应用.输入a的值为2,首先判断是否大于5,显然2不大于5,然后判断2与3的大小,显然2小于3,所以结果是b=5,因此结果应当输出2,5.答案A5执行下面的程序框图,如果输入的t∈[-1,3],则输出的s属于()A.[-3,4]B.[-5,2]C.[-4,3]D.[-2,5]解析当-1≤t<1时,s=3t,则s∈[-3,3).当1≤t≤3时,s=4t-t2.∵该函数的对称轴为t=2,∴该函数在[1,2]上单调递增,在[2,3]上单调递减.∴s max=4,s min=3.∴s∈[3,4].综上知s∈[-3,4].故选A.答案A6两个正整数490和910的最大公约数是()A.2B.10C.30D.70解析910=91×10,490=49×10.∵91=49×1+42,49=42×1+7,42=7×6,∴91与49的最大公约数为7.故910与490的最大公约数为70.答案D7下面的程序框图表示的算法的功能是()A.计算小于100的奇数的连乘积B.计算从1开始的连续奇数的连乘积C.从1开始的连续奇数的连乘积,当乘积大于100时,计算奇数的个数D.计算1×3×5×…×n≥100时的最小的n值解析题中程序框图表示的算法是确定使1×3×…×n≥100成立的最小整数n的值.答案D8某程序框图如图所示,运行后输出的倒数第二个数是()17 9 5 3A.16B.8C.4D.2解析当 n=1时,输出 a=3;当 n=2时,输出 a=2;当 n=3时,输出 a = 3 2;当 n=4时,输出 a = 5 4; 当 n=5时,输出 a = 9 8.5故输出的倒数第二个数是4.答案 C9 下面程序执行后输出的结果是( )n=5;S=0;while S<15S=S+n;n=n-1;endnA.-1B.0C.1D.2 解析∵5+4+3+2+1=15,∴当 n=1时进行最后一次循环,最后输出 n=n-1=1-1=0.答案 B10 执行两次下图所示的程序框图,若第一次输入的 a 的值为-1.2,第二次输入的 a 的值为 1.2,则第一次、第二次输出的 a 的值分别为( )A.0.2,0.2B.0.2,0.8C.0.8,0.2D.0.8,0.8解析第一次:a=-1.2<0,a=-1.2+1=-0.2,-0.2<0,a=-0.2+1=0.8>0,a=0.8≥1不成立,输出0.8.第二次:a=1.2<0不成立,a=1.2≥1成立,a=1.2-1=0.2≥1不成立,输出0.2.答案C二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上)11三个数72,120,168的最大公约数是.解析利用辗转相除法:120=72×1+48,72=48×1+24,48=24×2,所以72和120的最大公约数是24,又168=24×7,所以三个数的最大公约数是24.答案2412下面是求S=1+3+5+…+2 015的程序,在横线处填上正确的内容.S=;i=1;for i=1::S=;endprint(%io(2),S);答案0 2 2 015S+i13阅读某一问题的算法的程序框图(如图所示).此框图反映的算法功能是.答案计算任意实数x的绝对值|x|14执行如图所示的程序框图,如果输入a=1,b=2,则输出的a的值为.解析输入a=1,b=2,不满足a>8,故a=3;a=3不满足a>8,故a=5;a=5不满足a>8,故a=7;a=7不满足a>8,故a=9,满足a>8,终止循环.输出a=9.答案915用秦九韶算法计算多项式f(x)=3x6+4x5+5x4+6x3+7x2+8x+1当x=0.4时的值时,需要做乘法和加法的次数分别是.解析由于f(x)=(((((3x+4)x+5)x+6)x+7)x+8)x+1,因此需做乘法6次,加法6次.答案6,6三、解答题(本大题共5小题,共45分.解答时应写出文字说明、证明过程或演算步骤)16(8分)分别用更相减损之术与辗转相除法求161与253的最大公约数.解更相减损之术:(161,253)→(161,92)→(69,92)→(69,23)→(46,23)→(23,23).故161与253的最大公约数为23.辗转相除法:253÷161=1(余92),161÷92=1(余69),92÷69=1(余23),69÷23=3(余0),故161与253的最大公约数为23.17(8分)如图所示的程序框图.(1)试写出该程序框图的功能;(2)若输出的值为3,求输入x的值.2푥2-5,푥<0,解(1)该程序框图的功能是输入自变量x的值,输出函数y={.푥-1,푥≥0对应的函数值(2)若输出的值为3,当x<0时,2x2-5=3,解得x=2(舍去)或x=-2;当x≥0时,x-1=3,解得x=4.综上所得x=-2或x=4.18(9分)老师将一次测验的成绩分为3个等级:85~100为“A”;60~84为“B”;60以下为“C”.试用条件分支结构的框图表示某个学生成绩等级的算法.解程序框图如图所示.19(10分)已知如图所示的程序框图(未完成).设当箭头a指向①时,输出的结果为s=m,当箭头a指向②时,输出的结果为s=n,求m+n的值.解当箭头a指向①时,s和i的结果如下:0+ s 1 0+20+30+40+5i2 3 4 5 6因此,s=m=5.当箭头a指向②时,输出s和i的结果如下:0+ s 1 0+1+20+1+2+30+1+2+3+0+1+2+3+44 +5i2 3 4 5 6因此,s=n=1+2+3+4+5=15.故m+n=20.20(10分)相传古代印度国王在奖赏他聪明能干的宰相达依尔(国际象棋发明者)时,问他需要什么,达依尔说:“国王只要在国际象棋棋盘的第一格子上放一粒麦子,第二格子上放二粒,第三格子上放四粒,以后按比例每一格加一倍,一直放到第64格(国际象棋棋盘格数是8×8=64),我就感恩不尽,其他什么也不要了.”国王想:“这才有多少,还不容易!”于是让人扛来一袋小麦,但不到一会儿就用完了,再来一袋很快又没有了,结果全印度的粮食用完还不够, 国王很奇怪,怎么也算不清这笔账.请你设计一个程序框图表示其算法,来帮国王计算一下需要多少粒小麦,并用算法语句编写程序.解程序框图如图所示.程序如下:i=0;S=0;while i<64S=S+2^i;i=i+1;endprint(%io(2),S);。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
章末综合测评(一) 算法初步(满分:150分时间:120分钟)一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下面对算法的描述正确的一项是()A.算法只能用自然语言来描述B.算法只能用图形语言来表示C.同一问题可以有不同的算法D.同一问题的算法不同,结果必然不同C2.如图1所示的程序框图,下列说法正确的是()【导学号:49672133】图1A.该框图只含有顺序结构、条件结构B.该框图只含有顺序结构、循环结构C.该框图只含有条件结构、循环结构D.该框图包含顺序结构、条件结构、循环结构D[由框图知,三种逻辑结构均含有.]3.下列程序语句正确的是()A.输出语句PRINT A=4B.输入语句INPUT x=3C.赋值语句A=A*A+A-3D.赋值语句55=aC[输入语句、输出语句中输入、输出的是变量或数值,而不是等式.A、B均错;赋值语句格式是“变量=表达式”,D错;C对.]4.用辗转相除法,计算56和264的最大公约数时,需要做的除法次数是()【导学号:49672134】A.3B.4C.6 D.7B[由辗转相除法264=56×4+40,56=40×1+16,40=16×2+8,16=8×2,即最大公约数为8,做4次除法.]5.下列各进制数中,最小的是()A.1 002(3)B.210(6)C.1 000(4)D.111 111(2)A[1 002(3)=29,210(6)=78,1 000(4)=64,111 111(2)=63,故1 002(3)最小.] 6.对于程序:【导学号:49672135】试问,若输入m=-4,则输出的数为()A.9 B.-7C.5或-7 D.5D[由程序,先输入m,判断m>-4是否成立,因为m=-4,所以不成立,则执行m=1-m,最后输出结果为5.]7.如图2是求x1,x2,…,x10的乘积S的程序框图,图中空白框中应填入的内容为()图2A.S=S*(n+1) B.S=S*x n+1C.S=S*n D.S=S*x nD[由于求x1,x2,…,x10的乘积,故空白处应为“S=S*x n”.]8.阅读下面的程序:【导学号:49672136】上述程序的功能是()A.计算3×10的值B.计算39的值C.计算310的值D.计算1×2×3×…×10的值C[该程序使用了循环语句,在i不超过10的条件下,反复执行循环体,依次得到S的值为3,32,33,…,310,所以循环结束时,输出结果为310.] 9.用秦九韶算法求多项式f(x)=4x5-x2+2当x=3时的值时,需要做乘法运算和加法(或减法)运算的次数分别为()A.4,2 B.5,3C.5,2 D.6,2C[f(x)=4x5-x2+2=((((4x)x)x-1)x)x+2,所以需要做5次乘法运算和2次加(减)法运算.]10.考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图3所示的程序框图,运行相应程序,输出的结果i=()图3A.4 B.5C.6 D.7D[模拟算法:开始:a=10,i=1,a=1不成立;a是奇数,不成立,a=5,i=2,a=1不成立;a是奇数,不成立,a=16,i=3,a=1不成立;a是奇数,不成立,a=8,i=4,a=1不成立;a是奇数,不成立,a=4,i=5,a=1不成立;a是奇数,不成立,a=2,i=6,a=1不成立;a是奇数,不成立,a =1,i=7,a=1成立;输出i=7,结束算法.]11.阅读如图4所示的程序框图,运行相应的程序,若输出的结果是4,则程序框图中的处理框“①”处应填写的是()【导学号:49672137】图4A .n =n -1B .n =n -2C .n =n +1D .n =n +2C [因为起始n =1,输出的n =4,所以排除A 、B.若“①”处填n =n +1.则S =11-2=-1,n =2,判断-1≠2,继续循环;S =11-(-1)=12,n =3,判断12≠2,继续循环;S =11-12=2,n =4,判断2=2,则输出n 的值为4,故选C.]12.对于任意函数f (x ),x ∈D ,可按如图5构造一个数字发生器,其工作原理如下:图5①输入数据x 0∈D ,经过数字发生器,输出x 1=f (x 0);②若x 1∉D ,则数字发生器结束工作;若x 1∈D ,则将x 1反馈回输入端,再输出x 2=f (x 1),并依此规律继续下去.现定义f (x )=2x +1,D =(0,1 000).若输入x 0=0,当发生器结束工作时,输出数据的总个数为()A.8 B.9C.10 D.11C[依题中规律,当输入x0=0时,可依次输出1,3,7,15,31,63,127,255,511,1 023,共10个数据.]二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题纸的横线上)13.若运行下面的程序,输出的结果为5,则横线处应填写的内容为________.【导学号:49672138】2或-2[程序的功能是求所输入的两个数的平方和,由题意得12+y2=5,y=±2.]14.执行下面的程序后输出的第3个数是________.2[第一次输出的数是1,第二次输出的数是x=1+12=32,第三次输出的数是x=32+12=2.]15.运行如图6所示的程序框图,若输出的y值的范围是[0,10],则输入的x 的取值范围是________.图6[-7,9][本题中的程序框图是计算分段函数y =⎩⎪⎨⎪⎧3-x ,x <-1,x 2,-1≤x ≤1,x +1,x >1的函数值.当0≤3-x ≤10时,-7≤x <-1;当0≤x 2≤10时,-1≤x ≤1;当0≤x +1≤10时,1<x ≤9.故输入的x 的取值范围是[-7,9].]16.张老师给学生出了一道题:试画一个程序框图,计算S =1+13+15+17+19.同学们有如下四种画法,其中错误的程序框图是________(填相应的序号).【导学号:49672139】图7③ [③中,当i =7时,执行最后一次循环,此时S =S +17,与题意不符;①②④均正确.]三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)下面给出了一个问题的算法: 第一步,输入x .第二步,若x ≥4,则y =2x -1;否则,y =x 2-2x +3. 第三步,输出y .问题:(1)这个算法解决的问题是什么? (2)当输入的x 值为多少时,输出的y 值最小?[解] (1)这个算法解决的问题是求分段函数y =⎩⎨⎧2x -1,x ≥4,x 2-2x +3,x <4的函数值.(2)当x ≥4时,y =2x -1≥7;当x <4时,y =x 2-2x +3=(x -1)2+2≥2,所以y min =2,此时x =1.即当输入的x 值为1时,输出的y 值最小.18.(本小题满分12分)分别用辗转相除法和更相减损术求282和470的最大公约数.【导学号:49672140】[解] 辗转相除法:470=1×282+188,282=1×188+94,188=2×94,∴282与470的最大公约数为94.更相减损术:470与282分别除以2得235和141.∴235-141=94,141-94=47,94-47=47.∴470与282的最大公约数为47×2=94.]19.(本小题满分12分)下面给出一个用循环语句编写的程序:(1)指出程序所用的是何种循环语句,并指出该程序的算法功能;(2)请用另一种循环语句的形式把该程序写出来.[解](1)本程序所用的循环语句是WHILE循环语句,其功能是计算12+22+32+…+92的值.(2)用UNTIL语句改写程序如下:20.(本小题满分12分)到某银行办理个人异地汇款业务时,银行要收取一定的手续费,汇款不超过100元时,收取1元的手续费;超过100元时,按汇款的1%收取手续费,但最高收取50元的手续费.请你按照银行的规定,设计一个算法,要求输入汇款额x(元)时,输出银行收取的手续费y(元),并画出程序框图.【导学号:49672141】[解]算法步骤如下:第一步,输入x.第二步,如果x≤100,那么y=1;否则,执行第三步.第三步,如果x≤5 000,那么y=0.01x;否则,y=50.第四步,输出y.程序框图如图.21.(本小题满分12分)如图8(1),在边长为4的正方形ABCD的边上有一点P沿着折线BCDA由点B(起点)向点A(终点)运动.设点P运动的路程为x,△APB的面积为y,且y与x之间的函数关系式用如图8(2)所示的程序框图给出.图8(1)写出框图中①,②,③处应填写的式子;(2)若输出的面积y值为6,则程序输入x的值为多少?并指出此时点P在正方形的什么位置上?[解](1)框图中①,②,③处应填写的式子分别为y=2x,y=8,y=24-2x.(2)若输出的面积y值为6,则2x=6或24-2x=6,解得x=3或x=9.当x=3时,此时点P在正方形的边BC上,且BP=3;当x=9时,此时点P在正方形的边DA上,且AP=3.22.(本小题满分12分)某商场第一年销售计算机6 000台,如果以后每年销售比上一年增加12%,那么从第一年起,大约经过几年可使总销量达到150 000台?画出解决此问题的程序框图,并写出程序.【导学号:49672142】[解]程序框图如图所示:程序如下:。
