北京市西城区(普通校)2014-2015学年高一上学期期末考试数学试题 Word版含答案

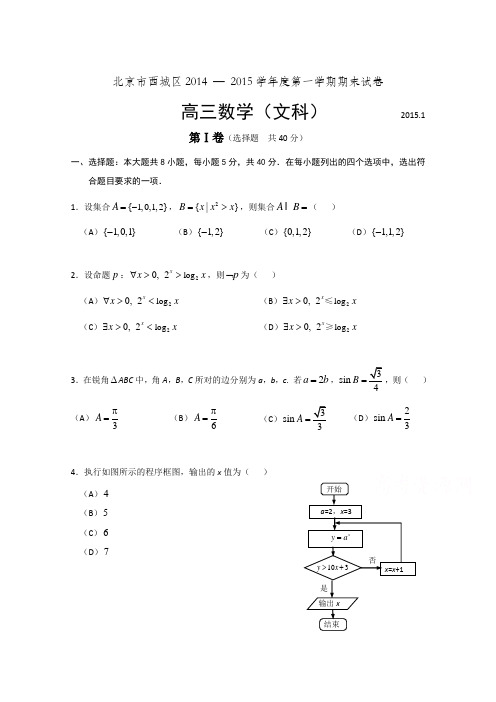
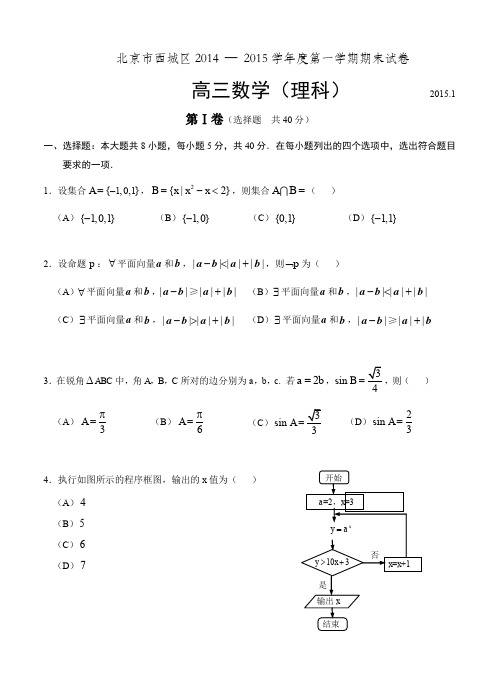
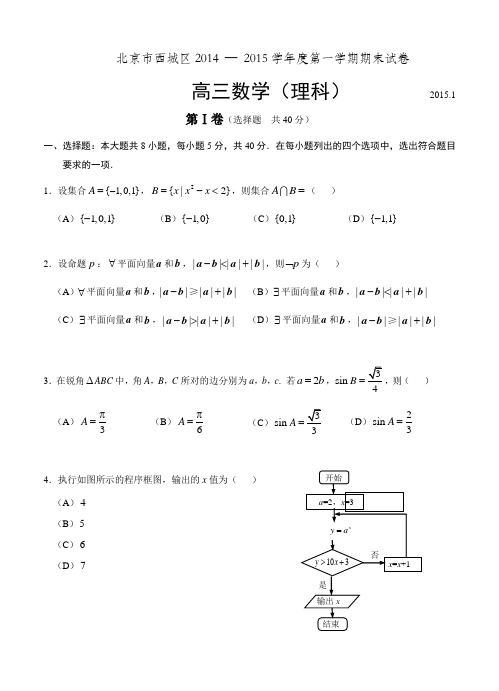
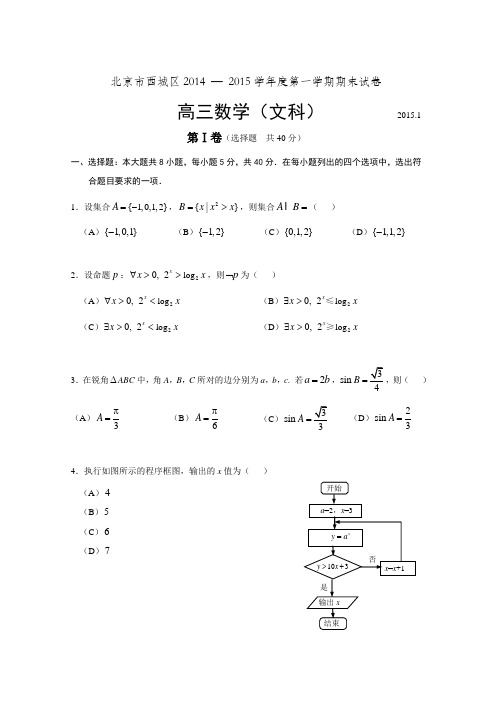
北京市西城区2014 — 2015学年度第一学期期末试卷高一数学 2015.1试卷满分：150分 考试时间：120分钟A 卷 [必修 模块4] 本卷满分：100分一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的.1．已知(0,2π)α∈，且sin 0<α，cos 0>α，则角α的取值范围是（ ） （A ）π(0,)2（B ）π(,π)2（C ）3π(π,)2（D ）3π(,2π)22．已知向量(2,8)=a ，(4,2)=-b ．若2=-c a b ，则向量=c （ ） （A ）(0,18)（B ）(8,14)（C ）(12,12)（D ）(4,20)-3．已知角α的终边经过点(3,4)P -，那么sin =α（ ） （A ）35（B ）45-（C ）34（D ）34-4．在△ABC 中，D 是BC 的中点，则AD =（ ） （A ）1()2AB AC +（B ）1()2AB AC -（C ）1()2AB BC +（D ）1()2AB BC -5．函数2(sin cos )y x x =-的最小正周期为（ ） （A ）2π（B ）3π2（C ）π（D ）π26．如果函数cos()y x =+ϕ的一个零点是3π，那么ϕ可以是（ ） （A ）6π （B ）6π-（C ）3π（D ）3π-7．如图，在矩形ABCD 中，2AB =，BC =， E 是CD的中点，那么AE DC ⋅=（ ）（A ）4（B ）2（C （D ）18．当[0,π]x ∈时，函数()cos f x x x =的值域是（ ）（A ）[2,1]-（B ）[1,2]-（C ）[1,1]-（D ）[-9．为得到函数πcos()6y x =+的图象，只需将函数sin y x =的图象（ ） （A ）向左平移π3个单位 （B ）向右平移π3个单位（C ）向左平移2π3个单位 （D ）向右平移2π3个单位10．已知a ，b 为单位向量，且m ⋅=a b ，则||t +a b ()t ∈R 的最小值为（ ）（A （B ）1（C ）||m（D二、填空题：本大题共6小题，每小题4分，共24分. 把答案填在题中横线上. 11．若向量(1,2)=a 与向量(,1)=-λb 共线，则实数=λ_____． 12．已知α是第二象限的角，且5sin 13α=，则cos =α_____． 13．若(,)22ππ∈-θ，且tan 1>θ，则θ的取值范围是_____． 14．已知向量(1,3)=a ，(2,1)=-b ，(1,1)=c ．若(,)=∈R c a +b λμλμ，则=λμ_____． 15．函数2()sin sin cos f x x x x =+⋅的最大值是_____．16．关于函数()sin(2)()6f x x x π=-∈R ，给出下列三个结论：① 对于任意的x ∈R ，都有2()cos(2)3f x x π=-； ② 对于任意的x ∈R ，都有()()22f x f x ππ+=-；③ 对于任意的x ∈R ，都有()()33f x f x ππ-=+．其中，全部正确结论的序号是_____．三、解答题：本大题共3小题，共36分. 解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分12分）已知tan 2=-α，其中(,)2π∈πα． （Ⅰ）求πtan()4-α的值； （Ⅱ）求sin 2α的值．18．（本小题满分14分）已知向量(cos ,sin )=ααa ，1(2=-b ，其中α是锐角． （Ⅰ）当30︒=α时，求||+a b ； （Ⅱ）证明：向量+a b 与-a b 垂直； （Ⅲ）若向量a 与b 夹角为60︒，求角α．19．（本小题满分10分）已知函数()sin cos f x a x b x =+，其中a ∈Z ，b ∈Z ．设集合{|()0}A x f x ==，{|(())0}B x f f x ==，且A B =．（Ⅰ）证明：0b =； （Ⅱ）求a 的最大值．B 卷 [学期综合] 本卷满分：50分一、填空题：本大题共5小题，每小题4分，共20分. 把答案填在题中横线上. 1．已知集合{,}A a b =，则满足{,,}A B a b c = 的不同集合B 的个数是_____． 2．若幂函数y x =α的图象过点(4,2)，则=α_____．3．函数2lg ,0,()4,0,x x f x x x >⎧=⎨-<⎩的零点是_____．4．设()f x 是定义在R 上的偶函数，且()f x 在[0,)+∞上是减函数．若()(2)f m f >，则 实数m 的取值范围是_____．5．已知函数()f x 的定义域为D ．若对于任意的1x D ∈，存在唯一的2x D ∈，使得M =成立，则称函数()f x 在D 上的几何平均数为M ．已知函数()31([0,1])g x x x =+∈，则()g x 在区间[0,1]上的几何平均数为_____．二、解答题：本大题共3小题，共30分.解答应写出文字说明，证明过程或演算步骤. 6．（本小题满分10分）已知函数()(2)()f x x x a =-+，其中a ∈R ． （Ⅰ）若()f x 的图象关于直线1x =对称，求a 的值； （Ⅱ）求()f x 在区间[0,1]上的最小值． 7．（本小题满分10分）已知函数()23xxf x a b =⋅+⋅，其中,a b 为常数．（Ⅰ）若0ab >，判断()f x 的单调性，并加以证明； （Ⅱ）若0ab <，解不等式：(1)()f x f x +>．8．（本小题满分10分）定义在R 上的函数()f x 同时满足下列两个条件：① 对任意x ∈R ，有(2)()2f x f x +≥+；② 对任意x ∈R ，有(3)()3f x f x +≤+． 设()()g x f x x =-．（Ⅰ）证明：(3)()(2)g x g x g x +≤≤+； （Ⅱ）若(4)5f =，求(2014)f 的值．北京市西城区2014 — 2015学年度第一学期期末试卷高一数学参考答案及评分标准 2015.1A 卷 [必修 模块4] 满分100分一、选择题：本大题共10小题，每小题4分，共40分.1.D ；2.B ；3.B ；4.A ；5.C ；6.A ；7.B ；8.A ；9.C ； 10.D . 二、填空题：本大题共6小题，每小题4分，共24分.11.12-； 12.1213-； 13. (,)42ππ；14.32； 15.12； 16. ① ② ③. 注：16题，少解不给分.三、解答题：本大题共3小题，共36分. 17.（本小题满分12分） （Ⅰ）解：因为 tan 2=-α，所以 πtan tanπ4tan()π41tan tan 4--=+⋅ααα 【 3分】 3=. 【 6分】（Ⅱ）解：由π(,π)2∈α，tan 2α=-， 得sin α=， 【 8分】cos α=. 【10分】 所以 4sin 22sin cos 5==-ααα. 【12分】18.（本小题满分14分） （Ⅰ）解：当30︒=α时，1)2=a ， 【 1分】 所以11(,)22+a b =， 【 2分】 所以||+=a b = 【 4分】 （Ⅱ）证明：由向量(cos sin )αα=，a，1(2=-b ， 得1(cos ,sin 2+=-ααa b，1(cos ,sin 2-=+ααa b ， 由 π(0,)2∈α，得向量+a b ，-a b 均为非零向量. 【 5分】 因为 222213()()||||(sin cos )()044+⋅-=-=+-+=ααa b a b a b ， 【 7分】所以向量+a b 与-a b 垂直. 【 8分】 （Ⅲ）解：因为||||1==a b ，且向量a 与b 夹角为60︒， 所以 1||||cos 602︒⋅=⋅=a b a b . 【10分】所以 11cos 22-+=αα， 即 π1sin()62-=α. 【12分】 因为 π02<<α， 所以 πππ663-<-<α， 【13分】 所以 ππ66-=α， 即3π=α. 【14分】19.（本小题满分10分） （Ⅰ）证明：显然集合A ≠∅．设 0x A ∈，则0()0f x =． 【 1分】 因为 A B =，所以 0x B ∈， 即 0(())0f f x =，所以 (0)0f =， 【 3分】 所以 0b =． 【 4分】 （Ⅱ）解：由（Ⅰ）得()sin f x a x =，a ∈Z ．① 当0a =时，显然满足A B =． 【 5分】 ② 当0a ≠时，此时{|sin 0}A x a x ==；{|sin(sin )0}B x a a x ==， 即{|sin ,}B x a x k k ==π∈Z ． 【 6分】因为 A B =，所以对于任意x ∈R ，必有sin a x k ≠π (k ∈Z ，且0)k ≠成立． 【 7分】所以对于任意x ∈R ，sin k x a π≠，所以 1k aπ>， 【 8分】 即 ||||a k <⋅π，其中k ∈Z ，且0k ≠．所以 ||a <π， 【 9分】 所以整数a 的最大值是3． 【10分】B 卷 [学期综合] 满分50分一、填空题：本大题共5小题，每小题4分，共20分.1. 4；2.12； 3. 2-，1； 4. (2,2)-； 5. 2. 注：3题，少解得2分，有错解不给分. 二、解答题：本大题共3小题，共30分. 6.（本小题满分10分）（Ⅰ）解法一：因为2()(2)()(2)2f x x x a x a x a =-+=+--， 所以，()f x 的图象的对称轴方程为22ax -=. 【 2分】 由212a-=，得0a =. 【 4分】 解法二：因为函数()f x 的图象关于直线1x =对称，所以必有(0)(2)f f =成立， 【 2分】 所以 20a -=， 得0a =. 【 4分】 （Ⅱ）解：函数()f x 的图象的对称轴方程为22ax -=. ① 当202a-≤，即 2a ≥时， 因为()f x 在区间(0,1)上单调递增，所以()f x 在区间[0,1]上的最小值为(0)2f a =-. 【 6分】② 当2012a-<<，即 02a <<时， 因为()f x 在区间2(0,)2a -上单调递减，在区间2(,1)2a-上单调递增， 所以()f x 在区间[0,1]上的最小值为222()()22a a f -+=-. 【 8分】 ③ 当212a-≥，即 0a ≤时，因为()f x 在区间(0,1)上单调递减，所以()f x 在区间[0,1]上的最小值为(1)(1)f a =-+. 【10分】7.（本小题满分10分）（Ⅰ）解：当0,0a b >>时，()f x 在R 上是增函数；当0,0a b <<时，()f x 在R 上是减函数； 【 1分】 证明如下：当0,0a b >>时，任取12,x x ∈R ，且12x x <，则210x x x ∆=->， 则 212121()()(22)(33)x x x xy f x f x a b ∆=-=-+-.因为 122122,0(22)0x x x x a a <>⇒->；又122133,0(33)0x x x xb b <>⇒->， 所以 21()()0y f x f x ∆=->，所以，当0,0a b >>时，()f x 在R 上是增函数.当0,0a b <<时，同理可得，()f x 在R 上是减函数. 【 5分】 （Ⅱ）解：由(1)()2230x xf x f x a b +-=⋅+⋅>，得 32()2xb a >-. （*） 【 6分】 ① 当0,0a b <>时，（*）式化为3()22xa b->， 解得32log ()2ax b>-. 【 8分】 ② 当0,0a b ><时，（*）式化为3()22xab-<， 解得32log ()2ax b<-. 【10分】 8.（本小题满分10分）（Ⅰ）证明：因为()()g x f x x =-，所以(2)(2)2g x f x x +=+--，(3)(3)3g x f x x +=+--．由条件①，②可得(2)(2)2()22()()g x f x x f x x f x x g x +=+--≥+--=-=； ③ 【 2分】 (3)(3)3()33()()g x f x x f x x f x x g x +=+--≤+--=-=． ④ 【 4分】所以(3)()(2)g x g x g x +≤≤+． （Ⅱ）解：由③得 (2)()g x g x +≥，所以(6)(4)(2)()g x g x g x g x +≥+≥+≥． 【 6分】由④得 (3)()g x g x +≤，所以(6)(3)()g x g x g x +≤+≤． 【 7分】 所以必有(6)()g x g x +=，即()g x 是以6为周期的周期函数． 【 8分】 所以(2014)(33564)(4)(4)41g g g f =⨯+==-=． 【 9分】 所以(2014)(2014)20142015f g =+=． 【10分】。