2020【浙教版】九年级数学下册第2章《切线长定理》同步测试(含答案)

合集下载

浙教版数学九年级下册《切线长定理》习题.docx

《切线长定理》习题1．一个直角三角形的斜边长为8，内切圆半径为1，则这个三角形的周长等于（)A．21 B．20 C．19 D．182．如图，P A、PB分别切⊙O于点A、B，AC是⊙O的直径，连结AB、BC、OP，则与∠P AB相等的角（不包括∠P AB本身)有（）A．1个B．2个C．3个D．4个3．如图，已知△ABC的内切圆⊙O与各边相切于点D、E、F，则点O是△DEF的（)A．三条中线的交点B．三条高的交点C．三条角平分线的交点D．三条边的垂直平分线的交点4．△ABC中，AB＝AC，∠A为锐角，CD为AB边上的高，I为△ACD的内切圆圆心，则∠AIB的度数是（）A．120°B．125°C．135°D．150°5．一个钢管放在V形架内，右图是其截面图，O为钢管的圆心．如果钢管的半径为25cm，∠MPN=60 ，则OP=（)A．50cm B．253cmC．3350cm D．503cm6．如图，P A、PB分别切圆O于A、B两点，C为劣弧AB上一点，∠APB=30°，则∠ACB=（）．B ACPOA．60°B．75°C．105°D．120°7．如图，在△ABC中，5cmAB AC==，cosB35=．如果⊙O的半径为10cm，且经过点B、C，那么线段AO=__________cm．8．如图，PA、PB分别切⊙O于点A、B，点E是⊙O上一点，且ο60=∠AEB，则=∠P_____度．9．如图，AE、AD、BC分别切⊙O于点E、D、F，若AD=20，求△ABC的周长．10．如图，已知AB为⊙O的直径，AD、BC、CD为⊙O的切线，切点分别是A、B、E，则有一下结论：（1）CO⊥DO；（2）四边形OFEG是矩形．试说明理由．GFECB初中数学试卷鼎尚图文**整理制作。

浙教版九年级下数学《2.2切线长定理》同步练习含答案

2.2 切线长定理同步练习一、单选题1、以下命题正确的是（）A、圆的切线一定垂直于半径；B、圆的内接平行四边形一定是正方形；C、直角三角形的外心一定也是它的内心；D、任何一个三角形的内心一定在这个三角形内2、下列说法：①三点确定一个圆；②垂直于弦的直径平分弦；③三角形的内心到三条边的距离相等；④圆的切线垂直于经过切点的半径．其中正确的个数是（）A、0B、2C、3D、43、如图，直角梯形ABCD中，以AD为直径的半圆与BC相切于E，BO交半圆于F，DF的延长线交AB于点P，连DE．以下结论：①DE∥OF；②AB+CD=BC；③PB=PF；④AD2=4AB•DC．其中正确的是（）A、①②③④B、只有①②C、只有①②④D、只有③④4、如图，在平面直角坐标系中，过格点A，B，C作一圆弧，点B与下列格点的连线中，能够与该圆弧相切的是（）A、点（0，3）B、点（2，3）C、点（5，1）D、点（6，1）5、如图，AB是⊙O的直径，BC交⊙O于点D，DE⊥AC于点E，要使DE是⊙O 的切线，还需补充一个条件，则补充的条件不正确的是（）A、DE=DOB、AB=ACC、CD=DBD、AC∥OD6、如图所示，⊙M与x轴相切于原点，平行于y轴的直线交圆于P，Q两点，P点在Q点的下方，若P点坐标是（2，1），则圆心M的坐标是（）A、（0，3）B、（0，2）C、（0，）D、（0，）7、．如图，半圆D的直径AB=4，与半圆O内切的动圆O1与AB切于点M，设⊙O1的半径为y，AM=x，则y关于x的函数关系式是( )A、y=-x2+xB、y=-x2+xC、y=-x2-xD、y=x2-x8、如图，两个同心圆，大圆的弦AB与小圆相切于点P，大圆的弦CD经过点P，且CD=13，PC=4，则两圆组成的圆环的面积是（）A、16πB、36πC、52πD、81π9、如图，在⊙O中，AD，CD是弦，连接OC并延长，交过点A的切线于点B，若∠ADC=30°，则∠ABO的度数为（）A、20°B、30°C、40°D、50°10、已知⊙O是以原点为圆心，为半径的圆，点P是直线上的一点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为( )A、3B、4C、D、11、如图，已知PA，PB分别切⊙O于点A、B，∠P=60°，PA=8，那么弦AB 的长是（）A、4B、8C、D、12、如图，以O为圆心的两个同心圆中，大圆的弦AB切小圆于点C，若∠AOB ＝120°，则大圆半径R与小圆半径r之间的关系满足( )A、R=2rB、R=3rC、R=rD、R=r13、如图，AE、AD和BC分别切⊙O于点E、D、F，如果AD=20，则△ABC的周长为（）A、20B、30C、40D、5014、如图，直线AB、CD、BC分别与⊙O相切于E、F、G，且AB∥CD，若OB=6cm，0C=8cm，则BE+CG的长等于（）A、13B、12C、11D、1015、如图，⊙O的半径为2，点O到直线l的距离为3，点P是直线l上的一个动点，PQ切⊙O于点Q，则PQ的最小值为（）A、B、C、3D、5二、填空题16、如图，直线AB与⊙O相切于点C，D是⊙O上的一点，∠CDE=22.5°，若EF∥AB，且EF=2，则⊙O的半径是________．17、如图，已知半圆O的直径AB＝4，沿它的一条弦折叠．若折叠后的圆弧与直径AB相切于点D，且AD:DB＝3:1，则折痕EF的长________ ．18、如图，⊙O是四边形ABCD的内切圆，切点分别为E、F、G、H，已知AB=5，CD=7，那么AD+BC= ________.19、如图，PA，PB是⊙O的切线，CD切⊙O于E，PA=6，则△PDC的周长为________.20、如图，AB为半⊙O的直径，C为半圆弧的三等分点，过B，C两点的半⊙O的切线交于点P，若AB的长是2a，则PA的长是________ ．三、解答题21、如图，在梯形ABCD中，AB∥CD，⊙O为内切圆，E为切点．若AO=8cm，DO=6cm，求OE的长．22、如图，PA、PB切⊙O于A、B两点，CD切⊙O于点E，分别交PA、PB 于点C、D．若PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根，求△PCD的周长．23、如图，AB是⊙O的直径，AC是弦，半径OD⊥AC于点E，过点D的切线与BA延长线交于点F．（1）求证：∠CDB=∠BFD；（2）若AB=10，AC=8，求DF的长．24、如图，点C在⊙O的直径BA的延长线上，AB=2AC，CD切⊙O于点D，连接CD，OD．（1）求角C的正切值：（2）若⊙O的半径r=2，求BD的长度．25、如图，△ABD是⊙O的内接三角形，E是弦BD的中点，点C是⊙O外一点且∠DBC=∠A，连接OE延长与圆相交于点F，与BC相交于点C．（1）求证：BC是⊙O的切线；（2）若⊙O的半径为6，BC=8，求弦BD的长．答案部分一、单选题1、【答案】D2、【答案】C3、【答案】C4、【答案】C5、【答案】A6、【答案】C7、【答案】A8、【答案】B9、【答案】B10、【答案】B 11、【答案】B 12、【答案】A 13、【答案】C 14、【答案】D 15、【答案】B二、填空题16、【答案】17、【答案】18、【答案】12 19、【答案】12 20、【答案】 a三、解答题21、【答案】解：∵AB∥CD，⊙O为内切圆，∴∠OAD+∠ODA=90°，∴∠AOD=90°，∵AO=8cm，DO=6cm，∴AD=10cm，∵OE⊥AD，∴AD•OE=OD•OA，∴OE=4.8cm．22、【答案】解：∵PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根，∴PA+PB=m，PA•PB=m﹣1，∵PA、PB切⊙O于A、B两点，∴PA=PB=，即•=m﹣1，即m2﹣4m+4=0，解得：m=2，∴PA=PB=1，∵PA、PB切⊙O于A、B两点，CD切⊙O于点E，∴AD=ED，BC=EC，∴△PCD的周长为：PD+CD+PC=PD+DE+EC+PC=PD+AD+BC+PC=PA+PB=2．23、【答案】解：（1）∵DF与⊙O相切，∴DF⊥OD，∵OD⊥AC，∴DF∥AC，∴∠CAB=∠BFD，∴∠CAB=∠BFD，∴∠CDB=∠BFD；（2）∵半径OD垂直于弦AC于点E，AC=8，∴AE=AC=．∵AB是⊙O的直径，∴OA=OD=AB=，在Rt△AEO中，OE===3，∵AC∥DF，∴△OAE∽△OFD．∴，∴=，∴DF=．24、【答案】解：（1）∵CD切⊙O于点D，∴CD⊥OD，又∵AB=2AC，∴OD=AO=AC=CO∴∠C=30°∴tan∠C=；（2）连接AD，∵AB是直径，∴∠ADB=90°，∵∠DOA=90°﹣30°=60°，又∵OD=OA，∴△DAO是等边三角形．∴DA=r=2，∴DB==．25、【答案】（1）证明：连接OB，如图所示：∵E是弦BD的中点，∴BE=DE，OE⊥BD，=，∴∠BOE=∠A，∠OBE+∠BOE=90°，∵∠DBC=∠A，∴∠BOE=∠DBC，∴∠OBE+∠DBC=90°，∴∠OBC=90°，即BC⊥OB，∴BC是⊙O的切线；（2）解：∵OB=6，BC=8，BC⊥OB，∴OC==10，∵△OBC的面积=OC•BE=O B•BC，∴BE===4.8，∴BD=2BE=9.6，即弦BD的长为9.6．。

浙教版九年级数学下册第2章直线与圆的位置关系2.2切线长定理同步测试-附答案

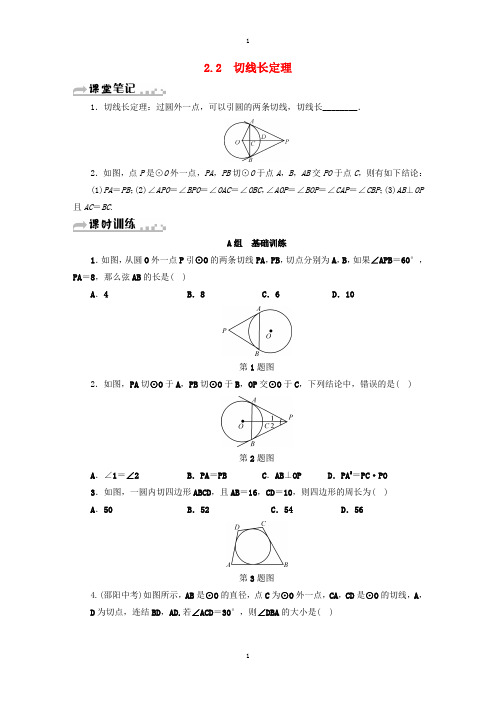
2.2 切线长定理1．切线长定理：过圆外一点，可以引圆的两条切线，切线长________．2．如图，点P是⊙O外一点，PA，PB切⊙O于点A，B，AB交PO于点C，则有如下结论：(1)PA＝PB；(2)∠APO＝∠BPO＝∠OAC＝∠OBC，∠AOP＝∠BOP＝∠CAP＝∠CBP；(3)AB⊥OP 且AC＝BC.A组基础训练1．如图，从圆O外一点P引⊙O的两条切线PA，PB，切点分别为A，B，如果∠APB＝60°，PA＝8，那么弦AB的长是( )A．4 B．8 C．6 D．10第1题图2．如图，PA切⊙O于A，PB切⊙O于B，OP交⊙O于C，下列结论中，错误的是( )第2题图A．∠1＝∠2 B．PA＝PB C．AB⊥OP D．PA2＝PC·PO3．如图，一圆内切四边形ABCD，且AB＝16，CD＝10，则四边形的周长为( )A．50 B．52 C．54 D．56第3题图4.(邵阳中考)如图所示，AB是⊙O的直径，点C为⊙O外一点，CA，CD是⊙O的切线，A，D为切点，连结BD，AD.若∠ACD＝30°，则∠DBA的大小是( )第4题图A．15° B．30° C．60° D．75°5．如图，过⊙O外一点P作⊙O的两条切线PA，PB，切点分别为A，B.下列结论中：①OP 垂直平分AB；②∠APB＝∠BOP；③△ACP≌△BCP；④PA＝AB；⑤若∠APB＝80°，则∠OBA ＝40°.正确的是________．第5题图1．如图，EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E＝46°，∠DCF＝32°，则∠A的度数是________°.第6题图7．如图，在△ABC中，已知∠ABC＝90°，在AB上取一点E，以BE为直径的⊙O恰与AC相切于点D，若AE＝2，AD＝4.则BE＝________，BC＝________.第7题图2．如图，⊙O与△ABC中AB、AC的延长线及BC边相切，且∠ACB＝90°，∠A，∠B，∠C所对的边长依次为3，4，5，则⊙O的半径是________．第8题图9．如图，AB为半圆O的直径，在AB的同侧作AC，BD切半圆O于点A，B，CD切半圆O 于点E.若AC＝4，BD＝9，求⊙O的半径．第9题图10．如图，PA，PB，DE分别切⊙O于点A，B，C，D在PA上，E在PB上．(1)若PA＝30，求△PDE的周长；(2)若∠P＝50°，求∠O的度数．第10题图B组自主提高11．如图，CA，CD分别切圆O1于A，D两点，CB、CE分别切圆O2于B，E两点，若∠1＝60°，∠2＝65°，判断AB、CD、CE的长度，下列关系何者正确( )第11题图A．AB>CE>CD B．AB＝CE>CD C．AB>CD>CE D．AB＝CD＝CE12．如图，直尺、三角尺都和⊙O相切，B是切点，且AB＝8cm.求⊙O的直径．第12题图13．如图，PA，PB分别切⊙O于点A，B，连结PO，AB相交于点D，C是⊙O上一点，∠C＝60°.(1)求∠APB的大小；(2)若PO＝20cm，求△AOB的面积．第13题图C组综合运用14．如图，在△ABC中，∠B＝90°，O是AB上一点，以O为圆心，OB长为半径的圆与AB交于点E，与AC相切于点D，直线ED交BC的延长线于点F.(1)求证：BC＝FC；(2)若AD∶AE＝2∶1，求tanF的值．第14题图2．2 切线长定理【课堂笔记】 1．相等【课时训练】 1－4.BDBD 5. ①③⑤ 6. 99 7. 6 6 8. 29. r ＝6.法一：可在△COD 中，连结OE ，有OE 2＝CE×DE＝36，∴r ＝6.法二：过C 作CH⊥BD 于点H ，在△CDH 中，CD ＝13，DH ＝5，∴CH ＝AB ＝12，即r ＝6.10. (1)∵PA、PB 是⊙O 切线，∴PA ＝PB ，∵DE 是⊙O 切线，∴DC ＝DA ，EC ＝EB ，∴△PDE 的周长＝PD ＋PE ＋DC ＋CE ＝PD ＋DA ＋PE ＋EB ＝PA ＋PB ＝60； (2)连结AO ，BO ，CO ，可证：∠AOD＝∠COD，∠COE ＝∠BOE，∴∠DOE ＝12∠AOB ，∵∠AOB ＋∠P＝180°，∠P ＝50°，∴∠AOB ＝130°，∴∠DOE ＝65°.11. A12. 连结AO ，BO ，∵AB 是⊙O 的切线，AC 是⊙O 的切线，∴∠ABO ＝90°，∠BAO ＝12∠BAC ＝60°，在Rt △AOB 中，OB ＝AB·tan ∠BAO ＝8×tan 60°＝83，∴⊙O 的直径为163cm .13. (1)∵PA，PB 分别为⊙O 的切线，∴OA ⊥PA ，OB ⊥PB ，∴∠OAP ＝∠OBP＝90°.∵∠C ＝60°，∴∠AOB ＝2∠C＝120°，∴在四边形APBO 中，∠APB ＝360°－∠OAP－∠OBP－∠AOB ＝360°－90°－90°－120°＝60°； (2)在Rt △PAO 与Rt △PBO 中，∵OA ＝OB ，PO ＝PO ，∴Rt △PAO ≌Rt △PBO ，∴∠APO ＝∠BPO＝12∠APB ＝30°，∴PO ⊥AB ，∴∠DAO ＝∠APO＝30°，∴OA ＝sin ∠APO ×OP ＝12×20＝10(cm )．在Rt △AOD 中，∠DAO ＝30°，OA ＝10cm ，∴AD ＝cos∠DAO ×OA ＝32×10＝53(cm )，OD ＝sin ∠DAO ×OA ＝12×10＝5(cm )，∴AB ＝2AD ＝103(cm )，∴S △AOB ＝12AB ×OD ＝12×103×5＝253(cm 2)．14. (1)连结BD.∵BE 为⊙O 的直径，∴∠BDE ＝90°，∴∠EBD ＝90°－∠BED.∵∠EBF ＝90°，∴∠F ＝90°－∠BEF.∴∠F＝∠EBD.∵AC 切⊙O 于点D ，∴∠EBD ＝∠ADE＝∠CDF.∴∠F＝∠CDF，∴DC ＝FC.∵OB⊥BC，∴BC 是⊙O 的切线，∴DC ＝BC.∴BC＝FC; (2)在△ADE 和△ABD 中，∵∠A ＝∠A，∠ADE ＝∠ABD，∴△ADE ∽△ABD ，DE BD ＝AE AD ＝12.又∵∠F＝∠EBD，∴tan F ＝tan ∠EBD ＝DE BD ＝12.。

浙教版数学九年级数学下册 2.2切线长2.3三角形的内切圆同步测试试题

切线长定理一、选择题（只有一个选项是正确的，请把它选出来）1. 点P是⊙O外一点，PA,PB是圆的切线，切点分别为A,B，若PA=12,则PB的长为（）（A）6. （B）8. （C）12. （D）14.2. (原创)如图1，点P是⊙O外一点，PA,PB是圆的切线，切点分别为A,B，PO与AB交于点C,则图中直角三角形的个数为（）（A）4个. （B）5个. （C）6个. （D）8个.图 13. 如图2，点P是⊙O外一点，PA,PB是圆的切线，切点分别为A,B，E点是劣弧AB上一点，过E点的切线CD，交PA，PB分别于点D,C，若圆的半径为3，PO=5，则三角形PCD的周长为（）（A）6. （B）8. （C）10. （D）12.图 24. (原创)如图3，点A是⊙O外一点，AB,AC是圆的切线，切点分别为B,C，若∠BOC=120°，则三角形ABC的形状是（）（A）等腰三角形. （B）等边三角形. （C）等腰直角三角形. （D）直角三角形.图 3二、填空题（答案要简洁）5. (原创) 如图4，点A是⊙O外一点，AB,AC是圆的切线，切点分别为B,C，若AB⊥AC，则四边形ABOC的形状是 .图 46. (原创)如图5，点P是⊙O外一点，PB,PA是圆的切线，切点分别为B,A，C是优弧AB上一点，且∠ACB=84°.则∠P的度数是 .图 57. (原创)如图6，点P是⊙O外一点，PB,PA是圆的切线，切点分别为B,A，C是PA的中点，CD切圆O于点D，则AD,PD,PB三者之间的关系是 .图 68. (原创) 如图7，已知点P是⊙O外一点，PB,PA是圆的切线，切点分别为B,A，B是OC 的中点，∠POB=70°，则∠APC的度数为 .图 7三、解答题9. (原创)如图8，已知半⊙O与等腰三角形ABC的边AB,AC分别相切，切点分为D,E，半圆的直径FG在边BC上.求证：DF=EG.图 810. (原创) 如图9，已知点P是⊙O外一点，PB,PA是圆的切线，切点分别为B,A，连接AB,PO 二线交于点E，以AB为一边作矩形ABCD，连接OB，若OB=3,PO=5，求矩形ABCD的面积.图 9三角形的内切圆一、选择题（只有一个选项是正确的，请把它选出来）1.三角形的内心是（）（A）三角形三条中线的交点.（B）三角形三条垂直平分线的交点.（C）三角形三条高线的交点.（D）三角形三条角平分线的交点.2. 如图1，⊙G是三角形ABC的内切圆，切点分别是D,E,F，则三角形EDF的形状是（）（A）直角三角形. （B）锐角三角形. （C）等边三角形. （D）无法确定.3. 如图2，⊙O是三角形ABC的内切圆，切点分别是D,E,F，∠C=78°，则∠EDF的度数是（）（A）51°. （B）62°. （C）78°. （D）84°.4. (原创) 如图3，圆与直角三角形ABC的三边都相切，切点分别是D,E,F，已知斜边AB=10,直角边BC=6,则CD,AE,BF 的长分别是（）（A ）2、6、4. （B ）2、4、6. （C ）2、4、5. （D ）2、5、4.二、填空题（答案要简洁）5. (原创) Rt △ABC 中，∠C=90°，AC=3cm ，BC=4cm ，r 为半径作圆与三角形的三边都相切，则点A 到圆心的距离为_______．6.三角形ABC 的内心与外心重合，则三角形ABC 的形状是．7. 如图4，Rt△ABC 的内切圆⊙O 与两直角边AB ，BC 分别相切与点D 、E ，过劣弧DE （不包括端点D ，E ）上任一点P 作⊙O 的切线MN 与AB ，BC 分别交于点M ，N ，若⊙O 的半径为r ，则Rt△MBN 的周长为 .８. (原创) 如图4，CD 是Rt△ABC 斜边AB 上高，⊙E 是三角形ABC 的内切圆，半径为R ，⊙F 是三角形ACD 的内切圆，半径为1R ，⊙G 是三角形BCD 的内切圆，半径为2R ，设三角形ABC 的三边长分别为a,b,c ，则12R R R= .(用a,b,c 表示)三、解答题9. 原创如图5，，CD是Rt△ABC斜边AB上高，⊙1O是三角形ACD的内切圆，半径为1R，⊙2O是三角形BCD的内切圆，半径为2R，设三角形ABC的三边长分别为a,b,c.（1）用a,b,c分别表示1R，2R；（2）计算12RR的值.10.原创如图6，Rt△ABC中，⊙O是三角形ABC的内切圆，半径为1R；如图7，⊙1O，⊙2o是两个等圆，两圆外切，且⊙1O与AB,BC都相切，⊙2o与AC,BC都相切，半径为2R；如图8，⊙1O，⊙2o，⊙3O是等圆，自左到右依次外切，且⊙1O与AB,BC都相切，⊙3O与AC,BC都相切，半径为3R，设三角形ABC的三边长分别为a,b,c.(1)求1R，2R，3R；(2)有n个等圆⊙1O，⊙2o，⊙3O…⊙nO，自左到右依次外切，且⊙1O与AB,BC都相切，⊙nO与AC,BC都相切，半径为2R，仔细观察（1）中的规律，直接写出nR.探究题：如图9，直角三角形ABC中，∠C=90°，AB=c,BC=a,AC=b，⊙0与直角三角形的三边相切，圆的半径r.则r=2()abcc a b c++．（2）如图10，直角三角形ABC中，∠C=90°，AB=c,BC=a,AC=b，⊙0、⊙I是两个等圆，且⊙0与直角三角形的两边相切，⊙I与直角三角形的两边相切，⊙0与⊙I相外切，圆的半径r.则r=22()abcc a b c ab+++．(3)如图11，直角三角形ABC中，∠C=90°，AB=c,BC=a,AC=b，⊙0、⊙I是n个等圆中的两个，且⊙0与直角三角形的两边相切，⊙I与直角三角形的两边相切，n个等圆两两相切，圆的半径r，则r= ．切线长定理一、选择题 1.（C ）提示：根据切线长定理PB=12. 2. （C ）提示：根据切线的性质，知道三角形PAO,PBO 是直角三角形，根据切线长定理，等腰三角形三线合一，知道三角形PAC,PBC,OAC,OBC 都是直角三角形. 3.（B ）提示：三角形PCD 的周长为PA+PB=2PA ，根据勾股定理，PA=4. 4.. （B ）提示：利用切线性质，四边形内角，确定∠A=60°. 二、填空题 5. 正方形提示：切线性质，得到两个直角，矩形+邻边相等. 6. 12°提示：利用圆心角与圆周角关系定理，得∠AOB=168°,利用四边形内角和定理可求. 7. 222AD PD PB +=提示：根据切线长定理，得PA=PB,AC=CD=CP ，所以三角形APD 是直角三角形. 8. 60°提示：切线长定理，等腰三角形三线合一，确定∠APO=∠OPB=∠BPC=20°.三、解答题 9.证明：连接OA ，因为AD,AE 是圆的切线，所以OA 平分∠BAC ，AD=AE ，所以AB-AD=AC-AE ，所以BD=CE. 因为OA 平分∠BAC,AB=AC ，所以OB=OC,所以OB-OF=OC-OG ，所以BF=CG ，因为∠B=∠C ，所以△DBF ≌△EGC ，所以DF=EG.10.解：因为PB 是圆的切线，所以三角形POB 是直角三角形，所以PB=4，所以BD=8.因为PA,PB 是圆的切线，所以PE ⊥AB ，所以PB g OB=PO g BE ，所以BE=125，所以AB=245，所以2222248()5BD AB -=-325, 所以矩形的面积AB g AD=245×325=76825.三角形的内切圆一、选择题 1.（D ）提示：根据三角形内心的定义判断. 2. （B ）提示：连接EG,FG ，则∠EGF ＜180°，所以12∠EGF ＜90°，所以∠EDF 是锐角，同理可证其余两个角也是锐角.3. （A ）提示：先求∠EOF=102°,后求解即可. 4.（A ）提示：先求AC=8,再求CF=2,AE=6,BF=4.二、填空题提示：r=1,AC 上点A 到切点的距离为2，根据勾股定理求解. 6. 等边三角形提示：等边三角形的三线合一判定. 7.2r提示：三角形的周长为2BD ，BD 就是r. ８.a bc+ 提示：设CD=h ，AD=x ，BD=y ，则R=2a b c +-，1R =2h x b +-，2R =2h y a+- 所以1R +2R =2h x b +-+2h y a +-=2()2h x y a b ++-+=2()2h c a b +-+，因为h=ab c ，所以1R +2R =222()()22ab ab c a b cc a b c c +-++-+= =2222()()()22ab a b a b ca b a b c c c++-++-+==()()22a b a b c a b a b c a b R c c c++-++-+==•g ,所以12R R R +=a b c+.三、解答题 9.解：（1）因为三角形ABC 的面积是定值，所以CD=abc.易证△ADC ∽△ACB ，所以AD=2b c，因为⊙1O 是三角形ACD 的内切圆，半径为1R ，所以AD-1R +CD-1R =AC所以1R =2AD CD AC +-=2()22b abbb a bc c c c+-+-=；同理可证， 2R =()2a a b c c+-；（2）因为1R =()2b a b c c +-，2R =()2a a b c c+-，所以12R R =b a .10. 解：（1）如图6 连接OA,OC,OB,因为⊙O 是三角形ABC 的内切圆，半径为1R ，三角形ABC 的三边长分别为a,b,c ，所以三角形AOC 的面积=12×AC ×1R ，三角形BOC 的面积=12×BC ×1R ，三角形AOB 的面积=12×AB ×1R ，三角形ABC 的面积=12×a ×b ，所以12×AC ×1R +12×BC ×1R +12×AB ×1R =12×a ×b ，所以1R =ab a c b ++；如图7 连接1O A, 1O C, 1O B, 等圆的半径为2R 三角形ABC 的三边长分别为a,b,c ，所以三角形A 1O C 的面积=12×AC ×22R ，三角形B 1O C 的面积=12×BC ×2R ，三角形A 1O B 的面积=12×AB ×2R ，三角形ABC 的面积=12×a ×b ，所以12×AC ×22R +12×BC ×2R +12×AB ×2R =12×a ×b ，所以2R =2ab a c b ++；同理可证，3R =3ab a c b++；（2）n R =ab a c nb ++.探究题：解：（1）连接OA,OC ，OB ，则三角形AOC 的面积=12×AC ×r ，三角形BOC 的面积=12×BC ×r ，三角形AOB 的面积=12×AB ×r ，三角形ABC 的面积=12×a ×b ，因为三角形AOC 的面积+三角形BOC 的面积+三角形AOB 的面积=三角形ABC 的面积，所以12×AC ×r+12×BC ×r+12×AB ×r=12×a ×b ，所以12（a+b+c ）r=12×a ×b,所以r=ab a b c ++，所以r=2()abc c a b c++．（2）连接OA,OC,IC,IB,OI,OE,IF,作高CD,交OI 于点G ，则三角形AOC 的面积=12×AC ×r ，三角形BIC 的面积=12×BC ×r ，三角形AOF 的面积=12×AF ×r ，三角形BIF 的面积=12×BF ×r ，三角形OIF 的面积=12×OI ×IF ，三角形OCI 的面积=12×OI ×CG ，三角形ABC 的面积=12×a ×b ，因为三角形AOC 的面积+三角形BIC 的面积+三角形AOF 的面积+三角形BIF 的面积+三角形OIF 的面积+三角形OCI 的面积=三角形ABC 的面积，所以12×AC ×r+12×BC ×r+12×AF ×r+12×BF ×r+12×OI ×IF+12×OI ×CG=12×a ×b ，所以12（a+b+c ）r+12×OI ×CD=12×a ×b,且CD=ab c ，整理得：r=22()abc c a b c ab +++．（3）规律隐藏在ab 分母中ab 的系数中，且系数与等圆的个数n 的关系是：系数=2（n-1）,于是结论为r=221()()abc c a b c n ab +++-.。

浙教版九年级数学下册2.2：切线长定理同步练习题(含解析)

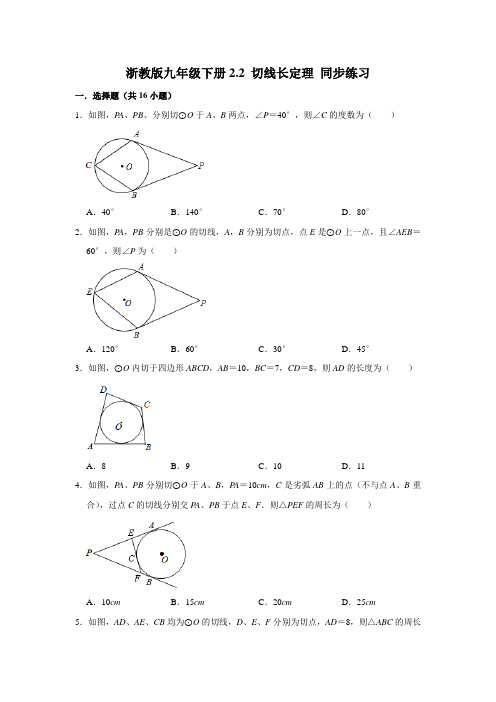
浙教版九年级下册2.2 切线长定理同步练习一．选择题（共16小题）1．如图，P A、PB、分别切⊙O于A、B两点，∠P＝40°，则∠C的度数为（）A．40°B．140°C．70°D．80°2．如图，P A，PB分别是⊙O的切线，A，B分别为切点，点E是⊙O上一点，且∠AEB＝60°，则∠P为（）A．120°B．60°C．30°D．45°3．如图，⊙O内切于四边形ABCD，AB＝10，BC＝7，CD＝8，则AD的长度为（）A．8B．9C．10D．114．如图，P A、PB分别切⊙O于A、B，P A＝10cm，C是劣弧AB上的点（不与点A、B重合），过点C的切线分别交P A、PB于点E、F．则△PEF的周长为（）A．10cm B．15cm C．20cm D．25cm5．如图，AD、AE、CB均为⊙O的切线，D、E、F分别为切点，AD＝8，则△ABC的周长为（）A．8B．10C．12D．166．如图，⊙O是四边形ABCD的内切圆，切点依次是E、F、G、H，下列结论一定正确的有（）个①AF＝BG②CG＝CH③AB+CD＝AD+BC④BG＜CG．A．1B．2C．3D．47．如图，AB、AC是⊙O的切线，B、C为切点，∠A＝50°，点P是圆上异于B、C，且在上的动点，则∠BPC的度数是（）A．65°B．115°C．115°或65°D．130°或65°8．如图，已知P A，PB分别切⊙O于点A、B，∠P＝60°，P A＝8，那么弦AB的长是（）A．4B．8C．4D．89．如图所示，P A，PB是⊙O的切线，且∠APB＝40°，下列说法不正确的是（）A．P A＝PB B．∠APO＝20°C．∠OBP＝70°D．∠AOP＝70°10．如图，AE、AD和BC分别切⊙O于点E、D、F，如果AD＝20，则△ABC的周长为（）A．20B．30C．40D．5011．如图，从圆O外一点P引圆O的两条切线P A，PB，切点分别为A，B．如果∠APB＝60°，P A＝8，那么弦AB的长是（）A．4B．8C．D．12．如图，圆O的圆心在梯形ABCD的底边AB上，并与其它三边均相切，若AB＝10，AD ＝6，则CB长（）A．4B．5C．6D．无法确定13．如图，一圆内切四边形ABCD，且AB＝16，CD＝10，则四边形的周长为（）A．50B．52C．54D．5614．如图，若△ABC的三边长分别为AB＝9，BC＝5，CA＝6，△ABC的内切圆⊙O切AB、BC、AC于D、E、F，则AF的长为（）A．5B．10C．7.5D．415．已知⊙O的半径是4，P是⊙O外的一点，且PO＝8，从点P引⊙O的两条切线，切点分别是A，B，则AB＝（）A．4B．C．D．16．如图，P A、PB分别切⊙O于A、B两点，如果∠P＝60°，P A＝2，那么AB的长为（）A．1B．2C．3D．4二．填空题（共4小题）17．如图，四边形ABCD是⊙O的外切四边形，且AB＝10，CD＝15，则四边形ABCD的周长为．18．如图，菱形ABCD，∠B＝60°，AB＝4，⊙O内切于菱形ABCD，则⊙O的半径为．19．如图，P A，PB是⊙O的切线，A，B为切点，∠OAB＝38°，则∠P＝°．20．如图，四边形ABCD外切于圆，AB＝16，CD＝10，则四边形的周长是．三．解答题（共7小题）21．如图，P A、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠BAC＝20°，求∠P 的度数．22．如图，P A、PB是⊙O的切线，CD切⊙O于点E，△PCD的周长为12，∠APB＝60°．求：（1）P A的长；（2）∠COD的度数．23．如图，P A、PB是⊙O的切线，切点分别是A、B，直线EF也是⊙O的切线，切点为Q，交P A、PB于点E、F，已知P A＝12cm，∠P＝40°①求△PEF的周长；②求∠EOF的度数．24．如图，P A、PB、DE切⊙O于点A、B、C、D在P A上，E在PB上，（1）若P A＝10，求△PDE的周长．（2）若∠P＝50°，求∠O度数．25．如图，P A，PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P＝60°．（1）求∠BAC的度数；（2）当OA＝2时，求AB的长．26．已知：如图，P A、PB是⊙O的切线，切点分别是A、B，Q为AB上一点，过Q点作⊙O 的切线，交P A、PB于E、F点，已知P A＝12cm，求△PEF的周长．27．如图，已知AB为⊙O的直径，P A，PC是⊙O的切线，A，C为切点，∠BAC＝30°．（Ⅰ）求∠P的大小；（Ⅱ）若AB＝2，求P A的长（结果保留根号）．参考答案一．选择题（共16小题）1．如图，P A、PB、分别切⊙O于A、B两点，∠P＝40°，则∠C的度数为（）A．40°B．140°C．70°D．80°【分析】连接OA，OB根据切线的性质定理，切线垂直于过切点的半径，即可求得∠OAP，∠OBP的度数，根据四边形的内角和定理即可求的∠AOB的度数，然后根据圆周角定理即可求解．【解答】解：∵P A是圆的切线．∴∠OAP＝90°，同理∠OBP＝90°，根据四边形内角和定理可得：∠AOB＝360°﹣∠OAP﹣∠OBP﹣∠P＝360°﹣90°﹣90°﹣40°＝140°，∴∠ACB＝∠AOB＝70°．故选：C．2．如图，P A，PB分别是⊙O的切线，A，B分别为切点，点E是⊙O上一点，且∠AEB＝60°，则∠P为（）A．120°B．60°C．30°D．45°【分析】连接OA，BO，由圆周角定理知可知∠AOB＝2∠E＝120°，P A、PB分别切⊙O 于点A、B，利用切线的性质可知∠OAP＝∠OBP＝90°，根据四边形内角和可求得∠P ＝180°﹣∠AOB＝60°．【解答】解：连接OA，BO；∵∠AOB＝2∠E＝120°，∴∠OAP＝∠OBP＝90°，∴∠P＝180°﹣∠AOB＝60°．故选：B．3．如图，⊙O内切于四边形ABCD，AB＝10，BC＝7，CD＝8，则AD的长度为（）A．8B．9C．10D．11【分析】根据圆外切四边形的性质对边和相等进而得出AD的长．【解答】解：∵⊙O内切于四边形ABCD，∴AD+BC＝AB+CD，∵AB＝10，BC＝7，CD＝8，∴AD+7＝10+8，解得：AD＝11．故选：D．4．如图，P A、PB分别切⊙O于A、B，P A＝10cm，C是劣弧AB上的点（不与点A、B重合），过点C的切线分别交P A、PB于点E、F．则△PEF的周长为（）A．10cm B．15cm C．20cm D．25cm【分析】根据切线长定理由P A、PB分别切⊙O于A、B得到PB＝P A＝10cm，由于过点C的切线分别交P A、PB于点E、F，再根据切线长定理得到EA＝EC，FC＝FB，然后三角形周长的定义得到△PEF的周长＝PE+EF+PF＝PE+EC+FC+PF，用等线段代换后得到三角形PEF的周长等于P A+PB．【解答】解：∵P A、PB分别切⊙O于A、B，∴PB＝P A＝10cm，∵EA与EC为⊙的切线，∴EA＝EC，同理得到FC＝FB，∴△PEF的周长＝PE+EF+PF＝PE+EC+FC+PF＝PE+EA+FB+PF＝P A+PB＝10+10＝20（cm）．故选：C．5．如图，AD、AE、CB均为⊙O的切线，D、E、F分别为切点，AD＝8，则△ABC的周长为（）A．8B．10C．12D．16【分析】由AD、AE、CB均为⊙O的切线，D、E、F分别为切点，根据切线长定理，可得CE＝CF，BD＝BF，AE＝AD＝8，继而可求得△ABC的周长为AE+AD的和．【解答】解：∵AD、AE、CB均为⊙O的切线，D、E、F分别为切点，∴CE＝CF，BD＝BF，AE＝AD＝8，∴△ABC的周长为：AC+BC+AB＝AC+CF+BF+AB＝AC+CE+BD+AB＝AE+AD＝16．故选：D．6．如图，⊙O是四边形ABCD的内切圆，切点依次是E、F、G、H，下列结论一定正确的有（）个①AF＝BG②CG＝CH③AB+CD＝AD+BC④BG＜CG．A．1B．2C．3D．4【分析】根据切线长定理（从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线，平分两条切线的夹角）对以下选项进行分析．【解答】解：如图，连接OE、OF、OH、OG．①∵⊙O是四边形ABCD的内切圆，切点依次是E、F、G、H，∴BF＝BG、AF＝AE，只有当点F是边AB的中点时，AF＝BF＝BG，否则，等式AF＝BG不成立；故本选项不一定正确；②根据题意，知，CG、CH都是⊙O的切线，∴CG＝CH．故本选项正确；③根据题意，知AF＝AE，DH＝DE，BF＝BG，CG＝CH，则AF+BF+CH+DH＝AE+BG+CG+DE，即AB+CD＝AD+BC．故本选项正确；④当点G是边BC的中点时，BG＝CG．故本选项错误；综上所述，正确的说法有2个；故选：B．7．如图，AB、AC是⊙O的切线，B、C为切点，∠A＝50°，点P是圆上异于B、C，且在上的动点，则∠BPC的度数是（）A．65°B．115°C．115°或65°D．130°或65°【分析】连接OB、OC，根据四边形的内角和定理，求得∠BOC＝130°，再由圆周角定理求得∠P的度数即可．【解答】解：如图，连接OB、OC，∵AB、AC是⊙O的切线，∴∠OBA＝∠OCA＝90°，∵∠A＝50°，∴∠BOC＝130°，∵∠BOC＝2∠P，∴∠BPC＝65°；故选：AC．8．如图，已知P A，PB分别切⊙O于点A、B，∠P＝60°，P A＝8，那么弦AB的长是（）A．4B．8C．4D．8【分析】根据切线长定理和等边三角形的判定方法，发现等边三角形即可求解．【解答】解：∵P A，PB分别切⊙O于点A、B，∴P A＝PB，又∠P＝60°，∴△APB是等边三角形，∴AB＝P A＝8．故选：B．9．如图所示，P A，PB是⊙O的切线，且∠APB＝40°，下列说法不正确的是（）A．P A＝PB B．∠APO＝20°C．∠OBP＝70°D．∠AOP＝70°【分析】根据切线长定理得A，B是正确的；再根据切线的性质定理以及直角三角形的两个锐角互余得D是正确的；根据切线的性质定理得C错误．【解答】解：∵P A，PB是⊙O的切线，且∠APB＝40°，∴P A＝PB，∠APO＝∠BPO，∠A＝∠B＝90°，∴∠OBP＝∠OAP，∴C是错误的．故选：C．10．如图，AE、AD和BC分别切⊙O于点E、D、F，如果AD＝20，则△ABC的周长为（）A．20B．30C．40D．50【分析】根据切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，将△ABC 的周长转化为切线长求解．【解答】解：据切线长定理有AD＝AE，BE＝BF，CD＝CF；则△ABC的周长＝AB+BC+AC＝AB+BF+CF+AC＝AB+BE+AC+CD＝AD+AE＝2AD＝40．故选：C．11．如图，从圆O外一点P引圆O的两条切线P A，PB，切点分别为A，B．如果∠APB＝60°，P A＝8，那么弦AB的长是（）A．4B．8C．D．【分析】根据切线长定理知P A＝PB，而∠P＝60°，所以△P AB是等边三角形，由此求得弦AB的长．【解答】解：∵P A、PB都是⊙O的切线，∴P A＝PB，又∵∠P＝60°，∴△P AB是等边三角形，即AB＝P A＝8，故选：B．12．如图，圆O的圆心在梯形ABCD的底边AB上，并与其它三边均相切，若AB＝10，AD ＝6，则CB长（）A．4B．5C．6D．无法确定【分析】方法1、设圆O的半径是R，圆O与AD、DC、CB相切于点E、F、H，连接OE、OD、OF、OC、OH，则圆的半径R，可以看作△BOC，△COD，△AOD的高，根据S梯形ABCD＝S△BOC+S△COD+S△DOA，以及梯形的面积公式即可求解．方法2、利用切线的性质得出∠ADO＝∠ODC，进而得出∠ADO＝∠AOD，即可得出OA ＝6，即：OB＝4，同理：BC＝OB即可得出结论．【解答】解：方法1、设圆O的半径是R，圆O与AD、DC、CB相切于点E、F、H，连接OE、OD、OF、OC、OH．设CD＝y，CB＝x．设S梯形ABCD＝S则S＝（CD+AB）R＝（y+10）R﹣﹣﹣﹣（1）S＝S△BOC+S△COD+S△DOA＝xR+yR+×6R﹣﹣﹣﹣（2）联立（1）（2）得x＝4；方法2、连接OD．OC∵AD，CD是⊙O的切线，∴∠ADO＝∠ODC，∵CD∥AB，∴∠ODC＝∠AOD，∴∠ADO＝∠AOD∴AD＝OA∵AD＝6，∴OA＝6，∵AB＝10，∴OB＝4，同理可得OB＝BC＝4，故选：A．13．如图，一圆内切四边形ABCD，且AB＝16，CD＝10，则四边形的周长为（）A．50B．52C．54D．56【分析】根据切线长定理，可以证明圆外切四边形的性质：圆外切四边形的两组对边和相等，从而可求得四边形的周长．【解答】解：由题意可得圆外切四边形的两组对边和相等，所以四边形的周长＝2（16+10）＝52．故选：B．14．如图，若△ABC的三边长分别为AB＝9，BC＝5，CA＝6，△ABC的内切圆⊙O切AB、BC、AC于D、E、F，则AF的长为（）A．5B．10C．7.5D．4【分析】由切线长定理，可知：AF＝AD，CF＝CE，BE＝BD，用未知数设AF的长，然后表示出BD、CF的长，即可表示出BE、CE的长，根据BE+CE＝5，可求出AF的长．【解答】解：设AF＝x，根据切线长定理得AD＝x，BD＝BE＝9﹣x，CE＝CF＝CA﹣AF ＝6﹣x，则有9﹣x+6﹣x＝5，解得x＝5，即AF的长为5．故选：A．15．已知⊙O的半径是4，P是⊙O外的一点，且PO＝8，从点P引⊙O的两条切线，切点分别是A，B，则AB＝（）A．4B．C．D．【分析】在Rt△POA中，用勾股定理，可求得P A的长，进而可根据∠APO的正弦值求出AC的长，即可求出AB的长．【解答】解：如图所示，P A、PB切⊙O于A、B，因为OA＝4，PO＝8，则AP＝＝4，∠APO＝30°，∵∠APB＝2∠APO＝60°故△P AB是等边三角形，AB＝AP＝4故选：C．16．如图，P A、PB分别切⊙O于A、B两点，如果∠P＝60°，P A＝2，那么AB的长为（）A．1B．2C．3D．4【分析】由切线长定理知P A＝PB，根据已知条件即可判定△P AB是等边三角形，由此可求得AB的长．【解答】解：∵P A、PB分别切⊙O于A、B，∴P A＝PB；∵∠P＝60°，∴△P AB是等边三角形；∴AB＝P A＝2，故选B．二．填空题（共4小题）17．如图，四边形ABCD是⊙O的外切四边形，且AB＝10，CD＝15，则四边形ABCD的周长为50．【分析】根据切线长定理得到AE＝AH，BE＝BF，CF＝CG，DH＝DG，得到AD+BC＝AB+CD＝25，根据四边形的周长公式计算，得到答案．【解答】解：∵四边形ABCD是⊙O的外切四边形，∴AE＝AH，BE＝BF，CF＝CG，DH＝DG，∴AD+BC＝AB+CD＝25，∴四边形ABCD的周长＝AD+BC+AB+CD＝25+25＝50，故答案为：50．18．如图，菱形ABCD，∠B＝60°，AB＝4，⊙O内切于菱形ABCD，则⊙O的半径为．【分析】作辅助线，构建直角△AOB，分别计算OA、OB的长，根据面积法可得OE的长．【解答】解：设AB和BC上的切点分别为E、F，连接OA、OE、OB、OF，则OE⊥AB，OF⊥BC，∵⊙O内切于菱形ABCD，∴OE＝OF，∴OB平分∠ABC，∵∠ABC＝60°，∴∠ABO＝30°，同理得∠BAO＝60°，∴∠AOB＝90°，∴AO＝AB＝2，OB＝2，∴S△AOB＝AB•OE＝AO•OB，4OE＝2×，OE＝，故答案为：．19．如图，P A，PB是⊙O的切线，A，B为切点，∠OAB＝38°，则∠P＝76°．【分析】由切线的性质得出P A＝PB，P A⊥OA，得出∠P AB＝∠PBA，∠OAP＝90°，由已知得出∠PBA＝∠P AB＝90°﹣∠OAB＝52°，再由三角形内角和定理即可得出结果．【解答】解：∵P A，PB是⊙O的切线，∴P A＝PB，P A⊥OA，∴∠P AB＝∠PBA，∠OAP＝90°，∴∠PBA＝∠P AB＝90°﹣∠OAB＝90°﹣38°＝52°，∴∠P＝180°﹣52°﹣52°＝76°；故答案为：76．20．如图，四边形ABCD外切于圆，AB＝16，CD＝10，则四边形的周长是52．【分析】利用圆外切四边形的性质定理可以得出，四边形的周长是对边和的2倍，即可得．【解答】解：由题意可得圆外切四边形的两组对边和相等，所以四边形的周长＝2（16+10）＝52．故答案为：52．三．解答题（共7小题）21．如图，P A、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠BAC＝20°，求∠P 的度数．【分析】根据切线长定理得等腰△P AB，运用三角形内角和定理求解即可．【解答】解：根据切线的性质得：∠P AC＝90°，所以∠P AB＝90°﹣∠BAC＝90°﹣20°＝70°，根据切线长定理得P A＝PB，所以∠P AB＝∠PBA＝70°，所以∠P＝180°﹣70°×2＝40°．22．如图，P A、PB是⊙O的切线，CD切⊙O于点E，△PCD的周长为12，∠APB＝60°．求：（1）P A的长；（2）∠COD的度数．【分析】（1）可通过切线长定理将相等的线段进行转换，得出三角形PDE的周长等于P A+PB的结论，即可求出P A的长；（2）根据三角形的内角和求出∠ADC和∠BEC的度数和，然后根据切线长定理，得出∠EDO和∠DEO的度数和，再根据三角形的内角和求出∠DOE的度数．【解答】解：（1）∵CA，CE都是圆O的切线，∴CA＝CE，同理DE＝DB，P A＝PB，∴三角形PDE的周长＝PD+CD+PC＝PD+PC+CA+BD＝P A+PB＝2P A＝12，即P A的长为6；（2）∵∠P＝60°，∴∠PCE+∠PDE＝120°，∴∠ACD+∠CDB＝360°﹣120°＝240°，∵CA，CE是圆O的切线，∴∠OCE＝∠OCA＝∠ACD；同理：∠ODE＝∠CDB，∴∠OCE+∠ODE＝（∠ACD+∠CDB）＝120°，∴∠COD＝180﹣120°＝60°．23．如图，P A、PB是⊙O的切线，切点分别是A、B，直线EF也是⊙O的切线，切点为Q，交P A、PB于点E、F，已知P A＝12cm，∠P＝40°①求△PEF的周长；②求∠EOF的度数．【分析】①根据切线长定理得出P A＝PB，EB＝EQ，FQ＝F A，由PE+EF+PF＝PE+EQ+FQ+PF即可求出答案．②连接OE，OF，求出∠OEF+∠OFE的度数，即可得出∠EOF的度数．【解答】解：①∵P A、PB是⊙O的切线，∴P A＝PB，又∵直线EF是⊙O的切线，∴EB＝EQ，FQ＝F A，∴△PEF的周长＝PE+PF+EF＝PE+PF+EB+F A＝P A+PB＝2P A＝24cm；②连接OE，OF，则OE平分∠BEF，OF平分∠AFE，则∠OEF+∠OFE＝（∠P+∠PFE）+∠（P+∠PEF）＝（180°+40°）＝110°，∴∠EOF＝180°﹣110°＝70°．24．如图，P A、PB、DE切⊙O于点A、B、C、D在P A上，E在PB上，（1）若P A＝10，求△PDE的周长．（2）若∠P＝50°，求∠O度数．【分析】（1）于P A、PB、DE都是⊙O的切线，可根据切线长定理将切线P A、PB的长转化为△PDE的周长；（2）连接OA、OC、0B，利用切线长定理即可得到∠O＝∠AOB，根据四边形的内角和可得∠AOB+∠P＝180°，进而求出∠O的度数．【解答】解：（1）∵P A、PB、DE分别切⊙O于A、B、C，∴P A＝PB，DA＝DC，EC＝EB；∴C△PDE＝PD+DE+PE＝PD+DA+EB+PE＝P A+PB＝10+10＝20；∴△PDE的周长为20；（2）连接OA、OC、0B，∵OA⊥P A，OB⊥PB，OC⊥DE，∴∠DAO＝∠EBO＝90°，∴∠P+∠AOB＝180°，∴∠AOB＝180°﹣50°＝130°∵∠AOD＝∠DOC，∠COE＝∠BOE，∴∠DOE＝∠AOB＝×130°＝65°．25．如图，P A，PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P＝60°．（1）求∠BAC的度数；（2）当OA＝2时，求AB的长．【分析】（1）根据切线长定理推出AP＝BP，根据等腰三角形性质和三角形的内角和定理求出∠P AB＝60°，求出∠P AO＝90°即可；（2）根据直角三角形性质求出OP，根据勾股定理求出AP，根据等边三角形的判定和性质求出即可．【解答】解：（1）∵P A，PB是⊙O的切线，∴AP＝BP，∵∠P＝60°，∴∠P AB＝60°，∵AC是⊙O的直径，∴∠P AC＝90°，∴∠BAC＝90°﹣60°＝30°．（2）连接OP，则在Rt△AOP中，OA＝2，∠APO＝30°，∴OP＝4，由勾股定理得：，∵AP＝BP，∠APB＝60°，∴△APB是等边三角形，∴．26．已知：如图，P A、PB是⊙O的切线，切点分别是A、B，Q为AB上一点，过Q点作⊙O 的切线，交P A、PB于E、F点，已知P A＝12cm，求△PEF的周长．【分析】根据切线长定理得出P A＝PB，EB＝EQ，FQ＝F A，代入PE+EF+PF＝PE+EQ+FQ+PF即可求出答案．【解答】解：∵P A、PB是⊙O的切线，切点分别是A、B，∴P A＝PB＝12，∵过Q点作⊙O的切线，交P A、PB于E、F点，∴EB＝EQ，FQ＝F A，∴△PEF的周长是：PE+EF+PF＝PE+EQ+FQ+PF，＝PE+EB+PF+F A＝PB+P A＝12+12＝24，答：△PEF的周长是24．27．如图，已知AB为⊙O的直径，P A，PC是⊙O的切线，A，C为切点，∠BAC＝30°．（Ⅰ）求∠P的大小；（Ⅱ）若AB＝2，求P A的长（结果保留根号）．【分析】（Ⅰ）根据切线的性质及切线长定理可证明△P AC为等边三角形，则∠P的大小可求；（Ⅱ）由（Ⅰ）知P A＝PC，在Rt△ACB中，利用30°的特殊角度可求得AC的长．【解答】解：（Ⅰ）∵P A是⊙O的切线，AB为⊙O的直径，∴P A⊥AB，∴∠BAP＝90°；∵∠BAC＝30°，∴∠CAP＝90°﹣∠BAC＝60°．又∵P A、PC切⊙O于点A、C，∴P A＝PC，∴△P AC为等边三角形，∴∠P＝60°．（Ⅱ）如图，连接BC，则∠ACB＝90°．在Rt△ACB中，AB＝2，∠BAC＝30°，∵cos∠BAC＝，∴AC＝AB•cos∠BAC＝2cos30°＝．∵△P AC为等边三角形，∴P A＝AC，∴P A＝．。

九年级下册第2章直线与圆的位置关系2、2切线长定理习题新版浙教版

(1)求证：OD∥BE；
证明：连结 OE， ∵AM，DE 是⊙O 的切线，切点分别为点 A，E， ∴DA＝DE，易证△ AOD≌△EOD， ∴∠AOD＝∠EOD＝12∠AOE，又∵∠ABE＝12∠AOE， ∴∠AOD＝∠ABE，∴OD∥BE.
(2)猜想：OF与CD有何数量关系？并说明理由．解：OF＝12CD. 理由：∵AM，BN，DC 是⊙O 的切线， ∴AD＝DE，BC＝CE，∴AD＋BC＝DE＋CE. 即 AD＋BC＝CD. 由 AB 是⊙O 的直径，且点 F 是 CD 的中点，易得 OF＝12(AD＋BC)＝12CD.即 OF＝12CD.
2 如图，从⊙O 外一点 P 引⊙O 的两条切线 PA，PB，切点分别为 A，B.如果∠APB＝60°，PA＝8，那么弦 AB 的长是( B ) A．4 B．8 C．4 3 D．8 3
3 如图，PA，PB为圆O的切线，切点分别为 A，B，PO 交AB于点C，PO的延长线交圆O于点D.下列结论不一定成立的是( B ) A．△BPA为等腰三角形 B．AB与PD相互垂直平分 C．点A，B都在以PO为直径的圆上 D．PC为△BPA的边AB上的中线
10 【中考·甘肃】如图，在Rt△ABC中，∠ACB＝90°，以BC为直径的⊙O交AB于点D，切线DE交AC于点E.
(1)求证：∠A＝∠ADE；
证明：如图，连结OD. ∵DE是⊙O的切线，∴∠ODE＝90°. ∴∠ADE＋∠BDO＝90°. ∵∠ACB＝90°，∴∠A＋∠B＝90°. ∵OD＝OB，∴∠B＝∠BDO. ∴∠A＝∠ADE.
【点拨】如图，连结OC，OD，OE. ∵BC切⊙O于点E，AC切⊙O于点D， ∴OE⊥BC，OD⊥AC. ∴∠OEB＝∠OEC＝∠ODC＝∠ODA＝∠ACB＝90°. ∴四边形ODCE是矩形．又∵DO＝OE，∴四边形ODCE是正方形．

九年级数学下册第2章直线与圆的位置关系2.2切线长定理同步测试浙教版

浙教版九年级下册数学 2.2：切线长定理同步练习(含解析)

2.2切线长定理同步练习一．选择题1．如图，P A、PB分别切⊙O于A、B，P A＝10cm，C是劣弧AB上的点（不与点A、B重合），过点C的切线分别交P A、PB于点E、F．则△PEF的周长为（）A．10cm B．15cm C．20cm D．25cm2．如图，圆O的圆心在梯形ABCD的底边AB上，并与其它三边均相切，若AB＝10，AD ＝6，则CB长（）A．4B．5C．6D．无法确定3．图，在矩形ABCD中，AB＝3，BC＝2，以BC为直径在矩形内作半圆，自点A作半圆的切线AE，则sin∠CBE＝（）A．B．C．D．4．如图，P A、PB、分别切⊙O于A、B两点，∠P＝40°，则∠C的度数为（）A．40°B．140°C．70°D．80°5．如图，在▱ABCD中，过A、B、C三点的圆交AD于E，且与CD相切．若AB＝4，BE ＝5，则DE的长为（）A．3B．4C．D．6．如图，P A、PB、CD分别切⊙O于A、B、E，CD交P A、PB于C、D两点，若∠P＝40°，则∠P AE+∠PBE的度数为（）A．50°B．62°C．66°D．70°7．如图，在等腰三角形△ABC中，O为底边BC的中点，以O为圆心作半圆与AB，AC相切，切点分别为D，E．过半圆上一点F作半圆的切线，分别交AB，AC于M，N．那么的值等于（）A．B．C．D．18．如图，四边形ABCD中，AD平行BC，∠ABC＝90°，AD＝2，AB＝6，以AB为直径的半⊙O切CD于点E，F为弧BE上一动点，过F点的直线MN为半⊙O的切线，MN交BC于M，交CD于N，则△MCN的周长为（）A．9B．10C．3D．29．如图，在平面直角坐标系xOy中，直线AB经过点A（6，0）、B（0，6），⊙O的半径为2（O为坐标原点），点P是直线AB上的一动点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为（）A．B．3C．3D．10．如图中，CA，CD分别切圆O1于A，D两点，CB、CE分别切圆O2于B，E两点．若∠1＝60°，∠2＝65°，判断AB、CD、CE的长度，下列关系何者正确（）A．AB＞CE＞CD B．AB＝CE＞CD C．AB＞CD＞CE D．AB＝CD＝CE 二．填空题11．如图，小明同学测量一个光盘的直径，他只有一把直尺和一块三角板，他将直尺、光盘和三角板如图放置于桌面上，并量出AB＝3cm，则此光盘的直径是cm．12．已知：P A切⊙O于点A，PB切⊙O于点B，点C是⊙O上异于A、B的一点，过点C作⊙O的切线分别交P A和PB于点D、E，若P A＝10cm，DE＝7cm，则△PDE的周长为cm．13．已知直角梯形ABCD的四条边长分别为AB＝2，BC＝CD＝10，AD＝6，过B、D两点作圆，与BA的延长线交于点E，与CB的延长线交于点F，则BE﹣BF的值为．14．已知：P A、PB、EF分别切⊙O于A、B、D，若P A＝15cm，那么△PEF周长是cm．若∠P＝50°，那么∠EOF＝．15．如图，△ABC是一张三角形的纸片，⊙O是它的内切圆，点D是其中的一个切点，已知AD＝10cm，小明准备用剪刀沿着与⊙O相切的任意一条直线MN剪下一块三角形（△AMN），则剪下的△AMN的周长为．三．解答题16．如图，P A、PB、CD是⊙O的切线，切点分别为点A、B、E，若△PCD的周长为18cm，∠APB＝60°，求⊙O的半径．17．如图，在梯形ABCD中，AB∥CD，⊙O为内切圆，E为切点．（1）求证：AO2＝AE•AD；（2）若AO＝4cm，AD＝5cm，求⊙O的面积．18．如图，AB、BC、CD分别与⊙O相切于E、F、G，且AB∥CD，BO＝6，CO＝8．（1）判断△OBC的形状，并证明你的结论；（2）求BC的长；（3）求⊙O的半径OF的长．参考答案一．选择题1．解：∵P A、PB分别切⊙O于A、B，∴PB＝P A＝10cm，∵EA与EC为⊙的切线，∴EA＝EC，同理得到FC＝FB，∴△PEF的周长＝PE+EF+PF＝PE+EC+FC+PF＝PE+EA+FB+PF＝P A+PB＝10+10＝20（cm）．故选：C．2．解：方法1、设圆O的半径是R，圆O与AD、DC、CB相切于点E、F、H，连接OE、OD、OF、OC、OH．设CD＝y，CB＝x．设S梯形ABCD＝S则S＝（CD+AB）R＝（y+10）R﹣﹣﹣﹣（1）S＝S△BOC+S△COD+S△DOA＝xR+yR+×6R﹣﹣﹣﹣（2）联立（1）（2）得x＝4；方法2、连接OD．OC∵AD，CD是⊙O的切线，∴∠ADO＝∠ODC，∵CD∥AB，∴∠ODC＝∠AOD，∴∠ADO＝∠AOD∴AD＝OA∵AD＝6，∴OA＝6，∵AB＝10，∴OB＝4，同理可得OB＝BC＝4，故选：A．3．解：取BC的中点O，则O为圆心，连接OE，AO，AO与BE的交点是F ∵AB，AE都为圆的切线∴AE＝AB∵OB＝OE，AO＝AO∴△ABO≌△AEO（SSS）∴∠OAB＝∠OAE∴AO⊥BE在直角△AOB里AO2＝OB2+AB2∵OB＝1，AB＝3∴AO＝易证明△BOF∽△AOB∴BO：AO＝OF：OB∴1：＝OF：1∴OF＝sin∠CBE＝＝故选：D．4．解：∵P A是圆的切线．∴∠OAP＝90°，同理∠OBP＝90°，根据四边形内角和定理可得：∠AOB＝360°﹣∠OAP﹣∠OBP﹣∠P＝360°﹣90°﹣90°﹣40°＝140°，∴∠ACB＝∠AOB＝70°．故选：C．5．解：连接CE；∵，∴∠BAE＝∠EBC+∠BEC；∵∠DCB＝∠DCE+∠BCE，由弦切角定理知：∠DCE＝∠EBC，由平行四边形的性质知：∠DCB＝∠BAE，∴∠BEC＝∠BCE，即BC＝BE＝5，∴AD＝5；由切割线定理知：DE＝DC2÷DA＝，故选：D．6．解：∵P A、PB、CD分别切⊙O于A、B、E，CD交P A、PB于C、D两点，∴CE＝CA，DE＝DB，∴∠CAE＝∠CEA，∠DEB＝∠DBE，∴∠PCD＝∠CAE+∠CEA＝2∠CAE，∠PDC＝∠DEB+∠DBE＝2∠DBE，∴∠CAE＝∠PCD，∠DBE＝∠PDC，即∠P AE＝∠PCD，∠PBE＝∠PDC，∵∠P＝40°，∴∠P AE+∠PBE＝∠PCD+∠PDC＝（∠PCD+∠PDC）＝（180°﹣∠P）＝70°．故选：D．7．解：连OM，ON，如图∵MD，MF与⊙O相切，∴∠1＝∠2，同理得∠3＝∠4，而∠1+∠2+∠3+∠4+∠B+∠C＝360°，AB＝AC∴∠2+∠3+∠B＝180°；而∠1+∠MOB+∠B＝180°，∴∠3＝∠MOB，即有∠4＝∠MOB，∴△OMB∽△NOC，∴＝，∴BM•CN＝BC2，∴＝．故选：B．8．解：作DH⊥BC于H，如图，∵四边形ABCD中，AD平行BC，∠ABC＝90°，∴AB⊥AD，AB⊥BC，∵AB为直径，∴AD和BC为⊙O切线，∵CD和MN为⊙O切线，∴DE＝DA＝2，CE＝CB，NE＝NF，MB＝MF，∵四边形ABHD为矩形，∴BH＝AD＝2，DH＝AB＝6，设BC＝x，则CH＝x﹣2，CD＝x+2，在Rt△DCH中，∵CH2+DH2＝DC2，∴（x﹣2）2+62＝（x+2）2，解得x＝，∴CB＝CE＝，∴△MCN的周长＝CN+CM+MN＝CN+CM+NF+MF＝CN+CM+NF+MB＝CE+CB＝9．故选：A．9．解：连接OP、OQ．∵PQ是⊙O的切线，∴OQ⊥PQ；根据勾股定理知PQ2＝OP2﹣OQ2，∵当PO⊥AB时，线段PQ最短；又∵A（﹣6，0）、B（0，6），∴OA＝OB＝6，∴AB＝6∴OP＝AB＝3，∵OQ＝2，∴PQ＝＝，故选：D．10．解：∵∠1＝60°，∠2＝65°，∴∠ABC＝180°﹣∠1﹣∠2＝180°﹣60°﹣65°＝55°，∴∠2＞∠1＞∠ABC，∴AB＞BC＞AC，∵CA，CD分别切圆O1于A，D两点，CB、CE分别切圆O2于B，E两点，∴AC＝CD，BC＝CE，∴AB＞CE＞CD．故选：A．二．填空题11．解：∵∠CAD＝60°，∴∠CAB＝120°，∵AB和AC与⊙O相切，∴∠OAB＝∠OAC，∴∠OAB＝∠CAB＝60°∵AB＝3cm，∴OA＝6cm，∴由勾股定理得OB＝3cm，∴光盘的直径6cm．故答案为：6．12．解：分两种情况：①点C在劣弧AB上时，如图，当根据切线长定理得：AD＝CD，BE＝CE，P A＝PB，则△PDE的周长＝PD+DE+PE＝PD+CD+CE+PE＝PD+AD+PE+BE＝P A+PB＝2P A＝20cm．②点C在优弧AB上时，如图，当根据切线长定理得：AD＝CD，BE＝CE，P A＝PB，则△PDE的周长＝PD+DE+PE＝2P A+2DE＝20+2×7＝34cm．综上，△PDE的周长为20或34cm．故答案为：20或34．13．解：延长CD交⊙O于点G，设BE，DG的中点分别为点M，N，则易知AM＝DN，∵BC＝CD＝10，由割线定理得，CB•CF＝CD•CG，∵CB＝CD，∴BF＝DG，∴BE﹣BF＝BE﹣DG＝2（BM﹣DN）＝2（BM﹣AM）＝2AB＝4．故答案为：4．14．解：∵P A、PB、EF分别切⊙O于A、B、D，∴P A＝PB＝15cm，ED＝EA，FD＝DB，∴PE+EF+PF＝PE+ED+PF+FD＝P A+PB＝30（cm）即△PEF周长是30cm；∵P A、PB为⊙O的切线，∴∠P AO＝∠PBO＝90°，而∠P＝50°，∴∠AOB＝360°﹣90°﹣90°﹣50°＝130°；连OD，如图，∴∠ODE＝∠ODF＝90°，易证得Rt△OAE≌Rt△ODE，Rt△OFD≌Rt△OFB，∴∠1＝∠2，∠3＝∠4，∴∠2+∠3＝∠AOB＝65°，则∠EOF＝65°．15．解：∵△ABC是一张三角形的纸片，⊙O是它的内切圆，点D是其中的一个切点，AD ＝10cm，∴设E、F分别是⊙O的切点，故DM＝MF，FN＝EN，AD＝AE，∴AM+AN+MN＝AD+AE＝10+10＝20（cm）．故答案是：20cm．三．解答题16．解：连接OA，OP，则OA⊥P A，根据题意可得：CA＝CE，DE＝DB，P A＝PB，∵PC+CE＝DE+PD＝18，∴PC+CA+DB+PD＝18，∴P A＝×18＝9（cm），∵P A、PB是⊙O的切线，∴∠APO＝∠APB＝30°，在Rt△AOP中，PO＝2AO，AO＞0，故OA2+92＝（2AO）2，解得：OA＝3，故⊙O的半径为：3cm．17．（1）证明：根据切线长定理可知：∵∠OAE+∠ODA＝（∠BAD+∠ADC）＝90°，∴∠AOD＝90°，∵∠OAE＝∠OAE，∠AOD＝∠AEO＝90°，∴△AOE∽△ADO，∴＝，即AO2＝AE•AD；（2）解：在Rt△AOD中，OD＝＝3（cm），∵S△AOD＝×AD×EO＝×AO×OD即5×EO＝4×3，∴EO＝（cm），∵OE是⊙O的半径，∴S圆O＝πr2＝π（cm2）．18．（1）答：△OBC是直角三角形．证明：∵AB、BC、CD分别与⊙O相切于E、F、G，∴∠OBE＝∠OBF＝∠EBF，∠OCG＝∠OCF＝∠GCF，∵AB∥CD，∴∠EBF+∠GCF＝180°，∴∠OBF+∠OCF＝90°，∴∠BOC＝90°，∴△OBC是直角三角形；（2）解：∵在Rt△BOC中，BO＝6，CO＝8，∴BC＝＝10；（3）解：∵AB、BC、CD分别与⊙O相切于E、F、G，∴OF⊥BC，∴OF＝＝＝4.8．。

2019-2020学年度最新浙教版九年级数学下册《切线长定理》单元考点练习及答案解析一

2.2《切线长定理》同步提升练习题一、选择题1．下列说法：①三点确定一个圆；②垂直于弦的直径平分弦；③三角形的内心到三条边的距离相等；④圆的切线垂直于经过切点的半径．其中正确的个数是（）A、0B、2C、3D、42．如图，在平面直角坐标系中，过格点A，B，C作一圆弧，点B与下列格点的连线中，能够与该圆弧相切的是（）A、点（0，3）B、点（2，3）C、点（5，1）D、点（6，1）3．已知⊙O的半径是4，P是⊙O外的一点，且PO＝8，从点P 引⊙O的两条切线，切点分别是A，B，则AB＝0A．4B．4 2C．4 3D．2 34．如图，AB，CD分别为⊙O1，⊙O2的弦，AC，BD为两圆的公切线且交于点P.若PC＝2，CD＝3，DB＝6，则△PA B的周长为()A．6B．9 C．12D．145.如图，半圆D的直径AB=4，与半圆O内切的动圆O1与AB切于点M，设⊙O1的半径为y，AM=x，则y关于x的函数关系式是 ()A 、y=-x 2+xB 、y=-x 2+xC 、y=-x 2-xD 、y=x 2-x6、如图，在⊙O 中，AD ，C D 是弦，连接OC 并延长，交过点A 的切线于点B ，若∠ADC=30°，则∠ABO 的度数为A 、20°B 、30°C 、40°D 、50°7、如图，AE 、AD 和BC 分别切⊙O 于点E 、D 、F ，如果AD=20，则△ABC 的周长为（）A 、20B 、30C 、40D 、508、如图，直线AB 、CD 、B C 分别与⊙O 相切于E 、F 、G ，且AB ∥CD ，若OB =6cm ，0C =8cm ，则BE+CG 的长等于（）A 、13B 、12C 、11D 、10二、填空题9．如图，P 是⊙O 外一点，PA ，PB 分别和⊙O 相切于点A ，B ，C 是AB ︵上任意一点，过点C 作⊙O 的切线，分别交PA ，PB 于点D ，E，若△PDE的周长为12，则PA的长为____．10．如图，EB，EC是⊙O的两条切线，B，C是切点，A，D是⊙O上的两点．若∠E＝46°，∠DCF＝32°，则∠A的度数是___．11. 如图，⊙O的半径OC是⊙O1的直径，且有OC垂直于⊙O的直径AB.⊙O1的切线AD交OC的延长线于点E，切点为D，已知⊙O1的半径为r，则AO1＝5r，DE＝___12、如图，⊙O是四边形AB CD的内切圆，切点分别为E、F、G、H，已知AB=5，CD=7，那么A D+B C=______.13、如图，PA，PB是⊙O的切线，CD切⊙O于E，PA=6，则△PDC 的周长为_____.14、如图，AB为半⊙O的直径，C为半圆弧的三等分点，过B，C 两点的半⊙O的切线交于点P，若AB的长是2a，则PA的长是________三、解答题15．如图，AB为半圆O的直径，在AB的同侧作AC，BD切半圆O 于点A，B，CD切半圆O于点E.请分别写出一对相等的角．一对相等的线段和一对相似三角形16．如图，直尺、三角尺和⊙O相切，AB＝8 cm.求⊙O的直经17．如图，已知CA，CD分别切⊙O1于点A，D，C B，CE分别切⊙O2于点B，E.若∠1＝60°，∠2＝65°，比较AB，CD，CE的长度，下列关系正确的是A．AB>CE>CD B．AB＝CE>CDC．AB>CD>CE D．AB＝CD＝CE18．如图，在△ABC中，∠B＝90°，O是AB上一点，以O为圆心，OB长为半径的圆与AB交于点E，与AC相切于点D，直线ED 交BC的延长线于点F.(1)求证：BC＝FC；(2)若AD∶AE＝2∶1，求tanF的值．19．如图，以Rt△ABC的直角边AB为直径作⊙O，与斜边AC交于点D，过点D作⊙O的切线交BC于点E.(1)求证：EB＝EC＝ED；(2)试问：在线段DC上是否存在点F，满足BC2＝4DF·D C？若存在，作出点F，并予以证明；若不存在，请说明理由．答案：15.【解】答案不唯一，如：∠ACO＝∠OCD，A C＝CE，△ACO∽△OCD16.【解】连结OE，OA，O B，如解图∵AC，AB都是⊙O的切线，切点分别是E，B，∴∠OBA＝∠OEA＝90°，AE＝AB.又∵OA＝OA，∴Rt△OAE≌Rt△OAB(HL)，∴∠OAE＝∠OAB＝12∠BAC.∵∠CAD＝60°，∴∠BAC＝120°，∴∠OAB＝12×120°＝60°，∴∠BOA＝30°，∴OA＝2AB＝16 cm.∴OB＝OA2－AB2＝162－82＝8 3(c m)，∴⊙O的直径是16 3cm.17.【解】∵∠1＝60°，∠2＝65°，∴∠ABC＝180°－∠1－∠2＝55°∴∠2>∠1>∠ABC∴AB>BC>AC∵CA，CD分别切⊙O1于点A，D，CB，CE分别切⊙O2于点B，E，∴AC＝CD，BC＝CE∴AB>CE>CD18.【解】(1)连结BD.∵BE为⊙O的直径，∴∠BDE＝90°，∴∠EBD＝90°－∠BED.∵∠EBF＝90°，∴∠F＝90°－∠BEF.∴∠F＝∠EBD.∵AC切⊙O于点D，∴∠EBD＝∠ADE＝∠CDF.∴∠F＝∠CDF，∴DC＝FC∵OB⊥BC，∴BC是⊙O的切线，∴BC ＝FC.(2)在△ADE 和△ABD 中，∵∠A ＝∠A ，∠ADE ＝∠ABD∴△ADE ∽△ABD ，∴DE BD ＝AE AD ＝12. 又∵∠F ＝∠EBD ，∴tan F ＝tan ∠EBD ＝DE BD ＝12. 19.【解】 (1)连结OD ，BD.∵ED ，EB 是⊙O 的切线，∴ED ＝EB ，∠E DO ＝∠EBO.∵OD ＝OB ，OE ＝OE∴△ODE ≌△OBE ，∴∠DEO ＝∠BEO∴OE 垂直平分BD.又∵AB 是⊙O 的直径，∴AD ⊥BD.∴AD ∥OE.即OE ∥AC.又∵O 为AB 的中点，∴OE 为△ABC 的中位线∴EB ＝EC ＝ED.(2)在△DEC 中，∵ED ＝EC ，∴∠C ＝∠CDE ，∴∠DEC ＝180°－2∠C.①当∠DEC>∠C 时，有180°－2∠C>∠C ，即0°<∠C<60°，在线段DC 上存在点F 满足BC 2＝4DF ·DC.在△DEC 中，过点E 作∠DEF ＝∠C ，EF 交CD 于点F ，则点F 即为所求．证明如下：在△DCE 和△DEF 中，∵∠CDE ＝∠EDF ，∠C ＝∠DEF∴△DEF ∽△DCE ，∴DE 2＝DF ·DC ，即⎝ ⎛⎭⎪⎪⎫12BC 2＝DF ·DC ， ∴BC 2＝4DF ·DC.②当∠DEC ＝∠C 时，△DEC 为等边三角形，即∠DEC ＝∠C ＝60°. 此时，点C 即为满足条件的点F ，∴DF ＝DC ＝DE ，仍有BC 2＝4DE 2＝4DF ·DC.③当∠DEC<∠C 时，有180°－2∠C<∠C ，即60°<∠C<90°，所作的∠DEF>∠DEC ，此时点F 在DC 的延长线上，故线段DC 上不存在满足条件的点F.。

浙教版数学九年级下册2.2切线长定理.doc

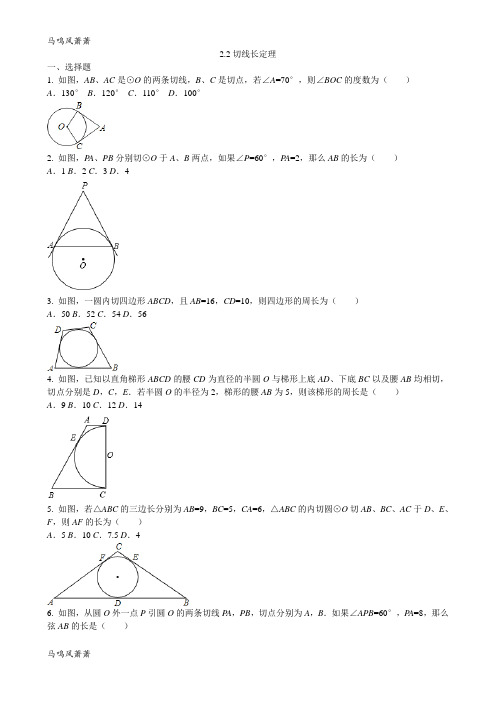
2.2切线长定理一、选择题1. 如图，AB、AC是⊙O的两条切线，B、C是切点，若∠A=70°，则∠BOC的度数为（）A．130°B．120°C．110°D．100°2. 如图，P A、PB分别切⊙O于A、B两点，如果∠P=60°，P A=2，那么AB的长为（）A．1 B．2 C．3 D．43. 如图，一圆内切四边形ABCD，且AB=16，CD=10，则四边形的周长为（）A．50 B．52 C．54 D．564. 如图，已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切，切点分别是D，C，E．若半圆O的半径为2，梯形的腰AB为5，则该梯形的周长是（）A．9 B．10 C．12 D．145. 如图，若△ABC的三边长分别为AB=9，BC=5，CA=6，△ABC的内切圆⊙O切AB、BC、AC于D、E、F，则AF的长为（）A．5 B．10 C．7.5 D．46. 如图，从圆O外一点P引圆O的两条切线P A，PB，切点分别为A，B．如果∠APB=60°，P A=8，那么弦AB的长是（）A ．4B ．8C ．34D ．38二、填空题7. 如图，⊙O 的半径为3cm ，点P 到圆心的距离为6cm ，经过点P 引⊙O 的两条切线，这两条切线的夹角为 .8. 如图，⊙O 与△ABC 中AB 、AC 的延长线及BC 边相切，且∠ACB =90°，∠A ，∠B ，∠C 所对的边长依次为3，4，5，则⊙O 的半径是 .9. 如图：EB 、EC 是⊙O 的两条切线，B 、C 是切点，A 、D 是⊙O 上两点，如果∠E =46°，∠DCF =32°，则∠A 的度数是 °.10. 如图，⊙O 的半径为3cm ，点P 到圆心的距离为6cm ，经过点P 引⊙O 的两条切线，则∠APO =°.11. 如图，P A 、PB 分别切⊙O 于A 、B ．P A =5，在劣弧AB 上取点C ，过C 作⊙O 的切线，分别交P A ，PB 于D ，E ，则△PDE 的周长等于 .12.如图，已知PA，PB分别切⊙O于A、B，CD切⊙O于E，PO=13，AO=5，则△PCD周长为 .三、解答题13.已知：⊙O的半径为3cm，点P和圆心O的距离为6cm，经过点P和⊙O的两条切线，求这两条切线的夹角及切线长．参考答案2.2切线长定理一、选择题1.C2.B3.B4.D5.A6.B二、填空题7.60度8.29.9910.3011.1012.24三、解答题13.初中数学试卷鼎尚图文**整理制作。

2.2切线长定理-20春浙教版九年级数学下册同步测试

2.2__切线长定理__[学生用书B66]1．[2019·杭州]如图2－2－1，P为⊙O外一点，P A，PB分别切⊙O于A，B两点，若P A＝3，则PB＝(B)图2－2－1A．2 B．3 C．4 D．52．如图2－2－2，△MBC中，∠B＝90°，∠C＝60°，MB＝23，点A在MB上，以AB为直径作⊙O与MC相切于点D，则CD的长为(C)图2－2－2A. 2B. 3 C．2 D．33．[2019·广州]平面内，⊙O的半径为1，点P到O的距离为2，过点P可作⊙O 的切线条数为(C)A．0条B．1条C．2条D．无数条4．如图2－2－3，四边形ABCD的边AB，BC，CD，DA和⊙O分别相切于点L，M，N，P.若四边形ABCD的周长为20，则AB＋CD等于(C)图2－2－3A．5 B．8 C．10 D．125．[2019·益阳]如图2－2－4，P A，PB为⊙O的切线，切点分别为A，B，PO交AB于点C，PO的延长线交⊙O于点D，下列结论不一定成立的是(D)图2－2－4A．P A＝PB B．∠BPD＝∠APDC．AB⊥PD D．AB平分PD6．[2019·温州]如图2－2－5，⊙O分别切∠BAC的两边AB，AC于点E，F，点P在优弧EDF上．若∠BAC＝66°，则∠EPF等于__57__度．【解析】如答图，连结OE ，OF .∵⊙O 分别切∠BAC 的两边AB ，AC 于点E ，F ，∴OF ⊥AC ，OE ⊥AB ，∴∠BAC ＋∠EOF ＝180°，∵∠BAC ＝66°，∴∠EOF ＝114°.∵点P 在优弧EDF ︵上，∴∠EPF ＝12∠EOF ＝57°.7．如图2－2－6，AB ，AC ，BD 是⊙O 的切线，P ，C ，D 为切点，如果AB ＝5，AC ＝3，则BD 的长为__2__．图2－2－6【解析】 ∵AC ，AP 为⊙O 的切线，∴AC ＝AP ， ∵BP ，BD 为⊙O 的切线，∴BP ＝BD ， ∴BD ＝PB ＝AB －AP ＝5－3＝2.8．如图2－2－7，P 为⊙O 外一点，P A ，PB 是⊙O 的切线，A ，B 为切点，P A ＝3，∠P ＝60°，则图中阴影部分的面积为3．【解析】如答图，连结OA ，OB ，OP . ∵∠APB ＝60°，∴∠APO ＝30°， ∵P A ＝3且OA ⊥AP ，∴OA ＝1，∴S △APO ＝32，∴S 四边形OAPB ＝2S △APO ＝3，又∵∠AOP ＝60°，∴∠AOB ＝120°， ∴S 扇形AOB ＝120×π×12360＝13π，∴S 阴影＝S 四边形OAPB －S 扇形AOB ＝3－π3.9．[2019·资阳]如图2－2－8，AC 是⊙O 的直径，P A 切⊙O 于点A ，PB 切⊙O 于点B ，且∠APB ＝60°. (1)求∠BAC 的度数；(2)若P A ＝1，求点O 到弦AB 的距离．图2－2－8 第9题答图解：(1)∵P A 切⊙O 于点A ，PB 切⊙O 于点B ， ∴P A ＝PB ，∠P AC ＝90°，∵∠APB ＝60°，∴△APB 是等边三角形， ∴∠BAP ＝60°，∴∠BAC ＝90°－∠BAP ＝30°；(2)作OD ⊥AB 于D ，如答图，则AD ＝BD ＝12AB ，由(1)得△APB 是等边三角形， ∴AB ＝P A ＝1，∴AD ＝12，∵∠BAC ＝30°，∴AD ＝3OD ＝12， ∴OD ＝36，即点O 到弦AB 的距离为36.10．如图2－2－9，P A ，PB 是⊙O 的切线，CD 切⊙O 于点E ，△PCD 的周长为12，∠P ＝60°.求：图2－2－9(1)P A 的长； (2)∠COD 的度数．解：(1)∵CA ，CE 都是⊙O 的切线， ∴CA ＝CE ，同理：DE＝DB，P A＝PB，∴△PCD的周长＝PD＋CD＋PC＝PD＋PC＋CA＋BD＝P A＋PB＝2P A＝12，即P A的长为6；(2)∵∠P＝60°，∴∠PCE＋∠PDE＝120°，∴∠ACD＋∠CDB＝360°－120°＝240°，∵CA，CE是⊙O的切线，∴∠OCE＝∠OCA＝12∠ACD；同理，∠ODE＝12∠CDB，∴∠OCE＋∠ODE＝12(∠ACD＋∠CDB)＝120°，∴∠COD＝180－120°＝60°.11．如图2－2－10，直尺、三角尺都和⊙O相切，B是切点，且AB＝8 cm.求⊙O 的直径．图2－2－10 第11题答图解：如答图，设三角尺与⊙O相切于点E，三角尺斜边所在直线为AC，连结OE，OA，OB.∵AC，AB都是⊙O的切线，切点分别是E，B，∴∠OBA＝∠OEA＝90°.又∵OB＝OE，OA＝OA，∴Rt△OBA≌Rt△OEA，∴∠OAB＝∠OAE＝12∠BAC.∵∠CAD＝60°，∴∠BAC＝120°，∴∠OAB＝12×120°＝60°，∴∠BOA＝30°，∴OA＝2AB＝16(cm)．由勾股定理，得OB＝OA2－AB2＝162－82＝83(cm)，即⊙O的半径是8 3 cm，∴⊙O的直径是16 3 cm.12．[2019·天津]已知P A，PB分别与⊙O相切于点A，B，∠APB＝80°，C为⊙O 上一点．(1)如图2－2－11①，求∠ACB的大小；(2)如图②，AE为⊙O的直径，AE与BC相交于点D.若AB＝AD，求∠EAC的大小．图2－2－11解：(1)如答图①，连结OA，OB，∵P A，PB是⊙O的切线，∴∠OAP＝∠OBP＝90°，∴∠AOB＝360°－90°－90°－80°＝100°，由圆周角定理，得∠ACB＝12∠AOB＝50°；第12题答图(2)如答图②，连结CE，∵AE为⊙O的直径，∴∠ACE＝90°，∵∠ACB＝50°，∴∠BCE＝90°－50°＝40°，∴∠BAE＝∠BCE＝40°，∵AB＝AD，∴∠ABD＝∠ADB＝70°，∴∠EAC＝∠ADB－∠ACB＝20°.13．[2018·北京]如图2－2－12，AB是⊙O的直径，过⊙O外一点P作⊙O的两条切线PC，PD，切点分别为C，D，连结OP，CD.(1)求证：OP⊥CD；(2)连结AD，BC，若∠DAB＝50°，∠CBA＝70°，OA＝2，求OP的长．图2－2－12 第13题答图解：(1)证明：如答图，连结OC，OD，∵PC，PD切⊙O于点C，D，∴PC＝PD，∴点P在线段CD的垂直平分线上，∵OC＝OD，∴点O在线段CD的垂直平分线上，∴OP⊥CD；(2)∵OA＝OD，∠DAB＝50°，∴∠DOA＝80°，同理，∠BOC＝40°，∴∠COD＝180°－∠AOD－∠BOC＝60°，∵OC＝OD，PD＝PC，OP＝OP，∴△OPC≌△OPD，∴∠POD＝∠POC＝30°，∵PD切⊙O于点D，∴OD⊥DP，在Rt△OPD中，cos∠DOP＝ODOP＝2OP，∴OP＝2cos30°＝433.14．如图2－2－13，P A，PB分别切⊙O于点A，B，连结PO，AB相交于点D，C是⊙O上一点，∠C＝60°.(1)求∠APB的大小；(2)若PO＝20 cm，求△AOB的面积．图2－2－13解：(1)∵P A，PB分别为⊙O的切线，∴OA⊥P A，OB⊥PB，∴∠OAP＝∠OBP＝90°.∵∠C＝60°，∴∠AOB＝2∠C＝120°，∴在四边形APBO中，∠APB＝360°－∠OAP－∠OBP－∠AOB＝360°－90°－90°－120°＝60°；(2)∵在Rt△P AO与Rt△PBO中，OA＝OB，PO＝PO，∴Rt△P AO≌Rt△PBO(HL)，∴∠APO＝∠BPO＝12∠APB＝30°.∵P A＝PB，PD＝PD，∴△P AD≌△PBD(SAS)，∴AD＝BD，∴PO⊥AB，∴∠DAO＝∠APO＝30°，∴OA＝OP·sin∠APO＝20×12＝10(cm)．∵在Rt△AOD中，∠DAO＝30°，OA＝10 cm，∴AD＝OA·cos∠DAO＝10×32＝53(cm)，OD＝OA·sin∠DAO＝10×12＝5(cm)，∴AB＝2AD＝103(cm)，∴S△AOB ＝12AB·OD＝12×103×5＝253(cm2)．15．如图2－2－14，直线AB，BC，CD分别与⊙O相切于E，F，G，且AB∥CD，OB＝6 cm，OC＝8 cm.求：图2－2－14(1)∠BOC的度数；(2)BE＋CG的长；(3)⊙O的半径．第15题答图解：(1)根据切线长定理得BE＝BF，CF＝CG，∠OBF＝∠OBE，∠OCF＝∠OCG.∵AB∥CD，∴∠ABC＋∠BCD＝180°，∴∠OBF＋∠OCF＝90°，∴∠BOC＝90°；(2)由(1)知∠BOC＝90°.∵OB＝6 cm，OC＝8 cm，∴由勾股定理得BC＝10 cm，∴BE＋CG＝BC＝10(cm)；(3)如答图，连结OF.∵OF⊥BC，∴OF＝OB·OCBC＝4.8(cm)．。

浙教版九年级数学下第二章同步练习2.1直线与圆的位置关系切线的判定

浙教版九年级数学下第二章同步练习2．1直线与圆的位置关系切线的判定学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列说法中，不正确的是（）A．与圆只有一个交点的直线是圆的切线B．经过半径的外端，且垂直于这条半径的直线是圆的切线C．与圆心的距离等于这个圆的半径的直线是圆的切线D．垂直于半径的直线是圆的切线2．已知⊙O的直径为4cm,圆心到直线l1, l2, l3, l4的距离分别为2cm,cm cm,则与⊙O相切的直线有（）,2tan45,1.9A．1条B．2条C．3条D．4条3．正方形ABCD中，点P是对角线AC上的任意一点（不包括端点），以P为圆心的圆与AB相切，则AD与⊙P的位置关系是（）A．相离B．相切C．相交D．不确定4．若⊙O的半径为R，直线l与⊙O有公共点，若圆心到直线l的距离为d，则d与R 的大小关系是（）．A．d＞R B．d＜R C．d≥R D．d≤R5．如图，AB是⊙O的直径，BC交⊙O于点D，DE⊥AC于点E，要使DE是⊙O的切线，还需补充一个条件，则补充的条件不正确的是（）A．DE=DO B．AB=ACC．CD=DB D．AC∥OD6．如图，在直角坐标系中，⊙O的半径为1，则直线与⊙O的位置关系是( )A．相离B．相交C．相切D．以上三种情形都有可能7．如图,AB与⊙O切于点B,AO=6 cm, AB=4 cm,则☉O的半径r等于( )A．4 cm B．C．2cm D．3cm8．如图,CB为⊙O的直径,P是CB的延长线上的一点,且OB=BP,∠AOC=120°,则PA与⊙O 的位置关系是( )A．相离B．相切C．相交D．不确定9．如图，在等腰直角三角形ABC中，AB=AC=8，O为BC的中点，以O为圆心作半圆，使它与AB，AC都相切，切点分别为D，E，则⊙O的半径为（）A．8 B．6 C．5 D．410．如图，AB是⊙O的弦，若∠PAB=40°，若使PA是⊙O的切线，则∠AOB=（）.A．80°B．60°C．40°D．20°二、填空题11．当点P 在⊙O 上时, 经过点P 能作________条直线与⊙O 相切. 若过点P 能作⊙O 的两条切线,则点P 必在⊙O _________(填”上”或”外”或”内”)12．已知直线l ，在l 上取一点A ，过A 点与l 相切的圆有______个.13．如图,已知30MAN ∠=︒，O 为边AN 上一点，以O 为圆心，2为半径作⊙O，交AN 于D E ，两点，设AD x =．当x =_______时，⊙O 与AM 相切.14．已知：如图：AB 是⊙O 的直径，BD ＝OB ，∠C AB ＝30°．请根据已知条件和所给图形，写出三个正确结论（除AO ＝OB ＝BD 外）；①_________；②_________；③_________．15．如图，⊙O 的半径为4 cm ，BC 是直径，若AB ＝10 cm ，则AC ＝_______cm 时，AC 是⊙O 的切线16．如图，已知ABC ∠是直角，在射线BC 上取一点O 为圆心、12BO 为半径画圆，射线BA 绕点B 顺时针旋转__________度时与圆O 第一次相切.17．如图，⊙O 的半径为4 cm ，BC 是直径，若AB ＝10 cm ，则AC ＝_____cm 时，AC 是⊙O 的切线．18．如图，△ABC 的一边AB 是⊙O 的直径，请你添加一个条件，使BC 是⊙O 的切线，你所添加的条件为______．三、解答题19．如图，AB是⊙O的弦，OC OA⊥交AB于点C，过点B的直线交OC的延长线于点E，当CE BE=时，直线BE与⊙O有怎样的位置关系？并证明你的结论．20．已知：如图，△ABC内接于⊙O，点D在OC的延长线上，sinB＝12，∠CAD＝30°．（1）求证：AD是⊙O的切线；（2）若OD⊥AB，BC＝5，求AD的长．21．如图所示，△ABC内接于⊙O，AC是⊙O的直径，点D是劣弧AB的中点，过点D 作直线BC的垂线，分别交CB，CA的延长线于E，F两点．(1)求证：EF是⊙O的切线；(2)若EF＝8，EC＝6，求⊙O的半径．22．如图，在△ABC中，BA＝BC，以AB为直径作半圆⊙O，交AC于点D．连接DB，过点D作DE⊥BC，垂足为点E.求证：DE为⊙O的切线．23．如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别交AC，BC于点D，E，点F在AC的延长线上，且∠CBF＝12∠CA B．求证：直线BF是⊙O的切线.24．如图，已知AB是⊙O的直径，AC为弦，且平分∠BAD，AD⊥CD，垂足为D．(1) 求证：CD是⊙O的切线；(2) 若⊙O的直径为4，AD=3，试求∠BAC的度数．参考答案1．D【解析】试题分析：利用切线的性质进行判断后即可得到答案．A．与圆只有一个交点的直线是圆的切线,正确；B．经过半径的外端，且垂直于这条半径的直线是圆的切线，正确；C．与圆心的距离等于这个圆的半径的直线是圆的切线，正确；D．垂直于半径的直线是圆的切线，错误.故选D.考点: 切线的判定．2．B【解析】【分析】把⊙O的半径为2cm与圆心到直线l1, l2, l3, l4的距离分别分别进行比较，根据直线与圆的位置关系的知识即可解答.【详解】∵⊙O的直径为4cm,∴⊙O的半径为2cm，=⨯=，2>1.9，∵2=2，2=2tan45212∴⊙O与l1，l3相切，与l2，l4相交，故选B.【点睛】本题考查了直线与圆的位置关系的知识，解决本题的关键是熟记位置关系及名称. 在判断直线与圆的位置关系时，通常要得到圆心到直线的距离d和圆的半径r，然后再利用d与r的大小关系进行判断.直线与圆的位置关系：①当d＞r时，直线与圆相离；②当d=r时，直线与圆相切；③当d＜r时，直线与圆相交.3．B【解析】分析：根据正方形的对角线平分一组对角，以及角平分线上的点到角两边的距离相等，得点P到AD的距离等于点P到AB的距离．所以若以P为圆心的圆与AB相切，则AD 与⊙P的位置关系是相切．详解：∵点P到AD的距离等于点P到AB的距离，以P为圆心的圆与AB相切，∴AD与⊙P的位置关系是相切．故选B．点睛：综合运用了正方形的性质和角平分线的性质．4．D【解析】【分析】直线l与⊙O有公共点，则可得圆与直线相交或相切，根据圆和直线的位置关系，可以得出d与R的大小关系.【详解】∵直线l与⊙O有公共点，∴直线l与⊙O相交或相切.∵圆心到直线l的距离是d，∴可得d≤R.故选D.【点睛】本题考查了直线与圆的位置关系的知识，解决本题的关键是熟记位置关系及名称. 在判断直线与圆的位置关系时，通常要得到圆心到直线的距离d和圆的半径r，然后再利用d与r的大小关系进行判断.直线与圆的位置关系：①当d＞r时，直线与圆相离；②当d=r时，直线与圆相切；③当d＜r时，直线与圆相交.5．A【详解】：根据AB=AC，连接AD，利用圆周角定理可以得到点D是BC的中点，OD是△ABC的中位线，OD∥AC，然后由DE⊥AC，得到∠ODE=90°，可以证明DE是⊙O的切线．根据CD=BD，AO=BO，得到OD是△ABC的中位线，同上可以证明DE是⊙O的切线．根据AC∥OD，AC⊥DE，得到∠EDO=90°，可以证明DE是⊙O的切线．故选A.6．C【解析】【分析】只需求得圆心到直线的距离，再根据圆心到直线的距离和圆的半径之间的大小关系进行分析．【详解】圆心O到直线y x=-+的距离是1，它等于圆的半径1，则直线和圆相切，故选：C.【点睛】考查直线与圆的位置关系，算出圆心O到直线的距离是解题的关键.7．B【解析】【分析】连接OB，由切线的性质可知，∠ABO=90°，然后根据勾股定理求解即可.【详解】连接OB，∵AB与⊙O切于点B,∴∠ABO=90°，r=故选B.【点睛】此题主要考查圆的切线的性质及勾股定理的应用.通过切线的性质定理得到△ABO是直角三角形是解决本题的关键.8．B【分析】连接AC，AB，由∠AOC=120°可求出∠C=∠CAO=30°，从而根据30°的角所对的直角边等于斜边的一半得AB=12BC,由等量代换可知AB=12OP,从而根据三角形中一边上的中线等于其所在边的一半，那么这个三角形为直角三角形可证明P A与⊙O相切.【详解】连接AC，AB，∵∠AOC=120°，OA=OC，∴∠C=∠CAO=30°，∴AB=12 BC,∵OB=BP, ∴BC=OP,∴AB=12 OP,∴△OAP是直角三角形，∴∠OAP=90°，∴P A与⊙O相切.故选B.【点睛】本题考查了等腰三角形的性质，直角三角形的判定与性质，切线的判定等知识，熟练掌握切线的判定方法是解答本题的关键.经过半径外端点并且垂直于这条半径的直线是圆的切线.9．D【解析】解：连接OA，OD，∵AB，AC都与⊙O相切，∴∠BAO=∠CAO，OD⊥AB，∵在等腰直角三角形ABC中，AB=AC=8，∴AO⊥BC，∴∠B=∠BAO=45°，=4√2，∴OB=AB•cos∠B=8×√22=4．∴在Rt△OBD中，OD=OB•sin∠B=4√2×√22故选D．10．A【解析】【分析】根据P A为圆O的切线，可求出∠P AO=90°，从而求出∠BAO=50°，然后利用等腰三角形的性质可求出∠AOB的值.【详解】∵P A为圆O的切线，∴P A⊥AO，∴∠P AO=90°，又∠P AB=40°，∴∠BAO=90°-40°=50°，又∵OA=OB，∴∠BAO=∠B=50°，则∠AOB=180°-50°-50°=80°．故选A.【点睛】本题考查了切线的性质，等腰直角三角形的性质，熟练掌握切线的性质是解答本题的关键. 切线的性质：①圆的切线垂直于经过切点的半径；②经过圆心且垂直于切线的直线必经过切点；③经过切点且垂直于切线的直线必经过圆心．11．一外【解析】【分析】根据切线的定义求解即可.【详解】如图，当点P在⊙O上时, 经过点P能作一条直线与⊙O相切. 若过点P能作⊙O的两条切线,则点P必在⊙O外.故答案为：一；外.【点睛】本题考查了切线的定义，经过半径的外端，且与半径垂直的直线是圆的切线，熟练掌握切线的定义是解答本题的关键.12．无数【解析】【分析】根据切线的定义求解即可.【详解】如图，过点A作l的垂线m，以m上任一点为圆心，以该点与点A的距离为半径画圆，则所得的圆与l相切，∵m上有无数个点，∴能作无数个圆与l相切.故答案为：无数.【点睛】本题考查了切线的定义，经过半径的外端，且与半径垂直的直线是圆的切线，熟练掌握切线的定义是解答本题的关键.13．2【分析】过O点作OF⊥AM于F．根据切线的性质知OF=r=2．然后在直角△AOF中，由“30°角所对的直角边是斜边的一半”求得线段AO的长度．则AD=AO-r．【详解】过O点作OF⊥AM于F．当OF=r=2时，⊙O与AM相切．∵∠AFO=90°，∠MAN=30°，∴AO=2OF=4，∴x=AD=AO-OD=AO-r=2cm．即当x为2时，⊙O与AM相切．故答案为2.【点睛】本题考查了切线的性质．运用切线的性质来进行计算或证明，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．14．答案不唯一，AB=2BD；∠ACD=120°；△BCD∽△CAD.【解析】【分析】首先连接OC，BC，由AB是⊙O的直径，BD=OB，∠CAB=30°，易得△OBC是等边三角形，△ACD是等腰三角形，继而可得CD是⊙O的切线．【详解】连接OC，BC，①∵BD＝OB，AO=OB，∴BD=AO=OB，∴AB=2BD；②∵AB是⊙O的直径，∴∠ACB=90°，∵OA=OC，∴∠ACO=∠CAB＝30°∴∠COB=60°，∴△OBC是等边三角形，∵BD=OB，∴BD=OB=BC=OC，∴∠D=∠BCD=12∠CBO=30°，∴∠ACD=30°+60°+30°=120°；③∠A=∠BCD=30°，∠D=∠D，∴△BCD∽△CAD．故答案为：此题答案不唯一，如①B=2BD；②∠ACD=120°；③△BCD∽△CAD．【点睛】此题考查了圆周角定理的推论、等边三角形的判定与性质、等腰三角形的性质与判定、三角形外角的性质以及相似三角形的判定．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．15．6【解析】【分析】若AC是是⊙O的切线，则∠C=90°，然后根据勾股定理即可求出AC的长.【详解】∵⊙O的半径为4 cm，∴BC=10 cm，若AC是是⊙O的切线，则∠C=90°，∴6AC==.故答案为：6.【点睛】本题考查了切线的判定方法，如果直线与圆只有一个公共点，这时直线与圆的位置关系叫做相切，这条直线叫做圆的切线，这个公共点叫做切点；经过半径外端点并且垂直于这条半径的直线是圆的切线.16．60【分析】根据题意，画出旋转过程中，与圆相切时的切线BA1，切点为D,连接OD，根据切线的性质可得∠ODB=90°，然后根据已知条件，即可得出∠OBD=30°，从而求出旋转角∠ABA1．【详解】解：如下图所示，射线BA1为射线BA与圆第一次相切时的切线，切点为D,连接OD∴∠ODB=90°根据题意可知：12 OD BO=∴∠OBD=30°∴旋转角：∠ABA1=∠ABC－∠OBD=60°故答案为：60【点睛】此题考查的是切线的性质和旋转角，掌握切线的性质是解决此题的关键．17．6【解析】【分析】根据切线的判定定理当∠BCA=90°时,AC是⊙O的切线,然后根据勾股定理计算AC.【详解】∵⊙O的半径为4 cm，∴BC=8cm，∵BC是直径，∴∠BCA=90°时,AC是⊙O的切线,∴6===.AC cm故答案为6.【点睛】本题考查了切线的判定:过半径的外端点与半径垂直的性质为圆的切线.也考查了勾股定理. 18．∠ABC=90°（答案不唯一）．【解析】【分析】根据切线的判定方法知，能使BC成为切线的条件就是能使AB垂直于BC的条件，从而得出答案即可.【详解】当∠ABC=90°时，BC与圆相切．故添加的条件可以是∠ABC=90°，或AB⊥BC等，答案不唯一．19．相切；证明见解析.【解析】【分析】）连接OB，由等腰三角形的性质可得∠A=∠ABO，∠EBC=∠ECB，由OC⊥OA可知∠A+∠ACO=90°，由等量代换得∠OBE=90°，则OB⊥BE，故BE与⊙O相切. 【详解】解：连结OB, 则OB=OA, ∴∠A=∠ABO.∵CE=BE, ∴∠EBC=∠ECB=∠ACO.∵OC⊥OA, ∴∠A+∠ACO=90°.∴∠OBC+∠EBC=90°, 即BE与⊙O相切.【点睛】本题考查的是切线的判定，等腰三角形的性质，要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可．20．（1）证明见解析；（2）【解析】【分析】（1）连接OA ，由于sinB=12，那么可求∠B =30°，利用圆周角定理可求∠AOC =60°，而OA =OB ，那么△AOC 是等边三角形，从而有∠OAC =60°，易求∠OAD =90°，即AD 是⊙O 的切线；（2）由垂径定理定理得OC 垂直平分AB ，从而AC ＝BC ＝5，然后利用正切函数求解即可.【详解】（1）证明：如图，连结OA ，因为sin ∠B ＝12，所以∠B ＝30°，故∠O ＝60°，又OA ＝OC ，所以△ACO 是等边三角形，故∠OAC ＝60°，因为∠CAD ＝30°，所以∠OAD ＝90°，所以AD 是⊙O 的切线（2）解：因为OD ⊥AB ，所以OC 垂直平分AB ，则AC ＝BC ＝5，所以OA ＝5，在△OAD 中，∠OAD ＝90°，由正切定义，有tan ∠AOD ＝AD OA，所以AD ＝【点睛】本题考查了锐角三角函数的知识、圆周角定理、等边对等角、等边三角形的判定和性质、切线的判定、垂径定理、线段垂直平分线的判定和性质，熟练掌握各知识点是解答本题的关键．21．（1）证明见解析；（2）15 4.【解析】【分析】（1）连接OD交AB于点G，依据垂径定理的推论可以得出OD⊥AB，结合题意易得AB∥EF，进而不难得到OD⊥EF，即可证明结论；（2）先根据勾股定理求出CF的长，由（1）知OD∥CE，然后利用平行线分线段成比例列式求解即可求出⊙O的半径.【详解】(1)证明：连结OD，∵D是的中点，∴OD⊥AB.又∵AC为⊙O的直径，∴BC⊥AB，∴OD∥CE.又∵CE⊥EF，∴OD⊥EF，即EF是⊙O的切线．(2)在Rt△CEF中，EF＝8，EC＝6，由勾股定理得CF＝10，设⊙O的半径为r，∵OD∥CE，∴＝，解得r＝.故⊙O的半径为.【点睛】本题主要考查了切线的判定，圆周角定理的推论，垂径定理定理的推论，平行线分线段成比例定理.证明一条直线是圆的切线常用的方法有：①若图形中已给出直线与圆的公共点，但未给出过点的半径，则可先连结过此点的半径，再证其与直线垂直；②若图形中未给出直线与圆的公共点，则需先过圆心作该直线的垂线，再证垂足到圆心的距离等于半径.22．证明见解析.【解析】【分析】连接OD，利用等腰三角形的性质可得∠BAC＝∠BCA，∠BAC＝∠ODA，从而∠BCA＝∠ODA，可证OD∥BC，利用平行线的性质可证∠ODE＝90°从而可证DE为⊙O的切线. 【详解】解：连接OD，∵AB＝BC，∴∠BAC＝∠BCA.∵OA＝OD，∴∠BAC＝∠ODA.∴∠BCA ＝∠ODA，∴OD∥BC，∵DE⊥BC，∴∠DEC＝90°，∴∠ODE＝90°，∴DE为⊙O的切线.【点睛】本题考查了等腰三角形的性质，平行线的判定与性质，切线的判定等知识，熟练掌握切线的判定方法是解答本题的关键. 经过半径外端点并且垂直于这条半径的直线是圆的切线. 23．证明见解析.【分析】连结AE.由AB是⊙O的直径得∠AEB＝90°.然后由等腰三角形的性质和等量代换可证∠CBF ＋∠2＝90°，即∠ABF＝90°，从而可证直线BF是⊙O的切线.【详解】解：连结AE.∵AB是⊙O的直径，∴∠AEB＝90°.∴∠1＋∠2＝90°.∵AB＝AC，∴∠1＝∠CAB.∵∠CBF＝∠CAB，∴∠1＝∠CBF.∴∠CBF＋∠2＝90°，即∠ABF＝90°.∵AB是⊙O 的直径，∴直线BF是⊙O的切线.【点睛】本题考查了圆周角定理的推论，切线的判定，等腰三角形的性质等知识. 半圆（或直径）所对圆周角是直角，90°的圆周角所对的弦是直径；经过半径外端点并且垂直于这条半径的直线是圆的切线.24．（1）证明见解析；（2）30°. 【解析】【分析】(1)连接OC ,证先利用角平分线的定义和等腰三角形的性质证明∠OCA =∠DAC ，从而OC ∥AD ，由平行线的性质可得OC ⊥CD ，从而得出CD 是⊙O 切线；(2)连接BC ,证明△ACB ∽△ADC ,求出AC 的长度,再求出∠BAC 的余弦,得出∠BAC 的度数.【详解】解：(1) 连结OC.∵AC 平分BAD ∠，∴∠BAC=∠DAC.又OA=OC, ∴∠BAC=∠OCA, ∴∠OCA=∠DAC, ∴OC ∥AD.∵AD ⊥CD, ∴OC ⊥CD, ∴CD 是⊙O 的切线.(2) 连结BC. ∵AB 是⊙O 的直径, ∴∠ACB=90°, ∴∠ACB=∠ADC=90°.又∠BAC=∠DAC, ∴△ACB ∽△ADC. ∴, AC AB AD AC=, , ∴AC=在Rt △ACB 中, cos ∠BAC=AC AB 2=, ∴∠BAC=30°.【点睛】本题主要考查了等腰三角形的性质，平行线的判定与性质，圆的切线的判定及锐角三角函数的知识.连接半径是证明切线的一种常用辅助线的做法,求角的度数可以借助于三角函数.。

2020—2021年浙教版九年级数学下册《切线长定理》单元考点练习及答案解析四.docx

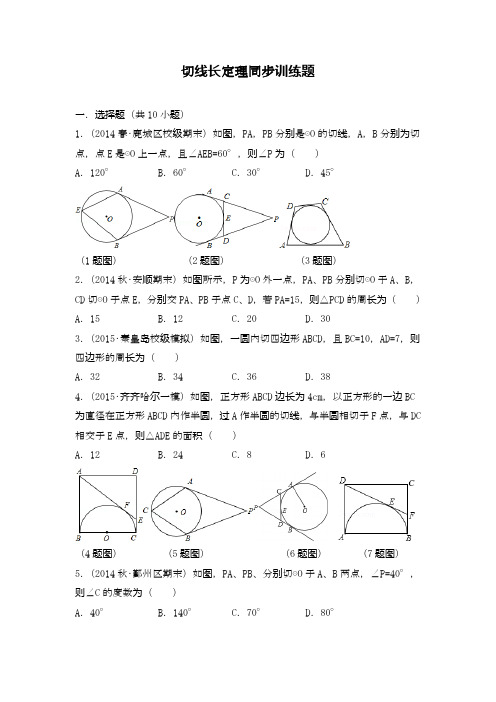
切线长定理同步训练题一．选择题（共10小题）1．（2014春•鹿城区校级期末）如图，PA，PB分别是⊙O的切线，A，B分别为切点，点E是⊙O上一点，且∠AEB=60°，则∠P为（）A．120°B．60°C．30°D．45°（1题图）（2题图）（3题图）2．（2014秋•安顺期末）如图所示，P为⊙O外一点，PA、PB分别切⊙O于A、B，CD切⊙O于点E，分别交PA、PB于点C、D，若PA=15，则△PCD的周长为（）A．15 B．12 C．20 D．303．（2015•秦皇岛校级模拟）如图，一圆内切四边形ABCD，且BC=10，AD=7，则四边形的周长为（）A．32 B．34 C．36 D．384．（2015•齐齐哈尔一模）如图，正方形ABCD边长为4cm，以正方形的一边BC 为直径在正方形ABCD内作半圆，过A作半圆的切线，与半圆相切于F点，与DC 相交于E点，则△ADE的面积（）A．12 B．24 C．8 D．6（4题图）（5题图）（6题图）（7题图）5．（2014秋•鄞州区期末）如图，PA、PB、分别切⊙O于A、B两点，∠P=40°，则∠C的度数为（）A．40°B．140°C．70°D．80°6．（2014秋•亭湖区校级月考）如图，PA，PB切⊙O于A、B两点，CD切⊙O于点E，交PA，PB于C，D．若△PCD的周长等于3，则PA的值是（）A． B．C．D．7．（2015•高港区二模）矩形ABCD中，AB=4，AD=3，以AB为直径在矩形内作半圆．DE切⊙O于点E（如图），则tan∠CDF的值为（）A． B．C．D．8．（2014秋•夏津县校级期末）如图，P为⊙O外一点，PA，PB分别切⊙O于A，B，CD切⊙O于点E，分别交PA，PB于点C，D．若PA=5，则△PCD的周长和∠COD分别为（）A．5，（90°+∠P）B．7，90°+C．10，90°﹣∠P D．10，90°+∠P（8题图）（9题图）（10题图）9．（2015•武汉模拟）如图，Rt△ABC中，∠ACB=90°，以AC为直径的⊙O交AB 于点D，过点D作⊙O的切线，与边BC交于点E，若AD=，AC=3．则DE长为（）A． B．2 C．D．10．（2014秋•岳池县期末）如图，从⊙O外一点P引圆的两条切线PA、PB，切点分别是A、B，如果∠APB=60°，线段PA=10，那么弦AB的长是（）A．10 B．12 C．5D．10二．填空题（共10小题）11．（2015•滨海县一模）如图，一圆外切四边形ABCD，且AB=16，CD=10，则四边形的周长为．（11题图）（12题图）（13题图）（15题图）12．（2015•婺城区模拟）PA、PB切⊙O于A、B两点，CD切⊙O于点E，交PA、PB 于C、D，若⊙O的半径为r，△PCD的周长等于3r，则tan∠APB的值是．13．（2015•屏山县校级模拟）如图，⊙I为△ABC的内切圆，AB=9，BC=8，AC=10，点D、E分别为AB、AC上的点，且DE为⊙I的切线，则△ADE的周长为．14．（2014秋•长汀县期末）已知P是⊙O外一点，PA切⊙O于A，PB切⊙O于B．若PA=6，则PB= ．15．（2014秋•崇安区校级期中）如图，AB、AC、BD是⊙O的切线，P、C、D为切点，如果AB=5，AC=3，则BD的长为．16．（2014秋•永定县校级期末）如图，PA、PB分别切圆O于A、B，并与圆O的切线DC分别相交于C、D．已知△PCD的周长等于14cm，则PA= cm．（16题图）（17题图）（18题图）17．（2014秋•如皋市校级月考）如图，PA、PB分别切圆O于A、B，并与圆O的切线，分别相交于C、D，已知△PCD的周长等于10cm，则PA= cm．18．（2014秋•嘉鱼县校级月考）如图，以正方形ABCD的边BC为直径作半圆O，过点D作直线切半圆于点F，交AB于点E，则△ADE和直角梯形EBCD的周长之比为．19．（2015春•叙永县校级月考）如图，⊙O是四边形ABCD的内切圆，切点分别为E、F、G、H，已知AB=5，CD=7，那么AD+BC= ．（19题图）（20题图）（21题图）20．（2012秋•茌平县校级期末）如图所示，DE是△ABC的内切圆I的切线，又BC=2cm，△ADE的周长为4cm，则△ABC的周长是cm.三．解答题（共5小题）21．（2014秋•临洮县校级月考）如图示，PA，PB分别与⊙O相切于点A，B，⊙O 的切线EF分别交PA，PB于点E，F，切点C在弧AB上，若PA=12，则△PEF的周长是？22．（2014秋•琼海校级期中）如图，PA，PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P=60°．（1）求∠BAC的度数；（2）当OA=2时，求AB的长．23．（2014秋•张家港市期末）如图，Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E；（1）求证：BE=CE；（2）若以O、D、E、C为顶点的四边形是正方形，⊙O的半径为r，求△ABC的面积；（3）若EC=4，BD=，求⊙O的半径OC的长．24．（2015•潍坊模拟）如图，PA、PB切⊙O于A、B，若∠APB=60°，⊙O半径为3，求阴影部分面积．25．（2014秋•仙游县期中）已知：AB为⊙O的直径，∠A=∠B=90°，DE与⊙O相切于E，⊙O的半径为，AD=2．①求BC的长；②延长AE交BC的延长线于G点，求EG的长．参考答案一．选择题（共10小题）1．B 2．D 3．B 4．D 5．C 6．A 7．B 8．C 9．B 10．A 二．填空题（共10小题）11．52 12．13．11 14．6 15．2 16．7 17．518．6：7 19．12 20．8三．解答题（共5小题）21．解：∵PA、PB分别与⊙O相切于点A、B，⊙O的切线EF分别交PA、PB于点E、F，切点C在弧AB上，∴AE=CE，FB=CF，PA=PB=12，∴△PEF的周长=PE+EF+PF=PA+PB=24．22．解：（1）∵PA，PB是⊙O的切线，∴AP=BP，∵∠P=60°，∴∠PAB=60°，∵AC是⊙O的直径，∴∠PAC=90°，∴∠BAC=90°﹣60°=30°．（2）连接OP，则在Rt△AOP中，OA=2，∠APO=30°，∴OP=4，由勾股定理得：，∵AP=BP，∠APB=60°，∴△APB是等边三角形，∴．23．（1）证明：连接CD，由AC是直径知CD⊥AB；DE、CE都是切线，所以DE=CE，∠EDC=∠ECD；又∠B+∠ECD=90°，∠BDE+∠EDC=90°；所以∠B=∠BDE，所以BE=DE，从而BE=CE；（2）解：连接OD，当以O、D、E、C为顶点的四边形是正方形时，DE=EC=OC=OD=r；从而BE=r，即△ABC是一个等腰直角三角形；AC=AB=2r，S△ABC=2r2；（3）解：若EC=4，BD=4，则BC=8；在Rt△BDC中，cos∠CBD==；所以∠CBD=30°；在Rt△ABC中，=tan30°，即AC=BCtan30°=8×=，OC==；另解：设OC=r，AD=x；由EC=4，BD=4得BC=8，DC=4；则：，解得；即OC=．（23题图）（24题图）（25题图）24．解：连接PO与AO，∵PA、PB切⊙O于A、B，若∠APB=60°，∴OA⊥PA，∠APO=∠APB=30°，∴∠AOP=60°，∵⊙O半径为3，∴OA=3，PO=6，∴PA==3，∴S△PAO=AO•PA=×3×3=，S扇形AOC==π，∴S阴影=2×（S△PAO﹣S扇形AOC）=2×（﹣π）=9﹣3π．∴阴影部分面积为：9﹣3π．25．解：①过点D作DF⊥BC于点F，∵AB为⊙O的直径，∠A=∠B=90°，∴四边形ABFD是矩形，AD与BC是⊙O的切线，∴DF=AB=2，BF=AD=2，∵DE与⊙O相切，∴DE=AD=2，CE=BC，设BC=x，则CF=BC﹣BF=x﹣2，DC=DE+CE=2+x，在Rt△DCF中，DC2=CF2+DF2，即（2+x）2=（x﹣2）2+（2）2，解得：x=，即BC=；②∵AB为⊙O的直径，∠A=∠B=90°，∴AD∥BC，∴△ADE∽△GCE，∴AD：CG=DE：CE，AE：EG=AD：CG，∵AD=DE=2，∴CG=CE=BC=，∴BG=BC+CG=5，∴AE：EG=4：5，在Rt△ABG中，AG==3，∴EG=AG=．。

【优选整合】浙教版九年级下册数学22切线长定理测试.doc

2.2切线长定理过圆外一点，对以引圆的两条切线，切线长如图，点P 是OO 外一点，PA, PB 切O0于点A, B, AB 交P0于点C,则有如下结论：(])FA = PB ； (2)ZAP0= ZBPO= ZOAC= ZOBC, ZAOP= ,BOP= ZCAP= ZCBP ； (3)AB 丄OP 且 AC=BC.耳课时训练 0A 组基础训练1.如图，从圆O 外一点P 引。

O 的两条切线PA, PB,切点分别为A, B,如果ZAPB = 60° , PA=8,那么弦AB 的长是()如图，PA 切OO 于A, PB 切OO 于B, OP 交OO 于C,下列结论中，错误的是()A. B.82. C. 第1题图A. Z1 = Z2B. PA=PB3. 如图，一圆内切四边形ABCD,且AB = 16, CD=10,A・50 B. 52 C. 54 D.56则四边形的周长为()第3题图点，连结BD, AD •若ZACD=30° ,则ZDBA 的大小是（）如图，CA, CD 分别切圆O 于A, D 两点，CB 、CE 分别切圆Ch 于B, E 两点，若Zl=60°, Z ,判断AB 、CD 、CE 的长度，下列关系何者正确（）的边长依次为3, 4, 5,则的半径是 ________________7. 如图，EB 、EC 是。

0的两条切线，B 、C 是切点，A 、D 是上两点，如果ZE=46° , ZDCF= 32° ,则ZA 的度数是 __________ ° •8. 如图，过OO 外一点P 作OO 的两条切线PA, PB,切点分别为A, B.下列结论中：①0P 垂直平分 AB ；②ZAPB = ZBOP ； ©AACP^ABCP ；④PA = AB ；⑤若ZAPB = 80° ,则ZOBA = 40° •正确的是15°B. 30° 5. 2=65°C. 6. AB>CE>CDAB>CD>CE 如图，（DO 与AABC 中AB 、第7题图 ,ZA, ZB, ZC 所对B. AB=CE>CD9.如图，AB为半圆0的直径，在AB的同侧作AC, BD切半圆O于点A, B, CD切半圆O于点E. 请分别写出一对相等的角，一对相等的线段和一对相似三角形.10.如图，PA, PB, DE分别切于点A, B, C,⑴若PA=30,求APDE的周长;(2)若ZP=50°,求ZO的度数.D在PA上，E在PB上. 第9题图第10题图11.如图，直尺、三角尺都和OO相切，B是切点，且AB = 8cm求。