匀变速直线运动的位移与时间的关系公式
2.3 匀变速直线运动的位移与时间的关系

2.3 匀变速直线运动的位移与时间的关系
2021.09.16
学习目标
1、能利用v-t图像得出匀变速直线运动的位移与时间关系式 = 0 +
1
2 ,进一步体会利用物理图像分析物体运动规律的研究方法。
2
2、能推导出匀变速直线运动的速度与位移关系式 2 − 02 = 2,体
(2)飞机在航母上降落时,需用阻拦索使飞机迅速停下来。若某次
飞机着舰时的速度为 80 m/s,飞机钩住阻拦索后经过 2.5 s 停下来。将这
段运动视为匀减速直线运动,此过程中飞机加速度的大小及滑行的距离各
是多少?
上面这种分析问题的方法具有一般意义,原则上对于处理
拓
展 任意形状的 v-t 图像都适用。对于图 所示的运动物体的位移,
1
2 ,是一个二次函数。
2
2、公式的适用条件:只适用于匀变速直线运动。
3、公式的矢量性:
0 、 、 均为矢量,应用公式解决问题时,应先选取正方
向。一般以0 的方向为正方向,若物体做匀加速运动,a取正值,
若物体做匀减速运动,则a取负值。
4、公式的特殊情况:
1 2
(1)如果v0=0,则x= at ,物体做初速度为0的匀加速直线运动。
刚好减为0。
【特别提醒】如果在所研究的问题中,已知量和未知
量都不涉及时间,利用这个公式求解,往往会更简便。
【例题2】动车铁轨旁两相邻里程碑之间的距离是1km。某同学乘坐
动车时,通过观察里程碑和车厢内电子屏上显示的动车速度来估算动车
减速进站时的加速度大小。当他身边的窗户经过某一里程碑时,屏幕显
示的动车速度是126km/h。动车又前进了 3 个里程碑时,速度变为 54
匀变速直线运动中位移与时间的关系

匀变速直线运动中位移与时间的关系一、匀速直线运动的位移时间关系1、匀速直线运动的速度始终保持不变,所以 vt x =2、从v-t 图像看位移匀变速直线运动的速度时间图像是一条平行于时间轴的直线即 v观察v-t 图像发现面积刚好就是 0v 位移,其中0v 是高,t 是底。
o t t 面积 位移二、匀变速直线运动的位移时间关系问题:匀速直线运动中位移大小可以用v-t 图像与坐标轴位的面积表示。
这个结论能否用于匀变速直线运动呢?1、我们知道对于变速运动的描述,最初使用的是平均速度即tx v ∆∆= ① 我们由①式出发稍微做一个变形就可以得到t v x ∆=∆ ② 2、我们来看一下匀变速直线运动的v-t 图像v0vo t我们观察图形会发现是一个梯形,所以我们不能用底乘以高即0v t 表示示其面积,那为什么就不行呢?因为这个图像中我们可以看出来从0到t 时刻存在一个很大的速度变化量即v ∆。
若从梯形中间做一条线,将其一分为二,我们在观察,还是不想矩形,但是会发现看其中一半是v ∆变小了,如果我们一直这样分下去会发现对一个细长的小梯形来说v ∆ 0,也就是说这个细长的梯形就可以看做一个矩形了,那么我们就可以用他的面积来表示位移的大小了。
于是我们就将梯形划分成许多细长的小梯形,所有小梯形的面积之和就是这段时间内物体的位移大小,也是整个梯形的面积。
故我们可以用梯形的面积来代表晕变速直线运动的位移大小。
所以我们求位移就可以通过求解梯形的面积。
解梯形的面积高下底上底⨯+==2s x t v v x t ⨯+=20––––––③高中位线⨯==s xt v x t ⨯=2––––––④ 因为at v v t +=0,所以我们将③式做一个简单的变形会得到2021at t v x += 这就是匀变速直线运动中位移与时间的关系,即位移公式3.对比将 ④三式进行对比会发现202t tv v v v +== 即中间时刻的速度等于平均速度等于初末速度之和的一半例:汽车刹车前的速度0v =5m/s ,a=-0.42s m ,求(1)开始刹车后20s 内滑行的距离?(2)汽车从刹车开始,位移x=30m 所用的时间?(3)在静止前2.5s 内滑行的距离?解:(1)错解:由2021at t v x +=可知x =5⨯202204.021⨯⨯-=20m 正解:法1:由a v at v v t 0t 0-v t =+=可知刹车制停的时间 又已知s m v /50= 2/4.0s m a -= 0=t v故t=12.5s 由于12.5<20,所以在t=12.5s 以后车就静止不动了。
匀变速直线运动的位移与时间的关系公式

匀变速直线运动的位移与时间的关系公式
匀变速直线运动的位移与时间的关系公式可以由运动学公式推导得到,具体分为两种情况:
1. 匀速直线运动的位移与时间的关系公式:
位移 = 速度 ×时间
其中,位移表示物体在运动过程中从起点到终点的距离,速度表示物体的运动速度,时间表示运动的时间长度。
2. 变速直线运动的位移与时间的关系公式:
位移 = 初速度 ×时间 + 0.5 ×加速度 ×时间²
其中,初速度表示运动开始时的速度,加速度表示运动过程中的加速度。
这个公式描述了的位移与时间的关系可以用来计算变速直线运动下物体在不同时间点的位置。
注意,这个公式的适用条件是运动过程中加速度是一个常量。
另外还有一种特殊情况,匀变速直线运动中,如果物体的位移与时间的关系符合二次函数的形式,可以使用二次函数公式来描述位移与时间的关系。
例如:位移 = a ×时间² + b ×时间 + c,其中a、b和c是常数。
初中物理 匀变速直线运动的位移与时间的关系

2、本节采用的探究方法——
理论探究法
(四)、证实猜想
物体作匀变速直线运动时,在V—t图象中图线 所围的梯形面积可以精确表示位移的大小
匀变速直线位移公式:
x = v0 t + 2—1 a t 2
匀
变 二.匀变速直线运动的位移
速 直 线 运
1.位移公式: x = v0 t + 2—1 a t 2
2.对位移公式的理解:
动 ⑴反映了位移随时间的变化规律。
=360m
对比计算值与图象所围面积
近似值与精确值相差 Δx3=375m-360m
=15m 相对误差= 4%
2、计算结果分析 (1)、将时间3等分:相对误差= 20%; (2)、将时间5等分:相对误差=12%; (3)、将时间15等分:相对误差=4%.
VOtFra bibliotek3、归纳总结:
将时间t等分的份数越多,时 间间隔Δt就越小,在Δt内速度的变 化就越小, 物体在Δt内的运动就 越接近匀速直线运动,用匀速运动 替代匀变速运动就越精确,同时图 象所围的阶梯形面积就越逼近梯形。 这种方法叫微元法
=300m
对比计算值与图象所围面积
V
近似值与精确值相差 Δx1=375m-300m
=75m 相对误差=20%
O
t
(2)、将时间(t=15s) 5等分,运用已知的规律 分别算出t=3s、6s、9s、 12s、15s时刻的速度, 将每一个时间间隔 ( Δt=3s )内物体的运 动近似作为匀速直线运 动来处理,得到15s内位 移的近似值;
(1)、将时间(t=15s)3等分,运用已知的 规律分别算出t=5s、10s、15s各时刻的速度, 将每一个时间间隔(Δt=5s)内物体的运动近 似作为匀速直线运动来处理,得到15s内位 移的近似值;
高一物理匀变速直线运动的位移与时间的关系

一、匀速直线运动的位移
匀速直线运动,物体的位移对应着v-t图 像中的一块矩形的面积。
二、匀变速直线运动的位移
1、 匀变速直线运动,物体的位移对 应着v-t图像中图线与时间轴之间包围 公式 v=(v0+v)/2
课堂训练
1、一辆汽车以1m/s2的加速度加速行驶了 12s,驶过了180m,求汽车开始加速时的 速度是多少? 9m/s 2、骑自行车的人以5m/s的初速度匀减速上 一个斜坡,加速度的大小为0.4m/s2,斜坡 长30m,骑自行车的人通过斜坡需要多少 时间? 10s
3、以10m/s的速度匀速行驶的汽车刹车后 做匀减速运动。若汽车刹车后第2s内的 位移为6.25m(刹车时间超过2s),则 刹车后6s内汽车的位移是多大? a=-2.5m/s2 20m 4、以10m/s的速度行驶的汽车关闭油门后 后做匀减速运动,经过6s停下来,求汽 车刹车后的位移大小。 30m
小结
一、匀速直线运动的位移 1、匀速直线运动,物体的位移对应着v-t图像中 的一块矩形的面积。 2、公式:S = v t 二、匀变速直线运动的位移与时间的关系 1、 匀变速直线运动,物体的位移对应着v- t图 像 中图线与时间轴之间包围的梯形面积。 2、公式 3、平均速度公式
v=(v0+v)/2
[课堂探究]
三、匀变速直线运动的位移与 速度的关系
v2 - v02 = 2 a s
匀变速直线运动公式
1、速度公式 v = v0 + at
2、位移公式 S = v0 t+1/2 at2 3、推论
v2 - v02 = 2 a s
4、平均速度公式 v=(v0+v)/ 2
课堂训练
1、射击时,火药在枪筒里燃烧。燃气膨胀, 推动弹头加速运动。我们把子弹在枪筒里 的运动看做是匀加速直线运动,假设子弹 的加速度是a=5×105m/s,枪筒长 x= 0.64m,我们计算子弹射出枪口时的速度。
匀变速直线运动的位移与时间的关系
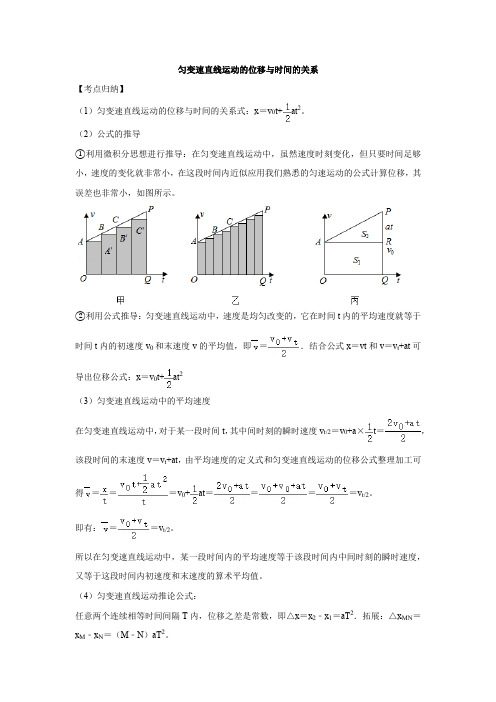
匀变速直线运动的位移与时间的关系【考点归纳】(1)匀变速直线运动的位移与时间的关系式:x=v0t+at2。
(2)公式的推导①利用微积分思想进行推导:在匀变速直线运动中,虽然速度时刻变化,但只要时间足够小,速度的变化就非常小,在这段时间内近似应用我们熟悉的匀速运动的公式计算位移,其误差也非常小,如图所示。
②利用公式推导:匀变速直线运动中,速度是均匀改变的,它在时间t内的平均速度就等于时间t内的初速度v0和末速度v的平均值,即=.结合公式x=vt和v=v t+at可导出位移公式:x=v0t+at2(3)匀变速直线运动中的平均速度在匀变速直线运动中,对于某一段时间t,其中间时刻的瞬时速度v t/2=v0+a×t=,该段时间的末速度v=v t+at,由平均速度的定义式和匀变速直线运动的位移公式整理加工可得===v0+at====v t/2。
即有:==v t/2。
所以在匀变速直线运动中,某一段时间内的平均速度等于该段时间内中间时刻的瞬时速度,又等于这段时间内初速度和末速度的算术平均值。
(4)匀变速直线运动推论公式:任意两个连续相等时间间隔T内,位移之差是常数,即△x=x2﹣x1=aT2.拓展:△x MN=x M﹣x N=(M﹣N)aT2。
推导:如图所示,x1、x2为连续相等的时间T内的位移,加速度为a。
【命题方向】例1:对基本公式的理解汽车在平直的公路上以30m/s的速度行驶,当汽车遇到交通事故时就以7.5m/s2的加速度刹车,刹车2s内和6s内的位移之比()A.1:1B.5:9C.5:8D.3:4分析:求出汽车刹车到停止所需的时间,汽车刹车停止后不再运动,然后根据位移时间公式求出2s内和6s内的位移。
解:汽车刹车到停止所需的时间>2s所以刹车2s内的位移=45m。
t0<6s,所以刹车在6s内的位移等于在4s内的位移。
=60m。
所以刹车2s内和6s内的位移之比为3:4.故D正确,A、B、C错误。
匀变速直线运动的位移与时间的关系

笔记
知识回顾 匀变速直线运动的速度与时间的关系
v=v0 + at
注意事项: 1、默认情况是以初速度方向为正方向。 2、如果是减速运动,则a取负值
笔记 一、匀速直线运动的位移
笔记 1、公式法
笔记 笔记 笔记
做匀速直线运动的物体在时间t 内的位移:
x= vt
v
作业与检测 第73页
设刹车过程的时间为t2,由速度公式有: v=v0+at2
得:t2
v
v0 a
0 30 S 5
6S
由位移公式:x2 v0t2
30 6m
1
1 2
at22
(-5)
62m
2
90m
应保持的车距为:x=x1+x2 =15m+90m=105m
补充例解:新课程导学 第20页
4.如图所示是一个物体沿直线运动的图象.求: (1)第5秒末的速度大小; (2)0-60S内的总路程; (3)在v-t坐标中作出0-60S内物体的速度-
解:(3)0-10S的速度为:v1=2m/s
10S-40S内速度为:v2=0 40S-60S内速度为:
v/(m/s)
4 x/m
3
v3
x t
0 20 60 40
m
/
s
-1m
/
s
2 1 0
-1
20 40 60 t/s
速度图象如图所示:
-2 -3
-4
(2)选向东为正方向
初速度:v0 =10m/s 加速度:a=-5m/s2 (减速)
时间:t=5 s
位移:x=?。
由位移公式:
x
v0t
匀变速直线运动位移与时间的关系

)
【解析】
子弹运动的逆过程可看成初速度为零、末速度为 v 的匀加速
直线运动,子弹通过连续相等位移的时间之比为 1∶( 2-1)∶( 3- 2).则 子弹实际运动通过连续相等位移的时间之比为 t1∶t2∶t3= ( 3- 2)∶( 2 - 1)∶1,故 D 正确. 1 由 x= at2 知,子弹运动的逆过程由右向左穿过第 1 块、前 2 块、前 3 块 2 的时间之比 t1∶t2∶t3=1∶ 2∶ 3,再根据 v=at 知,子弹由右向左依次“穿 出”3 个木块的速度之比为 1∶ 2∶ 3.则子弹实际运动依次穿入每个木块时 的速度之比 v1∶v2∶v 3= 3∶ 2∶1,故 B 正确.
1 2 由位移公式: x v0t at 2
又由速度公式: 可得:
2
v=v0+at
2 0
v v 2ax
对公式vt2-v0=2ax的理解与应用 1.该公式仅适用于匀变速直线运动. 2.公式中四个矢量v0、vt、a、x要规定统一的正方 向. 3.当v0=0时,公式简化为vt2=2ax;当vt=0时,公 式简化为-v02=2ax. 4.在分析和解决不需要知道运动时间的问题时,使 用vt2-v02=2ax往往会使问题变得简单、方便.
起第1个T内,第2个T内,第3个T内……的位移之比为
xⅠ∶xⅡ∶xⅢ∶……=1∶3∶5∶……,所以,所求位移之
比为1∶(3+5)∶(7+9+11)∶……=13∶23∶33∶……,D
对.
【答案】 D
4.如右图所示,在水平面上固定着三个完全相同的木
匀变速直线运动的位移与时间的关系 课件

四、刹车类问题
v0=72 km/h=20 m/s
例4:一辆汽车正在平直的公路上以72 km/h的速度行驶,司机
看见红色信号灯便立即踩下制动器,此后,汽车开始做匀减速
直线运动.设汽车减速过程的加速度大小为5 m/s2,求:
(1)开始制动后,前2 s内汽车行驶的距离. 注意:判断 (2)开始制动后,前5 s内汽车行驶的距离. 经过多久停下来!
0~5 s:匀加速运动 5 s~15 s:匀速运动 15 s~20 s:匀减速运动 20 s~25 s:反向的匀加速运动
解析 最大高度为题图中t 轴上方梯形
的面积:S1= 600 m.
开始回头
图象在t 轴上方:位移为正 图象在t 轴下方:位移为负
25 s时直升机所在高度为S1与面积S△CED的差: S2= S1-S△CED= (600-100) m= 500 m.
直线运动.设汽车减速过程的加速度大小为5 m/s2,求:
(1)开始制动后,前2 s内汽车行驶的距离. 注意:判断 (2)开始制动后,前5 s内汽车行驶的距离. 经过多久停下来!
解析
汽车运动的总时间 t v v0 0 20m/s 4s
a
5m/s2
(1)因为t1= 2 s < t,所以汽车2 s 末没有停止运动
匀变速直线运动的位移与时间的关系
一、匀速直线运动的位移
1.位移公式:vt 2.由v-t 图象求位移:矩形的面积
二、匀变速直线运动的位移
1.位移在v-t 图象中的表示: t 轴
2.位移与时间的关系:
x=v0t+at2/2
x=at2/2
面积
一. 用v-t 图象求位移 【问题设计】 某物体以5 m/s 的速度做匀速直线运动,求物体在8 s内的位移. 画出物体运动的v-t 图象. 物体的位移用v-t 图象能反映出来吗?
匀变速直线运动位移与时间的关系

• 变式训练3 火车沿平直铁轨匀加速前进, 通过一路标时的速度为10.8km/h,1min后变 成54km/h,又需经一段时间,火车的速度 才能达到64.8km/h.求所述过程中,火车的 位移是多少?
推论二
2.逐差相等:在任意两个连续相等的时间间隔 T 内,位移之差是一个常量,即 Δx=xⅡ-xⅠ=aT2 推导:时间 T 内的位移 x1=v0T+12aT2① 在时间 2T 内的位移 x2=v02T+21a(2T)2② 则 xⅠ=x1,xⅡ=x2-x1③ 由①②③得 Δx=xⅡ-xⅠ=aT2 此推论常有两方面的应用:一是用以判断物体是
( AC ) A.0~2 s 内的加速度为 1 m/s2 B.0~5 s 内的位移为 10 m C.第 1 s 末与第 3 s 末的速度方向相同
D.第 1 s 末与第 5 s 末加速度方向相同
5.一小球沿斜面由静止开始匀加速滚下(斜面 足够长),已知小球在第4 s末的速度为4 m/s.求: (1)第6 s末的速度; (2)前6 s内的位移; (3)第6 s内的位移.
• 变式训练2 某物体做直线运动的v-t图象 如图所示,通过图象回答下列问题:
• (1)物体在OA、AB、BC阶段各做什么运动, 加速度为多大?
• (2)物体在2s末和7s末的即时速度为多大?
• (3)物体的最大位移是多少?全过程的位移 为多少?全过程的路程是多少?第7s内的 位移是多少?
在匀变速直线运动中,对于某一段时间 t,其中间时
【答案】 BCD
对速度图象的意义理解不透,导致错误出现
如右图所示为甲、乙两物体运动 的 v-t 图象,由图象可知( AD ) A.甲做匀变速直线运动,乙做 匀速直线运动 B.甲、乙两物体在 t=0 时刻的 位置不一样 C.甲、乙两物体在 t=2 s 时相遇 D.前 4 s 内甲、乙两物体的位移大小相等
匀变速直线运动的位移与时间关系的推导

0
先微分再求总和的方法----微元法
结论
匀变速直线运动的 v-t 图象与时间轴所 围的面积表示位移。
课堂讲义
匀变速直线运动的位移与时间的关系
一、匀变速直线运动的位移公式及有关计算 1 2 1 .位移时间公式x=v0t+ at 的推导
如图所示,在匀变速直线运动中运用“无限分割、逐 步逼近”的微分思想可得 v - t 图象与时间轴所围成的 “面积”表示位移. 无限分割 迁移 再分割 v 逐渐逼近
温馨提示:请画出运动草图然后求解
2
0
速度图线和时间轴所包围的梯形面积为 1 与之对应的物体的位移 x = ( v0 +v)t 2 由速度公式v=v0+at
1 S = (OC +AB ) OA 2
t/s
1 2 x =v0t + at 2
科学 方法
⊿t 内是简单的匀速直线运动---- 化简
分割许多很小的时间间隔⊿t---- 微分 “无限逼近”的思维方法----极限思想 先微分再求总和的方法----微元法
匀变速直线运动的位移与时间关系的推导
一、匀变速直线运动的位移公式及有关计算 1 2 1 .位移时间公式x=v0t+ at 的推导
如图所示,在匀变速直线运动中运用“无限分割、逐 步逼近”的微分思想可得 v - t 图象与时间轴所围成的 “面积”表示位移. 无限分割 迁移 再分割 v 逐渐逼近
2
0
t/s
探究小结----图象分析1
v/m/s
v/m/s
18
18 14
14
10
0 v/m/s
x=48m
2 4
10
t/s 0
x=52m
1 2 3 4
匀变速直线运动的位移与时间的关系

匀变速直线运动的位移与时间的关系本讲要点:1、知道匀速直线运动的位移与时间的关系, 通过近似推导位移公式的过程,体验微元法的特点和技巧,能把瞬时速度的求法与此比较;2、理解匀变速直线运动的位移与时间的关系及其应用;3、理解v-t图象中图线与t轴所夹的面积表示物体在这段时间内运动的位移. 同步课堂:一、匀变速直线运动的平均速度V=v0+v/2注意:此公式仅适用于匀变速直线运动二、位移与时间的关系式X=V0t+at2/2说明:以V0为正方向,特体做匀加速运动,a与V0同向,a取正,物体做匀减速运动,a与V0反向,a取负。
特例:假设V0为零,那么X=at2/2三、位移和速度的关系v2-v02=2ax特例:假设V0为零,那么v2 =2ax二、重点难点:1、理解匀变速直线运动位移公式(a) (b) (c)1、用许多小段的匀速运动来模拟匀变速直线运动运动的时间分得越强,很小段的匀速运动越多,速度跳跃的幅度越小,这种模拟的运动更接近均匀变化的变速运动,同时,众多的小矩形面积之和更接近梯形的面积。
当运动的时间分得非常非常细,相邻匀速运动之间的跳跃中高度非常非常小,很多很多的小矩形面积就能准确地代表特体的位移,这时“很多很多〞小矩形顶端的“锯齿形〞就看不出来了,这时小矩形合在一起就成了一个梯形。
2、匀变速直线运动的位移——图象和t轴所围的梯形的面积v/(ms-1)t/sx =12(V 0+V t )·t(1) ——位移方程从(1)式可知,由x =v ·t ,02tV V v (2) 匀变速直线运动平均速度公式又由V =V 0+at(3) ——速度方程 x =V 0t +12at 2(4) ——位移方程又由(3)、(4)消去t ,V 2-V 02=2ax(5) ——位移和速度关系方程上述(1)、(3)、(4)、(5)四个方程均为矢量方程,每个方程均牵涉到四个物理量,在每个方程中,当知道其它三个量时,就可以求出第4个物理量,不过由于四个方程均可由其它两个方程导出,所以在一个过程中仅能解出两个未知数。
2-3 匀变速直线运动位移与时间的关系(刘)

二、匀变速直线运动的位移
结论:对于匀变速 结论: 直线运动,物体的位移 直线运动,物体的位移 也对应着 v-t 图象中图 线与时间轴所围的图形 线与时间轴所围的图形 面积” “面积”。
v
v v4 v3 v2 v1 v0 O t1 t2 t3 t4 t
t
1 则有: 则有: = (v0 + v)t − − − (1) 又 v = v0 + at - - - (2) x 2
∆x = aT
2
一个滑块沿斜面滑下,依次通过斜面上的 、 、 一个滑块沿斜面滑下,依次通过斜面上的A、B、 C三点,如图示,已知 三点, 三点 如图示,已知AB=6m,BC=10m,滑块经 , , 两段位移的时间都是2s 过AB、BC两段位移的时间都是 ,求:⑴ 滑块 、 两段位移的时间都是 运动的加速度; 滑块在A、 点的瞬时速度 运动的加速度; ⑵ 滑块在 、C点的瞬时速度 解:由匀变速直线运动的推论
v 0 +v v = vt = 2 2
1、汽车以l0m/s速度在平直公路上匀速行驶, 汽车以l0m/s速度在平直公路上匀速行驶 速度在平直公路上匀速行驶, 刹车后做匀减速运动,经2s速度为6m/s。求: 速度为6m/s。 刹车后做匀减速运动, 2s速度为 ⑴刹车后2s内前进的距离; 刹车后2s内前进的距离; 内前进的距离 ⑵ 刹车后8s内前进的距离。 刹车后8s内前进的距离 内前进的距离。
例题: 例题:一辆汽车以 1m/s2 的加速度加速行驶 12s, 180m, 了12s,驶过了 180m,汽车开始加速时的速 度为多少? 度为多少?
解:以初速度方向为正方向, 初速度方向为正方向 a = 1 m/s2 , x = 180 m, 根据 x = v0 t + at2/2, 得 t = 12 s ,
匀变速直线运动的位移与时间关系的推导

课堂讲义
匀变速直线运动的位移与时间的关系
一、匀变速直线运动的位移公式及有关计算
1 .位移时间公式x=v0t+
1 2
at2的推导
如图所示,在匀变速直线运动中运用“无限分割、逐
步逼近”的微分思想可得v-t图象与时间轴所围成的
“面积”表迁示移位移. 再分割
无限分割
先微分再求总和的方法----微元法
温馨提示:请画出运动草图然后求解
v/m/s
v/m/s
18
18
14
14
10
x=48m
10
x=52m
0 v/m/s
18 14 10
0
2
4
t/s 0 1 2
3
4
t/s
结论 ⊿t 越小,就是用
更多的但是更窄的小
x=54m
矩形面积代表物体的
位移!
t/s
v/m/s
18 14 10
v/m/s
18 14 10
01
2
3
4
t/s0
1
2
3
4
t/s
v/m/s
匀变速直线运动的位移与时间关系的推导
一、匀变速直线运动的位移公式及有关计算
1 .位移时间公式x=v0t+
1 2
at2的推导
如图所示,在匀变速直线运动中运用“无限分割、逐
步逼近”的微分思想可得v-t图象与时间轴所围成的
“面积”表迁示移位移. 再分割
无限分割-图象分析1
结论
18
⊿t 趋近零(“无限逼
14
近”的思维方法----极限思
想),无数个小矩形合在一
10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
匀变速直线运动的位移与时间的关系公式
1. 匀变速直线运动是指物体在一条直线上以恒定的加速度运动。
位移与时间的关系可以用公式来描述,该公式为:s = ut + (1/2)at^2,其中s表示位移,u 表示初速度,t表示时间,a表示加速度。
2. 公式中的第一项ut代表匀速直线运动的位移,即物体在没有加速度的情况下,根据初速度和时间的乘积计算得出的位移。
这是因为在匀速直线运动中,速度保持不变,位移与速度和时间的乘积成正比。
3. 公式中的第二项(1/2)at^2表示加速度对位移的影响。
加速度是速度的变化率,即速度每秒变化的大小。
当物体受到加速度的作用时,速度会随时间的推移而改变,从而导致位移的增加。
这一项表示加速度对位移的贡献,通过加速度和时间的平方的乘积来计算。
4. 公式的推导基于物体在匀变速直线运动过程中的运动规律。
根据牛顿第二定律,物体所受的合力等于质量乘以加速度。
在匀变速直线运动中,物体所受的合力是恒定的,所以加速度也是恒定的。
5. 利用物体运动的三个基本公式:v = u + at,s = ut + (1/2)at^2,v^2 = u^2 + 2as,其中v表示末速度,u表示初速度,s表示位移,t表示时间,a表示加速度。
可以推导出位移与时间的关系公式。
6. 通过将末速度v代入第一个公式,得到v = u + at,可以解出时间的表达式t = (v - u) / a。
7. 将时间t代入第二个公式s = ut + (1/2)at^2中,得到s = u((v - u) / a) + (1/2)a((v - u) / a)^2,化简得到s = (u(v - u) + (1/2)a(v - u)^2) / a。
8. 进一步化简得到位移与时间的关系公式s = (2u(v - u) + a(v - u)^2) / (2a),这就是匀变速直线运动的位移与时间的关系公式。
9. 该公式表示了位移与时间之间的关系,其中包含了初速度、末速度和加速度的影响。
当初速度、末速度和加速度为正值时,位移随时间的增加而增加;当初速度、末速度和加速度为负值时,位移随时间的增加而减小。
10. 通过该公式,我们可以计算匀变速直线运动中任意时间点的位移。
只需知道初速度、末速度和加速度的数值,以及经过的时间,就可以利用这个公式进行计算。
总结起来,匀变速直线运动的位移与时间的关系公式是s = (2u(v - u) + a(v - u)^2) / (2a)。
这个公式描述了物体在匀变速直线运动过程中的位移与时间的关系,通过初速度、末速度和加速度来计算位移。
