第5章 均匀平面波
电磁场与电磁波期末复习知识点归纳

哈密顿算子:矢量微分算子( Hamilton、nabla、del )
ex
x
ey
y
ez
z
★ 标量场的梯度
gradu u u xˆ u yˆ u zˆ ( xˆ yˆ zˆ)u x y z x y z
★ 矢量场的散度计算公式:
divA= • A Ax Ay Az x y z
1
2=∞ nˆ • D1 s
nˆ E1 0 nˆ B1 0
nˆ H1 Js
2、理想介质表面上 的边界条件
1=0
2=0
nˆ • (D1 D2) 0 nˆ (E1 E2 ) 0
nˆ B1 B2 0
nˆ H1 H2 0
第三章 静态电磁场及其边值问题的解
静电场中: E 0
圆柱坐标和球坐标的公式了解:
Bx By Bz
圆柱坐标系中的体积微元: dV=(d)(d)(dz)= d d dz
分析的问题具有圆柱对称性时可表示为:dV=2ddz
球坐标系中的体积微元: dV=(rsind)(rd)(dr)
分析的问题具有球对称性 时可表示为:
=r2sindrdd dV=4r2dr
★ 标量场的等值面方程 u x, y, z 常数C
程的解都是唯一的。这就是边值问题的唯一性定理
◇ 唯一性定理的意义:是间接求解边值问题的理论依据。
● 镜像法求解电位问题的理论依据是“唯一性定理”。
点电荷对无限大接地导体平面的镜像
z
r1
P
q h
r r2 介质
x
h
介质
q
点电荷对接地导体球面的镜像。
P
r
a
r2
o θ q
d
’d
第五讲 平面波

= ηHr
× erz
r A
⋅
(
r B
×
r C)
=
r B
⋅
r (C
×
r A)
=
r C
⋅(
r A
×
r B)
( ) erz
erz
⋅ ⋅
r H r E
= =
erz erz
⋅ ⋅
⎜⎛⎝ηη1Hrer×z
×
r E
⎟⎞
erz
⎠ =
η=Hrerz⋅⋅(⎜⎛⎝erezrz××erηz1)
r E =
⎟⎞ ⎠ 0
=
1
η
r E
=
yˆ 1
η
E(z,t)
3. 本征阻抗(特征阻抗)
计算式 η = ωμ = ωμ = μ k ω με ε
单位:欧姆(Ω)
η数值等于电场强度与对应磁场强度的振幅之比,并且仅决定于媒质的
电磁参数。
真空中 ④结论:
η0 =
μ0 = 120π ≈ 377 (Ω ) ε0
x
Ex = Emx cos(ω t − kz + ϕ x )
亥姆霍兹方程的解
结论
①亥姆霍兹方程的解代表正弦电磁波,进一步说,它们代表着等相位面(又
称波面)为平面的平面电磁波。如果将不同nˆ 的平面波进行叠加,还可以表
示等相位面为柱面或球面等其它形式的电磁波。
②从电场和磁场的叉积关系可以看出,电磁波的电场矢量、磁场矢量与波矢量
方向两两正交,且满足右手螺旋关系 Eˆ × Hˆ = kˆ。电场和磁场只有垂直于传播
在理想电介质中的波动方程解表示为
Ei (rv,t) = Ei m cos[ω
电磁场思考题

第一章1.什么是矢量场的通量?通量的值为正、负或0分别表示什么意义?解答:矢量场F 穿出闭合曲面S 的通量为:dS e F dS F sn s ⎰⎰==··ψ 当⎰>s dS F 0·时,表示穿出闭合曲面S 的通量多于进入的通量,此时闭合曲面内必有发出矢量线的源,成为正通量源。
当⎰<s dS F 0·时,表示穿出闭合曲面S 的通量少于进入的通量,此时闭合曲面内必有汇集矢量线的源,成为负通量源。
当⎰=sdS F 0·时,表示穿出闭合曲面S 的通量等于进入的通量,此时闭合曲面内正通量源与负通量源的代数和为0,或者闭合面内无通量源。
2.什么是散度定理?它的意义是什么?解答:矢量分析中的一个重要定理:⎰⎰⋅=⋅∇v sdS FdV F 称为散度(高斯)定理。
意义:矢量场F 的散度F ⋅∇在体积V 上的体积分等于矢量场F 在限定该体积的闭合面S 上的面积分,是矢量的散度的体积分与该矢量的闭合曲面积分之间的一个变换关系。
3.什么是矢量场的环流?环流的值为正、负或0分别表示什么意义?解答:矢量场F 沿场中的一条闭合回路C 的曲线积分,⎰⋅=Γc dl F ,称为矢量场F 沿闭合路径C 的环流。
⎰>⋅c dl F 0或⎰<⋅cdl F 0,表示场中有产生该矢量的源,称为漩涡源。
⎰=⋅cdl F 0,表示场中没有产生该矢量场的源。
4.什么是斯托克斯定理?它的意义是什么? 斯托克斯定理能用于闭合曲面吗?解答:在矢量场F 所在的空间中,对于任一以曲线C 为周界的曲面S ,存在如下重要关系式: ⎰⎰⋅=⋅⨯∇s cdl F dS F ,称为斯托克斯定理。
意义:矢量场F 的旋度F ⨯∇在曲面S 上的面积分等于矢量场F 在限定曲面的闭合曲线C 上的线积分,是矢量旋度的曲面积分与该矢量沿闭合曲线积分之间的一个变换关系。
能用于闭合曲面。
5.无旋场和无散场的区别是什么?解答:无旋场F 的旋度处处为0,即0≡⨯∇F ,它是由散度源所产生的,它总可以表示为某一标量场的梯度,即()0=∇⨯∇u 。
电磁场与电磁波(第4版)教学指导书 第5章 平面电磁波

第5章 平面电磁波5.1基本内容概述本章讨论均匀平面波在无界空间传播的特性,主要内容为:均匀平面波在无界的理想介质中的传播特性和导电媒质中的传播特性,电磁波的极化,均匀平面波在各向异性媒质中的传播、相速与群速。
5.1.1理想介质中的均匀平面波1.均匀平面波函数在正弦稳态的情况下,线性、各向同性的均匀媒质中的无源区域的波动方程为220k ∇+=E E对于沿z 轴方向传播的均匀平面波,E 仅是z 坐标的函数。
若取电场E 的方向为x 轴,即x x E =E e ,则波动方程简化为222d 0d x x E k E z+= 沿+z 轴方向传播的正向行波为()j jkz x m z E e e φ-=E e (5.1)与之相伴的磁场强度复矢量为()()z kz z ωμ=⨯H e E 1j jkz ym E e e φη-=e (5.2)电场强度和磁场强度的瞬时值形式分别为(,)Re[()]cos()j t x m z t z e E t kz ωωφ==-+E E e (5.3)(,)Re[()]cos()j t m y Ez t z e t kz ωωφη==-+H H e (5.4)2.均匀平面波的传播参数 (1)周期2T πω=(s),表示时间相位相差2π的时间间隔。
(2)相位常数k =(rad/m ),表示波传播单位距离的相位变化。
(3)波长kπλ2=(m ),表示空间相位相差2π的两等相位面之间的距离。
(4)相速p v kω==m/s ),表示等相位面的移动速度。
(5)波阻抗(本征阻抗)x y E H η==Ω),描述均匀平面波的电场和磁场之间的大小及相位关系。
在真空中,37712000≈===πεμηη(Ω) 3.能量密度与能流密度在理想介质中,均匀平面波的电场能量密度等于磁场能量密度,即221122εμ=E H电磁能量密度可表示为22221122e m w w w εμεμ=+=+==E H E H (5.5)瞬时坡印廷矢量为21zη=⨯=S E H e E (5.6)平均坡印廷矢量为211Re 22av z η*⎡⎤=⨯=⎣⎦S E H e E (5.7) 4.沿任意方向传播的平面波对于任意方向n e 传播的均匀平面波,定义波矢量为n x x y y z z k k k k ==++k e e e e (5.8)则00()n jk j --==e r k r E r E e E e (5.9)()()1n η=⨯H r e E r (5.10)00n =e E (5.11)5.1.2电磁波的极化1.极化的概念波的极化表征在空间给定点上电场强度矢量的取向随时间变化的特性, 并用电场强度矢量的端点在空间描绘出的轨迹来描述。
在自由空间传播的均匀平面电磁波

在自由空间传播的均匀平面电磁波(空间中没有自由电荷,没有传导电流),电场和磁场都没有和波传播方向平行的分量,都和传播方向垂直。
此时,电矢量E,磁矢量H和传播方向k两两垂直。
只是在这种情况下,才可以说电磁波是横波。
沿一定途径(比如说波导)传播的电磁波为导行电磁波。
根据麦克斯韦方程,导行电磁波在传播方向上一般是有E和H分量的。
光的传播形态分类:根据传播方向上有无电场分量或磁场分量,可分为如下三类,任何光都可以这三种波的合成形式表示出来。
1、TEM波:在传播方向上没有电场和磁场分量,称为横电磁波。
若激光在谐振腔中的传播方向为z方向,那么激光的电场和磁场将没有z方向的分量!实际的激光模式是准TEM模,即允许Ez、Hz分量的存在,但它们必须<<横向分量,因为较大的Ez意味着波矢方向偏离光轴较大,容易溢出腔外,所以损耗大,难于形成振荡。
2、TE波(即是物光里的s波):在传播方向上有磁场分量但无电场分量,称为横电波。
在平面光波导(封闭腔结构)中,电磁场分量有Ey, Hx, Hz,传播方向为z方向。
3、TM波(即是物光里的p波):在传播方向上有电场分量而无磁场分量,称为横磁波。
在平面光波导(封闭腔结构)中,电磁场分量有Hy, Ex, Ez,传播方向为z方向。
微波工程、电磁场理论等课程中有关于TEM、TE、TM模的更为详细的描述。
均匀平面波的电场与磁场相位相同

时间相位变化 2 所经历的时间称为电磁波的周期,以 T 表示,而 一秒内相位变化 2 的次数称为频率,以 f 表示。那么由 T 2 π 的关系 式,得 2π 1 T f
空间相位 kz 变化 2 所经过的距离称为波长,以 表示。那么由关 系式 k 2π,得 2π k 由上可见,电磁波的频率是描述相位随时间的变化特性,而波长描述相 位随空间的变化特性。 由上式又可得
因在给定的区域中, E 0, H 0 ,由上两式得
E z H z 0 z z
考虑到
2 Ez 2 Ez 2 Ez 2 Ez Ez 2 2 0 2 2 x y z z 2H z 2H z 2H z 2H z 2 Hz 0 2 2 2 2 x y z z
上式称为非齐次波动方程。
式中
J (r , t ) J (r , t ) E (r , t ),
其中J (r , t ) 是外源。电荷体密度 (r, t)与传导电流 (E ) 的关系为
(E ) t
若所讨论的区域中没有外源,即 J ' = 0 ,且媒质为理想介质, 即 = 0,此时传导电流为零,自然也不存在体分布的时变电荷,
Ex ( z) Ex0e jkz
式中Ex0 为 z = 0 处电场强度的有效值。
Ex(z) 对应的瞬时值为
Ez(z, t)
Ex ( z, t ) 2Ex0 sin( t kz)
电场强度随着时间 t 及空间 z 的 变化波形如图示。
可见,电磁波向正 z 方向传播。
O
2
t1 = 0 t 2
若所讨论的时变场为正弦电磁场,则上式变为
2 2 E (r ) k E (r ) 0 2 2 H (r ) k H (r ) 0
电磁场与电磁波(第4版)第5章 均匀平面波在无界空间中的传播

电磁场与电磁波第5章 均匀平面波在无界空间中的传播1C.Y.W@SDUWH2010电磁场与电磁波第5章 均匀平面波在无界空间中的传播2均匀平面波的概念 波阵面:空间相位相同的点构成的曲面,即等相位面 平面波:等相位面为无限大平面的电磁波 均匀平面波:电磁波的场矢量只沿着它的传播方向变化,等相 位面上电场和磁场的方向、振幅都保持不变的平面波。
均匀平面波是电磁波的一种理想 情况,其特性及分析方法简单,但又 表征了电磁波的重要特性。
实际应用中的各种复杂形式的电 磁波可看成是由许多均匀平面波叠加 的结果。
另外,在距离波源足够远的 地方,呈球面的波阵面上的一小部分 也可以近似看作均匀平面波。
C.Y.W@SDUWH 2010波阵面xE波传播方向o yzH均匀平面波电磁场与电磁波第5章 均匀平面波在无界空间中的传播3本章内容5.1 理想介质中的均匀平面波 5.2 电磁波的极化 5.3 均匀平面波在导电媒质中的传播 5.4 色散与群速 5.5 均匀平面波在各向异性媒质中的传播C.Y.W@SDUWH2010电磁场与电磁波第5章 均匀平面波在无界空间中的传播45.1 理想介质中的均匀平面波5.1.1 理想介质中的均匀平面波函数 5.1.2 理想介质中的均匀平面波的传播特点 5.1.3 沿任意方向传播的均匀平面波C.Y.W@SDUWH2010电磁场与电磁波第5章 均匀平面波在无界空间中的传播55.1.1 理想介质中的均匀平面波函数 设在无限大的无源空间中,充满线性、各向同性的均匀理想 介质。
均匀平面波沿 z 方向传播,则电场强度和磁场强度都不是 x 和 y 的函数,即∂E ∂E ∂H ∂H = =0, = =0 ∂x ∂y ∂x ∂yd2E d2H + k 2E = 0 , + k 2H = 0 dz 2 dz 2∂Ez =0 ∂zHz = 0∂Ex ∂E y ∂Ez + + =0 由于 ∇ ⋅ E = ∂x ∂y ∂zEz = 0∂ 2 Ez + k 2 Ez = 0 ∂z 2同理 ∇ ⋅ H =∂H x ∂H z + + =0 ∂x ∂y ∂z∂H y结论:均匀平面波的电场强度和磁场强度都垂直于波的传播 方向 —— 横电磁波(TEM波)C.Y.W@SDUWH 2010电磁场与电磁波第5章 均匀平面波在无界空间中的传播6在直角坐标系中:∇ 2 F = ex∇ 2 Fx + ey ∇ 2 Fy + ez ∇ 2 Fz 即 (∇2 F )i = ∇ 2 Fi(i = x, y, z )2 2教材第28页 式(1.7.5)2 2 如:(∇ F )φ ≠ ∇ Fφ注意:对于非直角分量, (∇2 F )i ≠ ∇2 Fi 由电场强度满足波动方程 ∇ E + k E = 0ex ∇ 2 Ex + ey ∇ 2 E y + ez ∇ 2 Ez + k 2 (ex Ex + ey E y + ez Ez ) = 0 即⎧∇ 2 Ex + k 2 Ex = 0 ⎪ 2 2 ⎨∇ E y + k E y = 0 ⎪ 2 ∇ Ez + k 2 Ez = 0 ⎩⎧ ∂ 2 Ex ∂ 2 Ex ∂ 2 Ex + + 2 + k 2 Ex = 0 ⎪ 2 2 ∂y ∂z ⎪ ∂x ⎪ ∂2 Ey ∂2 Ey ∂2 Ey ⎪ + + + k 2 Ey = 0 ⎨ 2 2 2 ∂y ∂z ⎪ ∂x ⎪ ∂2 E ∂2 E ∂2 E z + 2 z + k 2 Ez = 0 ⎪ 2z + ∂x ∂y 2 ∂z ⎪ ⎩2010C.Y.W@SDUWH电磁场与电磁波第5章 均匀平面波在无界空间中的传播7对于沿 z 方向传播的均匀平面波,电场强度 E 和磁场强度 H 的分量 Ex 、Ey 和 H x 、H y 满足标量亥姆霍兹方程,即d 2 Ex + k 2 Ex = 0 dz 2 d2Ey + k 2Ey = 0 dz 2 2 d Hx + k 2H x = 0 dz 2 d2H y + k 2H y = 0 dz 2以上四个方程都是二阶常微分方程,它们具有相同的形式,因 而它们的解的形式也相同。
第五章微波传输基本理论

2.第n菲涅尔区的半径Fn
第n菲涅尔区边界的某个点P到TR连线的距 离为第n菲涅尔区的半径Fn.
Fn TP d1 Fn (d1 ) 2d1
2 2 2
Fn PR d 2 Fn d 2 2d 2
2 2
2
因第n菲涅尔区定义: TP+PR=d+nλ/2
所以:
Fn
nd1d 2 d
5.1.4.2 传播衰落现象
衰落?一般是指信号电平随时间的随机起伏。 按引起衰落的原因可以分为
吸收型衰落:主要是由于传播媒质电参数的变化,使得 信号在媒质中的衰减发生相应的变化而引起的。这种衰 落跟天气有很大的关系,而且信号电平的变化缓慢,所 以称为慢衰落。此外,由地形起伏、建筑物及障碍物的 遮蔽等引起的阴影衰落也称慢衰落。 干涉型衰落:主要是由于随机多径干涉现象引起的。这 种衰落的信号电平变化很快,所以称为快衰落。
各种波段波的特性
长波的穿射能力最强,电磁波靠地波传播,但其收发信 天线的占用场地很大,常用于海上通信。 中波比较稳定,主要用于广播。 短波在传输过程中,碰到电离层会发生反射现象因而其 传输距离很远,故短波常用于远距离通信或广播。但极 易受电离层变化的影响,信号会时强时弱。 超短波的传输特性同光波一样,是沿直线传播的,要求 通信双方之间(两微波站之间)没有阻挡物,信号方能 传输到对方。 微波传输特性也和光波一样,只能沿直线传播即视距传 播,绕射能力弱,且在传播中遇到不均匀的介质时,将 产生折射和反射。
TPn R d
2
n
各相邻费涅尔区在R处产生的电波场强相位相差1800
由费涅尔区半径公式可知,第一费涅尔区的 面积为πF21 ;第二费涅尔区的面积为: πF22- πF21 = π(√ 2 F1 )2- πF21 = πF21 第三费涅尔区的面积为: 2 2 2 2 F3 F2 ( 3F1 ) ( 2F1 ) =πF21 可见个相邻费涅尔区面积相等。但它们离R 的距离不相等。第一费涅尔区离R最近,在R 处产生的电场E1最大,其他依次减小,近似 为等差级数,考虑到相位相反,使R点的总 电场强度E=1/2 E1
电磁场与电磁波(第4版)第5章部分习题参考解答

5.1 在自由空间中,已知电场3(,)10sin() V/m y E z t e t z ωβ=−G G,试求磁场强度。
(,)H z t G解:以余弦为基准,重新写出已知的电场表示式3π(,)10cos( V/m 2y E z t e t z ωβ=−−G G这是一个沿方向传播的均匀平面波的电场,其初相角为z +90−D 。
与之相伴的磁场为300311π(,)(,)10cos(210πcos() 2.65sin() A/m120π2z z y x x H z t e E z t e e t z e t z e t z ωβηηωβωβ=×=×−−=−−−=−−G G G G G G G5.2 理想介质(参数为0μμ=、r 0εεε=、0σ=)中有一均匀平面波沿x 方向传播,已知其电场瞬时值表达式为9(,)377cos(105) V/m y E x t e t x =−G G试求:(1) 该理想介质的相对介电常数;(2) 与(,)E x t G相伴的磁场;(3) 该平面波的平均功率密度。
(,)H x t G 解:(1) 理想介质中的均匀平面波的电场E G应满足波动方程2220EE tμε∂∇−=∂G G据此即可求出欲使给定的E G满足方程所需的媒质参数。
方程中222929425cos(105)y y y y y E E e E e e t x x∂∇=∇==−−∂G G G G 221892237710cos(105)y y y E E e e t t x∂∂==−×−∂∂G G G x = 故得91899425cos(105)[37710cos(105)]0t x t x με−−+×−即18189425251037710με−==×× 故181882r 0025102510(310) 2.25εμε−−×==×××=其实,观察题目给定的电场表达式,可知它表征一个沿x +方向传播的均匀平面波,其相速为98p 10210 m/s 5v k ω===× 而8p 310v ====×故2r 3() 2.252ε==(2) 与电场相伴的磁场E G H G 可由0j E ωμ∇×=−H G G求得。
均匀平面波的概念和波动方程

1, 均匀平面电磁波的概念
2, 时变电磁场的波动方程
3, 均匀平面波的特性
什么是电磁波?
在自由空间,麦克斯韦方程:
可见:
Jc=。,Pv =。
VxH = e — dt
V7百一渔
N xE = —//-dt
时变的电场可以产生时变的磁场,时变的磁场又可以产生时变的 磁电场, 同时在空间上向邻近点推移,这样就产生了以一定速度向前 传播的电磁波动。
(4)均匀平面电磁波:
任意时刻,如果在平面等相位面上,每一点的电场强度均相同, 这种电 磁波:
Vx H = J +亜 c dt
丿 V x E =--
<
dt
▽ . D = pN
i V.B = o
在自由空间:Jc=O/v=O (Vx H = 8 竺 dt
该电磁波动称为电磁波。
例如:水波
问题:一个点源所发射的电 磁 波的等相位面是什么样?
1 ,均匀平面电磁波的概念
(1) 等相位面:
在某一时刻,空间具有相同相位的点构成的面称为等相位面。 等相 位面又称为波阵面。
(2) 球面波:等相位面是球面的电磁波称为球面波。 (3) 平面波:等相位面是平面的电磁波称为平面电磁波。
可见:HZ与时间t无关,不属于时变场部分。Hz = 0 结论:磁场只有Hx和
Hy分量,说明磁场矢量也位于xOy平面上。
磁场强度可表示为:亘二jHx+ayH
结论: 对传播方向而言,电场和磁场只有横向分量,没有纵向分量,
这种平面电磁波称为横电磁波,简写为TEM波。
小结:
1、 均匀平面电磁波的概念 2、 时变电磁场的波动方程
D= 8E B=
《电磁场与电磁波》(第4版)谢处方第4-5章
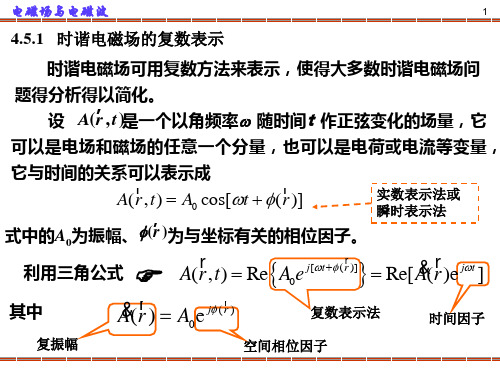
E ( z , t ) Re[ex jExm cos(k z z )e j t ]
j ( t ) 2 Re[ex Exm cos(k z z )e ]
ex Exm cos(k z z ) cos( t ) 2
式中H0 、ω、β、μ都是常数。试求:(1)瞬时坡印廷矢量; (2)平均坡印廷矢量。 解:(1)E 和H 的瞬时值为
jt x a H ( x, z , t ) Re[ He ] ex H 0 sin sin(t z ) a x ez H 0 cos cos(t z ) a
电磁场与电磁波
第5章 均匀平面波在无界媒质中的传播
13
例4.5.6 已知截面为 a b的矩形金属波导中电磁场的复矢量为 a x j z E ey j H 0 sin e a a x x j z H (ex j H 0 sin ez H 0 cos )e a a
jt a x E ( x, z, t ) Re[ Ee ] ey H 0 sin sin(t z ) a
电磁场与电磁波
第5章 均匀平面波在无界媒质中的传播
14
所以瞬时坡印廷矢量 S ( x, z, t ) E ( x, z, t ) H ( x, z, t )
A(r , t ) A0 cos[t (r )]
式中的A0为振幅、 ( r )为与坐标有关的相位因子。
实数表示法或 瞬时表示法
利用三角公式 其中
复振幅
j ( r ) A(r ) A0e
j [t ( r )] (r )e jt ] A(r , t ) Re A0e Re[ A
第5章 均匀平面波1

v E0
ω
ϕ
v k
第五章 均匀平面波在无界空间中的传播
2、波的频率和周期 频率: 频率: ω = 2π f 周期: 周期: T = 1 f
v 3、波数 k 、波长 λ 与波矢量 k
波数k: 长为 2π 距离内包含的波长数。 波数k: 距离内包含的波长数。
2π 2π 1 = 波长: 波长: λ = k = ω µε f µε
第五章 均匀平面波在无界空间中的传播
第5章
均匀平面波在无界空间中传播 均匀平面波在无界空间中传播
理想介质中的均匀平面波 5.1 理想介质中的均匀平面波 电磁波的极化 5.2 电磁波的极化 5.3 均匀平面波在导电媒质中的传播 均匀平面波在导电媒质中 导电媒质中的传播 5.4 色散与群速
5.5 均匀平面波在各向异性媒质中的传播
Ex = Re[( A1e − jkz + A2 e jkz )e jωt ]
第五章 均匀平面波在无界空间中的传播
通解的物理意义: 通解的物理意义:
ωt = 0
Ex
ωt =
π
4
ωt =
☺☺ 2π
π
2
kz 3π
+ 首先考察 Em e − jkz 。 其实数 形式为: 形式为:
π
0
+ x
不同时刻 E 的波形
∂2 ∂2 ∂2 ∇ = 2+ 2+ 2 ∂x ∂y ∂z
2
v E ( x, y , z )
v E ( Ex , 0, 0 )
⇓
v E ( Ex , E y , E z )
v E ( z)
思路: 思路:
时谐场
沿着z方向传播 均匀平面波
均匀平面波的概念和波动方程

6.2 均匀平面电磁波的概念和特性1、均匀平面电磁波的概念2、时变电磁场的波动方程3、均匀平面波的特性在自由空间,麦克斯韦方程:EH t HE tεμ∂∇⨯=∂∂∇⨯=-∂c v 0,0==J ρ可见:时变的电场可以产生时变的磁场,时变的磁场又可以产生时变的磁电场,同时在空间上向邻近点推移,这样就产生了以一定速度向前传播的电磁波动。
该电磁波动称为电磁波。
什么是电磁波?例如:水波问题:一个点源所发射的电磁波的等相位面是什么样?1、均匀平面电磁波的概念(1)等相位面:在某一时刻,空间具有相同相位的点构成的面称为等相位面。
等相位面又称为波阵面。
(2)球面波:等相位面是球面的电磁波称为球面波。
(3)平面波:等相位面是平面的电磁波称为平面电磁波。
(4)均匀平面电磁波:任意时刻,如果在平面等相位面上,每一点的电场强度均相同,这种电磁波称为均匀平面电磁波。
2、时变电磁场的波动方程从麦克斯韦方程出发:c v 0∂∇⨯=+∂∂∇⨯=-∂∇⋅=∇⋅=DH J t BE tD B ρ在自由空间:HB E D με==0=⋅∇=⋅∇∂∂-=⨯∇∂∂=⨯∇H E tH E t E Hμεc v 0,0==J ρ对第一方程两边取旋度:)(E t H ⨯∇∂∂=⨯∇⨯∇ε()H t t εμ∂∂=-∂∂22Htμε∂=-∂根据矢量运算:22()H H H H∇⨯∇⨯=∇∇⋅-∇=-∇由此可得:222tH H ∂∂=∇με——磁场的波动方程同理可得:222tE E ∂∂=∇με——电场的波动方程3、均匀平面波的特性x yzO对均匀平面波而言,在直角坐标系,假设电磁波沿z 方向传播,等相位面平面平行于xOy 平面。
如图所示:0,0=∂∂=∂∂yx所以:22222222HH z t E Ez tμεμε∂∂=∂∂∂∂=∂∂(1)均匀平面波满足一维波动方程。
(2)均匀平面波是横电磁波(TEM 波)根据麦克斯韦第一方程:tE H ∂∂=⨯∇ε结论:电场只有E x 和E y 分量,说明电场矢量位于xOy 平面上。
波的反射和折射
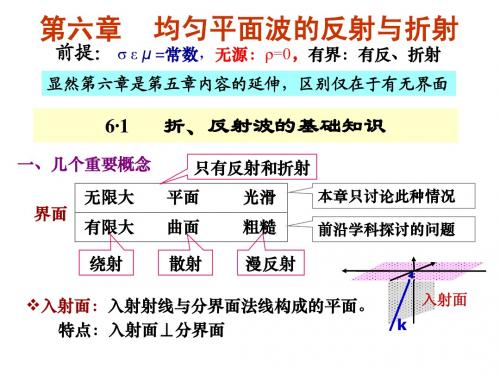
反
E− Ⅰ
H−
z
σ1 = 0
σ2 = ∞
& 5、由边值条件: E 1 t = E 2 t | z = 0 = 0 、由边值条件: &
则:1+R=0 → R=-1
& 6、故: E1 、
7、时域: 、时域:
& = ex Eio ( e − jk1z − e jk1z )
2j 2j
& = ex 2Eio sin k1ze
−j
π
2
π E1 = ex 2 2 Eio sin k1 z cos ω t − = ex 2 2 Eio sin k1 z sin ω t 2 & & & & & & = 1 e × E 则: 1 = H i + H r = 1 ( e z × E i − e z × E r ) & H 8、∵ H 、 η1 η k & & 2 Eio 2 E io − jk1z & 即: = e cos k1 z H1 e + e jk1 z 2 = e y y
入射面 k 本章只讨论此种情况 前沿学科探讨的问题
入射面:入射射线与分界面法线构成的平面。 入射面:入射射线与分界面法线构成的平面。 特点:入射面⊥ 特点:入射面⊥分界面
表示入射; 表示反射 表示反射; 表示透(折 射 设:i 表示入射;r表示反射;t 表示透 折)射; 垂直入射 θ =0:垂直入射 入射角: 入射角:入射射线与分界面法线夹角 i 斜入射 θi ≠0:斜入射 电磁波垂直入射时,电场和磁场总是平行分界面的。 电磁波垂直入射时,电场和磁场总是平行分界面的。 斜入射时,电场或磁场可能与分界面不平行。 斜入射时,电场或磁场可能与分界面不平行。 线极化 平行极化: 平行极化:Ei 的方向与入射面平行 圆极化 入射方式 垂直极化: 垂直极化: Ei 的方向与入射面垂直 椭圆极化
第5章部分习题参考解答

μ 0ε 0
其实,观察题目给定的电场表达式,可知它表征一个沿 + x 方向传播的均匀平面 ω 109 波,其相速为 vp = = = 2 ×108 m/s k 5 1 1 1 1 1 而 vp = = = = × 3 × 108
με
μ 0ε r ε 0
εr
μ 0ε 0
εr
3 故 ε r = ( ) 2 = 2.25 2
G G 5.1 在自由空间中,已知电场 E ( z , t ) = ey 103 sin(ωt − β z ) V/m ,试求磁场强度 G H ( z, t ) 。 解:以余弦为基准,重新写出已知的电场表示式 G π G E ( z , t ) = ey 103 cos(ωt − β z − ) V/m 2 这是一个沿 + z 方向传播的均匀平面波的电场,其初相角为 −90D 。与之相伴的磁 场为 G 1 G G 1 G G π H ( z , t ) = ez × E ( z , t ) = ez × ey 103 cos(ωt − β z − ) η0 η0 2
无损耗媒质中的波阻抗为
9 4
G E E 50 η= G = m = = 500 Ω H H m 0.1
又由于
η=
故
μ r μ0 μr = η0 ε rε 0 εr
(2)
μr η 500 2 ) = ( )2 = ( ε r η0 377
联立式(1)和式(2),得
μr = 1.99 , ε r = 1.13 5.8 在自由空间中,一均匀平面波的相位常数为 β 0 = 0.524 rad/m ,当该波进入到 理想介质后,其相位常数变为 β = 1.81 rad/m 。设该理想介质的 μr = 1 ,试求该理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
均匀平面波在无界空间中的传播
本章重点: 1.理想介质中的均匀平面波; 2.均匀平面波在导电媒质中的传播。 本章难点: 1.均匀平面波在磁化铁氧体中的传播。
均匀平面波
5.1 理想介质中的均匀平面波
• 5.1.1 理想介质中的均匀平面波函数 • 沿z轴方向传播的均匀平面波满足的亥姆霍兹方程:
5.2
平面波的极化
y
5.2.1 极化概念 用电场强度E 矢量末端随时间变化的轨迹来描述波的极化。 一般情况下,沿+z方向传播的均匀平面 波, Ex 和 E y 分量都存在,且其振幅和相 位不一定相等。
Ex Exm cos(t kz 1 ) , Ey Eym cos(t kz 2 )
式中:A1 E1m e j1 , A2 E2m e j2
• 瞬时表达式:
E x ( z, t ) Re Ex ( z)e
jt
E1m cos(t kz 1) E2m cos(t kz 2 )
磁场与电场的关系:
H
1
ez E
(5.1.21)
• • 或:
上式中消去t 得 2 2 Ey 2Ex E y Ex 2 cos sin 2 2 E xm E ym E xm E ym 可以证明,椭圆的长轴与 x 轴的夹角为 2 E E ym cos tan2 xm 2 2
Exm E ym
y
x
椭圆极化与圆极化类同,分右旋极化和左旋极化。 ◇ 当 90
E z, t e x E x z, t e x Em cos t kz xE
4 rad/m 3
Em 104 V/m
2f 2108 rad/s
k
?
由条件t=0,z=1/8 m时,电场等于其振幅值。 得 1 0 k xE 0 8 1 4 1 xE k rad 8 3 8 6
k
• (3)求相对介电常数:
r
2 v0
v
2
r
4,
r 0 4 0
⑷求电场振幅中的常数
• 由横波条件: 5 2E y0 4 • 得: • ⑸求磁场强度矢量
H
E0 en 0
3 5 5 0, E y 0 2
1
en E0e
jke n r
Em en 0
沿任意方向传播的平面电磁波
• 在理想介质中传播的均匀平面波矢量为
E
2 103 e x E y 0e y 5e z cos 30 108 t 4 5x 2 y 4 z
• • • • •
⑴求波的传播方向; ⑵求波的频率、波长、相速; ⑶若介质的μ=μ0,求ε; ⑷求电场振幅中的常数; ⑸求磁场强度矢量。
合成后
2 2 2 2 E Ex Ey E xm E ym cos t E y E ym tan const Ex Exm
合成波电场大小随时间变化, 但矢端轨迹与x轴夹角不变。
5.2.3
圆极化波
若 E x和 E y 振幅相同,相位差90°。则合成波为园极化波。
图 理想介质中均匀平面电磁波的电场和磁场空间分布
电场矢量
E E0e jken r
相伴的磁场 1 H en E
例5.1.1 频率为100MHz的正弦均匀平面波在各向同性的均匀理想介质中沿+z 方向传播,介质的特性参数为 r 4, r 1, 0 。设电场沿x方向,即 E ex Ex 当t=0,z=1/8 m时,电场等于其振幅值 104 V/m 。试求 (1)电场和磁场的瞬时表 达式;(2)波的传播速度;(3)平均坡印廷矢量。 解: (1)以余弦形式写出电场强度表示式
波动方程:
5.3.5 5.3.6
其中γ2= -ω2μεc。
直角坐标系中,对于沿+z 方向传播的均匀平面电磁波,如 果假定电场强度只有x分量Ex,那么式(5.3.5)的一个解为
E ex Eme z
令γ=β-jα,则E=exE0e-j
(β-jα)z=e xE0e
5.3.8
-αze-jβz。显然电场强度的复振幅
1
c
ez E
2
5.3.15
1 5.3.16a 1 2 1 5.3.16b 1 2
2
其中:
c 1 j j
以因子e-αz随z的增大而减小,表明α是说明每单位距离衰减程度
的常数,称为电磁波的衰减常数。β表示每单位距离落后的相位, 称为相位常数。γ=β-jα称为传播常数。因此电场强度的瞬时值可 以表示为
E( z, t ) ex Eme
az
cos(t z 0 )
其中Em、φ0分别表示电场强度的振幅值和初相角,即 j0 因为
o E E E , 0, 90 令 xm ym m 1 2
得
Ex Em cost , Ey Em sin t
y
E
x x
合成后
2 E E t
即
t
合成波电场大小不变, 但矢端轨迹与x 轴夹角 随时间变化。
圆极化的平面波
若以右手的四指随E的矢端运动,则姆指就指出了波的传播方向,表示的圆极
1 90 ,2 0 得到左旋圆极化波。 化波称为右旋圆极化波。显然,
o
5.2.4 椭圆极化波 若 E x和 E y 振幅、相位都不相同。则合成波为椭圆极化波。
令
1 0,2
得 Ex Exm cost , Ey Eym cos t
E0 E0 jkz jkz (ex jey )e (ex jey )e 2 2
上式右边第一项为一左旋圆极化波,第二项为一右旋圆极化波,
而且两者振幅相等,均为E0/2。
5.3 均匀平面波在导电媒质中的传播
5.3.1 导电媒质中均匀平面波
无源、无界的导电媒质中麦克斯韦方程组为
5.2.2 直线极化波 x
直线极化的平面波
取z=0
取 1 2 0
Ex Exm cos(t 1 ) , Ey Eym cos(t 2 ) 若 E x和E y 的相位相同或相差 ,则合成波为直线极化波。 Ex Exm cost , Ey Eym cost
则
4 E z, t ex104 cos 2108 t z V/m 3 6 1 1 104 4 H z, t ez E z, t e y Ex e y cos 2108 t z 60 3 6
A/m
(2) 波的传播速度
1 1 3 108 v 1.5 108 2 4 0 0
m/s
(3) 平均坡印廷矢量
1 Sav Re E H 2
E ex10 e
4 j z 4 6 3
z 104 j H ey e 3 6 60
y y
x x
椭圆、圆与直线极化的 关系
例 5.2.2
证明任一线极化波总可以分解为两个振幅相等旋
向相反的圆极化波的叠加。 解: 假设线极化波沿 +z 方向传播。不失一般性,取x 轴平 行于电场强度矢量E,则
E ( z ) ex E0e
jkz
ex E0e
jkz
1 1 jkz jkz jey E0e jey E0e 2 2
H E jE H jH H 0 E 0
安培环路定律可以写为
H j j E jc E
其中:
c j 1 j
2E 2E 0 2H 2H 0
0
, Eym Ezm Em 时, 椭圆极化 → 圆极化。
椭圆极化的平面波
◇ 当 0 时, 椭圆极化 → 直线极化。 若 E 的变化轨迹在 x 轴上( 0 ) ,称为 x 轴取 向的线极化波。 若 E 的变化轨迹在 y 轴上 ( 90 ) ,称为 y 轴取 向的线极化波。
c 1
1 2 4
1 2
c e
j
称为导电媒质的波阻抗, 它是一个复数。 上式中,
1 arctan 0 ~ 2 4
5.3.14
导电媒质的本征阻抗是一个复数,其模小于理想介质的本征 阻抗,幅角在 0~π/4 之间变化,具有感性相角。这意味着电场强 度和磁场强度在空间上虽然仍互相垂直,但在时间上有相位差, 二者不再同相,电场强度相位超前磁场强度相位。这样磁场强度 可以重写为
• 波矢量: • 沿波矢量
k en k e x k x e y k y e z k z
(5.1.27)
k 方向传播的平面波
E r E me jk r (5.1.28)
• 相伴的磁场强度矢量:
H r 1
e n E me jk r
(5.1.29)
• 横波条件:
d Ex k 2 Ex 0 dz2 d 2Ey dz2 d 2H x dz2 d 2H y k 2Ey 0 k 2H x 0
2
2
(5.1.1)
(5.1.2) (5.1.3)
k Hy 0 dz2
(5.1.4)
方程(5.1.1)的通解:
