八年级下数学压轴题和答案解析.docx
人教版八年级下册数学期末压轴题专题训练(含答案)

人教版八年级下册数学期末压轴题专题训练1.如图,已知长方形的边AD =8,AB =4,动点M 从点A 出发,以每秒2个单位长度的速度沿A →D →A 的路径匀速运动,同时,动点N 从点C 出发,沿C →B 方向以每秒1个单位长度的速度匀速运动,当其中一个动点到达终点时,另一点也随之停止运动,设运动时间为t 秒.(1)如(图一),当运动时间为1秒时,求MN 的长度;(2)当0≤t ≤4时,直接写出AMN 为直角三角形时的运动时间t 的值; (3)如(图二),当4<t <8时,判断AMN 的形状,并说明理由.2.(1)感知:如图①,在正方形ABCD 中,E 为边AB 上一点(点E 不与点AB 重合),连接DE ,过点A 作AF DE ⊥,交BC 于点F ,证明:DE AF =.(2)探究:如图②,在正方形ABCD 中,E ,F 分别为边AB ,CD 上的点(点E ,F 不与正方形的顶点重合),连接EF ,作EF 的垂线分别交边AD ,BC 于点G ,H ,垂足为O .若E 为AB 中点,1DF =,4AB =,求GH 的长.(3)应用:如图③,在正方形ABCD 中,点E ,F 分别在BC ,CD 上,BE CF =,BF ,AE 相交于点G .若3AB =,图中阴影部分的面积与正方形ABCD 的面积之比为2:3,则ABG 的面积为______,ABG 的周长为______.3.如图.菱形ABCD的对角线AC,BD交于点O.尺规作图:过点A作直线BC的垂线(不写作法和证明,保留作图痕迹).该垂线与BC交于点E,F为AD边上一点,DF=AE,连接OF,若OD=2AO,请猜想CE与OF的数量关系,并证明你的猜想.4.图1、图2分别是65的网格,网格中每个小正方形的边长均为1,线段AB的端点在小正方形的顶点上,请在图1、图2中各画一个图形,分别满足以下要求:(1)在图1中画一个以线段AB为一边的菱形(非正方形),所画菱形各顶点必须在小正方形的顶点上.(2)在图2中画一个以线段AB为一边的等腰三角形,所画等腰三角形各顶点必须在小正方形的顶点上,且所画等腰三角形的面积为52.5.如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.(1)求证:△ABE≌△CDF;(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.⊥,垂6.如图,在ABCD中,E,F分别为AD,BC的中点,AG BD⊥,CH BD足分别为G,H,连接EG,EH,FG,FH.(1)求证:四边形GEHF是平行四边形;BC=,当BD=______时,GEHF是矩形.(2)若2AB=,37.如图1,在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB 于E.(1)发现:如图1,连接CE,则△BCE的形状是_______________,∠CDB=____________°;(2)探索:如图2,点P为线段AC上一个动点,当点P在CD之间运动时,连接BP,作∠BPQ=60°,PQ交射线DE于Q,连接BQ,即△BPQ是等边三角形;思路:在线段BD上截取点H,使DH=DP,得等边△DPH,由∠DPQ=∠HPB,PD=PH,∠QDP=∠BHP,易证△PDQ≌△PHB(ASA),得PQ=PB,即△BPQ是等边三角形.试判断线段DQ、DP、AD之间的关系,并说明理由;(3)类比:如图3,当点P在AD之间运动时连接BP,作∠BPQ=60°,PQ交射线DE于Q,连接BQ.①试判断△BPQ的形状,并说明理由;②若AD=2,设AP=x,DQ=y,请直接写出y与x之间的函数关系式.8.下面是小东设计的“作平行四边形ABCD,使∠B=45°,AB=2cm,BC=3cm”的作图过程.作法:如图,①画∠B=45°;②在∠B的两边上分别截取BA=2cm,BC=3cm.③以点A为圆心,BC长为半径画弧,以点C为圆心,AB长为半径画弧,两弧相交于点D;则四边形ABCD为所求的平行四边形.根据小东设计的作图过程:(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明.证明:∵AB=,CB=,∴四边形ABCD为所求的平行四边形()(填推理的依据).9.如图,已知菱形ABCD中,分别以C、D为圆心,大于1CD的长为半径作弧,两弧2分别相交于M、N两点,直线MN交CD于点F,交对角线AC于点E,连接BE、DE.(1)求证:BE=CE;(2)若∠ABC=72°,求∠ABE的度数.10.如图,四边形ABCD是一个正方形,E、F分别在AD、DC边上,且DE=CF,AF、BE交于O点,请说出线段AF和BE的关系,并证明你的结论.11.如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:(1)在网格中画出平行四边形ABCD;(2)线段AC的长为,CD的长为,AD的长为,△ACD为三角形,平行四边形ABCD的面积为.12.两个不全等的直角三角形ABC 和DEF 重叠在一起,其中∠A =60°,AC =1.固定△ABC 不动,将△DEF 进行如下操作:(1)如图(1),△DEF 沿线段AB 向右平移(D 点在线段AB 内移动),连接DC 、CF 、FB ,四边形CDBF 的形状在不断的变化,但它的面积不变化,请求出其面积;(2)如图(2),当D 点移到AB 的中点时,请你猜想四边形CDBF 的形状,并说明理由.13.如图,长方形ABCD 中,E 是AD 的中点,将ABE △沿BE 折叠后得到GBE ,且G 点在长方形ABCD 内部,延长BG 交DC 于点F .(1)求证:GE DE =;(2)若9DC =,DF 2CF =,求AD 的长;(3)若DC n DF =⋅,求22AD AB 的值.14.在正方形ABCD 中,点E 是CD 边上任意一点.连接AE ,过点B 作BF ⊥AE 于F .交AD 于H .(1)如图1,过点D 作DG ⊥AE 于G ,求证:△AFB ≌△DGA ;(2)如图2,点E 为CD 的中点,连接DF ,求证:FH +FE ;(3)如图3,AB =1,连接EH ,点P 为EH 的中点,在点E 从点D 运动到点C 的过程中,点P 随之运动,请直接写出点P 运动的路径长.15.已知如图,四边形ABCD 是平行四边形.(1)尺规作图:作∠ABC 的角平分线交CD 的延长线于E ,交AD 于F (不写作法和证明,但要保留作图痕迹).(2)请在(1)的情况下,求证:DE =DF .16.如图,在Rt ABC ∆中,90ACB ∠=︒,CD 是斜边AB 上的中线,1AC CD ==,求直角边BC 的长.17.如图:正方形ABCD 中,点E 、F 分别在边BC 、CD 上,BE =CF ,连接AE ,BF 交于点O ,点M 为AB 中点,连接OM ,求证:12OM AB =.18.如图,在四边形ABCD 中,90ABD ACD ∠=∠=︒,E ,F 分别是BC 、AD 的中点.(1)若10AD =,求BF 的长; (2)求证:EF BC ⊥.19.如图,四边形ABDE 和四边形ACFG 都是正方形,CE 与BG 交于点M ,点M 在△ABC 的外部.(1)求证:BG =CE ; (2)求证:CE ⊥BG ; (3)求:∠AME 的度数.20.如图,△ABC中,D是AB边上任意一点,F是AC中点,过点C作CE//AB交DF 的延长线于点E,连接AE,CD.(1)求证:四边形ADCE是平行四边形;(2)若∠B=30°,∠CAB=45°,AC ,求AB的长.21.如图,△ABC中,∠C=90°.(1)尺规作图:作边BC的垂直平分线,与边BC,AB分别交于点D和点E;(保留作图痕迹,不要求写作法)(2)若点E是边AB的中点,AC=BE,求证:△ACE是等边三角形.22.已知:如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC 的平行线交BE的延长线于点F,且AF=DC,连接CF.(1)求证:D是BC的中点;(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.23.如图,四边形ABCD 是平行四边形.(1)尺规作图(不写作法,保留作图痕迹);作出ABC ∠的角平分线BE ,交AD 于点E ;在线段BC 上截取BF BA =,连接EF ;(2)在(1)所作图中,请判断四边形ABFE 的形状,并说明理由.24.如图,矩形ABCD 中,E 、F 分别为边AD 和BC 上的点,BE =DF ,求证:DE =BF .25.已知:在ABC 中,90BAC ∠=︒,AB AC =,点D 为直线BC 上一动点(点D 不与B 、C 重合).以AD 为边作正方形ADEF ,连接CF .(1)如图①,当点D 在线段BC 上时, ①求证:ABD △≌ACF ; ②ACF ∠的大小=______°;③若8BC =,2CD =,则CF 的长=______;(2)如图②,当点D 在线段BC 的延长线上时,其它条件不变,则CF 、BC 、CD 三条线段之间的关系是:CF =______;其它条件不变:①CF、BC、CD三条线段之间的关系是:CF ______;△的形状,并说明②若连接正方形的对角线AE、DF,交点为O,连接OC,探究AOC理由.26.已知:如图,▱ABCD中,延长BC至点E,使CE=BC,连接AE交CD于点O.(1)求证:CO=DO;(2)取AB中点F,连接CF,△COE满足什么条件时,四边形AFCO是正方形?请说明理由.参考答案:1.解:过点N作NR⊥AD于R.∵四边形ABCD是矩形,∴∠C=∠D=∠DRN=90°,∴四边形CDRN是矩形,∴RN=CD=4,CN=DR=1,∵AM=2,AD=8,∴RM=AD-AM-DR=8-2-1=5,∵∠MRN=90°,∴MN=(2)解:当0≤t≤4时,如果AM=BN,则△AMN是直角三角形,∴2t=8-t,∴t=83,当t=4时,点M与D重合,点N位于BC的中点,此时△AMN是等腰直角三角形,综上所述,当△AMN是直角三角形时,t的值为83或4.(3)解:∵当t=4时,△AMN是等腰直角三角形,∵点M的运动速度大于点N的运动速度,且M,N同时到达终点,即点M在点N的右侧,∴当4<t<8时,△AMN是锐角三角形.2.证明:∵四边形ABCD是正方形,∴AD AB =,90DAE ABF ∠=∠=︒,∵AF DE ⊥,∴90DAF BAF ∠+∠=︒,90DAF ADE ∠+∠=︒, ∴ADE BAF ∠=∠,在DAE △和ABF 中,ADE BAF AD AB DAE ABF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴DAE △≌ABF (ASA ),∴DE AF =.探究:解:分别过点A 、D 作AN GH ∥,DM EF ∥,分别交BC 、AB 于点N 、M ,如图②所示:∵四边形ABCD 是正方形,∴AB CD ∥,AB CD =,90DAB B ∠=∠=︒,∴四边形DMEF 是平行四边形,∴1ME DF ==,DM EF =, ∵AN GH ∥,GH EF ⊥,∴DM GH ⊥,同理,四边形AGHN 是平行四边形,∴GH AN =,∵DM EF ∥,GH EF ⊥,∴AN DM ⊥,∴90DAN ADM ∠+∠=︒,∵90DAN BAN ∠+∠=︒,∴ADM BAN ∠=∠,在ADM △和BAN 中,90ADM BAN AD AB DAM ABN ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩,∴ADM △≌BAN (ASA ),∴DM AN =,∴EF GH DM AN ===,∵E 为AB 中点,∴122AE AB ==, ∴211AM AE ME =-=-=,∴DM ==∴GH =应用:解:∵AB =3,∴S 正方形ABCD =3×3=9,∵阴影部分的面积与正方形ABCD 的面积之比为2:3,∴阴影部分的面积为:23×9=6, ∴空白部分的面积为:9﹣6=3,在△ABE 和△BCF 中,90BECF ABE BCF AB BC ,∴△ABE ≌△BCF (SAS ),∴∠BEA =∠BFC ,S △ABG =S 四边形CEGF ,∴S △ABG =12×3=32,∠FBC +∠BEA =90°, ∴∠BGE =90°,∴∠AGB =90°,设AG =a ,BG =b , 则12ab =32, ∴2ab =6,∵a 2+b 2=AB 2=32,∴a 2+2ab +b 2=32+6=15,即(a +b )2=15,而0,a b +>∴a +bBG +AG∴△ABG, 故答案为:323. 3.解:所作图形如图所示:结论:CE =OF .理由:∵四边形ABCD 是菱形,∴AC ⊥BD ,OA =OC ,AD ∥BC ,∵AE ⊥BC ,OF ⊥AD ,∴AE ⊥AD ,∴∠AEC =∠DAE =∠AOD =∠DFO =90°,∴∠EAC +∠DAO =90°,∠FDO +∠DAO =90°,∴∠CAE =∠ODF ,∵OD =2AO ,AC =2AO ,∴AC =OD ,在△AEC 和△DFO 中,AEC DFO CAE ODF AC DO ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AEC ≌△DFO (AAS ),∴CE =OF .4.解:所画菱形如图所示;(答案不唯一)(2)解根据勾股定理,AB = 所画等腰三角形的面积为52, ∴作以线段AB 为直角边的等腰直角三角形即可,所画三角形如图所示.5.证明:∵四边形ABCD 是平行四边形,∴AB =CD ,AB CD ∥,OB =OD ,OA =OC ,∴∠ABE =∠CDF ,∵点E ,F 分别为OB ,OD 的中点, ∴12BE OB =,12DF OD =, ∴BE =DF ,在△ABE 和△CDF 中,AB CD ABE CDF BE DF =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CDF(SAS).(2)解:当AC =2AB 时,可使四边形EGCF 为矩形;理由如下:∵△ABE ≌△CDF ,∴∠AEB =∠CFD ,∴∠AEO =∠CFO ,∴AE CF ∥,∵EA =EG ,OA =OC ,∴EO 是△AGC 的中位线,∴EO GC ∥,∴四边形EGCF 是平行四边形,∵AC =2AB ,AC =2AO ,∴AB =AO ,∵E 是OB 的中点,∴AE ⊥OB ,∴∠OEG =90°,∴平行四边形EGCF 是矩形.6.解:∵AG BD ⊥于G ,∴90AGD ∠=︒.∵在Rt AGD 中,E 为AD 的中点, ∴12EG ED AD ==,同理12HF BF BC ==. ∵在ABCD 中,AD BC =,∴EG FH =.∵在EGD 中,EG ED =,∴EDG EGD ∠=∠,同理在BFH △中,HBF FHB ∠=∠.∵在ABCD 中,AD BC ∥,∴EDG HBF ∠=∠.∴EGD FHB ∠=∠.∴EG FH ∥.又∵EG FH =,∴四边形GEHF 是平行四边形.(2)连接EF ,则EF =AB =CD =2,若四边形GEHF 是矩形,则EF =GH =2,在RtAGD 和Rt ΔCHB 中,41AGD CHB AD CB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ΔAGD ≅ΔCHB (AAS ),∴DG =BH ;∴DG -GH =BH -GH ,即BG =DH ,设BG =DH =x ,在Rt △ABG 中,AG 2=AB 2-BG 2=4-x 2,在Rt △AGD 中,AG 2=AD 2-DG 2=9-DG 2=9-(2+x )2,∴4-x 2=9-(2+x )2,解得x =14, ∴BD =BG +GH +HD =14+2+1452= . 7.解:如图1,∵在Rt △ABC 中,∠ACB =90°,∠A =30°,∴∠ABC =60°,∵BD 是△ABC 的角平分线,∴∠ABD =∠CBD =12∠ABC =30°,∴∠ABD =∠A ,∠CDB =90°-∠CBD =60°,∴AD =BD ,又DE ⊥AB ,∴AE =BE =12AB ,又∠ACB =90°,∴CE =12AB =BE ,又∠ABC =60°,∴△BCE 是等边三角形,故答案为:等边三角形,60;(2)解:AD =DQ +DP ,理由为:在线段BD 上截取点H ,使DH =DP ,如图2,∵∠CDB =60°,∴△DPH 为等边三角形,∴DP =PH ,∠DPH =∠DHP =60°,又∠BPQ =60°,∴∠DPQ +∠QPH =∠HPB +∠QPH =60°,∠BHP =120°,∴∠DPQ =∠HPB ,∵∠A =30°,DE ⊥AB ,∴∠QDP =∠A +∠AED =30°+90°=120°,∴∠QDP =∠BHP ,在△PDQ ≌△PHB 中, DPQ HPB PD PHQDP BHP ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△PDQ ≌△PHB (ASA ),∴DQ =BH ,PQ =PB ,∵AD =BD ,∠BPQ =60°,∴△BPQ 为等边三角形,AD =BD =BH +DH =DQ +DP ,即AD =DQ +DP ;(3)解:①△BPQ 为等边三角形,理由为:延长BD 至F ,使DF =DP ,连接PF ,设DQ 和BP 相交于O ,如图3, ∵∠PDF =∠CDB =60°,∴△PDF 为等边三角形,∴PF =DP ,∠F =∠PDF =∠DPF =60°,∵∠A =30°,DE ⊥AB ,∴∠PDQ =90°-∠A =60°,∴∠F =∠PDQ =60°,∵∠DPF +∠DPB =∠BPQ +∠DPB ,又∠BPQ =60°,∴∠BPF =∠QPD ,在△PBF 和△PQD 中,F PDQ PF DPBPF QPD ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△PBF ≌△PQD (ASA ),∴PB =PQ ,BF =DQ ,又∠BPQ =60°,∴△BPQ 为等边三角形;②∵ DF =DP ,BF =DQ ,AD =BD ,∴DQ =BF =BD +DF =AD +DP ,∵AD =2, AP =x ,DQ =y ,∴y =2+2-x ,即y =-x +4.8.(1)补全图形如下,.(2)∵AB =CD ,CB =AD∴四边形ABCD 为所求的平行四边形(两组对边分别相等的四边形是平行四边形). 故答案为:CD ,AD ,两组对边分别相等的四边形是平行四边形.9.证明:∵四边形ABCD 是菱形,∴CB =CD ,∠ACB =∠ACD ,在△ECB 和△ECD 中,CE CE ECB ECD CB CD =⎧⎪∠=∠⎨⎪=⎩,∴△ECB ≌△ECD (SAS ),∴BE =DE ,由作图可知,MN 垂直平分线段CD ,∴EC =ED ,∴BE =CE .(2)解:∵BA =BC ,∠ABC =72°,∴∠BAC =∠BCA =12(180°﹣72°)=54°,∵EB =EC ,∴∠EBC =∠ECB =54°,∴∠ABE =∠ABC ﹣∠EBC =18°.10.解:AF⊥BE,AF=BE,证明如下:证明:∵正方形ABCD∴AB=AD=DC,∠D=∠BAD=90°∵CF=DE∴AE=AD-DE,DF=DC-CF∴AE=DF在△AEB和△AFD中AB=AD, ∠D=∠BAD, AE=DF∴△ABE≌△DAF(SAS)∴∠ABE=∠F AD,AF=BE∵∠BAD=90°∴∠ABE+∠AEB=90°∴∠F AD +∠AEB=90°∴∠AOE=90°,AF⊥BE.∴AF=BE,AF⊥BE.11.解:如图所示:平行四边形ABCD即为所求;(2)解:AC,CD =,5=AD ,∴222AC CD AD += ,∴△ACD 是直角三角形,∴平行四边形ABCD 的面积为122102ACD S=⨯ . 12.解:过点C 作CG AE ⊥,垂足是点G .由题可知,//CF AE ,CF AD BE ==,则四边形CDBF 是梯形.在直角ABC ∆中,90ACB ∠=︒,60A ∠=︒,1AC =,22AB AC ∴==, 在直角ACG ∆中,90CGA ∠=︒,60A ∠=︒,1AC =,30ACG ∴∠=︒,1111222AG AC ==⨯=,CG ∴=.()()111122222CDBF S CE DB CG AD DB CG AB CG ∴=+⋅=+⋅=⋅=⨯=梯形; (2)证明:四边形CDBF 是菱形. 理由如下:在直角ABC ∆中,D 是AB 的中点,AD DB CD ∴==,由(1)CF AD =,CF DB CD ∴==,又//CF AE ,∴四边形CDBF 是平行四边形.CD BD =,∴四边形CDBF 是菱形.13.证明∵GBE 是由ABE △折叠而成,∴△ABE ≌△GBE ,∴AE GE =,∵E 是AD 的中点,∴AE DE =,∴GE DE =;(2)解:连接EF ,∵DF 2CF =, ∴229633DF DC ==⨯=, ∴963CF DC DF =-=-=.∵四边形ABCD 是长方形,∴AD BC =,9AB DC ==,90A C D ∠=∠=∠=︒.∵△ABE ≌△GBE ,∴9BG AB ==,90A BGE FGE ∠=∠=∠=︒.在Rt EGF 和Rt EDF 中,∵GE DE =,EF EF =∴Rt △EGF ≌Rt △EDF (HL ),∴6GF DF ==.∴9615BF BG GF =+=+=,在Rt BCF 中,∵15BF =,3CF =,∴BC =.∴AD BC ==(3)解:设DF a =,则AB DC n DF na ==⋅=,∴()1CF DC DF na a n a =-=-=-,又∵BG AB na ==,GF DF a ==,∴()1BF BG GF na a n a =+=+=+,在Rt BCF 中,∵()1BF n a =+,()1CF n a =-,∴ ()()22222222114BC BF CF n a n a na =-=+--=,∴ 2224AD BC na ==, ∴2222244AD na AB n a n==. 14.证明:∵四边形ABCD 是正方形,∴AB =AD ,∠BAD =90°∵DG ⊥AE ,BF ⊥AE∴∠AFB =∠DGA =90°∵∠F AB +∠DAG =90°,∠DAG +∠ADG =90°∴∠BAF =∠ADG在△AFB 和△DGA 中∵AFB DGABAF ADG AB AD∠=∠⎧⎪∠=∠⎨⎪=⎩∴△AFB≌△DGA(AAS).(2)证明:如图2,过点D作DK⊥AE于K,DJ⊥BF交BF的延长线于J由题意知∠BAH=∠ADE=90°,AB=AD=CD∵BF⊥AE∴∠AFB=90°∵∠DAE+∠EAB=90°,∠EAB+∠ABH=90°∴∠DAE=∠ABH在△ABH和△DAE中∵BAH ADE AB ADABH DAE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABH≌△DAE(ASA)∴AH=DE∵点E为CD的中点∴DE=EC=12CD∴AH=DH∴DE=DH∵DJ⊥BJ,DK⊥AE∴∠J=∠DKE=∠KFJ=90°∴四边形DKFJ是矩形∴∠JDK =∠ADC =90°∴∠JDH =∠KDE在△DJH 和△DKE 中∵J DKE JDH KDE DH DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△DJH ≌△DKE (AAS )∴DJ =DK ,JH =EK∴四边形DKFJ 是正方形∴FK =FJ =DK =DJ∴DFFJ2FJ =∴FH +FE =FJ ﹣HJ +FK +KE =2FJDF .(3)解:如图3,取AD 的中点Q ,连接PQ ,延长QP 交CD 于R ,过点P 作PT ⊥CD 于T ,PK ⊥AD 于K ,设PT =b由(2)得△ABH ≌△DAE (ASA )∴AH =DE∵∠EDH =90°,点P 为EH 的中点∴PD =12EH =PH =PE∵PK ⊥DH ,PT ⊥DE∴∠PKD=∠KDT=∠PTD=90°∴四边形PTDK是矩形∴PT=DK=b,PK=DT∵PH=PD=PE,PK⊥DH,PT⊥DE ∴PT是△DEH的中位线∴DH=2DK=2b,DE=2DT∴AH=DE=1﹣2b∴PK=12DE=12﹣b,QK=DQ﹣DK=12﹣b∴PK=QK∵∠PKQ=90°∴△PKQ是等腰直角三角形∴∠KQP=45°∴点P在线段QR上运动,△DQR是等腰直角三角形∴QR DQ∴点P.15.解:(1)尺规作图如下:(2)四边形ABCD是平行四边形,,AB CE AD BC∴,,ABE E CBE DFE∴∠=∠∠=∠,BE平分ABC∠,ABE CBE∴∠=∠,E DFE ∴∠=∠,DE DF ∴=.16.解:在Rt △ABC 中,CD 是斜边AB 上的中线, ∴AB =2CD =2,由勾股定理得,BC . 17.证明:∵四边形ABCD 是正方形,∴AB =BC ,∠ABE =∠BCF =90°,又BE =CF ,∴△ABE ≌△BCF (SAS ).∴∠BAE =∠CBF .∵∠ABO +∠CBF =90°,∴∠ABO +∠BAO =90°,即∠AOB =90°. 在Rt △ABO 中,M 点是斜边AB 中点, ∴12OM AB =. 18.(1) 解: 90ABD ∠=︒, F 为AD 的中点,10,AD = 1 5.2BFAD (2) 证明:如图,连接,CF90ABD ACD ∠=∠=︒, F 是AD 的中点,11,,22CF AD BF AD ,CF BF ∴=E 是BC 的中点,.EF BC19.解:证明:在正方形ABDE 和ACFG 中,AB AE =,AC AG =,90BAE CAG ∠=∠=︒, BAE BAC CAG BAC ∴∠+∠=∠+∠,即CAE BAG ∠=∠,在ABG ∆和AEC ∆中,{AB AECAE BAG AC AG=∠=∠=,()ABG AEC SAS ∴∆≅∆,BG CE ∴=;(2)解:证明:设BG 、CE 相交于点N ,ABG AEC ∆≅∆,ACE AGB ∴∠=∠,9090180NCF NGF ACF AGF ∠+∠=∠+∠=︒+︒=︒,360()360(18090)90CNG NCF NGF F ∴∠=︒-∠+∠+∠=︒-︒+︒=︒, BG CE ∴⊥;(3)解:过A 作BG,CE 的垂线段交于点P ,Q ,ABG AEC ∆≅∆,,ABP AEQ AB AE ∴∠=∠=,90APB AQE ∠=∠=︒,()ΔΔABP AEQ AAS ∴≅,∴=AP AQ ,AM ∴是角平分线,45AMC ∴∠=︒,135AME .20.证明:∵AB //CE ,∴∠CAD =∠ACE ,∠ADE =∠CED .∵F 是AC 中点,∴AF =CF .在△AFD 与△CFE 中,CAD ACE ADE CED AF CF ∠∠⎧⎪∠∠⎨⎪⎩=== , ∴△AFD ≌△CFE (AAS ),∴DF =EF ,∴四边形ADCE 是平行四边形;(2)解:过点C 作CG ⊥AB 于点G ,∵∠CAB =45°,∴AG CG =,在△ACG 中,∠AGC =90°,∴222AG CG AC +=,∵AC=∴CG=AG=1,∵∠B=30°,∴12CG BC=,∴2BC=,在Rt△BCG中,BG==,∴1AB AG BG=+=.21.解:如图所示,直线DE即为所求;,(2)证明:∵∠ACB=90°,点E是边AB的中点,∴AE=BE=CE=12 AB,∵AC=BE,∴AC=AE=CE,∴△ACE是等边三角形.22.证明:E是AD的中点,AE DE∴=,//AF BC∴,FAE BDE∴∠=∠,AFE DBE∠=∠.在AFE∆和DBE∆中,FAE BDEAFE DBE AE DE∠=∠⎧⎪∠=∠⎨⎪=⎩,()AFE DBE AAS ∴∆≅∆,AF BD ∴=.AF DC =,BD DC ∴=.即:D 是BC 的中点.(2)解:四边形ADCF 是矩形;证明:AF DC =,//AF DC ,∴四边形ADCF 是平行四边形,AB AC =,BD DC =,AD BC ∴⊥即90ADC ∠=︒,∴平行四边形ADCF 是矩形.23.(1)如图所示,BE 就是所求的ABC ∠的角平分线.BF BA =,(2)四边形ABFE 为菱形.理由如下:∵BE 是ABC ∠的平分线,∴∠ABE =∠FBE∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠AEB =∠EBF ,∴∠ABE =∠AEB∴AB =AE∵BF BA =∴AE =BF∴四边形ABFE 为平行四边形,∵BF BA =,∴四边形ABFE 为菱形.24.证明:∵四边形ABCD 是矩形,∴AB =CD ,AD =BC ,∠A =∠D =90°,在Rt △ABE 和Rt △CDF 中,BE CF AB CD =⎧⎨=⎩, ∴Rt △ABE ≌Rt △CDF (HL ),∴AE =CF ,∴DE =BF .25.(1)①证明:∵四边形ADEF 是正方形,∴AD AF =,90DAF ∠=︒,∵90BAC ∠=︒,∴BAD CAF ∠=∠,在ABD △和ACF 中,{AB ACBAD CAF AD AF=∠=∠=,∴ABD △≌ACF (SAS ).②∵ABD △≌ACF ,∴ABD ACF ∠=∠,∵90BAC ∠=︒,AB AC =,∴45ABD ACB ∠=∠=︒,∴45ACF ∠=︒.故答案为:45.③∵ABD △≌ACF ,∴=CF BD ,∵826BD BC CD =-=-=.∴CF =6,故答案为:6.(2)(2)CF BC CD =+,由(1)同理可证ABD △≌ACF 得:CF BD BC CD ==+. 故答案为:BC CD +.(3)(3)①由(1)同理可证ABD △≌ACF 得:CF BD CD BC ==-. 故答案为:CD BC -.②AOC △为等腰三角形,理由如下:∵90BAC ∠=︒,AB AC =,∴18045135ABD ∠=︒-︒=︒,∵四边形ADEF 是正方形,∴AD AF =,90DAF ∠=︒,∴BAD CAF ∠=∠,同理可证BAD ≌CAF ,∴135ACF ABD ∠=∠=︒,∴90FCD ACF ACB ∠=∠-∠=︒,∴FCD 为直角三角形,∵正方形ADEF 中,O 为DF 的中点, ∴12OC DF =,12OA AE =,AE DF =, ∴OC OA =,∴AOC △是等腰三角形.26.证明:∵四边形ABCD 是平行四边形,∴AD=BC,AD//BC,∴∠DAE=∠E,∵CE=BC,∴CE=AD,又∵∠AOD=∠COE,∴△AOD≌△EOC(AAS),∴CO=DO;(2)解:当CO=EO,∠COE=90°时,四边形AOCF是正方形;理由如下:∵CO=DO,∴CO=1CD,2又∵F是AB的中点,∴AF=1AB,2∵四边形ABCD是平行四边形,∴AB=CD,AB//CD,∴AF=CO,AF//CO,∴四边形AFCO是平行四边形,∵△AOD≌△EOC,∴AO=EO,∵CO=EO,∴AO=CO,∴平行四边形AFCO是菱形,∵∠COE=90°,∴菱形AFCO是正方形.。
填空题压轴题-2022-2023学年八年级数学下册期末解答压轴题必刷专题训练(华师大版)(解析版)

填空题压轴题【答案】145【详解】解:如图以DAB V 和FAQ △中:DA =∴()SAS DAB FAQ V V ≌,【答案】①②③④⑤⑥【详解】解:如图,过点∵四边形ABCD 是正方形,∴A C D ÐÐÐ==∴AEB EBC ÐÐ=∵FEB EBC ÐÐ=∴AEB BEF ÐÐ=5.如图,已知在△ABC中,AB 作平行四边形MCNB,连接MN【答案】24 5【详解】如图,设MN、BC交于点6.如图,在平面直角坐标系xoyAB AD为边作使2DP AP=,以,【答案】49【详解】解:∵四边形ABCD是平行四边形,∴AD∥BC,AB//CD∴∠E=∠DAE,又∵AE平分∠BAD,【答案】①④⑤【详解】解:∵四边形ABCD ∴AB CD =,AD BC =.设点P 到AB ,BC ,CD ,DA【答案】()453,【详解】解:从正方形的观点考虑,右下角对应的横坐标为1时,共有右下角对应的横坐标为2时,共有右下角对应的横坐标为3时,共有右下角对应的横坐标为4时,共有【答案】10 21【详解】解:设1A,2A,3A【答案】(10112-,10112)【详解】解:∵过点(1,0)作∴1A (1,2),把2y =代入y x =-得2x =-,即把2x =-代入2y x =得4y =-,即同理可得4A (4,4-),5A (32),…直线21y kx k =+-与直线(1)2y k x k =+++那么,COD ABDC S S =V 四边形【答案】22n+【详解】解:对于直线y=x+1∵A0B1∥x轴,∴B1的纵坐标为将y=1代入1122y x=+中得:∴A0B1=1=20,∵A1B1∥y轴,∴A1的横坐标为【答案】404432æöç÷èø【详解】解:∵直线1l :112y x =-+与直线2l :332y x =-+与y 轴交于点B ,∴AB 2\=,112BC AB ==,∵BC ⊥AB ,∴()1,3C -,∴四边形PECF 是矩形,∴PC=EF,∴PA=EF,故②正确;∵BD 是正方形ABCD 的对角线,∴∠ABD=∠BDC=∠DBC=45°,∵∠PFC=∠BCD=90°,∴PF∥BC,∴∠DPF=45°,∵∠DFP=90°,∴△FPD 是等腰直角三角形,故①正确;在△PAB 和△PCB 中,AB CB ABP CBP BP BP ìïÐÐíïî=== , ∴△PAB≌△PCB,∴∠BAP=∠BCP,在矩形PECF 中,∠PFE=∠FPC=∠BCP,∴∠PFE=∠BAP.故④正确;∵点P 是正方形对角线BD 上任意一点,∴AD 不一定等于PD ,只有∠BAP=22.5°时,AD=PD ,故③错误,故答案为①②④.38.如图,在矩形ABCD 中,5AB =,12BC =,P 是矩形ABCD 内一点,沿PA 、PB 、PC 、PD 把这个矩形剪开,然后把两个阴影三角形拼成一个四边形,则这个四边形的面积为_________;这个四边形周长的最小值为________.【答案】 30 26【详解】如解图①,过点P 作PE AB ^于点E ,延长EP 交CD 于点F ,∵四边形ABCD 是矩形,∴90ABC BCD Ð=Ð=°,5CD AB ==.∴四边形EBCF 是矩形.∴EF BC =.又∵12BC =,故答案为:30,26.39.如图,在△ABC 中,Ð,90BAC Ð=°,点A 为(3P 、A 、C 为顶点的三角形和△全等,则P 点坐标为___________【答案】(6)2-,或(81),或则90AOB AMP Ð=Ð=°,在AOB V 和V AMP 中,AOB OAB AB ÐìïÐíïî∴(AAS)AOB AMP V V ≌,∴3AM AO ==,2MP OB == ,∴此时点P 的坐标为(6)2-,;②如图,过点C 作CP AC ^,使CP AB =,则(HL)ABC CPA V V ≌.过P 作PF x ^轴于F ,过点C 作CE x ^轴于点E ,作CD y ^轴于点D .∵90OBA OAB Ð+Ð=°,90EAC OAB Ð+Ð=°,∴OBA EAC Ð=Ð.又∵90BOA AEC Ð=Ð=°,AB AC =,∴(AAS)BOA AEC V V ≌,∴3OD CE OA ===,2AE OB ==,∴5CD OE ==.∵CD x ∥轴,∴DCA FAC Ð=Ð.∵45BCA PAC Ð=Ð=°,∴DCA BCA FAC PAC Ð-Ð=Ð-Ð,即DCB FAP Ð=Ð.又∵90CDB AFP Ð=Ð=°,CB AP =,∴(AAS)CDB AFP V V ≌,∴321PF BD OD OB ==-=-=,5AF CD ==,∴358OF OA AF =+=+=,∴此时点P 的坐标为(81),;③如图,作CP AC ^,使CP AB =,连接BP ,则(SAS)ABC CPA V V ≌,∵90BAC PCA Ð=Ð=°,且CP AB = ,∴四边形ABPC 是矩形,∴90AB BP ABP =Ð=°, ,即90ABO PBM Ð+Ð=°,过点P 作PM y ^轴,则90BPM PBM Ð+Ð=°,∴ABO BPM Ð=Ð,在△AOB 和△BMP 中,AOB BMP ABO BPM AB BP Ð=ÐìïÐ=Ðíï=î,∴()AOB BMP AAS V V ≌,∴3BM OA ==,2PM OB == ,∴此时点P 的坐标为(25),;④当点P 与点B 重合时,点P 的坐标为(0)2,.综上可知,点P 的坐标为(6)2-,或(81),或(25),或(0)2,.。
八年级下册---平行四边形压轴题解析

八年级下册---平行四边形压轴题一.选择题(共15小题)1.(2012•玉环县校级模拟)如图,菱形ABCD中,AB=3,DF=1,∠DAB=60°,∠EFG=15°,FG⊥BC,则AE=()C D2.(2015•泰安模拟)如图,已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF,则下列结论:①CP平分∠BCD;②四边形ABED为平行四边形;③CQ将直角梯形ABCD分为面积相等的两部分;④△ABF为等腰三角形,其中不正确的有()3.(2014•武汉模拟)如图∠A=∠ABC=∠C=45°,E、F分别是AB、BC的中点,则下列结论,①EF⊥BD,②EF=BD,③∠ADC=∠BEF+∠BFE,④AD=DC,其中正确的是()4.(2014•市中区一模)在正方形ABCD中,点E为BC边的中点,点B′与点B关于AE对称,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠ADB′=75°;④∠CB′D=135°.其中正确的是()5.(2014•江阴市二模)在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE、BE、FA⊥AE交DP于点F,连接BF,FC.下列结论:①△ABE≌△ADF;②FB=AB;③CF⊥DP;④FC=EF其中正确的是()6.(2014•武汉模拟)如图,正方形ABCD的三边中点E、F、G.连ED交AF于M,GC 交DE于N,下列结论:①GM⊥CM;②CD=CM;③四边形MFCG为等腰梯形;④∠CMD=∠AGM.其中正确的有()7.(2013•绍兴模拟)如图,△ABC纸片中,AB=BC>AC,点D是AB边的中点,点E在边AC上,将纸片沿DE折叠,使点A落在BC边上的点F处.则下列结论成立的个数有()①△BDF是等腰直角三角形;②∠DFE=∠CFE;③DE是△ABC的中位线;④BF+CE=DF+DE.8.(2013•惠山区校级一模)如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=.下列结论:①△APD≌△AEB﹔②点B到直线AE的距离为﹔③EB⊥ED﹔④S△APD+S△APB=0.5+.其中正确结论的序号是()9.(2013•江苏模拟)在正方形ABCD外取一点E,连接AE、BE、DE,过A作AE的垂线交ED于点P,若AE=AP=1,PB=,下列结论:①△APD≌△AEB;②点B到直线AE的距离为;③S正方形ABCD=4+;其中正确的是()10.(2013•武汉模拟)如图,正方形ABCD的对角线相交于O点,BE平分∠ABO交AO 于E点,CF⊥BE于F点,交BO于G点,连结EG、OF.则∠OFG的度数是()11.(2012•武汉)在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点11+﹣11+11+或12.(2012•河南模拟)如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB 于点G,则S△CEF:S△DGF等于()13.(2012•杭州模拟)如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH (不重叠无缝隙).若①②③④四个平行四边形面积的和为28cm2,四边形ABCD面积是18cm2,则①②③④四个平行四边形周长的总和为()于点F.若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG、BG,∠BDG的大小是()15.(2012•碑林区校级模拟)如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=()八年级下册---平行四边形压轴题参考答案与试题解析一.选择题(共15小题)1.(2012•玉环县校级模拟)如图,菱形ABCD中,AB=3,DF=1,∠DAB=60°,∠EFG=15°,FG⊥BC,则AE=()C D,AE=AH+HE=1+.2.(2015•泰安模拟)如图,已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF,则下列结论:①CP平分∠BCD;②四边形ABED为平行四边形;③CQ将直角梯形ABCD分为面积相等的两部分;④△ABF为等腰三角形,其中不正确的有(),,,3.(2014•武汉模拟)如图∠A=∠ABC=∠C=45°,E、F分别是AB、BC的中点,则下列结论,①EF⊥BD,②EF=BD,③∠ADC=∠BEF+∠BFE,④AD=DC,其中正确的是()EF=ACEF=AC4.(2014•市中区一模)在正方形ABCD中,点E为BC边的中点,点B′与点B关于AE对称,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠ADB′=75°;④∠CB′D=135°.其中正确的是()=,==,5.(2014•江阴市二模)在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE、BE、FA⊥AE交DP于点F,连接BF,FC.下列结论:①△ABE≌△ADF;②FB=AB;③CF⊥DP;④FC=EF其中正确的是()6.(2014•武汉模拟)如图,正方形ABCD的三边中点E、F、G.连ED交AF于M,GC 交DE于N,下列结论:①GM⊥CM;②CD=CM;③四边形MFCG为等腰梯形;④∠CMD=∠AGM.其中正确的有()7.(2013•绍兴模拟)如图,△ABC纸片中,AB=BC>AC,点D是AB边的中点,点E在边AC上,将纸片沿DE折叠,使点A落在BC边上的点F处.则下列结论成立的个数有()①△BDF是等腰直角三角形;②∠DFE=∠CFE;③DE是△ABC的中位线;④BF+CE=DF+DE.8.(2013•惠山区校级一模)如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=.下列结论:①△APD≌△AEB﹔②点B到直线AE的距离为﹔③EB⊥ED﹔④S△APD+S△APB=0.5+.其中正确结论的序号是(),判断出PE=AE=BE==×1+×=0.5+的距离为9.(2013•江苏模拟)在正方形ABCD外取一点E,连接AE、BE、DE,过A作AE的垂线交ED于点P,若AE=AP=1,PB=,下列结论:①△APD≌△AEB;②点B到直线AE的距离为;③S正方形ABCD=4+;其中正确的是()PD BE=,所以=2+,PB=,由勾股定理得:BE=,PD=BE=,PD BE=,=2+.故选项10.(2013•武汉模拟)如图,正方形ABCD的对角线相交于O点,BE平分∠ABO交AO 于E点,CF⊥BE于F点,交BO于G点,连结EG、OF.则∠OFG的度数是()11.(2012•武汉)在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点11+﹣11+11+或AE=代入求出BE=DF=3﹣,,在BE=DF=3CF=5+3CE+CF=11+12.(2012•河南模拟)如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB 于点G,则S△CEF:S△DGF等于(),13.(2012•杭州模拟)如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH (不重叠无缝隙).若①②③④四个平行四边形面积的和为28cm2,四边形ABCD面积是18cm2,则①②③④四个平行四边形周长的总和为()×EM=xx14.(2012•淄博模拟)则在▱ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG、BG,∠BDG的大小是()15.(2012•碑林区校级模拟)如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=()。
八年级下压轴 50题(含答案及解析)

三.解答题(共46小题)
5.如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE= ,求AB的长;
(4)如图2,将线段AB绕点B沿顺时针方向旋转至BD,且OD⊥AD,延长DO交直线y=x+5于点P,求点P的坐标.
18.如图,在平面直角坐标系xoy中,直线y=﹣2x+4交y轴于点A,交x轴于点B.点C在y轴的负半轴上,且△ABC的面积为8,直线y=x和直线BC相交于点D.
(1)求直线BC的解析式;
(1)求证:∠BFC=∠BEA;
(2)求证:AM=BG+GM.
9.如图,正方形ABCD的对角线相交于点O.点E是线段DO上一点,连接CE.点F是∠OCE的平分线上一点,且BF⊥CF与CO相交于点M.点G是线段CE上一点,且CO=CG.
(1)若OF=4,求FG的长;
(2)求证:BF=OG+CF.
10.(1)如图①,两个正方形的边长均为3,求三角形DBF的面积.
(1)当点P运动到边AB的中点处时,点A′与点B′重合于点F处,过点C作CK⊥EF于Kห้องสมุดไป่ตู้求CK的长;
(2)当点P运动到某一时刻,若P,A',B'三点恰好在同一直线上,且A'B'=4,试求此时AP的长.
21.小华思考解决如下问题:
原题:如图1,点P,Q分别在菱形ABCD的边BC,CD上,∠PAQ=∠B,求证:AP=AQ.
16.如图,矩形OABC的两条边OA、OC分别在y轴和x轴上,已知点B坐标为(4,﹣3).把矩形OABC沿直线DE折叠,使点C落在点A处,直线DE与OC、AC、AB的交点分别为D、F、E.
中学数学八年级下册 期末压轴题(含答案)

八年级下册期末压轴题一.填空题(共1小题)1.(2018春•西城区期末)在查阅勾股定理证明方法的过程中,小红看到一种利用“等积变形﹣﹣同底等高的两个平行四边形的面积相等”证明勾股定理的方法,并尝试按自己的理解将这种方法介绍给同学.(1)根据信息将以下小红的证明思路补充完整:①如图1,在△ABC中,∠ACB=90°,四边形ADEC,四边形BCFG,四边形ABPQ都是正方形.延长QA交DE于点M,过点C作CN∥AM交DE的延长线于点N,可得四边形AMNC的形状是;②在图1中利用“等积变形”可得S正方形ADEC=;③如图2,将图1中的四边形AMNC沿直线MQ向下平移MA的长度,得到四边形A′M′N′C′,即四边形QACC′;④设CC′交AB于点T,延长CC′交QP于点H,在图2中再次利用“等积变形”可得S四边形QACC'=,则有S正方形ADEC=;⑤同理可证S正方形BCFG=S四边形HTBP,因此得到S正方形ADEC+S正方形BCFG=S正方形ABPQ,进而证明了勾股定理.(2)小芳阅读完小红的证明思路后,对其中的第③步提出了疑问,请将以下小红对小芳的说明补充完整:图1中△≌△,则有=AB=AQ,由于平行四边形的对边相等,从而四边形AMNC沿直线MQ向下平移MA的长度,得到四边形QACC′.二.解答题(共42小题)2.(2020春•海淀区校级期末)已知△ABC中,∠BAC=90°,AB=AC,点M为BC的中点,点P为AB边上一动点,点N为线段BM上一动点,以点P为旋转中心,将△BPN逆时针旋转90°得到△DPE,且点B的对应点为D,点N的对应点为E.(1)当点N与点M重合,且点P不是AB的中点时.①依据题意补全图1;②证明:以A,M,E,D为顶点的四边形是矩形.(2)连接EM,若AB=4,写出一个BN的值,使得EM=EA成立,并证明.3.(2020春•海淀区校级期末)∠MON=45°,点P在射线OM上,点A,B在射线ON上(点B与点O在点A的两侧),且AB=1,以点P为旋转中心,将线段AB逆时针旋转90°,得到线段CD(点C与点A对应,点D与点B对应).(1)如图,若OA=1,OP=,依题意补全图形;(2)若OP=,当线段AB在射线ON上运动时,线段CD与射线OM有公共点,求OA的取值范围.(要写过程)4.(2019•都江堰市模拟)定义:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根为x1,x2(x1<x2),分别以x1,x2为横坐标和纵坐标得到点M(x1,x2),则称点M为该一元二次方程的衍生点.(1)若方程为x2﹣2x=0,写出该方程的衍生点M的坐标.(2)若关于x的一元二次方程x2﹣(2m+1)x+2m=0(m<0)的衍生点为M,过点M 向x轴和y轴作垂线,两条垂线与坐标轴恰好围成一个正方形,求m的值.(3)是否存在b,c,使得不论k(k≠0)为何值,关于x的方程x2+bx+c=0的衍生点M 始终在直线y=kx﹣2(k﹣2)的图象上,若有请直接写出b,c的值,若没有说明理由.5.(2020春•海淀区校级期末)如图,在正方形ABCD中,AB=6,M是CD边上一动点(不与D点重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB到点F,使得BF=DM,连接EF,AF.(1)当DM=2时,依题意补全图1;(2)在(1)的条件下,求线段EF的长;(3)当点M在CD边上运动时,能使△AEF为等腰三角形,请直接写出此时DM与AD 的数量关系.6.(2019春•朝阳区期末)对于平面直角坐标系xOy中的图形M和点P(点P在M内部或M上),给出如下定义:如果图形M上存在点Q,使得0≤PQ≤2,那么称点P为图形M 的和谐点.已知点A(﹣4,3),B(﹣4,﹣3),C(4,﹣3),D(4,3).(1)在点P₁(﹣2,1),P2(﹣1,0),P3(3,3)中,矩形ABCD的和谐点是;(2)如果直线y=上存在矩形ABCD的和谐点P,直接写出点P的横坐标t的取值范围;(3)如果直线y=上存在矩形ABCD的和谐点E,F,使得线段EF上的所有点(含端点)都是矩形ABCD的和谐点,且EF,直接写出b的取值范围.7.(2017春•昌平区期末)(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.①如果AD=4,BD=9,那么CD=;②如果以CD的长为边长作一个正方形,其面积为S1,以BD,AD的长为邻边长作一个矩形,其面积为S2,则S1S2(填“>”、“=”或“<”).(2)基于上述思考,小泽进行了如下探究:①如图2,点C在线段AB上,正方形FGBC,ACDE和EDMN,其面积比为1:4:4,连接AF,AM,求证AF⊥AM;②如图3,点C在线段AB上,点D是线段CF的黄金分割点,正方形ACDE和矩形CBGF的面积相等,连接AF交ED于点M,连接BF交ED延长线于点N,当CF=a时,直接写出线段MN的长为.8.(2018春•浉河区期末)如图1,点A(a,b)在平面直角坐标系xOy中,点A到坐标轴的垂线段AB,AC与坐标轴围成矩形OBAC,当这个矩形的一组邻边长的和与积相等时,点A称作“垂点”,矩形称作“垂点矩形”.(1)在点P(1,2),Q(2,﹣2),N(,﹣1)中,是“垂点”的点为;(2)点M(﹣4,m)是第三象限的“垂点”,直接写出m的值;(3)如果“垂点矩形”的面积是,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标;(4)如图2,平面直角坐标系的原点O是正方形DEFG的对角线的交点,当正方形DEFG 的边上存在“垂点”时,GE的最小值为.9.(2018春•丰台区期末)如图,菱形ABCD中,∠BAD=60°,过点D作DE⊥AD交对角线AC于点E,连接BE,取BE的中点F,连接DF.(1)请你根据题意补全图形;(2)请用等式表示线段DF、AE、BC之间的数量关系,并证明.10.(2018春•丰台区期末)在平面直角坐标系xOy中,M为直线l:x=a上一点,N是直线l外一点,且直线MN与x轴不平行,若MN为某个矩形的对角线,且该矩形的边均与某条坐标轴垂直,则称该矩形为直线l的“伴随矩形”.如图为直线l的“伴随矩形”的示意图.(1)已知点A在直线l:x=2上,点B的坐标为(3,﹣2)①若点A的纵坐标为0,则以AB为对角线的直线l的“伴随矩形”的面积是;②若以AB为对角线的直线l的“伴随矩形”是正方形,求直线AB的表达;(2)点P在直线l:x=m上,且点P的纵坐标为4,若在以点(2,1),(﹣2,1),(﹣2,﹣1),(2,﹣1)为顶点的四边形上存在一点Q,使得以PQ为对角线的直线l的“伴随矩形”为正方形,直接写出m的取值范围.11.(2019春•海淀区期末)如图,在平面直角坐标系xOy中,直线y=kx+7与直线y=x﹣2交于点A(3,m)(1)求k,m的值;(2)已知点P(n,n),过点P作垂直于y轴的直线与直线y=x﹣2交于点M,过点P 作垂直于x轴的直线与直线y=kx+7交于点N(P与N不重合).若PN≤2PM,结合图象,求n的取值范围.12.(2019春•海淀区期末)在Rt△ABC中,∠BAC=90°,点O是△ABC所在平面内一点,连接OA,延长OA到点E,使得AE=OA,连按OC,过点B作BD与OC平行,并使∠DBC=∠OCB,且BD=OC,连按DE.(1)如图一,当点O在Rt△ABC内部时,①按题意补全图形;②猜想DE与BC的数量关系,并证明.(2)若AB=AC(如图二),且∠OCB=30°,∠OBC=15°,求∠AED的大小.13.(2017春•西城区期末)如图所示,在平面直角坐标系xOy中,B,C两点的坐标分别为B(4,0),C(4,4),CD⊥y轴于点D,直线l经过点D.(1)直接写出点D的坐标;(2)作CE⊥直线l于点E,将直线CE绕点C逆时针旋转45°,交直线l于点F,连接BF.①依题意补全图形;②通过观察、测量,同学们得到了关于直线BF与直线l的位置关系的猜想,请写出你的猜想;③通过思考、讨论,同学们形成了证明该猜想的几种思路:思路1:作CM⊥CF,交直线l于点M,可证△CBF≌△CDM,进而可以得出∠CFB=45°,从而证明结论.思路2:作BN⊥CE,交直线CE于点N,可证△BCN≌△CDE,进而证明四边形BFEN 为矩形,从而证明结论.…请你参考上面的思路完成证明过程.(一种方法即可)解:(1)点D的坐标为,(2)①补全图形,②直线BF与直线l的位置关系是,③证明:14.(2017春•西城区期末)如图,在由边长都为1个单位长度的小正方形组成的6×6正方形网格中,点A,B,P都在格点上请画出以AB为边的格点四边形(四个顶点都在格点的四边形),要求同时满足以下条件:条件1:点P到四边形的两个顶点的距离相等;条件2:点P在四边形的内部或其边上;条件3:四边形至少一组对边平行.(1)在图①中画出符合条件的一个▱ABCD,使点P在所画四边形的内部;(2)在图②中画出符合条件的一个四边形ABCD,使点P在所画四边形的边上;(3)在图③中画出符合条件的一个四边形ABCD,使∠D=90°,且∠A≠90°.15.(2017春•西城区期末)如图,在平面直角坐标系xOy中,动点A(a,0)在x轴的正半轴上,定点B(m,n)在第一象限内(m<2≤a),在△OAB外作正方形ABCD和正方形OBEF,连接FD,点M为线段FD的中点,作BB1⊥x轴于点B1,作FF1⊥x轴于点F1.(1)填空:由≌△,及B(m,n)可得点F的坐标为,同理可得点D的坐标为;(说明:点F,点D的坐标用含m,n,a的式子表示)(2)直接利用(1)的结论解决下列问题:①当点A在x轴的正半轴上指定范围内运动时,点M总落在一个函数图象上,求该函数的解析式(不必写出自变量x的取值范围);②当点A在x轴的正半轴上运动且满足2≤a≤8时,求点M所经过的路径的长.16.(2019春•西城区期末)四边形ABCD是正方形,AC是对角线,E是平面内一点,且CE<BC,过点C作FC⊥CE,且CF=CE.连接AE、AF,M是AF的中点,作射线DM 交AE于点N.(1)如图1,若点E,F分别在BC,CD边上.求证:①∠BAE=∠DAF;②DN⊥AE;(2)如图2,若点E在四边形ABCD内,点F在直线BC的上方,求∠EAC与∠ADN 的和的度数.17.(2019春•西城区期末)如图1,在菱形ABCD中,对角线AC,BD相交于点O,AC=4cm,BD=2cm,E,F分别是AB,BC的中点,点P是对角线AC上的一个动点,设AP =xcm,PE=y1cm,PF=y2cm.小明根据学习函数的经验,分别对这两种函数随自变量的变化而变化的情况进行了探究,下面是小明探究过程,请补充完整:(1)画函数y1的图象①按表中自变量的值进行取点、画图、测量,得到了y1与x的几组对应值:x/cm00.51 1.52 2.53 3.54y1/cm 1.120.50.71 1.12 1.58 2.06 2.55 3.04②在图2所给坐标系中描出补全后的表中的各对应值为坐标的点,画出函数y1的图象;(2)画函数y2的图象,在同一坐标系中,画出函数y2的图象;(3)根据画出的函数y1的图象、函数y2的图象,解决问题①函数y1的最小值是;②函数y1的图象与函数y2的图象的交点表示的含义是;③若PE=PC,AP的长约为cm18.(2019春•西城区期末)平面直角坐标系xOy中,对于点M和图形W,若图形W上存在一点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称点M与图形W是“中心轴对称”.对于图形W1和图形W2,若图形W1和图形W2分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形W1和图形W2是“中心轴对称”的.特别地,对于点M和点N,若存在一条经过原点的直线l,使得点M与点N关于直线l对称,则称点M和点N是“中心轴对称”的.(1)如图1,在正方形ABCD中,点A(1,0),点C(2,1),①下列四个点P1(0,1),P2(2,2),P3(﹣,0),P4(﹣,﹣)中,与点A是“中心轴对称”的是;②点E在射线OB上,若点E与正方形ABCD是“中心轴对称”的,求点E的横坐标x E的取值范围;(2)四边形GHJK的四个顶点的坐标分别为G(﹣2,2),H(2,2),J(2,﹣2),K (﹣2,﹣2),一次函数y=x+b图象与x轴交于点M,与y轴交于点N,若线段MN 与四边形GHJK是“中心轴对称”的,直接写出b的取值范围.19.(2019春•大兴区期末)有这样一个问题:探究函数y=+1的图象与性质.小东根据学习函数的经验,对函数y=+1的图象与性质进行了探究.下面是小东的探究过程,请补充完整:(1)函数y=+1的自变量x的取值范围是;(2)如表是y与x的几组对应值.x…﹣3﹣2﹣112345…y…393m…求m的值;(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(4)结合函数的图象,写出该函数的一条性质:.20.(2019春•大兴区期末)如图1,四边形ABCD是平行四边形,A,B是直线l上的两点,点B关于AD的对称点为M,连接CM交AD于F点.(1)若∠ABC=90°,如图1,①依题意补全图形;②判断MF与FC的数量关系是;(2)如图2,当∠ABC=135°时,AM,CD的延长线相交于点E,取ME的中点H,连结HF.用等式表示线段CE与AF的数量关系,并证明.21.(2019春•大兴区期末)在平面直角坐标系xOy中,记y与x的函数y=a(x﹣m)2+n (m≠0,n≠0)的图象为图形G,已知图形G与y轴交于点A,当x=m时,函数y=a (x﹣m)2+n有最小(或最大)值n,点B的坐标为(m,n),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线.(1)如图1,若函数y=(x﹣2)2+1的图象记为图形G,求图形G的伴随直线的表达式;(2)如图2,若图形G的伴随直线的表达式是y=x﹣3,且伴随四边形的面积为12,求y与x的函数y=a(x﹣m)2+n(m>0,n<0)的表达式;(3)如图3,若图形G的伴随直线是y=﹣2x+4,且伴随四边形ABCD是矩形,求点B 的坐标.22.(2019春•石景山区期末)正方形ABCD中,点P是直线AC上的一个动点,连接BP,将线段BP绕点B顺时针旋转90°得到线段BE,连接CE.(1)如图1,若点P在线段AC上,①直接写出∠ACE的度数为°;②求证:P A2+PC2=2PB2;(2)如图2,若点P在CA的延长线上,P A=1,PB=,①依题意补全图2;②直接写出线段AC的长度为.23.(2020春•浦东新区期末)在平面直角坐标系xOy中,若P,Q为某个矩形不相邻的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.图1为点P,Q的“相关矩形”的示意图.已知点A的坐标为(1,2).(1)如图2,点B的坐标为(b,0).①若b=﹣2,则点A,B的“相关矩形”的面积是;②若点A,B的“相关矩形”的面积是8,则b的值为.(2)如图3,点C在直线y=﹣1上,若点A,C的“相关矩形”是正方形,求直线AC 的表达式;(3)如图4,等边△DEF的边DE在x轴上,顶点F在y轴的正半轴上,点D的坐标为(1,0).点M的坐标为(m,2),若在△DEF的边上存在一点N,使得点M,N的“相关矩形”为正方形,请直接写出m的取值范围.24.(2016春•无锡期末)已知:如图1,在平面直角坐标中,A(12,0),B(6,6),点C 为线段AB的中点,点D与原点O关于点C对称.(1)利用直尺和圆规在图1中作出点D的位置(保留作图痕迹),判断四边形OBDA的形状,并说明理由;(2)在图1中,动点E从点O出发,以每秒1个单位的速度沿线段OA运动,到达点A 时停止;同时,动点F从点O出发,以每秒a个单位的速度沿OB→BD→DA运动,到达点A时停止.设运动的时间为t(秒).①当t=4时,直线EF恰好平分四边形OBDA的面积,求a的值;②当t=5时,CE=CF,请直接写出a的值.25.(2019春•东城区期末)有这样一个问题:探究函数y=﹣3的图象与性质.小亮根据学习函数的经验,对y=﹣3的图象与性质进行了探究下面是小亮的探究过程,请补充完整:(1)函数y=3中自变量x的取值范围是(2)下表是y与x的几组对应值.x…﹣3﹣2﹣102345…y…﹣﹣﹣4﹣5﹣7m﹣1﹣2﹣﹣…求m的值;(1)在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;(2)根据画出的函数图象,发现下列特征:该函数的图象与直线x=1越来越靠近而永不相交,该函数的图象还与直线越来越靠近而永不相交.26.(2019春•东城区期末)在正方形ABCD中,点E是射线AC上一点,点F是正方形ABCD 外角平分线CM上一点,且CF=AE,连接BE,EF.(1)如图1,当E是线段AC的中点时,直接写出BE与EF的数量关系;(2)当点E不是线段AC的中点,其它条件不变时,请你在图2中补全图形,判断(1)中的结论是否成立,并证明你的结论;(3)当点B,E,F在一条直线上时,求∠CBE的度数.(直接写出结果即可)27.(2019春•东城区期末)对于平面直角坐标系xOy中的点P和正方形给出如下定义:若正方形的对角线交于点O,四条边分别和坐标轴平行,我们称该正方形为原点正方形.当原点正方形上存在点Q,满足PQ≤1时,称点P为原点正方形的友好点.(1)当原点正方形边长为4时,①在点P1(0,0),P2(﹣1,1),P3(3,2)中,原点正方形的友好点是;②点P在直线y=x的图象上,若点P为原点正方形的友好点,求点P横坐标的取值范围;(2)一次函数y=﹣x+2的图象分别与x轴,y轴交于点A,B,若线段AB上存在原点正方形的友好点,直接写出原点正方形边长a的取值范围.28.(2019春•昌平区期末)如图,△ABC中,AB=BC=5cm,AC=6cm,点P从顶点B出发,沿B→C→A以每秒1cm的速度匀速运动到A点,设运动时间为x秒,BP长度为ycm.某学习小组对函数y随自变量x的变化而变化的规律进行了探究.下面是他们的探究过程,请补充完整:(1)通过取点,画图,测量,得到了x(秒)与y(cm)的几组对应值:x01234567891011y0.0 1.0 2.0 3.0 4.0 4.5 4.14 4.5 5.0要求:补全表格中相关数值(保留一位小数);(2)在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当x约为时,BP=CP.29.(2019春•昌平区期末)在矩形ABCD中,AB=3,AD=2,点E是射线DA上一点,连接EB,以点E为圆心EB长为半径画弧,交射线CB于点F,作射线FE与CD延长线交于点G.(1)如图1,若DE=5,则∠DEG=°;(2)若∠BEF=60°,请在图2中补全图形,并求EG的长;(3)若以E,F,B,D为顶点的四边形是平行四边形,此时EG的长为.30.(2019春•昌平区期末)在平面直角坐标系中,过一点分别作x轴,y轴的垂线,如果由这点、原点及两个垂足为顶点的矩形的周长与面积相等,那么称这个点是平面直角坐标系中的“巧点”.例如,图1中过点P(4,4)分別作x轴,y轴的垂线,垂足为A,B,矩形OAPB的周长为16,面积也为16,周长与面积相等,所以点P是巧点.请根据以上材料回答下列问题:(1)已知点C(1,3),D(﹣4,﹣4),E(5,﹣),其中是平面直角坐标系中的巧点的是;(2)已知巧点M(m,10)(m>0)在双曲线y=(k为常数)上,求m,k的值;(3)已知点N为巧点,且在直线y=x+3上,求所有满足条件的N点坐标.31.(2019春•延庆区期末)已知:在正方形ABCD中,点H在对角线BD上运动(不与B,D重合)连接AH,过H点作HP⊥AH于H交直线CD于点P,作HQ⊥BD于H交直线CD于点Q.(1)当点H在对角线BD上运动到图1位置时,则CQ与PD的数量关系是.(2)当H点运动到图2所示位置时①依据题意补全图形.②上述结论还成立吗?若成立,请证明.若不成立,请说明理由.(3)若正方形边长为,∠PHD=30°,直接写出PC长.32.(2019春•延庆区期末)对于一次函数y=kx+b(k≠0),我们称函数y[m]=为它的m分函数(其中m为常数).例如,y=3x+2的4分函数为:当x≤4时,y[4]=3x+2;当x>4时,y[4]=﹣3x﹣2.(1)如果y=x+1的﹣1分函数为y[﹣1],①当x=4时,y[﹣1];当y[﹣1]=﹣3时,x=.②求双曲线y=与y[﹣1]的图象的交点坐标;(2)如果y=﹣x+2的0分函数为y[0],正比例函数y=kx(k≠0)与y=﹣x+2的0分函数y[0]的图象无交点时,直接写出k的取值范围.33.(2017春•西城区校级期末)如图1,在等腰△ABC中,AB=AC,∠BAC=a,点P是线段AB的中点,点E是线段CB延长线上一点,且PE=PC,将线段PC绕点P顺时针旋转α得到PD,连接BD.(1)如图2,若α=60°,其他条件不变,先补全图形,然后探究线段BD和BC之间的数量关系,并说明理由.(2)如图3,若α=90°,其他条件不变,探究线段BP、BD和BC之间的等量关系,并说明理由.34.(2017春•西城区校级期末)某学习小组有a个男生,b个女生,其中a和b同时满足以下三个条件:①男生人数不少于女生人数;②a,b是一元二次方程mx2﹣(3m+8)x+24=0的两个实数根;③男生和女生的总人数不超过10人.请根据以上信息,回答下面两个问题:(1)求整数m的值?(2)若T=ma+b,求T的所有可能的值?35.(2017春•西城区校级期末)设p,q都是实数,且p<q.我们规定:如果变量x的取值范围为p≤x≤q,则把实数L=q﹣p叫做变量x的取值宽度.如果反比例函数y=在p ≤x≤q的函数值y的取值宽度与自变量x的取值宽度相等,则称此函数在p≤x≤q上具有“等宽性”.例如:函数y=的函数值y的取值范围为≤y≤2,故而函数y=具有“等宽性”.(1)下列函数哪些函数具有“等宽性”:(填序号)①y=(1≤x≤2);②y=﹣(﹣2≤x≤﹣1);③y=﹣(1≤x≤6);④y=﹣(﹣4≤x≤﹣1);(2)已知函数y=﹣在a≤x≤﹣1上具有“等宽性”,求a的值;(3)已知直线y=kx+b与函数y=﹣交于A(x1,y1)、B(x2,y2)两点,且函数y=﹣在x1≤x≤x2上具有“等宽性”,则k=.36.(2018春•海淀区期末)在正方形ABCD中,连接BD,P为射线CB上的一个动点(与点C不重合),连接AP,AP的垂直平分线交线段BD于点E,连接AE,PE.提出问题:当点P运动时,∠APE的度数,DE与CP的数量关系是否发生改变?探究问题:(1)首先考察点P的两个特殊位置:①当点P与点B重合时,如图1﹣1所示,∠APE=°,用等式表示线段DE与CP之间的数量关系:;②当BP=BC时,如图1﹣2所示,①中的结论是否发生变化?直接写出你的结论:;(填“变化”或“不变化”)(2)然后考察点P的一般位置:依题意补全图2﹣1,2﹣2,通过观察、测量,发现:(1)中①的结论在一般情况下(填“成立”或“不成立”)(3)证明猜想:若(1)中①的结论在一般情况下成立,请从图2﹣1和图2﹣2中任选一个进行证明;若不成立,请说明理由.37.(2018春•海淀区期末)在平面直角坐标系xOy中,A(O,2),B(4,2),C(4,0).P 为矩形ABCO内(不包括边界)一点,过点P分别作x轴和y轴的平行线,这两条平行线分矩形ABCO为四个小矩形,若这四个小矩形中有一个矩形的周长等于OA,则称P 为矩形ABCO的矩宽点.例如:下图中的为矩形ABCO的一个矩宽点.(1)在点D(,),E(2,1),F(,)中,矩形ABCO的矩宽点是;(2)若G(m,)为矩形ABCO的矩宽点,求m的值;(3)若一次函数y=k(x﹣2)﹣1(k≠0)的图象上存在矩形ABCO的矩宽点,则k的取值范围是.38.(2019春•曲阜市期末)如图,在菱形ABCD中,CE⊥AB交AB延长线于点E,点F为点B关于CE的对称点,连接CF,分别延长DC,CF至点G,H,使FH=CG,连接AG,DH交于点P.(1)依题意补全图1;(2)猜想AG和DH的数量关系并证明;(3)若∠DAB=70°,是否存在点G,使得△ADP为等边三角形?若存在,求出CG的长;若不存在,说明理由.39.(2018春•朝阳区期末)在平面直角坐标系xOy中,对于与坐标轴不平行的直线l和点P,给出如下定义:过点P作x轴,y轴的垂线,分别交直线l于点M,N,若PM+PN≤4,则称P为直线l的近距点,特别地,直线上l所有的点都是直线l的近距点.已知点A(﹣,0),B(0,2),C(﹣2,2).(1)当直线l的表达式为y=x时,①在点A,B,C中,直线l的近距点是;②若以OA为边的矩形OAEF上所有的点都是直线l的近距点,求点E的纵坐标n的取值范围;(2)当直线l的表达式为y=kx时,若点C是直线l的近距点,直接写出k的取值范围.40.(2018春•昌平区期末)如图,将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3).动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动秒时,动点P从点A出发以相同的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).(1)OP=,OQ=;(用含t的代数式表示)(2)当t=1时,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处.①求点D的坐标;②如果直线y=kx+b与直线AD平行,那么当直线y=kx+b与四边形P ABD有交点时,求b的取值范围.41.(2018春•昌平区期末)在四边形ABCD中,E、F分别是边BC、CD的中点,连接AE,AF.(1)如图1,若四边形ABCD的面积为5,则四边形AECF的面积为;(2)如图2,延长AE至G,使EG=AE,延长AF至H,使FH=AF,连接BG、GH、HD、DB.求证:四边形BGHD是平行四边形;(3)如图3,对角线AC、BD相交于点M,AE与BD交于点P,AF与BD交于点N.直接写出BP、PM、MN、ND的数量关系.42.(2018春•西城区期末)在矩形ABCD中,BE平分∠ABC交CD边于点E.点F在BC 边上,且FE⊥AE.(1)如图1,①∠BEC=°;②在图1已有的三角形中,找到一对全等的三角形,并证明你的结论;(2)如图2,FH∥CD交AD于点H,交BE于点M.NH∥BE,NB∥HE,连接NE.若AB=4,AH=2,求NE的长.43.(2018春•西城区期末)在△ABC中,M是BC边的中点.(1)如图1,BD,CE分别是△ABC的两条高,连接MD,ME,则MD与ME的数量关系是;若∠A=70°,则∠DME=°;(2)如图2,点D,E在∠BAC的外部,△ABD和△ACE分别是以AB,AC为斜边的直角三角形,且∠BAD=∠CAE=30°,连接MD,ME.①判断(1)中MD与ME的数量关系是否仍然成立,并证明你的结论;②求∠DME的度数;(3)如图3,点D,E在∠BAC的内部,△ABD和△ACE分别是以AB,AC为斜边的直角三角形,且∠BAD=∠CAE=α,连接MD,ME.直接写出∠DME的度数(用含α的式子表示).八年级下册期末压轴题参考答案与试题解析一.填空题(共1小题)1.(2018春•西城区期末)在查阅勾股定理证明方法的过程中,小红看到一种利用“等积变形﹣﹣同底等高的两个平行四边形的面积相等”证明勾股定理的方法,并尝试按自己的理解将这种方法介绍给同学.(1)根据信息将以下小红的证明思路补充完整:①如图1,在△ABC中,∠ACB=90°,四边形ADEC,四边形BCFG,四边形ABPQ都是正方形.延长QA交DE于点M,过点C作CN∥AM交DE的延长线于点N,可得四边形AMNC的形状是平行四边形;②在图1中利用“等积变形”可得S正方形ADEC=S四边形AMNC;③如图2,将图1中的四边形AMNC沿直线MQ向下平移MA的长度,得到四边形A′M′N′C′,即四边形QACC′;④设CC′交AB于点T,延长CC′交QP于点H,在图2中再次利用“等积变形”可得S四边形QACC'=S四边形QATH,则有S正方形ADEC=S四边形QATH;⑤同理可证S正方形BCFG=S四边形HTBP,因此得到S正方形ADEC+S正方形BCFG=S正方形ABPQ,进而证明了勾股定理.(2)小芳阅读完小红的证明思路后,对其中的第③步提出了疑问,请将以下小红对小芳的说明补充完整:图1中△ADM≌△ABC,则有AM=AB=AQ,由于平行四边形的对边相等,从而四边形AMNC沿直线MQ向下平移MA的长度,得到四边形QACC′.【分析】根据平行四边形的性质、正方形的性质、全等三角形的判定和性质、等高模型即可解决问题;【解答】解:(1)∵四边形ACED是正方形,∴AC∥MN,∵AM∥CN,∴四边形AMNC是平行四边形,∴S正方形ADEC=S平行四边形AMNC,∵AD=AC,∠D=∠ACB,∠DAC=∠MAB,∴∠DAM=∠CAB,∴△ADM≌△ACB,∴AM=AB=AQ,∴图1中的四边形AMNC沿直线MQ向下平移MA的长度,得到四边形A′M′N′C′,即四边形QACC′,∴S四边形QACC′=S四边形QATH,则有S正方形ADEC=S四边形QATH,∴同理可证S正方形BCFG=S四边形HTBP,因此得到S正方形ADEC+S正方形BCFG=S正方形ABPQ;故答案为平行四边形,S四边形AMNC,S四边形QATH,S四边形QATH;(2)由(1)可知:△ADM≌△ACB,∴AM=AB=AQ,故答案为ADM,ACB,AM;【点评】本题考查平行四边形的性质、正方形的性质、全等三角形的判定和性质、等高模型等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,属于中考创新题目.二.解答题(共42小题)2.(2020春•海淀区校级期末)已知△ABC中,∠BAC=90°,AB=AC,点M为BC的中点,点P为AB边上一动点,点N为线段BM上一动点,以点P为旋转中心,将△BPN 逆时针旋转90°得到△DPE,且点B的对应点为D,点N的对应点为E.(1)当点N与点M重合,且点P不是AB的中点时.①依据题意补全图1;②证明:以A,M,E,D为顶点的四边形是矩形.(2)连接EM,若AB=4,写出一个BN的值,使得EM=EA成立,并证。
上海(沪)八年级第二学期期末数学压轴题及答案(可转为word)
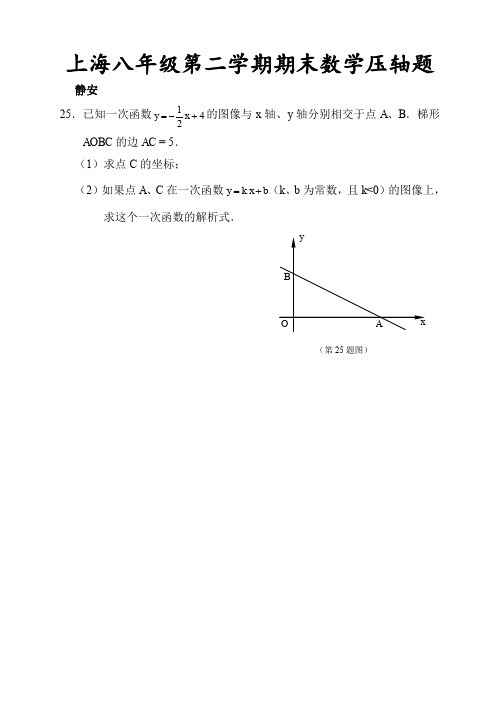
0 8k b, ∴ „„„„„„„„„„„„„„„„„„„„„„„„„(1 分) 4 5k b,
4 k , 3 „„„„„„„„„„„„„„„„„„„„„„„„„(1 分) ∴ 32 b . 3
4 32 .„„„„„„„„„„„„(1 分) x 3 3 26.解: (1)BF +AG= AE.„„„„„„„„„„„„„„„„„„„„„„(1 分) 证明如下:过点 F 作 FH⊥DA,垂足为 H, ∵在正方形 ABCD 中,∠DAE=∠B=90°,∴四边形 ABFH 是矩形.„(1 分) ∴FH=AB=DA.∵BD⊥FG,∴∠G=90°–∠ADE=∠DEA. 又∴∠DAE=∠FHG=90°,∴△FHG≌△DAE. „„„„„„„„„„(1 分) ∴GH=AE,即 HA+AG=AE.∵BF=HA,∴BF+AG=AE.„„„„„„(1 分)
本题满分12分其中第1小题5分第2小题3分第3小题4bcaebcdfdfaeefad四边形aefd是平行四边形efad5aedf?????????????????????????1abcd5rtabertdcfbecfefbccfbecf3在rtabeabaeaebqapaepdcqqcdpabqp当四边形abqp与四边形qcdp的面积相等时3当四边形abqp是平行四边形时pqab当四边形qcdp是平行四边形时可得pqcdcdabpqab此时cqpd11时pqab
FB 3 ,且 AC 10 ,求 FC 的值. BD 5
A
D
F
E
B
C
26. 在梯形 ABCD 中, ∠ABC= 90 , AD∥BC, BC>AD, AB=8cm, BC=18cm, CD=10 cm,点 P 从点 B 开始沿 BC 边向终点 C 以每秒 3cm 的速度移动,点 Q 从点 D 开始沿 DA 边向终点 A 以每秒 2cm 的速度移动,设运动时间为 t 秒. (1)求四边形 ABPQ 为矩形时 t 的值; (2)若题设中的“BC=18cm”改变为“BC= k cm” ,其它条件都不变,要 使四边形 PCDQ 是等腰梯形,求 t 与 k 的函数关系式,并写出 k 的取值范围; (3)在移动的过程中,是否存在 t 使 P、Q 两点 的距离为 10cm ,若存在求 t 的值. 若不存在请说明 理由?
八年级下册数学期末压轴题汇总(含解析)

(近三年)长春市八年级下数学期末压轴题(23.24题)长春市绿园区2020.7八下数学期末试题:24.(10分)如图,在矩形ABCD 中,AB=4,BC=10,E 、F 分别为BC 、AD 的中点,点P 从点A 出发,以每秒2个单位长度的速度沿AD 向终点D 速运动,作PQ ⊥BC 于Q ,当点P 不与点F 重合时,设四边形PQEF 的面积为S ,点P 的运动时间为t(秒)(1)当点P 与点D 重合时,求t 的值(2)用含t 的代数式表示线段PF (3)求S 与t 之间的函数关系式(4)当四边形PQEF 的对角线互相垂直时,直接写出的值24.(12分)如图,在平面直角坐标系中,A(-2,1),B(1,1).直线y =kx +3与y 轴相交于点C(1)在平面直角坐标系中标记出点C 的位置(2)当直线y =kx +3与直线y =2x 平行时,k 的值为;(3)当直线y =kx +3恰好经过点A 时,求直线y =kx +3的函数关系式;(4)当直线y =kx +3与线段AB 有公共点时,直接写出k 的取值范围。
B A PFDQE C01234-1-2-3-4xyAB -2-3-41234-1答案:23.(1)由题意,得2t =10(1分)t =5(2分)(2)当0≤t <25时,PF =5-2t 当25<t ≤5时,PF =2t -5(5分)(3)当0≤t <25时,S =20-8t当25<t ≤5时,S =8t -20(8分)(4)t =21或t =29(10分)评分说明:第(2)问写成PF =∣5-2t ∣或PF=∣2t -5∣扣1分第(2)间写成当0≤t ≤25一时,PF =5-2t 当25<t ≤5时,PF =2t -5不扣分第(2)、(3)问两个关系式各1分,取值范围共1分24.(1)点C 标记在(0,3)的位置(2分)(2)2(4分)(3)把(-2,1)代入y =kx +3得1=-2k +3(6分)解,得k =1(8分)∴y =x +3(10分)(4)k ≤-2或k ≥1(12分)评分说明:第(1)问只要位置标记正确即可给分长春市朝阳区2020.7数学八下期末试题23.(10分)如图在Rt ∆ABC 中∠C =90º,过点A 作线段AD 平行射线BC ,AB=10,BC=6,AD=15。
人教版八年级下册压轴题训练(含答案)

人教版八年级下册压轴题训练(含答案)压轴题训练01一.解答题(共3小题)1.如图①,已知抛物线y=ax2+bx+c的图象经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P 是抛物线上的一个动点,设其横坐标为m.(1)求抛物线的解析式;(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m 为何值时,四边形AOPE 面积最大,并求出其最大值;(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.【分析】(1)利用对称性可得点D的坐标,利用交点式可得抛物线的解析式;(2)设P(m,m2﹣4m+3),根据OE的解析式表示点G的坐标,表示PG的长,根据面积和可得四边形AOPE的面积,利用配方法可得其最大值;(3)存在四种情况:如图3,作辅助线,构建全等三角形,证明△OMP≌△PNF,根据|OM|=|PN|,列方程可得点P的坐标;同理可得其他图形中点P的坐标.【解答】解:(1)如图1,设抛物线与x轴的另一个交点为D,由对称性得:D(3,0),设抛物线的解析式为:y=a(x﹣1)(x﹣3),把A(0,3)代入得:3=3a,a=1,∴抛物线的解析式;y=x2﹣4x+3;(2)如图2,∵△AOE的面积是定值,所以当△OEP面积最大时,四边形AOPE面积最大,设P(m,m2﹣4m+3),∵OE平分∠AOB,∠AOB=90°,∴∠AOE=45°,∴△AOE是等腰直角三角形,∴AE=OA=3,∴E(3,3),易得OE的解析式为:y=x,过P作PG∥y轴,交OE于点G,∴G(m,m),∴PG=m﹣(m2﹣4m+3)=﹣m2+5m﹣3,∴S四边形AOPE=S△AOE+S△POE,=×3×3+PG?AE,=+×3×(﹣m2+5m﹣3),=﹣+,=﹣(m﹣)2+,∵﹣<0,∴当m=时,S有最大值是;(3)分四种情况:①当P在对称轴的左边,且在x轴下方时,如图3,过P作MN⊥y 轴,交y轴于M,交l于N,∵△OPF是等腰直角三角形,且OP=PF,易得△OMP≌△PNF,∴OM=PN,∵P(m,m2﹣4m+3),则﹣m2+4m﹣3=2﹣m,解得:m=(舍)或,∴P的坐标为(,);②当P在对称轴的左边,且在x轴上方时,如图3,同理得:2﹣m=m2﹣4m+3,解得:m1=(舍)或m2=,③当P在对称轴的右边,且在x轴下方时,如图4,过P作MN⊥x轴于N,过F作FM⊥MN于M,同理得△ONP≌△PMF,∴PN=FM,则﹣m2+4m﹣3=m﹣2,解得:x=或(舍);P的坐标为(,);④当P在对称轴的右边,且在x轴上方时,同理得m2﹣4m+3=m﹣2,解得:m=或(舍)P的坐标为:(,);综上所述,点P的坐标是:(,)或(,)或(,)或(,).【点评】本题属于二次函数综合题,主要考查了二次函数的综合应用,相似三角形的判定与性质以及解一元二次方程的方法,解第(2)问时需要运用配方法,解第(3)问时需要运用分类讨论思想和方程的思想解决问题.压轴题训练04一.解答题(共1小题)1.如图,已知直线l的解析式为y=x﹣1,抛物线y=ax2+bx+2 经过点A(m,0),B(2,0),D(1,)三点.(1)求抛物线的解析式及A点的坐标,并在图示坐标系中画出抛物线的大致图象;(2)已知点P(x,y)为抛物线在第二象限部分上的一个动点,过点P作PE垂直x轴于点E,延长PE与直线l交于点F,请你将四边形P AFB的面积S表示为点P的横坐标x的函数,并求出S的最大值及S最大时点P的坐标;(3)将(2)中S最大时的点P与点B相连,求证:直线l上的任意一点关于x轴的对称点一定在PB所在直线上.压轴题训练02参考答案与试题解析一.解答题(共1小题)1.如图,已知直线l的解析式为y=x﹣1,抛物线y=ax2+bx+2经过点A(m,0),B(2,0),D(1,)三点.(1)求抛物线的解析式及A点的坐标,并在图示坐标系中画出抛物线的大致图象;(2)已知点P(x,y)为抛物线在第二象限部分上的一个动点,过点P作PE垂直x轴于点E,延长PE与直线l交于点F,请你将四边形P AFB的面积S表示为点P的横坐标x的函数,并求出S的最大值及S最大时点P的坐标;(3)将(2)中S最大时的点P与点B相连,求证:直线l上的任意一点关于x轴的对称点一定在PB所在直线上.【分析】(1)根据待定系数法可求抛物线的解析式,再根据A (m,0)在抛物线上,得到0=﹣m2﹣m+2,解方程即可得到m的值,从而得到A点的坐标;(2)根据四边形P AFB的面积S=AB?PF,可得S=﹣(x+2)2+12,根据函数的最值可得S的最大值是12,进一步得到点P的坐标为;(3)根据待定系数法得到PB所在直线的解析式为y=﹣x+1,设Q(a,a﹣1)是y =x﹣1上的一点,则Q点关于x轴的对称点为(a,1﹣a),将(a,1﹣a)代入y =﹣x+1显然成立,依此即可求解.【解答】解:(1)∵抛物线y=ax2+bx+2经过点B(2,0),D(1,),∴,解得a=﹣,b=﹣,∴抛物线的解析式为y=﹣x2﹣x+2,∵A(m,0)在抛物线上,∴0=﹣m2﹣m+2,解得:m1=﹣4,m2=2(舍去),∴A点的坐标为(﹣4,0).如图所示:(2)∵直线l的解析式为y=x﹣1,∴S=AB?PF=×6?PF=3(﹣x2﹣x+2+1﹣x)=﹣x2﹣3x+9=﹣(x+2)2+12,其中﹣4<x<0,∴S的最大值是12,此时点P的坐标为(﹣2,2);(3)∵直线PB经过点P(﹣2,2),B(2,0),∴PB所在直线的解析式为y=﹣x+1,设Q(a,a﹣1)是y=x﹣1上的一点,则Q点关于x轴的对称点为(a,1﹣a),将(a,1﹣a)代入y=﹣x+1显然成立,∴直线l上的任意一点关于x轴的对称点一定在PB所在直线上.【点评】本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求抛物线的解析式,待定系数法求直线的解析式,函数的最值问题,四边形的面积求法,以及关于x 轴的对称点的坐标特征.压轴题训练03姓名:班级;学号:一.解答题(共3小题)1.已知平面直角坐标系xOy(如图),双曲线y=(k≠0)与直线y=x+2都经过点A(2,m).(1)求k与m的值;(2)此双曲线又经过点B(n,2),过点B的直线BC与直线y =x+2平行交y轴于点C,联结AB、AC,求△ABC的面积;(3)若(2)的条件下,设直线y=x+2与y轴交于点D,在射线CB上有一点E,如果以点A、C、E所组成的三角形与△ACD相似,且相似比不为1,求点E的坐标.2.如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC 所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=(k >0)的图象经过点D且与边BA交于点E,连接DE.(1)连接OE,若△EOA的面积为2,则k=;(2)连接CA、DE与CA是否平行?请说明理由;(3)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.3.已知如图,二次函数图象经过点A(﹣6,0),B(0,6),对称轴为直线x=﹣2,顶点为点C,点B关于直线x=﹣2的对称点为点D.(1)求二次函数的解析式以及点C和点D的坐标;(2)联结AB、BC、CD、DA,点E在线段AB上,联结DE,若DE平分四边形ABCD 的面积,求线段AE的长;(3)在二次函数的图象上是否存在点P,能够使∠PCA=∠BAC?如果存在,请求出点P的坐标;若不存在,请说明理由.参考答案与试题解析一.解答题(共3小题)1.已知平面直角坐标系xOy(如图),双曲线y=(k≠0)与直线y=x+2都经过点A(2,m).(1)求k与m的值;(2)此双曲线又经过点B(n,2),过点B的直线BC与直线y =x+2平行交y轴于点C,联结AB、AC,求△ABC的面积;(3)若(2)的条件下,设直线y=x+2与y轴交于点D,在射线CB上有一点E,如果以点A、C、E所组成的三角形与△ACD相似,且相似比不为1,求点E的坐标.【解答】解:(1)∵直线y=x+2都经过点A(2,m),∴m=2+2=4,则A(2,4),∵双曲线y=(k≠0)经过点A,∴k=2×4=8;(2)∵双曲线经过点B(n,2),∴2n=8,解得n=4,∴B(4,2),由题意可设直线BC解析式为y=x+b,把B点坐标代入可得2=4+b,解得b=﹣2,∴直线BC解析式为y=x﹣2,∴C(0,﹣2),∴AC===2,BC===4,AB===2,∴BC2+AB2=AC2,∴△ABC是以AC为斜边的直角三角形,∴S△ABC=AB?BC=×2×4=8;(3)∵直线y=x+2与y轴交于点D,∴D(0,2),∴AD==2,且AC=2如图所示,∵AD∥CE,∴∠DAC=∠ACE,若∠ACD=∠EAC,则AE∥CD,四边形AECD为平行四边形,此时△ADC≌△CEA,不满足条件,∴∠ACD=∠AEC,∴△ACD∽△CAE,∴=,即=,解得CE=10,∵E点在直线BC上,∴可设E(x,x﹣2)(x>0),又∵C(0,﹣2),∴CE==x,∴x=10,解得x=10,∴E点坐标为(10,8).2.如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC 所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=(k >0)的图象经过点D且与边BA交于点E,连接DE.(1)连接OE,若△EOA的面积为2,则k=4;(2)连接CA、DE与CA是否平行?请说明理由;(3)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.【解答】解:(1)连接OE,如,图1,∵Rt△AOE的面积为2,∴k=2×2=4.(2)连接AC,如图1,设D(x,5),E(3,),则BD=3﹣x,BE=5﹣,=,∴,又∵∠B=∠B,∴△BDE∽△BCA,∴∠BED=∠BAC,∴DE∥AC.(3)假设存在点D满足条件.设D(x,5),E(3,),则CD =x,BD=3﹣x,BE=5﹣,AE=.作EF⊥OC,垂足为F,如图2,易证△B′CD∽△EFB′,∴,即=,∴B′F=,∴OB′=B′F+OF=B′F+AE=+=,∴CB′=OC﹣OB′=5﹣,在Rt△B′CD中,CB′=5﹣,CD=x,B′D=BD=3﹣x,由勾股定理得,CB′2+CD2=B′D2,(5﹣)2+x2=(3﹣x)2,解这个方程得,x1=1.5(舍去),x2=0.96,∴满足条件的点D存在,D的坐标为D(0.96,5).3.已知如图,二次函数图象经过点A(﹣6,0),B(0,6),对称轴为直线x=﹣2,顶点为点C,点B关于直线x=﹣2的对称点为点D.(1)求二次函数的解析式以及点C和点D的坐标;(2)联结AB、BC、CD、DA,点E在线段AB上,联结DE,若DE平分四边形ABCD 的面积,求线段AE的长;(3)在二次函数的图象上是否存在点P,能够使∠PCA=∠BAC?如果存在,请求出点P的坐标;若不存在,请说明理由.【解答】解:(1)∵二次函数经过A(﹣6,0),B(0,6),对称轴为直线x=2,∴二次函数图象经过(2,0),设二次函数解析式为y=a(x+6)(x﹣2),把B(0,6)代入得:6=﹣12a,即a=﹣,∴二次函数解析式为y=﹣(x+6)(x﹣2)=﹣x2﹣2x+6=﹣(x+2)2+8,则C(﹣2,8),D(﹣4,6);(2)如图1所示,由题意得:AB=6,BC=CD=2,BD=4,∵BD2=CD2+BC2,∴∠DCB=90°,∵直线AB的解析式为y=x+6,直线DC解析式为y=x+10,∴DC∥AB,∴四边形ABCD为直角梯形,若S梯形ABCD=2S△ADE,即×2×(2+6)=2××2×AE,解得:AE=4;(3)如图2,在二次函数的图象上存在点P,使∠PCA=∠BAC,直线CP与AB交于点G,可得GA=GC,∵A(﹣6,0),C(﹣2,8),直线AB解析式为y=x+6,设G (x,x+6),∴=,两边平方得:2x2+24x+72=2x2+8,移项合并得:24x=﹣64,解得:x=﹣,经检验是原方程的根且符合题意,∴G(﹣,),设直线CG解析式为y=kx+b,把C与G坐标代入得:,解得:,∴直线CG解析式为y=7x+22,联立得:,解得:或(经检验不合题意,舍去),∴P坐标为(﹣16,﹣90);由(2)得到四边形ABCD为直角梯形,AB∥CD,∴∠DCA=∠BAC,此时P与D重合,即P(﹣4,6),综上,满足题意P的坐标为(﹣16,﹣90)或(﹣4,6).。
八年级下册数学压轴题(含答案)

八年级下压轴题1.如图,四边形OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=15,OC=12,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.(1)求CE和OD的长;(2)求直线DE的表达式;(3)直线y=kx+b与AE所在的直线垂直,当它与矩形OABC有公共点时,求出b的取值范围.【答案】解:(1)依题意可知,折痕AD是四边形OAED的对称轴,∴在Rt△ABE中,AE=AO=15,AB=OC=12,BE=√AE2−AB2=√152−122=9,∴CE=15−9=6,在Rt△DCE中,DC2+CE2=DE2,又∵DE=OD,∴(12−OD)2+62=OD2,∴OD=7.5.(2)∵CE=6,∴E(6,12).∵OD=7.5,∴D(0,7.5),设直线DE的解析式为y=mx+n,∴{n=7.56m+n=12,解得{m =34n =152, ∴直线DE 的解析式为y =34x +152.(3)∵直线y =kx +b 与AE 所在的直线垂直,DE ⊥AE ,∴直线y =kx +b 与DE 平行,∴直线为y =34x +b ,∴当直线经过A 点时,0=34×15+b ,则b =−454,当直线经过C 点时,则b =12,∴当直线y =kx +b 与矩形OABC 有公共点时,−454≤b ≤12. 2. 如图,在平面直角坐标系中,直线l 1:y =34x 与直线l 2:y =kx +b(k ≠0)相交于点A(a,3),直线l 2与y 轴交于点B(0,−5).(1)求直线l 2的函数解析式;(2)将△OAB 沿直线l 2翻折得到△CAB ,使点O 与点C 重合,AC 与x 轴交于点D.求证:四边形AOBC 是菱形;(3)在直线BC 下方是否存在点P ,使△BCP 为等腰直角三角形?若存在,直接写出点P 坐标;若不存在,请说明理由.【答案】解:(1)∵直线l₁:y =34x 与直线l₂:y =kx +b 相交于点A(a,3),∴A(4,3),∵直线交l₂交y 轴于点B(0,−5),∴y =kx −5,把A(4,3)代入得,3=4k −5,∴k =2,∴直线l 2的解析式为y =2x −5;(2)∵OA =√32+42=5,∴OA =OB ,∵将△OAB 沿直线l₂翻折得到△CAB ,∴OB =OC ,OA =AC ,∴OA=OB=BC=AC,∴四边形AOBC是菱形;(3)如图,过C作CM⊥OB于M,则CM=OD=4,∵BC=OB=5,∴BM=3,∴OB=2,∴C(4,−2),过P1作P1N⊥y轴于N,∵△BCP是等腰直角三角形,∴∠CBP1=90°,∴∠MCB=∠NBP1,∵BC=BP1,∴△BCM≌△P1BN(AAS),∴BN=CM=4,∴P1(3,−9);同理可得,P2(7,−6),P3(72,−112).综上所述,点P的坐标是(3,−9)或(7,−6)或P(72,−112).3.如图,在Rt△ABC中,∠C=90°,∠A=45°,AC=10cm,点D从点A出发沿AC方向以1cm/s的速度向点C匀速运动,同时点E从点B出发沿BA方向以√2cm/s的速度向点A匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D,E运动的时间是t(0<t≤10)s.过点E作EF⊥BC于点F,连接DE,DF.(1)用含t的式子填空;BE=______cm,CD=______cm.(2)试说明,无论t为何值,四边形ADEF都是平行四边形;(3)当t为何值时,△DEF为直角三角形?请说明理由.【答案】√2t t【解析】解:(1)由题意:BE=√2t(cm),AD=t(cm),故答案为√2t,t.(2)如图2中,∵CA=CB,∠C=90°,∴∠A=∠B=45°,∵EF⊥BC,∴∠EFB=90°,∴∠FEB=∠B=45°,∴EF=BF,∵BE=√2t,∴EF=BF=t,∴AD=EF,∵∠EFB=∠C=90°,∴AD//EF,∴四边形ADFE是平行四边形.(3)①如图3−1中,当∠DEF=90°时,易证四边形EFCD是正方形,此时AD=DE= CD,t=5.②如图3−2中,当∠EDF=90时,∵DF//AC,∴∠AED=∠EDF=90°,∵∠A=45°,∴AD=√2AE,∴t=√2(10√2−√2t),,解得t=203③当∠EFD=90°,△DFE不存在.s.综上所述,满足条件的t的值为5s或2034.如图,在矩形ABCO中,点C在x轴上,点A在y轴上,点B的坐标是(−9,12).矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,且直线BD与OA、x轴分别交于点D、F.(1)求线段BO的长;(2)求△OBD的面积;(3)在x轴上是否存在点M,使得以A、B、F、M为顶点的四边形是平行四边形?若存在,请求出满足条件的M点的坐标;若不存在,请说明理由.【答案】解:(1)∵四边形AB CO是矩形,∴∠BCO=90°.在Rt△BCO中,∵BO2=BC2+OC2,∴BO=√122+92=15.(2)设OD=x,∵四边形ABCO是矩形,∴∠BAD=90°.∵矩形ABCO沿直线BD折叠,使得点A落在对角线OB上的点E处,∴△BAD≌△BED,∴BE=BA=9,AD=ED=12−x,∠BED=∠BAD=90°,∴∠OED=90°,EO=BO−BE=15−9=6.在Rt△DEO中,OD2=OE2+DE2,∴x2=62+(12−x)2,解得x=152,即OD=152,∴S△OBD=12OD⋅AB=1354;(3)由(2)知,OD=152得D(0,152),设直线BD的解析式为y=kx+b,∵B(−9,12),D(0,152),∴{−9k+b=12 b=152,解得{k =−12b =152, ∴直线BD 的解析式为y =−12x +152.当y =0时,x =15,∴OF =15.又∵AB =9,∴FM =9, ∴在x 轴上存在点M ,使得以A 、B 、F 、M 为顶点的四边形是平行四边形.满足条件的点M 的坐标为(6,0)或(24,0).5. 如图,在平面直角坐标系中,O 为坐标原点,矩形OABC 的顶点A(12,0)、C(0,9),将矩形OABC 的一个角沿直线BD 折叠,使得点A 落在对角线OB 上的点E 处,折痕与x 轴交于点D .(1)线段OB 的长度为______;(2)求直线BD 所对应的函数表达式;(3)若点Q 在线段BD 上,在线段BC 上是否存在点P ,使以D ,E ,P ,Q 为顶点的四边形是平行四边形?若存在,请求出点P 的坐标;若不存在,请说明理由.【答案】解:(1)15;(2)如图,设AD =x ,则OD =OA −AD =12−x ,根据折叠的性质,DE =AD =x ,BE =AB =9,又OB =15,∴OE =OB −BE =15−9=6,在Rt △OED 中,OE 2+DE 2=OD 2,即62+x 2=(12−x)2,解得 x =92, ∴OD =12−92=152,∴点D(152,0),设直线BD 所对应的函数表达式为:y =kx +b(k ≠0),B(12,9), 则{12k +b =9152k +b =0,解得{k =2b =−15, ∴直线BD 所对应的函数表达式为:y =2x −15.(3)过点E 作EP//BD 交BC 于点P ,过点P 作PQ//DE 交BD 于点Q ,则四边形DEPQ 是平行四边形,再过点E 作EF ⊥OD 于点F ,由12⋅OE ⋅DE =12⋅DO ⋅EF ,得EF =6×92152=185,即点E 的纵坐标为185, 又点E 在直线OB :y =34x 上,∴185=34x,解得x=245,∴E(245,185),由于PE//BD,所以可设直线PE:y=2x+n,∵E(245,185)在直线EP上,∴185=2×245+n,解得n=−6,∴直线EP:y=2x−6,令y=9,则9=2x−6,解得x=152,∴P(152,9).6.如图,直线y=−12x+3与x轴、y轴分别相交于A,B两点,P是线段AB上的一个动点(不与AB两点重合),点M的坐标为(4,0),设P点的横坐标为x,设△OPM 的面积为S.(1)求点A,B的坐标;(2)求S关于x的函数解析式,并写出自变量x的取值范围;(3)当S=12S△AOB时,求点P的坐标;(4)画出函数S的图象.【答案】解:(1)针对于直线y=−12x+3,令x=0,∴y=3,∴B(0,3),令y=0,∴−12x+3=0,∴x=6,∴A(6,0);(2)∵点P在直线y=−12x+3上,且P点的横坐标为x,∴P(x,−12x+3),∵M(4,0),∴OM=4,∴S=S△OPM=12OM×|y P|=2y P=2(−12x+3)=−x+6(0<x<6);(3)由(1)知,A(6,0),B(0,3),∴S△AOB=12OA×OB=9,由(2)知,S=−x+6(0<x<6);当S=12S△AOB时,∴−x+6=92,∴x=32,∴y=−12x+3=94,∴P(32,94 );(4)由(2)知,S=−x+6(0<x<6),∴函数S的图象如图所示:7.如图,直线l1:y=kx+245与x轴、y轴分别相交于A、B两点,直线l2:y=−2x+b 与x轴、y轴、直线l1分别相交于点C、D、P.已知点A的坐标为(6,0),点D的坐标为(0,6),点M 是x 轴上的动点. (1)求k ,b 的值及点P 的坐标;(2)当△POM 为等腰三角形时,求点M 的坐标;(3)是否存在以点M 、O 、D 为顶点的三角形与△AOB 全等?若存在,请求出点M 的坐标;若不存在,请说明理由.【答案】解:(1)∵直线l 1:y =kx +245与x 轴相交于A(6,0),∴6k +245=0,∴k =−45,∴直线l 1:y =−45x +245①∵直线l 2:y =−2x +b 与y 轴相交于点D(0,6), ∴b =6,∴直线l 2:y =−2x +6②, 联立①②解得,{x =1y =4,∴P(1,4);(2)∵点M 是x 轴上的动点, ∴设M(m,0), ∵P(1,4),∴OP =√17,OM =|m|,MP =√(m −1)2+16, ∵△POM 为等腰三角形, ∴当OM =OP 时, ∴√17=|m|, ∴m =±√17, ∴M(−√17,0)或(√17,0)当OM=MP时,∴|m|=√(m−1)2+16,∴m=172,∴M(172,0),当OP=MP时,∴√17=√(m−1)2+16,∴m=0(舍)或m=2,∴M(2,0),即:点M的坐标为(−√17,0)或(√17,0)或(172,0)或(2,0);(3)∵点A的坐标为(6,0),点D的坐标为(0,6),∴OA=OD=6,∵点M在x轴上,∴∠AOB=∠DOM=90°,∵以点M、O、D为顶点的三角形与△AOB全等,∴△AOB≌△DOM,∴OM=OB,∵直线l1:y=−45x+245与y轴相交于B,∴B(0,245),∴OB=245,∴OM=245,∴M(245,0)或(−245,0).8.在平面直角坐标系中,一次函数的图象与x轴交于点A,与y轴交于点B,且与正比例函数的图象交于点C(3,4).(1)求、的值;(2)若D点是线段OC上的动点,过D作DE∥y轴交AC于点E.①设D点的横坐标为,线段DE的长为,则与的函数关系式为_______;②连接AD,若△AOD为等腰三角形,请求出点D的坐标;(3)在平面内是否存在点Q,使以O、A、C、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,请说明理由.【详解】(1)∵正比例函数的图象过点C(3,4),∴,解得:,∴正比例函数为,∵一次函数的图象过点C(3,4),∴,解得:,∴一次函数解析式为:;(2)①∵D在正比例函数上,∴ D点的纵坐标为:,∵E点在一次函数上,∴ E点的纵坐标为:,∴ DE =;②∵点A是一次函数与x轴的交点,∴ A(-3,2),即OA=3,而D的坐标为(,),∵∠AOD是钝角,一定是等腰三角形的顶角,∴OD=OA,∴OD=,解得:,则,∴点D的坐标为(,);(3)根据图象分析:①当OA作为平行四边形的边时,则CQ∥OA,CQ=OA,此时Q(0,4),(6,4),②当OA作为平行四边形的对角线时,则OQ∥AC,OQ=AC,此时Q(-6,-4),综上所述,存在,点Q的坐标为(0,4),(6,4),(-6,-4).9.如图1,在平面直角坐标系xOy中,直线l1:y1=kx+b与l2: y2=kx+3相交于点C(1,2),直线l1与x轴交于点A (-1,0)、直线l2与x轴交于B点.(1) 求直线l1的解析式(表达式) ;(2)判断△ABC的形状并说明理由; (3)在x轴上是否存在点P,使△ACP为等腰三角形?若存在,请直接写出P 点的坐标;若不存在,请说明理由;(4) 如图2,设直线l2与y轴交于点D,点为线段BD上的一个动点,过点M 作ME⊥y轴于点E,作MF⊥x轴于点F,连接EF,问是否存在点M,使EF的值最小?若存在,求出此时EF 的值.10.如图,直线y=kx -3与x 轴、y 轴分别交于B ⎪⎭⎫ ⎝⎛0,23、C 两点,(1)求k 值;(2)若点A(x ,y)是直线y=kx -3上在第一象限内的一个动点,当点A 在运动过程中,试写出△AOB 的面积S 与x 的函数关系式;(不要求写出自变量的取值范围) (3)探究:①当A 点运动到什么位置时,△AOB 的面积为49,并说明理由; ②在①成立的情况下,x 轴上是否存在一点P ,使△AOP 是等腰三角形?若存在,请直接写出满足条件的所有P 点坐标;若不存在,请说明理由.答案解析(1)把B 的坐标代入y=kx -3,得:k -3=0,解得:k=2; (2)OB=,则S=×(2x -3)=x -;(3)①根据题意得:x -=,解得:x=3,则A 的坐标是(3,3);②OA==3,当O是△AOP的顶角顶点时,P的坐标是(-3,0)或(3,0);当A是△AOP的顶角顶点时,P与过A的与x轴垂直的直线对称,则P的坐标是(6,0);当P是△AOP的顶角顶点时,P在OA的中垂线上,OA的中点是(,),与OA垂直的直线的斜率是:-1,设直线的解析式是:y=-x+b,把(,)代入得:=-+b,解得:b=,则直线的解析式是:y=-x+,令y=0,解得:x=,则P的坐标是(,0).故P的坐标是:(-3,0)或(3,0)或(6,0)或(,0).。
人教版八年级数学下册经典压轴题考点及例题解析

人教版八年级数学下册经典压轴题考点及例题解析例题1古希腊数学家把数 1 , 3 , 6 , 10 ,15 , 21 ,...... 叫做三角形数,它有一定的规律性。
若把第一个三角形数记为 a1 ,第二个三角形数记为 a2 ,......,第 n 个三角形数记为 an ,则 an + a(n+1) = ?答案:(n + 1)^2 。
例题2在平面直角坐标系中,对于平面内任意一点 P(a , b)若规定以下三种变换:① f(a , b)= (-a , b),如 f(2 , 5)= (-2 , 5);② g(a , b) = (b , a), 如 g(2 , 5)= (5 , 2);③ h(a , b)= (-a , -b),如 h(2 , 5)= (-2 , -5)。
根据以上变换,那么 f(h(5 , -3))等于多少?答案:(5,3)。
例题3如图,已知等腰直角△ABC 的直角边长为 1 ,以 Rt△ABC 的斜边 AC 为直角边,画第二个等腰 Rt△ACD ,在以 Rt△ACD 的斜边 AD 为直角边,画第三个等腰 Rt△ADE , ... ,依次类推到第五个等腰 Rt△AFG ,则由这五个等腰直角三角形所构成的图形的面积是多少?答案:31/2 。
例题4如图所示,直线 OP 经过点 P(4,4√3),过 x 轴上的点 1、3、5、7、9、11 ......分别作 x 轴的垂线,与直线 OP 相交得到一组梯形,其阴影部分梯形的面积从左至右依次记为 S1 , S2 , S3 , ... , Sn , 则 Sn 关于 n 的函数关系式是?答案:Sn = 4√3 (2n - 1)。
例题5现将 1、√2、√3、√6 四个数按下列方式排列。
若规定(m , n)表示第 m 排从左到右第 n 个数,则(5 , 4)与(15 , 7)表示的两数之积是多少?答案:2√3 。
例题6现将一块直角三角形的花圃进行改造,已知两直角边长分别为 6 m 、8 m 。
八年级下册数学期末压轴题(含答案)

八年级数学下册期末压轴题练习(含答案)一、填空题:1.如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ 的最小值为 .2.如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6,则另一直角边BC的长为.3.如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AE PQ的周长取最小值时,四边形AEPQ 的面积是.4.如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A.点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.现给出以下四个命题(1)∠APB=∠BPH;(2)当点P在边AD上移动时,△PDH的周长不发生变化; (3)∠PBH=450 ; (4)BP=BH.其中正确的命题是.5.如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值是.二、综合题:6. (1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.(3)运用(1)(2)解答中所积累的经验和知识,完成下题:如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD的面积.7.如图,已知等腰Rt△ABC和△CDE,AC=BC,CD=CE,连接BE、AD,P为BD中点,M为AB中点、N为DE中点,连接PM、PN、MN.(1)试判断△PMN的形状,并证明你的结论;(2)若CD=5,AC=12,求△PMN的周长.8.已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转.(1)①当E点旋转到DA的延长线上时(如图1),△ABE与△ADG的面积关系是:.②当E点旋转到CB的延长线上时(如图2),△ABE与△ADG的面积关系是:(2)当正方形AEFG旋转任意一个角度时(如图3),(1)中的结论是否仍然成立?若成立请证明,若不成立请说明理由.(3)已知△ABC,AB=5cm,BC=3cm,分别以AB、BC、CA为边向外作正方形(如图4),则图中阴影部分的面积和的最大值是 cm2.9.一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为,周长为;(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为,周长为;(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.10.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.参考答案1.答案为:3.3.答案为:4.5.2.答案为:7;解法一:如图1所示,过O作OF⊥BC,过A作AM⊥OF,∵四边形ABDE为正方形,∴∠AOB=90°,OA=OB,∴∠AOM+∠BOF=90°,又∠AMO=90°,∴∠AOM+∠OAM=90°,∴∠BOF=∠OAM,在△AOM和△BOF 中,,∴△AOM≌△BOF(AAS),∴AM=OF,OM=FB,又∠ACB=∠AMF=∠CFM=90°,∴四边形ACFM为矩形,∴AM=CF,AC=MF=5,∴OF=CF,∴△OCF为等腰直角三角形,∵OC=6,∴根据勾股定理得:CF2+OF2=OC2,解得:CF=OF=6,∴FB=OM=OF﹣FM=6﹣5=1,则BC=CF+BF=6+1=7.故答案为:7.解法二:如图2所示,过点O作OM⊥CA,交CA的延长线于点M;过点O作ON⊥BC于点N.易证△OMA≌△ONB,∴OM=ON,MA=NB.∴O点在∠ACB的平分线上,∴△OCM为等腰直角三角形.∵OC=6,∴CM=ON=6.∴MA=CM﹣AC=6﹣5=1,∴BC=CN+NB=6+1=7.故答案为:7.4.答案为:(1)(2)(3).5.答案为:2;解:作D 关于AE 的对称点D′,再过D′作D′P′⊥AD于P′,∵DD′⊥AE,∴∠AFD=∠AFD′,∵AF=AF,∠DAE=∠CAE,∴△DAF≌△D′AF,∴D′是D关于AE的对称点,AD′=AD=4,∴D′P′即为DQ+PQ的最小值,∵四边形ABCD是正方形,∴∠DAD′=45°,∴AP′=P′D′,∴在Rt△AP′D′中,P′D′2+AP′2=AD′2,AD′2=16,∵AP′=P′D',2P′D′2=AD′2,即2P′D′2=16,∴P′D′=2,即DQ+PQ的最小值为2,6. (1)证明:∵四边形ABCD是正方形,∴BC=CD,∠B=∠CDF=90°,∵∠ADC=90°,∴∠FDC=90°.∴∠B=∠FDC,∵BE=DF,∴△CBE≌△CDF(SAS).∴CE=CF.(2)证明:如图2,延长AD至F,使DF=BE,连接CF.由(1)知△CBE≌△CDF,∴∠BCE=∠DCF.∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∠GCE=45°,∴∠GCF=∠GCE=45°.∵CE=CF,GC=GC,∴△ECG≌△FCG.∴GE=GF,∴GE=GF=DF+GD=BE+GD.(3)解:如图3,过C作CG⊥AD,交AD延长线于G.在直角梯形ABCD中,∵AD∥BC,∴∠A=∠B=90°,又∵∠CGA=90°,AB=BC,∴四边形ABCG为正方形.∴AG=BC.…∵∠DCE=45°,根据(1)(2)可知,ED=BE+DG.…∴10=4+DG,即DG=6.设AB=x,则AE=x﹣4,AD=x﹣6,在Rt△AED中,∵DE2=AD2+AE2,即102=(x﹣6)2+(x﹣4)2.解这个方程,得:x=12或x=﹣2(舍去).…∴AB=12.∴S梯形ABCD=0.5(AD+BC)•AB=0.5×(6+12)×12=108.即梯形ABCD的面积为108.…7.解:(1)①∵正方形ABCD和正方形AEFG有公顶点A,将正方形AEFG绕点A旋转,E 点旋转到DA的延长线上,∴AE=AG,AB=AD,∠EAB=∠GAD,∴△ABE≌△ADG(SAS),∴△ABE的面积=△ADG的面积;②作GH⊥DA交DA的延长线于H,如图2,∴∠AHG=90°,∵E点旋转到CB的延长线上,∴∠ABE=90°,∠HAB=90°,∴∠GAH=∠EAB,在△AHG和△AEB中,∴△AHG≌△AEB,∴GH=BE,∵△ABE的面积=0.5EB•AB,△ADG的面积=0.5GH•AD,∴△ABE的面积=△ADG的面积;(2)结论仍然成立.理由如下:作GH⊥DA交DA的延长线于H,EP⊥BA交BA的延长线于P,如图3,∵∠PAD=90°,∠EAG=90°,∴∠PAE=∠GAH,在△AHG和△AEP中,∴△AHG≌△AEP(AAS),∴GH=BP,∵△ABP的面积=0.5EP•AB,△ADG的面积=0.5GH•AD,∴△ABP的面积=△ADG的面积;(3)∵AB=5cm,BC=3cm,∴AC==4cm,∴△ABC的面积=0.5×3×4=6(cm2);根据(2)中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=18cm2.故答案为相等;相等;18.8.解:(1)∵AM=MC=AC=a,则∴重叠部分的面积是△ACB的面积的一半为0.25a2,周长为(1+)a.(2)∵重叠部分是正方形∴边长为0.5a,面积为0.25a2,周长为2a.(3)猜想:重叠部分的面积为0.25a2.理由如下:过点M分别作AC、BC的垂线MH、MG,垂足为H、G 设MN与AC的交点为E,MK与BC的交点为F∵M是△ABC斜边AB的中点,AC=BC=a∴MH=MG=0.5a又∵∠HME+∠HMF=∠GMF+∠HMF,∴∠HME=∠GMF,∴Rt△MHE≌Rt△MGF∴阴影部分的面积等于正方形CGMH的面积∵正方形CGMH的面积是MG•MH=0.5a×0.5a =0.25a2,∴阴影部分的面积是0.25a2.9.(1)证明:∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°,∵∠EAF=45°,∴∠GAE=45°,在△AGE与△AFE中,,∴△AGE≌△AFE(SAS);(2)证明:设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.则△ADF≌△ABG,DF=BG.由(1)知△AEG≌△AEF,∴EG=EF.∵∠CEF=45°,∴△BME、△DNF、△CEF均为等腰直角三角形,∴CE=CF,BE=BM,NF=DF,∴a﹣BE=a﹣DF,∴BE=DF,∴BE=BM=DF=BG,∴∠BMG=45°,∴∠GME=45°+45°=90°,∴EG2=ME2+MG2,∵EG=EF,MG=BM=DF=NF,∴EF2=ME2+NF2;(3)解:EF2=2BE2+2DF2.如图所示,延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由(1)知△AEH≌△AEF,则由勾股定理有(GH+BE)2+BG2=EH2,即(GH+BE)2+(BM﹣GM)2=EH2又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,即2(DF2+BE2)=EF2。
压轴题:一元一次不等式及不等式组综合专练20题(解析版)八年级数学下学期期末精选题汇编(北师大版)

压轴题02:一元一次不等式及不等式组综合专练20题(解析版)一、单选题1.已知关于x 的不等式组100x x a ->⎧⎨-≤⎩,有以下说法: ①如果它的解集是1<x ≤4,那么a =4;①当a =1时,它无解;①如果它的整数解只有2,3,4,那么4≤a <5;①如果它有解,那么a ≥2.其中说法正确的个数为( )A .1个B .2个C .3个D .4个【答案】C【分析】分别求出每个不等式的解集,再根据各结论中a 的取值情况逐一判断即可.【详解】解:由x ﹣1>0得x >1,由x ﹣a ≤0得x ≤a ,①如果它的解集是1<x ≤4,那么a =4,此结论正确;①当a =1时,它无解,此结论正确;①如果它的整数解只有2,3,4,那么4≤a <5,此结论正确;①如果它有解,那么a >1,此结论错误;故选:C .【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.2.正整数n 小于100,并且满足等式236n n n n ⎡⎤⎡⎤⎡⎤++=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,其中[]x 表示不超过x 的最大整数,例如:[][]1.5122==,,则满足等式的正整数的个数为() A .2B .3C .12D .16【答案】D【分析】利用不等式[x ]≤x 即可求出满足条件的n 的值.【详解】 解:若2n ,3n ,6n 有一个不是整数, 则22n n ⎡⎤⎢⎥⎣⎦<或者33n n ⎡⎤⎢⎥⎣⎦<或者66n n ⎡⎤⎢⎥⎣⎦<, ∴][][236236n n n n n n n ⎡⎤++++=⎢⎥⎣⎦<, ∴2n ,3n ,6n 都是整数,即n 是2,3,6的公倍数,且n <100, ∴n 的值为6,12,18,24,......96,共有16个,故选:D .【点睛】本题主要考查不等式以及取整,关键是要正确理解取整的定义,以及[x ]≤x <[x ]+1式子的应用,这个式子在取整中经常用到.3.定义,图象与x 轴有两个交点的函数y =24()24()x x m x x m -+≥⎧⎨+<⎩叫做关于直线x =m 的对称函数,它与x 轴负半轴交点记为A ,与x 轴正半轴交点记为B 例如:如图:直线l :x =1,关于直线l 的对称函数y =24(1)24(1)x x x x -+≥⎧⎨+<⎩与该直线l 交于点C ,当直线y =x 与关于直线x =m 的对称函数有两个交点时,则m 的取值范围是( )A .0≤m ≤43B .-2<m ≤43C .-2<m ≤2D .-4<m <0【答案】B【分析】 根据定义x 轴上存在,A B 即可求得22m -<<,根据题意联立,24,y x y x =⎧⎨=+⎩,24,y x y x =⎧⎨=-+⎩即可求得m 的范围,结合定义所求范围即可求解 【详解】①一次函数图象与x 轴最多只有一个交点,且关于m 的对称函数()24,24()x x m y x x m ⎧-+≥=⎨+<⎩,与x 轴有两个交点, ①组成该对称函数的两个一次函数图象的部分图象都与x 轴有交点.①240x ±+=解得2x =或2-①22m -<<.①直线y =x 与关于直线x =m 的对称函数有两个交点,①直线y =x 分别与直线24()y x x m =-+≥和24()y x x m =+<各有一个交点.对于直线y =x 与直线24()y x x m =+<,联立可得,24,y x y x =⎧⎨=+⎩解得4,4x y =-⎧⎨=-⎩, ①直线y =x 与直线24()y x x m =+<必有一交点(4,4)--.对于直线y =x 与直线24()y x x m =-+≥,联立可得,24,y x y x =⎧⎨=-+⎩解得4,343x y ⎧=⎪⎪⎨⎪=⎪⎩, ①22m -<<, ①43x =必须在x m ≥的范围之内才能保证直线y =x 与直线24()y x x m =-+≥有交点. ①43m ≤. ①423m -<≤. ①m 的取值范围是423m -<≤. 故选B【点睛】本题考查了新定义,两直线交点问题,一次函数的性质,掌握一次函数的性质,数形结合是解题的关键.4.如图,长方形ABKL ,延CD 第一次翻折,第二次延ED 翻折,第三次延CD 翻折,这样继续下去,当第五次翻折时,点A 和点B 都落在①CDE =α内部(不包含边界),则α的取值值范围是( )A .3645α︒<≤B .3036α︒<≤C .3645α︒≤<D .3036α︒<<【答案】D【分析】 利用翻折前后角度总和不变,由折叠的性质列代数式求解即可;【详解】解:第一次翻折后2a +①BDE =180°,第二次翻折后3a +①BDC =180°,第三次翻折后4a +①BDE =180°,第四次翻折后5a +①BDC =180°,若能进行第五次翻折,则①BDC ≥0,即180°-5a ≥0,a ≤36°,若不能进行第六次翻折,则①BDC ≤a ,即180°-5a ≤a ,a ≥30°,当a =36°时,点B 落在CD 上,当a =30°时,点B 落在ED 上,①30°<a <36°,故选:D ;【点睛】本题考查了图形的规律,折叠的性质,一元一次不等式的应用;掌握折叠前后角度的变化规律是解题关键.5.关于x 的不等式组255332x x x x a +⎧>-⎪⎪⎨+⎪<+⎪⎩ 只有5个整数解,则a 的取值范围是( ) A .1162a -<<-B .1162a -≤<-C .1162a -<≤-D .1162a -≤≤- 【答案】C【分析】先解x 的不等式组255332x x x x a +⎧>-⎪⎪⎨+⎪<+⎪⎩,然后根据整数解的个数确定a 的不等式组,解出取值范围即可. 【详解】 解:不等式组255332x x x x a +⎧>-⎪⎪⎨+⎪<+⎪⎩, 解得:2032x x a <⎧⎨>-⎩, 不等式组只有5个整数解,即解只能是15x =,16,17,18,19,a ∴的取值范围是:32143215a a -≥⎧⎨-<⎩, 解得:1162a -<≤-. 故选:C .【点睛】 本题考查了一元一次不等式组的整数解,难度适中,关键是根据整数解的个数确定关于a 的不等式组.6.若实数a 使得关于x 的不等式组52232x a x x x +≤-⎧⎪⎨--<⎪⎩有且只有2个整数解,且使得关于x 的一次函数()15y a x a =+-+不过第四象限,则符合条件的所有整数a 的和为( )A .7B .9C .12D .14【答案】C【分析】先解不等式组,根据不等式组的解只有2个整数解,列出关于a 的不等式,求出此时a 的取值范围;再根据一次函数的图像不过第四象限,列出关于a 的不等式组,再次求出a 的取值范围,两项综合求出a 最终的取值范围,则问题得解.【详解】 52232x a x x x +≤-⎧⎪⎨--<⎪⎩①② 解不等式①得:24a x +≥, 解不等式①得:4<x ,不等式有解,则解为:244a x +≤<, ①不等式组有两个整数解,则这两个整数解为3,2, ①2124a +≤<,解得26a ≤<; ①一次函数()15y a x a =+-+不过第四象限,①则有1050a a +⎧⎨-+≥⎩>,解得15a -≤<; 综上:25a ≤<①a 的整数值有:3,4,5,则其和为:3+4+5=12,故选:C .【点睛】本题考查了解不等式组和一次函数的图像的性质,根据不等式组只有两个整数解和函数不过第四象限等条件求出a 的取值范围是解答本题的关键.7.对于实数,a b ,定义符号{},min a b 其意义为:当a b ≥时,{},min a b b =;当a b <时,{},min a b a =.例如:21{},1min -=-,若关于x 的函数2{}1,3y min x x =--+,则该函数的最大值是( )A .1B .43C .53D .2【答案】C【分析】根据定义先列不等式:213x x --+和213x x --+,确定其{21y min x =-,3}x -+对应的函数,画图象可知其最大值.【详解】解:由题意得:213y x y x =-⎧⎨=-+⎩,解得:4353x y ⎧=⎪⎪⎨⎪=⎪⎩, 当213x x --+时,43x, ∴当43x 时,{21y min x =-,3}3x x -+=-+,由图象可知:此时该函数的最大值为53; 当213x x --+时,43x, ∴当43x 时,{21y min x =-,3}21x x -+=-, 由图象可知:此时该函数的最大值为53; 综上所述,{21y min x =-,3}x -+的最大值是当43x =所对应的y 的值, 如图所示,当43x =时,53y =,故选:C【点睛】本题考查了新定义、一元一次不等式及一次函数的交点问题,认真阅读理解其意义,并利用数形结合的思想解决函数的最值问题.8.已知正整数a ,b ,c ,d 满足:a <b <c <d ,a +b +c +d =2022,22222022d c b a -+-=,则这样的4元数组(a ,b ,c ,d )共有( )A .251组B .252组C .502组D .504组【答案】D【分析】根据题意得出321a b c d +≤+≤+≤,继而得出()()()()()()222220222022d c b a d c d c b a b a d c b a =-+-=-++-+≥+++=,再由已知条件构造()10102a c a a =+≥++,即可解答.【详解】因为a ,b ,c ,d 为正整数,且a b c d <<<,所以321a b c d +≤+≤+≤.所以()()()()()()222220222022d c b a d c d c b a b a d c b a =-+-=-++-+≥+++=.因此1d c -=,1b a -=,即1d c =+,1b a =+.所以()()112022a b c d a a c c +++=+++++=,因此1010a c +=.又2a c +≤,所以()10102a c a a =+≥++,因此1504a ≤≤.所以符合条件的4元数组(),,,a b c d 为(),1,1010,1011a a a a +--,其中1504a ≤≤.所以符合条件的4元数组有504组.故选:D .【点睛】本题考查了整式的应用,解题的关键是根据题目已知等式构造不等式,属于竞赛题.二、填空题9.重庆云阳巴阳镇精准化发展枇杷产业切实带动低收入农户增收,成为一大“亮点”——“万亩枇杷,醉美巴阳”成为了重庆云阳的一大名片.今年5月又是一个丰收季,全镇枇杷种植面积达1万余亩,种植了“普通”、“白肉”、“大五星”三个品种的枇杷,其中6000亩用于村民集体采摘,其余部分用于游客自助采摘.这6000亩中种植“白肉”枇杷的面积是“普通”枇杷面积的2倍,“大五星”枇杷面积不超过“白肉”枇杷面积的1.2倍,种植“白肉”的面积不超过2300亩,现在正值采摘季节,若干村民进行采摘,每人每天可以采摘“普通”枇杷1.8亩,或“白肉”枇杷1.2亩,或“大五星”枇杷2亩,这6000亩枇杷预计20天采摘完,则需要村民_______人参与采摘.【答案】191人【分析】设“普通”枇杷面积x 亩,则“白肉”枇杷面积为2x 亩,“大五星”枇杷面积为()60003x -亩,有m 人采摘,采摘“普通”枇杷a 天, “白肉”枇杷为b 天,“大五星”枇杷为()20a b --天,先求解x 的范围,再用含m 的代数式表示x ,再解不等式组即可得到答案.【详解】解:设“普通”枇杷面积x 亩,则“白肉”枇杷面积为2x 亩,“大五星”枇杷面积为()60003x -亩,有m 人采摘,采摘“普通”枇杷a 天, “白肉”枇杷为b 天,“大五星”枇杷为()20a b --天,根据题意得:600032 1.222300x x x -≤⨯⎧⎨≤⎩ 解得:100001150,9x ≤≤同时可得:()1.81.2222060003am x bm xm a b x ⎧=⎪=⎨⎪--=-⎩55,,93am x bm x ∴== 101040224060003,93m ma mb m x x x ∴--=--=- 整理得:36054000,13m x -=∴ 10000360540001150,913m -≤≤ 1300003605400014950,9m ∴≤-≤ 616000360689509m ∴≤≤, 1019190191,8136m ∴≤≤ m 为正整数,∴ 191.m =故答案为:191.【点睛】本题考查不等式组的实际应用,解题的关键是仔细阅读找出题中的等量关系与不等关系列方程与不等式组.10.某商家需要更换店面的瓷砖,商家打算用1500元购买彩色和单色两种地砖进行搭配,并且把1500元全部花完.已知每块彩色地砖25元,每块单色地砖15元,根据需要,购买的单色地砖数要超过彩色地砖数的2倍,并且单色地砖数要少于彩色地砖数的3倍,那么符合要求的一种购买方案是________.【答案】购买24块彩色地砖,60块单色地砖 或 购买27块彩色地砖,55块单色地砖【分析】设购买x 块彩色地砖,购买单色地砖y 块,进而由题意得到2x <y <3x ,再根据总费用为1500元,且x 、y 均为正整数,将y 用x 的代数式表示,然后解一元一次不等式组即可求解.【详解】解:设购买x 块彩色地砖,购买单色地砖y 块,则2x <y <3x ,25x +15y =1500, ①1500255100(1)153x y x , 又已知有:23xy x ,①510033510023x x x x ⎧-<⎪⎪⎨⎪->⎪⎩,解得3003001411x , 又x 为正整数,且30021.414,30027.311,①x =22,23,24,25,26,27;由(1)式中,x y ,均为正整数,①x 必须是3的倍数,①24x =或27x =,当24x =时,单色砖的块数为15002425=6015; 当27x =时,单色砖的块数为15002725=5515; 故符合要求的购买方案为:购买24块彩色地砖,60块单色地砖 或 购买27块彩色地砖,55块单色地砖.【点睛】本题考查了一元一次不等式的实际应用,本题的关键点是将单色砖的块数用彩色砖的块数的代数式表示,进而解不等式组,注意实际问题考虑解为正整数的情况.11.春暖花开,又到了踏青赏花的好季节,某植物园决定在今年4月份购进一批花苗:绣球花苗、蔷薇花苗、铁线莲花苗和月季花苗.已知每株绣球花苗的价格是每株蔷薇花苗价格的12,每株月季花苗的价格是每株铁线莲花苗价格的3倍.另外,购进的绣球花苗数量是铁线莲花苗数量的2倍,蔷薇花苗的数量是月季花苗数量的3倍,且铁线莲花苗和蔷薇花苗的总数量不超过600株.已知一株绣球花苗和一株铁线莲花苗的价格之和为30元,最后,购进绣球花苗和蔷薇花苗的总费用比铁线莲花苗和月季花苗的总费用多14400元,则今年4月用于购进铁线莲花苗和月季花苗的总费用的最大值为______元.【答案】7200.【分析】根据题意可设蔷薇花苗价格为x 元,每株铁线莲花苗价格为y 元,则绣球花苗价格为12x 元,月季花苗为3y 元,根据已知关系列出不等关系3600a b +,表示购进铁线莲花苗和月季花苗的总费用,利用不等关系求解.【详解】解:设每株蔷薇花苗价格为x 元,每株铁线莲花苗价格为y 元,则绣球花苗价格为12x 元,月季花苗为3y 元,由题意得,1302x y +=①,设购进铁线莲花苗数量为a ,月季花苗数量为b ,则绣球花苗为2a ,蔷薇花苗为3b , 由题意可知,3600a b +,1231440032x a x b a y b y ⨯+⨯-=⋅+⨯, 整理得(3)()14400a b x y +-=,3600a b +, 24x y ∴-①,由①得602x y =-代入①得,60224y y --,解得12y ,用于购进铁线莲花苗和月季花苗的总费用为,3(3)ay by a b y +=+,3600a b +,12y ,∴用于购进铁线莲花苗和月季花苗的总费用的最大值为600127200⨯=(元),故答案为:7200. 【点睛】本题以购买的最大费用为背景考查了一元一次不等式的应用,关键根据数量关系表示未知量,然后根据不等关系求解.12.小李和小张大学毕业后准备合伙开一家工作室创业.他们在某写字楼租了一间空高为3米的房间作办公地点(如图),准备装修后开始办公.小李和小张分别提出两套装修方案(如表格).其中,每平方米木地板的装修费用与每平方米木质吊顶的装修费用之和等于每平方米复合材料墙面的装修费用;每平方米地砖的装修费用与每平方米乳胶漆的装修费用之和等于每平方米木质墙面的装修费用,以上各项装修单价均为整数.每平方米木地板、木质墙面、木质吊顶的装修费用之和不少于600元;每平方米复合材料墙面比木质墙面的装修费用多,且差价不大于90元,不少于80元.经测算,小李方案的总装修费用比小张方案的总装修费用多1260元.若x ,y 均为整数,且满足y<x<2y ,则小张的方案装修总费用最少为________元.【答案】234041401260y y +- 【分析】设每平方米木地板a 元,木制吊顶b 元,地砖m 元,乳胶漆n 元,则复合材料墙面()a b +元,木质墙面m n 元,根据题意列出不等式组,得到340345a b m n +≥⎧⎨+≥⎩,根据“小李方案的总装修费用比小张方案的总装修费用多1260元”列式即可求解. 【详解】解:设每平方米木地板a 元,木制吊顶b 元,地砖m 元,乳胶漆n 元, 则复合材料墙面()a b +元,木质墙面m n 元,根据题意可得6008090a b m n a b m n +++≥⎧⎨≤+--≤⎩,解得340345a b m n +≥⎧⎨+≥⎩,小李的总花费()()()()()2336xya xyb m n y x xy a b m n x y ++++=++++, 小张的总花费()()()()()2336xym xyn a b y x xy m n a b x y ++++=++++, ①()()()()()()661260xy a b m n x y xy m n a b x y ++++-+-++=, ①2y x y <<,①()()()61260xy a b m n x y ++++-()23406345126034041401260y y y y y y ≥⋅⨯+⨯+-=+-, 故答案为:234041401260y y +-. 【点睛】本题考查不等式组的实际应用,根据题意列出不等式是解题的关键.13.如图,设BAC θ∠=(090θ︒<<︒).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点1A开始,用等长的小棒依次向右摆放,其中12A A为第一根小棒,且11223341AA A A A A A A====⋅⋅⋅=,若只能摆放4根小棒,则θ的范围为________.【答案】18°≤θ<22.5°.【分析】根据等边对等角可得①BAC=①AA2A1,①A2A1A3=①A2A3A1,①A3A2A4=①A3A4A2,再根据三角形的一个外角等于与它不相邻的两个内角的和可得θ1=2θ,θ2=3θ,θ3=4θ,求出第三根小木棒构成的三角形,然后根据三角形的内角和定理和外角性质列出不等式组求解即可.【详解】解:如图,①小木棒长度都相等,①①BAC=①AA2A1,①A2A1A3=①A2A3A1,①A3A2A4=①A3A4A2,由三角形外角性质得,θ1=2θ,θ2=3θ,θ3=4θ;①只能摆放4根小木棒,①490 590θθ︒︒⎧<⎨≥⎩,解得18°≤θ<22.5°.故答案为:18°≤θ<22.5°.【点睛】本题考查了等腰三角形等边对等角的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,也考查了一元一次不等式组的应用,列出不等式组是解题的关键.14.若不等式231x x x a-+++-≥对一切数x都成立,则a的取值范围是________.【答案】5a ≤ 【分析】要使不等式231x x x a -+++-≥对一切数x 都成立,则a 需小于等于231x x x -+++-的最小值,再分3x <-、31x -≤<、12x ≤<和2x ≥四种情况,分别化简绝对值求出最小值即可得.【详解】要使不等式231x x x a -+++-≥对一切数x 都成立,则a 需小于等于231x x x -+++-的最小值, 由题意,分以下四种情况: (1)当3x <-时,2312313x x x x x x x -+++-=---+-=-,此时39x ->; (2)当31x -≤<时,2312316x x x x x x x -+++-=-+++-=-,此时569x <-≤; (3)当12x ≤<时,2312314x x x x x x x -+++-=-+++-=+,此时546x ≤+<; (4)当2x ≥时,2312313x x x x x x x -+++-=-+++-=,此时36x ≥;综上,231x x x -+++-的最小值为5, 则5a ≤, 故答案为:5a ≤. 【点睛】本题考查了化简绝对值、一元一次不等式组等知识点,将问题转化为求231x x x -+++-的最小值是解题关键.15.已知非负实数x y 、、z 满足123234x y z ---==,记23M x y z =++.则M 的最大值减去最小值的差为________. 【答案】283. 【分析】 设123234x y z k ---===,将x y 、、z 用k 表示出来,由x y 、、z 均为非负实数得关于k 的不等式组,求出k 取值范围,再将23M x y z =++转化为k 的代数式,由k 的范围即可确定M 的最大值和最小值,从而即可求差. 【详解】 设123234x y z k ---===, ①21x k =+,23y k =-,43z k =+, ①0x ≥,0y ≥,0z ≥,①210230430k k k +≥⎧⎪-≥⎨⎪+≥⎩, 解不等式组得1223k -≤≤,①23M x y z =++,①()()()21238142343M k k k k =+++=+-+, ①58108143k ≤+≤,即58103M ≤≤, M 的最大值为583,最小值为10, M 的最大值减去最小值的差58281033=-=, 故答案为:283. 【点睛】本题主要考查了不等式的性质的应用,解题关键是设比例式值为k ,通过已知确定k 的取值范围. 三、解答题16.商店销售10台A 型和20台B 型电脑的利润为40000元,销售20台A 型和10台B 型电脑的利润为3500元.(1)求每台A 型电脑和B 型电脑的销售利润;(2)该商店计划一次购进两种型号的电脑共100台,其中B 型电脑的进货量不超过A 型电脑的2倍,设购进A 型电脑x 台,这100台电脑的销售总利润为y 元. ①求y 关于x 的函数关系式:①该商店购进A 型、B 型电脑各多少台,才能使销售总利润最大?(3)实际进货时,厂家对A 型电脑出厂价下调()0100m m <<元,且限定商店最多购进A 型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.【答案】(1)A 100元,B 150元;(2)①5015000y x =-+;①A 34台,B 66台;(3)当050m <<时,A 34台B 66台;当50m =时,A 34~70内均可;当50100m <<时,A 70台B 30台 【分析】(1)设每台A 型加湿器和B 型加湿器的销售利润分别为a 元,b 元,然后根据题意列出二元一次方程组解答即可;(2)①据题意得即可确定y 关于x 的函数关系式,利用A 型利润与B 型利润即可求出总利润y 与x 的关系,并确定x 的范围即可;①根据一次函数的增减性,解答即可;(3)根据题意列出函数数关系式,分以下三种情况①0<m<50,①m=50,① 50 <m < 100时,m-50 >0结合函数的性质,进行求解即可. 【详解】(1)设每台A 型电脑的销售利润为a 元,每台B 型电脑的销售利润为b 元,根据题意得:1020400020103500a b a b +=⎧⎨+=⎩ 解得=100150a b ⎧⎨=⎩ 答:每台A 型电脑的销售利润为100元,每台B 型电脑的销售利润为150元;(2)①设购进A 型电脑x 台,每台A 型电脑的销售利润为100元,A 型电脑销售利润为100x 元, 每台B 型电脑的销售利润为150元,B 型电脑销售利润为()150100x -元()100150100y x x =+-,即这100台电脑的销售总利润为:5015000y x =-+;1002x x -≤,解得1333x ≥.且x 为正整数,150********y x x ⎛⎫=-+≥ ⎪⎝⎭,其中x 为正整数,①5015000y x =-+中,k=500-<,y ∴随x 的增大而减小.x 为正整数,1333x ≥ ①当34x =时,y 取得最大值,此时10066x -=.答:商店购进A 型电脑34台,B 型电脑66台,才能使销售总利润最大; (3)根据题意得()()100150100y m x x =++-,即()5015000y m x =-+,其中133703x ≤≤,且x 为正整数.①当050m <<时,k=500m -<,y ∴随x 的增大而减小,①当34x =时,y 取得最大值,即商店购进34台A 型电脑和66台B 型电脑才能获得最大利润; ①当50m =时,k=500m -=,15000y ∴=,即商店购进A 型电脑数量满足133703x ≤≤的整数时,均获得最大利润;①当50 <m < 100时,k=500m ->,y ∴随x 的增大而增大.①当70x =时,y 取得最大值.即商店购进70台A 型电脑和30台B 型电脑才能获得最大利润. 【点睛】本题主要考查了一次函数的应用,二元一次方程组及一元一次不等式的应用,掌握一次函数的增减性是解答本题的关键.17.某市A ,B 两个蔬菜基地得知黄岗C ,D 两个灾民安置点分别急需蔬菜240t 和260t 的消息后,决定调运蔬菜支援灾区,已知A 蔬菜基地有蔬菜200t ,B 蔬菜基地有蔬菜300t ,现将这些蔬菜全部调运C ,D 两个灾区安置点,从A 地运往C ,D 两处的费用分别为每吨20元和25元,从B 地运往C ,D 两处的费用分别为每吨15元和18元.设从B 地运往C 处的蔬菜为x 吨. (1)请填写下表,用含x 的代数式填空,结果要化简:(2)设A ,B 两个蔬菜基地的总运费为w 元,求出w 与x 之间的函数关系式,并求总运费最小的调运方案;(3)经过抢修,从B 地到C 处的路况得到进一步改善,缩短了运输时间,运费每吨减少m 元()0m >,其余线路的运费不变,试讨论总运费最小的调动方案.【答案】(1)()240x -,()40x -,()300x -;(2)29200w x =+;A →C :200吨,A →D : 0吨,B →C :40吨,B →D :260吨;(3)2m =时,在40240x ≤≤的前提下调运方案的总费用不变;215m <<时,240x =总费用最小,其调运方案为:A →C :0吨,A →D : 200吨,B →C :240吨,B →D :60吨; 【分析】(1)根据题意,从A 处调运到C 处的数量为(240-x )t ;从A 处调往D 处的数量为[200-(240-x )]t ;则从B 调运到D 处的数量为(300-x )t ;(2)根据调运总费用等于四种调运单价乘以对应的吨数的积的和,易得w 与x 的函数关系,根据调运的数量非负即可不等式组,求得x 的范围,从而可求得总费用的最小的调运方案;(3)由题意可得w 与x 的关系式,根据x 的取值范围不同而有不同的解,分情况讨论:当0<m <2时;当m =2时;当2<m <15时,根据一次函数的性质即可解决. 【详解】 (1)填表如下:故答案为:()240x -,()40x -,()300x -;(2)w 与x 之间的函数关系为:()()()202402540151830029200w x x x x x =-+-++-=+ 由题意得:240040003000x x x x -≥⎧⎪-≥⎪⎨≥⎪⎪-≥⎩ ①40240x ≤≤①在29200w x =+中,20> ①w 随x 的增大而增大 ①当40x =时,总运费最小此时调运方案为:(3)由题意得()()()()2024025401518300w x x m x x =-+-+-+- 即()29200w m x =-+,其中40240x ≤≤ ①02m <<,(2)中调运方案总费用最小;2m =时,在40240x ≤≤的前提下调运方案的总费用不变;215m <<时,240x =总费用最小,其调运方案如下:【点睛】本题是一次函数在实际问题中的应用,具有较强的综合性与较大的难度.它考查了一次函数的性质,求一次函数的解析式,解一元一次方程组等知识,用到分类讨论思想.18.如图,在长方形ABCD 中,AB =4,AD =2.P 是BC 的中点,点Q 从点A 出发,以每秒1个单位长度的速度沿A →D →C →B →A 的方向终点A 运动,设点Q 运动的时间为x 秒. (1)点Q 在运动的路线上和点C 之间的距离为1时,x = 秒. (2)若①DPQ 的面积为S ,用含x 的代数式表示S (0≤x <7).(3)若点Q 从A 出发3秒后,点M 以每秒3个单位长度的速度沿A →B →C →D 的方向运动,M 点运动到达D 点后立即沿着原路原速返回到A 点.当M 与Q 在运动的路线上相距不超过2时,请直接写出相应x 的取值范围.【答案】(1)5或7;(2)42(02)11(26)2212(67)x x S x x x x -≤<⎧⎪⎪=-<≤⎨⎪-<<⎪⎩,(3)45x ≤≤或79x ≤≤或1012x ≤≤.【分析】(1)根据题意,点Q 与点C 的距离为1,设Q 运动的路程为a ,则61a -=,根据速度为1,进而求得时间x ;(2)分三种情况讨论,①点Q 在AD 边上运动;①点Q 在CD 边上运动;①点Q 在BC 边上运动;根据情形写出①DPQ 的面积即可;(3)分三种情形讨论,①M 点未到达D 点时,①M 点原路原速返回时,根据情形分相遇和追及问题写出路程差不超过2时,①当M 点回到点A ,当M 与Q 在运动的路线上相距不超过2时,列出不等式组求解即可,注意两点运动的总时间会影响取值范围,即M 点先停止运动. 【详解】 (1)4,2AB AD ==,∴246AD DC +=+=,设Q 运动的路程为a ,依题意则,61a -=, 解得5a =或7a =,速度为每秒1个单位长度,515x ∴=÷=或者717x =÷=,故答案为:5或7;(2)速度为每秒1个单位长度,Q 运动的时间为x 秒. ∴点Q 的路程为1x x ,①点Q 在AD 边上运动;2,4AD CD BC ===,∴2DQ DA AQ x =-=-,11(2)422S DQ DC x ∴=⨯=⨯-⨯42x =-(02x ≤<),①点Q 在CD 边上运动;P 是BC 的中点,112PC BC ∴==,2DQ x AD x =-=-,111(2)11222S DQ CP x x =⨯=-⨯=-(26x <≤), ①点Q 在CP 边上运动,6PQ t AD DC t =--=-,11(6)421222S PQ CD x x ∴=⨯=-⨯=-(67x <<), 综合①①①得:42(02)11(26)2212(67)x x S x x x x -≤<⎧⎪⎪=-<≤⎨⎪-<<⎪⎩,(3)速度为每秒1个单位长度,Q 运动的时间为x秒.∴点Q 的路程为1x x ,设M 的运动时间为t ,根据题意,Q 从A 出发3秒后,M 才出发,则3t x =-,即3x t =+,M 的路程为3t ,Q 点的路程为3t +,42410DC BC AB ++=++=,∴M 点全路程所用时间为2010233⨯÷=秒, 则Q 点的全路程所用时间为12112÷=秒,分三种情形讨论,①M 点未到达D 点时,Q 点出发3秒后,,M Q 共同完成的路程为39AD DC BC AB +++-=根据题意,当M 与Q 在运动的路线上相距不超过2时,则,9(33)2t t -++≤,即9(33)2(33)92t t t t -++≤⎧⎨++-≤⎩, 解得12t ≤≤,45x ∴≤≤,①M 点原路原速返回时,根据题意,当M 与Q 在运动的路线上相距不超过2时,则,(310)2t t --≤,即(310)2(310)2t t t t --≤⎧⎨--≤⎩,解得46t ≤≤,79x ∴≤≤.①当M 点回到点A ,根据题意,当M 与Q 在运动的路线上相距不超过2时,则1012x ≤≤; 综合①①①可得x 的取值范围为45x ≤≤或79x ≤≤或1012x ≤≤.【点睛】本题考查了动点问题,路程问题,一元一次不等式的应用,弄清动点运动的方向和路程是解题的关键. 19.在平面直角坐标系xOy 中,对于M 、N 两点给出如下定义:若点M 到x 、y 轴的距离中的最大值等于点N 到x 、y 轴的距离中的最大值,则称M 、N 两点互为“等距点”,例如:点P (2,2)与Q (-2,-1)到x 轴、y 轴的距离中的最大值都等于2,它们互为“等距点”.已知点A 的坐标为(1,3).(1)在点B (5,3)、C (﹣3,1)、D (﹣2,﹣2)中,点 与点A 互为“等距点”(2)已知直线l :4y kx k =--① 若k =1,点E 在直线l 上,且点E 与点A 互为“等距点”,求点E 的坐标;①若直线l 上存在点F ,使得点F 与点A 互为“等距点”,求k 的取值范围(直接写出结果).【答案】(1)C ;(2)①(2,3)E -或(3,2)-;① 12k ≥或14k ≤-. 【分析】(1)根据新定义“等距点”的定义即可求解; (2)①k=1可得5y x =- 设,5E m m -(), 讨论353m m =-=或 即可,①设(),4F f kf k --,根据点F与点A 互为“等距点”,分两种情况讨论即可:343f kf k ⎧=⎪⎨--≤⎪⎩和343f kf k ⎧≤⎪⎨--=⎪⎩. 【详解】解:(1)①点A (1,3)到x 、y 轴的距离中最大值为3,点C (﹣3,1)到x 、y 轴的距离中最大值为3,①与A 点是“等距点”的点是C .(2)①①直线l :4y kx k =--当k=1时,5y x =- ,①点A (1,3)到x 、y 轴的距离中最大值为3,点E 到点A 互为“等距点”,点E 到坐标轴的最大距离为3,设,5Em m -() , ①EM m =,5EN m =- ①353m m ⎧=⎪⎨-≤⎪⎩或35=3m m ⎧≤⎪⎨-⎪⎩解得:3m =或=2m当3m =时,52m -=-,点E (3,﹣ 2),当=2m 时,53m -=-,点E (2,﹣3),故点E (3,﹣ 2)或E (2,﹣3),① 点F 在直线l :4y kx k =--上,设(),4F f kf k --, ①343f kf k ⎧=⎪⎨--≤⎪⎩①②或343f kf k ⎧≤⎪⎨--=⎪⎩③④ 由①得到:3f =±,当3f =时,243k -≤,解得1722k ≤≤, 当3f =-时,443k --≤,解得7144k -≤≤-, 由①得到:43kf k --=±,当43kf k --=,即7k f k+=时,则73k k +≤, 解得72k ≥或74k ≤-, 当43kf k --=-,即1k f k+=时,则13k k +≤, 解得12k ≥或14k ≤-, 综上所述:12k ≥或14k ≤-. 【点睛】本题考查新定义的应用和点坐标到坐标轴之间的距离,涉及到一元一次不等式,解题的关键是正确理解题意,学会利用分类讨论的思想.20.在平面直角坐标系中,若P 、Q 两点的坐标分别为()11,P x y 和()22,Q x y ,则定12x x -和12y y -中较小的一个(若它们相等,则任取其中一个)为P 、Q 两点的“直角距离小分量”,记为min (,)d P Q .例如:(2,3),(0,2)P Q -,因为12122,0,|20|2x x x x =-=-=--=;12123,2,|32|1y y y y ==-=-=,而|32||20|-<--,所以min (,)|32|1d P Q =-=.(1)请直接写出()3,2A -和()1,1B -的直角距离小分量()min ,d A B =_________;(2)点D 是坐标轴上的一点,它与点()3,1C -的直角距离小分量()min ,2d C D =,求出点D 的坐标; (3)若点(1,22)M m m +-满足以下条件:a )点M 在第一象限;b )点M 与点()5,0N 的直角距离小分量()min ,2d M N <c )45MON ∠>︒,O 为坐标原点.请写出满足条件的整点(横纵坐标都为整数的点)M 的坐标_______.【答案】(1)3;(2)(0,1)D 或(0,3)D -;(3)(5,6)M 或(6,8)【分析】(1)根据新概念求得即可;(2)分两种情况,根据“直角距离小分量”的定义得出即可;(3)根据题意得出10220m m +>⎧⎨->⎩,解出m 的取值范围,再由45MON ∠>︒可推导出2211OM m K m -=>+,解出m 的取值范围,根据横纵坐标都为整数的点取m 的值即可.【详解】解:(1)(3,2)A -,(1,1)B -,|31|4∴+=>|21|3--=,()min ,3d A B ∴=;故答案为3;(2)点D 是坐标轴上的一点,若D 在x 轴上,设(a,0)D ,由于|01|12+=<与题意矛盾,故点D 是在y 轴上的一点,|1|2b ∴+=,解得:1b =或3-,(0,1)D ∴或(0,3)D -;(3)由题意得:10220m m +>⎧⎨->⎩, 解得1m , |15||4|,|220|2|1|m m m m +-=---=-,∴[]222(4)2(1)312m m m ---=-+, 当12m <<时,()min ,2|1|2d M N m =-<,解得:02m <<,当2m ≥时,()min ,|4|2d M N m =-<,解得:26m <<,m ∴的取值范围是:02m <<或26m <<,45MON ∠>︒恰好为OM l 的倾斜角,1OM K ∴>,2211OM m K m -=>+, 解得:1m <-或3m >综上:m 的取值范围是:36m <<,横纵坐标都为整数,4m ∴=和5,(5,6)M ∴或(6,8),故答案为:(5,6)M 或(6,8).【点睛】本题考查了坐标与图形的性质,解一元一次不等式组,解题的关键是根据新概念列出不等式组.。
八年级下册数学压轴题(含答案)

八年级下册数学压轴题(含答案)四边形AOBC的对角线互相平分,且相等,故为菱形;又因为OC经过翻折后落在AB上,且AC与x轴垂直,故OC垂直于AB,故AO=OC=OB=BC,故AOBC是一个菱形;3)设点P的坐标为(x,y),则BPC为直角三角形,且BP=PC,又因为BP在y轴下方,故y<0,且BP与BC垂直,故BP的斜率为-2;设BP的解析式为y=-2x+b,且B点坐标为(0,-5),则有b=-5;又因为BP=PC,故PC的解析式为y=2x+b,且C点坐标为(a,0),代入得a=5;又因为XXX在BC下方,故y<0,代入得y=-2x-5;代入BP的解析式得x=5/3,代入得y=-25/3;故存在点P(5/3,-25/3),使△BCP为等腰直角三角形。
题目:在平面直角坐标系中,已知点A(0,0),B(5,0),C(0,5√2),D从A出发沿AC方向以1m/s的速度向C匀速运动,同时点E从B出发沿BA方向以√2m/s的速度向A匀速运动。
当其中一个点到达终点时,另一个点也随之停止运动。
设点D,E运动的时间是t(0<t≤10)秒。
过点E作EF⊥BC于点F,连接DE,DF。
1)求BE和CD的长度。
2)试说明,无论t为何值,四边形ADEF都是平行四边形。
3)当t为何值时,△DEF为直角三角形?请说明理由。
解法:1)由题意可知,BE=√2t,CD=t,故BE=√2t,CD=t。
2)如图所示,由题意可得,∠C=90°,∠A=45°,故∠B=45°。
又因为EF⊥BC,所以∠EFB=90°,∠FEB=45°,所以BE=EF。
又因为AE=√2t,DE=CD,所以DE=√2t。
因此,四边形ADEF的对角线相等,且相互平分,所以ADEF是平行四边形。
3)如图所示,当EF⊥BC时,由勾股定理可知,DE²=DF²+EF²,即(√2t)²=(t+BE)²+(5√2-BF)²。
【常考压轴题】一次函数实际应用压轴—2023-2024学年八年级数学下册(人教版)(解析版)

一次函数实际应用压轴题型1:利用一次函数解决方案问题题型2:利用一次函数解决销售利润问题题型3:利用一次函数解决行程问题题型4:利用一次函数解决运输问题题型1:利用一次函数解决方案问题【典例1】我校将举办一年一度的秋季运动会,需要采购一批某品牌的乒乓球拍和配套的乒乓球,一副球拍标价80元,一盒球标价25元.体育商店提供了两种优惠方案,具体如下:方案甲:买一副乒乓球拍送一盒乒乓球,其余乒乓球按原价出售;方案乙:按购买金额打9折付款.学校欲购买这种乒乓球拍10副,乒乓球x(x≥10)盒.(1)请直接写出两种优惠办法实际付款金额y甲(元),y乙(元)与x(盒)之间的函数关系式.(2)如果学校需要购买15盒乒乓球,哪种优惠方案更省钱?(3)如果学校提供经费为1800元,选择哪个方案能购买更多乒乓球?【答案】(1)y甲=25x+550,y乙=22.5x+720;(2)方案甲更省钱;(3)学校提供经费为1800元,选择方案甲能购买更多乒乓球.【解答】解:(1)由题意得:y甲=10×80+25(x﹣10)=25x+550,y乙=25×0.9x+80×0.9×10=22.5x+720,(2)根据(1)中解析式,y甲=25x+550,y乙=22.5x+720,当x=15时y甲=25×15+550=925(元),y乙=22.5×15+720=1057.5(元),∵925<1057.5,∴方案甲更省钱;(3)根据(1)中解析式,y甲=25x+550,y乙=22.5x+720,当y甲=1800元时,1800=25x+550,解得:x=50,当y乙=1800元时,1800=22.5x+720,解得:x=48,∵50>48,∴学校提供经费为1800元,选择方案甲能购买更多乒乓球.【变式1-1】已知用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有34吨货物,计划同时租用A型和B型车辆,一次运完,且恰好每辆车都载满货物.根据以上信息,解答下列问题:(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?(2)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.共有几种租车方案,哪种方案租车费用最少?【答案】(1)1辆A型车载满货物一次可运货3吨,1辆B型车载满货物一次可运货4吨;(2)该物流公司共有三种租车方案,方案1:租用A型车10辆,B型车1辆;方案2:租用A型车6辆,B型车4辆;方案3:租用A型车2辆,B型车7辆.方案3租用A型车2辆、B型车7辆最省钱,最少租车费为1040元.【解答】解:(1)设1辆A型车载满货物一次可运货x吨,1辆B型车载满货物一次可运货y吨,依题意,得:,解得:.答:1辆A型车载满货物一次可运货3吨,1辆B型车载满货物一次可运货4吨.(2)设A型车租a辆,B型车租b辆,依题意,得:3a+4b=34,∴a=.∵a,b均为非负整数,∴,,,∴该物流公司共有三种租车方案,方案1:租用A型车10辆,B型车1辆;方案2:租用A型车6辆,B型车4辆;方案3:租用A型车2辆,B型车7辆.方案1所需租金:100×10+120×1=1120(元),方案2所需租金:100×6+120×4=1080(元),方案3所需租金:100×2+120×7=1040(元).∵1120>1080>1040,∴方案3租用A型车2辆、B型车7辆最省钱,最少租车费为1040元.【变式1-2】2022年秋,郑州新冠疫情牵动全国,社会各界筹集的医用,建设等物资不断从各地向郑州汇集.这期间,恰逢春节承运资源短缺,紧急情况下,多家物流企业纷纷开通特别通道,驰援郑州,为生产药品,口罩,医疗器械等紧急物资的企业提供全方位支持.已知用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B 型车载满货物一次可运货11吨,某物流公司计划租用这两种车辆运输物资.根据以上信息,解答下列问题:(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?(2)若A型车每辆需租金90元/次,B型车每辆需租金110元/次.物流公司计划共租用8辆车,请写出总租车费用w A型车数量a(辆)的函数关系式.(3)如果汽车租赁公司的A型车只剩了6辆,B型车还有很多.在(2)的条件下,请选出最省钱的租车车方案,并求出最少租车费用.【答案】(1)1辆A型车和1辆B型车都装满货物一次可分别运货3吨、4吨;(2)w=﹣20a+880;(3)租6辆A型车,2辆B型车,租车费用最少,最少费用为760元.【解答】解:(1)设1辆A型车和1辆B型车都装满货物一次可分别运货x吨、y吨,由题意得:,解得,∴1辆A型车和1辆B型车都装满货物一次可分别运货3吨、4吨.(2)由题意可得:w=90a+110(8﹣a)=﹣20a+880;(3)在一次函数w=﹣20a+880中,∵﹣20<0,∴w随a的增大而小;由题意知:a≤6,则当a=6时,总租车费用最少,最少费用为:w=﹣20×6+880=760.8﹣6=2.∴最省钱的租车方案为租6辆A型车,2辆B型车,租车费用最少,最少费用为760元.题型2:利用一次函数解决销售利润问题【典例2】2023年第一届全国学生(青年)运动会在南宁市某中学初中部举行火炬传递仪式,有幸参与该盛事的学校的九年级1000名学生将在火炬传递经过的校道两边为火炬手摇旗呐喊,年级制定的活动经费初步方案是采购一些手摇式小国旗,每面小国旗售价为0.8元.经过进一步商讨之后,年级决定再补购印有运动会吉祥物“壮壮”和“美美”的头戴式小彩旗若干个.询问甲、乙两家吉祥物特许经销商,他们考虑到学校情况给出了不同的销售方案.甲经销商的销售方案是每个头戴式小彩旗卖2.2元.乙经销商的方案是:购买不超过200个头戴式小彩旗,每个售价2.5元;若超过200个,则超过部分每个售价2元.(1)设向乙经销商购买x个头戴式小彩旗,所需费用为y元,求出y关于x的函数关系式;(2)年级最终决定必须要买1000面小国旗及若干个头戴式小彩旗,最终总费用不低于1600元,不超过2000元.若向甲、乙两家经销商中的一家购买头戴式小彩旗,年级该向哪一家购买头戴式小彩旗最合算?【答案】(1)y=;(2)当总费用大于或等于1600而小于1900元时,向甲经销商购买最合算;当购买小彩旗费用为1900元时,两家一样合算;当购买总费用大于1900元而小于或等于2000元时,向乙经销商购买最合适.【解答】解:(1)当0≤x≤200时,y=2.5x;当x>200时,y=200×2.5+2(x﹣200)=2x+100;综上,y关于x的函数关系式为y=.(2)设在甲、乙两家经销商购买x个头戴式小彩旗所需费用分别为y1元、y2元,则y1=2.2x.由(1)得,y2=.它们的函数图象如图所示:∵最终总费用不低于1600元,不超过2000元,购买1000面小国旗的费用是1000×0.8=800(元),∴购买头戴式小彩旗的费用最少800元,最多1200元,即800≤y1≤1200,800≤y2≤1200.当y1=y2时,2.2x=2x+100x=500,此时y1=y2=1100.由图象可知,当购买头戴式小彩旗的费用低于1100元时,向甲经销商购买最合算;当购买头戴式小彩旗费用为1100元时,两家一样合算;当购买头戴式小彩旗费用大于1100元时,向乙经销商购买最合适.综上,当总费用大于或等于1600而小于1900元时,向甲经销商购买最合算;当购买小彩旗费用为1900元时,两家一样合算;当购买总费用大于1900元而小于或等于2000元时,向乙经销商购买最合适.【变式2-1】“互联网+”让我国经济更具活力.牡丹花会期间,某网店直接从工厂购进A、B两款花会纪念钥匙扣进行销售,进货价和销售价如表:(1)网店第一次用1100元购进A、B两款钥匙扣共50件,求两款钥匙扣分别购进的件数;(2)第一次购进的花会纪念钥匙扣售完后,该网店计划再次购进A、B两款钥匙扣共240件(进货价和销售价都不变),且第二次进货总价不高于5800元.网店这次应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?【答案】(1)购进A款钥匙扣30件,B款钥匙扣20件;(2)当购进40件A款钥匙扣,200件B款钥匙扣时,才能获得最大销售利润,最大销售利润是2800元.【解答】解:(1)设购进A款钥匙扣x件,B款钥匙扣y件,根据题意得:答:购进A款钥匙扣30件,B款钥匙扣20件;(2)设购进m件A款钥匙扣,则购进(240﹣m)件B款钥匙扣,根据题意得:20m+25(240﹣m)≤5800,解得:m≥40.设再次购进的A、B两款钥匙扣全部售出后获得的总利润为w元,则w=(30﹣20)m+(37﹣25)(240﹣m)=﹣2m+2880.∵﹣2<0,∴w随m的增大而减小,∴当m=40时,w取得最大值,最大值=﹣2×40+2880=2800(元),此时240﹣40=200(元).答:当购进40件A款钥匙扣,200件B款钥匙扣时,才能获得最大销售利润,最大销售利润是2800元.【变式2-2】2023年杭州亚运会期间,吉祥物徽章受到了众多人的喜爱.某网店直接从工厂购进A款礼盒120盒,B款礼盒50盒,两款礼盒全部售完.两款礼盒的进货价和销售价如下表:(1)求该网店销售这两款礼盒所获得的总利润.(2)网店计划用第一次所获的销售利润再次去购买A、B两款礼盒共80盒.该如何设计进货方案,使网店获得最大的销售利润?最大销售利润是多少?【答案】(1)该网店销售这两款礼盒所获得的总利润为2200元;(2)该网店购进A款礼盒和B款礼盒各40盒网店获得最大的销售利润,最大利润为920元.【解答】解:(1)120×(45﹣30)+50(33﹣25)=1800+400=2200(元),答:该网店销售这两款礼盒所获得的总利润为2200元;(2)设购进x盒A款礼盒,则购进(80﹣x)盒B款礼盒,网店所获利润为y元,根据题意得:y=(45﹣30)x+(33﹣25)(80﹣x)=7x+640,又∵30x+25(80﹣x)≤2200,∴x≤40,∵7>0,∴y随x的增大而增大,∴当x=40时,y有最大值,最大值为920,∴该网店购进A款礼盒和B款礼盒各40盒网店获得最大的销售利润,最大利润为920元.【变式2-3】“书香中国,读领未来”,4月23日是世界读书日,我市某书店同时购进A,B 两类图书,已知购进3本A类图书和4本B类图书共需160元;购进6本A类图书和2本B类图书共需170元.(1)A,B两类图书每本的进价各是多少元?(2)该书店计划用2000元购进这两类图书,设购进A类x本,B类y本.①求y关于x的关系式;②进货时,A类图书的购进数量不少于50本,已知A类图书每本的售价为28元,B类图书每本的售价为40元,如何进货才能使书店所获利润最大?最大利润为多少元?【答案】(1)A类图书每本的进价是20元,B类图书每本的进价是25元;(2)①;②购进A类图书50本,B类图书40本时,才能使书店所获利润最大,最大利润为1000元.【解答】解:(1)设A类图书每本的进价是a元,B类图书每本的进价是b元,根据题意得:,解得:,答:A类图书每本的进价是20元,B类图书每本的进价是25元;(2)①根据题意得:20x+25y=2000,∴y关于x的关系式为;②设书店所获利润为w元,根据题意得:W=(28﹣20)x+(40﹣25)y=8x+15y==﹣4x+1200∵﹣2<0,∴W随x的增大而减小,∵A类图书的购进数量不少于50本,∴x≥50,∴当x=50时,W4×50+1200=1000,此时,答:购进A类图书50本,B类图书40本时,才能使书店所获利润最大,最大利润为1000元.【变式2-4】为迎接新春佳节的到来,一水果店计划购进甲、乙两种新出产的水果共160千克,这两种水果的进价、售价如表所示:(1)若该水果店预计进货款为1000元,则这两种水果各购进多少千克?(2)若该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍,应怎样安排进货才能使水果店在销售完这批水果时获利最多?此时利润为多少元?【答案】(1)甲种水果购进110千克,则乙种水果购进50千克;(2)安排购买甲种水果40kg,乙种水果120千克,才能使水果店在销售完这批水果时获利最多,此时利润为600元.【解答】解:(1)设甲种水果购进x千克,则乙种水果购进(160﹣x)千克,由题意可得:5x+9(160﹣x)=1000,解得x=110,∴160﹣x=50,答:甲种水果购进110千克,则乙种水果购进50千克;(2)设购进甲种水果m千克,则乙种水果购进(160﹣m)千克,获得的利润为w元,由题意可得:w=(8﹣5)m+(13﹣9)(160﹣m)=﹣m+640,∴w随m的增大而减小,∵该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍,∴160﹣m≤3m,解得m≥40,∴当m=40时,w取得最大值,此时w=600,160﹣m=120,答:安排购买甲种水果40kg,乙种水果120千克,才能使水果店在销售完这批水果时获利最多,此时利润为600元.【变式2-5】随着“双减”政策的逐步落实,其中增加中学生体育锻炼时间的政策引发社会的广泛关注,体育用品需求增加,某商店决定购进A、B两种羽毛球拍进行销售,已知每副A种球拍的进价比每副B种球拍贵20元,用2800元购进A种球拍的数量与用2000元购进B种球拍的数量相同.(1)求A、B两种羽毛球拍每副的进价;(2)若该商店决定购进这两种羽毛球拍共100副,考虑市场需求和资金周转,用于购买这100副羽毛球拍的资金不超过5900元,那么该商店最多可购进A种羽毛球拍多少副?(3)若销售A种羽毛球拍每副可获利润25元,B种羽毛球拍每副可获利润20元,在第(2)问条件下,如何进货获利最大?最大利润是多少元?【答案】见试题解答内容【解答】解:(1)设A种羽毛球拍每副的进价为x元,根据题意,得,解得x=70,经检验,x=70是原分式方程的根,且符合题意,70﹣20=50(元),答:A种羽毛球拍每副的进价为70元,B种羽毛球拍每副的进价为50元;(2)设该商店购进A种羽毛球拍m副,根据题意,得70m+50(100﹣m)≤5900,解得m≤45,m为正整数,答:该商店最多购进A种羽毛球拍45副;(3)设总利润为w元,w=25m+20(100﹣m)=5m+2000,∵5>0,∴w随着m的增大而增大,当m=45时,w取得最大值,最大利润为5×45+2000=2225(元),此时购进A种羽毛球拍45副,B种羽毛球拍100﹣45=55(副),答:购进A种羽毛球拍45副,B种羽毛球拍55副时,总获利最大,最大利润为2225元.【变式2-6】新春佳节来临,某公司组织10辆汽车装运苹果、芦柑、香梨三种水果共60吨去外地销售,要求10的车辆都不少于2辆,根据下表提供的信息,解答以下问题:(1)设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围(2)用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w 的最大值.【答案】见试题解答内容【解答】解:(1)设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,则运香梨的车辆(10﹣x﹣y)辆.7x+6y+5(10﹣x﹣y)=60,∴y=﹣2x+10(2≤x≤4);(2)w=7×0.15x+6×0.2(﹣2x+10)+5×0.1[10﹣x﹣(﹣2x+10)],即w=﹣0.85x+12,∵﹣0.85<0,∴w随x的增大而减小,∴当x=2时,w有最大值10.3万元,∴装运苹果的车辆2辆,装运芦柑的车辆6辆,运香梨的车辆2辆时,此次销售获利最大,最大利润为10.3万元.【变式2-7】商店销售1台A型和2台B型电脑的利润为400元,销售2台A型和1台B 型电脑的利润为350元,该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润y 元.(1)①求y关于x的函数关系式;②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?(2)实际进货时,厂家对A型电脑出厂价下调了m(0<m≤50)元,且限定商店最多的进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出售这100台电脑销售总利润最大的进货方案.【答案】(1)①y=﹣50x+15000,②商店购进34台A型电脑和66台B型电脑的销售利润最大.(2)①当0<m<50时,商店购进34台A型电脑和66台B型电脑的销售利润最大.②m=50时,商店购进A型电脑数量满足33≤x≤70的整数时,均获得最大利润.【解答】解:(1)设每台A型电脑销售利润为a元,每台B型电脑的销售利润为b元;根据题意得:,解得∴y=100x+150(100﹣x),即y=﹣50x+15000,②据题意得,100﹣x≤2x,解得x≥33,∵y=﹣50x+15000,﹣50<0,∴y随x的增大而减小,∵x为正整数,∴当x=34时,y取最大值,则100﹣x=66,即商店购进34台A型电脑和66台B型电脑的销售利润最大.(2)据题意得,y=(100+m)x+150(100﹣x),即y=(m﹣50)x+15000,33≤x≤70①当0<m<50时,y随x的增大而减小,∴当x=34时,y取最大值,即商店购进34台A型电脑和66台B型电脑的销售利润最大.②m=50时,m﹣50=0,y=15000,即商店购进A型电脑数量满足33≤x≤70的整数时,均获得最大利润.【变式2-8】某水果种植基地为响应政府号召,大力种植优质水果.某超市看好甲、乙两种优质水果的市场价值,决定开始销售这两种水果.已知该超市购进甲种水果10千克和乙种水果3千克共需要197元;若购进甲种水果15千克和乙种水果6千克,则共需要324元.(1)求甲、乙两种水果每千克的进价分别是多少元?(2100千克进行销售,甲种水果的售价为20元/千克,乙种水果的售价为24元/千克.其中甲种水果的数量不少于20千克,但不超过60千克.若超市当天购进的水果当天售完(运输和销售过程中水果的损耗忽略不计),写出每天销售这两种水果获得的利润w(元)与购进甲种水果的数量a(千克)之间的关系式,并求出a为何值时能获得最大利润?最大利润是多少元?【答案】(1)甲种水果每千克的进价是14元,乙种水果每千克的进价是19元;(2)每天销售这两种水果获得的利润w(元)与购进甲种水果的数量a(千克)之间的关系式为w=a+500;当a=60时,能获得最大利润,最大利润是560元.【解答】解:(1)设甲种水果每千克的进价是x元,乙种水果每千克的进价是y元,根据题意得:,解得,答:甲种水果每千克的进价是14元,乙种水果每千克的进价是19元;(2)由题意得:w=(20﹣14)a+(24﹣19)(100﹣a)=6a+5(100﹣a)=a+500,∵1>0,20≤a≤60,∴当a=60时,w最大,最大值为560,∴每天销售这两种水果获得的利润w(元)与购进甲种水果的数量a(千克)之间的关系式为w=a+500;当a=60时,能获得最大利润,最大利润是560元.【变式2-9】某商店销售A型和B型两种型号的电脑,销售一台A型电脑可获利120元,销售一台B型电脑可获利140元.该商店计划一次购进两种型号的电脑共100台,其中B 型电脑的进货量不超过A型电脑的3倍.设购进A型电脑x台,这100台电脑的销售总利润为y元.(1)求y与x的函数关系式,并求出自变量x的取值范围;(2)该商店购进A型、B型电脑各多少台,才能使销售利润最大?最大利润是多少?【答案】见试题解答内容【解答】解:(1)由题意可得,A型电脑的总利润为:120x,B型电脑的总利润为:140(100﹣x),∴A、B电脑的总利润:y=120x+140(100﹣x)=﹣20x+14000,∴y与x的函数关系式为:y=﹣20x+14000,又B型电脑的进货量不超过A型电脑的3倍,∴100﹣x≤3x,解得:x≥25,∴自变量x的取值范围为:25≤x≤100,且x为正整数,∴y=﹣20x+14000(25≤x≤100,且x为正整数);(2)∵y=﹣20x+14000,且﹣20<0,∴y随x的增大而减小,∵25≤x≤100,且x为正整数,∴x=25时,y有最大值为:﹣20×25+14000=13500,∴A型电脑进货25台,B型电脑进货75台,销售利润最大为13500元.【变式2-10】在近期“抗疫”期间,某药店销售A,B两种型号的口罩,已知销售80只A 型和45只B型的利润为21元,销售40只A型和60只B型的利润为18元.(1)求每只A型口罩和B型口罩的销售利润;(2)该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不少于A 型口罩的进货量且不超过它的3倍,则该药店购进A型、B型口罩各多少只,才能使销售总利润y最大?最大值是多少?【答案】(1)每只A型口罩销售利润为0.15元,每只B型口罩销售利润为0.2元;(2)药店购进A型口罩500只、B型口罩1500只,才能使销售总利润最大,总利润最大为375元.【解答】解:(1)设每只A型口罩销售利润为a元,每只B型口罩销售利润为b元,根据题意得:,解得,答:每只A型口罩销售利润为0.15元,每只B型口罩销售利润为0.2元;(2)根据题意得,y=0.15x+0.2(2000﹣x),即y=﹣0.05x+400;根据题意得,,解得500≤x≤1000,∴y=﹣0.05x+400(500≤x≤1000),∵﹣0.05<0,∴y随x的增大而减小,∵x为正整数,∴当x=500时,y取最大值为375元,则2000﹣x=1500,即药店购进A型口罩500只、B型口罩1500只,才能使销售总利润最大为375元.【变式2-11】第19届亚运会已于2023年9月23日至10月8日在中国浙江杭州成功举行.这国关注,举世瞩目.杭州亚运会三个吉祥物分别取名“琮琮”“宸宸”“莲莲”.某专卖店购进A,B两种杭州亚运会吉祥物礼盒进行销售.A种礼盒每个进价160元,售价220元;B种礼盒每个进价120元,售价160元.现计划购进两种礼盒共100个,其中A种礼盒不少于60个.设购进A种礼盒x个,两种礼盒全部售完,该专卖店获利y元.(1)求y与x之间的函数关系式;(2)若购进100个礼盒的总费用不超过15000元,求最大利润为多少元?(3)在(2)的条件下,该专卖店对A种礼盒以每个优惠m(0<m<20)元的价格进行优惠促销活动,B种礼盒每个进价减少n元,售价不变,且m﹣n=4,若最大利润为4900元,请直接写出m的值.【答案】(1)y与x之间的函数关系式为y=20x+4000;(2)最大利润为5500元;(3)m=10.【解答】解:(1)由题意得:y=(220﹣160)x+(160﹣120)×(100﹣x)=20x+4000,∴y与x之间的函数关系式为y=20x+4000;(2)由题意得:,∴60≤x≤75,∵y=20x+4000中,20>0,∴y随x的增大而增大,∴当x=75时,y有最大值,最大值=20×75+4000=5500(元),∴最大利润为5500元;(3)∵m﹣n=4,∴n=m﹣4,由题意得:y=(220﹣160﹣m)x+(160﹣120+n)(100﹣x)=(60﹣m)x+(40+n)×100﹣(40+n)x=(24﹣2m)x+100m+3600.∵60≤x≤75,0<m<20,∴当0<m<12时,24﹣2m>0,∴y随x的增大而增大,∴当x=75时,y最大=(24﹣2m)×75+100m+3600=4900,∴m=10,符合题意;当m=12时,y=100×12+3600=4800≠4950,不合题意;当12<m<20时,24﹣2m<0,∴y随x的增大而减小.∴当x=60时,y最大=(24﹣2m)×60+100m+3600=4900,∴m=7,不合题意,舍去.综上,m=10.题型3:利用一次函数解决行程问题【典例3】2023年12月18日,甘肃积石山县发生6.2级地震,全国各地连夜出发实施紧急救援.一辆货车先从甲地出发运送赈灾物资到灾区,稍后一辆轿车从甲地急送医疗团队到灾区,已知甲地与灾区的路程是330km,货车行驶时的速度是60km/h.两车离甲地的路程s(km)与时间t(h)的函数图象如图.(1)求出a的值;(2)求轿车离甲地的路程s(km)与时间t(h)的函数表达式;(3)问轿车比货车早多少时间到达灾区?【答案】(1)1.5h;(2)s=100t﹣150(1.5≤t≤4.8);(3)轿车比货车早1.2h到达灾区.【解答】解:(1)∵货车的速度是60km/h,∴a==1.5(h);(2)由图象可得点(1.5,0),(3,150),设直线的表达式为s=kt+b,把(1.5,0),(3,150)代入得:,解得,∴s=100t﹣150(1.5≤t≤4.8);(3)由图象可得货车走完全程需要+0.5=6(h),∴货车到达乙地需6h,∵s=100t﹣150,s=330,解得t=4.8,∴两车相差时间为6﹣4.8=1.2(h),∴货车还需要1.2h才能到达,即轿车比货车早1.2h到达灾区.【变式3-1】我市莲池区开展了“阳光体育,强身健体”系列活动,小明积极参与,他每周末和哥哥一起练习赛跑.哥哥先让小明跑若干米,哥哥追上小明后,小明的速度降为原来的一半,已知他们所跑的路程y(m)与哥哥跑步的时间x(s)之间的函数图象如图.(1)哥哥的速度是m/s,哥哥让小明先跑了米,小明后来的速度为m/s.(2)哥哥跑几秒时,哥哥追上小明?(3)求哥哥跑几秒时,两人相距10米?【答案】(1)8,14,3;(2)7;(3)2或9.【解答】解:(1)根据图象可知,哥哥的速度是24÷3=8(m/s),哥哥让小明先跑了14m;在哥哥追上小明之前,小明的速度为(32﹣14)÷3=6(m/s),∴在哥哥追上小明之后,小明的速度为6÷2=3(m/s),故答案为:8,14,3.(2)设哥哥跑t秒时,哥哥追上小明.14+6t=8t,解得t=7,∴哥哥跑7秒时,哥哥追上小明.(3)设哥哥所跑的路程y与哥哥跑步的时间x之间的函数关系式为y=kx(k为常数,且k≠0).将x=3,y=24代入y=kx,得3k=24,解得k=8,∴y=8x;小明所跑的路程y与哥哥跑步的时间x之间的函数关系式:当哥哥追上小明时,哥哥所跑的路程为8×7=56(m),∴图象交点坐标为(7,56).当0≤x<7时,设y=k1x+b1(k1、b1为常数,且k1≠0).将x=0,y=14和x=7,y=56代入y=k1x+b1,得,解得,∴y=6x+14(0≤x<7);哥哥出发后8s时,小明跑的总路程为56+(8﹣7)×3=59(m),∴坐标(8,59)对应的点在图象l3上.当x≥7时,设y=k2x+b2(k2、b2为常数,且k2≠0).将x=7,y=56和x=8,y=59代入y=k2x+b2,得,解得,∴y=3x+35(x≥7);综上,y=.两人相距10米时:当0≤x<7时,|6x+14﹣8x|=10,整理得|x﹣7|=5,解得x=2或12(不符合题意,舍去);当x>7时,|3x+35﹣8x|=10,整理得|x﹣7|=2,解得x=5(不符合题意,舍去)或9;∴哥哥跑2秒或910米.【变式3-2】一辆汽车和一辆摩托车分别从A,B两地去同一城市C,它们离A地的路程随时间变化的图象如图所示,已知汽车的速度为60km/h,摩托车比汽车晚1个小时到达城市C.(1)求摩托车到达城市C所用的时间;(2)求摩托车离A地的路程y(km)关于时间x(h)的函数表达式;(3)当x为何值时,摩托车和汽车相距30km.【答案】(1)4小时;(2)y=40x+20;(3)或小时.【解答】解:(1)根据图象信息,得到A到C点的距离为180千米,∵汽车的速度为60km/h,∴汽车到达中点的用时,∵摩托车比汽车晚1个小时到达城市C,∴摩托车到达城市C的时间为4小时.(2)设解析式为y=kx+b,把(0,20),(4,180)分别代入解析式得:,解得,故摩托车离A地的路程y(km)关于时间x(h)的函数表达式为y=40x+20.(3)根据题意,得到汽车的函数解析式为y=60x,根据题意,得:60x﹣(40x+20)=30,解得,40x+20+30=180,x=,故经过或小时,摩托车和汽车相距30km.【变式3-3】已知A,B两港口相距150海里,甲船从A港行驶到B港后,休息一段时间,速度不变,沿原航线返回,同时,乙船从A港出发驶向B港,甲、乙两船离A港的距离s(海里)与甲船行驶时间t(小时)之间的函数关系如图所示,当两船相遇时,两船到A 港的距离为90海里,乙船在行驶过程中,速度不变.(假设甲、乙两船沿同一航线航行)(1)直接写出M点的坐标;(2)分别求线段DM、EF的表达式;(3)甲船行驶多少小时后两船在甲船返航过程中相距30海里?【答案】(1)(13,0);(2)s=﹣30t+390(8≤t≤13),;(3)9.6小时或10.4小时.【解答】解:(1)∵甲船返回时速度不变,∴返回时间为5小时,8+5=13,所以,点M的坐标为(13,0),故答案为:(13,0);(2)由图可知:点D(8,150),设DM所在直线的解析式为:s=kt+b,把点D(8,150),点M(13,0)分别代入解析式,得:,解得,故线段DM的表达式为:s=﹣30t+390(8≤t≤13);甲船的速度=150÷5=30(海里/时),(150﹣90)÷30=2(小时),∴乙船的速度为:90÷2=45(海里/时),∴乙船行驶的时间为:(小时),此时,故点G(10,90),由图可知:点E(8,0),设直线EF的表达式为s=mt+n,把点G(10,90),点E(8,0)分别代入解析式,得:,解得,故线段EF的表达式为:;(3)设甲船行驶x小时后两船相距30海里,①若相遇前相距30海里,则(30+45)×(x﹣8)=150﹣30,解得x=9.6,②若相遇后再相距30海里,则(30+45)×(x﹣8)=150+30,解得x=10.4,所以,甲船行驶9.6小时或10.4小时后,两船相距30海里.【变式3-4】甲、乙两车早上从A城车站出发匀速前往B城车站,在整个行程中,两车离开A城的距离s与时间t的对应关系如图所示.(1)A,B两城之间距离是多少?(2)求甲、乙两车的速度分别是多少?(3)乙车出发多长时间追上甲车?(4)从乙车出发后到甲车到达B城车站这一时间段,在何时间点两车相距40km?【答案】(1)A、B两城之间距离是300千米;(2)甲、乙两车的速度分别是60千米/小时和100千米/小时;(3)乙车出发1.5小时追上甲车;(4)分别在上午6:30,8:30,9:20这三个时间点两车相距40千米.【解答】解:(1)由图象可知A、B两城之间距离是300千米;(2)由图象可知,甲的速度==60(千米/小时),乙的速度==100(千米/小时),∴甲、乙两车的速度分别是60千米/小时和100千米/小时;(3)设乙车出发x小时追上甲车,由题意:60(x+1)=100x,解得:x=1.5,∴乙车出发1.5小时追上甲车;(4)设乙车出发后到甲车到达B城车站这一段时间内,甲车与乙车相距40千米时甲车行驶了m小时,①当甲车在乙车前时,得:60m﹣100(m﹣1)=40,解得:m=1.5,。
(完整)八年级下数学压轴题及答案.docx
.八年级下数学压轴题1.已知,正方形ABCD中,∠ MAN=45°,∠ MAN 绕点 A 顺时针旋转,它的两边分别交CB、 DC(或它们的延长线)于点M、 N, AH⊥ MN 于点 H.( 1)如图①,当∠MAN 绕点 A 旋转到 BM=DN 时,请你直接写出AH 与 AB 的数量关系:;(2)如图②,当∠ MAN 绕点 A 旋转到 BM≠ DN 时,( 1)中发现的 AH 与 AB 的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠ MAN=45°, AH⊥ MN 于点 H,且 MH=2 , NH=3,求 AH 的长.(可利用( 2)得到的结论).2.如图,△ ABC 是等边三角形,点 D 是边 BC上的一点,以AD 为边作等边△ADE,过点C 作 CF∥ DE交 AB 于点 F.(1)若点 D 是 BC边的中点(如图①),求证: EF=CD;(2)在( 1)的条件下直接写出△ AEF和△ ABC的面积比;(3)若点 D 是 BC 边上的任意一点(除 B、 C 外如图②),那么( 1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由..3.( 1)如图 1,在正方形ABCD中, E 是 AB 上一点, F 是 AD 延长线上一点,且DF=BE.求证: CE=CF;(2)如图 2,在正方形 ABCD中, E 是 AB 上一点, G 是 AD 上一点,如果∠ GCE=45°,请你利用( 1)的结论证明: GE=BE+GD.(3)运用( 1)( 2)解答中所积累的经验和知识,完成下题:如图 3,在直角梯形ABCD中, AD∥ BC( BC> AD),∠ B=90°,AB=BC,E 是 AB 上一点,且∠ DCE=45°, BE=4, DE=10,求直角梯形ABCD的面积..4.如图,正方形ABCD中, E 为 AB 边上一点,过点 D 作 DF⊥ DE,与 BC 延长线交于点F.连接 EF,与 CD边交于点 G,与对角线 BD 交于点 H.(1)若 BF=BD= ,求 BE 的长;(2)若∠ ADE=2∠ BFE,求证: FH=HE+HD..5.如图,将一三角板放在边长为 1 的正方形ABCD上,并使它的直角顶点P 在对角线AC 上滑动,直角的一边始终经过点B,另一边与射线DC 相交于 Q.探究:设A、 P 两点间的距离为x.(1)当点 Q 在边 CD上时,线段 PQ 与 PB 之间有怎样的数量关系?试证明你的猜想;(2)当点 Q 在边 CD上时,设四边形 PBCQ的面积为 y,求 y 与 x 之间的函数关系,并写出函数自变量x 的取值范围;( 3)当点 P 在线段 AC 上滑动时,△ PCQ是否可能成为等腰三角形?如果可能,指出所有能使△ PCQ成为等腰三角形的点Q 的位置.并求出相应的x 值,如果不可能,试说明理由..6.Rt△ ABC与 Rt△FED是两块全等的含30°、60°角的三角板,按如图(一)所示拼在一起, CB 与 DE 重合.( 1)求证:四边形ABFC为平行四边形;( 2)取 BC 中点 O,将△ ABC 绕点 O 顺时钟方向旋转到如图(二)中△A′B′位C置′,直线 B'C'与 AB、 CF分别相交于 P、 Q 两点,猜想 OQ、 OP 长度的大小关系,并证明你的猜想;( 3)在( 2)的条件下,指出当旋转角至少为多少度时,四边形PCQB为菱形?(不要求证明).7.如图,在正方形ABCD中,点 F 在 CD边上,射线AF 交 BD 于点 E,交 BC的延长线于点 G.(1)求证:△ ADE≌△ CDE;(2)过点 C 作 CH⊥ CE,交 FG于点 H,求证: FH=GH;(3)设 AD=1,DF=x,试问是否存在 x 的值,使△ ECG为等腰三角形?若存在,请求出x 的值;若不存在,请说明理由..8.在平行四边形ABCD中,∠ BAD 的平分线交直线BC于点 E,交直线 DC 于点 F.(1)在图 1 中证明 CE=CF;( 2)若∠ ABC=90°, G 是 EF的中点(如图2),直接写出∠ BDG 的度数;( 3)若∠ ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图 3),求∠ BDG的度数..9.如图,已知 ?ABCD中, DE⊥ BC 于点 E,DH⊥ AB 于点 H,AF 平分∠ BAD,分别交 DC、DE、 DH 于点 F、 G、 M,且 DE=AD.(1)求证:△ ADG≌△ FDM.(2)猜想 AB 与 DG+CE之间有何数量关系,并证明你的猜想..10.如图,在正方形 ABCD 中, E、 F 分别为 BC、 AB 上两点,且 BE=BF,过点 B 作 AE 的垂线交 AC 于点 G,过点 G 作 CF的垂线交 BC于点 H 延长线段 AE、GH 交于点 M.(1)求证:∠ BFC=∠ BEA;(2)求证: AM=BG+GM..11.如图所示,把矩形纸片OABC 放入直角坐标系xOy 中,使OA、OC 分别落在x、 y 轴的正半轴上,连接AC,且 AC=4,(1)求 AC 所在直线的解析式;(2)将纸片 OABC折叠,使点 A 与点 C重合(折痕为 EF),求折叠后纸片重叠部分的面积.(3)求 EF所在的直线的函数解析式..12.已知一次函数的图象与坐标轴交于A、B 点(如图),AE 平分∠ BAO,交x 轴于点 E.(1)求点 B 的坐标;(2)求直线 AE 的表达式;(3)过点 B 作 BF⊥ AE,垂足为 F,连接 OF,试判断△ OFB的形状,并求△ OFB的面积.(4)若将已知条件“AE平分∠ BAO,交 x 轴于点 E”改变为“点 E 是线段 OB上的一个动点(点 E 不与点 O、 B 重合)”,过点 B 作 BF⊥ AE,垂足为 F.设 OE=x, BF=y,试求 y 与 x 之间的函数关系式,并写出函数的定义域..13.如图,直线l1的解析表达式为:y=﹣ 3x+3,且 l1与 x 轴交于点D,直线 l2经过点 A,B,直线 l1, l2交于点 C.(1)求点 D 的坐标;(2)求直线 l 2的解析表达式;(3)求△ ADC的面积;( 4)在直线l 2上存在异于点 C 的另一点P,使得△ ADP 与△ ADC 的面积相等,请直接写出点 P 的坐标..14.如图 1,在平面直角坐标系中,O 是坐标原点,长方形OACB的顶点 A、B 分别在 x 轴与 y 轴上,已知OA=6, OB=10.点 D 为 y 轴上一点,其坐标为(0, 2),点 P 从点 A 出发以每秒 2 个单位的速度沿线段 AC﹣ CB的方向运动,当点 P 与点 B 重合时停止运动,运动时间为 t 秒.(1)当点 P 经过点 C 时,求直线 DP 的函数解析式;(2)①求△ OPD的面积 S关于 t 的函数解析式;②如图②,把长方形沿着OP 折叠,点 B 的对应点B′恰好落在A C 边上,求点P的坐标.( 3)点 P 在运动过程中是否存在使△BDP 为等腰三角形?若存在,请求出点P 的坐标;若不存在,请说明理由..15.如图,在平面直角坐标系中,已知O 为原点,四边形ABCD为平行四边形,A、 B、C 的坐标分别是A(﹣ 5, 1), B(﹣ 2, 4), C( 5, 4),点D 在第一象限.( 1)写出 D 点的坐标;( 2)求经过 B、 D 两点的直线的解析式,并求线段BD 的长;( 3)将平行四边形 ABCD先向右平移 1 个单位长度,再向下平移 1 个单位长度所得的四边形 A1 1 1 1四个顶点的坐标是多少?并求出平行四边形ABCD与四边B C DA1B1C1D1重叠部分的面积..16.如图,一次函数的图象与x 轴、 y 轴交于点A、B,以线段 AB 为边在第一象限内作等边△ABC,( 1)求△ ABC 的面积;( 2)如果在第二象限内有一点P( a,);试用含有a 的代数式表示四边形ABPO的面积,并求出当△ABP 的面积与△ ABC的面积相等时 a 的值;( 3)在 x 轴上,是否存在点M,使△ MAB 为等腰三角形?若存在,请直接写出点M 的坐标;若不存在,请说明理由...2018 年 06 月 17 日梧桐听雨的初中数学组卷参考答案与试题解析一.解答题(共16 小题)1.已知,正方形ABCD中,∠ MAN=45°,∠ MAN 绕点 A 顺时针旋转,它的两边分别交CB、 DC(或它们的延长线)于点M 、N,AH⊥ MN 于点 H.( 1)如图①,当∠ MAN 绕点 A 旋转到 BM=DN 时,请你直接写出AH 与 AB 的数量关系:AH=AB;(2)如图②,当∠ MAN 绕点 A 旋转到 BM≠ DN 时,( 1)中发现的 AH 与 AB 的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠ MAN=45°, AH⊥ MN 于点 H,且 MH=2 , NH=3,求 AH 的长.(可利用( 2)得到的结论)【解答】解:( 1)如图① AH=AB.( 2)数量关系成立.如图②,延长CB至 E,使 BE=DN.∵ ABCD是正方形,∴AB=AD,∠ D=∠ ABE=90°,在 Rt△ AEB和 Rt△ AND 中,,∴Rt△ AEB≌ Rt△AND,∴AE=AN,∠ EAB=∠NAD,∵∠ DAN+∠ BAN=45°,∴∠ EAB+∠ BAN=45°,∴∠ EAN=45°,∴∠ EAM=∠ NAM=45°,在△ AEM 和△ ANM 中,,.∵ AB、 AH 是△ AEM 和△ ANM 对应边上的高,∴AB=AH.( 3)如图③分别沿AM 、AN 翻折△ AMH 和△ ANH,得到△ ABM 和△ AND,∴BM=2, DN=3,∠ B=∠ D=∠BAD=90°.分别延长 BM 和 DN 交于点 C,得正方形 ABCD,由(2)可知,AH=AB=BC=CD=AD.设AH=x,则MC=x﹣ 2, NC=x﹣ 3,在 Rt△ MCN 中,由勾股定理,得MN 2=MC2+NC2∴52=( x﹣ 2)2 +(x﹣ 3)2( 6 分)解得 x1=6, x2 =﹣ 1.(不符合题意,舍去)∴AH=6.2.如图,△ ABC 是等边三角形,点 D 是边 BC上的一点,以AD 为边作等边△ADE,过点C作 CF∥ DE 交 AB 于点 F.( 1)若点 D 是 BC边的中点(如图①),求证: EF=CD;( 2)在( 1)的条件下直接写出△ AEF和△ ABC的面积比;(3)若点 D 是 BC 边上的任意一点(除 B、 C 外如图②),那么( 1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由...【解答】(1)证明:∵△ ABC是等边三角形, D 是 BC的中点,∴ AD⊥ BC,且∠ BAD= ∠ BAC=30°,∵△ AED是等边三角形,∴AD=AE,∠ ADE=60°,∴∠ EDB=90°﹣∠ ADE=90°﹣ 60°=30°,∵ED∥CF,∴∠ FCB=∠ EDB=30°,∵∠ ACB=60°,∴∠ ACF=∠ ACB﹣∠ FCB=30°,∴∠ ACF=∠ BAD=30°,在△ ABD 和△ CAF中,,∴△ ABD≌△ CAF(ASA),∴AD=CF,∵ AD=ED,∴ED=CF,又∵ ED∥ CF,∴四边形 EDCF是平行四边形,∴EF=CD.( 2)解:△ AEF和△ ABC的面积比为:1: 4;(易知AF=BF ,延长EF交AD于H,△AEF的面积..=?EF?AH= ? CB ?AD= ? ?BC?AD,由此即可证明)(3)解:成立.理由如下:∵ ED∥ FC,∴∠ EDB=∠FCB,∵∠ AFC=∠ B+∠ BCF=60°+∠ BCF,∠ BDA=∠ ADE+∠EDB=60°+∠ EDB ∴∠ AFC=∠ BDA,在△ ABD 和△ CAF中,∴△ ABD≌△ CAF(AAS),∴AD=FC,∵ AD=ED,∴ED=CF,又∵ ED∥ CF,∴四边形 EDCF是平行四边形,∴EF=DC.3.(1)如图 1,在正方形 ABCD中,E 是 AB 上一点, F 是 AD 延长线上一点,且 DF=BE.求证: CE=CF;(2)如图 2,在正方形 ABCD中, E 是 AB 上一点, G 是 AD 上一点,如果∠ GCE=45°,请你利用( 1)的结论证明: GE=BE+GD.(3)运用( 1)( 2)解答中所积累的经验和知识,完成下题:如图 3,在直角梯形ABCD中, AD∥ BC( BC>AD),∠ B=90°, AB=BC,E 是 AB 上一点,且∠ DCE=45°, BE=4, DE=10,求直角梯形ABCD的面积...【解答】( 1)明:∵四形ABCD是正方形,∴BC=CD,∠ B=∠CDF=90°,∵∠ ADC=90°,∴∠FDC=90°.∴∠B=∠ FDC,∵BE=DF,∴△ CBE≌△ CDF( SAS).∴CE=CF.(2)明:如 2 ,延 AD 至 F,使 DF=BE,接 CF.由( 1)知△CBE≌△ CDF,∴∠ BCE=∠ DCF.∴∠ BCE+∠ ECD=∠DCF+∠ ECD,即∠ ECF=∠ BCD=90°,又∠ GCE=45°,∴∠ GCF=∠ GCE=45°.∵CE=CF,GC=GC,∴△ ECG≌△ FCG.∴GE=GF,∴GE=GF=DF+GD=BE+GD.(3)解:如 3, C作 CG⊥ AD,交 AD 延于 G.在直角梯形ABCD中,∵ AD∥ BC,∴∠A=∠B=90°,又∵∠ CGA=90°, AB=BC,∴四形 ABCG正方形.∴AG=BC.⋯( 7 分)∵∠ DCE=45°,根据( 1)( 2)可知, ED=BE+DG.⋯( 8 分)∴10=4+DG,即 DG=6.AB=x, AE=x 4, AD=x 6,在Rt△ AED中,..∵DE2=AD2+AE2,即 102 =( x 6)2+(x 4)2.解个方程,得: x=12 或 x= 2(舍去).⋯(9 分)∴ AB=12.∴ S 梯形ABCD= ( AD+BC) ?AB= ×( 6+12)× 12=108.即梯形 ABCD的面108.⋯( 10 分)4.如,正方形 ABCD中, E AB 上一点,点 D 作 DF⊥ DE,与 BC 延交于点F.接 EF,与 CD 交于点 G,与角 BD 交于点 H.(1)若 BF=BD= ,求 BE 的;(2)若∠ ADE=2∠ BFE,求: FH=HE+HD.【解答】( 1)解:∵四形ABCD正方形,∴∠ BCD=90°,BC=CD,∴Rt△ BCD中, BC2+CD2=BD2,即 BC2=()2( BC)2,∴BC=AB=1,∵DF⊥ DE,∴∠ ADE+∠ EDC=90°=∠EDC+∠ CDF,∴∠ ADE=∠ CDF,在△ ADE 和△ CDF中,∵,∴△ ADE≌△ CDF( ASA),..∴ AE=CF=BF﹣ BC=﹣1,∴ BE=AB﹣ AE=1﹣(﹣1)=2﹣;(2)证明:在 FE 上截取一段 FI,使得 FI=EH,∵△ADE≌△CDF,∴ DE=DF,∴△ DEF为等腰直角三角形,∴∠ DEF=∠ DFE=45°=∠DBC,∵∠ DHE=∠ BHF,∴∠ EDH=∠ BFH(三角形的内角和定理),在△ DEH和△ DFI中,∵,∴△ DEH≌△ DFI( SAS),∴DH=DI,又∵∠ HDE=∠BFE,∠ ADE=2∠BFE,∴∠ HDE=∠ BFE= ∠ ADE,∵∠ HDE+∠ ADE=45°,∴∠ HDE=15°,∴∠ DHI=∠ DEH+∠ HDE=60°,即△ DHI 为等边三角形,∴DH=HI,∴FH=FI+HI=HE+HD.5.如图,将一三角板放在边长为 1 的正方形ABCD上,并使它的直角顶点P 在对角线AC 上滑动,直角的一边始终经过点B,另一边与射线DC 相交于 Q.探究:设 A、 P 两点间的距离为x.(1)当点 Q 在边 CD上时,线段 PQ 与 PB 之间有怎样的数量关系?试证明你的猜想;(2)当点 Q 在边 CD上时,设四边形 PBCQ的面积为 y,求 y 与 x 之间的函数关系,并..写出函数自变量x 的取值范围;( 3)当点 P 在线段 AC 上滑动时,△ PCQ是否可能成为等腰三角形?如果可能,指出所有能使△ PCQ成为等腰三角形的点Q 的位置.并求出相应的x 值,如果不可能,试说明理由.【解答】解:( 1) PQ=PB,(1 分)过P 点作 MN ∥ BC分别交 AB、 DC于点 M、 N,在正方形 ABCD中, AC 为对角线,∴ AM=PM ,又∵ AB=MN,∴MB=PN,∵∠BPQ=90°,∴∠ BPM+∠ NPQ=90°;又∵∠ MBP+∠BPM=90°,∴∠ MBP=∠ NPQ,在Rt△ MBP≌Rt△ NPQ 中,∵∴Rt△ MBP≌Rt△ NPQ,( 2 分)∴PB=PQ.(2)∵ S 四边形PBCQ=S△PBC+S△PCQ,∵AP=x,∴AM=x,∴CQ=CD﹣ 2NQ=1﹣ x,又∵ S△PBC= BC?BM= ?1?( 1﹣x) =﹣x,S△PCQ= CQ?PN=(1﹣x) ?( 1﹣x),..=﹣+,∴ S 四边形PBCQ=﹣x+1 .( 0≤ x≤).(4分)( 3)△ PCQ可能成为等腰三角形.①当点 P 与点 A 重合时,点Q 与点 D 重合,PQ=QC,此时, x=0.( 5 分)②当点 Q 在 DC的延长线上,且CP=CQ时,(6 分)有:QN=AM=PM=x,CP=﹣x,CN=CP=1﹣x,CQ=QN﹣ CN=x﹣( 1﹣x)=x﹣ 1,∴当﹣ x=x﹣ 1 时, x=1.( 7 分).6.Rt△ ABC 与 Rt△FED是两块全等的含30°、60°角的三角板,按如图(一)所示拼在一起, CB与 DE 重合.( 1)求证:四边形ABFC为平行四边形;( 2)取 BC 中点 O,将△ ABC 绕点 O 顺时钟方向旋转到如图(二)中△A′B′位C置′,直线B'C'与 AB、 CF分别相交于 P、Q 两点,猜想 OQ、OP 长度的大小关系,并证明你的猜想;( 3)在( 2)的条件下,指出当旋转角至少为多少度时,四边形PCQB为菱形?(不要求证明)..【解答】( 1)证明:∵△ABC≌△ FCB,∴AB=CF, AC=BF.∴四边形ABFC为平行四边形.(2)解: OP=OQ,理由如下:∵OC=OB,∠ COQ=∠BOP,∠ OCQ=∠ PBO,∴△ COQ≌△ BOP.∴OQ=OP.( 3)解: 90°.理由:∵ OP=OQ,OC=OB,∴四边形PCQB为平行四边形,∵BC⊥ PQ,∴四边形PCQB为菱形.7.如图,在正方形 ABCD中,点 F 在 CD 边上,射线 AF 交 BD 于点 E,交 BC 的延长线于点G.(1)求证:△ ADE≌△ CDE;(2)过点 C作 CH⊥ CE,交 FG 于点 H,求证: FH=GH;(3)设 AD=1,DF=x,试问是否存在 x 的值,使△ ECG为等腰三角形?若存在,请求出x的值;若不存在,请说明理由.【解答】( 1)证明:∵四边形ABCD是正方形,∴DA=DC,∠ 1=∠ 2=45°,DE=DE,∴△ ADE≌△ CDE...(2)证明:∵△ADE≌△CDE,∴∠ 3=∠4,∵ CH⊥ CE,∴∠ 4+∠5=90°,又∵∠ 6+∠ 5=90°,∴∠ 4=∠6=∠ 3,∵AD∥ BG,∴∠ G=∠3,∴∠ G=∠6,∴ CH=GH,又∵∠ 4+∠ 5=∠ G+∠7=90°,∴∠ 5=∠7,∴ CH=FH,∴ FH=GH.( 3)解:存在符合条件的x 值此时,∵∠ ECG> 90°,要使△ ECG为等腰三角形,必须CE=CG,∴∠ G=∠8,又∵∠ G=∠ 4,∴∠ 8=∠4,∴∠ 9=2∠4=2∠ 3,∴∠ 9+∠3=2∠ 3+∠ 3=90°,∴∠ 3=30°,∴ x=DF=1× tan30 °=.8.在 ?ABCD中,∠ BAD 的平分线交直线BC于点 E,交直线DC于点 F.(1)在图 1 中证明 CE=CF;(2)若∠ ABC=90°,G 是 EF 的中点(如图 2),直接写出∠ BDG的度数;(3)若∠ ABC=120°, FG∥ CE, FG=CE,分别连接 DB、 DG(如图 3),求∠ BDG 的度数...【解答】( 1)证明:如图1,∵AF 平分∠ BAD,∴∠ BAF=∠ DAF,∵四边形 ABCD是平行四边形,∴ AD∥ BC,AB∥ CD,∴∠ DAF=∠ CEF,∠ BAF=∠F,∴∠ CEF=∠ F.∴CE=CF.( 2)解:连接GC、 BG,∵四边形ABCD为平行四边形,∠ABC=90°,∴四边形ABCD为矩形,∵AF 平分∠ BAD,∴∠DAF=∠ BAF=45°,∵∠DCB=90°,DF∥ AB,∴∠DFA=45°,∠ ECF=90°∴△ ECF为等腰直角三角形,∵G 为 EF中点,∴EG=CG=FG, CG⊥ EF,∵△ ABE 为等腰直角三角形,AB=DC,∴BE=DC,∵∠ CEF=∠ GCF=45°,∴∠ BEG=∠DCG=135°在△ BEG与△ DCG中,∵,∴△ BEG≌△ DCG,∴BG=DG,..∵CG⊥ EF,∴∠ DGC+∠ DGA=90°,又∵∠ DGC=∠ BGA,∴∠ BGA+∠ DGA=90°,∴△ DGB为等腰直角三角形,∴∠ BDG=45°.(3)解:延长 AB、 FG交于 H,连接 HD.∵ AD∥ GF, AB∥ DF,∴四边形 AHFD 为平行四边形∵∠ABC=120°, AF 平分∠ BAD∴∠ DAF=30°,∠ ADC=120°,∠ DFA=30°∴△ DAF 为等腰三角形∴AD=DF,∴CE=CF,∴平行四边形AHFD为菱形∴△ ADH,△ DHF 为全等的等边三角形∴DH=DF,∠ BHD=∠ GFD=60°∵FG=CE, CE=CF,CF=BH,∴ BH=GF在△ BHD 与△ GFD中,∵,∴△ BHD≌△ GFD,∴∠ BDH=∠GDF∴∠ BDG=∠ BDH+∠HDG=∠GDF+∠ HDG=60°..9.如图,已知 ?ABCD中, DE⊥ BC于点 E,DH⊥ AB 于点 H,AF 平分∠ BAD,分别交 DC、DE、 DH 于点 F、G、 M,且 DE=AD.(1)求证:△ ADG≌△ FDM.(2)猜想 AB 与 DG+CE之间有何数量关系,并证明你的猜想.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AB∥ CD,AD∥ BC,∴∠ BAF=∠ DFA,∵ AF 平分∠ BAD,∴∠ DAF=∠ DFA,∴AD=FD,∵DE⊥ BC, DH⊥ AB,∴∠ ADG=∠ FDM=90°,在△ ADG 和△ FDM 中,,∴△ ADG≌△ FDM( ASA).(2) AB=DG+EC.证明:延长GD 至点 N,使 DN=CE,连接 AN,∵DE⊥ BC, AD∥ BC,∴∠ ADN=∠DEC=90°,..在△ ADN 和△ DEC中,,∴△ ADN≌△ DEC( SAS),∴∠ NAD=∠CDE, AN=DC,∵∠ NAG=∠NAD+∠ DAG,∠ NGA=∠ CDE+∠ DFA,∴∠ NAG=∠NGA,∴AN=GN=DG+CE=DC,∵四边形 ABCD是平行四边形,∴AB=CD,∴AB=DG+EC.10.如图,在正方形ABCD 中, E、 F 分别为 BC、 AB 上两点,且BE=BF,过点B 作 AE 的垂线交 AC 于点 G,过点 G 作 CF的垂线交BC于点 H 延长线段AE、 GH 交于点 M.( 1)求证:∠ BFC=∠ BEA;( 2)求证: AM=BG+GM.【解答】证明:( 1)在正方形 ABCD中, AB=BC,∠ ABC=90°,在△ ABE和△ CBF中,,..∴△ ABE≌△ CBF( SAS),∴∠ BFC=∠BEA;(2)连接 DG,在△ ABG 和△ ADG 中,,∴△ ABG≌△ ADG( SAS),∴BG=DG,∠2=∠3,∵ BG⊥AE,∴∠ BAE+∠ 2=90°,∵∠ BAD=∠ BAE+∠4=90°,∴∠ 2=∠3=∠ 4,∵ GM⊥ CF,∴∠ BCF+∠ 1=90°,又∠ BCF+∠ BFC=90°,∴∠ 1=∠BFC=∠ 2,∴∠ 1=∠3,在△ ADG 中,∠ DGC=∠3+45°,∴∠ DGC 也是△ CGH 的外角,∴D、G、 M 三点共线,∵∠ 3=∠4(已证),∴AM=DM ,∵DM=DG+GM=BG+GM,∴ AM=BG+GM.11.如图所示,把矩形纸片OABC 放入直角坐标系xOy 中,使OA、OC 分别落在x、 y 轴的正半轴上,连接AC,且 AC=4,..(1)求 AC所在直线的解析式;(2)将纸片 OABC折叠,使点 A 与点 C 重合(折痕为 EF),求折叠后纸片重叠部分的面积.(3)求 EF所在的直线的函数解析式.【解答】解:( 1)∵=,∴可设 OC=x,则 OA=2x,在Rt△ AOC中,由勾股定理可得 OC2+OA2=AC2,∴ x2+( 2x)2=(4 )2,解得 x=4( x=﹣ 4 舍去),∴ OC=4, OA=8,∴A( 8, 0), C(0, 4),设直线 AC 解析式为 y=kx+b ,∴,解得,∴直线 AC 解析式为y=﹣x+4;( 2)由折叠的性质可知AE=CE,设AE=CE=y,则 OE=8﹣ y,在Rt△ OCE中,由勾股定理可得 OE2+OC2=CE2,∴( 8﹣ y)2+42=y2,解得 y=5,∴AE=CE=5,∵∠ AEF=∠CEF,∠ CFE=∠ AEF,∴∠ CFE=∠ CEF,∴CE=CF=5,∴S△CEF= CF?OC= × 5× 4=10,..即重叠部分的面积为10;(3)由( 2)可知 OE=3, CF=5,∴ E(3 ,0), F( 5,4 ),设直线 EF的解析式为 y=k′x+b′,∴,解得,∴直线 EF的解析式为y=2x﹣ 6.12.已知一次函数的图象与坐标轴交于A、B 点(如图),AE 平分∠ BAO,交x 轴于点 E.(1)求点 B 的坐标;(2)求直线 AE 的表达式;(3)过点 B 作 BF⊥ AE,垂足为 F,连接 OF,试判断△ OFB的形状,并求△ OFB的面积.(4)若将已知条件“AE平分∠ BAO,交 x 轴于点 E”改变为“点 E 是线段 OB上的一个动点(点 E 不与点 O、B 重合)”,过点 B 作 BF⊥AE,垂足为 F.设 OE=x,BF=y,试求 y 与 x 之间的函数关系式,并写出函数的定义域...【解答】解:( 1)对于 y=﹣x+6,当x=0 时, y=6;当 y=0 时, x=8,∴ OA=6, OB=8,在 Rt△ AOB中,根据勾股定理得: AB=10,则 A( 0, 6), B(8,0);( 2)过点 E 作 EG⊥ AB,垂足为 G(如图 1 所示),∵ AE 平分∠ BAO, EO⊥AO,EG⊥ AG,∴ EG=OE,在 Rt△ AOE和 Rt△ AGE中,,∴Rt△ AOE≌Rt△ AGE(HL),∴AG=AO,设OE=EG=x,则有 BE=8﹣ x, BG=AB﹣ AG=10﹣ 6=4,在Rt△ BEG中, EG=x, BG=4, BE=8﹣ x,根据勾股定理得: x2+4 2=( 8﹣ x)2,解得: x=3,∴E(3 ,0),设直线 AE 的表达式为 y=kx+b( k≠ 0),将A( 0, 6), E( 3,0)代入 y=kx+b 得:,解得:,则直线 AE 的表达式为y=﹣ 2x+6;( 3)延长 BF 交 y 轴于点 K(如图 2 所示),..∵AE 平分∠ BAO,∴∠ KAF=∠ BAF,又BF⊥AE,∴∠ AFK=∠ AFB=90°,在△ AFK和△ AFB 中,∵,∴△ AFK≌△ AFB,∴FK=FB,即F 为KB 的中点,又∵△ BOK为直角三角形,∴OF= BK=BF,∴△ OFB 为等腰三角形,过点 F 作 FH⊥ OB,垂足为H(如图 2 所示),∵OF=BF, FH⊥ OB,∴OH=BH=4,∴F 点的横坐标为 4,设F( 4, y),将 F( 4, y)代入 y=﹣ 2x+6 ,得: y=﹣ 2,∴ FH=| ﹣2| =2,则 S△OBF= OB?FH= × 8× 2=8;(4)在 Rt△ AOE中, OE=x, OA=6,根据勾股定理得:AE==,又BE=OB﹣ OE=8﹣ x, S△ABE= AE?BF= BE?AO(等积法),∴ BF==(0<x<8),又BF=y,则 y=(0<x<8).13.如图,直线l1的解析表达式为:y=﹣ 3x+3,且 l1与 x 轴交于点D,直线 l2经过点 A,B,直线 l 1, l2交于点 C.(1)求点 D 的坐标;(2)求直线 l2的解析表达式;..(3)求△ ADC的面积;(4)在直线 l 2上存在异于点 C 的另一点 P,使得△ ADP 与△ ADC 的面积相等,请直接写出点 P 的坐标.【解答】解:( 1)由 y=﹣ 3x+3,令 y=0,得﹣ 3x+3=0,∴x=1,∴D( 1,0);( 2)设直线l 2的解析表达式为y=kx+b,由图象知: x=4,y=0; x=3,,代入表达式y=kx+b,∴,∴,∴直线 l2的解析表达式为;( 3)由,解得,∴ C(2,﹣ 3),∵ AD=3,∴ S△ADC=× 3× |﹣3| =;( 4)△ ADP 与△ ADC 底边都是AD,面积相等所以高相等,△ADC 高就是点 C 到直线AD 的距离,即 C 纵坐标的绝对值=| ﹣ 3| =3,则 P 到 AD 距离 =3,∴ P 纵坐标的绝对值=3,点 P 不是点 C,∴点 P 纵坐标是3,∵ y=1.5x﹣6 ,y=3,..∴1.5x﹣ 6=3x=6,所以 P( 6,3).14.如图 1,在平面直角坐标系中,O 是坐标原点,长方形OACB的顶点 A、B 分别在 x轴与 y 轴上,已知OA=6, OB=10.点 D 为 y 轴上一点,其坐标为(0, 2),点 P 从点 A出发以每秒 2 个单位的速度沿线段AC﹣CB 的方向运动,当点 P 与点 B 重合时停止运动,运动时间为t 秒.(1)当点 P 经过点 C 时,求直线 DP 的函数解析式;(2)①求△ OPD 的面积 S关于 t 的函数解析式;②如图②,把长方形沿着 OP 折叠,点 B 的对应点 B′恰好落在 AC 边上,求点 P 的坐标.( 3)点P 在运动过程中是否存在使△BDP 为等腰三角形?若存在,请求出点P 的坐标;若不存在,请说明理由.【解答】解:( 1)∵ OA=6, OB=10,四边形OACB为长方形,∴C( 6, 10).设此时直线DP 解析式为y=kx+b,把( 0,2 ), C(6, 10)分别代入,得,解得则此时直线DP 解析式为y=x+2;( 2)①当点P 在线段 AC 上时, OD=2,高为 6, S=6;当点 P 在线段 BC 上时, OD=2,高为 6+10﹣2t=16 ﹣2t ,S=× 2×(16﹣2t)=﹣2t+16;②设 P( m, 10),则 PB=PB′=m,如图 2,∵OB′=OB=10, OA=6,∴ AB′==8,..∴B′C=10﹣ 8=2,∵ PC=6﹣ m,∴m2=22+( 6﹣ m)2,解得 m=则此时点 P 的坐标是(,10);( 3)存在,理由为:若△ BDP为等腰三角形,分三种情况考虑:如图3,①当 BD=BP1=OB﹣ OD=10﹣ 2=8,在Rt△ BCP1中, BP1=8, BC=6,根据勾股定理得: CP1==2 ,∴AP1=10﹣ 2 ,即 P1(6, 10﹣ 2 );②当BP2 =DP2时,此时 P2( 6,6);③当DB=DP3=8 时,在 Rt△ DEP 中, DE=6,3根据勾股定理得:P3E==2,∴ AP3=AE+EP3=2+2,即 P3( 6, 2+2),综上,满足题意的P 坐标为( 6, 6)或( 6, 2+2)或( 6, 10﹣ 2)...15.如图,在平面直角坐标系中,已知O 为原点,四边形ABCD为平行四边形,A、 B、C 的坐标分别是A(﹣ 5,1), B(﹣ 2, 4),C( 5, 4),点 D 在第一象限.( 1)写出 D 点的坐标;( 2)求经过B、D 两点的直线的解析式,并求线段BD 的长;( 3)将平行四边形ABCD 先向右平移 1 个单位长度,再向下平移 1 个单位长度所得的四边形 A1B1C1 D1四个顶点的坐标是多少?并求出平行四边形ABCD与四边形 A1 B1 C1D1重叠部分的面积.【解答】解:( 1)∵ B(﹣ 2, 4), C( 5, 4),∴BC=5﹣(﹣ 2) =5+2=7,∵ A(﹣ 5,1),∴点 D 的横坐标为﹣ 5+7=2,∴点D 的坐标为( 2, 1);( 2)设直线 BD 的解析式为 y=kx+b,将 B(﹣ 2, 4)、D( 2, 1)代入得:,解得,∴经过 B、 D 两点的直线的解析式为y=﹣x+,过 B 点作 AD 的垂线,垂足为E,则 BE=4﹣ 1=3,DE=2﹣(﹣ 2)=2+2=4,..在 Rt△ BDE中, BD===5;( 3)∵ ?ABCD向右平移1 个单位长度,再向下平移 1 个单位长度,∴A1(﹣ 4, 0),B1(﹣ 1, 3), C1( 6,3) D1( 3,0 ),∴重叠部分的底边长 7﹣ 1=6,高为 3﹣1=2,∴重叠部分的面积S=6× 2=12.16.如图,一次函数的图象与x 轴、 y 轴交于点A、B,以线段AB 为边在第一象限内作等边△ABC,( 1)求△ ABC的面积;( 2)如果在第二象限内有一点P( a,);试用含有a 的代数式表示四边形ABPO的面积,并求出当△ABP的面积与△ ABC的面积相等时 a 的值;(3)在 x 轴上,是否存在点 M,使△ MAB 为等腰三角形?若存在,请直接写出点 M 的坐标;若不存在,请说明理由.【解答】解:( 1)分别令 y=0 和 x=0,得一次函数y=x+1 的图象与x 轴.y 轴的交点坐标分别是A(,0),B(0,1),即OA=,OB=1,∴ AB==2∵△ ABC为等边三角形,∴ S△ABC=;( 2)如图 1, S△AOB=,S△AOP=,S△BOP=| a| ?OB=﹣.∴ S 四边形ABPO=S△AOB+S△BOP=,而 S△ABP=S 四边形ABPO﹣S△APO,..∴当 S△ABP=S△ABC时,=,解得 a=﹣;( 3)如图 2,满足条件的点M 有 4 个:M 1(﹣,0),M 2(﹣ 2,0),M3(,0),M 4(+2,0)..。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级下数学压轴题1.已知,正方形 ABCD中,∠MAN=45°,∠ MAN绕点 A 顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、 N, AH⊥ MN于点 H.( 1)如图①,当∠MAN 绕点 A 旋转到BM=DN时,请你直接写出AH 与 AB 的数量关系:;(2)如图②,当∠ MAN绕点 A 旋转到 BM≠ DN时,( 1)中发现的 AH与 AB的数量关系还成立吗如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠ MAN=45°, AH⊥ MN于点 H,且 MH=2,NH=3,求 AH的长.(可利用(2)得到的结论)2.如图,△ ABC是等边三角形,点 D 是边 BC上的一点,以AD为边作等边△ ADE,过点C 作 CF∥ DE交 AB 于点 F.( 1)若点 D 是 BC边的中点(如图①),求证: EF=CD;( 2)在( 1)的条件下直接写出△AEF和△ ABC的面积比;(3)若点 D 是 BC边上的任意一点(除 B、C 外如图②),那么( 1)中的结论是否仍然成立若成立,请给出证明;若不成立,请说明理由.3.( 1)如图 1,在正方形 ABCD中, E 是 AB上一点, F 是 AD延长线上一点,且DF=BE.求证: CE=CF;(2)如图 2,在正方形 ABCD中,E 是 AB上一点, G是 AD上一点,如果∠ GCE=45°,请你利用( 1)的结论证明: GE=BE+GD.(3)运用( 1)( 2)解答中所积累的经验和知识,完成下题:如图 3,在直角梯形ABCD中, AD∥ BC( BC> AD),∠ B=90°, AB=BC, E 是 AB 上一点,且∠ DCE=45°, BE=4,DE=10,求直角梯形ABCD的面积.4.如图,正方形 ABCD中,E 为 AB边上一点,过点 D 作 DF⊥ DE,与 BC延长线交于点F.连接EF,与 CD边交于点 G,与对角线 BD交于点 H.(1)若 BF=BD= ,求 BE 的长;(2)若∠ ADE=2∠ BFE,求证: FH=HE+HD.5.如图,将一三角板放在边长为 1 AC上滑动,直角的一边始终经过点的正方形ABCD上,并使它的直角顶点B,另一边与射线DC相交于 Q.P 在对角线探究:设A、P 两点间的距离为x.(1)当点 Q在边 CD上时,线段 PQ与 PB 之间有怎样的数量关系试证明你的猜想;(2)当点 Q在边 CD上时,设四边形 PBCQ的面积为 y,求 y 与 x 之间的函数关系,并写出函数自变量 x 的取值范围;(3)当点 P 在线段 AC上滑动时,△ PCQ是否可能成为等腰三角形如果可能,指出所有能使△ PCQ成为等腰三角形的点Q的位置.并求出相应的x 值,如果不可能,试说明理由.6. Rt △ ABC与 Rt △ FED是两块全等的含30°、 60°角的三角板,按如图(一)所示拼在一起, CB与 DE重合.(1)求证:四边形 ABFC为平行四边形;(2)取 BC中点 O,将△ ABC绕点 O顺时钟方向旋转到如图(二)中△ A′B′C′位置,直线 B'C' 与 AB、 CF 分别相交于P、 Q两点,猜想OQ、 OP长度的大小关系,并证明你的猜想;( 3)在( 2)的条件下,指出当旋转角至少为多少度时,四边形PCQB为菱形(不要求证明)7.如图,在正方形ABCD中,点 F 在 CD边上,射线AF 交 BD于点 E,交 BC的延长线于点 G.(1)求证:△ ADE≌△ CDE;(2)过点 C 作 CH⊥ CE,交 FG于点 H,求证: FH=GH;(3)设 AD=1,DF=x,试问是否存在 x 的值,使△ ECG为等腰三角形若存在,请求出x 的值;若不存在,请说明理由.8.在平行四边形ABCD中,∠ BAD的平分线交直线BC于点 E,交直线DC于点 F.(1)在图 1 中证明 CE=CF;(2)若∠ ABC=90°, G是 EF 的中点(如图 2),直接写出∠ BDG的度数;(3)若∠ ABC=120°, FG∥ CE,FG=CE,分别连接 DB、 DG(如图 3),求∠ BDG的度数.9.如图,已知? ABCD中, DE⊥ BC于点 E, DH⊥ AB于点 H, AF 平分∠ BAD,分别交DC、DE、 DH于点 F、G、 M,且 DE=AD.(1)求证:△ ADG≌△ FDM.(2)猜想 AB与 DG+CE之间有何数量关系,并证明你的猜想.10.如图,在正方形ABCD中, E、 F 分别为 BC、AB 上两点,且B E=BF,过点 B 作 AE的垂线交 AC于点 G,过点 G作 CF的垂线交BC于点 H延长线段AE、 GH交于点 M.(1)求证:∠ BFC=∠ BEA;(2)求证: AM=BG+GM.11.如图所示,把矩形纸片OABC放入直角坐标系xOy 中,使 OA、 OC分别落在x、y 轴的正半轴上,连接AC,且 AC=4,(1)求 AC所在直线的解析式;(2)将纸片 OABC折叠,使点 A 与点 C 重合(折痕为 EF),求折叠后纸片重叠部分的面积.(3)求 EF 所在的直线的函数解析式.12.已知一次函数的图象与坐标轴交于A、B 点(如图),AE平分∠ BAO,交 x 轴于点 E.(1)求点 B 的坐标;(2)求直线 AE的表达式;(3)过点 B 作 BF⊥ AE,垂足为 F,连接 OF,试判断△ OFB的形状,并求△ OFB的面积.(4)若将已知条件“ AE 平分∠ BAO,交 x 轴于点E”改变为“点 E 是线段OB 上的一个动点(点 E 不与点 O、 B 重合)”,过点 B 作 BF⊥ AE,垂足为F.设 OE=x,BF=y,试求y 与 x 之间的函数关系式,并写出函数的定义域.13.如图,直线 l 1的解析表达式为:y=﹣ 3x+3 ,且 l 1与 x 轴交于点D,直线 l 2经过点 A,B,直线 l 1, l 2交于点 C.(1)求点 D 的坐标;(2)求直线 l 2的解析表达式;(3)求△ ADC的面积;(4)在直线 l 2上存在异于点 C 的另一点 P,使得△ ADP与△ ADC的面积相等,请直接写出点 P 的坐标.14.如图 1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点 A、 B 分别在 x 轴与y 轴上,已知OA=6,OB=10.点 D 为y 轴上一点,其坐标为(0, 2),点P 从P 与点 B 重合时点 A 出发以每秒 2 个单位的速度沿线段AC﹣ CB的方向运动,当点停止运动,运动时间为t 秒.(1)当点 P 经过点 C 时,求直线 DP的函数解析式;(2)①求△ OPD的面积 S 关于 t 的函数解析式;②如图②,把长方形沿着OP折叠,点 B 的对应点B′恰好落在AC边上,求点P的坐标.( 3)点 P 在运动过程中是否存在使△BDP为等腰三角形若存在,请求出点P 的坐标;若不存在,请说明理由.15.如图,在平面直角坐标系中,已知O为原点,四边形ABCD为平行四边形, A、B、C 的坐标分别是A(﹣ 5,1), B(﹣ 2, 4),C( 5, 4),点 D在第一象限.(1)写出 D 点的坐标;(2)求经过 B、 D 两点的直线的解析式,并求线段BD的长;( 3)将平行四边形ABCD先向右平移1 个单位长度,再向下平移 1 个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少并求出平行四边形ABCD与四边A1B1C1D1重叠部分的面积.16.如图,一次函数的图象与x 轴、 y 轴交于点A、B,以线段 AB为边在第一象限内作等边△ABC,( 1)求△ ABC的面积;( 2)如果在第二象限内有一点P(a,);试用含有a 的代数式表示四边形ABPO的面积,并求出当△ABP的面积与△ ABC的面积相等时 a 的值;( 3)在 x 轴上,是否存在点M,使△ MAB为等腰三角形若存在,请直接写出点M的坐标;若不存在,请说明理由.2018 年 06 月 17 日梧桐听雨的初中数学组卷参考答案与试题解析一.解答题(共16 小题)1.已知,正方形 ABCD中,∠MAN=45°,∠ MAN绕点 A 顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、 N, AH⊥ MN于点 H.( 1)如图①,当∠MAN绕点 A 旋转到 BM=DN时,请你直接写出AH 与 AB 的数量关系:AH=AB ;(2)如图②,当∠ MAN绕点 A 旋转到 BM≠ DN时,( 1)中发现的 AH与 AB的数量关系还成立吗如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠ MAN=45°, AH⊥ MN于点 H,且 MH=2,NH=3,求 AH的长.(可利用(2)得到的结论)【解答】解:( 1)如图① AH=AB.( 2)数量关系成立.如图②,延长CB至 E,使 BE=DN.∵ ABCD是正方形,∴AB=AD,∠ D=∠ABE=90°,在 Rt △ AEB和 Rt △AND中,,∴Rt △ AEB≌ Rt △ AND,∴AE=AN,∠ EAB=∠NAD,∵∠DAN+∠BAN=45°,∴∠EAB+∠BAN=45°,∴∠ EAN=45°,∴∠ EAM=∠NAM=45°,在△ AEM和△ ANM中,,∴△ AEM≌△ ANM.∴S△AEM=S△ANM, EM=MN,∵AB、 AH是△ AEM和△ ANM对应边上的高,∴ AB=AH.( 3)如图③分别沿 AM、 AN翻折△ AMH和△ ANH,得到△ ABM和△ AND,∴BM=2,DN=3,∠ B=∠ D=∠BAD=90°.分别延长 BM和 DN交于点 C,得正方形 ABCD,由( 2)可知, AH=AB=BC=CD=AD.设 AH=x,则 MC=x﹣ 2, NC=x﹣ 3,在 Rt △MCN中,由勾股定理,得222 MN=MC+NC∴52=( x﹣ 2)2+( x﹣ 3)2( 6 分)解得 x1=6,x2=﹣ 1.(不符合题意,舍去)∴AH=6.2.如图,△ ABC是等边三角形,点 D 是边 BC上的一点,以AD为边作等边△ ADE,过点C 作 CF∥DE交 AB于点 F.( 1)若点 D 是 BC边的中点(如图①),求证: EF=CD;( 2)在( 1)的条件下直接写出△AEF和△ ABC的面积比;(3)若点 D 是 BC边上的任意一点(除 B、 C 外如图②),那么( 1)中的结论是否仍然成立若成立,请给出证明;若不成立,请说明理由.【解答】(1)证明:∵△ ABC是等边三角形, D 是 BC的中点,∴ AD⊥ BC,且∠ BAD= ∠BAC=30°,∵△ AED是等边三角形,∴AD=AE,∠ ADE=60°,∴∠ EDB=90°﹣∠ ADE=90°﹣ 60°=30°,∵ED∥ CF,∴∠ FCB=∠EDB=30°,∵∠ ACB=60°,∴∠ ACF=∠ ACB﹣∠ FCB=30°,∴∠ ACF=∠BAD=30°,在△ ABD和△ CAF中,,∴△ ABD≌△ CAF(ASA),∴AD=CF,∵ AD=ED,∴ED=CF,又∵ ED∥CF,∴四边形 EDCF是平行四边形,∴EF=CD.( 2)解:△ AEF和△ ABC的面积比为: 1: 4;(易知AF=BF ,延长EF交AD于H,△AEF的面积=? EF? AH= ? CB ? AD= ? ? BC? AD,由此即可证明)(3)解:成立.理由如下:∵ ED∥FC,∴∠ EDB=∠ FCB,∵∠ AFC=∠ B+∠BCF=60° +∠ BCF,∠ BDA=∠ ADE+∠EDB=60° +∠ EDB∴∠ AFC=∠ BDA,在△ ABD和△ CAF中,∴△ ABD≌△ CAF(AAS),∴AD=FC,∵ AD=ED,∴ED=CF,又∵ ED∥CF,∴四边形 EDCF是平行四边形,∴EF=DC.3.( 1)如图 1,在正方形ABCD中,E 是 AB上一点, F 是 AD延长线上一点,且 DF=BE.求证: CE=CF;( 2)如图 2,在正方形ABCD中, E 是 AB上一点, G是 AD上一点,如果∠ GCE=45°,请你利用( 1)的结论证明:GE=BE+GD.( 3)运用( 1)( 2)解答中所积累的经验和知识,完成下题:如图 3,在直角梯形ABCD中, AD∥ BC( BC> AD),∠ B=90°, AB=BC,E 是 AB上一点,且∠ DCE=45°, BE=4, DE=10,求直角梯形ABCD的面积.【解答】( 1)证明:∵四边形ABCD是正方形,∴BC=CD,∠ B=∠ CDF=90°,∵∠ ADC=90°,∴∠FDC=90°.∴∠B=∠FDC,∵ BE=DF,∴△ CBE≌△ CDF(SAS).∴CE=CF.(2)证明:如图 2,延长 AD至 F,使 DF=BE,连接 CF.由( 1)知△ CBE≌△ CDF,∴∠ BCE=∠ DCF.∴∠ BCE+∠ ECD=∠DCF+∠ ECD,即∠ ECF=∠BCD=90°,又∠ GCE=45°,∴∠ GCF=∠GCE=45°.∵CE=CF,GC=GC,∴△ ECG≌△ FCG.∴ GE=GF,∴GE=GF=DF+GD=BE+GD.( 3)解:如图3,过 C作 CG⊥ AD,交 AD延长线于G.在直角梯形ABCD中,∵AD∥ BC,∴∠ A=∠B=90°,又∵∠ CGA=90°, AB=BC,∴四形ABCG正方形.∴AG=BC.⋯( 7 分)∵∠ DCE=45°,根据( 1)( 2)可知, ED=BE+DG.⋯( 8 分)∴10=4+DG,即DG=6.AB=x, AE=x 4, AD=x 6,在Rt △AED中,222222∵ DE=AD+AE,即 10 =( x 6) +( x 4).解个方程,得:x=12 或 x= 2(舍去).⋯( 9 分)∴ AB=12.∴ S 梯形ABCD=( AD+BC) ? AB= ×( 6+12)× 12=108.即梯形 ABCD的面108.⋯( 10 分)4.如,正方形 ABCD中,E AB上一点,点 D 作 DF⊥ DE,与 BC延交于点F.接EF,与 CD交于点 G,与角 BD交于点 H.( 1)若 BF=BD= ,求 BE的;( 2)若∠ ADE=2∠BFE,求: FH=HE+HD.【解答】( 1)解:∵四边形ABCD正方形,∴∠ BCD=90°, BC=CD,222∴ Rt △ BCD中, BC+CD=BD,222即 BC=()﹣(BC),∴ BC=AB=1,∵ DF⊥ DE,∴∠ ADE+∠EDC=90°=∠ EDC+∠ CDF,∴∠ ADE=∠ CDF,在△ ADE和△ CDF中,∵,∴△ ADE≌△ CDF(ASA),∴ AE=CF=BF﹣ BC=﹣1,∴ BE=AB﹣ AE=1﹣(﹣1)=2﹣;(2)证明:在 FE 上截取一段 FI ,使得 FI=EH,∵△ ADE≌△ CDF,∴ DE=DF,∴△ DEF为等腰直角三角形,∴∠DEF=∠DFE=45°=∠ DBC,∵∠ DHE=∠ BHF,∴∠ EDH=∠ BFH(三角形的内角和定理),在△ DEH和△ DFI 中,∵,∴△ DEH≌△ DFI (SAS),∴DH=DI,又∵∠ HDE=∠ BFE,∠ ADE=2∠ BFE,∴∠ HDE=∠ BFE= ∠ ADE,∵∠ HDE+∠ADE=45°,∴∠ HDE=15°,∴∠ DHI=∠ DEH+∠HDE=60°,即△ DHI 为等边三角形,∴DH=HI,∴FH=FI+HI=HE+HD.5.如图,将一三角板放在边长为 1 的正方形ABCD上,并使它的直角顶点P 在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于 Q.探究:设A、 P 两点间的距离为x.(1)当点 Q在边 CD上时,线段 PQ与 PB 之间有怎样的数量关系试证明你的猜想;(2)当点 Q在边 CD上时,设四边形 PBCQ的面积为 y,求 y 与 x 之间的函数关系,并写出函数自变量 x 的取值范围;(3)当点 P 在线段 AC上滑动时,△ PCQ是否可能成为等腰三角形如果可能,指出所有能使△ PCQ成为等腰三角形的点 Q的位置.并求出相应的 x 值,如果不可能,试说明理由.【解答】解:( 1)PQ=PB,(1 分)过P 点作 MN∥ BC分别交 AB、 DC于点 M、 N,在正方形ABCD中,AC为对角线,∴ AM=PM,又∵ AB=MN,∴ MB=PN,∵∠ BPQ=90°,∴∠ BPM+∠NPQ=90°;又∵∠ MBP+∠BPM=90°,∴∠ MBP=∠ NPQ,在 Rt △ MBP≌ Rt △NPQ中,∵∴Rt △ MBP≌ Rt △ NPQ,( 2 分)∴PB=PQ.(2)∵ S 四边形PBCQ=S△PBC+S△PCQ,∵AP=x,∴ AM= x,∴CQ=CD﹣ 2NQ=1﹣ x,又∵ S△PBC= BC? BM= ? 1? ( 1﹣x) =﹣x,S△PCQ= CQ? PN= ( 1﹣x) ? ( 1﹣x),=﹣+,∴ S 四边形PBCQ=﹣x+1.( 0≤x≤).(4分)( 3)△ PCQ可能成为等腰三角形.①当点 P 与点 A 重合时,点Q与点 D重合,PQ=QC,此时, x=0.( 5 分)②当点 Q在 DC的延长线上,且CP=CQ时,( 6 分)有: QN=AM=PM= x, CP=﹣x,CN=CP=1﹣x, CQ=QN﹣CN=x﹣( 1﹣x)=x﹣1,∴当﹣ x=x﹣ 1 时, x=1.(7 分).6. Rt △ABC与 Rt △ FED是两块全等的含30°、 60°角的三角板,按如图(一)所示拼在一起, CB与 DE重合.(1)求证:四边形 ABFC为平行四边形;(2)取 BC中点 O,将△ ABC绕点 O顺时钟方向旋转到如图(二)中△ A′B′C′位置,直线 B'C' 与 AB、CF分别相交于 P、Q两点,猜想 OQ、 OP长度的大小关系,并证明你的猜想;( 3)在( 2)的条件下,指出当旋转角至少为多少度时,四边形PCQB为菱形(不要求证明)【解答】( 1)证明:∵△ABC≌△ FCB,∴AB=CF, AC=BF.∴四边形 ABFC为平行四边形.(2)解: OP=OQ,理由如下:∵OC=OB,∠ COQ=∠ BOP,∠ OCQ=∠ PBO,∴△ COQ≌△ BOP.∴OQ=OP.(3)解: 90°.理由:∵ OP=OQ, OC=OB,∴四边形 PCQB为平行四边形,∵ BC⊥ PQ,∴四边形 PCQB为菱形.7.如图,在正方形ABCD中,点 F 在 CD边上,射线 AF 交 BD于点 E,交 BC的延长线于点G.(1)求证:△ ADE≌△ CDE;(2)过点 C 作 CH⊥ CE,交 FG于点 H,求证: FH=GH;( 3)设 AD=1, DF=x,试问是否存在x 的值,使△ ECG为等腰三角形若存在,请求出x 的值;若不存在,请说明理由.【解答】( 1)证明:∵四边形ABCD是正方形,∴DA=DC,∠ 1=∠2=45°, DE=DE,∴△ ADE≌△ CDE.(2)证明:∵△ ADE≌△ CDE,∴∠ 3=∠4,∵ CH⊥ CE,∴∠ 4+∠5=90°,又∵∠ 6+∠5=90°,∴∠ 4=∠6=∠ 3,∵AD∥ BG,∴∠ G=∠3,∴∠ G=∠6,∴ CH=GH,又∵∠4+∠5=∠G+∠7=90°,∴∠ 5=∠7,∴ CH=FH,∴ FH=GH.( 3)解:存在符合条件的x 值此时,CE=CG,∵∠ ECG>90°,要使△ECG为等腰三角形,必须∴∠ G=∠8,又∵∠ G=∠ 4,∴∠ 8=∠4,∴∠ 9=2∠ 4=2∠ 3,∴∠ 9+∠3=2∠ 3+∠3=90°,∴∠ 3=30°,∴x=DF=1×tan30 °= .8.在 ? ABCD中,∠ BAD的平分线交直线BC于点 E,交直线DC于点 F.(1)在图 1 中证明 CE=CF;(2)若∠ ABC=90°, G是 EF 的中点(如图 2),直接写出∠ BDG的度数;(3)若∠ ABC=120°, FG∥CE, FG=CE,分别连接 DB、DG(如图 3),求∠ BDG的度数.【解答】( 1)证明:如图1,∵AF 平分∠ BAD,∴∠ BAF=∠ DAF,∵四边形 ABCD是平行四边形,∴AD∥ BC, AB∥ CD,∴∠ DAF=∠ CEF,∠ BAF=∠F,∴∠ CEF=∠ F.∴CE=CF.( 2)解:连接GC、 BG,∵四边形 ABCD为平行四边形,∠ ABC=90°,∴四边形 ABCD为矩形,∵AF 平分∠ BAD,∴∠ DAF=∠BAF=45°,∵∠ DCB=90°, DF∥ AB,∴∠ DFA=45°,∠ ECF=90°∴△ ECF为等腰直角三角形,∵G为 EF中点,∴EG=CG=FG, CG⊥EF,∵△ ABE为等腰直角三角形,AB=DC,∴BE=DC,∵∠ CEF=∠GCF=45°,∴∠ BEG=∠DCG=135°在△ BEG与△ DCG中,∵,∴△ BEG≌△ DCG,∴BG=DG,∵ CG⊥ EF,∴∠ DGC+∠DGA=90°,又∵∠ DGC=∠ BGA,∴∠ BGA+∠DGA=90°,∴△ DGB为等腰直角三角形,∴∠ BDG=45°.(3)解:延长 AB、 FG交于 H,连接 HD.∵ AD∥ GF, AB∥ DF,∴四边形 AHFD为平行四边形∵∠ ABC=120°, AF 平分∠BAD∴∠ DAF=30°,∠ ADC=120°,∠ DFA=30°∴△ DAF为等腰三角形∴AD=DF,∴CE=CF,∴平行四边形AHFD为菱形∴△ ADH,△ DHF为全等的等边三角形∴DH=DF,∠ BHD=∠GFD=60°∵ FG=CE, CE=CF,CF=BH,∴BH=GF在△ BHD与△ GFD中,∵,∴△ BHD≌△ GFD,∴∠ BDH=∠ GDF∴∠ BDG=∠ BDH+∠HDG=∠ GDF+∠HDG=60°9.如图,已知? ABCD中, DE⊥ BC于点 E, DH⊥AB 于点 H, AF 平分∠ BAD,分别交DC、DE、 DH于点 F、 G、M,且 DE=AD.(1)求证:△ ADG≌△ FDM.(2)猜想 AB 与 DG+CE之间有何数量关系,并证明你的猜想.【解答】证明:( 1)∵四边形ABCD是平行四边形,∴AB∥ CD, AD∥ BC,∴∠ BAF=∠ DFA,∵ AF 平分∠ BAD,∴∠ DAF=∠ DFA,∴AD=FD,∵DE⊥ BC, DH⊥ AB,∴∠ ADG=∠FDM=90°,在△ ADG和△ FDM中,,∴△ ADG≌△ FDM(ASA).(2) AB=DG+EC.证明:延长GD至点 N,使 DN=CE,连接 AN,∵DE⊥ BC, AD∥ BC,∴∠ADN=∠DEC=90°,在△ ADN和△ DEC中,,∴△ ADN≌△ DEC(SAS),∴∠ NAD=∠ CDE,AN=DC,∵∠ NAG=∠ NAD+∠DAG,∠ NGA=∠ CDE+∠ DFA,∴∠ NAG=∠ NGA,∴AN=GN=DG+CE=DC,∵四边形 ABCD是平行四边形,∴AB=CD,∴AB=DG+EC.10.如图,在正方形ABCD中, E、 F 分别为 BC、AB 上两点,且B E=BF,过点 B 作 AE的垂线交 AC于点 G,过点 G作 CF 的垂线交BC于点 H 延长线段AE、GH交于点 M.(1)求证:∠ BFC=∠ BEA;(2)求证: AM=BG+GM.【解答】证明:( 1)在正方形ABCD中, AB=BC,∠ ABC=90°,在△ ABE和△ CBF中,,∴△ ABE≌△ CBF(SAS),∴∠ BFC=∠ BEA;(2)连接 DG,在△ ABG和△ ADG中,,∴△ ABG≌△ ADG(SAS),∴BG=DG,∠ 2=∠ 3,∵ BG⊥ AE,∴∠ BAE+∠2=90°,∵∠ BAD=∠ BAE+∠4=90°,∴∠ 2=∠3=∠ 4,∵ GM⊥ CF,∴∠ BCF+∠1=90°,又∠ BCF+∠BFC=90°,∴∠ 1=∠BFC=∠ 2,∴∠ 1=∠3,在△ ADG中,∠ DGC=∠ 3+45°,∴∠ DGC也是△ CGH的外角,∴D、 G、M三点共线,∵∠ 3=∠4(已证),∴AM=DM,∵DM=DG+GM=BG+GM,∴ AM=BG+GM.11.如图所示,把矩形纸片OABC放入直角坐标系xOy 中,使 OA、 OC分别落在 x、y 轴的正半轴上,连接AC,且 AC=4,(1)求 AC所在直线的解析式;(2)将纸片 OABC折叠,使点 A 与点 C 重合(折痕为 EF),求折叠后纸片重叠部分的面积.(3)求 EF 所在的直线的函数解析式.【解答】解:( 1)∵=,∴可设 OC=x,则 OA=2x,在 Rt △AOC中,由勾股定理可得222 OC+OA=AC,∴x2+( 2x)2=( 4 )2,解得 x=4( x= ﹣4 舍去),∴OC=4,OA=8,∴A( 8,0), C( 0, 4),设直线 AC解析式为 y=kx+b ,∴,解得,∴直线 AC解析式为y=﹣x+4;(2)由折叠的性质可知 AE=CE,设 AE=CE=y,则 OE=8﹣ y,在 Rt △ OCE中,由勾股定理可得222 OE+OC=CE,∴( 8﹣ y)2+42=y2,解得 y=5,∴ AE=CE=5,∵∠ AEF=∠ CEF,∠ CFE=∠AEF,∴∠ CFE=∠ CEF,∴ CE=CF=5,∴ S△CEF=CF? OC= × 5× 4=10,即重叠部分的面积为10;(3)由( 2)可知 OE=3,CF=5,∴ E( 3,0), F( 5, 4),设直线 EF 的解析式为 y=k′x+b′,∴,解得,∴直线 EF 的解析式为y=2x﹣ 6.12.已知一次函数的图象与坐标轴交于A、B 点(如图),AE平分∠ BAO,交 x 轴于点 E.(1)求点 B 的坐标;(2)求直线 AE的表达式;(3)过点 B 作 BF⊥ AE,垂足为 F,连接 OF,试判断△ OFB的形状,并求△ OFB的面积.(4)若将已知条件“ AE 平分∠ BAO,交 x 轴于点 E”改变为“点 E 是线段 OB上的一个动点(点 E 不与点 O、 B 重合)”,过点 B 作 BF⊥AE,垂足为F.设 OE=x,BF=y,试求y 与 x 之间的函数关系式,并写出函数的定义域.【解答】解:( 1)对于 y=﹣x+6,当x=0 时, y=6;当 y=0 时, x=8,∴OA=6,OB=8,在Rt △AOB中,根据勾股定理得: AB=10,则 A( 0, 6), B(8, 0);( 2)过点 E 作 EG⊥ AB,垂足为 G(如图 1 所示),∵ AE 平分∠ BAO,EO⊥ AO, EG⊥ AG,∴ EG=OE,在Rt △AOE和 Rt△ AGE中,,∴Rt △ AOE≌ Rt △ AGE( HL),∴AG=AO,设OE=EG=x,则有 BE=8﹣ x, BG=AB﹣AG=10﹣ 6=4,在Rt △ BEG中, EG=x, BG=4, BE=8﹣x,根据勾股定理得:222x+4 =( 8﹣ x),解得: x=3,∴ E( 3,0),设直线 AE的表达式为y=kx+b ( k≠ 0),将A( 0,6), E(3, 0)代入 y=kx+b 得:,解得:则直线,AE的表达式为y=﹣2x+6;(3)延长 BF 交 y 轴于点 K(如图 2 所示),∵ AE平分∠ BAO,∴∠ KAF=∠ BAF,又BF⊥ AE,∴∠ AFK=∠AFB=90°,在△ AFK和△ AFB中,∵,∴△ AFK≌△ AFB,∴FK=FB,即F 为KB 的中点,又∵△ BOK为直角三角形,∴OF= BK=BF,∴△ OFB为等腰三角形,过点 F 作 FH⊥ OB,垂足为 H(如图 2 所示),∵OF=BF, FH⊥ OB,∴OH=BH=4,∴F 点的横坐标为 4,设F( 4, y),将 F( 4, y)代入 y= ﹣2x+6,得: y= ﹣ 2,∴ FH=| ﹣2|=2 ,则 S△OBF= OB? FH= ×8× 2=8;(4)在 Rt △ AOE中, OE=x, OA=6,根据勾股定理得:AE==,又BE=OB﹣ OE=8﹣x, S△ABE= AE? BF= BE? AO(等积法),∴ BF==(0<x<8),又BF=y,则 y=(0<x<8).13.如图,直线 l 1的解析表达式为:y=﹣ 3x+3 ,且 l 1与 x 轴交于点D,直线 l 2经过点 A,B,直线 l 1, l 2交于点 C.(1)求点 D的坐标;(2)求直线 l 2的解析表达式;(3)求△ ADC的面积;(4)在直线 l 2上存在异于点 C 的另一点 P,使得△ ADP与△ ADC的面积相等,请直接写出点 P 的坐标.【解答】解:( 1)由 y=﹣3x+3,令 y=0,得﹣ 3x+3=0,∴x=1,∴D( 1,0);( 2)设直线l 2的解析表达式为y=kx+b ,由图象知: x=4, y=0; x=3,,代入表达式y=kx+b ,∴,∴,∴直线 l 2的解析表达式为;( 3)由,解得,∴ C( 2,﹣ 3),∵ AD=3,∴ S△ADC=× 3×|﹣3|=;( 4)△ ADP与△ ADC底边都是A D,面积相等所以高相等,△ADC高就是点 C 到直线 AD 的距离,即 C 纵坐标的绝对值=| ﹣ 3|=3 ,则 P 到 AD距离 =3,∴ P 纵坐标的绝对值=3,点 P 不是点 C,∴点 P 纵坐标是3,∵ y=﹣ 6, y=3,∴﹣ 6=3x=6,所以 P(6, 3).14.如图 1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点 A、 B 分别在 x 轴与 y 轴上,已知OA=6, OB=10.点 D 为 y 轴上一点,其坐标为(0, 2),点 P 从点 A 出发以每秒 2 个单位的速度沿线段AC﹣ CB的方向运动,当点 P 与点 B 重合时停止运动,运动时间为t 秒.( 1)当点 P 经过点 C 时,求直线DP的函数解析式;( 2)①求△ OPD的面积 S关于 t 的函数解析式;②如图②,把长方形沿着OP折叠,点 B 的对应点 B′恰好落在AC边上,求点 P 的坐标.( 3)点 P 在运动过程中是否存在使△BDP为等腰三角形若存在,请求出点P 的坐标;若不存在,请说明理由.【解答】解:( 1)∵ OA=6,OB=10,四边形OACB为长方形,∴C( 6,10).设此时直线DP解析式为 y=kx+b ,把( 0,2), C( 6, 10)分别代入,得,解得则此时直线DP解析式为 y= x+2;( 2)①当点P 在线段 AC上时, OD=2,高为 6, S=6;× 2×( 16﹣ 2t )=﹣ 2t+16 ;当点 P 在线段 BC上时, OD=2,高为 6+10﹣ 2t=16 ﹣ 2t ,S=②设 P(m, 10),则 PB=PB′=m,如图2,∵OB′=OB=10, OA=6,∴AB′==8,∴B′C=10﹣ 8=2,∵ PC=6﹣m,∴m2=22+( 6﹣ m)2,解得 m=则此时点 P 的坐标是(, 10);( 3)存在,理由为:若△ BDP为等腰三角形,分三种情况考虑:如图3,①当 BD=BP1=OB﹣ OD=10﹣ 2=8,在Rt △ BCP1中, BP1=8, BC=6,根据勾股定理得: CP1==2,∴ AP1=10﹣2,即 P1( 6, 10﹣ 2);②当 BP2=DP2时,此时 P2( 6, 6);3③当 DB=DP=8时,在Rt △ DEP3中, DE=6,根据勾股定理得:P E==2,3∴ AP3=AE+EP3=2+2,即 P3(6, 2+2),综上,满足题意的P 坐标为( 6, 6)或( 6, 2+2)或( 6, 10﹣ 2).15.如图,在平面直角坐标系中,已知O为原点,四边形ABCD为平行四边形,A、 B、C 的坐标分别是A(﹣ 5, 1), B(﹣ 2,4), C( 5, 4),点 D 在第一象限.( 1)写出 D 点的坐标;(2)求经过 B、D 两点的直线的解析式,并求线段BD的长;(3)将平行四边形 ABCD先向右平移 1 个单位长度,再向下平移 1 个单位长度所得的四边形 A1B1C1D1四个顶点的坐标是多少并求出平行四边形ABCD与四边形A1B1C1D1重叠部分的面积.【解答】解:( 1)∵ B(﹣ 2, 4), C( 5, 4),∴BC=5﹣(﹣ 2)=5+2=7,∵ A(﹣ 5, 1),∴点 D 的横坐标为﹣ 5+7=2,∴点 D 的坐标为( 2, 1);( 2)设直线 BD的解析式为 y=kx+b ,将 B(﹣ 2, 4)、D( 2, 1)代入得:,解得,∴经过 B、 D两点的直线的解析式为y=﹣x+,过 B 点作 AD的垂线,垂足为E,则 BE=4﹣ 1=3,DE=2﹣(﹣ 2) =2+2=4,在 Rt △BDE中, BD===5;( 3)∵ ? ABCD向右平移1 个单位长度,再向下平移 1 个单位长度,∴A1(﹣ 4, 0), B1(﹣ 1, 3),C1( 6, 3)D1( 3,0),∴重叠部分的底边长 7﹣ 1=6,高为 3﹣1=2,∴重叠部分的面积S=6× 2=12.16.如图,一次函数的图象与 x 轴、 y 轴交于点 A、B,以线段 AB为边在第一象限内作等边△ ABC,( 1)求△ ABC的面积;( 2)如果在第二象限内有一点P( a,);试用含有 a 的代数式表示四边形 ABPO的面积,并求出当△ABP的面积与△ ABC的面积相等时 a 的值;(3)在 x 轴上,是否存在点 M,使△ MAB为等腰三角形若存在,请直接写出点 M的坐标;若不存在,请说明理由.【解答】解:( 1)分别令 y=0 和 x=0,得一次函数y=x+1 的图象与x 轴.y 轴的交点坐标分别是A(,0),B(0,1),即OA=,OB=1,∴ AB==2∵△ ABC为等边三角形,△ ABC∴ S =;( 2)如图 1, S =, S =, S = |a| ? OB=﹣.△ AOB△ AOP△BOP∴ S 四边形ABPO=S△AOB+S△BOP=,而S△ABP=S 四边形ABPO﹣ S△APO,∴当 S△ABP=S△ABC时,=,解得 a=﹣;。
