第五章对流传热分析..
V4-第五章-对流传热的理论基础-2014

单位时间热对流传递到微元体的净热量: 1 + 2
t t Q对流 c p u v dxdy y x
Q导热 + Q对流 = U热力学能
单位时间导入导出的净热量: 单位时间热力学能的增量:
2t 2t Q导热 2 dxdy+ 2 dxdy x y
t y
y 0
h
t
t y
y 0
λ:流体导热系数; ∂t/∂y: 贴壁流体层的温度梯度 注意与导热问题第三类边界条件的区别
例5-1: 热边界层中特定位置x处的温度分布由下式给出 , t ( y) A By Cy 2 其中 A,B,C为常数。试求相应的局部换热系数hx的表达式。 分析:计算hx的公式主要有:对流换热微分方程式和努塞尔数准则。根据 本例条件,应该采用对流换热微分方程式计算。 解:
惯性力 体积力 压力梯度 粘性力
能量守恒方程:热力学第一定律 Q=∆E+W
[导入与导出的净热量] + [热对流传递的净热量] + [内热源发热量]
= [总能量的增量] + [对外膨胀功]
Q — Q导热 Q对流 Q内热源
E — U 热力学能 U K(动能)
假设: 无内热源,低速流动,流体不对外作功
1. 流动边界层及其厚度的定义
普朗特 实验发现:流体近壁面流动时基于粘性力的速度梯度 主要存在于近壁面的薄层,主流区速度梯度很小。
yx
du dy
速度边界层的定义 固壁表面附近流体速度剧烈变化的薄层称为速度边界 层 ,速度边界层外的主流区速度梯度视为零。
Ludwig Prandtl 1875-1953
Q导热 + Q对流 = U热力学能
传热学 第5章
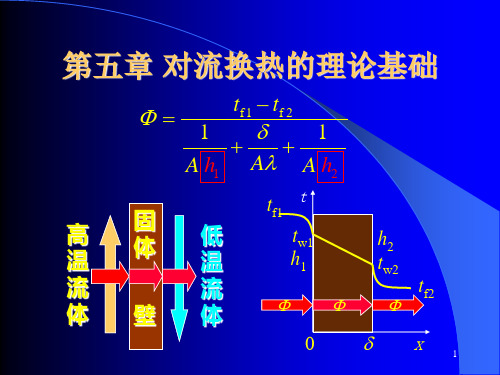
x x x dx q x dy q x dxdy
qx qx qx dy qx dx dy dxdy x x 2 t t dxdy 2 dxdy x x x
体积力
Du p Fx 2 u d x
粘性力
19
质量守恒
y
微元体
u v 0 x y
dy
0
dx
x
20
y dy
微元体
0
dx
x
2v 2v v v v p u v 2 Fy y方向: 2 x y y x y
36
5.3 边界层型对流传热
粘性流动的N-S方程很难获得分析解
流体的黏滞作用仅仅局限在靠近壁面的 薄层内 薄层之外,速度梯度很小,黏滞作用可 忽略不计
37
5.3.1 流动边界层
固体表面附近流体速度发生剧烈变化的 薄层。 流体速度从0到主流速度的99%的范围。
u 0.99u
y t 2 dxdy y
2
23
x y
t t 2 dxdy 2 x y
2 2
y dy
y+dy h y+dy
x h x
0 dx
x+dx h x+dx
y h y
2t 2t t t t cp u v 2 2 x y x y
31
定解条件
(1)几何条件
说明对流换热表面的几何形状、尺寸,壁面与
流体之间的相对位置,壁面的粗糙度等。
第五章 对流换热概述

在x方向上流入的净热量
2t 2 dxdy y
u t ucptdy c p u dx t dx dy x x u t u t ucp tdy c p dy ut tdx udx dxdx x x x x u t u t c p t dxdy c p u dxdy c p dxdxdy x x x x
二、对流传热的基本公式 ( h 的确定方式)
q ht
W m2 Leabharlann qA hAt无滑移边界条件
W
t A y
y 0
令上两式相等则有
t Ah t A y
t h t y
y 0
则
y 0
§5-2
一、假设条件
对流换热问题的数学描述
为简化分析,对于常见影响对流换热问题的主要因素,做如 下假设: (1) 流动是二维的; (2) 流体为不可压缩的牛顿流体; (3) 流体物性为常数,无内热源; (4) 流速不高,忽略粘性耗散(摩擦损失) ; (5) 流体为连续性介质
v ~ 01 y
导数的数量级由因变量与自变量的数量级确定,所以
u ~ 01 x
a~02 的数量级为1,
这样可以对微分方程组进行简化(数量级一致)
u v 0 x y
1 1
2u 2u u u p u v 2 x y x x y 2
§5-3 边界层分析及边界层微分方程组
一.边界层的概念
1. 流动(速度)边界层: 靠近壁面处流体速度发生显著变化的薄层 边界层的厚度(boundary layer thickness): 达到主流速度的99%处至固体壁面的垂直距离
传热学 第五章 对流传热

思路:
定性地分析对流传热的影响因素
深入讨论对流传热过程的数学描述 导出边界层问题的简化方程
给出相应的求解方法
3
2. 对流传热的特点 (1) 导热与热对流同时存在的复杂热传递过程 (2) 流固之间存在温差 (3) 必须有直接接触(流体与壁面)和宏观运动 (4) 由于流体的粘性,受壁面摩擦阻力的影响,紧贴壁面处会 形成速度梯度很大的边界层
自然对流:流体因各部分温度不同而引起的密度差所产生的 浮升力所推动的流动
5
(2) 流动状态
层流:(Laminar flow )流体微团沿主流方向做有规则的 分层运动,整个流场呈一簇互相平行的流线
湍流:(Turbulent flow )流体质点做复杂无规则的运动,
流体各部分之间发生剧烈的混合。
(3) 流体有无相变
15
2. 动量守恒方程
牛顿第二运动定律: 作用在微元体上各外力的总和等于控制体中流体动量的变化率
F = ma
作用力:体积力(重力、离心力、电磁力) 表面力:切应力、z应力
16
应力形式的运动微分方程:
(1)
牛顿流体的本构关系:
1)达朗伯原理——两相邻正交截面上的剪切力互等 2)斯托克斯三假设
a) 流体各向同性,任一质点在的各个方向上物理性质都相同 b) 应力分量与变形速度成正比 c) 变形速度为零:切应力为零,法向应力为流体静压强 P
Note: 第三类边界条件中的h为已知量
12
§5-2 对流传热问题的数学描述
为便于分析,以二维对流传热问题为研究对象: 假设:a) 流体为连续性介质 b) 流体为不可压缩的牛顿流体
c) 所有物性参数(?、cp、?、? )为常量 d) 粘性耗散热忽略不计 控制变量:速度 u、v;压力 p;温度 t 控制方程:连续性方程、动量方程、能量方程
《传热学》第五章 对流换热分析PPT演示课件

24
求解结果 局部表面传热系数:
或可写成:
其中:
——准则方程
——无量纲流速 ——无量纲物性 ——无量纲换热强度
准则方程的意义——
把微分方程所反映的众多因素间的规律用少数几个准则来概括, 从而减少变量个数,以便于进行对流换热问题的分析、实验研究 和数据处理。
将上式在x,y两个方向代入牛顿第二定律,得到Navier-Stokes方程: 对于不可压缩流体:
11
将其代入Navier-Stokes方程,并采用连续方程化简,得到:
对稳态流动:
惯性力
体积力 压强梯度 黏滞力
当只有重力场作用时:
12
四、能量微分方程式
推导依据—— 内能增量=导热热量+对流热量 1.导热热量:
外掠平板全板长平均换热准则方程:
29
第六节 相似理论基础
相似原理的意义——通过实验寻找现象的规律以及指导推广应用实验。
一、物理相似的基本概念
1.几何相似
LA、LB——几何相似准则
30
2.物理现象相似
以管内流动为例,当两管各r之比满足下列 关系时:
若: 则速度场相似。 以外掠平板为例,当x,y坐标满足下列关系时:
《传热学》
1
第五章 对流换热分析
研究对象——流体与固体壁面之间的传热过程
研究目的——确定牛顿冷却定律
中的h
对流表面 传热系数
局部对流表面传热系数hx 平均对流表面传热系数
Isaac Newton(1642-1727)
确定对流表面传热系数的四种方法
分析法
类比法 数值法 实验法
传热学第五章对流换热

1.流动边界层(Velocity boundary layer )
如果流体为没有粘性流体,流体流过平板时,流速在截 面上一直保持不变。 如果流体为粘性流体,情况会如何呢?我们用一测速仪 来测量壁面附近的速度分布。测量发现在法向方向上, 即y方向上,壁面上速度为零,随着y方向的增加,流速 急剧增加,到达一薄层后,流速接近或等于来流速度, 德国科学家普朗特L.Prandtl研究了这一现象,并且在 1904年第一次提出了边界层的、分类 三、对流换热的机理 四、影响因素 五、研究方法 六、h的物理意义
一.定义
流体流过与其温度不同的固体表面时所发生的热量交换称为 对流换热。 对流换热与热对流不同, 既有热对流,也有导热; 不是基本传热方式。 对流换热遵循牛顿冷却定律:
qw tw
x
y
t∞
u∞
图5-1 对流换热过程示意
圆管内强制对流换热 其它形式截面管道内的对流换热 外掠平板的对流换热 外掠单根圆管的对流换热 外掠圆管管束的对流换热 外掠其它截面形状柱体的对流换热 射流冲击换热
外部流动
对 流 换 热
有相变
自然对流(Free convection) 混合对流 沸腾换热 凝结换热
大空间自然对流 有限空间自然对流
大容器沸腾 管内沸腾 管外凝结 管内凝结
λ ∂t 换热微分方程(描写h的本质,hx = − ∆t ( ∂y ) y =0 dA) 连续性方程(描写流体流动状态,即质量守恒) 动量微分方程(描写流动状态,即动量守恒) 能量微分方程(描写流体中温度场分布)
对流换热微分方程组 先作假设: (1)仅考虑二维问题; (2)流体为不可压缩的牛顿流体,稳定流动; (3)常物性,无内热源; (4)忽略由粘性摩擦而产生的耗散热。 以二维坐标系中的微元体为分析对象,根据热力学第一定 律,对于这样一个开口系统,有:
传热学第五章对流换热

§5-1 §5-2 §5-3 §5-4 §5-5 §5-6 §5-7 §5-8
对流换热
Convective heat transfer
对流换热概说 对流换热的数学描写 对流换热边界层微分方程组 对流换热边界层积分方程组 相似理论与量纲分析 管内受迫流动 横向外掠圆管的对流换热 自然对流换热及实验关联式
λ ∂t 换热微分方程(描写h的本质,hx = − ∆t ( ∂y ) y =0 dA) 连续性方程(描写流体流动状态,即质量守恒) 动量微分方程(描写流动状态,即动量守恒) 能量微分方程(描写流体中温度场分布)
对流换热微分方程组 先作假设: (1)仅考虑二维问题; (2)流体为不可压缩的牛顿流体,稳定流动; (3)常物性,无内热源; (4)忽略由粘性摩擦而产生的耗散热。 以二维坐标系中的微元体为分析对象,根据热力学第一定 律,对于这样一个开口系统,有:
同理:() dτ qm hout − qm hin ≈ ρcp (
y
H y + dy − H y =
∂t ∂v ⋅ v + ⋅ t )dxdydτ ∂y ∂y
(qm h)out − (qm h)in ∴ ∂t ∂t ∂u ∂v = ρ c p (u + v )dxdy + ρ c p t ( + )dxdy ∂x ∂y ∂x ∂y ∂t ∂t = ρ c p (u + v )dxdy (d ) ∂x ∂y
1.流动边界层(Velocity boundary layer )
如果流体为没有粘性流体,流体流过平板时,流速在截 面上一直保持不变。 如果流体为粘性流体,情况会如何呢?我们用一测速仪 来测量壁面附近的速度分布。测量发现在法向方向上, 即y方向上,壁面上速度为零,随着y方向的增加,流速 急剧增加,到达一薄层后,流速接近或等于来流速度, 德国科学家普朗特L.Prandtl研究了这一现象,并且在 1904年第一次提出了边界层的概念。
传热学 第五章 对流原理.

层流边界层 紊流核心区
过渡区 紊流边界层 层流底层 主流区 速度边界层厚度 临界距离
层流
过渡流
湍流
u
y
x
xc
层流底层 缓冲层
根据流体力学知识,层流边界层厚度 xv 5x 5x 5 vf vf x Re x
在层流边界层内的速度分布线为抛物线型; 在紊流边界层内,层流底层部分的速度 分布较陡,接近于直线,而在底层以外 的区域,由于流体微团的紊流运动,动 量传递被强化了,速度变化趋于平缓。
如果流体的流动是由于流体冷热部分的密度不同 引起的浮升力造成的,则称为自然对流。暖气 片的散热,蒸汽或其他热流体输送管道的热量 损失,都与这类换热有关。 一般来讲:强迫对流 换热优于自然对流。
二、 在分析对流换热时,还应分清流体的流态。 流体力学告诉我们,流体受迫在流道内流 动时可以有两种不同性质的流态。流体分 层地平行于流道的壁面流动,呈现层流状 态。但当流动状态到超过某一临界值时, 流体的流动出现了旋涡,而且在不断地发 展和扩散,引起不规则的脉动,使流动呈 现紊流状态。
α =q/(tf-tw) W
对流换热系数 α表征着对流换热的强弱 。
在数值上,它等于流体和壁面之间的温度 差为 1℃时,通过对流换热交换的热流密 度。单位为W/(m2·℃)。 对流换热量以及相应的换热系数的大小,将 更多地取决于流体的运动性质和情况。
一、速度边界层
流体力学指出,具有粘性且能湿润固 体壁面的流体,流过壁面会产生粘性力。 根据牛顿粘性(内摩擦)定律,流体粘性 力 τ 与垂直于运动方程速度梯度 (dv/dy ) 成正比,即: τ=μ(dv/dy) N/m2 (5-2) 式中,μ 称为流体的动力粘度,单位为Pa· s 或kg/(m· s)。
传热学第五章_对流换热原理-1

Velocity = v Velocity = 0
Velocity Temperature
Boundary Boundary
Layer
Layer
HOT SURFACE, TEMP = TH
3. 热边界层厚度δt和流动边界层厚度δ的区 别与联系
(2) 边界层产生原因:
由于粘性的作用,流体与 壁面之间产生一粘滞力, 粘滞力使得靠近壁面处的 速度逐渐下降,最后使壁 面上的流体速度降为零, 流体质点在壁面上产生一 薄层。随着流体的流动, 粘滞力向内传递,形成的 薄层又阻碍邻近流体层中 微粒运动的作用,依此类 推,形成的薄层又阻碍邻 近流体层微粒运动,到一 定程度,粘滞力不再起作 用。
➢ 如果流体为粘性流体,情况会如何呢?我们用一测速仪来 测量壁面附近的速度分布。测量发现在法向方向上,即y 方向上,壁面上速度为零,随着y方向的增加,流速急剧 增加,到达一薄层后,流速接近或等于来流速度,普朗特 研究了这一现象,并且在1904年第一次提出了边界层的概 念。
普朗特在仔细观察了粘性流体流过固体表面的特性后提出了 突破性的见解。他认为,粘滞性起作用的区域仅仅局限在 靠近壁面的薄层内。在此薄层以外,由于速度梯度很小粘 滞性所造成的切应力可以略而不计,于是该区域中的流动 可以作为理想流体的无旋流动。这种在固体表面附近流体 速度发生剧烈变化的薄层称为流动边界层(又称速度边界 层).图5—5示出了产生流动边界层的两种常见情形。如 图5—5a所示,从y=o处u=0开始,流体的速度随着离开 壁面距离y的增加而急剧增大,经过一个薄层后u增长到接 近主流速度。这个薄层即为流动边界层,其厚度视规定的 接近主流速度程度的不同而不同。通常规定达到主流速度 的99%处的距离y为流动边界层的厚度,记为δ 。
第五章对流换热

第五章对流换热思考题1、在对流换热过程中,紧靠壁面处总存在一个不动的流体层,利用该层就可以计算出交换的热量,这完全是一个导热问题,但为什么又说对流换热是导热与对流综合作用的结果。
答:流体流过静止的壁面时,由于流体的粘性作用,在紧贴壁面处流体的流速等于零,壁面与流体之间的热量传递必然穿过这层静止的流体层。
在静止流体中热量的传递只有导热机理,因此对流换热量就等于贴壁流体的导热量,其大小取决于热边界层的厚薄,而它却受到壁面流体流动状态,即流动边界层的强烈影响,故层流底层受流动影响,层流底层越薄,导热热阻越小,对流换热系数h也就增加。
所以说对流换热是导热与对流综合作用的结果。
2、试引用边界层概念来分析并说明流体的导热系数、粘度对对流换热过程的影响。
答:依据对流换热热阻主要集中在热边界层区域的导热热阻。
层流边界层的热阻为整个边界层的导热热阻。
紊流边界层的热阻为层流底层的导热热阻。
导热系数越大,将使边界层导热热阻越小,对流换热强度越大;粘度越大,边界层(层流边界层或紊流边界层的层流底层)厚度越大,将使边界层导热热阻越大,对流换热强度越小。
3、由对流换热微分方程知,该式中没有出现流速,有人因此得出结论:表面传热系数h与流体速度场无关。
试判断这种说法的正确性?答:这种说法不正确,因为在描述流动的能量微分方程中,对流项含有流体速度,即要获得流体的温度场,必须先获得其速度场,“流动与换热密不可分”。
因此表面传热系数必与流体速度场有关。
4、试引用边界层概念来分析并说明流体的导热系数、粘度对对流换热过程的影响。
答:依据对流换热热阻主要集中在热边界层区域的导热热阻。
层流边界层的热阻为整个边界层的导热热阻。
紊流边界层的热阻为层流底层的导热热阻。
导热系数越大,将使边界层导热热阻越小,对流换热强度越大;粘度越大,边界层(层流边界层或紊流边界层的层流底层)厚度越大,将使边界层导热热阻越大,对流换热强度越小。
5、对管内强制对流换热,为何采用短管和弯管可以强化流体的换热?答:采用短管,主要是利用流体在管内换热处于入口段温度边界层较薄,因而换热强的特点,即所谓的“入口效应”,从而强化换热。
第五章对流传热分析

第五章对流换热分析通过本章的学习,读者应熟练掌握对流换热的机理及其影响因素,边界层概念及其应用,以及在相似理论指导下的实验研究方法,进一步提出针对具体换热过程的强化传热措施。
5.1 内容提要及要求5.1.1 对流换热概述1.定义及特性对流换热指流体与固体壁直接接触时所发生的热量传递过程。
在对流换热过程中,流体内部的导热与对流同时起作用。
牛顿冷却公式q h(t w t f ) 是计算对流换热量的基本公式,但它仅仅是对流换热表面传热系数h 的定义式。
研究对流换热的目的是揭示表面传热系数与影响对流换热过程相关因素之间的内在关系,并能定量计算不同形式对流换热问题的表面传热系数及对流换热量。
2.影响对流换热的因素(1)流动的起因:流体因各部分温度不同而引起密度差异所产生的流动称为自然对流,而流体因外力作用所产生的流动称为受迫对流,通常其表面传热系数较高。
(2)流动的状态:流体在壁面上流动存在着层流和紊流两种流态。
(3)流体的热物理性质:流态的热物性主要指比热容、导热系数、密度、粘度等,它们因种类、温度、压力而变化。
(4)流体的相变:冷凝和沸腾是两种最常见的相变换热。
(5)换热表面几何因素:换热表面的形状、大小、相对位置及表面粗糙度直接影响着流体和壁面之间的对流换热。
综上所述,可知表面传热系数是如下参数的函数h f u, t w , t f , , c p , ,,, l这说明表征对流换热的表面传热系数是一个复杂的过程量,不同的换热过程可能千差万别。
3.分析求解对流换热问题分析求解对流换热问题的实质是获得流体内的温度分布和速度分布,尤其是近壁处流体内的温度分布和速度分布,因为在对流换热问题中“流动与换热是密不可分”的。
同时,分析求解的前提是给出正确地描述问题的数学模型。
在已知流体内的温度分布后,可按如下的对流换热微分方程获得壁面局部的表面传热系数由上式可有h xtt x yW/(m 2 K)w,x其中为过余温度,h xxyW/(m 2 K)w,x对流换热问题的边界条件有两类,第一类为壁温边界条件,即壁温分布为已知,待求的是流体的壁面法向温度梯度;第二类为热流边界条件,即已知壁面热流密度,待求的是壁温。
传热学 第五章 对流换热

t qw
n w
第三类边界条件?
思考
对流换热微分方程表明,在边界上垂直于壁面的热量传 递完全依靠导热,那么在对流换热过程中流体的流动起 什么作用?
hx
tw t
x
t y
y0,x
c
p
t
u t x
v
t y
2t x2
2t y 2
流场决定温度场
小结
我们学习了 影响对流换热的一些因素; 对流换热微分方程:对流换热系数的定义 对流换热微分方程组:连续性方程、动量方程、能量方程
A qxdA
A
hx
tw
t
x
dA
h
1 A
A hxdA
对流换热的 核心问题
对流换热的影响因素
对流换热是流体的导热和热对流两种基本传热方式共同作用的结果。 影响因素:
1)流动的起因:强迫对流换热与自然对流换热 2) 流动的状态:层流和紊流 3) 流体有无相变 4) 流体的物理性质
5) 换热表面的几何因素
v
t y
2t x2
2t y 2
2) 对流换热的单值性条件
(1) 几何条件 (2) 物理条件 (3) 时间条件 (4) 边界条件
1904年,德国科学家普朗特(L. Prandtl)提出著名 的边界层概念后,上述方程的求解才成为可能。
第一类边界条件 t w f x, y, z,
q 第二类边界条件 w f x, y, z,
采用氢冷须注意其密封结构,否则泄露后会发生爆炸。
5) 换热表面的几何因素
强迫对流
(1)管内的流动
(2)管外的流动
自然对流
(3)热面朝上
(4)热面朝下
对流换热分类
传热学第五章

第五章 对流传热原理
第一节 概 述
对流传热种类 自然对流传热
空气 水 强迫对流传热 气体 高压水蒸汽
对流传热系数的大致范围
h[W/(m2﹒K)]
对流传热种类
水
3~10
液态金属
200~1000
气-液相变传热
水沸腾
20~100
水蒸汽凝结
500~3500
有机蒸汽凝结
表 5-1 h[W/(m2﹒K)] 1000~15000 3000~110000
第五章 对流传热原理
第二节 边界层概念
4、流动状态判据(P78)
(2)上述流体纵掠等温平壁中:
边界层由层流向湍流过渡的距离xc称为临界长度,对应的
临界雷诺数为
Re c
u xc
u xc
5 105
Re x Re c ,为层流边界层
Re x Re c ,为湍流边界层
综上所述,影响对流传热系数h的主要因素,可 定性地用函数形式表示为:
h=(v,tw,tf,λ,ρ,cp,η,αV,γ,lc,φ)
式中:γ为汽化潜热; lc为描述传热面大小的特征长度; φ为壁面的几何形状因素,包括形状、位置等。
第五章 对流传热原理
第一节 概 述
四、研究对流传热的方法(P76)
研究对流传热的方法,即确定对流传热系数h的方法大致有 以下四种:
例如,同一根圆管,管内流动和管外流动(横掠)的强迫对流 传热是截然不同的,如图5-1a)所示。
再如,同一水平壁自然对流散热,热面朝上时气流旺盛,热面 朝下时气流较弱,因此具有不同的传热强度,见图5-1b)
第五章 对流传热原理
第一节 概 述
图5-1 几何因素的影响
传热学第五章对流传热的理论基础

实验数据如何整理(整理成什么样函数关系) 强制对流:Nu f (Re,Pr); Nux f ( x' , Re,Pr)
自然对流换热:Nu f (Gr, Pr) 混合对流换热:Nu f (Re, Gr, Pr)
Nu — 待定特征数 (含有待求的 h)
Re,Pr,Gr — 已定特征数
特征关联式的具体函数形式、定性温度、特征长度等的确 定需要通过理论分析,同时又具有一定的经验性。
2
流体流过固体表面时,。。。
普朗特边界层理论:粘性流体流过固体表面时,粘滞性 起作用的区域仅仅局限在靠近壁面的薄层内。
3
2. 对流传热系数
u∞ ; t ∞
tw
由傅里叶定律:
q t y w
W m2
对流传热的定义式: q ht h tw t [W/m2 ]
在边界层不脱落的前提下:
q ht = t y w
x为当前点与板前缘的距离。 Pr=
a
1
1
hx x
0.332
u x
2
a
3
Nux 0.332Re1x 2 Pr1 3
上述理论解与实验值吻合。
注意:层流
18
2. 对于外掠平板层流分析解的几个讨论
(1)局部对流传热系数,平均对流传热系数
局部对流传热系数
Nux
hx x
11
0.332Rex 2 Pr 3
第五章 对流传热的理论基础
1
5.1 对流传热概述
1. 对流传热的定义、研究对象
流体流过固体表面时,流体与固体之间的热量传递。
工程上约定的计算习惯:
若tw t,Φ hA(tw t ) W 若tw t,Φ hA(t tw ) W
传热学5第五章
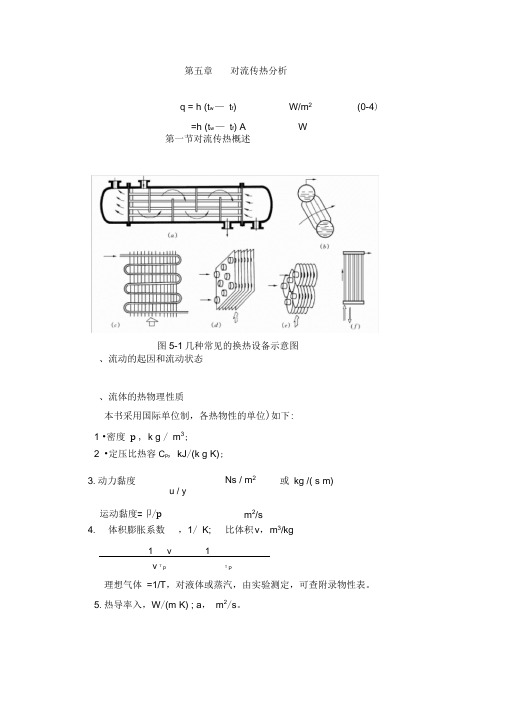
(0-4)第五章 对流传热分析q = h (t w — t f ) W/m 2 =h (t w — t f ) A W、流动的起因和流动状态、流体的热物理性质本书采用国际单位制,各热物性的单位)如下: 1 •密度 p , k g / m 3; 2 •定压比热容C p , kJ /(k g K); 3.动力黏度Ns / m 2或 kg /( s m)u / y运动黏度=卩/pm 2/s4. 体积膨胀系数 ,1/ K;比体积v ,m 3/kg1v1v TpT P理想气体 =1/T ,对液体或蒸汽,由实验测定,可查附录物性表。
5.热导率入,W /(m K) ; a , m 2/s 。
第一节对流传热概述图5-1几种常见的换热设备示意图、流体的相变四、换热表面几何因素h f u,t w, t f, ,C p, , , ,l (5-1)第二节对流传热微分方程组、对流传热过程微分方程式式中图5-3连续性方程的推导x 方向:M x udyM x M x dx M x x dxxy 方向:M y vdxM y M y dy M ydyy (5-3)、动量微分方程式tq xy w ,xW/m 2(1)q xh x (t wt f )xh x t x⑵th x tt xy w,x(5-2a)t t wh x ---------------------------Xy w,x(5-2b)其中wf x't f t w 01、连续性方程Y 卅严霧如图5-4动量微分方程的推导dxdy DUd(1) 微元体的质量X加速度:Du u u u= u v——d x yDv v v v= u v——d x y(2) 微元体所受的外力:体积力:X dx dyY dx dy表面力:(——-——汪)dx dyx y(—y——y ) dx dyy xu u u x yx x 方向:P ( u v ) = X + ----------------------------x y x yx y yx22z uuu 、p u u P (u v ) =X —+ 2 2 x yxxy22,vv v 、p v v P (uv ):=Y —+22 xyyxy(1)(2) (3)⑷vvvy xyy 方向: P ( u v ) = 丫 + —(5-4a)(4)黏滞x方向导入的净能量三(x+ x dx ) xy方向导入的净能量三2ydx dyx方向热对流传递的净能量三x—(x+ x dx) xdx dy⑴惯性力项,即质量与加速度之积;(2)体积力;⑶压强梯度; 力。
传热学(第四版)第五章:对流传热的理论基础

第五章 对流换热
9
层流到湍流的转变:Reynolds数(1880年~1883年)
澄清了当时流体流动实验结果 的混乱。
第五章 对流换热
10
边界层理论(1904年、1908年)
普朗特边界层理论在流体力学 发展史上具有划时代的意义。
第五章 对流换热
11
对流传热理论蓬勃发展(1910年以后)
1921年 波尔豪森 热边界层 1930年 Schmit等 竖壁附近空气的自然对流 。。。。。。
第五章 对流换热
14
边界层的特征: (1)薄;(2)沿平板长度层流过渡到湍流。
第五章 对流换热
15
N-S方程
u v 0 x y
u
u
u
x
v
u
y
Fx
p x
(
2u x2
2u y 2
)
v
u
v
x
v
v
y
Fy
p y
(
2v x2
2v y 2
)
由于 u v, y x
u v 0 x y
u
u
x
v
u
y
dp dx
第五章 对流换热
12
5 速度边界层理论(回忆流体力学知识)
研究背景
边界层理论是在研究流体流过固体表面时阻力特性这一问题
时提出来的。 Fd
A
wdA,
w
u
y w
第五章 对流换热
13
流体流过固体表面时,。。。
普朗特边界层理论:粘性流体流过固体表面时,粘滞性起作用 的区域仅仅局限在靠近壁面的薄层内。 Prandtl’s idea of the boundary layer: a thin region on the surface of a body in which viscous effects are very important and outside of which the fluid behaves essentially as if it were inviscid.
第五章对流传热理论基础

简化
流动
普朗特 速度边界层
类比
对流换热
波尔豪森 热边界层
38
传热学
一、流动边界层
1、流动边界层及其厚度 定义:当流体流过固体壁面时,由于流 体粘性的作用,使得在固体壁面附近存 在速度发生剧烈变化的薄层称为流动 边界层或速度边界层。
实际流动 ≈ 边界层区粘性流动+主流区无粘性理想流动
大空间自然对流 有限空间自然对流
沸腾换热 有相变
凝结换热
大容器沸腾 管内沸腾
管外凝结 管内凝结
14
传热学
六、研究对流传热的方法(确定h的方法)
四种:1)分析法;2)实验法;3)比拟法;4)数值法
适当介绍
重点介绍 一定介绍
不作介绍
1)分析法
解析:二维、楔形流、平板 边界层积分方程(近似解析)
2)实验法
u∞
y δ
0x xc
粘性底层
掠过平板时边界层的形成与发展
湍流核心 缓冲层
41
传热学
层流: 流体做有秩序的分层流动,各层互不干扰,只有分子扩散,
无大微团掺混
湍流: 流体微团掺混,紊乱的不规则脉动
粘性底层 :速度梯度较大、分子扩散—导热
湍流边界层
缓冲层 :导热+对流 湍流核心 :质点脉动强化动量传递,速度变化
换热表面的形状、大小、换热表面与流体运动方向的 相对位置及换热表面的状态(光滑或粗糙)
内部流动对流传热:管内或槽内 外部流动对流传热:外掠平板、圆管、管束
10
传热学
11
传热学
(5) 流体的热物理性质:
热导率 [W (m C)] 比热容 c [J (kg C)]
传热学5-对流换热分析

Mx
M x dx x
M y vdx
单位时间内、沿x轴方向、 经x表面流入微元体的质量 单位时间内、沿x轴方向、经 x+dx表面流出微元体的质量
M x udy
M x M x dx M x dx x
单位时间内、沿x轴方向流入微元体的净质量:
M x M x dx
无论流体流动与否, p 都存在;而 ii只存在于流动时
同一点处各方向的 p 都相同;而 ii与表面方向有关
推导过程见P110 动量微分方程 — Navier-Stokes方程(N-S方程)
u u u p u u ( u v ) Fx ( 2 2 ) x y x x y
M x ( u ) dx dxdy x x
单位时间内、沿 y 轴方向流入微元体的净质量:
M y M y dy
单位时间内微元体 内流体质量的变化:
( v) dy dxdy y y
M y
( dxdy) dxdy
Mx
速度场和温度场由对流换热微分方程组确定: 质量守恒方程、动量守恒方程、能量守恒方程
2 质量守恒方程(连续性方程) 流体的连续流动遵循质量守恒规律
(x, y) 处取出边长为 dx、dy 的微元体(z方向为单位长度),M 为质量 流量 [kg/s]
从流场中
Mx
M x dx x
M y vdx
热的核心问题
研究对流换热的方法:
(1)分析法 (2)实验法 (3)比拟法 (4)数值法
传热系数大致范围
5 对流换热的影响因素
对流换热是流体的导热和对流两种基本传热方式 共同作用的结果。其影响因素主要有以下五个方面: (1)流动起因 (2)流动状态 (3)流体有无相变
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 对流换热分析通过本章的学习,读者应熟练掌握对流换热的机理及其影响因素,边界层概念及其应用,以及在相似理论指导下的实验研究方法,进一步提出针对具体换热过程的强化传热措施。
5.1内容提要及要求5.1.1 对流换热概述1.定义及特性对流换热指流体与固体壁直接接触时所发生的热量传递过程。
在对流换热过程中,流体内部的导热与对流同时起作用。
牛顿冷却公式w f ()q h t t =-是计算对流换热量的基本公式,但它仅仅是对流换热表面传热系数h 的定义式。
研究对流换热的目的是揭示表面传热系数与影响对流换热过程相关因素之间的内在关系,并能定量计算不同形式对流换热问题的表面传热系数及对流换热量。
2.影响对流换热的因素(1)流动的起因:流体因各部分温度不同而引起密度差异所产生的流动称为自然对流,而流体因外力作用所产生的流动称为受迫对流,通常其表面传热系数较高。
(2)流动的状态:流体在壁面上流动存在着层流和紊流两种流态。
(3)流体的热物理性质:流态的热物性主要指比热容、导热系数、密度、粘度等,它们因种类、温度、压力而变化。
(4)流体的相变:冷凝和沸腾是两种最常见的相变换热。
(5)换热表面几何因素:换热表面的形状、大小、相对位置及表面粗糙度直接影响着流体和壁面之间的对流换热。
综上所述,可知表面传热系数是如下参数的函数()w f p ,,,,,,,,h f u t t c l λραμ=这说明表征对流换热的表面传热系数是一个复杂的过程量,不同的换热过程可能千差万别。
3.分析求解对流换热问题分析求解对流换热问题的实质是获得流体内的温度分布和速度分布,尤其是近壁处流体内的温度分布和速度分布,因为在对流换热问题中“流动与换热是密不可分”的。
同时,分析求解的前提是给出正确地描述问题的数学模型。
在已知流体内的温度分布后,可按如下的对流换热微分方程获得壁面局部的表面传热系数2x x w,xW/(m K)t h t y λ∆⎛⎫∂=-⋅ ⎪∂⎝⎭由上式可有2x x w,xW/(m K)h y λθ∆θ⎛⎫∂=-⋅ ⎪∂⎝⎭其中θ为过余温度,t t θ=-。
对流换热问题的边界条件有两类,第一类为壁温边界条件,即壁温分布为已知,待求的是流体的壁面法向温度梯度;第二类为热流边界条件,即已知壁面热流密度,待求的是壁温。
由于对流换热问题的分析求解常常要求解包括连续性方程、动量微分方程和能量微分方程在内的一系列方程,因此它的求解过程比导热问题要困难得多。
5.1.2 对流换热微分方程组1.连续性方程二维常物性不可压缩流体稳态流动连续性方程:0u x yυ∂∂+=∂∂ 2.动量微分方程式动量微分方程式描述流体速度场,可从分析微元体的动量守恒中建立。
它又称纳斯-斯托克斯方程,简称N·S 方程。
2222u u u pu u u X x y x x y ρυμτ⎛⎫⎛⎫∂∂∂∂∂∂++=-++ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭2222pu Y x y y x y υυυυυρυμτ⎛⎫⎛⎫∂∂∂∂∂∂++=-++ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭3.能量微分方程式能量微分方程式描述流体的温度场,由能量守恒原理分析进出微元体的各项能量来建立。
22p 22t t t t t c u x y x y ρυλτ⎛⎫⎛⎫∂∂∂∂∂++=+ ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭5.1.3 边界层分析及边界层换热微分方程组1.边界层的概念由于对流换热的热阻大小主要取决于紧靠壁面附近的流体流动状况,而该区域中速度和温度的变化最为剧烈。
因此,将固体壁面附近流体速度急剧变化的薄层称为流动边界层,而将温度急剧变化的薄层称为热边界层。
流动边界层的厚度δ通常规定为在壁面法线方向达到主流速度99%处的距离,即0.99u u ∞=。
而热边界层的厚度t δ为沿该方向达到主流过余温度99%处的距离,即f 0.99θθ=。
t δ不一定等于δ,两者之比决定于流体的物性。
读者应熟练掌握流动边界层和热边界层的特点及两者的区别,这是进行边界层分析的前提。
2.边界层的特性 (1)边界层极薄,其厚度δ、t δ与壁面尺寸相比都是很小的量。
(2)边界层内法线方向速度梯度和温度梯度非常大。
(3)边界层内存在层流和紊流两种流态。
(4)引入边界层的概念后,流场可分为边界层区和主流区。
边界层区是流体粘性起作用的区域,而主流区可视为无粘性的理想流体。
(建议增加关于管内(受限空间)流动时的边界层分析,因为学生容易误解,管内流动情况下边界层也很薄。
)3.边界层微分方程组二维稳态无内热源层流边界层对流换热方程组由动量微分方程、连续性方程、能量微分方程组成,即221d d u u p u u x y x yυνρ∂∂∂+=-+∂∂∂ 0u x yυ∂∂+=∂∂ 22t t t u a x y yυ∂∂∂+=∂∂∂ 利用边界层理论,可将原本需整个流场求解的问题,转化为可分区(主流区和边界层区)求解的问题。
其中,主流区按理想流体看待,而边界层区用边界层微分方程组求解。
4.外掠平板层流换热边界层微分方程式分析求解 由常物性流体外掠平板层流边界层换热微分方程组22u u u u x y yυν∂∂∂+=∂∂∂ 0u x yυ∂∂+=∂∂ 22t t t u a x y yυ∂∂∂+=∂∂∂ x w,xΔt h t y λ⎛⎫∂=- ⎪∂⎝⎭可求解得到如下结论:(1)边界层厚度及局部摩擦系数1/2x5.0Re xδ-= 1/3tPr δδ-= f,x 1/2x0.332Re 2C -= (2)常壁温平板局部表面传热系数1/21/32x x0.332Re Pr W/(m K)h xλ=⋅1/21/3Nu 0.332Re Pr=其中普朗特准则Pr aν=,反映流体物性对换热影响的大小;努谢尔特准则Nu hlλ=,反映对流换热强弱的程度。
5.1.4 边界层换热积分方程组及求解1.概述分析平板层流边界层换热问题的一种近似方法是,通过分析流体流过边界层任一微元宽度时的质量、动量及能量守恒关系,导出边界层积分方程组。
它与边界层微分方程组的不同在于,它不要求对边界层内每一微元都满足守恒定律,而是只要求包括固体边界及边界层外边界在内的有限大小的控制容积满足守恒定律即可。
2.边界层积分方程组 (1)边界层动量积分方程式00d d()d ()d d d w u u u u y u u y x x δδρρτ∞∞∞-+-=⎰⎰ (2)边界层能量积分方程式f 0w d()d d t u t t y a x y δ⎛⎫∂-= ⎪∂⎝⎭⎰ 3.求解结果常物性流体外掠平板层流边界层速度分布曲线33122u y y u δδ∞⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭无量纲温度分布3w f w f t t 3122t t y y t t θθδδ⎛⎫⎛⎫-==- ⎪ ⎪-⎝⎭⎝⎭离平板前沿x 处的流动边界层厚度的无量纲表达式1/2x4.64Re xδ=局部摩擦系数f,x 1/2x0.323Re 2C -= 离平板前沿x 处的热边界层厚度的无量纲表达式1/3t1/2x4.52Pr Re xδ-=局部表面传热系数1/21/32x x0.332Re Pr W/(m K)h xλ=⋅1/21/3Nu 0.332Re Pr=(建议增加积分解与分析解结果的比较,说明今后在计算过程中如何选取公式)5.1.5 动量传递和热量传递的类比紊流总粘滞应力为层流粘滞应力与紊流粘滞应力之和,即()2t m d N/m d l u yτττρνε=+=+紊流总热流密度为层流导热量和紊流传递热量之和,即()2t p h d W/m d l t q q q c a yρε=+=-+柯比朋类比律2/3x f,x Pr /2St C ⋅=(建议说明为什么可以类比、类比的原则是什么)5.1.6 相似理论基础1.相似原理 研究对流换热的主要方法是在相似理论指导下的实验方法,相似理论使个别的实验数据上升到能够代表整个相似群(?)的高度。
(建议再展开一些,许多学生不明白相似原理的用途)(1)相似性质1)用相同形式且具有相同内容的微分方程式所描述的现象称为同类现象。
只有同类现象才能谈相似问题。
(边界条件是否要相同)2)彼此相似的现象,其相关的物理量场分别相似。
3)彼此相似的现象,其同名相似准则必定相等。
(2)相似准则间的关系1)物理现象中的各物理量不是单个起作用,而是由各准则数组成联合作用。
因此方程的解只能是由这些准则组成的函数关系式,称为准则关联式。
2)按准则关联式的内容整理实验数据,就能得到反映现象变化规律的实用关联式,从而解决了实验数据如何整理的问题。
(3)判别相似的条件凡同类现象,单值性条件(几何条件、物理条件、边界条件、时间条件等)相似,同名的已定准则相等,现象必定相似。
学习相似理论时,读者应深入理解并充分掌握以下问题,如怎样安排实验、测量什么参数、如何整理实验数据,如何推广应用所得的实验关联式。
对于同一组实验数据,不同人采用不同的准则关系式形式,完全可能得到不同的实验关联式。
衡量一个实验关联式的好坏应该考虑该公式是否将所有实验数据拟合后的偏差最小,同时其参数范围是否广泛等。
教材中介绍的所有实验关联式都是前人经过大量实验研究并用相似理论方法整理出来的研究成果,学习时要充分理解并注意其使用方法及参数范围。
2.对流换热常用准则数及其物理意义 (1)雷诺准则,Re ulν=,它表示流体流动时惯性力与粘滞力的相对大小。
(2)格拉晓夫准则,32ΔGr g t l αν=,它表示浮升力与粘滞力的相对大小。
(3)普朗特准则,Pr aν=,它表示流体的动量传递能力与热量传递能力的相对大小。
(4)努谢尔特准则,Nu hlλ=,它表示壁面法向无量纲过余温度梯度的大小。
在受迫对流换热问题中,引入无量纲准则数后,原本影响因素众多的表面传热系数就变为Nu =f (Re ,Pr)。
由此可知,根据准则数安排实验,可大大减少实验次数,并减少实验的盲目性。
(关于准则的物理意义,建议稍微展开一点解释,因为教材中关于此问题的解释不容易被学生理解。
许多学生是死记硬背下来的)3.实验数据的整理方法通常,对流换热问题的准则关联式可表示为如下形式Nu (Re,Pr,Gr)f =-----5.2公式小结5.2.1 外掠平板层流换热流动边界层厚度1/2x4.64Re xδ=热边界层厚度1/3t1/2x4.52Pr Re xδ-=局部摩擦系数f,x 1/2x0.323Re 2C -= 局部表面传热系数1/21/32x x 0.332Re PrW/(m K)h xλ=⋅1/21/3x x Nu 0.332Re Pr= 平均表面传热系数1/21/320.664Re Pr W/(m K)h lλ=⋅1/21/3Nu 0.664Re Pr =5.2.2外掠平板紊流换热局部摩擦系数1/5f,x x0.0592Re C -= 局部表面传热系数关联式4/51/3x x Nu 0.0296Re Pr= 平均表面传热系数关联式0.81/3Nu (0.037Re 870)Pr =-5.3习题解析(以下几式中的矩形符号表示“正比于”或“相当于”的意思)例5.1 利用数量级分析的方法,对流体外掠平板的流动,从动量微分方程可导出边界层厚度有如下的变化关系式Re xδ试证明之。
