Mathematica函数大全(内置)
Mathematica的常用函数

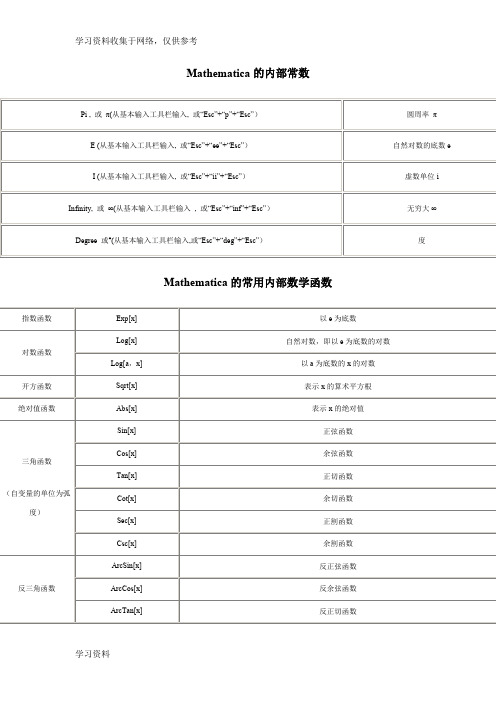
Mathematica的内部常数Pi , 或π(从基本输入工具栏输入, 或“Esc”+“p”+“Esc”)圆周率πE (从基本输入工具栏输入, 或“Esc”+“ee”+“Esc”)自然对数的底数eI (从基本输入工具栏输入, 或“Esc”+“ii”+“Esc”)虚数单位iInfinity, 或∞(从基本输入工具栏输入, 或“Esc”+“inf”+“Esc”)无穷大∞Degree 或°(从基本输入工具栏输入,或“Esc”+“deg”+“Esc”)度Mathematica的常用内部数学函数指数函数Exp[x]以e为底数对数函数Log[x]自然对数,即以e为底数的对数Log[a,x]以a为底数的x的对数开方函数Sqrt[x]表示x的算术平方根绝对值函数Abs[x]表示x的绝对值三角函数(自变量的单位为弧度)Sin[x]正弦函数Cos[x]余弦函数Tan[x]正切函数Cot[x]余切函数Sec[x]正割函数Csc[x]余割函数反三角函数ArcSin[x]反正弦函数ArcCos[x]反余弦函数ArcTan[x]反正切函数ArcCot[x]反余切函数ArcSec[x]反正割函数ArcCsc[x]反余割函数双曲函数Sinh[x]双曲正弦函数Cosh[x]双曲余弦函数Tanh[x]双曲正切函数Coth[x]双曲余切函数Sech[x]双曲正割函数Csch[x]双曲余割函数反双曲函数ArcSinh[x]反双曲正弦函数ArcCosh[x]反双曲余弦函数ArcTanh[x]反双曲正切函数ArcCoth[x]反双曲余切函数ArcSech[x]反双曲正割函数ArcCsch[x]反双曲余割函数求角度函数ArcTan[x,y]以坐标原点为顶点,x轴正半轴为始边,从原点到点(x,y)的射线为终边的角,其单位为弧度数论函数GCD[a,b,c,...]最大公约数函数LCM[a,b,c,...]最小公倍数函数Mod[m,n]求余函数(表示m除以n的余数)Quotient[m,n]求商函数(表示m除以n的商)Divisors[n]求所有可以整除n的整数FactorInteger[n]因数分解,即把整数分解成质数的乘积Prime[n]求第n个质数PrimeQ[n]判断整数n是否为质数,若是,则结果为True,否则结果为FalseRandom[Integer,{m,n}]随机产生m到n之间的整数排列组合函数Factorial[n]或n!阶乘函数,表示n的阶乘复数函数Re[z]实部函数Im[z]虚部函数Arg(z)辐角函数Abs[z]求复数的模Conjugate[z]求复数的共轭复数Exp[z]复数指数函数求整函数与截尾函数Ceiling[x]表示大于或等于实数x的最小整数Floor[x]表示小于或等于实数x的最大整数Round[x]表示最接近x的整数IntegerPart[x]表示实数x的整数部分FractionalPart[x]表示实数x的小数部分分数与浮点数运算函数N[num]或num//N把精确数num化成浮点数(默认16位有效数字)N[num,n]把精确数num化成具有n个有效数字的浮点数NumberForm[num,n]以n个有效数字表示numRationalize[float]将浮点数float转换成与其相等的分数Rationalize[float,dx]将浮点数float转换成与其近似相等的分数,误差小于dx最大、最小函数Max[a,b,c,...]求最大数Min[a,b,c,...]求最小数符号函数Sign[x]Mathematica中的数学运算符a+b 加法a-b减法a*b (可用空格键代替*)乘法a/b (输入方法为:“ Ctrl ” + “ / ” ) 除法a^b (输入方法为:“ Ctrl ” + “ ^ ” )乘方-a 负号Mathematica的关系运算符==等于<小于>大于<=小于或等于>=大于或等于!=不等于注:上面的关系运算符也可从基本输入工具栏输入。
Mathematica的常用函数.doc

Mathematica的内部常数Pi , 或π(从基本输入工具栏输入, 或“Esc”+“p”+“Esc”)圆周率πE (从基本输入工具栏输入, 或“Esc”+“ee”+“Esc”)自然对数的底数eI (从基本输入工具栏输入, 或“Esc”+“ii”+“Esc”)虚数单位iInfinity, 或∞(从基本输入工具栏输入, 或“Esc”+“inf”+“Esc”)无穷大∞Degree 或°(从基本输入工具栏输入,或“Esc”+“deg”+“Esc”)度Mathematica的常用内部数学函数指数函数Exp[x]以e为底数对数函数Log[x]自然对数,即以e为底数的对数Log[a,x]以a为底数的x的对数开方函数Sqrt[x]表示x的算术平方根绝对值函数Abs[x]表示x的绝对值三角函数(自变量的单位为弧度)Sin[x]正弦函数Cos[x]余弦函数Tan[x]正切函数Cot[x]余切函数Sec[x]正割函数Csc[x]余割函数反三角函数ArcSin[x]反正弦函数ArcCos[x]反余弦函数ArcTan[x]反正切函数ArcCot[x]反余切函数ArcSec[x]反正割函数ArcCsc[x]反余割函数双曲函数Sinh[x]双曲正弦函数Cosh[x]双曲余弦函数Tanh[x]双曲正切函数Coth[x]双曲余切函数Sech[x]双曲正割函数Csch[x]双曲余割函数反双曲函数ArcSinh[x]反双曲正弦函数ArcCosh[x]反双曲余弦函数ArcTanh[x]反双曲正切函数ArcCoth[x]反双曲余切函数ArcSech[x]反双曲正割函数ArcCsch[x]反双曲余割函数求角度函数ArcTan[x,y]以坐标原点为顶点,x轴正半轴为始边,从原点到点(x,y)的射线为终边的角,其单位为弧度数论函数GCD[a,b,c,...]最大公约数函数LCM[a,b,c,...]最小公倍数函数Mod[m,n]求余函数(表示m除以n的余数)Quotient[m,n]求商函数(表示m除以n的商)Divisors[n]求所有可以整除n的整数FactorInteger[n]因数分解,即把整数分解成质数的乘积Prime[n]求第n个质数PrimeQ[n]判断整数n是否为质数,若是,则结果为True,否则结果为FalseRandom[Integer,{m,n}]随机产生m到n之间的整数排列组合函数Factorial[n]或n!阶乘函数,表示n的阶乘复数函数Re[z]实部函数Im[z]虚部函数Arg(z)辐角函数Abs[z]求复数的模Conjugate[z]求复数的共轭复数Exp[z]复数指数函数求整函数与截尾函数Ceiling[x]表示大于或等于实数x的最小整数Floor[x]表示小于或等于实数x的最大整数Round[x]表示最接近x的整数IntegerPart[x]表示实数x的整数部分FractionalPart[x]表示实数x的小数部分分数与浮点数运算函数N[num]或num//N把精确数num化成浮点数(默认16位有效数字)N[num,n]把精确数num化成具有n个有效数字的浮点数NumberForm[num,n]以n个有效数字表示numRationalize[float]将浮点数float转换成与其相等的分数Rationalize[float,dx]将浮点数float转换成与其近似相等的分数,误差小于dx最大、最小函数Max[a,b,c,...]求最大数Min[a,b,c,...]求最小数符号函数Sign[x]Mathematica中的数学运算符a+b 加法a-b减法a*b (可用空格键代替*)乘法a/b (输入方法为:“ Ctrl ” + “ / ” ) 除法a^b (输入方法为:“ Ctrl ” + “ ^ ” )乘方-a 负号Mathematica的关系运算符==等于<小于>大于<=小于或等于>=大于或等于!=不等于注:上面的关系运算符也可从基本输入工具栏输入。
mathematica函数

(1) functionsSqrt[x],Exp[x],Log[x],Log[b,x],Sin[x],Cos[x],Tan[x],ArcSin[x],ArcCos[x],ArcTan[x],n!,Abs[x],Round[x],Mod[n,m],Random[], Max[x,y,z,…….],Min[x,y,z,…….],FactorInteger[n](2) symbolsPi : π 3.14159 E: e 2.71828 Degree: π/180 I: Infinity : ∂(3) Complex number:Re[z] : real part;Im[z]:imaginary part;Conjugate[z] :the complex conjugate ;Abs[z]:absolute value |z|;Arg[z]:the argument of z3. Algebraic Calculations:Expand[expr] , Factor[expr],Simplify and FullSimplify,Together and Apart,Collect and FactorTerms,TrigExpand, TrigFactor, TrigReduce, FunctionExpand, ComplexExpand and PowerExpand,TrigToExp and ExpToTrig4. Differentiation and Integration:D[f,x]:partial derivativeD[f,x1,x2,.]:multiple derivativesD[f,{x,n}]:repeated derivativeDt[f]:total differentialDt[f,x]:total derivativeIntegrate[f,x]: the indefinite integralIntegrate[f,x,y]:the multiple integralIntegrate[f,{x,xmin,xmax}]: the indefinite integralIntegrate[f, {x,xmin,xmax},{y,ymin,ymax}]: the multiple integral5. Sum and Product:Sum[f,{i,imin,imax}], Sum[f,{i,imin,imax,di}], Sum[f,{i,imin,imax},{j,jmin,jmax}],Product[f,{i,imin,imax}]6. Solving Equations and Inequalities:Solve[lhs == rhs , x] solve an equation , giving a list of rules for xSolve[{lhs1 == rhs1 , lhs2 == rhs2,…},{x,y,…}]solve a set of simultaneous equations for x,y,...Eliminate[{lhs1 == rhs1 , lhs2 == rhs2,…},{x,y,…}]eliminate x,… in a set of simultaneous equationsReduce[{lhs1 == rhs1 , lhs2 == rhs2,…},{x,y,…}]give a set of simplified equations, including all possible solutions Reduce[{ineqs},{x,y,…}]reduce a collection of inequalitiesMinimize[{expr , ineq},{x,y,…}]minimize expr while satisfying ineqsMaximize[{expr , ineq},{x,y,…}] maximize expr while satisfying ineqs7. Differential Equations:Dsolve[eqns,y[x],x] solve a differential equation for y[x] , taking x as the independent variable.Dsolve[eqns,y,x] give a solution for y in pure function form.8.Power Series:Series[expr,{x,x0,n}] find the power series expansion of expr about the point x = x0 to at most n th orderNormal[series] truncate a power series to give an ordinary expression9. Numerical Mathematics:N[expr]: numerical value of an expressionNIntegrate[f,{i,imin,imax}]:numerical approximation to the Integrate[f,x]NIntegrate[f,{x,xmin,xmax},{y,ymin,ymax}]:numerical approximation to the Integrate[f ,x,y]NSum[f,{i,imin,Infinity}]:numerical approximation to the sum[f]NProduct[f,{i,imin, Infinity}]:numerical approximation to product[f]FindRoot[lhs == rhs , {x,x0}]:search for the numerical solutiont to an equation , starting with x =x0FindRoot[{lhs1 == rhs1 , lhs2 == rhs2,…},{x,x0},{y,y0}...]:search for the numerical solutiont to equations, starting with x =x0 ,y ==y0 ,…FindMinimum[f,{x,x0}]:search for a local minimum of f , starting at x == x0FindMinimum[f,{x,x0},{y,y0},…]:search for a local minimum in several variablesFindMaximum[f,{x,x0}]:search for a local maximum of f , starting at x == x0FindMaximum[f,{x,x0},{y,y0},…] :search for a local maximum in several variablesNSolve[lhs == rhs ,x]:numerical approximation to all solutions of an equationNSolve[{lhs1 == rhs1, lhs2 == rhs2,…},{x,y…}]:numerical approximation to all solutions of equationsFindMinimum[f,{x,x0}]:search for a minimum of f , starting with x = x0NMinimize[f, x]:attempt to find the global minimum of fNMinimize[f, {x,y,…}]:minimize fNMinimize[f, ineqs,{x,y,…}]: minimize f subject to the constraints ineqsNMaximize[f,x]:attempt to find the global maximum of fNMaximize[f,{x,y,…}]:maximize fNMaximize[f, ineqs,{x,y,…}x]: maximize f subject to the constraints ineqsNDSolve[eqns,y,{x,xmin,xmax}]:solve numerically for the function y,with the independent variable x in the range xmin to xmaxNDSolve[eqns,{y1,y2,…},{x,xmin,xmax}]:solve a system of equations for y i10. Manipulating Numerical Data:Fit[{y1,y2,…},{f1,f2,…},x] fit the values y n to a linear combination of functions f iFit[{{x1,y1},{x2,y2},…},{f1,f2,…},x]11. Statistics:Mean[data]:average valueMedian[data]:central valueVariance[data]:varianceStandardDeviation[data]:standard deviationQuantile[data,q]:q th quantileTotal[data]:total of values12. List and Matrix:Table[f,{imax}],Table[f{i,imax}],Table[f,{i,imin,imax,di}],Table[f,{i,imin,imax},{j,jmin,jmax}],Table[f,{i,imin,imax,di},{j,jmin,jmax,di}];T[[i]] or Part[t,i] , T[[{i1,i2,…}]] or Part[t,{ i1,i2,…}] , T[[i,j,…]] or Part[t,i,j,…]Array[a , n] , Array[f,{m,n}];Range[n] , Range[n1,n2] , Range[n1,n2,dn];Length[list];Cross[a,b];Norm[v];IndentityMatrix[n], DiagonalMatrix[n]Dimensions[list];MatrixForm[list],ColumnForm[list],TableForm[list];Inverse[m];MatrixPower[m,n];Det[m],Tr[m],Transpose[m];Eigenvalues[m], EigenVectors[m];Join[list1,list2,…],Union[list1,list2,…];13. Graphics and Sound:Plot[f,{x,xmin,xmax}] , Plot[{f1,f2,…},{x,xmin,xmax}]Plot[Evaluate[f],{x,xmin,xmax}]:first evaluate f ,then choose specific numerical values of xPlot[Evaluate[Table[f,…]],{x,xmin,xmax}]:generate a list of functions , and then plot themPlot[Evaluate[y[x] /.solution],{x,xmin,xmax}]:plot a numerical solution to a differential equation obtained from NDSolve Frame -> True , AxesLabel ->{“x name” , “y name”},GridLines -> Automatic, AspectRatio->numerical(the range of the axes y), PlotRange->{ymin ,ymax },FrameTicks -> None or Automatic, Ticks -> None or AutomaticShow[GraphicsArray[{plot1,plot2,…}]],Show[GraphicsArray[{plot1},{plot2},…]],Show[GraphicsArray[{plot1,plot2,…},{},…]], Show[GraphicsArray[plots, GraphicsSpacing->{l,c}]]Play[f,{t,0, tmax}]:play a sound with amplitude f as a function of tome t in seconds.14. Advanced Graphics:ContourPlot[f,{x, xmin, xmax},{y, ymin, ymax}] : make a contour plot of f as a function of x and yColorFunction -> Automatic Contours -> numerical(the total number of contours , or the list of z values for contours) PlotRange -> Automatic ContourShading -> True or False PlotPoints -> numerical Compiled -> True or FalseDensityPlot[f,{x, xmin, xmax},{y, ymin, ymax}] : make a density plot of fColorFunction -> Automatic PlotPoints -> numerical Compiled -> True or False Mesh -> True or FalsePlot3D[f,{x, xmin, xmax},{y, ymin, ymax}]Axes -> True or False , AxesLabel -> {“xlabel”,”ylabel”,”zlabel”}, Boxed-> True or False, ColorFunction->Automatic, TextStyle, FormateType, DisplayFunction, FaceGrids-> None or All, HiddenSurface-> True or False, Lighting-> True or False, Mesh-> True or False, PlotRange->{{z,zmin,zmax},{x, xmin, xmax},{y, ymin, ymax}}, Shading-> True or False, ViewPoint -> {x, y, z}, PlotPoints ->numerical, Compiled -> True or FalseShow[ContourGraphics[g]] : convert to a contour plot;Show[DensityGraphics[g]] : convert to a density plot;Show[SurfaceGraphics[g]] : convert to a surface plot;Show[Graphics[g]] : convert to a tow-dimensional image;ListPlot[{y1,y2,…}],ListPlot[{{x1,y1},{x2,y2},…}],ListPlot[list,PlotJoined->True],ListPlot3D[{{z11,z12,..},{z21,z22,…},…}], ListContourPlot[array], ListDensityPlot[array]ParametricPlot[{fx , fy},{t, tmin, tmax}], ParametricPlot[{fx , fy},{gx,gy},…, {t, tmin, tmax}], ParametricPlot[{fx , fy},{t, tmin, tmax}, AspectRadio->Automatic]ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax}],ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax},{u,umin,umax}],ParametricPlot3D [{fx,fy,fz},{gx,gy,gz},…]LogPlot[f, {x, xmin, xmax}]:generate a log-linear plot;LogLogPlot[f,{x, xmin, xmax}]:generate a log-log plot;LogListPlot[list]:generate a log-linear plot from a list of data;LogLogListPlot[list]:generate a log-log plot from a list of data;PolarPlot[r,{t, tmin, tmax}]:generate a polar plot of the radius r as a function of angle t;ErrorListPlot[{x1,y1,dy1},{x2,y2,dy2},…]:generate a plot of data with error bars;TextListPlot[{x1,x2,”s1”}, {x2,y2,”s2”}, …]:plot a list of data with each point given by the text string s.BarChart[list]:plot a list of data as a bar chart;PieChart[list]:plot a list of data as a pie chart;PlotVectorField[{fx,fy},{x,xmin,xmax},{y,ymin,ymax}]:plot the vector field corresponding to the vector function f; ListPlotVectorField[{fx,fy},{x,xmin,xmax},{y,ymin,ymax}]:plot the vector field corresponding to the two-dimensional array of vector function f;SphericalPlot3D[r,{theta, min, max},{phi, min, max}]:generate a three-dimensional spherical plot.。
mathematica命令大全

Mathematica 8 命令大全Mathematica的内部常数Pi , 或π(从基本输入工具栏输入, 或“Esc”+“p”+“Esc”)圆周率πE (从基本输入工具栏输入, 或“Esc”+“ee”+“Esc”)自然对数的底数eI (从基本输入工具栏输入, 或“Esc”+“ii”+“Esc”)虚数单位iInfinity, 或∞(从基本输入工具栏输入, 或“Esc”+“inf”+“Esc”)无穷大∞Degree 或°(从基本输入工具栏输入,或“Esc”+“deg”+“Esc”)度Mathematica的常用内部数学函数指数函数Exp[x] 以e为底数对数函数Log[x] 自然对数,即以e为底数的对数Log[a,x] 以a为底数的x的对数开方函数Sqrt[x] 表示x的算术平方根绝对值函数Abs[x] 表示x的绝对值三角函数(自变量的单位为弧度)Sin[x] 正弦函数Cos[x] 余弦函数Tan[x] 正切函数Cot[x] 余切函数Sec[x] 正割函数Csc[x] 余割函数反三角函数ArcSin[x] 反正弦函数ArcCos[x] 反余弦函数ArcTan[x] 反正切函数ArcCot[x] 反余切函数ArcSec[x] 反正割函数ArcCsc[x] 反余割函数双曲函数Sinh[x] 双曲正弦函数Cosh[x] 双曲余弦函数Tanh[x] 双曲正切函数Coth[x] 双曲余切函数Sech[x] 双曲正割函数Csch[x] 双曲余割函数反双曲函数ArcSinh[x] 反双曲正弦函数ArcCosh[x] 反双曲余弦函数ArcTanh[x] 反双曲正切函数ArcCoth[x] 反双曲余切函数ArcSech[x] 反双曲正割函数ArcCsch[x] 反双曲余割函数求角度函数ArcTan[x,y]以坐标原点为顶点,x轴正半轴为始边,从原点到点(x,y)的射线为终边的角,其单位为弧度数论函数GCD[a,b,c,...] 最大公约数函数LCM[a,b,c,...] 最小公倍数函数Mod[m,n] 求余函数(表示m除以n的余数) Quotient[m,n] 求商函数(表示m除以n的商)Divisors[n] 求所有可以整除n的整数FactorInteger[n] 因数分解,即把整数分解成质数的乘积Prime[n] 求第n个质数PrimeQ[n] 判断整数n是否为质数,若是,则结果为True,否则结果为False Random[Integer,{m,n}] 随机产生m到n之间的整数排列组合函数Factorial[n]或n!阶乘函数,表示n的阶乘复数函数Re[z] 实部函数Im[z] 虚部函数Arg(z) 辐角函数Abs[z] 求复数的模Conjugate[z] 求复数的共轭复数Exp[z] 复数指数函数求整函数与截尾函数Ceiling[x] 表示大于或等于实数x的最小整数Floor[x] 表示小于或等于实数x的最大整数Round[x] 表示最接近x的整数IntegerPart[x] 表示实数x的整数部分FractionalPart[x] 表示实数x的小数部分分数与浮点数运算函数N[num]或num//N 把精确数num化成浮点数(默认16位有效数字)N[num,n] 把精确数num化成具有n个有效数字的浮点数NumberForm[num,n] 以n个有效数字表示num Rationalize[float] 将浮点数float转换成与其相等的分数Rationalize[float,dx] 将浮点数float转换成与其近似相等的分数,误差小于dx最大、最小函数Max[a,b,c,...] 求最大数Min[a,b,c,...] 求最小数符号函数Sign[x]Mathematica中的数学运算符加法a+ba-b 减法a*b (可用空格键代替*) 乘法a/b (输入方法为:“ Ctrl ” + “ / ” )除法a^b (输入方法为:“ Ctrl ” + “ ^ ” )乘方-a 负号Mathematica的关系运算符等于==< 小于> 大于<= 小于或等于>= 大于或等于!= 不等于注:上面的关系运算符也可从基本输入工具栏输入。
整理mathematica数学常用命令大全
Mathematica的内部常数Mathematica的常用内部数学函数Mathematica中的数学运算符Mathematica的关系运算符注:上面的关系运算符也可从基本输入工具栏输入。
如何用mathematica求多项式的最大公因式和最小公倍式如何用mathematica求整数的最大公约数和最小公倍数如何用mathematica进行整数的质因数分解如何用mathematica求整数的正约数如何用mathematica判断一个整数是否为质数n个质数如何用mathematica求第如何用mathematica配方Mathematica没有提供专门的配方命令,但是我们可以非常轻松地自定义一个函数进行配方。
如何用mathematica进行多项式运算如何用mathematica进行分式运算如何用Mathematica进行因式分解如何用Mathematica展开如何用Mathematica进行化简如何用Mathematica合并同类项如何用Mathematica进行数学式的转换如何用Mathematica进行变量替换如何用mathematica进行复数运算如何在mathematica中表示集合与数学中表示集合的方法相同,格式如下:下列命令可以生成特殊的集合:如何用Mathematica求集合的交集、并集、差集和补集如何mathematica用排序如何在Mathematica中解方程注:方程的等号必须用:= =如何在Mathematica中解方程组Solve[{方程组},{变元组}]注:方程的等号必须用:= =如何在Mathematica中解不等式先加载:Algebra`InequalitySolve` ,加载方法为:<<Algebra`InequalitySolve`然后执行解不等式的命令InequalitySolve,此命令的使用格式如下:<--mstheme-->如何在Mathematica中解不等式组先加载:Algebra`InequalitySolve` ,加载方法为:<<Algebra`InequalitySolve`然后执行解不等式组的命令InequalitySolve,此命令的使用格式如下:<--mstheme-->如何在Mathematica中解不等式组先加载:Algebra`InequalitySolve` ,加载方法为:<<Algebra`InequalitySolve` 然后执行解不等式组的命令InequalitySolve,此命令的使用格式如下:<--mstheme-->如何用mathematica表示分段函数如何用mathematica求反函数对系统内部的函数生效,但对自定义的函数不起任何作用,也许是方法不对。
Mathmatica中函数

Mathmatica中
的
常用函数
Mathmatica提供的数学常数:Pi 圆周率
E 自然对数的底e
I 虚数单位
Infinity 无限大∞
-Infinity 负无限大 -∞ComplexInfinity 复平面上的无穷远点Binomia[n, m] 二项式系数等等
表1 Mathematica 中的常用函数
表2 关于集合元素的常用函数
表3 Mathematica 常用的多项式运算
*上面最后三个运算方括号中的x代表把多项式的变元定义为x,以区别于多项式中可能包含的其它变量。
表4 Mathematica常用有理分式运算
表5 常用的几种求解方程的输入方式
表6 Mathematica 常用微积分运算
表7 矩阵的输入和裁剪方法
有时需要从一个矩阵中抽出一些行和列,甚至子矩阵,我们称这种运算为矩陈的
裁剪。
有时需要从一个矩阵中抽出一些行和列,甚至子矩阵,我们称这种运算为矩陈的裁剪。
表8 Mathematica提供的矩阵剪裁运算
表9 Mathematica 中常用矩阵运算
表10 Mathematica 中解线性方程组
的函数
表11 Mathematica 中常用数值算法
表12 画图中的特别说明部分摘要
表13 绘制函数图形常用的输入形式
表14 Mathematica 三维绘图的特别说
明项
表15 绘制三维图形Mathematica 的输入方法。
Mathematica函数大全(内置)

Mathematica函数大全--运算符及特殊符号一、运算符及特殊符号Line1;执行Line,不显示结果Line1,line2顺次执行Line1,2,并显示结果name关于系统变量name的信息name关于系统变量name的全部信息!command执行Dos命令n! N的阶乘!!filename显示文件内容<Expr>> filename打开文件写Expr>>>filename打开文件从文件末写() 结合率[]函数{}一个表<*Math Fun*> 在c语言中使用math的函数(*Note*)程序的注释#n第n个参数##所有参数rule& 把rule作用于后面的式子%前一次的输出%%倒数第二次的输出%n第n个输出var::note变量var的注释"Astring "字符串Context ` 上下文a+b 加a-b减a*b或a b 乘a/b除a^b 乘方base^^num以base为进位的数lhs&&rhs且lhs||rhs或!lha非++,-- 自加1,自减1+=,-=,*=,/= 同C语言>,<,>=,<=,==,!=逻辑判断(同c)lhs=rhs立即赋值lhs:=rhs建立动态赋值lhs:>rhs建立替换规则expr//funname相当于filename[expr]expr/.rule将规则rule应用于exprexpr//.rule 将规则rule不断应用于expr知道不变为止param_ 名为param的一个任意表达式(形式变量)param__名为param的任意多个任意表达式(形式变量)二、系统常数Pi 3.1415....的无限精度数值E 2.17828...的无限精度数值Catalan 0.915966..卡塔兰常数EulerGamma 0.5772....高斯常数GoldenRatio 1.61803...黄金分割数Degree Pi/180角度弧度换算I复数单位Infinity无穷大-Infinity负无穷大ComplexInfinity复无穷大Indeterminate不定式三、代数计算Expand[expr]展开表达式Factor[expr]表达式因式分解Factor[poly,Modulus->p] Z p域分解Factor[poly,Extension->{a1, a2,… }] 代数数域分解Factor[poly,GaussianIntegers->True] 复整数域分解Factor[poly,Extension->Automatic]poly的系数所在数域分解(以下函数都可在各数域内进行)Simplify[expr]化简表达式FullSimplify[expr]将特殊函数等也进行化简PowerExpand[expr]展开所有的幂次形式ComplexExpand[expr,{x1,x2...}]按复数实部虚部展开FunctionExpand[expr]化简expr中的特殊函数Collect[expr, x]合并同次项Collect[expr, {x1,x2,...}]合并x1,x2,...的同次项Together[expr]通分Apart[expr]部分分式展开Apart[expr, var] 对var的部分分式展开Cancel[expr]约分ExpandAll[expr]展开表达式ExpandAll[expr, patt] 展开表达式FactorTerms[poly]提出共有的数字因子FactorTerms[poly, x] 提出与x无关的数字因子FactorTerms[poly, {x1,x2...}]提出与xi无关的数字因子Coefficient[expr, form]多项式expr中form的系数Coefficient[expr, form, n]多项式expr中form^n的系数Exponent[expr, form]表达式expr中form的最高指数Numerator[expr] 表达式expr的分子Denominator[expr]表达式expr的分母ExpandNumerator[expr]展开expr的分子部分ExpandDenominator[expr]展开expr的分母部分ExpandDenominator[expr]展开expr的分母部分TrigExpand[expr]展开表达式中的三角函数TrigFactor[expr]给出表达式中的三角函数因子TrigFactorList[expr]给出表达式中的三角函数因子的表TrigReduce[expr]对表达式中的三角函数化简TrigToExp[expr] 三角到指数的转化ExpToTrig[expr]指数到三角的转化RootReduce[expr]ToRadicals[expr]四、解方程Solve[eqns, vars]从方程组eqns中解出varsSolve[eqns, vars, elims] 从方程组eqns中削去变量elims,解出vars DSolve[eqn, y, x]解微分方程,其中y是x的函数DSolve[{eqn1,eqn2,...},{y1,y2...},x]解微分方程组,其中yi是x的函数DSolve[eqn, y, {x1,x2...}]解偏微分方程RSolve[eqn, a[n], n] 解函数方程例1、RSolve u x2x1u x1zu x2,u x,x{{u[x] BesselJ[x,z] C[1]+BesselY[x,z] C[2]}} 2、RSolve[{y[x+2]==ay[x+1]+y[x],y[0]==0,y[1]==1},y,x]RSolve[{eqn1, eqn2, … }, {a1[n], a2[n], …}, n]RSolve[eqn, a[n1, n2, …], {n1, n2, …}]Resolve[expr]Resolve[expr, dom]FindInstance[expr, vars]求不定方程的特解FindInstance[expr, vars, dom]求不定方程的特解(在dom数域内)FindInstance[expr, vars, dom, n]求不定方程的n个特解Eliminate[eqns, vars] 把方程组eqns中变量vars约去SolveAlways[eqns, vars] 给出等式成立的所有参数满足的条件Reduce[eqns, vars] 化简并给出所有可能解的条件Reduce x22y21&&x0&&y0&&x y Integers,x,y LogicalExpand[expr] 用&&和||将逻辑表达式展开InverseFunction[f] 求函数f的逆函数Root[f, k] 求多项式函数的第k个根Roots[lhs==rhs, var] 得到多项式方程的所有根五、微积分函数D[f, x]求f[x]的微分∂f/∂xD[f, {x, n}]求f[x]的n阶微分n f x nD[f,x1,x2..] 求f[x]对x1,x2...偏微分x1x2...fDt[f, x]求f[x]的全微分df/dxDt[f]求f[x]的全微分dfDt[f, {x, n}] n阶全微分df^n/dx^nDt[f,x1,x2..]对x1,x2..的偏微分d d x1d d x2...fIntegrate[f, x] f[x]对x在的不定积分Integrate[f, {x, xmin, xmax}] f[x]对x在区间(xmin,xmax)的定积分Integrate[f, {x, xmin, xmax}, {y, ymin, ymax}] f[x,y]的二重积分Limit[expr, x->x0] x趋近于x0时expr的极限Limit[expr, x->x0, Direction -> 1] x趋近于x0+时expr的极限Limit[expr, x->x0, Direction ->-1] x趋近于x0-时expr的极限Residue[expr, {x,x0}] expr在x0处的留数Series[f, {x, x0, n}] 给出f[x]在x0处的幂级数展开Series[f, {x, x0,nx}, {y, y0, ny}]先对y幂级数展开,再对xNormal[expr]化简并给出最常见的表达式(可截断Series的误差O[x])SeriesCoefficient[series, n]给出级数中第n次项的系数SeriesCoefficient[series, {n1,n2...}]' 或Derivative[n1,n2...][f]一阶导数InverseSeries[s, x] 给出逆函数的级数ComposeSeries[serie1,serie2...] 给出两个基数的组合SeriesData[x,x0,{a0,a1,..},nmin,nmax,den]表示一个在x0处x的幂级数,其中aii 为系数O[x]^n n阶小量x^nO[x, x0]^n n阶小量(x-x0)^n六、多项式函数Variables[poly]给出多项式poly中独立变量的列表CoefficientList[poly, var]给出多项式poly中变量var的系数CoefficientList[poly, {var1,var2...}]给出多项式poly中变量var(i)的系数列? PolynomialMod[poly, m] poly中各系数mod m同余后得到的多项式,m可为整式PolynomialQuotient[p, q, x]以x为自变量的两个多项式之商式p/q PolynomialRemainder[p, q, x] 以x为自变量的两个多项式之余式PolynomialGCD[poly1,poly2,...] poly(i)的最大公因式PolynomialLCM[poly1,poly2,...] poly(i)的最小公倍式PolynomialReduce[poly, {poly1,poly2,...},{x1,x2...}]得到一个表{{a1,a2,...},b}其中Sum[ai*polyi]+b=polyResultant[poly1,poly2,var] 约去poly1,poly2中的varFactor[poly] 因式分解(在整式范围内)FactorTerms[poly] 提出poly 中的数字公因子FactorTerms[poly, {x1,x2...}] 提出poly 中与xi 无关项的数字公因子FactorList[poly] 给出poly 各个因子及其指数{{poly1,exp1},{...}...}FactorSquareFreeList[poly] 同上FactorTermsList[poly,{x1,x2...}] 给出各个因式列表,第一项是数字公因子,第二项是与xi 无关的因式,其后是与xi 有关的因式按升幂的排排?Cyclotomic[n, x] C n x k x e 2i k n (割圆多项式,即单位根的极小多项式)Decompose[poly, x] 迭代分解,给出{p1,p2,...},其中p1(p2(...))=polyInterpolatingPolynomial[data, var] 在数据data 上的插值多项式 data 可以写为{f1,f2..}相当于{{x1=1,y1=f1}..} data 可以写为{{x1,f1,df11,df12,..},{x2,f2,df21..} 可以指定数据点上的n 阶导数值RootSum[f, form] 得到f[x]=0的所有根,并求得Sum[form[xi]]七、随机函数Random[type,range] 产生type 类型且在range 范围内的均匀分布随机数,type 可以为Integer,Real,Complex,不写默认为Real ,range 为{min,max},不写默认为{0,1} Random[] 0~1上的随机实数SeedRandom[n] 以n 为seed 产生伪随机数 如果采用了 <在 2.0版本为 <<"D:\\Math\\PACKAGES\\STATISTI\\Continuo.m"Random[distribution]可以产生各种分布如Random[BetaDistribution[alpha, beta]]stribution[alpha, beta]}Random[NormalDistribution[miu,sigma]]等常用的分布如BetaDistribution,CauchyDistribution,ChiDistribution, NoncentralChiSquareDistribution,ExponentialDistribution, ExtremeValueDistribution,NoncentralFRatioDistribution,GammaDistribution,HalfNormalDistribution, LaplaceDistribution, LogNormalDistribution,LogisticDistribution,RayleighDistribution,NoncentralStudentTDistribution,UniformDistribution, WeibullDistribution八、数值函数N[expr] 表达式的机器精度近似值N[expr, n]表达式的n位近似值,n为任意正整数NSolve[lhs==rhs, var]求方程数值解NSolve[eqn, var, n] 求方程数值解,结果精度到n位NDSolve[eqns, y, {x, xmin, xmax}]微分方程数值解NDSolve[eqns, {y1,y2,...}, {x, xmin, xmax}]FindRoot[lhs==rhs, {x,x0}]以x0为初值,寻找方程数值解FindRoot x52,x,1,WorkingPrecision100精确到100位有效数字FindRoot[lhs==rhs, {x, xstart, xmin, xmax}]NSum[f, {i,imin,imax,di}] 数值求和,di为步长NSum[f, {i,imin,imax,di}, {j,..},..] 多维函数求和NProduct[f, {i, imin, imax, di}]函数求积NIntegrate[f, {x, xmin, xmax}] 函数数值积分优化函数:FindMinimum[f, {x,x0}]以x0为初值,寻找函数最小值FindMinimum[f, {x, xstart, xmin, xmax}]LinearProgramming[c,m,b]解线性组合c.x在m.x>=b&&x>=0约束下的最小值,x,b,c为向量,m为矩阵LatticeReduce[{v1,v2...}]向量组vi的极小无关组数据处理:Fit[data,funs,vars]用指定函数组对数据进行最小二乘拟和data可以为{{x1,y1,..f1},{x2,y2,..f2}..}多维的情况emp: Fit[{10.22,12,3.2,9.9}, {1, x, x^2,Sin[x]}, x]Interpolation[data]对数据进行差值,data同上,另外还可以为{{x1,{f1,df11,df12}},{x2,{f2,.}..}指定各阶导数InterpolationOrder默认为3次,可修改ListInterpolation[array]对离散数据插值,array可为n维ListInterpolation[array,{{xmin,xmax},{ymin,ymax},..}] FunctionInterpolation[expr,{x,xmin,xmax}, {y,ymin,ymax},..]以对应expr[xi,yi]的为数据进行插值Fourier[list] 对复数数据进行付氏变换InverseFourier[list]对复数数据进行付氏逆变换Min[{x1,x2...},{y1,y2,...}]得到每个表中的最小值Max[{x1,x2...},{y1,y2,...}]得到每个表中的最大值Select[list, crit] 将表中使得crit为True的元素选择出来Count[list, pattern] 将表中匹配模式pattern的元素的个数Sort[list] 将表中元素按升序排列Sort[list,p]将表中元素按p[e1,e2]为True的顺序比较list 的任两个元素e1,e2,实际上Sort[list]中默认p=Greater集合论:Union[list1,list2..] 表listi的并集并排序Intersection[list1,list2..]表listi的交集并排序Complement[listall,list1,list2...]从全集listall中对listi的差集九、虚数函数Re[expr]复数表达式的实部Im[expr] 复数表达式的虚部Abs[expr] 复数表达式的模Arg[expr]复数表达式的辐角Conjugate[expr] 复数表达式的共轭十、数的头及模式及其他操作Integer _Integer整数Real _Real实数Complex _Complex复数Rational_Rational 有理数(*注:模式用在函数参数传递中,如MyFun[Para1_Integer,Para2_Real]规定传入参数的类型,另外也可用来判断If[Head[a]==Real,...]*) IntegerDigits[n,b,len]数字n以b近制的前len个码元RealDigits[x,b,len]类上FromDigits[list] IntegerDigits的反函数Rationalize[x,dx] 把实数x有理化成有理数,误差小于dxChop[expr, delta]将expr中小于delta的部分去掉,dx默认为10^-10 Accuracy[x]给出x小数部分位数,对于Pi,E等为无限大Precision[x]给出x有效数字位数,对于Pi,E等为无限大SetAccuracy[expr, n] 设置expr显示时的小数部分位数SetPrecision[expr, n] 设置expr显示时的有效数字位数十一、区间函数Interval[{min, max}] 区间[min, max](* Solve[3 x+2==Interval[{-2,5}],xx]*) IntervalMemberQ[interval, x] x在区间内吗?IntervalMemberQ[interval1,interval2]区间2在区间1内吗?IntervalUnion[intv1,intv2...] 区间的并IntervalIntersection[intv1,intv2...]区间的交十二、矩阵操作a.b.c或Dot[a, b, c]矩阵、向量、张量的点积Inverse[m] 矩阵的逆Transpose[list]矩阵的转置Transpose[list,{n1,n2..}]将矩阵list 第k行与第nk列交换Det[m]矩阵的行列式Eigenvalues[m]特征值Eigenvectors[m]特征向量Eigensystem[m]特征系统,返回{eigvalues,eigvectors}LinearSolve[m, b] 解线性方程组m.x==bNullSpace[m] 矩阵m的零空间,即m.NullSpace[m]==零向量RowReduce[m] m化简为阶梯矩阵Minors[m, k] m的所有k*k阶子矩阵的行列式的值(伴随阵,好像是) MatrixPower[mat, n] 阵mat自乘n次MatrixExp[mat]e matOuter[f,list1,list2..] listi中各个元之间相互组合,并作为f的参数的到的矩矩? Outer[Times,list1,list2]给出矩阵的外积SingularValues[m] m的奇异值,结果为{u,w,v},m=Conjugate[Transpose[u]].DiagonalMatrix[w].vPseudoInverse[m] m的广义逆QRDecomposition[m] QR分解SchurDecomposition[m] Schur分解LUDecomposition[m] LU分解Norm[z]=Abs[z];Norm[v]=Sqrt[v.Conjugate[v]];向量的模(内积开平方)Norm[v, p]=Total[Abs[v^p]]^(1/p)。
(完整版)mathematica命令大全
<< Statistics`DescriptiveStatistics`
或者加载整个统计函数库,加载方法为:
<<Statistics`
求数据data的众数。
数据data的格式为:{ a1,a2,…}
Mode[data]
如何用mathematica求方差和标准差
首先要加载Statistics`DescriptiveStatistics`函数库,加载方法为:
<< Statistics`DescriptiveStatistics`
或者加载整个统计函数库,加载方法为:
<<Statistics`
求数据data的样本方差。
数据data的格式为:{ a1,a2,…} Variance[data]
VarianceMLE[data] 求数据data的母体方差。
数据data的格式为:{ a1,a2,…} StandardDeviation[data] 求数据data的样本标准差。
数据data的格式为:{a1,a2,…} StandardDeviationMLE[data] 求数据data的母体标准差。
数据data的格式为:{ a1,a2,…}
如何用mathematica求协方差和相关系数
首先要加载Statistics`MultiDescriptiveStatistics`函数库,加载方法为:
<< Statistics`MultiDescriptiveStatistics`
或者加载整个统计函数库,加载方法为:
<<Statistics`
求数据data1和data2的样本协方差。
数据的格式为:{a1,a2,…}。
手册:mathematica命令大全
<< Statistics`DescriptiveStatistics`
或者加载整个统计函数库,加载方法为:
<<Statistics`
求数据data的众数。
数据data的格式为:{ a1,a2,…}
Mode[data]
如何用mathematica求方差和标准差
首先要加载Statistics`DescriptiveStatistics`函数库,加载方法为:
<< Statistics`DescriptiveStatistics`
或者加载整个统计函数库,加载方法为:
<<Statistics`
求数据data的样本方差。
数据data的格式为:{ a1,a2,…} Variance[data]
VarianceMLE[data] 求数据data的母体方差。
数据data的格式为:{ a1,a2,…} StandardDeviation[data] 求数据data的样本标准差。
数据data的格式为:{a1,a2,…} StandardDeviationMLE[data] 求数据data的母体标准差。
数据data的格式为:{ a1,a2,…}
如何用mathematica求协方差和相关系数
首先要加载Statistics`MultiDescriptiveStatistics`函数库,加载方法为:
<< Statistics`MultiDescriptiveStatistics`
或者加载整个统计函数库,加载方法为:
<<Statistics`
求数据data1和data2的样本协方差。
数据的格式为:{a1,a2,…}。
mathematica_函数表
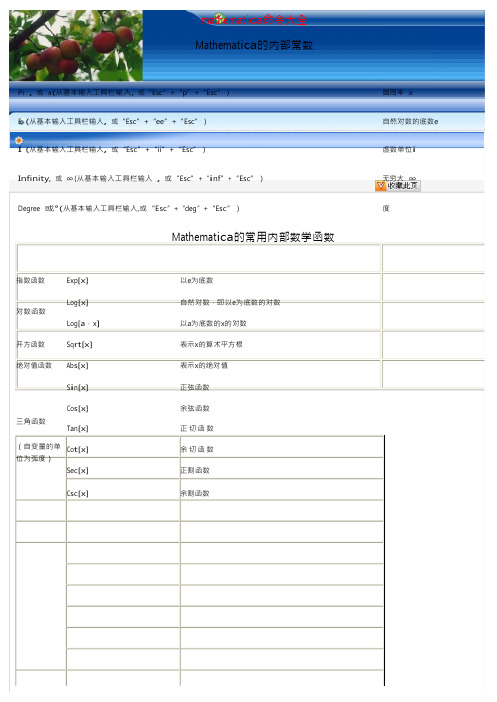
mathemat ica 命令大全Mathemat ica 的内部常数Pi , 或 π(从基本输入工具栏输入, 或“Esc ”+“p ”+“Esc ”)圆周率 πE (从基本输入工具栏输入, 或“Esc ”+“ee ”+“Esc ”)自然对数的底数eI (从基本输入工具栏输入, 或“Esc ”+“ii ”+“Esc ”)虚数单位i无穷大 ∞A r c Sin[x]反正弦函数A r cCos[x]反余弦函数A r cTan[x]反正切函数反三角函数A r cCot[x]反余切函数A r cSec[x]反正割函数A r cCsc[x]反余割函数S i n h[x]双曲正弦函数Co s h[x]双曲余弦函数Tanh[x] 双曲正切函数双曲函数Co t h[x]双曲余切函数Sech[x] 双曲正割函数C sc h[x]双曲余割函数A r cSinh[x]反双曲正弦函数A r c Cosh[x]反双曲余弦函数A r c Tanh[x]反双曲正切函数反双曲函数A r c Coth[x]反双曲余切函数A r c Sec h[x]反双曲正割函数A r c Csc h[x]反双曲余割函数求角度函数A r cTan[x,y]以坐标原点为顶点,x轴正半轴为始边,从原点到点(x,y)的射线为终边的角,其单位为弧度GCD[a,b,c,〃〃〃]最大公约数函数L C M[a,b,c,〃〃〃]最小公倍数函数M od[m,n]求余函数(表示m除以n的余数)Q u o ti e n t[m,n]求商函数(表示m除以n的商)数论函数D i v isors[n]求所有可以整除n的整数Fa c to rI n te ge r[n]因数分解,即把整数分解成质数的乘积P r i me[n]求第n个质数P r i meQ[n]判断整数n是否为质数,若是,则结果为T r u e,否则结果为F a lseR an do m[Int e g e r,{m,n}]随机产生m到n之间的整数排列组合函数Fa c torial[n]或n!阶乘函数,表示n的阶乘R e[z]实部函数I m[z]虚部函数A r g(z)辐角函数复数函数Ab s[z]求复数的模Co n juga te[z]求复数的共轭复数E x p[z]复数指数函数C e i ling[x]表示大于或等于实数x的最小整数F l o o r[x]表示小于或等于实数x的最大整数求整函数与截尾函数Ro u nd[x]表示最接近x的整数I n t e ge r P ar t[x]表示实数x的整数部分F r a ctio nalP a rt[x]表示实数x的小数部分N[num]或nu m//N把精确数n um化成浮点数(默认16位有效数字)N[n um,n]把精确数n um化成具有n个有效数字的浮点数分数与浮点数运算函数N u m b e r Form[nu m,n]以n个有效数字表示nu mR a t iona l iz e[f l o at]将浮点数flo at转换成与其相等的分数R a t iona l iz e[f l o a t,dx]将浮点数flo at转换成与其近似相等的分数,误差小于d x最大、最小函数M a x[a,b,c,〃〃〃]求最大数M i n[a,b,c,〃〃〃]求最小数符号函数S i g n[x]Mathemat ica中的数学运算符a+b加法a-b 减法a*b (可用空格键代替*)乘法a/b (输入方法为:“Ctr l”+ “/ ”)除法a^b (输入方法为:“Ctr l”+ “^ ”)乘方-a 负号Mathemat ica的关系运算符==等于<小于>大于<=小于或等于>=大于或等于!= 不等于注:上面的关系运算符也可从基本输入工具栏输入。
Mathematica的常用函数.doc

Mathematica的内部常数Pi , 或π(从基本输入工具栏输入, 或“Esc”+“p”+“Esc”)圆周率πE (从基本输入工具栏输入, 或“Esc”+“ee”+“Esc”)自然对数的底数eI (从基本输入工具栏输入, 或“Esc”+“ii”+“Esc”)虚数单位iInfinity, 或∞(从基本输入工具栏输入, 或“Esc”+“inf”+“Esc”)无穷大∞Degree 或°(从基本输入工具栏输入,或“Esc”+“deg”+“Esc”)度Mathematica的常用内部数学函数指数函数Exp[x]以e为底数对数函数Log[x]自然对数,即以e为底数的对数Log[a,x]以a为底数的x的对数开方函数Sqrt[x]表示x的算术平方根绝对值函数Abs[x]表示x的绝对值三角函数(自变量的单位为弧度)Sin[x]正弦函数Cos[x]余弦函数Tan[x]正切函数Cot[x]余切函数Sec[x]正割函数Csc[x]余割函数反三角函数ArcSin[x]反正弦函数ArcCos[x]反余弦函数ArcTan[x]反正切函数ArcCot[x]反余切函数ArcSec[x]反正割函数ArcCsc[x]反余割函数双曲函数Sinh[x]双曲正弦函数Cosh[x]双曲余弦函数Tanh[x]双曲正切函数Coth[x]双曲余切函数Sech[x]双曲正割函数Csch[x]双曲余割函数反双曲函数ArcSinh[x]反双曲正弦函数ArcCosh[x]反双曲余弦函数ArcTanh[x]反双曲正切函数ArcCoth[x]反双曲余切函数ArcSech[x]反双曲正割函数ArcCsch[x]反双曲余割函数求角度函数ArcTan[x,y]以坐标原点为顶点,x轴正半轴为始边,从原点到点(x,y)的射线为终边的角,其单位为弧度数论函数GCD[a,b,c,...]最大公约数函数LCM[a,b,c,...]最小公倍数函数Mod[m,n]求余函数(表示m除以n的余数)Quotient[m,n]求商函数(表示m除以n的商)Divisors[n]求所有可以整除n的整数FactorInteger[n]因数分解,即把整数分解成质数的乘积Prime[n]求第n个质数PrimeQ[n]判断整数n是否为质数,若是,则结果为True,否则结果为FalseRandom[Integer,{m,n}]随机产生m到n之间的整数排列组合函数Factorial[n]或n!阶乘函数,表示n的阶乘复数函数Re[z]实部函数Im[z]虚部函数Arg(z)辐角函数Abs[z]求复数的模Conjugate[z]求复数的共轭复数Exp[z]复数指数函数求整函数与截尾函数Ceiling[x]表示大于或等于实数x的最小整数Floor[x]表示小于或等于实数x的最大整数Round[x]表示最接近x的整数IntegerPart[x]表示实数x的整数部分FractionalPart[x]表示实数x的小数部分分数与浮点数运算函数N[num]或num//N把精确数num化成浮点数(默认16位有效数字)N[num,n]把精确数num化成具有n个有效数字的浮点数NumberForm[num,n]以n个有效数字表示numRationalize[float]将浮点数float转换成与其相等的分数Rationalize[float,dx]将浮点数float转换成与其近似相等的分数,误差小于dx最大、最小函数Max[a,b,c,...]求最大数Min[a,b,c,...]求最小数符号函数Sign[x]Mathematica中的数学运算符a+b 加法a-b减法a*b (可用空格键代替*)乘法a/b (输入方法为:“ Ctrl ” + “ / ” ) 除法a^b (输入方法为:“ Ctrl ” + “ ^ ” )乘方-a 负号Mathematica的关系运算符==等于<小于>大于<=小于或等于>=大于或等于!=不等于注:上面的关系运算符也可从基本输入工具栏输入。
Mathematica常用函数
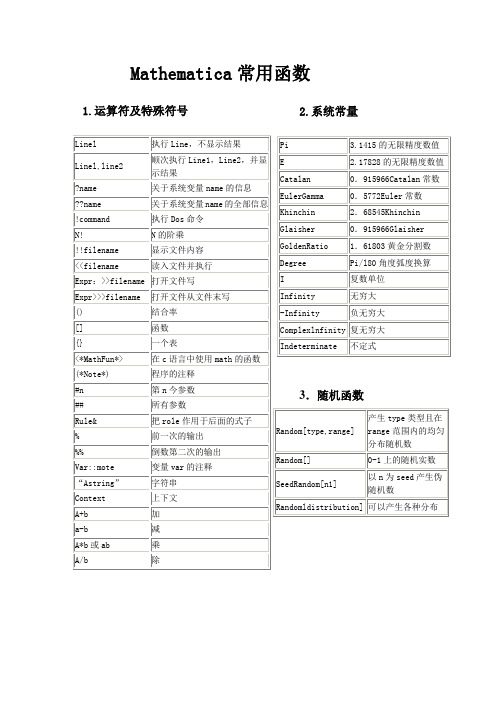
Mathematica 常用函数1.运算符及特殊符号2.系统常量3.随机函数4.代数计算5.解方程6.微积分7.多项式函数8.数值函数9.表相关函数(1)制表函数(2)元素操作(3)表的操作10.绘图函数(1)二维绘图(2)二维设置(3)三维绘图(4)三维设置(5)密度图(6)图形显示(7)图元函数(8)着色及其他11.流程控制函数Mathematica可进行矩阵的各种运算,如矩阵求逆、矩阵的转置、矩阵与向量的乘法等.下面列出主要的运算.记k为常数,u,v为向量,A,B为矩阵k*A------------------------常数乘矩阵k+u-----------------------向量u的每一个元素加上ku+v----------------------向量的对应元素相加u.v-----------------------向量的内积u*v-----------------------向量的对应元素相乘A.u---------------------矩阵乘向量u.A-----------------------向量乘矩阵A.B--------------------------矩阵乘矩阵Transpose[A]-----------------求矩阵A的转置阵Inverse[A]--------------------求矩阵A的逆矩阵Det[A]-------------------------求矩阵A的行列式Eigenvalues[A]-----------------求数字阵A的特征值Eigentvectors[A]---------------求数字阵A的特征向量LinearSolve[A,v]---------------求解线性方程组Ax=vChop[%n]-------------------舍去第n个输出中无实际意义小量矩阵可以左乘以向量或右乘以向量, Mathematica也不区分“行”,或“列”向量,自动进行可能的运算.例:In[1]:=A={{a,b},{c,d}}; v={x,y};In[2]:=A.v (A左乘以v)Out[2]={ax+by,cx+dy}In[3]:=v.A (A右乘以v)Out[3]={ax+cy,bx+dy}In[4]:=Inverse[A]Out[4]=如果矩阵的元素是近似数,则求出的逆矩阵也是近似的。
mathematica 常用函数
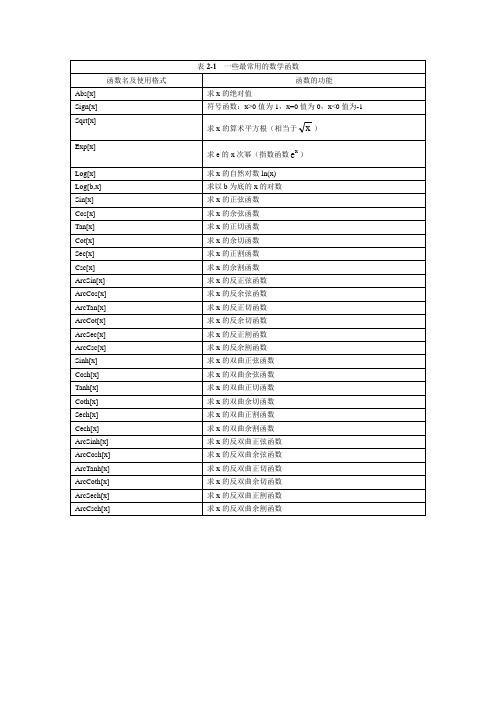
函数名及使用格式
函数的功能
Abs[x]
求x的绝对值
Sign[x]
符号函数:x>0值为1,x=0值为0,x<0值为-1
Sqrt[x]
求x的算术平方根(相当于 )
Exp[x]
求e的x次幂(指数函数 )
Log[x]
求x的自然对数ln(x)
Log[b,x]
求以b为底的x的对数
Sin[x]
求x的正弦函数
Cos[x]
求x的余弦函数
Tan[x]
求x的正切函数
Cot[x]
求x的余切函数
Sec[x]
求x的正割函数
Csc[x]
求x的余割函数
ArcSin[x]
求x的反正弦函数
ArcCos[x]
求x的反余弦函数
ArcTan[x]
求x的反正切函数
ArcCot[x]
求x的反余切函数
ArcSec[x]
求x的反正割函数
FactorInteger [n]
求出整数n的所有质数(素数)因子
Round[x]
求最接近于x的整数
Floor[x]
求不大于x的最大整数(即高斯函数)
Ceiling[x]
求不小于x的最小整数
IntegerPart[x]
求x的整数部分
FractionalPart[x]
求x的小数部分
Mod[m,n]
求m除以n的余数,即取模运算
n!!
求n的双阶乘n(n-2)(n-4)…
Binomial[n,m]
求组合数(二项式系数)
Permutations[{n1,n2,…}]
列出序列{n1,n2,…}的所有排列
整理mathematica数学常用命令大全

Mathematica的内部常数Mathematica的常用内部数学函数Mathematica中的数学运算符Mathematica的关系运算符注:上面的关系运算符也可从基本输入工具栏输入。
如何用mathematica求多项式的最大公因式和最小公倍式如何用mathematica求整数的最大公约数和最小公倍数如何用mathematica进行整数的质因数分解如何用mathematica求整数的正约数如何用mathematica判断一个整数是否为质数n个质数如何用mathematica求第如何用mathematica配方Mathematica没有提供专门的配方命令,但是我们可以非常轻松地自定义一个函数进行配方。
如何用mathematica进行多项式运算如何用mathematica进行分式运算如何用Mathematica进行因式分解如何用Mathematica展开如何用Mathematica进行化简如何用Mathematica合并同类项如何用Mathematica进行数学式的转换如何用Mathematica进行变量替换如何用mathematica进行复数运算如何在mathematica中表示集合与数学中表示集合的方法相同,格式如下:下列命令可以生成特殊的集合:如何用Mathematica求集合的交集、并集、差集和补集如何mathematica用排序如何在Mathematica中解方程注:方程的等号必须用:= =如何在Mathematica中解方程组Solve[{方程组},{变元组}]注:方程的等号必须用:= =如何在Mathematica中解不等式先加载:Algebra`InequalitySolve` ,加载方法为:<<Algebra`InequalitySolve`然后执行解不等式的命令InequalitySolve,此命令的使用格式如下:<--mstheme-->如何在Mathematica中解不等式组先加载:Algebra`InequalitySolve` ,加载方法为:<<Algebra`InequalitySolve`然后执行解不等式组的命令InequalitySolve,此命令的使用格式如下:<--mstheme-->如何在Mathematica中解不等式组先加载:Algebra`InequalitySolve` ,加载方法为:<<Algebra`InequalitySolve` 然后执行解不等式组的命令InequalitySolve,此命令的使用格式如下:<--mstheme-->如何用mathematica表示分段函数如何用mathematica求反函数对系统内部的函数生效,但对自定义的函数不起任何作用,也许是方法不对。
Mathematica常用函数

Mathematica常用函数基本运算a+b+c 加a-b 减a b c 或a*b*c 乘a/b 除-a 负号a^b 次方Mathematica 数字的形式256 整数2.56 实数11/35 分数2+6I 复数常用的数学常数Pi 圆周率,π=3.141592654…E 尤拉常数,e=2.71828182…Degree 角度转换弧度的常数,Pi/180I 虚数,其值为√-1Infinity 无限大指定之前计算结果的方法% 前一个运算结果%% 前二个运算结果%%…%(n个%) 前n个运算结果%n 或Out[n] 前n个运算结果复数的运算指令a+bI 复数Conjugate[a+bI] 共轭复数Re[z], Im[z] 复数z的实数/虚数部分Abs[z] 复数z的大小或模数(Modulus)Arg[z] 复数z的幅角(Argument)Mathematica 输出的控制指令expr1; expr2; expr3 做数个运算,但只印出最后一个运算的结果expr1; expr2; expr3; 做数个运算,但都不印出结果expr; 做运算,但不印出结果常用数学函数Sin[x],Cos[x],Tan[x],Cot[x],Sec[x],Csc[x] 三角函数,其引数的单位为弧度Sinh[x],Cosh[x],Tanh[x],… 双曲函数ArcSin[x],ArcCos[x],ArcTan[x] 反三角函数ArcCot[x],ArcSec[x],ArcCsc[x]ArcSinh[x],ArcCosh[x],ArcTanh[x],… 反双曲函数Sqrt[x] 根号Exp[x] 指数Log[x] 自然对数Log[a,x] 以a为底的对数Abs[x] 绝对值Round[x] 最接近x的整数Floor[x] 小于或等于x的最大整数Ceiling[x] 大于或等于x的最小整数Mod[a,b] a/b所得的馀数n! 阶乘Random[] 0至1之间的随机数(最新版本已经不用这个函数,改为使用RandomReal[])Max[a,b,c,...],Min[a,b,c,…] a,b,c,…的极大/极小值数值设定x=a 将变数x的值设为ax=y=b 将变数x和y的值均设为bx=. 或Clear[x] 除去变数x所存的值变数使用的一些法则xy 中间没有空格,视为变数xyx y x乘上y3x 3乘上xx3 变数x3x^2y 为x^2 y次方运算子比乘法的运算子有较高的处理顺序四个处理指令Expand[expr] 将expr展开Factor[expr] 将expr因式分解Simplify[expr] 将expr化简成精简的式子FullSimplify[expr] Mathematica 会尝试更多的化简公式,将expr化成更精简的式子多项式/分式转换ExpandAll[expr] 把算式全部展开Together[expr] 将expr各项通分在并成一项Apart[expr] 把分式拆开成数项分式的和Apart[expr,var] 视var以外的变数为常数,将expr拆成数项的和Cancel[expr] 把分子和分母共同的因子消去分母/分子运算Denominator[expr] 取出expr的分母Numerator[expr] 取出expr的分子ExpandDenominator[expr] 展开expr的分母ExpandNumerator[expr] 展开expr的分子多项式转换函数Collect[expr,x] 将expr表示成x的多项式,如Collect[expr,{x,y,…}] 将expr分别表示成x,y,…的多项式FactorTerms[expr] 将expr的数值因子提出,如4x+2=2(2x+1)FactorTerms[expr,x] 将expr中把所有不包含x项的因子提出FactorTerms[e xpr,{x,y,…}] 将expr中把所有不包含{x,y,...}项的因子提出函数和指数运算TrigExpand[expr] 将三角函数展开TrigFactor[expr] 将三角函数所组成的数学式因式分解TrigReduce[expr] 将相乘或次方的三角函数化成一次方的基本三角函数之组合ExpToTrig[expr] 将指数函数化成三角函数或双曲函数TrigToExp[expr] 将三角函数或双曲函数化成指数函数复数、次方乘积ComplexExpand[expr] 假设所有的变数都是实数来对expr展开ComplexExpand[expr,{x,y,…}] 假设x,y,..等变数均为复数来对expr展开PowerExpand[expr] 将项次、系数最高次方Coefficient[expr,form] 于expr中form的系数Exponent[expr,form] 于expr中form的最高次方Part[expr,n] 或expr[[n]] 在expr项中第n个项代换运算子expr/.x->value 将expr里所有的x均代换成valueexpr/.{x->value1,y->value2,…} 执行数个不同变数的代换expr/.{{x->value1},{x->value2},…} 将expr代入不同的x值expr//.{x->value1,y->value2,…} 重复代换到expr不再改变为止求解方程式的根Solve[lhs==rhs,x] 解方程式lhs==rhs,求xNsolve[lhs==rhs,x] 解方程式lhs==rhs的数值解Solve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] 解联立方程式,求x,y,…NSolve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] 解联立方程式的数值解FindRoot[lhs==rhs,{x,x0}] 由初始点x0求lhs==rhs的根四种括号(term) 圆括号,括号内的term先计算f[x] 方括号,内放函数的引数{x,y,z} 大括号或串列括号,内放串列的元素p[[i ]] 或Part[p,i] 双方括号,p的第i项元素p[[i,j]] 或Part[p,i,j] p的第i项第j个元素缩短输出指令expr//Short 显示一行的计算结果Short[expr,n] 显示n行的计算结果Command; 执行command,但不列出结果查询物件Command 查询Command的语法及说明Command 查询Command的语法和属性及选择项Aaaa* 查询所有开头为Aaaa的物件定义之查询与清除f[x_]= expr 立即定义函数f[x]f[x_]:= expr 延迟定义函数f[x]f[x_,y_,…] 函数f有两个以上的引数f 查询函数f的定义Clear[f] 或f=. 清除f的定义Remove[f] 将f自系统中清除掉含有预设值的Patterna_+b_. b的预设值为0,即若b从缺,则b以0代替x_ y_ y的预设值为1x_^y_ y的预设值为1条件式的自订函数lhs:=rhs/;condition 当condition成立时,lhs才会定义成rhsIf指令If[test,then,else] 若test为真,则回应then,否则回应elseIf[test,then,else,unknow] 同上,若test无法判定真或假时,则回应unknow 极限Limit[expr,x->c] 当x趋近c时,求expr的极限Limit[expr,x->c,Direction->1]Limit[expr,x->c,Direction->-1]微分D[f,x] 函数f对x作微分D[f,x1,x2,…] 函数f对x1,x2,…作微分D[f,{x,n}] 函数f对x微分n次D[f,x,NonConstants->{y,z,…}] 函数f对x作微分,将y,z,…视为x的函数全微分Dt[f] 全微分dfDt[f,x] 全微分Dt[f,x1,x2,…] 全微分Dt[f,x,Constants->{c1,c2,…}] 全微分,视c1,c2,…为常数不定积分Integrate[f,x] 不定积分∫f dx定积分Integrate[f,{x,xmin,xmax}] 定积分Integrate[f,{x,xmin,xmax},{y,ymin,ymax}] 定积分数列之和与积Sum[f,{i,imin,imax}] 求和Sum[f,{i,imin,imax,di}] 求数列和,引数i以di递增Sum[f,{i,imin,imax},{j,jmin,jmax}]Product[f,{i,imin,imax}] 求积Product[f,{i,imin,imax,di}] 求数列之积,引数i以di递增Product[f,{i,imin,imax},{j,jmin,jmax}]泰勒展开式Series[expr,{x,x0,n}] 对expr于x0点作泰勒级数展开至(x-x0)n项Series[expr,{x,x0,m},{y,y0,n}] 对x0和y0展开关系运算子a==b 等于a>b 大于a>=b 大于等于a<b 小于a<=b 小于等于a!=b 不等于逻辑运算子!p notp||q||… orp&&q&&… andXor[p,q,…] exclusive orLogicalExpand[expr] 将逻辑表示式展开二维绘图指令Plot[f,{x,xmin,xmax}]画出f在xmin到xmax之间的图形Plot[{f1,f2,…},{x,xmin,xmax}]同时画出数个函数图形Plot[f,{x,xmin,xmax},option->value]指定特殊的绘图选项,画出函数f的图形Plot几种指令选项预设值说明AspectRatio 1/GoldenRatio 图形高和宽之比例,高/宽Axes True 是否把坐标轴画出AxesLabel Automatic 为坐标轴贴上标记,若设定为AxesLabel->{?ylabel?},则为y轴之标记。
Mathematica画图函数命令大全

二维作图Plot[f,{x,xmin,xmax}] 一维函数f[x]在区间[xmin,xmax]上的函数曲?Plot[,f2.{f1.},{x,xmin,xmax}] 在一张图上画几条曲线ListPlo t[{y1,y2,..}] 绘出由离散点对(n,yn)组成的图ListPlo t[{{x1,y1},{x2,y2},..}] 绘出由离散点对(xn,yn)组成的图Plarame tricPo t[{fx,fy},{t,tmin,tmax}] 由参数方程在参数变化范围内的曲线Paramet ricPlo t[{{fx,fy},{gx,gy},...},{t,tmin,tmax}]在一张图上画多条参数曲线选项:PlotRan ge->{0,1} 作图显示的值域范围AspectR atio->1/GoldenR atio生成图形的纵横比PlotLab el ->label 标题文字Axes ->{False,True} 分别制定是否画x,y轴AxesLab el->{xlabel,ylabel}x,y轴上的说明文字Ticks->None,Automat ic,fun用什么方式画轴的刻度AxesOri gin ->{x,y} 坐标轴原点位置AxesSty le->{{xstyle}, {ystyle}}设置轴线的线性颜色等属性Frame ->True,False 是否画边框FrameLa bel ->{xmlabel,ymlabel,xplabel,yplabel}边框四边上的文字FrameTi cks同Ti cks 边框上是否画刻度GridLin es 同Ticks图上是否画栅格线FrameSt yle ->{{xmstyle},{ymstyle}设置边框线的线性颜色等属性ListPlo t[data,PlotJoi ned->True] 把离散点按顺序连线PlotSyt le->{{style1},{style2},..}曲线的线性颜色等属性PlotPoi nts->15 曲线取样点,越大越细致三维作图Plot3D[f,{x,xmin,xmax}, {y,ymin,ymax}]二维函数f[x,y]的空间曲面Plot3D[{f,s}, {x,xmin,xmax}, {y,ymin,ymax}]同上,曲面的染色由s[x,y]值决定ListPlo t3D[array] 二维数据阵ar ray的立体高度图ListPlo t3D[array,shades]同上,曲面的染色由s hades[数据]值决定Paramet ricPlo t3D[{fx,fy,fz},{t,tmin,tmax}]二元数方程在参数变化范围内的曲线二元数方程在参数变化范围内的曲线Paramet ricPlo t3D[{{fx,fy,fz},{gx,gy,gz},...},{t,tmin,tmax}]多条空间参数曲线选项:ViewPoi nt ->{x,y,z} 三维视点,默认为{1.3,-2.4,2}Boxed -> True,False 是否画三维长方体边框BoxRati os->{sx,sy,sz} 三轴比例BoxStyl e 三维长方体边框线性颜色等属性Lightin g ->True 是否染色LightSo urces->{s1,s2..} si为某一个光源si={{dx,dy,dz},color}color为灯色,向dx,dy,dz方向照射Ambient Light->颜色函数慢散射光的光源Mesh->True,False 是否画曲面上与x,y轴平行的截面的截线MeshSty le 截线线性颜色等属性MeshRan ge->{{xmin,xmax}, {ymin,ymax}}网格范围ClipFil l->Automat ic,None,color,{bottom,top}指定图形顶部、底部超界后所画的颜色Shading ->False,True 是否染色HiddenS urface->True,False 略去被遮住不显示部分的信息等高线Contour Plot[f,{x,xmin,xmax},{y,ymin,ymax}]二维函数f[x,y]在指定区间上的等高线图ListCon tourPl ot[array] 根据二维数组a rray数值画等高线选项:Contour s->n 画n条等高线Contour s->{z1,z2,..} 在zi处画等高线Contour Shadin g -> False 是否用深浅染色Contour Lines-> True 是否画等高线Contour Style-> {{style1},{style2},..}等高线线性颜色等属性FrameTi cks 同上密度图Density Plot[f,{x,xmin,xmax},{y,ymin,ymax}]二维函数f[x,y]在指定区间上的密度图ListDen sityPl ot[array] 同上图形显示Show[graphic s,options] 显示一组图形对象,options为选项设置Show[g1,g2...] 在一个图上叠加显示一组图形对象Graphic sArray[{g1,g2,...}]在一个图上分块显示一组图形对象Selecti onAnim ate[noteboo k,t]把选中的not ebook中的图画循环放映选项:(此处选项适用于全部图形函数)Backgro und->颜色函数指定绘图的背景颜色RotateL abel -> True 竖着写文字TextSty le 此后输出文字的字体,颜色大小等ColorFu nction->Hue等把其作用于某点的函数值上决定某点的颜色RenderA ll->False 是否对遮挡部分也染色MaxBend曲线、曲面最大弯曲度图元函数Graphic s[prim, options]prim为下面各种函数组成的表,表示一个二维图形对象Graphic s3D[prim, options]prim为下面各种函数组成的表,表示一个三维图形对象Surface Graphi cs[array, shades]表示一个由ar ray和sh ade决定的曲面对象Contour Graphi cs[array]表示一个由ar ray决定的等高线图对象Density Graphi cs[array]表示一个由ar ray决定的密度图对象以上定义图形对象,可以进行对变量赋值,合并显示等操作,也可以存盘Point[p] p={x,y}或{x,y,z},在指定位置画点Line[{p1,p2,..}]经由pi点连线Rectang le[{xmin, ymin}, {xmax, ymax}] 画矩形Cuboid[{xmin,ymin,zmin},{xmax,ymax,zmax}]由对角线指定的长方体Polygon[{p1,p2,..}] 封闭多边形Circle[{x,y},r] 画圆Circle[{x,y},{rx,ry}] 画椭圆,rx,ry为半长短轴Circle[{x,y},r,{a1,a2}] 从角度a1~a2的圆弧Disk[{x, y}, r] 填充的园、衷病⒃ 弧等参数同上Raster[array,ColorFu nction->f] 颜色栅格Text[expr,coords]在坐标coor ds上输出表达式PostScr ipt["string"] 直接用Post Script图元语言写Scaled[{x,y,..}] 返回点的坐标,且均大于0小于1颜色函数(指定其后绘图的颜色)GrayLev el[level] 灰度level为0~1间的实数RGBColo r[red, green, blue] RGB颜色,均为0~1间的实数Hue[h, s, b] 亮度,饱和度等,均为0~1间的实数CMYKCol or[cyan, magenta, yellow, black] CMYK颜色其他函数(指定其后绘图的方式)Thickne ss[r] 设置线宽为rPointSi ze[d] 设置绘点的大小Dashing[{r1,r2,..}] 虚线一个单元的间隔长度ImageSi ze->{x, y} 显示图形大小(像素为单位)ImageRe soluti on->r 图形解析度r个dpi小(像素为单位)ImageRe soluti on->r 图形解析度r个dpiImageMa rgins->{{left,right},{bottom,top}}四边的空白ImageRo tated->False 是否旋转90度显示。
整理mathematica数学常用命令大全

Mathematica的内部常数Mathematica的常用内部数学函数Mathematica中的数学运算符Mathematica的关系运算符注:上面的关系运算符也可从基本输入工具栏输入。
如何用mathematica求多项式的最大公因式和最小公倍式如何用mathematica求整数的最大公约数和最小公倍数如何用mathematica进行整数的质因数分解如何用mathematica求整数的正约数如何用mathematica判断一个整数是否为质数如何用mathematica求第n个质数如何用mathematica求阶乘如何用mathematica配方Mathematica没有提供专门的配方命令,但是我们可以非常轻松地自定义一个函数进行配方。
如何用mathematica进行多项式运算如何用mathematica进行分式运算如何用Mathematica进行因式分解如何用Mathematica展开如何用Mathematica进行化简如何用Mathematica合并同类项如何用Mathematica进行数学式的转换如何用Mathematica进行变量替换如何用mathematica进行复数运算如何在mathematica中表示集合与数学中表示集合的方法相同,格式如下:下列命令可以生成特殊的集合:如何用Mathematica求集合的交集、并集、差集和补集如何mathematica用排序如何在Mathematica中解方程注:方程的等号必须用:= =如何在Mathematica中解方程组Solve[{方程组},{变元组}]注:方程的等号必须用:= =如何在Mathematica中解不等式先加载:Algebra`InequalitySolve` ,加载方法为:<<Algebra`InequalitySolve`然后执行解不等式的命令InequalitySolve,此命令的使用格式如下:<--mstheme-->如何在Mathematica中解不等式组先加载:Algebra`InequalitySolve` ,加载方法为:<<Algebra`InequalitySolve`然后执行解不等式组的命令InequalitySolve,此命令的使用格式如下:<--mstheme-->如何在Mathematica中解不等式组先加载:Algebra`InequalitySolve` ,加载方法为:<<Algebra`InequalitySolve` 然后执行解不等式组的命令InequalitySolve,此命令的使用格式如下:<--mstheme-->如何用mathematica表示分段函数如何用mathematica求反函数对系统内部的函数生效,但对自定义的函数不起任何作用,也许是方法不对。
Mathematica的常用函数.doc

Mathematica的内部常数Pi , 或π(从基本输入工具栏输入, 或“Esc”+“p”+“Esc”)圆周率πE (从基本输入工具栏输入, 或“Esc”+“ee”+“Esc”)自然对数的底数eI (从基本输入工具栏输入, 或“Esc”+“ii”+“Esc”)虚数单位iInfinity, 或∞(从基本输入工具栏输入, 或“Esc”+“inf”+“Esc”)无穷大∞Degree 或°(从基本输入工具栏输入,或“Esc”+“deg”+“Esc”)度Mathematica的常用内部数学函数指数函数Exp[x]以e为底数对数函数Log[x]自然对数,即以e为底数的对数Log[a,x]以a为底数的x的对数开方函数Sqrt[x]表示x的算术平方根绝对值函数Abs[x]表示x的绝对值三角函数(自变量的单位为弧度)Sin[x]正弦函数Cos[x]余弦函数Tan[x]正切函数Cot[x]余切函数Sec[x]正割函数Csc[x]余割函数反三角函数ArcSin[x]反正弦函数ArcCos[x]反余弦函数ArcTan[x]反正切函数ArcCot[x]反余切函数ArcSec[x]反正割函数ArcCsc[x]反余割函数双曲函数Sinh[x]双曲正弦函数Cosh[x]双曲余弦函数Tanh[x]双曲正切函数Coth[x]双曲余切函数Sech[x]双曲正割函数Csch[x]双曲余割函数反双曲函数ArcSinh[x]反双曲正弦函数ArcCosh[x]反双曲余弦函数ArcTanh[x]反双曲正切函数ArcCoth[x]反双曲余切函数ArcSech[x]反双曲正割函数ArcCsch[x]反双曲余割函数求角度函数ArcTan[x,y]以坐标原点为顶点,x轴正半轴为始边,从原点到点(x,y)的射线为终边的角,其单位为弧度数论函数GCD[a,b,c,...]最大公约数函数LCM[a,b,c,...]最小公倍数函数Mod[m,n]求余函数(表示m除以n的余数)Quotient[m,n]求商函数(表示m除以n的商)Divisors[n]求所有可以整除n的整数FactorInteger[n]因数分解,即把整数分解成质数的乘积Prime[n]求第n个质数PrimeQ[n]判断整数n是否为质数,若是,则结果为True,否则结果为FalseRandom[Integer,{m,n}]随机产生m到n之间的整数排列组合函数Factorial[n]或n!阶乘函数,表示n的阶乘复数函数Re[z]实部函数Im[z]虚部函数Arg(z)辐角函数Abs[z]求复数的模Conjugate[z]求复数的共轭复数Exp[z]复数指数函数求整函数与截尾函数Ceiling[x]表示大于或等于实数x的最小整数Floor[x]表示小于或等于实数x的最大整数Round[x]表示最接近x的整数IntegerPart[x]表示实数x的整数部分FractionalPart[x]表示实数x的小数部分分数与浮点数运算函数N[num]或num//N把精确数num化成浮点数(默认16位有效数字)N[num,n]把精确数num化成具有n个有效数字的浮点数NumberForm[num,n]以n个有效数字表示numRationalize[float]将浮点数float转换成与其相等的分数Rationalize[float,dx]将浮点数float转换成与其近似相等的分数,误差小于dx最大、最小函数Max[a,b,c,...]求最大数Min[a,b,c,...]求最小数符号函数Sign[x]Mathematica中的数学运算符a+b 加法a-b减法a*b (可用空格键代替*)乘法a/b (输入方法为:“ Ctrl ” + “ / ” ) 除法a^b (输入方法为:“ Ctrl ” + “ ^ ” )乘方-a 负号Mathematica的关系运算符==等于<小于>大于<=小于或等于>=大于或等于!=不等于注:上面的关系运算符也可从基本输入工具栏输入。
整理mathematica数学常用命令大全

Mathematica的内部常数Mathematica的常用内部数学函数Mathematica中的数学运算符Mathematica的关系运算符注:上面的关系运算符也可从基本输入工具栏输入。
如何用mathematica求多项式的最大公因式和最小公倍式如何用mathematica求整数的最大公约数和最小公倍数如何用mathematica进行整数的质因数分解如何用mathematica求整数的正约数如何用mathematica判断一个整数是否为质数n个质数如何用mathematica求第如何用mathematica配方Mathematica没有提供专门的配方命令,但是我们可以非常轻松地自定义一个函数进行配方。
如何用mathematica进行多项式运算如何用mathematica进行分式运算如何用Mathematica进行因式分解如何用Mathematica展开如何用Mathematica进行化简如何用Mathematica合并同类项如何用Mathematica进行数学式的转换如何用Mathematica进行变量替换如何用mathematica进行复数运算如何在mathematica中表示集合与数学中表示集合的方法相同,格式如下:下列命令可以生成特殊的集合:如何用Mathematica求集合的交集、并集、差集和补集如何mathematica用排序如何在Mathematica中解方程注:方程的等号必须用:= =如何在Mathematica中解方程组Solve[{方程组},{变元组}]注:方程的等号必须用:= =如何在Mathematica中解不等式先加载:Algebra`InequalitySolve` ,加载方法为:<<Algebra`InequalitySolve`然后执行解不等式的命令InequalitySolve,此命令的使用格式如下:<--mstheme-->如何在Mathematica中解不等式组先加载:Algebra`InequalitySolve` ,加载方法为:<<Algebra`InequalitySolve`然后执行解不等式组的命令InequalitySolve,此命令的使用格式如下:<--mstheme-->如何在Mathematica中解不等式组先加载:Algebra`InequalitySolve` ,加载方法为:<<Algebra`InequalitySolve` 然后执行解不等式组的命令InequalitySolve,此命令的使用格式如下:<--mstheme-->如何用mathematica表示分段函数如何用mathematica求反函数对系统内部的函数生效,但对自定义的函数不起任何作用,也许是方法不对。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Mathematica函数大全--运算符及特殊符号一、运算符及特殊符号Line1;执行Line,不显示结果Line1,line2顺次执行Line1,2,并显示结果name关于系统变量name的信息name关于系统变量name的全部信息!command执行Dos命令n! N的阶乘!!filename显示文件内容<Expr>> filename打开文件写Expr>>>filename打开文件从文件末写() 结合率[]函数{}一个表<*Math Fun*> 在c语言中使用math的函数(*Note*)程序的注释#n第n个参数##所有参数rule& 把rule作用于后面的式子%前一次的输出%%倒数第二次的输出%n第n个输出var::note变量var的注释"Astring "字符串Context ` 上下文a+b 加a-b减a*b或a b 乘a/b除a^b 乘方base^^num以base为进位的数lhs&&rhs且lhs||rhs或!lha非++,-- 自加1,自减1+=,-=,*=,/= 同C语言>,<,>=,<=,==,!=逻辑判断(同c)lhs=rhs立即赋值lhs:=rhs建立动态赋值lhs:>rhs建立替换规则expr//funname相当于filename[expr]expr/.rule将规则rule应用于exprexpr//.rule 将规则rule不断应用于expr知道不变为止param_ 名为param的一个任意表达式(形式变量)param__名为param的任意多个任意表达式(形式变量)二、系统常数Pi 3.1415....的无限精度数值E 2.17828...的无限精度数值Catalan 0.915966..卡塔兰常数EulerGamma 0.5772....高斯常数GoldenRatio 1.61803...黄金分割数Degree Pi/180角度弧度换算I复数单位Infinity无穷大-Infinity负无穷大ComplexInfinity复无穷大Indeterminate不定式三、代数计算Expand[expr]展开表达式Factor[expr]表达式因式分解Factor[poly,Modulus->p] Z p域分解Factor[poly,Extension->{a1, a2,… }] 代数数域分解Factor[poly,GaussianIntegers->True] 复整数域分解Factor[poly,Extension->Automatic]poly的系数所在数域分解(以下函数都可在各数域内进行)Simplify[expr]化简表达式FullSimplify[expr]将特殊函数等也进行化简PowerExpand[expr]展开所有的幂次形式ComplexExpand[expr,{x1,x2...}]按复数实部虚部展开FunctionExpand[expr]化简expr中的特殊函数Collect[expr, x]合并同次项Collect[expr, {x1,x2,...}]合并x1,x2,...的同次项Together[expr]通分Apart[expr]部分分式展开Apart[expr, var] 对var的部分分式展开Cancel[expr]约分ExpandAll[expr]展开表达式ExpandAll[expr, patt] 展开表达式FactorTerms[poly]提出共有的数字因子FactorTerms[poly, x] 提出与x无关的数字因子FactorTerms[poly, {x1,x2...}]提出与xi无关的数字因子Coefficient[expr, form]多项式expr中form的系数Coefficient[expr, form, n]多项式expr中form^n的系数Exponent[expr, form]表达式expr中form的最高指数Numerator[expr] 表达式expr的分子Denominator[expr]表达式expr的分母ExpandNumerator[expr]展开expr的分子部分ExpandDenominator[expr]展开expr的分母部分ExpandDenominator[expr]展开expr的分母部分TrigExpand[expr]展开表达式中的三角函数TrigFactor[expr]给出表达式中的三角函数因子TrigFactorList[expr]给出表达式中的三角函数因子的表TrigReduce[expr]对表达式中的三角函数化简TrigToExp[expr] 三角到指数的转化ExpToTrig[expr]指数到三角的转化RootReduce[expr]ToRadicals[expr]四、解方程Solve[eqns, vars]从方程组eqns中解出varsSolve[eqns, vars, elims] 从方程组eqns中削去变量elims,解出vars DSolve[eqn, y, x]解微分方程,其中y是x的函数DSolve[{eqn1,eqn2,...},{y1,y2...},x]解微分方程组,其中yi是x的函数DSolve[eqn, y, {x1,x2...}]解偏微分方程RSolve[eqn, a[n], n] 解函数方程例1、RSolve u x2x1u x1zu x2,u x,x{{u[x] BesselJ[x,z] C[1]+BesselY[x,z] C[2]}} 2、RSolve[{y[x+2]==ay[x+1]+y[x],y[0]==0,y[1]==1},y,x]RSolve[{eqn1, eqn2, … }, {a1[n], a2[n], …}, n]RSolve[eqn, a[n1, n2, …], {n1, n2, …}]Resolve[expr]Resolve[expr, dom]FindInstance[expr, vars]求不定方程的特解FindInstance[expr, vars, dom]求不定方程的特解(在dom数域内)FindInstance[expr, vars, dom, n]求不定方程的n个特解Eliminate[eqns, vars] 把方程组eqns中变量vars约去SolveAlways[eqns, vars] 给出等式成立的所有参数满足的条件Reduce[eqns, vars] 化简并给出所有可能解的条件Reduce x22y21&&x0&&y0&&x y Integers,x,y LogicalExpand[expr] 用&&和||将逻辑表达式展开InverseFunction[f] 求函数f的逆函数Root[f, k] 求多项式函数的第k个根Roots[lhs==rhs, var] 得到多项式方程的所有根五、微积分函数D[f, x]求f[x]的微分∂f/∂xD[f, {x, n}]求f[x]的n阶微分n f x nD[f,x1,x2..] 求f[x]对x1,x2...偏微分x1x2...fDt[f, x]求f[x]的全微分df/dxDt[f]求f[x]的全微分dfDt[f, {x, n}] n阶全微分df^n/dx^nDt[f,x1,x2..]对x1,x2..的偏微分d d x1d d x2...fIntegrate[f, x] f[x]对x在的不定积分Integrate[f, {x, xmin, xmax}] f[x]对x在区间(xmin,xmax)的定积分Integrate[f, {x, xmin, xmax}, {y, ymin, ymax}] f[x,y]的二重积分Limit[expr, x->x0] x趋近于x0时expr的极限Limit[expr, x->x0, Direction -> 1] x趋近于x0+时expr的极限Limit[expr, x->x0, Direction ->-1] x趋近于x0-时expr的极限Residue[expr, {x,x0}] expr在x0处的留数Series[f, {x, x0, n}] 给出f[x]在x0处的幂级数展开Series[f, {x, x0,nx}, {y, y0, ny}]先对y幂级数展开,再对xNormal[expr]化简并给出最常见的表达式(可截断Series的误差O[x])SeriesCoefficient[series, n]给出级数中第n次项的系数SeriesCoefficient[series, {n1,n2...}]' 或Derivative[n1,n2...][f]一阶导数InverseSeries[s, x] 给出逆函数的级数ComposeSeries[serie1,serie2...] 给出两个基数的组合SeriesData[x,x0,{a0,a1,..},nmin,nmax,den]表示一个在x0处x的幂级数,其中aii 为系数O[x]^n n阶小量x^nO[x, x0]^n n阶小量(x-x0)^n六、多项式函数Variables[poly]给出多项式poly中独立变量的列表CoefficientList[poly, var]给出多项式poly中变量var的系数CoefficientList[poly, {var1,var2...}]给出多项式poly中变量var(i)的系数列? PolynomialMod[poly, m] poly中各系数mod m同余后得到的多项式,m可为整式PolynomialQuotient[p, q, x]以x为自变量的两个多项式之商式p/q PolynomialRemainder[p, q, x] 以x为自变量的两个多项式之余式PolynomialGCD[poly1,poly2,...] poly(i)的最大公因式PolynomialLCM[poly1,poly2,...] poly(i)的最小公倍式PolynomialReduce[poly, {poly1,poly2,...},{x1,x2...}]得到一个表{{a1,a2,...},b}其中Sum[ai*polyi]+b=polyResultant[poly1,poly2,var] 约去poly1,poly2中的varFactor[poly] 因式分解(在整式范围内)FactorTerms[poly] 提出poly 中的数字公因子FactorTerms[poly, {x1,x2...}] 提出poly 中与xi 无关项的数字公因子FactorList[poly] 给出poly 各个因子及其指数{{poly1,exp1},{...}...}FactorSquareFreeList[poly] 同上FactorTermsList[poly,{x1,x2...}] 给出各个因式列表,第一项是数字公因子,第二项是与xi 无关的因式,其后是与xi 有关的因式按升幂的排排?Cyclotomic[n, x] C n x k x e 2i k n (割圆多项式,即单位根的极小多项式)Decompose[poly, x] 迭代分解,给出{p1,p2,...},其中p1(p2(...))=polyInterpolatingPolynomial[data, var] 在数据data 上的插值多项式 data 可以写为{f1,f2..}相当于{{x1=1,y1=f1}..} data 可以写为{{x1,f1,df11,df12,..},{x2,f2,df21..} 可以指定数据点上的n 阶导数值RootSum[f, form] 得到f[x]=0的所有根,并求得Sum[form[xi]]七、随机函数Random[type,range] 产生type 类型且在range 范围内的均匀分布随机数,type 可以为Integer,Real,Complex,不写默认为Real ,range 为{min,max},不写默认为{0,1} Random[] 0~1上的随机实数SeedRandom[n] 以n 为seed 产生伪随机数 如果采用了 <在 2.0版本为 <<"D:\\Math\\PACKAGES\\STATISTI\\Continuo.m"Random[distribution]可以产生各种分布如Random[BetaDistribution[alpha, beta]]stribution[alpha, beta]}Random[NormalDistribution[miu,sigma]]等常用的分布如BetaDistribution,CauchyDistribution,ChiDistribution, NoncentralChiSquareDistribution,ExponentialDistribution, ExtremeValueDistribution,NoncentralFRatioDistribution,GammaDistribution,HalfNormalDistribution, LaplaceDistribution, LogNormalDistribution,LogisticDistribution,RayleighDistribution,NoncentralStudentTDistribution,UniformDistribution, WeibullDistribution八、数值函数N[expr] 表达式的机器精度近似值N[expr, n]表达式的n位近似值,n为任意正整数NSolve[lhs==rhs, var]求方程数值解NSolve[eqn, var, n] 求方程数值解,结果精度到n位NDSolve[eqns, y, {x, xmin, xmax}]微分方程数值解NDSolve[eqns, {y1,y2,...}, {x, xmin, xmax}]FindRoot[lhs==rhs, {x,x0}]以x0为初值,寻找方程数值解FindRoot x52,x,1,WorkingPrecision100精确到100位有效数字FindRoot[lhs==rhs, {x, xstart, xmin, xmax}]NSum[f, {i,imin,imax,di}] 数值求和,di为步长NSum[f, {i,imin,imax,di}, {j,..},..] 多维函数求和NProduct[f, {i, imin, imax, di}]函数求积NIntegrate[f, {x, xmin, xmax}] 函数数值积分优化函数:FindMinimum[f, {x,x0}]以x0为初值,寻找函数最小值FindMinimum[f, {x, xstart, xmin, xmax}]LinearProgramming[c,m,b]解线性组合c.x在m.x>=b&&x>=0约束下的最小值,x,b,c为向量,m为矩阵LatticeReduce[{v1,v2...}]向量组vi的极小无关组数据处理:Fit[data,funs,vars]用指定函数组对数据进行最小二乘拟和data可以为{{x1,y1,..f1},{x2,y2,..f2}..}多维的情况emp: Fit[{10.22,12,3.2,9.9}, {1, x, x^2,Sin[x]}, x]Interpolation[data]对数据进行差值,data同上,另外还可以为{{x1,{f1,df11,df12}},{x2,{f2,.}..}指定各阶导数InterpolationOrder默认为3次,可修改ListInterpolation[array]对离散数据插值,array可为n维ListInterpolation[array,{{xmin,xmax},{ymin,ymax},..}] FunctionInterpolation[expr,{x,xmin,xmax}, {y,ymin,ymax},..]以对应expr[xi,yi]的为数据进行插值Fourier[list] 对复数数据进行付氏变换InverseFourier[list]对复数数据进行付氏逆变换Min[{x1,x2...},{y1,y2,...}]得到每个表中的最小值Max[{x1,x2...},{y1,y2,...}]得到每个表中的最大值Select[list, crit] 将表中使得crit为True的元素选择出来Count[list, pattern] 将表中匹配模式pattern的元素的个数Sort[list] 将表中元素按升序排列Sort[list,p]将表中元素按p[e1,e2]为True的顺序比较list 的任两个元素e1,e2,实际上Sort[list]中默认p=Greater集合论:Union[list1,list2..] 表listi的并集并排序Intersection[list1,list2..]表listi的交集并排序Complement[listall,list1,list2...]从全集listall中对listi的差集九、虚数函数Re[expr]复数表达式的实部Im[expr] 复数表达式的虚部Abs[expr] 复数表达式的模Arg[expr]复数表达式的辐角Conjugate[expr] 复数表达式的共轭十、数的头及模式及其他操作Integer _Integer整数Real _Real实数Complex _Complex复数Rational_Rational 有理数(*注:模式用在函数参数传递中,如MyFun[Para1_Integer,Para2_Real]规定传入参数的类型,另外也可用来判断If[Head[a]==Real,...]*) IntegerDigits[n,b,len]数字n以b近制的前len个码元RealDigits[x,b,len]类上FromDigits[list] IntegerDigits的反函数Rationalize[x,dx] 把实数x有理化成有理数,误差小于dxChop[expr, delta]将expr中小于delta的部分去掉,dx默认为10^-10 Accuracy[x]给出x小数部分位数,对于Pi,E等为无限大Precision[x]给出x有效数字位数,对于Pi,E等为无限大SetAccuracy[expr, n] 设置expr显示时的小数部分位数SetPrecision[expr, n] 设置expr显示时的有效数字位数十一、区间函数Interval[{min, max}] 区间[min, max](* Solve[3 x+2==Interval[{-2,5}],xx]*) IntervalMemberQ[interval, x] x在区间内吗?IntervalMemberQ[interval1,interval2]区间2在区间1内吗?IntervalUnion[intv1,intv2...] 区间的并IntervalIntersection[intv1,intv2...]区间的交十二、矩阵操作a.b.c或Dot[a, b, c]矩阵、向量、张量的点积Inverse[m] 矩阵的逆Transpose[list]矩阵的转置Transpose[list,{n1,n2..}]将矩阵list 第k行与第nk列交换Det[m]矩阵的行列式Eigenvalues[m]特征值Eigenvectors[m]特征向量Eigensystem[m]特征系统,返回{eigvalues,eigvectors}LinearSolve[m, b] 解线性方程组m.x==bNullSpace[m] 矩阵m的零空间,即m.NullSpace[m]==零向量RowReduce[m] m化简为阶梯矩阵Minors[m, k] m的所有k*k阶子矩阵的行列式的值(伴随阵,好像是) MatrixPower[mat, n] 阵mat自乘n次MatrixExp[mat]e matOuter[f,list1,list2..] listi中各个元之间相互组合,并作为f的参数的到的矩矩? Outer[Times,list1,list2]给出矩阵的外积SingularValues[m] m的奇异值,结果为{u,w,v},m=Conjugate[Transpose[u]].DiagonalMatrix[w].vPseudoInverse[m] m的广义逆QRDecomposition[m] QR分解SchurDecomposition[m] Schur分解LUDecomposition[m] LU分解Norm[z]=Abs[z];Norm[v]=Sqrt[v.Conjugate[v]];向量的模(内积开平方)Norm[v, p]=Total[Abs[v^p]]^(1/p)。
