Mathematica的常用函数

Mathematica教程-2常用的数学函数

。
Round[x]: 最接近x的整数 Floor[x]: 不大于x的最大整数 Ceiling[x]: 不小于x的最小整数 Abs[x]: x的绝对值或复数的摸 x+Iy : 复数x+iy；Re[z]: 复数z的实部 Im[z]: 复数z的虚部；Arg[z]: 复数z的幅角 Divisors[n]: 能整除n的所有整数组成的表 Mod[m,n]: m被n除的正余数 Quotient[m,n]: m/n的整数部分 GCD[n1,n2……]: 求n1,n1，……的最大公因数 LCM[n1,n2……]: 求n1,n2，……的最小公倍数
函数的立即定义
立即定义函数的语法如下f[x_]=expr函数名为f, 自变量为x，expr是表达式。在执行时会把expr 中的x都换为f的自变量x(不是x_)。函数的自变量具有局部性，只对所在的函数起作用。函数执行结束后也就没有了，不会改变其它全局定义的同名变量的值。例: 定义函数f(x)=x*Sinx+x2, 对定义的函数求函数值，并绘制它的图形。
当然使用If命令也可以定义上面的函数
表
将一些相互关联的元素放在一起，使它们成为一个整体。既可以对整体操作，也可以对整体中的一个元素单独进行操作。在 Mathematica中这样的数据结构就称作表（List）。表主要有三个用法：表｛a,b,c｝可以表示一个向量；表{{a,b},{c,d}}可表示一个矩阵。
常用函数的命令格式
三角函数：Sin[x]，Cos[x] ，Tan[x] ，Cot[x] 等
反三角函数：ArcSin[x] ，ArcCos[x] ，ArcTan[x]等双曲函数与反双曲函数：Sinh[x] ，Cosh[x] ，Tanh[x]， ArcSinh[x]，ArcCosh[x]，ArcTanh[x] 指数函数E^x（或Exp[x]），指数函数a^x

mathematica 初中数学

在Mathematica中，我们可以使用各种内置函数和运算符来执行初中数学中的各种计算。

例如，我们可以使用内置的数学函数来计算平方、平方根、立方、立方根等。

平方可以使用#^2表示，例如3^2将返回9。

平方根可以使用#^2 & [#]表示，例如Sqrt[3]将返回1.732。

立方可以使用#^3表示，例如4^3将返回64。

立方根可以使用#^(1/3)表示，例如CubeRoot[64]将返回4。

此外，我们还可以使用内置的数学函数来计算三角函数、指数函数和对数函数等。

例如，我们可以使用Sin[#]来计算正弦值，使用Cos[#]来计算余弦值，使用Tan[#]来计算正切值。

指数函数可以使用#^#2表示，例如3^2将返回9。

对数函数可以使用Log[#1, #2]表示，例如Log[10, 1000]将返回3。

此外，我们还可以使用内置的数学运算符来进行加法、减法、乘法和除法等基本运算。

例如，我们可以使用#1 + #2来执行加法运算，使用#1 - #2来执行减法运算，使用#1 * #2来执行乘法运算，使用#1 / #2来执行除法运算。

Mathematica的内部常数Pi , 或π(从基本输入工具栏输入, 或“Esc”+“p”+“Esc”）圆周率πE (从基本输入工具栏输入, 或“Esc”+“ee”+“Esc”）自然对数的底数eI (从基本输入工具栏输入, 或“Esc”+“ii”+“Esc”）虚数单位iInfinity, 或∞(从基本输入工具栏输入, 或“Esc”+“inf”+“Esc”）无穷大∞Degree 或°(从基本输入工具栏输入,或“Esc”+“deg”+“Esc”）度Mathematica的常用内部数学函数指数函数Exp[x]以e为底数对数函数Log[x]自然对数，即以e为底数的对数Log[a，x]以a为底数的x的对数开方函数Sqrt[x]表示x的算术平方根绝对值函数Abs[x]表示x的绝对值三角函数（自变量的单位为弧度）Sin[x]正弦函数Cos[x]余弦函数Tan[x]正切函数Cot[x]余切函数Sec[x]正割函数Csc[x]余割函数反三角函数ArcSin[x]反正弦函数ArcCos[x]反余弦函数ArcTan[x]反正切函数ArcCot[x]反余切函数ArcSec[x]反正割函数ArcCsc[x]反余割函数双曲函数Sinh[x]双曲正弦函数Cosh[x]双曲余弦函数Tanh[x]双曲正切函数Coth[x]双曲余切函数Sech[x]双曲正割函数Csch[x]双曲余割函数反双曲函数ArcSinh[x]反双曲正弦函数ArcCosh[x]反双曲余弦函数ArcTanh[x]反双曲正切函数ArcCoth[x]反双曲余切函数ArcSech[x]反双曲正割函数ArcCsch[x]反双曲余割函数求角度函数ArcTan[x，y]以坐标原点为顶点，x轴正半轴为始边，从原点到点（x，y）的射线为终边的角，其单位为弧度数论函数GCD[a,b,c,．．．]最大公约数函数LCM[a,b,c,．．．]最小公倍数函数Mod[m,n]求余函数(表示m除以n的余数)Quotient[m，n]求商函数（表示m除以n的商）Divisors[n]求所有可以整除n的整数FactorInteger[n]因数分解，即把整数分解成质数的乘积Prime[n]求第n个质数PrimeQ[n]判断整数n是否为质数，若是，则结果为True，否则结果为FalseRandom[Integer，{m，n}]随机产生m到n之间的整数排列组合函数Factorial[n]或n！阶乘函数，表示n的阶乘复数函数Re[z]实部函数Im[z]虚部函数Arg(z)辐角函数Abs[z]求复数的模Conjugate[z]求复数的共轭复数Exp[z]复数指数函数求整函数与截尾函数Ceiling[x]表示大于或等于实数x的最小整数Floor[x]表示小于或等于实数x的最大整数Round[x]表示最接近x的整数IntegerPart[x]表示实数x的整数部分FractionalPart[x]表示实数x的小数部分分数与浮点数运算函数N[num]或num//N把精确数num化成浮点数（默认16位有效数字）N[num，n]把精确数num化成具有n个有效数字的浮点数NumberForm[num，n]以n个有效数字表示numRationalize[float]将浮点数float转换成与其相等的分数Rationalize[float，dx]将浮点数float转换成与其近似相等的分数，误差小于dx最大、最小函数Max[a，b，c，．．．]求最大数Min[a，b，c，．．．]求最小数符号函数Sign[x]Mathematica中的数学运算符a+b 加法a-b减法a*b (可用空格键代替*)乘法a/b (输入方法为：“ Ctrl ” + “ / ” ) 除法a^b (输入方法为：“ Ctrl ” + “ ^ ” )乘方-a 负号Mathematica的关系运算符==等于<小于>大于<=小于或等于>=大于或等于!=不等于注：上面的关系运算符也可从基本输入工具栏输入。

mathematica中分别绘制以下五类基本初等函数幂函数指数函数

mathematica中分别绘制以下五类基本初等函数幂函数指数函数一、文档概述本篇文章将介绍如何在Mathematica中分别绘制五类基本初等函数：幂函数、指数函数。

我们将通过详细的步骤和示例来展示如何使用Mathematica的绘图功能来创建这些函数的图像。

二、基本概念和准备1. 幂函数：幂函数是数学中常见的一种函数形式，其表达式为f(x)=x^n, 其中n为实数。

2. 指数函数：指数函数是另一种常见的函数形式，其表达式为f(x)=a^x, 其中a为常数，通常大于1。

三、绘图步骤1. 绘制幂函数(1) 打开Mathematica，创建一个新的绘图窗口。

(2) 使用`Plot`函数，将幂函数的表达式作为参数传入。

例如，要绘制x^2的图像，可以使用以下代码：`Plot[x^2, {x, -10, 10}, PlotStyle -> {Thick, Black}]`。

(3) 调整绘图范围和样式，使图像更清晰易读。

2. 绘制指数函数(1) 重复第一步，打开新的绘图窗口。

(2) 使用`Plot`函数，将指数函数的表达式作为参数传入。

例如，要绘制a^x的图像，其中a=2，可以使用以下代码：`Plot[2^x, {x, -10, 10}, PlotStyle -> {Thick, Blue}]`。

(3) 根据需要调整绘图范围和样式。

四、总结与扩展1. 通过上述步骤，我们成功地在Mathematica中绘制了幂函数和指数函数的图像。

通过调整参数和样式，我们可以得到更美观、更专业的图像。

2. 除了幂函数和指数函数，Mathematica还支持其他基本初等函数的绘制，如对数函数、三角函数等。

通过扩展这些基本知识，我们可以更好地掌握和使用Mathematica的绘图功能。

3. 在实际应用中，我们还可以将多个基本初等函数的图像结合在一起，形成复杂的函数图像，以更好地理解和分析数学问题。

4. 除了手动绘制图像，Mathematica还提供了许多强大的工具和功能，如符号计算、数值计算、数据可视化等，可以帮助我们更高效地解决数学问题。

Mathematica常用函数的中文说明及使用方法

Mathematica常⽤函数的中⽂说明及使⽤⽅法Mathematica常⽤函数的中⽂说明及使⽤⽅法---------------------------------------------------------------------注：为了对Mathematica有⼀定了解,使同学系统掌握Mathematica的强⼤功能，将常⽤函数的中⽂说明及使⽤⽅法总结如下，希望能对⼤家有所帮助。

---------------------------------------------------------------------⼀、运算符及特殊符号Line1; 执⾏Line，不显⽰结果Line1,line2 顺次执⾏Line1，2，并显⽰结果name 关于系统变量name的信息name 关于系统变量name的全部信息!command 执⾏Dos命令n! N的阶乘!!filename 显⽰⽂件内容<Expr>> filename 打开⽂件写Expr>>>filename 打开⽂件从⽂件末写() 结合率[] 函数{} ⼀个表<*Math Fun*> 在c语⾔中使⽤math的函数(*Note*) 程序的注释#n 第n个参数## 所有参数rule& 把rule作⽤于后⾯的式⼦% 前⼀次的输出%% 倒数第⼆次的输出%n 第n个输出var::note 变量var的注释"Astring " 字符串Context ` 上下⽂a+b 加a-b 减a*b或a b 乘a/b 除a^b 乘⽅base^^num 以base为进位的数lhs&&rhs 且lhs||rhs 或!lha ⾮++,-- ⾃加1，⾃减1+=,-=,*=,/= 同C语⾔>,<,>=,<=,==,!= 逻辑判断（同c）lhs=rhs ⽴即赋值lhs:=rhs 建⽴动态赋值lhs:>rhs 建⽴替换规则lhs->rhs 建⽴替换规则expr//funname 相当于filename[expr]expr/.rule 将规则rule应⽤于exprexpr//.rule 将规则rule不断应⽤于expr知道不变为⽌param_ 名为param的⼀个任意表达式（形式变量）param__ 名为param的任意多个任意表达式（形式变量）⼆、系统常数Pi 3.1415....的⽆限精度数值E 2.17828...的⽆限精度数值Catalan 0.915966..卡塔兰常数EulerGamma 0.5772....⾼斯常数GoldenRatio 1.61803...黄⾦分割数Degree Pi/180⾓度弧度换算I 复数单位Infinity ⽆穷⼤-Infinity 负⽆穷⼤ComplexInfinity 复⽆穷⼤Indeterminate 不定式三、代数计算Expand[expr] 展开表达式Factor[expr] 展开表达式Simplify[expr] 化简表达式FullSimplify[expr] 将特殊函数等也进⾏化简PowerExpand[expr] 展开所有的幂次形式ComplexExpand[expr,{x1,x2...}] 按复数实部虚部展开FunctionExpand[expr] 化简expr中的特殊函数Collect[expr, x] 合并同次项Collect[expr, {x1,x2,...}] 合并x1,x2,...的同次项Together[expr] 通分Apart[expr] 部分分式展开Apart[expr, var] 对var的部分分式展开Cancel[expr] 约分ExpandAll[expr] 展开表达式ExpandAll[expr, patt] 展开表达式FactorTerms[poly] 提出共有的数字因⼦FactorTerms[poly, x] 提出与x⽆关的数字因⼦FactorTerms[poly, {x1,x2...}] 提出与xi⽆关的数字因⼦Coefficient[expr, form] 多项式expr中form的系数Coefficient[expr, form, n] 多项式expr中form^n的系数Exponent[expr, form] 表达式expr中form的最⾼指数Numerator[expr] 表达式expr的分⼦Denominator[expr] 表达式expr的分母ExpandNumerator[expr] 展开expr的分⼦部分ExpandDenominator[expr] 展开expr的分母部分TrigExpand[expr] 展开表达式中的三⾓函数TrigFactor[expr] 给出表达式中的三⾓函数因⼦TrigFactorList[expr] 给出表达式中的三⾓函数因⼦的表TrigReduce[expr] 对表达式中的三⾓函数化简TrigToExp[expr] 三⾓到指数的转化ExpToTrig[expr] 指数到三⾓的转化RootReduce[expr]ToRadicals[expr]四、解⽅程Solve[eqns, vars] 从⽅程组eqns中解出varsSolve[eqns, vars, elims] 从⽅程组eqns中削去变量elims,解出vars DSolve[eqn, y, x] 解微分⽅程，其中y是x的函数DSolve[{eqn1,eqn2,...},{y1,y2...},x]解微分⽅程组，其中yi是x的函数DSolve[eqn, y, {x1,x2...}] 解偏微分⽅程Eliminate[eqns, vars] 把⽅程组eqns中变量vars约去SolveAlways[eqns, vars] 给出等式成⽴的所有参数满⾜的条件Reduce[eqns, vars] 化简并给出所有可能解的条件LogicalExpand[expr] ⽤&&和||将逻辑表达式展开InverseFunction[f] 求函数f的逆函数Root[f, k] 求多项式函数的第k个根Roots[lhs==rhs, var] 得到多项式⽅程的所有根五、微积分函数D[f, x] 求f[x]的微分D[f, {x, n}] 求f[x]的n阶微分D[f,x1,x2..] 求f[x]对x1,x2...偏微分Dt[f, x] 求f[x]的全微分df/dxDt[f] 求f[x]的全微分dfDt[f, {x, n}] n阶全微分df^n/dx^nDt[f,x1,x2..] 对x1,x2..的偏微分Integrate[f, x] f[x]对x在的不定积分Integrate[f, {x, xmin, xmax}] f[x]对x在区间(xmin,xmax)的定积分Integrate[f, {x, xmin, xmax}, {y, ymin, ymax}] f[x,y]的⼆重积分Limit[expr, x->x0] x趋近于x0时expr的极限Residue[expr, {x,x0}] expr在x0处的留数Series[f, {x, x0, n}] 给出f[x]在x0处的幂级数展开Series[f, {x, x0,nx}, {y, y0, ny}]先对y幂级数展开，再对xNormal[expr] 化简并给出最常见的表达式SeriesCoefficient[series, n] 给出级数中第n次项的系数SeriesCoefficient[series, {n1,n2...}]'或Derivative[n1,n2...][f] ⼀阶导数InverseSeries[s, x] 给出逆函数的级数ComposeSeries[serie1,serie2...] 给出两个基数的组合SeriesData[x,x0,{a0,a1,..},nmin,nmax,den]表⽰⼀个在x0处x的幂级数，其中ai为系数O[x]^n n阶⼩量x^nO[x, x0]^n n阶⼩量(x-x0)^n六、多项式函数Variables[poly] 给出多项式poly中独⽴变量的列表CoefficientList[poly, var] 给出多项式poly中变量var的系数CoefficientList[poly, {var1,var2...}]给出多项式poly中变量var(i)的系数列表PolynomialMod[poly, m] poly中各系数mod m同余后得到的多项式，m可为整式PolynomialQuotient[p, q, x] 以x为⾃变量的两个多项式之商式p/q PolynomialRemainder[p, q, x] 以x为⾃变量的两个多项式之余式PolynomialGCD[poly1,poly2,...] poly(i)的最⼤公因式PolynomialLCM[poly1,poly2,...] poly(i)的最⼩公倍式PolynomialReduce[poly, {poly1,poly2,...},{x1,x2...}]得到⼀个表{{a1,a2,...},b}其中Sum[ai*polyi]+b=polyResultant[poly1,poly2,var] 约去poly1,poly2中的varFactor[poly] 因式分解（在整式范围内）FactorTerms[poly] 提出poly中的数字公因⼦FactorTerms[poly, {x1,x2...}] 提出poly中与xi⽆关项的数字公因⼦FactorList[poly]给出poly各个因⼦及其指数{{poly1,exp1},{...}...}FactorSquareFreeList[poly]FactorTermsList[poly,{x1,x2...}] 给出各个因式列表，第⼀项是数字公因⼦，第⼆项是与xi⽆关的因式，其后是与xi有关的因式按升幂的排列Cyclotomic[n, x] n阶柱函数Decompose[poly, x] 迭代分解，给出{p1,p2,...},其中p1(p2(...))=poly InterpolatingPolynomial[data, var] 在数据data上的插值多项式data可以写为{f1,f2..}相当于{{x1=1,y1=f1}..}data可以写为{{x1,f1,df11,df12,..},{x2,f2,df21..}可以指定数据点上的n阶导数值RootSum[f, form] 得到f[x]=0的所有根，并求得Sum[form[xi]]七、随机函数Random[type,range] 产⽣type类型且在range范围内的均匀分布随机数type可以为Integer,Real,Complex,不写默认为Realrange为{min,max}，不写默认为{0,1}Random[] 0～1上的随机实数SeedRandom[n] 以n为seed产⽣伪随机数如果采⽤了 <在2.0版本为 <<"D:\\Math\\PACKAGES\\STATISTI\\Continuo.m" Random[distribution]可以产⽣各种分布如Random[BetaDistribution[alpha, beta]]Random[NormalDistribution[miu,sigma]]等常⽤的分布如BetaDistribution,CauchyDistribution,ChiDistribution, NoncentralChiSquareDistribution,ExponentialDistribution, ExtremeValueDistribution,NoncentralFRatioDistribution, GammaDistribution,HalfNormalDistribution, LaplaceDistribution, LogNormalDistribution,LogisticDistribution,RayleighDistribution,NoncentralStudentTDistribution, UniformDistribution, WeibullDistribution⼋、数值函数N[expr] 表达式的机器精度近似值N[expr, n] 表达式的n位近似值，n为任意正整数NSolve[lhs==rhs, var] 求⽅程数值解NSolve[eqn, var, n] 求⽅程数值解，结果精度到n位NDSolve[eqns, y, {x, xmin, xmax}]微分⽅程数值解NDSolve[eqns, {y1,y2,...}, {x, xmin, xmax}]微分⽅程组数值解FindRoot[lhs==rhs, {x,x0}] 以x0为初值，寻找⽅程数值解FindRoot[lhs==rhs, {x, xstart, xmin, xmax}]NSum[f, {i,imin,imax,di}] 数值求和，di为步长NSum[f, {i,imin,imax,di}, {j,..},..] 多维函数求和NProduct[f, {i, imin, imax, di}]函数求积NIntegrate[f, {x, xmin, xmax}] 函数数值积分优化函数：FindMinimum[f, {x,x0}] 以x0为初值，寻找函数最⼩值FindMinimum[f, {x, xstart, xmin, xmax}]ConstrainedMin[f,{inequ},{x,y,..}]inequ为线性不等式组，f为x,y..之线性函数，得到最⼩值及此时的x,y..取值ConstrainedMax[f, {inequ}, {x, y,..}]同上LinearProgramming[c,m,b] 解线性组合c.x在m.x>=b&&x>=0约束下的最⼩值，x,b,c为向量,m为矩阵LatticeReduce[{v1,v2...}] 向量组vi的极⼩⽆关组数据处理：Fit[data,funs,vars]⽤指定函数组对数据进⾏最⼩⼆乘拟和data可以为{{x1,y1,..f1},{x2,y2,..f2}..}多维的情况emp: Fit[{10.22,12,3.2,9.9}, {1, x, x^2,Sin[x]}, x]Interpolation[data]对数据进⾏差值,data同上，另外还可以为{{x1,{f1,df11,df12}},{x2,{f2,.}..}指定各阶导数InterpolationOrder默认为3次，可修改ListInterpolation[array]对离散数据插值，array可为n维ListInterpolation[array,{{xmin,xmax},{ymin,ymax},..}] FunctionInterpolation[expr,{x,xmin,xmax}, {y,ymin,ymax},..]以对应expr[xi,yi]的为数据进⾏插值Fourier[list] 对复数数据进⾏付⽒变换InverseFourier[list] 对复数数据进⾏付⽒逆变换Min[{x1,x2...},{y1,y2,...}]得到每个表中的最⼩值Max[{x1,x2...},{y1,y2,...}]得到每个表中的最⼤值Select[list, crit] 将表中使得crit为True的元素选择出来Count[list, pattern] 将表中匹配模式pattern的元素的个数Sort[list] 将表中元素按升序排列Sort[list,p] 将表中元素按p[e1,e2]为True的顺序⽐较list的任两个元素e1,e2,实际上Sort[list]中默认p=Greater集合论：Union[list1,list2..] 表listi的并集并排序Intersection[list1,list2..] 表listi的交集并排序Complement[listall,list1,list2...]从全集listall中对listi的差集九、虚数函数Re[expr] 复数表达式的实部Im[expr] 复数表达式的虚部Abs[expr] 复数表达式的模Arg[expr] 复数表达式的辐⾓Conjugate[expr] 复数表达式的共轭⼗、数的头及模式及其他操作Integer _Integer 整数Real _Real 实数Complex _Complex 复数Rational_Rational 有理数(*注：模式⽤在函数参数传递中，如MyFun[Para1_Integer,Para2_Real]规定传⼊参数的类型，另外也可⽤来判断If[Head[a]==Real,...]*) IntegerDigits[n,b,len] 数字n以b近制的前len个码元RealDigits[x,b,len] 类上FromDigits[list] IntegerDigits的反函数Rationalize[x,dx] 把实数x有理化成有理数，误差⼩于dxChop[expr, delta] 将expr中⼩于delta的部分去掉,dx默认为10^-10 Accuracy[x] 给出x⼩数部分位数,对于Pi,E等为⽆限⼤Precision[x] 给出x有效数字位数,对于Pi,E等为⽆限⼤SetAccuracy[expr, n] 设置expr显⽰时的⼩数部分位数SetPrecision[expr, n] 设置expr显⽰时的有效数字位数⼗⼀、区间函数Interval[{min, max}] 区间[min, max](* Solve[3 x+2==Interval[{-2,5}],x]*) IntervalMemberQ[interval, x] x在区间内吗？IntervalMemberQ[interval1,interval2] 区间2在区间1内吗？IntervalUnion[intv1,intv2...] 区间的并IntervalIntersection[intv1,intv2...] 区间的交⼗⼆、矩阵操作a.b.c 或 Dot[a, b, c] 矩阵、向量、张量的点积Inverse[m] 矩阵的逆Transpose[list] 矩阵的转置Transpose[list,{n1,n2..}]将矩阵list 第k⾏与第nk列交换Det[m] 矩阵的⾏列式Eigenvalues[m] 特征值Eigenvectors[m] 特征向量Eigensystem[m] 特征系统，返回{eigvalues,eigvectors}LinearSolve[m, b] 解线性⽅程组m.x==bNullSpace[m] 矩阵m的零空间，即m.NullSpace[m]==零向量RowReduce[m] m化简为阶梯矩阵Minors[m, k] m的所有k*k阶⼦矩阵的⾏列式的值(伴随阵，好像是) MatrixPower[mat, n] 阵mat⾃乘n次Outer[f,list1,list2..] listi中各个元之间相互组合，并作为f的参数的到的矩阵Outer[Times,list1,list2]给出矩阵的外积SingularValues[m] m的奇异值，结果为{u,w,v},m=Conjugate[Transpose[u]].DiagonalMatrix[w].vPseudoInverse[m] m的⼴义逆QRDecomposition[m] QR分解SchurDecomposition[m] Schur分解LUDecomposition[m] LU分解⼗三、表函数(*“表”，我认为是Mathematica中最灵活的⼀种数据类型 *)(*实际上表就是表达式，表达式也就是表，所以下⾯list==expr *) (*⼀个表中元素的位置可以⽤于⼀个表来表⽰ *)表的⽣成{e1,e2,...} ⼀个表，元素可以为任意表达式，⽆穷嵌套Table[expr,{imax}] ⽣成⼀个表，共imax个元素Table[expr,{i, imax}] ⽣成⼀个表，共imax个元素expr[i]Table[expr,{i,imin,imax},{j,jmin,jmax},..] 多维表Range[imax] 简单数表{1,2,..,imax}Range[imin, imax, di] 以di为步长的数表Array[f, n] ⼀维表，元素为f[i] (i从1到n)Array[f,{n1,n2..}] 多维表，元素为f[i,j..] (各⾃从1到ni) IdentityMatrix[n] n阶单位阵DiagonalMatrix[list] 对⾓阵元素操作Part[expr, i]或expr[[i]]第i个元expr[[-i]] 倒数第i个元expr[[i,j,..]] 多维表的元expr[[{i1,i2,..}] 返回由第i(n)的元素组成的⼦表First[expr] 第⼀个元Last[expr] 最后⼀个元Head[expr] 函数头，等于expr[[0]]Extract[expr, list] 取出由表list制定位置上expr的元素值Take[list, n] 取出表list前n个元组成的表Take[list,{m,n}] 取出表list从m到n的元素组成的表Drop[list, n] 去掉表list前n个元剩下的表，其他参数同上Rest[expr] 去掉表list第⼀个元剩下的表Select[list, crit] 把crit作⽤到每⼀个list的元上，为True的所有元组成的表表的属性Length[expr] expr第⼀曾元素的个数Dimensions[expr] 表的维数返回{n1,n2..},expr为⼀个n1*n2...的阵TensorRank[expr] 秩Depth[expr] expr最⼤深度Level[expr,n] 给出expr中第n层⼦表达式的列表Count[list, pattern] 满⾜模式的list中元的个数MemberQ[list, form] list中是否有匹配form的元FreeQ[expr, form] MemberQ的反函数Position[expr, pattern] 表中匹配模式pattern的元素的位置列表Cases[{e1,e2...},pattern]匹配模式pattern的所有元素ei的表表的操作Append[expr, elem] 返回在表expr的最后追加elem元后的表Prepend[expr, elem] 返回在表expr的最前添加elem元后的表Insert[list, elem, n] 在第n元前插⼊elemInsert[expr,elem,{i,j,..}]在元素expr[[{i,j,..}]]前插⼊elemDelete[expr, {i, j,..}] 删除元素expr[[{i,j,..}]]后剩下的表DeleteCases[expr,pattern]删除匹配pattern的所有元后剩下的表ReplacePart[expr,new,n] 将expr的第n元替换为newSort[list] 返回list按顺序排列的表Reverse[expr] 把表expr倒过来RotateLeft[expr, n] 把表expr循环左移n次RotateRight[expr, n] 把表expr循环右移n次Partition[list, n] 把list按每n各元为⼀个⼦表分割后再组成的⼤表Flatten[list] 抹平所有⼦表后得到的⼀维⼤表Flatten[list,n] 抹平到第n层Split[list] 把相同的元组成⼀个⼦表，再合成的⼤表FlattenAt[list, n] 把list[[n]]处的⼦表抹平Permutations[list] 由list的元素组成的所有全排列的列表Order[expr1,expr2] 如果expr1在expr2之前返回1,如果expr1在expr2之后返回-1,如果expr1与expr2全等返回0Signature[list] 把list通过两两交换得到标准顺序所需的交换次数(排列数)以上函数均为仅返回所需表⽽不改变原表AppendTo[list,elem] 相当于list=Append[list,elem];PrependTo[list,elem] 相当于list=Prepend[list,elem];⼗四、绘图函数⼆维作图Plot[f,{x,xmin,xmax}] ⼀维函数f[x]在区间[xmin,xmax]上的函数曲线Plot[{f1,f2..},{x,xmin,xmax}] 在⼀张图上画⼏条曲线ListPlot[{y1,y2,..}] 绘出由离散点对(n,yn)组成的图ListPlot[{{x1,y1},{x2,y2},..}] 绘出由离散点对(xn,yn)组成的图ParametricPlot[{fx,fy},{t,tmin,tmax}] 由参数⽅程在参数变化范围内的曲线ParametricPlot[{{fx,fy},{gx,gy},...},{t,tmin,tmax}]在⼀张图上画多条参数曲线选项：PlotRange->{0,1} 作图显⽰的值域范围AspectRatio->1/GoldenRatio⽣成图形的纵横⽐PlotLabel ->label 标题⽂字Axes ->{False,True} 分别制定是否画x,y轴AxesLabel->{xlabel,ylabel}x,y轴上的说明⽂字Ticks->None,Automatic,fun⽤什么⽅式画轴的刻度AxesOrigin ->{x,y} 坐标轴原点位置AxesStyle->{{xstyle}, {ystyle}}设置轴线的线性颜⾊等属性Frame ->True,False 是否画边框FrameLabel ->{xmlabel,ymlabel,xplabel,yplabel}边框四边上的⽂字FrameTicks同Ticks 边框上是否画刻度GridLines 同Ticks 图上是否画栅格线FrameStyle ->{{xmstyle},{ymstyle}设置边框线的线性颜⾊等属性ListPlot[data,PlotJoined->True] 把离散点按顺序连线PlotSytle->{{style1},{style2},..}曲线的线性颜⾊等属性PlotPoints->15 曲线取样点，越⼤越细致三维作图Plot3D[f,{x,xmin,xmax}, {y,ymin,ymax}]⼆维函数f[x,y]的空间曲⾯Plot3D[{f,s}, {x,xmin,xmax}, {y,ymin,ymax}]同上，曲⾯的染⾊由s[x,y]值决定ListPlot3D[array] ⼆维数据阵array的⽴体⾼度图ListPlot3D[array,shades]同上，曲⾯的染⾊由shades[数据]值决定ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax}]⼆元数⽅程在参数变化范围内的曲线ParametricPlot3D[{{fx,fy,fz},{gx,gy,gz},...},{t,tmin,tmax}]多条空间参数曲线选项：ViewPoint ->{x,y,z} 三维视点，默认为{1.3,-2.4,2}Boxed -> True,False 是否画三维长⽅体边框BoxRatios->{sx,sy,sz} 三轴⽐例BoxStyle 三维长⽅体边框线性颜⾊等属性Lighting ->True 是否染⾊LightSources->{s1,s2..} si为某⼀个光源si={{dx,dy,dz},color}color为灯⾊，向dx,dy,dz⽅向照射AmbientLight->颜⾊函数慢散射光的光源Mesh->True,False是否画曲⾯上与x,y轴平⾏的截⾯的截线MeshStyle 截线线性颜⾊等属性MeshRange->{{xmin,xmax}, {ymin,ymax}}⽹格范围ClipFill->Automatic,None,color,{bottom,top}指定图形顶部、底部超界后所画的颜⾊Shading ->False,True 是否染⾊HiddenSurface->True,False 略去被遮住不显⽰部分的信息等⾼线ContourPlot[f,{x,xmin,xmax},{y,ymin,ymax}]⼆维函数f[x,y]在指定区间上的等⾼线图ListContourPlot[array] 根据⼆维数组array数值画等⾼线选项：Contours->n 画n条等⾼线Contours->{z1,z2,..} 在zi处画等⾼线ContourShading -> False 是否⽤深浅染⾊ContourLines -> True 是否画等⾼线ContourStyle -> {{style1},{style2},..}等⾼线线性颜⾊等属性FrameTicks 同上密度图DensityPlot[f,{x,xmin,xmax},{y,ymin,ymax}]⼆维函数f[x,y]在指定区间上的密度图ListDensityPlot[array] 同上图形显⽰Show[graphics,options] 显⽰⼀组图形对象，options为选项设置Show[g1,g2...] 在⼀个图上叠加显⽰⼀组图形对象GraphicsArray[{g1,g2,...}]在⼀个图上分块显⽰⼀组图形对象SelectionAnimate[notebook,t]把选中的notebook中的图画循环放映选项：(此处选项适⽤于全部图形函数)Background->颜⾊函数指定绘图的背景颜⾊RotateLabel -> True 竖着写⽂字TextStyle 此后输出⽂字的字体，颜⾊⼤⼩等ColorFunction->Hue等把其作⽤于某点的函数值上决定某点的颜⾊RenderAll->False 是否对遮挡部分也染⾊MaxBend 曲线、曲⾯最⼤弯曲度⼗四、绘图函数（续）图元函数Graphics[prim, options]prim为下⾯各种函数组成的表，表⽰⼀个⼆维图形对象Graphics3D[prim, options]prim为下⾯各种函数组成的表，表⽰⼀个三维图形对象SurfaceGraphics[array, shades]表⽰⼀个由array和shade决定的曲⾯对象ContourGraphics[array]表⽰⼀个由array决定的等⾼线图对象DensityGraphics[array]表⽰⼀个由array决定的密度图对象以上定义图形对象，可以进⾏对变量赋值，合并显⽰等操作，也可以存盘Point[p] p={x,y}或{x,y,z}，在指定位置画点Line[{p1,p2,..}]经由pi点连线Rectangle[{xmin, ymin}, {xmax, ymax}] 画矩形Cuboid[{xmin,ymin,zmin},{xmax,ymax,zmax}]由对⾓线指定的长⽅体Polygon[{p1,p2,..}] 封闭多边形Circle[{x,y},r] 画圆Circle[{x,y},{rx,ry}] 画椭圆，rx,ry为半长短轴Circle[{x,y},r,{a1,a2}] 从⾓度a1～a2的圆弧Disk[{x, y}, r] 填充的园、椭圆、圆弧等参数同上Raster[array,ColorFunction->f] 颜⾊栅格Text[expr,coords] 在坐标coords上输出表达式PostScript["string"] 直接⽤PostScript图元语⾔写Scaled[{x,y,..}] 返回点的坐标，且均⼤于0⼩于1颜⾊函数(指定其后绘图的颜⾊)GrayLevel[level] 灰度level为0~1间的实数RGBColor[red, green, blue] RGB颜⾊，均为0~1间的实数Hue[h, s, b] 亮度，饱和度等，均为0~1间的实数CMYKColor[cyan, magenta, yellow, black] CMYK颜⾊其他函数(指定其后绘图的⽅式)Thickness[r] 设置线宽为rPointSize[d] 设置绘点的⼤⼩Dashing[{r1,r2,..}] 虚线⼀个单元的间隔长度ImageSize->{x, y} 显⽰图形⼤⼩(像素为单位)ImageResolution->r 图形解析度r个dpiImageMargins->{{left,right},{bottom,top}}四边的空⽩ImageRotated->False 是否旋转90度显⽰流程控制—————————————————————————————————————⼗五、流程控制分⽀If[condition, t, f] 如果condition为True,执⾏t段，否则f段If[condition, t, f, u] 同上，即⾮True⼜⾮False，则执⾏u段Which[test1,block1,test2,block2..] 执⾏第⼀为True的testi对应的blockiSwitch[expr,form1,block1,form2,block2..]执⾏第⼀个expr所匹配的formi所对应的blocki段循环Do[expr,{imax}] 重复执⾏expr imax次Do[expr,{i,imin,imax}, {j,jmin,jmax},...]多重循环While[test, body] 循环执⾏body直到test为FalseFor[start,test,incr,body]类似于C语⾔中的for，注意"，"与";"的⽤法相反examp: For[i=1;t =x,i^2<10,i++,t =t+i;Print[t]]异常控制Throw[value] 停⽌计算，把value返回给最近⼀个Catch处理Throw[value, tag] 同上，Catch[expr] 计算expr,遇到Throw返回的值则停⽌Catch[expr, form] 当Throw[value, tag]中Tag匹配form时停⽌其他控制Return[expr] 从函数返回，返回值为exprReturn[ ] 返回值NullBreak[ ] 结束最近的⼀重循环Continue[ ] 停⽌本次循环，进⾏下⼀次循环Goto[tag] ⽆条件转向Label[Tag]处Label[tag] 设置⼀个断点Check[expr,failexpr] 计算expr,如果有出错信息产⽣，则返回failexpr的值Check[expr,failexpr,s1::t1,s2::t2,...]当特定信息产⽣时则返回failexprCheckAbort[expr,failexpr]当产⽣abort信息时放回failexprInterrupt[ ] 中断运⾏Abort[ ] 中断运⾏TimeConstrained[expr,t] 计算expr，当耗时超过t秒时终⽌MemoryConstrained[expr,b]计算expr，当耗⽤内存超过b字节时终⽌运算交互式控制Print[expr1,expr2,...] 顺次输出expri的值examp: Print[ "X=" , X//N , " " ,f[x+1]];Input[ ] 产⽣⼀个输⼊对话框，返回所输⼊任意表达式Input["prompt"] 同上，prompt为对话框的提⽰Pause[n] 运⾏暂停n秒函数编程—————————————————————————————————————⼗六、函数编程(*函数编程是Mathematica中很有特⾊也是最灵活的⼀部分，它充分体现了 *)(*Mathematica的“⼀切都是表达式”的特点，如果你想使你的Mathematica程 *)(*序快于⾼级语⾔,建议你把本部分搞通*)纯函数Function[body]或body& ⼀个纯函数，建⽴了⼀组对应法则，作⽤到后⾯的表达式上Function[x, body] 单⾃变量纯函数Function[{x1,x2,...},body]多⾃变量纯函数#，#n 纯函数的第⼀、第n个⾃变量## 纯函数的所有⾃变量的序列examp: #1^#2& [2,3] 返回第⼀个参数的第⼆个参数次⽅映射Map[f,expr]或f/@expr 将f分别作⽤到expr第⼀层的每⼀个元上得到的列表Map[f,expr,level] 将f分别作⽤到expr第level层的每⼀个元上Apply[f,expr]或f@@expr 将expr的“头”换为fApply[f,expr,level] 将expr第level层的“头”换为fMapAll[f,expr]或f//@expr把f作⽤到expr的每⼀层的每⼀个元上MapAt[f,expr,n] 把f作⽤到expr的第n个元上MapAt[f,expr,{i,j,...}] 把f作⽤到expr[[{i,j,...}]]元上MapIndexed[f,expr] 类似MapAll,但都附加其映射元素的位置列表Scan[f, expr] 按顺序分别将f作⽤于expr的每⼀个元Scan[f,expr,levelspec] 同上，仅作⽤第level层的元素复合映射Nest[f,expr,n] 返回n重复合函数f[f[...f[expr]...]]NestList[f,expr,n] 返回0重到n重复合函数的列表{expr,f[expr],f[f[expr]]..} FixedPoint[f, expr] 将f复合作⽤于expr直到结果不再改变,即找到其不定点FixedPoint[f, expr, n] 最多复合n次，如果不收敛则停⽌FixedPointList[f, expr] 返回各次复合的结果列表FoldList[f,x,{a,b,..}] 返回{x,f[x,a],f[f[x,a],b],..}Fold[f, x, list] 返回FoldList[f,x,{a,b,..}]的最后⼀个元ComposeList[{f1,f2,..},x]返回{x,f1[x],f2[f1[x]],..}的复合函数列表Distribute[f[x1,x2,..]] f对加法的分配率Distribute[expr, g] 对g的分配率Identity[expr] expr的全等变换Composition[f1,f2,..] 组成复合纯函数f1[f2[..fn[ ]..]Operate[p,f[x,y]] 返回p[f][x, y]Through[p[f1,f2][x]] 返回p[f1[x],f2[x]]Compile[{x1,x2,..},expr]编译⼀个函数，编译后运⾏速度可以⼤⼤加快Compile[{{x1,t1},{x2,t2}..},expr] 同上，可以制定函数参数类型⼗七、替换规则lhs->rhs 建⽴了⼀个规则，把lhs换为rhs,并求rhs的值lhs:>rhs 同上，只是不⽴即求rhs的值，知道使⽤该规则时才求值Replace[expr,rules] 把⼀组规则应⽤到expr上，只作⽤⼀次expr /. rules 同上expr //.rules 将规则rules不断作⽤到expr上，直到⽆法作⽤为⽌Dispatch[{lhs1->rhs1,lhs2->rhs2,...}]综合各个规则，产⽣⼀组优化的规则组查询函数、串函数—————————————————————————————————————⼗⼋、查询函数(*查询函数⼀般是检验表达式是否满⾜某些特殊形式，并返回True或False*)(*可以在Mathematica中⽤“?*Q”查询到 *)ArgumentCountQ MatrixQAtomQ MemberQDigitQ NameQEllipticNomeQ NumberQEvenQ NumericQExactNumberQ OddQFreeQ OptionQHypergeometricPFQ OrderedQInexactNumberQ PartitionsQIntegerQ PolynomialQIntervalMemberQ PrimeQInverseEllipticNomeQ SameQLegendreQ StringMatchQLetterQ StringQLinkConnectedQ SyntaxQLinkReadyQ TrueQListQ UnsameQLowerCaseQ UpperCaseQMachineNumberQ ValueQMatchLocalNameQ VectorQMatchQ⼗九、字符串函数"text" ⼀个串，头为_String"s1"<>"s2"<>..或StringJoin["s1","s2",..] 串的连接StringLength["string"] 串长度StringReverse["string"] 串反转StringTake["string", n] 取串的前n个字符的⼦串，参数同Take[]StringDrop["string", n] 参见Drop,串也就是⼀个表StringInsert["string","snew",n] 插⼊，参见Insert[]StringPosition["string", "sub"] 返回⼦串sub在string中起⽌字母位置StringReplace["string",{"s1"->"p1",..}] ⼦串替换StringReplacePart["string", "snew", {m, n}]把string第m~n个字母之间的替换为snewStringToStream["string"] 把串当作⼀个输⼊流赋予⼀个变量Characters["string"] 把串"string"分解为每⼀个字符的表ToCharacterCode["string"] 把串"string"分解为每⼀个字符ASCII值的表FromCharacterCode[n] ToCharacterCode的逆函数FromCharacterCode[{n1,n2,..}]ToCharacterCode的逆函数ToUpperCase[string] 把串的⼤写形式ToLowerCase[string] 把串的⼩写形式CharacterRange["c1","c2"] 给出ASCII吗在c1到c2之间的字符列表ToString[expr] 把表达式变为串的形式ToExpression[input] 把⼀个串变为表达式Names["string"] 与?string同，返回与string同名的变量列表。

符号计算系统Mathematica的常用系统函数

符号计算系统Mathematica的常用系统函数Mathematica是一个很大的用计算机作数学的软件系统，仅在2.0版的系统中就定义了800多个函数。

这里摘选了Mathematica2.0版的部分函数和命令，其中不包括Mathematica软件包中的函数定义，因篇幅所限，对于一些函数只作了简要说明，可在任意版本中用“？？函数名”或“？？命令名”的形式得到该版本中函数和命令的更详细的使用说明.所提供的函数和命令对Mathematica2.0以后的版本仍然适用.（一）数学常数ComplexInfinity 复无穷大Degree 1°对应的弧度值，为π/180 DirectedInfinity 有方向的无穷E 自然对数的底e≈2.718 28I 虚单位i=1Indeterminate 不定值Infinity 正无穷Pi 圆周率π≈3.141 59…（二）数学函数Abort[ ] 产生中止运算过程的急停。

AbortProtect[expr ] expr的运算完成后执行中止运算过程的Abort[ ]命令.Abs[x] 给出实数x的绝对值，或给出复数x的模。

如果x不是数，则Abs[x]不作运算..AbsoluteDashing[{d1，d2，…}] 图形的样式指令，虚线线段重复循环使用d1，d2，…的长度.AbsolutePointSize[d] 图形的样式指令，d是图形上点的半径.AbsoluteThickness[d] 图形的样式指令，d是图形上直线的绝对宽度.Accuracy[x] 给出x的小数点以后的位数，如果x不是一个数，Accuracy[x]给出x 中所有数的精度的最小值，整数的精度为无穷大.Apart[expr] 将有理式写成一系列最简分式之和.Apart[expr，var] 将var以外的变量都作为常数.Append[expr，elem] 给出将元素elem追加到expr后的结果，expr的值不变.AppendTo[s，elem] 将元素elem追加到s中.Apply[f，expr] f作用于expr.例如，Apply[Plus，2，3]的值为5.ArcCos[z] 复数z的反余弦arccos z.ArcaCosh[z] 复数z的反双曲余弦arccosh z.ArcCot[z] 复数z的反余切arccot z.ArcCoth[z] 复数z的反双曲余切arccoth z.ArcCsc[z] 复数z的反余割arccsc z.ArcCsch[z] 复数z的反双曲余割arccsch z.ArcSec[z] 复数z的反正割arcsec z.ArcSech[z] 复数z的反双曲正割arcsech z.ArcSin[z] 复数z的反正弦arcsin z.ArcSinh[z] 复数z的反双曲正弦arcsinh z.ArcTan[z] 复数z的反正切arctan z.ArcTanh[z] 复数z的反双曲正切arctanh z.Arg[z] 给出复数z的辐角。

Mathematica常用语句

Mathematica常用语句一、常用常量PiπE eDegree 度(π/180)GoldenRatio 黄金分割比(0.618)Infinity 无穷大∞I 虚数单位ix=. 取消赋值xClear[x] 取消赋值x二、初等函数Log[x] ln xLog[a,x] log a xExp[x] x eSqrt[x] xSin[x] sin(x)Cos[x] cos(x)Tan[x] tan(x)Cot[x] cot(x)ArcSin[x] arcsin(x)ArcCos[x] arccos(x)三、函数的定义f[x_]:= 定义一元函数f[x_,y_]:= 定义二元函数四、常用函数：Plus[n1,n2,] 求和N[x,n] 取x的n位有效数字Abs[x] 取x的绝对值(x为复数时为取x的模) Sign[x] 符号函数Round[x] 最接近x的整数(可比x大也可比x小) Floor[x] 不大于x的最大整数Ceiling[x] 不小于x的最大整数Max[x1,x2,] 取变量x1,x2,的最大值Min[x1,x2,] 取变量x1,x2,的最小值Re[z] 取复数z的实部In[z] 取复数z的虚部Conjugate[z] 取复数z的共轭Arg[z] z的辐角Quotient[m,n] 取商函数(m被n除的整数部分)Mod[m,n] 取余函数(m被n除的余数部分)n！n的阶乘n！！n的双阶乘Binomial[n,m] 二项式系数mCn% 最近一次输出结果%% 倒数第二次输出%n 第n个输出结果Solve[方程] 解方程Fit[] 曲线拟合函数Simplify[] 用于化简的函数If语句If[条件,t,f]满足条件：执行t否则执行fIf[条件,t,f,u] 满足条件：执行t否则执行f无法判别执行u Which语句Which[条件1,t1,条件2,t2] 满足条件i执行ti五、表1、表的建立表名={元素1，元素2,}{循环变量n，循环初值n0，循环终值ni，步长增量d}(d为1时可省)Range[循环初值n0，循环终值ni，步长增量d](d为1时可省；n0为1时也可省)Table[通项公式f(m,n,)，{m,m0,mi,d1}，{ n,n0,ni,d1}]Array[f,n] 生成长为n，元素是f[i]的表Array[f,n,n0] 生成长为n，元素是f[i]且从f[n0]开始的表Array[f,{m,n}] 生成长为{m,n}，元素是f[i,j]的二维数表Array[f,{n1,n2,}] 把f作用到n1,n2,构成的表2、表的调整Length[t] 求表中元素个数(即表长)T[[n]] 表t中第n个元素T[[-n]] 表t中倒数第n个元素First[t] 表t中第一个元素Last[t] 表t中最后一个元素T[[i,j]] 表t中第i个子表中的第j个元素T[[{n1,n2,}]]或Part[t,{n1,n2,}] 由表t中n1,n2,等元素组成的数表Position[t,x] 元素x在表t中的位置Take[t,{m,n}] 从表t中取出m~n的元素Rest[t] 去掉表t中第一个元素Drop[t,{m,n}] 从表t中去掉m~n的元素Prepend[t,a] 将a加到表t的第一位Append[t,a] 将a加到表t的最后一位Insert[t,a,k] 将a加到表t的第k位Raplace[t,a,k] 用a替换表t的第k位Apply[f,t] 将函数f作用到表t的每一位Sort[t] 将元素依标准排列(数字按大小，字母按abc) Reverse[t] 将元素按顺序倒排RatateLeft[t,k] 将元素向左轮换k位RatateRight[t,k] 将元素向右轮换k位Partition[t,n] 将表t分成n个元素的块Partition[t,n,d]Transpose[t] 将表t转置Join[t1,t2] 将t1和t2合并，但是不去掉重复元素Union[t1,t2,] 并集运算Intersection[t1,t2,] 交集运算Complement[t1,t2] 从t1中去掉t2中的元素六、绘图1、绘图函数Plot[f[x],{x,a,b}] 画f[x]在区间[a,b]上的函数图象ParametricPlot[{x[t],y[t]},{t,a,b }] 画参数图ListPlot[{x1,y2},{x2,y2},] 绘制点图Plot3D[f[x,y],{x,x0,x1},{y,y0,y1}] 三维图像ParametricPlot3D[{x[t],y[t],z[t]},{t,t0,t1}]参数三维图2、绘图函数修饰项①二维绘图所用的修饰项PlotRange->{a,b} 确定函数值得范围(a~b)PlotStyle->{RGBColor[a,b,c]}确定曲线颜色P lotStyle->{AbsoluteThickness[n]}确定曲线粗细(n=1、2、)②三维绘图所用的修饰项PlotPoints->{a,b} 网格数a×b个PlotRange->{a,b} 确定函数值得范围(a~b)Axes->True/False 是否显示坐标轴Boxed->True/False 是否加立体框Mesh->True/False 是否加网格Shading ->True/False 是否在曲面着色HiddenSurface-> True/False 被挡部分是否隐藏ViewPoint->{a,b,c} 调整观察角度七、极限与导数Limit[f[x],x->a] alim ()x f x → (a 可以是∞) Limit[f[x],x->a,Direction->1]求右极限 Limit[f[x],x->a,Direction->1]求左极限 D[f[x],x]df dx 或f x ∂∂ D[f[x],{x,k}]k 阶导数或k 阶偏导 D[f,x1,x2, ,xk] 1k f x x ∂∂∂D[f[x],x,NonConstants->{v1,v2,}] 求导时vi 是关于x 的函数 Dt[f,x]复合函数f 关于x 的导数 Dt[f,{x,k}]复合函数f 关于x 的k 阶导数 Dt[f,{x,k},Constants->{c1,c2,}] 求导的时候ci 看为常数Dt[f]全微分 f `[x]一阶导数( ` 是1前面的那个) f ``[x]二阶导数 Simplify[] 用于化简的函数FindMinimum[f,{x,x0}] 在x0附近求极值点(求极大值用-f)FindMinimum[f,{x,{x0,x1}}] 以x0，x1为初始值搜索极值 (用于无导数)FindMinimum[f,{x, {x,x0,a,b}] 求以x0为初始值搜索[a,b]区间的极值FindMinimum[f,{x, {x,a,b}] 求在[a,b]间的极值FindMinimum[f,{x, {x,x0},{y,y0}]多元函数极值八、积分Integrate[f,x] 不定积分(f:被积函数,x:积分变量)Integrate[f,{x,a,b}] 定积分(f:被积函数,x:积分变量,a:上限,b:下限) Integrate[f,{x,x0,x1},{y,y0,y1},] 多重积分NIntegrate[f,{x,a,b}] 定积分近似值九、微分方程DSolve[方程组,函数f[x],变量x] 解微分方程(方程组可含有初边值条件) NDSolve[方程组,函数符号,变量符号及范围] 解微分方程数值解十、线性代数Array[a,{m,n}] 建一个m行n列的矩阵，元素为a[i,j]IndenityMatrix[n] 建一个n阶单位阵DiagonalMatrix[t] 建一个对角线上为表中元素的方阵MatrixForm[A] 将矩阵A按矩阵形式输出Det[A] 求方阵A的行列式Transpose[A] 矩阵A的转置Inverse[A ] 方阵A的逆矩阵A*B A与B对应元素相乘Dot[a,b]或a.b 数量积(.右下角)Cross[a,b]或a⨯b 向量积(⨯在输入模块上)Minors[M,k] 矩阵M的所有可能的k阶子式组成的矩阵RowReduce[A] 求A的行约化矩阵LinearSolve[A,B] 求满足Ax=B的一个解NullSpace[A] 求Ax=0的基础解析Eigenvalues[M]求方阵M 的特征值 Eigenvectors[M]求方阵M 的特征向量 Eiginsystem[M] 求方阵M 的特征值和特征向量十一、级数Series[f,{x,x0,n}] 将函数f 做泰勒展开到0()n x x SeriesCoefficient[s,n] 求级数s 中第n 阶的系数Normal[s] 舍去级数s 的余项部分 FourierTrigSeries[f[x],x,k, FourierParameters->{a,1T }]f[x]的k 阶傅里叶展开(T:周期,a:基本周期区间中心) 十二、概率Mean[d]求均值 Median[d]求中位数 Quartiles[d]求0.25分位数,中位数,0.75分位数 Quantile [d,k]求k 分位数 Variance[d]求方差(无偏估计是的方差) StandardDeviation[d] 求标准差(无偏估计是的标准差) VarianceMLE[d] 求方差(总体方差的极大似然估计) StandardDeviationMLE[d]求标准差SampleRange[d] 极差CentralMoment[d,k] k 阶中心距(k=2、3、4)Skewness[d]偏度 Kurtosis[d] 峰度BinCounts[d,{a,b,k}] 将a~b 按长度k 等分小区间，求出在每个小区间的数据个数Max[x1,x2,] 取变量x1,x2,的最大值Min[x1,x2,] 取变量x1,x2,的最小值Length[t] 求表中元素个数(即表长) BarChart[bc] 画直方图(bc为数据对)。

Mathematica中的常用函数汇总

Mathematica中的常用函数汇总数值函数:N[expr]表达式的机器精度近似值N[expr, n] 表达式的n位近似值，n为任意正整数NSolve[lhs==rhs, var] 求方程数值解NSolve[eqn, var, n] 求方程数值解，结果精度到n位NDSolve[eqns, y, {x, xmin, xmax}]微分方程数值解NDSolve[eqns, {y1,y2,...}, {x, xmin, xmax}] 微分方程组数值解FindRoot[lhs==rhs, {x,x0}] 以x0为初值，寻找方程数值解FindRoot[lhs==rhs, {x, xstart, xmin, xmax}]NSum[f, {i,imin,imax,di}] 数值求和，di为步长NSum[f, {i,imin,imax,di}, {j,..},..] 多维函数求和NProduct[f, {i, imin, imax, di}]函数求积NIntegrate[f, {x, xmin, xmax}] 函数数值积分优化函数：FindMinimum[f, {x,x0}] 以x0为初值，寻找函数最小值FindMinimum[f, {x, xstart, xmin, xmax}]ConstrainedMin[f,{inequ},{x,y,..}]inequ为线性不等式组，f为x,y..之线性函数，得到最小值及此时的x,y..取值ConstrainedMax[f, {inequ}, {x, y,..}]同上LinearProgramming[c,m,b] 解线性组合c.x在m.x>=b&&x>=0约束下的最小值，x,b,c为向量,m为矩阵LatticeReduce[{v1,v2...}] 向量组vi的极小无关组数据处理：Fit[data,funs,vars]用指定函数组对数据进行最小二乘拟和data可以为{{x1,y1,..f1},{x2,y2,..f2}..}多维的情况emp: Fit[{10.22,12,3.2,9.9}, {1, x, x^2,Sin[x]}, x]Interpolation[data]对数据进行差值,data同上，另外还可以为{{x1,{f1,df11,df12}},{x2,{f2,.}..}指定各阶导数InterpolationOrder默认为3次，可修改ListInterpolation[array]对离散数据插值，array可为n维ListInterpolation[array,{{xmin,xmax},{ymin,ymax},..}]FunctionInterpolation[expr,{x,xmin,xmax}, {y,ymin,ymax},..]以对应expr[xi,yi]的为数据进行插值Fourier[list] 对复数数据进行付氏变换InverseFourier[list] 对复数数据进行付氏逆变换Min[{x1,x2...},{y1,y2,...}]得到每个表中的最小值Max[{x1,x2...},{y1,y2,...}]得到每个表中的最大值Select[list, crit] 将表中使得crit为True的元素选择出来Count[list, pattern] 将表中匹配模式pattern的元素的个数Sort[list] 将表中元素按升序排列Sort[list,p] 将表中元素按p[e1,e2]为True的顺序比较list的任两个元素e1,e2,实际上Sort[list]中默认p=Greater集合论：Union[list1,list2..] 表listi的并集并排序Intersection[list1,list2..] 表listi的交集并排序Complement[listall,list1,list2...]从全集listall中对listi的差集虚数函数:Re[expr] 复数表达式的实部Im[expr] 复数表达式的虚部Abs[expr] 复数表达式的模Arg[expr] 复数表达式的辐角Conjugate[expr] 复数表达式的共轭数的头及模式及其他操作:Integer _Integer 整数Real _Real 实数Complex _Complex 复数Rational_Rational 有理数(*注：模式用在函数参数传递中，如MyFun[Para1_Integer,Para2_Real]规定传入参数的类型，另外也可用来判断If[Head[a]==Real,...]*)IntegerDigits[n,b,len] 数字n以b近制的前len个码元RealDigits[x,b,len] 类上FromDigits[list] IntegerDigits的反函数Rationalize[x,dx] 把实数x有理化成有理数，误差小于dxChop[expr, delta] 将expr中小于delta的部分去掉,dx默认为10^-10Accuracy[x] 给出x小数部分位数,对于Pi,E等为无限大Precision[x] 给出x有效数字位数,对于Pi,E等为无限大SetAccuracy[expr, n] 设置expr显示时的小数部分位数SetPrecision[expr, n] 设置expr显示时的有效数字位数区间函数：Interval[{min, max}] 区间[min, max](* Solve[3 x+2==Interval[{-2,5}],x]*)IntervalMemberQ[interval, x] x在区间内吗？IntervalMemberQ[interval1,interval2] 区间2在区间1内吗？IntervalUnion[intv1,intv2...] 区间的并IntervalIntersection[intv1,intv2...] 区间的交矩阵操作a.b.c 或Dot[a, b, c] 矩阵、向量、张量的点积Inverse[m] 矩阵的逆Transpose[list] 矩阵的转置Transpose[list,{n1,n2..}]将矩阵list 第k行与第nk列交换Det[m] 矩阵的行列式Eigenvalues[m] 特征值Eigenvectors[m] 特征向量Eigensystem[m] 特征系统，返回{eigvalues,eigvectors}LinearSolve[m, b] 解线性方程组m.x==bNullSpace[m] 矩阵m的零空间，即m.NullSpace[m]==零向量RowReduce[m] m化简为阶梯矩阵Minors[m, k] m的所有k*k阶子矩阵的行列式的值(伴随阵，好像是)MatrixPower[mat, n] 阵mat自乘n次Outer[f,list1,list2..] listi中各个元之间相互组合，并作为f的参数的到的矩阵Outer[Times,list1,list2]给出矩阵的外积SingularValues[m] m的奇异值，结果为{u,w,v},m=Conjugate[Transpose[u]].DiagonalMatrix[w].v PseudoInverse[m] m的广义逆QRDecomposition[m] QR分解SchurDecomposition[m] Schur分解LUDecomposition[m] LU分解运算符及特殊符号：Line1; 执行Line，不显示结果Line1,line2 顺次执行Line1，2，并显示结果?name 关于系统变量name的信息??name 关于系统变量name的全部信息!command 执行Dos命令n! N的阶乘!!filename 显示文件内容<<filename 读入文件并执行Expr>> filename 打开文件写Expr>>>filename 打开文件从文件末写() 结合率[] 函数{} 一个表<*Math Fun*> 在c语言中使用math的函数(*Note*) 程序的注释#n 第n个参数## 所有参数rule& 把rule作用于后面的式子% 前一次的输出%% 倒数第二次的输出%n 第n个输出var::note 变量var的注释"Astring " 字符串Context ` 上下文a+b 加a-b 减a*b或a b 乘a/b 除a^b 乘方base^^num 以base为进位的数lhs&&rhs 且lhs||rhs 或!lha 非++,-- 自加1，自减1+=,-=,*=,/= 同C语言>,<,>=,<=,==,!= 逻辑判断（同c）lhs=rhs 立即赋值lhs:=rhs 建立动态赋值lhs:>rhs 建立替换规则lhs->rhs 建立替换规则expr//funname 相当于filename[expr] expr/.rule 将规则rule应用于exprexpr//.rule 将规则rule不断应用于expr知道不变为止param_ 名为param的一个任意表达式（形式变量）param__ 名为param的任意多个任意表达式（形式变量）系统常数:Pi 3.1415....的无限精度数值E 2.17828...的无限精度数值Catalan 0.915966..卡塔兰常数EulerGamma 0.5772....高斯常数GoldenRatio 1.61803...黄金分割数Degree Pi/180角度弧度换算I 复数单位Infinity 无穷大-Infinity 负无穷大ComplexInfinity 复无穷大Indeterminate 不定式代数计算:Expand[expr] 展开表达式Factor[expr] 展开表达式Simplify[expr] 化简表达式FullSimplify[expr] 将特殊函数等也进行化简PowerExpand[expr] 展开所有的幂次形式ComplexExpand[expr,{x1,x2...}] 按复数实部虚部展开FunctionExpand[expr] 化简expr中的特殊函数Collect[expr, x] 合并同次项Collect[expr, {x1,x2,...}] 合并x1,x2,...的同次项Together[expr] 通分Apart[expr] 部分分式展开Apart[expr, var] 对var的部分分式展开Cancel[expr] 约分ExpandAll[expr] 展开表达式ExpandAll[expr, patt] 展开表达式FactorTerms[poly] 提出共有的数字因子FactorTerms[poly, x] 提出与x无关的数字因子FactorTerms[poly, {x1,x2...}] 提出与xi无关的数字因子Coefficient[expr, form] 多项式expr中form的系数Coefficient[expr, form, n] 多项式expr中form^n的系数Exponent[expr, form] 表达式expr中form的最高指数Numerator[expr] 表达式expr的分子Denominator[expr] 表达式expr的分母ExpandNumerator[expr] 展开expr的分子部分ExpandDenominator[expr] 展开expr的分母部分TrigExpand[expr] 展开表达式中的三角函数TrigFactor[expr] 给出表达式中的三角函数因子TrigFactorList[expr] 给出表达式中的三角函数因子的表TrigReduce[expr] 对表达式中的三角函数化简TrigToExp[expr] 三角到指数的转化ExpToTrig[expr] 指数到三角的转化RootReduce[expr] ToRadicals[expr]。

Mathematica常用函数

Mathematica函数及使用方法----------------------------------------------------------注：为了对Mathematica 有一定了解的同学系统掌握Mathematica的强大功能，我们把它的一些资料性的东西整理了一下，希望能对大家有所帮助。

----------------------------------------------------------一、运算符及特殊符号Line1; 执行Line，不显示结果Line1,line2 顺次执行Line1，2，并显示结果?name 关于系统变量name的信息??name 关于系统变量name的全部信息!command 执行Dos命令n! N的阶乘!!filename 显示文件内容< Expr>> filename 打开文件写Expr>>>filename 打开文件从文件末写() 结合率[] 函数{} 一个表<*Math Fun*> 在c语言中使用math的函数(*Note*) 程序的注释#n 第n个参数## 所有参数rule& 把rule作用于后面的式子% 前一次的输出%% 倒数第二次的输出%n 第n个输出var::note 变量var的注释"Astring " 字符串Context ` 上下文a+b 加a-b 减a*b或a b 乘a/b 除a^b 乘方base^^num 以base为进位的数lhs&&rhs 且lhs||rhs 或!lha 非++,-- 自加1，自减1+=,-=,*=,/= 同C语言>,<,>=,<=,==,!= 逻辑判断（同c）lhs=rhs 立即赋值lhs:=rhs 建立动态赋值lhs:>rhs 建立替换规则lhs->rhs 建立替换规则expr//filename 相当于filename[expr] expr/.rule 将规则rule应用于exprexpr//.rule 将规则rule不断应用于expr知道不变为止param_ 名为param的一个任意表达式（形式变量）param__ 名为param的任意多个任意表达式（形式变量）—————————————————————————————————————二、系统常数Pi 3.1415....的无限精度数值E 2.17828...的无限精度数值Catalan 0.915966..卡塔兰常数EulerGamma 0.5772....高斯常数GoldenRatio 1.61803...黄金分割数Degree Pi/180角度弧度换算I 复数单位Infinity 无穷大-Infinity 负无穷大ComplexInfinity 复无穷大Indeterminate 不定式—————————————————————————————————————三、代数计算Expand[expr] 展开表达式Factor[expr] 展开表达式Simplify[expr] 化简表达式FullSimplify[expr] 将特殊函数等也进行化简PowerExpand[expr] 展开所有的幂次形式ComplexExpand[expr,{x1,x2...}] 按复数实部虚部展开FunctionExpand[expr] 化简expr中的特殊函数Collect[expr, x] 合并同次项Collect[expr, {x1,x2,...}] 合并x1,x2,...的同次项Together[expr] 通分Apart[expr] 部分分式展开Apart[expr, var] 对var的部分分式展开Cancel[expr] 约分ExpandAll[expr] 展开表达式ExpandAll[expr, patt] 展开表达式FactorTerms[poly] 提出共有的数字因子FactorTerms[poly, x] 提出与x无关的数字因子FactorTerms[poly, {x1,x2...}] 提出与xi无关的数字因子Coefficient[expr, form] 多项式expr中form的系数Coefficient[expr, form, n] 多项式expr中form^n的系数Exponent[expr, form] 表达式expr中form的最高指数Numerator[expr] 表达式expr的分子Denominator[expr] 表达式expr的分母ExpandNumerator[expr] 展开expr的分子部分ExpandDenominator[expr] 展开expr的分母部分TrigExpand[expr] 展开表达式中的三角函数TrigFactor[expr] 给出表达式中的三角函数因子TrigFactorList[expr] 给出表达式中的三角函数因子的表TrigReduce[expr] 对表达式中的三角函数化简TrigToExp[expr] 三角到指数的转化ExpToTrig[expr] 指数到三角的转化RootReduce[expr]ToRadicals[expr]—————————————————————————————————————四、解方程Solve[eqns, vars] 从方程组eqns中解出varsSolve[eqns, vars, elims] 从方程组eqns中削去变量elims,解出varsDSolve[eqn, y, x] 解微分方程，其中y是x的函数DSolve[{eqn1,eqn2,...},{y1,y2...},x]解微分方程组，其中yi是x的函数DSolve[eqn, y, {x1,x2...}] 解偏微分方程Eliminate[eqns, vars] 把方程组eqns中变量vars约去SolveAlways[eqns, vars] 给出等式成立的所有参数满足的条件Reduce[eqns, vars] 化简并给出所有可能解的条件LogicalExpand[expr] 用&&和||将逻辑表达式展开InverseFunction[f] 求函数f的逆函数Root[f, k] 求多项式函数的第k个根Roots[lhs==rhs, var] 得到多项式方程的所有根—————————————————————————————————————五、微积分函数D[f, x] 求f[x]的微分D[f, {x, n}] 求f[x]的n阶微分D[f,x1,x2..] 求f[x]对x1,x2...偏微分Dt[f, x] 求f[x]的全微分df/dxDt[f] 求f[x]的全微分dfDt[f, {x, n}] n阶全微分df^n/dx^nDt[f,x1,x2..] 对x1,x2..的偏微分Integrate[f, x] f[x]对x在的不定积分Integrate[f, {x, xmin, xmax}] f[x]对x在区间(xmin,xmax)的定积分Integrate[f, {x, xmin, xmax}, {y, ymin, ymax}] f[x,y]的二重积分Limit[expr, x->x0] x趋近于x0时expr的极限Residue[expr, {x,x0}] expr在x0处的留数Series[f, {x, x0, n}] 给出f[x]在x0处的幂级数展开Series[f, {x, x0,nx}, {y, y0, ny}]先对y幂级数展开，再对xNormal[expr] 化简并给出最常见的表达式SeriesCoefficient[series, n] 给出级数中第n次项的系数SeriesCoefficient[series, {n1,n2...}]'或Derivative[n1,n2...][f] 一阶导数InverseSeries[s, x] 给出逆函数的级数ComposeSeries[serie1,serie2...] 给出两个基数的组合SeriesData[x,x0,{a0,a1,..},nmin,nmax,den]表示一个在x0处x的幂级数，其中ai为系数O[x]^n n阶小量x^nO[x, x0]^n n阶小量(x-x0)^n—————————————————————————————————————八、数值函数N[expr] 表达式的机器精度近似值N[expr, n] 表达式的n位近似值，n为任意正整数NSolve[lhs==rhs, var] 求方程数值解NSolve[eqn, var, n] 求方程数值解，结果精度到n位NDSolve[eqns, y, {x, xmin, xmax}]微分方程数值解NDSolve[eqns, {y1,y2,...}, {x, xmin, xmax}]微分方程组数值解FindRoot[lhs==rhs, {x,x0}] 以x0为初值，寻找方程数值解FindRoot[lhs==rhs, {x, xstart, xmin, xmax}]NSum[f, {i,imin,imax,di}] 数值求和，di为步长NSum[f, {i,imin,imax,di}, {j,..},..] 多维函数求和NProduct[f, {i, imin, imax, di}]函数求积NIntegrate[f, {x, xmin, xmax}] 函数数值积分优化函数：FindMinimum[f, {x,x0}] 以x0为初值，寻找函数最小值FindMinimum[f, {x, xstart, xmin, xmax}]ConstrainedMin[f,{inequ},{x,y,..}]inequ为线性不等式组，f为x,y..之线性函数，得到最小值及此时的x,y..取值ConstrainedMax[f, {inequ}, {x, y,..}]同上LinearProgramming[c,m,b] 解线性组合c.x在m.x>=b&&x>=0约束下的最小值，x,b,c为向量,m为矩阵LatticeReduce[{v1,v2...}] 向量组vi的极小无关组数据处理：Fit[data,funs,vars]用指定函数组对数据进行最小二乘拟和data可以为{{x1,y1,..f1},{x2,y2,..f2}..}多维的情况emp: Fit[{10.22,12,3.2,9.9}, {1, x, x^2,Sin[x]}, x]Interpolation[data]对数据进行差值,data同上，另外还可以为{{x1,{f1,df11,df12}},{x2,{f2,.}..}指定各阶导数InterpolationOrder默认为3次，可修改ListInterpolation[array]对离散数据插值，array可为n维ListInterpolation[array,{{xmin,xmax},{ymin,ymax},..}] FunctionInterpolation[expr,{x,xmin,xmax}, {y,ymin,ymax},..]以对应expr[xi,yi]的为数据进行插值Fourier[list] 对复数数据进行付氏变换InverseFourier[list] 对复数数据进行付氏逆变换Min[{x1,x2...},{y1,y2,...}]得到每个表中的最小值Max[{x1,x2...},{y1,y2,...}]得到每个表中的最大值Select[list, crit] 将表中使得crit为True的元素选择出来Count[list, pattern] 将表中匹配模式pattern的元素的个数Sort[list] 将表中元素按升序排列Sort[list,p] 将表中元素按p[e1,e2]为True的顺序比较list的任两个元素e1,e2,实际上Sort[list]中默认p=Greater集合论：Union[list1,list2..] 表listi的并集并排序Intersection[list1,list2..] 表listi的交集并排序Complement[listall,list1,list2...]从全集listall中对listi的差集—————————————————————————————————————九、虚数函数Re[expr] 复数表达式的实部Im[expr] 复数表达式的虚部Abs[expr] 复数表达式的模Arg[expr] 复数表达式的辐角Conjugate[expr] 复数表达式的共轭—————————————————————————————————————十、数的头及模式及其他操作Integer _Integer 整数Real _Real 实数Complex _Complex 复数Rational_Rational 有理数(*注：模式用在函数参数传递中，如MyFun[Para1_Integer,Para2_Real]规定传入参数的类型，另外也可用来判断If[Head[a]==Real,...]*)IntegerDigits[n,b,len] 数字n以b近制的前len个码元RealDigits[x,b,len] 类上FromDigits[list] IntegerDigits的反函数Rationalize[x,dx] 把实数x有理化成有理数，误差小于dxChop[expr, delta] 将expr中小于delta的部分去掉,dx默认为10^-10Accuracy[x] 给出x小数部分位数,对于Pi,E等为无限大Precision[x] 给出x有效数字位数,对于Pi,E等为无限大SetAccuracy[expr, n] 设置expr显示时的小数部分位数SetPrecision[expr, n] 设置expr显示时的有效数字位数—————————————————————————————————————十一、区间函数Interval[{min, max}] 区间[min, max](* Solve[3 x+2==Interval[{-2,5}],x]*) IntervalMemberQ[interval, x] x在区间内吗？IntervalMemberQ[interval1,interval2] 区间2在区间1内吗？IntervalUnion[intv1,intv2...] 区间的并IntervalIntersection[intv1,intv2...] 区间的交—————————————————————————————————————十二、矩阵操作a.b.c 或 Dot[a, b, c] 矩阵、向量、张量的点积Inverse[m] 矩阵的逆Transpose[list] 矩阵的转置Transpose[list,{n1,n2..}]将矩阵list 第k行与第nk列交换Det[m] 矩阵的行列式Eigenvalues[m] 特征值Eigenvectors[m] 特征向量Eigensystem[m] 特征系统，返回{eigvalues,eigvectors}LinearSolve[m, b] 解线性方程组m.x==bNullSpace[m] 矩阵m的零空间，即m.NullSpace[m]==零向量RowReduce[m] m化简为阶梯矩阵Minors[m, k] m的所有k*k阶子矩阵的行列式的值(伴随阵，好像是)MatrixPower[mat, n] 阵mat自乘n次Outer[f,list1,list2..] listi中各个元之间相互组合，并作为f的参数的到的矩阵Outer[Times,list1,list2]给出矩阵的外积SingularValues[m] m的奇异值，结果为{u,w,v},m=Conjugate[Transpose[u]].DiagonalMatrix[w].vPseudoInverse[m] m的广义逆QRDecomposition[m] QR分解SchurDecomposition[m] Schur分解LUDecomposition[m] LU分解—————————————————————————————————————十三、表函数(*“表”，我认为是Mathematica中最灵活的一种数据类型 *)(*实际上表就是表达式，表达式也就是表，所以下面list==expr *)(*一个表中元素的位置可以用于一个表来表示 *)表的生成{e1,e2,...} 一个表，元素可以为任意表达式，无穷嵌套Table[expr,{imax}] 生成一个表，共imax个元素Table[expr,{i, imax}] 生成一个表，共imax个元素expr[i] Table[expr,{i,imin,imax},{j,jmin,jmax},..] 多维表Range[imax] 简单数表{1,2,..,imax}Range[imin, imax, di] 以di为步长的数表Array[f, n] 一维表，元素为f[i] (i从1到n)Array[f,{n1,n2..}] 多维表，元素为f[i,j..] (各自从1到ni) IdentityMatrix[n] n阶单位阵DiagonalMatrix[list] 对角阵元素操作Part[expr, i]或expr[[i]]第i个元expr[[-i]] 倒数第i个元expr[[i,j,..]] 多维表的元expr[[{i1,i2,..}] 返回由第i(n)的元素组成的子表First[expr] 第一个元Last[expr] 最后一个元Head[expr] 函数头，等于expr[[0]]Extract[expr, list] 取出由表list制定位置上expr的元素值Take[list, n] 取出表list前n个元组成的表Take[list,{m,n}] 取出表list从m到n的元素组成的表Drop[list, n] 去掉表list前n个元剩下的表，其他参数同上Rest[expr] 去掉表list第一个元剩下的表Select[list, crit] 把crit作用到每一个list的元上，为True的所有元组成的表表的属性Length[expr] expr第一曾元素的个数Dimensions[expr] 表的维数返回{n1,n2..},expr为一个n1*n2...的阵TensorRank[expr] 秩Depth[expr] expr最大深度Level[expr,n] 给出expr中第n层子表达式的列表Count[list, pattern] 满足模式的list中元的个数MemberQ[list, form] list中是否有匹配form的元FreeQ[expr, form] MemberQ的反函数Position[expr, pattern] 表中匹配模式pattern的元素的位置列表Cases[{e1,e2...},pattern]匹配模式pattern的所有元素ei的表表的操作Append[expr, elem] 返回在表expr的最后追加elem元后的表Prepend[expr, elem] 返回在表expr的最前添加elem元后的表Insert[list, elem, n] 在第n元前插入elemInsert[expr,elem,{i,j,..}]在元素expr[[{i,j,..}]]前插入elem Delete[expr, {i, j,..}] 删除元素expr[[{i,j,..}]]后剩下的表DeleteCases[expr,pattern]删除匹配pattern的所有元后剩下的表ReplacePart[expr,new,n] 将expr的第n元替换为newSort[list] 返回list按顺序排列的表Reverse[expr] 把表expr倒过来RotateLeft[expr, n] 把表expr循环左移n次RotateRight[expr, n] 把表expr循环右移n次Partition[list, n] 把list按每n各元为一个子表分割后再组成的大表Flatten[list] 抹平所有子表后得到的一维大表Flatten[list,n] 抹平到第n层Split[list] 把相同的元组成一个子表，再合成的大表FlattenAt[list, n] 把list[[n]]处的子表抹平Permutations[list] 由list的元素组成的所有全排列的列表Order[expr1,expr2] 如果expr1在expr2之前返回1,如果expr1在expr2之后返回-1,如果expr1与expr2全等返回0Signature[list] 把list通过两两交换得到标准顺序所需的交换次数(排列数)以上函数均为仅返回所需表而不改变原表AppendTo[list,elem] 相当于list=Append[list,elem];PrependTo[list,elem] 相当于list=Prepend[list,elem];--—————————————————————————————————————十四、绘图函数二维作图Plot[f,{x,xmin,xmax}] 一维函数f[x]在区间[xmin,xmax]上的函数曲线Plot[{f1,f2..},{x,xmin,xmax}] 在一张图上画几条曲线ListPlot[{y1,y2,..}] 绘出由离散点对(n,yn)组成的图ListPlot[{{x1,y1},{x2,y2},..}] 绘出由离散点对(xn,yn)组成的图ParametricPlot[{fx,fy},{t,tmin,tmax}] 由参数方程在参数变化范围内的曲线ParametricPlot[{{fx,fy},{gx,gy},...},{t,tmin,tmax}]在一张图上画多条参数曲线选项：PlotRange->{0,1} 作图显示的值域范围AspectRatio->1/GoldenRatio生成图形的纵横比PlotLabel ->label 标题文字Axes ->{False,True} 分别制定是否画x,y轴AxesLabel->{xlabel,ylabel}x,y轴上的说明文字Ticks->None,Automatic,fun用什么方式画轴的刻度AxesOrigin ->{x,y} 坐标轴原点位置AxesStyle->{{xstyle}, {ystyle}}设置轴线的线性颜色等属性Frame ->True,False 是否画边框FrameLabel ->{xmlabel,ymlabel,xplabel,yplabel}边框四边上的文字FrameTicks同Ticks 边框上是否画刻度GridLines 同Ticks 图上是否画栅格线FrameStyle ->{{xmstyle},{ymstyle}设置边框线的线性颜色等属性ListPlot[data,PlotJoined->True] 把离散点按顺序连线PlotSytle->{{style1},{style2},..}曲线的线性颜色等属性PlotPoints->15 曲线取样点，越大越细致三维作图Plot3D[f,{x,xmin,xmax}, {y,ymin,ymax}]二维函数f[x,y]的空间曲面Plot3D[{f,s}, {x,xmin,xmax}, {y,ymin,ymax}]同上，曲面的染色由s[x,y]值决定ListPlot3D[array] 二维数据阵array的立体高度图ListPlot3D[array,shades]同上，曲面的染色由shades[数据]值决定ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax}]二元数方程在参数变化范围内的曲线ParametricPlot3D[{{fx,fy,fz},{gx,gy,gz},...},{t,tmin,tmax}] 多条空间参数曲线选项：ViewPoint ->{x,y,z} 三维视点，默认为{1.3,-2.4,2}Boxed -> True,False 是否画三维长方体边框BoxRatios->{sx,sy,sz} 三轴比例BoxStyle 三维长方体边框线性颜色等属性Lighting ->True 是否染色LightSources->{s1,s2..} si为某一个光源si={{dx,dy,dz},color} color为灯色，向dx,dy,dz方向照射AmbientLight->颜色函数慢散射光的光源Mesh->True,False 是否画曲面上与x,y轴平行的截面的截线MeshStyle 截线线性颜色等属性MeshRange->{{xmin,xmax}, {ymin,ymax}}网格范围ClipFill->Automatic,None,color,{bottom,top}指定图形顶部、底部超界后所画的颜色Shading ->False,True 是否染色HiddenSurface->True,False 略去被遮住不显示部分的信息等高线ContourPlot[f,{x,xmin,xmax},{y,ymin,ymax}]二维函数f[x,y]在指定区间上的等高线图ListContourPlot[array] 根据二维数组array数值画等高线选项：Contours->n 画n条等高线Contours->{z1,z2,..} 在zi处画等高线ContourShading -> False 是否用深浅染色ContourLines -> True 是否画等高线ContourStyle -> {{style1},{style2},..}等高线线性颜色等属性FrameTicks 同上密度图DensityPlot[f,{x,xmin,xmax},{y,ymin,ymax}]二维函数f[x,y]在指定区间上的密度图ListDensityPlot[array] 同上图形显示Show[graphics,options] 显示一组图形对象，options为选项设置Show[g1,g2...] 在一个图上叠加显示一组图形对象GraphicsArray[{g1,g2,...}]在一个图上分块显示一组图形对象SelectionAnimate[notebook,t]把选中的notebook中的图画循环放映选项：(此处选项适用于全部图形函数)Background->颜色函数指定绘图的背景颜色RotateLabel -> True 竖着写文字TextStyle 此后输出文字的字体，颜色大小等ColorFunction->Hue等把其作用于某点的函数值上决定某点的颜色RenderAll->False 是否对遮挡部分也染色MaxBend 曲线、曲面最大弯曲度绘图函数（续）图元函数Graphics[prim, options]prim为下面各种函数组成的表，表示一个二维图形对象Graphics3D[prim, options]prim为下面各种函数组成的表，表示一个三维图形对象SurfaceGraphics[array, shades]表示一个由array和shade决定的曲面对象ContourGraphics[array]表示一个由array决定的等高线图对象DensityGraphics[array]表示一个由array决定的密度图对象以上定义图形对象，可以进行对变量赋值，合并显示等操作，也可以存盘Point[p] p={x,y}或{x,y,z}，在指定位置画点Line[{p1,p2,..}]经由pi点连线Rectangle[{xmin, ymin}, {xmax, ymax}] 画矩形Cuboid[{xmin,ymin,zmin},{xmax,ymax,zmax}]由对角线指定的长方体Polygon[{p1,p2,..}] 封闭多边形Circle[{x,y},r] 画圆Circle[{x,y},{rx,ry}] 画椭圆，rx,ry为半长短轴Circle[{x,y},r,{a1,a2}] 从角度a1～a2的圆弧Disk[{x, y}, r] 填充的园、椭圆、圆弧等参数同上Raster[array,ColorFunction->f] 颜色栅格Text[expr,coords] 在坐标coords上输出表达式PostScript["string"] 直接用PostScript图元语言写Scaled[{x,y,..}] 返回点的坐标，且均大于0小于1颜色函数(指定其后绘图的颜色)GrayLevel[level] 灰度level为0~1间的实数RGBColor[red, green, blue] RGB颜色，均为0~1间的实数Hue[h, s, b] 亮度，饱和度等，均为0~1间的实数CMYKColor[cyan, magenta, yellow, black] CMYK颜色其他函数(指定其后绘图的方式)Thickness[r] 设置线宽为rPointSize[d] 设置绘点的大小Dashing[{r1,r2,..}] 虚线一个单元的间隔长度ImageSize->{x, y} 显示图形大小(像素为单位)ImageResolution->r 图形解析度r个dpiImageMargins->{{left,right},{bottom,top}}四边的空白ImageRotated->False 是否旋转90度显示—————————————————————————————————————十五、流程控制分支If[condition, t, f] 如果condition为True,执行t段，否则f段If[condition, t, f, u] 同上，即非True又非False，则执行u段Which[test1,block1,test2,block2..] 执行第一为True的testi对应的blocki Switch[expr,form1,block1,form2,block2..]执行第一个expr所匹配的formi所对应的blocki段循环Do[expr,{imax}] 重复执行expr imax次Do[expr,{i,imin,imax}, {j,jmin,jmax},...]多重循环While[test, body] 循环执行body直到test为FalseFor[start,test,incr,body]类似于C语言中的for，注意"，"与";"的用法相反examp: For[i=1;t =x,i^2<10,i++,t =t+i;Print[t]]异常控制Throw[value] 停止计算，把value返回给最近一个Catch处理Throw[value, tag] 同上，Catch[expr] 计算expr,遇到Throw返回的值则停止Catch[expr, form] 当Throw[value, tag]中Tag匹配form时停止其他控制Return[expr] 从函数返回，返回值为exprReturn[ ] 返回值NullBreak[ ] 结束最近的一重循环Continue[ ] 停止本次循环，进行下一次循环Goto[tag] 无条件转向Label[Tag]处Label[tag] 设置一个断点Check[expr,failexpr] 计算expr,如果有出错信息产生，则返回failexpr的值Check[expr,failexpr,s1::t1,s2::t2,...]当特定信息产生时则返回failexpr CheckAbort[expr,failexpr]当产生abort信息时放回failexprInterrupt[ ] 中断运行Abort[ ] 中断运行TimeConstrained[expr,t] 计算expr，当耗时超过t秒时终止MemoryConstrained[expr,b]计算expr，当耗用内存超过b字节时终止运算交互式控制Print[expr1,expr2,...] 顺次输出expri的值examp: Print[ "X=" , X//N , " " ,f[x+1]];Input[ ] 产生一个输入对话框，返回所输入任意表达式Input["prompt"] 同上，prompt为对话框的提示Pause[n] 运行暂停n秒—————————————————————————————————————十六、函数编程(*函数编程是Mathematica中很有特色也是最灵活的一部分，它充分体现了 *)(*Mathematica的“一切都是表达式”的特点，如果你想使你的Mathematica程 *) (*序快于高级语言,建议你把本部分搞通*)纯函数Function[body]或body& 一个纯函数，建立了一组对应法则，作用到后面的表达式上Function[x, body] 单自变量纯函数Function[{x1,x2,...},body]多自变量纯函数#，#n 纯函数的第一、第n个自变量## 纯函数的所有自变量的序列examp: ^& [2,3] 返回第一个参数的第二个参数次方映射Map[f,expr]或f/@expr 将f分别作用到expr第一层的每一个元上得到的列表Map[f,expr,level] 将f分别作用到expr第level层的每一个元上Apply[f,expr]或f@@expr 将expr的“头”换为fApply[f,expr,level] 将expr第level层的“头”换为fMapAll[f,expr]或f//@expr把f作用到expr的每一层的每一个元上MapAt[f,expr,n] 把f作用到expr的第n个元上MapAt[f,expr,{i,j,...}] 把f作用到expr[[{i,j,...}]]元上MapIndexed[f,expr] 类似MapAll,但都附加其映射元素的位置列表Scan[f, expr] 按顺序分别将f作用于expr的每一个元Scan[f,expr,levelspec] 同上，仅作用第level层的元素复合映射Nest[f,expr,n] 返回n重复合函数f[f[...f[expr]...]]NestList[f,expr,n] 返回0重到n重复合函数的列表{expr,f[expr],f[f[expr]]..} FixedPoint[f, expr] 将f复合作用于expr直到结果不再改变,即找到其不定点FixedPoint[f, expr, n] 最多复合n次，如果不收敛则停止FixedPointList[f, expr] 返回各次复合的结果列表FoldList[f,x,{a,b,..}] 返回{x,f[x,a],f[f[x,a],b],..}Fold[f, x, list] 返回FoldList[f,x,{a,b,..}]的最后一个元ComposeList[{f1,f2,..},x]返回{x,f1[x],f2[f1[x]],..}的复合函数列表Distribute[f[x1,x2,..]] f对加法的分配率Distribute[expr, g] 对g的分配率Identity[expr] expr的全等变换Composition[f1,f2,..] 组成复合纯函数f1[f2[..fn[ ]..]Operate[p,f[x,y]] 返回p[f][x, y]Through[p[f1,f2][x]] 返回p[f1[x],f2[x]]Compile[{x1,x2,..},expr]编译一个函数，编译后运行速度可以大大加快Compile[{{x1,t1},{x2,t2}..},expr] 同上，可以制定函数参数类型—————————————————————————————————————十七、替换规则lhs->rhs 建立了一个规则，把lhs换为rhs,并求rhs的值lhs:>rhs 同上，只是不立即求rhs的值，知道使用该规则时才求值Replace[expr,rules] 把一组规则应用到expr上，只作用一次expr /. rules 同上expr //.rules 将规则rules不断作用到expr上，直到无法作用为止Dispatch[{lhs1->rhs1,lhs2->rhs2,...}]综合各个规则，产生一组优化的规则组>************************************************************************< Mathematica的常见问题>************************************************************************<===================================1).Mathematica 可以定义变量为实数么？1. 在Simplify/FullSimplify可以使用\[Element]，如Simplify[Re[a+b*I],a\[Element]Reals]2. 可以使用ComplexExpand[]来展开表达式，默认：符号均为实数：Unprotect[Abs];Abs[x_] := Sqrt[Re[x]^2 + Im[x]^2];ComplexExpand[Abs[a + b*I], a]3. 使用/:，对符号关联相应的转换规则x /: Im[x] = 0;x /: Re[x] = x;y /: Im[y] = 0;y /: Re[y] = y;Re[x+y*I]===================================2).Mathematica中如何中断运算？Alt+. 直接终止当前执行的运算Alt+, 询问是否终止或者继续如果不能终止，用菜单Kernel\Quit Kernal\Local来退出当前运算===================================3).请高手推荐Mathematica参考书我迄今为止看到的最好的一本就是Mathematica自己带的帮助里面的The Mathematica Book，内容全面，循序渐近，非常容易学习使用。

Mathematica常用函数

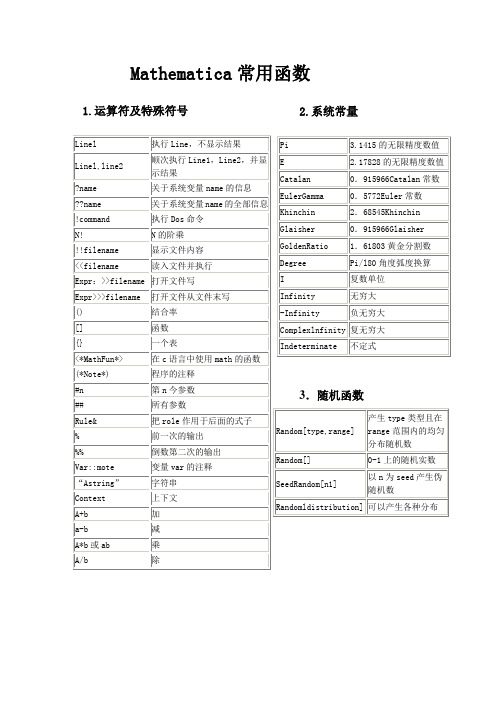
Mathematica 常用函数1.运算符及特殊符号2.系统常量3．随机函数4．代数计算5．解方程6．微积分7．多项式函数8．数值函数9．表相关函数(1)制表函数(2)元素操作(3)表的操作10．绘图函数(1)二维绘图(2)二维设置(3)三维绘图(4)三维设置(5)密度图(6)图形显示(7)图元函数(8)着色及其他11．流程控制函数Mathematica可进行矩阵的各种运算,如矩阵求逆、矩阵的转置、矩阵与向量的乘法等.下面列出主要的运算.记k为常数,u,v为向量,A,B为矩阵k*A------------------------常数乘矩阵k+u-----------------------向量u的每一个元素加上ku+v----------------------向量的对应元素相加u.v-----------------------向量的内积u*v-----------------------向量的对应元素相乘A.u---------------------矩阵乘向量u.A-----------------------向量乘矩阵A.B--------------------------矩阵乘矩阵Transpose[A]-----------------求矩阵A的转置阵Inverse[A]--------------------求矩阵A的逆矩阵Det[A]-------------------------求矩阵A的行列式Eigenvalues[A]-----------------求数字阵A的特征值Eigentvectors[A]---------------求数字阵A的特征向量LinearSolve[A,v]---------------求解线性方程组Ax=vChop[%n]-------------------舍去第n个输出中无实际意义小量矩阵可以左乘以向量或右乘以向量, Mathematica也不区分“行”,或“列”向量,自动进行可能的运算.例:In[1]:=A={{a,b},{c,d}}; v={x,y};In[2]:=A.v (A左乘以v)Out[2]={ax+by,cx+dy}In[3]:=v.A (A右乘以v)Out[3]={ax+cy,bx+dy}In[4]:=Inverse[A]Out[4]=如果矩阵的元素是近似数，则求出的逆矩阵也是近似的。

用mathematica解常微分方程

用mathematica解常微分方程用Mathematica解常微分方程常微分方程（Ordinary Differential Equation，ODE）是数学中的一个重要分支，它描述了未知函数的导数与自变量之间的关系。

在物理学、工程学、生物学等领域中，常微分方程是描述自然现象和过程的重要工具。

为了解决常微分方程，我们可以利用数值方法或符号计算工具。

其中，Mathematica是一种非常强大的符号计算软件，可以帮助我们解决各种数学问题，包括求解常微分方程。

Mathematica提供了多种函数和方法来求解常微分方程，下面将介绍其中的一些常用函数和使用方法。

1. DSolve函数DSolve函数是Mathematica中用于求解常微分方程的主要函数之一。

它可以解析地求解一阶和高阶常微分方程。

例如，我们可以使用DSolve函数求解一阶线性常微分方程dy/dx + p(x)y = q(x)，其中p(x)和q(x)是已知函数。

下面是一个示例：```mathematicaDSolve[y'[x] + x*y[x] == x^2, y[x], x]```这个命令将求解方程y'[x] + x*y[x] = x^2，并给出其通解。

2. NDSolve函数NDSolve函数是Mathematica中用于数值求解常微分方程的函数。

对于不能通过解析方法求解的常微分方程，我们可以使用NDSolve 函数进行数值求解。

例如，我们可以使用NDSolve函数求解二阶常微分方程y''[x] + p(x)*y'[x] + q(x)*y[x] = r(x)，其中p(x)、q(x)和r(x)是已知函数。

下面是一个示例：```mathematicaNDSolve[{y''[x] + x*y'[x] + y[x] == Sin[x], y[0] == 0, y'[0] == 1}, y[x], {x, 0, 10}]```这个命令将求解方程y''[x] + x*y'[x] + y[x] = Sin[x]，并给出其在x=0到x=10之间的数值解。

mathematica 常用函数

表2-1一些最常用的数学函数
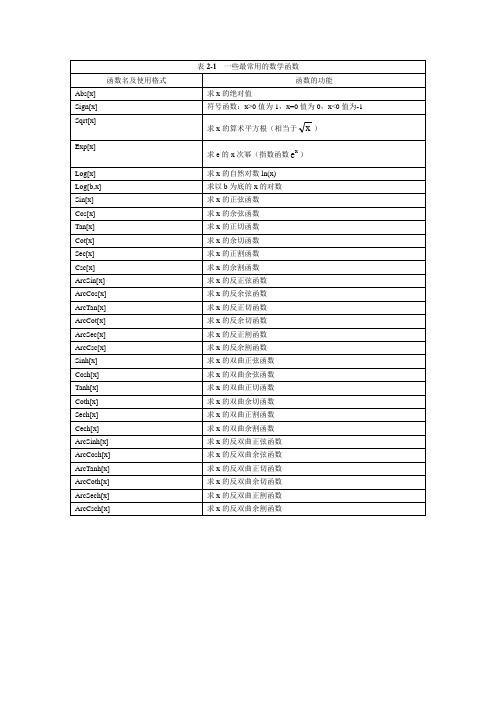
函数名及使用格式
函数的功能
Abs[x]
求x的绝对值
Sign[x]
符号函数：x>0值为1，x=0值为0，x<0值为-1
Sqrt[x]
求x的算术平方根（相当于）
Exp[x]
求e的x次幂（指数函数）
Log[x]
求x的自然对数ln(x)
Log[b,x]
求以b为底的x的对数
Sin[x]
求x的正弦函数
Cos[x]
求x的余弦函数
Tan[x]
求x的正切函数
Cot[x]
求x的余切函数
Sec[x]
求x的正割函数
Csc[x]
求x的余割函数
ArcSin[x]
求x的反正弦函数
ArcCos[x]
求x的反余弦函数
ArcTan[x]
求x的反正切函数
ArcCot[x]
求x的反余切函数
ArcSec[x]
求x的反正割函数
FactorInteger [n]
求出整数n的所有质数（素数）因子
Round[x]
求最接近于x的整数
Floor[x]
求不大于x的最大整数（即高斯函数）
Ceiling[x]
求不小于x的最小整数
IntegerPart[x]
求x的整数部分
FractionalPart[x]
求x的小数部分
Mod[m,n]
求m除以n的余数，即取模运算
n!!
求n的双阶乘n(n-2)(n-4)…
Binomial[n,m]
求组合数（二项式系数）
Permutations[{n1,n2,…}]
列出序列{n1,n2,…}的所有排列

Mathematica常用函数

Mathematica函数及使用方法----------------------------------------------------------注：为了对Mathematica 有一定了解的同学系统掌握Mathematica的强大功能，我们把它的一些资料性的东西整理了一下，希望能对大家有所帮助。

----------------------------------------------------------一、运算符及特殊符号Line1; 执行Line，不显示结果Line1,line2 顺次执行Line1，2，并显示结果?name 关于系统变量name的信息??name 关于系统变量name的全部信息!command 执行Dos命令n! N的阶乘!!filename 显示文件内容< Expr>> filename 打开文件写Expr>>>filename 打开文件从文件末写() 结合率[] 函数{} 一个表<*Math Fun*> 在c语言中使用math的函数(*Note*) 程序的注释#n 第n个参数## 所有参数rule& 把rule作用于后面的式子% 前一次的输出%% 倒数第二次的输出%n 第n个输出var::note 变量var的注释"Astring " 字符串Context ` 上下文a+b 加a-b 减a*b或a b 乘a/b 除a^b 乘方base^^num 以base为进位的数lhs&&rhs 且lhs||rhs 或!lha 非++,-- 自加1，自减1+=,-=,*=,/= 同C语言>,<,>=,<=,==,!= 逻辑判断（同c）lhs=rhs 立即赋值lhs:=rhs 建立动态赋值lhs:>rhs 建立替换规则lhs->rhs 建立替换规则expr//filename 相当于filename[expr] expr/.rule 将规则rule应用于exprexpr//.rule 将规则rule不断应用于expr知道不变为止param_ 名为param的一个任意表达式（形式变量）param__ 名为param的任意多个任意表达式（形式变量）—————————————————————————————————————二、系统常数Pi 3.1415....的无限精度数值E 2.17828...的无限精度数值Catalan 0.915966..卡塔兰常数EulerGamma 0.5772....高斯常数GoldenRatio 1.61803...黄金分割数Degree Pi/180角度弧度换算I 复数单位Infinity 无穷大-Infinity 负无穷大ComplexInfinity 复无穷大Indeterminate 不定式—————————————————————————————————————三、代数计算Expand[expr] 展开表达式Factor[expr] 展开表达式Simplify[expr] 化简表达式FullSimplify[expr] 将特殊函数等也进行化简PowerExpand[expr] 展开所有的幂次形式ComplexExpand[expr,{x1,x2...}] 按复数实部虚部展开FunctionExpand[expr] 化简expr中的特殊函数Collect[expr, x] 合并同次项Collect[expr, {x1,x2,...}] 合并x1,x2,...的同次项Together[expr] 通分Apart[expr] 部分分式展开Apart[expr, var] 对var的部分分式展开Cancel[expr] 约分ExpandAll[expr] 展开表达式ExpandAll[expr, patt] 展开表达式FactorTerms[poly] 提出共有的数字因子FactorTerms[poly, x] 提出与x无关的数字因子FactorTerms[poly, {x1,x2...}] 提出与xi无关的数字因子Coefficient[expr, form] 多项式expr中form的系数Coefficient[expr, form, n] 多项式expr中form^n的系数Exponent[expr, form] 表达式expr中form的最高指数Numerator[expr] 表达式expr的分子Denominator[expr] 表达式expr的分母ExpandNumerator[expr] 展开expr的分子部分ExpandDenominator[expr] 展开expr的分母部分TrigExpand[expr] 展开表达式中的三角函数TrigFactor[expr] 给出表达式中的三角函数因子TrigFactorList[expr] 给出表达式中的三角函数因子的表TrigReduce[expr] 对表达式中的三角函数化简TrigToExp[expr] 三角到指数的转化ExpToTrig[expr] 指数到三角的转化RootReduce[expr]ToRadicals[expr]—————————————————————————————————————四、解方程Solve[eqns, vars] 从方程组eqns中解出varsSolve[eqns, vars, elims] 从方程组eqns中削去变量elims,解出varsDSolve[eqn, y, x] 解微分方程，其中y是x的函数DSolve[{eqn1,eqn2,...},{y1,y2...},x]解微分方程组，其中yi是x的函数DSolve[eqn, y, {x1,x2...}] 解偏微分方程Eliminate[eqns, vars] 把方程组eqns中变量vars约去SolveAlways[eqns, vars] 给出等式成立的所有参数满足的条件Reduce[eqns, vars] 化简并给出所有可能解的条件LogicalExpand[expr] 用&&和||将逻辑表达式展开InverseFunction[f] 求函数f的逆函数Root[f, k] 求多项式函数的第k个根Roots[lhs==rhs, var] 得到多项式方程的所有根—————————————————————————————————————五、微积分函数D[f, x] 求f[x]的微分D[f, {x, n}] 求f[x]的n阶微分D[f,x1,x2..] 求f[x]对x1,x2...偏微分Dt[f, x] 求f[x]的全微分df/dxDt[f] 求f[x]的全微分dfDt[f, {x, n}] n阶全微分df^n/dx^nDt[f,x1,x2..] 对x1,x2..的偏微分Integrate[f, x] f[x]对x在的不定积分Integrate[f, {x, xmin, xmax}] f[x]对x在区间(xmin,xmax)的定积分Integrate[f, {x, xmin, xmax}, {y, ymin, ymax}] f[x,y]的二重积分Limit[expr, x->x0] x趋近于x0时expr的极限Residue[expr, {x,x0}] expr在x0处的留数Series[f, {x, x0, n}] 给出f[x]在x0处的幂级数展开Series[f, {x, x0,nx}, {y, y0, ny}]先对y幂级数展开，再对xNormal[expr] 化简并给出最常见的表达式SeriesCoefficient[series, n] 给出级数中第n次项的系数SeriesCoefficient[series, {n1,n2...}]'或Derivative[n1,n2...][f] 一阶导数InverseSeries[s, x] 给出逆函数的级数ComposeSeries[serie1,serie2...] 给出两个基数的组合SeriesData[x,x0,{a0,a1,..},nmin,nmax,den]表示一个在x0处x的幂级数，其中ai为系数O[x]^n n阶小量x^nO[x, x0]^n n阶小量(x-x0)^n—————————————————————————————————————八、数值函数N[expr] 表达式的机器精度近似值N[expr, n] 表达式的n位近似值，n为任意正整数NSolve[lhs==rhs, var] 求方程数值解NSolve[eqn, var, n] 求方程数值解，结果精度到n位NDSolve[eqns, y, {x, xmin, xmax}]微分方程数值解NDSolve[eqns, {y1,y2,...}, {x, xmin, xmax}]微分方程组数值解FindRoot[lhs==rhs, {x,x0}] 以x0为初值，寻找方程数值解FindRoot[lhs==rhs, {x, xstart, xmin, xmax}]NSum[f, {i,imin,imax,di}] 数值求和，di为步长NSum[f, {i,imin,imax,di}, {j,..},..] 多维函数求和NProduct[f, {i, imin, imax, di}]函数求积NIntegrate[f, {x, xmin, xmax}] 函数数值积分优化函数：FindMinimum[f, {x,x0}] 以x0为初值，寻找函数最小值FindMinimum[f, {x, xstart, xmin, xmax}]ConstrainedMin[f,{inequ},{x,y,..}]inequ为线性不等式组，f为x,y..之线性函数，得到最小值及此时的x,y..取值ConstrainedMax[f, {inequ}, {x, y,..}]同上LinearProgramming[c,m,b] 解线性组合c.x在m.x>=b&&x>=0约束下的最小值，x,b,c为向量,m为矩阵LatticeReduce[{v1,v2...}] 向量组vi的极小无关组数据处理：Fit[data,funs,vars]用指定函数组对数据进行最小二乘拟和data可以为{{x1,y1,..f1},{x2,y2,..f2}..}多维的情况emp: Fit[{10.22,12,3.2,9.9}, {1, x, x^2,Sin[x]}, x]Interpolation[data]对数据进行差值,data同上，另外还可以为{{x1,{f1,df11,df12}},{x2,{f2,.}..}指定各阶导数InterpolationOrder默认为3次，可修改ListInterpolation[array]对离散数据插值，array可为n维ListInterpolation[array,{{xmin,xmax},{ymin,ymax},..}] FunctionInterpolation[expr,{x,xmin,xmax}, {y,ymin,ymax},..]以对应expr[xi,yi]的为数据进行插值Fourier[list] 对复数数据进行付氏变换InverseFourier[list] 对复数数据进行付氏逆变换Min[{x1,x2...},{y1,y2,...}]得到每个表中的最小值Max[{x1,x2...},{y1,y2,...}]得到每个表中的最大值Select[list, crit] 将表中使得crit为True的元素选择出来Count[list, pattern] 将表中匹配模式pattern的元素的个数Sort[list] 将表中元素按升序排列Sort[list,p] 将表中元素按p[e1,e2]为True的顺序比较list的任两个元素e1,e2,实际上Sort[list]中默认p=Greater集合论：Union[list1,list2..] 表listi的并集并排序Intersection[list1,list2..] 表listi的交集并排序Complement[listall,list1,list2...]从全集listall中对listi的差集—————————————————————————————————————九、虚数函数Re[expr] 复数表达式的实部Im[expr] 复数表达式的虚部Abs[expr] 复数表达式的模Arg[expr] 复数表达式的辐角Conjugate[expr] 复数表达式的共轭—————————————————————————————————————十、数的头及模式及其他操作Integer _Integer 整数Real _Real 实数Complex _Complex 复数Rational_Rational 有理数(*注：模式用在函数参数传递中，如MyFun[Para1_Integer,Para2_Real]规定传入参数的类型，另外也可用来判断If[Head[a]==Real,...]*)IntegerDigits[n,b,len] 数字n以b近制的前len个码元RealDigits[x,b,len] 类上FromDigits[list] IntegerDigits的反函数Rationalize[x,dx] 把实数x有理化成有理数，误差小于dxChop[expr, delta] 将expr中小于delta的部分去掉,dx默认为10^-10Accuracy[x] 给出x小数部分位数,对于Pi,E等为无限大Precision[x] 给出x有效数字位数,对于Pi,E等为无限大SetAccuracy[expr, n] 设置expr显示时的小数部分位数SetPrecision[expr, n] 设置expr显示时的有效数字位数—————————————————————————————————————十一、区间函数Interval[{min, max}] 区间[min, max](* Solve[3 x+2==Interval[{-2,5}],x]*) IntervalMemberQ[interval, x] x在区间内吗？IntervalMemberQ[interval1,interval2] 区间2在区间1内吗？IntervalUnion[intv1,intv2...] 区间的并IntervalIntersection[intv1,intv2...] 区间的交—————————————————————————————————————十二、矩阵操作a.b.c 或 Dot[a, b, c] 矩阵、向量、张量的点积Inverse[m] 矩阵的逆Transpose[list] 矩阵的转置Transpose[list,{n1,n2..}]将矩阵list 第k行与第nk列交换Det[m] 矩阵的行列式Eigenvalues[m] 特征值Eigenvectors[m] 特征向量Eigensystem[m] 特征系统，返回{eigvalues,eigvectors}LinearSolve[m, b] 解线性方程组m.x==bNullSpace[m] 矩阵m的零空间，即m.NullSpace[m]==零向量RowReduce[m] m化简为阶梯矩阵Minors[m, k] m的所有k*k阶子矩阵的行列式的值(伴随阵，好像是)MatrixPower[mat, n] 阵mat自乘n次Outer[f,list1,list2..] listi中各个元之间相互组合，并作为f的参数的到的矩阵Outer[Times,list1,list2]给出矩阵的外积SingularValues[m] m的奇异值，结果为{u,w,v},m=Conjugate[Transpose[u]].DiagonalMatrix[w].vPseudoInverse[m] m的广义逆QRDecomposition[m] QR分解SchurDecomposition[m] Schur分解LUDecomposition[m] LU分解—————————————————————————————————————十三、表函数(*“表”，我认为是Mathematica中最灵活的一种数据类型 *)(*实际上表就是表达式，表达式也就是表，所以下面list==expr *)(*一个表中元素的位置可以用于一个表来表示 *)表的生成{e1,e2,...} 一个表，元素可以为任意表达式，无穷嵌套Table[expr,{imax}] 生成一个表，共imax个元素Table[expr,{i, imax}] 生成一个表，共imax个元素expr[i] Table[expr,{i,imin,imax},{j,jmin,jmax},..] 多维表Range[imax] 简单数表{1,2,..,imax}Range[imin, imax, di] 以di为步长的数表Array[f, n] 一维表，元素为f[i] (i从1到n)Array[f,{n1,n2..}] 多维表，元素为f[i,j..] (各自从1到ni) IdentityMatrix[n] n阶单位阵DiagonalMatrix[list] 对角阵元素操作Part[expr, i]或expr[[i]]第i个元expr[[-i]] 倒数第i个元expr[[i,j,..]] 多维表的元expr[[{i1,i2,..}] 返回由第i(n)的元素组成的子表First[expr] 第一个元Last[expr] 最后一个元Head[expr] 函数头，等于expr[[0]]Extract[expr, list] 取出由表list制定位置上expr的元素值Take[list, n] 取出表list前n个元组成的表Take[list,{m,n}] 取出表list从m到n的元素组成的表Drop[list, n] 去掉表list前n个元剩下的表，其他参数同上Rest[expr] 去掉表list第一个元剩下的表Select[list, crit] 把crit作用到每一个list的元上，为True的所有元组成的表表的属性Length[expr] expr第一曾元素的个数Dimensions[expr] 表的维数返回{n1,n2..},expr为一个n1*n2...的阵TensorRank[expr] 秩Depth[expr] expr最大深度Level[expr,n] 给出expr中第n层子表达式的列表Count[list, pattern] 满足模式的list中元的个数MemberQ[list, form] list中是否有匹配form的元FreeQ[expr, form] MemberQ的反函数Position[expr, pattern] 表中匹配模式pattern的元素的位置列表Cases[{e1,e2...},pattern]匹配模式pattern的所有元素ei的表表的操作Append[expr, elem] 返回在表expr的最后追加elem元后的表Prepend[expr, elem] 返回在表expr的最前添加elem元后的表Insert[list, elem, n] 在第n元前插入elemInsert[expr,elem,{i,j,..}]在元素expr[[{i,j,..}]]前插入elem Delete[expr, {i, j,..}] 删除元素expr[[{i,j,..}]]后剩下的表DeleteCases[expr,pattern]删除匹配pattern的所有元后剩下的表ReplacePart[expr,new,n] 将expr的第n元替换为newSort[list] 返回list按顺序排列的表Reverse[expr] 把表expr倒过来RotateLeft[expr, n] 把表expr循环左移n次RotateRight[expr, n] 把表expr循环右移n次Partition[list, n] 把list按每n各元为一个子表分割后再组成的大表Flatten[list] 抹平所有子表后得到的一维大表Flatten[list,n] 抹平到第n层Split[list] 把相同的元组成一个子表，再合成的大表FlattenAt[list, n] 把list[[n]]处的子表抹平Permutations[list] 由list的元素组成的所有全排列的列表Order[expr1,expr2] 如果expr1在expr2之前返回1,如果expr1在expr2之后返回-1,如果expr1与expr2全等返回0Signature[list] 把list通过两两交换得到标准顺序所需的交换次数(排列数)以上函数均为仅返回所需表而不改变原表AppendTo[list,elem] 相当于list=Append[list,elem];PrependTo[list,elem] 相当于list=Prepend[list,elem];--—————————————————————————————————————十四、绘图函数二维作图Plot[f,{x,xmin,xmax}] 一维函数f[x]在区间[xmin,xmax]上的函数曲线Plot[{f1,f2..},{x,xmin,xmax}] 在一张图上画几条曲线ListPlot[{y1,y2,..}] 绘出由离散点对(n,yn)组成的图ListPlot[{{x1,y1},{x2,y2},..}] 绘出由离散点对(xn,yn)组成的图ParametricPlot[{fx,fy},{t,tmin,tmax}] 由参数方程在参数变化范围内的曲线ParametricPlot[{{fx,fy},{gx,gy},...},{t,tmin,tmax}]在一张图上画多条参数曲线选项：PlotRange->{0,1} 作图显示的值域范围AspectRatio->1/GoldenRatio生成图形的纵横比PlotLabel ->label 标题文字Axes ->{False,True} 分别制定是否画x,y轴AxesLabel->{xlabel,ylabel}x,y轴上的说明文字Ticks->None,Automatic,fun用什么方式画轴的刻度AxesOrigin ->{x,y} 坐标轴原点位置AxesStyle->{{xstyle}, {ystyle}}设置轴线的线性颜色等属性Frame ->True,False 是否画边框FrameLabel ->{xmlabel,ymlabel,xplabel,yplabel}边框四边上的文字FrameTicks同Ticks 边框上是否画刻度GridLines 同Ticks 图上是否画栅格线FrameStyle ->{{xmstyle},{ymstyle}设置边框线的线性颜色等属性ListPlot[data,PlotJoined->True] 把离散点按顺序连线PlotSytle->{{style1},{style2},..}曲线的线性颜色等属性PlotPoints->15 曲线取样点，越大越细致三维作图Plot3D[f,{x,xmin,xmax}, {y,ymin,ymax}]二维函数f[x,y]的空间曲面Plot3D[{f,s}, {x,xmin,xmax}, {y,ymin,ymax}]同上，曲面的染色由s[x,y]值决定ListPlot3D[array] 二维数据阵array的立体高度图ListPlot3D[array,shades]同上，曲面的染色由shades[数据]值决定ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax}]二元数方程在参数变化范围内的曲线ParametricPlot3D[{{fx,fy,fz},{gx,gy,gz},...},{t,tmin,tmax}] 多条空间参数曲线选项：ViewPoint ->{x,y,z} 三维视点，默认为{1.3,-2.4,2}Boxed -> True,False 是否画三维长方体边框BoxRatios->{sx,sy,sz} 三轴比例BoxStyle 三维长方体边框线性颜色等属性Lighting ->True 是否染色LightSources->{s1,s2..} si为某一个光源si={{dx,dy,dz},color} color为灯色，向dx,dy,dz方向照射AmbientLight->颜色函数慢散射光的光源Mesh->True,False 是否画曲面上与x,y轴平行的截面的截线MeshStyle 截线线性颜色等属性MeshRange->{{xmin,xmax}, {ymin,ymax}}网格范围ClipFill->Automatic,None,color,{bottom,top}指定图形顶部、底部超界后所画的颜色Shading ->False,True 是否染色HiddenSurface->True,False 略去被遮住不显示部分的信息等高线ContourPlot[f,{x,xmin,xmax},{y,ymin,ymax}]二维函数f[x,y]在指定区间上的等高线图ListContourPlot[array] 根据二维数组array数值画等高线选项：Contours->n 画n条等高线Contours->{z1,z2,..} 在zi处画等高线ContourShading -> False 是否用深浅染色ContourLines -> True 是否画等高线ContourStyle -> {{style1},{style2},..}等高线线性颜色等属性FrameTicks 同上密度图DensityPlot[f,{x,xmin,xmax},{y,ymin,ymax}]二维函数f[x,y]在指定区间上的密度图ListDensityPlot[array] 同上图形显示Show[graphics,options] 显示一组图形对象，options为选项设置Show[g1,g2...] 在一个图上叠加显示一组图形对象GraphicsArray[{g1,g2,...}]在一个图上分块显示一组图形对象SelectionAnimate[notebook,t]把选中的notebook中的图画循环放映选项：(此处选项适用于全部图形函数)Background->颜色函数指定绘图的背景颜色RotateLabel -> True 竖着写文字TextStyle 此后输出文字的字体，颜色大小等ColorFunction->Hue等把其作用于某点的函数值上决定某点的颜色RenderAll->False 是否对遮挡部分也染色MaxBend 曲线、曲面最大弯曲度绘图函数（续）图元函数Graphics[prim, options]prim为下面各种函数组成的表，表示一个二维图形对象Graphics3D[prim, options]prim为下面各种函数组成的表，表示一个三维图形对象SurfaceGraphics[array, shades]表示一个由array和shade决定的曲面对象ContourGraphics[array]表示一个由array决定的等高线图对象DensityGraphics[array]表示一个由array决定的密度图对象以上定义图形对象，可以进行对变量赋值，合并显示等操作，也可以存盘Point[p] p={x,y}或{x,y,z}，在指定位置画点Line[{p1,p2,..}]经由pi点连线Rectangle[{xmin, ymin}, {xmax, ymax}] 画矩形Cuboid[{xmin,ymin,zmin},{xmax,ymax,zmax}]由对角线指定的长方体Polygon[{p1,p2,..}] 封闭多边形Circle[{x,y},r] 画圆Circle[{x,y},{rx,ry}] 画椭圆，rx,ry为半长短轴Circle[{x,y},r,{a1,a2}] 从角度a1～a2的圆弧Disk[{x, y}, r] 填充的园、椭圆、圆弧等参数同上Raster[array,ColorFunction->f] 颜色栅格Text[expr,coords] 在坐标coords上输出表达式PostScript["string"] 直接用PostScript图元语言写Scaled[{x,y,..}] 返回点的坐标，且均大于0小于1颜色函数(指定其后绘图的颜色)GrayLevel[level] 灰度level为0~1间的实数RGBColor[red, green, blue] RGB颜色，均为0~1间的实数Hue[h, s, b] 亮度，饱和度等，均为0~1间的实数CMYKColor[cyan, magenta, yellow, black] CMYK颜色其他函数(指定其后绘图的方式)Thickness[r] 设置线宽为rPointSize[d] 设置绘点的大小Dashing[{r1,r2,..}] 虚线一个单元的间隔长度ImageSize->{x, y} 显示图形大小(像素为单位)ImageResolution->r 图形解析度r个dpiImageMargins->{{left,right},{bottom,top}}四边的空白ImageRotated->False 是否旋转90度显示—————————————————————————————————————十五、流程控制分支If[condition, t, f] 如果condition为True,执行t段，否则f段If[condition, t, f, u] 同上，即非True又非False，则执行u段Which[test1,block1,test2,block2..] 执行第一为True的testi对应的blocki Switch[expr,form1,block1,form2,block2..]执行第一个expr所匹配的formi所对应的blocki段循环Do[expr,{imax}] 重复执行expr imax次Do[expr,{i,imin,imax}, {j,jmin,jmax},...]多重循环While[test, body] 循环执行body直到test为FalseFor[start,test,incr,body]类似于C语言中的for，注意"，"与";"的用法相反examp: For[i=1;t =x,i^2<10,i++,t =t+i;Print[t]]异常控制Throw[value] 停止计算，把value返回给最近一个Catch处理Throw[value, tag] 同上，Catch[expr] 计算expr,遇到Throw返回的值则停止Catch[expr, form] 当Throw[value, tag]中Tag匹配form时停止其他控制Return[expr] 从函数返回，返回值为exprReturn[ ] 返回值NullBreak[ ] 结束最近的一重循环Continue[ ] 停止本次循环，进行下一次循环Goto[tag] 无条件转向Label[Tag]处Label[tag] 设置一个断点Check[expr,failexpr] 计算expr,如果有出错信息产生，则返回failexpr的值Check[expr,failexpr,s1::t1,s2::t2,...]当特定信息产生时则返回failexpr CheckAbort[expr,failexpr]当产生abort信息时放回failexprInterrupt[ ] 中断运行Abort[ ] 中断运行TimeConstrained[expr,t] 计算expr，当耗时超过t秒时终止MemoryConstrained[expr,b]计算expr，当耗用内存超过b字节时终止运算交互式控制Print[expr1,expr2,...] 顺次输出expri的值examp: Print[ "X=" , X//N , " " ,f[x+1]];Input[ ] 产生一个输入对话框，返回所输入任意表达式Input["prompt"] 同上，prompt为对话框的提示Pause[n] 运行暂停n秒—————————————————————————————————————十六、函数编程(*函数编程是Mathematica中很有特色也是最灵活的一部分，它充分体现了 *)(*Mathematica的“一切都是表达式”的特点，如果你想使你的Mathematica程 *) (*序快于高级语言,建议你把本部分搞通*)纯函数Function[body]或body& 一个纯函数，建立了一组对应法则，作用到后面的表达式上Function[x, body] 单自变量纯函数Function[{x1,x2,...},body]多自变量纯函数#，#n 纯函数的第一、第n个自变量## 纯函数的所有自变量的序列examp: ^& [2,3] 返回第一个参数的第二个参数次方映射Map[f,expr]或f/@expr 将f分别作用到expr第一层的每一个元上得到的列表Map[f,expr,level] 将f分别作用到expr第level层的每一个元上Apply[f,expr]或f@@expr 将expr的“头”换为fApply[f,expr,level] 将expr第level层的“头”换为fMapAll[f,expr]或f//@expr把f作用到expr的每一层的每一个元上MapAt[f,expr,n] 把f作用到expr的第n个元上MapAt[f,expr,{i,j,...}] 把f作用到expr[[{i,j,...}]]元上MapIndexed[f,expr] 类似MapAll,但都附加其映射元素的位置列表Scan[f, expr] 按顺序分别将f作用于expr的每一个元Scan[f,expr,levelspec] 同上，仅作用第level层的元素复合映射Nest[f,expr,n] 返回n重复合函数f[f[...f[expr]...]]NestList[f,expr,n] 返回0重到n重复合函数的列表{expr,f[expr],f[f[expr]]..} FixedPoint[f, expr] 将f复合作用于expr直到结果不再改变,即找到其不定点FixedPoint[f, expr, n] 最多复合n次，如果不收敛则停止FixedPointList[f, expr] 返回各次复合的结果列表FoldList[f,x,{a,b,..}] 返回{x,f[x,a],f[f[x,a],b],..}Fold[f, x, list] 返回FoldList[f,x,{a,b,..}]的最后一个元ComposeList[{f1,f2,..},x]返回{x,f1[x],f2[f1[x]],..}的复合函数列表Distribute[f[x1,x2,..]] f对加法的分配率Distribute[expr, g] 对g的分配率Identity[expr] expr的全等变换Composition[f1,f2,..] 组成复合纯函数f1[f2[..fn[ ]..]Operate[p,f[x,y]] 返回p[f][x, y]Through[p[f1,f2][x]] 返回p[f1[x],f2[x]]Compile[{x1,x2,..},expr]编译一个函数，编译后运行速度可以大大加快Compile[{{x1,t1},{x2,t2}..},expr] 同上，可以制定函数参数类型—————————————————————————————————————十七、替换规则lhs->rhs 建立了一个规则，把lhs换为rhs,并求rhs的值lhs:>rhs 同上，只是不立即求rhs的值，知道使用该规则时才求值Replace[expr,rules] 把一组规则应用到expr上，只作用一次expr /. rules 同上expr //.rules 将规则rules不断作用到expr上，直到无法作用为止Dispatch[{lhs1->rhs1,lhs2->rhs2,...}]综合各个规则，产生一组优化的规则组>************************************************************************< Mathematica的常见问题>************************************************************************<===================================1).Mathematica 可以定义变量为实数么？1. 在Simplify/FullSimplify可以使用\[Element]，如Simplify[Re[a+b*I],a\[Element]Reals]2. 可以使用ComplexExpand[]来展开表达式，默认：符号均为实数：Unprotect[Abs];Abs[x_] := Sqrt[Re[x]^2 + Im[x]^2];ComplexExpand[Abs[a + b*I], a]3. 使用/:，对符号关联相应的转换规则x /: Im[x] = 0;x /: Re[x] = x;y /: Im[y] = 0;y /: Re[y] = y;Re[x+y*I]===================================2).Mathematica中如何中断运算？Alt+. 直接终止当前执行的运算Alt+, 询问是否终止或者继续如果不能终止，用菜单Kernel\Quit Kernal\Local来退出当前运算===================================3).请高手推荐Mathematica参考书我迄今为止看到的最好的一本就是Mathematica自己带的帮助里面的The Mathematica Book，内容全面，循序渐近，非常容易学习使用。

Mathematica常用函数的中文说明及使用方法

I 复数单位
Infinity 无穷大
-Infinity 负无穷大
ComplexInfinity 复无穷大
Indeterminate 不定式
三、代数计算
---------------------------------------------------------------------
一、运算符及特殊符号
Line1; 执行Line，不显示结果
Line1,line2 顺次执行Line1，2，并显示结果
Dt[f] 求f[x]的全微分df
Dt[f, {x, n}] n阶全微分df^n/dx^n
Dt[f,x1,x2..] 对x1,x2..的偏微分
Catalan 0.915966..卡塔兰常数
EulerGamma 0.5772....高斯常数
GoldenRatio 1.61803...黄金分割数
Degree Pi/180角度弧度换算
ExpandDenominator[expr] 展开expr的分母部分
TrigExpand[expr] 展开表达式中的三角函数
TrigFactor[expr] 给出表达式中的三角函数因子
Coefficient[expr, form] 多项式expr中form的系数
Coefficient[expr, form, n] 多项式expr中form^n的系数
Exponent[expr, form] 表达式expr中form的最高指数
lhs->rhs 建立替换规则
expr//funname 相当于filename[expr]
expr/.rule 将规则rule应用于expr

Mathematica学习笔记(自己总结)

Mathematica 学习笔记一、Mathematica介绍Mathematica在Notebook界面下，可以通过交互方式完成各种运算，如函数作图，求极限，解方程等，也可以编写结构化程序。

在Mathematical系统中定义了许多功能强大的内建函数（built-in function），这些函数分为两类：一类是数学意义上的函数：二类是命令意义上的函数：注意：Mathematica严格区分大小写，一般地，内建函数的首写字母必须大写，有时一个函数名由几个单词构成，则每个单词的首字母也必须大写，例如求局部极小值函数FindMinimum [f[x], {x, x0}]二、表达式的输入1、 Mathematica中提供了两种格式的数学表达式，形如 x/(2+3x)+y*(x-w) 的称为一维格式，形如x2+3x +yx−w称为二维格式。

可以使用快捷方式输入二维格式，也可以使用基本工具栏输入二维格式。

2、特殊符号的输入三、数据类型和常数1、数值类型在Mathematica中，基本的数值类型有四种：整数、有理数、实数和复数。

如果计算机的内存足够大，Mathematica可以表示任意长度的精确实数，而不受所用的计算机字长的影响。

整数与整数的计算结果仍是精确地整数或是有理数。

在Mathematica中允许使用分数，用有理数表示化简过的分数。

当两个整数相除而不能整除时，系统就用有理数来表示，即有理数是由两个整数的比来组成。

实数有两种方法表示：一种是小数点，另一种是指数方法表示的。

实数也可以与整数，有理数进行混合运算，结果还是一个实数。

复数是由实部和虚部组成，实部和虚部可以用整数，实数，有理数表示，在Mathematica中，用i表示虚数单位，如：3+0.7i2、不同类型数的转换在Mathematica的不同应用中，通常对数字的类型要求是不同的。

例如在公式推导中的数字常用整数或有理数表示，而在数值计算中数字常用实数表示。

Mathematica常用函数

Mathematica常用函数基本运算a+b+c 加a-b 减a b c 或a*b*c 乘a/b 除-a 负号a^b 次方Mathematica 数字的形式256 整数2.56 实数11/35 分数2+6I 复数常用的数学常数Pi 圆周率，π=3.141592654…E 尤拉常数，e=2.71828182…Degree 角度转换弧度的常数，Pi/180I 虚数，其值为√-1Infinity 无限大指定之前计算结果的方法% 前一个运算结果%% 前二个运算结果%%…%(n个%) 前n个运算结果%n 或Out[n] 前n个运算结果复数的运算指令a+bI 复数Conjugate[a+bI] 共轭复数Re[z], Im[z] 复数z的实数/虚数部分Abs[z] 复数z的大小或模数(Modulus)Arg[z] 复数z的幅角(Argument)Mathematica 输出的控制指令expr1; expr2; expr3 做数个运算，但只印出最后一个运算的结果expr1; expr2; expr3; 做数个运算，但都不印出结果expr; 做运算，但不印出结果常用数学函数Sin[x],Cos[x],Tan[x],Cot[x],Sec[x],Csc[x] 三角函数，其引数的单位为弧度Sinh[x],Cosh[x],Tanh[x],… 双曲函数ArcSin[x],ArcCos[x],ArcTan[x] 反三角函数ArcCot[x],ArcSec[x],ArcCsc[x]ArcSinh[x],ArcCosh[x],ArcTanh[x],… 反双曲函数Sqrt[x] 根号Exp[x] 指数Log[x] 自然对数Log[a,x] 以a为底的对数Abs[x] 绝对值Round[x] 最接近x的整数Floor[x] 小于或等于x的最大整数Ceiling[x] 大于或等于x的最小整数Mod[a,b] a/b所得的馀数n! 阶乘Random[] 0至1之间的随机数（最新版本已经不用这个函数，改为使用RandomReal[]）Max[a,b,c,...]，Min[a,b,c,…] a,b,c,…的极大/极小值数值设定x=a 将变数x的值设为ax=y=b 将变数x和y的值均设为bx=. 或Clear[x] 除去变数x所存的值变数使用的一些法则xy 中间没有空格，视为变数xyx y x乘上y3x 3乘上xx3 变数x3x^2y 为x^2 y次方运算子比乘法的运算子有较高的处理顺序四个处理指令Expand[expr] 将expr展开Factor[expr] 将expr因式分解Simplify[expr] 将expr化简成精简的式子FullSimplify[expr] Mathematica 会尝试更多的化简公式，将expr化成更精简的式子多项式/分式转换ExpandAll[expr] 把算式全部展开Together[expr] 将expr各项通分在并成一项Apart[expr] 把分式拆开成数项分式的和Apart[expr,var] 视var以外的变数为常数，将expr拆成数项的和Cancel[expr] 把分子和分母共同的因子消去分母/分子运算Denominator[expr] 取出expr的分母Numerator[expr] 取出expr的分子ExpandDenominator[expr] 展开expr的分母ExpandNumerator[expr] 展开expr的分子多项式转换函数Collect[expr,x] 将expr表示成x的多项式，如Collect[expr,{x,y,…}] 将expr分别表示成x,y,…的多项式FactorTerms[expr] 将expr的数值因子提出，如4x+2=2(2x+1)FactorTerms[expr,x] 将expr中把所有不包含x项的因子提出FactorTerms[e xpr,{x,y,…}] 将expr中把所有不包含{x,y,...}项的因子提出函数和指数运算TrigExpand[expr] 将三角函数展开TrigFactor[expr] 将三角函数所组成的数学式因式分解TrigReduce[expr] 将相乘或次方的三角函数化成一次方的基本三角函数之组合ExpToTrig[expr] 将指数函数化成三角函数或双曲函数TrigToExp[expr] 将三角函数或双曲函数化成指数函数复数、次方乘积ComplexExpand[expr] 假设所有的变数都是实数来对expr展开ComplexExpand[expr,{x,y,…}] 假设x,y,..等变数均为复数来对expr展开PowerExpand[expr] 将项次、系数最高次方Coefficient[expr,form] 于expr中form的系数Exponent[expr,form] 于expr中form的最高次方Part[expr,n] 或expr[[n]] 在expr项中第n个项代换运算子expr/.x->value 将expr里所有的x均代换成valueexpr/.{x->value1,y->value2,…} 执行数个不同变数的代换expr/.{{x->value1},{x->value2},…} 将expr代入不同的x值expr//.{x->value1,y->value2,…} 重复代换到expr不再改变为止求解方程式的根Solve[lhs==rhs,x] 解方程式lhs==rhs，求xNsolve[lhs==rhs,x] 解方程式lhs==rhs的数值解Solve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] 解联立方程式，求x,y,…NSolve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] 解联立方程式的数值解FindRoot[lhs==rhs,{x,x0}] 由初始点x0求lhs==rhs的根四种括号(term) 圆括号，括号内的term先计算f[x] 方括号，内放函数的引数{x,y,z} 大括号或串列括号，内放串列的元素p[[i ]] 或Part[p,i] 双方括号，p的第i项元素p[[i,j]] 或Part[p,i,j] p的第i项第j个元素缩短输出指令expr//Short 显示一行的计算结果Short[expr,n] 显示n行的计算结果Command; 执行command，但不列出结果查询物件Command 查询Command的语法及说明Command 查询Command的语法和属性及选择项Aaaa* 查询所有开头为Aaaa的物件定义之查询与清除f[x_]= expr 立即定义函数f[x]f[x_]:= expr 延迟定义函数f[x]f[x_,y_,…] 函数f有两个以上的引数f 查询函数f的定义Clear[f] 或f=. 清除f的定义Remove[f] 将f自系统中清除掉含有预设值的Patterna_+b_. b的预设值为0，即若b从缺，则b以0代替x_ y_ y的预设值为1x_^y_ y的预设值为1条件式的自订函数lhs:=rhs/;condition 当condition成立时，lhs才会定义成rhsIf指令If[test,then,else] 若test为真，则回应then，否则回应elseIf[test,then,else,unknow] 同上，若test无法判定真或假时，则回应unknow 极限Limit[expr,x->c] 当x趋近c时，求expr的极限Limit[expr,x->c,Direction->1]Limit[expr,x->c,Direction->-1]微分D[f,x] 函数f对x作微分D[f,x1,x2,…] 函数f对x1,x2,…作微分D[f,{x,n}] 函数f对x微分n次D[f,x,NonConstants->{y,z,…}] 函数f对x作微分，将y,z,…视为x的函数全微分Dt[f] 全微分dfDt[f,x] 全微分Dt[f,x1,x2,…] 全微分Dt[f,x,Constants->{c1,c2,…}] 全微分，视c1,c2,…为常数不定积分Integrate[f,x] 不定积分∫f dx定积分Integrate[f,{x,xmin,xmax}] 定积分Integrate[f,{x,xmin,xmax},{y,ymin,ymax}] 定积分数列之和与积Sum[f,{i,imin,imax}] 求和Sum[f,{i,imin,imax,di}] 求数列和，引数i以di递增Sum[f,{i,imin,imax},{j,jmin,jmax}]Product[f,{i,imin,imax}] 求积Product[f,{i,imin,imax,di}] 求数列之积，引数i以di递增Product[f,{i,imin,imax},{j,jmin,jmax}]泰勒展开式Series[expr,{x,x0,n}] 对expr于x0点作泰勒级数展开至(x-x0)n项Series[expr,{x,x0,m},{y,y0,n}] 对x0和y0展开关系运算子a==b 等于a>b 大于a>=b 大于等于a<b 小于a<=b 小于等于a!=b 不等于逻辑运算子!p notp||q||… orp&&q&&… andXor[p,q,…] exclusive orLogicalExpand[expr] 将逻辑表示式展开二维绘图指令Plot[f,{x,xmin,xmax}]画出f在xmin到xmax之间的图形Plot[{f1,f2,…},{x,xmin,xmax}]同时画出数个函数图形Plot[f,{x,xmin,xmax},option->value]指定特殊的绘图选项，画出函数f的图形Plot几种指令选项预设值说明AspectRatio 1/GoldenRatio 图形高和宽之比例，高/宽Axes True 是否把坐标轴画出AxesLabel Automatic 为坐标轴贴上标记，若设定为AxesLabel->{?ylabel?}，则为y轴之标记。

mathematica 范数

mathematica范数
Mathematica支持多种范数计算，可以使用Norm函数来计算范数。常见的范数有L1范数、L2范数和无穷范数。
具体用法如下：
- L1范数：Norm[m, 1]，其中m为向量或矩阵
- L2范数：Norm[m, 2]，其中m为向量或矩阵
-无穷范数：Norm[m, Infinity]，其中m为向量或矩阵
例如，计算向量{1, 2, 3}的L1范数和L2范数可以使用以下代码：
```
vec = {1, 2, 3};
L1Norm = Norm[vec, 1]
L2Norm = Norm[vec, 2]
```
Hale Waihona Puke 结果为L1范数为6，L2范数为√14。
同样地，计算矩阵的范数也可以使用Norm函数，例如：
```
matrix = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
L1Norm = Norm[matrix, 1]
L2Norm = Norm[matrix, 2]
```
注意，对于矩阵的范数计算，可以选择对矩阵的每一行求范数（Norm[matrix, 1]），或者对矩阵的每一列求范数（Norm[matrix, Infinity]）。