Mathematica语句基本命令

合集下载

Mathematica基本运算指令

Mathematica基本运算指令基本运算a+b+c 加a-b 减a b c 或 a*b*c 乘a/b 除-a 负号a^b 次方Mathematica 数字的形式256 整数2.56 实数11/35 分数2+6I 复数常用的数学常数Pi 圆周率，π=3.141592654…E 尤拉常数，e=2.71828182…Degree 角度转换弧度的常数，Pi/180I 虚数，其值为√-1Infinity 无限大指定之前计算结果的方法% 前一个运算结果%% 前二个运算结果%%…%(n个%) 前n个运算结果%n 或 Out[n] 前n个运算结果复数的运算指令a+bI 复数Conjugate[a+bI] 共轭复数Re[z], Im[z] 复数z的实数/虚数部分Abs[z] 复数z的大小或模数(Modulus)Arg[z] 复数z的幅角(Argument)Mathematica 输出的控制指令expr1; expr2; expr3 做数个运算，但只印出最后一个运算的结果expr1; expr2; expr3; 做数个运算，但都不印出结果expr; 做运算，但不印出结果常用数学函数Sin[x],Cos[x],Tan[x],Cot[x],Sec[x],Csc[x] 三角函数，其引数的单位为弧度Sinh[x],Cosh[x],Tanh[x],… 双曲函数ArcSin[x],ArcCos[x],ArcTan[x] 反三角函数ArcCot[x],ArcSec[x],ArcCsc[x]ArcS inh[x],ArcCosh[x],ArcTanh[x],…反双曲函数Sqrt[x] 根号Exp[x] 指数Log[x] 自然对数Log[a,x] 以a为底的对数Abs[x] 绝对值Round[x] 最接近x的整数Floor[x] 小于或等于x的最大整数Ceiling[x] 大于或等于x的最小整数Mod[a,b] a/b所得的馀数n! 阶乘Random[] 0至1之间的随机数（最新版本已经不用这个函数，改为使用RandomReal[]）Max[a,b,c,...]，Min[a,b,c,…] a,b,c,…的极大/极小值数值设定x=a 将变数x的值设为ax=y=b 将变数x和y的值均设为bx=. 或 Clear[x] 除去变数x所存的值变数使用的一些法则xy 中间没有空格，视为变数xyx y x乘上y3x 3乘上xx3 变数x3x^2y 为 x^2 y次方运算子比乘法的运算子有较高的处理顺序四个处理指令Expand[expr] 将 expr展开Factor[expr] 将 expr因式分解Simplify[expr] 将 expr化简成精简的式子FullSimplify[expr] Mathematica 会尝试更多的化简公式，将expr化成更精简的式子多项式/分式转换ExpandAll[expr] 把算式全部展开Together[expr] 将 expr各项通分在并成一项Apart[expr] 把分式拆开成数项分式的和Apart[expr,var] 视var以外的变数为常数，将 expr拆成数项的和Cancel[expr] 把分子和分母共同的因子消去分母/分子运算Denominator[expr] 取出expr的分母Numerator[expr] 取出expr的分子ExpandDenominator[expr] 展开expr的分母ExpandNumerator[expr] 展开expr的分子多项式转换函数Collect[expr,x] 将 expr表示成x的多项式，如Collect[expr,{x,y,…}] 将 expr分别表示成x,y,…的多项式FactorTerms[expr] 将 expr的数值因子提出，如 4x+2=2(2x+1)FactorTerms[expr,x] 将 expr中把所有不包含x项的因子提出FactorTerms[exp r,{x,y,…}] 将 expr中把所有不包含{x,y,...}项的因子提出函数和指数运算TrigExpand[expr] 将三角函数展开TrigFactor[expr] 将三角函数所组成的数学式因式分解TrigReduce[expr] 将相乘或次方的三角函数化成一次方的基本三角函数之组合ExpT oTrig[expr] 将指数函数化成三角函数或双曲函数TrigToExp[expr] 将三角函数或双曲函数化成指数函数复数、次方乘积ComplexExpand[expr] 假设所有的变数都是实数来对expr展开ComplexExpand[expr,{x,y,…}] 假设x,y,..等变数均为复数来对 expr展开PowerExpand[expr] 将项次、系数最高次方Coefficient[expr,form] 于 expr中form的系数Exponent[expr,form] 于 expr中form的最高次方Part[expr,n] 或 expr[[n]] 在 expr项中第n个项代换运算子expr/.x->value 将 expr里所有的x均代换成valueexpr/.{x->value1,y->value2,…} 执行数个不同变数的代换expr/.{{x->value1},{x->value2},…} 将 expr代入不同的x值expr//.{x->value1,y->value2,…} 重复代换到 expr不再改变为止求解方程式的根Solve[lhs==rhs,x] 解方程式lhs==rhs，求xNsolve[lhs==rhs,x] 解方程式lhs==rhs的数值解Solve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] 解联立方程式，求x,y,…NSolve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] 解联立方程式的数值解FindRoot[lhs==rhs,{x,x0}] 由初始点x0求lhs==rhs的根四种括号(term) 圆括号，括号内的term先计算f[x] 方括号，内放函数的引数{x,y,z} 大括号或串列括号，内放串列的元素p[[i ]] 或 Part[p,i] 双方括号，p的第i项元素p[[i,j]] 或 Part[p,i,j] p的第i项第j个元素缩短输出指令expr//Short 显示一行的计算结果Short[expr,n] 显示n行的计算结果Command; 执行command，但不列出结果查询物件Command 查询Command的语法及说明Command 查询Command的语法和属性及选择项Aaaa* 查询所有开头为Aaaa的物件定义之查询与清除f[x_]= expr 立即定义函数f[x]f[x_]:= expr 延迟定义函数f[x]f[x_,y_,…] 函数f有两个以上的引数f 查询函数f的定义Clear[f] 或 f=. 清除f的定义Remove[f] 将f自系统中清除掉含有预设值的Patterna_+b_. b的预设值为0，即若b从缺，则b以0代替x_ y_ y的预设值为1x_^y_ y的预设值为1条件式的自订函数lhs:=rhs/;condition 当condition成立时，lhs才会定义成rhs If指令If[test,then,else] 若test为真，则回应then，否则回应elseIf[test,then,else,unknow] 同上，若test无法判定真或假时，则回应unknow 极限Limit[expr,x->c] 当x趋近c时，求expr的极限Limit[expr,x->c,Direction->1]Limit[expr,x->c,Direction->-1]微分D[f,x] 函数f对x作微分D[f,x1,x2,…] 函数f对x1,x2,…作微分D[f,{x,n}] 函数f对x微分n次D[f,x,NonConstants->{y,z,…}] 函数f对x作微分，将y,z,…视为x的函数全微分Dt[f] 全微分dfDt[f,x] 全微分Dt[f,x1,x2,…] 全微分Dt[f,x,Constants->{c1,c2,…}] 全微分，视c1,c2,…为常数不定积分Integrate[f,x] 不定积分∫f dx定积分Integrate[f,{x,xmin,xmax}] 定积分Integrate[f,{x,xmin,xmax},{y,ymin,ymax}] 定积分数列之和与积Sum[f,{i,imin,imax}] 求和Sum[f,{i,imin,imax,di}] 求数列和，引数i以di递增Sum[f,{i,imin,imax},{j,jmin,jmax}]Product[f,{i,imin,imax}] 求积Product[f,{i,imin,imax,di}] 求数列之积，引数i以di递增Product[f,{i,imin,imax},{j,jmin,jmax}]泰勒展开式Series[expr,{x,x0,n}] 对expr于x0点作泰勒级数展开至(x-x0)n 项Series[expr,{x,x0,m},{y,y0,n}] 对x0和y0展开关系运算子a==b 等于a>b 大于a>=b 大于等于aa<=b 小于等于a!=b 不等于逻辑运算子!p notp||q||… orp&&q&&… andXor[p,q,…] exclusive orLogicalExpand[expr] 将逻辑表示式展开二维绘图指令Plot[f,{x,xmin,xmax}]画出f在xmin到xmax之间的图形Plot[{f1,f2,…},{x,xmin,xmax}]同时画出数个函数图形Plot[f,{x,xmin,xmax},option->value]指定特殊的绘图选项，画出函数f的图形Plot几种指令选项预设值说明AspectRatio 1/GoldenRatio 图形高和宽之比例，高/宽Axes True 是否把坐标轴画出AxesLabel Automatic 为坐标轴贴上标记，若设定为AxesLabel->{?ylabel?}，则为y轴之标记。

整理mathematica数学常用命令大全

整理mathematica数学常⽤命令⼤全Mathematica的内部常数Mathematica的常⽤内部数学函数Mathematica中的数学运算符Mathematica的关系运算符注：上⾯的关系运算符也可从基本输⼊⼯具栏输⼊。

如何⽤mathematica求多项式的最⼤公因式和最⼩公倍式如何⽤mathematica求整数的最⼤公约数和最⼩公倍数如何⽤mathematica进⾏整数的质因数分解如何⽤mathematica求整数的正约数如何⽤mathematica判断⼀个整数是否为质数如何⽤mathematica求第n个质数如何⽤mathematica求阶乘如何⽤mathematica配⽅Mathematica没有提供专门的配⽅命令,但是我们可以⾮常轻松地⾃定义⼀个函数进⾏配⽅。

如何⽤mathematica进⾏多项式运算如何⽤mathematica进⾏分式运算如何⽤Mathematica进⾏因式分解如何⽤Mathematica展开如何⽤Mathematica进⾏化简如何⽤Mathematica合并同类项如何⽤Mathematica进⾏数学式的转换如何⽤Mathematica进⾏变量替换如何⽤mathematica进⾏复数运算如何在mathematica中表⽰集合与数学中表⽰集合的⽅法相同，格式如下：下列命令可以⽣成特殊的集合：如何⽤Mathematica求集合的交集、并集、差集和补集如何mathematica⽤排序如何在Mathematica中解⽅程注：⽅程的等号必须⽤：= =如何在Mathematica中解⽅程组Solve[{⽅程组}，{变元组}]注：⽅程的等号必须⽤：= =如何在Mathematica中解不等式先加载：Algebra`InequalitySolve` ，加载⽅法为：<然后执⾏解不等式的命令InequalitySolve，此命令的使⽤格式如下：<--mstheme-->如何在Mathematica中解不等式组先加载：Algebra`InequalitySolve` ，加载⽅法为：<然后执⾏解不等式组的命令InequalitySolve，此命令的使⽤格式如下：<--mstheme-->如何在Mathematica中解不等式组先加载：Algebra`InequalitySolve` ，加载⽅法为：<<--mstheme-->如何⽤mathematica表⽰分段函数如何⽤mathematica求反函数对系统内部的函数⽣效，但对⾃定义的函数不起任何作⽤，也许是⽅法不对。

mathematica循环语句

mathematica循环语句在Mathematica中，循环语句是一种重要的编程结构，可以帮助我们有效地处理大量的数据或重复的任务。

下面我们来看看一些常用的循环语句及其用法。

1. For循环：For循环是最常见的循环语句之一，在Mathematica中的语法结构为For[init, test, incr, body]，其中init是初始化语句，test是循环条件，incr是迭代语句，body是循环体。

通过For循环，我们可以方便地对一个范围内的数据进行遍历和处理。

2. While循环：While循环是另一种常见的循环语句，其语法结构为While[test, body]，其中test是循环条件，body是循环体。

While 循环会在每次迭代前检查循环条件是否成立，只有在条件为真时才会执行循环体。

3. Do循环：Do循环是一种简单而灵活的循环语句，在Mathematica中的语法结构为Do[expr, n]，表示对表达式expr进行n次迭代。

Do循环适合于需要重复执行特定次数的任务。

4. Nest循环：Nest循环是一种递归循环语句，在Mathematica中的语法结构为Nest[f, x, n]，表示对函数f进行n次嵌套调用。

Nest循环通常用于处理具有递归结构的问题。

5. Table循环：Table循环是一种快速生成数据的循环语句，在Mathematica中的语法结构为Table[expr, {i, n}]，表示对表达式expr进行n次迭代，并将结果保存在列表中。

Table循环常用于生成序列数据或矩阵数据。

6. Map循环：Map循环是一种高阶函数循环语句，在Mathematica 中的语法结构为Map[f, data]，表示对数据data中的每个元素应用函数f。

Map循环可以简化对数据的处理过程。

7. Select循环：Select循环是一种条件过滤循环语句，在Mathematica中的语法结构为Select[data, test]，表示从数据data中筛选出满足条件test的元素。

mathmatic 基本用法

mathmatic 基本用法Mathematica是一种强大的数学软件，它具有广泛的数学计算和可视化功能。

基本用法包括使用Mathematica进行数学运算、求解方程、绘制图表等。

1.数学运算：Mathematica可以进行基本的数学运算，如加减乘除、幂运算、三角函数、对数函数等。

例如，可以输入"2+3"得到结果"5"，输入"Sin[π/2]"得到结果"1"。

2.方程求解：Mathematica可以求解各种类型的方程。

例如，可以输入"Solve[x^2 - 3x + 2 == 0, x]"来求解这个二次方程，得到结果"x == 1 || x == 2"。

3.符号计算：Mathematica可以进行符号计算，包括展开、化简、因式分解等。

例如，可以输入"Simplify[(x^2 + x - 6)/(x + 3)]"来化简这个表达式，得到结果"x - 2"。

4.绘图功能：Mathematica可以生成各种类型的图表，包括二维曲线图、三维曲面图、柱状图、散点图等。

例如，可以输入"Plot[Sin[x], {x, 0, 2π}]"来绘制正弦函数的曲线图。

除了基本用法外，Mathematica还有许多其他功能，如矩阵计算、微积分、概率统计、符号推导、动态演示等。

它还提供了大量的内置函数和算法，可以用于求解复杂的数学问题。

使用Mathematica还可以进行科学计算、工程计算、数据分析等各种应用领域。

总之，Mathematica是一款功能强大的数学软件，可以帮助用户进行各种数学计算和可视化操作。

mathematica循环语句

mathematica循环语句1. For循环For循环是最基本的循环语句，它的语法格式为：For[循环变量, 初始值, 终止值, 步长, 循环体]。

其中循环变量是一个变量名，初始值和终止值是循环变量的初始值和终止值，步长是循环变量每次增加或减少的量，循环体是要执行的语句块。

2. While循环While循环是一种条件循环语句，它的语法格式为：While[条件, 循环体]。

其中条件是一个逻辑表达式，循环体是要执行的语句块。

当条件为True时，就一直执行循环体，直到条件为False为止。

3. Do-While循环Do-While循环也是一种条件循环语句，它的语法格式为：Do[循环体]; While[条件]。

其中循环体是要执行的语句块，条件是一个逻辑表达式。

先执行一次循环体，然后判断条件是否为True，如果是则继续执行循环体，直到条件为False为止。

4. Nest循环Nest循环是一种嵌套循环语句，它的语法格式为：Nest[循环体, {循环变量1, 初始值1, 终止值1, 步长1}, {循环变量2, 初始值2, 终止值2, 步长2}, ...]。

其中循环体是要执行的语句块，循环变量1、循环变量2等是循环变量的变量名，初始值、终止值、步长是循环变量的初始值、终止值和步长。

5. Table循环Table循环是一种生成列表的循环语句，它的语法格式为：Table[表达式, {循环变量, 初始值, 终止值, 步长}]。

其中表达式是要生成的列表项，循环变量是一个变量名，初始值、终止值、步长是循环变量的初始值、终止值和步长。

6. Map循环Map循环是一种将函数应用于列表元素的循环语句，它的语法格式为：Map[函数, 列表]。

其中函数是要应用的函数，列表是要操作的列表。

7. Select循环Select循环是一种根据条件选择列表元素的循环语句，它的语法格式为：Select[列表, 条件]。

其中列表是要操作的列表，条件是一个逻辑表达式，用来判断列表元素是否符合条件。

mathematica命令大全

mathematica命令大全如何用mathematica求平均值首先要加载Statistics`DescriptiveStatistics`函数库，加载方法为：<< Statistics`DescriptiveStatistics`或者加载整个统计函数库，加载方法为：<<Statistics`Mean[data]求数据data的算术平均数。

数据data 的格式为：{a1,a2,…}HarmonicMean[data]求数据data的调和平均数。

数据data的格式为：{a1,a2,…} GeometricMean[data]求数据data的几何平均数。

数据data的格式为：{a1,a2,…}如何用mathematica求中位数首先要加载Statistics`DescriptiveStatistics`函数库，加载方法为：<< Statistics`DescriptiveStatistics`或者加载整个统计函数库，加载方法为：<<Statistics`Median[data]求数据data的中位数。

数据data的格式为：{ a1,a2,…}如何用mathematica求众数首先要加载Statistics`DescriptiveStatistics`函数库，加载方法为：<< Statistics`DescriptiveStatistics`或者加载整个统计函数库，加载方法为：<<Statistics`Mode[data]求数据data的众数。

数据data的格式为：{ a1,a2,…}如何用mathematica求方差和标准差首先要加载Statistics`DescriptiveStatistics`函数库，加载方法为：<< Statistics`DescriptiveStatistics`或者加载整个统计函数库，加载方法为：<<Statistics`Variance[data]求数据data的样本方差。

Mathematica基本命令

线形用来设定图象所使用的线形，其设定值Dashing[{实线长度，虚线长度}]。
线宽用来设定曲线的宽度，其设定值为Thickness[宽度]。线宽是一个相对数，以占整个图的宽度的比来衡量，线宽应在[0，1]之间选择。
例1：画出y=sin(x) 的图形，并设定曲线的颜色和线宽，函数图象用虚线绘出。
散点图的常用选项 PlotStyle 一>PointSize[x] ：设定散点图中每个点的大小 PlotJoined一>True ：用线段连接绘制的点例2：根据立方表的 y 值作出函数的散点图。
修饰整幅图的外观（第二类选择项）
Background一>GrayLevel [x](或 RGBColor [x,y,z])：指定图的背景颜色
Automatic,设置None则不显示刻度记号 Frame一>True ：在图形周围是否加框 FrameLabel一>“xxxx”：确定框的周围是否加标志，默认值为
False 例4：画出f(x)=Sinx的图象，但不显示刻度，且标注坐标名称，
x轴为time，y轴为height。
图形的组合与再现
Show[图形名称，选择项]: 再现一个已做好的图形 Show[图1，图2，…，选择项]：再现一组已做好图形 Show[GraphicsArray[{plot1,plot2,…}]]：将图形横向并排 Show[GraphicsArray[{plot1},{plot2},…}]]：将图形垂直排列 Show[GraphicsArray[{{plot1,plot2},…}]]：将图形以二维矩阵的
PlotLabel一>“xxxx” ：确定图的标题为 xxxx 例3：利用参数作图方法同时画出单位圆x2+y2=1和抛物线y= x2

mathmatics常用命令

基本操作1、 a*b 可表示为a b (中间加空格)2、 N[expr,n] 指定结果数字位数，而N[expr]可得到默认小数位数的近似值3、 Abs[x] 绝对值4、 % 表示上一个运算结果 %% 表示上面倒数第二个运算结果 ……以此类推 %n 输出行Out[n]上的结果代号5、 /. 替代符如定义p 代表一多项式，则 p/.a->x 表示用a 代替p 中的x6、取消变量赋值 Clear[p]数的操作1、GCD[a,b,c] 计算a ，b ，c 的最大公约数2、LCM[a,b,c] 计算a ，b ，c 的最小公倍数多项式操作1、 Expand[expr] 将多项式展开2、 Factor[expr] 将多项式分解因式3、 Simplify[expr] 将多项式化简4、 Together[expr] 对有理式通分5、 Apart[expr] 对有理式拆分6、 Collect[expr,x] 对多项式中的x 合并同类项7、 Coefficient[expr,form] 给出expr 中form 项前的系数8、 Exponent[expr,form] 给出expr 中form 项的最高次数函数功能1、一元函数 f[x_]:=expr2、二元函数 f[x_,y_]:=expr3、分段函数 f[x_]:=expr1; x 范围f[x_]:=expr2; x 的范围4、函数调用如f[3] 或 f[3,4]导数和积分1、 D[f,{x,n}] 求函数f 关于变量x 的n 次偏导，默认为1次求导2、 D[f,x] 求函数f 的全导数3、 Integrate[f,x] 求不定积分，也可以用符号()f x dx ⎰表示4、 Integrate[f,{x,a,b}] 求定积分，也可以用符号()ba f x dx ⎰表示5、 Integrate[f,{x,a,b},{y,c,d}] 求二重积分，也可以用符号()bda c dx f x dy ⎰⎰表示求解方程和方程组1、一元简单代数方程求解 Solve[expr = = 0，x]2、多元简单代数方程求解 Solve[{expr1==0,expr2==0},{x,y}]3、一元超越方程求解 FindRoot[expr==0,{x,a}] 其中a 为要求根的初始值，求解结果依赖初始值的选择4、多元超越方程求解FindRoot[{expr1==0,expr2==0},{x,a},{y,b}] 其中a ，b 为初始值表与矩阵1、表与Table函数（1）一维表如a={1，2，3}（2）二维表如aa={{1，2，3}，{2，3，4}}（3）从表中取出元素a[[]] 如a[[2]]得到结果为{2,3,4}aa[[2,3]]得到结果为4（4）Table 可以生成有规律的表，可以用下标计算如Table[i^2,{i,1,6}] 结果为{1，4，9，16，25，36}Table[i-j,{i,3},{j,2}] 结果为{{0，-1}，{1，0}，{2，1}} 2、矩阵的表示（1）行向量{{a，b，c}} 列向量{{a}，{b}，{c}}（2）表//MatrixForm 可以将表直观的反应出来（3）DiagonalMatrix[{a,b,c}] 产生对角阵（4）IdentityMatrix[n] 产生n维单位阵3、矩阵的运算（1）数乘* 矩阵乘法·（2）Det[A] 求方阵A的行列式（3）Minors[A,k] 给出矩阵A的所有k阶子式（4）Transpose[A] 对矩阵A转置（5）Dimensions[A] 给出矩阵A的维数（6）Inverse[A] 求方阵A的逆矩阵（7）RowReduce[A] 用初等行变换将矩阵化为规范阶梯阵（8）MatrixPower[A,n] 求方阵的n次幂A n基本作图函数1、一般作图Plot[f,{x,xmin,xmax}]2、离散点作图ListPlot[{{x1,y1},{x2,y2},{x3,y3},{x4,y4}},其他命令]Prolog →AbsolutePointSize[n] 改变n可以调整点的大小PlotJoined →True 用光滑曲线把散点图连起来3、参数方程作图ParametricPlot[{fx,fy},{t,min,max},其他命令]AspectRatio →n 调整坐标的横纵坐标显示比为n4、利用函数包做特殊图形导入<<类名`包名`（1）极坐标方程图像的绘制<<Graphics`Graphics`PolarPlot[f,{t,min,max}]（2）隐函数方程图像的绘制<<Graphics`ImplicitPlot`ImplicitPlot[f==0,{x,min,max}]5、三维作图Plot3D[f,{x,min,max},{y,min,max},其他命令]PlotRange →{a，b} 设置y轴的显示范围PlotPoints →n 设置取点密度，n越大，图形越精细。

Mathematica常用命令

Mathe‎m atic‎a常用命令‎软件学习‎2010-‎10-19‎21:0‎2:15 ‎阅读127‎评论0 ‎字号：‎大中小订‎阅 .‎M athe‎m atic‎a的内部常‎数Pi ‎,或π(‎从基本输入‎工具栏输入‎,或“E‎s c”+“‎p”+“E‎s c”）圆‎周率πE‎(从基本‎输入工具栏‎输入, 或‎“Esc”‎+“ee”‎+“Esc‎”）自然对‎数的底数e‎I (从‎基本输入工‎具栏输入,‎或“Es‎c”+“i‎i”+“E‎s c”）虚‎数单位i‎I nfin‎i ty, ‎或∞(从基‎本输入工具‎栏输入 ,‎或“Es‎c”+“i‎n f”+“‎E sc”）‎无穷大∞‎D egre‎e或°(‎从基本输入‎工具栏输入‎,或“Es‎c”+“d‎e g”+“‎E sc”）‎度Mat‎h emat‎i ca的常‎用内部数学‎函数指数‎函数Exp‎[x]以e‎为底数对‎数函数Lo‎g[x]自‎然对数，即‎以e为底数‎的对数L‎o g[a，‎x]以a为‎底数的x的‎对数开方‎函数Sqr‎t[x]表‎示x的算术‎平方根绝‎对值函数A‎b s[x]‎表示x的绝‎对值三角‎函数（自‎变量的单位‎为弧度）S‎i n[x]‎正弦函数‎C os[x‎]余弦函数‎Tan[‎x]正切函‎数Cot‎[x]余切‎函数Se‎c[x]正‎割函数C‎s c[x]‎余割函数‎反三角函数‎A rcSi‎n[x]反‎正弦函数‎A rcCo‎s[x]反‎余弦函数‎A rcTa‎n[x]反‎正切函数‎A rcCo‎t[x]反‎余切函数‎A rcSe‎c[x]反‎正割函数‎A rcCs‎c[x]反‎余割函数‎双曲函数S‎i nh[x‎]双曲正弦‎函数Co‎s h[x]‎双曲余弦函‎数Tan‎h[x]双‎曲正切函数‎Coth‎[x]双曲‎余切函数‎S ech[‎x]双曲正‎割函数C‎s ch[x‎]双曲余割‎函数反双‎曲函数Ar‎c Sinh‎[x]反双‎曲正弦函数‎ArcC‎o sh[x‎]反双曲余‎弦函数A‎r cTan‎h[x]反‎双曲正切函‎数Arc‎C oth[‎x]反双曲‎余切函数‎A rcSe‎c h[x]‎反双曲正割‎函数Ar‎c Csch‎[x]反双‎曲余割函数‎求角度函‎数ArcT‎a n[x，‎y]以坐标‎原点为顶点‎，x轴正半‎轴为始边，‎从原点到点‎（x，y）‎的射线为终‎边的角，其‎单位为弧度‎数论函数‎G CD[a‎,b,c,‎．．．]最‎大公约数函‎数LCM‎[a,b,‎c,．．．‎]最小公倍‎数函数M‎o d[m,‎n]求余函‎数(表示m‎除以n的余‎数)Qu‎o tien‎t[m，n‎]求商函数‎（表示m除‎以n的商）‎Divi‎s ors[‎n]求所有‎可以整除n‎的整数F‎a ctor‎I nteg‎e r[n]‎因数分解，‎即把整数分‎解成质数的‎乘积Pr‎i me[n‎]求第n个‎质数Pr‎i meQ[‎n]判断整‎数n是否为‎质数，若是‎，则结果为‎T rue，‎否则结果为‎F alse‎Rand‎o m[In‎t eger‎，{m，n‎}]随机产‎生m到n之‎间的整数‎排列组合函‎数Fact‎o rial‎[n]或n‎！阶乘函数‎，表示n的‎阶乘复数‎函数Re[‎z]实部函‎数Im[‎z]虚部函‎数Arg‎(z)辐角‎函数Ab‎s[z]求‎复数的模‎C onju‎g ate[‎z]求复数‎的共轭复数‎Exp[‎z]复数指‎数函数求‎整函数与截‎尾函数Ce‎i ling‎[x]表示‎大于或等于‎实数x的最‎小整数F‎l oor[‎x]表示小‎于或等于实‎数x的最大‎整数Ro‎u nd[x‎]表示最接‎近x的整数‎Inte‎g erPa‎r t[x]‎表示实数x‎的整数部分‎Frac‎t iona‎l Part‎[x]表示‎实数x的小‎数部分分‎数与浮点数‎运算函数N‎[num]‎或num/‎/N把精确‎数num化‎成浮点数（‎默认16位‎有效数字）‎N[nu‎m，n]把‎精确数nu‎m化成具有‎n个有效数‎字的浮点数‎Numb‎e rFor‎m[num‎，n]以n‎个有效数字‎表示num‎Rati‎o nali‎z e[fl‎o at]将‎浮点数fl‎o at转换‎成与其相等‎的分数R‎a tion‎a lize‎[floa‎t，dx]‎将浮点数f‎l oat转‎换成与其近‎似相等的分‎数，误差小‎于dx最‎大、最小函‎数Max[‎a，b，c‎，．．．]‎求最大数‎M in[a‎，b，c，‎．．．]求‎最小数符‎号函数Si‎g n[x]‎Math‎e mati‎c a中的数‎学运算符‎a+b 加‎法a-b‎减法a*‎b (可用‎空格键代替‎*)乘法‎a/b (‎输入方法为‎：“ Ct‎r l ” ‎+ “ /‎” ) ‎除法a^‎b (输入‎方法为：“‎Ctrl‎” + ‎“ ^ ”‎)乘方‎-a 负号‎Math‎e mati‎c a的关系‎运算符=‎=等于<‎小于>大‎于<=小‎于或等于‎>=大于或‎等于!=‎不等于注‎：上面的关‎系运算符也‎可从基本输‎入工具栏输‎入。

(完整版)mathematica命令大全

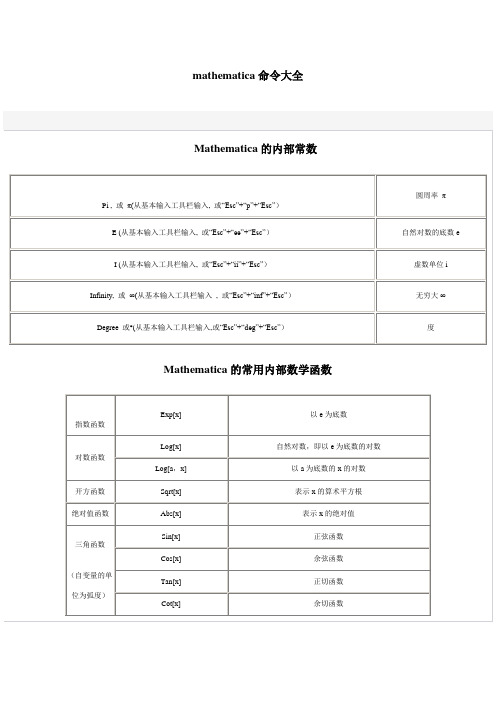
<< Statistics`DescriptiveStatistics`
或者加载整个统计函数库，加载方法为：
<<Statistics`
求数据data的众数。

数据data的格式为：{ a1,a2,…}
Mode[data]
如何用mathematica求方差和标准差
首先要加载Statistics`DescriptiveStatistics`函数库，加载方法为：
<< Statistics`DescriptiveStatistics`
或者加载整个统计函数库，加载方法为：
<<Statistics`
求数据data的样本方差。

数据data的格式为：{ a1,a2,…} Variance[data]
VarianceMLE[data] 求数据data的母体方差。

数据data的格式为：{ a1,a2,…} StandardDeviation[data] 求数据data的样本标准差。

数据data的格式为：{a1,a2,…} StandardDeviationMLE[data] 求数据data的母体标准差。

数据data的格式为：{ a1,a2,…}
如何用mathematica求协方差和相关系数
首先要加载Statistics`MultiDescriptiveStatistics`函数库，加载方法为：
<< Statistics`MultiDescriptiveStatistics`
或者加载整个统计函数库，加载方法为：
<<Statistics`
求数据data1和data2的样本协方差。

数据的格式为：{a1,a2,…}。

手册：mathematica命令大全

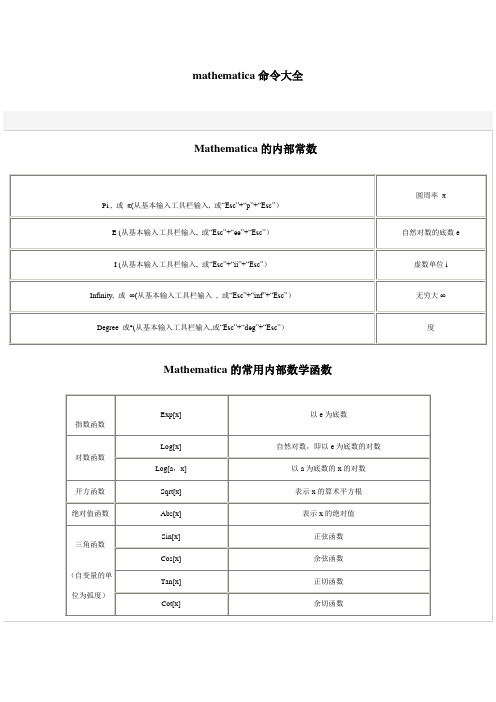
<< Statistics`DescriptiveStatistics`
或者加载整个统计函数库，加载方法为：
<<Statistics`
求数据data的众数。

数据data的格式为：{ a1,a2,…} Variance[data]
VarianceMLE[data] 求数据data的母体方差。

数据data的格式为：{ a1,a2,…} StandardDeviation[data] 求数据data的样本标准差。

数据data的格式为：{a1,a2,…} StandardDeviationMLE[data] 求数据data的母体标准差。

数据的格式为：{a1,a2,…}。

Mathematica语句基本命令

Mathematica语句基本命令Mathematica的内部常数Pi , 或π(从基本输入工具栏输入, 或“Esc”+“p”+“Esc”）圆周率π E (从基本输入工具栏输入, 或“Esc”+“ee”+“Esc”）自然对数的底数e I (从基本输入工具栏输入, 或“Esc”+“ii”+“Esc”）虚数单位iInfinity, 或∞(从基本输入工具栏输入, 或“Esc”+“inf”+“Esc”）无穷大∞Degree 或°(从基本输入工具栏输入,或“Esc”+“deg”+“Esc”）度Mathematica的常用内部数学函数指数函数Exp[x]以e为底数对数函数Log[x]自然对数，即以e为底数的对数Log[a，x]以a为底数的x的对数开方函数Sqrt[x]表示x的算术平方根绝对值函数Abs[x]表示x的绝对值三角函数（自变量的单位为弧度）Sin[x]正弦函数Cos[x]余弦函数Tan[x]正切函数Cot[x]余切函数Sec[x]正割函数Csc[x]余割函数反三角函数ArcSin[x]反正弦函数ArcCos[x]反余弦函数ArcTan[x]反正切函数ArcCot[x]反余切函数ArcSec[x]反正割函数ArcCsc[x]反余割函数双曲函数Sinh[x]双曲正弦函数Cosh[x]双曲余弦函数Tanh[x]双曲正切函数Coth[x]双曲余切函数Sech[x]双曲正割函数Csch[x]双曲余割函数反双曲函数ArcSinh[x]反双曲正弦函数ArcCosh[x]反双曲余弦函数ArcTanh[x]反双曲正切函数ArcCoth[x]反双曲余切函数ArcSech[x]反双曲正割函数ArcCsch[x]反双曲余割函数求角度函数ArcTan[x，y]以坐标原点为顶点，x轴正半轴为始边，从原点到点（x，y）的射线为终边的角，其单位为弧度数论函数GCD[a,b,c,．．．]最大公约数函数LCM[a,b,c,．．．]最小公倍数函数Mod[m,n]求余函数(表示m除以n的余数)Quotient[m，n]求商函数（表示m除以n的商）Divisors[n]求所有可以整除n的整数FactorInteger[n]因数分解，即把整数分解成质数的乘积Prime[n]求第n个质数PrimeQ[n]判断整数n是否为质数，若是，则结果为True，否则结果为False Random[Integer，{m，n}]随机产生m到n之间的整数排列组合函数Factorial[n]或n！阶乘函数，表示n的阶乘复数函数Re[z]实部函数Im[z]虚部函数Arg(z)辐角函数Abs[z]求复数的模Conjugate[z]求复数的共轭复数Exp[z]复数指数函数求整函数与截尾函数Ceiling[x]表示大于或等于实数x的最小整数Floor[x]表示小于或等于实数x的最大整数Round[x]表示最接近x的整数IntegerPart[x]表示实数x的整数部分FractionalPart[x]表示实数x的小数部分分数与浮点数运算函数N[num]或num//N把精确数num化成浮点数（默认16位有效数字）N[num，n]把精确数num化成具有n个有效数字的浮点数NumberForm[num，n]以n个有效数字表示numRationalize[float]将浮点数float转换成与其相等的分数Rationalize[float，dx]将浮点数float转换成与其近似相等的分数，误差小于dx最大、最小函数Max[a，b，c，．．．]求最大数Min[a，b，c，．．．]求最小数符号函数Sign[x]Mathematica中的数学运算符a+b 加法a-b减法a*b (可用空格键代替*)乘法a/b (输入方法为：“ Ctrl ” + “ / ” ) 除法a^b (输入方法为：“ Ctrl ” + “ ^ ” )乘方-a 负号Mathematica的关系运算符==等于<小于>大于<=小于或等于>=大于或等于!=不等于注：上面的关系运算符也可从基本输入工具栏输入。

mathematica命令大全

楼主大中小发表于 2005-11-20 21:55 只看该作者[分享]mathematica命令大全Mathematica函数大全一、运算符及特殊符号Line1; 执行Line，不显示结果Line1,line2 顺次执行Line1，2，并显示结果?name 关于系统变量name的信息??name 关于系统变量name的全部信息!command 执行Dos命令n! N的阶乘!!filename 显示文件内容Expr>> filename 打开文件写Expr>>>filename 打开文件从文件末写() 结合率[] 函数{} 一个表<*Math Fun*> 在c语言中使用math的函数(*Note*) 程序的注释#n 第n个参数## 所有参数rule& 把rule作用于后面的式子% 前一次的输出%% 倒数第二次的输出%n 第n个输出var::note 变量var的注释"Astring " 字符串Context ` 上下文a+b 加a-b 减a*b或a b 乘a/b 除a^b 乘方base^^num 以base为进位的数lhs&&rhs 且lhs||rhs 或!lha 非++,-- 自加1，自减1+=,-=,*=,/= 同C语言>,<,>=,<=,==,!= 逻辑判断（同c）lhs=rhs 立即赋值lhs:=rhs 建立动态赋值lhs:>rhs 建立替换规则lhs->rhs 建立替换规则expr//funname 相当于filename[expr]expr/.rule 将规则rule应用于exprexpr//.rule 将规则rule不断应用于expr知道不变为止param_ 名为param的一个任意表达式（形式变量）param__ 名为param的任意多个任意表达式（形式变量）二、系统常数Pi 3.1415....的无限精度数值E 2.17828...的无限精度数值Catalan 0.915966..卡塔兰常数EulerGamma 0.5772....高斯常数GoldenRatio 1.61803...黄金分割数Degree Pi/180角度弧度换算I 复数单位Infinity 无穷大-Infinity 负无穷大ComplexInfinity 复无穷大Indeterminate 不定式三、代数计算Expand[expr] 展开表达式Factor[expr] 展开表达式Simplify[expr] 化简表达式FullSimplify[expr] 将特殊函数等也进行化简PowerExpand[expr] 展开所有的幂次形式ComplexExpand[expr,{x1,x2...}] 按复数实部虚部展开FunctionExpand[expr] 化简expr中的特殊函数Collect[expr, x] 合并同次项Collect[expr, {x1,x2,...}] 合并x1,x2,...的同次项Together[expr] 通分Apart[expr] 部分分式展开Apart[expr, var] 对var的部分分式展开Cancel[expr] 约分ExpandAll[expr] 展开表达式ExpandAll[expr, patt] 展开表达式FactorTerms[poly] 提出共有的数字因子FactorTerms[poly, x] 提出与x无关的数字因子FactorTerms[poly, {x1,x2...}] 提出与xi无关的数字因子Coefficient[expr, form] 多项式expr中form的系数Coefficient[expr, form, n] 多项式expr中form^n的系数Exponent[expr, form] 表达式expr中form的最高指数Numerator[expr] 表达式expr的分子Denominator[expr] 表达式expr的分母ExpandNumerator[expr] 展开expr的分子部分ExpandDenominator[expr] 展开expr的分母部分ExpandDenominator[expr] 展开expr的分母部分TrigExpand[expr] 展开表达式中的三角函数TrigFactor[expr] 给出表达式中的三角函数因子TrigFactorList[expr] 给出表达式中的三角函数因子的表TrigReduce[expr] 对表达式中的三角函数化简TrigToExp[expr] 三角到指数的转化ExpToTrig[expr] 指数到三角的转化RootReduce[expr]ToRadicals[expr]搜索更多相关主题的帖子: mathematica大全命令name变量TOP沙发大中小发表于 2005-11-20 21:58 只看该作者回复：（ABBYABBIE）[分享]mathematica命令大全四、解方程Solve[eqns, vars] 从方程组eqns中解出vars Solve[eqns, vars, elims] 从方程组eqns中削去变量elims,解出vars DSolve[eqn, y, x] 解微分方程，其中y是x的函数DSolve[{eqn1,eqn2,...},{y1,y2...},x]解微分方程组，其中yi是x的函数DSolve[eqn, y, {x1,x2...}] 解偏微分方程Eliminate[eqns, vars] 把方程组eqns中变量vars约去SolveAlways[eqns, vars] 给出等式成立的所有参数满足的条件Reduce[eqns, vars] 化简并给出所有可能解的条件LogicalExpand[expr] 用&&和||将逻辑表达式展开InverseFunction[f] 求函数f的逆函数Root[f, k] 求多项式函数的第k个根Roots[lhs==rhs, var] 得到多项式方程的所有根五、微积分函数D[f, x] 求f[x]的微分D[f, {x, n}] 求f[x]的n阶微分D[f,x1,x2..] 求f[x]对x1,x2...偏微分Dt[f, x] 求f[x]的全微分df/dxDt[f] 求f[x]的全微分dfDt[f, {x, n}] n阶全微分df^n/dx^nDt[f,x1,x2..] 对x1,x2..的偏微分Integrate[f, x] f[x]对x在的不定积分Integrate[f, {x, xmin, xmax}] f[x]对x在区间(xmin,xmax)的定积分Integrate[f, {x, xmin, xmax}, {y, ymin, ymax}] f[x,y]的二重积分Limit[expr, x->x0] x趋近于x0时expr的极限Residue[expr, {x,x0}] expr在x0处的留数Series[f, {x, x0, n}] 给出f[x]在x0处的幂级数展开Series[f, {x, x0,nx}, {y, y0, ny}]先对y幂级数展开，再对xNormal[expr] 化简并给出最常见的表达式SeriesCoefficient[series, n] 给出级数中第n次项的系数SeriesCoefficient[series, {n1,n2...}]'或Derivative[n1,n2...][f] 一阶导数InverseSeries[s, x] 给出逆函数的级数ComposeSeries[serie1,serie2...] 给出两个基数的组合SeriesData[x,x0,{a0,a1,..},nmin,nmax,den]表示一个在x0处x的幂级数，其中ai为系数O[x]^n n阶小量x^nO[x, x0]^n n阶小量(x-x0)^nDt[f, x] 求f[x]的全微分df/dxDt[f] 求f[x]的全微分dfDt[f, {x, n}] n阶全微分df^n/dx^nDt[f,x1,x2..] 对x1,x2..的偏微分Integrate[f, x] f[x]对x在的不定积分Integrate[f, {x, xmin, xmax}] f[x]对x在区间(xmin,xmax)的定积分Integrate[f, {x, xmin, xmax}, {y, ymin, ymax}] f[x,y]的二重积分Limit[expr, x->x0] x趋近于x0时expr的极限Residue[expr, {x,x0}] expr在x0处的留数Series[f, {x, x0, n}] 给出f[x]在x0处的幂级数展开Series[f, {x, x0,nx}, {y, y0, ny}]先对y幂级数展开，再对xNormal[expr] 化简并给出最常见的表达式SeriesCoefficient[series, n] 给出级数中第n次项的系数SeriesCoefficient[series, {n1,n2...}] '或Derivative[n1,n2...][f] 一阶导数InverseSeries[s, x] 给出逆函数的级数ComposeSeries[serie1,serie2...] 给出两个基数的组合SeriesData[x,x0,{a0,a1,..},nmin,nmax,den]表示一个在x0处x的幂级数，其中aiO[x]^n n阶小量x^nO[x, x0]^n n阶小量(x-x0)^n六、多项式函数Variables[poly] 给出多项式poly中独立变量的列表CoefficientList[poly, var] 给出多项式poly中变量var的系数CoefficientList[poly, {var1,var2...}]给出多项式poly中变量var(i)的系数列?PolynomialMod[poly, m] poly中各系数mod m同余后得到的多项式，m可为整式PolynomialQuotient[p, q, x] 以x为自变量的两个多项式之商式p/qPolynomialRemainder[p, q, x] 以x为自变量的两个多项式之余式PolynomialGCD[poly1,poly2,...] poly(i)的最大公因式PolynomialLCM[poly1,poly2,...] poly(i)的最小公倍式PolynomialReduce[poly, {poly1,poly2,...},{x1,x2...}]得到一个表{{a1,a2,...},b}其中Sum[ai*polyi]+b=polyResultant[poly1,poly2,var] 约去poly1,poly2中的varFactor[poly] 因式分解（在整式范围内）FactorTerms[poly] 提出poly中的数字公因子FactorTerms[poly, {x1,x2...}] 提出poly中与xi无关项的数字公因子FactorList[poly]给出poly各个因子及其指数{{poly1,exp1},{...}...}FactorSquareFreeList[poly]FactorTermsList[poly,{x1,x2...}] 给出各个因式列表，第一项是数字公因子，第二项是与xi无关的因式，其后是与xi有关的因式按升幂的排排?Cyclotomic[n, x] n阶柱函数Decompose[poly, x] 迭代分解，给出{p1,p2,...},其中p1(p2(...))=poly InterpolatingPolynomial[data, var] 在数据data上的插值多项式data可以写为{f1,f2..}相当于{{x1=1,y1=f1}..}data可以写为{{x1,f1,df11,df12,..},{x2,f2,df21..}可以指定数据点上的n阶导数值RootSum[f, form] 得到f[x]=0的所有根，并求得Sum[form[xi]]七、随机函数Random[type,range] 产生type类型且在range范围内的均匀分布随机数type可以为Integer,Real,Complex,不写默认为Realrange为{min,max}，不写默认为{0,1}Random[] 0～1上的随机实数SeedRandom[n] 以n为seed产生伪随机数如果采用了 <在2.0版本为 <<"D:\\Math\\PACKAGES\\STATISTI\\Continuo.m"Random[distribution]可以产生各种分布如Random[BetaDistribution[alpha, beta]]stribution[alpha, beta]]Random[NormalDistribution[miu,sigma]]等常用的分布如BetaDistribution,CauchyDistribution,ChiDistribution, NoncentralChiSquareDistribution,ExponentialDistribution,ExtremeValueDistribution,NoncentralFRatioDistribution, GammaDistribution,HalfNormalDistribution, LaplaceDistribution, LogNormalDistribution,LogisticDistribution, RayleighDistribution,NoncentralStudentTDistribution,UniformDistribution, WeibullDistribution八、数值函数N[expr] 表达式的机器精度近似值N[expr, n] 表达式的n位近似值，n为任意正整数NSolve[lhs==rhs, var] 求方程数值解NSolve[eqn, var, n] 求方程数值解，结果精度到n位NDSolve[eqns, y, {x, xmin, xmax}]微分方程数值解NDSolve[eqns, {y1,y2,...}, {x, xmin, xmax}]微分方程组数值解FindRoot[lhs==rhs, {x,x0}] 以x0为初值，寻找方程数值解FindRoot[lhs==rhs, {x, xstart, xmin, xmax}]NSum[f, {i,imin,imax,di}] 数值求和，di为步长NSum[f, {i,imin,imax,di}, {j,..},..] 多维函数求和NProduct[f, {i, imin, imax, di}]函数求积NIntegrate[f, {x, xmin, xmax}] 函数数值积分优化函数：FindMinimum[f, {x,x0}] 以x0为初值，寻找函数最小值FindMinimum[f, {x, xstart, xmin, xmax}]ConstrainedMin[f,{inequ},{x,y,..}]inequ为线性不等式组，f为x,y..之线性函数，得到最小值及此时的x,y..取值ConstrainedMax[f, {inequ}, {x, y,..}]同上LinearProgramming[c,m,b] 解线性组合c.x在m.x>=b&&x>=0约束下的最小值，x,b,c为向量,m为矩阵LatticeReduce[{v1,v2...}] 向量组vi的极小无关组数据处理：Fit[data,funs,vars]用指定函数组对数据进行最小二乘拟和data可以为{{x1,y1,..f1},{x2,y2,..f2}..}多维的情况emp: Fit[{10.22,12,3.2,9.9}, {1, x, x^2,Sin[x]}, x]Interpolation[data]对数据进行差值,data同上，另外还可以为{{x1,{f1,df11,df12}},{x2,{f2,.}..}指定各阶导数InterpolationOrder默认为3次，可修改ListInterpolation[array]对离散数据插值，array可为n维ListInterpolation[array,{{xmin,xmax},{ymin,ymax},..}] FunctionInterpolation[expr,{x,xmin,xmax}, {y,ymin,ymax},..]以对应expr[xi,yi]的为数据进行插值Fourier对复数数据进行付氏变换InverseFourier对复数数据进行付氏逆变换Min[{x1,x2...},{y1,y2,...}]得到每个表中的最小值变换Min[{x1,x2...},{y1,y2,...}]得到每个表中的最小值Max[{x1,x2...},{y1,y2,...}]得到每个表中的最大值Select[list, crit] 将表中使得crit为True的元素选择出来Count[list, pattern] 将表中匹配模式pattern的元素的个数Sort将表中元素按升序排列Sort[list,p] 将表中元素按p[e1,e2]为True的顺序比较list的任两个元素e1,e2,实际上Sort中默认p=Greater集合论：Union[list1,list2..] 表listi的并集并排序Intersection[list1,list2..] 表listi的交集并排序Complement[listall,list1,list2...]从全集listall中对listi的差集九、虚数函数Re[expr] 复数表达式的实部Im[expr] 复数表达式的虚部Abs[expr] 复数表达式的模Arg[expr] 复数表达式的辐角Conjugate[expr] 复数表达式的共轭十、数的头及模式及其他操作复制内容到剪贴板Integer _Integer 整数Real _Real 实数Complex _Complex 复数Rational_Rational 有理数(*注：模式用在函数参数传递中，如MyFun[Para1_Integer,Para2_Real] 规定传入参数的类型，另外也可用来判断If[Head[a]==Real,...]*) IntegerDigits[n,b,len] 数字n以b近制的前len个码元RealDigits[x,b,len] 类上FromDigits[list] IntegerDigits的反函数Rationalize[x,dx] 把实数x有理化成有理数，误差小于dxChop[expr, delta] 将expr中小于delta的部分去掉,dx默认为10^-10 Accuracy[x] 给出x小数部分位数,对于Pi,E等为无限大Precision[x] 给出x有效数字位数,对于Pi,E等为无限大SetAccuracy[expr, n] 设置expr显示时的小数部分位数SetPrecision[expr, n] 设置expr显示时的有效数字位数十一、区间函数Interval[{min, max}] 区间[min, max](* Solve[3x+2==Interval[{-2,5}],xx]*)IntervalMemberQ[interval, x] x在区间内吗？IntervalMemberQ[interval1,interval2] 区间2在区间1内吗？IntervalUnion[intv1,intv2...] 区间的并IntervalIntersection[intv1,intv2...] 区间的交十二、矩阵操作a.b.c 或 Dot[a, b, c] 矩阵、向量、张量的点积Inverse[m] 矩阵的逆Transpose[list] 矩阵的转置Transpose[list,{n1,n2..}]将矩阵list 第k行与第nk列交换Det[m] 矩阵的行列式Eigenvalues[m] 特征值Eigenvectors[m] 特征向量特征值Eigenvectors[m] 特征向量Eigensystem[m] 特征系统，返回{eigvalues,eigvectors}LinearSolve[m, b] 解线性方程组m.x==bNullSpace[m] 矩阵m的零空间，即m.NullSpace[m]==零向量RowReduce[m] m化简为阶梯矩阵Minors[m, k] m的所有k*k阶子矩阵的行列式的值(伴随阵，好像是)MatrixPower[mat, n] 阵mat自乘n次Outer[f,list1,list2..] listi中各个元之间相互组合，并作为f的参数的到的矩矩?Outer[Times,list1,list2]给出矩阵的外积SingularValues[m] m的奇异值，结果为{u,w,v},m=Conjugate[Transpose[u]].DiagonalMatrix[w].vPseudoInverse[m] m的广义逆QRDecomposition[m] QR分解SchurDecomposition[m] Schur分解LUDecomposition[m] LU分解十三、表函数(*“表”，我认为是Mathematica中最灵活的一种数据类型 *) (*实际上表就是表达式，表达式也就是表，所以下面list==expr *)(*一个表中元素的位置可以用于一个表来表示 *)表的生成{e1,e2,...} 一个表，元素可以为任意表达式，无穷嵌套Table[expr,{imax}] 生成一个表，共imax个元素Table[expr,{i, imax}] 生成一个表，共imax个元素expr[i]Table[expr,{i,imin,imax},{j,jmin,jmax},..] 多维表Range[imax] 简单数表{1,2,..,imax}Range[imin, imax, di] 以di为步长的数表Array[f, n] 一维表，元素为f[i] (i从1到n)Array[f,{n1,n2..}] 多维表，元素为f[i,j..] (各自从1到ni)IdentityMatrix[n] n阶单位阵DiagonalMatrix[/i][/i][/u][list][u][i][i] 对角阵元素操作Part[expr, i]或expr[[i]]第i个元expr[[-i]] 倒数第i个元expr[[i,j,..]] 多维表的元expr[[{i1,i2,..}] 返回由第i(n)的元素组成的子表First[expr] 第一个元Last[expr] 最后一个元Head[expr] 函数头，等于expr[[0]]Extract[expr, list] 取出由表list制定位置上expr的元素值Take[list, n] 取出表list前n个元组成的表Take[list,{m,n}] 取出表list从m到n的元素组成的表Drop[list, n] 去掉表list前n个元剩下的表，其他参数同上Rest[expr] 去掉表list第一个元剩下的表Select[list, crit] 把crit作用到每一个list的元上，为True的所有元组成的表表的属性Length[expr] expr第一曾元素的个数Dimensions[expr] 表的维数返回{n1,n2..},expr为一个n1*n2...的阵TensorRank[expr] 秩Depth[expr] expr最大深度Level[expr,n] 给出expr中第n层子表达式的列表Count[list, pattern] 满足模式的list中元的个数MemberQ[list, form] list中是否有匹配form的元FreeQ[expr, form] MemberQ的反函数Position[expr, pattern] 表中匹配模式pattern的元素的位置列表Cases[{e1,e2...},pattern]匹配模式pattern的所有元素ei的表表的操作Append[expr, elem] 返回在表expr的最后追加elem元后的表Prepend[expr, elem] 返回在表expr的最前添加elem元后的表Insert[list, elem, n] 在第n元前插入elemInsert[expr,elem,{i,j,..}]在元素expr[[{i,j,..}]]前插入elemDelete[expr, {i, j,..}] 删除元素expr[[{i,j,..}]]后剩下的表DeleteCases[expr,pattern]删除匹配pattern的所有元后剩下的表ReplacePart[expr,new,n] 将expr的第n元替换为new Sort[/i][/i][/i][/u][list][u][i][i][i] 返回list按顺序排列的表Reverse[expr] 把表expr倒过来RotateLeft[expr, n] 把表expr循环左移n次RotateRight[expr, n] 把表expr循环右移n次Partition[list, n] 把list按每n各元为一个子表分割后再组成的大表Flatten[/i][/i][/i][/u][list][u][i][i][i] 抹平所有子表后得到的一维大表Flatten[list,n] 抹平到第n层Split[/i][/i][/i][/u][list][u][i][i][i] 把相同的元组成一个子表，再合成的大表FlattenAt[list, n] 把list[[n]]处的子表抹平FlattenAt[list, n] 把list[[n]]处的子表抹平Permutations[/i][/i][/i][/u][list][u][i][i][i] 由list的元素组成的所有全排列的列表Order[expr1,expr2] 如果expr1在expr2之前返回1,如果expr1在expr2之后返回-1,如果expr1与expr2全等返回0Signature[/i][/i][/i][/u][list][u][i][i][i] 把list通过两两交换得到标准顺序所需的交换次数(排列数)以上函数均为仅返回所需表而不改变原表AppendTo[list,elem] 相当于list=Append[list,elem];PrependTo[list,elem] 相当于list=Prepend[list,elem];十四、绘图函数二维作图Plot[f,{x,xmin,xmax}] 一维函数f[x]在区间[xmin,xmax]上的函数曲?Plot[{f1,f2..},{x,xmin,xmax}] 在一张图上画几条曲线ListPlot[{y1,y2,..}] 绘出由离散点对(n,yn)组成的图ListPlot[{{x1,y1},{x2,y2},..}] 绘出由离散点对(xn,yn)组成的图ParametricPlot[{fx,fy},{t,tmin,tmax}] 由参数方程在参数变化范围内的曲线ParametricPlot[{{fx,fy},{gx,gy},...},{t,tmin,tmax}]在一张图上画多条参数曲线选项：PlotRange->{0,1} 作图显示的值域范围AspectRatio->1/GoldenRatio生成图形的纵横比PlotLabel ->label 标题文字Axes ->{False,True} 分别制定是否画x,y轴AxesLabel->{xlabel,ylabel}x,y轴上的说明文字Ticks->None,Automatic,fun用什么方式画轴的刻度AxesOrigin ->{x,y} 坐标轴原点位置AxesStyle->{{xstyle}, {ystyle}}设置轴线的线性颜色等属性Frame ->True,False 是否画边框FrameLabel ->{xmlabel,ymlabel,xplabel,yplabel}边框四边上的文字FrameTicks同Ticks 边框上是否画刻度GridLines 同Ticks 图上是否画栅格线FrameStyle ->{{xmstyle},{ymstyle}设置边框线的线性颜色等属性ListPlot[data,PlotJoined->True] 把离散点按顺序连线PlotSytle->{{style1},{style2},..}曲线的线性颜色等属性PlotPoints->15 曲线取样点，越大越细致三维作图Plot3D[f,{x,xmin,xmax}, {y,ymin,ymax}]二维函数f[x,y]的空间曲面Plot3D[{f,s}, {x,xmin,xmax}, {y,ymin,ymax}]同上，曲面的染色由s[x,y]值决定ListPlot3D[array] 二维数据阵array的立体高度图ListPlot3D[array,shades]同上，曲面的染色由shades[数据]值决定ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax}]二元数方程在参数变化范围内的曲线二元数方程在参数变化范围内的曲线ParametricPlot3D[{{fx,fy,fz},{gx,gy,gz},...},{t,tmin,tmax}]多条空间参数曲线选项：ViewPoint ->{x,y,z} 三维视点，默认为{1.3,-2.4,2}Boxed -> True,False 是否画三维长方体边框BoxRatios->{sx,sy,sz} 三轴比例BoxStyle 三维长方体边框线性颜色等属性Lighting ->True 是否染色LightSources->{s1,s2..} si为某一个光源si={{dx,dy,dz},color}color为灯色，向dx,dy,dz方向照射AmbientLight->颜色函数慢散射光的光源Mesh->True,False 是否画曲面上与x,y轴平行的截面的截线MeshStyle 截线线性颜色等属性MeshRange->{{xmin,xmax}, {ymin,ymax}}网格范围ClipFill->Automatic,None,color,{bottom,top}指定图形顶部、底部超界后所画的颜色Shading ->False,True 是否染色HiddenSurface->True,False 略去被遮住不显示部分的信息等高线ContourPlot[f,{x,xmin,xmax},{y,ymin,ymax}]二维函数f[x,y]在指定区间上的等高线图ListContourPlot[array] 根据二维数组array数值画等高线选项：Contours->n 画n条等高线Contours->{z1,z2,..} 在zi处画等高线ContourShading -> False 是否用深浅染色ContourLines -> True 是否画等高线ContourStyle -> {{style1},{style2},..}等高线线性颜色等属性FrameTicks 同上密度图DensityPlot[f,{x,xmin,xmax},{y,ymin,ymax}]二维函数f[x,y]在指定区间上的密度图ListDensityPlot[array] 同上图形显示Show[graphics,options] 显示一组图形对象，options为选项设置Show[g1,g2...] 在一个图上叠加显示一组图形对象GraphicsArray[{g1,g2,...}]在一个图上分块显示一组图形对象SelectionAnimate[notebook,t]把选中的notebook中的图画循环放映选项：(此处选项适用于全部图形函数)Background->颜色函数指定绘图的背景颜色RotateLabel -> True 竖着写文字TextStyle 此后输出文字的字体，颜色大小等ColorFunction->Hue等把其作用于某点的函数值上决定某点的颜色RenderAll->False 是否对遮挡部分也染色MaxBend 曲线、曲面最大弯曲度图元函数Graphics[prim, options]prim为下面各种函数组成的表，表示一个二维图形对象Graphics3D[prim, options]prim为下面各种函数组成的表，表示一个三维图形对象SurfaceGraphics[array, shades]表示一个由array和shade决定的曲面对象ContourGraphics[array]表示一个由array决定的等高线图对象DensityGraphics[array]表示一个由array决定的密度图对象以上定义图形对象，可以进行对变量赋值，合并显示等操作，也可以存盘Point[p] p={x,y}或{x,y,z}，在指定位置画点Line[{p1,p2,..}]经由pi点连线Rectangle[{xmin, ymin}, {xmax, ymax}] 画矩形Cuboid[{xmin,ymin,zmin},{xmax,ymax,zmax}]由对角线指定的长方体Polygon[{p1,p2,..}] 封闭多边形Circle[{x,y},r] 画圆Circle[{x,y},{rx,ry}] 画椭圆，rx,ry为半长短轴Circle[{x,y},r,{a1,a2}] 从角度a1～a2的圆弧Disk[{x, y}, r] 填充的园、衷病⒃弧等参数同上Raster[array,ColorFunction->f] 颜色栅格Text[expr,coords] 在坐标coords上输出表达式PostScript["string"] 直接用PostScript图元语言写Scaled[{x,y,..}] 返回点的坐标，且均大于0小于1颜色函数(指定其后绘图的颜色)GrayLevel[level] 灰度level为0~1间的实数RGBColor[red, green, blue] RGB颜色，均为0~1间的实数Hue[h, s, b] 亮度，饱和度等，均为0~1间的实数CMYKColor[cyan, magenta, yellow, black] CMYK颜色其他函数(指定其后绘图的方式)Thickness[r] 设置线宽为rPointSize[d] 设置绘点的大小Dashing[{r1,r2,..}] 虚线一个单元的间隔长度ImageSize->{x, y} 显示图形大小(像素为单位)ImageResolution->r 图形解析度r个dpi小(像素为单位)ImageResolution->r 图形解析度r个dpiImageMargins->{{left,right},{bottom,top}}四边的空白ImageRotated->False 是否旋转90度显示回复：（ABBYABBIE）[分享]mathematica命令大全十五、流程控制分支If[condition, t, f] 如果condition为True,执行t段，否则f段If[condition, t, f, u] 同上，即非True又非False，则执行u段Which[test1,block1,test2,block2..] 执行第一为True的testi对应的blocki Switch[expr,form1,block1,form2,block2..]执行第一个expr所匹配的formi所对应的blocki段循环Do[expr,{imax}] 重复执行expr imax次Do[expr,{i,imin,imax}, {j,jmin,jmax},...]多重循环While[test, body] 循环执行body直到test为False For[start,test,incr,body]类似于C语言中的for，注意"，"与";"的用法相反examp: For[i=1;t =x,i^2<10,i++,t =t+i;Print[t]]异常控制Throw[value] 停止计算，把value返回给最近一个Catch处理Throw[value, tag] 同上，Catch[expr] 计算expr,遇到Throw返回的值则停止Catch[expr, form] 当Throw[value, tag]中Tag匹配form时停止? 其他控制Return[expr] 从函数返回，返回值为exprReturn[ ] 返回值NullBreak[ ] 结束最近的一重循环Continue[ ] 停止本次循环，进行下一次循环Goto[tag] 无条件转向Label[Tag]处Label[tag] 设置一个断点Check[expr,failexpr] 计算expr,如果有出错信息产生，则返回failexpr的值Check[expr,failexpr,s1::t1,s2::t2,...]当特定信息产生时则返回failexpr CheckAbort[expr,failexpr]当产生abort信息时放回failexprInterrupt[ ] 中断运行Abort[ ] 中断运行TimeConstrained[expr,t] 计算expr，当耗时超过t秒时终止MemoryConstrained[expr,b]计算expr，当耗用内存超过b字节时终止运算交互式控制Print[expr1,expr2,...] 顺次输出expri的值examp: Print[ "X=" , X//N , " " ,f[x+1]];Input[ ] 产生一个输入对话框，返回所输入任意表达式Input["prompt"] 同上，prompt为对话框的提示Pause[n] 运行暂停n秒的提示Pause[n] 运行暂停n秒十六、函数编程(*函数编程是Mathematica中很有特色也是最灵活的一部分，它充分体现了 *) (*Mathematica的“一切都是表达式”的特点，如果你想使你的Mathematica程 *)(*序快于高级语言,建议你把本部分搞通*)纯函数Function[body]或body& 一个纯函数，建立了一组对应法则，作用到后面的表达达式?Function[x, body] 单自变量纯函数Function[{x1,x2,...},body]多自变量纯函数#，#n 纯函数的第一、第n个自变量## 纯函数的所有自变量的序列examp: #1^#2& [2,3] 返回第一个参数的第二个参数次方映射Map[f,expr]或f/@expr 将f分别作用到expr第一层的每一个元上得到的列表Map[f,expr,level] 将f分别作用到expr第level层的每一个元上Apply[f,expr]或f@@expr 将expr的“头”换为fApply[f,expr,level] 将expr第level层的“头”换为fMapAll[f,expr]或f//@expr把f作用到expr的每一层的每一个元上MapAt[f,expr,n] 把f作用到expr的第n个元上MapAt[f,expr,{i,j,...}] 把f作用到expr[[{i,j,...}]]元上MapIndexed[f,expr] 类似MapAll,但都附加其映射元素的位置列表Scan[f, expr] 按顺序分别将f作用于expr的每一个元Scan[f,expr,levelspec] 同上，仅作用第level层的元素复合映射Nest[f,expr,n] 返回n重复合函数f[f[...f[expr]...]]NestList[f,expr,n] 返回0重到n重复合函数的列表{expr,f[expr],f[f[exprr]]..} FixedPoint[f, expr] 将f复合作用于expr直到结果不再改变,即找到其不定点FixedPoint[f, expr, n] 最多复合n次，如果不收敛则停止FixedPointList[f, expr] 返回各次复合的结果列表FoldList[f,x,{a,b,..}] 返回{x,f[x,a],f[f[x,a],b],..}Fold[f, x, list] 返回FoldList[f,x,{a,b,..}]的最后一个元ComposeList[{f1,f2,..},x]返回{x,f1[x],f2[f1[x]],..}的复合函数列表Distribute[f[x1,x2,..]] f对加法的分配率Distribute[expr, g] 对g的分配率Identity[expr] expr的全等变换Composition[f1,f2,..] 组成复合纯函数f1[f2[..fn[ ]..]Operate[p,f[x,y]] 返回p[f][x, y]br> Operate[p,f[x,y]] 返回p[f][x, y]Through[p[f1,f2][x]] 返回p[f1[x],f2[x]]Compile[{x1,x2,..},expr]编译一个函数，编译后运行速度可以大大加快Compile[{{x1,t1},{x2,t2}..},expr] 同上，可以制定函数参数类型十七、替换规则lhs->rhs 建立了一个规则，把lhs换为rhs,并求rhs的值lhs:>rhs 同上，只是不立即求rhs的值，知道使用该规则时才求值Replace[expr,rules] 把一组规则应用到expr上，只作用一次expr /. rules 同上expr //.rules 将规则rules不断作用到expr上，直到无法作用为止Dispatch[{lhs1->rhs1,lhs2->rhs2,...}]综合各个规则，产生一组优化的规则组十八、查询函数(*查询函数一般是检验表达式是否满足某些特殊形式，并返回True或False*) (*可以在Mathematica中用“?*Q”查询到 *)ArgumentCountQ MatrixQAtomQ MemberQDigitQ NameQEllipticNomeQ NumberQEvenQ NumericQExactNumberQ OddQFreeQ OptionQHypergeometricPFQ OrderedQInexactNumberQ PartitionsQIntegerQ PolynomialQIntervalMemberQ PrimeQInverseEllipticNomeQ SameQLegendreQ StringMatchQLetterQ StringQLinkConnectedQ SyntaxQLinkReadyQ TrueQListQ UnsameQLowerCaseQ UpperCaseQMachineNumberQ ValueQMatchLocalNameQ VectorQMatchQ十九、字符串函数"text" 一个串，头为_String"s1"<>"s2"<>..或StringJoin["s1","s2",..] 串的连接StringLength["string"] 串长度StringReverse["string"] 串反转StringTake["string", n] 取串的前n个字符的子串，参数同Take[] StringDrop["string", n] 参见Drop,串也就是一个表StringInsert["string","snew",n] 插入，参见Insert[] StringPosition["string", "sub"] 返回子串sub在string中起止字母位置StringReplace["string",{"s1"->"p1",..}] 子串替换StringReplacePart["string", "snew", {m, n}]把string第m~n个字母之间的替换为snewStringToStream["string"] 把串当作一个输入流赋予一个变量Characters["string"] 把串"string"分解为每一个字符的表ToCharacterCode["string"] 把串"string"分解为每一个字符ASCII值的表FromCharacterCode[n] ToCharacterCode的逆函数FromCharacterCode[{n1,n2,..}]ToCharacterCode的逆函数ToUpperCase[string] 把串的大写形式ToLowerCase[string] 把串的小写形式CharacterRange["c1","c2"] 给出ASCII吗在c1到c2之间的字符列表ToString[expr] 把表达式变为串的形式ToExpression[input] 把一个串变为表达式Names["string"] 与?string同，返回与string同名的变量列表。

Mathematica命令符集

Mathematica命令符集（基于Mathematica4.0）1、Mathematica中的数及运算N[算式，精度]——求近似值Pi 圆周率π E 自然常数e EulerGamma 欧拉常数γDegree 角度单位π/180 I 虚单位i Infinity，-Infinity ∞，-∞Re[a+I b] 求实部Im[a+I b] 求虚部Abs[a+I b] 求模Arg[a+I b] 求辐角Conjugate[a+I b] 求共轭2、变量和函数常用函数z^s 幂函数Sqrt[z]Exp[z] Log[z] Log[b,x] 指数/对数函数Sin[z] Cos[z] Tan[z] Cot[z] Sec[z] Csc[z] 三角函数ArcSin[z] ArcCos[z] ArcTan[z] ArcCot[z] ArcSec[z] ArcCsc[z] 反三角函数Sinh[z] Cosh[z] Tanh[z] Coth[z] Sech[z] Csch[z] 双曲函数ArcSinh[z] ArcCosh[z] ArcTanh[z] ArcCoth[z] ArcSech[z] ArcCsch[z] 反双曲函数ComplexExpand[f] (分离复函数的实部和虚部)ComplexExpand[f[x+I y]] (默认x，y为实变量)ComplexExpand[f[x，y]，{x，y}] (指明x，y为复变量)Sign[x] |x|/x，x≠0Round[x] 最接近的整数（四舍五入）Mod[n，m] （整数相除的）余数Quotient[n，m] （整数相除的）商n! n!! 阶乘双阶乘Binomial[n，m] 二项式系数n!/m!(n-m)!Multinominal[n，m，…] 组合数(n+m+…)!/n!m!BernoulliB[n] 伯努利数B nBernoulliB[n，x] 伯努利多项式B n(x)EulerE[n] 欧拉数E nEulerE[n，x] 欧拉多项式E n(x)KroneckerDelta[n] n=0时为1，否则为0 KroneckerDelta[n，m，…] n=m=…=0时为1，否则为0常用特殊函数（部分）UnitStep[x] η函数（亥维赛的单位阶跃函数）Gamma[z] Γ函数Γ(z)Beta[p,q] Β函数Β(p,q)PolyGamma[z] ψ函数ψ(z)MoebiusMu[n] 默比乌斯函数μ(n)Zeta[z] 黎曼ζ函数ζ(z)Erf[z] 误差函数erf(z)Erfc[z] 余误差函数erfc(z)LegendreP[n,x] 勒让德多项式P n(x)LegendreP[nu,x]，LegendreQ[nu,x] 勒让德函数Pυ(x)，Qυ(x) LegendreP[nu,mu,x]，LegendreQ[nu,mu,x] 连带勒让德函数Pμυ(x)，Qμυ(x) SphericalHarmonicY[l,m,u,v] 球面调和函数Y m l(u，v)BesselJ[nu,z]，BesselY[nu,z] 贝塞耳函数Jυ(z)，Nυ(z)BesselI[nu,z]，BesselK[nu,z] 虚宗量贝塞耳函数Iυ(z)，Kυ(z) AiryAi[z]，AiryBi[z] 艾里函数Ai(z)，Bi(z) SinIntegral[z] 正弦积分Si(z)CosIntegral[z] 余弦积分Ci(z)SinhIntegral[z] 双曲正弦积分Shi(z) CoshIntegral[z] 双曲余弦积分Chi(z) ExpIntegralEi[z]，ExpIntegralE[n,z] 指数积分Ei(z)，E n(z) LogIntegral[z] 对数积分li(z)FresnelC[z]，FresnelS[z] 菲涅尔积分C(z)，S(z) GegenbauerC[n,m,z] 盖根鲍尔多项式C(m)n(z) ChebyshevT[n,z]，ChebyshevU[z] 切比雪夫多项式T n(z)，U n(z) JacobiP[n,a,b,z] 雅克比多项式P(a,b)n(z)HermiteH[n,z] 厄米多项式H n(z)LaguerrelL[n,z]，LaguerrelL[n,a,z] 拉盖尔多项式L n(z)，Lαn(z) Hypergeometric2F1[a,b,c,z] 超几何函数F(a;b;c;z) Hypergeometric1F1[a,b,z] 合流超几何函数F(a;b;z)3、极限&微积分(1).求极限Limit[f[x],x->x0] Limit[f[x],x->x0,Direction->1] Limit[f[x],x->x0,Direction-> -1](2).求导数D[f[x],x] D[f[x,y],x,NonConstants->{y}](3).求高阶导数D[f[x],x,x,x] 或 D[f[x],{x,3}](4).求偏导数D[f[x,y,z],y] D[f[x,y,z],x,y](5).一元函数的不定积分Integral[f[x],x](6).多元函数的不定积分Integral[f[x,y], x,y](7).定积分Integral[f[x],{x,a,b}]4、幂级数展开与求和(1). 展开Series[f[x],{x,x0,k}](2). 求和Sum[f[n],{n,k,l}] Sum[f[m,n],{m,m1,m2},{n,n1,n2}](3). 连乘积Product[f[n],{n,k,l}](4). 求留数Residue[f[z],{z,z0}](5). 部分分式Apart[f[x]]（如果有理分式是多元函数，则可按指定变量进行部分分式，其余变量均视为常数，如Apart[f[x,y],y]）(6).Z变换ZTransform[f[n],n,z]InverseZTransform[F[n],n,z]5、求解微分方程(1).求解常微分方程DSolve[{eqn,y[0]==?},y[x],x](2).求解偏微分方程DSolve [eqn,u[x,t],{x,t}]E.g. DSolve [x·D[u[x,t],x]+t·D[u[x,t],t]==Exp[x·t],u[x,t],{x,t}]6、L变换和F变换(1).Laplace变换LaplaceTransform[f[t], t, p]InverseLaplaceTransform[F[p], p, t](2).Fourier变换FourierTransform[f[x],x,k]InverseFourierTransform[F[k], k, x]7、Mathematica作图作图指令：图形类型（二维/三维）+函数表达式，自变量（及函数）取值范围+选择项基本选择项选择项意义缺省项AspectRatio 图的高宽比 1/GoldenRatio Axes 是否画坐标轴 Automatic AxesLabel 坐标轴标记 None ColorOutput 图形颜色 $Automatic DefaultColor 默认颜色 $Automatic DisplayFunction 是否显示图形 $DisplayFunction PlotLabel 图题 None PlotPoints 函数值取点数 25PlotRange 函数值范围 Automatic Ticks 轴上刻度 Automatic对选择项赋值，写作options ->value，（value可以是具体数值，也可以是None，All，True，False，Automatic等）。

个人整理Mathematica 画图命令集

个人整理Mathematica 画图命令集二维作图命令：Plot[f,{x,xmin,xmax}] 一维函数f[x]在区间[xmin,xmax]上的函数曲?Plot[,f2.{f1.},{x,xmin,xmax}] 在一张图上画几条曲线ListPlot[{y1,y2,..}] 绘出由离散点对(n,yn)组成的图ListPlot[{{x1,y1},{x2,y2},..}] 绘出由离散点对(xn,yn)组成的图PlarametricPot[{fx,fy},{t,tmin,tmax}] 由参数方程在参数变化范围内的曲线ParametricPlot[{{fx,fy},{gx,gy},...},{t,tmin,tmax}]在一张图上画多条参数曲线选项：PlotRange->{0,1} 作图显示的值域范围AspectRatio->1/GoldenRatio 生成图形的纵横比PlotLabel ->label 标题文字Axes ->{False,True} 分别制定是否画x,y 轴AxesLabel->{xlabel,ylabel}x,y 轴上的说明文字Ticks->None,Automatic,fun 用什么方式画轴的刻度AxesOrigin ->{x,y} 坐标轴原点位置AxesStyle->{{xstyle}, {ystyle}}设置轴线的线性颜色等属性Frame ->True,False 是否画边框FrameLabel ->{xmlabel,ymlabel,xplabel,yplabel} 边框四边上的文字FrameTicks 同Ticks 边框上是否画刻度GridLines 同Ticks 图上是否画栅格线FrameStyle ->{{xmstyle},{ymstyle}设置边框线的线性颜色等属性ListPlot[data,PlotJoined->True] 把离散点按顺序连线PlotSytle->{{style1},{style2},..}曲线的线性颜色等属性PlotPoints->15 曲线取样点，越大越细致三维作图命令：Plot3D[f,{x,xmin,xmax}, {y,ymin,ymax}] 二维函数f[x,y]的空间曲面Plot3D[{f,s}, {x,xmin,xmax}, {y,ymin,ymax}]同上，曲面的染色由s[x,y]值决定ListPlot3D[array] 二维数据阵array 的立体高度图ListPlot3D[array,shades]同上，曲面的染色由shades[数据]值决定ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax}] 二元数方程在参数变化范围内的曲线ParametricPlot3D[{{fx,fy,fz},{gx,gy,gz},...},{t,tmin,tmax}]多条空间参数曲线选项：ViewPoint ->{x,y,z} 三维视点，默认为{1.3,-2.4,2}Boxed -> True,False 是否画三维长方体边框BoxRatios->{sx,sy,sz} 三轴比例BoxStyle 三维长方体边框线性颜色等属性Lighting ->True 是否染色LightSources->{s1,s2..} si 为某一个光源si={{dx,dy,dz},color} color 为灯色，向dx,dy,dz 方向照射AmbientLight->颜色函数慢散射光的光源Mesh->True,False 是否画曲面上与x,y 轴平行的截面的截线MeshStyle 截线线性颜色等属性MeshRange->{{xmin,xmax}, {ymin,ymax}}网格范围ClipFill->Automatic,None,color,{bottom,top}指定图形顶部、底部超界后所画的颜色Shading ->False,True 是否染色HiddenSurface->True,False 略去被遮住不显示部分的信息等高线命令：ContourPlot[f,{x,xmin,xmax},{y,ymin,ymax}] 二维函数f[x,y]在指定区间上的等高线图ListContourPlot[array] 根据二维数组array 数值画等高线选项：Contours->n 画n 条等高线Contours->{z1,z2,..} 在zi 处画等高线ContourShading -> False 是否用深浅染色ContourLines -> True 是否画等高线ContourStyle -> {{style1},{style2},..}等高线线性颜色等属性FrameTicks 同上密度图命令：DensityPlot[f,{x,xmin,xmax},{y,ymin,ymax}]二维函数f[x,y]在指定区间上的密度图ListDensityPlot[array] 同上图形显示命令：Show[graphics,options] 显示一组图形对象，options 为选项设置Show[g1,g2...] 在一个图上叠加显示一组图形对象GraphicsArray[{g1,g2,...}]在一个图上分块显示一组图形对象SelectionAnimate[notebook,t]把选中的notebook 中的图画循环放映选项：(此处选项适用于全部图形函数)Background->颜色函数指定绘图的背景颜色RotateLabel -> True 竖着写文字TextStyle 此后输出文字的字体，颜色大小等ColorFunction->Hue 等把其作用于某点的函数值上决定某点的颜色RenderAll->False 是否对遮挡部分也染色MaxBend 曲线、曲面最大弯曲度图元函数Graphics[prim, options] prim 为下面各种函数组成的表，表示一个二维图形对象Graphics3D[prim, options] prim 为下面各种函数组成的表，表示一个三维图形对象SurfaceGraphics[array, shades]表示一个由array 和shade 决定的曲面对象ContourGraphics[array]表示一个由array 决定的等高线图对象DensityGraphics[array]表示一个由array 决定的密度图对象以上定义图形对象，可以进行对变量赋值，合并显示等操作，也可以存盘Point[p] p={x,y}或{x,y,z}，在指定位置画点Line[{p1,p2,..}]经由pi 点连线Rectangle[{xmin, ymin}, {xmax, ymax}] 画矩形Cuboid[{xmin,ymin,zmin},{xmax,ymax,zmax}]由对角线指定的长方体Polygon[{p1,p2,..}] 封闭多边形Circle[{x,y},r] 画圆Circle[{x,y},{rx,ry}] 画椭圆，rx,ry 为半长短轴Circle[{x,y},r,{a1,a2}] 从角度a1～a2 的圆弧Disk[{x, y}, r] 填充的园、弧等参数同上Raster[array,ColorFunction->f] 颜色栅格Text[expr,coords] 在坐标coords 上输出表达式PostScript["string"] 直接用PostScript 图元语言写Scaled[{x,y,..}] 返回点的坐标，且均大于0 小于1 颜色函数(指定其后绘图的颜色)GrayLevel[level] 灰度level 为0~1 间的实数RGBColor[red, green, blue] RGB 颜色，均为0~1 间的实数Hue[h, s, b] 亮度，饱和度等，均为0~1 间的实数CMYKColor[cyan, magenta, yellow, black] CMYK 颜色其他函数(指定其后绘图的方式)Thickness[r] 设置线宽为rPointSize[d] 设置绘点的大小Dashing[{r1,r2,..}] 虚线一个单元的间隔长度ImageSize->{x, y} 显示图形大小(像素为单位)ImageResolution->r 图形解析度r个dpi 小(像素为单位)ImageResolution->r 图形解析度r个dpiImageMargins->{{left,right},{bottom,top}}四边的空白ImageRotated->False 是否旋转90 度显示。

Mathematica基本指令

,Mathematica 令Mathematica 令 List, List 令來.A =81,1,2,3<81,1,2,3<令A 81,1,2,3< 量 Count @A,1D 2Count 數 1 A 數 Position @A,2D883<<Position 數 2 A 81,1,2,3< FreeQ @A,4D True FreeQ @A,2D FalseFreeQ 數 A MemberQ @A,1D TrueMemberQ 數 1 A若 , Table 數 .Table @i^2,8i,1,10<D81,4,9,16,25,36,49,64,81,100<Set1=Table @i +4 j,8i,1,3<,8j,1,2<D 885,9<,86,10<,87,11<<i +4 j 1≤i ≤3,1≤j ≤2H L . Set1 3×2 , MatrixForm TableForm .MatrixForm @Set1Di k j j j j j j59610711y {z z z z z zSet1êêTableForm59610711Set1@@1DD85,9<Set1 1Set1@@3,2DD11Set1@@3DD@@2DD11Set1 3 2 兩Drop@Set1,1D886,10<,87,11<<Drop 數 Set1 1Drop@Set1,−2D885,9<<Drop 數 Set1 數兩Set1885,9<,86,10<,87,11<<:Set1 Drop 數 ,若 Set1=Drop@Set1,1D Set2=Drop@Set1,1DFirst@Set1D85,9<First 數, Set1 .Last@Set1D87,11<Last 數, Set1 .Take@Set1,2D885,9<,86,10<<Take@Set1,−2D886,10<,87,11<<Take 數, Set1 數 .Append 數, 20 Set1 .Prepend@Set1,21D821,85,9<,86,10<,87,11<<Prepend 數, 21 Set1 .:Set1 Append Prepend 數 ,若 AppendTo PrependTo 數AppendTo@Set1,20D885,9<,86,10<,87,11<,20<PrependTo@Set1,21D821,85,9<,86,10<,87,11<,20<Delete@Set1,2D821,86,10<,87,11<,20<Delete 數, Set1 .Insert@Set1,22,2D821,22,85,9<,86,10<,87,11<,20<Insert 數, 22 Set1 2 .Flatten@Set1D821,5,9,6,10,7,11,20<Flatten 數, Set1 .Join@Set1,823,24,25<D821,85,9<,86,10<,87,11<,20,23,24,25<Join 數, 兩列.Union@81,1,3,5<D81,3,5<Union@81,2<,82,3<D81,2,3<Union 數, 聯 .Sort@Set1D820,21,85,9<,86,10<,87,11<<Sort 數, Set1 .Complement@X,A D 數, X\A.Intersection@Set1,820,21<D820,21<Intersection 數, 兩 .Permutations@8a,b,c,d<D88a,b,c,d<,8a,b,d,c<,8a,c,b,d<,8a,c,d,b<,8a,d,b,c<,8a,d,c,b<, 8b,a,c,d<,8b,a,d,c<,8b,c,a,d<,8b,c,d,a<,8b,d,a,c<,8b,d,c,a<, 8c,a,b,d<,8c,a,d,b<,8c,b,a,d<,8c,b,d,a<,8c,d,a,b<,8c,d,b,a<, 8d,a,b,c<,8d,a,c,b<,8d,b,a,c<,8d,b,c,a<,8d,c,a,b<,8d,c,b,a<<Permutations 數, 列.M1=DiagonalMatrix@81,2,3<D881,0,0<,80,2,0<,80,0,3<<DiagonalMatrix 數, .Dimensions@M1D83,3<Dimension 數, 度.IdentityMatrix@5D881,0,0,0,0<,80,1,0,0,0<,80,0,1,0,0<,80,0,0,1,0<,80,0,0,0,1<<IdentityMatrix 數, .Range@5D81,2,3,4,5<Range@4,7D84,5,6,7<Range@4,18,3D84,7,10,13,16<Range 數, 連數 .Table@Random@D,8i,1,2<,8j,1,3<D880.480437,0.0218922,0.97713<,80.022056,0.409796,0.795632<<Random 數, 亂數.81,2<==82,1<False兩81,2<≠82,1<True兩不Table@If@i≥j,1,0D,8i,1,3<,8j,1,3<D881,0,0<,81,1,0<,81,1,1<<If 數 .x=1;While@x≤5,Print@x D;x=x+1D12345While 數 ..不1.v r=b k2.H v−1L=r H k−1L3.b≥v4.k<v2≤v≤10,1≤b≤10,1≤r≤10,1≤k≤10,1≤λ≤10 參數no=0;Do@If@λ∗H v−1L==r∗H k−1L&&v∗r==b∗k&&b>=v&&k<v, Print@"v=",v,",b=",b,",r=",r,",k=",k,",λ=",λD;no=no+1D, 8v,2,10<,8b,1,10<,8r,1,10<,8k,1,10<,8λ,1,2<D;Print@" 數 ",no Dv=3,b=3,r=2,k=2,λ=1v=3,b=6,r=4,k=2,λ=2v=4,b=4,r=3,k=3,λ=2v=4,b=6,r=3,k=2,λ=1v=5,b=10,r=4,k=2,λ=1v=6,b=10,r=5,k=3,λ=2v=7,b=7,r=3,k=3,λ=1v=7,b=7,r=4,k=4,λ=2數 81.λ∗H v−1LH k−1L 數2.v∗λ∗H v−1LH k−1L∗k 數3.k<v2≤v≤10,2≤k≤10,1≤λ≤2 參數Do@If@IntegerQ@λ∗H v−1LêH k−1LD&&IntegerQ@v∗λ∗H v−1LêHH k−1L∗k LD&&k<v, Print@"v=",v,",k=",k,",λ=",λDD,8v,2,10<,8k,2,10<,8λ,1,2<Dv=3,k=2,λ=1v=3,k=2,λ=2v=4,k=2,λ=1v=4,k=2,λ=2v=4,k=3,λ=2v=5,k=2,λ=1v=5,k=2,λ=2v=6,k=2,λ=1v=6,k=2,λ=2v=6,k=3,λ=2v=7,k=2,λ=1v=7,k=2,λ=2v=7,k=3,λ=1v=7,k=3,λ=2v=7,k=4,λ=2v=8,k=2,λ=1v=8,k=2,λ=2v=9,k=2,λ=1v=9,k=2,λ=2v=9,k=3,λ=1v=9,k=3,λ=2v=10,k=2,λ=1v=10,k=2,λ=2v=10,k=3,λ=2v=10,k=4,λ=2, 數數數,FunctionName@varible_D數列 .H .L若數, 來.Fun1@x_D:=2x^2+3Fun1@3D21Fun1@5D53FibonacciFib@n_D:=Fib@n−1D+Fib@n−2DFib@1D=1;Fib@2D=1;Fib@10D55Timing@Fib@20DD80.031Second,6765<Fib@30DêêTiming84.391Second,832040<Fib@50D$Aborted, 念. 利念 Fibonacci 數Fib1@n_D:=Fib1@n D=Fib1@n−1D+Fib1@n−2DFib1@1D=1;Fib1@2D=1;Fib1@3D2Fib1@20DêêTiming80.Second,6765<Fib1@30DêêTiming80.Second,832040<Fib1@100DêêTiming80.Second,354224848179261915075<H .L 數若 , :FunctionName@varible_D:=Module@8local varible<,state1;state2;...state n DState 數 Output.81,2,3<+84,5,6<85,7,9<81,2,3<+84,5,6,7<Thread::tdlen:Objects of unequal length in81,2,3<+84,5,6,7<cannot be combined. 81,2,3<+84,5,6,7<兩 Size ,, 數不 SizeSetSum@Set1_,Set2_D:=Module@8L1=Length@Set1D,L2=Length@Set2D,Set3<, Set3=8<;Do@AppendTo@Set3,Set1@@i DD+Set2@@j DDD,8i,1,L1<,8j,1,L2<D;Set3=Union@Set3DDSetSum@81,2,3<,84,5,6,7<D85,6,7,8,9,10<,Affine ProjectiveMod@10,5DMod1@m_,n_D:=If@Mod@m,n D=!=0,Mod@m,n D,n DMod1@10,5D5Mod@k,n D 落 80,1,...,n−1<, Mod1@k,n D 落 81,2,...,n<Line1@m_,k_,n_D:=Module@8Set1<,Set1=8<;Do@AppendTo@Set1,8x,Mod1@m x+k,n D<D,8x,1,n<D;Set1DLine2@k_,n_D:=Module@8Set1<,Set1=8<;Do@AppendTo@Set1,8k,m<D,8m,1,n<D;Set1DLine2@3,7D883,1<,83,2<,83,3<,83,4<,83,5<,83,6<,83,7<<AffinePlane@n_D:=Module@8Set1<,Set1=8<;Do@AppendTo@Set1,Line1@m,k,n DD,8m,1,n<,8k,1,n<D;Do@AppendTo@Set1,Line2@k,n DD,8k,1,n<D;Set1Dê;PrimeQ@n DAffinePlane@5D8881,2<,82,3<,83,4<,84,5<,85,1<<,881,3<,82,4<,83,5<,84,1<,85,2<<, 881,4<,82,5<,83,1<,84,2<,85,3<<,881,5<,82,1<,83,2<,84,3<,85,4<<, 881,1<,82,2<,83,3<,84,4<,85,5<<,881,3<,82,5<,83,2<,84,4<,85,1<<, 881,4<,82,1<,83,3<,84,5<,85,2<<,881,5<,82,2<,83,4<,84,1<,85,3<<, 881,1<,82,3<,83,5<,84,2<,85,4<<,881,2<,82,4<,83,1<,84,3<,85,5<<, 881,4<,82,2<,83,5<,84,3<,85,1<<,881,5<,82,3<,83,1<,84,4<,85,2<<, 881,1<,82,4<,83,2<,84,5<,85,3<<,881,2<,82,5<,83,3<,84,1<,85,4<<, 881,3<,82,1<,83,4<,84,2<,85,5<<,881,5<,82,4<,83,3<,84,2<,85,1<<, 881,1<,82,5<,83,4<,84,3<,85,2<<,881,2<,82,1<,83,5<,84,4<,85,3<<, 881,3<,82,2<,83,1<,84,5<,85,4<<,881,4<,82,3<,83,2<,84,1<,85,5<<, 881,1<,82,1<,83,1<,84,1<,85,1<<,881,2<,82,2<,83,2<,84,2<,85,2<<, 881,3<,82,3<,83,3<,84,3<,85,3<<,881,4<,82,4<,83,4<,84,4<,85,4<<, 881,5<,82,5<,83,5<,84,5<,85,5<<,881,1<,81,2<,81,3<,81,4<,81,5<<, 882,1<,82,2<,82,3<,82,4<,82,5<<,883,1<,83,2<,83,3<,83,4<,83,5<<, 884,1<,84,2<,84,3<,84,4<,84,5<<,885,1<,85,2<,85,3<,85,4<,85,5<<<ProjectivePlane@n_D:=Module@8Set1<,Set1=8<;Do@AppendTo@Set1,Union@Line1@m,k,n D,8m<DD,8m,1,n<,8k,1,n<D;Do@AppendTo@Set1,Union@Line2@k,n D,8n+1<DD,8k,1,n<D;AppendTo@Set1,Range@1,n+1DD;Set1Dê;PrimeQ@n DProjectivePlane@5D881,81,2<,82,3<,83,4<,84,5<,85,1<<,81,81,3<,82,4<,83,5<,84,1<,85,2<<,81,81,4<,82,5<,83,1<,84,2<,85,3<<, 81,81,5<,82,1<,83,2<,84,3<,85,4<<,81,81,1<,82,2<,83,3<,84,4<,85,5<<, 82,81,3<,82,5<,83,2<,84,4<,85,1<<,82,81,4<,82,1<,83,3<,84,5<,85,2<<, 82,81,5<,82,2<,83,4<,84,1<,85,3<<,82,81,1<,82,3<,83,5<,84,2<,85,4<<, 82,81,2<,82,4<,83,1<,84,3<,85,5<<,83,81,4<,82,2<,83,5<,84,3<,85,1<<, 83,81,5<,82,3<,83,1<,84,4<,85,2<<,83,81,1<,82,4<,83,2<,84,5<,85,3<<, 83,81,2<,82,5<,83,3<,84,1<,85,4<<,83,81,3<,82,1<,83,4<,84,2<,85,5<<, 84,81,5<,82,4<,83,3<,84,2<,85,1<<,84,81,1<,82,5<,83,4<,84,3<,85,2<<, 84,81,2<,82,1<,83,5<,84,4<,85,3<<,84,81,3<,82,2<,83,1<,84,5<,85,4<<, 84,81,4<,82,3<,83,2<,84,1<,85,5<<,85,81,1<,82,1<,83,1<,84,1<,85,1<<, 85,81,2<,82,2<,83,2<,84,2<,85,2<<,85,81,3<,82,3<,83,3<,84,3<,85,3<<, 85,81,4<,82,4<,83,4<,84,4<,85,4<<,85,81,5<,82,5<,83,5<,84,5<,85,5<<, 86,81,1<,81,2<,81,3<,81,4<,81,5<<,86,82,1<,82,2<,82,3<,82,4<,82,5<<, 86,83,1<,83,2<,83,3<,83,4<,83,5<<,86,84,1<,84,2<,84,3<,84,4<,84,5<<, 86,85,1<,85,2<,85,3<,85,4<,85,5<<,81,2,3,4,5,6<<,DifferenceSet Difference SystemDifference1@Set1_,n_D:=Module@8M,k<,k=Length@Set1D;M=Table@0,8i,1,k<,8j,1,k<D;Do@M@@i,j DD=Mod@Set1@@i DD−Set1@@j DD,n D,8i,1,k<,8j,1,k<D;M=Drop@Sort@Flatten@M DD,k D;MDDifference1@81,2,4<,7D81,2,3,4,5,6<Difference2@Set1__,n_D:=Module@8M,k<,k=Length@Set1D;M=8<;Do@AppendTo@M,Difference1@Set1@@i DD,n DD,8i,1,k<D;M=Sort@Flatten@M DD;MDDifference2@881,3,4,5<,81,2,5,7<<,9D81,1,1,2,2,2,3,3,3,4,4,4,5,5,5,6,6,6,7,7,7,8,8,8<DifferenceSetQ@Set1_,n_D:=Module@8Set2,Set3,a<, Set2=Difference1@Set1,n D;a=Count@Set2,First@Set2DD;Set3=8<;Do@AppendTo@Set3,Range@1,n−1DD,8i,1,a<D;Set3=Sort@Flatten@Set3DD;Set2 Set3DSet1 Z n Difference SetDifferenceSetQ@81,2,4<,7DTrueDifferenceSystemQ@Set1__,n_D:=Module@8Set2,Set3,a<, Set2=Difference2@Set1,n D;a=Count@Set2,First@Set2DD;Set3=8<;Do@AppendTo@Set3,Range@1,n−1DD,8i,1,a<D;Set3=Sort@Flatten@Set3DD;Set2 Set3DDifferenceSystemQ@881,3,4,9,10,12<,82,5,6,7,8,11<<,13D TrueJacobiSymbol@4,13D1LegenderSymbol@a_,m_D:=JacobiSymbol@a,m DDifferenceSet@n_D:=Module@8Set1<,Set1=8<;Do@If@LegenderSymbol@a,n D 1,AppendTo@Set1,a DD,8a,1,n−1<D;Set1Dê;Mod@n,4D 3&&PrimeQ@n Dn 數 4k+3, Difference SetDifferenceSet@19D81,4,5,6,7,9,11,16,17<DifferenceSystem@n_D:=Module@8Set1,Set2<,Set1=8<;Set2=8<;Do@If@LegenderSymbol@a,n D 1,AppendTo@Set1,a D,AppendTo@Set2,a DD ,8a,1,n−1<D;8Set1,Set2<Dê;Mod@n,4D 1&&PrimeQ@n Dn 數 4k+1, Difference SystemDifferenceSystem@13D881,3,4,9,10,12<,82,5,6,7,8,11<<六,拉拉LatinSquareQ@M_D:=Module@8L,Do1,M1<,M1=M;L=Length@M1D;Do1=True;If@Length@Union@Flatten@M1DDD=!=L,Do1=False D;Do@If@Length@Union@M1@@i DD DD=!=L,Do1=False D,8i,1,L<D;M1=Transpose@M1D;Do@If@Length@Union@M1@@i DD DD=!=L,Do1=False D,8i,1,L<D;Do1D數 M 拉LatinSquareQ@881,2<,82,1<<DTrueOrthogonalLatinSquareQ@M1_,M2_D:=Module@8m1,m2,L,Set1<, m1=M1;m2=M2;Set1=8<;L=Length@m1D;Do@AppendTo@Set1,8m1@@i,j DD,m2@@i,j DD<D,8i,1,L<,8j,1,L<D;Length@Union@Set1DD L^2Dê;H Length@M1D Length@M2DL&&LatinSquareQ@M1D&&LatinSquareQ@M2D 數兩拉M1=881,2,3<,83,1,2<,82,3,1<<;M2=881,2,3<,82,3,1<,83,1,2<<;OrthogonalLatinSquareQ@M1,M2DTrueTwoOrthogonalLatinSquare@n_D:=Module@8m1,m2,L,Set1<,m1=Table@Mod1@i+j−1,n D,8i,1,n<,8j,1,n<D;m2=Table@Mod1@−i+j+1,n D,8i,1,n<,8j,1,n<D;Set1=8<;AppendTo@Set1,m1D;AppendTo@Set1,m2D;Set1Dê;OddQ@n Dn 數 , n 拉a=TwoOrthogonalLatinSquare@7D8881,2,3,4,5,6,7<,82,3,4,5,6,7,1<,83,4,5,6,7,1,2<,84,5,6,7,1,2,3<, 85,6,7,1,2,3,4<,86,7,1,2,3,4,5<,87,1,2,3,4,5,6<<,881,2,3,4,5,6,7<,87,1,2,3,4,5,6<,86,7,1,2,3,4,5<,85,6,7,1,2,3,4<, 84,5,6,7,1,2,3<,83,4,5,6,7,1,2<,82,3,4,5,6,7,1<<<OrthogonalLatinSquareQ@a@@1DD,a@@2DDDTrue,6k+1 6k+3; n 6k+1 6k+3 , n .ModuloInverse@a_,n_D:=Mod@a EulerPhi@n D−1,n Dê;GCD@a,n D 1STS@n_Integer D:=Module@8m=nê3,L=8<,k<,Do@AppendTo@L,8i,i+m,i+2*m<D,8i,m<D;Do@k=Mod1@H i+j L*ModuloInverse@2,m D,m D;AppendTo@L,8i,j,k+m<D;AppendTo@L,8i+m,j+m,k+2m<D;AppendTo@L,8i+2m,j+2m,k<D,8i,1,m-1<,8j,i+1,m<D;LDê;H Mod@n,6D==3LSTS@9D881,4,7<,82,5,8<,83,6,9<,81,2,6<,84,5,9<,87,8,3<,81,3,5<,84,6,8<,87,9,2<,82,3,4<,85,6,7<,88,9,1<<STS@15D881,6,11<,82,7,12<,83,8,13<,84,9,14<,85,10,15<,81,2,9<,86,7,14<, 811,12,4<,81,3,7<,86,8,12<,811,13,2<,81,4,10<,86,9,15<,811,14,5<, 81,5,8<,86,10,13<,811,15,3<,82,3,10<,87,8,15<,812,13,5<,82,4,8<, 87,9,13<,812,14,3<,82,5,6<,87,10,11<,812,15,1<,83,4,6<,88,9,11<, 813,14,1<,83,5,9<,88,10,14<,813,15,4<,84,5,7<,89,10,12<,814,15,2<<STS@n_Integer D:=Module@8m=H n-1Lê6,v,k<,v=Table@8i,2*m+i,4*m+i<,8i,m<D;Do@AppendTo@v,8m+i,2*m+i,n<D;AppendTo@v,83*m+i,4*m+i,n<D;AppendTo@v,85*m+i,i,n<D,8i,m<D;For@a=1,a<=2*m-1,a++,For@b=a+1,b<=2*m,b++,If@EvenQ@a+b D,k=H a+b Lê2;AppendTo@v,8a,b,k+2*m<D;AppendTo@v,8a+2*m,b+2*m,k+4*m<D;AppendTo@v,8a+4*m,b+4*m,k<DD;H*Even*LIf@OddQ@a+b D,k=H a+b-1Lê2;AppendTo@v,8a,b,k+3*m<D;AppendTo@v,8a+2*m,b+2*m,k+5*m<D;AppendTo@v,8a+4*m,b+4*m,k+m<DD H*Odd*LDD;v Dê;H Mod@n,6D==1LSTS@7D881,3,5<,82,3,7<,84,5,7<,86,1,7<,81,2,4<,83,4,6<,85,6,2<<STS@25D881,9,17<,82,10,18<,83,11,19<,84,12,20<,85,9,25<,813,17,25<,821,1,25<, 86,10,25<,814,18,25<,822,2,25<,87,11,25<,815,19,25<,823,3,25<, 88,12,25<,816,20,25<,824,4,25<,81,2,13<,89,10,21<,817,18,5<, 81,3,10<,89,11,18<,817,19,2<,81,4,14<,89,12,22<,817,20,6<,81,5,11<, 89,13,19<,817,21,3<,81,6,15<,89,14,23<,817,22,7<,81,7,12<,89,15,20<, 817,23,4<,81,8,16<,89,16,24<,817,24,8<,82,3,14<,810,11,22<,818,19,6<, 82,4,11<,810,12,19<,818,20,3<,82,5,15<,810,13,23<,818,21,7<, 82,6,12<,810,14,20<,818,22,4<,82,7,16<,810,15,24<,818,23,8<, 82,8,13<,810,16,21<,818,24,5<,83,4,15<,811,12,23<,819,20,7<, 83,5,12<,811,13,20<,819,21,4<,83,6,16<,811,14,24<,819,22,8<, 83,7,13<,811,15,21<,819,23,5<,83,8,17<,811,16,25<,819,24,9<, 84,5,16<,812,13,24<,820,21,8<,84,6,13<,812,14,21<,820,22,5<, 84,7,17<,812,15,25<,820,23,9<,84,8,14<,812,16,22<,820,24,6<, 85,6,17<,813,14,25<,821,22,9<,85,7,14<,813,15,22<,821,23,6<, 85,8,18<,813,16,26<,821,24,10<,86,7,18<,814,15,26<,822,23,10<, 86,8,15<,814,16,23<,822,24,7<,87,8,19<,815,16,27<,823,24,11<<,HadamardHadamardMatrixQ@M_D:=M.Transpose@M D Length@M D IdentityMatrix@Length@M DDM1=881,1<,81,−1<<881,1<,81,−1<<HadamardMatrixQ@M1DTrueKronecker Product來 HadamardMatrixKroneckerProduct@M_,N_D:=Module@8M1,N1,LM,LN<,M1=M;N1=N;LM=Length@M1D;LN=Length@N1D;Do@M1@@i,j DD=M1@@i,j DD N1,8i,1,LM<,8j,1,LM<D;Partition@Flatten@M1D,LM∗LN,LM∗LN DDHadamardMatrix@n_D:=Module@8m<,m=881,1<,81,−1<<;HadamardMatrix@2D=m;KroneckerProduct@m,HadamardMatrix@nê2DDDHadamardMatrix @2^3D êêTableForm 111−1111−1111−1−1−1−11111−1111−1111−1−1−1−11111−1111−1111−1−1−1−11−1−1−11−1−1−11−1−1−11111−1HadamardMatrix @2^4D êêMatrixFormi k j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j j 111−1111−1111−1−1−1−11111−1111−1111−1−1−1−11111−1111−1111−1−1−1−11−1−1−11−1−1−11−1−1−11111−1111−1111−1111−1−1−1−11111−1111−1111−1−1−1−11111−1111−1111−1−1−1−11−1−1−11−1−1−11−1−1−11111−1111−1111−1111−1−1−1−11111−1111−1111−1−1−1−11111−1111−1111−1−1−1−11−1−1−11−1−1−11−1−1−11111−1−1−1−11−1−1−11−1−1−11111−1−1−1−11−1−1−11−1−1−11111−1−1−1−11−1−1−11−1−1−11111−1111−1111−1111−1−1−1−11y {z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z z ,Z 2 codesum 數 A B 裡量 CodeSum @A_,B_D :=Module @8L1,A1,B1,C <,L1=Length @A D ;A1=A;B1=B;C =Table @,8L1<D ;Do @C @@i DD =Mod @A1@@i DD +B1@@i DD ,2D ,8i,1,L1<D ;C DCodeSum @80,1,1,0<,80,1,1,1<D80,0,0,1<CodeSum 數 80,1,1,0<,80,1,1,1< 量 Count 數 1Count@CodeSum@80,1,1,0<,80,1,1,1<D,1D1Weight 數 A 1Weight@A_D:=Count@A,1DWeight 數 81,1,1,1,1< 1Weight@81,1,1,1,1<D5CodeDistance 數CodeDistance@A_,B_D:=Weight@CodeSum@A,B DDCodeDiameter 數 C1 量異數數量CodeDiameter@C1_D:=Module@8L1,A1,B1<,L1=Length@C1D;A1=C1;B1=8<;Do@AppendTo@B1,CodeDistance@A1@@i DD,A1@@j DDDD,8i,1,L1−1<,8j,i+1,L1<D;B1=Sort@Union@B1DD;Take@B1,1D@@1DDDCodeDiameter 數 881,1,1<,81,0,1<< 量異數數量 CodeDiameter@881,1,1<,81,0,1<<D1Z2 度 5 2K=80,1<;Set2=Flatten@Outer@List,K,K,K,K,K,K D,5D880,0,0,0,0,0<,80,0,0,0,0,1<,80,0,0,0,1,0<,80,0,0,0,1,1<, 80,0,0,1,0,0<,80,0,0,1,0,1<,80,0,0,1,1,0<,80,0,0,1,1,1<, 80,0,1,0,0,0<,80,0,1,0,0,1<,80,0,1,0,1,0<,80,0,1,0,1,1<, 80,0,1,1,0,0<,80,0,1,1,0,1<,80,0,1,1,1,0<,80,0,1,1,1,1<, 80,1,0,0,0,0<,80,1,0,0,0,1<,80,1,0,0,1,0<,80,1,0,0,1,1<, 80,1,0,1,0,0<,80,1,0,1,0,1<,80,1,0,1,1,0<,80,1,0,1,1,1<, 80,1,1,0,0,0<,80,1,1,0,0,1<,80,1,1,0,1,0<,80,1,1,0,1,1<, 80,1,1,1,0,0<,80,1,1,1,0,1<,80,1,1,1,1,0<,80,1,1,1,1,1<, 81,0,0,0,0,0<,81,0,0,0,0,1<,81,0,0,0,1,0<,81,0,0,0,1,1<, 81,0,0,1,0,0<,81,0,0,1,0,1<,81,0,0,1,1,0<,81,0,0,1,1,1<, 81,0,1,0,0,0<,81,0,1,0,0,1<,81,0,1,0,1,0<,81,0,1,0,1,1<, 81,0,1,1,0,0<,81,0,1,1,0,1<,81,0,1,1,1,0<,81,0,1,1,1,1<, 81,1,0,0,0,0<,81,1,0,0,0,1<,81,1,0,0,1,0<,81,1,0,0,1,1<, 81,1,0,1,0,0<,81,1,0,1,0,1<,81,1,0,1,1,0<,81,1,0,1,1,1<, 81,1,1,0,0,0<,81,1,1,0,0,1<,81,1,1,0,1,0<,81,1,1,0,1,1<, 81,1,1,1,0,0<,81,1,1,1,0,1<,81,1,1,1,1,0<,81,1,1,1,1,1<<離數令<<DiscreteMath\combinatorica.mKSubsets 數 81,2,3,4,5< 3 來列不KSubsets@81,2,3,4,5<,3D881,2,3<,81,2,4<,81,2,5<,81,3,4<,81,3,5<,81,4,5<,82,3,4<,82,3,5<,82,4,5<,83,4,5<<RandomKSubset 數 26 亂數 7 數Set3=RandomKSubset@2^6,7D87,11,14,22,25,35,49<A=Part@Set2,Set3D880,0,0,1,1,0<,80,0,1,0,1,0<,80,0,1,1,0,1<,80,1,0,1,0,1<,80,1,1,0,0,0<,81,0,0,0,1,0<,81,1,0,0,0,0<< CodeDiameter@A D2Do@Set3=RandomKSubset@2^6,16D;Print@A=Part@Set2,Set3DD;Print@CodeDiameter@A DD,8i,1,5<D 880,0,0,0,0,0<,80,0,0,0,0,1<,80,0,1,1,0,1<,80,1,0,0,1,1<, 80,1,0,1,0,0<,80,1,1,0,0,1<,80,1,1,0,1,1<,80,1,1,1,1,1<, 81,0,0,0,0,0<,81,0,0,1,0,0<,81,0,0,1,1,0<,81,0,0,1,1,1<, 81,0,1,1,0,0<,81,1,0,0,0,1<,81,1,0,0,1,0<,81,1,0,1,1,0<<1880,0,0,0,0,1<,80,0,0,0,1,0<,80,0,0,0,1,1<,80,0,0,1,0,0<, 80,0,0,1,1,1<,80,0,1,0,1,1<,80,1,0,1,0,0<,81,0,0,0,1,0<, 81,0,0,1,0,1<,81,0,0,1,1,1<,81,0,1,0,0,1<,81,0,1,0,1,1<, 81,0,1,1,0,1<,81,1,1,0,1,1<,81,1,1,1,0,1<,81,1,1,1,1,1<<1880,0,0,1,0,1<,80,0,1,1,1,1<,80,1,0,1,0,1<,80,1,0,1,1,0<, 80,1,1,0,1,0<,80,1,1,1,0,0<,80,1,1,1,1,0<,81,0,0,0,0,0<, 81,0,0,0,0,1<,81,0,0,0,1,1<,81,0,0,1,1,0<,81,0,1,0,0,1<, 81,1,0,0,0,0<,81,1,0,0,1,1<,81,1,1,0,1,0<,81,1,1,1,0,0<<1880,0,0,0,0,0<,80,0,0,1,1,1<,80,0,1,0,0,1<,80,0,1,0,1,1<, 80,0,1,1,0,1<,80,1,0,0,0,1<,80,1,0,1,0,1<,80,1,1,1,0,1<, 81,0,0,0,1,1<,81,0,1,0,0,1<,81,0,1,1,0,0<,81,0,1,1,0,1<, 81,0,1,1,1,0<,81,1,0,0,0,0<,81,1,0,1,0,1<,81,1,1,0,0,1<<1880,0,0,0,1,0<,80,0,0,0,1,1<,80,0,0,1,0,0<,80,0,0,1,0,1<, 80,0,0,1,1,0<,80,0,1,1,0,1<,80,0,1,1,1,1<,80,1,0,0,0,0<, 80,1,1,0,1,1<,80,1,1,1,1,0<,81,0,0,1,1,1<,81,0,1,0,1,1<, 81,0,1,1,0,0<,81,0,1,1,1,1<,81,1,1,0,0,1<,81,1,1,1,0,1<<1Z2 codesum 數 A 裡量CodeSum@A_D:=Module@8L1,L2,A1,C<,L1=Length@A D;L2=Length@A@@1DDD;A1=A;C=Table@0,8L2<D;Do@Do@C@@i DD=C@@i DD+A1@@j,i DD,8j,1,L1<D;C@@i DD=Mod@C@@i DD,2D,8i,1,L2<D;CDCodeSum @881,1,1,1<,81,0,1,0<,81,1,1,0<,81,0,1,1<<D80,0,0,0<Z 2 GeneratedCode 數 S 量來 GeneratedCode @S_D :=Module @8Set1,Set2,N1,N2,N3,List1<,Set1=S;Set2=S;N1=Length @S D ;N2=Length @Set1@@1DDD ;PrependTo @Set1,Table @0,8N2<DD ;Do @List1=KSubsets @Range @N1D ,k D ;N3=Length @List1D ;Do @AppendTo @Set1,CodeSum @Set2@@List1@@i DD DDDD ,8i,1,N3<D ,8k,2,N1<D ;Union @Set1D DGeneratedCode @881,0,0,0,1,1,1<,80,1,0,0,1,1,0<,80,0,1,0,1,0,1<,80,0,0,1,0,1,1<<D 880,0,0,0,0,0,0<,80,0,0,1,0,1,1<,80,0,1,0,1,0,1<,80,0,1,1,1,1,0<,80,1,0,0,1,1,0<,80,1,0,1,1,0,1<,80,1,1,0,0,1,1<,80,1,1,1,0,0,0<,81,0,0,0,1,1,1<,81,0,0,1,1,0,0<,81,0,1,0,0,1,0<,81,0,1,1,0,0,1<,81,1,0,0,0,0,1<,81,1,0,1,0,1,0<,81,1,1,0,1,0,0<,81,1,1,1,1,1,1<<ConnectTwoMatricesV 數 A B J ABN ConnectTwoMatricesV @A_,B_D :=Join @A,B DConnectTwoMatricesH 數 A B @AB DConnectTwoMatricesH @A_,B_D :=Transpose @Join @Transpose @A D ,Transpose @B DDDConnectTwoMatricesH ConnectTwoMatricesV 數 881,2<,83,4<<,885,6<,87,8<< 來ConnectTwoMatricesH @881,2<,83,4<<,885,6<,87,8<<D êêMatrixForm J12563478NConnectTwoMatricesV @881,2<,83,4<<,885,6<,87,8<<D êêMatrixFormi k j j j j j j j j j j j 12345678y {z z z z z z z z z z z Z 2 CodeProduct 數 A B CodeProduct @A_,B_D :=Mod @A.B,2DCodeProduct@80,1,1,0<,81,1,1,1<D 0。

手册：mathematica命令大全

<< Statistics`DescriptiveStatistics`或者加载整个统计函数库，加载方法为：<<Statistics`求数据data的众数。

数据data的格式为：{ a1,a2,…}Mode[data]如何用mathematica求方差和标准差首先要加载Statistics`DescriptiveStatistics`函数库，加载方法为：<< Statistics`DescriptiveStatistics`或者加载整个统计函数库，加载方法为：<<Statistics`求数据data的样本方差。

数据data的格式为：{ a1,a2,…} Variance[data]VarianceMLE[data] 求数据data的母体方差。

数据data的格式为：{ a1,a2,…} StandardDeviation[data] 求数据data的样本标准差。

数据data的格式为：{a1,a2,…} StandardDeviationMLE[data] 求数据data的母体标准差。

数据data的格式为：{ a1,a2,…}如何用mathematica求协方差和相关系数首先要加载Statistics`MultiDescriptiveStatistics`函数库，加载方法为：<< Statistics`MultiDescriptiveStatistics`或者加载整个统计函数库，加载方法为：<<Statistics`求数据data1和data2的样本协方差。

数据的格式为：{a1,a2,…}.可编辑。

Mathematica常用指令

Mathematica常⽤指令表达式：Plot[4 x - 9, {x, 0, 9}]f[x_] = x^3Plot[f[x], {x, 0, 9}]a = Plot[4 x - 9, {x, 0, 9}]b = Plot[x^3, {x, 0, 3}] 两图画在⼀个坐标系Show[a, b]a = Plot[4 x - 9, {x, 0, 9}]b = Plot[x^3, {x, 0, 3}] 两图画在⼀起（⼀排）c = GraphicsArray[{a, b}]Show[c]a = Plot[4 x - 9, {x, 0, 9}]b = Plot[x^3, {x, 0, 3}]c = GraphicsArray[{a}, {b}] 两图画在⼀起（两排）Show[c]⼆维画图：Automatic 默认值DisplayFunction -> Identity 不出现图DisplayFunction -> $DisplayFunction 出现图PlotRange -> All 画出所有点，指定区域点PlotStyle -> {RGBColor[1, 0, 0]} 图像颜⾊PlotStyle -> {Dashing[{0.01}]} 图像成虚线PlotStyle -> {Thickness[0.01]} 图像粗细AxesLabel -> {"x/t", "y/cm"} 坐标标签PlotLabel -> {"s-t"} 图像标签Frame -> True 图像边框Axes -> {True, True} 坐标轴的显⽰AxesOrigin -> {0, -5} 设置坐标原点GridLines -> {{-π, -π/2, 0, π/2, π}, {-1，-0.5，0, 0.5, 1}}给坐标轴分⽹格TextStyle -> {FontSize -> 30} 坐标字体⼤⼩AspectRatio -> Automatic 坐标⽐例⼀致Ticks -> {{0, 1, 2, 3}, {0,10,20}} 在坐标轴上显⽰特定点ParametricPlot[x(t),y(t)},{t,0,6,}] 画参数⽅程三维画图：PlotPoints -> 100 像素Boxed -> False 显⽰边框BoxRatios -> {1，1，2} 三维⽐例Mesh -> False 在曲⾯上不显⽰⽹格ViewPoint -> {0, 0, 1} 图的观察⽅向HiddenSurface -> False 图⽰⽆遮挡解⽅程：Solve[a x + b == c x + d, x]Solve[{2 x + 3 y == 3, 3 x - 5 y == 9}, {x, y}]NSolve[7 x + 3 == 2, 30]或N[Solve[7 x + 3 == 2], 30]Roots[x^2 + 2 x + 1 == 0, x]或NRoots[x^3 + 3 == 0, x] 解⼀元⽅程求解超越⽅程：先画图确定跟的位置，在⽤FindRoot解：Plot[{Sin[x], x^2 - 1}, {x, -π, π}]FindRoot[Sin[x] == x^2 - 1, {x, 1}]Factor[x^2 + 2 x + 1] 分解因式Expand[(x^2 + 2 x + 1)( x^2 - 1)] 展开多项式Collect[x^3y^2z^4 + x^4y^5z^2x^2y^3z^2, y] 按Y升次幂排列PowerExpand[Log[x\^y]] 展开或化简TrigExpand[Sin[3 x]] 按三⾓函数形式展开微分：Limit[(x^5 - 32)/(x^3 - 8), x -> 2] 求极限Limit[32/x, x -> 0, Direction -> 1（-1）] 左（右）极限f'[x] 求导D[f[x], {x, 3}] 以X为变量求3阶导数D[f[x], {x, 3}] /. x -> 2 f''[2]Series[Exp[x], {x, 3, 5}] 在3点展开⾄5次⽅D[x^3 y^4 z^2, x] 对x求偏导D[x^3 y^4 z^2, {x, 2}] 对x求⼆次偏导D[x^3 Sin[y], x, y] /. {x -> 2, y -> π} 定点求导常微分⽅程：DSolve[y'[x] == x + y[x], y[x], x] 解微分⽅程，y是x的函数DSolve[{y'[x] == x + y[x], y[0] == 0}, y[x], x] 初始条件NDSolve[{y'[x] == x + y[x], y[0] == 0}, y[x], x] 数值解矩阵：{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}} // MatrixForm ⽣成矩阵Table[x^2, {x, 1, 5}] ⽣成x取值1到5的x^2的值Table[x+y, {x, 1, 5}，{y，1, 7}] ⽣成5*7的矩阵，矩阵元的值是x+y f[x_] = 2 x^2 Array[f, 1, 5] ⽣成x=1到5的2 x^2的值IdentityMatrix[3] ⽣成3阶单位矩阵a[[3,4]] a矩阵的（3，4）矩阵元a[4] a矩阵的第四⾏a[[all,5]] a矩阵的第5列a[[{2,3,5},all]] a矩阵的第2，3，5⾏{q,w,e}={2+3,1+2,2} q=5，w=3，e=2Table[Random[Integer,{0,9}],{i,1,4},{j,1,4}] 随机产⽣矩阵元为0~9的4⾏4列的矩阵z.q 矩阵点乘Cross[z,q] 矩阵叉乘Inverse[a] 逆矩阵Transpose[a] 转置Det[a] 求⾏列式Tr[a] 求迹MatrixPower[a,2] 矩阵的3次⽅LinearSolve[a,aa]//MatrixForm 解线性⽅程组Eigenvalues[s] s矩阵的本征值Eigenvectors[s]s矩阵的本征向量Eigensystem[s]s矩阵的{本征值}，{本征向量} Eigenvalues[N[s]] s矩阵的本征值的数值表⽰命令语句：If[x ≤y, 1, 2] ifx ≤y，then 1，else 2If[Abs[q - w] == 1, 1, If[q == w, 2, 0] ifabs[q - w] == 1，then 1，elseif q == w，then 2，else 0 While[1,2] For[初始化，条件，更新，语句]。

Mathematica常用语句

Mathematica常用语句一、常用常量PiπE eDegree 度(π/180)GoldenRatio 黄金分割比(0.618)Infinity 无穷大∞I 虚数单位ix=. 取消赋值xClear[x] 取消赋值x二、初等函数Log[x] ln xLog[a,x] log a xExp[x] x eSqrt[x] xSin[x] sin(x)Cos[x] cos(x)Tan[x] tan(x)Cot[x] cot(x)ArcSin[x] arcsin(x)ArcCos[x] arccos(x)三、函数的定义f[x_]:= 定义一元函数f[x_,y_]:= 定义二元函数四、常用函数：Plus[n1,n2,] 求和N[x,n] 取x的n位有效数字Abs[x] 取x的绝对值(x为复数时为取x的模) Sign[x] 符号函数Round[x] 最接近x的整数(可比x大也可比x小) Floor[x] 不大于x的最大整数Ceiling[x] 不小于x的最大整数Max[x1,x2,] 取变量x1,x2,的最大值Min[x1,x2,] 取变量x1,x2,的最小值Re[z] 取复数z的实部In[z] 取复数z的虚部Conjugate[z] 取复数z的共轭Arg[z] z的辐角Quotient[m,n] 取商函数(m被n除的整数部分)Mod[m,n] 取余函数(m被n除的余数部分)n！n的阶乘n！！n的双阶乘Binomial[n,m] 二项式系数mCn% 最近一次输出结果%% 倒数第二次输出%n 第n个输出结果Solve[方程] 解方程Fit[] 曲线拟合函数Simplify[] 用于化简的函数If语句If[条件,t,f]满足条件：执行t否则执行fIf[条件,t,f,u] 满足条件：执行t否则执行f无法判别执行u Which语句Which[条件1,t1,条件2,t2] 满足条件i执行ti五、表1、表的建立表名={元素1，元素2,}{循环变量n，循环初值n0，循环终值ni，步长增量d}(d为1时可省)Range[循环初值n0，循环终值ni，步长增量d](d为1时可省；n0为1时也可省)Table[通项公式f(m,n,)，{m,m0,mi,d1}，{ n,n0,ni,d1}]Array[f,n] 生成长为n，元素是f[i]的表Array[f,n,n0] 生成长为n，元素是f[i]且从f[n0]开始的表Array[f,{m,n}] 生成长为{m,n}，元素是f[i,j]的二维数表Array[f,{n1,n2,}] 把f作用到n1,n2,构成的表2、表的调整Length[t] 求表中元素个数(即表长)T[[n]] 表t中第n个元素T[[-n]] 表t中倒数第n个元素First[t] 表t中第一个元素Last[t] 表t中最后一个元素T[[i,j]] 表t中第i个子表中的第j个元素T[[{n1,n2,}]]或Part[t,{n1,n2,}] 由表t中n1,n2,等元素组成的数表Position[t,x] 元素x在表t中的位置Take[t,{m,n}] 从表t中取出m~n的元素Rest[t] 去掉表t中第一个元素Drop[t,{m,n}] 从表t中去掉m~n的元素Prepend[t,a] 将a加到表t的第一位Append[t,a] 将a加到表t的最后一位Insert[t,a,k] 将a加到表t的第k位Raplace[t,a,k] 用a替换表t的第k位Apply[f,t] 将函数f作用到表t的每一位Sort[t] 将元素依标准排列(数字按大小，字母按abc) Reverse[t] 将元素按顺序倒排RatateLeft[t,k] 将元素向左轮换k位RatateRight[t,k] 将元素向右轮换k位Partition[t,n] 将表t分成n个元素的块Partition[t,n,d]Transpose[t] 将表t转置Join[t1,t2] 将t1和t2合并，但是不去掉重复元素Union[t1,t2,] 并集运算Intersection[t1,t2,] 交集运算Complement[t1,t2] 从t1中去掉t2中的元素六、绘图1、绘图函数Plot[f[x],{x,a,b}] 画f[x]在区间[a,b]上的函数图象ParametricPlot[{x[t],y[t]},{t,a,b }] 画参数图ListPlot[{x1,y2},{x2,y2},] 绘制点图Plot3D[f[x,y],{x,x0,x1},{y,y0,y1}] 三维图像ParametricPlot3D[{x[t],y[t],z[t]},{t,t0,t1}]参数三维图2、绘图函数修饰项①二维绘图所用的修饰项PlotRange->{a,b} 确定函数值得范围(a~b)PlotStyle->{RGBColor[a,b,c]}确定曲线颜色P lotStyle->{AbsoluteThickness[n]}确定曲线粗细(n=1、2、)②三维绘图所用的修饰项PlotPoints->{a,b} 网格数a×b个PlotRange->{a,b} 确定函数值得范围(a~b)Axes->True/False 是否显示坐标轴Boxed->True/False 是否加立体框Mesh->True/False 是否加网格Shading ->True/False 是否在曲面着色HiddenSurface-> True/False 被挡部分是否隐藏ViewPoint->{a,b,c} 调整观察角度七、极限与导数Limit[f[x],x->a] alim ()x f x → (a 可以是∞) Limit[f[x],x->a,Direction->1]求右极限 Limit[f[x],x->a,Direction->1]求左极限 D[f[x],x]df dx 或f x ∂∂ D[f[x],{x,k}]k 阶导数或k 阶偏导 D[f,x1,x2, ,xk] 1k f x x ∂∂∂D[f[x],x,NonConstants->{v1,v2,}] 求导时vi 是关于x 的函数 Dt[f,x]复合函数f 关于x 的导数 Dt[f,{x,k}]复合函数f 关于x 的k 阶导数 Dt[f,{x,k},Constants->{c1,c2,}] 求导的时候ci 看为常数Dt[f]全微分 f `[x]一阶导数( ` 是1前面的那个) f ``[x]二阶导数 Simplify[] 用于化简的函数FindMinimum[f,{x,x0}] 在x0附近求极值点(求极大值用-f)FindMinimum[f,{x,{x0,x1}}] 以x0，x1为初始值搜索极值 (用于无导数)FindMinimum[f,{x, {x,x0,a,b}] 求以x0为初始值搜索[a,b]区间的极值FindMinimum[f,{x, {x,a,b}] 求在[a,b]间的极值FindMinimum[f,{x, {x,x0},{y,y0}]多元函数极值八、积分Integrate[f,x] 不定积分(f:被积函数,x:积分变量)Integrate[f,{x,a,b}] 定积分(f:被积函数,x:积分变量,a:上限,b:下限) Integrate[f,{x,x0,x1},{y,y0,y1},] 多重积分NIntegrate[f,{x,a,b}] 定积分近似值九、微分方程DSolve[方程组,函数f[x],变量x] 解微分方程(方程组可含有初边值条件) NDSolve[方程组,函数符号,变量符号及范围] 解微分方程数值解十、线性代数Array[a,{m,n}] 建一个m行n列的矩阵，元素为a[i,j]IndenityMatrix[n] 建一个n阶单位阵DiagonalMatrix[t] 建一个对角线上为表中元素的方阵MatrixForm[A] 将矩阵A按矩阵形式输出Det[A] 求方阵A的行列式Transpose[A] 矩阵A的转置Inverse[A ] 方阵A的逆矩阵A*B A与B对应元素相乘Dot[a,b]或a.b 数量积(.右下角)Cross[a,b]或a⨯b 向量积(⨯在输入模块上)Minors[M,k] 矩阵M的所有可能的k阶子式组成的矩阵RowReduce[A] 求A的行约化矩阵LinearSolve[A,B] 求满足Ax=B的一个解NullSpace[A] 求Ax=0的基础解析Eigenvalues[M]求方阵M 的特征值 Eigenvectors[M]求方阵M 的特征向量 Eiginsystem[M] 求方阵M 的特征值和特征向量十一、级数Series[f,{x,x0,n}] 将函数f 做泰勒展开到0()n x x SeriesCoefficient[s,n] 求级数s 中第n 阶的系数Normal[s] 舍去级数s 的余项部分 FourierTrigSeries[f[x],x,k, FourierParameters->{a,1T }]f[x]的k 阶傅里叶展开(T:周期,a:基本周期区间中心) 十二、概率Mean[d]求均值 Median[d]求中位数 Quartiles[d]求0.25分位数,中位数,0.75分位数 Quantile [d,k]求k 分位数 Variance[d]求方差(无偏估计是的方差) StandardDeviation[d] 求标准差(无偏估计是的标准差) VarianceMLE[d] 求方差(总体方差的极大似然估计) StandardDeviationMLE[d]求标准差SampleRange[d] 极差CentralMoment[d,k] k 阶中心距(k=2、3、4)Skewness[d]偏度 Kurtosis[d] 峰度BinCounts[d,{a,b,k}] 将a~b 按长度k 等分小区间，求出在每个小区间的数据个数Max[x1,x2,] 取变量x1,x2,的最大值Min[x1,x2,] 取变量x1,x2,的最小值Length[t] 求表中元素个数(即表长) BarChart[bc] 画直方图(bc为数据对)。