Mathematica常用指令

合集下载

Mathematica基本运算指令

Mathematica基本运算指令基本运算a+b+c 加a-b 减a b c 或 a*b*c 乘a/b 除-a 负号a^b 次方Mathematica 数字的形式256 整数2.56 实数11/35 分数2+6I 复数常用的数学常数Pi 圆周率，π=3.141592654…E 尤拉常数，e=2.71828182…Degree 角度转换弧度的常数，Pi/180I 虚数，其值为√-1Infinity 无限大指定之前计算结果的方法% 前一个运算结果%% 前二个运算结果%%…%(n个%) 前n个运算结果%n 或 Out[n] 前n个运算结果复数的运算指令a+bI 复数Conjugate[a+bI] 共轭复数Re[z], Im[z] 复数z的实数/虚数部分Abs[z] 复数z的大小或模数(Modulus)Arg[z] 复数z的幅角(Argument)Mathematica 输出的控制指令expr1; expr2; expr3 做数个运算，但只印出最后一个运算的结果expr1; expr2; expr3; 做数个运算，但都不印出结果expr; 做运算，但不印出结果常用数学函数Sin[x],Cos[x],Tan[x],Cot[x],Sec[x],Csc[x] 三角函数，其引数的单位为弧度Sinh[x],Cosh[x],Tanh[x],… 双曲函数ArcSin[x],ArcCos[x],ArcTan[x] 反三角函数ArcCot[x],ArcSec[x],ArcCsc[x]ArcS inh[x],ArcCosh[x],ArcTanh[x],…反双曲函数Sqrt[x] 根号Exp[x] 指数Log[x] 自然对数Log[a,x] 以a为底的对数Abs[x] 绝对值Round[x] 最接近x的整数Floor[x] 小于或等于x的最大整数Ceiling[x] 大于或等于x的最小整数Mod[a,b] a/b所得的馀数n! 阶乘Random[] 0至1之间的随机数（最新版本已经不用这个函数，改为使用RandomReal[]）Max[a,b,c,...]，Min[a,b,c,…] a,b,c,…的极大/极小值数值设定x=a 将变数x的值设为ax=y=b 将变数x和y的值均设为bx=. 或 Clear[x] 除去变数x所存的值变数使用的一些法则xy 中间没有空格，视为变数xyx y x乘上y3x 3乘上xx3 变数x3x^2y 为 x^2 y次方运算子比乘法的运算子有较高的处理顺序四个处理指令Expand[expr] 将 expr展开Factor[expr] 将 expr因式分解Simplify[expr] 将 expr化简成精简的式子FullSimplify[expr] Mathematica 会尝试更多的化简公式，将expr化成更精简的式子多项式/分式转换ExpandAll[expr] 把算式全部展开Together[expr] 将 expr各项通分在并成一项Apart[expr] 把分式拆开成数项分式的和Apart[expr,var] 视var以外的变数为常数，将 expr拆成数项的和Cancel[expr] 把分子和分母共同的因子消去分母/分子运算Denominator[expr] 取出expr的分母Numerator[expr] 取出expr的分子ExpandDenominator[expr] 展开expr的分母ExpandNumerator[expr] 展开expr的分子多项式转换函数Collect[expr,x] 将 expr表示成x的多项式，如Collect[expr,{x,y,…}] 将 expr分别表示成x,y,…的多项式FactorTerms[expr] 将 expr的数值因子提出，如 4x+2=2(2x+1)FactorTerms[expr,x] 将 expr中把所有不包含x项的因子提出FactorTerms[exp r,{x,y,…}] 将 expr中把所有不包含{x,y,...}项的因子提出函数和指数运算TrigExpand[expr] 将三角函数展开TrigFactor[expr] 将三角函数所组成的数学式因式分解TrigReduce[expr] 将相乘或次方的三角函数化成一次方的基本三角函数之组合ExpT oTrig[expr] 将指数函数化成三角函数或双曲函数TrigToExp[expr] 将三角函数或双曲函数化成指数函数复数、次方乘积ComplexExpand[expr] 假设所有的变数都是实数来对expr展开ComplexExpand[expr,{x,y,…}] 假设x,y,..等变数均为复数来对 expr展开PowerExpand[expr] 将项次、系数最高次方Coefficient[expr,form] 于 expr中form的系数Exponent[expr,form] 于 expr中form的最高次方Part[expr,n] 或 expr[[n]] 在 expr项中第n个项代换运算子expr/.x->value 将 expr里所有的x均代换成valueexpr/.{x->value1,y->value2,…} 执行数个不同变数的代换expr/.{{x->value1},{x->value2},…} 将 expr代入不同的x值expr//.{x->value1,y->value2,…} 重复代换到 expr不再改变为止求解方程式的根Solve[lhs==rhs,x] 解方程式lhs==rhs，求xNsolve[lhs==rhs,x] 解方程式lhs==rhs的数值解Solve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] 解联立方程式，求x,y,…NSolve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] 解联立方程式的数值解FindRoot[lhs==rhs,{x,x0}] 由初始点x0求lhs==rhs的根四种括号(term) 圆括号，括号内的term先计算f[x] 方括号，内放函数的引数{x,y,z} 大括号或串列括号，内放串列的元素p[[i ]] 或 Part[p,i] 双方括号，p的第i项元素p[[i,j]] 或 Part[p,i,j] p的第i项第j个元素缩短输出指令expr//Short 显示一行的计算结果Short[expr,n] 显示n行的计算结果Command; 执行command，但不列出结果查询物件Command 查询Command的语法及说明Command 查询Command的语法和属性及选择项Aaaa* 查询所有开头为Aaaa的物件定义之查询与清除f[x_]= expr 立即定义函数f[x]f[x_]:= expr 延迟定义函数f[x]f[x_,y_,…] 函数f有两个以上的引数f 查询函数f的定义Clear[f] 或 f=. 清除f的定义Remove[f] 将f自系统中清除掉含有预设值的Patterna_+b_. b的预设值为0，即若b从缺，则b以0代替x_ y_ y的预设值为1x_^y_ y的预设值为1条件式的自订函数lhs:=rhs/;condition 当condition成立时，lhs才会定义成rhs If指令If[test,then,else] 若test为真，则回应then，否则回应elseIf[test,then,else,unknow] 同上，若test无法判定真或假时，则回应unknow 极限Limit[expr,x->c] 当x趋近c时，求expr的极限Limit[expr,x->c,Direction->1]Limit[expr,x->c,Direction->-1]微分D[f,x] 函数f对x作微分D[f,x1,x2,…] 函数f对x1,x2,…作微分D[f,{x,n}] 函数f对x微分n次D[f,x,NonConstants->{y,z,…}] 函数f对x作微分，将y,z,…视为x的函数全微分Dt[f] 全微分dfDt[f,x] 全微分Dt[f,x1,x2,…] 全微分Dt[f,x,Constants->{c1,c2,…}] 全微分，视c1,c2,…为常数不定积分Integrate[f,x] 不定积分∫f dx定积分Integrate[f,{x,xmin,xmax}] 定积分Integrate[f,{x,xmin,xmax},{y,ymin,ymax}] 定积分数列之和与积Sum[f,{i,imin,imax}] 求和Sum[f,{i,imin,imax,di}] 求数列和，引数i以di递增Sum[f,{i,imin,imax},{j,jmin,jmax}]Product[f,{i,imin,imax}] 求积Product[f,{i,imin,imax,di}] 求数列之积，引数i以di递增Product[f,{i,imin,imax},{j,jmin,jmax}]泰勒展开式Series[expr,{x,x0,n}] 对expr于x0点作泰勒级数展开至(x-x0)n 项Series[expr,{x,x0,m},{y,y0,n}] 对x0和y0展开关系运算子a==b 等于a>b 大于a>=b 大于等于aa<=b 小于等于a!=b 不等于逻辑运算子!p notp||q||… orp&&q&&… andXor[p,q,…] exclusive orLogicalExpand[expr] 将逻辑表示式展开二维绘图指令Plot[f,{x,xmin,xmax}]画出f在xmin到xmax之间的图形Plot[{f1,f2,…},{x,xmin,xmax}]同时画出数个函数图形Plot[f,{x,xmin,xmax},option->value]指定特殊的绘图选项，画出函数f的图形Plot几种指令选项预设值说明AspectRatio 1/GoldenRatio 图形高和宽之比例，高/宽Axes True 是否把坐标轴画出AxesLabel Automatic 为坐标轴贴上标记，若设定为AxesLabel->{?ylabel?}，则为y轴之标记。

整理mathematica数学常用命令大全之欧阳音创编

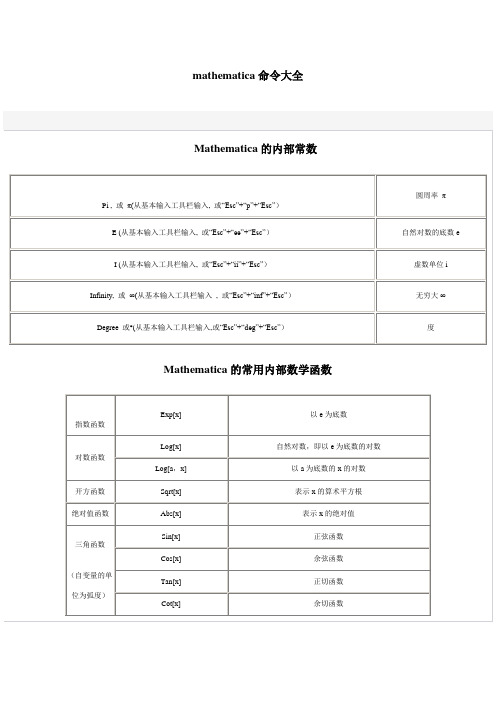
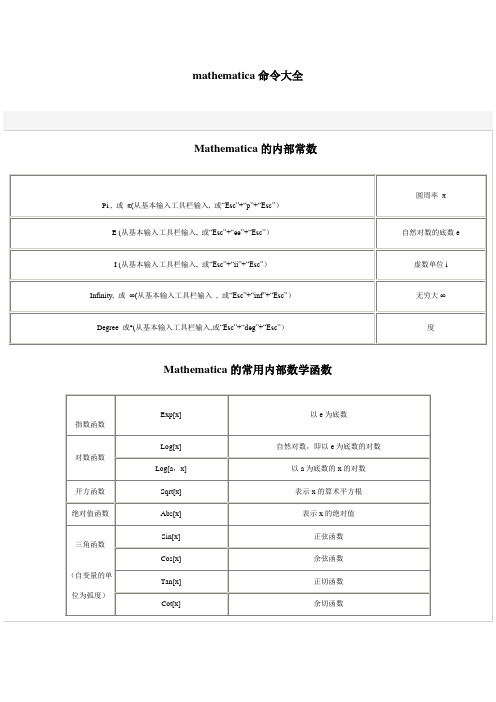
Mathematica的内部常数Mathematica的常用内部数学函数Mathematica中的数学运算符Mathematica的关系运算符注：上面的关系运算符也可从基本输入工具栏输入。

如何用mathematica求多项式的最大公因式和最小公倍式如何用mathematica求整数的最大公约数和最小公倍数如何用mathematica进行整数的质因数分解如何用mathematica求整数的正约数如何用mathematica判断一个整数是否为质数如何用mathematica求第n个质数如何用mathematica求阶乘如何用mathematica配方Mathematica没有提供专门的配方命令,但是我们可以非常轻松地自定义一个函数进行配方。

如何用mathematica进行多项式运算如何用mathematica进行分式运算如何用Mathematica进行因式分解如何用Mathematica展开如何用Mathematica进行化简如何用Mathematica合并同类项如何用Mathematica进行数学式的转换如何用Mathematica进行变量替换如何用mathematica进行复数运算如何在mathematica中表示集合与数学中表示集合的方法相同，格式如下：下列命令可以生成特殊的集合：如何用Mathematica求集合的交集、并集、差集和补集如何mathematica用排序如何在Mathematica中解方程注：方程的等号必须用： = =如何在Mathematica中解方程组Solve[{方程组}，{变元组}]注：方程的等号必须用： = =如何在Mathematica中解不等式先加载：Algebra`InequalitySolve` ，加载方法为：<<Algebra`InequalitySolve`然后执行解不等式的命令InequalitySolve，此命令的使用格式如下：<--mstheme-->如何在Mathematica中解不等式组先加载：Algebra`InequalitySolve` ，加载方法为：<<Algebra`InequalitySolve`然后执行解不等式组的命令InequalitySolve，此命令的使用格式如下：<--mstheme-->如何在Mathematica中解不等式组先加载：Algebra`InequalitySolve` ，加载方法为：<<Algebra`InequalitySolve`然后执行解不等式组的命令InequalitySolve，此命令的使用格式如下：<--mstheme-->如何用mathematica表示分段函数如何用mathematica求反函数对系统内部的函数生效，但对自定义的函数不起任何作用，也许是方法不对。

整理mathematica数学常用命令大全

整理mathematica数学常⽤命令⼤全Mathematica的内部常数Mathematica的常⽤内部数学函数Mathematica中的数学运算符Mathematica的关系运算符注：上⾯的关系运算符也可从基本输⼊⼯具栏输⼊。

如何⽤mathematica求多项式的最⼤公因式和最⼩公倍式如何⽤mathematica求整数的最⼤公约数和最⼩公倍数如何⽤mathematica进⾏整数的质因数分解如何⽤mathematica求整数的正约数如何⽤mathematica判断⼀个整数是否为质数如何⽤mathematica求第n个质数如何⽤mathematica求阶乘如何⽤mathematica配⽅Mathematica没有提供专门的配⽅命令,但是我们可以⾮常轻松地⾃定义⼀个函数进⾏配⽅。

如何⽤mathematica进⾏多项式运算如何⽤mathematica进⾏分式运算如何⽤Mathematica进⾏因式分解如何⽤Mathematica展开如何⽤Mathematica进⾏化简如何⽤Mathematica合并同类项如何⽤Mathematica进⾏数学式的转换如何⽤Mathematica进⾏变量替换如何⽤mathematica进⾏复数运算如何在mathematica中表⽰集合与数学中表⽰集合的⽅法相同，格式如下：下列命令可以⽣成特殊的集合：如何⽤Mathematica求集合的交集、并集、差集和补集如何mathematica⽤排序如何在Mathematica中解⽅程注：⽅程的等号必须⽤：= =如何在Mathematica中解⽅程组Solve[{⽅程组}，{变元组}]注：⽅程的等号必须⽤：= =如何在Mathematica中解不等式先加载：Algebra`InequalitySolve` ，加载⽅法为：<然后执⾏解不等式的命令InequalitySolve，此命令的使⽤格式如下：<--mstheme-->如何在Mathematica中解不等式组先加载：Algebra`InequalitySolve` ，加载⽅法为：<然后执⾏解不等式组的命令InequalitySolve，此命令的使⽤格式如下：<--mstheme-->如何在Mathematica中解不等式组先加载：Algebra`InequalitySolve` ，加载⽅法为：<<--mstheme-->如何⽤mathematica表⽰分段函数如何⽤mathematica求反函数对系统内部的函数⽣效，但对⾃定义的函数不起任何作⽤，也许是⽅法不对。

Mathematica语句基本命令

Mathematica的内部常数Pi , 或π(从基本输入工具栏输入, 或“Esc”+“p”+“Esc”）圆周率π E (从基本输入工具栏输入, 或“Esc”+“ee”+“Esc”）自然对数的底数e I (从基本输入工具栏输入, 或“Esc”+“ii”+“Esc”）虚数单位iInfinity, 或∞(从基本输入工具栏输入 , 或“Esc”+“inf”+“Esc”）无穷大∞Degree 或°(从基本输入工具栏输入,或“Esc”+“deg”+“Esc”）度Mathematica的常用内部数学函数指数函数Exp[x]以e为底数对数函数Log[x]自然对数，即以e为底数的对数Log[a，x]以a为底数的x的对数开方函数Sqrt[x]表示x的算术平方根绝对值函数Abs[x]表示x的绝对值三角函数（自变量的单位为弧度）Sin[x]正弦函数Cos[x]余弦函数Tan[x]正切函数Cot[x]余切函数Sec[x]正割函数Csc[x]余割函数反三角函数ArcSin[x]反正弦函数ArcCos[x]反余弦函数ArcTan[x]反正切函数ArcCot[x]反余切函数ArcSec[x]反正割函数ArcCsc[x]反余割函数双曲函数Sinh[x]双曲正弦函数Cosh[x]双曲余弦函数Tanh[x]双曲正切函数Coth[x]双曲余切函数Sech[x]双曲正割函数Csch[x]双曲余割函数反双曲函数ArcSinh[x]反双曲正弦函数ArcCosh[x]反双曲余弦函数ArcTanh[x]反双曲正切函数ArcCoth[x]反双曲余切函数ArcSech[x]反双曲正割函数ArcCsch[x]反双曲余割函数求角度函数ArcTan[x，y]以坐标原点为顶点，x轴正半轴为始边，从原点到点（x，y）的射线为终边的角，其单位为弧度数论函数GCD[a,b,c,．．．]最大公约数函数LCM[a,b,c,．．．]最小公倍数函数Mod[m,n]求余函数(表示m除以n的余数)Quotient[m，n]求商函数（表示m除以n的商）Divisors[n]求所有可以整除n的整数FactorInteger[n]因数分解，即把整数分解成质数的乘积Prime[n]求第n个质数PrimeQ[n]判断整数n是否为质数，若是，则结果为True，否则结果为False Random[Integer，{m，n}]随机产生m到n之间的整数排列组合函数Factorial[n]或n！阶乘函数，表示n的阶乘复数函数Re[z]实部函数Im[z]虚部函数Arg(z)辐角函数Abs[z]求复数的模Conjugate[z]求复数的共轭复数Exp[z]复数指数函数求整函数与截尾函数Ceiling[x]表示大于或等于实数x的最小整数Floor[x]表示小于或等于实数x的最大整数Round[x]表示最接近x的整数IntegerPart[x]表示实数x的整数部分FractionalPart[x]表示实数x的小数部分分数与浮点数运算函数N[num]或num//N把精确数num化成浮点数（默认16位有效数字）N[num，n]把精确数num化成具有n个有效数字的浮点数NumberForm[num，n]以n个有效数字表示numRationalize[float]将浮点数float转换成与其相等的分数Rationalize[float，dx]将浮点数float转换成与其近似相等的分数，误差小于dx最大、最小函数Max[a，b，c，．．．]求最大数Min[a，b，c，．．．]求最小数符号函数Sign[x]Mathematica中的数学运算符a+b 加法a-b减法a*b (可用空格键代替*)乘法a/b (输入方法为：“ Ctrl ” + “ / ” ) 除法a^b (输入方法为：“ Ctrl ” + “ ^ ” )乘方-a 负号Mathematica的关系运算符==等于<小于>大于<=小于或等于>=大于或等于!=不等于注：上面的关系运算符也可从基本输入工具栏输入。

mathmatic 基本用法

mathmatic 基本用法Mathematica是一种强大的数学软件，它具有广泛的数学计算和可视化功能。

基本用法包括使用Mathematica进行数学运算、求解方程、绘制图表等。

1.数学运算：Mathematica可以进行基本的数学运算，如加减乘除、幂运算、三角函数、对数函数等。

例如，可以输入"2+3"得到结果"5"，输入"Sin[π/2]"得到结果"1"。

2.方程求解：Mathematica可以求解各种类型的方程。

例如，可以输入"Solve[x^2 - 3x + 2 == 0, x]"来求解这个二次方程，得到结果"x == 1 || x == 2"。

3.符号计算：Mathematica可以进行符号计算，包括展开、化简、因式分解等。

例如，可以输入"Simplify[(x^2 + x - 6)/(x + 3)]"来化简这个表达式，得到结果"x - 2"。

4.绘图功能：Mathematica可以生成各种类型的图表，包括二维曲线图、三维曲面图、柱状图、散点图等。

例如，可以输入"Plot[Sin[x], {x, 0, 2π}]"来绘制正弦函数的曲线图。

除了基本用法外，Mathematica还有许多其他功能，如矩阵计算、微积分、概率统计、符号推导、动态演示等。

它还提供了大量的内置函数和算法，可以用于求解复杂的数学问题。

使用Mathematica还可以进行科学计算、工程计算、数据分析等各种应用领域。

总之，Mathematica是一款功能强大的数学软件，可以帮助用户进行各种数学计算和可视化操作。

关于数论MATHEMATICA相关指令

∑fa 加到 b
∑∑ f
i=m j =r n
n
s
∏f
i=m
Moebius μ-函數 σk(n)=
d n ,d >0
∑d
k
，σ0(n)表 n 的正因數個數
σ1(n)表 n 的正因數和 JacobiSymbol[n,m] ExtendedGCD[m,n]
n 當 m 為奇質數時就是 Legendre 符號 m 給出{g,{r,s}}，其中 g 為 m,n 的最大公因數， g=rm+sn
f[x_]:=expr fac[n_]:=n fac[n-1];fac[0]=1; Nest[f,x,n] NestList[f,x,n] For[start,test,increment,expr] While[test,expr] Do[expr,{i,imin,imax,di}]
定義函數 f[] 定義遞歸函數 fac[n] 以 x 為初值，用函數 f[]來疊代 n 次同 Nest[]指令，但會把每次疊代的結果記錄下來，形成數列{f[x],f[f[x]],...} 以 start 為初值 increment 為增量作 expr ，的運算，直到 test 不成立為止作 expr 的迴圈運算，直到 test 不成立 i 從 i=imin 到 i=imax 間距 di 來計算 expr
數論 MATHEMATICA 相關指令
Mod[k,n] Quotient[m,n] GCD[n1,n2,...] LCM[n1,n2,...] IntegerDigits[n,b] Floor[x] FactorInteger[n] Divisors[n] Prime[k] PrimePi[x] PrimeQ[n] Min[x1,x2,...] Max[x1,x2,...] n! EulerPhi[n] Sum[f,{i,m,n}] Sum[f,{i,m,n,d}] Sum[f,{i,m,n},{j,r,s}] Product[f,{i,m,n}] MoebiusMu[n] DivisorSigma[k,n] k (mod n)(k 被 n 除的餘數) m 被 n 除的商(即 m/n 的整數部分) 最大公因數最小公倍數將 n 化為以 b 為基底的數小於等於 x 的最大整數列出 n 的質因數分解列出 n 的所有正因數第 k 個質數小於等於 x 的質數個數詢問 n 是否為質數？ x1,x2,...中最小 x1,x2,...中最大 n 階乘尤拉φ-函數：小於等於 n 與 n 互質的正整數個數

mathematica执行命令(共20页)

Mathmatic 函数(hánshù)表一、运算符及特殊符号Line1; 执行(zhíxíng)Line，不显示(xiǎnshì)结果Line1,line2 顺次(shùncì)执行Line1，2，并显示结果?name 关于系统变量name的信息??name 关于系统变量name的全部信息!command 执行Dos命令n! N的阶乘!!filename 显示文件内容<Expr>> filename 打开文件写Expr>>>filename 打开文件从文件末写() 结合率[] 函数{} 一个表<*Math Fun*> 在c语言中使用math的函数(*Note*) 程序的注释#n 第n个参数## 所有参数rule& 把rule作用于后面的式子% 前一次的输出%% 倒数第二次的输出%n 第n个输出二、系统(xìtǒng)常数Pi 3.1415....的无限(wúxiàn)精度数值E 2.17828...的无限精度(jīnɡ dù)数值Catalan 0.915966..卡塔兰常数(chángshù) EulerGamma 0.5772....高斯常数GoldenRatio 1.61803...黄金分割数Degree Pi/180角度弧度换算I 复数单位Infinity 无穷大-Infinity 负无穷大ComplexInfinity 复无穷大Indeterminate 不定式三、代数计算Expand[expr] 展开表达式Expand[expr] 展开表达式Factor[expr] 展开表达式Simplify[expr] 化简表达式FullSimplify[expr] 将特殊函数等也进行化简PowerExpand[expr] 展开所有的幂次形式ComplexExpand[expr,{x1,x2...}] 按复数实部虚部展开FunctionExpand[expr] 化简expr中的特殊函数Collect[expr, x] 合并同次项Collect[expr, {x1,x2,...}] 合并x1,x2,...的同次项Together[expr] 通分Apart[expr] 部分分式展开Apart[expr, var] 对var的部分分式展开Cancel[expr] 约分ExpandAll[expr] 展开表达式ExpandAll[expr, patt] 展开表达式FactorTerms[poly] 提出共有的数字因子FactorTerms[poly, x] 提出与x无关的数字因子FactorTerms[poly, {x1,x2...}] 提出与xi无关的数字因子Coefficient[expr, form] 多项式expr中form的系数Coefficient[expr, form, n] 多项式expr中form^n的系数Exponent[expr, form] 表达式expr中form的最高指数Numerator[expr] 表达式expr的分子Denominator[expr] 表达式expr的分母ExpandNumerator[expr] 展开expr的分子部分ExpandDenominator[expr] 展开expr的分母部分TrigExpand[expr] 展开表达式中的三角函数TrigFactor[expr] 给出表达式中的三角函数因子TrigFactorList[expr] 给出表达式中的三角函数因子的表TrigReduce[expr] 对表达式中的三角函数化简TrigToExp[expr] 三角到指数的转化ExpToTrig[expr] 指数到三角的转化RootReduce[expr]ToRadicals[expr]四、解方程Solve[eqns, vars] 从方程组eqns中解出vars Solve[eqns, vars, elims] 从方程组eqns中削去变量(biànliàng)elims,解出varsDSolve[eqn, y, x] 解微分方程(wēi fēn fānɡchénɡ)，其中y是x的函数(hánshù)DSolve[{eqn1,eqn2,...},{y1,y2...},x]解微分方程(wēi fēn fānɡ chénɡ)组，其中yi是x的函数DSolve[eqn, y, {x1,x2...}] 解偏微分方程Eliminate[eqns, vars] 把方程组eqns中变量vars约去SolveAlways[eqns, vars] 给出等式成立的所有参数满足的条件Reduce[eqns, vars] 化简并给出所有可能解的条件LogicalExpand[expr] 用&&和||将逻辑表达式展开InverseFunction[f] 求函数f的逆函数Root[f, k] 求多项式函数的第k个根Roots[lhs==rhs, var] 得到多项式方程的所有根五、微积分函数D[f, x] 求f[x]的微分D[f, {x, n}] 求f[x]的n阶微分D[f,x1,x2..] 求f[x]对x1,x2...偏微分Dt[f, x] 求f[x]的全微分df/dxDt[f] 求f[x]的全微分dfDt[f, {x, n}] n阶全微分df^n/dx^nDt[f,x1,x2..] 对x1,x2..的偏微分Integrate[f, x] f[x]对x在的不定积分Integrate[f, {x, xmin, xmax}] f[x]对x在区间(xmin,xmax)的定积分Integrate[f, {x, xmin, xmax}, {y, ymin, ymax}]f[x,y]的二重积分Limit[expr, x->x0] x趋近于x0时expr的极限Residue[expr, {x,x0}] expr在x0处的留数Series[f, {x, x0, n}] 给出f[x]在x0处的幂级数展开Series[f, {x, x0,nx}, {y, y0, ny}]先对y幂级数展开，再对xNormal[expr] 化简并给出最常见的表达式SeriesCoefficient[series, n] 给出级数中第n次项的系数SeriesCoefficient[series, {n1,n2...}]'或Derivative[n1,n2...][f] 一阶导数InverseSeries[s, x] 给出逆函数的级数ComposeSeries[serie1,serie2...] 给出两个基数的组合SeriesData[x,x0,{a0,a1,..},nmin,nmax,den]表示一个在x0处x的幂级数? O[x]^n n阶小量x^nO[x, x0]^n n阶小量(x-x0)^n八、数值(shùzí)函数N[expr] 表达式的机器(jī qì)精度近似值N[expr, n] 表达式的n位近似值，n为任意(rènyì)正整数NSolve[lhs==rhs, var] 求方程(fāngchéng)数值解NSolve[eqn, var, n] 求方程数值解，结果精度到n 位NDSolve[eqns, y, {x, xmin, xmax}]微分方程数值解NDSolve[eqns, {y1,y2,...}, {x, xmin, xmax}]微分方程组数值解FindRoot[lhs==rhs, {x,x0}] 以x0为初值，寻找方程数值解FindRoot[lhs==rhs, {x, xstart, xmin, xmax}] NSum[f, {i,imin,imax,di}] 数值求和，di为步长NSum[f, {i,imin,imax,di}, {j,..},..] 多维函数求和NProduct[f, {i, imin, imax, di}]函数求积NIntegrate[f, {x, xmin, xmax}] 函数数值积分优化函数：FindMinimum[f, {x,x0}] 以x0为初值，寻找函数最小值FindMinimum[f, {x,x0}] 以x0为初值，寻找函数最小值FindMinimum[f, {x, xstart, xmin, xmax}] ConstrainedMin[f,{inequ},{x,y,..}]inequ为线性不等式组，f为x,y..之线性函数，得到最小值及此时的x,y..取值ConstrainedMax[f, {inequ}, {x, y,..}]同上LinearProgramming[c,m,b] 解线性组合c.x在m.x>=b&&x>=0约束下的最小值，x,b,c为向量,m为矩阵LatticeReduce[{v1,v2...}] 向量组vi的极小无关组数据处理：Fit[data,funs,vars]用指定函数组对数据进行最小二乘拟和data可以为{{x1,y1,..f1},{x2,y2,..f2}..}多维的情况emp: Fit[{10.22,12,3.2,9.9}, {1, x, x^2,Sin[x]}, x] Interpolation[data]对数据进行差值,data同上，另外还可以为{{x1,{f1,df11,df12}},{x2,{f2,.}..}指定各阶导数InterpolationOrder默认为3次，可修改ListInterpolation[array]对离散数据插值，array可为n维ListInterpolation[array,{{xmin,xmax},{ymin,ymax}, ..}]FunctionInterpolation[expr,{x,xmin,xmax},{y,ymin,ymax},..]以对应expr[xi,yi]的为数据进行插值Fourier[list] 对复数数据进行付氏变换InverseFourier[list] 对复数数据进行付氏逆变换Min[{x1,x2...},{y1,y2,...}]得到每个表中的最小值Max[{x1,x2...},{y1,y2,...}]得到每个表中的最大值Select[list, crit] 将表中使得crit为True的元素选择出来Count[list, pattern] 将表中匹配模式pattern的元素的个数Sort[list] 将表中元素按升序排列Sort[list,p] 将表中元素按p[e1,e2]为True的顺序比较list的任两个元素e1,e2,实际上Sort[list]中默认p=Greater集合论：Union[list1,list2..] 表listi的并集并排序Intersection[list1,list2..] 表listi的交集并排序Complement[listall,list1,list2...]从全集listall中对listi的差集九、虚数(xūshù)函数Re[expr] 复数(fùshù)表达式的实部Im[expr] 复数(fùshù)表达式的虚部Abs[expr] 复数(fùshù)表达式的模Arg[expr] 复数表达式的辐角Conjugate[expr] 复数表达式的共轭十、数的头及模式及其他操作Integer _Integer 整数Real _Real 实数Complex _Complex 复数Rational_Rational 有理数(*注：模式用在函数参数传递中，如MyFun[Para1_Integer,Para2_Real]规定传入参数的类型，另外也可用来判断If[Head[a]==Real,...]*)IntegerDigits[n,b,len] 数字n以b近制的前len个码元RealDigits[x,b,len] 类上FromDigits[list] IntegerDigits的反函数Rationalize[x,dx] 把实数x有理化成有理数，误差小于dxChop[expr, delta] 将expr中小于delta的部分去掉,dx默认为10^-10Accuracy[x] 给出x小数部分位数,对于Pi,E等为无限大Precision[x] 给出x有效数字位数,对于Pi,E等为无限大SetAccuracy[expr, n] 设置expr显示时的小数部分位数SetPrecision[expr, n] 设置expr显示时的有效数字位数十一、区间函数Interval[{min, max}] 区间[min, max](* Solve[3x+2==Interval[{-2,5}],x*)IntervalMemberQ[interval, x] x在区间内吗？IntervalMemberQ[interval1,interval2] 区间2在区间1内吗？IntervalUnion[intv1,intv2...] 区间的并IntervalIntersection[intv1,intv2...] 区间的交十二、矩阵操作a.b.c 或 Dot[a, b, c] 矩阵、向量、张量的点积Inverse[m] 矩阵的逆Transpose[list] 矩阵的转置Transpose[list,{n1,n2..}]将矩阵list 第k行与第nk 列交换Det[m] 矩阵的行列式Eigenvalues[m] 特征值Eigenvectors[m] 特征向量Eigensystem[m] 特征系统，返回{eigvalues,eigvectors}LinearSolve[m, b] 解线性方程组m.x==b NullSpace[m] 矩阵m的零空间，即m.NullSpace[m]==零向量RowReduce[m] m化简为阶梯矩阵Minors[m, k] m的所有k*k阶子矩阵的行列式的值(伴随阵，好像是)MatrixPower[mat, n] 阵mat自乘n次Outer[f,list1,list2..] listi中各个元之间相互组合，并作为f的参数的到的矩? Outer[Times,list1,list2]给出矩阵的外积SingularValues[m] m的奇异值，结果为{u,w,v}, m=Conjugate[Transpose[u]].DiagonalMatrix[w].v PseudoInverse[m] m的广义逆QRDecomposition[m] QR分解SchurDecomposition[m] Schur分解LUDecomposition[m] LU分解十四、绘图(huì tú)函数二维作图Plot[f,{x,xmin,xmax}] 一维函数(hánshù)f[x]在区间(qū jiān)[xmin,xmax]上的函数(hánshù)曲? Plot[{f1,f2..},{x,xmin,xmax}] 在一张图上画几条曲线ListPlot[{y1,y2,..}] 绘出由离散点对(n,yn)组成的图ListPlot[{{x1,y1},{x2,y2},..}] 绘出由离散点对(xn,yn)组成的图ParametricPlot[{fx,fy},{t,tmin,tmax}] 由参数方程在参数变化范围内的曲线ParametricPlot[{{fx,fy},{gx,gy},...},{t,tmin,tmax}] 在一张图上画多条参数曲线选项：PlotRange->{0,1} 作图显示的值域范围AspectRatio->1/GoldenRatio生成图形的纵横比PlotLabel ->label 标题文字Axes ->{False,True} 分别制定是否画x,y轴AxesLabel->{xlabel,ylabel}x,y轴上的说明文字Ticks->None,Automatic,fun用什么方式画轴的刻度AxesOrigin ->{x,y} 坐标轴原点位置AxesStyle->{{xstyle}, {ystyle}}设置轴线的线性颜色等属性Frame ->True,False 是否画边框FrameLabel ->{xmlabel,ymlabel,xplabel,yplabel} 边框四边上的文字FrameTicks同Ticks 边框上是否画刻度GridLines 同Ticks 图上是否画栅格线FrameStyle ->{{xmstyle},{ymstyle}设置边框线的线性颜色等属性ListPlot[data,PlotJoined->True] 把离散点按顺序连线PlotSytle->{{style1},{style2},..}曲线的线性颜色等属性PlotPoints->15 曲线取样点，越大越细致三维作图Plot3D[f,{x,xmin,xmax}, {y,ymin,ymax}]二维函数f[x,y]的空间曲面Plot3D[{f,s}, {x,xmin,xmax}, {y,ymin,ymax}]同上，曲面的染色由s[x,y]值决定ListPlot3D[array,shades]同上，曲面的染色由shades[数据]值决定ParametricPlot3D[{fx,fy,fz},{t,tmin,tmax}]二元数方程在参数变化范围内的曲线ParametricPlot3D[{{fx,fy,fz},{gx,gy,gz},...},{t,tmin, tmax}]多条空间参数曲线选项：ViewPoint ->{x,y,z} 三维视点，默认为{1.3,-2.4,2} Boxed -> True,False 是否画三维长方体边框BoxRatios->{sx,sy,sz} 三轴比例BoxStyle 三维长方体边框线性颜色等属性Lighting ->True 是否染色LightSources->{s1,s2..} si为某一个光源si={{dx,dy,dz},color}color为灯色，向dx,dy,dz方向照射AmbientLight->颜色函数慢散射光的光源Mesh->True,False 是否画曲面上与x,y轴平行的截面的截线MeshStyle 截线线性颜色等属性MeshRange->{{xmin,xmax}, {ymin,ymax}}网格范围ClipFill->Automatic,None,color,{bottom,top}指定图形顶部、底部超界后所画的颜色Shading ->False,True 是否染色HiddenSurface->True,False 略去被遮住不显示部分的信息等高线ContourPlot[f,{x,xmin,xmax},{y,ymin,ymax}]二维函数f[x,y]在指定区间上的等高线图ListContourPlot[array] 根据二维数组array数值画等高线选项：Contours->n 画n条等高线Contours->{z1,z2,..} 在zi处画等高线ContourShading -> False 是否用深浅染色ContourLines -> True 是否画等高线ContourStyle -> {{style1},{style2},..}等高线线性颜色等属性FrameTicks 同上密度图DensityPlot[f,{x,xmin,xmax},{y,ymin,ymax}]二维函数f[x,y]在指定区间上的密度图ListDensityPlot[array] 同上图形显示Show[graphics,options] 显示一组图形对象，options为选项设置Show[g1,g2...] 在一个图上叠加显示一组图形对象GraphicsArray[{g1,g2,...}]在一个图上分块显示一组图形对象SelectionAnimate[notebook,t]把选中的notebook中的图画循环放映选项：(此处选项适用于全部图形函数) Background->颜色函数指定绘图的背景颜色RotateLabel -> True 竖着写文字TextStyle 此后输出文字的字体，颜色大小等ColorFunction->Hue等把其作用于某点的函数值上决定某点的颜色RenderAll->False 是否对遮挡部分也染色MaxBend 曲线、曲面最大弯曲度十四、绘图(huì tú)函数（续）图元函数(hánshù)Graphics[prim, options]prim为下面各种(ɡè zhǒnɡ)函数组成的表，表示一个二维图形对象Graphics3D[prim, options]prim为下面各种函数组成(zǔ chénɡ)的表，表示一个三维图形对象SurfaceGraphics[array, shades]表示一个由array和shade决定的曲面对象ContourGraphics[array]表示一个由array决定的等高线图对象DensityGraphics[array]表示一个由array决定的密度图对象以上定义图形对象，可以进行对变量赋值，合并显示等操作，也可以存盘Point[p] p={x,y}或{x,y,z}，在指定位置画点Line[{p1,p2,..}]经由pi点连线Rectangle[{xmin, ymin}, {xmax, ymax}] 画矩形Cuboid[{xmin,ymin,zmin},{xmax,ymax,zmax}]由对角线指定的长方体Polygon[{p1,p2,..}] 封闭多边形Circle[{x,y},r] 画圆Circle...内容摘要。

Mathematica常用命令

Mathe‎m atic‎a常用命令‎软件学习‎2010-‎10-19‎21:0‎2:15 ‎阅读127‎评论0 ‎字号：‎大中小订‎阅 .‎M athe‎m atic‎a的内部常‎数Pi ‎,或π(‎从基本输入‎工具栏输入‎,或“E‎s c”+“‎p”+“E‎s c”）圆‎周率πE‎(从基本‎输入工具栏‎输入, 或‎“Esc”‎+“ee”‎+“Esc‎”）自然对‎数的底数e‎I (从‎基本输入工‎具栏输入,‎或“Es‎c”+“i‎i”+“E‎s c”）虚‎数单位i‎I nfin‎i ty, ‎或∞(从基‎本输入工具‎栏输入 ,‎或“Es‎c”+“i‎n f”+“‎E sc”）‎无穷大∞‎D egre‎e或°(‎从基本输入‎工具栏输入‎,或“Es‎c”+“d‎e g”+“‎E sc”）‎度Mat‎h emat‎i ca的常‎用内部数学‎函数指数‎函数Exp‎[x]以e‎为底数对‎数函数Lo‎g[x]自‎然对数，即‎以e为底数‎的对数L‎o g[a，‎x]以a为‎底数的x的‎对数开方‎函数Sqr‎t[x]表‎示x的算术‎平方根绝‎对值函数A‎b s[x]‎表示x的绝‎对值三角‎函数（自‎变量的单位‎为弧度）S‎i n[x]‎正弦函数‎C os[x‎]余弦函数‎Tan[‎x]正切函‎数Cot‎[x]余切‎函数Se‎c[x]正‎割函数C‎s c[x]‎余割函数‎反三角函数‎A rcSi‎n[x]反‎正弦函数‎A rcCo‎s[x]反‎余弦函数‎A rcTa‎n[x]反‎正切函数‎A rcCo‎t[x]反‎余切函数‎A rcSe‎c[x]反‎正割函数‎A rcCs‎c[x]反‎余割函数‎双曲函数S‎i nh[x‎]双曲正弦‎函数Co‎s h[x]‎双曲余弦函‎数Tan‎h[x]双‎曲正切函数‎Coth‎[x]双曲‎余切函数‎S ech[‎x]双曲正‎割函数C‎s ch[x‎]双曲余割‎函数反双‎曲函数Ar‎c Sinh‎[x]反双‎曲正弦函数‎ArcC‎o sh[x‎]反双曲余‎弦函数A‎r cTan‎h[x]反‎双曲正切函‎数Arc‎C oth[‎x]反双曲‎余切函数‎A rcSe‎c h[x]‎反双曲正割‎函数Ar‎c Csch‎[x]反双‎曲余割函数‎求角度函‎数ArcT‎a n[x，‎y]以坐标‎原点为顶点‎，x轴正半‎轴为始边，‎从原点到点‎（x，y）‎的射线为终‎边的角，其‎单位为弧度‎数论函数‎G CD[a‎,b,c,‎．．．]最‎大公约数函‎数LCM‎[a,b,‎c,．．．‎]最小公倍‎数函数M‎o d[m,‎n]求余函‎数(表示m‎除以n的余‎数)Qu‎o tien‎t[m，n‎]求商函数‎（表示m除‎以n的商）‎Divi‎s ors[‎n]求所有‎可以整除n‎的整数F‎a ctor‎I nteg‎e r[n]‎因数分解，‎即把整数分‎解成质数的‎乘积Pr‎i me[n‎]求第n个‎质数Pr‎i meQ[‎n]判断整‎数n是否为‎质数，若是‎，则结果为‎T rue，‎否则结果为‎F alse‎Rand‎o m[In‎t eger‎，{m，n‎}]随机产‎生m到n之‎间的整数‎排列组合函‎数Fact‎o rial‎[n]或n‎！阶乘函数‎，表示n的‎阶乘复数‎函数Re[‎z]实部函‎数Im[‎z]虚部函‎数Arg‎(z)辐角‎函数Ab‎s[z]求‎复数的模‎C onju‎g ate[‎z]求复数‎的共轭复数‎Exp[‎z]复数指‎数函数求‎整函数与截‎尾函数Ce‎i ling‎[x]表示‎大于或等于‎实数x的最‎小整数F‎l oor[‎x]表示小‎于或等于实‎数x的最大‎整数Ro‎u nd[x‎]表示最接‎近x的整数‎Inte‎g erPa‎r t[x]‎表示实数x‎的整数部分‎Frac‎t iona‎l Part‎[x]表示‎实数x的小‎数部分分‎数与浮点数‎运算函数N‎[num]‎或num/‎/N把精确‎数num化‎成浮点数（‎默认16位‎有效数字）‎N[nu‎m，n]把‎精确数nu‎m化成具有‎n个有效数‎字的浮点数‎Numb‎e rFor‎m[num‎，n]以n‎个有效数字‎表示num‎Rati‎o nali‎z e[fl‎o at]将‎浮点数fl‎o at转换‎成与其相等‎的分数R‎a tion‎a lize‎[floa‎t，dx]‎将浮点数f‎l oat转‎换成与其近‎似相等的分‎数，误差小‎于dx最‎大、最小函‎数Max[‎a，b，c‎，．．．]‎求最大数‎M in[a‎，b，c，‎．．．]求‎最小数符‎号函数Si‎g n[x]‎Math‎e mati‎c a中的数‎学运算符‎a+b 加‎法a-b‎减法a*‎b (可用‎空格键代替‎*)乘法‎a/b (‎输入方法为‎：“ Ct‎r l ” ‎+ “ /‎” ) ‎除法a^‎b (输入‎方法为：“‎Ctrl‎” + ‎“ ^ ”‎)乘方‎-a 负号‎Math‎e mati‎c a的关系‎运算符=‎=等于<‎小于>大‎于<=小‎于或等于‎>=大于或‎等于!=‎不等于注‎：上面的关‎系运算符也‎可从基本输‎入工具栏输‎入。

mathematica命令大全

Mathematica的内部常数Pi , 或π(从基本输入工具栏输入, 或“Esc”+“p”+“Esc”）圆周率πE (从基本输入工具栏输入, 或“Esc”+“ee”+“Esc”）自然对数的底数eI (从基本输入工具栏输入, 或“Esc”+“ii”+“Esc”）虚数单位iInfinity, 或∞(从基本输入工具栏输入, 或“Esc”+“inf”+“Esc”）无穷大∞Degree 或°(从基本输入工具栏输入,或“Esc”+“deg”+“Esc”）度Mathematica的常用内部数学函数指数函数Exp[x]以e为底数对数函数Log[x]自然对数，即以e为底数的对数Log[a，x]以a为底数的x的对数开方函数Sqrt[x]表示x的算术平方根绝对值函数Abs[x]表示x的绝对值三角函数（自变量的单位为弧度）Sin[x]正弦函数Cos[x]余弦函数Tan[x]正切函数Cot[x]余切函数Sec[x]正割函数Csc[x]余割函数反三角函数ArcSin[x]反正弦函数ArcCos[x]反余弦函数ArcTan[x]反正切函数ArcCot[x]反余切函数ArcSec[x]反正割函数ArcCsc[x]反余割函数双曲函数Sinh[x]双曲正弦函数Cosh[x]双曲余弦函数Tanh[x]双曲正切函数Coth[x]双曲余切函数Sech[x]双曲正割函数Csch[x]双曲余割函数反双曲函数ArcSinh[x]反双曲正弦函数ArcCosh[x]反双曲余弦函数ArcTanh[x]反双曲正切函数ArcCoth[x]反双曲余切函数ArcSech[x]反双曲正割函数ArcCsch[x]反双曲余割函数求角度函数ArcTan[x，y]以坐标原点为顶点，x轴正半轴为始边，从原点到点（x，y）的射线为终边的角，其单位为弧度数论函数GCD[a,b,c,．．．]最大公约数函数LCM[a,b,c,．．．]最小公倍数函数Mod[m,n]求余函数(表示m除以n的余数)Quotient[m，n]求商函数（表示m除以n的商）Divisors[n]求所有可以整除n的整数FactorInteger[n]因数分解，即把整数分解成质数的乘积 Prime[n]求第n个质数PrimeQ[n]判断整数n是否为质数，若是，则结果为True，否则结果为FalseRandom[Integer，{m，n}]随机产生m到n之间的整数排列组合函数Factorial[n]或n！阶乘函数，表示n的阶乘复数函数Re[z]实部函数Im[z]虚部函数Arg(z)辐角函数Abs[z]求复数的模Conjugate[z]求复数的共轭复数Exp[z]复数指数函数求整函数与截尾函数Ceiling[x]表示大于或等于实数x的最小整数Floor[x]表示小于或等于实数x的最大整数Round[x]表示最接近x的整数IntegerPart[x]表示实数x的整数部分FractionalPart[x]表示实数x的小数部分分数与浮点数运算函数N[num]或num//N把精确数num化成浮点数（默认16位有效数字）N[num，n]把精确数num化成具有n个有效数字的浮点数NumberForm[num，n]以n个有效数字表示numRationalize[float]将浮点数float转换成与其相等的分数 Rationalize[float，dx]将浮点数float转换成与其近似相等的分数，误差小于dx最大、最小函数Max[a，b，c，．．．]求最大数Min[a，b，c，．．．]求最小数符号函数Sign[x]Mathematica中的数学运算符a+b 加法a-b减法a*b (可用空格键代替*)乘法a/b (输入方法为：“Ctrl ” + “/ ” ) 除法a^b (输入方法为：“Ctrl ” + “^ ” )乘方-a 负号Mathematica的关系运算符==等于<小于>大于<=小于或等于>=大于或等于!=不等于注：上面的关系运算符也可从基本输入工具栏输入。

(完整版)mathematica命令大全

<< Statistics`DescriptiveStatistics`
或者加载整个统计函数库，加载方法为：
<<Statistics`
求数据data的众数。

数据data的格式为：{ a1,a2,…}
Mode[data]
如何用mathematica求方差和标准差
首先要加载Statistics`DescriptiveStatistics`函数库，加载方法为：
<< Statistics`DescriptiveStatistics`
或者加载整个统计函数库，加载方法为：
<<Statistics`
求数据data的样本方差。

数据data的格式为：{ a1,a2,…} Variance[data]
VarianceMLE[data] 求数据data的母体方差。

数据data的格式为：{ a1,a2,…} StandardDeviation[data] 求数据data的样本标准差。

数据data的格式为：{a1,a2,…} StandardDeviationMLE[data] 求数据data的母体标准差。

数据data的格式为：{ a1,a2,…}
如何用mathematica求协方差和相关系数
首先要加载Statistics`MultiDescriptiveStatistics`函数库，加载方法为：
<< Statistics`MultiDescriptiveStatistics`
或者加载整个统计函数库，加载方法为：
<<Statistics`
求数据data1和data2的样本协方差。

数据的格式为：{a1,a2,…}。

mathmatics常用命令

基本操作1、 a*b 可表示为a b (中间加空格)2、 N[expr,n] 指定结果数字位数，而N[expr]可得到默认小数位数的近似值3、 Abs[x] 绝对值4、 % 表示上一个运算结果 %% 表示上面倒数第二个运算结果 ……以此类推 %n 输出行Out[n]上的结果代号5、 /. 替代符如定义p 代表一多项式，则 p/.a->x 表示用a 代替p 中的x6、取消变量赋值 Clear[p]数的操作1、GCD[a,b,c] 计算a ，b ，c 的最大公约数2、LCM[a,b,c] 计算a ，b ，c 的最小公倍数多项式操作1、 Expand[expr] 将多项式展开2、 Factor[expr] 将多项式分解因式3、 Simplify[expr] 将多项式化简4、 Together[expr] 对有理式通分5、 Apart[expr] 对有理式拆分6、 Collect[expr,x] 对多项式中的x 合并同类项7、 Coefficient[expr,form] 给出expr 中form 项前的系数8、 Exponent[expr,form] 给出expr 中form 项的最高次数函数功能1、一元函数 f[x_]:=expr2、二元函数 f[x_,y_]:=expr3、分段函数 f[x_]:=expr1; x 范围f[x_]:=expr2; x 的范围4、函数调用如f[3] 或 f[3,4]导数和积分1、 D[f,{x,n}] 求函数f 关于变量x 的n 次偏导，默认为1次求导2、 D[f,x] 求函数f 的全导数3、 Integrate[f,x] 求不定积分，也可以用符号()f x dx ⎰表示4、 Integrate[f,{x,a,b}] 求定积分，也可以用符号()ba f x dx ⎰表示5、 Integrate[f,{x,a,b},{y,c,d}] 求二重积分，也可以用符号()bda c dx f x dy ⎰⎰表示求解方程和方程组1、一元简单代数方程求解 Solve[expr = = 0，x]2、多元简单代数方程求解 Solve[{expr1==0,expr2==0},{x,y}]3、一元超越方程求解 FindRoot[expr==0,{x,a}] 其中a 为要求根的初始值，求解结果依赖初始值的选择4、多元超越方程求解FindRoot[{expr1==0,expr2==0},{x,a},{y,b}] 其中a ，b 为初始值表与矩阵1、表与Table函数（1）一维表如a={1，2，3}（2）二维表如aa={{1，2，3}，{2，3，4}}（3）从表中取出元素a[[]] 如a[[2]]得到结果为{2,3,4}aa[[2,3]]得到结果为4（4）Table 可以生成有规律的表，可以用下标计算如Table[i^2,{i,1,6}] 结果为{1，4，9，16，25，36}Table[i-j,{i,3},{j,2}] 结果为{{0，-1}，{1，0}，{2，1}} 2、矩阵的表示（1）行向量{{a，b，c}} 列向量{{a}，{b}，{c}}（2）表//MatrixForm 可以将表直观的反应出来（3）DiagonalMatrix[{a,b,c}] 产生对角阵（4）IdentityMatrix[n] 产生n维单位阵3、矩阵的运算（1）数乘* 矩阵乘法·（2）Det[A] 求方阵A的行列式（3）Minors[A,k] 给出矩阵A的所有k阶子式（4）Transpose[A] 对矩阵A转置（5）Dimensions[A] 给出矩阵A的维数（6）Inverse[A] 求方阵A的逆矩阵（7）RowReduce[A] 用初等行变换将矩阵化为规范阶梯阵（8）MatrixPower[A,n] 求方阵的n次幂A n基本作图函数1、一般作图Plot[f,{x,xmin,xmax}]2、离散点作图ListPlot[{{x1,y1},{x2,y2},{x3,y3},{x4,y4}},其他命令]Prolog →AbsolutePointSize[n] 改变n可以调整点的大小PlotJoined →True 用光滑曲线把散点图连起来3、参数方程作图ParametricPlot[{fx,fy},{t,min,max},其他命令]AspectRatio →n 调整坐标的横纵坐标显示比为n4、利用函数包做特殊图形导入<<类名`包名`（1）极坐标方程图像的绘制<<Graphics`Graphics`PolarPlot[f,{t,min,max}]（2）隐函数方程图像的绘制<<Graphics`ImplicitPlot`ImplicitPlot[f==0,{x,min,max}]5、三维作图Plot3D[f,{x,min,max},{y,min,max},其他命令]PlotRange →{a，b} 设置y轴的显示范围PlotPoints →n 设置取点密度，n越大，图形越精细。

Mathematica常用语句

Mathematica常用语句一、常用常量PiπE eDegree 度(π/180)GoldenRatio 黄金分割比(0.618)Infinity 无穷大∞I 虚数单位ix=. 取消赋值xClear[x] 取消赋值x二、初等函数Log[x] ln xLog[a,x] log a xExp[x] x eSqrt[x] xSin[x] sin(x)Cos[x] cos(x)Tan[x] tan(x)Cot[x] cot(x)ArcSin[x] arcsin(x)ArcCos[x] arccos(x)三、函数的定义f[x_]:= 定义一元函数f[x_,y_]:= 定义二元函数四、常用函数：Plus[n1,n2,] 求和N[x,n] 取x的n位有效数字Abs[x] 取x的绝对值(x为复数时为取x的模) Sign[x] 符号函数Round[x] 最接近x的整数(可比x大也可比x小) Floor[x] 不大于x的最大整数Ceiling[x] 不小于x的最大整数Max[x1,x2,] 取变量x1,x2,的最大值Min[x1,x2,] 取变量x1,x2,的最小值Re[z] 取复数z的实部In[z] 取复数z的虚部Conjugate[z] 取复数z的共轭Arg[z] z的辐角Quotient[m,n] 取商函数(m被n除的整数部分)Mod[m,n] 取余函数(m被n除的余数部分)n！n的阶乘n！！n的双阶乘Binomial[n,m] 二项式系数mCn% 最近一次输出结果%% 倒数第二次输出%n 第n个输出结果Solve[方程] 解方程Fit[] 曲线拟合函数Simplify[] 用于化简的函数If语句If[条件,t,f]满足条件：执行t否则执行fIf[条件,t,f,u] 满足条件：执行t否则执行f无法判别执行u Which语句Which[条件1,t1,条件2,t2] 满足条件i执行ti五、表1、表的建立表名={元素1，元素2,}{循环变量n，循环初值n0，循环终值ni，步长增量d}(d为1时可省)Range[循环初值n0，循环终值ni，步长增量d](d为1时可省；n0为1时也可省)Table[通项公式f(m,n,)，{m,m0,mi,d1}，{ n,n0,ni,d1}]Array[f,n] 生成长为n，元素是f[i]的表Array[f,n,n0] 生成长为n，元素是f[i]且从f[n0]开始的表Array[f,{m,n}] 生成长为{m,n}，元素是f[i,j]的二维数表Array[f,{n1,n2,}] 把f作用到n1,n2,构成的表2、表的调整Length[t] 求表中元素个数(即表长)T[[n]] 表t中第n个元素T[[-n]] 表t中倒数第n个元素First[t] 表t中第一个元素Last[t] 表t中最后一个元素T[[i,j]] 表t中第i个子表中的第j个元素T[[{n1,n2,}]]或Part[t,{n1,n2,}] 由表t中n1,n2,等元素组成的数表Position[t,x] 元素x在表t中的位置Take[t,{m,n}] 从表t中取出m~n的元素Rest[t] 去掉表t中第一个元素Drop[t,{m,n}] 从表t中去掉m~n的元素Prepend[t,a] 将a加到表t的第一位Append[t,a] 将a加到表t的最后一位Insert[t,a,k] 将a加到表t的第k位Raplace[t,a,k] 用a替换表t的第k位Apply[f,t] 将函数f作用到表t的每一位Sort[t] 将元素依标准排列(数字按大小，字母按abc) Reverse[t] 将元素按顺序倒排RatateLeft[t,k] 将元素向左轮换k位RatateRight[t,k] 将元素向右轮换k位Partition[t,n] 将表t分成n个元素的块Partition[t,n,d]Transpose[t] 将表t转置Join[t1,t2] 将t1和t2合并，但是不去掉重复元素Union[t1,t2,] 并集运算Intersection[t1,t2,] 交集运算Complement[t1,t2] 从t1中去掉t2中的元素六、绘图1、绘图函数Plot[f[x],{x,a,b}] 画f[x]在区间[a,b]上的函数图象ParametricPlot[{x[t],y[t]},{t,a,b }] 画参数图ListPlot[{x1,y2},{x2,y2},] 绘制点图Plot3D[f[x,y],{x,x0,x1},{y,y0,y1}] 三维图像ParametricPlot3D[{x[t],y[t],z[t]},{t,t0,t1}]参数三维图2、绘图函数修饰项①二维绘图所用的修饰项PlotRange->{a,b} 确定函数值得范围(a~b)PlotStyle->{RGBColor[a,b,c]}确定曲线颜色P lotStyle->{AbsoluteThickness[n]}确定曲线粗细(n=1、2、)②三维绘图所用的修饰项PlotPoints->{a,b} 网格数a×b个PlotRange->{a,b} 确定函数值得范围(a~b)Axes->True/False 是否显示坐标轴Boxed->True/False 是否加立体框Mesh->True/False 是否加网格Shading ->True/False 是否在曲面着色HiddenSurface-> True/False 被挡部分是否隐藏ViewPoint->{a,b,c} 调整观察角度七、极限与导数Limit[f[x],x->a] alim ()x f x → (a 可以是∞) Limit[f[x],x->a,Direction->1]求右极限 Limit[f[x],x->a,Direction->1]求左极限 D[f[x],x]df dx 或f x ∂∂ D[f[x],{x,k}]k 阶导数或k 阶偏导 D[f,x1,x2, ,xk] 1k f x x ∂∂∂D[f[x],x,NonConstants->{v1,v2,}] 求导时vi 是关于x 的函数 Dt[f,x]复合函数f 关于x 的导数 Dt[f,{x,k}]复合函数f 关于x 的k 阶导数 Dt[f,{x,k},Constants->{c1,c2,}] 求导的时候ci 看为常数Dt[f]全微分 f `[x]一阶导数( ` 是1前面的那个) f ``[x]二阶导数 Simplify[] 用于化简的函数FindMinimum[f,{x,x0}] 在x0附近求极值点(求极大值用-f)FindMinimum[f,{x,{x0,x1}}] 以x0，x1为初始值搜索极值 (用于无导数)FindMinimum[f,{x, {x,x0,a,b}] 求以x0为初始值搜索[a,b]区间的极值FindMinimum[f,{x, {x,a,b}] 求在[a,b]间的极值FindMinimum[f,{x, {x,x0},{y,y0}]多元函数极值八、积分Integrate[f,x] 不定积分(f:被积函数,x:积分变量)Integrate[f,{x,a,b}] 定积分(f:被积函数,x:积分变量,a:上限,b:下限) Integrate[f,{x,x0,x1},{y,y0,y1},] 多重积分NIntegrate[f,{x,a,b}] 定积分近似值九、微分方程DSolve[方程组,函数f[x],变量x] 解微分方程(方程组可含有初边值条件) NDSolve[方程组,函数符号,变量符号及范围] 解微分方程数值解十、线性代数Array[a,{m,n}] 建一个m行n列的矩阵，元素为a[i,j]IndenityMatrix[n] 建一个n阶单位阵DiagonalMatrix[t] 建一个对角线上为表中元素的方阵MatrixForm[A] 将矩阵A按矩阵形式输出Det[A] 求方阵A的行列式Transpose[A] 矩阵A的转置Inverse[A ] 方阵A的逆矩阵A*B A与B对应元素相乘Dot[a,b]或a.b 数量积(.右下角)Cross[a,b]或a⨯b 向量积(⨯在输入模块上)Minors[M,k] 矩阵M的所有可能的k阶子式组成的矩阵RowReduce[A] 求A的行约化矩阵LinearSolve[A,B] 求满足Ax=B的一个解NullSpace[A] 求Ax=0的基础解析Eigenvalues[M]求方阵M 的特征值 Eigenvectors[M]求方阵M 的特征向量 Eiginsystem[M] 求方阵M 的特征值和特征向量十一、级数Series[f,{x,x0,n}] 将函数f 做泰勒展开到0()n x x SeriesCoefficient[s,n] 求级数s 中第n 阶的系数Normal[s] 舍去级数s 的余项部分 FourierTrigSeries[f[x],x,k, FourierParameters->{a,1T }]f[x]的k 阶傅里叶展开(T:周期,a:基本周期区间中心) 十二、概率Mean[d]求均值 Median[d]求中位数 Quartiles[d]求0.25分位数,中位数,0.75分位数 Quantile [d,k]求k 分位数 Variance[d]求方差(无偏估计是的方差) StandardDeviation[d] 求标准差(无偏估计是的标准差) VarianceMLE[d] 求方差(总体方差的极大似然估计) StandardDeviationMLE[d]求标准差SampleRange[d] 极差CentralMoment[d,k] k 阶中心距(k=2、3、4)Skewness[d]偏度 Kurtosis[d] 峰度BinCounts[d,{a,b,k}] 将a~b 按长度k 等分小区间，求出在每个小区间的数据个数Max[x1,x2,] 取变量x1,x2,的最大值Min[x1,x2,] 取变量x1,x2,的最小值Length[t] 求表中元素个数(即表长) BarChart[bc] 画直方图(bc为数据对)。

手册：mathematica命令大全

<< Statistics`DescriptiveStatistics`
或者加载整个统计函数库，加载方法为：
<<Statistics`
求数据data的众数。

数据data的格式为：{ a1,a2,…} Variance[data]
VarianceMLE[data] 求数据data的母体方差。

数据data的格式为：{ a1,a2,…} StandardDeviation[data] 求数据data的样本标准差。

数据data的格式为：{a1,a2,…} StandardDeviationMLE[data] 求数据data的母体标准差。

数据的格式为：{a1,a2,…}。

Mathematica常用命令

TrigFactorList[expr] 给出表达式中的三角函数因子的表
TrigReduce[expr] 对表达式中的三角函数化简
TrigToExp[expr] 三角到指数的转化
ExpToTrig[expr] 指数到三角的转化
RootReduce[expr]
ToRadicals[expr]
DSolve[{eqn1,eqn2,...},{y1,y2...},x]解微分方程组，其中yi是x的函数
DSolve[eqn, y, {x1,x2...}] 解偏微分方程
Eliminate[eqns, vars] 把方程组eqns中变量vars约去
SolveAlways[eqns, vars] 给出等式成立的所有参数满足的条件
ListInterpolation[array]对离散数据插值，array可为n维
NSolve[lhs==rhs, var] 求方程数值解
NSolve[eqn, var, n] 求方程数值解，结果精度到n位
NDSolve[eqns, y, {x, xmin, xmax}]微分方程数值解
NDSolve[eqns, {y1,y2,...}, {x, xmin, xmax}]
expr//funname 相当于filename[expr]
expr/.rule 将规则rule应用于expr
expr//.rule 将规则rule不断应用于expr知道不变为止
param_ 名为param的一个任意表达式（形式变量）
param__ 名为param的任意多个任意表达式（形式变量）
O[x]^n n阶小量x^n
O[x, x0]^n n阶小量(x-x0)^n

Mathematica命令符集

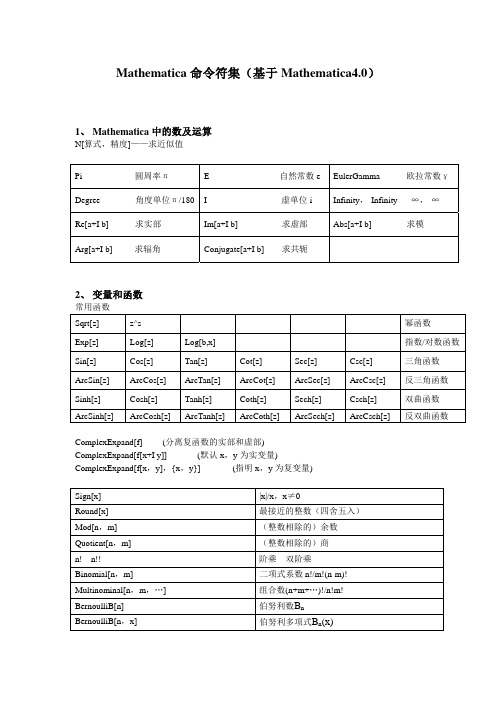
Mathematica命令符集（基于Mathematica4.0）1、Mathematica中的数及运算N[算式，精度]——求近似值Pi 圆周率π E 自然常数e EulerGamma 欧拉常数γDegree 角度单位π/180 I 虚单位i Infinity，-Infinity ∞，-∞Re[a+I b] 求实部Im[a+I b] 求虚部Abs[a+I b] 求模Arg[a+I b] 求辐角Conjugate[a+I b] 求共轭2、变量和函数常用函数z^s 幂函数Sqrt[z]Exp[z] Log[z] Log[b,x] 指数/对数函数Sin[z] Cos[z] Tan[z] Cot[z] Sec[z] Csc[z] 三角函数ArcSin[z] ArcCos[z] ArcTan[z] ArcCot[z] ArcSec[z] ArcCsc[z] 反三角函数Sinh[z] Cosh[z] Tanh[z] Coth[z] Sech[z] Csch[z] 双曲函数ArcSinh[z] ArcCosh[z] ArcTanh[z] ArcCoth[z] ArcSech[z] ArcCsch[z] 反双曲函数ComplexExpand[f] (分离复函数的实部和虚部)ComplexExpand[f[x+I y]] (默认x，y为实变量)ComplexExpand[f[x，y]，{x，y}] (指明x，y为复变量)Sign[x] |x|/x，x≠0Round[x] 最接近的整数（四舍五入）Mod[n，m] （整数相除的）余数Quotient[n，m] （整数相除的）商n! n!! 阶乘双阶乘Binomial[n，m] 二项式系数n!/m!(n-m)!Multinominal[n，m，…] 组合数(n+m+…)!/n!m!BernoulliB[n] 伯努利数B nBernoulliB[n，x] 伯努利多项式B n(x)EulerE[n] 欧拉数E nEulerE[n，x] 欧拉多项式E n(x)KroneckerDelta[n] n=0时为1，否则为0 KroneckerDelta[n，m，…] n=m=…=0时为1，否则为0常用特殊函数（部分）UnitStep[x] η函数（亥维赛的单位阶跃函数）Gamma[z] Γ函数Γ(z)Beta[p,q] Β函数Β(p,q)PolyGamma[z] ψ函数ψ(z)MoebiusMu[n] 默比乌斯函数μ(n)Zeta[z] 黎曼ζ函数ζ(z)Erf[z] 误差函数erf(z)Erfc[z] 余误差函数erfc(z)LegendreP[n,x] 勒让德多项式P n(x)LegendreP[nu,x]，LegendreQ[nu,x] 勒让德函数Pυ(x)，Qυ(x) LegendreP[nu,mu,x]，LegendreQ[nu,mu,x] 连带勒让德函数Pμυ(x)，Qμυ(x) SphericalHarmonicY[l,m,u,v] 球面调和函数Y m l(u，v)BesselJ[nu,z]，BesselY[nu,z] 贝塞耳函数Jυ(z)，Nυ(z)BesselI[nu,z]，BesselK[nu,z] 虚宗量贝塞耳函数Iυ(z)，Kυ(z) AiryAi[z]，AiryBi[z] 艾里函数Ai(z)，Bi(z) SinIntegral[z] 正弦积分Si(z)CosIntegral[z] 余弦积分Ci(z)SinhIntegral[z] 双曲正弦积分Shi(z) CoshIntegral[z] 双曲余弦积分Chi(z) ExpIntegralEi[z]，ExpIntegralE[n,z] 指数积分Ei(z)，E n(z) LogIntegral[z] 对数积分li(z)FresnelC[z]，FresnelS[z] 菲涅尔积分C(z)，S(z) GegenbauerC[n,m,z] 盖根鲍尔多项式C(m)n(z) ChebyshevT[n,z]，ChebyshevU[z] 切比雪夫多项式T n(z)，U n(z) JacobiP[n,a,b,z] 雅克比多项式P(a,b)n(z)HermiteH[n,z] 厄米多项式H n(z)LaguerrelL[n,z]，LaguerrelL[n,a,z] 拉盖尔多项式L n(z)，Lαn(z) Hypergeometric2F1[a,b,c,z] 超几何函数F(a;b;c;z) Hypergeometric1F1[a,b,z] 合流超几何函数F(a;b;z)3、极限&微积分(1).求极限Limit[f[x],x->x0] Limit[f[x],x->x0,Direction->1] Limit[f[x],x->x0,Direction-> -1](2).求导数D[f[x],x] D[f[x,y],x,NonConstants->{y}](3).求高阶导数D[f[x],x,x,x] 或 D[f[x],{x,3}](4).求偏导数D[f[x,y,z],y] D[f[x,y,z],x,y](5).一元函数的不定积分Integral[f[x],x](6).多元函数的不定积分Integral[f[x,y], x,y](7).定积分Integral[f[x],{x,a,b}]4、幂级数展开与求和(1). 展开Series[f[x],{x,x0,k}](2). 求和Sum[f[n],{n,k,l}] Sum[f[m,n],{m,m1,m2},{n,n1,n2}](3). 连乘积Product[f[n],{n,k,l}](4). 求留数Residue[f[z],{z,z0}](5). 部分分式Apart[f[x]]（如果有理分式是多元函数，则可按指定变量进行部分分式，其余变量均视为常数，如Apart[f[x,y],y]）(6).Z变换ZTransform[f[n],n,z]InverseZTransform[F[n],n,z]5、求解微分方程(1).求解常微分方程DSolve[{eqn,y[0]==?},y[x],x](2).求解偏微分方程DSolve [eqn,u[x,t],{x,t}]E.g. DSolve [x·D[u[x,t],x]+t·D[u[x,t],t]==Exp[x·t],u[x,t],{x,t}]6、L变换和F变换(1).Laplace变换LaplaceTransform[f[t], t, p]InverseLaplaceTransform[F[p], p, t](2).Fourier变换FourierTransform[f[x],x,k]InverseFourierTransform[F[k], k, x]7、Mathematica作图作图指令：图形类型（二维/三维）+函数表达式，自变量（及函数）取值范围+选择项基本选择项选择项意义缺省项AspectRatio 图的高宽比 1/GoldenRatio Axes 是否画坐标轴 Automatic AxesLabel 坐标轴标记 None ColorOutput 图形颜色 $Automatic DefaultColor 默认颜色 $Automatic DisplayFunction 是否显示图形 $DisplayFunction PlotLabel 图题 None PlotPoints 函数值取点数 25PlotRange 函数值范围 Automatic Ticks 轴上刻度 Automatic对选择项赋值，写作options ->value，（value可以是具体数值，也可以是None，All，True，False，Automatic等）。

Mathematica学习（2）-mathematica命令

Mathematica学习（2）-mathematica命令Mathematica的内部常数 Pi , 或π(从基本输⼊⼯具栏输⼊, 或“Esc”+“p”+“Esc”）圆周率πE (从基本输⼊⼯具栏输⼊, 或“Esc”+“ee”+“Esc”）⾃然对数的底数eI (从基本输⼊⼯具栏输⼊, 或“Esc”+“ii”+“Esc”）虚数单位iInfinity, 或 ∞(从基本输⼊⼯具栏输⼊ , 或“Esc”+“inf”+“Esc”）⽆穷⼤ ∞Degree 或°(从基本输⼊⼯具栏输⼊,或“Esc”+“deg”+“Esc”）度Mathematica的常⽤内部数学函数　指数函数Exp[x]以e为底数对数函数Log[x]⾃然对数，即以e为底数的对数Log[a，x]以a为底数的x的对数开⽅函数Sqrt[x]表⽰x的算术平⽅根绝对值函数Abs[x]表⽰x的绝对值三⾓函数（⾃变量的单位为弧度）Sin[x]正弦函数Cos[x]余弦函数Tan[x]正切函数Cot[x]余切函数Sec[x]正割函数Csc[x]余割函数反三⾓函数ArcSin[x]反正弦函数ArcCos[x]反余弦函数ArcTan[x]反正切函数ArcCot[x]反余切函数ArcSec[x]反正割函数ArcCsc[x]反余割函数双曲函数Sinh[x]双曲正弦函数Cosh[x]双曲余弦函数Tanh[x]双曲正切函数Coth[x]双曲余切函数Sech[x]双曲正割函数Csch[x]双曲余割函数反双曲函数ArcSinh[x]反双曲正弦函数ArcCosh[x]反双曲余弦函数ArcTanh[x]反双曲正切函数ArcCoth[x]反双曲余切函数ArcSech[x]反双曲正割函数ArcCsch[x]反双曲余割函数求⾓度函数ArcTan[x，y]以坐标原点为顶点，x轴正半轴为始边，从原点到点（x，y）的射线为终边的⾓，其单位为弧度数论函数GCD[a,b,c,．．．]最⼤公约数函数LCM[a,b,c,．．．]最⼩公倍数函数Mod[m,n]求余函数(表⽰m除以n的余数)Quotient[m，n]求商函数（表⽰m除以n的商）Divisors[n]求所有可以整除n的整数FactorInteger[n]因数分解，即把整数分解成质数的乘积Prime[n]求第n个质数PrimeQ[n]判断整数n是否为质数，若是，则结果为True，否则结果为FalseRandom[Integer，{m，n}]随机产⽣m到n之间的整数排列组合函数Factorial[n]或n！阶乘函数，表⽰n的阶乘复数函数Re[z]实部函数Im[z]虚部函数Arg(z)辐⾓函数Abs[z]求复数的模Conjugate[z]求复数的共轭复数Exp[z]复数指数函数求整函数与截尾函数Ceiling[x]表⽰⼤于或等于实数x的最⼩整数Floor[x]表⽰⼩于或等于实数x的最⼤整数Round[x]表⽰最接近x的整数IntegerPart[x]表⽰实数x的整数部分FractionalPart[x]表⽰实数x的⼩数部分分数与浮点数运算函数N[num]或num//N把精确数num化成浮点数（默认16位有效数字） N[num，n]把精确数num化成具有n个有效数字的浮点数NumberForm[num，n]以n个有效数字表⽰numRationalize[float]将浮点数float转换成与其相等的分数Rationalize[float，dx]将浮点数float转换成与其近似相等的分数，误差⼩于dx 最⼤、最⼩函数Max[a，b，c，．．．]求最⼤数Min[a，b，c，．．．]求最⼩数符号函数Sign[x]Mathematica中的数学运算符a+b 加法a-b减法a*b (可⽤空格键代替*)乘法a/b (输⼊⽅法为：“ Ctrl ” + “ / ” ) 除法a^b (输⼊⽅法为：“ Ctrl ” + “ ^ ” )乘⽅-a 负号Mathematica的关系运算符　==等于<⼩于>⼤于<=⼩于或等于>=⼤于或等于!=不等于注：上⾯的关系运算符也可从基本输⼊⼯具栏输⼊。

整理mathematica数学常用命令大全之欧阳语创编

Mathematica的内部常数Mathematica的常用内部数学函数Mathematica中的数学运算符Mathematica的关系运算符注：上面的关系运算符也可从基本输入工具栏输入。

如何用mathematica进行多项式运算如何用mathematica进行分式运算如何用Mathematica进行因式分解如何用Mathematica展开如何用Mathematica进行化简如何用Mathematica合并同类项如何用Mathematica进行数学式的转换如何用Mathematica进行变量替换如何用mathematica进行复数运算如何在mathematica中表示集合与数学中表示集合的方法相同，格式如下：下列命令可以生成特殊的集合：如何用Mathematica求集合的交集、并集、差集和补集如何mathematica用排序如何在Mathematica中解方程注：方程的等号必须用： = =如何在Mathematica中解方程组Solve[{方程组}，{变元组}]注：方程的等号必须用： = =如何在Mathematica中解不等式先加载：Algebra`InequalitySolve` ，加载方法为：<<Alg ebra`InequalitySolve`然后执行解不等式的命令InequalitySolve，此命令的使用格式如下：<--mstheme-->如何在Mathematica中解不等式组先加载：Algebra`InequalitySolve` ，加载方法为：<<Alg ebra`InequalitySolve`然后执行解不等式组的命令InequalitySolve，此命令的使用格式如下：<--mstheme-->如何在Mathematica中解不等式组先加载：Algebra`InequalitySolve` ，加载方法为：<<Algebra`InequalitySolve`然后执行解不等式组的命令InequalitySolve，此命令的使用格式如下：<--mstheme-->如何用mathematica表示分段函数如何用mathematica求反函数对系统内部的函数生效，但对自定义的函数不起任何作用，也许是方法不对。

手册：mathematica命令大全

<< Statistics`DescriptiveStatistics`或者加载整个统计函数库，加载方法为：<<Statistics`求数据data的众数。

数据data的格式为：{ a1,a2,…}Mode[data]如何用mathematica求方差和标准差首先要加载Statistics`DescriptiveStatistics`函数库，加载方法为：<< Statistics`DescriptiveStatistics`或者加载整个统计函数库，加载方法为：<<Statistics`求数据data的样本方差。

数据data的格式为：{ a1,a2,…} Variance[data]VarianceMLE[data] 求数据data的母体方差。

数据data的格式为：{ a1,a2,…} StandardDeviation[data] 求数据data的样本标准差。

数据data的格式为：{a1,a2,…} StandardDeviationMLE[data] 求数据data的母体标准差。

数据data的格式为：{ a1,a2,…}如何用mathematica求协方差和相关系数首先要加载Statistics`MultiDescriptiveStatistics`函数库，加载方法为：<< Statistics`MultiDescriptiveStatistics`或者加载整个统计函数库，加载方法为：<<Statistics`求数据data1和data2的样本协方差。

数据的格式为：{a1,a2,…}.可编辑。

Mathematica常用指令

Mathematica常⽤指令表达式：Plot[4 x - 9, {x, 0, 9}]f[x_] = x^3Plot[f[x], {x, 0, 9}]a = Plot[4 x - 9, {x, 0, 9}]b = Plot[x^3, {x, 0, 3}] 两图画在⼀个坐标系Show[a, b]a = Plot[4 x - 9, {x, 0, 9}]b = Plot[x^3, {x, 0, 3}] 两图画在⼀起（⼀排）c = GraphicsArray[{a, b}]Show[c]a = Plot[4 x - 9, {x, 0, 9}]b = Plot[x^3, {x, 0, 3}]c = GraphicsArray[{a}, {b}] 两图画在⼀起（两排）Show[c]⼆维画图：Automatic 默认值DisplayFunction -> Identity 不出现图DisplayFunction -> $DisplayFunction 出现图PlotRange -> All 画出所有点，指定区域点PlotStyle -> {RGBColor[1, 0, 0]} 图像颜⾊PlotStyle -> {Dashing[{0.01}]} 图像成虚线PlotStyle -> {Thickness[0.01]} 图像粗细AxesLabel -> {"x/t", "y/cm"} 坐标标签PlotLabel -> {"s-t"} 图像标签Frame -> True 图像边框Axes -> {True, True} 坐标轴的显⽰AxesOrigin -> {0, -5} 设置坐标原点GridLines -> {{-π, -π/2, 0, π/2, π}, {-1，-0.5，0, 0.5, 1}}给坐标轴分⽹格TextStyle -> {FontSize -> 30} 坐标字体⼤⼩AspectRatio -> Automatic 坐标⽐例⼀致Ticks -> {{0, 1, 2, 3}, {0,10,20}} 在坐标轴上显⽰特定点ParametricPlot[x(t),y(t)},{t,0,6,}] 画参数⽅程三维画图：PlotPoints -> 100 像素Boxed -> False 显⽰边框BoxRatios -> {1，1，2} 三维⽐例Mesh -> False 在曲⾯上不显⽰⽹格ViewPoint -> {0, 0, 1} 图的观察⽅向HiddenSurface -> False 图⽰⽆遮挡解⽅程：Solve[a x + b == c x + d, x]Solve[{2 x + 3 y == 3, 3 x - 5 y == 9}, {x, y}]NSolve[7 x + 3 == 2, 30]或N[Solve[7 x + 3 == 2], 30]Roots[x^2 + 2 x + 1 == 0, x]或NRoots[x^3 + 3 == 0, x] 解⼀元⽅程求解超越⽅程：先画图确定跟的位置，在⽤FindRoot解：Plot[{Sin[x], x^2 - 1}, {x, -π, π}]FindRoot[Sin[x] == x^2 - 1, {x, 1}]Factor[x^2 + 2 x + 1] 分解因式Expand[(x^2 + 2 x + 1)( x^2 - 1)] 展开多项式Collect[x^3y^2z^4 + x^4y^5z^2x^2y^3z^2, y] 按Y升次幂排列PowerExpand[Log[x\^y]] 展开或化简TrigExpand[Sin[3 x]] 按三⾓函数形式展开微分：Limit[(x^5 - 32)/(x^3 - 8), x -> 2] 求极限Limit[32/x, x -> 0, Direction -> 1（-1）] 左（右）极限f'[x] 求导D[f[x], {x, 3}] 以X为变量求3阶导数D[f[x], {x, 3}] /. x -> 2 f''[2]Series[Exp[x], {x, 3, 5}] 在3点展开⾄5次⽅D[x^3 y^4 z^2, x] 对x求偏导D[x^3 y^4 z^2, {x, 2}] 对x求⼆次偏导D[x^3 Sin[y], x, y] /. {x -> 2, y -> π} 定点求导常微分⽅程：DSolve[y'[x] == x + y[x], y[x], x] 解微分⽅程，y是x的函数DSolve[{y'[x] == x + y[x], y[0] == 0}, y[x], x] 初始条件NDSolve[{y'[x] == x + y[x], y[0] == 0}, y[x], x] 数值解矩阵：{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}} // MatrixForm ⽣成矩阵Table[x^2, {x, 1, 5}] ⽣成x取值1到5的x^2的值Table[x+y, {x, 1, 5}，{y，1, 7}] ⽣成5*7的矩阵，矩阵元的值是x+y f[x_] = 2 x^2 Array[f, 1, 5] ⽣成x=1到5的2 x^2的值IdentityMatrix[3] ⽣成3阶单位矩阵a[[3,4]] a矩阵的（3，4）矩阵元a[4] a矩阵的第四⾏a[[all,5]] a矩阵的第5列a[[{2,3,5},all]] a矩阵的第2，3，5⾏{q,w,e}={2+3,1+2,2} q=5，w=3，e=2Table[Random[Integer,{0,9}],{i,1,4},{j,1,4}] 随机产⽣矩阵元为0~9的4⾏4列的矩阵z.q 矩阵点乘Cross[z,q] 矩阵叉乘Inverse[a] 逆矩阵Transpose[a] 转置Det[a] 求⾏列式Tr[a] 求迹MatrixPower[a,2] 矩阵的3次⽅LinearSolve[a,aa]//MatrixForm 解线性⽅程组Eigenvalues[s] s矩阵的本征值Eigenvectors[s]s矩阵的本征向量Eigensystem[s]s矩阵的{本征值}，{本征向量} Eigenvalues[N[s]] s矩阵的本征值的数值表⽰命令语句：If[x ≤y, 1, 2] ifx ≤y，then 1，else 2If[Abs[q - w] == 1, 1, If[q == w, 2, 0] ifabs[q - w] == 1，then 1，elseif q == w，then 2，else 0 While[1,2] For[初始化，条件，更新，语句]。