【倍速课时学练】2013-2014学年七年级数学下册 5.1.3 同位角、内错角、同旁内角课件 (新版)新人教版
新人教版数学七年级下册 第五章相交线与平行线5.1.3同位角、内错角、同旁内角同步练习

新人教版数学七年级下册第五章相交线与平行线5.1.3同位角、内错角、同旁内角同步练习姓名:________ 班级:________ 成绩:________一、选择题(共15题) (共15题;共30分)1. (2分)若∠1与∠2是同位角,且∠1=60°,则∠2是()A . 60°B . 120°C . 120°或60°D . 不能确定2. (2分) (2015高二上·太和期末) 如图,与∠α构成同旁内角的角有()A . 1个B . 2个C . 5个D . 4个3. (2分)如图,图中∠1与∠2是同位角的是()A . (2)(3)B . (1)(2)(3)C . (2)(3)(4)D . (3)(4)4. (2分)如图,下列说法正确的是()A . ∠2和∠B是同位角B . ∠2和∠B是内错角C . ∠1和∠A是内错角D . ∠3和∠B是同旁内角5. (2分)如图,∠ADE和∠CED是()A . 同位角B . 内错角C . 同旁内角D . 互为补角6. (2分)如图,下列说法错误的是()A . ∠1与∠2是同内角B . ∠1与∠4是同旁内角C . ∠5与∠3是内错角D . ∠5与∠2是内错角7. (2分)下列说法中,正确的是()A . 内错角相等B . 同旁内角互补C . 同角的补角相等D . 相等的角是对顶角8. (2分)如图中,是同旁内角的是()A . ∠1与∠2B . ∠3与∠2C . ∠3与∠4D . ∠1与∠49. (2分)两条直线被第三条直线所截,则()A . 同位角一定相等B . 内错角一定相等C . 同旁内角一定互补D . 以上结论都不对10. (2分)如图所示,两只手的食指和拇指在同一平面内,它们构成的一对角可以看成()A . 内错角B . 同位角C . 同旁内角D . 对顶角11. (2分)下列说法:①两条直线被第三条直线所截,内错角相等;②相等的角是对顶角;③互余的两个角一定都是锐角;④互补的两个角一定有一个为钝角,另一个角为锐角.其中正确的有()A . 1个B . 2个C . 3个D . 4个12. (2分) (2017七下·静宁期中) 两条直线被第三条直线所截,则()A . 同位角不一定相等B . 内错角必相等C . 同旁内角必互补D . 同位角定相等13. (2分)下列图形中,∠1和∠2不是同位角的是()A .B .C .D .14. (2分)如图所示,与∠α构成同位角的角的个数为()A . 1B . 2C . 3D . 415. (2分)如图,下列6种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠2与∠4是内错角;④∠4与∠5是同旁内角;⑤∠2与∠4是同位角;⑥∠2与∠5是内错角.其中正确的有()A . 1个B . 2个C . 3个D . 4个二、填空题(共5题) (共5题;共18分)16. (10分)如图,已知直线a,b被直线c,d所截,直线a,c,d相交于点O,按要求完成下列各小题.(1)在图中的∠1~∠9这9个角中,同位角共有多少对?请你全部写出来;(2)∠4和∠5是什么位置关系的角?∠6和∠8之间的位置关系与∠4和∠5的相同吗?17. (1分)如图,直线a∥b,∠1=110°,∠2=55°,则∠3的度数为________.18. (1分)如图,与∠CAB成内错角的是________.19. (4分)如图,在△ABC中,∠ABC=90,过点B作三角形ABC的AC边上的高BD,过D点作三角形ABD的AB边上的高DE.∠A的同位角是________ .∠ABD的内错角是________ .点B到直线AC的距离是线段________ 的长度.点D到直线AB的距离是线段________ 的长度.20. (2分)如图,与∠1构成同位角的是________,与∠2构成同旁内角的是________.三、解答题(共6题) (共6题;共40分)21. (15分) (2018七下·赵县期末) 如图,已知直线A B∥CD,∠A=∠C=100°,点E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF(1)直线AD与BC有何位置关系?请说明理由(2)求∠DBE的度数.(3)若平行移动AD,在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在求出∠ADB;若不存在,请说明理由.22. (5分)如图,∠1,∠2,∠3,∠4及∠A,∠B,∠C中有多少对同位角、内错角、同旁内角?请一一写出来.23. (5分)图中的∠1与∠C、∠2与∠B、∠3与∠C,各是哪两条直线被哪一条直线所截形成的同位角?24. (5分)如图,(1)指出直线AB,CD被AC所截形成的内错角;(2)指出直线AB,CD被BE所截形成的同位角;(3)找出图中∠1的所有同旁内角25. (5分)在图中,先标上适当的字母,再回答下列问题;(1)∠1的同位角有哪些角?将它们分别写出来;(2)∠1的内错角有哪些角?将它们分别写出来;(3)∠1的同旁内角有哪些角?将它们分别写来.26. (5分)如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.参考答案一、选择题(共15题) (共15题;共30分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、二、填空题(共5题) (共5题;共18分)16-1、16-2、17-1、18-1、19-1、20-1、三、解答题(共6题) (共6题;共40分) 21-1、21-2、21-3、22-1、23-1、24-1、25-1、26-1、。
北师大版初中数学七年级下册全册课时练(一课一练)

北师大版初中数学七年级下册全册课时练
(一课一练)
本文档提供了北师大版初中数学七年级下册全册课时练的内容。
以下是每个课时练的简要介绍:
1. 第一节:数的基本性质
- 包括正整数、零、负整数、小数之间的大小比较
- 计算有理数的加减法
- 三角形的内角和为180度
2. 第二节:带负号的小数
- 了解带负号的小数
- 比较带负号的小数的大小
- 计算带负号的小数的加减法
3. 第三节:正数和负数的乘除法
- 正数和正数的乘法、除法
- 负数和负数的乘法、除法
- 正数和负数的乘法、除法
4. 第四节:数轴上的加减法
- 利用数轴进行加减法运算
- 数轴上的正数加法、减法
- 数轴上的负数加法、减法
5. 第五节:有理数的乘方
- 计算有理数的乘方
- 同底数的幂相乘的规律
- 幂的定义及性质
6. 第六节:有理数的乘方
- 计算有理数的乘方
- 同底数的幂相除的规律
- 幂的定义及性质
以上是北师大版初中数学七年级下册全册课时练的内容简介。
通过完成这些习题,学生将能够巩固和提高他们在数学方面的理解和能力。
七年级数学下册同步精品讲义(人教版):第02课 同位角、内错角、同旁内角(教师版)

能力拓展
与截线的位置关系 截线的同旁
截线两侧 截线同侧
考法 01
【典例 1】如图,∠B 的同位角可以是 ( )
同位角的判断
A.∠1
B.∠2
C.∠3D.∠4ຫໍສະໝຸດ 【答案】D【分析】
直接利用两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)
第 02 课 同位角、内错角、同旁内角
目标导航
课程标准 1.了解“三线八角”模型特征; 2.掌握同位角、内错角、同旁内角的概念,并能从图形中识别它们.
知识精讲
知识点 01 同位角、内错角、同旁内角的概念
1. “三线八角”模型 如图,直线 AB、CD 与直线 EF 相交(或者说两条直线 AB、CD 被第三条直线 EF 所截),构成八个角,简称 为“三线八角”,如图.
的同旁,则这样一对角叫做同位角,进而得出答案.
【详解】
∠B 的同位角可以是:∠4.
故选 D.
【点睛】
此题主要考查了同位角的定义,正确把握定义是解题关键.
【即学即练】如图,直线 AB , CD 被射线 CE 所截,与 1 构成同位角的是( )
A. 2
B. 3
C. 4
D. 5
【答案】D
【分析】
两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,
A.②③
B.①②③
C.①②④
D.①④
【答案】C
【分析】
根据同位角的定义逐一判断即得答案.
【详解】
图①中的∠1 与∠2 是同位角,
人教版 数学七年级下册课时练 第五章 相交线与平行线 5.1.3 同位角、内错角、同旁内角
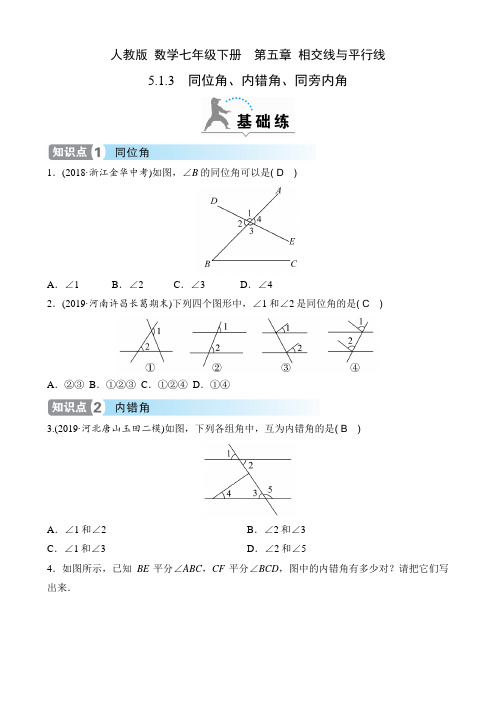
人教版数学七年级下册第五章相交线与平行线5.1.3同位角、内错角、同旁内角1.(2018·浙江金华中考)如图,∠B的同位角可以是( D)A.∠1 B.∠2 C.∠3 D.∠42.(2019·河南许昌长葛期末)下列四个图形中,∠1和∠2是同位角的是( C)A.②③ B.①②③ C.①②④ D.①④3.(2019·河北唐山玉田二模)如图,下列各组角中,互为内错角的是( B)A.∠1和∠2 B.∠2和∠3C.∠1和∠3 D.∠2和∠54.如图所示,已知BE平分∠ABC,CF平分∠BCD,图中的内错角有多少对?请把它们写出来.解:有4对,分别是∠ABC与∠BCF,∠ABC与∠BCD,∠EBC与∠BCF,∠EBC与∠BCD.5.(2019·安徽淮南大通区期中)如图,与∠4是同旁内角的是( C)A.∠1 B.∠2 C.∠3 D.∠56.如图,直线AB,CD,MN两两相交,则图中的同旁内角有( B)A.8对 B.6对 C.4对 D.2对7.在下列图形内各画一条直线,使得与∠A是同旁内角的角分别有3个和4个.解:如图1,与∠A是同旁内角的角有3个,分别是∠1,∠B,∠C.如图2,与∠A是同旁内角的角有4个,分别是∠1,∠B,∠C,∠2.8.如图,下列结论正确的是( D)A.∠5与∠2是对顶角B.∠1与∠3是同位角C.∠2与∠3是同旁内角D.∠1与∠2是同旁内角9.如图,如果∠1=50°,∠2=100°,那么∠3的同位角等于__80°__,∠3的内错角等于__80°__,∠3的同旁内角等于__100°__.10.如图所示,∠1,∠2,∠3,∠4,∠5中有哪几对同位角?哪几对内错角?哪几对同旁内角?解:从图1这两种“F”形图形可知:同位角有∠1和∠4,∠5和∠3.图1从图2这两种“Z”形图形可知:内错角有∠1和∠5,∠4和∠3.图2从图3这三种“U”形图形可知:同旁内角有∠4和∠2,∠4和∠5,∠5和∠2.图3易错点不能准确识别同位角、同旁内角11.如图所示,与∠A是同位角的是__∠EBD,∠CBD__,与∠A是同旁内角的是__∠C,∠ABE,∠ABC__.12.(2018·广东广州中考)如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是( B)A.∠4,∠2 B.∠2,∠6C.∠5,∠4 D.∠2,∠413.(2019·河南信阳罗山期中)如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是__①②__(填序号).14.如图所示,把一根筷子的一端放在水里,一端露出水面,筷子变弯了,它真的弯了吗?其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变. (1)请指出与∠1是同位角的角; (2)请指出与∠2是内错角的角.解:(1)与∠1是同位角的有∠C ,∠MOF ,∠AOF . (2)与∠2是内错角的有∠MOE ,∠AOE .15.(2019·山东济南槐荫区期末)两条直线被第三条直线所截,∠1与∠2是同旁内角,∠2与∠3是内错角.(1)画出示意图,标出∠1,∠2,∠3;(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2,∠3的度数. 解:(1)如图所示:(2)设∠3=x °,则∠2=2x °,∠1=4x °.因为∠1+∠3=180°,所以x +4x =180,解得x =36, 所以∠3=36°,∠2=72°,∠1=144°.16.(2019·湖北武汉六中月考)一个“跳棋棋盘”如图所示,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动后,到达终点角,跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上(棋子的落点在相应角的顶点处),如从起始位置∠1跳到终点位置∠3的路径有:路径1:∠1――→同旁内角∠9――→内错角∠3;路径2:∠1――→内错角∠12――→内错角∠6――→同位角∠10――→同旁内角∠3. (1)写出从∠1到∠8途经一个角的一条路径;(2)从起始∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点∠8? (3)找出从起始∠1跳到终点∠8的路径,要求跳遍所有的角,且不能重复. 解:(1)∠1――→同旁内角∠9――→内错角∠8(路径不唯一). (2)能.路径:∠1――→同位角∠10――→内错角∠5――→同旁内角∠8.(3)∠1――→同旁内角∠9――→同旁内角∠2――→内错角∠10――→同旁内角∠3――→同旁内角∠4――→内错角∠11――→同旁内角∠5――→同旁内角∠6――→内错角∠12――→同旁内角∠7――→同旁内角∠8(路径不唯一).。
人教版七年级数学下册5-1-3 同位角、内错角、同旁内角 习题(含答案及(6)

5.1.3 同位角、内错角、同旁内角学校:__________ 姓名:__________ 班级:__________ 考号:__________一、单选题1.如图所示,下列说法,正确的有( )①∠1与∠2是同旁内角;②∠1与∠ACE是内错角;③∠B与∠4是同位角;④∠1与∠3是内错角.A.①③④B.③④C.①②④D.①②③④2.如图,与∠B是同旁内角的角有( )A.1个B.2个C.3个D.4个3.如图所示,有下列五种说法:①∠1和∠4是同位角;②∠3和∠5是内错角;③∠2和∠6旁内角;④∠5和∠2是同位角;⑤<1和∠3是同旁内角;其中正确的是()A.①②③④B.①②③④C.①②③④⑤D.①②④⑤4.如图∠1与∠2是同位角的个数有()A.1个B.2个C.3个D.4个5.如图所示,下列说法不正确的是()A.∠1和∠2是同旁内角B.∠1和∠3是对顶角C.∠3和∠4是同位角D.∠1和∠4是内错角6.如图所示,同位角共有()对.A.1 B.2 C.3 D.47.如图,下列说法中,错误的是()A.∠4与∠B是同位角B.∠B与∠C是同旁内角C.∠2与∠C是同位角D.∠1与∠3是内错角二、填空题1.根据图形填空:(1)若直线ED,BC被直线AB所截,则∠1和____是同位角;(2)若直线ED,BC被直线AF所截,则∠3和____是内错角;(3)∠1和∠3是直线AB,AF被直线____所截构成的_______;(4)∠2和∠4是直线____,____被直线BC所截构成的_____.2.如图,∠ABC与_____是同位角;∠ADB与________是内错角;∠ABC与___________是同旁内角.3.图中的内错角是________ .三、解答题1.如图,试判断∠1与∠2,∠1与∠7,∠1与∠BAD,∠2与∠9,∠2与∠6,∠5与∠8各对角的位置关系.参考答案一、单选题1.D解析:根据同位角、内错角、同旁内角的定义进行解答即可.详解:①∠1与∠2是直线AB、BC被直线AC所截形成的同旁内角,故正确;②∠1与∠ACE是直线AB、CE被直线AC所截形成的内错角,故正确;③∠B与∠4是直线AB、CD被直线BE所截形成的同位角,故正确;④∠1与∠3是直线AB、CD被直线AC所截形成的内错角,故正确,故选D.点睛:本题考查了三线八角,在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.2.C解析:与∠B是同旁内角的角有∠C, ∠BAC, ∠BAE共3个.故选C.3.D解析:如图,①∠1和∠4是直线AC和直线BC被直线AB截得的同位角,所以①正确;②∠3和∠5是直线BC和直线AB被直线AC截得的内错角,所以②正确;③∠2和∠6是直线AB和直线AC被直线CB截得的内错角,所以③错误;④∠5和∠2是直线AC和直线BC被直线AB截得的同位角,所以④正确;⑤∠1和∠3是直线BC和直线AB被直线AC截得的同旁内角,所以⑤正确.故答案选D.点睛:(1)准确识别同位角、内错角、同旁内角的关键,是弄清两角是由哪两条直线被哪条直线截得,这其中的关键是辨别出截线,在截线的两旁的是内错角,在截线的同旁的为同位角或同旁内角;(2)辨别截线方法:先找出两角的边所在直线,公共直线即是截线.4.D详解:第一个图中∠1与∠2符合同位角的位置特征,是同位角;第二个图中∠1与∠2符合同位角的位置特征,是同位角;第三个图中∠1与∠2符合同位角的位置特征,是同位角;第四个图中∠1与∠2符合同位角的位置特征,是同位角,故选D.5.A分析:根据对顶角、邻补角、同位角、内错角定义判断即可.详解:A. ∠1和∠2是邻补角,故此选项错误;B. ∠1和∠3是对顶角,此选项正确;C. ∠3和∠4是同位角,此选项正确;D. ∠1和∠4是内错角,此选项正确;故选A.点睛:此题考查对顶角,邻补角,同位角,内错角,同旁内角,解题关键在于掌握各性质定义.6.B解析:试题如图所示:∠1和∠2,∠3和∠4是同位角,共2对,故选B .7.A解析:试题A. ∠4与∠B 应为同旁内角,说法错误;B. ∠B 与∠C 是同旁内角,说法正确;C. ∠2与∠C 是同位角,说法正确;D. ∠1与∠3是内错角,说法正确;故选A.二、填空题1.∠2 ∠4 ED 内错 AB AF 同位分析:根据同位角、内错角的定义进行分析解答即可,两个角分别在截线的两侧,且在两条直线之间,具有这样位置关系的一对角互为内错角,两个角都在截线的同旁,又分别处在被截的两条线的同侧,具有这样位置关系的一对角叫做同位角.详解:(1)若直线ED ,BC 被直线AB 所截,则∠1和∠2是同位角;(2)若直线ED ,BC 被直线AF 所截,则∠3和∠4是内错角;(3)∠1和∠3是直线AB ,AF 被直线ED 所截构成的内错角;(4)∠2和∠4是直线AB ,AF 被直线BC 所截构成的同位角.点睛:本题主要考查内错角、同位角的定义,解答此类题确定三线八角是关键,可直接从截线入手.2.∠EAD ∠DBC,∠EAD ∠DAB,∠BCD解析:试题根据同位角,内错角和同旁内角的概念进行判断,(1)ABC ∠与EAD ∠是同位角;(2)ADB ∠与DBC EAD ∠∠,是内错角;(3)ABC ∠与DAB BCD ∠∠,是同旁内角.故答案为:()()()1.2.,3.,.EAD DBC EAD DAB BCD ∠∠∠∠∠3.∠A与∠AEC;∠B与∠BED详解:解:根据内错角的定义得:∠A与∠AEC;∠B与∠BED;故答案为:∠A与∠AEC;∠B与∠BED.三、解答题1.∠1与∠2是同旁内角,∠1与∠7是同位角,∠1与∠BAD是同旁内角,∠2与∠9没有特殊的位置关系,∠2与∠6是内错角,∠5与∠8是对顶角.解析:根据同旁内角、同位角、内错角和对顶角的概念即可解答.详解:由图可知:∠1与∠2是同旁内角.∠1与∠7是同位角.∠1与∠BAD是同旁内角.∠2与∠9没有特殊的位置关系.∠2与∠6是内错角.∠5与∠8是对顶角.点睛:本题考查的知识点是同旁内角、同位角、内错角和对顶角,解题的关键是熟练的掌握同旁内角、同位角、内错角和对顶角.。
2021年人教版七年级数学下册第五章《5.1.3同位角、内错角、同旁内角》公开课课件1

b a
a
b
5
14
c
23
6
12 34
c
2.如右图,其中内错角共有____对; 同位角共有____对;同旁内角共有 ____对.
六、归纳小结
1.你能总结一下同位角、内错角、同旁内角分别 具有哪些特征吗?
2.你认为在图形中识别同位角、内错角、同旁内 角的关键是什么?
3.本节课的学习,你在数学思想方法方面还有哪 些收获?
另一边
各有一
5
在截线 的同侧,
边在同 一直线
两角方
(截线)
1
向相同.
上
具有这种位置关系的一对角叫做同位角. 图中除∠1和∠5外,还有同位角吗?若有请指出来. 特征:两角的边组成字母F.
辨认同位角
下列各图中的∠1与∠2,哪些是同位角?哪些不是?
内错角
问题4.观察图中的∠3和∠5,它们有怎样的位置关系?
七、布置作业
教科书 习题5.1第11题,复习题5第7题
初稿:丁浩勇(安徽省无为县刘渡中心学校) 修改:夏晓华(安徽省庐江县第三中学) 审校:张永超(安徽省合肥市教育局教研室)
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2021/2/42021/2/4Thursday, February 04, 2021
5 3
另一边 在截线 的两侧, 两角方 向相反.
各有一 边在同 一直线 (截线) 上.
具有这种位置关系的一对角叫做内错角. 图中除∠3和∠5外,还有内错角吗?若有请指出来. 特征:两角的边组成字母Z.
同旁内角
问题5.观察图中的∠3和∠6,它们具有怎样的位置关系?
同位角、内错角、同旁内角 浙教版七年级数学下册一课一练(含答案)

1.2 同位角、内错角、同旁内角课课练一、单选题1.如图,下列各角与∠A是同位角的是()A.∠1B.∠2C.∠3D.∠42.如图,下列两个角是同旁内角的是()A.∠1与∠2B.∠1与∠3C.∠1与∠4D.∠2与∠4 3.如图,下列说法错误的是()A.∠1与∠3是对顶角B.∠3与∠4是内错角C.∠2与∠6是同位角D.∠3与∠5是同旁内角4.如图,直线a,b,c被射线l和m所截,则下列关系正确的是()A.∠1与∠2是对顶角B.∠1与∠3是同旁内角C.∠3与∠4是同位角D.∠2与∠3是内错角5.如图,∠A与∠1是()A.同位角B.内错角C.同旁内角D.对顶角6.如图,已知两直线l1与l2被第三条直线l3所截,则下列说法中错误的是()A.∠2与∠4是邻补角B.∠2与∠3是对顶角C.∠1与∠4是内错角D.∠1与∠2是同位角7.如图,∠1和∠2不是同旁内角的是()A.B.C.D.8.如图,下列说法中错误的是().A.∠FBC和∠ACE是内错角B.∠ABD和∠ACH是同位角C.∠GBD和∠HCE是同位角D.∠GBC和∠BCE是同旁内角9.如图,AB∥CD,EF分别与AB,CD交于点B,F.若∠E=20°,∠EFC=130°,则∠A的度数是()A.20°B.30°C.40°D.50°10.如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,如果∠EFG=64°,那么∠EGD的大小是()A.122°B.124°C.120°D.126°二、填空题11.如图,∠1与∠2是直线和被直线所截的一对角.12.如图,若AB,AF被ED所截,则∠1与是内错角.13.如图,∠1和∠2是角,∠2和∠3是角.14.如图,与∠B构成同位角的角是.15.如图,下列结论:①∠2与∠3是内错角;②∠2与∠B是同位角;③∠A与∠B是同旁内角;④∠A与∠ACB不是同旁内角,其中正确的是(只填序号).16.如图,共有对同位角,有对内错角,有对同旁内角.17.如图,直线AB,CD被直线EF所截,如果∠2=100°,那么∠1的同位角等于度.18.如图,同旁内角有对.19.如图,与∠1是同旁内角的是,与∠2是内错角的是.20.如图,有下列3个结论:①能与∠DEF构成内错角的角的个数是2;②能与∠EFB构成同位角的角的个数是1;③能与∠C构成同旁内角的角的个数是4,以上结论正确的是.21.将一把直尺和一块直角三角板如图放置,如果∠α=43°,则∠β的度数是度.22.如图,AB∥CD,∠A=35°,∠C=80°,则∠E=.23.请完成下面的解答过程.如图,∠1=∠B,∠C=110°,求∠3的度数.解:∵∠1=∠B,∴AD∥()∴∠C+=180°.(两直线平行,同旁内角互补)∵∠C=110°,∴∠2=°.∴∠3==70°.()三、解答题24.如图所示的图形中,同位角有多少对。
人教版七年级数学下册《同位角、内错角、同旁内角》拓展练习
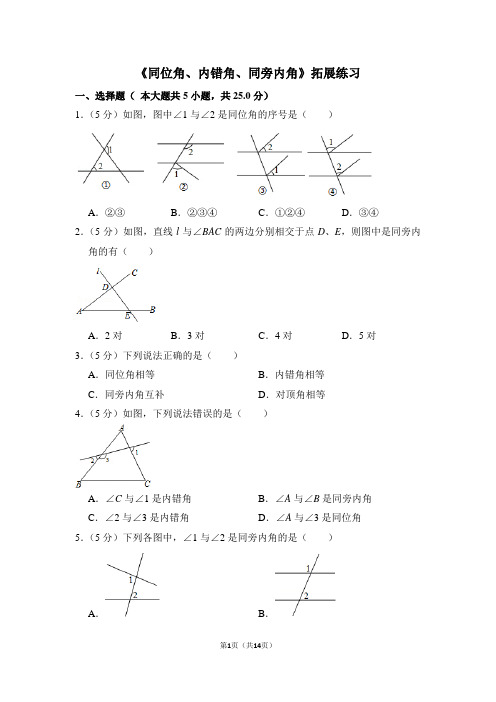
《同位角、内错角、同旁内角》拓展练习一、选择题(本大题共5小题,共25.0分)1.(5分)如图,图中∠1与∠2是同位角的序号是()A.②③B.②③④C.①②④D.③④2.(5分)如图,直线l与∠BAC的两边分别相交于点D、E,则图中是同旁内角的有()A.2对B.3对C.4对D.5对3.(5分)下列说法正确的是()A.同位角相等B.内错角相等C.同旁内角互补D.对顶角相等4.(5分)如图,下列说法错误的是()A.∠C与∠1是内错角B.∠A与∠B是同旁内角C.∠2与∠3是内错角D.∠A与∠3是同位角5.(5分)下列各图中,∠1与∠2是同旁内角的是()A.B.C.D.二、填空题(本大题共5小题,共25.0分)6.(5分)如图所示,直线AB,CD被DE所截,则∠1和∠是同位角,∠1和∠是内错角,∠1和∠是同旁内角.7.(5分)四条直线两两相交,且任意三条不相交于同一点,则四条直线共可构成的同位角有组.8.(5分)如图,按角的位置关系填空:∠3与∠2是;∠B与∠3 是.(填“同位角、内错角、同旁内角”)9.(5分)如图1,三条直线两两相交,且不共点,则图中同旁内角有对;如图2,四条直线两两相交,任三条直线不经过同一点,则图中的同旁内角有对.10.(5分)如图,与∠1构成内错角的角是.三、解答题(本大题共5小题,共50.0分)11.(10分)已知:如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径,路径1:∠1﹣同旁内角→∠9﹣内错角→∠3.路径2:∠1一内错角→∠12一内错角→∠6﹣同位角→∠10﹣同旁内角→∠3.试一试:(1)从起始∠1跳到终点角∠8;(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点∠8?12.(10分)读图1~图4,回答下列问题.(1)请你写出图1、图2、图3和图4中分别有几对同旁内角?(2)观察图形,请写出图n(n是正整数)中有几对同旁内角?13.(10分)如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=∠COF.(1)求∠FOG的度数;(2)写出一个与∠FOG互为同位角的角;(3)求∠AMO的度数.14.(10分)如图所示,同位角一共有对,分别是;内错角一共有对,分别是;同旁内角一共有对,分别是..15.(10分)如图,有四条互相不平行的直线L1、L2、L3、L4所截出的八个角.请你任意选择其中的三个角(不可选择未标注的角),尝试找到它们的关系,并选择其中一组予以证明.《同位角、内错角、同旁内角》拓展练习参考答案与试题解析一、选择题(本大题共5小题,共25.0分)1.(5分)如图,图中∠1与∠2是同位角的序号是()A.②③B.②③④C.①②④D.③④【分析】根据同位角的定义逐个判断即可.【解答】解:图①中∠1和∠2是同位角,图②中∠1和∠2是同位角,图③中∠1和∠2不是同位角,图④中∠1和∠2是同位角,故选:C.【点评】本题考查了同位角的定义,能够理解同位角的定义是解此题的关键,数形结合思想的运用.2.(5分)如图,直线l与∠BAC的两边分别相交于点D、E,则图中是同旁内角的有()A.2对B.3对C.4对D.5对【分析】根据第三条截线可能是直线AB、直线AC、直线l,结合同旁内角的定义,数出同旁内角即可.【解答】解:直线AC与直线AB被直线l所截形成的同旁内角有:∠ADE与∠AED、∠CDE与∠BED;直线AC与直线DE被直线AB所截形成的同旁内角有:∠DAE与∠DEA;直线AB与直线DE被直线AC所截形成的同旁内角有:∠EAD与∠EDA;故选:C.【点评】本题考查了同位角、内错角、同旁内角的定义,要结合图形,熟记同位角、内错角、同旁内角的位置特点.3.(5分)下列说法正确的是()A.同位角相等B.内错角相等C.同旁内角互补D.对顶角相等【分析】根据同位角、内错角、同旁内角的定义以及对顶角的性质解答.【解答】解:只有两直线平行时,同位角相等或内错角相等或同旁内角互补,故选项A、B、C错误.对顶角是相等的,故选项D是正确的.故选:D.【点评】本题考查同位角、内错角、同旁内角的定义以及对顶角的性质,属于基础题,熟记概念或性质进行解答即可.4.(5分)如图,下列说法错误的是()A.∠C与∠1是内错角B.∠A与∠B是同旁内角C.∠2与∠3是内错角D.∠A与∠3是同位角【分析】根据内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角可得答案.【解答】解:如图所示:A、∠C与∠1是内错角,正确,不合题意;B、∠B与∠A是同旁内角,正确,不合题意;C、∠3与∠2是邻补角,此选项错误,符合题意;D、∠A与∠3是同位角,正确,不合题意;故选:C.【点评】此题主要考查了三线八角,在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.5.(5分)下列各图中,∠1与∠2是同旁内角的是()A.B.C.D.【分析】根据内错角、同旁内角、同位角的概念逐一判断可得.【解答】解:A、∠1与∠2是内错角,此选项错误;B、此图形中∠1与∠2不构成直接关系,此选项错误;C、∠1与∠2是同旁内角,此选项正确;D、∠1与∠2是同位角,此选项错误;故选:C.【点评】本题主要考查内错角、同旁内角、同位角,掌握内错角、同旁内角、同位角的概念是解题的关键.二、填空题(本大题共5小题,共25.0分)6.(5分)如图所示,直线AB,CD被DE所截,则∠1和∠3是同位角,∠1和∠5是内错角,∠1和∠2是同旁内角.【分析】利用同位角,内错角,同旁内角的定义判断即可.【解答】解:如图所示,直线AB,CD被DE所截,则∠1和∠3是同位角,∠1和∠5是内错角,∠1和∠2是同旁内角,故答案为:3,5,2【点评】此题考查了同位角,内错角,同旁内角,熟练掌握各自的定义是解本题的关键.7.(5分)四条直线两两相交,且任意三条不相交于同一点,则四条直线共可构成的同位角有48组.【分析】每条直线都与另3条直线相交,有3个交点.每2个交点决定一条线段,共有3条线段.4条直线两两相交且无三线共点,共有3×4=12条线段.每条线段各有4组同位角,可知同位角的总组数.【解答】解:∵平面上4条直线两两相交且无三线共点,∴共有3×4=12条线段.又∵每条线段各有4组同位角,∴共有同位角12×4=48组,故答案为:48.【点评】本题考查了同位角的定义.注意在截线的同旁找同位角.要结合图形,熟记同位角的位置特点.两条直线被第三条直线所截所形成的八个角中,有4组同位角.8.(5分)如图,按角的位置关系填空:∠3与∠2是内错角;∠B与∠3 是同旁内角.(填“同位角、内错角、同旁内角”)【分析】直接利用内错角以及同旁内角的定义得出答案.【解答】解:∠3与∠2是内错角;∠B与∠3 是同旁内角.故答案为:内错角,同旁内角.【点评】此题主要考查了内错角、同旁内角的定义,正确把握相关定义是解题关键.9.(5分)如图1,三条直线两两相交,且不共点,则图中同旁内角有6对;如图2,四条直线两两相交,任三条直线不经过同一点,则图中的同旁内角有24对.【分析】如图1,按两条直线被第三条直线所截,得出同旁内角的对数,发现可以形成6对同旁内角;如,图2,根据总结出的结论得出.【解答】解:如图1,直线EF与直线AB被直线CD所截时,所构成的同旁内角有:∠1与∠2,∠2与∠3,同理,每一条直线做截线时,都有两对同旁内角,所以一共有6对同旁内角;如图2,不交于同一点的四条直线两两相交,设这四条直线分别为a、b、c、d,可以分为:①a、b、c;②a、b、d;③a、c、d;④b、c、d,每三条直线都构成了6对同旁内角,所以这四组线中一共有24对同旁内角;故答案为:6,24.【点评】本题考查了同位角、内错角、同旁内角.解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.10.(5分)如图,与∠1构成内错角的角是∠DEF或∠DEC.【分析】根据内错角的定义即可判断,注意有两解.【解答】解:∠1与∠DEF可以看成直线AB与直线EF被直线DE所截的内错角,∠1与∠DEC可以看成直线AB与直线AC被直线DE所截的内错角,故答案为∠DEF或∠DEC.【点评】本题看成内错角、同位角、同旁内角等知识,解题的关键是理解内错角的定义,属于基础题.三、解答题(本大题共5小题,共50.0分)11.(10分)已知:如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径,路径1:∠1﹣同旁内角→∠9﹣内错角→∠3.路径2:∠1一内错角→∠12一内错角→∠6﹣同位角→∠10﹣同旁内角→∠3.试一试:(1)从起始∠1跳到终点角∠8;(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点∠8?【分析】(1)路径:∠1→∠12→∠8;(2)路径:∠1→∠10→∠5→∠8.【解答】解:(1)路径∠1∠12∠8;(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能跳到终点∠8.其路径为:路径:∠1∠10∠5∠8.【点评】考查了同位角、内错角、同旁内角.解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.12.(10分)读图1~图4,回答下列问题.(1)请你写出图1、图2、图3和图4中分别有几对同旁内角?(2)观察图形,请写出图n(n是正整数)中有几对同旁内角?【分析】根据同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角进行分析即可,进而求出每个图形中同旁内角的个数,进而得出答案.【解答】解:(1)图1中:有2对同旁内角;图2中:有8对同旁内角;图3中:有18对同旁内角;图4中:有32对同旁内角;(2)图n(n是正整数)中有2n2对同旁内角.【点评】此题主要考查了三线八角,关键是掌握同旁内角的边构成“U”形.13.(10分)如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=∠COF.(1)求∠FOG的度数;(2)写出一个与∠FOG互为同位角的角;(3)求∠AMO的度数.【分析】(1)根据对顶角相等可得∠DOF的度数,再根据角平分线的定义可求∠FOG的度数;(2)根据同位角的定义可求与∠FOG互为同位角的角;(3)根据邻补角的性质可求∠COF,再根据已知条件和对顶角相等可求∠AMO 的度数.【解答】解:(1)∵∠COM=120°,∴∠DOF=120°,∵OG平分∠DOF,∴∠FOG=60°;(2)与∠FOG互为同位角的角是∠BMF;(3)∵∠COM=120°,∴∠COF=60°,∵∠EMB=∠COF,∴∠EMB=30°,∴∠AMO=30°.【点评】本题考查了同位角的定义,角平分线定义,对顶角、邻补角定义的应用,能综合运用知识点进行推理和计算是解此题的关键.14.(10分)如图所示,同位角一共有6对,分别是∠1和∠5,∠2和∠6,∠3和∠7∠4和∠8,∠7和∠9,∠4和∠9;内错角一共有4对,分别是∠1和∠7,∠4和∠6,∠5和∠9,∠2和∠9;同旁内角一共有4对,分别是∠1和∠6,∠1和∠9.∠4和∠7,∠6和∠9.【分析】利用同位角,内错角,以及同旁内角定义判断即可得到结果.【解答】解:同位角一共有6对,分别是∠1和∠5,∠2和∠6,∠3和∠7,∠4和∠8,∠7和∠9,∠4和∠9;内错角一共有4对,分别是∠1和∠7,∠4和∠6,∠5和∠9,∠2和∠9;同旁内角一共有4对,分别是∠1和∠6,∠1和∠9,∠4和∠7,∠6和∠9.故答案为:6,∠1和∠5,∠2和∠6,∠3和∠7,∠4和∠8,∠7和∠9,∠4和∠9;4,∠1和∠7,∠4和∠6,∠5和∠9,∠2和∠9;4,∠1和∠6,∠1和∠9,∠4和∠7,∠6和∠9【点评】此题考查了同位角,内错角,以及同旁内角,熟练掌握各自的定义是解本题的关键.15.(10分)如图,有四条互相不平行的直线L1、L2、L3、L4所截出的八个角.请你任意选择其中的三个角(不可选择未标注的角),尝试找到它们的关系,并选择其中一组予以证明.【分析】根据三角形的外角和为360°,三角形的内角和为180°以及三角形外角和定理即可写出三个角之间的数量关系.【解答】解:如∠2+∠4+∠6=360°,∠1+∠5+∠7=180°,∠2=∠5+∠7,∠3=∠1+∠8,已知如图:有四条互相不平行的直线L1、L2、L3、L4所截出的八个角,求证:∠1+∠5+∠7=180°,证明:∵∠DAC+∠7+∠5=180°,又∵∠1=∠DAC,∴∠1+∠5+∠7=180°.【点评】此题主要考查了对顶角的性质以及三角形的内角和定理,正确的应用三角形内角和定理是解决问题的关键.。
人教版七年级数学下册5-1-3 同位角、内错角、同旁内角 习题(含答案及(2)

5.1.3 同位角、内错角、同旁内角学校:__________ 姓名:__________ 班级:__________ 考号:__________一、单选题1.如图,是同位角关系的是( )A.∠3和∠4B.∠1和∠4C.∠2和∠4D.不存在2.如图,与∠1互为同旁内角的角共有()个.A.1 B.2 C.3 D.43.已知∠1与∠2是同旁内角,若∠1=60°,则∠2的度数是( )A.60°B.120°C.60°或120°D.不能确定4.如图,按各组角的位置判断错误的是()A.∠1与∠4是同旁内角B.∠3与∠4是内错角C.∠5与∠6是同旁内角D.∠2与∠5是同位角5.如图,直线a,b被直线c所截,则下列说法中错误的是( )A.∠1与∠2是邻补角B.∠1与∠3是对顶角C.∠2与∠4是同位角D.∠3与∠4是内错角6.如图,与∠4是同旁内角的是( )A.∠1B.∠2C.∠3D.∠57.如图,能与∠a构成同旁内角的角有()A.5个B.4个C.3个D.2个二、填空题1.若平面上4条直线两两相交且无三线共点,则共有同旁内角________对.2.如图,与∠1是同位角的角是___,与∠1是内错角的角是___,与∠1是同旁内角的角是___.3.如图,如果∠2=100°,那么∠1的同位角等于______,∠1的内错角等于_____,∠1的同旁内角等于____.三、解答题1.如图,由∠1=∠2能判断AB∥DF吗?若不能判断AB∥DF,你认为还需要再添加一个什么样的条件?并说明理由.参考答案一、单选题1.B解析:根据同位角的性质可得选项A中的∠1和∠2不是同位角;选项B中的∠1和∠3不是同位角;选项C中的∠1和∠4是同位角;选项D中的∠2和∠3不是同位角.故选B.2.C解析:根据AB和AC被BC所截得出∠2,根据BC和AC被AB所截得出∠CAB,根据DE和BC被AB所截得出∠EAB,即可得出答案.详解:与∠1互为同旁内角的是:∠CAB、∠2、∠EAB,共3个.故选C.点睛:本题考查了对同旁内角的定义的理解和运用,关键是能找出符合条件的所有情况,题目比较好,是一道比较容易出错的题目.3.D分析:同旁内角只有在两条线平行的情况下才是互补的.详解:两直线平行线,同旁内角互补.但是在不知道直线平行的情况下,同旁内角的关系是不确定的. 点睛:本题考查了平行线的性质,熟悉掌握平行线的性质是解题的关键.4.C解析:试题分析:A、∠1和∠A是同旁内角,说法正确;B、∠3和∠4是内错角,说法正确;C、∠5和∠6不是两条直线被第三条直线截成的角,说法错误;D、∠2和∠5是同位角,说法正确.故选C.考点:1.同位角2.内错角3.同旁内角.5.D详解:解:∠3与∠4是同旁内角.故选:D6.C解析:根据同位角、内错角、同旁内角、对顶角的定义逐个判断即可.详解:A、∠1和∠4是内错角,不是同旁内角,故本选项错误;B、∠2和∠4是同位角,不是同旁内角,故本选项错误;C、∠3和∠4是同旁内角,故本选项正确;D、∠4和∠5是邻补角,不是同旁内角,故本选项错误;故选C.点睛:本题考查了同位角、内错角、同旁内角、对顶角的定义的应用,能熟记同位角、内错角、同旁内角、对顶角的定义是解此题的关键,注意:数形结合思想的应用.7.A解析:如图有5个同旁内角,故选A.点睛:(1)“同位角相等、内错角相等”、“同旁内角互补”都是平行线的性质的一部分内容,切不可忽视前提“两直线平行”,否则同位角,内错角不一定相等,同旁内角不一定互补.(2)从角的关系得到两直线平行,是平行线的判定;从平行线得到角相等或互补关系,是平行线的性质.二、填空题1.24解析:根据三线八角的特点,对四条直线产生的6个交点,两两一组进行分类求解即可.详解:解:如图所示观测点A和点B,同旁内角有2对;A和C有2对;A和D,没有同旁内角;A和E有2对;A 和F有2对.B和C有2对;B和D有2对;B和E有2对;B和F没有同旁内角.C和D有2对,C和E没有同旁内角,C和F有2对.D和E有2对;D和F有2对.E和F有2对.共有2×12=24对.故答案是:24.点睛:本题主要考察三线八角中的同旁内角,正确理解同旁内角和准确的分类是解题的关键.2.∠4 ∠2 ∠5解析:根据同位角、内错角和同旁内角的特征(同位角形如“F”,内错角形如“Z”,同旁内角形如“U”)判断即可.详解:∠1与∠4的两条边组成“F”形的图案,故∠1的同位角是∠4;∠1与∠2的两条边组成“Z”形的图案,故∠1的内错角是∠2;∠1与∠5的两条边组成“U”形的图案,故∠1的同旁内角是∠5.故答案是:∠4;∠2;∠5点睛:本题主要考察三线八角中三种角的找法,正确区分同位角、内错角和同旁内角的特点是解题的关键.3.80° 80° 100°解析:试题根据图形可知,∠1的同位角与∠2互补,则∠1的同位角等于80°,∠1的内错角与∠2互补,则∠1的内错角等于80°,∠1的同旁内角与∠2是对顶角,则∠1的同旁内角等于100°.故答案为80°;80°;100°.三、解答题1.不能,理由见解析.解析:分析:∠1=∠2不是AB,DF两条直线的内错角或同位角,不符合平行线的判定条件;如果∠CBD=∠EDB,则∠CBD+∠1=∠EDB+∠2,即∠ABD=∠FDB,满足AB∥DF的条件.详解:不能,添加条件:∠CBD=∠EDB,∵∠CBD=∠EDB,∠1=∠2,∴∠CBD+∠1=∠EDB+∠2,即∠ABD=∠FDB,∴AB∥DF.点睛:正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.。
人教版七年级下册数学课时练《5.1.3 同位角、内错角、同旁内角》(2)(含答案)

臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,《5.1.3同位角、内错角、同旁内角》课时练学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图,下列说法错误的是().A .1Ð与2Ð是内错角B .1Ð与4Ð是同位角C .2Ð与4Ð是内错角D .2Ð与3Ð是同旁内角2.已知图(1)~(4),在上述四个图中,1Ð与2Ð是同位角的有().A .(1)(2)(3)B .(1)(2)C .(1)(3)D .(1)3.在下图中,1Ð和2Ð是同位角的是()A .(1)、(2)B .(1)、(3)C .(2)、(3)D .(2)、(4)4.下列图形中,1Ð与2Ð是同位角的是()A .B .C .D .5.如图,与C Ð是同旁内角的有()A .2个B .3个C .4个D .5个6.如图,B Ð的内错角是()A .1ÐB .2ÐC .3ÐD .4Ð二、填空题7.如图所示,1Ð与2Ð是________角,2Ð与4Ð是______角,2Ð与3Ð是__________角.8.如图,直线AB ,CD 被直线EF 所截,如果∠2=100°,那么∠1的同位角等于____度.9.如图所示,B Ð的同旁内角有______________.10.如图,∠1与∠2是直线_____和_____被直线_____所截的一对_____角.11.如图,有下列判断:①∠A 与∠1是同位角;②∠A 与∠B 是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是______(填序号).12.如图,直线,,AB CD EF 与直线,,GH IJ KL 分别相交,图中的同位角共有__________对.三、解答题13.分别指出下列图中的同位角、内错角、同旁内角.14.如图,∠1和∠2,∠3和∠4各是哪两条直线被哪一条直线所截形成的?它们各是什么位置关系的角?15.如图,∠B 与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C 进行同样的讨论.16.请在下图的基础上分别画出符合下列条件的角:(1)1Ð与BOC Ð是对顶角;(2)2Ð与AOB Ð是同位角;(3)3Ð与AOC Ð是内错角;(4)4Ð与AOB Ð是同旁内角.17.如图,已知AC 与EH 交于点B ,BF 与AC 交于点D .问图中同位角和对顶角各有几对?并具体写出各对同位角和对顶角.18.如图,直线AB ,CD 被直线EF 所截,点G ,H 为它们的交点,∠AGE 与它的同位角相等,HP 平分∠GHD ,∠AGH ∶∠BGH =2∶7,试求∠CHG 和∠PHD 的度数.参考答案1.B2.C 3.B 4.D 5.C 6.A 7.同位同旁内内错8.809.,,,BCA BDC A BCDÐÐÐÐ10.a b c 内错11.①②③12.15613.解:如图1,同位角有:∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8;内错角有:∠3与∠6,∠4与∠5;同旁内角有:∠3与∠5,∠4与∠6.如图2,同位角有:∠1与∠3,∠2与∠4;同旁内角有:∠3与∠2.14.解:如图1:∠1和∠2,是DC ,AB 两条直线被直线BD 所截形成,它们是内错角;∠3和∠4是两条AD ,BC 直线被直线BD 所截形成,它们是内错角;如图2:∠1和∠2,是DC ,AB 两条直线被直线BC 所截形成,它们是同旁内角;∠3和∠4是两条AD ,BC 直线被直线AE 所截形成,它们是同位角.15.解:∠B 与∠DAB 是内错角,是直线DE 和BC 被AB 所截而成;∠B 与∠BAE 是同旁内角,是直线DE 和BC 被AB 所截而成;∠B 与∠BAC 是同旁内角,是直线AC 和BC 被AB 所截而成;∠B 与∠C 是同旁内角,是直线AB 和AC 被CB 所截而成;∠C 与∠EAC 是内错角,是直线DE 和BC 被AC 所截而成;∠C 与∠DAC 是同旁内角,是直线DE 和BC 被AC 所截而成;∠C 与∠BAC 是同旁内角,是直线AB 和BC 被AC 所截而成;∠C 与∠B 是同旁内角,是直线AB 和AC 被CB 所截而成.16.如图所示(答案不唯一):17.同位角有7对,分别为:A Ð与HBC Ð,A Ð与FBC Ð,A Ð与GDB Ð,FBC Ð与FDG Ð,FBH Ð与FDG Ð,ABD Ð与ADF Ð,EBD Ð与ADF Ð;对顶角有4对,分别为:EBC Ð与ABH Ð,ABE Ð与HBC Ð,ADB Ð与FDG Ð,ADF Ð与GDB Ð.18.解:∵∠AGE 的同位角是∠CHG ,且∠CHG =∠AGE .∵∠AGH ∶∠BGH =2∶7,∴∠BGH =180°×79=140°,∴∠CHG =∠AGE =∠BGH =140°,∴∠GHD =180°-∠CHG =40°,又∵HP 平分∠GHD ,∴∠PHD =12∠GHD =20°.。
人教版数学七年级下册 5.1.3同位角、内错角、同旁内角课时练
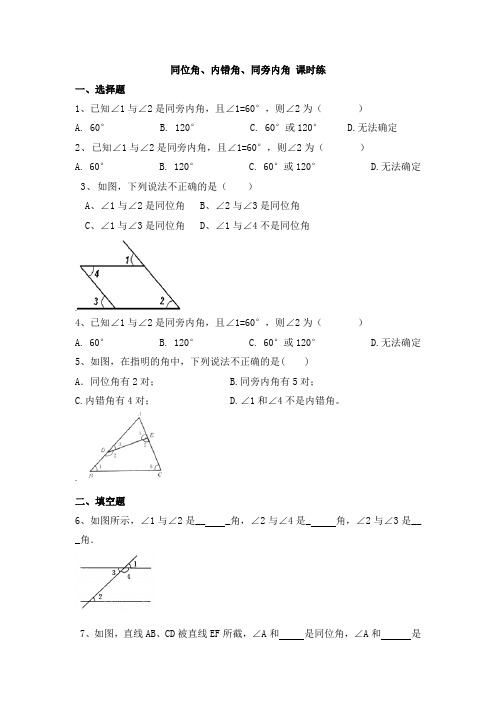
同位角、内错角、同旁内角课时练一、选择题1、已知∠1与∠2是同旁内角,且∠1=60°,则∠2为()A. 60°B. 120°C. 60°或120°D.无法确定2、已知∠1与∠2是同旁内角,且∠1=60°,则∠2为()A. 60°B. 120°C. 60°或120°D.无法确定3、如图,下列说法不正确的是()A、∠1与∠2是同位角B、∠2与∠3是同位角C、∠1与∠3是同位角D、∠1与∠4不是同位角4、已知∠1与∠2是同旁内角,且∠1=60°,则∠2为()A. 60°B. 120°C. 60°或120°D.无法确定5、如图,在指明的角中,下列说法不正确的是( )A.同位角有2对; B.同旁内角有5对;C.内错角有4对;D.∠1和∠4不是内错角。
二、填空题6、如图所示,∠1与∠2是__ _角,∠2与∠4是_ 角,∠2与∠3是__ _角.7、如图,直线AB、CD被直线EF所截,∠A和是同位角,∠A和是内错角,∠A和是同旁内角.8、已知∠1与∠2是同旁内角,且∠1=60°,则∠2为__________.9、如图,与∠1是内错角的是_______.10、如图,∠DAB和∠ABC的位置关系是________三、解答题11、如图(1)说出∠A与∠1互为什么角?(2) ∠B与∠2是否是同位角;(3)写出与∠2成内错角的角。
12. 三条直线两两相交于不同的三点,形成12个角,其中同位角有几对,内错角有几对,同旁内角有几对?13、如图∠1与∠2,∠3与∠4, ∠1与∠4分别是哪两条直线被哪一条直线所截形成的什么角?14、(1)DE 和BC 被AB 截得∠ADE 和∠ B 是什么角?(2)DE 和BC 被AC 截得∠DEC和∠ C 是什么角?15、如图,直线DE 、BC 被直线AB 所截.⑴∠1与∠2、∠1与∠3、∠1与∠4各是什么角?⑵如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?A D EB C16、如图, 直线DE截AB, AC, 构成八个角:①指出图中所有的同位角、内错角、同旁内角.②∠A与∠5, ∠A与∠6, ∠A与∠8, 分别是哪一条直线截哪两条直线而成的什么角?17、如图说出下列各对角是由哪两条直线被哪条直线所截形成的什么角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
l3
2 1 3 4 6 5 7 8
l1
l2
截线 同位角 内错角 同旁内角
同旁 两旁 同旁
被截线
同侧 内侧 内侧
结构特征
F Z U
A 1 4 E 5
∠1与∠2是一对同位角, ∠3与∠4是一对内错角, ∠2与∠4是一对同旁内角. D
(2)如果把图看成是直线 CD,EF被直线AB所截, B C 那么∠1与∠5是一对什么 角?∠4与∠5呢? (3) 哪两条直线被哪一条直 ∠1与∠5是一对同旁内角, ∠4与∠5 线所截, ∠ 2与∠ 5是同位角 是一对内错角.
E
1
C B E D
Q C
B A
F
2.看图填空: (1)若ED,BF被AB所截, 则∠ 1与 ∠2 是同位角;B E 1 3 Nhomakorabea2A
D 4 F
(2)若ED,BC被AF所截, 则∠3与 ∠4 是内错角;
(3)∠1与∠3是AB和AF被 ED 所截 构成的 内错 角; (4)∠2 与∠4是 AB 和 AF BC所截构成的 同位 角。 被
同旁内角:
E
2 1
①在直线AB、CD的内侧
②在直线EF的同侧 B
A C
3
6
4 5 8
4
5
7
D ∠3和∠6 F
同位角、内错角和同旁内角的结构特征:
l3
2 1 3 4 6 5 7 8
l1
l2
能力挑战: 看图填空
A E
2 1 3
D
4
B
F
C
(1)若ED,BF被AB所截, ∠2 是同位角。 则∠1与_____
4
1
3 7
8
2
5 6
例2
如图:直线DE交∠ABC的边BA于 点 F. 如果内错角∠1与∠2相等,那么你 能找出图中其它相等的角吗?请说明理 同位角∠1与∠4相等 由。 有互补的角吗?
同旁内角∠1与∠3互补
B D F A 4
2
1
E
3
C
课内练习
P
l
A D 5 2 3 6 F 4
3..燕子风筝的骨架如图 所示,它是以直线 l 为 对称轴的轴对称图形。 已知∠1=∠4=45O问 ∠2为多少度? ∠5呢?你 还能说出哪些角的度数? 4.找出图中所有的同位 角、内错角、同旁内角.
如图:直线a、b被直线 l 截的8个角中
l 1
同位角:∠1与∠5;
a
5 b 8
2
3
4
∠2与∠6; ∠4与∠8; ∠3与∠7. 内错角:∠3与∠5;
∠4与∠6.
6 7
同旁内角: ∠4与∠5; ∠3与∠6.
2、下列各图中 1 与2 哪些是同位角?哪些不是?
1
2 ( 1 2 ( ) )
1
2
( 1
同位角:
E
2 1 3 6
①在直线EF的同侧
B
②在直线AB、CD的同一旁
1
A
C
4
5 5
7
8
D
F ∠2和∠6;∠3和∠7;∠4和∠8
观察
问题:2、观察∠3与∠5的位置关
内错角:①在直线EF的两侧
E
2
1 3 6
②在直线AB、CD的内侧
B
4
5 3 5
A C
7
8
D ∠4和∠6
F
观察
问题3:观察∠4与∠5的位置关系
2 3
A D
A 1 1 1 2 2 B 2 C 2 3 3 1 4 4 3
D 4 1
(1) 1 4 1
4
4 1 1 B
4 1 4
4
4
C A 3 3 (2) 3 2 2 2 3 3 3 3
D
2 B
2
2
C
合作学习:
E D C
A F
B
请找出图中所有的同位角、内错角和同旁内角。
请用三根竹条或小木棍 制作一个如图的风筝骨架。 把它画成几何图形,并用适 当的方法表示图中的角,然 后分别指出其中所有的对顶 角、同位角、内错角和同旁 内角。
∠3与∠4呢?(内错角) ∠ 2与∠4呢? (同旁内角
练一练:
D
1 4
A
E B
5
2
3
F C
(2)如果把图看成是直线CD,EF被直线AB所截 那么∠1与∠5是一对什么角? (同旁内角)
∠4与∠5呢? (内错角)
练一练:
D
1 4
A
E B
5
2
3
F C
(3)哪两条直线被哪一条直线所截,∠2与∠5 是同位角? (直线AB和CD被直线EF所截)
A
如何找截线和 被截线?
D B
2 1 3 4 5 8 6 7
E
C
截线
被截线
练一练:
如图,直线AB,CD被直线EF所截,请找出一 对同位角,一对内错角和一对同旁内角。
B P A Q C D F
E
练一练:
D
1 4
A
E B
5
2
3
F C
(1)如果把图看成是直线AB,EF被直线CD所截 那么∠1与∠2是一对什么角? (同位角)
2 (
)
)
课堂练习
1
识别哪些角是同位角、内错角、 同旁内角。
1 1 2 2 1 (4) (5)
2
(1)
1 (2)
2
2
(3)
同位角
b a
同位角
同位角
同位角
1
1 2 (8)
1 2
1
1
(6)
2
c
2
(7)
2
(10)
(9)
同位角
内错角
同旁内角
例1:如图,直线DE截直线AB,AC,构成8个
角。指出所有的同位角、内错角和同旁内角。
直线AB,CD被直线EF所截
2
3
F
课堂练习: 1、如图,(1) 内错角 。 __________ (2) 和 和
1 4
AB CD BD 是直线_____与直线____被直线______所截形成的
AD BC BD 内错角 是直线_____与直线____被直线______所截形成的_________。
5.1.3 同位角、内错角、同 旁内角
1.两条直线相交有几个角? (4个) 2.两条直线与第三条直线相交呢? (8个)
3.你能找出这8个角的
关系吗? ∠1与∠3,∠2与∠4,
l3
2
1 4
3 6 7
8 5
l1
l2
∠5与∠7,∠6与∠8
分别是对顶角。
4.这些角还有其它的关系吗
观察
问题:1、观察∠1与∠5的位置关系
例1 如图,直线DE截AB,AC,构成8个角。指出
所有的同位角、内错角和同旁内角。 1.若DE,AB被AC所截呢?
2.若DE,AC被AB所截呢?
关键:要先分 清哪两条直线 被哪一条直线 所截
D
2
3 4 1
A
5
6
8 7
E C
B
课内练习
1.(1)如果把图看成是直线AB,EF被 直线CD所截,那么∠1与∠2是一对什 么角?∠3与∠4呢?∠2与∠4呢?
能力挑战: 看图填空
A E
2 1 3
D
4
B
F
C
(2)若ED,BC被AF所截, ∠4 是内错角。 则∠3与_____
能力挑战: 看图填空
A E
2 1 3
D
4
B
F
C
(3)∠1与∠3是AB和AF被 DE 所截构成的_______ 内错 角。 _____
能力挑战: 看图填空
A E
2 1 3
D
4
B
F
C
AB 和_____ AF 被 (4)∠2与∠4是_____ 同位 角。 BC所截构成的______
