中考数学压轴题分类练习几何中的变换专题无答案

合集下载

2023年九年级数学中考复习几何图形变换综合压轴题专题训练(含答案)

2023年春九年级数学中考复习《几何图形变换综合压轴题》专题训练（附答案）1．如图，△ABC和△ECD都是等边三角形，直线AE，BD交于点F．（1）如图1，当A，C，D三点在同一直线上时，∠AFB的度数为，线段AE与BD的数量关系为．（2）如图2，当△ECD绕点C顺时针旋转α（0°≤α＜360°）时，（1）中的结论是否还成立？若不成立，请说明理由；若成立，请就图2给予证明．（3）若AC＝4，CD＝3，当△ECD绕点C顺时针旋转一周时，请直接写出BD长的取值范围．2．如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D、E两点分别在AC、BC上，且DE∥AB，将△CDE绕点C按顺时针方向旋转，记旋转角为α．（1）问题发现：当α＝0°时，的值为；（2）拓展探究：当0°≤α＜360°时，若△EDC旋转到如图2的情况时，求出的值；（3）问题解决：当△EDC旋转至A、B、E三点共线时，若CE＝5，AC＝4，直接写出线段AD的长．3．已知：如图1，线段AD＝5，点B从点A出发沿射线AD方向运动，以AB为底作等腰△ABC，使得AC＝BC＝AB．（1）如图2，当AB＝10时，求证：CD⊥AB；（2）当△BCD是以BC为腰的等腰三角形时，求BC的长；（3）当AB＞5时，在线段BC上是否存在点E，使得△BDE与△ACD全等，若存在，求出BC的长；若不存在，请说明理由；（4）作点A关于直线CD的对称点A′，连接CA′当CA′∥AB时，CA′＝（请直接写出答案）．4．如图1，在△ABC中，AE⊥BC于点E，AE＝BE，D是AE上的一点，且DE＝CE，连接BD，CD．（1）试判断BD与AC的位置关系是：；数量关系是：；（2）如图2，若将△DCE绕点E旋转一定的角度后，试判断BD与AC的位置关系和数量关系是否发生变化，并说明理由；（3）如图3，若将（2）中的等腰直角三角形都换成等边三角形，其他条件不变．①试猜想BD与AC的数量关系为：；②你能求出BD与AC的夹角度数吗？如果能，请直接写出夹角度数；如果不能，请说明理由．5．如图，平面直角坐标系中O为原点，Rt△ABC的直角顶点A在y轴正半轴上，斜边BC 在x轴上，已知B、C两点关于y轴对称，且C（﹣8，0）．（1）请直接写出A、B两点坐标；（2）动点P在线段AB上，横坐标为t，连接OP，请用含t的式子表示△POB的面积；（3）在（2）的条件下，当△POB的面积为24时，延长OP到Q，使得PQ＝OP，在第一象限内是否存在点D，使得△OQD是等腰直角三角形，如果存在，求出D点坐标；如果不存在，请说明理由．6．如图1，已知△ABC中，∠ACB＝90°，AC＝BC＝6，点D在AB边的延长线上，且CD ＝AB．（Ⅰ）求BD的长度；（Ⅱ）如图2，将△ACD绕点C逆时针旋转α（0°＜α＜360°）得到△A'CD'．①若α＝30°，A'D'与CD相交于点E，求DE的长度；②连接A'D、BD'，若旋转过程中A'D＝BD'时，求满足条件的α的度数．（Ⅲ）如图3，将△ACD绕点C逆时针旋转α（0°＜α＜360°）得到△A'CD'，若点M 为AC的中点，点N为线段A'D'上任意一点，直接写出旋转过程中线段MN长度的取值范围．7．如图①，将两个等腰直角三角形纸片OAB和OCD放置在平面直角坐标系中，点O（0，0），点A（0，+1），点B（+1，0），点C（0，1），点D（1，0）．（Ⅰ）求证：AC＝BD；（Ⅱ）如图②，现将△OCD绕点O顺时针方向旋转，旋转角为α（0°＜α＜180°），连接AC，BD，这一过程中AC和BD是否仍然保持相等？说明理由；当旋转角α的度数为时，AC所在直线能够垂直平分BD；（Ⅲ）在（Ⅱ）的情况下，将旋转角α的范围扩大为0°＜α＜360°，那么在旋转过程中，求△BAD的面积的最大值，并写出此时旋转角α的度数．（直接写出结果即可）8．在△ABC中，AB＝AC，∠BAC＝α，过点A作直线l平行于BC，点D是直线l上一动点，连接CD，射线DC绕点D顺时针旋转α交直线AB于点E．（1）如图1，若α＝60°，当点E在线段AB上时，请直接写出线段AC，AD，AE之间的数量关系，不用证明；（2）如图2，若α＝60°，当点E在线段BA的延长线上时，（1）中的结论是否成立？若成立，请证明；若不成立，请写出正确结论，并证明．（3）如图3，若α＝90°，BC＝6，AD＝，请直接写出AE的长．9．有一根直尺短边长4cm，长边长10cm，还有一块锐角为45°的直角三角形纸板，它的斜边长为16cm，如图甲，将直尺的短边DE与直角三角形纸板的斜边AB重合，且点D 与点A重合．将直尺沿射线AB方向平移，如图乙，设平移的长度为xcm，且满足0≤x ≤12，直尺和三角形纸板重叠部分的面积为Scm2．（1）当x＝0cm时，S＝；当x＝12cm时，S＝．（2）当0＜x＜8（如图乙、图丙），请用含x的代数式表示S．（3）是否存在一个位置，使重叠部分面积为28cm2？若存在求出此时x的值．10．如图①，C为线段BD上的一点，BC≠CD，分别以BC，BD为边在BD的上方作等边△ABC和等边△CDE，连接AE，F，G，H分别是BC，AE，CD的中点，连接FG，GH，FH．（1）△FGH的形状是；（2）将图①中的△CDE绕点C顺时针旋转，其他条件不变，（1）的结论是否成立？结合图②说明理由；（3）若BC＝2，CD＝4，将△CDE绕点C旋转一周，当A，E，D三点共线时，直接写出△FGH的周长．11．已知，射线AB∥CD，P是直线AC右侧一动点，连接AP，CP，E是射线AB上一动点，过点E的直线分别与AP，CP交于点M，N，与射线CD交于点F，设∠BAP＝∠1，∠DCP＝∠2．（1）如图1，当点P在AB，CD之间时，求证：∠P＝∠1+∠2；（2）如图2，在（1）的条件下，作△PMN关于直线EF对称的△P'MN，求证：∠3+∠4＝2（∠1+∠2）；（3）如图3，当点P在AB上方时，作△PMN关于直线EF对称的△P'MN，（1）（2）的结论是否仍然成立，若成立，请说明理由；若不成立，请直接写出∠P，∠1，∠2之间数量关系，以及∠3，∠4与∠1，∠2之间数量关系．12．（1）如图1，平面直角坐标系中A（0，a），B（a，0）（a＞0）．C为线段AB的中点，CD⊥x轴于D，若△AOB的面积为2，则△CDB的面积为．（2）如图2，△AOB为等腰直角三角形，O为直角顶点，点E为线段OB上一点，且OB＝3OE，C与E关于原点对称，线段AB交x轴于点D，连CD，若CD⊥AE，试求的值．（3）如图3，点C、E在x轴上，B在y轴上，OB＝OC，△BDE是以B为直角顶点的等腰直角三角形，直线CB、ED交于点A，CD交y轴于点F，试探究：是否为定值？如果是定值，请求出该定值；如果不是，请求出其取值范围．13．在△ABC中，AB＝AC，∠BAC＝90°．（1）如图1，点P，Q在线段BC上，AP＝AQ，∠BAP＝15°，求∠AQB的度数；（2）点P，Q在线段BC上（不与点B，C重合），AP＝AQ，点Q关于直线AC的对称点为M，连接AM，PM．①依题意将图2补全；②用等式表示线段BP，AP，PC之间的数量关系，并证明．14．【问题背景】如图1，在Rt△ABC中，AB＝AC，D是直线BC上的一点，将线段AD绕点A逆时针旋转90°至AE，连接CE，求证：△ABD≌△ACE；【尝试应用】如图2，在图1的条件下，延长DE，AC交于点G，BF⊥AB交DE于点F，求证：FG＝AE；【拓展创新】如图3，A是△BDC内一点，∠ABC＝∠ADB＝45°，∠BAC＝90°，BD ＝，直接写出△BDC的面积为．15．在平面直角坐标系中，A（a，0），B（0，b）分别是x轴负半轴和y轴正半轴上一点，点C与点A关于y轴对称，点P是x轴正半轴上C点右侧一动点．（1）当2a2+4ab+4b2+2a+1＝0时，求A，B的坐标；（2）当a+b＝0时，①如图1，若D与P关于y轴对称，PE⊥DB并交DB延长线于E，交AB的延长线于F，求证：PB＝PF；②如图2，把射线BP绕点B顺时针旋转45o，交x轴于点Q，当CP＝AQ时，求∠APB的大小．16．已知：在Rt△ABC中，∠C＝90°，∠B＝30°，BC＝6，左右作平行移动的等边三角形DEF的两个顶点E、F始终在边BC上，DE、DF分别与AB相交于点G、H．（1）如图1，当点F与点C重合时，点D恰好在斜边AB上，求△DEF的周长；（2）如图2，在△DEF作平行移动的过程中，图中是否存在与线段CF始终相等的线段？如果存在，请指出这条线段，并加以证明；如果不存在，请说明理由；（3）假设C点与F点的距离为x，△DEF与△ABC的重叠部分的面积为y，求y与x的函数关系式，并写出定义域．17．在△ABC中，∠C＝90°，AC＝2，BC＝2，点D为边AC的中点（如图），点P、Q 分别是射线BC、BA上的动点，且BQ＝BP，联结PQ、QD、DP．（1）求证：PQ⊥AB；（2）如果点P在线段BC上，当△PQD是直角三角形时，求BP的长；（3）将△PQD沿直线QP翻折，点D的对应点为点D'，如果点D'位于△ABC内，请直接写出BP的取值范围．18．定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．（1）已知点M，N是线段AB的勾股分割点，若AM＝2，MN＝3，求BN的长．（2）如图2，在等腰直角△ABC中，AC＝BC，∠ACB＝90°，点M，N为边AB上两点满足∠MCN＝45°，求证：点M，N是线段AB的勾股分割点；阳阳同学在解决第（2）小题时遇到了困难，陈老师对阳阳说：要证明勾股分割点，则需设法构造直角三角形，你可以把△CBN绕点C逆时针旋转90°试一试．请根据陈老师的提示完成第（2）小题的证明过程．19．问题背景如图（1），△ABD，△AEC都是等边三角形，△ACD可以由△AEB通过旋转变换得到，请写出旋转中心、旋转方向及旋转角的大小．尝试应用如图（2），在Rt△ABC中，∠ACB＝90°，分别以AC，AB为边，作等边△ACD和等边△ABE，连接ED，并延长交BC于点F，连接BD．若BD⊥BC，求的值．拓展创新如图（3），在Rt△ABC中，∠ACB＝90°，AB＝2，将线段AC绕点A顺时针旋转90°得到线段AP，连接PB，直接写出PB的最大值．20．【教材呈现】如图是苏科版九年级下册数学教材第92页的第17题．一块直角三角形木板，它的一条直角边AC长为1.5m，面积为1.5m2．甲乙两人分别按图1、图2把它加工成一个正方形的桌面，请说明哪个正方形的面积较大．【解决问题】（1）记图1、图2中的正方形面积分别为S1，S2，则S1S2．（填“＞”、“＜”或“＝”）．【问题变式】若木板形状是锐角三角形A1B1C1．某数学兴趣小组继续思考：按图3、图4、图5三种方式加工，分别记所得的正方形面积为S3、S4、S5，哪一个正方形的面积最大呢？（2）若木板的面积S仍为1.5m2．小明：记图3中的正方形为“沿B1C1边的内接正方形”，图4中的正方形为“沿A1C1边的内接正方形”，依此类推．以图3为例，求“沿B1C1边的内接正方形DEFG”的面积．设EF ＝x ，B 1C 1＝a ，B 1C 1边上的高A 1H ＝h ，则S ＝ah ．由“相似三角形对应高的比等于相似比”易得x ＝；同理可得图4、图5中正方形边长，再比较大小即可．小红：若要内接正方形面积最大，则x 最大即可；小莉：同一块木板，面积相同，即S 为定值，本题中S ＝1.5，因此，只需要a +h 最小即可．我们可以借鉴以前研究函数的经验，令y ＝a +h ＝a +＝a +（a ＞0）．下面来探索函数y ＝a +（a ＞0）的图象和性质．①根据如表，画出函数的图象：（如图6）a… 1 2 3 4 … y … 12 9 6 4 3 3 4 4…②观察图象，发现该函数有最小值，此时a 的取值；A ．等于2；B ．在1～之间；C ．在～之间；D ．在～2之间．（3）若在△A 1B 1C 1中（如图7），A 1B 1＝5，A 1C 1＝，高A 1H ＝4．①结合你的发现，得到S 3、S 4、S 5的大小关系是（用“＜”连接）． ②小明不小心打翻了墨水瓶，已画出最大面积的内接正方形的△A 1B 1C 1原图遭到了污损，请用直尺和圆规帮他复原△A 1B 1C 1．（保留作图痕迹，不写作法）参考答案1．解：（1）∵△ABC是等边三角形，∴AC＝BC，∠BAC＝∠ACB＝60°，∵△ECD是等边三角形，∴CE＝CD，∠DCE＝60°，∴∠ACB＝∠DCE＝60°，∴∠ACB+∠BCE＝∠DCE+∠BCE，即∠ACE＝∠BCD，在△ACE和△BCD中，，∴△ACE≌△BCD（SAS），∴AE＝BD，∠CAE＝∠CBD，在△ABF中，∠AFB＝180°﹣（∠BAF+∠ABF）＝180°﹣（∠BAF+∠CBF+∠ABC）＝180°﹣（∠BAC+∠ABC）＝180°﹣（60°+60°）＝60°，∴∠AFB＝60°，故答案为：∠AFB＝60°，AE＝BD；（2）（1）中结论仍成立，证明：∵△ABC是等边三角形，∴AC＝BC，∠BAC＝∠ACB＝60°，∵△ECD是等边三角形，∴CE＝CD，∠DCE＝60°，∴∠ACB＝∠DCE＝60°，∴∠ACB+∠BCE＝∠DCE+∠BCE，即∠ACE＝∠BCD，在△ACE和△BCD中，，∴△ACE≌△BCD（SAS），∴AE＝BD，∠CAE＝∠CBD，∵∠AFB+∠CBD＝∠ACB+∠CAE，∴∠AFB＝∠ACB，∵∠ACB＝60°，∴∠AFB＝60°；（3）在△BCD中，BC+CD＞BD，BC﹣CD＜BD，∴点D在BC的延长线上时，BD最大，最大为4+3＝7，当点D在线段BC上时，BD最小，最小为4﹣3＝1，∴1≤BD≤7，即BD长的取值范围为1≤BD≤7．2．解：（1）∵∠BAC＝90°，AB＝AC，∴△ABC为等腰直角三角形，∠B＝45°，∵DE∥AB，∴∠DEC＝∠B＝45°，∠CDE＝∠A＝90°，∴△DEC为等腰直角三角形，∴cos∠C＝＝，∵DE∥AB，∴＝＝，故答案为：；（2）由（1）知，△BAC和△CDE均为等腰直角三角形，∴＝＝，又∠BCE＝∠ACD＝α，∴△BCE∽△ACD，∴＝＝，即＝；（3）①如图3﹣1，当点E在线段BA的延长线上时，∵∠BAC＝90°，∴∠CAE＝90°，∴AE＝＝＝3，∴BE＝BA+AE＝4+3＝7；由（2）知，＝．故AD＝．②如图3﹣2，当点E在线段BA上时，AE＝＝＝3，∴BE＝BA﹣AE＝4﹣3＝1，由（2）知，＝．故AD＝．综上所述，AD的长为或，故答案为：或．3．解：（1）如图2中，∵AB＝10，AD＝5，∴AD＝DB，∵CA＝CB，AD＝DB，∴CD⊥AB．（2）如图1中，当AB＜AD时，BC＝BD．设AB＝10k，则AC＝BC＝6k，∵AD＝5，∴10k+6k＝5，∴k＝，∴BC＝6k＝．如图1﹣1中，当AB＞AD时，BC＝BD，同法可得10k﹣6k＝5，解得k＝，∴BC＝6k＝，综上所述，BC的值为或．（3）如图3﹣1中，当△ADC≌△BED时，BD＝AC＝BC，由（2）可知，BC＝．如图3﹣2中，当△ADC≌△BCE时，点E与C重合，此时AB＝10k＝10，∴k＝1，BC＝6k＝6．综上所述，BC的值为或6．（4）如图3中，当CA′∥AB时，∵CA′∥AB，∴∠ADC＝∠A′CD，由翻折可知，∠A′CD＝∠ACD，∴∠ACD＝∠ADC，∴AC＝AD＝5，∴CA′＝CA＝5．故答案为5．4．解：（1）结论：BD＝AC，BD⊥AC．理由：延长BD交AC于F．∵AE⊥CB，∴∠AEC＝∠BED＝90°．在△AEC和△BED中，，∴△AEC≌△BED（SAS），∴AC＝BD，∠CAE＝∠EBD，∵∠AEC＝90°，∴∠ACB+∠CAE＝90°，∴∠CBF+∠ACB＝90°，∴∠BFC＝90°，∴AC⊥BD，故答案为：BD⊥AC，BD＝AC．（2）如图2中，不发生变化，设DE与AC交于点O，BD与AC交于点F．理由是：∵∠BEA＝∠DEC＝90°，∴∠BEA+∠AED＝∠DEC+∠AED，∴∠BED＝∠AEC，在△BED和△AEC中，，∴△BED≌△AEC（SAS），∴BD＝AC，∠BDE＝∠ACE，∵∠DEC＝90°，∴∠ACE+∠EOC＝90°，∵∠EOC＝∠DOF，∴∠BDE+∠DOF＝90°，∴∠DFO＝180°﹣90°＝90°，∴BD⊥AC；（3）①如图3中，结论：BD＝AC，理由是：∵△ABE和△DEC是等边三角形，∴AE＝BE，DE＝EC，∠BEA＝∠DEC＝60°，∴∠BEA+∠AED＝∠DEC+∠AED，∴∠BED＝∠AEC，在△BED和△AEC中，，∴△BED≌△AEC（SAS），∴BD＝AC，故答案为：BD＝AC．②能；设BD与AC交于点F，由①知，△BED≌△AEC，∴∠BDE＝∠ACE，∴∠DFC＝180°﹣（∠BDE+∠EDC+∠DCF）＝180°﹣（∠ACE+∠EDC+∠DCF）＝180°﹣（60°+60°）＝60°，即BD与AC的夹角中的锐角的度数为60°．5．解：（1）∵B、C两点关于y轴对称，且C（﹣8，0），∴点B（8，0），BO＝CO，又∵AO⊥BC，∴AC＝AB，∵∠CAB＝90°，AC＝AB，CO＝BO，∴AO＝CO＝BO＝8，∴点A（0，8）；（2）如图1，过点P作PM⊥OB于M，∵点P的横坐标为t，∴OM＝t，∴MB＝8﹣t，∵∠CAB＝90°，AC＝AB，∴∠ABO＝45°，∴∠BPM＝∠ABO＝45°，∴PM＝MB＝8﹣t，∴S△POB＝×OB×PM＝×8×（8﹣t）＝32﹣4t；（3）∵△POB的面积为24，∴32﹣4t＝24，∴t＝2，∴点P（2，6），如图2，当点Q为直角顶点时，过点Q作HG⊥y轴，过点D作DG⊥HG于点G，∵PQ＝OP，点P（2，6），∴点Q（4，12），∵∠OQD＝90°＝∠OHQ＝∠QGD，∴∠OQH+∠DQG＝90°＝∠OQH+∠HOQ，∴∠HOQ＝∠GQD，又∵OQ＝QD，∴△OHQ≌△QGD（AAS），∴OH＝QG＝12，HQ＝GD＝4，∴HG＝16，∴点D（16，8）；当点D为直角顶点时，过点Q作HG⊥y轴，过点D作DG⊥HG于点G，过点D作DN ⊥y轴于N，同理可求△QDG≌△ODN，∴ON＝QG，DN＝DG，∵DN＝QG+HQ＝4+QG，DG＝HN＝12﹣ON，∴ON＝QG＝4，DN＝DG＝8，∴点D（8，4），综上所述：点D（16，8）或（8，4）．6．解：（Ⅰ）如图1，过点C作CH⊥AB于H，∵∠ACB＝90°，AC＝BC＝6，CH⊥AB，∴AB＝CD＝6，CH＝BH＝AB＝3，∠CAB＝∠CBA＝45°，∴DH＝＝＝3，∴BD＝DH﹣BH＝3﹣3；（Ⅱ）①如图2，过点E作EF⊥CD'于F，∵将△ACD绕点C逆时针旋转α（0°＜α＜360°）得到△A′CD′，∴CD＝CD'＝6，∠DCD'＝30°＝∠CDA＝∠CD'A'，∴CE＝D'E，又∵EF⊥CD'，∴CF＝D'F＝3，EF＝，CE＝2EF＝2，∴DE＝DC﹣CE＝6﹣2；②如图2﹣1，∵∠ABC＝45°，∠ADC＝30°，∴∠BCD＝15°，∴∠ACD＝105°，∵将△ACD绕点C逆时针旋转α（0°＜α＜360°）得到△A′CD′，∴AC＝A'C，CD＝CD'，∠ACA'＝∠DCD'＝α，∴CB＝CA'，又∵A′D＝BD′，∴△A'CD≌△BCD'（SSS），∴∠A'CD＝∠BCD'，∴105°﹣α＝15°+α，∴α＝45°；如图2﹣2，同理可证：△A'CD≌△BCD'，∴∠A'CD＝∠BCD'，∴α﹣105°＝360°﹣α﹣15°，∴α＝225°，综上所述：满足条件的α的度数为45°或225°；（Ⅲ）如图3，当A'D'⊥AC时，N是AC与A'D'的交点时，MN的长度最小，∵∠A'＝45°，A'D'⊥AC，∴∠A'＝∠NCA'＝45°，∴CN＝A'N＝3，∵点M为AC的中点，∴CM＝AC＝3，∴MN的最小值＝NC﹣CM＝3﹣3；如图4，当点A，点C，点D'共线，且点N与点D'重合时，MN有最大值，此时MN＝CM+CN＝6+3，∴线段MN的取值范围是3﹣3≤MN≤6+3．7．解：（Ⅰ）∵点A（0，+1），点B（+1，0），点C（0，1），点D（1，0），∴OA＝+1，OB＝+1，OC＝1，OD＝1，∴AC＝OA﹣OC＝+1﹣1＝，BD＝+1﹣1＝，∴AC＝BD；（Ⅱ）由题意知，OA＝OB，OC＝OD，∠AOB＝∠COD＝90°，∴∠AOC＝∠AOB﹣∠COB＝90°﹣∠COB，∠BOD＝∠COD﹣∠COB＝90°﹣∠COB，∴∠AOC＝∠BOD，∴△AOC≌△BOD（SAS），∴AC＝BD，∠OAC＝∠OBD，如图1（注：点C在x轴上，为了不要出现误解，点C没画在x轴上），延长AC交BD 于D，连接BC，在Rt△AOB中，OA＝OB，∴∠OAB＝∠OBA＝45°，∴∠CAB+∠ABD＝∠OAB﹣∠OAC+∠ABO+∠BOD＝∠OAB+∠OBA＝90°，∴AC⊥BD，∵AC垂直平分BD，∴CD＝BC，设点C的坐标为（m，n），∴m2+n2＝1①，由旋转知，CD＝＝，∵B（+1，0），[m﹣（+1）]2+n2＝2②，联立①②解得，m＝1，n＝0，∴点C在x轴上，∴旋转角为∠AOC＝90°，故答案为：90°；（Ⅲ）如图2，∵OA＝OB＝+1，∴AB＝OA＝2+，过点O作OH⊥AB于H，∴S△AOB＝OA•OB＝AB•OH，∴OH＝＝＝＝，过点D作DG⊥AB于G，S△ABD＝AB•DG＝（2+）DG，要使△ABD的面积最大，则DG最大，由旋转知，点D是以O为圆心，1为半径的圆上，∴点D在HO的延长线上时，DG最大，即DG的最大值为D'H＝OD'+OH＝1+＝，∴S△ABD最大＝AB•D'H＝（2+）×＝，在Rt△AOB中，OA＝OB，OH⊥AB，∴∠BOH＝45°，∴旋转角∠BOD'＝180°﹣45°＝135°．8．解：（1）AC＝AE+AD．证明：连接CE，∵线段DC绕点D顺时针旋转α交直线AB于点E，α＝60°，∵AB＝AC，∠BAC＝60°，∴CB＝CA＝AB，∠ACB＝60°，∵AD∥BC，∴∠DAF＝∠ACB＝60°，∵∠FDC＝∠EAF＝60°，∠AFE＝∠DFC，∴△AFE∽△DFC，∴，∴，∵∠AFD＝∠EFC，∴△AFD∽△EFC，∴∠DAF＝∠FEC＝60°，∴△DEC是等边三角形，∴CD＝CE，∠ECD＝60°，∴∠BCE＝∠ACD，∴△BCE≌△ACD（SAS），∴BE＝AD，∴AB＝AE+BE＝AE+AD，∴AC＝AE+AD；（2）不成立，AD＝AC+AE．理由如下：在AC的延长线上取点F，使AF＝AD，连接DF，当α＝60°时，∠BAC＝∠EDC＝60°，∵AB＝AC，∴△ABC是等边三角形，∴AB＝AC＝BC∠BCA＝60°，∵l∥BC，∴∠DAC＝∠BCA＝60°，∠EAD＝∠ABC＝60°，∵AF＝AD，∴∠ADF＝∠AFD＝60°，AD＝FD＝AF，∴∠EDC＝∠ADF＝60°，∴∠EDC﹣∠ADC＝∠ADF﹣∠ADC，即∠EDA＝∠CDF，∵AD＝FD，∠EAD＝∠AFD＝60°，∴△EAD≌△CFD（ASA），∴AE＝CF，∴AD＝AF＝AC+CF＝AC+AE；（3）AE的长为或．当点E在线段AB上，过点D作直线l的垂线，交AC于点F，如图3所示．∵△ABC中，∠BAC＝90°，AC＝AB，∴∠ACB＝∠B＝45°．∵直线l∥BC，∴∠DAF＝∠ACB＝45°．∵FD⊥直线l，∴∠DAF＝∠DF A＝45°．∴AD＝FD．∵∠EDC＝∠ADF＝90°，∴∠ADE＝∠FDC．由（1）可知DC＝DE，∴△ADE≌△FDC（SAS），∴AE＝CF．∵AD＝，∴AF＝2，∵BC＝6，∴AC＝AB＝3，∴AE＝AC﹣AF＝3﹣2．当点E在线段AB的延长线上时，如图4所示．过点D作直线l的垂线，交AB于点M，同理可证得△ADC≌△MDE（SAS），∴AC＝EM＝3，∵AD＝，∴AM＝2，∴EM+AM＝3+2．综合以上可得AE的长为3+2或3﹣2．9．解：（1）当x＝0cm时，S＝4×4÷2＝8cm2；当x＝12cm时，S＝4×4÷2＝8cm2．故答案为：8cm2；8cm2．（2）①当0＜x＜4时，∵△CAB为等腰直角三角形，∴∠CAB＝45°，∴△ADG和△AEF都是等腰直角三角形，∴AD＝DG＝x，AE＝EF＝x+4，∴梯形GDEF的面积＝×（GD+EF）×DE＝×（x+x+4）×4＝4x+8．②如图所示：过点C作CM⊥AB于点M．当4＜x＜8时，梯形GDMC的面积＝（GD+CM）×DM＝（x+8）（8﹣x）＝﹣x2+32，梯形CMEF的面积＝（EF+CM）×ME＝[16﹣（x+4）+8][（x+4）﹣8]＝（20﹣x）（x﹣4）＝﹣x2+12x﹣40，S＝梯形GDMC的面积+梯形CMEF的面积＝（﹣x2+32）+（﹣x2+12x﹣40）＝﹣x2+12x ﹣8．综合以上可得，S＝．（3）当0＜x＜4时s最大值小于24，当x＝4时，S＝24cm2，所以当S＝28cm2时，x必然大于4，即﹣x2+12x﹣8＝28，解得x1＝x2＝6，当x＝6cm时，阴影部分面积为28cm2．当8＜≤12时，由对称性可知s的最大值也是小于24，不合题意舍去．∴当x＝6cm时，阴影部分面积为28cm2．10．解：（1）∵△ABC和△CDE都是等边三角形，∴∠B＝∠DCE＝60°，AB＝BC，CE＝CD，∴CE∥AB，∵BC≠CD，∴CE≠AB，∴四边形ABCE是梯形，∵点F，G分别是BC，AE的中点，∴FG是梯形ABCE的中位线，∴FG∥AB，∴∠GFC＝60°，同理：∠GHB＝60°，∴∠FGH＝180°﹣∠GFC﹣∠GHB＝60°＝∠GFC＝∠GHB，∴△FGH是等边三角形，故答案为：等边三角形；（2）成立，理由如下：如图1，取AC的中点P，连接PF，PG，∵△ABC和△CDE都是等边三角形，∴AB＝BC，CE＝CD，∠BAC＝∠ACB＝∠ECD＝∠B＝60°，又F，G，H分别是BC，AE，CD的中点，∴FP＝AB，FC＝BC，CH＝CD，PG＝CE，PG∥CE，PF∥AB，∴FP＝FC，PG＝CH，∠GPC+∠PCE＝180°，∠FPC＝∠BAC＝60°，∠PFC＝∠B＝60°，∴∠FPG＝∠FPC+∠GPC＝60°+∠GPC，∠GPC＝180°﹣∠PCE，∴∠FCH＝360°﹣∠ACB﹣∠ECD﹣∠PCE＝360°﹣60°﹣60°﹣（180°﹣∠GPC）＝60°+∠GPC，∴∠FPG＝∠FCH，∴△FPG≌△FCH（SAS），∴FG＝FH，∠PFG＝∠CFH，∴∠GFH＝∠GFC+∠CFH＝∠GFC+∠PFG＝∠PFC＝60°，∴△FGH为等边三角形；（3）①当点D在AE上时，如图2，∵△ABC是等边三角形，∴∠ACB＝60°，AC＝BC＝2，∵△CDE是等边三角形，∴∠CED＝∠CDE＝60°，CE＝CD＝DE＝4，过点C作CM⊥AE于M，∴DM＝EM＝DE＝2，在Rt△CME中，根据勾股定理得，CM＝＝＝2，在Rt△AMC中，根据勾股定理得，AM＝＝＝4，∴AD＝AM﹣DM＝4﹣2＝2，∵∠ACB＝∠DCE＝60°，∴∠ACB﹣∠DCB＝∠DCE﹣∠DCB，∴∠ACD＝∠BCE，连接BE，在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴BE＝AD＝2，∠ADC＝∠BEC，∵∠ADC＝180°﹣∠CDE＝120°，∴∠BEC＝120°，∴∠BEA＝∠BEC﹣∠CED＝60°，过点B作BN⊥AE于N，∴∠BNE＝90°，在Rt△BNE中，∠EBN＝90°﹣∠BEA＝30°，∴EN＝BE＝1，∴BN＝EN＝，DN＝DE﹣EN＝3，连接BD，根据勾股定理得，BD＝＝＝2，∵点H是CD的中点，点F是BC的中点，∴FH是△BCD的中位线，∴FH＝BD＝，由（2）知，△FGH是等边三角形，∴△FGH的周长为3FH＝3，②当点D在AE的延长线上时，如图3，同①的方法得，FH＝，∴△FGH的周长为3FH＝3，即满足条件的△FGH的周长为3或3．11．（1）证明：如图1中，过点P作PT∥AB．∵AB∥CD，AB∥PT，∴AB∥PT∥CD，∴∠1＝∠APT，∠2＝∠CPT，∴∠APC＝∠APT+∠CPT＝∠1+∠2．（2）证明：如图2中，连接PP′．∵∠3＝∠MPP′+∠MP′P，∠4＝∠NPP′+∠NP′P，∠APC＝∠MP′N，∴∠3+∠4＝2∠APC，∵∠APC＝∠1+∠2，∴∠3+∠4＝2（∠1+∠2）．（3）结论不成立．结论是：∠P＝∠2﹣∠1，∠4﹣∠3＝2（∠2﹣∠1）．理由：如图3中，设PC交AB于E，AP交NP′于F．∵AB∥CD，∴∠PEB＝∠2，∵∠PEB＝∠1+∠P，∴∠2＝∠P+∠1，∴∠P＝∠2﹣∠1．∵∠4＝∠P+∠PFN，∠PFN＝∠3+∠P′，∠P＝∠P′，∴∠4＝∠P+∠3+∠P，∴∠4﹣∠3＝2∠P＝2（∠2﹣∠1），∴∠4﹣∠3＝2（∠2﹣∠1）．12．解：（1）∵A（0，a），B（a，0）（a＞0），∴OA＝a，OB＝a，∵△AOB的面积为2，∴S△AOB＝×a×a＝2，∴a＝2（负值舍去），∴A（0，2），B（2，0），∵C为线段AB的中点，∴C（1，1），∴OD＝BD＝CD＝1，∴S△CDB＝×1×1＝．故答案为：．（2）连AC，过点D作DM⊥BC于M，∵△AOB是等腰直角三角形，∴AO⊥BO，AO＝BO，∠B＝∠OAB＝45°，又CO＝EO，∴AO是CE的垂直平分线，∴AE＝AC，不妨设AE、CD交于F，AO、CD交于G，∴∠CGA＝∠OAE+∠AFC＝∠OCD+∠COA，∵∠AFC＝∠COA＝90°，∴∠OAE＝∠OCD＝∠OAC，又∵∠CAD＝∠CAO+∠OAB＝∠OCD+∠B＝∠CDA，∴CD＝CA＝EA，∴△AOE≌△CMD（AAS），∴OE＝DM，∴＝＝＝3，∴＝2；（3）＝2，理由如下：作点C关于y轴的对称点N，连接BN，作DM∥BC交y轴于M，∵OB＝OC＝ON，∠BON＝90°，∴△BON等腰直角三角形，∴∠BNO＝∠BMD＝45°，∴∠MBD＝∠OBE+∠DBE＝∠OBE+∠BOE＝∠BEN，又∵BD＝BE，∴△BMD≌△ENB（AAS），∴EN＝BM，BN＝DM＝BC，又∵∠BFC＝∠DFM，∠BCF＝∠FDM，∴△BCF≌△MDF（AAS），∴BF＝MF，∴CO﹣EO＝NO﹣EO＝NE＝BM＝2BF，即＝2．13．解：（1）∵在△ABC中，AB＝AC，∠BAC＝90°，∴∠B＝∠C＝45°，∵∠APQ是△ABC的一个外角，∴∠APQ＝∠B+∠BAP，∵∠BAP＝15°，∴∠APQ＝60°，∵AP＝AQ，∴∠APQ＝∠AQB＝60°．（2）①图形如图2所示．②解：结论：PC2+BP2＝2AP2．理由：连接MC．∵AB＝AC，∠BAC＝90°，∴∠B＝∠ACB＝45°，∵AP＝AQ，∴∠APQ＝∠AQP，∴∠BAP＝∠CAQ，∴△ABP≌△ACQ（SAS），∴BP＝CQ，∵点Q关于直线AC的对称点为M，∴AQ＝AM，CQ＝CM，∠CAM＝∠CAQ，∠ACM＝∠ACQ＝45°，∴AP＝AM，∠B＝∠ACM＝45°，∠BAP＝∠CAM，BP＝CM，∴∠BAC＝∠P AM＝90°，在Rt△APM中，AP＝AM，∠P AM＝90°，∴PM＝，∵∠ACQ＝∠ACM＝45°，∴∠PCM＝90°，在Rt△PCM中，∠PCM＝90°，∴PC2+CM2＝PM2，∴PC2+BP2＝2AP2．14．【问题背景】证明：如图1，∵∠BAC＝∠DAE＝90°，∴∠DAB＝∠EAC，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）．【尝试应用】证明：如图2，过点D作DK⊥DC交FB的延长线于K．∵DK⊥CD，BF⊥AB，∴∠BDK＝∠ABK＝90°，∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠ACB＝45°，∴∠DBK＝∠K＝45°，∴DK＝DB，∵△ABD≌△ACE，∴∠ABD＝∠ACE＝135°，DB＝EC＝DK，∴∠ECG＝45°，∵BF⊥AB，CA⊥AB，∴AG∥BF，∴∠G＝∠DFK，在△ECG和△DKF中，，∴△ECG≌△DKF（AAS），∴DF＝EG，∵DE＝AE，∴DF+EF＝AE，∴EG+EF＝AE，即FG＝AE．【拓展创新】解：如图3中，过点A作AE⊥AD交BD于E，连接CE．．∵∠ADB＝45°，∠DAE＝90°，∴△ADE与△ABC都是等腰直角三角形，同法可证△ABD≌△ACE，∴CE＝BD＝2，∵∠AEC＝∠ADB＝45°，∴∠CED＝∠CEB＝90°，∴S△BDC＝•BD•CE＝×2×2＝6．故答案为：6．15．解：（1）∵2a2+4ab+4b2+2a+1＝0，∴（a+2b）2+（a+1）2＝0，∵（a+2b）2≥0 （a+1）2≥0，∴a+2b＝0，a+1＝0，∴a＝﹣1，b＝，∴A（﹣1，0）B（0，）．（2）①证明：如图1中，∵a+b＝0，∴a＝﹣b，∴OA＝OB，又∵∠AOB＝90°，∴∠BAO＝∠ABO＝45°，∵D与P关于y轴对称，∴BD＝BP，∴∠BDP＝∠BPD，设∠BDP＝∠BPD＝α，则∠PBF＝∠BAP+∠BP A＝45°+α，∵PE⊥DB，∴∠BEF＝90°，∴∠F＝90o﹣∠EBF，又∠EBF＝∠ABD＝∠BAO﹣∠BDP＝45°﹣α，∴∠F＝45o+α，∴∠PBF＝∠F，∴PB＝PF．②解：如图2中，过点Q作QF⊥QB交PB于F，过点F作FH⊥x轴于H．可得等腰直角△BQF，∵∠BOQ＝∠BQF＝∠FHQ＝90°，∴∠BQO+∠FQH＝90°，∠FQH+∠QFH＝90°，∴∠BQO＝∠QFH，∵QB＝QF，∴△FQH≌△QBO（AAS），∴HQ＝OB＝OA，∴HO＝AQ＝PC，∴PH＝OC＝OB＝QH，∴FQ＝FP，又∠BFQ＝45°∴∠APB＝22.5°．16．解：（1）在Rt△ABC中，∠C＝90°，∠B＝30°，BC＝6，∴AC＝2，∠A＝60°，∵△DEF是等边三角形，∴∠DCE＝60°，∴∠ACD＝30°，∴∠ADC＝90°，∴CD＝AC＝3，∴△DEF的周长＝9；（2）解：结论：CF＝DG．理由：∵BC＝6，EF＝DF＝DE＝3，∴CF+BE＝BC﹣EF＝6﹣3＝3，∵△DEF是等边三角形，∴∠DEF＝60°，∵∠DEF＝∠B+∠EGB，∴∠B＝∠EGB＝∠DGE＝30°，∴EG＝BE，∵EG+DG＝CF+BE＝3，∴CF＝DG；（3）∵S△DEF＝×32＝，S△DGH＝•GH•DH＝•x•x＝x2，y＝S△DFE﹣S△DHG＝﹣x2（0≤x≤3）．17．解：（1）在Rt△ABC中，AC＝2，BC＝2，根据勾股定理得，AB＝＝＝4，∴＝，∵BQ＝BP，∴＝，∴，∵∠QBP＝∠CBA，∴△BPQ∽△BAC，∴∠BQP＝∠ACB＝90°，∴PQ⊥AB；（2）∵点D是AC的中点，∴AD＝CD＝AC＝1，由（1）知，PQ⊥AB，∴∠AQP＝90°，∴∠PQD＜90°，∵△PQD是直角三角形，∴①当∠DPQ＝90°时，如图1，在Rt△ABC中，AC＝2，AB＝4，∴sin∠ABC＝＝，∴∠ABC＝30°，∴∠QPB＝90°﹣∠ABC＝60°，∴∠DPC＝90°﹣∠BPQ＝30°，∴CP＝＝＝，∴BP＝BC﹣CP＝，②当∠PDQ＝90°时，∴∠ADQ+∠PDC＝90°，如图2，过Q作QE⊥AC于E，∴∠DEQ＝90°＝∠ACB，∴∠ADQ+∠DQE＝90°，∴∠DQE＝∠PDC，∴△EQD∽△CDP，∴，∴，设BP＝t，则CP＝BC﹣BP＝2﹣t，在Rt△BQP中，BQ＝BP cos30°＝t，∴AQ＝AB﹣BQ＝4﹣t，在Rt△AEQ中，QE＝AQ cos30°＝（4﹣t）•＝2﹣t，AE＝AQ＝2﹣t，∴DE＝AD﹣AE＝t﹣1，∴，∴t＝或t＝（大于2，舍去）∴BP＝；即BP＝或；（3）；理由：如图3，①当点D'恰好落在边BC上时，由折叠知，PD'＝PD，PQ⊥DD'，由（1）知，PQ⊥AB，∴DD'∥AB，∴∠DD'C＝∠ABC＝30°，∴CD'＝CD＝，设BP＝m，则CP＝BC﹣BP＝2﹣m，∴DP＝D'P＝CD'﹣CP＝m﹣，在Rt△CDP中，根据勾股定理得，DP2＝CP2+CD2，∴（m﹣）2＝（2﹣m）2+1，∴m＝，②当点D'落在D时，即PQ过点D，在Rt△CDP'中，∠P'＝90°﹣∠DD'P'＝30°，∴CP'＝＝＝，∴BP'＝BC+CP'＝，综上：．18．（1）解：当MN最长时，BN＝＝＝；当BN最长时，BN＝＝＝，综合以上可得BN的长为或；（2）证明：如图，把△CBN绕点C逆时针旋转90°，得到△CAN'，连接MN'，∴△AN'C≌△BNC，∴CN'＝CN，∠ACN'＝∠BCN，∠CBN＝∠CAN'，∵∠MCN＝45°，∴∠N'CA+∠ACM＝∠ACM+∠BCN＝45°，∴∠MCN'＝∠BCM，∴△MN'C≌△MNC（SAS），∴MN'＝MN，∵AC＝BC，∠ACB＝90°，∴∠B＝∠CAM＝45°，∴∠CAN'＝45°，∴∠MAN'＝∠CAN'+∠CAM＝45°+45°＝90°，在Rt△MN'A中，AN'2+AM2＝N'M2，∴BN2+AM2＝MN2，∴点M，N是线段AB的勾股分割点．19．问题背景解：∵△ABD，△AEC都是等边三角形，∴∠BAD＝60°，∠CAE＝60°，AD＝AB，AC＝AE，∴∠BAD+∠BAC＝∠CAE+∠BAC，∴∠DAC＝∠BAE，∴△ACD≌△AEB（SAS），∴△ACD可以由△AEB绕点A顺时针旋转60°得到，即旋转中心是点A，旋转方向是顺时针，旋转角是60°；尝试应用∵△ACD和△ABE都是等边三角形，∴AC＝AD，AB＝AE，∠CAD＝∠BAE＝60°，∴∠CAB＝∠DAE，∴△ADE≌△ACB（SAS），∴∠ADE＝∠ACB＝90°，DE＝CB，∵∠ADE＝90°，∴∠ADF＝90°，∵∠ADC＝∠ACD＝60°，∴∠DCF＝∠CDF＝30°，∴CF＝DF，∵BD⊥BC，∴∠BDF＝30°，∴BF＝DF，设BF＝x，则CF＝DF＝2x，DE＝3x，∴；拓展创新∵∠ACB＝90°，∴点C在以AB为直径的圆上运动，取AB的中点D，连接CD，∴CD＝AB＝1，如图，过点A作AE⊥AB，且使AE＝AD，连接PE，BE，∵将线段AC绕点A顺时针旋转90°得到线段AP，∴∠P AC＝90°，P A＝AC，∵∠EAD＝90°，∴∠P AE＝∠CAD，∴△CAD≌△P AE（SAS），∴PE＝CD＝1，∵AB＝2，AE＝AD＝1，∴BE＝＝＝，∴BP≤BE+PE＝+1，当且仅当P、E、B三点共线时取等号，∴BP的最大值为+1．20．解：（1）由AC长为1.5m，△ABC的面积为1.5m2，可得BC＝2m，如图①，设加工桌面的边长为xcm，∵DE∥CB，∴△ADE∽△ACB，∴＝，即＝，解得：x＝；如图②，设加工桌面的边长为ym，过点C作CM⊥AB，分别交DE、AB于点N、M，∵AC＝1.5m，BC＝2m，∴AB＝＝＝2.5（m），∵△ABC的面积为1.5m2，∴CM＝m，∵DE∥AB，∴△CDE∽△CAB，∴＝，即＝，解得：y＝，∴x＞y，即S1＞S2，故答案为：＞．（2）①函数图象如图6所示：②观察图象，发现该函数有最小值，此时a的取值～2之间．故选D．（3）①由（2）可知，S5＜S4＜S3．故答案为：S5＜S4＜S3．②如图7，△A1B1C1即为所求作．。

中考数学复习专题四几何变换压轴题试题(2)

中考数学复习专题四几何变换压轴题试题(2)类型一图形的旋转变换几何图形的旋转变换是近年来中考中的常考点，多与三角形、四边形相结合．解决旋转变换问题，首先要明确旋转中心、旋转方向和旋转角，关键是找出旋转前后的对应点，利用旋转前后两图形全等等性质解题．如图，在菱形ABCD中，AB＝2，∠BAD＝60°，过点D作DE⊥AB于点E，DF⊥BC于点F.(1)如图1，连接AC分别交DE，DF于点M，N，求证：MN＝AC；(2)如图2，将∠EDF以点D为旋转中心旋转，其两边DE′，DF′分别与直线AB，BC相交于点G，P.连接GP，当△DGP的面积等于3时，求旋转角的大小并指明旋转方向．【分析】 (1)连接BD，由∠BAD＝60°，得到△ABD为等边三角形，进而证明点E是AB的中点，再根据相似三角形的性质解答；(2)分∠EDF顺时针旋转和逆时针旋转两种情况，然后根据旋转的性质解题．1．(20__·潍坊)边长为6的等边△ABC中，点D，E分别在AC，BC边上，DE∥AB，EC＝2.(1)如图1，将△DEC沿射线EC方向平移，得到△D′E′C′，边D′E′与AC的交点为M，边C′D′与∠ACC′的角平分线交于点N.当CC′多大时，四边形MCND′为菱形？并说明理由．(2)如图2，将△DEC绕点C旋转∠α(0°<α<360°)，得到△D′E′C，连接AD′，BE′.边D′E′的中点为P.①在旋转过程中，AD′和BE′有怎样的数量关系？并说明理由；②连接AP，当AP最大时，求AD′的值．(结果保留根号)图1 图22．(20__·成都)如图1，△ABC中，∠ABC＝45°，AH⊥BC于点H，点D在AH上，且DH＝CH，连接BD.(1)求证：BD＝AC；(2)将△BHD绕点H旋转，得到△EHF(点B，D分别与点E，F对应)，连接AE.①如图2，当点F落在AC上时(F不与C重合)，若BC＝4，tan C＝3，求AE的长；②如图3，当△EHF是由△BHD绕点H逆时针旋转30°得到时，设射线CF与AE相交于点G，连接GH，试探究线段GH与EF之间满足的等量关系，并说明理由．类型二图形的翻折变换几何图形的翻折变换也是近年来中考中的常考点，多与三角形、四边形相结合．翻折变换的实质是对称，翻折部分的两图形全等，找出对应边、对应角，再结合勾股定理、相似的性质与判定解题．(20__·苏州)如图，在△ABC中，AB＝10，∠B＝60°，点D，E分别在AB，BC上，且BD＝BE＝4，将△BDE沿DE所在直线折叠得到△B′DE(点B′在四边形ADEC内)，连接AB′，则AB′的长为____．【分析】作DF⊥B′E于点F，B′G⊥AD于点G，由∠B＝60°，BD＝BE，得到△BDE是等边三角形，由对称的性质得到△B′DE也是等边三角形，从而GD＝B′F，然后利用勾股定理求解．、3．(20__·安徽)在三角形纸片ABC中，∠A＝90°，∠C＝30°，AC＝30 cm，将该纸片沿过点B的直线折叠，使点A落在斜边BC上的一点E处，折痕记为BD(如图1)，剪去△CDE后得到双层△BDE(如图2)，再沿着过△BDE某顶点的直线将双层三角形剪开，使得展开后的平面图形中有一个是平行四边形，则所得平行四边形的周长为40或cm.图1 图24．如图，在矩形ABCD中，点E在边CD上，将矩形沿AE折叠，使点D落在边BC上的点F处，过点F作FG∥CD，交AE于点G，连接DG.(1)求证：四边形DEFG为菱形；(2)若CD＝8，CF＝4，求的值．类型三图形的相似图形的相似常以三角形、四边形为背景，与旋转、翻折、动点相结合，考查三角形相似的性质及判定，难度较大，是中考中常考的几何压轴题．与动点相关的相似三角形，要根据动点的运动情况讨论相似三角形的对应边、对应角，进而判定相似三角形，再利用相似三角形的性质解题．(20__·青岛)如图，在矩形ABCD中，AB＝6 cm，BC＝8 cm，对角线AC，BD交于点O.点P从点A出发，沿AD方向匀速运动，速度为1 cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为1 cm/s；当一个点停止运动时，另一个点也停止运动．连接PO并延长，交BC于点E，过点Q作QF∥AC，交BD于点F.设运动时间为t(s)(0＜t＜6) ，解答下列问题：(1)当t为何值时，△AOP是等腰三角形；(2)设五边形OECQF的面积为S(cm2)，试确定S与t的函数关系式．【分析】 (1)根据勾股定理求出AC的值，然后分类讨论：当AP＝PO时，求出t的值；当AP＝AO时，求出t的值；(2)过点E作EH⊥AC于点H，过点Q作QM⊥AC于点M，过点D作DN⊥AC于点N，交QF于点G，分别用t表示出EH，DN，DG，再利用面积的和差计算即可．5．(20__·常德)如图，Rt△ABC中，∠BAC＝90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC于F.(1)如图1，若BD＝BA，求证：△ABE≌△DBE；(2)如图2，若BD＝4DC，取AB的中点G，连接CG交AD于点M.求证：①GM＝2MC；②AG2＝AF·AC.图1 图2参考答案【例1】 (1)如图，连接BD，设BD交AC于点O，∵在菱形ABCD中，∠D AB＝60°，AD＝AB，∴△ABD为等边三角形．∵DE⊥AB，∴点E为AB的中点．∵AE∥CD，∴＝＝.同理＝.∴M，N是线段AC的三等分点，∴MN＝AC.(2)∵AB∥CD，∠BAD＝60°，∴∠ADC＝120°.∵∠ADE＝∠CDF＝30°，∴∠EDF＝60°.当∠EDF顺时针旋转时，由旋转的性质知，∠EDG＝∠FDP，∠GDP＝∠EDF＝60°.∵DE＝DF＝，∠DEG＝∠DFP＝90°，∴△DEG≌△DFP，∴DG＝DP，∴△DGP是等边三角形．则S△DGP＝DG2.由DG2＝3，又∵DG＞0，解得DG＝2.∴cos∠EDG＝＝＝，∴∠EDG＝60°.∴当顺时针旋转60°时，△DGP的面积是3.同理，当逆时针旋转60°时，△DGP的面积也是3.综上所述，当∠EDF以点D为旋转中心，顺时针或逆时针旋转60°时，△DGP的面积是3.【变式训练】1．解：(1)当CC′＝时，四边形MCND′为菱形．理由：由平移的性质得CD∥C′D′，DE∥D′E′.∵△ABC为等边三角形，∴∠B＝∠ACB＝60°，∴∠ACC′＝180°－60°＝120°.∵CN是∠ACC′的角平分线，∴∠NCC′＝60°.∵AB∥DE，DE∥D′E′，∴AB∥D′E′，∴∠D′E′C′＝∠B＝60°，∴∠D′E′C′＝∠NCC′，∴D′E′∥CN.∴四边形MCND′为平行四边形．∵∠ME′C′＝∠MCE′＝60°，∠NCC′＝∠NC′C＝60°，∴△MCE′和△NCC′为等边三角形，故MC＝CE′，NC＝CC′.又E′C′＝2，CC′＝，∴CE′＝CC′＝，∴MC＝CN，∴四边形MCND′为菱形．(2)①AD′＝BE′.理由：当α≠180°时，由旋转的性质得∠ACD′＝∠BCE′.由(1)知AC＝BC，CD′＝CE′，∴△ACD′≌△BCE′，∴AD′＝BE′.当α＝180°时，AD′＝AC＋CD′，BE′＝BC＋CE′，即AD′＝BE′.综上可知，AD′＝BE′.②连接CP，在△ACP中，由三角形三边关系得，AP<AC＋CP，∴当A，C，P三点共线时AP最大，如图所示．此时，AP＝AC＋CP.在△D′CE′中，由P为D′E′中点，得AP⊥D′E′，PD′＝，∴CP＝3，∴AP＝6＋3＝9.在Rt△APD′中，由勾股定理得AD′＝＝＝2.2．解：(1)在Rt△AHB中，∠ABC＝45°，∴AH＝BH.∵∠BHD＝∠AHC＝90°，DH＝CH，∴△BHD≌△AHC，∴BD＝AC.(2)①在Rt△AHC中，∵tan C＝3，∴＝3.设CH＝_，则BH＝AH＝3_，∴BC＝BH＋CH＝4_＝4，∴_＝1，∴AH＝3，CH＝1.由旋转的性质知，∠EHF＝∠BHD＝∠AHC＝90°，EH＝AH＝3，CH＝DH＝FH，∴∠EHA＝∠FHC，＝＝1，∴△EHA∽△FHC，∴∠EAH＝∠C，∴tan∠EAH＝tan C＝3.如图，过点H作HP⊥AE于点P，则HP＝3AP，AE＝2AP.在Rt△AHP中，AP2＋HP2＝AH2，即AP2＋(3AP)2＝9.∴AP＝，∴AE＝.②由①知，△AEH和△FHC都为等腰三角形，设AH交CG于点Q，∴∠GAH＝∠HCG，∴△AGQ∽△CHQ，∴＝，∴＝，∠AGQ＝∠CHQ＝90°.∵∠AQC＝∠GQH，∴△AQC∽△GQH.又∵旋转角为30°，∴∠EHA＝∠FHC＝120°，∴∠QAG＝30°，∴＝＝＝＝2.【例2】如图，作DF⊥B′E于点F，B′G⊥AD于点G，∵∠B＝60°，BD＝BE＝4，∴△BDE是边长为4的等边三角形．∵将△BDE沿DE所在的直线折叠得到△B′DE，∴△B′DE也是边长为4的等边三角形，∴GD＝B′F＝2.∵B′D＝4，∴B′G＝＝2.∵AB＝10，∴AG＝10－6＝4，∴AB′＝＝2.故答案为2.【变式训练】3．40或4．(1)证明：由折叠的性质知，DG＝FG，ED＝EF，∠AED＝∠AEF，∵FG∥CD，∴∠FGE＝∠AED，∴∠FGE＝∠AEF，∴FG＝FE，∴DG＝GF＝EF＝DE，∴四边形DEFG为菱形．(2)解：设DE＝_，根据折叠的性质，EF＝DE＝_，EC＝8－_，在Rt△EFC中，FC2＋EC2＝EF2，即42＋(8－_)2＝_2.解得_＝5，CE＝8－_＝3.∴＝.【例3】(1)∵在矩形ABCD中，AB＝6 cm，BC＝8 cm，∴AC＝10 cm.①当AP＝PO时，如图，过点P作PM⊥AO，∴AM＝AO＝.∵∠PMA＝∠ADC＝90°，∠PAM＝∠CAD，∴△APM∽△ACD，∴＝，∴AP＝t＝.②当AP＝AO时，t＝5.∵0＜t＜6，∴t＝或t＝5均符合题意，∴当t＝或t＝5时，△AOP是等腰三角形．(2)如图，过点E作EH⊥AC于点H，过点Q作QM⊥AC于点M，过点D作DN⊥AC于点N，交QF于点G，∵四边形ABCD是矩形，∴AD∥BC，∴∠PAO＝∠ECO.∵点O是对角线AC的中点，∴AO＝CO.又∵∠AOP＝∠COE，∴△AOP≌△COE，∴CE＝AP＝t.∵△CEH∽△CAB，∴＝，∴EH＝.∵S△ADC＝AD·DC＝DN·AC，∴DN＝＝.∵QM∥DN，∴△CQM∽△CDN，∴＝，即＝.∴QM＝，∴DG＝－＝.∵FQ∥AC，∴△DFQ∽△DOC，∴＝＝，∴FQ＝，∴S＝S△OEC＋S△OCD－S△DFQ＝OC·EH＋OC·DN－DG·FQ＝－t2＋t＋12，即S与t的函数关系式为S＝－t2＋t＋12.【变式训练】5．证明：(1)在Rt△ABE和Rt△DBE中，∴△ABE≌△DBE.(2)①如图，过点G作GH∥AD交BC于H，∵AG＝BG，∴BH＝DH.∵BD＝4DC，设DC＝1，则BD＝4，∴BH＝DH＝2.∵GH∥AD，∴＝＝，∴GM＝2MC.②如图，过点C作CN⊥AC交AD的延长线于N，则CN∥AG，∴△AGM∽△NCM，∴＝.由①知GM＝2MC，∴AG＝2NC.∵∠BAC＝∠AEB＝90°，∴∠ABF＝∠CAN＝90°－∠BAE，∴△ACN∽△BAF，∴＝.∵AB＝2AG，∴＝，∴2CN·AG＝AF·AC，∴AG2＝AF·AC.。

2022年中考数学复习专题几何压轴题题型分类整理

专题训练一平移问题基本模型经过平移，对应线段平行（或共线）且相等，对应角相等，对应点所连接的线段平行（或共线）且相等，因此可以通过平移构造平行四边形，转移线段和角.（基本模型图1）（基本模型图2）如图1，将线段CD 进行平移可得到线段EA ，连接EC ，AD. 根据平移的性质，得CD ∥EA.∴四边形CDAE 是平行四边形.∴EC ∥AD.同理，四边形CDFA 、四边形CDBG 和四边形CDHB 均为平行四边形. 如图2，平移线段AB ，即可得到▱ABCP 、▱ABDM 、▱ABND 和▱ABQC. 典型题在Rt △BAC 中，∠A=90°，D,E 分别为AB ，AC 上的点.（1）如图1，CE=AB ，BD=AE ，过点C 作CF ∥EB ，且CF=EB ，连接DF 交EB 于点G ，连接BF ，求EBDC 的值; （2）如图2,若CE=kAB ，BD=kAE ，EB DC =12，求k 的值.（典型题图1）（典型题图2）拓展题1.如图，在四边形ABCD中，AD∥BC，∠BAC=90°－1∠CAD，AC与BD相交于点E，且∠BEC=60°,若AD=5，2BD=15，求AC的长.（1题图）2.如图,在△ABC中，点D在AB的延长线上，点E在BC上，AC=BC=AD=DE，BE=BD，求∠BAC的度数.（2题图）3.阅读下面材料:数学课上，老师出示了下列问题:（1）如图1，过点B作AB的垂线BD，延长AB到点C,使AC=BD，延长BD到点E，使ED=CB，连接AE，CD，且CD的延长线交AE于点F，求∠AFC的度数;（2）如图2,在△ABC中,AB=AC=5m，D是边BC上一点，连接AD，延长CB到点E，使BE=kAD，过点E作EF，求EF的长.(用含m，k的式子表示)⊥AD，交AD的延长线于点F.若AF=kCD,tanC= 34（3题图1）（3题图2）同学们经过思考后，交流了自己的想法:小明:“通过观察和度量，发现∠AFC的度数等于45°”小伟:“通过平移线段AC，BD，ED，BC中的一条线段，可以构造两个全等三角形，进而可以获得等腰直角三角形,那么∠AFC的度数等于45°这一结论也就显而易见了.”……老师:“只要类比小伟平移线段构造全等三角形的思路与方法，那么（2）的问题就能迎刃而解.”请你根据上面的材料，完成上面的两个问题的解答过程.4.如图，在四边形ABCD中，AD∥BC，AD+BC=BD,AC与BD 相交于点F。

九年级数学几何模型压轴题专题练习(解析版)

九年级数学几何模型压轴题专题练习（解析版）一、初三数学旋转易错题压轴题（难）1.如图 1,在 Rt∆ΛSC 中，Z4 = 90o, AB=AC f点 D, E 分别在边 AB, AC 上，AD=AE f连接DC,点M, P, N分别为DE, DC, BC的中点.（1）观察猜想：图1中，线段PM与PN的数量关系是_,位置关系是_；（2〉探究证明：把AADF绕点A逆时针方向旋转到图2的位置，连接BD, CE,判断APMN的形状，并说明理由；（3）拓展延伸：把AADF绕点A在平面内自由旋转，若AD=4, AB=IO f请直接写出APMN面积的最人值.【答案】（I）PM=PΛ∕, PM丄PN；（2） APMN是等腰直角三角形.理由见解析；（3）49 S A.PMN⅜⅛大=.【解析】【分析】（1）由已知易得加=C利用三角形的中位线得出PM = ；CE , PN = ；BD,即可2 2得出数量关系，再利用三角形的中位线得出PM//CE得出ZDPM = ZDc4,最后用互余即可得出位置关系；（2）先判断出MBQ三AACE,得出皮） = CE,同（1）的方法得出PM=-BD i2PN = LBD t即可得出PM = PN,同（1）的方法由2ZMPN = ZDCE+ ZDCB+ ZDBC= ZACB+ ZABC ,即可得出结论；（3〉方法1：先判断出MN最人时，APMN的面积最大，进而求出AN, AM,即可得出MN最）＜=AM + AN,最后用面积公式即可得出结论.方法2：先判断出BD最大时，WMN的面积最大，而Br）最人是AB + AD = 14,即可得出结论.【详解】解：（1）•••点P, N是BC, CD的中点，.∙.PN□BD, PN = -BD,2•••点P, M是CD，DE的中点，..PM//CE9 PM=丄CE ,2∙.∙AB=AC, AD=AE^:.BD = CE ,:.PM = PN,-PN//BD f.∙. ZDPN = ZADC,'：PMIlCE.:.ZDPM = ZDCA,∙.∙ ZfiAC = 90。

2021年中考九年级数学第一轮专题复习：四边形综合压轴题分类练习(无答案)

2021年中考九年级数学第一轮专题复习：四边形综合压轴题分类练习1、如图1，四边形ABCD的对角线AC，BD相交于点O，OA＝OC，OB＝OD+CD．（1）过点A作AE∥DC交BD于点E，求证：AE＝BE；（2）如图2，将△ABD沿AB翻折得到△ABD'．①求证：BD'∥CD；②若AD'∥BC，求证：CD2＝2OD•BD．2、如图，在矩形ABCD中，E是AD上的一点，沿CE将△CDE对折，点D刚好落在AB边的点F上．（1）求证：△AEF∽△BFC．（2）若AB＝20cm，BC＝16cm，求tan∠DCE．45，3、如图，在四边形ABCD中，AD∥BC,E是BC的中点，AD=5，BC=12，，∠C=0点P 是BC 边上一动点，设PB 长为x.(1)当x 的值为时，以点P 、A 、D 、E 为顶点的四边形为直角梯形. (2)当x 的值为时，以点P 、A 、D 、E 为顶点的四边形为平行四边形.(3)点P 在BC 边上运动的过程中，以点P 、A 、D 、E 为顶点的四边形能否构成菱形？试说明理由.4、如图，在正方形ABCD 中，对角线AC 与BD 相交于点E ，AF 平分∠BAC ，交BD 于点F.（1）EF+AC =AB ；（2）点C 1从点C 出发，沿着线段CB 向点B 运动（不与点B 重合），同时点A 1从点A 出发，沿着BA 的延长线运动，点C 1与点A 1运动速度相同，当动点C 1停止运动时，另一动点A 1也随之停止运动.如图，AF 1平分∠B A 1 C 1，交BD 于F 1，过F 1作F 1E 1⊥A 1 C 1，垂足为E 1，试猜想F 1E 1，A 1 C 1与AB 之间的数量关系，并证明你的猜想. （3）在（2）的条件下，当A 1 E 1=3，C 1 E 1=2时，求BD 的长.21215、在四边形ABCD中，E、F分别是BD、BC上的点，∠BAE＝∠BDA．（1）如图1，求证：AB2＝BE•BD；（2）如图2，若四边形ABCD是平行四边形，A、E、F三点在同一条直线上，，∠ABC＝60°，求的值；（3）如图3，若A、E、F不在同一条直线，∠DEF＝∠C，AB＝2，BD＝4，，，则CD＝（直接写出结果）．6、如图，在四边形ABCD中，AB∥CD,其中AB=12 cm,CD=6cm ,梯形的高为4，点P从开始沿AB边向点B以每秒3cm的速度移动，点Q从开始沿CD边向点D以每秒1cm的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达终点时运动停止。

2020中考数学压轴题突破与提升专题练习坐标系中的几何问题(无答案)

2020中考数学压轴题突破与提升专题练习坐标系中的几何问题一．例题解析1.已知：如图1，等边ABC ∆的边长为x轴上且()10A ，AC 交y 轴于点E ，过点E 作EF ∥AB 交BC 于点F ．（1）直接写出点B C 、的坐标；（2）若直线()10y kx k =-≠将四边形EABF 的面积两等分，求k 的值；（3）如图2，过点A B C 、、的抛物线与y 轴交于点D ，M 为线段OB 上的一个动点，过x 轴上一点()2,0G -作DM 的垂线，垂足为H ，直线GH 交y 轴于点N ，当M 点在线段OB 上运动时，现给出两个结论：① GNM CDM ∠=∠ ②MGN DCM ∠=∠，其中有且只有一个结论是正确的，请你判断哪个结论正确，并证明．图2图1【解析】解：（1）()10B +；()13C ，．（2）过点C 作CP AB ⊥于P ，交EF 于点Q ，取PQ 的中点R ．∵ABC ∆是等边三角形，()10A ． ∴60EAO ∠=︒ ．在Rt EOA ∆中，90EOA ∠=︒．∴(tan 6013EO AO =⋅︒=-=．∴(0,3E ．∵EF ∥AB 交BC 于F ，()13C ，．∴1R ⎛ ⎝⎭．（就是四边形对角线的中点，横坐标自然和C 一样，纵坐标就是E 的纵坐标的一半）∵直线1y kx =-将四边形EABF 的面积两等分． ∴直线1y kx =-必过点1R ⎛⎝⎭．∴1k -，∴k =（3）正确结论：①GNM CDM ∠=∠．证明：可求得过A B C 、、的抛物线解析式为222y x x =-++∴()02D ，． ∵()20G -，． ∴OG OD =．由题意90GON DOM ∠=∠=︒．又∵GNO DNH ∠=∠ ∴NGO MDO ∠=∠ ∴NGO ∆≌MDO ∆∴GNO DMO ∠=∠，OM ON = ∴45ONM NMO ∠=∠=︒过点D 作DT CP ⊥于T ∴1DT CT == ∴45CDT DCT ∠=∠=︒ 由题意可知DT ∥AB ∴TDM DMO ∠=∠∴454545TDM DMO GNO ∠+︒=∠+︒=∠+︒ ∴TDM CDT GNO ONM ∠+∠=∠+∠即：GNM CDM ∠=∠．（这一问点多图杂，不行就直接另起一个没有抛物线干扰的图）GPNM HTD C BA O xy例2.如图,在平面直角坐标系xoy 中,抛物线21410189y x x =--与ｘ正半轴交于点A,与ｙ轴交于点B,过点B 作x 轴的平行线BC,交抛物线于点C,连结AC ．现有两动点P 、Q 分别从O 、C 两点同时出发,点P 以每秒4个单位的速度沿OA 向终点A 移动,点Q 以每秒1个单位的速度沿CB 向点B 移动,点P 停止运动时,点Q 也同时停止运动,线段OC,PQ 相交于点D,过点D 作DE∥OA,交CA 于点E,射线QE 交x 轴于点F ．设动点P,Q 移动的时间为t(单位:秒) (1)求A,B,C 三点的坐标;(2)当t 为何值时,四边形PQCA 为平行四边形?请写出计算过程;(3)当0＜t ＜92时,△P QF 的面积是否总为定值?若是,求出此定值,若不是,请说明理由;(4)当t _________时,△P QF 为等腰三角形? 【解析】解：(1) 21(8180)18y x x =--，令0y =得281800x x --=，()()18100x x -+=∴18x =或10x =-∴(18,0)A ；在21410189y x x =--中，令0x =得10y =即(0,10)B -；由于BC ∥OA ，故点C 的纵坐标为－10，由2141010189x x -=--得8x =或0x =即(8,10)C -于是，(18,0),(0,10),(8,10)A B C --（2）若四边形PQCA 为平行四边形，由于QC ∥PA.故只要QC=PA 即可 ∵184,PA t CQ t =-= ∴184t t -= 得185t =（3）设点P 运动t 秒，则4,OP t CQ t ==，0 4.5t <<，说明P 在线段OA 上，且不与点O 、A 重合，由于QC ∥OP 知△QDC ∽△PDO ，故144QD QC t DP OP t === ∴4AF t OP ==∴18PF PA AF PA OP =+=+= 又点Q 到直线PF 的距离10d =∴1118109022PQF S PF d ∆==⨯⨯=g g∴△PQF 的面积总为90（4）由上知，(4,0),(184,0),(8,10)P t F t Q t +--，0 4.5t <<。

德州市中考数学一轮复习课件专题四：几何变换压轴题

几何变换是德州市中考的常考点，多与三角形、四边形、圆相结合，考查形式多样化．德州市近五年中考对此问题的考查：2017年中考试题第11题考查了旋转变换，第 23题考查了翻折变换；2016年中考试题第12题考查了旋转
变换，第23题考查了类比变换；2015年中考试题第6题考查了旋转变换，第23题考查了类比变换；2014年中考试题第 12题考查了翻折变换，第23题考查了类比变换；2013年中考试题第23题考查了类比变换．
(3)
6．我们把两条中线互相垂直的三角形称为“中垂三角形”．例如图1，图2，图3中，AF，BE是△ABC的中线，AF⊥BE，垂足为P，像△ABC这样的三角形均为“中垂三角形”．设BC＝ a，AC＝b，AB＝c. 【特例探索】 (1)如图1，当∠ABE＝45°，c＝2 2 时，a＝，b＝；如图2，当∠ABE＝30°，c＝4时，a＝，b＝；
类型一图形的旋转变换几何图形的旋转变换是近年来中考中的常考点，多与
三角形、四边形相结合．解决旋转变换问题，首先要明确旋转中心、旋转方向和旋转角，关键是找出旋转前后的对应点，利用旋转前后两图形全等等性质解题．
例1 如图，O是等边△ABC内一点，OA＝3，OB＝4，OC＝5，
将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，
4．(2017·淄博)如图，将矩形纸片ABCD沿直线MN折叠，顶点B恰好与CD边上的动点P重合(点P不与点C，D重合)，折痕为MN，点M，N分别在边AD，BC上．连接MB，MP，BP，BP与 MN相交于点F. (1)求证：△BFN∽△BCP； (2)①在图2中，作出经过M，D，P三点的⊙O(要求保留作图痕迹，不写作法)；
【分析】作DF⊥B′E于点F，B′G⊥AD于点G，由∠B＝ 60°，BD＝BE，得到△BDE是等边三角形，由对称的性质得到△B′DE也是等边三角形，从而GD＝B′F，然后利用勾股定理求解．【自主解答】如图，作DF⊥B′E于点F，B′G⊥AD于点G， ∵∠B＝60°，BD＝BE＝4， ∴△BDE是边长为4的等边三角形．

压轴题27选择压轴题(几何篇)-2023年中考数学压轴题专项训练(全国通用)(原卷版)

2023年中考数学压轴题专项训练压轴题27选择压轴题（几何篇）一．选择题（共40小题）1．（2023•朝阳区校级三模）如图，AB是⊙O的直径，将OB绕着点O逆时针旋转40°得到OC，P是⊙O 上一点，且与点C在AB的异侧，连结P A、PC、AC，若P A＝PC，则∠P AB的大小是（）A．20°B．35°C．40°D．70°2．（2023•河北区二模）如图，在平面直角坐标系中，菱形OABC的顶点A在x轴上，且∠COA＝45°，OA ＝4，则点B的坐标为（）A．(4+2√2，2√2)B．(2√2，2√2)C．(2+2√2，2）D．(√2，2)3．（2023•奉贤区二模）如图，矩形ABCD中，AB＝1，∠ABD＝60°，点O在对角线BD上，圆O经过点C．如果矩形ABCD有2个顶点在圆O内，那么圆O的半径长r的取值范围是（）A．0＜r≤1B．1＜r≤√3C．1＜r≤2D．√3＜r≤24．（2023•广灵县模拟）如图，在Rt△ABC中，∠C＝90°，BC＝3，AC＝6，点O，D，E是AB边上的点，以点O为圆心，DE长为直径的半圆O与AC相切于点M，与BC相切于点N，则图中阴影部分的面积为（）A ．5B ．9﹣2πC ．9﹣πD ．5﹣π5．（2023•普陀区二模）如图，△ABC 中，∠BAC ＝60°，BO 、CO 分别平分∠ABC 、∠ACB ，AO ＝2，下面结论中不一定正确的是（）A ．∠BOC ＝120°B ．∠BAO ＝30°C ．OB ＝3D ．点O 到直线BC 的距离是16．（2023•瓯海区模拟）如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD 与正方形EFGH ，连结DH 并延长交AB 于点K ，若DF 平分∠CDK ，则DH HK =（）A ．2√33B ．65C ．√5−1D ．4√577．（2023•花溪区模拟）勾股定理是人类数学文化的一颗璀璨明珠，是用代数思想解决几何问题的最重要工具也是数形结合的组带之一，如图，秋千静止时，踏板离地的垂直高度BE ＝1m ，将它往前推6m 至C 处时（即水平距离CD ＝6m ），踏板离地的垂直高度CF ＝4m ，它的绳索始终拉直，则绳索AC 的长是（）A ．152mB ．92mC ．6mD ．212m8．（2023•承德一模）如图，在菱形ABCD 中，AC 、BD （AC ＞BD ）相交于点O ，E 、F 分别为OA 和OC 上的点（不与点A 、O 、C 重合）．其中AE ＝OF ．过点E 作GH ⊥AC ，分别交AD 、AB 于点G 、H ；过点F 作IJ ⊥AC 分别交CD 、CB 于点J 、I ；连接GJ 、HI ，甲、乙、丙三个同学给出了三个结论：甲：随着AE 长度的变化，GH +IJ ＝BD 始终成立．乙：随着AE 长度的变化，四边形GHIJ 可能为正方形．丙：随着AE 长度的变化，四边形GHIJ 的面积始终不变，都是菱形ABCD 面积的一半．下列选项正确的是（）A ．甲、乙、丙都对B ．甲、乙对，丙不对C ．甲、丙对，乙不对D ．甲不对，乙、丙对 9．（2023•石家庄二模）如图，在平行四边形ABCD 中，对角线AC ，BD 交于点O ，E ，F 分别是OB 与OD 的中点，依连接点A ，E ，C ，F ，A ，当四边形AECF 是矩形时，与线段BE 相等的线段有（）A ．4条B ．5条C ．6条D ．7条10．（2023•青山区二模）如图，边长为2的正方形ABCD 的对角线AC 与BD 相交于点O ，E 是BC 边上一点，F 是BD 上一点，连接DE ，EF ．若△DEF 与△DEC 关于直线DE 对称，则OF 的长为（）A ．√22B ．2√2−2C ．2−√2D ．√2−111．（2023•柳城县一模）七巧板是我国古代劳动人民的发明之一，被誉为“东方魔板”，它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的．（清）陆以活《冷庐杂识》卷中写道：近又有七巧图，其式五，其数七，其变化之式多至千余，体物肖形，随手变幻，盖游戏之具，足以排闷破寂，故世俗皆喜为之．如图，是一个用七巧板拼成的装饰图，放入长方形ABCD 内，装饰图中的三角形顶点E ，F 分别在边AB ，BC 上，三角形①的边GD 在边AD 上，则BF BE 的值为（）A ．1+√22B ．√22C ．2+√24D ．2+√2212．（2023•泉州模拟）如图，在矩形ABCD 中，AB ＝2，BC ＝4，将△ABC 沿BC 的方向平移至△A 'B 'C '，使得A ′E ＝A ′F ，其中E 是A ′B ′与AC 的交点，F 是A ′C ′与CD 的交点，则CC ′的长为（）A ．52−√52B ．112−√5C ．5−√5D ．92−√5 13．（2023•定远县二模）如图，在Rt △ABC 中，∠BAC ＝90°，AB ＝3，BC ＝5，点P 为BC 边上任意一点，连接P A ，以P A ，PC 为邻边作平行四边形P AQC ，连接PQ ，则PQ 长度的最小值为（）A ．3B ．2.5C ．2.4D ．214．（2023•烟台一模）如图，在矩形ABCD 中，AB ＝12，AD ＝10，点E 在AD 上，点F 在BC 上，且AE ＝CF ，连结CE ，DF ，则CE +DF 的最小值为（）A ．26B ．25C ．24D ．2215．（2023•郯城县一模）如图，在Rt △ABC 中，∠BAC ＝90°，AB ＝6，BC ＝10，点P 为BC 边上任意一点，连接P A ，以P A ，PC 为邻边作平行四边形P AQC ，连接PQ ，则PQ 长度的最小值为（）A ．4.8B ．5C ．2.4D ．416．（2023•白云区一模）如图，正方形ABCD 的面积为3，点E 在边CD 上，且CE ＝1，∠ABE 的平分线交AD 于点F ，点M ，N 分别是BE ，BF 的中点，则下列结论错误的是（）A ．FD =√2MNB ．△DEF 是等腰直角三角形C ．BN ＝1D ．tan ∠FBE =√317．（2023•九龙坡区校级模拟）如图，在正方形ABCD 中，O 为AC 、BD 的交点，△DCE 为直角三角形，∠CED ＝90°，OE =3√2，若CE •DE ＝6，则正方形的面积为（）A ．20B ．22C ．24D ．2618．（2023•杭州一模）如图，有两张矩形纸片ABCD 和EFGH ，AB ＝EF ＝2cm ，BC ＝FG ＝8cm ．把纸片ABCD 交叉叠放在纸片EFGH 上，使重叠部分为平行四边形，且B 点D 与点G 重合，当两张纸片交叉所成的角α最小时，tan α等于（）A ．14B ．815C ．12D ．81719．（2023•高明区二模）矩形ABCD 和直角三角形EFG 的位置如图所示，点A 在EG 上，点D 在EF 上，若∠2＝55°，则∠1等于（）A．155°B．135°C．125°D．105°20．（2023•余姚市一模）如图，由两个正三角形组成的菱形内放入标记为①，②，③，④的四种不同大小的小正三角形5个，其中编号①的有2个．设未被覆盖的浅色阴影部分的周长为C1，深色阴影部分的周长为C2，若要求出C1﹣C2的值，只需知道其中两个小正三角形的边长，则这两个小三角形的编号为（）A．①②B．②③C．①③D．②④21．（2023•衡水二模）如图，点P是正方形ABCD的边BC上一点，点M是对角线BD上一点，连接PM 并延长交BA的延长线于点Q，交AD于点G，取PQ的中点N．连接AN．若AQ＝PC，有下面两个结论：①DM＝DG，②AN⊥BD，则这两个结论中，正确的是（）A．①对B．②对C．①②都对D．①②都不对22．（2023•新乡二模）如图，在矩形ABCD中，点B（0，4），点C（2，0），BC＝2CD，先将矩形ABCD 沿y轴向下平移至点B与点O重合，再将平移后的矩形ABCD绕点O逆时针旋转90°得到矩形EOMN，则点D的对应点N的坐标为（）A．（3，3）B．（4，4）C．（3，4）D．（4，3）23．（2023•荆门一模）如图，菱形ABCD各边的中点分别是E、F、G、H，若EH＝2EF，则下列结论错误的是（）A．EH⊥EF B．EH＝AC C．∠B＝60°D．AB=√5EF24．（2023•中原区校级二模）如图，在Rt△ABO中，AB＝OB，顶点A的坐标为（2，0），以AB为边向△ABO的外侧作正方形ABCD，将组成的图形绕点O逆时针旋转，每次旋转45°，则第98次旋转结束时，点D的坐标为（）A．（1，﹣3）B．（﹣1，3）C．（﹣1，2+√2）D．（1，3）25．（2023•中原区模拟）如图，▱ABCD的边BC在x轴的负半轴上，点B与原点O重合，DE⊥AB，交BA 的延长线于点E，已知∠ABC＝60°，AB＝4，BC＝6，则点E的坐标为（）A．（﹣2，﹣，2√3）B．（﹣3，3√3）C．（−72，72√3）D．（−52√3，52）26．（2023•武邑县二模）如图，N是正六边形ABCDEF对角线CF上一点，延长FE，CD相交于点M，若S△ABN＝2，则S五边形ABCMF＝（）A．10B．12C．14D．1627．（2023•承德一模）如图，正六边形的两条对角线AE、BE把它分成Ⅰ、Ⅱ、Ⅲ三部分，则该三部分的面积比为（）A．1：2：3B．2：2：4C．1：2：4D．2：3：528．（2023•罗湖区二模）如图，AB为圆O的直径，C为圆O上一点，过点C作圆O的切线交AB的延长线于点D，DB=13AD，连接AC，若AB＝8，则AC的长度为（）A．2√3B．2√5C．4√3D．4√529．（2023•杭州一模）如图，过⊙O外一点A作⊙O的切线AD，点D是切点，连结OA交⊙O于点B，点C是⊙O上不与点B，D重合的点．若∠A＝α°，则∠C的度数为（）A．(45−12α)°B．12α°C．2α°D．(45+12α)°30．（2023•西宁一模）如图，扇形纸片AOB的半径为3，沿AB所在直线折叠扇形纸片，圆心D恰好落在AB̂上的点C处，则阴影部分的面积是（）A．3π−9√32B．3π−3√32C．2π−3√32D．2π−9√3231．（2023•太原一模）如图，在扇形纸片OAB 中，∠AOB ＝105°，OA ＝6、点C 是半径OA 上的点、沿直线BC 折叠△OBC 得到△DBC ，点O 的对应点D 落在AB̂上，图中阴影部分的面积为（）A ．9π−92B ．9π−182C ．9π﹣18D ．12π﹣1832．（2023•西山区校级模拟）如图，分别以等边△ABC 的三个顶点为圆心，边长为半径画弧，得到的封闭图形是莱洛三角形，若AB 为6，则图中阴影部分的面积为（）A ．18π−27√3B ．6π−9√3C ．12π−9√3D ．18π−18√333．（2023•莆田模拟）如图，在⊙O 中，∠AOB ＝120°，点C 在AB̂上，连接AC ，BC ，过点B 作BD ⊥AC 的延长线于点D ，当点C 从点A 运动到点B 的过程中，∠CBD 的度数（）A ．先增大后减小B ．先减小后增大C ．保持不变D ．一直减小 34．（2023•蚌埠二模）如图是某芯片公司的图标示意图，其设计灵感源于传统照相机快门的机械结构，圆O 中的阴影部分是一个正六边形，其中心与圆心O 重合，且AB ＝BC ，则阴影部分面积与圆的面积之比为（）A ．3√38πB ．√32πC ．√3πD ．2√39π35．（2023•鄞州区校级模拟）如图，AB 为⊙O 的直径，将弧BC 沿BC 翻折，翻折后的弧交AB 于D ．若BC ＝4√5，sin ∠ABC =√55，则图中阴影部分的面积为（）A ．256πB ．253πC ．8D ．1036．（2023•九龙坡区模拟）如图，在⊙O 中，AB 是圆的直径，过点B 作⊙O 的切线BC ，连接AC 交⊙O 于点D ，点E 为弧AD 中点，连接AE ，若AE ＝AO ，AB ＝6，则CD 的长为（）A ．2B ．3√32C ．√3D ．3√337．（2023•宁德模拟）“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形．如图，以等边三角形ABC 的三个顶点为圆心，以边长为半径画弧，三段圆弧围成的图形就是“莱洛三角形”．若等边三角形ABC 的边长为2，则该“莱洛三角形”的周长等于（）A ．2πB ．2π−√3C ．23πD ．2π+√338．（2023•虹口区二模）如图，在矩形ABCD 中，对角线AC 与BD 相交于点O ，AB ＝5，BC ＝12．分别以点O 、D 为圆心画圆，如果⊙O 与直线AD 相交、与直线CD 相离，且⊙D 与⊙O 内切，那么⊙D 的半径长r 的取值范围是（）A ．12＜r ＜4B ．52＜r ＜6C ．9＜r ＜252D ．9＜r ＜1339．（2023•苏州一模）东南环立交是苏州中心城区城市快速内环道路系统的重要节点，也是江苏省最大规模的城市立交．左图是该立交桥的部分道路示意图（道路宽度忽略不计），A 为立交桥入口，D 、G 为出口，其中直行道为AB 、CD 、FG ，且AB ＝CD ＝FG ；弯道是以点O 为圆心的一段弧，且BC 、CE 、EF 所在的圆心角均为90°．甲、乙两车由A 口同时驶入立交桥，均以16m /s 的速度行驶，从不同出口驶出，其间两车到点O 的距离y （m ）与时间x （s ）的对应关系如右图所示．结合题目信息，下列说法错误的是（）A ．该段立交桥总长为672mB ．从G 口出比从D 口出多行驶192mC ．甲车在立交桥上共行驶22sD ．甲车从G 口出，乙车从D 口出40．（2023•滨城区一模）如图，点A ，B 是半径为2的⊙O 上的两点，且AB =2√3，则下列说法正确的是（）A ．圆心O 到AB 的距离为√3B ．在圆上取异于A ，B 的一点C ，则△ABC 面积的最大值为3√3C ．以AB 为边向上作正方形，与⊙O 的公共部分的面积为3+√34πD ．取AB 的中点C ，当AB 绕点O 旋转一周时，点C 运动的路线长为3π。

中考数学总复习《几何压轴题》专项提升练习题(附答案)

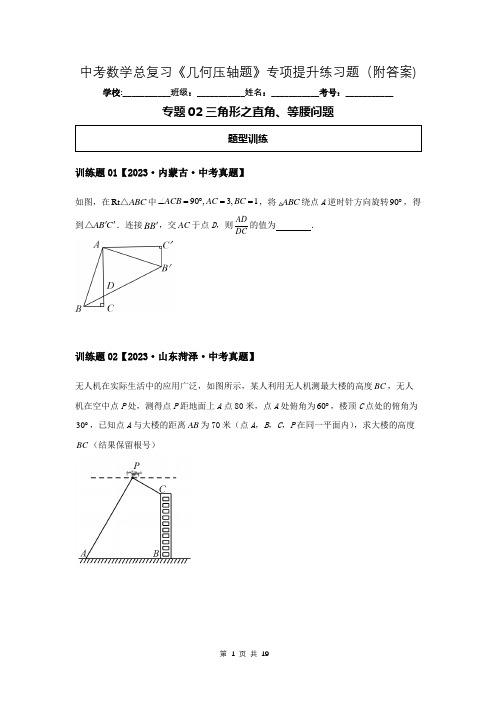
中考数学总复习《几何压轴题》专项提升练习题（附答案)学校:___________班级：___________姓名：___________考号：___________专题02三角形之直角、等腰问题题型训练训练题01【2023·内蒙古·中考真题】如图，在Rt ABC △中90,3,1ACB AC BC ∠=︒==，将ABC 绕点A 逆时针方向旋转90︒，得到AB C ''△．连接BB '，交AC 于点D ，则AD DC 的值为．训练题02【2023·山东菏泽·中考真题】无人机在实际生活中的应用广泛，如图所示，某人利用无人机测最大楼的高度BC ，无人机在空中点P 处，测得点P 距地面上A 点80米，点A 处俯角为60︒，楼顶C 点处的俯角为30︒，已知点A 与大楼的距离AB 为70米（点A ，B ，C ，P 在同一平面内），求大楼的高度BC （结果保留根号）训练题03【2023·广东·中考真题】2023年5月30日，神舟十六号载人飞船发射取得圆满成功，3名航天员顺利进驻中国空间站，如图中的照片展示了中国空间站上机械臂的一种工作状态，当两臂10m AC BC ==，两臂夹角100ACB ∠=︒时，求A ，B 两点间的距离．(结果精确到0.1m ，参考数据sin500.766︒≈ cos500.643︒≈ tan50 1.192︒≈)训练题04【2023·湖北黄冈·中考真题】综合实践课上，航模小组用航拍无人机进行测高实践．如图，无人机从地面CD 的中点A 处竖直上升30米到达B 处，测得博雅楼顶部E 的俯角为45︒，尚美楼顶部F 的俯角为30︒，已知博雅楼高度CE 为15米，则尚美楼高度DF 为米．（结果保留根号）训练题05【2023·河北沧州·模拟预测】如图1，嘉淇在量角器的圆心O 处下挂一铅锤，制作了一个简易测角仪．将此测角仪拿到眼前，使视线沿着仪器的直径刚好到达树的最高点M ．(1)在图1中，过点A 画出水平线，并标记观测M 的仰角α．若铅垂线在量角器上的读数为53︒，求α的值；(2)如图2，已知嘉淇眼睛离地1.5米，站在B 处观测M 的仰角为（1）中的α，向前走1.25米到达D 处，此时观测点M 的仰角为45︒，求树MN 的高度．（注：3tan 374︒≈ 3sin 375︒≈ 4cos375≈︒）训练题06【2023·四川成都·八年级期末联考】如图在等腰Rt EDF 中 90EDF ∠=︒ 2DE DF == DG EF ⊥于点G 点M N 分别是DE DG 上的动点且DN EM = 则FM FN +的最小值为．训练题07【2022·陕西西安·滨河期末】如图直线y ＝x ﹣3分别交x 轴 y 轴于B A 两点点C （0 1）在y 轴上点P 在x 轴上运动则2PC ＋PB 的最小值为．训练题08【2021·四川甘孜·中考真题】如图腰长为22+2的等腰ABC 中顶角∠A ＝45° D 为腰AB 上的一个动点将ACD 沿CD 折叠点A 落在点E 处当CE 与ABC 的某一条腰垂直时 BD 的长为．训练题09【2022·福建泉州·九年级联考】如图 ABC 和AGF 是等腰直角三角形 90BAC G ∠=∠=︒ AGF 的边AF AG 交边BC 于点D E ．若4=AD 3AE = 则BEDC 的值是．训练题10【2021·宁夏固元·联考一模】如图在直角△BAD中延长斜边BD到点C 使得BD=2DC 连接AC 如果则的值是（）A．B．C．D．答案&解析5 tanB3=tan CAD∠3 3351315训练题01【2023·内蒙古·中考真题】【答案】5【简证】因为tan 311tan 4522ABC CD ABD α∠=⎧⇒=⇒=⎨∠=︒⎩ 故5AD DC =【常规法】解：过点D 作DF AB ⊥于点F∵90ACB ∠=︒ 3AC = 1BC =∴223110AB =+=∵将ABC 绕点A 逆时针方向旋转90︒得到AB C ''△∴==10AB AB ' 90BAB '∠=︒∴ABB '是等腰直角三角形∴45ABB '∠=︒又∵DF AB ⊥∴45FDB ∠=︒∴DFB △是等腰直角三角形∴DF BF =∵1122ADB S BC AD DF AB =⨯⨯=⨯⨯ 即=10AD DF ∵ 90C AFD ∠=∠=︒ CAB FAD ∠=∠∴AFDACB ∴DF AF BC AC= 即3AF DF = 又∵=10AF DF -45°α∴10=4 DF∴105=10=42AD⨯51=3=22CD-∴52==512ADCD故答案为：5．训练题02【2023·山东菏泽·中考真题】【答案】大楼的高度BC 为303m ．【分析】如图过P 作PH AB ⊥于H 过C 作CQ PH ⊥于Q 而CB AB ⊥ 则四边形CQHB 是矩形可得QH BC = BH CQ = 求解3sin 60804032PH AP =︒=⨯= cos6040AH AP =︒= 可得704030CQ BH ==-= tan 30103PQ CQ =︒= 可得403103303BC QH ==-=．【详解】解：如图过P 作PH AB ⊥于H 过C 作CQ PH ⊥于Q 而CB AB ⊥则四边形CQHB 是矩形 ∴QH BC = BH CQ =由题意可得：80AP = 60PAH ∠=︒ 30PCQ ∠=︒ 70AB = ∴3sin 60804032PH AP =︒=⨯= cos6040AH AP =︒= ∴704030CQ BH ==-= ∴tan 30103PQ CQ =︒=∴403103303BC QH ==-= ∴大楼的高度BC 为303m ．训练题03【2023·广东·中考真题】【答案】15.3m【分析】连接AB 作作CD AB ⊥于D 由等腰三角形“三线合一”性质可知2AB AD = 1502ACD ACB ∠=∠=︒ 在Rt ACD △中利用sin AD ACD AC∠=求出AD 继而求出AB 即可．【详解】解：连接AB 作CD AB ⊥于D∵AC BC = CD AB ⊥∴CD 是边AB 边上的中线也是ACB ∠的角平分线∴2AB AD = 1502ACD ACB ∠=∠=︒ 在Rt ACD △中 10m AC = 50ACD ∠=︒ sin AD ACD AC ∠= ∴sin 5010AD ︒= ∴10sin50100.7667.66AD =︒≈⨯=∴()227.6615.3215.3m AB AD =≈⨯=≈答：A B 两点间的距离为15.3m ．训练题04【2023·湖北黄冈·中考真题】【答案】3053-/5330-+【分析】过点E 作EM AB ⊥于点M 过点F 作FN AB ⊥于点N 首先证明出四边形ECAM 是矩形得到15AM CE == 然后根据等腰直角三角形的性质得到15AC EM BM === 进而得到15==AD AC 然后利用30︒角直角三角形的性质和勾股定理求出53BN = 即可求解．【详解】如图所示过点E 作EM AB ⊥于点M 过点F 作FN AB ⊥于点N由题意可得四边形ECAM 是矩形 ∴15AM CE == ∵30AB = ∴15BM AB AM =-= ∵博雅楼顶部E 的俯角为45︒ ∴45EBM ∠=︒ ∴45BEM ∠=︒ ∴15AC EM BM ===∵点A 是CD 的中点 ∴15==AD AC 由题意可得四边形AMFN 是矩形 ∴15NF AD == ∵尚美楼顶部F 的俯角为30︒ ∴60NBF ∠=︒ ∴30BFN ∠=︒ ∴2BF BN =∴在Rt BNF △中 222BNNF BF += ∴()222152BN BN +=∴解得53BN =∴3053FD AN AB BN ==-=-．故答案为：3053-．训练题05【2023·河北沧州·模拟预测】【答案】(1)37︒(2)树MN 的高度为5.25米【分析】(1)根据互余的性质计算即可．(2) 过点A 作AP MN ⊥ 垂足为P 则 1.5PN AB ==米．设MN x =米．解直角三角形求解即可．【详解】（1）如图1；905337α=︒-︒=︒；（2）如图过点A 作AP MN ⊥ 垂足为P 则 1.5PN AB ==米．设MN x =米．在Rt APM △中 4( 1.5)tan 373MP AP x ==-︒（米）在Rt MCP 中 1.5CP MP x ==-（米） 4( 1.5)( 1.5) 1.253AC AP CP x x ∴=-=---=（米）解得 5.25x =．答：树MN 的高度为5.25米．训练题06【2023·四川成都·八年级期末联考】【答案】23【分析】过点E 作AE EF ⊥ 使得2AE DF == 证得AEM FDN ≅ 利用全等三角形的性质证得FN AM = 求FM FN +的最小值即求FM AM +的最小值此时只有A M F 在一条直线上时 FM AM +的最小即为AF 的长在Rt AEF 中利用勾股定理即可求解．【详解】解：过点E 作AE EF ⊥ 使得2AE DF == 如图所示∵等腰Rt EDF 中 90EDF ∠=︒ 2DE DF ==∴45DEF ∠=︒ 222222EF =+=∴9045AEM DEF ∠=︒-∠=︒∵等腰Rt EDF 中 90EDF ∠=︒ 2DE DF == DG EF ⊥∴45FDN ∠=︒∴FDN AEM ∠=∠在AEM △和FDN 中AE DF AEM FDN EM DN =⎧⎪∠=∠⎨⎪=⎩∴AEM FDN≅()SAS ∴FN AM =∴求FM FN +的最小值即求FM AM +的最小值此时只有A M F 在一条直线上时 FM AM +的最小即为AF 的长∴在Rt AEF 中()222222223AF AE EF =+=+=的最小值为23即FM FN故答案为：23训练题07【2022·陕西西安·滨河期末】【答案】4【分析】过P作PD⊥AB于D依据△AOB是等腰直角三角形可得∠BAO＝∠ABO＝45°＝∠BPD进而得到△BDP是等腰直角三角形故PD22=PB当C P D在同一直线上时CD⊥AB PC+PD的最小值等于垂线段CD的长求得CD的长即可得出结论．【详解】如图所示过P作PD⊥AB于D∵直线y＝x﹣3分别交x轴y轴于B A两点令x＝0 则y＝﹣3；令y＝0 则x＝3∴A（0 ﹣3）B（3 0）∴AO＝BO＝3又∵∠AOB＝90°∴△AOB是等腰直角三角形∴∠BAO＝∠ABO＝45°＝∠BPD∴△BDP是等腰直角三角形∴PD22=PB∴2PC+PB2=（PC22+PB）2=（PC+PD）当C P D在同一直线上即CD⊥AB时PC+PD的值最小最小值等于垂线段CD 的长此时△ACD是等腰直角三角形又∵点C（0 1）在y轴上∴AC＝1+3＝4∴CD22=AC＝22即PC+PD的最小值为22∴2PC+PB的最小值为222⨯=4 故答案为：4．训练题08【2021·四川甘孜·中考真题】【答案】2或22【分析】分两种情况：当CE ⊥AB 时设垂足为M 在Rt △AMC 中 ∠A ＝45° 由折叠得：∠ACD ＝∠DCE ＝22.5° 证明△BCM ≌△DCM 得到BM ＝DM 证明△MDE 是等腰直角三角形即可得解；当CE ⊥AC 时根据折叠的性质等腰直角三角形的判定与性质计算即可；【详解】当CE ⊥AB 时如图设垂足为M 在Rt △AMC 中 ∠A ＝45°由折叠得：∠ACD ＝∠DCE ＝22.5°∵等腰△ABC 中顶角∠A ＝45°∴∠B ＝∠ACB ＝67.5°∴∠BCM ＝22.5°∴∠BCM ＝∠DCM在△BCM 和△DCM 中90BMC DMC CM CM BCM DCM ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴△BCM ≌△DCM （ASA ）∴BM ＝DM由折叠得：∠E ＝∠A ＝45° AD ＝DE∴△MDE 是等腰直角三角形∴DM ＝EM设DM ＝x 则BM ＝x DE 2=x∴AD 2=x ．∵AB＝22+2∴2x2x＝22+2 解得：x2=∴BD＝2x＝22；当CE⊥AC时如图∴∠ACE＝90°由折叠得：∠ACD＝∠DCE＝45°∵等腰△ABC中顶角∠A＝45°∴∠E＝∠A＝45°AD＝DE∴∠ADC＝∠EDC＝90°即点D E都在直线AB上且△ADC△DEC△ACE都是等腰直角三角形∵AB＝AC＝＝22+2∴AD22=AC＝22BD＝AB﹣AD＝（22+2）﹣（22）2=综上BD的长为2或22．故答案为：2或22．训练题09【2022·福建泉州·九年级联考】【答案】916【分析】利用等腰直角三角形的性质先证明AED BEA ∽ 可得34BE AE AB AD ==,设3BE x = 则4AB x AC ==,再证明ADE CDA △∽△ 可得34AC AE CD AD == 可得163CD x = 从而可得结论．【详解】解：∵ABC 和AGF 是等腰直角三角形 ∴45,B F FAG AB AC ∠=∠=∠=︒=∵AEB AED ∠=∠∴AED BEA ∽∴AD AE DE AB BE AE ==,而4=AD 3AE = ∴34BE AE AB AD == 设3BE x = 则4AB x AC ==同理可得：ADE CDA △∽△∴AD AE DE CD AC AD == ∴34AC AE CD AD == ∴BE AC AB CD = ∴344x x x CD =,即163CD x = ∴3916163BE x CD x ==.训练题10【2021·宁夏固元·联考一模】【答案】D【详解】解：如图延长AD 过点C 作CE ⊥AD 垂足为E∵ 即∴设AD ＝5x 则AB ＝3x∵∠CDE ＝∠BDA ∠CED ＝∠BAD∴△CDE ∽△BDA∴∴CE ＝ DE ＝∴AE ＝ ∴tan ∠CAD ＝．5tanB 3=53AD AB =12CE DE CD AB AD BD ===32x 52x 152x 15CE AE =。

中考数学几何压轴题汇编

中考28汇编1．如图，在四边ABCD 中，BC=DC ，∠BAD+∠BCD=180°，AC ⊥BC ，O 是AB 的中点（1）如图1，求证：∠OCD=∠OBC（2）如图2，E 是AC 上一点，连接OE 并延长交AD 于点F ，连接BD ，分别交AC 、OC 于点M 、N ，若∠FOC=3∠CBD ，BN DM 76，试探究线段OE 和EF 之间的数量关系，并证明你的结论。

DCAO NMFEDCBA（图1）（图2）2．△ABC ，∠ACB=90°，点D 在BC 上，点E 在AD 上，∠CEB=90°，∠CED=∠CBA ，CE 的延长线交AB 于点F ，连接DF 。

（1）如图1，求证：∠EFD=∠DBE ；（2）如图2，若32cos =∠CAB ，DF 与BE 交于点G ，猜想GF 与DB 之间的数量关系并证明。

FEDCBAGFEDCBA（图1）（图2）3．已知，如图1，等腰直角△ABC中，AC=BC，等腰直角△CDE中，CD=DE，AD∥BC，CE与AB 相交于点F，AB与CD相交于点O，连接BE（1）求证：F为CE中点；（2）如图2，过点D作DG⊥BE于G，连接AE交DG于点H，连接HF，请探究线段HF与BC 之间的数量及位置关系，并证明你的结论。

OF EDC B A（图1）OGHFEDC BA（图2）4如图在四边形ABCD 中，连结BD 、AC 相交于F ，AB=BC ，AD=DE=DC ，∠ABC+∠EDC=180°，且AB AE AD ⋅=2。

（1）如图1，求证：∠ADE=2∠DCA ；（2）如图2，过点B 作BH ⊥CD 于点H ，交AC 于点G ，连结EC 交BD 于点P ，交BH 于点Q ，若31tan =∠ACD ，试探究线段PE 与PQ 之间的数量关系，并证明你的结论。

PG H QFEDCBAFEDCBA（图1）（图2）5．在Rt △ABC 中，∠ACB=90°，54sin =B ，作CH ⊥AB 于点H ，D 、K 分别为边AB 、AC 上的点，连接CD 、DK ，在射线DK 上取一点E ，使∠DCE=∠B ，且CE CD CK BC ⋅=⋅54。

2021年全国中考数学真题分类汇编--函数：函数与几何(压轴题2)(无答案)

中考真题分类汇编（函数）----函数与几何（2）1.（2021•四川省眉山市）如图，直线y＝x+6与x轴交于点A，与y轴交于点B．直线MN∥AB，且与△AOB的外接圆⊙P相切，与双曲线y＝﹣在第二象限内的图象交于C、D两点．（1）求点A，B的坐标和⊙P的半径；（2）求直线MN所对应的函数表达式；（3）求△BCN的面积．2.（2021•四川省南充市）如图，已知抛物线y＝ax2+bx+4（a≠0）与x轴交于点A（1，0）和B，与y轴交于点C，对称轴为直线x＝．（1）求抛物线的解析式；（2）如图1，若点P是线段BC上的一个动点（不与点B，C重合），过点P作y轴的平行线交抛物线于点Q，连接OQ，当线段PQ长度最大时，判断四边形OCPQ的形状并说明理由；（3）如图2，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且∠DQE＝2∠ODQ．在y轴上是否存在点F，得△BEF为等腰三角形？若存在，求点F 的坐标；若不存在，请说明理由．3. （2021•遂宁市）如图，已知二次函数的图象与x 轴交于A 和B （－3，0）两点，与y 轴交于C （0，－3），对称轴为直线1x =-，直线y ＝－2x ＋m 经过点A ，且与y 轴交于点D ，与抛物线交于点E ，与对称轴交于点F ．（1）求抛物线的解析式和m 的值；（2）在y 轴上是否存在点P ，使得以D 、E 、P 为顶点的三角形与△AOD 相似，若存在，求出点P 的坐标；若不存在，试说明理由；（3）直线y ＝1上有M 、N 两点（M 在N 的左侧），且MN ＝2，若将线段MN 在直线y ＝1上平移，当它移动到某一位置时，四边形MEFN 的周长会达到最小，请求出周长的最小值（结果保留根号）．4. (2021•四川省自贡市) 如图，抛物线(1)()y x x a =+-（其中1a >）与x 轴交于A 、B 两点，交y 轴于点C ．（1）直接写出OCA ∠的度数和线段AB 的长（用a 表示）；（2）若点D 为ABC 的外心，且BCD △与ACO △104，求此抛物线的解析式；（3）在（2）的前提下，试探究抛物线(1)()y x x a =+-上是否存在一点P ，使得CAP DBA ∠=∠？若存在，求出点P 的坐标；若不存在，请说明理由．5. （2021•天津市）已知抛物线22y ax ax c =-+（a ，c 为常数，0a ≠）经过点()0,1C -，顶点为D ．（Ⅰ）当1a =时，求该抛物线的顶点坐标；（Ⅱ）当0a >时，点()0,1E a +，若22DE DC =，求该抛物线的解析式；（Ⅲ）当1a <-时，点()0,1F a -，过点C 作直线l 平行于x 轴，(),0M m 是x 轴上的动点，()3,1N m +-是直线l 上的动点．当a 为何值时，FM DN +的最小值为10，并求此时点M ，N 的坐标．6. 2021•湖北省恩施州）如图，在平面直角坐标系中，四边形ABCD 为正方形，点A ，B 在x 轴上，抛物线y ＝x 2+bx +c 经过点B ，D （﹣4，5）两点，且与直线DC 交于另一点E ．（1）求抛物线的解析式；（2）F 为抛物线对称轴上一点，Q 为平面直角坐标系中的一点，是否存在以点Q ，F ，E ，B 为顶点的四边形是以BE 为边的菱形．若存在，请求出点F 的坐标；若不存在，请说明理由；（3）P 为y 轴上一点，过点P 作抛物线对称轴的垂线，垂足为M ，连接ME ，BP ，探究EM+MP+PB是否存在最小值．若存在，请求出这个最小值及点M的坐标；若不存在，请说明理由．7.（2021•浙江省金华市）在平面直角坐标系中，点A的坐标为（﹣，0），点B在直线l：y＝x上，过点B作AB的垂线，过原点O作直线l的垂线，两垂线相交于点C．（1）如图，点B，C分别在第三、二象限内，BC与AO相交于点D．①若BA＝BO，求证：CD＝CO．②若∠CBO＝45°，求四边形ABOC的面积．（2）是否存在点B，使得以A，B，C为顶点的三角形与△BCO相似？若存在，求OB 的长；若不存在，请说明理由．8.（2021•湖北省荆门市）如图，抛物线y＝ax2+bx+c交x轴于A（﹣1，0），B（3，0）两点，交y轴于点C（0，﹣3），点Q为线段BC上的动点．（1）求抛物线的解析式；（2）求|QO|+|QA|的最小值；（3）过点Q作PQ∥AC交抛物线的第四象限部分于点P，连接P A，PB，记△P AQ与△PBQ面积分别为S1，S2，设S＝S1+S2，求点P坐标，使得S最大，并求此最大值．9.（2021•江苏省盐城市）学习了图形的旋转之后，小明知道，将点P绕着某定点A顺时针旋转一定的角度α，能得到一个新的点P′，经过进一步探究，小明发现，当上述点P 在某函数图象上运动时，点P′也随之运动，并且点P′的运动轨迹能形成一个新的图形．试根据下列各题中所给的定点A的坐标、角度α的大小来解决相关问题．【初步感知】如图1，设A（1，1），α＝90°，点P是一次函数y＝kx+b图象上的动点，已知该一次函数的图象经过点P1（﹣1，1）．（1）点P1旋转后，得到的点P1′的坐标为（1，3）；（2）若点P′的运动轨迹经过点P2′（2，1），求原一次函数的表达式．【深入感悟】如图2，设A（0，0），α＝45°，点P是反比例函数y＝﹣（x＜0）的图象上的动点，过点P′作二、四象限角平分线的垂线，垂足为M，求△OMP′的面积．【灵活运用】如图3，设A （1，﹣），α＝60°，点P 是二次函数y ＝x 2+2x +7图象上的动点，已知点B （2，0）、C （3，0），试探究△BCP ′的面积是否有最小值？若有，求出该最小值；若没有，请说明理由．10. （2021•重庆市A ）如图，在平面直角坐标系中，抛物线2y x bx c =++经过A （0，﹣1），B （4，1）．直线AB 交x 轴于点C ，P 是直线AB 下方抛物线上的一个动点．过点P 作PD ⊥AB ，垂足为D ，PE ∥x 轴，交AB 于点E ．（1）求抛物线的函数表达式；（2）当△PDE 的周长取得最大值时，求点P 的坐标和△PDE 周长的最大值；（3）把抛物线2y x bx c =++平移，使得新抛物线的顶点为（2）中求得的点P ．M 是新抛物线上一点，N 是新抛物线对称轴上一点，直接写出所有使得以点A ，B ，M ，N 为顶点的四边形是平行四边形的点M 的坐标，并把求其中一个点M 的坐标的过程写出来．11.（2021•重庆市B ）如图，在平面直角坐标系中，抛物线y ＝ax 2+bx ﹣4（a ≠0）与x 轴交于点A （﹣1，0），B （4，0），与y 轴交于点C ．（1）求该抛物线的解析式；（2）直线l 为该抛物线的对称轴，点D 与点C 关于直线l 对称，点P 为直线AD 下方抛物线上一动点，连接P A ，PD ，求△P AD 面积的最大值．（3）在（2）的条件下，将抛物线y ＝ax 2+bx ﹣4（a ≠0）沿射线AD 平移4个单位，得到新的抛物线y 1，点E 为点P 的对应点，点F 为y 1的对称轴上任意一点，在y 1上确定一点G ，使得以点D ，E ，F ，G 为顶点的四边形是平行四边形，写出所有符合条件的点G 的坐标，并任选其中一个点的坐标，写出求解过程．12. （2021•湖北省十堰市）已知抛物线25y ax bx =+-与x 轴交于点()1,0A -和()5,0B -，与y 轴交于点C ，顶点为P ，点N 在抛物线对称轴上且位于x 轴下方，连AN 交抛物线于M ，连AC 、CM ．（1）求抛物线的解析式；（2）如图1，当tan 2ACM ∠=时，求M 点的横坐标；（3）如图2，过点P 作x 轴的平行线l ，过M 作MD l ⊥于D ，若3MD MN =，求N 点的坐标．13. （2021•湖南省张家界市）如图，已知二次函数c bx ax y ++=2的图象经过点)3,2(-C ，且与x 轴交于原点及点)0,8(B . (1)求二次函数的表达式；(2)求顶点A 的坐标及直线AB 的表达式；（3）判断ABO ∆的形状，试说明理由；（4）若点P 为⊙O 上的动点，且⊙O 的半径为 22，一动点E 从点A 出发，以每秒2个单位长度的速度沿线段AP 匀速运动到点P ，再以每秒1个单位长度的速度沿线段PB 匀速运动到点B 后停止运动，求点E 的运动时间t 的最小值.14. （2021•海南省）已知抛物线y ＝ax 2+x +c 与x 轴交于A 、B 两点，与y 轴交于C 点，且点A 的坐标为（﹣1，0）、点C 的坐标为（0，3）．（1）求该抛物线的函数表达式；（2）如图1，若该抛物线的顶点为P ，求△PBC 的面积；（3）如图2，有两动点D 、E 在△COB 的边上运动，速度均为每秒1个单位长度，它们分别从点C 和点B 同时出发，点D 沿折线COB 按C →O →B 方向向终点B 运动，点E_y _x _ A _ B _ O _ C _ P沿线段BC 按B →C 方向向终点C 运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动时间为t 秒，请解答下列问题： ①当t 为何值时，△BDE 的面积等于；②在点D 、E 运动过程中，该抛物线上存在点F ，使得依次连接AD 、DF 、FE 、EA 得到的四边形ADFE 是平行四边形，请直接写出所有符合条件的点F 的坐标．15. （2021•广西玉林市）已知抛物线：234y ax ax a =--（0a >）与x 轴交点为A ，B（A 在B 的左侧），顶点为D ．（1）求点A ，B 的坐标及抛物线的对称轴；（2）若直线32y x =-与抛物线交于点M ，N ，且M ，N 关于原点对称，求抛物线的解析式；（3）如图，将（2）中抛物线向上平移，使得新的抛物线的顶点D 在直线7:8l y =上，设直线l 与y 轴的交点为O '，原抛物线上的点P 平移后的对应点为点Q ，若O P O Q ''=，求点P ，Q 的坐标．16. （2021•广西贺州市）如图，抛物线2y x bx c =++与x 轴交于A 、B 两点，且()1,0A -，对称轴为直线2x =．（1）求该抛物线的函数达式；（2）直线l 过点A 且在第一象限与抛物线交于点C ．当45CAB ∠=︒时，求点C 的坐标；（3）点D 在抛物线上与点C 关于对称轴对称，点P 是抛物线上一动点，令(,)P P P x y ，当1P x a ≤≤，15a ≤≤时，求PCD 面积的最大值（可含a 表示）．17. 2021•山东省济宁市）如图，直线y ＝﹣x +分别交x 轴、y 轴于点A ，B ，过点A 的抛物线y ＝﹣x 2+bx +c 与x 轴的另一交点为C ，与y 轴交于点D （0，3），抛物线的对称轴l 交AD 于点E ，连接OE 交AB 于点F ．（1）求抛物线的解析式；（2）求证：OE ⊥AB ；（3）P 为抛物线上的一动点，直线PO 交AD 于点M ，是否存在这样的点P ，使以A ，O ，M 为顶点的三角形与△ACD 相似？若存在，求点P 的横坐标；若不存在，请说明理由．18 . (2021•内蒙古包头市) 如图，在平面直角坐标系中，抛物线24y x x =-+经过坐标原点，与x 轴正半轴交于点A ，点(,)M m n 是抛物线上一动点．（1）如图1，当0m >，0n >，且3n m =时，①求点M 的坐标： ②若点15,4B y ⎛⎫ ⎪⎝⎭在该抛物线上，连接OM ，BM ，C 是线段BM 上一动点（点C 与点M ，B 不重合），过点C 作//CD MO ，交x 轴于点D ，线段OD 与MC 是否相等？请说明理由；（2）如图2，该抛物线的对称轴交x 轴于点K ，点7,3E x ⎛⎫ ⎪⎝⎭在对称轴上，当2m >，0n >，且直线EM 交x 轴的负半轴于点F 时，过点A 作x 轴的垂线，交直线EM 于点N ，G 为y 轴上一点，点G 的坐标为180,5⎛⎫ ⎪⎝⎭，连接GF ．若2EF NF MF +=，求证：射线FE 平分AFG ∠．19. （2021•齐齐哈尔市）综合与探究如图，在平面直角坐标系中，抛物线2()20y ax x c a =++≠与x 轴交于点A 、B ，与y 轴交于点C ，连接BC ，1OA =，对称轴为2x =，点D 为此抛物线的顶点．（1）求抛物线的解析式；（2）抛物线上C，D两点之间的距离是__________；（3）点E是第一象限内抛物线上的动点，连接BE和CE．求BCE面积的最大值；（4）点P在抛物线对称轴上，平面内存在点Q，使以点B、C、P、Q为顶点的四边形为矩形，请直接写出点Q的坐标．。

2023年中考数学真题汇编几何综合压轴问题专项练习(共40题)(解析版)

几何综合压轴问题专项练习答案（40题）(1)将CDE 绕顶点C 旋转一周，请直接写出点M ，N 距离的最大值和最小值；(2)将CDE 绕顶点C 逆时针旋转120︒（如图2），求MN 【答案】(1)最大值为3，最小值为1(2)7【分析】（1）根据直角三角形斜边上的中线，得出,CM CN 解；（2）过点N 作NP MC ⊥，交MC 的延长线于点P ，根据旋转的性质求得进而可得1CP =，勾股定理解Rt ,Rt NCP MCP ，即可求解．【详解】（1）解：依题意，112CM DE ==，12CN AB =当M 在NC 的延长线上时，,M N 的距离最大，最大值为（2）解：如图所示，过点N 作NP MC ⊥，交MC 的延长线于点∵CDE 绕顶点C 逆时针旋转∴120BCE ∠=︒，∵45BCN ECM ∠=∠=︒，∴MCN BCM ECM ∠=∠-∠=∴60NCP ∠=︒，∴30CNP ∠=︒，∴112CP CN ==，在Rt CNP 中，2NP NC =-在Rt MNP △中，MP MC CP =+∴2234MN NP MP =+=+【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半，勾股定理，旋转的性质，含(1)如图1，求证：DE BF =；(2)如图2，若2AD BF =，的延长线恰好经过DE 的中点【答案】(1)见解析(2)22BE =+△∵点G 是DE 的中点，∴GH 是FCD 的中位线，∴11122GH CD AD ===，设BE a =，则CH EH ==(1)如图1，求AB边上的高CH的长．''．(2)P是边AB上的一动点，点,C D同时绕点P按逆时针方向旋转90︒得点,C D①如图2，当点C'落在射线CA上时，求BP的长．△是直角三角形时，求BP的长．②当AC D''∴90C PQ PC Q '∠+∠='︒∵90C PQ CPH ∠+∠='︒∴PC Q CPH ∠=∠'．由旋转知PC PC '=，设C D ''与射线BA 的交点为作CH AB ⊥于点H ．∵PC PC ⊥'，∴90CPH TPC ∠'+∠=︒，∵C D AT ''⊥，∴90PC T TPC ∠'+∠='︒，【答案】（1）①见解析；②AD DF BD =+，理由见解析；【分析】（1）①证明：ABE CBD ∠=∠，再证明ABE ≅△可得DF DC =．证明AE DF =，从而可得结论；（2）如图，过点B 作BE AD ⊥于点E ，得90BED ∠=︒，证明2DE BD =，证明2AB BC =，ABE CBD ∠=∠，可得②AD DF BD=+．理由如下：∵DF和DC关于AD对称，=．∴DF DC=，∵AE CD∴AE DF=．∴AD AE DE DF BD=+=+∵DF 和DC 关于AD 对称，∴DF DC =，ADF ADC ∠=∠．∵CD BD ⊥，∴45ADF ADC ∠=∠=︒，∴45EBD ∠=︒．∴2DE BD =．∵AB AC AF ==，∴()11222HF BF BD DF ==-=，222262210BC BD CD =+=+=∴2221022AF AC BC ===⨯=25HF (2)知识应用：如图2Y是菱形；①求证：ABCD②延长BC至点E，连接OE交【答案】(1)见解析5∴1BG BO GC OD==，∴115222CG BC AD ===，∴552OF GC ．处从由60PC P C PCP ''=∠=︒，，可知PCP '△为①三角形，故PP PC '=，又P A PA ''=，故PA PB PC PA PB PP A B '''++=++≥，由②可知，当B ，P ，P '，A 在同一条直线上时，PA PB PC ++取最小值，如图2，最小值为(3)如图5，设村庄A ，B ，C 的连线构成一个三角形，且已知4km 23km AC BC ==，，建一中转站P 沿直线向A ，B ，C 三个村庄铺设电缆，已知由中转站P 到村庄A ，B ，C 元/km ，a 元/km ，2a 元/km ，选取合适的P 的位置，可以使总的铺设成本最低为___________用含的式子表示）∵ACP A CP ''∠=∠，∴ACP BCP A CP BCP ∠+∠=∠+∠''又∵60PCP '∠=︒过点A '作A H BC '⊥，垂足为H ，∵60ACB ∠=︒，90ACA '∠=︒，∴30A CH '∠=︒，1猜想证明：(1)如图2，试判断四边形AEDG的形状，并说明理由．问题解决；(2)如图3，将图2中左侧折叠的三角形展开后，重新沿MN折叠，使得顶点B与点∵1122 CHGS CH HG=⋅=∴154302CG HE⋅=⨯=，①求证：PD PB =；②将线段DP 绕点P 逆时针旋转，化时，DPQ ∠的大小是否发生变化？请说明理由；③探究AQ 与OP 的数量关系，并说明理由．【答案】（1）①见解析；②不变化，（2）AQ CP =，理由见解析【分析】（1）①根据正方形的性质证明②作,PM AB PN AD ⊥⊥，垂足分别为点∵四边形ABCD 是正方形，∴45DAC BAC ∠=∠=︒，∴四边形AMPN 是矩形，∴90MPN ∠=︒，∵四边形ABCD 是正方形，∴45BAC ∠=︒，90AOB ∠=∴45AEP ∠=︒，四边形OPEF=作PM AB⊥于点M，则QM MB=，∴QA BE=．∴AQ CP（1）求BCF ∠的度数；（2）求CD 的长．深入探究：（3）若90BAC ∠<︒，将BMN 绕点B 顺时针旋转α，得到BEF △，连接AE ，CF 满足0360α︒<<︒，点,,C E F 在同一直线上时，利用所提供的备用图探究BAE ∠与ABF ∠的数量关系，并说明理由．【答案】初步尝试：（1）1MN AC =；MN AC ∥；（2）特例研讨：（1）30BCF ∠=︒；（2）CD∵MN 是BAC 的中位线，∴MN AC ∥，∴90BMN BAC ∠=∠=︒∵将BMN 绕点B 顺时针旋转α∴,BE BM BF BN ==；BEF ∠=∵点,,A E F 在同一直线上时，2∵,ADN BDE ANB BED ∠=∠∠=∠∴ADN BDE ∽,∴2222DN AN DE BE ===,设DE x =，则2DN x =，在Rt ABE △中，2,2BE AE ==在Rt ADN △中，22AD DN AN =+∵AB AC =，∴A ABC CB =∠∠，设ABC ACB θ∠=∠=，则1802BAC θ∠=︒-，∵MN 是ABC 的中位线，∴MN AC∥∴MNB MBN θ∠=∠=，∵将BMN 绕点B 顺时针旋转α，得到BEF △，∴EBF MBN ≌，MBE NBF α∠=∠=，∴EBF EFB θ∠=∠=∴1802BEF θ∠=︒-，∵点,,C E F 在同一直线上，∴2BEC θ∠=∴180BEC BAC ∠+∠=︒，∴,,,A B E C 在同一个圆上，∴EAC EBC αθ∠=∠=-∴()()1802BAE BAC EAC θαθ∠=∠-∠=︒---180αθ=︒--∵ABF αθ∠=+，∴180BAE ABF ∠∠=+︒；如图所示，当F 在EC 上时，∵,BEF BAC BC BC∠=∠=∴,,,A B E C 在同一个圆上，设ABC ACB θ∠=∠=，则1802BAC BEF θ∠=∠=︒-，将BMN 绕点B 顺时针旋转α，得到BEF △，设NBF β∠=，则EBM β∠=，则360αβ+=︒，∴ABF θβ∠=-，∵BFE EBF θ∠=∠=,EFB FBC FCB∠=∠+∠∴ECB FCB EFB FBC θβ∠=∠=∠-∠=-，∵ EBEB =∴EAB ECB θβ∠=∠=-∴BAE ∠ABF=∠综上所述，BAE ABF ∠=∠或180BAE ABF ∠∠=+︒【点睛】本题考查了圆周角定理，圆内接四边形对角互补，相似三角形的性质与判定，旋转的性质，中位线的性质与判定，等腰三角形的性质与判定，三角形内角和定理，三角形外角的性质，勾股定理，熟练掌握以上知识是解题的关键．10．（2023·湖北黄冈·统考中考真题）【问题呈现】CAB △和CDE 都是直角三角形，90,,ACB DCE CB mCA CE mCD ∠=∠=︒==，连接AD ，BE ，探究AD ，BE 的位置关系．(1)如图1，当1m =时，直接写出AD ，BE 的位置关系：____________；(2)如图2，当1m ≠时，（1）中的结论是否成立？若成立，给出证明；若不成立，说明理由．【拓展应用】(3)当3,47,4m AB DE ===时，将CDE 绕点C 旋转，使,,A D E 三点恰好在同一直线上，求（2）解：成立；理由如下：∵90DCE ACB ∠=∠=︒，∴DCA ACE ACE ∠+∠=∠+（3）解：当点E 在线段AD设AD y =，则AE AD DE =+根据解析（2）可知，DCA △∴3BE BC m AD AC===，勾股定理，解题的关键是熟练掌握三角形相似的判定方法，画出相应的图形，注意分类讨论．(1)若点P 在AB 上，求证：A P AP '=；(2)如图2．连接BD ．①求CBD ∠的度数，并直接写出当180n =时，x 的值；②若点P 到BD 的距离为2，求tan A MP '∠的值；∵PM 平分A MA '∠∴90PMA ∠=︒∴PM AB∥∴DNM DBA V V ∽∴DN DM MN DB DA BA ==∵8,6,90AB DA A ==∠=︒，∴2226BD AB AD =+=+∴2103sin 3BQ BP DBA ===∠，∵90PQB CBD DAB ∠=∠=∠=︒，∴90QPB PBQ DBA ∠=︒-∠=∠，∵A MP AMP ' ≌，∴90PA M A '∠=∠=︒，（2）如图②，在矩形ABCD 的BC 边上取一点E ，将四边形ABED 沿DE 翻折，使点B '处，若24,6BC CE AB ⋅==，求BE 的值；（3）如图③，在ABC 中，45,BAC AD BC ∠=︒⊥，垂足为点,10,D AD AE ==于点F ，连接DF ，且满足2DFE DAC ∠=∠，直接写出53BD EF +的值．∵EF BC ∥，∴2CDF DFE ∠=∠=∴CDH FDH ∠=∠，又∵DH DH =，CHD ∠∴(ASA CHD FHD ≌【点睛】本题考查矩形的性质、翻折性质、勾股定理、相似三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质、锐角三角函数等知识，综合性强，较难，属于中考压轴题，熟练掌握相关知识的联系与运用，添加辅助线求解是解答的关键．13．（2023·湖南郴州·=，连接点E，使CE AD(1)如图1，当点D在线段AB上时，猜测线段CF与BD的数量关系并说明理由；(2)如图2，当点D在线段AB的延长线上时，①线段CF与BD的数量关系是否仍然成立？请说明理由；②如图3，连接AE．设4AB=，若AEB DEB∠=∠，求四边形BDFC的面积．【答案】(1)1CF BD=，理由见解析∴60,ADG ABC AGD ∠=∠=︒∠=∠∴ADG △为等边三角形，∴AD AG DG ==，∵AD CE =，AD AB AG AC -=-∴DG CE =，BD CG =，于点由①知：ADG △为等边三角形，∵ABC 为等边三角形，∴4,AB AC BC BH CH =====∴2223AH AB BH =-=，(1)若正方形ABCD 的边长为2，E 是AD 的中点．①如图1，当90FEC ∠=︒时，求证：AEF DCE ∽△△；②如图2，当2tan 3FCE ∠=时，求AF 的长；(2)如图3，延长CF ，DA 交于点G ，当1,sin 3GE DE FCE =∠=时，求证：，可得结论；正方形ABCD 中，①ADC BAD ∠=∠ ∴AEF CED ∠+∠=AEF ECD ∴∠=∠，延长DA ，CF 交于点G ，作GH CE ⊥，垂足为H ，90EDC EHG ∠=∠=︒ 且∠问题探究：(1)先将问题特殊化，如图（2），当90α=︒时，直接写出GCF ∠的大小；(2)再探究一般情形，如图（1），求GCF ∠与α的数量关系．问题拓展：(3)将图（1）特殊化，如图（3），当120α=︒时，若12DG CG =，求BE CE 的值．故答案为：45︒．（2）解：在AB上截取ANABC BAE AEB∠+∠+∠=∠=∠，ABC AEF22⎝⎭（3）解：过点A作CD的垂线交CD的延长线于点【点睛】此题考查菱形性质、三角形全等、三角形相似，解题的关键是熟悉菱形性质、三角形全等、三角形相似．16．（2023·山西·统考中考真题）问题情境：“综合与实践沿对角线剪开，得到两个全等的三角形纸片，表示为∠=∠=︒∠=∠．将ABCACB DEF A D90,和DFE△(1)数学思考：谈你解答老师提出的问题；(2)深入探究：老师将图2中的DBE绕点B逆时针方向旋转，使点问题．∠①“善思小组”提出问题：如图3，当ABE②“智慧小组”提出问题：如图AH的长．请你思考此问题，直接写出结果．【答案】(1)正方形，见解析(2)①AM BE=，见解析；【分析】（1）先证明四边形形；∠（2）①由已知ABE【点睛】本题考查了旋转的性质、全等三角形的判定与性质、正方形的判定与性质、相似三角形的判定与性质、三角函数、勾股定理等知识点，适当添加的辅助线、构造相似三角形是解题的关键．17．（2023·湖北十堰·统考中考真题）过正方形E ，连接AE ，直线AE 交直线(1)如图1，若25CDP ∠=︒，则DAF ∠=___________(2)如图1，请探究线段CD ，EF ，AF 之间的数量关系，并证明你的结论；(3)在DP 绕点D 转动的过程中，设AF a =，EF 【答案】(1)20︒。

中考数学压轴题分类练习几何中的最定值专题无答案

几何中的最（定）值专题1．如图，在ABC 中， C 90 ， AB 10cm，BC 8cm ，点P 从点 A 沿AC 向点C 以 1cm / s 的速度运动，同时点Q 从点C沿CB向点B 以2cm/ s的速度运动(点Q运动到点 B 停止)，在运动过程中，四边形PABQ 的面积最小值为（）A．19cm2B．16m2 C.15m2D．12m22．正方形ABCD 的边长为1，点 O 是 BC 边上的一个动点（与B,C 不重合)，以O为极点在BC所在直线的上方作MON 90 .(1)当OM 经过点 A时，①请直接填空： ON （可能，不行能）过 D 点；（图 1 仅供剖析）②如图 2, 在ON 上截取，过 E 点作 EF 垂直于直线BC, 垂足为点 F ，册EH CD于 H ，求证：四边形EFCH OE OA为正方形 .（2）当OM 可是点 A时，设 OM 交边 AB于G ,且 OG 1. 在ON 上存在点 P ,过 P点作 PK 垂直于直线 BC ,垂足为点 K ，使得S PKO 4 S OBG，连结 GP ，求四边形 PKBG 的最大面积 .3．在平面直角坐标系xOy 中，抛物线y ax2 bx 2过点A( 2,0) ，，与 y 轴交于点C.（ 1）求抛物线y ax 2 bx 2 的函数表达式；（ 2）若点D在抛物线y ax2 bx 2的对称轴上，求ACD 的周长的最小值；（ 3）在抛物线y ax2 bx 2 的对称轴上能否存在点P ，使ACP 是直角三角形？若存在，直接写出点P 的坐标，若不存在，请说明原因.4．如图，在⊙O中，直径 CD垂直于可是圆心O的弦 AB，垂足为点N，连结 AC，点 E在 AB上，且 AE=CE．2（ 1）求证：AC=AE?AB；（ 2）过点B作⊙O的切线交EC的延伸线于点P，试判断 PB与 PE能否相等，并说明原因；（ 3）设⊙O半径为 4，点N为OC中点，点Q在⊙ O上，求线段PQ的最小值．5．如图，抛物线y 2 x2 bx c 经过点3,0 ，C 0, 2 ，直线 l : y 2 x 2 交 y 轴于点，且与抛物线3 3 3交于，D两点．为抛物线上一动点（不与， D 重合）．（ 1）求抛物线的分析式；（ 2）当点在直线l下方时，过点作//x 轴交于点，//y 轴交l于点．求的最大值；（ 3）设F为直线l 上的点，以， C ，， F为极点的四边形可否组成平行四边形？若能，求出点F的坐标；若不可以，请说明原因．6．已知抛物线y ax2 bx c ，此中2a b 0 c ，且 a b c 0 .（ 1）直接写出对于x 的一元二次方程 ax 2 bx c 0 的一个根；（ 2）证明：抛物线y ax2 bx c 的极点A在第三象限；（ 3）直线 y x m 与 x, y 轴分别订交于B, C两点，与抛物线y ax2 bx c 订交于 A, D 两点.设抛物线y ax 2c 的对称轴与x轴订交于 E ,假如在对称轴左边的抛物线上存在点 F ,使得 ADF 与 BOC 相像.而且bxSADF 1S ADE，求此时抛物线的表达式 . 27．如图，AB 是O 的直径， AC BC, AB 2 ，连结 AC ．（ 1）求证：CAB 450；（ 2）若直线l 为O的切线，C是切点，在直线l 上取一点D，使BD AB, BD 所在的直线与AC 所在的直线订交于点 E ，连结 AD ．①尝试究 AE 与 AD 之间的数目关系，并证明你的结论；② EB能否为定值？假如，恳求出这个定值；若不是，请说明原因．CD8．如图，动点M在以O为圆心，AB为直径的半圆弧上运动（点M不与点A、B及AB的中点F重合），连结OM.过点 M 作 MEAB 于点 E ，以 BE 为边在半圆同侧作正方形 BCDE ，过 M 点作 O 的切线交射线 DC 于点 N ，连结 BM 、BN .（ 1）研究：如左图，当M 动点在 AF 上运动时；①判断OEM MDN 能否建立？请说明原因；②设 ME NCk ， k 能否为定值？假如，求出该定值，若不是，请说明原因；MN③设MBN，能否为定值？假如，求出该定值，若不是，请说明原因；（ 2）拓展：如右图，当动点 M 在 FB 上运动时；分别判断（ 1）中的三个结论能否保持不变？若有变化，请直接写出正确的结论 . （均不用说明原因）8. 已知抛物线 yx 2 bx 3 （ b 是常数）经过点 A( 1,0) .（ 1）求该抛物线的分析式和极点坐标；（ 2） P(m ，t) 为抛物线上的一个动点， P 对于原点的对称点为 P' .①当点 P' 落在该抛物线上时，求 m 的值；②当点 P' 落在第二象限内， P' A 2 获得最小值时，求m 的值 .9. 在平面直角坐标系xOy 中的点 P 和图形 M ，给出以下的定义：若在图形M 上存在一点 Q ，使得 P 、 Q 两点间的距离小于或等于 1，则称 P 为图形 M 的关系点．（ 1）当 O 的半径为 2 时，①在点11 3 5中，O 的关系点是 _______________ ．P12,0 ,P22 ,2 , P 32 ,0②点 P 在直线 y x 上，若 P 为 O 的关系点，求点 P 的横坐标的取值范围．（ 2）C 的圆心在 x 轴上，半径为 2，直线 yx 1与 x 轴、 y 轴交于点 A 、 B ．若线段 AB 上的全部点都是 C的关系点，直接写出圆心C 的横坐标的取值范围．10. 如图，在平面直角坐标系中，抛物线yax 2bx 1 交 y 轴于点 A ，交 x 轴正半轴于点 B(4,0) ，与过 A 点的直线订交于另一点 D(3, 5) ，过点 D 作 DCx 轴，垂足为 C .2（ 1）求抛物线的表达式；（ 2）点P在线段OC上（不与点O C重合），过P作PN x轴，交直线AD于M，交抛物线于点N，连结CM，、求PCM 面积的最大值；（ 3）若P是x轴正半轴上的一动点，设OP 的长为，能否存在，使以点M、C、D、 N 为极点的四边形是平行四边形？若存在，求出的值；若不存在，请说明原因.。