Eigenvalue bounds in the gaps of Schrodinger operators and Jacobi matrices

合集下载

inequalities for graph eigenvalues

1
Introduction
We consider the Laplacian and eigenvalues of graphs and induced subgraphs. Although an induceas a graph in its own right, it is natural to consider an induced subgraph S as having a boundary (formed by edges joining vertices in S and vertices not in S but in the “ host ” graph). The host graph then can be regarded as a special case of a subgraph with no boundary. This paper consists of three parts. In the ﬁrst part (Section 2-5), we give deﬁnitions and describe basic properties for the Laplacian of graphs. We introduce the Neumann eigenvalues for induced subgraphs and the heat kernel for graphs and induced subgraphs. Then we establish the following lower bound for the Neumann eigenvalues of induced subgraphs. 1
Abstract For an induced subgraph S of a graph, we show that its Neumann eigenvalue λS can be lower-bounded by using the heat kernel Ht (x, y ) of the subgraph. Namely, √ 1 Ht (x, y ) dx λS ≥ inf y ∈S 2t dy x ∈S where dx denotes the degree of the vertex x. In particular, we derive lower bounds of eigenvalues for convex subgraphs which consist of lattice points in an d-dimensional Riemannian manifolds M with convex boundary. The techniques involve both the (discrete) heat kernels of graphs and improved estimates of the (continuous) heat kernels of Riemannian manifolds. We prove eigenvalue lower bounds for convex subgraphs of the form cǫ2 /(dD(M ))2 where ǫ denotes the distance between two closest lattice points, D(M ) denotes the diameter of the manifold M and c is a constant (independent of the dimension d and the number of vertices in S , but depending on the how “dense” the lattice points are). This eigenvalue bound is useful for bounding the rates of convergence for various random walk problems. Since many enumeration problems can be approximated by considering random walks in convex subgraphs of some appropriate host graph, the eigenvalue inequalities here have many applications.

氢键的应用

© XXXX American Chemical Society
how the standard perception of halogen substituents, which assumes an isotropic negative electron density around the halogen, was replaced by a description that takes the σ-hole into account. Halogen bonds have been found to occur in a multitude of inorganic, organic, and biological systems.4,5 In an early study from the 1950s, Hassel and Hvoslef solved the crystal structure of the equimolar Br2:dioxane adduct and found Br···O contacts featuring distances substantially below the sum of the van der Waals radii of both atoms, indicating a strong attractive interaction between both atoms.6,7 In 1984, a search of the Cambridge crystallographic data ﬁles for short iodine···N/O/S contacts revealed that these interactions are also formed in biologically relevant systems, being employed by nature for the molecular recognition of thyroid hormones at their target proteins such as transthyretin.8 In protein−ligand environments, halogen bonds can be formed between a halogenated ligand and any accessible Lewis base in the binding pocket.9 Probably because of its presence in every amino acid, the backbone carbonyl oxygen function is the most prominent Lewis base involved in halogen bonds in protein binding sites, as found from an analysis of the Protein Data Bank (PDB).10,11 Additionally, halogen bonds can be formed involving side chain groups, such as hydroxyls in serine, threonine, and tyrosine, carboxylate groups in aspartate and glutamate, sulfurs in cysteine and methionine, nitrogens in histidine, and the π surfaces of phenylalanine, tyrosine, histidine, and tryptophan. Several examples for these contacts are given in Figure 2.

energyS

k = the number of closed walks in G of length k ; λ i i
Interlacing: if H = G − u has eigenvalues µ1 ≥ µ2 ≥ . . . ≥ µn−1 , then
λ1 ≥ µ1 ≥ λ2 ≥ µ2 ≥ . . . ≥ λn−1 ≥ µn−1 ≥ λn .
Energy of Graphs – p.13/58
Trees are Ok! (3)
For example, the following special problems have been solved in this way: max and min E. for trees with perfect matchings; min E. for trees with a given maximum matching size; max E. for trees with n vertices and max degree ∆; min E. for trees with n vertices and max deg ∆ ≥ ⌈ n+1 3 ⌉; min E. for trees with n vertices and k pendant vertices; min E. for unicyclic graphs; max E. for bipartite unicyclic graphs; max and min E. for hexagonal chains; min E. for chains with polygons of 4n − 2 vertices.
The Coulson integral formula (1940):
1 E (G ) = π

微积分介值定理的英文

微积分介值定理的英文The Intermediate Value Theorem in CalculusCalculus, a branch of mathematics that has revolutionized the way we understand the world around us, is a vast and intricate subject that encompasses numerous theorems and principles. One such fundamental theorem is the Intermediate Value Theorem, which plays a crucial role in understanding the behavior of continuous functions.The Intermediate Value Theorem, also known as the Bolzano Theorem, states that if a continuous function takes on two different values, then it must also take on all values in between those two values. In other words, if a function is continuous on a closed interval and takes on two different values at the endpoints of that interval, then it must also take on every value in between those two endpoint values.To understand this theorem more clearly, let's consider a simple example. Imagine a function f(x) that represents the height of a mountain as a function of the distance x from the base. If the function f(x) is continuous and the mountain has a peak, then theIntermediate Value Theorem tells us that the function must take on every height value between the base and the peak.Mathematically, the Intermediate Value Theorem can be stated as follows: Let f(x) be a continuous function on a closed interval [a, b]. If f(a) and f(b) have opposite signs, then there exists a point c in the interval (a, b) such that f(c) = 0.The proof of the Intermediate Value Theorem is based on the properties of continuous functions and the completeness of the real number system. The key idea is that if a function changes sign on a closed interval, then it must pass through the value zero somewhere in that interval.One important application of the Intermediate Value Theorem is in the context of finding roots of equations. If a continuous function f(x) changes sign on a closed interval [a, b], then the Intermediate Value Theorem guarantees that there is at least one root (a value of x where f(x) = 0) within that interval. This is a powerful tool in numerical analysis and the study of nonlinear equations.Another application of the Intermediate Value Theorem is in the study of optimization problems. When maximizing or minimizing a continuous function on a closed interval, the Intermediate Value Theorem can be used to establish the existence of a maximum orminimum value within that interval.The Intermediate Value Theorem is also closely related to the concept of connectedness in topology. If a function is continuous on a closed interval, then the image of that interval under the function is a connected set. This means that the function "connects" the values at the endpoints of the interval, without any "gaps" in between.In addition to its theoretical importance, the Intermediate Value Theorem has practical applications in various fields, such as economics, biology, and physics. For example, in economics, the theorem can be used to show the existence of equilibrium prices in a market, where supply and demand curves intersect.In conclusion, the Intermediate Value Theorem is a fundamental result in calculus that has far-reaching implications in both theory and practice. Its ability to guarantee the existence of values between two extremes has made it an indispensable tool in the study of continuous functions and the analysis of complex systems. Understanding and applying this theorem is a crucial step in mastering the powerful concepts of calculus.。

The algebraic eigenvalue problem代数特征值问题

CLARENDON PRESS • OXFORD 1965
Contents
1. THEORETICAL BACKGROUND Page
Introduction Definitions Eigenvalues and eigenvectors of the transposed matrix Distinct eigenvalues Similarity transformations Multiple eigenvalues and canonical forms for general matrices Defective system of eigenvectors The Jordan (classical) canonical form The elementary divisors Companion matrix of the characteristic polynomial of A Non-derogatory matrices The Frobenius (rational) canonical form Relationship between the Jordan and Frobenius canonical forms Equivalence transformations Lambda matrices Elementary operations Smith's canonical form The highest common factor offc-rowedminors of a A-matrix Invariant factors of (A —XI) The triangular canonical form Hermitian and symmetric matrices Elementary properties of Hermitian matrices Complex symmetric matrices Reduction to triangular form by unitary transformations Quadratic forms Necessary and sufficient conditions for positive definiteness Differential equations with constant coefficients Solutions corresponding to non-linear elementary divisors Differential equations of higher order Second-order equations of special form Explicit solution of By = —Ay Equations of the form (AB— XI)x — 0 The minimum polynomial of a vector The minimum polynomial of a matrix Cayley-Hamilton theorem Relation between minimum polynomial and canonical forms Principal vectors Elementary similarity transformations Properties of elementary matrices Reduction to triangular canonical form by elementary similarity transformations Elementary unitary transformations Elementary unitary Hermitian matrices Reduction to triangular form by elementary unitary transformations Normal matrices Commuting matrices

拉格朗日乘子法

z 设长方体的三个棱长为x，y，z，则其体积f 为三个边长的乘积：f(x,y,z)=xyz.要求表面积为a 的平方于是长方体的6面的面积可以写成2xy+2xz+2yz=a2 即 2xy+2xz+2yz-a2 =0它也就是本问题中仅有一个约束条件。根据前面介绍的拉格朗日方法制造一个新函数F，并且放进一个未知的常数C ，于是有 F=xyz+C(2xy+2xz+2yz-a2 )
z 2. assume that the energy of the oscillators are quantized E = nhν = nhc / λ we see that at shortwavelength oscillators is very large. This energy is too large for the walls to supply it, so the shortwavelength oscillators remain unexcited.
z 上面的n 个方程连同约束条件给的m 个方程式已经可以解出n+m 个未知数。它们就是n 个x（即x1,x2,…,xn ）和m 个C (即C1 ,C2 ,…， Cm )。于是我们就得到了这个函数达到极值时的各个自变量的值。可以看到约束条件不同，得到的各个x 值也不同。这样就利用拉格朗日方法解决了问题
11.2(b)
z Describe how a wavefunction determines the dynamical properties of a system and how those properties may be perdicted.
z 1. In quantum mechanics all dynamical properties of a physical system have associated with them a corresponding operator. The system itself is described by a wavefunction.

薛定谔—麦克斯韦尔方程径向解的存在性和多重性(英文)

In 1887, the German physicist Erwin Schrödinger proposed a radial solution to the Maxwell-Schrödinger equation. This equation describes the behavior of an electron in an atom and is used to calculate its energy levels. The radial solution was found to be valid for all values of angular momentum quantum number l, which means that it can describe any type of atomic orbital.The existence and multiplicity of this radial solution has been studied extensively since then. It has been shown that there are infinitely many solutions for each value of l, with each one corresponding to a different energy level. Furthermore, these solutions can be divided into two categories: bound states and scattering states. Bound states have negative energies and correspond to electrons that are trapped within the atom; scattering states have positive energies and correspond to electrons that escape from the atom after being excited by external radiation or collisions with other particles.The existence and multiplicity of these solutions is important because they provide insight into how atoms interact with their environment through electromagnetic radiation or collisions with other particles. They also help us understand why certain elements form molecules when combined together, as well as why some elements remain stable while others decay over time due to radioactive processes such as alpha decay or beta decay.。

How large can the first eigenvalue be on a surface of genus two

a rX iv:mat h /59398v1[mat h.SP]18Se p25How large can the ﬁrst eigenvalue be on a surface of genus two?Dmitry Jakobson ∗Michael Levitin †Nikolai Nadirashvili ‡Nilima Nigam §Iosif Polterovich ¶11September 2005Abstract Sharp upper bounds for the ﬁrst eigenvalue of the Laplacian on a surface of a ﬁxed area are known only in genera zero and one.We investigate the genus two case and conjecture that the ﬁrst eigenvalue is maximized on a singular surface which is realized as a double branched covering over a sphere.The six ramiﬁcation points are chosen in such a way that this surface has a complex structure of the Bolza surface.We prove that our conjecture follows from a lower bound on the ﬁrst eigenvalue of a certain mixed Dirichlet-Neumann boundary value problem on a half-disk.The latter can be studied numerically,and we present conclusive evidence supporting the conjecture.Keywords:Laplacian,ﬁrst eigenvalue,surface of genus two,mixed boundary value problem.1Introduction and main results1.1Upper bounds on theﬁrst eigenvalueLet M be a closed surface of genusγand let g be the Riemannian metric on M.Denote by∆the Laplace-Beltrami operator on M,and byλ1the smallest positive eigenvalue of the Laplacian.Let the area Area(M)beﬁxed.How large canλ1be on such a surface?Sharp bounds for theﬁrst eigenvalue are known only for the sphere([H],see also[SY]),the projective plane([LY]),the torus([Ber],[N]),and the Klein bottle ([JNP],[EGJ]).The present paper is concerned with the surface of genus2.Let M be orientable and letΠ:M→S2be a non-constant holomorphic map(or,conformal branched covering)of degree d.It was proved in[YY]thatλ1Area(M)≤8πd.(1.1.1) Any Riemann surface of genusγcan be represented as a branched cover over S2of degree d= γ+32 .(1.1.2) In general,(1.1.2)is not sharp,for example forγ=1([N]).Let M=P be a surface of genusγ=2.Then(1.1.2)impliesλ1Area(P)≤16π.(1.1.3) The aim of this paper is to show,using a mixture of analytic and numerical tools, that(1.1.3)is sharp.Main results of this paper were announced(without proofs) in[JLNP,section4].1.2The Bolza surfaceLetΠ:P→S2be a branched covering of degree d=2.The Riemann-Hurwitz formula(see[GH])implies that this cover is ramiﬁed at6points.We choose these points to be the intersections of the round sphere S2centered at the origin with the coordinate axes in R3.The surface P can be realized as(z,w)∈C2:w2=F(z):=z(z−1)(z−i)This surface has the conformal structure of the Bolza surface.It has an octahe-dral group of holomorphic automorphisms and its symmetry group is the largest among surfaces of genus two[I,KW].Interestingly enough,the Bolza surface appears in some other extremal problems,in particular for systoles(see[KS]).To simplify calculations it is convenient to rotate the equatorial plane byπ/4. The equation of P becomesP:= (z,w)∈C2:w2=F(z):=z(z−eπi/4)(z−e3πi/4)u 2,where the scalar product ·,· and the norm · are taken in the space L2(P,g0). The Sobolev space H10(P,g0)of functions supported away from the singularities is obtained by the closure of C∞0(P,g0):={v∈C∞(P,g0)|Since(P,g0)is a double cover of the standard S2,we haveArea(P,g0)=2Area(S2)=8π.Therefore,in order to prove Conjecture1.3.1it suﬃces to show thatλ1(P,g0)=λ1(S2)=2.(1.3.2)Unfortunately,we are unable to prove(1.3.2),and therefore establish Con-jecture1.3.1.We can however reduce the conjecture to the following spectral problem on a quarter-sphere Q⊂S2that can be treated using numerical ly,let,in usual spherical coordinates(φ,θ),Q={(φ,θ):0<φ<π/2,0<θ<π}.We split the boundary∂Q into two parts:∂Q=Finally,we note that the spectral problem(1.3.3)easily reduces via the stere-ographic projection to the following mixed Dirichlet-Neumann problem on a half-disk D:={(r,ψ)∈R2:r<1,0<ψ<π}(here(r,ψ)are usual planar polar coordinates):−∆v=4Λ(1+r2)2v on D,v|∂2D=0,(∂v/∂n)|∂1D=0.(1.3.7)We refer to[JLNP]for a further discussion on Dirichlet-Neumann swap isospec-trality.Figure1:Geometry of boundary value problems(1.3.6)(left)and(1.3.7)(right). Here and further on,the solid red line denotes Dirichlet boundary condition and the dashed blue line—the Neumann one.Remark1.3.8.One can check that a surface with aﬁnite number of conical singularities can be approximated by a sequence of smooth surfaces of the same genus and area in such a way that the corresponding sequence of theﬁrst non-zero eigenvalues converges toλ1on the original surface.Thus,Conjecture1.3.1 means that(1.1.3)is sharp in the class of smooth metrics,although the equality is not necessarily attained.For a general result about the convergence of the whole spectrum see[Ro].52Symmetries2.1Hyperelliptic involutionLet T:P→P,T2=Id be a map that intertwines the preimages of points of S2under a two-sheeted coveringΠ:P→S2.Clearly,the Laplace operator∆commutes with T.By the spectral theorem,we can consider separately the restrictions of the Laplacian onto the spaces of functions which are either even or odd with respect to T.The even functions on P can be identiﬁed with the functions on S2. Therefore,asλ1(S2)=2,we haveλ1(P)≤2,and the equality in(1.3.2)will be achieved if and only if theﬁrst eigenvalueλodd1of the Laplacian acting on the odd subspace satisﬁesλodd1≥2.2.2Isometries of PConsider the following isometries of S2(as usual,we identify S2and C by stere-ographic projection):σ1:z→¯z or(χ,η,ξ)→(χ,−η,ξ),σ2:z→−¯z or(χ,η,ξ)→(−χ,η,ξ),(2.2.1)σ3:z→1/¯z or(χ,η,ξ)→(χ,η,−ξ).Here z=x+iy is a point in the equatorial plane upon which a point(χ,η,ξ)∈S2 is stereographically projected.The hyperelliptic involution T is given by T:(z,w)→(z,−w).For1≤j≤3,a symmetryσj of S2has two corresponding symmetries s j and T◦s j satisfyingΠ◦s j=Π◦T◦s j=σj◦Π.(2.2.2) Those symmetries,with account of(1.2.1)are given by the explicit formulaes1:(z,w)→(¯z,¯z/¯w),s2:(z,w)→(−¯z,i¯w),(2.2.3)s3:(z,w)→(1/¯z,¯w/¯z).As an illustration,we demonstrate how the last of these formulae is obtained:if w2=F(z),then by(1.2.1),F 1¯z(1/¯z−eπi/4)(1/¯z−e3πi/4)F(z)thus giving the expression for s3.It easily seen that all s j commute with T and satisfys2j=Id,j=1,2,3;(2.2.4)s1s3=s3s1,s2s3=s3s2;s2s1=T s1s2.Remark2.2.5.In the proof of Theorem1.3.5we will use only the symmetries s1and s3.Calculations for s2are presented for the sake of completeness(see Remark3.4.1).2.3Fixed point sets of isometriesLet Fix(S)denote aﬁxed point set of a mapping S.As easily seen from(2.2.1), the sets Fix(σj),for j=1,2,3,lie in the union of the coordinate lines and a unit circle of C,and we introduce the following notation for future reference.The coordinate lines are divided into two rays each by the ramiﬁcation point r0:=0, and we denotea1:={z=t,t>0},a2:={z=it,t>0},a3:={z=t,t<0},a4:={z=it,t<0}.The circle is divided into four arcs by the ramiﬁcation points r1:=e−πi/4, r2:=eπi/4,r3:=e3πi/4,and r4:=e−3πi/4,and we denote the arcs bya k+4:={z=e tπi/4,t∈(2k−3,2k−1)},k=1,2,3,4,so that the arc a5goes from r1to r2,the arc a6goes from r2to r3,the arc a7 goes from r3to r4,andﬁnally a8goes from r4to r1.In this notation,theﬁxed point sets Fix(σj)are written asFix(σ1)=a1∪a3,Fix(σ2)=a2∪a4,Fix(σ3)=a5∪a6∪a7∪a8.(2.3.1) Note that each of the rays a j(j=1,2,3,4)intersects an arc a j+4at a single point which we denote z j:z1=1,z2=i,z3=−1,z4=−i,see Figure2.7Figure2:Ramiﬁcation points,rays,arcs and intersections 2.4Fixed point sets of s1,s2,s3Each of the points z j has exactly two pre-images p(m)j :=(w(m)j,z j)∈Π−1z j,m=1,2,where w(1,2)j are the solutions of the equation(w j)2=F(z j),with Fgiven in(1.2.1).These solutions are easily found from(1.2.1);we are of course at liberty to choose which of the two solutions is denoted w(1)j and which is8denoted w(2)j.For deﬁniteness we setw(1)1=i,w(2)1=−i;w(1)2=1+i2,w(2)2=−1+i2; w(1)3=1,w(2)3=−1;w(1)4=1−i2,w(2)4=−1−i2.(2.4.1)For future use,we need to know the images of points p(m)j under the sym-metries s l,l=1,2,3.These are easily calculated from(2.2.3);it turns out thats l p(m)j =p(n)kwith some indices k∈{1,2,3,4},n∈{1,2}.The results of thecalculations are summarized in the following Table1.(j,m)(k,n)l=2(1,1)(1,1)(1,2)(1,2)(1,2)(1,1)(2,1)(2,2)(3,1)(3,2)(3,2)(3,2)(3,1)(3,1)(4,2)(4,1)the notation we postulate that b(m)k∋w(m)k′,k′=((k−1)mod4)+1,e.g. w(1)1∈b(1)1∩b(1)5,w(2)3∈b(2)3∩b(2)7,etc.We now have at our disposal all the information we need in order to obtain theﬁxed point sets of s1,s2,s3.We start with the following two simple Lemmas. Lemma2.4.2.ΠFix(s j)⊆Fix(σj).Proof.Let z∈ΠFix(s j).Then there exists p∈P such thatΠp=z and s j p= p.ThusΠs j p=z and by(2.2.2)σjΠp=σj z=z,so that z∈Fix(σj). Lemma2.4.3.Let a k⊆Fix(σj).Then,for m=1,2,either b(m)k⊆Fix(s j)or b(m)k⊆Fix(T◦s j).Proof.We haveΠb(m)k =a k,so thatσjΠb(m)k=σj a k=a k,and so by(2.2.2)Πs j b(m)k =a k=Πb(m)k=ΠT b(m)k.The result follows from the obvious observa-tion:ifΠα=Πβ,then eitherα=βorα=Tβ.The lemmas lead to the followingProposition2.4.4.Fix(s1)=b(1)1∪b(2)1,Fix(T s1)=b(1)3∪b(2)3,Fix(s2)=b(1)2∪b(2)2,Fix(T s2)=b(1)4∪b(2)4,Fix(s3)=b(1)6∪b(2)6∪b(1)8∪b(2)8,Fix(T s3)=b(1)5∪b(2)5∪b(1)7∪b(2)7.Proof.By Lemmas2.4.2and2.4.3,for any given j theﬁxed sets Fix(s j)and Fix(T s j)consist only of the pre-images of the components a k of the correspond-ingﬁxed sets Fix(σj)(given by(2.3.1)).However we still need to describe whichcomponent b(m)k,m=1,2,lies in Fix(s j)and which in Fix(T s j).As each com-ponent b k(m)is uniquely determined by the point w(m)kgiven by(2.4.1),it issuﬃcient just to check in Table1whether s j w(m)k =w(m)kor T s j w(m)k=w(m)k.For example,toﬁnd Fix(s2)we need only to inspect b(m)2and b(m)4.As,byTable1,s2w(m)2=w(m)2and T s2w(m)4=w(m)4,we have Fix(s2)=b(1)2∪b(2)2andFix(T s2)=b(1)4∪b(2)4.The rest of Proposition2.4.4is obtained in the same manner.103Proof of Theorem1.3.5We divide the proof of Theorem1.3.5into several steps.3.1Even eigenfunctions with respect to TConsider the subspace V+⊂L2(P)consisting of all even eigenfunctions with respect to T.Any such eigenfunction has a well-deﬁned projection on S2.There-fore,if there exists aﬁrst eigenfunction of P that belongs to V+,its projection is an eigenfunction on S2and hence the corresponding eigenvalue is greater or equal than two(recall thatλ1(S2)=2).Hence,in this case the Conjecture1.3.1 is veriﬁed.3.2Use of symmetries s1,s3.Denote by G13the subgroup of the automorphism group of P generated by the symmetries{T,s1,s3}.It follows from(2.2.4)that G13is commutative.Note also that all the elements of G13commute with the Laplacian on P.Therefore,we can choose a basis of L2(P)consisting of joint eigenfunctions of all s∈G13and∆.Given a joint eigenfunction f of all s∈G13,we denote byµ(f,s)the corresponding eigenvalue of s,i.e.f(sx)=µ(f,s)f(x).Since s2j=T2=Id for j=1,3,we see thatµ(f,s)=±1for all s∈G13.3.3Odd eigenfunctions with respect to TConsider now the space V−⊂L2(P)consisting of all eigenfunctions of the Laplacian which are odd with respect to T.Letφ1be a joint eigenfunction of {T,s1,s3,∆},corresponding to the smallest eigenvalue of∆ V−Now,sinceµ(φ1,T)=−1and s23T=T,we haveµ(φ1,s1)µ(φ1,s1T)=µ(φ1,T)=−1,and similarlyµ(φ1,s3)µ(φ1,s3T)=−1.Without loss of generality we may assume thatµ(φ1,s1)=−1.We recall from section2.3that theﬁxed point set Fix s1consists of the arcs b(1)1,b(2)1. Thusφ1must vanish on these arcs.11Consider now the symmetries s3,s3T.We must have one of the following two cases:i)µ(φ1,s3T)=−1,µ(φ1,s3)=1;ii)µ(φ1,s3)=−1,µ(φ1,s3T)=1.Considerﬁrst Case i).Proposition3.3.1.In Case i)the functionφ1vanishes on the arcsb(1)1,b(2)1,b(1)5,b(2)5,b(1)7,b(2)7,and its normal derivative∂nφ1vanishes on the arcsb(1)3,b(2)3,b(1)6,b(2)6,b(1)8,b(2)8.Proof.By Proposition2.4.4,theﬁxed-point set of s3T consists of the arcs b15,b25,b17,b27.Accordingly,φ1vanishes on all those arcs,as well as on b11,b21. Moreover,φ1hasµ(φ1,s3)=µ(φ1,s1T)=1.It follows that the normal deriva-tive of∂nφ1vanishes on theﬁxed-point sets of those symmetries.It remains to apply once more Proposition2.4.4in order to complete the proof.Consider next Case ii).Proposition3.3.2.In Case ii)the functionφ1vanishes on the arcsb(1)3,b(2)3,b(1)6,b(2)6,b(1)8,b(2)8,and its normal derivative∂nφ1vanishes on the arcsb(1)1,b(2)1,b(1)5,b(2)5,b(1)7,b(2)7.Proposition3.3.2is proved in the same way as Proposition3.3.1.3.4Final step of the proofSinceφ1is an odd function with respect to the hyperelliptic involution T,its projection upon S2is not well-deﬁned.However,the projection of|φ1|to S2is well-deﬁned.Denote it byψ1.In Case i),the functionψ1can be chosen as a test function for the mixed Dirichlet-Neumann boundary value problem(1.3.3).Assume now Conjecture121.3.4is true and theﬁrst eigenvalue of(1.3.3)satisﬁesΛ1≥2.Then the Rayleigh quotient ofψ1and hence ofφ1satisﬁes the same inequality.But this means thatψ1cannot be theﬁrst eigenfunction on P since we get a contradiction with(1.1.3).Therefore,theﬁrst eigenfunction of P is even with respect to T, and as was shown in section3.1this implies Conjecture1.3.1.Similarly,in Case ii),the functionψ1can be chosen as a test function for the mixed Dirichlet-Neumann boundary volume problem which is obtained from (1.3.3)by swapping the Dirichlet and the Neumann conditions.However,it was shown in[JLNP]that this problem is isospectral to(1.3.3).Therefore, repeating the same arguments as above we prove that Conjecture1.3.1holds. This completes the proof of Theorem1.3.5.Remark3.4.1.In the proof of Theorem1.3.5we have used only the symmetries s1and s3.Alternatively,we could have used s2and s3.One can check directly using Proposition2.4.4that applying s2one obtains a mixed Dirichlet-Neumann boundary value problem which is equivalent to(1.3.3)and hence no additional information about theﬁrst eigenfunction is obtained.3.5A family of extremal surfaces of genus twoThe purpose of this section is to prove the followingCorollary3.5.1.Conjecture1.3.4implies that there exists a continuous family P t of surfaces of genus2such thatλ1Area(P t)=16π.Proof.Consider the Riemann surface P t deﬁned by the equation(z,w):w2=z z−e i(π/2−t) z−e i(π/2+t)(1+r2)2v on D,v|∂1(t)=0,(∂v/∂n)|∂2(t)=0.(3.5.2)and−∆v=4ΛHere∂1(t):={(r,0):r∈(0,1)}∪{(1,ψ):|ψ−π/2|<t}and∂(t)D:= {(r,π):r∈(0,1)}∪{(1,ψ):π/2>|ψ−π/2|>t}.We remark that for t=π/4these two problems are not ing Dirichlet-Neumann bracketing it is easy to see that(3.5.2)has a smallerﬁrst eigenvalue than(3.5.3)if t<π/4and a larger one if t>π/4.Denote the minimalﬁrst eigenvalue of the two problems byΛ1(t).According to Conjec-ture2and numerical calculations,Λ1(π/4)>2.Since theﬁrst eigenvalues of both problems depend continuously and monotonically on parameter t,and since Λ1(0)=Λ1(π/2)=0.75(see section1.3),there exist numbers t∗1∈(0,π/4) and t∗2∈(π/4,π/2)such thatΛ1(t∗1)=Λ1(t∗2)=2and soΛ1(t)≥2for t∈[t∗1,t∗2].Arguing is above,we deduce that for all surfaces P t corresponding to these values of t,estimate(1.1.3)is sharp.This completes the proof of the theorem.Corollary3.5.1implies that16πis a degenerate maximum forλ1Area(M) for surfaces of genus two.This is not the case for surfaces of lower genus on which the metric maximizing theﬁrst eigenvalue is unique.Note also that the extremal metrics in genera zero and one are analytic,while the surfaces P t have singular points.4Numerical investigations4.1Basics of the Finite Element MethodIn this section we describe the numerical experiments used to estimate theﬁrst eigenvalue of(1.3.7).We deﬁne the space H as the closure of{v∈C∞(D)|dD.(4.1.1)(1+r2)2We useﬁnite elements to approximate the eigenvalues and eigenfunctions of (4.1.1).The general procedure we follow is:1.Discretize the region D using a triangular mesh T h= N h i=1τi,with a sizeof an individual triangleτ∈T h parameterized by h>0.142.Introduce aﬁnite-dimensional subspace V h of H,consisting ofﬁnite ele-ment basis functions{φi}N h i=1on T h;3.Denote(v h,λh)∈V h×R,with v h=(v1,v2,...,v N h)t,the solution oftheﬁnite-dimensional generalized eigenvalue problemA h v h=λhB h v h,(4.1.2)where(A h)ij:= D∇φi·∇φj dD,(B h)ij:= D4φiφjFigure3:Aﬁnite element meshλh N h No.ofArnoldi iterates2.00434573363e-052882.36301118569625118.16135748742e-0846082.301112381849409112.79565739833e-1073728dD,(1+r2)2satisﬁed|Err|<5×10−10.The results are tabulated in Table2.Experiment2:This experiment was conducted using MATLAB’sﬁnite el-ement package PDEToolbox,and the eigenvalue solve was performed using ARPACK routines.A sequence of triangular meshes was created,starting from the coarsest mesh,and reﬁning5times.The major diﬀerence between this and the previous experiment is in the manner in which the zero Dirichlet data is enforced.16λh No.ofTriangles772.4040011835691850410612.305829341498988064163372.28276090970583129024258881dD,(1+r2)2satisﬁed|Err|<5×10−10.The results are presented in Table4.In each of the experiments above,we found that the computed eigenvalues appeared to converge to a value greater than2.27.The associated eigenfunctions also appear to converge to a function whose contour lines are shown in Figure4.17λh N h No.ofArnoldi iterates -1.5494060025e-05288-7.89999667122e-071152-3.8455570927e-084608-1.87263030138e-0918432-8.78059287464e-1173728fellowship and Alfred P.Sloan Foundation fellowship.The research of N.Nig. and I.P.was partially supported by NSERC and FQRNT.References[ArDu]M.Armentano and R.Duran,Asymptotic lower bounds for eigenvalues by nonconformingﬁnite element methods,Electron.Trans.Numer.Anal.17 (2004),93–101.[Bab]I.Babuska and J.Osborn,Eigenvalue problems,in Handbook of Numerical Analysis Vol.II,Finite Element Methods(Part1).Edited by P.G.Ciarlet and J.L.Lions.1991,Elsevier.[Ber]M.Berger,Sur les premi`e res valeurs propres des vari´e t´e s riemanniennes, Compositio Math.26(1973),129–149.[Br]D.Braess,Finite elements,Cambridge University Press,1997.[EGJ]A.El Souﬁ,H.Giacomini,M.Jazar,Greatest least eigenvalue of the Laplacian on the Klein bottle,preprint math.MG/0506585(2005).[GovL]G.Golub,C.van Loan,Matrix Computations,3rd Ed.,John Hopkins University Press,Baltimore,1996.[GH]P.Griﬃths,J.Harris,Principles of algebraic geometry,Wiley,N.Y.,1978.[Gun]R.Gunning,Lectures on Riemann surfaces,Jacobi varieties,Mathematical Notes,No.12.,Princeton Univ.Press,1972.[H]J.Hersch,Quatre propri´e t´e s isop´e rim´e triques de membranes sph´e rique ho-mog`e nes,C.R.Acad.Paris270(1970),1645–1648.[I]J.Igusa,Arithmetic varierty of moduli for genus two,Annals of Math.72(1960),612–649.[JLNP].D.Jakobson,M.Levitin,N.Nadirashvili,I.Polterovich,Spectral prob-lems with mixed Dirichlet-Neumann boundary conditions:isospectrality and beyond,to appear in p.Appl.Math.(2005).[JNP]D.Jakobson,N.Nadirashvili,I.Polterovich,Extremal metric for theﬁrst eigenvalue on the Klein bottle,to appear in Canadian J.Math.(2005).19[KW]H.Karcher,M.Weber,The geometry of Klein’s Riemann surface.The eightfold way,MSRI Publ.35(1999),9–49,Cambridge Univ.Press.[KS]M.Katz,S.Sabourau,An optimal systolic inequality for CAT(0)metrics in genus two,preprint math.DG/0501017(2005).[Ke]J.Keller,Singularities at the tip of a plane angular sector,J.Math.Phys.40(1999),no.2,1087–1092.[LY]P.Li,S.-T.Yau.A new conformal invariant and its applications to the Willmore conjecture and theﬁrst eigenvalue of compact surfaces,Invent.Math.69(1982),269–291.[N]N.Nadirashvili,Berger’s isoperimetric problem and minimal immersions of surfaces,GAFA6(1996),877–897.[Ro]J.Rowlett,Spectral convergence of the Laplacian on a compact manifold with degenerating metric,to appear as a part of the Stanford University Ph.D.thesis under the supervision of R.Mazzeo.[SY]R.Schoen and S.-T.Yau,Lectures on Diﬀerential Geometry,International Press,1994.[TrBa]L.N.Trefethen and D.Bau III,Numerical Linear Algebra,SIAM,1997.[YY]P.Yang,S.-T.Yau,Eigenvalues of the Laplacian of compact Riemann surfaces and minimal submanifolds,Ann.Scuola Norm.Sup.Pisa Cl.Sci.(4) 7(1980),no.1,55–63.20。

école d’été CIMPA Systèmes d’équations polynomiales de la géométrie algébrique au

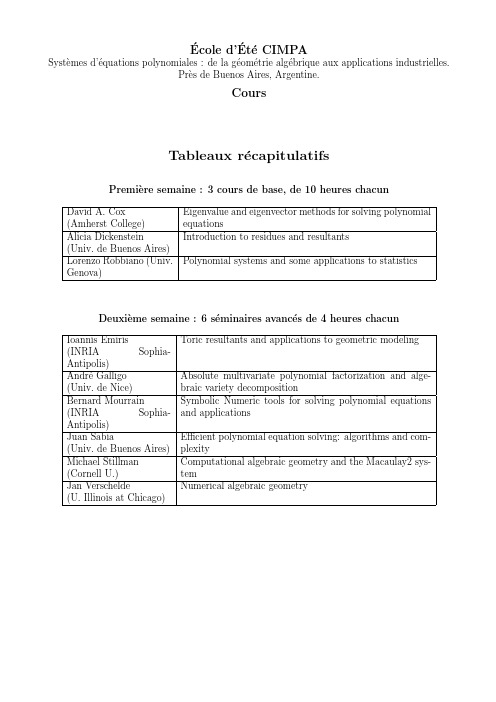
´Ecole d’´Et´e CIMPASyst`e mes d’´e quations polynomiales:de la g´e om´e trie alg´e brique aux applications industrielles.Pr`e s de Buenos Aires,Argentine.CoursTableaux r´e capitulatifsPremi`e re semaine:3cours de base,de10heures chacunDavid A.Cox (Amherst College)Eigenvalue and eigenvector methods for solving polynomial equationsAlicia Dickenstein(Univ.de Buenos Aires)Introduction to residues and resultantsLorenzo Robbiano(Univ.Genova)Polynomial systems and some applications to statisticsDeuxi`e me semaine:6s´e minaires avanc´e s de4heures chacun Ioannis Emiris(INRIA Sophia-Antipolis)Toric resultants and applications to geometric modelingAndr´e Galligo (Univ.de Nice)Absolute multivariate polynomial factorization and alge-braic variety decompositionBernard Mourrain (INRIA Sophia-Antipolis)Symbolic Numeric tools for solving polynomial equations and applicationsJuan Sabia(Univ.de Buenos Aires)Eﬃcient polynomial equation solving:algorithms and com-plexityMichael Stillman (Cornell U.)Computational algebraic geometry and the Macaulay2sys-temJan Verschelde(U.Illinois at Chicago)Numerical algebraic geometryR´e sum´e s disponiblesDavid A.Cox,Eigenvalue and eigenvector methods for solving polynomial equa-tions.Bibliography:W.Auzinger and H.J.Stetter,An Elimination Algorithm for the Computation of all Zeros of a System of Multivariate Polynomial Equations,In Proc.Intern.Conf.on Numerical Math.,Intern.Series of Numerical Math.,vol.86,pp.12–30,Birkh¨a user,Basel,1988,H.M.M¨o ller and H.J.Stetter,Multivariate Polynomial Equations with Multiple Zeros Solved by Matrix Eigenproblems,Numer.Math.,70:311-329,1995.Paper of Moller-Tenberg.Alicia Dickenstein,Introduction to residues and resultants.Some basics of commutative algebra and Groebner bases:Zero dimensional ideals and their quotients,complete intersections.Review of residues in one variable.Multidimensional polynomial residues:properties and applications.Introduction to elimination theory.Resultants.The classical projective case:all known determinantal formulas of resultants.Relation between residues and resultants.Applications to polynomial system solving.Bibliography:E.Becker,J.P.Cardinal,M.-F.Roy and Z.Szafraniec,Multivariate Bezoutians,Kronecker symbol and Eisenbud-Levine formula.In Algorithms in Algebraic Geometry and Applications,L.Gonz´a lez-Vega&T. Recio eds.,Progress in Mathematics,vol.143,p.79–104,Ed.Birkh¨a user,1996.J.P.Cardinal and B.Mourrain,Algebraic Approach of Residues and Applications,In The Mathematics of Numerical Analysis,Lectures in Applied Mathematics,vol.32,pp.189–210,1996,AMS.E.Cattani,A.Dickenstein and B.Sturmfels,Residues and Resultants,J.Math.Sciences,Univ.Tokyo, 5:119–148,1998.E.Cattani,A.Dickenstein&B.Sturmfels:Computing Multidimensional Residues.Algorithms in Algebraic Geometry and Applications,L.Gonz´a lez-Vega&T.Recio eds.,Progress in Mathematics,vol. 143,p.135–164,Ed.Birkh¨a user,1996.D.Cox,J.Little and D.O’Shea,Using Algebraic Geometry,Springer GTM,1998.C.D’Andrea&A.Dickenstein,Explicit Formulas for the Multivariate Resultant,J.Pure&Applied Algebra,164/1-2:59–86,2001.M.Elkadi and B.Mourrain,G´e om´e trie Alg´e brique Eﬀective en dimension0:de la th´e orie`a la pratique, Notes de cours,DEA de Math´e matiques,Universit´e de Nice.2001.I.M.Gelfand,M.Kapranov and A.Zelevinsky:Discriminants,Resultants,and Multidimensional Deter-minants,Birkh¨a user,Boston,1994.J.-P.Jouanolou:Formes d’inertie et r´e sultant:un Formulaire.Advances in Mathematics126(1997), 119–250.E.Kunz,K¨a hler diﬀerentials,Appendices,F.Vieweg&Son,1986.A.Tsikh,Multidimensional residues and Their Applications,Trans.of Math.Monographs,vol.103, AMS,1992.Lorenzo Robbiano,Polynomial systems and some applications to statistics.In theﬁrst part of my lectures we study systems of polynomial equations from the point of view of Groebner bases.In the second part we introduce problems from Design of Experiments,a branch of Statistics,and show how to use computational commutative algebra to solve some of them.Bibliography:Kreuzer and L.Robbiano,Computational Commutative Algebra,vol.1.Springer,2000.L.Robbiano,Groebner Bases and Statistics.In Groebner Bases and Applications,Proc.Conf.33Years of Groebner Bases,London Mathematical Society Lecture Notes Series,B.Buchberger and F.Winkler (eds.),Cambridge University Press,Vol.251(1998),pp.179–204.Ioannis Emiris,Toric resultants and applications to geometric modeling.Toric(or sparse)elimination theory uses combinatorial and discrete geometry to model the struc-ture of a given system of algebraic equations.The basic objects are the Newton polytope of a polynomial,the Minkowski sum of a set of convex polytopes,and a mixed polyhedral subdivision of such a Minkowski sum.It is thus possible to describe certain algebraic properties of the given system by combinatorial means.In particular,the generic number of isolated roots is given by the mixed volume of the corresponding Newton polytopes.This also gives the degree of the toric(or sparse) resultant,which generalizes the classical projective resultant.This seminar will provide an introduction to the theory of toric elimination and toric resultants, paying special attention to the algorithmic and computational issues involved.Diﬀerent matrices expressing the toric resultants shall be discussed,and eﬀective methods for their construction will be deﬁned based on discrete geometric operations,as well as linear algebra,including the subdivision-based methods and the incremental algorithm which is especially relevant for the systems studied by A.Zelevinsky and B.Sturmfels.Toric resultant matrices generalizing Macaulay’s matrix exhibit a structure close to that of Toeplitz matrices,which may reduce complexity by almost one order of magnitude.These matrices reduce the numeric approximation of all common roots to a problem in numerical linear algebra,as described in the courses of this School.In addition to a survey of recent results,the seminar shall point to open questions regarding the theory and the practice of toric elimination methods for system solving.Available software on Maple(from library multires)and in C(from library ALP)shall be de-scribed,with exercises designed to familiarize the user with is main aspects.The goal is to providean arsenal of eﬃcient tools for system solving by exploiting the fact that systems encountered in engineering applications are,more often than not,characterized by some structure.This claim shall be substantiated by examples drawn from several application domains discussed in other courses of this School including robotics,vision,molecular biology and,most importantly,geometric and solid modeling and design.Bibliography:J.F.Canny and I.Z.Emiris,A Subdivision-Based Algorithm for the Sparse Resultant,J.ACM,47(3):417–451,2000.J.Canny and P.Pedersen,An Algorithm for the Newton Resultant,Tech.report1394Comp.Science Dept.,Cornell University,1993.D.Cox,J.Little and D.O’Shea,Using Algebraic Geometry,Springer GTM,1998.C.D’Andrea,Macaulay-style formulas for the sparse resultant,Trans.of the AMS,2002.To appear.C.D’Andrea and I.Z.Emiris,Solving Degenerate Polynomial Systems,In Proc.AMS-IMS-SIAM Conf. on Symbolic Manipulation,Mt.Holyoke,Massachusetts,pp.121–139,AMS Contemporary Mathematics, 2001.I.Emiris,Notes creuses sur l’´e limination creuse,Notes au DEA de Maths,U.Nice,2001,ftp://ftp-sop.inria.fr/galaad/emiris/publis/NOTcreuxDEA.ps.gz.I.Z.Emiris,A General Solver Based on Sparse Resultants:Numerical Issues and Kinematic Applications, INRIA Tech.report3110,1997.I.Z.Emiris and J.F.Canny.Eﬃcient incremental algorithms for the sparse resultant and the mixed volume.J.Symbolic Computation,20(2):117–149,August1995.I.Z.Emiris and B.Mourrain,Matrices in elimination theory,put.,28:3–44,1999.I.M.Gelfand,M.Kapranov and A.Zelevinsky,Discriminants,Resultants,and Multidimensional Deter-minants,Birkh¨a user,Boston,1994.B.Mourrain and V.Y.Pan,Multivariate Polynomials,Duality and Structured Matrices,plexity, 16(1):110–180,2000.B.Sturmfels,On the Newton Polytope of the Resultant,J.of binatorics,3:207–236,1994.B.Sturmfels and A.Zelevinsky,Multigraded Resultants of Sylvester Type,J.of Algebra,163(1):115–127, 1994.Bernard Mourrain,Symbolic Numeric tools for solving polynomial equations and applications.This course will be divided into a tutorial part and a problem solving part.In theﬁrst part, we will gives an introductive presentation of symbolic and numeric methods for solving equations. We will brieﬂy recall well-known analytic methods and less known subdivision methods and will move to algebraic methods.Such methods are based on the study of the quotient algebra A of the polynomial ring modulo the ideal I=(f1,...,f m).We show how to deduce the geometry of the solutions,from the structure of A and in particular,how solving polynomial equations reduces to eigencomputations on these multiplication operators.We will mention a new method for computingthe normal of elements in A,used to obtain a representation of the multiplication operators.based on these formulations.We will describe iterative methods exploiting the properties of A,and which can be applied to select a root(among the other roots),which maximize or minimize some criterion, or to count or isolate the roots in a given domain.A major operation in eﬀective algebraic geometry is the projection,which is closely related to the theory of resultants.We present diﬀerent notions and constructions of resultants and diﬀerent geometric methods for solving systems of polynomial equationsIn a second part,we will consider problems from diﬀerent areas such CAD,robotics,computer vision,computational biology,...and show how to apply the methods that we have presented be-fore.Practical experimentations in maple with the package multires and with the library ALP (environment for symbolic and numeric computations)will illustrate these developments.Bibliography:David Cox,John Little and Donal O’Shea:Ideals,Varieties,and Algorithms,second edition,Under-graduate Texts in Mathematics,Springer,1997.D.Eisenbud,Commutative Algebra with a view toward Algebraic Geometry,Berlin,Springer-Verlag, Graduate Texts in Math.150,1994.M.Elkadi and B.Mourrain.G´e om´e trie Alg´e brique Eﬀective en dimension0:de la th´e orie`a la pratique, Notes de cours,DEA de Math´e matiques,Universit´e de Nice.2001.B.Mourrain,An introduction to algebraic methods for solving polynomial equations,Tutorial in Work-shop on Constructive Algebra and Systems Theory,Acad.Art and Science,Amsterdam,2000,2001,sub-mitted.http://www-sop.inria.fr/galaad/mourrain/Cours/2001tutorial.ps.gz.B.Mourrain and H.Prieto,A framework for Symbolic and Numeric Computations,Rapport de Recherche 4013,INRIA,2000.L.Bus´e,M.Elkadi and B.Mourrain,Residual Resultant of Complete Intersection,J.Pure&Applied Algebra,2001.I.Z.Emiris and B.Mourrain,Matrices in elimination theory,put.,28:3–44,1999.Juan Sabia,Eﬃcient polynomial equation solving:algorithms and complexity.This course intends to familiarize the assistants with the notion of algebraic complexity when solving polynomial equation systems.First,it will deal with the notion of dense representation of multivariate polynomials.Some results about the algebraic complexities of the eﬀective Nullstel-lensatz,of quantiﬁer elimination processes and of decomposition of varieties when using this model will be exposed.Then it will be shown how these complexities are essentially optimal in the dense representation model.This leads to a change of encoding of polynomials to get lower bounds for the complexity:the sparse representation and the straight-line program representation will be discussed. Finally,some complexity results in the straight-line program representation model will be shown (eﬀective Nullstellensatz,quantiﬁer elimination procedures,deformation techniques,for example).Bibliography:D.Brownawell,Bounds for the degrees in the Nullstellensatz,Ann.Math.2nd Series,126(3)(1987) 577-591.L.Caniglia,A.Galligo and J.Heintz,Some new eﬀective bounds in computational geometry,Lecture Notes in Computer Science357,Springer,Berlin(1989),131-151.A.L.Chistov and D.Y.Grigor’ev,Subexponential time solving systems of algebraic equations,LOMI preprint E-9-83,Steklov Institute,Leningrad(1983).A.L.Chistov and D.Y.Grigor’ev,Complexity of quantiﬁer elimination in the theory of algebraically closedﬁelds,Lecture Notes in Computer Science176,Springer,Berlin(1984),17-31.M.Elkadi and B.Mourrain,A new algorithm for the geometric decomposition of a variety,Proceedings of the1999International Symposium on Symbolic and Algebraic Computation(1999).N.Fitchas,A.Galligo and J.Morgenstern,Precise sequential and parallel complexity bounds for quan-tiﬁer elimination over algebraically closedﬁelds,J.Pure Appl.Algebra67(1990)1-14.M.Giusti and J.Heintz,Algorithmes-disons rapides-pour la d´e composition d’une vari´e t´e alg´e brique en composantes irr´e ductibles et´e quidimensionnelles,Progress in Mathematics94,Birkhauser(1991)169-193.M.Giusti,J.Heintz and J.Sabia,On the eﬃciency of eﬀective Nullstellensatz,plexity3, (1993)56-95.J.Heintz and C.P.Schorr,Testing polynomials which are easy to compute,Monographie30de l’Enseignement Math´e matique(1982)237-254.G.Jeronimo and J.Sabia,Eﬀective equidimensional decomposition of aﬃne varieties,to appear in J. Pure Appl.Algebra(2001).G.Lecerf,Computing an equidimensional decomposition of an algebraic variety by means of geometric resolutions,Proceedings of the ISSAC2000Conference(ACM)(2000).J.Kollar,Sharp eﬀective Nullstellensatz,J.AMS1(1988),963-975.S.Puddu and J.Sabia,An eﬀective algorithm for quantiﬁer elimination over algebraically closedﬁelds using straight-line programs,J.Pure Appl.Algebra129(1998),173-200.Jan Verschelde,Numerical algebraic geometry.In a1996paper,Andrew Sommese and Charles Wampler began developing new area,”Numerical Algebraic Geometry”,which would bear the same relation to”Algebraic Geometry”that”Numerical Linear Algebra”bears to”Linear Algebra”.To approximate all isolated solutions of polynomial systems,numerical path following techniques have been proven reliable and eﬃcient during the past two decades.In the nineties,homotopy methods were developed to exploit special structures of the polynomial system,in particular its sparsity.For sparse systems,the roots are counted by the mixed volume of the Newton polytopes and computed by means of polyhedral homotopies.In Numerical Algebraic Geometry we apply and integrate homotopy continuation methods to describe solution components of polynomial systems.One special,but important problem in Symbolic Computation concerns the approximate factorization of multivariate polynomials with approximate complex coeﬃcients.Our algorithms to decompose positive dimensional solution sets of polynomial systems into irreducible components can be considered as symbolic-numeric,or perhaps rather as numeric-symbolic,since numerical interpolation methods are applied to produce symbolic results in the form of equations describing the irreducible components.Applications from mechanical engineering motivated the development of Numerical Algebraic Geometry.The performance of our software on several test problems illustrate the eﬀectiveness of the new methods.Bibliography:J.Verschelde,Polynomial Homotopies for Dense,Sparse and Determinantal Systems,MSRI Preprint Number1999-041.Sophia-Antipolis,18th of March,2002.。

eigenvalue

u = Aa, v = Ab ⇒ u ⋅ v = a ⋅ b
» The norm is also invariant to orthogonal transformation
Similarity Transformations
Eigenbasis
» If a nxn matrix has n distinct eigenvalues, the eigenvectors form a basis for Rn » The eigenvectors of a symmetric matrix form an orthonormal basis for Rn » If a nxn matrix has repeated eigenvalues, the eigenvectors may not form a basis for Rn (see text)
0 if j ≠ k a ak = 1 if j = k
T j
Orthogonal transformation
» y = Ax where A is an orthogonal matrix » Preserves the inner product between any two vectors
(a, b) ≤ a b
» Unit vector: ||a|| = 1
a+b ≤ a + b
Linear Transformation
Properties of a linear operator F
F ( v + x) = F ( v ) + F (x) F (cx) = cF ( x)
» Linear operator example: multiplication by a matrix » Nonlinear operator example: Euclidean norm

A Robust Optimization Approach to Inventory theory

A Robust Oபைடு நூலகம்timization Approach to Inventory Theory
Sloan School of Management and Operations Research Center, Massachusetts Institute of Technology, E53-363, Cambridge, Massachusetts 02139, dbertsim@ Department of Industrial and Systems Engineering, Lehigh University, Mohler Building, Bethlehem, Pennsylvania 18015, aurelie.thiele@
1. Introduction
Optimal supply chain management has been extensively studied in the past with much theoretical success. Dynamic programming has long emerged as the standard tool for this purpose, and has led to signiﬁcant breakthroughs as early as 1960, when Clark and Scarf (1960) proved the optimality of base-stock policies for series systems in their landmark paper. Although dynamic programming is a powerful technique as to the theoretical characterization of the optimal policy for simple systems, the complexity of the underlying recursive equations over a growing number of state variables makes it ill suited for the computation of the actual policy parameters, which is crucial for real-life applications. Approximation algorithms have been developed to address those issues. These include stochastic approximation (see Koshner and Clark 1978) and inﬁnitesimal perturbation analysis (IPA) (see Glasserman 1991, Ho and Cao 1991), where a class of policies, e.g., base-stock, characterized by a set of parameters, is optimized using simulation-based methods (see Fu 1994, Glasserman and Tayur 1995, Kapuscinski and Tayur 1999). IPA-based methods assume knowledge of the underlying probability distributions and restrict their attention to cer150

Consensus and Cooperation in Networked Multi-Agent Systems

Consensus and Cooperation in Networked Multi-Agent SystemsAlgorithms that provide rapid agreement and teamwork between all participants allow effective task performance by self-organizing networked systems.By Reza Olfati-Saber,Member IEEE,J.Alex Fax,and Richard M.Murray,Fellow IEEEABSTRACT|This paper provides a theoretical framework for analysis of consensus algorithms for multi-agent networked systems with an emphasis on the role of directed information flow,robustness to changes in network topology due to link/node failures,time-delays,and performance guarantees. An overview of basic concepts of information consensus in networks and methods of convergence and performance analysis for the algorithms are provided.Our analysis frame-work is based on tools from matrix theory,algebraic graph theory,and control theory.We discuss the connections between consensus problems in networked dynamic systems and diverse applications including synchronization of coupled oscillators,flocking,formation control,fast consensus in small-world networks,Markov processes and gossip-based algo-rithms,load balancing in networks,rendezvous in space, distributed sensor fusion in sensor networks,and belief propagation.We establish direct connections between spectral and structural properties of complex networks and the speed of information diffusion of consensus algorithms.A brief introduction is provided on networked systems with nonlocal information flow that are considerably faster than distributed systems with lattice-type nearest neighbor interactions.Simu-lation results are presented that demonstrate the role of small-world effects on the speed of consensus algorithms and cooperative control of multivehicle formations.KEYWORDS|Consensus algorithms;cooperative control; flocking;graph Laplacians;information fusion;multi-agent systems;networked control systems;synchronization of cou-pled oscillators I.INTRODUCTIONConsensus problems have a long history in computer science and form the foundation of the field of distributed computing[1].Formal study of consensus problems in groups of experts originated in management science and statistics in1960s(see DeGroot[2]and references therein). The ideas of statistical consensus theory by DeGroot re-appeared two decades later in aggregation of information with uncertainty obtained from multiple sensors1[3]and medical experts[4].Distributed computation over networks has a tradition in systems and control theory starting with the pioneering work of Borkar and Varaiya[5]and Tsitsiklis[6]and Tsitsiklis,Bertsekas,and Athans[7]on asynchronous asymptotic agreement problem for distributed decision-making systems and parallel computing[8].In networks of agents(or dynamic systems),B con-sensus[means to reach an agreement regarding a certain quantity of interest that depends on the state of all agents.A B consensus algorithm[(or protocol)is an interaction rule that specifies the information exchange between an agent and all of its neighbors on the network.2 The theoretical framework for posing and solving consensus problems for networked dynamic systems was introduced by Olfati-Saber and Murray in[9]and[10] building on the earlier work of Fax and Murray[11],[12]. The study of the alignment problem involving reaching an agreement V without computing any objective functions V appeared in the work of Jadbabaie et al.[13].Further theoretical extensions of this work were presented in[14] and[15]with a look toward treatment of directed infor-mation flow in networks as shown in Fig.1(a).Manuscript received August8,2005;revised September7,2006.This work was supported in part by the Army Research Office(ARO)under Grant W911NF-04-1-0316. R.Olfati-Saber is with Dartmouth College,Thayer School of Engineering,Hanover,NH03755USA(e-mail:olfati@).J.A.Fax is with Northrop Grumman Corp.,Woodland Hills,CA91367USA(e-mail:alex.fax@).R.M.Murray is with the California Institute of Technology,Control and Dynamical Systems,Pasadena,CA91125USA(e-mail:murray@).Digital Object Identifier:10.1109/JPROC.2006.8872931This is known as sensor fusion and is an important application of modern consensus algorithms that will be discussed later.2The term B nearest neighbors[is more commonly used in physics than B neighbors[when applied to particle/spin interactions over a lattice (e.g.,Ising model).Vol.95,No.1,January2007|Proceedings of the IEEE2150018-9219/$25.00Ó2007IEEEThe common motivation behind the work in [5],[6],and [10]is the rich history of consensus protocols in com-puter science [1],whereas Jadbabaie et al.[13]attempted to provide a formal analysis of emergence of alignment in the simplified model of flocking by Vicsek et al.[16].The setup in [10]was originally created with the vision of de-signing agent-based amorphous computers [17],[18]for collaborative information processing in ter,[10]was used in development of flocking algorithms with guaranteed convergence and the capability to deal with obstacles and adversarial agents [19].Graph Laplacians and their spectral properties [20]–[23]are important graph-related matrices that play a crucial role in convergence analysis of consensus and alignment algo-rithms.Graph Laplacians are an important point of focus of this paper.It is worth mentioning that the second smallest eigenvalue of graph Laplacians called algebraic connectivity quantifies the speed of convergence of consensus algo-rithms.The notion of algebraic connectivity of graphs has appeared in a variety of other areas including low-density parity-check codes (LDPC)in information theory and com-munications [24],Ramanujan graphs [25]in number theory and quantum chaos,and combinatorial optimization prob-lems such as the max-cut problem [21].More recently,there has been a tremendous surge of interest V among researchers from various disciplines of engineering and science V in problems related to multia-gent networked systems with close ties to consensus prob-lems.This includes subjects such as consensus [26]–[32],collective behavior of flocks and swarms [19],[33]–[37],sensor fusion [38]–[40],random networks [41],[42],syn-chronization of coupled oscillators [42]–[46],algebraic connectivity 3of complex networks [47]–[49],asynchro-nous distributed algorithms [30],[50],formation control for multirobot systems [51]–[59],optimization-based co-operative control [60]–[63],dynamic graphs [64]–[67],complexity of coordinated tasks [68]–[71],and consensus-based belief propagation in Bayesian networks [72],[73].A detailed discussion of selected applications will be pre-sented shortly.In this paper,we focus on the work described in five key papers V namely,Jadbabaie,Lin,and Morse [13],Olfati-Saber and Murray [10],Fax and Murray [12],Moreau [14],and Ren and Beard [15]V that have been instrumental in paving the way for more recent advances in study of self-organizing networked systems ,or swarms .These networked systems are comprised of locally interacting mobile/static agents equipped with dedicated sensing,computing,and communication devices.As a result,we now have a better understanding of complex phenomena such as flocking [19],or design of novel information fusion algorithms for sensor networks that are robust to node and link failures [38],[72]–[76].Gossip-based algorithms such as the push-sum protocol [77]are important alternatives in computer science to Laplacian-based consensus algorithms in this paper.Markov processes establish an interesting connection between the information propagation speed in these two categories of algorithms proposed by computer scientists and control theorists [78].The contribution of this paper is to present a cohesive overview of the key results on theory and applications of consensus problems in networked systems in a unified framework.This includes basic notions in information consensus and control theoretic methods for convergence and performance analysis of consensus protocols that heavily rely on matrix theory and spectral graph theory.A byproduct of this framework is to demonstrate that seem-ingly different consensus algorithms in the literature [10],[12]–[15]are closely related.Applications of consensus problems in areas of interest to researchers in computer science,physics,biology,mathematics,robotics,and con-trol theory are discussed in this introduction.A.Consensus in NetworksThe interaction topology of a network of agents is rep-resented using a directed graph G ¼ðV ;E Þwith the set of nodes V ¼f 1;2;...;n g and edges E V ÂV .TheFig.1.Two equivalent forms of consensus algorithms:(a)a networkof integrator agents in which agent i receives the state x j of its neighbor,agent j ,if there is a link ði ;j Þconnecting the two nodes;and (b)the block diagram for a network of interconnecteddynamic systems all with identical transfer functions P ðs Þ¼1=s .The collective networked system has a diagonal transfer function and is a multiple-input multiple-output (MIMO)linear system.3To be defined in Section II-A.Olfati-Saber et al.:Consensus and Cooperation in Networked Multi-Agent Systems216Proceedings of the IEEE |Vol.95,No.1,January 2007neighbors of agent i are denoted by N i ¼f j 2V :ði ;j Þ2E g .According to [10],a simple consensus algorithm to reach an agreement regarding the state of n integrator agents with dynamics _x i ¼u i can be expressed as an n th-order linear system on a graph_x i ðt Þ¼X j 2N ix j ðt ÞÀx i ðt ÞÀÁþb i ðt Þ;x i ð0Þ¼z i2R ;b i ðt Þ¼0:(1)The collective dynamics of the group of agents following protocol (1)can be written as_x ¼ÀLx(2)where L ¼½l ij is the graph Laplacian of the network and itselements are defined as follows:l ij ¼À1;j 2N i j N i j ;j ¼i :&(3)Here,j N i j denotes the number of neighbors of node i (or out-degree of node i ).Fig.1shows two equivalent forms of the consensus algorithm in (1)and (2)for agents with a scalar state.The role of the input bias b in Fig.1(b)is defined later.According to the definition of graph Laplacian in (3),all row-sums of L are zero because of P j l ij ¼0.Therefore,L always has a zero eigenvalue 1¼0.This zero eigenvalues corresponds to the eigenvector 1¼ð1;...;1ÞT because 1belongs to the null-space of L ðL 1¼0Þ.In other words,an equilibrium of system (2)is a state in the form x Ã¼ð ;...; ÞT ¼ 1where all nodes agree.Based on ana-lytical tools from algebraic graph theory [23],we later show that x Ãis a unique equilibrium of (2)(up to a constant multiplicative factor)for connected graphs.One can show that for a connected network,the equilibrium x Ã¼ð ;...; ÞT is globally exponentially stable.Moreover,the consensus value is ¼1=n P i z i that is equal to the average of the initial values.This im-plies that irrespective of the initial value of the state of each agent,all agents reach an asymptotic consensus regarding the value of the function f ðz Þ¼1=n P i z i .While the calculation of f ðz Þis simple for small net-works,its implications for very large networks is more interesting.For example,if a network has n ¼106nodes and each node can only talk to log 10ðn Þ¼6neighbors,finding the average value of the initial conditions of the nodes is more complicated.The role of protocol (1)is to provide a systematic consensus mechanism in such a largenetwork to compute the average.There are a variety of functions that can be computed in a similar fashion using synchronous or asynchronous distributed algorithms (see [10],[28],[30],[73],and [76]).B.The f -Consensus Problem and Meaning of CooperationTo understand the role of cooperation in performing coordinated tasks,we need to distinguish between un-constrained and constrained consensus problems.An unconstrained consensus problem is simply the alignment problem in which it suffices that the state of all agents asymptotically be the same.In contrast,in distributed computation of a function f ðz Þ,the state of all agents has to asymptotically become equal to f ðz Þ,meaning that the consensus problem is constrained.We refer to this con-strained consensus problem as the f -consensus problem .Solving the f -consensus problem is a cooperative task and requires willing participation of all the agents.To demonstrate this fact,suppose a single agent decides not to cooperate with the rest of the agents and keep its state unchanged.Then,the overall task cannot be performed despite the fact that the rest of the agents reach an agree-ment.Furthermore,there could be scenarios in which multiple agents that form a coalition do not cooperate with the rest and removal of this coalition of agents and their links might render the network disconnected.In a dis-connected network,it is impossible for all nodes to reach an agreement (unless all nodes initially agree which is a trivial case).From the above discussion,cooperation can be infor-mally interpreted as B giving consent to providing one’s state and following a common protocol that serves the group objective.[One might think that solving the alignment problem is not a cooperative task.The justification is that if a single agent (called a leader)leaves its value unchanged,all others will asymptotically agree with the leader according to the consensus protocol and an alignment is reached.However,if there are multiple leaders where two of whom are in disagreement,then no consensus can be asymptot-ically reached.Therefore,alignment is in general a coop-erative task as well.Formal analysis of the behavior of systems that involve more than one type of agent is more complicated,partic-ularly,in presence of adversarial agents in noncooperative games [79],[80].The focus of this paper is on cooperative multi-agent systems.C.Iterative Consensus and Markov ChainsIn Section II,we show how an iterative consensus algorithm that corresponds to the discrete-time version of system (1)is a Markov chainðk þ1Þ¼ ðk ÞP(4)Olfati-Saber et al.:Consensus and Cooperation in Networked Multi-Agent SystemsVol.95,No.1,January 2007|Proceedings of the IEEE217with P ¼I À L and a small 90.Here,the i th element of the row vector ðk Þdenotes the probability of being in state i at iteration k .It turns out that for any arbitrary graph G with Laplacian L and a sufficiently small ,the matrix P satisfies the property Pj p ij ¼1with p ij !0;8i ;j .Hence,P is a valid transition probability matrix for the Markov chain in (4).The reason matrix theory [81]is so widely used in analysis of consensus algorithms [10],[12]–[15],[64]is primarily due to the structure of P in (4)and its connection to graphs.4There are interesting connections between this Markov chain and the speed of information diffusion in gossip-based averaging algorithms [77],[78].One of the early applications of consensus problems was dynamic load balancing [82]for parallel processors with the same structure as system (4).To this date,load balancing in networks proves to be an active area of research in computer science.D.ApplicationsMany seemingly different problems that involve inter-connection of dynamic systems in various areas of science and engineering happen to be closely related to consensus problems for multi-agent systems.In this section,we pro-vide an account of the existing connections.1)Synchronization of Coupled Oscillators:The problem of synchronization of coupled oscillators has attracted numer-ous scientists from diverse fields including physics,biology,neuroscience,and mathematics [83]–[86].This is partly due to the emergence of synchronous oscillations in coupled neural oscillators.Let us consider the generalized Kuramoto model of coupled oscillators on a graph with dynamics_i ¼ Xj 2N isin ð j À i Þþ!i (5)where i and !i are the phase and frequency of the i thoscillator.This model is the natural nonlinear extension of the consensus algorithm in (1)and its linearization around the aligned state 1¼...¼ n is identical to system (2)plus a nonzero input bias b i ¼ð!i À"!Þ= with "!¼1=n P i !i after a change of variables x i ¼ð i À"!t Þ= .In [43],Sepulchre et al.show that if is sufficiently large,then for a network with all-to-all links,synchroni-zation to the aligned state is globally achieved for all ini-tial states.Recently,synchronization of networked oscillators under variable time-delays was studied in [45].We believe that the use of convergence analysis methods that utilize the spectral properties of graph Laplacians willshed light on performance and convergence analysis of self-synchrony in oscillator networks [42].2)Flocking Theory:Flocks of mobile agents equipped with sensing and communication devices can serve as mobile sensor networks for massive distributed sensing in an environment [87].A theoretical framework for design and analysis of flocking algorithms for mobile agents with obstacle-avoidance capabilities is developed by Olfati-Saber [19].The role of consensus algorithms in particle-based flocking is for an agent to achieve velocity matching with respect to its neighbors.In [19],it is demonstrated that flocks are networks of dynamic systems with a dynamic topology.This topology is a proximity graph that depends on the state of all agents and is determined locally for each agent,i.e.,the topology of flocks is a state-dependent graph.The notion of state-dependent graphs was introduced by Mesbahi [64]in a context that is independent of flocking.3)Fast Consensus in Small-Worlds:In recent years,network design problems for achieving faster consensus algorithms has attracted considerable attention from a number of researchers.In Xiao and Boyd [88],design of the weights of a network is considered and solved using semi-definite convex programming.This leads to a slight increase in algebraic connectivity of a network that is a measure of speed of convergence of consensus algorithms.An alternative approach is to keep the weights fixed and design the topology of the network to achieve a relatively high algebraic connectivity.A randomized algorithm for network design is proposed by Olfati-Saber [47]based on random rewiring idea of Watts and Strogatz [89]that led to creation of their celebrated small-world model .The random rewiring of existing links of a network gives rise to considerably faster consensus algorithms.This is due to multiple orders of magnitude increase in algebraic connectivity of the network in comparison to a lattice-type nearest-neighbort graph.4)Rendezvous in Space:Another common form of consensus problems is rendezvous in space [90],[91].This is equivalent to reaching a consensus in position by a num-ber of agents with an interaction topology that is position induced (i.e.,a proximity graph).We refer the reader to [92]and references therein for a detailed discussion.This type of rendezvous is an unconstrained consensus problem that becomes challenging under variations in the network topology.Flocking is somewhat more challenging than rendezvous in space because it requires both interagent and agent-to-obstacle collision avoidance.5)Distributed Sensor Fusion in Sensor Networks:The most recent application of consensus problems is distrib-uted sensor fusion in sensor networks.This is done by posing various distributed averaging problems require to4In honor of the pioneering contributions of Oscar Perron (1907)to the theory of nonnegative matrices,were refer to P as the Perron Matrix of graph G (See Section II-C for details).Olfati-Saber et al.:Consensus and Cooperation in Networked Multi-Agent Systems218Proceedings of the IEEE |Vol.95,No.1,January 2007implement a Kalman filter [38],[39],approximate Kalman filter [74],or linear least-squares estimator [75]as average-consensus problems .Novel low-pass and high-pass consensus filters are also developed that dynamically calculate the average of their inputs in sensor networks [39],[93].6)Distributed Formation Control:Multivehicle systems are an important category of networked systems due to their commercial and military applications.There are two broad approaches to distributed formation control:i)rep-resentation of formations as rigid structures [53],[94]and the use of gradient-based controls obtained from their structural potentials [52]and ii)representation of form-ations using the vectors of relative positions of neighboring vehicles and the use of consensus-based controllers with input bias.We discuss the later approach here.A theoretical framework for design and analysis of distributed controllers for multivehicle formations of type ii)was developed by Fax and Murray [12].Moving in formation is a cooperative task and requires consent and collaboration of every agent in the formation.In [12],graph Laplacians and matrix theory were extensively used which makes one wonder whether relative-position-based formation control is a consensus problem.The answer is yes.To see this,consider a network of self-interested agents whose individual desire is to minimize their local cost U i ðx Þ¼Pj 2N i k x j Àx i Àr ij k 2via a distributed algorithm (x i is the position of vehicle i with dynamics _x i ¼u i and r ij is a desired intervehicle relative-position vector).Instead,if the agents use gradient-descent algorithm on the collective cost P n i ¼1U i ðx Þusing the following protocol:_x i ¼Xj 2N iðx j Àx i Àr ij Þ¼Xj 2N iðx j Àx i Þþb i (6)with input bias b i ¼Pj 2N i r ji [see Fig.1(b)],the objective of every agent will be achieved.This is the same as the consensus algorithm in (1)up to the nonzero bias terms b i .This nonzero bias plays no role in stability analysis of sys-tem (6).Thus,distributed formation control for integrator agents is a consensus problem.The main contribution of the work by Fax and Murray is to extend this scenario to the case where all agents are multiinput multioutput linear systems _x i ¼Ax i þBu i .Stability analysis of relative-position-based formation control for multivehicle systems is extensively covered in Section IV.E.OutlineThe outline of the paper is as follows.Basic concepts and theoretical results in information consensus are presented in Section II.Convergence and performance analysis of consensus on networks with switching topology are given in Section III.A theoretical framework for cooperative control of formations of networked multi-vehicle systems is provided in Section IV.Some simulationresults related to consensus in complex networks including small-worlds are presented in Section V.Finally,some concluding remarks are stated in Section VI.RMATION CONSENSUSConsider a network of decision-making agents with dynamics _x i ¼u i interested in reaching a consensus via local communication with their neighbors on a graph G ¼ðV ;E Þ.By reaching a consensus,we mean asymptot-ically converging to a one-dimensional agreement space characterized by the following equation:x 1¼x 2¼...¼x n :This agreement space can be expressed as x ¼ 1where 1¼ð1;...;1ÞT and 2R is the collective decision of the group of agents.Let A ¼½a ij be the adjacency matrix of graph G .The set of neighbors of a agent i is N i and defined byN i ¼f j 2V :a ij ¼0g ;V ¼f 1;...;n g :Agent i communicates with agent j if j is a neighbor of i (or a ij ¼0).The set of all nodes and their neighbors defines the edge set of the graph as E ¼fði ;j Þ2V ÂV :a ij ¼0g .A dynamic graph G ðt Þ¼ðV ;E ðt ÞÞis a graph in which the set of edges E ðt Þand the adjacency matrix A ðt Þare time-varying.Clearly,the set of neighbors N i ðt Þof every agent in a dynamic graph is a time-varying set as well.Dynamic graphs are useful for describing the network topology of mobile sensor networks and flocks [19].It is shown in [10]that the linear system_x i ðt Þ¼Xj 2N ia ij x j ðt ÞÀx i ðt ÞÀÁ(7)is a distributed consensus algorithm ,i.e.,guarantees con-vergence to a collective decision via local interagent interactions.Assuming that the graph is undirected (a ij ¼a ji for all i ;j ),it follows that the sum of the state of all nodes is an invariant quantity,or P i _xi ¼0.In particular,applying this condition twice at times t ¼0and t ¼1gives the following result¼1n Xix i ð0Þ:In other words,if a consensus is asymptotically reached,then necessarily the collective decision is equal to theOlfati-Saber et al.:Consensus and Cooperation in Networked Multi-Agent SystemsVol.95,No.1,January 2007|Proceedings of the IEEE219average of the initial state of all nodes.A consensus algo-rithm with this specific invariance property is called an average-consensus algorithm [9]and has broad applications in distributed computing on networks (e.g.,sensor fusion in sensor networks).The dynamics of system (7)can be expressed in a compact form as_x ¼ÀLx(8)where L is known as the graph Laplacian of G .The graph Laplacian is defined asL ¼D ÀA(9)where D ¼diag ðd 1;...;d n Þis the degree matrix of G with elements d i ¼Pj ¼i a ij and zero off-diagonal elements.By definition,L has a right eigenvector of 1associated with the zero eigenvalue 5because of the identity L 1¼0.For the case of undirected graphs,graph Laplacian satisfies the following sum-of-squares (SOS)property:x T Lx ¼12Xði ;j Þ2Ea ij ðx j Àx i Þ2:(10)By defining a quadratic disagreement function as’ðx Þ¼12x T Lx(11)it becomes apparent that algorithm (7)is the same as_x ¼Àr ’ðx Þor the gradient-descent algorithm.This algorithm globallyasymptotically converges to the agreement space provided that two conditions hold:1)L is a positive semidefinite matrix;2)the only equilibrium of (7)is 1for some .Both of these conditions hold for a connected graph and follow from the SOS property of graph Laplacian in (10).Therefore,an average-consensus is asymptotically reached for all initial states.This fact is summarized in the following lemma.Lemma 1:Let G be a connected undirected graph.Then,the algorithm in (7)asymptotically solves an average-consensus problem for all initial states.A.Algebraic Connectivity and Spectral Propertiesof GraphsSpectral properties of Laplacian matrix are instrumen-tal in analysis of convergence of the class of linear consensus algorithms in (7).According to Gershgorin theorem [81],all eigenvalues of L in the complex plane are located in a closed disk centered at Áþ0j with a radius of Á¼max i d i ,i.e.,the maximum degree of a graph.For undirected graphs,L is a symmetric matrix with real eigenvalues and,therefore,the set of eigenvalues of L can be ordered sequentially in an ascending order as0¼ 1 2 ÁÁÁ n 2Á:(12)The zero eigenvalue is known as the trivial eigenvalue of L .For a connected graph G , 290(i.e.,the zero eigenvalue is isolated).The second smallest eigenvalue of Laplacian 2is called algebraic connectivity of a graph [20].Algebraic connectivity of the network topology is a measure of performance/speed of consensus algorithms [10].Example 1:Fig.2shows two examples of networks of integrator agents with different topologies.Both graphs are undirected and have 0–1weights.Every node of the graph in Fig.2(a)is connected to its 4nearest neighbors on a ring.The other graph is a proximity graph of points that are distributed uniformly at random in a square.Every node is connected to all of its spatial neighbors within a closed ball of radius r 90.Here are the important degree information and Laplacian eigenvalues of these graphsa Þ 1¼0; 2¼0:48; n ¼6:24;Á¼4b Þ 1¼0; 2¼0:25; n ¼9:37;Á¼8:(13)In both cases, i G 2Áfor all i .B.Convergence Analysis for Directed Networks The convergence analysis of the consensus algorithm in (7)is equivalent to proving that the agreement space characterized by x ¼ 1; 2R is an asymptotically stable equilibrium of system (7).The stability properties of system (7)is completely determined by the location of the Laplacian eigenvalues of the network.The eigenvalues of the adjacency matrix are irrelevant to the stability analysis of system (7),unless the network is k -regular (all of its nodes have the same degree k ).The following lemma combines a well-known rank property of graph Laplacians with Gershgorin theorem to provide spectral characterization of Laplacian of a fixed directed network G .Before stating the lemma,we need to define the notion of strong connectivity of graphs.A graph5These properties were discussed earlier in the introduction for graphs with 0–1weights.Olfati-Saber et al.:Consensus and Cooperation in Networked Multi-Agent Systems220Proceedings of the IEEE |Vol.95,No.1,January 2007。

On the fundamental eigenvalue ratio of the p-Laplacian

a r X i v :m a t h /0411013v 1 [m a t h .S P ] 31 O c t 2004On the fundamental eigenvalue ratio of the p –LaplacianJacqueline Fleckinger ♥,Evans M.Harrell II♣,Fran¸c ois de Th´e lin♠AbstractIt is shown that the fundamental eigenvalue ratioλ2Ω|u |p ,(1)we refer to [8,9,16].In this article Ωwill be a smooth,bounded Euclidean domain,andu will vary in the Sobolev space W 1,p0(Ω),corresponding to Dirichlet conditions on the boundary.Several useful estimates are available in the linear case for the lowest two eigenvalues,especially the lowest,or fundamental,eigenvalue,and some of these have been extended to the nonlinear cases.For instance,see [16,17,18].In this article we seek information on the ratio of the ﬁrst two eigenvalues,which to our knowledge has not been much studied except when p =2,for which case it is known,for example,that the ratio is bounded universally above by the ratio attained when Ωis a ball [2].We are guided by some earlier analysis of the case p =2in [11,12,13]as well as [2,3],but the unavailability of the spectral theorem eliminates some essential parts of the analysis.Therefore we attempt to rely instead on certain integral inequalities as in [10].Let us recall some properties of the Dirichlet p–Laplacian:1.The p–Laplacian is deﬁned for u∈W1,p(Ω)by∆p u:=∇· |∇u|p−2|∇u| .(Here wealways equip the p–Laplacian with zero Dirichlet boundary conditions.)2.It is then natural to deﬁne an eigenvalueλj as a value ofλfor which the eigenvalueproblem−∆p u:=λ|u|p−2u inΩ;u=0on∂Ω(2) has a nontrivial solution.3.It is not,however,known whether every such quantity is a variational eigenvalue as forthe case p=2.Of course it is also possible to consider the“variational eigenvalues”but it is not known in general whether these numbers coincide.Nevertheless,it has long been known that theﬁrst eigenvalueλ1,which is isolated and simple,is theinﬁmum,for u∈W1,p0(Ω),of the“Rayleigh quotient”deﬁned by(1).4.The inﬁmum is achieved for a multiple of a functionϕ1that may be chosen positive on Ω.Henceforth we impose the normalization Ωϕp1=1.The pair(λ1,ϕ1)is referred to as the“principal eigenpair.”5.In1996Anane and Tsouli[1]gave a characterization of the variational eigenvalues ofthe Dirichlet p–Laplacian For any positive integer j,letλj:=infC∈C j maxu∈C Ω|∇u|p2p(p−1)ˆk=2(p−2)2p mˆk=1(5) Our main result is2Theorem1.LetΩbe a smooth,N–dimensional bounded Euclidean domain,and denote the two lowest Dirichlet eigenvalues for the p–Laplacian byλ1,λ2.If p≤2and N>p,thenΓ:=λ2−λ1≤ˆm p N pλ1≤1+ˆm p p2p pλ1,(8) or,equivalently,λ22p p .(9) We prepare the proof with two estimates.Theﬁrst is a standard(and known) uncertainty–principle inequality:Lemma2.Given a bounded domainΩ∈I R N,with N>p,for any u∈W1,p(Ω),Ω u N−p p Ω|∇u|p2,where x=(x1,...,x N)are the Cartesian coordinates and where x p:=(x p1+···+x pN )1/p.In particular, Ωϕ1N−p pλ1,(10) This follows easily from an inequality of Boggio,as shown in[10].Lemma3.Given a bounded domainΩ∈I R N,if p≥2,1N pλ1.Proof.1= Ωϕp1=1N Ωx·ϕp−11∇ϕ1≤pp−1as usual,by H¨o lder’s inequality.Therefore1≤ pIf p=2,this establishes the claim.Otherwise,p>2,that is,p′<p,and by H¨o lder’s inequality,1≤ p(p−1)1 p−1≤ p N pλ1 Ω x p2ϕp1 .Proof of Theorem1.For a uniﬁed treatment,we writeΓ:=λ2−ˆkλ1,noting that for p≤2,ˆk=1.Letδbe a given real constant and setω:={x=(x1,...,x N)∈Ω,with x k<δ}.Assume thatδis chosen so that meas(ω)>0and meas(Ω\ω)>0.In otherwordsδmin<δ<δmax.Now choose g∈C10(Ω)such that g(x)xk =δ=0.We deﬁneC:={ϕ1·Gα,β:α∈I R,β∈I R;|α|p+|β|p=1},whereGα,β:=g(x)(αχω+βχΩ\ω).(12) It is easy to see that the set C has the following properties;(1)C=−C(changeαto−αandβto−β).(2)γ(C)=2.From the variational characterization(4),for any k,anyδ,and any function g∈C10(Ω)satisfying g(x)|xk =δ=0,it follows thatλ2≤max|α|p+|β|p=1R(α,β),(13)whereR(α,β):=N(α,β)Therefore:Γ=λ2−ˆkλ1≤ˆm p max|α|p+|β|p=1|α|p ω|ϕ1∇g|p+|β|p Ω\ω|ϕ1∇g|pct+d(1−t)for0≤t≤1.Unless this expression is constant and equal to bc=a+bd or else whent=1as aωϕp1|x j−δ|p, Ω\ωϕp1ωϕp1|x j−δ|p→+∞,while Ω\ωϕp1ωϕp1|x j−δ|p= Ω\ωϕp1 Ωϕp1|x j−δ|p.HenceΩϕp1|x j−δ|p≤ˆm pΓ·N.ThereforeΓ≤ˆm p Nx p≤1x 2p≤pCombining(17)with(15),we derive(6)and(7)for p≤2.In case p≥2,a tighter bound can be derived.Since for p≥2,12p12λ1=2p.Since the Hardyconstant in one dimension is pp λ2(p)√[8]Pavel Dr´a bek,Pavel Krejˇc´i,and Peter Tak´a c,editors and authors,NonlinearDiﬀerential Equations,Boca Raton,FL:CRC Press,1999.[9]Pavel Dr´a bek,A.Kufner,and F.Nicolosi,Nonlinear Elliptic Equations,Sin-gular and Degenerate Case,Pilsen,Czech Republic,Univ.or West Bohemia,1996[10]Jacqueline Fleckinger Evans M.Harrell II,and Fran¸c ois de Th´e lin,Bound-ary behavior and L q estimates for solutions of equations containing the p–Laplacian,Electronic J.Diﬀ.Eqns.1999(1999)No.38,1–19.[11]Evans M.Harrell II and Joachim Stubbe,On trace identities and univer-sal eigenvalue estimates for some partial diﬀerential operators,Trans.Amer.Math.Soc.349(1997)1797–1809.[12]Evans M.Harrell II,General Bounds for the Eigenvalues of Schr¨o dinger Oper-ators,in Maximum Principles and Eigenvalue Problems in Partial DiﬀerentialEquations,P.W.Schaefer,editor.Essex,England:Longman House,and NewYork:Wiley,1988,146–166.[13]Evans M.Harrell II,Some Geometric Bounds on Eigenvalue Gaps,Commun.in Partial Diﬀ.Eqs.18(1993)179–198.[14]Petri Juutinen and Peter Lindqvist,On the higher eigenvalues for the∞–eigenvalue problem,preprint2003.[15]Lew Lefton and Dongming Wei,Numerical approximation of theﬁrst eigenpairof the p–Laplacian usingﬁnite elements and the penalty method,Numer.Funct.Anal.and Optimiz.18(1997)389–399.[16]Peter Lindqvist,On a nonlinear eigenvalue problem,preprint2000(updateof P.Lindqvist,On a nonlinear eigenvalue problem).Fall School in Analysis(Jyv¨a skyl¨a,1994),33–54,Report,68,Univ.Jyv¨a skyl¨a,Jyv¨a skyl¨a,Finland,1995.[17]Matei,Ana-Maria.First eigenvalue for the p–Laplace operator.NonlinearAnal.39(2000),no.8,Ser.A:Theory Methods,1051–1068.[18]H.Takeuchi,On theﬁrst eigenvalue of the p–Laplacian in a Riemannian man-ifold,Tokyo J.Math.21(1998).7。

Eigenvalues of a real supersymmetric tensor

Abstract In this paper, we deﬁne the symmetric hyperdeterminant, eigenvalues and E-eigenvalues of a real supersymmetric tensor. We show that eigenvalues are roots of a one-dimensional polynomial, and when the order of the tensor is even, E-eigenvalues are roots of another one-dimensional polynomial. These two one-dimensional polynomials are associated with the symmetric hyperdeterminant. We call them the characteristic polynomial and the E-characteristic polynomial of that supersymmetric tensor. Real eigenvalues (E-eigenvalues) with real eigenvectors (E-eigenvectors) are called H-eigenvalues (Z-eigenvalues). When the order of the supersymmetric tensor is even, H-eigenvalues (Z-eigenvalues) exist and the supersymmetric tensor is positive deﬁnite if and only if all of its H-eigenvalues (Z-eigenvalues) are positive. An m th-order n -dimensional supersymmetric tensor where m is even has exactly n (m − 1)n −1 eigenvalues, and the number of its E-eigenvalues is strictly less than n (m − 1)n −1 when m ≥ 4. We show that the product of all the eigenvalues is equal to the value of the symmetric hyperdeterminant, while the sum of all the eigenvalues is equal to the sum of the diagonal elements of that supersymmetric tensor, multiplied by (m − 1)n −1 . The n (m − 1)n −1 eigenvalues are distributed in n disks in C. The centers and radii of these n disks are the diagonal elements, and the sums of the absolute values of the corresponding off-diagonal elements, of that supersymmetric tensor. On the other hand, E-eigenvalues are invariant under orthogonal transformations. © 2005 Elsevier Ltd. All rights reserved.

计量经济学中英文词汇对照

Controlled experiments Conventional depth Convolution Corrected factor Corrected mean Correction coefficient Correctness Correlation coefficient Correlation index Correspondence Counting Counts Covaห้องสมุดไป่ตู้iance Covariant Cox Regression Criteria for fitting Criteria of least squares Critical ratio Critical region Critical value
Asymmetric distribution Asymptotic bias Asymptotic efficiency Asymptotic variance Attributable risk Attribute data Attribution Autocorrelation Autocorrelation of residuals Average Average confidence interval length Average growth rate BBB Bar chart Bar graph Base period Bayes' theorem Bell-shaped curve Bernoulli distribution Best-trim estimator Bias Binary logistic regression Binomial distribution Bisquare Bivariate Correlate Bivariate normal distribution Bivariate normal population Biweight interval Biweight M-estimator Block BMDP(Biomedical computer programs) Boxplots Breakdown bound CCC Canonical correlation Caption Case-control study Categorical variable Catenary Cauchy distribution Cause-and-effect relationship Cell Censoring

宏观应力的存在将使衍射峰产生偏移时相应的布拉格公式

宏观应力的存在将使衍射峰产生偏移时相应的布拉格公式下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!摘要：本文将讨论宏观应力对衍射峰产生偏移的影响，以及相应的布拉格公式的推导过程。

In this part

2
In the single antenna Additive White Gaussian Noise (AWGN) channel, 1 bit per second per hertz can be
achieved with every 3dB increase at high SNR. 3 By realistic, we mean models representing our state of knowledge of reality which might be diﬀerent from reality.
and related documents can be downloaded at http://www.ﬂ
January 14, 2004 SUBMITTED VERSION
2
I. Introduction The problem of modelling channels is crucial for the eﬃcient design of wireless systems [4]. The wireless channel suﬀers from constructive/destructive interference signaling [5] and yields a randomized channel with certain statistics to be discovered. Recently ([6], [7]), the need to increase spectral eﬃciency has motivated the use of multiple antennas at both the transmitter and the receiver side. Hence, in the case of i.i.d Gaussian entries of the MIMO link and perfect channel knowledge at the receiver, it has been proved [8] that the ergodic capacity increase is min(nr ,nt ) bits per second per hertz for every 3dB increase (nr is the number of receiving antennas and nt is the number of transmitting antennas) at high Signal to Noise Ratio (SNR)2 . However, for realistic3 channel models, results are still unknown and may seriously put into doubt the MIMO hype. As a matter of fact, the actual design of eﬃcient codes is tributary of the channel model available: the transmitter has to know in what environment the transmission occurs in order to provide the codes with the adequate properties: as a typical example, in Rayleigh fading channels, when coding is performed, the hamming distance (also known as the number of distinct components of the multi-dimensional constellation) plays a central role whereas maximizing the Euclidean distance is the commonly approved design criteria for Gaussian channels (see Giraud and Belﬁore [9] or Boutros and Viterbo [10]). As a consequence, channel modelling is the key in better understanding the limits of transmissions in wireless and noisy environments. In particular, questions of the form: ”what is the highest transmission rate on a propagation environment where we only know the mean of each path, the variance of each path and the directions of arrival?” are crucially important. It will justify the use (or not) of MIMO technologies for a given state of knowledge. Let us ﬁrst introduce the modelling constraints. We assume that the transmission takes place between a mobile transmitter and receiver. The transmitter has nt antennas and the receiver has nr antennas. Moreover, we assume that the input transmitted signal goes through a time invariant linear ﬁlter channel. Finally, we assume that the interfering noise

Competing Species Near a Degenerate Limit

Contents
1 Introduction 2 Preliminaries 3 Invasion of new species 4 Two similar competing species 4.1 Dynamics of (1.8) for τ ≪ 1 and µ bounded away from zero . . . . . . . . . 4.2 Dynamics of (1.8) for τ ≪ 1 and µ < µ1,∗ . . . . . . . . . . . . . . . . . . . . 4.3 Coexistence or Fixation? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 The case τ ≫ 1 2 13 16 18 uction
ut = µ∆u + u(α(x) − u − v ), vt = µ∆v + v (β (x) − u − v ), (1.1a) (1.1b)
We study the following semilinear parabolic system
in Ω × (0, ∞), where Ω is a bounded region in RN with smooth boundary ∂ Ω. On ∂ Ω × (0, ∞), we impose the homogeneous Neumann boundary condition ∂v ∂u = = 0, ∂n ∂n (1.1c)
Abstract We consider a competitive reaction diﬀusion model of two species in a bounded domain which are identical in all aspects except for their birth rates which diﬀer according to a function g. Under fairly weak hypothesis, the semitrivial solutions always exist. Our analysis provides a description of the stability of these solutions as a function of the diﬀusion rate µ and the diﬀerence between the birth rates g. In the case in which the magnitude of g is small we provide a fairly complete characterization of the stability in terms of the zeros of a single function. In particular, we are able to show that for any ﬁxed number n, one can choose the diﬀerence function g from an open set of possibilities in such a way that the stability of the semitrivial solutions changes at least n times as the diﬀusion µ is varied over (0, ∞). This result allows us to make conclusions concerning the existence of co-existent states. Furthermore, we show that under these hypothesis, co-existent states are unique if they exist.

谱方法和边界值法求解二维薛定谔方程硕士学位论文1 精品推荐

硕士学位论文谱方法和边界值法求解二维薛定谔方程摘要薛定谔方程是物理系统中量子力学的基础方程，它可以清楚地说明量子在系统中随时间变化的规律。

通过求解微观系统所对应的薛定谔方程，我们能够得到其波函数以及对应的能量，从而计算粒子的分布概率，进一步来了解其性质。

在化学和物理等诸多科学研究领域当中，薛定谔方程求解的结果都与实际很相符。

近年来，很多学者通过各种方法研究具有复杂势函数的薛定谔方程，解释了很多重要的物理现象，因此对薛定谔方程的求解具有相当重要的意义。

本文主要是用Galerkin-Chebyshev谱方法和边界值法求解二维薛定谔方程。

首先运用Galerkin-Chebyshev谱方法来对空间导数进行近似，离散二维薛定谔方程，从而将原问题转化为复数域上的线性常微分方程组。

然后用边界值法求解该方程组，所求得的数值解即为原问题的解，之后进行误差分析。

最后利用Matlab进行数值模拟，给出数值解的图像以及误差曲面图像，结果显示此方法精度高且具有很好的稳定性。

关键词：薛定谔方程；Galerkin-Chebyshev谱方法；边界值法；数值解；精度高；稳定AbstractThe Schrödinger equation is the basic equations of quantum mechanics in the physical system. It can clearly describe the regular of the quantum evolves over time. By solving the Schrödinger equation which the micro system correspond, we can get the wave function and energy, and thus calculate the probability distribution of the particles, further understand the nature of it.In chemistry, physics and other fields of scientific research, the results of solving the Schrodinger equation are basically consistent with the actual.In recent years, many researchers used a variety of methods to investigate the Schrödinger equation with complex potential function, and explained a lot of important phenomena.Thus solving the Schrödinger equation has very important significance.The main purpose of this paper is to solve the two dimensional Schrödinger equation through the Galerkin-Chebyshev spectral method and the boundary value method. First we use the spectral method to approximate the spatial derivation, discretize the two dimensional Schrödinger equation，and transform the original problem into a set of linear ordinary differential equations in the complex number field.Then by using the boundary value method to solve the equations, that the numerical solutions is the solutions of the original problem, and then analyze the error. Finally we use Matlab to conduct the numerical simulation, and give the images of the numerical solutions and errors, which show that the methods have high precision and good stability.Keywords: Schrödinger equation, Galerkin-Chebyshev spectral method, boundary value method, numerical solutions, high precision, stability目录摘要 (I)Abstract ................................................................................................................. I II 第1章绪论. (5)1.1课题研究的背景和意义 (5)1.2国内外研究现状 (6)1.3本文的主要研究内容 (6)第2章预备知识 (8)2.1克罗内克积的简介 (8)2.2Chebyshev多项式介绍及其性质 (9)2.3Chebyshev正交逼近的性质 (10)2.4投影算子的性质 (11)2.5本章小结 (12)第3章Galerkin-Chebyshev谱方法和边界值法 (13)3.1用Galerkin-Chebyshev谱方法求解椭圆型方程 (13)3.2用边界值法求解常微分方程 (14)3.3本章小结 (18)第4章求解二维薛定谔方程 (19)4.1区域和边界条件的处理 (19)4.1.1 区域的处理 (19)4.1.2 边界条件的处理 (21)4.2二维薛定谔方程的求解 (24)4.3误差分析 (25)4.4本章小结 (30)第5章数值模拟 (31)结论 (36)参考文献 (37)哈尔滨工业大学学位论文原创性声明及使用授权说明 .....错误！未定义书签。

线性代数教学资料—chapter 4

2
Li Jie
THE EIGENVALUE PROBLEM
Core sections
• The eigenvalue problem for (2×2) matrices • Eigenvalues and the characteristic polynomial • Eigenvectors and eigenspaces • Similarity transformations and diagonalization
of A are precisely the roots of p( ) 0.
p( ) det( A I ) characteristic polynomial p( ) det( A I ) 0 characteristic equation
20
Li Jie
1 1 1
where A I is the matrix given by
A

0
3 3
1 1 1 0 0
2 1 1
A

I

0
3
3

0

0

2 1 1 0 0
1 1 1

0
3
3

2 1 1
In section 4.1 we introduce the eigenvalue problem for the special case of (2×2) matrices; this special case can be handled using ideas developed in Chapter 1.