第二章玻尔模型
2玻尔模型-2

锂、钠、钾、铷、铯、钫的原子序数分别是3、11、19、37、55、 87, 各层上的原子数
原子序数 元素 K s 1 2 3 H He Li 1 2 2 1 s L p s M p d s N p
4
5 6 7 8 9 10 11
Be
B C N O F Ne Na
2
2 2 2 2 2 2 2
2
2 2 2 2 2 2 2 1 2 3 4 5 6 6 1
r
e
v
r
Ze
b
a
1 mZ 2 e 4 En 2 ( 2 2 ) n 8 0 h
这与玻尔理论的结果相同。
n 1,2,3,
能量只决定于主量子数n,而与 nϕ 无关。能量n重简 并(也称为退化)。
相对论修正
Ze2 能量: E Ek 4 0 r 2 h 0 半径: rn n 2 mZe2
此外: 电子在椭圆轨道中运动,角动量不变而速度变化,所 以电子质量在改变。结果是电子的轨道不闭合,椭圆 轨道有一个连续进动。
n相同而nϕ不同的轨道,速度 变化情况不同,因而质量的变 化和进动的情况不同。因此这 些轨道运动的能量略有差别。
一个电子轨道 的进动
索末菲按相对论的力学原理进行推算,求得氢原子的能 量等于 2 2 2 m0 c Z n 3 Z E 1 n 2 n n 4 其中第一项就是玻尔理论的结果,第二项起是相对论效 应。可见同一n而nϕ不同的轨道运动具有不同的能量。 但第二项代表的数值比第一项要小得多。
E 8.84eV ,4.89eV ,3.96eV
253.6nm的谱线较强,说明这可能相应于原子获取能 量后,由基态跃迁到第一激发态,再退激发而发出的 辐射。而它相应的能量间隔为 4.89eV。 由此,可推测8.84eV相应于第二激发态。3.96eV几乎 正好等于这两个激发态之间的能量差。由此能级图:
原子物理学第一、二章:卢瑟福模型、玻尔模型

第一章:原子的位形:卢斯福模型
第五节:行星模型的意义及困难 2.原子的同一性
任何元素的原子都是确定的,某一元素的所 有原子之间是无差别的,这种原子的同一性是 经典的行星模型无法理解的。
3.原子的再生性 一个原子在同外来粒子相互作用以后,这个 原子可以恢复到原来的状态,就象未曾发生过 任何事情一样。原子的这种再生性,是卢瑟福 模型所无法说明的.
Automic Physics 原子物理学
第二章:原子的量子态:玻尔模型
第一节 第二节 第三节 第四节 第五节 背景知识 玻尔模型 光 谱
夫兰克--赫兹实验 玻尔理论的推广
第二章:原子的量子态:玻尔模型
第一节:背景知识
卢瑟福模型把原子看成由带正电的原子核和围绕核运动的一 些电子组成,这个模型成功地解释了α粒子散射实验中粒子的 大角度散射现象
2
1
hv
e
c2
1
上式中的 h 就是著名的普朗克常量,其曲线与实验值 完全吻合,而这一公式是普朗克根据实验数据猜出来的。 由此公式当v->0和v->∞时分别都可得到与瑞利--金斯和 维恩公式相同的形式。
第二章:原子的量子态:玻尔模型
第一节:背景知识
此公式虽然符合实验事实但其在公布时仍没有理论根据,就在普朗克公式公 布当天,另一位物理学家鲁本斯将普朗克的结果与他的最新测量数据进行核对, 发现两者以惊人的精确性相符合。 第二天鲁本斯就把这一喜讯告诉了普朗克,从而使普朗克决心:“不惜一切 代价,找到一个理论解释。”
可是当我们准备进入原子内部作进一步的考察时,却发现已经 建立的物理规律无法解释原子的稳定性,同一性和再生性。 玻尔(N.Bohr)基于卢瑟福原子模型,原子光谱的实验规 律以及普朗克的量子化概念,于1913年提出了新的原子模型并 成功地建立了氢原子理论,解释了氢光谱的产生,玻尔理论还 可以准确地推出巴尔末公式,并能算出里德伯常数的理论值。 不过当玻尔理论应用于复杂一些的原子时,就与实验事实 产生了较大的出入。这说明玻尔理论还很粗略,直到1925年量 子力学建立以后,人们才建立了较为完善的原子结构理论。
第二章 原子的玻尔—索末菲理论 (4)
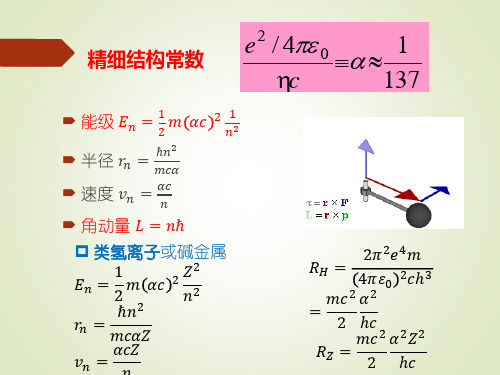
principal
diffuse
fundament al
(next in alphabet after f)
g
4
18
5th shell and higher (theoretically)
原子实极化和轨道贯穿
碱金属原子的光谱可以用类似氢原子的公式表示。这些原 子的能级,当n较大时,非常近氢原子的能级,只有当 n较小 时差别较大。如果考虑到碱金属原子化学上是一价的,它们 容易电离成为带一个单位电荷的离子等情况,可以设想上节 讨论过的那些光谱也是由于单电子的活动产生的。
此式中第一项就是玻尔理论的结果,第二项起则是相对论效 应的修正。显然,对同一n不同nφ,第二项的数值是不同的。 由此可见,同一n而nφ不同的那些轨道运动具有不同的能量。 这样,原来的能级简并在考虑了相对论修正后就消除了。不 过,第二项代表的数值比第一项小得多,所以分裂的能级只 有微小的差别。这个差别被称为能级的精细结构,与它相联 系的常数α称为精细结构常数。索末菲的功绩之一就是引入了 这一十分重要的常数。
n nr n 1,2,3,; n 1,2,3,,n.
上式所表达的是索末菲推广到椭圆轨道后得到的结果,把 它们与玻尔的圆运动情况相比较,不难看出:能量的表达 式没变,但轨道的半径有了长、短半轴之分,且出现了两 个量子数n和nφ。这个结果所包含的物理意义是:轨道的 长半轴和体系的能量只决定于主量子数 n,而与nφ无关; 轨道角动量决定于角量子数nφ,形状取决于 之比。
①椭圆轨道推广 索末菲认为电子绕原子核在一个平面上作椭圆运动,是一 个二维的运动。描述椭圆运动中电子的位置,可用平面极坐 标中的坐标φ和r,与这两个坐标对应的广义动量就是角动量 L 和动量Pr。这体系的能量可表示为
第2章 玻尔理论

3.光谱 3.光谱 α粒子的大角度散射,肯定了原子核的存在,但核外电 粒子的大角度散射,肯定了原子核的存在, 的大角度散射 子的分布及运动情况仍然是个迷, 子的分布及运动情况仍然是个迷,而光谱是原子结构的反 因此研究原子光谱是揭示这个迷的必由之路。 映,因此研究原子光谱是揭示这个迷的必由之路。 电磁波谱
n = 1, 2 , 3 ....
一个硬性的规定常常是在建立一个新理 论开始时所必须的。 论开始时所必须的。
三、关于氢原子的主要结果
1、量子化轨道半径 电子定态轨道角动量满足量子化条件: 电子定态轨道角动量满足量子化条件: 圆周运动: 圆周运动:
me rn vn = nh
2 vn Ze 2 me = rn 4πε 0 rn2
back next 目录 结束
1 1 1 1 2 ( )A = RA ( 2 − 2 )Z = RA ( m 2 − n 2 ) λ m n ( z ) (Z )
1
对He+,Z=2 ,
( )He+
1
λ
1
1 1 = RA ( m 2 − n 2 ) ( 2 ) (2)
设m=4,则n=5,6,7… 则 …
back
next
目录
结束
毕克林系与巴尔末系的区别 (1)毕克林系的谱线比巴尔末系多; (1)毕克林系的谱线比巴尔末系多; 毕克林系的谱线比巴尔末系多 不同,即使n=k的相应谱线, n=k的相应谱线 (2)RHe+与RH不同,即使n=k的相应谱线,位置 也不同。 也不同。 3.类氢离子公式 3.类氢离子公式
跃迁频率: 跃迁频率:
En − Em ν = h
(3) 角动量量子化假设 为保证定态假设中能量取不连续值, 取不连续值, 为保证定态假设中能量取不连续值,必须 rn 取不连续值, 如何做到? 如何做到?
原子物理学第2章原子的量子态全解

的温度升高时,单色辐射能量密度
最大值向短波方向移动.
0 1 2 3 4 λ(µm) 绝对黑体辐射能量密度按波长分布(实验)曲线
第二章 原子的量子态:玻尔模型
Manufacture: Zhu Qiao Zhong
4
物体辐射总能量按波长分布决定于温度.
800K
1000K
1200K
固体在温度升高时颜色的变化
矛盾二:经典的光强和时间决定光电流大小;而光电效应中只有 在光的频率大于红限时才会发生光电效应.
矛盾三:经典的驰豫时间(or:响应时间)较长 (若光强很小,电 子需较长时间吸收足够能量才能逸出),而光电效应不超过10-9s.
实验表明:光强为1μW/m2的光照射到钠靶上即有光电流产生, 这相当于500W的光源照在6.3km处的钠靶.
第二章 原子的量子态:玻尔模型
Manufacture: Zhu Qiao Zhong
10
“在目前业已基本建成的科学大厦中,物理学家似乎只要 做一些零碎的修补工作就行了;然而在物理学晴朗天空的 远处,还飘着两朵令人不安的愁云.”
——《19世纪笼罩在热和光的动力论上的阴影》 1900年4月27日于不列颠皇家科学院
1)光电流与入射光强度的关系
光电子
单色光
I
e
Is
A
V
遏止电压
光强较强 光强较弱
第二章 原子的量子态:玻尔模型
Ua o
U
Manufacture: Zhu Qiao Zhong
15
第二章 原子的量子态:玻尔模型
Manufacture: Zhu Qiao Zhong
16
2)光电子初动能与入射光频率呈线性关系,而与入射光强度
玻尔模型的原理和应用

玻尔模型的原理和应用1. 简介玻尔模型,又称为玻尔-索末菲模型,是位于量子力学早期阶段的一种模型。
它由丹麦物理学家尼尔斯·玻尔于1913年提出,用于解释氢原子的光谱线的产生机制。
玻尔模型成功地揭示了原子的稳定结构和能级的离散性质,并为后来量子力学的发展奠定了基础。
本文将介绍玻尔模型的原理及其在物理学和化学中的应用。
2. 玻尔模型的原理玻尔模型基于以下几个假设:1.电子只能在规定的轨道上运动,每个轨道对应一个特定的能级。
2.电子在轨道上运动时,不会辐射能量。
3.电子只有在跃迁到另一个较低能级的轨道上时,才会辐射出能量(光子),形成光谱线。
根据这些假设,玻尔推导得到了以下关于氢原子能级的公式:$$E = -\\frac{{2\\pi^2me^4Z^2}}{{h^2n^2}}$$其中,E为能级,m为电子质量,e为电子电荷,Z为原子核中质子数,h为普朗克常数,n为轨道的主量子数。
这个公式表明了能级与主量子数n的平方反比,能级越低,主量子数越小;能级越高,主量子数越大。
同时,这个公式也说明了能级的离散性质,即只有特定的能级值是允许的。
3. 玻尔模型的应用3.1 光谱线的解释玻尔模型的最初目的是解释氢原子光谱线的产生机制。
根据玻尔模型,当电子从一个较高的轨道跃迁到一个较低的轨道时,会释放出一个光子,其频率与能级差相关,从而形成光谱线。
通过对氢原子光谱线的研究,玻尔模型成功地解释了氢原子光谱线的频率和能级之间的关系。
3.2 原子结构的研究玻尔模型的成功启示了科学家们研究其他原子结构的思路。
通过将玻尔模型的原理推广到其他原子和离子系统中,科学家们能够预测和解释不同原子的能级结构和光谱线。
玻尔模型为我们理解原子的结构和性质提供了一个重要的基础。
3.3 量子力学的发展玻尔模型的提出对后来量子力学的发展产生了重要的影响。
玻尔模型的成功解释了氢原子光谱线和能级结构的实验现象,同时也暴露出了经典物理学的局限性。
原子物理课件cap2

黑体辐射
困难。然而,历史很快作出了判断,1922年,
爱因斯坦因光电效应获诺贝尔物理奖。
光电效应
光 谱
back
next
目录
结束
(一)光谱 • 光谱是电磁辐射(不论在可见区或在可见区外)的波 长成分和强度分布的记录;有时只是波长成分的记录。 • 光谱是研究原子结构的重要途径之一。 (二)光谱仪 光谱仪:能将混合光按不同波长成分展开成光谱的仪 器。 光谱仪的组成:光源、分光器、记录仪,若装有照相 设备,则称为摄谱仪。
back
next
目录
结束
第二章:原子的量子态:玻尔模型
第一节:背景知识 例如,用光强为 1 / m 2 的光照到钠金属表 面,根据经典理论的推算,至少要 107 秒(约 合120多天)的时间来积聚能量,才会有光电 子产生;事实上,只要ν >ν 0 ,就立即有光电 子产生,可见理论与实验产生了严重的偏离. 此外,按照经典理论,决定电子能量的是光 强,而不是频率.但实验事实却是:
光电效应
光 谱
back
next
目录
结束
第二章:原子的量子态:玻尔模型
第一节:背景知识 早在1887年,德国物理学家赫兹第一个观察 到用紫光照射的尖端放电特别容易发生,这实 际上是光电效应导致的.由于当时还没有电子 的概念,所以对其机制不是很清楚. 直到1897年汤姆逊发现了电子.人们才注意 到一定频率的光照射在金属表面上时,有大量 电子从表面逸出,人们称之为光电效应。光 电效应呈现出以下特点: 1.对一定金属有一个临界频率v0 ,当ν <ν 时,无论光强多大,无电子产生;
黑体辐射实验
前者导致了相对论的诞生后,后者导致了量 子论的诞生。
实验验证之一:光谱
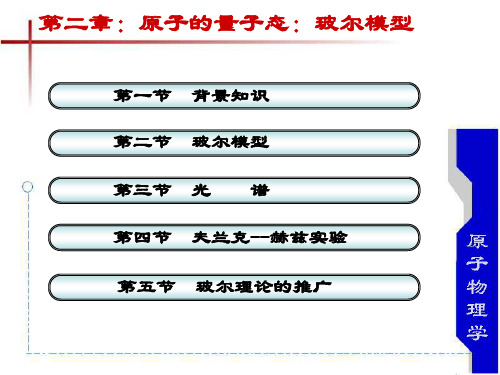
λmaxT=2.898×10-3mK。
维恩位移公式
量子假说根据之一黑体辐射
R( ,T ) c E( ,T )
4
腔内热平衡时的辐 射场的能量密度
1896年,维恩以经典物理为基础,认为能量的吸收和
hv
Tmax
W逸出
1 2
mvmax 2
W逸出
T
1.当光的强度与频率一定时, 当光照在金属表面时,电流几 乎同时产生。(<1 ns)
2.当减速势和光频率固定时, 光电流与光强成正比,即单位 时间内逸出的电子数目正比于 光的强度。
3.当光的强度和频率固定时,光电流随减速势增加而减 小,说明光电子的最大能量和光强无关。
基尔霍夫在光学理论方面的贡献是给出了惠更斯-菲 涅耳原理的更严格的数学形式。
热辐射方面的研究成就:1859年,基尔霍夫证明, 黑体辐射与热辐射达到平衡时,辐射能量密度随频率变 化的曲线与位置只与黑体的热力学温度有关,而与空腔 的形式和组成物质无关。利用黑体可撇开材料的具体性 质来普遍研究热辐射本身的规律
=nhv(n=1,2,3,……)
这一概念严重偏离了经典物理;因此,这一假设提 出后的5年时间内,没有引起人的注意,并且在这以后 的十多年时间里,普朗克很后悔当时的提法,在很多场 合他还极力的掩饰这种不连续性是“假设量子论”。
量子假说根据之二 光电效应
赫兹,(1857-1894) 德国物理学家,生 于汉堡。早在少年时代就被光学和力学 实验所吸引。十九岁入德累斯顿工学院 学工程,由于对自然科学的爱好,次年 转入柏林大学,在物理学教授亥姆霍兹 指导下学习。1885年任卡尔鲁厄大学物 理学教授。1889年,接替克劳修斯担任 波恩大学物理学教授,直到逝世。
玻尔的原子模型5

第二章 原子的量子态:玻尔模型一、学习要点:1背景知识(1)黑体辐射:黑体、黑体辐射、维恩位移律、普朗克黑体辐射公式、能量子假说 (2)光电效应:光电效应、光电效应实验规律、爱因斯坦方程、光量子(光子) (3)氢原子光谱:线状谱、五个线系(记住名称、顺序)、广义巴尔末公式2211()R n n ν=-'、 光谱项()2nR n T =、并合原则:()()T n T n ν'=-2.玻尔氢原子理论:(1)玻尔三条基本假设的实验基础和内容(记熟) (2)圆轨道理论(会推导):氢原子中假设原子核静止,电子绕核作匀速率圆周运动222200002244,0.053Z Z n e e n r n a a nm m e m e πεπε===≈;13714,Z Z 40202≈===c e n c n e c e n πεααπευ; ()24222220Z Z 1()42e n m e R hc E hcT n n nπε∞=-=-=-,n =1,2,3,…… (3)实验验证:(a )氢原子五个线系的形成24223220211,Z ()(4)e m e R R h c n n πνπε∞∞==-'(会推导)非量子化轨道跃迁 21()2n h mv E E ν∞=+- (b )夫朗克-赫兹实验:原理、装置、.结果及分析;原子的电离电势、激发电势 3.类氢离子(+++Li,He ,正电子偶素,-μ原子等)(1) He +光谱:毕克林系的发现、波数公式、与氢原子巴耳末系的异同等(2)理论处理:计及原子核的运动,电子和原子核绕共同质心作匀速率圆周运动eem m m m μ'⋅='+, 正负电荷中心之距Ze n r n 22204μπε =.能量2242202Z )41(n e E n μπε-=,里德伯常数变化11A eR R m m ∞=+'(3)重氢(氘)的发现 4.椭圆轨道理论索末菲量子化条件q q n h n pdq ,⎰=为整数a nn b n e m a n e m E n p e n ϕϕϕπεπε==-==,Z 4,2Z )41(,222022422,n n n ,,3,2,1;,3,2,1 ==ϕn 一定,n E 一定,长半轴一定,有n 个短半轴,有n 个椭圆轨道(状态),即n E 为n 度简并。
第二章 第4节 玻尔的原子模型 能级

第4节玻尔的原子模型__能级一、玻尔的原子结构理论(1)电子围绕原子核运动的轨道不是任意的,而是一系列分立的、特定的轨道,当电子在这些轨道上运动时,原子是稳定的,不向外辐射能量,也不吸收能量,这些状态称为定态。
(2)当原子中的电子从一定态跃迁到另一定态时,才发射或吸收一个光子,其光子的能量hν=E n-E m,其中E n、E m分别是原子的高能级和低能级。
(3)以上两点说明玻尔的原子结构模型主要是指轨道量子化和能量量子化。
[特别提醒]“跃迁”可以理解为电子从一种能量状态到另一种能量状态的瞬间过渡。
二、用玻尔的原子结构理论解释氢光谱1.玻尔的氢原子能级公式E n=E1n2(n=1,2,3,…),其中E1=-13.6 eV,称基态。
2.玻尔的氢原子中电子轨道半径公式r n=n2r1(n=1,2,3,…),其中r1=0.53×10-10 m。
3.玻尔理论对氢光谱解释按照玻尔理论,从理论上求出里德伯常量R H的值,且与实验符合得很好。
同样,玻尔理论也很好地解释甚至预言了氢原子的其他谱线系。
三、玻尔原子结构理论的意义1.玻尔理论的成功之处第一次将量子观念引入原子领域,提出了定态和跃迁的概念,成功地解释了氢原子光谱的实验规律。
2.玻尔理论的局限性不能说明谱线的强度和偏振情况;不能解释有两个以上电子的原子的复杂光谱。
1.判断:(1)玻尔的原子结构假说认为电子的轨道是量子化的。
()(2)电子吸收某种频率条件的光子时会从较低的能量态跃迁到较高的能量态。
()(3)电子能吸收任意频率的光子发生跃迁。
()(4)玻尔理论只能解释氢光谱的巴尔末系。
()答案:(1)√(2)√(3)×(4)×2.思考:卢瑟福的原子模型与玻尔的原子模型有哪些相同点和不同点?提示:(1)相同点:①原子有带正电的核,原子质量几乎全部集中在核上。
②带负电的电子在核外运转。
(2)不同点:卢瑟福模型:库仑力提供向心力,r的取值是连续的。
玻尔模型解析

玻尔模型解析玻尔模型是物理学家尼尔斯·玻尔在1913年提出的,该模型用于解释原子中电子的行为和电子能级的排布。
它被认为是理解和描述原子结构的一种简化模型。
本文将对玻尔模型的原理和应用进行详细解析。
一、玻尔模型的原理玻尔模型基于下面几个假设:1. 氢原子中的电子绕着原子核作圆周运动,类似于一个行星绕着太阳运行。
这种运动被称为量子化运动,即只能存在特定的能量级别。
2. 电子在特定轨道上运动时,不会辐射出能量。
只有当电子从一个轨道跃迁到另一个轨道时,才会吸收或辐射能量。
3. 电子只能处于特定的能级,不会停留在能级之间的状态。
根据这些假设,玻尔模型可以推导出以下几个关键结论:1. 电子的能级与距离原子核的距离相关。
能级越高,距离核心的距离越远。
2. 跃迁时,电子会吸收或放出特定能量的光子。
吸收的光子能量与跃迁前后的能级差相关。
3. 能级越高,电子的能量越大,光子的频率越高。
二、玻尔模型的应用玻尔模型的提出对原子物理学的发展起到了重要作用。
它的应用主要包括以下几个方面:1. 解释氢光谱根据玻尔模型,氢原子的电子处于特定的能级,当电子从一个能级跃迁到另一个能级时,会放出特定频率的光子。
这就解释了氢光谱中的发射线为何是不连续的,每条发射线对应着一个特定的能级差。
2. 描述原子结构玻尔模型将原子中的电子比作行星绕太阳运行,这种图像有助于人们形象地理解原子结构。
通过描述电子的分布和能级,可以更好地解释化学反应和分子的形成。
3. 基础教学工具玻尔模型作为原子结构的简化模型被广泛应用于物理和化学的教学中。
它为学生提供了一个更容易理解的框架,并为他们进一步学习原子结构的复杂理论打下基础。
综上所述,玻尔模型是理解原子结构和描述电子行为的一种简化模型。
它通过将原子中的电子比作绕核的行星,解释了实验中观察到的现象,并为进一步研究原子物理学提供了基础。
尽管玻尔模型在解释较为简单的系统中有效,但随着科学技术的进展,我们已经发现了更为复杂的原子结构和电子行为,这使得玻尔模型在现代物理学中的应用受到了一定的限制。
量子力学玻尔模型的解析

量子力学玻尔模型的解析量子力学是一门探究微观世界的科学,而玻尔模型则是其中的一个经典模型。
它被用来解析氢原子等单电子系统的能级结构以及光谱辐射等现象。
本文将介绍玻尔模型的基本原理和解析方法。
1. 玻尔模型的基本原理玻尔模型是以经典物理学为基础的量子力学模型。
它基于以下三个假设:(1) 原子中的电子绕核运动的轨道是圆形的。
(2) 电子在轨道中运动时不会辐射,只有在跃迁时才会发射或吸收能量。
(3) 跃迁时电子从一个轨道到另一个轨道,能量差等于发射或吸收的光子能量。
根据这三个假设,可以推导出玻尔模型的基本结论:原子的能级是量子化的,能级之间的跃迁只能发生在某些特定的频率下。
2. 玻尔模型的能级结构解析玻尔模型的能级结构可以通过以下公式来计算:E_n = -\frac{me^4}{2\epsilon_0^2 h^2 n^2}其中E_n表示第n级能量,m表示电子质量,e表示元电荷,\epsilon_0表示真空介电常数,h表示普朗克常数,n表示能级数。
可以看到,当n增大时,能级间隔越来越小,电子跃迁的能量不再集中在某一频率范围内,而是变得连续。
这是因为玻尔模型只适用于单电子系统,而在实际的多电子原子系统中,电子之间的相互作用会使能级分裂。
此外,玻尔模型还可以解析氢原子等的光谱线性质。
对于氢原子,其发射或吸收光子的波长可以通过以下公式计算:\frac{1}{\lambda} = R_H (\frac{1}{n_f^2}-\frac{1}{n_i^2})其中R_H表示里德伯常量,n_i和n_f表示跃迁前后电子的能级。
通过这个公式,可以计算出氢原子发射光谱和吸收光谱的波长。
此外,玻尔模型还可以解析氦原子等的双电子系统的能级结构。
3. 玻尔模型的局限性和发展尽管玻尔模型为量子力学的发展奠定了重要的基础,但其本身仍有很多局限性。
例如,电子的轨道不一定是圆形的,电子的运动速度无法用经典物理学描述等。
因此,玻尔模型只能用来解析单电子系统下的一些基本现象,而在实际中通常需要引入更为复杂的模型来描述多电子系统。
原子物理学 原子的量子态:玻尔模型 (2.3.3)--第二章补充内容

4
1 2
mo
(c)2 n2
1
1 4
n
2
能量整体下
对椭圆轨道相对论修正 : 轨道的进动使得在 n 相同 nf 不同的轨道上运动时能量略有差别。索末菲按相对论
力学原理推得:
�
� 12
�
�
E
mc2
mc2
� �1 � � �
轨道运动频率。
今天,推广至:任何一种新理论,不论它的 特性和细节,当把它应用到普遍性较小的理 论适用的情况时,必定可化为与它相应的、 已牢固确定的旧理论!
2. 玻尔理论成就
• 第一次把光谱的实验事实纳入一个理论体 系中
• 提出了动态的原子结构轮廓;提出了经 典理论有的不适用于原子内部
• 提出了微观体系特有的量子规律,如 能量量子化、角动量量子化,频率条 件等,启发了原子物理向前发展的途 径。
提出对应原理:在主量子数 n- 〉 的
极限条件下,量子规律趋向经典规律, 得到一致的结果。
例:氢原子理论结果符合对应原理的要求
两能级差: DE
Rhc[
1 n2
1 m2
]
n很大,时 Dn n m << n
DE
2RhcDn n3
nᅲ ᅲ
ᅲ0
能级趋于连续,量子 化特性消失。
还如:n 时,原子辐射频率趋于经典电子
1
v2 c2
物体动能:
T
m0c 2
1
1
1
v c
第二节 玻尔模型

1
令
1 1 2 R m( c) , 2 hc
R 109737.315cm
back
next
目录
结束
第二章:原子的量子态:玻尔模型
第二节:玻尔模型
R 称为里德伯常数,光谱公式为
~
玻尔假设 电子的运 动 氢光谱的 解释
1 2 1 v RZ 2 '2 n n
Ze 2 v2 2 m 即 40 r r 1
代入量子化条件 解得
Ze 2 r 2 40 mv 1
40 n 2 h 2 nh Vn ; rn 2 4 mZe2 2mr
back next 目录 结束
L mvr nh
第二章:原子的量子态:玻尔模型
第二节:玻尔模型
所以
1 mv0 2 En 2 因为 En 是一定的,而 v0 是任意的,所以可
以产生连续的 λ 值,对应连续的光谱,这 就是各系限外出现连续谱的原因。
back next
hc
目录
结束
第二章:原子的量子态:玻尔模型
第二节:玻尔模型
我们曾经定义光谱项
RH Tn 2 , n
前面已由
玻尔假设 电子的运 动 氢光谱的 解释
当 Z=1 时即为里德伯方程。试验中 R 的经 验值为
RH 109677.58cm1
比较 R 与 RH ,我们发现两者符合的很好, 但仍存在微小的差别。
back next 目录 结束
第二章:原子的量子态:玻尔模型
第二节:玻尔模型
我们已经知道,所有的光谱线分为一系列线 系,每个线系的谱线都从最大波长到最小波 长(系线);可是试验中观察到在系限之外 还有连续变化的谱线。这是怎么回事呢? 如果定义距核无穷远处的势能为0,那么位 于r=∞处的电子势能为0,但可具有任意的 1 动能 2
原子物理第3讲第二章玻尔模型资料
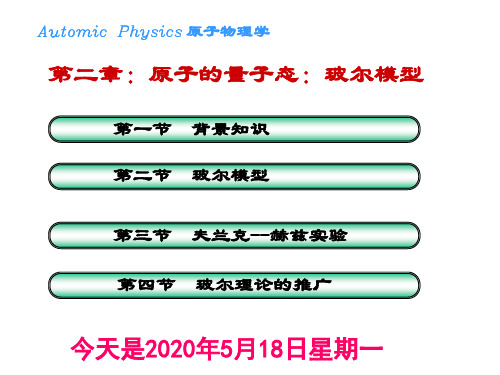
电离能:将一个基态电子电离至少需要的能量。对氢,13.6eV.
电离电势:U
eU E E1
U
E
e
E1
U 13.6V
玻尔理论的成功之二
自 氢原子能级图
由
态 n E / eV 0
激 n4 发 n3
0.85 1.51
态
n2
3.4
第一激发电势:U1
eU1 E2 E1
U1
E2
e
E1
U1 10.2V
)](nm)
n = 2 时对应最长波长 max 121.5nm
n = ∞时对应最短波长 min 91.2nm
帕邢系
1/[1.097
102
(
1 32
1 n2
)](nm)
53 1282nm
玻尔理论基于
•卢瑟福的原子核模型 •氢原子光谱的巴尔末公式 •普朗克能量子概念
玻尔(Niels henrik David Bohr,1885-1962)
一、玻尔基本假设(1913年)
(1) 定态(stationary state)假设
定态假说:电子在原子中,可以在一些特定的圆轨道上运动, 而不辐射电磁波,这时原子处于稳定状态(简称定态),每一 个定态都与一定的能量相对应;
电子轨道 rn 和能量分立(能级)En
n 1, 2, 3, K
——主量子数
v%
RH
1 m2
1 n2
m=1,2,3,4,5……. ------里德堡公式
n=m + 1, m + 2 , m + 3 或(广义的巴尔末公式)
例题1:
计算赖曼系的最短波长和最长波长 计算帕邢系第二条谱线的波长
第二章 4 玻尔的原子模型 能级

4 玻尔的原子模型 能级[学习目标] 1.知道玻尔原子结构理论的基本假设的主要内容.2.了解能级、跃迁、能量量子化及基态、激发态等概念.3.能用玻尔原子理论简单解释氢原子光谱.4.会计算原子跃迁时吸收或辐射光子的能量.一、玻尔的原子结构理论1.定态假设:电子围绕原子核运动的轨道不是任意的,而是一系列分立的、特定的轨道.当电子在这些轨道上运动时,原子是稳定的,不向外辐射能量,也不吸收能量,这些状态称为定态.2.跃迁假设:原子处在定态的能量用E n 表示,此时电子以r n 的轨道半径绕核运动,n 称为量子数.当原子中的电子从一定态跃迁到另一定态时,才发射或吸收一个光子,光子的能量hν=E n -E m ,式中E n 和E m 分别是原子的高能级和低能级,其中h 是普朗克常量,h =6.626×10-34 J·s ,ν是光子的频率.3.轨道量子化假设:围绕原子核运动的电子轨道半径只能是某些分立值,称之为轨道量子化.二、用玻尔的原子结构理论解释氢光谱1.氢原子的能级公式:E n =E 1n 2(n =1,2,3,…),E 1=-13.6 eV ,E 2=-3.4 eV ,…对应的轨道半径r n =n 2r 1(n =1,2,3,…),r 1=0.53×10-10 m.2.基态:能量最低的状态叫做基态.3.激发态:除基态之外的其他状态叫做激发态.4.吸收或辐射光子的能量hν=E n -E m =E 1(1n 2-1m 2). 三、玻尔原子结构理论的意义1.玻尔的原子结构理论比较完满地解释了氢光谱,他用能级跃迁的概念阐明了光谱的吸收和发射,第一次将量子概念引入原子模型,推动了量子力学的发展.2.局限性它不能说明谱线的强度和偏振情况.在解释有两个以上电子的原子的复杂光谱时也遇到了困难,玻尔的理论是不完善的.1.判断下列说法的正误.(1)玻尔认为电子运行轨道半径是任意的,就像人造地球卫星,能量大一些的电子,轨道半径就会大点.(×)(2)玻尔认为原子的能量是量子化的,不能连续取值.(√)(3)当电子从能量较高的定态轨道跃迁到能量较低的定态轨道时,会放出任意能量的光子.(×)(4)处于基态的原子是不稳定的,会自发地向其他能级跃迁,放出光子.(×)(5)玻尔的原子理论模型可以很好地解释氦原子的光谱现象.(×)2.电子处在n=4轨道上比处在n=3轨道上离核的距离(填“远”或“近”),能量值(填“大”或“小”).答案远大一、玻尔的原子结构理论1.按照经典理论,核外电子在库仑引力作用下绕原子核做圆周运动.我们知道,库仑引力和万有引力形式上有相似之处,电子绕原子核的运动与卫星绕地球的运动也一定有某些相似之处,那么若将卫星—地球模型缩小是否就可以变为电子—原子核模型呢?答案不可以.在玻尔理论中,电子的轨道半径只可能是某些分立的数值,而卫星的轨道半径可按需要任意取值.2.氢原子吸收或辐射光子的频率条件是什么?它和氢原子核外电子的跃迁有什么关系?答案电子从能量较高的定态轨道(其能量记为E n)跃迁到能量较低的定态轨道(其能量记为E m)时,会放出能量为hν的光子(h是普朗克常量),这个光子的能量由前后两个能级的能量差决定,即hν=E n-E m(n>m).这个式子称为频率条件,又称辐射条件.当电子从较低的能量态跃迁到较高的能量态,吸收的光子的能量同样由频率条件决定.1.轨道量子化(1)轨道半径只能够是一些不连续的、某些分立的数值.(2)氢原子中电子轨道的最小半径为r1=0.053 nm,其余轨道半径满足r n=n2r1,式中n称为量子数,对应不同的轨道,只能取正整数.2.能量量子化(1)电子在可能轨道上运动时,尽管是圆周运动,但它并不释放能量,原子是稳定的,这样的状态称之为定态.(2)由于原子的可能状态(定态)是不连续的,具有的能量也是不连续的.这样的能量值称为能级,能量最低的状态称为基态,其他状态叫做激发态.3.跃迁:原子从一种定态(设能量为E n)跃迁到另一种定态(设能量为E m)时,它辐射(或吸收)一定频率的光子,光子的能量由这两种定态的能量差决定,高能级低能级E m.E n发射光子hν=E n-E m吸收光子hν=E n-E m可见,电子如果从一个轨道到另一个轨道,不是以螺旋线的形式改变半径大小的,而是从一个轨道上“跳跃”到另一个轨道上.玻尔将这种现象叫做电子的跃迁.特别提醒(1)处于基态的原子是稳定的,而处于激发态的原子是不稳定的.(2)原子的能量与电子的轨道半径相对应,轨道半径大,原子的能量大,轨道半径小,原子的能量小.但半径越大,电子动能越小,半径越小,动能越大.命题角度1对玻尔理论的理解例1(多选)按照玻尔理论,下列表述正确的是()A.核外电子运动轨道半径可取任意值B.氢原子中的电子离原子核越远,氢原子的能量越大C.电子跃迁时,辐射或吸收光子的能量由能级的能量差决定,即hν=E m-E n(m>n)D.氢原子从激发态向基态跃迁的过程,可能辐射能量,也可能吸收能量答案BC解析根据玻尔理论,核外电子运动的轨道半径是确定的值,而不是任意值,A错误;氢原子中的电子离原子核越远,氢原子的能量越大,B正确;由跃迁规律可知C正确;氢原子从激发态向基态跃迁的过程中,应辐射能量,D错误.命题角度2氢原子的能量和能量变化例2氢原子的核外电子从距核较近的轨道跃迁到距核较远的轨道的过程中()A.原子要吸收光子,电子的动能增大,原子的电势能增大B.原子要放出光子,电子的动能减小,原子的电势能减小C.原子要吸收光子,电子的动能增大,原子的电势能减小D.原子要吸收光子,电子的动能减小,原子的电势能增大答案 D解析根据玻尔理论,氢原子的核外电子在离核较远的轨道上运动,氢原子的能量较大,必须吸收一定能量的光子后,电子才能从离核较近的轨道跃迁到离核较远的轨道,故B 错误;氢原子的核外电子绕核做圆周运动,由原子核对电子的库仑力提供向心力,即:k e 2r 2=m v 2r,又E k =12m v 2,所以E k =ke 22r.由此式可知:电子离核越远,即r 越大时,电子的动能越小,故A 、C 错误;r 变大时,库仑力对核外电子做负功,因此电势能增大,故D 正确.原子的能量及变化规律1.原子的能量:E n =E k n +E p n .2.电子绕氢原子核运动时:k e 2r n 2=m v n 2r n, 故E k n =12m v n 2=ke 22r n电子轨道半径越大,电子绕核运动的动能越小.3.当电子的轨道半径增大时,库仑引力做负功,原子的电势能增大,反之,电势能减小.4.电子的轨道半径增大时,说明原子吸收了光子,从能量较低的轨道跃迁到了能量较高的轨道上.即电子轨道半径越大,原子的能量E n 越大.针对训练1 (多选)关于对氢原子能级公式E n =E 1n2的理解,下列说法中正确的是( ) A .原子的定态能量E n 是指核外电子动能和电子与核之间的电势能的总和B .E n 是负值C .E n 是指核外电子的动能,只能取正值D .从公式中可以看出,随着电子运动半径的增大,原子总能量减少答案 AB二、玻尔理论对氢原子光谱的解释如何解释氢气导电发光现象?它的谱线为什么又是分立的?答案 (1)通常情况下原子处于基态,基态是最稳定的状态.氢气在放电管中受到高速运动的电子的撞击,跃迁到激发态.处于激发态的原子是不稳定的,会自发地向能量较低的能级跃迁,放出光子,最终又回到基态.(2)氢原子从高能级向低能级跃迁时,放出的光子能量等于前后两个能级的能量差.由于原子的能级是分立的,所以放出的光子的能量也是分立的.因此原子的发射光谱只有一些分立的亮线.由于不同的原子具有不同的结构,能级各不相同,因此辐射或吸收的光子也不相同,这就是不同元素的原子具有不同的特征谱线的原因.1.氢原子能级图(如图1所示)图1(1)能级图中n 称为量子数,E 1代表氢原子的基态能量,即量子数n =1时对应的能量,其值为-13.6 eV.E n 代表电子在第n 个轨道上运动时氢原子的能量.(2)作能级图时,能级横线间的距离和相应的能级差相对应,能级差越大,间隔越宽,所以量子数越大,能级越密,竖直线的箭头表示原子跃迁方向,长度表示辐射光子能量的大小,n =1是原子的基态,n →∞是原子电离时对应的状态.2.能级跃迁:处于激发态的原子是不稳定的,它会自发地向较低能级跃迁,经过一次或几次跃迁到达基态.所以一群氢原子处于量子数为n 的激发态时,可能辐射出的光谱线条数为N=C 2n =n (n -1)2. 3.光子的发射:原子由高能级向低能级跃迁时以光子的形式放出能量,发射光子的频率由下式决定.hν=E n -E m (E n 、E m 是始末两个能级且n >m ),能级的能量差越大,放出光子的频率就越高.4.光子的吸收:原子只能吸收一些特定频率的光子,原子吸收光子后会从较低能级向较高能级跃迁,吸收光子的能量仍满足hν=E n -E m (n >m ).例3 如图2所示是氢原子的能级图,大量处于n =4激发态的氢原子向低能级跃迁时,一共可以辐射出6种不同频率的光子,其中巴尔末系是指氢原子由高能级向n =2能级跃迁时释放的光子,则( )图2A .6种光子中能量最小的是n =4激发态跃迁到基态时产生的B .6种光子中有2种属于巴尔末系C .使n =4能级的氢原子跃迁到n =10能级需要0.85 eV 的能量D .6种光子中频率最大的是n =2激发态跃迁到基态时产生的答案 B解析 n =4激发态跃迁到基态时产生光子的能量最大,频率最大,故A 、D 错误;其中巴尔末系是指氢原子由高能级向n =2能级跃迁时释放的光子,6种光子中只有从n =4→n =2与n =3→n =2的属于巴尔末系,故B 正确;n =4能级的氢原子具有的能量为-0.85 eV ,n =10能级的氢原子具有的能量为-0.136 eV ,故要使n =4能级的氢原子跃迁到n =10能级,需要0.714 eV 的能量,故C 错误.针对训练2 如图3所示为氢原子的能级图.用光子能量为13.06 eV 的光照射一群处于基态的氢原子,则可能观测到氢原子发射的不同波长的光有( )图3A .15种B .10种C .4种D .1种答案 B解析 基态的氢原子的能量为-13.6 eV ,吸收13.06 eV 的能量后变成-0.54 eV ,原子跃迁到n =5能级,由于氢原子是大量的,故辐射的光子种类是C 25=5×(5-1)2=10种. 1.(玻尔理论)根据玻尔理论,下列关于氢原子的论述正确的是( )A .当氢原子由能量为E n 的定态向低能级跃迁时,氢原子要辐射的光子能量为hν=E nB .电子沿某一轨道绕核运动,若圆周运动的频率为ν,则其发光的频率也是νC .一个氢原子中的电子从一个半径为r a 的轨道自发地直接跃迁到另一个半径为r b 的轨道,已知r a >r b ,则此过程原子要辐射某一频率的光子D .氢原子吸收光子后,将从高能级向低能级跃迁答案 C解析 氢原子由能量为E n 的定态向低能级跃迁时,辐射的光子能量等于能级差,与E n 不同,故A错误;电子沿某一轨道绕核运动,处于某一定态,不向外辐射能量,故B错误;电子由半径大的轨道跃迁到半径小的轨道,能级降低,因而要辐射某一频率的光子,故C正确;原子吸收光子后能量增加,能级升高,故D错误.2.(能级跃迁与光谱)(2020·永春一中高二期末)图4甲所示为氢原子的能级图,图乙为氢原子的光谱.已知谱线a对应氢原子从n=4能级跃迁到n=2能级时的辐射光,则谱线b可能对应氢原子时的辐射光.(填选项前的字母)图4A.从n=5能级跃迁到n=3能级B.从n=4能级跃迁到n=3能级C.从n=5能级跃迁到n=2能级D.从n=3能级跃迁到n=2能级答案 C解析从题图乙看出,谱线a对应的波长大于谱线b对应的波长,所以谱线a对应的光子频率小于谱线b对应的光子频率,谱线a对应的光子的能量小于谱线b对应的光子的能量,因谱线a对应氢原子从n=4能级跃迁到n=2能级时的辐射光,所以谱线b对应的光子能量大于n=4与n=2间的能级的能量差,结合各选项分析可知C项可能,故选C.3.(能级跃迁)(2019·全国卷Ⅰ)氢原子能级示意图如图5所示.光子能量在1.63 eV~3.10 eV 的光为可见光.要使处于基态(n=1)的氢原子被激发后可辐射出可见光光子,最少应给氢原子提供的能量为()图5A.12.09 eV B.10.20 eV C.1.89 eV D.1.51 eV答案 A解析因为可见光光子的能量范围是1.63 eV~3.10 eV,所以处于基态的氢原子至少要被激发到n=3能级,要给氢原子提供的能量最少为E=(-1.51+13.60) eV=12.09 eV,故选项A 正确.考点一玻尔原子模型1.(多选)由玻尔理论可知,下列说法中正确的是()A.电子绕核运动有加速度,就要向外辐射电磁波B.处于定态的原子,其电子做变速运动,但它并不向外辐射能量C.原子内电子的可能轨道是连续的D.原子内电子的轨道半径越大,原子的能量越大答案BD解析按照经典物理学的观点,电子绕核运动有加速度,一定会向外辐射电磁波,很短时间内电子的能量就会消失,与客观事实相矛盾;而由玻尔理论可知选项A、C错误,B正确.原子内电子的轨道半径越大,原子的能量越大,选项D正确.2.(多选)(2020·银川一中模拟)玻尔在他提出的原子模型中所做的假设有()A.原子处于称为定态的能量状态时,电子在轨道上绕核转动,但并不向外辐射能量B.原子的不同能量状态与电子沿不同的圆轨道绕核运动相对应,而电子的可能轨道的分布是不连续的C.电子从一个轨道跃迁到另一个轨道时,辐射(或吸收)一定频率的光子D.电子跃迁时辐射的光子的频率等于电子绕核做圆周运动的频率答案ABC3.(多选)光子的发射和吸收过程是()A.原子从基态跃迁到激发态要放出光子,放出光子的能量等于原子在始、末两个能级的能量差B.原子不能从低能级向高能级跃迁C.原子吸收光子后从低能级跃迁到高能级,放出光子后从较高能级跃迁到较低能级D.原子无论是吸收光子还是放出光子,吸收的光子或放出的光子的能量恒等于始、末两个能级的能量差答案CD解析由玻尔理论的跃迁假设知,原子处于激发态不稳定,可自发地向低能级发生跃迁,以光子的形式放出能量,光子的吸收是光子发射的逆过程,原子在吸收光子后,会从较低能级向较高能级跃迁,但不管是吸收光子还是放出光子,光子的能量总等于始、末两个能级的能量差,即hν=E m-E n(m>n),故选项C、D正确,A、B错误.4.(2020·洛阳市统考)氢原子的核外电子由离核较远的轨道跃迁到离核较近的轨道上,下列说法正确的是()A.氢原子的能量减少B.氢原子的能量不变C.核外电子受力变小D.氢原子要吸收一定频率的光子答案 A解析核外电子从离核较远的轨道跃迁到离核较近的轨道的过程中,原子能级减小,总能量可知,轨道半径减小,则核外电子受力变大,故C 减少,所以A正确,B错误;根据F=ke2r2错误;从离核较远的轨道跃迁到离核较近的轨道的过程中,总能量减少,要放出一定频率的光子,故D错误.考点二能级跃迁对氢原子光谱的解释5.一群氢原子处于同一较高的激发态,它们向较低激发态或基态跃迁的过程中() A.可能吸收一系列频率不同的光子,形成光谱中的若干条暗线B.可能发出一系列频率不同的光子,形成光谱中的若干条亮线C.只吸收频率一定的光子,形成光谱中的一条暗线D.只发出频率一定的光子,形成光谱中的一条亮线答案 B6.(2019·无锡高二检测)已知处于某一能级n上的一群氢原子向低能级跃迁时,能够发出10种不同频率的光,下列能表示辐射光波长最长的跃迁的示意图是()答案 A解析根据玻尔理论,波长最长的跃迁对应着频率最小的跃迁,即放出的光子能量最小,根据氢原子能级图,可知对应的是从n=5能级到n=4能级的跃迁,选项A正确.7.(多选)(2020·湖北七市联考)如图1所示是氢原子的能级图,大量处于n=5激发态的氢原子向低能级跃迁时,一共可以辐射出10种不同频率的光子.其中赖曼系是指氢原子由高能级向n=1能级跃迁时释放的光子,则()图1A.10种光子中波长最短的是n=5激发态跃迁到基态时产生的B.10种光子中有4种属于赖曼系C.使n=5能级的氢原子电离至少要0.85 eV的能量D.从n=2能级跃迁到基态释放光子的能量等于从n=3能级跃迁到n=2能级释放光子的能量答案AB解析n=5激发态跃迁到基态时产生的光子的能量最大、波长最短,选项A正确;从n=5,4,3,2激发态跃迁到n=1时发出的4种光子属于赖曼系,所以选项B正确;由题图知,n=5能级的电离能为0.54 eV,所以选项C错误;从n=2能级跃迁到基态释放光子的能量大于从n=3能级跃迁到n=2能级释放光子的能量,所以选项D错误.8.(多选)μ子与氢原子核(质子)构成的原子称为μ氢原子(hydrogen muon atom).它在原子核物理的研究中有重要作用.图2为μ氢原子的能级示意图,假定光子能量为E的一束光照射容器中大量处于n=2能级的μ氢原子,μ氢原子吸收光子后,发出频率为ν1、ν2、ν3、ν4、ν5和ν6的光子,且频率依次增大,则()图2A.μ氢原子吸收光子后处于n=5能级B.μ氢原子吸收光子后处于n=4能级C.E等于h(ν6-ν4)D.E等于h(ν5-ν2)答案BC解析大量μ氢原子吸收光子后发出6种频率的光子,则由C2n=6,解得n=4,因此μ氢原子吸收光子后处于n=4能级,选项A错误,B正确;hν1=E4-E3,hν2=E3-E2,hν3=E4-E2,hν4=E2-E1,hν5=E3-E1,hν6=E4-E1,由能级跃迁规律得,E=E4-E2=h(ν6-ν4),选项C正确,D错误.9.(多选)一群处于基态的氢原子吸收某种光子后,向外辐射了ν1、ν2、ν3三种频率的光子,且ν1>ν2>ν3,则()A.被氢原子吸收的光子的能量为hν1B.被氢原子吸收的光子的能量为hν2C.ν1=ν2+ν3D.ν3=ν2+ν1答案AC解析氢原子吸收光子能向外辐射出三种频率的光子,说明氢原子从基态跃迁到了n=3激发态(如图所示),在n=3激发态不稳定,向低能级跃迁,发出光子,其中从n=3能级跃迁到基态向外辐射的光子能量最大,为hν1,从n=2能级跃迁到基态向外辐射的光子能量比从n=3能级跃迁到n =2能级向外辐射的光子能量大,氢原子一定是吸收了能量为hν1的光子,关系式hν1=hν2+hν3,即ν1=ν2+ν3成立,故A、C正确.10.(多选)(2020·萧山中学期末)按照玻尔原子理论,氢原子的能级图如图3所示,下列判断正确的是()图3A.用能量为12.01 eV的光子照射一群处于基态的氢原子,可观测到多种不同频率的光B.大量处于n=4激发态的氢原子向基态跃迁时,可能发出6条不同的光谱线C.氢原子从n=4激发态跃迁到n=2激发态需要吸收光子D.氢原子的核外电子由高能级跃迁到低能级时,氢原子的电势能减小,电子的动能增大答案BD解析氢原子发生能级跃迁吸收或放出的光子能量等于两能级的能量差,A错误;大量处于n=4激发态的氢原子向基态跃迁时可发出的不同的光谱线条数为C24=6,B正确;氢原子由高能级向低能级跃迁时辐射光子,C错误;氢原子的核外电子由高能级跃迁到低能级时,轨道半径减小,因库仑力做正功,故氢原子电势能减小,电子的动能增大,D正确.11.氢原子核外电子从外层轨道(半径为r b)向内层轨道(半径为r a)跃迁时(r a<r b),电子动能的增量ΔE k=E k a-E k b,电势能的增量ΔE p=E p a-E p b,则下列表述正确的是()A.ΔE k<0,ΔE p<0,ΔE k+ΔE p=0B.ΔE k<0,ΔE p>0,ΔE k+ΔE p=0C.ΔE k>0,ΔE p<0,ΔE k+ΔE p>0D.ΔE k>0,ΔE p<0,ΔE k+ΔE p<0答案 D解析 根据向心力公式m v 2r =k e 2r 2,得E k =12m v 2=ke 22r,即半径越大动能越小,所以ΔE k >0;当电子从外层轨道向内层轨道跃迁时,库仑引力做正功,电势能减小,所以ΔE p <0;又由于内层轨道比外层轨道原子的能级低,所以ΔE k +ΔE p <0,D 正确.12.氢原子第n 能级的能量为E n =E 1n2,其中E 1是基态能量,而n =1,2,3,…,若一氢原子发射能量为-316E 1的光子后处于比基态能量高出-34E 1的激发态,则氢原子发射光子前后分别处于第几能级?答案 氢原子发射光子前后分别处于第4能级与第2能级解析 设氢原子发射光子前后分别处于第n 与第m 能级,则依题意有E 1n 2-E 1m 2=-316E 1,E 1m2-E 1=-34E 1,由以上两式可以解得m =2,n =4. 13.如图4所示为氢原子最低的四个能级,当氢原子在这些能级间跃迁时,图4(1)最多有可能放出几种能量的光子?(2)在哪两个能级间跃迁时,所发出的光子波长最长?最长波长是多少?(普朗克常量h =6.63×10-34 J·s ,电子电荷量e =1.6×10-19 C ,结果保留三位有效数字)答案 (1)6种 (2)第4能级向第3能级 1.88×10-6 m解析 (1)由N =C 2n ,可得N =C 24=6种.(2)氢原子由第4能级向第3能级跃迁时,能级的能量差最小,辐射的光子能量最小,波长最长,根据hν=hc λ=E 4-E 3=[-0.85-(-1.51)] eV =0.66 eV ,λ=hc E 4-E 3=6.63×10-34×3×1080.66×1.6×10-19m ≈ 1.88×10-6 m.。
高中物理 课件 第2章 第3节 玻尔的原子模型

2.能量量子化 (1)电子在可能轨道上运动时,虽然是变速运动,但它并不释放能量,原子是 稳定的,这样的状态也称之为定态. (2)由于原子的可能状态(定态)是不连续的,具有的能量也是不连续的.这样的 能量值,称为能级,能量最低的状态称为基态,基态最稳定,其他的状态叫作激发 态,对氢原子,以无穷远处为势能零点时,其能级公式 En=n12E1(n=1,2,3,…)
2.玻尔原子理论的主要内容 (1)原子只能处于一系列能量 不连续 的状态中,这些状态叫作 定态 . (2)原子从一种定态跃迁到另一种定态时,吸收(或辐射)一定 频率 的光子能
量 hν ,其中h为普朗克常量,h= 6.63×10-34J·s ,ν为光的频率. (3)原子的不同能量状态对应于电子的不同 运行轨道 .只有电子的轨道半
【解析】 原子由能量为 En 的定态向低能级跃迁时,辐射的光子能量等于能 级差,A 正确;电子沿某一轨道绕核运动,处于某一定态,不向外辐射能量,故 B 错;电子由半径大的轨道跃迁到半径小的轨道,能级降低,因而要辐射某一频率 的光子,故 C 正确;原子吸收光子后能量增加,能级升高,故 D 错.氢原子辐射 光子后,原子能量减小,原子从高能级向低能级跃迁,E 正确.
知
识
点 一
学
第3节 玻尔的原子模型
业 分
层
测 评
知 识 点 二
学习目标
1.知道玻尔理论的基本假设的主要内 容.(重点) 2.了解能级、跃迁、能量量子化以及 基态、激发态等概念.(重点) 3.理解原子发射和吸收光子的频率与 能级差的关系.(难点)
知识脉络
玻尔原子模型
[先填空] 1.卢瑟福的原子核式结构模型能够很好地解释α粒子与金箔中原子碰撞所得 到的信息,但不能解释原子光谱是 特征光谱 和原子的 稳定性 .
第二章 原子的玻尔—索末菲理论 (4)

碱金属原子的光谱
玻尔理论已经成功讨论和解释了氢原子和类氢离子的结 构和光谱,这里要讨论的是另一类与氢原子类似结构的原 子——碱金属原子,包括锂Li、钠Na、钾K、铷Rb、铯Cs和 钫Fr,原子序数分别为3、11、19、37、55和87。这些元素 在周期表中属同一族,有相仿的化学性质,都是一价的。它 们的电离电势都比较小,易被电离,具有金属的一般性质。 对与氢原子类似结构的两大类原子来说,在谁更像氢原子的 问题上各有所长。从核外只有一个电子 e 这个角度看,显然类氢离子优于碱金 e 属原子,但从最外层那个电子所感受 到的那个“原子实”的作用来说,碱金 属原子中原子实的净电荷Z是1,在这 一点上又优于类氢离子。
2 Ze E T V m m0 c 2 4 0 r
根据类氢离子的玻尔理论上式可以写为
cZ 2 2 2 2 2 E m m0 c 2 m m m0 c mv m m0 c mc n m0 c mc 1 m0 c
按照玻尔 — 索末菲理论 Hα 线应为n=3到n=2的跃迁,n=3为 三条能级, n=2 为二条能级,考 虑能级跃迁的选择定则 △ =±1,就得到了三条Hα 线,与实验完全符合,但这完全 是巧合,有人称索末菲理论是物 理学中最值得纪念的失败。
图中的s,p,d,f,g,…等字母代表 4,…等值。
=0,1,2,3,
精细结构常数
e / 40 1 c 137
2
光谱
类氢离子,毕克林系 折合质量,里德堡常数随不同类氢离子变化
Franck-Hertz实验
广义量子化条件和索末菲理论
A. 广义量子化条件
玻尔在氢原子理论中得出,只有满足角动量量子化条件
第二章 原子的玻尔—索末菲理论 小结

Bohr模型
处理原子结构的方法:对于电子绕原子核运 动,用经典力学处理;对于电子轨道半径, 则用量子条件来处理。也就是所谓的半经典 的量子论。只对电子的径向运动采取量子理 论,而对其角向运动采取量子理论。
之所以先量子化径向运动,由于卢瑟福模型 电子塌缩就是与轨道半径有关。只要量子化 而不收缩,塌缩问题就解决了。 解释了近30年的巴尔末公式之谜。 解释了类氢离子光谱。
光谱
光谱是用光谱仪测量的。光谱仪的种类繁多,但其基 本结构原理却几乎都一样,大致由三部分组成:光源;分光 器;记录仪。 连续光谱 固体热辐射 线状光谱 带状光谱 发射光谱
样品光源 分光器 纪录仪
原子发光 分子发光
I
吸收光谱
连续光源 样品 分光器 纪录仪
I
氢原子光谱及其经验规律
巴耳末公式
2n 2 Rc Rc 4 与经典比较 n n3
2Rc e 3 2 n 1 40 mr 3
e2 2 rn 3 n 40 16 2 R 2 c 2 m 1
2 e m R 2 40 ch 3
2 4
h 2
4 0 2 2 h rn n ; 2 2 me
原子实极化和轨道贯穿
电偶极子
碱金属原子光谱的精细结构
me 4 1 En 2 2 2 4 0 2 n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 原子的量子态:玻尔模型
一、学习要点:
1、背景知识
(1)黑体辐射:黑体、黑体辐射、维恩位移律、普朗克黑体辐射公式、能量子假说
(2)光电效应:光电效应、光电效应实验规律、爱因斯坦方程、光量子(光子)
(3)氢原子光谱:线状谱、五个线系(记住名称、顺序)、里德伯公式2211()R n n ν
=-' 、 光谱项()2n R
n T =、并合原则:()()T n T n ν
'=- 2、玻尔氢原子理论:
(1)玻尔三条基本假设
(2)圆轨道理论:氢原子中假设原子核静止,电子绕核作匀速率圆周运动
2
22
200002244,0.053Z Z n e e n r n a a nm m e m e
πεπε===≈ ;
13714,Z Z 40202≈===c e n c n e c e n πεααπευ; ()2422
2220Z Z 1()42e n m e R hc E hcT n n n πε∞=-=-=- ,n =1,2,3,…… (3)实验验证:
(a )里德伯常量的验证()()22
1
11[]H R T n T n n n νλ'≡=-=-' ,(1)e A A m R R R m ∞==+ 类氢离子222
11[]A A R Z n n ν=-' (b )夫朗克-赫兹实验:原理、装置、.结果及分析;原子的电离电势、激发电势
3、椭圆轨道理论
n 称为主量子数, n=1,2,3……; l 称角量子数,n 取定后,l=0,1,2,…,n-1。
4、碱金属原子
由于原子实极化和轨道贯穿效应,使得价电子能量降低(相当于Z*>1 )。
光谱(四个线系):
第二章自测
1.选择题
(1)若氢原子被激发到主量子数为n 的能级,当产生能级跃迁时可能发生的所有谱线总条数应为:
A .n-1
B .n(n-1)/2
C .n(n+1)/2
D .n
(2)氢原子光谱赖曼系和巴耳末系的系线限波长分别为:
A.R/4 和R/9
B.R 和R/4
C.4/R 和9/R
D.1/R 和4/R
(3)氢原子赖曼系的线系限波数为R,则氢原子的电离电势为:
A .3Rhc/4 B. Rhc C.3Rhc/4e D. Rhc/e
(4)氢原子基态的电离电势和第一激发电势分别是:
A .13.6V 和10.2V
B –13.6V 和-10.2V C.13.6V 和3.4V; D. –13.6V 和-3.4V
(5)由玻尔氢原子理论得出的第一玻尔半径0a 的数值是:
A.5.291010-⨯m
B.0.529×10-10m
C. 5.29×10-12m
D.529×10-12m
(6)根据玻尔理论,若将氢原子激发到n=5的状态,则: A.可能出现10条谱线,分别属四个线系 B.可能出现9条谱线,分别属3个线系
C.可能出现11条谱线,分别属5个线系
D.可能出现1条谱线,属赖曼系
(7)欲使处于基态的氢原子发出αH 线,则至少需提供多少能量(eV )?
A.13.6
B.12.09
C.10.2
D.3.4
(8)氢原子被激发后其电子处在第四轨道上运动,按照玻尔理论在观测时间内最多能看到几条线?
A.1
B.6
C.4
D.3
(9)氢原子光谱由莱曼、巴耳末、帕邢、布喇开系…组成.为获得红外波段原子发射光谱,则轰击基态氢原子的最小动能为:
A .0.66 eV B.12.09eV C.10.2eV D.12. 75eV
(10)用能量为12.7eV 的电子去激发基态氢原子时,受激氢原子向低能级跃迁时最多可能出现几条光谱线(不考虑自旋); A.3 B.10 C.1 D.4
(11)有速度为1.875m/s 106
⨯的自由电子被一质子俘获,放出一个光子而形成基态氢原子,则光子的频率(Hz )为:
A .3.3⨯1015 B.2.4⨯1015 C.5.7⨯1015 D.2.1⨯1016
(12)按照玻尔理论基态氢原子中电子绕核运动的线速度约为光速的:
A.1/10倍
B.1/100倍 C .1/137倍 D.1/237倍
(13)已知一对正负电子绕其共同的质心转动会暂时形成类似于氢原子的结构的―正电子素‖那么该―正电子素‖由第一激发态跃迁时发射光谱线的波长应为:
A .3∞R /8 B.3∞R /4 C.8/3∞R D.4/3∞R
(14)电子偶素是由电子和正电子组成的原子,基态电离能量为:
A.-3.4eV
B.+3.4eV
C.+6.8eV
D.-6.8eV
(15)根据玻尔理论可知,氦离子H e +的第一轨道半径是:
A .20a B. 40a C. 0a /2 D. 0a /4
(16)一次电离的氦离子 H e +处于第一激发态(n=2)时电子的轨道半径为:
A.0.53⨯10-10m
B.1.06⨯10-10m
C.2.12⨯10-10m
D.0.26⨯10-10m
(17)假设氦原子(Z=2)的一个电子已被电离,如果还想把另一个电子电离,若以eV 为单位至少需提供的能量为: A .54.4 B.-54.4 C.13.6 D.3.4
(18)在H e +离子中基态电子的结合能是:
A.27.2eV
B.54.4eV
C.19.77eV
D.24.17eV
(19)夫—赫实验的结果表明:
A 电子自旋的存在;
B 原子能量量子化
C 原子具有磁性;
D 原子角动量量子化
(20)夫—赫实验使用的充气三极管是在:
A.相对阴极来说板极上加正向电压,栅极上加负电压
B.板极相对栅极是负电压,栅极相对阴极是正电压
C.板极相对栅极是正电压,栅极相对阴极是负电压
D.相对阴极来说板极加负电压,栅极加正电压
2.计算题
1、 试由氢原子里德伯常数计算基态氢原子的电离电势和第一激发电势.
2、 能量为12.6eV 的电子射入氢原子气体中,气体将发出哪些波长的辐射?
3、已知氢和重氢的里德伯常数之比为0.999728,而它们的核质量之比为m H /m D =0.50020.计算
质子质量与电子质量之比.
解: 由H
e H m m R R /11+=∞和D e D m m R R /11+=∞知: 999728.0/1/50020.01/1/1=++=++=H
e H e H e D e D H m m m m m m m m R R 解得: 5.1836/=e H m m
4、已知锂原子光谱主线系最长波长nm 7.670=λ,辅线系系限波长nm 9.351=∞λ,求锂
原子第一激发电势和电离电势。
5、钠原子基态为3s ,已知其主线系第一条线(共振线)波长为589.6nm ,漫线系第一条线
的波长为819.3nm ,基线系第一条线的波长为1845.9nm ,主线系的系限波长为241.3nm ,试求3S,3P,3D,4F 各谱项的项值。
3.思考题
1、解释下列概念:光谱项、定态、简并、电子的轨道磁矩、对应原理.
2、简述玻尔对原子结构的理论的贡献和玻尔理论的地位与不足.
3、为什么通常总把氢原子中电子状态能量作为整个氢原子的状态能量?
4、对波尔的氢原子在量子态时,势能是负的,且数值大于动能,这意味着什么?当氢原子总能量为正时,又是什么状态?
5、为什么氢原子能级,随着能量的增加,越来越密?
6、解释下述的概念或物理量,并注意它们之间的关系:激发和辐射;定态、基态、激发态和
电离态;能级和光谱项:线系和线系限;激发能,电离能;激发电位、共振电位、电离电位;。
