高三物理一轮复习——功能关系能量守恒定律学案

合集下载

高三物理一轮复习导学案：5-功能关系与能量守恒定律

2012届高三物理一轮复习导学案六、机械能（5）【课题】功能关系与能量守恒定律【导学目标】1．了解几种常见的功能关系。

2．能用功能关系解决常见的力学问题。

【知识要点】一、摩擦力做功1.静摩擦力做功的特点静摩擦力存在于相对静止的两个物体之间，当两物体相对地面静止时，静摩擦力对两个物体都不做功；当两物体相对地面运动时，静摩擦力对两个物体要么都不做功，要么做功为一正一负，代数和为零．因此得出以下结论：（1）静摩擦力可以做正功、负功，也可以不做功．一对静摩擦力做的总功必定为零。

（2）在静摩擦力做功的过程中，只有机械能的相互转移（静摩擦力起看传递机械能的作用），而没有机械能转化成其他形式的能。

2.滑动摩擦力做功的特点（1）滑动摩擦力可以对物体做正功，也可以对物体做负功，还可以不做功。

（2）一对滑动摩擦力做功的过程中，能量的变化有两种情况：一是相互摩擦的物体之间机械能的转移；二是机械能转化为内能；转化为内能的量值等于滑动摩擦力与其相对路程的乘积。

（3）相互摩擦的系统内，一对滑动摩擦力所做的功总是负值，其绝对值恰等于滑动摩擦力与其相对路程的乘积，即恰等于系统损失的机械能。

二、功能关系1．功能关系：做功的过程就是转化过程，做多少功就有多少某种形式的能转化为其他形式的能。

功是能量转化的。

2．常见力做功与能量转化的对应关系重力做功：弹簧弹力做功：合外力做功：除重力以外其它力做功：滑动摩擦力做功：三、能的转化和守恒定律能量既不会凭空产生，也不会凭空消失，它只能从一种形式为别的形式，或从一个物体到另一个物体．在转化或转移的过程中其总量不变，这就是能的转化和守恒定律．能的转化与守恒定律可从两个方面理解：1、某种形式的能量减少，一定存在另外形式的能量增加，且减少量和增加量相等。

2、某个物体的能量减少，一定存在别的物体的能量增加，且减少量和增加量相等。

【典型剖析】[例1]如图所示，A物体放在B物体的左侧，用水平恒力F将A拉至B的右端，第一次B固定在地面上，F做功为W1，产生热量Q1，第二次让B在光滑地面上自由滑动，F做功为W2，产生热量为Q2，则应有（）A．W1<W2，Q1＝Q2 B．W1＝W2，Q1＝Q2C ．W 1<W 2，Q 1<Q 2D ．W 1＝W 2，Q 1<Q 2[例2] 一物块以150Ｊ的初动能由地面沿一个很长的斜面往上滑行，当它到达最高点时，重力势能等于120Ｊ。

高三物理一轮复习功能关系训练导学案

功能关系、能量守恒定律训练课【学习目标】掌握功能关系、能量守恒定律。

【课堂检测】1．滑块以速率v 1靠惯性沿固定斜面由底端向上运动, 当它回到出发点时速率为v 2, 且v 2< v 1若滑块向上运动的位移中点为A ,取斜面底端重力势能为零，则（） A ．上升时机械能减小，下降时机械能增大。

B ．上升时机械能减小，下降时机械能也减小。

C ．上升过程中动能和势能相等的位置在A 点上方。

D ．上升过程中动能和势能相等的位置在A 点下方。

2、如图所示，木块质量为M ，放在光滑水平面上，一颗质量为m 的子弹以初速度v 0水平射入木块中，射入深度为d ，平均阻力为f ．设木块离原点s 远时开始匀速前进，最终速度为v ，下列判断正确的是( )A ．2212021v -v m m fd =B ．2212021)(v -v m M m fs +=C ．2212021)()(v -v m M m d s f +=+ D ．上面公式均不正确3、如图所示，质量为m 的物体自倾角为30°的固定斜面顶端匀加速滑至底端，物体加速度为，顶点距地面高为h ，重量加速度为g 。

则下列说法错误的是（）A.重力势能减少mghB.动能增加mgh/2C.机械能变化mghD.内能增加mgh/24． “街头篮球”是中学生喜爱的运动项目。

假设某队员在一次投篮过程中对篮球做功为W ，出手高度为h 1，篮筐距地面高度为h 2，球的质量为m ，不计空气阻力，则篮球进筐时的动能为：（）A ．W+21mgh mgh-； B ．12mgh mgh -－W ； C ．21mgh mgh+－W ； D ．W+12mgh mgh-。

5、质量为1kg 的物体被人用手由静止向上提高1m ，这时物体的速度是2m/s ，（g=10m/2s ），下列说法中正确的是：（）A ．手对物体做功12JB ．合外力对物体做功12JC ．合外力对物体做功2JD ．物体克服重力做功10J6、如图所示，一个滑雪运动员从左侧斜坡距离坡底8m 处由静止滑下．以坡底为零势能参考面，当下滑到距离坡底1s处时，运动员的动能和势能恰好相等；到坡底后运动员又靠惯性冲上右侧斜坡．若不计经过坡底时的机械能损失，当上滑到距离坡底2s处时，运动员的动能和势能再次相等，上滑的最大距离为4m ，在此全过程中，下列说法正确的是A.摩擦力对运动员所做的功等于运动员动能的变化B.重力和摩擦力对运动员所做的总功等于运动员机械能的变化C.124,2s m s m <>D.124,2s m s m><7、把甲图中的小球举高到绳子的悬点O 处，然后释放，让小球自由下落，利用传感器和计算机测量绳子快速变化的拉力的瞬时值，乙图为绳子拉力 F 随时间 t 变化的图线，由此图线所提供的信息，可以确定 ( ) A ．t 2时刻小球速度最大B ．t 1～t 2期间小球速度先增大后减小C ．t 3时刻小球动能最小D ．t 1和t 4时刻小球动能相等 8、滑块静止于光滑水平面上，与之相连的轻质弹簧处于自然伸直状态，现用恒定的水平外力F 作用于弹簧右端，在向右移动14g一段距离的过程中拉力F做了l0 J的功．在上述过程中（）A．弹簧的弹性势能增加了10 J B．滑块的动能增加了10 JC．滑块和弹簧组成的系统机械能增加了10 JD．滑块和弹簧组成的系统机械能守恒9．如图所示，由理想电动机带动的传送带以速度v保持水平方向的匀速传动，传送带把A处的无初速度放人的一个工件（其质量为m）运送到B处。

高考一轮复习：功能关系

2014届高三第一轮复习《功能关系能量守恒定律》学案班级姓名功是能量变化的量度，做功是一个过程，通过做功这个过程实现了能量的转化，它体现了一个因果关系，体现了状态与过程的关系，即E W ∆=。

其个性化的功表现如下：1.合外力对物体做功等于物体动能的变化K E W ∆=2.重力对物体所做的功等于物体重力势能的减少量P E W ∆-=3.弹簧弹力所做的功等于弹簧弹性势能的减少量弹E W ∆-=4.除重力及弹簧弹力以外的其它力对物体所做的功等于物体机械能的变化E W ∆=5.电场力所做的功等于物体电势能的减少量电E W ∆-=6.分子力所做的功等于分子势能的减少量分E W ∆-=7.一对滑动摩擦力对系统做的总功总是负值，其绝对值等于滑动摩擦力与相对位移（相对路程）的乘积即 fs 相=Q 。

【例1】质量为m 的物体，在距地面h 高处以g/3的加速度由静止竖直下落到地面，下列说法中正确的是（）A.物体的重力势能减少 mgh /3B.物体的机械能减少2 mgh /3C.物体的动能增加mgh /3D.重力做功mgh【变式1】如图所示，用水平恒力F 将质量为m 的物体沿倾角为α、高为h 的斜面由静止开始从底端推到顶端，其速度达到v ，物体与斜面之间的动摩擦因数为μ．下面说法中正确的是（）A.F 做的功为Fhcot αB.物体机械能增加mgh+m v 2/2C.转变成内能的部分是μ（F+mg·cot α）hD.物体克服阻力所做功为μmgcos αh【变式2】质量为m 的带正电的物体处于竖直向上的匀强电场中，已知带电物体所受电场力的大小为物体所受重力的1/4 ，现将物体从距地面高h 处以一定初速度竖直下抛，物体以g/4的加速度竖直下落到地面（空气阻力恒定），则在物体的下落过程中( )A.物体的重力势能减少mgh /4，电势能减少mgh /4B.由物体与周围空气组成的系统的内能增加了mgh /4C.物体的动能增加mgh /4D.物体的机械能减少mgh /4【例2】质量为M 的长木板放在光滑的水平面上，一质量为m 的滑块以某一速度沿木板表面从A 点滑到B 点，在板上前进了L ，而木板前进了l ，如图所示，若滑块与木板间的动摩擦因数为μ，求：(1)摩擦力对滑块和木板做的功；(2)系统产生的热量.【变式1】如图所示，长为L 的小车置于光滑的水平面上，小车前端放一小物块，用大小为F 的水平力将小车向右拉动一段距离s,物块刚好滑到小车的左端.物块与小车间的摩擦力为f,在此过程中( )（a ）A.系统产生的内能为fLB.系统增加的机械能为FsC.物块增加的动能为fLD.小车增加的动能为Fs-fL 【变式2】如图所示，质量为m 的物体在水平传送带上由静止释放，传送带由电动机带动，始终保持以速度v 匀速运动，物体与传送带间的动摩擦因数为μ，物体最后能与传送带保持相对静止.对于物体从开始释放到与传送带相对静止这一过程，下列说法正确的是( )A.电动机多做的功为21mv 2、 B.摩擦力对物体做的功为mv 2 C.传送带克服摩擦力做的功为21mv 2 D.电动机增加的功率为μmgv 【变式3】如图中（a ）所示，一倾角为37o 的传送带以恒定速度运行．现将一质量m =2kg 的小物体以某一初速度放上传送带，物体相对地面的速度随时间变化的关系如图（b ）所示．（取沿传送带向上为正方向，g =10m/s 2，sin37o =0.6，cos37o =0.8）求：（1）0~10s 内物体位移的大小；（2）物体与传送带间的动摩擦因数；（3）0~10s 内物体机械能增量及与传送带摩擦产生的热量Q ．解：(1)从图b 中求出物体位移s=（4+8）×6/2-3×2/2=33m （2分）(2)由图象知，物体在传送带上滑动时的加速度a =l.5m/s 2对此过程中物体分析得，μmg cos θ-mg sin θ=ma ，得μ=15/16=0.9375(3)物体被送上的高度h =s sin θ=19.8m ，重力势能增量△E p=mgh =396J动能增量△E k =22211122mv mv =27J 机械能增加△E =△E p+△E k =423J （3分）0~10s 内只有前6s 发生相对滑动．0~6s 内传送带运动距离s 带=6×6m=36m 0~6s 内物体位移s 物=9m△x =s 带-s 物=27m产生的热量Q =μmg cos θ·△x =405J （4分）【例3】节能混合动力车是一种可以利用汽油及所储存电能作为动力来源的汽车．有一质量m ＝1 000 kg 的混合动力轿车，在平直公路上以v 1＝90 km/h 匀速行驶，发动机的输出功率为P ＝50 kW.当驾驶员看到前方有80 km/h 的限速标志时，保持发动机功率不变，立即启动利用电磁阻尼带动的发电机工作给电池充电，使轿车做减速运动，运动L ＝72 m 后，速度变为v 2＝72 km/h.此过程中发动机功率的15用于轿车的牵引，45用于供给发电机工作，发动机输送给发电机的能量最后有50%转化为电池的电能．假设轿车在上述运动过程中所受阻力保持不变．求：(1)轿车以90 km/h在平直公路上匀速行驶时，所受阻力F 阻的大小；(2)轿车从90 km/h 减速到72 km/h 过程中，获得的电能E 电；(3)轿车仅用其在上述减速过程中获得的电能E 电维持72 km/h 匀速运动的距离L ′.2000N; J 4103.6⨯;31.5m【综合应用1】如图所示，AB 是倾角为θ的粗糙直轨道，BCD 是光滑的圆弧轨道，AB 恰好在B 点与圆弧相切，圆弧的半径为R.一个质量为m 的物体(可以看做质点)从直轨道上的P 点由静止释放．已知P 点与圆弧的圆心O 等高，物体与轨道AB 间的动摩擦因数为μ.求：(1)物体做往返运动的整个过程中在AB 轨道上通过的总路程；(2)最终当物体通过圆弧轨道最低点E 时，对圆弧轨道的压力；(3)为使物体能顺利到达圆弧轨道的最高点D ，释放点距B 点的距离L ′应满足什么条件？(1)R μ (2)(3－2cos θ)mg (3)3＋2cos θ2(sin θ－μcos θ)·R 解析 (1)摩擦力对物体始终做负功，故物体最终在圆心角为2θ的圆弧上做往复运动．设物体在AB 轨道上通过的总路程为x ，则全程应用动能定理得：mgR cos θ－μmg cos θ·x＝0 解得：x ＝R μ(2)最终当物体通过圆弧最低点E 时，设速度为v E ，在E 点：F N －mg ＝m v 2E R① 从B →E 由动能定理得：mgR (1－cos θ)＝12m v 2E② ①②两式联立，得：F N ＝(3－2cos θ)mg由牛顿第三定律得物体对轨道的压力为(3－2cos θ)mg(3)若物体刚好到D 点，设速度为v D ，则mg ＝m v 2D R③ 对全过程由动能定理得mgL ′sin θ－μmg cos θ·L ′－mgR (1＋cos θ)＝12m v 2D④ ③④联立，得L ′＝3＋2cos θ2(sin θ－μcos θ)R【综合应用2】如图所示，半圆形光滑轨道竖直固定，半径R =0.1m ，其右侧一定水平距离处固定一个斜面体。

2021高中物理一轮复习学案--第五章第4讲功能关系能量守恒定律

第4讲功能关系能量守恒定律ZHI SHI SHU LI ZI CE GONG GU知识梳理·自测巩固1．功能关系(1)功是__能量转化__的量度，即做了多少功就有多少__能量__发生了转化。

(2)做功的过程一定伴随着__能量的转化__，而且__能量的转化__必须通过做功来实现。

2．能量守恒定律(1)内容：能量既不会消灭，也__不会创生__。

它只会从一种形式__转化__为其他形式，或者从一个物体__转移__到另一个物体，而在转化和转移的过程中，能量的总量__保持不变__。

(2)表达式：ΔE减＝__ΔE增__。

思考：飞船返回舱进入地球大气层以后，由于它的高速下落，而与空气发生剧烈摩擦，返回舱的表面温度达到1 000摄氏度。

(1)进入大气层很长一段时间，返回舱加速下落，返回舱表面温度逐渐升高。

该过程动能和势能怎么变化？机械能守恒吗？(2)返回舱表面温度越高，内能越大。

该过程中哪两种形式的能量之间发生转化？机械能和内能的总量变化吗？[答案](1)动能增加，势能减少，不守恒。

(2)机械能向内能转化，不变。

思维诊断：(1)力对物体做了多少功，物体就有多少能。

( ×)(2)物体在速度增大时，其机械能可能在减小。

( √)(3)重力和弹簧弹力之外的力做功的过程是机械能和其他形式能量转化的过程。

( √)(4)一对互为作用力与反作用力的摩擦力做的总功，等于系统增加的内能。

( √)自测巩固ZI CE GONG GU1．(2019·重庆一诊)如图所示，一物块在粗糙斜面上由静止释放，运动到水平面上后停止，则运动过程中，物块与地球组成系统的机械能( B )A．不变B．减少C．增大D．无法判断[解析]本题考查摩擦力做功问题。

物块在粗糙斜面上由静止释放后，重力与摩擦力对物块做功，其中摩擦力做功是将物块机械能的一部分转化为内能，所以物块与地球组成系统的机械能减少，故A、C、D错误，B正确。

2．(2019·江苏盐城月考)火箭发射回收是航天技术的一大进步。

2024届高考一轮复习物理教案(新教材鲁科版)：功能关系能量守恒定律

第4讲功能关系能量守恒定律目标要求 1.熟练掌握几种常见的功能关系，并会用于解决实际问题.2.掌握一对摩擦力做功与能量转化的关系.3.会应用能量守恒观点解决综合问题．考点一功能关系的理解和应用1．对功能关系的理解(1)做功的过程就是能量转化的过程，不同形式的能量发生相互转化是通过做功来实现的． (2)功是能量转化的量度，功和能的关系，一是体现在不同的力做功，对应不同形式的能转化，具有一一对应关系，二是做功的多少与能量转化的多少在数值上相等． 2．常见的功能关系能量功能关系表达式势能重力做的功等于重力势能减少量W ＝E p1－E p2＝－ΔE p弹力做的功等于弹性势能减少量电场力做的功等于电势能减少量分子力做的功等于分子势能减少量动能合外力做的功等于物体动能变化量 W ＝E k2－E k1＝12m v 2－12m v 02机械能除重力和弹力之外的其他力做的功等于机械能变化量W 其他＝E 2－E 1＝ΔE 摩擦产生的内能一对相互作用的滑动摩擦力做功之和的绝对值等于产生的内能 Q ＝f ·s 相对电能克服安培力做的功等于电能增加量W 电能＝E 2－E 1＝ΔE1．一个物体的能量增加，必定有别的物体的能量减少．( √ ) 2．合力做的功等于物体机械能的改变量．( × )3．克服与势能有关的力(重力、弹簧弹力、电场力等)做的功等于对应势能的增加量．( √ ) 4．滑动摩擦力做功时，一定会引起机械能的转化．( √ )功的正负与能量增减的对应关系(1)物体动能的增加与减少要看合外力对物体做正功还是做负功．(2)势能的增加与减少要看对应的作用力(如重力、弹簧弹力、电场力等)做负功还是做正功．(3)机械能的增加与减少要看重力和弹簧弹力之外的力对物体做正功还是做负功．考向1功能关系的理解例1(多选)如图所示，楔形木块abc固定在水平面上，粗糙斜面ab与水平面的夹角为60°，光滑斜面bc与水平面的夹角为30°，顶角b处安装一定滑轮．质量分别为M、m(M>m)的两滑块A和B，通过不可伸长的轻绳跨过定滑轮连接，轻绳与斜面平行．两滑块由静止释放后，沿斜面做匀加速运动，A、B不会与定滑轮碰撞．若不计滑轮的质量和摩擦，在两滑块沿斜面运动的过程中()A．轻绳对滑轮作用力的方向竖直向下B．拉力和重力对M做功之和大于M动能的增加量C．拉力对M做的功等于M机械能的增加量D．两滑块组成系统的机械能损失等于M克服摩擦力做的功答案BD解析根据题意可知，两段轻绳的夹角为90°，轻绳拉力的大小相等，根据平行四边形定则可知，合力方向与轻绳方向的夹角为45°，所以轻绳对滑轮作用力的方向不是竖直向下的，故A错误；对M受力分析，受到重力、斜面的支持力、轻绳的拉力以及滑动摩擦力作用，根据动能定理可知，M动能的增加量等于拉力、重力以及摩擦力做功之和，而摩擦力做负功，则拉力和重力对M做功之和大于M动能的增加量，故B正确；由除重力和弹力之外的力对物体做的功等于物体机械能的变化量可知，拉力和摩擦力对M做的功之和等于M机械能的增加量，故C错误；对两滑块组成系统分析可知，除了重力之外只有摩擦力对M做功，所以两滑块组成的系统的机械能损失等于M克服摩擦力做的功，故D正确．例2(多选)如图所示，质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面，其减速运动的加速度大小为34g ，此物体在斜面上能够上升的最大高度为h ，则在这个过程中物体( )A ．重力势能增加了mghB ．机械能损失了12mghC ．动能损失了mghD ．克服摩擦力做功14mgh答案 AB解析加速度大小a ＝34g ＝mg sin 30°＋f m ，解得摩擦力f ＝14mg ，机械能损失量等于克服摩擦力做的功，即fs ＝14mg ·2h ＝12mgh ，故B 项正确，D 项错误；物体在斜面上能够上升的最大高度为h ，所以重力势能增加了mgh ，故A 项正确；动能损失量为克服合力做功的大小，动能损失量ΔE k ＝F 合s ＝34mg ·2h ＝32mgh ，故C 项错误．考向2 功能关系与图像的结合例3 (多选)(2020·全国卷Ⅰ·20)一物块在高3.0 m 、长5.0 m 的斜面顶端从静止开始沿斜面下滑，其重力势能和动能随下滑距离s 的变化如图中直线Ⅰ、Ⅱ所示，重力加速度取10 m/s 2.则( )A ．物块下滑过程中机械能不守恒B ．物块与斜面间的动摩擦因数为0.5C ．物块下滑时加速度的大小为6.0 m/s 2D ．当物块下滑2.0 m 时机械能损失了12 J答案AB解析由E－s图像知，物块动能与重力势能的和减小，则物块下滑过程中机械能不守恒，故A正确；由E－s图像知，整个下滑过程中，物块机械能的减少量为ΔE＝30 J－10 J＝20 J，重力势能的减少量ΔE p＝mgh＝30 J，又ΔE＝μmg cos α·s，其中cos α＝s2－h2s＝0.8，h＝3.0m，g＝10 m/s2，则可得m＝1 kg，μ＝0.5，故B正确；物块下滑时加速度的大小a＝g sin α－μg cos α＝2.0 m/s2，故C错误；物块下滑2.0 m时损失的机械能为ΔE′＝μmg cos α·s′＝8 J，故D错误．考点二摩擦力做功与能量转化两种摩擦力做功特点的比较类型比较静摩擦力做功滑动摩擦力做功不同点能量的转化只有机械能从一个物体转移到另一个物体，而没有机械能转化为其他形式的能(1)一部分机械能从一个物体转移到另一个物体(2)一部分机械能转化为内能，此部分能量就是系统机械能的损失量一对摩擦力的总功一对静摩擦力所做功的代数和总等于零一对滑动摩擦力做功的代数和总是负值，总功W＝－fs相对，即发生相对滑动时产生的热量相同点做功情况两种摩擦力对物体可以做正功，也可以做负功，还可以不做功例4(多选)如图所示，一个长为L，质量为M的木板，静止在光滑水平面上，一个质量为m的物块(可视为质点)，以水平初速度v0，从木板的左端滑向另一端，设物块与木板间的动摩擦因数为μ，当物块与木板相对静止时，物块仍在长木板上，物块相对木板的位移为d，木板相对地面的位移为s，重力加速度为g.则在此过程中()A．摩擦力对物块做的功为－μmg(s＋d)B．摩擦力对木板做的功为μmgsC．木板动能的增量为μmgdD．由于摩擦而产生的热量为μmgs答案AB解析根据W＝Fl cos θ，其中l指物体的位移，而θ指力与位移之间的夹角，可知摩擦力对物块做的功W1＝－μmg(s＋d)，摩擦力对木板做的功W2＝μmgs，A、B正确；根据动能定理可知木板动能的增量ΔE k＝W2＝μmgs，C错误；由于摩擦而产生的热量Q＝f·Δx＝μmgd，D 错误．例5(多选)(2019·江苏卷·8)如图所示，轻质弹簧的左端固定，并处于自然状态．小物块的质量为m，从A点向左沿水平地面运动，压缩弹簧后被弹回，运动到A点恰好静止．物块向左运动的最大距离为s，与地面间的动摩擦因数为μ，重力加速度为g，弹簧未超出弹性限度．在上述过程中()A．弹簧的最大弹力为μmgB．物块克服摩擦力做的功为2μmgsC．弹簧的最大弹性势能为μmgsD．物块在A点的初速度为2μgs答案BC解析物块处于最左端时，弹簧的压缩量最大，然后物块先向右加速运动再减速运动，可知弹簧的最大弹力大于滑动摩擦力μmg，选项A错误；物块从开始运动至最后回到A点过程，由功的定义可得物块克服摩擦力做的功为2μmgs，选项B正确；物块从最左侧运动至A点过程，由能量守恒定律可知E p＝μmgs，选项C正确；设物块在A点的初速度大小为v0，对整个过程应用动能定理有－2μmgs＝0－12，解得v0＝2μgs，选项D错误．2m v0考点三能量守恒定律的理解和应用1．内容能量既不会凭空产生，也不会凭空消失，它只能从一种形式转化为其他形式，或者从一个物体转移到别的物体，在转化或转移的过程中，能量的总量保持不变．2．理解(1)某种形式的能量减少，一定存在其他形式的能量增加，且减少量和增加量一定相等；(2)某个物体的能量减少，一定存在其他物体的能量增加，且减少量和增加量一定相等．例6(2023·福建省百校联合测评)如图甲所示，轻弹簧下端固定在倾角为θ＝37°的粗糙斜面底端，质量为m＝1 kg的物块从轻弹簧上端上方某位置由静止释放，测得物块的动能E k与其通过的路程s的关系如图乙所示(弹簧始终处于弹性限度内)，图像中O～s1＝0.4 m之间为直线，其余部分为曲线，s2＝0.6 m时物块的动能达到最大．弹簧的长度为l时，弹性势能为E p＝12k(l0－l)2，其中k为弹簧的劲度系数，l0为弹簧的原长．物块可视为质点，不计空气阻力，物块接触弹簧瞬间无能量损失，取重力加速度g＝10 m/s2，sin 37°＝0.6，cos 37°＝0.8.则()A．物块与斜面间的动摩擦因数为0.2B．弹簧的劲度系数k为25 N/mC．s3为0.8 mD．物块在斜面上运动的总路程大于s3答案 D解析物块接触弹簧前，由动能定理得mgs1sin θ－μmgs1cos θ＝E k1，解得μ＝0.25，故A错误；由能量守恒定律得mgs2sin θ＝μmgs2cos θ＋E k2＋12k(s2－s1)2，解得k＝20 N/m，故B错误；由能量守恒定律得mgs3sin θ＝μmgs3cos θ＋12k(s3－s1)2，解得s3＝(0.6＋0.25) m，故C错误；物块的路程为s3时mg sin θ＋μmg cos θ<k(s3－s1)，物块还会反向沿斜面向上运动，所以物块在斜面上运动的总路程大于s3，故D正确．例7如图所示，固定斜面的倾角θ＝30°，物体A与斜面之间的动摩擦因数μ＝34，轻弹簧下端固定在斜面底端，弹簧处于原长时上端位于C点，用一根不可伸长的轻绳通过轻质光滑的定滑轮连接物体A和B，滑轮右侧绳子始终与斜面平行，A的质量为2m＝4 kg，B的质量为m＝2 kg，初始时物体A到C点的距离L＝1 m，现给A、B一初速度v0＝3 m/s，使A开始沿斜面向下运动，B向上运动，物体A将弹簧压缩到最短后又恰好能弹回到C点．已知重力加速度大小g＝10 m/s2，不计空气阻力，整个过程中轻绳始终处于伸直状态．求在此过程中：(1)物体A 向下运动刚到C 点时的速度大小； (2)弹簧的最大压缩量； (3)弹簧的最大弹性势能．答案 (1)2 m/s (2)0.4 m (3)6 J解析 (1)在物体A 向下运动刚到C 点的过程中，对A 、B 组成的系统应用能量守恒定律可得 μ·2mg cos θ·L ＝12×3m v 02－12×3m v 2＋2mgL sin θ－mgL ，解得v ＝2 m/s.(2)对A 、B 组成的系统分析，在物体A 从C 点压缩弹簧至最短后恰好返回到C 点的过程中，系统动能的减少量等于因摩擦产生的热量，即12×3m v 2－0＝μ·2mg cos θ·2x其中x 为弹簧的最大压缩量解得x ＝0.4 m.(3)设弹簧的最大弹性势能为E pm ，从C 点到弹簧被压缩至最短过程中由能量守恒定律可得 12×3m v 2＋2mgx sin θ－mgx ＝μ·2mg cos θ·x ＋E pm ，解得E pm ＝6 J.应用能量守恒定律解题的步骤1．首先确定初、末状态，分清有几种形式的能在变化，如动能、势能(包括重力势能、弹性势能、电势能)、内能等．2．明确哪种形式的能量增加，哪种形式的能量减少，并且列出减少的能量ΔE 减和增加的能量ΔE 增的表达式．例8 如图所示，一自然长度小于R 的轻弹簧左端固定，在水平面的右侧，有一底端开口的光滑圆环，圆环半径为R ，圆环的最低点与水平轨道相切，用一质量为m 的小物块(可看作质点)压缩弹簧右端至P 点，P 点到圆环最低点距离为2R ，小物块释放后，刚好过圆环的最高点，已知重力加速度为g ，小物块与水平面间的动摩擦因数为μ.(1)弹簧的弹性势能为多大？(2)改变小物块的质量，仍从P 点释放，要使小物块在运动过程中不脱离轨道，小物块质量满足的条件是什么？答案 (1)2μmgR ＋52mgR(2)m 1≤m 或m 2≥4μ＋54μ＋2m解析 (1)小物块恰好过圆环最高点，则由牛顿第二定律有mg ＝m v 2R从小物块释放至运动到最高点的过程中，由能量守恒定律有E p ＝μmg ·2R ＋mg ·2R ＋12m v 2，联立可解得E p ＝2μmgR ＋52mgR(2)要使小物块在运动过程中不脱离轨道，有两种情况：①小物块能够通过最高点；②小物块在运动过程中最高到达与圆心等高处．①设小物块质量为m 1，在最高点满足m 1g ≤m 1v 12R ，从小物块释放至运动到最高点的过程满足E p ＝2μm 1gR ＋2m 1gR ＋12m 1v 12，解得m 1≤m②设小物块质量为m 2，当小物块运动的最高点不高于圆心时，满足h ≤R ，此时E p ＝2μm 2gR ＋m 2gh ，解得m 2≥4μ＋54μ＋2m .课时精练1.(多选)如图所示，在粗糙的桌面上有一个质量为M 的物块，通过轻绳跨过定滑轮与质量为m 的小球相连，不计轻绳与滑轮间的摩擦，在小球下落的过程中，下列说法正确的是( )A ．小球的机械能守恒B ．物块与小球组成的系统机械能守恒C ．若小球匀速下降，小球减少的重力势能等于物块与桌面间摩擦产生的热量D ．若小球加速下降，小球减少的机械能大于物块与桌面间摩擦产生的热量答案CD解析在小球下落的过程中，轻绳的拉力对小球做负功，小球的机械能减少，故A错误；由于物块要克服摩擦力做功，物块与小球组成的系统机械能不守恒，故B错误；若小球匀速下降，系统的动能不变，则根据能量守恒定律可知，小球减少的重力势能等于物块与桌面间摩擦产生的热量，故C正确；若小球加速下降，则根据能量守恒定律可知，小球减少的机械能等于物块与桌面间摩擦产生的热量及物块增加的动能之和，所以小球减少的机械能大于物块与桌面间摩擦产生的热量，故D正确．2．某同学用如图所示的装置测量一个凹形木块的质量m，弹簧的左端固定，木块在水平面上紧靠弹簧(不连接)并将其压缩，记下木块右端位置A点，静止释放后，木块右端恰能运动到B1点．在木块槽中加入一个质量m0＝800 g的砝码，再将木块左端紧靠弹簧，木块右端位置仍然在A点，静止释放后木块离开弹簧，右端恰能运动到B2点，测得AB1、AB2长分别为27.0 cm和9.0 cm，则木块的质量m为()A．100 g B．200 g C．300 g D．400 g答案 D解析根据能量守恒定律，有μmg·AB1＝E p，μ(m0＋m)g·AB2＝E p，联立解得m＝400 g，D正确．3．风力发电机是由风力带动叶片转动，叶片再带动转子(磁极)转动，使定子(线圈，不计电阻)中产生电流，实现风能向电能的转化．若叶片长为l，设定的额定风速为v，空气的密度为ρ，额定风速下发电机的输出功率为P，则风能转化为电能的效率为()A.2Pπρl2v3 B.6Pπρl2v3 C.4Pπρl2v3 D.8Pπρl2v3答案 A解析风能转化为电能的工作原理为将风的动能转化为输出的电能，设风吹向发电机的时间为t，则在t时间内吹向发电机的风柱的体积为V＝v t·S＝v tπl2，则风柱的质量M＝ρV＝ρv tπl2，因此在t时间内吹过的风的动能为E k＝12M v2＝12ρv tπl2·v2，在t时间内发电机输出的电能E＝P·t，则风能转化为电能的效率为η＝EE k ＝2Pπρl2v3，故A正确，B、C、D错误．4.(多选)如图所示，在竖直平面内有一半径为R的圆弧轨道，半径OA水平、OB竖直，一个质量为m 的小球自A 点的正上方P 点由静止开始自由下落，小球沿轨道到达最高点B 时恰好对轨道没有压力．已知AP ＝2R ，重力加速度为g ，则小球从P 点运动到B 点的过程中( )A ．重力做功2mgRB ．机械能减少mgRC ．合外力做功12mgRD ．克服摩擦力做功12mgR答案 CD解析小球从P 点运动到B 点的过程中，重力做的功W G ＝mg (2R －R )＝mgR ，故A 错误；小球沿轨道到达最高点B 时恰好对轨道没有压力，则有mg ＝m v B 2R ，解得v B ＝gR ，则此过程中机械能的减少量为ΔE ＝mgR －12m v B 2＝12mgR ，故B 错误；根据动能定理可知，合外力做功W 合＝12m v B 2－0＝12mgR ，故C 正确；根据功能关系可知，小球克服摩擦力做的功等于机械能的减少量，则W 克f ＝ΔE ＝12mgR ，故D 正确．5．一木块静置于光滑水平面上，一颗子弹沿水平方向飞来射入木块中．当子弹进入木块的深度达到最大值2.0 cm 时，木块沿水平面恰好移动1.0 cm.在上述过程中系统损失的机械能与子弹损失的动能之比为( )A ．1∶2B ．1∶3C ．2∶3D ．3∶2 答案 C解析根据题意，子弹在摩擦力作用下的位移为s 1＝(2＋1) cm ＝3 cm ，木块在摩擦力作用下的位移为s 2＝1 cm ；系统损失的机械能转化为内能，根据功能关系，有ΔE 系统＝Q ＝f ·Δs ＝f (s 1－s 2)；子弹损失的动能等于子弹克服摩擦力做的功，故ΔE k 子弹＝fs 1；所以ΔE 系统ΔE k 子弹＝23，所以C 正确，A 、B 、D 错误．6．(多选)(2023·福建省厦门外国语学校月考)商场的智能扶梯如图所示，扶梯与水平面之间的夹角为θ，扶梯没有站人时以较小的速度v 1匀速向上运动，当质量为m 的人踏上自动扶梯的水平踏板时，扶梯会自动以加速度a 向上匀加速运动，经过时间t 加速到较大速度v 2后再次匀速向上运动．已知在扶梯加速过程中人上升的竖直高度为h ，人手未接触扶梯扶手，重力加速度为g .则( )A ．扶梯在加速过程中人处于超重状态B ．加速过程中踏板对人的摩擦力不做功C ．加速过程扶梯对人做的功为12m (v 22－v 12)D ．当扶梯以速度v 2匀速运动时，支持力做功的功率为mg v 2sin θ 答案 AD解析扶梯在加速过程中，竖直方向上，人所受的合力向上，支持力大于重力，因此人处于超重状态，A 正确；加速过程中，踏板对人摩擦力水平向右，人在水平向右的方向上有位移，因此摩擦力对人做正功，B 错误；根据能量守恒定律，加速过程扶梯对人做的功W ＝12m (v 22－v 12)＋mgh ，C 错误；扶梯匀速运动时，支持力等于重力，因此支持力做功的功率P ＝mg v 2sin θ，D 正确．7.(2023·江苏南京市十一校调研)如图所示，倾角θ＝30°的粗糙斜面固定在地面上，长为l 、质量为m 、粗细均匀、质量分布均匀的软绳置于斜面上，其上端与斜面顶端平齐，重力加速度为g .用细线将物块与软绳连接，物块由静止释放后向下运动，直到软绳刚好全部离开斜面(此时物块未到达地面)，在此过程中( )A ．物块的机械能逐渐增加B ．软绳的重力势能共减少了14mglC ．物块减少的重力势能等于软绳克服摩擦力所做的功D ．软绳减少的重力势能大于其增加的动能与克服摩擦力所做的功之和答案 B解析物块克服细线的拉力做功，其机械能逐渐减少，A 错误；软绳重力势能减少量ΔE p 减＝mg ·l 2－mg ·l 2sin θ＝14mgl ，B 正确；因为物块的机械能减小，则物块的重力势能减小量大于物块的动能增加量，机械能的减小量等于拉力做功的大小，由于拉力做功大于克服摩擦力做功，所以物块重力势能的减少量大于软绳克服摩擦力所做的功，C 错误；细线的拉力对软绳做正功，对物块做负功，则物块的机械能减小，软绳的机械能增加，软绳重力势能的减少量一定小于其动能的增加量，故软绳重力势能的减少量小于其动能的增加量与克服摩擦力所做功的和，D 错误．8．(多选)(2023·重庆市调研)将一初动能为E 的物体(可视为质点)竖直上抛，物体回到出发点时，动能为E2，取出发点位置的重力势能为零，整个运动过程可认为空气阻力大小恒定，则该物体动能与重力势能相等时，其动能为( ) A.E 4 B.3E10 C.3E 7 D.4E 9答案 BC解析设上升的最大高度为h ，根据功能关系有f ·2h ＝E －E 2＝E2，根据能量守恒可得E ＝mgh＋fh ，求得mgh ＝34E ，fh ＝14E ，求得f ＝13mg ，若在上升阶段离出发点H 处动能和重力势能相等，由能量守恒定律有E k ＋mgH ＝E －fH ，E k ＝E p ＝mgH ，联立解得E k ＝mgH ＝37E ，若在下降阶段离出发点H ′处动能和重力势能相等，由能量守恒定律有E k ′＋mgH ′＝E －f (2h －H ′)，E k ′＝E p ′＝mgH ′，联立解得E k ′＝mgH ′＝310E ，故选B 、C.9．(2023·山西太原市高三模拟)如图甲所示，一物块置于粗糙水平面上，其右端通过水平弹性轻绳固定在竖直墙壁上．用力将物块向左拉至O 处后由静止释放，用传感器测出物块的位移s 和对应的速度，作出物块的动能E k －s 关系图像如图乙所示．其中，0.10～0.25 m 间的图线为直线，其余部分为曲线．已知物块与水平面间的动摩擦因数为0.2，取g ＝10 m/s 2，弹性绳的弹力与形变始终符合胡克定律，可知( )A ．物块的质量为0.2 kgB ．弹性绳的劲度系数为50 N/mC ．弹性绳弹性势能的最大值为0.6 JD ．物块被释放时，加速度的大小为8 m/s 2 答案 D解析根据动能定理可得μmg Δs ＝ΔE k ，代入数据可得m ＝ΔE k μg Δs ＝0.300.2×10×(0.25－0.10) kg＝1 kg ，所以A 错误；由题图乙可知动能最大时弹性绳弹力等于滑动摩擦力，则有k Δs 1＝μmg ，Δs 1＝0.10 m －0.08 m ＝0.02 m ，解得k ＝100 N/m ，所以B 错误；根据能量守恒定律有E pm ＝μmg s m ＝0.2×1×10×0.25 J ＝0.5 J ，所以C 错误；物块被释放时，加速度的大小为a ＝k Δs m －μmg m ＝100×0.10－0.2×1×101m/s 2＝8 m/s 2，所以D 正确． 10.如图所示，在某竖直平面内，光滑曲面AB 与粗糙水平面BC 平滑连接于B 点，BC 右端连接内壁光滑、半径r ＝0.2 m 的14细圆管CD ，管口D 端正下方直立一根劲度系数为k ＝100 N/m的轻弹簧，弹簧一端固定于地面上，另一端恰好与管口D 端平齐．一个质量为1.0 kg 的物块放在曲面AB 上，现从距BC 的高度为h ＝0.6 m 处由静止释放物块，它与BC 间的动摩擦因数μ＝0.5，物块进入管口C 端时，它对上管壁有N ＝2.5mg 的作用力，通过CD 后，在压缩弹簧过程中物块速度最大时弹簧的弹性势能E p ＝0.5 J ．重力加速度g 取10 m/s 2.求：(1)在压缩弹簧过程中物块的最大动能E km ； (2)物块最终停止的位置．答案 (1)6 J (2)停在BC 上距离C 端0.3 m 处(或距离B 端0.2 m 处)解析 (1)在压缩弹簧过程中，物块速度最大时所受合力为零．设此时物块离D 端的距离为x 0，则有kx 0＝mg ，解得x 0＝mgk＝0.1 m 在C 点，物块受到上管壁向下的作用力N ′＝2.5mg 和重力，有N ′＋mg ＝m v C 2r ，解得v C ＝7 m/s.物块从C 点到速度最大时，由能量守恒定律有mg (r ＋x 0)＝E p ＋E km －12m v C 2，解得E km ＝6 J(2)物块从A 点运动到C 点的过程中，由动能定理得mgh －μmgs ＝12m v C 2－0解得B 、C 间距离s ＝0.5 m物块与弹簧作用后返回C 处时动能不变，物块的动能最终消耗在与BC 水平面相互作用的过程中．设物块第一次与弹簧作用返回C 处后，物块在BC 上运动的总路程为s ′，由能量守恒定律有：μmgs ′＝12m v C 2，解得s ′＝0.7 m ，故最终物块在BC 上距离C 点为x 1＝0.5 m －(0.7 m－0.5 m)＝0.3 m(或距离B 端为x 2＝0.7 m －0.5 m ＝0.2 m)处停下．11．(多选)(2023·山东济南市十一校检测)如图所示为某缓冲装置的模型图，一轻杆S 被两个固定薄板夹在中间，轻杆S 与两薄板之间的滑动摩擦力大小均为f ，轻杆S 露在薄板外面的长度为l .轻杆S 前端固定一个劲度系数为3fl 的轻弹簧．一质量为m 的物体从左侧以大小为v 0的速度撞向弹簧，能使轻杆S 向右侧移动l 6.已知弹簧的弹性势能E p ＝12kx 2，其中k 为劲度系数，x 为形变量．最大静摩擦力等于滑动摩擦力，弹簧始终在弹性限度内．下列说法正确的是( )A ．欲使轻杆S 发生移动，物体m 运动的最小速度为1010v 0 B ．欲使轻杆S 发生移动，物体m 运动的最小速度为63v 0C ．欲使轻杆S 左端恰好完全进入薄板，物体m 运动的速度大小为62v 0D ．欲使轻杆S 左端恰好完全进入薄板，物体m 运动的速度大小为263v 0答案 BD解析当轻杆刚要移动时，对轻杆受力分析，设此时弹簧弹力大小为F ，压缩量为x ，由平衡条件知F ＝kx ＝2f ，代入k 的值可得x ＝23l ，设欲使轻杆S 发生移动，物体m 运动的最小速度为v1，则由能量守恒定律有12m v12＝12k(23l)2，由题意知，物体以大小为v0的速度撞向弹簧，能使轻杆S向右侧移动l6，由能量守恒定律有12m v02＝2f×l6＋12m v12，联立可得v1＝63v0，故A错误，B正确；设物体m的运动速度大小为v2时，轻杆S左端恰好完全进入薄板，则由能量守恒定律有12m v22＝2f×l＋12m v12，可解得v2＝263v0，故C错误，D正确．。

高三物理一轮复习功能关系能量守恒导学案

班级：组别：姓名：组内评价：教师评价：（等第）课题：功能关系、能量守恒定律【学习目标】理解功能关系，掌握能量守恒定律。

【重点难点】功能关系的应用【自主学习】教师评价：（等第）一、功能关系1．功能关系：做功的过程就是转化过程，做多少功就有多少某种形式的能转化为其他形式的能。

2．功是能量转化的。

3．常见力做功与能量转化的对应关系：⑴重力所做的功等于能的变化⑵弹簧的弹力所做的功等于能的变化⑶合外力所做的功等于能的增加⑷只有重力和弹簧的弹力做功，守恒⑸重力和弹簧的弹力以外的力所做的功等于能的增加⑹克服一对滑动摩擦力所做的净功等于能的增加⑺电场力所做的功等于能的减少⑻克服安培力所做的功等于能的增加二、能的转化和守恒定律能量既不会凭空产生，也不会凭空消失，它只能从一种形式为别的形式，或从一个物体到另一个物体．在转化或转移的过程中其总量不变，这就是能的转化和守恒定律．表达式：自主测评：1、质量为3kg的物体在空中以8m/s2的加速度竖直下降2m的过程中，物体的机械能 (填“增加”或“减少”) J，重力势能(“增加”或“减少”) J，动能(“增加”或“减少”) J．2、以初速度v0竖直上抛一个质量为m的小球，小球运动过程中所受阻力F阻大小不变，上升最大高度为h，则抛出过程中，人手对小球做的功为（）3、水平地面上原来分散平放着n块砖，每块砖的质量均为m，厚度均为d，某人以靠墙的一块砖做底，将分散的砖一块一块的仍平放着叠放起来，则在这一过程中，此人至少做功（）4、如图所示轻弹簧一端固定在墙上的O点，处于自然长度状态时，另一端在B点．今将一质量为m的物体靠在弹簧的右端，并用力向左推物体，压缩弹簧至A点，然后由静止释放物体，物体在水平面上滑行到C点停止．已知AC距离为S，若将物体拴接在弹簧的右侧，同样将其推至A点，再由静止释放，弹簧与物体将振动至最后静止，则振动的总路程L与S相比较，下列关系正确的是( )A．L一定小于S B．L一定等于SC．L一定大于S D．L小于、等于S都有可能5：一滑块放在如图所示的凹形斜面上，斜面固定于水平地面，用拉力F沿斜面向下拉小滑块，小滑块沿斜面运动了一段距离．若已知在这过程中，拉力F所做的功为A，斜面对滑块的作用力所做的功为B，重力所做的功为C，空气阻力所做的功为D，则小滑块的动能的增量为，重力势能的增量为，机械能的增量为．6：在离地面高为h处竖直上抛一质量为m的物块，抛出时的速度为v0，当它落到地面时速度为v，用g表示重力加速度，则在此过程中物块克服空气阻力所做的功等于（）7. 2010·江苏如图所示，平直木板AB 倾斜放置，板上的P 点距A 端较近，小物块与木板间的动摩擦因数由A 到B 逐渐减小，先让物块从A 由静止开始滑到B 。

高三物理一轮复习优质学案1：5.4功能关系能量守恒定律

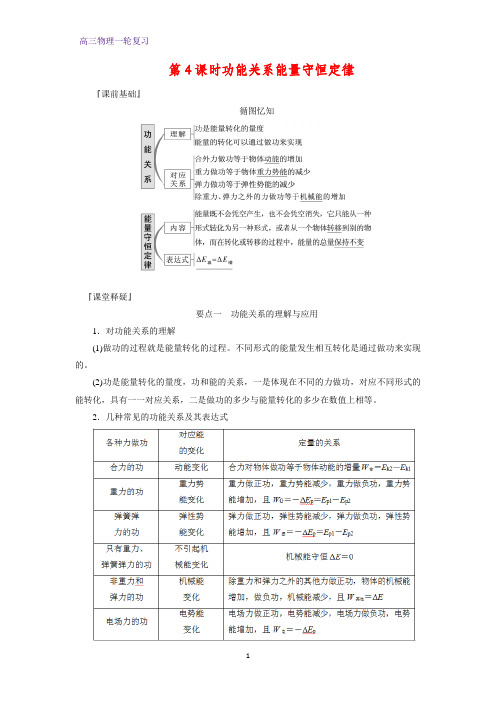
第4课时功能关系能量守恒定律『课前基础』循图忆知『课堂释疑』要点一功能关系的理解与应用1．对功能关系的理解(1)做功的过程就是能量转化的过程。

不同形式的能量发生相互转化是通过做功来实现的。

(2)功是能量转化的量度，功和能的关系，一是体现在不同的力做功，对应不同形式的能转化，具有一一对应关系，二是做功的多少与能量转化的多少在数值上相等。

2．几种常见的功能关系及其表达式[多角练通]1.(2015·商丘模拟)自然现象中蕴藏着许多物理知识，如图5-4-1所示为一个盛水袋，某人从侧面缓慢推袋壁使它变形，则水的势能()图5-4-1A．增大B．变小C．不变D．不能确定2．(2015·唐山模拟)轻质弹簧右端固定在墙上，左端与一质量m＝0.5 kg的物块相连，如图5-4-2甲所示。

弹簧处于原长状态，物块静止且与水平面间的动摩擦因数μ＝0.2。

以物块所在处为原点，水平向右为正方向建立x轴。

现对物块施加水平向右的外力F，F随x轴坐标变化的情况如图乙所示。

物块运动至x＝0.4 m处时速度为零。

则此时弹簧的弹性势能为(g取10 m/s2)()图5-4-2A．3.1 J B．3.5 JC．1.8 J D．2.0 J3．(2014·广东高考)如图5-4-3是安装在列车车厢之间的摩擦缓冲器结构图。

图中①和②为楔块，③和④为垫板，楔块与弹簧盒、垫板间均有摩擦。

在车厢相互撞击使弹簧压缩的过程中()图5-4-3A．缓冲器的机械能守恒B．摩擦力做功消耗机械能C．垫板的动能全部转化为内能D．弹簧的弹性势能全部转化为动能要点二摩擦力做功与能量的关系1．两种摩擦力做功的比较2．求解相对滑动物体的能量问题的方法(1)正确分析物体的运动过程，做好受力分析。

(2)利用运动学公式，结合牛顿第二定律分析物体的速度关系及位移关系。

(3)公式Q＝F f·s相对中s相对为两接触物体间的相对位移，若物体在传送带上做往复运动时，则s相对为总的相对路程。

高三物理一轮复习优质学案：功能关系能量守恒定律

能力课功能关系能量守恒定律[热考点]功能关系的理解和应用1.力学中常见的功能关系2.应用功能关系解决具体问题应注意以下三点(1)若只涉及动能的变化用动能定理。

(2)只涉及重力势能的变化，用重力做功与重力势能变化的关系分析。

(3)只涉及机械能变化，用除重力和弹簧的弹力之外的力做功与机械能变化的关系分析。

『例1』(2016·全国卷Ⅱ，21)(多选)如图1，小球套在光滑的竖直杆上，轻弹簧一端固定于O点，另一端与小球相连。

现将小球从M点由静止释放，它在下降的过程中经过了N点。

已知在M、N两点处，弹簧对小球的弹力大小相等，且∠ONM<∠OMN<π2。

在小球从M点运动到N点的过程中()图1A.弹力对小球先做正功后做负功B.有两个时刻小球的加速度等于重力加速度C.弹簧长度最短时，弹力对小球做功的功率为零D.小球到达N 点时的动能等于其在M 、N 两点的重力势能差解析因M 和N 两点处弹簧对小球的弹力大小相等，且∠ONM <∠OMN <π2，M 处的弹簧处于压缩状态，N 处的弹簧处于伸长状态，则弹簧的弹力对小球先做负功后做正功再做负功，选项A 错误；当弹簧水平时，竖直方向的力只有重力，加速度为g ；当弹簧处于原长位置时，小球只受重力，加速度为g ，则有两个时刻的加速度大小等于g ，选项B 正确；弹簧长度最短时，即弹簧水平，弹力与速度垂直，弹力对小球做功的功率为零，选项C 正确；由动能定理得，W F ＋W G ＝ΔE k ，因M 和N 两点处弹簧对小球的弹力大小相等，弹性势能相等，则由弹力做功特点知W F ＝0，即W G ＝ΔE k ，选项D 正确。

答案 BCD『变式训练1』 (2017·江苏泰州模拟)一个系统的机械能增大，究其原因，下列推测正确的是( ) A.可能是重力对系统做了功 B.一定是合外力对系统做了功 C.一定是系统克服合外力做了功 D.可能是摩擦力对系统做了功解析只有重力做功，系统的机械能守恒，选项A 错误；除重力、弹力之外的力做正功时，系统机械能增加，做负功时则减少，故选项B 、C 错误；如果摩擦力对系统做正功，则系统机械能增加，故选项D 正确。

高三总复习功能关系能量守恒定律导学案

年级：高三学科：物理班级：学生姓名：制作人：不知名编号：2023－33第4讲功能关系能量守恒定律学习目标：结合运动学公式、牛顿运动定律、圆周运动规律、机械能守恒定律、功能关系、动量守恒定律等知识进行综合考查。

预学案1、三大类功能关系：（1）第一大类：做正功，能量减少；做负功，能量增加。

W=-∆E P重力做功↔重力势能的变化W G=-∆E P；电场力做功↔电势能的变化W F=--∆E P；弹簧弹力做功↔弹性势能的变化W F=-∆E P；分子力做功↔分子势能的变化W F=--∆E P。

(2) 第二大类：：做正功，能量增加；做负功，能量减少。

W=∆E P合力做功↔动能的变化W合=∆E K；单个物体除重力外其他力做功或系统除重力、弹簧弹力以外其他力做功↔机械能的变化W其=∆E（3）第三大类：两个特殊的功能关系a.滑动摩擦力与两物体间相对滑行距离的乘积等于产生的内能,即F f x相对=Q。

B.电磁感应过程中克服安培力做的功等于产生的电能,即W克安=E电。

2、能量守恒定律（1）内容：能量既不会凭空产生,也不会凭空消失。

它只能从一种形式______为另一种形式,或者从一个物体_______ 到另一个物体,而在转化和转移的过程中,能量的总量__________。

（2）表达式:ΔE减=ΔE增。

探究案探究一：功能关系的理解及应用。

总复习大本P108 典例1、典例2、多维训练1、2。

探究二:功能关系的综合应用。

总复习大本P110 典例3、典例4、多维训练1、2。

检测案1、(多选)(2022·武汉模拟)如图所示,轻质弹簧下端固定在水平面上,弹簧原长为L,质量为m的小球从距弹簧上端高度为h的P点由静止释放,小球与弹簧接触后立即与弹簧上,弹簧端粘连,并在竖直方向上运动。

一段时间后,小球静止在O点,此时,弹簧长度为L2的弹性势能为E p,重力加速度为g,弹簧始终在弹性限度内。

下列说法正确的是()A.弹簧的劲度系数为2mgLB.小球在运动过程中,球与弹簧组成的系统机械能守恒C.小球第一次下落过程中速度最大位置在O点)D.E p<mg(h+L22、如图所示的离心装置中,光滑水平轻杆固定在竖直转轴的O点,小圆环A和轻质弹簧套在轻杆上,长为2L的细线和弹簧两端分别固定于O和A,质量为m的小球B固定在细线的中点,装置静止时,细线与竖直方向的夹角为37°,现将装置由静止缓慢加速转动,当细线与竖直方向的夹角增大到53°时,A、B间细线的拉力恰好减小到零,弹簧弹力与静止时大小相等、方向相反,重力加速度为g,取sin37°=0.6,cos37°=0.8,求:(1)装置静止时,弹簧弹力的大小F;(2)环A的质量M;(3)上述过程中装置对A、B所做的总功W。

高三物理一轮复习学案(37) 功能关系

2019级高三物理一轮复习学案（37）功能关系目标导航1、理解掌握各种力做功对应的功能关系2、理解能量守恒定律并熟练应用一、功能关系做功的过程是能量转化的过程，功是能的转化的量度。

具体关系有： 1.物体动能的增量由外力做的总功来量度：W 外=2.物体重力势能的增量由重力做的功来量度：W G =3．弹簧弹性势能的增量由弹簧弹力做的功来量度：W 弹=4.物体机械能的增量由除重力之外的其它力做功来量度：W 其=5.一对互为作用力反作用力的滑动摩擦力做的总功，用来量度该过程系统由于摩擦而减小的机械能，也就是系统增加的内能。

f d =Q （d 为这两个物体间相对移动的路程）。

6.一对互为作用力反作用力的静摩擦力对系统不做功。

二、能量的转化和守恒定律列能量守恒定律方程式的两条基本思路：１.某种形式的能减少，一定存在其他形式的能增加，且减少量和增加量一定相等。

２.某个物体的能量减少，一定存在其他物体的能量增加，且减少量一定与增加量相等。

【课中案】例1.质量为m 的物体(可视为质点)以某一速度由底端冲上倾角为30°的固定斜面，上升的最大高度为h ，其加速度大小为3g/4.在这个过程中，物体( )A ．重力势能增加了mghB ．动能损失了mghC ．动能损失了3mgh 2D ．机械能损失了mgh 2例2．如图所示，质量为m 的物块从A 点由静止开始下落，加速度是g/2，下落H 到B 点后与一轻弹簧接触，又下落h 后到达最低点C ，在由A 运动到C 的过程中，空气阻力恒定，则( )A ．物块机械能守恒B ．物块和弹簧组成的系统机械能守恒C ．物块机械能减少mg(H+h)/2D ．物块和弹簧组成的系统机械能减少mg(H+h)/2例3．如图所示，质量为M 的木块放在光滑的水平面上，质量为m 的子弹以速度v 0沿水平方向射中木块，并最终留在木块中与木块一起以速度v 运动。

已知当子弹相对木块静止时，木块前进距离为L ，子弹进入木块的深度为s ，若木块对子弹的阻力f 视为恒定，则下列关系式中正确的是（）A ．221Mv fL = C ．()2202121mv mv s L f -=+ B ．221mv fs = D ．()2202121v m M mv fs +-=【课后案】1．韩晓鹏是我国首位在冬奥会雪上项目夺冠的运动员。

高三物理一轮复习精品学案4：5.4功能关系能量守恒定律

第4课时功能关系能量守恒定律考纲解读1.知道功是能量转化的量度，掌握重力的功、弹力的功、合力的功与对应的能量转化关系.2.知道自然界中的能量转化，理解能量守恒定律，并能用来分析有关问题『知识要点』一功能关系的应用力学中几种常见的功能关系二1．静摩擦力做功的特点(1)静摩擦力可以做功，也可以做功，还可以功．(2)相互作用的一对静摩擦力做功的代数和总等于(3)静摩擦力做功时，只有机械能的相互转移，不会转化为内能．2．滑动摩擦力做功的特点(1)滑动摩擦力可以做功，也可以做功，还可以功．(2)相互间存在滑动摩擦力的系统内，一对滑动摩擦力做功将产生两种可能效果：①机械能全部转化为内能；②有一部分机械能在相互摩擦的物体间转移，另外一部分转化为内能．(3)摩擦生热的计算：Q＝F f x相对．其中x相对为相互摩擦的两个物体间的相三能量守恒定律及应用1．内容能量既不会凭空，也不会凭空消失，它只能从一种形式为另一种形式，或者从一个物体到别的物体，在转化或转移的过程中，能量的总量．2．表达式ΔE减＝．3．基本思路(1)某种形式的能量减少，一定存在其他形式的能量增加，且减少量和增加量一定相等；(2)某个物体的能量减少，一定存在其他物体的能量增加且减少量和增加量一定相等『课后检测』1．(多选)(2015年东莞调研)由于某种原因，人造地球卫星的轨道半径减小了，那么( ) A ．卫星受到的万有引力增大，线速度减小 B ．卫星的向心加速度增大，周期减小 C ．卫星的动能、重力势能和机械能都减小 D ．卫星的动能增大，重力势能减小，机械能减小2．(多选)(2015年惠州三模)如图5－4－7所示，足够长的传送带以恒定速率沿顺时针方向运转．现将一个物体轻轻放在传送带底端，物体在第一阶段被加速到与传送带具有相同的速度，第二阶段匀速运动到传送带顶端．则下列说法中正确的是( )图5－4－7A ．第一阶段和第二阶段摩擦力对物体都做正功B ．第一阶段摩擦力对物体做的功等于第一阶段物体动能的增加量C ．第二阶段摩擦力对物体做的功等于第二阶段物体机械能的增加量D ．两个阶段摩擦力对物体所做的功等于物体机械能的减少量3．(多选)(2015年广东六校一模)如图5－4－8所示，M 为固定在水平桌面上的有缺口的方形木块，abcd 为半径是R 的34光滑圆弧形轨道，a 为轨道的最高点，de 面水平且有一定长度．今将质量为m 的小球在d 点的正上方高为h 处由静止释放，让其自由下落到d 处切入轨道内运动，不计空气阻力，则( )图5－4－8A ．只要h 大于R ，释放后小球就能通过a 点B ．只要改变h 的大小，就能使小球通过a 点后，既可能落回轨道内，又可能落到de 面上C ．无论怎样改变h 的大小，都不可能使小球通过a 点后落回轨道内D ．调节h 的大小，可以使小球飞出de 面之外(即e 的右侧)4．(2015年湖南段考)如图5－4－9，一滑块经水平轨道AB 进入竖直平面内的四分之一圆弧轨道BC ．已知滑块的质量m ＝0.60 kg ，在A 点时的速度v A ＝8.0 m/s ，AB 长s ＝5.0 m ，滑块与水平轨道间的动摩擦因数μ＝0.15，圆弧轨道的半径R ＝2.0 m ，滑块离开C 点后竖直上升h ＝0.20 m ，取g ＝10 m/s 2.求：图5－4－9(1)滑块经过B 点时的速度大小；(2)滑块经过B 点时圆弧轨道对它的支持力的大小； (3)滑块在圆弧轨道BC 段克服摩擦力所做的功．5．(2012年海南卷)如图5－4－10，在竖直平面内有一固定光滑轨道，其中AB 是长为R 的水平直轨道，BCD 是圆心为O 、半径为R 的34圆弧轨道，两轨道相切于B 点．在外力作用下，一小球从A 点由静止开始做匀加速直线运动，到达B 点时撤除外力．已知小球刚好能沿圆轨道经过最高点C ，重力加速度大小为g .求：图5－4－10(1)小球在AB 段运动的加速度的大小； (2)小球从D 点运动到A 点所用的时间．『答案』1.『答案』BD2.『答案』AC3.『答案』CD『解析』要使小球到达最高点a ，则在最高点小球速度最小时有mg ＝m v 2R ，得最小速度v ＝gR ，由机械能守恒定律得mg (h －R )＝12mv 2，得h ＝32R ，即h 必须大于或等于32R ，小球才能通过a 点，A 错误；小球若能到达a 点，并从a 点以最小速度平抛，有R ＝12gt 2，x ＝vt＝2R ，所以，无论怎样改变h 的大小，都不可能使小球通过a 点后落回轨道内，B 错误、C 正确；如果h 足够大，小球可能会飞出de 面之外，D 正确．4.『答案』(1)7.0 m/s (2)20.7 N (3)1.5 J『解析』(1)滑块从A 到B 做匀减速直线运动，由动能定理：－fs ＝12mv 2B －12mv 2A 摩擦力f ＝μmg 联立解得vB ＝7.0 m/s.(2)滑块经过B 点时，由牛顿第二定律 N －mg ＝m v 2B R解得N ＝20.7 N.(3)滑块离开C 点后做竖直上抛运动，由运动学公式 v 2C ＝2gh从B 到C 的过程中，设摩擦力做功为W f ，由动能定理－mgR ＋W f ＝12mv 2C －12mv 2B联立解得W f ＝－1.5 J.故滑块在圆弧轨道BC 段克服摩擦力做的功为W ′f ＝1.5 J.5.『答案』 (1)a ＝52g (2)()5－3Rg『解析』(1)小球在BCD 段运动时，受到重力mg 、轨道正压力N 的作用，如图所示．据题意，N ≥0，且小球在最高点C 所受轨道正压力为零N C ＝0设小球在C 点的速度大小为v C ，根据牛顿第二定律有mg ＝m v 2CR小球从B 点运动到C 点，机械能守恒．设B 点处小球的速度大小为v B ，有 12mv 2B ＝12mv 2C＋2mgR 由于小球在AB 段由静止开始做匀加速运动，设加速度大小为a ，由运动学公式有v 2B＝2aR .解得a ＝52g .(2)设小球在D 处的速度大小为v D ，下落到A 点时的速度大小为v ，由机械能守恒有 12mv 2B ＝12mv 2D ＋mgR 12mv 2B ＝12mv 2 设从D 点运动到A 点所用的时间为t ，由运动学公式得 gt ＝v －v D 解得t ＝(5－3)R g.。

高考物理一轮复习功能关系能量守恒定律学案新人教

第四节功能关系能量守恒定律(对应学生用书第89页)[教材知识速填]知识点1 功能关系1．内容(1)功是能量转化的量度，即做了多少功就有多少能量发生了转化．(2)做功的过程一定伴随着能量的转化，而且能量的转化必须通过做功来实现．2．做功对应变化的能量形式(1)合外力的功等于物体的动能的变化．(2)重力做功引起物体重力势能的变化．(3)弹簧弹力做功引起弹性势能的变化．(4)除重力和系统内弹力以外的力做功等于物体机械能的变化．易错判断(1)做功的过程一定会有能量转化．(√)(2)力对物体做了多少功，物体就有多少能．(×)(3)力对物体做功，物体的总能量一定增加．(×)知识点2 能量守恒定律1．内容能量既不会凭空产生，也不会凭空消失，它只能从一种形式转化为另一种形式，或者从一个物体转移到另一个物体，在转化和转移的过程中，能量的总量保持不变．2．适用范围能量守恒定律是贯穿物理学的基本规律，是各种自然现象中普遍适用的一条规律．3．表达式ΔE减＝ΔE增，E初＝E末．易错判断(1)能量在转化或转移的过程中，其总量会不断减少．(×)(2)能量的转化和转移具有方向性，且现在可利用的能源有限，故必须节约能源．(√)(3)滑动摩擦力做功时，一定会引起能量的转化．(√)[教材习题回访]考查点：对功能关系理解1．(粤教版必修2P89T2)(多选)平直公路上行驶中的汽车制动后滑行一段距离，最后停下；流星在夜空中坠落并发出明亮的光焰；降落伞在空中匀速下降；条形磁铁在下落过程中穿过闭合线圈，线圈中产生电流．上述不同现象中所包含的相同的物理过程是( )A ．物体克服阻力做功B ．物体动能转化为其他形式的能量C ．物体势能转化为其他形式的能量D ．物体机械能转化为其他形式的能量 [答案] AD考查点：能量的转化与守恒2．(沪科版必修2P 77T 5改编)上端固定的一根细线下面悬挂一摆球，摆球在空气中摆动，摆动的幅度越来越小，对此现象下列说法正确的是( )A ．摆球机械能守恒B ．总能量守恒，摆球的机械能正在减少，减少的机械能转化为内能C ．能量正在消失D ．只有动能和重力势能的相互转化 [答案] B考查点：功能关系的计算3．(沪科版必修2P 55T 1)(多选)某人用手将质量为1 kg 的物体由静止向上提起1 m ，这时物体的速度为2 m/s ，g 取10 m/s 2，下列说法中正确的是( )A ．手对物体做功12 JB ．合外力做功2 JC ．合外力做功12 JD ．物体克服重力做功10 J [答案] ABD考查点：能量的转化与守恒4．(人教版必修2P 82T 2改编)三峡水力发电站是我国最大的水力发电站，平均水位落差约135 m ，水的流量约1.35×104m 3/s.船只通航需要约3 500 m 3/s 的流量，其余流量全部用来发电．水流冲击水轮机发电时，水流减少的机械能有20%转化为电能．(1)按照以上数据估算，三峡发电站的发电功率是多少？(2)设三口之家生活用电平均为0.5 kW ，如果三峡电站全部用于城市生活用电，它大约可以满足多少个百万人口城市的生活用电？[解析](1)用于发电的水流量Q ＝(1.35×104－3.5×103) m 3/s ＝1.0×104m 3/s 发电功率P ＝mgh t ×20%＝ρVgh t ×20%＝ρQgh×20%＝2.7×109W.(2)可供给用户数n ＝2.7×1090.5×103＝5.4×106人口数为N ＝3n ＝16.2×106故可满足16个百万城市的生活用电[答案](1)2.7×109 W (2)16个(对应学生用书第90页)对功能关系的理解及应用几种常见功能关系的对比各种力做功对应能的变化定量关系合力的功动能变化合力对物体做功等于物体动能的增量W合＝E k2－E k1重力的功重力势能变化重力做正功，重力势能减少，重力做负功，重力势能增加，且W G＝－ΔE p＝E p1－E p2弹簧弹力的功弹性势能变化弹力做正功，弹性势能减少，弹力做负功，弹性势能增加，且W弹＝－ΔE p＝E p1－E p2只有重力、弹簧弹力做功不引起机械能变化机械能守恒ΔE＝0非重力和弹力的功机械能变化重力和弹力之外的力做正功，物体的机械能增加，做负功，机械能减少，且W其他＝ΔE一对相互作用的滑动摩擦力做的总功内能变化作用于系统的一对滑动摩擦力一定做负功，系统内能增加Q＝fs相对[题组通关]1．(多选)悬崖跳水是一项极具挑战性的极限运动，需要运动员具有非凡的胆量和过硬的技术．跳水运动员进入水中后受到水的阻力而做减速运动，设质量为m的运动员刚入水时的速度为v，水对他的阻力大小恒为F，那么在他减速下降深度为h的过程中，下列说法正确的是(g为当地的重力加速度)( ) A．他的动能减少了(F－mg)hB．他的重力势能减少了mgh－12 mv2C．他的机械能减少了FhD．他的机械能减少了mghAC [合力做的功等于动能的变化，合力做的功为(mg－F)h，动能减少了(F－mg)h，A正确；重力做的功等于重力势能的变化，故重力势能减小了mgh，B错误；重力以外的力做的功等于机械能的变化，故机械能减少了Fh，C正确，D错误．]2．(2020·陕西西安联考)(多选)如图541所示，将质量为2m的重物悬挂在轻绳的一端，轻绳的另一端系一质量为m的环，环套在竖直固定的光滑直杆上，光滑定滑轮与直杆的距离为d.杆上的A点与定滑轮等高，杆上的B 点在A 点正下方距离为d 处．现将环从A 处由静止释放，不计一切摩擦阻力，下列说法正确的是( ) 【导学号：84370232】图541A ．环到达B 处时，重物上升的高度h ＝d2B ．环到达B 处时，环与重物的速度大小相等C ．环从A 到B ，环减少的机械能等于重物增加的机械能D ．环能下降的最大高度为43d[题眼点拨] ①“轻绳”和“光滑直杆”说明质量为m 的环下滑过程中，与重物组成的系统机械能守恒；②“到达B 处”要利用环沿绳的速度分量等于重物上升的速度． CD [环到达B 处时，对环的速度进行分解，可得v 环cos θ＝v 物，由题图中几何关系可知θ＝45°，则v 环＝2v 物，B 错；因环从A 到B ，环与重物组成的系统机械能守恒，则环减少的机械能等于重物增加的机械能，C 对；当环到达B 处时，由题图中几何关系可得重物上升的高度h ＝(2－1)d ，A 错；当环下落到最解得H ＝43低点时，设环下落高度为H ，由机械能守恒有mgH ＝2mg(H 2＋d 2－d)，d ，故D 正确．]对能量守恒定律的理解及应用1．对能量守恒定律的两点理解(1)某种形式的能量减少，一定存在其他形式的能量增加，且减少量和增加量一定相等． (2)某个物体的能量减少，一定存在其他物体的能量增加，且减少量和增加量一定相等．2．能量转化问题的解题思路(1)当涉及滑动摩擦力做功，机械能不守恒时，一般应用能的转化和守恒定律．(2)解题时，首先确定初、末状态，然后分析状态变化过程中哪种形式的能量减少，哪种形式的能量增加，求出减少的能量总和ΔE 减和增加的能量总和ΔE 增，最后由ΔE 减＝ΔE 增列式求解．[多维探究]考向1 能量守恒定律的简单应用1. 蹦极是一项既惊险又刺激的运动，深受年轻人的喜爱．如图542所示，蹦极者从P 处由静止跳下，到达A 处时弹性绳刚好伸直，继续下降到最低点B 处，B 离水面还有数米距离．蹦极者(视为质点)在其下降的整个过程中，重力势能的减少量为ΔE 1、绳的弹性势能的增加量为ΔE 2、克服空气阻力做的功为W ，则下列说法正确的是( )图542A ．蹦极者从P 到A 的运动过程中，机械能守恒B ．蹦极者与绳组成的系统从A 到B 的过程中，机械能守恒C ．ΔE 1＝W ＋ΔE 2D ．ΔE 1＋ΔE 2＝WC [下落过程中有空气阻力做功，所以机械能不守恒，A 、B 项错误；根据能量守恒，在下落的全过程，有ΔE 1＝W ＋ΔE 2，故C 项正确，D 项错误．]如图所示，A 、B 、C 质量分别为m A ＝0.7 kg ，m B ＝0.2 kg ，m C ＝0.1 kg ，B 为套在细绳上的圆环，A 与水平桌面的动摩擦因数μ＝0.2，另一圆环D 固定在桌边外侧，离地面高h 2＝0.3 m ．当B 、C 从静止下降h 1＝0.3 m ，C 穿环而过，B 被D 挡住，不计绳子质量和滑轮的摩擦，取g ＝10 m/s 2，若开始时A 离桌边足够远．试求：(1)物体C 穿环瞬间的速度；(2)物体C 能否到达地面？如果能到达地面，其速度多大？[解析](1)由能量守恒定律得：(m B ＋m C )gh 1＝12(m A ＋m B ＋m C )v 21＋μm A gh 1可求得：v 1＝256 m/s.(2)设物体C 到达地面时的速度为v 2，由能量守恒定律得： m C gh 2＝12(m A ＋m C )v 22－12(m A ＋m C )v 21＋μm A gh 2可求得：v 2＝6610 m/s ，故物体C 能到达地面，到达地面时的速度为6610m/s. [答案](1)25 6 m/s (2)能 6610m/s 考向2 涉及弹簧(或橡皮绳)类的能量守恒问题2．在儿童乐园的蹦床项目中，小孩在两根弹性绳和蹦床的协助下实现上下弹跳．如图543所示，某次蹦床活动中小孩静止时处于O 点，当其弹跳到最高点A 后下落可将蹦床压到最低点B ，小孩可看成质点，不计空气阻力，下列说法正确的是( )图543A．从A运动到O，小孩重力势能减少量大于动能增加量B．从O运动到B，小孩动能减少量等于蹦床弹性势能增加量C．从A运动到B，小孩机械能减少量小于蹦床弹性势能增加量D．若从B返回到A，小孩机械能增加量等于蹦床弹性势能减少量A [从A运动到O，小孩重力势能减少量等于动能增加量与弹性绳的弹性势能的增加量之和，选项A正确；从O运动到B，小孩动能和重力势能的减少量等于弹性绳和蹦床的弹性势能的增加量，选项B错误；从A运动到B，小孩机械能减少量大于蹦床弹性势能增加量，选项C错误；若从B返回到A，小孩机械能增加量等于蹦床和弹性绳弹性势能减少量之和，选项D错误．] 3．(2020·河南名校联考)如图544所示，在某竖直平面内，光滑曲面AB与水平面BC平滑连接于B点，BC右端连接内壁光滑、半径r＝0.2 m的四分之一细圆管CD，管口D端正下方直立一根劲度系数k＝100 N/m的轻弹簧，弹簧一端固定，另一端恰好与管口D端平齐．一个质量为1 kg的小球放在曲面AB 上，现从距BC的高度h＝0.6m处静止释放小球，它与BC间的动摩擦因数μ＝0.5，小球进入管口C 端时，它对上管壁有F N＝2.5mg的作用力，通过CD后，在压缩弹簧过程中小球速度最大时弹簧的弹性势能E p＝0.5 J．重力加速度g取10 m/s2.求：图544(1)小球在C处受到的向心力大小；(2)在压缩弹簧过程中小球的最大动能E km；(3)小球最终停止的位置.【导学号：84370233】[题眼点拨] ①“对上管壁有F N的作用力”要想到在c点时向心力的来源；②“速度最大时弹簧的弹性势能E p＝0.5 J”要利用速度最大时小球重力等于弹簧弹力的条件分析弹簧的形变量．[解析](1)小球进入管口C端时，它与圆管上管壁有大小为F N＝2.5mg的相互作用力，故对小球由牛顿第二定律有F N＋mg＝F n解得F n＝35 N.(2)在压缩弹簧过程中，速度最大时合力为零．设此时小球离D 端的距离为x 0，则有kx 0＝mg 解得x 0＝mgk＝0.1 m 在C 点，有F n ＝mv 2Cr解得v C ＝7 m/s由能量守恒定律有mg(r ＋x 0)＝E p ＋(E km －12mv 2C )解得E km ＝mg(r ＋x 0)＋12mv 2C －E p ＝6 J.(3)小球从A 点运动到C 点过程，由动能定理得 mgh －μmgs＝12mv 2C解得B 、C 间距离s ＝0.5 m小球与弹簧作用后返回C 处动能不变，小球的动能最终消耗在与BC 水平面相互作用的过程中．设小球与弹簧作用后在BC 上运动的总路程为s′，由能量守恒定律有 μmgs′＝12mv 2C解得s′＝0.7 m故最终小球在BC 上距离C 为0.5 m －(0.7 m －0.5 m)＝0.3 m(或距离B 端为0.7 m －0.5 m ＝0.2 m)处停下．[答案](1)35 N (2)6 J (3)停在BC 上距离C 端0.3 m 处(或距离B 端0.2 m 处)如图所示，固定斜面的倾角θ＝30°，物体A 与斜面之间的动摩擦因数μ＝32，轻弹簧下端固定在斜面底端，弹簧处于原长时上端位于C 点．用一根不可伸长的轻绳通过轻质光滑的定滑轮连接物体A 和B ，滑轮右侧绳子与斜面平行，A 的质量为2m ，B 的质量为m ，初始时物体A 到C 点的距离为L.现给A 、B 一初速度v 0>gL ，使A 开始沿斜面向下运动，B 向上运动，物体A 将弹簧压缩到最短后又恰好能弹到C 点．已知重力加速度为g ，不计空气阻力，整个过程中，轻绳始终处于伸直状态，求：(1)物体A 向下运动刚到C 点时的速度； (2)弹簧的最大压缩量； (3)弹簧的最大弹性势能．[解析](1)A 与斜面间的滑动摩擦力F f ＝2μ mgcos θ，物体A 向下运动到C 点的过程中，根据能量守恒定律可得：2mgLsin θ＋12·3mv 20＝12·3mv 2＋mgL ＋F f L解得v ＝v 20－gL.(2)从物体A 接触弹簧，将弹簧压缩到最短后又恰回到C 点，对系统应用动能定理－F f ·2x＝0－12×3mv 2 解得x ＝v 202g －L2.(3)弹簧从压缩到最短到恰好能弹到C 点的过程中，对系统根据能量守恒定律可得：E p ＋mgx ＝2mgxsin θ＋F f x 所以E p ＝F f x ＝3mv 204－3mgL4.[答案](1)v 20－gL (2)v 202g －L2(3)3mv 204－3mgL 4考向3 能量守恒定律与图象的结合问题4．(多选)如图545所示，一质量为m 的小球以初动能E k0从地面竖直向上抛出，已知运动过程中受到恒定阻力f ＝kmg 作用(k 为常数且满足0<k<1)．图中两条图线分别表示小球在上升过程中动能和重力势能与其上升高度之间的关系(以地面为零势能面)，h 0表示上升的最大高度．则由图可知，下列结论正确的是( )图545A ．E 1是最大势能，且E 1＝E k0k ＋2B ．上升的最大高度h 0＝E k0k ＋1mgC ．落地时的动能E k ＝kE k0k ＋1D ．在h 1处，物体的动能和势能相等，且h 1＝E k0k ＋2mgBD [因小球上升的最大高度为h 0，由图可知其最大势能E 1＝E k0k ＋1，又E 1＝mgh 0，得h 0＝E k0k ＋1mg ，A 项错误，B 项正确．由图可知，小球上升过程中克服阻力做功为E k0－E k0k ＋1，因小球所受阻力恒定，且上升和下落高度相等，则小球下落过程中克服阻力做功为E k0－E k0k ＋1，则小球落地时的动能E k ＝E k0k ＋1－⎝ ⎛⎭⎪⎫E k0－E k0k ＋1＝1－k k ＋1E k0，C 项错误．在h 1处，小球的动能和势能相等，则有E k0－(mg ＋f)h 1＝mgh 1，解得h 1＝E k0k ＋2mg，D 项正确．]摩擦力做功与能量的转化关系1．对摩擦生热的理解(1)从功的角度看，一对滑动摩擦力对系统做的功等于系统内能的增加量．(2)从能量的角度看，是其他形式能量的减少量等于系统内能的增加量．2．两种摩擦力做功情况比较静摩擦力滑动摩擦力不同点能量的转化方面只有能量的转移，而没有能量的转化既有能量的转移，又有能量的转化一对摩擦力的总功方面一对静摩擦力所做功的代数和等于零一对滑动摩擦力所做功的代数和不为零，总功W＝－F f·l相对，产生的内能Q＝F f·l相对相同点正功、负功、不做功方面两种摩擦力对物体可以做正功、负功，还可以不做功[母题] 如图546所示，在竖直平面内，粗糙的斜面轨道AB的下端与光滑的圆弧轨道BCD相切于B，C 是最低点，圆心角∠BOC＝37°，D与圆心O等高，圆弧轨道半径R＝1.0 m，现有一个质量为m＝0.2 kg 可视为质点的小物体，从D点的正上方E点处自由下落，D、E距离h＝1.6 m，小物体与斜面AB之间的动摩擦因数μ＝0.5.sin 37°＝0.6，cos 37°＝0.8，g取10 m/s2.求：图546(1)小物体第一次通过C点时对轨道的压力；(2)要使小物体不从斜面顶端飞出，斜面至少要多长；(3)若斜面已经满足(2)要求，请首先判断小物体是否可能停在斜面上．再研究小物体从E点开始下落后，整个过程中系统因摩擦所产生的热量Q.【导学号：84370234】[题眼点拨] ①“粗糙斜面”要利用μ＝0.5分析物体是否会停在斜面上；②“光滑圆弧”要想到物体有可能最终在圆弧上往复性运动．[解析](1)小物体从E点到C点，由能量守恒定律得mg(h＋R)＝12mv2C①在C点，由牛顿第二定律得F N－mg＝mv2CR②联立①②式解得F N＝12.4 N.根据牛顿第三定律可知小物体对轨道的压力大小为12.4 N，方向竖直向下．(2)从E→D→C→B→A 过程，由动能定理得 W G ＋W f ＝0③ W G ＝mg[(h ＋Rcos 37°)－L AB sin 37°] ④ W f ＝－μmgcos 37°·L AB⑤联立③④⑤式解得L AB ＝2.4 m.(3)因为mgsin 37°>μmgcos 37°(或μ<tan 37°)，所以，小物体不会停在斜面上．小物体最后以C 为中心，B 为一侧最高点沿圆弧轨道做往返运动，从E 点开始直至运动稳定，系统因摩擦所产生的热量Q ＝ΔE p⑥ΔE p ＝mg(h ＋Rcos 37°)⑦联立⑥⑦式解得Q ＝4.8 J.[答案](1)12.4 N 方向竖直向下 (2)2.4 m (3)小物体不会停在斜面上 4.8 J[母题迁移]迁移1 传送带问题中摩擦力做功分析1.如图547所示，质量为m 的物体在水平传送带上由静止释放，传送带由电动机带动，始终保持以速度v 匀速运动，物体与传送带间的动摩擦因数为μ，物体经过一段时间能保持与传送带相对静止，对于物体从静止释放到相对静止这一过程中，下列说法正确的是( )图547A ．电动机做的功为12mv 2B ．摩擦力对物体做的功为mv 2C ．传送带克服摩擦力做的功为12mv 2D ．电动机增加的功率为μmgvD [由能量守恒可知，电动机做的功等于物体获得的动能和由于摩擦而产生的内能，选项A 错误；对物体受力分析知，仅有摩擦力对物体做功，由动能定理知，其大小应为12mv 2，选项B 错误；传送带克服摩擦力做功等于摩擦力与传送带对地位移的乘积，可知这个位移是物体对地位移的两倍，即W ＝mv 2，选项C 错误；由功率公式知电动机增加的功率为μmgv，选项D 正确．]如图所示，绷紧的传送带与水平面的夹角θ＝30°，皮带在电动机的带动下，始终保持v 0＝2 m/s 的速率运行，现把一质量为m ＝10 kg 的工件(可看做质点)轻轻放在皮带的底端，经过时间1.9 s ，工件被传送到h ＝1.5 m 的高处，g 取10 m/s 2，求：(1)工件与传送带间的动摩擦因数；(2)电动机由于传送工件多消耗的电能．[解析](1)由题图可知，皮带长x ＝h sin θ＝3 m ．工件速度达v 0前，做匀加速运动的位移x 1＝v t 1＝v 02t 1 匀速运动的位移为x －x 1＝v 0(t －t 1)解得加速运动的时间t 1＝0.8 s加速运动的位移x 1＝0.8 m所以加速度a ＝v 0t 1＝2.5 m/s 2 由牛顿第二定律有：μmgcos θ－mgsin θ＝ma解得：μ＝32. (2)从能量守恒的观点，显然电动机多消耗的电能用于增加工件的动能、势能以及克服传送带与工件之间发生相对位移时摩擦力做功产生的热量．在时间t 1内，皮带运动的位移x 皮＝v 0t 1＝1.6 m在时间t 1内，工件相对皮带的位移x 相＝x 皮－x 1＝0.8 m在时间t 1内，摩擦生热Q ＝μmgcos θ·x 相＝60 J工件获得的动能E k ＝12mv 20＝20 J 工件增加的势能E p ＝mgh ＝150 J电动机多消耗的电能W ＝Q ＋E k ＋E p ＝230 J.[答案](1)32(2)230 J 迁移2 “滑块—木板”问题中摩擦力做功分析2．(2020·衡水四调)如图548甲所示，质量M ＝1.0 kg 的长木板A 静止在光滑水平面上，在木板的左端放置一个质量m ＝1.0 kg 的小铁块B ，铁块与木板间的动摩擦因数μ＝0.2，对铁块施加水平向右的拉力F ，F 大小随时间变化如图乙所示，4 s 时撤去拉力．可认为A 、B 间的最大静摩擦力与滑动摩擦力大小相等，取重力加速度g ＝10 m/s 2.求：甲乙图548(1)0～1 s 内，A 、B 的加速度大小a A 、a B ；(2)B 相对A 滑行的最大距离x ；(3)0～4 s 内，拉力做的功W ；(4)0～4 s 内系统产生的摩擦热Q.[题眼点拨] ①“木板A 静止在光滑水平面上”说明若水平方向对木板A 施力，木板A 会做加速运动；②“F 大小随时间变化如图乙所示”，要根据数据分析A 、B 两物体是否发生相对滑动．[解析](1)在0～1 s 内，A 、B 两物体分别做匀加速直线运动根据牛顿第二定律得μmg＝Ma AF 1－μmg＝ma B代入数据得a A ＝2 m/s 2，a B ＝4 m/s 2.(2)t 1＝1 s 后，拉力F 2＝μmg，铁块B 做匀速运动，速度大小为v 1：木板A 仍做匀加速运动，又经过时间t 2，速度与铁块B 相等．v 1＝a B t 1又v 1＝a A (t 1＋t 2)解得t 2＝1 s设A 、B 速度相等后一起做匀加速运动，运动时间t 3＝2 s ，加速度为aF 2＝(M ＋m)aa ＝1 m/s 2木板A 受到的静摩擦力f ＝Ma<μmg，A 、B 一起运动x ＝12a B t 21＋v 1t 2－12a A (t 1＋t 2)2 代入数据得x ＝2 m.(3)时间t 1内拉力做的功W 1＝F 1x 1＝F 1·12a B t 21＝12 J 时间t 2内拉力做的功W 2＝F 2x 2＝F 2v 1t 2＝8 J时间t 3内拉力做的功W 3＝F 2x 3＝F 2(v 1t 3＋12at 23)＝20 J 4 s 内拉力做的功W ＝W 1＋W 2＋W 3＝40 J.(4)系统的摩擦热Q 只发生在t 1＋t 2时间内，铁块与木板相对滑动阶段，此过程中系统的摩擦热Q ＝μmg·x＝4 J.[答案](1)2 m/s 2 4 m/s 2 (2)2 m (3)40 J (4)4 J3利用Q＝F f x相对计算热量Q时，关键是对相对路程x相对的理解.例如：如果两物体同向运动，x相对为两物体对地位移大小之差；如果两物体反向运动，x相对为两物体对地位移大小之和；如果一个物体相对另一个物体往复运动，则x相对为两物体相对滑行路径的总长度.高考理综物理模拟试卷注意事项：1. 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

人教版高考物理一轮复习学案设计专题：功能关系,能量守恒定律

高考物理一轮复习学习讲义[小题快练]能量在转移或转化过程中，其总量会不断减少．( × )在物体的机械能减少的过程中，动能有可能是增大的．( √ )既然能量在转移或转化过程中是守恒的，故没有必要节约能源．( × )滑动摩擦力做功时，一定会引起机械能的转化．( √ )．自然现象中蕴藏着许多物理知识，如图所示为一个盛水袋，某人从侧面缓慢推袋壁使它变形，( A )B．变小D．不能确定如图所示，在升降机内有一固定的光滑斜面体，一轻弹簧的一端连在位于斜面体下方的重力势能增加量一定等于mgh的动能增加量等于斜面的支持力和弹簧的弹力对其做功的代数和的机械能增加量等于斜面的支持力和弹簧的弹力对其做功的代数和2.求解相对滑动物体的能量问题的方法(1)正确分析物体的运动过程，做好受力分析．(2)利用运动学公式，结合牛顿第二定律分析物体的速度关系及位移关系(3)公式W＝F f·l相对中l相对为两接触物体间的相对位移，若物体在传送带上做往复运动时，则总的相对路程．B．W1＝WB．h＝H 3D．H3＜h＜如图所示，固定斜面的倾角θ＝30°，物体A与斜面之间的动摩擦因数为μ固定在斜面底端，弹簧处于原长时上端位于C点，用一根不可伸长的轻绳通过轻质光滑的定滑轮，滑轮右侧绳子与斜面平行，A的质量为2m＝4 kg，B的质量为点的距离为L＝1 m，现给A、B一初速度v0＝3 m/s，使A开始沿斜面向下运动，点时的速度大小；．有两个时刻小球的加速度等于重力加速度．弹簧长度最短时，弹力对小球做功的功率为零，物块不能滑到斜面顶端，但上滑最大高度一定增大点时速度的大小；点时弹簧的弹性势能；点，从静止开始释放．已知点左下方，与C 点水平相距72v C；受到轨道支持力的大小F N；h.点：竖直方向上的分速度v＝gt＝10×2 m/s＝20 m/s ．从人被弹簧弹起到弹簧第一次恢复原长，人一直向上加速运动滑动到底端时动能较大滑动到底端时动能较大滑动过程中克服摩擦力做的功较多2＋mgh2＋mgh2 m/s212.5 cm 12.5 cm的位移为多少时，B从A的右端滑出？求上述过程中滑块与木块之间产生的内能．点时速度v C的大小；及水平距离x；(1)物体做往返运动的整个过程中在AB 轨道上通过的总路程； (2)最终当物体通过圆弧轨道最低点E 时，对圆弧轨道的压力大小；(3)为使物体能顺利到达圆弧轨道的最高点D ，释放点距B 点的距离L ′应满足什么条件？解析 (1)物体在P 点及最终到B 点的速度都为零，对全过程由动能定理得 mgR cos θ－μmg cos θ·s ＝0①得s ＝Rμ.(2)设物体在E 点的速度为v E ，由机械能守恒定律有mgR (1－cos θ)＝12mv 2E ② 在E 点时由牛顿第二定律有N －mg ＝mv 2E R ③ 联立②③式解得N ＝(3－2cos θ)mg .由牛顿第三定律可知物体对圆弧轨道E 点的压力大小为(3－2cos θ)mg . (3)设物体刚好通过D 点时的速度为v D ，由牛顿第二定律有： mg ＝m v 2DR，得：v D ＝gR ④设物体恰好通过D 点时，释放点距B 点的距离为L 0，在粗糙直轨道上重力的功 W G 1＝mgL 0sin θ⑤滑动摩擦力的功：W f ＝－μmg cos θ·L 0⑥在光滑圆弧轨道上重力的功W G 2＝－mgR (1＋cos θ)⑦ 对全过程由动能定理得W G 1＋W f ＋W G 2＝12mv 2D ⑧ 联立④⑤⑥⑦⑧式解得：L 0＝＋2cos θRθ－μcos θ则L ′≥＋2cos θRθ－μcos θ.答案 (1)Rμ (2)(3－2cos θ)mg (3)L ′≥＋2cos θRθ－μcos θ§课后作业§1．如图，半圆形光滑轨道固定在水平地面上，半圆的直径与地面垂直，一小物块以速度v 从轨道v28gv22gB．0.2 mD．0.8 m．如图所示，建筑工地上载人升降机用不计质量的细钢绳跨过定滑轮与一电动机相连，通电后电．升降机匀加速上升过程中，升降机底板对人做的功等于人增加的动能．升降机匀加速上升过程中，升降机底板对人做的功大于人增加的机械能．升降机匀速上升过程中，升降机底板对人做的功等于人增加的机械能动能的增加机械能的增加0.8 m．物块对板做功的功率保持不变的运动时间；。

高三物理一轮复习——功能关系 能量守恒定律学案

高三物理一轮复习导学案：5-功能关系与能量守恒定律

高三物理一轮复习功能关系训练导学案

高考一轮复习：功能关系

2021高中物理一轮复习学案--第五章 第4讲 功能关系 能量守恒定律

2024届高考一轮复习物理教案(新教材鲁科版)：功能关系 能量守恒定律

高三物理一轮复习 功能关系能量守恒导学案

高三物理一轮复习优质学案1：5.4功能关系 能量守恒定律

高三物理一轮复习优质学案：功能关系 能量守恒定律