奥数染色问题
小学奥数杂题染色问题【三篇】

小学奥数杂题染色问题【三篇】
解析:对房间染色,使最下面的两个房间染成黑色,与黑色相邻的
房染成白色,
则图中有7个黑色房间和5个白色房间.
如果要想不重复地走过每一个房间,黑色与白色房间数应该相等.故题中的想法是不能实现的.
点评:完成本题也可根据要求据图中的房间实际找下路线,看是
否能够找到.
【第二篇】
展览会有36个展室(如图),每两相邻展室之间均有门相通.能不能从入
口进去,不重复地参观完全部展室后,从出口出来呢?
答案:
不能.对展室实行染色,使相邻两房间分别是黑色和白色的.此时入
口处展室的颜色与出口处展室的颜色是相同的,而不重复参观完36个
展室,入口与出口展室的颜色应该不相同.
【第三篇】
染色问题基本解法:
三面涂色和顶点相关 8个顶点。
两面染色和棱长相关。
即新棱长(棱长-2)×12
一面染色和表面积相关。
同样用新棱长计算表面积公式(棱长-2)×(棱长-2)*6
0面染色和体积相关。
用新棱长计算体积公式(棱长-2)×(棱长-2)×(棱长-2)
长方体的解法和立方体同理,即计算各种公式前长、宽、高都要先减2再利用公式计算。
小学奥数专题15:染色问题
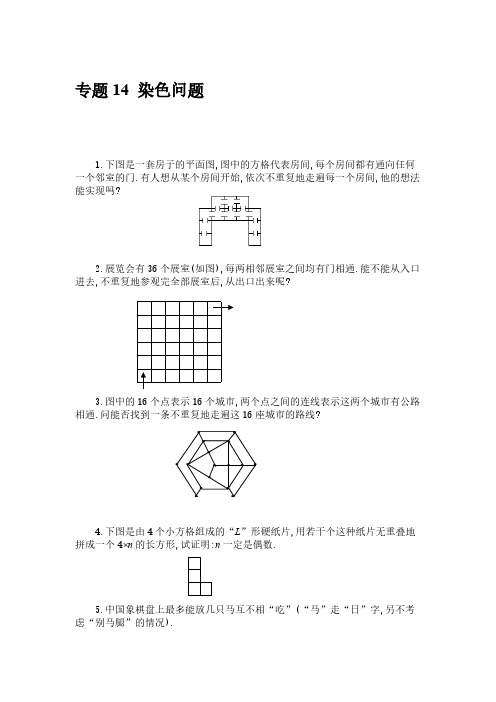
专题14 染色问题1.下图是一套房子的平面图,图中的方格代表房间,每个房间都有通向任何一个邻室的门.有人想从某个房间开始,依次不重复地走遍每一个房间,他的想法能实现吗?2.展览会有36个展室(如图),每两相邻展室之间均有门相通.能不能从入口进去,不重复地参观完全部展室后,从出口出来呢?3.图中的16个点表示16个城市,两个点之间的连线表示这两个城市有公路相通.问能否找到一条不重复地走遍这16座城市的路线?4.下图是由4个小方格组成的“L ”形硬纸片,用若干个这种纸片无重叠地拼成一个4 n 的长方形,试证明:n 一定是偶数.5.中国象棋盘上最多能放几只马互不相“吃”(“马”走“日”字,另不考虑“别马腿”的情况).6.能否用一个田字和15个4⨯1矩形覆盖8⨯8棋盘?7.能否用1个田字和15个T 字纸片,拼成一个8⨯8的正方形棋盘?8.在8⨯8棋盘上,马能否从左下角的方格出发,不重地走遍棋盘,最后回到起点?若能请找出一条路,若不能,请说明理由.9.下面三个图形都是从4⨯4的正方形分别剪去两个1⨯1的小方格得到的,问可否把它们分别剪成1⨯2的七个小矩形?(1)(2) (3)10.把三行七列的21个小格组成的矩形染色,每个小格染上红、蓝两种色中的一种.求证:总可以找到4个同色小方格,处于某个矩形的4个角上(如图)红红红红11.17个科学家互相通信,在他们的通信中共讨论3个问题,而任意两个科学家之间仅讨论1个问题.证明:至少有3个科学家,他们彼此通信讨论的是同一个问题.12.用一批1⨯2⨯4的长方体木块,能不能把一个容积为6⨯6⨯6的正方体木箱充塞填满?说明理由.13.在平面上有一个27⨯27的方格棋盘,在棋盘的正中间摆好81枚棋子,它们被罢成一个9⨯9的正方形.按下面的规则进行游戏:每一枚棋子都可沿水平方向或竖直方向越过相邻的棋子,放进紧挨着这枚棋子的空格中,并把越过的这格棋子取出来.问:是否存在一种走法,使棋盘上最后恰好剩下一枚棋子?14.12⨯12的超极棋盘上,一匹超级马每步跳至3⨯4矩形的另一角(如图).问能否从任一点出发遍历每一格恰一次,再回到出发点(这种情况又称马有“回路”)?123———————————————答 案—————————————————————— 1. 不能.对房间染色,使最下面的两个房间染成黑色,与黑色相邻的房染成白色,则图中有7个黑色房间和5个白色房间.如果要想不重复地走过每一个房间,黑色与白色房间数应该相等.故题中的想法是不能实现的. 2. 不能.对展室进行染色,使相邻两房间分别是黑色和白色的.此时入口处展室的颜色与出口处展室的颜色是相同的,而不重复参观完36个展室,入口与出口展室的颜色应该不相同. 3. 不能.对这16个城市进行黑白相间的染色,一种颜色有9个,另一种颜色有7个.而要不重复地走遍这16个城市,黑色与白色的个数应该相等. 4. 如图,对4⨯n 长方形的各列分别染上黑色和白色.任一L 形纸片所占的3黑1白,第二类占3白1黑.设第一类有a 个,第二类有b 个,因为涂有两种颜色的方格数相等,故有3b +a =3a +b ,即a =b ,也就是说第一类与第二类相等,因此各种颜色的方格数都是4的倍数,总数是8的倍数,从而n 是偶然.5. 将棋盘黑白相间染色,由“马”的走法可知,放在黑点上的“马”,只能吃放在某些白点上的马.整个棋盘上黑、白点的个数均为45,故可在45个黑点放上马,它们是不能互吃的.6. 如图的方式对棋盘染色.那么一个田字形盖住1个或3个白格,而一个4⨯1的矩形盖住2个白格.这样一来一个田字和15个4⨯1的矩形能盖住的白格数是一个奇数,但上图中的白格数是一个偶数,因此一个田字形和15个4⨯1的矩n 个7. 将棋盘里黑白相间涂色.一个田字形盖住2个白格,一个T字形盖住3个或1个白格.故1个田字和15个T字盖住的白格数是一个奇数,但棋盘上的白格数是一个偶数.因此一个田字形和15个T字形不能盖住8⨯8的棋盘.8. 将棋盘黑白相间地染色后,马的走法是从一种颜色的格子跳到另一种颜色.棋盘上有32个白格与32个黑格,故马可能跳遍整个棋盘.图中给出了一种走法.564158355039603347445540593451384257464936533261454843543162375220530632211161329642141714251061922782312151287183269249. 先对4⨯4的棋盘黑白相间的涂色(如图),这道题的实际问题是问7个1⨯2矩形能否分别复盖剪去A、B;剪去A、C;剪去A、D的三个棋盘.若7个1⨯2矩形可以复盖剪残的棋盘,因为每个1⨯2矩形均可盖住一个白格和一个黑格,所以棋盘的白格与黑格数目应该相等.都是7个.而剪去A格和C格的棋盘(2)有5个白格8个黑格,剪去A、D的棋盘(3)有5个白格8个黑格,因此这两个剪损的棋盘均不能被7,也就不能剪成7个1⨯2的矩形.棋盘(1)可以被7个1⨯2的矩形所复盖.下面给出一种剪法:A11277B26543654310. 在第一行的7格中必有4格同色,不妨设这4格位于前4个位置,且均为红色.然后考虑前4列构成的3⨯4矩形.若第二行和第3行中出现2个或2个以上的红色格子.则该行的两个红色格子与第一行的红色格子就组成一个4角同为红色格子的矩形.若不然,则第2、3行中都至少有3个蓝格在前4列中,不妨设第2行前3格为蓝色,显然第三行中的前3格中至少有2个蓝格,故在二、三行的前4列中必存在四角都是蓝色的矩形.11. 将17个科学家用17个点代表,两点之间连结的线段表示两个科学家之间讨论的问题.用三种颜色给这些线段染色,表示三个问题,于是问题就变成:给17个点之间的所有连结线段用三种颜色染色,必有同色三角形.从任意一点,不妨设从A 向其他16点A 1,A 2,…A 16共可连成16条线段,用三种颜色染色,由抽屉原则可知,必有6条线段同色.设这6条线段为AA 1,AA 2,…AA 6且同为红色.考虑A 1,A 2,A 3,A 4,A 5,A 6这六点之间的连线,若有一条为红色,(如A 1A 2为红色) ,则三角形AA 1A 2为红色的同色三角形.若这六点之间的连线中,没有一条是红色的,则它们之间只能涂两种颜色.考虑从A 1引出的五条线段A 1A 2 A 1A 3 A 1A 4 A 1A 5 A 1A 6,由抽屉原理知,其中必有三条是同色的.不妨设这三条为A 1A 2 A 1A 3 A 1A 4,且同为蓝色.若三角形A 2A 3A 4的三边中有一条为蓝色的,则有一个蓝色的三角形存在;若三角形A 2A 3A 4三边都不是蓝色的,则它的三边是同为第三色的同色三角形.12. 把正方体木箱分成27个小正方体,每个小正方体的体积为2⨯2⨯2=8.将这些正方体如右图黑白相间染上色.显然黑色2⨯2⨯2的正方体有14个,白色2⨯2⨯2小正方体有13个.每一个这样的正方体相当于8个1⨯1⨯1的小正方体.将1⨯2⨯4的长方体放入木箱,无论怎么放,每个长方体木块盖住8个边长为1的单位正方体,其中有4个黑色的,4个白色的.木箱共含6⨯6⨯6=216个单位正方体,26个长方体木块共盖住8⨯26=208个单位正方体,其中黑白各占104个,余下216-208=8个单位正方体是黑色的.但是第27个1⨯2⨯4长方体木块不管怎样A A 1A 2A 3A 4A 5A 6A 1A 2A 3A4放,也无法盖住这8个黑色单位正方体.13. 如图,将整个棋盘的每一格都分别染上红、白、黑三种颜色,这种染色方式将棋盘分成了三个部分.按照游戏规则,每走一步,有两种颜色方格中的棋子数分别减少了1个,而第三种颜色的棋子数增加了一个.这表明每走一步,每个部.因为一开始时,81枚棋子摆成一个9 9的正方形,显然三个部分的棋子数是相同的,从而每走一步,三部分中的棋子数的奇偶性是相同的.如果走了若干步以后,棋盘上恰好剩下一枚棋子,则两部分上的棋子数为偶数,而另一部分上的棋子数为奇数.这种结果是不可能出现的.14. 用两种方法对超级棋盘染色.首先,将棋盘黑白相间染色,则马每跳一步,它所在的方格就要改变一次颜色.不妨设第奇数步跳入白格.其次,将棋盘的第3,4,5及8,9,10这六行染成黑色,其余六行染成白色.在此种染色方式下,马从白格一定跳入黑格.又因黑白格总数相同,马要遍历每一格恰一次又回到出发点,因此,马从黑格只能跳入白格而不能跳入黑格.不妨设马第奇数步跳入白格.但是对于一种满足要求跳法,在两种染色方式下第奇数步跳入的格子的全体是不同的,这显然是不可能的,故题目要求的跳法是不存在的.。
小学奥数杂题染色问题【三篇】

小学奥数杂题染色问题【三篇】
导读:本文小学奥数杂题染色问题【三篇】,仅供参考,如果觉得很不错,欢迎点评和分享。
【第一篇】 1.如图是一套房子的平面图,图中的方格代表房间,每个房间都有通向任何一个邻室的门.有人想从某个房间开始,依次不重复地走遍每一个房间,他的想法能实现吗?
解析:对房间染色,使最下面的两个房间染成黑色,与黑色相邻的房染成白色,
则图中有7个黑色房间和5个白色房间.
如果要想不重复地走过每一个房间,黑色与白色房间数应该相等.故题中的想法是不能实现的.
点评:完成本题也可根据要求据图中的房间实际找下路线,看是否能够找到.【第二篇】展览会有36个展室(如图),每两相邻展室之间均有门相通.能不能从入口进去,不重复地参观完全部展室后,从出口出来呢? 答案:不能.对展室进行染色,使相邻两房间分别是黑色和白色的.此时入口处展室的颜色与出口处展室的颜色是相同的,而不重复参观完36个展室,入口与出口展室的颜色应该不相同. 【第三篇】染色问题基本解法:三面涂色和顶点有关8个顶点。
两面染色和棱长有关。
即新棱长(棱长-2)×12一面染色和表面积有关。
同样用新棱长计算表面积公式(棱长-2)×(棱长-2)*6 0面染色和体积有关。
用新棱长计算体积公式(棱
长-2)×(棱长-2)×(棱长-2)长方体的解法和立方体同理,即计算各种公式前长、宽、高都要先减2再利用公式计算。
奥数 染色问题【范本模板】

1. 如右图,对A,B,C,D,E五个区域分别用红黄绿蓝白五种颜色中的某一种来着色,规定相邻的区域着不同色,问有多少种不同的着色方案?【组合十讲P37】2 用红黄蓝三种颜色涂在右图的圆圈中,每个圆圈中,每个圆圈只涂一种颜色,并且要使每条连线两端的圆圈涂上不同颜色,问一共有多少种不同的涂法?3.某植物园计划在A,B,C,D,E五个地块栽种四种不同颜色的郁金香,每个地块内的郁金香必须同色,相邻的(有公共边界的)地块郁金香不能同色,不相邻可以同色,问共有多少种不同的方案?4。
如图对A,B,C,D,E,F,G七个区域分别采用红,黄,绿,蓝,白五种颜色中的某一种来着色,规定相邻的区域不能同色,那么有多少种不同的着色方案?5.用红,黄,蓝,三种颜色把如图的8个小圆圈涂上颜色,每个圆圈只涂一种颜色,并且有连线的两个圆圈不能同色,那么有多少种不同涂色方案?【希望杯P107】6. 一根划分成相等5段的钢管,若要用红,白两种颜色分别对每一段着色,问共有几种不同的涂色方案?(倒置后相同的两种涂色方案视为同种)8。
如图用4种颜色对A,B,C,D,E五个区域涂色,要求相邻的区域涂不同的颜色,那么,共有几种涂法?9。
用三种颜色染正方体的6条边,相邻边不同色,有多少种染法?【教程P133】10. 如图,用红,黄,蓝三种颜色给一个五边形的各个顶点染色,同一边的两段点不能同色,且顶点A 必须染红色,请问:有多少种不同的染色方案?【高斯导引P76】11。
如图一个圆环被分成8部分,先将每一部分染上红,黄,蓝三种颜色之一,要求相邻两部分颜色不同,共有多少种不同染色方案?12. 如图,用4种不同的颜色将图中的圆圈分别涂色,要求有线段连接的两个相邻的圆圈必须涂不同的颜色,共有几种涂法?(不许旋转翻转)13 给一个正四面体的4个面染色,每个面只允许用一种颜色,且4个面的颜色互不相同,现有5种颜色可选,共有多少种不同的染色方案?14. 用4种颜色为一个正方体的6个面染色,要求每个面只能用1种颜色,且乡邻面的颜色必须不同,如果将正方体经过反转后颜色相同视为同一种,那么共有多少种不同的染色方案?17.用红,黄,蓝三种颜色对右图进行染色,要求相邻两块颜色不同,共有多少种不同的染色方案? 【简明读本P191】1。
六级奥数专题染色问题.docx

二十染色问题(1)年级班姓名得分( 编者按 : 由于内容本身的限制 , 本讲不设填空题 )1.某影院有 31 排, 每排 29 个座位 . 某天放映了两场电影 , 每个座位上都坐了一个观众 . 如果要求每个观众在看第二场电影时必须跟他 ( 前、后、左、右 ) 相邻的某一观众交换座位 , 这样能办到吗为什么2.如图是一所房子的示意图 , 图中数字表示房间号码 , 每间房子都与隔壁的房间相通 . 问能否从 1 号房间开始 , 不重复的走遍所有房间又回到 1 号房间1234567893.在一个正方形的果园里 , 种有 63 棵果树、加上右下角的一间小屋 , 整齐地排列成八行八列 ( 见图 ( a)). 守园人从小屋出发经过每一棵树 , 不重复也不遗漏( 不许斜走 ), 最后又回到小屋 , 行吗如果有 80 棵果树 , 连小屋在内排成九行九列( 图( b)) 呢(a)(b)4.一个 8 8 国际象棋 ( 下图 ) 去掉对角上两格后 , 是否可以用 31 个 2 1 的“骨牌” ( 形如)把象棋盘上的62个小格完全盖住5.如果在中国象棋盘上放了多于45 只马 , 求证 : 至少有两只马可以“互吃”.6. 空间 6 个点 , 任三点不共线 , 对以它们为顶点的线段随意涂以红色或蓝色 , 是否必有两个同色三角形7.如图 , 把正方体分割成 27 个相等的小正方体 , 在中心的那个小正方体中有一只甲虫 , 甲虫能从每个小正方体走到与这个正方体相邻的 6 个小正方体中的任一个中去 . 如果要求甲虫能走到每个小正方体一次 , 那么甲虫能走遍所有的正方体吗8.中国象棋的马走“日”字 , 车走横线或竖线 , 下图是半张中国象棋盘 , 试回答下面的问题 :A B一只马从起点出发 , 跳了 n 步又回到起点 . 证明 : n 一定是偶数 .9.中国象棋的马走“日”字 , 车走横线或竖线 , 下图是半张中国象棋盘 , 试回答下面的问题 :A B一只马能否跳遍这半张棋盘, 每一点都不重复 , 最后一步跳回起点10.中国象棋的马走“日”字 , 车走横线或竖线 , 下图是半张中国象棋盘 , 试回答下面的问题 :A B证明 : 一只马不可能从位置 B 出发 , 跳遍半张棋盘而每个点都只经过一次 ( 不要求最后一步跳回起点 ).11.中国象棋的马走“日”字 , 车走横线或竖线 , 下图是半张中国象棋盘 , 试回答下面的问题 :A B一只马能否从位置 B 出发 , 用 6 步跳到位置 A 为什么12.中国象棋的马走“日”字 , 车走横线或竖线 , 下图是半张中国象棋盘 , 试回答下面的问题 :A B一只车从位置 A 出发 , 在这半张棋盘上走 , 每步走一格 , 走了若干步后到了位置 B. 证明 : 至少有一个格点没被走过或被走了不止一次 .8 的国际象棋棋盘能不能被剪成 7 个 2 2 的正方形和 9 个 4 1 的长方形如果可以 , 请给出一种剪法 ; 如果不行 , 请说明理由 .14.( 表 1) 是由数字 0,1 交替构成的 ,( 表 2) 是由 ( 表 1) 中任选、、三种形式组成的图形 , 并在每个小方格全部加 1 或减 1, 如此反复多次进行形成的 , 试问 ( 表 2) 中的 A格上的数字是多少并说明理由 .1010101001010101101010100101010010101010010101011010101001010101表1111111111111111111111111111111111 1 1 1 1 1 A 11 1 1 1 1 1 11 1 1 1 1 1 1 11 1 1 1 1 1 1 11表2———————————————答案——————————————————————1.把影院的座位画成黑白相的矩形.(29 31), 共有 899 个小方格 . 不妨假定四角黑格 , 共有黑格 450 个, 白格 449 个.要求看第二影 , 每位众必跟他相的某一众交位置 , 即要求每一黑白格必互 , 因黑白格的数不相等 , 因此是不可能的 .2.将号奇数的房染成黑色 , 号偶数的房染成白色 . 从 1 号房出 , 只能按黑白黑白⋯⋯的次序,当走遍九个房在黑色房中 , 个房不与 1 号房相 , 故不能不重复地走遍所有房又回到 1 号房 .3.(a) 行, 走法如所示 .(a)(b) 不行 , 将小屋染成黑色 , 果染成黑白相的色 ,(b) 中有 41 个黑色的 ,40 个白色的 . 从小屋出 , 按黑白黑白⋯⋯的次序,当走遍 80 棵后 , 到达的的色是黑色 , 与小屋不相 , 故不可能最后回到小屋 .4.不能 . 原因是每一个 2 1 的矩形骨牌一定恰好盖住一个黑格和一个白格,31 个的骨牌恰好盖住 31 个黑格和 31 个白格 .但是国象棋棋上角两格的色是相同的 , 把它去掉后剩下的是 30 个白格 ,32 个黑格 , 或 32 个白格 ,30 个黑格 , 因此不能盖住 .5.中国象棋棋盘上有 90 个交叉点 , 把棋盘分成 10 个小部分 , 每部分有33=9 个交叉点 , 由抽屉原则知 , 至少有一个小部分内含有 6 只马 .将这一小部分的 9 个交叉点分别涂上黑色及白色 . 总有两只马在不同颜色交叉点上 , 故一定有两只马“互吃”.6.设这六个点为 A、 B、 C、 D、 E、 F. 我们先证明存在一个同色的三角形 :考虑由 A 点引出的五条线段 AB、AC、AD、AE、AF,其中必有三条被染成了相同的颜色 , 不妨设 AB、AC、AD三条同为红色 . 再考虑三角形 BCD的三边 : 若其中有一条为红色 , 则存在一个红色三角形 ; 若这三条都不是红色 , 则三角形 BCD为蓝色三角形 .BCAD下面再来证明有两个同色三角形, 不妨设三角形 ABC的三边同为红色 .(1)若三角形 DEF也是红色三角形 , 则存在两个同色三角形 .(2)若三角形 DEF中有一条边为蓝色 ( 不妨设 DE), 下面考虑 DA、DB、 DC三条线段,其中必有两条同色 .①若其中有两条是红色的 , 如 DA、DB是红色的 , 则三角形 DAB为第二个同色三角形 ( 图 1).D AE B C( 图 1)②若其中有两条是蓝色的 , 设 DA、DB为蓝色 ( 图 2). 此时在 EA、EB两条线段中 , 若有一条为蓝色 , 则存在一个蓝色三角形 ; 若两条都是红色的 , 则三角形 EAB 为红色三角形 .综上所述 , 一定有两个同色三角形 .7.甲虫不能走遍所有的立方体 .我们将大正方体如图分割成 27 个小正方体 , 涂上黑白相间的两种颜色 , 使得中心的小正方体染成白色 , 再使两个相邻的小正方体染上不同的颜色 . 显然在 27 个小正文体中 ,14 个是黑的 ,13 个是白的 . 甲虫从中间的白色正方体出发 , 每走一步 , 小正方体就改变一种颜色 . 故它走 27 步, 应该经过 14 个白色的小正方体 ,13 个黑色的小正方体 . 因此在 27 步中至少有一个白色的小正方体 , 甲虫进去过两次 . 故若要求甲虫到每个小正方体只去一次 , 甲虫就不能走遍所有的小正方体 .8.将棋上的各点按黑白相的方式染上黑白二色 .由“ 步”的行走 , 当“ ”从黑点出 , 下一步只能跳到白点 , 以后依次是黑、白、黑、白⋯⋯要回到原出点 ( 黑点 ), 它必跳偶数步 .9.不能 . 半象棋共有 45 个格点 , 从起点出跳遍半棋 , 起点与最后一步同色 . 故不可能从最后一步跳回起点 .10.与 B 点同色的点 ( 白点 ) 有 22 个, 异色的点 ( 黑色 ) 有 23 个. 从 B 点出 , 跳了 42 步 , 已跳遍了所有的白色 , 剩下两个黑点 , 但是不能跳两个黑点 .11.不能 . 因 A、B 两点异色 , 从 B 到 A 所跳的步数是一个奇数 .12.“ ”每走一步 , 所在的格点就会改一次色 . 因 A、B 两点异色 , 故从 A 到B“ ”走的步数是一个奇数 . 但半棋共有 45 个格点 , 不重复地走遍半棋要 44 步,但44 是一个偶数 .13.如 8 8 的棋染色 , 每一个 4 1 的方形能盖住 2 白 2 黑小方格 , 而每一个 2 2 的正方形能盖住 1 白 3 黑或 1 黑 3 白小方格 , 那么 7 个 22的正方形盖住的黑色小方格数是一个奇数, 但中黑格数32 是一个偶数 . 故种剪法是不存在的 .+1+1-1-1+1+1+1+1+1-1-1+1+1+1+1+1-1-1-1-1 -1+1 +1-1-1-1-1 -1+1 +1-1 -114.如下所示 , 将表 (1) 黑白相地染色 .表(1)本题条件允许如图所示的 6 个操作 , 这 6 个操作无论实行在那个位置上 , 白格中的数字之和减去黑格中的数字之和总是一个常数 , 所以表 1 中白格中数字之和与黑格中数字之和的差即 32, 等于表 2 中白格中数字之和与黑格中数字之和的差即(31+A)-32, 于是 (31+A)-32=32, 故 A=33.二十染色问题(2)年级班姓名得分1.下图是一套房子的平面图 , 图中的方格代表房间 , 每个房间都有通向任何一个邻室的门 . 有人想从某个房间开始 , 依次不重复地走遍每一个房间 , 他的想法能实现吗2.展览会有 36 个展室 ( 如图 ), 每两相邻展室之间均有门相通 . 能不能从入口进去 , 不重复地参观完全部展室后 , 从出口出来呢3.图中的 16 个点表示 16 个城市 , 两个点之间的连线表示这两个城市有公路相通 . 问能否找到一条不重复地走遍这 16 座城市的路线4.下图是由 4 个小方格组成的“ L”形硬纸片 , 用若干个这种纸片无重叠地拼成一个 4 n 的长方形 , 试证明 : n 一定是偶数 .5.中国象棋盘上最多能放几只马互不相“吃” ( “马”走“日”字 , 另不考虑“别马腿”的情况 ).6.能否用一个田字和 15 个 4 1 矩形覆盖 8 8 棋盘7. 能否用 1 个田字和 15 个 T 字纸片 , 拼成一个 88 的正方形棋盘8.在 8 8 棋盘上 , 马能否从左下角的方格出发 , 不重地走遍棋盘 , 最后回到起点若能请找出一条路 , 若不能 , 请说明理由 .9. 下面三个图形都是从 4 4 的正方形分别剪去两个 1 1 的小方格得到的 , 问可否把它们分别剪成 1 2 的七个小矩形(1)(2)(3)10.把三行七列的 21 个小格组成的矩形染色 , 每个小格染上红、蓝两种色中的一种 . 求证 : 总可以找到 4 个同色小方格 , 处于某个矩形的 4 个角上 ( 如图 ) 1红红红红2个科学家互相通信 , 在他们的通信中共讨论 3 个问题 , 而任意两个科学家之间仅讨论 1 个问题 . 证明 : 至少有 3个科学家 , 他们彼此通信讨论的是同一个问题 .12. 用一批 1 2 4 的长方体木块 , 能不能把一个容积为 6 6 6 的正方体木箱充塞填满说明理由 .13.在平面上有一个 27 27 的方格棋盘 , 在棋盘的正中间摆好 81 枚棋子 , 它们被罢成一个 9 9 的正方形 . 按下面的规则进行游戏 : 每一枚棋子都可沿水平方向或竖直方向越过相邻的棋子 , 放进紧挨着这枚棋子的空格中 , 并把越过的这格棋子取出来 . 问: 是否存在一种走法 , 使棋盘上最后恰好剩下一枚棋子12 的超极棋盘上 , 一匹超级马每步跳至 3 4 矩形的另一角 ( 如图 ). 问能否从任一点出发遍历每一格恰一次 , 再回到出发点 ( 这种情况又称马有“回路”)OO———————————————答案——————————————————————1.不能 . 对房间染色 , 使最下面的两个房间染成黑色 , 与黑色相邻的房染成白色 , 则图中有 7 个黑色房间和 5 个白色房间 . 如果要想不重复地走过每一个房间 ,黑色与白色房间数应该相等. 故题中的想法是不能实现的.2.不能 . 对展室进行染色, 使相邻两房间分别是黑色和白色的 . 此时入口处展室的颜色与出口处展室的颜色是相同的 , 而不重复参观完 36 个展室 , 入口与出口展室的颜色应该不相同 .3.不能 . 对这 16 个城市进行黑白相间的染色 , 一种颜色有 9 个, 另一种颜色有7 个. 而要不重复地走遍这 16 个城市 , 黑色与白色的个数应该相等 .4.如图 , 对 4 n 长方形的各列分别染上黑色和白色 . 任一 L 形纸片所占的方格只有两类 : 第一类占 3 黑 1 白, 第二类占 3 白 1 黑.n个设第一类有 a 个, 第二类有 b 个, 因为涂有两种颜色的方格数相等, 故有3b+a=3a+b, 即a=b, 也就是说第一类与第二类相等, 因此各种颜色的方格数都是4 的倍数 , 总数是 8 的倍数 , 从而 n 是偶然 .5.将棋盘黑白相间染色 , 由“马”的走法可知 , 放在黑点上的“马” , 只能吃放在某些白点上的马 . 整个棋盘上黑、白点的个数均为45, 故可在45 个黑点放上马 , 它们是不能互吃的 .6.如图的方式对棋盘染色 . 那么一个田字形盖住 1 个或 3 个白格 , 而一个4 1 的矩形盖住 2 个白格 . 这样一来一个田字和 15 个 4 1 的矩形能盖住的白格数是一个奇数 , 但上图中的白格数是一个偶数 , 因此一个田字形和 15 个 4 1 的矩形不能复盖 8 8 的棋盘 .7.将棋盘里黑白相间涂色 . 一个田字形盖住 2 个白格 , 一个 T 字形盖住 3 个或 1 个白格 . 故 1 个田字和 15 个 T 字盖住的白格数是一个奇数 , 但棋盘上的白格数是一个偶数 . 因此一个田字形和 15 个 T 字形不能盖住 8 8 的棋盘 .8.将棋盘黑白相间地染色后 , 马的走法是从一种颜色的格子跳到另一种颜色. 棋盘上有 32 个白格与 32 个黑格 , 故马可能跳遍整个棋盘 . 图中给出了一种走法 .564158355039603347445540593451384257464936533261454843543162375220530632211161329642141714251061922782312151287183269249. 先对 4 4 的棋盘黑白相间的涂色 ( 如图 ), 这道题的实际问题是问7 个1 2 矩形能否分别复盖剪去 A、B;剪去 A、C;剪去 A、D的三个棋盘 . 若 7 个 12矩形可以复盖剪残的棋盘 , 因为每个 1 2 矩形均可盖住一个白格和一个黑格, 所以棋的白格与黑格数目相等 . 都是 7 个. 而剪去 A 格和 C 格的棋 (2) 有 5 个白格 8 个黑格 , 剪去 A、D 的棋 (3) 有 5 个白格 8 个黑格 , 因此两个剪的棋均不能被 7 个1 2 矩形复盖 , 也就不能剪成 7 个 1 2 的矩形 .ABCD棋 (1) 可以被 7 个 1 2 的矩形所复盖 . 下面出一种剪法 :A11277B26543654310.在第一行的 7 格中必有 4 格同色 , 不妨 4 格位于前 4 个位置 , 且均色 .然后考前 4 列构成的 3 4 矩形 . 若第二行和第 3 行中出 2 个或 2 个以上的色格子 . 行的两个色格子与第一行的色格子就成一个 4 角同色格子的矩形 .若不然 , 第 2、3 行中都至少有 3 个格在前 4 列中 , 不妨第 2 行前 3 格色 , 然第三行中的前 3 格中至少有 2 个格,故在二、三行的前 4 列中必存在四角都是色的矩形 .11.将 17 个科学家用 17 个点代表 , 两点之的段表示两个科学家之的 . 用三种色些段染色 , 表示三个 , 于是就成 :17 个点之的所有段用三种色染色, 必有同色三角形 .从任意一点 , 不妨从 A 向其他 16 点 A1, A2 , ⋯ A16共可成 16 条段 , 用三种色染色 , 由抽原可知 , 必有 6 条段同色 . 6 条段 AA1, AA2 , ⋯AA6且同色 .考 A1, A2, A3, A4, A5, A6六点之的 , 若有一条色 ,( 如 A1A2色 ) ,则三角形 AA1 A2为红色的同色三角形 .A1A2A3AA4A5A6若这六点之间的连线中 , 没有一条是红色的 , 则它们之间只能涂两种颜色 . 考虑从 A1引出的五条线段 A1A2 A1A3 A1A4 A1A5 A1A6, 由抽屉原理知 , 其中必有三条是同色的 . 不妨设这三条为 A1A2 A1 A3 A1A4, 且同为蓝色 . 若三角形 A2A3A4的三边中有一条为蓝色的 , 则有一个蓝色的三角形存在 ; 若三角形 A2A3 A4三边都不是蓝色的 , 则它的三边是同为第三色的同色三角形 . A2A3A1A412. 把正方体木箱分成27 个小正方体 , 每个小正方体的体积为 2 2 2=8.将这些正方体如右图黑白相间染上色. 显然黑色 2 2 2 的正方体有 14 个, 白色2 2 2 小正方体有 13 个 . 每一个这样的正方体相当于8 个 1 1 1 的小正方体 .将 1 2 4 的长方体放入木箱 , 无论怎么放 , 每个长方体木块盖住8个边长为1 的单位正方体 , 其中有 4 个黑色的 ,4 个白色的 . 木箱共含 6 6 6=216个单位正方体 ,26 个长方体木块共盖住 8 26=208个单位正方体 , 其中黑白各占 104 个 , 余下216-208=8 个单位正方体是黑色的 . 但是第 27 个 1 2 4 长方体木块不管怎样放 , 也无法盖住这 8 个黑色单位正方体 .13.如图 , 将整个棋盘的每一格都分别染上红、白、黑三种颜色 , 这种染色方式将棋盘分成了三个部分 . 按照游戏规则 , 每走一步 , 有两种颜色方格中的棋子数分别减少了 1 个, 而第三种颜色的棋子数增加了一个 . 这表明每走一步 , 每个部分的棋子的奇偶性要发生改变 .因为一开始时 ,81 枚棋子摆成一个 9 9 的正方形 , 显然三个部分的棋子数是相同的 , 从而每走一步 , 三部分中的棋子数的奇偶性是相同的 . 如果走了若干步以后, 棋盘上恰好剩下一枚棋子 , 则两部分上的棋子数为偶数 , 而另一部分上的棋子数为奇数 . 这种结果是不可能出现的 .14.用两种方法对超级棋盘染色 .首先 , 将棋盘黑白相间染色 , 则马每跳一步 , 它所在的方格就要改变一次颜色.不妨设第奇数步跳入白格.其次 , 将棋盘的第 3,4,5 及 8,9,10 这六行染成黑色 , 其余六行染成白色 . 在此种染色方式下 , 马从白格一定跳入黑格 . 又因黑白格总数相同 , 马要遍历每一格恰一次又回到出发点 , 因此 , 马从黑格只能跳入白格而不能跳入黑格 . 不妨设马第奇数步跳入白格 .但是对于一种满足要求跳法 , 在两种染色方式下第奇数步跳入的格子的全体是不同的 , 这显然是不可能的 , 故题目要求的跳法是不存在的 .。
小学奥数专题15:染色问题

专题14 染色问题1.下图是一套房子的平面图,图中的方格代表房间,每个房间都有通向任何 一个邻室的门.有人想从某个房间开始,依次不重复地走遍每一个房间,他的想法能实现吗?2.展览会有36个展室(如图),每两相邻展室之间均有门相通.能不能从入口 进去,不重复地参观完全部展室后,从出口出来呢?3.图中的16个点表示16个城市,两个点之间的连线表示这两个城市有公路 相通.问能否找到一条不重复地走遍这16座城市的路线?4.下图是由4个小方格组成的“L ”形硬纸片,用若干个这种纸片无重叠地 拼成一个4 n 的长方形,试证明:n 一定是偶数.5.中国象棋盘上最多能放几只马互不相“吃”(“马”走“日”字,另不考虑“别马腿”的情况).6.能否用一个田字和15个4⨯1矩形覆盖8⨯8棋盘?7.能否用1个田字和15个T 字纸片,拼成一个8⨯8的正方形棋盘?8.在8⨯8棋盘上,马能否从左下角的方格出发,不重地走遍棋盘,最后回到起点?若能请找出一条路,若不能,请说明理由.9.下面三个图形都是从4⨯4的正方形分别剪去两个1⨯1的小方格得到的,问可否把它们分别剪成1⨯2的七个小矩形?10.把三行七列的21个小格组成的矩形染色,每个小格染上红、蓝两种色中的一种.求证:总可以找到4个同色小方格,处于某个矩形的4个角上(如图)11.17个科学家互相通信,在他们的通信中共讨论3个问题,而任意两个科学家之间仅讨论1个问题.证明:至少有3个科学家,他们彼此通信讨论的是同一个问题.12.用一批1⨯2⨯4的长方体木块,能不能把一个容积为6⨯6⨯6的正方体木箱充塞填满?说明理由.13.在平面上有一个27⨯27的方格棋盘,在棋盘的正中间摆好81枚棋子,它们被罢成一个9⨯9的正方形.按下面的规则进行游戏:每一枚棋子都可沿水平方向或竖直方向越过相邻的棋子,放进紧挨着这枚棋子的空格中,并把越过的这格棋子取出来.问:是否存在一种走法,使棋盘上最后恰好剩下一枚棋子?14.12⨯12的超极棋盘上,一匹超级马每步跳至3⨯4矩形的另一角(如图).问能否从任一点出发遍历每一格恰一次,再回到出发点(这种情况又称马有“回12 3———————————————答 案——————————————————————1. 不能.对房间染色,使最下面的两个房间染成黑色,与黑色相邻的房染成白色,则图中有7个黑色房间和5个白色房间.如果要想不重复地走过每一个房间,黑色与白色房间数应该相等.故题中的想法是不能实现的.2. 不能.对展室进行染色,使相邻两房间分别是黑色和白色的.此时入口处展室的颜色与出口处展室的颜色是相同的,而不重复参观完36个展室,入口与出口展室的颜色应该不相同.3. 不能.对这16个城市进行黑白相间的染色,一种颜色有9个,另一种颜色有7个.而要不重复地走遍这16个城市,黑色与白色的个数应该相等.4. 如图,对4⨯n 长方形的各列分别染上黑色和白色.任一L 形纸片所占的方3黑1白,第二类占3白1黑.设第一类有a 个,第二类有b 个,因为涂有两种颜色的方格数相等,故有3b +a =3a +b ,即a =b ,也就是说第一类与第二类相等,因此各种颜色的方格数都是4的倍数,总数是8的倍数,从而n 是偶然.5. 将棋盘黑白相间染色,由“马”的走法可知,放在黑点上的“马”,只能吃放在某些白点上的马.整个棋盘上黑、白点的个数均为45,故可在45个黑点放上马,它们是不能互吃的.6. 如图的方式对棋盘染色.那么一个田字形盖住1个或3个白格,而一个4⨯1的矩形盖住2个白格.这样一来一个田字和15个4⨯1的矩形能盖住的白格数是一个奇数,但上图中的白格数是一个偶数,因此一个田字形和15个4⨯1的矩形n 个7. 将棋盘里黑白相间涂色.一个田字形盖住2个白格,一个T字形盖住3个或1个白格.故1个田字和15个T字盖住的白格数是一个奇数,但棋盘上的白格数是一个偶数.因此一个田字形和15个T字形不能盖住8⨯8的棋盘.8. 将棋盘黑白相间地染色后,马的走法是从一种颜色的格子跳到另一种颜色.棋盘上有32个白格与32个黑格,故马可能跳遍整个棋盘.图中给出了一种走法.9. 先对4⨯4的棋盘黑白相间的涂色(如图),这道题的实际问题是问7个1⨯2矩形能否分别复盖剪去A、B;剪去A、C;剪去A、D的三个棋盘.若7个1⨯2矩形可以复盖剪残的棋盘,因为每个1⨯2矩形均可盖住一个白格和一个黑格,所以棋盘的白格与黑格数目应该相等.都是7个.而剪去A格和C格的棋盘(2)有5个白格8个黑格,剪去A、D的棋盘(3)有5个白格8个黑格,因此这两个剪损的棋盘均不能被7个也就不能剪成7个1⨯2的矩形.棋盘(1).下面给出一种剪法:10. 在第一行的7格中必有4格同色,不妨设这4格位于前4个位置,且均为红色.然后考虑前4列构成的3⨯4矩形.若第二行和第3行中出现2个或2个以上的红色格子.则该行的两个红色格子与第一行的红色格子就组成一个4角同为红色格子的矩形.若不然,则第2、3行中都至少有3个蓝格在前4列中,不妨设第2行前3格为蓝色,显然第三行中的前3格中至少有2个蓝格,故在二、三行的前4列中必存在四角都是蓝色的矩形.11. 将17个科学家用17个点代表,两点之间连结的线段表示两个科学家之间讨论的问题.用三种颜色给这些线段染色,表示三个问题,于是问题就变成:给17个点之间的所有连结线段用三种颜色染色,必有同色三角形.从任意一点,不妨设从A向其他16点A1,A2,…A16共可连成16条线段,用三种颜色染色,由抽屉原则可知,必有6条线段同色.设这6条线段为AA1,AA2,…AA6且同为红色.考虑A1,A2,A3,A4,A5,A6这六点之间的连线,若有一条为红色,(如A1A2为红色) ,则三角形AA1A2为红色的同色三角形.若这六点之间的连线中,没有一条是红色的,则它们之间只能涂两种颜色.考虑从A1引出的五条线段A1A2A1A3A1A4A1A5A1A6,由抽屉原理知,其中必有三条是同色的.不妨设这三条为A1A2A1A3A1A4,且同为蓝色.若三角形A2A3A4的三边中有一条为蓝色的,则有一个蓝色的三角形存在;若三角形A2A3A4三边都不是蓝色的,则它的三边是同为第三色的同色三角形.12. 把正方体木箱分成27个小正方体,每个小正方体的体积为2⨯2⨯2=8.将这些正方体如右图黑白相间染上色.显然黑色2⨯2⨯2的正方体有14个,白色2⨯2⨯2小正方体有13个.每一个这样的正方体相当于8个1⨯1⨯1的小正方体.将1⨯2⨯4的长方体放入木箱,无论怎么放,每个长方体木块盖住8个边长为1的单位正方体,其中有4个黑色的,4个白色的.木箱共含6⨯6⨯6=216个单位正方体,26个长方体木块共盖住8⨯26=208个单位正方体,其中黑白各占104个,余下216-208=8个单位正方体是黑色的.但是第27个1⨯2⨯4长方体木块不管怎样放,也无法盖住这8个黑色单位正方体.13. 如图,将整个棋盘的每一格都分别染上红、白、黑三种颜色,这种染色方式将棋盘分成了三个部分.按照游戏规则,每走一步,有两种颜色方格中的棋子数分别减少了1个,而第三种颜色的棋子数增加了一个.这表明每走一步,每个部.AA1 A2A3A4A5A6A1A2A3A4因为一开始时,81枚棋子摆成一个9 9的正方形,显然三个部分的棋子数是相同的,从而每走一步,三部分中的棋子数的奇偶性是相同的.如果走了若干步以后,棋盘上恰好剩下一枚棋子,则两部分上的棋子数为偶数,而另一部分上的棋子数为奇数.这种结果是不可能出现的.14. 用两种方法对超级棋盘染色.首先,将棋盘黑白相间染色,则马每跳一步,它所在的方格就要改变一次颜色.不妨设第奇数步跳入白格.其次,将棋盘的第3,4,5及8,9,10这六行染成黑色,其余六行染成白色.在此种染色方式下,马从白格一定跳入黑格.又因黑白格总数相同,马要遍历每一格恰一次又回到出发点,因此,马从黑格只能跳入白格而不能跳入黑格.不妨设马第奇数步跳入白格.但是对于一种满足要求跳法,在两种染色方式下第奇数步跳入的格子的全体是不同的,这显然是不可能的,故题目要求的跳法是不存在的.。
小学奥数-长方体正方体染色问题、三视图-知识点+例题+练习-(分类全面)精选全文完整版
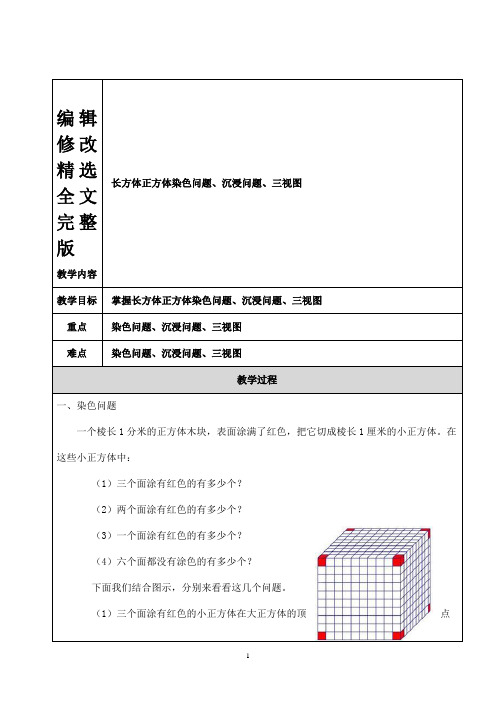
可编辑修改精选长方体正方体染色问题、沉浸问题、三视图全文完整版教学内容教学目标掌握长方体正方体染色问题、沉浸问题、三视图重点染色问题、沉浸问题、三视图难点染色问题、沉浸问题、三视图教学过程一、染色问题一个棱长1分米的正方体木块,表面涂满了红色,把它切成棱长1厘米的小正方体。
在这些小正方体中:(1)三个面涂有红色的有多少个?(2)两个面涂有红色的有多少个?(3)一个面涂有红色的有多少个?(4)六个面都没有涂色的有多少个?下面我们结合图示,分别来看看这几个问题。
(1)三个面涂有红色的小正方体在大正方体的顶点处,正方体有8个顶点,所以三个面涂有红色的有8个。
(2)两个面涂有红色的小正方体在大正方体的棱上,每条棱上有8个,正方体有12条棱,所以两个面涂有红色的有8×12=96个。
(3)一个面涂有红色的小正方体在大正方体的面上,每个面上有8×8=64个,正方体有6个面,所以一个面涂有红色的有8×8×6=384个。
(4)六个面都没有涂色的在大正方体的中间,有两种算法:算法1: 1000-8-96-384=512(个);算法2: 8×8×8=512(个)。
公式:(1)正方体有8个顶点、12条棱、6个面假设把棱n等分(n≥3),那么:N的三次方个小立方体组成的立方体的表面图涂上颜色,则未被涂色的小立方体有(n-2)3个.一面被涂色的小立方体为(n-2)2*6个.两面被涂色的小立方体有(n-2)*12个.三面被涂色的有8个.(2)长方体, 有a*b*c个立方体组成的长方体表面涂上颜色.则未被涂色的小立方体有(a-2)*(b-2)*(c-2)个一面被涂色的小立方体有(a-2)* (b-2)*2+(b-2)* (c-2)*2+(c-2)* (a-2)*2两面被涂色的小立方体有(a-2)*4+(b-2)*4+(c-2)*4三面被涂色的有8个【例 1】下图是333⨯⨯正方体,如果将其表面涂成红色,那么其中一面、两面、三面被涂成红色的小正方体及未被涂色的小正方体各有多少块?0面:1; 1面:6;两面:2;三面:8【巩固】下图是456⨯⨯长方体,如果将其表面涂成红色,那么其中一面、两面、三面被涂成红色的小正方体及未被涂色的小正方体各有多少块?看如右下图,那么他最少用了_____块木块。
最新小学奥数染色与操作问题学生版

模块一:染色问题【巩固】 右图是某一湖泊的平面图,图中所有曲线都是湖岸.(1)如果P 点在岸上,那么A 点是在岸上还是在水中?(2)某人过此湖泊,他下水时脱鞋,上岸时穿鞋.如果他从A 点出发走到某 点B ,他穿鞋与脱鞋的总次数是奇数,那么B 点是在岸上还是在水中?为 什么?一、染色问题这里的染色问题不是要求如何染色,然后问有多少种染色方法的那类题目,它指的是一种解题方法.染色方法是一种将题目研究对象分类的形象化方法,通过将问题中的对象适当染色,我们可以更形象地观察分析出其中所蕴含的关系,再经过一定的逻辑推理,便能得出问题的答案.这类问题不需要太多的数学知识,但技巧性,逻辑性较强,要注意学会几种典型的染色问题.二、操作问题例题11第十一讲染色与操作问题六年级一班全班有35名同学,共分成5排,每排7人,坐在教室里,每个座位的前后左右四个位置都叫做它的邻座.如果要让这35名同学各人都恰好坐到他的邻座上去,能办到吗?为什么?【巩固】某班有45名同学按9行5列坐好.老师想让每位同学都坐到他的邻座(前后左右)上去,问这能否办到?【巩固】有一次车展共6×6=36个展室,如右图,每个展室与相邻的展室都有门相通,入口和出口如图所示.参观者能否从入口进去,不重复地参观完每个展室再从出口出来?例题44例题33例题22右图是某一套房子的平面图,共12个房间,每相邻两房间都有门相通.请问:你能从某个房间出发,不重复地走完每个房间吗?在一个正方形的果园里,种有63棵果树,加上右下角的一间小屋,整齐地排列成八行八列,如图(1).守园人从小屋出发经过每一棵树,不重复也不遗漏(不许斜走),最后又回到小屋,行吗?如果有80棵果树,如图(2),连小屋排成九行九列呢?右图是半张中国象棋盘,棋盘上已放有一只马. 众所周知,马是走“日”字的. 请问:这只马能否不重复地走遍这半张棋盘上的每一个点,然后回到出发点?【巩固】下图是由40个小正方形组成的图形,能否将它剪裁成20个相同的长方形?【巩固】下面的三个图形都是从4×4的正方形纸片上剪去两个1×1的小方格后得到的. 问:能否把它们分 别剪成1×2的七个小矩形?【巩固】能否用9个所示的卡片拼成一个6×6的棋盘?【巩固】9个1×4的长方形不能拼成一个6×6的正方形,请你说明理由!例题66例题55右图是由14个大小相同的方格组成的图形. 试问能不能剪裁成7个由相邻两方格组成的长方形? 用11个和5个能否盖住8×8的大正方形?【巩固】用若干个2×2和3×3的小正方形不能拼成一个11×11的大正方形,请你说明理由!模块二:操作问题例题1010例题99例题88例题77【巩固】对于表(1),每次使其中的任意两个数减去或加上同一个数,能否经过若干次后(各次减去或加上的数可以不同),变为表(2)?为什么?右图是一个圆盘,中心轴固定在黑板上.开始时,圆盘上每个数字所对应的黑板处均写着0.然后转动圆盘,每次可以转动90°的任意整数倍,圆盘上的四个数将分别正对着黑板上写数的位置,将圆盘上的数加到黑板上对应位置的数上.问:经过若干次后,黑板上的四个数是否可能都是999?有7个苹果要平均分给12个小朋友,园长要求每个苹果最多分成5份.应该怎样分?有一位老人,他有三个儿子和十七匹马.他在临终前对他的儿子们说:“我已经写好了遗嘱,我把马留给你们,你们一定要按我的要求去分.”老人去世后,三兄弟看到了遗嘱.遗嘱上写着:“我把十七匹马全都留给我的三个儿子.长子得12,次子得13,给幼子19.不许流血,不许杀马.你们必须遵从父亲的遗愿!”请你帮助他们分分马吧!【巩固】甲、乙、丙、丁分29头羊. 甲、乙、丙、丁分别得1111,,,25610,应如何分?【巩固】9个金币中,有一个比真金币轻的假金币,你能用天平称两次就找出来吗(天平无砝码)?【巩固】 大桶能装5千克油,小桶能装4千克油,你能用这两只桶量出6千克油吗?怎么量?【巩固】 有一个小朋友叫小满,他学会了韩信分油的方法,心里很是得意. 一天,他遇到了两位农妇. 两位农妇有两个各装满了10升奶的罐子,还有一个5升和一个4升的小桶,她们请求小满就用这些容器将罐子中的奶给两个小桶中各倒入2升奶.小满按照韩信分油的方法,略加变通,就将奶分好了!你说说具体的做法!例题1313例题1212例题11118个金币中,有一个比真金币轻的假金币,你能用天平称两次就找出来吗(天平无砝码)据说有一天,韩信骑马走在路上,看见两个人正在路边为分油发愁.这两个人有一只容量10斤的篓子,里面装满了油;还有一只空的罐和一只空的葫芦,罐可装7斤油,葫芦可装3斤油.要把这10斤油平分,每人5斤. 但是谁也没有带秤,只能拿手头的三个容器倒来倒去.应该怎样分呢?有大,中,小3个瓶子,最多分别可以装入水1000克,700克和300克.现在大瓶中装满水,希望通过水在3个瓶子间的流动使得中瓶和小瓶上标出100克水的刻度线,问最少要倒几次水老师在黑板上画了9个点,要求同学们用一笔画出一条通过这9个点的折线(只许拐三个弯儿).你能办到吗?例题1717例题1616例题1515例题1414练习11一只电动老鼠从左下图的A 点出发,沿格线奔跑,并且每到一个格点不是向左转就是向右转。
五年级奥数排列组合之染色

东坡踏翠 (打一中国数学家)
答案:苏步青
介绍一位数学家的成就或故事.
恭喜!恭喜! 请按这个按钮! 傻瓜哈!罚哈你!再对按自!己 说:“你太粗心了!
没做出来啊?罚!你 是哪队的就学哪队的 叫声。哈哈!
泰山中无人无水。 (猜一数字)
答案:三
旭日东升。 (猜一数字)
答案ቤተ መጻሕፍቲ ባይዱ九
语言不通口难开。 (猜一数字)
一个数字3,走在 路上翻了一个跟头, 结果不小心以翻了 一个。(打一成语)
答案:三翻两次
俄国大文豪托尔斯泰在谈到 对人的评价时说:“一个人 就好像一个分数,它的实际 才能好比分子,而他对自己 的估价好比分母。分母越大, 则分数值就越小。”
把这句话背下来。
两只鸟儿并排飞,一 只瘦来一只肥,一年 中来一次,一月当中 来三回。(打一数字)
一个点或同一条线段只能经过一
次.这只甲虫最多有多少种不同
的走法? A
B
C
D
E
例3:从学校到少年宫有4条 东西向的马路和3条南北向的 马路相通,小杰从学校步行到 少年宫(只许向东或向南行进), 最多有多少种走法?
学校
少年宫
如图,从P到Q共有多少种 不同的最短路线?
P
Q
如图,长方体有12条棱,8个顶 点,一只小蚂蚁从A点出发沿 棱爬行,要经过每个顶点一次,且 只经过一次.问共有多少种不同 的走法?
例1:用红、黄、蓝三色 给边长分别为3、4、5、 6、7的五边形的各边 染色,要求相邻两边 不许同色,共有多少 种不同染法?
例3:地图上有A、B、C、
D、E五个国家用五种颜
色去染,要求相邻国家染
不同的颜色。问:有多少
种不同染法?
四年级数学奥数题知识点《染色问题》专项训练及答案

四年级数学奥数题知识点《染色问题》专项训练
及答案
题型:染色问题难度:★★
如图,把A、B、C、D、M这五个部分用5种不同的颜色染色,且相邻的部分不能使用同一种颜色,有的颜色也可以不用,不相邻的部分可以使用同一种颜色,那么这幅图一共有多少种不同的染色方法?
【答案解析】
如果5种颜色全部使用,那么共有5×4×3×2×1=120种染色方法。
如果只使用4种颜色,可以是B和D同色,也可以是A和C 同色,那么共有5×4×3×2×2=240种染色方法。
如果只使用3种颜色,那么有B和D同色并且A和C同色,共有5×4×3=60种染色方法。
120+240+60=420,所以这幅图一共有420种不同的染色方法。
题型:染色问题难度:★★
如图,9条小线段组成了4个小三角形,现在将每条线段分别染上红、黄、蓝三种颜色之一,使得每个三角形三条边的颜色互不相同,那么共有多少种不同的染色方式?
【答案解析】
任选一个小三角形的一条边,当这条边的颜色确定时,这个小三角形的染色方法有2种,同时每种方法都会确定与其相邻的小三角形的一条边的颜色。
24×3=48,所以共有48种不同的染色方式。
小学奥数模块教程染色问题(一)

染色问题(一)染色问题是一种将题目研究对象分类的形象化方法,通过将问题中的对象适当染色,我们可以更形象地观察分析出其中蕴含的关系,再经过一定的逻辑推理,便能得出问题的答案。
因此,这里的染色问题指的是一种解题方法。
这类问题不需要太多的数学知识,但技巧性、逻辑性较强,要注意学会集中典型的染色方法。
根据具体题目的研究对象,染色方法大致可以分为对点染色、对线段染色、对方格染色和对区域染色。
对方格染色常用的是黑白方格相间染色,也叫自然染色。
例1如右图,在5×5方格的A格中有一只爬虫,它每次总是朝上下左右方向爬到相邻的方格中。
那么他能否不重复的爬满每个方格再回A到A格中?解:有小虫的爬法,可黑白相间对方格自然染色,于是小虫只能由黑格爬到白格或白格爬到黑格。
所以它由A出发回到A,即黑格爬到黑格,必须经过偶数步。
而小方格为5×5=25个,每格爬过一次,就应该为25步,不是偶数。
于是这只爬虫不可能不重复地爬遍每格再回到A格。
例2 有一次车展有6×6=36个展室,如图。
每格展室与相邻的展室都有门相通,入口和出口如图所示。
参观者能否从入口进去,不重复地参观完每格展室在从出口出来?解:如图,对每个展室黑白相间染色,同样每次只能冲黑格到白格或者从白格到黑格。
入口和出口都是白格,故线路黑白相间,首位都是白格,于是应该白格比合格多1个,而实际上白格、黑格都是18个,故不能做到不重复走遍每个展室。
例3 右图是某一套房子的平面图,共12个房间,每相邻两间房间都有门相通。
请问,你能从某个房间出发,不重复地走完每个房间吗?解:如图所示,将房间黑白相间染色,发现只有5个黑格、7个白格。
因为每次只能从黑到白或者白到黑,路线必然是黑白相间,显然应该从多的白格开始。
但路线上1白1黑......直至5白5黑后还多余2白格,不可能从白到黑。
故无法实现不重复地走遍每个房间。
小结:染色问题的解题技巧主要在于染色具体方案的构造,其基本原则是使题目条件出现一定的规律,以利于解题。
(完整版)六年级奥数专题01:染色问题.doc

二十染色问题(1)年级班姓名得分(编者按 : 由于内容本身的限制 ,本讲不设填空题 )1.某影院有 31 排,每排 29 个座位 .某天放映了两场电影 ,每个座位上都坐了一个观众 .如果要求每个观众在看第二场电影时必须跟他 (前、后、左、右 )相邻的某一观众交换座位 ,这样能办到吗 ?为什么 ?2.如图是一所房子的示意图 ,图中数字表示房间号码 ,每间房子都与隔壁的房间相通 .问能否从 1 号房间开始 ,不重复的走遍所有房间又回到 1 号房间 ?1 2 34 5 67 8 93.在一个正方形的果园里 ,种有 63 棵果树、加上右下角的一间小屋 ,整齐地排列成八行八列 (见图 (a)).守园人从小屋出发经过每一棵树 ,不重复也不遗漏 (不许斜走 ),最后又回到小屋 ,行吗 ?如果有 80 棵果树 ,连小屋在内排成九行九列 (图 (b)) 呢?(a) (b)4.一个 8 8 国际象棋 (下图 )去掉对角上两格后,是否可以用31 个 2 1 的“骨牌”(形如)把象棋盘上的62 个小格完全盖住?5.如果在中国象棋盘上放了多于45 只马 ,求证 :至少有两只马可以“互吃”.6.空间 6 个点 ,任三点不共线 ,对以它们为顶点的线段随意涂以红色或蓝色 ,是否必有两个同色三角形 ?7.如图 ,把正方体分割成 27 个相等的小正方体 ,在中心的那个小正方体中有一只甲虫 ,甲虫能从每个小正方体走到与这个正方体相邻的 6 个小正方体中的任一个中去 .如果要求甲虫能走到每个小正方体一次 ,那么甲虫能走遍所有的正方体吗?8.中国象棋的马走“日”字 ,车走横线或竖线 ,下图是半张中国象棋盘 ,试回答下面的问题 :A B一只马从起点出发 ,跳了 n 步又回到起点 .证明 :n 一定是偶数 .9.中国象棋的马走“日”字 ,车走横线或竖线 ,下图是半张中国象棋盘 ,试回答下面的问题 :A B一只马能否跳遍这半张棋盘,每一点都不重复 ,最后一步跳回起点 ?10.中国象棋的马走“日”字 ,车走横线或竖线 ,下图是半张中国象棋盘 ,试回答下面的问题 :A B证明 :一只马不可能从位置 B 出发 ,跳遍半张棋盘而每个点都只经过一次 (不要求最后一步跳回起点 ).11.中国象棋的马走“日”字 ,车走横线或竖线 ,下图是半张中国象棋盘 ,试回答下面的问题 :A B一只马能否从位置 B 出发 ,用 6 步跳到位置 A?为什么 ?12.中国象棋的马走“日”字 ,车走横线或竖线 ,下图是半张中国象棋盘 ,试回答下面的问题 :A B,走了若干步后到了位一只车从位置 A 出发 ,在这半张棋盘上走 ,每步走一格置 B.证明 :至少有一个格点没被走过或被走了不止一次.9 个 4 1 的长方13.8 8 的国际象棋棋盘能不能被剪成7 个 2 2 的正方形和形?如果可以 ,请给出一种剪法 ;如果不行 ,请说明理由 .14.(表1)是由数字 0,1 交替构成的 ,(表 2)是由 (表1)中任选、、三种形式组成的图形 ,并在每个小方格全部加 1 或减 1,如此反复多次进行形成的 , 试问 (表 2)中的 A 格上的数字是多少 ?并说明理由 .1 0 1 0 1 0 1 00 1 0 1 0 1 0 11 0 1 0 1 0 1 00 1 0 1 0 1 0 01 0 1 0 1 0 1 00 1 0 1 0 1 0 11 0 1 0 1 0 1 00 1 0 1 0 1 0 1表11 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 A 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1表2———————————————答案——————————————————————1.把影院的座位画成黑白相的矩形 .(29 31),共有 899 个小方格 .不妨假定四角黑格 ,共有黑格 450 个,白格 449 个.要求看第二影 ,每位众必跟他相的某一众交位置 ,即要求每一黑白格必互 ,因黑白格的数不相等 ,因此是不可能的 .2.将号奇数的房染成黑色 ,号偶数的房染成白色 .从 1 号房出 ,只能按黑白黑白⋯⋯的次序,当走遍九个房在黑色房中 ,个房不与 1 号房相 ,故不能不重复地走遍所有房又回到 1 号房 .3.(a)行,走法如所示 .(a)(b)不行 ,将小屋染成黑色 ,果染成黑白相的色 ,(b)中有 41 个黑色的 ,40 个白色的 .从小屋出 ,按黑白黑白⋯⋯的次序,当走遍80 棵后 ,到达的的色是黑色,与小屋不相 ,故不可能最后回到小屋 .4. 不能 .原因是每一个 2 1 的矩形骨牌一定恰好盖住一个黑格和一个白格,31 个的骨牌恰好盖住 31 个黑格和 31 个白格 .但是国象棋棋上角两格的色是相同的 ,把它去掉后剩下的是 30 个白格 ,32 个黑格 ,或 32 个白格 ,30 个黑格 ,因此不能盖住 .5.中国象棋棋上有 90个交叉点 ,把棋分成 10个小部分 ,每部分有 3 3=9 个交叉点 ,由抽原知 ,至少有一个小部分内含有 6 只 .将一小部分的 9 个交叉点分涂上黑色及白色 .有两只在不同色交叉点上 ,故一定有两只“互吃”.6.六个点 A 、 B、 C、D、E、F.我先明存在一个同色的三角形 : 考由 A 点引出的五条段 AB 、AC 、 AD 、 AE、 AF,其中必有三条被染成了相同的色 ,不妨 AB 、AC 、AD 三条同色 .再考三角形 BCD 的三 : 若其中有一条色 ,存在一个色三角形 ;若三条都不是色 ,三角形 BCD 色三角形 .BCAD下面再来明有两个同色三角形,不妨三角形 ABC 的三同色 .(1)若三角形 DEF 也是色三角形 ,存在两个同色三角形 .(2)若三角形 DEF 中有一条色 (不妨 DE), 下面考 DA 、 DB 、DC三条段,其中必有两条同色.①若其中有两条是色的 ,如 DA 、DB 是色的 ,三角形 DAB 第二个同色三角形( 1).D AE B C(1)②若其中有两条是色的 , DA 、 DB 色 ( 2).此在 EA、 EB 两条段中 ,若有一条色 ,存在一个色三角形 ;若两条都是色的 ,三角形 EAB 色三角形 .上所述 ,一定有两个同色三角形.D AE B C(2)7.甲虫不能走遍所有的立方体 .我将大正方体如分割成 27 个小正方体 ,涂上黑白相的两种色 ,使得中心的小正方体染成白色 ,再使两个相的小正方体染上不同的色 .然在 27 个小正文体中 ,14 个是黑的 ,13 个是白的 .甲虫从中的白色正方体出 ,每走一步 , 小正方体就改一种色 .故它走 27 步, 14 个白色的小正方体 ,13 个黑色的小正方体 .因此在 27 步中至少有一个白色的小正方体,甲虫去两次 .故若要求甲虫到每个小正方体只去一次,甲虫就不能走遍所有的小正方体 .8.将棋上的各点按黑白相的方式染上黑白二色.由“ 步”的行走 ,当“ ”从黑点出 ,下一步只能跳到白点 ,以后依次是黑、白、黑、白⋯⋯要回到原出点 (黑点 ),它必跳偶数步 .9.不能 .半象棋共有 45 个格点 ,从起点出跳遍半棋 ,起点与最后一步同色 .故不可能从最后一步跳回起点 .10.与 B 点同色的点 (白点 )有 22 个,异色的点 (黑色 )有 23 个.从 B 点出 ,跳了 42 步时 ,已经跳遍了所有的白色 ,还剩下两个黑点 ,但是马不能够连续跳过两个黑点 .11.不能 .因为 A、 B 两点异色 ,从 B 到 A 所跳的步数是一个奇数 .12.“车”每走一步 ,所在的格点就会改变一次颜色 .因 A、B 两点异色 ,故从 A 到B“车”走的步数是一个奇数 .但半张棋盘共有 45 个格点 ,不重复地走遍半张棋盘要 44 步,但 44 是一个偶数 .13.如图对 8 8 的棋盘染色 ,则每一个 4 1 的长方形能盖住 2 白 2 黑小方格 , 而每一个 2 2 的正方形能盖住 1 白 3 黑或 1 黑 3 白小方格 ,那么 7 个 2 2 的正方形盖住的黑色小方格数总是一个奇数 ,但图中黑格数为 32 是一个偶数 .故这种剪法是不存在的 .+1 +1 - 1 - 1 +1 +1 +1+1 +1 - 1 - 1 +1 +1 +1+1 +1 - 1 - 1- 1 - 1 - 1 +1 +1 - 1 - 1- 1 - 1 - 1 +1 +1 - 1 - 114.如下图所示 ,将表 (1)黑白相间地染色 .表(1)本题条件允许如图所示的 6 个操作 ,这 6 个操作无论实行在那个位置上 ,白格中的数字之和减去黑格中的数字之和总是一个常数 ,所以表 1 中白格中数字之和与黑格中数字之和的差即 32,等于表 2 中白格中数字之和与黑格中数字之和的差即(31+A)-32,于是 (31+A)-32=32, 故 A=33.二十染色问题(2)年级班姓名得分1.下图是一套房子的平面图 ,图中的方格代表房间 ,每个房间都有通向任何一个邻室的门 .有人想从某个房间开始 ,依次不重复地走遍每一个房间 ,他的想法能实现吗 ?2.展览会有 36 个展室 (如图 ),每两相邻展室之间均有门相通 .能不能从入口进去 ,不重复地参观完全部展室后 ,从出口出来呢 ?3.图中的 16 个点表示 16 个城市 ,两个点之间的连线表示这两个城市有公路相通 .问能否找到一条不重复地走遍这 16 座城市的路线 ?4.下图是由 4 个小方格组成的“L”形硬纸片 ,用若干个这种纸片无重叠地拼成一个 4 n 的长方形 ,试证明 :n 一定是偶数 .5.中国象棋盘上最多能放几只马互不相“吃” (马“”走“日”字,另不考虑“别马腿”的情况 ).6.能否用一个田字和15 个 4 1 矩形覆盖 8 8 棋盘 ?7.能否用 1 个田字和 15 个 T 字纸片 ,拼成一个 8 8 的正方形棋盘 ?8.在 8 8 棋盘上 ,马能否从左下角的方格出发 ,不重地走遍棋盘 ,最后回到起点 ? 若能请找出一条路 ,若不能 ,请说明理由 .9.下面三个图形都是从 4 4 的正方形分别剪去两个 1 1 的小方格得到的 ,问可否把它们分别剪成 1 2 的七个小矩形 ?(1)(2)(3)10.把三行七列的 21 个小格组成的矩形染色 ,每个小格染上红、蓝两种色中的一种 .求证 :总可以找到 4 个同色小方格 ,处于某个矩形的 4 个角上 (如图 ) 1红红红红2311.17个科学家互相通信 ,在他们的通信中共讨论 3 个问题 ,而任意两个科学家之间仅讨论 1 个问题 .证明 :至少有 3 个科学家 ,他们彼此通信讨论的是同一个问题 .12.用一批 1 2 4 的长方体木块 ,能不能把一个容积为 6 6 6 的正方体木箱充塞填满 ?说明理由 .13.在平面上有一个 27 27 的方格棋盘 ,在棋盘的正中间摆好 81 枚棋子 ,它们被罢成一个 9 9 的正方形 .按下面的规则进行游戏 :每一枚棋子都可沿水平方向或竖直方向越过相邻的棋子 ,放进紧挨着这枚棋子的空格中 ,并把越过的这格棋子取出来 .问 :是否存在一种走法 ,使棋盘上最后恰好剩下一枚棋子 ?14.12 12 的超极棋盘上 ,一匹超级马每步跳至 3 4 矩形的另一角 (如图 ).问能否从任一点出发遍历每一格恰一次 ,再回到出发点 (这种情况又称马有“回路”)?OO———————————————答案——————————————————————1.不能 .对房间染色 ,使最下面的两个房间染成黑色 ,与黑色相邻的房染成白色,则图中有 7 个黑色房间和 5 个白色房间 .如果要想不重复地走过每一个房间 , 黑色与白色房间数应该相等 .故题中的想法是不能实现的 .2.不能 .对展室进行染色 ,使相邻两房间分别是黑色和白色的 .此时入口处展室的颜色与出口处展室的颜色是相同的,而不重复参观完36 个展室,入口与出口展室的颜色应该不相同 .3.不能 .对这 16 个城市进行黑白相间的染色 ,一种颜色有 9 个,另一种颜色有7 个 .而要不重复地走遍这 16 个城市 ,黑色与白色的个数应该相等 .4.如图 ,对 4 n 长方形的各列分别染上黑色和白色 .任一 L 形纸片所占的方格只有两类 :第一类占 3 黑 1 白 ,第二类占 3 白 1 黑 .n个设第一类有 a 个 , 第二类有 b 个 ,因为涂有两种颜色的方格数相等,故有3b+a=3a+b,即 a=b,也就是说第一类与第二类相等,因此各种颜色的方格数都是 4 的倍数 ,总数是 8 的倍数 ,从而 n 是偶然 .5.将棋盘黑白相间染色 ,由“马”的走法可知 ,放在黑点上的“马”,只能吃放在某些白点上的马 .整个棋盘上黑、白点的个数均为 45,故可在 45 个黑点放上马 ,它们是不能互吃的 .6.如图的方式对棋盘染色 .那么一个田字形盖住 1 个或 3 个白格 ,而一个 4 1 的矩形盖住 2 个白格 .这样一来一个田字和 15 个 4 1 的矩形能盖住的白格数是一个奇数 ,但上图中的白格数是一个偶数 ,因此一个田字形和 15 个 4 1 的矩形不能复盖8 8 的棋盘 .7.将棋盘里黑白相间涂色 .一个田字形盖住 2 个白格 ,一个 T 字形盖住 3 个或1 个白格 .故 1 个田字和 15 个 T 字盖住的白格数是一个奇数 ,但棋盘上的白格数是一个偶数 .因此一个田字形和 15 个 T 字形不能盖住 8 8 的棋盘 .8.将棋盘黑白相间地染色后 ,马的走法是从一种颜色的格子跳到另一种颜色 .棋盘上有 32 个白格与 32 个黑格 ,故马可能跳遍整个棋盘 .图中给出了一种走法 .56 41 58 35 50 39 60 3347 44 55 40 59 34 51 3842 57 46 49 36 53 32 6145 48 43 54 31 62 37 5220 5 30 63 22 11 16 1329 64 21 4 17 14 25 106 19 2 278 23 12 151 28 7 18 3 26 9 249.先 4 4 的棋黑白相的涂色 (如 ),道的是 7 个 1 2 矩形能否分复盖剪去A、B;剪去 A、C;剪去 A、 D 的三个棋 .若 7 个 1 2 矩形可以复盖剪残的棋 ,因每个 12 矩形均可盖住一个白格和一个黑格 ,所以棋的白格与黑格数目相等 .都是 7 个.而剪去 A 格和 C 格的棋 (2)有 5 个白格8 个黑格 ,剪去 A、D 的棋 (3)有 5 个白格 8 个黑格 ,因此两个剪的棋均不能被7 个 1 2 矩形复盖 ,也就不能剪成 7 个 1 2 的矩形 .ABCD棋 (1)可以被 7 个 1 2 的矩形所复盖 .下面出一种剪法 :A 1 1 27 7 B 26 5 4 36 5 4 310.在第一行的 7 格中必有 4 格同色 ,不妨 4 格位于前 4 个位置 ,且均色 .然后考前 4 列构成的 3 4 矩形 .若第二行和第 3 行中出 2 个或 2 个以上的色格子 .行的两个色格子与第一行的色格子就成一个 4 角同色格子的矩形 .若不然 ,第 2、3 行中都至少有 3 个格在前 4 列中 ,不妨第 2 行前 3 格色 ,然第三行中的前 3 格中至少有 2 个格,故在二、三行的前 4 列中必存在四角都是色的矩形 .11.将 17 个科学家用 17 个点代表 ,两点之的段表示两个科学家之的 .用三种色些段染色 ,表示三个 ,于是就成 : 17个点之的所有段用三种色染色,必有同色三角形 .从任意一点 ,不妨从 A 向其他 16 点 A1,A2, ⋯A16共可成 16 条段 ,用三种色染色 ,由抽原可知 ,必有 6 条段同色 . 6 条段 AA1,AA2, ⋯AA6且同色 .考 A1,A2,A3,A4,A5,A6六点之的 ,若有一条色 ,(如 A1A2色 ) , 三角形 AA1A2色的同色三角形 .A1 A2A3A A4A 5A6若这六点之间的连线中 ,没有一条是红色的 ,则它们之间只能涂两种颜色.考虑从 A1引出的五条线段 1 21 3 1 41 51 6 由抽屉原理知其中必有三A A A A A A A A A A , , 的三条是同色的 .不妨设这三条为 A1 2 1 3 1 4 且同为蓝色若三角形 2 3 4A A A A A , . A A A边中有一条为蓝色的 ,则有一个蓝色的三角形存在 ;若三角形 A2A3A4三边都不是蓝色的 ,则它的三边是同为第三色的同色三角形 .A2A3A1A412.把正方体木箱分成 27 个小正方体 ,每个小正方体的体积为 2 2 2=8.将这些正方体如右图黑白相间染上色 .显然黑色 2 2 2 的正方体有 14 个,白色 2 2 2小正方体有 13 个.每一个这样的正方体相当于8 个 1 1 1 的小正方体 .将1 2 4 的长方体放入木箱 ,无论怎么放 ,每个长方体木块盖住 8 个边长为 1 的单位正方体 ,其中有 4 个黑色的 ,4 个白色的 .木箱共含 6 6 6=216 个单位正方体,26 个长方体木块共盖住 8 26=208 个单位正方体 ,其中黑白各占 104 个 ,余下216-208=8 个单位正方体是黑色的 .但是第 27 个 1 2 4 长方体木块不管怎样放 , 也无法盖住这 8 个黑色单位正方体 .13.如图 ,将整个棋盘的每一格都分别染上红、白、黑三种颜色 ,这种染色方式将棋盘分成了三个部分 .按照游戏规则 ,每走一步 ,有两种颜色方格中的棋子数分别减少了 1 个,而第三种颜色的棋子数增加了一个 .这表明每走一步 ,每个部分的棋子的奇偶性要发生改变 .因为一开始时 ,81 枚棋子摆成一个 9 9 的正方形 ,显然三个部分的棋子数是相同的 ,从而每走一步 ,三部分中的棋子数的奇偶性是相同的 .如果走了若干步以后 , 棋盘上恰好剩下一枚棋子 ,则两部分上的棋子数为偶数 ,而另一部分上的棋子数为奇数 .这种结果是不可能出现的 .14.用两种方法对超级棋盘染色 .首先 ,将棋盘黑白相间染色,则马每跳一步 ,它所在的方格就要改变一次颜色. 不妨设第奇数步跳入白格.其次 ,将棋盘的第 3,4,5 及 8,9,10 这六行染成黑色 ,其余六行染成白色 .在此种染色方式下 ,马从白格一定跳入黑格 .又因黑白格总数相同 ,马要遍历每一格恰一次又回到出发点 ,因此 ,马从黑格只能跳入白格而不能跳入黑格 .不妨设马第奇数步跳入白格 .但是对于一种满足要求跳法 ,在两种染色方式下第奇数步跳入的格子的全体是不同的 ,这显然是不可能的 ,故题目要求的跳法是不存在的 .。
奥数染色问题题目及答案.doc
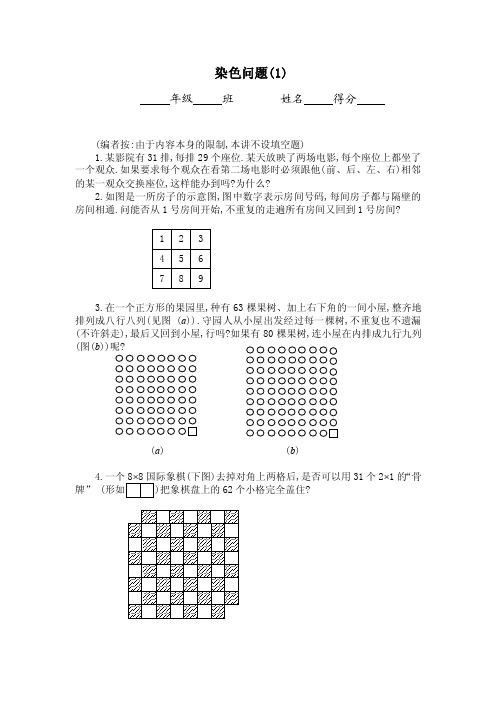
染色问题(1)年级班姓名得分(编者按:由于内容本身的限制,本讲不设填空题)1.某影院有31排,每排29个座位.某天放映了两场电影,每个座位上都坐了一个观众.如果要求每个观众在看第二场电影时必须跟他(前、后、左、右)相邻的某一观众交换座位,这样能办到吗?为什么?2.如图是一所房子的示意图,图中数字表示房间号码,每间房子都与隔壁的房间相通.问能否从1号房间开始,不重复的走遍所有房间又回到1号房间?1 2 34 5 67 8 93.在一个正方形的果园里,种有63棵果树、加上右下角的一间小屋,整齐地排列成八行八列(见图 (a)).守园人从小屋出发经过每一棵树,不重复也不遗漏(不许斜走),最后又回到小屋,行吗?如果有80棵果树,连小屋在内排成九行九列(图(b))呢?(a) (b)4.一个8⨯8国际象棋(下图)去掉对角上两格后,是否可以用31个2⨯1的“骨牌” (形如 )把象棋盘上的62个小格完全盖住?5.如果在中国象棋盘上放了多于45只马,求证:至少有两只马可以“互吃”.6.空间6个点,任三点不共线,对以它们为顶点的线段随意涂以红色或蓝色,是否必有两个同色三角形?7.如图,把正方体分割成27个相等的小正方体,在中心的那个小正方体中有一只甲虫,甲虫能从每个小正方体走到与这个正方体相邻的6个小正方体中的任一个中去.如果要求甲虫能走到每个小正方体一次,那么甲虫能走遍所有的正方体吗?8.中国象棋的马走“日”字,车走横线或竖线,下图是半张中国象棋盘,试回答下面的问题:一只马从起点出发,跳了n 步又回到起点.证明:n 一定是偶数.9.中国象棋的马走“日”字,车走横线或竖线,下图是半张中国象棋盘,试回答下面的问题:一只马能否跳遍这半张棋盘,每一点都不重复,最后一步跳回起点?10.中国象棋的马走“日”字,车走横线或竖线,下图是半张中国象棋盘,试回答下面的问题:ABA B证明:一只马不可能从位置B 出发,跳遍半张棋盘而每个点都只经过一次(不要求最后一步跳回起点).11.中国象棋的马走“日”字,车走横线或竖线,下图是半张中国象棋盘,试回答下面的问题:一只马能否从位置B 出发,用6步跳到位置A ?为什么?12.中国象棋的马走“日”字,车走横线或竖线,下图是半张中国象棋盘,试回答下面的问题:一只车从位置A 出发,在这半张棋盘上走,每步走一格,走了若干步后到了位置B .证明:至少有一个格点没被走过或被走了不止一次.13.8⨯8的国际象棋棋盘能不能被剪成7个2⨯2的正方形和9个4⨯1的长方形?如果可以,请给出一种剪法;如果不行,请说明理由.14.(表1)是由数字0,1交替构成的,(表2)是由(表1)中任选 、 、三种形式组成的图形,并在每个小方格全部加1或减1,如此反复多次进行形成的,试问(表2)中的A 格上的数字是多少?并说明理由.1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1ABABA B表 11 1 1 1 1 1 1 11 1 1 1 1 1 1 11 1 1 1 1 1 1 11 1 1 1 1 1 1 11 1 1 1 1 1 A 11 1 1 1 1 1 1 11 1 1 1 1 1 1 11 1 1 1 1 1 1 1表 2———————————————答案——————————————————————1. 把影院的座位图画成黑白相间的矩形.(29⨯31),共有899个小方格.不妨假定四角为黑格,则共有黑格450个,白格449个.要求看第二场电影,每位观众必须跟他相邻的某一观众交换位置,即要求每一黑白格必须互换,因黑白格的总数不相等,因此是不可能的.2. 将编号为奇数的房间染成黑色,编号为偶数的房间染成白色.从1号房间出发,只能按黑白黑白……的次序,当走遍九个房间时应在黑色房间中,这个房间不与1号房间相邻,故不能不重复地走遍所有房间又回到1号房间.3. 图(a)行,走法如图所示.图(a)图(b)不行,将小屋染成黑色,果树染成黑白相间的颜色,则图(b)中有41个黑色的,40个白色的.从小屋出发,按黑白黑白……的次序,当走遍80棵树后,到达的树的颜色还是黑色,与小屋不相邻,故不可能最后回到小屋.4. 不能.原因是每一个2⨯1的矩形骨牌一定恰好盖住一个黑格和一个白格,31个这样的骨牌恰好盖住31个黑格和31个白格.但是国际象棋棋盘上对角两格的颜色是相同的,把它们去掉后剩下的是30个白格,32个黑格,或32个白格,30个黑格,因此不能盖住.5. 中国象棋棋盘上有90个交叉点,把棋盘分成10个小部分,每部分有3 3=9个交叉点,由抽屉原则知,至少有一个小部分内含有6只马.将这一小部分的9个交叉点分别涂上黑色及白色.总有两只马在不同颜色交叉点上,故一定有两只马“互吃”.6. 设这六个点为A 、B 、C 、D 、E 、F.我们先证明存在一个同色的三角形: 考虑由A 点引出的五条线段AB 、AC 、AD 、AE 、AF,其中必有三条被染成了相同的颜色,不妨设AB 、AC 、AD 三条同为红色.再考虑三角形BCD 的三边:若其中有一条为红色,则存在一个红色三角形;若这三条都不是红色,则三角形BCD 为蓝色三角形.下面再来证明有两个同色三角形,不妨设三角形ABC 的三边同为红色. (1)若三角形DEF 也是红色三角形,则存在两个同色三角形.(2)若三角形DEF 中有一条边为蓝色(不妨设DE),下面考虑DA 、DB 、DC 三 条线段,其中必有两条同色.①若其中有两条是红色的,如DA 、DB 是红色的,则三角形DAB 为第二个同色三角形(图1).②若其中有两条是蓝色的,设DA 、DB 为蓝色(图2).此时在EA 、EB 两条线段中,若有一条为蓝色,则存在一个蓝色三角形;若两条都是红色的,则三角形EAB 为红色三角形.综上所述,一定有两个同色三角形.7. 甲虫不能走遍所有的立方体.我们将大正方体如图分割成27个小正方体,涂上黑白相间的两种颜色,使得中心的小正方体染成白色,再使两个相邻的小正方体染上不同的颜色.显然在27A B DCA BC D E (图1) A BCDE (图2)个小正文体中,14个是黑的,13个是白的.甲虫从中间的白色正方体出发,每走一步,小正方体就改变一种颜色.故它走27步,应该经过14个白色的小正方体,13个黑色的小正方体.因此在27步中至少有一个白色的小正方体,甲虫进去过两次.故若要求甲虫到每个小正方体只去一次,甲虫就不能走遍所有的小正方体.8. 将棋盘上的各点按黑白相间的方式染上黑白二色.由“马步”的行走规则,当“马”从黑点出发,下一步只能跳到白点,以后依次是黑、白、黑、白……要回到原出发点(黑点),它必须跳偶数步.9. 不能.半张象棋盘共有45个格点,马从起点出发跳遍半张棋盘,则起点与最后一步同色.故不可能从最后一步跳回起点.10. 与B 点同色的点(白点)有22个,异色的点(黑色)有23个.马从B 点出发,跳了42步时,已经跳遍了所有的白色,还剩下两个黑点,但是马不能够连续跳过两个黑点.11. 不能.因为A 、B 两点异色,从B 到A 所跳的步数是一个奇数.12. “车”每走一步,所在的格点就会改变一次颜色.因A 、B 两点异色,故从A 到B “车”走的步数是一个奇数.但半张棋盘共有45个格点,不重复地走遍半张棋盘要44步,但44是一个偶数.13. 如图对8⨯8的棋盘染色,则每一个4⨯1的长方形能盖住2白2黑小方格,而每一个2⨯2的正方形能盖住1白3黑或1黑3白小方格,那么7个2⨯2的正方形盖住的黑色小方格数总是一个奇数,但图中黑格数为32是一个偶数.故这种剪法是不存在的.14. 如下图所示,将表(1)黑白相间地染色.+1 +1 +1 +1-1 -1 -1 -1+1 +1 +1 +1 +1 +1-1 -1 -1 -1 -1 -1+1 +1 +1 +1+1 +1-1 -1 -1 -1-1 -1表(1)本题条件允许如图所示的6个操作,这6个操作无论实行在那个位置上,白格中的数字之和减去黑格中的数字之和总是一个常数,所以表1中白格中数字之和与黑格中数字之和的差即32,等于表2中白格中数字之和与黑格中数字之和的差即(31+A)-32,于是(31+A)-32=32,故A=33.。
小学奥数——染色问题(答案)

第9讲 染色问题【知识要点】染色方法是一种对题目所研究的对象用直观形象的染色来进行分类的方法。
象国际象棋的棋盘那样,我们可以把研究的对象染上不同的颜色,使问题变得浅显明了、一目了然,有利于我们观察、分析对象之间的关系,再利用奇偶性、抽屉原理等多种知识对染色图形进行分析,从而达到对原问题的解决。
【典型例题】例1、教室中有7排位子,每排7张,每张位子上坐一个同学,如果一周后,每个同学都必须和他相邻的(前、后、左、右)某一个同学换位子,问:这种交换可能成功吗?为什么? 解:如右图所示黑白相间涂色,白色共有25个,黑色24个,要实现题意要求,一个白色位置必须和一个黑色位置互换,黑白座位应该一样多才行,所以办不到。
例2、如图是一所房子的示意图,图中数字表示房间号码,每间房子都与隔壁的房间相通.问能否从1号房间开始,不重复的走遍所有房间又回到1号房间? 解:如图所示每一个奇数号房间旁边一定是偶数号房间,反之亦然,那么奇数号房间一定走到偶数号,偶数号一定走到奇数号,从一号开始走奇数步一定是到偶数号房间,走偶数步一定是到奇数号房间,要不重复的走遍所有房间回到1号房间,共要走9步,应该走到偶数号房间,而1是奇数,所以办不到。
例3、一个8⨯8国际象棋(下图)去掉对角上两格后,是否可以用31个2⨯1的“骨牌” (形如 )把象棋盘上的62个小格完全盖住?解:任意一个2⨯1的“骨牌”一定是一白一黑的,所以若要用31个这样的骨牌覆盖这个棋盘,白黑格数应该一样多,而此棋盘中有32个黑格,30个白格,所以办不到。
例4、线段AB 的两个端点,一个标以红色,一个标以蓝色。
在此线段中任意插入2008个分点,每个分点任意涂上红色或蓝色,这样分得2009条不重叠的小线段,如果把两端涂色不同的线段叫做奥运线段,奥运线段的条数是奇数还是偶数? 解:原本的线段AB 就是一条奥运线段,然后不管中间插入的点是什么颜色的,都会破坏原来的奥运线段从而变成一条两端同色一条奥运线段,再然后如果在一条奥运线段中间插入任意颜色的点,奥运线段会被破坏,但是又会生成一条较短的,那么奥运线段的数量总数不变;如果在一条两端同色的线段中间插入不同色 1 2 3 4 5 6 7 8 9的点,一下就增加2条奥运线段,不改变奥运线段数量的奇偶性。
小学奥数模块教程染色问题(一)

染色问题(一)染色问题是一种将题目研究对象分类的形象化方法,通过将问题中的对象适当染色,我们可以更形象地观察分析出其中蕴含的关系,再经过一定的逻辑推理,便能得出问题的答案。
因此,这里的染色问题指的是一种解题方法。
这类问题不需要太多的数学知识,但技巧性、逻辑性较强,要注意学会集中典型的染色方法。
根据具体题目的研究对象,染色方法大致可以分为对点染色、对线段染色、对方格染色和对区域染色。
对方格染色常用的是黑白方格相间染色,也叫自然染色。
例1如右图,在5×5方格的A格中有一只爬虫,它每次总是朝上下左右方向爬到相邻的方格中。
那么他能否不重复的爬满每个方格再回A到A格中?解:有小虫的爬法,可黑白相间对方格自然染色,于是小虫只能由黑格爬到白格或白格爬到黑格。
所以它由A出发回到A,即黑格爬到黑格,必须经过偶数步。
而小方格为5×5=25个,每格爬过一次,就应该为25步,不是偶数。
于是这只爬虫不可能不重复地爬遍每格再回到A格。
例2 有一次车展有6×6=36个展室,如图。
每格展室与相邻的展室都有门相通,入口和出口如图所示。
参观者能否从入口进去,不重复地参观完每格展室在从出口出来?解:如图,对每个展室黑白相间染色,同样每次只能冲黑格到白格或者从白格到黑格。
入口和出口都是白格,故线路黑白相间,首位都是白格,于是应该白格比合格多1个,而实际上白格、黑格都是18个,故不能做到不重复走遍每个展室。
例3 右图是某一套房子的平面图,共12个房间,每相邻两间房间都有门相通。
请问,你能从某个房间出发,不重复地走完每个房间吗?解:如图所示,将房间黑白相间染色,发现只有5个黑格、7个白格。
因为每次只能从黑到白或者白到黑,路线必然是黑白相间,显然应该从多的白格开始。
但路线上1白1黑......直至5白5黑后还多余2白格,不可能从白到黑。
故无法实现不重复地走遍每个房间。
小结:染色问题的解题技巧主要在于染色具体方案的构造,其基本原则是使题目条件出现一定的规律,以利于解题。
四年级奥数染色问题的知识点

四年级奥数染色问题的知识点小朋友们,咱们来聊聊四年级奥数里神奇的染色问题!啥是染色问题呢?这就好像是给一个大拼图上色,只不过这个拼图可复杂啦!比如说,有一个方格阵,咱要给它们染上不同的颜色,然后看看能发现啥有趣的规律。
就像咱们玩跳棋,每个格子都得有自己独特的颜色,不能乱套。
你想想,如果颜色乱七八糟的,那得多乱呀!染色问题里常常会有一些特别的条件。
比如说,要求相邻的格子不能是同一种颜色。
这就好像你的好朋友不能和你穿一样的衣服去学校,不然多没个性!那怎么解决这些染色问题呢?这可得好好动动脑筋。
咱们可以一个一个格子地去考虑,就像走迷宫,一步一步来,可不能着急。
先选好第一个格子的颜色,然后再想下一个和它挨着的格子该用啥颜色。
比如说有个九宫格,咱们先给左上角的格子染成红色,那它旁边的格子就不能是红色啦,可能就得是蓝色或者黄色。
这是不是有点像排座位,不能让关系好的总坐在一起,得打乱了才有新鲜感!再比如说,给一个图形的顶点染色。
每个顶点就像是一个小将军,它们也得有自己独特的标志颜色。
而且还要注意,相邻顶点的颜色不能一样,不然它们就分不清自己的队伍啦!还有那种复杂的立体图形染色,这可就像是给一个大城堡涂颜色,每个面都得漂漂亮亮的,还不能重样。
解决染色问题的时候,咱们得细心,就像给妈妈准备礼物,得用心包装,不能马虎。
小朋友们,染色问题是不是很有趣呀?只要咱们认真思考,多尝试,就一定能解决这些难题,就像超级英雄打败大怪兽一样厉害!我相信你们都能在奥数的世界里玩得开心,学得快乐!总之,四年级奥数的染色问题虽然有点难,但只要咱们用心,就能找到其中的乐趣和秘密,成为奥数小高手!。
小学奥数染色与操作问题学生版

模块一:染色问题【巩固】 右图是某一湖泊的平面图,图中所有曲线都是湖岸.(1)如果P 点在岸上,则A 点是在岸上还是在水中?(2)某人过此湖泊,他下水时脱鞋,上岸时穿鞋.如果他从A 点出发走到某 点B ,他穿鞋与脱鞋的总次数是奇数,则B 点是在岸上还是在水中?为 什么?一、染色问题这里的染色问题不是要求如何染色,然后问有多少种染色方法的那类题目,它指的是一种解题方法.染色方法是一种将题目研究对象分类的形象化方法,通过将问题中的对象适当染色,我们可以更形象地观察分析出其中所蕴含的关系,再经过一定的逻辑推理,便能得出问题的答案.这类问题不需要太多的数学知识,但技巧性,逻辑性较强,要注意学会几种典型的染色问题.二、操作问题例题11第十一讲染色与操作问题六年级一班全班有35名同学,共分成5排,每排7人,坐在教室里,每个座位的前后左右四个位置都叫做它的邻座.如果要让这35名同学各人都恰好坐到他的邻座上去,能办到吗为什么?【巩固】 某班有45名同学按9行5列坐好.老师想让每位同学都坐到他的邻座(前后左右)上去,问这能否办到【巩固】有一次车展共6×6=36个展室,如右图,每个展室与相邻的展室都有门相通,入口和出口如图所示. 参观者能否从入口进去,不重复地参观完每个展室再从出口出来例题44例题33例题22右图是某一套房子的平面图,共12个房间,每相邻两房间都有门相通.请问:你能从某个房间出发,不重复地走完每个房间吗在一个正方形的果园里,种有63棵果树,加上右下角的一间小屋,整齐地排列成八行八列,如图(1).守园人从小屋出发经过每一棵树,不重复也不遗漏(不许斜走),最后又回到小屋,行吗?如果有80棵果树,如图(2),连小屋排成九行九列呢?右图是半张中国象棋盘,棋盘上已放有一只马. 众所周知,马是走“日”字的. 请问:这只马能否不重复地走遍这半张棋盘上的每一个点,然后回到出发点?【巩固】下图是由40个小正方形组成的图形,能否将它剪裁成20个相同的长方形?【巩固】下面的三个图形都是从4×4的正方形纸片上剪去两个1×1的小方格后得到的. 问:能否把它们分 别剪成1×2的七个小矩形?【巩固】能否用9个所示的卡片拼成一个6×6的棋盘?【巩固】9个1×4的长方形不能拼成一个6×6的正方形,请你说明理由!例题66例题55右图是由14个大小相同的方格组成的图形. 试问能不能剪裁成7个由相邻两方格组成的长方形? 用11个和5个能否盖住8×8的大正方形【巩固】用若干个2×2和3×3的小正方形不能拼成一个11×11的大正方形,请你说明理由!模块二:操作问题【巩固】甲、乙、丙、丁分29头羊. 甲、乙、丙、丁分别得1111,,,25610,应如何分?例题1010例题99例题88例题77【巩固】对于表(1),每次使其中的任意两个数减去或加上同一个数,能否经过若干次后(各次减去或加上的数可以不同),变为表(2)?为什么?右图是一个圆盘,中心轴固定在黑板上.开始时,圆盘上每个数字所对应的黑板处均写着0.然后转动圆盘,每次可以转动90°的任意整数倍,圆盘上的四个数将分别正对着黑板上写数的位置,将圆盘上的数加到黑板上对应位置的数上.问:经过若干次后,黑板上的四个数是否可能都是999?有7个苹果要平均分给12个小朋友,园长要求每个苹果最多分成5份.应该怎样分?有一位老人,他有三个儿子和十七匹马.他在临终前对他的儿子们说:“我已经写好了遗嘱,我把马留给你们,你们一定要按我的要求去分.”老人去世后,三兄弟看到了遗嘱.遗嘱上写着:“我把十七匹马全都留给我的三个儿子.长子得12,次子得13,给幼子19.不许流血,不许杀马.你们必须遵从父亲的遗愿!”请你帮助他们分分马吧!【巩固】9个金币中,有一个比真金币轻的假金币,你能用天平称两次就找出来吗(天平无砝码)【巩固】 大桶能装5千克油,小桶能装4千克油,你能用这两只桶量出6千克油吗怎么量?【巩固】 有一个小朋友叫小满,他学会了韩信分油的方法,心里很是得意. 一天,他遇到了两位农妇. 两位农妇有两个各装满了10升奶的罐子,还有一个5升和一个4升的小桶,她们请求小满就用这些容器将罐子中的奶给两个小桶中各倒入2升奶.小满按照韩信分油的方法,略加变通,就将奶分好了!你说说具体的做法!例题1313例题1212例题11118个金币中,有一个比真金币轻的假金币,你能用天平称两次就找出来吗(天平无砝码)据说有一天,韩信骑马走在路上,看见两个人正在路边为分油发愁.这两个人有一只容量10斤的篓子,里面装满了油;还有一只空的罐和一只空的葫芦,罐可装7斤油,葫芦可装3斤油.要把这10斤油平分,每人5斤. 但是谁也没有带秤,只能拿手头的三个容器倒来倒去.应该怎样分呢?有大,中,小3个瓶子,最多分别可以装入水1000克,700克和300克.现在大瓶中装满水,希望通过水在3个瓶子间的流动使得中瓶和小瓶上标出100克水的刻度线,问最少要倒几次水例题1717练习22例题1616例题1515例题1414练习11一只电动老鼠从左下图的A 点出发,沿格线奔跑,并且每到一个格点不是向左转就是向右转。
高中数学奥林匹克竞赛讲座:14染色问题与染色方法

竞赛讲座14-染色问题与染色方法1.小方格染色问题最简单的染色问题是从一种民间游戏中发展起来的方格盘上的染色问题.解决这类问题的方法后来又发展成为解决方格盘铺盖问题的重要技巧.例1 如图29-1(a),3行7列小方格每一个染上红色或蓝色.试证:存在一个矩形,它的四个角上的小方格颜色相同.证明由抽屉原则,第1行的7个小方格至少有4个不同色,不妨设为红色(带阴影)并在1、2、3、4列(如图29-1(b)).在第1、2、3、4列(以下不必再考虑第5,6,7列)中,如第2行或第3行出现两个红色小方格,则这个问题已经得证;如第2行和第3行每行最多只有一个红色小方格(如图29-1(c)),那么在这两行中必出现四角同为蓝色的矩形,问题也得到证明.说明:(1)在上面证明过程中除了运用抽屉原则外,还要用到一种思考问题的有效方法,就是逐步缩小所要讨论的对象的范围,把复杂问题逐步化为简单问题进行处理的方法.(2)此例的行和列都不能再减少了.显然只有两行的方格盘染两色后是不一定存在顶点同色的矩形的.下面我们举出一个3行6列染两色不存在顶点同色矩形的例子如图29-2.这说明3行7列是染两色存在顶点同色的矩形的最小方格盘了.至今,染k色而存在顶点同色的矩形的最小方格盘是什么还不得而知.例2 (第2届全国部分省市初中数学通讯赛题)证明:用15块大小是4×1的矩形瓷砖和1块大小是2×2的矩形瓷砖,不能恰好铺盖8×8矩形的地面.分析将8×8矩形地面的一半染上一种颜色,另一半染上另一种颜色,再用4×1和2×2的矩形瓷砖去盖,如果盖住的两种颜色的小矩形不是一样多,则说明在给定条件不完满铺盖不可能.证明如图29-3,用间隔为两格且与副对角线平行的斜格同色的染色方式,以黑白两种颜色将整个地面的方格染色.显然,地面上黑、白格各有32个.每块4×1的矩形砖不论是横放还是竖盖,且不论盖在何处,总是占据地面上的两个白格、两个黑格,故15块4×1的矩形砖铺盖后还剩两个黑格和两个白格.但由于与副对角线平行的斜格总是同色,而与主对角线平行的相邻格总是异色,所以,不论怎样放置,一块2×2的矩形砖,总是盖住三黑一白或一黑三白.这说明剩下的一块2×2矩形砖无论如何盖不住剩下的二黑二白的地面.从而问题得证.例3 (1986年北京初二数学竞赛题)如图29-4(1)是4个1×1的正方形组成的“L”形,用若干个这种“L”形硬纸片无重迭拼成一个m×n(长为m 个单位,宽为n个单位)的矩形如图29-4(2).试证明mn必是8的倍数.证明∵m×n矩形由“L”形拼成,∴m×n是4的倍数,∴m、n中必有一个是偶数,不妨设为m.把m×n矩形中的m列按一列黑、一列白间隔染色(如图29-4(2)),则不论“L”形在这矩形中的放置位置如何(“L”形的放置,共有8种可能),“L”形或占有3白一黑四个单位正方形(第一种),或占有3黑一白四个单位正方形(第二种).设第一种“L”形共有p个,第二种“L”形共q个,则m×n矩形中的白格单位正方形数为3p+q,而它的黑格单位正方形数为p+3q.∵m为偶数,∴m×n矩形中黑、白条数相同,黑、白单位正方形总数也必相等.故有3p+q=p+3q,从而p=q.所以“L”形的总数为2p个,即“L”形总数为偶数,所以m×n 一定是8的倍数.2.线段染色和点染色下面介绍两类重要的染色问题.(1) 线段染色.较常见的一类染色问题是发样子组合数学中图论知识的所谓“边染色”(或称“线段染色”),主要借助抽屉原则求解.例4 (1947年匈牙利数学奥林匹克试题)世界上任何六个人中,一定有3个人或者互相认识或者互相都不认识.我们不直接证明这个命题,而来看与之等价的下述命题例5 (1953年美国普特南数学竞赛题)空间六点,任三点不共线,任四点不共面,成对地连接它们得十五条线段,用红色或蓝色染这些线段(一条线段只染一种颜色).求证:无论怎样染,总存在同色三角形.证明设A、B、C、D、E、F是所给六点.考虑以A为端点的线段AB、AC、AD、AE、AF,由抽屉原则这五条线段中至少有三条颜色相同,不妨设就是AB、AC、AD,且它们都染成红色.再来看△BCD的三边,如其中有一条边例如BC是红色的,则同色三角形已出现(红色△ABC);如△BCD三边都不是红色的,则它就是蓝色的三角形,同色三角形也现了.总之,不论在哪种情况下,都存在同色三角形.如果将例4中的六个人看成例5中六点,两人认识的连红线,不认识的连蓝线,则例4就变成了例5.例5的证明实际上用染色方法给出了例4的证明.例6 (第6届国际数学奥林匹克试题)有17位科学家,其中每一个人和其他所有人的人通信,他们的通信中只讨论三个题目.求证:至少有三个科学家相互之间讨论同一个题目.证明用平面上无三点共线的17个点A1,A2,…,A17分别表示17位科学家.设他们讨论的题目为x,y,z,两位科学家讨论x连红线,讨论y连蓝线,讨论z连黄线.于是只须证明以这17个点为顶点的三角形中有一同色三角形.考虑以A1为端点的线段A1A2,A1A3,…,A1A17,由抽屉原则这16条线段中至少有6条同色,不妨设A1A2,A1A3,…,A1A7为红色.现考查连结六点A2,A3,…,A7的15条线段,如其中至少有一条红色线段,则同色(红色)三角形已出现;如没有红色线段,则这15条线段只有蓝色和黄色,由例5知一定存在以这15条线段中某三条为边的同色三角形(蓝色或黄色).问题得证.上述三例同属图论中的接姆赛问题.在图论中,将n点中每两点都用线段相连所得的图形叫做n点完全图,记作k n.这些点叫做“顶点”,这些线段叫做“边”.现在我们分别用图论的语言来叙述例5、例6.定理1 若在k6中,任染红、蓝两色,则必有一只同色三角形.定理2 在k17中,任染红、蓝、黄三角,则必有一只同色三角形.(2)点染色.先看离散的有限个点的情况.例7 (首届全国中学生数学冬令营试题)能否把1,1,2,2,3,3,…,1986,1986这些数排成一行,使得两个1之间夹着一个数,两个2之间夹着两个数,…,两个1986、之间夹着一千九百八十六个数?请证明你的结论.证明将1986×2个位置按奇数位着白色,偶数位着黑色染色,于是黑白点各有1986个.现令一个偶数占据一个黑点和一个白色,同一个奇数要么都占黑点,要么都占白点.于是993个偶数,占据白点A1=993个,黑色B1=993个.993个奇数,占据白点A2=2a个,黑点B2=2b个,其中a+b=993.因此,共占白色A=A1+A2=993+2a个.黑点B=B1+B2=993+2b个,由于a+b=993(非偶数!)∴a≠b,从而得A≠B.这与黑、白点各有1986个矛盾.故这种排法不可能.“点”可以是有限个,也可以是无限个,这时染色问题总是与相应的几何问题联系在一起的.例8 对平面上一个点,任意染上红、蓝、黑三种颜色中的一种.证明:平面内存在端点同色的单位线段.证明作出一个如图29-7的几何图形是可能的,其中△ABD、△CBD、△AEF、△GEF 都是边长为1的等边三角形,CG=1.不妨设A点是红色,如果B、E、D、F中有红色,问题显然得证.当B、E、D、F都为蓝点或黄点时,又如果B和D或E和F同色,问题也得证.现设B和D异色E和F异色,在这种情况下,如果C或G为黄色或蓝点,则CB、CD、GE、GF中有两条是端点同色的单位线段,问题也得证.不然的话,C、G均为红点,这时CG是端点同色的单位线段.证毕.还有一类较难的对区域染色的问题,就不作介绍了.练习二十九1.6×6的方格盘,能否用一块大小为3格,形如的弯角板与11块大小为3×1的矩形板,不重迭不遗漏地来铺满整个盘面.2.(第49届苏联基辅数学竞赛题)在两张1982×1983的方格纸涂上红、黑两种颜色,使得每一行及每一列都有偶数个方格是黑色的.如果将这两张纸重迭时,有一个黑格与一个红格重合,证明至少还有三个方格与不同颜色的方格重合.3.有九名数学家,每人至多会讲三种语言,每三名中至少有2名能通话,那么其中必有3名能用同一种语言通话.4.如果把上题中的条件9名改为8名数学家,那么,这个结论还成立吗?为什么?5.设n=6(r-2)+3(r≥3),求证:如果有n名科学家,每人至多会讲3种语言,每3名中至少有2名能通话,那么其中必有 r名能用同一种语言通话.6.(1966年波兰数学竞赛题)大厅中会聚了100个客人,他们中每人至少认识67人,证明在这些客人中一定可以找到4人,他们之中任何两人都彼此相识.7.(首届全国数学冬令营试题)用任意方式给平面上的每一个点染上黑色或白色.求证:一定存在一个边长为1或的正三角形,它三个顶点是同色的.练习二十九1.将1、4行染红色、2、5行染黄色、3、6行染蓝色,然后就弯角板盖住板面的不同情况分类讨论.2.设第一张纸上的黑格A与第二张纸上的红格A′重合.如果在第一张纸上A所在的列中,其余的黑格(奇数个)均与第二张纸的黑格重合,那么由第二张纸上这一列的黑格个数为偶数,知必有一黑格与第一张纸上的红格重合,即在这一列,第一张纸上有一方格B与第二张纸上不同颜色的方格B′重合.同理在A、B所在行上各有一个方格C、D,第二张纸上与它们重合的方格C′、D′的颜色分别与C、D不同.3.把9名数学家用点A1,A2,…,A9表示.两人能通话,就用线连结,并涂某种颜色,以表示不同语种。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.如右图,对 A,B,C,D,E五个区域分别用红黄绿蓝白五种颜色中的某一种来着色,规定相邻的区域着不同色,问有
多少种不同的着色方案?【组合十讲 P37】
2用红黄蓝三种颜色涂在右图的圆圈中,每个圆圈中,每个圆圈只涂一种颜色,并且要使每条连线两端的圆圈涂上
不同颜色,问一共有多少种不同的涂法?
3.某植物园计划在 A,B,C,D,E五个地块栽种四种不同颜色的郁金香,每个地块内的郁金香必须同色,相邻的(有公共
边界的)地块郁金香不能同色,不相邻可以同色,问共有多少种不同的方案?
4.如图对 A,B,C,D,E,F,G七个区域分别采用红,黄,绿,蓝,白五种颜色中的某一种来着色,规定相邻的区域不能
同色,那么有多少种不同的着色方案?
5.用红,黄,蓝,三种颜色把如图的8 个小圆圈涂上颜色,每个圆圈只涂一种颜色,并且有连线的两个
圆圈不能同色,那么有多少种不同涂色方案?【希望杯P107】
6.一根划分成相等 5 段的钢管,若要用红,白两种颜色分别对每一段着色,问共有几种不同的涂色方案?(倒置后相
同的两种涂色方案视为同种)
8.如图用 4 种颜色对 A,B,C,D,E五个区域涂色,要求相邻的区域涂不同的颜色,那么,共有几种涂法?
9. 用三种颜色染正方体的 6 条边,相邻边不同色,有多少种染法?【教程P133】
A 10. 如图,用红,黄,蓝三种颜色给一个五边形的各个顶点染色,同一边的两段点不能同色,且顶点必须染红色,
请问:有多少种不同的染色方案?【高斯导引 P76】
11.如图一个圆环被分成 8 部分,先将每一部分染上红,黄,蓝三种颜色之一,要求相邻两部分颜色不同,共有多少
种不同染色方案?
12.如图,用 4 种不同的颜色将图中的圆圈分别涂色,要求有线段连接的两个相邻的圆圈必须涂不同的颜色,共有
几种涂法?(不许旋转翻转)
13 给一个正四面体的 4 个面染色,每个面只允许用一种颜色,且 4 个面的颜色互不相同,现有 5 种颜色可选,共有多少种不同的染色方案?
14.用 4 种颜色为一个正方体的 6 个面染色,要求每个面只能用 1 种颜色,且乡邻面的颜色必须不同,如果将正方体
经过反转后颜色相同视为同一种,那么共有多少种不同的染色方案?
17.用红,黄,蓝三种颜色对右图进行染色,要求相邻两块颜色不同,共有多少种不同的染色方案?【简明读本
P191】
1.某影院有 31 排,每排 29 个座位 .某天放映了两场电影 ,每个座位上都坐了一个观众 .如果要求每个观众在看第二场电影时必须跟他 (前、后、左、右 )相邻的某一观众交换座位 ,这样能办到吗 ?为什么 ?
2.如图是一所房子的示意图 ,图中数字表示房间号码 ,每间房子都与隔壁的房间相通 .问能否从 1 号房间开始,不重复的走遍所有房间又回到 1 号房间 ?
1 2 3
4 5 6
7 8 9
3.在一个正方形的果园里 ,种有 63 棵果树、加上右下角的一间小屋 ,整齐地排列成八行八列 (见图 (a)).守园人从小屋出发经过每一棵树 ,不重复也不遗漏 (不许斜走 ),最后又回到小屋 ,行吗 ?如果有 80 棵果树 ,连小屋在内排成九行九列 (图 (b))呢?
(a) (b)
4.一个 8 8 国际象棋 (下图 )去掉对角上两格后62 个小格完全盖住 ? ,是否可以用31 个 2 1 的“骨牌”形(如)把象棋盘
上的。
