借助DDS的精密频率的一种替代方法毕业论文外文文献翻译及原文
直接数字频率合成器中英文对照外文翻译文献

中英文资料外文翻译文献All About Direct Digital SynthesisWhat is Direct Digital Synthesis?Direct digital synthesis (DDS) is a method of producing an analog waveform—usually a sine wave—by generating a time-varying signal in digital form and then performing a digital-to-analog conversion. Because operations within a DDS device are primarily digital, it can offer fast switching between output frequencies, fine frequency resolution, and operation over a broad spectrum of frequencies. With advances in design and pro cess technology, today’s DDS devices are very compact and draw little power.Why would one use a direct digital synthesizer (DDS)? Aren’t there other methods for easily generating frequencies?The ability to accurately produce and control waveforms of various frequencies and profiles has become a key requirement common to a number of industries. Whether providing agile sources of low-phase-noise variable-frequencies with good spurious performance for communications, or simply generating a frequency stimulus in industrial or biomedical test equipment applications, convenience, compactness, and low cost are important design considerations.Many possibilities for frequency generation are open to a designer, ranging from phase-locked-loop (PLL)-based techniques for very high-frequency synthesis, to dynamic programming of digital-to-analog converter (DAC) outputs to generate arbitrary waveforms at lower frequencies. But the DDS technique is rapidly gaining acceptance for solving frequency- (or waveform) generation requirements in both communications and industrial applications because single-chip IC devices can generate programmable analog output waveforms simply and with high resolution and accuracy.Furthermore, the continualimprovements in both processtechnolog y and design haveFigure 1. The AD9833-a one-chip waveformgenerator.resulted in cost and power consumption levels that were previously unthinkably low. For example, the AD9833, a DDS-based programmable waveform generator (Figure1), operating at 5.5 V with a 25-MHz clock, consumes a maximum power of 30 milliwatts.What are the main benefits of using a DDS?DDS devices like the AD9833 are programmed through a high speed serial peripheral-interface (SPI), and need only an external clock to generate simple sine waves. DDS devices are now available that can generate frequencies from less than 1 Hz up to 400 MHz (based on a 1-GHz clock). The benefits of their low power, low cost, and single small package, combined with their inherent excellent performance and the ability to digitally program (and re-program) the output waveform, make DDS devices an extremely attractive solution —preferable to less-flexible solutions comprising aggregations of discrete elements.What kind of outputs can I generate with a typical DDS device?DDS devices are not limited to purelysinusoidal outputs. Figure 2 shows thesquare-, triangular-, and sinusoidal outputsavailable from an AD9833.How does a DDS device create a sinewave?Here’s a breakdown of the internalcircuitry of a DDS device: its maincomponents are a phase accumulator, ameans of phase-to-amplitude conversion(often a sine look-up table), and a DAC.These blocks are represented in Figure 3.A DDS produces a sine wave at a given frequency. The frequency depends on two variables, the reference-clock frequency and the binar y number programmed into the frequency register (tuning word).Figure 2. Square-, triangular-, and sinusoidal outputs from a DDS.The binary number in thefrequency register providesthe main input to the phaseaccumulator. If a sinelook-up table is used, theFigure 3. Components of a direct digital synthesizer. phase accumulator computesa phase (angle) address for the look-up table, which outputs the digital value of amplitude—corresponding to the sine of that phase angle—to the DAC. The DAC, in turn, converts that number to a corresponding value of analog voltage or current. To generate a fixed-frequency sine wave, a constant value (the phase increment—which is determined by the binary number) is added to the phase accumulator with each clock cycle. If the phase increment is large, the phase accumulator will step quickly through the sine look-up table and thus generate a high frequency sine wave. If the phase increment is small, the phase accumulator will take many more steps, accordingly generating a slower waveform.What do you mean by a complete DDS?The integration of a D/A converter and a DDS onto a single chip is commonly known as a complete DDS solution, a property common to all DDS devices from ADI.Let’s talk some more about the phase accumulator. How does it work?Continuous-time sinusoidal signals have a repetitive angular phase range of 0 to 2 .The digital implementation is no different. The counter’s carry function allows the phase accumulator to act as a phase wheel in the DDS implementation.To understand this basic function, visualize the sine-wave oscillation as a vector rotating around a phase circle (see Figure 4). Each designated point on the phase wheel corresponds to the equivalent point on acycle of a sine wave. As the vector rotatesaround the wheel, visualize that the sine of theangle generates a corresponding output sineFigure 4. Digital phase wheel.wave. One revolution of the vector around the phase wheel, at a constant speed, results in one complete cycle of the output sine wave. The phase accumulator provides the equally spaced angular values accompanying the vector’s linear rotation around the phase wheel. The contents of the phase accumulator correspond to the points on the cycle of the output sine wave.The phase accumulator is actually a modulo- M counter that increments its stored number each time it receives a clock pulse. The magnitude of the increment is determined by the binary-coded input word (M). This word forms the phase step size between reference-clock updates; it effectively sets how many points to skip around the phase wheel. The larger the jump size, the faster the phase accumulator overflows and completes its equivalent of a sine-wave cycle. The number of discrete phase points contained in the wheel is determined by the resolution of the phase accumulator (n), which determines the tuning resolution of the DDS. For an n = 28-bit phase accumulator, an M value of 0000...0001 would result in the phase accumulator overflowing after 28 reference-clock cycles (increments). If the M value is changed to 0111...1111, the phase accumulator will overflow after only 2 reference-clock cycles (the minimum required by Nyquist). This relationship is found in the basic tuning equation for DDS architecture:nC out f M f 2⨯= where:fOUT = output frequency of the DDSM = binary tuning wordfC = internal reference clock frequency (system clock)n = length of the phase accumulator, in bitsChanges to the value of M result in immediate and phase-continuous changes in the output frequency. No loop settling time is incurred as in the case of a phase-locked loop.As the output frequency is increased, the number of samples per cycle decreases. Since sampling theory dictates that at least two samples per cycle are required toreconstruct the output waveform, the maximum fundamental output frequency of a DDS is fC/2. However, for practical applications, the output frequency is limited to somewhat less than that, improving the quality of the reconstructed waveform and permitting filtering on the output.When generating a constant frequency, the output of the phase accumulator increases linearly, so the analog waveform it generates is inherently a ramp.Then how is that linear output translated into a sine wave?A phase -to - amplitude lookup table is used to convert the phase-accumulator’s instantaneous output value (28 bits for AD9833)—with unneeded less-significant bits eliminated by truncation—into the sine-wave amplitude information that is presented to the (10 -bit) D/A converter.The DDS architecture exploitsthe symmetrical nature of a sinewave and utilizes mapping logicto synthesize a complete sinewave from one-quarter-cycle ofdata from the phase accumulator.Figure 5. Signal flow through the DDS architecture. The phase-to- amplitude lookuptable generates the remaining data by reading forward then back through the lookup table. This is shown pictorially in Figure 5.What are popular uses for DDS?Applications currently using DDS-based waveform generation fall into two principal categories: Designers of communications systems requiring agile (i.e., immediately responding) frequency sources with excellent phase noise and low spurious performance often choose DDS for its combination of spectral performance and frequency-tuning resolution. Such applications include using a DDS for modulation, as a reference for a PLL to enhance overall frequency tunability, as a local oscillator (LO), or even for direct RF transmission.Alternatively, many industrial and biomedical applications use a DDS as aprogrammable waveform generator. Because a DDS is digitally programmable, the phase and frequency of a waveform can be easily adjusted without the need to change the external components that would normally need to be changed when using traditional analog-programmed waveform generators. DDS permits simple adjustments of frequency in real time to locate resonant frequencies or compensate for temperature drift. Suchapplications include using a DDS in adjustable frequency sources to measure impedance (for example in an impedance-based sensor), to generate pulse-wave modulated signals for micro-actuation, or to examine attenuation in LANs or telephone cables.What do you consider to be the key advantages of DDS to designers ofreal-world equipment and systems?Today’s cost- competitive, high - performance, functionally integrated DDS ICs are becoming common in both communication systems and sensor applications. The advantages that make them attractive to design engineers include:• digitally controlled micro-hertz frequency-tuning and sub-degree phase-tuning capability,• extremely fast hopping speed in tuning output frequency (or phase); phase - continuous frequency hops with no overshoot/undershoot or analog-related loop settling-time anomalies,• the digital architecture of DDS eliminates the need for the manual tuning and tweaking related to component aging and temperature drift in analog synthesizer solutions, and• the digital control interface of the DDS architecture facilitates an environment where systems can be remotely controlled and optimized with high resolution under processor control.How would I use a DDS device for FSK encoding?Binary frequency-shift keying (usually referred to simply as FSK) is one of the simplest forms of data encoding. The data is transmitted by shifting the frequency of a continuous carrier to one of two discrete frequencies (hence binary). One frequency,f1, (perhaps the higher) is designated as the mark frequency (binary one) and the other, f0, as the space frequency (binary zero). Figure 6 shows an example of the relationship between the mark-space data and the transmitted signal.This encoding scheme is easilyimplemented using a DDS. The DDSfrequency tuning word, representing theoutput frequencies, is set to theappropriate values to generate f0 and f1as they occur in the pattern of 0s and 1sto be transmitted. The user programs thetwo required tuning words into the device before transmission. In the case of the AD9834, two frequency registers are available to facilitate convenient FSK encoding. A dedicated pin on the device(FSELECT) accepts the modulating signal and selects the appropriate tuning word (or frequency register). The block diagram in Figure 7 demonstrates a simpleimplementation of FSK encoding.And how about PSK coding?Phase-shift keying (PSK) is anothersimple form of data encoding. In PSK, thefrequency of the carrier remains constantand the phase of the transmitted signal isvaried to convey the information.Of the schemes to accomplish PSK, the simplest-known as binary PSK (BPSK)—uses just two signal phases, 0 degrees and 180 degrees. BPSK encodes 0 phase shift for a logic 1 input and 180 phase shift for a logic 0 input. The state of each bit is determined according to the state of the preceding bit. If the phase of the wave does not change, the signal state stays the same (low or high). If the phase of the wave reverses (changes by 180 degrees), then the signal state changes (from low to high, or from high to low). Figure 6. FSK modulation. Figure 7. A DDS-based FSK encoder.PSK encoding is easily implemented with DDS ICs. Most of the devices have a separate input register (a phase register) that can be loaded with a phase value. This value is directly added to the phase of the carrier without changing its frequency. Changing the contents of this register modulates the phase of the carrier, thus generating a PSK output signal. For applications that require high speed modulation, the AD9834 allows the preloaded phase registers to be selected using a dedicated toggling input pin (PSELECT), which alternates between the registers and modulates the carrier as required.More sophisticated forms of PSK employ four- or eight- wave phases. This allows binary data to be transmitted at a faster rate per phase change than is possible with BPSK modulation. In four-phase modulation (quadrature PSK or QPSK), the possible phase angles are 0, +90, –90, and 180 degrees; each phase shift can represent two signal elements. The AD9830, AD9831, AD9832, and AD9835 provide four phase registers to allow complex phase modulation schemes to be implemented by continuously updating different phase offsets to the registers.Can multiple DDS devices be synchronized for, say, I-Q capability?It is possible to use two single DDS devices that operate on the same master clock to output two signals whose phase relationship can then be directly controlled. In Figure 8, two AD9834s are programmed using one reference clock, with the same reset pin being used to update both parts. Using this setup, it is possible to do I-Q modulation.A reset must be asserted after power-upand prior to transferring any data to the DDS.This sets the DDS output to a known phase,which serves as the common reference pointthat allows synchronization of multiple DDSdevices. When new data is sent simultaneouslyto multiple DDS units, a coherent phase relationship can be maintained, and their relative phase offset can be predictably shifted by means of the phase-offset register. Figure 8. Multiple DDS ICs in synchronous mode.The AD9833 and AD9834 have 12 bits of phase resolution, with an effective resolution of 0.1 degree. [For further details on synchronizing multiple DDS units please see Application Note AN-605.]What are the key performance specs of a DDS based system?Phase noise, jitter, and spurious-free dynamic range (SFDR).Phase noise is a measure (dBc/Hz) of the short-term frequency instability of the oscillator. It is measured as the single-sideband noise resulting from changes in frequency (in decibels below the amplitude at the operating frequency of the oscillator using a 1-Hz bandwidth) at two or more frequency displacements from the operating frequency of the oscillator. This measurement has particular application to performance in the analog communications industry.Do DDS devices have good phase noise?Noise in a sampled system depends on many factors. Reference-clock jitter can be seen as phase noise on the fundamental signal in a DDS system; and phase truncation may introduce an error level into the system, depending on the code word chosen. For a ratio that can be exactly expressed by a truncated binary-coded word, there is no truncation error. For ratios requiring more bits than are available, the resulting phase noise truncation error results in spurs in a spectral plot. Their magnitudes and distribution depends on the code word chosen. The DAC also contributes to noise in the system. DAC quantization or linearity errors will result in both noise and harmonics. Figure 9shows a phase noise plot for a typicalDDS device—in this case anAD9834.What about jitter?Jitter is the dynamicdisplacement of digital signal edgesfrom their long-term averagepositions, measured in degrees rms. A Figure 9. Typical output phase noise plotfor the AD9834. Output frequency is 2MHz and M clock is 50 MHz.perfect oscillator would have rising and falling edges occurring at precisely regular moments in time and would never vary. This, of course, is impossible, as even the best oscillators are constructed from real components with sources of noise and other imperfections. A high-quality, low-phase-noise crystal oscillator will have jitter of less than 35 picoseconds (ps) of period jitter, accumulated over many millions of clock edgesJitter in oscillators is caused by thermal noise, instabilities in the oscillator electronics, external interference through the power rails, ground, and even the output connections. Other influences include external magnetic or electric fields, such as RF interference from nearby transmitters, which can contribute jitter affecting the oscillator’s output. Even a simple amplifier, inve rter, or buffer will contribute jitter to a signal.Thus the output of a DDS device will add a certain amount of jitter. Since every clock will already have an intrinsic level of jitter, choosing an oscillator with low jitter is critical to begin with. Dividing down the frequency of a high-frequency clock is one way to reduce jitter. With frequency division, the same amount of jitter occurs within a longer period, reducing its percentage of system time.In general, to reduce essential sources of jitter and avoid introducing additional sources, one should use a stable reference clock, avoid using signals and circuits that slew slowly, and use the highest feasible reference frequency to allow increased oversampling.Spurious-Free Dynamic Range (SFDR)refers to the ratio (measured in decibels) between the highest level of the fundamental signal and the highest level of any spurious, signal—including aliases and harmonically related frequency components—in the spectrum. For the very best SFDR, it is essential to begin with a high-quality oscillator.SFDR is an important specification in an application where the frequency spectrum is being shared with other communication channels and applications. If a transmitter’s output sends spurious signals into other frequ ency bands, they cancorrupt, or interrupt neighboring signals.Typical output plots taken from an AD9834 (10-bit DDS) with a 50MHz master clock are shown in Figure10. In (a), the output frequency is exactly 1/3 of the master clock frequency (MCLK). Because of the judicious choice of frequencies, there are no harmonic frequencies in the 25-MHz window, aliases are minimized, and the spurious behavior appears excellent, with all spurs at least 80 dB below the signal (SFDR = 80 dB). The lower frequency setting in (b) has more points to shape the waveform (but not enough for a really clean waveform), and gives a more realistic picture; the largest spur, at the second-harmonic frequency, is about 50 dB below thesignal (SFDR = 50 dB).(a) f OUT = 16.667MHz (b) f OUT = 4.8MHz.Figure 10. Output of an AD9834 with a 50MHz master clockDo you have tools that make iteasier to program and predict theperformance of the DDS?The on-line interactive designtool is an assistant for selectingtuning words, given a referenceclock and desired outputfrequencies and/or phases. Therequired frequency is chosen, and idealized output harmonics are Figure 11. Screen presentation provided by an interactive design tool.A sinx/x presentation of a typical device output.shown after an external reconstruction filter has been applied. An example is shown in Figure 11. Tabular data is also provided for the major images and harmonics.How will these tools help me program the DDS?All that’s needed is therequired frequency output andthe system’s reference clockfrequency. The design tool willoutput the full programmingsequence required to programthe part. In the example inFigure 12, the MCLK is set toFigure 12. Typical display of programming sequence.25 MHz and the desired outputfrequency is set to 10MHz. Once the update button is pressed, the full programming sequence to program the part is contained in the Init Sequence register.How can I evaluate your DDS devices?All DDS devices have an evaluation board available for purchase. They come with dedicated software, allowing the user to test/evaluate the part easily within minutes of receiving the board. A technical note accompanying each evaluation board contains schematic information and shows best recommended board-design and layout practice.关于直接数字频率合成器什么是直接数字频率合成器?直接数字频率合成器(DDS)是一种通过产生一个以数字形式时变的信号,然后执行由数字至模拟转换的方法。
基于单片机的DDS信号发生器设计毕业论文

摘要本文首先介绍了信号发生器的发展以及直接数字频率合成技术(DDS)的现状和发展趋势,然后介绍了DDS的原理结构及其主要构成部分。
再根据系统的要求,比较合理地采用了DDS技术,以单片机AT89S52和AD9850芯片为核心,设计了一种结构简单性能优良的信号发生器。
最后详细分析了该信号发生器的系统结构,软硬件设计和具体电路实现。
信号发生器的硬件部分包括三个模块,分别是单片机主控制模块,DDS模块和信号频率显示模块。
软件部分主要开发基于单片机AT89S52的数据处理和控制程序,以及信号发生器的外部通信程序。
最终完成实验电路板的制作,并通过电路板的调试,实现电路工作正常。
根据系统的最终测试结果可知该信号发生器具有输出信号波形精度高,频带宽等特点。
关键词:信号发生器;DDS;AT98S52;AD9850;频率;ABSTRACTThis article describes the development of the signal generator, the status and development trends of direct digital frequency synthesis (DDS) technology at first, then introduces the principle of DDS structure and its main components. According to system requirements, more rational use of DDS technology, single-chip AT89S52 and AD9850 chip as the core, has designed a simple structure and excellent performance of the signal generator. Finally, there is a detailed analysis of the signal generator system architecture, hardware and software design and specific circuit implementation. The hardware portion of the signal generator consists of three modules, namely, single-chip main control module, DDS module and signal frequency display module. Some of the major software development based on MCU AT89S52 data processing and control procedures, as well as external communication signal generator program. Completing the pilot circuit board production, and through the debug board to realize the circuit is working properly. According to the results of final test, the system shows that the output signal waveform signal generator has high accuracy, bandwidth and other characteristics.Keywords: Signal Generator; DDS; AT98S52; AD9850; Frequency目录摘要 (I)ABSTRACT .................................................................................................................. I I 第1章绪论 (1)1.1 课题背景 (1)1.2 课题的主要研究目的和意义 (1)第2章 DDS简介 (3)2.1 DDS结构 (3)2.2 频率预置与调节电路 (4)2.3 累加器 (4)2.4 控制相位和控制波形的加法器 (5)2.5 波形存储器 (5)2.6 D/A转换器 (5)2.7 低通滤波器 (6)第3章系统整体设计方案 (7)3.1 系统设计原理 (7)3.2 总体设计框图 (7)第4章系统各模块组成 (8)4.1 单片机控制模块 (8)4.1.1 AT89S52单片机介绍 (8)4.1.2 AT89S52功能特性描述 (8)4.1.3 时钟电路 (11)4.1.4 复位电路 (11)4.2 按键控制模块 (12)4.3 LCD显示模块 (13)4.4 AD9850 与单片机连接模块 (13)4.4.1 AD9850简介 (13)4.4.2 AD9850的控制字与控制时序 (16)4.4.3 单片机与AD9850的接口 (18)第5章软件设计与硬件调试 (20)5.1 程序流程图 (20)5.2 软件测试 (21)5.3 硬件电路制作 (21)5.4 硬件电路调试 (22)第6章结束语 (27)致谢 (28)参考文献 (29)附录1 原理图 (30)附录2 主程序代码 (31)第1章绪论1.1 课题背景信号发生器[1],它是一种悠久的测量仪器,最早出现于十九世纪20年代。
毕业论文:基于DDS技术实现的频率可跳变的频率合成器设计(终稿)-精品

基于DDS技术实现的频率可跳变的频率合成器摘要:本文首先对频率合成技术现状和未来发展进行了简要说明,同时对直接数字频率合成技术理论作了比较详细的分析,另还对本设计选用的一些芯片进行了介绍。
在此基础上,采用外部输入时钟方式,由控制、电平转换、频率合成、低通滤波、放大等模块构成频率合成器。
在实现过程中,以直接数字频率合器(DDS)为核心,通过单片机对其进行初始化、工作状态设置和实时地向其输入频率控制字和频率更新信号,实现DDS输出频率的跳变,最后再通过滤波和放大,得到一个能满足一定使用要求且频率可跳变频率源。
关键词:频率合成;单片机;直接数字频率合成(DDS);低通滤波;Design of Frequency Synthesizer with Frequency-HoppingBased on DDS TechnologyAbstract: In this paper, the frequency of technical status and future development of a summary statement, the Direct Digital Synthesis techniques of a more detailed analysis, and the other is also on the choice of a number of chip design was introduced.On this basis, the use of external input clock, from control, power conversion, frequency synthesis, low-pass filtering, amplification modules constitute Synthesis. In the process of achieving, with a direct digital frequency (DDS) as the core, through its SCM initialized, the state set-up and real-time control to the input frequency and frequency of updates word signal, the output frequency of DDS Hopping, and then through the filtering and amplification, with a meet certain requirements and the use of frequency hopping frequency source.Keywords: Synthesis; SCM; Direct Digital Synthesis (DDS); low pass filter;第 1 章 绪 论1.1频率合成技术概述随着现代通信与电子系统的发展,对频率合成技术在多个性能方面提出了更高的要求,希望频率源能输出一个更为稳定且在一定频率范围内可跳变频率信号。
电子信息工程 外文翻译 外文文献 英文文献 借助DDS的精密频率的一种替代方法

An alternative method of precise frequency by the aid of a DDS ContentsA method of frequency measurement based on a closed loop composed mainly of a Frequency Comparator (FC) and a Direct Digital Synthesizer (DDS) is presented in this paper. The DDS serves as reference sinewave signal generator acting at one of the FC's inputs. The FC accepts the hard-limited waveform of the DDS as well as the unknown frequency. From the comparison of the two signals a logic output that controls an up/down counter is produced. The counter's output acting as the Frequency Setting Word (FSW) instructs the DDS to produce a new sinewave closer in frequency to the unknown one. When the loop settles, the FSW gives the digital estimate of the unknown frequency. Advantage is taken from the inherent high resolution of the DDS and noise immunity of the loop, to design an equally precise and immune frequency meter. All the additional associated stages up to the instrument's display are presented.1 IntroductionThe most commonly used frequency measurement technique adopts counters that count the pulses of the unknown frequency during a predefined time window (aperture). Apart from this, techniques where the pulses of a reference frequency are counted during one or more periods of the unknown one are also common. In the latter case, the period instead of the frequency is estimated .Some papers in [1] in the literature deal with the problem of low frequency measurement and are focusing in the frequency range of cardiac (heart) signals (a few hertz) or in the mains frequency (50-60 Hz).These techniques are actually measuring the period of the signals and use some way to calculate its reciprocal, the frequency. In [2], the frequency is calculated by the method of look-up tables. Others [4-6] are microprocessor or microcontroller based.The above methods can be characterized as open-loop methods i.e. digital counters are used to count during a predefined tinle interval and calculate the result afterwards. Its closed-loop form characterizes the proposed method in this paper. By the term "closed-loop" we denote some sort of feedback. A waveform with a known (controlled) frequency is produced within the circuit and is fed back to the frequency comparison stage which consecutively forces it to approximate the unknown (input) frequency. The device that produces the above mentioned waveform of controlled frequency is a Direct Digital Synthesizer.2 Direct Digital SynthesisA typical Direct Digital Synthesizer consists of a RAM containing samples of a sinewave (sine look-up table, LUT). These samples are swept in a controlled manner by the aid of a Frequency Setting Word (FSW), which determines the phase step. A typical FSW is 32-bit wide, but 48-bit synthesizers leading in higher frequency resolution are also available. A phase accumulator produces the successive addresses of the sine look-up table and generates a digitized sine wave output. The digital part of the DDS, the phase accumulator and the LUT, is called Numerically Controlled Oscillator (NCO). The final stage, which in contrast to the previous one is mostlyanalog, consists of a D/A converter followed by a filter. The filter smoothes the digitized sinewave, producing a continuous output signal. In the applications where a square wave output is needed, this is obtained by a hard limiter after the filter. It is not equivalent to use e.g. the MSB of the accumulator's output instead of the filtered and hard limited waveform because significant jitter will be encountered.The frequency of the output signal for an n-bit system is calculated in the following way; If the phase step is equal to one, the accumulator will count by ones, taking 2n clock cycles to address the entire LUT and to generate one cycle of the output sinewave. This is the lowest frequency that the system can generate and is also its frequency resolution. Setting the FSW equal to two, results in the accumulator counting by twos, taking 12n - clock cycles to complete one cycle of the output sinewave. It can easily be shown that for any integer m, where m<12n -, the number of clock cycles taken to generate one cycle of the output sine wave is 2n /m, and the output frequency (fDDS) and the frequency resolution (fres) are given by the following formulas : fDDS=2n m fclk ⨯ fres= fclk/2nFor n = 32 and having a clock frequency of fclk = 33 MHz, the frequency resolution is 7.68 mHz. If n is increased to 48, with the same clock frequency, a resolution of 120 nHz is possible.3 The proposed frequency measurement technique The idea that led to our present design came from the extremely high frequency resolution of the DDS devices and is enforced by the noise immunity of its closed loop form. A (known) frequency source, the DDS, is employed in a closed loop and is forced progressively to produce an output with a frequency equal to the unknown input . A rule of thumb in the DDS systems is that the maximum acceptable synthesized frequency is about 25% of the clock frequency (well below the Nyquist limit). According to this, our prototype that uses a 33 MHz clock would effectively count up to 8 MHz. Looking at the GaAs products, we can see that recently available DDS devises can operate at clock frequencies up to the extent of 400 MHz. Therefore, by the present method, frequency counters working up to 100 MHz can be designed. The resolution will depend on the number of FSW bits and the clock frequency. The clock frequency fclk of the DDS is very critical because as it decreases, the resolution of the proposed method (defined as fclk/2n ) becomes finer i.e. it improves. The impact of the clock frequency decrease is the subsequent decrease of its maximum output frequency that limits the counter's maximum count. The major blocks have been shown . Among them are the Frequency Comparator and the DDS. To overcome some disadvantages of the specific frequency comparator a correction stage has been incorporated. This stage is also used for the measurement extraction in order to display the correct reading.3.1 Operation of the circuit The circuit operates in such a way that at the beginning of a new measurement the DDS output frequency would be controlled in a successive approximation way.The initial DDS frequency would be half of it's maximum. In addition, the frequency step of the approximation would equal the 1/4 of the DDS maximum frequency. On every approximation the frequency step is divided by two and added or subtracted to the FSW of the DDS, depending on the output of the Frequency Comparator. The approximation procedure stops when the step size decreases to one. After that, an up/down counter substitutes the approximation mechanism.The digital FSW, after the appropriate correction and decoding, is presented in an output device i.e. an LCD display or any other suitable means. Alternatively, it can be digitally recorded or it can be read by a computer.As conclusion of this initial approach we could say that the proposed method is based on a Digital Controlled Synthesizer which is forced to produce a frequency almost equal to the unknown one.3.2 Frequency comparisonThe frequency comparator seems to be the most critical stage of the design. The implementation is based on a modified phase/frequency comparator proposed by Philips in the 74HC4046 PLL device. It consists primarily of two binary counters, counting up to two and an RS flip-flop.The function of the frequency comparator is based on the principle that the lower frequency, i.e. larger period, includes (embraces) at least one or more full periods of the higher frequency (smaller period). This means that two or more rising edges of the higher frequency waveform are included within the lower frequency period. Considering the above, the circuit operates as follows: When the first counter (#1) encounters two rising edges of the unknown frequency in one period of the DDS, it sets the output of the RS flip-flop. The logic "1" of the RS flip-flop acting at the U/D control input of the Up/Down counter forces the DDS to rise its output frequency. On the contrary, when the second counter (#2) counts two rising edges of the DDS output within a period of the unknown frequency it resets the RS flip-flop's output. This action decreases the frequency of the DDS.At a first glance one could think that the synthesized frequency could reach the measured one (fin) and then the operation of the counter stops. Unfortunately this is not the case. A dynamic mechanism takes place instead. The circuit needs some time to realize the correct frequency relation. We will refer to this time as "hysteresis". Hysteresis depends on the initial timing relation of the DDS output and on the unknown frequency. Initially, during the hysteresis period, the indication regarding the larger frequency is ambiguous i.e. it can be erroneous. The ambiguity settles when two rising edges of the higher frequency waveform occur during one period of the lower one. If we consider the case of the DDS frequency to be equal to the unknown one, we will find that the comparator's output will toggle, indicating alternatively that the DDS frequency is higher or lower than the unknown. This is actually an acceptable and expected condition, because (as in a voltage comparator) an equality indication could not exist. In our case this is not a problem because the circuit is embedded in a closed loop. The loop will act in a manner that after some short time, the hysteresis, the situation will be reversed and so on. The duration of hysteresis is variable. This situation is controlled, as will be explained later. Although an analogimplementation of the frequency comparator would look more robust to noise we insisted to the digital implementation for three reasons: ease of implementation in VLSI or Programmable Logic Devices (PLDs) with no need of analog components, wide frequency range of operation and shorter response time.3.3 Interaction between frequency comparator and digital synthesizerAfter the successive approximation of the unknown frequency the Frequency Comparator "realizes" that the synthesized frequency is higher (lower) than the unknown one and produces a logic 0 (1) at the output which commands the up/down counter to count in the down (up) direction. As previously mentioned, the output of this counter is considered to be the FSW to the DDS stage. In the case when the DDS frequency was initially lower, the synthesized frequency will increase progressively to reach the unknown one. This will not be "realized" by the frequency comparator and the synthesized frequency will keep on increasing for some clock cycles, until the comparator detects the correct relation of it's two input frequencies, the unknown one and the DDS output. The same phenomenon will be observed for the opposite (decreasing) case also. This is due to hysteresis that was mentioned earlier.When DDS output (fDDS) has approached fin, due to hysteresis, no specific frequency is synthesized. Instead, it swings between f1 and f2, where f1 and f2are the two extreme values of the frequency swing lying symmetrically around fin. The DDS output can be considered as a frequency modulated carrier by a triangular waveform. The triangular waveform is the analog representation of the FSW applied to the DDS. lower trace shows a typical output of the Frequency Comparator. In the same figure, upper trace, is shown in analog form the FSW variation as it is trying to approach the correct value. This waveform has been captured using an auxiliary hardware circuit: A digital-to-analog converter (DAC) was connected to the output of the U/D counter (MSBs) in order to study the operation. This DAC is not shown in the block diagram of the circuit. Stated differently, the lower trace is the U/D command (input) to the counter while the upper trace is a hypothetical "frequency modulating" waveform. It is obvious that the term "hypothetical" is used because there is not such a waveform available somewhere in the circuit (except for the auxiliary DAC). Instead, its numerical equivalent exists. The magnitude of the slope of the elements of the triangular waveform is constant for constant input frequency and depends on the clock of the U/D counter (horizontal axis) and the voltage reference of the DAC (vertical axis). This slope is k • fin.3.4 Description of the prototype hardwareFor evaluation purposes two prototypes have been built and tested in the laboratory. The first approach was a low frequency instrument (operating up to 15 KHz) . The purpose of this implementation was to study the principles of operation of the proposed method. Next, a higher frequency prototype was built which will be described in more detail here. In order to implement the digital part of the prototype, (Frequency Comparator, Successive Counter, Correction Stage) two PLD devices from Altera (EPF 8064LC68-12) were used. These devices are interconnected with the DDS, which is the Q2240I-3S1 from Qualcomm. The DDS has a 32-bit input and a 12-bit output for the sine lookup table (LUT). The 12-bit output of the LUT is fedinto the D/A converter, the AD9713B from Analog Devices. Its analog output is connected to an I/V amplifier (current-to-voltage converter).The generated sinewave has upper harmonics, due to the DAC operation. These harmonics are removed from the filters that follow the DAC. The correction stage is implemented partially on the PLDs and partially on the microcontroller. Based on the up-down command of the frequency comparator we store the two extreme values, FSW1 and FSW2, which are then transferred into the micro-controller (Atmel AT89C52), transformed into numerical representation and fed to the LCD Display. The micro-controller also controls the whole operation of the prototype.The behaviour of the instrument was according to the expected and was alike to a conventional bench frequency counter. The speed of measurement was checked using lower trace, obtained by the aid of a digital oscilloscope. Each state, high or low, of this waveform corresponds to the time required for one measurement.4 ConclusionIn this paper an alternative method of frequency measurement has been proposed. It has been pointed out that in most cases this method is faster than conventional methods for the same frequency resolution. On the other hand, the precision of the method can be very high due to the inherent high frequency resolution characteristic of the DDS that is employed. This synthesizer, which can be thought as an oscillator, is driven to "oscillate" in the region of the unknown input frequency. A comparison with conventional methods has been given and two prototypes have been built and tested in the laboratory.The second major advantage of this method is that if repetitive frequency measurements are to be taken, the instrument remains locked and the frequency measurement does not restart from the beginning, but instead is automatically driven to lower or higher values. In other words, the loop has the capability to follow the changes in the frequency of the input signal. In the conventional counting techniques the counting procedure is repeated (restarted) for each new measurement.Another important advantage is the noise immunity of the system, due to its closed loop nature. A detailed study of the noise behavior has not been carried out in this paper. This is mainly because the aim of this text is to present an alternative principle of frequency measurement. Moreover, the final output of the system is taken after some further processing (measurement correction) which also contributes to the noise immunity.借助DDS 的精密频率的一种替代方法内容频率测量的方法基于闭环组成,主要是一个频率比较器(FC)和直接数字合成器(DDS),对此在本文中进行了介绍。
基于DDS技术的可调高精度信号源设计

罗嗣乔 何春晖
摘 要 :针对频率转换器与码同步器的测试过程需要逐赫兹可调的高精度信号源这一问题, 提出了一种以 DDS 频率合成器为基础的逐赫兹可 用液晶模块显示频率, 可发生正弦波与方波, 并讨论分析了稳定频率与改善方波波形 调的高精度信号源设计。此信号发生器以单片机为控制核心, 的方法。 关键词 :DDS;信号源;单片机
Á Ã Â Ä Á Å Æ Â Ã Ç È Â Á É Ä Á Â Ã Ä Å Á Â Á
科 技 论 坛
(91245 部队, 辽宁 葫芦岛 125000 )
图 1 系统整体框图 图 2 DDS 原理简图 法 频率稳定度指标是 DDS 系统的重要指 标, 方波边沿的好坏直接关系到所带负载 的性能。为了系统能更稳定、 更有效地工 作, 有必要讨论一下提高频率稳定度与改 善方波波形的方法。 4.1 提高频率稳定度的方法 。 使用 图 3 DDS 频谱示意图 图 4 AD9850 与单片机的接口 AD9850 DDS 芯片进行数字调整频率的方法比采 用压控振荡器(VCO)的方法在频率精度上提高了 l f f l f f 为进一步提高输出频率的频率稳定度, 可采 Sa ( ) exp( j ) [ 2 (l f f )] 很多。 f f 用如下方法: 4.1.1 采用高频率参考时钟。根据 其中 Sa( · )为抽样函数, Sa(t)= ;δ· ( )为单 DDS 分频原理, 理论上 DDS 的相位噪声应比钟源 δ(t)= lim Sa kt , 频谱如图 3。 位冲激信号, 的相位噪声改善 20log(2N/K)dB。 在相同的短稳条件 2.3 AD9850 与 8096 单片机接口。8096 单片 下, 参考时钟频率高, 分频数大, 可以改善输出信 机对 DDS 芯片 AD9850 的控制是通过向其写入 号的频率精度及频率稳定度。4.1.2 采用更为精确 频率控制字实现的。可以依次串行写入 40 比特, 的时钟频率源作为 AD9850 的参考时钟输入。尽 分 5 次写 管普通晶振在温度适宜的条件下可以达到 10- 6 量 也可以并行写人, 一次写 1 字节(8 比特), 完。 因此, AD9850 与 8096 单片机的接口有并行与 级的频率稳定度, 但在温度变化较大的情况下, 应 串行两种方式。本文考虑到 AD9850 应尽量少占 当采用数字温度补偿晶振代替普通晶振,频率稳 用单片机接口, 留出键盘接口和液晶模块接口, 因 定度可以达到 10- 6 量级(- 10℃~+60℃)。 在要求很 此采用了串行写入的方式,使用 8096 单片机 P2 高的环境条件下,必须采用恒温晶振或普通晶振 口的 1 根 I/O 线和 P3 口的 3 根 I/O 线来控制 加恒温槽, 使频率稳定度达到 10- 8 量级。 考虑到恒 AD9850。其中, P3.0 为串行数据端口, P3.1 为串行 温晶振成本较高, 本系统暂不采用。 数据时钟, 如图 4 所示。 4.2 改善方波波形的方法。在实用中, 用户有 为了满足 AD9850 写入时序, 在单片机的编 时需要得到方波信号。 在本系统输出方波后, 为了 程时使用了空指令、 重复上次指令等方法来延时, 改善通过比较器后的方波波形的边沿,使上升沿 以满足 AD9850 写入频率控制字时序的要求。 4.2.1 采用 和下降沿更加陡峭, 可以采用如下方法: 3 单片机控制过程 片外更高性能的高速电压比较器来将正弦波转化 会使方波性 单片机是整个系统的控制核心, 按照顺序负 为方波。片内 DDS 环境的噪声很大, 责完成 LCD 液晶模块的初始化、 AD9850 复位、 从 能降低, 边沿出现抖动。 选择合适的片外高性能比 键盘读入用户键入数字等任务。单片机依次扫描 较器, 既可以提供适当的输出逻辑电平, 又避免了 4×4 键盘的行线与列线,当读到有键按下时转向 片内 DDS 的噪声耦合干扰输出波形。 4.2.2 采用更 相应的处理程序。当用户键入 “确认” 时, 单片机向 为稳定的时钟频率源作为 AD9850 的参考时钟输 液晶模块写入 ASCII 字符,供液晶显示屏显示当 入。很明显,输出的边沿抖动等于输入的边沿抖 前频率。 最后, 单片机完成向 AD9850 写入频率控 动, 改善输入的边沿可以使输出波形变陡峭。 4.2.3 在单片机得 采用性能优良的低通滤波器抑制输出谐波分量, 制字, 更新 AD9850 输出频率等任务。 到用户从键盘输入的数字后, 还必须做数字转换, 使输出谐波低于 - 65dB。如果输出频率的带宽较 根据键值计算出二进制的频率控制字,也就是 窄, 甚至可以采用带通滤波器代替低通滤波器, 因 AD9850 的 32 位的频率调谐码,然后才能串行写 为带通滤波器可以更好地滤除比所需要的频率更 入 AD9850。 数据全部写入 AD9850 后,按照 低频率或更高频率的噪声。本设计尝试了用无源 AD9850 控制时序,由单片机发出一个脉冲触发, 带通滤波器代替低通滤波器,虽然通过无源滤波 才能更新 AD9860 的当前输出频率。 器后信号幅度有衰减,但有效地滤除了低频的干 ( 下转 136 页 ) 4 提高频率稳定度及改善方波波形边沿的方 扰。
南理工dds电类综合实验报告(dds)直接数字频率合成器设计大学论文

南京理工大学研究生电类综合实验实验报告作者: 袁一超学号:514101001333学院(系):机械工程学院专业: 航天工程题目: (DDS)直接数字频率合成器设计指导者:花汉兵姜萍2015年6月电类综合实验(实验报告)中文摘要电类综合实验(实验报告)外文摘要电类综合实验(实验报告)第I 页共II 页目次1设计内容 (1)2方案论证 (1)2.1DDS 概念 (1)2.2DDS 的组成及工作原理 (1)2.3DDS 的工作流流程图 (1)2.4DDS 的总体框图 (2)3设计要求 (3)3.1设计基本要求 (3)3.2设计提高部分要求 (3)4各基本电路子模块设计原理 (3)4.1脉冲发生电路 (3)4.1.1二分频 (4)4.1.2三分频 (4)4.1.3八分频 (4)4.1.4十分频 (5)4.1.5千分频 (5)4.1.6总脉冲电路图 (5)4.2频率和相位调节电路 (5)4.2.1设计原理 (5)4.2.2频率和相位调节电路总图 (6)4.3累加器 (8)4.3.1累加器的原理 (8)4.3.2电路 (8)4.3.3波形仿真 (9)4.4加法器 (9)4.4.1设计原理 (9)4.4.2电路图 (10)4.5波形存储器(ROM) (10)4.5.1波形存储器(ROM)的原理 (10)4.5.2存储器(ROM)的设计 (11)4.6DDS电路 (15)4.6.1设计原理 (15)4.6.2电路总图 (15)4.7测频电路 (15)4.7.1设计原理 (15)4.7.2测频电路电路图 (16)4.8动态显示电路 (17)4.8.1设计原理 (17)电类综合实验(实验报告)第II 页共II 页4.8.2电路图 (17)4.9消颤电路 (18)4.9.1设计原理 (18)4.9.2电路图 (18)5整体封装图 (18)6管脚分配仿真下载 (19)6.1管脚分配 (19)6.2仿真 (19)6.3下载 (20)结论 (21)参考文献 (22)电类综合实验(实验报告)第1 页共22 页1设计内容设计一个频率及相位均可控制的具有正弦和余弦输出的直接数字频率合成器(Direct Digital Frequency Synthesizer 简称DDFS或DDS)。
基于DDS的信号发生器的设计的相关英文文献
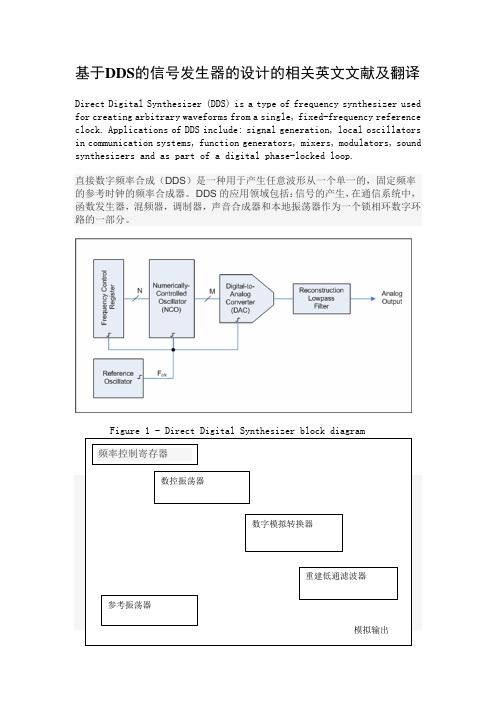
基于DDS的信号发生器的设计的相关英文文献及翻译Direct Digital Synthesizer (DDS) is a type of frequency synthesizer used for creating arbitrary waveforms from a single, fixed-frequency reference clock. Applications of DDS include: signal generation, local oscillators in communication systems, function generators, mixers, modulators,sound synthesizers and as part of a digital phase-locked loop.直接数字频率合成(DDS)是一种用于产生任意波形从一个单一的,固定频率的参考时钟的频率合成器。
DDS的应用领域包括:信号的产生,在通信系统中,函数发生器,混频器,调制器,声音合成器和本地振荡器作为一个锁相环数字环路的一部分。
Figure 1 - Direct Digital Synthesizer block diagram图1 - 直接数字频率合成器框图A basic Direct Digital Synthesizer consists of a frequency reference (often a crystal or SAW oscillator), a numerically controlled oscillator (NCO) and a digital-to-analog converter (DAC) as shown in Figure 1.The reference provides a stable time base for the system and determines the frequency accuracy of the DDS. It provides the clock to the NCO which produces at its output a discrete-time, quantized version of the desired output waveform (often a sinusoid) whose period is controlled by the digital word contained in the Frequency Control Register. The sampled, digital waveform is converted to an analog waveform by the DAC. The output reconstruction filter rejects the spectral replicas produced by the zero-order hold inherent in the analog conversion process.A DDS has many advantages over its analog counterpart, the phase-locked loop (PLL), including much better frequency agility, improved phase noise, and precise control of the output phase across frequency switching transitions. Disadvantages include spurious due mainly to truncation effects in the NCO, crossing spurious resulting from high order (>1) Nyquist (尼奎斯特定理) images, and a higher noise floor at large frequency offsets due mainly to the Digital-to-analog converter.Because a DDS is a sampled system, in addition to the desired waveform at output frequency Fout, Nyquist images are also generated (the primaryimage is at Fclk -Fout, where Fclkis the reference clock frequency). In orderto reject these undesired images, a DDS is generally used in conjunction with an analog reconstruction lowpass filter as shown in Figure 1.The output frequency of a DDS is determined by the value stored in the frequency control register (FCR) (see Fig.1), which in turn controls the NCO's phase accumulator step size. Because the NCO operates in the discrete-time domain, it changes frequency instantaneously at the clock edge coincident with a change in the value stored in the FCR. The DDS output frequency settling time is determined mainly by the phase response of the reconstruction filter. An ideal reconstruction filter with a linear phase response (meaning the output is simply a delayed version of the input signal) would allow instantaneous frequency response at its output because a linear system can not create frequencies not present at its input.The superior close-in phase noise performance of a DDS stems from the fact that it is a feed-forward system. In a traditional phase locked loop (PLL), the frequency divider in the feedback path acts to multiply the phase noise of the reference oscillator and, within the PLL loop bandwidth, impresses this excess noise onto the VCO output. A DDS on the other hand, reduces the reference clock phase noise by the ratio f clk/f out,because its output is derived by fractional division of the clock. Reference clock jitter translates directly to the output, but this jitter is a smaller percentage of the output period (by the ratio above). Since the maximum output frequency is limited to f clk/2, the output phase noise at close-in offsets is always at least 6dB below the reference clock phase-noise.At offsets far removed from the carrier, the phase-noise floor of a DDS is determined by the power sum of the DAC quantization noise floor and the reference clock phase noise floor.一个DDS以上的锁相回路(PLL),其模拟对应,许多优势,包括更好的频率灵活性,提高了相位噪声,整个频率转换开关的输出相位的精确控制。
数字频率合成器的外文翻译资料

英文原文Modulating Direct Digital Synthesizer In the pursuit of more complex phase continuous modulation techniques, the control of the output waveform becomes increasingly more difficult with analog circuitry. In these designs, using a non-linear digital design eliminates the need for circuit board adjustments over yield and temperature. A digital design that meets these goals is a Direct Digital Synthesizer DDS. A DDS system simply takes a constant reference clock input and divides it down a to a specified output frequency digitally quantized or sampled at the reference clock frequency. This form of frequency control makes DDS systems ideal for systems that require precise frequency sweeps such as radar chirps or fast frequency hoppers. With control of the frequency output derived from the digital input word, DDS systems can be used as a PLL allowing precise frequency changes phase continuously. As will be shown, DDS systems can also be designed to control the phase of the output carrier using a digital phase word input. With digital control over the carrier phase, a high spectral density phase modulated carrier can easily be generated.This article is intended to give the reader a basic understanding of a DDS design, and an understanding of the spurious output response. This article will also present a sample design running at 45MHz in a high speed field programmable gate array from QuickLogic.A basic DDS system consists of a numerically controlled oscillator (NCO) used to generate the output carrier wave, and a digital to analog converter (DAC) used to take the digital sinusoidal word from the NCO and generate a sampled analog carrier. Since the DAC output is sampled at the reference clock frequency, a wave form smoothing low pass filter is typically used to eliminate alias components. Figure 1 is a basic block diagram of a typical DDS system design.The generation of the output carrier from the reference sample clock input is performed by the NCO. The basic components of the NCO are a phase accumulator and a sinusoidal ROM lookup table. An optional phase modulator can also be include in the NCO design. This phase modulator will add phase offset to the output of the phase accumulator just before the ROM lookup table. This will enhance the DDS system design by adding thecapabilities to phase modulate the carrier output of the NCO. Figure 2 is a detailed block diagram of a typical NCO design showing the optional phase modulator.FIGURE 1: Typical DDS System.FIGURE 2: Typical NCO Design.To better understand the functions of the NCO design, first consider the basic NCO design which includes only a phase accumulator and a sinusoidal ROM lookup table. The function of these two blocks of the NCO design are best understood when compared to the graphical representat ion of Euler’s formula ej wt = cos( wt) + jsin( wt). The graphical representation of Euler’s formula, as shown in Figure 3, is a unit vector rotating around the center axis of the real and imaginary plane at a velocity of wrad/s. Plotting the imaginary component versus time projects a sine wave while plotting the real component versus time projects a cosine wave. The phase accumulator of the NCO is analogous, or could be considered, the generator of the angular velocity component wrad/s. The phase accumulator is loaded, synchronous to the reference sample clock, with an N bit frequency word.This frequency word is continuously accumulated with the last sampled phase value by an N bit adder. The output of the adder is sampled at the reference sample clock by an N bit register. When the accumulator reaches the N bit maximum value, the accumulator rolls over and continues. Plotting the sampled accumulator values versus time produces a saw tooth wave form as shown below in Figure 3.FIGURE 3 Euler’s Equation Re presented GraphicallyThe sampled output of the phase accumulator is then used to address a ROM lookup table of sinusoidal magnitude values. This conversion of the sampled phase to a sinusoidal magnitude is analogous to the projection of the real or imaginary component in time. Since the number of bits used by the phase accumulator determines the granularity of the frequency adjustment steps, a typical phase accumulator size is 24 to 32 bits. Since the size of the sinusoidal ROM table is directly proportional to the addressing range, not all 24 or 32 bits of the phase accumulator are used to address the ROM sinusoidal table. Only the upper Y bits of the phase accumulator are used to address the sinusoidal ROM table, where Y < N bits and Y is typically but not necessarily equal to D, and D is the number of output magnitude bits from the sinusoidal ROM table.Since an NCO outputs a carrier based on a digital representation of the phase and magnitude of the sinusoidal wave form, designers have complete control overfrequency, phase, and even amplitude of the output carrier. By adding a phase port and a phase adder to the basic NCO design, the output carrier of the NCO can be M array phase modulated where M equals the number of phase port bits and where M is less than or equal to the Y number of bits used to address the sinusoidal ROM table. For system designs that require amplitude modulation such as QAM, a magnitude port can be added to adjust the sinusoidal ROM table output. Note that this port is not shown in Figure 2 and that this feature is not demonstrated in the sample QuickLogic FPGA design. Finally, frequency modulation is a given with the basic NCO design. The frequency port can directly adjust the carrier output frequency. Since frequency words are loaded into the DDS synchronous to the sample clock, frequency changes are phase continuous.Although DDS systems give the designer complete control of complex modulation synthesis, the representation of sinusoidal phase and magnitude in a non-linear digital format introduces new design complexities. In sampling any continuous-time signal, one must consider the sampling theory and quantization error.To understand the effects of the sampling theory on a DDS system, it is best to look at the DDS synthesis processes in both the time and frequency domain. As stated above, the NCO generates a sinusoidal wave form by accumulating the phase at a specified rate and then uses the phase value to address a ROM table of sinusoidal amplitude values. Thus, the NCO is essentially taking a sinusoidal wave form and sampling it with the rising or falling edge of the NCO input reference sampling clock. Figure 4 shows the time and frequency domain of the NCO processing. Note that this representation does not assume quantization.Based on the loaded frequency word, the NCO produces a set of amplitude output values at a set period. The frequency domain representation of this sinusoid is an impulse function at the specified frequency. The NCO, however, outputs discrete digital samples of this sinusoid at the NCO reference clock rate. In the time domain, the NCO output is a function of the sampling clock edge strobes multiplied by the sinusoid wave form producing a train of impulses at the sinusoid amplitude. In the frequency domain, the sampling strobes of the reference clock produce a train of impulses at frequencies of K times the NCO clock frequency where K = ... - 1, 0, 1, 2 .... Since the sampling clock was multiplied by the sinusoid in the time domain, the frequency domain components of the sinusoid and the sampling clock need to be convolved to produce the frequency domain representation of the NCO output.The frequency domain results are the impulse function at the fundamental frequency of the sinusoid and the alias impulse functions occurring at K times the NCO clock frequency plus or minus the fundamental frequency. The fundamental and alias component occur at:K*Fclk - FoutK*Fclk + FoutWhere K = ... -1, 0 , 1, 2 ..... and K = 0 is the NCO sinusoid fundamental frequencyFout is the specified NCO sinusoid output frequencyFclk is the NCO reference clock frequencyFIGURE 4 NCO Output Representation Time and Frequency DomainThe DAC of the DDS system takes the NCO output values and translates these values into analog voltages. Figure 4 shows the time and frequency domain representations of the DAC processing starting with the NCO output. The DAC output is a sample and hold circuit that takes the NCO digital amplitude words and converts the value into an analog voltage and holds the value for one sample clock period. The time domain plot of the DAC processing is the convolution of the NCO sampled output values with a pulse of one sample clock period. The frequency domain plot of the sampling pulse is a sin(x)/x function with the first null at the sample clock frequency. Since the time domain was convolved, the frequency domain is multiplied. This multiplication dampens the NCO output with the sin(x)/x envelope. This attenuation at the DAC output can be calculated as follows and a sample output spectrum is shown in Figure 5:Atten(F) = 20log[(sin(pF/Fclk)/pF/Fclk)] Where F is the output frequency Fclk is the sample clock frequencyFIGURE 5: DAC Output Representation in Time and Frequency Domain Aside from the sampling theory, the quantization of the real values into digital form must also be considered in the performance analysis of a DDS system. The spurious response of a DDS system is primarily dictated by two quantization parameters. These parameters are the phase quantization by the phase accumulator and the magnitude quantization by the ROM sinusoidal table and the DAC.As mentioned above, only the upper Y bits of the phase accumulator are used to address the ROM lookup table. It should be noted, however, that using only the upper Y bits of the phase accumulator introduces a phase truncation. When a frequencyword containing a non-zero value in the lower (N-Y-1:0) bits is loaded into the DDS system, the lower non-zero bits will accumulate to the upper Y bits and cause a phase truncation. The frequency at which the phase truncation occurs can be calculated by the following:Ftrunc = FW(N-Y- 1:0)/2N-Y* Fclk.A phase truncation will periodically (at the Ftrunc rate) phase modulate the output carrier forward 2p/28 to compensate for frequency word granularity greater than 2Y. The phase jump caused by the accumulation of phase truncated bits produces spurs around the fundamental.These spurs are located plus and minus the truncation frequency from the fundamental frequency and the magnitude of the spurs will be - 20log(2Y)dBc. A sample output of a phase truncation spur is shown in Figure 5.In a typical NCO design, the ROM sinusoidal table will hold a ¼ sine wave (0 , p/2) of magnitude values. The ROM table is generated by taking all possible phase value addresses and map to a real magnitude sine value rounded to the nearest D bits. Thus, the maximum error output is ±- ½ LSB giving a worst case spur of -20log(2D)dBc.Like the NCO ROM table, a DAC quantizes the digital magnitude values. A DAC, however, outputs an analog voltage corresponding to the digital input value. When designing the NCO sinusoidal ROM table, one should take some empirical data on the DAC linearity to better understand the interaction between the ROM table and the DAC. The quantization for a DAC is specified against an ideal linear plot of digital input versus analog output. Two linearity parameters, differential and integral linearity, are used to specify a DAC’s performance.Differential linearity is the output step size from bit to bit. A DAC must guarantee a differential linearity of a maximum 1 LSB. When an input code is increased, the DAC output must increase. If the DAC voltage does not increase versus an increase digital input value, the DAC is said to be missing codes. Thus, a 10 bit DAC that has a differential linearity of greater that 1 LSB is only accurate to 9 or less bits. The number of accurate output bits will specify the DDS spurious performance as -20log(2dl) where dl is the number differential linear bits..Integral linearity is a measure of the DAC’s overall linear performance versus an ideal linear straight line. The straight line plot can be either a “best straight line” where DC offsets are possible at both the min and max outputs of the DAC, or thestraight line can cross the end points of the min and max output values. A DAC will tend to have a characteristic curve that is traversed over the output range. Depending on the shape and symmetry (symmetry about the half way point of the DAC output) of this curve, output harmonics of the DDS fundamental output frequency will be produced. As these harmonics approach and cross the Nyquist frequency of Fclk/2, the harmonics become under sampled and reflect back into the band of interest, 0 to Fclk/2. This problem is best illustrated by setting the NCO output to Fclk/4 plus a slight offset. The third harmonic will fall minus 3 folds the small offset from the fundamental and the second harmonic will cross the Nyquist frequency by 2 folds the small offset leaving a reflected image back in the band of interest A sample plot of this frequency setup is shown in Figure 5.Other DAC characteristic that will produce harmonic distortion is any disruption of the symmetry of the output wave form such as a different rise and fall time. These characteristics can typically be corrected by board components external to the DAC such as an RF transformer, board layout issues, attenuation pads etc.Given the complexities of the DDS system, engineers should consider implementing the design using separate devices for the numerically controlled oscillator, the digital to analog converter, and the low pass filter. This approach allows for signal observation at many points in the system, yet is compact enough to be practical as an end-solution. Alternatively, the discrete implementation can serve as a prototyping vehicle for a single-chip mixed signal ASIC.The author developed a version of the design using a Harris HI5721 evaluation board for the DAC. The NCO at the heart of the DDS design, and a random generator to test signal modulation, was implemented into about 65% of a QuickLogic field programmable gate array (FPGA). This FPGA, a QL16x24B 4000-gate device, was chosen for its high performance, ease-of-use, and powerful development tools.The NCO design included following:Developed in Verilog with the 8 bit CLA adder schematiccaptured and net listed to Verilog32 bit frequency word input32 phase accumulator pipelined over 8 bits8 bit phase moudulation word input8 bit sine ROM look-up tableThe design was described mostly in Verilog, with an 8 bit carry look ahead addermodified from QuickLogic’s macro library netlisted to Verilog. The whole design cycle was less than four days (two days to describe the design and a day and a half to prototype the hardware). Everything worked perfectly the first time, with the design running at an impressive 45MHz as predicted by the software simulation tools.Plots used in the article to illustrate DDS performance parameters were provided from the test configuration.Figure 6 below shows the external IO interface to the NCO design .The function of each signal is described in the following table.Signal Function TableFREQWORD[31:0] This input is the frequency control word to the NCO. This word controls the phase accumulator rate, and thus, the output frequency of the DACOUT sinusoidal wave form. The output carrier frequency is calculated by the following :PHASEWORD[7:0] This input is the phase modulation control word to the NCO. This word controls the phase offset following the phase accumulator. This phase offset is used to phase modulate the output carrier.FWWRN This input is the low asserted frequency word write strobe. This strobe input registers the FREQWORD input on the rising edge. This strobe can be asynchronous to the SYSCLK.SYSCLK This is the reference system clock input to the NCO. This clock is the sampling clock of the output carrier.PNCLK This input is the pseudo-noise generator clock input. This clock sets the data rate of the I and Q data outputs.RESETN This input is a low asserted global reset. When asserted, the internal phase and frequency word registers are cleared stopping the output carrier at 0 radians.DACOUT[7:0] This output is the sinusoidal DAC amplitude word. This word is valid on the rising edge of the DACCLK. The sinusoidal wave form output is represented by the following :f(t) = sin(2pFout(t) + Pout)DACCLK This output is the DAC clock strobe. This clock is the SYSCLK feed back to an output pin compensating for the latency of the NCO IO pins. The DACOUT amplitude words will be valid on the rising edge of the DACCLK.SIN This output is a single bit digital sine wave output. This sine wave output comes from the MSB of the phase accumulator. The output frequency of this pin is controlled by the frequency word input.COS This output is a single bit digital cosine wave output. This cosine wave output comes form the MSB and next most significant bit of the phase accumulator. The output frequency of this pin is controlled by the frequency word input.MSIN This output is a single bit digital sine wave output. This sine wave output comes from the MSB of the phase modulator. The output frequency of this pin is controlled by the frequency word input and phase offset bythe phase word input. This sine wave output is the same as the SIN output with a phase offset of plus 2p/28 * PHASEWORD.MCOS This output is a single bit digital cosine wave output. This cosine wave output comes form the MSB and next most significant bit of the phase modulator. The output frequency of this pin is controlled by the frequency word input and the phase offset by the phase word input. This cosine wave outputis the same as the COS output with a phase offset of plus 2p/28 * PHASEWORD.IDATA This output is a 25 - 1 pseudo noise random pattern. This output is not a functional part of the NCO design but used to demonstrate phasemodulation using the phase port.QDATA This output is a 25 - 1 pseudo noise random pattern. This output is not a functional part of the NCO design but used to demonstrate phase modulation using the phase port.Figure 6: The External IO InterfaceTop Level (dds.v)The top level of the NCO design instantiates the functional blocks of the NCO design and the PN generator block.PN Generator (pngen.v)This module is not part of the NCO design but is used to produce a sample random data pattern to modulate the carrier output. This module uses the PNCLK input to clock two Gold code 5 bit PN generators. The outputs of the PN generators are IDATA and QDATA outputs.The lower level block of this NCO design consist of a synchronous frequencyword input register, a synchronous phase word input register, a 32 bit pipe lined phase accumulator, an 8 bit phase adder, and a sin lockup table. A detailed description of each of the NCO blocks and the PN generator are provided in the following sections.Load Frequency Word (loadfw.v)The load frequency word block is a synchronizing loading circuit. The FREQWORD[31:0] input drives a the data input to the 32 bit fwreg register that is sampled on the rising edge of the FWWRN write strobe. The FWWRN strobe also drives the data input to a metastable flip flop fwwrnm that is used in conjunction with a synchronous register fwwrns to produce a FWWRN rising edge strobe. This rising edge strobe loadp1 is then piped for an additional 3 clock cycles producing the load strobes loadp2, loadp3, and loadp4. The load strobes are used to signal when to update the synchronous pipe line 8 bit registers pipefw1, pipefw2, pipefw3, and pipefw4 to the sampled frequency word content. The pipe line registers are concatenated to produce the 32 bit synchronous frequency word output SYNCFREQ[31:0] that is staggered to compensate for the 32 bit pipe lined phase adder.Phase Word Accumulator (phasea.v)The phase accumulator block is a 32 bit accumulator that is pipe lined in 8 bit sections. This module instanciates a schematic captured carry lock ahead CLA adder that has a carry in and carry out port. The synchronous frequency word, staggered to match the pipe lined accumulator, is loaded into the B input of the CLA adders. The sum output of the CLA adders are registered in the pipe registered with the output tied back to the A input of the CLA adders. The carry output of the CLA adders is registered in the pipec registers with the output tied to the next most significant CLA adder carry input. The most significant sum output register pipe4 is assigned to the PHASE output port giving a phase value quantized to 8 bits. A digital sine and cosine value is also calculated from the pipe4 register and brought out of the chip as SIN and COS.Load Phase Word (loadpw.v)The load phase word block is a synchronizing loading circuit. The PHASEWORD[7:0] input drives the data input to the 32 bit pwreg register that is sampled on the rising edge of the PWWRN write strobe. The PWWRN strobe also drives the data input to a metastable flip flop pwwrnm that is used in conjunction with a synchronous register pwwrns to produce a FWWRN rising edge strobe. This risingedge strobe load is used to signal when to update the synchronous phase word register phswd. The phswd register is assigned to the synchronous phase word output SYNCPHSWD[7:0].Phase Modulator (phasemod.v)The phase modulator block is used to phase offset the phase accumulator 8 bit quantized output with the synchronous phase word from the load phase word block. This module instantiates a CLA adder with the A input tied to the synchronous phase output and the B input tied to the phase accumulator output. The sum output of the adder is registered in the mphsreg register and assigned to the MODPHASE output port. A modulated version of the sine and cosine values are calculated and brought out of the chip as MSIN and MCOS.Sine Lockup (sinlup.v)This module takes the modulated phase value form the phase modulator block and translated the quantized 8 bit value into a sine wave form amplitude value quantized to 8 bits. The translation from phase to amplitude is performed by a sine ROM table that in instantiated in this module. The ROM table is reduced to a ¼ of the symmetrical sine wave form and the MSB of the sine wave form is equivalent to the modulated phase input.This module performs the calculations to reconstruct a complete period of the sine wave form from the ¼ representation of the ROM table and the MSB of the modulated phase input. To better understand the processing of this module, consider the following. The modulated phase value is a 0 to 2p value quantized to 8 bits 2p/28. The quantized value for p/2, p, 3p/2, and 2p are 0x3F, 0x7F, 0xBF, and 0xFF. The amplitude values for 0 to p/2 is stored in the ROM table. The amplitude values for p/2 to p are the ROM table output in the reverse order. The amplitude values for p to 3p/2 are the same output as the amplitude value from 0 to p/2 with the output from the ROM table inverted. Finally the amplitude value for 3p/2 to 2p are the same as for p to 3p/2 with the ROM table accessed in reverse.This module manages the address values to the ROM table and the amplitude outputs to form the complete period of the sine wave form. The first process of generating the sine wave function is the addressing of the ROM table such that phase angles p/2 to p and 3p/2 to 2p are addressed in the reverse order. Reverse addressing is accomplished by simply inverting the ROM table address input vector. The phase modulated address input is inverted when the MODPHASE[6] is one and is then registered in the phaseadd register. The phase address is used to address the ROM sinetable with the output registered in the qwavesin_ff register. To construct the negative amplitude values of the sine wave form, the MSB of the modulate phase word input is registered twice in modphase_msb1_ff and modphase_msb2_ff, compensating for the two cycle latency of the phaseadd and qwavesin_ff registers. The delayed MSB bit is used to invert the ROM table output when one. The altered ROM table output and the invert of the delayed modulated phase word MSB are finally registered in by the dac_ff register and then assigned to the DACOUT output port.Sine ROM Table (romtab.v)This module is the sine wave form ROM table. This table converts the phase word input to a sine amplitude output. To conserve area, only ¼ of the symmetrical sine wave form is stored in the ROM. The sine values stored in this table are the 0 to p/2 unsigned values quantized to 8 bits. Thus, the ROM table requires a 6 bit phase address input and outputs a 7 bit amplitude output. The sinlup module processes the phase and amplitude values to produce a complete sine period.Dan Morelli has over 9 years of design and management experience. His areas of expertise include spread spectrum communications (involving GPS, TDRSS, and 802.11), PC chip set and system architecture, cell library development (for ECL devices) and ASIC development. He has been published and has multiple patents awarded and pending. Dan currently works for Accelent Systems Inc., an electronic design consulting company, where he is a founder and the VP of Engineering.附录4:中文译文数字频率合成器在探讨许多复杂的相位连续的调制技术中,对模拟电路中输出波形的控制已经越来越困难。
外文翻译及原文翻译

本科毕业设计(论文)外文翻译译文学生姓名:王惠院(系):电子工程学院仪器系专业班级:测控0701指导教师:刘选朝完成日期: 20 11 年 3 月 7 日咨询应用工程师- 33关于直接数字频率合成器的问题作者Eva Murphy [eva.murphy@]Colm Slattery [colm.slattery@]什么是直接数字频率合成器?直接数字频率合成器(DDS)是一种产生模拟波形(通常是正弦波)的仪器,这种仪器是生成一个数字形式的时变信号,然后执行数字到模拟的转换。
因为用一个DDS设备操作主要是数字形式,所以它可以提供输出频率之间的快速转换,较高的频率分辨率并且可以在一个宽频带上进行操作。
随着设计和工艺技术的进步,现在的DDS器件都非常小巧,在低功率下也可以工作。
为什么我们要使用直接数字频率合成器(DDS)?难道就没有其他产生频率的简单方法吗?能够准确地产生和控制各种频率和轮廓的波形的能力已成为一个通用于多个行业重要要求。
在通信系统中能否利用良好的杂散性提供低相位噪声可变频率的活跃来源,或仅产生用于工业或生物医学测试设备的应用的频率刺激,便利、简洁和低成本是重要的设计考虑因素。
频率产生的多种可能性对设计师来说是开放的,从锁相回路(PLL)——极高频率合成的基础技术,到以数模转换器(DAC)的动态编制程序输出来产生低频任意波形。
但是DDS技术迅速在解决频率(或波形)产生的通信和工业应用要求上得到接受,因为单芯片集成电路器件可以简单的产生可编程模拟输出波形,具有较高的分辨率和精度。
此外,在这两种工艺技术和设计的不断改进也使得成本和功耗较从前降低了许多。
例如,AD9833——基于DDS的可编程波形发生器(图1)在5.5 V的电压下工作工作具有25 MHz的时钟,消耗的最大功率为30毫瓦。
图1 单片波形发生器使用直接数字频率合成器(DDS)的主要优点有哪些?像AD9833 之类的DDS器件都可通过一个高速串行外设接口(SPI)进行编程,并且只需要一个外部时钟来生成简单的正弦波。
一种能改善DDS输出精度的技术

一种能改善DDS输出精度的技术屈八一;米婕;陈瑞洁;董绍峰;陈晓龙;周渭【摘要】In today's widely used direct digital frequency synthesis technology,there is a slight difference between the actual output frequency and the frequency to be generated due to the rounding of the frequency control word.In this paper,the phase accumulation process in the direct digital frequency synthesizer is controlled to basically realize a direct digital frequency synthesis technique without the mantissa frequency. The design and control process is optimized by the phase difference variation characteristics between the actual output frequency and the theoretical frequency.Experimental results show that the technical scheme can effectively reduce the influence of the mantissa frequency in the direct digital frequency synthesis technology by nearly ten thousand times,and the control process has a little effect on the phase noise, frequency stability,and other indicators of the output signal.%为改善直接数字式频率合成技术中存在对频率控制字取整造成的实际输出频率和拟产生频率有微小差异的问题.文中对直接数字式频率合成器中的相位累加过程进行了控制,实现了一种可输出精确频率的直接数字式频率合成技术.利用实际输出频率和理论频率之间的相位差变化特性优化设计控制过程.实验结果表明该技术方案有效,能将直接数字式频率合成技术中尾数频率的影响减小至1/104,而控制过程对输出信号的相位噪声和频率稳定度等指标几乎无影响.【期刊名称】《西安电子科技大学学报(自然科学版)》【年(卷),期】2018(045)003【总页数】5页(P58-62)【关键词】直接数字式频率合成;频率精度;频率合成器;小数频率控制字【作者】屈八一;米婕;陈瑞洁;董绍峰;陈晓龙;周渭【作者单位】长安大学信息工程学院,陕西西安 710064;长安大学信息工程学院,陕西西安 710064;长安大学信息工程学院,陕西西安 710064;西安电子科技大学机电工程学院,陕西西安 710071;西安电子科技大学机电工程学院,陕西西安710071;西安电子科技大学机电工程学院,陕西西安 710071【正文语种】中文【中图分类】TM935.15直接数字式频率合成技术(Direct Digital Synthesizer,DDS)是一种广泛应用的频率合成技术.它具有很多优势,例如,变频速度快、频率分辨率高等特点.目前国内外针对DDS的主要研究内容是提高DDS的运行频率,降低输出信号的杂散和噪声,研制能输出多种信号的DDS芯片等方面,也有关于DDS理论的研究工作[1-4].DDS的尾数频率是一个基本问题,产生尾数频率的原因是频率控制字只能是整数,而实际计算出来频率控制字往往带小数[5-6].若要输出高准确度的点频[7-9],小数部分的影响会使得合成器输出的频率和理论值之间存在差异.虽然直接数字式频率合成技术已广泛应用,但是关于消除其尾数频率方面的工作研究甚少.尾数频率没有被重视的一个原因是大量用到直接数字式频率合成技术的场合,它不影响其应用,例如在跳频通讯中; 另外,很多人认为以目前DDS的频率分辨率,实用中只要微调DDS的参考源的频率,便能由该DDS输出一个精准频率[5].这个观点虽然是正确的,但是在原子频标的频率链中采用直接数字式频率合成器将会产生一个系统误差,若设计的是二级频标,这个系统误差则通过校准可以消除,但是对于一级频标,要消除这个系统误差需要大量的精密测量[10-12].若是能直接消除上述尾数频率,则很有价值.文中依据输出理论频率和实际频率的相位差变化规律,对实际信号进行相位修正,实现了一种无尾数的直接数字式频率合成技术,即可输出精确频率的直接数字式频率合成技术.由于技术方案中的附件电路都是数字电路,因此具有能在芯片上集成的优势.该技术与ADI公司在AD9913中采用的基于附加累加器来扩展频率控制字位数的方法比较[6],在理论上不制约DDS内核的速度.1 无尾数频率的直接数字式频率合成理论DDS的输出频率f0、参考时钟频率fc、相位累加器的长度N以及频率控制字K 之间的关系为f0=K fc2N .(1)为消除DDS尾数频率的影响,首先利用式(1)求得频率控制字K.设K为K下取整的数据,控制频率控制字为K时的持续时间为t1,控制频率控制字为K+1时的持续时间为t2,设 t= t1+ t2,设时间t内输出信号的平均频率f0,依据频率的定义即频率为单位时间内完成的周期性变化的次数有时间t内输出信号的平均频率(2)可见只要Kt1+K+1t2t=K ,(3)则输出信号的平均频率就等于拟产生的理想频率.对式(3)化简可得,只要满足:t2t=K-K ,(4)即,t2t=t2(t1+t2),等于用式(1)求得的频率控制字的小数部分,输出信号的平均频率就等于拟产生的理想频率.2 实现方案设计设计了两种方案来实现.方案1 基于单片机的控制实现DDS模块的频率,控制字在K和 K+1 按一定规律变化的方案,其原理框图如图1所示.图中的频率变换模块用于对外部参考源信号fREF进行处理,其输出是单片机的时钟信号fMCU和DDS模块的时钟信号fc.利用单片机中的计数器对fMCU计数实现发送给DDS模块的频率控制字在K 和 K+1 之间交替变换.利用键盘实现对DDS模块输出频率值的设定,显示模块的作用是显示DDS模块输出信号的一些信息.图1 基于方案1改善DDS输出信号的频率准确度的原理框图图2 基于方案2改善DDS输出信号的频率准确度的原理框图方案2 将直接对DDS技术中的相位累加过程进行控制以使得频率控制字能在K和K+1 之间快速交替变换.方案如图2所示,主控单片机依据输出频率值计算出频率控制字K并依据K的小数部分设计出一组数据.移位寄存器对设计的数据进行移位操作,每来1个时钟周期,移位寄存器将输出1位.上述移位寄存器、N相位累加器、N位累加寄存器等都将在现场可编程门阵列(Field Programmable Gate Array,FPGA)中实现.写入随机存取存储器(Random Access Memory,RAM)的数据的产生方法如下: 设 fc= 100 MHz,f0= 10.23 MHz,当采用图2方案时,希望在 10 000 个时钟周期fc内能移出 8 912 个0和 1 088 个1,由于 8 912= 1 088× 8+208,因此送给移位寄存器的基本数据的低9位可以是000000001b,但若全部都是该数据,则在 10 000 个时钟周期fc内少了208个1,可以在后面的208个字空间中写入的数据的低9位是 000010001b.设计的数据的高7位全部补零,高7位对移位结果无影响,因为只有低9位数据接入后级移位寄存器,移位寄存器完整移出一个数据需要9个时钟周期.可以计算出分别写 000000001b 和 000010001b 的地址范围.由于 10 000/ 9= 1 111.11,需要的RAM空间的大小为 1 111 个字,若从0地址开始顺序写入,则写入000000001b 的地址范围为0至902,写入 000010001b 的地址范围为903至 1 110.3 性能分析由式(1)计算出的频率控制字往往是无理数.为了便于实现,实际中只考虑小数部分的前4位.因此采用上述方法能将DDS中尾数频率的影响减小至 1/104,但并没有完全消除尾数频率的影响.其次,采用文中所述方法获得的输出信号不是传统意义上的单一频率信号.输出信号的频率在两个频率之间的跳变使得输出信号的频谱很复杂.但由于上述两个频率之间的频差非常小,且跳变的速度非常快,特别是采用方案2时,频率的跳变往往在几个时钟周期内就发生一次,这使得输出信号和单一频率信号几乎无差别.下面对文中所述方法给输出信号造成的相位抖动进行计算和分析.设上述两信号的频率分别为f1和f2且f1≈f2,设它们在时间τ内的累积相位差为Δφ(τ),累积相位时差为Δt(τ),则(5)而Δφ(τ)=2πΔt(τ).累积相位差Δφ(τ)和累积相位时差Δt(τ)呈线性关系.设计算出的频率控制字的小数部分有很多位,小数部分的前4位对应的数字为M,在 10 000 个时钟信号fc的周期内,控制频率控制字为K时的持续时间为 10 000- M个时钟周期,控制频率控制字为 K+1 时的持续时间为M个时钟周期,如此,则在上述 10 000 个时钟信号fc的周期内,输出信号的平均频率基本等于拟产生的理想频率,而输出信号和理想输出的最大相位抖动出现在 (10 000- M)fc时刻,基于式(1)和式(5),可求得最大相位抖动为若采用的频率控制为48位,设输出频率为10 MHz,则由式(6)可得上述最大相位抖动为3.55×10-18 s.采用方案2时,控制输出频率值的频率控制字在K和K+1 之间能以更快的速度变化,因此输出信号的最大相位抖动比由式(6)计算出的结果更小,即输出信号的频率稳定性和频谱纯度也将更好.目前时频领域中,若输出信号相位抖动小于 0.1 ps 以上,则能满足大多数应用的需求.方案1和方案2比较,方案1较容易实现和实验.理论上,采用方案2获得的输出信号的频率稳定性和频谱纯度将更好,因为采用方案2时控制输出频率值的频率控制字能以更快的速度在K和 K+1 之间变化.方案2更具有实用价值,因为它可以被用于对DDS芯片的改进设计中.方案2中相比较传统DDS芯片增加的硬件电路当研究成熟时完全可以做到DDS芯片上.图3 基于方案1的实验框图4 实验结果和分析4.1 实验设计对方案1进行了实验,以检验方案的正确性并测试上述控制及附加电路对DDS频率合成器输出信号的影响.主要检测输出信号的频率准确度、单边带相位噪声及频率稳定度.实验框图如图3所示.让AD9852模块分别按传统方法和方案1描述的方法输出10.23MHz,测量并记录上述指标.实验中对单边带相位噪声和频率稳定度的测量由TSC 5125A完成,其参考源为HP8662输出的 10 MHz 参考信号; 对频率准确度的测量采用Agilent 53132A完成,采用了时差法求输出信号的频率误差[9],53132A的参考源也为HP8662输出的 10 MHz 参考信号,取样时间长度为3天.4.2 实验结果和分析传统方法获得的10.23 MHz的单边带相位相位噪声如图4(a)所示,其频率稳定度见表1中的数据,频率误差为 -3.81×10-15,它与理论计算结果基本相等.由方案1获得的 10.23 MHz 单边带相位相位噪声如图4(b)所示,其频率稳定度见表1中的数据,频率误差为零.采用时差法测频率误差时存在一定的误差,且会受到Agilent 53132A分辨率的影响.采用方案1获得的 10.23 MHz 的频率误差为零.因为在3天的取样时间内,若 10.23 MHz 的频率误差非常小,它生成的 1 PPS 信号和 10 MHz 基准信号的累积相位误差非常小,小于Agilent 53132A的分辨率,因此获得了频率误差为零的测量结果.可见采用方案1获得的 10.23 MHz 的频率误差非常小,远小于传统方法获得的输出信号的频率误差,同时测量结果表明采用方案1时,对输出信号的相位噪声指标和频率稳定度指标基本无影响,这符合理论分析结果.因为DDS跳频过程中引起的最大相位抖动非常小,跳频速度又非常快,产生的输出信号的最大相位抖动远小于皮秒量级,使得整个跳频过程对输出信号的影响基本可以忽略.这证明了方案1的正确性和有效性.文中未对方案2的进行验证.由于采用方案2时频率控制字在K和 K+1 之间能以更快的速度变化,输出信号的最大相位抖动更小.因此可确信方案2的正确性和有效性.图4 两种方法获得的10.23 MHz的相噪曲线表1 两种方法获得的10.23 MHz信号的频率稳定度测量结果频率稳定度传统方法输出10.23MHz方案1描述的方法输出10.23MHz1ms级频率稳定度5.45×10-105.47×10-1010ms级频率稳定度6.86×10-106.83×10-10100ms级频率稳定度6.50×10-116.47×10-111s级频率稳定度8.20×10-128.00×10-1210s级频率稳定度4.60×10-124.60×10-1220级频率稳定度3.80×10-123.90×10-125 结束语在直接数字式频率合成技术中,通过控制频率控制字在两个相邻整数值K和K+1之间快速且规律的跳变的方法,能很好地解决直接数字式频率合成技术中存在的由于对频率控制字取整造成的实际输出频率和拟产生频率有微小差异的问题.文中设计了两套实现方案并对其中之一进行了实验,实验结果表明,设计的方案正确且有效,能比较容易地将原尾数频率的影响减小至 1/104,且对获得的输出信号的相位噪声指标和频率稳定度指标几乎无影响.该技术在时频测控领域及DDS芯片的改进研究中有一定的参考价值和实用价值.参考文献:[1] ZHAO Z Y, LI X Y, CHANG W G. LFM-CW Signal Generator Based on Hybrid DDS-PLL Structure[J]. Electronics Letters, 2013, 49(6): 381-382. [2] ZHOU Z H, LA RUE G S. A 12-bit Nonlinear DAC for Direct Digital Frequency Synthesis[J]. IEEE Transactions on Circuits and Systems Ⅰ: Regular Papers, 2008, 55(9): 2459-2468.[3] AVITABILE G, CANNONE F, VANIA A. Phase Shifter Based on DDS-driven Offset-PLL[J]. Electronics Letters, 2006, 42(25): 1438-1439.[4] GHOSH M, CHIMAKURTHY L S J, DAI F F, et al. A Novel DDS Architecture Using Nonlinear ROM Addressing with Improved Compression Ratio and Quantization Noise[C]//Proceedings of the 2004 IEEE International Symposium on Circuits and Systems. Piscataway: IEEE, 2004: II705-II708.[5] 刘马良, 朱樟明, 郭旭龙, 等. 一种4路内插CORDIC的14位吉赫兹DDS IP 核[J]. 西安电子科技大学学报,2013, 40(6): 62-66.LIU Maliang, ZHU Zhangming, GUO Xulong, et al. 4 Channel Interpolated 14 bit High Speed CORDIC DDS IP Core[J]. Journal of Xidian University,2013, 40(6): 62-66.[6] 张俊安, 李广军, 张瑞涛, 等. 单片直接数字频率合成器产品发展综述[J]. 微电子学, 2015, 45(5): 676-680.ZHANG Jun’an, LI Guangjun, ZHANG Ruitao, et al. An Overview of Direct Digital Frequency Synthesizer IC[J]. Microelectronics, 2015, 45(5): 676-680.[7] de CARO D, STROLLO A G M. High Performance Direct Digital Frequency Synthesizers Using Piecewise Polynomial Approximation[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2005, 52(2): 324-337.[8] 屈八一, 宋焕生, 周渭, 等. 一种新型不同频直接鉴相的锁相环[J]. 西安电子科技大学报, 2014, 41(2): 172-177.QU Bayi, SONG Huansheng, ZHOU Wei, et al. Novel Phase Locked Loop with Direct Phase Detection for Two Frequency Different Signals[J]. Journal of Xidian University, 2014, 41(2): 172-177.[9] LANGLOIS J M P, AL-KHALILI D. Phase to Sinusoid Amplitude Conversion Techniques for Direct Digital Frequency Synthesis[J]. IEE Proceedings: Circuits, Devices and Systems, 2004, 151(6): 519-528. [10] GALLEANI L, TAVELLA P. Robust Detection of Fast and Slow Frequency Jumps of Atomic Clocks[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2017, 64(2): 475-485.[11] ZHAN L, LIU Y, YAO W, et al. Utilization of Chip-scale Atomic Clock for Synchrophasor Measurements[J]. IEEE Transactions on Power Delivery, 2016, 31(5): 2299-2300.[12] 白丽娜, 周渭, 都倩倩, 等. 一种新颖的铯原子钟频率信号处理的线路技术[J].西安电子科技大学学报, 2015, 42(2): 71-76.BAI Lina, ZHOU Wei, DU Qianqian, et al. Novel Cesium Atomic Clock Frequency Signal Processing Circuit Technology[J]. Journal of Xidian University, 2015, 42(2): 71-76.。
基于DDS正弦波函数发生器的设计(文献综述)

基于LMP核和DDS的正弦波函数发生器设计摘要:在频率合成领域中,直接数字合成(DDS)是近年来新的技术,它是从相位概念出发直接合成所需波形的一种新的全数字技术的频率合成方法。
此次正弦波函数发生器的设计是利用VHDL语言和Quartus II开发环境进行设计。
首先对VHDL和Quartus II开发环境进行了介绍,接着对DDS工作原理进行了阐述,最后提出了两种方法并进行了比较和做出了选择。
关键词:DDS;正弦波函数发生器;VHDL;Quartus II1.前言1.1 课题研究背景在一些电子设备的电路板故障检测仪中,往往需要频率、幅度都能由计算机自动调节的信号源。
采用诸如MAX038信号发生器芯片外加电阻及切换开关等器件虽然也能调节频率和幅度,但这种调节是离散的,且电路复杂,使用不方便。
而采用直接数字合成芯片DDS及外加D/A转换芯片构成的可控信号源,可产生正弦波、调频波、调幅波及方波等,并且其信号的频率和幅度可由微机来精确控制,调节非常方便。
另外随着21世纪的到来,人类正在跨入信息时代。
现代通信系统的发展方向是功能更强,体积更小,速度更快,功耗更低。
1.2 课题研究目的和意义正弦信号发生器作为电子技术领域中最基本的电子仪器,广泛应用于航空航天测控、通信系统、电子对抗、电子测量、科研等各个领域中。
随着电子信息技术的发展,对其性能的要求也越来越高,如要求频率稳定性高、转换速度快,具有调幅、调频、调相等功能,另外还经常需要两路正弦信号不仅具有相同的频率,同时要有确定的相位差。
随着数字信号处理和集成电路技术的发展,直接数字频率合成(DDS)的应用也越来越广泛。
DDS具有相位和频率分辨率高、稳定度好、频率转换时间短、输出相位连续、可以实现多种数字与模拟调制的优点,而可编程门阵列(FPGA)具有集成度高、通用性好、设计灵活、编程方便、可以实现芯片的动态重构等特点,因此可以快速地完成复杂的数字系统。
由于模拟调相方法有生产性差、调试不方便、调制度控制不精确等缺点,因此采用数字方法实现各种模拟调制也越来越普遍。
DDs的论文

常量K被称为相位增量,也叫频率控制字。
DDS方程为:
(2-1)
fO为输出频率,fC为时钟频率.当M=1时,DDS输出最低频率(也即频率分辨率)为fc/2n,而DDS的最大输出频率由Nyquist采样定理决定,采样的频率应大于或等于信号频率带宽的二倍,即fc/2,也就是说K的最大值为2(n-1)。因此,只要N足够大,DDS可以得到很细的频率间隔。要改变DDS的输出频率,只要改变频率控制字K即可。
PLL一般由数字鉴相器、分频器、模拟环路滤波和压控振荡器组成,因其具有相位噪声低,杂散抑制好,输出频率高,价格便宜等优点至今仍在频率合成器领域占有重要地位。目前已有许多性能优良的单片PLL频率合成器面市,PLL频率合成利用了相位反馈控制原理来稳频,在频率切换速度要求不高,但相对相位噪声、杂散有较高要求时,PLL频率合成有特殊的优势。PLL式频综输出的频率分辨率越高时,其频率切换速度就越慢。如果要提高切换速度,就必须牺牲分辨率,这是PLL的工作机理所致,无法通过性能优化来解决。所以在选择锁相式频率合成时除了考虑频谱纯度外,还要考查其它性能是否满足要求。
由于DDS具有以上优良性能与市场地位,作为一名电子信息专业学生并且在毕业后立志从事电子信息方面的相关工作,那么对其的了解学习掌握更是势在必行。因此此次设计就是以DDS信号源为基础,采用AD9850芯片与C51芯片相结合,通过在硬件与软件上的双重实践,来充分了解与掌握到DDS的基本原理,工作过程及其在带宽,转换时间,相位连续等方面的优良性能。
由于作者的知识水平与学识素养的局限性,此次设计定出现不少待完善处,望阅者不吝赐教。
第1章绪 论
1.1设计目的及意义
信号源即信号发生器,是用来产生各种电子信号的仪器。
自20世纪90年代以来,电子通信技术的突飞猛进的发展,人们对信号源的要求越来越高,而作为电子通信系统的“心脏”的频率合成器,也要不停地接受人们精良细致的择选淘汰,传统的模拟信号源因其倍频、分频等工作原理而在体积、时间、功耗各方面都存在欠缺,现今已不能满足人们的要求。比如要设计一频率范围为0—15MHZ的信号源,其包括了超低频---高频范围,如用传统电路来完成则要求分别独立设计各个频率范围内的信号源,使用上不方便且频率准确度和频率稳定度极差。而DDS以其优良的全数字化与弥补于前两代在各种性能上的不足而正在成为频率合成世家的主导力量。
用DDS产生任意精准频率的方法[发明专利]
![用DDS产生任意精准频率的方法[发明专利]](https://img.taocdn.com/s3/m/54d8592008a1284ac85043f3.png)
专利名称:用DDS产生任意精准频率的方法专利类型:发明专利
发明人:舒炳江,刘文焘,蒋宇志
申请号:CN201110403820.1
申请日:20111207
公开号:CN102571036A
公开日:
20120711
专利内容由知识产权出版社提供
摘要:本发明提出的一种用DDS产生任意精准频率的方法,旨在提供一种输出时钟和输入系统时钟不成整数倍时,产生精准输出频率的方法。
本发明通过下述技术方案予以实现:在由频率控制字、相位累加器、正弦查找表、数模转换器组成的直接数字频率合成器(DDS)中,采用一个跨接于上述相位累加器两端的相位溢出控制逻辑模块,控制DDS的溢出时刻,DDS通过相位溢出控制逻辑,将公式中的相位累加器的最大值2,更改成能被f整除的数A,使其和输入频率的关系满足整数倍关系(N为整数)和关系式式中,f为输出频率,f为输入频率,A是相位累加器的最大值,是输出频率的频率控制字。
本发明解决了现有技术不能对输入频率和输出频率不成整数倍时,不能产生精准输出频率的问题。
申请人:中国电子科技集团公司第十研究所
地址:610036 四川省成都市金牛区外西营康西路85号
国籍:CN
代理机构:成飞(集团)公司专利中心
代理人:郭纯武
更多信息请下载全文后查看。
借助DDS的精密频率的一种替代方法外文资料翻译

借助DDS的精密频率的一种替代方法外文资料翻译外文出处: Arthur Schwilch ,Christoph Goste li 附件: 1、外文资料翻译译文,2、外文原文。
指导教师评语:该生的外文翻译,紧扣论文的主题,语句较通顺,翻译较准确,说明前期准备阶段的文献调研做了一定的工作,达到了预期的目的。
签名:2012 年 4 月 20 日附件1:外文资料翻译译文借助DDS的精密频率的一种替代方法频率测量的方法基于闭环组成,主要是一个频率比较器(FC)和直接数字合成器(DDS),对此在本文中进行了介绍。
DDS作为标准信号发生器在FC的投入之中扮演一定的角色。
FC接受了DDS的硬限幅波形以及未知的频率。
从比较两个信号的输出,控制逻辑向上/向下计数器产生了。
计数器的输出频率设定字(FSW)代理指示的DDS产生一个新的正弦波频率接近未知之一。
当循环沉淀,频率设定字给出了未知的高频数字估计。
优势是从DDS固有的高分辨率和环路噪声免疫力而来,从而设计同样精确和不受影响的频率计。
所有额外相关的阶段都被仪器的显示器显示出来。
1简介最常用的测频技术采用计数在预定的时间窗口(光圈)的未知频率的脉冲的计数器。
此外,凡任何参考频率的脉冲在一个或多个未知一期计算方法也很常见。
在后一种情况下,代替频率的周期只是估计的。
本文献的第[1]部分的某些文件处理了低频率的测量问题并集中在心脏(心脏)信号的频率范围(几赫兹)或在电源频率(50-60赫兹)。
这些技术实际上是在测量讯号的时间,并使用一些方法来计算它的倒数,即频率。
在第[2]中,频率由查找表的方法计算。
其他[4-6]的内容是关于微处理器或以微控制器为基础的。
上述方法的特点是开环方法,即数字计数器来计数在预定tinle间隔,之后计算结果。
其闭环形式刻画了本文提出的方法。
这个术语“闭环”我们用来记一些反馈排序。
一个已知(控制)的频率波形在电路中产生,并反馈到强制它来接近未知的(输入)的频率的频率比较阶段。
DDS正弦信号发生器设计外文文献

DDS devices to produce high-quality waveform: a simple, efficient and flexibleAbstract: Direct digital frequency synthesis (DDS) technology for the generation and regulation of high-quality waveforms, widely used in medical, industrial, instrumentation, communications, defense and many other areas. This article will briefly describe the technology, on its strengths and weaknesses, examine some application examples, and also introduced some new products that contribute to the promotion1.IntroductionA key requirement in many industries is an exact production, easy operation and quick change of different frequencies, different types of waveforms. Whether it is broadband transceiver requires low phase noise and excellent spurious-free dynamic performance of agile frequency source, or for industrial measurement and control system needs a stable frequency excitation, fast, easy and economical to produce adjustable waveform while maintaining phase continuity capabilities are critical to a design standard, which is what the advantages of direct digital frequency synthesis.2.Frequency synthesis taskThe growing congestion of the spectrum, coupled with lower power consumption, quality of never-ending demand for higher measuring equipment, these factors require the use of the new frequency range, requires a better use of existing frequency range. A result, the search for better control, in most cases, by means of frequency synthesizer for frequency generation. These devices use a given frequency, fC of to generate a target frequency (and phase) fOUT the general relationship can be simply expressed as:fOUT = εx× fCAmong them, the scale factor εx, sometimes known as the normalized frequency.The equation is usually gradual approximation of the real number algorithms. When the scale factor is a rational number, two relatively prime numbers (output frequency and reference frequency) than the harmonic. However, in most cases, εx may belong to a broader set of real numbers, the approximation process is within the acceptable range will be truncatedThe frequency synthesizer a practical way to achieve is the direct digital frequency synthesis (of DDFS), usually referred to as direct digital synthesis (DDS). This technique using digital data processing to generate a frequency and phase adjustable output, the output anda fixed frequency reference clock source fC. related. DDS architecture, the reference or the system clock frequency divided by a scale factor to produce the desired frequency, the scale factor is controlled by the binary tuning word programmable.In short, direct digital frequency synthesizer to convert a bunch of clock pulses into an analog waveform, usually a sine wave, triangle wave or square wave. Shown in Figure 1, its main parts: the phase accumulator (to produce the output waveform phase angle data), relative to digital converter, (above the phase data isconverted to the instantaneous output amplitude data), and digital-to-analog converter (DAC) (the magnitude of data into a sampled analog data points)Figure 2-1 DDS function of the system block diagram.For the sine wave output, relative to digital converter is usually a sine lookup table (Figure 2). Phase accumulator unit count N a relative to the frequency of fC, according to the following equation:The number of pulses of the fC:M is the resolution of the tuning word (24-48)N corresponds to the smallest increment of phase change of the phase accumulator output wordFigure2-2 Typical DDS architecture and signal path (with DACs).Changing N will immediately change the output phase and frequency, so the system has its own continuous phase characteristics, which is one of the key attributes of many applications. No loop settling time, which is different from the analog system, such as phase-locked loops (PLLs). DAC is usually a high-performance circuit, designed specifically for the DDS core (phase accumulator and phase amplitude converter). In most cases, the results of the device (usually single-chip) is generally referred to as the pure DDS or the C-DDS.Actual DDS devices are generally multiple registers, in order to achieve a different frequency and phasemodulation scheme. Such as phase register, their storage phase of increase in the output phase of the phase accumulator. In this way, the corresponding delay output sine wave phase in a phase tuning word. This is useful for phase modulation applications for communication systems. The resolution of the adder circuit determines the number of bits of the phase tuning word, therefore, also decided to delay the resolution.Integrated in a single device on the engine of a DDS and a DAC has both advantages and disadvantages, however, whether integrated or not, need a DAC to produce ultra-high purity high-quality analog signal. DAC will convert digital sinusoidal output to an analog sine wave may be single-ended or differential. Some of the key requirements for low phase noise, excellent wideband (WB) and narrowband (NB), spurious-free dynamic range (SFDR), and low power consumption. If the external device, the DAC must be fast enough to handle the signal, so the built-in parallel port device is very common.3.DDS and other solutionsThe frequency analog phase-locked loops (PLLs), clock generator, and the use of FPGA dynamic programming of the output of the DAC. By examining the spectrum of performance and power of these technologies, a simple comparison, Table 1 shows the qualitative results of the comparisonTable 3-1DDS with competing technologies - Advanced comparePower consumption Spectral purity RemarksDDS Low Middle Ease of tuningDiscrete DAC+FPGA Middle Middle-High With tuning capabilitiesAnalog PLL Milddle High Difficult tuningPhase-locked loop is a feedback loop and its components: a phase comparator, a divider and a pressure-controlled oscillator (VCO), phase comparator reference frequency and output frequency (usually the output frequency is N)frequency) were compared. The error voltage generated by the phase comparator is used to adjust the VCO, thus the output frequency. When the loop is established, the output frequency and / or phase with the reference frequency to maintain a precise relationship. PLL has long been considered in a particular frequency range, high fidelity and consistent signal low phase noise and high spurious free dynamic range (SFDR) are ideal for applications.PLL can not be precisely and quickly tuning the frequency output waveform, and the slow response, which limits their applicability for fast frequency hopping and part of the frequency shift keying and phase shift keying applications.Other programs, including integrated DDS engine field programmable gate arrays (FPGAs) - a synthetic sine wave output with the off-the-shelf DAC - though the PLL frequency-hopping problem can be solved, but there own shortcomings. The defects of the major systems work and interface power requirements, high cost, large size, and system developers must also consider the additional software, hardware and memory. For example, using the DDS engine option in the modern FPGA to generate the 10 MHz output signal dynamic range is 60 dB up to 72 kB memory space. In addition, designers need to accept and be familiar with thesubtle balance DDS core architecture. .From a practical point of view (see Table 2), thanks to the rapid development of CMOS technology and modern digital design techniques, as well as the improvement of the DAC topology, DDS technology has been able to achieve unprecedented low power consumption in a wide range of applications, spectrum performance and cost levels. Although the pure DDS products in performance and design flexibility to achieve the level of high-end DAC technology and FPGA, but the advantages of DDS in terms of size, power consumption, cost and simplicity, making it the primary choice for many applications.Table 3-2 Benchmark Analysis Summary - frequency generation technique (<50 MHz)Phase -locked loop DAC + FPGA DDS Spectral performance High High MiddleSystem power requirements High High MiddleDigital frequency tuning No Yes YesTuning response time High Low LowSolution size Middle High LowWaveform flexibility Low Middle HighCost Middle High LowDesign reuse Middle Low HighImplementation complexity Middle High LowAlso be noted that the DDS device for digital methods to produce the output waveform, it can simplify some of the architecture of the solution, or the waveform of digital programming to create the conditions. Usually with a sine wave to explain the functions and working principle of the DDS, but using modern DDS ICs can easily generate a triangle wave or square wave (clock) output, thereby eliminating the former case the lookup table, and the latter case the DAC the need to integrate a simple and accurate enough.4. Performance and limitations of the DDS4.1 Image and envelope: Sin (x) xx roll-offThe actual output of the DAC is not a continuous sine wave, but a series of pulses with a sinusoidal time envelope. The corresponding spectrum is a series of image and signal aliasing. Image along the sin (x) / x envelope distribution (see Figure 3 | margin | graph). The need for the filter to suppress frequencies outside the target band, but can not inhibit the high-level in the passband aliasing (for example, caused due to DAC non-linear)The Nyquist criterion requires that each cycle requires at least two sampling points in order to rebuild the desired output waveform. The Mirroring response arising from sampling the output frequency K, CLOCK ×OUT In this example, which CLOCK = 25 25 MHz and fOUT = 5 MHz, the first and second mirror frequency appear in (see Figure 3) fCLOCK × fOUT, o 20 MHz and 30 MHz. The third and fourth mirror frequency at 45 MHz and 55 MHz. Note, sin (x) / x value of zero at multiples of the sampling frequency.When fOUT greater than the Nyquist bandwidth (1/2 f CLOCK), the first mirror frequency will appear in the Nyquist bandwidth, the occurrence of aliasing (such as 15 MHz signal aliasing down to 10 MHz). Can not use the traditional quist anti-aliasing filter to filter out aliasing mirror frequency from the outputFigure 4-1 Sin, in Figure 3.DDS, (x) / x roll-off.In a typical DDS application, the use of a low-pass filter to suppress the mirror frequency response of the output spectrum. To make the low-pass filter cutoff frequency to remain at reasonable levels, and keep it simple filter design, a feasible approach is the use of an economic low-pass output filter bandwidth limited to about 40% of the frequency of clock.Any given mirror frequency relative to the amplitude of the fundamental formula of sin (x) / x calculation. Because the function of the frequency roll-off, the basic output of the amplitude and the output frequency is inversely proportional to decrease; in the DDS system, reduce the amount of DC-Nyquist bandwidth range of -3.92 dB.Significant reduction in frequency in the first mirror - the fundamental 3 dB range. In order to simplify the DDS application filtering, frequency plan must be formulated and analyzed to mirror the frequency and magnitude of the sin (x) / x response in the OUT and CLOCK target frequency spectrum requirements. Other unwanted frequencies in the output spectrum (such as integral and differential linearity error of the DAC, the surge of energy associated with the DAC and clock feed through noise) does not follow the sin (x) / x roll-off response. These unwanted frequencies will be harmonic and spurious energy in the output spectrum in many places - but its magnitude is generally far below the mirror frequency response. DDS devices to the general background noise, substrate noise, thermal noise effects, ground coupling and other signal source coupling factor cumulative portfolio decisions. DDS devices, the noise floor performance of stray and jitter by the circuit board layout, power quality, and - most importantly - Enter the profound impact of the quality of the reference clock.4.2ShakeThe edge of the perfect clock source will be the precise time interval, the interval will never change. Of course, this is not possible; even the best oscillator is also the ideal components constitute, with noise and other defects. Quality and low phase noise crystal oscillator jitter picosecond, and is built up from one millionthe number of clock edge. The factors leading to jitter external interference, thermal noise, the oscillator circuit instability and power, ground and output connections bring, all these factors will interfere with the timing characteristics of the oscillator. In addition, the oscillator by the external magnetic field or electric field and the nearby transmitter RF interference. Oscillator circuit, a simple amplifier, inverter or buffer to signal additional jitter.Therefore, the choice of a low-jitter, and the edge of steep stable reference clock oscillator is critical. Higher frequency reference clock allows a larger sample, and divide to some extent, reduce the jitter, because the signal to divide a long time to produce the same amount of jitter, which can reduce the jitter on the signal percentage.4.3 Noise - including the phase noiseThe sampling system noise depends on many factors, the most important factor is the reference clock jitter, this jitter performance of phase noise on fundamental signal. In the DDS system, the register output of the truncated phase may bring the system error code. The binary word does not lead to the truncation error. But for non-binary word, phase noise truncation error in the spectrum spurious. Spurious frequency / amplitude depends on the code word. Quantification and linearity error of the DAC will be brought to the system harmonic noise. Time-domain error (such as owed to the red / overshoot and code errors) will increase the output signal distortion.5. Application5.1 DDS applications can be divided into two categories:Require agile frequency source for data coding and modulation applications, communications and radar systemsRequire measurement of the universal frequency synthesizer features and programmable tuning, scanning, and motivational skills, industrial and optical applicationsBoth cases, the trend toward higher spectral purity (low phase noise and higher spurious free dynamic range), also low power and small size requirements to accommodate the remote ordemand for battery-powered devices.5.2 Modulation / data encoding, and synchronization of the DDSDDS products first appeared on the radar and military applications and the development of some of its characteristics (performance improvements, cost and size, etc.) DDS technology is becoming more prevalent in the modulation and data encoding applications. This section will discuss the two data encoding scheme in the DDS system.5.3 Binary frequency shift keyingThe launch of the data is a continuous carrier frequency in two discrete frequency (binary one, ie, pass number, a binary 0, namely, the transformation between the space). Figure 4 shows the relationship between the data and transmit signals.Figure 5-1 binary FSK modulation.Binary 1 and 0 for two different frequencies f0 and f1, respectively. This encoding scheme can be easily DDS device. On behalf of the output frequency of the DDS frequency tuning word change to f0 and f1, will launch the 1 and 0. To transform the output frequency shall dedicated pin FSELECT, containing the appropriate tuning word registers (see Figure 5)Figure 5-2 AD9834 or AD9838 DDS tuning word selector realization of the FSK encoding.5.4 Phase shift keying (PSK)In PSK, the carrier frequency remains the same, by changing the phase of the transmitted signal to transmit information. Can take advantage of a variety of programs to achieve PSK,. The easiest way is often referred to as binary PSK (BPSK), using only two signal phase: 0 ° (logic 1) and 180 ° (logic 0). Members state depends on the status of the former one. If the wave phase remains unchanged, the signal state will remain the same (low or high). Wave phase change 180 °, ie, phase inversion, the signal state will change (low into high or high to low). PSK coding in DDS products can be easily achieved, because most devices have a separate input register (phase register), and phase values can be loaded. This value is added directly to the carrier phase, without changing its frequency. Change the contents of the register will be modulated carrier phase, resulting in a PSK output. For applications that require high-speed modulation, built-in phase register of the AD9834 and AD9838 allow PSELECT pin signal transformation, according to need modulated carrierin the preloaded phase registers.The more complex the PSK four or eight-wave phase. Thus, whenever the phase change of binary data transfer rate will be higher than the BPSK modulation. In the four-phase modulation (Quadrature PSK), in the phase angle of 0 ° to +90 °, -90 ° and +180 °; each phase to transform the two signals may represent a factor AD9830, AD9831, AD9832, and the AD9835 provides four phase registers, can be continuously updated register of different phase shift, the complex phase modulation scheme.5.5 The use of synchronous mode of multiple DDS devices to achieve the I / QMultiple DDS components to achieve the many applications of the I / Q sine wave or square wave signal of known phase relationship between two or more synchronous mode. A common example is the same phase and quadrature modulation (I / Q) in this technique, the phase angle of 0 ° and 90 ° from the carrier frequency signal information. To run two separate DDS components, you can use the same source clock to output can directly control and manipulate the signal of the phase relationship. In Figure 6, with a reference clock on the AD9838 device programming; the RESET pin is used to update the two devices. In this way, you can achieve a simple I / Q modulationRESET after power and initialized before any data to the DDS transmission. DDS output results can be placed in a known phase, making it a common reference point of view, in order to synchronize multiple DDS devices. When new data is sent to multiple DDS devices, the DDS can remain relevant phase relationship, or by the phase offset register can predict the relative phase shift between the adjustments of multiple DDS. The AD983x series of DDS products have a 12 phase resolution, the effective resolution of 0.1 °.Figure 5-3 Synchronize the two DDS components.DDS器件产生高质量波形:简单、高效而灵活摘要:直接数字频率合成(DDS)技术用于产生和调节高质量波形,广泛用于医学、工业、仪器仪表、通信、国防等众多领域。
DDS信号发生器外文资料翻译

Design of Digital Controlled Signal Generator Based on DDS and MCUYinjun Chena, Zehuai YuanFaculty of Electronic Information and Mechanical Electrical Engineering, Zhaoqing University,Zhaoqing 526061, ChinaKeywords: DDS; MCU; Signal generator; Phase Accumulator; DACAbstract. Its advantage to use DDS chip is output signal frequency bigger, and precision higher, But users can't change the output signal waveforms. The MCU can produce the required arbitrary waveforms, but its program execution of the order limit the speed.So we use their Synergy to design the digital controlled signal generator. The System has the advantage of output good quality waveform, frequency of precision and stability ,and high frequency, empty, amplitude and phase is to step into the need.IntroductionThe digitally synthesized sine waveform (Direct Digital Synthesis, DDS) is a well-known method and has been applied to many embedded applications [1]. This technique can be used to create a positive digital sine waveform. Compared to other frequency composing method, Direct Digital Frequency Synthesis(DDS) has been the most popular trend in modern frequency synthetic technique for its excellent characteristics. The signal source that the DDS technology realizes can carry out accurate controlling on DDS frequency , extent , phase exporting wave form's etc. by numerical control circuit, the system making use of this method has many merits such as stability, reliably and accuracy.The commercial DDS chip can only export a sine wave for the data in the ROM form already has been solidified. If needing to come into being any wave form, it may come true by the way that FPGA adopts DDS IP core or hardware describe language etc, however,the cost of This way cost is high; on the other hand, any wave form can be achieved by making use of micro controller unit (MCU) to carry out figure frequency combining and DA converting. The experiment and applying testing have shown that the numerical control signal source composed of STM32 micro controller and DDS chip can work well.DDS and wave form programming patternThe core of DDS system is phase accumulator carriage, and it is composed of a ADR and one unit phase register. When any clock comes, the phase register increases by with the step length, phase register output and phase control word add together, and then the output is imported to sine inquiry form address.The sine inquiring form includes the numeral extent information of one-period sine wave, each address corresponds to the phase dot of 0~360 degrees of the sine wave. The mapping digital signal drives DAC and outputs analog value. The output sine circle and frequency areThe phase register will return to the original state when the 2N/M fc clock is finished. Accordingly, the DDS system output a sine wave when the sine inquiring form finish a circle. The output sine circle and frequency is TO --output sine wave circle, unit: s; TC --external referenced clock circle, unit: s; M --accumulated step length of phase register, constant; f out --output sine wave frequency, unit: Hz; f c --external referenced clock frequency, unit: Hz; N --phase accumulator digit, constant.The relationship among the frequency control word, and the output signal frequency and the referenced clock frequency are:Frequency control word is directly proportional to the output signal frequency. In order to describe clearly, the sine wave form is as one vector turns around phase circle, the phase circle matches along with a cycle sine wave. Every sampling pots in wave form corresponds to a phase dot of the phase circle.To synthesis the required frequency signal, it needs to accomplish the following steps1. Controlling every sampling increment of phase and accumulating them (frequency control word K), output 2 pi cumulated phase (using phase accumulator).2. Converting 2 pi accumulating phase into the corresponding sine amplitude, use ROM to store the corresponding phase-extent form of sine function in general.3. Use DAC to change extent code into the signal simulating voltage.4. The voltage signal that DAC exports is ladder wave form , the required simulation voltage out is achieved after LPF smoothing.Numerical control DDS signal source system designs analysisSystem uses the STM32 as control core and the AD9850 as generator. STM32 is 32-bit ARM-based micro controller with 128 K byte flash memory.The two signal output of STM32 can be achieved by controlling AD9850 and DAC0832 output simultaneously. The system designs block diagram is shown in Fig. 1. One signal output can generate 30 MHz sine wave and rectangular wave by controlling AD9850, the other output generate any wave form with its frequency less than 10 KHz by numerical frequency mixture of DAC0832.Fig. 1 System designs block diagramHardware designAD9850 moduleAD9850 contains the DDS system and high-speed comparator. The AD9850 can realize the entire numerical frequency combining. The core of the programmable DDS is the phase accumulator, it is composed of a ADR and a N bit phase register, N is for 24 ~ 32.After connecting to the accurate clock source and writing the frequency phase control word, AD9850 can generate the frequency-programmable and phase-programmable output of analog sine wave, which can be used as the direct frequency signal source or be transferred into rectangular wave through high-speed comparator.With the 125 MHz clock, 32-bit frequency control word can carry out the output frequency resolution ratio of AD9850 with 0.0291 Hz[4].DAC0832 moduleThe circuit exports the phase data sheet to DAC0832 from STM32 and gets corresponding wave form by DA converting. The step-by-step adjusting phase amounts can create arbitrary frequency, the PWM signal from the STM32 transfers into the corresponding voltage by low-passfilter, therefore, the referenced voltage of DAC0832 is controlled, furthermore, the output wave form extent is tuned appropriately. The digital to analog conversion circuit is shown in Fig.2Fig. 2 DAC circuitPWM converting DA circuitThe low-pass filtered PWM signal from STM32 is then stable using the voltage follower, which will yield a stable output voltage; the voltage can be adjusted by tuning the PWM dutyfactor. The system output three PWM signals, which controls AD9850 output extent, dutyfactor and the output extent of DAC0832, respectively,. Fig. 3 shows the PWM controls DA transferring circuit.Fig. 3 PWM controlled DA converting circuitFig. 4 Export amplification and the wave filtering circuit. (a) amplification circuit; (b) filteringcircuitAmplification and wave filtering circuitThe amplification circuit will export amplified wave form and modify the factor of amplification. An excellent smooth output waveform can be achieved by using the low-pass active power filtering. The amplification circuit and the filtering circuit is showed in Fig. 4.Software designAnd the system software mainly include AD9850 driving module, DAC0832 driving module, the step-by-step automation module, PWM-converting-DA module and uC/GUI figure supporting system implanted in procedure. The operation interface is full of humanization for themulti-window pattern is adopted. The design process of the system software is shown in Fig. 5.Implanted uC/GUIThe numerical control signal source has used the uC/GUI software sufficiently to establish many windows and control buttons. By means of invoking the corresponding windows and control with the feedback information, the peripheral equipment operated under the control of the system.The external equipment is mainly separated into two drivers, the drive being an AD9850 module and DAC0832 module drive, respectively. The two modules can be controlled by means of the outside interruption and timing interruption.AD9850 DriveAD9850 has 40 control words, among them, 32-bit is used for frequency control, 5-bit is used for the phase control, 1-bit is used for the power source dormancy control, 2-bit is used to choose operation pattern.Fig. 5 Systematic procedure flow chartThis 40 control words may arrive at AD9850 by concurrence way or serial way, in the concurrence way, 8 data highway generals can transfer the data to a register.After repeating 5 times, the 40-bit data is loaded into the frequency / phase data register (for refreshing DDS output frequency and phase) at the FQ-UD rising edge, meanwhile, the address pointer is reset to the first input registerThen the 8-bit data is loaded at the W-CLK rising edge, and the pointer is set to the next input register. After repeating 5 times of W-CLK rising edge, the W-CLK rising edge will work no longer until the reset signal comes or the address pointer is reset to the first input register by the FQ-UD rising edge.The procedure operate AD9850 module through the bottom function, asvoid ad9850(double frequency, //frequencyunsigned char phase, //phaseunsigned char mode, //patternunsigned char power //source)The DAC0832 driven moduleIn the design of the numerical control signal source, DAC0832 is defined as single buffered pattern, when the 8 bit Parallel data D0~D7 is input, the DA will transfer data in the CS.The bottom function of void DA0832(u8 value)can invoke Out_To_DDS0832(double Frequency,u8 type) function and control the defined wave form and frequency.This function is based on figure frequency composes principle, it transfers the input frequency into corresponding control word, and then combing phase step-by-step expect, output wave form data sheet in memory.The extent and dutyfactor can be tuned through invoking Adjust_Vpp() and Adjust Duty() Step-by-step automation procedureA step-by-step automation procedure brick is added to the design to define the frequency range, step-by-step rate , step-by-step amounts , ascending or lapse, cycling pattern.The step-by-step automation function can be realized through invoking AutoStep(AutoStepStr*AS) and passing memory structure type to a function.Test the experiment and data analysisThe DDS numerical control signal source can import the various changeable control words by a touching screen, and then accurately control the signal frequency, dutyfactor, extent and phase. Figure 6 shows the corresponding experimental wave forms.Fig. 6 The oscillograph exports experiment picture (a) 1 KHz wave form output; (b) 1 MHz waveform output; (c) 20 MHz wave form output.With the oscillograph testing, it shows that the circuit work stably and rightly. The various parametric index exhibit fine numerical control effect.a. Output frequency range: 1Hz—30MHz,peak-to-peak value: 50mV~10V;dutyfactor:10%~100%, difference≤1%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
毕业设计(论文)外文文献翻译文献、资料中文题目:借助DDS的精密频率的一种替代方法文献、资料英文题目:文献、资料来源:文献、资料发表(出版)日期:院(部):专业:班级:姓名:学号:指导教师:翻译日期: 2017.02.14An alternative method of precise frequency by the aid of a DDSContentsA method of frequency measurement based on a closed loop composed mainly of a Frequency Comparator (FC) and a Direct Digital Synthesizer (DDS) is presented in this paper. The DDS serves as reference sinewave signal generator acting at one of the FC's inputs. The FC accepts the hard-limited waveform of the DDS as well as the unknown frequency. From the comparison of the two signals a logic output that controls an up/down counter is produced. The counter's output acting as the Frequency Setting Word (FSW) instructs the DDS to produce a new sinewave closer in frequency to the unknown one. When the loop settles, the FSW gives the digital estimate of the unknown frequency. Advantage is taken from the inherent high resolution of the DDS and noise immunity of the loop, to design an equally precise and immune frequency meter. All the additional associated stages up to the instrument's display are presented.1 IntroductionThe most commonly used frequency measurement technique adopts counters that count the pulses of the unknown frequency during a predefined time window (aperture). Apart from this, techniques where the pulses of a reference frequency are counted during one or more periods of the unknown one are also common. In the latter case, the period instead of the frequency is estimated .Some papers in [1] in the literature deal with the problem of low frequency measurement and are focusing in the frequency range of cardiac (heart) signals (a few hertz) or in the mains frequency (50-60 Hz).These techniques are actually measuring the period of the signals and use some way to calculate its reciprocal, the frequency. In [2], the frequency is calculated by the method of look-up tables. Others [4-6] are microprocessor or microcontroller based.The above methods can be characterized as open-loop methods i.e. digital counters are used to count during a predefined tinle interval and calculate the result afterwards. Its closed-loop form characterizes the proposed method in this paper. By the term "closed-loop" we denote some sort of feedback. A waveform with a known (controlled) frequency is produced within the circuit and is fed back to the frequency comparison stage which consecutively forces it to approximate the unknown (input) frequency. The device that produces the above mentioned waveform of controlled frequency is a Direct Digital Synthesizer.2 Direct Digital SynthesisA typical Direct Digital Synthesizer consists of a RAM containing samples of a sinewave (sine look-up table, LUT). These samples are swept in a controlled manner by the aid of a Frequency Setting Word (FSW), which determines the phase step. A typical FSW is 32-bit wide, but 48-bit synthesizers leading in higher frequency resolution are also available. A phase accumulator produces the successive addresses of the sine look-up table and generates a digitized sine wave output. The digital part of the DDS, the phase accumulator and the LUT, is called Numerically Controlled Oscillator (NCO). The final stage, which in contrast to the previous one is mostly analog, consists of a D/A converter followed by a filter. The filter smoothes the digitized sinewave, producing a continuous output signal. In the applications where a square wave output is needed, this is obtained by a hard limiter after the filter. It is not equivalent to use e.g. the MSB of the accumulator's output instead of the filtered and hard limited waveform because significant jitter will be encountered.The frequency of the output signal for an n-bit system is calculated in the following way; If the phase step is equal to one, the accumulator will count by ones, taking2n clock cycles toaddress the entire LUT and to generate one cycle of the output sinewave. This is the lowest frequency that the system can generate and is also its frequency resolution. Setting the FSW equal to two, results in the accumulator counting by twos, taking 12n - clock cycles to complete onecycle of the output sinewave. It can easily be shown that for any integer m, where m<12n -, thenumber of clock cycles taken to generate one cycle of the output sine wave is 2n /m, and theoutput frequency (f DDS ) and the frequency resolution (fres) are given by the following formulas : f DDS =2nm fclk ⨯ fres= fclk/2n For n = 32 and having a clock frequency of fclk = 33 MHz, the frequency resolution is 7.68 mHz. If n is increased to 48, with the same clock frequency, a resolution of 120 nHz is possible. 3 The proposed frequency measurement technique The idea that led to our present design came from the extremely high frequency resolution of the DDS devices and is enforced by the noise immunity of its closed loop form. A (known) frequency source, the DDS, is employed in a closed loop and is forced progressively to produce an output with a frequency equal to the unknown input . A rule of thumb in the DDS systems is that the maximum acceptable synthesized frequency is about 25% of the clock frequency (well below the Nyquist limit). According to this, our prototype that uses a 33 MHz clock would effectively count up to 8 MHz. Looking at the GaAs products, we can see that recently available DDS devises can operate at clock frequencies up to the extent of 400 MHz. Therefore, by the present method, frequency counters working up to 100 MHz can be designed. The resolution will depend on the number of FSW bits and the clock frequency. The clock frequency fclk of the DDS is very critical because as it decreases, the resolution of the proposed method (defined as fclk/2n ) becomes finer i.e. it improves. The impact of the clock frequency decrease is the subsequent decrease of its maximum output frequency that limits the counter's maximum count. The major blocks have been shown . Among them are the Frequency Comparator and the DDS. To overcome some disadvantages of the specific frequency comparator a correction stage has been incorporated. This stage is also used for the measurement extraction in order to display the correct reading.3.1 Operation of the circuitThe circuit operates in such a way that at the beginning of a new measurement the DDS output frequency would be controlled in a successive approximation way. The initial DDS frequency would be half of it's maximum. In addition, the frequency step of the approximation would equal the 1/4 of the DDS maximum frequency. On every approximation the frequency step is divided by two and added or subtracted to the FSW of the DDS, depending on the output of the Frequency Comparator. The approximation procedure stops when the step size decreases to one. After that, an up/down counter substitutes the approximation mechanism.The digital FSW, after the appropriate correction and decoding, is presented in an output device i.e. an LCD display or any other suitable means. Alternatively, it can be digitally recorded or it can be read by a computer. As conclusion of this initial approach we could say that the proposed method is based on a Digital Controlled Synthesizer which is forced to produce a frequency almost equal to the unknown one.3.2 Frequency comparisonThe frequency comparator seems to be the most critical stage of the design. Theimplementation is based on a modified phase/frequency comparator proposed by Philips in the 74HC4046 PLL device. It consists primarily of two binary counters, counting up to two and an RS flip-flop.The function of the frequency comparator is based on the principle that the lower frequency, i.e. larger period, includes (embraces) at least one or more full periods of the higher frequency (smaller period). This means that two or more rising edges of the higher frequency waveform are included within the lower frequency period. Considering the above, the circuit operates as follows: When the first counter (#1) encounters two rising edges of the unknown frequency in one period of the DDS, it sets the output of the RS flip-flop. The logic "1" of the RS flip-flop acting at the U/D control input of the Up/Down counter forces the DDS to rise its output frequency. On the contrary, when the second counter (#2) counts two rising edges of the DDS output within a period of the unknown frequency it resets the RS flip-flop's output. This action decreases the frequency of the DDS.At a first glance one could think that the synthesized frequency could reach the measured one (fin) and then the operation of the counter stops. Unfortunately this is not the case. A dynamic mechanism takes place instead. The circuit needs some time to realize the correct frequency relation. We will refer to this time as "hysteresis". Hysteresis depends on the initial timing relation of the DDS output and on the unknown frequency. Initially, during the hysteresis period, the indication regarding the larger frequency is ambiguous i.e. it can be erroneous. The ambiguity settles when two rising edges of the higher frequency waveform occur during one period of the lower one. If we consider the case of the DDS frequency to be equal to the unknown one, we will find that the comparator's output will toggle, indicating alternatively that the DDS frequency is higher or lower than the unknown. This is actually an acceptable and expected condition, because (as in a voltage comparator) an equality indication could not exist. In our case this is not a problem because the circuit is embedded in a closed loop. The loop will act in a manner that after some short time, the hysteresis, the situation will be reversed and so on. The duration of hysteresis is variable. This situation is controlled, as will be explained later. Although an analog implementation of the frequency comparator would look more robust to noise we insisted to the digital implementation for three reasons: ease of implementation in VLSI or Programmable Logic Devices (PLDs) with no need of analog components, wide frequency range of operation and shorter response time.3.3 Interaction between frequency comparator and digital synthesizerAfter the successive approximation of the unknown frequency the Frequency Comparator "realizes" that the synthesized frequency is higher (lower) than the unknown one and produces a logic 0 (1) at the output which commands the up/down counter to count in the down (up) direction. As previously mentioned, the output of this counter is considered to be the FSW to the DDS stage. In the case when the DDS frequency was initially lower, the synthesized frequency will increase progressively to reach the unknown one. This will not be "realized" by the frequency comparator and the synthesized frequency will keep on increasing for some clock cycles, until the comparator detects the correct relation of it's two input frequencies, the unknown one and the DDS output. The same phenomenon will be observed for the opposite (decreasing) case also. This is due to hysteresis that was mentioned earlier.When DDS output (f DDS) has approached fin, due to hysteresis, no specific frequency is synthesized. Instead, it swings between f1 and f2, where f1 and f2are the two extreme values of thefrequency swing lying symmetrically around fin. The DDS output can be considered as a frequency modulated carrier by a triangular waveform. The triangular waveform is the analog representation of the FSW applied to the DDS. lower trace shows a typical output of the Frequency Comparator. In the same figure, upper trace, is shown in analog form the FSW variation as it is trying to approach the correct value. This waveform has been captured using an auxiliary hardware circuit: A digital-to-analog converter (DAC) was connected to the output of the U/D counter (MSBs) in order to study the operation. This DAC is not shown in the block diagram of the circuit. Stated differently, the lower trace is the U/D command (input) to the counter while the upper trace is a hypothetical "frequency modulating" waveform. It is obvious that the term "hypothetical" is used because there is not such a waveform available somewhere in the circuit (except for the auxiliary DAC). Instead, its numerical equivalent exists. The magnitude of the slope of the elements of the triangular waveform is constant for constant input frequency and depends on the clock of the U/D counter (horizontal axis) and the voltage reference of the DAC (vertical axis). This slope is k • fin.3.4 Description of the prototype hardwareFor evaluation purposes two prototypes have been built and tested in the laboratory. The first approach was a low frequency instrument (operating up to 15 KHz) . The purpose of this implementation was to study the principles of operation of the proposed method. Next, a higher frequency prototype was built which will be described in more detail here. In order to implement the digital part of the prototype, (Frequency Comparator, Successive Counter, Correction Stage) two PLD devices from Altera (EPF 8064LC68-12) were used. These devices are interconnected with the DDS, which is the Q2240I-3S1 from Qualcomm. The DDS has a 32-bit input and a 12-bit output for the sine lookup table (LUT). The 12-bit output of the LUT is fed into the D/A converter, the AD9713B from Analog Devices. Its analog output is connected to an I/V amplifier (current-to-voltage converter).The generated sinewave has upper harmonics, due to the DAC operation. These harmonics are removed from the filters that follow the DAC. The correction stage is implemented partially on the PLDs and partially on the microcontroller. Based on the up-down command of the frequency comparator we store the two extreme values, FSW1 and FSW2, which are then transferred into the micro-controller (Atmel AT89C52), transformed into numerical representation and fed to the LCD Display. The micro-controller also controls the whole operation of the prototype.The behaviour of the instrument was according to the expected and was alike to a conventional bench frequency counter. The speed of measurement was checked using lower trace, obtained by the aid of a digital oscilloscope. Each state, high or low, of this waveform corresponds to the time required for one measurement.4 ConclusionIn this paper an alternative method of frequency measurement has been proposed. It has been pointed out that in most cases this method is faster than conventional methods for the same frequency resolution. On the other hand, the precision of the method can be very high due to the inherent high frequency resolution characteristic of the DDS that is employed. This synthesizer, which can be thought as an oscillator, is driven to "oscillate" in the region of the unknown input frequency. A comparison with conventional methods has been given and two prototypes have been built and tested in the laboratory.The second major advantage of this method is that if repetitive frequency measurements areto be taken, the instrument remains locked and the frequency measurement does not restart from the beginning, but instead is automatically driven to lower or higher values. In other words, the loop has the capability to follow the changes in the frequency of the input signal. In the conventional counting techniques the counting procedure is repeated (restarted) for each new measurement.Another important advantage is the noise immunity of the system, due to its closed loop nature. A detailed study of the noise behavior has not been carried out in this paper. This is mainly because the aim of this text is to present an alternative principle of frequency measurement. Moreover, the final output of the system is taken after some further processing (measurement correction) which also contributes to the noise immunity.借助DDS的精密频率的一种替代方法内容频率测量的方法基于闭环组成,主要是一个频率比较器(FC)和直接数字合成器(DDS),对此在本文中进行了介绍。
