江苏省无锡市长泾二中2019—2020学年上初二第九周随堂练习(第三章勾股定理,无答案)
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、如图,△ABC是的内接等边三角形,AB=1.点D,E在圆上,四边形为矩形,则这个矩形的面积是()A. B. C. D.12、如图,Rt△ABC中,∠C=90°,∠B=30°,AC=.按以下步骤作图:①以A为圆心,以小于AC长为半径画弧,分别交AC,AB于点E、D;②分别以D,E为圆心,以大于DE长为半径画弧,两弧相交于点P;③连接AP交BC于点F.那么BF的长为()A. B.3 C.2 D.3、菱形的周长为20cm,两邻角的比为1:2,则较长的对角线长为().A.4.5cmB.4cmC. cmD. cm4、下列各组线段能构成直角三角形的一组是()A.5cm,9cm,12cmB.7cm,12cm,13cmC.30cm,40cm,50cm D.3cm,4cm,6cm5、在△ABC中,∠A=90°,对应三条边分别为a、b、c,则a、b、c满足的关系为()A.a 2+b 2=c 2B.a 2+c 2=b 2C.b 2+c 2=a 2D.b+c=a6、如图,在矩形ABCD中,E为AD的中点,∠BED的平分线交BC于点F,若AB=3,BC=8,则FC的长度为()A.6B.5C.4D.37、如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P 是AB上的动点,则PC+PD的最小值为()A.4B.5C.6D.78、直角三角形的两条边长为5和12,它的斜边长为()A.13B.C.13或D.13或129、如图,在Rt△ABC中,∠ACB=90°,AC=5 cm,BC=12 cm,则其斜边上的高为()A.6 cmB.8.5 cmC. cmD. cm10、如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是()A.互相平分B.相等C.互相垂直D.互相垂直平分11、如图①,在边长为2cm的正方形ABCD中,点P以每秒1cm的速度从点A出发,沿AB→BC的路径运动,到点C停止,过点P作PQ∥BD,PQ与边AD(或边CD)交于点Q,PQ的长度y(cm)与点P的运动时间x(秒)的函数图象如图②所示.当点P运动3秒时,PQ的长是()A. cmB. cmC. cmD. cm12、如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D 作DF⊥AB于点E,交⊙O于点F,OE=1cm,DF=2cm,则CB的长为( )A.4-B.5-C.2D.413、如图,四边形ABCD中∠DAB=60°,∠B=∠D=90°,BC=1,CD=2,则对角线AC的长为()A. B. C. D.14、已知线段AB,按如下步骤作图:①作射线AC,使AC⊥AB;②作∠BAC的平分线AD;③以点A为圆心,AB长为半径作弧,交AD于点E;④过点E作EP⊥AB于点P,则AP:AB=()A. B. C. D.15、一棵大树在一次强台风中于离地面米处折断倒下,倒下部分与地面成夹角,这棵大树在折断前的高度为()A. 米B. 米C. 米D. 米二、填空题(共10题,共计30分)16、如图,已知在矩形中,,,沿着过矩形顶点的一条直线将折叠,使点的对应点落在矩形的边上,则折痕的长为________.17、如图,在平面直角坐标系xOy中,已知点A(0,),B(-1,0),菱形ABCD的顶点C在x轴的正半轴上,其对角线BD的长为________。
苏科版八年级数学上册第三章《勾股定理》专题练习.docx

初中数学试卷马鸣风萧萧第三章《勾股定理》专题练习(时间:90分钟满分:100分)一、选择题(每小题3分,共30分)1.直角三角形两锐角的平分线所成钝角的度数是( )A.115°B.125°C.135°D.无法确定2.有四个三角形,分别满足下列条件:①一个内角等于另外两个内角之和;②三个内角之比为3:4:5;③三边之比为5:12:13;④三边长分别为7,24,25.其中直角三角形有( )A.1个B.2个C.3个D.4个3.在Rt△ABC中,∠C=90°,周长为60,斜边与一条直角边之比为13:5,则这个三角形三边长分别为( )A.5,4,3 B.13,12,5 C.10,8,6 D.26,24,104.一等腰三角形底边长为10 cm,腰长为13 cm,则腰上的高为( )A.12 cm B.6013cm C.12013cm D.135cm5.如图,在把易拉罐中的水倒入一个圆水杯的过程中,若水杯中的水在点P与易拉罐刚好接触,则此时水杯中的水深为( )A.2 cm B.4 cm C.6 cm D.8 cm6.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )A.42 B.32 C.37或33 D.42或327.如图,一架长2.5 m的梯子,斜靠在竖直的墙上,这时梯子顶端离地面2.4 m,为了安装壁灯.梯子顶端离地面降至2m,请你计算一下,此时梯子底端应再向远离墙的方向移动( )A.0.4 m B.0.8 m C.1.2 m D.不能确定8.如图,在一个高为3m,长为5m的楼梯表面铺地毯,则地毯长度为( )A.7 m B.8 m C.9 m D.10 m9.如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( ) A.600 m B.500 m C.400 m D.300 m10.在一次课外社会实践中,王强想知道学校旗杆的高,但不能爬上旗杆也不能把绳子解下来,可是他发现旗杆上的绳子垂到地面上还多1 m,当他拿着绳子的下端沿水平方向走5m后,发现绳子下端刚好接触地面,则旗杆的高为( )A.13 m B.12 m C.4m D.10 m二、填空题(每小题3分,共24分)11.在△ABC中,若AC2+BC2=AB2,则∠C=_______;若∠A=90°,则AC2+_______=_______.12.直角三角形两条直角边的长分别为6,8,则斜边上的高长为_______.13.在Rt△ABC中,∠B=90°,BC=3 cm,AC=4 cm,则AB=_______cm.14.如图,在四边形ABCD中,∠BAD=90°,AD=3 cm,AB=4 cm,BC=12 cm,CD =13 cm,则∠DBC=_______.15.如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,1.21,1.44,正放置的四个正方形的面积分别为S1,S2,S3,S4,则S1+2S2+2S3+S4=_______.16.如图,在长、宽都是3,高是8的长方体纸箱的外部,一只蚂蚁从顶点A沿纸箱表面爬到顶点B,那么它所爬行的最短路线的长是_______.17.如图,在△ABC中,CE平分∠ACB,CF平分外角∠ACD,且EF∥BC交AC于点M,若CM=5,则CE2+CF2=_______.18.如图,在△ABC中,AB=BC=2,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D',则(BD')2=_______.三、解答题(共46分)19.(6分)假期中,小明和同学们到某海岛上去探宝旅游,按照探宝图,他们登陆后先往东走8 km,又往北走2 km,遇到障碍后又往西走了3 km,再折向北走到6 km处往东一拐,仅走了1 km就找到宝藏,问登陆点A到宝藏埋藏点B的距离是多少千米?20.(8分)如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3 m,BC=4 m,CD=12 m,DA=13 m,∠B=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?21.(8分)在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,过点D作DE⊥DF,交AB于点E,交BC于点F,若AE=4.FC=3,求EF的长.22.(8分)周老师在一次“探究性学习”课中,设计了如下数表:(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:a=_______;b=_______;c=_______;(2)猜想:以a,b,c为边长的三角形是否是直角三角形?证明你的猜想.23.(8分)实践与探究问题情境:勾股定理是一条古老的数学定理,它有多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行了证明,著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.问题1 请你根据图①中的直角三角形叙述勾股定理(用文字及符号语言叙述);探究2 以图①中的直角三角形为基础,可以构造出以a,b为底,以a+b为高的直角梯形(如图②),请你利用图②,尝试验证证明勾股定理;拓展3 利用图②中的直角梯形,我们可以证明a bc+<2,其证明步骤如下:∵BC=a+b,AD=_______,又在直角梯形ABCD中,BC_______AD(填“>”“<”或“=”),即_______.∴a bc+<2.24.(8分)我们给出如下新定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.(1)如图①,请你在图中画出以格点为顶点,OA,OB为勾股边且对角线相等的勾股四边形OAMB:(2)如图②,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD,DC.若∠DCB=30°,则四边形ABCD是勾股四边形,为什么?参考答案1.C2.C3.D4.C5.C6.D7.B8.A9.B 10.B 11.90° AB 2 BC 2 12.24513.7 14.90° 15.3.65 16.10 17.100 18.519.AB =10 km .20.3600(元).21.5.22.(1)a =n 2-1,b =2n ,c =n 2+1.(2)是直角三角形23.(1)直角三角形中两直角边的平方和等于斜边的平方,用式子表示为在△ABC 中,如果∠C =90°,那么a 2+b 2=c 2.(2)c < a +b<c24.(1)如图①,勾股四边形OAMB(或OAM'B).(2)是勾股四边形.。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、下列能构成直角三角形三边长的是()A.1,2,3B.C.D.4,5,62、如图,在4×4的正方形网格中,所有线段的端点都在格点处,则这些线段的长度是无理数的有()A.1 条B.2条C.3条D.4条3、满足下列条件的三角形中,不是直角三角形的是()A.三内角之比为1:2:3B.三边长的平方之比为1:2:3C.三边长之比为3:4:5D.三内角之比为3:4:54、正方形网格中,△ABC如图放置,则sin∠BAC=()A. B. C. D.5、已知直角三角形两边的长为3和4,则第三边的长为()A.5B.C.5或﹣1D.以上都不对6、如图,在方格纸中,假设每个小正方形的面积为2,则图中的四条线段中长度是有理数的有()A.1条B.2条C.3条D.4条7、如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为( )A. B. C. D.8、如图,菱形ABCD中,,,M为AB的中点.动点P在菱形的边上从点B出发,沿的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,,则表示y与x的函数关系的图象大致为()A. B. C. D.9、一个直角三角形,有两边长分别为6和8,下列说法正确的是()A.第三边一定为10B.三角形的周长为25C.三角形的面积为48 D.第三边可能为1010、如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+MN的最小值为()A.6B.8C.12D.1011、如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC 交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为2,则线段CF 的最小值是()A.2B.1C. -1D. -212、如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若DE=1,则BC的长为()A.3B.C.2+D.2+13、如图,在△ABC中,AB=AC,AD、CE是△ABC的两条中线,P是AD上一个动点,则下列线段的长度等于BP+EP最小值的是()A.BCB.CEC.ADD.AC14、下列三边的长不能成为直角三角形三边的是()A.3,4,5B.4,5,6C.6,8,10D.5,12,1315、如图①,在边长为2cm的正方形ABCD中,点P以每秒1cm的速度从点A出发,沿AB→BC的路径运动,到点C停止,过点P作PQ∥BD,PQ与边AD(或边CD)交于点Q,PQ的长度y(cm)与点P的运动时间x(秒)的函数图象如图②所示.当点P运动3秒时,PQ的长是()A. cmB. cmC. cmD. cm二、填空题(共10题,共计30分)16、在△ABC中,AB=10,AC=17,BC边上的高为8,则△ABC的面积为________.17、如下图,已知四边形OABC为正方形,边长为6,点A,C分别在x轴、y轴的正半轴上,点D在OA上,且点D的坐标为(2,0),点P是OB上的一个动点,则PD+PA的最小值是________.18、如图所示,直线 y=x+2 与两坐标轴分别交于 A、B 两点,点 C 是 OB 的中点,D、E 分别是直线 AB、y 轴上的动点,则△CDE 周长的最小值是________.19、如图,在Rt△ABC中,∠C=90°,AC=6,∠A=60°,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是________.20、如图,将等腰直角三角形ABC(∠B=90°)沿EF折叠,使点A落在BC边的中点A处,BC=8,那么线段AE的长度为________.121、在中,,,,则线段AC的长为________.22、如图,一个池塘,其底面是边长为10尺的正方形,一棵芦苇生长在它的中央,高出水面的部分为1尺.如果把这根芦苇沿与水池边垂直的方向拉向岸边,芦苇的顶部恰好碰到岸边的,则这根芦苇的长度是________尺.23、如图,在平行四边形ABCD中,AB=8,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=2,则AE的长为________.24、如图,在等腰△ABC中,底边BC=16,底边上的高AD=6,则腰AB=________.25、如图,BD为长方形ABCD的对角线,BD=10,∠ABD=30°,求长方形ABCD的面积________.三、解答题(共5题,共计25分)26、如图所示,△ABC和△AEF为等边三角形,点E在△ABC内部,且E到点A,B,C的距离分别为3,4,5,求∠AEB的度数.27、如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=16,AB=CD=34.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,求DE的长.28、在四边ABCD中,∠D=90°,AD= ,CD=2,BC=3,AB=5,,求:四边形ABCD的面积.29、阅读:能够成为直角三角形三条边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为:其中m>n>0,m,n是互质的奇数.应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.30、由于大风,山坡上的一棵树甲被从点A处拦腰折断,如图,其树恰好落在另一棵树乙的根部C处,已知AB=1米,BC=5米,已知两棵树的水平距离为3米,请计算出这棵树原来的高度(结果保留根号)参考答案一、单选题(共15题,共计45分)1、C2、B4、D5、D6、B7、A8、B9、D10、D11、C12、D13、B14、B15、C二、填空题(共10题,共计30分)16、17、18、20、21、22、23、24、25、三、解答题(共5题,共计25分)29、。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、如图,在ABC中,AC=BC,∠ACB=90°,过点C作CD⊥AB交∠CAB的平分线AE于点O,点P是AC延长线上一点,OP=OB,现有下列结论:①∠OCP=∠OEB;②∠POB=90°;③CP=OD;④SCOP =SCOE;⑤PC2+BC2=OP2+OB2.其中正确的有()A.1个B.2个C.3个D.4个2、如图,直线l为等腰梯形ABCD的对称轴,点P在直线l上,且PC+PB最小,则点P应位于()A.点P1处 B.点P2处 C.点P3处 D.点P4处3、要登上某建筑物,靠墙有一架梯子,底端离建筑物3m,顶端离地面4m,则梯子的长度为()A.2mB.3mC.4mD.5m4、已知直角三角形的两边长是方程x2﹣7x+12=0的两根,则第三边长为()A.7B.5C.D.5或5、如图,四边形ABCD是正方形,直线a,b,c分别通过A、D、C三点,且a ∥b∥c.若a与b之间的距离是3,b与c之间的距离是5,则正方形ABCD的面积是()A.16B.30C.34D.646、设边长为3的正方形的对角线长为a,下列关于a的四种说法:① a是无理数;② a可以用数轴上的一个点来表示;③ 3<a<4;④ a是18的算术平方根.其中,所有符合题意说法的序号是A.①④B.②③C.①②④D.①③④7、a、b、c为△ABC三边,满足下列条件的三角形不是直角三角形的是()A.∠C=∠A-∠BB.a:b:c = 1 : :C.∠A∶∠B∶∠C=5∶4∶3D. ,8、直角三角形两直角边分别为5、12,则这个直角三角形斜边上的高为().A.6B.8.5C.D.9、三角形的三边长分别为6,8,10,它的最长边上的高为()A.6B.4.8C.2.4D.810、在边长为2的正方形ABCD中,P为AB上一动点,E为AD中点,PE交CD 延长线于Q,过E作EF⊥PQ交BC延长线于F,则下列结论:①△APE≅△DQE;②PQ=EF;③当P为AB中点时,CF= ;④若H为QC中点,当P从A移动到B 时,线段EH扫过的面积为.其中正确的是()A.①②B.①②④C.②③④D.①②③11、下列数组中,不是勾股数组的是 ( )A.8,12,15B.7,25,24C.5,12,13D.3k,4k,5k(k为正整数)12、已知一个直角三角形的两条边长分别是6和8,则第三边长是()A.10B.8C.2D.10或213、若直角三角形的两直角边长分别为5、12,则这个直角三角形的斜边长是()A.13B.C.169D.14、如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+ 的值最小时,线段PD的长是()A. B. C. D.15、如图,在四边形ABCD中,AB=BC=2 ,AD=2,∠B=∠D=90°,则CD 等于()A.2B.C.2D.二、填空题(共10题,共计30分)16、如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,AE=CD,若⊙O的半径为5,则弦CD的长为________.17、如图,半径为且坐标原点为圆心的圆交轴、轴于点、、、,过圆上的一动点(不与重合)作,且在右侧)⑴连结,当时,则点的横坐标是________.⑵连结,设线段的长为,则的取值范围是________.18、如图,在中,,.将绕点B 逆时针旋转60°,得到,则边的中点D与其对应点的距离是________.19、如图,将矩形纸片ABCD沿直线AF翻折,使点B恰好落在CD边的中点E 处,点F在BC边上,若CD=6,则AD=________.20、如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要________元钱.21、如图,每个小正方形的边长为1,在△ABC中,点D为AB的中点,则线段CD的长为________.22、如图,已知直线AB∥CD,AB与CD之间的距离为,∠BAC=60°,则AC=________.23、如图,已知图中每个小方格的边长为1,则点C到AB所在直线的距离等于________.24、如图,在由12个边长都为1且有一个锐角为60°的小菱形组成的网格中,点P是其中的一个顶点,以点P为直角顶点作格点直角三角形(即顶点均在格点上的三角形),请你写出所有可能的直角三角形斜边的长________ .25、如图,AD是的中线,,把沿着直线AD对折,点C落在点E的位置,如果,那么线段BE的长度为________.三、解答题(共5题,共计25分)26、如图,在Rt△ABC中,∠C=90°,BC=8,tanB= ,点D在BC上,且BD=AD,求AC的长和cos∠ADC的值.27、如图(1),在∆ABC中,AB=BC=5,AC=6,∆ABC沿BC方向平移得到△ECD,连接AE、AC和BE相交于点O。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、如图中的小正方形边长都相等,若△MNP≌△MEQ,则点Q可能是图中的()A.点AB.点BC.点CD.点D2、如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方A、B、C、D的边长分别是3、5、2、3,则最大正方形E 的面积是()A.13B.26C.34D.473、在正方形网格中,△ABC的位置如图所示,则cosB的值为()A. B. C. D.4、满足下列条件的,不是直角三角形的是()A. B. C.D.5、若菱形两条对角线的长分别为6和8,则这个菱形的边长为( )A.5B.10C.20D.146、如图,一只蚂蚁从长宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B 点,那么它所行的最短路线的长是()A.(3 +8)cmB.10cmC.14cmD.无法确定7、已知如图,在正方形ABCD中,AD=4,E,F分别是CD,BC上的一点,且∠EAF=45°,EC=1,将△ADE绕点A沿顺时针方向旋转90°后与△ABG重合,连接EF,过点B作BM∥AG,交AF于点M,则以下结论:①DE+BF=EF,②BF= ,= 中正确的是()③AF= ,④S△MEFA.①②③B.②③④C.①③④D.①②④8、若直角三角形两直角边长分别为5,12,则斜边上的高为()A.6B.8C.D.9、在Rt△ABC中,∠C=90°,BC=1,AB=2,则tanA等于()A. B. C. D.10、如图,在正方形中,点在边上,且将沿对折至延长交边于点连接,下列结论:①;②;③.其中正确的是()A.①②B.①③C.②③D.①②③11、如图,在Rt△ABC中,∠C=90°,CDEF为内接正方形,若AE=2cm,BE=1cm,则图中阴影部分的面积为()A.1cm 2B. cm 2C. cm 2D.2cm 212、如图,在中,,,,将绕点逆时针旋转得到,使得点落在上,则的值为()A. B. C. D.13、在△ABC中,AB=10,AC=2 ,BC边上的高AD=6,则另一边BC等于()A.10B.8C.6或10D.8或1014、如图,已知在平面直角坐标系xOy中,抛物线y= 与y轴交于点A,顶点为B,直线l:y=- x+b经过点A,与抛物线的对称轴交于点C,点P 是对称轴上的一个动点,若AP+ PC的值最小,则点P的坐标为()A.(3,1)B.(3,)C.(3,)D.(3,)15、如图,点D是正△ABC内的一点,DB=3,DC=4,DA=5,则∠BDC的度数是()A.120°B.135°C.140°D.150°二、填空题(共10题,共计30分)16、如图,已知正方形ABCD的边长是4,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,则PD+PG的最小值为________.17、如图,在中,,点在上,点为外一点,且为等边三角形,,若,,则的边长为________.18、四根小木棒的长分别是5,8,12,13,任选三根组成三角形,其中有________个直角三角形。
苏科版八年级上册数学第三章 勾股定理含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、如图,在中,,E为中点,连接,,若,则的长为()A. B. C. D.2、已知a、b、c为的三边,且满足,则是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形3、如图,周长为16的菱形ABCD中,点E,F分别在边AB,AD上,AE=1,AF=3.P为BD上一动点,则线段EP+FP的长最短为()A.3B.4C.5D.64、如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与CB,CA分别相交于点E,F,则线段EF长度的最小值是()A.2.4B.2C.2.5D.5、如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600米,E为弧CD上一点,且OE⊥CD,垂足为F,OF=米,则这段弯路的长度为()A.200π米B.100π米C.400π米D.300π米6、如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1, l2, l3上,且l1, l2之间的距离为2,l2, l3之间的距离为3,则AC的长是()A. B. C.4 D.77、下列几组数能作为直角三角形的三边长的是()A.6,8,10B.4,5,7C.2,3,4D.1,2,38、在4×5网格中,A,B,C为如图所示的格点(小正方形的顶点),则下列等式正确的是()A.sinA=B.cosA=C.tanA=D.cosA=9、若直角三角形的两边长分别为a,b,且满足+|b﹣4|=0,则该直角三角形的第三边长为()A.5B.C.4D.5或10、下列四组数据不能作为直角三角形的三边长的是()A.6、8、10B.5、12、13C.12、18、22D.9、12、1511、如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为()A.20B.25C.30D.4012、我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形.现有一个对角线长分别为6和8的菱形,它的中点四边形的对角线长是( )A.5B.C.6D.1013、在△ABC中,∠C=90°,BC=2,sinA= ,则边AC的长是()A. B.3 C. D.14、如图,中,平分,交于点,,,,则的长为()A. B. C. D.15、△ABC中∠A,∠B,∠C的对边分别是a、b、c,下列命题为真命题的是( )A.如果∠A=2∠B=3∠C,则△ABC是直角三角形B.如果∠A:∠B:∠C=3:4:5,则△ABC是直角三角形 C.如果a:b:c=1:2:2,则△ABC 是直角三角形 D.如果a:b:c=3:4:,则△ABC是直角三角形二、填空题(共10题,共计30分)16、如图7,正方形①,②的一边在同一直线上,正方形③的一个顶点也在该直线上,且有两个顶点分别与正方形①,②的两个顶点重合,若正方形①,②的面积分别3cm2和4cm2,则正方形③的面积为________cm2.17、已知的对角线,相交于点,是等边三角形,且,则的长为________.18、如图,将一根长为20cm的筷子置于底面直径为5cm,高为12cm的圆柱形水杯中,筷子露在杯子外面的长度为________cm.19、如果一个四边形有且只有三个顶点在圆上,那么称这个四边形是该圆的“联络四边形”,已知圆的半径长为,这个圆的一个联络四边形是边长为的菱形,那么这个菱形不在圆上的顶点与圆心的距离是________.20、如图,圆柱形玻璃板,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离________cm.21、在Rt△ABC中,,,,则=________.22、如图,有一块直角三角形纸片,两直角边cm,cm,现将直角边沿直线折叠,使它落在斜边上,且与重合,则________.23、一个三角形的三边长分别为6,8,10,则这个三角形最长边上的高是________.24、在等腰Rt△ABC中,∠C=90°,AC=1,过点C作直线l∥AB,F是l上的一点,且AB=AF,则点F到直线BC的距离为________.25、等腰三角形的腰长为1cm,底边长为cm,则它的底角的正切值为________.三、解答题(共5题,共计25分)26、如图,中,于D.求及的长.27、如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km 处?28、如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?29、水池中有水,水面是一个边长为10尺的正方形,水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的终点,它的顶端恰好到达池边的水面.水的深度和这根芦苇的长度分别是多少?30、如图,在中,,,,求:的面积和的度数.参考答案一、单选题(共15题,共计45分)1、A2、D3、B4、A5、A6、A7、A8、D9、D10、C11、A12、A13、A14、A15、D二、填空题(共10题,共计30分)16、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、。
苏科版八年级上册数学第三章 勾股定理 含答案

15、C
二、填空题(共10题,共计30分)
16、
17、
18、
19、
20、
21、
22、
23、
24、
25、
三、解答题(共5题,共计25分)
26、
27、
28、
29、
30、
苏科版八年级上册数学第三章勾股定理含答案
一、单选题(共15题,共计45分)
1、下列各组数中,以a,b,c为边长的三角形不是直角三角形的是()
A.a=3,b=4,c=5 B.a=4,b=5,c=6 C.a=6,b=8,c=10 D.a=5,b=12,c=13
2、如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
21、如图,把矩形纸片 沿 折叠,使点B落在边 上的点 处,点A落在点 处,已知 .则 ________.
22、如图,已知正方形ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,则DE=________.
23、现有两根木棒的长度分别为40cm和50cm,若要钉成一个直角三角形木架,则所需木棒长度为________.
29、如图所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EF的长.
30、如图,在四边形 中, , , , .
求 的度数.
参考答案
一、单选题(共15题,共计45分)
1、B
2、C
3、A
4、D
5、C
6、C
7、C
8、D
9、C
10、B
11、C
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、下列各组线段a、b、c能构成直角三角形的是()A. ,,B. ,,C. ,,D. ,,2、如图,平面直角坐标系中,长方形OABC,点A,C分别在x轴,y轴的正半轴上,点B(6,3),现将△OAB沿OB翻折至△OA′B位置,OA′交BC于点P.则点P的坐标为()A.(,3)B.(,3)C.(,3)D.()3、如图,长方形ABCD中,AB=4,BC=3,将其沿直线MN折叠,使点C与点A重合,则CN的长为().A. B. C. D.4、如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD 内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为()A. B.2 C.2 D.5、下列各组数中,能成为直角三角形的三条边长的是()A.3,5,7B.1,,2C.4,6,7D.5,7,86、如图,大正方形是由49个边长为l的小正方形拼成的,A,B,C,D四个点是小正方形的顶点,由其中三个点为顶点的直角三角形的个数是()A.1B.2C.3D.47、△ABC中,∠C=90°,AC=8,BC=6,则cosA的值是()A. B. C. D.8、如图,周长为的菱形中,点分别在边上,为上一动点,则线段长度的最小值为()A. B. C. D.9、如图,△ABC中,D为AB的中点,BE⊥AC,垂足为E.若DE=4,AE=6,则BE的长度是()A.10B.2C.8D.210、如图所示,△ABC中,∠A=90°,D是AC上一点,且∠ADB=2∠C,P是BC 上任一点,PE⊥BD于点E,PE⊥AC于点F,下列结论:①△DBC是等腰三角形;②∠C=30°;③PE+PF=AB;④PE2+AF2=BP2.其中结论正确的序号是()A.只有①②③B.只有①③④C.只有②④D.①②③④11、勾股定理是人类最伟大的科学发明之一.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大的正方形内,三个阴影部分面积分别记为,,,若已知,,,则两个较小正方形纸片的重叠部分(四边形)的面积为()A.5B.5.5C.5.8D.612、如图,用8块相同的小长方形拼成一个大长方形,则大长方形对角线的长为()A.10 cmB.72cmC.10 cmD.10cm13、如图,中,是的中点,,垂足为.若,则的长度是()A.4B.6C.8D.1014、下列几组数中不能作为直角三角形的三边长的是()A.9,40,41B.8,10,12C.6,8,10D.7,24,2515、在Rt△ABC中,∠B=90°,BC=15,AC=17,以AB为直径作半圆,则此半圆的面积为()A.16πB.12πC.10πD.8π二、填空题(共10题,共计30分)16、如图,在长方形ABCD的边AD上找一点P,使得点P到B、C两点的距离之和最短,则点P的位置应该在________.17、已知是腰长为的等腰直角三角形,以的斜边为直角边,画第二个等腰再以的斜边为直角边,画第三个等腰,…,依此类推,第个等腰直角三角形的斜边长是________.18、如图,一棵大树在离地面4米高的处折断,树顶落在离树底端的5米远处,则大树折断前的高度是________米(结果保留根号).19、如图,正方形ABCD 中,边AB=6 ,点E 在边BC 上,且BE=2 ,点F 为边CD 上的一个动点,以 EF为直角边作直角三角形,,且,点 G在直线 EF的左上方,连接BG ,当点F 在边 CD上运动时,的周长的最小值为________.20、如图,在△ABC中,∠B=90°,AB= ,将AC沿AE折叠,使点C与点D 重合,且DE⊥BC,则AE=________.21、在平面直角坐标系中,O为坐标原点,设点P(1,t)在反比例函数y=的图象上,过点P作直线l与x轴平行,点Q在直线l上,满足QP=OP.若反比例函数y=的图象经过点Q,则k=________ .22、在中,,BC=6,DE是斜边AB的中垂线,交AC于点E,的周长为14,则AB=________23、如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D,E分别是AB,AC的中点,点G,F在BC边上(均不与端点重合),DG∥EF.将△BDG绕点D顺时针旋转180°,将△CEF绕点E逆时针旋转180°,拼成四边形MGFN,则四边形MGFN周长l的取值范围是________.24、如图,在Rt△ABC中,∠B=90°,AB=3 cm,AC=5 cm,将△ABC折叠,使点C与点A重合,得折痕DE,则△ABE的周长等于________.25、如图,在矩形ABCD中,AB=3,E为AD的中点,F为CD上一点,且DF=2CF,沿BE将△ABE翻折,如果点A恰好落在BF上,则AD=________.三、解答题(共5题,共计25分)26、如图所示,△ABC和△AEF为等边三角形,点E在△ABC内部,且E到点A,B,C的距离分别为3,4,5,求∠AEB的度数.27、如图,在中,,,,平分交于D点,E,F分别是,上的动点,求的最小值.28、如图,海中有一小岛A,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?29、如图,Rt△ABC中,∠ACB=90°,cosA= ,D为AB上一点,且AD:BD=1:2,若BC=3 ,求CD的长.30、如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.(1)求抛物线顶点A的坐标;(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状.参考答案一、单选题(共15题,共计45分)1、C2、A3、B4、B5、B6、B7、A8、C9、D10、B11、D12、A13、B14、B15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、25、三、解答题(共5题,共计25分)28、30、。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、在等边三角形ABC中,D,E分别是BC,AC的中点,点P是线段AD上的一个动点,当△PCE的周长最小时,P点的位置在().A.A点处B.D点处C.AD的中点处D.△ABC三条高线的交点处2、如图,各正方形的边长均为1,则四个阴影三角形中,一定相似的一对是()A.①②B.①③C.②③D.②④3、已知a=3,b=4,若a,b,c能组成直角三角形,则c=()A.5B.C.5或D.5或64、如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为()A.6B.8C.16D.555、如图,在矩形ABCD中,O是对角线AC、BD的交点,点E,F分别是OD,OC 的中点.如果AC=10,BC=8,那么EF的长为()A.6B.5C.4D.36、如图,分别以直角△ABC的三边AB,BC,CA为直径向外作半圆.设直线AB左边阴影部分的面积为S1,右边阴影部分的面积和为S2,则()A.S1=S2B.S1<S2C.S1>S2D.无法确定7、如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3, H 是AF的中点,那么CH的长是( )A.2.5B.C.D.28、如图,点A(a,3),B(b,1)都在双曲线y= 上,点C,D,分别是x 轴,y轴上的动点,则四边形ABCD周长的最小值为()A. B. C. D.9、如图,已知等边△ABC的边长为6,点D为AC的中点,点E为BC的中点,点P为BD上一点,则PE+PC的最小值为()A.3B.3C.2D.310、以下列选项中的数为长度的三条线段中,不能组成直角三角形的是()A.8,15,17B.4,6,8C.3,4,5D.6,8,1011、如图,正方形中的数表示该正方形的面积,则字母B所代表的正方形的面积是()A.12B.144C.13D.19412、如图所示,已知在三角形纸片中,,,,在边上取一点,以为折痕,使的一部分与重合,与延长线上的点重合,则的长度为()A. B. C. D.13、在△ABC中,∠A、∠B、∠C的对边分别为a,b,c,下列说法中错误的是()A.如果,那么B.如果,那么C.如果,那么D.如果,那么14、在如图的方格纸中,每个小方格都是边长为1的正方形,点A、B是方格纸中的两个格点(即正方形的顶点),在这个5×5的方格纸中,找出格点C使△ABC的面积为2个平方单位,则满足条件的格点C的个数是()A.5B.4C.3D.215、如图,正六边形ABCDEF内接于,过点O作弦BC于点M,若的半径为4,则弦心距OM的长为()A. B. C.2 D.二、填空题(共10题,共计30分)16、如图,在Rt△ABC中,∠C=90°,AC=3,以AB为一边向三角形外作正方形ABEF,正方形的中心为O,且OC=4 ,则BC=________.17、如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为弧AN 的中点,P是直径MN上一动点,则PA+PB的最小值为________.18、如图,△ABC是等腰三角形,AB=AC=5,BC=6,E为BA延长线上的一点,AE= AB,D为BC的中点,则DE的长为________.19、如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则的值为________.20、已知如图,△ABC为等腰三角形,D为CB延长线上一点,连AD且∠DAC=45°,BD=1,CB=4,则AC长为________.21、如图,⊙O的半径是,△ABC是⊙O的内接三角形,过圆心O分别作AB,BC,AC的垂线,垂足为E,F,G,连接EF,若OG=1,则EF的长为________ .22、如图所示的图案是我国汉代数学家赵爽在注解《周髀算经》中“赵爽弦图”经修饰后的图形,四边形与四边形均为正方形,点H是的中点,阴影部分的面积为24,则的长为________..23、如图,在中,,,,将绕点顺时针旋转后得到,将线段绕点逆时针旋转后得到线段,分別以、为圆心,、长为半径画弧和弧,连接,则图中阴影部分的面积是________.24、长方形的一条对角线的长为10cm,一边长为6cm,它的面积是________cm2.25、如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为________.三、解答题(共5题,共计25分)26、如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“反演点”.如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.27、如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C.(1)求证:四边形ABCD是正方形;(2)连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段MN、ND、DH之间的数量关系,并说明理由.(3)若EG=4,GF=6,BM=3,求AG、MN的长.28、如图,有一只小鸟从小树顶飞到大树顶上,请问它飞行的最短路程是多少米(先画出示意图,然后再求解).29、已知如图,.求四边形的面积.30、如图,已知⊙O的半径长为R=5,弦AB 与弦CD平行,他们之间距离为7,AB=6求:弦CD的长.参考答案一、单选题(共15题,共计45分)1、D2、A3、C4、C5、D6、A7、B8、B9、D10、B11、B12、A13、D14、A15、A二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、30、。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、如图,在中,,,,在数轴上,以点为圆心,长为半径画弧,交数轴于点,则点表示的数是()A. B. C. D.2、如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为A.90°B.60°C.45°D.30°3、如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为()A. B.4 C.2 D.64、如图:在等腰梯形ABCD中,AD∥BC,过D作DF⊥BC于F,若AD=2,BC=4,DF=2,则DC的长为()A.1B.C.2D.5、已知,如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距()A.25海里B.30海里C.35海里D.40海里6、如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E。
若DE=1,则BC的长为()A.2+B.C.D.37、平面直角坐标系中,点P(2,0)平移后对应的点为Q(5,4),则平移的距离为()A.3B.4C.5D.78、勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,已知∠BAC=90°,AB=6,AC=8,点D、E、F、G、H、I都在矩形KLMJ的边上,则矩形KLMJ的周长为()A.40B.44C.84D.889、已知的三边长为a,b,c,且,则()A.a边的对角是直角B.b边的对角是直角C.c边的对角是直角 D.不是直角三角形10、满足下列条件的△ABC中,不是直角三角形的是( )A.b²=c²-a²B.a:b:c=3:4:5C.∠C=∠A-∠BD.∠A:∠B:∠C=3:4:511、如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM= MF.其中正确结论的是()A.①③④B.②④⑤C.①③④⑤D.①③⑤12、把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D =30°,斜边AB=4,CD=5.把三角板DCE绕着点C顺时针旋转15°得到△D 1CE1(如图2),此时AB与CD1交于点O,则线段AD1的长度为()A. B. C. D.413、如图,是的中线,,把沿着直线对折,点落在点的位置.如果,那么以线段为边长的正方形的面积为().A.6B.72C.12D.1814、如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AE平分∠BAC,ED⊥AB,则ED的长()A.3B.4C.5D.615、适合下列条件的△ABC中,直角三角形的个数为()①∠A=32°,∠B=58°;②a=6,∠A=45°;③a= ,b= ,c= ;④a=7,b=24,c=25;⑤a=2,b=3,c=4.A.2个B.3个C.4个D.5个二、填空题(共10题,共计30分)16、如图,在四边形ABCD中,AB=AD,BC=CD,∠A=60°,点E为AD边上一点,连接BD、CE,CE与BD交于点F,且CE∥AB,若AB=,CE=,则BC的长为________.17、已知中,∠C=90°, a+b=14, c=10,则的面积等于________.18、已知在中,半径,弦,且,,则AB与CD的距离为________.19、已知直角三角形的两条直角边是3和5,则第三条边是________20、如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A 落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则cos∠EFG的值为________.21、如图,在四边形ABCD中,AB=1,BC=1,CD=2,则四边形ABCD的面积是________.22、直角三角形两条边的长度分别为3cm,4cm,那么第三条边的长度是________cm.23、Rt△ABC两直角边的长分别为6cm和8cm,则斜边上的中线长为________24、如图,中,,是的垂直平分线,交于点E,交于点D.连接.若,,则的周长为________.25、如图,直角梯形ABCD中,AD∥BC,∠ADC=∠BAC=90°,AB=2,CD=,则AD的长为________.三、解答题(共5题,共计25分)26、如图,方格纸上每个小正方形的面积为1.⑴在方格纸上,以线段AB为边画正方形ABCD,并计算所画正方形ABCD的面积.⑵请你在图上分别画出面积为5正方形A1B1C1D1和面积为10的正方形A 2B2C2D2,正方形的各个顶点都在方格纸的格点上.27、已知把长为和的三根细木棒首尾相连,能搭成一个直角三角形.如果把这三根细木棒的长度分别扩大为原来的倍,那么所得的三根细木棒能不能搭成一个直角三角形,为什么?28、已知△ABC的三边分别为k2-1,2k,k2+1(k>1),求证:△ABC是直角三角形.29、如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):(1)利用网格确定该圆弧所在圆的圆心D点的位置,并写出D点的坐标为;(2)连接AD、CD,则⊙D的半径为,∠ADC的度数为;(3)若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.30、如图,在四边形BCDE中,∠C=∠BED=90°,∠B=60°,延长CD、BE,两线相交于点A,已知CD=2,DE=1,求Rt△ABC的面积.参考答案一、单选题(共15题,共计45分)1、A2、C3、C4、B5、D6、A7、C8、C10、D11、C12、A13、D14、A15、A二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、27、28、29、30、。
苏科版八年级上册数学第三章 勾股定理 含答案

苏科版八年级上册数学第三章勾股定理含答案一、单选题(共15题,共计45分)1、CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=8,则BE的长是()A.8B.2C.2或8D.3或72、如图,所有的四边形是正方形,所有的三角形都是直角三角形,其中最大的正方形边长为13 cm,则图中所有的正方形的面积之和为()A.169cm 2B.196cm 2C.338cm 2D.507cm 23、正方形ABCD的边长为4,P 为BC上的动点,连接PA,作PQ⊥PA,PQ交CD 于Q,连接AQ ,则AQ的最小值是()A.5B.C.D.44、下列长度的三条线段能组成钝角三角形的是( )A.3,4,4B.3,4,5C.3,4,6D.3,4,75、如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为()A.4B.6C.8D.6、如图,小方格的面积是1,图中以格点为端点且长度为5的线段有( )A.5条B.4条C.3条D.2条7、如图,正方形ABCD的边长为4,点E在对角线BD上,且,EF⊥AB,垂足为F,则EF的长为()A.1B.C.D.8、在4×5网格中,A,B,C为如图所示的格点(小正方形的顶点),则下列等式正确的是()A.sinA=B.cosA=C.tanA=D.cosA=9、下列说法正确的是()A.已知a、b、c是三角形的三边长,则a 2+b 2=c 2B.在直角三角形中,两边的平方和等于第三边的平方C.在Rt△ABC中,∠C=90°,a、b、c 分别是∠A,∠B,∠C的对边,则a 2+b 2=c 2D.在Rt△ABC中,∠B=90°,a、b、c分别是∠A,∠B,∠C的对边,则a 2+b 2=c 210、三角形的三边长为a,b,c,且满足(a+b)2=c2+2ab,则这个三角形是( )A.直角三角形B.等边三角形C.钝角三角形D.锐角三角形11、如图,一根长25m 梯子,斜立在一竖直的墙上,这时梯足距墙底端7m,如果梯子的顶端下滑4m,那么梯足将滑动()A.15mB.9mC.8mD.7m12、如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边=6+3 ;其中正确的结论是()形AOBO′A.①②③B.①③④C.②③④D.①②13、如果,AB是⊙O的切线,A为切点,OB=5 ,AB=5,AC是⊙O的弦,OH⊥AC,垂足为H,若OH=3,则弦AC的长为()A.5B.6C.8D.1014、如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积分别是9、25、1、9,则最大正方形E的边长是()A.12B.44C.2D.无法确定15、如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波g拉底月牙”,当AC=4,BC=2时,则阴影部分的面积为()A.4B.4πC.8πD.8二、填空题(共10题,共计30分)16、如图所示,以直角三角形的一直角边和斜边为边长所作正方形A、C的面积分别为9和25,则以另一直角边为边长的正方形B的面积为________.17、点A、C为半径是4的圆周上两点,点B为弧AC的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆半径的中点上,则该菱形的边长为________.18、如图,矩形OABC的对角线OB长为6,顶点A,C在坐标轴上,反比例函数(k>0,x>0)的图象交边BC于点E,交边AB于点D,连结DE,若CE=2BE,则DE的长为 ________;19、如图所示,折叠长方形的一边AD,使点D落在边BC的点F处,已知AB=8cm,BC=10cm,则EC的长为________ cm.20、如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是________.21、如图,在四边形中,,点E是的中点.若,,则________.22、如图,在△ABC中,tanB= ,AB=10,AC=2 ,将线段AB绕点A旋转到AD,使AD∥BC,连接CD,则CD=________.23、如果一个矩形较短的边长为5cm,两条对角线所夹的角为60°,则这个矩形的面积是________.24、如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB=2 .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=________.25、已知:在矩形ABCD中,AB=4,AD=10,点P是BC上的一点,若∠APD=90°,则AP=________.三、解答题(共5题,共计25分)26、如图,在Rt△ABC中,∠C=90°,BC=8,tanB= ,点D在BC上,且BD=AD,求AC的长和cos∠ADC的值.27、如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.28、如图,水平放置的一个油管的截面半径为13cm,其中有油部分油面宽AB 为24cm,求截面上有油部分油面高CD(单位:cm).29、如图,某学校(A点)与公路(直线L)的距离为300米,又与公路车站(D点)的距离为500米,现要在公路上建一个小商店(C点),使之与该校A 及车站D的距离相等,求商店与车站之间的距离.30、如图,把一张长方形纸折叠,使点与点重合,折痕.若AB=4,BC=8,求 AF 的长参考答案一、单选题(共15题,共计45分)1、C2、D3、A4、C5、D6、B7、C8、D10、A11、C12、A13、C14、C15、A二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、27、29、。
2019-2020学年苏科版八年级上册第三章勾股定理过关检测随堂练习(解析版)

2019-2020学年苏科版八年级上册第三章勾股定理过关检测随堂练习(解析版)[测试范围:第3章 勾股定理 时间:40分钟 分值:100分]一、选择题(每小题4分,共24分)1.以a ,b ,c 为边长,不能组成直角三角形的是( ) A .a =6,b =8,c =10 B .a =0.3,b =0.4,c =0.5 C .a =8,b =15,c =17 D .a =13,b =14,c =152.如果一个三角形的三边长分别为6,8,10,那么最长边上的高为( ) A .2.4 B .4.8 C .6 D .83.在△ABC 中,∠C =90°,AB =2,则AC 2+BC 2+AB 2的值是( ) A .2 B .4 C .6 D .84.如图3-Z -1,在△ABC 中,AB =AC =5,BC =8,D 是线段BC 上的动点(不与端点B ,C 重合).若线段AD 长为正整数,则点D 的个数共有( )图3-Z -1A .5个B .4个C .3个D .2个5.已知在Rt △ABC 中,∠C =90°,a +b =14,c =10,则△ABC 的面积为( ) A .48 B .24 C .96 D .206.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图3-Z -2所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a ,较短直角边长为b .若ab =8,大正方形的面积为25,则小正方形的边长为( )图3-Z-2A.9 B.6 C.4 D.3二、填空题(每小题4分,共24分)7.如图3-Z-3所示,图中阴影部分正方形的面积是________.图3-Z-38.如图3-Z-4,在△ABC中,CD⊥AB于点D,E是AC的中点.若AD=6 cm,DE =5 cm,则CD的长为________cm.图3-Z-49.如果△ABC的三边长分别为a,b,c,且满足关系式(a+2b-60)2+|b-18|+(c-30)2=0,那么△ABC是__________三角形.10.若直角三角形中,斜边长比一直角边长大2,且另一直角边长为6,则斜边长为________.11.如图3-Z-5,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C2的长为________.图3-Z-512.如图3-Z-6所示,△ABC为等边三角形,AD为BC边上的高,且AB=2,则正方形ADEF的面积为________.图3-Z-4三、解答题(共52分)13.(6分)如图3-Z-7,在四边形ABCD中,∠C=90°,BD平分∠ABC,AD=3,E 为AB上一点,AE=4,ED=5,求CD的长.图3-Z-714.(6分)在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.图3-Z-815.(8分)如图3-Z-9所示,将长方形ABCD沿直线BD折叠,使点C落在点C′处,BC′交AD于点E,AD=16,AB=8,求DE的长.图3-Z-916.(8分)如图3-Z-10所示,某人到岛上去探宝,从A处登陆后先往东走4 km,又往北走1.5 km,遇到障碍后又往西走2 km,再转向北走到4.5 km处往东一拐,仅走0.5 km就找到了宝藏.则登陆点A与宝藏埋藏点B之间的距离是多少?(提示:42.25=6.52)图3-Z-1017.(12分)如图3-Z-11,在△ABD中,AC⊥BD于点C,E为AC上一点,连接BE,DE,DE的延长线交AB于点F,已知DE=AB,∠CAD=45°.(1)求证:DF⊥AB;(2)利用图中阴影部分面积完成勾股定理的证明,已知:在△ABC中,∠ACB=90°,BC =a,AC=b,AB=c.求证:a2+b2=c2.图3-Z-1118.(12分)如图3-Z-12,在Rt△ABC中,∠B=90°,AB=7 cm,AC=25 cm.点P 从点A沿AB方向以1 cm/s的速度运动至点B,点Q从点B沿BC方向以6 cm/s的速度运动至点C,P,Q两点同时出发.(1)求BC的长;(2)当点P,Q运动2 s时,求P,Q两点之间的距离;(3)P,Q两点运动几秒时,AP=CQ?图3-Z-12教师详解详析1.D2.[解析] B 因为62+82=102,由勾股定理的逆定理可以判断此三角形是直角三角形,利用直角三角形面积的两种表达形式可得ab =ch (其中a ,b 为直角边长,c 为斜边长,h 为斜边上的高).3.[解析] D ∵∠C =90°,AB =2,∴AC 2+BC 2=AB 2=4.∴AC 2+BC 2+AB 2=4+4=8.故选D.4.[解析] C 如图,过点A 作AE ⊥BC 于点E .∵AB =AC ,∴EC =BE =12BC =4.∴AE 2=52-42=9,即AE =3.∵D 是线段BC 上的动点(不与端点B ,C 重合),∴3≤AD <5.∵线段AD 的长为正整数,∴点D 的个数共有3个.故选C.5.[解析] B ∵a +b =14,∴(a +b )2=196.∴2ab =196-(a 2+b 2)=96.∴ab =48.∴12ab =12×48=24.故选B. 6.[解析] D 由题意可知中间小正方形的边长为a -b . ∵每一个直角三角形的面积为12ab =12×8=4,∴4×12ab +(a -b )2=25.∴(a -b )2=25-16=9.∴a -b =3.故选D. 7.[答案] 64 cm 2[解析] 设正方形的边长为x cm.由勾股定理,得x 2+152=172,∴x 2=64.∴图中阴影部分正方形的面积为64 cm 2.8.[答案] 8[解析] ∵CD ⊥AB 于点D ,E 是AC 的中点,∴DE 是Rt △ACD 边AC 的中线.∵AD =6 cm ,DE =5 cm ,∴AC =2DE =10 cm.根据勾股定理,得AD 2+CD 2=AC 2,∴CD 2=64.∴CD =8 cm.故答案为8.9.[答案] 直角[解析] ∵(a +2b -60)2+|b -18|+(c -30)2=0,∴a+2b-60=0,b-18=0,c-30=0.∴a=24,b=18,c=30.∵242+182=302,∴△ABC是直角三角形.故答案为直角.10.[答案] 10[解析] 设一直角边长为a,则斜边长为a+2.∵另一直角边长为6,∴(a+2)2=a2+62,解得a=8,∴a+2=8+2=10.11.[答案] 27[解析] ∵∠ACB=∠AC′B′=90°,AC=BC=3,∴AB2=18,∠CAB=45°.∵△ABC和△A′B′C′大小、形状完全相同,∴∠C′AB′=∠CAB=45°,AB′2=AB2=18.∴∠CAB′=90°.∴B′C2=AC2+AB′2=9+18=27.12.[答案] 3[解析] ∵在等边三角形ABC中,AD为BC边上的高,∴AD也是BC边上的中线,即D 为BC的中点,∴BD=DC=1.∵AD⊥BC,∴AD2+BD2=AB2.∴AD2=AB2-BD2=22-12=3.∴正方形ADEF的面积为3.13.解:∵AD=3,AE=4,ED=5,∴AD2+AE2=ED2.∴∠A=90°.∴DA⊥AB.∵∠C=90°,∴CD⊥BC.∵BD平分∠ABC,∴CD=AD.∵AD=3,∴CD=3.14.解:在△ABC中,AB=15,BC=14,AC=13,设BD=x,则CD=14-x.在Rt△ABD中,由勾股定理,得AD2=AB2-BD2=152-x2.在Rt△ACD中,由勾股定理,得AD2=AC2-CD2=132-(14-x)2,∴152-x2=132-(14-x)2,解得x=9.∴AD=12.故S △ABC =12BC ·AD =12×14×12=84.15.[解析] 先根据折叠的性质得出CD =C ′D ,∠C =∠C ′=90°,再设DE =x ,则AE =16-x ,由全等三角形的判定定理得出Rt △ABE ≌Rt △C ′DE ,可得出BE =DE =x ,在Rt △ABE 中利用勾股定理即可求出x 的值,进而得出DE 的长.解:由折叠的性质,得CD =C ′D =AB =8,∠C =∠C ′=90°. 设DE =x ,则AE =16-x .在△ABE 和△C ′DE 中,⎩⎨⎧∠A =∠C ′=90°,∠AEB =∠C ′ED ,AB =C ′D ,∴△ABE ≌△C ′DE ,∴BE =DE =x . 在Rt △ABE 中,由勾股定理,得 AB 2+AE 2=BE 2,即82+(16-x )2=x 2, 解得x =10,即DE =10.16.解:如图,过点B 作BC ⊥AD 于点C ,则AC =4-2+0.5=2.5(km),BC =4.5+1.5=6(km).在Rt △ABC 中,由勾股定理,得AB 2=AC 2+BC 2=2.52+62=6.52,∴AB =6.5(km). 答:登陆点A 与宝藏埋藏点B 之间的距离是6.5 km. 17.证明:(1)∵AC ⊥BD ,∠CAD =45°, ∴AC =DC ,∠ACB =∠DCE =90°,在Rt △ABC 与Rt △DEC 中,⎩⎨⎧AC =DC ,AB =DE ,∴Rt △ABC ≌Rt △DEC (HL). ∴∠BAC =∠EDC .∵∠EDC +∠CED =90°,∠CED =∠AEF , ∴∠AEF +∠BAC =90°.∴∠AFE =90°.∴DF ⊥AB .(2)∵S △BCE +S △ACD =S △ABD -S △ABE ,∴12a 2+12b 2=12·c ·DF -12·c ·EF =12·c ·(DF -EF )=12·c ·DE =12c 2. ∴a 2+b 2=c 2.18.解:(1)∵在Rt △ABC 中,∠B =90°,AB =7 cm ,AC =25 cm ,∴BC 2=AC 2-AB 2=252-72=242.∴BC =24 cm.(2)连接PQ .由题意知BP =7-2=5(cm),BQ =6×2=12(cm).在Rt △BPQ 中,由勾股定理,得PQ 2=BP 2+BQ 2=52+122=132,∴PQ =13 cm. (3)设P ,Q 两点运动t s 时,AP =CQ ,则t =24-6t ,解得t =247.答:P ,Q 两点运动247 s 时,AP =CQ .。
2019-2020学年苏科版初二数学第一学期第3章《勾股定理》单元测试题(含答案)
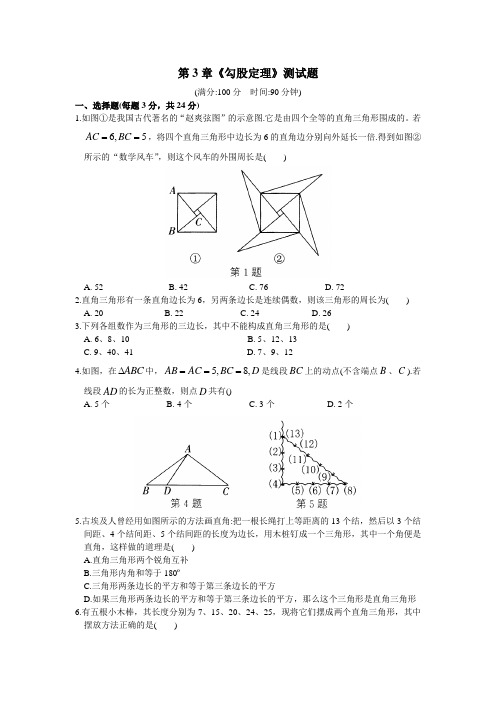
第3章《勾股定理》测试题(满分:100分 时间:90分钟)一、选择题(每题3分,共24分)1.如图①是我国古代著名的“赵爽弦图”的示意图.它是由四个全等的直角三角形围成的。
若6,5AC BC ==,将四个直角三角形中边长为6的直角边分别向外延长一倍.得到如图②所示的“数学风车”,则这个风车的外围周长是( )A. 52B. 42C. 76D. 722.直角三角形有一条直角边长为6,另两条边长是连续偶数,则该三角形的周长为( ) A. 20 B. 22 C. 24 D. 263.下列各组数作为三角形的三边长,其中不能构成直角三角形的是( ) A. 6、8、10 B. 5、12、13 C. 9、40、41 D. 7、9、124.如图,在ABC ∆中,5,8,AB AC BC D ===是线段BC 上的动点(不含端点B 、C ).若线段AD 的长为正整数,则点D 共有()A. 5个B. 4个C. 3个D. 2个5.古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( ) A.直角三角形两个锐角互补 B.三角形内角和等于180ºC.三角形两条边长的平方和等于第三条边长的平方D.如果三角形两条边长的平方和等于第三条边长的平方,那么这个三角形是直角三角形 6.有五根小木棒,其长度分别为7、15、20、24、25,现将它们摆成两个直角三角形,其中摆放方法正确的是( )7.四个全等的直角三角形按如图所示的方式围成正方形ABCD ,过各较长直角边的中点作垂线,围成面积为S 的小正方形EFGH ,已知AM 为Rt ABM ∆的较长直角边,4AM EF =,则正方形ABCD 的面积为( )A. 18SB. 17SC. 16SD. 15S8.如图,圆柱形容器的底面周长是2lcm ,高为17 cm ,在外侧底面S 处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1 cm 的点F 处有一苍蝇,急于捕获苍蝇充饥的蜘蛛所走的最短路线长度是( )A. 20 cmB. 22 cmC. 23 cmD. 24 cm 二、填空题(每题3分,共24分)9.如图,在ABC ∆中,10AB AC ==c m ,12BC =c m ,AD BC ⊥于点D ,则 AD = cm.10.如图①,这个图案是我国汉代的赵爽在注解《周骸算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图②所示,其中四边形ABCD 和四边形EFGH 都是正方形,ABF ∆、BCG ∆、CDH ∆、DAE ∆是四个全等的直角三角形.若2,8EF DE ==,则AB 的长为 .11.如图,正方形ABDE 、CDFI 、EFGH 的面积分别为25、9、16,AEH ∆、BDC ∆、GFI ∆的面积分别为1S 、2S 、3S ,则123S S S ++= .12.如图,在ABC ∆中,5,12,13,A C B C A B CD ===是AB 边上的中线,则CD = .13.如图,长方体的高为3 cm ,底面是正方形,边长为2 cm ,现使一绳子从点A 出发,沿长方体表面到达C 处,则绳子最短是 cm.14.如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形,若小正方形与大正方形的面积之比为1:13,则直角三角形较短的直角边a 与较长的直角边b 的比值为 .15.我国古代有这样一道数学问题: “枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A 处缠绕而上,绕五周后其末端恰好到达点B 处,则问题中葛藤的最短长度是 尺.16.观察下列各组数:(3,4,5),(5,12,13),(7,24,25),(9,40,41),…,可发现,23142-=,251122-=,271242-=,…,请写出第5组数: .三、解答题(共52分)17.(8分)如图,某住宅小区在施工过程中留下了一块空地,已知4AD =米,3CD =米,90ADC ∠=︒,13AB =米,12BC =米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?18. (8分)某路段限速标志规定:小汽车在此路段上行驶速度不得超过70千米/时.如图,一辆小汽车在一条城市街道上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30米的C 处,过了2秒后,小汽车行驶到B 处,测得小汽车与车速检测仪间距离50米. (1)求BC 的长;(2)这辆小汽车超速了吗?19. (8分)(1)如图①,在ABC ∆中,3,4,5,BC AC AB D ===为AB 边上一点,且ACD ∆ 与BCD ∆的周长相等,则AD = .(2)如图②,在ABC ∆中,,2BC a AC ==,222AB BC AC =+,E 为BC 边上一点,且ABE ∆与ACE ∆的周长相等;F 为AC 边上一点,且ABF ∆与BCF ∆的周长相等.求CE CF g 的值(用含a 、b 的式子表示).20. (8分)如图,在ABC ∆中,90C ∠=︒,点P 在AC 上运动,点D 在AB 上,PD 始终保持与PA 相等,BD 的垂直平分线交BC 于点E ,交BD 于点F ,连接DE . (1)判断DE 与DP 的位置关系.并说明理由; (2)若6,8,2AC BC PA ===,求线段DE 的长.21.(8分)如图①,有四个同样大小的直角三角形,两条直角边分别为a 、()b a b <,斜边为c ,拼成一个正方形,中间留有一个小正方形.(1)利用它们之间的面积关系,探索出关于a 、b 、c 的等式.(2)利用(1)中发现的直角三角形中两直角边a 、b 和斜边c 之间的关系。
苏科版数学初二上册第三章勾股定理章节练习

苏科版数学初二上册第三章勾股定理章节练习A . 1,a b c ==B . 53,1,44a b c ===C . 2,3,a b c ==D . 7,23,24a b c === 【答案】D【解析】 该题考察的是勾股定理的逆定理.A 、2221+=,能组成直角三角形; B 、22235144⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭,能组成直角三角形;C 、22223+=,能组成直角三角形; D 、22272324+>,不能组成直角三角形;应选D .2 三角形的三边长区分为22a b +、2ab 、22a b -〔a 、b 都是正整数〕,那么这个三角形是〔 〕A . 直角三角形B . 钝角三角形C . 锐角三角形D . 不确定【答案】A【解析】 依据勾股定理的逆定理可知,当三角形中三边的关系为:222a b c +=时,那么三角形为直角三角形,∵()()()22222222a b ab a b -+=+,∴三角形为直角三角形. 3 假设三角形的一个角是另一个角的3倍,那么我们称这个三角形为〝智慧三角形〞.以下各组数据中,能作为一个智慧三角形三边长的一组是〔 〕A . 1,2,3B . 1,1C . 1,1D . 12【答案】D【解析】 此题考察特殊角直角三角形,D 选项三角形,三内角为30,60,90︒︒︒4 △ABC 中,∠A 、∠B 、∠C 的对边的区分用a 、b 、c 来表示,且其满足关系:222200121620a b c a b c +++=++,试判别ABC △的外形.【答案】 直角三角形【解析】 原式可化简为()()()22268100a b c -+-+-=,由非正数的性质知,6a =,8b =,10c =.因此222a b c +=.5 三角形的三边区分为a 、b 、c ,且1a m =-,b =,1c m =+〔1m >〕.〔1〕这个三角形一定是直角三角形吗?为什么?〔2〕试给出一组直角三角形的三边的长,使它的最小边不小于20,另两边的差为2,三边均为正整数.【答案】 〔1〕这个三角形一定是直角三角形;〔2〕100m =,99a =,101c =【解析】 〔1〕∵222221214211m m m m m m m -+=-++=++=+()((),∴这个三角形一定是直角三角形;〔2〕取100m =,那么99a =,101c =.6 罕见勾股数有:3、____、____;5、____、____;6、____、____;7、____、____;8、____、____;9、____、____【答案】 4;5;12;13;8;10;24;25;15;17;12;15【解析】 罕见勾股数有:3、4、5;5、12、13;6、8、10;7、24、25;8、15、17;9、12、15. 7 如图,将△ABC 放在正方形网格图中〔图中每个小正方形的边长均为1〕,点A ,B ,C 恰恰在网格图中的格点上,那么△ABC 中BC 的高是〔 〕 A . 10 B . 10 C . 10 D . 5 【答案】A【解析】 该题考察的是等腰直角三角形的性质.依据图形可得:5AB AC ==,10BC =,故△ABC 为等腰直角三角形,90BAC ∠=︒,故BC 边上的初等于斜边BC 的一半,故10BC =. 应选A . 8 将一个有45°角的三角板的直角顶点放在一张宽为3cm 的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,那么三角板的最大边的长为〔 〕A . 3cmB . 6cmC . 32cmD . 62cm【答案】D【解析】过点C 作CD ⊥AD ,∴CD=3,在直角三角形ADC 中,∵∠CAD=30°,∴AC=2CD=2×3=6,又∵三角板是有45°角的三角板,∴AB=AC=6,∴BC 2=AB 2+AC 2=62+62=72,∴BC=62,应选:D .9 如图,D 为ABC △外一点,BD AD ⊥,BD 平分ABC △的一个外角,C CAD ∠=∠,假定5AB =,3BC =,那么BD 的长为〔 〕A . 1B . 1.5C . 2D . 3【答案】D【解析】 此题考察勾股定理及等腰三角形的判定与性质.如图,设CB 与AD 延伸线交于E 点.又∵BD 平分∠ABE ,BD ⊥AD ,∴在RT △ABD中,由勾股定理失掉3BD =. 10 如图是一株美丽的勾股树,其中一切的四边形都是正方形,一切的三角形都是直角三角形.假定正方形A ,B ,C ,D 的边长区分是3,5,2,3,那么最大正方形E 的面积是〔 〕A . 13B . 26C . 47D . 94【答案】C【解析】依据勾股定理的几何意义,可得A 、B 的面积和为S 1,C 、D 的面积和为S 2,S 1+S 2=S 3,于是S 3=S 1+S 2, 即S 3=9+25+4+9=47.应选C .11 如图,在Rt △ABC 中,∠C=90°,BC=1,D 在AC 上,将△ADB 沿直线BD 翻折后,点A 落在点E 处,假设AD ⊥ED ,那么△ABE 的面积是〔 〕A . 1B .C .D .【答案】A【解析】∵∠C=90°,BC=1,∴,∴∠BAC=30°,∵△ADB 沿直线BD 翻折后,点A 落在点E 处,∴BE=BA=2,∠BED=∠BAD=30°,DA=DE ,∵AD ⊥ED ,∴BC ∥DE ,∴∠CBF=∠BED=30°,在Rt △BCF 中,,BF=2CF=, ABC D∴EF=2-23, 在Rt △DEF 中,FD=12EF=1-3,ED=3FD=3-1, ∴S △ ABE =S △ ABD +S △ BED +S △ ADE=2S △ ABD +S △ ADE=2×12BC•AD+12AD•ED =2×12×1×〔3-1〕+12×〔3-1〕〔3-1〕 =1.应选A .12 如图,在四边形ABCD 中,∠A=120°,∠C=60°,AB=2,AD=DC=4,那么BC 边的长为 .【答案】 6【解析】 连结BD ,作DM ⊥AB 于M ,DN ⊥BC 于N ,∵∠BAD=120°,∴∠MAD=180°﹣120°=60°,∵AD=4,∴AM=2,DM=2,∵∠C=60°,∴DN=2,NC=2,在Rt △BDM 与Rt △BDN 中,∴Rt △BDM ≌Rt △BDN 〔HL 〕,∴BN=BM=2+2=4,∴BC=BN+NC=6.故答案为:6.13 如图,长方体的高5BC =cm ,一只小蚂蚁从A 点爬到BC 上某一点P ,再爬到D 点去吃糖,假设小蚂蚁走的最短路程是13cm ,那么AB BE +=宽长____cm【答案】 12【解析】 如图展开,衔接AD 交BC 于P ,此时小蚂蚁走的路程最短,13AD =cm ,5BC DE ==cm ,90E ∠=︒,在Rt △AED 中,由勾股定理得:2213512cm AE =-(),即12AB BE +=宽长cm ,14 如图,在Rt △ABC 中,∠ACB=90°,AC=6,BC=8,AD 是∠BAC 的平分线.假定P ,Q 区分是AD 和AC 上的动点,那么PC+PQ 的最小值是〔 〕A . 125B . 4C . 245D . 5 【答案】C【解析】如图,过点C 作CM ⊥AB 交AB 于点M ,交AD 于点P ,过点P 作PQ ⊥AC 于点Q ,∵AD 是∠BAC 的平分线.∴PQ=PM ,这时PC+PQ 有最小值,即CM 的长度,∵AC=6,BC=8,∠ACB=90°,∴AB=22AC BC +=2268+=10.∵S △ ABC =12AB•CM=12AC•BC , ∴CM=AC BC AB =6810⨯=245, 即PC+PQ 的最小值为245. 应选:C .15 如图,圆柱形玻璃容器高20cm ,底面圆的周长为48cm ,在外侧距下底1cm 的点A 处有一蜘蛛,与蜘蛛相对的圆柱描画器的上口外侧距上口1cm 的点B 处有一只苍蝇,那么蜘蛛捕捉苍蝇所走的最短路途长度为 .【答案】 30cm【解析】 把圆柱沿过B 点的母线剪开,然后展开如图,A′点为点A 展开后的对应点,作BH ⊥MN 于H ,BH=×48=24,MH=1,A′N=1,∴A′H=20﹣1﹣1=18,在Rt △A′BH 中,A′B==30〔cm 〕.16 照应〝绿色环保,疏通出行〞的召唤,越来越多的市民选择乘地铁出行,为保证市民方便出行,我市新建了多条地铁线路,与旧地铁线路相比,新建地铁车站出入口上下楼梯的高度普遍添加,原楼梯BD 长20米,在楼梯水平长度〔BC 〕不发作改动的前提下,楼梯的倾斜角由30°增大到45°,2 1.414≈3 1.732〕【答案】 新修建的楼梯高度将会添加约7米【解析】 该题考察的是解直角三角形. 由题意,可知△ABC 和△BDC 都是直角三角形,∵在Rt △BDC 中,20BD =,30DBC ∠=︒,∴依据勾股定理22222010103BC BD CD =-=-=……………………………2分∵在Rt △ABC 中,45ABC ∠=︒,∴103AC BC ==………………………… ………………………………………3分∴10310AD AC CD =-=-,………………………………………………………4分∴7AD ≈米,…………………………………………………………………………5分17 :如图,线段AB 、DE 表示一个斜靠在墙上的梯子的两个不同的位置,假定CB =3m ,∠ABC =45°,要使∠EDC =60°,那么需BD =__________m .【答案】3【解析】该题考察的是特殊直角三角形.△ABC是等腰直角三角形;△EDC是含30°的直角三角形,18某开发区有一块四边形的空地ABCD,如下图,现方案在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,假定每平方米草皮需求200元,问要多少投入?【答案】7200〔元〕【解析】该题考察的是勾股定理的运用.如图,衔接BD,在Rt△ABD中,222222345BD AB AD=+=+=,在△CBD中,2213CD=,2212BC=,而22212513+=,即222BC BD CD+=,所以需费用362007200⨯=〔元〕.19如下图,B.C两个乡镇相距25千米,有一个自然维护区A与B相距15千米,与C相距20千米,以点A为圆心,10千米为半径是自然维护区的范围,如今要在B.C两个乡镇之间修一条蜿蜒的公路,请问:这条公路能否会穿过自然维护区?试经过计算加以说明.【答案】不会穿过【解析】该题考察的是解三角形.由题得,25BC=,15AB=,20AC=,在△ABC中,由于222AB AC BC+=,设BC边上的高为h,∴11502ABCS BC h∆=⋅=,解得12h=,∴这条公路不会穿过自然维护区.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二数学第三章随堂练习
班级:姓名:
一、精心选一选
1、下列图形中,不是轴对称图形的有( )
A 、1个
B 、2个
C 、3个
D 、4个
2、下列说法正确的是( )
A 、形状相同的两个三角形全等
B 、面积相等的两个三角形全等
C 、完全重合的两个三角形全等
D 、所有的等边三角形全等
3、如图:已知AB =AC ,添加下列条件仍不能..
使△ABD ≌△ACD 的是( ) A 、∠B =∠C =90° B 、AD 平分∠BAC C 、AD 平分∠BDC D 、BD =CD
4、在四边形ABCD 中,AB =AD ,BC =CD ,则两对角线AC 与BD 的关系是()
A 、AC 垂直平分BD
B 、BD 垂直平分AC
C 、AC 与B
D 互相垂直平分 D 、BD 平分∠ADC
5、已知∠AOB 的平分线上一点P 到OA 的距离为5,Q 是OB 上任意一点,则( )
A. PQ ⩾ 5
B. PQ > 5
C. PQ ⩽5
D. PQ <5
6、下列长度的各组线段中,能够组成直角..
三角形的是( ) A 、5、6、7 B 、5、11、12 C 、7、20、25 D 、8、15、17
7、若直角三角形斜边上的高和中线分别是6cm 和8cm ,则它的面积是( )
A 、224cm
B 、248cm
C 、296cm
D 、无法确定
8、三角形的三边长分别为6、8、10,那它最长边上的高为( )
A 、4.8
B 、5
C 、6
D 、8
9、下列说法:①等腰三角形的两底角相等;②线段垂直平分线上的点到两边的距离相等;③成轴对称的
两个图形中,对应点的连线被对称轴垂直平分;④全等三角形的对应边上的高相等;⑤在直角三角形中,30°角所对的直角边是斜边的一半.以上结论正确的个数为( )
A 、5个
B 、2个
C 、3个
D 、4个
10、如图:等腰△ABC 的底边BC 长为6,面积是18,腰AC 的垂直平分线EF 分别交AC ,AB 边于E ,F 点.若
点D 为BC 边的中点,点M 为线段EF 上一动点,则△CDM 周长的最小值为( )
A 、6
B 、8
C 、9
D 、10
二、细心填一填
11、一个等腰三角形的两边长分别为4cm 和8cm ,则周长是_________cm .
12、在平面镜里看到背后墙上,电子钟示数如图所示,这时的实际时间应该是______.
13、△ABC 中,∠ACB =90°,E 是AB 的中点,如果AB =6,则CE =.
14、等腰△ABC 的周长为25,底边BC =7,AB 的垂直平分线DE 交AB 于点D ,交AC 于点E ,则△BEC 的周长为. 15、如图,△ABC 是等边三角形,D ,E ,F 分别是AB ,BC ,CA 边上一点,且AD=BE=CF .则△DEF 的形状是________.
16、在△ABC 中,底角∠A =80°,若∠B =__________时,△ABC 是等腰三角形.
17、如图,在△ABC 中,AD ⊥BC 于D ,CE ⊥AB 于E ,AD 、CE 交于点H ,已知EH
=EB =3,AE =4,则CH 的长是.
18、如图,点P 是∠AOB 内任意一点,OP=5cm ,点M 和点N 分别是射线OA 和射
线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是_______°
三、认真答一答:
19、如图,在长度为1个单位长度的小正方形组成的正方形网格中,△ABC的三个顶点A、B、C都在格点
上.
(1)在图中画出与△ABC关于直线l成轴对称的△A1B1C1;
(2)在直线l上找出一点Q,使得 QA+QC1的值最小;(保留痕迹并标上字母Q)
(3)在正方形网格中存在_______个格点,使得该格点与B、C两点构成以BC为底边的等腰三角形。
20、如图已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠D=∠B,AD∥BC.
求证:DF=BE.
21、如图已知:∠A=∠D=90°,AC=DB,AC、DB相交于点O,求证:OB=OC;
22、如图所示,在一棵树的10m 高处有两只猴子,其中一只猴子爬下树走到离树20m 处的池塘A 处,另一只爬到树顶后直接跃向池塘的A 处,距离以直线计算,如果两只猴子所经过的距离相等,试问这棵树有多高?
23、如图:已知在△ABC 中,AD ⊥BC 于D ,E 是AB 的中点,
(1)E 点一定在的垂直平分线上;
(2)如果AD =16cm ,AC =20cm ,F 点在AC 边上从A 点向C 点运动、速度是2cm/s ,求当运动几秒钟时.△ADF 是等腰三角形?
24、如图:已知AB ∥CD ,BC ⊥CD ,且CD =2AB =12,BC =8,E 是AD 的中点,
(1)请你用直尺(无刻度)画出一条线段与BE 相等;并证明之;
(2)求BE 的长.
25、如图⑴:已知在△ABC 中,AB =AC ,P 是底边BC 上一点,作PD ⊥AB 于D ,PE ⊥AC 于E ,BF ⊥AC 于F ,求证:PD +PE =BF.
【思路梳理】:如⑵图:连接AP ,必有,因为△ABP 、△ACP 和△ABC 的底相等,所以三条高PD 、PE 和BF 满足关系:PD +PE =BF.
ABC APC APB S S S ∆∆∆=+
【变式应用】:如图⑶:已知在△ABC中,AB=AC,P是底边BC的反向延长线上一点,作PD⊥AB于D,PE ⊥AC于E,BF⊥AC于F,求证:PE-PD=BF.
【联想拓展】:已知某三角形的三条边分别是5cm、12 cm、13 cm,在平面上有一点P,它到此三角形的三边的距离相等,则这个距离等于.
26、⑴、如图1:将长方形ABCD(∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC)折叠,使BC落在
对角线BD上,折痕为BE,点C落在点F处,若∠ADB=48°,则∠DBE的度数为________°.
⑵、小明手中有一张长方形纸片ABCD,AB=12,AD=27.
【画一画】:如图2:点E在这张长方形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为MN(点M、N分别在边AD、BC上),利用直尺和圆规画出折痕MN(不写作法,保留作图痕迹,并用黑色水笔把线段MN描清楚).
【算一算】:如图3:点F在这张长方形纸片的边BC上,将纸片折叠,使FB落在线段FD上,折痕为GF,点A、B分别落在点E、H处,若△DCF的周长等于48,求DH和AG的长.。
