初三中考重点题型分析(二)
中考命题研究中考物理 第二编 重点题型突破 专题二 填空题(无答案)

专题二填空题,专题特征) 填空题大都是一个缺字少词或少句少结果的不完整陈述,要求应试者通过回忆、理解、判断、计算等思维活动,填入准确的字、词、句或数据或单位,使全题表述完整,使问题有一个明确的结果,全题有的填一处,有的要填几处。
怀化物理卷中占20分。
(一)填空题的类型1.记忆型填空题。
这类题主要考查对物理概念、定理、定律以及物理量的符号、单位的记忆能力。
【例1】改变内能有两种方式:____________和________。
光在真空中传播的速度是________m/s。
【例2】1标准大气压等于________毫米汞柱,密度的公式是________,单位是________。
【分析】这类题所填内容源于课本,关键是平时多看书,对重要的物理概念、定理、定律、公式和单位要强化记忆,确保解答时准确、迅速。
2.计算型填空题。
这类题必须通过计算才能填空。
它的特点是题目中有物理过程、有数据,解答时要利用物理公式计算,最后将结果填入题中空白处。
【例3】弹簧秤下挂一质量为79克的铁块,当它投入水中时,弹簧秤的示数是________牛。
(ρ铁=7.9×103kg/m3,ρ水=1.0×103kg/m3,g取10N/kg)【分析】这类题解答的关键是:细心审题,弄清物理过程,正确运用物理公式,代入数据准确,单位统一,在稿纸上求出结果。
3.解释现象型填空题。
这类题考查应试者观察生活、实验中的物理现象并作出解释的能力。
【例4】缝衣针头做得很尖是为了________,缝衣时总要把针在头发上擦一擦是为了________。
【分析】解答这类题的关键是:平时注意留心观察生活、实践中的物理现象,经过头脑中周密思考,找出现象中依据的物理知识,然后加以解释。
4.图示型填空题。
题目中给出图形,要求应试者析图、标图或根据图形填入适当的物理知识。
【例5】如图所示,竖直放置的试管中装有液体,若将试管倾斜(液体不溢出)时,试管底部受到液体压强将________(选填“变大”、“变小”或“不变”)。
专题02 物态变化-2023年中考物理毕业班二轮热点题型归纳与变式演练(全国通用)(解析版)

专题02 物态变化目录一、热点题型归纳【题型一】温度【题型二】熔化和凝固【题型三】汽化和液化【题型四】升华和凝华【题型五】三个图像二、最新模考题组练【题型一】温度【典例分析】用实验室常用温度计测量烧杯中热水的温度时,下列说法正确的是()。
A.温度计的感温泡可以碰到容器壁;B.将感温泡浸入热水马上读出温度;C.读数时温度计可以离开被测热水;D.读数时如图所示,测量数据偏大【答案】D【解析】A.温度计感温泡不可以碰到容器底或容器壁,否则会造成所测温度不准确,故A错误;B.将感温泡浸没热水后,应待温度计示数稳定后,再读数,故B错误;C.读数时温度计不应离开热水来读数,否则会造成读数有偏差,故C错误;D.读数时,视线应与刻度值保持水平,图中俯视读数或导致测量结果偏大,故D正确。
故选D。
【提分秘籍】1.温度:温度是用来表示物体冷热程度的物理量。
我们常说热的物体温度高,冷的物体温度低,如果两个物体冷热程度一样,它们的温度相同。
2.温度计:温度计是利用液体的热胀冷缩原理制成的。
3.温度计的使用方法(1)使用前:观察它的量程、分度值(每个小刻度表示多少温度),估测是否适合测量待测物体的温度,待测温度不能超过温度计的量程(否则会损坏温度计);并看清温度计的分度值,以便准确读数。
(2)测量时:温度计的玻璃泡应全部浸入被测液体中,不能紧靠容器壁和容器底部;温度计玻璃泡浸入被测液体中稍候一会儿,待温度计的示数稳定后再读数;读数时玻璃泡要继续留在被测液体中,视线与温度计中液柱的上表面相平,并估测到最小刻度的下一位。
4.体温计体温计是专门用来测量人体体温的,测量范围:35℃~42℃;分度值为0.1℃,体温计读数时可以离开人体。
【变式演练】1.(2022·湖北鄂州·统考中考真题)妈妈对你说,今天降温了,看看墙上挂的寒暑表,自己选择合适的衣服。
如图所示,关于该寒暑表,下列说法正确的是()A.寒暑表的量程是﹣50~50℃B.寒暑表的分度值是0.1℃C.寒暑表的示数是21℃D.寒暑表的示数是39℃【答案】C【解析】A.寒暑表的量程是-35~50℃,故A错误;B.寒暑表的分度值是1℃,故B错误;CD.由寒暑表的分度值和液柱指示刻度可知,寒暑表的示数是21℃,故C正确,D错误。
中考物理重要测量仪器考试要点及题型分析:专题2 机械秒表(停表)问题(含解析)

中考物理重要测量仪器考试要点及题型分析专题02 机械秒表(停表)一、用机械秒表(停表)测量时间问题学啥1.机械停表的构造与用途如图甲秒表的主要构造有:A.启动、停止按钮;B.回零按钮;C.分钟刻度:读取整分钟数(包括半分钟);D.秒钟刻度(读取秒数)。
甲乙2.机械停表的使用方法对于甲图秒表,使用秒表前首先要上好发条,按压启动按钮,表启动,再次按下该按钮,秒表指针停止转动,按压回零按钮,分针与秒针都归零. 即三次按下按钮:一“走时”,二“停止”,三“复零”,对于乙图秒表,使用前,转动秒表上端带滚花的手轮,上紧发条使用时,分为开始、停止、秒表清零三步。
(1)第一次按下手轮,开始记时,指针开始走动;(2)第二次按下手轮,停止记时,指针停止走动,读出时间,读数时视线应垂直与所读刻度;(3)第三次按下手轮,秒表清零,指针复位。
3.机械停表的原理与读数方法秒表是利用周期性振动的等时性制成的.它的读数方法是:①首先读出小刻度盘中的整分钟数(包括半分钟);②然后读出大刻度盘的秒刻度数;③将两个读数统一单位后先后相加即将两个读数统一单位后相加即得最后读数。
4.会使用钟表或停表测量时间使用停表时(1)测量前:要注意小圈的指针所指数字的单位是min;大圈指针所指数字的单位是s,常用的停表秒针走两圈为1min,即分针走1格。
要注意分针和秒针的分度值(2)测量时:先读分针指示的示数,观察分针是否过半格,再秒针所指的示数。
二、用机械秒表(停表)测量时间问题考法【例题1】下图所示秒表的读数是_______。
【答案】579 s【解析】秒表读数问题是难点,原因就是平时使用的次数不多,训练的少。
要加大实践的力度就会突破这个难点。
这个问题应该属于今后中考命题的热点素材。
抓住秒表使用与读数规则是关键。
首先读出秒表分钟数是9min=540s然后观察剩余值是否已过半刻度,是。
再读出剩余部分的秒数39s。
最后将两个读数统一单位后相加即得最后读数为579秒。
【卷2】题型二 关注生产实际-2023年中考化学必练题型聚焦(解析版)

题型二关注生产实际1.某实践小组参观本地矿泉水厂,该厂矿泉水含钙、钾等矿物质,其生产流程示意图如下,回答下列问题。
(1)矿泉水中的钙、钾指的是_______(填“元素”或“单质”)。
(2)活性炭过滤器中活性炭的作用是________________________________________。
(3)超滤是利用薄膜(仅允许小分子和离子通过)进行物质分离的技术。
若水源中含有下列物质,推测该流程中“超滤”的主要作用是除去_______(填字母序号)。
A.难溶性大颗粒B.可溶性无机盐C.可溶性高分子化合物(4)臭氧的化学式O3的微观意义是________________________________________(写出1点即可)。
(5)生活中,你提倡饮用白开水还是矿泉水,理由是________________________________________。
2.2021年3月的全国两会上,“碳达峰”“碳中和”被首次写人政府工作报告。
我国承诺,力争于2030年前二氧化碳的排放量达到峰值,之后逐步降低。
以下是二氧化碳的捕集流程。
分析流程,结合NaOH的溶解度表,回答下列问题:(1)捕捉室中氢氧化钠溶液的溶质质量分数最高是________(精确到1%)。
(2)X的化学式是________________。
(3)分离室中将物质分离的方法是____________________。
(4)上述流程中发生分解反应的化学方程式是___________________________________________。
(5)上述流程中可循环利用的物质是_______________。
3.“奋斗者号”万米深潜,新型钛合金Ti-62A功不可没。
工业上利用钛铁矿(主要成分是FeTiO3,还含一定量Fe2O3杂质)提炼金属钛并制备绿矾(FeSO4·7H2O)的流程如下图。
请分析制备过程,回答下列问题。
资料:FeTiO3 +3H2SO4= Ti( SO4)2 + FeSO4 +3H2O(1)“粉碎”的目的是____________________________________________________________。
初三英语试卷分析_教学反思.doc

初三英语试卷分析_教学反思九年级英语试卷分析(一)在教育局教研室统筹安排和指导下,我们老师进行了认真监考和阅卷,现将本次考试分析如下:一、试题分析本次试题严格按照山西省中考题型来出,.注重实际情景和具体语境中考察学生对基础知识理解和运用,有较强探究性和灵活性。
试卷突出了语言交际能力,力求体现课程标准精神。
试卷着重考查了学生理解和运用语言能力,重视考查学生英语基础知识、基本技能,考查学生运用所学知识分析问题、解决问题能力。
考试范围为UNITS1-13所学内容,侧重于UNITS8-13,总体难度适中,听力第四题和任务型阅读难度较大。
试卷选材有一定时代感和知识性,在选材上既注意了所选材料在题材和体裁上多样性,又注意了所选材料思想性和教育性。
注重教育学生跨文化意识培养,较好地落实了新课标中关于对文化意识培养理念。
增加学生阅读量,拓展学生知识面,提高学生综合运用语言能力。
二、作答情况分析I、听力,四道大题各有侧重.第一题情景反应,主要失分题有:1小题,广告语EVERYTHINGISPOSSIBLE。
学生对生活不了解而不知道。
8小题学生只听SHEIS16YEARSOLD.就着急选择,而不听HOWOLDISTHEBOY?和SHEIS2YEARSOLDERTHANME。
9小题学生听到ATTENTOSEVEN就选7:10,对于时间表达法不清楚,不知道TO与PAST意义。
第三大题语篇理解中12,14,15小题,失分也很严重,这几个题都是听数字,并且学生需要扑捉信息太长,同学们听起来很吃力。
第四题听力填空,难度较大,考生做此类题目,普遍存在许多问题,失分最为严重,90%多学生得零分。
同时同学们单词记忆和书写不能过关。
II、单项填空题,难度不是很大,主要失分题有:16,18,29等题。
本次考试题紧抠所学内容并包含以前语法知识。
好学生做题情况较好,70%学生得分在10分以上,但不及格同学基础较差,结果不是很好。
III、完形填空,是综合性较强题型,集中考查阅读理解与语言运用能力为一体,检测考生综合运用语言能力。
【中考2022】初中物理重点题型复习 题型二 作图题 (含答案)

题型二作图题模块1 光学作图(2020·湖北十堰)如图,空气中某点光源S发出的一条光线射向水面,在水面发生反射和折射,反射光线经过P点。
请在图中作出这条入射光线、对应的反射光线和折射光线的大致方向(保留作图痕迹)。
思路点拨先作出S关于水面的对称点,得到S经过反射形成的虚像S′。
连接S′P,与水面的交点O即为入射点,连接SO即为入射光线,连接OP即为反射光线。
再根据折射规律作出折射光线。
(2020·福建)如图所示,点光源S位于凸透镜一侧。
在图中画出S发出的两条光线通过凸透镜后的折射光线。
思路点拨先确定所给的光线的特点,再根据透镜的光学特点作图是关键。
类型❶光的反射作图1.(2021·贵州黔东南)如图所示,A、B是镜前一点光源S发出的光线经平面镜MN反射后的两条反射光线,请在图中画出点光源S的位置。
2.(2022·改编)如图所示,光射到平面镜上,使其沿水平方向传播,请在图中画出平面镜的位置。
类型❷光的折射作图3.(2021·淄博)“珍爱生命,注意安全”是我们应具备的安全意识。
由于光的折射,池水看起来比实际的浅,夏季要特别注意防范溺水事故,用A、A′分别表示池底和看到的“池底”,请在图中画出人眼看到池底的光路图。
4.(2021·内蒙古赤峰)如图所示,请画出激光束从三棱镜折射入空气时,法线的位置和折射光线的大致位置。
类型❸平面镜成像作图5.(2021·四川德阳)如图所示,A′O′是AO在平面镜中的像,请根据平面镜成像特点在图中画出平面镜的位置。
6.(2020·四川广元)根据平面镜成像特点画出点光源S发出的光经平面镜反射后过A点的反射光线。
7.(2020·泰安改编)利用一块平面镜使图中的一束光竖直射入井中,请你通过作图标出平面镜的位置,并标出反射角的度数。
类型❹根据光线画透镜8.(2019·东营)根据入射光线和折射光线,请在图中虚线框内画出适当类型的透镜。
中考生物重点题型二 资料分析题

第二部分福建中考重点题型集训题型二资料分析题类型一传染病、免疫与健康(必考)1. (2019龙岩5月质检)2019年1月2日,“糖丸之父”顾方舟病逝。
他研制的脊灰糖丸活疫苗,使中国于2000年实现了无脊灰状态,这意味着千百万儿童远离了小儿麻痹症。
脊髓灰质炎是一种急性传染病,脊髓灰质炎病毒常侵犯中枢神经系统,损害脊髓前角运动神经细胞,导致肢体松弛性麻痹,多见于儿童,故又名小儿麻痹症。
请回答:(1)中枢神经系统包括________和脊髓。
(2)脊髓灰质是神经元的________集中出现的部位。
(3)脊髓前角运动神经细胞受损,会影响肢体肌肉的收缩,肌肉属于反射弧结构中的________。
(4)小儿麻痹症的病原体是______________。
(5)儿童免疫力较低,从传染病流行的环节看,他们属于____________。
(6)从免疫的角度看,脊灰糖丸活疫苗属于________(填“抗原”或“抗体”)。
2. (2018宁德5月质检)根据资料回答:资料一:据报道,淄博一男子不幸患上尿毒症,他母亲用自己的一颗肾脏给了儿子第二次生命。
肾移植时,患者的免疫系统会对异体器官产生排斥,因此移植手术后需长期使用免疫抑制剂药物。
资料二:2017年,一则“106名学生染艾滋”的消息引起网友的关注与热议。
艾滋病是由于感染艾滋病病毒引起的,主要传播途径有血液传播、母婴传播、性传播等。
中学生感染艾滋病可能性最大的途径是血液传播。
(1)资料中属于传染病的是________,其病原体是由____________和蛋白质外壳组成。
(2)血液流经肾脏后,血液中尿素含量________。
(3)从免疫学角度来说,被移植的肾脏相当于______(填“抗原”或“抗体”)。
(4)请你结合生活实际说说如何避免感染艾滋病?________________________________________________________________________。
中考数学10道经典题型分析
中考数学10道经典题型分析跟大家分享一下近期初三数学总复习的一些好的题目,相信总有一款题目你会感兴趣。
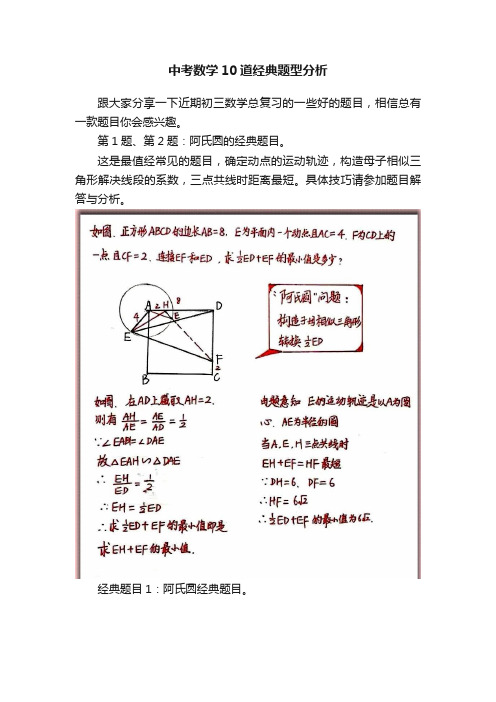
第1题、第2题:阿氏圆的经典题目。
这是最值经常见的题目,确定动点的运动轨迹,构造母子相似三角形解决线段的系数,三点共线时距离最短。
具体技巧请参加题目解答与分析。
经典题目1:阿氏圆经典题目。
经典题目2:阿氏圆问题。
第3题:费马点问题。
费马点问题也是最值问题最常见的题型,三线线段之和最短,通过旋转构造全等三角形,实现线段的转换(移到同一直线上),四点共圆时,线段之和最短。
经典题目3:胡不归问题。
第4题:胡不归问题。
胡不归问题同样的线段最值常见问题,AB+kCD的最值问题,首先要解决其中一条线段的K值,阿氏圆通常采用构造母子相似三角形来解决这个问题,而胡不归通常采用三角函数来解决这个问题。
这道综合题还是很不错的,值得练一练。
经典题目4:胡不归问题。
第5,6题:二次函数中的a,b,c问题。
在选择题中,这也算是比较有点难度的问题了,而且考试的频率往往非常高,需要熟练掌握。
基本的技巧我已经在下面列出了。
经典题目5:二次函数多结论问题。
经典题目7:二次函数多结论问题。
第7题:相似三角形综合题目。
这是一次模拟测验的倒数第2题,三角形综合题。
这道题比较好,是因为它不只一种解法,尤其是在第3问中,有不同的作辅助线的方法,有点意思。
经典题目7:三角形综合题。
第8题:中考压轴题模拟题。
这是深圳南山区联考模拟卷的压轴题,最后一问其实并不难,根据题意不难理解,动点的运动轨迹是某个圆的一段弧,在同一个圆中,同弧(弦)所对的圆周角相等,从而可以确定动点的运动轨迹,三点共线时,由距离最短。
具本思路和过程可参照下面答案。
经典题目8:中考压轴题目。
第9题:平行四边形的存在性问题。
这道题目真的很不错,弄懂这道题目,平行四边形的存在性问题就基本弄懂了。
我在参考答案中列举了三种常见的方法,其中包括点的坐标平移法,中点坐标(平行四边形对角顶点坐标之间的关系要熟练掌握)等。
初三语文试卷分析与反思10篇

初三语文试卷分析与反思10篇初三语文试卷分析与反思10篇初三语文试卷分析与反思(一):填空题默写题考察了《过零丁洋》《诗经·蒹葭》《岳阳楼记》和《浣溪沙》(一曲新词酒一杯),四篇都是重点备考的对象,不多说。
名著阅读考察了《孟子》,也是学生需重点注意的名著之一。
其考查形式给各位考生的备考供给了一个方向,即名著的相关文学常识、涉及到名著的课文的具体资料(包括提到的重要地点、时间、人物、事件、主题)都应当成为重点记忆的对象。
选择题题量六道,东城与西城一样,题型上稍有创新,将关联词替换成了病句。
其六种题型中,字音字形与西城海淀一样,都涉及到对新增二十个词语的考察。
其他题,病句题不难,而标点、语意衔接及修辞则是十分难为各位考生了。
标点所考察的书名号用法及引号与其他符号的位置关系会难倒一批考生;语意衔接考察的是上下文资料及语法结构的严格一致,语感稍差的同学都选不出来;修辞手法中所附的材料可用“不知所云”来评价,材料过于晦涩,且主题太不明显,中考不太会出这样的材料。
综合性学习第一题,整合并概括材料信息。
材料形式为“表格+文字材料”,文字材料中概括两个要点并不难,表格的概括相对较难,表此刻表头不够清晰,能做出的同学需有较好的逻辑思维。
第二题,概括采访记录。
思路跟2011年中考一致,基本上需概括的关键词都在各个材料的第一句话中,要概括的自我的理解也只是各个看法的整合,这使得本题很容易。
第三题,考察学生对材料进行高度概括的本事,比前两题难,但若掌握了方法,本题也容易。
仔细审题可知,标题中已知部分对应的是材料最终一段,所以学生需概括的即是一二段的资料,一段写“爱心分队”诞生,二段写“分队用爱心传递温暖”,将这两个意思概括为与标题已知部分格式一致的句子即可。
文言文阅读从篇目上看,考察的是《陈涉世家》,就预测性来说,不算成功。
题型则是一贯的实词解释、句子翻译与文意理解,可分析之处不多。
现代文阅读文学类阅读:王蒙《新疆的歌》相对海淀、西城文学类阅读都选择“亲情”主题的文章,东城选取的主题比较晦涩,王蒙的《新疆的歌》,是一篇主题偏向于地域文化的抒情散文,理解上来说,会比《苏醒中的母亲》及《母亲》都难。
初三政治考试分析

初三政治考试分析(一)本次期中考试试卷系从兄弟学校引进,考试内容为人教版教材九年级两个单元1-5课内容。
试卷包括选择题,简答题、材料分析题、实践探究题四种题型。
选择题共三十道题,每题一分合计三十分。
关于责任与角色的内容1分,涉及对外开放3分个人与集体、个人利益与集体利益关系2分,不言代价与回报、热心公益2分,民族关系问题2分,祖国统一两岸关系3分,科教兴国战略3分,保护环境与实施可持续发展战略4分,名族文化与民族精神3分,计划生育1分,关于三个代表1分,青少年历史使命1分,主要矛盾、根本任务2分,取得各项成绩的根本原因和原因2分。
选择题注重理解和分析能力,学生得分最高分为28分(有一道题目答案存在争议),最低分为15分,总体状况不理想,这除了试题本身较难这一原因外,还可能在于学生平时书本还不够熟练,对知识的领会还不够深,今后要加强这些方面的训练。
简答题10分,考的是教科书的循环使用利国利民,利在何处,重点考查的是学生对事物的分析和评价,学会从多个角度分析和认识问题,对应的知识点是节约资源,保护环境,实施可持续发展战略,社会责任感等,联系实际还为国家和家庭能够节省了经费,减轻了国家和家庭的经济负担培养了学生爱护课本等良好的行为习惯培养其珍惜资源爱护环境的意识和强烈的社会责任感等。
这一题材料来源与学生生活实际,学生很熟悉,所以作答相对较容易,大部分学生都能说出所以然。
材料分析题两大题,关于国际局势变化和对外开放的内容16分,涉及中华文化的24分,共计40分。
文化方面的内容包括讲到文化你会想到什么?如何正确对待外来文化?京剧进入九年义务教育音乐课程谈谈自己的看法。
前面的题目基本上都比较客观,只有最后一题对京剧进入义务教育音乐课程的题目考察学生在掌握教材知识的基础上,应用知识去分析问题、解决问题的能力,同时也考察学生对我国传统文化的正确认识和情感。
此题能反映出学生的正确情感和解题技巧与能力,部分学生发挥很好,有部分学生情感正确,理论联系实际能力差,语言苍白无力,难以说服打动人,得分不理想。
中考数学题型归类与解析2---整式及运算(解析版)

中考数学题型归类与解析2 整式及运算一、单选题1.(2021·浙江丽水市·中考真题)计算:()24a a -⋅的结果是( )A .8aB .6aC .8aD .6a -【答案】B【分析】根据乘方的意义消去负号,然后利用同底数幂的乘法计算即可.【解析】解:原式24246a a a a +=⋅==.故选B .【小结】此题考查的是幂的运算性质,掌握同底数幂的乘法法则是解题关键.2.(2021·四川资阳市·中考真题)下列计算正确的是( )A .2242a a a +=B .23a a a ⋅=C .22(3)6a a =D .623+=a a a【答案】B【分析】根据合并同类项,同底数幂的乘法,积的乘方法则进行计算作出判断.【解析】解:A . 2222a a a +=,故此选项不符合题意; B . 23a a a ⋅=,正确,故此选项符合题意;C . 22(3)9a a =,故此选项不符合题意;D . 62,a a 不是同类项,不能合并计算,故此选项不符合题意;故选:B .【小结】本题考查合并同类项,同底数幂的乘法,积的乘方计算,掌握计算法则准确计算是解题关键.3.(2021·四川自贡市·中考真题)已知23120x x --=,则代数式2395x x -++的值是( )A .31B .31-C .41D .41-【答案】B【分析】根据题意,可先求出x 2-3x 的值,再化简()22395=3+53x x x x -++--,然后整体代入所求代数式求值即可.【解析】解:∵23120x x --=,∴23=12x x -,∴()223395=3+5=312+5=31x x x x -++---⨯-.故选:B .【小结】此题考查了代数式求值,此题的关键是代数式中的字母表示的数没有明确告知,而是隐含在题设中,得出23=12x x -,是解题的关键.4.(2021·四川乐山市·中考真题)某种商品m 千克的售价为n 元,那么这种商品8千克的售价为( )A .8n m (元)B .8n m (元)C .8m n (元)D .8m n(元) 【答案】A【分析】先求出1千克售价,再计算8千克售价即可;【解析】∵m 千克的售价为n 元,∴1千克商品售价为n m, ∴8千克商品的售价为8n m (元); 故答案选A .【小结】本题主要考查了列代数式,准确分析列式是解题的关键.5.(2021·四川泸州市·中考真题)关于x 的一元二次方程2220x mx m m ++-=的两实数根12,x x ,满足122x x =,则2212(2)(2)x x ++的值是( )A .8B .16C . 32D .16或40【答案】C【分析】根据一元二次方程根与系数的关系,即韦达定理,先解得2m =或1m =-,再分别代入一元二次方程中,利用完全平方公式变形解题即可.【解析】解:一元二次方程2220x mx m m ++-=21,2,a b m c m m ===-2122c m x am x ==-= 220m m --=(2)(1)0m m ∴-+=2m ∴=或1m =-当2m =时,原一元二次方程为2420x x ++=12=24b m ax x +-=-=-, 22221212122)+2((2)(2)()+4=x x x x x x +∴++,221212122=()2x x x x x x ++-221212212212)+(2)(2)=)(2(4+4x x x x x x x x -∴+++22=2+2(4)424⨯--⨯+32=当1m =-时,原一元二次方程为2220x x +=-2(2)41240∆=--⨯⨯=-<原方程无解,不符合题意,舍去,故选:C .【小结】本题考查一元二次方程根与系数的关系,韦达定理等知识,涉及解一元二次方程,是重要考点,难度较易,掌握相关知识是解题关键.6.(2021·四川泸州市·中考真题)已知1020a =,10050b =,则1322a b ++的值是( ) A .2B .52C .3D .92【答案】C【分析】根据同底数幂的乘法31010010a b ⋅=,可求23a b +=再整体代入即可.【解析】解: ∵1020a =,10050b =,∴2310100102050100010a b a b +⋅==⨯==,∴23a b +=, ∴()()1311233332222a b a b ++=++=+=. 故选:C .【小结】本题考查幂的乘方,同底数幂的乘法逆运算,代数式求值,掌握幂的乘方,同底数幂的乘法法则,与代数式值求法是解题关键.7.(2021·云南中考真题)按一定规律排列的单项式:23456,4,9,16,25a a a a a ,……,第n 个单项式是( )A .21n n a +B .21n n a -C .1n n n a +D .()21n n a +【答案】A【分析】根据题目中的单项式可以发现数字因数是从1开始的正整数的平方,字母的指数从1开始依次加1,然后即可写出第n 个单项式,本题得以解决.【解析】解:∵一列单项式:23456,4,9,16,25a a a a a ,...,∴第n 个单项式为21n n a +,故选:A .【小结】本题考查数字的变化类、单项式,解答本题的关键是明确题意,发现单项式的变化特点,求出相应的单项式.8.(2021·浙江金华市·中考真题)某超市出售一商品,有如下四种在原标价基础上调价的方案,其中调价后售价最低的是()A.先打九五折,再打九五折B.先提价50%,再打六折C.先提价30%,再降价30%D.先提价25%,再降价25%【答案】B【分析】设原件为x元,根据调价方案逐一计算后,比较大小判断即可.【解析】设原件为x元,∵先打九五折,再打九五折,∴调价后的价格为0.95x×0.95=0.9025x元,∵先提价50%,再打六折,∴调价后的价格为1.5x×0.6=0.90x元,∵先提价30%,再降价30%,∴调价后的价格为1.3x×0.7=0.91x元,∵先提价25%,再降价25%,∴调价后的价格为1.25x×0.75=0.9375x元,∵0.90x<0.9025x<0.91x<0.9375x故选B【小结】本题考查了代数式,打折,有理数大小比较,准确列出符合题意的代数式,并能进行有理数大小的比较是解题的关键.9.(2021·浙江温州市·中考真题)某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米a 元;超过部分每立方米()1.2a +元.该地区某用户上月用水量为20立方米,则应缴水费为( )A .20a 元B .()2024a +元C .()17 3.6a +元D .()20 3.6a +元【答案】D【分析】分两部分求水费,一部分是前面17立方米的水费,另一部分是剩下的3立方米的水费,最后相加即可.【解析】解:∵20立方米中,前17立方米单价为a 元,后面3立方米单价为(a +1.2)元, ∴应缴水费为17a +3(a +1.2)=20a +3.6(元),故选:D .【小结】本题考查的是阶梯水费的问题,解决本题的关键是理解其收费方式,能求出不同段的水费,本题较基础,重点考查了学生对该种计费方式的理解与计算方法等.10.(2021·甘肃武威市·中考真题)对于任意的有理数,a b ,如果满足2323a b a b ++=+,那么我们称这一对数,a b 为“相随数对”,记为(),a b .若(),m n 是“相随数对”,则()323[]21m m n ++-=( )A .2-B .1-C .2D .3【答案】A先根据新定义,可得9m +4n =0,将整式()21]2[33m m n ++-去括号合并同类项化简得942m n +-,然后整体代入计算即可.【解析】解:∵(),m n 是“相随数对”, ∴2323m n m n ++=+, 整理得9m +4n =0,()323213642942[]2m m n m m n m n ++-=++-=+-=-.故选择A .【小结】本题考查新定义相随数对,找出数对之间关系,整式加减计算求值,掌握新定义相随数对,找出数对之间关系,整式加减计算求值是解题关键.11.(2021·山东临沂市·中考真题)实验证实,放射性物质在放出射线后,质量将减少,减少的速度开始较快,后来较慢,实际上,物质所剩的质量与时间成某种函数关系.下图为表示镭的放射规律的函数图象,据此可计算32mg 镭缩减为1mg 所用的时间大约是( )A .4860年B .6480年C .8100年D .9720年【分析】根据物质所剩的质量与时间的规律,可得答案.【解析】解:由图可知:1620年时,镭质量缩减为原来的12, 再经过1620年,即当3240年时,镭质量缩减为原来的21142=, 再经过1620×2=3240年,即当4860年时,镭质量缩减为原来的31182=, ...,∴再经过1620×4=6480年,即当8100年时,镭质量缩减为原来的511232=, 此时132132⨯=mg , 故选C .【小结】本题考查了函数图象,规律型问题,利用函数图象的意义是解题关键.12.(2021·山东泰安市·中考真题)下列运算正确的是( )A .235235x x x +=B .()3326x x -=-C .()222x y x y +=+D .()()2322349x x x +-=- 【答案】D【分析】分别根据合并同类项法则、积的乘方运算法则、完全平方公式、平方差公式进行判断即可.【解析】解:A 、x 2和x 3不是同类项,不能合并,此选项错误;B 、()3328x x -=-,此选项错误;C 、()2222x y x xy y +=++,此选项错误;D 、()()23223(23)(23)49x x x x x +-=+-=-,此选项正确, 故选:D .【小结】本题考查了同类项、积的乘方、完全平方公式、平方差公式,熟记公式,掌握运算法则是解答的关键.13.(2021·江苏连云港市·中考真题)下列运算正确的是( )A .325a b ab +=B .22523a b -=C .277a a a +=D .()22112x x x -+-=【答案】D【分析】根据同类项与合并同类项、全完平方差公式的展开即可得出答案.【解析】解:A ,3a 与2b 不是同类项,不能合并,故选项错误,不符合题意;B ,25a 与22b 不是同类项,不能合并得到常数值,故选项错误,不符合题意;C ,合并同类项后2787a a a a +=≠,故选项错误,不符合题意;D ,完全平方公式:()22211221x x x x x =-++-=-,故选项正确,符合题意; 故选:D .【小结】本题考查了代数式的运算,同类项合并及完全平方差公式,解题的关键是:掌握相关的运算法则.14.(2021·安徽)计算23()x x ⋅-的结果是( )A .6xB .6x -C .5xD .5x -【答案】D【分析】利用同底数幂的乘法法则计算即可【解析】解:52233=-()x x x x +⋅-=-故选:D【小结】本题考查同底数幂的乘法法则,正确使用同底数幂相乘,底数不变,指数相加是关键15.(2021·陕西中考真题)计算:()23a b -=( ) A .621a b B .62a b C .521a bD .32a b - 【答案】A【分析】根据积的乘方,幂的乘方以及负整数指数幂运算法则计算即可.【解析】解:()23621a b a b -=, 故选:A .【小结】本题考查积的乘方,幂的乘方以及负整数指数幂等知识点,熟记相关定义与运算法则是解答本题的关键.16.(2021·湖南衡阳市·中考真题)下列运算结果为6a 的是( )A .23a a ⋅B .122a a ÷C .()23aD .2312a ⎛⎫ ⎪⎝⎭ 【答案】C【分析】根据同底数幂相乘、同底数幂相除、幂的乘方法则逐项计算即可.【解析】A 选项,23235a a a a +⋅==,不符合题意;B 选项,12210122=a a a a -=÷,不符合题意;C 选项,()23326=a a a ⨯=,符合题意;D 选项,22233611=1224a a a ⨯⎛⎫⋅= ⎪⎝⎭⎛⎫ ⎪⎝⎭,不符合题意. 故选:C .【小结】本题考查同底数幂相乘、同底数幂相除、幂的乘方和积的乘方法则.同底数幂相乘,底数不变,指数相加;同底数幂相除,底数不变,指数相减;幂的乘方,底数不变,指数相乘;积的乘方,等于把积的每一个因式的积的乘方,再把所得的幂相乘.17.(2021·浙江台州市·中考真题)已知(a +b )2=49,a 2+b 2=25,则ab =( )A .24B .48C .12D .【答案】C【分析】利用完全平方公式计算即可.【解析】解:∵()222249a b a b ab +=++=,2225a b +=, ∴4925122ab -==, 故选:C .【小结】本题考查整体法求代数式的值,掌握完全平方公式是解题的关键.18.(2021·浙江台州市·中考真题)将x 克含糖10%的糖水与y 克含糖30%的糖水混合,混合后的糖水含糖( )A .20%B .+100%2x y ⨯C .+3100%20x y ⨯D .+3 100%10+10x y x y ⨯ 【答案】D【分析】先求出两份糖水中糖的重量,再除以混合之后的糖水总重,即可求解.【解析】 解:混合之后糖的含量:10%30%3100%1010x y x y x y x y ++=⨯++, 故选:D .【小结】本题考查列代数式,理解题意是解题的关键.19.(2021·江苏苏州市·中考真题)已知两个不等于0的实数a 、b 满足0a b +=,则b a a b +等于( ) A .2-B .1-C .1D .2【答案】A【分析】先化简式子,再利用配方法变形即可得出结果.【解析】 解:∵22=b a b a a b ab++, ∴()2222==a b ab b a b a a b ab ab +-++, ∵两个不等于0的实数a 、b 满足0a b +=, ∴()22-2===-2a b ab b a ab a b ab ab+-+, 故选:A .【小结】本题考查分式的化简、配完全平方、灵活应用配方法是解题的关键.20.(2021·上海中考真题)下列单项式中,23a b 的同类项是( )A .32a bB .232a bC .2a bD .3ab【答案】B【分析】比较对应字母的指数,分别相等就是同类项【解析】∵a 的指数是3,b 的指数是2,与23a b 中a 的指数是2,b 的指数是3不一致, ∴32a b 不是23a b 的同类项,不符合题意; ∵a 的指数是2,b 的指数是3,与23a b 中a 的指数是2,b 的指数是3一致, ∴232a b 是23a b 的同类项,符合题意;∵a 的指数是2,b 的指数是1,与23a b 中a 的指数是2,b 的指数是3不一致,∴2a b 不是23a b 的同类项,不符合题意;∵a 的指数是1,b 的指数是3,与23a b 中a 的指数是2,b 的指数是3不一致, ∴3ab 不是23a b 的同类项,不符合题意;故选B【小结】本题考查了同类项,正确理解同类项的定义是解题的关键.21.(2021·四川广安市·中考真题)下列运算中,正确的是( )A .2510a a a ⋅=B .222()a b a b -=-C .()23636a a -=D .22232a b a b a b -+=- 【答案】D【分析】根据同底数幂的乘法,合并同类项,幂的乘方和积的乘方,完全平方公式分别判断即可.【解析】解:A 、257a a a ⋅=,故选项错误;B 、222()2a b a b ab -=+-,故选项错误;C 、()23639a a -=,故选项错误;D 、22232a b a b a b -+=-,故选项正确;故选D .【小结】本题考查了同底数幂的乘法,合并同类项,幂的乘方和积的乘方,完全平方公式,解题的关键是掌握各自的运算法则.22.(2021·四川眉山市·中考真题)下列计算中,正确的是( )A .5315a a a ⨯=B .53a a a ÷=C .()423812a b a b -=D .()222a b a b +=+ 【答案】C【分析】逐一分析各选项中的计算结果,利用计算公式进行计算即可得到正确选项.【解析】解:A 选项中,538a a a ⨯=;B 选项中,532a a a ÷=;C 选项正确;D 选项中,()2222a b a ab b +=++;故选:C .【小结】本题综合考查了同底数幂的乘法计算、同底数幂的除法计算、幂的乘方运算、积的乘方运算、完全平方公式等内容,解决本题的关键是牢记对应法则和公式即可.23.(2021·湖南岳阳市·中考真题)下列运算结果正确的是( )A .32a a -=B .248a a a ⋅=C .()()2224a a a +-=-D .()22a a -=- 【答案】C【分析】逐一分析各选项,利用对应法则进行计算即可判断出正确选项.【解析】解:A 选项中:32a a a -=,因此错误;B 选项中:246·a a a =,因此错误;C 选项中:()()2224a a a +-=-,因此正确;D 选项中:()22a a -=,因此错误;故选:C .【小结】本题考查了合并同类项、同底数幂的乘法、平方差公式、乘方的运算性质等内容,解决本题的关键是牢记相关运算法则和公式即可.24.(2021·浙江台州市·中考真题)下列运算中,正确的是( )A .a 2+a =a 3B .(-ab )2=-ab 2C .a 5÷a 2=a 3D .a 5・a 2=a 10【答案】C【分析】根据合并同类项、积的乘方、同底数幂相除、同底数幂相乘的法则分别计算即可.【解析】解:A .2a 与a 不是同类项,不能合并,故该项错误;B .()222b a ab =-,故该项错误;C .523a a a ÷=,该项正确;D .527a a a ⋅=,该项错误;故选:C .【小结】本题考查整式的运算,掌握合并同类项、积的乘方、同底数幂相除、同底数幂相乘的法则是解题的关键.25.(2021·四川成都市·中考真题)下列计算正确的是( )A .321mn mn -=B .()22346m n m n = C .()34m m m -⋅=D .()222m n m n +=+ 【答案】B【分析】利用合并同类项法则可判定A ,利用积的乘方法则与幂的乘方法则可判定B ,利用同底数幂乘法法则可判定C ,利用完全平方公式可判定D .【解析】解:A . 321mn mn mn -=≠,故选项A 计算不正确;B.()()()222232346m n m n m n =⋅=,故选项B 计算正确; C . ()3344m m m m m m -⋅=-⋅=-≠,故选项C 计算不正确;D . ()222222m n m mn n m n +=++≠+,故选项D 计算不正确.故选择B .【小结】本题考查同类项合并,积的乘方与幂的乘方,同底数幂乘法,完全平方公式,掌握同类项合并,积的乘方与幂的乘方,同底数幂乘法,完全平方公式是解题关键.26.(2021·山东临沂市·中考真题)计算3325a a 的结果是( )A .610aB .910aC .37aD .67a【答案】A【分析】直接利用单项式乘以单项式运算法则计算得出答案.【解析】解:6332510a a a =⋅,故选:A .【小结】此题主要考查了单项式乘以单项式,正确掌握相关运算法则是解题关键.27.(2021·浙江宁波市·中考真题)计算()3a a ⋅-的结果是( )A .2aB .2a -C .4aD .4a -【答案】D【分析】根据单项式乘以单项式和同底数幂的运算法则解答即可.【解析】解:原式4a =-.故选:D【小结】本题考查了整式的乘法,属于基础题目,熟练掌握运算法则是关键.28.(2021·重庆中考真题)计算63a a ÷的结果是( )A .63aB .52aC .62aD .53a【答案】D【分析】根据单项式除以单项式法则、同底数幂除法法则解题.【解析】解:63a a ÷=53a ,故选:D .【小结】本题考查同底数幂相除、单项式除以单项式等知识,是重要考点,难度较易,掌握相关知识是解题关键.二、填空题29.(2021·上海中考真题)计算:72=x x÷_____________.【答案】5x【分析】根据同底数幂的除法法则计算即可【解析】∵72=÷5x,x x故答案为: 5x.【小结】本题考查了同底数幂的除法,熟练掌握运算的法则是解题的关键.30.(2021·天津中考真题)计算42a a a+-的结果等于_____.【答案】5a【分析】根据合并同类项的性质计算,即可得到答案.【解析】()+-=+-=424215a a a a a故答案为:5a.【小结】本题考查了整式加减的知识;解题的关键是熟练掌握合并同类项的性质,从而完成求解.31.(2021·江苏扬州市·中考真题)计算:22-=__________.20212020【答案】4041 【分析】利用平方差公式进行简便运算即可. 【解析】 解:2220212020-=()()2021202020212020+⨯- =40411⨯ =4041故答案为:4041. 【小结】本题考查了平方差公式的应用,解题时注意运算顺序.32.(2021·浙江嘉兴市·中考真题)观察下列等式:22110=-,22321=-,22532=-,…按此规律,则第n 个等式为21n -=__________________. 【答案】()221n n --. 【分析】第一个底数是从1开始连续的自然数的平方,减去从0开始连续的自然数的平方,与从1开始连续的奇数相同,由此规律得出答案即可. 【解析】解:∵22110=-,22321=-, 22532=-,…∴第n 个等式为:()22211n n n -=--故答案是:()221n n --. 【小结】本题考查了数字的变化类,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题的关键.33.(2021·四川遂宁市·中考真题)如图都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第___个图形共有210个小球.【答案】20 【分析】根据已知图形得出第n 个图形中黑色三角形的个数为1+2+3++n =()12n n +,列一元二次方程求解可得. 【解析】解:∵第1个图形中黑色三角形的个数1, 第2个图形中黑色三角形的个数3=1+2, 第3个图形中黑色三角形的个数6=1+2+3, 第4个图形中黑色三角形的个数10=1+2+3+4, ……∴第n 个图形中黑色三角形的个数为1+2+3+4+5++n =()12n n +,当共有210个小球时,()12102n n +=,解得:20n =或21-(不合题意,舍去), ∴第20个图形共有210个小球. 故答案为:20. 【小结】本题考查了图形的变化规律,解一元二次方程,解题的关键是得出第n 个图形中黑色三角形的个数为1+2+3+……+n .34.(2021·湖南岳阳市·中考真题)已知1x x +=1x x+=______. 【答案】0 【分析】把1x x+=直接代入所求的代数式中,即可求得结果的值. 【解析】10x x+== 故答案为:0. 【小结】本题考查了求代数式的值,涉及二次根式的减法运算,整体代入法是解决本题的关键. 35.(2021·江苏苏州市·中考真题)若21m n +=,则2366m mn n ++的值为______. 【答案】3 【分析】根据21m n +=,将式子2366m mn n ++进行变形,然后代入求出值即可. 【解析】 ∵ 21m n +=,∴2366m mn n ++=3m (m +2n )+6n =3m +6n =3(m +2n )=3. 故答案为:3. 【小结】本题考查了代数式的求值,解题的关键是利用已知代数式求值.36.(2021·江苏扬州市·中考真题)将黑色圆点按如图所示的规律进行排列,图中黑色圆点的个数依次为:1,3,6,10,……,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为___________.【答案】1275 【分析】首先得到前n 个图形中每个图形中的黑色圆点的个数,得到第n 个图形中的黑色圆点的个数为()12n n +,再判断其中能被3整除的数,得到每3个数中,都有2个能被3整除,再计算出第33个能被3整除的数所在组,为原数列中第50个数,代入计算即可. 【解析】解:第①个图形中的黑色圆点的个数为:1,第②个图形中的黑色圆点的个数为:()1222+⨯=3,第③个图形中的黑色圆点的个数为:()1332+⨯=6,第④个图形中的黑色圆点的个数为:()1442+⨯=10,...第n个图形中的黑色圆点的个数为()12n n+,则这列数为1,3,6,10,15,21,28,36,45,55,66,78,91,...,其中每3个数中,都有2个能被3整除,33÷2=16...1,16×3+2=50,则第33个被3整除的数为原数列中第50个数,即50512⨯=1275,故答案为:1275.【小结】此题考查了规律型:图形的变化类,关键是通过归纳与总结,得到其中的规律.37.(2021·陕西中考真题)幻方,最早源于我国,古人称之为纵横图.如图所示的幻方中,各行、各列及各条对角线上的三个数字之和均相等,则图中a的值为______.【答案】-2【分析】先通过计算第一行数字之和得到各行、各列及各条对角线上的三个数字之和,再利用第二列三个数之和得到a 的值. 【解析】解:由表第一行可知,各行、各列及各条对角线上的三个数字之和均为1616--+=-, ∴626a -++=-, ∴2a =-, 故答案为:2-. 【小结】本题考查了数字之间的关系,解决本题的关键是读懂题意,正确提取表中数据,找到它们之间的关系等,该题对学生的观察分析能力有一定的要求,同时也考查了学生对有理数的和差计算的基本功.38.(2021·甘肃武威市·中考真题)一组按规律排列的代数式:2335472,2,2,2a b a b a b a b +-+-,…,则第n 个式子是___________.【答案】()12112n n n a b +-+-⋅【分析】根据已知的式子可以看出:每个式子的第一项中a 的次数是式子的序号;第二项中b 的次数是序号的2倍减1,而第二项的符号是第奇数项时是正号,第偶数项时是负号. 【解析】解:∵当n 为奇数时,()111n +-=;当n 为偶数时,()111n +-=-,∴第n 个式子是:()1211?2n n n a b +-+-.故答案为:()1211?2n n n a b +-+- 【小结】本题考查了多项式的知识点,认真观察式子的规律是解题的关键.39.(2021·重庆中考真题)某销售商五月份销售A 、B 、C 三种饮料的数量之比为3:2:4,A 、B 、C 三种饮料的单价之比为1:2:1.六月份该销售商加大了宣传力度,并根据季节对三种饮料的价格作了适当的调整,预计六月份三种饮料的销售总额将比五月份有所增加,A 饮料增加的销售占六月份销售总额的115,B 、C 饮料增加的销售额之比为2:1.六月份A 饮料单价上调20%且A 饮料的销售额与B 饮料的销售额之比为2:3,则A 饮料五月份的销售数量与六月份预计的销售数量之比为_____________. 【答案】910【分析】设销售A 饮料的数量为3x ,销售B 种饮料的数量2x, 销售C 种饮料的数量4x ,A 种饮料的单价y . B 、C 两种饮料的单价分别为2y 、y .六月份A 饮料单价上调20%,总销售额为m ,可求A 饮料销售额为3xy+115m ,B 饮料的销售额为91210xy m +,C 饮料销售额:171420xy m +,可求=15m xy ,六月份A 种预计的销售额4xy ,六月份预计的销售数量103x ,A 饮料五月份的销售数量与六月份预计的销售数量之比103:3x x 计算即可【解析】解:某销售商五月份销售A 、B 、C 三种饮料的数量之比为3:2:4,设销售A 饮料的数量为3x ,销售B 种饮料的数量2x, 销售C 种饮料的数量4x ,A 、B 、C 三种饮料的单价之比为1:2:1.,设A 种饮料的单价y . B 、C 两种饮料的单价分别为2y 、y .六月份A 饮料单价上调20%后单价为(1+20%)y,总销售额为m ,A 饮料增加的销售占六月份销售总额的115A 饮料销售额为3xy+115m , A 饮料的销售额与B 饮料的销售额之比为2:3,B 饮料的销售额为31913=215210xy m xy m ⎛⎫++ ⎪⎝⎭ B 饮料的销售额增加部分为3134215xy m xy ⎛⎫+- ⎪⎝⎭∴C 饮料增加的销售额为131342215xy m xy ⎡⎤⎛⎫+- ⎪⎢⎥⎝⎭⎣⎦∴C 饮料销售额:13117134+42215420xy m xy xy xy m ⎡⎤⎛⎫+-=+ ⎪⎢⎥⎝⎭⎣⎦∴191171315210420xy m xy m xy m m +++++= ∴=15m xy六月份A 种预计的销售额1315415xy xy xy +⨯=, 六月份预计的销售数量()1041+20%y 3xy x ÷=∴A 饮料五月份的销售数量与六月份预计的销售数量之比1093:9:10=310x x = 故答案为910【小结】本题考查销售问题应用题,用字母表示数,列代数式,整式的加减法,单项式除以单项式,掌握销售额=销售单价×销售数量是解题关键40.(2021·四川凉山彝族自治州·中考真题)如图,用火柴棍拼成一个由三角形组成的图形,拼第一个图形共需要3根火柴棍,拼第二个图形共需要5根火柴棍;拼第三个图形共需要7根火柴棍;……照这样拼图,则第n 个图形需要___________根火柴棍.【答案】2n +1 【分析】分别得到第一个、第二个、第三个图形需要的火柴棍,找到规律,再总结即可. 【解析】 解:由图可知:拼成第一个图形共需要3根火柴棍, 拼成第二个图形共需要3+2=5根火柴棍, 拼成第三个图形共需要3+2×2=7根火柴棍, ...拼成第n 个图形共需要3+2×(n -1)=2n +1根火柴棍, 故答案为:2n +1. 【小结】此题考查图形的变化规律,找出图形之间的联系,得出运算规律解决问题.三、解答题41.(2021·湖南衡阳市·中考真题)计算:()()()()22224x y x y x y x x y ++-++-. 【答案】23x【分析】利用完全平方公式,平方差公式,单项式乘以多项式的法则,计算合并同类项即可 【解析】解:()()()()22224x y x y x y x x y ++-++-222224x 444x y y x y x xy =+++-+-23x =.【小结】本题考查了完全平方公式,平方差公式,单项式乘以多项式,合并同类项,熟练掌握公式,准确合并计算是解题的关键.42.(2021·浙江金华市·中考真题)已知16x =,求()()()2311313x x x -++-的值. 【答案】1 【分析】直接利用完全平方差公式展开及平方差公式展开后,合并同类项化简,再将16x =代入进去计算. 【解析】解:原式229611962x x x x =-++-=-+ 当16x =时,原式16216=-⨯+=. 故答案是:1.【小结】本题考查了代数式的化简求值,解题的关键是:先利用完全平方差公式,平方差公式,合并同类项运算法则化简,然后代值计算.43.(2021·浙江温州市·中考真题)(1)计算:()0438⨯-+--.(2)化简:()()215282a a a -++. 【答案】(1)-6;(2)22625a a -+.【分析】(1)直接利用有理数乘法法则以及绝对值的性质、二次根式的性质、零指数幂的性质分别化简得出答案;(2)直接利用完全平方公式以及单项式乘以多项式运算法则计算再合并即可得出答案.【解析】解:(1)()0438⨯-+- 12831=-+-+6=-;(2)()()215282a a a -++ 2210254a a a a =-+++22625a a =-+.【小结】此题主要考查了实数运算、整式的混合运算,正确掌握相关运算法则是解题关键.44.(2021·四川南充市·中考真题)先化简,再求值:2(21)(21)(23)x x x +---,其中1x =-.【答案】1210x -,-22【分析】利用平方差公式和完全平方公式,进行化简,再代入求值,即可求解.【解析】解:原式=2241(4129)x x x ---+=22414129x x x --+-=1210x -,当x =-1时,原式=()12110⨯--=-22.【小结】本题主要考查整式的化简求值,熟练掌握完全平方公式和平方差公式,是解题的关键.45.(2021·浙江宁波市·中考真题)(1)计算:()()()2113a a a +-++. (2)解不等式组:21930x x +<⎧⎨-≤⎩①②. 【答案】(1)610a +;(2)34x ≤<.【分析】(1)根据平方差公式和完全平方公式进行多项式乘法,再将结果合并同类项即可; (2)先解出①,得到4x <,再解出②,得到3x ≥,由大小小大中间取得到解集.【解析】解:(1)原式22169a a a =-+++610a =+.(2)解不等式①,得4x <,解不等式②,得3x ≥,所以原不等式组的解是34x ≤<.【小结】本题主要考查了整式的混合运算和解不等式组,关键在于平方差公式、完全平方公式以及不等式基本性质的应用,特别注意不等式的基本性质3,不等号的方向要改变.46.(2021·重庆中考真题)计算:(1)2(23)()a a b a b ++-;(2)22293211x x x x x x ⎛⎫--÷+ ⎪+++⎝⎭. 【答案】(1)223++a ab b ;(2)-31x x + 【分析】(1)根据单项式乘以多项式以及完全平方公式计算即可;(2)利用分式的混合运算法则进行计算即可.【解析】解:(1)2(23)()a a b a b ++-2222+3+2+=a ab a ab b -22=3++a ab b (2)22293211x x x x x x ⎛⎫--÷+ ⎪+++⎝⎭()()()222+3-3+3=11+x x x x x x x ⎛⎫-÷ ⎪++⎝⎭()()()2+3-31=31x x x x x +++ -3=1x x + 【小结】本题考查了整式的混合运算和分式的混合运算,熟练掌握运算法则是解题的关键.47.(2021·浙江中考真题)计算:()()()211x x x x +++-.【答案】21x +【分析】利用单项式乘多项式、平方差公式直接求解即可.【解析】解:原式2221x x x =++-21x =+.【小结】本题考查整式的乘法,掌握单项式乘多项式法则和平方差公式是解题的关键.48.(2021·四川乐山市·中考真题)已知2612(1)(2)A B x x x x x --=----,求A 、B 的值. 【答案】A 的值为4,B 的值为-2【分析】根据分式、整式加减运算,以及二元一次方程组的性质计算,即可得到答案.【解析】(2)(1)12(1)(2)(1)(2)A B A x B x x x x x x x ---=+------, ∴(2)(1)26(1)(2)(1)(2)A xB x x x x x x -+--=----, ∴(2)(1)26A x B x x -+-=-,即()(2)26A B x A B x +-+=-.∴226A B A B +=⎧⎨+=⎩, 解得:42A B =⎧⎨=-⎩∴A 的值为4,B 的值为2-.【小结】本题考查了分式、整式、二元一次方程组的知识;解题的关键是熟练掌握分式加减运算、整式加减运算、二元一次方程组的性质,从而完成求解.49.(2021·安徽)某矩形人行道由相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成,图1表示此人行道的地砖排列方式,其中正方形地砖为连续排列.[观察思考]当正方形地砖只有1块时,等腰直角三角形地砖有6块(如图2);当正方形地砖有2块时,等腰直角三角形地砖有8块(如图3);以此类推,[规律总结](1)若人行道上每增加1块正方形地砖,则等腰直角三角形地砖增加块;(2)若一条这样的人行道一共有n(n为正整数)块正方形地砖,则等腰直角三角形地砖的块数为(用含n的代数式表示).[问题解决](3)现有2021块等腰直角三角形地砖,若按此规律再建一条人行道,要求等腰直角三角形地砖剩余最少,则需要正方形地砖多少块?n ;(3)1008块【答案】(1)2 ;(2) 24【分析】(1)由图观察即可;(2)由每增加一块正方形地砖,即增加2块等腰直角三角形地砖,(3)再结合题干中的条件正方形地砖只有1块时,等腰直角三角形地砖有6块,递推即可;利用上一小题得到的公式建立方程,即可得到等腰直角三角形地砖剩余最少时需要正方形地砖的数量.【解析】。
初三语文试卷分析

初三语文试卷分析(一)一、总体分析这一份模拟考卷,可以说是命题者花了一定心思,出的非常成功。
考卷突出了检查学生初中三学年所掌握的知识和所具有的语文能力,重视语文基础知识的考查,突出对学生语文素养的考查,对今后的中考复习具有较强的指导性。
虽然难度系数有一定提升,但符合今年中考的命题导向。
本试题满分为120分,考试时间为150分钟。
在参加的考生中最高分为101分,最低分为6分,其中以80----90分的居多,较往常相比确实有点难度。
二、试卷分析本次试卷在结构上,主要分为以下几大块:(一)语文知识积累与运用。
主要考查了汉字的书写,拼音的正确读法、病句的修改、古诗文名句默写、运用、名著积累、语言的实际运用等几个方面,很有针对性地考查学生对语文基础知识的掌握。
本次试卷在结构上,主要分为以下几大块:1、汉字书写。
这一题不是简简单单的规范抄写而是要求学生从多个词语中选择拼音、写法正确的一项综合性较强。
2、病句修改注重与课本接轨,既考查了对文本的熟悉又巧妙的考察了学生的修改病句的知识。
3、名句填空。
第1----4题是机械型默写,即给出上句,要求写出下句,或给出下句,要求填出上句。
难度较小,除个别的有错别字,其余得分不错。
第5题和第6题是理解性填空还是比较简单的,也容易得分。
最后一个是考查学生的筛选能力。
有新意的是加进了对现代文名篇名段的考察,体现了中考的立足课本,以本为主的思想。
4、名著积累。
名著题不是简单的考名著知识而是将语言的运用与其结合起来,可谓一举二得。
5、语言运用题。
这道题既联系了实际,又考察了学生的语法知识,是一道综合性较强的题。
学生要想选对须仔细思索。
(二)阅读(一)古诗文阅读文言文阅读延续了传统的比较阅读,选择了《爱莲说》与《岳阳楼记》进行比较阅读,在题型的设计上也是由易到难,由课内的知识识记到课外的理解运用。
特别是第7小题前面考文题后面考作者有一定的迷惑性。
第10题在文言文中考察了修辞的作用,可谓巧妙。
中考数学复习讲义课件 重点中学自主招生试题分类专题 题型二 方程与不等式

18.已知关于x的方程x2-2(k-3)x+k2-4k-1=0. (1)若这个方程有实数根,求k的取值范围; (2)若以方程x2-2(k-3)x+k2-4k-1=0的两个根 为横坐标、纵坐标的点恰在反比例函数y=m/x的图 象上,求满足条件的m的最小值.
用水加满,这时容器内纯酒精与水之比为13,则容
器的容积为()
9.满足等式 x y+y x- 2021x- 2021y+ 2021xy=2021 的
正整数对的个数是( B)
A.1
B.2
C.3
D.4
[解析] 由 x y+y x- 2021x- 2021y+ 2021xy=2021,得 ( xy- 2021)( x+ y+ 2021)=0. ∵ x+ y+ 2021>0,∴ xy- 2021=0, ∴ xy= 2021,故 xy=2021. 又 2021 是质数,且 x,y 都为正整数,
题型精讲
C
[归纳总结] 求代数式的值是经典题目,方法很多 很灵活,但基本思路要么变换已知,要么变换未知, 要么已知未知一起变,直到能代入求值.其中整体 思想的运用不容忽视,因为很多方程不需解,只需 变换成可以整体代入的形式即可求值. [易错分析] 解答本题时容易忽略题目中的隐含条 件,即二次根式有意义的条件,误将x=4和x=5代 入式子错选D答案.
m+1=1,2,3,6, m=0,1,2,5,
即
m-1=1,3,
m=2,4,
S△ABC=12×2 3× (2+ 2)2-( 3)2= 9+12 2. 综上,△ABC 的面积为 1 或 9+12 2.
[2020中考生物]第二部分重点题型探究题型二识图题第九类神经系统的组成与生理活动习题01213119
![[2020中考生物]第二部分重点题型探究题型二识图题第九类神经系统的组成与生理活动习题01213119](https://img.taocdn.com/s3/m/3b3d864fb14e852459fb578e.png)
题型二识图题第九类神经系统的组成与生理活动习题1.(2018·山东临沂)节能减排,绿色出行.公共自行车已遍布临沂市各县区,“小绿”为市民出行带来了方便,也成为一道亮丽的风景.在骑自行车时需要人体的各种器官、系统的协调才能完成.请据图分析回答:(1)在骑车时,你需“眼观六路”.物像会落在眼球的[]上,最后在[]形成清晰的视觉.为保护视力、预防近视,你应该做到 (答出一条具体措施).(2)当你行至路口时,发现红灯则应停车等待,此反射类型属于反射.(3)骑车时,一不明物体突然从眼前飞过,你会不由自主的迅速眨眼.完成此眨眼反射的基本途径是 (用图中数字、字母和箭头表示).(4)在紧急情况下, 的分泌会增加,可以增加中枢神经系统的兴奋性,使人体反应灵敏,还能充分调动人体的潜力,以应对紧急情况.(5)由上述感受可知,通过的共同调节作用,人体的各项生理活动相互协调,使人体成为一个统一的整体.2.(2018·湖南湘潭)2018年3月14日凌晨著名物理学家霍金因病去世,享年76岁.他因患肌肉萎缩性侧索硬化症(ALS)禁锢在轮椅上达50年之久.ALS俗称“渐冻人症”,是一种运动神经元(负责支配效应器活动的神经元)疾病,患病者会出现肌肉无力、萎缩等症状,据图回答问题:(1)神经元是神经系统的基本单位.(2)霍金因运动神经元死亡,基本不能完成运动,但调节心跳、呼吸的基本生命中枢正常,至少说明下列哪一结构一定完好无损? .A.大脑B.小脑C.脑干D.脊髓(3)ALS患者因长期不能运动,导致肌肉萎缩,发生萎缩的结构主要是 (填图中字母).(4)医生用小锤叩击霍金膝盖下方的韧带时,他 .A.有感觉,不发生膝跳反射B.没感觉,发生膝跳反射C.有感觉,发生膝跳反射D.没感觉,不发生膝跳反射(5)霍金虽然不能运动,但视觉和听觉都相当敏锐,产生听觉的部位是 .3.请根据神经系统的结构示意图回答下列问题:(1)请用图中字母结合箭头写出“缩手反射”活动的反射途径: . (2)有人只有在看到自己下肢的情况下,才知道下肢的具体活动情况,则此人可能损伤的部位是[] .(3)由(1)(2)可知,脊髓具有功能.(4)人在吃梅、看梅、谈梅时都能分泌唾液,其中不需大脑皮层参与就能完成的反射活动是 .4.(2018·山东青岛二模)世界卫生组织的事故调查显示,大约50%~60%的交通事故与酒后驾驶有关,请结合下图回答问题:(1)醉酒者常表现出出汗、走路摇晃等现象,这是由于酒精麻痹了造成的.(2)某人在“酒驾”交通事故中受伤,医生用针刺其指尖,此人立刻缩手,该反射的神经中枢在 ,请用甲图中的数字和箭头表示缩手反射的神经冲动传导途径: . (3)对醉酒者采用吹气检测醉驾程度,吹气时,膈肌处于(填“收缩”或“舒张”)状态.(4)酒驾者血液中酒精随血液循环在身体内流动,最先进入乙图中的[Ⅰ] ,当血液流经肾脏时,葡萄糖浓度出现了丁图所示的变化,发生此变化的原因是丙图中的(填字母)进行了作用.(5)醉酒的人常表现出面红耳赤的状态,此时体内(填“胰岛素”或“肾上腺素”)水平比正常值高.5.(2018·甘肃兰州模拟)醉驾害己、害人、害社会.请你根据反射弧模式图回答下列问题:(1)对酒驾者可采用酒精测试仪检测醉酒,吹气时,受检者膈肌处于状态.(2)醉酒者常表现为思维混乱、反应迟钝、动作不协调等,这是由于酒精麻醉了造成的.(3)某醉驾者被撞成了“植物人”,生命体征只有心跳、呼吸和血压,你认为他未受损的中枢部分最可能是 .(4)医生用针刺某伤者的指尖,此人有感觉但不能缩手,则其受伤部位是图中的 (填序号并答出所有可能性).(5)若事故中某醉驾者的血液从上臂伤口的b处喷出且为鲜红色,你认为较为科学的急救方法是 .A.用手指压住a端血管,并用纱布包扎B.用手指压住c端血管,并用纱布包扎C.用手指压住ac两端血管,并用纱布包扎D.不用手指压住血管,直接用纱布包扎(6)有些同学骑车时喜欢戴着耳机高分贝听歌,这样不仅为交通安全埋下隐患,而且长期如此最有可能损伤 ,使听力渐进式减退.①外耳道②鼓膜③听小骨④耳蜗⑤听觉神经⑥听觉中枢A.①②B.②④C.②⑤D.③⑥参考答案1.(1)③视网膜 A 大脑皮层的视觉中枢不走路看书,不在强光下看书,不躺卧看书,读写姿势要正确,认真做眼保健操等(合理科学即可) (2)条件 (3)⑨→⑦→B→⑥→⑧(4)肾上腺素 (5)神经系统和激素【解析】(1)外界物体反射来的光线,经过角膜、房水,由瞳孔进入眼球内部,再经过①晶状体和玻璃体的折射作用,在视网膜上能形成清晰的物像,物像刺激了③视网膜上的感光细胞,这些感光细胞产生的神经冲动沿着视神经传到大脑皮层的视觉中枢,就形成视觉.为保护视力、预防近视,你应该做到不走路看书,不在强光下看书,不躺卧看书,读写姿势要正确,认真做眼保健操等(答出一条具体措施).(2)行驶到路口时,发现红灯立即刹车,此反射类型属于条件反射,完成此反射活动的神经中枢位于图中的A大脑皮层内.(3)反射弧包括感受器、传入神经、神经中枢、传出神经、效应器,用数字、字母和箭头表示膝跳反射的基本途径:⑨→⑦→B→⑥→⑧.(4)紧急情况时,肾上腺素分泌增加,可以增加神经系统或者中枢神经系统兴奋性.(5)人体的各项生命活动常常同时受神经系统和激素的调节,正是由于这两种调节方式的相互协调,相互影响,各器官、系统的活动才能协调一致,使人体成为一个复杂、协调、统一的整体.2.(1)结构与功能 (2)C (3)E (4)A (5)大脑皮层听觉中枢【解析】(1)神经元是神经系统结构与功能的基本单位.(2)脑干中有呼吸中枢、心血管运动中枢等,调节心跳、呼吸、血压等人体基本的生命活动.可见霍金的脑干是完好的.(3)效应器是运动神经末梢支配的肌肉或腺体.ALS患者因长期不能运动,导致肌肉萎缩,发生萎缩的结构是E效应器.(4)霍金患肌肉萎缩性侧索硬化症(ALS),ALS俗称“渐冻人症”,是一种运动神经元疾病,可见反射弧中D传出神经(运动神经)受伤.人体的传出神经受损,反射弧不完整,神经冲动就不能由传出神经传到效应器,效应器就无法做出反应,即反射活动不能进行.但是神经冲动仍然可以通过脊髓传到大脑的感觉中枢,产生感觉.(5)外界的声波经过外耳道传到鼓膜,引起鼓膜的振动;振动通过听小骨传到内耳,刺激耳蜗内的听觉感受器,产生神经冲动;神经冲动通过与听觉有关的神经传递到大脑皮层的听觉中枢,就形成了听觉.3.(1)A→B→E→C→D (2)A 感受器(3)反射(4)吃梅【解析】本题主要考查反射弧的结构和功能、脊髓的功能以及反射的类型.(1)神经调节的基本方式是反射,反射活动的结构基础为反射弧,反射弧由感受器、传入神经、神经中枢、传出神经、效应器五部分组成.缩手反射的反射途径为A感受器→B传入神经→E神经中枢→C传出神经→D效应器.(2)在反射弧的五个组成部分中,感受器可以接受外界刺激,并能产生神经冲动,神经冲动通过传入神经传到脊髓中特定的神经中枢,神经中枢的神经元接受了“这种信号”后,立刻产生神经冲动,并将它传给传出神经,传出神经迅速地将来自中枢的神经冲动传给效应器,于是就产生了反射活动.有人只有在看到自己下肢的情况下,才知道下肢的具体活动情况,则此人最可能损伤的部位是A感受器.(3)由(1)(2)可知,脊髓具有反射功能.(4)简单的反射活动不需要大脑皮层的参与就能完成.吃梅是简单反射,不需要大脑皮层的参与就能完成.4.(1)小脑(2)脊髓灰质①→③→⑤→④→②(3)舒张(4)右心房 D重吸收(5)肾上腺素【解析】本题主要考查神经系统的结构和功能、反射弧的组成和功能、尿液的形成过程以及激素的作用等知识点.(1)脑位于颅腔内,包括大脑、小脑和脑干三部分.小脑位于脑干背侧,大脑的后下方,小脑的主要功能是使运动协调、准确,维持身体的平衡;饮酒过量的人常常表现走路不稳,这是由于酒精麻痹了小脑.(2)图甲中①是感受器,②是效应器,③是传入神经,④是传出神经,⑤是神经中枢.缩手反射是简单反射,神经中枢在脊髓灰质内.缩手反射的神经冲动传导途径为①感受器→③传入神经→⑤神经中枢→④传出神经→②效应器.(3)当膈肌和肋间外肌舒张时,肋骨与胸骨因本身重力及弹性而回位,结果胸廓缩小,肺也随之回缩,造成肺内气压大于外界气压,肺内气体排出肺,形成被动的呼气运动.故司机吹气时膈肌处于舒张状态.(4)酒精随血液循环在身体内流动,进入下腔静脉,然后进入右心房.丁图中,葡萄糖浓度变为0,是因为当原尿流经肾小管时,原尿中的葡萄糖被肾小管全部重新吸收回血液.(5)肾上腺素能使心肌收缩力加强、兴奋性增高.5.(1)舒张 (2)小脑 (3)脑干 (4)④或⑤ (5)A (6)B【解析】(1)司机吹气时膈肌舒张,胸廓和肺缩小,肺内气压增大.(2)饮酒过量的人常常表现走路不稳,这是由于酒精麻醉了小脑造成的.(3)脑干中具有调节呼吸、心跳和血压等的神经中枢,“植物人”的生命体征只有心跳、呼吸和血压,所以其脑干没有受损.(4)此人有感觉但不能缩手,表明①感受器产生的神经冲动能通过②传入神经传到神经中枢,再经过脊髓的白质上行传到大脑皮层,形成感觉,不能完成反射活动,可能是④传出神经或⑤效应器受损.(5)某醉驾者的血液从伤口喷出且为鲜红色,可以判断是动脉出血,因而应该在近心端用指压法或止血带止血,因此应按住a端血管.(6)戴着耳机高分贝听歌,会影响鼓膜把声波转化为振动以及耳蜗把振动转化为神经冲动,故选B.。
中考道德与法治复习讲义中考题型揭秘 题型二 非选择题 题解题方法(道德与心理知识)——漫画题

【案例2】【2021年重庆中考A卷13】最好的成长在行走 的路上,把孩子放在大自然的体验馆中挑战自我,锻炼 坚韧意志,提升合作探究等综合素养,成为越来越多父 母的选择。以下几位孩子正在参加丛林穿越探险夏令营 活动。请你阅读他们的故事,并运用道德与心理的相关 知识回答问题。
请运用生命、责任、诚信相关知识,给漫画中的故事 设计一个结局并谈谈理由考。点(范4围分)
结局2:最终觉得不能违背保证书,同时意识到可能 的安全风险,给救援队和自己带来不必要的麻烦等放 弃了违规穿越。理由:他们懂得对自己的生命负责, 有安全意识、自我保护意识;他们有责任意识,懂得 对自己负责、对他人负责;他们有诚信意识,懂得信 守承诺。
答题要求及内容
【答案】结局1:几位同学违规穿越丛林被困遇到危 险(包括生命危险、跌落摔伤、遭遇野兽袭击等), 向景区救援人员求救。理由:他们缺乏对生命负责任 的态度,缺乏安全意识、自我保护意识和安全防范能 力,使自己陷于危险中;他们缺乏责任意识,不懂得 对自己负责,对他人负责,使自己和他人陷于危险中;
2.从不同考点入手分析。考生可找出漫画中体现了 生命、亲情、责任、关爱他人、服务社会、诚信、 尊重、文明有礼等考点的部分内容,将体现的考点 与漫画材料相对应进行作答。
二、试题示例
漫画题目暗含考点范明确考点范围 围
【案例1】阅读漫画《因为爱》,运用道德与心理
知识回答问题。
因为 爱》
考点范围
请结合材料,从“生命”和“亲情”角度,谈谈你对 漫画的理解。(4分) 【答案】①漫画中丈夫每天喝酒应酬、深夜回家,没 有做到珍爱生命、爱护身体;②孩子考试没考好、听 到父母吵架感到心烦,说明面对挫折,我们可能产生 难过、愤怒、不满等负面情绪;③孩子威胁父母不回 家,没有明白生活难免有挫折,要正确认识和对待挫 折;④丈夫道出自己应酬的用意,妻子理解丈夫的不 易,体现出爱在家人间,家是心灵的港湾,家人间要 用沟通来传递爱/家人之间要相互体谅和包容;⑤丈夫
中考生物重点题型突破:题型二 实验题

题型二实验题1. (滨州A卷)如图所示是制作临时玻片标本的流程图,图中空格中依次应该填写的是()第1题图A. 滴、展、染B. 染、展、滴C. 展、滴、染D. 滴、染、展2. (新疆维吾尔自治区)探究实验为避免误差,需要计算平均值,但也有个别例外。
下列计算不需要计算平均值的是()A. 测定种子的发芽率B. 探究植物对空气湿度的影响C. 探究蚂蚁的通讯D. 烟草浸出液对水蚤心率的影响3. (安徽)某生物兴趣小组探究“光照对蚯蚓生活的影响”,设计的实验方案如下表,其中需要修改的内容是()A. 蚯蚓数量B. 光照条件C. 温度D. 土壤4. (巢湖)某同学欲验证叶是蒸腾作用的主要器官,其实验装置及处理应是( )5. (百色)为探究唾液对淀粉的消化作用,某同学设置如图实验装置,已知试管A 实验材料是:淀粉液+唾液,则试管B 实验材料应为( )第5题图A. 淀粉液+碘液B. 唾液+碘液蚯蚓数量 光照条件 温度土壤20只 阴暗 适宜 一层湿土 20只明亮适宜一层干土C. 淀粉液+清水D. 唾液+清水6. (枣庄)试剂的正确选择和使用是实验成功的关键因素之一。
下列实验中,所用试剂与使用目的不符的是()7. (天门)用显微镜观察小鱼尾鳍的血液流动,实验过程中观察到如下图像,下列叙述正确的是()第7题图A. 观察时发现物像模糊,应用擦镜纸将反光镜擦拭干净B. 观察时选用16×目镜、10×物镜,则物像的放大倍数是26倍C. 观察时视野过亮,则应该换用平面镜或选用小光圈D. 视野中发现红细胞从左往右流动,则实际上红细胞从左往右流动8.(威海)下列探究实验与其依据的生物学原理的对应关系,错误的是()A. 探究馒头在口腔中的变化——淀粉在唾液淀粉酶的作用下被分解B. 探究光对鼠妇生活的影响——生物影响环境C. 检测不同环境中的细菌和真菌——细菌和真菌的生存需要一定的条件D. 探究植物对空气湿度的影响——植物通过蒸腾作用将水分散失到大气中9. (泰安)下列关于观察与实验的叙述,正确的是()A. 观察花的结构、草履虫的运动、蚯蚓的形态,都要用到放大镜、显微镜等工具B. 探究蚂蚁的通讯时,捕获到的蚂蚁要先饲养一段时间,实验前让其处于饥饿状态C. 显微镜的目镜、物镜、通光孔在一条直线上,调好反光镜就可以看到明亮的视野D. 制作人的口腔上皮细胞时,载玻片上滴加的液体和染色的液体分别是清水、碘液10. (来宾)下列实验中,实验材料与使用目的不相符的是()11. (聊城)下表所示实验或探究活动中,相关操作与所要达到的目的对应错误的是()名称操作目的在载玻片的培养液里放几限制草履虫的运动速度A 观察草履虫丝棉花纤维12. (福建)下列实验中,材料用具与使用目的不一致的是()13. (益阳)对下列相关实验或探究活动的描述错误的是()A. 测定反应速度:要多次重复实验,并计算平均值B. 观察人血涂片:视野中最多的是红细胞C. 演示实验模拟人体呼吸运动:玻璃罩模拟肺D. 观察小鱼尾鳍血液流动:视野中可见红细胞单行通过毛细血管14. (娄底)学校生物兴趣小组想探究“酒精对细胞的影响”进行了如下实验:①取相同的新鲜杨梅各5颗分别放入编号为1号和2号的杯子中,②1号杯中加入适量的清水,2号杯中加入等量的高度白酒,③一段时间后观察,现象如下图所示,请你推测2号杯中液体颜色变红的主要原因是()第14题图A. 酒精破坏了细胞的细胞膜B. 酒精破坏了细胞的细胞壁C. 酒精破坏了细胞的细胞质D. 酒精破坏了细胞的细胞核15. (潍坊A卷)初中生物教材中,著名科学家与其相关学说或科学实验对应错误的是()16.(庆阳)某校研究性学习小组同学进行“绿豆种子萌发的环境条件”的探究活动,实验条件及结果如表所示。
中考热点:(一)构造三角形外接圆解四类难题;(二)圆+三角函数综合题型

中考热点:构造三角形外接圆解四类难题一、问题导读在解证几何题时,四点共圆已经被一些学生所了解或重视,然而作三角形的外接圆还没有被学生重视,使对许多几何题的证明难于入手.下面介绍作三角形外接圆这个辅助圆的思路和方法,以期待对你的学习有所帮助。
二、典例精析类型1 作三角形外接圆,求含有乘积式问题例1.已知AD是△ABC的角平分线,求证:ABAC=AD+BDCD.【分析】作辅助圆,根据同弧所对的圆周角相等和角平分线证明相似得出比例式,再证△BAD∽△ECD,根据相似三角形的性质得出ADED=BDDC,即可得出答案.【解答】证明:作△ABC的外接圆O,延长AD交⊙O于E,连接CE,∵AE平分∠BAC,∴∠BAD=∠EAC,∵∠B=∠E,∴△ABD∽△AEC,∴AB/AE=AD/AC,∴ABAC=ADAE=AD(AD+DE)=AD2+ADED,∵∠B=∠E,∠BAD=∠DCE,∴△BAD∽△ECD,∴AD/CD=BD/ED,∴ADED=BDDC,∴ABAC=ADAE=AD+BDDC.【点评】本题考查了相似三角形的性质和判定,圆周角定理的应用,解此题的关键是推出△ABD∽△AEC 和△BAD∽△ECD,主要考查学生的推理能力.例2.如图,ABCD是圆内接四边形,AB、DC的延长线交于E,AD、BC的延长线交于F,EP、FQ切圆于P、Q两点,求证:EP+FQ=EF.【分析】作辅助圆,构建四点共圆的四边形,利用切割线定理列式:EP2=ECED,FQ2=FCFB,得出结论.【解答】证明:作△BCE的外接圆,交EF于G,连接CG,∵A、B、C、D四点共圆,∴∠FDC=∠ABC,∵B、C、G、E四点共圆,∴∠ABC=∠CGE,∴∠FDC=∠ABC=∠CGE,∴F、D、C、G四点共圆,由切割线定理得:EP=ECED,FQ=FCFB,EF=(EG+GF)EF=EGEF+GFEF=ECED+FCFB,∴EP+FQ=EF.【点评】本题考查了切割线定理和圆内接四边形的性质,本题运用了圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角);反之也成立;在证明线段的平方和时,一方面考虑利用勾股定理来求,另一方面考虑利用切割线定理列式得出.类型2 作三角形外接圆,利用圆中的角证明线段的和差倍半问题例3.四边形ABCD内接于圆,另一圆的圆心在边AB上且与其余三边相切,求证:AD+BC=AB.【分析】先画图,设AB上的圆心为P,由等腰三角形的性质得,∠CMB=∠PDC,则M,P,C,D四点共圆,从而得出∠AMD=∠ADM,最后证得AD+BC=AB.【解答】证明:设AB上的圆心为P,在AB上取一点M,使MB=BC,连接MC,MD,PD,PC 等腰△CMB中,∠CMB=∠MCB,∴∠CMB=1/2(∠MCB+∠CMB)=1/2(180°﹣∠B),=1/2∠ADC (圆内接四边形ABCD的对角相加为180°),=∠PDC (设圆P切AD于E,切DC于F,有PE=PF,Rt△PDE和Rt△PDF中,一对儿直角边相等,且斜边是公共的,∴两Rt△全等,可得PD平分∠CDA),∴M,P,C,D四点共圆,∴∠AMD=∠DCP=1/2∠DCB (同理,可证PC平分∠DCB),=1/2(180°﹣∠A)(ABCD的另一对儿对角和为180°,=1/2(∠ADM+∠AMD),∴∠AMD=∠ADM∴AD=AM,∴AD+BC=AM+MB=AB.例4.如图,在△ABC中,AB=AC,D是底边BC上一点,E是线段AD上一点且∠BED=2∠CED=∠A.求证:BD=2CD.【分析】首先作DO∥AB交AC于O,得出O为△EDC的外心,进而得出△ACE∽△ADF,即有AD/AC=AF/AE,即可得出△ADO∽△BAE,即可得出BD=2CD.【解答】证明:作DO∥AB交AC于O.则由AB=AC易知OD=OC,且∠DOC=∠BAC=2∠CED,所以O为△EDC的外心,取F为△EDC的外接圆与AC的交点,连接DF,则OF=OC=OD,∠ACE=∠ADF.所以△ACE∽△ADF,即有AD/AC=AF/AE.再由DO∥AB,∠ADO=∠BAE,∠AOD=180﹣∠DOC=180°﹣∠A=180°﹣∠BED=∠AEB,所以△ADO∽△BAE,即得OD/AE=AD/AB=AF/AE.故AF=OD=OC=1/2CF,从而AO=2OC.由DO∥AB,得:BD=2CD.类型3 作三角形的外接圆,利用圆中的角判断三角形的形状例5.已知:AD是△ABC的中线,若∠ABC+∠CAD=90.试判断△ABC的形状.分析:作△ABC的外接圆.使分散的∠ABC.∠CAD集中在一起,从而知道中线AD在外接圆的直径上.根据圆中弦的定理,可判断△ABC的形状.解:作△ABC的外接圆.延长AD交外接圆于E.连结BE.∵∠EBC=∠CAD,又∠ABC+∠CAD=90°,∴∠ABC+∠EBC=90°,即∠ABE=90°.AE是△ABC的外接圆的直径.又AD是BC边上的中线.(1)当BC不是外接圆的直径时,即BC为弦,则 AD⊥BC,AD是BC边的中垂线.△ABC为等腰三角形.(2)当BC是外接圆的直径时,∠CAB=90°,△ABC为直角三角形.例6. 设P、Q为线段BC 上两定点,且BP=CQ.A为BC外一动点.当点A运动到使∠BAP=∠CAQ时,△ABC是什么三角形?分析:作△ABC的外接圆,能把角等转化为弦等,构造全等三角形.证明:作△ABC的外接圆,延长AP、AQ分别交外接圆于E、F.连结BE、CF.∵∠BAP=∠CAQ,即∠BAE=∠CAF,∴BE=FC, 弧BE=弧CF,∴弧BF=弧CE, ∴∠EBP=∠FCQ,又BP=CQ,∴△BEP≌△CFQ.∠E=∠F,在△ABE和△ACF中,∠E=∠F,∠BAE=∠CAF,BE=CF.∴△ABE≌△ACF,AB=AC, ∴△ABC是等腰三角形.类型4 作三角形的外接圆,解几何综合题例7.已知:A、B、C三点不在同一直线上.(1)若点A、B、C均在半径为R的⊙O上,i)如图①,当∠A=45°,R=1时,求∠BOC的度数和BC的长;ii)如图②,当∠A为锐角时,求证:sinA=BC/2R;(2)若定长线段BC的两个端点分别在∠MAN的两边AM、AN(B、C均与A不重合)滑动,如图③,当∠MAN=60°,BC=2时,分别作BP⊥AM,CP⊥AN,交点为P,试探索在整个滑动过程中,P、A两点间的距离是否保持不变?请说明理由.【分析】(1)i)根据圆周角定理得出∠BOC=2∠A=90°,再利用勾股定理得出BC的长;ii)作直径CE,则∠E=∠A,CE=2R,利用sinA=sinE=BC/2R,得出即可;(2)首先证明点A、B、P、C都在⊙K上,再利用sin60°=BC/AP,得出AP=2/ sin60°=4√3/3(定值).【解答】(1)i)∵A、B、C均在⊙O上,∴∠BOC=2∠A=2×45°=90°,∵OB=OC=1,∴BC=√2,注:也可延长BO或过O点作BC的垂线构造直角三角形求得BC.ii)证法一:如图②,连接EB,作直径CE,则∠E=∠A,CE=2R,∴∠EBC=90°∴sinA=sinE=BC/2R,证法二:如图③.连接OB、OC,作OH⊥BC于点H,则∠A=1/2∠BOC=∠BOH,BH=1/2BC∴sinA=sin∠BOH=BH/OB=1/2BC/R=BC/2R,(2)如图④,连接AP,取AP的中点K,连接BK、CK,在Rt△APC中,CK=1/2AP=AK=PK,同理得:BK=AK=PK,∴CK=BK=AK=PK,∴点A、B、P、C都在⊙K上,∴由(1)ii)可知sin60°=BC/AP∴AP=2/ sin60°=4√3/3(定值),故在整个滑动过程中,P、A两点间的距离不变.【点评】此题主要考查了圆周角定理以及解直角三角形和四点共圆等知识,根据已知得出点A、B、P、C 都在⊙K上以及sin60°=BC/AP是解题关键.中考热点:圆+三角函数综合题型一、问题导读“圆”这一部分知识,多年来都是中考的重点,锐角三角函数大家也不算陌生,那么当圆遇上三角函数又会出现什么呢?下面就和大家分享一下圆偶遇三角函数之后所发生的一个小片段吧!当然如果想了解具体发生了什么,首先得记住他们的暗号喔,通过下面问题的探讨,不难发现它们携手并进暗号呢。
初三级各科目知识重难点分析
第一部分初三年级各科目知识重难点分析
数学
初三上册该知识点与其他年级知识点的分析
分式
1、分式的乘除法
2、分式的加减法
3、分式方程中考易以计算题的形式出现。
1 与初二上册的一元一次不等式,初二上册二元一次方程构成了应用题的重要部分。
2 这三种方程是初中学习解方程的重点,不会解方程计算题就得不了分,应用题更是无法去完整解答。
相似图形
1、线段的比
2、比例线段
3、形状相同的图形
4、相似三角形
5、相似多边形中考易出选择和填空。
中考中易出现多边形的性质应用。
证明(一)
1、定义与命题
2、证明的必要性
3、公理与定理
4、平行线的判定定理
5、平行线的性质定理
6、三角形内角和定理中考定义命题易以填空、选择的形式出现。
内角和定理易结合三角形证明的题以综合运用大题的形式出现。
中考易出选择题或作为后面大题的基础。
数据的收集与处理
1、数据收集
2、数据整理
3、频数和频率
4、数据的波动
二次根式
1、二次根式的性质
2、二次根式的加减法
3、二次根式的乘除法中考经常以计算题的形式出现,需注意计算的步骤要严谨。
初三下册与其他年级哪些知识点相关
1 / 11。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三中考重点题型分析(二)
1、如图:将一张长为70cm 的长方形纸片ABCD 沿对称轴EF 折叠后得到如图所示的形状,若折叠后AB 与CD 的距离为60cm ,则原纸片的宽度为:
A 、10 cm
B 、15 cm
C 、20 cm
D 、30 cm
第1题图
2、探究性学习小组的同学接受了测量同样型号圆柱工件直径的任务,他们使用的工具是有一个角是600的直角三角板和刻度尺,小明的测量方法如图甲所示,测得PC=12cm ,小亮的测量方法如图乙所示,则与QA 的值最接近的是:
A 、8cm
B 、7 cm
C 、6 cm
D 、5 cm
3、如图:在△ABC 中有一点O ,AO 的延长线交BC 于点D ,若S △OBD =4,S △AOC =9,那么△ABC 的面积的最小值为:
A 、24
B 、25
C 、26
D 、27
第
2题
图 第3
题图 第5题图 第4题图 4、如图:在Rt △ABC 中,∠C=900
,正方形CEDF 的顶点都落在△ABC 的边上,且AD=3,BD=4,则S 阴影=
A 、4
B 、5
C 、6
D 、12 5、梯形ABCD 中,AD ∥BC ,∠ABC 的平分线B
E 与CD 垂直且CE=2ED ,则图中12S S :=
A 、15:7
B 、1:2
C 、7:8
D 、16:7 6、将半径为2cm 的圆形纸板沿着挖空的部分方格纸板(小方格的边长为2cm)的
内侧滚动一周,回到开始位置后,圆心经过的路线的长度为(精确到0.01cm): A 、36 cm B 、42.28 cm C 、40.28 cm D 、40 cm
7、如图:在△ABC 中,BD 平分∠ABC ,AD ⊥BD ,垂足为D ,DE ∥BC ,若DE=2,BC=10,则AB= ________。
8、如图:△ABC 中,AC 的垂直平分线交AC 于E ,交BC 于D ,△ABD 的周长为12cm ,AE=5cm ,则△ABC 的周长为:____________________。
9、如图:花丛中有一路灯杆AB ,在灯光下,小明在D 点处的影长为DE=3米,沿BD 方向行走到达G 点后,DG=5米,这时小明的影长GH=5米,如果小明的身高为1.7米,则路灯杆AB 高为:_______________(保留两个有效数字)。
第7题图 第8题图 第9题图
10、如果2007个整数122007,,...,a a a 满足下列条件:10,a =212,a a =-+322,a a =-+
2007...,a =20062a -+,则1232007...a a a a ++++=__________________。
11.有一边长为2的正方形纸片ABCD ,先将正方形ABCD 对折,设折痕为EF (如图(3));再沿过点D 的折痕将角A 反折,使得点A 落在EF 的H 上(如图(4)),折痕交AE 于点G ,则EG 的长度为 (A
)6 (B
)3
(C
)8-(D
)4-
12、街道旁边有一根电线杆AB 和一块半圆广告牌,有一天,小明突然发现,在太阳照射下,电线杆的顶端A 的影子刚好落在半圆形广告牌的最高处G ,而半圆形广告牌的影子刚好落在地面上一点E 。
已知BC=5米,半圆的直径是6米,DE=2米,根据以上数据,你能计算出电线杆的高度吗?试试看。
13、如图12,A B C △是O 的内接三角形,A C B C =,
D 为O 中 AB 上一点,
延长D A 至点E ,使C E C D =.
(1)求证:AE BD =;
(2)若A C B C ⊥
,求证:AD BD +=.
14、某工厂生产的某种产品按质量分为1 0个档次.第1档次(最低档次)的产品一天能生产7 6件,每件利润10元.每提高一个档次,每件利润增加2元,但一天产量减少4件.
(1)若生产第x 档次的产品一天的总利润为y 元(其中x 为正整数,且1≤x ≤10),求出y 关于x 的函数关系式;
(2)若生产第x 档次的产品一天的总利润为1080元,求该产品的质量档次.
E
图
13
F (3)
A
B
C
D
E F
G
H
(4)
(第11题)。
