信与系统公式大全带公式证明

信号与系统典型公式

(八) 直流信号 (二)对称性

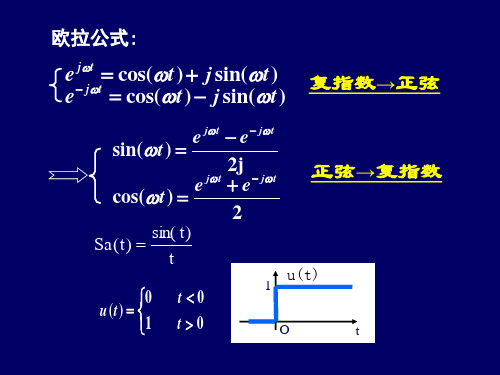
( t )e

j t
dt 1
F [1] 2 ( )
若f (t ) F ( )则F (t ) 2f ( )即F F (t ) 2 f ( )
(四)尺度变换特性
1 F [ f (at )] F( ) a a
若

t2
t1
f1 ( t ) f 2 ( t )dt 0 (p326式(6-53))
则称f1(t)与f2(t)在区间（t1,t2）上(相互)正交。对复值函数f1(t)，f2(t)(p329)
f1 ( t ), f 2 ( t )正交 f1 ( t ) f *2 ( t )dt 0
更一般的三角函数形式傅里叶级数（FS）
f (t ) a 0 [a n cos( n 1 t ) b n sin( n 1 t )]
n 1

f (t) c0 cn cos( n1t n ) d 0 d n sin( n1t n )
n 1 n 1
f(t)的直流分量=其任意周期的直流分量
f(t)=fD(t)+fA(t)，
f(t)的功率=fD(t)的功率+fA(t)功率三、偶分量与奇分量分解
f(t)=fe(t)+fo(t)
f(t)的功率=fe(t)功率+fo(t)功率且
f (t ) f ( t ) f（t） e 2
f (t ) f ( t ) f（t） o 2
时域卷积定理若
F[ f1 (t )] F1 ( )
F[ f2 (t )] F2 ()
则
F[ f1 (t )* f2 (t )] F1 () F2 ()

信号与系统重点概念公式总结

信号与系统重点概念及公式总结：第一章：概论1.信号：信号是消息的表现形式。

（消息是信号的具体内容）2.系统：由若干相互作用和相互依赖的事物组合而成的具有特定功能的整体。

第二章：信号的复数表示：1.复数的两种表示方法：设C 为复数，a 、b 为实数。

常数形式的复数C=a+jb a 为实部，b 为虚部；或C=|C|e j φ，其中，22||b a C +=为复数的模，tan φ=b/a ，φ为复数的辐角。

（复平面）2.欧拉公式：wt j wt e jwtsin cos +=（前加-，后变减）第三章：正交函数集及信号在其上的分解1.正交函数集的定义：设函数集合)}(),(),({21t f t f t f Fn =如果满足：ni K dt t f ji dt t f t f iT T i T T j i 2,1)(0)()(21212==≠=⎰⎰则称集合F 为正交函数集如果n i K i,2,11==，则称F 为标准正交函数集。

如果F 中的函数为复数函数条件变为：ni K dt t f t f ji dt t f t f iT T i i T T j i 2,1)()(0)()(2121**==⋅≠=⋅⎰⎰其中)(*t f i 为)(t f i 的复共轭。

2.正交函数集的物理意义：一个正交函数集可以类比成一个坐标系统；正交函数集中的每个函数均类比成该坐标系统中的一个轴；在该坐标系统中，一个函数可以类比成一个点；点向这个坐标系统的投影（体现为该函数与构成坐标系的函数间的点积）就是该函数在这个坐标系统中的坐标。

3.正交函数集完备的概念和物理意义：如果值空间中的任一元素均可以由某正交集中的元素准确的线性表出，我们就称该正交集是完备的，否则称该正交集是不完备的。

如果在正交函数集()()()()t g n ,t g ,t g ,t g 321之外，不存在函数x （t ）()∞<<⎰2120t t dt t x ，满足等式：()()⎰=210t t i dt t g t x ，则此函数集称为完备正交函数集。

信号与系统概念公式总结

⎰T 1 11i信号与系统概念，公式集：第一章：概论1.信号：信号是消息的表现形式。

（消息是信号的具体内容）2.系统：由若干相互作用和相互依赖的事物组合而成的具有特定功能的整体。

第二章：信号的复数表示：1.复数的两种表示方法：设 C 为复数，a 、b 为实数。

常数形式的复数 C=a+jb a 为实部，b 为虚部；或 C=|C|e j φ，其中，| C |=复数的辐角。

（复平面）a 2 +b 2 为复数的模，tan φ=b/a ，φ为2.欧拉公式：e jwt= cos wt +j sin wt （前加-，后变减）第三章：正交函数集及信号在其上的分解1.正交函数集的定义：设函数集合F = { f 1 (t ), f 2 (t ), f n ( t )}T 21如果满足： T 2f i (t ) f 2j (t )dt = 0i ≠ j ⎰Tf i (t )dt = K ii = 1,2 n 则称集合 F 为正交函数集如果K i = 1i = 1,2, n ，则称 F 为标准正交函数集。

如果 F 中的函数为复数函数T 2f (t) ⋅ f * (t )dt = 0i ≠ j⎰T i j条件变为： T2*⎰T f i (t ) ⋅ f i (t )dt = K ii = 1,2 n其中 f *(t ) 为 f i (t) 的复共轭。

2.正交函数集的物理意义：一个正交函数集可以类比成一个坐标系统；正交函数集中的每个函数均类比成该坐标系统中的一个轴；在该坐标系统中，一个函数可以类比成一个点；点向这个坐标系统的投影（体现为该函数与构成坐标系的函数间的点积）就是该函数2 1 11 1 1t 222**在这个坐标系统中的坐标。

3.正交函数集完备的概念和物理意义：如果值空间中的任一元素均可以由某正交集中的元素准确的线性表出，我们就称该正交集是完备的，否则称该正交集是不完备的。

如果在正交函数集 g 1 (t ), g 2 (t ), g 3 (t ), g n(t ) 之外，不存在函数 x （ t ）t 20 < ⎰ x 2(t )dt < ∞ ，满足等式： ⎰x (t )g (t )dt = 0 ，则此函数集称为完备正交函数集。

信号与系统公式归纳

为实虚奇
实信号的奇偶分解
帕斯瓦尔定理
双边拉普拉斯变换
单边拉普拉斯变换
双边Z变换
单边Z变换
公式
性质
信号
拉普拉斯变换
收敛域
信号
拉普拉斯变换
信号
Z变换
收敛域
信号
Z变换
线性
至少
至少
时移
（除了可能增加或除去0或点）
尺度变换
S域平移
的比例伸缩
时域尺度变换
共轭
卷积
至少
时
至少
时域微分
至少
至少
S域微分
至少
时域积分
至少
积分/求和
（仅当才为有限值且为周期的）
（仅当才为有限值且为周期的）
（频域微分）
（频域微分）
实信号的共轭对称性
为实信号
为实信号
为实信号
为实信号
实偶信号
为实偶信号
为实偶函数
为实偶信号
为实偶数
为实偶信号
为实偶
为实偶信号
为实偶
实奇信号
为实奇信号
为纯虚奇函数
为实奇信号
为纯虚奇数
为实奇信号
为实虚奇
为实奇信号
初值定理
终值定理
若，且在不包括任何冲激或高阶奇异函数，则
初值定理
若，，则
初值定理
连续时间基本傅立叶变换对
离散时间基本傅立叶变换对
信号
傅立叶变换
傅立叶级数系数
信号
傅立叶变换
1
1
拉普拉斯变换
Z变换
信号
变换
收敛域
信号
变换
收域
1
全部s

信号与系统-公式

r 2

C1k C0
k
j
Z域尺度变换
z ak f k F , a z a a
k m f k z
f k k m
1,2 a jb
e j
k C cos k D sin k 或A k cos k , 其中Ae
z
1

km
Pm k Pm 1k
m r m
m 1

m 1
Pk P0 1
k Pm k Pm 1k
Pa
k
k

Pk P0 1
时域积分
f
1
t F 0
F j j
不等于特征根时等于特征单根时
t
尺度变换
f at
1 a
F j
a
F j
1,2 j
C cos t D sin t 或A cos t , 其中Ae
j
C jD
时移特性
f t t0 e
jt0
r 重共轭复根
r 1 r 2 Ar 1t cos t r 1 Ar 2t cos t r 2
t A0t r 2 cos t 0 e
频移特性
f t e
j0 t
F j 0
微分方程激励 f t
微分方程特征根单实根
不同特征根所对应的齐次解齐次解
yh t
对称性
傅里叶变换的性质
时域f t F j 频域 F jt 2 f

(完整版),信号与系统-公式总结,推荐文档

an (s p1)(s p2 )(s pn ) (s p1) (s p2 )
(s pn )
k i (s pi )F (s) |s pi
(i 1, 2,n)
变变变变变变变变变变
et ut 1
s α
z变变变变变变变
z
z
a
a n u( n) anu(n
1)
za za
⑵留数法
留数法是将拉普拉斯反变换的积分运算转换为求被积函数各极点上留数的运算，即
an
1
, a 1
n0
1 a
第二章傅立叶变换
1 正变换： F () f (t)e jtdt
2 傅立叶变换的性质性质 ※时移
※时频展缩
※※频移
逆变换： f (t) 1 F ()e jtd
2
时域
f (t t0 )
f (at) a 0 f (at b) a 0
f (t)e j0t
信号
名称
f (t)
波形图
F () F () e j()
频谱图
※※ 矩形
脉冲 E[u(t ) u(t )]
E
Sa(
)
2
冲激
脉冲
E (t)
E
※※
直流
E
函数
2 E ()
※ 冲激序列
T 1 (t )
1 1 ( )
1
2 T1
第三章拉普拉斯变换
1 定义
双边拉普拉斯变换 F (s) f (t)estdt
z
z i0 z pi
根据收敛域给出反变换
N
A： if z R ，则 f (n) 为因果序列（右边序列），即 f (n) Ai pinu(n) i 1

信号与系统的公式汇总分类

称
值
s→∞
值
z→∞
z→∞
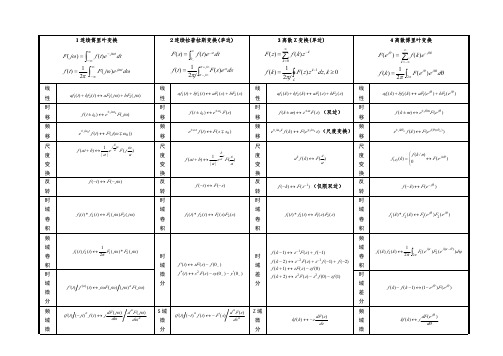
帕斯
∫ ∫ E = ∞ | f (t) |2dt = 1 ∞ | F ( jω) |2 dω
−∞
2π −∞
帕
终
f (∞) = lim sF (s), s = 0 在收敛域
s→0
终
f (∞) = lim(z −1)F (z) （右边信号）斯
瓦
值
值
z→1
瓦
内
尔
尔
∑ ∫ ∞ | f (k) |2 = 1 | F (e jθ ) |2 dθ
域 f (k + 1) ↔ zF (z) − zf (0)
积
时
微
f ′′(t) ↔ s 2 F (s) − sy(0− ) − y′(0− )
差
f (k + 2) ↔ z2F (z) − z2 f (0) − zf (1)
时
域
分 f ′(t) f (n) (t) ↔ jωF( jω) ( jω)n F ( jω)
1 n! s 2 s n+1
1
1
s +α (s +α)2
kε (k) akε (k)
z (z −1) 2
z z−a
(k + 1)akε (k) kak −1ε (k)
cos(βt)ε (t) sin(βt)ε (t) cosh(βt)ε (t) sinh(βt)ε (t) e−αt cos(βt)ε (t) e−αt sin(βt)ε (t)
s s2 +β 2
β s2 +β 2
s s2 −β 2
β s2 −β 2
s+α (s +α)2 + β 2

信号与系统公式大全

信号与系统公式大全1.傅里叶变换公式：F(ω) = ∫f(t)e^(-jωt)dtf(t)=∫F(ω)e^(jωt)dω2.傅里叶级数公式：f(t) = a_0/2 + ∑[a_n*cos(nωt) + b_n*sin(nωt)] a_n = (2/T)∫[f(t)*cos(nωt)]dtb_n = (2/T)∫[f(t)*sin(nωt)]dt3.傅里叶变换与傅里叶级数之间的关系：F(ω)=2π∑[a_n*δ(ω-nω_0)+b_n*δ(ω+nω_0)]a_n=f(nT)/Tb_n=04.系统均方根误差公式：E = √(∫[y(t)-x(t)]^2dt)5.窄带系统的频率响应公式：H(ω)=，H(0)，*e^(jφ)φ=∠H(ω)-∠H(0)6.线性时不变系统的冲激响应公式：h(t)=L^{-1}[H(ω)]7.卷积公式：y(t)=h(t)*x(t)=∫h(τ)x(t-τ)dτ8.卷积定理：F_y(ω)=H(ω)F_x(ω)9.线性时不变系统的输入-输出关系公式：y(t)=x(t)*h(t)10.系统频率响应的幅度与相位关系：H(ω)=，H(ω)，*e^(j∠H(ω))11.奇谐信号的频谱：F(ω)=∑[C_k*δ(ω-2kπ/T)]C_k = (2/T)∫[f(t)*sin(kωt)]dt12.偶谐信号的频谱：F(ω)=∑[C_k*δ(ω-2kπ/T)]C_k = (2/T)∫[f(t)*cos(kωt)]dt13.系统频率响应的单位脉冲响应关系：H(ω) = ∫h(t)e^(-jωt)dt以上是信号与系统中的一些重要公式，这些公式是理解和分析信号与系统的基础。

在学习时，我们可以通过掌握这些公式，理解它们的意义和用途，以便更好地应用在实际问题中。

同时，信号与系统还涉及到很多其他的公式和定理，如采样定理、拉普拉斯变换、Z变换等，这些内容超过1200字无法一一列举。

如果对这些公式有更进一步的了解，推荐阅读相关的教材和参考资料，以便更好地理解信号与系统的知识。

考研信号与系统公式分类与汇总(最实用版)

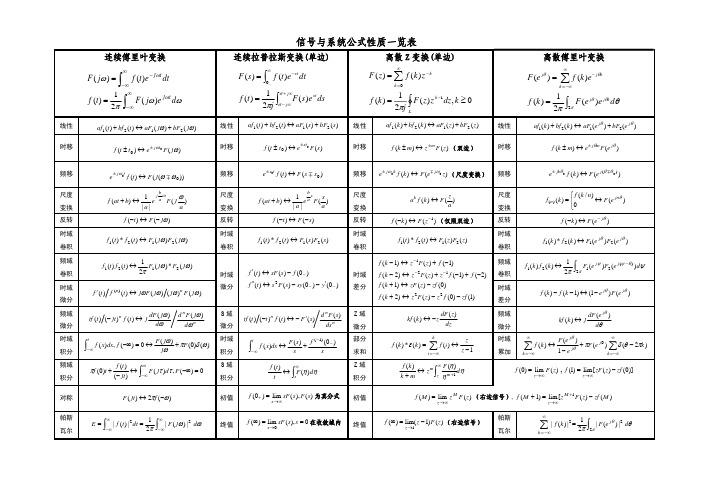
S域微分时域积分 S域积分
tf (t) (−t)n f (t) ↔ − F ′(s) d n F (s) ds n
∫t f (x)dx ↔ F (s) + f (−1) (0− )
−∞
s
s
∫ f (t) ↔
∞
F (η)dη
t
s
频移
尺度变换反转时域卷积
时域差分
Z域微分部分求和 Z域积分
频域卷积时域差分频域微分时域累加
∫ f1 (k )
f 2 (k )
↔
1 2π
2π F1(e jψ )F2 (e j(ψ −θ ) )dψ
f (k) − f (k −1) ↔ (1− e jθ )F (e jθ )
kf (k) ↔ j dF (e jθ ) dθ
∑ ∑ ∞ f (k)
k =−∞
af1 (k) + bf 2 (k) ↔ aF1 (z) + bF2 (z)
时移
f (t ± t0 ) ↔ e±st0 F (s)
时移
f (k ± m) ↔ z ±m F (z) （双边）
离散傅里叶变换
∞
∑ F (e jθ ) = f (k)e− jθk k =−∞
∫ f (k) = 1 F (e jθ )e jθkdθ
连续傅里叶变换
∫ F ( jω) = ∞ f (t)e − jωt dt −∞
∫ f (t) = 1 ∞ F ( jω)e jωt dω 2π −∞
线性时移
af1(t) + bf2 (t) ↔ aF1( jω) + bF2 ( jω) f (t ± t0 ) ↔ e± jωt0 F ( jω)

信号与系统概念公式总结

信号与系统概念，公式集：第一章：概论1.信号：信号是消息的表现形式。

（消息是信号的具体内容）2.系统：由若干相互作用和相互依赖的事物组合而成的具有特定功能的整体。

第二章：信号的复数表示：1.复数的两种表示方法：设C 为复数，a 、b 为实数。

常数形式的复数C=a+jb a 为实部，b 为虚部；或C=|C|e j φ，其中，22||b a C +=为复数的模，tan φ=b/a ，φ为复数的辐角。

（复平面）2.欧拉公式：wt j wt e jwtsin cos +=（前加-，后变减）第三章：正交函数集及信号在其上的分解1.正交函数集的定义：设函数集合)}(),(),({21t f t f t f Fn =如果满足：ni K dt t f ji dt t f t f iT T i T T j i 2,1)(0)()(21212==≠=⎰⎰则称集合F 为正交函数集如果n i K i,2,11==，则称F 为标准正交函数集。

如果F 中的函数为复数函数条件变为：ni K dt t f t f ji dt t f t f iT T i i T T j i 2,1)()(0)()(2121**==⋅≠=⋅⎰⎰其中)(*t f i 为)(t f i 的复共轭。

2.正交函数集的物理意义：一个正交函数集可以类比成一个坐标系统；正交函数集中的每个函数均类比成该坐标系统中的一个轴；在该坐标系统中，一个函数可以类比成一个点；点向这个坐标系统的投影（体现为该函数与构成坐标系的函数间的点积）就是该函数在这个坐标系统中的坐标。

3.正交函数集完备的概念和物理意义：如果值空间中的任一元素均可以由某正交集中的元素准确的线性表出，我们就称该正交集是完备的，否则称该正交集是不完备的。

如果在正交函数集()()()()t g n ,t g ,t g ,t g 321之外，不存在函数x （t ）()∞<<⎰2120t t dt t x ，满足等式：()()⎰=210t t i dt t g t x ，则此函数集称为完备正交函数集。

信号与系统主要公式和内容摘要

信号与系统主要公式和内容摘要一．单位冲激信号()t δ的基本特性： 1. √()()()()()0t x dt t t t x dt t t t x =+=-⎰⎰∞∞-∞∞-δδ2.()()()⎩⎨⎧><=⎰0ab ab dt t t b aϕδϕ3.()()t aat δδ1=4. √ ()()()()000t t t x t t t x -=-δδ5. ()()t t δδ=- 偶函数6.()()t dtt du δ= ()()t u d t =⎰∞-ττδ 7. ()()()t x t t x =*δ ()()()00t t x t t t x -=-*δ 8. ()()()2121t t t t t t t --=-*-δδδ 9. ()()()t x t t x '='*δ ()()()ττd x t u t x t⎰∞-=*10. 若：()()()t x t x t y 21*=则：()()()()()t x t x t x t x t y 2121'*=*'=' ()()()()()()()()t x t x t x t x t y 1212111---*=*=()()()212211t t t y t t x t t x --=-*- 二．单位脉冲序列[]n δ的基本特性： 1. [][]∑+∞=-=k k n n u δ [][]∑-∞==nk k n u δ √[][][]1--=n u n u n δ2. √[][][][]000n n n x n n n x -=-δδ√[][][]n x n n x =*δ √[][][]00n n x n n n x -=-*δ 3. [][][]k n k x n x k -=∑∞-∞=δ特殊：()()()()t r t tu t u t u ==* [][]()[]n u n n u n u 1+=* 1欧拉公式：()()()[]()[]⎪⎪⎪⎩⎪⎪⎪⎨⎧-=+=+=--t j t j t j t j t j e e j t Sin e e t Cos t jSin t Cos e ααααααααα2121三．线性时不变系统（LTI 系统）的主要特性 1. 线性：（1）无初值：()()()()t y a t y a t x a t x a 22112211+→+ [][][][]n y a n y a n x a n x a 22112211+→+ （2）含初值：若：()()()t y x t f 1110→⎥⎦⎤⎢⎣⎡ ()()()t y x t f 2220→⎥⎦⎤⎢⎣⎡ 则：()()()()()()t y t y x t f x t f 21221100βαβα+→⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡[][][][][][]k y k y x k f x k f 21221100βαβα+→⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡ 2. 时不变性：()()00t t y t t x -→- [][]00n n y n n x -→- 3. 微（差）分性：()()dtt dy dt t dx → [][]k n y k n x -→- 4. 积分（累加）特性：()()⎰⎰→ttd y d x 0ττττ [][]∑∑==→Nk Nk k y k x 05. 因果性：若：()0=t h ，当0<t 时 √若：[]0=n h ，当0<n 时 6. 稳定性：()∞<⎰∞∞-ττd h √[]∑∞-∞=∞<k k h27. 卷积特性： ()()()()()()()ττττττd t x h d t h x t h t x t y f ⎰⎰∞∞-∞∞--=-=*=[][][][][][][]k n x k h k n h k x n h n x n y k k f -=-=*=∑∑∞-∞=∞-∞=有：()()()ωωωj H j X j Y f =()()()S H S X S Y f =()()()Z H Z X Z Y f =四．信号的基本运算： 1. 相加：()()()t x t x t y 21+= [][][]n x n x n y 21+=2. 相乘：()()()t x t x t y 21= [][][]n x n x n y 21=3. 幅度加权：()()t x t y α= [][]n x n y α=4. 反折：()()t x t y -= [][]n x n y -=5. 时移：()()0t t x t y -= [][]0n n x n y -=00>t （或00>n ）为右移，00<t （或00<n ）为左移 6. 尺度变换：（1）连续时间信号的尺度变换：()()at x t y =1>a 时，表示()t x 在时间轴上被压缩a 倍 1<a 时，表示()t x 在时间轴上被扩展a 倍（2）离散时间信号的内插与抽取：内插：[]⎥⎦⎤⎢⎣⎡→L k f k f , L 为正整数[]0f 不动，在序列2点之间插入1-L 个零点 3抽取：[][]Mk f k f →， M 为正整数[]0f 不动，在原序列中每隔1-M 点抽取一点 7. 微分（差分）： ()()dtt dx t y =[][][]1--=n x n x n y8. 积分（累加）： ()()ττd x t y t⎰∞-= [][]∑-∞==nk k x n y9. 卷积()()()()()()()ττττττd t x x d t x x t x t x t y -=-=*=⎰⎰∞∞-∞∞-122121[][][][][][][]k n x k x k n x k x n x n x n y k k -=-=*=∑∑∞-∞=∞-∞=122121五．几何级数的求值公式：1. ⎪⎪⎩⎪⎪⎨⎧=+≠--=+=∑1111121220a n a a a a n n n n2. ⎪⎪⎩⎪⎪⎨⎧=+-≠--=+=∑11111212121a n n a a a a a n n n n n n210n n ≤<3.aa n n -=∑+∞=110 1<a 4. a a a n n-=∑+∞=11 1<a 5. a a a n n n n-=∑+∞=1111<a六．傅里叶变换、拉普拉斯变换、Z 变换 1.LTI 系统对虚指数信号的响应：→t j e ω()()t j e j H t y ωω=→()()()tjn n n n tjn n e jn H C t y eC t f 000ωωω∑∑∞-∞=∞-∞==→=42.傅里叶级数公式： ()∑∞-∞==n tjn n eC t x0ω 其中：()dt e t x T C tjn Tn 01ω-⎰= 3. 傅里叶变换公式（系统稳定）：（1）非周期信号：()()ωωπωd ej X t x tj ⎰∞+∞-=21()()dt e t x j X t j ωω-∞+∞-⎰=条件：()⎰∞+∞-∞<dt t x 或()⎰∞+∞-∞<dt t x 2（2）周期信号：()∑∞-∞==k t jk k e a t xω()()∑∞-∞=-=k k k a j X 02ωωδπω 002T πω=()dt e t x T a tjk Tk 01ω-⎰=4. 拉普拉斯变换公式： ()()dt et x S XtS -∞-⎰=0 ()()dS e S X j t x t S j j ⎰∞+∞-=σσπ215. Z 变换公式： ()[]n n Z n x Z X -∞=∑=[]()dZ Z Z X j n x n C121-⎰=π6. 典型信号的三种变换公式：（1）√()1−→←FTt δ√()1−→←LT t δ √()()n LTn S t −→←δROC:整个S 平面√[]1−→←Zn δ ROC:整个Z 平面 (2) √()00t j FTe t t ωδ-−→←-√()00t S LT e t t -−→←-δ ROC:整个S 平面√[]00nZ Z n n -−→←-δROC:整个Z 平面(可能去除0=Z )(3) ()()ωπδω+−→←j t u FT15()St u LT1−→← ROC:{}0>S R e √ []111--−→←Zn u ZROC: 1>Z (4) ()ωj a t u eFTat+−→←-1{}0>a R e√()a S t u eLTat+−→←-1ROC: {}a S R e -> []111--−→←aZn u a Z nROC: a Z > (5) ()()21ωj a t u teFTat+−→←- {}0>a R e()()21a S t u teLTat+−→←- ROC: {}a S R e ->()[]()21111--−→←+aZ k u a k Zk ROC: a Z >(6)()∑∑+∞-∞=+∞-∞=-−→←k kFTk tjk kk a ea 020ωωδπω(7) ()020ωωπδω-−→←FT tj e()020ωωπδω+−→←-FTt j e(8) ()ωπδ21−→←FT(9) √()()[]000ωωδωωδπω++-−→←FTt Cos()220)(ωω+−→←S S t u t Cos LTROC: {}0>S R e(10) ()()[]000ωωδωωδπω--+−→←j t Sin FT()2020)(ωωω+−→←S t u t Sin LTROC: {}0>S R e (11) ()∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛-−→←-k FTn T kT nT t πωδπδ226（12） −→←FTT ASa T )(211ω（13） −→←FTtt ASin πλ√()()21ωSa t p FT−→← ()()()2211ωSa t p t p FT−→←* 七．傅里叶变换、拉普拉斯变换、Z 变换的主要性质设：()S X ：ROC {}0Re σ>S ()Z X ：ROC Rf Z > 1. 线性：()()()()ωωj bY j aX t by t ax FT+−→←+()()()()S bY S aX t by t ax lT +−→←+ ROC ：公共收敛域 [][]()()Z bY Z aX n by n ax ZT +−→←+ ROC ：公共收敛域2. 时移： √()()ωωj X e t t xt j FT00-−→←-√()()S X e t t xt S LT 00-−→←- 要求：右移，即00>tROC ：未变因果序列：√[][]()Z X Z n n u n n xn ZT00-−→←-- 要求：右移，即00>nROC ：未变非因果序列：√[][]()[]111-+−→←--x Z X Z n u n x ZT√ [][]()[][]21212-+-+−→←---x x Z Z X Zn u n x ZT73. 频移：()()[]00ωωω-−→←j X t x e FTt j()()00S S X t x e LT tS -−→← ROC: {}00Re σ>-S S []⎪⎭⎫ ⎝⎛−→←a Z X n x a ZT n ROC: Rf a Z >()[]()Z X n x ZTn -−→←-1 ROC:Rf Z >-4．反折：()()ωj X t x FT -−→←-()()S X t x LT -−→←- ROC: {}0Re σ>-S5．尺度变换：()⎪⎭⎫ ⎝⎛−→←a j X a at x FT ω1 √()⎪⎭⎫ ⎝⎛−→←a S X a at x LT1 ROC ：0Re σ>⎭⎬⎫⎩⎨⎧a S6．卷积：√()()()()ωωj Y j X t y t x FT−→←*()()()()S Y S X t y t x LT−→←* ROC ：公共收敛域 [][]()()Z Y Z X n y n x ZT −→←* ROC ：公共收敛域7．时域微分：()()ωωj X j t x dtd FT−→←：未修正不含初值：√()()S SX t x dt d LT −→← √()()S X S t x dtd n LTn n −→← 含初值： √()()()--−→←0x S SX t x dt d LT √ ()()()()--'--−→←00222x Sx S X S t x dtd LT 8．频域微分： 8()()ωωj X d djt tx FT−→← ()()S X dSd t tx LT-−→← ROC ：未变[]()dZZ dX Z n nx ZT-−→← ROC ：未变9．积分(累加)：()()()()ωδπωωττ01X j X j d x FTt +−→←⎰∞- ()()S X Sd x LTt1−→←⎰-ττ ROC ：{})0,max(Re 0σ>S []()Z X Zn x ZT kn 111-=-−→←∑ ROC ：),1max(Rf Z > 10．调制（频域卷积）：()()()(){}ωωπj Y j X t y t x FT *−→←2111．对偶：若：()()ωj F t g FT−→← 则：()()ωπ-−→←g jt F FT2 八．系统函数： 1.连续系统：()()∑∑===Nk M k kk k k k k dt t x d b dt t y d a 00√()()()()()∑∑====Nk kk kMk k j a j b j X j Y j H 00ωωωωω√()()()∑∑====Nk kk Mk kk f Sa Sb S X S Y S H 0()()ωωπωd ej H t h tj ⎰∞∞-=21()()dS e S H j t h t S j j ⎰∞+∞-=σσπ212. 离散系统：[][]∑∑==-=-Mk kN k kk n x b k n y a 0√()()()k Nk k Mk Kk f Z a Zb Z X Z Y Z H -==-∑∑==[]()dZ Z Z H j n h n C121-⎰=π3. 系统的因果性：（1）连续系统：S 域一个具有有理系统函数H(S)的LTI 系统，其因果性等价于H(S)的ROC 位于S 平面上最右边极点的右半平面。

信号与系统公式总结

信号与系统公式总结在信号与系统的学习过程中，公式总结是非常重要的，它可以帮助我们更好地理解和掌握知识。

下面将对信号与系统中常见的公式进行总结，希望能够对大家的学习有所帮助。

一、基本概念公式总结。

1. 信号的分类：连续时间信号，x(t)。

离散时间信号，x[n]2. 基本信号：单位冲激函数，δ(t)或δ[n]阶跃函数，u(t)或u[n]3. 基本性质：奇偶性，x(t) = x(-t)，x[n] = x[-n]周期性，x(t) = x(t+T)，x[n] = x[n+N]二、时域分析公式总结。

1. 基本运算：时移性质，x(t-t0)或x[n-n0]反褶性质，x(-t)或x[-n]放大缩小，Ax(t)或Ax[n]2. 基本运算公式：加法，x1(t) + x2(t)或x1[n] + x2[n]乘法，x1(t)x2(t)或x1[n]x2[n]三、频域分析公式总结。

1. 傅里叶变换：连续时间信号，X(ω) = ∫x(t)e^(-jωt)dt。

离散时间信号，X(e^jω) = Σx[n]e^(-jωn)。

2. 傅里叶变换性质：线性性质，aX1(ω) + bX2(ω)。

时移性质，x(t-t0)对应X(ω)e^(-jωt0)。

频移性质，x(t)e^(jω0t)对应X(ω-ω0)。

四、系统分析公式总结。

1. 系统性质：线性性，y(t) = ax1(t) + bx2(t)。

时不变性，y(t) = x(t-t0)对应h(t-t0)。

2. 系统时域分析：离散卷积，y[n] = Σx[k]h[n-k]连续卷积，y(t) = ∫x(τ)h(t-τ)dτ。

3. 系统频域分析：系统函数，H(ω) = Y(ω)/X(ω)。

五、采样定理公式总结。

1. 采样定理：连续信号采样，x(t)对应x[n]，x[n] = x(nT)。

重建滤波器，h(t) = Tsinc(πt/T)。

六、傅里叶级数公式总结。

1. 傅里叶级数：周期信号的傅里叶级数展开。

信号与系统重点概念公式总结

信号与系统重点概念及公式总结：第一章：概论1.信号：信号是消息的表现形式。

（消息是信号的具体内容）2.系统：由若干相互作用和相互依赖的事物组合而成的具有特定功能的整体。

第二章：信号的复数表示：1.复数的两种表示方法：设C 为复数，a 、b 为实数。

常数形式的复数C=a+jb a 为实部，b 为虚部；或C=|C|e j φ，其中，22||b a C +=为复数的模，tan φ=b/a ，φ为复数的辐角。

（复平面）2.欧拉公式：wt j wt e jwt sin cos +=（前加-，后变减）第三章：正交函数集及信号在其上的分解1.正交函数集的定义：设函数集合)}(),(),({21t f t f t f F n =如果满足：ni K dt t f ji dt t f t f i T T i T T j i 2,1)(0)()(21212==≠=⎰⎰则称集合F 为正交函数集如果n i K i ,2,11==，则称F 为标准正交函数集。

如果F 中的函数为复数函数条件变为：ni K dt t f t f j i dt t f t f i T T i i T T j i 2,1)()(0)()(2121**==⋅≠=⋅⎰⎰其中)(*t f i 为)(t f i 的复共轭。

2.正交函数集的物理意义：一个正交函数集可以类比成一个坐标系统；正交函数集中的每个函数均类比成该坐标系统中的一个轴；在该坐标系统中，一个函数可以类比成一个点；点向这个坐标系统的投影（体现为该函数与构成坐标系的函数间的点积）就是该函数在这个坐标系统中的坐标。

3.正交函数集完备的概念和物理意义：如果值空间中的任一元素均可以由某正交集中的元素准确的线性表出，我们就称该正交集是完备的，否则称该正交集是不完备的。

如果在正交函数集()()()()t g n ,t g ,t g ,t g 321之外，不存在函数x （t ）()∞<<⎰2120t t dt t x ，满足等式：()()⎰=210t t i dt t g t x ，则此函数集称为完备正交函数集。

信号与系统公式

信号与系统概念，公式集：一：概念1.信号：信号是消息的表现形式。

（消息是信号的具体内容）2.系统：由若干相互作用和相互依赖的事物组合而成的具有特定功能的整体。

二：信号的复数表示：1.复数的两种表示方法：设C 为复数，a 、b 为实数。

常数形式的复数C=a+jb a 为实部，b 为虚部；或C=|C|e j φ，其中，22||b a C +=为复数的模，tan φ=b/a ，φ为复数的辐角。

（复平面）2.欧拉公式：wt j wt e jwtsin cos +=（前加-，后变减）三：正交函数集及信号在其上的分解1.正交函数集的定义：设函数集合)}(),(),({21t f t f t f Fn =如果满足：ni K dt t f ji dt t f t f iT T i T T j i 2,1)(0)()(21212==≠=⎰⎰则称集合F 为正交函数集如果n i K i,2,11==，则称F 为标准正交函数集。

如果F 中的函数为复数函数条件变为：ni K dt t f t f ji dt t f t f iT T i i T T j i 2,1)()(0)()(2121**==⋅≠=⋅⎰⎰其中)(*t f i 为)(t f i 的复共轭。

2.正交函数集的物理意义：一个正交函数集可以类比成一个坐标系统；正交函数集中的每个函数均类比成该坐标系统中的一个轴；在该坐标系统中，一个函数可以类比成一个点；点向这个坐标系统的投影（体现为该函数与构成坐标系的函数间的点积）就是该函数在这个坐标系统中的坐标。

3.正交函数集完备的概念和物理意义：如果值空间中的任一元素均可以由某正交集中的元素准确的线性表出，我们就称该正交集是完备的，否则称该正交集是不完备的。

如果在正交函数集()()()()t g n ,t g ,t g ,t g 321之外，不存在函数x （t ）()∞<<⎰2120t t dt t x ，满足等式：()()⎰=210t t i dt t g t x ，则此函数集称为完备正交函数集。

信号与系统概念公式总结

信号与系统概念，公式集：第一章：概论1.信号：信号是消息的表现形式。

（消息是信号的具体内容）2.系统：由若干相互作用和相互依赖的事物组合而成的具有特定功能的整体。

第二章：信号的复数表示：1.复数的两种表示方法：设C 为复数，a 、b 为实数。

常数形式的复数C=a+jb a 为实部，b 为虚部；或C=|C|e j φ，其中，22||b a C +=为复数的模，tan φ=b/a ，φ为复数的辐角。

（复平面）2.欧拉公式：wt j wt e jwtsin cos +=（前加-，后变减）第三章：正交函数集及信号在其上的分解1.正交函数集的定义：设函数集合)}(),(),({21t f t f t f Fn =如果满足：ni K dt t f ji dt t f t f iT T i T T j i 2,1)(0)()(21212==≠=⎰⎰则称集合F 为正交函数集如果n i K i,2,11==，则称F 为标准正交函数集。

如果F 中的函数为复数函数条件变为：ni K dt t f t f ji dt t f t f iT T i i T T j i 2,1)()(0)()(2121**==⋅≠=⋅⎰⎰其中)(*t f i 为)(t f i 的复共轭。

2.正交函数集的物理意义：一个正交函数集可以类比成一个坐标系统；正交函数集中的每个函数均类比成该坐标系统中的一个轴；在该坐标系统中，一个函数可以类比成一个点；点向这个坐标系统的投影（体现为该函数与构成坐标系的函数间的点积）就是该函数在这个坐标系统中的坐标。

3.正交函数集完备的概念和物理意义：如果值空间中的任一元素均可以由某正交集中的元素准确的线性表出，我们就称该正交集是完备的，否则称该正交集是不完备的。

如果在正交函数集()()()()t g n ,t g ,t g ,t g 321之外，不存在函数x （t ）()∞<<⎰2120t t dt t x ，满足等式：()()⎰=210t t i dt t g t x ，则此函数集称为完备正交函数集。

信号与系统的公式汇总分类 - 副本

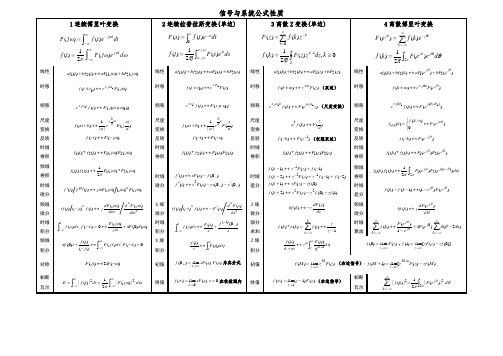
信号与系统公式性质1连续傅里叶变换⎰⎰∞∞-∞∞--==ωωπωωωd e j F t f dtet f j F t j tj )(21)()()(2连续拉普拉斯变换(单边) ⎰⎰∞+∞-∞-==-j j st stds e s F j t f dte tf s F σσπ)(21)()()(03离散Z 变换(单边) ⎰∑≥==-∞=-Lk k kk dz z z F j k f z k f z F 0,)(21)()()(10π4离散傅里叶变换⎰∑==∞-∞=-πθθθθθπ2)(21)()()(d e eF k f e k f e F k j j k kj j 线性 )()()()(2121ωωj bF j aF t bf t af +↔+线性 )()()()(2121s bF s aF t bf t af +↔+线性 )()()()(2121z bF z aF k bf k af +↔+线性 )()()()(2121θθj j e bF e aF k bf k af +↔+时移)()(00ωωj F e t t f t j ±↔± 时移)()(00s F e t t f st ±↔± 时移)()(z F z m k f m ±↔±（双边）时移)()(θθj m j e F e m k f ±↔± 频移 ))(()(00ωωω j F t f e t j ↔±频移 )()(00s s F t f e t s ↔±频移 )()(00z e F k f e j k j ωω ↔±（尺度变换）频移 )()()(00θθθ j jk e F k f e ↔±尺度变换 )(||1)(aj F e a b at f a bj ωω↔+尺度变换 )(||1)(asF e a b at f s a b↔+尺度变换 )()(azF k f a k ↔尺度变换 )(0)/()()(θjn n e F n k f k f ↔⎩⎨⎧=反转 )()(ωj F t f -↔- 反转 )()(s F t f -↔- 反转 )()(1-↔-z F k f （仅限双边）反转 )()(θj e F k f -↔-时域卷积 )()()(*)(2121ωωj F j F t f t f ↔时域卷积)()()(*)(2121s F s F t f t f ↔时域卷积)()()(*)(2121z F z F t f t f ↔时域卷积 )()()(*)(2121θθj j e F e F k f k f ↔ 频域卷积 )(*)(21)()(2121ωωπj F j F t f t f ↔时域微分)0()0()()()0()()(2---'--↔''-↔'y sy s F s t f f s sF t f时域差分)1()0()()2()0()()1()2()1()()2()1()()1(22121zf f z z F z k f zf z zF k f f f zz F z k f f z F z k f --↔+-↔+-+-+↔--+↔----频域卷积 ψπθψπψd e F eF k f k f j j )()(21)()()(22121-⎰↔时域微分 )()()()()()(ωωωωj F j j F j t f t f n n ↔'时域差分 )()1()1()(θθj j e F e k f k f -↔--频域微分 nn nd j F d d j dF jt f jt t tf ωωωω)()()()()(↔-S 域微分 nn nds s F d s F t f t t tf )()()()()('-↔-Z 域微分 dzz dF zk kf )()(-↔频域微分 θθd e dF jk kf j )()(↔时域积分 )()0()(0)(,)(ωδπωωF j j F f dx x f t+↔=-∞⎰∞-时域积分 sf s s F dx x f t)0()()()1(--∞-+↔⎰部分求和 1)()(*)(-↔=∑-∞=z zi f k k f ki ε 时域累加∑∑∞-∞=∞-∞=-+-↔k j j j k k e F e e F k f )2()(1)()(0πθδπθθ频域积分 0)(,)()()()0(=-∞↔-+⎰∞-F d j F jt t f t f ωττπS 域积分 ⎰∞↔s d F tt f ηη)()(Z 域积分 ηηηd F z mk k f z m m⎰∞+↔+1)()()(lim )0(z F f z →∞=,)]0()([lim )1(zf z zF f z -=→∞对称 )(2)(ωπ-↔f jt F初值)(),(lim )0(s F s sF f s →∞+=为真分式初值)(lim )(z F z M f M z ∞→=（右边信号）,)()([lim )1(1M zf z F z M f M z -=++∞→帕斯瓦尔⎰⎰∞∞-∞∞-==ωωπd j F dt t f E 22|)(|21|)(| 终值0),(lim )(0==∞→s s sF f s 在收敛域内终值)()1(lim )(1z F z f z -=∞→（右边信号）帕斯瓦尔⎰∑∞-∞==πθθπ222|)(|21|)(|d e F k f j k常用连续傅里叶变换、拉普拉斯变换、Z 变换对一览表连续傅里叶变换对⎰∞∞--=dt et f j F tj ωω)()(拉普拉斯变换对（单边）⎰∞--=0)()(dt e t f s F stZ 变换对（单边） ∑∞=-=0)()(k k z k f z F函数 )(t f傅里叶变换)(ωj F 函数 )(t f 象函数)(s F函数0),(≥k k f象函数函数0),(≥k k f象函数1)(t δ )(21ωπδ )(t δ1)(k δ10),(≥-m m k δmz -)()()(t t n δδ'nj j )(ωω)(t δ's11-z z 0),(≥-m m k εm z z z-⋅-1)(t ε)(1ωπδω+j )(t εs1)(k ε1-z z )(2k k ε32)1(-+z z z )(t t ε21)(ωωδπ-'j )()(t t t t nεε12!1+n s n s )(k k ε2)1(-z z )()1(k a k k ε+ 22)(a z z - 0,)()(>--αεεααt te t e t t2)(11ωαωαj j ++)()(t te t e t t εεαα--2)(11αα++s s)(k a k ε az z - )(1k ka k ε-2)(a z z - )sin()cos(00t t ωω)]()([)]()([0000ωωδωωδπωωδωωδπ--+-++j)()cos(t t εβ22β+s s)(k e k εααe z z -)(k ka k ε2)(a z az -t 1)sgn(ωπj -)()sin(t t εβ 22ββ+s)(k ekj εββj e z z -)(2k a k kε322)(a z z a az -+||t22ω-)()cosh(t t εβ22β-s s )(2)(k aa a kk ε-- 22a z z - )(2)(k aa a kk ε-+ 222a z z - tj e0ω±)(20ωωπδ)()sinh(t t εβ22ββ-s )(2)1(k k k ε- 3)1(-z z)(2)1(k kk ε+ 32)1(-z z )()cos(t t etεβα-22)(βαωαω+++j j)()cos(t t etεβα-22)(βαα+++s s )(k ba b a kk ε-- ))((b z a z z--)(11k ba b a k k ε--++ ))((2b z a z z -- )()sin(t t e t εβα-22)(βαωβ++j)()sin(t t etεβα-22)(βαβ++s)()cos(k k εβ1cos 2)cos (2+--ββz z z z)()sin(k k εβ1cos 2sin 2+-ββz z z),(||>-αεαt et222ωαα+)()(10t b t b ε+210ss b b +)()cos(k k εθβ+1cos 2)cos(cos 22+---βθβθz z z z)()sin(k k εθβ+1cos 2)sin(sin 22+--+βθβθz z z znt t)()(2)(2)(ωδπωδπn n j j ')()(10t e b b b t εααα---)(01α++s s b s b)()cos(k k a k εβ22cos 2)cos (a az z a z z +--ββ)()sin(k k a k εβ22cos 2sin a az z az +-ββ)sgn(tωj 2)()]sin([13t t t εβββ-)(1222β+s s)()cosh(k k a k εβ22cosh 2)cosh (aaz z a z z +--ββ)()sinh(k k a k εβ22cosh 2sinh a az z az +-ββ)0(,0,0,>⎪⎩⎪⎨⎧><--αααt e t e tt 222ωαω+-j)()sin()]1[213t t t εβββ-222)(1β+s0),(>k k ka kε⎪⎭⎫ ⎝⎛-a z z ln )(!k k a kε za e⎪⎪⎩⎪⎪⎨⎧><=2||,02||),cos()(τττπt t t t f 22)2()2()2cos(2ωτπωτπτ-⋅)()sin(21t t t εββ222)(β+s s)(!)(ln k k a kε za1)!2(1k z1cosh∑∞-∞=Ωn tjn n e FTn F n n πωδπ2,)(2=ΩΩ-∑∞-∞= )()]cos()[sin(21t t t t εββββ+ 2222)(β+s s)(11k k ε+ ⎪⎭⎫ ⎝⎛-1ln z z z )(121k k ε+ 11ln21-+z z z ∑∞-∞=-=n T nT t t )()(δδTn n πωδωδ2)()(=ΩΩ-Ω=∑∞-∞=Ω )()cos(t t t εβ22222)(ββ+-s s)(])([1010t e b b e b b tt εαββαβαβα----+--))((01βα+++s s b s b⎪⎪⎩⎪⎪⎨⎧><=2||,02||,1)(τττt t t g⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛2sin 22ωτωωττSateb t b b αα-+-])[(110201)(α++s b s b)(]))(())(())(([221022102210t e b b b eb b b e b b b ttt εγβγαγγβγβαββαγαβααγβα-----+-+--+-+--+-))()((0122γβα+++++s s s b s b s btWt Wt Sa Wππ)sin()(= ⎪⎪⎩⎪⎪⎨⎧><=2||,02||,1)(W W j F ωωω)()sin(t t Ae t εθβα+-,其中ββαθ)(10j b b Ae j --=2201)(βα+++s b s b)(])()2()([2210221022210t eb b b te b b b e b b b ttt εαβαβαβαβααβαββααβ-----+--⋅-+-+-+-)()(20122βα++++s s b s b s b⎪⎪⎩⎪⎪⎨⎧><-=∆2||,02||,||21)(τττt t t t f ⎪⎭⎫⎝⎛422ωττSa )(])(21)2([22210212t e t b b b teb b eb t ttεαααααα---+-+-+3122)(α+++s b s b s b)()]sin([222210t t A e b b b t εθββγγγγ++++--其中)()(1220βγβββθj jb b b Ae j ++-=))((220122βγ++++s s b s b s b⎪⎪⎩⎪⎪⎨⎧><+=2||,02||),2(1)(ττττt t t t f⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--212ωτωωτSa ejj ⎥⎦⎤⎢⎣⎡-⨯⎥⎦⎤⎢⎣⎡+-↔⎪⎪⎪⎩⎪⎪⎪⎨⎧><<--<=4)(sin 4)(sin )(82||,02||2),||21(2||,1)(1112111ττωττωττωττττττττt t t t t f)()]sin()([222210t t Ae e b b b t t εθββγαγγαγ+++-+---其中)()()(2210βαγββαβαθj j b j b b Ae j +--+--=)]))[((220122βαγ+++++s s b s b s b双边拉普拉斯变换与双边Z 变换对一览表双边拉普拉斯变换对 ⎰∞∞--=dt e t f s F st)()(双边Z 变换对∑∞-∞=-=k kzk f z F )()(函数象函数)(s F 和收敛域函数象函数)(z F 和收敛域 )(t δ 1，整个S 平面)(k δ1，整个Z 平面)()(t n δns ，有限S 平面)(k nδ∆0||,)1(>-z z z nn)(t ε0}Re{,1>s s)(k ε1||,1>-z z z)(t t ε0}Re{,12>s s )()1(k k ε+ 1||,)1(22>-z z z)()!1(1t n t n ε-- 0}Re{,1>s s n)()!1(!)!1(k n k n k ε--+1||,)1(>-z z z nn)(t --ε 0}Re{,1<s s)1(---k ε1||,1<-z z z)(t t --ε 0}Re{,12<s s )1()1(--+-k k ε 1||,)1(22<-z z z)()!1(1t n t n ----ε 0}Re{,1<s sn )1()!1(!)!1(----+-k n k n k ε 1||,)1(<-z z z nn)(t e at ε-}Re{}Re{,1a s as ->+ )(k a k ε||||,a z az z>- )(t teatε- }Re{}Re{,)(12a s a s ->+)()1(k a n nε+||||,)(22a z a z z >-)()!1(1t e n t atn ε--- }Re{}Re{,)(1a s a s n->+ )()!1(!)!1(k a n k n k nε--+||||,)(a z a z z nn>-)(t e at ---ε }Re{}Re{,1a s as -<+ )1(---k a k ε||||,a z az z<- )()!1(1t e n t at n -----ε }Re{}Re{,)(1a s a s n-<+)1()!1(!)!1(----+-k a n k n k n ε ||||,)(a z a z z nn<- )()cos(t t εβ 0}Re{,22>+s s sβ)()cos(k k εβ 1cos 2cos 22+--ββz z z z)()sin(t t εβ 0}Re{,22>+s s ββ)()sin(k k εβ 1cos 2sin 2+-ββz z z)()cos(t t etεβα-}Re{}Re{,)(22a s s s ->+++βαα)()cos(k k a kεβ 1cos 2cos 22+--ββza z za z)()sin(t t e t εβα- }Re{}Re{,)(22a s s ->++βαβ)()sin(k k a k εβ1cos 2sin 2+-ββza z za0}Re{,||>-a et α}Re{}Re{}Re{,222a s a as a->>-- 1||,||<a a k |1|||||,)1)(()1(2a z a az a z z a <<---}Re{),sgn(||>-a t e t α}Re{}Re{}Re{,222a s a a s s->>-1||sgn,||<a a k|1|||||,)1)(()(2az a az a z z z a <<---卷积积分一览表⎰∞∞--=τττd t f f t f t f )()()(*)(121)(1t f)(2t f)(*)(21t f t f)(1t f)(2t f)(*)(21t f t f)(t f )(t δ')(t f ')(t f)(t δ)(t f)(t f)(t ελλd f t⎰∞-)()(t ε )(t ε)(t t ε)(t e t εα-)(t ε)()1(1t e t εαα--)(t ε)(t t ε)(212t t ε )(1t e t εα-)(2t e t εα-2112),()(121ααεαααα≠----t e e t t )(t e t εα- )(t e t εα-)(t te t εα- )(t t ε )(t e t εα- )(1122t e t t εαααα⎪⎪⎭⎫ ⎝⎛+--)(t te t εα-)(t e t εα-)(212t e t tεα-卷积和一览表∑∞-∞=-=i i k f i ft f t f )()()(*)(121 )(1t f)(2t f)(*)(21t f t f)(1t f)(2t f)(*)(21t f t f)(k f)(k δ)(k f)(k f)(k ε ∑-∞=ki i f )()(k ε )(k ε )()1(k k ε+ )(k k ε)(k ε)()1(21k k k ε+)(k a k ε)(k ε0),(111≠--+a k aa k ε )(1k a k ε )(2k a kε21211211),(a a k a a a a k k ≠--++ε )(k a k ε )(k a k ε)()1(k a k k ε+)(k k ε)(k a k ε)()1()1()(12k a a a k a k k εε--+- )(k k ε )(k k ε)()1()1(61k k k k ε-+)()cos(1k k a k εθβ+)(k a k ε⎥⎦⎤⎢⎣⎡-=-+---++++2112122211211cos sin arctan )(cos )cos(])1(cos[a a a k a a a a a k a k k ββϕεβϕθϕθβ关于)(t δ、)(k δ函数公式一览表)()0()()(t f t t f δδ=)()()()(000t t t f t t t f -=-δδ)()()()(t t t t δδδδ'-=-'=- )()0()()0()()(t f t f t t f δδδ'-'=')0()()(f dt t t f =⎰∞∞-δ)()()(00t f dt t t t f =-⎰∞∞-δ)(|)(|1)([1i ni i t t t f t f -'=∑=δδ)0()1()()()()(n n n f dt t t f -=⎰∞∞-δ)(||1)(t a at δδ=⎰⎰∞-∞∞-==tt d dt t )()(1)(εττδδ)()(0)(t d dt t tδττδδ='='⎰⎰∞-∞∞-)()()()()()(00000t t t f t t t f t t t f -'--'=-'δδδ)(1||1)()()(t a a at n nn δδ⋅=)()()()(k k k ak δδδδ=-=∑∞-∞===k f k k f k f k k f )0()()()()0()()(δδδ)()()(00t f dt t t t f '-=-'⎰∞∞-δ。

信号与系统概念公式总结

信号与系统概念，公式集：第一章：概论1.信号：信号是消息的表现形式。

（消息是信号的具体内容）2.系统：由若干相互作用和相互依赖的事物组合而成的具有特定功能的整体。

第二章：信号的复数表示：1.复数的两种表示方法：设C 为复数，a 、b 为实数。

常数形式的复数C=a+jb a 为实部，b 为虚部；或C=|C|e j φ，其中，22||b a C +=为复数的模，tan φ=b/a ，φ为复数的辐角。

（复平面）2.欧拉公式：wtj wt ejwtsin cos +=（前加-，后变减）第三章：正交函数集及信号在其上的分解1.正交函数集的定义：设函数集合)}(),(),({21t f t f t f F n =如果满足：ni K dt t f ji dt t f t f iT T i T T j i 2,1)(0)()(21212==≠=⎰⎰则称集合F 为正交函数集如果n i K i ,2,11==，则称F 为标准正交函数集。

如果F 中的函数为复数函数条件变为：ni K dt t f t f ji dt t f t f iT T i i T T j i 2,1)()(0)()(2121**==⋅≠=⋅⎰⎰其中)(*t f i 为)(t f i 的复共轭。

2.正交函数集的物理意义：一个正交函数集可以类比成一个坐标系统；正交函数集中的每个函数均类比成该坐标系统中的一个轴；在该坐标系统中，一个函数可以类比成一个点；点向这个坐标系统的投影（体现为该函数与构成坐标系的函数间的点积）就是该函数在这个坐标系统中的坐标。

3.正交函数集完备的概念和物理意义：如果值空间中的任一元素均可以由某正交集中的元素准确的线性表出，我们就称该正交集是完备的，否则称该正交集是不完备的。

如果在正交函数集()()()()t g n ,t g ,t g ,t g 321之外，不存在函数x （t ）()∞<<⎰2120t t dtt x，满足等式：()()⎰=210t t i dt t g t x ，则此函数集称为完备正交函数集。

信 与系统公式大全 带公式证明

信号与系统 典型公式

信号与系统重点概念公式总结

信号与系统概念公式总结

信号与系统公式归纳

信号与系统-公式

(完整版),信号与系统-公式总结,推荐文档

信号与系统的公式汇总分类

信号与系统公式大全

考研信号与系统公式分类与汇总(最实用版)

信号与系统概念公式总结

信号与系统主要公式和内容摘要

信号与系统公式总结

信号与系统重点概念公式总结

信号与系统公式

信号与系统概念公式总结

信号与系统的公式汇总分类 - 副本

信号与系统概念公式总结

信与系统公式大全带公式证明

信号与系统典型公式