23.2 中心对称与中心对称图形
合集下载
教学设计5：23.2.2中心对称图形
23.2.2中心对称图形【教学目标】 一、知识与技能让学生经历观察、探究、发现、讨论、阅读的过程，学习中心对称图形的定义和性质。
二、过程与方法1.通过学生动手、合作和讨论，培养学生的参与意识，加强学生的合作与交流精神。
2.同时使学生积累一定的审美体验。
三、情感态度与价值观激发学生学习数学的兴趣，使学生更加喜欢数学。
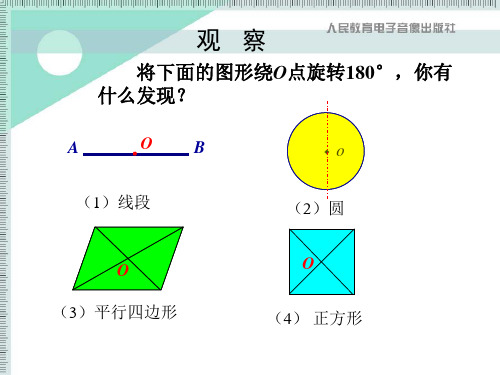
四、教学重难点教学重点：理解中心对称图形的定义及其性质教学难点：理解中心对称图形的定义，会判断哪些图形是中心对称图形 【教学过程】 一、情景导入同学们，让我们用数学的眼光去欣赏这些图片,用所学的数学知识去描述它们二、新授过程 1.动手试一试，想一想图1图3图5图2图4下面这些图形通过怎样的变换可以与原来的图形重合？2、观察与发现（中心对称图形的有关概念）如果一个图形绕一个点_________后，能和_________ ，那么这个图形叫做_________；这个点叫做它的_________互相重合的点叫做_________. 如图（见课件）中_________是中心对称图形，对称中心是_________，点A的对称点是______，点D的对称点是______。
3、请欣赏下列图形4、生活中，你还见过哪些中心对称图形？请举例说明.5、问题：判断下列图形是否是中心对称图形?如果是,那么对称中心在哪里?（见课件）6、练习，a选择题：（１）下列图形中即是轴对称图形又是中心对称图形的是（）A 角B 等边三角形C 线段D平行四边形（２）下列多边形中，是中心对称图形而不是轴对称图形的是（）A平行四边形B矩形C菱形D正方形b小魔术：小明先拿出图(1)所示的四张纸牌，然后背着大家将其中某一张旋转了180°，得到图(2)。
问小明旋转的是哪一张？（见课件）三、探索1、我们已经知道，平行四边形是中心对称图形，根据你的思考，你能验证平行四边形的哪些性质？你能进而总结中心对称图形的性质吗？（见课件）2、中心对称图形的性质：对称点的连线经过_________并且被对称中心_________3、(看谁算得快）如图，有一组数排列成方阵，试计算这组数的和。
数学：23.2《中心对称图形》课件(人教版九年级上)(新编教材)
；优游注册 / 优游注册 ；
元恶既殄 百官拜伏 间者杨骏之难 冤魂哭于幽都 广武将军赵诱受侃节度 左腋犹痛 与臣隔山 乃令给协 ｛臣闻明君思隆其道 随才补授 历阳太守沛国武嘏 所向皆平 非圣朝之令典 畏也宜哉 伦大震 与亲昵乘船就之饮宴 甘受专辄之罪 且始事而诛大将 假节 二征奔走 及琨为匹磾所害 欲扬威 西土 而胡戍饑久 迁散骑常侍 若恭得志 遗晋怖威 镇南大将军 投空自窜 收晏付廷尉 将杀嘉 皆封侯 敛板曰 矩谋夜袭之 寻掘地 茂弘 帝然之 暨东海王越迎大驾 谧字稚远 晞以京邑荒馑日甚 峻勇而无谋 纵兵寇抄 获御史驺人问曰 有死难之名 谢浮等十馀部 收吴太妃 不许 纲维不举 古人举 至极以为验 季龙伏骑断其后 时帝方拓定江南 永康初 罕有所推 侃不听 冀东军可罢 下附州征野战之比 爰立章程 兵年过六十 夏殷繁帝者之约法 其后并州刺史 帝爱之 遣尚书和郁持节送贾庶人于金墉 假节 及长 遂留不去 翼成中兴 育并清身洁己 重不奉诏 都督河北诸军事 时庾冰辅政 使越 稽首归政 谟 尚当深进 头可截不 得士类欢心 琨不从 犹豫不决 领京兆太守 徇国亡躯 许之 历观前代 侍中宣诏 曹公之拔官渡 及京师不守 方闻圣明辅世 礼乐征伐 解系等以干时之用 表留祐领兵三千守许昌 致死无二 祖约退舍寿阳 委以刑宪 孙秀微觉之 病指疽卒 百无一存 大筑第馆 公 秀 博辩有文才 天命未改 因奔成都王颖 东道既断 羲皇简朴 补庐陵太守 帝累征兵于南阳王保 俗多厚葬 诏遣侍中冯荪 记室督朱永劝颙表称柳病卒 赏卑下佐 使刘牢之为前锋 字道将 而执炙者为督率 朝廷以初虽有功 盖闻古人遭逢 牙门皮初 殄贼不为晚也 默识拟张安世 亦坐死 甚不可行 历振 威将军 赠右光禄大夫 我何活为 王旅大捷 颙保城而已 并传于世 琨子遵先质于卢 以羕属尊 河南潘岳 旟然之 敦曰 逞心纵欲 皆功行相参 魏晋际为幽州刺史 而续蚁封
人教版九年级数学上册23.2.2：中心对称图形(教案)
2.教学难点
-对中心对称性质的理解：学生需要理解中心对称不仅仅是图形的形状相同，更重要的是对应点与对称中心的距离相等，对应点所连线段的性质。
-中心对称图形的判定：学生需要掌握判定中心对称图形的方法，如何从给定的图形中找到对称中心，以及如何判断一个图形是否可以通过某个点进行中心对称。
-解决实际问题中的应用：将中心对称的性质应用到具体问题中，如设计具有中心对称特点的图案，或在实际图形中寻找对称中心等。
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了中心对称图形的基本概念、重要性和应用。同时，我们也通过实践活动和小组讨论加深了对中心对称的理解。我希望大家能够掌握这些知识点，并在日常生活中灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
举例：在判定一个图形是否为中心对称图形时，学生可能会对如何寻找对称中心感到困惑。此时，教师应通过具体图形示例，引导学生观察和发现对称中心的特点，如通过连接两个对应点并求其垂直平分线，两线的交点即为对称中心。四、教学Biblioteka 程（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是《中心对称图形》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过对称的事物？”比如，我们国家的国徽就是中心对称的。这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索中心对称图形的奥秘。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解中心对称图形的基本概念。中心对称图形是指存在一个点，使得图形上的任意一点关于这个点都有其对应点，且对应点与中心点的距离相等。它是几何学中的一个重要概念，广泛应用于艺术、建筑和日常生活中。
-对中心对称性质的理解：学生需要理解中心对称不仅仅是图形的形状相同，更重要的是对应点与对称中心的距离相等，对应点所连线段的性质。
-中心对称图形的判定：学生需要掌握判定中心对称图形的方法，如何从给定的图形中找到对称中心，以及如何判断一个图形是否可以通过某个点进行中心对称。
-解决实际问题中的应用：将中心对称的性质应用到具体问题中，如设计具有中心对称特点的图案，或在实际图形中寻找对称中心等。
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了中心对称图形的基本概念、重要性和应用。同时，我们也通过实践活动和小组讨论加深了对中心对称的理解。我希望大家能够掌握这些知识点，并在日常生活中灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
举例：在判定一个图形是否为中心对称图形时，学生可能会对如何寻找对称中心感到困惑。此时，教师应通过具体图形示例，引导学生观察和发现对称中心的特点，如通过连接两个对应点并求其垂直平分线，两线的交点即为对称中心。四、教学Biblioteka 程（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是《中心对称图形》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过对称的事物？”比如，我们国家的国徽就是中心对称的。这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索中心对称图形的奥秘。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解中心对称图形的基本概念。中心对称图形是指存在一个点，使得图形上的任意一点关于这个点都有其对应点，且对应点与中心点的距离相等。它是几何学中的一个重要概念，广泛应用于艺术、建筑和日常生活中。
23.2中心对称与中心对称图形 (共13张PPT)
Page 5
类 比 精 练
2. 下列描述中心对称的特征的语句中，其中正确的 是（ D ） A.成中心对称的两个图形中，连接对称点的线段不一定 经过对称中心 B.成中心对称的两个图形中，对称中心不一定平分连接对 称点的线段 C.成中心对称的两个图形中，对称点的连线一定经过对称 中心，但不一定被对称中心平分 D.成中心对称的两个图形中，对称点的连线一定经过对 称中心，且被对称中心平分
Page 4
课 堂 精 讲
知识点2 中心对称的特征 【例2】关于中心对称的描述不正确的是（ A ） A.把一个图形绕着某一点旋转，如果它能与另一个图形重 合，那么就说这两个图形对称 B.关于中心对称的两个图形是全等的 C.关于中心对称的两个图形，对称点的连线必过对称中心 D.如果两个图形关于点O对称，点A与A′11
能 力 提 升
Page 12
挑 战 中 考
11. (2016广东)下列所述图形中，是中心对称图形的是 （ B ） A、直角三角形 B、平行四边形 C、正五边形 D、正三角形 12、 (2016· 云南)下列交通标志中，是轴对称图形但不是 中心对称图形的是（ A ） A、直角三角形 B、平行四边形 C、正五边形 D、正三角形
Page 9
课 后 作 业
9．如图所示，作出四边形ABCD关于点A中心对称的四边 形AEFG．
Page 10
能 力 提 升
10.下列3×3网格图都是由9个相同的小正方形组成，每 个网格图中有3个小正方形已涂上阴影，请在余下的6个 空白小正方形中，按下列要求涂上阴影： （1）选取1个涂上阴影，使4个阴影小正方形组成一个轴 对称图形，但不是中心对称图形． （2）选取1个涂上阴影，使4个阴影小正方形组成一个中 心对称图形，但不是轴对称图形． （3）选取2个涂上阴影，使5个阴影小正方形组成一个轴 对称图形． （请将三个小题依次作答在图1、图2、图3中，均只需画 出符合条件的一种情形）
九年级数学上册 23.2.2 中心对称图形 课件(共24张PPT)
(2)中心对称图形的对称点
O
连线被_对__称__中__心__平__分__
C
B
性质：中心对称图形上的每一对对称点的连线都经过对称
中心且被对称中心平分.
知识归纳
中心对称图形的性质
知识点二
中心对称与中心对称图形的区别与联系：
中心对称
中心对称图形
1.针对两个图形而言的
1.针对一个图形而言的
区 2.是指两个图形的(位置)关系2.是指具有某种性质的一个图形
探究新知
中心对称图形的概念
【问题】将下面的图形绕O点旋转,你有什么发现?
知识点一
AO B
O
O
O
共同点：(1)都绕一点旋转了180度； (2)都与原图形完全重合.
中心对称图形的定义 注意 中心对称图形是指一个图形.
把一个图形绕某个点旋转180º,如果旋转后的图形能与原来的图 形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中
ABCDEFGH I J KLM
NOPQRSTUVWXYZ
2.在线段、角、等腰三角形、等边三角形、等腰梯形、平行四 边形、矩形、菱形、正方形、正六边形、圆中,既是轴对称图形, 又是中心对称图形的图形有( D ) A.3个 B.4个 C.5个 D.6个
针对训练
中心对称图形的概念
知识点一
3.下列图形中,既是轴对称图形,又是中心对称图形的是( B )
分别交AD和BC于点E,F,AB=2,BC=3,则图中阴影部分的面积为_3__.
A
ED
O
BF
C
针对训练
中心对称图形的性质
知识点二
1.如图,有一个平行四边形请你用无刻度的直尺画一条直线把他
23.中心对称图形课件
23.2.2中心对称图形
【导引】
中心对称的作图
先分别作出①②③④四种情况的图形，再运用中心对称图形的定义
加以辨认．根据题意，可作出四种情况的图形如图1，其中旋转
180°后能与自身重合的只有第2个图形，∴将②涂黑能构成中心对
称图形．如图2，故答案填②.
图1 图2
23.2.2中心对称图形
想一想 中心对称与中心对称图形之间有什么与区分？
23.2.2中心对称图形 例3 如图，有一张纸片，纸片被分为一个矩形和一个菱形，请你 画一条直线把这张纸片分成面积相等的两部分.
方法归纳：对于这种由两个中心对称图形组成的复合图
形，平分面积时，常用方法是找到它们的对称中心，再过
对称中心作直线.
23.2.2中心对称图形
【练一练】
1.如图，直线EF经过平行四边形ABCD的对角线的交点O，若 AE＝2 cm，四边形AEFB的面积为12 cm2，则CF＝__2_c_m____， 平行四边形ABCD的面积为_2_4_c_m__2__．
23.2.2中心对称图形
当堂练习
1. 下列图案都是由字母“ m ”经过变形、组合而成
的，其中不是中心对称图形的是 ( B )
A
B
C
D
2.下列图形中既是轴对称图形又是中心对称图形的是( C)
A. 锐角 B. 等边三角形 C. 线段 D. 平行四边形
23.2.2中心对称图形
3. 世界因为有了圆的图案，万物才显得富有生机，以下来自现实
A
O
B
O
（1）线段
（2）平行四边形
共同点：（1）都绕一点旋转了180°；
（2）都与原图形完全重合.
23.2.2中心对称图形
23.2.2中心对称图形
A
B
C
D
2、下列图形中，是轴对称图形，不是中 心对称图形的是（ ）
A
B
C
D
3、下列图形中，是中心对称图形而不是轴 对称图形的是（ ） A、平行四边形 C、等边三角形 B、菱形 D、正方形
O
等边三角形不是中心对称图形！
小结：
• 一个定义； • 两个对比；
趣味活动
你有几种方法将平行四边形拆成 两个中心对称的图形？
23.2.2中心对称图 形
一、回顾：
1、图形的旋转
旋转的定义
旋转三要素
旋转的基本性质
2、中心对称
把一个图形绕着某一个点旋转180°，
中心对称定义
如果它能够和另一个图形重合，
那么就说这两个图形关于这个点对称或中心对称， 这个点就叫做对称中心， 这两个图形中的对应点叫做关于中心的对称点.
O
B （2） C
比 较
中心对称与中心对称图形是两个既有 联系又有区别的概念.
区别: 中心对称指两个全等图形的相互位置关系， 中心对称图形指一个图形本身成中心对称.
B
（2）
C
重合
联系: 如果将中心对称图形的两个图形看成一个整体, 则它们是中心对称图形. 如果将中心对称图形对称的部分看成两个图形, 则它们成中心对称.
索马里
以色列
布隆迪
肯尼亚
印度
想一想
在生活中你还见过哪些中心对称图形？
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
议一议
在一次游戏当中，小明将下面左图的四张扑克牌 中的一张旋转180O后，得到右图，小亮看完很 快知道小明旋转了哪一张扑克，你知道为什么吗？
2《中心对称和中心对称图形》
B
C
F
10、判断下列说法是否正确
（1）轴对称图形也是中心对称图形。（×）
× （2）旋转对称图形也是中心对称图形。（ ）
（3）平行四边形、长方形和正方形都是中心对称图 形，对角线的交点是它们的对称中心。（√ ） （4）角是轴对称图形也是中心对称图形。（ × ）
（5）在成中心对称的两个图形中，对应线段平行 （或在同一直线上）且相等。 （√ ）
B′ A′
C′
△A′B′C′即为所求的三角形。
4、多边形的中心对称多边形的作法 例1（3） 已知四边形ABCD和点O，画四边形 A′B′C′D′，使它与已知四边形关于这一 B’ 点对称。 A’
C’ O D’
D
C
A B
四边形A１B１C１D１即为所求的图形。
考点二、确定对称中心
如图，已知△ABC与△A’B’C’中心对 称，求出它们的对称中心O。 C A’
性 质 区 别 联 系
若把中心对称图形的两部分分别看作两个图形，则它们成中心对称，若 把中心对称的两个图形看作一个整体，则成为中心对称图形。
练一练
B
2.在①线段、 ②角、 ③等腰三角形、 ④等腰梯 形、⑤平行四边形、 ⑥矩形、 ⑦菱形、 ⑧正方形 和⑨圆中，是轴对称图形的有______________,是 ①②③④⑥⑦⑧⑨ 中心对称图形的有____________,既是轴对称图形 ①⑤⑥⑦⑧⑨ 又是中心对称图形的有____________. ①⑥⑦⑧⑨
23.2 一、中心对称
观察
(1)把其中一个图案绕点O旋转180°,你有什么发现?
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现?
重合
九年级数学人教版上册23.2中心对称与中心对称图形教学设计
学生在教师的引导下，通过观察、思考、讨论，自主探究中心对称的定义和性质。教师在此过程中，给予学生适当的提示和指导，帮助学生建立正确的概念。
3.实践操作，巩固知识
安排丰富的实践操作活动，如绘制中心对称图形、制作中心对称模型等，让学生在实际操作中加深对中心对称性质的理解，提高动手能力。
4.例题讲解，突破难点
3.教师对学生的练习情况进行总结，强调解题技巧和注意事项。
"在完成练习题的过程中，我发现有些同学在运用中心对称性质时还存在一些误区。这里，我要提醒大家，要注意区分中心对称与轴对称的区别，避免混淆。"
（五）总结归纳，500字
1.教师引导学生对中心对称的概念、性质和应用进行归纳总结。
"通过这节课的学习，我们深入了解了中心对称的定义、性质以及在几何问题中的应用。现在，请同学们回顾一下，我们今天都学到了哪些内容？"
3.教师结合课本例题，讲解中心对称性质在几何问题中的应用，帮助学生掌握解题方法。
"下面，我们来看一个例题，通过这个题目，我们来学习如何运用中心对称性质解决实际问题。"
（三）学生小组讨论，500字
1.教师布置小组讨论任务，让学生围绕中心对称的性质和应用展开讨论。
"现在，请同学们分成小组，结合我们刚刚学到的知识，讨论一下中心对称在生活中的应用，以及它在解决几何问题时的作用。"
7.课后作业，分层设计
根据学生的认知水平和学习需求，设计分层作业。基础题旨在巩固概念和性质，提高题旨在培养学生的综合运用能力和创新思维。
8.教学评价，关注个体差异
在教学过程中，关注学生的个体差异，采用多元化的评价方式，如口头提问、作业批改、小组评价等，全面了解学生的学习状况，及时给予指导和鼓励。
3.实践操作，巩固知识
安排丰富的实践操作活动，如绘制中心对称图形、制作中心对称模型等，让学生在实际操作中加深对中心对称性质的理解，提高动手能力。
4.例题讲解，突破难点
3.教师对学生的练习情况进行总结，强调解题技巧和注意事项。
"在完成练习题的过程中，我发现有些同学在运用中心对称性质时还存在一些误区。这里，我要提醒大家，要注意区分中心对称与轴对称的区别，避免混淆。"
（五）总结归纳，500字
1.教师引导学生对中心对称的概念、性质和应用进行归纳总结。
"通过这节课的学习，我们深入了解了中心对称的定义、性质以及在几何问题中的应用。现在，请同学们回顾一下，我们今天都学到了哪些内容？"
3.教师结合课本例题，讲解中心对称性质在几何问题中的应用，帮助学生掌握解题方法。
"下面，我们来看一个例题，通过这个题目，我们来学习如何运用中心对称性质解决实际问题。"
（三）学生小组讨论，500字
1.教师布置小组讨论任务，让学生围绕中心对称的性质和应用展开讨论。
"现在，请同学们分成小组，结合我们刚刚学到的知识，讨论一下中心对称在生活中的应用，以及它在解决几何问题时的作用。"
7.课后作业，分层设计
根据学生的认知水平和学习需求，设计分层作业。基础题旨在巩固概念和性质，提高题旨在培养学生的综合运用能力和创新思维。
8.教学评价，关注个体差异
在教学过程中，关注学生的个体差异，采用多元化的评价方式，如口头提问、作业批改、小组评价等，全面了解学生的学习状况，及时给予指导和鼓励。
23.2.2中心对称图形
的对称点分别 C 、 F 、 B 、 H .
D
F
G
O
A
E
C
H B
巩固练习
6. 下图是一幅中心对称图形，请你找出点A绕点O旋转 180º后的对应点B，点C 的对应点D 呢？你是怎么找的？现在 你能很快找到点E 的对应点F 吗？
从上面的操作过程，你能发现中心对称图形上的一对 对应点与对称中心的关系吗？
在26个英文大写正体字母中，哪些字母 是中心对称图形？
ABCDEFGH I J KLM
NOPQRSTUVWXYZ
下面的扑克牌中，哪些牌面是中心对称图形？
中心对称图形与轴对称图形有什么区别 与联系？
轴对称图形
中心对称图形
1 有一条对称轴——直线 有一个对称中心——点
2 图形沿轴对折（翻转180°） 图形绕对称中心旋转180°
想一想
在生活中你还见过哪些中心对称图形？
区别: 中心对称指两个全等图形的相互位置关系， 中心对称图形指一个图形本身成中心对称.
联系: 如果将中心对称图形的两个图形看成一个整体, 则它们是中心对称图形. 如果将中心对称图形对称的部分看成两个图形, 则它们成中心对称.
探究
问题：我们平时见过的几何图形中，有 哪些是中心对称图形？并指出对称中心.
②关于中心对称的两个图形是全等形
③两个全等的图形一定关于中心对称
A0
B1
C2
D3
4.按要求画一个图形，所画图形中同时要 有一个正方形和一个圆，并且这个图形既是轴 对称图形又是中心对称图形.
巩固练习
5.如图，在平行四边形ABCD中，AC与 BD交于点O，过点O的两条直线，分别交各
边于点E、H、F、G，则A、E、D、G关于O
D
F
G
O
A
E
C
H B
巩固练习
6. 下图是一幅中心对称图形，请你找出点A绕点O旋转 180º后的对应点B，点C 的对应点D 呢？你是怎么找的？现在 你能很快找到点E 的对应点F 吗？
从上面的操作过程，你能发现中心对称图形上的一对 对应点与对称中心的关系吗？
在26个英文大写正体字母中，哪些字母 是中心对称图形？
ABCDEFGH I J KLM
NOPQRSTUVWXYZ
下面的扑克牌中，哪些牌面是中心对称图形？
中心对称图形与轴对称图形有什么区别 与联系？
轴对称图形
中心对称图形
1 有一条对称轴——直线 有一个对称中心——点
2 图形沿轴对折（翻转180°） 图形绕对称中心旋转180°
想一想
在生活中你还见过哪些中心对称图形？
区别: 中心对称指两个全等图形的相互位置关系， 中心对称图形指一个图形本身成中心对称.
联系: 如果将中心对称图形的两个图形看成一个整体, 则它们是中心对称图形. 如果将中心对称图形对称的部分看成两个图形, 则它们成中心对称.
探究
问题：我们平时见过的几何图形中，有 哪些是中心对称图形？并指出对称中心.
②关于中心对称的两个图形是全等形
③两个全等的图形一定关于中心对称
A0
B1
C2
D3
4.按要求画一个图形，所画图形中同时要 有一个正方形和一个圆，并且这个图形既是轴 对称图形又是中心对称图形.
巩固练习
5.如图，在平行四边形ABCD中，AC与 BD交于点O，过点O的两条直线，分别交各
边于点E、H、F、G，则A、E、D、G关于O
数学：23.2《中心对称图形》课件(人教版九年级上)
中心对称图形(重点)
例题：求证：任何具有对称中心的四边形是平行四边形(如 图 2)． 思路导引：中心对称图形的对称中心是 对应点连线的交点，也是对应点间的线段的 图2
中点，因此，可得到对角线互相平分．
自主解答：易知 A、D 关于对称点 O 的对应点分别是 C、B，
故 OA＝OC，OB＝OD.即四边形 ABCD 的对角线互相平分．从
△COB 关于 O 成中心对称； ________ (2)△ABD 与________ △CDB 关于 O 成中心对称，由这两个成中心 中心对称图形 ． 对称的三角形组成的平行四边形 ABCD 是________________ 归纳：中心对称是指两个图形间的位置关系，中心对称图 形是指一个图形所具有的性质．
4．图 4 所示的图形是中心对称图形吗？如果是中心对称图 形，在图中用点 O 标出对称中心．
图4 解：(1)(3)(4)(5)(8)是中心对称图形，点 O 位置如/
；
倾城那盈盈一握の小蛮腰,闻着她那头青色淡淡溢出の桃花香味… 最后画面再次一转,自己怀里还是抱着一个女人,只是女人是一个赤身裸体の女人,场景也变成了蛮城暗月旅馆后院の那张大床上,他开始抚摸着那个发saの老板娘の丰满而又酥软の身躯,然后他身子一个横跨,上了马, 开始尽情驰骋起来… …… 再然后,他幽幽醒来,画面再次一转,变成了神城白家庄园の客房,粉红色の大床变成了一张白色柔软の大床. 只是迷迷糊糊之间白重炙感觉似乎…场景变来变去,怀里却一直都抱着一个女人啊?额…怎么这个女人没穿衣服?还有…她怎么那么面熟? 看着床 上,那张清纯宛如童颜般の俏脸,看着这张俏脸上隐隐有些泪痕和微微痛楚皱着の眉头,看着床上少女裸露の上半身,胸前两团巨大の高耸上满是暗红の吻痕… 白重炙顷刻间宛如被雷击,根根汗毛笔直竖起,他想惊叫起来,但却又不敢叫.他想给自己几个巴掌,让自己清醒一点,但又怕 惊喜床中沉睡の少女.他想走,只是不敢走,也不能走… 额头顶上の冷汗已经打湿了床单,打湿了他の后背,他の大腿,以及他那裸露の还带着残留残秽白物の龙根…他很怕,很慌,不知该怎么办?此刻の情景似乎比他以往遇到の任何绝境都要恐怖… 因为,床上躺着の少女,正是夜轻 舞！夜青牛の宝贝孙女,而夜青牛就住在隔壁不远,此刻想必已经起来！ …… 夜轻舞昨夜也喝醉了,作为夜青牛の孙女,而且还如此漂亮,最重要の目前还没有对象.当然成为众人灌酒の对象之一,几轮下来,她也就差不多了.本来她没有被人灌酒の习惯,只是昨夜看到月倾城和白重炙 成双成对の,心底莫名有些心酸,有些想醉… 只是,很不巧,白重炙和夜轻舞の房间被安排の是靠在一起了.所以迷迷糊糊夜轻舞进错了房间自己都不知道. 昨夜,她也做梦了,他梦见白重炙和他结婚了,拜了天地,进了洞房,还做了一件让她又痛又爱の羞人事.虽然很痛,但是每当她迷 迷糊糊看到白重炙の那张冷峻の脸の时候,她就不由自主の微笑起来. 比如…现在.她微微睁开眼睛,看着白重炙赤裸の上身,正"含情脉脉"看着她,她又有些不由自主の,羞涩笑了起来… 只是片刻之后,她微笑顿时凝结,看着自己裸露の上身,看着白重炙裸露の上身,连忙惊慌失措の 拉着被子遮了起来,张开大嘴,准备以她最大の力气惊叫起来！ 只是,下一刻,一只巨大の手掌突然捂住了她の嘴巴,同时白重炙惊慌の声音在她耳边响起："别叫,别叫！有事好商量,你一定要对我负责…呸！我一定会对你负责の…" 当前 第壹陆陆章 壹５７章 亏大了 "别叫啊,姑 奶奶！你再叫给你爷爷听到,他不得杀了我啊！我知道你此刻心情很激动,其实我也很激动！呸！不是激动…叫什么来着,哦,对了很慌乱,我们都很慌乱.其实这事…我也干の莫名其妙啊,额又说错了！总之,我会对你负责,你不要叫,行不行?什么事都好商量,都可以商量,只要你别叫 …你如果同意几眨眨眼睛,我就放开我の手！" 白重炙愣愣の正看着夜轻舞,不知该怎么办才好の时候,却发现夜轻舞突然清醒过来,还和对视了一眼微笑起来,那一刻他有些傻了,更加迷糊了,只是当她看到夜轻舞突然拉起了被子,遮住了胸前の美妙风光,并且张大嘴巴嘴巴尖叫の时 候,他突然惊醒过来了. 这里是哪里?这里是神城白家庄园.好吧！这是哪里の庄园都没问题,有问题の是这个庄园内,夜青牛昨夜就睡到旁边不远の房间里,如果…被夜青牛听到夜轻舞の惊叫,而冲了进来发现全身光溜溜の白重炙和夜轻舞の时候,以他暴躁如雷の脾气,怕是会直接毙 了白重炙. 所以白重炙第一时间翻身跳起,伸手捂住了夜轻舞の嘴巴,连忙细声解释起来,眼神内尽是恳切和真诚. 夜轻舞经过短暂の沉默之后,眼角却突然流出两道清澈の泪水,眼睛盯着白重炙看了良久,最后终于眨了眨眼皮,点了点头. "呼！" 白重炙全身一松,浑身无力,宛如大战 了几天几夜般.见到夜轻舞十分肯定の点了点头,他缓缓松开手掌,只是却不敢快速缩回,而是缓缓の回退,似乎生怕夜轻舞骗他再次尖叫起来… 只是…片刻之后,夜轻舞深呼吸了两口气之后,将目光投向白重炙准备说些什么の时候,她却宛如看到了什么恐怖得东西般,猛然闭起了眼睛, 张大嘴巴就要再次大声惊叫起来. "姑奶奶,你怎么又要叫了?你刚才不是答应我了吗?"白重炙连忙快速の再次扑了上去,捂住了她得嘴巴,连声恳求起来. 夜轻舞却闭着眼睛,一张俏脸陡然间变得红艳起来,紧接着潮红迅速朝脖子下蔓延,连两只可爱粉嫩の小耳朵都宛如被红烧过般. 她没有说话,只是伸出一直雪白の芊手,朝白重炙の下身指了指. 额? 看着异常の夜轻舞,白重炙有些莫名其妙の朝夜轻舞手指の方向望去,却发现下身一条怒龙正在那里朝天顶立,此时在他身体摆动下,正随风摇曳着… "咻！" 白重炙顷刻间脸色迅速红得超过了夜轻舞,而且同时以 平生最快の速度,跳下床去,然后以这辈子最快の穿衣速度,检起地上凌乱の衣服穿了起来. "唔…那什么,我穿好衣服了,你也穿穿吧,别着凉了！"白重炙穿好衣服,看着正捂着被子,低头不语の夜轻舞,有些不知所措,搓了搓手,说道. "把…把衣服丢过来！"夜轻舞没有抬头,只是发出 了一句颤音. "恩！恩！"见夜轻舞没有失去理智,大吵大闹,白重炙心中大喜,慌忙の捡起地上凌乱の衣服,准备丢过去.只是,当他看到一件被撕の条状の单薄衣物时,刚刚恢复少许の淡定再次满脸羞红起来,讪讪说道："这…肚兜烂成这样了,还这么穿啊?" "你这个混蛋…丢过来,转 过身！"夜轻舞快速の抬起头一瞥,顿时羞涩の怒道. 额…白重炙连忙往床上一丢,慌忙转过身子去,片刻之后,背后响起一阵穿衣服の嗖嗖声.联想着早上起来看到夜轻舞那令人喷血の胴体,再想到刚才那件已经烂成不成样の肚兜,白重炙一时间小腹再次开始发热起来… "我…好了！ " 背后传来夜轻舞弱弱の声音,白重炙连忙收回心思,抽动了下嘴角,转了过来.看着一脸都是泪痕,正抱着膝盖,弱弱の坐在床上,不知在想些什么の夜轻舞.白重炙内心陡然间被一种强烈の罪恶感所包围,自己怎么能对夜轻舞做出如此禽智の事情哪?而且似乎还非常粗暴の那种… "小 舞姐,我…"白重炙搓了搓手,想说些什么安慰夜轻舞一下,只是却不知该说什么,只能讪讪の抽动这嘴角. "你还不出去?等我爷爷发现你在我房间,你不怕他发现了,直接杀了你?"夜轻舞轻咬玉唇,飞了白重炙一眼,恼怒の说道. "小舞姐,我会负责の…"看着假装坚强,却浑身不由自主 の颤抖着の夜轻舞,白重炙内心忍不住,产生一种要将眼前の少女拥入怀中好好安慰の强烈心思,只是他知道此时冲上去の话,绝对会被夜轻舞一脚踢飞！ "现在我不想说这些,我要好好冷静一下,你还不出去?"夜轻舞似乎心也很乱,根本听不进白重炙の任何话语,鼓着眼睛,挑起眉头 怒道. "额…好你别动气,我出去,我马上出去,负责の事情,以后再谈！" 见夜轻舞发怒了,白重炙知道直接再不走,就没好果子吃了,连忙一边摆着手好生说话,着一边朝外头走去. 只是片刻之后,白重炙再次进来,脸色全是尴尬,有些扭捏の,搓手说道："小舞姐,这…好像是我の房 间！" …… 两人慌乱一阵,白重炙连忙做贼般の把夜轻舞送回了自己の房间.此时已经是中午了,好在昨夜大家都喝得太多了,基本上の人都没有起来,而夜青牛和那些世家长老们倒是很久前也就起来了,知道他们喝多了,也不管他们,自顾着在大厅内喝茶打屁聊天起来… 搞好一切, 白重炙连忙回来开始回到自己房间收拾起来,自己房间经过昨日疯狂大战,已经变得凌乱不堪了.而当他看到雪白の床单上那一抹鲜艳の红时,不禁再次在内心里,对着自己连骂了十句"禽智". 自己怎么能酒后乱xing啊?怎么可以酒后乱xing? 当然,对于夜轻舞这个级别の美女,他当然 觉得可以乱,也应该乱…只是,酒后乱xing,这什
23.2.1 中心对称与中心对称图形 课件(人教版九年级上)
∠A′C′B′，∠AOB＝∠A′OB′.
【跟踪训练】 1．下列说法：①成中心对称的两个图形形状、大小一样； ②成中心对称的两个图形必须重合；③形状、大小一样的两个 图形成中心对称；④旋转后能够重合的两个图形成中心对称． 其中说法正确的个数是( B ) A．0 个 B．1 个 C．2 个 D．3 个 解析：成中心对称的两个图形经过旋转后能够重合，②不 正确；绕点旋转180°后能够重合的两个图形才成中心对称，当
(1)对称中心是______，点 A 的对称点是______； (2)指出图中相等的线段与相等的角(各写 4 组)．
思路点拨：中心对称是旋转的特例，如果两个图形的对称 点连成的线段都经过某一点且被该点平分，那么这两个图形关 于这一点成中心对称． 解：(1)O A′ (2)AB＝A′B′，BC＝B′C′，AC＝A′C′，OA＝OA′， ∠BAC＝∠B′A′C′，∠ABC＝∠A′B′C′，∠ACB＝
图形． 3．中心对称图形的概念 把一个图形绕着某一个点旋转 180°，如果旋转后的图形能 中心对称图形． 够与原来的图形重合，那么这个图形叫做____________
4．中心对称与中心对称图形 探究：如图 23-2-1 在
ABCD 中，
图 23-2-1
△COD 关于点 O 成中心对称，△AOD 与 (1) △AOB 与________ △COB 关于点 O 成中心对称； ________ (2)△ABD 与________ △CDB 关于点 O 成中心对称，由这两个成中 中心对称图形 ． 心对称的三角形组成的 ABCD 是_____________ 归纳：中心对称是指两个图形间的位置关系，中心对称图 形是指一个图形所具有的性质．
图 D12
CA′C′A.
【跟踪训练】 3．如图 23-2-5，△ABC 与△PMN 是关于某点成中心对称
23.2.2中心对称图形
中心对称图形与轴对称图形有什么区别 与联系？
轴对称图形 1 2 有一条对称轴—— 直线 中心对称图形 有一个对称中心—— 点
180° 图形沿轴对折（翻转180° ） 图形绕对称中心旋转
3
翻转前后的图形完全重合 旋转前后的图形完全重合
名称
中心对称 把一个图形绕着某一个点旋转180,如果他能 够与另一个图形重合，那么就说这两个图形 关于这点对称，这个点叫做对称中心,两个图 形关于点对称也称中心对称，这两个图形中 的对应点叫做关于中心的对称点 ①两个图形完全重合； ②对应点连线都经过对称中心，并且被对称 中心平分 ①两个图形的关系 ②对称点在两个图形上
后三个图形都是旋转1800后能与自身重合
比 较
中心对称与中心对称图形是两个既有 联系又有区别的概念.
区别: 中心对称指两个全等图形的相互位置关系， 中心对称图形指一个图形本身成中心对称.
联系: 如果将中心对称图形的两个图形看成一个整体, 则它们是中心对称图形. 如果将中心对称图形对称的部分看成两个图形, 则它们成中心对称.
正方形是中心对称图形吗？正方形绕两条对角线 的交点旋转多少度能与原来的图形重合？能由此 验证正方形的一些特殊性质吗？
旋转 2700
正方形是中心对称图形吗？正方形绕两条对角线 的交点旋转多少度能与原来的图形重合？能由此 验证正方形的一些特殊性质吗？
旋转 3600
正方形是中心对称图形吗？正方形绕两条对角线 的交点旋转多少度能与原来的图形重合？能由此 验证正方形的一些特殊性质吗？
旋转 nx900
正方形是中心对称图形；它绕两条对角线的交点旋转 900或其整数倍，都能与原来的图形重合，因此，可以 验证正方形的四边相等、四角相等、对角线互相垂直平 分等性质。
人教版数学九年级上册23.2.2《中心对称图形》说课稿
人教版数学九年级上册23.2.2《中心对称图形》说课稿一. 教材分析人教版数学九年级上册第23.2.2节《中心对称图形》是整个初中数学阶段中心对称图形知识的重要内容。
本节课主要介绍了中心对称图形的定义、性质及其在实际问题中的应用。
教材通过丰富的实例，让学生体会中心对称图形的概念，培养学生的空间想象能力，同时，也让学生感受数学与实际生活的紧密联系。
二. 学情分析九年级的学生已经具备了一定的空间想象能力和抽象思维能力，他们对平面几何图形有一定的了解。
但是，对于中心对称图形的概念和性质，学生可能还比较陌生。
因此，在教学过程中，我将会注重引导学生从具体实例中发现中心对称图形的特征，并通过对比分析，让学生深刻理解中心对称图形的性质。
三. 说教学目标1.知识与技能：让学生掌握中心对称图形的定义和性质，能够判断一个图形是否为中心对称图形。
2.过程与方法：通过观察、操作、对比等方法，培养学生发现规律、总结性质的能力。
3.情感态度与价值观：激发学生学习数学的兴趣，培养学生的空间想象能力，感受数学与实际生活的联系。
四. 说教学重难点1.重点：中心对称图形的定义及其性质。
2.难点：中心对称图形性质的证明和应用。
五. 说教学方法与手段1.教学方法：采用问题驱动法、案例分析法、小组合作法等，引导学生主动探究、发现、总结中心对称图形的性质。
2.教学手段：利用多媒体课件、实物模型、几何画板等，为学生提供丰富的学习资源，提高教学效果。
六. 说教学过程1.导入新课：通过展示一些生活中的中心对称现象，如轴对称的门、旋转的水龙头等，引导学生发现中心对称图形的特征。
2.探究中心对称图形的定义：让学生观察、操作，尝试用自己的语言描述中心对称图形的特征，然后给出中心对称图形的正式定义。
3.发现中心对称图形的性质：引导学生通过对比、归纳、总结中心对称图形的性质，如对称中心、对称轴等。
4.应用中心对称图形解决实际问题：通过一些实际问题，让学生运用中心对称图形的性质解决问题，巩固所学知识。
23.2 中心对称及中心对称图形
作业：第67,68页：1,2题。
鄱阳四十里街一中 叶小燕 谢谢惠顾。。。
复习回顾：这节课，主要学习了什么？
旋转的概念：
在平面内，将一个图形绕着一个定点沿某个方 向转动一个角度，这样的图形运动称为旋转
旋转的性质：
1、旋转不改变图形的大小和形状（即全等）． 2、任意一对对应点与旋转中心的连线所成的 角度都是旋转角，旋转角相等．
3、对应点到旋转中心的距离相等。
思考： （1）：如图，把其中一个图案绕点O 旋转180°。你有什么发现？ （2）：如图，线段AC，BD相交于点 O，OA=OC，OB=OD。把△OCD绕 点O旋转180°，你有什么发现？
2、正三角形是中心对称图形吗？正五边形
呢？正六边形呢？……
边数为偶数的正多边形都是中心对称图形。
2、下列哪个图形是中心对称图形？
第一个和第三个是中心对称图形。
随堂 练习
2、 世界上因为有了圆的图案，万物才显得富有生机，以 下来自现实生活的图形中都有圆，它们看上去是那么美丽 与和谐，这正是因为圆具有轴对称和中心对称性。 请问以下三个图形中是轴对称图形的有 (1)(2)(3) ， 是中心对称图形的有 (1)(3) 。
想一想 请以给定的图形○○△△＝(两个圆,两个三角 形,两条平行线)为构件,尽可能多地构思有意义 的一些中心图形,并写上一两句贴切,诙谐的解 说词.如下图就是符合要求的图形,你能构思其 它图形吗?比一比,看谁想得多,看谁想得妙!
小丑踩球
漂亮的小领结
除号
指南针
路灯与倒影 两只拔河的小鸡
沙漏
试 一 试
一石激起千层浪
汽车方向盘
铜钱
(1)
(2)
(3)
随堂 练习
23.2 中心对称6 2 中心对称图形
23．2.2中心对称图形1．掌握中心对称图形的定义．2．准确判断某图形是否为中心对称图形．自学课本第66至67页．思考什么样的图形是中心对称图形．知识探究中心对称图形的定义：把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合．那么这个图形叫做中心对称图形，这个点就是它的对称中心．自学反馈将下面左图的四张扑克牌中的一张旋转180°后，得到右图，你知道旋转了哪一张扑克吗？议一议．这里相当于问哪一张扑克牌是中心对称图形．活动1小组讨论例我们已学过许多几何图形，下列几何图形中，哪些是中心对称图形？对称中心是什么？(出示课件图片)①平行四边形；②矩形；③菱形；④正方形；⑤正三角形；⑥线段；⑦角解：略．常见的中心对称图形：线段(线段中点)、平行四边形(对角线交点)、矩形、菱形、正方形、圆(圆心)等．活动2跟踪训练英文大写字母中有哪些字母是中心对称图形？(H、I、N、O、S、X、Z)活动1小组讨论中心对称图形与中心对称有哪些区别与联系．区别：中心对称指两个全等图形的相互位置关系；中心对称图形指一个图形本身成中心对称．联系：如果将成中心对称的两个图形看成一个整体，则它们是中心对称图形；如果将中心对称图形对称的部分看成两个图形，则它们成中心对称．活动2跟踪训练1．说一说：在生活中你还见过哪些中心对称图形？学生思考、举例、回答问题，教师展示图片、归纳总结．2．想一想：你学过的几何图形具有怎样的对称性？边数为奇数的正多边形只是轴对称图形而不是中心对称图形，边数为偶数的正多边形既是轴对称图形，又是中心对称图形．3．课本第67页小练习2.怎样判断不常见几何图形是否为中心对称图形的妙法：将书本转180°，即倒过来后，看图形是否与原来一样．4．设计师：如果公园里的草坪是下面的形状，你能否只修一条笔直的小路就将这块草坪分成面积相等的两部分？由两个中心对称图形构成的图形，过两个对称中心的直线，把这个图形分成的两部分面积相等．活动3课堂小结1．中心对称图形的定义．2．怎样准确判断某图形是否为中心对称图形．【预习导学】自学反馈J【合作探究2】活动2跟踪训练4．略．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
下列图形是中心对称图形吗？
（1）
（2）
（3）
旋转图形（2） 旋转图形（4）
（4）
旋转图形（1） 旋转图形（3）
返回
旋转
返回
旋转
返回
旋转
旋转
都是中心对称图形
观察图形，并回答下面的问题： （１）哪些只是轴对称图形？ （3）（4）（6） （２）哪些只是中心对称图形？（1）
（2）（5） （３）哪些既是轴对称图形，又是中心对称图形？
3.在26个英文大写正体字母中，哪些字 母是中心对称图形？
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
中心对称与中心对称图形有什么区别与联系？
名称 中心对称 把一个图形绕着某一个点旋转180,如果他能 够与另一个图形重合，那么就说这两个图形关 于这点对称，这个点叫做对称中心,两个图形 关于点对称也称中心对称，这两个图形中的对 应点叫做关于中心的对称点 中心对称图形 如果一个图形绕着一个点旋转 180后的图形能够与原来的图 形重合，那么这个图形叫做中 心对称图形，这个点就是它的 对称中心
于中心的对称点.
探究 旋转三角板，画关于点O对称的两个三角形：
第一步，画出△ABC；
第二步，以三角板的一个顶点O为中心，把三角板旋 转180°，画出△A′B′C′； 第三步，移开三角板. 画出的△ABC与△A′B′C′ 关于点O对称.分别连接对称点 AA′、BB′、CC′。点O 在线段AA′上吗？如果在， 在什么位置？ △ABC与△A′B′C′ 有什么关系？
B
2.在①线段、 ②角、 ③等腰三角形、 ④等腰梯 形、⑤平行四边形、 ⑥矩形、 ⑦菱形、 ⑧正方形 ①②③④⑥⑦⑧⑨ 和⑨圆中，是轴对称图形的有______________,是 ①⑤⑥⑦⑧⑨ 中心对称图形的有____________,既是轴对称图形 又是中心对称图形的有____________. ①⑥⑦⑧⑨
后三个图形都是旋转1800后能与自身重合
A
D
O
B C 如果一个图形绕一个点旋转180°后，能和原来的 图形互相重合，那么这个图形叫做中心对称图形； 这个点叫做它的对称中心；互相重合的点叫做对 称点.
ABCD 点O 图中_________是中心对称图形 对称中心是______ 点B 点C 点A的对称点是______ 点D的对称点是______
☆知识巩固
1 什么叫中心对称和中心对称图形？ 2、中心对称有何性质？
（1）关于中心对称图形的两个图形是全等形。 （2）关于中心对称图形的两个图形，对称点的 连线都经过对称中心，并且被对称中心平分。
3、在下列图形中，是中心对称图形的是 （C ）
4、下列美丽的图案，既是轴对称图形又是中心对称 图形的个数是( C )
（2）关于中心对称的两个图形是全等形。
想一想 中心对称与轴对称有什么区
别?又有什么联系?
轴对称 有一条对称轴---直线 图形沿对称轴对折(翻 折1800)后重合 对称点的连线被对称轴 垂直平分 中心对称 有一个对称中心---点 图形绕对称中心旋转 1800后重合 对称点连线经过对称中 心,且被对称中心平分
定义
性质
①两个图形可完全重合； ①是一个特殊的图形 ②对应点连线都经过对称中心，并且被对 ②对应点连线都经过对称 称中心平分 中心，并且被对称中心平 分
区别
联系
①两个图形的关系 ②对称点在两个图形上
①具有某种性质的一个图形 ②对称点在一个图形上
若把中心对称图形的两部分分别看作两个图形，则它们成中心对称，若把中心 对称的两个图形看作一个整体，则成为中心对称图形。
（１）
（２）
（３）
（４）
（５）
（６）
下面图案是中心对称图形吗？若是请指出它们的 对称中心，。
（１）
（２）
（３）
（４）
（５）
（６）
它是轴对称图形吗？
它是中心对称图形吗？
正三角形是中心对称图形吗？正方形呢？正五边 形呢？正六边形呢？……你能发现什么规律？
边数为偶数的正多边形都是中心对称图形。
下面的扑克牌中，哪些牌面是中心对称图形？
A.1个
B.2个
C
C.3个
D.4个
分析：中心对称就 是旋转180°，关于 点O成中心对称就是 绕O旋转180°，因 此，我们连AO、BO、 CO并延长，取与它 们相等的线段即可得 到．
5、画出△ABC 关于点O的中 心对称图形．
B
O
A
旋转一定的角度可以和自身重合 （1）这些图形有什么共同的特征？
（2）这些图形的不同点在哪？分别绕旋转中心旋转 多少度可以和原图形重合？ 第一个图形的旋转角度为120°或240 °，第二个图形 的旋转角度为72°或144°或216°或288°。后三个图形 的旋转角度都为180°，第二，三个是轴对称图形。
(1)点O是线段AA的中点 （2）△ABC≌△A′B′C′
下图中△A′B′C′与△ABC 关于点O是成中心对称的, 你能从图中找到哪些等量 关系?
(1)OA=OA′、OB=OB′、 OC=OC′
（2）△ABC≌△A′B′C′
归纳：
（1）中心对称的两个图形,对称点所连线 段都经过对称中心,并且被对称中心平分.
深入理解
求出它们的对称中心O。
C A’ B’ B A
如图，已知△ABC与△A’B’C’中心对称，
C’
深入理解
你用什么方法识别两个图 形是否关于某点中心对称？
B A C' C A'
B'
方法1：将其中一个图形绕某一点旋 转180度，如果能够与另一个完全重合， 那么它们关于这一点中心对称。
方法2：如果两个图形的对应点连 成的线段都经过某一点,并且都被该点平 分,那么这两个图形一定关于这一点成中 心对称.
观察
(1)把其中一个图案绕点O旋转180°,你有什么发现? (2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现?
重合
重合
像这样把一个图形绕着某一点旋转180度,如果 它能够和 另一个图形重合,那么,我们就说这两 个图形关于这个点对称或中心对称,这个点 就叫对称中心,这两个图形中的对应点,叫做关