中考数学最值问题
初中数学最值问题专题

中考数学最值问题【例题1】(经典题)二次函数y二2 (x-3) 2-4的最小值为.【例题2】(2018江西)如图,AB是。
的弦,AB=5,点C是。
上的一个动点,且NACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是___ .C【例题3】(2019湖南张家界)已知抛物线y=ax2+bx+c (a不0)过点A(1, 0), B(3, 0)两点,与y 轴交于点C, OC=3.(1)求抛物线的解析式及顶点D的坐标;(2)过点A作AM^BC,垂足为M,求证:四边形ADBM为正方形;(3)点P为抛物线在直线BC下方图形上的一动点,当^PBC面积最大时,求P点坐标及最大面积的值;(4)若点Q为线段OC上的一动点,问AQ+ 2 QC是否存在最小值若存在,求出这个最小值;若不存在,请说明理由.1.(2018河南)要使代数式V-2^37有意义,则乂的( )A.最大值为2B.最小值为2C.最大值为-D.最大值为°3 3 2 22.(2018四川绵阳)不等边三角形AABC的两边上的高分别为4和12且第三边上的高为整数,那么此高的最大值可能为。
3.(2018齐齐哈尔)设a、b为实数,那么“2+“〃 +从一” 的最小值为04.(2018云南)如图,MN是。
的直径,MN=4, NAMN=40° ,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为.C5.(2018海南)某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为元/斤,并且两次降价的百分率相同.(1)求该种水果每次降价的百分率;(2)从第一次降价的第1天算起,第x天(x为正数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1WxV15)之间的函数关系式,并求出第几天时销售利润最大(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少元,则第15天在第14天的价格基础上最多可降多少元6.(2018湖北荆州)某玩具厂计划生产一种玩具熊猫,每日最高产量为40只,且每日产出的产品全部售出,已知生产x只玩具熊猫的成本为R (元),售价每只为P (元),且R、P与x的关系式分别为R = 500 + 30x , P = 170 —2x。
中考数学最值问题总结(含强化训练)

中考数学最值问题总结(含强化训练)在中学数学题中,最值题是常见题型,围绕最大(小)值所出的数学题是各种各样,就其解法,主要分为几何最值和代数最值两大部分。
一、解决几何最值问题的要领(1)两点之间线段最短;(2)直线外一点与直线上所有点的连线段中,垂线段最短;(3)三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值)。
二、解决代数最值问题的方法要领1.二次函数的最值公式二次函数y ax bx c =++2(a 、b 、c 为常数且a ≠0)其性质中有 ①若a >0当x b a=-2时,y 有最小值。
y ac b a min =-442; ②若a <0当x b a=-2时,y 有最大值。
y ac b a max =-442。
2.一次函数的增减性.一次函数y kx b k =+≠()0的自变量x 的取值范围是全体实数,图象是一条直线,因而没有最大(小)值;但当m x n ≤≤时,则一次函数的图象是一条线段,根据一次函数的增减性,就有最大(小)值。
3. 判别式法.根据题意构造一个关于未知数x 的一元二次方程;再根据x 是实数,推得∆≥0,进而求出y 的取值范围,并由此得出y 的最值。
4.构造函数法.“最值”问题中一般都存在某些变量变化的过程,因此它们的解往往离不开函数。
5. 利用非负数的性质.在实数范围内,显然有a b k k 22++≥,当且仅当a b ==0时,等号成立,即a b k 22++的最小值为k 。
6. 零点区间讨论法.用“零点区间讨论法”消去函数y 中绝对值符号,然后求出y 在各个区间上的最大值,再加以比较,从中确定出整个定义域上的最大值。
7. 利用不等式与判别式求解.在不等式x a ≤中,x a =是最大值,在不等式x b ≥中,x b =是最小值。
8. “夹逼法”求最值.在解某些数学问题时,通过转化、变形和估计,将有关的量限制在某一数值范围内,再通过解不等式获取问题的答案,这一方法称为“夹逼法”。
中考数学最值—阿氏圆问题(解析+例题)

中考数学最值——阿氏圆问题(点在圆上运动)(PA+k·PB型最值)【问题背景】与两个定点距离之比为一个不为0的常数的点的轨迹是一个圆,这个圆为阿氏圆。
这个定理叫阿波罗尼斯定理。
【知识储备】①三角形三边关系:两边之和大于第三边;两边之差小于第三边。
②两点之间线段最短。
③连接直线外一点和直线上各点的所有线段中,垂线段最短。
【模型分析】①条件:已知A、B为定点,P为 O上一动点,OPOB=k(0<k<1)。
②问题:P在何处时,PA+k·PB的值最小。
③方法:连接OP,OB,在OB上取点C,使OCOP =k,可得△POC∽△BOP,所以CPPB=OPOB=k,所以得CP=k·PB。
所以PA+k·PB=PA+CP≥AC,当P为AC与 O的交点时,PA+k·PB的最小值为AC。
总结:构造母子三角形相似若能直接构造△相似计算的,直接计算,不能直接构造△相似计算的,先把k提到括号外边,将其中一条线段的系数化成,再构造△相似进行计算。
【经典例题】已知∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点.(1)求12AP BP+的最小值为。
(2)求13AP BP+的最小值为。
【巩固训练】练习1:如图,点A、B在⊙O 上,且OA=OB=6,且OA⊥OB,点C是OA的中点,点D在OB 上,且OD=4,动点P在⊙O 上,则2PC+PD的最小值为;练习2:如图,在Rt△ABC中,∠ACB=90°,D为AC的中点,M为BD的中点,将线段AD绕A点任意旋转(旋转过程中始终保持点M为BD的中点),若AC=4,BC=3,那么在旋转过程中,线段CM长度的取值范围是__________。
练习3:Rt △ABC 中,∠ACB=90°,AC=4,BC=3,点D 为△ABC 内一动点,满足CD=2,则AD+32BD 的最小值为_______.练习4:如图,菱形ABCD 的边长为2,锐角大小为60°,⊙A 与BC 相切于点E ,在⊙A 上任取一点P ,则PB+23PD 的最小值为________.练习5:如图,已知菱形ABCD 的边长为4,∠B=60°,圆B 的半径为2,P 为圆B 上一动点,则PD+21PC 的最小值为_________.练习6:如图,等边△ABC 的边长为6,内切圆记为⊙O ,P 是圆上动点,求2PB+PC 的最小值.值。
2024年中考 数学总复习 题型训练四 几何最值问题

题型四几何最值问题类型一利用“垂线段最短”解决最值问题1. 如图,在△ABC中,AC=BC=6,AB=8,点D在AC边上,连接BD,以AD,BD为邻边作▱ADBE,连接DE,则DE的最小值为________.第1题图2. 如图,在△ABC中,AC=BC=6,S△ABC=12,点D为AB的中点,点M,N分别是CD 和BC上的动点,则BM+MN的最小值是________.第2题图3. 如图,四边形ABCD是菱形,对角线AC,BD相交于点O,点P是BD上一动点,点E 是BC上一动点,若AC=6,BD=63,则PC+PE的最小值为________.第3题图4. 如图,在△OAB中,已知∠AOB=35°,点P是边AB上一点,点M,N分别是射线OA,OB上异于点O的动点,连接PO,PM,MN,若∠BOP=10°,OP=6,则PM+MN的最小值为________.第4题图类型二 利用“两点之间线段最短”解决最值问题1. 如图,在矩形ABCD 中,AB =6,AD =8,点P 是矩形ABCD 内一点,记a =S △APB +S △CPD ,b =P A +PB +PC +PD ,则a +b 的最小值为________.第1题图2. 如图,在四边形ABCD 中,∠BAD =120°,∠B =∠D =90°,AB =1,AD =2,M ,N 分别为BC ,CD 边上的动点,则△AMN 周长的最小值为________.第2题图3. 如图,在Rt △ABC 中,∠C =90°,∠ABC =30°,BC =43 ,点D 为边BC 上的动点,点E 为边AB 的中点,连接DE ,DA ,则线段DE +DA 的最小值为________.第3题图4. 如图,在等腰Rt △ABC 中,AB =AC =22 ,∠A =90°,点P 是△ABC 内部一点,且满足S △BCP =12S △ABC ,则PB +PC 的最小值为________.第4题图5. 如图,二次函数y =-23 x 2-43x +2的图象与x 轴分别交于A ,B 两点(点A 在点B 左侧),与y 轴交于点C ,点P 是其对称轴上一点,连接PB ,PC ,BC ,则△PBC 的周长最小为________.第5题图类型三 利用“二次函数性质”解决最值问题(2021.9)1. 我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a ,b ,c, 记p =a +b +c 2,则其面积S =p (p -a )(p -b )(p -c ) .这个公式也被称为海伦-秦九韶公式.若p =5,c =4,则此三角形面积的最大值为( )A. 5B. 4C. 25D. 52. 如图,在矩形ABCD 中,AB =2,AD =3,P 是BC 上的任意一点(P 与B ,C 不重合),过点P 作AP ⊥PE ,垂足为P ,PE 交CD 于点E ,连接AE ,在点P 的运动过程中,线段CE 的最大值为________.第2题图3. 如图,在等腰△ABC 中,AC =BC =4,∠C =120°,点P 是AC 上一动点,PD ∥AB ,交BC 于点D ,连接AD ,则点P 在运动过程中,△APD 的面积的最大值为________.第3题图4. 如图,矩形ABCD中,AB=6,BC=4,点E,F分别为边AB,CD上的动点,且AE=CF,将线段EF绕点F逆时针旋转90°得到线段FG,连接DG.(1)当点E为AB的中点时,线段DG的长是________;(2)当点E在边AB上运动时,线段DG的最小值是________.第4题图类型四利用“辅助圆”解决最值问题(8年3考:2021.10、17,2020.17)1. 如图,在矩形ABCD中,AB=6,AD=25,E是边CD上一点,将△ADE沿直线AE 折叠得到△AFE,BF的延长线交边CD于点G,则DG长的最大值为________.第1题图2. 如图,在正方形ABCD中,E,F分别是AB,BC边上的动点(不与正方形的顶点重合),且AE=BF,CE,DF交于点M,连接BM,若AB=2,则BM的最小值为________.第2题图3.如图,在Rt△ABC中,∠C=90°,AB=10,BC=8,E,F分别是AC,BC边上的动点,且EF=AC,P是EF的中点,连接AP,BP,则△APB面积的最小值为________.第3题图4. 如图,已知△ABC为等边三角形,AB=6,将边AB绕点A顺时针旋转a(0°<a<120°),得到线段AD,连接CD,点E为CD上一点,且DE=2CE.连接BE,则BE的最小值为________.第4题图5. 如图,在△ABC中,∠C=45°,∠B=60°,BC=3+1,P为边AB上一动点,过点P 作PD⊥BC于点D,PE⊥AC于点E,连接DE,则DE的最小值为________.第5题图题型四 几何最值问题类型一 利用“垂线段最短”解决最值问题 1. 853【解析】如解图,设DE 与AB 交于点O ,∵四边形ADBE 是平行四边形,∴OB =OA ,DE =2OD ,∴当OD ⊥AC 时,DO 的值最小,即DE 的值最小,过点B 作BH ⊥AC 于点H ,则∠BHD =∠EDH =90°,易知AD ∥BE ,即AC ∥BE ,∴∠EBH =90°,∴四边形BHDE 是矩形,∴DE =BH ,∵AC =BC =6,AB =8,∴设CH =x ,则AH =6-x ,∵BA 2-AH 2=BH 2=BC 2-CH 2,即82-(6-x )2=62-x 2,解得x =23 ,∴CH =23,∴DE =BH =BC 2-CH 2 =853 .∴DE 的最小值为853.第1题解图2. 4 【解析】如解图,作点N 关于DC 的对称点N ′.∵AC =BC ,点D 为AB 的中点,∴点N ′在AC 上,连接MN ′,BN ′,∴BM +MN =BM +MN ′≥BN ′,∴当B ,M ,N ′三点共线,且BN ′⊥AC 时,BM +MN 取得最小值.∵AC =6,S △ABC =12,∴△ABC 中AC 边上的高为4,∴BM +MN 的最小值是4.第2题解图3. 33 【解析】如解图,作点E 关于BD 的对称点E ′,连接PE ′,∵四边形ABCD 是菱形,∴BA 与BC 关于BD 对称,∴点E ′位于BA 上,由对称的性质可知,PE =PE ′,∴当C ,P ,E ′三点重合,且CE ′⊥BA 时,PC +PE 的值最小,即为CE ′的长,∵四边形ABCD 是菱形,∴AO =CO =12 AC =3,BO =DO =12BD =33 ,AC ⊥BD ,AB =BC ,∴在Rt △BOC 中,BC =BO 2+CO 2 =6,tan ∠BCO =BO CO=3 ,∴∠BCO =60°,∴△ABC 是等边三角形,∴CE ′=BC ·sin 60°=33 ,∴PC +PE 的最小值为33 .第3题解图 4. 33 【解析】如解图,作点P 关于OA 的对称点P ′,连接OP ′,过点P ′作OB 的垂线交OA 于点M ,交OB 于点N ,此时PM +MN 的值最小,最小值为线段P ′N 的长.∵∠AOB =35°,∠BOP =10°,点P ′与点P 关于OA 对称,∴∠POA =∠P ′OA =25°,∴∠BOP ′=60°,OP ′=OP =6,在Rt △P ′ON 中,P ′N =OP ′·sin 60°=6×32=33 ,∴PM +MN 的最小值为33 .第4题解图类型二 利用“两点之间线段最短”解决最值问题1. 44 【解析】如解图,过点P 作EF ⊥AB ,分别交AB ,CD 于点E ,F ,连接AC ,BD ,则EF =AD =8,∵四边形ABCD 是矩形,∴∠ABC =90°,AB =CD =6,AD =BC =8,∴AC=AB 2+BC 2 =62+82 =10,∴BD =AC =10,∵S △APB +S △CPD =12 AB ·PE +12 CD ·PF =12AB ·EF =12×6×8=24,P A +PC ≥AC ,PB +PD ≥BD ,∴当A ,P ,C 三点共线,B ,P ,D 三点也共线时,P A +PB +PC +PD 有最小值,最小值为AC +BD =20,∴a +b 的最小值为24+20=44.第1题解图2. 27 【解析】如解图,分别作A 关于BC 和CD 的对称点A ′,A ″,连接A ′A ″,交BC 于点M ,交CD 于点N ,则A ′A ″即为△AMN 的周长最小值,作A ′H ⊥DA 交DA 的延长线于点H ,∴AA ′=2AB =2,AA ″=2AD =4,∵∠BAD =120°,∴∠HAA ′=60°,∴在Rt △A ′HA 中,AH =12 AA ′=1,∴A ′H =22-12 =3 ,A ″H =AH +AA ″=1+4=5,∴A ′A ″=A ′H 2+A ″H 2 =27 ,∴△AMN 的周长最小值为27 .第2题解图3. 43 【解析】如解图,作点E 关于BC 的对称点E ′,连接EE ′,交BC 于点F ,连接DE ′,AE ′,过点E ′作E ′G ⊥AC 交AC 的延长线于点G ,则DE =DE ′,EF =E ′F ,DE +DA =DE ′+DA ≥AE ′,∴当A ,D ,E ′在同一直线上时,DE +DA 的值最小,最小值为AE ′的长,∵∠ACB =90°,∠ABC =30°,BC =43 ,∴AC =33 BC =33×43 =4,∵点E 为边AB 的中点,∴EF 为△ABC 的中位线,∴EF =12 AC =2,CF =12BC =23 ,∴E ′F =EF =2=CG ,E ′G =CF =23 ,∴AG =AC +CG =4+2=6,∴AE ′=E ′G 2+AG 2 =(23)2+62 =43 ,∴DE +DA 的最小值为43 .第3题解图4. 25 【解析】如解图,过点A 作AD ⊥BC 于点D ,∵AB =AC =22 ,∠BAC =90°,∴AD =2,BC =4,∵S △BCP =12S △ABC ,∴点P 到BC 的距离为1,即点P 在AD 的垂直平分线l 上运动,作点B 关于直线l 的对称点B ′,连接B ′C 交直线l 于点P ′,连接BP ′,B ′P ,则BB ′⊥BC ,BP ′=B ′P ′,BP =B ′P ,∴BP +PC =B ′P +PC ≥B ′C ,当B ′,P ,C 三点共线,即点P 与点P ′重合时,BP +PC 的值最小,为B ′C 的长.在Rt △B ′BC 中,BB ′=2,BC =4,∴B ′C =BB ′2+BC 2 =25 ,∴PB +PC 的最小值为25 .第4题解图5. 13 +5 【解析】如解图,连接AC ,AP ,令y =0,得x =-3或1,∴点A (-3,0),点B (1,0),∴抛物线的对称轴是直线x =-1,OA =3,OB =1,令x =0,得y =2,∴点C (0,2),∴OC =2,∴BC =OB 2+OC 2 =5 ,AC =OA 2+OC 2 =13 ,∵△PBC 的周长为PB +PC +BC ,BC 为定值,∴要使△PBC 的周长最小,则PB +PC 最小即可,∵点A 与点B 关于对称轴对称,∴P A =PB ,∴PB +PC =P A +PC ≥AC ,∴PB +PC 的最小值为AC 的长,∴△PBC 的周长最小值=AC +BC =13 +5 .第5题解图类型三 利用“二次函数性质”解决最值问题1. C 【解析】∵p =5,c =4,∴S =5(5-a )(5-b )(5-4) =5(5-a )(5-b ) ,∵p =a +b +c 2 ,∴a +b =2p -c =6,∴b =6-a ,∴S =5(5-a )[5-(6-a )] =5(5-a )(a -1) =-5(a -3)2+20 ,∵-5<0,∴当a =3时,S 有最大值为20 =25 .2. 98【解析】∵四边形ABCD 是矩形,∴∠B =∠C =90°,∵AP ⊥PE ,∴∠APB +∠CPE =∠CPE +∠PEC =90°,∴∠APB =∠PEC ,∴△ABP ∽△PCE ,∴AB PC =BP CE,设BP =x ,CE =y ,则PC =3-x ,即23-x =x y,∴y =-12 x 2+32 x =-12 (x -32 )2+98 ,∵-12 <0,∴当x =32 时,y 有最大值,最大值是98 ,∴线段CE 的最大值为98 . 3. 3 【解析】如解图,过点C 作CE ⊥AB 于点E ,过点P 作PF ⊥AB 于点F ,设AP =x ,则CP =4-x ,∵AC =BC ,∠C =120°,∴∠BAC =∠B =30°,AE =BE ,∴CE =12AC =2,PF =12 AP =12x ,在Rt △AEC 中,由勾股定理得AE =42-22 =23 ,∴AB =2AE =43 ,∵PD ∥AB ,∴△PCD ∽△ACB ,∴PC AC =PD AB ,∴4-x 4 =PD 43,解得PD =3 (4-x ),∴S △APD =12 PD ·PF =12 ×3 (4-x )×12 x =-34 (x -2)2+3 ,∵-34<0,∴当x =2时,S △APD 有最大值,最大值为3 .第3题解图4. (1)1 【解析】∵点E 为AB 的中点,AE =CF ,∴点F 为CD 的中点,∴EF =FG =4,此时F ,D ,G 三点共线,∴DG =FG -FD =1; (2)255 【解析】如解图,过点F 作FH ⊥AB 于点H ,过点G 作IG ⊥CD 于点I ,则∠EHF =∠GIF =90°,由题意可知∠EFG =90°,EF =GF ,∴∠EFH +∠EFI =∠EFI +∠GFI =90°,∴∠EFH =∠GFI ,∴△EFH ≌△GFI (AAS),∴EH =GI ,设AE =a ,①当0<a <3时,如解图①,GI =EH =6-2a ,ID =FD -FI =FD -FH =6-a -4=2-a ,∴DG 2=ID 2+IG 2=(2-a )2+(6-2a )2=5a 2-28a +40=5(a -145 )2+45 ,∵5>0,∴当a =145 时,DG 2取最小值45,∴DG =255;②当3≤a <6时,如解图②,GI =EH =2a -6,ID =FI -FD =FH -AE +EH =4-a +2a -6=a -2,∴DG 2=ID 2+IG 2=(a -2)2+(2a -6)2=5a 2-28a +40=5(a -145)2+45 ,∵5>0,3≤a <6,∴当a =3时,DG 2取最小值1,∴DG =1,∵1>255,∴DG 的最小值为255.第4题解图类型四 利用“辅助圆”解决最值问题1. 2 【解析】如解图,以点A 为圆心,AD 长为半径画弧,过点B 作弧的切线交CD 于点G ,切点为F ,此时点E 和点G 重合,DG 的最大值即为DE 的长,∵四边形ABCD 是矩形,∴BC =AD =25 ,AB =CD =6,由折叠的性质可知,DE =EF ,AF =AD =25 ,设DE =EF =x ,则CE =CD -DE =6-x ,在Rt △ABF 中,由勾股定理得BF =AB 2-AF 2 =4,则BE =BF +EF =4+x ,在Rt △BEC 中,由勾股定理得BE 2=CE 2+BC 2,即(4+x )2=(6-x )2+(25 )2 ,解得x =2,即DG 的最大值为2.第1题解图 2. 5 -1 【解析】如解图,取CD 的中点O ,连接BO ,∵四边形ABCD 为正方形,∴AB =BC =CD =AD ,∠EBC =∠FCD =90°,∵AE =BF ,∴AE +BE =BF +CF ,∴BE =CF ,∴△EBC ≌△FCD (SAS),∴∠BCE =∠CDF ,∵∠BCE +∠DCE =∠BCD =90°,∴∠CDF +∠ECD =90°,∴∠CMD =90°,当点E ,F 分别在AB 和BC 上移动时,点M 在以CD 的中点O 为圆心,OC 长为半径的半圆上运动,要使BM 取得最小值,则需点B ,M ,O 在同一条直线上.∵AB =2,∴CO =1,∴BO =5 ,∴此时BM =5 -1,即BM 的最小值为5 -1.第2题解图3. 9 【解析】如解图,过点P 作PH ⊥AB 于点H ,则S △ABP =12AB ·PH =5PH ,∴当PH 最小时,△ABP 的面积最小.∵∠ACB =90°,AB =10,BC =8,∴AC =AB 2-BC 2 =6.∴EF=AC =6.连接CP ,则CP =12EF =3.∴点P 在以点C 为圆心,3为半径的圆弧上,过点C 作CH ′⊥AB 于点H ′,交⊙C 于点P ′,∵P ′H ′=CH ′-CP ′=CH ′-CP ≤CP +PH -CP =PH ,∴当点P 与点P ′重合,点H 与点H ′重合时,PH 最小,最小值为P ′H ′的长.∵S △ABC =12AC ·BC =12 AB ·CH ′,∴CH ′=AC ·BC AB =245 ,∴P ′H ′=CH ′-CP ′=245 -3=95 ,∴PH 的最小值是95 ,此时S △ABP =5PH =9,即△ABP 面积的最小值为9.第3题解图4. 27 -2 【解析】如解图,过点E 作EH ∥AD ,交AC 于点H ,∵△ABC 为等边三角形,∴AB =AC =6,由旋转的性质得AD =AB ,∴AD =AC ,∴∠D =∠ACD ,∵DE =2CE ,∴CE CD =CH CA =13 ,∠CEH =∠D =∠ACD ,∴CH =EH ,∵AC =6,∴CH =EH =2,取AH 的中点P ,连接EP ,则PH =EH ,∴∠EPH =∠PEH ,∵∠EPH +∠CEP +∠ACD =180°,∴2∠PEH +2∠CEH =180°,∴∠CEP =90°,∴点E 在以点H 为圆心,CP 为直径的圆弧上运动,连接BH ,∵EH 为定值2,∴当B ,E ,H 三点共线时,BE 的长最小,过点B 作BQ ⊥AC 于点Q ,则CQ =12AC =3,∴QH =CQ -CH =1,BQ =BC 2-CQ 2 =62-32 =33 ,∴BH =BQ 2+QH 2 =(33)2+12 =27 ,∴BE 的最小值为27 -2.第4题解图5. 32+64【解析】如解图,连接CP ,∵∠PDC =∠PEC =90°,∴∠PDC +∠PEC =180°,∴C ,D ,P ,E 四点共圆,圆心为点O ,且直径为CP ,∵BC =3 +1,∠ACB =45°,∠B =60°是定值,∴直径CP 最小时,∠DCE 所对的弦DE 最小,即CP ⊥AB 时,DE 的值最小,连接OD ,OE ,∵∠B =60°,CP ⊥AB ,BC =3 +1,∴∠BCP =30°,∴BP =12BC =3+12 ,CP =3 BP =3+32 ,∴OD =OE =12 CP =3+34,∵∠ACB =45°,∴∠DOE =2∠ACB =90°,∴△ODE 是等腰直角三角形,∴DE =2 OD =32+64,即DE 的最小值为32+64.第5题解图。
初中几何最值问题类型

初中几何最值问题类型
初中几何中的最值问题类型有以下几种:
1.最大值最小值问题:
求某个几何图形的最大面积或最小周长,如矩形、三角形等。
求抛物线的最高点或最低点,即顶点的坐标。
2.极值问题:
求函数图像与坐标轴的交点。
求函数在某个区间内的最大值或最小值,如求二次函数的最
值等。
3.最优化问题:
求物体从一个点到另一个点的路径问题,如两点之间的最短
路径、最快速度等。
4.最长边最短边问题:
求三角形的最长边或最短边,如用三根木棍构成三角形,求
最长边的长度。
5.相等问题:
求两个几何形状中的某个参数,使得它们的某个关系成立,
如求两个相似三角形的边长比、两个等腰三角形的底角角度等。
这些问题类型都需要通过合理的分析和运用相关的几何定理
来解决。
对于初中学生来说,熟练掌握基本的几何概念和定理,灵活运用数学思维和方法,可以较好地解决这些最值问题。
通
过多做练习和思考,培养几何思维和解决问题的能力。
初中数学定值定点最值问题

初中数学定值定点最值问题初中数学定值定点和最值问题是中考数学压轴题常考考点,对于定值定点问题可以采用特殊点,特殊值和特殊位置确定其值是多少,然后采用一般法去证明,最值问题一般是线段的和与差,最常用的方法是“化折为直”比如常见的“将军饮马问题”、“胡不归问题”、“阿氏圆问题”、“隐圆问题”。
例1.对于任意非零实数a,抛物线y=ax2+ax﹣6a总不经过点P(m+1,4﹣2m),则符合条件的点P的坐标为.变式1.若对于任意非零实数a,抛物线y=ax2+ax﹣2a总不经过点P(x0﹣3,x02﹣16),则写出符合条件的点P的坐标:.变式2.若对于任意非零实数a,抛物线y=ax2+ax﹣6a总不经过点P(m﹣2,m2﹣9),写出符合条件的点P的坐标:.变式3.若对于任意非零实数a,抛物线y=ax2+ax﹣2a总不经过点P(x0,2x0﹣6),写出符合条件的点P的坐标:.变式4.若对于任意非零实数a,抛物线y=ax2+ax﹣2a总不经过点P(m﹣3,m2﹣16),写出符合条件的点P的坐标:.变式5.若对于任意非零实数a,抛物线y=a(x+2)(x﹣1)总不经过点P(x0﹣3,x0﹣5)写出符合条件的点P的坐标:.变式6.若对于任意非零实数a,抛物线y=ax2+ax﹣2a总不经过点P(x0﹣3,x02﹣16),写出符合条件的点P的坐标:.例2.已知抛物线y=ax2﹣2anx+an2+n+3的顶点P在一条定直线l上.求直线l的解析式;例3.我们不妨约定:在平面直角坐标系中,若某函数图象上至少存在不同的两点关于y轴对称,则把该函数称之为“T函数”,其图象上关于y轴对称的不同两点叫做一对“T点”.若关于x的“T函数”y=ax2+bx+c(a>0,且a,b,c是常数)经过坐标原点O,且与直线l:y=mx+n(m≠0,n>0,且m,n是常数)交于M(x1,y1),N(x2,y2)两点,当x1,x2满足(1﹣x1)﹣1+x2=1时,直线l是否总经过某一定点?若经过某一定点,求出该定点的坐标;否则,请说明理由.例4.如图,已知P为正方形ABCD的外接圆的劣弧上任意一点,求证:为定值.例5.如图,在△ABC中,AB=5,AC=4,sin A=,BD⊥AC交AC于点D.点P为线段BD上的动点,则PC+PB的最小值为.例6.如图,在Rt△ABC中,∠A=90°,M为BC的中点,H为AB上一点,过点C作CG ∥AB,交HM的延长线于点G,若AC=8,AB=6,求四边形ACGH周长的最小值例7如图,已知二次函数y=ax2+bx+c的图象经过点C(2,﹣3),且与x轴交于原点及点B(8,0).若点P为⊙O上的动点,且⊙O的半径为2,一动点E从点A出发,以每秒2个单位长度的速度沿线段AP匀速运动到点P,再以每秒1个单位长度的速度沿线段PB匀速运动到点B后停止运动,求点E的运动时间t的最小值.例8.已知抛物线y=ax2+bx+c(a≠0)过点A(1,0),B(3,0)两点,与y轴交于点C,OC=3.若点Q为线段OC上的一动点,问:AQ+QC是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.例9.如图,A,B两点的坐标分别为A(4,3),B(0,﹣3),在x轴上找一点P,使线段P A+PB的值最小,则点P的坐标是.例10.如图,已知抛物线过点O(0,0),A(5,5),且它的对称轴为x=2,点B是抛物线对称轴上的一点,且点B在第一象限.当△OAB的面积为15时,P是抛物线上的动点,当P A﹣PB的值最大时,求P的坐标以及P A﹣PB的最大值.例11.如图1,在矩形ABCD中,AB=4,BC=6.点E是线段AD上的动点(点E不与点A,D重合),连接CE,过点E作EF⊥CE,交AB于点F.连接CF,过点B作BG⊥CF,垂足为G,连接AG.点M是线段BC的中点,连接GM.①求AG+GM的最小值;②当AG+GM取最小值时,求线段DE的长.例12.如图一所示,在平面直角坐标系中,抛物线y=ax2+2x+c经过点A(﹣1,0)、B(3,0),与y轴交于点C,顶点为点D.在线段CB上方的抛物线上有一动点P,过点P作PE ⊥BC于点E,作PF∥AB交BC于点F.当△PEF的周长为最大值时,求点P的坐标和△PEF的周长.。
2023年九年级数学中考专题复习——最值问题(将军饮马,胡不归,阿氏圆)

牛吃草最值问题:1.如图,AB 是⊙O 的直径,AB=8,点M 在⊙O 上,∠MAB=20°,N 是弧MB 的中点,P 是直径AB 上的一动点.若MN=1,则△PMN 周长的最小值为.2.如图,点P 是∠AOB 内一定点,点M 、N 分别在边OA 、OB 上运动,若∠AOB =45°,OP =32,则△PMN 周长的最小值为.3.如图,∠AOB 的边OB 与x 轴正半轴重合,点P 是OA 上一动点,点N(6,0)是OB 上的一定点,点M 是ON 中点,∠AOB=30∘,要使PM+PN 最小,则点P 的坐标为.4.如图,Rt △ABC 中,∠ACB=90º,∠CAB=30º, BC=1,将△ABC 绕点B 顺时针转动, 并把各边缩小为原来的一半,得到△DBE ,点A ,B ,E 在一直线上.P 为边DB 上的动点,则AP+CP 的最小值为 .5.点A 、B 均在由面积为1的相同小矩形组成的网格的格点上,建立坐标系如图所示.若P 是x 轴上使得PA PB -的值最大的点,Q 是y 轴上使得QA+QB 的值最小的点,则OP OQ ⋅= .N M O P B A Ay6.如图,当四边形PABN 的周长最小时,a =.7.矩形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,OA=3,OB =4,D 为边OB 的中点. 若E 、F 为边OA 上的两个动点,且EF =2,当四边形CDEF 的周长最小时,则点F 的坐标为8.如图,在Rt △ABO 中,∠OBA =90°,A (4,4),点C 在边AB 上,且=,点D 为OB 的中点,点P 为边OA 上的动点,当点P 在OA 上移动时,使四边形PDBC 周长最小的点P 的坐标为三角形条件及隐圆最值问题1.如图,在边长为2的菱形ABCD 中,∠A=60°,M 是AD 边的中点,N 是AB 边上一动点,将△AMN 沿MN 所在的直线翻折得到△A′MN ,连接A′C. 则A′C 长度的最小值是.N (a +2,0)P (a ,0)B (4,-1)A (1,-3)O y x F D C B A x y O E F D C B A x y O E2如图,矩形ABCD中,AB=4,BC=2,把矩形ABCD沿过点A的直线AE折叠点D落在矩形ABCD内部的点D处,则CD′的最小值是3.如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP的垂线,垂足为H,连结DH,若正方形的边长为4,则线段DH长度的最小值是.4.如图,AB为直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,取AP中点Q,连CQ,则线段CQ的最大值为5.如图,矩形ABCD中,AC与BD相交于点E,AD:AB=:1,将△ABD沿BD折叠,点A的对应点为F,连接AF交BC于点G,且BG=2,在AD边上有一点H,使得BH+EH的值最小,此时BH:CF=6.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为_____.7.如图,A(1,0)、B(3,0),以AB为直径作⊙M,射线OF交⊙M于E、F两点,C为弧AB的中点,D为EF的中点.当射线OF 绕O点旋转时,CD的最小值为________8.如图,点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是______9.AB是半圆O的直径,AB=10,弦AC长为8,点D是弧BC上一个动点,连接AD,作CP⊥AD,垂足为P,连接BP,则BP的最小值是_____10.直线y=x+4 分别与x 轴、y 轴相交与点M、N,边长为2 的正方形OABC 一个顶点O 在坐标系的原点,直线AN 与MC 相交与点P,若正方形绕着点O 旋转一周,则点P 到点(0,2)长度的最小值是__________11.如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是x−3与x轴、y轴分别交于A、B两点,P是以C(0,2)为圆心,2为半径的圆上一动点,连结PA、12.如图,已知直线y=34PB.则△PAB面积的最小值是_____.13.如图,C、D是以AB为直径的圆O上的两个动点(点C、D不与A、B重合),在运动过程中弦CD始终保持不变,M是弦CD 的中点,过点C作CP⊥AB于点P.若CD=3,AB=5,PM=x,则x的最大值是14.如图,已知A、B两点的坐标分别为(8,0)、(0,8),点C、F分别是直线x=﹣5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取得最小值时,tan∠BAD的值是15.如图,抛物线y=x2﹣4与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段P A的中点,连结OQ.则线段OQ的最大值是16.如图,正方形ABCD和Rt△AEF,AB=5,AE=AF=4,连接BF,DE.若△AEF绕着点A旋转,当∠ABF最大时,S△ADE =17.如图,在直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为18.在△ABC中,AB=4,∠C=60°,∠A>∠B,则BC的长的取值范围是19.如图,直线y=x+1与抛物线y=x2﹣4x+5交于A,B两点,点P是y轴上的一个动点,当△P AB的周长最小时,S△P AB=20..如图,△ABC是⊙O的内接三角形,且AB是⊙O的直径,点P为⊙O上的动点,且∠BPC=60°,⊙O的半径为6,则点P到AC距离的最大值是路径问题:1.如图,AB是⊙O的直径,M、N是(异于A、B)上两点,C是上一动点,∠ACB的角平分线交⊙O于点D,∠BAC 的平分线交CD于点E.当点C从点M运动到点N时,则C、E两点的运动路径长的比是2.如图,在圆心角为90°的扇形OAB中,OB=2,P为上任意一点,过点P作PE⊥OB于点E,设M为△OPE的内心,当点P从点A运动到点B时,则内心M所经过的路径长为3.如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧,点F从点A到点C的运动过程中,点E的运动路径长是4.等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.若AF=BE,当点E从点A运动到点C时,则点P经过的路径长为.5.如图,边长为2 的正方形ABCD 的两条对角线交于点O,把BA 与CD 分别绕点B 和点C 逆时针旋转相同的角度,此时正方形ABCD 随之变成四边形A′BCD′.设A′C,BD′交于点O′,若旋转了60°,则点O 运动到点O′所经过的路径长为6.已知等边三角形ABC 的边长为4,点D 是边BC 的中点,点E 在线段BA 上由点B 向点A 运动,连接DE,以DE 为边在DE 右侧作等边三角形DEF.设△DEF 的中心为O,则点 E 由点 B 向点 A 运动的过程中,点O 运动的路径长为胡不归型问题:当 k≠1 且 k 为正数时,若点 P 在某条直线上运动时,此时所求的最短路径问题称之为“胡不归”问题.那么对于当“PA + k·PB”的值最小时,点 P 的位置如何确定呢?过点 P 作 PQ⊥BN,垂足为 Q,如图3则 k·PB = PB·sin∠MBN = PQ.因此,本题求“PA + k·PB”的最小值转化为求“PA +PQ”的最小值,即 A,P,Q 三点共线时最小.1.如图,四边形ABCD是菱形,AB=4,且∠ABC=60°,M为对角线BD(不含B点)上任意一点,则AM+1BM的最小值为.22.在△ABC中,AB=AC=10,tan A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是阿氏圆模型问题:已知平面上两点 A,B,则所有满足 PA + k·PB(k≠1,且 k 为正数),若点 P 的轨迹是一个圆,当点 P 在圆周上运动的类型称之为“阿氏圆”(阿波罗尼斯圆)问题.如图所示,⊙O 的半径为 r,点 A,B 都在圆外,P 为⊙O 上的动点,已知 r = k·OB,连接 PA,PB,则当“PA + k·PB”的值最小时,P 点的位置如何确定?在线段 OB 上截取 OC 使 OC = k·r,则可说明△BPO∽△PCO,即 k·PB = PC.因此,求“PA + k·PB”的最小值转化为求“PA + PC”的最小值,即 A,P,C 三点共线时最小1.已知A(-4,-4)、B(0, 4)、C(0, -6)、 D(0, -1),AB与x轴交于点E,以点E为圆心,ED长为半径作圆,点M为⊙E上AM的最小值.一动点,求CM+122.如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连接AP,BP,则AP+1BP的最小值为.2旋转最值及路径问题:1.如图,点O在线段AB上,OA=1,OB=3,以O为圆心,OA长为半径作⊙O,点M在⊙O上运动,连接MB,以MB为腰作等腰Rt△MBC,使∠MBC=90°,M,B,C三点为逆时针顺序,连接AC,则AC长的取值范围为___________.2.如图,线段AB为⊙O的直径,AB=4,点C为OB的中点,点P在⊙O上运动,连接CP,以CP为一边向上作等边△CPD,连接OD,则OD的最大值为___________.3.如图,在直角坐标系中,已知点A(4,0),点B为y轴正半轴上一动点,连接AB,以AB为一边向下做等边△ABC,连接OC,则OC的最小值为__________4.如图,在Rt△ABC中,AB=BC=2,点P为AB边上一动点,连接CP,以CP为边向下作等腰RT△CPD,连接BD,则BD的最小值为____________.5..如图,在直角坐标系中,已知点A(4,0),点B为直线y=2上一动点,连接AB,以AB为底边向下做等腰Rt△ABC,∠ACB=90°,连接OC,则OC的最小值为__________6.如图,已知点A(3,0),C(0,-4),⊙C的半径为√5,点P为⊙C上一动点,连接AP,若M为AP的中点,连接OM,则OM的最大值为.7.如图,已知△ABC为等腰直角三角形,∠BAC=90°,AC=2,以点C为圆心,1为半径作圆,点P为⊙C上一动点,连结AP,并绕点A顺时针旋转90°得到AP′,连结CP′,则CP′的取值范围是.8.如图,Rt△ABC中,AC=6,BC=8,∠C=90°.点P是AB边上一动点,D是AC延长线上一点,且AC=CD,连接PD,过点D作.则当点P从点A运动到B点时,点E运动的路径长为DE⊥PD,连接PE,且tan∠DPE=252的一个定点,AC⊥x 轴于点M,交直线y=-x 于点N.若点P 是线段ON 上9.如图,点A 是第一象限内横坐标为3的一个动点,∠APB=30°,BA⊥PA,则点P 在线段ON 上运动时,A 点不变,B 点随之运动.当点P 从点O 运动到点N 时,点B 运动的路径长是旋转构图法(补形)问题:常见旋转模型:1.如图,在△ABC 中,AB=AC=32,∠BAC=120°,点D ,E 都在BC 上,∠DAE=60°,若BD=2CE ,则DE 的长为_____.2.在四边形ABCD 中,AD=4,CD =3,∠ABC=∠ACB =∠ADC=45°,则BD 的长为;3.如图,在△ABC 中,∠ABC=90°,将AB 边绕点A 逆时针旋转90°得到线段AD ,将AC 边绕点C 顺时针旋转90°得到线段CE ,AE 与BD 交于点F .若DF=2,EF=22,则BC 边的长为____________.A D CB E FDE CB A4.如图,菱形ABCD的对角线AC上有一动点P,BC=6,∠ABC=150°,则线段AP+BP+PD的最小值为5.如图,在△ABC中,∠ABC=30°,AB=4 ,BC=5 , P是△ABC内部的任意一点,连接PA , PB , PC,则PA + PB + PC 的最小值为.。
中考数学中的最值问题求法
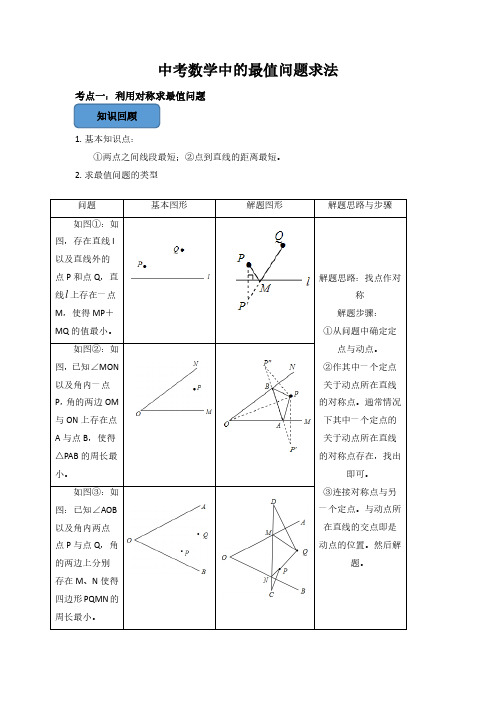
中考数学中的最值问题求法考点一:利用对称求最值问题1.基本知识点:①两点之间线段最短;②点到直线的距离最短。
2.求最值问题的类型ABCD的边长为6,点E在BC上,CE=2.点M是对角线BD上的一个动点,则EM+CM的最小值是()A.62B.35C.213D.413【分析】要求ME+MC的最小值,ME、MC不能直接求,可考虑通过作辅助线转化ME,MC的值,从而找出其最小值求解.【解答】解:如图,连接AE交BD于M点,∵A、C关于BD对称,∴AE就是ME+MC的最小值,∵正方形ABCD中,点E是BC上的一定点,且BE=BC﹣CE=6﹣2=4,∵AB=,∴AE==2,∴ME+MC的最小值是2.故选:C.2.(2022•资阳)如图,正方形ABCD的对角线交于点O,点E是直线BC上一动点.若AB =4,则AE+OE的最小值是()A.42B.25+2C.213D.210【分析】本题为典型的将军饮马模型问题,需要通过轴对称,作点A关于直线BC的对称点A',再连接A'O,运用两点之间线段最短得到A'O为所求最小值,再运用勾股定理求线段A'O的长度即可.【解答】解:如图所示,作点A关于直线BC的对称点A',连接A'O,其与BC的交点即为点E,再作OF⊥AB交AB于点F,∵A与A'关于BC对称,∴AE=A'E,AE+OE=A'E+OE,当且仅当A',O,E在同一条线上的时候和最小,如图所示,此时AE+OE=A'E+OE=A'O,∵正方形ABCD,点O为对角线的交点,∴,∵A与A'关于BC对称,∴AB=BA'=4,∴F A'=FB+BA'=2+4=6,在Rt△OF A'中,,故选:D.3.(2022•菏泽)如图,在菱形ABCD中,AB=2,∠ABC=60°,M是对角线BD上的一个动点,CF=BF,则MA+MF的最小值为()A.1B.2C.3D.2【分析】当MA+MF的值最小时,A、M、F三点共线,即求AF的长度,根据题意判断△ABC为等边三角形,且F点为BC的中点,根据直角三角形的性质,求出AF的长度即可.【解答】解:当A、M、F三点共线时,即当M点位于M′时,MA+MF的值最小,由菱形的性质可知,AB=BC,又∵∠ABC=60°,∴△ABC为等边三角形,∵F点为BC的中点,AB=2,∴AF⊥BC,CF=FB=1,∴在Rt△ABF中,AF==.故选:C.4.(2022•广安)如图,菱形ABCD的边长为2,点P是对角线AC上的一个动点,点E、F 分别为边AD、DC的中点,则PE+PF的最小值是()A.2B.3C.1.5D.5【分析】如图,取AB的中点T,连接PT,FT.首先证明四边形ADFT是平行四边形,推出AD=FT=2,再证明PE+PF=PT+PF,由PF+PT≥FT=2,可得结论.【解答】解:如图,取AB的中点T,连接PT,FT.∵四边形ABCD是菱形,∴CD∥AB,CD=AB,∵DF=CF,AT=TB,∴DF=AT,DF∥AT,∴四边形ADFT是平行四边形,∴AD=FT=2,∵四边形ABCD是菱形,AE=DE,AT=TB,∴E,T关于AC对称,∴PE=PT,∴PE+PF=PT+PF,∵PF+PT≥FT=2,∴PE+PF≥2,∴PE+PF的最小值为2.故选:A.5.(2022•赤峰)如图,菱形ABCD,点A、B、C、D均在坐标轴上.∠ABC=120°,点A (﹣3,0),点E是CD的中点,点P是OC上的一动点,则PD+PE的最小值是()3 A.3B.5C.22D.32【分析】根据题意得,E点关于x轴的对称点是BC的中点E',连接DE'交AC与点P,此时PD+PE有最小值,求出此时的最小值即可.【解答】解:根据题意得,E点关于x轴的对称点是BC的中点E',连接DE'交AC与点P,此时PD+PE有最小值为DE',∵四边形ABCD是菱形,∠ABC=120°,点A(﹣3,0),∴OA=OC=3,∠DBC=60°,∴△BCD是等边三角形,∴DE'=OC=3,即PD+PE的最小值是3,故选:A .6.(2022•安顺)已知正方形ABCD 的边长为4,E 为CD 上一点,连接AE 并延长交BC 的延长线于点F ,过点D 作DG ⊥AF ,交AF 于点H ,交BF 于点G ,N 为EF 的中点,M为BD 上一动点,分别连接MC ,MN .若91=∆∆FCEDCG S S ,则MC +MN 的最小值为 .【分析】由正方形的性质,可得A 点与C 点关于BD 对称,则有MN +CM =MN +AM ≥AN ,所以当A 、M 、N 三点共线时,MN +CM 的值最小为AN ,先证明△DCG ∽△FCE ,再由=,可知=,分别求出DE =1,CE =3,CF =12,即可求出AN .【解答】解:如图,连接AM ,∵四边形ABCD 是正方形, ∴A 点与C 点关于BD 对称, ∴CM =AM ,∴MN +CM =MN +AM ≥AN ,∴当A 、M 、N 三点共线时,MN +CM 的值最小, ∵AD ∥CF , ∴∠DAE =∠F ,∵∠DAE +∠DEH =90°, ∵DG ⊥AF ,∴∠CDG +∠DEH =90°, ∴∠DAE =∠CDG , ∴∠CDG =∠F , ∴△DCG ∽△FCE , ∵=,∴=,∵正方形边长为4,∴CF=12,∵AD∥CF,∴==,∴DE=1,CE=3,在Rt△CEF中,EF2=CE2+CF2,∴EF==3,∵N是EF的中点,∴EN=,在Rt△ADE中,EA2=AD2+DE2,∴AE==,∴AN=,∴MN+MC的最小值为,故答案为:,7.(2022•内江)如图,矩形ABCD中,AB=6,AD=4,点E、F分别是AB、DC上的动点,EF∥BC,则AF+CE的最小值是.【分析】延长BC到G,使CG=EF,连接FG,则四边形EFGC是平行四边形,得CE =FG,则AF+CE=AF+FG,可知当点A、F、G三点共线时,AF+CE的值最小为AG,利用勾股定理求出AG的长即可.【解答】解:延长BC到G,使CG=EF,连接FG,∵EF∥CG,EF=CG,∴四边形EFGC是平行四边形,∴CE=FG,∴AF+CE=AF+FG,∴当点A、F、G三点共线时,AF+CE的值最小为AG,由勾股定理得,AG===10,∴AF+CE的最小值为10,故答案为:10.8.(2022•贺州)如图,在矩形ABCD中,AB=8,BC=6,E,F分别是AD,AB的中点,∠ADC的平分线交AB于点G,点P是线段DG上的一个动点,则△PEF的周长最小值为.【分析】如图,在DC上截取DT,使得DT=DE,连接FT,过点T作TH⊥AB于点H.利用勾股定理求出FT=,EF=5,证明PE+PF=PF+PT≥FT,可得结论.【解答】解:如图,在DC上截取DT,使得DT=DE,连接FT,过点T作TH⊥AB于点H.∵四边形ABCD是矩形,∴∠A=∠ADT=90°,∵∠AHT=90°,∴四边形AHTD是矩形,∵AE=DE=AD=3.AF=FB=AB=4,∴AH=DT=3,HF=AF﹣AH=4﹣3=1,HT=AD=6,∴FT===,∵DG平分∠ADC,DE=DT,∴E、T关于DG对称,∴PE=PT,∴PE+PF=PF+PT≥FT=,∵EF===5,∴△EFP的周长的最小值为5+,故答案为:5+.9.(2022•娄底)菱形ABCD的边长为2,∠ABC=45°,点P、Q分别是BC、BD上的动点,CQ+PQ的最小值为.【分析】连接AQ,作AH⊥BC于H,利用SAS证明△ABQ≌△CBQ,得AQ=CQ,当点A、Q、P共线,AQ+PQ的最小值为AH的长,再求出AH的长即可.【解答】解:连接AQ,作AH⊥BC于H,∵四边形ABCD是菱形,∴AB=CB,∠ABQ=∠CBQ,∵BQ=BQ,∴△ABQ≌△CBQ(SAS),∴AQ=CQ,∴当点A、Q、P共线,AQ+PQ的最小值为AH的长,∵AB=2,∠ABC=45°,∴AH=,∴CQ+PQ的最小值为,故答案为:.10.(2022•眉山)如图,点P为矩形ABCD的对角线AC上一动点,点E为BC的中点,连接PE,PB,若AB=4,BC=43,则PE+PB的最小值为.【分析】作点B关于AC的对称点B',交AC于点F,连接B′E交AC于点P,则PE+PB 的最小值为B′E的长度;然后求出B′B和BE的长度,再利用勾股定理即可求出答案.【解答】解:如图,作点B关于AC的对称点B',交AC于点F,连接B′E交AC于点P,则PE+PB的最小值为B′E的长度,∵四边形ABCD为矩形,∴AB=CD=4,∠ABC=90°,在Rt△ABC中,AB=4,BC=4,∴tan∠ACB==,∴∠ACB=30°,由对称的性质可知,B'B=2BF,B'B⊥AC,∴BF=BC=2,∠CBF=60°,∴B′B=2BF=4,∵BE=BF,∠CBF=60°,∴△BEF是等边三角形,∴BE=BF=B'F,∴△BEB'是直角三角形,∴B′E===6,∴PE+PB的最小值为6,故答案为:6.11.(2022•滨州)如图,在矩形ABCD中,AB=5,AD=10.若点E是边AD上的一个动点,过点E作EF⊥AC且分别交对角线AC、直线BC于点O、F,则在点E移动的过程中,AF+FE+EC的最小值为.【分析】如图,过点E作EH⊥BC于点H.利用相似三角形的性质求出FH,EF,设BF=x,则DE=10﹣x﹣=﹣x,因为EF是定值,所以AF+CE的值最小时,AF+EF+CE 的值最小,由AF+CE=+,可知欲求AF+CE的最小值相当于在x轴上找一点P(x,0),使得P到A(0,5),B(,5)的距离和最小,如图1中,作点A关于x轴的对称点A′,连接BA′交x轴于点P,连接AP,此时P A+PB的值最小,最小值为线段A′B的长,由此即可解决问题.【解答】解:如图,过点E作EH⊥BC于点H.∵四边形ABCD是矩形,∴∠B=∠BAD=∠BHE=90°,∴四边形ABHE是矩形,∴EH=AB=5,∵BC=AD=10,∴AC===5,∵EF⊥AC,∴∠COF=90°,∴∠EFH+∠ACB=90°,∵∠BAC+∠ACB=90°,∴∠EFH=∠BAC,∴△EHF∽△CBA,∴==,∴==,∴FH=,EF=,设BF=x,则DE=10﹣x﹣=﹣x,∵EF是定值,∴AF+CE的值最小时,AF+EF+CE的值最小,∵AF+CE=+,∴欲求AF+CE的最小值相当于在x轴上找一点P(x,0),使得P到A(0,5),B(,5)的距离和最小,如图1中,作点A关于x轴的对称点A′,连接BA′交xz轴于点P,连接AP,此时P A+PB的值最小,最小值为线段A′B的长,∵A′(0,﹣5),B(,5),∴A′B==,∴AF+CE的最小值为,∴AF+EF+CE的最小值为+.解法二:过点C作CC′∥EF,使得CC′=EF,连接C′F.∵EF=CC′,EF∥CC′,∴四边形EFC′C是平行四边形,∴EC=FC′,∵EF⊥AC,∴AC⊥CC′,∴∠ACC=90°,∵AC′===,∴AF+EC=AF+FC′≥AC′=,∴AF+EF+CE的最小值为+.故答案为:+.12.(2022•自贡)如图,矩形ABCD中,AB=4,BC=2,G是AD的中点,线段EF在边AB上左右滑动,若EF=1,则GE+CF的最小值为.【分析】解法一:利用已知可以得出GC,EF长度不变,求出GE+CF最小时即可得出四边形CGEF周长的最小值,利用轴对称得出E,F位置,即可求出.解法二:设AE=x,则BF=3﹣x,根据勾股定理可得:EG+CF=+,由勾股定理构建另一矩形EFGH,根据线段的性质:两点之间线段最短可得结论.【解答】解:解法一:如图,作G关于AB的对称点G',在CD上截取CH=1,然后连接HG'交AB于E,在EB上截取EF=1,此时GE+CF的值最小,∵CH=EF=1,CH∥EF,∴四边形EFCH是平行四边形,∴EH=CF,∴G'H=EG'+EH=EG+CF,∵AB=4,BC=AD=2,G为边AD的中点,∴DG'=AD+AG'=2+1=3,DH=4﹣1=3,由勾股定理得:HG'==3,即GE+CF的最小值为3.解法二:∵AG=AD=1,设AE=x,则BF=AB﹣EF﹣AE=4﹣x﹣1=3﹣x,由勾股定理得:EG+CF=+,如图,矩形EFGH中,EH=3,GH=2,GQ=1,P为FG上一动点,设PG=x,则FP=3﹣x,∴EP+PQ=+,当E,P,Q三点共线时,EP+PQ最小,最小值是3,即EG+CF的最小值是3.故答案为:3.13.(2022•泰州)如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F、G与点C的距离分别为d2、d3,则d1+d2+d3的最小值为()A.2B.2C.22D.4【分析】连接AE,那么,AE=CG,所以这三个d的和就是AE+EF+FC,所以大于等于AC,故当AEFC四点共线有最小值,最后求解,即可求出答案.【解答】解:如图,连接AE ,∵四边形DEFG 是正方形,∴∠EDG =90°,EF =DE =DG ,∵四边形ABCD 是正方形,∴AD =CD ,∠ADC =90°,∴∠ADE =∠CDG ,∴△ADE ≌△CDG (SAS ),∴AE =CG ,∴d 1+d 2+d 3=EF +CF +AE ,∴点A ,E ,F ,C 在同一条线上时,EF +CF +AE 最小,即d 1+d 2+d 3最小,连接AC ,∴d 1+d 2+d 3最小值为AC ,在Rt △ABC 中,AC =AB =2,∴d 1+d 2+d 3最小=AC =2, 故选:C .14.(2022•安徽)已知点O 是边长为6的等边△ABC 的中心,点P 在△ABC 外,△ABC ,△P AB ,△PBC ,△PCA 的面积分别记为S 0,S 1,S 2,S 3.若S 1+S 2+S 3=2S 0,则线段OP 长的最小值是( )A .233B .235C .33D .237【分析】如图,不妨假设点P 在AB 的左侧,证明△P AB 的面积是定值,过点P 作AB 的平行线PM ,连接CO 延长CO 交AB 于点R ,交PM 于点T .因为△P AB 的面积是定值,推出点P 的运动轨迹是直线PM ,求出OT 的值,可得结论.【解答】解:如图,不妨假设点P 在AB 的左侧,∵S △P AB +S △ABC =S △PBC +S △P AC ,∴S 1+S 0=S 2+S 3,∵S 1+S 2+S 3=2S 0,∴S 1+S 1+S 0=2,∴S1=S0,∵△ABC是等边三角形,边长为6,∴S0=×62=9,∴S1=,过点P作AB的平行线PM,连接CO延长CO交AB于点R,交PM于点T.∵△P AB的面积是定值,∴点P的运动轨迹是直线PM,∵O是△ABC的中心,∴CT⊥AB,CT⊥PM,∴•AB•RT=,CR=3,OR=,∴RT=,∴OT=OR+TR=,∵OP≥OT,∴OP的最小值为,当点P在②区域时,同法可得OP的最小值为,如图,当点P在①③⑤区域时,OP的最小值为,当点P在②④⑥区域时,最小值为,∵<,故选:B.考点二:利用确定圆心的位置求最短路径通过确定圆心的位置,利用定点到圆心的距离加或减半径解题。
初中数学最值问题典型例题(含答案分析)

考查知识点:1、“两点之间线段最短”(2、代数计算最值问题 问题原型:饮马问题造桥选址问题(完全平方公式 出题背景变式:角、三角形、菱形、矩形、正方形、梯形、 解题总思路:找点关于线的对称点实现“折”转“直” 几何基本模型: 条件 问题 方法 中考数学最值问题总结 ,“垂线段最短”,“点关于线对称”,“线段的平移”。
3、二次函数中最值问题) 配方求多项式取值 二次函数顶点)圆、坐标轴、抛物线等。
如下左图, A 、B 是直线I 同旁的两个定点.在直线I 上确定一点P ,使PA PB 的值最小. 作点 A 关于直线I 的对称点A ,连结AB 交I 于 点P ,则PA PB AB 的值最小 例1、如图,四边形 ABCD 是正方形,△ ABE 是等边三 角形,M 为对角线BD (不含B 点) 上任意一点,将 BM 绕点B 逆时针旋转60°得到BN ,连接 EN 、AM 、CM . (1) 求证:△ AMB ENB ; (2) ①当M 点在何处时,AM+CM 的值最小;②当 M 点在何处时,AM+BM+CM 的值最小,并说明理由;(3) 当AM+BM+CM 的最小值为 ■■ ■■■ I 时,求正方形的边长。
例2、如图13,抛物线y=ax2+ bx + c(a丰(的顶点为(1,4 ),交x轴于A B,交y轴于D, 其中B点的坐标为(3,0 )(1)求抛物线的解析式(2)如图14,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则x轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小•若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由•(3)如图15,抛物线上是否存在一点T,过点T作x的垂线,垂足为M,过点M作直线MN// BD,交线段AD于点N,连接MD使厶DN WA BMD若存在,求出点T的坐标;若不存在,说明理由.例3、如图1,四边形AEFG与ABCD都是正方形,它们的边长分别为a,b(b >2a且点F在AD上(以下问题的结果可用a,b表示)(1) 求DBF;(2) 把正方形AEFG绕点A逆时针方向旋转45°得图2,求图2中的S^DBF;(3) 把正方形AEFG绕点A旋转任意角度,在旋转过程中DBF是否存在最大值,最小值?如果存在,试求出最大值、最小值;如果不存在,请说明理由。
中考数学复习《最值问题》

解:如图,∵高为 12 cm,底面周长为 10 cm,在容器内壁离容器底部 3 cm 的 点 B 处有一饭粒,此时蚂蚁正好在容器外壁,离容器上沿 3 cm 与饭粒相对的点 A 处,∴A′D=5 cm,BD=12-3+AE=12(cm),∴将容器侧面展开,作 A 关 于 EF 的对称点 A′,连结 A′B,则 A′B 即为最短距离,A′B= A′D2+BD2= 52+122=13(cm)
解:(1)如图所示 (2)如图,即为所求
(3)作点 C 关于 y 轴的对称点 C′,连结 CP,B1C′交 y 轴于点 P, 则点 P 即为所求.设直线 B1C′的解析式为 y=kx+b(k≠0),
-2k+b=-2, k=2, ∵B1(-2,-2),C′(1,4),∴ 解得 k+b=4, b=2,
7.图1、图2为同一长方体房间的示意图 ,图3为该长方体的表面展开 图.
(1)蜘蛛在顶点A′处.
①苍蝇在顶点B处时,试在图1中画出蜘蛛为捉住苍蝇,沿墙面爬行的 最近路线;
②苍蝇在顶点C处时,图2中画出了蜘蛛捉住苍蝇的两条路线,往天花
板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC,试通 过计算判断哪条路线更近;
两点距离之差的绝对值最大时,点P在直线AB上.先运用待定系数法求出直
线AB的解析式,再令y=0,求出x的值即可.
解:由题意可知,当点 P 到 A,B 两点距离之差的绝对值最大时, 点 P 在直线 AB 上.设直线 AB 的解析式为 y=kx+b,
b=1, k=1, ∵A(0,1),B(1,2),∴ 解得 ∴y=x+1, k+b=2, b=1,
令 y=0,得 0=x+1,解得 x=-1,∴点 P 的坐标是(-1,0)
中考数学最值问题总结

中考数学最值问题总结中考数学中最值问题是一个重要的考点,通常涉及到二次函数、一次函数、不等式等问题。
以下是一些常见的最值问题及解决方法:1. 二次函数最值问题二次函数的最值问题是最常见的最值问题之一。
解决这类问题的一般步骤是:首先确定自变量的取值范围,然后利用二次函数的顶点式或开口方向来求最值。
如果二次函数的开口向上,那么在顶点处取得最小值(当x<0时),在x轴上取得最大值(当x>0时)。
如果二次函数的开口向下,那么在顶点处取得最大值(当x<0时),在x轴上取得最小值(当x>0时)。
2. 一次函数最值问题一次函数的最值问题通常涉及到一次函数的单调性和自变量的取值范围。
如果一次函数是递增的,那么在自变量取值范围内的最大值是当x取最大值时的函数值,最小值是当x取最小值时的函数值。
如果一次函数是递减的,那么在自变量取值范围内的最大值是当x取最小值时的函数值,最小值是当x取最大值时的函数值。
3. 不等式最值问题不等式的最值问题通常涉及到不等式的性质和不等式的取值范围。
解决这类问题的一般步骤是:首先确定不等式的取值范围,然后利用不等式的性质来求最值。
如果是不等式左边是一个定值,右边是一个变量的形式,那么当变量取最大或最小值时,不等式取得最值。
如果是不等式两边都是变量,那么需要利用不等式的性质来求解。
4. 代数式的最值问题代数式的最值问题通常涉及到代数式的化简和代数式中字母的取值范围。
解决这类问题的一般步骤是:首先将代数式进行化简,然后根据代数式中字母的取值范围来确定最值。
如果代数式中包含有二次项,那么可以利用配方法将其化简为顶点式或开口方向式来求解最值。
如果代数式中包含有绝对值,那么需要先去掉绝对值符号再化简求解最值。
解决中考数学最值问题需要掌握各种知识点和方法,包括二次函数、一次函数、不等式、代数式等,同时需要注意自变量的取值范围和函数的单调性等问题。
中考数学《最值问题》及参考答案

中考数学《最值问题》及参考答案一、轴对称求最小值1.如图,四边形ABCD是边长为6的正方形,△ABC是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的值最小,求这个最小值.2.四边形ABCD中,∠BAD=122°,∠B=∠D=90°,在BC、CD上分别找一点M、N,当△AMN周长最小时,求∠MAN的度数.3.如图,∠AOB =45°,OC为∠AOB内部一条射线,点D为射线OC上一点,OD=√2,点E、F分别为射线0A、OB上的动点,求△DEF周长的最小值.二、垂线段最短求最值4.如图,矩形ABCD中,AD=3,AB=4,M为线段BD上一动点,MP⊥CD于点P,MQ⊥BC于点Q,求PQ 的最小值.5.如图,边长为6的等边三角形ABC中,E是对称轴AD上一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF,则在点E运动的过程中,求DF的最小值.6.如图所示,在RtΔABC中,∠C=90°,AC=4,BC=3,P为AB上一动点(不与A、 B重合),作PE ⊥AC于点E,PF⊥BC于点F,连接EF,求EF的最小值.7.如图,在ΔABC中,∠BAC=90,AB=6,BC=10,BD平分∠ABC,若P,Q分别是BD,AB上的动点,求PA+PQ的最小值.8.如图,Rt△ABC中,∠C=90°,以AB为边在AB上方作正方形ABDE,过点D作DF⊥CB,交CB的延长线于点F,连接BE,P,N分别为AC,BE上的动点,连接AN, PN,若DF=5,AC=9,求AN+PN的最小值.二、两点之间,线段最短求最值9.如图,等边△ABC的边长为4,过点B的直线l⊥AB,且△ABC与△A´B´C´公关于直线l对称,D为线段BC´上一动点,求AD+CD的最小值是( )10.如图,在长方形ABCD中,AB=3,AD=4,动点P满足S△PCD=14S长方形ABCD´,求点P到A,B两点的距离之和PA+PB的最小值.三、三角形三边的关系求最值问题11.如图,在平面直角坐标系中,平行四边形ABCD的坐标分别为A(-1,0)、B(0,2)、 C(4,2)、D(3,0),点P是AD边上的一个动点,若点A关于BP的对称点为A´,求则A´C的最小值.参考答案1.析:连接BP.因为点B 与点D 关于直线AC 对称,所以PB=PD .所以PD+PE =PB+PE≥BE,所以PD+PE 的最小值即为BE 的长.BE =AB =6,则PD+PE 的值最小为6.2.析:如图,延长AB 到A ´使得BA ´=AB,延长AD 到A ´使得DA"=AD,连接A ´A"与BC 、CD 分别交于点M 、N.∵∠ABC=∠ADC=90° ∴ A 、A ´关于BC 对称,A 、A"关于CD 对称,此时ΔAMN 的周长最小∵BA=BA ´,MB ⊥ AB ∴MA =MA ´同理:NA=NA" ∴∠A ´=∠MAB,∠A"=∠NAD∵∠AMN =∠A ´+∠MAB =2∠A ´,∠ANM =∠A"+∠NAD =2∠A"∴∠AMN +∠ANM = 2(∠A ´+∠A")∵∠BAD=122° ∴ ∠A ´+LA"=180°-∠BAD=58° ∴∠AMN +∠ANM=2x58°=116∴∠MAN =180-116°=64°3.析:作点D 作关于OA 的对称点P,点D 关于OB 的对称点Q,连接PQ,与OA 的交点为点E,与OB 的交点为点F.△DEF 的最小周长为DE +EF +QF =PE+EF+QF =PQ连接OP 、OQ,则OP=0Q=√2 ∵∠POQ =2∠AOB=90°∴ΔOPQ 是等腰直角三角形∴PQ =√2OD=2∴ΔDEF 的周长的最小值是2.4.析:如图,连接CM∵MP ⊥CD 于点P,MQ ⊥BC 于点Q ∴∠CPM =∠CQM=90°∴四边形ABCD 是矩形∴BC=AD=3,CD=AB=4,∠BCD=90°∴四边形PCQM 是矩形,PQ =CM∴BD =√32+42=5当CM ⊥BD 时,CM 最小,则PQ 最小,此时,S △BCD =1 2BD ·CM=12BC ·CD ∴PQ 的最小值为125.5.析:取线段AC 的中点G,连接EG∵ΔABC 为等边三角形,AD 为△ABC 的对称轴∴CD=CG=1 2AB=3,∠ACD =60° ∵ ∠ECF =60°∴∠FCD =∠ECG在ΔFCD 和ΔECG 中,FC =EC,∠FCD=∠ECG,DC=GC∴ΔFCD ≌AECG ∴DF =GE当EG ⊥AD 时,EG 最短,即DF 最短∵点G 为AC 的中点,EG=DF=1 2CD=32 6.析: 连接CP.∵∠C=90,AC=3,BC =4 ∴AB =√32+42=5∵PE ⊥AC,PF ⊥BC,∠C=90°∴四边形CFPE 是矩形∴EF =CP由垂线段最短可得CP ⊥AB 时,线段EF 的值最小S △ABC=1 2BC ·AC=12AB ·CP ∴1 2×4×3=12×5·CP ∴CP =2.4 7.如图,作点Q 关于直线BD 的对称点Q ´∵BD 平分∠ABC ∴点Q 在BC 上连接PQ ´,则PA+PQ 的最小值即为PA+PQ ´的最小值∴当A 、P 、Q ´三点共线且AQ ´⊥BC 时,PA+PQ 的值最小过点A 作AM ⊥BC 于点M,则PA+PQ 的最小值即为AM 的长∵AB=6,BC=10 ∴AC ²=10²-6²=64 ∴AC=8∵ S △ABC =1 2AM ·BC=1 2AB ·AC ∴AM=AB·AC BC =48 10=4.88.析:连接AD ,与BE 交于点O∵四边形ABDE 是正方形 ∴BE ⊥AD,OD =OA ,点A 与点D 关于直线BE 对称 求PN + AN 的最小值,只需D ,N ,P 在同一条直线上,由于P ,N 分别是AC 和BE 上的动点,过点D 作DP ⊥AC 于P 交BE 于点 N ,此时PN + AN =PN+ND=PD ,由△ABC ≌ △BDF 可知,BF= AC = 9,BC=DF=5,易知四边形DFCP 是矩形,CF=PD=BF+BC=9+5=149.析:如图,连接AD∵△ABC 是边长为4的等边三角形 ∴AB =BC=4,∠ABC=60° ∵△ABC 与△ A ´B ´C ´关于直线l 对称∴A ´B=BC,∠AB ´C ´=60°∴∠CBC ´=60°=∠A ´BD∴△BCD ≌△BA ´D(SAS)∴A ´D=CD ∴CD +AD =AD +A ´D当A 、D 、A ´三点共线时,AD+A ´D 最小,此时CD+AD 最小,最小为4+4=8.10.析:如图,设APC 的CD 边上的高是h.∵S △PCD =1 2S 长形ABCD ,AD=4 ∴1 2·CD ·h =1 4CD ·AD ∴h=12AD=2 ∵动点P 在与CD 平行且与CD 的距离是2的直线l 上连接AC 交直线l 于点P ´∵l//CD,AD=4,四边形ABCD 是长方形 ∴l ⊥AD,l ⊥BC∴直线l 是BC 边的垂直平分线 ∴BP ´=CP ´∴AP ´+BP ´=AP ´+CP ´ ∴ AC 的长是最短距离∴AC=√32+4=5,PA +PB 的最小值为5.11.析:连接BA ´∵AB=√5,BC =4若点A 关于BP 的对称点为A ´ ∴BA ´=BA=√5在△BA ´C 中,A ´C ≥BC-BA ´,即AC ´≥4-√5∴AC ´的最小值为4-√5。
二次函数中求线段,线段和,面积等最值问题—备战2024年中考数学(全国通用)(解析版)

二次函数中求线段,线段和,面积等最值问题(压轴通关) 目录【中考预测】预测考向,总结常考点及应对的策略【误区点拨】点拨常见的易错点【抢分通关】精选名校模拟题,讲解通关策略(含新考法、新情境等)二次函数中求线段,线段和,面积等最值问题是全国中考的热点内容,更是全国中考的必考内容。
每年都有一些考生因为知识残缺、基础不牢、技能不熟、答欠规范等原因导致失分。
1.从考点频率看,二次函数的图象和性质是考查的基础,也是高频考点、必考点。
2.从题型角度看,以解答题的最后一题或最后第二题为主,分值12分左右,着实不少!题型一 二次函数中求线段的最值问题【例1】(2024·安徽滁州·一模)已知抛物线()22131y x n x n =−++++交x 轴于点()10A −,和点B ,交y 轴于点C .(1)求抛物线的函数解析式;(2)如图1,已知点P 是位于BC 上方的抛物线上的一点,作PM BC ⊥,垂足为M ,求线段PM 长度的最大值;(3)如图2,已知点Q 是第四象限抛物线上一点,45ACQ ∠=︒,求点Q 的坐标.【答案】(1)234y x x =−++;(2)PM 的最大值为(3)点Q 的坐标为143439⎛⎫− ⎪⎝⎭,.【分析】(1)将点()10A −,代入()22131y x n x n =−++++,求得1n =,即可得解;(2)求得点B 和C 的坐标,推出45OAB OBC ∠=∠=︒,作PF x ⊥轴于点F ,交BC 于点E ,得到PEM △是等腰直角三角形,2PM PE =,设()234P m m m −++,,求得PM 关于m 的二次函数,利用二次函数的性质求解即可;(3)作BG CQ ⊥轴于点G ,作GH x ⊥轴于点H ,求得BC =ACO GCB ∠=∠,利用正切函数的定义求得BG ,证明HBG 是等腰直角三角形,求得()31G −,,再求得直线CG 的解析式,据此求解即可.【详解】(1)解:∵抛物线()22131y x n x n =−++++交x 轴于点()10A −,, ∴()121310n n −−+++=,解得1n =,∴抛物线的函数解析式为234y x x =−++; (2)解:当0x =时,4y =;当0y =时,2340x x −++=,解得4x =或=1x −;∴()40B ,,()04C ,,∴4OA OB ==,∴45OCB OBC ∠=∠=︒,作PF x ⊥轴于点F ,交BC 于点E ,∴9045PEM BEF OBC ∠=∠=︒−∠=︒,∴PEM △是等腰直角三角形,∴PM =,设直线BC 的解析式为4y kx =+,把()40B ,代入得044k =+,解得1k =−,∴直线BC 的解析式为4y x =−+,设()234P m m m −++,,则()4E m m −+,,∴))223442PM PE m m m m ==−+++−=−+∵0>,∴PM 有最大值,最大值为(3)解:作BG CQ ⊥轴于点G ,作GH x ⊥轴于点H ,∵()10A −,,()40B ,,()04C ,,∴1OA =,4OB OC ==,BC =∵45ACQ ∠=︒,45OCB ∠=︒,∴ACO GCB ∠=∠,∴tan tan ACO GCB ∠=∠,即OA BG OC BC =,∴14=∴BG ,∵45OBC ∠=︒,∴45HBG ∠=︒,∴HBG 是等腰直角三角形,∴1BH GH ==,∴413OH =−=,∴()31G −,,同理直线CG 的解析式为543y x =−+, 联立得235434x x x =−+++−,解得0x =或143x =; 当143x =时,514344339y =−⨯+=−, ∴点Q 的坐标为143439⎛⎫− ⎪⎝⎭,.【例2】(2024·江苏淮安·二模)如图,在平而直角坐标系中,二次函数2y =+的图象与x 轴分别交于点,O A ,顶点为B .连接,OB AB ,将线段AB 绕点A 按顺时针方向旋转60︒得到线段AC ,连接BC .点,D E 分别在线段,OB BC 上,连接,,,AD DE EA DE 与AB 交于点,60F DEA ∠=︒.(1)求点A ,B 的坐标;(2)随着点E 在线段BC 上运动.①EDA ∠的大小是否发生变化?请说明理由;②线段BF 的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由.【答案】(1)()20A ,,(B ;(2)①EDA ∠的大小不变,理由见解析;②线段BF 的长度存在最大值为12【分析】(1)0y =得20+=,解方程即可求得A 的坐标,把2y =+化为顶点式即可求得点B 的坐标;(2)①在AB 上取点M ,使得BM BE =,连接EM ,证明AED △是等边三角形即可得出结论;②证BDF OAD ∽,利用相似三角形的性质得BD BF OA OD =即22x BF x −=,解得()211122BF x =−−+进而利用二次函数的性质即可得解.【详解】(1)解:∵)221y x =+=−+∴顶点为(B ,令0y =,20+=,解得0x =或2x =,∴()20A ,;(2)解:①EDA ∠的大小不变,理由如下:在AB 上取点M ,使得BM BE =,连接EM ,∵)21y x =−∴抛物线对称轴为1x =,即1ON =,∵将线段AB 绕点A 按顺时针方向旋转60︒得到线段AC ,∴60BAC ∠=︒,AB AC =,∴BAC 是等边三角形,∴AB AC BC ==,60C ∠=︒,∵()20A ,,(B ,()00O ,,1ON =,∴2OA =,OB =2,AB =2=,∴OA OB AB ==,∴OAB 是等边三角形,2OA OB AC BC ====,∴60∠=∠=∠=︒OAB OBA AOB ,∵60MBE ∠=︒,BM BE =,∴BME 是等边三角形,∴60BME ABE ∠∠=︒=,ME BE BM ==,∴180120AME BME ∠∠=︒−=︒,BD EM ∥,∵120DBE ABO ABC ∠∠∠=+=︒,∴DBE AME ∠∠=,∵BD EM ∥,∴18012060FEM BED AEF MEA FEM ∠∠∠∠∠+=︒−︒=︒==+,∴BED MEA ∠∠=,∴BED MEA ≌,∴DE EA =,又60AED ∠=︒,∴AED △是等边三角形,∴60ADE ∠=︒,即ADE ∠的大小不变;②设OD x =,则2BD x =−,∵OAB 是等边三角形,60ADE ∠=︒,∴60DOA FBD ADE ∠∠∠===︒,∵BDA BDF ADE DOA OAD ∠∠∠∠∠=+=+,∴BDF OAD ∠∠=,∴BDF OAD ∽,∴BD BF OA OD =即22x BF x −=, ∴()211122BF x =−−+,∴当1x =时,BF 有最大值为12.【点睛】本题主要考查了二次函数的图像及性质,全等三角形的判定及性质,相似三角形的判定及性质以及等边三角形的判定及性质,题目综合性较强,熟练掌握各知识点是解题的关键.1.(2024·四川南充·一模)如图,已知抛物线2y x bx c =++与x 轴交于0()1,A -,B 两点,与y 轴交于点C (0,3)−.(1)求抛物线的解析式;(2)如图1,点P 是抛物线上位于第四象限内一动点,PD BC ⊥于点D ,求PD 的最大值及此时点P 的坐标;(3)如图2,点E 是抛物线的顶点,点M 是线段BE 上的动点(点M 不与B 重合),过点M 作MN x ⊥轴于N ,是否存在点M ,使CMN 为直角三角形?若存在,求出点M 的坐标;若不存在,请说明理由.【答案】(1)223y x x =−−(2)当32m =时,PD取得最大值为.此时315,24P ⎛⎫− ⎪⎝⎭ (3)CMN 为直角三角形时,点M 的坐标为:3,32⎛⎫− ⎪⎝⎭或()12【分析】(1)把点,A C 坐标代入函数的解析式,利用待定系数法求解即可;(2)先求线BC 的解析式,设点p 的横坐标为m ,再用m 的代数式表示PD 的长度建立二次函数求解即可;(3)先求直线BE 的解析式,再分三种情况,根据相似三角形的判定和性质求解即可.【详解】(1)由题意得103b c c −+=⎧⎨=−⎩,解得:23b c =−⎧⎨=−⎩.则抛物线的解析式为:223y x x =−−;(2)过点P 作PH x ⊥轴于点H ,交BC 于点G当0y =时,2230x x −−=,解得=1x −或3,∴(3,0)B设直线BC 的解析式为:1y kx b =+,则11303k b b +=⎧⎨=−⎩,解得:113k b =⎧⎨=−⎩∴3y x =−设点()2,23P m m m −−(03m <<),则3G m m −(,), ∴()()223233PG m m m m m =−−−−=−, ∵OB OC =,∴45OBC OCB ∠=∠=︒,∴45BGH ∠=︒∴45PGD BGH ∠=∠=︒,∴PD =.)22332228PD m m m ⎫=−+=−−+⎪⎝⎭ ∴当32m =时,PD取得最大值为8.此时315,24P ⎛⎫− ⎪⎝⎭. (3)在EB 上存在点M ,使CMN 为直角三角形.抛物线顶点(1,4)E −,设直线BE 的解析式为:22y k x b =+,则2222430k b k b +=−⎧⎨+=⎩,解得:2226k b =⎧⎨=−⎩,∴26y x =−.设26M n n −(,)13n ≤<(),①∵90CNM ONC ∠=︒−∠,∴90CNM ∠<︒,不可能为直角;②当90CMN ∠=︒时,则90CMN MNB ∠=∠=︒ ∴//MC x 轴,则263n −=−,∴32n =,∴3,32M ⎛⎫− ⎪⎝⎭. ③当90MCN ∠=︒时,过点M 作MF y ⊥轴于点F .∵90MCF NCO ∠+∠=︒,90CNO NCO ∠+∠=︒,∴MCF CNO ∠=∠,又90MFC CON ∠=∠=︒,∴MFC CON ∽, ∴CF MF NO CO =, ∴()3263n nn −−−=,∴2690n n +−=,解得:123,3n n ==−.∵13n ≤<,∴23n =−不合题意,应舍去,∴3n =∴()12M综上所述,CMN 为直角三角形时,点M 的坐标为:3,32⎛⎫− ⎪⎝⎭或()12.【点睛】本题考查用待定系数法求二次函数的解析式,构造二次函数求线段的最值,二次函数与直角三角形的存在性问题,相似三角形的判定和性质,难度较大,是中考的压轴题,解题的关键是数形结合,提高综合运用的能力.2.(23-24九年级下·江苏宿迁·阶段练习)如图,在平面直角坐标系中抛物线214y x bx c =++与x 轴交于点A ,B ,与y 轴交于点C ,其中()3,0B ,()0,3C −.(1)求该抛物线的表达式;(2)点P 是直线AC 下方抛物线上一动点,过点P 作PD AC ⊥于点D ,求PD 的最大值及此时点P 的坐标;(3)在(2)的条件下,将该抛物线向右平移5个单位,点E 为点P 的对应点,平移后的抛物线与y 轴交于点F ,Q 为平移后的抛物线的对称轴上任意一点.求出所有使得以QF 为腰的QEF △是等腰三角形的点Q 的坐标.【答案】(1)211344y x x =+−;(2)PD 的最大值为45,此时点52,2P ⎛⎫−− ⎪⎝⎭; (3)Q 点的坐标为9,12⎛⎫− ⎪⎝⎭或9,52⎛⎫ ⎪⎝⎭或97,24⎛⎫ ⎪⎝⎭.【分析】(1)待定系数法求二次函数解析式即可求解;(2)直线AC 的解析式为334y x =−−,过点P 作PE x ⊥轴于点E ,交AC 于点Q ,设211,344P t t t ⎛⎫+− ⎪⎝⎭,则3,34Q t t ⎛⎫−− ⎪⎝⎭,则45PD PQ =,进而根据二次函数的性质即可求解;(3)根据平移的性质得出219494216y x ⎛⎫=−− ⎪⎝⎭,对称轴为直线92x =,点52,2P ⎛⎫−− ⎪⎝⎭向右平移5个单位得到53,2E ⎛⎫− ⎪⎝⎭,()0,2F ,勾股定理分别表示出2EF ,2QE ,2QF 进而分类讨论即可求解. 【详解】(1)解:将点()3,0B ,()0,3C −,代入214y x bx c =++得,2133043b c c ⎧⨯++=⎪⎨⎪=−⎩,解得:143b c ⎧=⎪⎨⎪=−⎩,∴抛物线解析式为:211344y x x =+−; (2)∵211344y x x =+−与x 轴交于点A ,B ,当0y =时,2113044x x +−=,解得:124,3x x =−=, ∴()4,0A −, ∵()0,3C −, 设直线AC 的解析式为3y kx =−,∴430k −−=, 解得:34k =−,∴直线AC 的解析式为334y x =−−,如图所示,过点P 作PE x ⊥轴于点E ,交AC 于点Q ,设211,344P t t t ⎛⎫+− ⎪⎝⎭,则3,34Q t t ⎛⎫−− ⎪⎝⎭, ∴223111334444PQ t t t t t ⎛⎫=−−−+−=−− ⎪⎝⎭,∵AQE PQD ∠=∠,90AEQ QDP ∠=∠=︒,∴OAC QPD ∠=∠,∵4,3OA OC ==,∴5AC =, ∴4cos cos =5PD AO QPD OAC PQ AC ∠==∠=, ∴()222441141425545555PD PQ t t t t t ⎛⎫==−−=−−=−++ ⎪⎝⎭, ∴当2t =−时,PD 取得最大值为45,()()2211115322344442t t +−=⨯−+⨯−−=−, ∴52,2P ⎛⎫−− ⎪⎝⎭; (3)∵抛物线211344y x x =+−211494216x ⎛⎫=+− ⎪⎝⎭, 将该抛物线向右平移5个单位,得到219494216y x ⎛⎫=−− ⎪⎝⎭,对称轴为直线92x =, 点52,2P ⎛⎫−− ⎪⎝⎭向右平移5个单位得到53,2E ⎛⎫− ⎪⎝⎭, ∵平移后的抛物线与y 轴交于点F ,令0x =,则2194924216y ⎛⎫=⨯−= ⎪⎝⎭, ∴()0,2F , ∴22251173224EF ⎛⎫=++= ⎪⎝⎭, ∵Q 为平移后的抛物线的对称轴上任意一点,则Q 点的横坐标为92, 设9,2Q m ⎛⎫ ⎪⎝⎭,∴22295322QE m ⎛⎫⎛⎫=−++ ⎪ ⎪⎝⎭⎝⎭,()222922QF m ⎛⎫=+− ⎪⎝⎭, 当QF EF =时,()229117224m ⎛⎫+−= ⎪⎝⎭, 解得:1m =−或5m =,当QE QF =时,()222295932222m m ⎛⎫⎛⎫⎛⎫−++=+− ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 解得:74m =, 综上所述,Q 点的坐标为9,12⎛⎫− ⎪⎝⎭或9,52⎛⎫ ⎪⎝⎭或97,24⎛⎫ ⎪⎝⎭. 【点睛】本题考查了二次函数综合问题,解直角三角形,待定系数法求解析式,二次函数的平移,线段周长问题,特殊三角形问题,熟练掌握二次函数的性质是解题的关键.3.(2024·山西阳泉·一模)综合与探究 如图,二次函数213442y x x =−−的图象与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,对称轴与x 轴交于点D ,连接AC ,作直线BC .(1)求A ,B ,C 三点的坐标,并直接写出直线BC 的表达式;(2)如图1,若点P 是第四象限内二次函数图象上的一个动点,其横坐标为m ,过点P 分别作x 轴、y 轴的垂线,交直线BC 于点M ,N ,试探究线段MN 长的最大值;(3)如图2,若点Q 是二次函数图象上的一个动点,直线BQ 与y 轴交于点H ,连接CD ,在点Q 运动的过程中,是否存在点H ,使以H ,C ,B 为顶点的三角形与ACD 相似?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.【答案】(1)()20A −,,()80B ,,()04C −,,直线BC 的表达式为1y x 42=−;(2)线段MN长的最大值为(3)点Q 的坐标为3954⎛⎫− ⎪⎝⎭,或()46−,.【分析】(1)令0y =,求得x 的值,令0x =,求得y 的值,可求得A ,B ,C 三点的坐标,利用待定系数法即可求得直线BC 的表达式;(2)设213442P m m m ⎛⎫−− ⎪⎝⎭,,则142M m m ⎛⎫− ⎪⎝⎭,,证明PNM OBC ∠=∠,利用正切函数的定义推出2PN PM =,求得MN ,得到MN 关于m 的二次函数,利用二次函数的性质求解即可;(3)利用勾股定理求得AC =,5AD OC ==,作DG AC ⊥于点G ,用正切函数的定义推出OCA BCH ∠=∠,分BC BH =和BH CH =两种情况讨论,分别求得点H 的坐标,求得直线BH 的表达式,与二次函数的表达式联立求解即可.【详解】(1)解:令0y =,则2134042x x −−=,解得12x =−,28x =,令0x =,则4y =−,∴()20A −,,()80B ,,()04C −,,设直线BC 的表达式为4y kx =−,代入()80B ,得084k =−,解得12k =, ∴直线BC 的表达式为1y x 42=−; (2)解:∵()20A −,,()80B ,,()04C −,,∴2OA =,8OB =,4OC =, 设213442P m m m ⎛⎫−− ⎪⎝⎭,,则142M m m ⎛⎫− ⎪⎝⎭,,2211314422424PM m m m m m ⎛⎫=−−−−=−+ ⎪⎝⎭,∵PN OB ∥,PM OC ∥,∴PNM OBC ∠=∠, ∴41tan tan 82OC PNM OBC OB ∠=∠===,∴2PN PM =,MN ,∴)221244MN m m m ⎫=−+=−+⎪⎭∵0<,∴当4m =时,线段MN 长的最大值为 (3)解:∵()20A −,,()80B ,,()04C −,, ∴对称轴为直线2832x −+==, ∴()30D ,,∴()325AD =−−=,5CD ==,AC == ∴5AD DC ==,作DG AC ⊥于点G ,∴12AG CG AC ===∴DG == ∴tan 2DG DCA CG ∠==, ∵tan 2OB BCO OC ∠==,∴DCA BCH ∠=∠,以H ,C ,B 为顶点的三角形与ACD 相似,则分BC BH =和BH CH =两种情况讨论,①当BC BH =时,∵BO CH ⊥,∴OH OC =,∴()04H ,,同理求得直线BH 的表达式为142y x =−+, 联立得241234412x x x −−−+=,解得14x =−,28x =(舍去),()14462y =−⨯−+=,∴点Q 的坐标为()46−,;①当BH CH =时,设()0H t ,,则2264BH t =+,()2224816CH t t t =+=++,∴2264816t t t +=++,解得6t =,∴()06H ,,同理求得直线BH 的表达式为364y x =−+, 联立得261434432x x x −−−+=,解得15x =−,28x =(舍去),()3395644y =−⨯−+=,∴点Q 的坐标为3954⎛⎫− ⎪⎝⎭,; 综上,点Q 的坐标为3954⎛⎫− ⎪⎝⎭,或()46−,.【点睛】本题是二次函数的综合题,考查了待定系数法求一次函数的解析式,点的坐标表示三角形的面积,勾股定理,正切函数,解方程,熟练掌握待定系数法,勾股定理,正切函数是解题的关键.题型二 将军饮马河求二次函数中线段和最值问题【例1】(2024·天津津南·一模)综合与探究:如图,抛物线2y x bx c =−++上的点A ,C 坐标分别为()0,2,()4,0,抛物线与x 轴负半轴交于点B ,且2OM =,连接AC ,CM .(1)求点M 的坐标及抛物线的解析式;(2)点P 是抛物线位于第一象限图象上的动点,连接AP ,CP ,当PAC ACM S S =△△时,求点P 的坐标;(3)将抛物线沿x 轴的负方向平移得到新抛物线,点A 的对应点为点A ',点C 的对应点为点C ',当MA MC ''+的值最小时,新抛物线的顶点坐标为 ,MA MC ''+的最小值为 .【答案】(1)()0,2M −,2722y x x =−++ (2)()2,5P(3)1181,1216⎛⎫− ⎪⎝⎭,【分析】(1)根据点M 在y 轴负半轴且2OM =可得点M 的坐标为()0,2M −,利用待定系数法可得抛物线的解析式为2722y x x =−++;(2)过点P 作PF x ⊥轴于点F ,交线段AC 于点E ,用待定系数法求得直线AC 的解析式为122y x =−+,设点P 的横坐标为()04p p <<,则27,22P p p p ⎛⎫−++ ⎪⎝⎭,1,22E p p ⎛⎫−+ ⎪⎝⎭,故24(04)PE p p p =−+<<,先求得8ACM S =△,从而得到212882PAC S PE OC p p =⋅=−+=△,解出p 的值,从而得出点P 的坐标;(3)设抛物线沿x 轴的负方向平移m 个单位长度得到新抛物线,将点M 右平移m 个单位长度得到点M ',由平移的性质可知,,MA M A MC M C ''''==,MA MC ''+的值最小就是M A M C ''+最小值,作出点C 关于直线=2y −对称的对称点C '',连接AC ''交直线=2y −于点M ',连接M C '则此时M A M C ''+取得最小值,即为AC ''的长度,利用两点间的距离公式求这个长度,用待定系数法求出直线AC ''的解析式,从而确定M '的坐标,继而确定平移距离,将原抛物线的解析式化为顶点式,从而得到其顶点,继而确定新抛物线的顶点.【详解】(1)解:∵点M 在y 轴负半轴且2OM =,∴()0,2M −将()0,2A ,()4,0C 代入2y x bx c =−++,得:21640c b c =⎧⎨−++=⎩,解得722b c ⎧=⎪⎨⎪=⎩∴抛物线的解析式为2722y x x =−++(2)解:过点P 作PF x ⊥轴于点F ,交线段AC 于点E ,设直线AC 的解析式为()0y kx m k =+≠,将()0,2A ,()4,0C 代入y kx m =+,得:240m k m =⎧⎨+=⎩,解得122k m ⎧=−⎪⎨⎪=⎩,∴直线AC 的解析式为122y x =−+ 设点P 的横坐标为()04p p << 则27,22P p p p ⎛⎫−++ ⎪⎝⎭,1,22E p p ⎛⎫−+ ⎪⎝⎭, ∴2271224(04)22PE p p p p p p ⎛⎫=−++−−+=−+<< ⎪⎝⎭∵8ACM S =△,∴212882PAC S PE OC p p =⋅=−+=△,解得122p p ==, ∴()2,5P ;(3)1181,1216⎛⎫− ⎪⎝⎭,补充求解过程如下:设抛物线沿x 轴的负方向平移m 个单位长度得到新抛物线,将点M 向右平移m 个单位长度得到点M ',作出图形如下:由平移的性质可知,,MA M A MC M C ''''==,∴MA MC ''+的值最小就是M A M C ''+最小值, 显然点M '在直线=2y −上运用,作出点C 关于直线=2y −对称的对称点C '',连接AC ''交直线=2y −于点M ',连接M C '则此时M A M C ''+取得最小值,即为AC ''的长度,∵点C 关于直线=2y −C '',()4,0C ∴()4,4C ''−,∴()()min min MA MC M A M C AC ''''''+=+== 设直线AC ''的解析式是:11y k x b =+将点()0,2A ,()4,4C ''−代入得:111244b k b =⎧⎨+=−⎩,解得:11322k b ⎧=−⎪⎨⎪=⎩直线AC ''的解析式是:322y x =−+令3222y x =−+=−,解得:83x =, ∴8,23M ⎛⎫'− ⎪⎝⎭,∴平移的距离是83m = 又∵22778122416y x x x ⎛⎫=−++=−−+ ⎪⎝⎭, ∴平移前的抛物线的坐标是781416,⎛⎫ ⎪⎝⎭∴新抛物线的顶点坐标为7881,4316⎛⎫− ⎪⎝⎭即1181,1216⎛⎫− ⎪⎝⎭ 故答案是:1181,1216⎛⎫− ⎪⎝⎭,【例2】(2024·江苏宿迁·模拟预测)如图1,抛物线2y x bx =−+与x 轴交于点A ,与直线y x =−交于点()4,4B −,点()0,4C −在y 轴上.点P 从点B 出发,沿线段BO 方向匀速运动,运动到点O 时停止.(1)求抛物线2y x bx =−+的表达式;(2)当BP =1中过点P 作PD OA ⊥交抛物线于点D ,连接PC OD ,,判断四边形OCPD 的形状,并说明理由;(3)如图2,点P 从点B 开始运动时,点Q 从点O 同时出发,以与点P 相同的速度沿x 轴正方向匀速运动,点P 停止运动时点Q 也停止运动.连接BQ PC ,,求CP BQ +的最小值.【答案】(1)抛物线的表达式为23y x x =−+ (2)平行四边形,见解析(3)【分析】(1)利用待定系数法将B 点坐标代入抛物线2y x bx =−+中,即可求解.(2)作辅助线,根据题意,求出PD 的长,PD OC =,PD OC ∥,利用一组对边平行且相等的四边形是平行四边形即可得证.(3)作出图,证明()SAS CBP MOQ ≌,CP BQ +的最小值为MB ,根据勾股定理求出MB 即可解答. 【详解】(1)解: 抛物线2y x bx =−+过点(4,4)B −,1644b ∴−+=−,3b ∴=,23y x x ∴=−+.即抛物线的表达式为23y x x =−+. (2)解:四边形OCPD 是平行四边形,理由如下:如图1,作PD OA ⊥交x 轴于点H ,连接PC 、OD ,点P 在y x =−上,OH PH ∴=,45POH ∠=︒,连接BC ,4OC BC ==,OB ∴= 2BP =OP OB BP ∴=−=2OH PH ∴===,当2D x =时,4322D DH y ==−+⨯=,224PD DH PH ∴=+=+=, (0,4)C −,4OC ∴=,PD OC ∴=,OC x ⊥Q 轴,PD x ⊥轴,PD OC ∴∥,∴四边形OCPD 是平行四边形.(3)如图2,由题意得,BP OQ =,连接BC ,在OA 上方作OMQ ,使得45MOQ ∠=︒,OM BC =,4OC BC ==,BC OC ⊥,45CBP ∴∠=︒,CBP MOQ ∴∠=∠,BP OQ =,CBP MOQ ∠=∠,BC OM ,(SAS)CBP MOQ ∴△≌△,CP MQ ∴=,CP BQ MQ BQ MB ∴+=+≥(当M ,Q ,B 三点共线时最短),CP BQ ∴+的最小值为MB ,454590MOB MOQ BOQ ∠=∠+∠=︒+︒=︒,MB ∴即CP BQ +的最小值为答:CP BQ +的最小值为【点睛】本题主要考查待定系数法,二次函数图象与性质,平等四边形的判定,全等三角形的判定与性质以及勾股定理等知识,正确作出辅助线是解答醒的关键.1.(2024·宁夏银川·一模)如图,已经抛物线经过点()00O ,,()55A ,,且它的对称轴为2x =.(1)求此抛物线的解析式;(2)若点B 是抛物线对称轴上的一点,且点B 在第一象限,当OAB 的面积为15时;求点B 的坐标.(3)在(2)的条件下,P 是抛物线上的动点,求P 的坐标以及PA PB −的最大值.【答案】(1)24.y x x =- (2)()2,8B (3)()2,12,P - PA PB −的最大值为【分析】(1)根据题意可设抛物线为2,y ax bx =+再利用待定系数法求解抛物线的解析式即可; (2)设()2,,B y 且0,y > 记OA 与对称轴的交点为Q ,设直线OA 为:,y kx = 解得:1,k = 可得直线OA 为:,y x = 则()2,2,Q 利用()12OAB BOQ ABQ A O S S S BQ x x =+=⨯⨯−列方程,再解方程即可;(3)如图,连接AB ,延长AB 交抛物线于P ,则此时PA PB AB −=最大,由勾股定理可得最小值,再利用待定系数法求解AB 的解析式,联立一次函数与二次函数的解析式,解方程组可得P 的坐标.【详解】(1)解: 抛物线经过点(0,0)O ,∴设抛物线为:2,y ax bx =+抛物线过(5,5)A ,且它的对称轴为2x =.2555,22a b b a +=⎧⎪∴⎨−=⎪⎩ 解得:1,4a b =⎧⎨=−⎩∴抛物线为:24.y x x =-(2)解:如图,点B 是抛物线对称轴上的一点,且点B 在第一象限,设()2,,B y 且0,y > 记OA 与对称轴的交点为Q ,设直线OA 为:,y kx =55,k \= 解得:1,k =∴ 直线OA 为:,y x =()2,2,Q ∴ ()12OAB BOQ ABQ A O SS S BQ x x ∴=+=⨯⨯− 12515,2y =−⨯=解得:8y =或4,y =−∵0,y > 则8,y =()2,8.B ∴(3)如图,连接AB ,延长AB 交抛物线于P ,则此时PA PB AB −=最大,()()5,5,2,8,A BAB ∴=设AB 为:,y k x b ''=+ 代入A 、B 两点坐标,55,28k b k b '''+=⎧∴⎨+=⎩' ,解得:1,10k b =−⎧⎨='⎩'∴AB 为:10,y x =-+210,4y x y x x =−+⎧∴⎨=−⎩ 解得:52,,512x x y y ==−⎧⎧⎨⎨==⎩⎩()2,12.P ∴−【点睛】本题考查的是利用待定系数法求解二次函数的解析式,坐标与图形面积,三角形三边关系的应用,勾股定理的应用,确定PA PB −最大时P 的位置是解本题的关键.2.(2024·湖南怀化·一模)如图1,在平面直角坐标系中,抛物线2y x bx c =−++与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,5OB OC ==,顶点为D ,对称轴交x 轴于点E .图1 图2 图3(1)求抛物线的解析式、对称轴及顶点D 的坐标;(2)如图2,点Q 为抛物线对称轴上一动点,当Q 在什么位置时QA QC +最小,求出Q 点的坐标,并求出此时QAC △的周长;(3)如图3,在对称轴左侧的抛物线上有一点M ,在对称轴右侧的抛物线上有一点N ,满足90MDN ∠=︒.求证:直线MN 恒过定点,并求出定点坐标.【答案】(1)245y x x =−++,对称轴为直线2x =,顶点D 的坐标为()29,;(2)QAC △(3)直线MN 恒过定点,定点坐标为()28,.【分析】(1)求得点B 的坐标为()50,,点C 的坐标为()05,,利用待定系数法求解,再配成顶点式,即可得解;(2)先求得直线BC 的解析式,再求直线BC 与对称轴交点Q ,将AQ CQ +转化为BC ,在Rt AOC 中求AC ,在Rt BOC 中求BC 即可求解;(3)如图,过点D 作直线l 垂直y 轴,再过点M ,N 分别作直线l 的垂线,设点M 的坐标为()245m m m −++,,点N 的坐标为()245n n n −++,,证明MDH DNG ∽△△,求得()250mn m n −++=,再利用待定系数法求得直线MN 的解析式为()45y m n x mn =−−+++,据此求解即可. 【详解】(1)解:∵5OB OC ==,∴点B 的坐标为()50,,点C 的坐标为()05,,∴25505b c c −++=⎧⎨=⎩,解得4b =,∴抛物线的解析式为245y x x =−++, ∵()224529y x x x =−++=−−+,∴对称轴为直线2x =,顶点D 的坐标为()29,; (2)解:∵点A 与点()50B ,关于直线2x =对称,∴直线BC 与对称轴的交点为Q ,则Q 为QA QC +最小时位置,设直线BC 的解析式为5y kx =+,代入点()50B ,得055k =+,解得1k =−,∴直线BC 的解析式为5y x =−+,当2x =,253y =−+=,∴()23Q ,,∵点()10A −,,∵ACAQ CQ CB +===∴QAC △(3)解:如图,过点D 作直线l 垂直y 轴,再过点M ,N 分别作直线l 的垂线,垂足分别为H ,G ,设点M 的坐标为()245m m m −++,,点N 的坐标为()245n n n −++,,∵顶点D 的坐标为()29,, ∴()()222945442MH m m m m m =−−++=−+=−,2DH m =−,()()222945442GN n n n n n =−−++=−+=−,2DG n =−,由题意得90H G MDN ∠=∠=∠=︒,∴90MDH NDG DNG ∠=︒−∠=∠, ∴MDH DNG ∽△△, ∴MH HD DG NG =,即()()222222m mn n −−=−−,∴()()221m n −−=−, ∴()250mn m n −++=,∵点M 的坐标为()245m m m −++,,点N 的坐标为()245n n n −++,,设直线MN 的解析式为11y k x b =+,∴2112114545mk b m m nk b n n ⎧+=−++⎨+=−++⎩①②,−①②得()()()2214m n k m n m n −=−−+−, ∵m n ≠,∴14k m n =−−+,将14k m n =−−+代入①得()21445m m n b m m −−++=−++,求得15b mn =+;∴直线MN 的解析式为()45y m n x mn =−−+++, ∵()250mn m n −++=,即()25m n mn +=+, ∴()()428y m n x =−−+−+, ∴当20x −=即2x =时,8y =,∴无论m n 、为何值,直线MN 总会经过定点()28,, ∴直线MN 恒过定点,定点坐标为()28,.【点睛】本题考查了二次函数的综合运用.考查了待定系数法求函数解析式,相似三角形的判定和性质,熟练掌握二次函数的图象与性质、轴对称的性质,添加适当的辅助线,是解题的关键.3.(2024·安徽池州·二模)如图,抛物线2Ly ax bx c =++∶与x 正半轴交于点(3,0)A ,与y 轴交于点(0,3)B ,对称轴为直线1x =.(1)求直线AB 的解析式及抛物线的解析式;(2)如图①,点P 为第一象限抛物线上一动点,过点P 作PC x ⊥轴,垂足为C ,PC 交AB 于点D ,求当点P 的横坐标为多少时,PD AD +最大;(3)如图②,将抛物线2Ly ax bx c =++∶向左平移得到抛物线L ',直线AB 与抛物线L '交于M 、N 两点,若点B 是线段MN 的中点,求抛物线'L 的解析式.【答案】(1)3y x =−+,223y x x =−++;(2)点P 的横坐标为时,PD AD +有最大值; (3)2154y x x =−−+.【分析】(1)利用待定系数法解答即可求解;(2)设点P 的横坐标为t ,则()2,23P t t t −++,(,0)C t ,(,3)D t t −+,先证明ACD 为等腰直角三角形,得到)AD t =−,进而得到2PD AD t ⎛+=−+ ⎝⎭,根据二次函数的性质即可求解;(3)设平移后抛物线L '的解析式2()4y x m =−−+,联立函数解析式得23()4x x m −+=−−+,整理得,22(21)10x m x m −++−=,设()11,M x y ,()22,N x y ,则1x ,2x 是方程22(21)10x m x m −++−=的两根,由B 为MN 的中点可得210m +=,求出m 即可求解;本题考查了二次函数与一次函数的交点问题,待定系数法求函数解析式,二次函数的性质,二次函数图象的平移,掌握二次函数的图象和性质是解题的关键.【详解】(1)解:抛物线2L y ax bx c =++∶与x 正半轴交于点(3,0)A ,与y 轴交于点(0,3)B ,对称轴为直线1x =,930312a b c c b a ⎧⎪++=⎪∴=⎨⎪⎪−=⎩,解得123a b c =−⎧⎪=⎨⎪=⎩,∴抛物线L 的解析式为223y x x =−++;设直线AB 的解析式为3(0)y kx k =+≠,把(3,0)A 代入得,330k +=,解得1k =−,∴直线AB 的解析式为3y x =−+;(2)解:设点P 的横坐标为t ,则()2,23P t t t −++,(,0)C t ,(,3)D t t −+, 3AC t ∴=−,23PD t t =−+,(3,0)A ,(0,3)B −,3OA OB ∴==,AOB ∴为等腰直角三角形,45OAB ∴∠=︒,PC x ⊥轴, ACD ∴为等腰直角三角形,)AD t ∴==−,∴223PD AD t t t ⎛+=−++=− ⎝⎭,∴当t =时,PD AD +有最大值,即点P的横坐标为32时,PD AD +有最大值;(3)解:由(1)可知,直线AB 的解析式为3y x =−+,抛物线L 为:2223(1)4y x x x =−++=−−+,∴设平移后抛物线L '的解析式2()4y x m =−−+,联立函数解析式得,()234y x y x m =−+⎧⎪⎨=−−+⎪⎩,23()4x x m ∴−+=−−+,整理得,22(21)10x m x m −++−=, 设()11,M x y ,()22,N x y ,则1x ,2x 是方程22(21)10x m x m −++−=的两根,1221x x m ∴+=+,∵B 为MN 的中点,∴120x x +=,∴210m +=, 解得12m =−,∴抛物线L '的解析式22115424y x x x ⎛⎫=−++=−−+ ⎪⎝⎭.题型三 胡不归求二次函数中线段和最值问题【例1】(新考法,拓视野)(2024·陕西西安·三模)已知抛物线2(,,y ax bx c a b c =++为常数,0)a ≠与x 轴交于点()A −、点B 两点,与y 轴交于点()0,2C,对称轴为x =(1)求抛物线的表达式;(2)M 是抛物线上的点且在第二象限,过M 作MN AC ⊥于点N,求AN 的最大值.【答案】(1)22y x =−+(2)496【分析】(1)用待定系数法求解即可;(2)过点M 作MF y ∥轴,交AC 于点E ,先求出一次函数AC 的解析式,用解直角三角形的方法求出30OAC ∠=︒,表示出MN =,设2,2M m m ⎛⎫−+ ⎪⎝⎭,2E m ⎛⎫+ ⎪ ⎪⎝⎭,分别表示出EF ME AE MN ,,,,最后得到249=26AN m ⎛−+ ⎝⎭,求出最后结果即可.【详解】(1)解:点()A −,对称轴为x =(2a c ∴−−+=,2c =,2b a −=解得:1a =−,b = ∴抛物线的表达式为:22y x =−+;(2)如图,过点M 作MF y ∥轴,交AC 于点E ,设AC 的解析式为y kx b =+,02b b ⎧−+=⎪∴⎨=⎪⎩,2k b ⎧=⎪⎨⎪=⎩,∴AC的解析式为2y =+,2AO =2CO =,tan CO OAC AO ∴∠==,30OAC ∴∠=︒,90AFE MNE ∠=︒=∠,AEF MEN ∠=∠, 30M OAC ∴∠=∠=︒,2AE EF ∴=,12EN ME =,sin MN ME ACO ∴=⋅∠=,设2,2M m m ⎛⎫−+ ⎪⎝⎭,2E m ⎛⎫+ ⎪ ⎪⎝⎭,2EF ∴=+,2222ME m m ∴=−+−=−−,24AE EF ∴==+,21122EN ME m ==−,23MN m==−,AN ∴,AE EN=+2213422m m =+−−−224m =−+24926m ⎛=−++ ⎝⎭,20−<,∴当m =时,AN 的最大值为496.【例2】(2024·浙江·一模)如图,在平面直角坐标系中,抛物线24y ax bx =++交y 轴于点A ,交x 轴于点()6,0B −和点()2,0C ,连接AB 、AQ 、BQ ,BQ 与y 轴交于点N .(1)求抛物线表达式;(2)点713Q ⎛⎫⎪⎝⎭,,点M 在x 轴上,点E 在平面内,BME AOM ≌,且四边形ANEM 是平行四边形.①求点E 的坐标;②设射线AM 与BN 相交于点P ,交BE 于点H ,将BPH 绕点B 旋转一周,旋转后的三角形记为11BPH △,求11BP 的最小值. 【答案】(1)214433y x x =−−+(2)①()2,2E −−;②【分析】(1)将点B 、C 的坐标代入抛物线,利用待定系数法求得解析式;(2)①由Q 坐标求出BQ 解析式,然后根据四边形ANEM 是平行四边形和BME AOM ≌得出4BM OA ==,再分类讨论求得M 和E 的坐标;②求出AM 解析式,交点为P ,再求出H 坐标,然后由两点间距离公式求出BP 和BH 长度,因为旋转不改变长度,所以1BP长度不变,当H 旋转到x 轴上时,此时1OH 最短,所以此时1OH 等于BO BH −,然后代入计算即可.【详解】(1)解:①抛物线24y ax bx =++交y 轴于点A ,交x 轴于点()6,0B −和点()2,0C , ∴366404240a b a b −+=⎧⎨++=⎩,解得:1343a b ⎧=−⎪⎪⎨⎪=−⎪⎩ ∴214433y x x =−−+;(2)解:214433y x x =−−+4∴=OA ,设直线BQ 的解析式为1y kx b =+, ()6,0B −,713Q ⎛⎫ ⎪⎝⎭,∴117360k b k b ⎧+=⎪⎨⎪−+=⎩,解得1132k b ⎧=⎪⎨⎪=⎩,∴直线BQ 的解析式为123=+y x ,N Q 为BQ 与y 轴交点, ()0,2N ∴,2AN ∴=,四边形ANEM 是平行四边形,∴AN EM ∥且2EM AN ==,且点E 在点M 下方, 点M 在x 轴上,点E 在平面内,BME AOM ≌,4BM OA ∴==, ()6,0B −, ()2,0M ∴−或()10,0−,若M 为()2,0−,90BME AOM ∠=∠=︒,故()2,2E −−, 若M 为()10,0−,2OM ME ==,此时10OM =,(矛盾,舍去),综上,点E 的坐标为()2,2−−;②如图,设AM 的解析式为,y kx b =+抛物线24y ax bx =++交y 轴于点A ,∴点A 的坐标为(0,4),将点()0,4A 、()2,0M −的坐标代入y kx b =+得:420b k b =⎧⎨−+=⎩,解得24k b =⎧⎨=⎩,AM ∴的解析式为24y x =+,AM 与BQ 相交于点P ,∴24123y x y x =+⎧⎪⎨=+⎪⎩,解得6585x y ⎧=−⎪⎪⎨⎪=⎪⎩, 所以点P 的坐标为68,55⎛⎫− ⎪⎝⎭,设直线BE 的解析式为y mx n =+,将点B 、E 的坐标代入直线BE 的解析式得:2260m n m n −+=−⎧⎨−+=⎩,解得123m n ⎧=−⎪⎨⎪=−⎩, 所以直线BE 的解析式为132y x =−−,BE 与AM 相交于点H ,∴24132y x y x =+⎧⎪⎨=−−⎪⎩,解得14585x y ⎧=−⎪⎪⎨⎪=−⎪⎩, ∴点H 的坐标为148,55⎛⎫−− ⎪⎝⎭,BP ∴==BH ==1BP ∴当H 旋转到x 轴上时,此时1OH 最短,∴16OH BO BH =−=116BP ∴==⎭∴11BP的最小值为1.(2024·河南洛阳·一模)在平面直角坐标系中,抛物线212y x bx c =−++交x 轴于()4,0A 、B 两点,交y 轴于点()0,4C .(1)求抛物线表达式中的b 、c ;(2)点P 是直数AC 上方抛物线上的一动点,过点F 作PF y 轴交AC 于点E ,作PE AC ∥交x 轴于点F ,求PE 的最大值及此时点P 的坐标; (3)将该抛物线沿射线CA方向平移1y ,请直接写出新抛物线1y 的表达式______.【答案】(1)1b =,4c =(2)PE 取得最大值为254,此时335,28P ⎛⎫ ⎪⎝⎭.(3)()2115322y x =−−+【分析】本题考查了二次函数的综合,待定系数法求函数解析式: (1)利用待定系数法即可求解;(2)延长PE 交x 轴于H ,根据题意求得直线AC 的解析式为4y x =−+,OC OA =,设点()21,4042P p p p p ⎛⎫−++<< ⎪⎝⎭,则(),4E p p −+,(),0H p ,证得PHF是等腰直角三角形,从而求得232524PE PE PH p ⎛⎫=+=−−+⎪⎝⎭,即可求解; (3)先求得CA =,根据1y 由抛物线()2211941222y x x x =−++=−−+,向右和向下分别平移2个单位长度得到,进而可求解;掌握待定系数法求函数解析式及利用数学结合是解题的关键.【详解】(1)解:抛物线212y x bx c =−++交于()4,0A 和()0,4C ,8404b c c −++=⎧∴⎨=⎩,解得:14b c =⎧⎨=⎩. (2)延长PE 交x 轴于H()4,0A ,()0,4C ,∴直线AC 的解析式为4y x =−+,OC OA =, PE y ∥Q 轴,PE x ∴⊥轴, 90AOC ∴∠=︒,45OAC ∴∠=︒,PFAC ,45OFP ∴∠=︒,2PH PF ∴=,PE PE PH ∴+=+,设点()21,4042P p p p p ⎛⎫−++<< ⎪⎝⎭,则(),4E p p −+,(),0H p , ()221144222PE p p p p p ∴=−++−−+=−+,2142PH p p =−++,222211325243422224PE PF PE PH p p p p p p p ⎛⎫∴+=+=−+−++=−++=−−+⎪⎝⎭,PE ∴+的最大值为254,此时点P 的坐标为325,24⎛⎫ ⎪⎝⎭.(3)()4,0A ,()0,4C ,CA ∴=将抛物线y 沿射线CA 方向平移1y ,∴1y 由抛物线()2211941222y x x x =−++=−−+,向右和向下分别平移2个单位长度得到, ()2115322y x ∴=−−+,故答案为:()2115322y x =−−+.2.(2024·海南海口·一模)如图,抛物线2y ax bx c =++过点()1,0A −,()3,0B ,()0,3C .(1)求抛物线的解析式;(2)设点P 是第一象限内的抛物线上的一个动点, ①当P 为抛物线的顶点时,求证:PBC 直角三角形; ②求出PBC 的最大面积及此时点P 的坐标;③过点P 作PN x ⊥轴,垂足为N ,PN 与BC 交于点E.当PE 的值最大时,求点P 的坐标.【答案】(1)223y x x =−++(2)①PBC 是直角三角形;②315,24P ⎛⎫ ⎪⎝⎭;③57,24P ⎛⎫ ⎪⎝⎭【分析】(1)把A 、B 、C 三点坐标代入2y ax bx c =++求解即可; (2)①作PH y ⊥轴于点H ,易证PCH △和BOC 是等腰直角三角形,即可求出90PCB ∠=︒; ②先求出直线BC 的解析式,过点P 作PD x ⊥轴于点D ,交BC 于点E ,设点()2,23P x x x −++,则(),3E x x −+,故23PE x x =−+,23922PBC S x x ∆=−+,然后根据二次函数的性质求解即可; ③过点P 作PN x ⊥轴于点N ,交BC 于点E ,设点()2,23P x x x −++,则(),3E x x −+,故23PE x x =−+,判断BEN是等腰直角三角形得出BE =,即可求出25PE x x =−+,然后根据二次函数的性质求解即可. 【详解】(1)解:将点()1,0A −,()3,0B ,()0,3C 代入解析式得:09303a b c a b c c −+=⎧⎪++=⎨⎪=⎩,解得:123a b c =−⎧⎪=⎨⎪=⎩,∵抛物线的解析式为223y x x =−++;(2)解:①配方得()222314y x x x =−++−−+∴点P 的坐标为()1,4,作PH y ⊥轴于点H ,则1PH CH ==,∴45HCP ∠=︒又∵在Rt BOC 中,3OB OC ==, ∴45OCB ∠=︒, ∴90PCB ∠=︒∴PCB 是直角三角形②设直线BC 的解析式为y kx b =+,将点B 、C 代入得:303k b b +=⎧⎨=⎩,解得:13k b =−⎧⎨=⎩, ∴直线BC 的解析式为3y x =−+, ∵()3,0B ,∴3OB =, 设点()2,23P x x x −++(03x <<),过点P 作PD x ⊥轴于点D ,交BC 于点E ,如图所示:∴(),3E x x −+,∴()222333PE x x x x x=−++−−+=−+,∴()22211393327332222228PBCSPE OB x x x x x ⎛⎫=⨯⨯=⨯−+⨯=−+=−−+ ⎪⎝⎭,当32x =时,PBC 的最大面积为278,2915233344x x −++=−++=,∴315,24P ⎛⎫⎪⎝⎭③设点()2,23P x x x −++(03x <<),过点P 作PN x ⊥轴于点N ,交BC 于点E ,如图所示:∴(),3E x x −+,∴()222333PE x x x x x =−++−−+=−+, ∵()0,3C ,()3,0B ,∴3OC OB ==,3BN x =−,∴45OBC OCB ∠=∠=︒,∴45NEB OBC ∠=∠=︒,∴BE ==,∴()CE BC BE =−==,∴22525524PE x x x ⎛⎫=−+=−−+ ⎪⎝⎭, ∴当52x =时,PE 有最大值,此时57,24P ⎛⎫ ⎪⎝⎭. 【点睛】本题考查了二次函数综合问题,面积问题,线段问题,掌握二次函数的性质是解题的关键.3.(2023·山东济南·一模)抛物线()21122y x a x a =−+−+与x 轴交于(),0A b ,()4,0B 两点,与y 轴交于点()0,C c ,点P 是抛物线在第一象限内的一个动点,且在对称轴右侧.(1)求a ,b ,c 的值;(2)如图1,连接BC 、AP ,交点为M ,连接PB ,若14PMB AMB S S =V V ,求点P 的坐标; (3)如图2,在(2)的条件下,过点P 作x 轴的垂线交x 轴于点E ,将线段OE 绕点O 逆时针旋转得到OE ',旋转角为9(0)0αα︒<<︒,连接E B ',E C ',求34E B E C ''+的最小值. 【答案】(1)2a =,2b =−,4c = (2)53,2P ⎛⎫ ⎪⎝⎭(3)【分析】(1)利用待定系数法求解即可;(2)过点P 作PD x ⊥轴,交BC 于点D ,过点A 作y 轴的平行线交BC 的延长线于H ,求得BC l 的解析式,设21,42P m m m ⎛⎫−++ ⎪⎝⎭,则(),4D m m −+,利用相似三角形的判定与性质可得答案; (3)在y 轴上取一点F ,使得94OF =,连接BF ,由相似三角形的判定与性质可得34FE CE ''=,可得34E B E C BE E F '''+'+=,即可解答.【详解】(1)解:将()4,0B 代入()21122y x a x a =−+−+,得()84120a a −+−+=,2a ∴=,∴抛物线的解析式为2142y x x =−++,令0x =,则4y =,4c ∴=,令0y =,则21042x x =−++,14x ∴=,22x =−,()2,0A ∴−,即2b =−; ∴2a =,2b =−,4c =(2)过点P 作PD x ⊥轴,交BC 于点D ,过点A 作y 轴的平行线交BC 的延长线于H ,设BC l :y kx b =+,将()0,4,()4,0代入得440b k b =⎧⎨+=⎩解得:4b =,1k =−,BC l ∴:4y x =−+, 设21,42P m m m ⎛⎫−++ ⎪⎝⎭,则(),4D m m −+, ()221144222P D PD y y m m m m m =−=−++−−+=−+,PD HA ∥,AMH PMD ∴∽,PM PD MA HA ∴=,将2x =−代入4y x =−+,6HA ∴=,112142PMB AMBPM h S PM S AM AM h ⋅===⋅, 164PD PD HA ∴==,32PD ∴=, 231222m m ∴=−+,11(m ∴=舍),23m =,53,2P ⎛⎫∴ ⎪⎝⎭;(3)在y 轴上取一点F ,使得94OF =,连接BF ,根据旋转得性质得出:3OE OE '==,∵9494OF OC ⋅=⨯=, 2OE OFOC '∴=⋅,∴OE OC OF OE '=',COE FOE ''∠=∠,∴FOE E OC ''∽,。
2024年全国各地中考数学最值问题

例2024年全国各地中考数学最值问题1如图1,在平面直角坐标系中,已知A (3, 0),B (0, 2),过点B 作y 轴的垂线l ,P 为直线l 上一动点,连接PO 、P A ,则PO +P A 的最小值为__________一、两条线段和的最小值2024年成都市中考第13题.如图,在平行四边形ABCD中,AB=4,AD=5,∠ABC=30°,点M为直线BC上一动点,则MA+MD的最小值为__________。
如图1,抛物线21462y x x =-+与y 轴交于点A ,与x 轴左侧的一个交点为B ,线段CD 在抛物线的对称轴上移动(点C 在点D 的下方),且CD =3。
当AD +BC 的值最小时,点C 的坐标为________。
如图,在平行四边形ABCD中,AB=2,AD=4,E、F分别是边CD、AD上的动点,且CE=DF.当AE+CF的值最小时,则CE=__________.如图,已知A(4, 0),P(2,-3),点M在直线32x 上。
MN⊥y轴于点N,求NA+MP的最小值。
如图1,已知A(4, 0),B,点C为OB的中点,点D为线段OA上一动点(O 点除外),在OC右侧作平行四边形OCFD,联结BD、BF,求BD+BF的最小值。
如图,点K是抛物线y=-x2+2x+3的对称轴与x轴的交点,过点K的直线(不与对称轴重合)与抛物线交于点M、N,过抛物线的顶点G作直线l//x轴,点Q是直线l上一动点,求QM+QN的最小值。
如图,在Rt△ABC中,∠C=90°,点D、E分别在边AC和BC上,连结DE、AE、BD。
若AC+CD=5,BC+CE=8,求AE+BD的最小值。
已知D(1, 0)、M(3, 1)、N(2,-2),点E在线段MN上,点F在线段DN上,ME=NF,求DE+MF的最小值。
二、三条线段和的最小值例10 2024年绥化市中考第20题如图1,已知∠AOB=50°,点P为∠AOB内部一点,点M、N分别为射线OA、OB 上的动点,当△PMN的周长最小时,∠MPN=__________。
专题01 中考数学专题复习最值问题(阿氏圆)练习

中考数学专题复习最值问题(阿氏圆)练习1.如图,在Rt△ABC中,∠ACB=90°,CB=7,AC=9,以C为圆心、3为半径作⊙C,P为⊙C上一动点,连接AP、BP,则13AP+BP的最小值为()A.7B.C.4D.【答案】B【解析】思路引领:如图,在CA上截取CM,使得CM=1,连接PM,PC,BM.利用相似三角形的性质证明MP13=PA,可得13AP+BP=PM+PB≥BM,利用勾股定理求出BM即可解决问题.答案解析:如图,在CA上截取CM,使得CM=1,连接PM,PC,BM.∵PC=3,CM=1,CA=9,∴PC2=CM•CA,∴PC CM CA CP=,∵∠PCM=∠ACP,∴△PCM∽△ACP,∴13 PM PCPA AC==,∴PM13=PA,∴13AP+BP=PM+PB,∵PM+PB≥BM,在Rt△BCM中,∵∠BCM=90°,CM=1,BC=7,∴BM==∴13AP +BP ,∴13AP +BP 的最小值为.故选:B .2.如图,边长为4的正方形,内切圆记为⊙O ,P 是⊙O +PB 的最小值为________.【答案】【分析】+PB (PA PB )PB 即可解答.【解析】解:设⊙O 半径为r ,OP =r =12BC =2,OB r =,取OB PI ,∴OI =IB∵OP OI =,OB OP ==,∴OP OBOI OP= ,∠O 是公共角,∴△BOP ,∴PI PB =,∴PI ,∴AP =AP +PI ,∴当A 、P 、I 在一条直线上时,AP 最小,作IE ⊥AB 于E ,∵∠ABO =∴IE =BE =1,∴AE =AB −BE =3,∴AI =∴AP 最小值=AI+PB (PA PB ),+=.故答案是【点睛】本题是“阿氏圆”问题,解决问题的关键是构造相似三角形.3.如图,已知正方ABCD 的边长为6,圆B 的半径为3,点P 是圆B 上的一个动点,则12PD PC -的最大值为_______.【答案】152【分析】如图,连接BP ,在BC 上取一点M ,使得BM =32,进而证明BPM BCP △∽△,则在点P 运动的任意时刻,均有PM =12PC ,从而将问题转化为求PD -PM 的最大值.连接PD ,在△PDM 中,PD -PM <DM ,故当D 、M 、P 共线时,PD -PM =DM 为最大值,勾股定理即可求得DM .【解析】如图,连接BP ,在BC 上取一点M ,使得BM =32,31232BM BP ==Q ,3162BP BC ==BM BPBP BC\=PBM CBP Ð=ÐQ \BPM BCP△∽△12MP BM PC BP \==12MP PC \=12PD PC PD MD\-=-在△PDM 中,PD -PM <DM ,当D 、M 、P 共线时,PD -PM =DM 为最大值,Q 四边形ABCD 是正方形90C \Ð=°在Rt CDM V 中,152DM ===故答案为:152.【点睛】本题考查了圆的性质,相似三角形的性质与判定,勾股定理,构造12PC 是解题的关键.4.如图,在V 90,2B AB CB Ð=°==,以点B 为圆心作圆B 与AC 相切,点P 为圆B 上任一动点,则PA +的最小值是___________.【分析】作BH ⊥AC 于H ,取BC 的中点D ,连接PD ,如图,根据切线的性质得BH等腰直角三角形的性质得到BH 12=AC =接着证明△BPD ∽△BCP 得到PD =,所以PAPC =PA +PD ,而PA +PD ≥AD (当且仅当A 、P 、D 共线时取等号),从而计算出AD 得到PA 的最小值.【解析】解:作BH ⊥AC 于H ,取BC 的中点D ,连接PD ,如图,∵AC 为切线,∴BH 为⊙B 的半径,∵∠90°=CB =2,∴AC ==∴BH 12=AC∴BP =∵PB BC BD BP ==,而∠PBD =∠CBP ,∴△BPD∴PD PC ∴PD =,∴PA =PA +PD ,而PA +PD ≥AD (当且仅当A 、P 、D 共线时取等号),而AD =∴PA+即PA【点睛】:圆的切线垂直于经过切点的半径.解决问题的关键是利用相似比确定线段PD=.也考查了等腰直角三角形的性质.5.如图,在Rt ABCD中,AB=AC=4,点E,F分别是AB,AC的中点,点P是扇形AEF的 E F上任意一点,连接BP,CP,则12BP+CP的最小值是_____..【分析】在AB上取一点T,使得AT=1,连接PT,PA,CT.证明PAT BAPD D∽,推出PTPB=APAB=12,推出PT=12PB,推出12PB+CP=CP+PT,根据PC+PT≥TC,求出CT即可解决问题.【解析】解:在AB上取一点T,使得AT=1,连接PT,PA,CT.∵PA=2.AT=1,AB=4,∴PA2=4=AT•AB,∴PAAT=ABPA,∵∠PAT=∠PAB,∴PAT BAPD D∽,∴PTPB=APAB=12,∴PT=12PB,∴12PB+CP=CP+PT,∵PC+PT≥TC,在Rt ACTD中,∵∠CAT=90°,AT=1,AC=4,∴CT,∴12PB+PC,∴12PB+PC..【点睛】本题考查等腰直角三角形的性质,三角形相似的判定与性质,勾股定理的应用,三角形的三边关系,圆的基本性质,掌握以上知识是解题的关键.6.如图,已知正方形ABCD的边长为4,⊙B的半径为2,点P是⊙B上的一个动点,则PD﹣12 PC的最大值为_____.【答案】5【解析】分析: 由PD−12PC=PD−PG≤DG,当点P在DG的延长线上时,PD−12PC的值最大,最大值为DG=5.解析: 在BC上取一点G,使得BG=1,如图,∵221PBBG==,422BCPB==,∴PB BC BG PB=,∵∠PBG=∠PBC,∴△PBG∽△CBP,∴12 PG BGPC PB==,∴PG=12PC,当点P在DG的延长线上时,PD−12PC的值最大,最大值为DG=5.故答案为5点睛: 本题考查圆综合题、正方形的性质、相似三角形的判定和性质等知识,解题的关键是学会构建相似三角形解决问题,学会用转化的思想思考问题,把问题转化为两点之间线段最短解决,题目比较难,属于中考压轴题.7.如图1所示,⊙O的半径为r,点A、B都在⊙O外,P为⊙O上的动点,已知r=k·OB.连接PA、PB,则当“PA+k·PB”的值最小时,P点的位置如何确定?【解析】1:连接动点至圆心0(将系数不为1的线段两端点分别与圆心相连接),即连接OP 、OB ;2:计算连接线段OP 、OB 长度;3:计算两线段长度的比值k OPOB=;4:在OB 上截取一点C ,使得OC OPOP OB=构建母子型相似:5:连接AC ,与圆0交点为P ,即AC 线段长为PA +K *PB 的最小值.本题的关键在于如何确定“k ·PB ”的大小,(如图 2)在线段 OB 上截取 OC 使 OC =k ·r ,则可说明△BPO 与△PCO 相似,即 k ·PB =PC .∴本题求“PA +k ·PB ”的最小值转化为求“PA +PC ”的最小值,即 A 、P 、C 三点共线时最小(如图 3),时AC 线段长即所求最小值.8.如图,点A 、B 在O e 上,且OA =OB =6,且OA ⊥OB ,点C 是OA 的中点,点D 在OB 上,且OD =4,动点P 在O e 上.求2PC +PD 的最小值.【答案】【分析】连接OP ,在射线OA 上截取AE =6,连接PE .由题意易证OPC OEP V :V ,即得出2PE PC =,从而得出2PC PD PE PD +=+,由此可知当P 、D 、E 三点共线时,PE PD +最小,最小值为DE 的长,最后在Rt OED △中利用勾股定理求出DE 的长即可.【解析】如图,连接OP ,在射线OA 上截取AE =6,连接PE .∵C 是OA 的中点,∴1122OC OA OP ==.∴在△OPC 和△OEP 中,12COP POE OC OP OP OE Ð=Ðìïí==ïî,∴OPC OEP V :V ,∴1=2PC PE ,即2PE PC =,∴2PC PD PE PD +=+,.∴当P 、D 、E 三点共线时,PE PD +最小,最小值即为DE 的长,如图,在Rt OED △中,DE ===,∴2PC PD +的最小值为.【点睛】本题考查同圆半径相等、三角形相似的判定和性质和勾股定理等知识.正确作出辅助线并理解当P 、D 、E 三点共线时,PE PD +最小,最小值为DE 的长是解答本题的关键.9.如图,Rt △ABC ,∠ACB =90°,AC =BC =2,以C CDEF (C 、D 、E 、F 四个顶点按逆时针方向排列)可以绕点C 自由转动,且CD ,连接AF ,BD(1)求证:△BDC ≌△AFC(2)当正方形CDEF 有顶点在线段AB 上时,直接写出BD AD 的值;(3)直接写出正方形CDEF 旋转过程中,BD 的最小值.【答案】(1)见解析;(21 ;(3【分析】(1)利用SAS ,即可证明△FCA ≌△DCB ;(2)分两种情况当点D ,E 在AB 边上时和当点E ,F 在边AB(3)取AC 的中点M .连接DM ,BM .则CM =1,可证得△DCM ∽△ACD ,可得DM ,从而得到当B ,D ,M 共线时,BD 的值最小,即可求解.【解析】(1)证明: ∵四边形CDEF 是正方形,∴CF =CD ,∠DCF =∠ACB =90°,∴∠ACF =∠DCB ,∵AC =CB ,∴△FCA ≌△DCB (SAS );(2)解:①如图2中,当点D ,E 在AB 边上时,∵AC =BC =2,∠ACB =90°,∴sin 45ACAB ==°∵CD ⊥AB ,∴AD AC =´=∴BD =1==;②如图3中,当点E ,F 在边AB 上时.BD =CF =sin 452BC ´°==AD∴BD =综上所述,BD 1+(3)如图4中.取AC 的中点M .连接DM ,BM .则CM =1,∵CD CM =1,CA =2,∴CD 2=CM •CA ,∴CD CA =CMCD,∵∠DCM =∠ACD ,∴△DCM ∽△∴DM AD =CD AC ,∴DM ,∴BD =BD +DM ,∴当B ,D ,M 共线时,BD 的值最小,最小值BM ==【点睛】本题主要考查了相似三角形的判定和性质,全等三角形的判定和性质,正方形的性质,锐角三角函数,熟练掌握相关知识点是解题的关键.10.已知抛物线y =ax 2+bx +c 与x 轴交于A (﹣1,0),B (5,0)两点,C 为抛物线的顶点,抛物线的对称轴交x 轴于点D ,连接BC ,且tan∠CBD 4=3,如图所示.(1)求抛物线的解析式;(2)设P 是抛物线的对称轴上的一个动点.①过点P 作x 轴的平行线交线段BC 于点E ,过点E 作EF ⊥PE 交抛物线于点F ,连接FB 、FC ,求△BCF 的面积的最大值;②连接PB ,求35PC +PB 的最小值.【答案】(1)241620999x x -++;(2)①32;②245【解析】思路引领:(1)设抛物线的解析式为:y =a (x +1)(x ﹣5),可得对称轴为直线x =2,由锐角三角函数可求点C 坐标,代入解析式可求解析式;(2)①先求出直线BC 解析式,设P (2,t ),可得点E (534-t ,t ),点2315244F t t t æö--ç÷èø,,可求EF 的长,由三角形面积公式和二次函数性质可求解;②根据图形的对称性可知∠ACD =∠BCD ,AC =BC =5,过点P 作PG ⊥AC 于G ,可得PG 35=PC ,可得35PC PB PG PB +=+,过点B 作BH ⊥AC 于点H ,则PG +PB ≥BH ,即BH 是35PC +PB 的最小值,由三角形面积公式可求解.答案解析:(1)根据题意,可设抛物线的解析式为:y =a (x +1)(x ﹣5),∵抛物线的对称轴为直线x =2,∴D (2,0),又∵43CDtan CBD DBÐ==,∴CD =BD •tan∠CBD =4,即C (2,4),代入抛物线的解析式,得4=a (2+1)(2﹣5),解得 49a =-,∴二次函数的解析式为 ()()441599y x x =-+-=-x 2162099x ++;(2)①设P (2,t ),其中0<t <4,设直线BC 的解析式为 y =kx +b ,∴0542.k b k b =+ìí=+î,,解得 4320.3k b ì=-ïïíï=ïî即直线BC 的解析式为 42033y x =-+,令y =t ,得:354x t =-,∴点E (534-t ,t ),把354x t =- 代入()()4159y x x =-+-,得 24t y t æö=-ç÷èø,即2315244F t t t æö--ç÷èø,,∴221244t EF t t t t æö=--=-ç÷èø,∴△BCF 的面积12=´EF ×BD 32=(t 24t -)()223334(2)882t t t =--=--+,∴当t =2时,△BCF 的面积最大,且最大值为32;②如图,据图形的对称性可知∠ACD =∠BCD ,AC =BC =5,∴35AD sin ACD AC Ð==,过点P 作PG ⊥AC 于G ,则在Rt△PCG 中,35PG PC sin ACD PC =×Ð=,∴35PC PB PG PB +=+,过点B 作BH ⊥AC 于点H ,则PG +PB ≥BH ,∴线段BH 的长就是35PC PB +的最小值,∵11641222ABC S AB CD =´´=´´=V ,又∵1522ABC S AC BH BH =´´=V ,∴5122BH =,即245BH =,∴35PC PB +的最小值为245.11.问题提出:如图①,在Rt ABC △中,90C =o ∠,4CB =,6CA =,⊙C 的半径为2,P 为圆上一动点,连接AP 、BP ,求12AP BP +的最小值.(1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图①,连接CP ,在CB 上取一点D ,使1CD =,则12CD CP CP CB ==.又PCD BCP Ð=Ð,所以PCD D ∽BCP D .所以12PD CD BP CP ==.所以12PD PB =,所以12AP BP AP PD +=+.请你完成余下的思考,并直接写出答案:12AP BP +的最小值为________;(2)自主探索:在“问题提出”的条件不变的前提下,求13AP BP +的最小值;(3)拓展延伸:如图②,已知在扇形COD 中,90COD Ð=o ,6OC =,3OA =,5OB =,P 是 CD上一点,求2PA PB +的最小值.【答案】(1;(2(3)13.【分析】(1)根据题意可知最小值为AD 长度,利用勾股定理即可求出AD 长度.(2)连接CP ,在CA 上取一点D ,使23CD =,即可证明PCD V ∽ACP △,得到13PD AP =,即13AP BP PD BP +=+,所以13AP BP +的最小值为BD 长度,利用勾股定理即可求出BD 长度.(3)延长OC 到E ,使6CE =,连接PE ,OP ,即可证明OAP △∽OPE V ,得到2EP PA =,即2PA PB EP PB +=+,所以2PA PB +的最小值为BE 长度,利用勾股定理即可求出BE 长度.【解析】(1)根据题意可知,当A 、P 、D 三点共线时,12AP BP +最小,最小值AD ====.(2)连接CP ,在CA 上取一点D ,使23CD =,则有13CD CP CP CA ==,∵PCD ACP Ð=Ð,∴PCD D ∽ACP △,得13PD CD AP CP ==,∴13PD AP =,故13AP BP PD BP +=+,仅当B 、P 、D 三点共线时,13AP BP +的最小值BD ====.(3)延长OC 到E ,使6CE =,连接PE ,OP ,则12OA OP OP OE ==,∵AOP POE Ð=Ð,∴OAP △∽OPE D ,∴12OA OP AP OP OE EP ===,∴2EP PA =,∴2PA PB EP PB +=+,仅当E 、P 、B 三点共线时,13EP PB BE +====,即2PA PB +的最小值为13.【点睛】本题考查圆的综合,勾股定理,相似三角形的判定和性质.根据阅读材料的思路构造出PCD V ∽ACP △和OAP △∽OPE V 是解题的关键.本题较难.12.如图,抛物线2y ax bx c =++与x 轴交于A 0),B 两点(点B 在点A 的左侧),与y 轴交于点C ,且3OB OA =,OAC Ð的平分线AD 交y 轴于点D ,过点A 且垂直于AD 的直线l 交y 轴于点E ,点P 是x 轴下方抛物线上的一个动点,过点P 作PF x ^轴,垂足为F ,交直线AD 于点H .(1)求抛物线的解析式;(2)设点P 的横坐标为m ,当FH HP =时,求m 的值;(3)当直线PF 为抛物线的对称轴时,以点H 为圆心,12HC 为半径作⊙H ,点Q 为⊙H 上的一个动点,求14AQ EQ +的最小值.【答案】(1)y 13=x 2﹣3;(2);(3【分析】对于(1),结合已知先求出点B 和点C 的坐标,再利用待定系数法求解即可;对于(2),在Rt△OAC 中,利用三角函数的知识求出∠OAC 的度数,再利用角平分线的定义求出∠OAD 的度数,进而得到点D 的坐标;接下来求出直线AD 的解析式,表示出点P ,H ,F 的3),首先求出⊙H 的半径,在HA 上取一点K ,使得HK=14,此时K (15-8);然后由HQ 2=HK·HA ,得到△QHK∽△AHQ,再利用相似三角形的性质求出KQ=14AQ ,进而可得当E 、Q 、K 共线时,14AQ+EQ 的值最小,据此解答.【解析】(1)由题意A 0),B 0),C (0,﹣3),设抛物线的解析式为y =a (x(x ,把C (0,﹣3)代入得到a 13=,∴抛物线的解析式为y 13=x 2﹣3.(2)在Rt△AOC 中,tan∠OAC OCOA==,∴∠OAC =60°.∵AD OAC ,∴∠OAD =30°=D (0,﹣1),∴直线AD 的解析式为y =﹣1,由题意P (m ,13m 2,H (m ﹣1),F (m ,0).∵FH =PH ,∴1=﹣1﹣(13﹣3)解得m =,∴当时,m .(3)如图,∵PF 是对称轴,∴F 0),H (.∵AH ⊥AE ,∴∠EAO =60°,∴EO ==3,∴E (0,3).∵C (0,﹣3),∴HC ==2,AH =2FH =4,∴QH 12=CH =1,在HA 上取一点K ,使得HK14=,此时K (158-).∵HQ 2=1,HK •HA =1,∴HQ 2=HK •HA ,∴HQ KHAH HQ=.∵∠QHK =∠AHQ ,∴△QHK ∽△AHQ ,∴14KQ HQ AQ AH ==,∴KQ 14=AQ ,∴14AQ +QE =KQ +EQ ,∴当E 、Q 、K 共线时,14AQ +QE 的值最小,最小值==.【点睛】本题考查了相似三角形对应边成比例、两边成比例且夹角相等的两个三角形相似、待定系数法求二次函数的表达式、二次函数的图象与性质、数轴上两点间的距离公式,熟练掌握该知识点是本题解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学最值问题
类型一:线段和最小值
例1 如图,在菱形ABCD中,AB=12,∠ABC=60°,P在AD上,Q在AB上,AP=2,BQ=2,点K是BD 的一动点,则PK+QK的最小值为___.
变式1、如图,在菱形ABCD中,AB=12,∠ABC=60°,P在AD上,Q在AB上,AP=2,BQ=3,点K是BD的一动点,则PK+QK的最小值为___.
变式2、如图,在菱形ABCD中,AB=12,∠ABC=60°,P在AD上,AP=2,点Q是AB上的一动点,点K是BD上的一动点,则PK+QK的最小值为___.
例2 点A(1,-3),B(4,-1),P(a,0),则AP+BP的最小值是
__________.
变式1、若点N(a+2,0),连接AB、AP、BN,则当四边形ABNP周长最小时,
a=______
变式2、若点Q为(0,b),PQ、AQ、AB、BP, 则当四边形PQAB周长最小时,Q的坐标为_________
课后思考
1、如图,矩形ABCD中,AB=2,BC=3,分别以A.?D为圆心,1为半径画圆,E、F分别是A.?D上的一动点,P是BC上的一动点,则PE+PF的最小值是_________
类型二:线段的最值
例4、如图,∠MON=90°,矩形ABCD的顶点A.?B分别在边OM,ON上,当B在边ON上运动时,A
随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O最
大距离为___.
课后思考
1、如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在
直线折叠得到△EB′F,连接B′D,则B′D的最小值是___.
2、如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,
则线段CP长的最小值为___.
类型三:利用函数关系式求最值
例5 正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,当BM=___cm 时,四边形ABCN的面积最大,最大面积为___cm2.
课后思考
如图,已知半径为2的O与直线l相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线l的
垂线,垂足为C,PC与O交于点D,连接PA、PB,设PC的长为x(2<x<4)
当x为何值时,PD?PC的值最大?最大值是多少?
类型四:利用相似或三角函数转化求最值
例6、在平面直角坐标系中,一次函数x轴于点C,交y轴于点B,
D为(-1
2,0),A为射线BO上的动点,求1
2
AB+AD的最小值
课后思考
如图,圆柱形玻璃板,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离________cm.。
