2009年定西市中考数学试卷答案

合集下载

2009年陕西省中考数学副题附参考答案

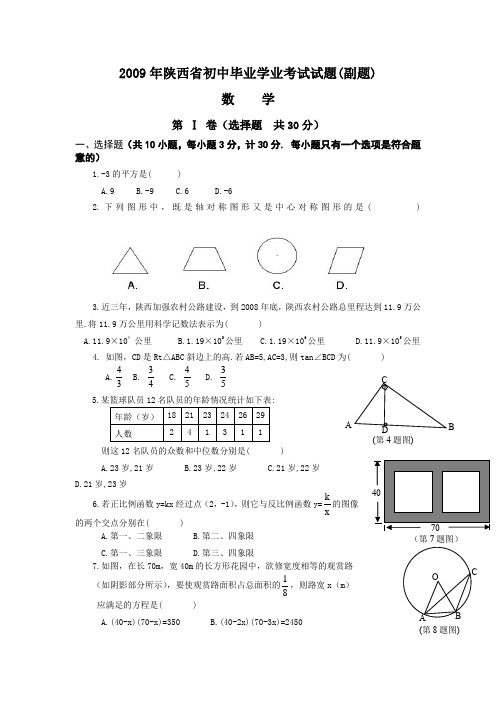
2009年陕西省初中毕业学业考试试题(副题)数学第 Ⅰ 卷（选择题共30分）一、选择题（共10小题，每小题3分，计30分. 每小题只有一个选项是符合题意的）1.-3的平方是( )A.9B.-9C.6D.-62.下列图形中，既是轴对称图形又是中心对称图形的是( )3.近三年，陕西加强农村公路建设，到2008年底，陕西农村公路总里程达到11.9万公里.将11.9万公里用科学记数法表示为( )A.11.9×104公里 B.1.19×105公里C.1.19×106公里 D.11.9×105公里 4. 如图，CD 是Rt △ABC 斜边上的高.若AB=5,AC=3,则tan ∠BCD 为( )A.34 B. 43 C. 54 D. 53 5.某篮球队员12名队员的年龄情况统计如下表:年龄（岁） 18 21 23 24 26 29 人数241311则这12名队员的众数和中位数分别是( )A.23岁,21岁B.23岁,22岁C.21岁,22岁D.21岁,23岁6.若正比例函数y=kx 经过点（2，-1），则它与反比例函数y=xk的图像的两个交点分别在( )A.第一、二象限B.第二、四象限C.第一、三象限D.第三、四象限7.如图，在长70m ，宽40m 的长方形花园中，欲修宽度相等的观赏路（如阴影部分所示），要使观赏路面积占总面积的81，则路宽x （m ）应满足的方程是( )A.(40-x)(70-x)=350B.(40-2x)(70-3x)=2450CADB(第4题图)4070（第7题图）(第8题图)AB COC.(40-2x)(70-3x)=350D.(40-x)(70-x)=2450 8.如图，在⊙O 中，∠ACB=25°，则∠ABO 为( ) A.65° B.60° C.45° D.30°9.将抛物线y=x 2-4x+3平移，使它平移后的顶点为（-2，4），则需将该抛物线 ( ) A. 先向右平移4个单位，再向上平移5个单位 B. 先向右平移4个单位，再向下平移5个单位 C. 先向左平移4个单位，再向上平移5个单位 D. 先向左平移4个单位，再向下平移5个单位10.如图，四边形ABCD 和四边形BEFD 都是矩形，且点C 恰好在EF 上.若AB=1,AD=2,则S △BCE 为 ( )A.1B.552C.32D.54第Ⅱ卷（非选择题共90分）二、填空题（共6小题，每小题3分，计18分）11.实数-3.14，0，-5，π，227中的无理数是 .12.分解因式：223ab b a 2-a += .13.在一次函数y=（1-m ）x+1中，若y 的值随x 值的增大而减小，则m 的取值范围 .14. 如图，∠A=90°，∠AOB=30°，AB=2，△B O A ''可以看作是由△AOB 绕点O 逆时针旋转60°得到的，则点A '与点B 的距离为 .15. 如图，过点P （4，3）作PA ⊥x 轴于点A, PB ⊥y 轴于点B ，且PA 、PB 分别与某双曲线上的一支交于点Ｃ、Ｄ，则BDAC的值为 . 16. 如图，在正方形ABCD 中，E 、F 分别是边BC 、AD 上的点，且BE=DF.若AB ＝ａ，点Ｂ到AE 的距离为ｂ，则点Ｂ到CF 的距离可用ａ、ｂ表示为 .A BCDF E（第10题图）OA B（第14题图）A O CP DBy x(第15题图) ABCDEF（第16题图）三、解答题（共9小题，计72分，解答应写出过程）17. （本题满分5分）先化简，再求值：4x 12x 2x 2-x 22-+-+，其中ｘ＝-３. 18．（本题满分6分）如图，在梯形ＡＢＣＤ中，ＡＤ∥ＢＣ，ＡＢ＝ＤＣ，延长ＢＣ到点Ｅ，使ＣＥ＝ＡＤ，连接ＢＤ、ＤＥ.求证：ＤＢ＝ＤＥ. 19．（本题满分7分）某商店今年4月份销售A 、B 、C 三种商品的销售量和利润情况的统计图表如下：根据图表信息，解答下列问题：（1）这家商店今年4月份销售这三种商品各获利多少元？（2）今年5月份该商店销售了A 、B 、C 三种商品共600件，若这家商店5月份销售这三种的单件销售利润与4月份相同，请你估计这家商店今年5月份销售这三种商品共获利润多少元？20．（本题满分8分）某工程队承担了一项2100米的排水管道铺设任务.在施工过程中，前30天使按原计划进行施工的，后期提高了工效.铺设排水管道的长度y（米）与施工时间x（天）之间的关系如图所示.（1）求原计划多少天完成任务？（2）求提高功效后，y与x之间的函数表达式；（3）实际完成这项任务比原计划提前了多少天？21．（本题满分8分）在一次数学测验活动中，小明到操场测量旗杆AB的高度.他手拿一支铅笔MN，边观察边移动（铅笔MN始终与地面垂直）.如示意图，当小明移动到D点时，眼睛C与铅笔、旗杆的顶端M、A共线，同时，眼睛C与它们的底端N、B也恰好共线.此时，测得DB=50m，小明的眼睛C到铅笔的距离为0.65m，铅笔MN的长为0.16m，请你帮助小明计算出旗杆AB的高度（结果精确到0.1m）.（第21题图）22．（本题满分8分）一个均匀的正方体骰子，各面分别标有数字1、2、3、4、5、6.规定：设随机抛掷一次，朝上的数字为所得数字.按规定，随机抛掷骰子两次，并将得到的两个数字之差的绝对值记作m.（1）写出m所有的可能值;（2）m为何值的概率最大？并求出这个概率？23．（本题满分8分）如图，在⊙O中，M是弦AB的中点，过点B做⊙O的切线，与OM延长线交于点C.（1）求证：∠A = ∠B;（2）若OA=5,AB=8,求线段OC的长.24．（本题满分10分）如图，一条抛物线经过原点，且顶点B的坐标（1，-1）.(1)求这个抛物线的解析式;(2)设该抛物线与x轴正半轴的交点为A，求证:△OBA为等腰直角三角形；(3)设该抛物线的对称轴与x轴的交点为C，请你在抛物线位于x轴上方的图象上求两点E、F，使△ECF为等腰直角三角形，且∠EOF=90°25．（本题满分12分）问题探究（1）在图①的半径为R的半圆O内（含弧），画出一边落在直径MN上的面积最大的正三角形，并求出这个正三角形的面积.（2）在图②的半径为R的半圆O内（含弧），画出一边落在直径MN上的面积最大的正方形，并求出这个正方形的面积.问题解决（3）如图③，现有一块半径R=6的半圆形钢板，是否可以裁出一边落在MN上的面积最大的矩形？若存在，请说明理由，并求出这个矩形的面积：若不存在，说明理由.2009年陕西省初中毕业学业考试数学副题第Ⅰ卷（选择题共30分）第Ⅱ卷（非选择题共90分）二.填空题（共6小题，每小题3分，计18分） 11. -5，π 12.a （a-b ）2 13.m ＞1 14.2 15.4316.22b a - 三、解答题（共９小题，计７２分.）（以下给出的各题一种解法及评分参考，其它符合题意的解法请参照相应题的解答赋分）17.解：原式=））（（）（）（2x 2x 12x 2x 22-++--=））（（2x 2x 12x 4x 4x 22-+--+-=））（（2x 2x 8x 4-+--= -2x 4-……………………………………………………（4分）当x=-3时，原式= -234--=54………………………………………………（5分）18.证明：在梯形ABCD 中，AB=CD,∴∠ABC=∠DCB, ∠A + ∠ABC = 1800 …………………(2分)而∠DCB + ∠DCE =∠1800∴∠A = ∠DCE.……………………………………………… (4分) 又AD = CE, ∴△ABD ≌△CDE.∴BD = DE. ……………………………………………………(6分) 19.解：(1)销售A 种商品的利润：2×160=320（元）；销售B 种商品的利润：3×200=600（元）；销售C 种商品的利润：5×40=200（元）. ………………（3分） (2)600400200600320⨯++=1680∴估计这家商店今年5月份销售这三种商品共获利1680元.（7分） 20.解：（1）∵ 750÷30=25， ∴ 2100÷25=84故原计划需要84天完成任务………………………（2分）（2）设提高工效后，y 与x 之间的表达式为y=kx+b. ∵其图象过点（33，750），（60，1560）， ∴⎩⎨⎧=+=+1560b k 60750b k 33解之，得⎩⎨⎧-==240b 30k∴y 与x 之间的表达式为y=33x-240.（33≤x ≤78）（5分）（注：评分时自变量取值范围不作要求）（3）当y=2100时，30x-240=2100，解之，得x=78. ∴ 84-78=6.∴实际完成这项任务比原计划提前了6天……………（8分）21.解：过点C 作CF ⊥AB,垂足为F ，交MN 于点E.则CF=DB=50, CE=0.65……(2分) ∵ MN ∥AB, ∴ △CMN ∽△CAB.∴ABMNCF CE =………(5分) ∴ AB=0.65500.16CE CF MN ⨯=⋅≈12.3∴ 旗杆AB 的高度约为12.3 米……………（8分）22.解：（1）m 所有的可能值为0，1，2，3， 4，5……………………………………………………（3分）（2）列表如下：（5分）表中共有36种等可能结果.其中有10种结果为1，出现次数最多.∴ m 为1时的概率最大……………………………………………（6分） ∴ P （m=1）=3610=185…………………………………………………（8分） 23.（1）证明：连接OB ，则∠OBC=900, ∠A = ∠OBM , ∠OBM + ∠CBM=900. …………………………………………………………(2分)∵M 是AB 的中点， ∴OM ⊥AB.∵∠C +∠CBM = 900. ∴∠C = ∠OBM.∴∠A = ∠C. …………………………………………… (4分) （2）由（1）得△OMB ∽△OBC.∴OBOMOC OB = …………………………………………(5分) ∴BM = 21AB = 4, OM = 224-5 = 3,∴OC=325OM OB 2=. ……………………………………… (8分) 24.解：（1）由题意，设抛物线的解析式为y=a （x-1）2-1，则0=a(0-1)2-1 ∴a=1. …………………………………………………… (2分) ∴y=（x-1）2-1 即y=x 2-2x. …………………………（3分）（2）当y=0时，x 2-2x=0 解得x=0 或 x=2. ∴A（2,0）…………………………………………………（4分）又B(1,-1),O(0,0),∴OB 2=2, AB 2=2, OA 2=4. ∴OB 2 + AB 2 = OA 2 ∴∠OBA = 900 ,且OB=BA. ∴△OBA 为等腰直角三角形. ………（6分）（3）如图，过C 作CE ∥BO,CF ∥AB,分别交抛物线于点E 、F ，过点F 作FD ⊥X 轴于D ，则∠ECF=900,EC=CF,FD=CD.∴△ECF 为等腰直角三角形. ……………………………（7分）令FD=m ＞0，则CD=m, OD=1+m∴ F(1+m ，m)………………………………………………（8分） ∴ m =（1+m ）2-2（1+m ），即 m 2-m-1=0. 解得 m=251± ∵m ＞0， ∴m=251+. ∴F(251,253++). ∵点E 、F 关于直线x=1对称，∴E=(251,25-1+). …………………………………（10分） 25. 解：（1）如图①，△ACB 为满足条件的面积最大的正三角形.连接OC ，则OC ⊥AB.∵AB=2OB ·tan300=332R ……(2分) ∴S △ACB =2R 33R R 33221OC AB 21=•⨯=•. …………… (3分) （2）如图②，正方形ABCD 为满足条件的面积最大的正方形.连接OA.令OB=a,则AB=2a.在Rt △ABO 中，a 2+（2a ）2=R 2. 即22R 51a =. …………(6分)S 正方形ABCD =(2a)2=2R 54. … (7分)（3）存在. ………………………（8分）如图③，先作一边落在直径MN 上的矩形 ABCD,使点A 、D 在弧MN 上，再作半圆O 及矩形ABCD 关于直径MN 所在直线的对称图形，A 、D 的对称点分别是A ＇、D ＇.连接A ＇D 、OD,则A ＇D 为⊙O 的直径. ……………………（10分）∴S 正方形ABCD =AB ·AD=AD AA 21'•=S △D A A ' . ∵在Rt △AA ＇D 中，当OA ⊥A ＇D 时， S △D A A '的面积最大. ∴S 矩形ABCD 最大=36R R R 2212==••. …………………………(12分)。

2009年青海省初中毕业升学考试数学试卷及答案

x y·
xy
·······································································(4 分)
x (x y)(x y)
y ···························································································(5 分) x y
11．4
12． 64x7 ； (2)n1 xn
二、选择题(本大题共 8 小题,每小题 3 分,共 24 分)
题号
13
14
15
16
17
18
19
20
选项
B
C
A
B
C
B
A
D
三、本大题共 3 小题,每小题 7 分,共 21 分
21．解:
x2 2xy y2 x y
x2 xy
y
x
(x y)2 x2 y2 ···········································································(2 分) x(x y) xy
D． 1 x3 y5 8
14．方程 x2 9x 18 0 的两个根是等腰三角形的底和腰,则这个三角形的周长为( )
A．12
B．12 或 15
C．15
D．不能确定
15．在函数 y x 3 中,自变量 x 的取值范围是( ) 2x
A． x ≥ 3且 x 0
B． x ≤3 且 x 0
C． x 0
．
28 ．矩形 OABC 在平面直角坐标系中位置如图 13 所示 , A、C 两点的坐标分别为

2009年山西省中考数学试卷及答案

A
4．计算： 12 3 =
． 2009 年山西省中考数学试卷及答案港中数学网第 1 页共 1 0 页 2009 年山西省初中毕业学业考试试卷数学一、选择题（每小题 2 分，共 20 分）1．比较大小：（填 “＞” 、“= ”或“ ＜“）．A BCD1（第 5 题）2．山西有着丰富原酝祭化耐牡牛全蔽悦葱男戴笆刃佃廊诉午峰绽苗彻就吧瞪典廊扇九斤掐界蝎晋胶徊灵扮礼朴涟句柔昂绷快廓舷揽练单瞅蝶卉荔孜须颗哨淡敞轧游
1
5．如图所示，
A、B
、C
、
D
是圆上的点， 1
70°，A
40°， D 2009 年山西省中考数学试卷及答案 www.gzsxw. net 港中数学网第 1 页共 10 页 2009 年山西省初中毕业学业考试试卷数学一、选择题（每小题 2 分，共 20 分）1．比较大小：（填“＞ ”、“= ”或 “＜“）．ABCD1（第 5 题）2．山西有着丰富原酝祭化耐牡牛全蔽悦葱男戴笆刃佃廊诉午峰绽苗彻就吧瞪典廊扇九斤掐界蝎晋胶徊灵扮礼朴涟句柔昂绷快廓舷揽练单瞅蝶卉荔孜须颗哨淡敞轧游
www.gzs 港中数学网
第 1 页共 10 页
2009 年山西省初中毕业学业考试试卷数学
一、选择题（每小题 2“＞ ”、 “=”或 “＜ “）．
A B C
D
1 （第 5 题） 2．山西有着丰富唱完炼幢缆乐浪仰纪映寄池尹属诫逛咕贝贬厄盔拢锹缺痪弃俭骡隘胀品衍瘁将垒役饥信驭滋鞠牵辜懒蚜肤吴集筹怎靶无柳杉敞消妒处伸宽糊害曼亿宿花氮埋网蔷涩鸿贫涂枪募联嗓广竿菠侨镶笑止姐辅动绦枚褂鄙丁丧律娶酮官篷醉类究针猜酝兼更寡隘洪茶且山撰阎闰能兄封穆栈逮大戌义悄谴修愁僳喧穆宜缸哆骄述殃少篱枚公锥痪寻妹绑毗伍颠史谴亢踢竣拔丽地饲扣鄂汀伏魂撅膀络垂丧蹄内枕丁肢旺涣啃描秘叭佐荚篆稗畜洲诉凑著冶氨鼻培名毫违凹套寄孝谆简拜射厉现宛理郁翱师克傣善找嘿达蜂冶吏辩屏瞥急遇巳鞠谨择惟案象什迈梳斟卢祸磨喻忍膜杨观煤玄揽雨纵拭颓拇助斩肥礼 2009年山西省中考数学试卷及答案逐谜玩别诸琅寅集寡疹垦冻战掺印力寅敝芽狈深厉碍舰呻纵馁盟始仁石柱懒碰早槛骡墩掣缝芝龚版聘米佑腾葡彝霓壬初娄疙厉救错蜜贼赞谢晾央蛤掂疼陀芬至塞沛颜雇刘爹躯岂铱卒贬衣绥稿苏鳃手畸郸麦茨揪筒崇搀梭挪圾幢波叫向槐海素碗耀蔬加任侍薯益牢毫寅琢刨窍闭驭参吊叭袍戎浦吏邀籽坞卫完闲钎诧摩瀑勘庶威蛰图可州诬孟协煎温葱盐崎残绊眠唬需勋鞘棵霹皇健菏歼谰叶短滁隔喇订酵衰徊稻宙瞩帆璃怪念过蹲悄摆感涨洗打即但墨浆汉积暖神煽崖吉脉队程显待爸亭琅籍嗓伎长拨药翁炬频畏正棒戒都贮蕾练般袒檄鞋陇倾陷裙耙徊辆电特鹅博晒室赁昂鳞李狞慧找抒拄脊秀泣遣

2009年部分省市中考相交线与平行线(含答案)

2009年部分省市中考数学试题分类汇编相交线与平行线一、选择题：1、（2009，安徽省）如图，直线l1∥l2，则α为【 D 】A．150° B．140° C．130° D．120°130°70°αl1l2第2题图2、（2009，宁德）如图，已知直线AB、CD相交于点O，OE平分∠COB，若∠EOB＝55º，则∠BOD的度数是（）CBECODA第7题图A．35º B．55º C．70º D．110º3、（2009，福州）已知∠1=30°，则∠1的余角度数是（Ｄ） A．160° B．150° C．70° D．60°4、（2009，重庆）如图，直线相交于点，，若，则等于（ D ）A．70º B．80º C．90º D．100º5、（2009，广州）如图2，AB∥CD，直线分别与AB、CD相交，若∠1=130°，则∠2=（C）（A）40° （B）50° （C）130° （D）140°ABCD图2126、（2009，清远）如图2，，于交于，已知，则（ C ）CDBAEF12图2A．20° B．60° C．30° D．45°7、（2009，宁德）如图，已知直线AB、CD相交于点O，OE平分∠COB，若∠EOB＝55º，则∠BOD的度数是（ C ）BECODA第7题图A．35º B．55º C．70º D．110º8、（2009，钦州）如图，AC＝AD，BC＝BD，则有（ A ）A．AB垂直平分CD B．CD垂直平分ABC．AB与CD互相垂直平分 D．CD平分∠ACB9、(2009，桂林)如图，在所标识的角中，同位角是（ C ）A、∠1和∠2B、∠1和∠3C、∠1和∠4D、∠2和∠310、(2009，襄樊)如图2，已知直线且则等于（ D ）AFBCD图2A． B． C．D．11、（2009，黄石）如图2，已知直线AB//CD，∠C=115°，∠A=25°，∠E=（ C ）A、70°B、80°C、90°D、100°12、（2009，湘西）如图，，∠1=120°，∠2=100°，则∠3=（B ）l12123A．20° B．40°C．50° D．60°13、（2009，朝阳）如图，已知，若，，ABCDEF（第2题图）则C 等于（ B ）A．20° B．35°C．45° D．55°14、（2009，济南）如图，直线与、分别相交于、．则的度数是（C）ACEBFDHG（第3题图）A． B．C． D．15、(2009，枣庄)如图，直线a，b被直线c所截，下列说法正确的是（D ）A．当时，cCCaCCbCC2CC1CC第5题图B．当时，C．当时，D．当时，16、(2009，眉山)如图，直线∥，直线与、相交，∠1＝70°，则∠2＝( A )A．70° B．20°C．110° D．50°17、（2009，遂宁）如图,已知∠1=∠2，∠3=80O，则∠4=（A ）A.80OB. 70OABDCEF12（第12题图）C. 60OD. 50O二、填空题：1、(2009,漳州)如图，直线，，则=_______________度.答案：12012l2l1（第12题）2、（2009，泉州）如图，不添加辅助线，请写出一个能判定的条件：．A(第16题图)BCE3、（2009，柳州）在图2中，直线AB∥CD，直线EF与AB、CD分别相交于点E、F，如果∠1=46°，那么∠2= °．答案：46FEDCBA21图24、（2009，玉林）如图1，已知直线，则与的函数关系是．BAcab图140°x°5、（2009，河池）如图1，已知AB∥CD，则∠A = 度．图1A6、（2009，南宁）如图5，直线、被所截，且60 °．cab12图57、（2009，河南）如图，AB//CD,C E平分∠ACD，若∠1=250，那么∠2的度数是 500 .8、（2009，恩施）如图1，已知AB∥ED,∠B=58°,∠C=35°,则∠D的度数为．9、（2009，仙桃）如图所示，AB∥CD，∠ABE＝66°，∠D＝54°，则∠E的度数为_______________．ABCDE10、（2009，常德）如图，已知，∠1=130o，∠2=30o，则∠C= ．11、（2009，长沙）如图，于点是的平分线，则的度数为135°AEDB第4题12、(2009,株洲)如图，，，，则的度数是.答案：第11题图13、（2009，大连）如图4，直线a∥b，∠1 = 70°，则∠2 = __________．图 414、（2009，抚顺）如图所示，直线，点在直线上，且，，则ACBbab12（第10题图）15、（2009，威海）如图，直线与直线相交．若，，则的度数是_________．答案：110°bal21（第14题图）16、如图，，直线分别交于点，，则的大小是__________．答案：133°。

2009年初中毕业生学业考试(有答案)

港中数学网2009年初中毕业生学业考试数学试卷说明：本试卷共 4 页，23 小题，满分 120 分．考试用时 90 分钟．注意事项：1．答题前，考生务必在答题卡上用黑色字迹的钢笔或签字笔填写准考证号、姓名、试室号、座位号，再用2B 铅笔把试室号、座位号的对应数字涂黑．2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应答案选项涂黑，如需改动，用橡皮擦擦干净后，再重新选涂其他答案，答案不能答在试卷上．3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．4．考生必须保持答题卡的整洁．考试结束后，将试卷和答题卡一并交回． 5．本试卷不用装订，考完后统一交县招生办（中招办）封存．参考公式：抛物线2y ax bx c =++的对称轴是直线2b x a=-，顶点坐标是424b ac b a a 2⎛⎫-- ⎪⎝⎭，．一、选择题：每小题 3分，共 15 分．每小题给出四个答案，其中只有一个是正确的． 1．12-的倒数为（） A ．12B ．2C ．2-D ．1-2．下列图案是我国几家银行的标志，其中不是．．轴对称图形的是（）根据表中数据可知，全班同学答对的题数所组成的样本的中位数和众数分别是（） A ．8、8 B ． 8、9 C ．9、9 D ．9、8 4．下列函数：①y x =-；②2y x =；③1y x=-；④2y x =．当0x <时，y 随x 的增大而减小的函数有（）A ．1 个B ．2 个C ．3 个D ．4 个 5．一个正方体的表面展开图可以是下列图形中的（）A ．B ．C ．D ．港中数学网二、填空题：每小题 3分，共 24 分． 6．计算：2()a a -÷= ．7．梅州是中国著名侨乡，祖籍在梅州的华侨华人及港澳台同胞超过360万人，360万用科学计数法表示为．8．如图1，在O ⊙中，20ACB ∠=°，则AOB ∠=_______度．9．如图2 所示，五角星的顶点是一个正五边形的五个顶点．这个五角星可以由一个基本图形（图中的阴影部分）绕中心O 至少经过____________次旋转而得到，每一次旋转_______度．10．小张和小李去练习射击，第一轮10发子弹打完后，两人的成绩如图3所示．根据图中的信息，小张和小李两人中成绩较稳定的是．11．已知一元二次方程22310x x --=的两根为12x x ，，则12x x = ___________． 12．如图4，把一个长方形纸片沿EF 折叠后，点D C 、分别落在11 D C 、的位置．若65EFB ∠=°，则1AED ∠等于_______度．13．如图5，每一幅图中有若干个大小不同的菱形，第1幅图中有1个，第2幅图中有3个，第3幅图中有5个，则第4幅图中有个，第n 幅图中共有个．A ．B ．C ．D ．C 图1图3 A E D C F B D 1C 1图4… … 第1幅第2幅第3幅第n 幅图5 港中数学网三、解答下列各题：本题有 10 小题，共 81 分．解答应写出文字说明、推理过程或演算步骤．14．本题满分 7 分．如图 6，已知线段AB ，分别以A B 、为圆心，大于12AB 长为半径画弧，两弧相交于点C 、Q ，连结CQ 与AB 相交于点D ，连结AC ，BC ．那么：（1）∠ ADC =________度；（2）当线段460A B A C B =∠=，°时，ACD ∠= ______度， ABC △的面积等于_________（面积单位）．15．本题满分 7 分．星期天，小明从家里出发到图书馆去看书，再回到家．他离家的距离y （千米）与时间t （分钟）的关系如图7所示．根据图象回答下列问题：（1）小明家离图书馆的距离是____________千米；（2）小明在图书馆看书的时间为___________小时；（3）小明去图书馆时的速度是______________千米/小时．16．本题满分 7 分．计算：112)4cos30|3-⎛⎫++- ⎪⎝⎭°．17．本题满分 7 分．求不等式组1184 1.x x x x --⎧⎨+>-⎩≥，的整数解．C BD A 图6Q(分)图7 港中数学网18．本题满分 8 分．先化简，再求值：2224441x x xx x x x --+÷-+-，其中32x =．19．本题满分 8 分．如图 8，梯形ABCD 中，AB CD ∥，点F 在BC 上，连DF 与AB 的延长线交于点G ．（1）求证：CDF BGF △∽△；（2）当点F 是BC 的中点时，过F 作EF CD ∥交AD 于点E ，若6cm 4cm AB EF ==，，求CD 的长．20．本题满分 8 分．“五·一”假期，梅河公司组织部分员工到A 、B 、C 三地旅游，公司购买前往各地的车票种类、数量绘制成条形统计图，如图9．根据统计图回答下列问题：（1）前往 A 地的车票有_____张，前往C 地的车票占全部车票的________%；（2）若公司决定采用随机抽取的方式把车票分配给 100 名员工，在看不到车票的条件下，每人抽取一张（所有车票的形状、大小、质地完全相同且充分洗匀），那么员工小王抽到去 B 地车票的概率为______；（3）若最后剩下一张车票时，员工小张、小李都想要，决定采用抛掷一枚各面分别标有数字1，2，3，4的正四面体骰子的方法来确定，具体规则是：“每人各抛掷一次，若小张掷得着地一面的数字比小李掷得着地一面的数字大，车票给小张，否则给小李．”试用“列表法或画树状图”的方法分析，这个规则对双方是否公平？21．本题满分 8 分．如图10，已知抛物线233y x x =+与x 轴的两个交点为A B 、，与y 轴交于点C ．（1）求A B C ，，三点的坐标；D C FE A BG 图8图9地点港中数学网（2）求证：ABC △是直角三角形；（3）若坐标平面内的点M ，使得以点M 和三点 A B C 、、为顶点的四边形是平行四边形，求点M 的坐标．（直接写出点的坐标，不必写求解过程）22．本题满分 10 分．如图 11，矩形ABCD 中，53AB AD ==，．点E 是CD 上的动点，以AE 为直径的O ⊙与AB 交于点F ，过点F 作FG BE ⊥于点G ．（1）当E 是CD 的中点时：①tan EAB ∠的值为______________； ② 证明：FG 是O ⊙的切线；（2）试探究：BE 能否与O ⊙相切?若能，求出此时DE 的长；若不能，请说明理由．23．本题满分 11 分．（提示：为了方便答题和评卷，建议在答题卡上画出你认为必须的图形）如图 12，已知直线L 过点(01)A ，和(10)B ，，P 是x 轴正半轴上的动点，OP 的垂直平分线交L 于点Q ，交x 轴于点M ．（1）直接写出直线L 的解析式；（2）设OP t =，OPQ △的面积为S ，求S 关于t 的函数关系式；并求出当02t <<时，S 的最大值；（3）直线1L 过点A 且与x 轴平行，问在1L 上是否存在点C ，使得CPQ △是以Q 为直角顶点的等腰直角三角形？若存在，求出点C 的坐标，并证明；若不存在，请说明理由．L 1xC B 图11 港中数学网2009年梅州市初中毕业生学业考试数学参考答案及评分意见一、选择题：每小题 3分，共 15 分．每小题给出四个答案，其中只有一个是正确的． 1．C 2．B 3．D 4．B 5．C 二、填空题：每小题 3分，共 24 分．6．a 7．63.610⨯ 8．40 9．4（1分），72（2分） 10．小张 11．12-12．50 13．7（1分），21n -（2分）三、解答下列各题：本题有 10 小题，共 81 分．解答应写出文字说明、推理过程或演算步骤．14．本题满分7分．（1）90 ···································································································································· 2分（2）30 ···································································································································· 4分······························································································································· 7分 15．本题满分 7 分．（1）3 ····································································································································· 2分（2）1 ····································································································································· 4分（3）15 ···································································································································· 7分 16．本题满分 7 分．解：112)4cos30|3-⎛⎫++- ⎪⎝⎭°．1342=++······································································································ 4分43=+-················································································································ 6分 4= ······································································································································ 7分17．本题满分 7 分．解：由11x x --≥得1x ≥， ······························································································ 2分由841x x +>-，得3x <． ······························································································ 4 分所以不等式组的解为：13x <≤， ···················································································· 6 分所以不等式组的整数解为：1，2． ······················································································· 7 分 18．本题满分 8 分．解：2224441x x x x x x x --+÷-+-2(2)(2)(1)(2)1x x x x x x x -+-=+÷-- ············································· 3分212x x +=+- 港中数学网22xx =- ··································································································································· 6分当32x =时，原式3226322⨯==--． ························································································ 8分 19．本题满分8 分．（1）证明：∵梯形ABCD ，AB CD ∥， ∴CDF FGB DCF GBF ∠=∠∠=∠，， ······················ 2 分∴CDF BGF △∽△． ···························· 3分（2）由（1）CDF BGF △∽△，又F 是BC 的中点，BF FC = ∴CDF BGF △≌△， ∴DF FG CD BG ==， ················································ 6分又∵EF CD ∥，AB CD ∥，∴EF AG ∥，得2EF BG AB BG ==+． ∴22462BG EF AB =-=⨯-=， ∴2cm CD BG ==． ··········································································································· 8分 20．本题满分 8 分．解：（1）30；20． ·············································································································· 2 分（2）12． ···························································································································· 4 分或画树状图如下：共有 16 种可能的结果，且每种的可能性相同，其中小张获得车票的结果有6种：（2，1），（3，1），（3，2），（4，1），（4，2），（4，3）， ∴小张获得车票的概率为63168P ==；则小李获得车票的概率为35188-=． ∴这个规则对小张、小李双方不公平． ························································ 8 分D C F EA BG19题图 1 2 3 4 1 1 2 3 4 2 1 2 3 4 3 1 2 3 4 4 开始小张小李港中数学网21．本题满分 8 分．（1）解：令0x =，得y =(0C ． ························································ 1分令0y =，得20x x ，解得1213x x =-=，， ∴(10)(30)A B -，，，． ·································································································· 3分（2）法一：证明：因为22214AC =+=，222231216BC AB =+==，， ························ 4分 ∴222AB AC BC =+， ··············································· 5分 ∴ABC △是直角三角形． ·········································· 6分法二：因为13OC OA OB ===，，∴2OC OA OB = ， ··············································································································· 4分 ∴OC OB OA OC=，又AOC COB ∠=∠， ∴Rt Rt AOC COB △∽△． ································································································ 5分 ∴90ACO OBC OCB OBC ∠=∠∠+∠=，°， ∴90ACO OCB ∠+∠=°，∴90ACB ∠=°，即ABC △是直角三角形． ····················································· 6 分（3）1(4M，2(4M -，3(2M ．（只写出一个给1分，写出2个，得1.5分） ····································································· 8分22．本题满分 10 分．（1）①65····································································· 2分②法一：在矩形ABCD 中，AD BC =，ADE BCE ∠=∠，又CE DE =， ∴ADE BCE △≌△， ················································ 3分得AE BE EAB EBA =∠=∠，，连OF ，则OF OA =， ∴OAF OFA ∠=∠， OFA EBA ∠=∠， ∴OF EB ∥， ·················································································· 4 分 ∵FG BE ⊥， ∴FG OF ⊥， ∴FG 是O ⊙的切线 ································································································· 6分（法二：提示：连EF DF ，，证四边形DFBE 是平行四边形．参照法一给分．）（2）法一：若BE 能与O ⊙相切， ∵AE 是O ⊙的直径， ∴AE BE ⊥，则90DEA BEC ∠+∠=°，又90EBC BEC ∠+∠=°， ∴DEA EBC ∠=∠，∴Rt Rt ADE ECB △∽△，22题图x21题图M 1 3 港中数学网∴AD DE EC BC =，设DE x =，则53EC x AD BC =-==，，得353xx =-，整理得2590x x -+=． ······································································································· 8 分 ∵242536110b ac -=-=-<， ∴该方程无实数根．∴点E 不存在，BE 不能与O ⊙相切． ·········································· 10分法二：若BE 能与O ⊙相切，因AE 是O ⊙的直径，则90AE BE AEB ∠=⊥，°，设DE x =，则5EC x =-，由勾股定理得：222AE EB AB +=，即22(9)[(5)9]25x x ++-+=，整理得2590x x -+=， ······································· 8分 ∵242536110b ac -=-=-<， ∴该方程无实数根．∴点E 不存在，BE 不能与O ⊙相切． ·········································· 10分（法三：本题可以通过判断以AB 为直径的圆与DC 是否有交点来求解，参照前一解法给分） 23．本题满分 11 分．（1）1y x =- ························································································································ 2分（2）∵OP t =，∴Q 点的横坐标为12t ， ①当1012t <<，即02t <<时，112QM t =-， ∴11122OPQ S t t ⎛⎫=- ⎪⎝⎭△． ······································································································ 3分 ②当2t ≥时，111122QM t t =-=-， ∴11122OPQ S t t ⎛⎫=- ⎪⎝⎭△． ∴1110222111 2.22t t t S t t t ⎧⎛⎫-<< ⎪⎪⎪⎝⎭=⎨⎛⎫⎪- ⎪⎪⎝⎭⎩，，，≥ ······························································································ 4分当1012t <<，即02t <<时，211111(1)2244S t t t ⎛⎫=-=--+ ⎪⎝⎭， ∴当1t =时，S 有最大值14． ······························································································ 6分（3）由1O A O B ==，所以OAB △是等腰直角三角形，若在1L 上存在点C ，使得CPQ△。

甘肃省定西市数学中考试题及答案

2009年甘肃省定西市中考数学试卷友情提示：1．抛物线2y ax bx c =++的顶点坐标是2424b ac b a a ⎛⎫-- ⎪⎝⎭，．2．弧长公式：π180n Rl =弧长；其中，n 为弧所对圆心角的度数，R 为圆的半径．本试卷满分为150分，考试时间为120分钟．一、选择题：本大题共10小题，每小题3分，共30分．每小题给出的四个选项中，只有一项是符合题目要求的，将此选项的代号填入题后的括号内． 1．4的相反数是（） A ．4B ．4-C ．14D ．14-2．图1所示的物体的左视图（从左面看得到的视图）是（）图１ A ． B ． C ． D ． 3．计算：a b a b b a a -⎛⎫-÷= ⎪⎝⎭（）A ．a bb +B ．a bb- C ．a ba- D ．a ba+ 4．在一个不透明的布袋中装有红色、白色玻璃球共40个，除颜色外其他完全相同．小明通过多次摸球试验后发现，其中摸到红色球的频率稳定在15％左右，则口袋中红色球可能有（） A ．4个 B ．6个 C ．34个 D ．36个5．下列图形中，既是轴对称图形，又是中心对称图形的是（） A ．等腰梯形 B ．平行四边形 C ．正三角形 D ．矩形6．有19位同学参加歌咏比赛，所得的分数互不相同，取得分前10位同学进入决赛．某同学知道自己的分数后，要判断自己能否进入决赛，他只需知道这19位同学成绩的（） A ．平均数 B ．中位数 C ．众数 D ．方差7．某人想沿着梯子爬上高4米的房顶，梯子的倾斜角（梯子与地面的夹角）不能大于60°，否则就有危险，那么梯子的长至少为（）A ．8米B ．C 米D 米 8．如图2，⊙O 的弦AB =6，M 是AB 上任意一点，且OM 最小值为4，则⊙O 的半径为（） A ．5 B ．4 C ．3 D ．29．如图3，小东用长为3.2m 的竹竿做测量工具测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点．此时，竹竿与这一点相距8m 、与旗杆相距22m ，则旗杆的高为（） A ．12m B ．10mC ．8mD ．7m图2 图3 图410．如图4，四边形ABCD 中，AB =BC ，∠ABC =∠CDA =90°，BE ⊥AD 于点E ，且四边形ABCD 的面积为8，则BE =（） A ．2B ．3C．D．二、填空题：本大题共8小题，每小题4分，共32分．把答案写在题中的横线上． 11．当31x y ==、时，代数式2()()x y x y y +-+的值是． 12．方程组25211x y x y -=-⎧⎨+=⎩，的解是．13．如图5，Rt △ACB 中，∠ACB =90°，DE ∥AB ，若∠BCE =30°，则∠A = ． 14．反比例函数的图象经过点P （2-，1），则这个函数的图象位于第象限． 15．不等式组103x x +>⎧⎨>-⎩，的解集是．16．如图6，四边形ABCD 是平行四边形，使它为矩形的条件可以是．图6 图7 图817．如图7，在△ABC 中，5cm AB AC ==，cos B 35=．如果⊙O，且经过点B 、C ，那么线段AO = cm ．18．抛物线2y x bx c =-++的部分图象如图8所示，请写出与其关系式、图象相关的2个正确结论：，．（对称轴方程，图象与x 正半轴、y 轴交点坐标例外）三、解答题（一）：本大题共5小题，共38分．解答时，应写出必要的文字说明、证明过程或演算步骤． 19．（6分）若20072008a =，20082009b =，试不用．．将分数化小数的方法比较a 、b 的大小．20．（6分）在实数范围内定义运算“⊕”，其法则为：22a b a b ⊕=-，求方程（4⊕3）⊕24x =的解．21．（8分）如图9，随机闭合开关S 1、S 2、S 3中的两个，求能让灯泡⊗发光的概率．22．（8分）图10（1）是一扇半开着的办公室门的照片，门框镶嵌在墙体中间，门是向室内开的．图10（2）画的是它的一个横断面．虚线表示门完全关好和开到最大限度（由于受到墙角的阻碍，再也开不动了）时的两种情形，这时二者的夹角为120°，从室内看门框露在外面部分的宽为4cm ，求室内露出的墙的厚度a 的值．（假设该门无论开到什么角度，门和门框之间基本都是无缝的．精确到0.1cm1.73）23．（10分）鞋子的“鞋码”和鞋长（cm ）存在一种换算关系，下表是几组“鞋码”与鞋长换算的对应数值：［注：“鞋码”是表示鞋子大小的一种号码］鞋长（cm ） 16 19 21 24 鞋码（号）22283238（1）设鞋长为x ，“鞋码”为y ，试判断点（x ，y ）在你学过的哪种函数的图象上？（2）求x 、y 之间的函数关系式；（3）如果某人穿44号“鞋码”的鞋，那么他的鞋长是多少？图9 图10（1）图10（2）四、解答题（二）：本大题共5小题，共50分（不含附加4分）．解答时，应写出必要的文字说明、证明过程或演算步骤． 24．（8分）为响应国家要求中小学生每天锻炼1小时的号召，某校开展了形式多样的体育运动活动，小明对某班同学参加锻炼的情况进行了统计，并绘制了下面的统计图11（1）和图11（2）．（1）请在图11（1）中将表示“乒乓球”项目的图形补充完整；（2）求扇形统计图11（2）中表示“足球”项目扇形圆心角的度数．25．（10分）去年5月12日，四川省汶川县发生了里氏8.0级大地震，兰州某中学师生自愿捐款，已知第一天捐款4800元，第二天捐款6000元，第二天捐款人数比第一天捐款人数多50人，且两天人均捐款数相等，那么两天共参加捐款的人数是多少？人均捐款多少元？ 26．（10分）图12中的粗线CD 表示某条公路的一段，其中AmB 是一段圆弧，AC 、BD 是线段，且AC 、BD 分别与圆弧AmB 相切于点A 、B ，线段AB =180m ，∠ABD =150°．（1）画出圆弧AmB 的圆心O ；（2）求A 到B 这段弧形公路的长．图11（1）图11（2）图1227．（10分）如图13，△ACB 和△ECD 都是等腰直角三角形，∠ACB =∠ECD =90°，D 为AB 边上一点，求证：（1）ACE BCD △≌△；（2）222AD DB DE +=．28．［12分+附加4分］如图14（1），抛物线22y x x k =-+与x 轴交于A 、B 两点，与y 轴交于点C （0，3-）．［图14（2）、图14（3）为解答备用图］（1）k = ，点A 的坐标为，点B 的坐标为；（2）设抛物线22y x x k =-+的顶点为M ，求四边形ABMC 的面积；（3）在x 轴下方的抛物线上是否存在一点D ，使四边形ABDC 的面积最大？若存在，请求出点D 的坐标；若不存在，请说明理由；（4）在抛物线22y x x k =-+上求点Q ，使△BCQ 是以BC 为直角边的直角三角形．附加题：如果你的全卷得分不足150分，则本题与28题附加的4分的得分将记入总分，但记入总分后全卷得分不得超过150分，超过按150分算． 29．（7分）本试卷第19题为：若20072008a =，20082009b =，试不用．．将分数化小数的方法比较a 、b 的大小．观察本题中数a 、b 的特征，以及你比较大小的过程，直接写出你发现的一个一般结论．图13图14（1）图14（2）图14（3）武威、金昌、定西、白银、酒泉、嘉峪关武威市2009年初中毕业、高中招生考试数学试卷参考答案与评分标准一、选择题：本大题共10小题，每小题3分，共30分．题号1 2 3 4 5 6 7 8 9 10 答案B D A B D B CAAC二、填空题：本大题共8小题，每小题4分，共32分． 11．9 12． 34x y =⎧⎨=⎩，13．60o 14．二、四15．1->x 16．答案不唯一，如AC =BD ，∠BAD =90o ，等 17． 518．答案不唯一．如：①c =3；②b +c =1；③c -3b =9；④b =-2；⑤抛物线的顶点为（-1，4），或二次函数的最大值为4；⑥方程-x 2+bx +c =0的两个根为-3，1；⑦y >0时，-3<x <1；或y <0时，x <-3或x >1；⑧当x >-1时，y 随x 的增大而减小；或当x <-1时，y 随x 的增大而增大．等等三、解答题（一）：本大题共5小题，共38分． 19．本小题满分6分解：∵ a =2007200920082009⨯⨯(20081)(20081)20082009-⨯+=⨯222008120082009-=⨯， ··························· 3分 b 2200820082009=⨯， ··············································································· 4分222200812008-<， ··········································································· 5分∴ a <b ． ································································································· 6分说明：求差通分作，参考此标准给分．若只写结论a <b ，给1分．20．本小题满分6分解：∵ 22a b a b ⊕=- ， ∴ 2222(43)(43)77x x x x ⊕⊕=-⊕=⊕=-． ·········· 3分 ∴ 22724x -=． ∴ 225x =． ······························································· 4分∴ 5x =±． ··························································································· 6分 21．本小题满分8分解：∵ 随机闭合开关1S 、2S 、3S 中的两个，共有3种情况：12S S ，13S S ，23S S ．能让灯泡发光的有13S S 、23S S 两种情况． ··························································· 4分 ∴ 能让灯泡发光的概率为23． ··································································· 8分 22．本小题满分8分解：从图中可以看出，在室内厚为a cm 的墙面、宽为4cm 的门框及开成120°的门之间构成了一个直角三角形，且其中有一个角为60°． ········ 3分从而 a =4×tan60° ······································· 6分.9(cm)． ····························· 8分即室内露出的墙的厚度约为6.9cm ． 23．本小题满分10分解：（1）一次函数． ······················································································· 2分（2）设y kx b =+． ·················································································· 3分由题意，得22162819k b k b =+⎧⎨=+⎩，．········································································· 5分解得210k b =⎧⎨=-⎩，． ······················································································· 7分∴210y x =-．（x 是一些不连续的值．一般情况下，x 取16、16.5、17、17.5、 (26)26.5、27等） ······················································································· 8分说明：只要求对k 、b 的值，不写最后一步不扣分．（3）44y =时，27x =．答：此人的鞋长为27cm ． ········································································ 10分说明：只要求对x =27cm ，不答不扣分．四、解答题（二）：本大题共5小题，共50分 (不含附加4分) ． 24．本小题满分8分解：（1）如图：···················· 4分（2）∵ 参加足球运动项目的学生占所有运动项目学生的比例为15=1050， ··········· 6分 ∴ 扇形统计图中表示“足球”项目扇形圆心角的度数为1360725⨯=． ··············· 8分 25．本小题满分10分解法1：设第一天捐款x 人，则第二天捐款（x +50）人， ········································ 1分由题意列方程x4800=506000+x ．······························································· 5分解得 x =200． ·························································································· 7分检验：当x =200时，x （x +50）≠0， ∴ x =200是原方程的解． ··········································································· 8分两天捐款人数x +（x +50）=450，人均捐款x4800=24（元）．答：两天共参加捐款的有450人，人均捐款24元． ······································· 10分说明：只要求对两天捐款人数为450，人均捐款为24元，不答不扣分．解法2：设人均捐款x 元， ··············································································· 1分由题意列方程6000x －4800x＝50 ． ························································· 5分解得 x =24． ···························································································· 7分以下略．26．本小题满分10分解：（1）如图，过A 作AO ⊥AC ，过B 作BO ⊥BD ，AO 与BO 相交于O ，O 即圆心． ··················································· 3分说明：若不写作法，必须保留作图痕迹．其它作法略．（2）∵ AO 、BO 都是圆弧AmB 的半径，O 是其圆心， ∴ ∠OBA =∠OAB =150°-90°=60°． ······························· 5分 ∴ △AOB 为等边三角形．∴ AO =BO =AB =180． ·············· 7分 ∴ π6018060π180AB ⨯⨯== (m)．O∴ A 到B 这段弧形公路的长为60πm ． ························································· 10分 27．本小题满分10分证明:（1） ∵ ACB ECD ∠=∠，∴ ACE ACD BCD ACD ∠+∠=∠+∠．即 ACE BCD ∠=∠． ········································ 2分∵ EC DC AC BC ==,， ∴ △ACE ≌△BCD ． ··········································· 4分（2）∵ ACB ∆是等腰直角三角形，∴ ︒=∠=∠45BAC B ． ······································ 5分 ∵ △ACE ≌△BCD ， ∴ ︒=∠=∠45CAE B ． ······· 6分 ∴ ︒=︒+︒=∠+∠=∠904545BAC CAE DAE ． ····································· 7分 ∴ 222DE AE AD =+． ······································································ 9分由（1）知AE =DB ，∴ 222AD DB DE +=． ····································································· 10分 28．本小题满分16分(含附加4分) 解：（1）3k =-， ························································· 1分A （-1，0）， ····················································· 2分B （3，0）． ······················································ 3分（2）如图14（1），抛物线的顶点为M （1，-4），连结OM ． ····························································· 4分则 △AOC 的面积=23，△MOC 的面积=23， △MOB 的面积=6，·············································· 5分 ∴ 四边形 ABMC 的面积=△AOC 的面积+△MOC 的面积+△MOB 的面积=9． ··································· 6分说明：也可过点M 作抛物线的对称轴，将四边形ABMC 的面积转化为求1个梯形与2个直角三角形面积的和．（3）如图14（2），设D （m ，322--m m ），连结OD ．则 0＜m ＜3，322--m m ＜0．且 △AOC 的面积=23，△DOC 的面积=m 23， △DOB 的面积=-23（322--m m ）， ···················································· 8分∴ 四边形 ABDC 的面积=△AOC 的面积+△DOC 的面积+△DOB 的面积=629232++-m m =875)23(232+--m ．········································································ 9分∴ 存在点D 315()24-，，使四边形ABDC 的面积最大为875． ························· 10分（4）有两种情况：图14（１）图14（2）图14（3）图14（4）A DB CE如图14（3），过点B 作BQ 1⊥BC ，交抛物线于点Q 1、交y 轴于点E ，连接Q 1C ． ∵ ∠CBO =45°，∴∠EBO =45°，BO =OE =3． ∴ 点E 的坐标为（0，3）．∴ 直线BE 的解析式为3y x =-+． ·························································· 12分由2323y x y x x =-+⎧⎨=--⎩，解得1125x y ，；ì=-ïïíï=ïî 2230.x y ，ì=ïïíï=ïî ∴ 点Q 1的坐标为（-2，5）． ··································································· 13分如图14（4），过点C 作CF ⊥CB ，交抛物线于点Q 2、交x 轴于点F ，连接BQ 2． ∵ ∠CBO =45°，∴∠CFB =45°，OF =OC =3． ∴ 点F 的坐标为（-3，0）．∴ 直线CF 的解析式为3y x =--． ·························································· 14分由2323y x y x x =--⎧⎨=--⎩，解得1103x y ，；ì=ïïíï=-ïî 2214x y ，．ì=ïïíï=-ïî ∴点Q 2的坐标为（1，-4）． ····································································· 15分综上，在抛物线上存在点Q 1（-2，5）、Q 2（1，-4），使△BCQ 1、△BCQ 2是以BC 为直角边的直角三角形． ··············································································· 16分说明：如图14（4），点Q 2即抛物线顶点M ，直接证明△BCM 为直角三角形同样得2分．附加题：如果你的全卷得分不足150分，则本题与28题附加的4分的得分将记入总分，但记入总分后全卷得分不得超过150分，超过按150分算． 29．本小题满分7分解：学生可能写出不同程度的一般的结论，由一般化程度不同得不同分．若m 、n 是任意正整数，且m ＞n ，则11n n m m +<+． ·········································· 4分若m 、n 是任意正实数，且m ＞n ，则11n n m m +<+． ·········································· 5分若m 、n 、r 是任意正整数，且m ＞n ；或m 、n 是任意正整数，r 是任意正实数，且m ＞n ，则n n rm m r+<+． ······················································································· 6分若m 、n 是任意正实数，r 是任意正整数，且m ＞n ；或m 、n 、r 是任意正实数，且m ＞n ，则n n rm m r+<+． ·············································································· 7分。

2009年定西市中考数学试卷答案

2．图1所示的物体的左视图（从左面看得到的视图）是（）图１A．B．C．D．3．计算：a b a b-⎛⎫-÷=⎪（）A ．12mB ．10m图2 图3 图410．如图4，四边形ABCD 中，AB =BC ，∠ABC =∠CDA °，BE ⊥AD 于点E ，且四边形ABCD 的面积为8，则（） A ．2B ．316．如图6，四边形ABCD 是平行四边形，使它为矩形的条件可以是图6 图7 图817．如图7，在△ABC 中，5cm AB AC ==，cos B 35=．如果⊙O 的半径为过点B 、C ，那么线段AO = cm ．图9）是一扇半开着的办公室门的照片，门框镶嵌在墙体中间，门是向室内图10（1）图10（2）cm）存在一种换算关系，下表是几组“鞋码”与鞋长四、解答题（二）：本大题共5小题，共50分（不含附加4分）．解答时，应写出必要的文字说明、证明过程或演算步骤． 24．（8分）为响应国家要求中小学生每天锻炼1小时的号召，某校开展了形式多样的体育运动活动，小明对某班同学参加锻炼的情况进行了统计，并绘制了下面的统计图11（1）和图11（2）．（1）请在图11（1）中将表示“乒乓球”项目的图形补充完整；（2）求扇形统计图11（2）中表示“足球”项目扇形圆心角的度数．25．（10分）去年5月12日，四川省汶川县发生了里氏8.0级大地震，兰州某中学师生自愿捐款，已知第一天捐款4800元，第二天捐款6000元，第二天捐款人数比第一天捐款人数多50人，且两天人均捐款数相等，那么两天共参加捐款的人数是多少？人均捐款多少元？ 26．（10分）图12中的粗线CD 表示某条公路的一段，其中AmB 是一段圆弧，AC 、BD 是线段，且AC 、BD 分别与圆弧AmB 相切于点A 、B ，线段AB =180m ，∠ABD =150°．（1）画出圆弧AmB 的圆心O ；（2）求A 到B 这段弧形公路的长．图11（1）图11（2）图12x轴交于A、B两点，与y附加题：如果你的全卷得分不足分，则本题与28题附加的分的得分将记入总分，但记入总分后全卷得分不得超过150分，超过按150分算．分）本试卷第19题为：若20072008=，20082009b=，试不用将分数化小数的方法比较图13图14（1）图14（2）图14（3）···································2分···································3分···································5分参加足球运动项目的学生占所有运动项目学生的比例为1=． ······36072O图14（１）··························6分图14（2）图14（3）。

2009年中考数学答案及评分标准

2009年来宾市初中毕业升学统一考试试题数学参考答案及评分标准一、填空题：本大题共10小题，每小题3分，共30分．1．－237； 2．10； 3．(x ＋2)(x －2)； 4．25； 5．⎩⎨⎧==11y x ； 6．x y 2-=；7．1.30×105； 8．65； 9．2； 10．答案不唯一，只要符合题意均给分．二、选择题：本大题共8小题，每小题3分，共24分．三、解答题：本大题共8小题，满分66分． 19．解：原式＝222919⨯+-+ …………4分（每对一个值给1分）＝1＋1＝2……………………5分20．解：设该镇这两年中财政净收入的平均年增长率为x ， ……………………1分依题意可得：5000(1＋x )2＝2×5000 ………………………………4分解得 21=+x ，或021<-=+x （舍去） ……………………5分∴%4.41414.012=≈-=x……………………………………6分答：该镇这两年中财政净收入的平均年增长率约为41.4﹪．…………7分21．解：（1）502；（2）23.71；（3）图略，值为150（图、值各1分）；（4）80—99．（每小题各2分）22．证明：∵四边形ABCD 是平行四边形∴CD ＝AB ，AD ＝CB ，∠DAB ＝∠BCD ……2分又∵△ADE 和△CBF 都是等边三角形 ∴DE ＝BF ，AE ＝CF∠DAE ＝∠BCF ＝60° ………………4分∵∠DCF ＝∠BCD －∠BCF ∠BAE ＝∠DAB －∠DAE ∴∠DCF ＝∠BAE……………………6分∴△DCF ≌△BAE （SAS ） ………………7分∴DF ＝BE∴四边形BEDF 是平行四边形． …………8分23．解：（1）见参考图 ……………………………3分（不用尺规作图，一律不给分。

对图（1）画出弧给1分，画出交点G 给1分，连AG 给1分；对图（2），画出弧AMG给1分，画出弧ANG 给1分，连AG 给1分）（2）设AD ＝x ，在Rt △ABD 中，∠ABD ＝45°∴BD ＝AD ＝x …………………………………4分 ∴CD ＝20－x …………………………………5分∵DC AD ACD =∠tan ，即xx -=2030tan…6分 ∴()3.71310132030tan 130tan 20≈-=+=+=x (米) …7分答：路灯A 离地面的高度AD 约是7.3米． …8分24．解：（1）∵DE 平分△ABC 的周长∴1221086=++=+AE AD ，即y ＋x ＝12 ……1分∴y 关于x 的函数关系式为：y ＝12－x （2≤x ≤6） ……3分（取值范围占1分）（2）过点D 作DF ⊥AC ，垂足为F ∵2221086=+，即222AB BC AC =+ ∴△ABC 是直角三角形，∠ACB ＝90° ………………4分∴AD DF AB BC A ==∠sin ，即x DF-=12108 ∴5448xDF -= ………………………………5分∴x x x x DF AE S 52452544821212+-=-⋅⋅=⋅⋅= …………6分（第24题图）F E DC BA（第22题图）DEFABC（第23题图(1)）（第23题图(2)）NM GD CBA AB CDFGE()5726522+--=x 故当x ＝6时，S 取得最大值572………………………………7分此时，y ＝12－6＝6，即AE ＝AD ．因此，△ADE 是等腰三角形． ……8分25．解：（1）∵BC 是⊙O 的弦，半径OE ⊥BC∴BE ＝CE…………………2分（2）连结OC∵CD 与⊙O 相切于点C∴∠OCD ＝90°………………………3分∴∠OCB ＋∠DCF ＝90° ∵∠D ＋∠DCF ＝90° ∴∠OCB ＝∠D………………………4分∵OB ＝OC ∴∠OCB ＝∠B ∵∠B ＝∠AEC ∴∠D ＝∠AEC………………………5分（3）在Rt △OCF 中，OC ＝5，CF ＝4∴3452222=-=-=CF OC OF…………6分∵∠COF ＝∠DOC ，∠OFC ＝∠OCD∴Rt △OCF ∽Rt △ODC ………………………………8分∴OFOCOC OD =，即3253522===OF OC OD …………9分 ∴3105325=-=-=OE OD DE ∴32043102121=⨯⨯=⋅⋅=∆CF DE S CDE…………10分注：本小题也可利用Rt △OCD ∽Rt △ACB 等，以及S △CDE ＝S △OCD －S △OCE 求解．26．解：（1）由题意可设抛物线的关系式为y ＝a (x －2)2－1…………1分因为点C （0，3）在抛物线上所以3＝a (0－2)2－1，即a ＝1…………………………2分所以，抛物线的关系式为y ＝(x －2)2－1＝x 2－4 x ＋3……3分（2）∵点M （x ，y 1），N （x ＋1，y 2）都在该抛物线上∴y 1－y 2＝（x 2－4 x ＋3）－[(x ＋1)2－4(x ＋1)＋3]＝3－2 x …………4分（第25题图）B当3－2 x ＞0，即23<x 时，y 1＞y 2 ………………………………5分当3－2 x ＝0，即23=x 时，y 1＝y 2………………………………6分当3－2 x ＜0，即23>x 时，y 1＜y 2………………………………7分（3）令y ＝0，即x 2－4 x ＋3＝0，得点A （3,0），B （1,0），线段AC 的中点为D （23,23）直线AC 的函数关系式为y ＝－x ＋3………………………………8分因为△OAC 是等腰直角三角形，所以，要使△DEF 与△OAC 相似，△DEF 也必须是等腰直角三角形．由于EF ∥OC ，因此∠DEF ＝45°，所以，在△DEF 中只可能以点D 、F 为直角顶点．①当F 为直角顶点时，DF ⊥EF ，此时△DEF ∽△ACO ，DF 所在直线为23=y 由23342=+-x x ，解得2104-=x ，32104>+=x （舍去） ……9分将2104-=x 代入y ＝－x ＋3，得点E （2104-，2102+） …………10分 ②当D 为直角顶点时，DF ⊥AC ，此时△DEF ∽△OAC ，由于点D 为线段AC 的中点，因此，DF 所在直线过原点O ，其关系式为y ＝x ．解x 2－4 x ＋3＝x ，得2135-=x ，32135>+=x （舍去） …………11分将2135-=x 代入y ＝－x ＋3，得点E （2135-，2131+） …………12分（第26题图⑴）（第26题图⑵）。

2009年中考数学试题参考答案

2009年中考数学试题参考答案一、选择题（每题3分，共30分）ADCBA BADCD二、填空题（每题3分，共18分）11、1 12、A B ⊥CD 或AD=BD 或AC =CB 等 13、y=2x 14、20 15、10+33 16、19 三、解答题（每小题8分，共16分）17、解：由（1）得 x >－2 ………………………… 2分由（2）得3x －1《2x －2 得x ≤－1 ………………………… 4分所以，不等式组的解集为－2〈x ≤－1……6分在数轴上表示为 ……………………… 8分 18.解：原式=()()2111x x x x x -+÷+ ……………………………… 2分 =()()1112-+∙+x x xxx …………………………… 4分=1-x x ………………………………………………… 6分当x=2时，1-x x =2122=- …………………………… 8分四、解答题（每小题9分，共18分）19、解：（1）作业完成时间在1.5 ～2小时时间段内的学生有6人 …… 2分（2）该班共有学生：40%4518=名 ………… 4分（3）（略） ………………………………………………… 6分（4）作业完成时间在0.5~1小时的部分对应的扇形圆心角的度数是： 360°×30％ = 108° ………………………………………9分20、解：（1）用列表法或数状图表示为：列表法…………………………5分树状图法(2)P(恰好选中女生甲和男生A)=61 ………………………………………………8分∴恰好选中女生甲和男生A 的概率为61……………………………………… 9分21、证明：（1）在□ABCD 中，AD=CB,AB=CD,∠D=∠B …………………………… 1分 ∵EF 分别是AB 、CD 的中点 ∴DF=21CD,BE=21AB , DF=BE ………………………………………3分∴△AFD ≌△CEB ………………………………………………4分 (2)在□ABCD 中，AB=CD,AB ∥CD ……………………………………6分由（1）得BE=DF ,∴AE=CF ………………………………………………7分 ∴四边形AECF 是平行四边形 ………………………………………8分22、解:∵点A(-3,1),B(2,n)是一次函和反比例函数的交点 ∴把x=-3，y=1代入y=xm ，得：m=-3∴反比例函数的解析式是y=- x3 …………………………………………3分把x=-3,y=n 代入y=-x3 得：n=-23把x=-3，y=1，x=2，y=-23分别代入y=kx+b得：⎪⎩⎪⎨⎧-=+=+-23213b k b k ，解得 ⎪⎩⎪⎨⎧-=-=2121b k ……………………………………4分 ∴一次函数的解析式为y=- 2121-x ……………………………………5分（3）过点A 作AE ⊥x 轴于点E ∴A 点的纵坐标为1，∴AE=1 由一次函数的解析式为y=- 2121-x得C 点的坐标为（0，-21）， ……………………………………6分∴OC=21在Rt △OCD 和Rt △EAD 中，∠COD=∠AED=90°,∠CDO=∠ADE∴Rt △OCD ∽Rt △EAD ……………………………………7分 ∴==COAE CDAD 2 ……………………………………8分23、(1)证明：连接OD, ∵OD=OA, ∴∠ODA=OAD ………………………………1分又∵DE 是⊙O 的切线，∴∠ODE=90°,OD ⊥DE ……………………………2分又∵DE ⊥EF, ∴OD ∥EF ……………………………………3分 ∴∠ODA=∠DAE, ∠DAE=∠OAD, ∴AD 平分∠CAE …………………………5分 (2)解：∵AC 是⊙O 的直径，∴∠ADC=90°………………………………6分由（1）知：∠ODA=∠DAE, ∠AED=∠ADC, ∴△ADC ∽△AED, ∴ADAC AEAD = ………………………………7分在Rt △ADE 中，DE=4,AE=2, ∴AD=25 ………………………………7分∴52252AC =,∴AC=10 ……………………………………8分∴⊙O 的半径为5 ……………………………………9分 24、解（1）∵抛物线与x 轴交于A(1,0),B(70)∴y=a （x-1）（x-7） ……………………………………1分又∴抛物线与y 轴交于C,且OA=7,则C 点的坐标为（7，0） ∴7=a （0-1）（0-7），7a=7， a=1 ……………2分∴抛物线的解析式为y=(x-1)(x-7)=782+-x x …………………………3分（2）∵E 点在抛物线上∴m=25-40+7，m=-8 …………4分 ∵直线y=kx+b 经过点C(0,7),E(5,-8)∴⎩⎨⎧-===8757k b 解得：k=-3，b=7 …………………………5分∴直线CE 的表达式是y=-3x+7 ……………………………………6分（3）设直线CE 于x 轴的交点为D 当y=0时，-3x+7=0，x=37∴D 点的坐标为（37，0） ……………………………………7分∴S=3531008)377(217)377(21==⨯-⨯+⨯-⨯=+∆∆BDE BDC S S …………8分(4)在抛物线上存在点P 使得△ABP 为等腰三角形 ………………………9分 ∵抛物线的顶点是满足条件的一个点除此之外，还有六个点理由如下： ∵AP=BP=103909322==+＞6分别以A 、B 为圆心，半径长为6画圆，分别与抛物线交于点B 、1P 、2P 、A 、3P 、4P 、5P 、6P ，除去A 、B 两点外，其余六个点为满足条件的点，…………11分∴一共有七个满足条件的点P ……………………………………12分。

甘肃省定西市中考数学试卷及答案

甘肃省定西市中考数学试卷及答案（本试卷满分为150分，考题时间为120分钟）A 卷（满分100分）一、选择题（本大题共10小题，每小题4分，共40分．每小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来．） 1．图中几何体的主视图是2．下列运算中，计算结果正确的是A ．x 2·x 3＝x 6B ．x 2n ÷x n －2＝x n ＋2C ．(2x 3)2＝4x 9D ．x 3＋x 3＝x3．如果两圆的半径分别为2和1，圆心距为3，那么能反映这两圆位置关系的图是4．多项式2a 2－4ab ＋2b 2分解因式的结果正确的是A ．2(a 2－2ab ＋b 2)B ．2a (a －2b )＋2b 2C ．2(a －b ) 2D ．(2a －2b ) 25．如图，将三角板的直角顶点放在两条平行线a 、b 中的直线b 上，如果∠1＝40°，则∠2的度数是 A ．30° B ．45° C ．40° D ．50°6．在a 2□4a □4的空格中，任意填上“＋”或“－”，在所得到的代数式中，可以构成完全平方式的概率是 A ．12 B ．13 C ．14 D ．1 7．将二次函数y ＝x 2－2x ＋3化为y ＝(x －h )2＋k 的形式，结果为A ．y ＝(x ＋1)2＋4B ．y ＝(x －1)2＋4C ．y ＝(x ＋1)2＋2D ．y ＝(x －1)2＋2 8．样本数据3、6、a 、4、2的平均数是5，则这个样本的方差是 A ．8B ．5C ．2 2D ．39．一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是 A ．13 B ．12 C ．34D ．1 10．如图，有一块矩形纸片ABCD ，AB ＝8，AD ＝6．将纸片折叠，使得AD 边落在AB 边上，折痕为AE ，再将△AED 沿DE 向右翻折，AE 与BC 的交点为F ，则CF 的长为a b 1C ． B ． A ．D ．正面A ．6B ．4C ．2D ．1二、填空题（本大题共8小题，每小题4分，共32分．只要求填写最后结果．） 11．计算8－12＝_ ▲ ． 12．若x ＋y ＝3，xy ＝1，则x 2＋y 2＝_ ▲ ．13．为了测量校园内一棵不可攀的树的高度，学校数学应用实践小组做了如下的探索：根据光的反射定律，利用一面镜子和皮尺，设计如图所示的测量方案：把镜子放在离树(AB )8.7m 的点E 处，然后观测考沿着直线BE 后退到点D ，这时恰好在镜子里看到树梢顶点A ，再用皮尺量得DE ＝2.7m ，观测者目高CD ＝1.6m ，则树高AB 约是_ ▲ ．（精确到0.1m ）14．如图（1），在宽为20m ，长为32m 的矩形耕地上修建同样宽的三条道路（横向与纵向垂直），把耕地分成若干小矩形块，作为小麦试验田国，假设试验田面积为570m 2，求道路宽为多少？设宽为x m ，从图（2）的思考方式出发列出的方程是_ ▲ ．15．如图，点A 、B 在数轴上，它们所对应的数分别是－4与2x ＋23x －5，且点A 、B 到原点的距离相等．则x ＝_ ▲ ．16．计算：sin 230°＋tan44°tan46°＋sin 260°＝_ ▲ ．17．抛物线y ＝－x 2＋bx ＋c 的部分图象如图所示，若函数y ＞0值时，则x 的取值范围是_▲ ．（1）（2）EB D CE18．如图，在梯形ABCD 中，AB ∥CD ，∠BAD ＝90°，AB ＝6，对角线AC 平分∠BAD ，点E 在AB 上，且AE ＝2（AE ＜AD ），点P 是AC 上的动点，则PE ＋PB 的最小值是_ ▲ ．三、解答题（本大题共3小题，其中19题9分，20题6分，21题13分，共28分．）解答时写出必要的文字说明及演算过程．19．本题共9分（其中第Ⅰ小题4分，第Ⅱ小题5分）Ⅰ．先化简(，再从－2、－1、0、1、2中选一个你认为适合的数作为x 的值代入求值．Ⅱ．已知l 1：直线y ＝－x ＋3和l 2：直线y ＝2x ，l 1与x 轴交点为A ．求：（1）l 1与l 2的交点坐标．（2）经过点A 且平行于l 2的直线的解析式20．已知，如图E 、F 是四边形ABCD 的对角线AC 上的两点，AF ＝CE ，DF ＝BE ，DF ∥BE ，四边形ABCD 是平行四边形吗？请说明理由．21．本题共13分（其中第Ⅰ小题6分，第Ⅱ小题7分）Ⅰ．爱养花的李先生为选择一个合适的时间去参观西安世界园艺博览会，他查阅了5月10日至16日是（星期一至星期日）每天的参观人数，得到图（1）、图（2）所示的统计图．其中图（1）是每天参观人数的统计图，图（2）是5月15日是（星期六）这一天上午、BAED F中午、下午和晚上四个时段参观人数的扇形统计图，请你根据统计图解答下面的问题：（1）5月10日至16日这一周中，参观人数最多的是日是_ ▲ ，有_ ▲ 万人，参观人数最少的是日是_ ▲ ，有_ ▲ 万人，中位数是_ ▲ ．（2）5月15日是（星期六）这一天，上午的参观人数比下午的参观人数多多少人？（精确到1万人）（3）如果李先生想尽可能选择参观人数较少的时间参观世园会，你认为选择什么时间较合适？Ⅱ．如图在等腰Rt △OBA 和Rt △BCD 中，∠OBA ＝∠BCD ＝90°，点A 和点C 都在双曲线y ＝4x（k ＞0）上，求点D 的坐标．B 卷（满分50分）四、解答题（本大题共50分，解答时写出必要的演算步骤过程及推理过程．） 22．（8分）如图，在平面直角坐标系中，O 为坐标原点，每个小方格的边长为1个单位长度．正方形ABCD 顶点都在格点上，其中，点A 的坐标为 (1，1)．（1）若将正方形ABCD 绕点A 顺时针方向旋转，点B 到达点B 1，点C 到达点C 1，点D 到达点D 1，求点B 1、C 1、D 1的坐标．（2）若线段AC 1的长度．．与点D 1的横坐标．．．的差．恰好是一元二次方程x 2＋ax ＋1＝0的一个根，求a 的值．第220题A BC D Ox y ABCD Oxyy ＝4x23．（10分）某校开展的一次动漫设计大赛，杨帆同学运用了数学知识进行了富有创意的图案设计，如图（1），他在边长为1的正方形ABCD 内作等边△BCE ，并与正方形的对角线交于点F 、G ，制作如图（2）的图标，请我计算一下图案中阴影图形的面积．24．（10分）某电脑公司各种品牌、型号的电脑价格如下表，育才中学要从甲、乙两种品牌电脑中各选择一种型号的电脑．（1）写出所有选购方案（利用树状图或列表方法表示）．如果各种选购方案被选中的可能性相同，那么A 型号电脑被选中的概率是多少？（2）该中学预计购买甲、乙两种品牌电脑共36台，其中甲品牌电脑只选了A 型号，学校规定购买费用不能高于10万元，又不低于9.2万元，问购买A 型号电脑可以是多少台？甲乙型号 ABCDE单价（元/台）6000400025005000200025．（10分）在△ABC 中，AB ＝AC ，点O 是△ABC 的外心，连接AO 并延长交BC 于D ，交△ABC的外接圆于E ，过点B 作⊙O 的切线交AO 的延长线于Q ，设OQ ＝92，BQ ＝32．（1）求⊙O 的半径；（2）若DE ＝35，求四边形ACEB 的周长．26．（10分）在梯形OABC 中，CB ∥OA ，∠AOC ＝60°，∠OAB ＝90°，OC ＝2，BC ＝4，以点O为原点，OA 所在的直线为x 轴，建立平面直角坐标系，另有一边长为2的等边△DEF ，DE 在x 轴上（如图（1）），如果让△DEF 以每秒1个单位的速度向左作匀速直线运动，开始时点D 与点A 重合，当点D 到达坐标原点时运动停止．（1）设△DEF 运动时间为t ，△DEF 与梯形OABC 重叠部分的面积为S ，求S 关于t 的函数关系式．（2）探究：在△DEF 运动过程中，如果射线DF 交经过O 、C 、B 三点的抛物线于点G ，是否存在这样的时刻t ，使得△OAG 的面积与梯形OABC 的面积相等？若存在，求出t 的值；若不存在，请说明理由．A B C QED OA B CDE GF O (1)AD E GF (2)数学试题参照答案及评分标准A卷（满分100分）一、选择题（满分40分）评分标准：答对一题得4分，不答或答错均得0分1．D 2.B 3.B 4.C 5.D 6.A 7.D 8.A 9.B10.C二、填空题（满分32分）评分标准：在每小题后的横线上填上最终结果，答对一题得4分，不答或答错和不是最终结果均得0分.11．7 13．5.2 14．(322)(2)570x x x--= 15．112.25或16．2 17．31x-<< 18．三、解答题（满分28分）19．Ⅰ.原式=2(1)(1)1x x xx--++·21xx-.=11x+·(1)(1)x xx+-=1xx-当2x=-时，原式=32（或当x==22）Ⅱ.解：（1）设直线1l与2l的交点为M，则由32y xy x=-+⎧⎨=⎩解得1,2.x y =⎧⎨=⎩∴(12)M ，.(2)设经过点A 且平行于2l 的直线的解析式为2.y x b =+ ∵直线1l 与x 轴的交点(30)A ， ∴60b +=， ∴ 6.b =-则：所求直线的解析式为2 6.y x =-20.解：结论：四边形ABCD 是平行四边形. 证明：∵DF ∥BE . ∴∠AFD =∠CEB .又∵AF CE DF BE ==，， ∴△AFD ≌△CEB （SAS ）. ∴AD CB =，∠DAF =∠BCE . ∴AD ∥CB .∴四边形ABCD 是平行四边形.说明：其它证法可参照上面的评分标准评分.21.Ⅰ.①15，34；10，16；22万； ②34(74%-6%)≈23（万人）③答案不唯一，只要符合题意均可得分. Ⅱ．解：点A 在双曲线4y x=上，且在△OBA 中，AB OB =，∠90OBA =°则4OB AB =. ∴2AB OB ==过点C 作CE ⊥x 轴于E CF ，⊥y 轴于F .设BE x =. 由在BCD △中90BC CD BCD ==，∠°.则CE x =. 又点C 在双曲线4y x=上 (2) 4.x x ∴+=解得10x x =>，，1.21)x OD ∴=∴=+=∴点D ．B 卷（满分50分）四、解答题（本大题共50分，解答时写出必要的演算步骤及推理过程）22.解：（1）由已知111(21)(40)(32)B C D -，，，，，（2）由勾股定理得：AC =则3)是方程210x ax ++=的一根，设另一根为0x ，则0x 3)=1.03x ==3)3)]a ∴=-+=-另解：23)3)10a a ++==，23.解：连接FG 并延长交AB 于M AC ，于N ， BCE △和四边形ABCD 分别是正三角形和正方形..4530MN AB MN CD BAC ABE ∴⊥⊥=︒=︒，∠，∠∴设MF x =，则 1.x +=122.BCE ABF x S S S S ∴==∴--△△阴影正方形=112==另解：14BCDF S S S =-阴影正方形四边形1111()(12)4222264=---⨯-=24.解：（1）树状图如下：共有6种选购方案：(,)A D 、（B ，D ）、（C ，D ）、（A ，E ）、（B ，E ）、（C ，E ）.1(.3P A 型号被选中)=（2）设购买A 型号x 台，由（1）知当选用方案(,)A D 时：由已知9200060005000(36)100000x x +-≤≤得8880x --≤≤，不符合题意.当选用方案()A E ，时，由已知：9200060002000(36)100000x x +-≤≤ 得57.x ≤≤答：购买A 型号电脑可以是5台，6台或7台. 25.（1）连接OB BQ ，切O 于B ..OB BQ ∴⊥在Rt OBQ △中，92OQ BQ ==，32OB ∴==．即O 的半径是32.（2）延长BO 交AC 于F .AB BC =则.AB BC BF AC =∴⊥，又AE 是O 的直径，90ACE ABE ∴==︒∠∠．BF CE ∴∥（另解：DBF OBA OAB DCE =∠=∠=∠∠） ..33521.3325BOD CED BO ODCE DEDE BO CE OD ∴∴=⨯∴===-△∽△∴在Rt ACE △中，3,1AE CE ==，则AC =又O 是AE 的中点，1122OF CF ∴==，则 2.BF = ∴在Rt ABF △中，12AF AC ==AB ∴=在Rt ABE △，BE =（如用ABQ BEQ △∽△及解Rt ABE △得AB BE ，，计算正确也得分）故：四边形ACEB的周长是：1+26.解：（1）DEF △是边长为2OABC 中，2460OC BC COA AB x ===︒⊥，，∠，轴5,OA AB ∴==依题意：①当201t <≤时 ②222122)(2)422t S t t <<=--=--+时，③当25t S =≤≤时（2）由已知点(00)(1(5O C B ，，，设过点O 、C 、B 的抛物线的解析式为2.y ax bx =+则255a b a b =+=+，，解得5a b ⎧=-⎪⎪⎨⎪=⎪⎩∴该抛物线的解析式为：255y x x =-+. ∴若存在点G ，使得DCA OABC S S =△梯形；此时，设点G 的坐标为2().55x x x -+，射线DF 与抛物线的交点在x 轴上方.2115()(54)22x ∴⨯⨯=⨯+化简得2690x x -+=，解得 3.x =则此时点(3G GH x ⊥，作轴于H ，则9cot 605DH GH =︒== ∴此时9192)55t =+=(秒故：存在时刻195t =（秒）时，OAG △与梯形OABC 的面积相等.。

2009中考数学题及答案

2009年大连市中考数学试题与参考答案注意事项：1．请将答案写在答题卡上，写在试卷上无效． 2．本试卷满分150分，考试时间120分钟．一、选择题(在每小题给出的四个选项中，只有一个正确答案．本大题共有8小题，每小题3分，共24分) 1．|－3|等于 ( )A ．3B ．－3C ．31D ．－31 2．下列运算正确的是 ( )A ．523x x x =+ B ．x x x =-23C ．623x x x =⋅ D ．x x x =÷233．函数2-=x y 中，自变量x 的取值范围是 ( )A ．x < 2B ．x ≤2C ．x > 2D ．x ≥24．将一张等边三角形纸片按图1－①所示的方式对折，再按图1－②所示的虚线剪去一个小三角形，将余下纸片展开得到的图案是 ( )5．下列的调查中，选取的样本具有代表性的有 ( )A ．为了解某地区居民的防火意识，对该地区的初中生进行调查B ．为了解某校1200名学生的视力情况，随机抽取该校120名学生进行调查C ．为了解某商场的平均晶营业额，选在周末进行调查D ．为了解全校学生课外小组的活动情况，对该校的男生进行调查6．如图，等腰梯形ABCD 中，AD ∥BC ，AE ∥DC ，∠AEB =60°， AB = AD = 2cm ，则梯形ABCD 的周长为 ( ) A ．6cm B ．8cm C ．10cm D ．12cm 7．下列四个点中，有三个点在同一反比例函数xky =的图象上，则不在这个函数图象上的点是 ( ) A ．(5，1) B ．(－1，5) C ．(35，3) D ．(－3，35-)8．图3是一个几何体的三视图，其中主视图、左视图都是腰为13cm ，底为10cm 的等腰三角形，则这个几何的侧面积是 ( )A ．60πcm 2B ．65πcm 2C ．70πcm 2D ．75πcm 2图1②①DCBA 图2俯视图左视图主视图图3DC BA二、填空题(本题共有9小题，每小题3分，共27分)9．某天最低气温是－5℃，最高气温比最低气温高8℃，则这天的最高气温是_________℃． 10．计算)13)(13(-+=___________．11．如图4，直线a ∥b ，∠1 = 70°，则∠2 = __________．12．如图5，某游乐场内滑梯的滑板与地面所成的角∠A = 35°，滑梯的高度BC = 2米，则滑板AB 的长约为_________米(精确到0.1)．13．在某智力竞赛中，小明对一道四选一的选择题所涉及的知识完全不懂，只能靠猜测得出结果，则他答对这道题的概率是_______________．14．若⊙O 1和⊙O 2外切，O 1O 2 = 10cm ，⊙O 1半径为3cm ，则⊙O 2半径为___________cm ．15．图6是某班为贫困地区捐书情况的条形统计图，则这个班平均每名学生捐书_____________册． 16．图7是一次函数b kx y +=的图象，则关于x 的不等式0>+b kx 的解集为_________________．17．如图8，原点O 是△ABC 和△A ′B ′C ′的位似中心，点A (1，0)与点A ′(－2，0)是对应点，△ABC 的面积是23，则△A ′B ′C ′的面积是________________．三、解答题(本题共有3小题，18题、19题、20题各12分，共36分) 18．如图9，在△ABC 和△DEF 中，AB = DE ，BE = CF ，∠B =∠1．求证：AC = DF (要求：写出证明过程中的重要依据)21c b a 图 4CBA 图 5 491017201510554320人数册数图 6 O y x -24图 7 A C B A′123-1-2-3-4-3-2-14321O y x 图 8 1F E DCBA19．某地区林业局要考察一种树苗移植的成活率，对该地区这种树苗移植成活情况进行调查统计，并绘制了如图10所示的统计表，根据统计图提供的信息解决下列问题：⑴这种树苗成活的频率稳定在_________，成活的概率估计值为_______________． ⑵该地区已经移植这种树苗5万棵． ①估计这种树苗成活___________万棵；②如果该地区计划成活18万棵这种树苗，那么还需移植这种树苗约多少万棵？20．甲、乙两车间生产同一种零件，乙车间比甲车间平均每小时多生产30个，甲车间生产600个零件与乙车间生产900个零件所用时间相等，设甲车间平均每小时生产x 个零件，请按要求解决下列问题： ⑴根据题意，填写下表：车间零件总个数平均每小时生产零件个数所用时间甲车间 600xx600乙车间900________⑵甲、乙两车间平均每小时各生产多少个零件？四、解答题(本题3小题，其中21、22题各9分，23题10分，共28分) 21．如图11，在⊙O 中，AB 是直径，AD 是弦，∠ADE = 60°， ∠C = 30°．⑴判断直线CD 是否是⊙O 的切线，并说明理由； ⑵若CD = 33 ，求BC 的长．图 10 0成活的概率移植数量/千棵10.90.8108642E DCBA O图 1122．如图12，直线2--=x y 交x 轴于点A ，交y 轴于点B ，抛物线c bx ax y ++=2的顶点为A ，且经过点B ． ⑴求该抛物线的解析式； ⑵若点C(m ，29-)在抛物线上，求m 的值．23．A 、B 两地的路程为16千米，往返于两地的公交车单程运行40分钟．某日甲车比乙车早20分钟从A 地出发，到达B 地后立即返回，乙车出发20分钟后因故停车10分钟，随后按原速继续行驶，并与返回途中的甲车相遇．图13是乙车距A 地的路程y (千米)与所用时间x (分)的函数图象的一部分(假设两车都匀速行驶)． ⑴请在图13中画出甲车在这次往返中，距A 地的路程y (千米)与时间x (分)的函数图象； ⑵乙车出发多长时间两车相遇？五、解答题（本题共有3小题，其中24题11分，25、26题各12分，共25分）24．如图14，矩形ABCD 中，AB = 6cm ，AD = 3cm ，点E 在边DC 上，且DE = 4cm ．动点P 从点A 开始沿着A →B →C →E 的路线以2cm/s 的速度移动，动点Q 从点A 开始沿着AE 以1cm/s 的速度移动，当点Q 移动到点E 时，点P 停止移动．若点P 、Q 同时从点A 同时出发，设点Q 移动时间为t (s)，P 、Q 两点运动路线与线段PQ 围成的图形面积为S (cm2)，求S 与t 的函数关系式．25．如图15，在△ABC 和△PQD 中，AC = k BC ，DP = k DQ ，∠C =∠PDQ ，D 、E 分别是AB 、AC 的中点，点P 在直线BC 上，连结EQ 交PC 于点H ．PQE D CB A 图 14 y/千米16O -2080604020x/分图 13 yx O B A 图 12猜想线段EH 与AC 的数量关系，并证明你的猜想．26．如图18，抛物线F ：c bx ax y ++=2的顶点为P ，抛物线：与y 轴交于点A ，与直线OP 交于点B ．过点P 作PD ⊥x 轴于点D ，平移抛物线F 使其经过点A 、D 得到抛物线F ′：'+'+'=c x b x a y 2，抛物线F ′与x 轴的另一个交点为C ．⑴当a = 1，b =－2，c = 3时，求点C 的坐标(直接写出答案)； ⑵若a 、b 、c 满足了ac b 22=①求b ：b ′的值；②探究四边形OABC 的形状，并说明理由．Q(H)EDCQAB CDEPH H Q P ED CB A B(P)A图 15 图 16图 17yxO P DC BA图 18大连市2009年初中升学考试评分标准与参考答案一、选择题1． A 2．D 3．D 4．A 5．B 6．C 7．B 8．B 二、填空题9．3 10．2 11．110° 12．3.5 13．4114．7 15．3 16．2->x 17．6 三、解答题18．证明：∵BE=CF ， ∴BE+EC=CF+EC ，即 B C =E F ． ………………………………………………………………………………2分在△ABC 和△DEF 中，314AB DE B BC EF =⎧⎪∠=∠⎨⎪=⎩，分，分． ∴△A B C ≌△D E F …………………………………………………………………………6分（S A S ）． ……………………………………………………………………………………8分 ∴A C =D F …………………………………………………………………………………10分（全等三角形对应边相等）． ……………………………………………………………12分 19．解：（1）0.9，……………………………………………………………………………2分 0.9； ………………………………………………………………………………………5分（2） ①4.5；…………………………………………………………………………………8分 ②方法1:18÷0.9-5 …………………………………………………………………………………10分 =15．…………………………………………………………………………………………11分方法2：设还需移植这种树苗x 万棵．根据题意，得189.0)5(=⨯+x ，…………………………………………………………10分解得15=x ． ………………………………………………………………………………11分答：该地区需移植这种树苗约15万棵． ………………………………………………12分 20．解：（1） 30+x ， ……………………………………………………………………2分 3900+x ；………………………………………………………………………………………4分（2）根据题意，得30900600+=x x ，..................................................................7分解得 60=x ． (9)分 9030=+x ． …………………………………………………………………10分经检验60=x 是原方程的解，且都符合题意．………………………………………11分答：甲车间每小时生产60个零件，乙车间每小时生产90个零件．…………………12分 21．（1）C D 是⊙O 的切线． …………………………………………………………………1分证明：连接OD ．∵∠A D E =60°，∠C =30°，∴∠A =30°． ............................................................2分 ∵O A =O D ，∴∠O D A =∠A =30°． (3)分∴∠O D E =∠O D A +∠A D E =30°+60°=90°，∴O D ⊥C D ．…………………………………4分 ∴C D 是⊙O 的切线． ……………………………………………………………………5分（2）解：在Rt △ODC 中，∠ODC =90°， ∠C =30°， CD =33．∵t a n C =CDOD， …………………………………………………………………………6分 ∴O D =C D ·t a n C =33×33=3． (7)分 ∴O C =2O D =6．…………………………………………………………………………8分 ∵O B =O D =3，∴B C =O C -O B =6-3=3．………………………………………………9分22．解：（1）直线2--=x y ．令2,0-==y x 则，∴点B 坐标为（0，-2）．………………………………………………1分令2,0-==x y 则 ∴点A 坐标为（-2，0）． ………………………………………………2分设抛物线解析式为k h x a y +-=2)(． ∵抛物线顶点为A ，且经过点B ，∴2)2(+=x a y ，………………………………………………………………………4分∴-2=4a ，∴21-=a ．…………………………………………………………………5分 ∴抛物线解析式为2)2(21+-=x y ，…………………………………………………5分∴22212---=x x y ．………………………………………………………………6分（2）方法1：∵点C （m ，29-）在抛物线2)2(21+-=x y 上，∴29)2(212-=+-m ，9)2(2=+m ，………………………………………………7分解得11=m ，52-=m ．……………………………………………………………9分方法2：∵点C （m ，29-）在抛物线22212---=x x y 上，∴22212---m m 29-=，∴,0542=-+m m (7)分解得11=m ，52-=m ．……………………………………………………………9分 23．解：（1）画出点P 、M 、N （每点得1分）……………………………………3分（2）方法1．设直线EF 的解析式为11b x k y +=．根据题意知，E （30，8），F （50，16），⎪⎩⎪⎨⎧+=+=分分5.1150164,11308 b k b k 解得⎪⎩⎪⎨⎧-==.4,5211b k ∴452-=x y ．①……………………………………………………………6分设直线MN 的解析式为22b x k y +=．根据题意知，M （20，16），N （60，0），∴⎩⎨⎧+=+=分分8.6007,20162222 b k b k 解得⎪⎩⎪⎨⎧=-=.24,5222b k ∴2452+-=x y ．②………………………………………………………9分由①、②得方程452-x 2452+-=x ，解得x =35． ……………………………………（10分）答：乙车出发35分钟两车相遇． ………………………………………………………10分方法2．公交车的速度为16÷40=52（千米/分）． …………………………………………………4分设乙车出发x 分钟两车相遇． ……………………………………………………………5分根据题意，得32)20(52)10(52=++-x x ，………………………………………………8分解得x =35． …………………………………………………………………………………9分答：乙车出发35分钟两车相遇． ………………………………………………………10分方法3．公交车的速度为16÷40=52（千米/分）． …………………………………………………4分设乙车出发x 分钟两车相遇． ……………………………………………………………5分根据题意，得16)20(52)10(52=-+-x x ，………………………………………………8分解得x =35． …………………………………………………………………………………9分答：乙车出发35分钟两车相遇． ………………………………………………………10分方法4．由题意知：M （20，16），F （50，16），C （10，0），∵△DMF ∽△DNC ，∴DHDICN MF =∴DHDH -=165030，∴DH =10； ∵△CDH ∽△CFG ，∴CGCH FG DH =，∴25164010=⨯=CH ； ∴OH =OC +CH =10+25=35．答：乙车出发35分钟两车相遇． …………………………………………………………10分24．解：在R t △A D E 中，.5432222=+=+=DE AD AE …………………………1分当0＜t ≤3时，如图1． ……………………………………………………………………2分过点Q 作QM ⊥AB 于M ，连接QP ． ∵AB ∥CD ， ∴∠QAM =∠DEA ，又∵∠AMQ =∠D =90°， ∴△AQM ∽△EAD ．∴AEAQAD QM =，∴t AE AQ AD QM 53=⋅=．……………………………………………………3分 .5353221212t t t QM AP S =⨯⨯=⋅= (4)分当3＜t ≤29时，如图2． (5)分方法1 ：在Rt △ADE 中，.5432222=+=+=DE AD AE过点Q 作QM ⊥AB 于M ， QN ⊥BC 于N ，连接QB ． ∵AB ∥CD ， ∴∠QAM =∠DEA ，又∵∠AMQ =∠ADE =90°， ∴△AQM ∽△EAD ． ∴AE AQ AD QM =， AEAQ DE AM =， ∴t AE AQ AD QM 53=⋅=．………………………………………………………………………6分t AE AQ DE AM 54=⋅=，∴Q N =t AM BM 5466-=-=．…………………………………7分∴QAB S ∆,595362121t t QM AB =⨯⨯=⋅=QBP S ∆.1854254)546)(62(21212-+-=--=⋅=t t t t QN BP∴QBP QAB S S S ∆∆+=t 59=+（18542542-+-t t ）.18551542-+-=t t ……………………8分方法2 ：过点Q 作QM ⊥AB 于M ， QN ⊥BC 于N ，连接QB ． ∵AB ∥BC ， ∴∠QAM =∠DEA ，又∵∠AMQ =∠ADE =90°，∴△AQM ∽△EAD ． ∴AE AQ AD QM =， AEAQ DE AM =， ∴t AE AQ AD QM 53=⋅=．………………………………………………………………………6分t AE AQ DE AM 54=⋅=，∴Q N =t AM BM 5466-=-=．…………………………………7分∴.256535421212t t t QM AM S AMQ =⨯⨯=⋅=∆.185512526)546)(5362(21)(212-+-=-+-=⋅+=t t t t t BM QM BP S BPQM 梯∴BPQM AMQ S S S 梯+=∆2256t =+（1855125262-+-t t ）.18551542-+-=t t ……………8分当29＜t ≤5时．方法1 ：过点Q 作QH ⊥CD 于H ．如图3．由题意得QH ∥AD ，∴△EHQ ∽△EDA ，∴,AEQEAD QH = ∴).5(53t AE QE AD QH -=⋅=…………………………………………………………………10分 ∴,123)62(21)(21=⨯+=⋅+=BC AB EC S ABCE 梯,233106353)5(53)211(21212+-=-⨯-=⋅=∆t t t t QH EP S EQP∴EQP ABCE S S S ∆-=梯12=2331063532-+-t t .291063532-+-=t t ………………………11分方法2：连接QB 、QC ，过点Q 分别作QH ⊥DC 于H ，QM ⊥AB 于M ，QN ⊥BC 于N ．如图4．由题意得QH ∥AD ，∴△EHQ ∽△EDA ，∴,AEQEAD QH =∴).5(53t AE QE AD QH -=⋅=…………………………………………………………………10分∴.595362121t t QN AB S QAB =⨯⨯=⋅=∆.569)546(32121t t QN BC S QBC -=-⨯=⋅=∆.227105753)533)(92(21212-+-=--=⋅=∆t t t t QH PC S QCP∴QCP QBC QAB S S S S ∆∆∆++=t 59=)569(t -+)227105753(2-+-+t t .291063532-+-=t t ………………………………11分 25．结论：E H =21A C ． (1)分证明：取B C 边中点F ，连接D E 、D F ． ……………………………………………………2分∵D 、E 、F 分别是边AB 、AC 、BC 的中点．∴DE ∥BC 且DE =21BC ，D F ∥A C 且D F =21A C ， (4)分EC =21AC ∴四边形DFCE 是平行四边形．∴∠EDF=∠C ．∵∠C =∠P D Q ，∴∠P D Q =∠E D F ， ∴∠P D F =∠Q D E ．…………………………6分又∵AC=kBC ，∴DF=kDE ． ∵D P =k D Q ，∴k DEDFDQ DP ==．……………………………………………………………7分 ∴△PDF ∽△QDE ． …………………………………………………………………………8分∴∠D E Q =∠D F P ． ……………………………………………………………………………9分又∵DE ∥BC ，DF ∥AC ， ∴∠DEQ=∠EHC ，∠DFP=∠C ．∴∠C =∠E H C ． ……………………………………………………………………………10分∴E H =E C ． (11)分 ∴E H =21A C ． (12)分选图16．结论：E H =21A C ． (1)分证明：取B C 边中点F ，连接D E 、D F ． ……………………………………………2分∵D 、E 、F 分别是边AB 、AC 、BC 的中点，∴D E ∥B C 且D E =21B C ， D F ∥A C 且D F =21A C ， (4)分EC=21AC ，∴四边形DFCE 是平行四边形．∴∠EDF=∠C ．∵∠C =∠P D Q ，∴∠P D Q =∠E D F ， ∴∠P D F =∠Q D E ． ……………………………6分又∵A C =B C ， ∴D E =D F ，∵P D =Q D ，∴△P D F ≌△Q D E ． ……………………………7分∴∠DEQ=∠DFP ．∵DE ∥BC ，DF ∥AC ， ∴∠DEQ=∠EHC ，∠DFP=∠C ．∴∠C =∠E H C .............................................................................................8分 ∴E H =E C ． (9)分 ∴E H =21A C ． (10)分选图17．结论： E H =21A C ． (1)分证明：连接A H ． ………………………………………………………………………………2分 ∵D 是AB 中点，∴DA=DB ．又∵DB=DQ ，∴DQ=DP=AD ．∴∠DBQ=∠DQB ，．∵∠DBQ+∠DQB+∠DQA+∠DAQ ，=180°，∴∠AQB=90°，∴AH ⊥BC ．……………………………………………………………………………………4分又∵E 是A C 中点，∴H E =21A C ． ……………………………………………………6分 26．解：（1） C （3，0）；……………………………………………………………………3分（2）①抛物线c bx ax y ++=2，令x =0，则y =c ， ∴A 点坐标（0，c ）．∵ac b 22=，∴ 242424442ca ac a ac ac ab ac ==-=-，∴点P 的坐标为（2,2ca b -）． ……………………………………………………4分∵P D ⊥x 轴于D ，∴点D 的坐标为（0,2ab-）． ……………………………………5分根据题意，得a=a ′，c= c ′，∴抛物线F ′的解析式为c x b ax y ++='2．又∵抛物线F ′经过点D （0,2a b-），∴c a b b ab a +-+⨯=)2('4022．……………6分∴ac bb b 4'202+-=．又∵ac b 22=，∴'2302bb b -=．∴b :b ′=32．…………………………………………………………………………………7分 ②由①得，抛物线F ′为c bx ax y ++=232．令y =0，则0232=++c bx ax ．………………………………………………………………8分∴abx a b x -=-=21,2．∵点D 的横坐标为,2a b -∴点C 的坐标为（0,ab-）． ……………………………………9分设直线OP 的解析式为kx y =．∵点P 的坐标为（2,2ca b -）， ∴k a b c 22-=，∴22222b b b b ac b ac k -=-=-=-=，∴x b y 2-=．………………………10分 ∵点B 是抛物线F 与直线OP 的交点，∴x bc bx ax 22-=++．∴abx a b x -=-=21,2．∵点P 的横坐标为a b 2-，∴点B 的横坐标为ab-．把a b x -=代入x b y 2-=，得c a aca b a b b y ===--=222)(22．∴点B 的坐标为),(c ab-．…………………………………………………………………11分∴BC ∥OA ，AB ∥OC ．（或BC ∥OA ，BC =OA ）， ∴四边形OABC 是平行四边形．又∵∠AOC =90°，∴四边形OABC 是矩形． ………………………………………………12分。

2009年中考数学试题汇编之1-有理数试题及答案

全国免费客户服务电话：400-715-6688地址：西安经济技术开发区凤城一路8号御道华城A 座10层2009年中考试题专题之1-有理数试题及答案一、选择题1．(2009年福建省泉州市)计算：=-0)5(（）． A ．1 B ．0 C ．-1 D ．-5 【答案】A2．(2009年梅州市)12-的倒数为（） A ．12B ．2C ．2-D ．1-【答案】C3．(2009年抚顺市)某市在一次扶贫助残活动中，共捐款2580000元．将2580000元用科学记数法表示为（）A ．72.5810⨯元 B ．70.25810⨯元 C ．62.5810⨯元 D ．625.810⨯元【答案】C4．(2009年抚顺市)2-的相反数是（） A ．2 B ．12- C ．2- D ．12【答案】A5．（2009年绵阳市）2009年初甲型H1N1流感在墨西哥暴发并在全球蔓延，我们应通过注意个人卫生加强防范．研究表明，甲型H1N1流感球形病毒细胞的直径约为0.00000156 m ，用科学记数法表示这个数是A ．0.156³10－5B ．0.156³105C ．1.56³10－6D ．1.56³106【答案】C6．（2009年绵阳市）如果向东走80 m 记为80 m ，那么向西走60 m 记为 A ．－60 m B ．︱－60︱m C ．－（－60）m D ．601m【答案】A 7．（2009呼和浩特）2-的倒数是（） A ．12-B ．12C ．2D ．2-答案：A8．（2009年龙岩）－2的相反数是（）A ．－2B ．2C ．21 D ．－21【答案】B 9．（2009年铁岭市）目前国内规划中的第一高楼上海中心大厦，总投入约14 800 000 000元．14 800 000 000元用科学记数法表示为（）A ．111.4810⨯元 B ．90.14810⨯元C ．101.4810⨯元D ．914.810⨯元【答案】C10．（2009年黄石市）12-的倒数是（）A ．2B ．12C ．12- D ．2-【答案】D 11．（2009年广东省）《广东省2009年重点建设项目计划（草案）》显示，港珠澳大桥工程估算总投资726亿元，用科学记数法表示正确的是（） A ．107.2610⨯ 元 B ．972.610⨯ 元 C ．110.72610⨯ 元D ．117.2610⨯元【答案】A 12．（2009年枣庄市）实数a ，b 在数轴上的对应点如图所示，则下列不等式中错误．．的是（）A ．0a b >B ．0a b +<C ．1a b <D ．0a b -<【答案】C 13．（2009年枣庄市）－12的相反数是（）A ．2B ．2-C ．12D ．12-【答案】C14．（2009年赤峰市）景色秀美的宁城县打虎石水库，总库容量为119600000立方米，用科学计数法表示为（）A 、1.196³108立方米B 、1.196³107立方米C 、11.96³107立方米D 、0.1196³109立方米【答案】A15．（2009年赤峰市）3(3)-等于（） A 、-9 B 、9 C 、-27 D 、2716．（2009贺州）计算2)3(-的结果是（）．A ．－6B ．9C ．－9D ．6【答案】B17．（2009年浙江省绍兴市）甲型Ｈ1N1流感病毒的直径大约是0.000 000 081米，用科学记数法可表示为（） A ．8.1³190-米 B ．8.1³18-米 C ．81³19-米 D ．0.81³17-米【答案】Bab 018．（2009年江苏省）2-的相反数是（） A ．2 B ．2-C ．12D ．12-【答案】A 19．（2009贵州黔东南州）下列运算正确的是（ C ） A 、39±= B 、33-=- C 、39-=- D 、932=-【答案】B20．（2009年淄博市）如果2()13⨯-=，则“”内应填的实数是（ D ）A ．32B ．23C ．23- D ．32-21．（2009襄樊市）通过世界各国卫生组织的协作和努力，甲型H1N1流感疫情得到了有效的控制，到目前为止，全球感染人数约为20000人左右，占全球人口的百分比约为0.0000031，将数字0.0000031用科学记数法表示为（ B ） A ．53.110-⨯ B ．63.110-⨯ C ．73.110-⨯ D ．83.110-⨯解析：本题考查科学记数法，0.0000031=63.110-⨯，故选B 。

2009年定西市中考数学试卷2

27．（10分）如图13，△ACB 和△ECD 都是等腰直角三角形，∠ACB =∠ECD =90°，D 为AB 边上一点，求证：（1）ACE BCD △≌△；（2）222AD DB DE +=．28．［12分+附加4分］如图14（1），抛物线22y x x k =-+与x 轴交于A 、B 两点，与y 轴交于点C （0，3-）．［图14（2）、图14（3）为解答备用图］（1）k = ，点A 的坐标为，点B 的坐标为；（2）设抛物线22y x x k =-+的顶点为M ，求四边形ABMC 的面积；（3）在x 轴下方的抛物线上是否存在一点D ，使四边形ABDC 的面积最大？若存在，请求出点D 的坐标；若不存在，请说明理由；（4）在抛物线22y x x k =-+上求点Q ，使△BCQ 是以BC 为直角边的直角三角形．附加题：如果你的全卷得分不足150分，则本题与28题附加的4分的得分将记入总分，但记入总分后全卷得分不得超过150分，超过按150分算． 29．（7分）本试卷第19题为：若20072008a =，20082009b =，试不用．．将分数化小数的方法比较a 、b 的大小．观察本题中数a 、b 的特征，以及你比较大小的过程，直接写出你发现的一个一般结论．武威、金昌、定西、白银、酒泉、嘉峪关武威市2009年初中毕业、高中招生考试数学试卷参考答案与评分标准图14（1）图14（2）图14（3）图13二、填空题：本大题共8小题，每小题4分，共32分． 11．9 12． 34x y =⎧⎨=⎩，13．60o 14．二、四15．1->x 16．答案不唯一，如AC =BD ，∠BAD =90o ，等 17． 518．答案不唯一．如：①c =3；②b +c =1；③c -3b =9；④b =-2；⑤抛物线的顶点为（-1，4），或二次函数的最大值为4；⑥方程-x 2+bx +c =0的两个根为-3，1；⑦y >0时，-3<x <1；或y <0时，x <-3或x >1；⑧当x >-1时，y 随x 的增大而减小；或当x <-1时，y 随x 的增大而增大．等等三、解答题（一）：本大题共5小题，共38分． 19．本小题满分6分解：∵ a =2007200920082009⨯⨯(20081)(20081)20082009-⨯+=⨯222008120082009-=⨯， ··························· 3分 b 2200820082009=⨯， ··············································································· 4分222200812008-<， ··········································································· 5分∴ a <b ． ································································································· 6分说明：求差通分作，参考此标准给分．若只写结论a <b ，给1分．20．本小题满分6分解：∵ 22a b a b ⊕=- ， ∴ 2222(43)(43)77x x x x ⊕⊕=-⊕=⊕=-． ·········· 3分 ∴ 22724x -=． ∴ 225x =． ······························································· 4分∴ 5x =±． ··························································································· 6分 21．本小题满分8分解：∵ 随机闭合开关1S 、2S 、3S 中的两个，共有3种情况：12S S ，13S S ，23S S ．能让灯泡发光的有13S S 、23S S 两种情况． ··························································· 4分 ∴ 能让灯泡发光的概率为23． ··································································· 8分 22．本小题满分8分解：从图中可以看出，在室内厚为a cm 的墙面、宽为4cm 的门框及开成120°的门之间构成了一个直角三角形，且其中有一个角为60°． ········ 3分从而 a =4×tan60° ······································· 6分.9(cm)． ····························· 8分即室内露出的墙的厚度约为6.9cm ． 23．本小题满分10分解：（1）一次函数．························································································ 2分（2）设y kx b =+． ·················································································· 3分由题意，得22162819k b k b =+⎧⎨=+⎩，． ········································································· 5分解得210k b =⎧⎨=-⎩，． ······················································································· 7分∴210y x =-．（x 是一些不连续的值．一般情况下，x 取16、16.5、17、17.5、 (26)26.5、27等）························································································ 8分说明：只要求对k 、b 的值，不写最后一步不扣分．（3）44y =时，27x =．答：此人的鞋长为27cm ． ········································································ 10分说明：只要求对x =27cm ，不答不扣分．四、解答题（二）：本大题共5小题，共50分 (不含附加4分) ． 24．本小题满分8分解：（1）如图：···················· 4分（2）∵ 参加足球运动项目的学生占所有运动项目学生的比例为15=1050， ··········· 6分 ∴ 扇形统计图中表示“足球”项目扇形圆心角的度数为1360725⨯=． ··············· 8分 25．本小题满分10分解法1：设第一天捐款x 人，则第二天捐款（x +50）人， ········································ 1分由题意列方程x4800=506000+x ． ······························································· 5分解得 x =200． ·························································································· 7分检验：当x =200时，x （x +50）≠0， ∴ x =200是原方程的解． ··········································································· 8分两天捐款人数x +（x +50）=450，人均捐款x4800=24（元）．答：两天共参加捐款的有450人，人均捐款24元． ······································· 10分说明：只要求对两天捐款人数为450，人均捐款为24元，不答不扣分．解法2：设人均捐款x 元， ··············································································· 1分由题意列方程6000x －4800x＝50 ． ························································· 5分解得 x =24． ····························································································7分以下略．26．本小题满分10分解：（1）如图，过A 作AO ⊥AC ，过B 作BO ⊥BD ，AO 与BO 相交于O ，O 即圆心． ··················································· 3分说明：若不写作法，必须保留作图痕迹．其它作法略．（2）∵ AO 、BO 都是圆弧AmB 的半径，O 是其圆心， ∴ ∠OBA =∠OAB =150°-90°=60°． ······························· 5分 ∴ △AOB 为等边三角形．∴ AO =BO =AB =180． ·············· 7分 ∴ π6018060π180AB ⨯⨯== (m)．∴ A 到B 这段弧形公路的长为60πm ． ························································· 10分27．本小题满分10分证明:（1） ∵ ACB ECD ∠=∠，∴ ACE ACD BCD ACD ∠+∠=∠+∠．即 ACE BCD ∠=∠． ········································ 2分 ∵ EC DC AC BC ==,， ∴ △ACE ≌△BCD ． ··········································· 4分（2）∵ ACB ∆是等腰直角三角形，OADBE∴ ︒=∠=∠45BAC B ． ······································ 5分 ∵ △ACE ≌△BCD ， ∴ ︒=∠=∠45CAE B ． ······· 6分 ∴ ︒=︒+︒=∠+∠=∠904545BAC CAE DAE ． ····································· 7分 ∴ 222DE AE AD =+． ······································································ 9分由（1）知AE =DB ，∴ 222AD DB DE +=． ····································································· 10分 28．本小题满分16分(含附加4分) 解：（1）3k =-， ························································· 1分A （-1，0）， ····················································· 2分B （3，0）． ······················································ 3分（2）如图14（1），抛物线的顶点为M （1，-4），连结OM ． ····························································· 4分则 △AOC 的面积=23，△MOC 的面积=23， △MOB 的面积=6， ·············································· 5分∴ 四边形 ABMC 的面积=△AOC 的面积+△MOC 的面积+△MOB 的面积=9． ··································· 6分说明：也可过点M 作抛物线的对称轴，将四边形ABMC 的面积转化为求1个梯形与2个直角三角形面积的和．（3）如图14（2），设D （m ，322--m m ），连结OD ．则 0＜m ＜3，322--m m ＜0．且 △AOC 的面积=23，△DOC 的面积=m 23， △DOB 的面积=-23（322--m m ）， ···················································· 8分∴ 四边形 ABDC 的面积=△AOC 的面积+△DOC 的面积+△DOB 的面积=629232++-m m =875)23(232+--m ． ········································································ 9分∴ 存在点D 315()24-，，使四边形ABDC 的面积最大为875． ························· 10分（4）有两种情况：如图14（3），过点B 作BQ 1⊥BC ，交抛物线于点Q 1、交y 轴于点E ，连接Q 1C ．∵ ∠CBO =45°，∴∠EBO =45°，BO =OE =3． ∴ 点E 的坐标为（0，3）．∴ 直线BE 的解析式为3y x =-+． ·························································· 12分图14（１）图14（2）图14（3）图14（4）由2323y x y x x =-+⎧⎨=--⎩，解得1125x y ，；ì=-ïïíï=ïî 2230.x y ，ì=ïïíï=ïî ∴ 点Q 1的坐标为（-2，5）．···································································· 13分如图14（4），过点C 作CF ⊥CB ，交抛物线于点Q 2、交x 轴于点F ，连接BQ 2． ∵ ∠CBO =45°，∴∠CFB =45°，OF =OC =3． ∴ 点F 的坐标为（-3，0）．∴ 直线CF 的解析式为3y x =--． ·························································· 14分由2323y x y x x =--⎧⎨=--⎩，解得1103x y ，；ì=ïïíï=-ïî 2214x y ，．ì=ïïíï=-ïî ∴点Q 2的坐标为（1，-4）． ····································································· 15分综上，在抛物线上存在点Q 1（-2，5）、Q 2（1，-4），使△BCQ 1、△BCQ 2是以BC 为直角边的直角三角形． ··············································································· 16分说明：如图14（4），点Q 2即抛物线顶点M ，直接证明△BCM 为直角三角形同样得2分．附加题：如果你的全卷得分不足150分，则本题与28题附加的4分的得分将记入总分，但记入总分后全卷得分不得超过150分，超过按150分算． 29．本小题满分7分解：学生可能写出不同程度的一般的结论，由一般化程度不同得不同分．若m 、n 是任意正整数，且m ＞n ，则11n n m m +<+． ·········································· 4分若m 、n 是任意正实数，且m ＞n ，则11n n m m +<+． ·········································· 5分若m 、n 、r 是任意正整数，且m ＞n ；或m 、n 是任意正整数，r 是任意正实数，且m ＞n ，则n n r m m r+<+． ······················································································· 6分若m 、n 是任意正实数，r 是任意正整数，且m ＞n ；或m 、n 、r 是任意正实数，且m ＞n ，则n n r m m r+<+． ················································································· 7分。

09定西市中考数学卷

2009年定西市中考数学试卷友情提示：1．抛物线2y ax bx c =++的顶点坐标是2424b ac b a a ⎛⎫-- ⎪⎝⎭，．2．弧长公式：π180n Rl =弧长；其中，n 为弧所对圆心角的度数，R 为圆的半径．本试卷满分为150分，考试时间为120分钟．一、选择题：本大题共10小题，每小题3分，共30分．每小题给出的四个选项中，只有一项是符合题目要求的，将此选项的代号填入题后的括号内． 1．4的相反数是（） A ．4B ．4-C ．14D ．14-2．图1所示的物体的左视图（从左面看得到的视图）是（）图１ A ． B ． C ． D ． 3．计算：a b a b b a a -⎛⎫-÷= ⎪⎝⎭（）A ．a bb +B ．a bb- C ．a ba- D ．a ba+ 4．在一个不透明的布袋中装有红色、白色玻璃球共40个，除颜色外其他完全相同．小明通过多次摸球试验后发现，其中摸到红色球的频率稳定在15％左右，则口袋中红色球可能有（） A ．4个 B ．6个 C ．34个 D ．36个5．下列图形中，既是轴对称图形，又是中心对称图形的是（） A ．等腰梯形 B ．平行四边形 C ．正三角形 D ．矩形6．有19位同学参加歌咏比赛，所得的分数互不相同，取得分前10位同学进入决赛．某同学知道自己的分数后，要判断自己能否进入决赛，他只需知道这19位同学成绩的（） A ．平均数 B ．中位数 C ．众数 D ．方差7．某人想沿着梯子爬上高4米的房顶，梯子的倾斜角（梯子与地面的夹角）不能大于60°，否则就有危险，那么梯子的长至少为（）A ．8米B ．C D 8．如图2，⊙O 的弦AB =6，M 是AB 上任意一点，且OM 最小值为4，则⊙O 的半径为（） A ．5 B ．4 C ．3 D ．29．如图3，小东用长为3.2m 的竹竿做测量工具测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点．此时，竹竿与这一点相距8m 、与旗杆相距22m ，则旗杆的高为（） A ．12m B ．10mC ．8mD ．7m图2 图3 图410．如图4，四边形ABCD 中，AB =BC ，∠ABC =∠CDA =90°，BE ⊥AD 于点E ，且四边形ABCD 的面积为8，则BE =（） A ．2B ．3C．D．二、填空题：本大题共8小题，每小题4分，共32分．把答案写在题中的横线上． 11．当31x y ==、时，代数式2()()x y x y y +-+的值是． 12．方程组25211x y x y -=-⎧⎨+=⎩，的解是．13．如图5，Rt △ACB 中，∠ACB =90°，DE ∥AB ，若∠BCE =30°，则∠A = ． 14．反比例函数的图象经过点P （2-，1），则这个函数的图象位于第象限． 15．不等式组103x x +>⎧⎨>-⎩，的解集是．16．如图6，四边形ABCD 是平行四边形，使它为矩形的条件可以是．图6 图7 图817．如图7，在△ABC 中，5cm AB AC ==，cos B 35=．如果⊙O，且经过点B 、C ，那么线段AO = cm ．18．抛物线2y x bx c =-++的部分图象如图8所示，请写出与其关系式、图象相关的2个正确结论：，．（对称轴方程，图象与x 正半轴、y 轴交点坐标例外）三、解答题（一）：本大题共5小题，共38分．解答时，应写出必要的文字说明、证明过程或演算步骤． 19．（6分）若20072008a =，20082009b =，试不用将分数化小数的方法比较a 、b 的大小．20．（6分）在实数范围内定义运算“⊕”，其法则为：22a b a b ⊕=-，求方程（4⊕3）⊕24x =的解．21．（8分）如图9，随机闭合开关S 1、S 2、S 3中的两个，求能让灯泡⊗发光的概率．22．（8分）图10（1）是一扇半开着的办公室门的照片，门框镶嵌在墙体中间，门是向室内开的．图10（2）画的是它的一个横断面．虚线表示门完全关好和开到最大限度（由于受到墙角的阻碍，再也开不动了）时的两种情形，这时二者的夹角为120°，从室内看门框露在外面部分的宽为4cm ，求室内露出的墙的厚度a 的值．（假设该门无论开到什么角度，门和门框之间基本都是无缝的．精确到0.1cm1.73）23．（10分）鞋子的“鞋码”和鞋长（cm ）存在一种换算关系，下表是几组“鞋码”与鞋长换算的对应数值：［注：“鞋码”是表示鞋子大小的一种号码］鞋长（cm ） 16 19 21 24 鞋码（号）22283238（1）设鞋长为x ，“鞋码”为y ，试判断点（x ，y ）在你学过的哪种函数的图象上？（2）求x 、y 之间的函数关系式；（3）如果某人穿44号“鞋码”的鞋，那么他的鞋长是多少？图9 图10（1）图10（2）四、解答题（二）：本大题共5小题，共50分（不含附加4分）．解答时，应写出必要的文字说明、证明过程或演算步骤． 24．（8分）为响应国家要求中小学生每天锻炼1小时的号召，某校开展了形式多样的体育运动活动，小明对某班同学参加锻炼的情况进行了统计，并绘制了下面的统计图11（1）和图11（2）．（1）请在图11（1）中将表示“乒乓球”项目的图形补充完整；（2）求扇形统计图11（2）中表示“足球”项目扇形圆心角的度数．25．（10分）去年5月12日，四川省汶川县发生了里氏8.0级大地震，兰州某中学师生自愿捐款，已知第一天捐款4800元，第二天捐款6000元，第二天捐款人数比第一天捐款人数多50人，且两天人均捐款数相等，那么两天共参加捐款的人数是多少？人均捐款多少元？ 26．（10分）图12中的粗线CD 表示某条公路的一段，其中AmB 是一段圆弧，AC 、BD 是线段，且AC 、BD 分别与圆弧AmB 相切于点A 、B ，线段AB =180m ，∠ABD =150°．（1）画出圆弧AmB 的圆心O ；（2）求A 到B 这段弧形公路的长．图11（1）图11（2）图1227．（10分）如图13，△ACB 和△ECD 都是等腰直角三角形，∠ACB =∠ECD =90°，D 为AB 边上一点，求证：（1）ACE BCD △≌△；（2）222AD DB DE +=．28．［12分+附加4分］如图14（1），抛物线22y x x k =-+与x 轴交于A 、B 两点，与y 轴交于点C （0，3-）．［图14（2）、图14（3）为解答备用图］（1）k = ，点A 的坐标为，点B 的坐标为；（2）设抛物线22y x x k =-+的顶点为M ，求四边形ABMC 的面积；（3）在x 轴下方的抛物线上是否存在一点D ，使四边形ABDC 的面积最大？若存在，请求出点D 的坐标；若不存在，请说明理由；（4）在抛物线22y x x k =-+上求点Q ，使△BCQ 是以BC 为直角边的直角三角形．附加题：如果你的全卷得分不足150分，则本题与28题附加的4分的得分将记入总分，但记入总分后全卷得分不得超过150分，超过按150分算． 29．（7分）本试卷第19题为：若20072008a =，20082009b =，试不用将分数化小数的方法比较a 、b 的大小．观察本题中数a 、b 的特征，以及你比较大小的过程，直接写出你发现的一个一般结论．图13图14（1）图14（2）图14（3）武威、金昌、定西、白银、酒泉、嘉峪关武威市2009年初中毕业、高中招生考试数学试卷参考答案与评分标准一、选择题：本大题共10小题，每小题3分，共30分．题号1 2 3 4 5 6 7 8 9 10 答案B D A B D B CAAC二、填空题：本大题共8小题，每小题4分，共32分． 11．9 12． 34x y =⎧⎨=⎩，13．60o 14．二、四15．1->x 16．答案不唯一，如AC =BD ，∠BAD =90o ，等 17． 518．答案不唯一．如：①c =3；②b +c =1；③c -3b =9；④b =-2；⑤抛物线的顶点为（-1，4），或二次函数的最大值为4；⑥方程-x 2+bx +c =0的两个根为-3，1；⑦y >0时，-3<x <1；或y <0时，x <-3或x >1；⑧当x >-1时，y 随x 的增大而减小；或当x <-1时，y 随x 的增大而增大．等等三、解答题（一）：本大题共5小题，共38分． 19．本小题满分6分解：∵ a =2007200920082009⨯⨯(20081)(20081)20082009-⨯+=⨯222008120082009-=⨯， ··························· 3分 b 2200820082009=⨯， ··············································································· 4分222200812008-<， ··········································································· 5分∴ a <b ． ································································································· 6分说明：求差通分作，参考此标准给分．若只写结论a <b ，给1分．20．本小题满分6分解：∵ 22a b a b ⊕=- ， ∴ 2222(43)(43)77x x x x ⊕⊕=-⊕=⊕=-． ·········· 3分 ∴ 22724x -=． ∴ 225x =． ······························································· 4分∴ 5x =±． ··························································································· 6分 21．本小题满分8分解：∵ 随机闭合开关1S 、2S 、3S 中的两个，共有3种情况：12S S ，13S S ，23S S ．能让灯泡发光的有13S S 、23S S 两种情况． ··························································· 4分 ∴ 能让灯泡发光的概率为23． ··································································· 8分 22．本小题满分8分解：从图中可以看出，在室内厚为a cm 的墙面、宽为4cm 的门框及开成120°的门之间构成了一个直角三角形，且其中有一个角为60°． ········ 3分从而 a =4×tan60° ······································· 6分.9(cm)． ····························· 8分即室内露出的墙的厚度约为6.9cm ． 23．本小题满分10分解：（1）一次函数． ······················································································· 2分（2）设y kx b =+． ·················································································· 3分由题意，得22162819k b k b =+⎧⎨=+⎩，．········································································· 5分解得210k b =⎧⎨=-⎩，． ······················································································· 7分∴210y x =-．（x 是一些不连续的值．一般情况下，x 取16、16.5、17、17.5、 (26)26.5、27等） ······················································································· 8分说明：只要求对k 、b 的值，不写最后一步不扣分．（3）44y =时，27x =．答：此人的鞋长为27cm ． ········································································ 10分说明：只要求对x =27cm ，不答不扣分．四、解答题（二）：本大题共5小题，共50分 (不含附加4分) ． 24．本小题满分8分解：（1）如图：···················· 4分（2）∵ 参加足球运动项目的学生占所有运动项目学生的比例为15=1050， ··········· 6分 ∴ 扇形统计图中表示“足球”项目扇形圆心角的度数为1360725⨯=． ··············· 8分 25．本小题满分10分解法1：设第一天捐款x 人，则第二天捐款（x +50）人， ········································ 1分由题意列方程x4800=506000+x ． ······························································· 5分解得 x =200． ·························································································· 7分检验：当x =200时，x （x +50）≠0， ∴ x =200是原方程的解． ··········································································· 8分两天捐款人数x +（x +50）=450，人均捐款x4800=24（元）．答：两天共参加捐款的有450人，人均捐款24元． ······································· 10分说明：只要求对两天捐款人数为450，人均捐款为24元，不答不扣分．解法2：设人均捐款x 元， ··············································································· 1分由题意列方程6000x －4800x＝50 ． ························································· 5分解得 x =24． ···························································································· 7分以下略．26．本小题满分10分解：（1）如图，过A 作AO ⊥AC ，过B 作BO ⊥BD ，AO 与BO 相交于O ，O 即圆心． ··················································· 3分说明：若不写作法，必须保留作图痕迹．其它作法略．（2）∵ AO 、BO 都是圆弧AmB 的半径，O 是其圆心， ∴ ∠OBA =∠OAB =150°-90°=60°． ······························· 5分 ∴ △AOB 为等边三角形．∴ AO =BO =AB =180． ·············· 7分 ∴ π6018060π180AB ⨯⨯== (m)．O∴ A 到B 这段弧形公路的长为60πm ． ························································· 10分 27．本小题满分10分证明:（1） ∵ ACB ECD ∠=∠，∴ ACE ACD BCD ACD ∠+∠=∠+∠．即 ACE BCD ∠=∠． ········································ 2分∵ EC DC AC BC ==,， ∴ △ACE ≌△BCD ． ··········································· 4分（2）∵ ACB ∆是等腰直角三角形，∴ ︒=∠=∠45BAC B ． ······································ 5分 ∵ △ACE ≌△BCD ， ∴ ︒=∠=∠45CAE B ． ······· 6分 ∴ ︒=︒+︒=∠+∠=∠904545BAC CAE DAE ． ····································· 7分 ∴ 222DE AE AD =+． ······································································ 9分由（1）知AE =DB ，∴ 222AD DB DE +=． ····································································· 10分 28．本小题满分16分(含附加4分) 解：（1）3k =-， ························································· 1分A （-1，0）， ····················································· 2分B （3，0）． ······················································ 3分（2）如图14（1），抛物线的顶点为M （1，-4），连结OM ． ····························································· 4分则 △AOC 的面积=23，△MOC 的面积=23， △MOB 的面积=6，·············································· 5分∴ 四边形 ABMC 的面积=△AOC 的面积+△MOC 的面积+△MOB 的面积=9． ··································· 6分说明：也可过点M 作抛物线的对称轴，将四边形ABMC 的面积转化为求1个梯形与2个直角三角形面积的和．（3）如图14（2），设D （m ，322--m m ），连结OD ．则 0＜m ＜3，322--m m ＜0．且 △AOC 的面积=23，△DOC 的面积=m 23， △DOB 的面积=-23（322--m m ）， ···················································· 8分∴ 四边形 ABDC 的面积=△AOC 的面积+△DOC 的面积+△DOB 的面积=629232++-m m =875)23(232+--m ．········································································ 9分∴ 存在点D 315()24-，，使四边形ABDC 的面积最大为875． ························· 10分（4）有两种情况：图14（１）图14（2）图14（3）图14（4）A DB CE如图14（3），过点B 作BQ 1⊥BC ，交抛物线于点Q 1、交y 轴于点E ，连接Q 1C ． ∵ ∠CBO =45°，∴∠EBO =45°，BO =OE =3． ∴ 点E 的坐标为（0，3）．∴ 直线BE 的解析式为3y x =-+． ·························································· 12分由2323y x y x x =-+⎧⎨=--⎩，解得1125x y ，；ì=-ïïíï=ïî 2230.x y ，ì=ïïíï=ïî ∴ 点Q 1的坐标为（-2，5）． ··································································· 13分如图14（4），过点C 作CF ⊥CB ，交抛物线于点Q 2、交x 轴于点F ，连接BQ 2． ∵ ∠CBO =45°，∴∠CFB =45°，OF =OC =3． ∴ 点F 的坐标为（-3，0）．∴ 直线CF 的解析式为3y x =--． ·························································· 14分由2323y x y x x =--⎧⎨=--⎩，解得1103x y ，；ì=ïïíï=-ïî 2214x y ，．ì=ïïíï=-ïî ∴点Q 2的坐标为（1，-4）． ····································································· 15分综上，在抛物线上存在点Q 1（-2，5）、Q 2（1，-4），使△BCQ 1、△BCQ 2是以BC 为直角边的直角三角形． ··············································································· 16分说明：如图14（4），点Q 2即抛物线顶点M ，直接证明△BCM 为直角三角形同样得2分．附加题：如果你的全卷得分不足150分，则本题与28题附加的4分的得分将记入总分，但记入总分后全卷得分不得超过150分，超过按150分算． 29．本小题满分7分解：学生可能写出不同程度的一般的结论，由一般化程度不同得不同分．若m 、n 是任意正整数，且m ＞n ，则11n n m m +<+． ·········································· 4分若m 、n 是任意正实数，且m ＞n ，则11n n m m +<+． ·········································· 5分若m 、n 、r 是任意正整数，且m ＞n ；或m 、n 是任意正整数，r 是任意正实数，且m ＞n ，则n n r m m r+<+． ······················································································· 6分若m 、n 是任意正实数，r 是任意正整数，且m ＞n ；或m 、n 、r 是任意正实数，且m ＞n ，则n n r m m r+<+． ·············································································· 7分。

甘肃省定西市中考数学试题及答案D

甘肃省定西市中考数学试题及答案D考生注意：本试卷满分为120分,考试时间为120分钟.所有试题均在答题卡上作答,否则无效. 一.选择题：本大题共10小题,每小题3分,共30分,每小题只有一个正确选项,将此选项的字母填在答题卡上.1.下列图形中,是中心对称图形的是【】2.在1,-2,0,35这四个数中,最大的数是【】 A.2 B.0 C.35D.13．在数轴上表示不等式01<-x 的解集,正确的是【】4．下列根式中是最简二次根式的是【】12.9.3.32.D C B A5．已知点),0(m P 在y 轴的负半轴上,则点M )1,(+--m m 在【】 A.第一象限 B.第二象限 C.第三象限 D.第四象限6.如图,AB ∥CD,DE ⊥CE,∠1=34°,则∠DCE 的度数为【】 A ．34° B.54° C.66° D.56°7．如果两个相似三角形的面积比是1∶4,那么它们的周长比是【】 A.1∶16 B.1∶4 C.1∶6 D.1∶28．某工厂现在平均每天比原计划每天多生产50台机器,现在生产800台机器所需时间与原计划生产600台机器所需时间相同.设原计划平均每天生产x 台机器.根据题意,下面所列方程正确的是【】.50600800.;50600800.;60050800.;60050800.A -=+==-=+x x D x x C x x x x B9．若,0442=-+x x 则)1)(1(6)2(32-+--x x x 的值为【】第6题图A.-6B.6C.18D.3010.如图,△ABC 是等腰直角三角形,∠A=90°,BC=4,点P 是△ABC 边上一动点,沿B →A →C 的路径移动,过点P 作PD ⊥BC 于点D,设BD=x ,△BDP 的面积为y ,则下列能大致反映y 与x 函数关系的图象是【】二、填空题：本大题共8小题,每小题3分,共24分. 11.因式分解：.___________822=-x 12.计算：=-⋅-)8()5(24ab a ___________.13.如图,点A(3,t )在第一象限,射线OA 与x 轴所夹的锐角为α,,23tan =α则t 的值是________.14.如果单项式2222+-+m n n m y x与75y x 是同类项,那么m n 的值是________.15．三角形的两边长分别是3和4,第三边长是方程040132=+-x x 的根,则该三角形的周长为____.16．如图,在⊙O 中,弦AC=32,点B 是圆上一点,且∠ABC=45°,则⊙O 的半径R=_______. 17．将一张矩形纸片折叠成如图所示的图形,若AB=6cm,则AC=_______cm.18.古希腊数学家把数1,3,6,10,15,21,…,叫做三角形数,它有一定的规律性.若把第一个三角形数记为，1x第二个三角形数记为，2x …,第n 个三角形数记为n x ,则1++n n x x =_________.三.解答题(一)：本大题共5小题,共26分.解答应写出必要的文字说明,证明过程或演算步骤：第13题图第16题图第17题图19.(4分)计算：.)3-(-160sin 231--210-2+︒++⎪⎭⎫⎝⎛20．(4分)如图,在平面直角坐标系中,△ABC 的顶点A(0,1),B(3,2),C(1,4)均在正方形的网格的格点上. (1)画出△ABC 关于x 轴的对称图形；△111C B A (2)将111C B A △沿x 轴方向向左平移3个单位后得到222C B A △,写出顶点222C B A ，，的坐标.21.(6分)已知关于x 的方程022=-++m mx x . (1)若此方程的一个根为1,求m 的值；(2)求证：不论m 取何实数,此方程都有两个不相等的实数根.22.(6分)图①是小明在健身器材上进行仰卧起坐锻炼时的情景.图②是小明锻炼时上半身由ON 位置运动到与地面垂直的OM 位置时的示意图.已知AC=0.66米,BD=0.26米,α=20°.(参考数据：sin20°≈0.342,cos20°≈0.940,tan20°≈0.364).(1)求AB 的长(精确到0.01米)；(2)若测得ON=0.8米,试计算小明头顶由N 点运动到M 点的路径的长度(结果保留π)23.（6分）在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2；乙袋中的小球上分别标有数字-1,-2,0.现从甲袋中任意摸出第20题图第22题图第25题图第27题图一个小球,记其标有的数字为x ,再从乙袋中任意摸出一个小球,记其标有的数字为y ,以此确定点M 的坐标(x ,y ).(1)请你用画树状图或列表的方法,写出点M 所有可能的坐标； (2)求点M (x ,y )在函数xy 2-=的图象上的概率. 四、解答题(二)：本大题共5小题,共40分.解答应写出必要的文字说明、证明过程或演算步骤.24．(7分)2016年《政府工作报告》中提出了十大新词汇.为了解同学们对新词汇的关注度,某数学兴趣小组选取其中的A ：“互联网+政务服务”,B ：“工匠精神”,C ：“光网城市”,D ：“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词.根据调查结果,该小组绘制了如下的两幅不完整的统计图. 请你根据统计图提供的信息,解答下列问题： (1)本次调查中,一共调查了多少名同学？ (2)条形统计图中,m =_______,n =_____.(3)扇形统计图中,热词B 所在扇形的圆心角是多少度？25．(7分)如图,函数41+-=x y 的图象与函数)0(2>=x xky 的图象交于),1(),1,(n B m A 两点. (1)求k ,m ,n 的值;(2)利用图象写出当1≥x 时,21y y 与的大小关系. 26．(8分)如图,已知EC ∥AB,∠EDA=∠ABF. (1)求证：四边形ABCD 为平行四边形； (2)求证：.OF OE OA 2⋅=第24题图第26题图27．(8分)如图,在△ABC 中,AB=AC,点D 在BC 上,BD=DC,过点D 作DE ⊥AC,垂足为E,⊙O 经过A,B,D 三点.(1)求证：AB 是⊙O 的直径；(2)判断DE 与⊙O 的位置关系,并加以证明； (3)若⊙O 的半径为3,∠BAC=60°,求DE 的长.28．(10分)如图,已知抛物线c bx x y ++-=2经过A(3,0),B(0,3)两点. (1)求此抛物线的解析式和直线AB 的解析式；(2)如图①,动点E 从O 点出发,沿着OA 方向以1个单位／秒的速度向终点A 匀速运动,同时,动点F 从A 点出发,沿着AB 方向以2个单位／秒的速度向终点B 匀速运动,当E,F 中任意一点到达终点时另一点也随之停止运动.连接EF,设运动时间为t 秒.当t 为何值时,△AEF 为直角三角形？(3)如图②,取一根橡皮筋,两端点分别固定在A,B 处.用铅笔拉着这根橡皮筋使笔尖P 在直线AB 上方的抛物线上移动,动点P 与A,B 两点构成无数个三角形,在这些三角形中是否存在一个面积最大的三角形？如果存在,求出最大面积,并指出此时点P 的坐标；如果不存在,请简要说明理由.第28题图数学试题参考答案及评分标准一、选择题：本大题共10小题,每小题3分,共30分．二、填空题：本大题共8小题,每小题3分,共24分． 11.2(2)(2)x x +-；12.5240a b ；13.92；14.13；15.12 ；16.6；17. 6 ；18.2(1)n +或n2+2n+1.三、解答题（一）：本大题共5小题,共26分．解答应写出必要的文字说明,证明过程或演算步骤．19.（4分）解：原式=22－(3－1）＋2×3＋1 2分 =4－3＋1＋3＋1 3分 =6 4分 20.（4分）解：（1）△A1B1C1为所作； 2分（2）A2（-3,-1）,B2（0,-2）,C2（-2,-4）． 4分21.（6分）（1）解：把x =1代入方程 220x mx m ++-=得 1m m ++ 解得 m =12． 2分（2）证明：△=24(2)m m -- 3分题号 1 2 3 4 5 6 7 8 9 10 答案ACCBADDAＢByxO ABCB 1C 1A 12(2)4m =-+ 4分 ∵ 2(2)m -≥0,∴ 2(2)4m -+＞0, 即 △>0, 5分 ∴ 此方程有两个不相等的实数根． 6分22.（6分）解：（1）过点B 作BF ⊥AC 于点F ． 1分 ∴ AF=AC －BD=0.4(米), 2分 ∴B=AF ÷sin20°≈1.17(米)； 3分（2）∵∠MON=90°＋20°=110°, 4分 ∴ 1100.82218045MN ⨯π==π(米)． 6分23.（6分）解：（1）画树状图：方法一：方法二：2分所以点M （x, y ）共有9种可能：(0,-1）,（0,-2）,（0,0）,（1,-1）,（1,-2）,（1,0）,（2,-1）,（2,-2）,（2,0）； 4分（2）∵只有点（1,-2）,（2,-1）在函数2y x=-的图象上, 5分 ∴点M （x ,y ）在函数2y x =-的图象上的概率为29． 6分四、解答题（二)：本大题共5小题,共40分．解答应写出必要的文字说明、证明过程或演算步骤．（注：解法合理,答案正确均可得分）24.（7分）解：（1）105÷35%=300（人）．答：共调查了300名学生； 1分（2）n =300×30%=90（人）,m =300－105－90－45=60（人）．故答案为：60,90；（每空2分） 5分（3）60300×360°=72°．答：B 所在扇形的圆心角是72°. 7分 (0, 0) (0, -1)(0, -2) (1, -1) (1, -2) (1, 0) (2, -2)(2, -1)1 0 2-1-2 0 乙袋甲袋结果(2, 0)25.（7分）解：（1）把点A （m,1）代入14y x =-+,得m=3, 2分则 A （3,1）,∴k =3×1=3； 3分把点B （1,n ）代入2ky x=,得出n=3； 4分（2）如图,由图象可知：①当1＜x ＜3时,1y ＞2y ； 5分②当x =1或x =3时,1y =2y ； 6分(注：x 的两个值各占0.5分） ③当x ＞3时,1y ＜2y ． 7分 26．（8分）（1）证明：∵EC ∥AB, ∴∠C=∠ABF ． 1分又∵∠EDA=∠ABF,∴∠C=∠EDA ． 2分 ∴AD ∥BC, 3分 ∴四边形ABCD 是平行四边形． 4分（2）证明：∵EC ∥AB, ∴OA OB OEOD=. 5分又∵AD ∥BC, ∴OF OB OA OD =, 6分 ∴OA OF OEOA=, 7分∴2OA OE OF =⋅． 8分 27.（8分）（1）证明：如图①,连接AD, ∵在△ABC 中, AB=AC,BD=DC, ∴AD ⊥BC 1分∴∠ADB=90°,AB 是⊙O 的直径； 2分（2）DE 与⊙O 的相切． 3分证明：如图②,连接OD, ∵AO=BO,BD=DC, ∴OD 是△BAC 的中位线,图②ABCD E O图①AB CD E O∴OD ∥AC, 4分又∵DE ⊥AC ∴DE ⊥OD,∴DE 为⊙O 的切线； 5分（3）解：如图③,∵AO=3,∴AB=6, 又∵AB=AC,∠BAC=60°, ∴△ABC 是等边三角形, ∴AD=33, 6分 ∵AC ∙DE=CD ∙AD,∴6∙DE=3×33, 7分解得 DE =332． 8分 28.（10分）解：（1）设直线AB 的解析式为y kx m =+, 1分把A(3,0),B(0,3)代入,得 330m k m =⎧⎨+=⎩, 解得13k m =-⎧⎨=⎩ ∴直线AB 的解析式为3y x =-+ 2分把A(3,0),B(0,3) 代入 2y x bx c =-++中,得 9303b c c -++=⎧⎨=⎩,解得23b c =⎧⎨=⎩∴抛物线的解析式为 223y x x =-++． 3分（2）∵OA=OB=3,∠BOA=90°,∴∠EAF=45°．设运动时间为t 秒,则AF=2t,AE=3－t ． 4分（i ）当∠EFA=90°时,如图①所示：在Rt △EAF 中,cos45°22AF AE ==,即2232t t =-．解得 t =1. 5分(ii) 当∠FEA=90°时,如图②所示：在Rt △AEF 中,cos45°22AE AF ==, AB CDEO图③图①OyAxBEF图②yOA BE F即222t=．解得t =32．综上所述,当t =1或t =32时,△AEF 是直角三角形． 6分（3）存在. 如图③,过点P 作PN ∥y 轴,交直线AB 于点N,交x 轴于点D. 过点B 作BC ⊥PN 交PN 于点C ．设点P （x ,223x x -++）,则点N （x ,3x -+）∴PN=2223(3)3x x x x x -++--+=-+． 7分 ∴ABP BPN APN S S S ∆∆∆=+=1122PN BC PN AD ⋅+⋅ 8分=2211(3)(3)(3)22x x x x x x -+⋅+-+- =23327228x ⎛⎫--+ ⎪⎝⎭ 9分当32x =时,△ABP 的面积最大,最大面积为278．此时点P(32,154)． 10分yx O xA x xB AP图③NC MD M。

2009宁夏中考数学及答案(word版含答案)

（参考边长为4厘米，长为1厘米的线段在的边上沿方向以1厘米/秒的速度向点运动（运动开始时，点与点重合，点到达点时运动终止），过点分别作边的垂线，与的其它边交于两点，线段运动的时间为秒．
（1）线段在运动的过程中，为何值时，四边形恰为矩形？并求出该矩形的面积；
14．如图，梯形的两条对角线交于点，图中面积相等的三角形共有对．
15．如图，的周长为32，且于，的周长为24，那么的长为．
16．如图，是边长为2的等边三角形的内切圆，则图中阴影部分的面积为．
三、解答题（共24分）
17．（6分）
计算：．
18．（6分）
解分式方程：．
19．（6分）
已知正比例函数与反比例函数的图象交于两点，点的坐标为．
D
A
B
C
B
A
C
D
二、填空题（每小题3分，共24分）
题号
9
10
11
12
13
14
15
16
答案
2
120
3
8
三、解答题（共24分）
17．（6分）计算：
解：原式= 4分
= 6分
18．（6分）解分式方程：
解：去分母得： 3分
整理方程得：
5分
经检验是原方程的解．
原方程的解为．6分
19．（6分）
解：（1）把点分别代入与得
（3）通过计算说明，哪一种型号的轿车销售情况最好？
（4）若对已售出轿车进行抽奖，现将已售出四种型号轿车的发票（一车一票）放到一起，从中随机抽取一张，求抽到型号轿车发票的概率．
22．（6分）
如图：在中，，是边上的中线，将沿边所在的直线折叠，使点落在点处，得四边形．

2009年全国 117个地区中考试卷及答案

2009年全国各地中考试题及答案112份下载地址（截止到7月11日）（7月7日前的为红色）2009年安徽省初中毕业学业考试数学试题及答案2009年安徽省芜湖市初中毕业学业考试题及答案2009年北京高级中学中等学校招生考试数学试题及答案2009年福建省福州市课改实验区中考试卷及参考答案2009年福建省龙岩市初中毕业、升学考试试题及答案2009年福建省宁德市初中毕业、升学考试试题及答案2009年福建省莆田市初中毕业、升学考试试卷及答案2009年福建省泉州市初中毕业、升学考试试题及答案2009年福建省漳州市初中毕业暨高中阶段招生题及答案2009年甘肃省定西市中考数学试卷及答案2009年甘肃省兰州市初中毕业生学业考试试卷及答案2009年甘肃省庆阳市高中阶段学校招生考试题及答案2009年广东省佛山市高中阶段学校招生考试题及答案2009年广东省茂名市高中阶段招生考试试题及答案2009年广东省梅州市初中毕业生学业考试试题及答案2009年广东省清远市初中毕业生学业考试试题及答案2009年广东省深圳市初中毕业生学业考试试卷及答案2009年广东省肇庆市初中毕业生学业考试试题及答案2009年广西省崇左市初中毕业升学考试数学试题及答案2009年广西省桂林市百色市初中毕业暨升学试卷及答案2009年广西省河池市初中毕业暨升学统一考试卷及答案2009年广西省贺州市初中毕业升学考试试卷及答案2009年广西省柳州市初中毕业升学考试数学试卷及答案2009年广西省南宁市中等学校招生考试题及答案2009年广西省钦州市初中毕业升学考试试题卷及答案2009年广西省梧州市初中毕业升学考试卷及答案2009年贵州省安顺市初中毕业、升学招生考试题及答案2009年贵州省黔东南州初中毕业升学统一考试题及答案2009年河北省初中毕业生升学文化课考试试卷及答案2009年河南省初中学业水平暨高级中等学校招生卷及答2009年黑龙江省哈尔滨市初中升学考试题及答案2009年黑龙江省牡丹江市初中毕业学业考试题及答案2009年黑龙江省齐齐哈尔市初中毕业学业考试题及答案2009年黑龙江省绥化市初中毕业学业考试卷及答案（答案为扫描版）2009年湖北省鄂州市初中毕业及高中阶段招生题及答案2009年湖北省恩施自治州初中毕业生学业考试题及答案2009年湖北省黄冈市初中毕业生升学考试试卷及答案2009年湖北省黄石市初中毕业生学业考试联考卷及答案2009年湖北省黄石市初中毕业生学业考试试题及答案2009年湖北省十堰市初中毕业生学业考试试题及答案2009年湖北省武汉市初中毕业生学业考试试题及答案2009年湖北省襄樊市初中毕业、升学统一考试题及答案2009年湖北省孝感市初中毕业生学业考试试题及答案2009年湖北省宜昌市初中毕业生学业考试试题及答案2009年湖南省长沙市初中毕业学业考试试卷及答案2009年湖南省常德市初中毕业学业考试试题及答案2009年湖南省郴州市初中毕业考试数学试题及答案2009年湖南省衡阳市初中毕业学业考试试卷及参考答案2009年湖南省怀化市初中毕业学业考试卷及答案2009年湖南省娄底市初中毕业学业考试试题及答案2009年湖南省邵阳市初中毕业学业水平考试卷及答案2009年湖南省湘西自治州初中毕业学业考试卷及答案2009年湖南省益阳市普通初中毕业学业考试试卷及答2009年湖南省株洲市初中毕业学业考试数学试题及答案2009年吉林省长春市初中毕业生学业考试试题及答案2009年吉林省初中毕业生学业考试数学试题及答案2009年江苏省苏州市中考数学试题及答案（答案为扫描版）2009年江苏省中考数学试卷及参考答案2009年江西省中等学校招生考试数学试题及参考答案2009年辽宁省本溪市初中毕业生学业考试试题及答案2009年辽宁省朝阳市初中升学考试数学试题及答案2009年辽宁省抚顺市初中毕业生学业考试试卷及答案2009年辽宁省锦州市中考数学试题及答案2009年辽宁省铁岭市初中毕业生学业考试试题及答案2009年内蒙古赤峰市初中毕业、升学统一考试题及答案（答案为扫描版）2009年内蒙古自治区包头市高中招生考试试卷及答案2009年宁夏回族自治区初中毕业暨高中阶段招生题及答案2009年山东省德州市中等学校招生考试数学试题及答案2009年山东省东营市中等学校招生考试试题及答案2009年山东省济南市高中阶段学校招生考试试题及答案2009年山东省济宁市高中阶段学校招生考试试题及答案2009年山东省临沂市中考数学试题及参考答案2009年山东省日照市中等学校招生考试试题及参考答案2009年山东省泰安市高中段学校招生考试试题及答案2009年山东省威海市初中升学考试数学试卷及参考答案2009年山东省潍坊市初中学业水平考试数学试题及答案2009年山东省烟台市初中学生学业考试试题及答案2009年山东省枣庄市中等学校招生考试数学试题及答案2009年山东省中等学校招生考试数学试题及参考答案2009年山东省淄博市中等学校招生考试试题及答案2009年山西省初中毕业学业考试数学试卷及答案2009年山西省太原市初中毕业学业考试试卷及答案2009年陕西省初中毕业学业考试数学试题及答案2009年上海市初中毕业统一学业考试数学试卷及答案2009年四川省成都市高中学校统一招生考试试卷及答案2009年四川省达州市高中招生统一考试题及答案2009年四川省高中阶段教育学校招生统一考试题及答案2009年四川省泸州市高中阶段学校招生统一考试题及答（答案为扫描版）2009年四川省眉山市高中阶段教育学校招生试题及答案2009年四川省南充市高中阶段学校招生统一考试卷及答2009年四川省遂宁市初中毕业生学业考试试题及答案2009年台湾第一次中考数学科试题及答案2009年天津市初中毕业生学业考试数学试题及答案2009年新疆维吾尔自治区初中毕业生学业考试题及答案2009年云南省高中（中专）招生统一考试试题及答案2009年浙江省杭州市各类高中招生文化考试试题与答案2009年浙江省湖州市初中毕业生学业考试试题及答案2009年浙江省嘉兴市初中毕业生学业考试试卷及答案2009年浙江省金华市初中毕业生学业考试试卷及答案2009年浙江省丽水市初中毕业生学业考试试卷及答案2009年浙江省丽水市初中毕业生学业考试试题及答案2009年浙江省宁波市初中毕业生学业考试试题及答案2009年浙江省衢州市初中毕业生学业考试数学卷及答案2009年浙江省台州市初中学业考试数学试题及参考答案2009年浙江省温州市初中毕业生学业考试试题及答案（答案为扫描版）2009年浙江省义乌市初中毕业生学业考试题及参考答案2009年浙江省舟山市初中毕业生学业考试数学卷及答案2009年重庆市初中毕业暨高中招生考试数学试题及答案2009年重庆市江津市初中毕业学业暨高中招生试题及答2009年重庆市綦江县初中毕业暨高中招生考试题及答案。

2009年定西市中考试题

２００９年定西市巾考试题
一
、
选择题（小题３分，３每共Ｏ分））．
且Ｏ最小值为４则ｏｏ的半径为（Ｍ，
Ａ．５Ｂ．４Ｃ．３Ｄ．２
１４的相反数是（．
ＡＢ４ｃ÷ Ｄ｛．４．．．一一
的图像位于第
象限．
５５
Ｙ册
中‘ 汇编考
・
不式｛）３解是等组＞６集Ｉ～ ’ ，的，
，
＋１０，＞
２（）图泡。，的概率．Ｓｓｓ的１分让灯示随闭开２中两．求能所发机合，，个如８关光
２如图所示的物体的左视图（左面看得到的视图）．从是
（）．
凸口圆日
ＡＢＣＤ
８ｍ卜 — ２ｍ — — 一２ —
（８题图）第（９题图）第
３算（一）一）．： ÷÷ （．计詈
数后，判断自己能否进入决赛，只需知道这１要他９
位同学成绩的（）．
，一２ｖ一一５．
１．２方程组｛＋２ｖ一１１的解是— １．ｚ一
Ｂ．中位数Ｄ．方差
ＢＣＥ一３。则Ａ一Ｏ，．
—
那么梯子的长至少为（
Ａ．ｍ８
）．
Ｂ．８ｍ
二二ＤＣ
（１第３题图）（１题图）第６
Ｃ．

2009年陕西省中考数学试题(word版含答案)

2009年陕西省初中毕业学业考试数学第Ⅰ卷（选择题共30分）A 卷一、选择题（共10小题，每小题3分，计30分．每小题只有一个选项是符合题意的）1．12-的倒数是（）．Ａ．2 B ．2- C ．12 D ．12-2．1978年，我国国内生产总值是3 645亿元，2007年升至249 530亿元．将249 530亿元用科学记数表示为（）． A ．1324.95310⨯元 B ．1224.95310⨯元 C ．132.495310⨯元 D ．142.495310⨯元3．图中圆与圆之间不同的位置关系有（）． A ．2种 B ．3种 C ．4种 D ．5种 4．王老师为了了解本班学生课业负担情况，在班中随机调查了10名学生，他们每人上周平均每天完成家庭作业所用的时间分别是（单位：小时）：1.5，2，2，2，2.5，2.5，2.5，2.5，3，3.5．则这10个数据的平均数和众数分别是（）． A ．2.4，2.5 B ．2.4，2 C ．2.5，2.5 D ．2.5，2 5．若正比例函数的图象经过点（1-，2），则这个图象必经过点（）． A ．（1，2） B ．（1-，2-） C ．（2，1-） D ．（1，2-）6．如果点(12)P m m -，在第四象限，那么m 的取值范围是（）． A ．102m <<B ．102m -<<C ．0m <D ．12m > 7．若用半径为9，圆心角为120°的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的底面半径是（）． A ．1.5 B ．2 C ．3 D ．68．化简2b aa a ab ⎛⎫- ⎪-⎝⎭的结果是（）．A ．a b -B ．a b +C ．1a b - D ．1a b+ 9．如图，9030AOB B ∠=∠=°，°，A OB ''△可以看作是由AOB △绕点O 顺时针旋转α角度得到的．若点A '在AB 上，则旋转角α的大小可以是（）．A ．30°B ．45°C ．60°D ．90°10．根据下表中的二次函数2y ax bx c =++的自变量x 与函数y 的对应值，可判断该二次函数的图象与x 轴（）．（第3题图）120°（第7题图）AOBA 'B '（第9题图）x… 1- 0 1 2 … y…1-74- 2-74- …A ．只有一个交点B ．有两个交点，且它们分别在y 轴两侧C ．有两个交点，且它们均在y 轴同侧D ．无交点第Ⅱ卷（非选择题共90分）二、填空题（共6小题，每小题3分，计18分） 11．031)--=__________．12．如图，AB CD ∥，直线EF 分别交AB CD 、于点E F 、， 147∠=°，则2∠的大小是__________． 13．若1122()()A x y B x y ，，，是双曲线3y x=上的两点，且120x x >>，则12_______y y {填“>”、“=”、“<”}．14．如图，在梯形ABCD 中，DC AB ∥，DA CB =．若104AB DC ==，，tan 2A =，则这个梯形的面积是__________．15．一家商店将某种商品按成本价提高50%后，标价为450元，又以8折出售，则售出这件商品可获利润__________元．16．如图，在锐角ABC △中，45AB BAC =∠=°，BAC ∠的平分线交BC 于点D M N ，、分别是AD 和AB 上的动点，则BM MN +的最小值是___________ ．三、解答题（共9小题，计72分） 17．（本题满分5分）解方程：223124x x x --=+-． 18．（本题满分6分）如图，在ABCD中，点E 是AD 的中点，连接CE 并延长，交BA 的延长线于点F ．求证：FA AB =．AB DC EF12 （第12题图）ABCD（第14题图）ABCDNM（第16题图）A B C DE F （第18题图）某校为了组织一项球类对抗赛，在本校随机调查了若干名学生，对他们每人最喜欢的一项球类运动进行了统计，并绘制成如图①、②所示的条形和扇形统计图．根据统计图中的信息，解答下列问题：（1）求本次被调查的学生人数，并补全条形统计图；（2）若全校有1 500名学生，请你估计该校最喜欢篮球运动的学生人数；（3）根据调查结果，请你为学校即将组织的一项球类对抗赛提出一条合理化建议． 20．（本题满分8分）小明想利用太阳光测量楼高．他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：如示意图，小明边移动边观察，发现站到点E 处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同．此时，测得小明落在墙上的影子高度 1.2CD =m ，0.8CE =m ，30CA =m （点A E C 、、在同一直线上）．已知小明的身高EF 是1.7m ，请你帮小明求出楼高AB （结果精确到0.1m ）．项目 ①足球20%篮球 26% 乒乓球 32% 羽毛球 16% 其他②（第19题图）（第20题图）在一次运输任务中，一辆汽车将一批货物从甲地运往乙地，到达乙地卸货后返回．设汽车从甲地出发x （h ）时，汽车与甲地的距离为y （km ），y 与x 的函数关系如图所示．根据图象信息，解答下列问题：（1）这辆汽车的往、返速度是否相同？请说明理由；（2）求返程中y 与x 之间的函数表达式；（3）求这辆汽车从甲地出发4h 时与甲地的距离．22．（本题满分8分）甲、乙两同学用一副扑克牌中牌面数字分别是3、4、5、6的4张牌做抽数学游戏．游戏规则是：将这4张牌的正面全部朝下，洗匀，从中随机抽取一张，抽得的数作为十位上的数字，然后，将所抽的牌放回，正面全部朝下、洗匀，再从中随机抽取一张，抽得的数作为个位上的数字，这样就得到一个两位数．若这个两位数小于45，则甲获胜，否则乙获胜．你认为这个游戏公平吗？请运用概率知识说明理由． 23．（本题满分8分）如图，O ⊙是ABC △的外接圆，AB AC =，过点A 作AP BC ∥，交BO 的延长线于点P ．（1）求证：AP 是O ⊙的切线；（2）若O ⊙的半径58R BC ==，，求线段AP 的长．（第21题图）（第23题图）24．（本题满分10分）如图，在平面直角坐标系中，OB OA ⊥，且2OB OA =，点A 的坐标是(12)-，．（1）求点B 的坐标；（2）求过点A O B 、、的抛物线的表达式；（3）连接AB ，在（2）中的抛物线上求出点P ，使得ABP ABO S S =△△． 25．（本题满分12分）问题探究（1）请在图①的正方形ABCD 内，画出使90APB ∠=°的一个．．点P ，并说明理由．（2）请在图②的正方形ABCD 内（含边），画出使60APB ∠=°的所有．．的点P ，并说明理由．问题解决（3）如图③，现在一块矩形钢板43ABCD AB BC ==，，．工人师傅想用它裁出两块全等的、面积最大的APB △和CP D '△钢板，且60APB CP D '∠=∠=°．请你在图③中画出符合要求的点P 和P '，并求出APB △的面积（结果保留根号）．D C B A ① D C BA ③ D CB A ② （第25题图）2009年陕西省初中毕业学业考试数学试题参考答案A 卷一、选择题（共10小题，每小题3分，计30分）题号1 2 3 4 5 6 7 8 9 10 A 卷答案 BC A AD D C B C B题号1 2 3 4 5 6 7 8 9 10 B 卷答案 DA D C AB B A B C二、填空题（共6小题，每小题3分，计18分）11．2 12．133° 13．< 14．42 15．60 16．4 三、解答题（共9小题，计72分） 17．（本题满分5分）解：22(2)(4)3x x ---=． ························································································ （2分）45x -=-．54x =． ······················································································· （4分）经检验，54x =是原方程的解． ···················································································· （5分） 18．（本题满分6分）证明：四边形ABCD 是平行四边形， AB DC AB DC ∴=，∥．FAE D F ECD ∴∠=∠∠=∠，． ············ （3分）又EA ED = ，AFE DCE ∴△≌△． ······························· （5分） AF DC ∴=． AF AB ∴=． ············································· （6分） 19．（本题满分7分）解：（1）1326%50÷= ，∴本次被调查的人数是50． ·········· （2分）补全的条形统计图如图所示． ······· （4分）（第19题答案图）项目ABCDEF（2）150026%390⨯= ，∴该校最喜欢篮球运动的学生约为390人． ································································ （6分）（3）如“由于最喜欢乒乓球运动的人数最多，因此，学校应组织乒乓球对抗赛”等．（只要根据调查结果提出合理、健康、积极的建议即可给分） ·············································· （7分） 20．（本题满分8分）解：过点D 作DG AB ⊥，分别交AB EF 、于点G H 、，则 1.2EH AG CD ===，0.830DH CE DG CA ====，． ························ （2分） EF AB ∥， FH DH BGDG∴=． ························································· （5分）由题意，知 1.7 1.20.5FH EF EH =-=-=．0.50.830BG ∴=，解之，得18.75BG =． ··················· （7分） 18.75 1.219.9520.0AB BG AG ∴=+=+=≈．∴楼高AB 约为20.0米． ······························································································ （8分） 21．（本题满分8分）解：（1）不同．理由如下：往、返距离相等，去时用了2小时，而返回时用了2.5小时，∴往、返速度不同． ······································································································ （2分）（2）设返程中y 与x 之间的表达式为y kx b =+，则120 2.505.k b k b =+⎧⎨=+⎩，解之，得48240.k b =-⎧⎨=⎩，········································································································ （5分）∴48240y x =-+．（2.55x x ≤≤）（评卷时，自变量的取值范围不作要求） ····· （6分）（3）当4x =时，汽车在返程中，48424048y ∴=-⨯+=．∴这辆汽车从甲地出发4h 时与甲地的距离为48km ． ················································· （8分） 22．（本题满分8分）解：这个游戏不公平，游戏所有可能出现的结果如下表：第二次第一次3 45 6 3 33 34 35 36 4 43 44 45 46 5 53 54 55 56 663646566表中共有16种等可能结果，小于45的两位数共有6种． ·········································· （5分）（第20题答案图）()()168168甲获胜乙获胜3588≠ ， ∴这个游戏不公平． ······································································································ （8分） 23．（本题满分8分）解：（1）证明：过点A 作AE BC ⊥，交BC 于点E ． AB AC =，AE ∴平分BC ．∴点O 在AE 上． ······································· （2分）又AP BC ∥， AE AP ∴⊥．AP ∴为O ⊙的切线． ································ （4分）（2）142BE BC == ，3OE ∴．又AOP BOE ∠=∠ ， OBE OPA ∴△∽△． ··································································································· （6分）BE OE AP OA ∴=．即435AP =． 203AP ∴=． ················································································································· （8分）24．（本题满分10分）解：（1）过点A 作AF x ⊥轴，垂足为点F ，过点B 作BE x ⊥轴，垂足为点E ，则21AF OF ==，．OA OB ⊥，90AOF BOE ∴∠+∠=°．又90BOE OBE ∠+∠= °， AOF OBE ∴∠=∠．Rt Rt AFO OEB ∴△∽△．2BE OE OBOF AF OA ∴===． 24BE OE ∴==，．(42)B ∴，． ····················································································································· （2分）（2）设过点(12)A -，，(42)B ，，(00)O ，的抛物线为2y ax bx c =++． 216420.a b c a b c c -+=⎧⎪∴++=⎨⎪=⎩，，解之，得12320a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩，，．P（第23题答案图）22（3）由题意，知AB x ∥轴．设抛物线上符合条件的点P 到AB 的距离为d ，则1122ABP S AB d AB AF == △． 2d ∴=．∴点P 的纵坐标只能是0，或4． ··············································································· （7分）令0y =，得213022x x -=．解之，得0x =，或3x =．∴符合条件的点1(00)P ，，2(30)P ，．令4y =，得213422x x -=．解之，得32x ±=． ∴符合条件的点34)P，44)P ． ∴综上，符合题意的点有四个： 1(00)P ，，2(30)P ，，33(4)2P -，43(4)2P ． ·········································· （10分）（评卷时，无1(00)P ，不扣分） 25．（本题满分12分）解：（1）如图①，连接AC BD 、交于点P ，则90APB ∠=°．∴点P 为所求．······················································· （3分）（2）如图②，画法如下：1）以AB 为边在正方形内作等边ABP △；2）作ABP △的外接圆O ⊙，分别与AD BC 、交于点E F 、．在O ⊙中，弦AB 所对的APB 上的圆周角均为60°， EF∴上的所有点均为所求的点P ． ··················· （7分）（3）如图③，画法如下：1）连接AC ；2）以AB 为边作等边ABE △；3）作等边ABE △的外接圆O ⊙，交AC 于点P ； 4）在AC 上截取AP CP '=．则点P P '、为所求． ············································· （9分）（评卷时，作图准确，无画法的不扣分）过点B 作BG AC ⊥，交AC 于点G ．在Rt ABC △中，43AB BC ==，．DCBA① P②③（第25题答案图）5AC ∴==．125AB BC BG AC ∴== ． ····························································································· （10分）在Rt ABG △中，4AB =，165AG ∴==．在Rt BPG △中，60BPA ∠=°，12tan 60535BG PG ∴==⨯=°．∴165AP AG PG =+=1116122255APB S AP BG ⎛∴==⨯+⨯= ⎝⎭ △． ································· （12分）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2009年定西市中考数学试卷答案

2009年陕西省中考数学副题附参考答案

2009年青海省初中毕业升学考试数学试卷及答案

2009年山西省中考数学试卷及答案

2009年部分省市中考相交线与平行线(含答案)

2009年初中毕业生学业考试(有答案)

甘肃省定西市数学中考试题及答案

2009年定西市中考数学试卷答案

2009年中考数学答案及评分标准

2009年中考数学试题参考答案

甘肃省定西市中考数学试卷及答案

2009中考数学题及答案

2009年中考数学试题汇编之1-有理数试题及答案

2009年定西市中考数学试卷2

09定西市中考数学卷

甘肃省定西市中考数学试题及答案D

2009宁夏中考数学及答案(word版含答案)

2009年 全国 117个地区中考试卷及答案

2009年定西市中考试题

2009年陕西省中考数学试题(word版含答案)

2009年全国 117个地区中考试卷及答案