线性系统理论(复习)(精选)
线性系统理论复习题纲
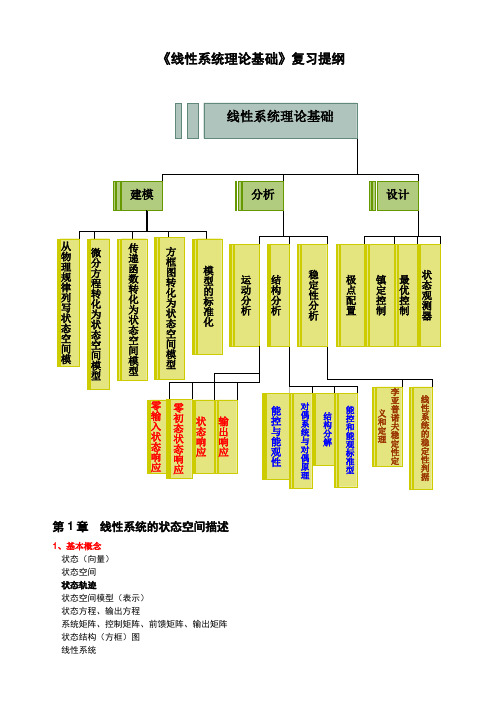
《线性系统理论基础》复习提纲第1章线性系统的状态空间描述1、基本概念状态(向量)状态空间状态轨迹状态空间模型(表示)状态方程、输出方程系统矩阵、控制矩阵、前馈矩阵、输出矩阵状态结构(方框)图线性系统时不变(定常)系统、时变系统连续时间系统、离散时间系统 状态线性变换矩阵的特征值、矩阵的特征向量 对角线标准型、约当标准型 模态标准型 正则型矩阵 范德蒙矩阵 传递函数矩阵2、知识要点%%知识点1:根据物理规律建立状态空间模型♦ 简单机械系统 ♦简单电气系统参考例题:例2.1.1,例2.1.2(P8)%%知识点2:微分方程模型转化为状态空间模型♦微分方程中不含输入导数项给定 ()(1)110n n n y a ya y a y bu --++++=&L ,选取状态向量12(1)n n x y x y x y -⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦&M M , 则有状态方程: 1122011010010n n n x x x x u x a a a x b -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦&&M O M M M&L输出方程: []⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n x x x y M Λ21001 例2.1.3 (注意:方框图在没有要求时可以不画出) ♦微分方程中包含输入函数导数项,且m n <给定()(1)()(1)110110n n m m n m m ya y a y a yb u b u b u b u ----++++=++++&&L L ,m n <,将其转化为()(1)110()(1)110n n n m m m m y a y a y a y u y b yb y b y b y ----⎧++++=⎪⎨=++++⎪⎩&%%%%L &%%%%L ,选取状态向量12(1)n n x yx y x y-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦%&%M M %,则有状态方程 120110100101n n x x u x a a a -⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦&&M O M M &L 输出方程 12011[,,,,0,,0]m n m n x x y b b b x --⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦L L 123M例2.1.4 ♦ 微分方程中包含输入函数导数项,且n m =若()(1)()(1)110110n n n n n n n ya y a y a yb u b u b u b u ----++++=++++&&L L ,让n y y b u =-%,则转化为如下微分方程的形式()(1)(1)(1)110111100()()()n n n n n n n n n y a y a y a y b a b u b a b u b a b u -----++++=-++-+-%%%%&L L 。
线性系统复习

k1
y(k) CAk x0 C Ak j1Bu( j)
0
j0
CeAtx0 h(t)*u(t)
CAk x0 h(k)*u(k)
h (t )DCe At B
h(k )DCA k 1B
传递函 数阵
H ( s) C ( sI A) 1 B
H ( z ) C ( zI A)1 B
u(k) u(t)
u (t) u (k) k T t (k 1)T y(k)
u(t)
u(k) 保持器 u(t) x Ax Bu
y Cx Du y(u)
x(k1)G(xk)H(uk) y(k)C(xk)D(uk)
{x Ax Bu
定1.理 给定线性y 定 Cx D常 u x系 0)(x统 0 (1
2 ,G
e At
1
0
0.5(
1-e-2T ) e-2T
1 0
0.091
0.819
H (
T e At dt)B
T 1
0
0 0
0.5(
1-e-2t ) e-2t
dt
×10
0.5T 0.25e-2T -0.5e-2T 0.5
Bu (k )
(k
)
(1)
已知 x(k 0 ), 及 u(k) k k 0
k 1
x(k) A k-k 0 x(k 0 )
A k-i- 1 Bu(i)
i k0
若令 k 0 0 , 则有 :
k 1
x(k) A k x( 0 )
A k-i- 1 Bu(i)
总复习(信号与线性系统必过知识点)

目录
• 信号与系统基本概念 • 线性时不变系统 • 信号的变换 • 系统的变换 • 信号与系统的应用
01 信号与系统基本概念
信号的描述与分类
信号的描述
信号是信息的载体,可以通过时间或空间的变化来传递信息 。信号的描述包括信号的幅度、频率、相位等特征。
信号的分类
拉普拉斯变换
拉普拉斯变换的定义
将一个信号从时域转换到复频域的过 程,通过将信号表示为无穷积分的形 式来实现。
拉普拉斯变换的性质
拉普拉斯变换的应用
在控制系统分析、电路分析等领域有 广泛应用,如系统稳定性分析、传递 函数求解等。
包括线性性、时移性、复频域平移性、 收敛性等。
Z变换
Z变换的定义
01
将一个序列信号从时域转换到复平面的过程,通过将信号表示
因果性
线性时不变系统的输出仅与当 前和过去的输入有关,而与未 来的输入无关。
稳定性
如果系统对所有非零输入信号 的响应最终都趋于零,则称该
系统是稳定的。
线性时不变系统的分析方法
01
02
03
频域分析法
通过傅里叶变换将时域信 号转换为频域信号,然后 分析系统的频率响应。
时域分析法
通过求解差分方程或常微 分方程来分析系统的动态 行为。
系统分析方法
系统分析是对系统进行建模、分析和综合的方法。常用的系统分析方法包括传递 函数分析、状态方程分析、根轨迹分析等。
02 线性时不变系统
线性时不变系统的性质
线性性
线性时不变系统对输入信号的 响应与输入信号的强度无关,
只与输入信号的形状有关。
时不变性
线性时不变系统的特性不随时 间变化,即系统对输入信号的 响应不会因为时间的推移而改 变。
线性系统复习

完全能观V对连续时间线性时变系统和指定初始时刻九匚£如果存在一个时刻輕几f"*使系统以A W F为初始状态的输HVW恒为零,即HCmtreivj.则称非零状态「切在时刻如为不能观测;如果状态空闻中所有非塞状态在时刻f松都不为不能观测,则称系统在时刻如为完全能观瀝,不完全能观一致完全能观r如果系统对任意时刻均为完全能观測,即能观测性与初始时刻如的选取无关・则称系统为救S全能观测.完全能控判据对H维连续时间线性时不变系统,系统完全能控的充分必要条件为能控性判别矩阵S松=[5 AE,才鱼…才T R满秩,即ranliQ=ftn维连续时间线性时不变系统完全能控的充分必要条件为:rank{Sf-A / Vs€ C或TOM耳人r-坨月]="&为系统特征值能控性指数令Q& =2炯…屮5对完全能控连续时间线性时不变系统,定义能控性指数为:"=使/71戚0=丹成立的最小正整数h完全能观判据对科维连续时间线性时不变系统,系统完全能观测的充分必要条件为能观测性判别矩阵CCA满秩,即fank Qf,=rt歼维连续时间线性时不变系统完全能观测的充分必要条件;Sf-ACrank=/?V5E C或rank 人/一川C ZMy…4,为系统特征值= A(t)X + 5® Y 二 c(t)XI 屮r = —/厂⑴屮卩+ C 丁⑴/b =£「(f)屮 rP = \b Ab A^b …才比]能观性指数 宦义:令西=cCA完全能观测胖堆连续時间线性时不变系统的能观测性指数 定义为訂使"皿必0=/|"成立的最小正整数4离散系统能控 结论4 H 维离散时间线性时不变系统X 茁十1} = GVW 十切 系统完全能达的充分必要条件为矩阵久“乩他…”切馬秩 离散系统能观 结论8 «维离散时间线性时不变系统完全能观测的充分必要 条件为Q"* =c ' CG cc*-'对偶系统满秩能控标准型 比—|W6=严%©=eP兀=PrcinkQ^=r<n^尸1=尸=[如,血…4「丨Oz …,qJ于是可得能控子系统动态方程V = 4 rV 十岀沙厂十和 ”=百*不能控子系统动态方程丘点-兀2丫己Xl — C 2七zrank 0。
线性系统理论第一章

第一章线性定常系统的状态空间描述及运动分析1.1 线性定常系统的传递函数描述传递函数描述局部的,有局限性的描述传递函数描述的是系统的输入--输出关系,即假定对系统结构的内部信息一无所知,只能得到系统的输入信息和输出信息,系统内部结构就像一个"黑箱"一样,因此,传递函数只能刻画系统的输入--输出特性,它被称为系统的输入--输出描述和外部描述.常用的数学工具:拉普拉斯变换主要适用于描述线性定常系统1.单变量情形回顾已知由下列常系数微分方程描述的定常系统其中 : 系统的输出 ; :系统的输入; : 时间; 均为常数 ,(希望input少,收益大)假定所有初始值(包括导数的值)全为0,对上式两边取拉普拉斯变换,得到其中为的拉普拉斯变换,则下式称为系统的传递函数 :传递函数为的真有理分式,则称系统为物理能实现的. 单输入--单输出系统的传递函数必为真有理分式.系统的特征多项式: 多项式系统的特征方程 : 代数方程系统的极点 : 特征方程的根或者说特征方程的零点系统的零点 : 多项式的零点传递函数的零点和极点 : 零极相消后剩下的系统的零点和极点 (若系统有相同的零点和极点,则称系统有零极点相消)2.传递函数矩阵考察多输入--多输出的线性定常系统.令输入变量组 : {} , 输出变量组 : {} 且假定系统的初始变量为 0 .用和分别表示和的拉普拉斯变换, 表示系统的由第个输入端到第个输出端的传递函数,其中则由系统的线性属性(即满足叠加原理) 可以导出:称由上式所定义的为系统的传递函数矩阵. 容易看出, 为的一个有理分式矩阵. 当的元传递函数除严格真还包含真有理分式时,即它的一个或一些元传递函数中分母和分子多项式具有相等的最高幂次时,称为真有理分式矩阵.通常,当且仅当为真的或严格真的时,它才是物理上可实现的.作为一个判别准则,当且仅当零阵时, 为严格真的;非零常阵传递函数矩阵为真的.1.2 线性定常系统的状态空间描述1. 状态和状态空间定义1.1 动力学系统的状态定义为完全的表征系统时间域行为的一个最小内部变量组.组成这个变量组的变量称为系统的状态变量,其中为初始时刻由初始变量构成的列向量称为系统的状态向量,简称为状态.状态空间则定义为状态向量取值的一个向量空间.几点解释:1. 状态向量组可完全的表征系统行为的属性.2. 状态变量组的最小性.3. 状态变量组在数学上的特征.4. 状态变量组包含了系统的物理特征.5. 状态变量组选取上的不唯一性定理1.1 系统任意选取的两个状态变量组之间为线性非奇异的关系2.动态系统的状态空间描述和输入--输出描述不同,状态空间描述中把系统动态过程的描述考虑为一个更加细致的过程,输入引起系统状态的变化,而状态和输入则决定了输出的变化."输入"引起"状态"的变化 ( 一个运动的过程)数学上必须采用微分方程或差分方程来表征并且称这个数学方程为系统的状态方程考虑最为一般的连续动态过程: (一个一阶非线性时变微分方程组)进而,在引入向量表示的基础上,还可将状态方程简洁的表示为向量方程的形式:其中"状态"和"输入"决定"输出"的变化 (一个变量见的转换过程)描述这种转换过程的数学表达式为变换方程,并且称之为系统的输出方程或量测方程.最一般的,一个连续的动力学系统的输出方程具有以下形式:表示为向量方程的形式为其中系统的状态空间描述由状态方程和输出方程组成.离散动态过程(离散系统)的状态空间的描述: 只在离散时刻取值,用来表示其状态空间过程描述只反映离散时刻的变量组间的因果关系和转换关系.通常,可采用两条可能的途径来组成系统的状态空间描述:一是分析途径,适用于结构和参数已知的系统;二是辨识的途径,适用于结构和参数难于搞清楚的系统.3.线性定常系统的状态空间描述限于考虑线性定常系统的连续动态过程,此时,向量函数将都具有线性的关系,且不显含时间 .从而线性定常系统的状态空间描述的表达式为其中维状态向量维控制输入向量维输出向量系统矩阵输入矩阵输出矩阵前馈矩阵以上统称为系统的系数矩阵,均为实常阵.线性定常系统也叫做线性时不变系统(linear time-invariant L TI),完全由系数矩阵决定.简记为.对于线性定常系统,我们分别称系统矩阵的特征值,特征向量,若尔当标准型,特征方程,特征多项式为系统的特征值,特征向量,若尔当标准型,特征方程,特征多项式,系统的特征值也称作系统的极点.若,则此系统为单输入线性定常系统;若,此系统为单输出线性定常系统;若,此系统为单输入--单输出系统,或单变量系统.考虑线性定常离散系统的状态空间描述,其一般形式为其中维状态向量维控制输入向量维输出向量阶实常系数矩阵简记为1.3 输入输出描述导出状态空间描述------------- 系统的实现问题(第五章详解)考虑单输入--单输出线性定常系统.表征此系统动态过程的输入-输出描述,时域为或等价的频域描述即传递函数其中和分别表示和的拉普拉斯变换对于由上式描述的系统,可以引进状态变量 ,将其写成状态空间描述形式,其中为维状态变量分别为的常矩阵由"上"写成"下",称为实现问题,实现不具有唯一性1. 当时,有如下结论:定理1.2 给定单输入--单输出线性定常系统的输入输出描述如"上",当时,其对应的一个状态空间描述为:2. 当时,已知"上"求其状态空间描述.先求极限然后令为严格真,直接按的形式写出即可.3. 当时, 此时输入输出关系为此时状态空间描述形式为:1.4 由状态空间描述导出的传递函数矩阵对于多输入--多输出线性定常系统,传递函数矩阵是表征系统输入输出特性的最基本的形式.1. 传递函数矩阵的表示的基本表达式定理1.3 对应于状态空间描述的传递函数矩阵为并且 ,当时, 为真的 , 时, 为严格真的,且有2.的实用关系式有给出的关系式在理论分析上很重要,但从计算的角度而言不方便,下面给出由计算的两个实用算式.定理1.4 给定状态空间描述的系数矩阵 , 求出则相应的传递函数矩阵可表示为注: 的根 : 系统的极点 ; 分子的根 : 系统的零点推论1.1 若的最小多项式为则系统的传递函数矩阵可表示为2. 脉冲响应矩阵和状态空间描述定理1.11 线性定常系统其中的实常阵的脉冲响应矩阵为将其写作更为常用的形式定理1.12 两个代数等价的线性定常系统具有相同的脉冲响应矩阵.定理1.13 两个代数等价的线性定常系统具有相同的输出零状态响应和输出零输入响应.3. 脉冲响应矩阵和传递函数矩阵定理1.14 分别表示线性定常系统的脉冲响应矩阵和传递函数矩阵,则有推论1.2 给定两个线性定常系统 ,设两者都具有相同的输入和输出维数,状态维数不一定相同,则两系统具有相同的脉冲响应矩阵(即相同的传递函数矩阵)的充要条件为1.8 线性定常离散系统的运动分析归结为对定常的线性差分方程进行求解.1. 线性定常离散系统的运动规律对于上述系统,其状态运动的表达式为或2. 脉冲传递函数矩阵取初始状态 , 则可得到系统的输入输出关系式为其中为线性定常离散系统的传递函数矩阵, 按习惯称为脉冲传递函数矩阵.G(z) 为 z 的有理分式矩阵,通常只讨论其为真的或严格真的情况,此时 G(z) 为物理可实现的. 1.9 线性定常系统的时间离散化1. 问题的提出把连续时间系统化为等价的离散时间系统的问题. (课本P22 或百度文库)2.线性定常系统按采样周期T的离散化线性定常系统引入三点基本假设,以保证系统离散化后的描述简单,且是可复原的1. 采样器的采样方式取为以常数 T 为周期的等间隔采样. 采样瞬时为2. 保持器为零阶的.3. 采样周期的值要满足香农(Shannon)采样定理所给出的条件香农定理:离散信号可以完满地复原为原来的连续信号的条件为采样频率满足.考虑到 , 故上式可化为定理1.15 上述系统的时间离散化模型为其中注 :定理1.15提供了线性定常连续系统时间离散化的算法, 离散化系统仍为定常系统.不管A是否奇异,离散化后系统矩阵G一定是非奇异的.。
线性系统 复习

5)坐标缩放性质(定标性质)—The scaling property
若: g(x) f (x) h(x)
6) 函数的卷积性质
则: f (ax) h(ax) 1 g(ax) a
f (x) (x) f ( ) (x )d f ( ) ( x)d f (x)
f (x) (x x0 ) f (x x0 )
2j
f0 ) (u
f0 )]
9.圆函数的FT
1 , r a
f
(r)
circ(
r a
)
1/ 2 0 ,
, r
r
a
a
1, r 1 f (r) circ(r) 1/ 2 , r 1
0 , r 1
FT[circ( r )] 2 a2 J1( 2a)
a
2a
FT[circ(r)] 2 J1( 2) 2
(a
2 f0 j2 u)2 (2
f0 )2
5).平移性:
若: F(u, v) FT[ f (x, y)]
则:
FT[ f (x x0, y y0 )] exp[ j2 (ux0 vy0 )]F (u, v)
❖空域中的平移造成频域中频谱的相移。
❖光场复振幅不具有平移不变性。但强度具有平移不性。
0
1.2-3.3 FT存在及应用条件(Requirements)
1.2-3.4 广义FT (极限意义下的FT,及δ函数的FT)
lim 1. 极限意义下的FT f (x)
gn ( x)
n
FT f (x) limFT gn(x) limGn(u)
n
n
FT
[sgn(
j
u
x)]
lim
信号与线性系统知识点总复习

信号与线性系统知识点总复习1.信号的基本概念信号是电子信息工程中的重要概念,简单来说就是随时间(或空间)变化的物理现象。
信号可以分为连续信号和离散信号两种。
连续信号可以用函数表示,离散信号可以用数列表示。
2.常见信号的分类常见的信号类型包括连续时间信号、离散时间信号、周期信号、非周期信号、奇函数信号、偶函数信号等。
不同类型的信号在数学表示和性质上有所差异。
3.连续时间信号的基本性质连续时间信号可以通过振幅、频率、相位等参数来描述。
它们具有线性性质、时移性、尺度变换性质和时间反转性质。
这些性质对于信号的分析和处理都是重要的基础。
4.离散时间信号的基本性质离散时间信号是在离散时间点上取值的信号,通常用数列表示。
离散时间信号具有线性性质、时移性、尺度变换性质和时间反转性质。
此外,离散时间信号还有抽样定理、离散时间傅立叶变换等重要概念。
5.线性系统的基本概念线性系统是输入和输出之间存在线性关系的系统,可以用线性常微分方程或差分方程表示。
线性系统具有叠加原理、时不变性、因果性等基本特性。
线性系统的频率响应是分析系统特性的重要工具。
6.线性时不变系统的冲激响应冲激响应是线性时不变系统的重要性质,它描述了系统对单位冲激输入的响应。
从冲激响应可以得到系统的频率响应、相位响应等信息。
7.线性时不变系统的频率响应频率响应描述了线性时不变系统对不同频率的输入信号的响应特性。
它可以通过线性时不变系统的冲激响应来计算,常用的方法有离散时间傅立叶变换、连续时间傅立叶变换、z变换等。
8.线性系统的稳定性分析稳定性是线性系统分析中的重要性质。
对于连续时间系统,稳定性可以通过系统的传递函数的极点位置来判断。
对于离散时间系统,稳定性可以通过系统的差分方程的极点位置来判断。
9.线性系统的频域分析频域分析是信号与系统分析中的重要方法,可以通过傅立叶变换、拉普拉斯变换和z变换等来将信号从时域转换到频域。
频域分析可以得到信号的频谱特性、频率响应等信息。
线性系统理论(2013.7.26)
定义 Φ(t ) e At L1[(sI A)1 ] 为系统状态转移矩阵
解状态方程的关键——求状态转移矩阵 。
13
已知状态方程及初始条件:x1(0)=1,x2(0)=0,求解该齐次方程。
1 0 x x 1 1
解:
(sI A)-1
1 s 1 0 (s - 1)2 1 s - 1
系统结构图:
U1(s) G1/s 11(s) Y1(s)
0 G21(s)
1/s(s+2) G12(s)
U2(s)
1 y1 s y 2 0
1 s( s 2) u1 1 u2 s2
1/(s+2) G22(s)
y c1m c1,m 1 c12 c11 X
2) 由系统结构图建立状态空间表达式
4
例 系统如图,试建立起状态空间表达式。 u
—
k x3 1 x2 1 s1 s2 s
x1
yHale Waihona Puke 解:由结构图X 1 ( s) 1 X 2 ( s) s
x1 x2
X 2 ( s) 1 X 3 ( s) s 2
y x1
5
5 矩阵的特征方程、特征值
1)方阵A的特征方程与特征值 设A 为n×n的方阵,如有一未知量λ ,则: 0 a11 a12 ... a1n a11 a12 a 21 a22 ... a 2 n a21 a 22 I A ... ... ... ... ... ... an1 an 2 ... ann an1 a n 2 0
线性系统理论考点汇总

4
系统运动的稳定性
考点 4.1. 渐进稳定: 对特征多项式det(sI − A)运用劳斯判据。 特 征 多 项 式 系 数 都 大 于0是 渐 进 稳 定 的的 必 要 条 件。 BIBO稳定: 传递函数的极点均具有负实部。 考点 4.2. 大范围渐进稳定。 步骤:1、V (x)c。 ˙ (x)负定。或V ˙ (x)半负定,系统状态方程的解 2、V 只有平衡状态(导数不恒为0)。 3、||x|| → ∞,V (x) → ∞ 考点 4.3. P A + AT P = Q,Q = −I 。 若P对称正定,则大范围渐进稳定。
考点 3.1. 系统是否能控/能观。 若A无特定形式:采用秩判据。 若A为 约 旦 规 范 形: 不 同 特 征 值 的 约 旦 块 末 行(首 列)非 零。 相 同 特 征 值 的 约 旦 块 末 行(首 列)线 性 无 关。 考点 3.2. 判断连续时间线性线性时变系统是否完 全能控。 M0 (t) = b(t) 0 (t) M1 (t) = −AM0 (t) + dM dt 对于任意的t,rank M0 (t) M1 (t) 满秩,系统完 全能控。 考点 3.3. 求线性时不变系统的能控性指数和能观 性指数。 使能控性判别阵rank B AB . . . 满秩。 A的最小幂次为α。能 控性指 数u=α+1 C 使能观性判别阵rank CA 的满秩。 ... A的最小幂次为β 。能观性指数v=β +1 考点 3.4. 已知状态空间表达式, 求能控规范性及 其变换阵。 步骤:1、列出特征多项式det(sI − A) 1 0 0 2、变换阵P = A2 B AB B a2 1 0 a1 a2 1 −1 −1 3、A = P AP , B = P B , C = CP 能观规范形形式上对偶。 考点 3.5. 定出三阶龙伯格能控规范形。 取能控性判别阵线性无关的三列,构造变换阵P −1 。 由P的块末行导出变换阵S −1 。 基于状态变换x = S −1 x,导出变换后系统的系数矩 阵。 考点 3.6. 传递函数的能控规范形实现。 提 出 直 接 传 递 矩 阵 化 简 后 分 母 必 须 为严 真 首 一 多 项式。 考 点 3.7. G(s)的 行 列 维 数 为 能 观 块 维 数 和 能 控 块 维数。 考点 3.8. 传递函数矩阵的最小实现。 考点 3.9. 按能控性分解。 取 能 控 性 判别 阵 的 非 零 向Q量q1 ,另取 线 性 无 关 非 零向量q2 ,构成变换矩阵Q。 基于状态变换x = Q−1 x,导出变换后系统的系数矩 阵 考点 3.10. 定出能控能观子系统。
线性系统理论全

稳定性判据与判定方法
稳定性判据
在控制工程中,常用的稳定性判据有Routh判据、Nyquist判据、 Bode判据等。这些判据通过分析系统的特征方程或频率响应来判 断系统的稳定性。
判定方法
除了使用稳定性判据外,还可以通过时域仿真、频域分析、根轨 迹法等方法来判定系统的稳定性。这些方法各有优缺点,适用于 不同类型的线性系统和不同的问题背景。
100%
线性偏差分方程
处理离散空间和时间的问题,如 数字滤波器和图像处理等。
80%
初始条件与边界条件
在差分方程中,初始条件确定系 统的起始状态。
状态空间模型
状态变量与状态方程
表示系统内部状态的变化规律 ,揭示系统动态特性。
输出方程
描述系统输出与状态变量和输 入的关系,反映系统对外部激 励的响应。
状态空间表达式的建立
复频域分析法
拉普拉斯变换
将时域信号转换为复频域信号,便于分析系统的稳定性和动态性 能。
系统函数
描述Байду номын сангаас统传递函数的复频域表示,反映系统的固有特性和对输入信 号的响应能力。
极点、零点与稳定性
通过分析系统函数的极点和零点分布,可以判断系统的稳定性以及 动态性能。
04
线性系统稳定性分析
BIBO稳定性
01
线性系统理论全
目
CONTENCT
录
• 线性系统基本概念 • 线性系统数学模型 • 线性系统分析方法 • 线性系统稳定性分析 • 线性系统能控性与能观性分析 • 线性系统优化与综合设计
01
线性系统基本概念
线性系统定义与性质
线性系统定义
满足叠加性与均匀性的系统。
线性系统性质
线性系统理论汇总

非线性序
序列中存在分支、闭合环路或者其他复杂 情形。
当实际问题被表示为数学形式,特别是解析 形式时,线性与非线性的区别显而易见,只 包含变量的一次项是线性特性,企业的均为 非线性特性。而没有给出数学表达式的实际 现象往往可以通过直观的判断。
能够用线性数学模型描述的系统
称为线性系统。
所具有线性基本特性:
一对多
变量之间的 关系
多对多 多对一
一对一•
变量之间最简单最 基本的对应关系
函数
线性函数
因变量和自变量成比例 的变化,即变化过程中 二者的比值不变,称 为线性函数
非线性函数
因变量和自变量之间的 变化过程中二者的比值 变化
最简单的一元线性函数的一般形式为: y=ax+b
a:代表因变量与自变量的不同比率 线性静态系统 b: 线性函数的截距
截距
有实际意义,函数形式为y=ax+b
没有实际意义,则 x1=x+ b/a
y=ax1
简单的变量关系用一元函数表示
较为复杂的变量关系须用多元函数表示 如,z=ax+by,函数所表示的图形就是3维空间 中的一张平面。
函数仅仅是描述一个变量对另一个变量的 依存关系,如果要表示多个变量之间的相互 依存关系,则应该用以下的数学形式:
y
x
x
t
不稳定结点,如组织溃散、文化感弱的团队会越来越难以 形成一个有机的有力整体。
y x
x t
稳定结点,如团队的建立,起初建立起来的团队是动荡 不稳定的,但是最后有一个趋于稳定有效的过程。
y x
y x
两张图分别表示稳定焦点和不稳定焦点,举例来说就如企 业团队在合作的过程中团队成员向团队核心人物靠拢或着 远离团队领导人。
线性系统复习题—答案 - 副本

1、已知线性定常系统状态方程为:Ax x =.其中,⎥⎦⎤⎢⎣⎡-=2310A (1)采用线性变换化A 为对角型;32231det )det(2-+=⎥⎦⎤⎢⎣⎡+--=-s s s s A SI 特征值:1,321=-=λλ鉴于系统矩阵是能控规范型,且特征值互异,故取变化矩阵⎥⎦⎤⎢⎣⎡-=1311P ⎥⎦⎤⎢⎣⎡-==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=--13,41434141 11AP P A P 故有则(2)求出状态转移矩阵)(t Φ;⎥⎦⎤⎢⎣⎡+--=-231)(s sA SI⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-++-++--++--++=⎥⎦⎤⎢⎣⎡+-+=--=--141343143343141341143341312)1)(3(1)()()(1s s s s s s s s s s s s A SI A SI adj A SI (主对换,负变号)()[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++-+-+=-=Φ∴------t t tt t t tt e e e e e e e e A SI L t 4143434341414341)(333311 (3)初始状态T x ]10[)0(=时,写出系统齐次状态方程)(t x 。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++-=Φ==--t t t t Ate e e e X t X e t X 41434141)0()()0()(332、已知系统方程为:[]x y u x x 110,121201112201=⋅⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⋅⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⋅(1)写出对偶系统的状态空间描述;;(2)写出原系统的能控矩阵c Q 、能观矩阵o Q ;(3)写出对偶系统的能控矩阵c Q 、能观矩阵o Q ;(4)运用对偶原理,判断原系统及其对偶系统的状态能控、能观测性。
原系统 :能控性: 能观测性:rank( )=3=n即原系统属于完全能控和完全能观系统。
对偶系统 : 根据对偶原理完全能控 完全能观测 完全能观测 完全能控推出,对偶系统属于完全能控和完全能观系统。
线性系统理论(复习)

u
u1
x1
1
y1
x2
2
y2 y
y1 1 0 x1
R
S2: x2 x2 3u2
y2 2x2
+
e(t)
i
C - uc
e
uc
RC
duc dt
,
x 1 x 1 u, RC RC
yx
解:
1 2 0 1
.
x
A1 B2C1
0 A2
x
B1
B2
D1
u
0 3
3 0
0 x1 3 u 1 0
例 线性定常系统的齐次状态方程为
x1 x2
0 2
1 x1
3
x2
求其状态转移矩阵 eAt
解
[sI
A]1
s 2
1
1
1 s 3
s 3
(s 1)(s
2)
2
1 s
s
2 1
s
1
2
2 s 1
s
2
2
s
1 1
s
1
2
1 s 1
s
2
2
于是
eAt L
1[sI
A]1
2et
x1
x2
[D1
D2
]u
G(s) G1(s) G2 (s)
:
p
x1 A1
xN
y C1
x1 B1
u
AN xN BN
CN
x1 x2
[D1
DN ]u
N
G(s) Gi (s) i 1
u1
例:求如下并联系统的状态空间描述 u
0 1 0
线性系统理论复习大纲

第一部分复习大纲1.什么是线性系统?线性系统一般怎样分类?2.状态空间的描述和输入输出描述的基本概念及其关系。
3.系统状态空间描述建模。
主要是指电路、力学装置、机电装置的状态空间描述数学模型。
4.状态方程的约当标准型及其性质。
5.传递函数矩阵概念。
传递函数矩阵与状态空间描述之间的关系(已知状态空间描述求传递函数矩阵和已知传递函数矩阵进行状态空间描述实现)。
6.线性坐标变换。
7.组合系统的状态空间描述,输入输出描述建模。
8.矩阵指数函数及其性质。
9.线性系统的运动求解,系统矩阵特征值,特征向量对运动的影响。
10.脉冲响应阵与传递函数阵的关系、卷积定理。
11.状态转移矩阵及其性质。
12.线性连续系统离散化及其性质、求解。
13.连续系统与离散系统的能控性、能达性、能观性、能测性及其判据。
14.能控性指数、能观性指数、对偶原理。
15.能控能观标准型及其结构分解,结构分解后各部分与输入输出描述,状态空间描述之间的关系,会对约当标准型进行结构分解并求传递函数。
16.线性系统内部稳定、BIBO稳定概念及其性质。
17.连续和离散系统的lyapunov稳定概念及其各种判别定理,会用lyapunov方法判断连续系统、离散系统的稳定性。
18.状态反馈、输入输出反馈性能比较。
19.极点配置及其算法。
20.镇定条件、镇定与极点配置的关系(算法不考,但对一个线性系统能进行是否能镇定条件判断)。
21.解耦控制形式、分类,各种解耦方法特点,系统能否解耦判断,会进行积分型解耦算法。
22.跟踪问题及其结构框图、内模原理(会建立跟踪问题的内模)、可跟踪条件。
23.各种线性二次型最优控制问题指标含义,掌握最优控制及其性能指标求法。
24.无限时间最优控制的稳定裕度,反馈增益可摄动范围及其物理意义。
25.状态观测器设计、分类及其特点,掌握全维和降维观测器设计方法。
26.状态观测器设计与状态反馈设计之间的关系问题。
第二部分复习大纲1.多项式、多项式矩阵的基本概念。
线性系统理论复习大纲

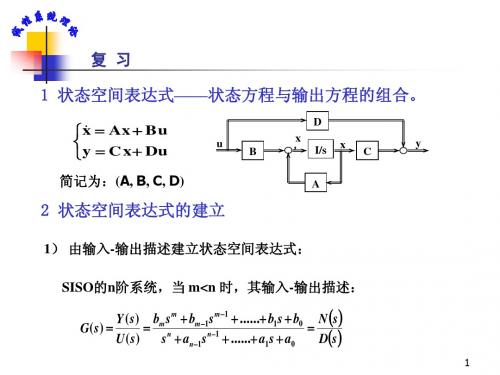
Chapter 2 Mathematical Descriptions of Systems定义2.1 一个系统在0t 时刻的状态是一组信息的组合,它和系统的输入0()()u t t t ≥一起可唯一确定系统的输出0()()y t t t ≥系统数学描述小结系统类型 内部描述 外部描述 分布、线性 0()(,)()tt y t G t u d τττ=⎰ 集中、线性()()()()x A t x B t uy C t xD t u=+=+ 0()(,)()tt y t G t u d τττ=⎰分布、线性、定常()()()()()()t y t G t u dy s G s u s i r r a t i o n a lτττ=-=⇒⎰集中、线性、定常 x A x B uy C x D u=+=+()()()()()()t y t G t u dy s G s u s r a t i o n a lτττ=-=⇒⎰Chapter 4 State-space Solutions and Realizations线性定常系统状态方程的解()()(0)()tAtA t x t e x eBu d τττ-=+⎰()()(0)()()tAt A t y t Ce x C eBu d Du t τττ-=++⎰111()()[(0)()]()()(0)[()]()xs sI A x B u s y s C sI A x C sI A B D us ---=-+=-+-+连续状态方程按采样时间T 离散化 0TA TAA d eB de B d ττ==⎰定义4.1 设P 为n n ⨯非奇异实矩阵,任等价变换x Px =,那么方程xAx Bu y C x Du=+=+ 与原方程代数等价。
(其中,11,,,A PAP B PB C C P D D --====)定理 4.1 两个线性定常系统状态方程为零状态态等价(具有相同的传递矩阵)的充分必要条件mmCA B CA B =定义4.2 设()X t 是()x A t x = 的任一基本矩阵,那么100(,)()()t t X t X t φ-=称该方程的状态转移矩阵,它同时也是方程00'(,)()(,)t t A t t t φφ=关于初始条件00(,)t t I φ=的唯一解。
研究生线性系统理论题

1.为什么要对连续系统进行离散化?离散化有哪些方法?它们各自的特点是什么?因为连续系统在电脑上无法实现,只能把连续系统离散化,而离散华是将连续变化的模拟量信号,转换成数字量(脉冲)信号,但是这里的离散化是非常密集的,在误差允许的范围内,可以非常的逼近原函数.这样就能用数字电子计算机(电脑)进行计算或处理。
1.前向差分法S平面左半平面得极点可能映射到Z平面单位圆外,这种方式所得到得离散滤波器可能不稳定2.后向差分法变换计算简单;S平面得左半平面映射到Z平面得单位圆内部一个小圆内因此如果D(s)稳定则变换后的D(z)也稳定;离散滤波器得过程特性及频率特性同原连续滤波器比较有一定得失真,需要较小得采样周期T。
3.双线性变换法如果D(s)稳定,则相应得D(z)也稳定;D(s)不稳定,则相应的D(z)也不稳定;所得D(z)的频率响应应在低频段与D(s)得频率响应相近,而在高频段相对于D(S)得频率响应有严重畸变。
4.脉冲响应不变法D(z)和D(s)有相同得单位脉冲响应序列;若D(z)稳定,则D(s)也稳定;D(z)存在着频率失真。
该法特别适用于频率特性为锐截止型的连续滤波器的离散化。
主要应用于连续控制器D(s)具有部分分式结构或能较容易地分解为并联结构,以及D(s)具有陡衰减特性,且为有限带宽得场合。
这时采样频率足够高,可减少频率混叠影响,从而保证D(z)得频率特性接近原连续控制器D(s)。
5.阶跃响应不变法若D(s)稳定,则相应的D(z)也稳定;D(z)和D(s)得阶跃响应序列相同;6.零极点匹配法需要先求出连续传递函数得全部零极点,计算复杂;能够保持变换前后特征频率处得增益不变;不改变系统得稳定区域,变换前后G(z)和G(s)的稳定特性不变2.多输入/多输出系统能控性和能观测性与系统传递函数矩阵的关系如何?在单输入单输出系统中,能控且能观测得充分必要条件是传递矩阵G (s )的分母与分子之间不发生因子相消。
线性系统理论复习

◆给定系统{A,B,C,D},当A的特征值两两相异时,利用特征向量组成变换矩阵,可化为对角形;当A的特征值不是两两相异时,有时可以化为对角形,有时不能化成对角形,只能化为约当形。
◆对n维线性时不变系统,若A为对角阵,且其特征值两两相异,系统完全能控的充分必要条件是B中不包含零行向量。
◆线性时不变系统引入坐标变换,其传递函数矩阵在线性非奇异变换下保持不变。
定义:称具有相同输入和输出的两个同维线性时不变系统代数等价,当且仅当它们的系统矩阵之间满足状态空间描述坐标变换中给出的关系。
代数等价的系统的基本特征是具有相同的代数结构特性,如特征多项式、特征值、极点、稳定性、能控性、能观测性等。
◆对完全能控单输入连续时间线性时不变系统,状态维数为n,则系统能控性指数μ=n。
结论①时间离散化属性:时间离散化不改变系统的时变或时不变属性。
②离散化系统属性:不管系统矩阵A(t)或A是非奇异或奇异,其离散化系统的系统矩阵G(k)和G必为非奇异。
◆如果A的特征值互不相同,则系统(A、B、C)为能控且能观测的充分必要条件是:传递矩阵G(s)的分母|sI-A|与分子之间不发生因子相消。
◆单输入、单输出系统(A、b、c)是能控且能观测的充分必要条件是:传递函数G(s)的分母|sI-A|与分子之间不发生因子相消◆单输入、单输出系统(A、b、c),如果A的特征值互不相同,若传递函数存在零、极点对消,则系统或是状态不能控或是状态不能观测的;若传递函数不存在零、极点对消,则系统是状态完全能控且完全能观测的。
◆对零初始条件p维输入和q维输出连续时间线性时不变系统,令初始时刻t0=0,则系统BIBO 稳定的充分必要条件为:真或严真传递函数矩阵G(s)的所有极点均具有负实部。
◆定义:称连续时间线性时不变系统在t0为内部稳定,是指由时刻t0任意非零初始状态引起的零输入响应Xou(t)对t∈[t0,+∞)有界,并满足渐近属性。
◆李亚普诺夫意义下稳定只能保证系统受扰运动相对于平衡状态的有界性,不能保证系统受扰运动相对于平衡状态的渐进性。
线性系统理论复习提纲

线性系统理论复习提纲闭卷部分内容:(40分)题型:判断改错、填空、简答(证明,传递函数、特征值等计算)1、第一章P4:什么是线性系统?(,要求会证明)例子:是否线性系统?什么是定常系统?(参数不随时间变化)例子:和那个是定常系统?2、第二章P17:动态系统的内部和外部描述(外部——输入输出描述,内部——基于内部结构分析的数学模型)。
例子:传递函数是线性定常系统的外部描述模型还是内部描述模型?第2.5和2.6节:给定矩阵A,求特征多项式、特征值;转换为约当标准形。
例子:(特征值互异时)试求系统矩阵A的特征多项式、特征值,并转换为约当标准形。
例子:(存在重特征值时)试求系统矩阵A的特征多项式、特征值,并转换为约当标准形。
第2.7节:已知系统的状态空间描述(A,B,C,D),写出其传递函数表达式。
例子:试求系统的传递函数矩阵。
第2.8节:两个线性定常系统代数等价是什么意思?线性系统在坐标变换下,哪些量发生变化,哪些不变?例子:若,,,系统和是否代数等价?例子:坐标变换是否改变系统的传递函数?3、第三章第3.1节:已知系统的状态空间描述为(A,B,C,D),写出其状态响应和输出响应表达式,并指出哪部分是零输入响应,哪部分是零初态响应。
第3.2节:特征值与状态响应模式的关系(P101 中间(1))。
例子:系统的运动模式是否存在振荡?第3.4节:给定(A, B, C, D),求其脉冲响应矩阵。
4、第四章第4.1节:简述状态和系统能控性的定义,并简单解释其物理意义。
第4.1节:简述状态和系统能观测性的定义,并简单解释其物理意义。
第4.2、4.3节:能控性和能观测性判别矩阵的形式(秩判据)。
例子:试判断系统是否完全能控、是否完全能观测。
第4.7节:能控和能观测规范形。
例子:判断对错并改正:完全能控的任意两个代数等价系统必具有相同的能控规范形。
完全能观测的任意两个代数等价系统必具有相同的能观测规范形。
5、第五章第5.1节:内部和外部稳定性的定义及其相互关系。
