线性系统理论课后答案

北航线性系统理论完整版答案

1-1 证明：由矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=12-n 1-n n- - - -1 0 1 0 00 0 1 0a a a a A可知A 的特征多项式为nn n n n n n n n n nn n n n a a a a a a a a a a a a a a a a a a a a a a a A I ++++++=+++++=+++=++=+=-+λλλλλλλλλλλλλλλλλλλλλλλ1-3-32-21-11-3-3122-2-1-n 13-n 2-n 21-1n 12-n 1-n 12-n 1-n n1- )1(-)1(- 00 0 1- )1(-)1(- 0 00 1-1 0 1- 0 00 1-若i λ是A 的特征值，则00 0 0 1 10 1- 0 0 0 1-111n 1-n i 12-n 1-n n =⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=++++=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--ni n i n i i i i i a a a a a a a λλλλλλλλ 所以[]Ti i 1-n i 2 1 λλλ 是属于i λ的特征向量。

1-7 解：由于()ττ--t e t g =，，可知当τ<t 时，()0≠τ，t g ，所以系统不具有因果性。

又由于()()0 ，，ττ-=t g t g ，所以系统是时不变的。

1-8 解：容易验证该系统满足齐次性与可加性，所以此系统是线性的。

由于()()t 0 t ⎩⎨⎧>≤-=-=ααββαβαt u t u P u Q P 而()()⎩⎨⎧+>+≤-=⎩⎨⎧>≤=βαβαβααβαβ t 0 t t 0 t t u t u Q u P Q ，故u P Q u Q P αββα≠，所以系统是时变的。

又因为()()()()()⎩⎨⎧>≤=⎩⎨⎧>≤=ααααα，，T T t u t u P u P P T T min t 0 min t t 0 t 而()()()()()()()⎩⎨⎧>≤=⎩⎨⎧>≤=ααααα，，，，T T t u T T t u P u P P P T T T min t 0 min t min t 0 min t ，故()()u P P P u P P T T T αα=，所以系统具有因果性。

线性系统理论课后答案

6 XI 给定图P2.12)和＜b)所示两个电路，试列写出其状态方S 和输出方程。

其中, 分别指定：⑹状态变组廿二叱•勺输入变M « = ef(r):输出支量尹=/(b)状态变宣组X 严气，输入变S“y(O；输出变量丿■“CP2 1解本题A 于由物理系统養立状态令问描述的基本题，意在训练正磧和熟塚运用电路定律列写岀电路的状态方程和输出方程•(1)列写P2・l(a)电路的状态方程和输山方程。

首先.考虎到电容C 和电感E 为给定电路中仅有的两个储能元件•电容端电压弋和流经电感电流了构成此电路的线性无关极人变*组，从而透取状态变*组州=%:和巧=i 符合定义要求。

基此，利用电路元件关系式和回路基尔《夫定律，定出电路方程为C 虬r dr L —+= e再由上述电路方程导出状态变量陀和i 的导》项，可得到状态变査方程规范形式，血C I •—=—(tU C d/ 1 心 1 d/L c L L表%=3山和dW/dn 并将上述方程组表为向量方程，就得到此电路的状态方程:继而.按约定输出y = A 可直接得到此电路的输出方程:(b)列写P2.i(b)电路的状态方程和«ta 方程•类似地.考虑到电容C ］和C2为给定电路中仅有的两个储能元件，电容端电压乜和七构成此电路的线性无关极大变fi 组，选取状态变量组二叱和可二叱2符合定义要求，基此，利用电路元件关系式和回路基尔霍夫定定出电路方程为dur GRpM 叱+叱之71RZ,皿6再由上述电路方程导出状态变量叱和叱的导数项，可得到状态变量方程规范形式: % 1 I 1少GR q GR 5 C,Kdr 表M 也C| /曲和 MqI方程：继而，按约定输出y =坯，可由电路导出：尸叱=%+七将其表为向*方程，就得萸i 此电路的皴出方程，八不叱~孫"6 +丽e并将上述方程组表为向量方程，就得封此电路的状态K2.6求出下列^输入输出描述的一个状态空同描述： (i) 施)二 2^2 十 18$+40u(s)『+ 6“ +11S+6 (ii) 型十妙⑴_u(j) (g + 3)2(zl)解本®属于由传递函数型输入输出描述导出狀态空间描述的基本fi 。

线性系统课后答案第5章

5.1Is the network shown in Fing5.2 BIBO stable ? If not , find a bounded input that will excite an unbound output 图5.2 的网络BIBO 是否稳定?如果不是.请举出一般激励无界输出的有界输入. From Fig5.2 .we can obtain that xy yu x =-=Assuming zero initial and applying Laplace transform then we have1)(ˆ)(ˆ)(ˆ2+==s ss us y s yt s sL s g L t g cos ]1[)]([)(211=+==-- because⎰⎰⎰∑⎰∞∞∞=π+π++-+==02002322121cos )1(cos |cos ||)(|x k k k k tdttdt dt t dt t g=1+∑∞=+π+π-π+π-021231)sin()2[sin()1(k k k=1+∑∞=+π-π--021231]sin [sin )1()1(k k k=1+∑∞=++-⋅--012122)1()1(k k k ）（=1+2∑∞=01k =∞Which is not bounded .thus the network shown in Fin5.2 is not BIBO stable ,If u(t)=sint ,then we have y(t)=⎰⎰τ-τ=τττ-ttt d t 0)sin(cos sin )cos(τd =⎰=τt t t td 0sin 21sin 21 we can see u(t)is bounded ,and the output excited by this input is not bounded5.2consider a system with an irrational function )(ˆs y.show that a necessary condition for the system to be BIBO stable is that |g(s)| is finite for all Res ≥ 0一个系统的传递函数是S 的非有理式。

线性系统课后答案第2章

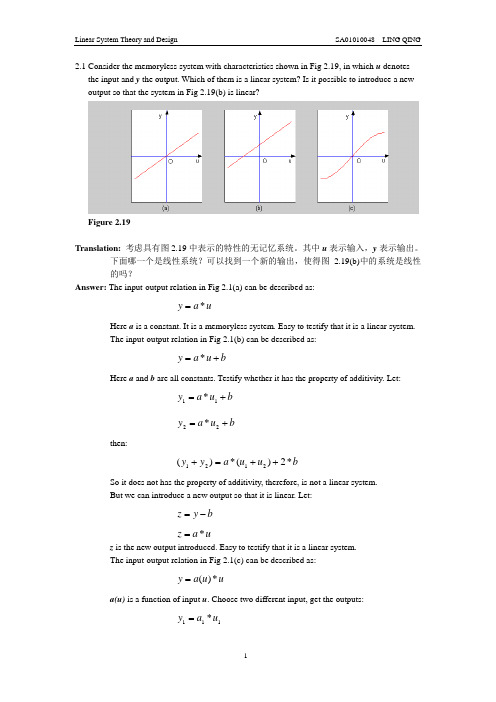
2.1 Consider the memoryless system with characteristics shown in Fig 2.19, in which u denotes the input and y the output. Which of them is a linear system? Is it possible to introduce a new output so that the system in Fig 2.19(b) is linear?Figure 2.19Translation: 考虑具有图2.19中表示的特性的无记忆系统。

其中u 表示输入，y 表示输出。

下面哪一个是线性系统？可以找到一个新的输出，使得图2.19(b)中的系统是线性的吗？Answer: The input-output relation in Fig 2.1(a) can be described as:u a y *=Here a is a constant. It is a memoryless system. Easy to testify that it is a linear system. The input-output relation in Fig 2.1(b) can be described as:b u a y +=*Here a and b are all constants. Testify whether it has the property of additivity. Let: b u a y +=11*b u a y +=22*then:b u u a y y *2)(*)(2121++=+So it does not has the property of additivity, therefore, is not a linear system.But we can introduce a new output so that it is linear. Let:b y z -=u a z *=z is the new output introduced. Easy to testify that it is a linear system.The input-output relation in Fig 2.1(c) can be described as:u u a y *)(=a(u) is a function of input u . Choose two different input, get the outputs:111*u a y =222*u a y =Assure:21a a ≠then:221121**)(u a u a y y +=+So it does not has the property of additivity, therefore, is not a linear system.2.2 The impulse response of an ideal lowpass filter is given by)(2)(2sin 2)(00t t t t t g --=ωωω for all t , where w and to are constants. Is the ideal lowpass filter causal? Is is possible to built the filter in the real world?Translation: 理想低通滤波器的冲激响应如式所示。

第一篇线性系统理论习题答案

⎡ s +1 ⎢s2 + s +1 ⎢ −1 = [1 0 1]⎢ 2 ⎢s + s +1 ⎢ 0 ⎢ ⎣
9－7 设有三维状态方程
⎡0 ⎤ ⎢1 ⎥ ⎢ ⎥ ⎢ ⎣1 ⎥ ⎦
1 s + s +1 s 2 s + s +1
2
0
⎤ 0 ⎥ ⎥ ⎡0 ⎤ s 2 + 2 s 1⎥ = 3 0 ⎥ ⎢ ⎢ s −1 ⎥ ⎥ 1 ⎥ ⎢ ⎣1⎥ ⎦ s − 1⎥ ⎦
⎡ R M ⎤ ⎡ R −1 ∵⎢ ⎥×⎢ ⎣0 T ⎦ ⎣ 0
− R −1 MT −1 ⎤ ⎡ R −1 ⎥=⎢ T− ⎦ ⎣ 0
⎡R M ⎤ ∴⎢ ⎥ ⎣0 T ⎦
9－10 解
−1
⎡ R −1 =⎢ ⎣ 0
− R −1 MT −1 ⎤ ⎥ T −1 ⎦
−1
对可控标准形 A 和 b ，计算 ( sI − A) b
+
v2
& 2 = x1 + y = x1 − C 2 x
写成矩阵形式为
1 1 x2 + U R2 R2
图 9－1 RLC 网络
⎡ R1 − & x ⎡ 1 ⎤ ⎢ L1 ⎢x ⎥=⎢ ⎣ &2 ⎦ ⎢ 0 ⎢ ⎣
⎤ ⎡ 1 ⎤ 0 ⎥ x ⎡ ⎤ ⎢ L ⎥ ⎥ ⎢ 1 ⎥ + ⎢ 1 ⎥U − 1 ⎥ ⎣ x2 ⎦ ⎢ − 1 ⎥ ⎢ R2 C 2 ⎥ ⎦ ⎣ R2 C 2 ⎥ ⎦
x1 ， x 2 有下列关系存在 x1 = x1 + x 2 x 2 = − x1 − 2 x 2
试求系统在 x 坐标中的状态方程。解 ①
&1 = x & = x2 x &2 = & & = −2 x1 − 3 x 2 + u x x

《线性系统理论》作业参考答案

x 11 e t x 21 , 21 0 , x
x11 ( t 0 ) 1 x 21 ( t 0 ) 0
，
x 12 e t x 22 , 22 0 , x
x12 ( t 0 ) 0 x 22 ( t 0 ) 1
解得
x12 e t e t 0 x11 1 ， x 21 0 x 21 1 1 (t ) x 0 e
( sI A )
1
s ( s 1) 0 2 det( sI A ) s ( s 1) 0 adj ( sI A ) 1
s 1 ( s 1) 0
2
s ( s 1) 1 s ( s 1) 1 s 1 1
2
所以 e
。
可以看出， f ( i ) 是 f ( A ) 的一个特征值。
1-3 解：(1) 特征多项式为 1 ( ) ( 1 ) .
4
验证
A 1 I 0 , ( A 1 I ) 2 0 , ( A 1 I ) 3 0 , ( A 1 I ) 4 0
At
e t 1 1 L [( sI A ) ] 0 0
e 1 1 0
t
t t 1 e te t e 1 。 t e
1-5 证明：因为 D 1 存在，所以由 D R p p
A det C B IA det D 0 BD A I D C
c
k 0
k
A
k
设 x 是属于 i 的一个非零特征向量，故
A x i x
.
2 2 因此 A x A Ax A i x i Ax i i x i x .

线性系统课后答案第4章

PROBLEMS OF CHAPTER 44.1 An oscillation can be generated by 一个振荡器可由下式描述：X X ⎥⎦⎤⎢⎣⎡-=0110 试证其解为：Show that its solution is )0(cos sin sin cos )(X t t t t t X ⎥⎦⎤⎢⎣⎡-=Proof: )0()0()(0110X eX e t X t At ⎥⎦⎤⎢⎣⎡-== ,the eigenvalues of A are j,-j;Let λββλ10)(+=h .If te h λλ=)(,then on the spectrum of A,thentj t e j j h t j t e j j h jt jt sin cos )(sin cos )(1010-==-=-+==+=-ββββ thenttsin cos 10==ββso ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡=+=t t t t t t A I A h cos sin sin cos 0110sin 1001cos )(10ββ )0(cos sin sin cos )0()0()(0110X t t t t X eX e t X t At ⎥⎦⎤⎢⎣⎡-===⎥⎦⎤⎢⎣⎡- 4.2 Use two different methods to find the unit-step response of 用两种方法求下面系统的单位阶跃响应：U X X ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=112210[]X Y 32=Answer: assuming the initial state is zero state.method1:we use (3.20) to compute⎥⎦⎤⎢⎣⎡-+++=⎥⎦⎤⎢⎣⎡+-=---s s s s s s A sI 212221221)(211then t At e t t tt tt A sI L e ---⎥⎦⎤⎢⎣⎡--+=-=sin cos sin 2sin sin cos ))((11 and )22(5)22(5)()()(221++=++=-=-s s s s s s s BU A sI C s Y then t e t y tsin 5)(-= for t>=0method2:ttt tt At tt A tt A te t e t e t e t e C Be e CA B d e C d Bu e C t y --------=⎥⎦⎤⎢⎣⎡---+⎥⎦⎤⎢⎣⎡--=-===⎰⎰sin 51sin 3cos 1sin 2cos 015.01)()()(010)(0)(τττττfor t>=04.3 Discretize the state equation in Problem 4.2 for T=1 and T=π.离散化习题4.3中的状态方程，T 分别取1和π Answer:][][][][][]1[0k DU k CX k Y k BU d e k X e k X TA AT +=⎪⎭⎫ ⎝⎛+=+⎰ααFor T=1,use matlab: [ab,bd]=c2d(a,b,1) ab =0.5083 0.3096 -0.6191 -0.1108 bd =1.0471 -0.1821[]][32][][1821.00471.1][1108.06191.03096.05083.0]1[k X k Y k U k X k X =⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--=+for T=π,use matlab:[ab,bd]=c2d(a,b,3.1415926) ab =-0.0432 0.0000 -0.0000 -0.0432 bd =1.5648 -1.0432[]][32][][0432.15648.1][0432.0000432.0]1[k X k Y k U k X k X =⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--=+ 4.4 Find the companion-form and modal-form equivalent equations of 求系统的等价友形和模式规范形。

北航线性系统理论答案

2-17 证明：①首先证明()T T T B C A ，，是()s G 的不可简约实现（该题有问题，不是()TT TCB A，，）。

由于()s G 是对称传递函数阵，故有()()T T T C sI B B A sI C 1-1-A --=，所以()TT TBC A，，是()s G 的实现。

又因为()[]n CA CA Crank CA C A C rank n Tn TT T T =⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=1-1- ，其可控；同理可证其可观，故系统()T T T B C A ，，是可控可观的。

所以其是()s G 的不可简约实现。

②证明P 的对称性。

由题设易知，由于()T T T B C A ，，是()s G 的不可简约实现，则存在非奇异阵P ，使得TT T BCPC PB A PAP===--11，，。

由T T T T T T P P I P P P CP P B C C PB =⇒=⇒==⇒=--11 所以P 是非奇异对称阵。

③证明P 的唯一性。

由T C PB =，很容易知道1-=B C P T ，故知P 是唯一的。

综上可知，命题得证。

2-18 解：[]1 1 3- 4 2301 4 0 2- 3-0 3 2- 6-0 02 0 0 0 0 1 -=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=C B A 。

a.① ><B A |由[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==65 17 5 2 3 3 3 3 00 0 0 1 1 1 1 32B A B A AB B U 所以)53012301(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡>=<，span B A 。

② η()⇔⋂=kCAker η064 27 118- 145-16 9 34- 43-4 3 10- 13-1 1 3- 4 032=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⇔=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡x x CACA CA C故)12101301(⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=，span η ③ ><⋂B A |η即任意>⇔<⋂∈B A x |η2153012301x x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=，同时有4312101301x x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=故0--1 1 5 22 3 3 31 0 0 00 1 1 14321=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡x x x x ，有)1301(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡>=<⋂span B A η ④ ⊥><⋂B A |η 易知，⇔>∈<⊥B A x |[]065 17 5 2 3 3 3 3 0 0 0 0 1 1 1 1 32=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=T TxB A B A AB B x，即 065 3 0 117 3 0 15 3 0 12 3 0 1=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡x 所以)0103-0010(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=><⊥，span B A 同③，可知⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=><⋂⊥0000|B A η⑤ ><⋂⊥B A |η)101-1-0123(⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⊥，span η同③可知⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡>=<⋂⊥0000|B A η⑥ ⊥⊥><⋂B A |η易知)0123(|⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=><⋂⊥⊥span B A η 综上可知，上述空间的维数加起来不等于4，故在上述空间的直和空间中不能取到状态空间的基底。

中国科学技术大学自动化专业《线性系统理论和设计》习题1-6章习题答案

1.7 证明：())()det(det )det(det )(det )det()det()(1111λλλλλλλA B A I T A I T T A I T AT T I B I AT T B B A ∆=-=⋅-⋅-=-=-=∆⇒=----相似，与设= 又因为特征值为特征方程()0λ∆=的根，故特征值也相同。

1.11 解：可以参照课本P18的例题1.12（1）,3,2,1)3)(2)(1()(,300020104132111===⇒---=∆⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=λλλλλλA A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==Λ∴⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⇒⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⇒=--3211000105411050140010)(1113211Q A Q Q q q q q A I ，，由λ（4）,2,1,1)2)(1)(1()(4344111432124==-==⇒-+-=∆⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--λλλλλλλA ，1241243111111()0,111122,()012,12,4822 2.P I A q q q u I A q q u λλλλλξλλη⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥==--=⇒==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦==-=⎡⎤⎢⎥⎢⎥==<=⎢⎥⎢⎥⎣⎦===对于，，由对于的特征值，其代数重数由计算其对应的特征向量计算出一个特征向量，即几何重数个数小于代数重数，即标准型中存在一个对应的约当块，约当块的阶数即的指数可以利用[]4443434123414418 1.682,()001110111121,,44114412121181211212q I A q q q c q q Q q q q q Q A Q λλ-=-=⇒⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥=⋅-=∴==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥-⎢⎥∴Λ==⎢⎥⎢⎥⎣⎦的式计算的广义特征向量由取1.12 证明：12n 222112n n 1n-1n-112n 21n 121n 1221n n 1n-3n-3221n 21n-22n-2n-2221n n 1111(1110()()0()()(0()()λλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλλ-⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎡⎤--⎢⎥--⎢⎥--⎢⎥==⎢⎥--⎢⎥⎢⎥--⎣⎦后一行减去前一行的倍）n-221n n 123n 2131n 1n-2n-2n-223n j i 1i j n)()111()()()()()λλλλλλλλλλλλλλλλλλ≤<≤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎡⎤⎢⎥⎢⎥=---=⎢⎥⎢⎥⎣⎦=-∏同理2.6 解：(d) 令24231211y x y x yx y x ====，，，，则状态空间方程为： u m m k m k m k mk ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--=0010020100000200112211x xx y ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=010*******y y (e) 令yx y x ==21，，则状态空间方程为： u e e t t ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=-10102x x[]x y 01= 2.7 解：(c)非线性方程： ⎩⎨⎧==21221u-x xx x[]x y 01= (d) 设⎪⎩⎪⎨⎧+=⇒=+⋅++-=⇒=+⋅+ux sx x u)(x s u x x sx x s )x (u 333221122121112，则状态空间方程可为：u ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-=310312x x[]x y 01= 另法：先求出传递函数2323s G(s)s s +=+-，按2.6（b ）方法求解。

线性系统理论+课后答案+(程兆林+马树萍+著)+科学出版社

0
t 0
⎡e −t ⎢ At 11. 解： e = ⎢ 0 ⎢0 ⎣
课
⎛ (4t − 1)e − t + e −2t ⎞ ⎟ =⎜ ⎜ (3 − 4t )e −t − 2e − 2t ⎟ . ⎝ ⎠
te− t e−t
x(t ) = e At x0 + ∫ e A(t −τ ) Bu (τ )dτ
= e x0 +
⎡ e −τ ⎢ ⎢0 ⎢0 ⎣
w.
⎞ ⎟dτ ⎟ ⎠
案网
e −τ − e −2τ ⎞⎛ 2 ⎞ −(t −τ ) ⎟⎜ dτ ⎜ ⎟ ⎟e 2e − 2τ − e −τ ⎟ ⎠⎝ 0 ⎠
τ e−τ
e
−τ
0
0 ⎤ ⎡0 ⎤ ⎥ ⎥ 0 ⎥⎢ ⎢1 ⎥ dτ −2τ ⎥ e ⎦⎢ ⎣ 4⎥ ⎦
co
x(t ) = e At x(0) + ∫ e A( t −τ ) Bu (τ )dτ
0
⎛ 2e − t − e −2t =⎜ ⎜ − 2e − t + 2e − 2 t ⎝ ⎛ 2e −τ − e −2τ +∫ ⎜ 0 ⎜ − 2e −τ + 2e − 2τ ⎝
t
e − t − e −2t ⎞⎛ 0 ⎞ ⎟⎜ ⎜ ⎟ ⎟ − e − t + 2e − t ⎟ ⎠⎝ 1 ⎠
w.
0
kh
C1 s n−1 + " + Cn−1 s + Cn + C0 . s n + a1s n−1 + " + an−1 s + an
9. 证明类似定理 1.4, 此处略.
w.
−1
1 0⎞ ⎛ 0 ⎛0⎞ ⎜ ⎟ ⎜ ⎟ 7．解：(1) A = ⎜ − 2 − 3 0 ⎟ ， B = ⎜ 1 ⎟ ， C = (0 0 1) . ⎜ − 1 1 3⎟ ⎜ 2⎟ ⎝ ⎠ ⎝ ⎠

线性系统理论习题答案ans1to6

-1 l 0 M
0 -1 l M
an -1 an - 2 -1 l l 0 0 M M
= l2 0
L L L O L 0 -1 l M
an - 2 an - 3 an - 4 = l + a1ln -1 + L + an
n
l -1 0 L 0 l -1 L 0 0 =l 0 l L 0 0 + (-1) n +1 an (-1) n -1 M M M M O M l + a1 an -1 an - 2 an - 3 L l + a1 L 0 0 L 0 + l (-1) n an -1 (-1) n - 2 + an = L L O M L l + a1
而Q AB = BA \ e
A+ B
\ F (t , t0 ) = e B (t - t 0 )
= e A × eB = eB × e A
e - At e( A + B )(t - t 0 )e At 0 = e - At e A( t - t 0 ) e B ( t - t 0 ) e At 0 = e - At e At e - At 0 e B (t -t 0 )e At 0 = e - At 0 e B ( t - t 0 ) e At 0 = e - At 0 e At 0 e B (t - t 0 ) = e B ( t - t 0 ) = F (t , t0 )
1-6 证明：由 A Î R p ´ q , B Î R q ´ p 得令C = ê
éA ëIq
Ipù éB ,D = ê ú 0û ëI p
Iq ù é I p + AB 0 ù é BA + I q ，则 CD = ê , DC = ê ú ú - Aû Iq û ë B ë 0

北航线性系统理论答案

1-1 证明：由矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=12-n 1-n n- - - -1 01 0 00 0 1 0a a a a A可知A 的特征多项式为nn n n n n n n n n nn n n n a a a a a a a a a a a a a a a a a a a a a a a A I ++++++=+++++=+++=++=+=-+λλλλλλλλλλλλλλλλλλλλλλλ1-3-32-21-11-3-3122-2-1-n 13-n 2-n 21-1n 12-n 1-n 12-n 1-n n 1- )1(-)1(- 0 00 1- )1(-)1(- 0 0 0 1-1 0 1- 0 00 1- 若i λ是A 的特征值，则00 0 01 1 01- 0 0 0 1- 111n 1-n i 12-n 1-n n =⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=++++=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--ni n i n i i i i i a a a a a a a λλλλλλλλ所以[]Ti i 1-n i 2 1 λλλ 是属于i λ的特征向量。

1-7 解：由于()ττ--t e t g =，，可知当τ<t 时，()0≠τ，t g ，所以系统不具有因果性。

又由于()()0 ，，ττ-=t g t g ，所以系统是时不变的。

1-8 解：容易验证该系统满足齐次性与可加性，所以此系统是线性的。

由于()()t 0 t ⎩⎨⎧>≤-=-=ααββαβαt u t u P u Q P 而()()⎩⎨⎧+>+≤-=⎩⎨⎧>≤=βαβαβααβαβ t 0 t t 0 t t u t u Q u P Q ，故u P Q u Q P αββα≠，所以系统是时变的。

又因为()()()()()⎩⎨⎧>≤=⎩⎨⎧>≤=ααααα，，T T t u t u P u P P T T min t 0 min t t 0 t 而()()()()()()()⎩⎨⎧>≤=⎩⎨⎧>≤=ααααα，，，，T T t u T T t u P u P P P T T T min t 0 min t mint 0 min t ，故()()u P P P u P P T T T αα=，所以系统具有因果性。

线性系统课后答案第3章

线性系统课后答案第3章3.1consider Fig3.1 ,what is the representation of the vector with respect to thebasis ? What is the representation of with respect ro ?图3.1中,向量关于的表⽰是什么? 关于的表⽰有是什么?If we draw from two lines in parallel with and , they tutersect at and as shown, thus the representation of with respect to the basis is , this can be verifiedfromTo find the representation of with respect to ,we draw from two lines inparallel with and , they intersect at -2 and , thus the representation of withrespect to , is , this can be verified from3.2 what are the 1-morm ,2-norm , and infinite-norm of the vectors , 问向量的1-范数,2-范数是什么?3.3 find two orthonormal vectors that span the same space as the two vectors in problem 3题3.2中的两个向量张成同⼀空间的两个标准正交向量.Schmidt orthonormalization praedure ,The two orthomormal vectors areIn fact , the vectors and are orthogonal because so we can only normalize thetwo vectors3.4 comsider an matrix A with , if all colums of A are orthonormal , then ,what can you say abort ? ⼀个阶矩阵A(), 如果A的所有列都是标准正交的,则问是怎么样?Let , if all colums of A are orthomormal , that isthenif A is a symmetric square matrix , that is to say , n=m for everythen3.5 find the ranks and mullities of the following matrices 求下列矩阵的秩和化零度3.6 Find bases of the range spaces of the matrices in problem 3.5 求题3.5中矩阵值域空间的基the last two columns of are linearly independent , so the set can be used as abasis of the range space of , all columns of are linearly independent ,so the setcan be used as a basis of the range spare oflet ,where denotes of are linearly independent , the third colums can beexpressed as , so the set can be used as a basis of the range space of3.7 consider the linear algebraic equation it has three equations and two unknowns does a solution exist in the equation ? is the solution unique ? doesa solution exist if ?线性代数⽅程有三个⽅程两个未知数, 问⽅程是否有解?若有解是否唯⼀?若⽅程是否有解?Let clearly and are linearly independent , so rank(A)=2 , is the sum of and,that is rank([A ])=2, rank(A)= rank([A ]) so a solution exists in A=Nullity(A)=2- rank(A)=0The solution is unique if , then rank([A ])=3 rank(A), that is to say theredoesn’t exist a solution in A=3.8 find the general solution of how many parameters do you have ?求⽅程的同解,同解中⽤了⼏个参数?Let we can readily obtain rank(A)= rank([A ])=3 so this lies in the rangespace of A and is a solution Nullity(A)=4-3=1 that means the dimension ofthe null space of A is 1 , the number of parameters in the general solution willbe 1 , A basis of the null space of A is thus the general solution of A= can be expressed an for any realis the only parameter3.9 find the solution in example 3.3 that has the smallest Euclidean norm 求例3中具有最⼩欧⽒范数的解,the general solution in example 3.3 is for any real andthe Euclidean norm of ishas the smallest Euclidean norm ,3.10 find the solution in problem 3.8 that has the smallest Euclidean norm 求题3.8中欧⽒范数最⼩的解,for any realthe Euclidean norm of is has the smallest Euclidean norm3.11 consider the equationwhere A is an matrix and is an column vector ,under what conditions on A andexist to meet the equation for any ?令A是的矩阵, 是的列向量,问在A和满⾜什么条件时,存在,对所有的,它们都满⾜⽅程write the equation in this formwhere is an matrix and is an column vector , from the equation we can see , exist to meet t equation for any ,if and only if under this condition , there will exist to meet the equation f 3.12 given what are the representations of A with respect to the basis and the basis , respectively? 给定请问A 关于和基的表⽰分别是什么?we have thus the representation of A with respect to the basis isthus the representation of A with respect to the basis is3.13 find Jordan-form representations of the following matrices写出下列矩阵的jordan 型表⽰:the characteristic polynomial of is thus the eigenvelues of are 1 ,2 , 3 , they are all distinct Jordan-form representation of will be diagonal .the eigenvectors associated with ,respectively can be any nonzero solution ofthus the jordan-form representation of with respect to isthe characteristic polynomial of is has eigenvalues the eigenvectorsassociated with are , respectively the we havethe characteristic polynomial of is theus the eigenvalues of are 1 ,1 and 2 , the eigenvalue 1 has multiplicity 2 , and nullity the has two tinearly independent eigenvectors associated with 1 , thus we havethe characteristic polynomial of is clearly has lnly one distinct eigenvalue 0with multiplicity 3 , Nullity(-0I)=3-2=1 , thus has only one independenteigenvector associated with 0 , we can compute the generalized , eigenvectorsof from equations below , then the representation of with respect to the basisis3.14 consider the companion-form matrix show that its characterisicpolynomial is given byshow also that if is an eigenvalue of A or a solution of then is an eigenvectorof A associated with证明友矩阵A的特征多项式并且,如果是的⼀个特征值, 的⼀个解, 那么向量是A 关于的⼀个特征向量proof:if is an eigenvalue of A , that is to say , then we havethat is to say is an eigenvetor oa A associated with3.15 show that the vandermonde determinant equals , thus we concludethat the matrix is nonsingular or equivalently , the eigenvectors are linearly independent if all eigenvalues are distinct ,证明vandermonde ⾏列式为, 因此如果所有的特征值都互不相同则该矩阵⾮奇异, 或者等价地说, 所有特征向量线性⽆关,proof: let a, b, c and d be the eigenvalues of a matrix A , and they are distinct Assuming the matrix is singular , that is abcd=0 , let a=0 , then we have and from vandermonde determinantso we can see ,that is to say are not distinetthis implies the assumption is not true , that is , the matrix is nonsingular let be the eigenvectors of A ,3.16 show that the companion-form matrix in problem 3.14 is nonsingular if and only if , under this assumption , show that its inverse equals 证明题3.14 中的友矩阵⾮奇异当且仅当, 且矩阵的逆为proof: as we know , the chacteristic polynomial is so let , we haveA is nonsingular if and only if3.17 consider with and T>0 show that is an generalized eigenvector of grade 3 and the three columns of constitute a chain of generalized eigenvectors of length 3 , venty矩阵A 中,T>0 , 证明是3 级⼴义特征向量, 并且矩阵Q 的3 列组成长度是3的⼴义特征向量链,验证Proof : clearly A has only one distinct eigenvalue with multiplicity 3 these two equation imply that is a generalized eigenvctorof grade 3 ,andthat is the three columns of Q consititute a chain of generalized eigenvectors of length 33.18 Find the characteristic polynomials and the minimal polynomials of the following matrices求下列矩阵的特征多项式和最⼩多项式,3.19 show that if is an eigenvalue of A with eigenvector then is an eigenvalue of with the same eigenvector证明如果是A 的关于的特征向量,那么是的特征值, 是关于的特征向量, proof let A be an matrix , use theorem 3.5 for any function we can definewhich equals on the spectrum of Aif is an eigenvalue of A , then we have andwhich implies that is an eigenvalue of with the same eigenvector3.20 show that an matrix has the property for if and only if A has eigenvalues 0 with multiplicity n and index m of less , such a matrix is called a nilpotent matrix证明的矩阵在当且仅当A的n 重0特征值指数不⼤于m ,这样的矩阵被称为归零矩阵,proof : if A has eigenvalues 0 with multiplicity n and index M or less then the Jordan-form representation of A is wherefrom the nilpotent property , we have so if andthenIf then where ,So we havewhich implies that A has only one distinct eigenvalue o with multiplicity n and index m or less ,3.21 given , find 求A的函数,the characteristic polynomial of A islet on the spectrum of A , we havethe we havethe computeto compute :3.22 use two different methods to compute for A1 and A4 in problem 3.13⽤两种⽅法计算题3.13 中A1和A4的函数method 1 : the Jordan-form representation of A1 with respect to the basis is method 2: the characteristic polynomial of is let on the spectrum of , we have the characteristic polynomial of is , let on the spectrum of ,we havethus3.23 Show that functions of the same matrix ; that is consequently we have 证明同⼀矩阵的函数具有可交换性，即因此有成⽴proof: let ( n is the order of A)let then we have3.24 let , find a B such that show that of for some I ,then B does not existlet , find a B such that Is it true that ,for any nonsingular c ,there exists a matrix B such that ?令证明若,则不存在B 使若 ,是否对任意⾮奇异C都存在B使, ?Let sowhere , if for some i , does not existfor we have , where then does mot exist , so B does mot exist , we can conclude that , it is mot true that , for any nonsingular C THERE EXISTS aB such that3.25 let and let m(s) be the monic greatest common divisor of all entries of Adj(Si-A) , Verify for the matrix in problem 3.13 that the minimal polynomial of A equals令, , 并且令m(s)是Adj(Si-A)的所有元素的第⼀最⼤公因⼦,利⽤题3.13 中验证A的最⼩多项式为verification : we can easily obtain that3.26 Define where are constant matrices theis definition is valid because the degree in s of the adjoint of (sI-A) is at most n-1 , verifywhere tr stands for the trase of a matrix and is defined as the sum of all its diagonal entries this process of computing is called the leverrier algorithm定义其中是A 的特征多项式是常数矩阵,这样定义是有效的, 因为SI-A 的伴随矩阵中S的阶次不超过N-1 验证其中矩阵的迹tr 定义为其对⾓元素之和, 这种计算和的程式被称为leverrier 算法.verification:’where3.27 use problem 3.26 to prove the cayley-hamilton theorem利⽤题3.26证明cayley-hamilton 定理proof:multiplying ith equation by yields ( )then we can see that is3.28 use problem 3.26 to show利⽤题3.26 证明上式,Proof: another : let3.29 let all eigenvalues of A be distinct and let be a right eigenvector of A associated with that is define and define,where is the ith row of P , show that is a left eigenvector of A associated with , that is 如果A的所有特征值互不相同, 是关于的⼀个右特征向量,即,定义并且其中是P 的第I ⾏, 证明是A的关于的⼀个左特征向量,即Proof: all eigenvalues of A are distinct , and is a right eigenvector of A associated with , and so we know thatThat isso , that is , is a left eigenvector of A associated with3.30 show that if all eigenvalues of A are distinct , then can be expressed as where and are right and left eigenvectors of A associated with 证明若A的所有特征值互不相同,则可以表⽰为其中和是A的关于的右特征值和左特征值,Proof: if all eigenvalues of A are distinct , let be a right eigenvector of A associated with , then is nonsingular , and where is aleft eigenvector of A associated with ,That is3.31 find the M to meet the lyapunov equation in (3.59) with what are the eigenvalues of the lyapunov equation ? is the lyapunov equation singular ? is the solution unique ?已知A,B,C,求M 使之满⾜(3.59) 的lyapunov ⽅程的特征值, 该⽅程是否奇异>解是否唯⼀?The eigenvalues of the Lyapunov equation areThe lyapunov equation is nonsingular M satisfying the equation3.32 repeat problem 3.31 for with two different C ,⽤本题给出的A, B, C, 重复题3.31 的问题,the eigenvalues of the lyapunov equation are the lyapunov equation is singular because it has zero eigenvalue if C lies in the range space of the lyapunov equation , then solution exist and are not unique,3.33 check to see if the following matrices are positive definite orsenidefinite 确定下列矩阵是否正定或者正半定,1. is not positive definite , nor is pesitive semidefinite2. it has a negative eigenvalue , so the second matrix is not positive definite , neither is positive demidefinte ,,3 the third matrix ‘s prindipal minors `that is all the principal minors of the thire matrix are zero or positive , so the matrix is positive semidefinite ,3.34 compute the singular values of the following matrices 计算下列矩阵的奇值,the eigenvalues of are 6 and 1 , thus the singular values of are and 1 ,the eigenvalues of are , thus the singular values of are3.35 if A is symmetric , what is the ralatimship between its eigenvalues and singular values ? 对称矩阵A 的特征值与奇异值之间有什么关系?If A is symmetric , then LET be an eigenvector of A associated with eigenvaue that is , thus we haveWhich implies is the eigenvalue of , (n is the order of A )So the singular values of A are where is the eigenvalue of A3.36 show证明上式成⽴let A is and B isuse (3.64) we can readily obtain3.37 show (3.65) 证明(3.65)proof: letthen we havebecausewe have det(NP)=det(QP)And3.38 Consider , where A is and has rank m is a solution ? if not , under what condition will it be a solution? Is a solution ?阶矩阵A 秩为m , 是不是⽅程的解? 如果不是, 那么在什么条件下,他才会成为该⽅程的解? 是不是⽅程的解?A is and has rank m so we know that , and is a square matrix of rankA=m , rank( ,So if ,then rank()If m=n , and rankA=m , so A is nonsingular , then we haverank()=rank(A)=m , and A=A that is is a solution ,RankA=MRank()=m is monsingular and exists , so we have , that is , is a solution of ,。

线性系统课后题答案

第一章数学基础1、加法不变性：R(S)中存在零元0，使得对()()S R s f ∈∀，都有()()s f s f =+0成立。

乘法不变性：R(S)中存在单位元1，使得对()()S R s f ∈∀，都有()()()s f s f s f =⋅=⋅11成立。

2、反证法证明：(1)加法不变性的唯一性假设在域F 中，存在0和0’，0≠0’，..t s αααα=+=+'0,0,对F ∈∀α成立。

以α+0=α为例，取α=0’，则0’+0=0’ 因为0’为零元，所以0’+0=0 所以0’=0，与假设矛盾。

（2）乘法不变性的唯一性假设在域F 中，存在1和1’，'11≠，..t s αααααα=⋅=⋅=⋅=⋅'1'1,11,对F ∈∀α成立。

以ααα=⋅=⋅11为例，取'1=α，则有'1'111'1=⋅=⋅ '1为单位元1'111'1=⋅=⋅∴'11=∴ 与假设矛盾3、试用反例证明你对下列问题的回答域交换环环 []R s 是是是 n n R *是是元素[]R s ∈的对角矩阵是是是 []p R s 是是是[]n np R s *是是其中：()p R s 是元素为常态的实有理分式（当s →∞，()R s 有界）；()n n p R s ⨯是元素属于()p R s 的n n ⨯矩阵证明：⑴[]R s 不是域。

如 ()1f +=s s ，显然()[]s R s f ∉-1。

（2）n nR* 不是交换环。

如⎥⎦⎤⎢⎣⎡=1010α，⎥⎦⎤⎢⎣⎡=0101β，显然22⨯∈R βα、。

但是βααβ≠。

（3）不是域。

如⎥⎦⎤⎢⎣⎡+=0001s α，1-α不存在。

（4）()p R s 不是域。

如∈+=1s 1α()p R s ，1-α=s+1.∞→∞→-1α时，s , 所以1-α∉()p R s 。

线性系统理论课后-答案

给定图P2.1(町和(b)所示两个电路，试列写岀其状态方程和输出方程。

其中, 分別指定：⑹状态变II组廿二陀・输入变量“ = 输出变畳尸=f(b)状态变量组齐= u c2 >输入变量输出变量y =(a) O)图P21解本题属于由物理系统尊立状态令间描述的基本题.意在训练正确和熟练运用电路定律列写出电路的状态方程和输出方程。

W列写P2.1(a)电路的状态方程和输川方程。

首先.考虑到电容C和电感I为给定电路中仅有的两个储能元件，电容端电压弋和流经电感电流/构成此电路的线性无关极人变裁组.从而选取状态变量组召=陀和勺符合定义耍求o基此，利用电路元件关系式利回路基尔霍夫定律.定出电路方程为cS d/再由上述电路方程导出状态变量陀和i的导数项..可得到状态变屋方程规范形式,dx 1 & 1丁二一"V u c —匸t + ~e d/ L c L L表u c x<to c/d/和i = d//dn并将上述方程组表为向量方程，就得到此电路的状态方程:继而，按约定输出y =几可直接得到此电路的输出方程：”[0 1卄(b)列写P2.1(b)电路的状态方程和輸出方程。

类似地，考虔到电容C]和C?为给定电路中仅有的两个储能元件，电容端电压呵和叱构成此电路的线性无关极大妾量组，选取状态变量组刁二呵和帀二叱2符合定义要求丿基此，利用电路元件关系式和回路基尔霍夫定律，定出电路方程为du cC&才4匕+七=€++M Q =€再由上述电路方程导出状态变最叱和叱:的导数项，可得到状态变量方程规范形式:表％二血c/击和击，并将上述方程组表为向最方程，就得到此电路的状态方程:继而，按约定输出y讥，可由电路导出:尸％% +七将其表为向量方程，就得到此电路的输出方程！T 1］卜融2・6求岀下列各输入输出描述的一个状态空树描述：⑴笳)—2?十18$+如1 i(s) ?+6?+11J 4-6(ii) 叫 n龜)(g+3)2(zl)解本题属于由传递函数型输入输出描述导出状态空间描述的基本题。