概率论与数理统计英文版总结
概率论及数理统计中英辞汇对照

absolute value 绝对值acceptable region 同意域additivity 可加性adjusted 调整的alternative hypothesis 对立假设analysis of covariance 协方差分析analysis of variance 方差分析arithmetic mean 算术平均值association 相关性assumption 假设assumption checking 假设查验availability 有效度average 均值Bbalanced 平稳的band 带宽bar chart 条形图beta-distribution 贝塔散布between groups 组间的bias 偏倚binomial distribution 二项散布binomial test 二项查验Ccalculate 计算case 个案category 类别center of gravity 重心central tendency 中心趋势chi-square distribution 卡方散布chi-square test 卡方查验classify 分类cluster analysis 聚类分析coefficient 系数coefficient of correlation 相关系数collinearity 共线性column 列compare 比较comparison 对照components 组成,分量compound 复合的confidence interval 置信区间consistency 一致性constant 常数continuous variable 持续变量control charts 操纵图correlation 相关covariance 协方差covariance matrix 协方差矩阵critical point 临界点critical value 临界值crosstab 列联表cubic 三次的,立方的cubic term 三次项cumulative distribution function 累加散布函数curve estimation 曲线估量Ddata 数据default 默许的definition 概念deleted residual 剔除残差density function 密度函数dependent variable 因变量description 描述design of experiment 实验设计deviations 不同df.(degree of freedom) 自由度diagnostic 诊断dimension 维discrete variable 离散变量discriminant function 判别函数discriminatory analysis 判别分析distance 距离distribution 散布D-optimal design D-优化设计Eeaqual 相等effects of interaction 交互效应[Last edit by happyjyl]efficiency 有效性eigenvalue 特点值equal size 等含量equation 方程error 误差estimate 估量estimation of parameters 参数估量estimations 估量量evaluate 衡量exact value 精准值expectation 期望expected value 期望值exponential 指数的exponential distributon 指数散布extreme value 极值Ffactor 因素,因子factor analysis 因子分析factor score 因子得分factorial designs 析因设计factorial experiment 析因实验fit 拟合fitted line 拟合线fitted value 拟合值fixed model 固定模型fixed variable 固定变量fractional factorial design 部份析因设计frequency 频数F-test F查验full factorial design 完全析因设计function 函数Ggamma distribution 伽玛散布geometric mean 几何均值group 组Hharmomic mean 调和均值heterogeneity 不齐性histogram 直方图homogeneity 齐性homogeneity of variance 方差齐性hypothesis 假设hypothesis test 假设查验Iindependence 独立independent variable 自变量independent-samples 独立样本index 指数index of correlation 相关指数interaction 交互作用interclass correlation 组内相关interval estimate 区间估量intraclass correlation 组间相关inverse 倒数的iterate 迭代Kkernal 核Kolmogorov-Smirnov test柯尔莫哥洛夫-斯米诺夫查验kurtosis 峰度Llarge sample problem 大样本问题layer 层least-significant difference 最小显著差数least-square estimation 最小二乘估量least-square method 最小二乘法level 水平level of significance 显著性水平leverage value 中心化杠杆值life 寿命life test 寿命实验likelihood function 似然函数likelihood ratio test 似然比查验linear 线性的linear estimator 线性估量linear model 线性模型linear regression 线性回归linear relation 线性关系linear term 线性项logarithmic 对数的logarithms 对数logistic 逻辑的lost function 损失函数Mmain effect 主效应matrix 矩阵maximum 最大值maximum likelihood estimation 极大似然估量mean squared deviation(MSD) 均方差mean sum of square 均方和measure 衡量media 中位数M-estimator M估量minimum 最小值missing values 缺失值mixed model 混合模型mode 众数model 模型Monte Carle method 蒙特卡罗法moving average 移动平均值multicollinearity 多元共线性multiple comparison 多重比较multiple correlation 多重相关multiple correlation coefficient 复相关系数multiple correlation coefficient 多元相关系数multiple regression analysis 多元回归分析multiple regression equation 多元回归方程multiple response 多响应multivariate analysis 多元分析Nnegative relationship 负相关nonadditively 不可加性nonlinear 非线性nonlinear regression 非线性回归noparametric tests 非参数查验normal distribution 正态散布null hypothesis 零假设number of cases 个案数Oone-sample 单样本one-tailed test 单侧查验one-way ANOVA 单向方差分析one-way classification 单向分类optimal 优化的optimum allocation 最优配制order 排序order statistics 顺序统计量origin 原点orthogonal 正交的outliers 异样值Ppaired observations 成对观测数据paired-sample 成对样本parameter 参数parameter estimation 参数估量partial correlation 偏相关partial correlation coefficient 偏相关系数partial regression coefficient 偏回归系数percent 百分数percentiles 百分位数pie chart 饼图point estimate 点估量poisson distribution 泊松散布polynomial curve 多项式曲线polynomial regression 多项式回归polynomials 多项式positive relationship 正相关power 幂P-P plot P-P概率图predict 预测predicted value 预测值prediction intervals 预测区间principal component analysis 主成份分析proability 概率probability density function 概率密度函数probit analysis 概率分析proportion 比例Qqadratic 二次的Q-Q plot Q-Q概率图quadratic term 二次项quality control 质量操纵quantitative 数量的,气宇的quartiles 四分位数Rrandom 随机的random number 随机数random number 随机数random sampling 随机取样random seed 随机数种子random variable 随机变量randomization 随机化range 极差rank 秩rank correlation 秩相关rank statistic 秩统计量regression analysis 回归分析regression coefficient 回归系数regression line 回归线reject 拒绝rejection region 拒绝域relationship 关系reliability 靠得住性repeated 重复的report 报告,报表residual 残差residual sum of squares 剩余平方和response 响应risk function 风险函数robustness 稳健性root mean square 标准差row 行run 游程run test 游程查验Ssample 样本sample size 样本容量sample space 样本空间sampling 取样sampling inspection 抽样查验scatter chart 散点图S-curve S形曲线separately 单独地sets 集合sign test 符号查验significance 显著性significance level 显著性水平significance testing 显著性查验significant 显著的,有效的significant digits 有效数字skewed distribution 偏态散布skewness 偏度small sample problem 小样本问题smooth 滑腻sort 排序soruces of variation 方差来源space 空间spread 扩展square 平方standard deviation 标准离差standard error of mean 均值的标准误差standardization 标准化standardize 标准化statistic 统计量statistical quality control 统计质量操纵std. residual 标准残差stepwise regression analysis 慢慢回归stimulus 刺激strong assumption 强假设stud. deleted residual 学生化剔除残差stud. residual 学生化残差subsamples 次级样本sufficient statistic 充分统计量sum 和sum of squares 平方和summary 归纳,综述Ttable 表t-distribution t散布test 查验test criterion 查验判据test for linearity 线性查验test of goodness of fit 拟合优度查验test of homogeneity 齐性查验test of independence 独立性查验test rules 查验法那么test statistics 查验统计量testing function 查验函数time series 时刻序列tolerance limits 允许限total 总共,和transformation 转换treatment 处置trimmed mean 截尾均值true value 真值t-test t查验two-tailed test 双侧查验Uunbalanced 不平稳的unbiased estimation 无偏估量unbiasedness 无偏性uniform distribution 均匀散布Vvalue of estimator 估量值variable 变量variance 方差variance components 方差分量variance ratio 方差比various 不同的vector 向量Wweight 加权,权重weighted average 加权平均值within groups 组内的ZZ score Z分数最优化方式辞汇英汉对照表Aactive constraint 活动约束active set method 活动集法analytic gradient 解析梯度approximate 近似arbitrary 强制性的argument 变量attainment factor 达到因子Bbandwidth 带宽be equivalent to 等价于best-fit 最正确拟合bound 边界Ccoefficient 系数complex-value 复数值component 分量constant 常数constrained 有约束的constraint 约束constraint function 约束函数continuous 持续的converge 收敛cubic polynomial interpolation method三次多项式插值法curve-fitting 曲线拟合Ddata-fitting 数据拟合default 默许的,默许的define 概念diagonal 对角的direct search method 直接搜索法direction of search 搜索方向discontinuous 不持续Eeigenvalue 特点值empty matrix 空矩阵equality 等式exceeded 溢出的Ffeasible 可行的feasible solution 可行解finite-difference 有限差分first-order 一阶GGauss-Newton method 高斯-牛顿法goal attainment problem 目标达到问题gradient 梯度gradient method 梯度法Hhandle 句柄Hessian matrix 海色矩阵Iindependent variables 独立变量inequality 不等式infeasibility 不可行性infeasible 不可行的initial feasible solution 初始可行解initialize 初始化inverse 逆invoke 激活iteration 迭代iteration 迭代JJacobian 雅可比矩阵LLagrange multiplier 拉格朗日乘子large-scale 大型的least square 最小二乘least squares sense 最小二乘意义上的Levenberg-Marquardt method列文伯格-马夸尔特法line search 一维搜索linear 线性的linear equality constraints 线性等式约束linear programming problem 线性计划问题local solution 局部解Mmedium-scale 中型的minimize 最小化mixed quadratic and cubic polynomial interpolation and extrapolation method混合二次、三次多项式内插、外插法multiobjective 多目标的Nnonlinear 非线性的norm 范数Oobjective function 目标函数observed data 测量数据optimization routine 优化进程optimize 优化optimizer 求解器over-determined system 超定系统Pparameter 参数partial derivatives 偏导数polynomial interpolation method 多项式插值法Qquadratic 二次的quadratic interpolation method 二次内插法quadratic programming 二次计划Rreal-value 实数值residuals 残差robust 稳健的robustness 稳健性,鲁棒性Sscalar 标量semi-infinitely problem 半无穷问题Sequential Quadratic Programming method序列二次计划法simplex search method 单纯形法solution 解sparse matrix 稀疏矩阵sparsity pattern 稀疏模式sparsity structure 稀疏结构starting point 初始点step length 步长subspace trust region method 子空间置信域法sum-of-squares 平方和symmetric matrix 对称矩阵Ttermination message 终止信息termination tolerance 终止容限the exit condition 退出条件the method of steepest descent 最速下降法transpose 转置Uunconstrained 无约束的under-determined system 负定系统Vvariable 变量vector 矢量Wweighting matrix 加权矩阵样条辞汇英汉对照表Aapproximation 逼近array 数组a spline in b-form/b-spline b样条a spline of polynomial piece/ppform spline 分段多项式样条Bbivariate spline function 二元样条函数break/breaks 断点Ccoefficient/coefficients 系数cubic interpolation 三次插值/三次内插cubic polynomial 三次多项式cubic smoothing spline 三次滑腻样条cubic spline 三次样条cubic spline interpolation三次样条插值/三次样条内插curve 曲线Ddegree of freedom 自由度dimension 维数Eend conditions 约束条件Iinput argument 输入参数interpolation 插值/内插interval 取值区间Kknot/knots 节点Lleast-squares approximation 最小二乘拟合Mmultiplicity 重次multivariate function 多元函数Ooptional argument 可选参数order 阶次output argument 输出参数Ppoint/points 数据点Rrational spline 有理样条rounding error 舍入误差(相对误差)Sscalar 标量sequence 数列(数组)spline 样条spline approximation 样条逼近/样条拟合spline function 样条函数spline curve 样条曲线spline interpolation 样条插值/样条内插spline surface 样条曲面smoothing spline 滑腻样条T tolerance 许诺精度Uunivariate function 一元函数Vvector 向量Wweight/weights 权重4 偏微分方程数值解辞汇英汉对照表Aabsolute error 绝对误差absolute tolerance 绝对容限adaptive mesh 适应性网格Bboundary condition 边界条件Ccontour plot 等值线图converge 收敛coordinate 坐标系Ddecomposed 分解的decomposed geometry matrix 分解几何矩阵diagonal matrix 对角矩阵Dirichlet boundary conditions Dirichlet边界条件Eeigenvalue 特点值elliptic 椭圆形的error estimate 误差估量exact solution 精准解Ggeneralized Neumann boundary condition推行的Neumann边界条件geometry 几何形状geometry description matrix 几何描述矩阵geometry matrix 几何矩阵graphical user interface(GUI)图形用户界面Hhyperbolic 双曲线的Iinitial mesh 初始网格Jjiggle 微调LLagrange multipliers 拉格朗日乘子Laplace equation 拉普拉斯方程linear interpolation 线性插值loop 循环Mmachine precision 机械精度mixed boundary condition 混合边界条件NNeuman boundary condition Neuman 边界条件node point 节点nonlinear solver 非线性求解器normal vector 法向量PParabolic 抛物线型的partial differential equation 偏微分方程plane strain 平面应变plane stress 平面应力Poisson's equation 泊松方程polygon 多边形positive definite 正定Qquality 质量Rrefined triangular mesh 加密的三角形网格relative tolerance 相对容限relative tolerance 相对容限residual 残差residual norm 残差范数Ssingular 奇异的。
(完整word版)英文版概率论与数理统计重点单词

概率论与数理统计中的英文单词和短语概率论与数理统计Probability Theory and Mathematical Statistics第一章概率论的基本观点Chapter 1Introduction of Probability Theory不确立性indeterminacy必定现象certain phenomenon随机现象random phenomenon试验experiment结果outcome频次数frequency number样本空间sample space出现次数frequency of occurrencen 维样本空间n-dimensional sample space样本空间的点point in sample space随机事件random event / random occurrence基本领件elementary event必定事件certain event不行能事件impossible event等可能事件equally likely event事件运算律operational rules of events事件的包括implication of events并事件union events交事件intersection events互不相容事件、mutually exclusive exvents/互斥事件/incompatible events互逆的mutually inverse加法定理addition theorem古典概率classical probability古典概率模型classical probabilistic model几何概率geometric probability 乘法定理product theorem概率乘法multiplication of probabilities条件概率conditional probability全概率公式、全formula of total probability概率定理贝叶斯公式、逆Bayes formula概率公式后验概率posterior probability先验概率prior probability独立事件independent event独立随机事件independent random event独立实验independent experiment两两独立pairwise independent两两独立事件pairwise independent events第二章随机变量及其散布Chapter2Random Variables and Distributions随机变量random variables失散随机变量discrete random variables概率散布律law of probability distribution一维概率散布one-dimension probability distribution 概率散布probability distribution两点散布two-point distribution伯努利散布Bernoulli distribution二项散布 / 伯努Binomial distribution利散布超几何散布hypergeometric distribution三项散布trinomial distribution多项散布polynomial distribution泊松散布Poisson distribution泊松参数Poisson theorem散布函数distribution function概率散布函数probability density function连续随机变量continuous random variable概率密度probability density概率密度函数probability density function概率曲线probability curve平均散布uniform distribution指数散布exponential distribution指数散布密度函exponential distribution density 数function正态散布、高斯normal distribution散布标准正态散布standard normal distribution正态概率密度函normal probability density function数正态概率曲线normal probability curve标准正态曲线standard normal curve柯西散布Cauchy distribution散布密度density of distribution第三章多维随机变量及其散布Chapter 3 Multivariate Random Variables and Distributions二维随机变量two-dimensional random variable结合散布函数joint distribution function二维失散型随机two-dimensional discrete random 变量variable二维连续型随机two-dimensional continuous random 变量variable结合概率密度joint probability variablen 维随机变量n-dimensional random variablen 维散布函数n-dimensional distribution functionn 维概率散布n-dimensional probability distribution边沿散布marginal distribution边沿散布函数marginal distribution function边沿散布律law of marginal distribution边沿概率密度marginal probability density二维正态散布two-dimensional normal distribution二维正态概率密two-dimensional normal probability 度density 二维正态概率曲two-dimensional normal probability 线curve条件散布conditional distribution条件散布律law of conditional distribution条件概率散布conditional probability distribution条件概率密度conditional probability density边沿密度marginal density独立随机变量independent random variables第四章随机变量的数字特点Chapter 4 Numerical Characteristics fo Random Variables数学希望、均值mathematical expectation希望值expectation value方差variance标准差standard deviation随机变量的方差variance of random variables均方差mean square deviation有关关系dependence relation有关系数correlation coefficient协方差covariance协方差矩阵covariance matrix切比雪夫不等式Chebyshev inequality第五章大数定律及中心极限制理Chapter 5 Law of Large Numbers and Central Limit Theorem大数定律law of great numbers切比雪夫定理的special form of Chebyshev theorem特别形式依概率收敛convergence in probability伯努利大数定律Bernoulli law of large numbers同散布same distribution列维 - 林德伯格independent Levy-Lindberg theorem定理、独立同分布中心极限制理辛钦大数定律Khinchine law of large numbers利亚普诺夫定理Liapunov theorem棣莫弗 - 拉普拉De Moivre-Laplace theorem斯定理第六章样本及抽样分布Chapter 6 Samples and Sampling Distributions统计量statistic整体population个体individual样本sample容量capacity统计剖析statistical analysis统计散布statistical distribution统计整体statistical ensemble随机抽样stochastic sampling / random sampling 随机样本random sample简单随机抽样simple random sampling简单随机样本simple random sample经验散布函数empirical distribution function样本均值sample average / sample mean样本方差sample variance样本标准差sample standard deviation标准偏差standard error样本 k 阶矩sample moment of order k样本中心矩sample central moment样本值sample value样本大小、样本sample size容量样本统计量sampling statistics 随机抽样散布random sampling distribution抽样散布、样本sampling distribution散布自由度degree of freedomZ 散布Z-distributionU 散布U-distribution第七章参数预计Chapter 7Parameter Estimations统计推测statistical inference参数预计parameter estimation散布参数parameter of distribution参数统计推测parametric statistical inference点预计point estimate / point estimation整体中心距population central moment整体有关系数population correlation coefficient整体散布population covariance整体协方差population covariance点预计量point estimator预计量estimator无偏预计unbiased estimate/ unbiasedestimation预计量的有效性efficiency of estimator矩法预计moment estimation整体均值population mean整体矩population moment整体 k 阶矩population moment of order k整体参数population parameter极大似然预计maximum likelihood estimation极大似然预计量maximum likelihood estimator极大似然法maximum likelihood method /maximum-likelihood method似然方程likelihood equation似然函数likelihood function区间预计interval estimation置信区间confidence interval置信水平confidence level置信系数confidence coefficient单侧置信区间one-sided confidence interval置信上限置信下限U 预计正态整体整体方差的预计confidence upper limit confidence lower limitU-estimatornormal populationestimation of population variance置信度方差比degree of confidence variance ratio第八章假定查验Chapter 8Hypothesis Testings参数假定假定查验两类错误统计假定统计假定查验查验统计量明显性查验统计明显性parametric hypothesis hypothesis testingtwo types of errors statistical hypothesis statistical hypothesis testing test statisticstest of significance statistical significance单边查验、单侧one-sided test查验单侧假定、单边one-sided hypothesis 假定两侧假定两侧查验明显水平拒绝域 / 否认区two-sided hypothesis two-sided testing significant level rejection region域接受地区acceptance regionU 查验F 查验方差齐性的查验拟合优度查验U-testF-testhomogeneity test for variances test of goodness of fit。
概率论与数理统计(英文) 第八章

8. Testing HypothesesOften, the problem confronting scientists or engineers is not so much the estimation of a population parameter as discussed in Chapter 7, but rather the formation of data-based decision procedure that can produce a conclusion about some scientific system.We shall now consider one of the most important problems that of testing statistical hypotheses.8.1 Statistical Hypotheses: General conceptsFirst, let us define what we mean by a statistical hypothesis.一个统计假设是关于总体某些参数所作的假设。
For example, suppose we wish to test the “honesty” of a coin. This is a statistical hypothesis, since the assumption of “honesty” is equivalentThe truth or falsity of a statistical hypothesis is never known with absolute certainly unless we examine the entire population. This, of course, would be impractical in most situations.Instead, we are force to take a sample from the population and use the data contained in this sample in deciding whether the hypothesis is true or false. In above example, suppose now in tossing the coin 100 times we obtain 60 heads, and from this information we are forced to reach a decision regarding the honesty of the coin.统计检验是统计推测假设是否正确H null hypothesis. 零假设H alternative hypothesis备择假设1A null hypothesis concerning a population parameter will always be stated so as to specify an exact value of the parameter,the alternative hypothesis allows for the possibility of several values.一般做法:Assuming that the null hypothesisH is true,Uses the sample data to decide:whether the evidence favorsH1 rather thanH and draws one of these two conclusions:(1) RejectH and accept 1H(2) AcceptH as trueThere is a difference in the forms of the alternative hypotheses given in Example 8.1.1 and 8.1.2.In Example 8.1.1, no directional difference is suggested for the value of μ; that is μmight be either larger or smaller than $14 ifH is true.1This type of test is called a two-tailed test of hypothesis. (双边检验) In Example 8.1.2, however, you are specifically interested in detecting a directional different in the value of p; that is, ifH is true,1the value of p is less than 0.03. This type of test is called a one-tailed test of hypothesis.(单边检验)8.2Testing a statistical Hypothesisthe statistical procedure(1)H0 : Hypothesis being tested 提出原假设(2)take a sample from the population(3)use the sample to decide: H0 is true or H0 is falseAccept or not H0To illustrate the testing of a statistical hypothesis, consider the following example.Since the sample size is large, the sampling distribution of X approximately normal with mean 14μ= and standard deviation, i.e. 2~(,)X Nn σμ , ~(0,1)X Z N = If the null hypothesis 0H is true, then the sample mean should not be toofar from the population mean 14μ=, i.e. 0||X k μ-<, where 0k is the specified value (depending on we need). If 0||X k μ-≥, it is reasonable todoubt 0H , and thus it may lead to reject 0H and accept 1H . Since0{||}{||{||}X X k Z k μ-≥=≥=≥, whereX Z = and k =, we consider ||Z k ≥ instead of 0||X k μ-≥. How do you decide the k ?Now we can calculate the test statistic . Suppose this sample produces a sample mean 15x = with standard deviation ˆ2s =, then the observed value of the test statistic is5 1.96x z ===>. It told us that the null hypothesis is not true. We decide to reject 0H .z -1.96 1.96reject region14μ=Comparing with /2{||}P Z z αα≥=, it is easy to see /2k z α=. Once k is fixed. FromZ k ≥We can fix the rejection regions 拒绝域(,)(,)k k -∞-+∞,when the test statistic Z falls on (,)(,)k k -∞-+∞, the researcher would reject the null hypothesis. From Z k <, we can fix the another region, called accept region(接受域). When the test statistic Z falls on (,)k k -, i.e. sample meanX fallson 00(kk μμ-+. We wouldacceptH.显著性水平It is a commonly accepted convention to consider a result significant if the calculated probability is less than α=0.05,and to term it highly significant if the calculated probability is less than α=0.01.3. H0 is true or false?In general, α= 0.05a result is significant-----if P{ the calculated event}≤0.05(显著)a result is highly significant----if α= 0.01, P{ the calculated event}≤α(高度显著)so in making a statistical test, αmust be decided first.Is equivalent to (等价于)On the basis of the 5% level of significant, we rejects Ho( the hypothesis that the coin is honest)以5%的显著水平拒绝假设Ho.To approach problem of hypothesis testing systematically, it will help to proceed as outlined in the following five steps.·From the result, we have to justify:Or (1) the hypothesis is correct, but a rare event has occurred.Or (2) the hypothesis is not correct.Two Types of ErrorsIt should be emphasized that the testing of statistical hypotheses does not constitute a mathematical proof of the truth or falsity of the hypothesis. Unfortunately, there is no absolute certainly that theconclusion reached will be correct. In fact, in testing statistical hypotheses, two types of incorrect conclusion are possible. (two types of error conclusion)The probability of committing a type I error is the relative frequency with which we reject a correct hypothesis, and this is precisely equal to the significance level α. The smaller the value of α, the smaller the chance of committing a type I error.α=P {type I error}P ={reject 0H 0H is true}The probability of committing a type II error is usually denoted by β.P β={type II error}P ={accept 0H 0H is false}In testing any null hypothesis, there are four possible situation that determine whether our decision is correct or in error. These four situation are summarized in the following table.For a given number of observations it can be shown that if α is given β can be determined, and that if α is decreased β is increased. This means that, for a fixed sample size, if the probability of committing a type I error is decreased, the probability of committing a type II error is increased, and vice versa. If we wish to decrease the chances of both types of error at the same time, it can be accomplished only by increasing the size of the sample.8.3 Hypotheses Concerning MeanIn this section we are concerned with testing hypotheses concerning population mean. There are two situation, single mean and two means. Let us first consider the single mean.Testing 0μμ= (Normal population and variance 2σ known)Following the outline of the preceding section, by writing we do: 1. 0H : 0μμ=, alternative hypotheses 1H : 0μμ≠2. The appropriate test statistic is~(0,1)X Z N =3. Find out critical value for fixed level of significance α/2{||}P Z z αα>=4. Calculation:/x z nμσ-= 5. DecisionWe would reject 0H if /2z z α≥ or /2z z α≤- and say the results is significant, otherwise accept 0H .Although it is easier to understand the critical region written in term of z , we write the same critical region in terms of the observation sample mean x . The following can be written as an identical decision procedure:Reject 0H if x b > or x a < Where 0/2a z nααμ=-, 0/2b z nααμ=+Hence, for a significant level α, the critical value of the random variable z and x are both depicted in Figure 8.3.1.Figure 8.3.1 critical region for the alternativehypothesis 0μμ≠Tests of one-tailed hypotheses on the mean involve the same statistic described in two-tailed case. The difference, of course, is the criticalregion is only in one tail of the standard normal distribution. As a result, we list them as follow:Alternative hypothesis type I error rejection regions1H : 0μμ< {}P Z z αα<-= z z α<- 1H : 0μμ> {}P Z z αα>= z z α>The following two examples illustrate tests on means for the case in which σ is known.Solution1. 0H : 18.3μ= 1:18.3H μ<2. The appropriate test statistic is ~(0,1)Z N = 3. 0.01α=. 4. Critical region:base on {}0.01P Z z α<-=,from the Table B 2.325z α=.5. Calculations.17x =, 1.2σ=, 100n =, 0 1.310.83 2.3250.12/ 1.2/100x z n σ-====-<-, 6. Decision.Since the value of test statistics 10.83z =- is less than critical value2.325z α-=-, we reject 0H in favor of 1H , and we would say that thissample is inferior on the basis of the 1% level of significance.Example 8.3.2 A manufacturer of sports equipment has level a new synthetic fishing line that he claims has a mean breaking strength of 8 kilograms with a standard deviation of 0.5 kilogram. If a random sample of 50 lines is tested and found to have a mean breaking strength of 7.8 kilograms. Can we conclude that the mean of breaking (5% level) different from the claimed by the manufacturer. Solution1. 0H : 8μ= 1H : 8μ≠2. test statistic 0~(0,1)/X Z N nσ=3. α=0.054. critical value:/2{||}0.05P Z z α>=From the Table , /2 1.96z α= 5. Calculations.7.8x =, 0.5σ=, 50n = 2.83x z ===-, 6. DecisionSince /2|| 2.83 1.96z z α=>=, we reject 0H and conclude that the mean of breaking different from the claimed by the manufacturer.Homework 8.1, 8.2---------------------------------1.P -valueIn problem like this, many research workers accompany the calculated value of Z with a corresponding tail probability , or P -value , which is the probability of getting a difference between x and 0μ greater than or equal to that actually observed.If the P -value is less than the level of significance α, indicating that the hypothesis is false, the result is termed significant.If we want to test the hypothesis is 0H : 0μμ=, then the P -value corresponding alternative hypothesis 1H is found as following:For instance, in the above example, the observed value of the test statistic is7.88 2.83x z μ--===-.Since the alternative hypothesis is two-tailed, we can find the P -value is{ 2.83}{ 2.83}{ 2.83}0.0230.0230.046P P Z P Z P Z =>=>+<-=+=.This P -value is less than α=0.05, which results in rejecting 0H .In fact, if the P -value is less than the level of significance α, theobserved value of the test statistic is fall down the critical region. (如果P-value 小于显著性水平,则观察值比落在拒绝域内) 2.方差未知,检验均值Testing 0μμ= (Normal population and variance 2σ unknown) The test we have described in this section is essentially an approximate large sample test: it is exact only when the population we are sampling is normal and σ is known. In many practical situations whereσis unknown, the sample size is large. We must make further approximation of substituting for it the sample standard deviation ˆs.(1)大样本Statistic for large sample test concerning mean is~(0,1)XZ N-=(2)小样本If the sample size is small and σis unknown, the tests just described can not be used. However, if the sample comes from a normal population (with a reasonable degree of approximation), we can make use of the theory discussed in chapter 5.3 and base the test of the null hypothesis 0μμ=on the statistic~(1)t t n=-. 等价于)1(~1/0---=ntnsXtμWheres=.Solution1. 0H : 21.5μ= 1H : 21.5μ<2. the appropriate statistic is~(1)X t t n =- (small sample. σ unknown) 3. α=0.05, 6n =,{(1)}P t t n αα<--=From the Table C: 0.05(1)(5) 2.015t n t α-== Critical region : 2.015t <- 4.Calculations:X X X - 2()X X -19 -1 1 18 -2 422 2 4 20 0 0 16 -4 16 25 5 25 120 0 50 And,12020.06x ==, s ===, 1.51.161.29x t -====-5. DecisionSince 1.16t =-≮ 2.015(5)t α-=, we accept 0H . The results do not indicate that batteries of this type have a shorter life than that claimed by the company.3 检验两正态总体均值之差Testing 12μμδ-= (Normal population)Now, let ’s consider a large-sample Test of Hypothesis for the Difference between two population means. (1)(方差已知)In many situations, the statistical question to be answered involves a comparison of two population means. For example, if two methods ofwelding are being considered for use with railroad rails, we may take samples and decide which is better by comparing their mean strength. Formulating the problem more generally, we shall consider two population having the means 1μ and 2μ and the variances of 21σ and22σ, and we shall want to test the null hypothesis 12μμδ-=, (120μμ-=)where δ is specified constant, on the basis of independent random sample of size 1n and 2n . We shall consider tests of this null hypothesis against each of the alternatives 12μμδ-<, 12μμδ->, and 12μμδ-≠. The test itself will depend on the difference between the sample means 12X X -, and if both samples come from normal population with known variance, it can be based on the statistic1212()~(0,1)X XX X Z N δσ---=here12X X σ-=when 21σ and 22σ are unknown, but 1n and 2n , or both are large (greater than or equal to 30), we can apply the central limit theorem andapproximate 1σ and 2σ with 1ˆsand 2ˆs , therefore the standard deviation of 12()X X -is estimated by ()12X X S -=.Critical region for testing 12μμδ-= (Normal populations and 1σand 2σ known, or large samples 1n , 230n >)Although δ can be any constant, it is worth nothing that in the great majority of problems its value is zero and we test the null hypothesis of no difference, namely, the null hypothesis 12μμ=.SolutionHere we wish to test the statistical hypothesis that the means of thetwo populations (distances traveled per gallon of gasoline for makes A and B, denoted by 1X and 2X , respectively) are identical. It is large sample because of 150n = and 270n =.1. 0H : 120μμ-= 1H : 120μμ-<2. the appropriate statistic is 1212()~(0,1)X XX X Z N δσ---=l,3. 0.05α={}P Z z αα<-=,From the Table B : 0.05 1.645z z α==Critical region: 1.645z <-4. Calculations:150X =, 11ˆ 2.5X s σ==, 150n =, 270X =, 22ˆ 3.0X sσ==, 270n =, Hence12X X σ-===0.50=== 1212()(17.018.6)0 1.603.200.500.50X XX X z δσ------====-5. DecisionSince 3.20 1.645z =-<-, we reject 0H and conclude that cars of make B consume less gasoline than those of make A. We can also calculate the P -value:{{ 3.20}0.0007P P Z P Z =<=<-=.Since the probability is less than 0.05, the result is significant. (2)(方差未知,但12σσσ==)The more prevalent situations involving test on two means are those in which 21σ and 22σ are unknown, at the same time 1n and 2n , or both are small. If the scientist involved is willing to assume that both distributions are normal and that 12σσσ==, the pooled t-test (often called the two-sample t-test) may be used. The test statistic is given by the following test procedure.12~(2)X X t t n n δ--=+- where222112212(1)(1)2s n s n s n n -+-=+-Solution1. 0H : 122μμ-= 1H : 122μμ->2. the appropriate statistic is 12~(2)X X t t n n =+-3. 0.05α=12{(2)}P t t n n αα>+-=From the Table C : 120.05(2)(20) 1.725t n n t α+-== Critical region: 1.725t > 4. Calculations:185X =, 41=s , 112n =, 281X =, 52=s , 210n =,Hence2)1()1(2122 221-+-+-=nns nsns4.478==1.04Xt===5. DecisionSince 1.04t=is not exceed to 1.725, we accept 0H. We are unable to conclude that the abrasive wear of material 1 exceeds that of material 2 by more than units.4 成对总体均值之差检验Paired-Difference Test. (The case of Paired variates)Many experiments are performed in such a way that each variate of one sample is paired with a particular varite of another sample.If, for example, the effectiveness of a fertilizer is to be determined, the experimenter might select 10 plots, treat half of each plot with the fertilizer, and leave the other half untreated to serve as a control. In this case, the yield from the treated and untreated halves of each plot constitute a set of paired variates, and we need to watch that the significant difference found between means (or not found) be due to the different conditions of the population and not due to the experimentalunits. So the t test with two populations be independent statistical test.To analyze paired experiments, we consider for each pair the difference between the variates i X and i Y , and denote this difference byi Di i i D X Y =- 1,2i n =This collection of (signed) differences in them treated as a random sample of size n from a population having mean 0u . We interpret00μ= as indicating the mean of the two responses are the same and 00μ> as indicating the mean responses of the first is higher than that ofthe second.Tests of the null hypothesis 0H : ,0D D u u =, are based on the ratioD u - where 1nii DD n==∑ 221()1nii DD D s n =-=-∑if n is small, we treat this ratio as~(1)D u t t n -=-Otherwise, we treat this ratio as~(0,1)D u z N -=SolutionWe cannot apply the independent samples test because the midterm and final records of student are correlated. Here there is the obvious pairing of these two observations1. 0H : ,0120D μμμ=-= 1H : 120μμ-≠2. 9n = is small sample, the appropriate statistic is~(1)D t t n μ-=-3. 0.05α=/2{||(1)}0.05P t t n α>-=From the Table : 0.0250.025(1)(8) 2.306t n t -== 4. Calculations:X Y D X Y =- D D - 2()D D -67 81 -14 -9 8177 82 -5 0 0 80 73 7 12 144 83 84 -1 4 16 92 87 5 10 100 54 68 -14 -9 81 89 97 -8 -3 9 67 76 -9 -4 16 85 91 -6 -1 14559D -==- Their mean is 5D =- and their standard deviation is483.75684481)(2===--=∑n D D s D532.00447.483D u t --⨯====- 5. Decision: Since || 2.0044t = is not more than 2.306. We accept 0H , these data confirm teacher ’s claim. Homework (1, 2, 10, 13)8.6 Tests for proportionTest of hypotheses concerning proportions are required in many areas.The politician is certainly interested in knowing what fraction of the voters will favor him in the next election.All manufacturing firms are concerned about the proportion ofdefective items when a shipment is made.The gambler depends on a knowledge of the proportion of outcomes that he considers favorable.We shall consider the problem of testing the hypothesis that theproportion of successes in a binomial experiment equals some specified value.That is, we are testing the null hypothesis 0H that 0p p =, where p is the parameter of the binomial distribution. The alternative hypothesis may be one of the usual one-tailed or two-tailed alternatives: 0p p <, 0p p >, or 0p p =.The appropriate random variable on which we base our decisioncriterion is the binomial random variable X , although we could just as well use the statistic /p X n =. Value of X that are far from the mean0np μ= will lead to the rejection of the null hypothesis. Because X is adiscrete binomial variable, it is unlikely that a critical region can be established whose size is exactly equal to a prespecified value of α. For this reason it is preferable, in dealing with small samples, to base our decisions on P -value . To test the hypothesis0010:,:H p p H p p =<,we use the binomial distribution to compute the P -value0{when }P P X x p p =≤=.The value x is the number of successes in our sample of size n .If P -value ≤ α, our test is significant at the α level and we reject 0H in favor of 1H .Similarly, to test the hypothesis0010:,:H p p H p p =>,we calculate0{when }P P X x p p =>=.Finally, to test the hypothesis0010:,:H p p H p p =≠we calculate02{when }P P X x p p =≤= if 0x np < or 02{when }P P X x p p =≥= if 0x np >.The steps for testing a null hypothesis about a proportion againstvarious alternatives using the binomial probability are as follows: 1. 00:H p p =.2. 1000:(or ,)H p p p p or p p ><≠3. Test statistic: Binomial variable X with 0p p =.4. Calculate: find x , the number of successes, and calculate theappropriate P -value.5. Decision: comparing with level of significance, draw appropriateconclusions based on the P -value.Solution 1. 0:0.70H p =. 2. 1:0.7H p ≠3. Test statistic: Binomial variable X with 0.7p = and n =154. Calculation: x =8 and 0(15)(0.7)10.5np ==, the P -value is82{8when 0.7}2(;15,0.7)0.2622x P P X p b x ==≤===∑5. Decision: Since 0.26330.10P α=>=, we do not reject 0H .Conclude that there is insufficient reason to doubt the builder ’s claim.When the hypothesized value 0p is very close to 0 or 1, the Possiondistribution, with parameter 0np μ=, may be used.When large n , as long as 0p is not extremely close to 0 or 1,thenormal-curve approximation, with parameters 0np μ= and 200np q σ=, is usually preferred.If we use the normal approximation, the z-value for testing 0p p = is given byz =which is a value of the standard normal variable Z. Hence, for a two-tailed test at the α-level of significance, the critical region is/2z z α<- and /2z z α>. For the one-tailed alternative 0p p <, the criticalregion is z z α<-, and for the alternative 0p p >,the critical region isz z α>.Solution1. 03:4H p =.2. 13:4H p >3. Test statistic: ~(0,1)Z N =4.Critical value: 0.05α=, based on {}0.05P Z z α>=, we can find0.05 1.645z = from the Table B.5. Calculation: n =228, 0(228)(3/4)171np ==, x =179, and1.15z ===6. Decision: Since 1.15 1.645z =<, the result does not represent a significant deviation from the theory and we do not reject 0H . Homework (1, 2, 10, 13)(8.4, 8.5, 8.8, 8.10, 8.13)8.4 Hypotheses concerning variance1.单个总体方差的检验In this section, we are concerned with testing hypotheses on population variance or standard deviation. First, we shall consider the case in single population, (the null hypothesis is 0H : 220σσ=, the alternative hypothesis is 1H : 220σσ< or 220σσ> or 220σσ≠)By Theorem 6.4.7, we base such tests on the fact that for a random sample from a normal population with variance 20σ, the statistic2220(1)n s χσ-=For testing the variance is a random variable having the Chi-square distribution with 1n - degree of freedom, i.e. 22220(1)~(1)n s n χχσ-=-Solution .1. 0H : 220.9σ= 1H : 220.9σ>2. the appropriate statistic is22220(1)~(1)n s n χχσ-=-3. for 0.05α= 10n =220.05{(9)}0.05P χχ>= 4. Critical value: From the Table20.05(9)16.92χ= 5. Calculations.221.2s =, 2200.9σ= 2(9)(1.44)16.00.81χ==≯20.0516.92(9)χ= 6. Decision:Since 216.0χ=is not exceed the critical value 20.05(9)16.92χ=, we accept 0H , and do not believe that 0.9σ> year. (The statistic 2χ is not significant)(小样本,样本方差理解为 2s大样本,样本方差理解为 2ˆs)2.两个总体方差的检验 (1)F 分布We already know, from Theorem 6.4.7, that if 21ˆS is the variance of a random sample of size 1n from a normal population with variance21σ, and 22ˆS is the variance of a random sample of size 2n from a normal population with variance 22σ, then)1(2212111~ˆ-n S n χσ and)1(2222222~ˆ-n S n χσ.Suppose that these two samples are independent random samples , which means that all the 21n n + random variables in these two random samples are independent. Then these two chi-square random variables arealso independent. Replacing X and Y in Theorem 6.6.1 by21211ˆσS n and22222ˆσS n leads to the following important conclusion.There is a special case when the two random samples are from a same normal population. Thus, 21σσ= and we have the result below.(2)两个总体方差的检验Now let us consider the case in the two populations case, we shall test the null hypothesis 0H that 2212σσ= against one of the usual alternatives2212σσ<, 2212σσ> or 2212σσ≠According to Theorem 6.6.1, if independent random samples of size 1nand 2n are taken from normal populations having the same variance, that2122s F s =is a random variable having the F distribution with 11n - and 21n - degrees of freedom, i.e.211222~(1,1)s F F n n s =--.Because there is a relationship between 12(,)F v v α and 121(,)F v v α- 121121(,)(,)F v v F v v αα-=we base the test on the statistic 2122s F s = and critical region for testing thenull hypothesis 2212σσ= against the alternative hypothesis 2212σσ< becomes 12(1,1)F F n n α>--For the two-tailed alternative 2212σσ≠ the critical region is)1,1(212/1--<-n n F F α or /212(1,1)F F n n α>-- where211222~(1,1)s F F n n s =--.In practice, we modify this test as in the preceding paragraph, so that we can use the table of F -distribution value corresponding to the right-hand tail.Let 2M S represent the larges of the two sample variances, 2m S thesmaller, and we write the corresponding sample size as M n and m n ,respectively. Thus, the test statistic becomes 22Mms F s = and the criticalregion is as shown in the following table:Solution1. Null hypothesis: 2212σσ=0H : 2212σσ=, 1H : 2212σσ≠ 2. The appropriate statistic is22~(1,1)MM m ms F F n n s =--3. For 0.05α=, compute /2{(1,1)}2M m P F F n n αα>--=4. Calculate14n =, 2211()11036.6713x x sn -===-∑, 26n =, 2222()5611.2015y y s n -===-∑ and 22122236.673.2711.20M m s s F s s ====,from Table E to get 0.05(3,5)14.9F =. 5. DecisionSince 3.27F =≯0.0514.9(3,5)F =, we conclude that the two variances can be assumed to be homogeneous.8.5 Relationship to confidence Interval Estimation 假设检验与区间估计的联系The reader should realize by now that the hypothesis-testing approach to statistical inference in this chapter is very closely related to the confidence interval approach in Chapter 7.Confidence interval estimation involves calculation of bounds for which it is “reasonable ” that the parameter in question is inside the bounds.For the case of a single population mean μ with 2σ known, the test statistic of both hypothesis testing and confidence interval estimation isX Z =. It turns out that the testing of 0H : 0μμ= against: 0μμ≠ at a significance level α is equivalent tocalculating a 100(1)%α- confidence interval on μ and reject 0H if 0μ is not inside the confidence interval.If 0μ is inside the confidence interval, then the null hypothesis is not rejected. The equivalence is very intuitive and quite simple to illustrate.Recall that with an observed value x failure to reject 0H at the significance level α implies that/2/2x z z αα-<< which is equivalent to/20/2x z x z ααμ-<<+The equivalence between hypotheses-testing and confidence interval estimation for comparing two means, two variances or other pair of statistics is similar. As a result, the student of statistics should not consider confidence interval estimation and hypothesis testing as separate forms of statistical inference. 8.20, 8.22, 8.248.7 Tests for independence 独立性检验The chi-squared test procedure discussed in Chapter 6 can also be used to test the hypothesis of the independence of two variables .Suppose that we wish to determine whether there might be a relationship between month of birth and intelligence.A random sample of 148 individuals(persons) are classified as to whether their birth are in summer, autumn, winter or spring and whether their IQ are in 55~69 or 40~54. The observed frequencies are presented in Table 8.7.1 Which is known as a contingency table.Table 8.7.1 The season of birth and IQ incidence (24⨯ Contingency Table 列联表)Summer Autumn Winter Spring Totals。
概率论与数理统计(英文) 第三章

3.R a n d o m V a r i a b l e s 3.1 Definition of Random VariablesIn engineering or scientific problems, we are not only interested in the probability of events, but also interested in some variables depending on sample points. (定义在样本点上的变量)For example, we maybe interested in the life of bulbs produced by a certain company, or the weight of cows in a certain farm, etc. These ideas lead to the definition of random variables.1. random variable definitionHere are some examples.Example 3.1.1 A fair die is tossed. The number X shown is a random variable, it takes values in the set {1,2,6}.Example 3.1.2The life t of a bulb selected at random from bulbs produced by company A is a random variable, it takes values in the interval (0,) .Since the outcomes of a random experiment can not be predicted in advance, the exact value of a random variable can not be predicted before the experiment, we can only discuss the probability that it takes some value or the values in some subset of R.2. Distribution functionNote The distribution function ()F X is defined on real numbers, not on sample space. Example 3.1.3Let X be the number we get from tossing a fair die. Then the distribution function of X is (Figure 3.1.1)Figure 3.1.1 The distribution function in Example 3.1.33. PropertiesThe distribution function ()F x of a random variable X has the following properties:SolutionBy definition,1≤==-=.(2000)(2000)10.6321P X F e-Question:What are the probabilities (2000)P X=?P X<and (2000)SolutionLet 1X be the total number shown, then the events 1{}X k = contains 1k - sample points, 2,3,4,5k =. Thus11()36k P X k -==, 2,3,4,5k = AndsoThusFigure 3.1.2 The distribution function in Example 3.1.53.2 Discrete Random Variables 离散型随机变量In this book, we study two kinds of random variables. ,,}n aAssume a discrete random variable X takes values from the set 12{,,,}n X a a a =. Let()n n P X a p ==,1,2,.n = (3.2.1)Then we have 0n p ≥, 1,2,,n = 1n n p=∑.the probability distribution of the discrete random variable X (概率分布)注意随机变量X 的分布所满足的条件(1) P i ≥0(2) P 1+P 2+…+P n =1离散型分布函数 And the distribution function of X is given by()()n n a xF x P X x p ≤=≤=∑ (3.2.2)Solutionn=3, p=1/2X p r1/8 13/8 23/8 31/8two-point distribution(两点分布)某学生参加考试得5分的概率是p , X 表示他首次得5分的考试次数,求X 的分布。
概率论与数理统计英文版总结电子教案

概率论与数理统计英文版总结Sample Space样本空间The set of all possible outcomes of a statistical experiment is called the sample space. Event 事件An event is a subset of a sample space.certain event(必然事件):The sample space S itself, is certainly an event, which is called a certain event, means that it always occurs in the experiment.impossible event(不可能事件):The empty set, denoted by∅, is also an event, called an impossible event, means that it never occurs in the experiment.Probability of events (概率)If the number of successes in n trails is denoted by s, and if the sequence of relative frequencies /s n obtained for larger and larger value of n approaches a limit, then this limit is defined as the probability of success in a single trial.“equally likely to occur”------probability(古典概率)If a sample space S consists of N sample points, each is equally likely to occur. Assume that the event A consists of n sample points, then the probability p that A occurs is()np P AN==Mutually exclusive(互斥事件)Mutually independent 事件的独立性Two events A and B are said to be independent if ()()()P A B P A P B=⋅IOr Two events A and B are independent if and only if(|)()P B A P B=.Conditional Probability 条件概率The multiplication theorem 乘法定理 If 12k ,,,A A A L are events, then12k 121312121()()(|)(|)(|)k k P A A A P A P A A P A A A P A A A A -=⋅⋅I I L I L I I L I If the events 12k ,,,A A A L are independent, then for any subset12{,,,}{1,2,,}m i i i k ⊂L L ,1212()()()()m m P A A A P A P A P A i i i i i i =I I L L(全概率公式 total probability)(贝叶斯公式Bayes ’ formula.)()(|)()i i P B A P B A P A =IUsing the theorem of total probability, we have1()(|)(|)()(|)i i i kjjj P B P A B P B A P B P A B ==∑ 1,2,,i k =L1. random variable definition2. Distribution functionNote The distribution function ()F X is defined on real numbers, not on sample space. 3. PropertiesThe distribution function ()F x of a random variable X has the following properties:3.2 Discrete Random Variables 离散型随机变量geometric distribution (几何分布)Binomial distribution(二项分布)poisson distribution(泊松分布)Expectation (mean) 数学期望2.Variance 方差 standard deviation (标准差)probability density function概率密度函数5. Mean(均值)6. variance 方差4.2 Uniform Distribution 均匀分布The uniform distribution, with the parameters a a nd b , has probability density function1for ,()0 elsewhere,a x b f x b a⎧<<⎪=-⎨⎪⎩4.5 Exponential Distribution 指数分布4.3 Normal Distribution 正态分布4.4 Normal Approximation to the Binomial Distribution (二项分布)4.7 Chebyshev’s Theorem (切比雪夫定理)Joint probability distribution (联合分布)In the study of probability, given at least two random variables X, Y, ..., that are defined on a probability space, the joint probability distribution for X, Y, ... is a probability distribution that gives the probability that each of X, Y, ... falls in any particular range or discrete set of values specified for that variable. 5.2 C onditional distribution 条件分布Consistent with the definition of conditional probability of events when A is the event X =x and B is the event Y =y , the conditional probability distribution of X given Y =y is defined as(,)(|)()X Y p x y p x y p y =for all x provided ()0Y p y ≠.5.3S tatistical independent 随机变量的独立性5.4 Covariance and Correlation 协方差和相关系数We now define two related quantities whose role in characterizing the interdependence of X and Y we want to examine.理We can find the steadily of the frequency of the events in large number of random phenomenon. And the average of large number of random variables are also steadiness. These results are the law of large numbers.population (总体)sample (样本、子样)中位数Sample Distributions 抽样分布1.sampling distribution of the mean 均值的抽样分布It is customary to write )(X E as X μ and )(X D as 2X σ.Here, ()E X μ= is called the expectation of the mean .均值的期望 n X σσ= is called the standard error of the mean. 均值的标准差7.1 Point Estimate 点估计Unbiased estimator(无偏估计量)minimum variance unbiased estimator(最小方差无偏估计量)3. Method of Moments 矩估计的方法confidence interval----- 置信区间lower confidence limits-----置信下限upper confidence limits----- 置信上限degree of confidence----置信度2.极大似然函数likelihood functionmaximum likelihood estimate(最大似然估计)8.1 Statistical Hypotheses(统计假设)显著性水平Two Types of Errors。
概率论与数理统计英文文献

Introduction to probability theory andmathematical statisticsThe theory of probability and the mathematical statistic are carries on deductive and the induction science to the stochastic phenomenon statistical rule, from the quantity side research stochastic phenomenon statistical regular foundation mathematics discipline, the theory of probability and the mathematical statistic may divide into the theory of probability and the mathematical statistic two branches. The probability uses for the possible size quantity which portrays the random event to occur. Theory of probability main content including classical generally computation, random variable distribution and characteristic numeral and limit theorem and so on. The mathematical statistic is one of mathematics Zhonglian department actually most directly most widespread branches, it introduced an estimate (rectangular method estimate, enormousestimate), the parameter supposition examination, the non-parameter supposition examination, the variance analysis and the multiple regression analysis, the fail-safe analysis and so on the elementary knowledge and the principle, enable the student to have a profound understanding tostatistics principle function. Through this curriculum study, enables the student comprehensively to understand, to grasp the theory of probability and the mathematical statistic thought and the method, grasps basic and the commonly used analysis and the computational method, and can studies in the solution economy and the management practice question using the theory of probability and the mathematical statistic viewpoint and the method.Random phenomenonFrom random phenomenon, in the nature and real life, some things are interrelated and continuous development. In the relationship between each other and developing, according to whether there is a causal relationship, very different can be divided into two categories: one is deterministic phenomenon. This kind of phenomenon is under certain conditions, will lead to certain results. For example, under normal atmospheric pressure, water heated to 100 degrees Celsius, is bound to a boil. This link is belong to the inevitability between things. Usually in natural science is interdisciplinary studies and know the inevitability, seeking this kind of inevitable phenomenon.Another kind is the phenomenon of uncertainty. This kind of phenomenon is under certain conditions, the resultis uncertain. The same workers on the same machine tools, for example, processing a number of the same kind of parts, they are the size of the there will always be a little difference. As another example, under the same conditions, artificial accelerating germination test of wheat varieties, each tree seed germination is also different, there is strength and sooner or later, respectively, and so on. Why in the same situation, will appear this kind of uncertain results? This is because, we say "same conditions" refers to some of the main conditions, in addition to these main conditions, there are many minor conditions and the accidental factor is people can't in advance one by one to grasp. Because of this, in this kind of phenomenon, we can't use the inevitability of cause and effect, the results of individual phenomenon in advance to make sure of the answer. The relationship between things is belong to accidental, this phenomenon is called accidental phenomenon, or a random phenomenon.In nature, in the production, life, random phenomenon is very common, that is to say, there is a lot of random phenomenon. Issue such as: sports lottery of the winning Numbers, the same production line production, the life of the bulb, etc., is a random phenomenon. So we say: randomphenomenon is: under the same conditions, many times the same test or survey the same phenomenon, the results are not identical, and unable to accurately predict the results of the next. Random phenomena in the uncertainties of the results, it is because of some minor, caused by the accidental factors.Random phenomenon on the surface, seems to be messy, there is no regular phenomenon. But practice has proved that if the same kind of a large number of repeated random phenomenon, its overall present certain regularity. A large number of similar random phenomena of this kind of regularity, as we observed increase in the number of the number of times and more obvious. Flip a coin, for example, each throw is difficult to judge on that side, but if repeated many times of toss the coin, it will be more and more clearly find them up is approximately the same number.We call this presented by a large number of similar random phenomena of collective regularity, is called the statistical regularity. Probability theory and mathematical statistics is the study of a large number of similar random phenomena statistical regularity of the mathematical disciplines.The emergence and development of probability theoryProbability theory was created in the 17th century, it is by the development of insurance business, but from the gambler's request, is that mathematicians thought the source of problem in probability theory.As early as in 1654, there was a gambler may tired to the mathematician PASCAL proposes a question troubling him for a long time: "meet two gamblers betting on a number of bureau, who will win the first m innings wins, all bets will be who. But when one of them wins a (a < m), the other won b (b < m) bureau, gambling aborted. Q: how should bets points method is only reasonable?" Who in 1642 invented the world's first mechanical addition of computer.Three years later, in 1657, the Dutch famous astronomy, physics, and a mathematician huygens is trying to solve this problem, the results into a book concerning the calculation of a game of chance, this is the earliest probability theory works.In recent decades, with the vigorous development of science and technology, the application of probability theory to the national economy, industrial and agricultural production and interdisciplinary field. Many of applied mathematics, such as information theory, game theory, queuing theory, cybernetics, etc., are based on the theory of probability.Probability theory and mathematical statistics is a branch of mathematics, random they similar disciplines are closely linked. But should point out that the theory of probability and mathematical statistics, statistical methods are each have their own contain different content.Probability theory, is based on a large number of similar random phenomena statistical regularity, the possibility that a result of random phenomenon to make an objective and scientific judgment, the possibility of its occurrence for this size to make quantitative description; Compare the size of these possibilities, study the contact between them, thus forming a set of mathematical theories and methods.Mathematical statistics - is the application of probability theory to study the phenomenon of large number of random regularity; To through the scientific arrangement of a number of experiments, the statistical method given strict theoretical proof; And determining various methods applied conditions and reliability of the method, the formula, the conclusion and limitations. We can from a set of samples to decide whether can with quite large probability to ensure that a judgment is correct, and can control the probability of error.- is a statistical method provides methods are used in avariety of specific issues, it does not pay attention to the method according to the theory, mathematical reasoning.Should point out that the probability and statistics on the research method has its particularity, and other mathematical subject of the main differences are:First, because the random phenomena statistical regularity is a collective rule, must to present in a large number of similar random phenomena, therefore, observation, experiment, research is the cornerstone of the subject research methods of probability and statistics. But, as a branch of mathematics, it still has the definition of this discipline, axioms, theorems, the definitions and axioms, theorems are derived from the random rule of nature, but these definitions and axioms, theorems is certain, there is no randomness.Second, in the study of probability statistics, using the "by part concluded all" methods of statistical inference. This is because it the object of the research - the range of random phenomenon is very big, at the time of experiment, observation, not all may be unnecessary. But by this part of the data obtained from some conclusions, concluded that the reliability of the conclusion to all the scope.Third, the randomness of the random phenomenon, refers to the experiment, investigation before speaking. After the real results for each test, it can only get the results of the uncertainty of a certain result. When we study this phenomenon, it should be noted before the test can find itself inherent law of this phenomenon.The content of the theory of probabilityProbability theory as a branch of mathematics, it studies the content general include the probability of random events, the regularity of statistical independence and deeper administrative levels.Probability is a quantitative index of the possibility of random events. In independent random events, if an event frequency in all events, in a larger range of stable around a fixed constant. You can think the probability of the incident to the constant. For any event probability value must be between 0 and 1.There is a certain type of random events, it has two characteristics: first, only a finite number of possible results; Second, the results the possibility of the same. Have the characteristics of the two random phenomenon called"classical subscheme".In the objective world, there are a large number of random phenomena, the result of a random phenomenon poses a random event. If the variable is used to describe each random phenomenon as a result, is known as random variables.Random variable has a finite and the infinite, and according to the variable values is usually divided into discrete random variables and the discrete random variable. List all possible values can be according to certain order, such a random variable is called a discrete random variable; If possible values with an interval, unable to make the order list, the random variable is called a discrete random variable.The content of the mathematical statisticsIncluding sampling, optimum line problem of mathematical statistics, hypothesis testing, analysis of variance, correlation analysis, etc. Sampling inspection is to pair through sample investigation, to infer the overall situation. Exactly how much sampling, this is a very important problem, therefore, is produced in the sampling inspection "small sample theory", this is in the case of the sample is small, the analysis judgment theory.Also called curve fitting and optimal line problem. Some problems need to be according to the experience data to find a theoretical distribution curve, so that the whole problem get understanding. But according to what principles and theoretical curve? How to compare out of several different curve in the same issue? Selecting good curve, is how to determine their error? ...... Is belong to the scope of the optimum line issues of mathematical statistics.Hypothesis testing is only at the time of inspection products with mathematical statistical method, first make a hypothesis, according to the result of sampling in reliable to a certain extent, to judge the null hypothesis.Also called deviation analysis, variance analysis is to use the concept of variance to analyze by a handful of experiment can make the judgment.Due to the random phenomenon is abundant in human practical activities, probability and statistics with the development of modern industry and agriculture, modern science and technology and continuous development, which formed many important branch. Such as stochastic process, information theory, experimental design, limit theory, multivariate analysis, etc.译文:概率论和数理统计简介概率论与数理统计是对随机现象的统计规律进行演绎和归纳的科学,从数量侧面研究随机现象的统计规律性的基础数学学科,概率论与数理统计又可分为概率论和数理统计两个分支。
概率论与数理统计英语

概率论与数理统计英语English: Probability theory and mathematical statistics are two branches of mathematics that deal with the concepts and tools used to understand randomness and uncertainty in various phenomena. Probability theory is concerned with quantifying uncertainty and making predictions about the likelihood of certain events occurring, while mathematical statistics uses probability theory to draw conclusions about populations based on sample data. These two fields are closely related and often used together in applications such as insurance, finance, engineering, and social sciences. Probability theory involves concepts such as random variables, probability distributions, and the laws of large numbers, while mathematical statistics covers topics such as estimation, hypothesis testing, and regression analysis. Together, they provide a framework for understanding uncertainty and making informed decisions in the face of incomplete information.中文翻译: 概率论和数理统计是数学的两个分支,涉及用于理解各种现象中的随机性和不确定性的概念和工具。
(完整word版)概率论与数理统计(英文)

3. Random Variables3.1 Definition of Random VariablesIn engineering or scientific problems, we are not only interested in the probability of events, but also interested in some variables depending on sample points. (定义在样本点上的变量)For example, we maybe interested in the life of bulbs produced by a certain company, or the weight of cows in a certain farm, etc. These ideas lead to the definition of random variables.1. random variable definitionHere are some examples.Example 3.1.1 A fair die is tossed. The number X shown is a random variable, it takes values in the set {1,2,6}.Example 3.1.2The life t of a bulb selected at random from bulbs produced by company A is a random variable, it takes values in the interval (0,) .Since the outcomes of a random experiment can not be predicted in advance, the exact value of a random variable can not be predicted before the experiment, we can only discuss the probability that it takes somevalue or the values in some subset of R.2. Distribution function Definition3.1.2 Let X be a random variable on the sample space S . Then the function()()F X P X x =≤. R x ∈is called the distribution function of XNote The distribution function ()F X is defined on real numbers, not on sample space.Example 3.1.3 Let X be the number we get from tossing a fair die. Then the distribution function of X is (Figure 3.1.1)0,1;(),1,1,2,,5;61, 6.if x n F x if n x n n if x <⎧⎪⎪=≤<+=⎨⎪≥⎪⎩Figure 3.1.1 The distribution function in Example 3.1.3 3. PropertiesThe distribution function ()F x of a random variable X has the following properties :(1) ()F x is non-decreasing.SolutionBy definition,1(2000)(2000)10.6321P X F e -≤==-=.(10003000)(3000)(1000)P X P X P X <≤=≤-≤1.50.5(3000)(1000)(1)(1)0.3834F F e e --=-=---= Question : What are the probabilities (2000)P X < and (2000)P X =? SolutionLet 1X be the total number shown, then the events 1{}X k = contains 1k - sample points, 2,3,4,5k =. Thus11()36k P X k -==, 2,3,4,5k = And512{1}{}k X X k ==-==so 525(1)()18k P X P X k ==-===∑ 13(1)1(1)18P X P X ==-=-=Thus0,1;5()(),11;181, 1.x F x P X x x x <-⎧⎪⎪=≤=-≤<⎨⎪≥⎪⎩Figure 3.1.2 The distribution function in Example 3.1.5The distribution function of random variables is a connection between probability and calculus. By means of distribution function, the main tools in calculus, such as series, integrals are used to solve probability and statistics problems.3.2 Discrete Random Variables 离散型随机变量In this book, we study two kinds of random variables. ,,}n aAssume a discrete random variable X takes values from the set 12{,,,}n X a a a =. Let()n n P X a p ==,1,2,.n = (3.2.1) Then we have 0n p ≥, 1,2,,n = 1n n p=∑.the probability distribution of the discrete random variable X (概率分布)注意随机变量X 的分布所满足的条件(1) P i ≥0(2) P 1+P 2+…+P n =1离散型分布函数And the distribution function of X is given by()()n n a xF x P X x p ≤=≤=∑ (3.2.2)Solutionn=3, p=1/2X p r01/813/823/831/8two-point distribution(两点分布)某学生参加考试得5分的概率是p, X表示他首次得5分的考试次数,求X的分布。
(完整word版)英文版概率论与数理统计重点单词
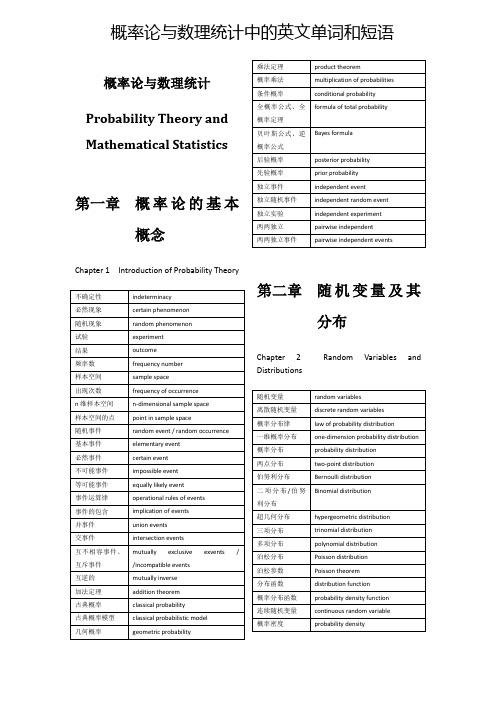
Bayes formula
后验概率
posterior probability
先验概率
prior probability
独立事件
independent event
独立随机事件
independent random event
独立实验
independent experiment
两两独立
classical probabilistic model
几何概率
geometric probability
乘法定理
product theorem
概率乘法
multiplication of probabilities
条件概率
conditional probability
全概率公式、全概率定理
formula of total probability
基本事件
elementary event
必然事件
certain event
不可能事件
impossible event
等可能事件
equally likely event
事件运算律
operational rules of events
事件的包含
implication of events
并事件
union events
似然方程
likelihood equation
似然函数
likelihood function
区间估计
interval estimation
置信区间
confidence interval
置信水平
confidence level
概率论与数理统计英文

4. Continuous Random Variable 连续型随机变量Continuous random variables appear when we deal will quantities that are measured on a continuous scale. For instanee, when we measure the speed of a car, the amount of alcohol in a pers on's blood, the ten sile stre ngth of new alloy.We shall lear n how to determ ine and work with probabilities relat ing to continu ous ran dom variables in this chapter. We shall introduce to the concept of the probability density function.4.1 Continuous Random Variable1. DefinitionDefinition 4.1.1 A function f(x) defined on (-〜:)is called a probability densityfunction (概率密度函数)if:(i) f (x) _0 for any x R;oO(ii) f(x) is in tergrable (可积的)on (-〜::)a nd f (x)dx = 1.-nODefinition 4.1.2Let f(x) be a probability density function. If X is a random variable having distribution functionxF(x)二P(X 乞x)二f(t)dt, (4.1.1)_oQthen X is called a continuous random variable having density function f(x). In this case,X2P(m :: X :: x2) = f (t)dt. (4.1.2)X i2. 几何意义()xF(x)二P(X ^x)二P((X,Y)|X zx, 0 乞丫乞f (X)) = f (t)dt-oOx2P(x , ::: X ::: x 2) = f(t)dtx13. NoteIn most applications, f(x) is either continuous or piecewise continuous having at most fin itely many disc on ti nuities. Note 1 For a random variable X, we have adistribution function . If X is discrete, it has a probability distribution . If X is continuous, it has a probability density function.Note 2 Let X be a continuous random variable, then for any real number x,P(X =x) =0.0 < P(X =x) * f (x)dxP(a 乞 X 乞 b)二 P(a 乞 X ::: b)二 P(a :: X <b) = P(a :: X ::: b)4. ExampleExample 4.1.2Find k so that the following can serve as the probability density of a continuous random variable:kf(xr FW)Solution To satisfy the conditions (4.1.1), k must be nonnegative, and to satisfy the condition (4.1.2) we must haveoaf (x)dx =JO O,1 so that k .(Cauchy distribution 柯西分布)Example 4.1.3 Calculating probabilities from the probability density functionIf a ran dom variable has the probability den sityFind the probability from that it will take on valueo 乞 p (x 二 X )空 limx * ;f (x)dx = 0 ■ x"x for x 0f(x)= 3e [0 for x 乞 0(a) betwee n 0 and 2; (b) greater tha n 1.Solution Evaluating the necessary integrals, we get2(a) P(0 辽 x 乞 2) = j 3e 'x dx =1 - e" =0.9975oO(b) P(x 〉1) = 3e'Xdx = e" =0.04981Example 4.1.4Determ ining the distributi on function of X, it is known工 3e'x for x 0f(x)=0 for x <0Solution Performing the necessary integrations, we get(0for x _ 0l x"x) 3e"dt = 1—e"x for x 0P(x _1) = F(1) =1 -e‘ =0.9502□5. meanIf the in tegral (4.1.3) does not con verges absolutely(绝对收敛 ),we say the mean of X does not exist.Definition 4.1.2 Let X be a continuous random variable having probability density functionf(x). Then the mean (or expectation) of X is defined by—E(X)二.xf (x)dx ,(4.1.3)-oOThe mean of continuous random variable has the similar properties as discrete random variable.If g(X) is an integrable function of a continuous random variable X, having density function f(x), mean of g(X) isooE(g (x ))「g(x)f(x)dx-JO Oprovided the in tegral con verges absolutely. Example 4.6.4Let X be a random variable having Cauchy distribution, the probability density function is give n by(a) Find E(X);二(1x 2)-::::xgw 」ox :10, elsewhere(b) LetFind E(g(X)). 00|x | Solution (a) Since the integral ----------------- 2 dx diverges(发散), E(X) does not exist.丿(1 + x )1(b) E(g(X))「g(x)f (x)dx = _:: 0 x ln2 -------- 2 dx-—— 二(1 x ) 2二6. variance Determining the mean and varianee using the probability density funetion 3e"xfor x 0 With referenee to the example 4.1.3: f (x)- <0 for x 兰 0find the mean and varianee of the given probability density. Solution Performing the necessary integrations, we getoO oo . 1 亠=xf(x)dx 二x 3e'x dx =_ 0 3 and c 2::1 1 =J (x_ A)2 f (x )dx = J(x__)3e :X dx =_0 3 9均匀分布 4.2 Uniform Distribution The uniform distributi on, with the parameters a and b, has probability den sity fun eti on一for a x : b, f(x)p b -a 0 elsewhere, whose graph is show n in Figure 4.2.1. f(x)1Figure 4.2.1 The uniform probability density in the interval (a, b)-beTo proof f (x)dx =1.*jtJdTo find the distribution function.The distribution function of the uniform distribution is9 for x < a,F(x) = < x _a for a 兰xeb,b -a 1 for x _ b.Note that all values of x from a and b are “ equally likely ”,in the sense that the probabixty that lies in an interval of width L X entirely contained in the interval from a to b is equal to =x/(b —a), regardless of the exact location of the interval.To find the mean and variance of the uniform distributi onAnd1 , a2 ab b 2----- d x 二 ------------b —a 3Thus,2a 2+ab+b 22 2(")2"-3I 2丿124.5 Exponential Distribution 指数分布Many random variables, such as the life of automotive parts, life of animals, time period between two calls arrives to an office, having a distribution called exponential distribution.Definition 4.5.1 A continuous variable X has an exponential distribution with parameter入(& A 0), if its density function is given byh 仝、 —e 九 for x 》0f(x) = 5(4.5.1)for x 兰 0Note Equati on (4.5.1) really gives a den sity fun cti on, since(丄 e ,dx = 1. 0 Z1dx =EXbx 2 a baxE(X) = J xf (x)dx = Jx 〒e^dx = h.: 0 1彳xE(X2) = J x2 f (x)dx = Jx2■—e 站x =2丸2..:: o'2 2 2D(X)二E(X ) -[E(X)] = ■.Example 4.5.1.Assume that the life Y of bulbs produced by company X has exponential distribution with mean ■ = 300(hrs).(a) Find the probability that a bulb selected at ran dom from the product of compa ny X haslife Ion ger tha n 450 hrs.(b) Select 5 bulbs ran domly from the product of compa ny X, what is the probability that at least 3 of them has life Ion ger tha n 450 hrs.Solution (a)P(Y 450) = 1 - P(Y 乞450)450 —x=1 _ 1 e^dx d5 =0.22310 300(b) The nu mber Z of bulb of bulbs with life Ion ger tha n 450 hrs has the bino mial distributi onB( n, p), where n=5, p=0.2231. ThusP(Z _3) =C;30.223130.77692C;0.223140.7769 0.2231^0.0772.****** homeworkP66 4.1, 4.3,4.5, 4.23, 4.24,4.264.3 Normal Distribution 正态分布The normal probability density usually referred to simply as the normal distribution , is by far the most important. It was studied first in the eighteenth century when scientists observed an ast onishing degree of regularity in errors of measureme nt. They found that the patter ns (distributi ons) they observed were closely approximated by a con ti nu ous distributi on which they referred to as the “ normacurve of errors and attributed to the laws of chanee. The normaldistribution is one of the frequently used distributions in both applied and theoretical probability.1. DefinitionThe equati on of the no rmal probability den sity, whose graph is show n in Figure 4.3.1, isf(x)二一1—e“"「八::x ::::V2^cf (x) _0.「f (x)dx =1. ???proof???_oOIt is often convenient to designate the face that X is normal with parameters J and - by2the notation X ~ )2. the property of the normal probability densitythe normal distribution function isx* 2 3 4 (x)二2二e2Figure 4.3.1 The normal probability densityThe distribution is characterized by two parameters, traditionally designated 士and 匚. (二0.) To proof(x) is an even function: ( _x) = (x),and :( -z) =1 :'7 (z).To find the probability that a random variable having the standard normal distribution will take on a value betwee n a and b, we use the equatio nP(a7z2b)二①(b)-①(a)as show n by the shaded are in Figure 4.3.3.Figure 433 P(a <b)5. find the probabilityExample 4.3.1 Calculating some standard normal distributionLet Z ~ N (0,1), take on a value(a) between -0.34 and 0.62;(b) greater than -0.65Solution ⑻From the Appe ndix BP(-0.34 ::Z 0.62)=门(0.62) —门(一0.34)=:」(0.62) -[1 —::」(0.34)]= 0.7324 -1 0.6331 = 0.3655.(b)P(Z -0.65) =1 -::」(-0,65)儿(0.65) =0.7422.X ~ Nd,we refer to the corresponding standardized random variable ,F z (z)二 P(Z 布 zF^Xlz )(t-J 2F dtuCTthen ~Z> 一 〜N(0,1). (sincee = t 一 ",dt 11dt )ffcr= G(z)X —Ahence Z~ N(0,1)Example X ~ N (1.5, 4) , find P(X <3)P(X :::3) =P(—3 :: X :::3) = P i —3—1.5 :: X 」:::3一1.511( 2 ▽ 2 ;»-3-1.5 R3-1.5、 =P( --------- Z ------------ )22= ::」(0.75) — :」( 一2.25) =「(0.75)—(1 一:」(2.25))=0.7734-(1-0.9878)=0.7612Example 4.3.2The actual amount of instant coffee that a filling machine puts into -ounce ” jars may be 4looked upon as a random variable having a normal distribution with 二 =0.04ounces. If only 2%of the jars to contain less tha n 4 oun ces, what should be the mean fill of these jars?Solution To find 亠 such thatdt jP(X 兰 x)= P(Zcrcr乞 x _)儿(x _) <i crSolutionThere are also problems in which we are given probabilities relating to standard normal distributionsand asked to find the corresponding values of z.Let z a be such that the probability is a that it will be exceeded by a random variable having the standard normal distribution. That is, P(Z zj 二:- as illustrated in Figure 4.3.5.Example 4.3.3 Two important values for z-..Find (a) z 0.01; (b) z 0.05. Solution(a) Since ❻(01)=1 -0.01=0.99, we look for the entry in appe ndix which is closest to 0.99 and get 0.9901 corresponding to z=2.33. Thus z 0.01=2.33.(b) Since Z 0&s (=1 -0.05=0.95, we look for the entry in Appe ndix which is closest to 0.95 and get 0.9495 and 0.9505 corresponding to z=1.64 and z=1.65. Thus, by interpolation, z 0.05=1.645.6. 3- TheoryP(X ::4) =P(Z ::4 - J 0.04)/(10.04)=0.02, we look for the entry in Appe ndix closest to 0.02 and get 0.0202 corresp onding toin dicated in Figure 4.3.4.4-^ 2.050.04z = -2.05. Assolving for ”,we find that J =4.082 ounces.Figure 4.3.4 P (Z _ -2.05)X ~ N 壬,)nd P(」X ::」;「),P()_2二:::X 2;「),P(」-3二:::X 3二)P=0.6826, P=0.9544, P=0.99744.4 Normal Approximation to the Binomial DistributionX ~ B(n, p), n is large (n>30), p is close to 0.50,X ~ B(n, p) :N (np, npq)Theorem 4.4.1 If X is a random variable having the binomial distribution with the parameters n and p, i.e. X ~ B(n, p) the limiting form of the distribution function of the standardized random variableas n = ' , is given by the standard normal distributiongraph--__ExampleFor an experiment in which 9 coins are tossed, Let X denotes the number of head occurrenee, con struct the probability distributi on of X.SolutionX 0 1 2 3 4 5 6 7 8 9 P 1 9 36 84 126 126 84 36 9 1 512 512 512 512 512 512 512 512 512 512NP1 9 36 84126 12684 36 91N=512r (or f)Figure 7-2Histogram and normal curve for expected frequencies of heads in tossing 9 coins 51 2 times.直方图与正态曲线非常接近,所以正态分布是二项概率分布的一个极好的逼近,当n足够大时.Example 4.4.1 A normal approximation to binomial probabilitiesIf 20% of the memory chips made in a certa in pla nt are defective, what are the probabilities that ina lot of 100 ran domly chose n for in specti onSolutionWhen the values of X are equal to -2, -1,0, 1,2, the random variable Y are equal t°匚斗・3,4,7 respectively. Then,P(Y =3) =P(X =0) =0.20,P(Y =4)二 P(X = -1) P(X =1) =0.20 0.25 =0.45 , P(Y =7)二 P(X 二-2) P(X =2) =0.15 0.20 =0.35,Thus, we getAndExample 462Suppose the random variable Y=aX+b, with a 0 . Determine F Y (y). Solution We n eed con sider two cases. y —b(1) a 0: Y 二 y iff X , athen,y — bP(Y < y)二 P(aX b 乞 y)二 P(X _ ') aimpliesy —bF Y (y) = F xr ).ay -b⑵ a ::0:Y _ y iff X --------- ,athus,y —b y —bP(Y < y) = P(aX b 乞 y) = P(X _ ---------- ) =1 _P(X :. ----- ),a aimpliesF Y (y)=1 —F x (m )+ P (x =□)•a a******den sity yields two cases that can be comb ined by the use of the absolute value to obta inf Y (y)^f X (宁.we know that if X ~ N (^\ - 2), then the corresponding standardized random variable , let usgive the proof aga in.1 k 1k here a : 一,b = - , Y X -一a a cr aIf X is continuous, so is Y. In this case,P(X=^lb )=0. Differentiating aF Y to obta in theX」〜N(0,1)cr1 ^J2Lf X (x)e 2二 ,using the result of example 4.6.2, we get4.7 Chebyshev ' s TheoremEarlier in this chapter we used examples to show how the sta ndard measures the variati on of a probability distribution, that is, how it reflects the concentration of probability in the neighborhood of the mean. Ifc is large there is a correspondingly higher probability of getting values farther away mean. Formally, the idea is expressed by the follow ing theorem.Theorem 4.7.1 If a probability distribution has mean ^and standard deviation q the probability of 1getting a value which deviates from (iby at least k H s at most —2 . Symbolically , k 21P(|X -「_2)乞kwhere P(| X __ k ;「) is the probability associated with the set of outcomes for which x ,the value of a random variable having the given probability distribution, is such that | X -」|丄 k 二.Then, the probability that a random variable will take on a value which deviates from the mean by at least 2 sta ndard deviati ons is at most 1/4, the probability that it will take on a value which deviates from the mean by at least 6 standard deviations is at most 1/36.deviates from the meanthe probability that a ran dom variablek=2P w 1/4k=6P w 1/36Proof As an example, we consider the case that X is a continuous variable with probability den sity f(x).1 fY(y )]a|fX ( a …)y .丄 e"d 1J 2wExample 4.6.3 Square Root Fun ctionSuppose the random variable Y = X ,and X 亠 0. Determine the distribution for Y.Solution The function g(x) = x is increasingon [0, ::) . Now X -y 肝 X _ y 2.22Thus for y _ 0, F y ( y)二 P(Y _ y) = P(X _ y ) = F x (y ), and if X is continuous, thus,fY(y)二dF Y (y) dyP{| X - 珥k;「} f(x)dxSo we haveThis completes the proof of Theorem 4.7.1.To get an alter native form of Chebyshev ' theorem, n ote that the |x -」|:: k 二 is the 1 complement of the event | x - ■打 _ k ;「; thus, P (| x - ■讣:k ;「) _ 1 …2 .k对比正态分布的3 c 定理?Example 4.7.1 A probability bound using Chebyshev ' s theoremThe number of customers who visit a car dealer 'showroom on a Saturday morning is a random variable with 卩=18 and c =2.5. With what probability can we assert that there will be more tha n 8 but fewer tha n 28 customers?Solution Let X be the nu mber of customers. Si nceP (8 :: X ::: 28) = P (8 一18 :: X -」28 —18) = P (| X -亠卜:10)B =1 0,k = 1 0/二1 0 /=2. 51 1 15P (|X —「*)_12 and P (8 :: X :: 28)-1 2 . k 2 42 16The most important feature of Chebyshe ' s theorem is that it applies to any probabilitydistribution for which ^and c exist.切比雪夫定理要求随机变量的 期望和方差存在However, it provides only an upper limit ( 上限)to the probability of getting a value that deviates from the mean by at least k standard deviations. For instance, we can assert in general that the probabilityP (| X 「二|一 2匚)乞 0.25,When a random variable X ~ B (16,0.50),21(x 「.S ) f (x )dx_k 2_2 . |x 』k 二 k C一:空 11 (x 「丄)f (x )dx=k 2_2; - k 2■' -16 0.50 =8,;丁八16 0.50 0.50 =2,the value of probability which differs from the mean by at least 2 standard deviations isP(|X _・i|_2;「)= P(|X _8|_4)=仁P(|X _8|::: 4)11= 1—' G;0.516 =1 —0.9232 = 0.0768.k出“ At most 0.25 ” does not tell us that the actual probability may be as small as 0.0768.问题思考1在P(|X —卩彥畑)兰疋,问P(|X —片沁)=?Homework jsjP69 27, 28, 29,304.29 Over the range of cyli ndrical parts manu factured on a computer con trolled lathe, the sta ndard deviation of the diameters is 0.0 02 mm.(a) What does Chebyshev ' theorem tell us about the probability that a new part will be with in 0.006 un its of the mean (ifor that run?(b) If the 400 parts are made duri ng the run, about what proporti on do you expect will lie in the in terval in Part (a)?例3.按规定,某车站每天8:00-9:00,9:00-10:00都恰有一辆客车到站,但到站的时刻是随机的,且两者到站的时间相互独立.其规律为一旅客8:20到车站,求他候车时间的数学期望. 解设旅客的候车时间为X(以分计).X的分布律为在上表中,1 3P{X =70} = P(AB)二P(A)P(B) -―—,6 6其中A为事件“第一班车在8:10到站” ,B为“第二班车在9:30到站” •候车时间的数学期望为3 2 1 3 2E(X) =10 +30 + 50 :—+ 70 :—+ 90 :—=27.22 (分).6 6 36 36 36例4某商店对某种家用电器的销售采用先使用后付款的方式.记使用寿命为X(以年计),规定:X <1 , 一台付款1500元;1 ::: X <2,一台付款2000元;2 X <3,一台付款2500元;X 3,一台付款3000元.设寿命X服从指数分布,概率密度为3 “P{2 X' 3}=.210e"°d x =e』-2- 汁“0779,P{X①^讣-沁“/3"07408.一台收费Y 的分布律为得E(X) =2732.15,即平均一台收费2732・15元.口(1) The probability mass is distributed symmetrically about the point t =」.The parameter ■-, which can be any real number, thus determines the center of the distribution.(2) The parameter - gives an indication of how the probability is spread around the center of the distributi on.3. The parameters J and 匚 are indeed its mean and its standard deviation.2EX=」,DX=二.4. standard normal distributionthe normal distribution with " = 0 and = 1, the normal probability density is1e _1°f(x) = <10 1. 0, x < 0试求该商店卖出一台家电的平均收费 (Y 元). 解 先求出寿命X 落在各个时间区间的概率,即有 P{X» 1e»Z。
概率论与数理统计(英文) 第五章

5. Random vectors and Joint Probability Distribution s随机向量与联合概率分布5.1 Concept of Joint Probability Distributions(1) Discrete Variables Case 离散型Often, trials are conducted where two random variables are observed simultaneously in order to determine not only their individual behavior but also the degree of relationship between them.( X, Y)For two discrete random variables X and Y, we write the probability that X will take the value x and Y will take the value y as P(X=x, Y=y). Consequently, P(X=x, Y=y) is the probability of the intersection of the events X=x and Y=y.(X=x, Y=y) ------ (X=x)∩(Y=y)The distribution of probability is specified by listing the probabilities associated with all possible pairs of values x and y, either by formula or in a table. We refer to the function p(x, y)=P(X=x, Y=y) and the corresponding possible values (X, Y) as the j oint probability distribution (联合分布)of X and Y.They satisfy(,)0, (,)1xyp x y p x y ≥=∑∑,where the sum is over all possible values of the variable.Example 5.1.1 Calculating probabilities from a discrete joint probability distributionLet X and Y have the joint probability distribution.(a) Find (1)P X Y +>;(b) Find the probability distribution ()()X p x P X x == of the individualrandom variable X . Solution(a) The event 1X Y +>is composed of the pairs of values (l,1), (2,0), and (2,l). Adding their corresponding probabilities(1)(1,1)(2,0)(2,1)0.20.100.3.P X Y p p p +>=++=++=(b) Since the event X =0 is composed of the two pairs of values (0,0) and (0,1), we add their corresponding probabilities to obtain(0)(0,0)(0,1)0.10.20.3P X p p ==+=+=.Continuing, we obtain (1)(1,0)(1,1)0.40.20.6P X p p ==+=+= and(2)(2,0)(2,1)0.100.1P X p p ==+=+=.In summary, (0)0.3X p =, (1)0.6X p = and (2)0.1X p =is the probabilitydistribution of X . Note that the probability distribution ()X p x of appears in the lower margin of this enlarged table. The probability distribution ()Y p y of Y appears in the right-hand margin of the table. Consequently, the individual distributions are called marginal probability distributions .(边缘分布)From the example, we see that for each fixed value of x , the marginalprobability distribution is obtained as()()(,)X yP X x p x p x y ===∑,where the sum is over all possible values of the second variable. Continuing, we obtain()()(,)Y xP Y y p y p x y ===∑.Example 3.5.3Suppose the number X of patent applications (专利申请)submitted by a company during a 1-year period is a random variable having thePoisson distribution with mean λ, (()!n e P X n n λλ-==)and the variousapplications independently have probability (0,1)p ∈ of eventually being approved.Determine the distribution of the number of patent applications during the 1-year period that are eventually approved.先求联合分布密度,再求边缘分布Solution Let Y be the number of patent application being eventually approved during 1-year period. Then the event {}Y k = is the union of mutually exclusive events {,}X n Y k == ()n k ≥.If X n =, then the random variable S has the binomial distribution with parameter n and p :(|)(1)k k n k n P Y k X n C p p -===-. (0)n k ≥≥ Thus(,)()(|)P X n Y k P X n P Y k X n ====== (1)!nk kn k n e C p p n λλ--=⋅⋅-when k>n, P(X=n, Y=k)=0,Hence the distribution of Y is()(,)(,)n n kP Y k P X n Y k P X n Y k ∞∞=========∑∑(1)!nk kn k n n ke C p p n λλ∞--==⋅⋅-∑!(1)!!()!nk n k n k n e p p n k n k λλ∞--==⋅⋅--∑(1)!()!kn kkn k n ke p p k n k λλλ-∞--==⋅⋅--∑()(1)(1)()()!!!mk k p m p p p e e ek m k λλλλλλ∞---=-==∑ ()!k pp e k λλ-= Thus, Y has the Poisson distribution of mean p λ. exercise从1,2,3,4,5五个数中不放回随机的接连地取3个,然后按大小排成123X X X <<,试求13(,)X X 的联合分布,x1,x3 独立吗?Homework Chap 5 1,(2) Continuous Variables Case 连续型随机向量There are many situations in which we describe an outcome by giving the values of several continuous random variables. For instance, we may measure the weight and the hardness of a rock, the pressure and the temperature of a gas. Suppose that X and Y are two continuous random variables. A function (,)f x y is called the joint probability density of these random variables, if the probability that , a X b c Y d ≤≤≤≤ is given by the multiple integral(, )(,)b da cP a X b c Y d f x y dxdy ≤≤≤≤=⎰⎰Thus, a function (,)f x y can serve as a joint probability density if all of the following hold:for all values of x and y , f is integrable on R 2 andTo extend the concept of a cumulative distribution function to the two variables case, we can define F (x , y )(, )(, )F x y P X x Y y =≤≤,and we refer to the corresponding function F as the joint cumulative distribution function of the two random variables.Example 5.1.2If the joint probability density of two random variables is given by236 for 0,0(,)0 elsewherex y e x y f x y --⎧>>=⎨⎩ Find the joint distribution function, and use it to find the probability(2,4)P X Y ≤≤.Solution By definition,23006 for 0, 0(,)(,)0 elsewhere y x yu vxe du e dv x y F x yf u v dudv ---∞-∞⎧>>⎪==⎨⎪⎩⎰⎰⎰⎰Thus,23(1)(1) for >0, >0(,)0 elsewhere x y e e x y F x y --⎧--=⎨⎩.Hence,412(2, 4)(2, 4)(1)(1)0.9817P X Y F e e --≤≤==--=.ExampleIf the joint probability density of two random variables is given by2,1,01(,)0,kxy x y x f x y ⎧≤≤≤≤=⎨⎩其他(a)find the k; (b)find the probability2((,)),{(,)|,01}P X Y D D x y x y x x ∈=≤≤≤≤solutionsince(,)1f x y dxdy ∞∞-∞-∞=⎰⎰24111001(,)()226x x kf x y dxdy dx kxydy k x dx ∞∞-∞-∞==-=⎰⎰⎰⎰⎰ hence k=6.21124001((,))663()4xx DP X Y D xydxdy dx xydy x x x dx ∈===-=⎰⎰⎰⎰⎰joint marginal densities 边缘密度Given the joint probability density of two random variables, the probability density of the X or Y can be obtained by integrating out another variable,The functions f X and f Y respectively are called the marginal density (边缘密度)of X and Y .,ExampleThe joint probability density of two random variables is given by26,1,01(,)0,xy x y x f x y ⎧≤≤≤≤=⎨⎩其他find the marginal density from the joint density when [0,1]x ∈,215()(,)633X xf x f x v dv xydy x x +∞-∞====-⎰⎰[0,1]x ∉,()0X f x =,hence 533,01()0,X x x x f x elsewhere ⎧-≤≤=⎨⎩23,01()0,Y y y f x elsewhere ⎧≤≤=⎨⎩exercises求服从B 上均匀分布的随机向量(X,Y )的分布密度及分布函数。
概率论与数理统计(英文) 第六章

(---24 | 25----)6. Fundamental Sampling Distributions and Data Descriptions抽样分布 6.1 Analysis of Data Mean 均值 Kx x x m K+++= 21mmm f f f f x f x f x m ++++++=212211,Median 中位数()⎪⎩⎪⎨⎧+=++2/)1(2/2121k k k d x x x MMean Deviation 平均差(均值离差)∑-=Kiim xKD M 1..方差()∑=-=Ki i m x K 1221σ标准差 ()∑=-=Ki i m x K 121σ 6.2 Random SamplingSampling is one of the most important concepts in the study of statistics. We need the fundamental ideas of populations and samples before studying particular statistical descriptions.population (总体)sample (样本)sampling (抽样)For example, in the study of the grade of Calculus course in some university of the year 2006, the grades of all the students who took this course constitute the population.a finite population(有限总体)infinite population(无限总体)This is a finite population. A example is the study of the length of newborns in China.The population is then the all possible lengths of the newborns in China, in the past, now or in the future. Such population is an infinite one.Since in many cases we are not able to investigate a whole population we are obliged to get conclusions regarding a population from its samples.sample (样本、子样)sampling(抽样)taking a sample: The process of performing an experiment to obtain a sample from the population is called sampling.sampling is done with replacement 有放回抽样sampling is done without replacement 无放回(有放回抽样,使样本点独立同分布)The purpose of the sampling is to find out something about the nature of the population.good sample——→good estimatesgood estimates concerning a population necessitate good sample.good sample-----random sample (随机样本)If ),,,(21n x x x f is the value of the joint distribution of such a set of random variables at ),,,(21n x x x , we can get that∏==ni i n x f x x x f 121)(),,,( (6.1.1)in which )(i x f is the population distribution at i x .6.3 Statistics 统计量We will discuss the definitionof the word statistic and someSample variance 子样方差Remark:The sample variance is sometimes defined as212)(11X X n S ni i --=∑= in some books.Here, X and 2S are both random variables. Suppose a set of values of observations of the random sample is n x x x ,,,21 , then the observation value of X and 2S are denoted as 观察值2121)(1ˆ,1x x n sx n x n i i ni i -==∑∑==.In the future, normally we use capital letters to represent random variables and use small letters to represent the observation values.顺序统计量With the definition of the order statistics, we are able to introduce some more terms that are also useful and important. 中位数Example 6.2.1 54321,,,,X X X X X is a random sample of size 5. If an observation of this sample yields the values 2, 5, 1, 4, 8. Then, we can get the value of statistics as the following.Sample mean : 4)84152(51=++++=xSample variance : 64)84152(51ˆ2222222=-++++=s)5()4()3()2()1(,,,,X X X X X : 1, 2, 4, 5, 8Sample median : 40=mSample range: 718=-=r □6.4 Sample Distributions 抽样分布It should be kept in mind that a statistic , being computed from samples, is a random variable .1.sampling distribution of the mean 均值的抽样分布Proof . First,μμ===⎪⎭⎫ ⎝⎛=∑∑∑===n i ni i n i i n X E n X n E X E 1111)(11)(.Second, since each pair of i X and j X , with j i ≠, are independent. We can get thatnn X D nX n D X D ni ni in i i 21221211)(1)1()(σσ∑∑∑=======. □It is customary to write )(X E as X μ and )(X D as 2X σ.Here, ()E X μ= is called the expectation of the mean .均值的期望nX σσ=is called the standard error of the mean . 均值的标准差This formula shows that the standard deviation of the distribution of X decreases when n , the sample size, is increased. It means that when n becomes larger, we can expect that the value of X to be closer to μ. 方差越小表示子样均值越靠近总体均值总体服从正态分布X ~),(2σμN ,则 ),(~2n N X σμ, 总体分布未知, 但n 够大,则X ~ N(μ, σ2/n)(子样均值也近似服从正态)Example 8-1 find P{X >68.9} Solution.Since2~(,)x X X N μσ,68.20x μμ==, 25.010050.2===n x σσ2~()X Nσμ~(0,1)Nso P{X>68.9}=68.968.20}0.25P->=P{Z > 2.8}=1-P{Z < 2.8}=0.5 – 0.4974=0.0026Distribution of the sample standard Deviation (子样标准差的分布)the population with mean=mstandard deviation=σ the sample standard deviation21)(1ˆX X n Sni i -=∑=for large nσμ=S ˆ,nS 2ˆσσ=此处并没有给出具体的分布,但告诉我们,当n 足够大时, *****子样标准差的均值 s ES μσ==, 和子样标准差的标准差S σ==Homework 6.1 6.6 6.8堂上练习设总体服从正态分布N(12,4) ,今抽取容量为5的样本X 1,X 2,X 3,X 4,X 5,试问:(1) 样本均值 X 大于13的概率是多少? (2) 样本均值X 的数学期望E X 、方差D X 、子样方差的数学期望是多少?(3) 如果(1,0,3,1,2)是样本的一个观察值,它的样本平均值和样本方差等于多少?数据处理(找数据的特征、规律) 1.直方图 histogramExample 6.3.2 We are interested in the distribution of peoples ’ age in some city. In our hand, we have a sample of the ages of 50 people who were randomly picked and the data are listed below:35 23 48 21 15 36 12 3 14 54 21 43 92 15 32 5 71 55 62 24 64 78 50 11 9 43 28 25 34 15 22 30 51 88 16 75 22 27 41 33 45 61 35 28 43 59 38 90 70 6 Find the frequency table and draw the histogram. Solution .We find that the minimum sample value in this example is 3)1(=x and the maximum sample value is 92)50(=x . So, we choose the range of the frequency table as ]100,0[ and divided it into 10 classes : [0, 10), [10, 20), [20, 30), [30, 40), [40, 50), [50, 60), [60, 70), [70, 80), [80, 90), [90, 100].Then, we count the number of sample values in each class and get the following frequency table.Table 6.3.1At last, using the horizontal axis to represent the classes and the vertical axis to represent the frequency, we can draw the histogram below. □In summery, for a random sample of size n , the process of drawing a histogram is as following: 方法步骤(1) Find the minimum sample value )1(x and maximum sample value)(n x . Decide the number of classes m (usually between 5 and 20) and thendecide a fitting range ],[0m a a of the frequency table so that 0a is a little less than )1(x and m a is a little bigger than )(n x .(2) Insert 1-m points into ],[0m a a : m m a a a a a <<<<<-1210 so that the range ],[0m a a is divided into m equal length classes: ),[10a a ,),[21a a , ,),[12--m m a a , ],[1m m a a -. The length of each class isma a m 0-. (3) Count for each class how many sample values are inside this class, and then get the frequency table.(4) Using the horizontal axis to represent the classes and the vertical axis to represent the frequency, draw the histogram at last.2.带频数的样本均值和样本方差For Table 6.3.1 , How to find the sample mean and sample variance?Table 6.3.1Example 6.3.2Find the sample mean and the sample variance if we have a random sample that is given in Table 6.3.1. Solution . By Definition 6.3.5, we get that()4.39295185475365555645835102571545501=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=x []64.5562)4.3995(1)4.3985(4)4.3975(3)4.3965(5)4.3955(6)4.3945(8)4.3935(10)4.3925(7)4.3915(4)4.395(501ˆ22222222222=⨯-+⨯-+⨯-+⨯-+⨯-+⨯-+⨯-+⨯-+⨯-+⨯-=s*****==mi i f N 16.5 Chi-square Distributions1.gamma distribution ,),(~βαΓXgamma function⎰∞--=Γ01)(dy e y y αα for 0>α.Gamma function has a few useful properties, such the recursion formula)1()1()(-Γ-=Γααα.Also, when n is a positive integer, we have)!1()(-=Γn n .At last, an important special value is π=Γ)21( Properties 性质(有可加性)The gamma densities with several special values of α and β are shown in Figure 6.5.1. The readers can get some idea about the shape of the gamma distribution.12340.51.01.52.02.5xf(x)α=1/2, β=1α=2, β=1/2α=10, β=1/5Figure 6.4.1: Graphs of gamma distribution),(~βαΓX2.特例(1)1=α and λβ=,),1(),(λβαΓ=Γ----- exponential distributionthe probability density of ),1(λΓ is⎪⎩⎪⎨⎧≤>=-0for 00for 1)(x x e x f xλλ(2) 2να= and 2=β,)2,2(),(νβαΓ=Γ---- chi-square distributionChi-square distribution)(2~νχX 卡方分布the parameter ν ----- degree of freedom (自由度). We will write)(2~νχX ifXis a random variable which follows achi-square distribution with the degree of freedom ν.Corollary 6.5.1 The mean and the variance of the chi-square distribution)(2~νχX is given byν=)(X E and ν2)(=X D .The chi-square distribution is closely related to the normal distribution and has many important applications in statistics. Let us list several meaningful properties below.卡方分布与正态分布有密切联系,在统计学中有重要的应用3.重要结论Proof . We omit the proof of part (i) since it is beyond the scope of this book. Let us show only the part (ii).In order to study the distribution of22σnS , we need the identity22112)()()(μμ-+-=-∑∑==X n X X Xni i ni i(6.5.5)In fact, the left hand side of (6.4.5) is21221121221222)2()(μμμμμμμn X n X n X X X X Xni i ni i ni i ni i i ni i+-=+-=+-=-∑∑∑∑∑=====and the right hand side of (6.5.5) is()μμμμμμμn X n X n X n X n X n X X n X n X n X n X X X X n X X ni i ni i ni i n i i ni i +-=+-+=+-+⎪⎭⎫ ⎝⎛+-=-+-∑∑∑∑∑=====222222)()(122212222112221-which proves (6.4.5). By the definition of 2S in (6.3.2), we have212)(∑=-=ni i X X nS . Substitute it into (6.4.5) and then divide both sides of(6.5.5) by 2σ to get22212/⎪⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛-∑=n X nS X ni i σμσσμ (6.5.6)We know that)1,0(~N X i σμ- and from Theorem 6.5.4, weconclude that )(212~n ni i X χσμ∑=⎪⎭⎫⎝⎛-. At the same time, by Theorem 6.4.1and Theorem 6.5.3, we get that )1(22~/χσμ⎪⎪⎭⎫⎝⎛-n X . Therefore, thanks Theorem 6.4.6, we have that)1(222~-n nS χσ.Let X be a random variable whose distribution is )5(2χ. Find thevalue a such that 05.0)(=≥a X P6.6 Student’s Distributions (t -Distribution)学生分布/****Consider the case that a random sample of size n from a normal population with the mean μ and the variance 2σ. In Corollary 6.3.1, we know that the random variable X is also a normal distribution),(2nN σμ. Furthermore,)1,0(~/N nX σμ-. (6.5.1)Of course this is an important conclusion in statistics. However, in application, the population standard deviation σ is usually unknown. Therefore, people start to seek a replacement of σ with an estimate. Naturally, the sample standard deviation S seems to be a good choice. Since in the later material, we will know that nn S E σ=-)1(, wereplacenσin (6.5.1) by1-n Sand it comes the problem: What is the exact distribution of 1/--n S X μ for a random sample from a normalpopulation?This problem was originally studied by W.S. Gosset, who wrote under the pen name “student” because the company where he worked, Guiness’ Brewery in Dublin, did not allow publication by the employees. Gosset found that the quantities resulting from this substitution no longer follows normal distribution, instead, it satisfied a different type of distribution which has been called Student’s t -distribution since then. Let us first introduce a more general situation which leads to the formal definition of t-distribution. ****/1.Student ’s distributionWe omit the detailed proof which is above the requirement of this book. If a random distribution T has the t-distribution with ν degrees of freedom, we will write )(~νt T for short.-3-2-11230.10.20.30.4xf(x)←ν=1←ν=5←Standard normal distributionFigure 6.6.1Figure 6.6.1 includes the graphs of standard normal distribution, t-distributions with 1 and 5 degrees of freedom. We can see that the curves of t-distributions resemble in general shape the normal distribution. Also, as ν increases, the t-distribution will get closer to the normal distribution. In fact, the standard normal distribution can be considered to be the limiting case for the )(νt distributions, that is, ∞=ν.With the help of Theorem 6.6.1, we are now able to obtain the distribution of1/--n S X μ which is the problem raised in the beginning ofthis section. It is treated in the following theorem.2. 应用Proof. LetnX Z /σμ-=and 22ˆσSn Y =.By the Corollary 6.4.1 and Theorem 6.5.7, we get that )1,0(~N Z and)1(2~-n Y χ, also, Z and Y are independent. Thus1/ˆ)1(ˆ/)1/(22--=--=-n SX n Sn n X n Y Z μσσμand by Theorem 6.5.1, we conclude that)1(~1/ˆ---n t n SX μ. □Let Y be a t -distribution with degrees of freedom n , find the value a such that (a) 10.0)(=>a Y P , when 5=n ; (b)10.0)(=≤a Y P , when 5=n .Homework 6.9, 6.14, 6.17αα=>)}({n t t P6.6 F-DistributionsIn this section, we will study another important distribution in practical applications of statistics, the F-distribution. It helps us to deal with the comparison of the variability of two samples. In order to obtain the F-distribution, we consider the ratio of two independent chi-square random variables, each divided by its own degrees of freedom. The distribution of this radio is presented in the following theorem.Theorem 6.6.1 is often applied in the cases when we are interested in comparing the variances of two normal populations or two samples from normal populations. For example, we may need to estimate the ratio2221σσ. Or, in many cases we need to check whether 21σσ=.We already know, from Theorem 6.4.7, that if 21S is the variance of a random sample of size 1n from a normal population with variance21σ, and 22S is the variance of a random sample of size 2n from anormal population with variance 22σ, thenSuppose that these two samples are independent random samples , which means that all the 21n n + random variables in these two random samples are independent. Then these two chi-square random variables are also independent. Replacing X and Y in Theorem 6.6.1 by21211ˆσS n and22222ˆσS n leads to the following important conclusion.There is a special case when the two random samples are from a same normal population. Thus, 21σσ= and we have the result below.The proof is left as an exercise. F-propertiesFind )7,3(),4,5(95.001.0F F (15.52 , 0.1125)Using the result in the previous exercise, show that nm m n f f ,,1,,1αα-=Ifαα=>)},({m n F F P ,Thenαα-=≤1)},({m n F F P , (1)),(~11n m F FF =, 11)},({1αα=>n m F F P 11}),(1{)},(1{)},({111αααα=<=>=>n m F F P n m F F P n m F F P (2) let,11αα-=),(1),(1m n F n m F αα=-。
概率论与数理统计(英文)

1.定义
定义4.1.1函数f(x)定义在 上,且满足下面两个条件
(i) ;
(ii)f(x)在 上可积且 .
那么f(x)就叫概率密度函数.
定义4.1.2设f(x)是一个概率密度函数。如果x是一个具有分布函数的随机变量且
(4.1.1)
那么x称为一个具有连续随机变量的密度函数f(x)。在这种情况下
定义4.5.1一个连续变量X有一个参数的指数分布,其密度函数为
定理4.5.1连续型随机变量X具有指数分布的均值和方差由下式给出
If the continuous random variable x withprobability density function
Called X in the (a, b) obey uniform distribution
4. Exponential Distribution指数分布
Many random variables, such as the life of automotive parts, life of animals, time period between two calls arrives to an office, having a distribution called exponential distribution.
Continuous Random Variable
1.Definition
Definition 4.1.1
A functionf(x) defined on is called aprobability density function(概率密度函数)if:
(i) ;
(ii)f(x) is intergrable on and .
概率与统计英语

概率与统计英语《概率论与数理统计》基本名词中英文对比表英文中文 Probability theory 概率论mathematical statistics 数理统计deterministic phenomenon 确定性现象random phenomenon 随机现象sample space 样本空间random occurrence 随机大事fundamental event 基本领件certain event 必定大事impossible event 不行能大事random test 随机实验incompatible events 互不相容大事frequency 频率classical probabilistic model 古典概型geometric probability 几何概率conditional probability 条件概率multiplication theorem 乘法定理Bayes's formula 贝叶斯公式Prior probability 先验概率Posterior probability 后验概率Independent events 互相自立大事Bernoulli trials 贝努利实验random variable 随机变量probability distribution 概率分布distribution function 分布函数discrete random variable 离散随机变量distribution law 分布律hypergeometric distribution 超几何分布random sampling model 随机抽样模型binomial distribution 二项分布Poisson distribution 泊松分布geometric distribution 几何分布probability density 概率密度continuous random variable 延续随机变量uniformly distribution 匀称分布exponential distribution 指数分布numerical character 数字特征mathematical expectation 数学期望variance 方差moment 矩central moment XXX矩n-dimensional random variable n-维随机变量two-dimensional random variable 二维离散随机变量joint probability distribution 联合概率分布joint distribution law 联合分布律joint distribution function 联合分布函数boundary distribution law 边缘分布律boundary distribution function 边缘分布函数exponential distribution 二维指数分布continuous random variable 二维延续随机变量joint probability density 联合概率密度boundary probability density 边缘概率密度conditional distribution 条件分布conditional distribution law 条件分布律conditional probability density 条件概率密度covariance 协方差dependency coefficient 相关系数normal distribution 正态分布limit theorem 极限定理standard normal distribution 标准正态分布logarithmic normal distribution 对数正态分布covariance matrix 协方差矩阵central limit theorem XXX极限定理Chebyshev's inequality 切比雪夫不等式Bernoulli's law of large numbers 贝努利大数定律statistics 统计量simple random sample 容易随机样本sample distribution function 样本分布函数sample mean 样本均值sample variance 样本方差sample standard deviation 样本标准差sample covariance 样本协方差sample correlation coefficient 样本相关系数order statistics 挨次统计量sample median 样本中位数sample fractiles 样本极差sampling distribution 抽样分布parameter estimation 参数估量estimator 估量量estimate value 估量值unbiased estimator 无偏估量unbiassedness 无偏性biased error 偏差mean square error 均方误差relative efficient 相对有效性minimum variance 最小方差asymptotic unbiased estimator 渐近无偏估量量uniformly estimator 全都性估量量moment method of estimation 矩法估量maximum likelihood method of estimation 极大似然估量法likelihood function 似然函数maximum likelihood estimator 极大似然估量值interval estimation 区间估量hypothesis testing 假设检验statistical hypothesis 统计假设simple hypothesis 容易假设composite hypothesis 复合假设rejection region 否决域acceptance domain 接受域test statistics 检验统计量linear regression analysis 线性回归分析1 概率论与数理统计词汇英汉对比表Aabsolute value 肯定值accept 接受acceptable region 接受域additivity 可加性adjusted 调节的alternative hypothesis 对立假设analysis 分析analysis of covariance 协方差分析analysis of variance 方差分析arithmetic mean 算术平均值association 相关性assumption 假设assumption checking 假设检验availability 有效度average 均值Bbalanced 平衡的band 带宽bar chart 条形图beta-distribution 贝塔分布between groups 组间的bias 偏倚binomial distribution 二项分布binomial test 二项检验Ccalculate 计算case 个案category 类别center of gravity 重心central tendency XXX趋势chi-square distribution 卡方分布chi-square test 卡方检验classify 分类cluster analysis 聚类分析coefficient 系数coefficient of correlation 相关系数collinearity 共线性column 列compare 比较comparison 对比components 构成,重量compound 复合的confidence interval 置信区间consistency 全都性constant 常数continuous variable 延续变量control charts 控制图correlation 相关covariance 协方差covariance matrix 协方差矩阵critical point 临界点critical value 临界值crosstab 列联表cubic 三次的,立方的cubic term 三次项cumulative distribution function 累加分布函数curve estimation 曲线估量Ddata 数据default 默认的definition 定义deleted residual 剔除残差density function 密度函数dependent variable 因变量description 描述design of experiment 实验设计deviations 差异df.(degree of freedom) 自由度diagnostic 诊断dimension 维discrete variable 离散变量discriminant function 判别函数discriminatory analysis 判别分析distance 距离distribution 分布D-optimal design D-优化设计Eeaqual 相等effects of interaction 交互效应efficiency 有效性eigenvalue 特征值equal size 等含量equation 方程error 误差estimate 估量estimation of parameters 参数估量estimations 估量量evaluate 衡量exact value 精确值expectation 期望expected value 期望值exponential 指数的exponential distributon 指数分布extreme value 极值 Ffactor 因素,因子factor analysis 因子分析factor score 因子得分factorial designs 析因设计factorial experiment 析因实验fit 拟合fitted line 拟合线fitted value 拟合值fixed model 固定模型fixed variable 固定变量fractional factorial design 部分析因设计frequency 频数F-test F检验full factorial design 彻低析因设计function 函数Ggamma distribution 伽玛分布geometric mean 几何均值group 组Hharmomic mean 调和均值heterogeneity 不齐性histogram 直方图homogeneity 齐性homogeneity of variance 方差齐性hypothesis 假设hypothesis test 假设检验Iindependence 自立independent variable 自变量independent-samples 自立样本index 指数index of correlation 相关指数interaction 交互作用interclass correlation 组内相关interval estimate 区间估量intraclass correlation 组间相关inverse 倒数的iterate 迭代Kkernal 核Kolmogorov-Smirnov test柯尔莫哥洛夫-斯米诺夫检验kurtosis 峰度Llarge sample problem 大样本问题layer 层least-significant difference 最小显著差数least-square estimation 最小二乘估量least-square method 最小二乘法level 水平level of significance 显著性水平leverage value XXX化杠杆值life 寿命life test 寿命实验likelihood function 似然函数likelihood ratio test 似然比检验 linear 线性的linear estimator 线性估量linear model 线性模型linear regression 线性回归linear relation 线性关系linear term 线性项logarithmic 对数的logarithms 对数logistic 规律的lost function 损失函数Mmain effect 主效应matrix 矩阵maximum 最大值maximum likelihood estimation 极大似然估量mean squared deviation(MSD) 均方差mean sum of square 均方和measure 衡量media 中位数M-estimator M估量minimum 最小值missing values 缺失值mixed model 混合模型mode 众数model 模型Monte Carle method 蒙特卡罗法moving average 移动平均值multicollinearity 多元共线性multiple comparison 多重比较multiple correlation 多重相关multiple correlation coefficient 复相关系数multiple correlation coefficient 多元相关系数multiple regression analysis 多元回归分析multiple regression equation 多元回归方程multiple response 多响应multivariate analysis 多元分析Nnegative relationship 负相关nonadditively 不行加性nonlinear 非线性nonlinear regression 非线性回归noparametric tests 非参数检验normal distribution 正态分布null hypothesis 零假设number of cases 个案数Oone-sample 单样本one-tailed test 单侧检验one-way ANOVA 单向方差分析one-way classification 单向分类optimal 优化的optimum allocation 最优配制order 排序order statistics 次序统计量origin 原点orthogonal 正交的outliers 异样值Ppaired observations 成对观测数据paired-sample 成对样本parameter 参数parameter estimation 参数估量partial correlation 偏相关partial correlation coefficient 偏相关系数partial regression coefficient 偏回归系数percent 百分数percentiles 百分位数pie chart 饼图point estimate 点估量poisson distribution 泊松分布polynomial curve 多项式曲线polynomial regression 多项式回归polynomials 多项式positive relationship 正相关power 幂P-P plot P-P概率图predict 预测predicted value 预测值prediction intervals 预测区间principal component analysis 主成分分析proability 概率probability density function 概率密度函数probit analysis 概率分析proportion 比例Qqadratic 二次的Q-Q plot Q-Q概率图quadratic term 二次项quality control 质量控制quantitative 数量的,度量的quartiles 四分位数Rrandom 随机的random number 随机数random number 随机数random sampling 随机取样random seed 随机数种子random variable 随机变量randomization 随机化range 极差rank 秩rank correlation 秩相关rank statistic 秩统计量regression analysis 回归分析regression coefficient 回归系数regression line 回归线reject 否决rejection region 否决域relationship 关系reliability 牢靠性repeated 重复的report 报告,报表residual 残差residual sum of squares 剩余平方和response 响应risk function 风险函数robustness 稳健性root mean square 标准差row 行run 游程run test 游程检验Ssample 样本sample size 样本容量sample space 样本空间sampling 取样sampling inspection 抽样检验scatter chart 散点图S-curve S形曲线separately 单独地sets 集合sign test 符号检验significance 显著性significance level 显著性水平significance testing 显著性检验significant 显著的,有效的significant digits 有效数字skewed distribution 偏态分布skewness 偏度small sample problem 小样本问题smooth 平滑sort 排序soruces of variation 方差来源space 空间spread 扩展square 平方standard deviation 标准离差standard error of mean 均值的标准误差standardization 标准化standardize 标准化statistic 统计量statistical quality control 统计质量控制std. residual 标准残差stepwise regression analysis 逐步回归stimulus 刺激strong assumption 强假设stud. deleted residual 同学化剔除残差stud. residual 同学化残差subsamples 次级样本sufficient statistic 充分统计量sum 和sum of squares 平方和summary 概括,综述Ttable 表t-distribution t分布test 检验test criterion 检验判据test for linearity 线性检验test of goodness of fit 拟合优度检验test of homogeneity 齐性检验test of independence 自立性检验test rules 检验法则test statistics 检验统计量testing function 检验函数time series 时光序列tolerance limits 容许限total 总共,和transformation 转换treatment 处理trimmed mean 截尾均值true value 真值t-test t检验two-tailed test 双侧检验Uunbalanced 不平衡的unbiased estimation 无偏估量unbiasedness 无偏性uniform distribution 匀称分布Vvalue of estimator 估量值variable 变量variance 方差variance components 方差重量variance ratio 方差比various 不同的vector 向量Wweight 加权,权重weighted average 加权平均值within groups 组内的ZZ score Z分数。
(完整版)概率论与数理统计英文版总结,推荐文档

x
F (x) P( X x) f (t)dt , (4.1.1)
The empty set, denoted by , is also an event, called an impossible event, means that it never
occurs in the experiment.
Probability of events (概率)
If the number of successes in n trails is denoted by s , and if the sequence of relative frequencies s / n obtained for larger and larger value of n approaches a limit, then this limit is defined as the
certain event(必然事件):
The sample space S itself, is certainly an event, which is called a certain event, means that it
always occurs in the experiment.
impossible event(不可能事件):
X12 3 4 …k …
P p q1p q2p q3p
qk-1 …
p
Binomial distribution(二项分布)
概率论与数理统计中的英文单词和短语
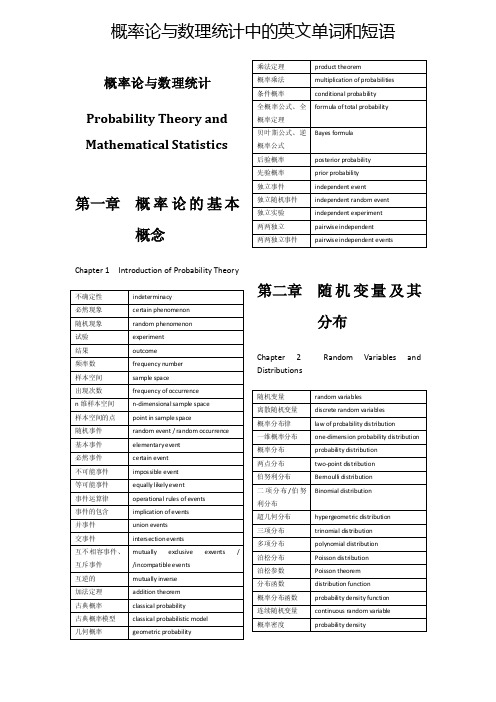
概率分布函数 probability density function
连续随机变量 continuous random variable
概率密度
probability density
概率密度函数 概率曲线
probability density function probability curve
均匀分布 指数分布
概率论与数理统计中的英文单词和短语
概率论与数理统计 Probability Theory and Mathematical Statistics
第一章 概 率 论 的 基 本 概念
乘法定理 概率乘法
product theorem multiplication of probabilities
条件概率 全概 率公式、 全 概率定理
二维正态概率曲 two-dimensional normal probability
线
curve
条件分布
conditional distribution
条件分布律
law of conditional distribution
条件概率分布 conditional probability distribution
条件概率密度 conditional probability distribution
边缘密度
marginal density
独立随机变量 independent random variables
第四章 随 机 变 量 的 数 字特征
第三章 多 维 随 机 变 量 及其分布
Chapter 3 Multivariate Random Variables and Distributions
概率论与数理统计(英文)第三章

3. Random Variables3.1 Definition of Random VariablesIn engineering or scientific problems, we are not only interested in the probability of events, but also interested in some variables depending on sample points. (定义在样本点上的变量)For example, we maybe interested in the life of bulbs produced by a certain company, or the weight of cows in a certain farm, etc. These ideas lead to the definition of random variables.1. random variable definitionHere are some examples.Example 3.1.1 A fair die is tossed. The number X shown is a random variable, it takes values in the set {1,2,6}.Example 3.1.2The life t of a bulb selected at random from bulbs produced by company A is a random variable, it takes values in the interval (0,) .Since the outcomes of a random experiment can not be predicted in advance, the exact value of a random variable can not be predicted before the experiment, we can only discuss the probability that it takes somevalue or the values in some subset of R.2. Distribution functionNote The distribution function ()F X is defined on real numbers, not on sample space.Example 3.1.3Let X be the number we get from tossing a fair die. Then the distribution function of X is (Figure 3.1.1)Figure 3.1.1 The distribution function in Example 3.1.3 3. PropertiesThe distribution function ()F x of a random variable X has the following properties:SolutionBy definition,1(2000)(2000)10.6321P X F e -≤==-=.Question : What are the probabilities (2000)P X < and (2000)P X =?SolutionLet 1X be the total number shown, then the events 1{}X k = contains 1k - sample points, 2,3,4,5k =. Thus11()36k P X k -==, 2,3,4,5k = AndsoThus Figure 3.1.2 The distribution function in Example 3.1.53.2 Discrete Random Variables 离散型随机变量In this book, we study two kinds of random variables. ,,}n aAssume a discrete random variable X takes values from the set 12{,,,}n X a a a =. Let()n n P X a p ==,1,2,.n = (3.2.1) Then we have 0n p ≥, 1,2,,n = 1n n p=∑.the probability distribution of the discrete random variable X (概率分布)注意随机变量X 的分布所满足的条件(1) P i ≥0(2) P 1+P 2+…+P n =1离散型分布函数 And the distribution function of X is given by()()n n a xF x P X x p ≤=≤=∑ (3.2.2)Solutionn=3, p=1/2X p r01/813/823/831/8two-point distribution(两点分布)某学生参加考试得5分的概率是p, X表示他首次得5分的考试次数,求X的分布。
概率论与数理统计(英文) 第二章

2. Probability (概率)2.1 Sample Space 样本空间statistical experiment (random experiment)----repeating----more than one outcome----know all the outcomes, but don ’t predict whichoutcome will be occurexample :toss an honest coin---- In this experiment there are only two possible outcomes:{head}, {tail}toss two honest coins---- In this experiment there are 4 possible outcomes:{H, H}, {H, T}, {T, H}, {T, T}Each outcome in a sample space is called a sample point of the sample space.Example 2.1.1 Consider the experiment of tossing a die. If we are interested in the number thatshows on the top face, the sample space would be{}11,2,3,4,5,6S =If we are interested only in whether the numbers is even or odd, the sample space is simply{}2,S even odd =Example 2.1.3 An experiment consists of flipping a coin and then flipping it a second time if ahead occurs. If a tail occurs on the first flip then a die is tossing once. To list the elements of thesample space providing the most information,we construct a diagram of Fig 2.1.1, which is called a tree diagram. Now the various paths alongthe branches of the tree give the distinct sample points. Starting with the top left branch andmoving to the right along the first path, we get the sample point HH, indicating the possibility thatheads occurs on two successive flips of the coin. The possibility that coin will show a tail followedby a 4 on the toss of the die is indicated by T4. Thus the sample space is{,,1,2,3,4,5,6}S HH HT T T T T T T =Fig .2.1.1 Tree diagram for Example 2.1.3 Definition 2.2.1 An event is a subset of a sample space.Example 2.2.1 Given the sample space {|0}S t t =≥. where t is the life in hours of a certainbulb, we are interest in the event B that a bulb burnt out before 200 hrs, i.e. the subset{|0200}B t t =≤< of S .Example 2.2.2 Assume that the unemployment rate r of a region is between 0 and 15%,i.e. wehave the sample space {|00.15}S r r =≤≤. If the event C “unemployment rate is low ”means that 0.04r ≤, then we have the subset {|00.04}C r r =≤≤ of S .You may have known operation of subsets, i.e.the complement of a subset (余集),the union of subset,(并集)the difference of subset (差集)intersection of subsets (交集),so we can say about the complement of an event, the union, difference and intersection ofevents.certain event (必然事件):The sample space S itself, is certainly an event, which is called a certain event, means thatit always occurs in the experiment.impossible event (不可能事件):The empty set, denoted by ∅, is also an event, called an impossible event, means that it neveroccurs in the experiment.Example 2.2.3 Consider the experiment of tossing a die, then{1,2,3,4,5,6}S =Let x be the number that shows on the top face, then the event {|,10}A x x S x =∈≤, isthe certain event, i.e. A S =.Then even {|,B x x S x =∈ is an irrational number }, (irrational-无理数)is the impossible event, i.e.B =∅.Let be the event consisting of all even numbers and be the event consisting of numbers divisible by 3. Find A , ,,A B A B A B .Solution We have {2,4,6,8},{3,6,9}.A B ==Thus{1,3,5,7,9}A = {2,3,4,6,8,9}A B = {6}A B = {3,9}A B = The relationship between events and the corresponding sample space can be illustrated graphical by means of Venn diagrams. In a Venn diagram, we represent the sample space by a rectangle and represent events by circles drawn inside the rectangle.Example 2.2.5 In Figure 2.2.1A B = regions 1 and 2, A D = regions 1,2 ,3 ,4 ,5 and 7,A B D = regions 2, 6 and 7A B D 1234567Fig 2.2.1 Venn diagram of Example 2.2.5The following list summarizes the rules of the operations of events.1. A ∅=∅2. A A ∅=3. A A A =4. A A =∅5. A A S =6. S =∅7. S ∅=8. A A =9. _________A B A B =10. _________A B A B =11. AB B A = 12. ()()AB C A B C = 13. ()()()AB C A C B C = 14. ()()()A B C A C B C =2.3 Probability of events1. relative frequency --------probability用频率定义概率Considering an Example.We plant 100 untreated cotton seeds.If 49 seeds germinate, that is, if there are 49 success (by success in statistics we mean the occurrence of the event under discussion) in 100 trials, we say that the relative frequency of success is 0.49.If we plant more and more seeds, a whole sequence of values for the respective relative frequencies is obtained. In general, these relative frequencies approach a limit value, we call this limit the probability of success in a single trial. From the data of Table 2.3.1 it appears that the relative frequencies are approaching the value 0.51, which we call the probability of a cotton seedling emerging from an untreated seed.relative frequencies are approaching the value 0.5252.0→n salways 1. Similarly, the probability of the impossible event is 0, and the probability of any event is always between 0 and 1.Note. In this definition , the word“limit”has a meaning which is different from the meaning you may have learned in calculus. We will discuss this problem later.Example 2.3.1Select 200 bulbs produced by company X at random of them 150 having life longer than 300hrs. Find the probability that the bulbs produced by company X have life longer than 300hrs.Solution.1500.75200p==Jixie-9-42.”equally likely to occur”------probability(古典概率,有限、等可能性)In many cases, the probability may be stated without experience. If we toss a properly balanced coin, we believe that the probability of getting a head is 0.5. We make this statement since in tossing a properly balanced coin, only two outcomes are possible and both outcome areIt should be pointed out that this definition is in a sense circular in nature, since the expression “equally likely to occur”itself involves the idea of probability. However, since this term is generally intuitively understood, the concept of “equally likely” will be left undefined.Solution.The sample space S consists of 20 sample points. The event {A= a white ball is drawn}consists of 4 sample points, thus the probability of drawing a white ball is4()0.2P A==.Solution The sample space is{S =(,)|,m n m n are positive integers 6}≤thus S consists of 36 sample points .Let {A =getting a total of 9},{B =getting a total greater of 9}Then we have{(3,6),(4,5),(5,4),(6,3)}A ={(4,6),(5,5),(6,4),(5,6),(6,5),(6,6)}B =Thus41()369P A == , 61()366P B ==. where ()p A is the probability that the event A occurs ./*******/Example 2.3.4 抽球问题Consecutively draw ballFrom a big pack which contains a white balls and b black balls, a ball is consecutively draw at random. what is the probability that the ball which be drawn in m-th time is white?抽球问题袋中有a 个白球,b 个黑球,从中依次任取一个球,且每次取出的球不再放回去,求第m 次取出的球是白球的概率。
(完整word)概率论与数理统计英文版总结,推荐文档

Sample Space样本空间The set of all possible outcomes of a statistical experiment is called the sample space.Event 事件An event is a subset of a sample space.certain event(必然事件):The sample space S itself, is certainly an event, which is called a certain event, means that it always occurs in the experiment.impossible event(不可能事件):The empty set, denoted by∅, is also an event, called an impossible event, means that it never occurs in the experiment.Probability of events (概率)If the number of successes in n trails is denoted by s, and if the sequence of relative frequencies /s n obtained for larger and larger value of n approaches a limit, then this limit is defined as the probability of success in a single trial.“equally likely to occur”------probability(古典概率)If a sample space S consists of N sample points, each is equally likely to occur. Assume that the event A consists of n sample points, then the probability p that A occurs is()np P AN==Mutually exclusive(互斥事件)Two events A and B are said to be independent if()()()P A B P A P B=⋅IOr Two events A and B are independent if and only if(|)()P B A P B=.Conditional Probability 条件概率The probability of an event is frequently influenced by other events.If 12k ,,,A A A L are events, then12k 121312121()()(|)(|)(|)k k P A A A P A P A A P A A A P A A A A -=⋅⋅I I L I L I I L I Ifthe events12k ,,,A A A L areindependent, then for any subset12{,,,}{1,2,,}m i i i k ⊂L L ,1212()()()()m m P A A A P A P A P A i i i i i i =I I L L(全概率公式 total probability)()(|)()i i P B A P B A P A =IUsing the theorem of total probability, we have1()(|)(|)()(|)i i i kjjj P B P A B P B A P B P A B ==∑ 1,2,,i k =L1. random variable definition2. Distribution functionNote The distribution function ()F X is defined on real numbers, not on sample space. 3. PropertiesThe distribution function ()F x of a random variable X has the following properties:3.2 Discrete Random Variables 离散型随机变量geometric distribution (几何分布)Binomial distribution(二项分布)poisson distribution(泊松分布)Expectation (mean) 数学期望2.Variance 方差standard deviation (标准差)probability density function概率密度函数5. Mean (均值)6. variance 方差.4.2 Uniform Distribution 均匀分布The uniform distribution, with the parameters a a nd b , has probability density function1for ,()0 elsewhere,a xb f x b a⎧<<⎪=-⎨⎪⎩4.5 Exponential Distribution 指数分布4.3 Normal Distribution正态分布1. Definition4.4 Normal Approximation to the Binomial Distribution (二项分布)4.7 C hebyshev’s Theorem (切比雪夫定理)Joint probability distribution (联合分布)In the study of probability, given at least two random variables X, Y , ..., that are defined on a probability space, the joint probabilitydistribution for X, Y , ... is a probability distribution that gives the probability that each of X, Y , ... falls in any particular range or discrete set of values specified for that variable. 5.2 C onditional distribution 条件分布Consistent with the definition of conditional probability of events when A is the event X =x and B is the event Y =y , the conditional probability distribution of X given Y =y is defined as(,)(|)()X Y p x y p x y p y =for all x provided ()0Y p y ≠. 5.3 S tatistical independent 随机变量的独立性5.4 Covariance and Correlation 协方差和相关系数We now define two related quantities whose role in characterizing the interdependence of X and Y we want to examine.理We can find the steadily of the frequency of the events in large number of random phenomenon. And the average of large number of random variables are also steadiness. These results are the law of large numbers.population (总体)A population may consist of finitely or infinitely many varieties. sample (样本、子样)中位数Sample Distributions 抽样分布1.sampling distribution of the mean 均值的抽样分布It is customary to write )(X E as X μ and )(X D as 2X σ.Here, ()E X μ= is called the expectation of the mean .均值的期望 n X σσ= is called the standard error of the mean. 均值的标准差7.1 Point Estimate 点估计Unbiased estimator(无偏估计量)minimum variance unbiased estimator (最小方差无偏估计量)3. Method of Moments 矩估计的方法confidence interval----- 置信区间lower confidence limits-----置信下限upper confidence limits----- 置信上限degree of confidence----置信度2.极大似然函数likelihood functionmaximum likelihood estimate(最大似然估计)8.1 Statistical Hypotheses(统计假设)显著性水平Two Types of Errors。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Sample Space样本空间
The set of all possible outcomes of a statistical experiment is called the sample space、
Event 事件
An event is a subset of a sample space、
certain event(必然事件):
The sample space S itself, is certainly an event, which is called a certain event, means that it always occurs in the experiment、
impossible event(不可能事件):
The empty set, denoted by∅, is also an event, called an impossible event, means that it never occurs in the experiment、
Probability of events (概率)
If the number of successes in n trails is denoted by s, and if the sequence of relative frequencies /s n obtained for larger and larger value of n approaches a limit, then this limit is defined as the probability of success in a single trial、
“equally likely to occur”------probability(古典概率)
If a sample space S consists of N sample points, each is equally likely to occur、Assume
that the event A consists of n sample points, then the probability p that A occurs is
()n
p P A
N
==
Mutually exclusive(互斥事件)
Mutually independent 事件的独立性
Two events A and B are said to be independent if
()()()
P A B P A P B
=⋅
I
Or Two events A and B are independent if and only if
(|)()
P B A P B
=、
Conditional Probability 条件概率
The probability of an event is frequently influenced by other events、
If 12k ,,,A A A L are events, then
12k 121312121()()(|)(|)(|)k k P A A A P A P A A P A A A P A A A A -=⋅⋅I I L I L I I L I If the events 12k ,,,A A A L are independent, then for any subset 12{,,,}{1,2,,}m i i i k ⊂L L ,
1212()()()()m m
P A A A P A P A P A i i i i i i =I I L L (全概率公式 total probability)
()(|)()
i i P B A P B A P A =I
Using the theorem of total probability, we have
1()(|)(|)()(|)i i i k j j
j P B P A B P B A P B P A B ==
∑ 1,2,,i k =L
1、 random variable definition
2、 Distribution function
Note The distribution function ()F X is defined on real numbers, not on sample space 、
3、 Properties
The distribution function ()F x of a random variable X has the following properties:
3、2 Discrete Random Variables 离散型随机变量
geometric distribution (几何分布)
Binomial distribution(二项分布)
poisson distribution(泊松分布)
Expectation (mean) 数学期望
2.Variance 方差standard deviation (标准差)
probability density function概率密度函数
5、 Mean(均值)
6、 variance 方差
、
4、2 Uniform Distribution 均匀分布
The uniform distribution, with the parameters a a nd b , has probability density function
1 for ,(
)0 elsewhere,
a x
b f x b a ⎧<<⎪=-⎨⎪⎩
4、5 Exponential Distribution 指数分布
4、3 Normal Distribution 正态分布
1、Definition
4、4 Normal Approximation to the Binomial Distribution(二项分布)
4、7 Chebyshev’s Theorem(切比雪夫定理)
Joint probability distribution(联合分布)
In the study of probability, given at least two random variables X, Y, 、、、, that are defined on a probability space, the joint probability distribution for X, Y, 、、、is a probability distribution that gives the probability that each of X, Y, 、、、falls in any particular range or discrete set of values specified for that variable、
5.2C onditional distribution 条件分布
Consistent with the definition of conditional probability of events when A is the event X=x and B is the event Y=y, the conditional probability distribution of X given Y=y is defined as
(,)(|)()
X Y p x y p x y p y = for all x provided ()0Y p y ≠、 5.3 S tatistical independent 随机变量的独立性
interdependence of X and Y we want to examine 、
number of random phenomenon 、 And the average of large number of random variables are also steadiness 、 These results are the law of large numbers 、
population (总体)
sample (样本、子样)
中位数
It is customary to write )(X E as X μ and )(X D as 2X σ、
Here, ()E X μ= is called the expectation of the mean 、均值的期望 n X σσ= is called the standard error of the mean 、 均值的标准差 7、1 Point Estimate 点估计
Unbiased estimator(无偏估计量)
minimum variance unbiased estimator(最小方差无偏估计量)
3、Method of Moments 矩估计的方法
confidence interval----- 置信区间lower confidence limits-----置信下限upper confidence limits----- 置信上限
degree of confidence----置信度
2.极大似然函数likelihood function
显著性水平
Two Types of Errors。
