拉格朗日中值定理的推广及其应用
拉格朗日中值定理证明及其应用

拉格朗日中值定理证明及其应用1. 引言1.1 拉格朗日中值定理的引入拉格朗日中值定理是微积分中一个非常重要的定理,它由法国数学家约瑟夫·拉格朗日在18世纪提出并证明。
这个定理在微积分的发展中具有重要的地位,被广泛应用于函数的性质研究和最值问题的求解中。
拉格朗日中值定理可以理解为函数在某个区间上的平均变化率等于某个点的瞬时变化率。
具体地说,如果一个函数在闭区间[a, b]上连续且可导,那么在开区间(a, b)内一定存在一个点c,使得函数在点c处的导数等于函数在区间[a, b]上的平均变化率。
这个定理的引入可以帮助我们更好地理解函数的变化规律。
在实际问题中,我们经常需要研究函数在某个区间上的性质,比如函数的波动情况、增减性、极值等。
拉格朗日中值定理提供了一个有效的工具,可以帮助我们准确地描述函数在某个区间上的特征,进而推导函数的性质并解决相关问题。
拉格朗日中值定理的引入为我们理解函数的变化规律提供了一种新的视角,为函数求值、曲线求导和最值问题等提供了重要的理论支撑。
在接下来的文章中,我们将深入探讨拉格朗日中值定理的数学表述、证明过程以及在不同领域中的应用。
1.2 拉格朗日中值定理的重要性拉格朗日中值定理作为微积分中的重要定理,具有非常重要的数学意义和实际应用价值。
在数学分析领域,拉格朗日中值定理是连接微积分中的微分和积分两个重要概念的桥梁,它可以帮助我们更深入地理解函数的性质和求值方法。
拉格朗日中值定理的重要性在于它提供了一种有效的方法来处理函数的平均变化率和瞬时变化率之间的关系。
通过该定理,我们可以准确地计算函数在某一区间上的平均斜率,并将其与函数在该区间某一点的瞬时斜率联系起来。
这对于研究函数的变化规律,求解函数的最值以及解决相关实际问题都具有重要作用。
拉格朗日中值定理还为我们提供了一种重要的数学工具,可以帮助我们证明一些关于函数的重要性质和定理。
通过应用拉格朗日中值定理,我们可以简化复杂的数学问题,减少证明的难度,提高证明的效率。
拉格朗日定理的应用

拉格朗日定理的应用
拉格朗日定理是微积分中的一个重要定理,是一种中间值定理。
它指出,如果函数在一定区间内连续,且在这个区间内它有导数,那么这个函数的某个导数值可以用这个函数在某个区间中的两个端点的函数值来表示。
拉格朗日定理经常用于解决函数近似值、最值、凸凹性等问题,下面我们来简单介绍一些其应用。
1. 求解最值
拉格朗日中值定理可以用来求解函数的最值。
假设函数在区间[a,b]上连续,且在(a,b)内有导数。
那么只需要找到函数在(a,b)内的驻点(即导数为零的点),再将这些驻点与区间端点比较,就能找到函数的最大值和最小值。
2. 证明函数单调性
如果函数在[a,b]上连续,且在(a,b)内有导数,那么拉格朗日定理可以用来证明函数在[a,b]上的单调性。
如果函数在[a,b]上的导数大于零,则函数单调递增,如果小于零,则函数单调递减。
3. 求解方程根
4. 求解不等式
拉格朗日定理可以用来求解不等式,比如可以通过拉格朗日中值定理证明柯西-施瓦茨不等式。
5. 刻画函数的凸凹性
综上所述,拉格朗日定理在微积分中有着广泛的应用,可以帮助我们解决许多重要的问题。
拉格朗日中值定理的应用

拉格朗日中值定理在极限的应用

拉格朗日中值定理在极限的应用拉格朗日中值定理是微积分学中的一条重要定理,它是用来描述函数在一定范围内的变化规律的。
在极限的应用中,拉格朗日中值定理可以帮助我们求解一些复杂的问题,并且得到更为准确的结果。
一、拉格朗日中值定理的基本概念拉格朗日中值定理是微积分学中的一条基本定理,它是由法国数学家拉格朗日提出的。
该定理的基本概念是:假设函数f(x)在区间[a,b]上连续,在(a,b)内可导,则存在一个点c∈(a,b),使得f(b)-f(a)=f'(c)(b-a)。
这个定理的意义在于,它告诉我们在一个区间内,函数的平均变化率等于函数在该区间内某一点的瞬时变化率。
这个点就是拉格朗日中值定理中的中值点。
二、拉格朗日中值定理在极限的应用在极限的应用中,拉格朗日中值定理可以帮助我们求解一些复杂的问题。
例如,在求解极限时,我们常常需要利用拉格朗日中值定理来证明某些极限的存在性,或者求出极限的具体值。
具体应用如下:1. 利用拉格朗日中值定理证明某些极限的存在性在求解一些复杂的极限时,我们常常需要利用拉格朗日中值定理来证明其存在性。
例如,对于函数f(x)=sinx/x,当x趋近于0时,我们需要证明它的极限存在。
根据拉格朗日中值定理,我们可以得到: f(x)-f(0)=f'(c)(x-0)其中,c∈(0,x)。
而f'(x)=cosx/x-sinx/x^2,因此:f(x)-f(0)=f'(c)(x-0)=cosc/x-sinc/x^2×x当x趋近于0时,c也趋近于0,因此cosc趋近于1,sinc趋近于0。
因此,上式可以化为:lim(x→0)(sinx/x)=lim(x→0)(cosc)=1从而证明了该极限的存在性。
2. 利用拉格朗日中值定理求解极限的具体值在一些情况下,我们可以利用拉格朗日中值定理求解极限的具体值。
例如,对于函数f(x)=x^2sin(1/x),当x趋近于0时,我们需要求出它的极限。
拉格朗日中值定理在高中数学中的应用

应用拉格朗日中值定理拉格朗日中值定理在高中数学中的应用一、定理与推论拉格朗日中值定理设函数f(x)满足如下条件:(1) f(x)在闭区间[a,b]上连续;(2) f(x)在开区间(a,b)内可导,则在(a,b)内至少存在一点ξ,使得 = f(ξ),其中b > a.推论1若在(a,b)内, f(x) ≡ 0,则在(a,b)内f(x)为一常数、推论2若在(a,b)内, f′(x) = g′(x),则在(a,b)内f(x) = g(x) + c(c为常数).二、应用举例以下从应用的角度说明在解题中如何运用拉格朗日中值定理及其推论.1、运用拉格朗日中值定理证明不等式例1试证当x∈[1,+∞)时,ln1 +x ≥ ln2 .分析与说明这类题原本在高等数学中就是常见题型,求解这类题的通常思路就是先将一边移到另一边,构造一个函数,然后对它求导. 近些年来,这类题倍受高考命题者青睐.证明令f(x) = ln1 +x - ln2,对函数f(x)求导,得f′(x) = xln1 +′ =[ln(1+x) -lnx]-、令函数g(t) = ln(t),则g(t)在[x,x + 1]上满足拉格朗日中值定理,于就是对ln(1 + x) - ln x应用拉格朗日中值定理得到ln(1 + x)-ln x = ξ∈(x,x + 1),所以有f′(x) = - > 0 (x > 0 ),因此,由上面的结论推出f(x)在x∈[1,+∞)上单调递增,所以f(x)≥f(1),即 ln1 +x -ln2 ≥ f(1) = 0 ?圯ln1 +x ≥ln2、2. 运用拉格朗日中值定理证明恒等式例2若x ≥ 1,求证:arctan x +arccos=、分析在三角函数部分解题中见到过这种题型,应用公式tan(α ± β) =,解得tan(α ± β) = 1, α ± β的值可能为. 但此种解法较繁琐,在这里用推论1证明.证明设f(x)=arctan x +arccos - ,则f′(x)≡0,即f(x) = c (c为常数)、又因为f(1)=arctan1-arccos1 - = 0,所以c = 0,故f(x) = 0,即arctan x +arccos=.3、运用拉格朗日中值定理求极限例3求 (cos -cos )、分析观察函数特征容易想到:若令f(t)=cos ,则f(t)在[x,x + 1](x ≥ 0)上显然满足拉格朗日中值定理的条件.解令f(t)=cos ,显然f(t)在[x,x + 1](x ≥0)上满足拉格朗日中值定理,得cos -cos =(-sin ξ) ,其中x <ξ < x + 1,所以 (cos -cos ) =(-sinξ)=0、4.运用拉格朗日中值定理证明方程根的存在唯一性例4设f(x)在[0,1]上可导,且0 <f(x) < 1,又对于(0,1)内的所有点x有f′(x)≠-1,证明方程f(x) + x - 1 = 0在(0,1)内有唯一实根.分析证明方程根的存在性就有可能用到介值定理、在用介值定理证明问题时,选取合适的辅助函数可收到事半功倍的效果、而在证明唯一性的时候较常用的方法就就是反证法,所以本题证明思路就就是先证存在性,再证唯一性.证明先证存在性.令?准(x) = f(x) + x - 1,则?准(x)在[0,1]上可导.因为0 <f(x) < 1.所以?准(0) = f(0) - 1 < 0,?准(1) = f(1)>0、由介值定理知?准(x)在 (0,1)内至少有一个零点, 即方程f(x) + x - 1 = 0在(0,1)内至少有一个实根.再证唯一性(反证法). 设方程f(x) + x - 1 = 0在 (0,1)内有两个实根x1,x2,不妨设0 < x1 < x2 < 1有f(x1)=1 - x1,f(x2) = 1 - x2,对f(x)在[x1,x2]上应用拉格朗日中值定理,有ξ∈(x1,x2),使f′(ξ) = = = -1 、这与题设f′(x)≠-1矛盾,唯一性得证.拉格朗日中值定理在高中数学中应用非常广泛,远不止以上这些,如利用导数来研究函数的某些性质、描绘函数的图像、解决极值、最值等问题非常简捷,在此就不一一列举了、【参考文献】[1]华东师范大学数学系.数学分析(第三版下册)[M].北京:高等教育出版社,2001、[2]贾俊芳.拉格朗日中值定理的应用.雁北师范学院学报[J].2004.(5):25-28、[3]李艳敏,叶伯英.关于微分中值定理的两点思考,高等数学研究[M].北京:高等教育出版社,2001、。
知识点29罗尔定理拉格朗日中值定理的应用

知识点29罗尔定理拉格朗日中值定理的应用罗尔定理和拉格朗日中值定理是微积分中的两个重要定理,它们在数学和物理学中有着广泛的应用。
下面将详细介绍这两个定理及其应用。
一、罗尔定理罗尔定理是微积分中的基本定理之一,它是拉格朗日中值定理的一个特殊情况。
罗尔定理是由法国数学家迪尔勒·罗尔在17世纪提出的。
罗尔定理的表述如下:设函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,并且满足f(a)=f(b),则在开区间(a,b)内至少存在一点c,使得f'(c)=0。
也就是说,如果一个函数在闭区间两个端点处的函数值相等,且在闭区间内可导,则在开区间内至少存在一个点使得函数的导数为0。
罗尔定理的应用非常广泛,以下是一些典型的应用场景:1.判断函数的极值点:对于一个函数f(x)在一个闭区间[a,b]上连续,在开区间(a,b)内可导,且在两个端点处的函数值相等,根据罗尔定理,至少存在一个点c使得f'(c)=0。
因此,可以通过判断函数的导数为0的点来确定函数的极值点。
2.判断函数的单调性:对于一个函数f(x)在一个闭区间[a,b]上连续,在开区间(a,b)内可导,且在两个端点处的函数值相等,根据罗尔定理,至少存在一个点c使得f'(c)=0。
如果f'(x)>0,表示函数在这个点的导数大于0,即函数在这个点附近是单调递增的;如果f'(x)<0,表示函数在这个点的导数小于0,即函数在这个点附近是单调递减的。
3.解方程:对于一些特定的方程,可以通过罗尔定理来证明方程在一些区间内存在解。
例如,对于方程f(x)=0,在一个开区间(a,b)内,如果f(a)=f(b),则根据罗尔定理,至少存在一个点c使得f'(c)=0,即方程存在解。
二、拉格朗日中值定理拉格朗日中值定理是微积分中的一个重要定理,它是由法国数学家约瑟夫·拉格朗日在18世纪提出的。
浅析定拉格朗日中值定理及其应用

浅析定拉格朗日中值定理及其应用中值定理证明是考研数学中最大的难点,综合性与灵活性很强。
拉格朗日中值定理是中值定理中重要的一项内容,也是考生们较难掌握的知识点。
我们可以从以下几部分来理解掌握拉格朗日定理的内容、证明、与应用。
一、拉格朗日中值定理的内容如果函数f(x)满足:(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;那么在开区间(a,b)内至少有一点ξ,使等式成立()f ξ'=()()f b f a b a --。
注:1.拉格朗日中值定理条件与罗尔定理及柯西中值定理条件相同,即“闭区间连续,开区间可导”。
2.拉格朗日中值定理与罗尔定理及柯西中值定理相互关联,罗尔定理是()()f a f b =时,拉格朗日中值定理的特殊情形。
拉格朗日中值定理又为()g x x =时,柯西中值定理的特殊情形。
积分中值定理同可看作拉格朗日中值定理的特殊情形。
二、拉格朗日中值定理的证明()()()()()()()()()()()()()()()()()()()[]()()()()()()a,b a,b ,,=0,f b f a f b a f b f a f b a f b f a F x f b af b f a F x f x f a x a b aF a F b f b f a F x a b F f b a ξξξξξξ-'=--'-=--'---=----==-''∃∈=-设为的原函数之一在上连续,在上可导,则使即。
注:1.考情:考研考试中曾考察过拉格朗日中值定理证明过程,拉格朗日中值定理的内容及证明是同学们必须掌握的知识内容。
2.学情:拉格朗日中值定理可被理解为罗尔定理的推广,同时拉格朗日中值定理也是通过罗尔定理来证明的。
在使用罗尔定理证明的过程中,最重要的一步就是构造函数。
在拉格朗日中值定理的证明过程中,()F x 的构造尤为重要,对原函数加减常数后求导无影响,故在式中添加了()f a -,并将x 写为()x a -。
拉格朗日中值定理的应用

高教论坛在数学分析中,微分中值定理主要包括罗尔中值定理、拉格朗日中值定理和柯西中值定理及泰勒公理等.微分中值定理是导数应用的重要基础,其中,拉格朗日中值定理的应用最为广泛。
下面,分别介绍拉格朗日中值定理的内容及其应用。
1拉格朗日中值定理的内容定理[1]:如果函数f(x)满足(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导.则在开区间(a,b)内至少存在一点ξ,使得注释:(1)拉格朗日中值定理又称为有限增量定理,该定理建立了函数与导数的关系,这样就可以利用导数的性质研究函数的性质。
(2)罗尔定理是拉格朗日中值定理的特例,柯西中值定理是拉格朗日中值定理的推广,拉格朗日公式恰好为0阶泰勒公式。
(3)拉格朗日中值定理可以证明等式和不等式,也可以研究函数的单调性、凹凸性及其连续性等性质。
2证明等式由于拉格朗日中值定理的结论本身就是一个等式,因此可以利用该定理证明某些等式。
例1[2]:闭区间[a,b]上连续,则在开区间(a,b)内至少存在一点ξ,使得证明:因f(x)连续,故它的原函数存在,设为F(x),由牛顿—莱布尼茨公式,有在区间[a,b]上,对函数F(x)应用拉格朗日中值定理,在开区间内至少存在一点ξ,使得故3不等式的证明拉格朗日中值定理中的ξ位于开区间(a,b)内,可以利用这一属性证明不等式。
例2[2]:证明当时,有.证明:设,显然f(t)在[0,x]上满足拉格朗自中值定理的条件,根据定理,应有即又由于,有,即4求极限利用拉格朗日中值定理可以解决某些特殊极限的计算问题。
例3[3]:求解:原式因为,所以当,有,故原式.5研究函数的性质利用拉格朗日中值定理可以研究函数的单调性、凹凸性及连续性.这里仅给出定理在函数一致连续方面的应用举例。
例4[4]:证明在上一致连续。
证明:由于f(x)在上一致连续,因此在[0,2]上一致连续,于是,使得当且时,有.另一方面,因为在上严格单调递减,所以在上恒有,于是,对,应用拉格朗日中值定理,得这样,对给定的ε,取,则当且时,有现取,则对,当时,一定有或,从而必有这表明f(x)在上一致连续。
拉格朗日中值定理在高考数学中的应用

拉格朗日中值定理在高考数学中的应用拉格朗日中值定理是高中数学中的一项重要定理,它不仅具有理论意义,还能在实际问题中得到广泛应用。
在高考数学中,拉格朗日中值定理经常被用来解决函数极值、最大值最小值、证明函数单调性等问题。
首先,我们来了解一下拉格朗日中值定理的定义。
对于连续函数f(x)在区间[a,b]上可导,且a<b,则存在一个介于a和b之间的数c,使得f(b)-f(a)=f'(c)(b-a)。
这个定理表明,对于一段区间上的函数,它的两个端点之间的变化量等于该函数在某点处的导数与自变量的差的乘积。
在实际问题中,我们经常会遇到需要求出函数的最大值和最小值的情况。
根据拉格朗日中值定理,若函数f(x)在区间[a,b]上可导且恰有一个极值点c,则f(x)在点c处取得最大值或最小值。
因此,我们可以通过求导数、解方程来求出函数的极值点,在这些点处比较函数值,进而得到函数的最大值和最小值。
此外,拉格朗日中值定理还可以用来证明函数的单调性。
若函数f(x)在区间[a,b]上可导,则f(x)在该区间上单调递增,当且仅当对于任意的x1、x2∈[a,b],都有f(x2)-f(x1)=f'(c)(x2-x1),其中c ∈(x1,x2)。
同理,若f(x)在区间[a,b]上可导,则f(x)在该区间上单调递减,当且仅当对于任意的x1、x2∈[a,b],都有
f(x1)-f(x2)=f'(c)(x1-x2),其中c∈(x2,x1)。
综上所述,拉格朗日中值定理在高考数学中的应用十分广泛。
通
过运用这个定理,我们可以更加深入地理解函数的特性,进而更加熟练地解决各种数学问题。
拉格朗日微分中值定理

拉格朗日微分中值定理的概念、证明和应用拉格朗日微分中值定理,又称拉氏定理、有限增量定理,是微分学中的基本定理之一,反映了可导函数闭区间上整体的平均变化率与区间内某点的局部变化率的关系。
它是罗尔中值定理的推广,同时也是柯西中值定理的特殊情形。
定理的内容和几何意义令f为闭区间[a,b]上的一个连续函数,且在开区间(a,b)内可导,其中a<b。
那么在(a,b)上存在某个ξ使得f′(ξ)=f(b)−f(a)b−a此定理称为拉格朗日中值定理,也简称均值定理。
在几何上,这表示曲线y=f(x)上存在一点(ξ,f(ξ))其切线的斜率等于由两点(a,f(a))和(b,f(b))所连接的直线的斜率。
如下图所示:定理的证明在不失去一般性的条件下,设对所有x∈[a,b],有f(a)≤f(x)≤f(b);因为f是闭区间[a,b]上的连续函数,取得最大值M和最小值m。
令g(x)=f(x)−f(b)−f(a)b−a(x−a)那么g在[a,b]上连续,在(a,b)上可导,且g(a)=g(b)=f(a)由罗尔定理,存在至少一点ξ∈(a,b),使得g′(ξ)=0即f′(ξ)=f(b)−f(a)b−a定理的应用拉格朗日中值定理在微分学中有着广泛的应用,例如:证明函数单调性、极值、凹凸性等性质;估计函数误差、求函数极限、判断函数收敛性等问题;推导洛必达法则、泰勒公式、积分第一中值定理等重要结论。
下面举几个例子说明。
例1:证明函数单调性设f(x)在[a,b]上连续,在(a,b)内可导,且对任意x∈(a,b)有f′(x)>0,则f(x)在[a,b]上单调递增。
证明:任取x1,x2∈[a,b]且x1<x2,由拉格朗日中值定理,存在ξ∈(x1,x2)使得f′(ξ)=f(x2)−f(x1) x2−x1由于f′(ξ)>0且x2−x1>0,所以有f(x2)−f(x1)>0即f(x2)>f(x1)这说明f(x)在[a,b]上单调递增。
拉格朗日中值定理现实应用

拉格朗日中值定理现实应用拉格朗日中值定理是微积分中的一条重要定理,它在实际生活中有着广泛的应用。
本文将以拉格朗日中值定理的现实应用为主题,探讨其在经济学、物理学和工程学等领域的具体应用。
拉格朗日中值定理在经济学中有着重要的应用。
经济学家常常使用拉格朗日中值定理来研究市场供需关系。
通过对供给和需求函数进行微分,并利用拉格朗日中值定理,可以找到市场均衡点的存在和唯一性。
这对于研究市场定价、市场波动以及市场调节机制等方面具有重要意义。
此外,拉格朗日中值定理还可以帮助经济学家分析市场失灵的原因,为政府制定经济政策提供理论依据。
拉格朗日中值定理在物理学中也有着广泛的应用。
物理学家常常利用拉格朗日中值定理来研究物体的运动。
例如,在研究自由落体运动时,可以利用拉格朗日中值定理证明在任意两个时间点之间,存在至少一个时间点,物体的瞬时速度等于物体平均速度。
这对于研究物体的加速度、速度变化以及运动轨迹等方面具有重要意义。
此外,拉格朗日中值定理还可以应用于力学、光学等领域,为物理学家提供了一种分析和解决问题的思路。
拉格朗日中值定理在工程学中也有着实际应用。
工程师常常通过拉格朗日中值定理来优化工程设计。
例如,在设计道路的坡度时,工程师可以利用拉格朗日中值定理来确定最合适的坡度。
通过对道路高度函数进行微分,并利用拉格朗日中值定理,可以找到最陡和最缓的坡度,以实现最佳的行车舒适度和安全性。
除此之外,拉格朗日中值定理还可以应用于电子电路设计、材料力学等领域,为工程师提供了一种优化设计和解决问题的方法。
拉格朗日中值定理在经济学、物理学和工程学等领域都有着重要的应用。
它不仅为解决实际问题提供了理论支持,而且为相关学科的发展和进步作出了贡献。
因此,深入理解和应用拉格朗日中值定理对于相关领域的研究和实践具有重要意义。
希望本文的介绍能够帮助读者更好地理解拉格朗日中值定理的实际应用,并且对读者在相关领域的学习和研究有所启发。
拉格朗日中值定理在微积分解题中的应用

拉格朗日中值定理在微积分解题中的应用拉格朗日中值定理是微积分中的一个重要定理,它是由法国数学家拉格朗日在18世纪提出的。
这个定理主要用于分析函数在闭区间上的平均变化率与瞬时变化率之间的关系,被广泛应用于微积分解题中。
接下来,我们将详细介绍拉格朗日中值定理在微积分解题中的应用。
我们来介绍一下拉格朗日中值定理的表述。
假设函数f(x)在闭区间[a, b]上连续,在开区间(a, b)上可导,那么在(a, b)内至少存在一点ξ,使得f'(ξ) = [f(b) - f(a)] / (b - a)这个等式就是拉格朗日中值定理的表述。
接下来,我们来看一下拉格朗日中值定理在微积分解题中的应用。
它可以用来证明某些函数在特定区间上的性质。
对于一个连续函数在闭区间上可导,我们可以利用拉格朗日中值定理来证明在该区间上存在唯一的最大值或最小值。
拉格朗日中值定理可以用来求解函数在特定区间上的平均变化率。
我们知道,函数在闭区间上的平均变化率可以用函数值之间的差值除以自变量之间的差值来表示。
而拉格朗日中值定理提供了一种简便的方法来计算这个平均变化率,不需要严格求解函数的导数,只需通过找到一个满足定理条件的ξ即可得到结果。
拉格朗日中值定理还可以用来证明微积分中的其他定理和公式。
它可以用来证明微分中值定理和泰勒定理。
这说明拉格朗日中值定理在微积分理论体系中具有重要地位,它是其他定理的基础之一。
拉格朗日中值定理还可以应用于一些实际问题的求解中。
在求解速度、加速度、斜率等问题时,我们常常会用到拉格朗日中值定理。
它能够帮助我们理解函数在特定区间上的变化规律,进而推导出一些实际问题的解析结果。
拉格朗日中值定理在微积分解题中具有重要的应用价值。
它不仅可以用来证明某些函数在特定区间上的性质,还可以用来求解函数在特定区间上的平均变化率,证明微积分中的其他定理和公式,以及应用于一些实际问题的求解中。
熟练掌握拉格朗日中值定理的应用,对于学习和理解微积分理论具有重要的意义。
论文拉格朗日中值定理及其应用

拉格朗日中值定理引言众所周至拉格朗日中值定理是几个中值定理中最重要的一个,是微分学应用的桥梁,在高等数学的一些理论推导中起着很重要的作用. 研究拉格朗日中值定理的证明方法,力求正确地理解和掌握它,是十分必要的. 拉格朗日中值定理证明的关键在于引入适当的辅助函数. 实际上,能用来证明拉格朗日中值定理的辅助函数有无数个,因此如果以引入辅助函数的个数来计算,证明拉格朗日中值定理的方法可以说有无数个. 但事实上若从思想方法上分,我们仅发现五种引入辅助函数的方法. 首先对罗尔中值定理拉格朗日中值定理及其几何意义作一概述. 1罗尔()Rolle 中值定理如果函数()x f 满足条件:()1在闭区间[]b a ,上连续;()2在开区间()b a ,内可导;(3)()()b f a f =,则在()b a ,内至少存在一点ζ ,使得()0'=ζf罗尔中值定理的几何意义:如果连续光滑曲线()x f y =在点B A ,处的纵坐标相等,那么,在弧 ⋂AB 上至少有一点()(),Cf ζζ ,曲线在C 点的切线平行于x 轴,如图1,注意 定理中三个条件缺少其中任何一个,定理的结论将不一定成立;但不能认为定理条件不全具备,就一定不存在属于()b a ,的ζ,使得()0'=ζf . 这就是说定理的条件是充分的,但非必要的.2拉格朗日()lagrange中值定理 若函数()x f 满足如下条件:()1在闭区间[]b a ,上连续;()2在开区间()b a ,内可导;则在()b a ,内至少存在一点ζ,使()()()ab a f b f f --=ζ'拉格朗日中值定理的几何意义:函数()x f y =在区间[]b a ,上的图形是连续光滑曲线弧⋂AB 上至少有一点C ,曲线在C 点的切线平行于弦AB . 如图2,从拉格朗日中值定理的条件与结论可见,若()x f 在闭区间[]b a ,两端点的函数值相等,即()()b f a f =,则拉格朗日中值定理就是罗尔中值定理. 换句话说,罗尔中值定理是拉格朗日中值定理的一个特殊情形.正因为如此,我们只须对函数()x f 作适当变形,便可借助罗尔中值定理导出拉格朗日中值定理. 3 证明拉格朗日中值定理3.1 教材证法证明 作辅助函数 ()()()()f b f aF x f x x b a-=--显然,函数()x F 满足在闭区间[]b a ,上连续,在开区间()b a ,内可导,而且()()F a F b =.于是由罗尔中值定理知道,至少存在一点ζ()b a <<ζ,使()()()()0''=---=ab a f b f f F ζζ.即()()()ab a f b f f --=ζ'。
拉格朗日(Lagrange)中值定理
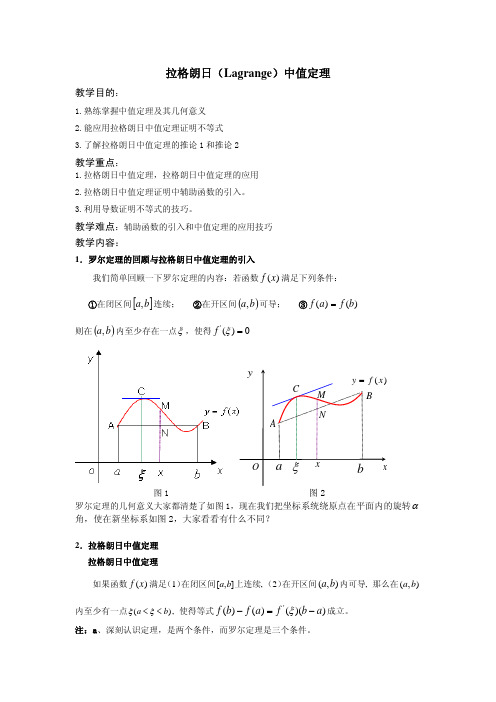
拉格朗日(Lagrange )中值定理教学目的:1.熟练掌握中值定理及其几何意义2.能应用拉格朗日中值定理证明不等式3.了解拉格朗日中值定理的推论1和推论2教学重点:1.拉格朗日中值定理,拉格朗日中值定理的应用2.拉格朗日中值定理证明中辅助函数的引入。
3.利用导数证明不等式的技巧。
教学难点:辅助函数的引入和中值定理的应用技巧 教学内容:1.罗尔定理的回顾与拉格朗日中值定理的引入我们简单回顾一下罗尔定理的内容:若函数满足下列条件: )(x f ①在闭区间[连续; ②在开区间]b a ,()b a ,可导; ③)()(b f a f = 则在(内至少存在一点)b a ,ξ,使得'()0f ξ=图1 图2罗尔定理的几何意义大家都清楚了如图1,现在我们把坐标系统绕原点在平面内的旋转α角,使在新坐标系如图2,大家看看有什么不同?2.拉格朗日中值定理 拉格朗日中值定理如果函数满足(1)在闭区间上连续, (2)在开区间内可导, 那么在内至少有一点)(x f (a <],[b a ),(b a ),(b a )b <ξξ, 使得等式成立。
)a )(()('b f a f −=−ξ)(b f 注:a 、深刻认识定理,是两个条件,而罗尔定理是三个条件。
b 、若加上,则)()(b f a f =()()'()0f b f a f b a b aξ−===−−,即:,拉格朗日定理变为罗尔定理,换句话说罗尔定理是拉格朗日定理的特例。
'()0f ξ=拉格朗日(微分)中值定理几何意义我们从几何的角度看一个问题,如下:设连续函数()y f x =,a 与是它定义区间内的两点(a b b <),假定此函数在(,上处处可导,也就是在(,内的函数图形上处处有不垂直于)a b )a b x 轴的切线,那么我们从图2上容易看到,差商()y f x b =(f a)a b Δ−Δ−就是割线的斜率,若我们把割线作平行于自身的移动,那么至少有一次机会达到离割线最远的一点AB AB ()C x ξ=处成为曲线的切线,而切线的斜率为()f ξ′,由于切线与割线是平行的,因此()()()f b f a f b aξ−′=−成立。
拉格朗日中值定理用法

拉格朗日中值定理用法1. 大家好啊!今天咱们来聊聊拉格朗日中值定理这个数学界的"明星定理"。
说实话,这个定理就像是数学界的"神探",特别擅长帮我们找到函数里藏着的秘密。
2. 这个定理说的是啥呢?简单来说,就是在一段平滑的曲线上,一定能找到一个点,在这个点的切线平行于曲线两端的连线。
就像荡秋千一样,总能找到一个时刻,秋千的速度正好等于平均速度。
3. 用这个定理解题可有意思了!比方说,要是遇到证明不等式的题目,拉格朗日中值定理就像是一把万能钥匙。
它告诉我们,函数在两点之间的变化量,等于某个中间点导数值乘以自变量的变化量。
4. 来看个实际例子:假如你想证明正弦函数在零到π之间的某个地方,斜率一定等于零。
用这个定理一套,就跟变魔术似的,马上就能找到答案。
5. 这个定理还特别爱帮忙估计误差。
就像买东西要算找零一样,它能告诉我们计算结果最多差多少。
这简直就是数学界的"验钞机",特别靠谱!6. 用这个定理解题有个小窍门:看到两点之间函数值的差,就要想到它。
就像见到下雨就知道要打伞一样,这是条件反射!7. 不过用这个定理也得注意几个坑:函数必须是连续的,还得能求导。
就像游泳必须会换气一样,这些基本条件缺一不可。
8. 这个定理最厉害的地方是,它能把复杂的问题变简单。
就像给你一个超级难的不等式,用它一推导,复杂的式子立马就乖乖听话了。
9. 在实际应用中,这个定理简直是处理变化率问题的一把好手。
比如要计算一个物体的平均速度,它立马就能帮你找到某个时刻的瞬时速度。
10. 解题时要记住,中值定理给出的只是存在性,告诉我们"有这么一点",但具体是哪个点,往往需要我们自己动脑筋去找。
11. 这个定理还特别喜欢和泰勒公式做朋友。
它们俩合起来简直就是数学界的"黄金搭档",能解决很多近似计算的问题。
12. 总的来说,拉格朗日中值定理就像是数学工具箱里的瑞士军刀,用途特别广。
论文拉格朗日中值定理及其应用.

拉格朗日中值定理引言众所周至拉格朗日中值定理是几个中值定理中最重要的一个,是微分学应用的桥梁,在高等数学的一些理论推导中起着很重要的作用. 研究拉格朗日中值定理的证明方法,力求正确地理解和掌握它,是十分必要的. 拉格朗日中值定理证明的关键在于引入适当的辅助函数. 实际上,能用来证明拉格朗日中值定理的辅助函数有无数个,因此如果以引入辅助函数的个数来计算,证明拉格朗日中值定理的方法可以说有无数个. 但事实上若从思想方法上分,我们仅发现五种引入辅助函数的方法. 首先对罗尔中值定理拉格朗日中值定理及其几何意义作一概述. 1罗尔()Rolle 中值定理如果函数()x f 满足条件:()1在闭区间[]b a ,上连续;()2在开区间()b a ,内可导;(3)()()b f a f =,则在()b a ,内至少存在一点ζ ,使得()0'=ζf罗尔中值定理的几何意义:如果连续光滑曲线()x f y =在点B A ,处的纵坐标相等,那么,在弧 ⋂AB 上至少有一点()(),Cf ζζ ,曲线在C 点的切线平行于x 轴,如图1,注意 定理中三个条件缺少其中任何一个,定理的结论将不一定成立;但不能认为定理条件不全具备,就一定不存在属于()b a ,的ζ,使得()0'=ζf . 这就是说定理的条件是充分的,但非必要的.2拉格朗日()lagrange中值定理 若函数()x f 满足如下条件:()1在闭区间[]b a ,上连续;()2在开区间()b a ,内可导;则在()b a ,内至少存在一点ζ,使()()()ab a f b f f --=ζ'拉格朗日中值定理的几何意义:函数()x f y =在区间[]b a ,上的图形是连续光滑曲线弧⋂AB 上至少有一点C ,曲线在C 点的切线平行于弦AB . 如图2,从拉格朗日中值定理的条件与结论可见,若()x f 在闭区间[]b a ,两端点的函数值相等,即()()b f a f =,则拉格朗日中值定理就是罗尔中值定理. 换句话说,罗尔中值定理是拉格朗日中值定理的一个特殊情形.正因为如此,我们只须对函数()x f 作适当变形,便可借助罗尔中值定理导出拉格朗日中值定理. 3 证明拉格朗日中值定理3.1 教材证法证明 作辅助函数 ()()()()f b f a F x f x x b a-=--显然,函数()x F 满足在闭区间[]b a ,上连续,在开区间()b a ,内可导,而且()()F a F b =.于是由罗尔中值定理知道,至少存在一点ζ()b a <<ζ,使()()()()0''=---=ab a f b f f F ζζ.即()()()ab a f b f f --=ζ'。
拉格朗日中值定理 直接无穷区间

拉格朗日中值定理是微积分中的重要定理之一,它在分析函数在某个区间上的平均增长率与函数导数之间建立了必然的联系。
而直接无穷区间则是指函数的定义域包含了无穷大范围的区间。
本文将深入探讨拉格朗日中值定理在直接无穷区间上的应用,以及其在实际问题中的意义。
1. 拉格朗日中值定理的基本原理拉格朗日中值定理是微积分理论中的一个重要定理,它表明了如果一个函数在某个闭区间上连续,在该区间内可导,则在开区间内一定存在至少一个点,使得函数在该点的导数等于函数在区间两端点处的函数值的增量与自变量增量的比值。
具体而言,设函数f(x)在闭区间[a, b]上连续,在开区间(a, b)内可导,那么一定存在ξ∈(a, b),使得f'(ξ) = (f(b) - f(a))/(b - a)。
2. 拉格朗日中值定理在直接无穷区间上的推论在实际问题中,很多函数的定义域并不仅限于有限的区间,而是涉及到直接无穷大的范围。
在这种情况下,拉格朗日中值定理同样可以发挥重要作用。
通过逐步推广区间长度至无穷大,我们可以得到在直接无穷区间上的拉格朗日中值定理推论:设函数f(x)在闭区间[a, +∞)上连续,在开区间(a, +∞)内可导,那么对于任意的x > a,总存在ξ∈(a, x),使得f'(ξ) = (f(x) - f(a))/(x - a)。
3. 拉格朗日中值定理的在实际问题中的应用拉格朗日中值定理在实际问题中有许多应用,特别是在求解函数在特定区间上的性质时。
以直接无穷区间为例,考虑一个函数f(x)在闭区间[a, +∞)上的增长情况,我们可以利用拉格朗日中值定理在该区间内的某一点ξ处的导数值来评价函数在该区间上的整体增长情况。
这对于研究函数的渐近性质或者求解极限时具有重要的意义。
4. 个人观点和理解拉格朗日中值定理作为微积分理论中的重要定理之一,在直接无穷区间上的应用对于深入理解函数在无限范围内的性质具有重要意义。
在实际问题中,我们经常需要研究函数在无穷范围内的增长情况,而了解拉格朗日中值定理在直接无穷区间上的推论可以帮助我们更好地解决这类问题。
拉格朗日中值定理在微积分解题中的应用

拉格朗日中值定理在微积分解题中的应用拉格朗日中值定理(Lagrange mean value theorem)是微积分中的一种工具,它可以用来探究函数在某个区间上的变化情况,也可以搭配其它工具推导出函数的某些性质,因此被广泛地应用在微积分解题中。
下面,本文将介绍拉格朗日中值定理在微积分解题中的应用。
一、函数单调性的判断当我们需要判断函数$f(x)$在某个区间上是否单调时,一种比较简单的方法是求出$f'(x)$,然后观察其符号。
但是,对于那些比较复杂的函数来说,求导并不是一件容易的事情,因此,我们可以考虑运用拉格朗日中值定理来推导$f(x)$在某个区间上的单调性。
设$f(x)$在区间$[a,b]$上连续且可导,且$f(a)<f(b)$,则存在$\xi\in(a,b)$,使得$f'(\xi)>0$。
上述结论的推导可以用反证法的思想,首先假设$f(x)$在区间$[a,b]$上是非单调的,那么必定存在$x_1<x_2<x_3$,使得$f(x_1)<f(x_2),f(x_3)>f(x_2)$,而根据费马定理的结论,存在$x_4\in(x_1,x_2)$,使得$f'(x_4)=0$,存在$x_5\in(x_2,x_3)$,使得$f'(x_5)=0$,那么分别对$[x_4,x_2]$和$[x_2,x_5]$应用拉格朗日中值定理,得出存在$\xi_1\in(x_4,x_2),\xi_2\in(x_2,x_5)$,使得$f''(\xi_1)>0,f''(\xi_2)<0$,但这与$f''(x)\geq0$矛盾,因此假设不成立,结论得证。
二、实数幂指数函数的等价无穷小在微积分中,我们经常需要比较两个函数在某个点附近的变化趋势,这时候我们可以利用实数幂指数函数的等价无穷小准则,尤其是拉格朗日中值定理可以为此提供较好的基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
嘉应学院本科毕业论文(设计)(2014届)题目:拉格朗日中值定理的推广及其应用姓名:徐佳琳学号: 101010045学院:数学学院专业:数学与应用数学(师范)指导老师:温坤文申请学位:学士学位嘉应学院教务处摘要拉格朗日中值定理是微分学的基础定理之一,在理论和应用上都有极其重要的意义.本文先对拉格朗日中值定理作了一定的阐述,并将其进行了推广,然后通过对几种类型问题的解决,对拉格朗日值定理的应用作一些探讨和归纳,以起到对定理的深入理解,熟悉掌握并能够正确应用的作用.字典关键词:拉格朗日中值定理,定理的推广及应用,极限,不等式,级数的敛散性.AbstractLagrange mean value theorem is one of the basic theorem of differential calculus,It has extremely important meaning in the theory and application.This article first to make the Lagrange theorem certain, and put it to the promotion, then through several types on the solution of the problem,and it will make some discussions and studies on the application of lagrange mean value theorem .It’s purpose is to have in-depth understanding of theorem, the role of expert knowledge and be able to correct application.Keywords: Lagrange mean value theorem,The generalization and application of the theorem, The limit, Inequality, The convergence and divergence of the series.1. 引言罗尔定理、拉格朗日中值定理、柯西定理以及泰勒公式是微分学的基本定理,这些定理都具有中值性,所以统称微分学中值定理,以拉格朗日中值定理为中心,他们之间的关系可用简图示意如下:以罗尔定理、拉格朗日中值定理和柯西中值定理组成的一组中值定理是整个微分学的理论基础,尤其是拉格朗日中值定理,他建立了函数值与导数值之间的定量联系,因而可用中值定理通过导数研究函数的性态,中值定理的主要作用在于理论分析和证明,例如为利用导数判断函数单调性、取极值、凹凸性、拐点等重要函数性态提供重要理论依据,从而把握函数图像的各种几何特征.拉格朗日中值定理是微分学的基础定理之一,拉格朗日中值定理作为微分中值定理的核心,它有许多推广,这些推广都有一个基本特点,就是把定理条件中可微性概念拓宽,然后推广微分中值表达公式.除此之外,拉格朗日中值定理在理论和应用上也有着极其重要的意义.该定理叙述简单明了,并有明确的几何意义,一般掌握问题不大,但要深刻认识定理的内容,特别是中值点的含义,就有较大难度.总之,微分学中值定理是沟通导数值与函数值之间的桥梁,是利用导数的局部性质推断函数的整体性质的工具,而著名的拉格朗日中值定理作为其中一个承上启下的定理,是应用数学研究函数在区间整体性态的有力工具,必须深刻认识定理的内容,熟练掌握定理的本质,在解题时游刃有余,若对定理的实质了解不够深刻的话,会进入不少误区.现借下文中的若干例子来对拉格朗日中值定理作一些探讨,以起到对定理深入理解、熟练掌握并正确应用的作用.2.拉格朗日中值定理定理2.1(拉格朗日中值定理)若函数满足下列条件:(i)在闭区间上连续;(ii) 在开区间内可导,则在内至少存在一点,使得.3. 拉格朗日中值定理的推广命题3.1 若函数在开区间内可导,函数极限都存在;则至少存在一点,使得.证明不妨记,,令函数则函数在闭区间上连续,函数在开区间内可导,.由拉格朗日中值定理,至少存在一点,使得又,,,所以.命题3.2 若函数在内可导,函数极限与都存在;则至少存在一点,使得证明令则复合函数在开区间内可导,其导数为由已知函数极限,与,都存在.由命题3.1,至少存在一点,使得,令,则时,,并且.所以,至少存在一点,使得命题3.3 若函数在开区间内可导,函数极限与都存在,则至少存在一点使得.证明令,且则复合函数在开区间内可导,其导数为由已知函数极限,与,都存在.由命题3.1,至少存在一点使得令则时,所以,至少存在一点使得命题3.4 若函数在开区间,使得证明令,且则复合函数在开区间内可导,其导数为由已知函数极限,与,都存在.由命题3.1,至少存在一点,使得令则时,所以,至少存在一点使得显然,有如下的推论:若把上述命题的第二个条件加强为:有关的函数极限存在且相等,则至少存在一点属于上述各区间,使得.于是我们得到了推广的罗尔中值定理.不难看出,推广的罗尔中值定理,有其明确的几何意义:在符合定理的条件下,曲线在点处有水平的切线.4. 拉格朗日中值定理的应用拉格朗日中值定理的应用广泛,可用于计算、证明、估算、判定等,在应用中灵活性较大,下面从求极限、证明不等式、判别级数敛散性等方面对拉格朗日中值定理的应用做进一步的研究.4.1 利用拉格朗日中值定理求极限用拉格朗日中值定理,最重要的是去找函数和相应的区间,而公式可变形为:它的左端是有特点的,恰好是在区间上的增量与的区间长度的比值.因此公式变形后就可以确定函数和相应的区间.例1.求极限:.解函数在或上运用拉格朗日中值定理,得(在与之间).故.例2.设连续,,有公式, (1)试求解对函数在或上运用拉格朗日中值定理,得,代入(1)式,得. (2)将按泰勒公式展开:, (3)由(2)(3)得,故.例3.求极限:.解令在或上对变量运用拉格朗日中值定理,得(在之间),故.4.2 利用拉格朗日中值定理证明不等式拉格朗日中值定理存在的形式并不是不等式的形式.那么怎么能用拉格朗日中值公式去证明不等式呢?我们知道,在拉格朗日中值公式中而不知道具体是多少,但根据在之间的取值却可以估计的取值范围.或者说可以估计出取值的上、下界,分别用取值的上、下界去代换拉格朗日中值公式中的就可以得到不等式.这就是用拉格朗日中值公式证明不等式的思想.例4.证明当时,.证明设,显然在区间上满足拉格朗日中值定理的条件,故有. (1)又,故(1)式为,则,即.例5.设函数在上连续,有二阶连续导数且,若有使得,则必有,使得.证明由题知,在,上分别满足拉格朗日中值定理的条件,则有,且.因且,故,又由题知在上满足拉格朗日中值定理,即.例6.证明:当时,.证明令,则在上满足拉格朗日中值定理的条件,故存在,使得,即.又因,故.当时,,即.所以当时,不等式成立.4.3 利用拉格朗日中值定理证明恒等式由拉格朗日中值定理知,函数在定义域内取两点(不妨设),有,那么若恒为0,则有,所以.由的任意性可知,在定义域内函数值恒等.即有下面一个推论:推论如果函数在开区间内的导数恒为零,那么在内是一个常数.利用这个推论可以证明一类反三角恒等式的题目.例7.证明恒等.证明令在时,有意义,且.所以,在时,(常数).又取内任一点,如,有,且,所以端点值也成立,由推论有恒等.4.4 利用拉格朗日中值定理证明等式用拉格朗日中值定理证明等式也是它的应用中很重要的一项,证明的目标在于凑出形式类似于拉格朗日中值定理的式子,寻找机会应用.例8.设在内可导,且,试证,使得.证明令,则在上满足拉格朗日中值定理条件,故存在,使得,由条件,可得,再令,则在上满足拉格朗日中值定理条件,故存在,使得,综合上述两式可得,即.4.5 利用拉格朗日中值定理研究函数在区间上的性质因为拉格朗日中值定理沟通了函数与其导数的联系,很多时候我们可以借助其导数,研究导数的性质从而了解函数在整个定义域区间上的整体认识.比如研究函数在区间上的符号、单调性、一致连续性,凸性等等,都可能用到拉格朗日中值定理的结论,通过对函数局部性质的研究把握整体性质,这是数学研究中一种重要的方法.例9.证明:若函数在有穷或无穷的区间内存在有界的导函数,则在内一致连续.证明设当时,对于,在以为端点的区间上由拉格朗日中值定理,有,在之间,那么对于,取,则当,且,就有(在之间),由一致连续定义可知,在内一致连续.4.6 利用拉格朗日中值定理证明估值问题证明估值问题,一般情况下选用泰勒公式证明比较简便,特别是二阶及二阶以上的导函数估值时.但对于某些积分估值,可以采用拉格朗日中值定理来证明.例10.设在上连续,且,试证:.证明若,不等式显然成立;若不恒等于0,,使,在及上分别用拉格朗日中值定理,有,从而,这里利用了,所以原不等式得证.4.7 利用拉格朗日中值定理判别级数的敛散性在级数敛散性的判别问题上,可以构造辅助函数,研究在各个区间上的特点,最后相加可以进行化简,利用级数敛散性的判别法则给出判断.例11.证明调和级数的敛散性.。
