课时微训练10
四年级下册语文课时训练类文阅读10 蝙蝠和雷达

类文阅读-10 蝙蝠和雷达苍蝇与宇宙飞船令人讨厌的苍蝇,与宏伟的航天事业似乎风马牛不相及,但科学家却把它们紧密地联系起来了。
苍蝇是声名狼藉的“逐臭之夫”,凡是腥臭污秽的地方,都有它们的踪迹。
苍蝇的嗅觉特别灵敏,远在几千米外的气味也能嗅到。
但是苍蝇并没有“鼻子”,它靠什么来充当嗅觉的呢? 原来,苍蝇的“鼻子”——嗅觉感受器分布在头部的一对触角上。
每个“鼻子”只有一个“鼻孔”与外界相通,内含上百个嗅觉神经细胞。
若有气味进入“鼻孔”,这些神经立即把气味刺激转变成神经电脉冲,送往大脑。
大脑根据不同气味物质所产生的神经电脉冲的不同,就可区别出不同气味的物质。
因此,苍蝇的触角像是一台灵敏的气体分析仪。
科学家由此得到启发,根据苍蝇嗅觉器的结构和功能,仿制成一种别具匠心的小型气体分析仪。
这种仪器的“探头”不是金属,而是活的苍蝇。
就是把非常纤细的微电极插到苍蝇的嗅觉神经上,将引导出来的神经电信号经电子线路放大后,送给分析器;分析器一经发现气味物质的信号,便能发出警报。
这种仪器已经被安装在宇宙飞船的座舱里,用来检测舱内气体的成分。
(《小学阅读指南(高年级版)(3-6年级)》2021年第2期)1.解释词语。
声名狼藉:别具匠心:2.画线的句子中,“鼻子”一词加引号是因为。
这和文章前面一句相呼应。
3.下列说法中,正确的是()。
A.苍蝇是非常脏的动物,所以它一无是处。
B.苍蝇是依靠嗅觉神经细胞闻到气味的。
C.科学家仿制的小型气体分析仪的探头是金属。
4.你还知道哪些模仿生物的发明呢?给大家简单介绍一下吧。
【参考答案】1.形容一个人的名誉坏到极点。
在技巧和艺术方面具有与众不同的巧妙构思。
2.这里说的鼻子并不是真正的鼻子但是苍蝇并没有“鼻子”3.B4.示例:科学家模仿鱼鳔的原理,发明了潜水艇。
飞行之王——蜻蜓蜻蜓被誉为昆虫世界里的“飞行之王”。
在闷热的夏季里,暴雨将至或骤雨初歇,蜻蜓常常三五成群在空中飞舞。
它好似一架飞机,而飞行技巧却远远高出于飞机之上。
七年级语文统编版(2024)上册《我的白鸽》课时优化训练(含解析)

18 我的白鸽——七年级语文统编版(2024)上册课时优化训练1.小文研读完课文,摘录了一些词语并将其分类。
请你从下列选项中,找出每对加粗字的读音都不同的一项( )A.豁朗/书声琅琅蜕变/脱胎换骨邋遢/踏歌而行B.骊山/玉米粒儿肮脏/情绪亢奋胆怯/情真意切C.屈膝/一团漆黑雏鸟/锥心刺骨博弈/神采奕奕D.客栈/风烛残年调动/乡村情调不舍/退避三舍2.小天从课文中提取了四个成语并试着运用它们写了四个句子。
其中有一个句子中加粗的成语使用不恰当,请你帮忙找出( )A.动物是大自然的瑰宝,是人类的朋友,用实际行动拯救濒危动物迫不及待。
B.在作者眼中,湖中游弋的白天鹅已经被拟人化了,柔美的身姿宛若一位亭亭玉立的美人。
C.那匹骏马已至风烛残年,只能静静回望曾经在草原上飞奔的岁月。
D.在热带雨林这片气象万千的土地上,动物们展现着自己蓬勃的生命力。
3.把下列句子组成语意连贯的一段话,填入文段横线处,顺序最恰当的一项是( )鸽子走路时头一顿一顿的姿态引发的争论已持续了数百年,其间涌现出过各种各样的理论。
甚至有许多人认为,鸽子的头与脚之间存在着类似曲柄结构的机械连接,因此脚步移动时头也会跟着晃动。
_________________①现在科学家普遍认为,以鸽子为代表,鸟类的这种奇特步态是为了增强视觉,更好地判断距离。
②然而真实原因可能比这些奇谈怪论更不可思议。
③这样可以增强鸽子判断距离的能力,在寻找食物和躲避危险时大有帮助。
④但是,通过头部快速频繁地点动,鸽子仅用一只眼睛,就能不断地从略微不同的位置获取图像,就好像双眼同时视物一样。
⑤鸽子的两只眼睛分别位于头部两侧,因此每只眼睛看到的世界都是平面的,缺乏立体视觉。
A.③②①④⑤B.①③⑤④②C.②①⑤④③D.⑤②④③①4.下列依次填入文段画线处句子,排列最恰当的一项是( )立夏有三候,初候___________;二候___________;三候___________。
新课标人教版小学五年级语文上册第3单元课时同步练习-10松鼠附答案

新课标人教版小学五年级语文上册第3单元课时同步练习-10松鼠(2)附答案基础积累不夯实基础,难建成高楼。
一、拼音小关卡。
用“\”画去括号里错误的读音。
1.窝口朝上,端端正正,很狭(xiǎ xiá)窄,勉(miǎn mián)强可以进出。
2.松鼠横渡溪流的时候,用一块树皮当作船,用自己的尾巴当作帆和舵(duó duò)。
二、词语游艺厅。
1.仿照例子,写汉字并组词。
例如:驯-(驯良)--__训__ --(训练)矫-()--________--()舵-()--________--( )2.写出下列词语的反义词。
轻快() 机警() 宽敞()敏捷() 光滑()强烈()3.选择合适的词语填入括号里,用另外一个造句。
干净整洁(1)松鼠的窝通常搭在树枝分杈的地方,又()又暖和。
造句:响亮明亮(2)松鼠的叫声很()。
造句:三、句子训练营。
1. 它们从来不..待在小树丛里,只.喜欢住在高大的老树上。
(用加点词造...接近人的住宅,也不句)_______________________________________________________________________________ ________2.“厉害”有两个意思,请根据它的不同意思造句。
(1)严厉:(2)难以对付或忍受;剧烈;猛烈:_______ _______________________________________________四、课文回眸室。
课文第1自然段介绍松鼠是一种________的小动物,乖巧,_______,很______ _。
接着从________、________、________、________、________和______几个方面具体来写松鼠的外形特征。
理解感悟重点难点,一网打尽。
五、课堂连线台。
同学甲:本文是一篇_____________,它的标题“松鼠”交代了说明的对象。
《卖油翁》课时训练

四川绵阳示范初中(富乐国际学校)2020年春初中语文(人教版)七年级下册课时训练班级姓名第三单元第12课卖油翁1.(独家原创试题)下列句中加点字的注音有误的一项是 ( )A.公亦以此自矜(jīn)尝射于家圃(pǔ)B.睨(nì)之久而不去但微颔(hàn)之C.康肃忿(pén)然曰以我酌(sháo)油知之D.以钱覆(fù)其口徐以杓酌油沥(lì)之2.下列句中加点虚词的意思相同的一项是 ( )A.公亦以此自矜以钱覆其口B.尝射于家圃乃取一葫芦置于地C.见其发矢十中八九以钱覆其口D.自钱孔入,而钱不湿笑而遣之3.(独家原创试题)下列句中加点词语解释有误的一项是 ( )A.但微颔之(点头)康肃忿然曰(气愤的样子)B.但手熟尔(同“耳”,相当于“罢了”)公亦以此自矜(自夸)C.有卖油翁释担而立(放下担子)康肃笑而遣之(打发)D.以我酌油知之(斟酌)睨之久而不去(斜着眼看,这里形容不在意的样子)4.下列语句没有词类活用现象的一项是 ( )A.尔安敢轻吾射B.康肃笑而遣之C.吾射不亦精乎D.无他,但手熟尔5.(独家原创试题)下列句子翻译不当的一项是 ( )A.陈康肃公善射,当世无双。
(陈尧咨擅长射箭,当世没有第二个人可与之媲美。
)B.尔安敢轻吾射!(你居然敢轻视我射箭!)C.徐以杓酌油沥之。
(慢慢地用勺舀油倒入葫芦。
)D.我亦无他,惟手熟尔。
[我也没有别的(奥妙),只是手法技艺熟练罢了。
]6.(独家原创试题)下列说法有误的一项是 ( )A.《卖油翁》选自《归田录》卷一。
有删节。
B.欧阳修,字永叔,号放翁,晚号六一居士,谥号文忠,北宋政治家、文学家。
C.欧阳修是北宋诗文革新运动的领袖,散文成就最高,唐宋八大家之一。
D.《归田录》是欧阳修晚年写的作品,不仅具有文学价值,还有重要的史料价值。
7.(独家原创试题)下面句子全部表现陈康肃骄傲自满的一项是 ( )①公亦以此自矜②但微颔之③尔安敢轻吾射④吾射不亦精乎⑤康肃笑而遣之A.①②③B.②④⑤C.②④③D.①③④8.(独家原创试题)学习了《卖油翁》一文,语文老师根据文意拟写了一副对联,有意空出了部分内容。
七年级生物能力培养与测试(上)答案

第一单元生物和生物圈第一章认识生物第一节生物的特征【教材助读·自主学习】1.放大镜摄像机2.营养繁殖遗传3.生物【课内探究·展示交流】探究一(1)呼气能进行呼吸(2)合拢能对外界刺激作出反应(3)能排出体内产生的废物(4)获得营养(5)繁殖生长(6)像不完全像遗传和变异的特性探究二(1)狮子(2)机器人和枯树叶生命【课时作业·高效训练】1.C [解析]观察是通过肉眼或借助仪器进行科学探究的基本方法之一。
2.B [解析]木材不是生物,木材燃烧是一种物理和化学反应,不属于生命现象。
3.D [解析]子代与亲代之间的相似性称为遗传。
4.A [解析]病毒是一类没有细胞结构的微小生物。
5.D [解析]图中植物表现出由小长大的生长现象。
6.(1)生物能对外界刺激作出反应(2)营养(3)生长和繁殖(4)生物微型专题探究(一)1.A [解析]生物能对外界刺激作出反应的最大特点是必须有“外界刺激”存在,其次是该刺激能使生物作出一定的反应。
“惟有葵花向日倾”中的外界刺激是阳光,向着太阳生长是葵花对阳光的刺激作出的反应。
2.D [解析]图示鱼“浮头”,鱼浮头的原因是水中的氧气不足,“浮头”的目的是吸入氧气。
第二节调查周边环境中的生物【教材助读·自主学习】1.目的对象整理分析2.(1)动物(2)陆生生物(3)作物家畜【课内探究·展示交流】探究一(1)年级越高,近视率也越高(2)七年级(3)除了自己注意用眼外,还应提醒同学们保护视力(答案不唯一,合理即可) 探究二(1)淡水水域(2)植物动物(3)水生动物两栖动物陆生动物探究三(4)植物动物其他生物【课时作业·高效训练】1.A [解析]用显微镜观察细胞属于观察活动。
2.D [解析]了解各种生物的生活环境是解答本题的关键。
3.A [解析]通过调查才能达到对校园生物进行了解的目的。
4.C5.A [解析]依据形态结构特点可将生物分为动物、植物和其他生物。
部编版四年级语文下册全册课时练习含答案
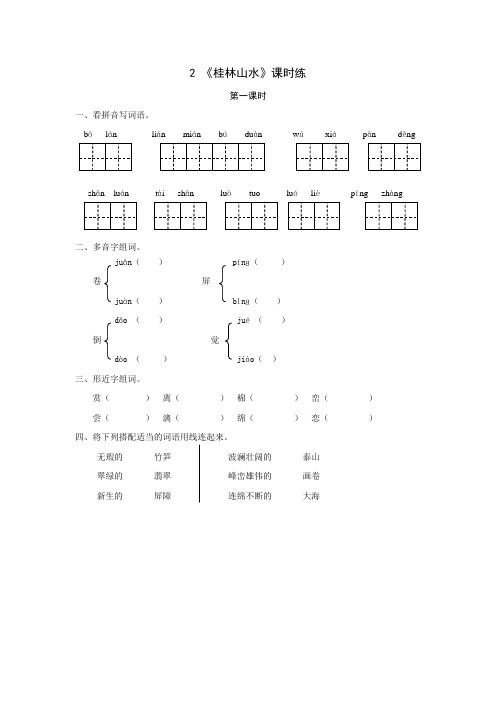
2 《桂林山水》课时练第一课时一、看拼音写词语。
bōlán lián mián búduàn wúxiápān dēngshān luán tài shān luòtuo luólièpíng zhàng二、多音字组词。
juǎn()pínɡ()卷屏juàn()bǐnɡ()dǎo()jué ()倒觉dào()jiào()三、形近字组词。
赏()离()棉()峦()尝()漓()绵()恋()四、将下列搭配适当的词语用线连起来。
无瑕的竹笋波澜壮阔的泰山翠绿的翡翠峰峦雄伟的画卷新生的屏障连绵不断的大海第二课时一、判断句子的正误,在正确的句子后面画“√”,错误的句子后面画“×”。
1.“形态万千”的意思是有一千种或一万种形态、姿态。
()2.“好像一不小心就会栽倒下来”是比喻句。
()3.这篇文章的中心思想是表达了作者对祖国山河的赞美之情。
()4.“这样的山围绕着这样的水”和“这样的水被这样的山围绕着”的意思是一样的。
()5.因为船桨激起的微波扩散出了一道道水纹,所以我才感觉到船在前进,岸在后移。
()二、根据课文内容填空。
1.“桂林山水甲天下”的意思是说,这句话在文中起的作用。
2.课文将、与漓江的水进行比较,是为了突出漓江水的特点;将、与桂林的山进行比较,是为了突出桂林山的特点。
三、请仿照例句为你熟悉的景色写一段话。
漓江的水真静啊,静得让你感觉不到它在流动;漓江的水真清啊,清得可以看见江底的沙石;漓江的水真绿啊,绿得仿佛那是一块无瑕的翡翠。
四、课内阅读。
这样的山(围绕环绕)着这样的水,这样的水(倒映倒立)着这样的山,(在再)加上空中云雾迷(濛蒙),山间绿树红花,江上竹筏小舟,让你感到像是走进了连(绵棉)不断的画卷,真是“舟行碧波上,人在画中游”。
四年级语文下册10《绿》课时练 提高篇(含答案)部编版

四年级语文下册10《绿》课时练提高篇一、看拼音写词语。
huā píng zhǐ huī nèn lǜdàn lǜjí zhōng yōng jǐ二、填空题1.写出下列词语的近义词或反义词。
近义词:出奇——( ) 集中——( ) 交叉——( )反义词:出奇——( ) 交叉——( ) 整齐——( )2.一音多字。
(1).yuán( )圈( )来公( ) ( )于( )旦(2).wéi( )护( )巾( )一( )抗敢作敢( )(3).yán( )色( )谨边( ) 屋( ) ( )究3.照样子写词语。
(1).浅绿(形容绿的词语):___________________、___________________(2).整齐(带有近义词的词语):___________________、___________________(3).姗姗来迟(AABC式词语):___________________、___________________(4).白雪皑皑(ABCC式词语):___________________、___________________ 4.改正下列词语中的错别字。
声色俱历( ) 青萃欲滴( ) 群雄分争( )浮光略影( ) 微不足到( ) 循规蹈距( )5.读下面的句子,体会加下划线的词语的作用。
(1)在我的窗前,有一棵白桦,仿佛涂上银霜,披了一身雪花。
____________________________________________________________________ (2)那草滩的绿,绿得娇嫩;那菜花的黄,黄得蓬勃;而那湖水的蓝,又是蓝得多么醉人啊!____________________________________________________________________ (3)到哪儿去找这么多的绿:墨绿、浅绿、嫩绿、翠绿、淡绿、粉绿……____________________________________________________________________ 三、根据课文内容判断对错,打上“√”或“×”。
北师大版七年级数学下册全册课时练习(一课一练)

北师大版七年级数学下册全册课时练习同底数幂的乘法题组同底数幂的乘法1.有下列式子:①34×34=316;②(-3)4×(-3)3=(-3)7;③-32×(-3)2=(-3)4;④24×22=28.其中计算正确的有( )A.1个B.2个C.3个D.4个【解析】选A.①34×34=38;③-32×(-3)2=-34;④24×22=26;故①③④错误,只有②正确.2.在等式a3·a2·( )=a11中,括号里面的代数式是 ( )A.a7B.a8C.a6D.a3【解析】选C.由a3·a2·( )=a11可得,a5·( )=a11,所以括号里的代数式为a6.3.计算a·a2的结果是( )A.aB.a2C.2a2D.a3【解析】选D.a·a2=a3.4.计算:(1)-a2·a5.(2)x3·x5·x+x6·x3.(3)(2x-1)2·(2x-1)3+(2x-1)4·(1-2x).【解析】(1)-a2·a5=-a2+5=-a7.(2)x3·x5·x+x6·x3=x3+5+1+x6+3=x9+x9=2x9.(3)(2x-1)2·(2x-1)3+(2x-1)4·(1-2x)=(2x-1)2+3+(2x-1)4·[-(2x-1)]=(2x-1)5+[-(2x-1)4+1]=(2x-1)5-(2x-1)5=0.【方法技巧】整式的混合运算顺序是先算乘方,再算乘除,最后算加减,在进行每一种运算时,要明确它们的运算性质.【变式训练】计算:(1)4×2n.(2)x·(-x)2·(-x)2n+1-x2n+2·x2.【解析】(1)原式=22×2n=22+n.(2)原式=-x·x2·x2n+1-x2n+2·x2=-x2n+1+2+1-x2n+2+2=-2x2n+4.题组同底数幂的乘法法则的应用1.如果3x=m,3y=n,那么3x+y等于 ( )A.m+nB.m-nC.mnD.【解析】选C.因为3x=m,3y=n,所以3x+y=3x×3y=mn.【方法指导】同底数幂的乘法法则的逆用法则a m·a n=a m+n(m,n都是正整数),从右向左为a m+n=a m·a n(m,n都是正整数),以此类推=a p·…·a q(p,…,q都是正整数).当幂的指数是和的形式时,可考虑变为同底数幂的乘法,结合已知条件灵活变形,使计算简便.2.x3m+2不等于( )A.x3m·x2B.x m·x2m+2C.x3m+2D.x m+2·x2m【解析】选C.A.x3m·x2=x3m+2;B.x m·x2m+2=x3m+2;C.x3m+2不能再进行运算;D.x m+2·x2m=x3m+2.3.已知2×2x=212,则x的值为( )A.5B.10C.11D.12【解析】选C.因为2×2x=212,所以x+1=12,解得x=11.4.计算22016-22015的结果是( )A.22015B.2C.1D.-22016【解题指南】把2016拆成2015+1,再逆用同底数幂的乘法法则计算.【解析】选A.原式=2×22015-22015=22015.5.已知2x+2=12,则2x=________.【解析】2x+2=2x·22=2x·4=12,因此2x=3.答案:36.(教材变形题·P3随堂练习T2)长方形的长是4.2×103cm,宽为2.5×102cm,求长方形的面积.【解析】4.2×103×2.5×102=10.5×105=1.05×106(cm2).答:长方形的面积为1.05×106cm2.7.计算:(1)(m-n)2(n-m)2(n-m)3.(2)x3·x n-1-x n-2·x4+x n+2.(3)(a+b)·(b+a)·(b+a)2+(a+b)2·(b+a)2.(4)-a2·(-a)2·(-a)2k·(-a)2k+1.【解析】(1)原式=(n-m)2(n-m)2(n-m)3=(n-m)2+2+3=(n-m)7.(2)原式=x3+n-1-x n-2+4+x n+2=x n+2-x n+2+x n+2=x n+2.(3)原式=(a+b)1+1+2+(a+b)2+2=(a+b)4+(a+b)4=2(a+b)4.(4)原式=-a2·(-a)2+2k+2k+1=-a2·(-a)4k+3=-a2·(-a4k+3)=a4k+5.1.为了求1+2+22+23+…+2100的值,可令S=1+2+22+23+…+2100,则2S=2+22+23+24+…+2101,因此2S-S=2101-1,所以1+2+22+23+…+2100=2101-1,仿照以上推理,求:1+5+52+53+…+52017的值.【解析】设S=1+5+52+53+ (52017)则5S=5+52+53+ (52018)所以5S-S=4S=5+52+53+…+52018-(1+5+52+53+…+52017)=52018-1,则S=.2.已知2m+3n能被19整除,求2m+3+3n+3能否被19整除.【解析】2m+3+3n+3=8×2m+27×3n=8×(2m+3n)+19×3n,由(2m+3n)能被19整除,19×3n能被19整除,所以2m+3+3n+3能被19整除.幂的乘方与积的乘方题组幂的乘方、积的乘方运算1.计算(-2a3)2的结果是( )A.-4a6B.4a5C.-4a5D.4a6【解析】选D.根据幂的乘方的运算性质,(-2a3)2=(-2)2a3×2=4a6.2.下列各式计算正确的是( )A.4a-a=3B.a4+a2=a3C.(-a3)2=a6D.a3·a2=6【解析】选 C.根据合并同类项法则“同类项的系数相加,所得的结果作为系数,字母和字母指数保持不变”,可知4a-a=3a,故选项A错误;选项B中“a4”和“a2”不是同类项,故不能进行加减运算,所以选项B错误;根据“(ab)n=a n b n”和“(a m)n=a mn”可知(-a3)2=a6成立,故选项C正确;根据“a m·a n=a m+n”,可知a3·a2=a5,故选项D 错误.3.(-a)3(-a)2(-a5)= ( )A.a10B.-a10C.a30D.-a30【解析】选A.(-a)3(-a)2(-a5)=(-a3)·a2(-a5)=a3+2+5=a10.4.计算:(a2)2= .【解析】(a2)2=a4.答案:a45.计算:(a4)3+m= .【解析】(a4)3+m=a4(3+m)=a12+4m.答案:a12+4m6.如果a n=5,b n=3,则(ab)n= .【解析】(ab)n=a n·b n=5×3=15.答案:157.计算下列各式,结果用幂的形式表示.(1)-23×22.(2)(-2)3×(-2)6.(3)(-x)3·x2·(-x)5.(4)-(-a4)·(-a3)·(-a2).【解析】(1)原式=-25.(2)原式=(-2)9=-29.(3)原式=x3·x2·x5=x10.(4)原式=a4·a3·a2=a9.题组逆用幂的乘方、积的乘方法则1.丁丁认为下列括号内都可以填a4,你认为使等式成立的只能是( )A.a12=( )3B.a12=( )4C.a12=( )2D.a12=( )6【解析】选A.a12=a4×3=(a4)3.2.若3×9m×27m=321,则m的值为( )A.3B.4C.5D.6【解析】选 B.3×9m×27m=3×(32)m×(33)m=3×32m×33m=31+2m+3m=31+5m=321,所以1+5m=21,5m=20,m=4.3.若m=2125,n=375,则m,n的大小关系正确的是( )A.m>nB.m<nC.m=nD.大小关系无法确定【解析】选A.m=2125=25×25=(25)25=3225,n=375=33×25=(33)25=2725,因为32>27,所以m>n.4.逆用积的乘方,小明很轻松地计算出:·22018==1,受他的启发,请你计算一下:×32018= .【解析】×32018=×32017×3=×3=1×3=3.答案:3.5.(2017·深圳市观澜中学质检)若10m=5,10n=3,则102m+3n= .【解析】因为10m=5,10n=3,所以102m+3n=102m×103n=(10m)2×(10n)3=52×33=25×27=675.答案:6756.如果2x+1×3x+1=62x-1,则x的值为.【解析】2x+1×3x+1=2x×2×3x×3=(2×3)x×2×3=6x×6=6x+1=62x-1,所以2x-1=x+1,x=2.答案:27.已知3x-5y-2=0,则8x·32-y的值为.【解析】8x·32-y=(23)x·(25)-y=23x·2-5y=23x-5y.因为3x-5y-2=0,所以3x-5y=2,所以23x-5y=22=4.答案:48.已知2n=3,则4n+1的值是.【解析】因为4n+1=22(n+1)=22n+2=(2n)2×4,把2n=3代入得32×4=9×4=36.答案:369.比较:218×310与210×315的大小.【解析】因为218×310=28×210×310=28×(2×3)10=256×610, 210×315=210×310×35=(2×3)10×35=243×610,又256>243,所以218×310>210×315.10.计算:(1)已知44·83=2x,求x的值.(2)x a=2,y a=3,求(xy)2a的值(3)当a3b2=72时,求a6b4的值.【解析】(1)44·83=(22)4·(23)3=28·29=217,所以x=17.(2)(xy)2a=[(xy)a]2=(x a y a)2=62=36.(3)a6b4=(a3)2(b2)2=(a3b2)2=722=5184.若22·16n=(22)9,解关于x的方程nx+4=2.【解析】22·16n=(22)9变形为22·24n=218,所以2+4n=18,解得n=4.此时方程为4x+4=2,解得x=-.同底数幂的除法题组同底数幂的除法1.计算(a4)3÷(a2)5的结果是( )A.aB.a2C.a3D.a4【解析】选B.(a4)3÷(a2)5=a12÷a10=a2.2.下列运算正确的是( )A.2a5-3a5=a5B.a2·a3=a6C.a7÷a5=a2D.(a2b)3=a5b3【解析】选C.A.原式=-a5,故本选项错误;B.原式=a5,故本选项错误;C.原式=a2,故本选项正确;D.原式=a6b3,故本选项错误.3.计算x7÷x4的结果等于.【解析】x7÷x4=x3.答案:x34.a5÷a2÷a= .【解析】a5÷a2÷a=a5-2-1=a2.答案:a25.已知x a=4,x b=16,则x3a-2b= .【解析】x3a-2b=x3a÷x2b=(x a)3÷(x b)2=43÷162=.答案:【变式训练】若3n=2,3m=5,则32m+3n-1= .【解析】因为3n=2,3m=5,所以32m+3n-1=(3m)2×(3n)3÷3=25×8÷3=.答案:6.计算:(1)(a3)3÷(a4)2.(2)(-a)5÷a3.(3)x m÷x÷x.(4)(x-2y)4÷(2y-x)2÷(x-2y).【解析】(1)原式=a9÷a8=a.(2)原式=-a5÷a3=-a2.(3)原式=x m-1-1=x m-2.(4)原式=(x-2y)4÷(x-2y)2÷(x-2y)=(x-2y)1=x-2y.题组零指数幂和负整数指数幂1.计算3-1等于( )A.3B.-C.-3D.【解析】选D.3-1=.2.计算:20·2-3= ( )A.-B.C.0D.8【解析】选B.20·2-3=1×=.3.若(x-3)0+2(3x-6)-2有意义,则x的取值范围是 ( )A.x>3B.x<2C.x≠3且x≠2D.以上都不对【解析】选C.由题意得x-3≠0,且3x-6≠0,解得x≠3且x≠2.4.若a=,b=,c=0.8-1,则a,b,c三数的大小关系是( )A.a<b<cB.a>b>cC.a>c>bD.c>a>b【解题指南】解决本题的两个步骤(1)求出a,b,c的值.(2)比较a,b,c的大小.【解析】选C.因为a===,b==1,c=0.8-1==,所以a>c>b.5.计算+a2·a3-a2÷a-3的结果为( )A.2a5-aB.2a5-C.a5D.a6【解析】选D.(a2)3+a2·a3-a2÷a-3=a6+a5-a5=a6.6.计算:x0·x3÷x-4= .【解析】x0·x3÷x-4=x3÷x-4=x3+4=x7.答案:x77.计算:(1)(-1)2016+-(3.14-π)0(2)++.【解析】(1)原式=1+4-1=4.(2)原式=-2+4+1=3.1.已知10a=20,10b=,求3a÷3b的值.【解析】因为10a=20,10b=,所以10a÷10b=10a-b=20÷=100=102,所以a-b=2,所以3a÷3b=3a-b=32=9.2.小颖学习了“幂的运算”后做这样一道题:若(2x-3)x+3=1,求x的值,她解出来的结果为x=1,老师说小颖考虑问题不全面,聪明的你能帮助小颖解决这个问题吗?小颖解答过程如下:解:因为1的任何次幂都为1,所以2x-3=1,x=2.且2+3=5,故(2x-3)x+3=(2×2-3)2+3=15=1,所以x=2.你是如何解答的?【解析】①因为1的任何次幂为1,所以2x-3=1,x=2.且2+3=5,所以(2x-3)x+3=(2×2-3)2+3=15=1,所以x=2;②因为-1的任何偶次幂也都是1,所以2x-3=-1,且x+3为偶数,所以x=1,当x=1时,x+3=4是偶数,所以x=1;③因为任何不是0的数的0次幂也是1,所以x+3=0,2x-3≠0,解得x=-3,综上所述,x=2或-3或1.同底数幂的除法题组用科学记数法表示绝对值较小的数1.某种细胞的直径是0.00000095米,将0.00000095用科学记数法表示为( )A.9.5×10-7B.9.5×10-8C.0.95×10-7D.95×10-8【解析】选A.0.00000095=9.5×10-7.2.每到四月,许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰,据测定,杨絮纤维的直径约为0.0000105m,该数值用科学记数法表示为( )A.1.05×105B.0.105×10-4C.1.05×10-5D.105×10-7【解析】选C.0.0000105=1.05×10-5.3.2011年3月,英国和新加坡研究人员制造出观测极限为0.00000005米的光学显微镜.下列将0.00000005米用科学记数法表示正确的是 ( )A.0.5×10-9米B.5×10-8米C.5×10-9米D.5×10-7米【解析】选B.0.00000005米=5×10-8米.4.我们身处在自然环境中,一年接受的宇宙射线及其他天然辐射照射量约为3100微西弗(1西弗等于1000毫西弗,1毫西弗等于1000微西弗),用科学记数法可表示为( )A.3.1×106西弗B.3.1×103西弗C.3.1×10-3西弗D.3.1×10-6西弗【解析】选C.3100微西弗=3.1毫西弗=3.1×10-3西弗.5.下列各数表示正确的是( )A.57000000=57×106B.0.0158(用四舍五入法精确到0.001)≈0.015C.1.804(用四舍五入法精确到十分位)≈1.8D.0.0000257=2.57×10-4【解析】选C.A.57000000=5.7×107,故A错误;B.0.0158(用四舍五入法精确到0.001)≈0.016,故B错误;C.1.804(用四舍五入法精确到十分位)≈1.8,故C正确;D.0.0000257=2.57×10-5,故D错误.6.(2017·常熟市期末)在人体血液中,红细胞的直径约为7.7×10-4cm,7.7×10-4用小数表示为( )A.0.000 077B.0.000 77C.-0.000 77D.0.0077【解析】选B.7.7×10-4用小数表示为0.00077.7.21世纪,纳米技术被广泛应用,纳米是长度计算单位,1纳米=10-9米.VCD光碟的两面有用激光刻成的小凹坑,已知小凹坑的宽度只有0.4微米(1微米=10-6米),试将小凹坑的宽度用纳米作为计算单位表示出来(结果用科学记数法表示). 【解析】0.4微米=(4×10-7米)÷10-9米=4×10-7-(-9)=4×102纳米.8.我们知道一粒大米大约是0.022g.现在请你计算:我国现在14亿人口,按每人三餐计算,若每人每餐节约一粒米,请问全国人民一年大约能节约多少t大米?如果用载重5 t的汽车来运输这些大米,需要多少辆车才能一次装完(一年按365天计算)?【解析】14亿=1.4×109,0.022g=2.2×10-8t.由题意可得2.2×10-8×1.4×109×3×365=3.3726×104(t).需要载重5t的汽车:≈6746(辆),即需要用6746辆汽车才能一次装完.1.观察下列计算过程:(1)因为33÷35===,33÷35=33-5=3-2,所以3-2=.(2)当a≠0时,因为a2÷a7===,a2÷a7=a2-7=a-5,所以a-5=,由此可归纳出规律是:a-p=(a≠0,p为正整数)请运用上述规律解决下列问题:(1)填空:3-10= ;x2×x5÷x9= .(2)3×10-4= .(写成小数形式)(3)把0.00000002写成如(2)的科学记数法a×10n的形式是: .【解析】(1)3-10=;x2×x5÷x9=x2+5-9=x-2=.(2)3×10-4=0.0003.(3)0.00000002=2×10-8.答案:(1)(2)0.0003 (3)2×10-82.一个水分子的质量约为3×10-26kg,一滴水中大约有1.67×1021个水分子,说明分子的质量和体积都很小.如果一只用坏的水龙头每秒钟漏2滴水,假设平均每20滴水为1mL.(1)试计算这只坏的水龙头一昼夜漏水的体积为多少升.(2)这只坏的水龙头一昼夜漏水的质量大约是多少千克?(保留两位小数)(3)你能从中得到什么启示,生活中该怎么做?【解析】(1)根据水龙头1s滴2滴水,一昼夜滴水量为2×60×60×24= 172800(滴).因为20滴为1mL,故一昼夜共漏水172800÷20=8640(mL)=8.64(L).(2)3×10-26×1.67×1021×2×60×60×24≈8.66(kg).所以一昼夜漏水的质量大约是8.66kg.(3)滴漏浪费巨大,应及时修理,定期检修;爱护和保护水资源,是每个公民应尽的责任和义务,从自身做起,像对待掌上明珠一样珍惜每一滴水等(答案不唯一).1.4 整式的乘法第一课时题组单项式乘单项式1.计算4x3·3x6的结果是( )A.7x6B.12x18C.12x9D.7x9【解析】选C.4x3·3x6=(4×3)×(x3·x6)=12x9.2.下列运算正确的是( )A.3x2+4x2=7x4B.2x3·3x3=6x3C.a÷a-2=a3D.=-a6b3【解析】选C.选项A是合并同类项,结果为7x2,故选项A错误;选项B,是同底数幂乘法,结果为6x6,故选项B错误;选项C是同底数幂除法,底数不变,指数相减,故选项C正确;选项D是积的乘方,结果为-a6b3,故选项D错误.3.-2a2bc×□=-6a6b2c,则□内应填的代数式是( )A.3a3bB.-3a3bC.3a4bD.-3a4b【解析】选C.-2×3=-6,a2·a4=a6,b·b=b2,所以□内应填的代数式是3a4b.4.a5·+a6·= .【解析】原式=a5·(-8a3)+a6·9a2=-8a8+9a8=a8.答案:a85.计算:(1)3a·a3-(2a2)2.(2)(-2a2x)3·bx.(3)-2(x-y)×3(x-y)2.【解析】(1)3a·a3-(2a2)2=3a4-4a4=-a4.(2)(-2a2x)3·bx=ax2[(-2)3a6x3]·bx=ax2[(-8)a6x3]·bx=-2a7bx6.(3)原式=(-2×3)(x-y)1+2=-6(x-y)3.6.先化简,再求值:-(-2a)3·(-b3)2+;其中a=-,b=2.【解析】原式=-(-8a3)·b6+=8a3b6-a3b6=a3b6.当a=-,b=2时,原式=××26=××64=-37.题组单项式乘单项式的应用1.一个长方体的底面积是4xy,高是3x,那么这个长方体的体积是 ( )A.7x2yB.7x2C.12x2D.12x2y【解析】选D.由题意,得4xy·3x=12x2y.2.计算(6×103)×(8×105)的结果是( )A.48×109B.4.8×109C.4.8×1016D.48×1015【解析】选B.(6×103)×(8×105)=48×108=4.8×109.3.长方形的长是1.6×103cm,宽是5×102cm,则它的面积是( )A.8×104cm2B.8×106cm2C.8×105cm2D.8×107cm2【解析】选C.(1.6×103)×(5×102)=(1.6×5)×(103×102)=8×105(cm2).【变式训练】如图是一个长方形场地,则它的面积为.【解析】由图可知长方形的长=2a+a+a+2a=6a,宽为3b,所以长方形的面积=6a·3b=18ab.答案:18ab4.已知3x n-3y5-n·(-8x3m y2n)=-24x4y9,m= ,n=【解析】3x n-3y5-n·(-8x3m y2n)=-24x n-3+3m y5-n+2n=,所以5-n+2n=9得n=4;把n=4代入n-3+3m=4得m=1.答案:1 45.三角表示3abc,方框表示-4x y w z,则×的结果是.【解析】×=9mn·(-4n2m5)=-36m6n3.答案:-36m6n36.如图所示,计算变压器铁芯片(图中阴影部分)的面积.(单位:cm)【解析】方法一:用整个长方形面积减去空白部分面积.(1.5a+2.5a)(a+2a+2a+2a+a)-2a·2.5a-2a·2.5a=4a·8a-5a2-5a2=32a2-10a2=22 a2(cm2).方法二:分割求和,即分割成4块的和.1.5a·(a+2a+2a+2a+a)+2.5a·a+2.5a·2a+2.5a·a=1.5a·8a+2.5a2+5a2+2.5a2 =12a2+2.5a2+5a2+2.5a2=22a2(cm2).形如的式子叫做二阶行列式,它的运算法则用公式表示为=ad-bc,比如:=2×3-1×5=1.请你按照上述法则,计算的结果.【解析】=-2ab×(-ab)2-a2b×(-3ab2)=5a3b3.1.4 整式的乘法第二课时题组单项式与多项式相乘1.下列计算不正确的是( )A.-x(3x-1)=-x2+1B.x(x-1)=x2-xC.m(n-m)=-m2+mnD.(x2-x-1)x=x3-1【解析】选A.A.-x(3x-1)=-x2+x,故此选项错误;B.x(x-1)=x2-x,正确;C.m(n-m)=-m2+mn,正确;D.(x2-x-1)x=x3-1,正确.2.化简x(y-x)-y(x-y)得( )A.x2-y2B.y2-x2C.2xyD.-2xy【解析】选B.x(y-x)-y(x-y)=xy-x2-xy+y2=y2-x2.3.下列计算正确的是( )A.a8÷a4=a2B.(2a2)3=6a6C.3a3-2a2=aD.3a(1-a)=3a-3a2【解析】选D.a8÷a4=a8-4=a4.可见A错误.(2a2)3=23(a2)3=8a6.可见B错误.多项式3a3-2a2不能化简,可见C错误.由单项式乘多项式的法则可知D正确.4.计算:2(x-y)+3y= .【解析】①去括号,得2(x-y)+3y=2x-2y+3y;②合并同类项,得2(x-y)+3y=2x+y. 答案:2x+y5.(1)计算(6a3-12a2+9a)= .【解析】(6a3-12a2+9a)=-4a7+8a6-6a5.答案:-4a7+8a6-6a56.计算:(1)3x2(-y-xy2+x2).(2)(-4xy)·(xy+3x2y-2).【解析】(1)3x2(-y-xy2+x2)=3x2·(-y)-3x2·(xy2)+3x2·x2=-3x2y-3x3y2+3x4.(2)(-4xy)·(xy+3x2y-2)=(-4xy)·xy+(-4xy)·3x2y+(-4xy)·(-2)=-4x2y2-12x3y2+8xy.【知识归纳】单项式与多项式相乘,其实质就是乘法分配律的应用,将单项式乘多项式转化为单项式乘单项式,再转化为同底数幂相乘.单项式与多项式相乘,结果是一个多项式,其项数与因式中多项式的项数相同,运算时可以用此来检验运算中是否漏乘.7.化简求值:3a(a2-2a+1)-2a2(a-3),其中a=2.【解析】3a(a2-2a+1)-2a2(a-3)=3a3-6a2+3a-2a3+6a2=a3+3a.当a=2时原式=23+3×2=8+6=14.题组单项式与多项式相乘的应用1.如果长方体的长为3a-4,宽为2a,高为a,则它的体积是( )A.3a2-4aB.a2C.6a3-8a2D.6a2-8a【解析】选C.由题意可得:长方体的体积是:(3a-4)×2a×a=(3a-4)×2a2=6a3-8a2.2.若三角形的底边为2m+1,底边上的高为2m,则此三角形的面积为 ( )A.4m2+2mB.4m2+1C.2m2+mD.2m2+m【解析】选C.因为三角形的底边为2m+1,底边上的高为2m,所以此三角形的面积为:×2m×(2m+1)=2m2+m.3.如果(x2-a)x+x的展开式中只含有x3这一项,那么a的值为( )A.1B.-1C.0D.不能确定【解析】选A.(x2-a)x+x=x3-ax+x=x3+(1-a)x,因为只含x3这一项所以1-a=0,a=1.4.已知2m-3n=-4,则代数式m(n-4)-n(m-6)的值为.【解析】m(n-4)-n(m-6)=mn-4m-mn+6n=-4m+6n=-2(2m-3n)=-2×(-4)=8.答案:85.若-2x2y(-x m y+3xy3)=2x5y2-6x3y n,则m= ,n= .【解析】-2x2y(-x m y+3xy3)=2x2+m y2-6x3y4=2x5y2-6x3y n,所以2+m=5,m=3,n=4.答案:3 46.若要使x(x2+a+3)=x(x2+5)+2(b+2)成立,则a,b的值分别为.【解析】已知等式变形得:x3+(a+3)x=x3+5x+2(b+2),可得a+3=5,2(b+2)=0,解得:a=2,b=-2.答案:2,-27.如图,一长方形地块用来建造住宅、广场、商厦,求这块地的面积.【解析】长方形地块的长为:(3a+2b)+(2a-b),宽为4a,这块地的面积为:4a·[(3a+2b)+(2a-b)]=4a·(5a+b)=4a·5a+4a·b=20a2+4ab.答:这块地的面积为20a2+4ab.某同学在计算一个多项式乘以-2a时,因抄错运算符号,算成了加上-2a,得到的结果是a2+2a-1,那么正确的计算结果是多少?【解析】因为计算一个多项式乘以-2a时,因抄错运算符号,算成了加上-2a,得到的结果是a2+2a-1,所以这个多项式为:a2+2a-1+2a=a2+4a-1,所以正确的计算结果是:-2a(a2+4a-1)=-2a3-8a2+2a.1.4 整式的乘法第三课时题组多项式与多项式相乘1.下列算式的计算结果等于x2-5x-6的是( )A.(x-6)(x+1)B.(x+6)(x-1)C.(x-2)(x+3)D.(x+2)(x-3)【解析】选A.A.(x-6)(x+1)=x2+x-6x-6=x2-5x-6,符合题意;B.(x+6)(x-1)=x2-x+6x-6=x2+5x-6,不符合题意;C.(x-2)(x+3)=x2+3x-2x-6=x2+x-6,不符合题意;D.(x+2)(x-3)=x2-3x+2x-6=x2-x-6,不符合题意.【规律总结】(x+a)(x+b)型多项式的乘法因为(x+a)(x+b)=x2+ax+bx+ab= x2+(a+b)x+ab,所以(x+a)(x+b)=x2+(a+b)x+ab.【变式训练】计算:(x+5)(x-4)= .【解析】(x+5)(x-4)=x2+x-20.答案:x2+x-202.下列计算正确的是( )A.(x+2)(2-x)=x2-4B.(2x+y2)(2x2-y2)=2x2-y4C.(3x2+1)(3x2-1)=9x4-1D.(x-2)(x+3)=x2-6【解析】选C.A.(x+2)(2-x)=-x2+4,故A选项错误;B.(2x+y2)(2x2-y2)=4x3-2xy2+2x2y2-y4,故B选项错误;C.(3x2+1)(3x2-1)=9x4-1,故C选项正确;D.(x-2)(x+3)=x2+x-6,故D选项错误.3.计算(2x2-4)= ( )A.-x2+2B.x3+4C.x3-4x+4D.x3-2x2-2x+4【解析】选D.(2x2-4)=(2x2-4)=x3-2x2-2x+4.4.若3x(2x-3)-(4-2x)x=8x2-3x+4,则x的值等于 ( )A. B.- C. D.-【解析】选B.3x(2x-3)-(4-2x)x=8x2-3x+4,6x2-9x-4x+2x2=8x2-3x+4,-13x+3x=4,-10x=4,x=-.5.计算:(1)(2x-1)(-1-2x)= .(2)(-a+2b)(a2+2ab+4b2)= .【解析】(1)(2x-1)(-1-2x)=-2x-4x2+1+2x=1-4x2.(2)(-a+2b)(a2+2ab+4b2)=-a3-2a2b-4ab2+2a2b+4ab2+8b3=-a3+8b3答案:(1)1-4x2(2)-a3+8b3【方法指导】多项式与多项式相乘1.第一步要先进行整理,在用一个多项式的每一项去乘另一个多项式的每一项时,要“依次”进行,不重复,不遗漏,且各个多项式中的项不能自乘.2.多项式是几个单项式的和,每一项都包括前面的符号,在计算时要正确确定积中各项的符号.6.化简:x(x+1)-(x+1)(x-2).【解析】原式=x2+x-(x2-x-2)= x2+x-x2+x+2=2x+2.题组多项式与多项式相乘的应用1.如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式,你认为其中正确的有( )①(2a+b)(m+n);②2a(m+n)+b(m+n);③m(2a+b)+n(2a+b);④2am+2an+bm+bn.A.①②B.③④C.①②③D.①②③④【解析】选D.①大长方形的长为2a+b,宽为m+n,利用长方形的面积公式,表示即可;①(2a+b)(m+n),故①正确;②长方形的面积等于左边、右边及中间的长方形面积之和,表示即可;②2a(m+n)+b(m+n),故②正确;③长方形的面积等于上下两个长方形面积之和,表示即可;③m(2a+b)+n(2a+b),故③正确;④长方形的面积等于6个长方形的面积之和,表示即可.④2am+2an+bm+bn,故④正确,则正确的有①②③④.2.若=x2+mx+n,则m,n分别为( )A.m=4,n=12B.m=-4,n=12C.m=-4,n=-12D.m=4,n=-12【解析】选D.原式 =x2+4x-12=x2+mx+n,所以m=4,n=-12.3.若(x+m)(x-8)中不含x的一次项,则m的值为 ( )A.8B.-8C.0D.8或-8【解析】选A.(x+m)(x-8)=x2-8x+mx-8m=x2+(m-8)x-8m.因为不含x的一次项,所以m-8=0,m=8.【变式训练】若多项式乘法(x+2y)(2x-ky-1)的结果中不含xy项,则k的值为( )A.4B.-4C.2D.-2【解析】选A.(x+2y)(2x-ky-1)=2x2-kxy-x+4xy-2ky2-2y=2x2+(4-k)xy-x-2ky2-2y,因为结果中不含xy项,所以4-k=0,解得k=4.4.若M=(a+3)(a-4),N=(a+2)(2a-5),其中a为有理数,则M,N的大小关系是( )A.M>NB.M<NC.M=ND.无法确定【解析】选B.因为M-N=(a+3)(a-4)-(a+2)(2a-5)=a2-a-12-2a2+a+10=-a2-2≤-2<0,所以M<N.5.已知:a+b=,ab=1,化简(a-2)(b-2)的结果是.【解析】(a-2)(b-2)=ab-2a-2b+4=ab-2(a+b)+4=1-2×+4=1-3+4=2.答案:26.解方程:(x+1)(x-1)=(x+2)(x-3).【解析】因为(x+1)(x-1)=(x+2)(x-3),所以x2-1=x2-x-6.解得:x=-5.7.如图,长为10cm,宽为6cm的长方形,在4个角剪去4个边长为xcm的小正方形后,按折痕做成一个有底无盖的长方体盒子,试求盒子的体积.【解析】根据题意可得:长方体盒子的长为(10-2x)cm,宽为(6-2x)cm,高为xcm. 所以长方体盒子的体积V=(10-2x)·(6-2x)·x=(4x2-32x+60)x=(4x3-32x2+60x)cm3.答:盒子的体积为(4x3-32x2+60x)cm3.1.(1)计算:(x+1)(x+2)= ,(x-1)(x-2)= ,(x-1)(x+2)= ,(x+1)(x-2)= .(2)你发现(1)小题有何特征,会用公式表示出来吗?(3)已知a,b,m均为整数,且(x+a)(x+b)=x2+mx+12,则m的可能取值有多少个? 【解析】(1)(x+1)(x+2)=x2+3x+2,(x-1)(x-2)=x2-3x+2,(x-1)(x+2)=x2+x-2,(x+1)(x-2)=x2-x-2.(2)可以发现题(1)中,左右两边式子符合(x+p)(x+q)=x2+(p+q)x+pq结构.(3)因为12可以分解以下6组数,12=1×12,2×6,3×4,(-1)×(-12),(-2)×(-6),(-3)×(-4),所以m=a+b应有6个值.2.你能化简(x-1)(x99+x98+…+x+1)吗?遇到这样的复杂问题时,我们可以先从简单的情形入手.然后归纳出一些方法.(1)分别化简下列各式:(x-1)(x+1)= ;(x-1)(x2+x+1)= ;(x-1)(x3+x2+x+1)= ;…(x-1)(x99+x98+…+x+1)= .(2)请你利用上面的结论计算:299+298+…+2+1.【解析】(1)(x-1)(x+1)=x2-1;(x-1)(x2+x+1)=x3-1;(x-1)(x3+x2+x+1)=x4-1;…(x-1)(x99+x98+…+x+1)=x100-1.答案:x2-1 x3-1 x4-1 x100-1(2)299+298+…+2+1=(2-1)×(299+298+…+2+1)=2100-1.平方差公式第一课时题组平方差公式1.下列式子不能用平方差公式计算的是( )A.(-x+y)(-x-y)B.(a-b)(b-a)C.(a-b)(a+b)D.(-x-1)(x-1)【解析】选B.A.(-x+y)(-x-y)中-x与-x相同,y与-y互为相反数,能用平方差公式;B.(a-b)(b-a)中a与-a互为相反数,-b与b互为相反数,不能用平方差公式;C.(a-b)(a+b)中a与a相同,-b与b互为相反数,能用平方差公式;D.(-x-1)(x-1)中-x与x互为相反数,-1与-1相同,能用平方差公式.2.化简(a+b+c)2-(a-b+c)2的结果为( )A.4ab+4bcB.4acC.2acD.4ab-4bc【解析】选A.(a+b+c)2-(a-b+c)2=(a+b+c+a-b+c)(a+b+c-a+b-c)=(2a+2c)(2b)=4ab+4bc.3.已知a+b=3,a-b=5,则a2-b2= ( )A.3B.8C.15D.-2【解析】选C.因为(a+b)(a-b)=a2-b2,而a+b=3,a-b=5,所以3×5=a2-b2=15.【变式训练】若a2-b2=,a-b=,则a+b的值为.【解析】(a+b)(a-b)=a2-b2=,a-b=,所以a+b=.4.等式(-a-b)( )(b2+a2)=a4-b4中,括号内应填( )A.a-bB.-a+bC.-a-bD.a+b【解析】选B.因为a4-b4=(a2+b2)(a2-b2),所以a2-b2=(-a-b)( ).( )应填(-a+b).5.计算(4x+3b)(4x-3b)= __.【解析】(4x+3b)(4x-3b)=(4x)2-(3b)2=16x2-9b2.答案:16x2-9b26.计算:(x+y+z)(x+y-z)=(A+B)(A-B),则A= ,B= .【解析】在x+y+z和x+y-z中完全相同的是x+y,z与-z互为相反数,所以A=x+y,B=z.答案:x+y z7.如果x+y=2,x2-y2=10,则x-y= _.【解析】x2-y2=(x+y)(x-y)=2(x-y)=10,所以x-y=5.答案:58.若(x+3a)(x-3a)=x2-36,则a的值为_. 【解析】(x+3a)(x-3a)=x2-9a2=x2-36,所以-9a2=-36,a2=4,因为(±2)2=4,所以a=±2.答案:±29.计算:(1).(2)(a+b-c)(-a+b+c).【解析】(1)===-x4.(2)(a+b-c)(-a+b+c)=[b+(a-c)][b-(a-c)]=b2-(a-c)2=b2-(a2-2ac+c2)=b2-a2+2ac-c2.1.计算:(2x+3y)(2x-3y)-(-3x+5y)(-3x-5y). 【解析】(2x+3y)(2x-3y)-(-3x+5y)(-3x-5y)=(2x)2-(3y)2-[(-3x)2-(5y)2]=4x2-9y2-9x2+25y2=16y2-5x2.2.计算:(1+x)(1-x)(1+x2)(1+x4).【解析】(1+x)(1-x)(1+x2)(1+x4)=(1-x2)(1+x2)(1+x4)=(1-x4)(1+x4)=1-x8.平方差公式第二课时题组利用平方差公式进行数的运算1.运用平方差公式计算40×39,可以变形为( )A.×B.×C.×D.×【解题指南】运用平方差公式进行数的简便运算应满足两点:一是把算式变形为相同两数的和与差;二是变成平方差公式的形式后两个因数的大小不变.【解析】选D.由÷2=40得,40×39=×.2.下列代数式的值是1的是( )A.20092-2008×2010B.20092-2009×2010C.20092-2009×2008D.20092-20082【解析】选A.A.20092-2008×2010=20092-(2009-1)(2009+1)=20092-20092+1=1,此选项正确;B.20092-2009×2010=20092-(2009.5-0.5)(2009.5+0.5)=20092-2009.52+0.25,计算结果不是1,此选项错误;C.20092-2009×2008=20092-(2008.5+0.5)(2008.5-0.5)=20092-2008.52+0.25,计算结果不是1,此选项错误; D.20092-20082=(2009+2008)(2009-2008)=4017,计算结果不是1,此选项错误.3.计算的结果是 ( )A.62500B.1000C.500D.250【解析】选C.原式=====500.4.计算142-13×15的结果是__.【解析】142-13×15=142-(14-1)(14+1)=142-142+1=1. 答案:15.计算:9×11×101×10001.【解析】9×11×101×10001=99×101×10001=(100-1)(100+1)×10001=(1002-1)×10001=9999×10001=(10000-1)(10000+1)=100002-1=99999999.6.利用整式乘法公式进行计算:992-1.【解析】原式=(99+1)×(99-1)=100×98=9800.题组利用平方差公式进行整式的运算1.计算(1+3x)(3x-1)+9的结果是( )A.18x2-2B.2-18x2C.0D.8x2【解析】选C.(1+3x)(3x-1)+9=(3x)2-1+9=9x2-1+1-9x2=0.2.代数式(y-1)(y+1)(y2+1)-(y4+1)的值是( )A.0B.2C.-2D.不能确定【解析】选C.(y-1)(y+1)(y2+1)-(y4+1)=(y2-1)(y2+1)-(y4+1)=y4-1-y4-1=-23.(2017·温州中考)化简:(1+a)(1-a)+a(a-2).【解析】原式=1-a2+a2-2a=1-2a.4.计算:-(3a-2b)(3a+2b).【解析】原式=a2-b2-(9a2-4b2)=a2-b2-9a2+4b2=-8a2+b2.5.解方程:(3-x)(3+x)-x(5-x)=4.【解析】(3-x)(3+x)-x(5-x)=4.9-x2-5x+x2=4.9-5x=4.-5x=-5.x=1.6.先化简,再求值:(x+2)(x-2)-x(x-1),其中x=-2.【解析】原式=x2-4-x2+x=x-4.把x=-2代入,得原式=-2-4=-6.1.若A=(2+1)(22+1)(24+1)(28+1)+1,则A的末位数字是__. 【解析】A=(2-1)(2+1)(22+1)(24+1)(28+1)+1=216.21的末位数字是2,22的末位数字是4,23的末位数字是8,24的末位数字是6,25的末位数字是2,26的末位数字是4,16÷4=4,所以216的末位数字是6.答案:62.乘法公式的探究及应用:(1)如图1所示,可以求出阴影部分面积是__.(写成两数平方差的形式)(2)若将图1中的阴影部分裁剪下来,重新拼成一个如图2的矩形,此矩形的面积是__.(写成多项式乘法的形式)(3)根据两图的阴影部分面积得到的乘法公式计算下列算式:(1-)(1-)(1-)(1-)…(1-)(1-).【解析】(1)a2-b2.(2)(a+b)(a-b).(3)原式=…=××××…××××=×=.完全平方公式题组完全平方公式1.下列各式,计算正确的是( )A.(2x-y)2=4x2-2xy+y2B.(a2+2b)2=a2+4a2b+4b2C.=x2+1+xD.(x-2y)2=x2-4xy+y2【解析】选C.A.(2x-y)2=4x2-4xy+y2,此选项错误;B.(a2+2b)2=a4+4a2b+4b2,此选项错误;C.=x2+1+x,此选项正确;D.(x-2y)2=x2-4xy+4y2,此选项错误.2.小虎在利用完全平方公式计算时,不小心用墨水将式子中的两项染黑:(2x+)2=4x2+12xy+,则被染黑的最后一项应该是 ( )A.3yB.9yC.9y2D.36y2【解析】选C.(2x)2=4x2,2·2x( )=12xy,所以括号里应填3y,(3y)2=9y2.3.计算(-2y-x)2的结果是( )A.x2-4xy+4y2B.-x2-4xy-4y2C.x2+4xy+4y2D.-x2+4xy-4y2【解析】选C.(-2y-x)2=x2+4xy+4y2.4.计算(2a-3)2的结果为__.【解析】(2a-3)2=4a2-2·2a·3+9=4a2-12a+9.答案:4a2-12a+95.(x- )2=x2-6xy+ .【解析】2·x( )=6xy,括号里应填3y,(3y)2=9y2.答案:3y 9y26.计算:(1)(-x+2y)2.(2)(m+n-2)(m+n+2).(3).(4)(a+b)2(a-b)2.【解析】(1)(-x+2y)2=x2+2·(-x)·2y+4y2=x2-4xy+4y2.(2)(m+n-2)(m+n+2)=(m+n)2-22=m2+2mn+n2-4.(3)===a4-2·a2·+=a4-a2+.(4)(a+b)2(a-b)2=[(a+b)(a-b)]2=(a2-b2)2=a4-2a2b2+b4.【方法技巧】完全平方公式应用的三个技巧1.公式右边共有3项.2.两个平方项符号永远为正.3.中间项的符号由等号左边两项的符号是否相同决定.题组完全平方公式的应用1.若a+b=3,a2+b2=7,则ab等于 ( )A.2B.1C.-2D.-1【解析】选B.因为(a+b)2=a2+2ab+b2,所以ab===1. 【变式训练】已知x+y=-6,x-y=5,则下列计算正确的是( )A.(x+y)2=36B.(y-x)2=-10C.xy=-2.75D.x2-y2=25【解析】选A.A.(x+y)2=(-6)2=36,正确;B.(y-x)2=(x-y)2=52=25,故本选项错误;C.因为(x+y)2-(y-x)2=4xy,(x+y)2-(y-x)2=36-25=11,所以4xy=11,xy=2.75,故本选项错误;D.x2-y2=(x+y)(x-y)=(-6)×5=-30,故本选项错误.2.若等式(x-4)2=x2-8x+m2成立,则m的值是( )A.16B.4C.-4D.4或-4【解析】选D.因为(x-4)2=x2-8x+16,所以m2=16,解得m=±4.3.一个正方形的边长增加了2cm,面积相应增加了32cm2,则原来这个正方形的边长为( )A.6cmB.5cmC.8cmD. 7cm【解析】选D.设原来正方形的边长为xcm.则(x+2)2-x2=32.x2+4x+4-x2=32.4x=28.x=7.4.设(5a+3b)2=(5a-3b)2+A,则A= ( )A.30abB.60abC.15abD.12ab【解析】选B.因为(5a+3b)2=25a2+30ab+9b2,所以25a2+9b2=(5a+3b)2-30ab.因为(5a-3b)2=25a2-30ab+9b2,所以25a2+9b2=(5a-3b)2+30ab.所以(5a+3b)2-30ab=(5a-3b)2+30ab.所以(5a+3b)2=(5a-3b)2+60ab.5.已知x2+y2+4x-6y+13=0,那么x y= __.【解析】因为x2+y2+4x-6y+13=0,所以x2+4x+4+y2-6y+9=0,即(x+2)2+(y-3)2=0,所以x+2=0,y-3=0,解得x=-2,y=3,所以x y=(-2)3=-8.答案:-81.已知x=m时,多项式x2+2x+n2的值为-1,则x=-m时,该多项式的值为. 【解析】当x=m时,m2+2m+n2=-1,则(m+1)2+n2=0,∴m+1=0,n=0,∴m=-1,n=0,∴x2+2x+n2=3.答案:32.乘法公式的探究及应用.图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.(1)请用两种不同的方法求图②中阴影部分的面积.方法一: _______________________________________.方法二: _______________________________________.(2)观察图②请你写出下列三个代数式:(a+b)2,(a-b)2,ab之间的等量关系.______________________________________________________.(3)根据(2)题中的等量关系,解决如下问题:已知:a-b=5,ab=-6,求:①a2+b2= ___.②(a+b)2= _.【解析】(1)方法一:阴影部分是正方形,正方形的边长是m-n,即阴影部分的面积是(m-n)2,方法二:阴影部分的面积S=(m+n)2-4mn,答案:(m-n)2(m+n)2-4mn(2)(a-b)2=(a+b)2-4ab.答案:(a-b)2=(a+b)2-4ab(3)①因为a-b=5,ab=-6,所以(a-b)2=52,所以a2-2ab+b2=25,a2+b2=25+2ab=25-12=13.答案:13②(a+b)2=(a-b)2+4ab=52+4×(-6)=1.答案:1完全平方公式第二课时题组利用完全平方公式进行数的运算1.运用完全平方公式计算89.82的最佳选择是( )A.(89+0.8)2B.(80+9.8)2C.(90-0.2)2D.(100-10.2)2【解析】选 C.A.(89+0.8)2=892+2×89×0.8+0.82,B.(80+9.8)2=802+2×80×9.8+9.82,C.89.82=(90-0.2)2=902-2×90×0.2+0.22,D.(100-10.2)2=1002-2×100×10.2+10.22,选项A,B,D都不如选项C计算简便.2.用乘法公式计算:3992= __.【解析】3992=(400-1)2=4002-2×400×1+12=160000-800+1=159201答案:1592013.计算3.76542+0.4692×3.7654+0.23462= __.【解析】3.76542+0.4692×3.7654+0.23462=3.76542+2×0.2346×3.7654+0.23462=(3.7654+0.2346)2=42=16.答案:164.利用整式乘法公式计算:(1)962. (2)2032.【解析】(1)962=(100-4)2=1002-2×100×4+42=10000-800+16=9216.(2)2032=(200+3)2=2002+2×200×3+32=40000+1200+9=41209.5.已知m=2016×2017-1,n=20162-2016×2017+20172,请尝试用一种简便方法比较m,n的大小.【解析】方法一:m=2016×2017-1,n=20162-2016×2017+20172=20162-2×2016×2017+20172+2016×2017=(2016-2017)2+2016×2017=2016×2017+1,因为2016×2017-1<2016×2017+1,所以m<n.方法二:n-m=20162-2016×2017+20172-(2016×2017-1)=20162-2016×2017+20172-2016×2017+1=20162-2×2016×2017+20172+1=(2016-2017)2+1=1+1=2>0,所以n-m>0,即n>m.题组与完全平方公式有关的整式运算1.(a+3b)2-(3a+b)2的计算结果是( )A.8(a-b)2B.8(a+b)2C.8b2-8a2D.8a2-8b2【解析】选C.(a+3b)2-(3a+b)2=a2+6ab+9b2-(9a2+6ab+b2)=a2+6ab+9b2-9a2-6ab-b2=-8a2+8b2.2.将正方形的边长由acm增加6cm,则正方形的面积增加了 ( )A.36cm2B.12acm2C.(36+12a)cm2D.以上都不对【解析】选C.(a+6)2-a2=a2+12a+36-a2=12a+36cm2.3.用乘法公式计算:(1)(a+2b-3c)(a-2b+3c).(2)(a+2b-3c)2.【解析】(1)(a+2b-3c)(a-2b+3c)=[a+(2b-3c)][a-(2b-3c)]=a2-(2b-3c)2=a2-(4b2-12bc+9c2)=a2-4b2+12bc-9c2.(2)(a+2b-3c)2=[(a+2b)-3c]2=(a+2b)2-2(a+2b)·3c+(3c)2=a2+4ab+4b2-6ac-12bc+9c2.4.下面是小颖化简整式的过程,仔细阅读后解答所提出的问题.解:x(x+2y)-(x+1)2+2x=x2+2xy-x2+2x+1+2x 第一步=2xy+4x+1 第二步(1)小颖的化简过程从第步开始出现错误.(2)对此整式进行化简.【解析】(1)括号前面是负号,去掉括号应变号,故第一步出错.答案:一(2)x(x+2y)-(x+1)2+2x=x2+2xy-x2-2x-1+2x=2xy-1.5.小明和小颖同时解答下面的习题,所用的方法不相同,但所得的结果相同,先阅读他们的解法,然后回答问题.计算:.小明的解答:=。
2022年人教版高考生物一轮考点复习过关 课时规范练10 光合作用、细胞呼吸综合

课时规范练10光合作用、细胞呼吸综合一、选择题1.(2021八省联考湖南卷)适宜的温度和光照条件下,在盛有水生动植物的鱼缸内(不考虑微生物的影响),物质代谢处于相对平衡状态的是()A.动物细胞呼吸释放的CO2量等于植物光合作用吸收的CO2量B.动物细胞呼吸吸收的O2量等于植物光合作用产生的O2量C.动植物细胞呼吸释放的CO2量等于植物光合作用吸收的CO2量D.动物细胞呼吸消耗的有机物量等于植物光合作用合成的有机物量2.(2021广东汕头三模)高等植物通过光合作用固定太阳能,同时也进行细胞呼吸释放能量。
下列关于高等植物光合作用和有氧呼吸的说法,正确的是()A.光合作用和有氧呼吸均产生还原性辅酶,且来源相同B.植物个体的所有细胞均能进行光合作用和有氧呼吸C.光合作用只在叶绿体中进行,有氧呼吸只在线粒体中进行D.光合作用和有氧呼吸都能产生ATP,但去向不同3.(2021山东泰安三模)下列有关农谚的解释,错误的是()4.(2021八省联考广东卷)下列所述生产与生活中的做法,合理的是()A.做面包时加入酵母菌并维持密闭状态B.水稻田适时排水晒田以保证根系通气C.白天定时给栽培大棚通风以保证氧气供应D.用不透气的消毒材料包扎伤口以避免感染5.(2021辽宁,2)植物工厂是通过光调控和通风控温等措施进行精细管理的高效农业生产系统,常采用无土栽培技术。
下列有关叙述错误的是()A.可根据植物生长特点调控光的波长和光照强度B.应保持培养液与植物根部细胞的细胞液浓度相同C.合理控制昼夜温差有利于提高作物产量D.适时通风可提高生产系统内的CO2浓度6.(2020浙江7月选考,25)将某植物叶片分离得到的叶绿体,分别置于含不同蔗糖浓度的反应介质溶液中,测量其光合速率,结果如下图所示。
图中光合速率用单位时间内单位叶绿素含量消耗的二氧化碳量表示。
下列叙述正确的是()A.测得的该植物叶片的光合速率小于该叶片分离得到的叶绿体的光合速率B.若分离的叶绿体中存在一定比例的破碎叶绿体,测得的光合速率与无破碎叶绿体的相比,光合速率偏大C.若该植物较长时间处于遮阴环境,叶片内蔗糖浓度与光合速率的关系与图中BC段对应的关系相似D.若该植物处于开花期,人为摘除花朵,叶片内蔗糖浓度与光合速率的关系与图中AB段对应的关系相似7.(2021湖南,7)绿色植物的光合作用是在叶绿体内进行的一系列能量和物质转化过程。
高中物理课时素养评价十弹力含解析粤教版1

弹力(25分钟·60分)一、选择题(本题共6小题,每题6分,共36分)1。
(2020·肇庆高一检测)如图所示,杯底对铅笔底端的弹力的方向是 ()A.垂直于杯底向上B。
垂直于杯底向下C.垂直于铅笔杆斜向左上方D.垂直于铅笔杆斜向右下方【解析】选A。
杯底对铅笔底端的弹力,是由于杯底发生弹性形变,要恢复原状,从而对铅笔产生弹力,弹力方向垂直杯底向上,故A正确,B、C、D错误;故选A.2。
足球运动是目前全球体育界最具影响力的项目之一,深受青少年喜爱。
如图所示为四种与足球有关的情景。
下列说法正确的是()【解析】选 C.静止在草地上的足球受到的弹力,与重力相平衡,但不是它的重力,故A错误;静止在光滑水平地面上的两个足球相互接触,若没有弹性形变,就没有受到相互作用的弹力,B错误;踩在脚下且静止在水平草地上的足球受到重力、支持力及人脚的压力的作用,故受到3个力的作用,故C正确;进球时,足球撞到网上,球网被撑开,由于网的形变,而使球受到了弹力;故D 错误;故选C。
3。
如图所示,为了观察桌面的微小形变,在一张大桌子上放两个平面镜M和N,让一束光依次被这两面镜子反射,最后射到墙上,形成一个光点。
实验中,用力按压两镜之间的桌面,观察到的现象是()A.桌面明显向下凹陷B.N镜明显向右倾斜C。
M镜明显向左倾斜 D.光点位置明显变化【解析】选D.用力按压桌面,桌面向下发生微小的凹陷,故A错误。
桌面不会发生明显凹陷,则N镜不会明显向右倾斜,M镜不会明显向左倾斜,故B、C错误.在两镜之间用力F向下按压桌面,M、N将向中间略微倾斜,光束的入射角减小,由光的反射定律可知,反射角减小会加倍,则光点位置明显变化,故D正确。
故选D。
4.关于弹性形变与非弹性形变,下列说法正确的是()A。
物体受力后发生的一切形变都可视为弹性形变B。
物体在去掉外力后,能够恢复原来形状的形变为非弹性形变C.当你坐在椅子上时,椅面发生的微小形变可视为弹性形变D。
《济南的冬天》课时训练(解析版)

2 济南的冬天★积累运用(2022秋·安徽省滁州市凤阳县宋集中学第一次月考)1.阅读下面文字,完成下列各题。
那水呢,不结冰,倒反在绿苹上冒着热气,水(zâo)真绿,把终年贮蓄的绿色全拿出来了,天儿越晴,水藻越绿,就凭着这些绿的精神,水也不忍得冻上,那些长枝的垂柳还要在水里照个影呢!看吧,由(chéng)清的河水慢慢往上看吧,空中,半空中,天上,自上而下全是那么清亮,那么蓝汪汪,整个是块空灵的蓝水晶。
(1)给划线词注音,根据拼音写汉字。
①水(zâo)②贮蓄③(chéng)清(2)文中有个错别字是“”,正确写法是“”(3)文中划线字“贮”查部,“贮”正确解释是A收藏;收获 B 储存;积存 C 储蓄(钱财)(4)在原文括号里填上适当的关联词语。
【答案】(1)藻;zhù;澄(2)“绿苹”;“绿萍”(3)贝;B (4)不但况且【解析】(1)考查汉字字音字形。
重点关注课文中常见易写错、易混淆的字词,熟读熟记。
水藻:水生藻类植物。
藻的一种,水中很多。
贮蓄:1.储存,积聚。
2.指储存的物品。
3.把节约下来或暂时不用的钱存起来。
多指存到银行里。
4.指积存的钱。
澄清:指杂质沉淀,液体变清;形容水清而透明。
(2)阅读语段,错别字是“绿苹”,正确写法是“绿萍”。
(3)考查字词的理解能力。
根据字词原义和结合文段内容进行理解。
文中加点字"贮"查“贝"部。
贮蓄:1.储存,积聚。
2.指储存的物品。
3.把节约下来或暂时不用的钱存起来多指存到银行里。
4.指积存的钱。
根据"把终年贮蓄的绿色全拿出来了”可知,“贮”的意思是储存,积存,故选B。
(4)考查关联词的运用。
解答此题,只要弄清楚句与句之间存在的关系,然后选用正确的关联词语就可以了。
根据"倒反”—词,可知第一个空应填关联词“不但”;根据句意,第二个空应填表示递进关系的关联词“况且。
_高中政治课时练习11源远流长的中华文化含解析新人教版必修

源远流长的中华文化(15分钟·30分)一、选择题(每小题5分,共15分)1.孔子的思想历经两千多年仍被传承,体现了中华文化的源远流长。
下列对中华文化能够源远流长的原因说法正确的是( )①汉字的使用②史书典籍的传承③社会制度的更替④中华文化是世界上最优秀的文化A.①②B.③④C.①③D.②④【解析】选A。
汉字的使用和史书典籍的传承是中华文化能够源远流长的重要原因,①②符合题意;社会制度的更替不是文化源远流长的原因,③不符合题意;各民族文化一律平等,没有高低优劣之分,④错误。
2.(2020·郑州高二检测)海峡两岸汉字节、巴黎汉字节、中国文字学高端论坛暨中国文字学会召开……近年来,这些以“汉字之美”为主题的文化活动逐渐红火起来。
人们之所以重视学习和研究汉字,是因为汉字( )①具有集形、音、义三者为一体的特点②是继承和传播中华文化的重要载体③对增强民族认同感发挥着重要作用④是记录和传承中华文明的唯一工具A.①②B.①④C.②③D.③④【解析】选C。
我们重视汉字是因为它是继承和传播中华文化的重要载体,对增强民族认同感发挥着不可替代的作用,②③符合题意。
形、音、义三者是汉字的特点,与题干不构成因果关系,排除①。
汉字不是记录和传承中华文明的唯一工具,④错误。
【补偿训练】1.中国有修史的传统,“国有史、方有志、家有谱”。
继承这一传统,有利于中华文化( )A.薪火相传,一脉相承B.以我为主,为我所用C.全盘继承,保持本色D.面向世界,博采众长【解析】选A。
修史有利于中华文化的传承,A符合题意;B、D涉及如何正确对待外来文化的问题,与题意不符;对待传统文化要在继承的基础上创新,C错误。
2.(2020·景德镇高二检测)下列史实体现了中华文化“源远流长,一脉相承”的是 ( )A.佛教从印度传到中国,并实现了中国化B.中国科技在15世纪之前一直处于世界前列C.藏族、蒙古族、柯尔克孜族都有本民族的英雄史诗D.孔子的“大同”“小康”一直是人们追求的理想社会【解析】选D。
微生物的基本培养技术 同步课时训练-高二下学期生物学生物人教版选择性必修三

1.2.1微生物的基本培养技术——高二生物学人教版(2019)选择性必修三同步课时训练【基础练习】1.培养过程中不希望培养液pH发生变化时,应该( )A.加酸B.加碱C.加缓冲液D.加无机盐2.培养微生物就需要配制培养基,所配制的培养基都需( )A.用蒸馏水配制B.高压灭菌C.进行倒平板处理D.加热融化琼脂3.用牛肉膏蛋白胨培养基采集和培养人体呼吸道细菌。
对于温度的控制合理的操作是( )A.接种在37℃环境中进行B.在常温环境中培养细菌C.倒平板时用沸腾的培养基D.培养基在121℃灭菌4.下列关于培养基的叙述中正确的是( )A.培养液的灭菌采取干热灭菌法B.制备培养基时灭菌后再调节pH值,培养基分装到培养皿后进行灭菌C.倒平板时将培养皿的盖拿开,以便于将锥形瓶中的培养基倒入培养皿D.可以通过适宜条件下培养未接种的培养基以确定培养基是否被污染5.下列操作不能达到灭菌目的的是( )A.使用高压蒸汽灭菌锅处理培养基B.在火焰上灼烧接种环C.使用干热灭菌箱处理金属用具D.防疫期间用石炭酸喷洒教室6.下列关于培养基的叙述,错误的是( )A.培养基是为微生物的生长、繁殖提供营养物质的基质B.根据微生物对碳源需要的差别,使用不同碳源的培养基C.可在培养基中加入磷酸氢二钾或磷酸二氢钾,用于维持pH的相对稳定D.制备牛肉膏蛋白胨固体培养基的操作顺序为计算、称量、溶化、倒平板、灭菌【能力提升】7.下列针对微生物纯培养的说法,错误的是( )A.倒平板操作中,等待平板冷却凝固后,要将平板倒置B.将单个微生物分散在固体培养基上的方法只有平板划线法C.若皿盖和皿底之间溅上培养基,则这个培养基不可再用D.微生物纯培养形成的菌落只出现在固体培养基表面或内部8.微生物培养过程中,要十分重视无菌操作,现代生物学实验中的许多方面也要进行无菌操作,防止杂菌污染,请分析下列操作中错误的有几项( )①煮沸消毒可以杀死微生物营养细胞和一部分芽孢②配制培养基时可以加入蒸馏水③培养基只能进行湿热灭菌,培养皿只能进行干热灭菌④加入培养基中的指示剂或染色剂不需要灭菌A.1项B.2项C.3项D.4项9.细菌需要从外界吸收营养物质并通过代谢来维持正常的生长和繁殖。
高中物理人教版5第十八章原子结构1电子的发现 课时训练10电子的发现

课时训练10电子的发现题组一阴极射线1.下面对阴极射线的认识正确的是()A.阴极射线是由阴极发出的粒子撞击玻璃管壁上的荧光而产生的B.只要阴阳两极间加有电压,就会有阴极射线产生C.阴极射线可以穿透薄铝片,这说明它是电磁波D.阴阳两极间加有高压时,电场很强,阴极中的电子受到很强的库仑力作用而脱离阴极解析:阴极射线是由阴极直接发出的,A错误;只有当两极间加有高压且阴极接电源负极时,阴极中的电子才会受到足够大的库仑力作用而脱离阴极成为阴极射线,B错误,D正确;可以穿透薄铝片的,可能是电磁波,也可能是更小的粒子,C错误。
答案:D2.(多选)关于阴极射线的性质,判断正确的是()A.阴极射线带负电B.阴极射线带正电C.阴极射线的比荷比氢离子的比荷大D.阴极射线的比荷比氢离子的比荷小解析:汤姆孙通过实验证实,阴极射线是带负电的粒子流;阴极射线所带的电荷量与氢离子相同,但质量比氢离子小得多,所以它的比荷比氢离子的比荷大。
答案:AC3.如果阴极射线像X射线一样,则下列说法正确的是()A.阴极射线管内的高电压能够对其加速而增加能量B.阴极射线通过偏转电场不会发生偏转C.阴极射线通过偏转电场能够改变方向D.阴极射线通过磁场时方向可能发生改变解析:X射线是电磁波,不带电,通过电场、磁场时不受力的作用,不会发生偏转、加速,选项B正确。
答案:B4.阴极射线是从阴极射线管的阴极发出的高速运动的粒子流。
若在如图所示的阴极射线管中部加上竖直向上的匀强电场,阴极射线将向(选填“外”“里”“上”或“下”)偏转;若使阴极射线不偏转,可在匀强电场区域再加一大小合适、方向垂直纸面向(选填“外”或“里”)的匀强磁场。
解析:阴极射线带负电,在竖直向上的匀强电场中受向下的静电力作用,将向下偏转;要使阴极射线不偏转,应使其再受一竖直向上的洛伦兹力与库仑力平衡,由左手定则可判断磁场方向垂直纸面向外。
答案:下外题组二电子的发现5.(多选)关于电荷量,下列说法中正确的是()A.物体所带电荷量可以是任意值B.物体所带电荷量只能是某些值C.物体所带电荷量的最小值为×10-19 CD.一个物体带×10-9 C的正电荷,这是它失去了×1010个电子的缘故解析:电荷量是量子化的,即物体带的电荷量只能是某一最小电荷量的整数倍,这一最小电荷量是×10-19C,A错误,B、C正确;物体带正电,是由于它失去了带负电的电子,D正确。
课时训练 定积分的概念与微积分基本定理(北师大版)

A 级 基础达标演练 (时间:40分钟 满分:60分)一、选择题(每小题5分,共25分)1.与定积分∫3π1-cos x d x 相等的是( ). A.2∫3π0sin x 2d x B.2∫3π0⎪⎪⎪⎪⎪⎪sin x 2d x C.⎪⎪⎪⎪⎪⎪2∫3π0sin x 2d x D .以上结论都不对解析 ∵1-cos x =2sin 2x2,∴∫3π1-cos x d x = ∫3π02|sin x 2|d x =2∫3π0|sin x 2|d x . 答案 B2.(2012·芜湖一中月考)⎠⎛0e 1+ln xx d x =( ).A .ln x +12ln 2x B.2e -1 C.32 D.12解析⎪⎪⎪⎠⎛0e1+ln x x d x =(ln x +ln 2x 2)e 1=32. 答案 C3.(2012·长春质检)以初速度40 m/s 竖直向上抛一物体,t 秒时刻的速度v =40-10t 2,则此物体达到最高时的高度为( ). A.1603 m B.803 m C.403 mD.203 m解析 v =40-10t 2=0,t =2,⎠⎛02(40-10t 2)d t =⎪⎪⎪⎝ ⎛⎭⎪⎫40t -103t 320=40×2-103×8=1603(m). 答案 A4.一物体在变力F (x )=5-x 2(力单位:N ,位移单位:m)作用下,沿与F (x )成30°方向作直线运动,则由x =1运动到x =2时F (x )作的功为( ). A. 3 J B.233 J C.433 JD .2 3 J解析 由于F (x )与位移方向成30°角.如图:F 在位移方向上的分力F ′=F ·cos 30°,W =⎠⎛12(5-x 2)·cos 30°d x=32⎠⎛12(5-x 2)d x=32⎝ ⎛⎪⎪⎪⎭⎪⎫5x -13x 321 =32×83=433(J). 答案 C5.(2011·全国新课标)由曲线y =x ,直线y =x -2及y 轴所围成的图形的面积为( ).A.103 B .4 C.163D .6解析 由y =x 及y =x -2可得,x =4,所以由y =x 及y =x -2及y 轴所围成的封闭图形面积为⎠⎛04(x -x +2)d x =⎝ ⎛⎭⎪⎫23x 32-12x 2+2x | 40=163.答案 C二、填空题(每小题4分,共12分)6.一物体以初速度v =9.8t +6.5 m/s 的速度自由落下,则下落后第二个4 s 内经过的路程是__________. 解析⎪⎪⎠⎛48(9.8t +6.5)d t =(4.9t 2+6.5t )84=4.9×64+6.5×8-4.9×16-6.5×4=313.6+52-78.4-26 =261.2(m). 答案 261.2 m7.(2012·榆林模拟)曲线y =1x 与直线y =x ,x =2所围成的图形的面积为____________. 答案 32-ln 28.⎠⎛3-3(9-x 2-x 3)d x =________. 答案 9π2三、解答题(共23分)9.(11分)如图在区域Ω={(x ,y )|-2≤x ≤2,0≤y ≤4}中随机撒900粒豆子,如果落在每个区域的豆子数与这个区域的面积近似成正比,试估计落在图中阴影部分的豆子数.解 区域Ω的面积为S 1=16. 图中阴影部分的面积 S 2=S 1-⎪⎪⎪⎠⎛2-2x 2d x =16-13x 32-2=323.设落在阴影部分的豆子数为m , 由已知条件m 900=S 2S 1,即m =900S 2S 1=600.因此落在图中阴影部分的豆子约为600粒.10.(12分)如图所示,直线y =k x 分抛物线y =x -x 2与x 轴所围图形为面积相等的两部分,求k 的值.解 抛物线y =x -x 2与x 轴两交点的横坐标为x 1=0,x 2=1, 所以,抛物线与x 轴所围图形的面积S =⎠⎛01(x -x 2)d x =⎪⎪⎪⎝ ⎛⎭⎪⎫x 22-13x 310=16. 又⎩⎨⎧y =x -x 2,y =k x , 由此可得,抛物线y =x -x 2与y =k x 两交点的横坐标为 x 3=0,x 4=1-k ,所以, S 2=∫1-k 0(x -x 2-k x )d x =⎝ ⎛⎪⎪⎪⎭⎪⎫1-k 2x 2-13x 31-k 0=16(1-k )3. 又知S =16, 所以(1-k )3=12,于是k =1- 312=1-342.B 级 综合创新备选 (时间:30分钟 满分:40分)一、选择题(每小题5分,共10分)1.(2012·洛阳模拟)已知a =∑i =1n1n ⎝ ⎛⎭⎪⎫i n 2,n ∈N *,b =⎠⎛01x 2d x ,则a ,b 的大小关系是( ). A .a >b B .a =b C .a <bD .不确定答案 A 2.下列积分中①⎠⎛1e 1x d x ;②⎠⎛2-2x d x ;③⎠⎛024-x 2πd x ;④∫π20cos 2x2(cos x -sin x )d x ,积分值等于1的个数是( ).A .1B .2C .3D .4 解析 ①⎪⎪⎪⎠⎛1e 1x d x =ln x e 1=1, ②⎪⎪⎪⎠⎛2-2x d x =12x 22-2=0,③⎠⎛024-x 2πd x =1π(14π22)=1,④∫π20cos 2x 2(cos x -sin x )d x =12∫π20(cos x +sin x )d x=12(sin x -cos)|0π2=1.答案 C二、填空题(每小题4分,共8分) 3.(2012·福州模拟)⎠⎛12|3-2x |d x =________.解析∵|3-2x |=⎩⎪⎨⎪⎧-2x +3,x ≤32,2x -3,x >32,∴⎠⎛12|3-2x |d x =∫321(3-2x )d x +⎠⎛232(2x -3)d x= |(3x -x 2)321+(x 2-3x )|232=12. 答案 124.(2012·新余模拟)抛物线y =-x 2+4x -3及其在点A (1,0)和点B (3,0)处的切线所围成图形的面积为________.解析 如图所示,因为y ′=-2x +4,y ′|x =1=2,y ′|x =3=-2,两切线方程为y =2(x -1)和y =-2(x -3). 由⎩⎨⎧y =2(x -1),y =-2(x -3)得x =2.所以S =⎠⎛12[2(x -1)-(-x 2+4x -3)]d x +⎠⎛23[-2(x -3)-(-x 2+4x -3)]d x=⎠⎛12(x 2-2x +1)d x +⎠⎛23(x 2-6x +9)d x = ⎪⎪⎪⎝ ⎛⎭⎪⎫13x 3-x 2+x 21+⎪⎪⎪⎝ ⎛⎭⎪⎫13x 3-3x 2+9x 32=23. 答案 23三、解答题(共22分)5.(10分)曲线C :y =2x 3-3x 2-2x +1,点P ⎝ ⎛⎭⎪⎫12,0,求过P 的切线l 与C 围成的图形的面积.解 设切点坐标为(x 0,y 0) y ′=6x 2-6x -2, 则y ′|x =x 0=6x 20-6x 0-2, 切线方程为y =(6x 20-6x 0-2)⎝ ⎛⎭⎪⎫x -12, 则y 0=(6x 20-6x 0-2)⎝ ⎛⎭⎪⎫x 0-12,即2x 30-3x 20-2x 0+1=(6x 20-6x 0-2)⎝⎛⎭⎪⎫x 0-12.整理得x 0(4x 20-6x 0+3)=0,解得x 0=0,则切线方程为y =-2x +1. 解方程组⎩⎨⎧y =-2x +1,y =2x 3-3x 2-2x +1, 得⎩⎨⎧x =0,y =1或⎩⎪⎨⎪⎧x =32,y =-2.由y =2x 3-3x 2-2x +1与y =-2x +1的图象可知 S =∫320[(-2x +1)-(2x 3-3x 2-2x +1)]d x =∫320(-2x 3+3x 2)d x =2732.6.(12分)由曲线y =x 2和直线x =0,x =1,y =t 2,t ∈(0,1)所围成的图形(如图阴影部分),求其面积的最小值.解 S 1=t 3-⎠⎛0t x 2d x =t 3-13t 3=23t 3,S 2=⎠⎛t 1x 2d x -(1-t )t 2=13-13t 3-(1-t )t 2,=23t 3-t 2+13,S 1+S 2=43t 3-t 2+13,t ∈(0,1).可由导数求得当t =12时,S 1+S 2取到最小值,最小值为14.。
备战2023 高考历史 全程复习 10 两次鸦片战争及国家出路的探索与列强侵略的加剧 课时训练

十两次鸦片战争及国家出路的探索与列强侵略的加剧一、选择题(本大题共12小题,每小题2分,共24分)1.(2021·湖州模拟)关于鸦片战争的起因,有西方学者认为“因为傲慢的清政府不肯在相互平等基础上与英国建立贸易关系,拒绝平等交往,故只有让英国来承担终结中国排外政策之使命。
”该观点()A.揭示了鸦片战争爆发的根源B.指出了清朝士大夫阶层的傲慢与无知C.抹杀了鸦片战争爆发的实质D.旨在说中英不平等贸易责任方在英国【解析】选C。
“因为傲慢的清政府不肯在相互平等基础上与英国建立贸易关系,拒绝平等交往”可知该学者认为鸦片战争的原因在于清政府拒绝与英国平等交往,并未意识到英国发动侵略战争的本质,故选C。
2.林则徐在《译编卷·澳门月刊》中写到:“前在一千七百三十七年,带来鸦片不过四千余箱,前时鸦片准纳税进口,至一千七百九十六年才禁止,一千八百三十六年又欲如前纳进口,奏而未允,其时已多至三万余箱”。
英国大肆对华销售鸦片主要是为了()A.损害中国人的健康B.加剧清廷的政治腐败C.削弱中国军队战斗力D.寻求中英贸易平衡【解析】选D。
根据所学可知,19世纪初,英国从中国大量输入茶叶和生丝,而销往中国市场的棉纺织品有限,对华贸易出现逆差,便借助鸦片走私寻求贸易平衡,故选D;损害中国人的健康、加剧清廷的政治腐败、削弱中国军队战斗力是鸦片走私的危害,排除A、B、C。
3.(2021·金华模拟)有学者说:“这场战争,自西方人1514年到中国起,是他们积326年窥探之后的一逞。
”下列项中,对“这场战争”表述正确的是()A.签订的条约实现了鸦片贸易合法化B.中国完全沦为半殖民地半封建社会C.这场战争成为了中国近代史的开端D.“亚罗号”事件是这场战争的借口【解析】选C。
自1514年起,经过326年,即1840年,西方人窥探中国的战争指鸦片战争,这场战争成为中国近代史的开端,故选C。
4.鸦片战争后,1842年签订的中英《南京条约》是中国近代史上第一个不平等条约。
人教部编版五年级上册语文第10课《牛郎织女(一)》课时练(含答案)

部编版五年级上册语文10. 牛郎织女(一)课时练一、填空题1. 拼一拼,写一写。
di ē ni áng h ǎn ji àn y í t àng x īn l áng(__________) (__________) (__________) (__________)h ūn l ǐ zh ǎng b èi g ē s ǎo q ī zi(__________) (__________) (__________) (__________)2. 比一比,再组词。
嫂________ 托________ 泳________ 恳________ 辈________搜________ 拖________ 咏________ 垦________ 悲________3. 根据意思写词语,并选择其中一个造句。
①眉头舒展,眼含笑意。
形容高兴愉快的样子。
________②虽然很好,但还有缺陷。
________③指结了婚,有了家业或建立了某项事业。
________④数数目时往往以五为单位,一五,一十,十五,二十……数下去,因此用“一五一十”比 喻叙述时清楚有序而无遗漏。
________⑤不受任何约束,形容自由自在。
________⑥形容舍不得离开。
________造句:________4. 写出加点词语的近义词。
(1) 牛郎照看..那头牛挺周到。
(________) (2) 姑娘听得出了神,又同情..他,又爱惜他,就把自己的情形..也告诉了他。
(________)(________) (3) 织女的身子老在机房里,手老在梭子上,劳累..不用说,自由也没有了,等于关在监狱里,实在难受。
(________)(________)..5.选择加点字正确的拼音,打“√”。
兄嫂.(sǎo shǎo)勤恳.(kén kěn)监狱.(yùyǜ)酿.酒(nàng niàng)瞌.睡(hēkē)拘.束(jújū)筛.选(sāi shāi)晚辈.(bèi biè)6.照样子,写词语。
高中数学人教A版选修2-2(课时训练):1.6微积分基本定理含答案

微积分根本定理[学习目的]1.直观理解并掌握微积分根本定理的含义. 2.会利用微积分根本定理求函数的定积分. [知识链接]1.导数与定积分有怎样的联络?答 导数与定积分都是微积分学中两个最根本、最重要的概念,运用它们之间的联络,我们可以找出求定积分的方法,求导数与定积分是互为逆运算.2.在下面图(1)、图(2)、图(3)中的三个图形阴影部分的面积分别怎样表示?答 根据定积分与曲边梯形的面积的关系知: 图(1)中S =⎠⎛ab f (x )d x ,图(2)中S =-⎠⎛ab f (x )d x ,图(3)中S =⎠⎛0b f (x )d x -⎠⎛a0f (x )d x .[预习导引] 1.微积分根本定理假设f (x )是区间[a ,b ]上的连续函数,并且F ′(x )=f (x ),那么⎠⎛ab f (x )d x =F (b )-F (a ).2.函数f (x )与其一个原函数的关系 (1)假设f (x )=c (c 为常数),那么F (x )=cx ; (2)假设f (x )=x n (n ≠-1),那么F (x )=1n +1·x n +1;(3)假设f (x )=1x ,那么F (x )=ln_x (x >0);(4)假设f (x )=e x ,那么F (x )=e x ;(5)假设f (x )=a x,那么F (x )=a xln a(a >0且a ≠1);(6)假设f (x )=sin x ,那么F (x )=-cos_x ; (7)假设f (x )=cos x ,那么F (x )=sin_x .要点一 求简单函数的定积分 例1 计算以下定积分 (1)⎠⎛123d x ; (2)⎠⎛02(2x +3)d x ;(3)⎠⎛3-1(4x -x 2)d x ; (4)⎠⎛12(x -1)5d x .解 (1)因为(3x )′=3,所以⎠⎛123d x =(3x )⎪⎪⎪21=3×2-3×1=3. (2)因为(x 2+3x )′=2x +3, 所以⎠⎛2(2x +3)d x =(x 2+3x )⎪⎪⎪2=22+3×2-(02+3×0)=10. (3)因为⎝⎛⎭⎫2x 2-x33′=4x -x 2, 所以⎠⎛3-1(4x -x 2)d x =⎝⎛⎭⎫2x 2-x 33⎪⎪⎪3-1 =⎝⎛⎭⎫2×32-333-⎣⎡⎦⎤2×(-1)2-(-1)33=203.(4)因为⎣⎡⎦⎤16(x -1)6′=(x -1)5, 所以⎠⎛21(x -1)5d x=16(x -1)6⎪⎪⎪21=16(2-1)6-16(1-1)6 =16. 规律方法 (1)用微积分根本定理求定积分的步骤: ①求f (x )的一个原函数F (x ); ②计算F (b )-F (a ). (2)本卷须知:①有时需先化简,再求积分;②f (x )的原函数有无穷多个,如F (x )+c ,计算时,一般只写一个最简单的,不再加任意常数c .跟踪演练1 求以下定积分: (1)∫π20(3x +sin x )d x ;(2)⎠⎛21⎝⎛⎭⎫e x -1x d x . 解 (1)∵⎝⎛⎭⎫32x 2-cos x ′=3x +sin x , ∴∫π20(3x +sin x )d x =⎝⎛⎭⎫32x 2-cos x ⎪⎪⎪⎪π20=⎣⎡⎦⎤32×⎝⎛⎭⎫π22-cos π2-⎝⎛⎭⎫32×0-cos 0=3π28+1; (2)∵(e x -ln x )′=e x -1x,∴⎠⎛21(e x-1x )d x =()e x -ln x ⎪⎪⎪21=(e 2-ln 2)-(e -0) =e 2-e -ln 2.要点二 求较复杂函数的定积分 例2 求以下定积分:(1)⎠⎛41x (1-x )d x ; (2)∫π202cos 2x2d x ;(3)⎠⎛41(2x +1x)d x . 解 (1)∵x (1-x )=x -x , 又∵⎝⎛⎭⎫23x 32-12x 2′=x -x .∴⎠⎛41x (1-x )d x =⎝⎛⎭⎫23x 32-12x 2⎪⎪⎪41 =⎝⎛⎭⎫23×432-12×42-⎝⎛⎭⎫23-12=-176. (2)∵2cos 2x2=1+cos x ,(x +sin x )′=1+cos x ,∴原式=∫π20(1+cos x )d x =(x +sin x )⎪⎪⎪⎪π20=π2+1.(3)∵⎝⎛⎭⎫2xln 2+2x ′=2x +1x,∴⎠⎛41(2x +1x)d x =⎝⎛⎭⎫2xln 2+2x ⎪⎪⎪41=⎝⎛⎭⎫24ln 2+24-⎝⎛⎭⎫2ln 2+2=14ln 2+2. 规律方法 求较复杂函数的定积分的方法:(1)掌握根本初等函数的导数以及导数的运算法那么,正确求解被积函数的原函数,当原函数不易求时,可将被积函数适当变形后求解,详细方法是能化简的化简,不能化简的变为幂函数、正、余弦函数、指数、对数函数与常数的和与差. (2)确定积分区间,分清积分下限与积分上限. 跟踪演练2 计算以下定积分: (1)∫π30(sin x -sin 2x )d x ;(2)⎠⎛0ln 2e x (1+e x )d x .解 (1)sin x -sin 2x 的一个原函数是-cos x + 12cos 2x ,所以∫π30(sin x -sin 2x )d x =⎝⎛⎭⎫-cos x +12cos 2x ⎪⎪⎪⎪π30=⎝⎛⎭⎫-12-14-⎝⎛⎭⎫-1+12=-14. (2)∵e x (1+e x )=e x +e 2x , ∴⎝⎛⎭⎫e x +12e 2x ′=e x +e 2x , ∴⎠⎛0ln 2e x (1+e x )d x =⎠⎛0ln 2()e x +e 2x d x=⎝⎛⎭⎫e x +12e 2x ⎪⎪⎪ln 2=e ln 2+12e 2ln 2-e 0-12e 0=2+12×4-1-12=52.要点三 定积分的简单应用例3 f (a )=⎠⎛10(2ax 2-a 2x )d x ,求f (a )的最大值.解 ∵⎝⎛⎭⎫23ax 3-12a 2x 2′=2ax 2-a 2x ,∴⎠⎛10(2ax 2-a 2x )d x =⎝⎛⎭⎫23ax 3-12a 2x 2⎪⎪⎪10=23a -12a 2, 即f (a )=23a -12a 2=-12⎝⎛⎭⎫a 2-43a +49+29 =-12⎝⎛⎭⎫a -232+29, ∴当a =23时,f (a )有最大值29.规律方法 定积分的应用表达了积分与函数的内在联络,可以通过积分构造新的函数,进而对这一函数进展性质、最值等方面的考察,解题过程中注意体会转化思想的应用. 跟踪演练3 f (x )=ax 2+bx +c (a ≠0),且f (-1)=2,f ′(0)=0,⎠⎛10f (x )d x =-2,求a 、b 、c的值.解 由f (-1)=2,得a -b +c =2. ① 又f ′(x )=2ax +b ,∴f ′(0)=b =0, ②而⎠⎛10f (x )d x =⎠⎛10(ax 2+bx +c )d x =⎝⎛⎭⎫13ax 3+12bx 2+cx ⎪⎪⎪1=13a +12b +c , ∴13a +12b +c =-2, ③由①②③式得a =6,b =0,c =-4. 要点四 求分段函数的定积分 例4 计算以下定积分:(1)假设f (x )=⎩⎪⎨⎪⎧x 2 (x ≤0)cos x -1 (x >0),求∫π2-1f (x )d x ;(2)⎠⎛30|x 2-4|d x .解 (1)∫π2-1f (x )d x =⎠⎛0-1x 2d x +∫π20(cos x -1)d x ,又∵⎝⎛⎭⎫13x 3′=x 2,(sin x -x )′=cos x -1∴原式=13x 3⎪⎪⎪0-1+(sin x -x )⎪⎪⎪⎪π20=⎝⎛⎭⎫0+13+⎝⎛⎭⎫sin π2-π2-(sin 0-0) =43-π2.(2)∵|x 2-4|=⎩⎪⎨⎪⎧x 2-4 (x ≥2或x ≤-2),4-x 2 (-2<x <2),又∵⎝⎛⎭⎫13x 3-4x ′=x 2-4,⎝⎛⎭⎫4x -13x 3′=4-x 2, ∴⎠⎛30|x 2-4|d x =⎠⎛20(4-x 2)d x +⎠⎛32(x 2-4)d x=⎝⎛⎭⎫4x -13x 3⎪⎪⎪20+⎝⎛⎭⎫13x 3-4x ⎪⎪⎪32 =⎝⎛⎭⎫8-83-0+(9-12)-⎝⎛⎭⎫83-8=233. 规律方法 (1)求分段函数的定积分时,可利用积分性质将其表示为几段积分和的形式; (2)带绝对值的解析式,先根据绝对值的意义找到分界点,去掉绝对值号,化为分段函数; (3)含有字母参数的绝对值问题要注意分类讨论. 跟踪演练4 求⎠⎛3-3(|2x +3|+|3-2x |)d x .解 ∵|2x +3|+|3-2x |=⎩⎪⎨⎪⎧-4x ,x <-32,6,-32≤x ≤32,4x ,x >32,∴⎠⎛3-3(|2x +3|+|3-2x |)d x=∫-32-3(-4x )d x +∫32-326d x +∫3324x d x=-2x 2⎪⎪⎪⎪-32-3+6x ⎪⎪⎪32-32+2x 2⎪⎪⎪⎪332=45.1.∫π2-π2(1+cos x )d x 等于( )A .πB .2C .π-2D .π+2答案 D解析 ∵(x +sin x )′=1+cos x , ∴⎪⎪∫π2-π2(1+cos x )d x =(x +sin x )π2-π2=π2+sin π2-⎣⎡⎦⎤-π2+sin ⎝⎛⎭⎫-π2=π+2. 2.假设⎠⎛1a ⎝⎛⎭⎫2x +1x d x =3+ln 2,那么a 的值是( ) A .5 B .4 C .3 D .2答案 D解析 ⎠⎛1a ⎝⎛⎭⎫2x +1x d x =⎠⎛1a 2x d x +⎠⎛1a 1xd x =x 2|a 1+ ln x ⎪⎪a1=a 2-1+ln a =3+ln 2,解得a =2.3.⎠⎛02⎝⎛⎭⎫x 2-23x d x =________. 答案 43解析 ⎠⎛02⎝⎛⎭⎫x 2-23x d x =⎠⎛02x 2d x -⎠⎛0223x d x =x 33⎪⎪⎪⎪20-x 2320=83-43=43. 4.f (x )=⎩⎨⎧4x -2π,0≤x ≤π2,cos x ,π2<x ≤π,计算⎠⎛0πf (x )d x .解 ⎠⎛0πf (x )d x =∫π20f (x )d x +错误!f (x )d x=∫π20(4x -2π)d x +错误!cos x d x ,取F 1(x )=2x 2-2πx ,那么F 1′(x )=4x -2π; 取F 2(x )=sin x ,那么F 2′(x )=cos x .所以∫π20(4x -2π)d x +错误!cos x d x =(2x 2-2πx )错误!+sin x ⎪⎪⎪ππ2=-12π2-1,即⎠⎛0πf (x )d x =-12π2-1.1.求定积分的一些常用技巧(1)对被积函数,要先化简,再求积分.(2)假设被积函数是分段函数,根据定积分“对区间的可加性〞,分段积分再求和.(3)对于含有绝对值符号的被积函数,要去掉绝对值符号才能积分.2.由于定积分的值可取正值,也可取负值,还可以取0,而面积是正值,因此不要把面积理解为被积函数对应图形在某几个区间上的定积分之和,而是在x 轴下方的图形面积要取定积分的相反数.一、根底达标1.物体做变速直线运动的位移函数s =s (t ),那么以下命题正确的选项是( ) ①它在时间段[a ,b ]内的位移是s =s (t )⎪⎪ba ; ②它在某一时刻t =t 0时,瞬时速度是v =s ′(t 0); ③它在时间段[a ,b ]内的位移是s =li m n →∞∑i =1n b -a n s ′(ξi ); ④它在时间段[a ,b ]内的位移是s =⎠⎛ab s ′(t )d t .A .①B .①②C .①②④D .①②③④答案 D2.假设F ′(x )=x 2,那么F (x )的解析式不正确的选项是( ) A .F (x )=13x 3B .F (x )=x 3C .F (x )=13x 3+1D .F (x )=13x 3+c (c 为常数)答案 B解析 假设F (x )=x 3,那么F ′(x )=3x 2,这与F ′(x )=x 2不一致,应选B. 3.⎠⎛01(e x +2x )d x 等于( )A .1B .e -1C .eD .e +1答案 C解析 ⎠⎛01(e x +2x )d x =(e x +x 2)|10=(e 1+12)-(e 0+02)=e.4.f (x )=⎩⎪⎨⎪⎧x 2,-1≤x ≤0,1,0<x ≤1,那么⎠⎛1-1f (x )d x 的值为( )A.32 B .43C .23D .-23答案 B解析 ⎠⎛1-1f (x )d x =⎠⎛0-1x 2d x +⎠⎛011d x =⎪⎪x 330-1+1=13+1=43,应选B. 5.设函数f (x )=ax 2+c (a ≠0),假设⎠⎛01f (x )d x =f (x 0),0≤x 0≤1,那么x 0的值为________.答案33解析 由得13a +c =ax 20+c ,∴x 20=13,又∵0≤x 0≤1,∴x 0=33. 6.(20xx·湖南)假设⎠⎛0T x 2d x =9,那么常数T 的值为________.答案 3解析 ⎠⎛0T x 2d x =⎪⎪13x 3T 0=13T 3=9,即T 3=27,解得T =3. 7.⎠⎛1-1(x 3+ax +3a -b )d x =2a +6且f (t )=⎠⎛0t (x 3+ax +3a -b )d x 为偶函数,求a ,b 的值.解 ∵f (x )=x 3+ax 为奇函数, ∴⎠⎛1-1(x 3+ax )d x =0,∴⎠⎛1-1(x 3+ax +3a -b )d x=⎠⎛1-1(x 3+ax )d x +⎠⎛1-1(3a -b )d x=0+(3a -b )[1-(-1)]=6a -2b . ∴6a -2b =2a +6,即2a -b =3, ①又f (t )=⎪⎪⎣⎡⎦⎤x 44+a 2x 2+(3a -b )x t 0 =t 44+at 22+(3a -b )t 为偶函数, ∴3a -b =0,② 由①②得a =-3,b =-9. 二、才能提升8.∫π20sin 2x2d x 等于( )A.π4B .π2-1C .2D .π-24答案 D解析 ∫π20sin 2x 2d x =∫π201-cos x 2d x =⎪⎪12(x -sin x )π20=π-24,应选D. 9.(20xx·江西)假设S 1=⎠⎛12x 2d x ,S 2=⎠⎛121x d x ,S 3=⎠⎛12e x d x ,那么S 1,S 2,S 3的大小关系为( )A .S 1<S 2<S 3B .S 2<S 1<S 3C .S 2<S 3<S 1D . S 3<S 2<S 1答案 B 解析 S 1=⎠⎛12x 2d x =13x 3⎪⎪21=73,S 2=⎪⎪⎪⎠⎛121x d x =ln x 21=ln 2<1,S 3=⎠⎛12e x d x =e x |21=e 2-e =e(e -1)>73,所以S 2<S 1<S 3,选B.10.设f (x )=⎩⎪⎨⎪⎧lg x ,x >0,x +⎠⎛0a 3t 2d t ,x ≤0.假设f [f (1)]=1,那么a =________.答案 1解析 因为x =1>0,所以f (1)=lg 1=0.又x ≤0时,f (x )=x +⎠⎛0a 3t 2d t =x +t 3|a 0=x +a 3,所以f (0)=a 3.因为f [f (1)]=1,所以a 3=1,解得a =1.11.设f (x )是一次函数,且⎠⎛01f (x )d x =5,⎠⎛01xf (x )d x =176,求f (x )的解析式.解 ∵f (x )是一次函数,设f (x )=ax +b (a ≠0),那么 ⎠⎛01f (x )d x =⎠⎛01(ax +b )d x =⎠⎛01ax d x +⎠⎛01b d x =12a +b =5, ⎠⎛01xf (x )d x =⎠⎛01x (ax +b )d x =⎠⎛01(ax 2)d x +⎠⎛a1b x d x =13a +12b =176. 由⎩⎨⎧12a +b =513a +12b =176,得⎩⎪⎨⎪⎧a =4b =3.即f (x )=4x +3.12.假设函数f (x )=⎩⎪⎨⎪⎧x 3,x ∈[0,1],x ,x ∈(1,2],2x ,x ∈(2,3].求⎠⎛03f (x )d x 的值.解 由积分的性质,知: ⎠⎛03f (x )d x =⎠⎛01f (x )d x +⎠⎛12f (x )d x +⎠⎛23f (x )d x =⎠⎛01x 3d x +⎠⎛12x d x +⎠⎛232x d x =x 44⎪⎪⎪⎪10+23x 3221⎪⎪+2x ln 232 =14+432-23+8ln 2-4ln 2=-512+432+4ln 2. 三、探究与创新13.求定积分⎠⎛3-4|x +a |d x . 解 (1)当-a ≤-4即a ≥4时,原式=⎠⎛3-4(x +a )d x = ⎪⎪⎝⎛⎭⎫x 22+ax 3-4=7a -72. (2)当-4<-a <3即-3<a <4时, 原式=⎠⎛-4-a [-(x +a )]d x +⎠⎛3-a(x +a )d x =⎝⎛⎭⎫-x 22-ax ⎪⎪-a -4+ ⎪⎪⎝⎛⎭⎫x 22+ax 3-a =a 22-4a +8+⎝⎛⎭⎫a 22+3a +92 =a 2-a +252. (3)当-a ≥3即a ≤-3时,原式=⎠⎛3-4[-(x +a )]d x = ⎪⎪⎝⎛⎭⎫-x 22-ax 3-4= -7a +72. 综上,得⎠⎛3-4|x +a |d x =⎩⎪⎨⎪⎧ 7a -72(a ≥4),a 2-a +252(-3<a <4),-7a +72(a ≤-3).。
2024届高三化学一轮复习+微专题课时训练:弱电解质的电离平衡

2024届新高考化学第一轮复习微专题课时训练弱电解质的电离平衡一、选择题(共15题)1、H2S水溶液中存在电离平衡:H2S H++HS-和HS-H++S2-。
若向H2S溶液中 ( )A.加水,平衡向右移动,溶液中氢离子浓度增大B.通入过量SO2气体,平衡向左移动,溶液pH增大C.滴加新制氯水,平衡向左移动,溶液pH减小D.加入少量硫酸铜固体(忽略体积变化),溶液中所有离子浓度都减小2、硼酸(H3BO3)大量用于玻璃工业,可以改善玻璃制品的耐热、透明性能,提高机械强度等。
硼酸水溶液呈弱酸性,原因是其能够结合水电离出来的氢氧根离子从而释放出氢离子。
以下说法正确的是() A.往纯水中加入少许硼酸,水的电离程度增加B.等浓度的硼酸与碳酸相比,硼酸酸性强C.H3BO3为三元酸D .1 mol H 3BO 3最多能和1 mol 甲醇发生酯化反应3、一定温度下,将一定质量的冰醋酸加水稀释过程中,溶液的导电能力变化如图所示,下列说法正确的是( )A .a 、b 、c 三点溶液的pH :c<a<bB .a 、b 、c 三点CH 3COOH 的电离程度:c <a <bC .用湿润的pH 试纸测量a 处溶液的pH ,测量结果偏小D .a 、b 、c 三点溶液用1 mol·L -1NaOH 溶液中和,消耗NaOH 溶液的体积:c <a <b4、由于血液中存在如下平衡过程: CO 2(g) CO 2(aq)、CO 2(aq)+H 2O(l)H 2CO 3(aq)、H 2CO 3(aq)H +(aq)+HCO -3(aq),使血液的pH 维持在7.35~7.45。
如超出这个范围会造成酸中毒(pH 过低)或碱中毒(pH 过高),急性中毒时需静脉注射NH 4Cl 或NaHCO 3进行治疗。
下列叙述正确的是( )A .血液中CO 2浓度过高会导致酸中毒,使血液中c HCO -3c H 2CO 3的值增大B .治疗碱中毒时,患者需降低呼吸频率,以增加血液中CO 2浓度C.急性酸中毒时,救治方式是静脉注射NH4Cl溶液D.酸或碱中毒时,会导致血液中的酶发生水解5、如图所示,烧杯中的溶液为2 mol·L-1 CH3COOH溶液,接通直流电源。
语文课时特训七年级上册答案

语文课时特训七年级上册答案【篇一:实用[附答案]2016-2017年人教版七年级语文上册练习:《我的老师》课时训练】识及运用。
1.给下面加点字注音或根据注音写出汉字纷2.下面的句子中每句都有两个错别字,把它们找出来填入表中,然后改正。
①一个老师排除孩子世界里的一件小小的咎纷,是多么平常;可是回想起来,那时候我却觉得是给了我漠大的支持!②我不知道你当时是不是察觉,一个孩子站在那里,对你是多么的依练!至于暑假,对于一个喜欢他的老师的孩子来说,又是多么慢长!3.下面是专门为老师拟写的一副对联,只有上联,没有下联,你能对出下联吗?上联:三尺讲台,三寸舌,三寸笔,三千桃李;下联:__________________________________。
4.综合性学习。
有些新闻图片,常常让人感动不已。
一个人、一件事,被定格在那一瞬间……(图片1)老人名叫阎琼玛,家住甘肃省迭部县腊子口乡朱立村,今年76岁。
虽然每天要打柴背柴,但老太太总是面带笑容。
那是一种发自内心的笑容,没有丝毫做作,没有丝毫埋怨。
几十年的风雨历程,这位老人早已习惯了艰难困苦,习惯了微笑面对人生。
是血的男孩从废墟中被救出。
就在武警官兵准备把他转移到安全地带时,他艰难地举起还能动弹的右手,虚弱而又标准地敬了一个少先队队礼。
担架上的小男孩不忘向援救他的官兵叔叔敬礼感恩的举动,让无数的人深受感动。
后来人们知道,这位小男孩名叫郎铮。
(1)给这两幅图片分别拟一个标题。
______________________________________________________ ___________________(2)假如见到阎琼玛老人或者郎铮小朋友,你会对其中的一位说点什么?______________________________________________________ _________________________________________________________________________ ___________________二.阅读理解、分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1课时微训练10一、选择题1.已知反应A 2(g)+2B 2(g) 2AB 2(g) ΔH <0,下列说法正确的是( )A .升高温度,正反应速率增加,逆反应速率减小B .升高温度有利于反应速率增加,从而缩短达到平衡的时间C .达到平衡后,升高温度或增加压强都有利于该反应平衡正向移动D .达到平衡后,降低温度或减小压强都有利于该反应平衡正向移动解析:升温正、逆反应速率都增大,A 错;升温平衡逆移,C 错;减压平衡逆移,D 错。
答案:B2.(2016·重点中学模拟)T ℃时,SO 3气体分解的热化学方程式为:2SO 3(g) 2SO 2(g)+O 2(g) ΔH =+196 kJ/mol ,现向5.0 L 恒容密闭容器中充入1.0 mol SO 3气体,反应一段时间后达到平衡,恢复到T ℃,测得此过程中从外界共吸收了19.6 kJ 的热量。
当温度不变时,改变某一反应条件,下列对应结论正确的是( )2变,平衡不移动,平衡常数不变,A 项错误。
容积不变时,再充入1.0 mol SO 3,平衡正向移动,但SO 3的转化率减小,B 项错误。
通过计算比较K 值和Q c 值的大小,可知C 项中:Q c >K ,反应逆向进行,反应达到平衡前,v (逆)>v (正),C 项错误。
D 中平衡与原平衡是等效平衡,原平衡中最终SO 3的物质的量为0.8 mol ,D 中达平衡时生成的SO 3也是0.8 mol ,据此算出放出的热量为78.4 kJ ,D 项正确。
答案:D3.(2016·银川一中月考)N 2O 5是一种新型硝化剂,在一定温度下可发生下列反应:2N 2O 5(g) 4NO 2(g)+O 2(g) ΔH >0T 1温度下的部分实验数据为:A .500 s 内N 2O 5分解速率为2.96×10-3 mol/(L· s)B .T 1温度下的平衡常数为K 1 =125,1 000 s 时转化率为50%C .其他条件不变时,T 2温度下反应到1 000 s 时测得N 2O 5(g)浓度为2.98 mol/L ,则T 1 <T 2D .T 1温度下的平衡常数为K 1 ,T 3温度下的平衡常数为K 3,若3T 1 >T 3,则K 1> K 3 解析:v =Δc Δt =(5.00-3.52)mol/L 500 s=2.96×10-3 mol/(L·s),故A 正确;T 1温度下,平衡常数K =c 4(NO 2)·c (O 2)c 2(N 2O 5)=54·1.252.52=125,N 2O 5的转化率=(5.00-2.50) mol/L 5.00 mol/L×100%=50%,故B 正确;该反应正向吸热,升高温度,平衡正向移动,N 2O 5的浓度减小,平衡常数增大,故C 错,D 正确。
答案:C4.(2016·保定期中)将一定量的氨基甲酸铵固体置于某容积恒定的真空容器中,发生反应:H 2NCOONH 4(s) 2NH 3(g)+CO 2(g),在不同温度下,该反应达平衡状态时,部分数据见下表。
下列说法正确的是( )21B .向容器中充入少量氢气,H 2NCOONH 4质量增加C .NH 3体积分数不变时,说明该反应一定达到平衡D .T 1、T 2时,H 2NCOONH 4转化的Δn (T 2)=2Δn (T 1)解析:由图表可知T 1时c (NH 3)=0.1 mol /L ,c (CO 2)=0.05 mol/L ,T 2时c (CO 2)=0.1 mol /L ,则c (NH 3)=0.2 mol/L 。
若T 2>T 1,升温,平衡正向移动,那么正反应为吸热反应,ΔH >0,故A 项错;向容器中4充入少量H 2,不改变各物质的浓度,平衡不会移动,故B 错;由于NH 3与CO 2的物质的量之比总是为2∶1,所以无论是否平衡,NH 3的体积分数都是23,故C 错;T 2时消耗的H 2NCOONH 4是T 1时的2倍,故D 正确。
答案:D5.(双选)(2016·珠海模拟)往一真空密闭容器中通入一定量的气体A ,在一定条件下发生如下反应:2A(g) B(g)+x C(g)反应达到平衡时,测得容器的压强增大了p %,若此时A 的转化率为a %,下列关系正确的是( )A .若x =1则p >aB .若x =2则p <aC .若x =3则p =aD .若x =4则p =a解析:设A 的物质的量为n ,则:2A(g) B(g)+x C(g) Δn2 mol [(1+x )-2]moln ×a % n ×p %解得:a (x -1)=2p讨论:若x =1则p =0,若x =2则a =2p若x =3则a =p ,若x =4则3a =2p故B 、C 正确。
答案:BC6.(2016·武汉调研)向甲、乙两个体积相同的恒容容器中,分别充入2 mol 气体R 和1 mol 气体R ,相同温度下,发生下列反应:x R M +N(正反应为吸热反应)。
两容器中R 的物质的量随时间的5变化如图所示。
下列说法正确的是()A .将甲升温,可使甲和乙中各物质的体积分数达到相同B .x =2,且M 、N 中仅有一种为气态C .曲线Ⅱ为甲中R 的物质的量—时间图象D .其他条件不变时,向乙中再加入1 mol M 、1 mol N ,达到新平衡时,则有1.0 mol<n (R)<1.2 mol解析:由题意可知,甲容器中R 的体积分数比乙容器中的大,甲容器升高温度,平衡要向正反应方向移动,R 的体积分数减小,故最终有可能使甲、乙容器中各物质的体积分数相等,故A 正确;由于甲容器中R 的体积分数比乙容器中的大,相当于压强越大,R 的体积分数越大,说明压强增大,平衡要向逆反应方向移动,故x 小于2,M 、N 均为气态,B 项错误;曲线Ⅱ为乙中R 的物质的量—时间图象,故C 项错误;再向乙中充入1 mol M 和1 mol N ,与甲容器中的平衡完全等效,则平衡时R 的物质的量为1.2 mol ,故D 项错误。
答案:A7.(2016·东城模拟)一密闭容器中发生反应:2SO 2(g)+O 2(g) 2SO 3(g) ΔH <0,如图表示该反应的速率(v )在某一时间段内的变化。
则下列时间段中,SO 3的百分含量最高的是( )6A .t 0→t 1B .t 2→t 3C .t 3→t 4D .t 4→t 5解析:分析图象可知在t 1时刻是升高了反应体系的温度,平衡向左移动,SO 3的百分含量降低;在t 3时刻是加入了催化剂,平衡不移动;t 4时刻是减小了反应体系的压强,平衡左移,SO 3的百分含量降低;综合分析t 0→t 1时间段SO 3的百分含量最高,故选A 。
答案:A8.T ℃时在2L 密闭容器中使X(g)与Y(g)发生反应生成Z(g)。
反应过程中X 、Y 、Z 的浓度变化如图1所示;若保持其他条件不变,温度分别为T 1和T 2时,Y 的体积百分含量与时间关系如图2所示。
则下列结论错误的是()A .容器中发生的反应可表示为:3X(g)+Y(g) 2Z(g)B .保持其他条件不变,升高温度,反应的化学平衡常数K 减小C .反应进行的前4 min 内,用X 表示的反应速率v (X)=0.0757mol·(L·min)-1 D .若改变反应条件,使反应进程如图3所示,则改变的条件是使用催化剂解析:由图①可知该反应方程式为3X(g)+Y(g) 2Z(g),故A 正确;由图②可知T 2>T 1,升高温度,V (Y)%减小,平衡正向移动,则反应的化学平衡常数K 增大,故B 错误;v (X)=Δc Δt=(2.0-1.4)mol/2L 4min=0.075 mol·(L·min)-1,故C 正确;图③与图①相比,平衡未变,但缩短了到达平衡的时间,应是使用了催化剂,故D 正确。
答案:B9.(2016·扬州月考)如图所示,甲、乙之间的隔板K 可以左右移动,甲中充入2 mol A 和1 mol B ,乙中充入2 mol C 和1 mol He ,此时K 停在0处。
在一定条件下发生可逆反应:2A(g)+B(g) 2C(g),反应达到平衡后,恢复到反应发生前时的温度。
下列有关说法不正确的是()A .根据隔板K 滑动与否可判断左右两边的反应是否达到平衡B .达到平衡后,隔板K 最终停留在左侧刻度0~2之间C .达到平衡时,甲容器中C 的物质的量大于乙容器中C 的物8质的量D .若平衡时K 停留在左侧1处,则活塞仍停留在右侧6处 解析:本题结合压强改变考查平衡的移动知识、判断到达平衡的标志及等效平衡的有关知识。
由题意可知:2A(g)+B(g) 2C(g),由于甲中充入2 mol A 和1 mol B ,所以反应向正反应方向移动。
A 中压强降低,所以活塞向甲容器中移动,最多能转化为2 molC ,但是由于反应是可逆反应,所以C 的物质的量在0~2 mol 之间,所以达到平衡后,隔板K 不再滑动,最终停留在左侧刻度0~2之间。
如果不充入He 气,甲、乙两容器实质为等效平衡,都相当于2 mol C 。
又因为保持恒压的条件,充入He 气,那么乙中2A(g)+B(g) 2C(g)反应体系的压强降低,所以到达平衡时,乙向逆方向反应的程度大于甲中,导致到达平衡时甲容器中C 的物质的量大于乙容器中C 的物质的量。
甲、乙容器中压强相等,若平衡时K 停留在左侧1处,则活塞应停留在右侧5~6之间。
所以A 、B 、C 正确,D 错误。
答案:D10.(2016·河南开封模拟)I 2在KI 溶液中存在下列平衡:I 2(aq)+I -(aq) I -3(aq)。
I 2、KI 混合溶液中,I -3的物质的量浓度c (I -3)与温度T 的关系如图所示(曲线上任何一点都表示平衡状态)。
下到说法正确的组合是( )9①反应I 2(aq)+I -(aq) I -3(aq)的ΔH >0②若温度为T 1、T 2,反应的平衡常数分别为K 1、K 2,则K 1>K 2 ③若反应进行到状态D 时,一定有v 正>v 逆④状态A 与状态B 相比,状态A 的c (I 2)大⑤保持温度不变,在该混合液中加水,c (I -3)/c (I 2)将变大A .②③B .①③⑤C .③④⑤D .①④⑤解析:由图象可知,随温度的升高,c (I -3)降低,平衡逆向移动了,则该反应正向是放热反应,ΔH <0,故①错误;由T 1到T 2,温度升高,平衡逆向移动,所以K 1>K 2,故②正确;若反应进行到状态D 未达平衡,若想达到平衡状态A ,仍需正向移动,故v 正>v 逆,③正确;由状态A 到状态B ,温度升高,平衡逆向移动,则B 状态时c (I 2)大,故④错;保持温度不变,在混合液中加水,K =c (I -3)c (I 2)·c (I -)不变,c (I -)减小,则c (I -3)/c (I 2)变小,故⑤错。
