2016年高考(490)湖南省常德市2016届高三3月模拟考试
【解析版】湖南省常德市2016届高三3月模拟考试数学(文)试题

2016年常德市高三年级模拟考试数学(文史类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分150分,时量120分钟.第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中, 只有一项是符合题目要求的.1.已知集合{|0}M x x =<,2{|20}N x x x =--<,则M N =A .{|10}x x -<<B .{|20}x x -<<C .{|2}x x <D .{|1}x x < 【考点】集合的运算【试题解析】,则。
故答案为:A 【答案】A2.复数z 满足i i z 2)1)(1(=+-,则=||z A .1 B .2C .5D .5【考点】复数乘除和乘方 【试题解析】因为,所以所以故答案为:C 【答案】C3.若:,p a b R +∈;22:2q a b ab +≥,则A .p 是q 充要条件B .p 是q 的充分条件,但不是q 的必要条件C .p 是q 的必要条件,但不是q 的充分条件D .p 既不是q 的充分条件,也不是q 的必要条件 【考点】充分条件与必要条件 【试题解析】因为对都成立,所以p 是q 的充分不必要条件。
故答案为:B 【答案】B4.已知平面向量b a ,为单位向量,||1a b +=,则向量b a ,的夹角为A .6π B .65π C .3π D .32π 【考点】数量积的应用 【试题解析】因为,所以故答案为:D【答案】D5.函数22,0,()|log |,0,x x f x x x ⎧=⎨>⎩≤则函数1()2y f x =-的零点个数为A .3B .2C .1D .0 【考点】零点与方程分段函数,抽象函数与复合函数【试题解析】时,令符合题意;时,令或符合题意。
所以函数的零点个数为3.故答案为:A 【答案】A6.设y x ,满足约束条件1,20,20,x x y y ⎧⎪-⎨⎪-⎩≥≤≤则23z x y =+-的最大值为A .8B .5C .2D .1 【考点】线性规划【试题解析】作可行域:A(1,2),B(,C(4,2).所以则的最大值为5. 故答案为:B 【答案】B7.现有一枚质地均匀且表面分别标有1、2、3、4、5、6的正方体骰子,将这枚骰子先后抛掷两次,这两次出现的点数之和大于点数之积的概率为A .13B .12C .23D . 1136【考点】古典概型【试题解析】一枚子先后抛掷两次的基本事件有36种, 其中两次出现的点数之和大于点数之积的事件有:(1,1),(1,2)1,3)(1,4),(1,5),(1,6), (2,1)(3,1),(4,1),(5,1),(6,1)共11种, 所以两次出现的点数之和大于点数之积的概率为:。
湖南省常德市2016届高三3月模拟考试理综试题(含答案)

下列有关说法错误的是
A .干细胞的分化方向与细胞中基因的执行情况有关
B .干细胞具有控制该种生物生长发育的全套遗传物质
C .干细胞分化后的细胞凋亡是由基因决定的
D .干细胞在癌变过程中细胞膜上的甲胎蛋白会减少
3.下列与生物遗传有关的说法错误的是
A .若生物体内核酸中嘌呤与嘧啶碱基的数目不相等,则说明该生物体内只含有
B . X 、 Z 均能与 Na2CO3溶液反应
C. X 、 Y 、 Z 均能使溴水褪色,且原理相同
D . X 可作缩聚反应单体, Y 可作加聚反应单体
10.已知电离平衡常数:
H 2CO3>HClO>HCO
-
3
。下列离子反应方程式正确的是
① NaClO 溶液中通入少量二氧化碳:
2ClO
-+ CO2+ H2O
D .新物种的形成意味着生物能以新的方式利用环境条件,为生物进一步发展开辟 新的前景
5.下列属于控制自变量的操作且正确的是 A .在探究过氧化氢酶最适 pH 的实验中,需要在同一温度下进行 B .在探究光照强弱对光合作用影响的实验中可用多盏功率相同的灯泡控制变量 C .在探究土壤微生物对淀粉的分解作用的实验中,两只烧杯中要放入等量的淀粉糊 D .在探索生长素类似物促进插条生根的最适浓度的实验中,用不同植物的插条作对照 6.右图中横坐标 Y 和纵坐标 X 表示两种不同必需营养 物质的浓度, 图中两条折线分别为生物 A 、B 对营养 物质 X 、 Y 的最低浓度要求线, m 为交点,①~⑥ 表示六个不同营养供应区域。下列说法错误的是
2016 年 常 德 市 高 三 年 级 模 拟 考 试
理科综合能力测试
本试卷分为选择题和非选择题两部分,共
湖南省常德市2016届高考历史三模试卷(3月份)

2016年湖南省常德市高考历史三模试卷(3月份)一、选择题(共12小题,每小题4分,满分48分)1.顾炎武在《日知录》中记载夏商周时写道:“七月流火,农夫之辞也;三星在户,妇人之语也;月离于毕,戍卒之作也;龙尾伏辰,儿童之谣也。
”材料反映夏商周时期()A.人们熟知人事与天象息息相关B.统治者借神权以加强王权C.人们认为有超人间的鬼神世界D.社会各阶层普遍注意天象2.考古数据显示,春秋战国时期,各地工艺虽有地方性的特色,基本上差别不大;各国文字,从出土的简牍与铭辞看,也出现大同小异的现象。
这说明春秋战国时期()A.文化统一为政治统一准备了条件B.文化统一与政治统一之趋势并驾齐驱C.争霸战争促进了文化的发展与交流D.文化发展呈现统一性与多样性共生的局面3.亚里士多德在《雅典政制》里写道:(梭伦把)法律颁写在木板上,竖立在巴西勒斯柱廊里,所有人都发誓恪守它们,9名执政官还要在那块石头跟前起誓,如果他们僭越了某条法律,他们将献塑一座金像。
这一记载说明梭伦为雅典执政官时()A.规定法律面前人人平等 B.处处维护平民的利益C.使雅典成为了民主国家 D.奉行法律至上的原则4.清末学者皮锡瑞在《经学历史》中写道:前汉武、宣之间,经学大昌……以《禹贡》治河,以《洪范》察变,以《春秋》决狱,以三百五篇当谏书,治一经得一经之益也。
由材料可知前汉武、宣年间()A.儒者治经学重在阐发义理B.儒学获得了独尊的地位C.儒学发挥了经世致用作用D.仅以儒学为据选拔人才5.唐初诏令,男20、女15即要结婚成家.唐玄宗又敕令,男15、女13,听婚嫁.其目的是()A.促进一家一户生产方式的增长B.促进男、女平等观念的形成C.打压早婚早育的传统风俗习惯D.恢复社会稳定维护封建统治6.有学者认为,明代皇帝的批红权原则上不可超越票拟而径自为之,票拟则经过批红而成为行政命令。
君主如主动下手诏、中旨处理政事,也必须送内阁“商确可否”。
“圣意所予夺,亦必下内阁议而后行”,内阁如不同意,便可将手诏、中旨“封还”“执奏”,拒绝拟旨。
【试卷】湖南省2016届高考数学模拟试卷三理含解析

【关键字】试卷2016年湖南省高考数学模拟试卷(理科)(三)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.若a为实数且(2+ai)(a﹣2i)=8,则a=()A.﹣1 B.0 C.1 D.22.已知集合A={x|﹣3<x<3},B={x|x(x﹣4)<0},则A∪B=()A.(0,4)B.(﹣3,4)C.(0,3)D.(3,4)3.“﹣1<x<2”是“|x﹣2|<1”的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件4.若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,叶为个位数,则这组数据的中位数和平均数分别是()A.91,91.5 B.91,92 C.91.5,91.5 D.91.5,925.设等差数列{an}的前n项和为Sn,已知a1=﹣9,a2+a8=﹣2,当Sn取得最小值时,n=()A.5 B.6 C.7 D.86.执行如图所示的程序框图,输出S的值为时,k是()A.5 B.3 C.4 D.27.函数y=sin(2x+φ),的部分图象如图,则φ的值为()A.或B. C. D.8.如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0(,﹣),角速度为1,那么点P到x轴距离d关于时间t的函数图象大致为()A. B. C. D.9.某几何体的三视图如图所示,图中的四边形都是边长为1的正方形,其中正视图、侧视图中的两条虚线互相笔直,则该几何体的体积是()A. B. C. D.10.设G是△ABC的重心,a,b,c分别是角A,B,C的对边,若a+b+c=,则角A=()A.90°B.60°C.45°D.30°11.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O﹣ABC体积的最大值为36,则球O的表面积为()A.36πB.64πC.144π D.256π12.已知A、B为双曲线E的左右顶点,点M在E上,AB=BM,三角形ABM有一个角为120°,则E的离心率为()A. B. C. D.2二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上.. 13.(x3+)5的展开式中x8的二项式系数是(用数字作答)14.已知函数f(x)=,且f(a)=﹣3,则f(6﹣a)=.15.若变量x,y满足约束条件,则z=2x+3y的最大值为.16.已知函数f(x)是定义在R上的可导函数,其导函数记为f′(x),若对于任意的实数x,有f(x)>f′(x),且y=f(x)﹣1是奇函数,则不等式f(x)<ex的解集为.三、解答题:本大题共5小题,满分60分,解答应写出文字说明、证明过程或演算步骤17.在△ABC中,内角A,B,C所对的边分别是a,b,c,已知△ABC的面积.(Ⅰ)求sinA与cosA的值;(Ⅱ)设,若tanC=2,求λ的值.18.为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作标本,如图是样本的茎叶图,规定:成绩不低于120分时为优秀成绩.(1)从甲班的样本中有放回的随机抽取2 个数据,求其中只有一个优秀成绩的概率;(2)从甲、乙两个班级的样本中分别抽取2名同学的成绩,记获优秀成绩的人数为X,求X的分布列和数学期望E(X)19.已知在四棱锥P﹣ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S 分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PD⊥CD,PD⊥PB,AB=BC=2AD=2.(Ⅰ)求证:①平面PAD⊥平面PBC;②RS∥平面PAD;(Ⅱ)若点Q在线段AB上,且CD⊥平面PDQ,求二面角C﹣PQ﹣D的余弦值.20.已知函数f(x)=2lnx﹣ax+a(a∈R).(Ⅰ)讨论f(x)的单调性;(Ⅱ)若f(x)≤0恒成立,证明:当0<x1<x2时,.21.已知椭圆C1:+x2=1(a>1)与抛物线C:x2=4y有相同焦点F1.(Ⅰ)求椭圆C1的标准方程;(Ⅱ)已知直线l1过椭圆C1的另一焦点F2,且与抛物线C2相切于第一象限的点A,设平行l1的直线l交椭圆C1于B,C两点,当△OBC面积最大时,求直线l的方程.选修4-1几何证明选讲22.如图,AB为圆O的直径,CB是圆O的切线,弦AD∥OC.(Ⅰ)证明:CD是圆O的切线;(Ⅱ)AD与BC的延长线相交于点E,若DE=3OA,求∠AEB 的大小.选修4-4坐标系与参数方程23.在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系.已知曲线C1:(t为参数),C2:(θ为参数).(Ⅰ)化C1,C2的方程为普通方程,并说明它们分别表示什么曲线;(Ⅱ)若C1上的点P对应的参数为t=,Q为C2上的动点,求PQ中点M到直线C3:ρ(cosθ﹣2sinθ)=7距离的最小值.选修4-5不等式选讲24.已知函数f(x)=|x﹣2|,g(x)=﹣|x+3|+m.(1)解关于x的不等式f(x)+a﹣1>0(a∈R);(2)若函数f(x)的图象恒在函数g(x)图象的上方,求m的取值范围.2016年湖南省高考数学模拟试卷(理科)(三)参考答案与试题解析一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.若a为实数且(2+ai)(a﹣2i)=8,则a=()A.﹣1 B.0 C.1 D.2【考点】复数代数形式的乘除运算.【专题】计算题;方程思想;数学模型法;数系的扩充和复数.【分析】利用复数代数形式的乘除运算化简,由复数相等的条件列式求得a值.【解答】解:由(2+ai)(a﹣2i)=8,得4a+(a2﹣4)i=8,∴,解得a=2.故选:D.【点评】本题考查复数代数形式的乘除运算,考查了复数相等的条件,是基础题.2.已知集合A={x|﹣3<x<3},B={x|x(x﹣4)<0},则A∪B=()A.(0,4) B.(﹣3,4)C.(0,3) D.(3,4)【考点】并集及其运算.【专题】集合.【分析】利用并集的性质求解.【解答】解:∵集合A={x|﹣3<x<3},B={x|x(x﹣4)<0}={x|0<x<4},∴A∪B={x|﹣3<x<4}=(﹣3,4).故选:B.【点评】本题考查并集的求法,是基础题,解题时要认真审题.3.“﹣1<x<2”是“|x﹣2|<1”的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【专题】计算题;综合法;不等式的解法及应用;简易逻辑.【分析】由|x﹣2|<1,解得1<x<3,即可判断出结论.【解答】解:由|x﹣2|<1,解得1<x<3,∴“﹣1<x<2”是“|x﹣2|<1”的既不充分也不必要条件.故选:D.【点评】本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.4.若某市8所中学参加中学生合唱比赛的得分用茎叶图表示(如图1),其中茎为十位数,叶为个位数,则这组数据的中位数和平均数分别是()A.91,91.5 B.91,92 C.91.5,91.5 D.91.5,92【考点】茎叶图.【专题】计算题;概率与统计.【分析】根据茎叶图中的数据,计算这组数据的中位数与平均数即可.【解答】解:把茎叶图中的数据按大小顺序排列,如下;87、88、90、91、92、93、94、97;∴这组数据的中位数为=91.5,平均数是(87+88+90+91+92+93+94+97)=91.5.故选:C.【点评】本题考查了利用茎叶图中的数据求中位数与平均数的应用问题,是基础题目.5.设等差数列{a n}的前n项和为S n,已知a1=﹣9,a2+a8=﹣2,当S n取得最小值时,n=()A.5 B.6 C.7 D.8【考点】等差数列的性质.【专题】等差数列与等比数列.【分析】利用等差数列的通项公式,可求得公差d=2,从而可得其前n项和为S n的表达式,配方即可求得答案.【解答】解:等差数列{a n}中,a1=﹣9,a2+a8=2a1+8d=﹣18+8d=﹣2,解得d=2,所以,S n=﹣9n+=n2﹣10n=(n﹣5)2﹣25,故当n=5时,S n取得最小值,故选:A.【点评】本题考查等差数列的性质,考查其通项公式与求和公式的应用,考查运算求解能力,属于基础题.6.执行如图所示的程序框图,输出S的值为时,k是()A.5 B.3 C.4 D.2【考点】循环结构.【专题】计算题;图表型;试验法;算法和程序框图.【分析】模拟执行程序,依次写出每次循环k的值,当k=5时,大于4,计算输出S的值为,从而得解.【解答】解:模拟执行程序,可得每次循环的结果依次为:k=2,k=3,k=4,k=5,大于4,可得S=sin=,输出S的值为.故选:A.【点评】本题主要考查了循环结果的程序框图,模拟执行程序正确得到k的值是解题的关键,属于基础题.7.函数y=sin(2x+φ),的部分图象如图,则φ的值为()A.或B.C.D.【考点】y=Asin(ωx+φ)中参数的物理意义;由y=Asin(ωx+φ)的部分图象确定其解析式.【专题】计算题;三角函数的图像与性质.【分析】由已知中函数的图象,通过坐标(,0)代入解析式,结合φ求出φ值,得到答案.【解答】解:由已知中函数y=sin(2x+φ)(φ)的图象过(,0)点代入解析式,结合五点法作图,sin(+φ)=0,+φ=π+2kπ,k∈Z,∵φ,∴k=0,∴φ=,故选:B.【点评】本题考查的知识点是由y=Asin(ωx+φ)的部分图象确定其解析式,特殊点是解答本题的关键.8.如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0(,﹣),角速度为1,那么点P到x轴距离d关于时间t的函数图象大致为()A.B.C.D.【考点】函数的图象.【分析】本题的求解可以利用排除法,根据某具体时刻点P的位置到到x轴距离来确定答案.【解答】解:通过分析可知当t=0时,点P到x轴距离d为,于是可以排除答案A,D,再根据当时,可知点P在x轴上此时点P到x轴距离d为0,排除答案B,故应选C.【点评】本题主要考查了函数的图象,以及排除法的应用和数形结合的思想,属于基础题.9.某几何体的三视图如图所示,图中的四边形都是边长为1的正方形,其中正视图、侧视图中的两条虚线互相垂直,则该几何体的体积是()A.B.C.D.【考点】由三视图求面积、体积.【专题】空间位置关系与距离.【分析】由三视图可知:该几何体是一个正方体,挖去一个四棱锥所得的组合体,分别计算正方体和四棱锥的体积,相减可得答案.【解答】解:由三视图可知:该几何体是一个正方体,挖去一个四棱锥所得的组合体,正方体的体积为1,四棱锥的体积为:×1×1×=,故组合体的体积V=1﹣=,故选:A【点评】本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.10.设G是△ABC的重心,a,b,c分别是角A,B,C的对边,若a+b+c=,则角A=()A.90° B.60° C.45° D.30°【考点】余弦定理;平面向量的基本定理及其意义.【专题】计算题;平面向量及应用.【分析】根据三角形重心的性质得到,可得.由已知向量等式移项化简,可得=,根据平面向量基本定理得到,从而可得a=b=c,最后根据余弦定理加以计算,可得角A的大小.【解答】解:∵G是△ABC的重心,∴,可得.又∵,∴移项化简,得.由平面向量基本定理,得,可得a=b=c,设c=,可得a=b=1,由余弦定理得cosA===,∵A为三角形的内角,得0°<A<180°,∴A=30°.故选:D【点评】本题给出三角形中的向量等式,求角A的大小,着重考查了三角形重心的性质、平面向量基本定理和利用余弦定理解三角形等知识,属于中档题.11.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O﹣ABC 体积的最大值为36,则球O的表面积为()A.36π B.64π C.144πD.256π【考点】球的体积和表面积.【专题】计算题;空间位置关系与距离.【分析】当点C位于垂直于面AOB的直径端点时,三棱锥O﹣ABC的体积最大,利用三棱锥O﹣ABC体积的最大值为36,求出半径,即可求出球O的表面积.【解答】解:如图所示,当点C位于垂直于面AOB的直径端点时,三棱锥O﹣ABC的体积最大,设球O的半径为R,此时V O﹣ABC=V C﹣AOB===36,故R=6,则球O的表面积为4πR2=144π,故选C.【点评】本题考查球的半径与表面积,考查体积的计算,确定点C位于垂直于面AOB的直径端点时,三棱锥O﹣ABC的体积最大是关键.12.已知A、B为双曲线E的左右顶点,点M在E上,AB=BM,三角形ABM有一个角为120°,则E的离心率为()A.B.C.D.2【考点】双曲线的简单性质.【专题】计算题;方程思想;数形结合法;圆锥曲线的定义、性质与方程.【分析】由题意画出图形,过点M作MN⊥x轴,得到Rt△BNM,通过求解直角三角形得到M 坐标,代入双曲线方程可得a与b的关系,结合隐含条件求得双曲线的离心率.【解答】解:设双曲线方程为(a>0,b>0),如图所示,|AB|=|BM|,∠AMB=120°,过点M作MN⊥x轴,垂足为N,则∠MBN=60°,在Rt△BMN中,∵BM=AB=2a,∠MBN=60°,∴|BN|=a,,故点M的坐标为M(2a,),代入双曲线方程得a2=b2,即c2=2a2,∴.故选:B.【点评】本题考查双曲线的简单性质,考查数形结合的解题思想方法,是中档题.二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上.. 13.(x3+)5的展开式中x8的二项式系数是10 (用数字作答)【考点】二项式定理.【专题】计算题;转化思想;二项式定理.【分析】由展开式的通项公式T r+1==2﹣r,令=8,解得r即可得出.【解答】解:展开式的通项公式T r+1==2﹣r,令=8,解得r=2,∴(x3+)5的展开式中x8的二项式系数是=10.故答案为:10.【点评】本题考查了二项式定理的应用,考查了推理能力与计算能力,属于中档题.14.已知函数f(x)=,且f(a)=﹣3,则f(6﹣a)= ﹣.【考点】分段函数的应用.【专题】计算题;分类讨论;方程思想;分类法.【分析】由函数f(x)=且f(a)=﹣3,求出a值,可得答案.【解答】解:∵函数f(x)=,∴当a≤1时,2a﹣2﹣2=﹣3,无解;当a>1时,﹣log2(a+1)=﹣3,解得a=7,∴f(6﹣a)=f(﹣1)=2﹣1﹣2﹣2=﹣,故答案为:﹣【点评】本题考查的知识点是分段函数的应用,函数求值,分类讨论思想,方程思想,难度中档.15.若变量x,y满足约束条件,则z=2x+3y的最大值为 1 .【考点】简单线性规划.【专题】数形结合;数形结合法;不等式的解法及应用.【分析】作出可行域,变形目标函数,平移直线y=﹣x数形结合可得结论.【解答】解:作出约束条件所对应的可行域(如图阴影),变形目标函数可得y=﹣x+z,平移直线y=﹣x可知,当直线经过点A(4,﹣1)时,目标函数取最大值,代值计算可得z的最大值为:2×4﹣3=1,故答案为:1.【点评】本题考查简单线性规划,准确作图是解决问题的关键,属中档题.16.已知函数f(x)是定义在R上的可导函数,其导函数记为f′(x),若对于任意的实数x,有f(x)>f′(x),且y=f(x)﹣1是奇函数,则不等式f(x)<e x的解集为(0,+∞).【考点】函数奇偶性的性质.【专题】函数的性质及应用.【分析】根据条件构造函数令g(x)=,由求导公式和法则求出g′(x),根据条件判断出g′(x)的符号,得到函数g(x)的单调性,再由奇函数的结论:f(0)=0求出g(0)的值,将不等式进行转化后,利用g(x)的单调性可求出不等式的解集.【解答】解:由题意令g(x)=,则=,∵f(x)>f′(x),∴g′(x)<0,即g(x)在R上是单调递减函数,∵y=f(x)﹣1为奇函数,∴f(0)﹣1=0,即f(0)=1,g(0)=1,则不等式f(x)<e x等价为<1=g(0),即g(x)<g(0),解得x>0,∴不等式的解集为(0,+∞),故答案为:(0,+∞).【点评】本题主要考查导数与函数的单调性关系,奇函数的结论的灵活应用,以及利用条件构造函数,利用函数的单调性解不等式是解决本题的关键,考查学生的解题构造能力和转化思想.三、解答题:本大题共5小题,满分60分,解答应写出文字说明、证明过程或演算步骤17.在△ABC中,内角A,B,C所对的边分别是a,b,c,已知△ABC的面积.(Ⅰ)求sinA与cosA的值;(Ⅱ)设,若tanC=2,求λ的值.【考点】余弦定理;两角和与差的余弦函数.【专题】计算题;转化思想;分析法;解三角形.【分析】(Ⅰ)由三角形面积公式及余弦定理化简已知等式可得,解得:sinA+2cosA=2,又sin2A+cos2A=1,从而解方程组即可得解.(Ⅱ)由tanC=2,可得sinC,cosC的值,可得,从而由正弦定理即可解得.【解答】(本题满分为14分)解:(Ⅰ)由题意可得:,…所以解得:sinA+2cosA=2,又因为sin2A+cos2A=1,解方程组可得.…(Ⅱ)∵tanC=2,C为三角形的内角,∴易得,…∴…∴.…【点评】本题主要考查了正弦定理,余弦定理,三角形面积公式,三角形内角和定理,同角三角函数关系式的应用,考查了三角函数恒等变换的应用,属于中档题.18.为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作标本,如图是样本的茎叶图,规定:成绩不低于120分时为优秀成绩.(1)从甲班的样本中有放回的随机抽取 2 个数据,求其中只有一个优秀成绩的概率;(2)从甲、乙两个班级的样本中分别抽取2名同学的成绩,记获优秀成绩的人数为X,求X 的分布列和数学期望E(X)【考点】离散型随机变量的期望与方差;茎叶图.【专题】概率与统计.【分析】(1)甲班抽取的5名学生的成绩为102,112,117,124,136,从中有放回地抽取两个数据,基本事件总数n=52=25,其中只有一个优秀成绩,包含的基本事件个数m=2×3+3×2=12,由此利用等可能事件概率计算公式能求出其中只有一个优秀成绩的概率.(2)由茎叶图知甲班抽取的5名学生中有2名学生成绩优秀,乙班抽取的5名学生中有1名学生成绩优秀,由此得X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X 的分布列和数学期望E(X).【解答】解:(1)甲班抽取的5名学生的成绩为102,112,117,124,136,从中有放回地抽取两个数据,基本事件总数n=52=25,其中只有一个优秀成绩,包含的基本事件个数m=2×3+3×2=12,∴其中只有一个优秀成绩的概率p==.(2)由茎叶图知甲班抽取的5名学生中有2名学生成绩优秀,乙班抽取的5名学生中有1名学生成绩优秀,由此得X的可能取值为0,1,2,3,P(X=0)==,P(X=1)=+=,P(X=2)=+=,P(X=3)==,∴X的分布列为:X 0 1 2 3PEX==.【点评】本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意排列组合知识的合理运用.19.已知在四棱锥P﹣ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,R、S分别是棱AB、PC的中点,AD∥BC,AD⊥AB,PD⊥CD,PD⊥PB,AB=BC=2AD=2.(Ⅰ)求证:①平面PAD⊥平面PBC;②RS∥平面PAD;(Ⅱ)若点Q在线段AB上,且CD⊥平面PDQ,求二面角C﹣PQ﹣D的余弦值.【考点】二面角的平面角及求法;直线与平面平行的判定;平面与平面垂直的判定.【专题】空间位置关系与距离;空间角.【分析】(Ⅰ)①由已知得AD⊥平面APB,从而PB⊥AD,由此能证明平面PAD⊥平面PBC.②取PB中点M,连结RM,SM,由已知推导出平面PAD∥平面SMR,由此能证明RS∥平面PAD.(Ⅱ)由已知得AP=1,BP=,PQ=,AQ=,BQ=,以Q为原点,QP为x轴,QB为y 轴,建立如图所示的空间直角坐标系,利用向量法能求出二面角C﹣PQ﹣D的余弦值.【解答】(Ⅰ)①证明:∵在四棱锥P﹣ABCD中,底面ABCD是直角梯形,平面PAB⊥平面ABCD,AD⊥AB,∴AD⊥平面APB,又PB⊂平面APB,∴PB⊥AD,∵PD⊥PB,AD∩PD=D,∴PB⊥平面PAD,∵PB⊂平面PBC,∴平面PAD⊥平面PBC.②证明:取PB中点M,连结RM,SM,∵R、S分别是棱AB、PC的中点,AD∥BC,∴SM∥CB∥AD,RM∥AP,又AD∩AP=A,∴平面PAD∥平面SMR,∵RS⊂平面SMR,∴RS∥平面PAD.(Ⅱ)解:由已知得,解得AP=1,BP=,PQ=,AQ=,BQ=,以Q为原点,QP为x轴,QB为y轴,建立如图所示的空间直角坐标系,则Q(0,0,0),P(),D(0,﹣,1),C(0,,2),∴,, =(0,,2),设平面PDQ的法向量,则,取y=2,得,设平面PCQ的法向量,则,取b=4,得=(0,4,﹣3),设二面角C﹣PQ﹣D的平面角为θ,∴cosθ=|cos<>|=||=,∴二面角C﹣PQ﹣D的余弦值为.【点评】本题考查平面与平面垂直的证明,考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要注意空间思维能力的培养.20.已知函数f(x)=2lnx﹣ax+a(a∈R).(Ⅰ)讨论f(x)的单调性;(Ⅱ)若f(x)≤0恒成立,证明:当0<x1<x2时,.【考点】利用导数研究函数的单调性;函数单调性的性质.【专题】导数的综合应用.【分析】(I)利用导数的运算法则可得f′(x),对a分类讨论即可得出其单调性;(II)通过对a分类讨论,得到当a=2,满足条件且lnx≤x﹣1(当且仅当x=1时取“=”).利用此结论即可证明.【解答】解:(Ⅰ)求导得f′(x)=,x>0.若a≤0,f′(x)>0,f(x)在(0,+∞)上递增;若a>0,当x∈(0,)时,f′(x)>0,f(x)单调递增;当x∈(,+∞)时,f′(x)<0,f(x)单调递减.(Ⅱ)由(Ⅰ)知,若a≤0,f(x)在(0,+∞)上递增,又f(1)=0,故f(x)≤0不恒成立.若a>2,当x∈(,1)时,f(x)递减,f(x)>f(1)=0,不合题意.若0<a<2,当x∈(1,)时,f(x)递增,f(x)>f(1)=0,不合题意.若a=2,f(x)在(0,1)上递增,在(1,+∞)上递减,f(x)≤f(1)=0,合题意.故a=2,且lnx≤x﹣1(当且仅当x=1时取“=”).当0<x1<x2时,f(x2)﹣f(x1)=2ln﹣2(x2﹣x1)<2(﹣1)﹣2(x2﹣x1)=2(﹣1)(x2﹣x1),∴<2(﹣1).【点评】熟练掌握利用导数研究函数的单调性、极值、等价转化、分类讨论的思想方法等是解题的关键.21.已知椭圆C1: +x2=1(a>1)与抛物线C:x2=4y有相同焦点F1.(Ⅰ)求椭圆C1的标准方程;(Ⅱ)已知直线l1过椭圆C1的另一焦点F2,且与抛物线C2相切于第一象限的点A,设平行l1的直线l交椭圆C1于B,C两点,当△OBC面积最大时,求直线l的方程.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程;直线与圆锥曲线的关系.【专题】圆锥曲线的定义、性质与方程.【分析】(Ⅰ)求出抛物线的F1(0,1),利用椭圆的离心率,求出a、b即可求解椭圆方程.(Ⅱ)F2(0,﹣1),由已知可知直线l1的斜率必存在,联立方程组,利用相切求出k,然后利用直线的平行,设直线l的方程为y=x+m联立方程组,通过弦长公式点到直线的距离求解三角形的面积,然后得到所求直线l的方程.【解答】解:(Ⅰ)∵抛物线x2=4y的焦点为F1(0,1),∴c=1,又b2=1,∴∴椭圆方程为: +x2=1.…(Ⅱ)F2(0,﹣1),由已知可知直线l1的斜率必存在,设直线l1:y=kx﹣1由消去y并化简得x2﹣4kx+4=0∵直线l1与抛物线C2相切于点A.∴△=(﹣4k)2﹣4×4=0,得k=±1.…∵切点A在第一象限.∴k=1…∵l∥l1∴设直线l的方程为y=x+m由,消去y整理得3x2+2mx+m2﹣2=0,…△=(2m)2﹣12(m2﹣2)>0,解得.设B(x1,y1),C(x2,y2),则,.…又直线l交y轴于D(0,m)∴…=当,即时,.…所以,所求直线l的方程为.…【点评】本题主要考查椭圆、抛物线的有关计算、性质,考查直线与圆锥曲线的位置关系,考查运算求解能力及数形结合和化归与转化思想.选修4-1几何证明选讲22.如图,AB为圆O的直径,CB是圆O的切线,弦AD∥OC.(Ⅰ)证明:CD是圆O的切线;(Ⅱ)AD与BC的延长线相交于点E,若DE=3OA,求∠AEB 的大小.【考点】与圆有关的比例线段;圆的切线的判定定理的证明.【专题】选作题;推理和证明.【分析】(Ⅰ)连接OD,由弦AD∥OC,易证得∠COB=∠COD,继而证得△COB≌△COD(SAS),即可得∠ODC=∠OBC,然后由BC与⊙O相切于点B,可得∠ODC=90°,即可证得CD是⊙O的切线.(Ⅱ)利用射影定理,求出AD,即可求∠AEB 的大小.【解答】(Ⅰ)证明:连接OD∵AD∥OC,∴∠A=∠COB,∠ADO=∠COD,∵OA=OD,∴∠A=∠ADO,∴∠COB=∠COD,在△COB和△COD中,OB=OD,∠COB=∠COD,OC=OC,∴△COB≌△COD(SAS),∴∠ODC=∠OBC,∵BC与⊙O相切于点B,∴OB⊥BC,∴∠OBC=90°,∴∠ODC=90°,即OD⊥CD,∴CD是⊙O的切线;(Ⅱ)解:设OA=1,AD=x,则AB=2,AE=x+3,由AB2=AD•AE得x(x+3)=4,∴x=1,∴∠OAD=60°,∠AEB=30°.【点评】此题考查了切线的判定与性质、全等三角形的判定与性质以及射影定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.选修4-4坐标系与参数方程23.在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系.已知曲线C1:(t为参数),C2:(θ为参数).(Ⅰ)化C1,C2的方程为普通方程,并说明它们分别表示什么曲线;(Ⅱ)若C1上的点P对应的参数为t=,Q为C2上的动点,求PQ中点M到直线C3:ρ(cosθ﹣2sinθ)=7距离的最小值.【考点】参数方程化成普通方程;简单曲线的极坐标方程.【专题】坐标系和参数方程.【分析】(Ⅰ)曲线C1:(t为参数),利用sin2t+cos2t=1即可化为普通方程;C2:(θ为参数),利用cos2θ+sin2θ=1化为普通方程.(Ⅱ)当t=时,P(﹣4,4),Q(8cosθ,3sinθ),故M,直线C3:ρ(cosθ﹣2sinθ)=7化为x﹣2y=7,利用点到直线的距离公式与三角函数的单调性即可得出.【解答】解:(Ⅰ)曲线C1:(t为参数),化为(x+4)2+(y﹣3)2=1,∴C1为圆心是(﹣4,3),半径是1的圆.C2:(θ为参数),化为.C2为中心是坐标原点,焦点在x轴上,长半轴长是8,短半轴长是3的椭圆.(Ⅱ)当t=时,P(﹣4,4),Q(8c osθ,3sinθ),故M,直线C3:ρ(cosθ﹣2sinθ)=7化为x﹣2y=7,M到C3的距离d==|5sin(θ+φ)+13|,从而当cossinθ=,sinθ=﹣时,d取得最小值.【点评】本题考查了参数方程化为普通方程、点到直线的距离公式公式、三角函数的单调性、椭圆与圆的参数与标准方程,考查了推理能力与计算能力,属于中档题.选修4-5不等式选讲24.已知函数f(x)=|x﹣2|,g(x)=﹣|x+3|+m.(1)解关于x的不等式f(x)+a﹣1>0(a∈R);(2)若函数f(x)的图象恒在函数g(x)图象的上方,求m的取值范围.【考点】绝对值不等式的解法;函数恒成立问题.【专题】计算题;压轴题.【分析】(1)不等式转化为|x﹣2|+|a﹣1>0,对参数a进行分类讨论,分类解不等式;(2)函数f(x)的图象恒在函数g(x)图象的上方,可转化为不等式|x﹣2|+|x+3|>m恒成立,利用不等式的性质求出|x﹣2|+|x+3|的最小值,就可以求出m的范围.【解答】解:(Ⅰ)不等式f(x)+a﹣1>0即为|x﹣2|+a﹣1>0,当a=1时,解集为x≠2,即(﹣∞,2)∪(2,+∞);当a>1时,解集为全体实数R;当a<1时,解集为(﹣∞,a+1)∪(3﹣a,+∞).(Ⅱ)f(x)的图象恒在函数g(x)图象的上方,即为|x﹣2|>﹣|x+3|+m对任意实数x恒成立,即|x﹣2|+|x+3|>m恒成立,文档来源为:从网络收集整理.word版本可编辑.欢迎下载支持. 又由不等式的性质,对任意实数x恒有|x﹣2|+|x+3|≥|(x﹣2)﹣(x+3)|=5,于是得m <5,故m的取值范围是(﹣∞,5).【点评】本题考查绝对值不等式的解法,分类讨论的方法,以及不等式的性质,涉及面较广,知识性较强.此文档是由网络收集并进行重新排版整理.word可编辑版本!21文档来源为:从网络收集整理.word版本可编辑.欢迎下载支持.。
湖南省常德市2016届高三文综3月模拟考试试题
2016年常德市高三年级模拟考试文科综合能力测试本试题卷分选择题和非选择题两部分,共15页。
时量150分钟,满分300分。
一、选择题:本部分共35小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
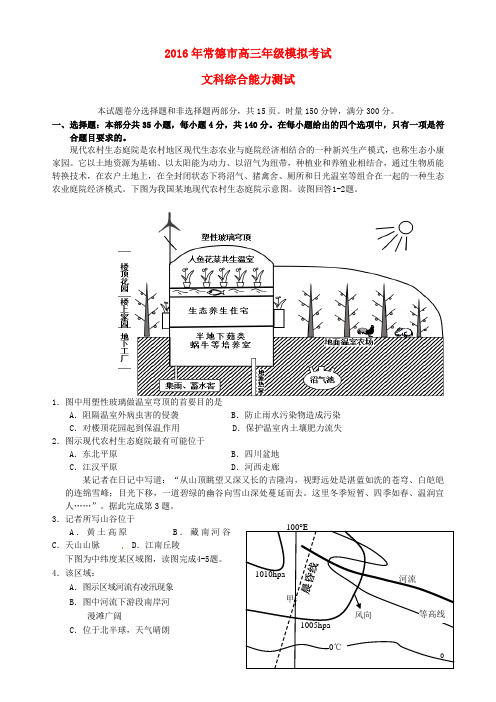
现代农村生态庭院是农村地区现代生态农业与庭院经济相结合的一种新兴生产模式,也称生态小康家园。
它以土地资源为基础、以太阳能为动力、以沼气为纽带,种植业和养殖业相结合,通过生物质能转换技术,在农户土地上,在全封闭状态下将沼气、猪禽舍、厕所和日光温室等组合在一起的一种生态农业庭院经济模式。
下图为我国某地现代农村生态庭院示意图。
读图回答1-2题。
1.图中用塑性玻璃做温室穹顶的首要目的是A .阻隔温室外病虫害的侵袭B .防止雨水污染物造成污染C .对楼顶花园起到保温作用D .保护温室内土壤肥力流失2.图示现代农村生态庭院最有可能位于A .东北平原B .四川盆地C .江汉平原D .河西走廊某记者在日记中写道:“从山顶眺望又深又长的吉隆沟,视野远处是湛蓝如洗的苍穹、白皑皑的连绵雪峰;目光下移,一道碧绿的幽谷向雪山深处蔓延而去。
这里冬季短暂、四季如春、温润宜人……”。
据此完成第3题。
3.记者所写山谷位于 A .黄土高原 B .藏南河谷C .天山山脉 D .江南丘陵下图为中纬度某区域图,读图完成4-5题。
4.该区域:A .图示区域河流有凌汛现象B .图中河流下游段南岸河漫滩广阔C .位于北半球,天气晴朗D .典型植被为亚热带常绿硬叶林5.朝鲜决定2015年8月15日起使用平壤时间(127°30´E 为标准时间),若此时甲地的区时为07:30,则此时的平壤时间为:A .06:20B .06:00C .09:20D .09:00抚养比是指非劳动年龄人口与劳动年龄人口之比。
下图为我国劳动人口增长和抚养比变化情况图。
读图完成6-7题。
6.我国劳动力人口最多的年份大约是A .1970年B .1985年C .2020年D .2050年7.2010年后总抚养比预测值上升最可能的原因是A .年龄结构变化B .死亡率上升C .延迟退休政策D .生育率上升读“我国各气候区城市热岛效应强度(以城乡温差最小值表示)图”,回答8~9题。
【高考模拟】湖南2016届高三下学期高考模拟(三)数学(文)试题Word版含答案

数学(文科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1.若复数()()1,z i bi b R =-∈对应的点在直线y x =上,则实数b 的值为( ) A .0 B .1 C .-1 D .32.若,,,a b c R a b ∈>,则下列不等式成立的是( ) A .1b a < B .22a b > C .2211a b c c >++ D .a c b c > 3. 0002sin 45cos15sin 30-的值等于( )A .12 B .2 C .1 4.已知某几何体的三视图如图所示,则该几何体的体积为( )A .83 B .8 C .5.已知点(),P x y 的可行域是如图阴影部分(含边界),若目标函数()2,0z x ay a =->取得最小值的最优解有无数个,则a 的取值为( )A .1B .2C .6D .86.如图12,F F 是双曲线221:13y C x -=与椭圆2C 的公共焦点,点A 是12,C C 在第一象限的公共点,若121F F F A =,则2C 的离心率是( )A .13 B .23 C .15 D .257.直线()11y k x =-+与椭圆2219x y m+=恒有交点,则m 的取值范围是( ) A .9,8⎛⎫+∞ ⎪⎝⎭ B .()9,99,8⎡⎫+∞⎪⎢⎣⎭ C .()9,99,8⎛⎫+∞ ⎪⎝⎭ D .9,8⎡⎫+∞⎪⎢⎣⎭8.如图,位于A 处的海面观测站获悉,在其正东方向相距40海里的B 处有一艘渔船遇险,并在原地等待营救.在A 处南偏西30°且相距20海里的C 处有一艘救援船,该船接到观测站通告后立即前往B 处求助,则sin ACB ∠=( )A .7 B .14 C .14 D .289.设命题0:p x R ∃∈,使()20020x x a a R ++=∈,则使得p 为真命题的一个充分不必要条件是( )A .2a >-B .2a <C .1a ≤D . 0a <10.如图,在等腰直角三角形ABO 中,设向量,,1,OA a OB b OA OB C ====为边AB 上靠近点A 的四等分点,过点C 作AB 的垂线l ,点P 为垂线l 上任意一点,则()OP b a -=( )A .12-B .12C .32-D .3211.已知正项数列{}n a 满足()110n n n a na ++-=,且11a =,不等式12231n n a a a a a a m ++++≥ 对任意*n N ∈恒成立,则实数m 的取值范围是( )A .1,2⎛⎤-∞ ⎥⎝⎦ B .1,2⎛⎫-∞ ⎪⎝⎭C .(],1-∞D .(),1-∞12.偶函数()f x 满足()()2f x f x =-,且当[]1,0x ∈-时,()cos12xf x π=-,若函数()()()log ,0,1a g x f x x a a =->≠有且仅有三个零点,则实数a 的取值范围是( )A .()3,5B .()2,4C .11,42⎛⎫⎪⎝⎭D .11,53⎛⎫ ⎪⎝⎭二、填空题:本大题共4个小题,每小题5分,共20分,将答案填在答题纸上.13.对具有线性相关关系的变量,y x 有一组观测数据()(),1,2,,8i i x y i = ,其回归直线方程是1ˆˆ3yx a =+,且()1238123828x x x x y y y y ++++=++++= ,请估算3x =时,y =____________.14.已知立方体,,F,G,H ABCD A B C D E ''''-分别是棱,.AD BB B C ''',DD '中点,从中任取两点确定的直线中,与平面AB D ''平行的有__________条.15.在数列{}n a 中,若存在一个确定的正整数T ,对任意*n N ∈满足n T n a a +=,则称{}n a 是周期数列,T 叫做它的周期.已知数列{}n x 满足()12211,1,n n n x x a a x x x ++==≤=-,当数列{}n x 的周期为3时,则{}n x 的前2016项的和2016S =___________.16.设函数()322ln f x x ex mx x =-+-,记()()f xg x x=,若函数()g x 至少存在一个零点,则实数m 的取值范围是_____________.三、解答题 :共70分.解答应写出文字说明、证明过程或演算步骤.17.(本题满分12分)某中学的高三一班中男同学有45名,女同学有15名,老师按照分层抽样的方法组建了一个4人的课外兴趣小组.(1)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出1名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;(3)在(2)中的实验结束后,第一次做实验的同学得到的试验数据为68,70,71,72,74,第二次做实验的同学得到的实验数据为69,70,70,72,74,请问哪位同学的实验更稳定?并说明理由. 18.(本题满分12分) 已知向量2cos,1,cos ,3cos 22x x a b x π+⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,设函数()()f x a b a =-. (1)若x R ∀∈,求()f x 的单调递增区间;(2)在ABC ∆中,角A B C 、、所对的边分别为,,a b c ,且()4,f A a ==求ABC ∆的面积S 的最大值. 19.(本题满分12分)在如图所示的几何体中,平面ACE ⊥平面ABCD ,四边形ABCD 平行四边形,090,//,1ACB EF BC AC BC AE EC ∠====.(1)求证:AE ⊥平面BCEF ; (2)求三棱锥D ACF -的体积. 20.(本题满分12分)已知圆()22:116A x y ++=,点()1,0B 是圆A 内一个定点,P 是圆A 上任意一点,线段BP 的垂直平分线l 和半径AP 相交于点Q .(1)当点P 在圆A 上运动时,求点Q 的轨迹曲线C 的方程;(2)若直线12,l l 是过点A 且相互垂直的两条直线,其中直线1l 交曲线C 于,E F 两点,直线2l 与圆A 相交于,M N 两点,求四边形MFNE 面积等于14时直线1l 的方程.21. (本小题满分 12分) 已知()ln x af x x e+=-.(1)若1x =是()f x 的极值点,讨论()f x 的单调性; (2)当2a ≥-时,证明:()f x 在定义域内无零点.请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.22.(本小题满分10分)选修4-1:几何证明选讲如图,已知AB 为圆O 的一条直径,以端点B 为圆心的圆交直线AB 于D C ,两点,交圆O 于,E F 两点,过点D 作垂直于AD 的直线,交直线AF 于H 点. (1)求证:,,,B D H F 四点共圆;(2)若2,AC AF ==BDF ∆外接圆的半径. 23. (本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线 B 是过点()1,1P -,倾斜角为4π的直线,以直角坐标系xOy 的原点为极点,x 轴正半轴为极轴建立极坐标,曲线A 的极坐标方程是22123sin ρθ=+.(1)求曲线A 的普通方程和曲线B 的一个参数方程; (2)曲线A 与曲线B 相交于,M N 两点,求MP NP 的值.24. (本小题满分10分)选修4-5:不等式选讲 已知函数()()()2,2f x x g x m x m R =-=-∈. (1)解关于x 的不等式()23f x x ->;(2)若不等式()()f x g x ≥对任意的x R ∈恒成立,求m 的取值范围.参考答案一、选择题1. B 【解析】因为()1z i bi b i =-=+,对应的点为(),1b ,所以1b =,选B . 2. C 【解析】取1,1a b ==-,排除选项A ,取0,1a b ==-,排除选项B ,取0c =,排除选项D ,显然2101c >+,对不等式a b >的两边同时乘211c +成立,故选C .3. C 【解析】()(000000000000000002sin 45cos15sin 302sin 45cos15sin 45152sin 45cos15sin 45cos15cos 45si sin 45cos15cos 45sin15sin 60-=--=--=+==故选C .4. A 【解析】该几何体是一个四棱锥,其底面是边长为2的等腰三角形,且垂直于底面,由此可得四棱锥的高为2,所以体积83V =,选A . 5. C 【解析】当0a >时,210,0a a >-<,当221641AC k a a -==⇒=-时,目标函数2z x ay =-在线段AC 上的所有点处都取得最小值,∴6a =,选C .6. B 【解析】由题意知,1214F F F A ==,∵122F A F A -=,∴22F A =,∴126F A F A +=,∵12=4F F ,∴2C 的离心率是4263=,选B7. B 【解析】()11y k x =-+恒过点()1,1P ,由点()1,1P 在椭圆内或椭圆上得:1119m+≤得98m ≥且9m ≠,选B . 8. A 【解析】在ABC ∆中,040,20,120AB AC ABC ==∠=.由余弦定理,得22202cos1202800BC AB AC AB AC =+-=,所以BC =10. A 【解析】以点O 为原点建立直角坐标系,所以()()311,0,0,1,,44A B C ⎛⎫⎪⎝⎭,不妨设P取点C ,∴()()31311,1,144442OP b a ⎛⎫-=-=-+=- ⎪⎝⎭,故选A .11. A 【解析】∵()110n n n a na ++-=,∴11n n a na n +=+,∴1211112n n n a n n n --==- . ∴122311111111111111112231122311n n a a a a a a n n n n n ++++=+++=-+-++-=-+++ ,∵12231n n a a a a a a m ++++≥ 恒成立,∴11122m ≤-=,故选A . 12. D 【解析】由()()2f x f x =-,可知函数()f x 图像关于1x =对称,又因为()f x 为偶函数,所以函数()f x 图像关于y 轴对称.所以函数()f x 的周期为2,要使函数()()log a g x f x x =-有且仅有三个零点,即函数()y f x =和函数log a y x =图形有且只有3个交点.由数形结合分析可知,0111log 31,53log 51a a a a <<⎧⎪⎪>-⇒<<⎨⎪<-⎪⎩,故D 正确.二、填空题 13.76 【解析】由题意知11,2x y ==,故样本中心为11,2⎛⎫⎪⎝⎭,代入回归直线方程1ˆˆ3y x a =+,得1ˆ6a =.所以3x =时,76y =. 14.6【解析】连接,EH,FG EG ,∵//EH FG ,∴EFGH 四点共面,由//,//,,EG AB EH AD EG EH E AB AD A ''''== ,可得平面EFGH 与平面AB D ''平行,所以符合条件的共6条.15. 1344 【解析】∵32111x x x a a =-=-=-,∴()2016672111344S a a =⨯++-=.16. 21,e e ⎛⎤-∞+ ⎥⎝⎦【解析】令()2ln 20xg x x ex m x =-+-=, ∴()2ln 20xm x ex x x =-++>, 设()2ln 2x h x x ex x =-++,令()()212ln 2,x f x x ex f x x =-+=,∴()221ln x f x x-'=,发现函数()()12,f x f x 在()0,x e ∈上都是单调递增,在[),x e ∈+∞上都是单调递减,∴函数()2ln 2xh x x ex x =-++在()0,x e ∈上单调递增,在[),x e ∈+∞上单调递减,∴当x e =时,()2max1h x e e =+,∴函数有零点需满足()max m h x ≤,即21m e e≤+.三、解答题17.【解析】(1)由题意可知,抽样比416015==,所以某同学被抽到的概率为115. 课外兴趣小组中男同学454360⨯=(人),女同学1(人)……………………………………………2分(2)把3名男同学和1名女同学分别记为123,,,a a a b ,则选取两名同学的基本事件有()()()()()()()()()()()()121312123231323123,,,,,,,,,,,,,,,,,,,,,,a a a a a b a a a a a b a a a a a b b a b a b a ,,共12个,其中恰有一名女同学的有6个. 所以选出的两名同学中恰有一名女同学的概率为61122P ==…………………………7分 (3)由题意可知两名同学做实验得到的数据的平均数及方差分别为:()()()()()()()()()()1222222212222222687071727471,5697070727471,5687170717171727174714,569717071707172717471 3.25x x s s ++++==++++==-+-+-+-+-==-+-+-+-+-==由于2212s s >,因此,第二位同学的实验更稳定…………………………………………12分 18.【解析】(1)()2cossin ,13cos 2cos ,1222x x x f x x ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭24cos sin 13cos sin cos 3324x x x x x x π⎛⎫=++-=-+=-+ ⎪⎝⎭…………………………………3分22,242k x k k Z πππππ-≤-≤+∈,即322,44k x k k Z ππππ-≤≤+∈, 所以()f x 的单调递增区间为32,2,44k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦…………………………………………6分 (2)因为()344f A A π⎛⎫=-+= ⎪⎝⎭,所以sin 42A π⎛⎫-=⎪⎝⎭又因为()0,A π∈,所以3,444A πππ⎛⎫-∈- ⎪⎝⎭,故44A ππ-=, 所以2A π=.........................................................8分于是在ABC ∆中,22210b c a +==,故221152222b c S bc +=≤=,当且仅当b c == 所以ABC ∆的面积的最大值为52………………………………………………………12分 19.【解析】①∵平面ACE ⊥平面ABCD ,且平面AC E 平面ABCD AC =,∵,BC AC BC ⊥⊂平面ABCD ,∴BC ⊥平面AEC ……………………………………………………………………………2分AE 平面AEC ,∴BC AE ⊥,……………………………………………3分又1AC AE EC ==, ∴222AC AE CE =+,∴AE EC ⊥………………………………………………………4分且BC EC C = ,∴AE ⊥平面BCEF ……………………………………………6分(2)设A C 的中点为G ,连接EG ,∵AE CE =,∴A EG C ⊥………………………………………………7分 ∵平面ACE ⊥平面ABCD ,且平面ACE 平面ABCD AC =, ∴EG ⊥平面ABCD …………………………………………9分 ∵//,EF BC EF ⊄平面ABCD ,所以点F 到平面ABCD 的距离就等于点E 到平面ABCD 的距离,即点F 到平面ABCD 的距离为EG 的长…………………………………………10分 ∴13D ACF F ACDE ACD ACD V V V S EG ---∆===, ∵111222ACD S AC AD EG AC ∆====,,………………………………………11分∴113D ACF V -=⨯=,即三棱锥D ACF -的体积为6…………………………………12分 20.【解析】(1)连接QB ,∵4,AQ QP QP QB +==,∴4AQ QB +=,故点Q 的轨迹是以点,A B 为焦点,24a =为长轴的椭圆,所以22,1,3a c b ===,点Q 的轨迹曲线C 的方程为:22143x y +=…………………………………………………5分 (2)①当直线1l 的斜率不存在时,则直线1l 的方程为:1x =-,直线2l 的方程为:0y =,故228,3b MN EF a===,∴183122MFNE S =⨯⨯=,不合题意,故直线1l 的斜率存在...............6分②当直线1l 的斜率存在时,设直线1l 的方程为:()()()11221,,,,y k x E x y F x y =+, ∴142MFNE S EF MN EF =⨯⨯=. 联立()221143y k x x y =+⎧⎪⎨+=⎪⎩, ∴()()22223484120k x k x k +++-=, ∴221212228412,3434k k x x x x k k--+==++,……………………………………………………8分 ∴2211234k EF k +==⨯+, ∴22211448121143434MFNEk S EF k k +⎛⎫==⨯=+= ⎪++⎝⎭…………………………………………10分 ∴243k =,∴k =, 此时,直线1l 的方程为)12yx =+或)12y x =-+……………………………………12分21.【解析】(1)∵()1x a f x e x+'=-,由1x =是()f x 的极值点,知()0f x '=, 故110a e +-=,∴1a =-,………………………………………………………………2分① 当01x <<时,1011,1x e e x-><=,则()0f x '>,所以()f x 在()0,1内单调递增; ② 当1x >时,10101,1x e e x -<<>=,则()0f x '<,所以()f x 在()1,+∞内单调递减……………5分(2)因为函数()f x 的定义域为()0,+∞,当2a ≥-时,2x a x e e +-≥,∴()2ln ln x a x f x x e x e +-=-≤-………………………………………6分令()()221ln ,x x g x x e g x e x --'=-=-,令()21x h x e x -=-,∴()2210x h x e x-'=--<, ∴()g x '在()0,+∞上递减,又()1110g e -'=->,()01202g e '=-<,……………………………8分 ∴()g x '在()0,+∞上有唯一的零点0x , ∴02010x e x --=,∴00001ln 2,2x x ex x =-+=-…………………………………………9分 当00x x <<时,则()0g x '>,所以()g x 在()00,x 内单调递增;当0x x >时,则()0g x '<,所以()g x 在()0,x +∞内单调递减.∴()()02000max 01ln 220x g x g x x e x x -==-=-+-<-=…………………………………11分 故当2a ≥-时,()0g x <,故()()0f x g x ≤<,所以当2a ≥-时,()f x 在定义域内无零点…………………………………………………12分22.【解析】(1)因为AB 为圆O 的一条直径,所以BF FH ⊥.又DH BD ⊥,故,,,B D F H 四点在以BH 为直径的圆上.所以,,,,B D F H 四点共圆…………………………………………………………4分(2)由题意得AH 与圆B 相切于点F ,由切割线定理得2AF AC AD = ,即(22,4AD AD == , 所以()11,12BD AD AC BF BD =-===, 又AFD ADH ∆∆ ,则DH AD BF AF =,得DH =连接BH (图略),由(1)可知,BH 为BDF ∆外接圆的直径.BH =,故BDF ∆的外接圆的半径为2………………………………………………………………10分23.【解析】(1)∵22123sin ρθ=+,∴()223sin 12ρθ+=,即曲线A 的普通方程为:22143x y +=, 曲线B的一个参数方程为:112x y ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数).......................................5分(2)设12,PM t PN t ==,∴12MP NP t t = .把11x y ⎧=-⎪⎪⎨⎪=+⎪⎩代入方程22143x y +=中,得:2231411222⎛⎫⎛⎫-+++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,整理得:27502t +-=,∴12121077t t t t +=-=-,∴12107MP NP t t ==......................................................10分 24.【解析】(1)由()223223x f x x x x ≥⎧->⇔⎨-->⎩或2223x x x <⎧⎨-->⎩, ∴x ∈∅或13x <-, 故原不等式的解集为1|3x x ⎧⎫<-⎨⎬⎩⎭..................................................5分 (2)由()()f x g x ≥,得22x m x -≥-对任意的x R ∈恒成立, 当0x =时,不等式22x m x -≥-成立;当0x ≠时,问题等价于22x m x -+≤对任意的非零实数恒成立, ∵22221x x x x ++-+≥=,∴1m ≤,即m 的取值范围是(],1-∞...............................................10分。
【英语】湖南省常德市2016届高三3月模拟考试

2016年常德市高三年级模拟考试英语本试卷分为四个部分,共12页。
时量120分钟。
满分150分。
第I卷第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上,录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题。
从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £ 19.15B. £ 9.18C. £ 9.15答案是C。
1. How would the woman get to the cinema?A. By bus.B. On foot.C. By taxi.2. What can we learn from the conversation?A. John will play.B. John will be punished.C. John will read books.3. What does the woman think of the acting?A. Very bad.B. Just so-so.C. Excellent.4. What are the speakers talking about?A. A restaurant.B. An apartment.C. An office.5. Where does the woman want to go?A. The Science Museum.B. The bus station.C. The Art Museum.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白,每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
英语高考模拟卷-常德市2016届高三3月模拟考试英语试题及答案

2016年常德市高三年级模拟考试英语本试卷分为四个部分,共12页。
时量120分钟。
满分150分。
第I卷第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上,录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题。
从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £ 19.15B. £ 9.18C. £ 9.15答案是C。
1. How would the woman get to the cinema?A. By bus.B. On foot.C. By taxi.2. What can we learn from the conversation?A. John will play.B. John will be punished.C. John will read books.3. What does the woman think of the acting?A. Very bad.B. Just so-so.C. Excellent.4. What are the speakers talking about?A. A restaurant.B. An apartment.C. An office.5. Where does the woman want to go?A. The Science Museum.B. The bus station.C. The Art Museum.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白,每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
常德市届高三3月模拟考试数学试题及答案(文)

2016年常德市高三年级模拟考试数学(文史类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分150分,时量120分钟.第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|0}M x x =<,2{|20}N x x x =--<,则MN =( )A .{|10}x x -<<B .{|20}x x -<<C .{|2}x x <D .{|1}x x <2.复数z 满足i i z 2)1)(1(=+-,则=||z ( )A .1B .2C .5D .53.若:,p a b R +∈;22:2q a b ab +≥,则( )A.p 是q 充要条件B.p 是q 的充分条件,但不是q 的必要条件C.p 是q 的必要条件,但不是q 的充分条件D.p 既不是q 的充分条件,也不是q 的必要条件 4.已知平面向量,为单位向量,||1a b +=,则向量,的夹角为( )A .6πB .65π C .3πD .32π 5.函数22,0,()|log |,0,x x f x x x ⎧=⎨>⎩≤则函数1()2y f x =-的零点个数为( )A .3B .2C .1D .06.设y x ,满足约束条件1,20,20,x x y y ⎧⎪-⎨⎪-⎩≥≤≤则23z x y =+-的最大值为( )A .8B .5C .2D .17.现有一枚质地均匀且表面分别标有1、2、3、4、5、6的正方体骰子,将这枚骰子先后抛掷两次,这两次出现的点数之和大于点数之积的概率为( ) A .13B .12C .23D .11368.右边程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n ”表示m 除以n 的余数),若输入的m ,n 分别为495,135,则输出的m = ( )A .0B .5C .45D .909.抛物线x y 82=的焦点F 与双曲线22221x y a b-=(0,a >0)b >右焦点重合,又P 为两曲线的一个公共交点,且5||=PF ,则双曲线的实轴长为( ) A .1B .2C .317-D .610.数列}{n a 满足:1132,51++=-=n n n n a a a a a ,则数列}{1+n n a a 前10项的和为( ) A .1021 B .2021 C .919 D .181911.某几何体的三视图如图所示,则该几何体外接球的表面积为( )A .32πB .3πC .6πD .24π12.已知函数2cos sin )(x x x x x f ++=,则不等式1(ln )(ln )2(1)f x f f x+<的解集为( )A .),(+∞eB .(0,)eC .1(0,)(1,)e eD .),1(e e第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分.第13题~第21题为必考题,第22题~第24题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡...中对应题号后的横线上.13.已知定义在R 上的函数()f x 满足(2)()0f x f x +-=,当(0,2]x ∈时,()2xf x =,则(2016)f = .14.在等比数列{}n a 中,12561,8,02n a a a a a +=+=>,则34a a += .15.已知圆C 的方程为228150x y x +++=,若直线2y kx =-上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 有公共点,则k 的取值范围为 .16.为了测得一铁塔AB 的高度,某人在塔底B 的正东方向C 处测得塔顶A 的仰角为45°,再由C 点沿北偏东30°方向走了20米后到达D 点,又测得塔顶A 的仰角为30°,则铁塔AB 的高度为 米.三、解答题:本大题共70分. 解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)已知函数2()cos 2cos (0)f x x x x ωωωω=+>,且()f x 的最小正周期为π.(Ⅰ)求ω的值及()f x 的单调递减区间; (Ⅱ)将函数()f x 的图象向右平移6π个长度单位后得到函数()g x 的图象,求当[0,]2x π∈时()g x 的最大值.18.(本小题满分12分)某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.下图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图.已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群” .(Ⅰ)求m ,n 的值,并求这100名学生月消费金额的样本平均数x (同一组中的数据用该组区间的中点值作代表);(Ⅱ)根据已知条件完成下面2×2列联表,并判断能否有90%的把握认为“高消费群”与性别有关?(参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++)19.(本小题满分12分)如图,四棱锥A BCDE -中,CD ⊥平面ABC ,BE ∥CD ,AB =BC CD =,AB BC ⊥,M 为AD 上一点,EM ⊥平面ACD .(Ⅰ)求证:EM ∥平面ABC .(Ⅱ)若22CD BE ==,求点D 到平面EMC 的距离.20.(本小题满分12分)已知椭圆1C :22221(0)x y a b a b +=>>焦距为抛物线2C :22(0)x py p =>的焦点F 是椭圆1C 的顶点.(Ⅰ)求1C 与2C 的标准方程;(Ⅱ)若2C 的切线交1C 于P ,Q 两点,且满足0FP FQ ⋅=,求直线PQ 的方程.21.(本小题满分12分)已知函数()ln mxf x x=,曲线()y f x =在点22(,())e f e 处的切线与直线20x y +=垂直(其中e 为自然对数的底数). (Ⅰ)求()f x 的解析式及单调递减区间;(Ⅱ)是否存在常数k ,使得对于定义域内的任意x ,()ln kf x x>+恒成立?若存在,求出k 的值;若不存在,请说明理由.请考生在第22、23、24三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.22.(本小题满分10分)选修4-1:几何证明选讲如图,已知AB AC =,圆O 是ABC △的外接圆,CD AB ⊥,CE 是圆O 的直径.过点B 作圆O 的切线交AC 的延长线于点F .(Ⅰ)求证:AB CB CD CE ⋅=⋅;(Ⅱ)若BC =,BF =,求ABC ∆的面积.23.(本小题满分10分)选修4-4:坐标系与参数方程已知曲线C 的参数方程是2cos sin x y θθ=⎧⎨=⎩(θ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,A 、B 的极坐标分别为(2,)A π、4(2,)3B π. (Ⅰ)求直线AB 的直角坐标方程;(Ⅱ)设M 为曲线C 上的动点,求点M 到直线AB 距离的最大值.24.(本小题满分10分)选修4-5:不等式选讲已知函数()|21||1|f x x x =+--. (Ⅰ)求不等式()2f x <的解集;(Ⅱ)若关于x 的不等式2()2a f x a -≤有解,求a 的取值范围.2016年常德市高三年级模拟考试数学(文史类)参考答案第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. A2.C3.B4. D5.A6.B7.D8.C9.B 10.A 11.C 12.D第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分. 把答案填在答题卡中对应题号后的横线上.13. 4 14. 2 15. 403k -≤≤ 16. 20三、解答题:本大题共70分,解答应写出文字说明、证明过程或演算步骤. 17.(本题满分12分)(Ⅰ)()21cos2f x x x ωω++=2sin(2)16x πω++∵22T πππω=⇒=,∴1ω= ……………………3分 从而()2sin(2)16f x x π=++,令3222262k x k πππππ+≤+≤+, 得263k x k ππππ+≤≤+,∴()f x 的单调减区间为2[,],63k k k Z ππππ++∈. ……………………6分 (Ⅱ)()2sin[2()]12sin(2)1666g x x x πππ=-++=-+, ……………………9分∵[0,]2x π∈,∴52666x πππ-≤-≤,∴当262x ππ-=,即3x π=时,max ()2113g x =⨯+=. ……………………12分18.(本题满分12分)(Ⅰ)由题意知 100()0.6m n +=且20.0015m n =+解得0.0025,0.0035m n == ……………………3分 所求平均数为:3000.154000.355000.256000.157000.10470x =⨯+⨯+⨯+⨯+⨯=(元) ……6分(Ⅱ)根据频率分布直方图得到如下2×2列联表:……………………9分根据上表数据代入公式可得22100(15403510)1001.332.7062575505075K ⨯⨯-⨯==≈<⨯⨯⨯所以没有90%的把握认为“高消费群”与性别有关. ……………………12分19.(本题满分12分)(Ⅰ)证明:取AC 的中点F ,连接BF ,因为BC AB =,所以AC BF ⊥,又因为⊥CD 平面ABC ,所以BF CD ⊥,所以⊥BF 平面ACD ,………………3分因为⊥EM 平面ACD ,所以EM ∥BF ,EM ⊄面ABC ,⊂BF 平面ABC ,所以EM ∥平面ABC ; ………………6分(Ⅱ)因为⊥EM 平面ACD ,EM ⊂面EMC ,所以平面⊥CME 平面ACD ,平面 C M E 平面A C D C M =,过点D 作直线DG ⊥CM ,则⊥DG 平面C M E ,…… 9分由已知⊥CD 平面ABC ,BE ∥CD ,BE CD BC AB 2===,可得DE AE =, 又AD EM ⊥,所以M 为AD 的中点,在ABC Rt ∆中,222==BC AC ,在ADC Rt ∆中,3222=+=AC CD AD ,2222212121=⨯⨯⨯==∆∆ACD CDM S S , 在DCM ∆中,321==AD CM ,由等面积法知221=⨯⨯DG CM ,所以362=DG ,即点D 到平面EMC 的距离为362. …………………12分 说明:用三棱锥的等体积方法求三棱锥CEM D -的高.按相应计分标准给分。
湖南省常德市2016届高三3月模拟考试数学(文)试题 含解析

2016年常德市高三年级模拟考试数学(文史类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,时量120分钟.第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中, 只有一项是符合题目要求的.1.已知集合{|0}=<,2M x x=--<,则M N={|20}N x x xA.{|10}x x<-<<C.{|2}x x<D.{|1}x x-<<B.{|20}x x【考点】集合的运算【试题解析】,则。
故答案为:A【答案】A2.复数z满足i(=+1)(1-,则=||z)iz2A.1B.2C.5D.5【考点】复数乘除和乘方【试题解析】因为,所以所以故答案为:C【答案】C3.若:,p a b R+∈;22+≥,则q a b ab:2A .p 是q 充要条件B .p 是q 的充分条件,但不是q 的必要条件C .p 是q 的必要条件,但不是q 的充分条件D .p 既不是q 的充分条件,也不是q 的必要条件【考点】充分条件与必要条件 【试题解析】因为对都成立, 所以p 是q 的充分不必要条件。
故答案为:B【答案】B4.已知平面向量b a ,为单位向量,||1a b +=,则向量b a ,的夹角为A .6πB .65πC .3πD .32π【考点】数量积的应用【试题解析】因为, 所以故答案为:D【答案】D5.函数22,0,()|log |,0,x x f x x x ⎧=⎨>⎩≤则函数1()2y f x =-的零点个数为 A .3 B .2 C .1 D .0【考点】零点与方程分段函数,抽象函数与复合函数【试题解析】时,令符合题意; 时,令或符合题意。
所以函数的零点个数为3.故答案为:A【答案】A 6.设y x ,满足约束条件1,20,20,x x y y ⎧⎪-⎨⎪-⎩≥≤≤则23z x y =+-的最大值为A .8B .5C .2D .1【考点】线性规划【试题解析】作可行域:A (1,2),B(,C(4,2). 所以则的最大值为5.故答案为:B【答案】B7.现有一枚质地均匀且表面分别标有1、2、3、4、5、6的正方体骰子,将这枚骰子先后抛掷两次,这两次出现的点数之和大于点数之积的概率为。
湖南省常德市2016届高三3月模拟考试理综物理试题 含答案

O x C 甲 B A 乙 t t 1 t 2 t 3 2016年常德市高三年级模拟考试理科综合能力测试 物理二、选择题:本题共8小题,每小题6分,在每小题给出的四个选项中,第14-18题只有一个选项符合题目要求,第19-21题有多个选项符合题目要求.全部选对的得6分,选对但不全的得3分,有选错的得0分.14.甲、乙两质点沿同一方向做直线运动,某时刻经过同一地点。
若以该时刻作为计时起点,得到两质点的x -t 图象如图所示。
图象中的OC 与AB 平行,CB 与OA 平行。
则下列说法中正确的是 A .t 1~t 2时间内甲和乙的距离越来越远 B .0~t 2时间内甲的速度和乙的速度始终不相等 C .0~t 3时间内甲和乙的位移相等 D .0~ t 3时间内甲的平均速度大于乙的平均速度 15.“神舟十号"飞船于2013年6月11日17时38分载着3名宇航员顺利升空.当“神十”在绕地球做半径为r 的匀速圆周运动时,若飞船舱内质量为m 的航天员站在台秤上,对台秤的压力为F N .用R 表示地球的半径,g 表示地球表面处的重力加速度,g ´表示飞船轨道所在处的重力加速度,不考虑地球自转。
则下列关系式中正确的是A .g ´=0B .22R g g r '=C .F N = mgD .2N 2R F mg r = 16.如图所示,斜面固定在水平面上,斜面上一个质量为m 的物块在沿斜面向下的拉力F 1作用下匀速下滑,在下滑过程中的某时刻在物块上再施加一个竖直向上的恒力F 2,且F 2<mg 。
则加F 2之后较短的一段时间内物块的运动状态是 A .仍匀速下滑 B .匀加速下滑 C .匀减速下滑 D .上述情况都有可能17.如图所示的电路中有一自耦变压器,其原线圈接在电压稳定的交流电源上,副线圈上连接了灯泡、定值电阻R 1、R 2,电流表和电压表都是理想电表,起初开关S 处于断开状态。
湖南省常德市高考数学一模试卷理(含解析)

湖南省常德市2016年高考数学一模试卷(理科)(解析版)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集U={x∈N|x≥1},集合A={x∈N|x2≥3},则∁U A=()A.∅B.{1} C.{1,2} D.{1,2,3}2.设i是虚数单位,表示复数z的共轭复数.若z=1﹣2i,则复数在复平面内对应的点位于()A.第一象限 B.第二象限 C.第三象限 D.第四象限3.已知向量,均为单位向量,它们的夹角为,则|+|=()A.1 B.C.D.24.已知随机变量X~N(1,σ2),若P(0<X<2)=0.4,则P(X≤0)=()A.0.6 B.0.4 C.0.3 D.0.25.已知函数,则=()A.﹣sin1 B.sin1 C.﹣1 D.16.如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=()A.0 B.5 C.45 D.907.已知3件次品和2件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,则第一次检测出的是次品且第二次检测出的是正品的概率为()A.B.C.D.8.已知圆C:x2+y2﹣2x﹣4y+1=0上存在两点关于直线l:x+my+1=0对称,经过点M(m,m)作圆的两条切线,切点分别为P,Q,则|PQ|=()A.3 B.C. D.9.函数是()A.最小正周期为π的奇函数B.最小正周期为π的偶函数C.最小正周期为的奇函数D.最小正周期为的偶函数10.不等式组的解集记为D,,有下面四个命题:p1:∀(x,y)∈D,z≥1;p2:∃(x,y)∈D,z≥1p3:∀(x,y)∈D,z≤2;p4:∃(x,y)∈D,z<0其中的真命题是()A.p1,p2B.p1,p3C.p1,p4D.p2,p311.某几何体的三视图如图所示,则该几何体外接球的表面积为()A. B.3πC.6πD.24π12.已知e为自然对数的底数,若对任意的x∈[0,1],总存在唯一的y∈[﹣1,1],使得x+y2e y ﹣a=0成立,则实数a的取值范围是()A.[1,e] B.C.(1,e] D.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中对应题号后的横线上.13.已知定义在R上的函数f(x)满足f(x+2)﹣f(x)=0,当x∈(0,2]时,f(x)=2x,则f(2016)= .14.已知(1﹣x)6=a0+a1x+a2x2+…+a6x6,则|a0|+|a1|+…+|a6|= .15.已知双曲线﹣=1(a>0,b>0)的左顶点为M,右焦点为F,过F的直线l与双曲线交于A,B两点,且满足:=2, =0,则该双曲线的离心率是.16.在四边形ABCD中,AB=7,AC=6,,CD=6sin∠DAC,则BD的最大值为.三、解答题:本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(12分)(2016常德一模)已知数列{a n}前n项和为S n,且满足3S n﹣4a n+2=0.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)令b n=log2a n,T n为{b n}的前n项和,求证:.18.(12分)(2016常德一模)某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.右图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图:已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群”.(Ⅰ)求m,n的值,并求这100名学生月消费金额的样本平均数(同一组中的数据用该组区间的中点值作代表);(Ⅱ)现采用分层抽样的方式从月消费金额落在[350,450),[550,650)内的两组学生中抽取10人,再从这10人中随机抽取3人,记被抽取的3名学生中属于“高消费群”的学生人数为随机变量X,求X的分布列及数学期望.19.(12分)(2016常德一模)如图所示的几何体中,ABC﹣A1B1C1为三棱柱,且AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,∠ADC=60°.(Ⅰ)若AA1=AC,求证:AC1⊥平面A1B1CD;(Ⅱ)若CD=2,AA1=λAC,二面角C﹣A1D﹣C1的余弦值为,求三棱锥C1﹣A1CD的体积.20.(12分)(2016常德一模)已知椭圆C1:的离心率为,焦距为,抛物线C2:x2=2py(p>0)的焦点F是椭圆C1的顶点.(Ⅰ)求C1与C2的标准方程;(Ⅱ)C1上不同于F的两点P,Q满足,且直线PQ与C2相切,求△FPQ的面积.21.(12分)(2016常德一模)已知函数,曲线y=f(x)在点(e2,f(e2))处的切线与直线2x+y=0垂直(其中e为自然对数的底数).(Ⅰ)求f(x)的解析式及单调减区间;(Ⅱ)若函数无零点,求k的取值范围.请考生在第22,23,24三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.[选修4-1:几何证明选讲]22.(10分)(2016常德一模)如图,已知AB=AC,圆O是△ABC的外接圆,CD⊥AB,CE是圆O的直径.过点B作圆O的切线交AC的延长线于点F.(Ⅰ)求证:ABCB=CDCE;(Ⅱ)若,,求△ABC的面积.[选修4-4:坐标系与参数方程]23.(2016常德一模)已知曲线C的参数方程是(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A,B的极坐标分别为A(2,π),.(Ⅰ)求直线AB的直角坐标方程;(Ⅱ)设M为曲线C上的动点,求点M到直线AB距离的最大值.[选修4-5:不等式选讲]24.(2016常德一模)己知函数f(x)=|2x+1|﹣|x﹣1|.(Ⅰ)求不等式f(x)<2的解集;(Ⅱ)若关于x的不等式f(x)≤a﹣有解,求a的取值范围.2016年湖南省常德市高考数学一模试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集U={x∈N|x≥1},集合A={x∈N|x2≥3},则∁U A=()A.∅B.{1} C.{1,2} D.{1,2,3}【分析】直接利用集合的补集求解即可.【解答】解:全集U={x∈N|x≥1},集合A={x∈N|x2≥3},则∁U A={1}.故选:B.【点评】本题考查集合的基本运算,补集的求法,是基础题.2.设i是虚数单位,表示复数z的共轭复数.若z=1﹣2i,则复数在复平面内对应的点位于()A.第一象限 B.第二象限 C.第三象限 D.第四象限【分析】利用复数的乘法运算法则化简求解,求出复数的对应点的坐标即可判断选项.【解答】解:z=1﹣2i,则复数=1﹣2i+i(1+2i)=-1﹣i,复数对应点的坐标(-1,﹣1)在第三象限.故选:C.【点评】本题考查复数的代数形式混合运算,复数的几何意义,是基础题.3.已知向量,均为单位向量,它们的夹角为,则|+|=()A.1 B.C.D.2【分析】由条件即可得到,且夹角为,从而进行数量积的运算便可求出,从而便可得出的值.【解答】解:根据题意,,;∴=;∴.故选:A.【点评】考查单位向量的概念,向量夹角的概念,以及向量数量积的运算及计算公式.4.已知随机变量X~N(1,σ2),若P(0<X<2)=0.4,则P(X≤0)=()A.0.6 B.0.4 C.0.3 D.0.2【分析】随机变量ξ服从正态分布N(1,σ2),得到曲线关于x=1对称,根据曲线的对称性得到小于等于0的概率和大于等于2的概率是相等的得到结果.【解答】解:随机变量ξ服从正态分布N(1,σ2),∴曲线关于x=1对称,∴P(X≤0)=(1﹣P(0<X<2))=×(1﹣0.4)=0.3.故选:C.【点评】本题主要考查正态分布曲线的特点及曲线所表示的意义、函数图象对称性的应用等基础知识,属于基础题.5.已知函数,则=()A.﹣sin1 B.sin1 C.﹣1 D.1【分析】利用分段函数、三角函数的性质求解.【解答】解:∵函数,∴f(﹣)=sin(﹣)=﹣sin=1,=f(1)=1.故选:D.【点评】本题考查函数值的求法,是基础题,解题时要认真审题,注意分段函数的性质的合理运用.6.如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=()A.0 B.5 C.45 D.90【分析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量m的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.【解答】解:第一次执行循环体,r=90,m=135,n=90,不满足退出循环的条件;第二次执行循环体,r=0,m=45,n=0,满足退出循环的条件;故输出的m值为45,故选:C【点评】本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答.7.已知3件次品和2件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,则第一次检测出的是次品且第二次检测出的是正品的概率为()A.B.C.D.【分析】利用相互独立事件概率乘法公式求解.【解答】解:∵3件次品和2件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,∴第一次检测出的是次品且第二次检测出的是正品的概率为:p==.故选:B.【点评】本题考查概率的求法,是基础题,解题时要认真审题,注意相互独立事件概率乘法公式的合理运用.8.已知圆C:x2+y2﹣2x﹣4y+1=0上存在两点关于直线l:x+my+1=0对称,经过点M(m,m)作圆的两条切线,切点分别为P,Q,则|PQ|=()A.3 B.C. D.【分析】由题意直线l:x+my+1=0过圆心C(1,2),从而得到m=﹣1.圆C半径r=2,当过点M(﹣1,﹣1)的切线的斜率不存在时,切线方程为x=﹣1,把x=﹣1代入圆C,得P(﹣1,2);当过点M(﹣1,﹣1)的切线的斜率存在时,设切线方程为y=k(x+1)﹣1,由圆心C(1,2)到切线y=k(x+1)﹣1的距离d=r,求出切线方程,与圆联立,得Q(,),由此能求出|PQ|.【解答】解:∵圆C:x2+y2﹣2x﹣4y+1=0上存在两点关于直线l:x+my+1=0对称,∴直线l:x+my+1=0过圆心C(1,2),∴1+2m+1=0.解得m=﹣1.圆C:x2+y2﹣2x﹣4y+1=0的圆心(1,2),半径r==2,当过点M(﹣1,﹣1)的切线的斜率不存在时,切线方程为x=﹣1,圆心C(1,2)到x=﹣1的距离为2,成立,把x=﹣1代入圆C:x2+y2﹣2x﹣4y+1=0,得y=2,∴P(﹣1,2),当过点M(﹣1,﹣1)的切线的斜率存在时,设切线方程为y=k(x+1)﹣1,圆心C(1,2)到切线y=k(x+1)﹣1的距离d==,解得k=,∴切线方程为y=(x+1)﹣1,即5x﹣12y﹣7=0,联立,得169x2﹣598x+529=0,解得x=,y=,∴Q(,),∴|PQ|==.故选:D.【点评】本题考查线段长的求法,是中档题,解题时要认真审题,注意圆的性质、点到直线的距离公式的合理运用.9.函数是()A.最小正周期为π的奇函数B.最小正周期为π的偶函数C.最小正周期为的奇函数D.最小正周期为的偶函数【分析】使用两角和差的三角函数公式化简函数解析式.【解答】解:y=[(cosx﹣sinx)﹣][(cosx﹣sinx)+]=(cosx﹣sinx)2﹣=﹣sin2x.∴函数y的周期T=.∵y=sinx是奇函数,∴y=﹣sin2x为奇函数.故选A.【点评】本题考查了三角函数的恒等变换,正弦函数的性质,属于中档题.10.不等式组的解集记为D,,有下面四个命题:p1:∀(x,y)∈D,z≥1;p2:∃(x,y)∈D,z≥1p3:∀(x,y)∈D,z≤2;p4:∃(x,y)∈D,z<0其中的真命题是()A.p1,p2B.p1,p3C.p1,p4D.p2,p3【分析】画出约束条件不是的可行域,利用目标函数的几何意义,求出范围,判断选项的正误即可.【解答】解:不等式组的可行域如图:的几何意义是可行域内的点与(﹣1,﹣1)连线的斜率,可知(﹣1,﹣1)与C连线的斜率最小,与B连线的斜率最大.可得C(2,1).最小值为: =,z≥,由,解得x=1,y=3,B(1,3).最大值为: =2.z≤2.可得选项p2,p3正确.故选:D.【点评】本题考查线性规划的解得应用,命题的真假的判断,正确画出可行域以及目标函数的几何意义是解题的关键.11.某几何体的三视图如图所示,则该几何体外接球的表面积为()A. B.3πC.6πD.24π【分析】根据三视图知几何体是三棱锥为长方体一部分,画出直观图,由长方体的性质求出该几何体外接球的半径,利用球的表面积公式求出该几何体外接球的表面积.【解答】解:根据三视图知几何体是:三棱锥P﹣ABC为长方体一部分,直观图如图所示:且长方体的长、宽、高分别是1、1、2,∴三棱锥P﹣ABC的外接球与长方体的相同,设该几何体外接球的半径是R,由长方体的性质可得,2R==,解得R=,∴该几何体外接球的表面积S=4πR2=6π,故选:C.【点评】本题考查由三视图求几何体外接球的表面积,在三视图与直观图转化过程中,以一个长方体为载体是很好的方式,使得作图更直观,考查空间想象能力.12.已知e 为自然对数的底数,若对任意的x ∈[0,1],总存在唯一的y ∈[﹣1,1],使得x+y 2e y﹣a=0成立,则实数a 的取值范围是( )A .[1,e]B .C .(1,e]D .【分析】由x+y 2e y ﹣a=0成立,解得y 2e y =a ﹣x ,根据题意可得:a ﹣1≥(﹣1)2e ﹣1,且a ﹣0≤12×e 1,解出并且验证等号是否成立即可得出. 【解答】解:由x+y 2e y﹣a=0成立,解得y 2e y=a ﹣x ,∴对任意的x ∈[0,1],总存在唯一的y ∈[﹣1,1],使得x+y 2e y﹣a=0成立, ∴a ﹣1≥(﹣1)2e ﹣1,且a ﹣0≤12×e 1,解得≤a ≤e ,其中a=1+时,y 存在两个不同的实数,因此舍去,a 的取值范围是.故选:B .【点评】本题考查了函数的单调性、不等式的性质,考查了推理能力与计算能力,属于中档题.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中对应题号后的横线上.13.已知定义在R 上的函数f (x )满足f (x+2)﹣f (x )=0,当x ∈(0,2]时,f (x )=2x ,则f (2016)= 4 .【分析】由题意可得函数为周期为2的周期函数,可得f (2016)=f (2),代值计算可得. 【解答】解:∵定义在R 上的函数f (x )满足f (x+2)﹣f (x )=0, ∴f (x+2)=f (x )即函数f (x )为周期为2的周期函数, 又∵当x ∈(0,2]时,f (x )=2x, ∴f (2016)=f (2)=22=4, 故答案为:4.【点评】本题考查函数的周期性,涉及指数的运算,属基础题.14.已知(1﹣x)6=a0+a1x+a2x2+…+a6x6,则|a0|+|a1|+…+|a6|= 64 .【分析】根据二项式定理可知a0,a2,a4,a6均为正数,a1,a3,a5均为负数,令x=﹣1即可求出结论.【解答】解:,由二项式定理可知a0,a2,a4,a6均为正数,a1,a3,a5均为负数,∴令x=﹣1,得(1+1)6=a0﹣a1+a2﹣…+a6=26=64,即|a0|+|a1|+…+|a6|=a0﹣a1+a2﹣…+a6=64.故答案为:64.【点评】本题考查了用赋值法求二项式展开式的各项系数和的应用问题,是基础题目.15.已知双曲线﹣=1(a>0,b>0)的左顶点为M,右焦点为F,过F的直线l与双曲线交于A,B两点,且满足:=2, =0,则该双曲线的离心率是 2 .【分析】由中点的向量表示形式可得F为AB的中点, =0可得MA⊥MB,由△ABM为等腰直角三角形,可得tan45°=,即有b2=a(c+a),由a,b,c的关系和离心率公式,计算即可得到所求值.【解答】解:由=2, =0可得:F为AB的中点,MA⊥MB,由双曲线的对称性,可得AB⊥x轴,令x=c,可得y=±b=±,由△ABM为等腰直角三角形,可得:tan45°===1,即有b2=a(c+a),即(c﹣a)(c+a)=a(c+a),可得c﹣a=a,即c=2a,即有e==2.故答案为:2.【点评】本题考查双曲线的离心率的求法,注意运用平面向量共线定理和向量垂直的条件,考查等腰三角形的性质,属于中档题.16.在四边形ABCD中,AB=7,AC=6,,CD=6sin∠DAC,则BD的最大值为8 .【分析】由CD=6sin∠DAC,可得CD⊥AD.点D在以AC为直径的圆上(去掉A,B,C).可得:当BD经过AC的中点O时取最大值,利用余弦定理可得:OB,可得BD的最大值=OB+AC.【解答】解:由CD=6sin∠DAC,可得CD⊥AD.∴点D在以AC为直径的圆上(去掉A,B,C).∴当BD经过AC的中点O时取最大值,OB2=32+72﹣2×3×7cos∠BAC=25,解得OB=5,∴BD的最大值=5+AC=8.故答案为:8.【点评】本题考查了余弦定理、圆的性质,考查了推理能力与计算能力,属于中档题.三、解答题:本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(12分)(2016常德一模)已知数列{a n}前n项和为S n,且满足3S n﹣4a n+2=0.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)令b n=log2a n,T n为{b n}的前n项和,求证:.【分析】(Ⅰ)当n=1,a1=2,当n≥2,求得a n=4a n﹣1,数列{a n}是首项为a1=2,公比为4的等比数列,再利用等比数列的通项公式即可得出,(Ⅱ)写出{b n}的通项公式,b n=2n﹣1,及前n项和T n=n2,采用裂项法,化简=<2.【解答】解:(Ⅰ)由3S n﹣4a n+2=0,令n=1,可得:a1=2;…(2分)当n≥2时,可得(3S n﹣4a n+2)﹣(3S n﹣1﹣4a n﹣1+2)=0⇒a n=4a n﹣1…(4分)所以数列{a n}是首项为a1=2,公比为4的等比数列,故: =22n﹣1…(6分)(Ⅱ),T n=1+3+…+(2n﹣1)=n2…(8分)≤…(11分)==<2…(12分)【点评】本题考查求数列通项公式及前n项和公式,属于中档题.18.(12分)(2016常德一模)某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.右图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图:已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群”.(Ⅰ)求m,n的值,并求这100名学生月消费金额的样本平均数(同一组中的数据用该组区间的中点值作代表);(Ⅱ)现采用分层抽样的方式从月消费金额落在[350,450),[550,650)内的两组学生中抽取10人,再从这10人中随机抽取3人,记被抽取的3名学生中属于“高消费群”的学生人数为随机变量X,求X的分布列及数学期望.【分析】(Ⅰ)由题意知 100(m+n)=0.6且2m=n+0.0015,由此能求出m,n的值,并求这100名学生月消费金额的样本平均数.(Ⅱ)由题意从[350,450)中抽取7人,从[550,650)中抽取3人,随机变量X的取值所有可能取值有0,1,2,3,分别求出相应的概率,由此能求出随机变量X的分布列及随机变量X的数学期望E(X).【解答】解:(Ⅰ)由题意知 100(m+n)=0.6且2m=n+0.0015,故m=0.0025,n=0.0035.…(3分)所求平均数为:(元)…(5分)(Ⅱ)由题意从[350,450)中抽取7人,从[550,650)中抽取3人…(7分)随机变量X的取值所有可能取值有0,1,2,3,…(9分)所以,随机变量X的分布列为随机变量X的数学期望E(X)=…(12分)【点评】本题考查频率分布直方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.19.(12分)(2016常德一模)如图所示的几何体中,ABC﹣A1B1C1为三棱柱,且AA1⊥平面ABC,四边形ABCD为平行四边形,AD=2CD,∠ADC=60°.(Ⅰ)若AA1=AC,求证:AC1⊥平面A1B1CD;(Ⅱ)若CD=2,AA1=λAC,二面角C﹣A1D﹣C1的余弦值为,求三棱锥C1﹣A1CD的体积.【分析】(Ⅰ)若AA1=AC,根据线面垂直的判定定理即可证明AC1⊥平面A1B1CD;(Ⅱ)建立坐标系,根据二面角C﹣A1D﹣C1的余弦值为,求出λ的值,根据三棱锥的体积公式进行计算即可.【解答】证明:(Ⅰ)若AA1=AC,则四边形ACC1A1为正方形,则AC1⊥A1C,∵AD=2CD,∠ADC=60°,∴△ACD为直角三角形,则AC⊥CD,∵AA1⊥平面ABC,∴CD⊥平面ACC1A1,则CD⊥A1C,∵A1C∩CD=C,∴AC1⊥平面A1B1CD;(Ⅱ)若CD=2,∵∠ADC=60°,∴AC=2,则AA1=λAC=2λ,建立以C为坐标原点,CD,CB,CC1分别为x,y,z轴的空间直角坐标系如图:则C(0,0,0),D(2,0,0),A(0,2,0),C1(0,0,2λ),A1(0,2,2λ),则=(2,﹣2,﹣2λ),=(2,0,0),=(0,2,0),设面CA1D的一个法向量为=(1,0,0).则=2x﹣2y﹣2λz=0,=2x=0,则x=0,y=﹣λz,令z=1,则y=﹣λ,则=(0,﹣λ,1)设面A1DC1的一个法向量为=(x,y,z)=2x﹣2y﹣2λz=0,=2y=0,则y=0,2x﹣2λz=0,令z=1,则x=λ,则=(λ,0,1),∵二面角C﹣A1D﹣C1的余弦值为,∴cos<,>===,即(1+λ2)(1+3λ2)=8,得λ=1,即AA1=AC,则三棱锥C1﹣A1CD的体积V=V===4.【点评】本题主要考查线面垂直的判断以及三棱锥体积的计算,根据二面角的关系建立坐标系求出λ的值是解决本题的关键.20.(12分)(2016常德一模)已知椭圆C1:的离心率为,焦距为,抛物线C2:x2=2py(p>0)的焦点F是椭圆C1的顶点.(Ⅰ)求C1与C2的标准方程;(Ⅱ)C1上不同于F的两点P,Q满足,且直线PQ与C2相切,求△FPQ的面积.【分析】(I)设椭圆C1的焦距为2c,依题意有,,由此能求出椭圆C1的标准方程;又抛物线C2:x2=2py(p>0)开口向上,故F是椭圆C1的上顶点,由此能求出抛物线C2的标准方程.(II)设直线PQ的方程为y=kx+m,设P(x1,y1),Q(x2,y2),则,,联立,得(3k2+1)x2+6kmx+3m2﹣12=0,由此利用根的判别式、韦达定理、弦长公式,结合已知条件能求出△FPQ的面积.【解答】解:(I)设椭圆C1的焦距为2c,依题意有,,解得,b=2,故椭圆C1的标准方程为.…(3分)又抛物线C2:x2=2py(p>0)开口向上,故F是椭圆C1的上顶点,∴F(0,2),∴p=4,故抛物线C2的标准方程为x2=8y.…(5分)(II)由题意得直线PQ的斜率存在.设直线PQ的方程为y=kx+m,设P(x1,y1),Q(x2,y2),则,,∴,…(6分)即(*)联立,消去y整理得,(3k2+1)x2+6kmx+3m2﹣12=0(**).依题意,x1,x2是方程(**)的两根,△=144k2﹣12m2+48>0,∴,,…(7分)将x1+x2和x1x2代入(*)得m2﹣m﹣2=0,解得m=﹣1,(m=2不合题意,应舍去).…(8分)联立,消去y整理得,x2﹣8kx+8=0,令△'=64k2﹣32=0,解得.…(10分)经检验,,m=﹣1符合要求.此时,,∴.…(12分)【点评】本题考查椭圆标准方程的求法,考查三角形面积的求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、弦长公式、椭圆性质的合理运用.21.(12分)(2016常德一模)已知函数,曲线y=f(x)在点(e2,f(e2))处的切线与直线2x+y=0垂直(其中e为自然对数的底数).(Ⅰ)求f(x)的解析式及单调减区间;(Ⅱ)若函数无零点,求k的取值范围.【分析】(Ⅰ)求出函数的导数,求得切线的斜率,由两直线垂直的条件,可得m=2,求得f (x)的解析式,可得导数,令导数小于0,可得减区间;(Ⅱ)可得g(x),函数g(x)无零点,即要在x∈(0,1)∪(1,+∞)内无解,亦即要在x∈(0,1)∪(1,+∞)内无解.构造函数.对k讨论,运用单调性和函数零点存在定理,即可得到k的范围.【解答】解:(Ⅰ)函数的导数为,又由题意有:,故.此时,由f'(x)≤0⇒0<x<1或1<x≤e,所以函数f(x)的单调减区间为(0,1)和(1,e].(Ⅱ),且定义域为(0,1)∪(1,+∞),要函数g(x)无零点,即要在x∈(0,1)∪(1,+∞)内无解,亦即要在x∈(0,1)∪(1,+∞)内无解.构造函数.①当k≤0时,h'(x)<0在x∈(0,1)∪(1,+∞)内恒成立,所以函数h(x)在(0,1)内单调递减,h(x)在(1,+∞)内也单调递减.又h(1)=0,所以在(0,1)内无零点,在(1,+∞)内也无零点,故满足条件;②当k>0时,,(1)若0<k<2,则函数h(x)在(0,1)内单调递减,在内也单调递减,在内单调递增.又h(1)=0,所以在(0,1)内无零点;易知,而,故在内有一个零点,所以不满足条件;(2)若k=2,则函数h(x)在(0,1)内单调递减,在(1,+∞)内单调递增.又h(1)=0,所以x∈(0,1)∪(1,+∞)时,h(x)>0恒成立,故无零点,满足条件;(3)若k>2,则函数h(x)在内单调递减,在内单调递增,在(1,+∞)内也单调递增.又h(1)=0,所以在及(1,+∞)内均无零点.又易知,而h(e﹣k)=k(﹣k)﹣2+2e k=2e k﹣k2﹣2,又易证当k>2时,h(e﹣k)>0,所以函数h(x)在内有一零点,故不满足条件.综上可得:k的取值范围为:k≤0或k=2.【点评】本题考查导数的运用:求切线的斜率和单调区间,考查函数方程的转化思想的运用,分类讨论的思想方法,以及函数零点存在定理的运用,考查化简整理的运算能力,属于难题.请考生在第22,23,24三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.[选修4-1:几何证明选讲]22.(10分)(2016常德一模)如图,已知AB=AC,圆O是△ABC的外接圆,CD⊥AB,CE是圆O的直径.过点B作圆O的切线交AC的延长线于点F.(Ⅰ)求证:ABCB=CDCE;(Ⅱ)若,,求△ABC的面积.【分析】(Ⅰ)连接AE,证明Rt△CBD∽Rt△CEA,结合AB=AC,即可证明:ABCB=CDCE;(Ⅱ)证明△ABF~△BCF,可得AC=CF,利用切割线定理有FAFC=FB2,求出AC,即可求△ABC 的面积.【解答】证明:(Ⅰ)连接AE,∵CE是直径,∴∠CAE=90°,又CD⊥AB,∴∠CDB=90°,∵∠CBD=∠CEA,故Rt△CBD∽Rt△CEA,…(2分)∴,∴ACCB=CDCE又AB=AC,∴ABCB=CDCE.…(5分)(Ⅱ)∵FB是⊙O的切线,∴∠CBF=∠CAB.∴在△ABF和△BCF中,,∴△ABF~△BCF,∴,∴FA=2AB=2AC,∴AC=CF…(7分)设AC=x,则根据切割线定理有FAFC=FB2∴x2x=8,∴x=2,∴.…(10分)【点评】本题主要考查了切线的性质及其应用,同时考查了相似三角形的判定和切割线定理等知识点,属于中档题.[选修4-4:坐标系与参数方程]23.(2016常德一模)已知曲线C的参数方程是(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,A,B的极坐标分别为A(2,π),.(Ⅰ)求直线AB的直角坐标方程;(Ⅱ)设M为曲线C上的动点,求点M到直线AB距离的最大值.【分析】(Ⅰ)由x=ρcosθ,y=ρsinθ,可得A,B的直角坐标,求得AB的斜率,由点斜式方程可得直线方程;(Ⅱ)运用点到直线的距离公式,结合三角函数的辅助角公式,由正弦函数的值域,即可得到所求最大值.【解答】解:(Ⅰ)将A、B化为直角坐标为A(2cosπ,2sinπ)、,即A、B的直角坐标分别为A(﹣2,0)、,即有,可得直线AB的方程为,即为.(Ⅱ)设M(2cosθ,sinθ),它到直线AB距离=,(其中)当sin(θ+φ)=1时,d取得最大值,可得.【点评】本题考查直角坐标和极坐标的互化,直线方程的求法和运用,同时考查三角函数的辅助角公式和正弦函数的值域的运用,属于中档题.[选修4-5:不等式选讲]24.(2016常德一模)己知函数f(x)=|2x+1|﹣|x﹣1|.(Ⅰ)求不等式f(x)<2的解集;(Ⅱ)若关于x的不等式f(x)≤a﹣有解,求a的取值范围.【分析】(Ⅰ)将f(x)写成分段函数式,讨论x的范围,解不等式,求交集即可得到所求解集;(Ⅱ)关于x的不等式f(x)≤a﹣有解,即为f(x)min≤a﹣,运用一次函数的单调性,求得最小值,解二次不等式即可得到所求范围.【解答】解:(Ⅰ)函数f(x)=|2x+1|﹣|x﹣1|=,当x≥1时,x+2<2,即x<0,可得x∈∅;当﹣<x<1时,3x<2,即x<,可得﹣<x<;当x≤﹣时,﹣x﹣2<2,即x>﹣4,可得﹣4<x≤﹣.综上可得,不等式的解集为(﹣4,);(Ⅱ)关于x的不等式f(x)≤a﹣有解,即为:f(x)min≤a﹣,由x≥1时,x+2≥3;﹣<x<1时,﹣<3x<3:x≤﹣时,﹣x﹣2≥﹣.可得f(x)min=﹣,即有a﹣≥﹣,解得﹣1≤a≤3.即有a的取值范围是[﹣1,3].【点评】本题考查绝对值不等式的解法,注意运用零点分区间法,考查不等式有解的条件,注意运用转化思想,求函数的最值,考查运算能力,属于中档题.。
湖南省常德市高三3月模拟考试语文试卷.pdf

2016年常德市高三年级模拟考试 注意事项: 1.本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分。
满分150分,考试时间150分钟。
2.答题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷 阅读题 甲 必考题 一、现代文阅读(9分,每小题3分) 阅读下面的文字,完成1~3题。
近年来,每逢春节便刷爆社交网络的返乡日记,道出的不仅仅是凋零的劳动力、解体的乡规民约、高昂的娶亲负担这些表面现象,浓郁的乡愁背后,实际上是当代中国人集体面临的现代化困境。
一篇又一篇的返乡日记,记述的是残留的小农经济形态解体过程中的乡村巨变和个人蜕变。
而这些看似无意识的自然流露,背后却有文化的深层推力。
文化影响着我们的思维习惯、性格特征、处事风格,而这些都可以在历史回溯中窥探其奥秘。
拥有几千年历史的中华大地饱经沧桑战火,但没有像其他任何一个古文明发源地那样分崩离析。
因为,以儒家文化为核心的中华文明深深植根于寻常百姓家,得到代际传承。
中华文明能够躲过岁月的刀斧、能够抗击少数民族的金戈铁马,其答案就在农耕社会的生产方式中。
中国有着长达数千年的农耕经济形态,农耕文明早在黄河中游和长江中下游流域形成,人们逐水而居,春播秋收,以家庭为单位进行农业生产,从肥沃的土地中收获上天的馈赠,过着与游牧民族饥饱不定、奔走疲惫的迁徙生涯截然不同的富足生活。
当农耕经济逐渐推广到整个中原大地,儒家文化也日渐从百家争鸣中脱颖而出。
汉武帝罢黜百家独尊儒术以后,儒家文化便在历史的长河中不断得到深化和扩充,并由上至下推行,深深渗入到寻常百姓的生活中,外化为柴米油盐酱醋茶和琴棋书画诗酒花,从而演绎出数千年来稳健发展的人情百态。
所以说,天人合一、尊老敬上、友善勤劳、守旧谨慎、善恶报应、祖宗家法这些传承数千年的文化观念,是与中国古代农耕社会相适应的社会意识形态,在根本上都是由农耕经济形态决定的。
农耕经济形态决定了传统中国人的存在样态,决定了传统中国人的处世风格,也塑造了传统中国人的国民性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年高考(490)湖南省常德市2016届高三3月模拟考试湖南省常德市2016届高三年级3月模拟考试语文注意事项:1.本试卷分第卷(阅读题)和第卷(表达题)两部分。
满分150分,考试时间150分钟。
2.答题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第卷阅读题甲必考题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成1~3题。
近年来,每逢春节便刷爆社交网络的返乡日记,道出的不仅仅是凋零的劳动力、解体的乡规民约、高昂的娶亲负担这些表面现象,浓郁的乡愁背后,实际上是当代中国人集体面临的现代化困境。
一篇又一篇的返乡日记,记述的是残留的小农经济形态解体过程中的乡村巨变和个人蜕变。
而这些看似无意识的自然流露,背后却有文化的深层推力。
文化影响着我们的思维习惯、性格特征、处事风格,而这些都可以在历史回溯中窥探其奥秘。
拥有几千年历史的中华大地饱经沧桑战火,但没有像其他任何一个古文明发源地那样分崩离析。
因为,以儒家文化为核心的中华文明深深植根于寻常百姓家,得到代际传承。
中华文明能够躲过岁月的刀斧、能够抗击少数民族的金戈铁马,其答案就在农耕社会的生产方式中。
中国有着长达数千年的农耕经济形态,农耕文明早在黄河中游和长江中下游流域形成,人们逐水而居,春播秋收,以家庭为单位进行农业生产,从肥沃的土地中收获上天的馈赠,过着与游牧民族饥饱不定、奔走疲惫的迁徙生涯截然不同的富足生活。
当农耕经济逐渐推广到整个中原大地,儒家文化也日渐从百家争鸣中脱颖而出。
汉武帝罢黜百家独尊儒术以后,儒家文化便在历史的长河中不断得到深化和扩充,并由上至下推行,深深渗入到寻常百姓的生活中,外化为柴米油盐酱醋茶和琴棋书画诗酒花,从而演绎出数千年来稳健发展的人情百态。
所以说,天人合一、尊老敬上、友善勤劳、守旧谨慎、善恶报应、祖宗家法这些传承数千年的文化观念,是与中国古代农耕社会相适应的社会意识形态,在根本上都是由农耕经济形态决定的。
农耕经济形态决定了传统中国人的存在样态,决定了传统中国人的处世风格,也塑造了传统中国人的国民性。
然而,社会意识观念必须适应社会存在,否则就会制约社会的经济发展。
当今的中国早已不是农耕经济形态下的中国,全球化的历史潮流已经席卷着我们进入现代化社会。
在社会主义现代化进程中,适宜传统农耕经济形态的中华文明已无法完全适应当今社会发展的新形势,而文化的滞后性必然导致这样的情形出现:随着现代化的推进,当代中国人不得不遭受从传统文化观念和生活样态中撕离出去的苦痛,在旧观念与新常态格格不入、新观念尚未形成确立之际,难免陷入传统性与现代性所构成的两难境地。
因此,如何审视传统性与现代性的交锋,不仅关系个人的安身立命,更关系国家的长远发展。
如果固守传统的价值观念和生活方式,这样的遗老不仅难以在现代工商业活动中收获事业成功,也难以在新旧价值观念的现实冲突中求得心灵安宁。
如果全盘抛弃传统文明,生搬硬套西方国家在他们的传统文明基础上生发演绎的现代文明,那不啻于邯郸学步,会使处在全球化浪潮中的我们成为无根浮萍,随波逐流,沦为附庸。
所以,理性清晰地思考传统文化,慎思明辨地融入现代发展,做出恰当的判断和抉择,我们才有可能走出现代性与传统性交织而成的圈牢。
(摘编自2016年2月24日光明网《光明时评》)1.下列关于原文内容的表述,不正确的一项是A.返乡日记记述的是村庄的沦落和个人的乡愁,但这种看似无意识的自然流露背后,却有着文化的深层推力。
B.中华大地饱经风霜却没有分崩离析,是因为以儒家文化为核心的中华文明植根于寻常百姓的生活中并代代相传。
C.中国有着长达数千年的农耕经济形态,然而,随着社会的发展,乡村的巨变宣告了小农经济形态的彻底瓦解。
D.农耕经济形态从根本上决定了友善勤劳、善恶报应、天人合一、守旧谨慎、祖宗家法这些传承数千年的文化观念。
2.下列理解和分析,不符合原文意思的一项是A.农耕社会的生产方式使中华文明躲过了岁月的刀斧、抗击了少数民族的金戈铁马,绵延发展了几千年。
B.儒家文化在汉武帝时期得到自上而下的推行,从此开始影响普通百姓的生活,并形成了稳健发展的人情百态。
C.浓浓的乡愁背后,是当代中国人集体性的现代化困境:传统的中华文明已不能完全适应当今社会发展的新形势。
D.社会的意识观念如果不能适应社会存在,不仅会对个人的安身立命造成阻碍,也会对国家的长远发展形成制约。
3.根据原文内容,下列理解和分析不正确的一项是A.由于文化的滞后,在现代化背景下演进的传统中华文明,让当代中国人陷入旧观念与新常态格格不入的两难境地。
B.随着社会主义现代化的推进,与中国古代农耕社会相适应的社会意识形态已制约了当代社会的经济发展。
C.传统中国人的存在样态,传统中国人的处世风格,乃至传统中国人的国民性,归根到底都受制于农耕经济形态。
D.只有抛弃传统价值观念和生活方式,才能在现代工商业活动中收获事业成功,并在新旧冲突中求得心灵安宁。
二、古代诗文阅读(36分)(一)文言文阅读(19分)阅读下面的文言文,完成4~7题。
刘世让字元钦,雍州醴泉人也。
仕隋徵仕郎。
高祖入长安,世让以湋川归国,拜通议大夫。
时唐弼余党寇扶风,世让自请安辑,许之,俄得数千人。
复为安定道行军总管,率兵以拒薛举,战败,世让及弟宝俱为举军所获。
举将至城下,令绐说城中曰:大军五道已趣长安,宜开门早降。
世让伪许之,因告城中曰:贼兵多少,极于此矣。
宜善自固,以图安全。
举重其执节,竟不之害。
太宗时屯兵高墌,世让潜遣宝逃归,言贼中虚实,高祖嘉之,赐其家帛千匹。
及贼平,得归,授彭州刺史。
寻领陕东道行军总管,与永安王孝基击吕崇茂于夏县,诸军败绩,世让与唐俭俱为贼所获。
狱中闻独孤怀恩有逆谋,逃还以告高祖。
时高祖方济河,将幸怀恩之营,闻难惊曰:刘世让之至,岂非天命哉!因劳之曰:卿往陷薛举,遣弟潜效款诚,今复冒危告难,是皆忧国忘身也。
寻封弘农郡公,赐庄一区、钱百万。
累并州总管,统兵屯于雁门。
突厥处罗可汗与高开道、苑君璋合众攻之,甚急。
鸿胪卿郑元璹先使在蕃,可汗令元璹来说之,世让厉声曰:大丈夫奈何为夷狄作说客耶!经月余,虏乃退。
及元璹还,述世让忠贞勇干,高祖下制褒美之,赐以良马。
未几,召拜广州总管。
将之任,高祖问以备边之策,世让答曰:突厥南寇,徒以马邑为其中路耳。
如臣所计请于崞城置一智勇之将多储金帛有来降者厚赏赐之数出奇兵略其城下芟践禾稼败其生业不出岁余彼当无食马邑不足图也。
高祖曰:非公无可任者。
乃使驰驿往经略之。
突厥惧其威名,乃纵反间,言世让与可汗通谋,将为乱。
高祖不之察,遂诛世让,籍没其家。
贞观初,突厥来降者言世让初无逆谋,始原其妻子。
(节选自《旧唐书刘世让传》)4.对下列句子中加点词语的解释,不正确的一项是(3分)A.令绐说城中曰绐:欺骗B.大军五道已趣长安趣:攻取C.将幸怀恩之营幸:指皇帝亲临D.籍没其家籍:登记财产5.下列对文中画波浪线部分的断句,正确的一项是(3分)A.如臣所计请于崞城置一智勇之将多储金帛有来降者厚赏赐之数出奇兵略其城下芟践禾稼败其生业不出岁余彼当无食马邑不足图也B.如臣所计请于崞城置一智勇之将多储金帛有来降者/厚赏赐之数出奇兵略其城下芟践禾稼败其生业不出岁余彼当无食马邑不足图也C.如臣所计请于崞城置一智勇之将多储金帛有来降者厚赏赐之数出奇兵略其城下芟践禾稼败其生业不出岁余彼当无食马邑不足图也D.如臣所计请于崞城置一智勇之将多储金帛有来降者/厚赏赐之数出奇兵略其城下芟践禾稼败其生业不出岁余彼当无食马邑不足图也6.下列对原文有关内容的概括和分析,不正确的一项是(3分)A.世让颇具谋略,他假装答应薛举,却趁机告诉城中人:敌兵的数目最多不过如此,应该好好地坚守,以保证安全。
B.世让听说怀恩有叛逆的阴谋,冒死从狱中逃出报告高祖,高祖很是感激,封他为弘农郡公,并赏赐了庄园和钱财。
C.世让忠贞勇敢,可汗命郑元璹劝说他投降,他厉声呵斥,击退敌军,高祖下旨褒奖他,不久授予他广州总管之职。
D.世让拒贼平叛,威名卓著,对皇帝忠心耿耿,但因突厥的反间计被高祖诛杀并抄家,还差点波及其妻儿。
7.把文中画横线的句子翻译成现代汉语。
(10分)(1)时唐弼余党寇扶风,世让自请安辑,许之,俄得数千人。
(2)卿往陷薛举,遣弟潜效款诚,今复冒危告难,是皆忧国忘身也。
(二)古代诗歌阅读(11分)阅读下面这首宋诗,完成8~9题。
(11分)道间即事黄公度花枝已尽莺将老,桑叶渐稀蚕欲眠。
半湿半晴梅雨道,乍寒乍暖麦秋天。
村垆沽酒谁能择,邮壁题诗尽偶然。
方寸怡怡无一事,粗裘粝食地行仙。
【注释】麦秋天:农历四月麦收季节。
地行仙:原是佛典中记载的长寿佛,后指人间安乐长寿的人。
8.请从炼字角度赏析诗歌首联。
(5分)9.这首诗的后两联抒发了什么样的感情?请简要分析。
(6分)(三)名篇名句默写(6分)10.补写出下列句子中的空缺部分。
(6分)(1)《诗经·氓》描述女主人公起早贪黑、辛勤劳作、没有尽头的句子是,。
(2)韩愈《马说》中,写千里马的悲惨遭遇的句子是,。
(3)辛弃疾《破阵子·为陈同甫赋壮词以寄之》中,两句,表达了诗人希望建功立业、报效君王的雄心壮志。
乙选考题请考生在第三、四两大题中选定其中一大题作答。
注意:作答时必须用2B铅笔在答题卡上把所选大题题号后的方框涂黑。
只能做所选大题内的小题,不得选做另一大题内的小题。
如果多做,则按所做的第一大题计分。
三、文学类文本阅读(25分)11.阅读下面的文字,完成(1)~(4)题。
(25分)全职主夫毕淑敏早上,告别伊利诺伊州的小镇,出发到芝加哥去。
行程的安排是:我和安妮先乘坐当地志愿者的车,一个半小时之后到达罗克福德车站,然后从那里再乘坐大巴,直抵芝加哥。
早起收拾行囊,在岳拉娜老奶奶家吃了早饭,安坐等待车夫到来。
私下揣摸:今天我们将有幸与谁同行?几天前,到小镇来的时候,是一对中年夫妇接站。
丈夫叫鲍比,妻子叫玛丽安。
丈夫开的车。
玛丽安面容疲惫但很健谈。
我说,看你很操劳辛苦的样子,还到车站迎接我们,非常感谢。
玛丽安说,疲劳感我的母亲患老年性痴呆十四年,前不久去世了。
但照料母亲成了我生命的一部分,母亲去世了,我一下子不知道干什么好了。
你猜,我选择了怎样的方式悼念母亲?我想出的办法是竞选议员,玛丽安说。
玛丽安沉浸在对自我远景的设想中。
她说,我要向大家呼吁,给我们的老年人更多的爱和财政拨款。
服侍老人不单是爱老年人,也是爱我们每一个人。
我到处游说……我对玛丽安生出了深深的敬佩。
有了来时和这位预备役议员的谈话,我就对去时与谁同车,抱有了浓烈的期待。
车夫来了。
一个很高大而帅气的男子,名叫约翰。
一见面,约翰连说了两句话,让我觉得行程不会枯燥。
第一句话是:出远门的人,走得慌忙,往往容易落下东西。
我帮你们装箱子,你们再好好检查一下,不要遗漏了宝贝。
