2011-工程数学-科学计算部分
工程数学线性代数

工程数学线性代数
工程数学线性代数是工程数学中的一个重要分支,它研究的是向量、张量、矩阵等有关的结构数学知识,也是工程师和工程数学科学家们日常解决工程问题的必备知识。
线性代数涉及到矩阵、向量等结构数学知识,它可以帮助我们解决复杂的数学问题,对于工程问题也有重要的启发性作用。
线性代数可以帮助我们构建、求解线性方程组,它就像一台求解复杂的数学问题的军械库一样。
线性代数的实用性不仅在数学研究方面,而且在工程应用中也是不可或缺的工具,在工程中有着广泛的应用。
线性代数虽然只是数学中的一小部分,但它对于工程数学应用却有着不可替代的作用。
它可以用来分析复杂的数学模型,并进行有效的求解,为工程的设计和建造提供参考。
例如,在建筑工程中,线性代数可以用来分析结构的物理组成、材料的性质以及施工的过程,可以提供最优的设计方案,以此来保证建筑的质量安全。
线性代数在工程数学中也有着广泛的应用,它可以用来分析、计算任意复杂的工程数学问题,并将结果应用于工程实践中,例如在控制系统设计过程中,可以用线性代数计算控制系统的稳定性、鲁棒性以及参数估计等,从而使控制系统的设计更加完善。
另外,线性代数也被用来计算机视觉,并在图像处理领域中发挥重要作用,例如检测图像中的边缘、色彩、噪声等。
线性代数在图像处理中起着至关重要的作用,它可以用来提高图像的质量,检测图像的特征,并从而更精确地识别物体。
综上所述,线性代数是工程数学中不可缺少的一个重要分支,它被应用于各个领域,以求解复杂的数学模型和工程问题。
它也可以用来提高图像处理的质量,从而使工程设计更加完善和先进。
总而言之,线性代数在工程数学中发挥着不可或缺的重要作用,值得研究和深入探索。
《工程数学》课程教学大纲
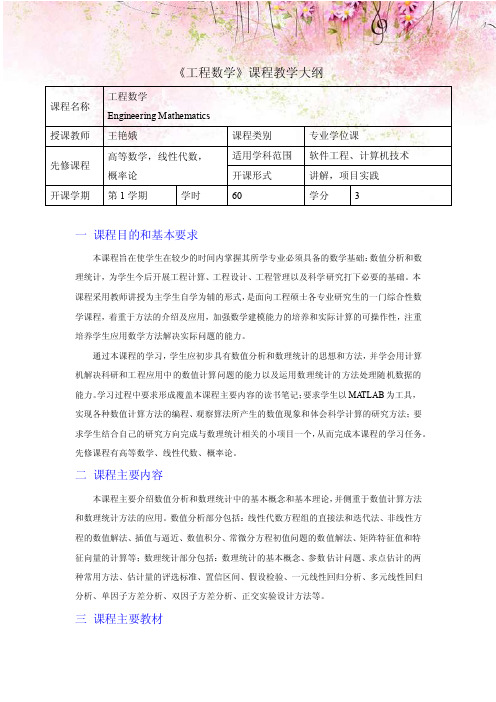
《工程数学》课程教学大纲课程名称工程数学Engineering Mathematics授课教师王艳娥课程类别专业学位课先修课程高等数学,线性代数,概率论适用学科范围软件工程、计算机技术开课形式讲解,项目实践开课学期第1学期学时60 学分 3一课程目的和基本要求本课程旨在使学生在较少的时间内掌握其所学专业必须具备的数学基础:数值分析和数理统计,为学生今后开展工程计算、工程设计、工程管理以及科学研究打下必要的基础。
本课程采用教师讲授为主学生自学为辅的形式,是面向工程硕士各专业研究生的一门综合性数学课程,着重于方法的介绍及应用,加强数学建模能力的培养和实际计算的可操作性,注重培养学生应用数学方法解决实际问题的能力。
通过本课程的学习,学生应初步具有数值分析和数理统计的思想和方法,并学会用计算机解决科研和工程应用中的数值计算问题的能力以及运用数理统计的方法处理随机数据的能力。
学习过程中要求形成覆盖本课程主要内容的读书笔记;要求学生以MA TLAB为工具,实现各种数值计算方法的编程、观察算法所产生的数值现象和体会科学计算的研究方法;要求学生结合自己的研究方向完成与数理统计相关的小项目一个,从而完成本课程的学习任务。
先修课程有高等数学、线性代数、概率论。
二课程主要内容本课程主要介绍数值分析和数理统计中的基本概念和基本理论,并侧重于数值计算方法和数理统计方法的应用。
数值分析部分包括:线性代数方程组的直接法和迭代法、非线性方程的数值解法、插值与逼近、数值积分、常微分方程初值问题的数值解法、矩阵特征值和特征向量的计算等;数理统计部分包括:数理统计的基本概念、参数估计问题、求点估计的两种常用方法、估计量的评选标准、置信区间、假设检验、一元线性回归分析、多元线性回归分析、单因子方差分析、双因子方差分析、正交实验设计方法等。
三课程主要教材[1]同济大学应用数学系编. 工程数学上下册. 同济大学出版社,2010年[2]于寅. 高等工程数学. 华中理工大学出版社,1995年[3]姚仰新等. 高等工程数学. 华南理工大学出版社,2007年[4]沈剑华. 数值计算基础. 上海:同济大学出版社,1999年[5]盛骤等. 概率论与数理统计. 高等教育出版社,2008年[6]施雨等. 概率论与数理统计应用. 西安交通大学出版社,2005年四考核方式考核方式为笔试占60%,项目成果占40%。
工程理论知识点总结

工程理论知识点总结工程理论是工程学科的基本理论体系,是工程科学与技术的理论基础。
工程理论是指导工程实践的科学理论体系,是工程实践的理论基础。
工程理论包括工程数学、工程力学、工程热力学、工程流体力学、工程材料力学、工程结构力学、工程振动与维修、工程传热传质传动、工程流体传动、工程机械传动、工程动力学、工程光学、工程声学、工程电磁学等理论。
这些理论对于各类工程实践具有很大的指导作用。
本文将从工程数学、工程力学、工程热力学、工程流体力学和工程材料力学等方面来总结工程理论的知识点。
一、工程数学工程数学是工程学科中的一个重要学科。
它是数学在工程中的应用,是把数学知识用于解决工程问题的一门学科。
工程数学包括微积分、线性代数、概率统计、数值计算等内容。
1. 微积分微积分是研究变化的数学分支。
它包括微分学和积分学两部分。
微分学研究函数的变化率,而积分学研究函数的面积、体积以及反函数。
微积分在工程中有着广泛的应用,例如在工程建筑中,可以利用微积分来计算建筑物的结构强度和稳定性。
2. 线性代数线性代数是一门研究向量、向量空间和线性变换的数学学科。
在工程学中,线性代数有着重要的应用。
例如在机械工程中,可以利用线性代数的知识来研究机械结构的运动规律。
3. 概率统计概率统计是研究随机现象的数学理论。
在工程中,很多问题都带有一定的随机性,例如零件的尺寸、机器的寿命等。
概率统计可以帮助工程师对这些随机现象进行分析和预测,提高工程设计的可靠性。
4. 数值计算数值计算是用数字方法对数学模型进行计算的一门学科。
在工程学中,很多问题由于过于复杂而无法用解析方法求解,这时就需要通过数值计算的方法来求解。
例如有限元分析、有限差分法等都是数值计算的应用。
二、工程力学工程力学是研究物体受力、受力后的变形和运动规律的学科,它是工程学的基础。
工程力学主要包括刚体力学、弹性力学、塑性力学和流体力学等内容。
1. 刚体力学刚体力学是研究刚体运动的学科。
工程数学1

工程数学1
工程数学1是一门基础课程,主要介绍工程领域中常用的数学方法和技巧。
该课程包括以下内容:
1. 微积分:研究函数的变化率和积分的概念和方法,包括导数、积分、常微分方程等。
2. 线性代数:研究向量空间、线性方程组以及线性变换的性质和运算规律,包括矩阵运算、特征值和特征向量等。
3. 微分方程:研究描述自然和工程现象的微分方程,包括一阶线性微分方程、高阶线性微分方程等。
4. 概率论与统计:研究随机现象的数学模型和统计分析方法,包括概率、随机变量、概率分布、统计参数估计与假设检验等。
5. 多元函数与偏微分方程:研究多元函数的导数和积分,以及描述物理和工程问题的偏微分方程。
6. 数值方法:研究利用计算机进行数值计算和近似计算的方法和技巧,包括数值积分、数值微分、差分方程、插值和拟合等。
工程数学1在工程专业中具有重要的应用价值,它为工程师提供了解决实际问题的数学工具和技能,可以应用于电子、机械、土木、化工、材料等各个工程领域。
工程数学1

工程数学1一、工程数学的概述工程数学是一门以应用为目的的数学分支,它以高等数学为基础,为各类工程技术人才提供必要的数学知识和方法。
工程数学在科学研究和工程技术领域中具有广泛的应用,它可以解决实际问题,优化工程设计,提高生产效率,降低成本,从而推动科学技术的发展和工程技术的进步。
二、工程数学的主要内容工程数学主要包括微积分、线性代数、概率论与数理统计、数学建模等。
微积分是研究函数的极限、连续、微分、积分等性质的分支,它在物理、化学、生物等领域有广泛应用。
线性代数研究向量、矩阵、线性方程组等概念,它在电子电路、计算机科学、运筹学等方面具有重要意义。
概率论与数理统计是研究随机现象的规律性和应用的科学,它在金融、保险、医学等领域具有广泛的应用。
数学建模是将实际问题抽象为数学问题,并利用数学方法求解的过程,它在工程技术、经济管理等领域具有重要意义。
三、工程数学的应用领域工程数学在各类工程专业中都有广泛的应用。
电子信息工程中,工程数学可以帮助分析和设计电子电路、通信系统等。
机械工程中,工程数学可以优化机械设计,提高机械性能。
土木工程中,工程数学可以解决结构分析、水资源利用等问题。
此外,工程数学在经济管理等领域也有广泛的应用,如优化生产计划、预测市场趋势等。
四、如何学习工程数学学习工程数学需要掌握以下几点:一是要理解基本概念和方法,打下扎实的理论基础;二是要加强实践与应用,将所学知识运用到实际问题中;三是要培养数学思维能力,学会用数学方法解决实际问题;四是注重与其他学科的结合,拓宽知识面,提高综合素质。
五、工程数学的前景与展望随着科技的飞速发展,工程数学在人工智能、大数据等领域具有广阔的前景。
在新型基础设施建设中,工程数学可以帮助优化工程设计,提高建设效率。
同时,跨学科研究与创新也为工程数学的发展提供了新的机遇。
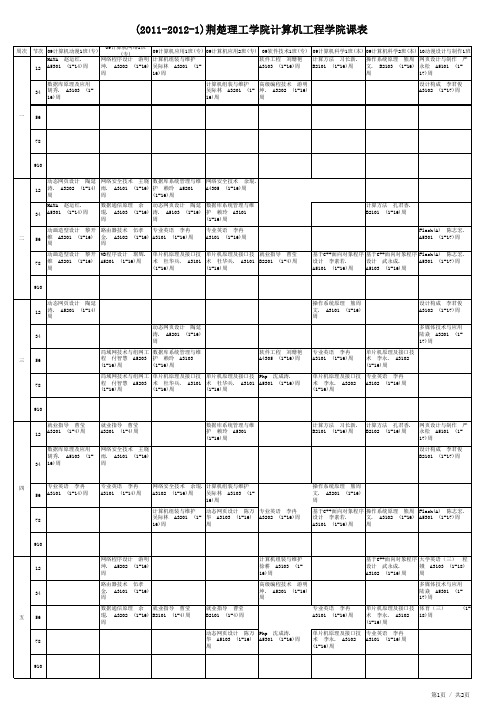
荆楚理工学院2011-2012-1计算机工程学院课表
12
34
三
56
78
局域网技术与组网工 单片机原理及接口技 单片机原理及接口技 Php 沈成涛. A5301 单片机原理及接口技 专业英语 李冉 程 付智慧 A5203 术 杜华兵. A3101 术 杜华兵. A3101 (1-16)周 术 李永. A3202 A3102 (1-16)周 (1-16)周 (1-16)周 (1-16)周 (1-16)周
汇编语言程序设计 贺体刚. B2201 (117)周 概率论与数理统计 盛集明. B2102 (117)周
78
910 数据结构 贺体刚. A3103 (1-17)周 工程数学 张玲 B2102 (1-17)周 数据库原理及应用 周良泽. A3201 (117)周 数据库原理及应用 周良泽. A5101 (117)周 多媒体技术及应用 陆焱 A3201 (1-17) 周 操作系统 熊周文. A3102 (1-17)周 操作系统 熊周文. A3102 (1-17)周 工程数学 张玲 B2102 (1-17)周 大学英语(三) 何 爱红. A3202 (118)周 汇编语言程序设计 贺体刚. A5101 (117)周 数据结构 余云霞. B2101 (1-17)周 sql server 应用开发 马克思主义基本原理 马克思主义基本原理 赖玲 A5201 (1-17) 何新明. B2101 (1- 何新明. B2101 (1周 18)周 18)周 大学英语(三) 何 爱红. A3202 (118)周 现代数据库技术 李祥 简明嵌入式系统硬件设 琴 A5301 (1-13)周 计与实现 李永. A4301 (1-13)周 简明嵌入式系统硬件设 现代数据库技术 李祥 计与实现 李永. 琴 A5301 (1-13)周 A4301 (1-13)周
工程数学(01) 绪论及几个关键问题

(b c) p(r )dr (a b) p(r )dr
0 n
n
dG 0 dn
p ( r ) dr a b bc p ( r ) dr
0 n
n
工程数学
工程数学
结果解释
n
p ( r ) dr a b bc p ( r ) dr
0 n
G(n) 0 [( a b)r (b c)( n r )] p(r )dr n (a b)np(r )dr
dG (a b)np(n) n (b c) p(r )dr 0 dn (a b)np(n) (a b) p(r )dr
工程数学
工程数学
三、舍入误差分析
1 1 2 1 3 1 2 1 3 1 4 1 11 3 x 6 1 1 13 x2 12 4 x3 47 1 5 60
(1)
Ax=b A可逆
由线性方程组的克莱姆(Cramer)规则可知,如果方程组 (1)的系数矩阵A的行列式(一般记为D=|A|)不等于零,那末,这 个方程组有唯一解,而且它们可以表示为 xi=Di/D (i=1,…,n)
这里,Di是指D中第i列元素用右端(b1,… bn)代替构成的行列 式。
工程数学
工程数学
第一章 计算环节的几个关键问题
第一节 数值算法
第二节 误差分析
第三节 效果评价(稳定性)
工程数学
工程数学
第ቤተ መጻሕፍቲ ባይዱ节
数值算法
算法:从给定的已知量出发,经过有限次四则运算及规
定的运算顺序,最后求出未知量的数值解,这样构成的
工程数学1

工程数学1
工程数学1通常是指大学本科阶段工科专业学生学习的一门数学课程。
这门课程旨在为工科学生提供数学基础知识,使他们能够在工程和科学领域中应用数学工具解决实际问题。
具体内容可能包括但不限于以下主题:
微积分:包括极限、导数、积分等基本概念,以及应用到工程问题的技能,如曲线的切线和曲率等。
线性代数:矩阵、行列式、线性方程组等内容,为工程问题的建模和求解提供数学工具。
常微分方程:解微分方程的基本方法,以及工程和科学领域中常见的微分方程建模问题。
多元统计:多变量函数、偏导数、多元积分等内容,为处理多变量工程问题提供数学支持。
复变函数:复数、复变函数的基本概念,以及在工程和科学中的应用。
离散数学:集合论、图论、逻辑等内容,为计算机科学等领域的学生提供数学基础。
这门课程的目标是培养学生具备将数学知识应用到实际工程问题中的能力,同时提供一个坚实的数学基础,以便他们在后续的工程专业课程中更好地理解和应用相关数学知识。
浙江省2011年10月高等教育自学考试 工程数学(一)试题 课程代码07961

07961# 工程数学(一)试题 第 1 页 共 5 页浙江省201 1年10月高等教育自学考试工程数学(一)试题课程代码:07961一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.设事件A 与B 相互独立,且P (A )>0,P (B )>0,则一定有( ) A.()1()P A B P A =- B. ()0P A B = C.P (A )=1-P (B )D. ()()P A B P B =2.掷2颗骰子,记事件A={2颗骰子出现点数之和等于7},则事件A 的概率为( ) A.16 B. 56 C.112D. 153.下列各函数中可以作为某个随机变量的分布函数的是( )A.1() 0,1x f x x <=≥⎩B. 1() 0,1x f x x <=≥⎩C. 21,11() 0,1x x f x x ⎧<⎪+=⎨⎪≥⎩D. 22,11() 0,1x x f x x ⎧<⎪+=⎨⎪≥⎩4.设随机变量X题4表则P ({0<X ≤3}-{X >2})=( ) A.0 B.0.2 C.0.5D.0.75.已知随机变量(X ,Y )服从二维正态分布,且E (X )=E (Y )=0,D (X )=1,D (Y )=4,ρXY =12,若07961# 工程数学(一)试题 第 2 页 共 5 页Z =aX +Y 与Y 的协方差为0,则a 等于( )A.2B.-2C.4D.-46.设二维连续随机变量(X 1,Y 1)与(X 2,Y 2)的概率密度为f 1(x ,y )与f 2(x ,y ),令f (x ,y )=af 1(x ,y )+bf 2(x ,y ),要使函数f (x ,y )是某个二维随机变量的概率密度,则a ,b 应满足( )A.a +b =1B.a ≥0,b ≥0且a +b =1C.0≤a ≤1,0≤b ≤1D.a >0,b >07.设随机变量X ~B (10,0.2),Y ~P (5),则E (2X +Y )等于( ) A.215 B.7 C.9D.1158.设随机变量X 1,X 2,…,X n ,…相互独立,且X i (i =1,2,…,n,…)都服从参数为3的指数分布,则当n 充分大时,随机变量Z n =11ni i X n =∑的概率分布近似服从( )A.N (11,39)B.N (11,39n)C.N (3,9)D.N (3,9n) 9.设总体X ~N (μ,σ2),X 1,X 2,…,X n 为样本,X 为样本均值,S 为样本标准差,则服从t (n -1)分布的统计量是( )A.C.10.设α,β分别是假设检验中第一、第二类错误的概率,且H 0,H 1分别为原假设和备择假设,则P {拒绝H 0\H 0为真}=( ) A.α B.βC.1-αD.1-β07961# 工程数学(一)试题 第 3 页 共 5 页二、填空题(本大题共15小题,每小题2分,共30分)请在每小题的空格中填上正确答案。
工程数学的作用和意义

工程数学的作用和意义
工程数学的作用和意义
一、定义
工程数学是一门综合性学科,是应用数学和计算机技术解决工程问题
的科学。
它是一种利用数学方法和技术为工程实践提供计算、分析和
解决方案的过程。
二、作用
1、为工程实践提供计算方案:工程数学可以帮助工程师设计出有效的
计算方案,并将其应用于实际的工程实践中,以解决实际的工程问题。
2、应用于研究:工程数学也可以应用于研究,它可以帮助工程师研究
新的技术,研究新材料,发现更好的设计方案等。
3、有助于决策分析:工程数学利用数学模型和统计技术,有助于分析
工程方案并作出有效的决策。
三、意义
1、丰富工程科学:工程数学使工程科学增添了多种数学模型、技术,成为工程科学的重要组成部分,为工程解决实际问题提供了有力的支持。
2、为实践提供新方法:工程数学为实践工作提供了新的解决方案,帮助实践者科学地选择最佳方案并达到最佳效果,增强了实践工作的高效性。
3、拓宽社会发展视野:工程数学为社会发展提供了诸多有益的建议和技术支持,引发了新的创新点,拓展了社会发展的视野。
四、结论
工程数学的作用和意义十分重要。
它为工程技术的发展提供了支持,为实践提供了有效的计算、分析和解决方案,丰富了工程科学,拓宽了社会的发展视野。
工程数学的诞生为我们的社会提供了更多强劲的发展动力,更好地服务于人类社会的发展。
《工程数学》广播电视大学历年期末试题及答案及中央电大工程数学形成性考核册答案

试卷代号:1080中央广播电视大学2011~2012学年度第一学期“开放本科”期末考试(半开卷)工程数学(本) 试题2012年1月一、单项选择题(每小题3分,共15分)1. 设A ,B 为三阶可逆矩阵,且0k >,则下列( )成立.A . AB A B +=+ B .AB A B '=C . 1AB A B -=D .kA k A =2. 设A 是n 阶方阵,当条件( )成立时,n 元线性方程组AX b =有惟一解.3.设矩阵1111A -⎡⎤=⎢⎥-⎣⎦的特征值为0,2,则3A 的特征值为( )。
A .0,2 B .0,6C .0,0D .2,64.若随机变量(0,1)X N :,则随机变量32Y X =-: ( ).5. 对正态总体方差的检验用( ).二、填空题(每小题3分,共15分)6. 设,A B 均为二阶可逆矩阵,则111O A B O ---⎡⎤=⎢⎥⎣⎦ .8. 设 A , B 为两个事件,若()()()P AB P A P B =,则称A 与B .9.若随机变量[0,2]X U :,则()D X = .10.若12,θθ都是θ的无偏估计,且满足 ______ ,则称1θ比2θ更有效。
三、计算题(每小题16分,共64分)11. 设矩阵234123231A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,111111230B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,那么A B -可逆吗?若可逆,求逆矩阵1()A B --. 12.在线性方程组123121232332351x x x x x x x x λλ++=⎧⎪-+=-⎨⎪++=⎩中λ取何值时,此方程组有解。
在有解的情况下,求出通解。
13. 设随机变量(8,4)X N :,求(81)P X -<和(12)P X ≤。
(已知(0.5)0.6915Φ=,(1.0)0.8413Φ=,(2.0)0.9773Φ=)14. 某切割机在正常工作时,切割的每段金属棒长服从正态分布,且其平均长度为10.5cm ,标准差为0.15cm 。
【工程数学课件】数值分析2.1

Ln nsin n
L2n Ln / cos 2n
n
L
192 3.1414524
384 3.1415576
Lˆ2n (4L2n Ln ) / 3
3.1415926
error 1.4e-004 3.5e-005 4.6e-010
3/16
➢通信卫星覆盖地球面积 实际问题
将地球考虑成一
个球体, 设R为地 球半径,h为卫星 高度,D为覆盖面 在切痕平面上的
《科学计算方法》1
科学计算的背景 关于计算误差讨论 浮点数与有效数字 算术运算的误差估计
➢数值分析——研究用计算机求解
数学问题的方法(算法)和理论 方程组求解、方程求根、数据插值、 数据拟合、数值积分、微分方程求解
➢科学计算方法与计算机有机结合 构造出强有力的工作平台
von Neumann
舍入误差:计算机表示的数的位数有限,通常用 四舍五入的办法取一数据的准确值为 x*,其近似值 为 x,则称
e(x)= x - x*
为 x 的绝对误差
而称
e(x) x x* er (x) x x ,
(x 0)
为 x 的相对误差
6/16
如果存在一个适当小的正数ε ,使得
投影(积分区域)
数学模型 获取数据
R
dxdy
D R2 x2 y2
数值方法、程序 数据结果
4/16
➢误差分类:
模型误差: 建立数学模型时所引起的误差;
观测误差:测量工具的限制或在数据的获取时随 机因素所引起的物理量的误差; 截断误差:求解数学模型时,用简单代替复杂, 或者用有限过程代替无限过程所引起的误差
e(x) x x
则称ε为绝对误差限。
工程数学教案

课程教案2011~2012学年第一学期课程编号课程名称工程数学主讲教师胡丽姣职称助教系(部)名称公共课部2011年09月28日题目:数列极限的定义 函数的极限 课时:2教学目的、要求:理解数列极限的概念,会用数列极限的性质求一些数列的极限,理解函数极限的概念;会用函数极限的定义和性质求一些函数在某点处的极限;重点:数列极限的定义,用数列极限的性质求一些数列的极限, 函数极限的定义,求函数在某点处的极限;难点:计算数列极限, 函数在无穷远处的极限的概念的理解。
内容: 1.数列的定义 无穷多个数 ,,,,,321n x x x x 按某些规律一个一个地进行排列,n x 为数列的第n 项,又是通项。
例:(1) ,1,,41,31,21,1:n 1n ⎭⎬⎫⎩⎨⎧; 趋近于0 01lim n =∞→n(2 ,11,,411,311,211,2:n 11n ++++⎭⎬⎫⎩⎨⎧+; 趋近于1 111lim n =⎪⎭⎫⎝⎛+∞→n(3){} ,2,,8,6,4,2:2n n(4)(){} ,0,2,,0,2,0,2:111--+n (5){}()是常数C C C C C ,,,,:CC =∞→n lim分析以上五个数列的特性,得出数列的极限概念。
2、极限的定义:设有数列{}n x ,A 为常数,当n 无限增大时,n x 无限趋近于A ,则数列极限存在或收敛,极限是A 或{}n x 收敛于A 。
记为()∞→→=∞→n A A x n n x lim n 或若{}n x 极限不存在,则{}n x 发散。
数列的几何解释:将A 及 ,,,,,321n x x x x 在数轴上一一表示出来,当n 无限增大时,数列{}n x 对应的点n x 聚集在A 点附近且无限趋近于A 点。
单调数列:{}n n x x x x x 321,则≤≤≤≤≤单调增加;{}n n x x x x x 321,则≥≥≥≥≥单调减少;{}n n x x x x x 321,则<<<<<严格单调增加;{}n n x x x x x 321,则>>>>>严格单调减少。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、 填空题 (每题3分, 共15分)
1. 取3.14159作为π的近似值,则其具有 6 位有效数字.
2. 矩阵A 1302⎡⎤
=⎢⎥⎣⎦
的-∞条件数cond (A)∞= 10 . 3. 对函数()(1)(2)f x x x x =--, 差商[0,1,2,3]f = 1 . 4. 求积分2
1()f x dx ⎰的Simpson 公式为
321
((1)4(
)(2)
)6
f f f ++ . 5.
求解常微分方程5dy
x dx
=的隐式Euler 公式为
115)n n n y y x ++=++
.
二、 计算题 (共35分)
1. (15分) 对方程组
123410312120145x x x -⎡⎤⎡⎤⎡⎤
⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦
, (1) 用Gauss 消去法求解方程组, 并写出由此得到的Doolittle 三角分解LU A =.
(2) 写出对应的Jacobi 迭代格式, 并求迭代矩阵的谱半径. 该格式是否收敛?
解:(1) 771111444
424
247
74103410
3410
3121201010145014
500---⎡⎤
⎡⎤⎡⎤⎢⎥
⎢⎥⎢⎥-→→⎢⎥⎢⎥⎢
⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦
, 解得1231x x x === 其LU 分解为71
44424
774101
0041012110010140100--⎡⎤⎡⎤
⎡⎤⎢⎥⎢⎥⎢⎥-=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦
(2) Jacobi 迭代格式为
(1)
()
3111441122513344000100k k x x x x x x +⎡⎤
⎡⎤⎡⎤
⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥
⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦
⎣⎦⎣⎦⎣⎦
其迭代矩阵的特征方程14
211
2
2
14
1()040
λ
λ
λλλ
--=-=, 故其谱半径1
2
, 收敛.
2. (12分) 已知函数)(x f 满足(1)1,(2)3,(3)7,f f f ===求其二次插值多项式. 若再补充条件(1)f '=3, 求其三次插值多项式.
解:利用Lagrange 插值公式,或Newton 插值公式,皆可得二次插值多项式
2()1L x x x =-+. 设三次插值多项式2()1(1)(2)(3)H x x x x x x α=-++---,
则(1)123H α'=+=, 得1α=. 于是2()1(1)(2)(3)H x x x x x x =-++---
325105x x x =-+-.
2. (8分) 对3
()f x dx ⎰的近似求积公式39
()(0)(2)44
Q f f f =
+, 求其代数精确度. 解:令2()1,,f x x x =代入,精确成立
令3()f x x =代入不精确成立. 故代数精确度为2.。
