材料力学10
材料力学10压杆稳定_2经验公式

这类杆称为中长杆(或中柔度杆),亦即直线公式适用于中长杆 (或中柔度杆)
说明: 当 ≤ s,称为粗短杆,则应按强度问题处理。
三、临界应力总图
压杆的临界应力 cr 可视作压杆柔度 的分段函数,即
π2E 2
cr
查表得 a = 461 MPa、b = 2.567 MPa
临界应力 临界力
cr a b 461 2.567 64.7 294.9 MPa Fcr cr A 162.7 kN
3)由于连杆在 x-y、x-z 两个平面内的柔度 z = 64.7、y = 57.4 比
π 2 EI min
0.7l 2
870 kN
2)两端固定但可沿轴向相对移动
长度因数 = 0.5, 立柱柔度
3600
zz
s
l
imin
0.5 3600 24
75 p
此时,立柱为中柔度杆,应用直线公式计算其临界力
由表 10-2 查得 a = 304 MPa,b = 1.12 MPa
临界应力 临界力
cr a b 304 1.12 75 220 MPa Fcr cr A 220 48.541 1068 kN
[例2] 图示连杆,已知材料为优质碳钢,弹性模量 E = 210×109 GPa, 屈服极限 s = 306 MPa。试确定该连杆的临界力Fcr ,并说明横截面的 设计是否合理。
解: 由于连杆在两 个方向上的约束情 况不同,故应分别 计算连杆在两个纵 向对称平面内的柔 度,柔度大的那个 平面即为失稳平面
1)计算柔度 在 x-y 平面(弯曲中性轴为 z 轴): 两端铰支
材料力学课件-10截面的静矩和形心位置

静矩在结构设计中的应用
抗弯设计
在结构设计时,需要考虑到截面的抗弯能力。静矩是计算 抗弯能力的重要参数,通过计算截面的静矩,可以确定截 面的抗弯刚度,从而优化结构设计。
稳定性分析
在分析结构的稳定性时,静矩也是一个重要的参数。通过 比较不同截面的静矩,可以判断结构的稳定性,并优化截 面设计。
材料选择
优化设计
通过深入了解静矩和形心位置, 可以更好地优化结构设计,提高 结构的稳定性和安全性践
静矩和形心位置不仅是理论上的 概念,更是指导实践的重要工具 。在实际工程中,这些概念的应 用有助于确保结构的可靠性和安 全性。
THANK YOU
感谢观看
静矩的计算方法
直接积分法
适用于规则截面,通过积分计算得到静矩。
表格法
根据已知的规则截面尺寸和载荷分布,查找表格 中的静矩值。
近似法
对于不规则截面,可以采用近似法估算静矩值。
静矩的性质
静矩具有方向性
根据右手定则判断矩心的方向。
静矩与截面尺寸和形状有关
不同尺寸和形状的截面具有不同的静矩值。
静矩是内力分布的面积分
03
位置,形心位置与截面的形状密切相关。
截面尺寸对形心位置的影响
01
同一形状的截面,尺寸不同时,其形心位置也会发生变化 。
02
例如,矩形截面长度和宽度不同时,其形心位置会有所偏 移。
03
截面尺寸对形心位置的影响:同一形状的截面,尺寸不同时, 其形心位置也会发生变化,但总是位于截面的面积中心。
04
在选择材料时,静矩也是重要的参考因素。不同材料的截 面静矩不同,选择合适的材料可以保证结构的稳定性和安 全性。
形心位置在结构设计中的应用
材料力学10组合变形

材料力学10组合变形组合变形是指当结构受到外力作用时,由于各个零件的不同材料及尺寸性质的差异,导致各个零件产生不同的变形现象,从而使整个结构发生整体的变形。
组合变形是结构力学的重要内容,对于工程结构的设计、安全性评估和结构稳定性分析都至关重要。
本文将介绍组合变形的概念、分析方法和影响因素。
组合变形的概念:组合变形是指由于结构中不同零件的尺寸和材料性质的不一致,而导致结构在受力时产生的整体变形。
组合变形分为两类:一是刚体体变形,即结构在受力作用下整体平移、旋转或缩放;二是构件本身变形,即结构中各零件由于尺寸和材料的不一致而产生的内部变形。
组合变形的分析方法:组合变形的分析方法主要有两种:力法和位移法。
力法是指根据梁的变形方程和杨氏模量的定义,通过计算各零件在各个截面上的张力或弯矩,从而得到整体的变形情况。
位移法是指根据构件的位移和应变关系,通过求解位移方程组,从而得到整体的变形情况。
力法和位移法都是基于弹性理论,适用于较小变形和线性弹性材料的情况。
组合变形的影响因素:组合变形的大小与结构的几何形状、零件尺寸和材料性质有关。
影响组合变形的因素主要有以下几个方面:1.结构的几何形状:结构的几何形状对组合变形有重要影响。
例如,在长梁的弯曲变形中,梁的长度和曲率半径都会影响变形的大小。
2.零件的尺寸:零件的尺寸对组合变形有重要影响。
例如,在梁的弯曲变形中,梁的截面积和转动惯量会影响变形的大小。
3.零件的材料性质:零件的材料性质对组合变形有重要影响。
例如,在梁的弯曲变形中,梁的弹性模量和截面剪切模量会影响变形的大小。
4.外力的作用方式:外力的作用方式对组合变形有重要影响。
例如,在梁的弯曲变形中,集中力和均布力对变形的影响是不同的。
除了以上几个因素外,结构的边界条件和连接方式也会影响组合变形的大小。
此外,在实际工程中,结构中可能存在的缝隙、温度变化、材料老化等因素也会对组合变形产生影响。
对于设计工程结构来说,合理控制组合变形是非常重要的。
材料力学第10章(动载荷)

Kd 2
二、水平冲击 mg v
d
Fd d , Pst st
Pst mg 其中: mgl st EA
Fd
st
Pst
mv2 冲击前:动 T1 能 2
冲击后: 应变能Vε 2 Fd d 2
2 F 2 st mv d mg
h
P
h
解:
st
Pl 1.7 102 (mm) EA
2h K d 1 1 st
2 500 1 1 243 2 1.7 10
l
l
d 2 A 4
P 2 103 0.028(MPa) st 4 A 7.1 10 d Kd st
假设: (1)冲击物为刚体; (2)不计冲击过程中的声、光、热等能量损耗(能量守恒);
(3)冲击过程中被冲击物的变形为线弹性变形过程。(保守计算)
一、自由落体冲击
P
冲击前: T 0
V P(h d )
B
h
A
冲击后:
1 Vε d Fd d 2
A
Δd
能量守恒: T V Vd
B
2h st
l
4 Pl 3 22mm st 3 EI
K d 1 1 2 50 3.35 22
40 C 30
d Kd st
M max Pl 50(MPa) st W W
d Kd st 161 MPa) (
A
Δd
Fd
B
1 P (h d ) Fd d 2 Fd d P st
2 Fd 1 Fd P (h st ) st P 2 P
材料力学第10章 组合变形

因此,截面O为危险截面。
危险截面上,由轴力引起的正应力均匀分布,其值
为
,由弯矩引起的正应力线性分布,其值为
。利用叠加原理,将拉伸及弯曲正应力叠加
后,危险截面上正应力沿截面高度的变化情况如图10.5
(e)所示,仍为线性分布。而且可以看出,最大拉应
力和最大压应力分别发生在O截面上、下边缘各点,其
值为
(10.4)
图10.5
依据上述分析,弯拉(压)组合变形时危险点处于单向应力状态,所以可将 截面上的σmax与材料的许用应力相比较建立其强度条件。对于拉压强度相等 的材料,强度条件为
对于抗拉与抗压性能不同的材料,强度条件为
下面举例说明弯拉(压)组合变形的强度计算。 例10.2如图10.6(a)所示的钢支架,已知载荷F=45 kN,尺寸如图。 (1)如材料为钢材,许用应力[σ]=160 MPa,试选择AC杆的工字钢型号。 (2)如材料为铸铁,许用拉应力[σt]=30 MPa,许用压应力[σc]=160 MPa,且AC杆截面形式和尺寸如图10.6(e)所示,A=15×10-3 m2,z0=75mm ,Iy=5.31×10-5 m4。试校核AC杆的强度。
其力矩矢量分别与y轴和z轴的正向一致(见图10.2(b))。 为了确定横截面上最大正应力点的位置,先求截面中性轴位置。记中性轴上 任一点的坐标为(y0,z0),由于中性轴上各点处的正应力均为零,所以由式 可得中性轴方程为
(10.2) 可见,中性轴是一条通过横截面形心的直线(见图10.2(c)),其与y轴的 夹角θ为
图10.3 例10.1如图10.4(a)所示,20a号工字钢悬臂梁承受均布载荷q和集中力
。已知钢的许用弯曲正应力[σ]=160 MPa,a=1 m。试求梁的许可 载荷集度[q]。 解由于梁所受到的横向力不在梁的两个纵向对称面内,此时可以将横向力向 两个纵向对称面分解(向y和z轴分解),从而将其看成是梁在其两个相互垂
材料力学10压杆的稳定性问题
F
不稳定平衡
C
C C
闽 南
临界荷载与约束形式、材料性能、杆件几何 及刚度有关。
B 分叉点
稳定平衡
Fcr FC
理
工 稳定性准则
学
最大工作压力 F < 临界荷载 Fcr
院
o
v
Pinned-pinned
材料力学 Mechanics of Materials
第十章 压杆稳定
闽 南 理 工 学 院
材料力学 Mechanics of Materials
L / i 11.732 / 0.01 173.2 p 100
材料力学 Mechanics of Materials
第十章 压杆稳定
压杆的稳定条件
图示支架,材料均为Q235 钢。弹性模量E=200GPa,
许用应力[]=160MPa。
A
C端受垂直载荷F=15kN作
用。已知AC梁是14号工字
闽
钢,其抗弯截面系数Wz= 102cm3, 截 面 积 A=21.5cm2。
南 BD为直径40mm的圆截面杆,
理 p=100,稳定安全系数nst=
材料力学 Mechanics of Materials
第十章 压杆稳定
临界应力
欧拉公式的适用范围
欧拉公式限于材料处于线弹性的情况。所以,欧拉公式也只能在
杆内压应力不超过比例极限p时才适用。于是要求
cr
2E 2
p
闽 南
称为杆的柔度或长细比
l
i
理 工 或者是 学
E
p
p
院
材料力学 Mechanics of Materials
材料力学 Mechanics of Materials
材料力学:第10章:应力状态分析_强度理论
y
§10-3 平面应力状态主应力及最大剪应力
( x , x )
( y , y )
例:分别用解析法和图解法求图示单元体的 (1)指定斜截面上的正应力和剪应力; (2)主应力值及主方向,并画在单元体上; (3)最大剪应力值。 单位:MPa
解:(一)使用解析法求解
x 80MPa, x 60MPa, x y
y 40MPa = 30 x y
cos 2 x sin 2
2 2 102 MPa x y sin 2 x cos 2 2 22.0MPa
max x y 105 x y max x y x y 2 105 MPa 2 x 65 MPa 2 2 x min 2 2 min 65 1 105MPa, 2 0, 3 65MPa 1 105MPa, 2 0, 3 65MPa 2 x tan 2 0 2 x 1 tan 2 0 x y 1 max 105 x y 0 22.5 0 22.5 或112.5 0 22.5态的概念
P
P
m
m
P
A B C D E
A D
B E
C
• 主平面 :剪应力为零的平面
• 主应力 :主平面上的正应力 • 主方向 :主平面的法线方向
• 可以证明:通过受力构件内的任一点,一定
存在三个互相垂直的主平面。 • 三个主应力用σ1、 σ2 、 σ3 表示,按代数值 大小顺序排列,即 σ1 ≥ σ2 ≥ σ3
材料力学第六版答案第10章
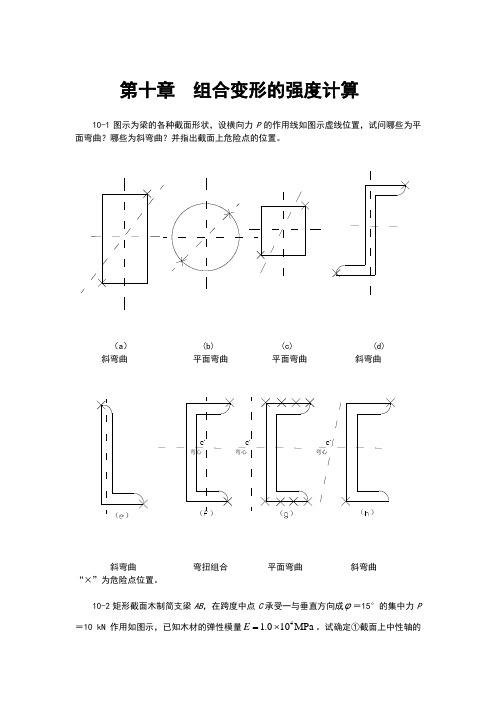
第十章 组合变形的强度计算10-1图示为梁的各种截面形状,设横向力P 的作用线如图示虚线位置,试问哪些为平面弯曲?哪些为斜弯曲?并指出截面上危险点的位置。
(a ) (b) (c) (d) 斜弯曲 平面弯曲 平面弯曲 斜弯曲弯心()()弯心弯心()()斜弯曲 弯扭组合 平面弯曲 斜弯曲“×”为危险点位置。
10-2矩形截面木制简支梁AB ,在跨度中点C 承受一与垂直方向成ϕ=15°的集中力P =10 kN 作用如图示,已知木材的弹性模量MPa 100.14⨯=E 。
试确定①截面上中性轴的位置;②危险截面上的最大正应力;③C 点的总挠度的大小和方向。
解:66.915cos 10cos =⨯==οϕP P y KN59.215sin 10sin =⨯==οϕP P z KN4310122015=⨯=z J 4cm 3310cm W z =335625121520cm J y =⨯=3750cm W y =25.74366.94max =⨯==l P M y z KN-M 94.14359.24m ax =⨯==l P M z y KN-MMPaW M W M yy z z 84.9107501094.110101025.763633maxmax max=⨯⨯+⨯⨯=+=--σ 中性轴:οο47.2515tan 562510tan tan tan 411=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛-=--ϕαy z J J 2849333105434.0101010104831066.948--⨯=⨯⨯⨯⨯⨯⨯==z y y EJ l P f m28933310259.010562510104831059.248--⨯=⨯⨯⨯⨯⨯⨯==y z z EJ l P f m 602.0259.05434.022=+=f cm方向⊥中性轴:ο47.25=α10-3 矩形截面木材悬臂梁受力如图示,P 1=800 N ,P 2=1600 N 。
浙江工业大学材料力学第10章答案

浙江⼯业⼤学材料⼒学第10章答案10.1 ⼀端固定⼀端铰⽀的⼯字形截⾯细长压杆,已知弹性模量GPa 208=E ,截⾯尺⼨200mm×100mm ×7mm ,杆长m l10=,试确定压杆的临界压⼒。
解:4337.16796532121869312200100mm I x =?-?=4332.11719831271861210072mm I y =?+?=因为x y I I <,故y I I =()()kN N l EI F cr 1.49101.49100007.02.117198310208323222=?===πµπ10.2 两端固定的圆截⾯钢质压杆,直径为50mm ,受轴向压⼒F 作⽤。
已知GPa 210=E 和MPa 200=p σ,试确定能够使⽤欧拉公式的最短压杆长度l 。
解:8.10120010210505.044322=??==≥??===πσπλµµλp p E l d l i l可得:mm l 2545≥10.3 截⾯为矩形h b ?的压杆,两端⽤柱销联接(在y x -平⾯内弯曲时,可视为两端铰⽀;在zx -平⾯内弯曲时,可视为两端固定)。
已知GPa 200=E ,MPa 200=p σ,试求:(1)当mm 30=b ,mm50=h 时,压杆的临界压⼒;(2)若使压杆在两个平⾯(y x -和z x -⾯)内失稳的可能性相同时,求b 和h 的⽐值。
解:43331250012503012mm bh I z =?==,1=z µ,故()()kNN l EI F z z cr 1171011723001312500102003232221=?===πµπ43311250012305012mm hb I y =?==,5.0=y µ,故()()kN N l EI F y y cr 1681016823005.0112500102003232222=?===πµπ故kN F cr 117=。
材料力学 第10章 弯曲应力及强度

a
Φ14
30 工件
Fa x
10.4 弯曲强度条件
例10-5 梁的载荷及截面尺寸如图所示,材料的容许拉应力
[t]=40MPa、容许压应力[c] =100MPa,试校核该梁的强度。
q=10kN/m
F=20kN
AB 2m
CD 3m 1m
q=10kN/m
A
B
FB M
F=20kN
C
D
FD
10kN.m
x
157.5 200 30
10.3 横力弯曲时梁的切应力
三、其它形状截面
T型截面
圆形截面
环形截面
max
z
max
FSS
* z,m
ax
I zb1
z
max
z
max
max
4 3
FS A
max
2
FS A
10.3 横力弯曲时梁的切应力
21 560
例10-2 56a号工字钢制成的简支梁如图所示,F=150kN,求最大 切应力及最大切应力所在截面上K点处的切应力。
ad bc
a
d
b
c
σσ
M
ττ
10.2 纯弯曲时梁的正应力
3. 变形几何关系
o1o2 dx ρdθ
k1k2 (ρ y)dθ Δl=k1k2 k1k2 ( ρ y)dθ ρdθ ydθ
dx 中性层
y o1
o2
k1
k2
dx 变形前
o
d
o1
o2
k1
k 2
变形后
10.2 纯弯曲时梁的正应力
第10章 弯曲应力及弯曲强度
10.1 引言 10.2 纯弯曲时梁的正应力 10.3 横力弯曲时梁的切应力 10.4 弯曲强度条件 10.5 提高梁弯曲强度的措施
材料力学第十章

fC
1 EI
AC
M
(
x1
)
Fs
0
M ( x1 Fs
)
dx
)
f ( x) 1 EI
x 0
F
(l
x1
)(
x
x1
)dx1
Fx 2 6EI
(3l
x)
§10-4 卡氏第二定理
例10-5 图示悬臂梁AB,B端作用铅垂力F,梁的EI已知,
1)求梁的挠曲线方程;2)若在梁中截面再作用力F,求自
x2
F=F0
A
1)dx段应变能:
dU 1(A)( d
x
)
2
d
xA
FQ2dx
2
2G
2GA
dx dx
2)l段应变能:
U
l
0dU
0l
FQ2 dx 2GA
FQ—横截面剪力; A—横截面面积;
—截面系数
矩形:=6/5;实心圆:=10/9;薄圆环:=2;
3)注意:在一般细长梁中,远小于弯矩应变能的 剪力应变能,通常忽略不计。
若=0.3,h/l=0.1,比值为0.0312。长梁忽略剪切应变能。
3)求C点挠度:W
1 2
FfC
U弯
F 2l3 96EI
fC
Fl 3 48EI
§10-2 弹性应变能的计算
四、非线性固体的应变能
1.应变能
F 非线性
与比能:
U*
线性
非线性
u*
线性
2.余能与
F1
余比能:
U
d1
1 d
u
1
应变能:线弹性
F
由端挠度fB。
材料力学 第十章组合变形(1,2,3)

1.2m
解:求支反力,由平衡方程
FB B
FA
' FA
F ' A 0,
FA FB 5kN
A
1.6m 1.6m
m g f A
10kN C
m FAy
作折杆的受力图,折杆及 受力对称,只需分析一半 即杆AC 将FA分解, 得杆的轴力 FN、弯矩M (x)
B
FAx
FN FAx 3kN
3 10 8 10 t 81.1 2 3 c d / 4 d / 32 81.9
3 3
M W
[例10-2]圆截面杆的偏心压缩时不产生拉 力的载荷作用范围
P
y
P
y
Pa
a
z
z
CL11TU12
P
y
Pa
y
P
y
Pa
z
z
z
P
y y
Pa
y
P
z
Pa
z P
y y
z
Pa
y
P
CL11TU10
解: X A 3kN, A 4kN Y
任意横截面x上的内力:
FN X A 3kN FS YA 4kN M ( x) YA x 4 x
1 1截面上危险截面, 其上:FN 3kN,M 8kN m
FN A
M W
t FN M c A W
CL11TU5
y0 Iz tg tg z0 Iz
为中性轴与z轴夹角
3.强度计算:
1)危险截面:当x=0时 M Z , M y 同时取最大,固定端处为危险面 2)危险点:危险面上 D1 , D2点 3)最大应力
材料力学课件第10章 动载荷zym

FNd
qd D Aρ D 2 2 = = ω 2 4
(3)截面应力: )截面应力: FNd ρ D 2ω 2 σd = = = ρv2 A 4 (4)强度条件: )强度条件:
σ d = ρ v 2 ≤ [σ ]
2、问题特点: 、问题特点: •截面应力与截面面积 无关。 截面应力与截面面积A无关 截面应力与截面面积 无关。 (三)扭转问题
2)强度计算: )强度计算: (1)确定危险截面: )确定危险截面: 为跨中截面。 为跨中截面。
l 1 l M = F −b − q 2 2 2 a l 1 = Aρ g 1 + − b l 2 g 4
2
(2)建立强度条件: )建立强度条件: M d Aρ g a l σd = = 1 + − b l ≤ [σ ] W 2W g 4 2、问题特点: 、问题特点: 设加速度为零时的应力为σst 则: 设加速度为零时的应力为σ 1 l Aρ g − b l M 2 4 = Aρ g l − b l σ st = st = W W 2W 4 a σ d = σ st 1 + = σ st K d g
P
v
∆d P 即:Fd = ∆ st
代入得: 代入得: 1P 2 1 1 ∆2 d v = ∆ d Fd = P 2g 2 2 ∆ st
∆d =
Kd =
P
∆ st
v2 ∆ st g ∆ st
v2 g ∆ st (10.9)
∆ d = K d ∆ st ,
Fd = K d P,
σ d = K dσ st
= 1057 ×106 Pa
§10 – 5
材料力学期末试卷10(带答案)

三明学院《材料力学》期末考试卷10(考试时间:120分钟)使用班级: 学生数: 任课教师: 考试类型 闭卷一.填空题(每题3,共30分)1. 构件所受的外力可以是各式各样的,有时是很复杂的。
材料力学根据构件的典型受力情况及截面上的内力分量可分为 拉伸或压缩 、 剪切 、 扭转 、 弯曲 四种基本变形。
2. 现代工程中常用的固体材料种类繁多,物理力学性能各异。
所以,在研究受力后物体(构件)内部的力学响应时,除非有特别提示,一般将材料看成由 连续性 、 均匀性 、 各向同性 的介质组成。
3. 为保证工程结构或机械的正常工作,构件应满足三个要求,即 强度 、 刚度 、 稳定性 。
4. 为了求解静不定问题,必须研究构件的 变形 ,从而寻找出 变形协调方程 。
5. 矩形截面梁的弯曲剪力为FS ,横截面积为A ,则梁上的最大切应力为A F s=σ 。
6. 用主应力表示的广义胡克定律是()[]32111σσμσε+-=E ;()[]331211σσμσε+-=E ; ()[]21331σσμσε+-=E 。
7. 压杆稳定问题中,欧拉公式成立的条件是:)E(Pσπλλλ211:=≥其中 。
8. 轴向拉压变形中,横向应变与轴向应变的关系是 μεε=' 。
9. 图示外伸梁受均布载荷作用,欲使C B A M M M -==,则要求a l /的比值为22/=a l ;欲使0=C M ,则要求比值为2/=a l 。
10. 图示矩形截面纯弯梁受弯矩M 作用,梁发生弹性变形,横截面上图示阴影面积上承担的弯矩为 7M/8 。
二.选择题(每题3分,共15分)1.平面弯曲梁的横截面上,最大正应力出现在( D ) A .中性轴;B .左边缘;C .右边缘;D .离中性轴最远处 。
2.第一强度理论适用于( A )A .脆性材料;B .塑性材料;C .变形固体;D .刚体。
3.在计算螺栓的挤压应力时,在公式bsbsbs A F =σ中,bsA 是(B )A .半圆柱面的面积;B .过直径的纵截面的面积;C .圆柱面的面积;D .横截面积。
材料力学 第10章 压杆稳定

μ=2
欧拉临界压力公式 :
Fcr
2 EI (l )2
应用欧拉公式时,应注意以下两点:
1、欧拉公式只适用于线弹性范围,即只适用于弹性稳定问题
2、 I 为压杆失稳发生弯曲时,截面对其中性轴的惯性矩。
对于各个方向约束相同的情形(例如球铰约束),I 取截面的 最小惯性矩,即 I=Imin;
Fcr
2 EI (l )2
压杆临界压力欧拉公式的一般形式
E——材料的弹性模量;
—长度系数(或约束系数),反映了杆端支承对临界载
荷的影响。
压杆临界力与外
l—压杆的计算长度或相当长度。 力有关吗??
l—压杆的实际长度。
I—压杆失稳发生弯曲时,截面对其中性轴的惯性矩。
适用条件:1.理想压杆;2.线弹性范围内
第10章 压杆稳定
第10章 压杆稳定
§10.1 §10.2 §10.3 §10.4 §10.5 §10.6
工程中的压杆稳定问题 理解
压杆稳定性概念 掌握
细长压杆临界压力的欧拉公式 掌握
压杆的临界应力 掌握
压杆的稳定性计算
掌握
提高压杆稳定性的措施
了解
关键术语
压杆,稳定性,屈曲,稳定失效,临界压力Fcr, 柔度λ(长细比),计算长度μl
重点 1、细长压杆临界压力的欧拉公式 2、压杆的临界应力 3、压杆临界载荷的欧拉公式的适用条件 4、压杆稳定性设计
难点 1、压杆临界压力的计算 2、压杆稳定性设计
§10.1 工程中的压杆稳定问题
构件的承载能力:
①强度 ②刚度 ③稳定性
工程中有些构件 具有足够的强度、刚 度,却不一定能安全 可靠地工作。
F
30mm
材料力学-10-压杆的稳定性问题

欢迎来到材料力学-10-压杆的稳定性问题演示文稿。今天,我们将探讨压杆的 定义、分类以及影响其稳定性的因素。
压杆的定义和分类
压杆是一种长而细的结构元素,主要通过压力来支撑负载。根据其截面形状,压杆可以分为圆形、方形 和矩形等不同类型。
欧拉公式简介
欧拉公式是用于计算压杆的临界压力的重要公式。它基于结构的刚度和截面的几何特性,帮助我们预测 压杆在不同加载条件下的稳定性。
实例分析
通过实例分析,我们将深入探讨具体的压杆结构,并分析其稳定性问题。了 解实际案例对于理解压杆稳定性的关键因素至关重要。
结论和要点
在本演示文稿中,我们回顾了压杆的定义和分类,介绍了欧拉公式及其应用,探讨了稳定性分析的关键 因素,并通过实例分析展示了压杆的真实应用。记住这些要点,您将能够更好公式
临界压力计算公式是通过将欧拉公式代入材料的弹性模量和截面的惯性矩,从而得出压杆在理想情况下 可能失稳的临界加载。
压杆的稳定性分析
压杆的稳定性分析涉及到考虑加载条件、几何形状以及材料性质等因素。我们将使用数学模型和工程实 践来评估压杆在给定条件下的稳定性。
缺陷对稳定性的影响
压杆的稳定性可能受到结构缺陷的影响,如划伤、弯曲或异物。我们将研究 这些因素如何改变压杆的临界压力和整体稳定性。
材料力学第10章 动载荷

Kd = 1 + 1 + 2H
∆st
P
Pl 3 + P ∆st = 48EI 4C
σ st max = Pl / 4 = Pl
W
4W
MF
Pl/4
σd max = Kdσ st max ≤ [σ ] [H] =
∆st
2 σ st max
[(
[σ ]
−1) −1]
2
等截面刚架,重物P自高度 处自由下落。 、 、 自高度h处自由下落 例:等截面刚架,重物 自高度 处自由下落。 E、I、 W已知 。 试求截面的最大竖直位移和刚架内的最大 已知。 已知 冲击正应力( 刚架的质量可略去不计, 冲击正应力 ( 刚架的质量可略去不计 , 且不计轴力 对刚架变形的影响) 对刚架变形的影响)。
第十章 动载荷
§10.1 概述 §10.2 动静法的应用 §10.3 强迫振动的应力计算 §10.4 杆件受冲击时的应力和变形 §10.5 冲击韧性
§10.1 概述
1)动载荷问题的特点: )动载荷问题的特点: 静载荷问题:载荷平稳地增加, 静载荷问题:载荷平稳地增加,不引起构件 的加速度——准静态。 准静态。 的加速度 准静态 动载荷问题:载荷急剧变化, 动载荷问题:载荷急剧变化,构件速度发生 急剧变化。 急剧变化。
2FNd = qd (2R)
qd FNd FNd
qd
σd =
FNd = ρR2ω2 = ρv2 A
注意: 无关! 注意:与A无关! 无关
4)匀减速转动(飞轮刹车) )匀减速转动(飞轮刹车) 例 4 : 飞 轮 转 速 n=100r/min , 转 动 惯 量 为 Ix=0.5kNms2 , 轴 直 径 d=100mm , 10 秒停转,求最大动应力。 秒停转,求最大动应力。 解:角速度: ω0 = nπ 角速度: 30 角加速度: 角加速度:α = −ω0 / t
《材料力学基础》10动载荷

水平方向冲击 。
求:杆在危险点处的 d 。
B
C
v
A
52
解:
B
冲击过程中小球动能减少为
C
v
T 1 mv2 1 P v2
2
2g
位能 没有改变
A
V=0
d
B
C
G
Pd
A
53
杆的应变能可用冲击力
B
Pd 所作的功表示。
C
v
Ud
1 2
Pd
d
d 是被击点处的冲击挠度
A
d
Pd a3 3EI
d
B
C
G
Pd
A
Pd
3EI a3
mn 截面上的轴力 FN(x) 等于 P
F N ( x) 0l
g
2
(
R0
)
A(
)d
d
l n
x
m
R1 R0
x dP
n FN(x)
转轴
27
最大的惯性力发生在叶根截
面上
F
N
max
2 A0[l2
g3
3 4
R0 l]
在叶根截面上的拉应力为
顶部
m 叶根
F N max 2 (1 R0)(1 5 R0)
A0 3g R1 4 R1
o
D
D 2 2
因为环是等截面的,所以相同长度的任一段质量相等。
19
加在环上的惯性力必然是沿轴线 均匀分布的线分布力。
其上的惯性力集度为
qd
(1
A )( D 2) g2
A 2 2g
D
qd
o
20
qd
材料力学第10章_梁的应力(1)

max
2 300 kNm
max
WZ
B
Wz
M
max
cm
3
B 1875
选择确定I字钢型号:INO50a
1875 1860 1875 100 % 0 .8 %
例 铸铁制作的悬臂梁,尺寸及受力如图示,图中F=20kN。梁的截面 为T字形,形心坐标yc=96.4mm。已知材料的拉伸许用应力和压缩许用应力 分别为[σ ]+=40MPa, [σ ]-=100MPa。试校核梁的强度是否安全。
Fa
Fb
C截面:
max
MC W zC
6
Fb
d 2
32
3
62 . 5 160 32
0 . 13
3
M
46 . 4 10 Pa 46 . 4 MPa
结论:轮轴安全
例 图示T形截面简支梁在中点承受集中力F=32kN,梁的长度L=2m。T形截 面的形心坐标yc=96.4mm,横截面对于z轴的惯性矩Iz=1.02×108mm4。求弯矩 最大截面上的最大拉应力和最大压应力。
y
(1)
(二)物理关系:
y
......
由纵向线应变的变化规律→正应力的分布规律。
在弹性范围内
d
E
O O1
E
Ey
...... (2)
A1
y
B1 x
E
Ey
1
为梁弯曲变形后的曲率
上式说明了横截面上正应力的分布规律,表明正应力沿截面高度
呈线性变化,距中性轴越远,应力值越大,在中性轴处正应力为零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b 先上升后下降 1)温度升高,
先下降后上升 b 最高 在250-350度之间,
兰脆:强度最高,塑性最低。 2)温度不断升高, s 不断下降 到400度时,屈服现象消失。
3)弹性模量E随温度升高而下降
§10–1 高温下材料的力学性能 二、温度对材料力学性能的影响 2、蠕变 1)蠕变现象 蠕变:在一定温度和不变应力下,材料随时间 增加而缓慢地发生塑性变形的现象称为蠕变。 沥青在自重作用 下会渐渐流动。
交变应力: 正应力、切应力
§10-3 交变应力下材料的疲劳极限 一、交变应力、循环特性、应力幅和平均应力 1、交变应力 交变应力: 随时间作周期性改变的应力称为交变应力。 活塞杆 连杆
y
A
©2001 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning™ is a trademark used herein under license.
实际结构疲劳试验装置
§10-3 交变应力下材料的疲劳极限 二、材料在交变应力作用下的破坏特点,疲劳极限 4、疲劳试验 1)疲劳试验装置 2)疲劳试件 一组光滑小试件
特点:
裂纹源、光滑区、粗糙区
颗粒状区域
光滑区域
§10-3 交变应力下材料的疲劳极限 二、材料在交变应力作用下的破坏特点,疲劳极限 3、疲劳破坏和特点 疲劳破坏过程 -累积损伤的形成
初始缺陷
滑
移
滑移带
初始裂纹(微裂纹)
脆性断裂
宏观裂纹扩展
宏观裂纹
§10-3 交变应力下材料的疲劳极限 二、材料在交变应力作用下的破坏特点,疲劳极限 4、疲劳试验
A—名义持久限。
N0—循环基数。
r—材料持久限。
§10-3 交变应力下材料的疲劳极限 二、材料在交变应力作用下的破坏特点,疲劳极限 3、疲劳破坏和特点 弹簧的疲劳失效
疲劳源
§10-3 交变应力下材料的疲劳极限 二、材料在交变应力作用下的破坏特点,疲劳极限 3、疲劳破坏和特点 1)抵抗断裂的极限应力低于强度极限,甚至屈服极限。 2)破坏有一个过程,构件需经过若干次应力循环才 突然破坏。 3)材料的破坏呈脆性断裂。
强度高:强度极限应力 b
n 材料的屈服强度 0.2
塑性好:延伸率
铸铁拉伸
§10–1 高温下材料的力学性能 一、常温、静载下的材料力学实验 低碳钢和铸铁材料的压缩实验
s 低碳钢:
铸铁: b
铸铁材料 b b
§10–1 高温下材料的力学性能 二、温度对材料力学性能的影响 1、短时高温下材料的力学性能
工程力学
工程力学
第十章 材料的力学性能
第十章 材料的力学性能
§10-1 高温下材料的力学性能 §10-2 冲击吸收功 §10-3 交变应力下材料的疲劳极限 §10-4 断裂韧度 §10-5 硬度
§10-6 提高和改善材料力学性能的途经
第十章 材料的力学性能 【本章重点内容】
1. 蠕变、应力松弛、疲劳极限、断裂韧度概念 2. 对称循环下的疲劳强度计算
tT
-在工作温度T下,经历t小时不发生断裂的持 久强度极限。
对在高温下长期承受静载的构件进行安全计算时, 考虑设备对蠕变变形限制量的具体要求,一般应使工作 应力小于相应的蠕变极限。
§10–1 高温下材料的力学性能 二、温度对材料力学性能的影响 3、应力松弛 应力松弛:在规定温度及初始变形或位移恒定的条下, 材料中的应力随时间而逐渐减小的现象称为应力松弛。 连接高温蒸汽管道的螺栓,拧紧后产生伸长变形, 因螺栓蠕变,其弹性变形量减小,塑性变形增加,螺 栓的应力降低,因此出现应力松弛。
伸长率随时间变化曲线
蠕变速度逐渐减小
第二阶段:
蠕变速度恒定
第三阶段:
蠕变速度不断增加, 直至断裂。
第一阶段
第二阶段 第三阶段
§10–1 高温下材料的力学性能 二、温度对材料力学性能的影响 2、蠕变 2)蠕变规律 蠕变曲线:试样在一定的拉力和温度下,蠕 变伸长率随时间变化的曲线。 各种金属的蠕变曲 线决定于材质,但 温度和应力的大小 也影响蠕变。 对给定材料,当应 力较小或温度较低 时,蠕变匀速阶段 长,蠕变速度也低 当应力大或温度高 时,蠕变只有第一 阶段和第三阶段。
用第一种方法表示蠕变:
用第二种方法表示蠕变:
T
t
700 0.2 100
T v
1600 105
700 C 100h 0.2% 600oC 1×10-5% / h
§10–1 高温下材料的力学性能 二、温度对材料力学性能的影响 2、蠕变 3)蠕变极限和持久极限强度
持久强度极限:在指定温度T和规定时间t内,使材料 因蠕变而不发生断裂的最大应力称为持久极限应力。
冲击力功 W k 断口面积 A
②“V”型口试件的冲击韧性:
k 冲击力功W
③ 冷脆:温度降低,冲击韧性下降的现象称为冷脆。
当温度降低到某一温度下时,材料在发生塑性变形之 前就因拉断而破坏,这就是材料的的冷脆。而上述温度则
称为脆性转变温度或简称转变温度。
§10–2 冲击吸收功 三、冲击吸收功的应用 由于冲击吸收功值不仅与材料有关,而且随试样的 形状、尺寸不同而显著改变。所以,由标准试样测得的 冲击吸收功值不能直接换算到实际构件上。 冲击吸收功值只适用于评定承 受一次冲击、或较大能量多次 冲击材料的抗断能力。
a max
m 0
§10-3 交变应力下材料的疲劳极限 一、交变应力、循环特性、应力幅和平均应力 3、几种特殊的交变应力
max m min
2)脉动循环 r min 0 max
a m max
2
a
t
m max min
3)静循环 min r 1 max
§10–2 冲击吸收功 二、冲击吸收功 为了评定材料在冲击载荷下脆性破坏的倾向,在工 程中广泛采用一次摆锤冲击试验,测定标准试样在一次 冲击载荷作用下折断时试样所吸收的冲击功。 冲击试验器
2 1
l
国家标准: 《金属夏比缺口冲击试验方法》 (GB/T 229-1994)
mg
试件
§10–2 冲击吸收功 二、冲击吸收功 ① “U”型口试件的冲击韧性:
min r max
max min
2
2)平均应力 m
3)应力幅 交变应力
a
max min
2
稳定交变应力:循环特征及循环周期都不变。
不稳定交变应力:循环特征及循环周期变化。
§10-3 交变应力下材料的疲劳极限 例10-1 发动机连杆大头螺钉工作时最大拉力Pmax =58.3kN, 最小拉力Pmin =55.8kN ,螺纹内径为 d=11.5mm,试求 a 、m 和 r。 解: max Pmax 458300 2 561MPa A 0.0115
伸长率随时间变化曲线
低熔点金属(铅、 锌等)在室温下有 蠕变。 高熔点金属钢等在 高温下有蠕变。
低碳钢300-350度
第一阶段
第二阶段 第三阶段
合金钢350-400度
§10–1 高温下材料的力学性能 二、温度对材料力学性能的影响 2、蠕变 2)蠕变规律 蠕变曲线:试样在一定的拉力和温度下,蠕 变伸长率随时间变化的曲线。 第一阶段:
§10–2 冲击吸收功 一、速度对材料力学性能的影响 当加载速度很慢时,金属材料的力学性能是稳定的, 因此可以按静载处理。当加载速度较快时,随着加载速 )升高,塑性指标( 度的增加,强度指标( ) s , b , 下降,材料脆性增加。 工程中的设备中,采掘机、锻压机等承受加速度很快 的冲击载荷;一般设备也会受到启动、急刹车或超载等引 起的冲击载荷作用,这时材料的脆性破坏倾向增加。 材料处于低温时,受到冲击载荷作用,脆性破坏的危 险性更大。
0
th
O
a c b
l
l
§10–1 高温下材料的力学性能 二、温度对材料力学性能的影响 3、应力松弛
温度不变 3 2 1
初始弹性应变不变
T1T2 T3
3 2 1
T3 T2 T1
初应力越大,松弛的初速率越大
温度越高,松弛的初速率越大
第十章 材料的力学性能
§10-2 冲击吸收功
第十章 材料的力学性能
§10–1 高温下材料的力学性能
§10–1 高温下材料的力学性能 一、常温、静载下的材料力学实验 拉伸实验:低碳钢 强度指标: s b
§10–1 高温下材料的力学性能 一、常温、静载下的材料力学实验 其它材料的拉伸实验
1-锰钢 2-硬铝 3-退火球墨铸铁 4-青铜
应力-应变曲线:
2)平均应力
a
t
m
T
max min
2
3)应力幅
4)循环周期
T
a
max min
2
§10-3 交变应力下材料的疲劳极限 一、交变应力、循环特性、应力幅和平均应力 3、几种特殊的交变应力 1) 对称循环
max m min a
T
t
r
min 1 max
2 1lFra bibliotek mg
试件
冲击试验对材料品质、内部 缺陷、脆性转化趋势和工艺 质量等方面较其它试验方法 敏感,能显示材料内部组织 结构的微小差异,所以广泛 应用于材料的品质和控制热 处理工艺质量等方面。
第十章 材料的力学性能
§10-3 交变应力下材料的疲劳极限
§10-3 交变应力下材料的疲劳极限 一、交变应力、循环特性、应力幅和平均应力 1、交变应力 交变应力: 随时间作周期性改变的应力称为交变应力。 传动轴 齿轮的齿
§10-3 交变应力下材料的疲劳极限 二、材料在交变应力作用下的破坏特点,疲劳极限 1、材料持久限(疲劳极限) 循环应力只要不超过某个“最大限度”,构件就可 以经历无数次循环而不发生疲劳破坏,这个限度值称 为“疲劳极限”,用r 表示。 2、 —N 曲线(应力—寿命曲线)
