八年级第二学期3月份月考数学试题
八年级数学第二学期3月份月考检测测试卷含答案

一、选择题1.下列根式是最简二次根式的是( ) A .4B .21x +C .12D .40.52.下列计算正确的是( ) A .325+=B .2222+=C .2651-=D .822-=3.2的倒数是( ) A .2B .22C .2-D .22-4.要使2020x -有意义,x 的取值范围是( ) A .x≥2020 B .x≤2020C .x> 2020D .x< 20205.下列运算正确的是( )A .52223-=y yB .428x x x ⋅=C .(-a-b )2=a 2-2ab+b 2D .27123-=6.下列说法错误的个数是( ) ①所有无限小数都是无理数;②()23-的平方根是3±;③2a a =;④数轴上的点都表示有理数 A .1个B .2个C .3个D .4个7.下列计算不正确的是 ( )A .35525-=B .236⨯=C 774=D 363693=+==8.12的下列说法中错误的是( ) A 1212的算术平方根 B .3124<< C 12不能化简 D 12是无理数9.若3235a =++,2610b =+a b 的值为( )A .12B .14C 23+D 610+10.下列各式计算正确的是( ) A .233= B ()255-=± C 523=D .3223=二、填空题11.比较实数的大小:(1)______ ;(2)14_______1212.若0a >化成最简二次根式为________. 13.能力拓展:1A =2A =;3:A =;4A =________.…n A :________.()1请观察1A ,2A ,3A 的规律,按照规律完成填空.()2比较大小1A 和2A()3-14.若a ,b ,c 是实数,且10a b c ++=,则2b c +=________. 15.观察下列等式:第1个等式:a 11=,第2个等式:a 2=,第3个等式:a 3,第4个等式:a 42=, …按上述规律,回答以下问题: (1)请写出第n 个等式:a n =__________. (2)a 1+a 2+a 3+…+a n =_________16.10=,则222516x y +=______.17..18.计算:2015·2016=________.19.n 的最小值为___20.函数y 中,自变量x 的取值范围是____________. 三、解答题21.计算:10099+【答案】910【解析】 【分析】先对代数式的每一部分分母有理化,然后再进行运算 【详解】10099++=2100992-++++=991224-+-++-=1- =1110- =910【点睛】本题看似计算繁杂,但只要找到分母有理化这个突破口,就会化难为易。
人教版八年级第二学期3月份月考数学试卷含答案
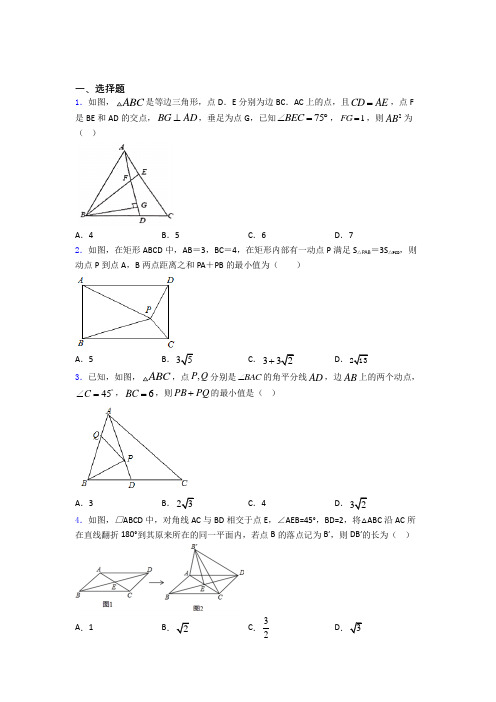
一、选择题1.如图,ABC 是等边三角形,点D .E 分别为边BC .AC 上的点,且CD AE =,点F 是BE 和AD 的交点,BG AD ⊥,垂足为点G ,已知75∠=︒BEC ,1FG =,则2AB 为( )A .4B .5C .6D .72.如图,在矩形ABCD 中,AB =3,BC =4,在矩形内部有一动点P 满足S △PAB =3S △PCD ,则动点P 到点A ,B 两点距离之和PA +PB 的最小值为( )A .5B .35C .332+D .2133.已知,如图,ABC ,点,P Q 分别是BAC ∠的角平分线AD ,边AB 上的两个动点,45C ︒∠=,6BC =,则PB PQ +的最小值是( )A .3B .23C .4D .324.如图,□ABCD 中,对角线AC 与BD 相交于点E ,∠AEB=45°,BD=2,将△ABC 沿AC 所在直线翻折180°到其原来所在的同一平面内,若点B 的落点记为B′,则DB′的长为( )A .1B 2C .32D 35.在ΔABC 中,211a b c =+,则∠A( ) A .一定是锐角B .一定是直角C .一定是钝角D .非上述答案 6.在ABC 中,90C ∠=︒,30A ∠=︒,12AB =,则AC =( )A .6B .12C .62D .63 7.ABC 三边长为a 、b 、c ,则下列条件能判断ABC 是直角三角形的是( ) A .a =7,b =8,c =10B .a =41,b =4,c =5C .a =3,b =2,c =5D .a =3,b =4,c =6 8.下列结论中,矩形具有而菱形不一定具有的性质是( ) A .内角和为360°B .对角线互相平分C .对角线相等D .对角线互相垂直 9.一个直角三角形的两条边的长度分别为3和4,则它的斜边长为( )A .5B .4C .7D .4或5 10.如图,是一张直角三角形的纸片,两直角边6,8AC BC ==,现将ABC 折叠,使点B 点A 重合,折痕为DE ,则BD 的长为( )A .7B .254C .6D .112二、填空题11.如图,在Rt ABC 中,90ACB ∠=︒,4AC =,2BC =,以AB 为边向外作等腰直角三角形ABD ,则CD 的长可以是__________.12.如图,在四边形ABCD 中,22AD =,3CD =,45ABC ACB ADC ∠=∠=∠=︒,则BD 的长为__________.13.如图,在ABC 中,D 是BC 边中点,106AB AC ==,,4=AD ,则BC 的长是_____________.14.在ABC ∆中,90BAC ∠=︒,以BC 为斜边作等腰直角BCD ∆,连接DA ,若22AB =,42AC =,则DA 的长为______.15.已知Rt △ABC 中,AC =4,BC =3,∠ACB =90°,以AC 为一边在Rt △ABC 外部作等腰直角三角形ACD ,则线段BD 的长为_____.16.在Rt △ABC 中,直角边的长分别为a ,b ,斜边长c ,且a +b =35,c =5,则ab 的值为______.17.如图,在锐角ABC ∆中,2AB =,60BAC ∠=,BAC ∠的平分线交BC 于点D ,M ,N 分别是AD 和AB 上的动点,则BM MN +的最小值是______.18.如图,在△ABC 中,AB =AC =10,BC =12,BD 是高,则点BD 的长为_____.19.如图的实线部分是由Rt ABC ∆经过两次折叠得到的.首先将Rt ABC ∆沿高CH 折叠,使点B 落在斜边上的点B '处,再沿CM 折叠,使点A 落在CB '的延长线上的点A '处.若图中90ACB ∠=︒,15cm BC =,20cm AC =,则MB '的长为______.20.四个全等的直角三角形按图示方式围成正方行ABCD ,过各较长直角边的中点作垂线,围成面积为4的小正方形EFGH,已知AM为Rt△ABM的较长直角边,AM=7EF,则正方形ABCD的面积为_______.三、解答题21.(1)计算:1312248233⎛⎫-+÷⎪⎪⎝;(2)已知a、b、c满足2|23|32(30)0a b c+-+--=.判断以a、b、c为边能否构成三角形?若能构成三角形,说明此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.22.如图,在△ABC中,AB=30 cm,BC=35 cm,∠B=60°,有一动点M自A向B以1 cm/s的速度运动,动点N自B向C以2 cm/s的速度运动,若M,N同时分别从A,B出发.(1)经过多少秒,△BMN为等边三角形;(2)经过多少秒,△BMN为直角三角形.23.在等腰Rt△ABC中,AB=AC,∠BAC=90°(1)如图1,D,E是等腰Rt△ABC斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90后,得到△AFC,连接DF①求证:△AED≌△AFD;②当BE=3,CE=7时,求DE的长;(2)如图2,点D 是等腰Rt △ABC 斜边BC 所在直线上的一动点,连接AD ,以点A 为直角顶点作等腰Rt △ADE ,当BD =3,BC =9时,求DE 的长.24.如图所示,已知ABC ∆中,90B ∠=︒,16AB cm =,20AC cm =,P 、Q 是ABC ∆的边上的两个动点,其中点P 从点A 开始沿A B →方向运动,且速度为每秒1cm ,点Q 从点B 开始沿B C A →→方向运动,且速度为每秒2cm ,它们同时出发,设出发的时间为ts .(1)则BC =____________cm ;(2)当t 为何值时,点P 在边AC 的垂直平分线上?此时CQ =_________?(3)当点Q 在边CA 上运动时,直接写出使BCQ ∆成为等腰三角形的运动时间.25.在ABC ∆中,AB AC =,CD 是AB 边上的高,若10,45AB BC ==.(1)求CD 的长.(2)动点P 在边AB 上从点A 出发向点B 运动,速度为1个单位/秒;动点Q 在边AC 上从点A 出发向点C 运动,速度为v 个单位秒()v>1,设运动的时间为()0t t >,当点Q 到点C 时,两个点都停止运动.①若当2v =时,CP BQ =,求t 的值.②若在运动过程中存在某一时刻,使CP BQ =成立,求v 关于t 的函数表达式,并写出自变量t 的取值范围.26.问题情境:综合实践活动课上,同学们围绕“已知三角形三边的长度,求三角形的面积”开展活动,启航小组同学想到借助正方形网格解决问题问题解决:图(1)、图(2)都是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,操作发现,启航小组同学在图(1)中画出△ABC ,其顶点A ,B ,C 都在格点上,同时构造长方形CDEF ,使它的顶点都在格点上,且它的边EF 经过点A ,ED 经过点B .同学们借助此图求出了△ABC 的面积.(1)在图(1)中,△ABC 的三边长分别是AB = ,BC = ,AC = .△ABC 的面积是 .(2)已知△PMN 中,PM =17,MN =25,NP =13.请你根据启航小组的思路,在图(2)中画出△PMN ,并直接写出△RMN 的面积 .27.如图,在平面直角坐标系中,点O 是坐标原点,ABC ∆,ADE ∆,AFO ∆均为等边三角形,A 在y 轴正半轴上,点0()6,B -,点(6,0)C ,点D 在ABC ∆内部,点E 在ABC ∆的外部,32=AD ,30DOE ∠=︒,OF 与AB 交于点G ,连接DF ,DG ,DO ,OE .(1)求点A 的坐标;(2)判断DF 与OE 的数量关系,并说明理由;(3)直接写出ADG ∆的周长.28.阅读下列一段文字,然后回答下列问题.已知在平面内有两点()111, P x y 、()222, P x y ,其两点间的距离()()22121212PP x x y y =-+-直于坐标轴时,两点间距离公式可化简为12x x -或1|y -2|y .(1)已知()2, 4A 、()3, 8B --,试求A 、B 两点间的距离______.已知M 、N 在平行于y 轴的直线上,点M 的纵坐标为4,点N 的纵坐标为-1,试求M 、N 两点的距离为______;(2)已知一个三角形各顶点坐标为()1, 6D 、()3, 3E -、()4, 2F ,你能判定此三角形的形状吗?说明理由.(3)在(2)的条件下,平面直角坐标系中,在x 轴上找一点P ,使PD PF +的长度最短,求出点P 的坐标及PD PF +的最短长度.29.已知,矩形ABCD 中,AB =4cm ,BC =8cm ,AC 的垂直平分线EF 分别交AD 、BC 于点E 、F ,垂足为O .(1)如图1,连接AF 、CE .求证:四边形AFCE 为菱形.(2)如图1,求AF 的长.(3)如图2,动点P 、Q 分别从A 、C 两点同时出发,沿△AFB 和△CDE 各边匀速运动一周.即点P 自A →F →B →A 停止,点Q 自C →D →E →C 停止.在运动过程中,点P 的速度为每秒1cm ,设运动时间为t 秒.①问在运动的过程中,以A 、P 、C 、Q 四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t 和点Q 的速度;若不可能,请说明理由.②若点Q 的速度为每秒0.8cm ,当A 、P 、C 、Q 四点为顶点的四边形是平行四边形时,求t 的值.30.已知ABC 是等边三角形,点D 是BC 边上一动点,连结AD()1如图1,若2BD =,4DC =,求AD 的长;()2如图2,以AD 为边作60ADE ADF ∠=∠=,分别交AB ,AC 于点E ,F . ①小明通过观察、实验,提出猜想:在点D 运动的过程中,始终有AE AF =,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的两种想法想法1:利用AD 是EDF ∠的角平分线,构造角平分线的性质定理的基本图形,然后通过全等三角形的相关知识获证.想法2:利用AD 是EDF ∠的角平分线,构造ADF 的全等三角形,然后通过等腰三角形的相关知识获证.请你参考上面的想法,帮助小明证明.(AE AF =一种方法即可)②小聪在小明的基础上继续进行思考,发现:四边形AEDF 的面积与AD 长存在很好的关系.若用S表示四边形AEDF的面积,x表示AD的长,请你直接写出S与x之间的关系式.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】结合等边三角形得性质易证△ABE≌△CAD,可得∠FBG=30°,BF=2FG=2,再求解∠ABE =15°,进而两次利用勾股定理可求解.【详解】∵△ABC为等边三角形∴∠BAE=∠C=60°,AB=AC,CD=AE∴△ABE≌△CAD(SAS)∴∠ABE=∠CAD∴∠BFD=∠ABE+∠BAD=∠CAD+∠BAF=∠BAC=60°,∵BG⊥AD,∴∠BGF=90°,∴∠FBG=30°,∵FG=1,∴BF=2FG=2,∵∠BEC=75°,∠BAE=60°,∴∠ABE=∠BEC﹣∠BAE=15°,∴∠ABG=45°,∵BG⊥AD,∴∠AGB=90°,∴2222BF FG-=-321AB2=AG2+BG2323)2=6.故选C.【点睛】本题考查全等三角形的判定与性质,等边三角形的性质,勾股定理,证明△ABG为等腰直角三角形是解题关键.2.B解析:B【分析】首先由PAB PCD S =3S △△,得知动点P 在与AB 平行且与AB 的距离为3的直线l 上,作点A 关于直线l 的对称点E ,连接AE 、BE ,则BE 的长就是所求的最短距离,然后在直角三角形ABE 中,由勾股定理求得BE 的值,即PA+PB 的最小值.【详解】解:∵PAB PCD S =3S △△, 设点P 到CD 的距离为h ,则点P 到AB 的距离为(4-h ), 则11AB (4-h)=3CD h 22⋅⋅⨯⋅⋅,解得:h=1,∴点P 到CD 的距离1,到AB 的距离为3, ∴如下图所示,动点P 在与AB 平行且与AB 的距离为3的直线l 上,作点A 关于直线l 的对称点E ,连接AE 、BE ,且两点之间线段最短,∴PA+PB 的最小值即为BE 的长度,AE=6,AB=3,∠BAE=90°,根据勾股定理:22222BE =AE AB =63=35++故选:B .【点睛】本题考查了轴对称—最短路线问题(两点之间线段最短),勾股定理,得出动点P 所在的位置是解题的关键.3.D解析:D【分析】先根据等腰三角形的性质得出AD 是线段QE 垂直平分线,再根据垂直平分线的性质、两点之间线段最短得出PB PQ +最小值为BE ,最后根据垂线段最短、直角三角形的性质得出BE 的最小值即可得.【详解】如图,作QE AD ⊥,交AC 于点E ,∵AD 平分∠BAC ,∴∠BAD=∠CAD ,AD ∴是线段QE 垂直平分线(等腰三角形的三线合一)PQ PE ∴=PB PQ PB PE ∴+=+由两点之间线段最短得:当点,,B P E 共线时,PB PE +最小,最小值为BE 点,P Q 都是动点BE ∴随点,P Q 的运动而变化由垂线段最短得:当BE AC ⊥时,BE 取得最小值在Rt BCE ∆中,456,C C B ∠=︒= 232BE CE BC ∴=== 即PB PQ +的最小值为32故选:D .【点睛】本题考查了等腰三角形的性质、垂直平分线的性质、两点之间线段最短等知识点,利用两点之间线段最短和垂线段最短确认PB PQ +的最小值是解题关键.4.B解析:B【解析】【分析】如图,连接BB′.根据折叠的性质知△BB′E 是等腰直角三角形,则2.又B′E 是BD 的中垂线,则DB′=BB′.【详解】∵四边形ABCD 是平行四边形,BD=2,∴BE=12BD=1. 如图2,连接BB′.根据折叠的性质知,∠AEB=∠AEB′=45°,BE=B′E .∴∠BEB′=90°,∴△BB′E 是等腰直角三角形,则22,又∵BE=DE ,B′E ⊥BD ,∴2故选B.【点睛】考查了平行四边形的性质以及等腰直角三角形性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.5.A解析:A【解析】【分析】根据211a b c=+以及三角形三边关系可得2bc>a 2,再根据(b-c)2≥0,可推导得出b 2 +c 2>a 2,据此进行判断即可得.【详解】∵211a b c =+,∴2b ca bc+ =,∴2bc=a(b+c),∵a、b、c是三角形的三条边,∴b+c>a,∴2bc>a·a,即2bc>a 2,∵(b-c)2≥0,∴b 2 +c 2 -2bc≥0,b 2 +c 2≥2bc,∴b 2 +c 2>a 2,∴一定为锐角,故选A.【点睛】本题考查了三角形三边关系、完全平方公式、不等式的传递性、勾股定理等,题目较难,得出b 2 +c 2>a 2是解题的关键.6.D解析:D【分析】根据直角三角形的性质求出BC,根据勾股定理计算,得到答案.【详解】解:∵∠C=90°,∠A=30°,∴BC=12AB=6,由勾股定理得,=故选:D.【点睛】本题考查的是直角三角形的性质、勾股定理,掌握在直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.7.B解析:B【分析】根据勾股定理逆定理对每个选项一一判断即可.【详解】A、∵72+82≠102,∴△ABC不是直角三角形;B、∵52+42=)2,∴△ABC是直角三角形;C、∵2222,∴△ABC不是直角三角形;D、∵32+42≠62,∴△ABC不是直角三角形;故选:B.【点睛】本题主要考查勾股定理逆定理,熟记定理是解题关键.8.C解析:C【分析】矩形与菱形相比,菱形的四条边相等、对角线互相垂直;矩形四个角是直角,对角线相等,由此结合选项即可得出答案.【详解】A、菱形、矩形的内角和都为360°,故本选项错误;B、对角互相平分,菱形、矩形都具有,故本选项错误;C、对角线相等菱形不具有,而矩形具有,故本选项正确D、对角线互相垂直,菱形具有而矩形不具有,故本选项错误,故选C.【点睛】本题考查了菱形的性质及矩形的性质,熟练掌握矩形的性质与菱形的性质是解题的关键. 9.D解析:D【分析】根据题意,可分为已知的两条边的长度为两直角边,或一直角边一斜边两种情况,根据勾股定理求斜边即可.【详解】当3和4为两直角边时,由勾股定理,得:5=;当3和4为一直角边和一斜边时,可知4为斜边.∴斜边长为4或5.故选:D .【点睛】本题考查了勾股定理,关键是根据题目条件进行分类讨论,利用勾股定理求解.10.B解析:B【分析】由折叠的性质得出AD=BD ,设BD=x ,则CD=8-x ,在Rt △ACD 中根据勾股定理列方程即可得出答案.【详解】解:∵将△ABC 折叠,使点B 与点A 重合,折痕为DE ,∴AD=BD ,设BD=x ,则CD=8-x ,在Rt △ACD 中,∵AC 2+CD 2=AD 2,∴62+(8-x )2=x 2,解得x=254 ∴BD=254. 故选:B .【点睛】本题考查了翻折变换的性质、勾股定理等知识,熟练掌握方程的思想方法是解题的关键.二、填空题11.【分析】在ABC 中计算AB ,情况一:作AE CE ⊥于E ,计算AE ,DE ,CE ,可得CD ;情况二:作BE CE ⊥于E ,计算BE ,CE ,DE ,可得CD ;情况三:作DE CE ''⊥,计算,,DF DE CE '',可得CD .【详解】∵90ACB ︒∠=,4,2AC BC ==,∴AB =情况一:当AD AB ==AE CE ⊥于E∴ 1122BC AC AB AE ⋅=⋅,即455AE =,1455DE = ∴22855CE AC AE =-= ∴22213CD CE DE =+=情况二:当25BD AB ==时,作BE CE ⊥于E ,∴1122BC AC AB BE ⋅=⋅,即455BE =,1455DE = ∴22255CE BC BE =-= ∴22210CD CE DE =+=情况三:当AD BD =时,作DE CE ''⊥,作BE CE ⊥于E∴1122BC AC AB BE ⋅=⋅, ∴45BE =355CE ∴= ∵ABD △为等腰直角三角形∴152BF DF AB === ∴955DE DF E F DF BE ''=+=+= 2535555CE EE CE BF CE ''=-=-=-= ∴2232CD CE E D ''=+=故答案为:210或213或32【点睛】本题考查了等腰直角三角形的探索,勾股定理的计算等,熟知以上知识是解题的关键. 12.5【分析】作AD′⊥AD ,AD′=AD 构建等腰直角三角形,根据SAS 求证△BAD ≌△CAD′,证得BD=CD′,∠DAD′=90°,然后在Rt △AD′D 和Rt △CD′D 应用勾股定理即可求解.【详解】作AD′⊥AD ,AD′=AD ,连接CD′,DD′,如图:∵∠BAC+∠CAD=∠DAD′+∠CAD ,∴∠BAD=∠CAD′,在△BAD 与△CAD′中,{BAD CAD AD AD ∠=∠='',∴△BAD ≌△CAD′(SAS ),∴BD=CD′,∠DAD′=90°,由勾股定理得DD′=22()4AD AD +=',∵∠D′DA+∠ADC=90°,∴由勾股定理得CD′=22(')5DC DD +=,∴BD=CD′=5故答案为5.【点睛】本题考查了全等三角形的判定与性质,勾股定理,等腰直角三角形,正确引出辅助线构造等腰直角三角形是本题的关键.13.413【分析】延长AD 至点E ,使得DE =AD =4,结合D 是中点证得△ADC ≌△EDB ,进而利用勾股定理逆定理可证得∠E =90°,再利用勾股定理求得BD 长进而转化为BC 长即可.【详解】解:如图,延长AD 至点E ,使得DE =AD =4,连接BE ,∵D 是BC 边中点, ∴BD =CD ,又∵DE =AD ,∠ADC =∠EDB ,∴△ADC ≌△EDB (SAS ),∴BE =AC =6,又∵AB =10,∴AE 2+BE 2=AB 2,∴∠E =90°,∴在Rt △BED 中,222264213BD BE DE =++=,∴BC =2BD =13故答案为:13【点睛】本题考查了全等三角形的判定及性质、勾股定理及其逆定理,正确作出辅助线是解决本题14.6或2.【分析】由于已知没有图形,当Rt△ABC固定后,根据“以BC为斜边作等腰直角△BCD”可知分两种情况讨论:①当D点在BC上方时,如图1,把△ABD绕点D逆时针旋转90°得到△DCE,证明A、C、E三点共线,在等腰Rt△ADE中,利用勾股定理可求AD长;②当D点在BC下方时,如图2,把△BAD绕点D顺时针旋转90°得到△CED,证明过程类似于①求解.【详解】解:分两种情况讨论:①当D点在BC上方时,如图1所示,把△ABD绕点D逆时针旋转90°,得到△DCE,则∠ABD=∠ECD,CE=AB=22,AD=DE,且∠ADE=90°在四边形ACDB中,∠BAC+∠BDC=90°+90°=180°,∴∠ABD+∠ACD=360°-180°=180°,∴∠ACD+∠ECD=180°,∴A、C、E三点共线.∴AE=AC+CE=42+22=62在等腰Rt△ADE中,AD2+DE2=AE2,即2AD2=(62)2,解得AD=6②当D点在BC下方时,如图2所示,把△BAD绕点D顺时针旋转90°得到△CED,则2,∠BAD=∠CED,AD=AE且∠ADE=90°,所以∠EAD=∠AED=45°,∴∠BAD=90°+45°=135°,即∠CED=135°,∴∠CED+∠AED=180°,即A、E、C三点共线.∴222在等腰Rt△ADE中,2AD2=AE2=8,解得AD=2.故答案为:6或2.【点睛】本题主要考查了旋转的性质、勾股定理,解决这类等边(或共边)的两个三角形问题,一般是通过旋转的方式作辅助线,转化线段使得已知线段于一个特殊三角形中进行求解.15.7或29或65【分析】分三种情形讨论:(1)如图1中,以点C所在顶点为直角时;(2)如图2中,以点D所在顶点为直角时;(3)如图3中,以点A所在顶点为直角时.【详解】(1)如图1中,以点C所在顶点为直角时.∵AC=CD=4,BC=3,∴BD=CD+BC=7;(2)如图2中,以点D所在顶点为直角时,作DE⊥BC与E,连接BD.在Rt△BDE中DE=2,BE=5,∴BD2229=+=;DE BE(3)如图3中,以点A所在顶点为直角时,作DE⊥BC于E,在Rt△BDE中,DE=4.BE=7,∴BD2265=+=.DE BE故答案为:7或29或65.【点睛】本题考查了勾股定理、等腰直角三角形等知识,解题的关键是学会用分类讨论的思想思考问题.16.10【分析】先根据勾股定理得出a2+b2=c2,利用完全平方公式得到(a+b)2﹣2ab=c2,再将a+b=35,c=5代入即可求出ab的值.【详解】解:∵在Rt△ABC中,直角边的长分别为a,b,斜边长c,∴a2+b2=c2,∴(a+b)2﹣2ab=c2,∵a+b=35,c=5,∴(35)2﹣2ab=52,∴ab=10.故答案为10.【点睛】本题考查勾股定理以及完全平方公式,灵活运用完全平方公式是解题关键.17.3.【分析】作点B关于AD的对称点B′,过点B′作B′N⊥AB于N交AD于M,根据轴对称确定最短路线问题,B′N的长度即为BM+MN的最小值,根据∠BAC=60°判断出△ABB′是等边三角形,再根据等边三角形的性质求解即可.【详解】如图,作点B关于AD的对称点B′,由垂线段最短,过点B′作B′N⊥AB于N交AD于M,B′N最短,由轴对称性质,BM=B′M,∴BM+MN=B′M+MN=B′N,由轴对称的性质,AD垂直平分BB′,∴AB=AB′,∵∠BAC=60°,∴△ABB′是等边三角形,∵AB=2,∴B′N=即BM+MN ..【点睛】本题考查了轴对称确定最短路线问题,等边三角形的判定与性质,确定出点M 、N 的位置是解题的关键,作出图形更形象直观.18.485【解析】试题分析:根据等腰三角形的性质和勾股定理可知BC 边上的高为8,然后根据三角形的面积法可得111012822BD ⨯⨯=⨯⨯,解得BD=485. 19.3【分析】根据题意利用折叠后图形全等,并利用等量替换和等腰三角形的性质进行综合分析求解.【详解】解:由题意可知','ACM A CM BCH B CH ≅≅,∵15cm BC =,20cm AC =,∴'15,'20,BC B C cm AC A C cm ====''20155A B cm =-=,∵90ACB ∠=︒,∴'A M AB ⊥(等量替换),CH AB ⊥(三线合一),∴25,AB cm = 利用勾股定理假设MB '的长为m ,'257AM AM m ==-,则有222(257)5m m +-=,解得3m =,所以MB '的长为3.【点睛】本题考查几何的翻折问题,熟练掌握并综合利用等量替换和等腰三角形的性质以及勾股定理分析是解题的关键.20.32【分析】由题意设AM=2a ,BM=b ,则正方形ABCD 的面积=224a b +,由题意可知EF=(2a-b)-2(a-b)=2a-b-2a +2b=b ,由此分析即可.【详解】解:设AM=2a .BM=b .则正方形ABCD 的面积=224a b +由题意可知EF=(2a-b)-2(a-b)=2a-b-2a +2b=b ,∵AM EF ,2,,2a a ∴== ∵正方形EFGH 的面积为4,∴24b =,∴正方形ABCD 的面积=2224+832.a b b ==故答案为32.【点睛】本题考查正方形的性质、勾股定理以及线段的垂直平分线的定义等知识,解题的关键是灵活运用所学知识解决问题.三、解答题21.(1)423;(2)以a 、b 、c 为边能构成三角形,此三角形的形状是直角三角形,【分析】(1)根据二次根式的加减法法则、除法法则和二次根式的性质求出即可;(2)先根据绝对值,偶次方、算术平方根的非负性求出a 、b 、c 的值,再根据勾股定理的逆定理得出三角形是直角三角形,再求出面积即可.【详解】解:(1)⎛÷ ⎝=÷=÷ =423; (2)以a 、b 、c 为边能构成三角形,此三角形的形状是直角三角形,理由是:∵a 、b 、c 满足2|a (c 0-=,∴a ﹣=0,﹣b =0,c 0,∴a =,b =,c∵,,∴以a 、b 、c 为边能组成三角形,∵a =,b =,c∴a 2+b 2=c 2,∴以a 、b 、c 为边能构成直角三角形,直角边是a 和b ,则此三角形的面积是12⨯. 【点睛】 此题考查了计算能力,掌握二次根式的加减法法则、除法法则和二次根式的性质,绝对值,偶次方、算术平方根的非负性,勾股定理的逆定理是解题的关键.22.(1) 出发10s 后,△BMN 为等边三角形;(2)出发6s 或15s 后,△BMN 为直角三角形.【分析】(1)设时间为x ,表示出AM=x 、BN=2x 、BM=30-x ,根据等边三角形的判定列出方程,解之可得;(2)分两种情况:①∠BNM=90°时,即可知∠BMN=30°,依据BN=12BM 列方程求解可得;②∠BMN=90°时,知∠BNM=30°,依据BM=12BN 列方程求解可得. 【详解】解 (1)设经过x 秒,△BMN 为等边三角形,则AM =x ,BN =2x ,∴BM =AB -AM =30-x ,根据题意得30-x =2x ,解得x =10,答:经过10秒,△BMN 为等边三角形;(2)经过x 秒,△BMN 是直角三角形,①当∠BNM =90°时,∵∠B =60°,∴∠BMN =30°,∴BN =12BM ,即2x =12(30-x), 解得x =6;②当∠BMN =90°时,∵∠B =60°,∴∠BNM =30°,∴BM =12BN ,即30-x =12×2x , 解得x =15,答:经过6秒或15秒,△BMN 是直角三角形.【点睛】本题考查勾股定理的逆定理,等边三角形的判定.23.(1)①见解析;②DE =297;(2)DE 的值为 【分析】(1)①先证明∠DAE=∠DAF,结合DA=DA,AE=AF,即可证明;②如图1中,设DE=x,则CD=7﹣x.在Rt△DCF中,由DF2=CD2+CF2,CF=BE=3,可得x2=(7﹣x)2+32,解方程即可;(2)分两种情形:①当点E在线段BC上时,如图2中,连接BE.由△EAD≌△ADC,推出∠ABE=∠C=∠ABC=45°,EB=CD=5,推出∠EBD=90°,推出DE2=BE2+BD2=62+32=45,即可解决问题;②当点D在CB的延长线上时,如图3中,同法可得DE2=153.【详解】(1)①如图1中,∵将△ABE绕点A逆时针旋转90°后,得到△AFC,∴△BAE≌△CAF,∴AE=AF,∠BAE=∠CAF,∵∠BAC=90°,∠EAD=45°,∴∠CAD+∠BAE=∠CAD+∠CAF=45°,∴∠DAE=∠DAF,∵DA=DA,AE=AF,∴△AED≌△AFD(SAS);②如图1中,设DE=x,则CD=7﹣x.∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°,∵∠ABE=∠ACF=45°,∴∠DCF=90°,∵△AED≌△AFD(SAS),∴DE=DF=x,∵在Rt△DCF中, DF2=CD2+CF2,CF=BE=3,∴x2=(7﹣x)2+32,∴x=297,∴DE=297;(2)∵BD=3,BC=9,∴分两种情况如下:①当点E在线段BC上时,如图2中,连接BE.∵∠BAC=∠EAD=90°,∴∠EAB=∠DAC,∵AE=AD,AB=AC,∴△EAB≌△DAC(SAS),∴∠ABE=∠C=∠ABC=45°,EB=CD=9-3=6,∴∠EBD=90°,∴DE2=BE2+BD2=62+32=45,∴DE =35; ②当点D 在CB 的延长线上时,如图3中,连接BE .同理可证△DBE 是直角三角形,EB =CD =3+9=12,DB =3,∴DE 2=EB 2+BD 2=144+9=153,∴DE =317,综上所述,DE 的值为35或317.【点睛】本题主要考查旋转变换的性质,三角形全等的判定和性质以及勾股定理,添加辅助线,构造旋转全等模型,是解题的关键.24.(1)12;(2)t=12.5s 时,13 cm ;(3)11s 或12s 或13.2s【分析】 (1)由勾股定理即可得出结论;(2)由线段垂直平分线的性质得到PC = PA =t ,则PB =16-t .在Rt △BPC 中,由勾股定理可求得t 的值,判断出此时,点Q 在边AC 上,根据CQ =2t -BC 计算即可;(3)用t 分别表示出BQ 和CQ ,利用等腰三角形的性质可分BQ =BC 、CQ =BC 和BQ =CQ 三种情况,分别得到关于t 的方程,可求得t 的值.【详解】(1)在Rt △ABC 中,BC 2222212016AC AB =-=-=(cm ).故答案为:12;(2)如图,点P 在边AC 的垂直平分线上时,连接PC ,∴PC = PA =t ,PB =16-t . 在Rt △BPC 中,222BC BP CP +=,即2221216)t t +-=(, 解得:t =252. ∵Q 从B 到C 所需的时间为12÷2=6(s ),252>6, ∴此时,点Q 在边AC 上,CQ =25212132⨯-=(cm );(3)分三种情况讨论:①当CQ =BQ 时,如图1所示,则∠C =∠CBQ .∵∠ABC =90°,∴∠CBQ +∠ABQ =90°,∠A +∠C =90°,∴∠A =∠ABQ ,∴BQ =AQ ,∴CQ =AQ =10,∴BC +CQ =22,∴t =22÷2=11(s ).②当CQ =BC 时,如图2所示,则BC +CQ =24,∴t =24÷2=12(s ).③当BC =BQ 时,如图3所示,过B 点作BE ⊥AC 于点E ,则BE 121648205AB BC AC ⋅⨯===, ∴CE 2222483612()55BC BE =-=-==7.2.∵BC=BQ,BE⊥CQ,∴CQ=2CE=14.4,∴BC+CQ=26.4,∴t=26.4÷2=13.2(s).综上所述:当t为11s或12s或13.2s时,△BCQ为等腰三角形.【点睛】本题考查了勾股定理、等腰三角形的性质、方程思想及分类讨论思想等知识.用时间t表示出相应线段的长,化“动”为“静”是解决这类问题的一般思路,注意方程思想的应用.25.(1)CD=8;(2)t=4;(3)12-=tvt(26t≤<)【分析】(1)作AE⊥BC于E,根据等腰三角形三线合一的性质可得BE=12BC,然后利用勾股定理求出AE,再用等面积法可求出CD的长;(2)①过B作BF⊥AC于F,易得BF=CD,分别讨论Q点在AF和FC之间时,根据△BQF≌△CPD,得到PD=QF,建立方程即可求出t的值;(3)同(2)建立等式关系即可得出关系式,再根据Q在FC之间求出t的取值范围即可.【详解】解:(1)如图,作AE⊥BC于E,∵AB=AC,∴BE=12BC=25在Rt△ABE中,()2222AE=AB BE=1025=45--∵△ABC的面积=11BC AE=AB CD 22⋅⋅∴BC AE4545 CD==AB⋅⨯(2)过B作BQ⊥AC,当Q在AF之间时,如图所示,∵△ABC的面积=11AC BF=AB CD22⋅⋅,AB=AC∴BF=CD在Rt△CPD和Rt△BQF中∵CP=BQ,CD=BF,∴Rt△CPD≌Rt△BQF(HL)∴PD=QF在Rt△ACD中,CD=8,AC=AB=10∴22AD=AC CD=6-同理可得AF=6∴PD=AD=AP=6-t,QF=AF-AQ=6-2t由PD=QF得6-t=6-2t,解得t=0,∵t>0,∴此种情况不符合题意,舍去;当Q点在FC之间时,如图所示,此时PD=6-t,QF=2t-6由PD=QF得6-t=2t-6,解得t=4,综上得t的值为4.(3)同(2)可知v>1时,Q在AF之间不存在CP=BQ,Q在FC之间存在CP=BQ,Q在F 点时,显然CP≠BQ,∵运动时间为t,则AP=t,AQ=vt,∴PD=6-t,QF=vt-6,由PD=QF得6-t=vt-6,整理得12-=t v t , ∵Q 在FC 之间,即AF <AQ ≤AC ∴610<≤vt ,代入12-=t v t得 61210<-≤t ,解得26t ≤<所以答案为12-=t v t (26t ≤<) 【点睛】本题考查三角形中的动点问题,熟练掌握勾股定理求出等腰三角形的高,利用全等三角形对应边相等建立方程是解题的关键.26.(1)13,17,10,112;(2)图见解析;7. 【分析】(1)利用勾股定理求出AB ,BC ,AC ,理由分割法求出△ABC 的面积.(2)模仿(1)中方法,画出△PMN ,利用分割法求解即可.【详解】解:(1)如图1中,AB =22AE BE +=2232+=13,BC =22BD CD +=2214+=17,AC =22AF CF +=2213+=10,S △ABC =S 矩形DEFC ﹣S △AEB ﹣S △AFC ﹣S △BDC =12﹣3﹣32﹣2=112, 故答案为13,17,10,112. (2)△PMN 如图所示.S △PMN =4×4﹣2﹣3﹣4=7,故答案为7.【点睛】此题重点考查学生对勾股定理的应用,熟练掌握勾股定理是解题的关键.27.(1)(0,3);(2)DF OE =;(3)93233+【分析】(1)由等边三角形的性质得出6OB =,12AB AC BC ===,由勾股定理得出OA ==A 的坐标;(2)由等边三角形的性质得出AD AE =,AF AO =,60FAO DAE ∠=∠=︒,证出FAD OAE ∠=∠,由SAS 证明FAD OAE ∆≅∆,即可得出DF OE =;(3)证出90AGO ∠=︒,求出9AG =,由全等三角形的性质得出AOE AFD ∠=∠,证出6090FDO AFD AOD ∠=∠+︒+∠=︒,由等边三角形的性质得12DG OF ==即可得出答案.【详解】解:(1)ABC ∆是等边三角形,点0()6,B -,点(6,0)C ,6OB ∴=,12AB AC BC ===,OA === ∴点A 的坐标为(0,;(2)DF OE =;理由如下:ADE ∆,AFO ∆均为等边三角形,AD AE ∴=,AF AO =,60FAO DAE ∠=∠=︒,FAD OAE ∴∠=∠,在FAD ∆和OAE ∆中,AF AO FAD OAE AD AE =⎧⎪∠=∠⎨⎪=⎩,()FAD OAE SAS ∴∆≅∆,DF OE ∴=;(3)60AOF ∠=︒,30FOB ∴∠=︒,60ABO ∠=︒,90AGO ∴∠=︒,AFO ∆是等边三角形,AO =·sin 609AG OA ∴=︒==, FAD OAE ∆≅∆,AOE AFD ∴∠=∠,30DOE AOD AOE ∠=︒=∠+∠,30AOD AFD ∴∠+∠=︒,FDO AFD FAO AOD ∠=∠+∠+∠,60603090FDO AFD AOD ∴∠=∠+︒+∠=︒+︒=︒,AG OF ⊥,AOF ∆为等边三角形,G ∴为斜边OF 的中点,1122DG OF ∴==⨯=ADG ∴∆的周长9AG AD DG =++=+【点睛】本题是三角形综合题目,考查了等边三角形的性质、勾股定理、坐标与图形性质、全等三角形的判定与性质、三角函数等知识;本题综合性强,有一定难度,熟练掌握等边三角形的性质,证明三角形全等是解题的关键.28.(1)13,5;(2)等腰直角三角形,理由见解析;(3)当P 的坐标为(1304,)时,PD+PF【解析】【分析】(1)根据阅读材料中A 和B 的坐标,利用两点间的距离公式即可得出答案;由于M 、N 在平行于y 轴的直线上,根据M 和N 的纵坐标利用公式1|y -2|y 即可求出MN 的距离; (2)由三个顶点的坐标分别求出DE ,DF ,EF 的长,即可判定此三角形的形状;(3)作F 关于x 轴的对称点F',连接DF',与x 轴交于点P ,此时PD PF +最短,最短距离为DF',P 的坐标即为直线DF'与x 轴的交点.【详解】解:(1)∵()2, 4A 、()3, 8B --∴AB 13==故A 、B 两点间的距离为:13.∵M 、N 在平行于y 轴的直线上,点M 的纵坐标为4,点N 的纵坐标为-1∴()MN 415=--=故M 、N 两点的距离为5.(2)∵()1, 6D 、()3, 3E -、()4, 2F∴DE 5==DF 5==EF ==∴DE=DF ,222DE DF EF +=∴△DEF 为等腰直角三角形(3)作F 关于x 轴的对称点F',连接DF',与x 轴交于点P ,此时DP+PF 最短设直线DF'的解析式为y=kx+b将D (1,6),F'(4,-2)代入得:642k b k b +=⎧⎨+=-⎩ 解得83263k b ⎧=-⎪⎪⎨⎪=⎪⎩∴直线DF'的解析式为:826y 33x =-+ 令y=0,解得13x 4=,即P 的坐标为(1304,) ∵PF=PF'∴PD+PF=PD+ PF'= DF'()()22146273-++=故当P 的坐标为(1304,)时,PD+PF 73 【点睛】本题属于一次函数综合题,待定系数法求一次函数解析式以及一次函数与x 轴的交点,弄清楚材料中的距离公式是解决本题的关键.29.(1)证明见解析;(2)AF =5cm ;(3)①有可能是矩形,P 点运动的时间是8,Q 的速度是0.5cm /s ;②t =203. 【解析】【分析】(1)证△AEO ≌△CFO ,推出OE=OF ,根据平行四边形和菱形的判定推出即可; (2)设AF=CF=a ,根据勾股定理得出关于a 的方程,求出即可;(3)①只有当P 运动到B 点,Q 运动到D 点时,以A 、P 、C 、Q 四点为顶点的四边形有可能是矩形,求出时间t ,即可求出答案;②分为三种情况,P 在AF 上,P 在BF 上,P 在AB 上,根据平行四边形的性质求出即可.【详解】(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠AEO=∠CFO,∵AC的垂直平分线EF,∴AO=OC,AC⊥EF,在△AEO和△CFO中∵AEO CFOAOE COF AO OC∠∠⎧⎪∠∠⎨⎪⎩===,∴△AEO≌△CFO(AAS),∴OE=OF,∵OA=OC,∴四边形AECF是平行四边形,∵AC⊥EF,∴平行四边形AECF是菱形;(2)解:设AF=acm,∵四边形AECF是菱形,∴AF=CF=acm,∵BC=8cm,∴BF=(8﹣a)cm,在Rt△ABF中,由勾股定理得:42+(8﹣a)2=a2,a=5,即AF=5cm;(3)解:①在运动过程中,以A、P、C、Q四点为顶点的四边形有可能是矩形,只有当P运动到B点,Q运动到D点时,以A、P、C、Q四点为顶点的四边形有可能是矩形,P点运动的时间是:(5+3)÷1=8,Q的速度是:4÷8=0.5,即Q的速度是0.5cm/s;②分为三种情况:第一、P在AF上,∵P的速度是1cm/s,而Q的速度是0.8cm/s,∴Q只能再CD上,此时当A、P、C、Q四点为顶点的四边形不是平行四边形;第二、当P在BF上时,Q在CD或DE上,只有当Q在DE上时,当A、P、C、Q四点为顶点的四边形才有可能是平行四边形,如图,∵AQ=8﹣(0.8t﹣4),CP=5+(t﹣5),∴8﹣(0.8t﹣4)=5+(t﹣5),t=203,第三情况:当P在AB上时,Q在DE或CE上,此时当A、P、C、Q四点为顶点的四边形不。
八年级(下)月考数学试卷(3月份)

八年级(下)月考数学试卷(3月份)一、选择题(每题3分,共30分)1.(3分)若在实数范围内有意义,则x的取值范围为()A.x≥0B.x≤0C.x=0D.x为任意实数2.(3分)△ABC三边为a、b、C,下列条件不能判定△ABC是直角三角形的是()A.a=,b=2,c=B.a=3,b=4,c=5C.b2=a2﹣c2D.∠A:∠B:∠C=1:2:33.(3分)下列二次根式中,化简后不能与进行合并的是()A.B.C.D.4.(3分)若平行四边形中两个内角的度数比为1:2,则其中较小的内角是()A.60°B.90°C.120°D.45°5.(3分)下列各命题的逆命题成立的是()A.两条直线平行,同位角相等B.如果两个实数相等,那么它们的绝对值相等C.等边三角形是锐角三角形D.全等三角形的对应角相等6.(3分)点D、E、F分别为△ABC三边的中点,若△DEF的周长为3,则△ABC的周长为()A.12B.9C.6D.1.57.(3分)甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B,若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是()A.北偏西30°B.南偏西30°C.南偏东60°D.南偏西60°8.(3分)如图,Rt△ABC中,∠C=90°,D为AB中点,E为BC上一点,且CE=2BE =2DE=6.则AB的长为()A.12B.6C.6D.39.(3分)如图,长方体的长宽高分别是3、4、2,一只蚂蚁要沿着长方体的外表面从A点爬到B点,最短路径长为()A.5B.C.3D.10.(3分)如图,△ABC为等腰直角三角形,∠ACB=90°.若∠AOB=45°,则OA、OB、OC之间满足()A.OA2+OB2=OC2B.OA2+OB2=2OC2C.OA2+OB2+OA•OB=2OC2D.OA2+OB2+OA•OB=2OC2二、填空题(每题3分,共18分)11.(3分)=;(3)2=;=.12.(3分)一个三角形的三边长为5、、,则该三角形的面积为.13.(3分)如图,E、F是▱ABCD对角线BD上的两点,请你添加一个适当的条件:,使四边形AECF是平行四边形.14.(3分)E为▱ABCD边AD上一点,将△ABE沿BE翻折得到△FBE,点F在BD上,且EF=DF.若∠C=52°,那么∠ABE=.15.(3分)A(3,4)是平面直角坐标系第一象限内一点,B为x轴正半轴上一点,若△AOB 为等腰三角形,则B点坐标为.16.(3分)如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=4.P为BC边上一点,以AP为边在右侧构造等边△APD.连接BD,Q为BD中点,则P点从C点运动到B点的过程中,Q点的运动路径长为.三、解答题(共72分)17.(8分)(1)计算(﹣)﹣(+);(2)(﹣)×.18.(8分)先化简再求值:,其中x=.19.(8分)如图,Rt△ABC中,∠C=90°(1)若AB=,AC=,求BC2(2)若AB=4,AC=1,求AB边上高.20.(8分)▱ABCD中,BD是对角线,CE⊥CD交BD于E点,AF⊥AB交BD于F点,连接AE、CF.求证:四边形AECF是平行四边形.21.(8分)按要求仅用无刻度的直尺作图,不要求写作法,但要保留作图痕迹.(1)如图1,正方形网格中的每个小正方形边长都为1,以格点A为顶点画一个△ABC,使其三边长分别为AB=,AC=,BC=;(2)在▱ABCD中,点E在BC边上,AB=BE,BF平分∠ABC交AD于点F.①在图2中,过点A画出△ABF的BF边上的高AG;②在图3中,过点C画出C到BF的垂线段CH.22.(10分)如图,在平行四边形ABCD中,AC、BD相交于O,OE⊥AC交CD于E点.(1)求证:OA平分∠BAE;(2)若平行四边形ABCD的周长为20,求△ADE的周长.23.(10分)如图,等腰Rt△ABD中,AB=AD,点M为边AD上一动点,点E在DA的延长线上,且AM=AE,以BE为直角边,向外作等腰Rt△BEG,MG交AB于N,连NE、DN.(1)求证:∠BEN=∠BGN.(2)求的值.(3)当M在AD上运动时,探究四边形BDNG的形状,并证明之.24.(12分)如图所示,在平面直角坐标系中A(a,0),B(b,0),D(0,d),以AB,AD 为邻边作平行四边形ABCD,其中a,b,d满足.(1)直接写出C点坐标;(2)如图2,线段BC的垂直平分线交y轴于点E,F为AD的中点,试判断∠EFB的大小,并说明理由;(3)如图3,点E(,0),F为x轴上的一点,∠ECF=45°,求F点的坐标.。
八年级数学第二学期3月份月考测试卷含答案

八年级数学第二学期3月份月考测试卷含答案一、选择题1.下列计算正确的是( )A =B .3=C 2=D2.a 的值可能是( ) A .2-B .2C .32D .83.下列各式成立的是( )A 3=B 3=C .22(3=- D .2-=4.下列二次根式中,是最简二次根式的是( )ABC .D5.化简 )ABC D6.化简二次根式 )A B C D 7.若化简1682+-x x -1x -的结果为5-2x ,则x 的取值范围是( ) A .为任意实数B .1≤x≤4C .x≥1D .x≤48.已知实数x ,y 满足(x y )=2008,则3x 2-2y 2+3x -3y -2007的值为( ) A .-2008 B .2008C .-1D .19.有意义,则实数m 的取值范围是( )A .m >﹣2B .m >﹣2且m ≠1C .m ≥﹣2D .m ≥﹣2且m ≠110.m 的值为( ) A .7B .11C .2D .111.已知实数x 、y 满足2y =,则yx 值是( )A .﹣2B .4C .﹣4D .无法确定12.下面计算正确的是( )A .BCD 2-二、填空题13.化简并计算:()()()()()()()1111...112231920xx x x x x x x ++++=+++++++________.(结果中分母不含根式)14.设四边形ABCD 是边长为1的正方形,以对角线AC 为边作第二个正方形ACEF ,再以对角线AE 为边作第二个正方形AEGH ,如此下去…….⑴记正方形ABCD 的边长为11a =,按上述方法所作的正方形的边长依次为234,,,,n a a a a ,请求出234,,a a a 的值;⑵根据以上规律写出n a 的表达式.15.实数a ,b 在数轴上的位置如图所示,则化简()22b a b +-﹣|a +b |的结果是_____.16.甲容器中装有浓度为a 40kg ,乙容器中装有浓度为b 90kg ,两个容器都倒出m kg ,把甲容器倒出的果汁混入乙容器,把乙容器倒出的果汁混入甲容器,混合后,两容器内的果汁浓度相同,则m 的值为_________. 17.已知实数m 、n 、p 满足等式33352m n m n m n p m n p -+--+----,则p =__________.18.使式子32xx -+有意义的x 的取值范围是______. 19.若a 、b 为实数,且b 2211a a -+-+4,则a+b =_____. 20.4x -x 的取值范围是_____. 三、解答题21.先阅读下列解答过程,然后再解答:2m n +,a b ,使a b m +=,ab n =,使得22m+====>a b)+=⨯=,==,由于437,43127,12m n+=,=即:2272===+。
八年级第二学期3月份月考数学试卷含解析

八年级第二学期3月份月考数学试卷含解析一、选择题1.下列计算正确的是( ) A .()25-=﹣5 B .4y =2y C .822aaa=D .235+=2.下列运算正确的是( ) A .732-= B .()255-=-C .1232÷=D .03812+=3.下列各式中,运算正确的是( )A .32222-=B .8383-=-C .2323+=D .()222-=-4.下列各式一定成立的是( ) A .2()a b a b +=+ B .222(1)1a a +=+ C .22(1)1a a -=-D .2()ab ab =5.若2()a b a b -=--则( ) A .0a b +=B .0a b -=C .0ab =D .220a b +=6.下列计算正确的是( ) A .531883+= B .()322326a ba b -=-C .222()a b a b -=- D .2422a ab a a b a -+⋅=-++7.若ab <0,则代数式可化简为( ) A .aB .aC .﹣aD .﹣a8.下列各式计算正确的是( ) A 235+=B .236=()C 824=D 236=9.下列运算一定正确的是( ) A 2a a =B ab a b =C .222()a b a b ⋅=⋅D ()0n mnaa m=≥ 10.下列各式计算正确的是( ) A .233= B ()255-=± C 523=D .3223=11.下列根式中是最简二次根式的是( ) A 23B 10C 9D 3a 12.3x -在实数范围内有意义,则x 的取值范围是( )A .x >0B .x >3C .x ≥3D .x ≤3二、填空题13.实数a 、b 满足22a -4a 436-12a a 10-b 4-b-2+++=+,则22a b +的最大值为_________.14.甲容器中装有浓度为a 的果汁40kg ,乙容器中装有浓度为b 的果汁90kg ,两个容器都倒出m kg ,把甲容器倒出的果汁混入乙容器,把乙容器倒出的果汁混入甲容器,混合后,两容器内的果汁浓度相同,则m 的值为_________. 15.已知a =﹣73+,则代数式a 3+5a 2﹣4a ﹣6的值为_____. 16.已知72x =-,a 是x 的整数部分,b 是x 的小数部分,则a-b=_______ 17.已知120654010144152118+++可写成235a b c ++的形式(,,a b c 为正整数),则abc =______.18.将1、2、3、6按右侧方式排列.若规定(m ,n )表示第m 排从左向右第n 个数,则(5,4)与(9,4)表示的两数之积是______.19.计算:652015·652016=________. 20.36,3,2315,,则第100个数是_______.三、解答题21.计算及解方程组: (11324-2-1-26() (2)262-153-2+(3)解方程组:251032x y x y x y -=⎧⎪+-⎨=⎪⎩【答案】(1)2)7;(3)102x y =⎧⎨=⎩.【分析】(1)首先化简绝对值,然后根据二次根式乘法、加减法法则运算即可; (2)首先根据完全平方公式化简,然后根据二次根式加减法法则运算即可; (3)首先将第二个方程化简,然后利用加减消元法即可求解. 【详解】(11-1+(11=1(22+)=34-=7-=7-(3)251032x y x y x y-=⎧⎪⎨+-=⎪⎩①②由②得:50x y -= ③ ②-③得: 10x = 把x=10代入①得:y=2∴原方程组的解是:102x y =⎧⎨=⎩【点睛】本题考查了二次根式的混合运算,加减消元法解二元一次方程,熟练掌握二次根式的运算法则是本题的关键.22.若x ,y 为实数,且y12.求x y y x ++2-xy y x +-2的值.【分析】根据二次根式的性质,被开方数大于等于0可知:1﹣4x ≥0且4x ﹣1≥0,解得x =14,此时y =12.即可代入求解. 【详解】解:要使y 有意义,必须140410x x -≥⎧⎨-≤⎩,即1414x x ⎧≤⎪⎪⎨⎪≥⎪⎩∴ x =14.当x =14时,y =12.又∵x y y x ++2-x yy x +-2=-| ∵x =14,y =12,∴ x y <y x.∴+当x =14,y =12时,原式=.【点睛】(a ≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.23.先阅读材料,再回答问题:因为)111=1=;因为1=,所以=1== (1=,= ; (2⋅⋅⋅+的值. 【答案】(12)9 【分析】(1)仿照例子,由1+=的值;由1+=1的值;(2)根据(1)中的规律可将每个二次根式分母有理化,可转化为实数的加减法运算,再寻求规律可得答案. 【详解】解:(1)因为1-=;因为1=1(2⋅⋅⋅+1=+⋅⋅⋅1=1019=-=.【点睛】本题考查了分母有理化,分子分母都乘以分母这两个数的差进行分母有理化是解题关键.24.(112===;……写出④ ;⑤ ;(2)归纳与猜想.如果n 为正整数,用含n 的式子表示这个运算规律; (3)证明这个猜想.【答案】(12=55==;(2=3)证明见解析. 【解析】 【分析】(1)根据题目中的例子直接写出结果; (2)根据(1)中的特例,可以写出相应的猜想;(3)根据(2)中的猜想,对等号左边的式子进行化简,即可得到等号右边的式子,从而可以解答本题. 【详解】解:(1)由例子可得,④5=25,6,(2)如果n 为正整数,用含nn, (3)证明:∵n 是正整数,n .n.故答案为5=25 n;(3)证明见解析. 【点睛】本题考查了二次根式的混合运算、数字的变化类,解答本题的关键是明确题意,找出所求问题需要的条件.25.观察下列等式:1==;==== 回答下列问题:(1(2)计算:【答案】(1(2)9 【分析】(1)根据已知的31=-n=22代入即可求解;(2)先利用上题的规律将每一个分数化为两个二次根式的差的形式,再计算即可. 【详解】解:(1=(2+99+=1100++-=1 =10-1 =9.26.计算:(1)11(2【答案】(12+;(2)【分析】(1)根据二次根式的加减法法则和乘除法法则进行计算,注意运算顺序与实数的混合运算顺序相同;(2)根据二次根式的加减法法则和乘除法法则进行计算,注意运算顺序与实数的混合运算顺序相同. 【详解】解:)1131-=2==【点睛】本题考查了二次根式的混合运算,二次根式的混合运算顺序与实数的混合运算顺序一样,先乘方,再乘除,最后加减,有括号时要先算括号里的或先去括号.27.一样的式子,其实我==3==,1===;以上这种化简的步骤叫做分母有理化还可以用以下方法化简:221111===-=(12)化简:2n+++【答案】(1-2.【解析】试题分析:(12看出5-3,根据平方差公式分解因式,最后进进约分即可.(2)先每一个二次根式分母有理化,再分母不变,分子相加,最后合并即可.试题解析:(1)=====(2)原式=122n++++=12.考点:分母有理化.28.(1)已知a2+b2=6,ab=1,求a﹣b的值;(2)已知b=,求a2+b2的值.【答案】(1)±2;(2)2.【分析】(1)先根据完全平方公式进行变形,再代入求出即可;(2)先分母有理化,再根据完全平方公式和平方差公式即可求解.【详解】(1)由a2+b2=6,ab=1,得a2+b2-2ab=4,(a-b)2=4,a-b=±2.(2)a ===b ===2222()22312a b a b ab +=+-=-=-=⎝⎭ 【点睛】本题考查了分母有理化、完全平方公式的应用,能灵活运用公式进行变形是解此题的关键.29.已知a,b(1)求a 2﹣b 2的值; (2)求b a +ab的值. 【答案】(1);(2)10 【分析】(1)先计算出a+b 、a-b 的值,然后将所求的式子因式分解后利用整体代入思想代入数值进行计算即可;(2)先计算ab 的值,然后将所求的式子通分,分子进行变形后利用整体代入思想代入相关数值进行计算即可. 【详解】(1)∵ab, ∴a +ba ﹣b=, ∴a 2﹣b 2=(a +b )(a ﹣b )==; (2)∵ab, ∴ab =)×)=3﹣2=1,则原式=22b a ab +=()22a b ab ab +-=(2211-⨯=10. 【点睛】本题考查了二次根式的化简求值,熟练掌握整体代入思想是解题的关键.30.化简求值:212(1)211x x x x -÷-+++,其中1x =.【答案】3【解析】分析:先把小括号内的通分,按照分式的减法和分式除法法则进行化简,再把字母的值代入运算即可. 详解:原式2112,2111x x x x x x -+⎛⎫=÷- ⎪++++⎝⎭2112,211x x x x x -+-=÷+++()211,11x x x x -+=⋅-+ 1.1x =+当1x =时,11x ==+ 点睛:考查分式的混合运算,掌握运算顺序是解题的关键.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】根据二次根式的性质对A 、B 进行判断;利用分母有理化对C 进行判断;利用二次根式的加减法对D 进行判断. 【详解】解:A 、原式=5,所以A 选项错误;B 、原式=,所以B 选项错误;Ca =,所以C 选项正确;D D 选项错误. 故选:C . 【点睛】本题主要考查了二次根式的性质以及合并同类项法则,正确化简各式是解题的关键.2.C【分析】由二次根式的性质,二次根式的混合运算,分别进行计算,即可得到答案.【详解】解:A A错误;B5=,故B错误;C2==,故C正确;D01213=+=,故D错误;故选:C.【点睛】本题考查了二次根式的性质,二次根式的混合运算,立方根,零指数幂,解题的关键是熟练掌握运算法则进行解题.3.A解析:A【分析】由合并同类项、二次根式的性质分别进行判断,即可得到答案.【详解】解:A、-=A正确;B=B错误;C、2不能合并,故C错误;D2=,故D错误;故选:A.【点睛】本题考查了二次根式的性质,合并同类项,解题的关键是熟练掌握运算法则进行解题.4.B解析:B【分析】分别利用二次根式的性质化简求出即可.【详解】解;A2=|a+b|,故此选项错误;B2+1,正确;C,无法化简,故此选项错误;D,故此选项错误;故选:B.本题考查了二次根式的性质与化简,正确掌握二次根式的性质是解题的关键.5.C解析:C【分析】直接利用二次根式的性质 ,将已知等式左边化简,可以得到a 与b 中至少有一个为0,进而分析得出答案即可.【详解】 解:∵ 2()a b a b -=--,∴a-b=-a-b , 或b-a=-a-b∴a= -a ,或b=-b, ∴a=0,或b=0, ∴ab=0, ∴0ab =.故选:C .【点睛】本题考查了二次根式的性质与化简,正确掌握二次根式的性质是解题的关键.6.D解析:D【分析】分别运用二次根式、整式的运算、分式的运算法则逐项排除即可.【详解】解:A. 53183253+=+,故A 选项错误;B. ()()()33322363228a b a b a b -=-=-,故B 选项错误;C. 222()2a b a ab b -=-+,故C 选项错误;D. ()()2224222a a a ab a b a a b a a b a +--++⋅=⋅=-++++,故D 选项正确. 故答案为D .【点睛】本题考查了二次根式、整式的运算、分式的运算,掌握相关运算法则是解答本题的关键.7.C解析:C【解析】【分析】二次根式有意义,就隐含条件b <0,由ab <0,先判断出a 、b 的符号,再进行化简即可.【详解】解:若ab <0,且代数式有意义; 故由b >0,a <0;则代数式故选:C .本题主要考查二次根式的化简方法与运用:当a>0时,,当a<0时,,当a=0时,.8.D解析:D【分析】根据二次根式的运算法则一一判断即可.【详解】A23B、错误,22312=();C8222232==D23236=⨯=故选:D.【点睛】本题考查二次根式的运算,解题的关键是熟练掌握二次根式的加减乘除运算法则,属于中考常考题型.9.C解析:C【分析】直接利用二次根式的性质与化简以及积的乘方运算法则分别计算即可得出答案.【详解】A2a|a|,故此选项错误;B.ab a b,则a,b均为非负数,故此选项错误;C.a2•b2=(a•b)2,正确;D n ma m n a(a≥0),故此选项错误.故选C.【点睛】本题主要考查了二次根式的性质与化简以及积的乘方运算,正确掌握相关运算法则是解题的关键.10.A解析:A【分析】根据二次根式的性质和运算法则逐一计算可得.【详解】A、233=此选项计算正确,符合题意;B、5=此选项计算错误,不符合题意;C-不是同类二次根式,不能合并,此选项计算错误,不符合题意;D、-=故选:A.【点睛】本题主要考查了利用二次根式的性质化简以及二次根式的加减运算,准确利用二次根式的性质计算是解题的关键.11.B解析:B【分析】根据最简二次根式的条件:①根号下不含能开得尽方的因数或因式;②根号下不含分母,据此逐项判断即可.【详解】解:A、被开方数含分母,故A不符合题意;B、被开方数不含分母;被开方数不含能开得尽方的因数或因式.,故B符合题意;C被开方数含能开得尽方的因数或因式,故C不符合题意;D、被开方数含能开得尽方的因数或因式,故D不符合题意;故选:B.【点睛】本题考查了最简二次根式,解题的关键是掌握最简二次根式的两个条件.12.C解析:C【详解】解:根据题意得:x-3≥0解得:x≥3故选C.二、填空题13.【分析】首先化简,可得|a-2|+|a-6|+|b+4|+|b-2|=10,然后根据|a-2|+|a-6|≥4,|b+4|+|b-2|≥6,判断出a,b的取值范围,即可求出的最大值.【详解】解析:【分析】=+,可得|a-2|+|a-6|+|b+4|+|b-10-b4-b-22|=10,然后根据|a-2|+|a-6|≥4,|b+4|+|b-2|≥6,判断出a,b的取值范围,即可求出22+的最大值.a b【详解】10-b 4-b-2=+,1042b b =-+--, ∴261042a a b b -+-=-+--, ∴264210a a b b -+-+++-=,∵264a a -+-≥,426b b ++-≥,∴ 264a a -+-=,42=6b b ++-,∴2≤a≤6,-4≤b≤2,∴22a b +的最大值为()226452+-=,故答案为52.【点睛】本题考查了二次根式的性质与化简,绝对值的意义,算术平方根的性质.解题的关键是要明确化简二次根式的步骤:①把被开方数分解因式;②利用算术平方根的性质,把被开方数中能开得尽方的因数(或因式)都开出来;③化简后的二次根式中的被开方数中每一个因数(或因式)的指数都小于根指数2. 14.【分析】分别求出甲,乙容器中原溶液中纯果汁的含量,再求出mkg 溶液中纯果汁的含量,最后利用混合后果汁的浓度相等列出关系式,求出m 即可.【详解】解:根据题意,甲容器中纯果汁含量为akg ,乙容器【分析】分别求出甲,乙容器中原溶液中纯果汁的含量,再求出mkg 溶液中纯果汁的含量,最后利=,求出m 即可. 【详解】, 甲容器倒出mkg 果汁中含有纯果汁makg ,乙容器倒出mkg 果汁中含有纯果汁mbkg ,,=,整理得,-6b=5ma-5mb,∴(a-b)=5m(a-b),∴m=.5故答案为:5【点睛】本题考查二次根式的应用,能够正确理解题意,化简二次根式是解题的关键.15.-4【分析】先将a进行化简,然后再进一步分组分解代数式,最后代入求得答案即可. 【详解】解:当a=-=-=-3时,原式=a3+6a2+9a-(a2+6a+9)-7a+3=a(a+3)2-(解析:-4【分析】先将a进行化简,然后再进一步分组分解代数式,最后代入求得答案即可.【详解】-3时,解:当a原式=a3+6a2+9a-(a2+6a+9)-7a+3=a(a+3)2-(a+3)2-7a+3=7a-7-7a+3=-4.故答案为:-4.【点睛】本题综合运用了二次根式的化简,提公因式及完全平方公式法分解因式,熟练掌握分母有理化的方法及因式分解的方法是解题的关键.16.【分析】先把x分母有理化求出x= ,求出a、b的值,再代入求出结果即可.【详解】∵∴∴∴【点睛】本题考查了分母有理化和估算无理数的大小的应用,解此题的关键是求a 、b 的值.解析:6【分析】先把x 分母有理化求出2 ,求出a 、b 的值,再代入求出结果即可.【详解】2x === ∵23<<∴425<< ∴4,242a b ==-=∴42)6a b -=-=【点睛】本题考查了分母有理化和估算无理数的大小的应用,解此题的关键是求a 、b 的值.17.【解析】【分析】根据题意,可得到=,利用平方关系把根号去掉,根据、、的系数相等的关系得到关于a ,b ,c 的三元方程组,解方程组即可.【详解】∵=∴,即.解得.【点睛】本题考查了解析:【解析】【分析】a ,b ,c 的三元方程组,解方程组即可.【详解】∴(22118=,即2222118235a b c =+++++. 2222352118,2120,2540,2144,a b c ab ac bc ⎧++=⎪=⎪∴⎨=⎪⎪=⎩ 解得15,4,18.a b c =⎧⎪=⎨⎪=⎩154181080abc ∴=⨯⨯=.【点睛】本题考查了二次根式的加减,解本题的关键是将等式平方去根号,利用等量关系中等式左、.18.【解析】试题解析:(5,4)表示第5排从左向右第4个数是:,(9,4)表示第9排从左向右第4个数,可以看出奇数排最中间的一个数都是1,第9排是奇数排,最中间的也就是这排的第5个数是1,那么第解析:【解析】试题解析:(5,4)表示第5排从左向右第4,(9,4)表示第9排从左向右第4个数,可以看出奇数排最中间的一个数都是1, 第9排是奇数排,最中间的也就是这排的第5个数是1,那么第4, ∴(5,4)与(9,4)故答案为19.【解析】原式=.故答案为.【解析】原式=20152015=20.【分析】原来的一列数即为,,,,,,于是可得第n个数是,进而可得答案.【详解】解:原来的一列数即为:,,,,,,∴第100个数是.故答案为:.【点睛】本题考查了数的规律探求,属于常考解析:【分析】,,于是可得第n进而可得答案.【详解】,∴第100=.故答案为:【点睛】本题考查了数的规律探求,属于常考题型,熟练掌握二次根式的性质、找到规律是解题的关键.三、解答题21.无22.无23.无24.无25.无26.无27.无28.无29.无30.无。
八年级第二学期3月份月考数学试卷含解析

一、选择题1.如果0,0a b <<,且6a b -= )A .6B .6-C .6或6-D .无法确定 2.下列计算,正确的是( )A .=B .=C .0=D .10=3.若2a <3=( ) A .5a - B .5a -C .1a -D .1a -- 4.下列各式计算正确的是( )A =B .2=C =D =5.下列计算正确的是( )A 2=±B 3=-C .(25=D .(23=-6.下列计算结果正确的是( )A B .3=C =D =7.下列运算正确的是( )A =B =C .3=D 2=8.1在3和4中x 的取值范围是1x ≥-;③3;④5=-58>.其中正确的个数为( ) A .1个 B .2个 C .3个 D .4个9.a 的值是( )A .2B .-1C .3D .-1或310.下列运算一定正确的是( )A a =B =C .222()a b a b ⋅=⋅D ()0n a m=≥ 二、填空题11.已知a ,b 是正整数,且满足是整数,则这样的有序数对(a ,b )共有____对.12.化简并计算:...+=________.(结果中分母不含根式)13.732x y -=-,则2x ﹣18y 2=_____.14.)30m -≤,若整数a 满足m a +=a =__________.15.若2x ﹣x 2﹣x=_____.16.已知,n=1的值________.17.若0xy >,则二次根式________.18.已知x ,y 为实数,y 求5x +6y 的值________.19.mn =________.20.下列各式:③4是最简二次根式的是:_____(填序号) 三、解答题21.已知1,2y =. 【答案】1【解析】【分析】根据已知和二次根式的性质求出x 、y 的值,把原式根据二次根式的性质进行化简,把x 、y 的值代入化简后的式子计算即可.【详解】1-8x≥0,x≤18 8x-1≥0,x≥18,∴x=18,y=12,∴原式532-==1222. 【点睛】本题考查的是二次根式的化简求值,把已知条件求出x 、y ,把要求的代数式进行正确变形是解题的关键,注意因式分解在化简中的应用.22.先将2x-x的值,代入后,求式子的值.【答案】答案见解析.【解析】试题分析:先把除式化为最简二次根式,再用二次根式的乘法法则化简,选取的x的值需要使原式有意义.试题解析:原式====要使原式有意义,则x>2.所以本题答案不唯一,如取x=4.则原式=223.小明在解决问题:已知2a2﹣8a+1的值,他是这样分析与解的:∵=2∴a﹣2=∴(a﹣2)2=3,a2﹣4a+4=3∴a2﹣4a=﹣1∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1请你根据小明的分析过程,解决如下问题:(1(2)若,求4a2﹣8a+1的值.【答案】(1)9;(2)5.【解析】试题分析:(1)此式必须在把分母有理化后才能实现化简,即各分式分子分母同乘以一个因式,使得1===.(2)先对a1,若就接着代入求解,计算量偏大.模仿小明做法,可先计算2(1)a-的值,就能较为简单地算出结果;也可对这个二次三项式进行配方,再代入求值.后两种方法都比直接代入计算量小很多.解:(1)原式=(21)(32+43++10099-+--⋯-)()) =100-1=10-1=9(2)∵212121(21)(21)a +===+--+, 解法一:∵22(1)(211)2a -=+-= ,∴2212a a -+= ,即221a a -=∴原式=24(2)14115a a -+=⨯+=解法二∴ 原式=24(211)1a a -+-+24(1)3a =--24(211)3=+--4235=⨯-=点睛:(1)把分母+a b 有理化的方法:分子分母同乘以分母的有理化因式a b -, 得22()()()()+-=-=-a b a b a b a b ,去掉根号,实现分母有理化.(2)当已知量为根式时,求这类二次三项式的值,直接代入求值,计算量偏大,若能巧妙利用完全平方公式或者配方法,计算要简便得多.24.先化简,再求值:a+212a a -+,其中a =1007.如图是小亮和小芳的解答过程.(1) 的解法是错误的;(2)错误的原因在于未能正确地运用二次根式的性质: ;(3)先化简,再求值:269a a -+a =﹣2018.【答案】(1)小亮(22a (a <0)(3)2013.【解析】试题分析:(12a ,判断出小亮的计算是错误的;(22a 的应用错误;(3)先根据配方法把被开方数配成完全平方,然后根据正确的性质化简,再代入计算即可. 试题解析:(1)小亮(22a (a <0)(3)原式=a+2(3-a )=6-a=6-(-2007)=2013.25.先化简,再求值:2222212⎛⎫----÷ ⎪-+⎝⎭x y x y x x xxy y,其中x y ==. 【答案】原式x y x-=-,把x y ==代入得,原式1=-. 【详解】试题分析:先将括号里面进行通分,再将能分解因式的分解因式,约分化简即可. 试题解析: 2222212⎛⎫----÷ ⎪-+⎝⎭x y x y x x x xy y ()()()222=x y x y x x x x x x y x y -⎛⎫---⋅ ⎪+-⎝⎭ =y x x y x x y---⋅+ x y x-=-把x y ==代入得:原式1==-+考点:分式的化简求值.26.在一个边长为(cm 的正方形的内部挖去一个长为()cm ,cm的矩形,求剩余部分图形的面积.【答案】【解析】试题分析:用大正方形的面积减去长方形的面积即可求出剩余部分的面积.试题解析:剩余部分的面积为:(2﹣()=()﹣(﹣)=(cm 2). 考点:二次根式的应用27.先化简,再求值:2443(1)11m m m m m -+÷----,其中2m =.【答案】22m m-+ 1. 【解析】 分析:先根据分式的混合运算顺序和运算法则化简原式,再将m 的值代入计算可得.详解:原式=221m m --()÷(31m -﹣211m m --) =221m m --()÷241m m -- =221m m --()•122m m m --+-()() =﹣22m m -+ =22m m -+当m ﹣2时,原式===﹣1+=1.点睛:本题主要考查分式的化简求值,解题的关键是掌握分式的混合运算顺序和运算法则.28.已知长方形的长a =b =. (1)求长方形的周长;(2)求与长方形等面积的正方形的周长,并比较其与长方形周长的大小关系.【答案】(1)2)长方形的周长大.【解析】试题分析:(1)代入周长计算公式解决问题;(2)求得长方形的面积,开方得出正方形的边长,进一步求得周长比较即可. 试题解析:(1)()11222223a b ⎛+=⨯=⨯⨯⨯=⨯= ⎝∴长方形的周长为 .(2)11 4.23=⨯⨯=正方形的面积也为4. 2.=周长为:428.⨯=8.>∴长方形的周长大于正方形的周长.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】=-a-(-b)=b-a=-6.故选B2.C解析:C【分析】A 、B 、C 、根据合并同类二次根式的法则即可判定;D 、利用根式的运算法则计算即可判定.【详解】解:A 、B 、D 不是同类二次根式,不能合并,故选项不符合题意;C =,故选项正确.故选:C .【点睛】此题主要考查二次根式的运算,应熟练掌握各种运算法则,且准确计算.3.D解析:D【分析】||a =,然后再根据a 的范围去掉绝对值后即可求解.【详解】|2|=-a ,且2a <,∴|2|2=-=-+a a ,原式|2|3231=--=-+-=--a a a ,故选:D . 【点睛】||a =这个公式是解决本题的关键.4.C解析:C【分析】计算出各个选项中的正确结果,即可得到哪个选项是正确【详解】A错误;∵2+B错误;=,故选项C正确;=,故选项D错误.2故选C.【点睛】本题考查二次根式的混合运算,解题的关键是明确二次根式的混合运算的计算方法.5.C解析:C【分析】直接利用二次根式的性质分别求解,即可得出答案.【详解】解:A,故A选项错误;B,故B选项错误;C选项:2=5,故C选项正确;D选项:2=3,故D选项错误,故选:C.【点睛】此题主要考查了二次根式的性质,正确求解二次根式是解题的关键.6.C解析:C【分析】根据二次根式的加法、减法、乘法、分母有理化逐一进行计算判断即可.【详解】A不能合并,故A选项错误;B.-=B选项错误;C=D==D选项错误,故选C.【点睛】本题考查了二次根式的运算,分母有理化,熟练掌握各运算法则是解题的关键.7.D解析:D【分析】利用二次根式的加减法对A、C进行判断;利用二次根式的性质对B进行判断;利用二次根式的除法法则对D进行判断.【详解】解:A A选项错误;B=B选项错误;C、=C选项错误;D2=,所以D选项正确.故选:D.【点睛】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.8.A解析:A【分析】答.【详解】解:①3104<<,415∴<<,故①错误;x的取值范围是1x≥-,故②正确;9=,9的平方根是3±,故③错误;④5=,故④错误;⑤∵159288-=,(229<,∴15028-<,即1528<,故⑤错误; 综上所述:正确的有②,共1个,故选:A .【点睛】本题考查了故算无理数的大小,解决本题的关键是掌握估算平方法比较无理数大小.9.C解析:C【分析】根据同类二次根式的性质即可求出答案.【详解】由题意可知:a 2-3=2a∴解得:a=3或a=-1当a=-1时,该二次根式无意义,故a=3故选C .【点睛】本题考查二次根式的概念,解题的关键是熟练正确理解最简二次根式以及同类二次根式的概念.10.C解析:C【分析】直接利用二次根式的性质与化简以及积的乘方运算法则分别计算即可得出答案.【详解】A |a |,故此选项错误;B .,则a ,b 均为非负数,故此选项错误;C .a 2•b 2=(a •b )2,正确;D mn a(a ≥0),故此选项错误. 故选C .【点睛】本题主要考查了二次根式的性质与化简以及积的乘方运算,正确掌握相关运算法则是解题的关键. 二、填空题11.7【解析】解:∵=+,∴a、b 的值为15,60,135,240,540.①当a=15,b=15时,即=4;②当a=60,b=60时,即=2;③当a=15,b=60时,即=3;④当a=60解析:7【解析】解:∵2,∴a、b的值为15,60,135,240,540.①当a=15,b=15时,即2=4;②当a=60,b=60时,即2=2;③当a=15,b=60时,即2=3;④当a=60,b=15时,即2=3;⑤当a=240,b=240时,即2=1;⑥当a=135,b=540时,即2=1;⑦当a=540,b=135时,即2=1;故答案为:(15,15)、(60、60)、(15,60)、(60,15)、(240,240)、(135,540)、(540,135).所有满足条件的有序数对(a,b)共有7对.故答案为:7.点睛:本题考查了二次根式的性质和化简,解决此题的关键是分类讨论思想,得出a、b可能的取值.12.【分析】根据=,将原式进行拆分,然后合并可得出答案.【详解】解:原式==.故答案为.【点睛】此题考查了二次根式的混合运算,解答本题的关键是将原式进行拆分,有一定的技巧性,注意仔细观解析:220400x x x- 【分析】-,将原式进行拆分,然后合并可得出答案. 【详解】解:原式===故答案为220400x x x-. 【点睛】 此题考查了二次根式的混合运算,解答本题的关键是将原式进行拆分,有一定的技巧性,注意仔细观察.13.【分析】直接利用二次根式的性质将已知化简,再将原式变形求出答案.【详解】解:∵一定有意义,∴x≥11,∴﹣|7﹣x|+=3y ﹣2,﹣x+7+x ﹣9=3y ﹣2,整理得:=3y ,∴x﹣解析:22【分析】直接利用二次根式的性质将已知化简,再将原式变形求出答案.【详解】一定有意义,∴x ≥11,|7﹣x =3y ﹣2,﹣x +7+x ﹣9=3y ﹣2,=3y ,∴x ﹣11=9y 2,则2x ﹣18y 2=2x ﹣2(x ﹣11)=22.故答案为:22.【点睛】本题考查二次根式有意义的应用,以及二次根式的性质应用,属于提高题.14.【分析】先根据确定m 的取值范围,再根据,推出,最后利用来确定a 的取值范围.【详解】解:为整数为故答案为:5.【点睛】本题考查的知识点是二次根式以及估算无理数的大小,利用解析:5【分析】)30m -≤确定m 的取值范围,再根据m a +=32a ≤≤,最后利用78<<来确定a 的取值范围.【详解】 解:()230m m --≤23m ∴≤≤m a +=a m ∴=32a ∴≤≤7528<<46a ∴<<a 为整数a ∴为5故答案为:5.【点睛】本题考查的知识点是二次根式以及估算无理数的大小,利用“逼近法”得出围是解此题的关键.15.【解析】【分析】根据完全平方公式以及整体的思想即可求出答案.【详解】解:∵2x﹣1= ,∴(2x﹣1)2=3∴4x2﹣4x+1=3∴4(x2﹣x)=2∴x2﹣x=故答案为【点解析:1 2【解析】【分析】根据完全平方公式以及整体的思想即可求出答案.【详解】解:∵2x﹣,∴(2x﹣1)2=3∴4x2﹣4x+1=3∴4(x2﹣x)=2∴x2﹣x=12故答案为1 2【点睛】本题考查二次根式的运算,解题的关键是熟练运用完全平方公式,本题属于基础题型.16.【解析】根据题意,把被开方数配方为完全平方,然后代入求解,可得====.故答案是:.【解析】根据题意,把被开方数配方为完全平方,然后代入求解,可得.17.-【分析】首先判断出x ,y 的符号,再利用二次根式的性质化简求出答案.【详解】解:∵,且有意义,∴,∴.故答案为.【点睛】此题主要考查了二次根式的性质与化简,正确掌握二次根式的性质是解析:【分析】首先判断出x ,y 的符号,再利用二次根式的性质化简求出答案.【详解】解:∵0xy > ∴00x y <,<,∴x ==.故答案为.【点睛】 此题主要考查了二次根式的性质与化简,正确掌握二次根式的性质是解题关键.即(0)(0)a a a a a ≥⎧==⎨-<⎩=(a ≥0,b >0). 18.-16【解析】试题分析:根据分式的有意义和二次根式有意义的条件,可知x2-9=0,且x-3≠0,解得x=-3,然后可代入得y=-,因此可得5x+6y=5×(-3)+6×(-)=-15-1=-16 解析:-16【解析】试题分析:根据分式的有意义和二次根式有意义的条件,可知x 2-9=0,且x-3≠0,解得x=-3,然后可代入得y=-16,因此可得5x+6y=5×(-3)+6×(-16)=-15-1=-16. 故答案为:-16.点睛:此题主要考查了分式的有意义和二次根式有意义,解题关键是利用二次根式的被开方数为非负数和分式的分母不为0,可列式求解.19.21【分析】根据二次根式及同类二次根式的定义列出方程组即可求出答案. 【详解】∵最简二次根式与是同类二次根式,∴ ,解得,,∴故答案为21.解析:21【分析】根据二次根式及同类二次根式的定义列出方程组即可求出答案.【详解】∴1221343nm m-=⎧⎨-=-⎩,解得,73mn=⎧⎨=⎩,∴7321.mn=⨯=故答案为21.20.②③【分析】根据最简二次根式的被开方数不含分母;被开方数不含能开得尽方的因数或因式,可得答案.【详解】②③是最简二次根式,故答案为②③.【点睛】本题考查最简二次根式的定义,解析:②③【分析】根据最简二次根式的被开方数不含分母;被开方数不含能开得尽方的因数或因式,可得答案.【详解】是最简二次根式,③4故答案为②③.【点睛】本题考查最简二次根式的定义,最简二次根式必须满足两个条件:被开方数不含分母;被开方数不含能开得尽方的因数或因式.三、解答题21.无22.无23.无24.无25.无26.无27.无28.无。
八年级第二学期3月份月考数学试卷含答案

一、选择题1.如果0,0a b <<,且6a b -=,则22a b -的值是( ) A .6 B .6- C .6或6- D .无法确定 2.下列计算,正确的是( ) A . 235+= B . 2323+= C . 8220-=D . 510-= 3.下列运算结果正确的是( )A .()299-=-B .623÷=C .()222-=D .255=-4.下列计算正确的是( )A .325+=B .1233-=C .326D .1234÷= 5.下列运算正确的是( ) A .235+= B .322-=3 C .2(2)-=﹣2 D .24322÷=6.如图,在矩形ABCD 中无重叠放入面积分别为16cm 2和12cm 2的两张正方形纸片,则图中空白部分的面积为( )A .(8﹣3cm 2B .(4﹣3cm 2C .(16﹣3cm 2D .(﹣3)cm 2 7.下列计算正确的是( )A 2510=B 623=C 12315=D .241=8.下列各式中正确的是( )A 36 6B 2(2)2--=-C 8 4D .2(7)=79.下列计算正确的是( )A 235=B .332-=C .222=D 393=10.下列运算一定正确的是( )A 2a a =B ab a b =C .222()a b a b ⋅=⋅D ()0n m n a a m=≥ 二、填空题11.已知3,3-1,则x 2+xy +y 2=_____.12.已知a 73+a 3+5a 2﹣4a ﹣6的值为_____.13.+的形式(,,a b c 为正整数),则abc =______.14.10=,则222516x y +=______. 15.若实数x ,y ,m 满足等式()223x y m +-=m+4的算术平方根为 ________.16.若6x ,小数部分为y ,则(2x y 的值是___.17.÷=________________ .18..19.=_______.20.古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式,称为海伦—秦九韶公式:如果一个三角形的三边长分别是a ,b ,c ,记2a b c p ++=,那么三角形的面积S =ABC 中,A ∠,B ,C ∠所对的边分别记为a ,b ,c ,若4a =,5b =,7c =,则ABC 面积是_______. 三、解答题21.计算:(1(2))((222+-+.【答案】(1)【分析】(1)先化简二次根式,再合并同类二次根式即可;(2)根据平方差公式化简,再化简、合并同类二次根式即可.【详解】(1==(2))((222+-+=2223--+ =5-4-3+2=022.先阅读下列解答过程,然后再解答:,a b,使a b m=,使得+=,ab n22m+====>)a b==,由于437,4312+=⨯=,m n7,12+=,=即:227===+。
人教版八年级数学第二学期3月份月考测试卷含答案

一、选择题1.如图,在△ABC中,∠C=90°,AD是△ABC的一条角平分线.若AC=6,AB=10,则点D到AB边的距离为()A.2 B.2.5 C.3 D.42.如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2016的值为()A.(22)2013B.(22)2014C.(12)2013D.(12)20143.如图,在△ABC中,∠A=90°,P是BC上一点,且DB=DC,过BC上一点P,作PE⊥AB于E,PF⊥DC于F,已知:AD:DB=1:3,BC=46,则PE+PF的长是()A.46B.6 C.42D.264.将6个边长是1的正方形无缝隙铺成一个矩形,则这个矩形的对角线长等于()A.37B.13C.37或者13D.37或者137 5.如图,OP=1,过点P作PP1⊥OP,且PP1=1,得OP1=2;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=3;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2018的值为( )A .2016B .2017C .2018D .20196.如图所示,有一个高18cm ,底面周长为24cm 的圆柱形玻璃容器,在外侧距下底1cm 的点S 处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm 的点F 处有一只苍蝇,则急于捕获苍蝇充饥的蜘蛛所走的最短路径的长度是( )A .16cmB .18cmC .20cmD .24cm7.如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )A .甲、乙都可以B .甲、乙都不可以C .甲不可以、乙可以D .甲可以、乙不可以8.如图,已知AB 是线段MN 上的两点,MN =12,MA =3,MB >3,以A 为中心顺时针旋转点M ,以点B 为中心顺时针旋转点N ,使M 、N 两点重合成一点C ,构成△ABC ,当△ABC 为直角三角形时AB 的长是( )A .3B .5C .4或5D .3或519.如图,BD 为ABCD 的对角线,45,DBC DE BC ︒∠=⊥于点E ,BF ⊥DC 于点F ,DE 、BF 相交于点H ,直线BF 交线段AD 的延长线于点G ,下列结论:①12CE BE =;②A BHE ∠=∠;③AB=BH;④BHD BDG ∠=∠;⑤222BH BG AG +=;其中正确的结论有( )A .①②③B .②③⑤C .①⑤D .③④10.下列条件中,不能..判定ABC 为直角三角形的是( ) A .::5:12:13a b c = B .A B C ∠+∠=∠C .::2:3:5A B C ∠∠∠=D .6a =,12b =,10c =二、填空题11.如图,在矩形 ABCD 中,AB =10,BC =5,若点 M 、N 分别是线段 AC 、AB 上的两个动点,则 BM+MN 的最小值为_____________________.12.将一副三角板按如图所示摆放成四边形ABCD ,发现只要知道其中一边的长就可以求出其它各边的长,若已知AD =32,则AB 的长为__________.13.如图,Rt ABC 中,90A ∠=︒,8AC =,6AB =,DE AC ⊥,13CD BC =,13CE AC =,P 是直线AC 上一点,把CDP 沿DP 所在的直线翻折后,点C 落在直线DE 上的点H 处,CP 的长是__________14.如图在三角形纸片ABC 中,已知∠ABC =90º,AC =5,BC=4,过点A 作直线l 平行于BC ,折叠三角形纸片ABC ,使直角顶点B 落在直线l 上的点P 处,折痕为MN ,当点P 在直线l 上移动时,折痕的端点M 、N 也随之移动,若限定端点M 、N 分别在AB 、BC 边上(包括端点)移动,则线段AP 长度的最大值与最小值的差为________________.15.如图,在△ABC 中,AB =AC ,∠BAC =120°,AC 的垂直平分线交 BC 于 F ,交 AC 于 E ,交 BA 的延长线于 G ,若 EG =3,则 BF 的长是______.16.如图,BAC 90∠=度,AB AC =,AE AD ⊥,且AE AD =,AF 平分DAE ∠交BC 于F ,若BD 6=,CF 8=,则线段AD 的长为______.17.如图,在四边形ABCD 中,AD =4,CD =3,∠ABC =∠ACB =∠ADC =45°,则2________BD =.18.如图所示,四边形ABCD 是长方形,把△ACD 沿AC 折叠到△ACD′,AD′与BC 交于点E ,若AD =4,DC =3,求BE 的长.19.观察:①3、4、5,②5、12、13,③7、24、25,……,发现这些勾股数的“勾”都是奇数,且从3起就没断过.根据以上规律,请写出第8组勾股数:______. 20.已知,在△ABC 中,BC=3,∠A=22.5°,将△ABC 翻折使得点B 与点A 重合,折痕与边AC 交于点P ,如果AP=4,那么AC 的长为_______三、解答题21.如图,△ABC 和EDC ∆都是等边三角形,7,3,2AD BD CD ===求:(1)AE长;(2)∠BDC 的度数:(3)AC 的长.22.如图,在两个等腰直角ABC 和CDE △中,∠ACB = ∠DCE=90°.(1)观察猜想:如图1,点E 在BC 上,线段AE 与BD 的数量关系是 ,位置关系是 ;(2)探究证明:把CDE △绕直角顶点C 旋转到图2的位置,(1)中的结论还成立吗?说明理由;(3)拓展延伸:把CDE △绕点C 在平面内自由旋转,若AC = BC=10,DE=12,当A 、E 、D 三点在直线上时,请直接写出 AD 的长.23.如图,△ABC 和△ADE 都是等腰三角形,其中AB =AC ,AD =AE ,且∠BAC =∠DAE . (1)如图①,连接BE 、CD ,求证:BE =CD ;(2)如图②,连接BE 、CD ,若∠BAC =∠DAE =60°,CD ⊥AE ,AD =3,CD =4,求BD 的长;(3)如图③,若∠BAC =∠DAE =90°,且C 点恰好落在DE 上,试探究CD 2、CE 2和BC 2之间的数量关系,并加以说明.24.如图1,在△ABC 中,AB =AC ,∠BAC =90°,D 为AC 边上一动点,且不与点A 点C 重合,连接BD 并延长,在BD 延长线上取一点E ,使AE =AB ,连接CE .(1)若∠AED =20°,则∠DEC = 度;(2)若∠AED =a ,试探索∠AED 与∠AEC 有怎样的数量关系?并证明你的猜想; (3)如图2,过点A 作AF ⊥BE 于点F ,AF 的延长线与EC 的延长线交于点H ,求证:EH 2+CH 2=2AE 2.25.如图,ABC ∆是等边三角形,,D E 为AC 上两点,且AE CD =,延长BC 至点F ,使CF CD =,连接BD .(1)如图1,当,D E 两点重合时,求证:BD DF =; (2)延长BD 与EF 交于点G . ①如图2,求证:60BGE ∠=︒;②如图3,连接,BE CG ,若30,4EBD BG ∠=︒=,则BCG ∆的面积为______________.26.如图, ABD 为边长不变的等腰直角三角形,AB AD =,90BAD ∠=︒,在 ABD 外取一点 E ,以A 为直角顶点作等腰直角AEP △,其中 P 在ABD 内部,90EAP ∠=︒,2AE AP ==,当E 、P 、D 三点共线时,7BP =.下列结论:①E 、P 、D 共线时,点B 到直线AE 的距离为5; ②E 、P 、D 共线时, 13ADP ABP S S ∆∆+=+;=532ABD S ∆+③;④作点 A 关于 BD 的对称点 C ,在 AEP 绕点 A 旋转的过程中,PC 的最小值为5+232-;⑤AEP △绕点A 旋转,当点E 落在AB 上,当点P 落在AD 上时,取BP 上一点N ,使得AN BN =,连接 ED ,则AN ED ⊥.其中正确结论的序号是___.27.如果一个三角形的两条边的和是第三边的两倍,则称这个三角形是“优三角形”,这两条边的比称为“优比”(若这两边不等,则优比为较大边与较小边的比),记为k . (1)命题:“等边三角形为优三角形,其优比为1”,是真命题还是假命题? (2)已知ABC 为优三角形,AB c =,AC b =,BC a =,①如图1,若90ACB ∠=︒,b a ≥,6b =,求a 的值. ②如图2,若c b a ≥≥,求优比k 的取值范围.(3)已知ABC 是优三角形,且120ABC ∠=︒,4BC =,求ABC 的面积. 28.我国古代数学家赵爽曾用图1证明了勾股定理,这个图形被称为“弦图”.2002年在北京召开的国际数学家大会(ICM 2002)的会标(图2),其图案正是由“弦图”演变而来.“弦图”是由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形请你根据图1解答下列问题:(1)叙述勾股定理(用文字及符号语言叙述); (2)证明勾股定理;(3)若大正方形的面积是13,小正方形的面积是1,求()2a b +的值.29.如图,点A 是射线OE :y =x (x ≥0)上的一个动点,过点A 作x 轴的垂线,垂足为B ,过点B 作OA 的平行线交∠AOB 的平分线于点C .(1)若OA =2,求点B 的坐标;(2)如图2,过点C 作CG ⊥AB 于点G ,CH ⊥OE 于点H ,求证:CG =CH .(3)①若点A 的坐标为(2,2),射线OC 与AB 交于点D ,在射线BC 上是否存在一点P 使得△ACP 与△BDC 全等,若存在,请求出点P 的坐标;若不存在,请说明理由.②在(3)①的条件下,在平面内另有三点P1(2,2),P2(2,22),P3(2+2,2﹣2),请你判断也满足△ACP与△BDC全等的点是.(写出你认为正确的点)30.如图,在△ABC中,D是边AB的中点,E是边AC上一动点,连结DE,过点D作DF⊥DE交边BC于点F(点F与点B、C不重合),延长FD到点G,使DG=DF,连结EF、AG.已知AB=10,BC=6,AC=8.(1)求证:△ADG≌△BDF;(2)请你连结EG,并求证:EF=EG;(3)设AE=x,CF=y,求y关于x的函数关系式,并写出自变量x的取值范围;(4)求线段EF长度的最小值.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】作DE⊥AB于E,由勾股定理计算出可求BC=8,再利用角平分线的性质得到DE=DC,设DE=DC=x,利用等等面积法列方程、解方程即可解答.【详解】解:作DE⊥AB于E,如图,在Rt△ABC中,BC221068,∵AD是△ABC的一条角平分线,DC⊥AC,DE⊥AB,∴DE=DC,设DE=DC=x,S△ABD=12DE•AB=12AC•BD,即10x=6(8﹣x),解得x=3,即点D到AB边的距离为3.故答案为C.【点睛】本题考查了角平分线的性质和勾股定理的相关知识,理解角的平分线上的点到角的两边的距离相等是解答本题的关键..2.C解析:C【分析】根据等腰直角三角形的性质可得出S2+S2=S1,写出部分S n的值,根据数的变化找出变化规律“S n=(12)n−3”,依此规律即可得出结论.【详解】解:在图中标上字母E,如图所示.∵正方形ABCD的边长为2,△CDE为等腰直角三角形,∴DE2+CE2=CD2,DE=CE,∴S2+S2=S1.观察,发现规律:S1=22=4,S2=12S1=2,S3=12S2=1,S4=12S3=12,…,∴S n=(12)n−3.当n=2016时,S2016=(12)2016−3=(12)2013.故选:C.【点睛】本题考查了等腰直角三角形的性质、勾股定理以及规律型中数的变化规律,解题的关键是找出规律“S n=(12)n−3”.本题属于中档题,难度不大,解决该题型题目时,写出部分S n的值,根据数值的变化找出变化规律是关键.3.C解析:C【解析】【分析】根据三角形的面积判断出PE+PF的长等于AC的长,这样就变成了求AC的长;在Rt△ACD 和Rt△ABC中,利用勾股定理表示出AC,解方程就可以得到AD的长,再利用勾股定理就可以求出AC的长,也就是PE+PF的长.【详解】∵△DCB为等腰三角形,PE⊥AB,PF⊥CD,AC⊥BD,∴S△BCD=12BD•PE+12CD•PF=12BD•AC,∴PE+PF=AC,设AD=x,BD=CD=3x,AB=4x,∵AC2=CD2-AD2=(3x)2-x2=8x2,∵AC2=BC2-AB2=(46)2-(4x)2,∴x=2,∴AC=42,∴PE+PF=42.故选C【点睛】本题考查勾股定理、等腰三角形的性质等知识,解题的关键是学会利用面积法证明线段之间的关系,灵活运用勾股定理解决问题,属于中考常考题型.4.C解析:C【分析】如图1或图2所示,分类讨论,利用勾股定理可得结论.【详解】当如图1所示时,AB=2,BC=3,∴AC=2223=13;当如图2所示时,AB=1,BC=6,∴AC=221+6=37;故选C.【点睛】本题主要考查图形的拼接,数形结合,分类讨论是解答此题的关键.5.D解析:D【解析】【分析】由勾股定理求出各边,再观察结果的规律.【详解】∵OP=1,OP1=2OP2=3,OP3=4=2,∴OP4=5,…,OP2018=2019.故选D【点睛】本题考查了勾股定理,读懂题目信息,理解定理并观察出被开方数比相应的序数大1是解题的关键.6.C解析:C【分析】首先画出圆柱的侧面展开图,进而得到SC=12cm,FC=18-2=16cm,再利用勾股定理计算出SF长即可.【详解】将圆柱的侧面展开,蜘蛛到达目的地的最近距离为线段SF的长,由勾股定理,SF2=SC2+FC2=122+(18-1-1)2=400,SF=20 cm,故选C.【点睛】本题考查了平面展开-最短路径问题,先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.7.A解析:A试题分析:剪拼如下图:乙故选A考点:剪拼,面积不变性,二次方根8.C解析:C【分析】设AB =x ,则BC =9-x ,根据三角形两边之和大于第三边,得到x 的取值范围,再利用分类讨论思想,根据勾股定理列方程,计算解答.【详解】解:∵在△ABC 中,AC =AM =3,设AB =x ,BC =9-x ,由三角形两边之和大于第三边得:3939x x x x +-⎧⎨+-⎩>>, 解得3<x <6,①AC 为斜边,则32=x 2+(9-x )2,即x 2-9x +36=0,方程无解,即AC 为斜边不成立,②若AB 为斜边,则x 2=(9-x )2+32,解得x =5,满足3<x <6,③若BC 为斜边,则(9-x )2=32+x 2,解得x =4,满足3<x <6,∴x =5或x =4;故选C .【点睛】本题考查三角形的三边关系,勾股定理等,分类讨论和方程思想是解答的关键.解析:B【分析】根据直角三角形的意义和性质可以得到解答.【详解】解:由题意,90BHE HBE C HBE A C ∠+∠=∠+∠=︒∠=∠,∴A BHE C ∠=∠=∠,②正确;∵∠DBC=45°,DE ⊥BC ,∴∠EDB=∠DBC=45°,∴BE=DE∴Rt BEH Rt DEC ≅,∴BH=CD=AB ,③正确;∵AB CD BF CD ⊥,,∴AB ⊥CD ,∴222AB BG AG +=即 222BH BG AG +=,⑤正确,∵没有依据支持①④成立,∴②③⑤正确故选B .【点睛】本题考查直角三角形的意义和性质,灵活应用有关知识求解是解题关键.10.D解析:D【分析】由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方或最大角是否是90︒即可.【详解】解:A 、22251213+=,ABC ∆∴是直角三角形,故能判定ABC ∆是直角三角形; B 、A B C ∠+∠=∠,90C ∴∠=︒,故能判定ABC ∆是直角三角形;C 、::2:3:5A B C ∠∠∠=,518090235C ∴∠=⨯︒=︒++,故能判定ABC ∆是直角三角形;D 、22261012+≠,ABC ∆∴不是直角三角形,故不能判定ABC ∆是直角三角形; 故选:D .【点睛】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,可利用勾股定理的逆定理和直角三角形的定义判断.二、填空题11.8【解析】如图作点B 关于AC 的对称点B ′,连接B ′A 交DC 于点E ,则BM+MN 的最小值等于的最小值作交于,则为所求;设,,由,,h+5=8,即BM+MN 的最小值是8.点睛:本题主要是利用轴对称求最短路线,题中应用了勾股定理与用不同方式表示三角形的面积从而求出某条边上的高,利用轴对称得出M 点与N 点的位置是解题的关键. 12.3【分析】利用勾股定理求出AC=6,在Rt △ABC 中,∠BAC=30°,得到12BC AB =,再利用勾股定理得到222AC BC AB +=,即可求出AB .【详解】在Rt △ACD 中,CD=AD=32∴226AD CD +=,在Rt △ABC 中,∠BAC=30°, ∴12BC AB =, ∵222AC BC AB +=, ∴22216()2AB AB +=,解得AB=3 故答案为:3【点睛】此题考查勾股定理,直角三角形30度角所对的直角边等于斜边的一半,正确理解勾股定理的三边的数量关系是解题的关键.13.53或203 【分析】 根据折叠后点C 的对应点H 与AC 的位置关系分类讨论,分别画出对应的图形,利用勾股定理求出各边的长,再根据折叠的性质与勾股定理列出对应的方程即可求出结论.【详解】解:①当折叠后点C 的对应点H 在AC 的下方时,如下图所示∵Rt ABC 中,90A ∠=︒,8AC =,6AB =,根据勾股定理可得2210AB AC += ∵13CD BC =,13CE AC =, ∴13CD BC ==103,13CE AC ==83 ∵DE AC ⊥根据勾股定理可得222CD CE -=由折叠的性质可得:DH=CD=103,CP=PH ∴EH=DH -DE=43设CP=PH=x ,则EP=CE -CP=83-x 在Rt △PEH 中,EP 2+EH 2=PH 2即(83-x )2+(43)2=x 2 解得:x=53即此时CP=53; ②当折叠后点C 的对应点H 在AC 的上方时,如下图所示根据折叠的性质可得DH=CD=103,CP=PH∴EH=DH+DE=16 3设CP=PH=y,则EP= CP-CE =y-8 3在Rt△PEH中,EP2+EH2=PH2即(y-83)2+(163)2=y2解得:y=20 3即此时CP=203.综上所述:CP=53或203.故答案为:53或203.【点睛】此题考查的是勾股定理和折叠问题,掌握利用勾股定理解直角三角形、折叠的性质和分类讨论的数学思想是解决此题的关键.1471【分析】分别找到两个极端,当M与A重合时,AP取最大值,当点N与C重合时,AP取最小,即可求出线段AP长度的最大值与最小值之差【详解】如图所示,当M 与A 重合时,AP 取最大值,此时标记为P 1,由折叠的性质易得四边形AP 1NB 是正方形,在Rt △ABC 中,2222AB=AC BC =54=3--,∴AP 的最大值为A P 1=AB=3如图所示,当点N 与C 重合时,AP 取最小,过C 点作CD ⊥直线l 于点D ,可得矩形ABCD ,∴CD=AB=3,AD=BC=4,由折叠的性质有PC=BC=4,在Rt △PCD 中,2222PD=PC CD =43=7--,∴AP 的最小值为AD PD=47-线段AP 长度的最大值与最小值之差为(1AP AP=347=71-- 71【点睛】本题考查勾股定理的折叠问题,可以动手实际操作进行探索.15.4【分析】根据线段垂直平分线得出AE=EC ,∠AEG=∠AEF=90°,求出∠B=∠C=∠G=30°,根据勾股定理和含30°角的直角三角形性质求出AE 和EF ,即可求出FG ,再求出BF=FG 即可【详解】∵AC 的垂直平分线FG ,∴AE=EC ,∠AEG=∠AEF=90°,∵∠BAC=120°,∴∠G=∠BAC-∠AEG=120°-90°=30°,∵∠BAC=120°,AB=AC ,∴∠B=∠C=12(180°-∠BAC )=30°, ∴∠B=∠G ,∴BF=FG ,∵在Rt △AEG 中,∠G=30°,EG=3,∴AG=2AE ,即(2AE )2=AE 2+32,∴3即CE=3,同理在Rt△CEF中,∠C=30°,CF=2EF,(2EF)2=EF2+(3)2,∴EF=1(负值舍去),∴BF=GF=EF+CE=1+3=4,故答案为4.【点睛】本题考查了勾股定理,含30°角的直角三角形性质,等腰三角形的性质和判定等知识点,能综合运用定理进行推理是解此题的关键.16.65【分析】由“SAS”可证ABD≌ACE,DAF≌EAF可得BD CE=,4B∠∠=,DF EF=,由勾股定理可求EF的长,即可求BC的长,由勾股定理可求AD的长.【详解】解:如图,连接EF,过点A作AG BC⊥于点G,AE AD⊥,DAE DAC290∠∠∠∴=+=,又BAC DAC190∠∠∠=+=,12∠∠∴=,在ABD和ACE中12AB ACAD AE=⎧⎪∠=∠⎨⎪=⎩,ABD∴≌()ACE SAS.BD CE∴=,4B∠∠=BAC90∠=,AB AC=,∴B345∠∠==4B45∠∠∴==,ECF3490∠∠∠∴=+=,222CE CF EF∴+=,222BD FC EF∴+=,AF平分DAE∠,DAF EAF ∠∠∴=,在DAF 和EAF 中AD AE DAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩,DAF ∴≌()EAF SAS .DF EF ∴=.222BD FC DF ∴+=.22222DF BD FC 68100∴=+=+=,∴DF 10=BC BD DF FC 610824∴=++=++=,AB AC =,AG BC ⊥, 1BG AGBC 122∴===, DG BG BD 1266∴=-=-=,∴22AD AG DG 65=+=故答案为65【点睛】考查等腰直角三角形的性质、勾股定理、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.17.41【解析】作AD′⊥AD ,AD′=AD ,连接CD′,DD ′,如图:∵∠BAC+∠CAD=∠DAD′+∠CAD ,即∠BAD=∠CAD′,在△BAD 与△CAD ′中,;BA CA BAD CAD AD AD ===⎧⎪∠∠'⎨⎪⎩∴△BAD ≌△CAD′(SAS ), ∴BD=CD′,∠DAD′=90°,由勾股定理得,∠D′DA+∠ADC=90°,由勾股定理得BD 2=41.故答案是:41.18.78【解析】 试题分析:根据矩形性质得AB=DC=6,BC=AD=8,AD ∥BC ,∠B=90°,再根据折叠性质得∠DAC=∠D′AC ,而∠DAC=∠ACB ,则∠D′AC=∠ACB ,所以AE=EC ,设BE=x ,则EC=4-x ,AE=4-x ,然后在Rt △ABE 中利用勾股定理可计算出BE 的长即可.试题解析:∵四边形ABCD 为矩形,∴AB=DC=3,BC=AD=4,AD∥BC,∠B=90°,∵△ACD 沿AC 折叠到△ACD′,AD′与BC 交于点E ,∴∠DAC=∠D′AC,∵AD∥BC,∴∠DAC=∠ACB,∴∠D′AC=∠ACB,∴AE=EC,设BE=x ,则EC=4﹣x ,AE=4﹣x ,在Rt△ABE 中,∵AB 2+BE 2=AE 2,∴32+x 2=(4﹣x )2,解得x=78, 即BE 的长为78. 19.17,144,145【分析】 由题意观察题干这些勾股数,根据所给的勾股数找出三个数之间的关系即可.【详解】解:因为这些勾股数的“勾”都是奇数,且从3起就没断过,所以从3、5、7…依次推出第8组的“勾”为17,继续观察可知弦-股=1,利用勾股定理假设股为m ,则弦为m+1,所以有22217(1)m m +=+,解得144m =,1145m +=,即第8组勾股数为17,144,145.故答案为17,144,145.【点睛】本题属规律性题目,考查的是勾股数之间的关系,根据题目中所给的勾股数及勾股定理进行分析即可.20.522,322++【分析】过B作BF⊥CA于F,构造直角三角形,分两种情况讨论,利用勾股定理以及等腰直角三角形的性质,即可得到AC的长.【详解】分两种情况:①当∠C为锐角时,如图所示,过B作BF⊥AC于F,由折叠可得,折痕PE垂直平分AB,∴AP=BP=4,∴∠BPC=2∠A=45°,∴△BFP是等腰直角三角形,∴BF=DF=22,又∵BC=3,∴Rt△BFC中,CF=221-=,BC BF∴AC=AP+PF+CF=5+22;②当∠ACB为钝角时,如图所示,过B作BF⊥AC于F,同理可得,△BFP是等腰直角三角形,∴BF=FP=22又∵BC=3,∴Rt△BCF中,221-=,BC BF∴AC=AF-CF=3+22故答案为:5+223+22【点睛】本题主要考查了折叠问题以及勾股定理的运用,解决问题的关键是分两种情况画出图形进行求解.解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.三、解答题21.(1)3;(2)150°;(3)13.【分析】(1)根据等边三角形的性质可利用SAS 证明△BCD ≌△ACE ,再根据全等三角形的性质即得结果;(2)在△ADE 中,根据勾股定理的逆定理可得∠AED =90°,进而可求出∠AEC 的度数,再根据全等三角形的性质即得答案;(3)过C 作CP ⊥DE 于点P ,设AC 与DE 交于G ,如图,根据等边三角形的性质和勾股定理可得PE 与CP 的长,进而可得AE =CP ,然后即可根据AAS 证明△AEG ≌△CPG ,于是可得AG =CG ,PG =EG ,根据勾股定理可求出AG 的长,进一步即可求出结果.【详解】解:(1)∵△ABC 和△EDC 都是等边三角形,∴BC =AC ,CD =CE =DE =2,∠ACB =∠DCE =60°,∴∠BCD =∠ACE ,在△BCD 与△ACE 中,∵BC =AC ,∠BCD =∠ACE ,CD =CE ,∴△BCD ≌△ACE ,∴AE =BD =3;(2)在△ADE 中,∵7,3,2AD AE DE ===, ∴DE 2+AE 2=()()222237+==AD 2, ∴∠AED =90°,∵∠DEC =60°,∴∠AEC =150°,∵△BCD ≌△ACE ,∴∠BDC =∠AEC =150°;(3)过C 作CP ⊥DE 于点P ,设AC 与DE 交于G ,如图,∵△CDE 是等边三角形,∴PE =12DE =1,CP 22213-=,∴AE =CP ,在△AEG 与△CPG 中,∵∠AEG =∠CPG =90°,∠AGE =∠CGP ,AE =CP ,∴△AEG ≌△CPG ,∴AG =CG ,PG =EG =12,∴AG ==,∴AC =2AG【点睛】本题考查了等边三角形的性质、全等三角形的判定和性质、勾股定理及其逆定理等知识,熟练掌握上述知识、灵活应用全等三角形的判定与性质是解题的关键.22.(1)AE BD =,AE BD ⊥;(2)成立,理由见解析;(3)14或2.【分析】(1)先根据等腰三角形的定义可得AC BC =,CE CD =,再根据三角形全等的判定定理与性质可得AE BD =,EAC DBC ∠=∠,然后根据直角三角形两锐角互余、等量代换即可得90AHD ∠=︒,由此即可得;(2)先根据三角形全等的判定定理与性质可得AE BD =,EAC DBC ∠=∠,再根据直角三角形两锐角互余可得90EAC AOC ∠+∠=︒,然后根据对顶角相等、等量代换可得90BOH DBC ∠∠+=︒,从而可得90OHB ∠=︒,由此即可得;(3)先利用勾股定理求出AB =,再分①点,,A E D 在直线上,且点E 位于中间,②点,,A E D 在直线上,且点D 位于中间两种情况,结合(1)(2)的结论,利用勾股定理求解即可得.【详解】(1)AE BD =,AE BD ⊥,理由如下:如图1,延长AE 交BD 于H ,由题意得:AC BC =,90ACE BCD ∠=∠=︒,CE CD =, ∴()ACE BCD SAS ≅,∴AE BD =,EAC DBC ∠=∠,∵90DBC BDC ∠+∠=︒,∴90EAC BDC ∠+∠=︒,∴0)9018(EAC BD A D C H ∠+∠∠︒==-︒,即AE BD ⊥,故答案为:AE BD =,AE BD ⊥;(2)成立,理由如下:如图2,延长AE 交BD 于H ,交BC 于O ,∵90ACB ECD ∠=∠=︒,∴ACB BCE ECD BCE ∠-∠=∠-∠,即ACE BCD ∠=∠,在ACE △和BCD 中,AC BC ACE BCD CE CD =⎧⎪∠=∠⎨⎪=⎩,∴()ACE BCD SAS ≅,∴AE BD =,EAC DBC ∠=∠,∵90ACB ∠=︒,∴90EAC AOC ∠+∠=︒,∵AOC BOH ∠=∠,∴90BOH DBC ∠∠+=︒,即90OBH BOH ∠+∠=︒,∴180()90OHB OBH BOH ∠=︒-∠+∠=︒,即AE BD ⊥;(3)设AD x =,10,90AC BC ACB ==∠=︒,2102AB AC ∴==,由题意,分以下两种情况:①如图3-1,点,,A E D 在直线上,且点E 位于中间,同理可证:AE BD =,AE BD ⊥,12DE =,12BD AE AD DE x ∴==-=-,在Rt ABD △中,222AD BD AB +=,即222(12)(102)x x +-=,解得14x =或2x =-(不符题意,舍去),即14AD =,②如图3-2,点,,A E D 在直线上,且点D 位于中间,同理可证:AE BD =,AE BD ⊥, 12DE =,12BD AE AD DE x ∴==+=+,在Rt ABD △中,222AD BD AB +=,即222(12)(102)x x ++=,解得2x =或14x =-(不符题意,舍去),即2AD =,综上,AD 的长为14或2.【点睛】本题考查了三角形全等的判定与性质、勾股定理等知识点,较难的是题(3),正确分两种情况讨论,并画出图形是解题关键.23.(1)证明见解析;(2)5;(3)CD 2+CE 2=BC 2,证明见解析.【分析】(1)先判断出∠BAE=∠CAD ,进而得出△ACD ≌△ABE ,即可得出结论.(2)先求出∠CDA=12∠ADE=30°,进而求出∠BED=90°,最后用勾股定理即可得出结论. (3)方法1、同(2)的方法即可得出结论;方法2、先判断出CD 2+CE 2=2(AP 2+CP 2),再判断出CD 2+CE 2=2AC 2.即可得出结论.【详解】解:∵∠BAC =∠DAE ,∴∠BAC +∠CAE =∠DAE +∠CAE ,即∠BAE =∠CAD .又∵AB =AC ,AD =AE ,∴△ACD ≌△ABE (SAS ),∴CD =BE .(2)如图2,连结BE ,∵AD =AE ,∠DAE =60°,∴△ADE 是等边三角形,∴DE =AD =3,∠ADE =∠AED =60°,∵CD ⊥AE ,∴∠CDA =12∠ADE =12×60°=30°, ∵由(1)得△ACD ≌△ABE ,∴BE =CD =4,∠BEA =∠CDA =30°,∴∠BED =∠BEA +∠AED =30°+60°=90°,即BE ⊥DE ,∴BD =22BE DE +=2234+=5.(3)CD 2、CE 2、BC 2之间的数量关系为:CD 2+CE 2=BC 2,理由如下:解法一:如图3,连结BE .∵AD =AE ,∠DAE =90°,∴∠D =∠AED =45°,∵由(1)得△ACD ≌△ABE ,∴BE =CD ,∠BEA =∠CDA =45°,∴∠BEC =∠BEA +∠AED =45°+45°=90°,即BE ⊥DE ,在Rt △BEC 中,由勾股定理可知:BC 2=BE 2+CE 2.∴BC 2=CD 2+CE 2.解法二:如图4,过点A 作AP ⊥DE 于点P .∵△ADE 为等腰直角三角形,AP ⊥DE ,∴AP =EP =DP .∵CD 2=(CP +PD )2=(CP +AP )2=CP 2+2CP •AP +AP 2,CE 2=(EP ﹣CP )2=(AP ﹣CP )2=AP 2﹣2AP •CP +CP 2,∴CD 2+CE 2=2AP 2+2CP 2=2(AP 2+CP 2),∵在Rt △APC 中,由勾股定理可知:AC 2=AP 2+CP 2,∴CD 2+CE 2=2AC 2.∵△ABC 为等腰直角三角形,由勾股定理可知:∴AB 2+AC 2=BC 2,即2AC 2=BC 2,∴CD 2+CE 2=BC 2.【点睛】本题是几何变换综合题,主要考查了全等三角形的判定和性质,勾股定理,等边三角形的判定和性质,等腰直角三角形的判定和性质,解(1)的关键是判断出∠BAE=∠CAD,解(2)(3)的关键是判断出BE⊥DE,是一道中等难度的中考常考题.24.(1)45度;(2)∠AEC﹣∠AED=45°,理由见解析;(3)见解析【分析】(1)由等腰三角形的性质可求∠BAE=140°,可得∠CAE=50°,由等腰三角形的性质可得∠AEC=∠ACE=65°,即可求解;(2)由等腰三角形的性质可求∠BAE=180°﹣2α,可得∠CAE=90°﹣2α,由等腰三角形的性质可得∠AEC=∠ACE=45°+α,可得结论;(3)如图,过点C作CG⊥AH于G,由等腰直角三角形的性质可得EH2EF,CH=2CG,由“AAS”可证△AFB≌△CGA,可得AF=CG,由勾股定理可得结论.【详解】解:(1)∵AB=AC,AE=AB,∴AB=AC=AE,∴∠ABE=∠AEB,∠ACE=∠AEC,∵∠AED=20°,∴∠ABE=∠AED=20°,∴∠BAE=140°,且∠BAC=90°∴∠CAE=50°,∵∠CAE+∠ACE+∠AEC=180°,且∠ACE=∠AEC,∴∠AEC=∠ACE=65°,∴∠DEC=∠AEC﹣∠AED=45°,故答案为:45;(2)猜想:∠AEC﹣∠AED=45°,理由如下:∵∠AED=∠ABE=α,∴∠BAE=180°﹣2α,∴∠CAE=∠BAE﹣∠BAC=90°﹣2α,∵∠CAE+∠ACE+∠AEC=180°,且∠ACE=∠AEC,∴∠AEC=45°+α,∴∠AEC﹣∠AED=45°;(3)如图,过点C作CG⊥AH于G,∵∠AEC﹣∠AED=45°,∴∠FEH=45°,∵AH⊥BE,∴∠FHE=∠FEH=45°,∴EF=FH,且∠EFH=90°,∴EH2EF,∵∠FHE=45°,CG⊥FH,∴∠GCH=∠FHE=45°,∴GC=GH,∴CH2CG,∵∠BAC=∠CGA=90°,∴∠BAF+∠CAG=90°,∠CAG+∠ACG=90°,∴∠BAF=∠ACG,且AB=AC,∠AFB=∠AGC,∴△AFB≌△CGA(AAS)∴AF=CG,∴CH2AF,∵在Rt△AEF中,AE2=AF2+EF2,2AF)2+2EF)2=2AE2,∴EH2+CH2=2AE2.【点睛】本题是综合了等腰直角三角形的性质,全等三角形的性质与判定的动点问题,三个问题由易到难,在熟练掌握各个相关知识的基础上找到问题之间的内部联系,层层推进去解答是关键.25.(1)见解析;(2)①见解析;②2.【分析】(1)当D、E两点重合时,则AD=CD,然后由等边三角形的性质可得∠CBD的度数,根据等腰三角形的性质和三角形的外角性质可得∠F的度数,于是可得∠CBD与∠F的关系,进而可得结论;(2)①过点E 作EH ∥BC 交AB 于点H ,连接BE ,如图4,则易得△AHE 是等边三角形,根据等边三角形的性质和已知条件可得EH=CF ,∠BHE =∠ECF =120°,BH =EC ,于是可根据SAS 证明△BHE ≌△ECF ,可得∠EBH =∠FEC ,易证△BAE ≌△BCD ,可得∠ABE =∠CBD ,从而有∠FEC =∠CBD ,然后根据三角形的内角和定理可得∠BGE =∠BCD ,进而可得结论; ②易得∠BEG =90°,于是可知△BEF 是等腰直角三角形,由30°角的直角三角形的性质和等腰直角三角形的性质易求得BE 和BF 的长,过点E 作EM ⊥BF 于点F ,过点C 作CN ⊥EF 于点N ,如图5,则△BEM 、△EMF 和△CFN 都是等腰直角三角形,然后利用等腰直角三角形的性质和30°角的直角三角形的性质可依次求出BM 、MC 、CF 、FN 、CN 、GN 的长,进而可得△GCN 也是等腰直角三角形,于是有∠BCG =90°,故所求的△BCG 的面积=12BC CG ⋅,而BC 和CG 可得,问题即得解决. 【详解】 解:(1)∵△ABC 是等边三角形,∴∠ABC =∠ACB =60°,当D 、E 两点重合时,则AD=CD ,∴1302DBC ABC ∠=∠=︒, ∵CF CD =,∴∠F =∠CDF , ∵∠F +∠CDF =∠ACB =60°,∴∠F =30°,∴∠CBD =∠F ,∴BD DF =;(2)①∵△ABC 是等边三角形,∴∠ABC =∠ACB =60°,AB=AC ,过点E 作EH ∥BC 交AB 于点H ,连接BE ,如图4,则∠AHE =∠ABC =60°,∠AEH =∠ACB =60°,∴△AHE 是等边三角形,∴AH=AE=HE ,∴BH =EC ,∵AE CD =,CD=CF ,∴EH=CF ,又∵∠BHE =∠ECF =120°,∴△BHE ≌△ECF (SAS ),∴∠EBH =∠FEC ,EB=EF ,∵BA=BC ,∠A =∠ACB =60°,AE=CD ,∴△BAE ≌△BCD (SAS ),∴∠ABE =∠CBD ,∴∠FEC =∠CBD ,∵∠EDG =∠BDC ,∴∠BGE =∠BCD =60°;②∵∠BGE =60°,∠EBD =30°,∴∠BEG =90°,∵EB=EF ,∴∠F =∠EBF =45°,∵∠EBG =30°,BG =4,∴EG =2,BE 3∴BF 226BE =232GF =,过点E 作EM ⊥BF 于点F ,过点C 作CN ⊥EF 于点N ,如图5,则△BEM 、△EMF 和△CFN 都是等腰直角三角形, ∴6BM ME MF ===, ∵∠ACB =60°,∴∠MEC =30°,∴2MC =, ∴62BC =+,266262CF =--=-, ∴()262312CN FN ==⨯-=-, ∴()2323131GN GF FN CN =-=---=-=, ∴45GCN CGN ∠=∠=︒,∴∠GCF =90°=∠GCB ,∴62CG CF ==-,∴△BCG 的面积=()()116262222BC CG ⋅=+-=. 故答案为:2.【点睛】本题考查了等腰三角形与等边三角形的判定和性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、30°角的直角三角形的性质和勾股定理等知识,涉及的知识点多、难度较大,正确添加辅助线、熟练掌握全等三角形的判定与性质是解①题的关键,灵活应用等腰直角三角形的性质和30°角的直角三角形的性质解②题的关键.26.②③⑤【分析】①先证得ABE ADP ≅,利用邻补角和等腰直角三角形的性质求得90PEB ∠=︒,利用勾股定理求出BE ,即可求得点B 到直线AE 的距离;②根据①的结论,利用APD ABP ABE APB S S S S ∆∆∆+=+AEP BEP S S ∆∆=+即可求得结论; ③在Rt AHB 中,利用勾股定理求得2AB ,再利用三角形面积公式即可求得ABD S ∆; ④当A P C 、、共线时,PC 最小,利用对称的性质,AB BC =的长,再求得AC 的长,即可求得结论;⑤先证得ABP ADE ≅,得到ABP ADE ∠=∠,根据条件得到ABP NAB ∠=∠,利用互余的关系即可证得结论.【详解】①∵ABD 与AEP 都是等腰直角三角形,∴90BAD ∠=︒,90EAP ∠=︒,AB AD =,AE AP =,45APE AEP ∠=∠=︒, ∴EAB PAD ∠=∠,∴()ABE ADP SAS ≅,∴180********AEB APD APE ∠=∠=︒-∠=︒-︒=︒,∴1354590PEB AEB AEP ∠=∠-∠=︒-︒=︒,∴222PE BE PB +=,∵2AE AP ==,90EAP ∠=︒, ∴22PE AE ==, ∴()22227BE +=, 解得:3BE =,作BH ⊥AE 交AE 的延长线于点H ,∵45AEP ∠=︒,90PEB ∠=︒, ∴180180904545HEB PEB AEP ∠=︒-∠-∠=︒-︒-︒=︒,∴26sin 453HB BE =︒==, ∴点B 到直线AE 6,故①错误; ②由①知:ABE ADP ≅,2EP =,3BE =∴APD ABP ABE APB S S S S ∆∆∆∆+=+AEP BEP S S ∆∆=+1122AE AP PE EB =⨯⨯+⨯⨯ 11222322=⨯ 13=,故②正确;③在Rt AHB 中,由①知:6EH HB ==∴62AH AE EH =+=,22222256623AB AH BH ⎛⎫⎛⎫=+=++=+ ⎪ ⎪ ⎪ ⎪⎭⎝⎭,21153222ABD S AB AD AB ∆=⋅==+,故③正确; ④因为AC 是定值,所以当A P C 、、共线时,PC 最小,如图,连接BC ,∵A C 、关于 BD 的对称,∴523AB BC ==+ ∴225231043AC BC ==+=+∴ min PC AC AP =-,10432=+⑤∵ABD 与AEP 都是等腰直角三角形,∴90BAD ∠=︒,90EAP ∠=︒,AB AD =,AE AP =, 在ABP 和ADE 中,AB AD BAP DAE AP AE =⎧⎪∠=∠⎨⎪=⎩,∴()ABP ADE SAS ≅,∴ABP ADE ∠=∠,∵AN BN =,∴ABP NAB ∠=∠,∴EAN ADE ∠=∠,∵90EAN DAN ∠+∠=︒,∴90ADE DAN ∠+∠=︒,∴AN DE ⊥,故⑤正确;综上,②③⑤正确,故答案为:②③⑤.【点睛】本题是三角形的综合题,主要考查了等腰直角三角形的性质,全等三角形的判定和性质,勾股定理的应用,三角形的面积公式,综合性强,全等三角形的判定和性质的灵活运用是解题的关键.27.(1)该命题是真命题,理由见解析;(2)①a 的值为92;②k 的取值范围为13k ≤<;(3)ABC ∆的面积为2033或1235. 【分析】 (1)根据等边三角形的性质、优三角形和优比的定义即可判断;(2)①先利用勾股定理求出c 的值,再根据优三角形的定义列出,,a b c 的等式,然后求解即可;②类似①分三种情况分析,再根据三角形的三边关系定理得出每种情况下,,a b c 之间的关系,然后根据优比的定义求解即可;(3)如图(见解析),设BD x =,先利用直角三角形的性质、勾股定理求出AC 、AB 的长及ABC ∆面积的表达式,再类似(2),根据优三角形的定义分三种情况分别列出等式,然后解出x 的值,即可得出ABC ∆的面积.【详解】(1)该命题是真命题,理由如下:设等边三角形的三边边长为a则其中两条边的和为2a ,恰好是第三边a 的2倍,满足优三角形的定义,即等边三角形为优三角形又因该两条边相等,则这两条边的比为1,即其优比为1故该命题是真命题;(2)①90,6CB b A ∠=︒=22236c a b a ∴=++根据优三角形的定义,分以下三种情况:当2a b c +=时,26236a a +=+,整理得24360a a -+=,此方程没有实数根。
八年级第二学期3月份月考数学试卷及解析

A. B. C. D.
11.已知实数x、y满足 ,则yx值是()
A.﹣2B.4C.﹣4D.无法确定
12.下列运算正确的是()
A. B. C. D.
二、填空题
13.已知a,b是正整数,且满足 是整数,则这样的有序数对(a,b)共有____对.
14.化简 ___________.
【答案】(1)6 ﹣3 ;(2)-6(3)甲的方差1.65;乙的方差0.76
【解析】
试题分析:(1)先去括号,再合并;
(2)先进行二次根式的乘法运算,然后去绝对值合并;
(3)先分别计算出甲乙的平均数,然后根据方差公式分别进行甲乙的方差.
试题解析:(1)原式=4 ﹣3 +2
=6 ﹣3 ;
(2)原式= ﹣3﹣2 + ﹣3
八年级第二学期3月份月考数学试卷及解析
一、选择题
1.若 ,则 的值用 、 可以表示为 ( )
A. B. C. D.
2.对于所有实数a,b,下列等式总能成立的是()
A. B.
C. D.
3.下列计算正确的是()
A. B.
C. D.
4. 的倒数是()
A. B. C. D.
5.下列式子中,是二次根式的是()
所以a-2=- .
所以(a-2)2=3,即a2-4a+4=3.
所以a2-4a=-1.
所以2a2-8a+1=2(a2-4a)+1=2×(-1)+1=-1.
请你根据小明的分析过程,解决如下问题:
(1)计算: =-.
(2)计算: +…+ ;
(3)若a= ,求4a2-8a+1的值.
【答案】(1) ,1;(2) 9;(3) 5
八年级第二学期3月份 月考检测数学试卷含答案

一、选择题1.若5,a =17=b ,则0.85的值用a 、b 可以表示为 ( ) A .10a b+ B .10-b aC .10ab D .b a2.若2a <,化简()223a --=( )A .5a -B .5a -C .1a -D .1a --3.计算32782-⨯的结果是( ) A .3B .3-C .23D .534.下列计算正确的是( ) A .2×3=6B .2+3=5C .8=42D .4﹣2=25.已知x 1=3+2,x 2=3-2,则x₁²+x₂²等于( ) A .8B .9C .10D .116.下列各式中,正确的是( ) A .42=±B .822-=C .()233-=- D .342=7.下列算式:(1)257+=;(2)5x 2x 3x -=;(3)8+502=4257+=;(4)33a 27a 63a +=,其中正确的是( ) A .(1)和(3) B .(2)和(4)C .(3)和(4)D .(1)和(4)8.下列计算不正确的是 ( )A .35525-=B .236⨯=C .7742=D .363693+=+==9.下列二次根式中,与3是同类二次根式的是( ) A .18B .13C 24D 0.310.使式子2124x x +-x 的取值范围是( ) A .x≥﹣2B .x >﹣2C .x >﹣2,且x ≠2D .x≥﹣2,且x ≠2二、填空题11.已知112a b +=,求535a ab b a ab b++=-+_____.12.已知2216422x x ---=,则22164x x -+-=________. 13.(1)已知实数a 、b 在数轴上的位置如图所示,化简()222144a a ab b +--+=_____________;(2)已知正整数p ,q 满足32016p q +=,则整数对()p q ,的个数是_______________;(3)△ABC 中,∠A=50°,高BE 、CF 所在的直线交于点O,∠BOC 的度数__________. 14.设12211112S =++,22211123S =++,32211134S =++,设12...n S S S S =+++,则S=________________ (用含有n 的代数式表示,其中n 为正整数).15.为了简洁、明确的表示一个正数的算术平方根,许多数学家进行了探索,期间经历了400余年,直至1637年法国数学家笛卡儿在他的《几何学》中开始使用“”表示算数平方根.我国使用根号是由李善兰(1811-1882年)译西方数学书时引用的,她在《代数备旨》中把图1所示题目翻译为: 22164?a x a x +=则图2所示题目(字母代表正数)翻译为_____________,计算结果为_______________.16.把1m m-_____________. 17.若a 、b 、c 均为实数,且a 、b 、c 均不为043252a cb=___________ 18.已知整数x ,y 满足20172019y x x =+--,则y =__________.19.28n n 为________.20.古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形的三边求面积的公式,称为海伦—秦九韶公式:如果一个三角形的三边长分别是a ,b ,c ,记2a b cp ++=,那么三角形的面积()()()S p p a p b p c =---ABC 中,A ∠,B ,C ∠所对的边分别记为a ,b ,c ,若4a =,5b =,7c =,则ABC 面积是_______.三、解答题21.先观察下列等式,再回答问题:=1+1=2;12=2 12;=3+13=313;… (1)根据上面三个等式提供的信息,请猜想第四个等式;(2)请按照上面各等式规律,试写出用 n (n 为正整数)表示的等式,并用所学知识证明.【答案】(1=144+=144;(2=211n n n n++=,证明见解析. 【分析】(1)根据“第一个等式内数字为1,第二个等式内数字为2,第三个等式内数字为3”,=414+=414;(2=n 211n n n++=”,再利用222112n n n n++=+()()开方即可证出结论成立.【详解】(1=1+1=2=212+=212;=313+=313;里面的数字分别为1、2、3,= 144+= 144.(2=1+1=2,=212+=212=313+=313=414+=414= 211n n n n++=.证明:等式左边==n 211n n n++==右边.=n 211n n n++=成立. 【点睛】本题考查了二次根式的性质与化简以及规律型中数的变化类,解题的关键是:(1)猜测出第四个等式中变化的数字为4;(2)找出变化规律=n 211n n n++=”.解决该题型题目时,根据数值的变化找出变化规律是关键.22.已知m ,n 满足m 4n=3+.【答案】12015【解析】 【分析】由43m n +=2﹣2)﹣3=0,将,代入计算即可.【详解】解:∵4m n +=3,)22﹣2)﹣3=0,)2﹣23=0,+13)=0,=﹣13,∴原式=3-23+2012=12015.【点睛】本题主要考查二次根式的混合运算,解题的关键是熟练掌握完全平方公式的运用及二次根式性质.23.解:设x222x =++2334x =+,x 2=10 ∴x =10.0.【分析】根据题意给出的解法即可求出答案即可. 【详解】设x两边平方得:x 2=2+2+即x 2=4+4+6, x 2=14∴x =.0,∴x . 【点睛】本题考查了二次根式的运算,解题的关键是正确理解题意给出的解法,本题属于中等题型.24.在学习了二次根式后,小明同学发现有的二次根式可以写成另一个二次根式的平方的形式.比如:2224312111-=-=-+=).善于动脑的小明继续探究:当a b m n 、、、为正整数时,若2a n +=+),则有22(2a m n =+,所以222a m n =+,2b mn =.请模仿小明的方法探索并解决下列问题:(1)当a b m n 、、、为正整数时,若2a n =+),请用含有mn 、的式子分别表示a b 、,得:a = ,b = ;(2)填空:13-( - 2;(3)若2a m +=(),且a m n 、、为正整数,求a 的值.【答案】(1)223a m n =+,2b mn =;(2)213--;(3)14a =或46. 【解析】 试题分析:(1)把等式)2a n +=+右边展开,参考范例中的方法即可求得本题答案;(2)由(1)中结论可得:2231324a m n b mn ⎧=+=⎨==⎩,结合a b m n 、、、都为正整数可得:m=2,n=1,这样就可得到:213(1-=-;(3)将()2a m +=+右边展开,整理可得:225a m n =+,62mn =结合a m n 、、为正整数,即可先求得m n 、的值,再求a 的值即可.试题解析:(1)∵2a n =+),∴223a m n +=++, ∴2232a m n b mn =+=,;(2)由(1)中结论可得:2231324a m nb mn ⎧=+=⎨==⎩ ,∵a b m n 、、、都为正整数,∴12m n =⎧⎨=⎩ 或21m n =⎧⎨=⎩ , ∵当m=1,n=2时,223713a m n =+=≠,而当m=2,n=1时,22313a m n =+=, ∴m=2,n=1,∴(2131--;(3)∵222()52a m m n +=+=++ ∴225a m n =+,62mn = , 又∵a m n 、、为正整数, ∴=1=3m n ,, 或者=3=1m n ,,∴当=1=3m n ,时,46a =;当=3=1m n ,,14a =, 即a 的值为:46或14.25.小明在解决问题:已知2a 2﹣8a+1的值,他是这样分析与解的:∵=2 ∴a﹣2=∴(a ﹣2)2=3,a 2﹣4a+4=3 ∴a 2﹣4a=﹣1∴2a 2﹣8a+1=2(a 2﹣4a )+1=2×(﹣1)+1=﹣1 请你根据小明的分析过程,解决如下问题:(1(2)若,求4a2﹣8a+1的值.【答案】(1)9;(2)5.【解析】试题分析:(1)此式必须在把分母有理化后才能实现化简,即各分式分子分母同乘以一个因式,使得1===.(2)先对a1,若就接着代入求解,计算量偏大.模仿小明做法,可先计算2(1)a-的值,就能较为简单地算出结果;也可对这个二次三项式进行配方,再代入求值.后两种方法都比直接代入计算量小很多.解:(1)原式=1)+++⋯(2)∵1a===,解法一:∵22(1)11)2a-=-=,∴2212a a-+=,即221a a-=∴原式=24(2)14115a a-+=⨯+=解法二∴原式=24(211)1a a-+-+24(1)3a=--211)3=--4235=⨯-=点睛:(1得22=-=-a b,去掉根号,实现分母有理化.(2)当已知量为根式时,求这类二次三项式的值,直接代入求值,计算量偏大,若能巧妙利用完全平方公式或者配方法,计算要简便得多.26.先化简,再求值:a,其中【答案】2a-1,【分析】先根据二次根式的性质进行化简,再代入求值即可.【详解】解:1a =-∴原式=1a a --=21a -当1a =-∴原式=(211-=1-【点睛】此题主要考查化简求值,正确理解二次根式的性质是解题关键.27.(1)计算:21)-(2)已知a ,b 是正数,4a b +=,8ab =【答案】(1)5-2 【分析】(1)根据完全平方公式、平方差公式可以解答本题;(2)先将所求式子化简,然后将a+b=4,ab=8代入化简后的式子即可解答本题. 【详解】解:(1)原式21)=-(31)(23)=---5=-;(2)原式=== a ,b 为正数, ∴原式=把4a b +=,8ab =代入,则原式== 【点睛】本题考查二次根式的化简求值,完全平方公式、平方差公式,解答本题的关键是明确二次根式化简求值的方法.28.2020(1)- 【答案】1 【分析】先计算乘方,再化简二次根式求解即可. 【详解】2020(1)-=1 =1. 【点睛】本题考查了二次根式的混合运算,先把二次根式化为最简二次根式,再合并即可.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】化简即可. 【详解】=1010ab. 故选C . 【点睛】的形式. 2.D解析:D 【分析】||a =,然后再根据a 的范围去掉绝对值后即可求解. 【详解】|2|=-a ,且2a <,∴|2|2=-=-+a a ,原式|2|3231=--=-+-=--a a a , 故选:D . 【点睛】||a =这个公式是解决本题的关键.3.A解析:A 【分析】先计算二次根式乘法,再合并同类二次根式即可. 【详解】原式= 故选:A . 【点睛】本题考查二次根式的运算,熟练掌握运算法则是解题关键.4.A解析:A 【解析】分析:根据二次根式的加、减、乘、除的法则计算逐一验证即可.详解: , 此选项正确;≠此选项错误;, 此选项错误;,此选项错误.故选A.点睛:本题考查了二次根式的混合运算,掌握二次根式的运算法则是解题的关键.5.C解析:C 【详解】12x x +==12321x x ==-=,所以()2221212122x x x x x x +=+-=(22112210-⨯=-=,故选:C . 【点睛】对于形如2212x x +的式子,改变其中两个字母的位置后,并不改变代数式的值,通常将具有这个特点的代数式称为轮换对称式,如1211+x x ,1221x x x x +,12x x -等,轮换对称式都可以用12x x +,12x x 来表示,所以求轮换对称式的值,一般是先将式子用12x x +,12x x 来表示,然后再整体代入计算.6.B解析:B【分析】本题可利用二次根式的化简以及运算法则判断A 、B 、C 选项;利用立方根性质判断D 选项.【详解】A,故该选项错误;B==C3=,故该选项错误; D 11223334=(2)2==,故该选项错误;故选:B .【点睛】本题考查二次根式以及立方根,二次根式计算时通常需要化为最简二次根式,然后按照运算法则求解即可,解题关键是细心.7.B解析:B【分析】根据二次根式的性质和二次根式的加法运算,分别进行判断,即可得到答案.【详解】(1(2),正确;(3,错误;(4)==故选:B .【点睛】本题考查了二次根式的加法运算,二次根式的性质,解题的关键是熟练掌握运算法则进行解题.8.D解析:D【解析】根据二次根式的加减法,合并同类二次根式,可知=故正确;=根据二次根式的性质和化简,=,故正确;根据二次根式的加减,不是同类二次根式,故不正确.故选D.9.B解析:B【详解】A不是同类二次根式,故此选项错误;B=不是同类二次根式,故此选项错误;CD不是同类二次根式,故此选项错误;故选B.10.C解析:C【分析】根据分式和二次根式有意义的条件(分式的分母不为零,二次根式的被开方数为非负数)即可得到结果.【详解】≠,解:由题意得:2x-40x∴≠±,2x+≥,又∵20∴x≥-2.x≠.∴x的取值范围是:x>-2且2故选C.【点睛】本题考查了分式和二次根式有意义的条件,解不等式,是基础题.二、填空题11.13【解析】【分析】由得a+b=2ab,然后再变形,最后代入求解即可.【详解】解:∵∴a+b=2ab∴故答案为13.【点睛】本题考查了已知等式求代数式的值,解答的关键是通过变形找解析:13【解析】【分析】 由112a b +=得a+b=2ab ,然后再变形535a ab b a ab b++-+,最后代入求解即可. 【详解】 解:∵112a b+= ∴a+b=2ab ∴()5353510ab 3===132ab a b ab a ab b ab a ab b a b ab ab+++++-++-- 故答案为13. 【点睛】本题考查了已知等式求代数式的值,解答的关键是通过变形找到等式和代数式的联系. 12.3【解析】设,则 可化为:,∴,两边同时平方得:,即:,∴,解得:,∴.故答案为:.点睛:本题的解题要点是:设原式中的,从而使原式结构变得简单,这样应用二次根式的相关运算法则化简变形解析:【解析】设24x a -====两边同时平方得:128a a +=++4=,∴3216a =,解得:12a =,===故答案为: 点睛:本题的解题要点是:设原式中的24x a -=,从而使原式结构变得简单,这样应用二次根式的相关运算法则化简变形即可求得a 的值,使问题得到解决.13.(1)2a -2b +1;(2)3;(3)130°或50°. 【解析】(1)∵-1<a<0,b>1,∴=|a+1|-|a-2b|=1+a-2b+a=2a-2b+1.(2)∵,∴,p=20解析:(1)2a -2b +1;(2)3;(3)130°或50°.【解析】(1)∵-1<a<0,b>1,=|a+1|-|a-2b|=1+a-2b+a=2a-2b+1.(2)==∴p=14x 3(其中x 为正整数),同理可得:q=14y 2(其中y 为正整数),则x+3y=12(x 、y 为正整数)∴963,,123x x x y y y ===⎧⎧⎧⎨⎨⎨===⎩⎩⎩, ∴整数对有(p,q )=(14⨯81,141⨯),或(1436,144)⨯⨯ ,或(149,149⨯⨯)。
人教版八年级数学第二学期3月份月考测试卷含答案

人教版八年级数学第二学期3月份月考测试卷含答案一、选择题1.下列计算正确的是( ) A .=1212⨯B .4-3=1C .63=2÷D .8=2±2.下列计算正确的是( ) A .336+=B .3323+=C .336⨯=D .3333+=3.下列方程中,有实数根的方程是( ) A .240x += B .210x -+= C .12x +=D .331x x -+-=.4.下列各式中,运算正确的是( )A .32222-=B .8383-=-C .2323+=D .()222-=-5.已知2225152x x ---=,则222515x x -+-的值为( ) A .3B .4C .5D .66.下列计算或判断:(1)±3是27的立方根;(2)33a =a ;(3)64的平方根是2;(4)22(8)±=±8;(5)65- =65+,其中正确的有( ) A .1个B .2个C .3个D .4个 7.若实数a ,b 满足+=3,﹣=3k ,则k 的取值范围是( )A .﹣3≤k ≤2B .﹣3≤k ≤3C .﹣1≤k ≤1D .k ≥﹣1 8.下列各式计算正确的是( )A 235+=B .236=()C 824=D 236=9.下列计算正确的是( ) A 235=B 623=C 23(3)86-=-D 321=10.下列计算正确的是( ) A .333=1B 23=5C .12=22D .322=52+11.下列二次根式中是最简二次根式的是( ) A 6B 18C 27D 1212.与根式1x-- ) A .xB .x x --C .x --D x -二、填空题13.若a ,b ,c是实数,且10a b c ++=,则2b c +=________.14.实数a 、b10-b 4-b-2=+,则22a b +的最大值为_________.15.已知实数m 、n 、p满足等式,则p =__________.16.把 17_____. 18.已知x,y,则x 2+xy +y 2的值为______. 19.如果0xy >.20.观察分析下列数据:0,,-3,的规律得到第10个数据应是__________.三、解答题21.阅读材料,回答问题:两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们就说这两个代数式a =,)111=11互为有理化因式.(1)1的有理化因式是 ;(2)这样,化简一个分母含有二次根式的式子时,采用分子、分母同乘以分母的有理化因式的方法就可以了,例如:3==,25384532++====-进行分母有理化. (3)利用所需知识判断:若a =,2b =ab ,的关系是 . (4)直接写结果:)1=.【答案】(1)1;(2)7-;(3)互为相反数;(4)2019【分析】(1)根据互为有理化因式的定义利用平方差公式即可得出;(2)原式分子分母同时乘以分母的有理化因式(2,化简即可;(3)将a=(4)化简第一个括号内的式子,里面的每一项进行分母有理化,然后利用平方差公式计算即可.【详解】解:(1)∵()()1111=,∴1的有理化因式是1;(22243743--==--(3)∵2a===,2b=-,∴a和b互为相反数;(4))1 ++⨯=)11⨯=)11=20201-=2019,故原式的值为2019.【点睛】本题考查了互为有理化因式的定义及分母有理化的方法,并考查了利用分母有理化进行计算及探究相关式子的规律,本题属于中档题.22.先观察下列等式,再回答问题:=1+1=2;12=212;=3+13=313;…(1)根据上面三个等式提供的信息,请猜想第四个等式;(2)请按照上面各等式规律,试写出用 n (n 为正整数)表示的等式,并用所学知识证明.【答案】(1=144+=144;(2=211n n n n++=,证明见解析. 【分析】(1)根据“第一个等式内数字为1,第二个等式内数字为2,第三个等式内数字为3”,=414+=414;(2=n 211n n n++=”,再利用222112n n n n++=+()()开方即可证出结论成立.【详解】(1=1+1=2=212+=212;=313+=313;里面的数字分别为1、2、3,= 144+= 144.(2=1+1=2,=212+=212=313+=313=414+=414= 211n n n n++=.证明:等式左边==n 211n n n++==右边.=n 211n n n++=成立. 【点睛】本题考查了二次根式的性质与化简以及规律型中数的变化类,解题的关键是:(1)猜测出第四个等式中变化的数字为4;(2)找出变化规律=n 211n n n++=”.解决该题型题目时,根据数值的变化找出变化规律是关键.23.阅读下面的解答过程,然后作答:m 和n ,使m 2+n 2=a 且,则a 可变为m 2+n 2+2mn ,即变成(m +n )2例如:∵=)2+)2=)2∴请你仿照上例将下列各式化简(12【答案】(1)2-【分析】参照范例中的方法进行解答即可. 【详解】解:(1)∵22241(1+=+=,1=(2)∵2227-=-=,∴==24.观察下列等式:1==;==== 回答下列问题:(1(2)计算:【答案】(1(2)9 【分析】(1)根据已知的31=-n=22代入即可求解;(2)先利用上题的规律将每一个分数化为两个二次根式的差的形式,再计算即可. 【详解】解:(1=(2+99+=1100++-=1 =10-1 =9.25.【分析】先化为最简二次根式,再将被开方数相同的二次根式进行合并. 【详解】. 【点睛】本题考查了二次根式的加减运算,在进行此类运算时,先把二次根式化为最简二次根式的形式后再运算.26.先观察下列等式,再回答下列问题:111111112=+-=+;111112216=+-=+1111133112=+-=+(1) (2)请你按照上面各等式反映的规律,用含n 的等式表示(n 为正整数).【答案】(1)1120(2)()111n n ++(n 为正整数)【解析】试题分析:(1)从三个式子中可以发现,第一个加数都是1,第二个加数是个分数,设分母为n,第三个分数的分母就是n+1,结果是一个带分数,整数部分是1,分数部分的分子也是1,分母是前项分数的分母的积.所以由此可计算给的式子;(2)根据(1)找的规律写出表示这个规律的式子.试题解析:(1)=1+14−141+=1120,1 1 20(2)1n−1n1+=1+()1n n1+ (n为正整数).a=,也考查了二次根式的运算.此题是一道阅读题目,通过阅读找出题目隐含的条件.总结:找规律的题目,都要通过仔细观察找出和数之间的关系,并用关系式表示出来.27.观察下列一组等式,然后解答后面的问题1)1=,1=,1=,1=⋯⋯(1)观察以上规律,请写出第n个等式:(n为正整数).(2(3【答案】(1)1=;(2)9;(3【分析】(1)根据规律直接写出,(2)先找出规律,分母有理化,再化简计算.(3)先对两个式子变形,分子有理化,变为分子为1,再比大小.【详解】解:(1)根据题意得:第n个等式为1=;故答案为1=;(2)原式111019==-=;(3-==,<∴>.【点睛】本题是一道利用规律进行求解的题目,解题的关键是掌握平方差公式.28.计算:(1;(2+2)2+2).【答案】(1-2)【分析】(1)直接化简二次根式进而合并得出答案; (2)直接利用乘法公式计算得出答案. 【详解】解:(1)原式=-(2)原式=3434++-=6+. 【点睛】本题考查了二次根式的运算,在进行二次根式运算时,可以运用乘法公式,运算率简化运算.29.(1|5-+;(2)已知实数a 、b 、c 满足|3|a +=,求2(b a +的值.【答案】(1)5;(2)4 【分析】(1)先利用二次根式的乘法法则和绝对值的意义计算,再进行回头运算即可; (2)先根据二次根式有意义的条件确定b 的值,再根据非负数的和的意义确定a ,c 的值,然后再计算代数式的值即可. 【详解】解:(15-+5)=+5=+5=(2)由题意可知:50 50 bb-≥⎧⎨-≥⎩,解得5b=由此可化简原式得,30a+=30a∴+=,20c-=3a∴=-,2c=22((534b a∴+=--=【点睛】可不是考查了二次根式的混合运算以及二次根式的化简求值,熟练掌握运算法则和运算顺序是解答此题的关键.30.计算:(1)-(2)【答案】(1)21【分析】(1)先把二次根式化为最简二次根式,然后合并即可;(2)先利用二次根式的乘除法则运算,再合并即可.【详解】解:(1)原式==(2)原式3+21==.【点睛】本题考查二次根式的混合运算:在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【解析】2÷故选A.2.B解析:B【分析】根据二次根式加法法则,二次根式的乘法法则计算后判断即可得到答案.【详解】=,=3∴A、C、D均错误,B正确,故选:B.【点睛】此题考查二次根式的加法法则,二次根式的乘法法则,熟记计算法则是正确解题的关键. 3.C解析:C【分析】=的形式,再根据二次根式成立的条件逐个进行判断即可.k【详解】解:A、x2+4=0,此时方程无解,故本选项错误;B10=,-,1∵算术平方根是非负数,∴此时方程无解,故本选项错误;C2=,∴x+1=4,∴x=3,故本选项正确;D1=,∴x-3≥0且3-x≥0,解得:x=3,代入得:0+0=1,此时不成立,故本选项错误;故选:C.【点睛】本题考查了二次根式的意义,能根据二次根式成立的条件进行判断是解此题的关键.4.A解析:A【分析】由合并同类项、二次根式的性质分别进行判断,即可得到答案.【详解】解:A、-=A正确;B=B错误;C、2不能合并,故C错误;D、()222-=,故D错误;故选:A.【点睛】本题考查了二次根式的性质,合并同类项,解题的关键是熟练掌握运算法则进行解题.5.C解析:C【解析】∵22---=,x x251522222222222 (2515)(2515)(25)(15)251510 ----+-=---=--+=x x x x x x x x,∴22-+-=.25155x x故选C.6.B解析:B【解析】根据立方根的意义,可知27的立方根是3,故(1)不正确;33a a=正确,故(2)正确;由64=8,可知其平方根为±22,故(3)不正确;根据算术平方根的意义,可知=+,故2288(),故(4)不正确;根据分母有理化的意义,可知65±=6-5(5)正确.故选B.7.C解析:C【解析】依据二次根式有意义的条件即可求得k的范围.解:若实数a,b满足+=3,又有≥0,≥0,故有0≤≤3 ①,0≤≤3,则﹣3≤-≤0 ②+②可得﹣3≤﹣≤3,又有﹣=3k,即﹣3≤3k≤3,化简可得﹣1≤k≤1.故选C.点睛:本题主要考查了二次根式的意义和性质.解题的关键在于二次根式具有双非负性,即≥0(a≥0),利用其非负性即可得到0≤≤3,0≤≤3,并对0≤≤3变形得到﹣3≤-≤0,进而即可转化为关于k的不等式组,求出k的取值范围.8.D解析:D【分析】根据二次根式的运算法则一一判断即可.【详解】AB、错误,212(;=C==D==故选:D.【点睛】本题考查二次根式的运算,解题的关键是熟练掌握二次根式的加减乘除运算法则,属于中考常考题型.9.B解析:B【分析】根据二次根式加减运算和二次根式的性质逐项排除即可.【详解】与A选项错误;===B选项正确;=-=,所以C选项错误;321与D选项错误;故选答案为B.【点睛】本题考查了二次根式加减运算和二次根式的性质,掌握同类二次根式的定义和二次根式的性质是解答本题的关键.10.C解析:C【解析】分析:根据二次根式的四则混合运算法则,二次根式的性质与化简逐项进行分析解答即可.详解:A.=,故本选项错误;B.不是同类二次根式,不能进行合并,故本选项错误;C.正确;D.不是同类二次根式,不能进行合并,故本选项错误.故选C.点睛:本题主要考查二次根式的化简,二次根式的四则运算法则,解题的关键是正确根据相关法则逐项进行分析解答.11.A解析:A【分析】根据最简二次根式的定义判断即可.【详解】A 是最简二次公式,故本选项正确;BCD =故选A .【点睛】本题考查了最简二次根式,掌握最简二次根式的定义是解题的关键.12.D解析:D【分析】先化简二次根式,再计算二次根式的乘法即可.【详解】由题意可得x 是负数,所以-x x-⋅=- 故选:D .【点睛】此题考查二次根式的化简,二次根式的乘法计算法则,正确化简二次根式是解题的关键,注意题目中x 的符号是负号,这是解题的难点. 二、填空题13.21【分析】结合态,根据完全平方公式的性质,将代数式变形,即可计算得,,的值,从而得到答案.【详解】∵∴∴∴∴∴∴∴.【点睛】本题考查了二次根式、完全平方公式的知识;解题的解析:21【分析】结合态,根据完全平方公式的性质,将代数式变形,即可计算得a ,b ,c 的值,从而得到答案.【详解】∵10a b c ++=∴100a b c ---=∴2221490⎡⎤⎡⎤⎡⎤-+-+-=⎣⎦⎣⎦⎣⎦∴2221)2)3)0++=∴123=== ∴111429a b c -=⎧⎪-=⎨⎪-=⎩∴2511a b c =⎧⎪=⎨⎪=⎩∴2251121b c +=⨯+=.【点睛】本题考查了二次根式、完全平方公式的知识;解题的关键是熟练掌握二次根式、完全平方公式、一元一次方程的性质,从而完成求解.14.【分析】首先化简,可得|a-2|+|a-6|+|b+4|+|b-2|=10,然后根据|a-2|+|a-6|≥4,|b+4|+|b-2|≥6,判断出a ,b 的取值范围,即可求出的最大值.【详解】解析:【分析】10-b 4-b-2=+,可得|a-2|+|a-6|+|b+4|+|b-2|=10,然后根据|a-2|+|a-6|≥4,|b+4|+|b-2|≥6,判断出a ,b 的取值范围,即可求出22a b +的最大值.【详解】10-b 4-b-2=+,1042b b =-+--, ∴261042a a b b -+-=-+--, ∴264210a a b b -+-+++-=,∵264a a -+-≥,426b b ++-≥,∴ 264a a -+-=,42=6b b ++-,∴2≤a≤6,-4≤b≤2,∴22a b +的最大值为()226452+-=,故答案为52.【点睛】本题考查了二次根式的性质与化简,绝对值的意义,算术平方根的性质.解题的关键是要明确化简二次根式的步骤:①把被开方数分解因式;②利用算术平方根的性质,把被开方数中能开得尽方的因数(或因式)都开出来;③化简后的二次根式中的被开方数中每一个因数(或因式)的指数都小于根指数2. 15.5【解析】试题解析:由题可知,∴,∴,∴,①②得,,解方程组得,∴.故答案为:5.解析:5【解析】试题解析:由题可知3030m n m n -+≥⎧⎨--≥⎩, ∴3m n +=,0=,∴35200m n p m n p +--=⎧⎨--=⎩①②,①-②得2620m n +-=,31m n +=,解方程组331m n m n +=⎧⎨+=⎩得41m n =⎧⎨=-⎩, ∴4(1)5p m n =-=--=.故答案为:5.16.﹣【解析】解:通过有意义可以知道≤0,≤0,所以=﹣=﹣.故答案为:.点睛:此题主要考查了二次根式的性质应用,正确判断二次根式的整体符号是解题关键.解析:【解析】解:通过a ≤0,,所以故答案为:点睛:此题主要考查了二次根式的性质应用,正确判断二次根式的整体符号是解题关键. 17.6【分析】利用二次根式乘除法法则进行计算即可.【详解】===6,故答案为6.【点睛】本题考查了二次根式的乘除法,熟练运用二次根式的乘除法法则是解题的关键.解析:6【分析】==进行计算即可.【详解】=6,故答案为6.【点睛】本题考查了二次根式的乘除法,熟练运用二次根式的乘除法法则是解题的关键. 18.4【详解】根据完全平方公式可得:原式=-xy==5-1=4.解析:4【详解】根据完全平方公式可得:原式=2()x y +-xy=251515151)222=5-1=4. 19.【分析】由,且,即知,,据此根据二次根式的性质化简可得. 【详解】∵,且,即,∴,,∴,故答案为:.【点睛】本题主要考查了二次根式的性质与化简,熟练掌握二次根式的性质是解题的关键.解析:-【分析】由0xy >,且20xy -≥,即•0y xy -≥知0x <,0y <,据此根据二次根式的性质化简可得.【详解】∵0xy >,且20xy -≥,即•0y xy -≥, ∴0x <,0y <,==-故答案为:-【点睛】本题主要考查了二次根式的性质与化简,熟练掌握二次根式的性质是解题的关键. 20.6【分析】通过观察可知,根号外的符号以及根号下的被开方数依次是:,,…,可以得到第13个的答案.【详解】解:由题意知道:题目中的数据可以整理为:,,…,∴第13个答案为:.故答案为6.解析:6【分析】 通过观察可知,根号外的符号以及根号下的被开方数依次是:11(1)30,21(1)31,31(1)32…1(1)3(1)n n ,可以得到第13个的答案.【详解】 解:由题意知道:题目中的数据可以整理为:11(1)30,21(1)31,31(1)32…1(1)3(1)n n ,∴第13个答案为:131(1)3(131)6.故答案为6.【点睛】此题主要考查了二次根式的运算以及学生的分析、总结、归纳的能力,规律型的习题一般是从所给的数据和运算方法进行分析,从特殊值的规律上总结出一般性的规律. 三、解答题21.无22.无23.无24.无25.无26.无27.无28.无29.无30.无。
八年级第二学期3月份 月考检测数学试题含答案

17.如图,把平面内一条数轴 x 绕点 O 逆时针旋转角 θ(0°<θ<90°)得到另一条数轴 y,x 轴和 y 轴构成一个平面斜坐标系.规定:已知点 P 是平面斜坐标系中任意一点,过点 P 作 y 轴的平行线交 x 轴于点 A,过点 P 作 x 轴的平行线交 y 轴于点 B,若点 A 在 x 轴上对 应的实数为 a,点 B 在 y 轴上对应的实数为 b,则称有序实数对(a,b)为点 P 的斜坐
C. 25cm
D. 40cm
2.如图,西安路与南京路平行,并且与八一街垂直,曙光路与环城路垂直.如果小明站在
南京路与八一街的交叉口,准备去书店,按图中的街道行走,最近的路程约为( )
A.600m
B.500m
C.400m
D.300m
3.如图,已知 MON 45 ,点 A、B 在边 ON 上, OA 3,点 C 是边 OM 上一个动点,
若 ABC 周长的最小值是 6,则 AB 的长是( )
A. 1 2
B. 3 4
C. 5 6
D.1
4.如图,P 为等边三角形 ABC 内的一点,且 P 到三个顶点 A,B,C 的距离分别为
3,4,5,则△ABC 的面积为( )
A. 9 25 3 4
B. 9 25 3 2
C.18 25 3
D.18 25 3 2
一、选择题 1.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为15cm ,在容器内壁离容器 底部 3cm 的点 B 处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿 3cm 的 点 A 处,若蚂蚁吃到蜂蜜需爬行的最短路径为 25cm ,则该圆柱底面周长为( )
八年级第二学期3月份月考数学试卷含解析

八年级第二学期3月份月考数学试卷含解析一、选择题1.下列计算正确的是( )A =B .3=C 2=D 2.对于所有实数a ,b ,下列等式总能成立的是( )A .2a b =+ B 22a b =+C a b =+D a b =+3.下列各式成立的是( )A 3=B 3=C .22(3=- D .2-=4. )A B C D5. ) A .-3B .3或-3C .9D .36.x 的取值范围是( ) A .x≥2020B .x≤2020C .x> 2020D .x< 20207.a b =--则( ) A .0a b +=B .0a b -=C .0ab =D .220a b +=8.已知a 满足2018a -a ,则a -2 0182=( ) A .0B .1C .2 018D .2 0199.设0a >,0b >=的值是( ) A .2B .14C .12D .315810.2的结果是( ) A .±3B .﹣3C .3D .911.已知实数x 、y 满足2y =,则yx 值是( )A .﹣2B .4C .﹣4D .无法确定12.下列运算中正确的是( )A .=B===C 3===D 1==二、填空题13.化简并计算:...+=________.(结果中分母不含根式)14.3=,且01x <<=______.15.若6x ,小数部分为y ,则(2x y 的值是___.16.已知a ,b 是正整数,若有序数对(a ,b )使得的值也是整数,则称(a ,b )是的一个“理想数对”,如(1,4)使得=3,所以(1,4)是的一个“理想数对”.请写出其他所有的“理想数对”: __________. 17.已知整数x ,y 满足y =,则y =__________.18.已知实数m 、n 、p 满足等式,则p =__________.19.有意义,则x 的取值范围是____.20.mn =________.三、解答题21.阅读下面问题: 阅读理解:==1;==2==-.应用计算:(1(21(n 为正整数)的值.归纳拓展:(398++【答案】应用计算:(12 归纳拓展:(3)9. 【分析】由阅读部分分析发现式子的分子、分母都乘以分母的有理化因式,为此(1分母利用平方差公式计算即可,(2(3)根据分母的特点各项分子分母乘以各分母的有理化因式,分母用公式计算化去分母,分子合并同类项二次根式即可. 【详解】(1(2(3+98+,(+98+,++99-, =10-1, =9. 【点睛】本题考查二次根式化简求值问题,关键找到各分母的有理化因式,用平方差公式化去分母.22.计算(1)2213113a a a a a a +--+-+-;(2)已知a 、b +b =0.求a 、b 的值 (3)已知abc =1,求111a b cab a bc b ac c ++++++++的值【答案】(1)22223a a a ----;(2)a =-3,b ;(3)1.【分析】(1)先将式子进行变形得到()()113113a a a a a a +--+-+-,此时可以将其化简为1113a a a a ⎛⎫⎛⎫--+ ⎪ ⎪+-⎝⎭⎝⎭,然后根据异分母的加减法法则进行化简即可;(2)根据二次根式及绝对值的非负性得到2a +6=0,b =0,从而可求出a 、b ; (3)根据abc =1先将所求代数式转化:11b ab abbc b abc ab a ab a ==++++++,2111c abc ac c a bc abc ab ab a ==++++++,然后再进行分式的加减计算即可.【详解】解:(1)原式=()()113113a a a a a a +--+-+- =1113a a a a ⎛⎫⎛⎫--+ ⎪ ⎪+-⎝⎭⎝⎭=1113a a --+- =()()()()3113a a a a -++-+-=22223a a a ----;(20b =,∴2a +6=0,b =0,∴a =-3,b ; (3)∵abc =1, ∴11b ab ab bc b abc ab a ab a ==++++++,2111c abc ac c a bc abc ab ab a ==++++++,∴原式=1111a ab ab a ab a ab a ++++++++=11a ab ab a ++++=1.【点睛】本题考查了分式的化简求值和二次根式、绝对值的非负性,分式中一些特殊求值题并非一味的化简,代入,求值,熟练掌握转化、整体思想等解题技巧是解答这类题目的关键.23.先观察下列等式,再回答问题:=1+1=2;12=2 12;=3+13=313;… (1)根据上面三个等式提供的信息,请猜想第四个等式;(2)请按照上面各等式规律,试写出用 n (n 为正整数)表示的等式,并用所学知识证明.【答案】(1=144+=144;(2=211n n n n++=,证明见解析. 【分析】(1)根据“第一个等式内数字为1,第二个等式内数字为2,第三个等式内数字为3”,=414+=414;(2=n 211n n n++=”,再利用222112n n n n++=+()()开方即可证出结论成立.【详解】(1=1+1=2=212+=212;=313+=313;里面的数字分别为1、2、3,= 144+= 144.(2=1+1=2,=212+=212=313+=313=414+=414= 211n n n n++=.证明:等式左边==n 211n n n++==右边.=n 211n n n++=成立. 【点睛】本题考查了二次根式的性质与化简以及规律型中数的变化类,解题的关键是:(1)猜测出第四个等式中变化的数字为4;(2)找出变化规律=n 211n n n++=”.解决该题型题目时,根据数值的变化找出变化规律是关键.24.已知m ,n 满足m 4n=3+.【答案】12015【解析】 【分析】由43m n +=2﹣2)﹣3=0,将,代入计算即可.【详解】解:∵4m n +=3,)22﹣2)﹣3=0,)2﹣23=0,+13)=0,=﹣13,∴原式=3-23+2012=12015.【点睛】本题主要考查二次根式的混合运算,解题的关键是熟练掌握完全平方公式的运用及二次根式性质.25.像2)=1=a (a ≥0)、﹣1)=b ﹣1(b ≥0)……两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因+1﹣1,﹣因式.进行二次根式计算时,利用有理化因式,可以化去分母中的根号.请完成下列问题: (1);(2)+;(3)的大小,并说明理由.【答案】(1(2)(3)< 【解析】分析:(1=1,确定互为有理化因式,由此计算即可;(2)确定分母的有理化因式为2与2+然后分母有理化后计算即可;(3与,,然后比较即可.详解:(1) 原式=9;(2)原式=2+=2+ (3)根据题意,-==,><,>点睛:此题是一个阅读题,认证读题,了解互为有理化因式的实际意义,以及特点,然后根据特点变形解题是关键.26.计算:(1(2|a ﹣1|,其中1<a 【答案】(1)1;(2)1 【分析】(1)根据二次根式的乘法法则计算;(2)由二次根式的非负性,a 的取值范围进行化简. 【详解】解:(1-1=2-1=1(2)∵1<a ,a ﹣1=2﹣a +a ﹣1=1. 【点睛】本题考查二次根式的性质、二次根式的乘法法则,主要检验学生的计算能力.27.计算(1(2)21)-【答案】(1)4;(2)3+ 【分析】(1)先把各根式化为最简二次根式,再去括号,合并同类项即可; (2)利用平方差公式和完全平方公式计算即可. 【详解】解:(1)解:原式=4=+4=-(2)解:原式()22161=---63=-+3=+ 【点睛】本题考查了二次根式的混合运算,注意先化简,再进一步利用计算公式和计算方法计算.28.(1)计算)(2201113-⎛⎫--•- ⎪⎝⎭(2)已知,,a b c 为实数且2c =2c ab-的值【答案】(1)13;(2)12-【分析】(1)利用完全平方公式、负整数指数幂、零指数幂分别计算再合并即可; (2)先依据二次根式有意义的条件,求得a 、b 、c 的值,然后再代入计算即可. 【详解】 (1))(2201113-⎛⎫--•- ⎪⎝⎭31=+⨯=4+9=13;(2)根据二次根式有意义的条件可得:∵()2303010a a b ⎧-≥⎪⎪-≥⎨⎪-+≥⎪⎩, ∴3a =,1b =-,∴2c =∴(()2223112c ab -=-⨯-=-【点睛】本题主要考查了二次根式的混合运算,二次根式有意义的条件以及二次根式的化简求值,熟练掌握二次根式有意义的条件是解题的关键.29.计算:(1)()22131)()2---+(2【答案】(1)12;(2) 【分析】(1)按照负整数指数幂、0指数幂、乘方的运算法则计算即可; (2)根据二次根式的加减乘除运算法则计算即可. 【详解】(1)解:原式= 9-1+4=12(2)【点睛】本题考查负整数指数幂、0指数幂、乘方以及二次根式的运算法则,熟练掌握二次根式的化简是关键.30.化简求值:212(1)211x x x x -÷-+++,其中1x =.【解析】分析:先把小括号内的通分,按照分式的减法和分式除法法则进行化简,再把字母的值代入运算即可. 详解:原式2112,2111x x x x x x -+⎛⎫=÷- ⎪++++⎝⎭2112,211x x x x x -+-=÷+++()211,11x x x x -+=⋅-+1.1x =+当1x =时,11x ==+ 点睛:考查分式的混合运算,掌握运算顺序是解题的关键.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】根据二次根式的运算法则逐项计算即可判断. 【详解】解:AB 、C 2÷=2,故错误;D ,故正确.故选D. 【点睛】本题考查了二次根式的四则运算.2.B解析:B 【详解】解:A 、错误,∵2=+a bB 、正确,因为a 2+b 2≥0a 2+b 2;CD =|a +b |,其结果a+b 的符号不能确定.故选B .3.A解析:A【分析】根据各个选项中的式子,可以计算出正确的结果,从而可以解答本题.【详解】解:A 3=,故A 正确;B -不能合并,故B 错误;C 、22(3=,故C 错误;D 、=D 错误; 故选:A .【点睛】本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.4.A解析:A【分析】根据二次根式的性质把每一项都化为最简二次根式,再根据同类二次根式的定义判断即可.【详解】解:A =B 3C 不是同类二次根式,不合题意;D 3 故选:A .【点睛】本题考查了同类二次根式的定义和二次根式的性质,属于基本题型,熟练掌握基本知识是解题关键.5.D【分析】根据二次根式的性质进行计算即可.【详解】|3|3=.故选:D.【点睛】(0)0(0)(0)a aa aa a><⎧⎪===⎨⎪-⎩.6.A解析:A【分析】先根据二次根式有意义的条件列出关于x的不等式,求出x的取值范围即可.【详解】∴x-2020≥0,解得:x≥2020;故选:A.【点睛】本题考查的是二次根式有意义的条件,熟知二次根式中的被开方数是非负数是解答此题的关键.7.C解析:C【分析】直接利用二次根式的性质,将已知等式左边化简,可以得到a与b中至少有一个为0,进而分析得出答案即可.【详解】解:∵a b=--,∴a-b=-a-b,或b-a=-a-b∴a= -a,或b=-b, ∴a=0,或b=0, ∴ab=0, ∴0ab=.故选:C.【点睛】本题考查了二次根式的性质与化简,正确掌握二次根式的性质是解题的关键.8.D解析:D【解析】根据二次根式的被开数的非负性,求的a的范围,然后再化简绝对值,最后,依据二次根式的定义进行变形即可.【详解】-=a成立,则a≥2019,解:等式2018a∴,,∴a-2019=20182,∴a-20182=2019.故选D.【点睛】本题主要考查的是二次根式有意义的条件,求得a的取值范围是解题的关键.9.C解析:C【分析】=变形后可分解为:)=0,从而根据a>0,b>0可得出a和b的关系,代入即可得出答案.【详解】由题意得:a=+15b,∴+)=0,=,a=25b,1.2故选C.【点睛】本题考查二次根式的化简求值,有一定难度,根据题意得出a和b的关系是关键.10.C解析:C【分析】根据二次根式的性质即可求出答案.【详解】原式=3,故选C.【点睛】本题考查二次根式的性质,解题的关键是熟练运用二次根式的性质,本题属于基础题型.解析:C【分析】依据二次根式中的被开方数是非负数求得x的值,然后可得到y的值,最后代入计算即可.【详解】y=,∵实数x、y满足2∴x=2,y=﹣2,-⨯=-4.∴yx=22故选:C.【点睛】本题主要考查的是二次根式有意义的条件,熟练掌握二次根式有意义的条件是解题的关键.12.B解析:B【分析】根据二次根式的乘除法则求出每个式子的值,再判断即可.【详解】=⨯==42,故本选项不符合题意;解: A. 67===,故本选项,符合题意;===,故本选项不符合题意;D. ==3,故本选项不符合题意;故选B.【点睛】本题考查二次根式的性质和二次根式的乘除法则,能灵活运用二次根式的乘除法则进行计算是解题关键.二、填空题13.【分析】根据=,将原式进行拆分,然后合并可得出答案.【详解】解:原式==.故答案为.此题考查了二次根式的混合运算,解答本题的关键是将原式进行拆分,有一定的技巧性,注意仔细观解析:220400x x x- 【分析】-,将原式进行拆分,然后合并可得出答案. 【详解】解:原式===故答案为220400x x x-. 【点睛】 此题考查了二次根式的混合运算,解答本题的关键是将原式进行拆分,有一定的技巧性,注意仔细观察.14..【分析】利用题目给的求出,再把它们相乘得到,再对原式进行变形凑出的形式进行计算.【详解】∵,∴,∴,∴,∵,∴,∴,∴原式.故答案是:.本题考查二次根式的运.【分析】,再把它们相乘得到1xx-,再对原式进行变形凑出1xx-的形式进行计算.【详解】3=,∴221239xx=++==,∴17xx+=,∴212725xx=-+=-=,∵01x<<,=,∴1xx=-=-∴原式====.故答案是:12.【点睛】本题考查二次根式的运算和乘法公式的应用,解题的关键是熟练运用乘法公式对式子进行巧妙运算.15.3【分析】先估算,再估算,根据6-的整数部分为x,小数部分为y,可得: x=2, y=,然后再代入计算即可求解.【详解】因为,所以,因为6-的整数部分为x,小数部分为y,所以x=2,解析:3【分析】先估算34<<,再估算263<<,根据6x ,小数部分为y ,可得: x =2, y=4然后再代入计算即可求解.【详解】因为34<,所以263<-<,因为6x ,小数部分为y ,所以x =2, y=4-,所以(2x y =(4416133=-=, 故答案为:3.【点睛】本题主要考查无理数整数部分和小数部分,解决本题的关键是要熟练掌握无理数估算方法和无理数整数和小数部分的求解方法. 16.(1,1)、(4,1)、(4,4)、(9,36)、(16,16)、(36,9)【解析】试题解析:当a=1,=1,要使为整数,=1或时,分别为4和3,得出(1,4)和(1,1)是的“理想数对”,解析:(1,1)、(4,1)、(4,4)、(9,36)、(16,16)、(36,9)【解析】试题解析:当a =1,要使或12时,分别为4和3,得出(1,4)和(1,1)是的“理想数对”,当a =412,要使+或12时,分别为3和2,得出(4,1)和(4,4)是的“理想数对”,当a =913,要使16时,=1,得出(9,36)是的“理想数对”,当a =1614,要使14时,=1,得出(16,16)是的“理想数对”,当a =3616,要使13时,=1,得出(36,9)是的“理想数对”, 即其他所有的“理想数对”:(1,1)、(4,1)、(4,4)、(9,36)、(16,16)、(36,9).故答案为:(1,1)、(4,1)、(4,4)、(9,36)、(16,16)、(36,9). 17.2018【解析】试题解析:,令,,显然,∴,∴,∵与奇偶数相同,∴,∴,∴.故答案为:2018.解析:2018【解析】 试题解析:y ===令a =b =显然0a b >≥,∴224036a b -=,∴()()4036a b a b +-=,∵()a b +与()-a b 奇偶数相同,∴20182a b a b +=⎧⎨-=⎩, ∴10101008a b =⎧⎨=⎩, ∴2018y a b =+=.故答案为:2018.18.5【解析】试题解析:由题可知,∴,∴,∴,①②得,,解方程组得,∴.故答案为:5.解析:5【解析】试题解析:由题可知3030m n m n -+≥⎧⎨--≥⎩, ∴3m n +=,0=, ∴35200m n p m n p +--=⎧⎨--=⎩①②, ①-②得2620m n +-=,31m n +=,解方程组331m n m n +=⎧⎨+=⎩得41m n =⎧⎨=-⎩, ∴4(1)5p m n =-=--=.故答案为:5.19.x≥0.【分析】直接利用二次根式有意义的条件进而分析得出答案.【详解】∵有意义,∴x≥0,故答案为x≥0.【点睛】此题主要考查了二次根式有意义的条件,正确把握定义是解题关键.解析:x≥0.【分析】直接利用二次根式有意义的条件进而分析得出答案.【详解】有意义,∴x≥0,故答案为x≥0.【点睛】此题主要考查了二次根式有意义的条件,正确把握定义是解题关键.20.21【分析】根据二次根式及同类二次根式的定义列出方程组即可求出答案. 【详解】∵最简二次根式与是同类二次根式,∴ ,解得,,∴故答案为21.解析:21【分析】根据二次根式及同类二次根式的定义列出方程组即可求出答案.【详解】∴1221343nm m-=⎧⎨-=-⎩,解得,73mn=⎧⎨=⎩,∴7321. mn=⨯=故答案为21.三、解答题21.无22.无23.无24.无25.无26.无27.无28.无29.无30.无。
八年级第二学期3月份 月考检测数学试卷含答案

一、选择题1.如图,点A 的坐标是(2)2,,若点P 在x 轴上,且APO △是等腰三角形,则点P 的坐标不可能是( )A .(2,0)B .(4,0)C .(-22,0)D .(3,0) 2.已知:△ABC 中,BD 、CE 分别是AC 、AB 边上的高,BQ =AC ,点F 在CE 的延长线上,CF =AB ,下列结论错误的是( ).A .AF ⊥AQB .AF=AQC .AF=AD D .F BAQ ∠=∠3.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由三角形较长直角边长为a ,较短直角边长为b ,若(a +b )2=21,大正方形的面积为13,则小正方形的面积为( )A .3B .4C .5D .6 4.如图,在ABC 中,,904C AC ︒∠==cm ,3BC =cm ,点D 、E 分别在AC 、BC上,现将DCE 沿DE 翻折,使点C 落在点'C 处,连接AC ',则AC '长度的最小值 ( )A .不存在B .等于 1cmC .等于 2 cmD .等于 2.5 cm 5.如图,在四边形ABCD 中,∠ABC =∠ACB =∠ADC =45︒,若AD =4,CD =2,则BD 的长为( )A .6B .27C .5D .25 6.如图,在△ABC 中,∠ACB =90°,AB 的中垂线交AC 于D ,P 是BD 的中点,若BC =4,AC =8,则S △PBC 为( )A .3B .3.3C .4D .4.57.如图,在等腰Rt △ABC 中,∠C =90°,AC =7,∠BAC 的角平分线AD 交BC 于点D ,则点D 到AB 的距离是( )A .3B .4C .7(21)-D .7(21)+8.已知一个直角三角形的两边长分别为3和5,则第三边长是( )A .5B .4C .34D .4或349.已知直角三角形纸片ABC 的两直角边长分别为6,8,现将ABC 按如图所示的方式折叠,使点A 与点B 重合,则BE 的长是( )A .72B .74C .254D .15410.我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知∠A =90°,BD =4,CF =6,设正方形ADOF 的边长为x ,则210x x +=( )A .12B .16C .20D .24二、填空题11.如图,在矩形 ABCD 中,AB =10,BC =5,若点 M 、N 分别是线段 AC 、AB 上的两个动点,则 BM+MN 的最小值为_____________________.12.等腰三角形的腰长为5,一腰上的高为3,则这个等腰三角形底边的长为________13.已知,如图:在平面直角坐标系中,O 为坐标原点,四边形OABC 是矩形,点A 、C 的坐标分别为A (10,0)、C (0,4),点D 是OA 的中点,点P 在BC 边上运动,当△ODP 是腰长为5的等腰三角形时,点P 的坐标为_____.14.在ABC ∆中,90BAC ∠=︒,以BC 为斜边作等腰直角BCD ∆,连接DA ,若22AB =,42AC =,则DA 的长为______.15.如图,已知△DBC 是等腰直角三角形,BE 与CD 交于点O ,∠BDC=∠BEC=90°,BF=CF ,若BC=8,OD=2,则OF=______.16.如图,在△ABC 中,∠C =90°,∠ABC =45°,D 是BC 边上的一点,BD =2,将△ACD 沿直线AD 翻折,点C 刚好落在AB 边上的点E 处.若P 是直线AD 上的动点,则△PEB 的周长的最小值是________.17.四边形ABCD 中AB =8,BC =6,∠B =90°,AD =CD =52,四边形ABCD 的面积是_______.18.如图,E 为等腰直角△ABC 的边AB 上的一点,要使AE =3,BE =1,P 为AC 上的动点,则PB +PE 的最小值为____________.19.如图所示,圆柱体底面圆的半径是2π,高为1,若一只小虫从A 点出发沿着圆柱体的外侧面爬行到C 点,则小虫爬行的最短路程是______20.已知,在△ABC 中,BC=3,∠A=22.5°,将△ABC 翻折使得点B 与点A 重合,折痕与边AC 交于点P ,如果AP=4,那么AC 的长为_______三、解答题21.在等边ABC 中,点D 是线段BC 的中点,120,EDF DE ∠=︒与线段AB 相交于点,E DF 与射线AC 相交于点F .()1如图1,若DF AC ⊥,垂足为,4,F AB =求BE 的长;()2如图2,将()1中的EDF ∠绕点D 顺时针旋转一定的角度,DF 仍与线段AC 相交于点F .求证:12BE CF AB +=.()3如图3,将()2中的EDF ∠继续绕点D 顺时针旋转一定的角度,使DF 与线段AC 的延长线交于点,F 作DN AC ⊥于点N ,若,DN FN =设,BE x CF y ==,写出y 关于x 的函数关系式.22.如图,在等腰直角三角形ABC 中,∠ACB =90°,AC=BC ,AD 平分∠BAC ,BD ⊥AD 于点D ,E 是AB 的中点,连接CE 交AD 于点F ,BD =3,求BF 的长.23.如图,在矩形ABCD 中,AB=8,BC=10,E 为CD 边上一点,将△ADE 沿AE 折叠,使点D 落在BC 边上的点F 处.(1)求BF 的长;(2)求CE 的长.24.定义:如图1,点M 、N 把线段AB 分割成AM 、MN 和BN ,若以AM 、MN 、BN 为边的三角形是一个直角三角形,则称点M 、N 是线段AB 的勾股分割点.(1)已知点M 、N 是线段AB 的勾股分割点,若2AM =,3MN =,求BN 的长; (2)如图2,在Rt ABC △中,AC BC =,点M 、N 在斜边AB 上,45MCN ∠=︒,求证:点M 、N 是线段AB 的勾股分割点(提示:把ACM 绕点C 逆时针旋转90︒);(3)在(2)的问题中,15ACM ∠=︒,1AM =,求BM 的长.25.已知ABC ∆中,AB AC =.(1)如图1,在ADE ∆中,AD AE =,连接BD 、CE ,若DAE BAC ∠=∠,求证:BD CE =(2)如图2,在ADE ∆中,AD AE =,连接BE 、CE ,若60DAE BAC ∠=∠=,CE AD ⊥于点F ,4AE =,5EC =,求BE 的长;(3)如图3,在BCD ∆中,45CBD CDB ∠=∠=,连接AD ,若45CAB ∠=,求AD AB 的值.26.如图,在ABC ∆中,90ACB ∠=︒,2BC AC =.(1)如图1,点D 在边BC 上,1CD =,5AD =,求ABD ∆的面积.(2)如图2,点F 在边AC 上,过点B 作BE BC ⊥,BE BC =,连结EF 交BC 于点M ,过点C 作CG EF ⊥,垂足为G ,连结BG .求证:2EG BG CG =+.27.如图,在四边形ABCD 中,=AB AD ,=BC DC ,=60A ∠︒,点E 为AD 边上一点,连接CE ,BD . CE 与BD 交于点F ,且CE ∥AB .(1)求证:CED ADB ∠=∠;(2)若=8AB ,=6CE . 求BC 的长 .28.如图,点A 是射线OE :y =x (x ≥0)上的一个动点,过点A 作x 轴的垂线,垂足为B ,过点B 作OA 的平行线交∠AOB 的平分线于点C .(1)若OA =52,求点B 的坐标; (2)如图2,过点C 作CG ⊥AB 于点G ,CH ⊥OE 于点H ,求证:CG =CH .(3)①若点A 的坐标为(2,2),射线OC 与AB 交于点D ,在射线BC 上是否存在一点P 使得△ACP 与△BDC 全等,若存在,请求出点P 的坐标;若不存在,请说明理由. ②在(3)①的条件下,在平面内另有三点P 1(2,2),P 2(2,22),P 3(2+2,2﹣2),请你判断也满足△ACP 与△BDC 全等的点是 .(写出你认为正确的点)29.如图1, △ABC 和△CDE 均为等腰三角形,AC=BC, CD=CE, AC>CD, ∠ACB=∠DCE=a ,且点A 、D 、E 在同一直线上,连结BE.(1)求证: AD=BE.(2)如图2,若a=90°,CM ⊥AE 于E.若CM=7, BE=10, 试求AB 的长.(3)如图3,若a=120°, CM ⊥AE 于E, BN ⊥AE 于N, BN=a, CM=b,直接写出AE 的值(用a, b 的代数式表示).30.如图1,点E 是正方形ABCD 边CD 上任意一点,以DE 为边作正方形DEFG ,连接BF ,点M 是线段BF 中点,射线EM 与BC 交于点H ,连接CM .(1)请直接写出CM 和EM 的数量关系和位置关系.(2)把图1中的正方形DEFG 绕点D 顺时针旋转45︒,此时点F 恰好落在线段CD 上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由.(3)把图1中的正方形DEFG 绕点D 顺时针旋转90︒,此时点E 、G 恰好分别落在线段AD 、CD 上,连接CE ,如图3,其他条件不变,若2DG =,6AB =,直接写出CM 的长度.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【详解】解:(1)当点P在x轴正半轴上,①以OA为腰时,∵A的坐标是(2,2),∴∠AOP=45°,OA=22,∴P的坐标是(4,0)或(22,0);②以OA为底边时,∵点A的坐标是(2,2),∴当点P的坐标为:(2,0)时,OP=AP;(2)当点P在x轴负半轴上,③以OA为腰时,∵A 的坐标是(2,2),∴OA= 22,∴OA=AP=22∴P 的坐标是(-22,0).故选D .2.C解析:C【分析】根据BD 、CE 分别是AC 、AB 边上的高,推导出EBH DCH ∠=∠;再结合题意,可证明FAC AQB △≌△,由此可得F BAQ ∠=∠,AF AQ =;再经90AEF ∠=得90F FAE ∠+∠=,从而证明AF ⊥AQ ;最后由勾股定理得222AQ AD QD =+,从而得到AF AD ≠,即可得到答案.【详解】如图,CE 和BD 相较于H∵BD 、CE 分别是AC 、AB 边上的高∴CE AB ⊥,BD AC ⊥∴90BEC BDC AEF ADQ ∠=∠=∠=∠=∴90EBH EHB DHC DCH ∠+∠=∠+∠=∵EHB DHC ∠=∠∴EBH DCH ∠=∠又∵BQ =AC 且CF =AB∴FAC AQB △≌△∴F BAQ ∠=∠,AF AQ =,故B 、D 结论正确;∵90AEF ∠=∴90F FAE ∠+∠=∴90BAQ FAE F FAE ∠+∠=∠+∠=∴AF ⊥AQ 故A 结论正确;∵90ADQ ∠=∴222AQ AD QD =+∵0QD ≠∴AQ AD ≠∴AF AD ≠故选:C .【点睛】本题考查了全等三角形、直角三角形、勾股定理、三角形的高等知识;解题的关键是熟练掌握全等三角形、直角三角形、勾股定理、三角形的高的性质,从而完成求解. 3.C解析:C【分析】观察图形可知,小正方形的面积=大正方形的面积-4个直角三角形的面积,利用已知2()a b + =21,大正方形的面积为13,可以得以直角三角形的面积,进而求出答案。
人教版八年级第二学期3月份月考数学试卷含答案

人教版八年级第二学期3月份月考数学试卷含答案一、选择题1.下列计算,正确的是( )A .=B .=C .0=D .10=2.下列各式成立的是( )A 3=B 3=C .22(3=- D .2-=3. )A B C D4.已知2a =,2b =的值为( ) A .4B .5C .6D .75.下列各式中,无意义的是( )A B C D .310-6.估计( ( ) A .4和5之间B .5和6之间C .6和7之间D .7和8之间7.下列式子中,为最简二次根式的是( )A B C D8.化简 )ABC D9.1在3和4中x 的取值范围是1x ≥-;③3;④5=-;⑤1528->.其中正确的个数为( ) A .1个B .2个C .3个D .4个10.若化简1682+-x x -1x -的结果为5-2x ,则x 的取值范围是( ) A .为任意实数B .1≤x≤4C .x≥1D .x≤411.下列二次根式中,最简二次根式是( )A B C D12.给出下列化简①(2=2=2=④11142-=,其中正确的是( ) A .①②③④B .①②③C .①②D .③④二、填空题13.若0a >,把4ab-化成最简二次根式为________. 14.已知a ,b 是正整数,且满足15152()a b +是整数,则这样的有序数对(a ,b )共有____对.15.计算(π-3)02-211(223)-4--22--()的结果为_____. 16.实数a ,b 在数轴上的位置如图所示,则化简()22b a b +-﹣|a +b |的结果是_____.17.若实数x ,y ,m 满足等式()23532322x y m x y m x y x y +--++-=+----,则m+4的算术平方根为________.18.将1、2、3、6按右侧方式排列.若规定(m ,n )表示第m 排从左向右第n 个数,则(5,4)与(9,4)表示的两数之积是______.19.已知整数x ,y 满足20172019y x x =+--,则y =__________.20.4102541025-+++=_______.三、解答题21.计算及解方程组:(1-1-) (2)2+(3)解方程组:251032x y x y x y -=⎧⎪+-⎨=⎪⎩【答案】(1)2)7;(3)102x y =⎧⎨=⎩.【分析】(1)首先化简绝对值,然后根据二次根式乘法、加减法法则运算即可; (2)首先根据完全平方公式化简,然后根据二次根式加减法法则运算即可; (3)首先将第二个方程化简,然后利用加减消元法即可求解. 【详解】(11-1+(11=1 (22+)=34-=7-=7-(3)251032x y x y x y-=⎧⎪⎨+-=⎪⎩①②由②得:50x y -= ③ ②-③得: 10x = 把x=10代入①得:y=2 ∴原方程组的解是:102x y =⎧⎨=⎩【点睛】本题考查了二次根式的混合运算,加减消元法解二元一次方程,熟练掌握二次根式的运算法则是本题的关键.22.先阅读材料,再回答问题:因为)111=1=;因为1=,所以=1== (1= ,= ; (2⋅⋅⋅+的值.【答案】(12)9 【分析】(1)仿照例子,由1+=的值;由1+=的值;(2)根据(1)中的规律可将每个二次根式分母有理化,可转化为实数的加减法运算,再寻求规律可得答案. 【详解】解:(1)因为1-=;因为1=1(2⋅⋅⋅+1=+⋅⋅⋅1=1019=-=.【点睛】本题考查了分母有理化,分子分母都乘以分母这两个数的差进行分母有理化是解题关键.23.)÷)(a ≠b ).【答案】-+a b【解析】试题分析:先计算括号内的,然后把除法转化为乘法,约分即可得出结论.试题解析:解:原式=a ab b aba b++-+÷()()()()()()a a ab b b a b a b a bab a b a b--+-+-+-=a b+÷()()2222a a ab b ab b a bab a b a b----++-=a b+·()()()ab a b a bab a b-+-+=-a b+.24.先化简,再求值:a+212a a-+,其中a=1007.如图是小亮和小芳的解答过程.(1)的解法是错误的;(2)错误的原因在于未能正确地运用二次根式的性质:;(3)先化简,再求值:269a a-+a=﹣2018.【答案】(1)小亮(22a(a<0)(3)2013.【解析】试题分析:(12a,判断出小亮的计算是错误的;(22a的应用错误;(3)先根据配方法把被开方数配成完全平方,然后根据正确的性质化简,再代入计算即可.试题解析:(1)小亮(22a(a<0)(3)原式=()23a-a+2(3-a)=6-a=6-(-2007)=2013.25.计算下列各式:(1()2112323-;(2【答案】(12;(2)【分析】先根据二次根式的性质化简,再合并同类二次根式即可.【详解】(1)原式2=-2=;(2)原式==.【点睛】本题考查了二次根式的加减,熟练掌握性质是解答本题的关键(0)(0)a aaa a≥⎧==⎨-<⎩,)0,0a b=≥≥=(a≥0,b>0).26.在一个边长为(cm的正方形的内部挖去一个长为()cm,cm的矩形,求剩余部分图形的面积.【答案】【解析】试题分析:用大正方形的面积减去长方形的面积即可求出剩余部分的面积.试题解析:剩余部分的面积为:(2﹣()=()﹣(﹣)=(cm2).考点:二次根式的应用27.一样的式子,其实我====,1===;以上这种化简的步骤叫做分母有理化还可以用以下方法化简:221111===-=(12)化简:2n+++【答案】(1-2.【解析】试题分析:(12看出5-3,根据平方差公式分解因式,最后进进约分即可.(2)先每一个二次根式分母有理化,再分母不变,分子相加,最后合并即可.试题解析:(1)=====(2)原式=122n++++=12.考点:分母有理化.28.计算:(1(2|a﹣1|,其中1<a【答案】(1)1;(2)1【分析】(1)根据二次根式的乘法法则计算;(2)由二次根式的非负性,a的取值范围进行化简.【详解】解:(1-1=2-1=1(2)∵1<a,a ﹣1=2﹣a +a ﹣1=1. 【点睛】本题考查二次根式的性质、二次根式的乘法法则,主要检验学生的计算能力.29.计算(1))(121123-⎛⨯-- ⎝⎭(2)已知:11,22x y ==,求22x xy y ++的值.【答案】(1)28-;(2)17. 【分析】(1)先利用完全平方公式和平方差公式计算二次根式的乘法、负指数幂运算,再计算二次根式的加减法即可得;(2)先求出x y +和xy 的值,再利用完全平方公式进行化简求值即可得. 【详解】(1)原式()((221312⎡⎤=⨯+--⎢⎥⎣⎦,(()1475452=⨯+---230=+28=-;(2)(1119,22x y==,1122x y∴+=+=,()11119112224xy =⨯=⨯-=,则()222x xy y x y xy ++=+-,22=-,192=-, 17=. 【点睛】本题考查了二次根式的混合运算、完全平方公式和平方差公式等知识点,熟练掌握二次根式的运算法则是解题关键.30.已知x²+2xy+y²的值.【答案】16【解析】分析:(1)根据已知条件先计算出x+y=4,再利用完全平方公式得到x²+2xy+y²=(x+y)²,然后利用整体代入的方法计算.本题解析:∵x² +2xy+y² =(x+y)²,∴当∴x²+2xy+y²=(x+y)²=(2−=16.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】A、B、C、根据合并同类二次根式的法则即可判定;D、利用根式的运算法则计算即可判定.【详解】解:A、B、D不是同类二次根式,不能合并,故选项不符合题意;C=,故选项正确.故选:C.【点睛】此题主要考查二次根式的运算,应熟练掌握各种运算法则,且准确计算.2.A解析:A【分析】根据各个选项中的式子,可以计算出正确的结果,从而可以解答本题.【详解】解:A3=,故A正确;B-不能合并,故B错误;C、22(3=,故C错误;D、=D错误;故选:A . 【点睛】本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.3.A解析:A 【分析】根据二次根式的性质把每一项都化为最简二次根式,再根据同类二次根式的定义判断即可. 【详解】解:A =B 3C 不是同类二次根式,不合题意;D 3故选:A . 【点睛】本题考查了同类二次根式的定义和二次根式的性质,属于基本题型,熟练掌握基本知识是解题关键.4.B解析:B 【分析】根据二次根式的混合运算和完全平方公式进行计算,即可得到结果. 【详解】解:∵2a =,2b =, ∴227a b ++2252527 55454745425=∴255故选:B . 【点睛】本题主要考查了二次根式的混合运算和完全平方公式,熟悉相关运算法则是解题的关键5.A解析:A 【分析】直接利用二次根式有意义的条件、负整数指数幂的性质分析得出答案.【详解】AB ,有意义,不合题意;C D 、33110=10-,有意义,不合题意; 故选A.【点睛】 此题主要考查了二次根式有意义的条件、负整数指数幂的性质,正确把握二次根式的定义是解题关键.6.A解析:A【分析】根据二次根式的混合运算法则进行计算,再估算无理数的大小.【详解】(=,∵4<6<9,∵<3,∴<5,故选:A .【点睛】此题考查了二次根式的混合运算,无理数的估算,正确掌握二次根式的运算法则、会进行无理数的大小估算是解题的关键.7.B解析:B【分析】根据最简二次根式的定义即可求出答案.【详解】=,故A 不是最简二次根式;是最简二次根式,故B 正确;,故C 不是最简二次根式;=D 不是最简二次根式;故选:B .【点睛】本题考查最简二次根式,解题的关键是正确理解最简二次根式的定义,本题属于基础题型.8.C解析:C【解析】 根据二次根式有意义的条件可知﹣1x>0,求得x <0,然后根据二次根式的化简,可得x. 故选C .9.A解析:A【分析】答.【详解】 解:①3104<<,415∴<<,故①错误;x 的取值范围是1x ≥-,故②正确;9=,9的平方根是3±,故③错误;④5=,故④错误;⑤∵159288-=,(229<,508-<58<,故⑤错误; 综上所述:正确的有②,共1个,故选:A .【点睛】本题考查了故算无理数的大小,解决本题的关键是掌握估算平方法比较无理数大小.10.B【解析】【分析】根据完全平方公式和2a=|a|,先把多项式化简为|x-4|-|1-x|,然后根据x的取值范围分别讨论,求出符合题意的x的值即可.【详解】解:原式=2x4-()-1x-=|x-4|-|1-x|,当x≤1时,此时1-x≥0,x-4<0,∴(4-x)-(1-x)=3,不符合题意,当1≤x≤4时,此时1-x≤0,x-4≤0,∴(4-x)-(x-1)=5-2x,符合题意,当x≥4时,此时x-4≥0,1-x<0,∴(x-4)-(x-1)=-3,不符合题意,∴x的取值范围为:1≤x≤4故选B.【点睛】本题主要考查绝对值及二次根式的化简,要注意正负号的变化,分类讨论.11.A解析:A【解析】试题分析:最简二次根式是指不能继续化简的二次根式,A、原式=;B、是最简二次根式,不能化简;C、原式=;D、原式=.考点:最简二次根式12.C解析:C【分析】根据二次根式的性质逐一进行计算即可求出答案.【详解】①原式=2,故①正确;②原式=2,故②正确;③原式340285==④原式3342==,故④错误,【点睛】本题考查二次根式的性质和化简,熟练掌握二次根式的性质是解题的关键.二、填空题13.【分析】先判断b的符号,再根据二次根式的性质进行化简即可.【详解】解:∵∴∴所以答案是:【点睛】本题考查了二次根式的性质.解析:【分析】先判断b的符号,再根据二次根式的性质进行化简即可.【详解】解:∵40,0 aab-≥>∴0b<2a bb b b=--所以答案是:【点睛】a=.14.7【解析】解:∵=+,∴a、b的值为15,60,135,240,540.①当a=15,b=15时,即=4;②当a=60,b=60时,即=2;③当a=15,b=60时,即=3;④当a=60解析:7【解析】解:∵2,∴a 、b 的值为15,60,135,240,540.①当a =15,b =15时,即2=4;②当a =60,b =60时,即2=2;③当a =15,b =60时,即2=3;④当a =60,b =15时,即2=3;⑤当a =240,b =240时,即2=1;⑥当a =135,b =540时,即2=1;⑦当a =540,b =135时,即2=1; 故答案为:(15,15)、(60、60)、(15,60)、(60,15)、(240,240)、(135,540)、(540,135).所有满足条件的有序数对(a ,b )共有 7对.故答案为:7.点睛:本题考查了二次根式的性质和化简,解决此题的关键是分类讨论思想,得出a 、b 可能的取值.15.﹣6【解析】根据零指数幂的性质,二次根式的性质,负整指数幂的性质,可知(π-3)0=1﹣(3﹣2)﹣4×﹣4=1﹣3+2﹣2﹣4=﹣6.故答案为﹣6.解析:﹣6【解析】根据零指数幂的性质01(0)a a =≠,二次根式的性质,负整指数幂的性质1(0)p p a a a -=≠,可知(π-3)0-21-2()=1﹣(3﹣)﹣﹣4=1﹣﹣﹣4=﹣6. 故答案为﹣6.16.3b【分析】先判断a,b的取值范围,并分别判断a-b,a+b的符号,再根据二次根式的性质和绝对值的性质化简,计算即可求解.【详解】解:由数轴可知:b>0,a﹣b<0,a+b<0,∴原式=|解析:3b【分析】先判断a,b的取值范围,并分别判断a-b,a+b的符号,再根据二次根式的性质和绝对值的性质化简,计算即可求解.【详解】解:由数轴可知:b>0,a﹣b<0,a+b<0,∴原式=|b|+|a﹣b|﹣|a+b|=b﹣(a﹣b)+(a+b)=b﹣a+b+a+b=3b,故答案为:3b【点睛】a=和绝对值的性质是解题的关键.17.3【解析】【分析】先根据二次根式有意义的条件得出x+y的值,再根据非负数的性质列出关于x,y,m的方程组,求出m的值,进而可得出结论.【详解】依题意得:,解得:x=1,y=1,m=5,∴3解析:3【解析】【分析】先根据二次根式有意义的条件得出x+y的值,再根据非负数的性质列出关于x,y,m的方程组,求出m的值,进而可得出结论.【详解】依题意得:35302302x y mx y mx y+--=⎧⎪+-=⎨⎪+=⎩,解得:x=1,y=1,m=5,∴==3.故答案为3.【点睛】本题考查了二次根式有意义得条件及非负数的性质,熟知二次根式具有非负性是解答此题的关键.18.【解析】试题解析:(5,4)表示第5排从左向右第4个数是:,(9,4)表示第9排从左向右第4个数,可以看出奇数排最中间的一个数都是1, 第9排是奇数排,最中间的也就是这排的第5个数是1,那么第解析:【解析】试题解析:(5,4)表示第5排从左向右第4,(9,4)表示第9排从左向右第4个数,可以看出奇数排最中间的一个数都是1,第9排是奇数排,最中间的也就是这排的第5个数是1,那么第4,∴(5,4)与(9,4)故答案为19.2018【解析】试题解析:,令,,显然,∴,∴,∵与奇偶数相同,∴,∴,∴.故答案为:2018.解析:2018【解析】 试题解析:y ===令a =b = 显然0a b >≥,∴224036a b -=,∴()()4036a b a b +-=,∵()a b +与()-a b 奇偶数相同,∴20182a b a b +=⎧⎨-=⎩, ∴10101008a b =⎧⎨=⎩, ∴2018y a b =+=.故答案为:2018.20.【分析】设,将等式的两边平方,然后根据完全平方公式和二次根式的性质化简即可得出结论.【详解】解:设,由算术平方根的非负性可得t≥0,则.故答案为:.【点睛】此题考查的是二【分析】t =,将等式的两边平方,然后根据完全平方公式和二次根式的性质化简即可得出结论.【详解】t =,由算术平方根的非负性可得t ≥0,则244t =+8=+8=+81)=+6=+2=1)∴=.1t.【点睛】此题考查的是二次根式的化简,掌握完全平方公式和二次根式的性质是解题关键.三、解答题21.无22.无23.无24.无25.无26.无27.无28.无29.无30.无。
人教版八年级第二学期3月份月考数学试卷
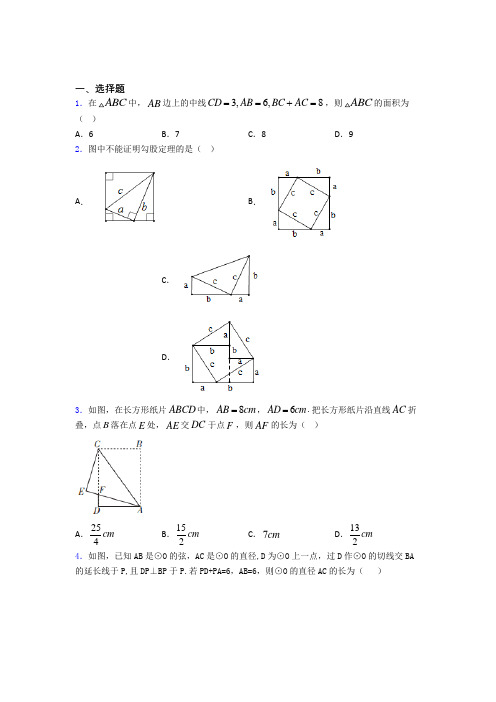
一、选择题1.在ABC 中,AB 边上的中线3,6,8CD AB BC AC ==+=,则ABC 的面积为( ) A .6B .7C .8D .92.图中不能证明勾股定理的是( )A .B .C .D .3.如图,在长方形纸片ABCD 中,8AB cm =,6AD cm =. 把长方形纸片沿直线AC 折叠,点B 落在点E 处,AE 交DC 于点F ,则AF 的长为( )A .254cm B .152cm C .7cmD .132cm 4.如图,已知AB 是⊙O 的弦,AC 是⊙O 的直径,D 为⊙O 上一点,过D 作⊙O 的切线交BA 的延长线于P,且DP⊥BP 于P.若PD+PA=6,AB=6,则⊙O 的直径AC 的长为( )A .5B .8C .10D .125.若直角三角形的三边长分别为-a b 、a 、+a b ,且a 、b 都是正整数,则三角形其中一边的长可能为() A .22B .32C .62D .826.如图,在ABC 中,CE 平分ACB ∠,CF 平分ACD ∠,且//EF BC 交AC 于M ,若3CM =,则22CE CF +的值为( )A .36B .9C .6D .187.如图,在数轴上点A 所表示的数为a ,则a 的值为( )A .15--B .15-C .5-D .15-+8.如图,在ABC 中,13AB =,10BC =,BC 边上的中线12AD =,请试着判定ABC 的形状是( )A .直角三角形B .等边三角形C .等腰三角形D .以上都不对9.小明学了在数轴上画出表示无理数的点的方法后,进行练习:首先画数轴,原点为O ,在数轴上找到表示数2的点A ,然后过点A 作AB ⊥OA ,使AB=3(如图).以O 为圆心,OB 的长为半径作弧,交数轴正半轴于点P ,则点P 所表示的数介于( )A .1和2之间B .2和3之间C .3和4之间D .4和5之间10.长度分别为9cm 、12cm 、15cm 、36cm 、39cm 五根木棍首尾连接,最多可搭成直角三角形的个数为( ) A .1个B .2个C .3个D .4个二、填空题11.如图,RT ABC ,90ACB ∠=︒,6AC =,8BC =,将边AC 沿CE 翻折,使点A 落在AB 上的点D 处;再将边BC 沿CF 翻折,使点B 落在CD 的延长线上的点B '处,两条折痕与斜边AB 分别交于点E 、F ,则B FC '△的面积为______.12.如图,这是由八个全等的直角三角形拼接而成,记图中正方形ABCD ,正方形EFGH ,正方形MNKT 的面积分别为 1S ,2S ,3S ,若123144S S S ++=,则2S 的值是__________.13.在△ABC 中,若222225,75a b a b c -+===,,则最长边上的高为_____. 14.在△ABC 中,AB=15,AC=13,高AD=12,则ABC ∆的周长为_______________. 15.如图,Rt ABC 中,90A ∠=︒,8AC =,6AB =,DE AC ⊥,13CD BC =,13CE AC =,P 是直线AC 上一点,把CDP 沿DP 所在的直线翻折后,点C 落在直线DE 上的点H 处,CP 的长是__________16.如图所示,“赵爽弦图”是由8个全等的直角三角形拼接而成的,记图中正方形ABCD ,正方形EFGH ,正方形MNKT 的面积分别为123,,S S S ,已知12310S S S ++=,则2S 的值是____.17.Rt △ABC 中,∠BAC =90°,AB =AC =2,以 AC 为一边.在△ABC 外部作等腰直角三角形ACD ,则线段 BD 的长为_____.18.如图,小正方形的边长为1,连接小正方形的三个格点可得△ABC ,则AC 边上的高的长度是_____________.19.一块直角三角形绿地,两直角边长分别为3m ,4m ,现在要将绿地扩充成等腰三角形,且扩充时只能延长长为3m 的直角边,则扩充后等腰三角形绿地的面积为____m 2. 20.如图,在等腰△ABC 中,AB =AC ,底边BC 上的高AD =6cm ,腰AC 上的高BE =4m ,则△ABC 的面积为_____cm 2.三、解答题21.如图,△ABC 和EDC ∆都是等边三角形,7,3,2AD BD CD ===求:(1)AE长;(2)∠BDC 的度数:(3)AC 的长.22.如图,在两个等腰直角ABC 和CDE △中,∠ACB = ∠DCE=90°.(1)观察猜想:如图1,点E 在BC 上,线段AE 与BD 的数量关系是 ,位置关系是 ;(2)探究证明:把CDE △绕直角顶点C 旋转到图2的位置,(1)中的结论还成立吗?说明理由;(3)拓展延伸:把CDE △绕点C 在平面内自由旋转,若AC = BC=10,DE=12,当A 、E 、D 三点在直线上时,请直接写出 AD 的长.23.定义:如图1,平面上两条直线AB 、CD 相交于点O ,对于平面内任意一点M ,点M 到直线AB 、CD 的距离分别为p 、q ,则称有序实数对(p ,q )是点M 的“距离坐标”,根据上述定义,“距离坐标”为(0,0)的点有1个,即点O . (1)“距离坐标”为(1,0)的点有 个;(2)如图2,若点M 在过点O 且与直线AB 垂直的直线l 上时,点M 的“距离坐标”为(p ,q ),且∠BOD = 150︒,请写出p 、q 的关系式并证明;(3)如图3,点M 的“距离坐标”为(1,3),且∠DOB = 30︒,求OM 的长.24.阅读与理解:折纸,常常能为证明一个命题提供思路和方法.例如,在ABC 中,AB AC >(如图),怎样证明C B ∠>∠呢?分析:把AC 沿A ∠的角平分线AD 翻折,因为AB AC >,所以,点C 落在AB 上的点C '处,即AC AC '=,据以上操作,易证明ACD AC D '△△≌,所以AC D C '∠=∠,又因为AC D B '∠>∠,所以C B ∠>∠.感悟与应用:(1)如图(a ),在ABC 中,90ACB ∠=︒,30B ∠=︒,CD 平分ACB ∠,试判断AC 和AD 、BC 之间的数量关系,并说明理由;(2)如图(b ),在四边形ABCD 中,AC 平分BAD ∠,16AC =,8AD =,12DC BC ==,①求证:180B D ∠+∠=︒; ②求AB 的长.25.如图1,在等腰直角三角形ABC 中,动点D 在直线AB (点A 与点B 重合除外)上时,以CD 为一腰在CD 上方作等腰直角三角形ECD ,且90ECD ∠=︒,连接AE .(1)判断AE 与BD 的数量关系和位置关系;并说明理由.(2)如图2,若4BD =,P ,Q 两点在直线AB 上且5EP EQ ==,试求PQ 的长. (3)在第(2)小题的条件下,当点D 在线段AB 的延长线(或反向延长线)上时,判断PQ 的长是否为定值.分别画出图形,若是请直接写出PQ 的长;若不是请简单说明理由. 26.如图,点A 是射线OE :y =x (x ≥0)上的一个动点,过点A 作x 轴的垂线,垂足为B ,过点B 作OA 的平行线交∠AOB 的平分线于点C .(1)若OA =2,求点B 的坐标;(2)如图2,过点C 作CG ⊥AB 于点G ,CH ⊥OE 于点H ,求证:CG =CH .(3)①若点A 的坐标为(2,2),射线OC 与AB 交于点D ,在射线BC 上是否存在一点P 使得△ACP 与△BDC 全等,若存在,请求出点P 的坐标;若不存在,请说明理由. ②在(3)①的条件下,在平面内另有三点P 122),P 2(2,2),P 3(2+2,2﹣2),请你判断也满足△ACP与△BDC全等的点是.(写出你认为正确的点)27.如图1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,(1)试说明△ABC是等腰三角形;(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒2cm的速度沿线段BA向点A 运动,同时动点N从点A出发以每秒1cm速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止. 设点M运动的时间为t(秒),①若△DMN的边与BC平行,求t的值;②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.图1 图2 备用图28.如图1,在正方形ABCD中,点E,F分别是AC,BC上的点,且满足DE⊥EF,垂足为点E,连接DF.(1)求∠EDF= (填度数);(2)延长DE交AB于点G,连接FG,如图2,猜想AG,GF,FC三者的数量关系,并给出证明;(3)①若AB=6,G是AB的中点,求△BFG的面积;②设AG=a,CF=b,△BFG的面积记为S,试确定S与a,b的关系,并说明理由.29.菱形ABCD中,∠BAD=60°,BD是对角线,点E、F分别是边AB、AD上两个点,且满足AE=DF,连接BF与DE相交于点G.(1)如图1,求∠BGD的度数;(2)如图2,作CH⊥BG于H点,求证:2GH=GB+DG;(3)在满足(2)的条件下,且点H在菱形内部,若GB=6,CH=3ABCD的面积.30.阅读下列材料,并解答其后的问题:我国古代南宋数学家秦九韶在其所著书《数学九章》中,利用“三斜求积术”十分巧妙的解决了已知三角形三边求其面积的问题,这与西方著名的“海伦公式”是完全等价的.我们也称这个公式为“海伦•秦九韶公式”,该公式是:设△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,△ABC的面积为S=()()()()a b c a b c a c b b c a+++-+-+-.(1)(举例应用)已知△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,且a=4,b =5,c=7,则△ABC的面积为;(2)(实际应用)有一块四边形的草地如图所示,现测得AB=(26+42)m,BC=5m,CD=7m,AD=46m,∠A=60°,求该块草地的面积.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】本题考查三角形的中线定义,根据条件先确定ABC为直角三角形,再根据勾股定理求得228AC BC=,最后根据12ABCAC BC∆=⋅求解即可.【详解】解:如图,在ABC中,AB边上的中线,∵CD=3,AB= 6,∴CD=3,AB= 6,∴CD= AD= DB ,12∠∠∴=,34∠=∠ , ∵1234180∠+∠+∠+∠=︒,∴1390∠+∠=︒, ∴ABC 是直角三角形,∴22236AC BC AB +==, 又∵8AC BC +=,∴22264AC AC BC BC +⋅+=,∴22264()643628AC BC AC BC ⋅=-+=-=, 又∵12ABC AC BC ∆=⋅, ∴128722ABC S ∆=⨯=, 故选B.【点睛】本题考查三角形中位线的应用,熟练运用三角形的中线定义以及综合分析、解答问题的能力,关键要懂得:在一个三角形中,如果获知一条边上的中线等于这一边的一半,那么就可考虑它是一个直角三角形,通过等腰三角形的性质和内角和定理来证明一个三是直角三角形.2.A解析:A 【分析】根据各个图象,利用面积的不同表示方法,列式证明结论222+=a b c ,找出不能证明的那个选项. 【详解】解:A 选项不能证明勾股定理;B 选项,通过大正方形面积的不同表示方法,可以列式()22142a b ab c +=⨯+,可得222+=a b c ;C 选项,通过梯形的面积的不同表示方法,可以列式()22112222a b ab c +=⨯+,可得222+=a b c ;D 选项,通过这个不规则图象的面积的不同表示方法,可以列式222112222c ab a b ab +⨯=++⨯,可得222+=a b c .故选:A . 【点睛】本题考查勾股定理的证明,解题的关键是掌握勾股定理的证明方法.3.A解析:A 【分析】由已知条件可证△CFE≌△AFD,得到DF=EF,利用折叠知AE=AB=8cm ,设AF=xcm ,则DF=(8-x)cm ,在Rt△AFD 中,利用勾股定理即可求得x 的值. 【详解】∵四边形ABCD 是长方形, ∴∠B=∠D=900,BC=AD,由翻折得AE=AB=8m ,∠E=∠B=900,CE=BC=AD 又∵∠CFE=∠AFD ∴△CFE≌△AFD ∴EF=DF设AF=xcm ,则DF=(8-x )cm 在Rt△AFD 中,AF 2=DF 2+AD 2,AD=6cm ,222(8)6x x =-+254x cm =故选择A. 【点睛】此题是翻折问题,利用勾股定理求线段的长度.4.C解析:C 【解析】分析:通过切线的性质表示出EC 的长度,用相似三角形的性质表示出OE 的长度,由已知条件表示出OC 的长度即可通过勾股定理求出结果. 详解:如图:连接BC ,并连接OD 交BC 于点E :∵DP ⊥BP ,AC 为直径; ∴∠DPB=∠PBC=90°.∴PD ∥BC,且PD 为⊙O 的切线.∴∠PDE=90°=∠DEB,∴四边形PDEB 为矩形,∴AB ∥OE ,且O 为AC 中点,AB=6.∴PD=BE=EC.∴OE=12AB=3. 设PA=x ,则OD=DE-OE=6+x-3=3+x=OC ,EC=PD=6-x..在Rt △OEC 中:222OE EC OC +=,即:()()222363x x +-=+,解得x=2.所以AC=2OC=2×(3+x )=10.点睛:本题考查了切线的性质,相似三角形的性质,勾股定理. 5.B解析:B【解析】由题可知(a-b )2+a 2=(a+b )2,解得a=4b ,所以直角三角形三边分别为3b ,4b ,5b ,当b=8时,4b=32,故选B .6.A解析:A【分析】先根据角平分线的定义、角的和差可得90ECF ∠=︒,再根据平行线的性质、等量代换可得,ACE CEF ACF F ∠=∠∠=∠,然后根据等腰三角形的定义可得,EM CM FM CM ==,从而可得6EF =,最后在Rt CEF 中,利用勾股定理即可得.【详解】 CE 平分ACB ∠,CF 平分ACD ∠,,1122ACB ACD BCE ACE DCF ACF ∴∠∠=∠=∠=∠∠=, 111(90222)ACB AC E D ACB ACD CF ACE ACF ∠=∠+∴∠+∠=∠∠∠=+=︒, //EF BC ,,BCE CEF DCF F ∠=∴∠∠=∠,,ACE CEF ACF F ∴∠=∠∠=∠,3,3EM CM FM CM ∴====,6EF EM FM ∴=+=,在Rt CEF 中,由勾股定理得:2222636CE CF EF +===,故选:A .【点睛】本题考查了角平分线的定义、平行线的性质、等腰三角形的定义、勾股定理等知识点,熟练掌握等腰三角形的定义是解题关键.7.A解析:A【分析】首先根据勾股定理得出圆弧的半径,然后得出点A 的坐标.【详解】∴由图可知:点A 所表示的数为: 1-故选:A【点睛】本题主要考查的就是数轴上点所表示的数,属于基础题型.解决这个问题的关键就是求出斜边的长度.在数轴上两点之间的距离是指两点所表示的数的差的绝对值.8.C解析:C【分析】利用勾股定理的逆定理可以推导出ABD △是直角三角形.再利用勾股定理求出A C ,可得出AB=AC ,即可判断.【详解】解:由已知可得CD=BD=5,22251213+=即222BD AD AB +=,ABD ∴是直角三角形,90ADB ∠=︒,90ADC ∴∠=︒222AD CD AC ∴+=13AC ∴=13AB AC ∴==故ABC 是等腰三角形.故选C【点睛】本题考查了勾股定理和它的逆定理,熟练掌握定理是解题关键.9.C解析:C【分析】利用勾股定理求出AB 的长,再根据无理数的估算即可求得答案.【详解】由作法过程可知,OA=2,AB=3,∵∠OAB=90°,∴==,∴P∵<∴34<<,即点P所表示的数介于3和4之间,故选C.【点睛】本题考查了勾股定理和无理数的估算,熟练掌握勾股定理的内容以及无理数估算的方法是解题的关键.10.B解析:B【解析】试题分析:解:∵92=81,122=144,152=225,362=1296,392=1521,∴81+144=225,225+1296=1521,即92+122=152,152+362=392,故选B.考点:勾股定理的逆定理点评:本题难度中等,主要考查了勾股定理的逆定理,解题的关键熟知勾股定理逆定理的内容.二、填空题11.96 25【分析】将△B´CF的面积转化为求△BCF的面积,由折叠的性质可得CD=AC=6,∠ACE=∠DCE,∠BCF=∠B´CF,CE⊥AB,可证得△ECF是等腰直角三角形,EF=CE,∠EFC=45°,由等面积法可求CE的长,由勾股定理可求AE的长,进而求得BF的长,即可求解.【详解】根据折叠的性质可知,CD=AC=6,∠ACE=∠DCE,∠BCF=∠B´CF,CE⊥AB,∴∠DCE+∠B´CF=∠ACE+∠BCF,∵∠ACB=90°,∴∠ECF=45°,且CE⊥AB,∴△ECF是等腰直角三角形,∴EF=CE,∠EFC=45°,∵S△ABC=12AC•BC=12AB•CE,∴AC•BC=AB•CE,∵根据勾股定理求得AB =10,∴CE =245, ∴EF =245,∵AE 185, ∴BF =AB−AE−EF =10-185-245=85, ∴S △CBF =12×BF ×CE =12×85×245=9625, ∴S △CB´F =9625, 故填:9625. 【点睛】此题主要考查了翻折变换,等腰三角形的判定和性质,勾股定理的应用等知识,根据折叠的性质求得相等的角是解决本题的关键.12.48【分析】用a 和b 表示直角三角形的两个直角边,然后根据勾股定理列出正方形面积的式子,求出2S 的面积.【详解】解:本图是由八个全等的直角三角形拼成的,设这个直角三角形两个直角边中较长的长度为a ,较短的长度为b ,即图中的AE a =,AH b =,则()221S AB a b ==+,2222S HE a b ==+,()223S TM a b ==-, ∵123144S S S ++=,∴()()2222144a b a b a b ++++-= 22222222144a b ab a b a b ab ++++++-=2233144a b +=2248a b +=,∴248S =.故答案是:48.【点睛】本题考查勾股定理,解题的关键是要熟悉赵爽弦图中勾股定理的应用.13.125【分析】解方程222225,7a b a b +=-=可求得a=4,b=3,故三角形ABC 是直角三角形,在利用三角形的面积转化得到斜边上的高.【详解】解:∵222225,7a b a b +=-=,将两个方程相加得:2232a =,∵a >0,∴a=4代入得:22425b +=,∵b >0,∴b=3,∵a=3,b=4,c=5满足勾股定理逆定理,∴△ABC 是直角三角形,如下图,∠ACB=90°,CD ⊥AB ,1122ABC S AC BC AB CD =⋅⋅=⋅⋅ , 即:1134522CD ⋅⋅=⋅⋅, 解得:CD=125, 故答案为:125. 【点睛】 本题考查求解三角形的高,解题关键是利用三角形的面积进行转化,在同一个三角形中,一个底乘对应高等于另一个底乘对应高.14.32或42【分析】根据题意画出图形,分两种情况:△ABC 是钝角三角形或锐角三角形,分别求出边BC ,即可得到答案【详解】当△ABC 是钝角三角形时,∵∠D=90°,AC=13,AD=12,∴222213125CD AC AD=-=-=,∵∠D=90°,AB=15,AD=12,∴222215129BD AB AD=-=-=,∴BC=BD-CD=9-5=4,∴△ABC的周长=4+15+13=32;当△ABC是锐角三角形时,∵∠ADC=90°,AC=13,AD=12,∴222213125CD AC AD=-=-=,∵∠ADB=90°,AB=15,AD=12,∴222215129BD AB AD=-=-=,∴BC=BD-CD=9+5=14,∴△ABC的周长=14+15+13=42;综上,△ABC的周长是32或42,故答案为:32或42.【点睛】此题考查勾股定理的实际应用,能依据题意正确画出图形分类讨论是解题的关键.15.53或203【分析】根据折叠后点C的对应点H与AC的位置关系分类讨论,分别画出对应的图形,利用勾股定理求出各边的长,再根据折叠的性质与勾股定理列出对应的方程即可求出结论.【详解】解:①当折叠后点C 的对应点H 在AC 的下方时,如下图所示∵Rt ABC 中,90A ∠=︒,8AC =,6AB =,根据勾股定理可得2210AB AC += ∵13CD BC =,13CE AC =, ∴13CD BC ==103,13CE AC ==83 ∵DE AC ⊥根据勾股定理可得222CD CE -=由折叠的性质可得:DH=CD=103,CP=PH ∴EH=DH -DE=43设CP=PH=x ,则EP=CE -CP=83-x 在Rt △PEH 中,EP 2+EH 2=PH 2 即(83-x )2+(43)2=x 2 解得:x=53即此时CP=53; ②当折叠后点C 的对应点H 在AC 的上方时,如下图所示根据折叠的性质可得DH=CD=103,CP=PH ∴EH=DH +DE=163设CP=PH=y ,则EP= CP -CE =y -83在Rt △PEH 中,EP 2+EH 2=PH 2即(y -83)2+(163)2=y 2 解得:y=203即此时CP=203. 综上所述:CP=53或203. 故答案为:53或203. 【点睛】 此题考查的是勾股定理和折叠问题,掌握利用勾股定理解直角三角形、折叠的性质和分类讨论的数学思想是解决此题的关键.16.103. 【分析】 根据八个直角三角形全等,四边形ABCD ,EFGH ,MNKT 是正方形,得出CG=NG ,CF=DG=NF ,再根据()21S CG DG =+,22S GF =,()23S NG NF =-,12310S S S ++=,即可得出答案.【详解】∵八个直三角形全等,四边形ABCD ,EFGH ,MNKT 是正方形∴CG=NG ,CF=DG=NF∴()2222122S CG DG CG DG CG DG GF CG DG =+=++=+22S GF =()22232S NG NF NG NF NG NF =-=+-∴2222212322310S S S GF CG DG GF NG NF NG NF GF ++=+⋅+++-⋅== ∴2103GF =故2103S = 故答案为103. 【点睛】 本题主要考查了勾股定理的应用,用到的知识点由勾股定理和正方形、全等三角形的性质.17.4或【分析】分三种情况讨论:①以A 为直角顶点,向外作等腰直角三角形DAC ;②以C 为直角顶点,向外作等腰直角三角形ACD ;③以AC 为斜边,向外作等腰直角三角形ADC .分别画图,并求出BD .【详解】①以A 为直角顶点,向外作等腰直角三角形DAC ,如图1.∵∠DAC =90°,且AD =AC ,∴BD =BA +AD =2+2=4;②以C 为直角顶点,向外作等腰直角三角形ACD ,如图2.连接BD ,过点D 作DE ⊥BC ,交BC 的延长线于E .∵△ABC 是等腰直角三角形,∠ACD =90°,∴∠DCE =45°.又∵DE ⊥CE ,∴∠DEC =90°,∴∠CDE =45°,∴CE =DE =2=在Rt △BAC 中,BC == BD ===③以AC 为斜边,向外作等腰直角三角形ADC ,如图3.∵∠ADC =90°,AD =DC ,且AC =2,∴AD =DC =AC sin45°=22= 又∵△ABC 、△ADC 是等腰直角三角形,∴∠ACB =∠ACD =45°,∴∠BCD=90°.又∵在Rt△ABC中,BC2222=+=22,∴BD222222210BC CD=+=+=()().故BD的长等于4或25或10.故答案为4或25或10.【点睛】本题考查了等腰直角三角形的性质、勾股定理等知识.解题的关键是分情况考虑问题,18.35 5【详解】四边形DEFA是正方形,面积是4;△ABF,△ACD的面积相等,且都是×1×2=1.△BCE的面积是:12×1×1=12.则△ABC的面积是:4﹣1﹣1﹣12=32.在直角△ADC中根据勾股定理得到:AC=222+1=5.设AC边上的高线长是x.则12AC•x=5x=32,解得:x=355.35 5.19.8或10或12或25 3【详解】解:①如图1:当BC=CD=3m时,AB=AD=5m,AC⊥BD,此时等腰三角形绿地的面积:12×6×4=12(m2);②如图2:当AC=CD=4m时,AC⊥CB,此时等腰三角形绿地的面积:12×4×4=8(m2);③如图3:当AD=BD时,设AD=BD=xm,在Rt△ACD中,CD=(x-3)m,AC=4m,由勾股定理,得AD2=DC2+CA2,即(x-3)2+42=x2,解得x=256,此时等腰三角形绿地的面积:12BD·AC=12×256×4=253(m2);④如图4,延长BC 到D ,使BD=AB=5m ,故CD=2m , 此时等腰三角形绿地的面积:12BD·AC=12×5×4=10(m 2); 综上所述,扩充后等腰三角形绿地的面积为8m 2或12m 2或10m 2或253m 2. 点睛:此题主要考查了等腰三角形的性质以及勾股定理的应用,解决问题的关键是根据题意正确画出图形.20.2【分析】 根据三角形等面积法求出32AC BC = ,在Rt△ACD 中根据勾股定理得出AC 2=14BC 2+36,依据这两个式子求出AC 、BC 的值.【详解】 ∵AD 是BC 边上的高,BE 是AC 边上的高, ∴12AC•BE=12BC•AD, ∵AD=6,BE =4, ∴AC BC =32, ∴22AC BC =94, ∵AB=AC ,AD⊥BC,∴BD=DC =12BC , ∵AC 2﹣CD 2=AD 2,∴AC 2=14BC 2+36, ∴221364BC BC +=94, 整理得,BC 2=3648⨯,解得:BC =∴△ABC 的面积为12×cm 2故答案为:【点睛】本题考查了三角形的等面积法以及勾股定理的应用,找出AC 与BC 的数量关系是解答此题的关键.三、解答题21.(12)150°;(3【分析】(1)根据等边三角形的性质可利用SAS 证明△BCD ≌△ACE ,再根据全等三角形的性质即得结果;(2)在△ADE 中,根据勾股定理的逆定理可得∠AED =90°,进而可求出∠AEC 的度数,再根据全等三角形的性质即得答案;(3)过C 作CP ⊥DE 于点P ,设AC 与DE 交于G ,如图,根据等边三角形的性质和勾股定理可得PE 与CP 的长,进而可得AE =CP ,然后即可根据AAS 证明△AEG ≌△CPG ,于是可得AG =CG ,PG =EG ,根据勾股定理可求出AG 的长,进一步即可求出结果.【详解】解:(1)∵△ABC 和△EDC 都是等边三角形,∴BC =AC ,CD =CE =DE =2,∠ACB =∠DCE =60°,∴∠BCD =∠ACE ,在△BCD 与△ACE 中,∵BC =AC ,∠BCD =∠ACE ,CD =CE ,∴△BCD ≌△ACE ,∴AE =BD(2)在△ADE 中,∵2AD AE DE ===,∴DE 2+AE 2=2222+==AD 2, ∴∠AED =90°,∵∠DEC =60°,∴∠AEC =150°,∵△BCD ≌△ACE ,∴∠BDC =∠AEC =150°;(3)过C 作CP ⊥DE 于点P ,设AC 与DE 交于G ,如图,∵△CDE 是等边三角形,∴PE =12DE =1,CP 22213-=,∴AE =CP ,在△AEG 与△CPG 中,∵∠AEG =∠CPG =90°,∠AGE =∠CGP ,AE =CP ,∴△AEG ≌△CPG ,∴AG =CG ,PG =EG =12, ∴AG ()222211332AE EG ⎛⎫+=+= ⎪⎝⎭, ∴AC =2AG 13【点睛】本题考查了等边三角形的性质、全等三角形的判定和性质、勾股定理及其逆定理等知识,熟练掌握上述知识、灵活应用全等三角形的判定与性质是解题的关键.22.(1)AE BD =,AE BD ⊥;(2)成立,理由见解析;(3)14或2.【分析】(1)先根据等腰三角形的定义可得AC BC =,CE CD =,再根据三角形全等的判定定理与性质可得AE BD =,EAC DBC ∠=∠,然后根据直角三角形两锐角互余、等量代换即可得90AHD ∠=︒,由此即可得;(2)先根据三角形全等的判定定理与性质可得AE BD =,EAC DBC ∠=∠,再根据直角三角形两锐角互余可得90EAC AOC ∠+∠=︒,然后根据对顶角相等、等量代换可得90BOH DBC ∠∠+=︒,从而可得90OHB ∠=︒,由此即可得; (3)先利用勾股定理求出102AB =,再分①点,,A E D 在直线上,且点E 位于中间,②点,,A E D 在直线上,且点D 位于中间两种情况,结合(1)(2)的结论,利用勾股定理求解即可得.【详解】(1)AE BD =,AE BD ⊥,理由如下:如图1,延长AE 交BD 于H ,由题意得:AC BC =,90ACE BCD ∠=∠=︒,CE CD =, ∴()ACE BCD SAS ≅,∴AE BD =,EAC DBC ∠=∠,∵90DBC BDC ∠+∠=︒,∴90EAC BDC ∠+∠=︒,∴0)9018(EAC BD A D C H ∠+∠∠︒==-︒,即AE BD ⊥,故答案为:AE BD =,AE BD ⊥;(2)成立,理由如下:如图2,延长AE 交BD 于H ,交BC 于O ,∵90ACB ECD ∠=∠=︒,∴ACB BCE ECD BCE ∠-∠=∠-∠,即ACE BCD ∠=∠,在ACE △和BCD 中,AC BC ACE BCD CE CD =⎧⎪∠=∠⎨⎪=⎩,∴()ACE BCD SAS ≅,∴AE BD =,EAC DBC ∠=∠,∵90ACB ∠=︒,∴90EAC AOC ∠+∠=︒,∵AOC BOH ∠=∠,∴90BOH DBC ∠∠+=︒,即90OBH BOH ∠+∠=︒,∴180()90OHB OBH BOH ∠=︒-∠+∠=︒,即AE BD ⊥;(3)设AD x =,10,90AC BC ACB ==∠=︒, 2102AB AC ∴==,由题意,分以下两种情况:①如图3-1,点,,A E D 在直线上,且点E 位于中间,同理可证:AE BD =,AE BD ⊥,12DE =,12BD AE AD DE x ∴==-=-,在Rt ABD △中,222AD BD AB +=,即222(12)(102)x x +-=, 解得14x =或2x =-(不符题意,舍去),即14AD =,②如图3-2,点,,A E D 在直线上,且点D 位于中间,同理可证:AE BD =,AE BD ⊥,12DE =,12BD AE AD DE x ∴==+=+,在Rt ABD △中,222AD BD AB +=,即222(12)(102)x x ++=,解得2x =或14x =-(不符题意,舍去),即2AD =,综上,AD 的长为14或2.【点睛】本题考查了三角形全等的判定与性质、勾股定理等知识点,较难的是题(3),正确分两种情况讨论,并画出图形是解题关键.23.(1)2;(2)32q p =;(3)27OM =【分析】(1)根据“距离坐标”的定义结合图形判断即可;(2)过M 作MN ⊥CD 于N ,根据已知得出MN q =,OM p =,求出∠MON =60°,根据含30度直角三角形的性质和勾股定理求出223MN MO NO p =-=即可解决问题;(3)分别作点M 关于AB 、CD 的对称点F 、E ,连接EF 、OE 、OF ,连接MF 、ME 分别交AB 、CD 于P 点、Q 点,首先证明OM OE OF EF ===,求出2MF =,23ME =,然后过F 作FG QM ⊥,交QM 延长线于G ,根据含30度直角三角形的性质求出1FG =,3MG =,再利用勾股定理求出EF 即可.【详解】解:(1)由题意可知,在直线CD 上,且在点O 的两侧各有一个,共2个,故答案为:2;(2)过M 作MN CD ⊥于N ,∵直线l AB ⊥于O ,150BOD ∠=︒,∴60MON ∠=︒,∵MN q =,OM p =,∴1122NO MO p ==, ∴2232MN MO NO p =-=, ∴3q p =; (3)分别作点M 关于AB 、CD 的对称点F 、E ,连接EF 、OE 、OF ,连接MF 、ME 分别交AB 、CD 于P 点、Q 点.∴OFP OMP △≌△,OEQ OMQ △≌△,∴FOP MOP ∠=∠,EOQ MOQ ∠=∠,OM OE OF ==,∴260EOF BOD ∠=∠=︒,∴△OEF 是等边三角形,∴OM OE OF EF ===,∵1MP =,3MQ =∴2MF =,3ME =,∵30BOD ∠=︒,∴150PMQ ∠=︒,过F 作FG QM ⊥,交QM 延长线于G ,∴30FMG ∠=︒,在Rt FMG △中,112FG MF ==,则3MG =, 在Rt EGF 中,1FG =,33EG ME MG =+=,∴22(33)127EF =+=,∴27OM =.【点睛】本题考查了轴对称的应用,含30度直角三角形的性质,勾股定理以及等边三角形的判定和性质等,正确理解题目中的新定义是解答本题的关键.24.(1)BC−AC =AD ;理由详见解析;(2)①详见解析;②AB=14【分析】(1)在CB 上截取CE =CA ,连接DE ,证△ACD ≌△ECD 得DE =DA ,∠A =∠CED =60°,据此∠CED =2∠CBA ,结合∠CED =∠CBA +∠BDE 得出∠CBA =∠BDE ,即可得DE =BE ,进而得出答案;(2)①在AB 上截取AM =AD ,连接CM ,先证△ADC ≌△AMC ,得到∠D =∠AMC ,CD =CM ,结合CD =BC 知CM =CB ,据此得∠B =∠CMB ,根据∠CMB +∠CMA =180°可得;②设BN =a ,过点C 作CN ⊥AB 于点N ,由CB =CM 知BN =MN =a ,CN 2=BC 2−BN 2=AC 2−AN 2,可得关于a 的方程,解之可得答案.【详解】解:(1)BC−AC =AD .理由如下:如图(a ),在CB 上截取CE =CA ,连接DE ,∵CD 平分∠ACB ,∴∠ACD =∠ECD ,又CD =CD ,∴△ACD ≌△ECD (SAS ),∴DE =DA ,∠A =∠CED =60°,∴∠CED =2∠CBA ,∵∠CED =∠CBA +∠BDE ,∴∠CBA =∠BDE ,∴DE =BE ,∴AD =BE ,∵BE =BC−CE =BC−AC ,∴BC−AC =AD .(2)①如图(b ),在AB 上截取AM =AD ,连接CM ,∵AC 平分∠DAB ,∴∠DAC =∠MAC ,∵AC =AC ,∴△ADC ≌△AMC (SAS ),∴∠D =∠AMC ,CD =CM =12,∵CD =BC =12,∴CM =CB ,∴∠B =∠CMB ,∵∠CMB +∠CMA =180°,∴∠B +∠D =180°;②设BN =a ,过点C 作CN ⊥AB 于点N ,∵CB =CM =12,∴BN =MN =a ,在Rt △BCN 中,2222212CN BC BN a --==,在Rt △ACN 中,2222216(8)CN AC AN a --+==, 则22221216(8)a a --+=, 解得:a =3,即BN =MN =3,则AB =8+3+3=14,∴AB=14.【点睛】本题考查了四边形的综合题,以及全等三角形的判定与性质、勾股定理、等腰三角形的判定与性质;本题有一定难度,需要通过作辅助线证明三角形全等才能得出结果.25.(1)AE=BD且AE⊥BD;(2)6;(3)PQ为定值6,图形见解析【分析】(1)由“SAS”可证△ACE≌△BCD,可得AE=BD,∠EAC=∠DBC=45°,可得AE⊥BD;(2)由等腰三角形的性质可得PA=AQ,由勾股定理可求PA的长,即可求PQ的长;(3)分两种情况讨论,由“SAS”可证△ACE≌△BCD,可得AE=BD,∠EAC=∠DBC,可得AE⊥BD,由等腰三角形的性质可得PA=AQ,由勾股定理可求PA的长,即可求PQ的长.【详解】解:(1)AE=BD,AE⊥BD,理由如下:∵△ABC,△ECD都是等腰直角三角形,∴AC=BC,CE=CD,∠ACB=∠ECD=90°,∠ABC=∠CAB=45°,∴∠ACE=∠DCB,且AC=BC,CE=CD,∴△ACE≌△BCD(SAS)∴AE=BD,∠EAC=∠DBC=45°,∴∠EAC+∠CAB=90°,∴AE⊥BD;(2)∵PE=EQ,AE⊥BD,∴PA=AQ,∵EP=EQ=5,AE=BD=4,∴,∴PQ=2AQ=6;(3)如图3,若点D在AB的延长线上,∵△ABC,△ECD都是等腰直角三角形,∴AC=BC,CE=CD,∠ACB=∠ECD=90°,∠ABC=∠CAB=45°,∴∠ACE=∠DCB,且AC=BC,CE=CD,∴△ACE≌△BCD(SAS)∴AE=BD,∠CBD=∠CAE=135°,且∠CAB=45°,∴∠EAB=90°,∵PE=EQ,AE⊥BD,∴PA=AQ,∵EP=EQ=5,AE=BD=4,∴,∴PQ=2AQ=6;如图4,若点D 在BA 的延长线上,∵△ABC ,△ECD 都是等腰直角三角形,∴AC=BC ,CE=CD ,∠ACB=∠ECD=90°,∠ABC=∠CAB=45°,∴∠ACE=∠DCB ,且AC=BC ,CE=CD ,∴△ACE ≌△BCD (SAS )∴AE=BD ,∠CBD=∠CAE=45°,且∠CAB=45°,∴∠EAB=90°,∵PE=EQ ,AE ⊥BD ,∴PA=AQ ,∵EP=EQ=5,AE=BD=4,∴AQ=22=2516=3EQ AE --,∴PQ=2AQ=6.【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,等腰三角形的性质,勾股定理等知识,证明AE ⊥BD 是本题的关键.26.(1)(5,0);(2)见解析;(3)①P (4,2),②满足△ACP 与△BDC 全等的点是P 1、P 2,P 3.理由见解析【分析】(1)由题意可以假设A (a ,a )(a >0),根据AB 2+OB 2=OA 2,构建方程即可解决问题;(2)由角平分线的性质定理证明CH=CF,CG=CF即可解决问题;(3)①如图3中,在BC的延长线上取点P,使得CP=DB,连接AP.只要证明△ACP≌△CDB(SAS),△ABP是等腰直角三角形即可解决问题;②根据SAS即可判断满足△ACP与△BDC全等的点是P1、P2,P3;【详解】解:(1)∵点A在射线y=x(x≥0)上,故可以假设A(a,a)(a>0),∵AB⊥x轴,∴AB=OB=a,即△ABO是等腰直角三角形,∴AB2+OB2=OA2,∴a2+a2=(52)2,解得a=5,∴点B坐标为(5,0).(2)如图2中,作CF⊥x轴于F.∵OC平分∠AOB,CH⊥OE,∴CH=CF,∵△AOB是等腰直角三角形,∴∠AOB=45°,∵BC∥OE,∴∠CBG=∠AOB=45°,得到BC平分∠ABF,∵CG⊥BA,CF⊥BF,∴CG=CF,∴CG=CH.(3)①如图3中,在BC的延长线上取点P,使得CP=DB,连接AP.由(2)可知AC平分∠DAE,∴∠DAC=12∠DAE=12(180°﹣45°)=67.5°,由OC平分∠AOB得到∠DOB=12∠AOB=22.5°,∴∠ADC=∠ODB=90°﹣22.5°=67.5°,∴∠ADC=∠DAC=67.5°,∴AC=DC,∠BDC=∠OBD+∠DOB=90°+22.5°=112.5°,∠ACD=180°﹣∠CAD﹣∠ADC=180°﹣67.5°﹣67.5°=45°,∠OCB=45°﹣22.5°=22.5°,∠ACP=180°﹣∠ACD﹣∠OCB=180°﹣45°﹣22.5°=112.5°,在△ACP和△CDB中,AC ADACP DB CP DB=⎧⎪∠=∠⎨⎪=⎩,∴△ACP≌△CDB(SAS),∴∠CAP=∠DCB=22.5°,∴∠BAP=∠CAP+∠DAC=22.5°+67.5°=90°,∴△ABP是等腰直角三角形,∴AP=AB=OB=2,∴P(4,2).②满足△ACP与△BDC全等的点是P1、P2,P3.理由:如图4中,由题意:AP1=BD,AC=CD,∠CAP1=∠CDB,根据SAS可得△CAP1≌△CDB;AP2=BD,AC=CD,∠CAP2=∠CDB,根据SAS可得△CAP2≌△CDB;AC=CD,∠ACP3=∠BDC,BD=CP3根据SAS可得△CAP3≌△DCB;故答案为P1、P2,P3.【点睛】本题考查全等三角形的判定和性质、等腰直角三角形的判定和性质、勾股定理、角平分线的性质定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.27.(1)见详解;(2)①t值为:103s或6s;②t值为:4.5或5或4912.【分析】(1)设BD=2x,AD=3x,CD=4x,则AB=5x,由勾股定理求出AC,即可得出结论;(2)由△ABC的面积求出BD、AD、CD、AC;①当MN∥BC时,AM=AN;当DN∥BC时,AD=AN;得出方程,解方程即可;②根据题意得出当点M在DA上,即2<t≤5时,△MDE为等腰三角形,有3种可能:如果DE=DM;如果ED=EM;如果MD=ME=2t-4;分别得出方程,解方程即可.【详解】解:(1)证明:设BD=2x,AD=3x,CD=4x,则AB=5x,在Rt△ACD中,AC=5x,∴AB=AC,∴△ABC是等腰三角形;(2)解:由(1)知,AB=5x,CD=4x,∴S△ABC=12×5x×4x=40cm2,而x>0,∴x=2cm,则BD=4cm,AD=6cm,CD=8cm,AB=AC=10cm.由运动知,AM=10-2t,AN=t,①当MN∥BC时,AM=AN,即10-2t=t,∴103t ;当DN∥BC时,AD=AN,∴6=t,得:t=6;∴若△DMN的边与BC平行时,t值为103s或6s.②存在,理由:Ⅰ、当点M在BD上,即0≤t<2时,△MDE为钝角三角形,但DM≠DE;Ⅱ、当t=2时,点M运动到点D,不构成三角形Ⅲ、当点M在DA上,即2<t≤5时,△MDE为等腰三角形,有3种可能.∵点E是边AC的中点,∴DE=12AC=5当DE=DM,则2t-4=5,∴t=4.5s;当ED=EM,则点M运动到点A,∴t=5s;当MD=ME=2t-4,如图,过点E作EF垂直AB于F,∵ED=EA,∴DF=AF=12AD=3,在Rt△AEF中,EF=4;∵BM=2t,BF=BD+DF=4+3=7,∴FM=2t-7在Rt△EFM中,(2t-4)2-(2t-7)2=42,∴t=49 12.综上所述,符合要求的t值为4.5或5或49 12.【点睛】本题主要考查了等腰三角形的性质,平行线的性质,三角形的面积公式,勾股定理,解本题的关键是分情况讨论.,理由见解析. 28.(1)45°;(2)GF=AG+CF,证明见解析;(3)①6;②s ab【解析】【分析】(1)如图1中,连接BE.利用全等三角形的性质证明EB=ED,再利用等角对等边证明EB=EF即可解决问题.(2)猜想:GF=AG+CF.如图2中,将△CDF绕点D旋转90°,得△ADH,证明△GDH≌△GDF(SAS)即可解决问题.(3)①设CF=x,则AH=x,BF=6-x,GF=3+x,利用勾股定理构建方程求出x即可.②设正方形边长为x,利用勾股定理构建关系式,利用整体代入的思想解决问题即可.【详解】解:(1)如图1中,连接BE.∵四边形ABCD是正方形,∴CD=CB,∠ECD=∠ECB=45°,∵EC=EC,∴△ECB≌△ECD(SAS),∴EB=ED,∠EBC=∠EDC,∵∠DEF=∠DCF=90°,∴∠EFC+∠EDC=180°,∵∠EFB+∠EFC=180°,∴∠EFB=∠EDC,∴∠EBF=∠EFB,∴EB=EF,∴DE=EF,∵∠DEF=90°,∴∠EDF=45°故答案为45°.(2)猜想:GF=AG+CF.如图2中,将△CDF绕点D旋转90°,得△ADH,。
人教版八年级第二学期3月份月考数学试卷含答案

人教版八年级第二学期3月份月考数学试卷含答案一、选择题1.下列各式计算正确的是( )A =B .2=C =D =2.下列各式计算正确的是( )AB .C =3D .3.下列各式计算正确的是( )A =B =C .23=D 2=-4.下列各式中,正确的是( )A 2=±B =C 3=-D 2=5.下列计算正确的是( )A =B 3=C =D .21=6.下列各式计算正确的是( )A .6232126()b a b a b a---⋅=B .(3xy )2÷(xy )=3xyC =D .2x •3x 5=6x 67.x 的取值范围是( ) A .13x ≥B .13x >C .13x ≤D .13x <8.下列各式中,正确的是( )A .B .a 3 • a 2=a 6C .(b+2a) (2a -b) =b 2 -4a 2D .5m + 2m = 7m 29.已知a 满足2018a -a ,则a -2 0182=( ) A .0B .1C .2 018D .2 01910.下列运算中错误的是( )A =B =C 2÷=D .2 (3=11.若|x 2﹣4x+4|x+y 的值为( ) A .3B .4C .6D .912.下列各组二次根式中,能合并的一组是( )A B 和C D 二、填空题13.定义:对非负实数x “四舍五入”到个位的值记为()f x z ,即:当n 为非负整数时,如果1122n x n -<+≤,则()f x n =z .如:(0)(0.48)0f f ==z z ,(0.64)(1.49)1f f ==z z ,(4)(3.68)4f f ==z z ,试解决下列问题:①f =z __________;②f =z __________;+=__________.14.已知,-1,则x 2+xy +y 2=_____.15.+的形式(,,a b c 为正整数),则abc =______.16.下面是一个按某种规律排列的数阵:根据数阵排列的规律,第 5 行从左向右数第 3 个数是 ,第 n (n 3≥ 且 n 是整数)行从左向右数第 n 2- 个数是 (用含 n 的代数式表示).17.÷=________________ .18.已知a ,b 是正整数,若有序数对(a ,b )使得的值也是整数,则称(a ,b )是的一个“理想数对”,如(1,4)使得=3,所以(1,4)是的一个“理想数对”.请写出其他所有的“理想数对”: __________. 19.已知整数x ,y 满足y =,则y =__________.20.把三、解答题21.计算:(1(2))((222+-+.【答案】(1) 【分析】(1)先化简二次根式,再合并同类二次根式即可; (2)根据平方差公式化简,再化简、合并同类二次根式即可. 【详解】(1==(2))((222+-+=2223--+ =5-4-3+2 =022.先阅读材料,再回答问题:因为)111=1=;因为1=,所以=1== (1= ,= ; (2⋅⋅⋅+的值.【答案】(12)9 【分析】(1)仿照例子,由1+=的值;由1+=1的值;(2)根据(1)中的规律可将每个二次根式分母有理化,可转化为实数的加减法运算,再寻求规律可得答案. 【详解】解:(1)因为1-=;因为1=1(2⋅⋅⋅+1=+⋅⋅⋅1=1019=-=.【点睛】本题考查了分母有理化,分子分母都乘以分母这两个数的差进行分母有理化是解题关键.23.阅读下面的解答过程,然后作答:m 和n ,使m 2+n 2=a 且,则a 可变为m 2+n 2+2mn ,即变成(m +n )2例如:∵=)2+)2=)2∴请你仿照上例将下列各式化简(12【答案】(1)2-【分析】参照范例中的方法进行解答即可. 【详解】解:(1)∵22241(1+=+=,1=(2)∵2227-=-=,∴==24.观察下列等式:1==;==== 回答下列问题:(1(2)计算:【答案】(1(2)9 【分析】(1)根据已知的31=-n=22代入即可求解;(2)先利用上题的规律将每一个分数化为两个二次根式的差的形式,再计算即可. 【详解】解:(1=(2+99+=1100++-=1 =10-1 =9.25.【分析】先化为最简二次根式,再将被开方数相同的二次根式进行合并. 【详解】. 【点睛】本题考查了二次根式的加减运算,在进行此类运算时,先把二次根式化为最简二次根式的形式后再运算.26.计算:【答案】【分析】先将括号内的二次根式进行化简并合并,再进行二次根式的乘法运算即可. 【详解】解:=== 【点睛】此题主要考查了二次根式的混合运算,熟练掌握运算法则是解答此题的关键.27.观察下列各式:11111122=+-=11111236=+-=111113412=+-= 请你根据上面三个等式提供的信息,猜想:(1=_____________ (2)请你按照上面每个等式反映的规律,写出用n (n 为正整数)表示的等式:______________;(3【答案】(1)1120;(211(1)n n =++;(3)1156,过程见解析【分析】(1)仿照已知等式确定出所求即可; (2)归纳总结得到一般性规律,写出即可; (3)原式变形后,仿照上式得出结果即可. 【详解】解:(1111114520=+-=; 故答案为:1120;(2111111(1)n n n n =+-=+++;11(1)n n =++;(31156== 【点睛】此题是一个阅读题目,通过阅读找出题目隐含条件.总结:找规律的题,都要通过仔细观察找出和数之间的关系,并用关系式表示出来.28.已知x y ==求下列各式的值: (1)22x xy y -+; (2).y xx y+ 【答案】(1) 72;(2)8. 【分析】计算出xy=12, (1)把x 2-xy+y 2变形为(x+y )2-3xy ,然后利用整体代入的方法计算;(2)把原式变形为2()2x y xyxy+-,然后利用整体代入的方法计算.【详解】∵x =,y ==32∴xy=12, (1)22x xy y -+ =(x+y )2-3xy,=2132-⨯=72; (2)y x x y +=2212()22812x y xy xy-⨯+-==.【点睛】本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.29.先化简,再求值:24224x x x x x x ⎛⎫÷- ⎪---⎝⎭,其中2x =. 【答案】22x x +-,1 【分析】先把分式化简,然后将x 、y 的值代入化简后的式子求值即可. 【详解】 原式(2)(2)22(2)2x x x x x x x x +-+=⋅=---,当2x =时,原式1==.【点睛】本题考查了分式的化简求值这一知识点,把分式化到最简是解题的关键.30.计算:(1)13⎛+-⨯ ⎝⎭(2))()2221+.【答案】(1)6-;(2)12-【分析】(1)原式化简后,利用二次根式乘法法则计算即可求出值; (2)原式利用平方差公式,以及完全平方公式计算即可求出值. 【详解】解:(1)原式=1(23⨯⨯-⨯=3=⨯⎭=6-;(2)原式=3﹣4+12﹣=12﹣.【点睛】此题考查了二次根式的混合运算,以及平方差公式、完全平方公式,熟练掌握运算法则及公式是解本题的关键.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】计算出各个选项中的正确结果,即可得到哪个选项是正确【详解】A错误;∵2+B错误;=,故选项C正确;=,故选项D错误.故选C.【点睛】本题考查二次根式的混合运算,解题的关键是明确二次根式的混合运算的计算方法.2.C解析:C【分析】根据二次根式的化简进行选择即可.【详解】AB、C,故本选项正确;D、=18,故本选项错误;故选:C.【点睛】本题考查了二次根式的混合运算,掌握二次根式的化简是解题的关键.3.C解析:C【分析】根据各个选项中的式子,可以计算出正确的结果,从而可以解答本题.【详解】,故选项A错误;=2,故选项B错误;C. 23=,故选项C正确;2=,故选项D错误;故选C.【点睛】本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.4.B解析:B【分析】本题可利用二次根式的化简以及运算法则判断A、B、C选项;利用立方根性质判断D选项.【详解】A,故该选项错误;B==C3=,故该选项错误;D11223334=(2)2==,故该选项错误;故选:B.【点睛】本题考查二次根式以及立方根,二次根式计算时通常需要化为最简二次根式,然后按照运算法则求解即可,解题关键是细心.5.A解析:A【分析】分别进行二次根式的乘除法、加减法运算,然后选择正确答案.【详解】解:======,原式计算错误;D. 2220=-=,原式计算错误;故应选:A【点睛】本题考查了二次根式的乘除法和加减法,掌握运算法则是解答本题的关键.6.D解析:D【分析】依据单项式乘以单项式、单项式除以单项式以及二次根式的加法法则对各项分别计算出结果,再进行判断即可得到结果.【详解】 A. 2321526()b a b a b a ---⋅=,故选项A 错误; B. (3xy )2÷(xy )=9xy ,故选项B 错误;C 错误;D. 2x •3x 5=6x 6,正确.故选:D .【点睛】此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.7.C解析:C【分析】根据二次根式的性质:被开方数大于或等于0,列不等式求解.【详解】解:依题意有当130x -≥时,原二次根式有意义; 解得:13x ≤; 故选:C .【点睛】本题考查了二次根式的基本性质(被开方数大于或等于0);解一元一次不等式,在解一元一次不等式的过程中要用到不等式的基本性质(1.不等式两边同时加上或同时减去一个数,不等号的方向不变;2.不等式两边同时乘以或同时除以一个正数,不等号的方向不变;3.不等式两边同时乘以或同时除以一个负数,不等号的方向改变.)熟记并灵活运用不等式的基本性质是解本题的关键.8.A解析:A【分析】比较两个二次根式的大小可判别A ,根据同底数幂的乘法、平方差公式、合并同类项的运算法则分别计算可判断B 、C 、D 的正误.【详解】A 、=,=∵1812>,∴>,故该选项正确;B 、3a •25a a =,故该选项错误;C 、()()22224b a a b a b +-=-,故该选项错误; D 、527m m m +=,故该选项错误;故选:A .【点睛】本题考查了二次根式大小的比较,同底数幂的乘法、平方差公式、合并同类项的运算,熟练掌握相关运算法则是解题的关键.9.D解析:D【解析】【分析】根据二次根式的被开数的非负性,求的a 的范围,然后再化简绝对值,最后,依据二次根式的定义进行变形即可.【详解】解:等式2018a -=a 成立,则a ≥2019,∴,,∴a-2019=20182,∴a-20182=2019.故选D .【点睛】本题主要考查的是二次根式有意义的条件,求得a 的取值范围是解题的关键.10.A解析:A【分析】根据合并同类二次根式的法则对A 进行判断;根据二次根式的乘法法则对B 进行判断;根据二次根式的除法法则对C 进行判断;根据二次根式的性质对D 进行判断.【详解】==2÷,故此项正确,不符合要求;D. 2 (3=,故此项正确,不符合要求;故选A .【点睛】本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.11.A解析:A【解析】根据题意得:|x 2–4x ,所以|x 2–4x +4|=0,即(x –2)2=0,2x –y –3=0,所以x =2,y =1,所以x +y =3.故选A .12.B解析:B【分析】先化简,再根据同类二次根式的定义解答即可.【详解】解:A 、是最简二次根式,被开方数不同,不是同类二次根式;BCD故选B .【点睛】本题考查的知识点是同类二次根式的定义,解题关键是熟记同类二次根式的定义.二、填空题13.3【解析】1、;2、根据题意,先推导出等于什么,(1)∵,∴,(2)再比较与的大小关系,①当n=0时,;②当为正整数时,∵,∴,∴,综合(1)、(2)可得:,解析:320172018【解析】1、(1.732)2z z f f ==;2、根据题意,先推导出f 等于什么,(1)∵2221142n n n n n ⎛⎫+<++=+ ⎪⎝⎭,12n <+, (2)12n -的大小关系,①当n=012n >-; ②当n 为正整数时,∵2212n n n ⎛⎫+-- ⎪⎝⎭1204n =->, ∴2212n n n ⎛⎫+>- ⎪⎝⎭,12n >-,综合(1)、(2)可得:1122n n -<+,∴f n =z ,∴3f =z .3、∵f n =z ,∴(2017z f +111112233420172018=++++⨯⨯-⨯ 111111112233420172018=-+-+-++- 112018=- 20172018=. 故答案为(1)2;(2)3;(3)20172018. 点睛:(1)解第②小题的关键是应用“完全平方公式”和“作差的方法”分别证明到当n 为非负整数时,1122n n -<+,从而得到f n =z ;(2)解题③的要点是:当n 为正整数时,111(1)1n n n n =-++. 14.10【解析】根据完全平方式的特点,可得x2+xy+y2=(x+y )2﹣xy=(2)2﹣(+1)(﹣1)=12﹣2=10.故答案为10.解析:10【解析】根据完全平方式的特点,可得x 2+xy+y 2=(x+y )2﹣xy=(2﹣1)=12﹣2=10.故答案为10.15.【解析】【分析】根据题意,可得到=,利用平方关系把根号去掉,根据、、的系数相等的关系得到关于a ,b ,c 的三元方程组,解方程组即可.【详解】∵=∴,即.解得.【点睛】本题考查了解析:【解析】【分析】a ,b ,c 的三元方程组,解方程组即可.【详解】∴(22118=,即2222118235a b c =+++++. 2222352118,2120,2540,2144,a b c ab ac bc ⎧++=⎪=⎪∴⎨=⎪⎪=⎩ 解得15,4,18.a b c =⎧⎪=⎨⎪=⎩154181080abc ∴=⨯⨯=.【点睛】本题考查了二次根式的加减,解本题的关键是将等式平方去根号,利用等量关系中等式左、.16.;.【分析】根据被开方数是连续的自然数写出即可;根据每一行的最后一个数的被开方数是所在的行数乘比行数大1的数写出第(n-1)行的最后一个数,然后被开方数加上(n-2)即可求解.【详解】观察表【分析】根据被开方数是连续的自然数写出即可;根据每一行的最后一个数的被开方数是所在的行数乘比行数大1的数写出第(n-1)行的最后一个数,然后被开方数加上(n-2)即可求解.【详解】观察表格中的数据可得,第5行从左向右数第3=∵第(n-1,∴第n(n≥3且n是整数)行从左向右数第n-2个数是..【点睛】本题是对数字变化规律的考查,观察出被开方数是连续自然数并且每一行的最后一个数的被开方数是所在的行数乘比行数大1的数是解题的关键.17.【解析】=,故答案为.解析:【解析】÷====-,故答案为18.(1,1)、(4,1)、(4,4)、(9,36)、(16,16)、(36,9)【解析】试题解析:当a=1,=1,要使为整数,=1或时,分别为4和3,得出(1,4)和(1,1)是的“理想数对”,解析:(1,1)、(4,1)、(4,4)、(9,36)、(16,16)、(36,9)【解析】试题解析:当a=1,要使或12时,分别为4和3,得出(1,4)和(1,1)是的“理想数对”,当a=412,要使+或12时,分别为3和2,得出(4,1)和(4,4)是的“理想数对”,当a=913,要使16时,=1,得出(9,36)是的“理想数对”,当a =1614,要使14时,=1,得出(16,16)是的“理想数对”,当a =3616,要使13时,=1,得出(36,9)是的“理想数对”, 即其他所有的“理想数对”:(1,1)、(4,1)、(4,4)、(9,36)、(16,16)、(36,9).故答案为:(1,1)、(4,1)、(4,4)、(9,36)、(16,16)、(36,9). 19.2018【解析】试题解析:,令,,显然,∴,∴,∵与奇偶数相同,∴,∴,∴.故答案为:2018.解析:2018【解析】 试题解析:y ===令a =b = 显然0a b >≥,∴224036a b -=,∴()()4036a b a b +-=,∵()a b +与()-a b 奇偶数相同,∴20182a b a b +=⎧⎨-=⎩, ∴10101008a b =⎧⎨=⎩, ∴2018y a b =+=.故答案为:2018.20.﹣【解析】解:通过有意义可以知道≤0,≤0,所以=﹣=﹣.故答案为:.点睛:此题主要考查了二次根式的性质应用,正确判断二次根式的整体符号是解题关键.解析:【解析】解:通过a ≤0,,所以故答案为:点睛:此题主要考查了二次根式的性质应用,正确判断二次根式的整体符号是解题关键.三、解答题21.无22.无23.无24.无25.无26.无27.无28.无29.无30.无。
八年级第二学期3月份月考数学试题及答案

一、选择题1.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=6,DC=2,点P是AB上的动点,则PC+PD的最小值为()A.8 B.10 C.12 D.142.如图,□ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为()A.1 B.2C.32D.33.在ΔABC中,211a b c=+,则∠A( )A.一定是锐角B.一定是直角C.一定是钝角D.非上述答案4.一个直角三角形两边长分别是12和5,则第三边的长是()A.13B.13或15C.13或119D.155.如图,△ABC中,AB=10,BC=12,AC=213,则△ABC的面积是().A.36 B.1013C.60 D.12136.《九章算术》中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是一根竹子,原高一丈(一丈=10尺)一阵风将竹子折断,某竹梢恰好抵地,抵地处离竹子底部6尺远,则折断处离地面的高度是()A.5.3尺B.6.8尺C.4.7尺D.3.2尺7.下列四组线段中,可以构成直角三角形的是()A .1、2、3B .2、3、4C .1、2、3D .4、5、68.如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形构成的大正方形,若直角三角形的两直角边长分别为5和3,则小正方形的面积为( )A .4B .3C .2D .19.为了庆祝国庆,八年级(1)班的同学做了许多拉花装饰教室,小玲抬来一架2.5米长的梯子,准备将梯子架到2.4米高的墙上,则梯脚与墙角的距离是( )A .0.6米B .0.7米C .0.8米D .0.9米 10.下列条件中,不能..判定ABC 为直角三角形的是( ) A .::5:12:13a b c = B .A B C ∠+∠=∠ C .::2:3:5A B C ∠∠∠=D .6a =,12b =,10c = 二、填空题11.如图,在△中,,∠90°,是边的中点,是边上一动点,则的最小值是__________.12.如图所示的网格是正方形网格,则ABC ACB ∠+∠=__________°(点A ,B ,C 是网格线交点).13.如图,在△ABC 中,OA =4,OB =3,C 点与A 点关于直线OB 对称,动点P 、Q 分别在线段AC 、AB 上(点P 不与点A 、C 重合),满足∠BPQ =∠BAO.当△PQB 为等腰三角形时,OP 的长度是_____.14.如图,这是由八个全等的直角三角形拼接而成,记图中正方形ABCD ,正方形EFGH ,正方形MNKT 的面积分别为 1S ,2S ,3S ,若123144S S S ++=,则2S 的值是__________.15.我国古代数学名著《九章算术》中有云:“今有木长二丈,围之三尺.葛生其下,缠木七周,上与木齐.问葛长几何?”大意为:有一根木头长2丈,上、下底面的周长为3尺,葛生长在木下的一方,绕木7周,葛梢与木头上端刚好齐平,则葛长是______尺.(注:l 丈等于10尺,葛缠木以最短的路径向上生长,误差忽略不计)16.如图,在ABC 中,D 是BC 边中点,106AB AC ==,,4=AD ,则BC 的长是_____________.17.如图,正方体的底面边长分别为2cm 和3cm ,高为5cm .若一只蚂蚁从P 点开始经过四个侧面爬行一圈到达Q 点,则蚂蚁爬行的最短路径长为_____cm .18.如图,△ABC 中,∠ACB=90°,AB=2,BC=AC ,D 为AB 的中点,E 为BC 上一点,将△BDE 沿DE 翻折,得到△FDE ,EF 交AC 于点G ,则△ECG 的周长是___________.19.如图,30AOB ∠=︒,点,M N 分别在,OA OB 上,且6,8OM ON ==,点,P Q 分别在,OB OA 上运动,则PM PQ QN ++的最小值为______.20.如图所示,四边形ABCD 是长方形,把△ACD 沿AC 折叠到△ACD′,AD′与BC 交于点E ,若AD =4,DC =3,求BE 的长.三、解答题21.如图,一架长25米的梯子,斜靠在竖直的墙上,这时梯子底端离墙7米.(1)此时梯子顶端离地面多少米?(2)若梯子顶端下滑4米,那么梯子底端将向左滑动多少米?22.如图1,在△ABC 中,AB =AC ,∠BAC =90°,D 为AC 边上一动点,且不与点A 点C 重合,连接BD 并延长,在BD 延长线上取一点E ,使AE =AB ,连接CE .(1)若∠AED =20°,则∠DEC = 度;(2)若∠AED =a ,试探索∠AED 与∠AEC 有怎样的数量关系?并证明你的猜想; (3)如图2,过点A 作AF ⊥BE 于点F ,AF 的延长线与EC 的延长线交于点H ,求证:EH 2+CH 2=2AE 2.23.已知a ,b ,c 满足88a a -+-=|c ﹣17|+b 2﹣30b +225, (1)求a ,b ,c 的值;(2)试问以a ,b ,c 为边能否构成三角形?若能构成三角形,求出三角形的周长和面积;若不能构成三角形,请说明理由.24.定义:如图1,点M 、N 把线段AB 分割成AM 、MN 和BN ,若以AM 、MN 、BN 为边的三角形是一个直角三角形,则称点M 、N 是线段AB 的勾股分割点.(1)已知点M 、N 是线段AB 的勾股分割点,若2AM =,3MN =,求BN 的长; (2)如图2,在Rt ABC △中,AC BC =,点M 、N 在斜边AB 上,45MCN ∠=︒,求证:点M 、N 是线段AB 的勾股分割点(提示:把ACM 绕点C 逆时针旋转90︒);(3)在(2)的问题中,15ACM ∠=︒,1AM =,求BM 的长.25.我们规定,三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差.如图1,在ABC ∆中,AO 是BC 边上的中线,AB 与AC 的“广益值”就等于22AO BO -的值,可记为22AB AC OA BO ∇=-(1)在ABC ∆中,若90ACB ∠=︒,81AB AC ∇=,求AC 的值.(2)如图2,在ABC ∆中,12AB AC ==,120BAC ∠=︒,求AB AC ∇,BA BC ∇的值.(3)如图3,在ABC ∆中,AO 是BC 边上的中线,24ABC S ∆=,8AC =,64AB AC ∇=-,求BC 和AB 的长.26.已知ABC ∆中,AB AC =.(1)如图1,在ADE ∆中,AD AE =,连接BD 、CE ,若DAE BAC ∠=∠,求证:BD CE =(2)如图2,在ADE ∆中,AD AE =,连接BE 、CE ,若60DAE BAC ∠=∠=,CE AD ⊥于点F ,4AE =,5EC =,求BE 的长;(3)如图3,在BCD ∆中,45CBD CDB ∠=∠=,连接AD ,若45CAB ∠=,求AD AB 的值.27.已知:如图,在ABC ∆中,90ACB ∠=,以点B 为圆心,BC 的长为半径画弧,交线段AB 于点D ,以点A 为圆心,AD 长为半径画弧,交线段AC 与点E .(1)根据题意用尺规作图补全图形(保留作图痕迹);(2)设,BC m AC n ==①线段AD 的长度是方程2220x mx n +-=的一个根吗?并说明理由.②若线段2AD EC =,求m n的值.28.如图,在四边形ABCD 中,=AB AD ,=BC DC ,=60A ∠︒,点E 为AD 边上一点,连接CE ,BD . CE 与BD 交于点F ,且CE ∥AB .(1)求证:CED ADB ∠=∠;(2)若=8AB ,=6CE . 求BC 的长 .29.如图1,在平面直角坐标系中,直线AB 经过点C (a ,a ),且交x 轴于点A (m ,0),交y 轴于点B (0,n ),且m ,n 满足6m -+(n ﹣12)2=0.(1)求直线AB 的解析式及C 点坐标;(2)过点C 作CD ⊥AB 交x 轴于点D ,请在图1中画出图形,并求D 点的坐标;(3)如图2,点E (0,﹣2),点P 为射线AB 上一点,且∠CEP =45°,求点P 的坐标.30.如图1,在正方形ABCD 中,点E ,F 分别是AC ,BC 上的点,且满足DE ⊥EF ,垂足为点E ,连接DF .(1)求∠EDF= (填度数);(2)延长DE 交AB 于点G ,连接FG ,如图2,猜想AG ,GF ,FC 三者的数量关系,并给出证明;(3)①若AB=6,G 是AB 的中点,求△BFG 的面积;②设AG=a ,CF=b ,△BFG 的面积记为S ,试确定S 与a ,b 的关系,并说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP,此时DP+CP=DP+PC′=DC′的值最小.由DC=2,BD=6,得到BC=8,连接BC′,由对称性可知∠C′BA=∠CBA=45°,于是得到∠CBC′=90°,然后根据勾股定理即可得到结论.【详解】解:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP.此时DP+CP=DP+PC′=DC′的值最小.∵DC=2,BD=6,∴BC=8,连接BC′,由对称性可知∠C′BA=∠CBA=45°,∴∠CBC′=90°,∴BC′⊥BC,∠BCC′=∠BC′C=45°,∴BC=BC′=8,根据勾股定理可得DC′=2222'+=+=.8610BC BD故选:B.【点睛】此题考查了轴对称﹣线路最短的问题,确定动点P为何位置时 PC+PD的值最小是解题的关键.2.B解析:B【解析】【分析】如图,连接BB′.根据折叠的性质知△BB′E是等腰直角三角形,则2.又B′E是BD 的中垂线,则DB′=BB′.【详解】∵四边形ABCD是平行四边形,BD=2,∴BE=12BD=1.如图2,连接BB′.根据折叠的性质知,∠AEB=∠AEB′=45°,BE=B′E.∴∠BEB′=90°,∴△BB′E是等腰直角三角形,则BB′=2BE=2,又∵BE=DE,B′E⊥BD,∴DB′=BB′=2.故选B.【点睛】考查了平行四边形的性质以及等腰直角三角形性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.3.A解析:A【解析】【分析】根据211a b c=+以及三角形三边关系可得2bc>a 2,再根据(b-c)2≥0,可推导得出b 2 +c 2>a 2,据此进行判断即可得.【详解】∵211a b c =+,∴2b ca bc+ =,∴2bc=a(b+c),∵a、b、c是三角形的三条边,∴b+c>a,∴2bc>a·a,即2bc>a 2,∵(b-c)2≥0,∴b 2 +c 2 -2bc≥0,b 2 +c 2≥2bc,∴b 2 +c 2>a 2,∴一定为锐角,故选A .【点睛】本题考查了三角形三边关系、完全平方公式、不等式的传递性、勾股定理等,题目较难,得出b 2 +c 2 >a 2 是解题的关键.4.C解析:C【分析】记第三边为c ,然后分c 为直角三角形的斜边和直角边两种情况,利用勾股定理求解即可.【详解】解:记第三边为c ,若c 为直角三角形的斜边,则2212513c =+=;若c 为直角三角形的直角边,则22125119c =-=.故选:C .【点睛】本题考查了勾股定理,属于基本题目,正确分类、熟练掌握勾股定理是解题的关键.5.A解析:A【分析】作AD BC ⊥于点D ,设BD x =,得222AB BD AD -=,222AC CD AD -=,结合题意,经解方程计算得BD ,再通过勾股定理计算得AD ,即可完成求解.【详解】如图,作AD BC ⊥于点D设BD x =,则12CD BC x x =-=-∴222AB BD AD -=,222AC CD AD -=∴2222AB BD AC CD -=-∵AB=10,AC=213∴(()22221021312x x -=-- ∴8x =∴22221086AD AB BD =-=-=∴△ABC的面积1112636 22BC AD=⨯=⨯⨯=故选:A.【点睛】本题考察了直角三角形、勾股定理、一元一次方程的知识,解题的关键是熟练掌握勾股定理的性质,从而完成求解.6.D解析:D【分析】根据题意结合勾股定理得出折断处离地面的长度即可.【详解】解:设折断处离地面的高度OA是x尺,根据题意可得:x2+62=(10-x)2,解得:x=3.2,答:折断处离地面的高度OA是3.2尺.故选D.【点睛】此题主要考查了勾股定理的应用,根据题意正确应用勾股定理是解题关键.7.A解析:A【分析】求出两小边的平方和、最长边的平方,看看是否相等即可.【详解】A、12+2)2=32∴以123,故本选项正确;B、22+32≠42∴以2、3、4为边组成的三角形不是直角三角形,故本选项错误;C、12+22≠32∴以1、2、3为边组成的三角形不是直角三角形,故本选项错误;D、42+52≠62∴以4、5、6为边组成的三角形不是直角三角形,故本选项错误;故选A..【点睛】本题考查了勾股定理的逆定理应用,掌握勾股定理逆定理的内容就解答本题的关键.8.A解析:A【分析】根据直角三角形的两直角边长分别为5和3,可计算出正方形的边长,从而得出正方形的面积.【详解】解:3和5为两条直角边长时,小正方形的边长=5-3=2,∴小正方形的面积22=4;综上所述:小正方形的面积为4;故答案选A .【点睛】本题考查了勾股定理及其应用,正确表示出直角三角形的面积是解题的关键. 9.B解析:B【解析】试题解析:依题意得:梯子、地面、墙刚好形成一直角三角形,梯高为斜边,利用勾股定(米).故选B .10.D解析:D【分析】由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方或最大角是否是90︒即可.【详解】解:A 、22251213+=,ABC ∆∴是直角三角形,故能判定ABC ∆是直角三角形;B 、A BC ∠+∠=∠,90C ∴∠=︒,故能判定ABC ∆是直角三角形; C 、::2:3:5A B C ∠∠∠=,518090235C ∴∠=⨯︒=︒++,故能判定ABC ∆是直角三角形;D 、22261012+≠,ABC ∆∴不是直角三角形,故不能判定ABC ∆是直角三角形; 故选:D .【点睛】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,可利用勾股定理的逆定理和直角三角形的定义判断.二、填空题11.【解析】如图,过点作⊥于点,延长到点,使,连接,交于点,连接,此时的值最小.连接,由对称性可知∠45°,,∴∠90°.根据勾股定理可得.12.45【分析】如下图,延长BA至网络中的点D处,连接CD. ABC ACB DAC∠+∠=∠,只需证△ADC是等腰直角三角形即可【详解】如下图,延长BA至网络中的点D处,连接CD设正方形网络每一小格的长度为1则根据网络,555BC=5,∴5其中BD、DC、BC边长满足勾股定理逆定理∴∠CDA=90°∵AD=DC∴△ADC是等腰直角三角形∴∠DAC=45°故答案为:45°【点睛】本题是在网格中考察勾股定理的逆定理,解题关键是延长BA,构造处△ABC的外角∠CAD13.1或7 8【分析】分为三种情况:①PQ BP =,②BQ QP =,③BQ BP =,由等腰三角形的性质和勾股定理可求解.【详解】解:分为3种情况:①当PB PQ =时,4=OA ,3OB =,∴5BC AB ===, C 点与A 点关于直线OB 对称,BAO BCO ∴∠=∠,BPQ BAO ∠=∠,BPQ BCO ∴∠=∠,APB APQ BPQ BCO CBP ∠=∠+∠=∠+∠,APQ CBP ∴∠=∠,在APQ 和CBP 中,BAO BCP APQ B PQ B P C P ∠=∠⎧⎪∠=∠⎨=⎪⎩, ()APQ CBP AAS ∴△≌△,∴5AP BC ==,1OP AP OA ∴=-=;②当BQ BP =时,BPQ BQP ∠=∠,BPQ BAO ∠=∠,BAO BQP ∴∠=∠,根据三角形外角性质得:BQP BAO ∠>∠,∴这种情况不存在;③当QB QP =时,QBP BPQ BAO ∠=∠=∠,PB PA ∴=,设OP x =,则4PB PA x ==-在Rt OBP △中,222PB OP OB =+,222(4)3x x ∴-=+, 解得:78x =; ∴当PQB △为等腰三角形时,1OP =或78; 【点睛】本题考查了勾股定理,等腰三角形的性质,全等三角形的性质和判定的应用,解题的关键是熟练掌握所学的性质进行解题,注意分类讨论.14.48【分析】用a 和b 表示直角三角形的两个直角边,然后根据勾股定理列出正方形面积的式子,求出2S 的面积.【详解】解:本图是由八个全等的直角三角形拼成的,设这个直角三角形两个直角边中较长的长度为a ,较短的长度为b ,即图中的AE a =,AH b =,则()221S AB a b ==+,2222S HE a b ==+,()223S TM a b ==-, ∵123144S S S ++=,∴()()2222144a b a b a b ++++-= 22222222144a b ab a b a b ab ++++++-=2233144a b +=2248a b +=,∴248S =.故答案是:48.【点睛】本题考查勾股定理,解题的关键是要熟悉赵爽弦图中勾股定理的应用.15.【分析】这种立体图形求最短路径问题,可以展开成为平面内的问题解决,展开后可转化下图,所以是个直角三角形求斜边的问题,根据勾股定理可求出.【详解】解:如图,一条直角边(即木棍的高)长20尺,另一条直角边长7×3=21(尺), 222021+=29(尺).答:葛藤长29尺.故答案为:29.【点睛】本题考查了平面展开最短路径问题,关键是把立体图形展成平面图形,本题是展成平面图形后为直角三角形按照勾股定理可求出解.16.413【分析】延长AD至点E,使得DE=AD=4,结合D是中点证得△ADC≌△EDB,进而利用勾股定理逆定理可证得∠E=90°,再利用勾股定理求得BD长进而转化为BC长即可.【详解】解:如图,延长AD至点E,使得DE=AD=4,连接BE,∵D是BC边中点,∴BD=CD,又∵DE=AD,∠ADC=∠EDB,∴△ADC≌△EDB(SAS),∴BE=AC=6,又∵AB=10,∴AE2+BE2=AB2,∴∠E=90°,∴在Rt△BED中,2222=+=+=,64213BD BE DE∴BC=2BD=413,故答案为:413.【点睛】本题考查了全等三角形的判定及性质、勾股定理及其逆定理,正确作出辅助线是解决本题的关键.17.55【解析】【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将长方体展开,然后利用两点之间线段最短解答.【详解】展开图如图所示:由题意,在Rt△APQ中,PD=10cm,DQ=5cm,∴蚂蚁爬行的最短路径长=PQ=2222PD QD+=+=55(cm),105故答案为:55.【点睛】本题考查了平面展开﹣最短路径问题,解答此类问题时要先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.18.2【分析】连接CE.根据“直角三角形斜边上的中线等于斜边的一半”、等腰三角形的性质以及折叠的性质推知EG+CG=EG+GF=EF=BE,【详解】解:(1)如图,连接CD、CF.∵Rt△ABC中,∠ACB=90°,AC=BC,D为AB边的中点,∴BD=CD=1.2 ,∵由翻折可知BD=DF,∴CD=BD=DF=1,∠DFE=∠B=∠DCA=45°,∴∠DCF=∠DFC,∴∠DCF-∠DCA=∠DFC-∠DFE,即∠GCF=∠GFC,∴GC=GF,∴EG+CG=EG+GF=EF=BE,∴△ECG的周长2,2.【点睛】本题考查了折叠的性质、勾股定理、直角三角形的性质,能将三角形的周长转移到已知线段上是解题的关键..19.10【分析】首先作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN 的最小值,易得△ONN′为等边三角形,△OMM′为等边三角形,∠N′OM′=90°,继而可以求【详解】作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN的最小值.根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°,OM′=OM=6,ON′=ON=8,∴△ONN′为等边三角形,△OMM′为等边三角形,∴∠N′OM′=90°.在Rt△M′ON′中,M′N′=22''OM ON=10.故答案为10.【点睛】本题考查了最短路径问题,根据轴对称的定义,找到相等的线段,得到直角三角形是解题的关键.20.7 8【解析】试题分析:根据矩形性质得AB=DC=6,BC=AD=8,AD∥BC,∠B=90°,再根据折叠性质得∠DAC=∠D′AC,而∠DAC=∠ACB,则∠D′AC=∠ACB,所以AE=EC,设BE=x,则EC=4-x,AE=4-x,然后在Rt△ABE中利用勾股定理可计算出BE的长即可.试题解析:∵四边形ABCD为矩形,∴AB=DC=3,BC=AD=4,AD∥BC,∠B=90°,∵△ACD沿AC折叠到△ACD′,AD′与BC交于点E,∴∠DAC=∠D′AC,∵AD∥BC,∴∠DAC=∠ACB,∴∠D′AC=∠ACB,∴AE=EC,设BE=x,则EC=4﹣x,AE=4﹣x,在Rt△ABE中,∵AB2+BE2=AE2,∴32+x2=(4﹣x)2,解得x=78,即BE的长为78.三、解答题21.(1)梯子顶端离地面24米(2)梯子底端将向左滑动了8米试题分析:(1)构建数学模型,根据勾股定理可求解出梯子顶端离地面的距离;(2)构建直角三角形,然后根据购股定理列方程求解即可.试题解析:(1)如图,∵AB=25米,BE=7米,梯子距离地面的高度AE=22257-=24米.答:此时梯子顶端离地面24米;(2)∵梯子下滑了4米,即梯子距离地面的高度CE=(24﹣4)=20米,∴222520-,CD CE-22∴DE=15﹣7=8(米),即下端滑行了8米.答:梯子底端将向左滑动了8米.22.(1)45度;(2)∠AEC﹣∠AED=45°,理由见解析;(3)见解析【分析】(1)由等腰三角形的性质可求∠BAE=140°,可得∠CAE=50°,由等腰三角形的性质可得∠AEC=∠ACE=65°,即可求解;(2)由等腰三角形的性质可求∠BAE=180°﹣2α,可得∠CAE=90°﹣2α,由等腰三角形的性质可得∠AEC=∠ACE=45°+α,可得结论;(3)如图,过点C作CG⊥AH于G,由等腰直角三角形的性质可得EH2EF,CH=2CG,由“AAS”可证△AFB≌△CGA,可得AF=CG,由勾股定理可得结论.【详解】解:(1)∵AB=AC,AE=AB,∴AB=AC=AE,∴∠ABE=∠AEB,∠ACE=∠AEC,∵∠AED=20°,∴∠ABE=∠AED=20°,∴∠BAE=140°,且∠BAC=90°∴∠CAE=50°,∵∠CAE+∠ACE+∠AEC=180°,且∠ACE=∠AEC,∴∠AEC=∠ACE=65°,∴∠DEC=∠AEC﹣∠AED=45°,故答案为:45;(2)猜想:∠AEC﹣∠AED=45°,理由如下:∵∠AED=∠ABE=α,∴∠BAE=180°﹣2α,∴∠CAE=∠BAE﹣∠BAC=90°﹣2α,∵∠CAE+∠ACE+∠AEC=180°,且∠ACE=∠AEC,∴∠AEC=45°+α,∴∠AEC﹣∠AED=45°;(3)如图,过点C作CG⊥AH于G,∵∠AEC﹣∠AED=45°,∴∠FEH=45°,∵AH⊥BE,∴∠FHE=∠FEH=45°,∴EF=FH,且∠EFH=90°,∴EH2EF,∵∠FHE=45°,CG⊥FH,∴∠GCH=∠FHE=45°,∴GC=GH,∴CH2CG,∵∠BAC=∠CGA=90°,∴∠BAF+∠CAG=90°,∠CAG+∠ACG=90°,∴∠BAF=∠ACG,且AB=AC,∠AFB=∠AGC,∴△AFB≌△CGA(AAS)∴AF=CG,∴CH2AF,∵在Rt△AEF中,AE2=AF2+EF2,2AF)2+2EF)2=2AE2,∴EH2+CH2=2AE2.【点睛】本题是综合了等腰直角三角形的性质,全等三角形的性质与判定的动点问题,三个问题由易到难,在熟练掌握各个相关知识的基础上找到问题之间的内部联系,层层推进去解答是关键.23.(1)a=8,b=15,c=17;(2)能,60【分析】(1)根据算术平方根,绝对值,平方的非负性即可求出a、b、c的值;(2)根据勾股定理的逆定理即可求出此三角形是直角三角形,由此得到面积和周长【详解】解:(1)∵a ,b ,c|c ﹣17|+b 2﹣30b +225,21||7(15)c b +-﹣,∴a ﹣8=0,b ﹣15=0,c ﹣17=0,∴a =8,b =15,c =17;(2)能.∵由(1)知a =8,b =15,c =17,∴82+152=172.∴a 2+c 2=b 2,∴此三角形是直角三角形,∴三角形的周长=8+15+17=40; 三角形的面积=12×8×15=60. 【点睛】此题考查算术平方根,绝对值,平方的非负性,勾股定理的逆定理判断三角形的形状.24.(12)见解析;(3)2【分析】(1)分两种分割法利用勾股定理即可解决问题;(2)如图,过点A 作AD ⊥AB ,且AD=BN .只要证明△ADC ≌△BNC ,推出CD=CN ,∠ACD=∠BCN ,再证明△MDC ≌△MNC ,可得MD=MN ,由此即可解决问题;(3)过点B 作BP ⊥AB ,使得BP=AM=1,根据题意可得△CPB ≌△CMA ,△CMN ≌△CPN ,利用全等性质推出∠BNP=30°,从而得到NB 和NP 的长,即得BM.【详解】解:(1)当MN 最长时,,当BN 最长时,(2)证明:如图,过点A 作AD ⊥AB ,且AD=BN ,在△ADC 和△BNC 中, AD BN DAC B AC BC =⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△BNC (SAS ),∴CD=CN ,∠ACD=∠BCN ,∵∠MCN=45°,∴∠DCA+∠ACM=∠ACM+∠BCN=45°,∴∠MCD=∠MCN ,在△MDC 和△MNC 中,CD CN MCD MCN CM CM =⎧⎪∠=∠⎨⎪=⎩,∴△MDC ≌△MNC (SAS ),∴MD=MN在Rt △MDA 中,AD 2+AM 2=DM 2,∴BN 2+AM 2=MN 2,∴点M ,N 是线段AB 的勾股分割点;(3)过点B 作BP ⊥AB ,使得BP=AM=1,根据(2)中过程可得:△CPB ≌△CMA ,△CMN ≌△CPN ,∴∠AMC=∠BPC=120°,AM=PB=1,∠CMN=∠CPN=∠A+∠ACM=45°+15°=60°,∴∠BPN=120°-60°=60°,∴∠BNP=30°,∴NP=2BP=2=MN ,∴BN=22213-=,∴BM=MN+BN=23+.【点睛】本题是三角形的综合问题,考查了全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.25.(1)AC=9;(2)AB ∇AC =-72,BA ∇BC =73【分析】(1)在Rt AOC ∆中,根据勾股定理和新定义可得AO 2-OC 2=81=AC 2;(2)①先利用含30°的直角三角形的性质求出AO =2,OB =23再用新定义即可得出结论; ②先构造直角三角形求出BE ,AE ,再用勾股定理求出BD ,最后用新定义即可得出结论;(3)作BD ⊥CD,构造直角三角形BCD,根据三角形面积关系求出BD,根据新定义和勾股定理逆定理得出三角形AOD 是直角三角形,根据中线性质得出OA 的长度,根据勾股定理求出OC,从而得出BC,再根据勾股定理求出CD,再求出AD,再运用勾股定理求出AB.【详解】(1)已知如图:AO 为BC 上的中线,在Rt AOC ∆中,AO 2-OC 2=AC 2因为81AB AC ∇=所以AO 2-OC 2=81所以AC 2=81所以AC=9.(2)①如图2,取BC 的中点D ,连接AO ,∵AB =AC ,∴AO ⊥BC ,在△ABC 中,AB =AC ,∠BAC =120°,∴∠ABC =30°,在Rt △AOB 中,AB =12,∠ABC =30°,∴AO =6,OB =2222126AB AO -=-=63,∴AB ∇AC =AO 2﹣BO 2=36﹣108=﹣72, ②取AC 的中点D ,连接BD ,∴AD =CD =12AC =6,过点B 作BE ⊥AC 交CA 的延长线于E ,在Rt △ABE 中,∠BAE =180°﹣∠BAC =60°,∴∠ABE =30°, ∵AB =12,∴AE =6,BE =222212663AB AE -=-=, ∴DE =AD +AE =12,在Rt △BED 中,根据勾股定理得,BD =()2222631267BE DE +=+= ∴BA ∇BC =BD 2﹣CD 2=216;(3)作BD ⊥CD,因为24ABC S ∆=,8AC =,所以BD=26ABC S AC ∆÷=,因为64AB AC ∇=-,AO 是BC 边上的中线,所以AO 2-OC 2=-64,所以OC 2-AO 2=64,由因为AC 2=82=64,所以OC 2-AO 2= AC 2所以∠OAC=90°所以OA=24228322ABC S AC ∆⨯÷=⨯÷= 所以OC=22228373AC OA +=+=所以BC=2OC=273,在Rt △BCD 中, CD=()2222276163BC BD -=-=所以AD=CD-AC=16-8=8所以AB=22228610AD BD +=+=【点睛】考核知识点:勾股定理逆定理,含30°直角三角形性质.借助辅助线构造直角三角形,运用勾股定理等直角三角形性质解决问题是关键.26.(1)详见解析;(241;(33【分析】(1)证∠EAC=∠DAB.利用SAS 证△ACE ≌△ABD 可得;(2)连接BD ,证1302FEA AED ∠=∠=,证△ACE ≌△ABD 可得30FEA BDA ∠=∠=,CE=BD=5,利用勾股定理求解;(3)作CE 垂直于AC,且CE=AC,连接AE,则90,45ACE CAE ∠=∠=,利用勾股定理得AE 2AB =,3AB ,根据(1)思路得3AB .【详解】(1) 证明:∵∠DAE=∠BAC ,∴∠DAE+∠CAD=∠BAC+∠CAD ,即∠EAC=∠DAB.在△ACE 与△ABD 中,AD AE EAC BAB AC AB =⎧⎪∠=∠⎨⎪=⎩, ∴△ACE ≌△ABD(SAS),∴BD CE =;(2)连接BD因为AD AE =, 60DAE BAC ∠=∠=,所以ADE ∆是等边三角形因为60DAE DEA EDA ∠=∠=∠=,ED=AD=AE=4因为CE AD ⊥ 所以1302FEAAED ∠=∠= 同(1)可知△ACE ≌△ABD(SAS),所以30FEA BDA ∠=∠=,CE=BD=5所以90BDE BDA ADE ∠=∠+∠=所以BE=22225441BD DE +=+=(3)作CE 垂直于AC,且CE=AC,连接AE,则90,45ACE CAE ∠=∠=所以222AB AC AC +因为AB AC =所以AE 2=又因为45CAB ∠=所以90ABE ∠=所以()222223BE AE AB AB AB AB =+=+= 因为45CBD CDB ∠=∠=所以BC=CD, 90BCD ∠=因为同(1)可得△ACD ≌△ECB(SAS)所以AD=BE=3AB 所以33AD AB AB AB==【点睛】考核知识点:等边三角形;勾股定理.构造全等三角形和直角三角形是关键.27.(1)详见解析;(2)①线段AD 的长度是方程2220x mx n +-=的一个根,理由详见解析;②512m n = 【分析】(1)根据题意,利用尺规作图画出图形即可;(2)①根据勾股定理求出AD ,然后把AD 的值代入方程,即可得到答案;②先得到出边长的关系,然后根据勾股定理,列出方程,解方程后得到答案.【详解】(1)解:作图,如图所示:(2)解:①线段AD 的长度是方程2220x mx n +-=的一个根.理由如下:依题意得, BD BC m ==,在Rt ABC 中,90ACB ∠=︒222BC AC AB ∴=+22AB m n =+22AD AB BD m n m ∴=-=+222AD m AD n ∴+-)()2222222m n m m m n m n =+++- 222222222222m n m m n m m m n m n =+-+++-0=;∴线段AD 的长度是方程22 20x mx n +-=的一个根②依题意得:,,AD AE BD BC AB AD BD ====2AD EC =2233AD AE AC n ∴=== 在RT ABC 中,90ACB ∠=222BC AC AB ∴+=22223m n n m ⎛⎫+=+ ⎪⎝⎭ 22224493m n n mn m +=++ 25493n mn = 512m n ∴= 【点睛】本题考查的是基本作图,勾股定理、一元二次方程的解法,掌握一元二次方程的求根公式、勾股定理是解题的关键.28.(1)见解析;(2)BC =.【分析】(1)由等边三角形的判定定理可得△ABD 为等边三角形,又由平行进行角度间的转化可得出结论.(2)连接AC 交BD 于点O ,由题意可证AC 垂直平分BD ,△ABD 是等边三角形,可得∠BAO=∠DAO=30°,AB=AD=BD=8,BO=OD=4,通过证明△EDF 是等边三角形,可得DE=EF=DF=2,由勾股定理可求OC ,BC 的长.【详解】(1)证明:∵AB AD =,=60A ∠︒,∴△ABD 是等边三角形.∴60ADB ∠=︒.∵CE ∥AB ,∴60CED A ∠=∠=︒.∴CED ADB ∠=∠.(2)解:连接AC 交BD 于点O ,∵AB AD =,BC DC =,∴AC 垂直平分BD .∴30BAO DAO ∠=∠=︒.∵△ABD 是等边三角形,8AB =∴8AD BD AB ===,∴4BO OD ==.∵CE ∥AB ,∴ACE BAO ∠=∠.∴6AE CE ==, 2DE AD AE =-=.∵60CED ADB ∠=∠=︒.∴60EFD ∠=︒.∴△EDF 是等边三角形.∴2EF DF DE ===,∴4CF CE EF =-=,2OF OD DF =-=.在Rt △COF 中, ∴2223OC CF OF =-=.在Rt △BOC 中, ∴22224(23)27BC BO OC =+=+= 【点睛】本题考查了等边三角形的性质和判定,勾股定理,熟练运用等边三角形的判定是本题的关键.29.(1)y =-2x +12,点C 坐标(4,4);(2)画图形见解析,点D 坐标(-4,0);(3)点P 的坐标(143-,643)【分析】(1)由已知的等式可求得m、n的值,于是可得直线AB的函数解析式,把点C的坐标代入可求得a的值,由此即得答案;(2)画出图象,由CD⊥AB知1AB CDk k=-可设出直线CD的解析式,再把点C代入可得CD的解析式,进一步可求D点坐标;(3)如图2,取点F(-2,8),易证明CE⊥CF且CE=CF,于是得∠PEC=45°,进一步求出直线EF的解析式,再与直线AB联立求两直线的交点坐标,即为点P.【详解】解:(1)∵6m-+(n﹣12)2=0,∴m=6,n=12,∴A(6,0),B(0,12),设直线AB解析式为y=kx+b,则有1260bk b=⎧⎨+=⎩,解得212kb=-⎧⎨=⎩,∴直线AB解析式为y=-2x+12,∵直线AB过点C(a,a),∴a=-2a+12,∴a=4,∴点C坐标(4,4).(2)过点C作CD⊥AB交x轴于点D,如图1所示,设直线CD解析式为y=12x+b′,把点C(4,4)代入得到b′=2,∴直线CD解析式为y=12x+2,∴点D坐标(-4,0).(3)如图2中,取点F(-2,8),作直线EF交直线AB于P,图2∵直线EC解析式为y=32x-2,直线CF解析式为y=-23x+203,∵32×(-23)=-1,∴直线CE⊥CF,∵EC=13CF=13∴EC=CF,∴△FCE是等腰直角三角形,∴∠FEC=45°,∵直线FE解析式为y=-5x-2,由21252y xy x=-+⎧⎨=--⎩解得143643xy⎧=-⎪⎪⎨⎪=⎪⎩,∴点P的坐标为(1464,33 -).【点睛】本题是一次函数的综合题,综合考查了坐标系中两直线的垂直问题、两条直线的交点问题和求特殊角度下的直线解析式,并综合了勾股定理和等腰直角三角形的判定和性质,解题的关键是熟知坐标系中两直线垂直满足121k k=-,一次函数的交点与对应方程组的解的关系.其中,第(3)小题是本题的难点,寻找到点F(-2,8)是解题的突破口. 30.(1)45°;(2)GF=AG+CF,证明见解析;(3)①6;②s ab=,理由见解析.【解析】【分析】(1)如图1中,连接BE.利用全等三角形的性质证明EB=ED,再利用等角对等边证明EB=EF即可解决问题.(2)猜想:GF=AG+CF.如图2中,将△CDF绕点D旋转90°,得△ADH,证明△GDH≌△GDF(SAS)即可解决问题.(3)①设CF=x,则AH=x,BF=6-x,GF=3+x,利用勾股定理构建方程求出x即可.②设正方形边长为x,利用勾股定理构建关系式,利用整体代入的思想解决问题即可.【详解】解:(1)如图1中,连接BE.∵四边形ABCD是正方形,∴CD=CB,∠ECD=∠ECB=45°,∵EC=EC,∴△ECB≌△ECD(SAS),∴EB=ED,∠EBC=∠EDC,∵∠DEF=∠DCF=90°,∴∠EFC+∠EDC=180°,∵∠EFB+∠EFC=180°,∴∠EFB=∠EDC,∴∠EBF=∠EFB,∴EB=EF,∴DE=EF,∵∠DEF=90°,∴∠EDF=45°故答案为45°.(2)猜想:GF=AG+CF.如图2中,将△CDF绕点D旋转90°,得△ADH,∴∠CDF=∠ADH,DF=DH,CF=AH,∠DAH=∠DCF=90°,∵∠DAC=90°,∴∠DAC+∠DAH=180°,∴H、A、G三点共线,∴GH=AG+AH=AG+CF,∵∠EDF=45°,∴∠CDF+∠ADG=45°,∴∠ADH+∠ADG=45°∴∠GDH=∠EDF=45°又∵DG=DG∴△GDH≌△GDF(SAS)∴GH=GF,∴GF=AG+CF.(3)①设CF=x,则AH=x,BF=6-x,GF=3+x,则有(3+x)2=(6-x)2+32,解得x=2∴S△BFG=12•BF•BG=6.②设正方形边长为x,∵AG=a,CF=b,∴BF=x-b,BG=x-a,GF=a+b,则有(x-a)2+(x-b)2=(a+b)2,化简得到:x2-ax-bx=ab,∴S=12(x-a)(x-b)=12(x2-ax-bx+ab)=12×2ab=ab.【点睛】本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数构建方程解决问题,属于中考常考题型.。
八年级第二学期3月份月考数学试题含答案

八年级第二学期3月份月考数学试题含答案一、选择题1.二次根式1x -中字母x 的取值可以是( ) A .2B .0C .12-D .-12.下列运算正确的是( ) A .235+=B .322-=3C .2(2)-=﹣2D .24322÷=3.下列二次根式中,最简二次根式是( ) A . 1.5B .13C .10D .274.已知实数a 在数轴上的位置如图所示,则化简2||(-1)a a +的结果为( )A .1B .﹣1C .1﹣2aD .2a ﹣1 5.下列各式中,运算正确的是( ) A 2(2)-=﹣2B 2+810C 28 4D .22=2 6.下列式子中,是二次根式的是( ) A 2B 32C xD .x7.下列各式中,正确的是( ) A 16B .16C 26628= D 42783=- 48.若化简2816x x -+的结果为2x ﹣5,则x 的取值范围是( ) A . x 为任意实数B .1≤x ≤4C .x ≥1D . x ≤49.下列各式中,不正确的是( ) A 233(3)(3)->-33648<C 2221a a +>+ D 2(5)5-=10.下列各式计算正确的是( ) A 2+3=5B .43-33=1 C .2333=63D 123=211.()23-A .﹣3B .3C .﹣9D .912.若a b >3a b - ) A .ab --B .-abC .a abD .-ab二、填空题13.将(0)a a -<化简的结果是___________________.14.732x y -=-,则2x ﹣18y 2=_____.15.下面是一个按某种规律排列的数阵:根据数阵排列的规律,第 5 行从左向右数第 3 个数是 ,第 n (n 3≥ 且 n 是整数)行从左向右数第 n 2- 个数是 (用含 n 的代数式表示). 16.若实数x ,y ,m 满足等式()223x y m +-=m+4的算术平方根为________.17.已知|a ﹣2007=a ,则a ﹣20072的值是_____.18.若0xy >,则二次根式________. 19.若实数a =,则代数式244a a -+的值为___.20.1=-==++……=___________.三、解答题21.计算:10099+【答案】910【解析】 【分析】先对代数式的每一部分分母有理化,然后再进行运算 【详解】10099++10099+++=9912233499100-+-+-++-=1100- =1110- =910【点睛】本题看似计算繁杂,但只要找到分母有理化这个突破口,就会化难为易。
人教版八年级第二学期3月份月考数学试题

一、选择题1.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为12cm ,在容器内壁离容器底部4 cm 的点B 处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,且离容器上沿4 cm 的点A 处,若蚂蚁吃到蜂蜜需爬行的最短路径为15 cm ,则该圆柱底面周长为( )cm .A .9B .10C .18D .202.如图,在等边△ABC 中,AB =15,BD =6,BE =3,点P 从点E 出发沿EA 方向运动,连结PD ,以PD 为边,在PD 右侧按如图方式作等边△DPF ,当点P 从点E 运动到点A 时,点F 运动的路径长是( )A .8B .10C .43D .123.如图所示,用四个全等的直角三角形和一个小正方形拼成一个大正方形已知大正方形的面积为49,小正方形的面积为4.用,表示直角三角形的两直角边(),请仔细观察图案.下列关系式中不正确的是( )A .B .C .D .4.如图,在ABC 中,CE 平分ACB ∠,CF 平分ACD ∠,且//EF BC 交AC 于M ,若3CM =,则22CE CF +的值为( )A .36B .9C .6D .185.在ABC 中,,,A B C ∠∠∠的对边分别是a b c 、、,下列条件中,不能说明ABC是直角三角形的是( )A .222b a c =-B .;C A B ∠=∠-∠ C .::3:4:5A B C ∠∠∠=D .::5:12:13a b c =6.如图,分别以直角ABC ∆三边为边向外作三个正方形,其面积分别用123,,S S S 表示,若27S =,32S =,那么1S =( )A .9B .5C .53D .457.如图,在△ABC 中,AB=8,BC=10,AC=6,则BC 边上的高AD 为( )A .8B .9C .245D .108.在ABC ∆中,::2BC AC AB =则△ABC 是( )A .等腰三角形B .钝角三角形C .直角三角形D .等腰直角三角形9.在△ABC 中,∠A ,∠B ,∠C 的对边分别记为a ,b ,c ,下列结论中不正确的是( ) A .如果∠A ﹣∠B =∠C ,那么△ABC 是直角三角形B .如果∠A :∠B :∠C =1:2:3,那么△ABC 是直角三角形C .如果 a 2:b 2:c 2=9:16:25,那么△ABC 是直角三角形D .如果 a 2=b 2﹣c 2,那么△ABC 是直角三角形且∠A =90°10.已知三角形的两边分别为3、4,要使该三角形为直角三角形,则第三边的长为( )A .5B 7C .57D .3或4二、填空题11.将一副三角板按如图所示摆放成四边形ABCD ,发现只要知道其中一边的长就可以求出其它各边的长,若已知AD =32AB 的长为__________.12.如图,在Rt ABC 中,90ACB ∠=︒,4AC =,2BC =,以AB 为边向外作等腰直角三角形ABD ,则CD 的长可以是__________.13.如图,四边形ABDC 中,∠ABD =120°,AB ⊥AC ,BD ⊥CD ,AB =4,CD =43,则该四边形的面积是______.14.如图,有一个圆柱,它的高等于12厘米,底面半径等于3厘米.在圆柱的下底面A 点有一只蚂蚁,它想吃到上底面上与A 点相对的C 点处的食物,需要爬行的最短路程是___________________(π的值取3).15.在△ABC 中,AB=15,AC=13,高AD=12,则ABC ∆的周长为_______________.16.如图,在Rt △ABC 中,∠ACB =90°,AB =7.5cm ,AC =4.5cm ,动点P 从点B 出发沿射线BC 以2cm/s 的速度移动,设运动的时间为t 秒,当△ABP 为等腰三角形时,t 的取值为_____.17.如图,在Rt ABC ∆中,90ABC ∠=,DE 垂直平分AC ,垂足为F ,//AD BC ,且3AB =,4BC =,则AD 的长为______.18.一块直角三角形绿地,两直角边长分别为3m ,4m ,现在要将绿地扩充成等腰三角形,且扩充时只能延长长为3m 的直角边,则扩充后等腰三角形绿地的面积为____m 2.19.如图,由两个直角三角形和三个正方形组成的图形,已知25AB = ,24AC = 其中阴影部分面积是_____________平方单位.20.如图,在等腰△ABC 中,AB =AC ,底边BC 上的高AD =6cm ,腰AC 上的高BE =4m ,则△ABC 的面积为_____cm 2.三、解答题21.在等边ABC 中,点D 是线段BC 的中点,120,EDF DE ∠=︒与线段AB 相交于点,E DF 与射线AC 相交于点F .()1如图1,若DF AC ⊥,垂足为,4,F AB =求BE 的长;()2如图2,将()1中的EDF ∠绕点D 顺时针旋转一定的角度,DF 仍与线段AC 相交于点F .求证:12BE CF AB +=.()3如图3,将()2中的EDF ∠继续绕点D 顺时针旋转一定的角度,使DF 与线段AC 的延长线交于点,F 作DN AC ⊥于点N ,若,DN FN =设,BE x CF y ==,写出y 关于x 的函数关系式.22.如图1,在△ABC 中,AB =AC ,∠BAC =90°,D 为AC 边上一动点,且不与点A 点C 重合,连接BD 并延长,在BD 延长线上取一点E ,使AE =AB ,连接CE .(1)若∠AED =20°,则∠DEC = 度;(2)若∠AED =a ,试探索∠AED 与∠AEC 有怎样的数量关系?并证明你的猜想; (3)如图2,过点A 作AF ⊥BE 于点F ,AF 的延长线与EC 的延长线交于点H ,求证:EH 2+CH 2=2AE 2.23.如图,△ABC 中,∠ACB =90°,AB =5cm ,BC =3cm ,若点P 从点A 出发,以每秒2cm 的速度沿折线A ﹣C ﹣B ﹣A 运动,设运动时间为t 秒(t >0).(1)若点P 在AC 上,且满足PA =PB 时,求出此时t 的值;(2)若点P 恰好在∠BAC 的角平分线上,求t 的值;(3)在运动过程中,直接写出当t 为何值时,△BCP 为等腰三角形.24.如图,将一长方形纸片OABC 放在平面直角坐标系中,(0,0)O ,(6,0)A ,(0,3)C ,动点F 从点O 出发以每秒1个单位长度的速度沿OC 向终点C 运动,运动23秒时,动点E 从点A 出发以相同的速度沿AO 向终点O 运动,当点E 、F 其中一点到达终点时,另一点也停止运动.设点E 的运动时间为t :(秒)(1)OE =_________,OF =___________(用含t 的代数式表示)(2)当1t =时,将OEF ∆沿EF 翻折,点O 恰好落在CB 边上的点D 处,求点D 的坐标及直线DE 的解析式;(3)在(2)的条件下,点M 是射线DB 上的任意一点,过点M 作直线DE 的平行线,与x 轴交于N 点,设直线MN 的解析式为y kx b =+,当点M 与点B 不重合时,设MBN ∆的面积为S ,求S 与b 之间的函数关系式.25.如图, ABD 为边长不变的等腰直角三角形,AB AD =,90BAD ∠=︒,在 ABD 外取一点 E ,以A 为直角顶点作等腰直角AEP △,其中 P 在ABD 内部,90EAP ∠=︒,2AE AP ==E 、P 、D 三点共线时,7BP =下列结论:①E 、P 、D 共线时,点B 到直线AE 5②E 、P 、D 共线时, 13ADP ABP S S ∆∆+==532ABD S ∆+③ ④作点 A 关于 BD 的对称点 C ,在 AEP 绕点 A 旋转的过程中,PC 的最小值为5+232;⑤AEP △绕点A 旋转,当点E 落在AB 上,当点P 落在AD 上时,取BP 上一点N ,使得AN BN =,连接 ED ,则AN ED ⊥.其中正确结论的序号是___.26.如图,在四边形ABCD 中,=AB AD ,=BC DC ,=60A ∠︒,点E 为AD 边上一点,连接CE ,BD . CE 与BD 交于点F ,且CE ∥AB .(1)求证:CED ADB ∠=∠;(2)若=8AB ,=6CE . 求BC 的长 .27.在ABC ∆中,AB AC =,CD 是AB 边上的高,若10,45AB BC ==.(1)求CD 的长.(2)动点P 在边AB 上从点A 出发向点B 运动,速度为1个单位/秒;动点Q 在边AC 上从点A 出发向点C 运动,速度为v 个单位秒()v>1,设运动的时间为()0t t >,当点Q 到点C 时,两个点都停止运动.①若当2v =时,CP BQ =,求t 的值.②若在运动过程中存在某一时刻,使CP BQ =成立,求v 关于t 的函数表达式,并写出自变量t 的取值范围.28.在ABC ∆中,90ACB ∠=︒,6AC BC ==,点D 是AC 的中点,点E 是射线DC 上一点,DF DE ⊥于点D ,且DE DF =,连接CF ,作FH CF ⊥于点F ,交直线AB 于点H .(1)如图(1),当点E 在线段DC 上时,判断CF 和FH 的数量关系,并加以证明; (2)如图(2),当点E 在线段DC 的延长线上时,问题(1)中的结论是否依然成立?如果成立,请求出当ABC △和CFH △面积相等时,点E 与点C 之间的距离;如果不成立,请说明理由.29.菱形ABCD 中,∠BAD =60°,BD 是对角线,点E 、F 分别是边AB 、AD 上两个点,且满足AE =DF ,连接BF 与DE 相交于点G .(1)如图1,求∠BGD 的度数;(2)如图2,作CH ⊥BG 于H 点,求证:2GH =GB +DG ;(3)在满足(2)的条件下,且点H 在菱形内部,若GB =6,CH =43,求菱形ABCD 的面积.30.如图,在△ABC 中,∠ACB =90°,AC =BC ,AB =2,CD 是边AB 的高线,动点E 从点A 出发,以每秒1个单位的速度沿射线AC 运动;同时,动点F 从点C 出发,以相同的速度沿射线CB 运动.设E 的运动时间为t (s )(t >0).(1)AE = (用含t 的代数式表示),∠BCD 的大小是 度;(2)点E 在边AC 上运动时,求证:△ADE ≌△CDF ;(3)点E 在边AC 上运动时,求∠EDF 的度数;(4)连结BE ,当CE =AD 时,直接写出t 的值和此时BE 对应的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】将容器侧面展开,建立A 关于上边沿的对称点A’,根据两点之间线段最短可知A’B 的长度为最短路径15,构造直角三角形,依据勾股定理可以求出底面周长的一半,乘以2即为所求.【详解】解:如图,将容器侧面展开,作A 关于EF 的对称点'A ,连接'A B ,则'A B 即为最短距离, 根据题意:'15A B cm =,12412BD AE cm =-+=,2222'15129A D A B BD ∴--'==.所以底面圆的周长为9×2=18cm.故选:C .【点睛】本题考查了平面展开——最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.2.D解析:D【分析】首先利用等边三角形的性质和含30°直角三角形的运用,判定△DPE ≌△FDH ,△DF 2Q ≌△ADE ,然后利用全等三角形的性质,得出点F 运动的路径长.【详解】∵△ABC 为等边三角形,∴∠B =60°,过D 点作DE ′⊥AB ,过点F 作FH ⊥BC 于H ,如图所示:则BE′=12BD=3,∴点E′与点E重合,∴∠BDE=30°,DE3BE3,∵△DPF为等边三角形,∴∠PDF=60°,DP=DF,∴∠EDP+∠HDF=90°∵∠HDF+∠DFH=90°,∴∠EDP=∠DFH,在△DPE和△FDH中,90PED DHFEDP DFHDP FD︒⎧∠=∠=⎪∠=∠⎨⎪=⎩,∴△DPE≌△FDH(AAS),∴FH=DE3∴点P从点E运动到点A时,点F运动的路径为一条线段,此线段到BC的距离为3当点P在E点时,作等边三角形DEF1,∠BDF1=30°+60°=90°,则DF1⊥BC,当点P在A点时,作等边三角形DAF2,作F2Q⊥BC于Q,则四边形DF1F2Q是矩形,∵∠BDE=30°,∠ADF2=60°,∴∠ADE+∠F2DQ=180°﹣30°﹣60°=90°,∵∠ADE+∠DAE=90°,∴∠F2DQ=∠DAE,在△DF2Q和△ADE中,222F QD DEA90F DQ DAEDF AD︒⎧∠=∠=⎪∠=∠⎨⎪=⎩,∴△DF2Q≌△ADE(AAS),∴DQ=AE=AB﹣BE=15﹣3=12,∴F1F2=DQ=12,∴当点P从点E运动到点A时,点F运动的路径长为12,故选:D.【点睛】此题主要考查等边三角形的性质以及全等三角形的判定与性质,解题关键是作好辅助线. 3.D【解析】【分析】利用勾股定理和正方形的面积公式,对公式进行合适的变形即可判断各个选项是否争取.【详解】A 中,根据勾股定理等于大正方形边长的平方,它就是正方形的面积,故正确; B 中,根据小正方形的边长是2它等于三角形较长的直角边减较短的直角边即可得到,正确;C 中,根据四个直角三角形的面积和加上小正方形的面积即可得到,正确;D 中,根据A 可得,C 可得,结合完全平方公式可以求得,错误.故选D.【点睛】本题考查勾股定理.在A 、B 、C 选项的等式中需理解等式的各个部分表示的几何意义,对于D 选项是由A 、C 选项联立得出的. 4.A解析:A【分析】先根据角平分线的定义、角的和差可得90ECF ∠=︒,再根据平行线的性质、等量代换可得,ACE CEF ACF F ∠=∠∠=∠,然后根据等腰三角形的定义可得,EM CM FM CM ==,从而可得6EF =,最后在Rt CEF 中,利用勾股定理即可得.【详解】 CE 平分ACB ∠,CF 平分ACD ∠,,1122ACB ACD BCE ACE DCF ACF ∴∠∠=∠=∠=∠∠=, 111(90222)ACB AC E D ACB ACD CF ACE ACF ∠=∠+∴∠+∠=∠∠∠=+=︒, //EF BC ,,BCE CEF DCF F ∠=∴∠∠=∠,,ACE CEF ACF F ∴∠=∠∠=∠,3,3EM CM FM CM ∴====,6EF EM FM ∴=+=,在Rt CEF 中,由勾股定理得:2222636CE CF EF +===,故选:A .【点睛】本题考查了角平分线的定义、平行线的性质、等腰三角形的定义、勾股定理等知识点,熟练掌握等腰三角形的定义是解题关键.解析:C【分析】此题考查的是直角三角形的判定方法,大约有以下几种:①勾股定理的逆定理,即三角形三边符合勾股定理;②三个内角中有一个是直角,或两个内角的度数和等于第三个内角的度数;根据上面两种情况进行判断即可.【详解】解:A 、由222b a c =-得a 2=b 2+c 2,符合勾股定理的逆定理,能够判定△ABC 为直角三角形,不符合题意;B 、由C A B ∠=∠-∠得∠C +∠B=∠A ,此时∠A 是直角,能够判定△ABC 是直角三角形,不符合题意;C 、∠A :∠B :∠C=3:4:5,那么∠A=45°、∠B=60°、∠C=75°,△ABC 不是直角三角形,故此选项符合题意;D 、a :b :c=5:12:13,此时c 2=b 2+ a 2,符合勾股定理的逆定理,△ABC 是直角三角形,不符合题意;故选:C .【点睛】此题主要考查了直角三角形的判定方法,只有三角形的三边长构成勾股数或三内角中有一个是直角的情况下,才能判定三角形是直角三角形.6.A解析:A【分析】根据勾股定理与正方形的性质解答.【详解】解:在Rt △ABC 中,AB 2=BC 2+AC 2,∵S 1=AB 2,S 2=BC 2,S 3=AC 2,∴S 1=S 2+S 3.∵S 2=7,S 3=2,∴S 1=7+2=9.故选:A .【点睛】本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.7.C解析:C【分析】本题根据所给的条件得知,△ABC 是直角三角形,再根据三角形的面积相等即可求出BC 边上的高.∵AB=8,BC=10,AC=6,∴62+82=102,∴△ABC是直角三角形,∠BAC=90°,则由面积公式可知,S△ABC=12AB⋅AC=12BC⋅AD,∴AD=245.故选C.【点睛】本题考查了勾股定理的逆定理,需要先证得三角形为直角三角形,再利用三角形的面积公式求得AD的值.8.D解析:D【分析】根据题意设出三边分别为k、k k,然后利用勾股定理的逆定理判定三角形为直角三角形,又有BC、AC边相等,所以三角形为等腰直角三角形.【详解】设BC、AC、AB分别为k,k k,∵k2+k2=k)2,∴BC2+AC2=AB2,∴△ABC是直角三角形,又BC=AC,∴△ABC是等腰直角三角形.故选D.【点睛】本题主要考查了直角三角形的判定,利用设k法与勾股定理证明三角形是直角三角形是难点,也是解题的关键.9.D解析:D【分析】根据直角三角形的判定和勾股定理的逆定理解答即可.【详解】选项A中如果∠A﹣∠B=∠C,由∠A+∠B+∠C=180°,可得∠A=90°,那么△ABC 是直角三角形,选项正确;选项B中如果∠A:∠B:∠C=1:2:3,由∠A+∠B+∠C=180°,可得∠A=90°,那么△ABC 是直角三角形,选项正确;选项C中如果 a2:b2:c2=9:16:25,满足a2+b2=c2,那么△ABC 是直角三角形,选项正确;选项D中如果 a2=b2﹣c2,那么△ABC 是直角三角形且∠B=90°,选项错误;【点睛】考查直角三角形的判定,学生熟练掌握勾股定理逆定理是本题解题的关键,并结合直角三角形的定义解出此题.10.C解析:C【分析】根据勾股定理和分类讨论的方法可以求得第三边的长,从而可以解答本题.【详解】由题意可得,当3和45,当斜边为4,故选:C【点睛】本题考查勾股定理,解答本题的关键是明确题意,利用勾股定理和分类讨论的数学思想解答.二、填空题11.【分析】利用勾股定理求出AC=6,在Rt △ABC 中,∠BAC=30°,得到12BC AB =,再利用勾股定理得到222AC BC AB +=,即可求出AB .【详解】在Rt △ACD 中,CD=AD=∴6=,在Rt △ABC 中,∠BAC=30°, ∴12BC AB =, ∵222AC BC AB +=, ∴22216()2AB AB +=,解得AB=故答案为:【点睛】此题考查勾股定理,直角三角形30度角所对的直角边等于斜边的一半,正确理解勾股定理的三边的数量关系是解题的关键.12.210或213或32【分析】在ABC 中计算AB ,情况一:作AE CE ⊥于E ,计算AE ,DE ,CE ,可得CD ;情况二:作BE CE ⊥于E ,计算BE ,CE ,DE ,可得CD ;情况三:作DE CE ''⊥,计算,,DF DE CE '',可得CD .【详解】∵90ACB ︒∠=,4,2AC BC ==,∴25AB =, 情况一:当25AD AB ==时,作AE CE ⊥于E∴ 1122BC AC AB AE ⋅=⋅,即45AE =,1455DE = ∴22855CE AC AE =-= ∴22213CD CE DE =+=情况二:当25BD AB ==时,作BE CE ⊥于E ,∴1122BC AC AB BE ⋅=⋅,即45BE =145DE =∴22255CE BC BE =-= ∴22210CD CE DE =+=情况三:当AD BD =时,作DE CE ''⊥,作BE CE ⊥于E ∴1122BC AC AB BE ⋅=⋅, ∴45BE =355CE ∴= ∵ABD △为等腰直角三角形 ∴152BF DF AB === ∴955DE DF E F DF BE ''=+=+= 25355CE EE CE BF CE ''=-=-=-= ∴2232CD CE E D ''=+=故答案为:1021332【点睛】本题考查了等腰直角三角形的探索,勾股定理的计算等,熟知以上知识是解题的关键.13.163【分析】延长CA 、DB 交于点E ,则60C ∠=°,30E ∠=︒,在Rt ABE ∆中,利用含30角的直角三角形的性质求出28BE AB ==,根据勾股定理求出43AE =.同理,在Rt DEC ∆中求出283CE CD ==,2212DE CE CD =-=,然后根据CDE ABE ABDC S S S ∆∆=-四边形,计算即可求解.【详解】解:如图,延长CA 、DB 交于点E ,∵四边形ABDC 中,120ABD ∠=︒,AB AC ⊥,BD CD ⊥,∴60C ∠=°,∴30E ∠=︒,在Rt ABE ∆中,4AB =,30E ∠=︒,∴28BE AB ==,2243AE BE AB ∴=-=.在Rt DEC ∆中,30E ∠=︒,43CD =,283CE CD ∴==,2212DE CE CD ∴=-=,∴1443832ABE S ∆=⨯⨯=, 143122432CDE S ∆=⨯⨯=, 24383=163CDE ABE ABDC S S S ∆∆∴=-=-四边形.故答案为:163.【点睛】本题考查了勾股定理,含30角的直角三角形的性质,图形的面积,准确作出辅助线构造直角三角形是解题的关键.14.15厘米【分析】要想求得最短路程,首先要画出圆柱的侧面展开图,把A 和C 展开到一个平面内.根据两点之间,线段最短,结合勾股定理即可求出蚂蚁爬行的最短路程.【详解】解:如图,展开圆柱的半个侧面是矩形,π=厘米,矩形的宽BC=12厘米.∴矩形的长是圆柱的底面周长的一半,即AB=39∴蚂蚁需要爬行最短路程2222=+=+=厘米.12915AC BC AB故答案为:15厘米【点睛】求两个不在同一平面内的两点之间的最短距离时,一定要展开到一个平面内,根据两点之间,线段最短.15.32或42【分析】根据题意画出图形,分两种情况:△ABC是钝角三角形或锐角三角形,分别求出边BC,即可得到答案【详解】当△ABC是钝角三角形时,∵∠D=90°,AC=13,AD=12,∴2222=-=-=,13125CD AC AD∵∠D=90°,AB=15,AD=12,∴2222=-=-=,BD AB AD15129∴BC=BD-CD=9-5=4,∴△ABC的周长=4+15+13=32;当△ABC是锐角三角形时,∵∠ADC=90°,AC=13,AD=12,∴2222CD AC AD-=-=,13125∵∠ADB=90°,AB=15,AD=12,∴2222=-=-,BD AB AD15129∴BC=BD-CD=9+5=14,∴△ABC的周长=14+15+13=42;综上,△ABC的周长是32或42,故答案为:32或42.【点睛】此题考查勾股定理的实际应用,能依据题意正确画出图形分类讨论是解题的关键.16.75或6或9 4【分析】当△ABP为等腰三角形时,分三种情况:①当AB=BP时;②当AB=AP时;③当BP=AP 时,分别求出BP的长度,继而可求得t值.【详解】在Rt△ABC中,BC2=AB2﹣AC2=7.52﹣4.52=36,∴BC=6(cm);①当AB=BP=7.5cm时,如图1,t=7.52=3.75(秒);②当AB=AP=7.5cm时,如图2,BP=2BC=12cm,t=6(秒);③当BP=AP时,如图3,AP=BP=2tcm,CP=(4.5﹣2t)cm,AC=4.5cm,在Rt△ACP中,AP2=AC2+CP2,所以4t2=4.52+(4.5﹣2t)2,解得:t=94,综上所述:当△ABP为等腰三角形时,t=3.75或t=6或t=94.故答案为:3.75或6或94.【点睛】此题是等腰三角形与动点问题,考查等腰三角形的性质,勾股定理,解题中应根据每两条边相等分情况来解答,不要漏解.17.25 8【分析】先根据勾股定理求出AC的长,再根据DE垂直平分AC得出FA的长,根据相似三角形的判定定理得出△AFD∽△CBA,由相似三角形的对应边成比例即可得出结论.【详解】∵Rt△ABC中,∠ABC=90°,AB=3,BC=4,∴AC=2222AB+BC=3+4=5;∵DE垂直平分AC,垂足为F,∴FA=12AC=52,∠AFD=∠B=90°,∵AD∥BC,∴∠A=∠C,∴△AFD∽△CBA,∴ADAC=FABC,即AD5=2.54,解得AD=258;故答案为258.【点睛】本题考查的是勾股定理及相似三角形的判定与性质,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.18.8或10或12或25 3【详解】解:①如图1:当BC=CD=3m时,AB=AD=5m,AC⊥BD,此时等腰三角形绿地的面积:12×6×4=12(m2);②如图2:当AC=CD=4m时,AC⊥CB,此时等腰三角形绿地的面积:12×4×4=8(m2);③如图3:当AD=BD时,设AD=BD=xm,在Rt△ACD中,CD=(x-3)m,AC=4m,由勾股定理,得AD2=DC2+CA2,即(x-3)2+42=x2,解得x=256,此时等腰三角形绿地的面积:12BD·AC=12×256×4=253(m2);④如图4,延长BC到D,使BD=AB=5m,故CD=2m,此时等腰三角形绿地的面积:12BD·AC=12×5×4=10(m2);综上所述,扩充后等腰三角形绿地的面积为8m2或12m2或10m2或253m2.点睛:此题主要考查了等腰三角形的性质以及勾股定理的应用,解决问题的关键是根据题意正确画出图形.19.49【分析】先计算出BC 的长,再由勾股定理求出阴影部分的面积即可.【详解】∵∠ACB=90︒,25AB = ,24AC =,∴22222252449BC AB AC =-=-=,∴阴影部分的面积=249BC =,故答案为:49.【点睛】此题考查勾股定理,能利用根据直角三角形计算得到所需的边长,题中根据勾股定理的图形得到阴影部分面积等于BC 的平方是解题的关键.20.【分析】 根据三角形等面积法求出32AC BC = ,在Rt△ACD 中根据勾股定理得出AC 2=14BC 2+36,依据这两个式子求出AC 、BC 的值.【详解】 ∵AD 是BC 边上的高,BE 是AC 边上的高, ∴12AC•BE=12BC•AD, ∵AD=6,BE =4, ∴AC BC =32, ∴22AC BC =94, ∵AB=AC ,AD⊥BC,∴BD=DC =12BC , ∵AC 2﹣CD 2=AD 2,∴AC 2=14BC 2+36, ∴221364BC BC +=94, 整理得,BC 2=3648⨯, 解得:BC=∴△ABC 的面积为12×cm 2故答案为:92. 【点睛】 本题考查了三角形的等面积法以及勾股定理的应用,找出AC 与BC 的数量关系是解答此题的关键.三、解答题21.(1)BE =1;(2)见解析;(3)()23y x =-【分析】(1)如图1,根据等边三角形的性质和四边形的内角和定理可得∠BED =90°,进而可得∠BDE =30°,然后根据30°角的直角三角形的性质即可求出结果;(2)过点D 作DM ⊥AB 于M ,作DN ⊥AC 于N ,如图2,根据AAS 易证△MBD ≌△NCD ,则有BM =CN ,DM =DN ,进而可根据ASA 证明△EMD ≌△FND ,可得EM =FN ,再根据线段的和差即可推出结论;(3)过点D 作DM ⊥AB 于M ,如图3,同(2)的方法和已知条件可得DM =DN =FN =EM ,然后根据线段的和差关系可得BE +CF =2DM ,BE ﹣CF =2BM ,在Rt △BMD 中,根据30°角的直角三角形的性质可得DM =3BM ,进而可得BE +CF =3(BE ﹣CF ),代入x 、y 后整理即得结果.【详解】解:(1)如图1,∵△ABC 是等边三角形,∴∠B =∠C =60°,BC =AC =AB =4.∵点D 是线段BC 的中点,∴BD =DC =12BC =2. ∵DF ⊥AC ,即∠AFD =90°,∴∠AED =360°﹣60°﹣90°﹣120°=90°,∴∠BED =90°,∴∠BDE =30°,∴BE =12BD =1;(2)过点D 作DM ⊥AB 于M ,作DN ⊥AC 于N ,如图2,则有∠AMD =∠BMD =∠AND =∠CND =90°.∵∠A =60°,∴∠MDN =360°﹣60°﹣90°﹣90°=120°.∵∠EDF =120°,∴∠MDE =∠NDF .在△MBD 和△NCD 中,∵∠BMD =∠CND ,∠B =∠C ,BD =CD ,∴△MBD ≌△NCD (AAS ),∴BM =CN ,DM =DN .在△EMD 和△FND 中,∵∠EMD =∠FND ,DM =DN ,∠MDE =∠NDF ,∴△EMD ≌△FND (ASA ),∴EM =FN ,∴BE +CF =BM +EM +CN -FN =BM +CN =2BM =BD =12BC =12AB ;(3)过点D 作DM ⊥AB 于M ,如图3,同(2)的方法可得:BM =CN ,DM =DN ,EM =FN .∵DN =FN ,∴DM =DN =FN =EM ,∴BE +CF =BM +EM +FN -CN =NF +EM =2DM =x +y ,BE ﹣CF =BM +EM ﹣(FN -CN )=BM +NC =2BM =x -y ,在Rt △BMD 中,∵∠BDM =30°,∴BD =2BM ,∴DM =22=3BD BM BM -,∴()3x y x y +=-,整理,得()23y x =-.【点睛】本题考查了等边三角形的性质、四边形的内角和定理、全等三角形的判定与性质、30°角的直角三角形的性质以及勾股定理等知识,具有一定的综合性,正确添加辅助线、熟练掌握上述知识是解题的关键.22.(1)45度;(2)∠AEC﹣∠AED=45°,理由见解析;(3)见解析【分析】(1)由等腰三角形的性质可求∠BAE=140°,可得∠CAE=50°,由等腰三角形的性质可得∠AEC=∠ACE=65°,即可求解;(2)由等腰三角形的性质可求∠BAE=180°﹣2α,可得∠CAE=90°﹣2α,由等腰三角形的性质可得∠AEC=∠ACE=45°+α,可得结论;(3)如图,过点C作CG⊥AH于G,由等腰直角三角形的性质可得EH=2EF,CH=2CG,由“AAS”可证△AFB≌△CGA,可得AF=CG,由勾股定理可得结论.【详解】解:(1)∵AB=AC,AE=AB,∴AB=AC=AE,∴∠ABE=∠AEB,∠ACE=∠AEC,∵∠AED=20°,∴∠ABE=∠AED=20°,∴∠BAE=140°,且∠BAC=90°∴∠CAE=50°,∵∠CAE+∠ACE+∠AEC=180°,且∠ACE=∠AEC,∴∠AEC=∠ACE=65°,∴∠DEC=∠AEC﹣∠AED=45°,故答案为:45;(2)猜想:∠AEC﹣∠AED=45°,理由如下:∵∠AED=∠ABE=α,∴∠BAE=180°﹣2α,∴∠CAE=∠BAE﹣∠BAC=90°﹣2α,∵∠CAE+∠ACE+∠AEC=180°,且∠ACE=∠AEC,∴∠AEC=45°+α,∴∠AEC﹣∠AED=45°;(3)如图,过点C作CG⊥AH于G,∵∠AEC﹣∠AED=45°,∴∠FEH=45°,∵AH⊥BE,∴∠FHE=∠FEH=45°,∴EF =FH ,且∠EFH =90°,∴EH EF ,∵∠FHE =45°,CG ⊥FH ,∴∠GCH =∠FHE =45°,∴GC =GH ,∴CH CG ,∵∠BAC =∠CGA =90°,∴∠BAF +∠CAG =90°,∠CAG +∠ACG =90°,∴∠BAF =∠ACG ,且AB =AC ,∠AFB =∠AGC ,∴△AFB ≌△CGA (AAS )∴AF =CG ,∴CH AF ,∵在Rt △AEF 中,AE 2=AF 2+EF 2,AF )2+EF )2=2AE 2,∴EH 2+CH 2=2AE 2.【点睛】本题是综合了等腰直角三角形的性质,全等三角形的性质与判定的动点问题,三个问题由易到难,在熟练掌握各个相关知识的基础上找到问题之间的内部联系,层层推进去解答是关键.23.(1) 2516;(2)83t =或6;(3)当153,5,210t =或194时,△BCP 为等腰三角形. 【分析】(1)设存在点P ,使得PA PB =,此时2PA PB t ==,42PC t =-,根据勾股定理列方程即可得到结论;(2)当点P 在CAB ∠的平分线上时,如图1,过点P 作PE AB ⊥于点E ,此时72BP t =-,24PE PC t ==-,541BE =-=,根据勾股定理列方程即可得到结论; (3)在Rt ABC 中,根据勾股定理得到4AC cm =,根据题意得:2AP t =,当P 在AC 上时,BCP 为等腰三角形,得到PC BC =,即423t -=,求得12t =,当P 在AB 上时,BCP 为等腰三角形,若CP PB =,点P 在BC 的垂直平分线上,如图2,过P 作PE BC ⊥于E ,求得194t =,若PB BC =,即2343t --=,解得5t =,PC BC =③,如图3,过C 作CF AB ⊥于F ,由射影定理得;2BC BF AB =⋅,列方程2234352t --=⨯,即可得到结论. 【详解】 解:在Rt ABC 中,5AB cm =,3BC cm =,4AC cm ∴=,(1)设存在点P ,使得PA PB =,此时2PA PB t ==,42PC t =-,在Rt PCB 中,222PC CB PB +=,即:222(42)3(2)t t -+=, 解得:2516t =, ∴当2516t =时,PA PB =; (2)当点P 在BAC ∠的平分线上时,如图1,过点P 作PE AB ⊥于点E ,此时72BP t =-,24PE PC t ==-,541BE =-=,在Rt BEP 中,222PE BE BP +=,即:222(24)1(72)t t -+=-,解得:83t =, 当6t =时,点P 与A 重合,也符合条件,∴当83t =或6时,P 在ABC ∆的角平分线上; (3)根据题意得:2AP t =,当P 在AC 上时,BCP 为等腰三角形,PC BC ∴=,即423t -=,12t ∴=, 当P 在AB 上时,BCP 为等腰三角形,CP PB =①,点P 在BC 的垂直平分线上,如图2,过P 作PE BC ⊥于E ,1322BEBC ∴==, 12PB AB ∴=,即52342t --=,解得:194t =, PB BC =②,即2343t --=,解得:5t =,PC BC =③,如图3,过C 作CF AB ⊥于F ,12BF BP ∴=, 90ACB ∠=︒,由射影定理得;2BC BF AB =⋅, 即2234352t --=⨯, 解得:5310t =, ∴当15319,5,2104t =或时,BCP 为等腰三角形. 【点睛】本题考查了等腰三角形的判定,三角形的面积,难度适中.利用分类讨论的思想是解(3)题的关键.24.(1)6-t ,t+23;(2)D(1,3),y=34-x+154;(3)1515215()4215215()2b b S b b ⎧-+≤<⎪⎪=⎨⎪->⎪⎩【分析】(1)根据点E ,F 的运动轨迹和速度,即可得到答案;(2)由题意得:DF=OF=53,DE=OE=5,过点E 作EG ⊥BC 于点G ,根据勾股定理得DG=4,进而得D(1,3),根据待定系数法,即可得到答案;(3)根据题意得直线直线MN 的解析式为:34y x b =-+,从而得M(443b -,3),分2种情况:①当点M 在线段DB 上时, ②当点M 在DB 的延长线上时,分别求出S 与b 之间的函数关系式,即可.【详解】∵(0,0)O ,(6,0)A ,(0,3)C ,∴OA=6,OC=3,∵AE=t×1= t , ∴OE =6-t ,OF =(t+23)×1=t+23, 故答案是:6-t ,t+23; (2)当1t =时,OE =6-t=5,OF =t+23=53, ∵将OEF ∆沿EF 翻折,点O 恰好落在CB 边上的点D 处,∴DF=OF=53,DE=OE=5, 过点E 作EG ⊥BC 于点G ,则EG=OC=3,CG=OE=5,∴4=,∴CD=CG-DG=5-4=1,∴D(1,3),设直线DE 的解析式为:y=kx+b ,把D(1,3),E(5,0)代入y=kx+b ,得350k b k b +=⎧⎨+=⎩ ,解得:34154k b ⎧=-⎪⎪⎨⎪=⎪⎩, ∴直线DE 的解析式为:y=34-x+154; (3)∵MN ∥DE ,∴直线直线MN 的解析式为:34y x b =-+, 令y=3,代入34y x b =-+,解得:x=443b -, ∴M(443b -,3). ①当点M 在线段DB 上时,BM=6-(443b -)=4103b -+, ∴1143(10)223S BM AB b =⋅=⨯⨯-+=215b -+, ②当点M 在DB 的延长线上时,BM=443b --6=4103b -,∴1143(10)223S BM AB b=⋅=⨯⨯-=215b-,综上所述:1515215()4215215()2b bSb b⎧-+≤<⎪⎪=⎨⎪->⎪⎩.【点睛】本题主要考查一次函数与几何图形的综合,掌握勾股定理与一次函数的待定系数法,是解题的关键.25.②③⑤【分析】①先证得ABE ADP≅,利用邻补角和等腰直角三角形的性质求得90PEB∠=︒,利用勾股定理求出BE,即可求得点B到直线AE的距离;②根据①的结论,利用APD ABP ABE APBS S S S∆∆∆+=+AEP BEPS S∆∆=+即可求得结论;③在Rt AHB中,利用勾股定理求得2AB,再利用三角形面积公式即可求得ABDS∆;④当A P C、、共线时,PC最小,利用对称的性质,AB BC=的长,再求得AC的长,即可求得结论;⑤先证得ABP ADE≅,得到ABP ADE∠=∠,根据条件得到ABP NAB∠=∠,利用互余的关系即可证得结论.【详解】①∵ABD与AEP都是等腰直角三角形,∴90BAD∠=︒,90EAP∠=︒,AB AD=,AE AP=,45APE AEP∠=∠=︒,∴EAB PAD∠=∠,∴()ABE ADP SAS≅,∴180********AEB APD APE∠=∠=︒-∠=︒-︒=︒,∴1354590PEB AEB AEP∠=∠-∠=︒-︒=︒,∴222PE BE PB+=,∵2AE AP==90EAP∠=︒,∴22PE==,∴22227BE+=,解得:3BE =,作BH ⊥AE 交AE 的延长线于点H ,∵45AEP ∠=︒,90PEB ∠=︒,∴180180904545HEB PEB AEP ∠=︒-∠-∠=︒-︒-︒=︒, ∴26sin 453HB BE =︒==, ∴点B 到直线AE 6,故①错误; ②由①知:ABE ADP ≅,2EP =,3BE =∴APD ABP ABE APB S S S S ∆∆∆∆+=+AEP BEP S S ∆∆=+ 1122AE AP PE EB =⨯⨯+⨯⨯ 11222322=⨯ 13=,故②正确;③在Rt AHB 中,由①知:6EH HB ==∴62AH AE EH =+=, 2222225662322AB AH BH ⎛⎫=+=+=+ ⎪ ⎪⎭⎝⎭, 21153222ABD S AB AD AB ∆=⋅==+ ④因为AC 是定值,所以当A P C 、、共线时,PC 最小,如图,连接BC ,∵A C 、关于 BD 的对称, ∴523AB BC ==+,∴225231043AC BC ==+=+,∴ min PC AC AP =-,10432=+-,故④错误;⑤∵ABD 与AEP 都是等腰直角三角形,∴90BAD ∠=︒,90EAP ∠=︒,AB AD =,AE AP =, 在ABP 和ADE 中,AB AD BAP DAE AP AE =⎧⎪∠=∠⎨⎪=⎩,∴()ABP ADE SAS ≅,∴ABP ADE ∠=∠,∵AN BN =,∴ABP NAB ∠=∠,∴EAN ADE ∠=∠,∵90EAN DAN ∠+∠=︒,∴90ADE DAN ∠+∠=︒,∴AN DE ⊥,故⑤正确;综上,②③⑤正确,故答案为:②③⑤.【点睛】本题是三角形的综合题,主要考查了等腰直角三角形的性质,全等三角形的判定和性质,勾股定理的应用,三角形的面积公式,综合性强,全等三角形的判定和性质的灵活运用是解题的关键.26.(1)见解析;(2)27BC =.【分析】(1)由等边三角形的判定定理可得△ABD 为等边三角形,又由平行进行角度间的转化可得出结论.(2)连接AC 交BD 于点O ,由题意可证AC 垂直平分BD ,△ABD 是等边三角形,可得∠BAO=∠DAO=30°,AB=AD=BD=8,BO=OD=4,通过证明△EDF 是等边三角形,可得DE=EF=DF=2,由勾股定理可求OC ,BC 的长.【详解】(1)证明:∵AB AD =,=60A ∠︒,∴△ABD 是等边三角形.∴60ADB ∠=︒.∵CE ∥AB ,∴60CED A ∠=∠=︒.∴CED ADB ∠=∠.(2)解:连接AC 交BD 于点O ,∵AB AD =,BC DC =,∴AC 垂直平分BD .∴30BAO DAO ∠=∠=︒.∵△ABD 是等边三角形,8AB =∴8AD BD AB ===,∴4BO OD ==.∵CE ∥AB ,∴ACE BAO ∠=∠.∴6AE CE ==, 2DE AD AE =-=.∵60CED ADB ∠=∠=︒.∴60EFD ∠=︒.∴△EDF 是等边三角形.∴2EF DF DE ===,∴4CF CE EF =-=,2OF OD DF =-=.在Rt △COF 中, ∴2223OC CF OF =-=.在Rt △BOC 中, ∴22224(23)27BC BO OC =+=+=. 【点睛】本题考查了等边三角形的性质和判定,勾股定理,熟练运用等边三角形的判定是本题的关键.27.(1)CD=8;(2)t=4;(3)12-=t v t (26t ≤<) 【分析】(1)作AE ⊥BC 于E ,根据等腰三角形三线合一的性质可得BE=12BC ,然后利用勾股定理求出AE ,再用等面积法可求出CD 的长;(2)①过B 作BF ⊥AC 于F ,易得BF=CD ,分别讨论Q 点在AF 和FC 之间时,根据△BQF ≌△CPD ,得到PD=QF ,建立方程即可求出t 的值;(3)同(2)建立等式关系即可得出关系式,再根据Q 在FC 之间求出t 的取值范围即可.【详解】解:(1)如图,作AE ⊥BC 于E ,∵AB=AC ,∴BE=12BC=25在Rt △ABE 中,()2222AE=AB BE=1025=45--∵△ABC的面积=11BC AE=AB CD 22⋅⋅∴BC AE4545 CD===8AB10⋅⨯(2)过B作BQ⊥AC,当Q在AF之间时,如图所示,∵△ABC的面积=11AC BF=AB CD22⋅⋅,AB=AC∴BF=CD在Rt△CPD和Rt△BQF中∵CP=BQ,CD=BF,∴Rt△CPD≌Rt△BQF(HL)∴PD=QF在Rt△ACD中,CD=8,AC=AB=10∴22AD=AC CD=6-同理可得AF=6∴PD=AD=AP=6-t,QF=AF-AQ=6-2t 由PD=QF得6-t=6-2t,解得t=0,∵t>0,∴此种情况不符合题意,舍去;当Q点在FC之间时,如图所示,此时PD=6-t,QF=2t-6。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级第二学期3月份月考数学试题一、选择题1.下列计算正确的是()A1BCD±2.)AB.C.D.3.下列计算正确的是()A=BCD=4.)5=()A.5+B.5+C.5+D.5.下列运算正确的是()A.3=B=C.=D=6.如果关于x的不等式组0,2223x mxx-⎧>⎪⎪⎨-⎪-<-⎪⎩的解集为2x>则符合条件的所有整数m的个数是().A.5 B.4 C.3 D.2 7.“分母有理化”是我们常用的一种化简的方法,如:7==+x=>,故0x>,由22332x==-=,解得x=结果为()A.5+B.5+C.5D.5-8.如图,是按一定规律排成的三角形数阵,按图中数阵的排列规律,第9行从左至右第5个数是()123A .BC .D9.若a b >)A.-B.- C. D.10.下列运算中正确的是( )A.= B===C3=== D1== 11.下列运算正确的是( ) A=B2= C= D9=12.在实数范围内有意义,则x 的取值范围是( )A .x >0B .x >3C .x ≥3D .x ≤3二、填空题13.已知a ,b是正整数,且满足是整数,则这样的有序数对(a ,b )共有____对.14.若2x ﹣x 2﹣x=_____.15.已知|a ﹣2007=a ,则a ﹣20072的值是_____.16.把 17.已知,n=1的值________.18.n 的最小值为___19.3y =,则2xy 的值为__________.20.1=-==++……=___________.三、解答题21.观察下列各式子,并回答下面问题.(1)试写出第n 个式子(用含n 的表达式表示),这个式子一定是二次根式吗?为什么? (2)你估计第16个式子的值在哪两个相邻整数之间?试说明理由.【答案】(1,该式子一定是二次根式,理由见解析;(215和16之间.理由见解析.【分析】(1)依据规律可写出第n 个式子,然后判断被开方数的正负情况,从而可做出判断;(2)将16n =代入,得出第16,再判断即可.【详解】解:(1该式子一定是二次根式,因为n 为正整数,2(1)0n n n n -=-≥,所以该式子一定是二次根式(215=16=,∴1516<<.15和16之间.【点睛】本题考查的知识点是二次根式的定义以及估计无理数的大小,掌握用“逼近法”估算无理数的大小的方法是解此题的关键.22.先阅读材料,再回答问题:因为)111=1=;因为1=,所以=1== (1= ,= ; (2⋅⋅⋅+的值.【答案】(12)9【分析】(1)仿照例子,由1+=的值;由1+=1的值;(2)根据(1)中的规律可将每个二次根式分母有理化,可转化为实数的加减法运算,再寻求规律可得答案.【详解】解:(1)因为1-=;因为1=(2⋅⋅⋅+1=+⋅⋅⋅1=1019=-=.【点睛】本题考查了分母有理化,分子分母都乘以分母这两个数的差进行分母有理化是解题关键.23.先化简,再求值:24211326x x x x -+⎛⎫-÷ ⎪++⎝⎭,其中1x =..【分析】根据分式的运算法则进行化简,再代入求解.【详解】原式=221(1)12(3)232(3)3(1)1x x x x x x x x x ---+⎛⎫⎛⎫÷=⋅= ⎪ ⎪+++--⎝⎭⎝⎭.将1x == 【点睛】此题主要考查分式的运算,解题的关键是熟知分式的运算法则.24.计算:10099+【答案】910【解析】【分析】 先对代数式的每一部分分母有理化,然后再进行运算【详解】10099++=2100992-++++=991224-+-++-=1-=1110-=910【点睛】本题看似计算繁杂,但只要找到分母有理化这个突破口,就会化难为易。
25.)÷)(a ≠b ). 【答案】【解析】试题分析:先计算括号内的,然后把除法转化为乘法,约分即可得出结论.试题解析:解:原式=()()a b a b --+-222226.小明在解决问题:已知2a2﹣8a+1的值,他是这样分析与解的:∵=2∴a﹣2=∴(a﹣2)2=3,a2﹣4a+4=3∴a2﹣4a=﹣1∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1请你根据小明的分析过程,解决如下问题:(1(2)若,求4a2﹣8a+1的值.【答案】(1)9;(2)5.【解析】试题分析:(1)此式必须在把分母有理化后才能实现化简,即各分式分子分母同乘以一个因式,使得1===.(2)先对a1,若就接着代入求解,计算量偏大.模仿小明做法,可先计算2(1)a-的值,就能较为简单地算出结果;也可对这个二次三项式进行配方,再代入求值.后两种方法都比直接代入计算量小很多.解:(1)原式=1)+++⋯(2)∵1a===,解法一:∵22(1)11)2a-=-=,∴2212a a-+=,即221a a-=∴原式=24(2)14115a a-+=⨯+=解法二∴原式=24(211)1a a-+-+24(1)3a=--211)3=--4235=⨯-=点睛:(1得22=-=-a b,去掉根号,实现分母有理化.(2)当已知量为根式时,求这类二次三项式的值,直接代入求值,计算量偏大,若能巧妙利用完全平方公式或者配方法,计算要简便得多.27.计算(1+(2+-÷(4)((3)2b【答案】(1)234)7.【分析】(1)先把各二次根式化为最简二次根式,然后合并即可;(2)先把各二次根式化为最简二次根式,然后合并即可;(3)根据二次根式的乘除法则运算;(4)利用平方差公式计算;【详解】(1+==;(2==;(3÷==;4(4)((22=- =7 【点睛】本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了平方差公式.28.计算②)21-【答案】① 【分析】 ①根据二次根式的加减法则计算;②利用平方差、完全平方公式进行计算.【详解】解:①原式=②原式=(5-2-=【点睛】本题考查二次根式的运算,熟练掌握完全平方公式、平方差公式是关键.29.2020(1)-【答案】1【分析】先计算乘方,再化简二次根式求解即可.【详解】2020(1)-=1=1.【点睛】本题考查了二次根式的混合运算,先把二次根式化为最简二次根式,再合并即可.30.(1)计算)(2201113-⎛⎫--•- ⎪⎝⎭(2)已知,,a b c为实数且2c =2c ab -的值 【答案】(1)13;(2)12-【分析】(1)利用完全平方公式、负整数指数幂、零指数幂分别计算再合并即可;(2)先依据二次根式有意义的条件,求得a 、b 、c 的值,然后再代入计算即可.【详解】(1))(2201113-⎛⎫--•- ⎪⎝⎭31=+⨯=4+9=13;(2)根据二次根式有意义的条件可得:∵()2303010a a b ⎧-≥⎪⎪-≥⎨⎪-+≥⎪⎩,∴3a =,1b =-,∴2c =∴(()2223112c ab -=-⨯-=-【点睛】本题主要考查了二次根式的混合运算,二次根式有意义的条件以及二次根式的化简求值,熟练掌握二次根式有意义的条件是解题的关键.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【解析】2÷故选A.2.A解析:A【分析】先计算二次根式乘法,再合并同类二次根式即可.【详解】原式=故选:A.【点睛】本题考查二次根式的运算,熟练掌握运算法则是解题关键.3.D解析:D【分析】直接利用二次根式的混合运算法则分别判断得出答案.【详解】解:AB=,故此选项不合题意;2C,故此选项不合题意;D=故选:D.【点睛】本题考查二次根式的混合运算,正确掌握相关运算法则是解题关键.4.B解析:B【分析】根据乘法分配律可以解答本题.【详解】)5=5+故选:B.【点睛】本题考查二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.5.A解析:A【分析】根据各个选项中的式子,可以计算出正确的结果,从而可以解答本题.【详解】A 、3=,故选项A 正确;B B 错误;C 、18=,故选项C 错误;D =D 错误;故选:A .【点睛】本题考查了二次根式的混合运算,解答本题的关键是明确二次根式混合运算的计算方法.6.C解析:C【分析】先求出两个不等式的解集,根据不等式组的解集为2x >可得出m ≤2的值是整数,得出|m|=3或2,于是m=-3,3,-2或2,由m ≤2,得m=-3,-2或2.【详解】 解:解不等式02x m ->得x >m , 解不等式223x x --<-得x >2, ∵不等式组解集为x >2,∴m ≤2,则|m|=3或2,∴m=-3,3,2或-2,由m ≤2得,m=-3,-2或2.即符合条件的所有整数m 的个数是3个.故选:C .【点睛】本题考查了解一元一次不等式组以及二次根式的性质,熟练运用一元一次不等式组的解法是解题的关键.7.D解析:D【分析】进行化简,然后再进行合并即可.【详解】设x =<∴0x<,∴266x=-+,∴212236x=-⨯=,∴x=∵5=-,∴原式5=-5=-故选D.【点睛】本题考查了二次根式的混合运算,涉及了分母有理化等方法,弄清题意,理解和掌握题中介绍的方法是解题的关键.8.B解析:B【解析】【分析】由图形可知,第n(n =案.【详解】由图形可知,第n(n =∴第8=,则第9行从左至右第5=,故选B.【点睛】本题主要考查数字的变化类,解题的关键是根据题意得出第n行最后一个数为9.D解析:D【分析】首先根据二次根式有意义的条件求得a、b的取值范围,然后再利用二次根式的性质进行化简即可;【详解】∴-a3b≥0∵a>b,∴a>0,b<0=-,a ab故选:D.【点睛】此题考查二次根式的性质及化简,解题的关键是根据二次根式有意义的条件判断字母的取值范围.10.B解析:B【分析】根据二次根式的乘除法则求出每个式子的值,再判断即可.【详解】=⨯==42,故本选项不符合题意;解: A. 67===,故本选项,符合题意;===,故本选项不符合题意;D. ==3,故本选项不符合题意;故选B.【点睛】本题考查二次根式的性质和二次根式的乘除法则,能灵活运用二次根式的乘除法则进行计算是解题关键.11.C解析:C【分析】根据二次根式的减法法则对A进行判断;根据二次根式的加法法则对B进行判断;根据二次根式的乘法则对C进行判断;根据二次根式的除法法则对D进行判断.【详解】解:A=,所以A选项错误;B=B选项错误;C=C选项正确;D3=,所以D选项错误.故选:C.【点睛】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.12.C解析:C解:根据题意得:x-3≥0解得:x≥3故选C.二、填空题13.7【解析】解:∵=+,∴a、b的值为15,60,135,240,540.①当a=15,b=15时,即=4;②当a=60,b=60时,即=2;③当a=15,b=60时,即=3;④当a=60解析:7【解析】解:∵2,∴a、b的值为15,60,135,240,540.①当a=15,b=15时,即2=4;②当a=60,b=60时,即2=2;③当a=15,b=60时,即2=3;④当a=60,b=15时,即2=3;⑤当a=240,b=240时,即2=1;⑥当a=135,b=540时,即2=1;⑦当a=540,b=135时,即2=1;故答案为:(15,15)、(60、60)、(15,60)、(60,15)、(240,240)、(135,540)、(540,135).所有满足条件的有序数对(a,b)共有7对.故答案为:7.点睛:本题考查了二次根式的性质和化简,解决此题的关键是分类讨论思想,得出a、b可能的取值.14.【解析】根据完全平方公式以及整体的思想即可求出答案.【详解】解:∵2x﹣1= ,∴(2x﹣1)2=3∴4x2﹣4x+1=3∴4(x2﹣x)=2∴x2﹣x=故答案为【点解析:1 2【解析】【分析】根据完全平方公式以及整体的思想即可求出答案.【详解】解:∵2x﹣,∴(2x﹣1)2=3∴4x2﹣4x+1=3∴4(x2﹣x)=2∴x2﹣x=12故答案为1 2【点睛】本题考查二次根式的运算,解题的关键是熟练运用完全平方公式,本题属于基础题型.15.2008【解析】分析:本题首先能够根据二次根式的被开方数为非负数的条件,得到a的取值范围;再根据a的取值范围,化简去掉绝对值;最后进行整理变形.详解:∵|a﹣2007|+=a,∴a≥2008,解析:2008【解析】分析:本题首先能够根据二次根式的被开方数为非负数的条件,得到a的取值范围;再根据a的取值范围,化简去掉绝对值;最后进行整理变形.详解:∵|a﹣2007=a,∴a≥2008,∴a﹣2007=a,=2007,两边同平方,得:a﹣2008=20072,∴a﹣20072=2008.故答案为:2008.点睛:解决此题的关键是能够得到a的取值范围,从而化简绝对值并变形.16.﹣【解析】解:通过有意义可以知道≤0,≤0,所以=﹣=﹣.故答案为:.点睛:此题主要考查了二次根式的性质应用,正确判断二次根式的整体符号是解题关键.解析:【解析】解:通过a≤0,,所以故答案为:点睛:此题主要考查了二次根式的性质应用,正确判断二次根式的整体符号是解题关键.17.【解析】根据题意,把被开方数配方为完全平方,然后代入求解,可得====.故答案是:.【解析】根据题意,把被开方数配方为完全平方,然后代入求解,可得.18.5【分析】因为是整数,且,则5n是完全平方数,满足条件的最小正整数n为5.【详解】∵,且是整数,∴是整数,即5n是完全平方数;∴n的最小正整数值为5.故答案为5.【点睛】主要考查了解析:5【分析】,则5n是完全平方数,满足条件的最小正整数n为5.【详解】∴是整数,即5n是完全平方数;∴n的最小正整数值为5.故答案为5.【点睛】主要考查了二次根式的定义,关键是根据乘除法法则和二次根式有意义的条件.二次根式有意义的条件是被开方数是非负数进行解答.19.【解析】试题分析:根据二次根式的意义和等式的特点,可知2x-5=0,解得x=,y=-3,代入可得=-2××3=-15.解析:15-【解析】试题分析:根据二次根式的意义和等式的特点,可知2x-5=0,解得x=52,y=-3,代入可得2xy=-2×52×3=-15.20.2018【分析】先根据已知等式归纳类推出一般规律,再根据二次根式的加减法与乘法运算法则即可得.【详解】第1个等式为:,第2个等式为:,第3个等式为:,归纳类推得:第n个等式为:(其中,解析:2018【分析】先根据已知等式归纳类推出一般规律,再根据二次根式的加减法与乘法运算法则即可得.【详解】第11=,第2=,第3=归纳类推得:第n 1=-n 为正整数),则2020++,2020=+,=, 20202=-,2018=,故答案为:2018.【点睛】本题考查了二次根式的加减法与乘法运算,依据已知等式,正确归纳出一般规律是解题关键.三、解答题21.无22.无23.无24.无25.无26.无27.无28.无29.无30.无。
