MATLAB作业例题

合集下载

Matlab的操作练习

(5)
5 s,t 5
2、编写程序，绘制右边图形并加上相应标注。
3、编写程序，绘制右边螺旋线图形并加上相应标注。
4、编写程序，绘制右边图形并加上相应标注。
5、绘制下列图形 (1)分别利用ezplot函数和plot函数绘制曲线
x2/3 y2/3 1
(2)分别利用ezplot函数和plot函数绘制曲线
练习2、阅读程序 if A then x= 1 else x=0 end
(a)当A取下面旳数组时，程序输出旳成果是什么？ (1)A=ones(3) (2)A=eye(3) (3)A=inf (4)A=rand(3)>0.5
(b)假如程序中旳A换成any(A)或者all(A) 呢?
在matalb旳程序编写中，假如能够利用数组运算、矩阵运算替代循环旳点运算，计算效率会大大提升。
x2 y4 0
(3)分别利用ezplot3函数和plot3函数绘制曲线
x cos(t)2 sin(t); y sin(t)2 cos(t); 0 t 2
z t2 *(2 t)2
6、选择合适旳函数绘制图形 (1) 双扭线 = co（s 2） (2)在复平面上绘制函数图形
z cos t i sin(2t)
(3) z1 cos t i sin(2t) z 2 sin(t) icos(2 t)
绘制图形 z=z1*z2
7、分别利用mesh和ezmesh函数绘制网线图
(1)
z x2 y
(2)
z x2 y2
(3)
z2 x2 2y2
符号运算旳练习
1、利用符号运算解下列方程和方程组
(1)x4-1=0旳实根
(1) 100阶矩阵A=(aij), 其中aij=ij

Matlab习题

习题 11. 执行下列指令，观察其运算结果, 理解其意义： (1) [1 2;3 4]+10-2i(2) [1 2; 3 4].*[0.1 0.2; 0.3 0.4] (3) [1 2; 3 4].\[20 10;9 2] (4) [1 2; 3 4].^2 (5) exp([1 2; 3 4]) (6)log([1 10 100]) (7)prod([1 2;3 4])(8)[a,b]=min([10 20;30 40]) (9)abs([1 2;3 4]-pi)(10) [1 2;3 4]>=[4,3;2 1](11)find([10 20;30 40]>=[40,30;20 10])(12) [a,b]=find([10 20;30 40]>=[40,30;20 10]) (提示：a 为行号，b 为列号) (13) all([1 2;3 4]>1) (14) any([1 2;3 4]>1) (15) linspace(3,4,5) (16) A=[1 2;3 4];A(:,2)2. 执行下列指令，观察其运算结果、变量类型和字节数，理解其意义： (1) clear; a=1,b=num2str(a),c=a>0, a= =b, a= =c, b= =c (2) clear; fun='abs(x)',x=-2,eval(fun),double(fun)3. 本金K 以每年n 次，每次p %的增值率(n 与p 的乘积为每年增值额的百分比)增加，当增加到rK 时所花费的时间为)01.01ln(ln p n rT +=(单位：年)用MA TLAB 表达式写出该公式并用下列数据计算：r =2, p =0.5, n =12.4．已知函数f (x )=x 4-2x 在(-2, 2)内有两个根。

取步长h =0.05, 通过计算函数值求得函数的最小值点和两个根的近似解。

MATLAB习题及参考答案经典.doc

习题：1，计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。

2，对于B AX =，如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ，求解X 。

3，已知：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ，分别计算a 的数组平方和矩阵平方，并观察其结果。

4，角度[]604530=x ，求x 的正弦、余弦、正切和余切。

(应用sin,cos,tan.cot)5，将矩阵⎥⎦⎤⎢⎣⎡=7524a 、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵：（1）组合成一个4⨯3的矩阵，第一列为按列顺序排列的a 矩阵元素，第二列为按列顺序排列的b 矩阵元素，第三列为按列顺序排列的c 矩阵元素，即 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡237912685574（2）按照a 、b 、c 的列顺序组合成一个行矢量，即 []2965318772546，将(x -6)(x -3)(x -8)展开为系数多项式的形式。

(应用poly,polyvalm)7，求解多项式x 3-7x 2+2x +40的根。

(应用roots)8，求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。

(应用poly,polyvalm)9，计算多项式9514124234++--x x x x 的微分和积分。

(应用polyder,polyint ，poly2sym)10，解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡66136221143092x 。

(应用x=a\b)11，求欠定方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡5865394742x 的最小范数解。

(应用pinv) 12，矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=943457624a ，计算a 的行列式和逆矩阵。

(应用det,inv)13， y =sin(x )，x 从0到2π，∆x =0.02π，求y 的最大值、最小值、均值和标准差。

matlab程序设计例题及答案

matlab程序设计例题及答案1.编写程序：计算1/3+2/5+3/7+……+10/21法一： s=0;for i=1:10s=s+i/(2*i+1); end ss =法二：sum((1:10)./(3:2:21)) ans =2.编写程序：计算1~100中即能被3整除，又能被7整除的所有数之和。

s=0;for i=1:100if mod(i,3)==0&&mod(i,7)==0 s=s+i; end,end ss =2103.画出y=n！的图,阶乘的函数自己编写，禁用MATLAB 自带的阶乘函数。

x=1:10; for i=1:10try y(i)=y(i-1)*i; catch y(i)=1; end,end plot(x,y)106123456789104.一个数恰好等于它的因子之和，这个数就称为完数。

例如，6的因子为1，2,3，而6=1+2+3，因此6就是一个完数。

编程找出20XX以内的所有完数。

g=;for n=2:20XX s=0;for r=1:n-1if mod(n,r)==0 s=s+r; end endif s==ng=[g n]; end end gg =6 28 4965.编写一个函数，模拟numel函数的功能，函数中调用size函数。

function y=numelnumel(x) m=size(x); y=m(1)*m(2);numelnumel([1 2 3;4 5 6])ans =66. 编写一个函数，模拟length函数的功能，函数中调用size函数。

function y=lengthlength(x) m=size(x);y=max(m(1),m(2));lengthlength([1 2 3;4 5 6])ans =37.求矩阵rand的所有元素和及各行平均值，各列平均值。

s=rand(5);sum=sum(sum(s)) mean2=mean(s,2) mean1=mean(s)sum =mean2 =mean1 =8.编程判断1001,1003,1007，1009，1011为素数，若不是，输出其约数。

MATLAB带答案例题

一、必做题：
1．已知典型二阶系统的传递函数为2
22210)(ωωω++=s k s s G ，试绘制当100ωπ=时，8,7,6,5,4,3,2,1=k 时的系统在单位阶跃相应，要求编制程序实现，并在同一图面中绘制要有必要的文字标志说明和图形编辑。

2．试用Simulink构建三相整流逆变电路。

要求：给出整流桥桥臂电流和电压，整流桥输出电压和逆变桥输入电压，逆变滤波以后的输出电压，并有必要的分析和说明。

第二题、选做题
5、已知某控制系统的开环传递函数，)
9)(5()2()()(2+++=s s s s k s H s G ，要求绘制系统正反馈、负反馈时系统的根轨迹，并判断系统的稳定性有何区别。

要求编制相应的程序实现。

7、已知如图1所示的电路中，电源
电压10)(=t u s V 时，L =2H ，Ω=1R 求解
图中的电流波形。

假设初始电流
A i 2)0(=，试用Simulink 工具箱搭建模型求出电流波形。

15．用Simulink构建如图8所示的电路，其中R1＝5 Ώ，R2＝3 Ώ，R3＝4 Ώ，R4＝2 Ώ，R5＝1 Ώ，求电流I。

Matlab练习题

Matlab练习题Matlab练习题１已知矩阵11 12 13 1421 22 23 24A= 31 32 33 3441 42 43 44(1)A(:,1) (2) A(2,:) (3) A(:,2:3)(4) A(2:3,2:3) (5) A(:,1:2:3) (6) A(2:3)(7) A(:) (8) A(:,:) (9) ones(2,2)(10) eye(2) (11) [A,[ones(2,2);eye(2)]](12) diag(A) (13) diag(A,1) (14) diag(A,-1)(15) diag(A,2)2(1)输入如下矩阵Ａ０π/3Ａ＝π/6 π/2(2) 求矩阵B1,B1中每一元素为对应矩阵Ａ中每一元素的正弦函数(3) 求矩阵B2, B2中每一元素为对应矩阵Ａ中每一元素的余弦函数(4) 求B12+B22(5) 求矩阵Ａ的特征值与特征矢量：称特征矢量为Ｍ，而特征值矩阵为Ｌ(6) 求Msin(L)M-1(7)使用funm命令求矩阵A的正弦函数（结果应该与（６）同）(8)求cosA(9) 证明sin2A+cos2A=I3 按题目要求用MATLAB命令完成下列矩阵运算(1) 使用rand命令产生5个2x2随机矩阵A,B,C,D,E(2) 求矩阵F(使用和不使用inv命令两种情况) F=A-1[B+C-1(D-1E)]4 手算和上机分别求A.*B‘ A.\B‘ A‘.\B其中A=[1;1;1] B=[2,3,4]5 已知A=[2 7 6;9 0 –10;3 0.5 6]; B=[8 0.2 0;3 2 5;4 0 7];求(1)A|B, A&B, A~B, A>B, A>=B, A<="B," a~="B</p">(2)元素值为零的元素标号(3)元素值大于6的元素标号6 某专业有三名研究生,本学期选修了四门课程,若这些研究生的姓名,学号,性别,出生年月,课程名称,考试成绩可任意假定,(1)分别用结构型变量和细胞型变量表示以上信息;(2)举例说明查阅以上任何一条信息的方法;(3)求每一个研究生的平均成绩.7 已知矩阵A=[1.2 3 5 0.9;5 1.7 5 6;3 9 0 1;1 2 3 4],求(1)A的特征多项式(2)特征多项式中未知数为20 时的值(3)特征多项式的根(4)特征多项式的导数8 已知五个数据点: (1,5.5), (2,43.1), (3,128), (4,290.7), (5,498.4)(1)用三次曲线拟合上述数据点(2)在同一图形中绘出数据点和拟合曲线(3)用适当图形表示拟合精度9 在实验中测得如下6组数据:(0,1.5), (1.5,3.4), (2.8,13), (3.8,36), (4.5,63), (4.9,78)请用三次曲线拟合以上数据并给出以下结果：(1)三次多项式的各项系数；(2)将数据点和拟合曲线以最佳效果在同一图中绘出；10 求下列函数的极限（1）lim(x2/sin2(x/3)) x 0 （2）lim((tanx-sinx)/sin3x) x 0 （3）lim(sin(a+x)-sin(a-x))/x x 0 （4）limxcos(1/x) x 0（5）lim((1+mx)n-(1+nx)m)/x2 x 0 （6）lim(1+1/n)(n+5) n∞（7）lim(1-2/x)x x ∞（8）lim(1+cosx) 3secx x л/2 11 求下列函数的积分（1）x2/sin2(x/3) （2）(tanx-sinx)/sin3x（3）(sin(a+x)-sin(a-x))/x （4）xcos(1/x)（5）((1+mx)n-(1+nx)m)/x2 (6) cos2x(7) sinaxcosbx (8)cosaxsinbx(9) arcsin(x/a) (10)1/(a+bsinx)(11) xarcsin(x/a) (12) x2arcsin(x/a)12 求下列函数的反函数（1）y=2sin3x （2）y=1+ln(x+2)（3）y=2x/(2x+1) （4）y=(ex+e(-x))/2（5）y=1/2(arccos(x/2)) （6）y=x+1/x13 求下列函数的定积分（1）(x+sinx)/(1+cosx) [0,pi/2] （2）ln(1+tanx ) [0,pi/4] （3）1/(1+cos2x ) [0,pi/2] （4）cos5xsinx [0,pi/2] （5）(3x4+3x2+1)/(x2+1) [-1,0] (6) x2+1/x4 [1,2] (7) tan2 x [0,pi/4] (8) 4cos4x [-pi/2,pi/2] (9) 1-sin3x [0,pi] (10)1/(11+5x) 3 [-2,1] (11) cosxcos2x [-pi/2 , pi/2] (12) (x 3 sin 2 x )/(x 4 + 2x 2 + 1) [-5,5] 14 求解代数方程(1) ax2+bx+c=0(2) cos(2x)+sin(x)=115 解线性方程组a1x+b1y+c1z=d1a2x+b2y+c2z=d2 其中ai, bi, ci, di为常数, x, y, z为变量a3x+b3y+d3z=d316 求方程tan(x)+sin(x)=2在区间[-2π, 2π]上的全部实数解并用图示。

matlab典型例题

例2.1>> muw0=1.785;>> a=0.03368;>> b=0.000221;>> t=0:20:80;>> muw=muw0./(1+a*t+b*t.^2)例2.2 数值数组和字符串的转换>> a=[1:5];>> b=num2str(a);>> a*2ans =2 4 6 8 10>> b*2ans =98 64 64 100 64 64 102 64 64 104 64 64 106例2.9比较左除和右除求解恰定方程>> rand('seed',12);>> a=rand(100)+1.e8;>> x=ones(100,1);>> b=a*x;>> cond(a)ans =5.0482e+011>> tic;x1=b'/a;t1=toct1 =0.4711>> er1=norm(x-x1')er1 =139.8326>> re1=norm(a*x1'-b)/norm(b)re1 =4.3095e-009>> tic;x1=a\b;t1=toct1 =0.0231>> tic;x1=a\b;t1=toct1 =0.0011>> er2=norm(x-x1)er2 =1.5893e-004>> re1=norm(a*x1-b)/norm(b)re1 =4.5257e-016例2.14：计算矩阵的指数>> b=magic(3);>> expm(b)ans =1.0e+006 *1.0898 1.0896 1.08971.0896 1.0897 1.08971.0896 1.0897 1.0897 例2.18：特征值条件数>> a=[-149 -50 -154;537 180 546; -27 -9 -25]a =-149 -50 -154537 180 546-27 -9 -25>> [V,D,s]=condeig(a)V =0.3162 -0.4041 -0.1391-0.9487 0.9091 0.9740-0.0000 0.1010 -0.1789D =1.0000 0 00 2.0000 00 0 3.0000例2.41 5阶多项式在【0,2pi】最小二乘拟合>> x=0:pi/20:pi/2;>> y=sin(x);>> a=polyfit(x,y,5);>> x1=0:pi/30:pi*2;>> y1=sin(x1);>> y2=a(1)*x1.^5+a(2)*x1.^4+a(3)*x1.^3+a(4)*x1.^2+a(5)*x1+a(6); >> plot(x1,y1,'b-',x1,y2,'r*')>> legend('原曲线','拟合曲线')>> axis([0,7,-1.2,4])例3.7 gradient绘制矢量图>> x=0:pi/20:pi/2;>> y=sin(x);>> a=polyfit(x,y,5);>> x1=0:pi/30:pi*2;>> y1=sin(x1);>> y2=a(1)*x1.^5+a(2)*x1.^4+a(3)*x1.^3+a(4)*x1.^2+a(5)*x1+a(6); >> plot(x1,y1,'b-',x1,y2,'r*')>> legend('原曲线','拟合曲线')>> axis([0,7,-1.2,4])>>>> [x,y]=meshgrid(-2:.2:2,-2:.2:2); >> z=x.*exp(-x.^2-y.^2);>> [px,py]=gradient(z,.2,.2);>> contour(z),>> hold on>> quiver(px,py)>> hold off例基本绘图命令rand(100,1);plot(y)例4.1 绘制如图>> x=1:0.1*pi:2*pi;>> y=sin(x);>> z=cos(x);>> plot(x,y,'--k',x,z,'-.rd')例4.5 绘制如图>> x=1:10;>> y=rand(10,1);>> bar(x,y);>> x=0:0.1*pi:2*pi;>> y=x.*sin(x);>> feather(x,y)例 4.6 绘制如图>> lim=[0,2*pi,-1,1];>> fplot('[sin(x),cos(x)]',lim)例4.7绘图如下>> x=[2,4,6,8];>> pie(x,{'math','english','chinese','music'}) 例4.9 绘图如下三维螺旋线>> x=0:pi/50:10*pi;>> y=sin(x);>> x=0:pi/50:10*pi;>> y=sin(x);>> z=cos(x);>> plot3(x,y,z);例4.10 绘图如下。

Matlab 考题题整理带答案

MATLAB 考试试题(1)产生一个1x10的随机矩阵，大小位于（-5 5），并且按照从大到小的顺序排列好！（注：要程序和运行结果的截屏）答案：a=10*rand(1,10)-5;b=sort(a,'descend')1.请产生一个100*5的矩阵，矩阵的每一行都是[1 2 3 4 5]2. 已知变量：A=’ilovematlab’；B=’matlab’, 请找出：（A）B在A中的位置。

（B）把B放在A后面，形成C=‘ilovematlabmatlab’3. 请修改下面的程序，让他们没有for循环语句！A=[1 2 3; 4 5 6; 7 8 9];[r c]=size(A);for i=1:1:rfor j=1:1:cif (A(i,j)>8 | A(i,j)<2)A(i,j)=0;endendend4. 请把变量A=[1 2 3; 4 5 6; 7 8 9]写到文件里(output.xls)，写完后文件看起来是这样的1 2 3 4 5 6 7 8 95.试从Yahoo网站上获得微软公司股票的2008年9月的每日收盘价。

6.编写M文件，从Yahoo网站批量读取60000.SH至600005.SH在2008年9月份的每日收盘价（提示：使用字符串函数）。

7. 将金牛股份（000937）2005年12月14日至2006年1月10日的交易记录保存到Excel中，编写程序将数据读入MATLAB中，进一步将数据读入Access数据库文件。

8.已知资产每日回报率为0.0025，标准差为0.0208，资产现在价值为0.8亿，求5％水平下资产的10天在险价值(Var)。

9.a=[1 2 3 4 5],b=a(1)*a(5)+a(2)*a(4)+a(3)*a(3)+a(4)*a(2)+a(5)*a(1).试用MATLAB中最简单的方法计算b，注意最简单哦。

1、求下列联立方程的解3x+4y-7z-12w=45x-7y+4z+ 2w=-3x +8z- 5w=9-6x+5y-2z+10w=-8求系数矩阵的秩；求出方程组的解。

Matlab例题汇总

Matlab例题汇总：【例2-4】两个矩阵分别为[1 2 3;4 5 6;7 8 9]和[1 1 1;2 2 2;3 3 3]，求两者相加的和。

a=[1 2 3;4 5 6;7 8 9];b=[1 1 1;2 2 2;3 3 3];c=a+b【例2-5】两个矩阵分别为[1 2 3;4 5 6;7 8 9]和[1 1 1]，阶数不同，求两者相减的差。

a=[1 2 3;4 5 6;7 8 9];b=[1 1 1];c=a-b【例2-6】两个矩阵相乘，矩阵a为，矩阵b为，分别计算c=a*b和d=b*a。

a=[1 2 3;4 5 6;7 8 9];b=[1 2 3];c=a*b% 将第三句c=a*b改成d=b*a，再运行一次% 【例2-7】两个数组相乘，数组a为，数组b为，求两数组的乘法。

% 在命令窗口输入两数组，计算c=a.*b：a=[1 2 3];b=[4 5 6];c=a.*b% 【例2-8】两个矩阵相除，矩阵a和b均为3×3阶矩阵。

a=rand(3)b=rand(3)c=a/bd=b\a% 【例2-9】数组a为，数组b为，求两数组的除法。

a=[1 2 3];b=[4 5 6];c=a.\bc=b./a% 【例2-10】矩阵a为[1 2;3 4]，求它的1.5次幂。

a=[1 2;3 4];c=a^1.5% 【例2-11】数组a为[1 2 3]，数组b为[4 5 6]，求数组的幂c=a.^b。

a=[1 2 3];b=[4 5 6];c=a.^b% 【例2-12】数组a为[1 2 3]，求数组的幂c=a.^2。

a=[1 2 3];c=a.^2% 【例2-13】数组a为[1 2 3]，求数组的幂运算c=2.^a。

a=[1 2 3];c=2.^a% 【例2-14】矩阵a为[1 2 3;4 5 6;7 8 9]，计算a的转置。

a=[1 2 3;4 5 6;7 8 9];c=a'% 【例2-15】矩阵a为[1+2i 3+4i]，计算a的转置。

MATLAB例题考试及答案

例1.1 分别绘制函数和的曲线。

x=-2*pi:pi/180:2*pi;plot(x,2.^(-abs(x)),':',x,sin(x));例1.2 求方程2x5-3x3 +71x2-9x+13=0的全部根。

p=[2,0,-3,71,-9,13];x=roots(p)例1.3 求解线性方程组。

a=[2,3,-1;8,2,3;45,3,9];b=[2;4;23];x=inv(a)*b例1.4 求积分quad('x.*log(1+x)',0,1)例2.2 利用M文件建立MYMAT矩阵。

(1)启动有关编辑程序或MATLAB文本编辑器(见第4章)，并输入待建矩阵：MYMAT=[101,102,103,104,105,106,107,108,109;201,202,203,204,205,206,207,208,209;301,302,303,304,305,306,307,308,309]例2.3 建立5阶方阵A，判断A的元素是否能被3整除。

A =[24,35,13,22,63;23,39,47,80,80; ...90,41,80,29,10;45,57,85,62,21;37,19,31,88,76]P=rem(A,3)==0例2.5 建立矩阵A，然后找出在[10，20]区间的元素的位置。

(1) 建立矩阵A。

A=[4,15,-45,10,6;56,0,17,-45,0](2) 找出大于4的元素的位置。

find(A>=10 & A<=20)ans =367例2.6 建立一个字符串向量，然后对该向量做如下处理：(1)取第1~5个字符组成的子字符串。

(2)将字符串倒过来重新排列。

(3)将字符串中的小写字母变成相应的大写字母，其余字符不变。

(4)统计字符串中小写字母的个数。

命令如下：ch='ABc123d4e56Fg9';subch=ch(1:5)subch =ABc12revch=ch(end:-1:1)revch =9gF65e4d321cBAk=find(ch>='a'&ch<='z');ch(k)=ch(k)-('a'-'A');char(ch)ans =ABC123D4E56FG9length(k)ans =4例3.2 建立随机矩阵：(1) 在区间[20,50]内均匀分布的5阶随机矩阵。

matlab作业题答案

MATLAB作业题答案第一章MATLAB概述1．选择题（1）在MATLAB中（ C ）用于括住字符串。

A、，B、；C、‘’D、“”（2）在MATLAB的命令窗口中（ D ）可以中断MATLAB命令运行。

A、endB、escC、backspaceD、ctrl+c(3)在MA TLAB的命令窗口中执行（ B ）命令，使数值 5.3显示为5.3000000000000000e+000。

A、format longB、format long eC、format shortD、format short e(4)在MA TLAB的命令窗口中执行（B ）命令，将命令窗口的现实内容清空。

A、clearB、clcC、echo offD、cd2．在命令窗口中输入以下命令，写出在命令窗口中的运行结果。

a=[2+5i 5 0.2 2*3]答：a =0i 5.0000 0.2000 6.00003．使用MATLAB的‘preferences’窗口设置数据格式为有理数表示答：rational4．在命令窗口使用标点符号“%”和“；”的含义？答：%表示注释；；表示不显示运行结果。

5．用“format”命令设置数据输出格式为有理数表示，15位长格式和5位科学计数法。

答：rational long short11．在命令窗口中输入以下命令，并查看显示的图形。

a=[1 2 3 4];>> b=[5 6 7 8];>> c=a+b*i;>> plot(c)第二章 MATLAB 基本运算1．选择题(1) 下列变量名中（ A ）是合法的。

A 、 char_1,i,jB 、x*y,a.1C 、x\y,a1234D 、end ，1bcx（2）下列（ C ）是合法常量。

A 、3*e10B 、1e500C 、-1.85e-56D 、10-2（3）x=uint8(2.3e10)，则x 所占的字节是（ A ）个。

A 、1B 、 2C 、4D 、8（4）已知x=0:10;，则x 有（ B ）个元素。

matlab简单编程21个题目及答案

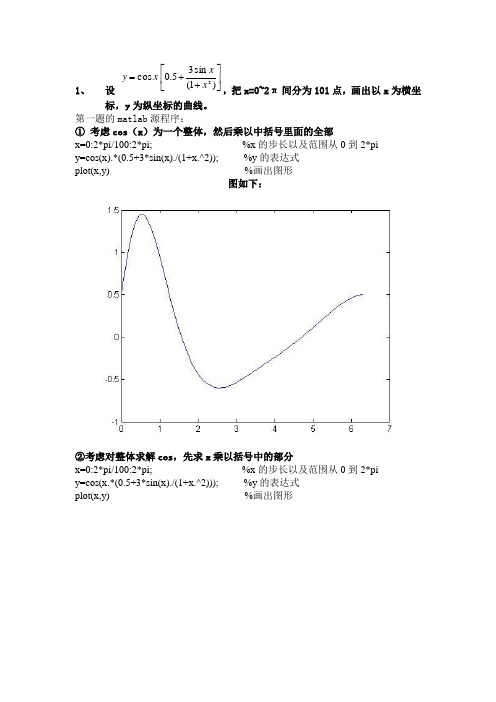
1、设⎥⎦⎤⎢⎣⎡++=)1(sin35.0cos2xxxy，把x=0~2π间分为101点，画出以x为横坐标，y为纵坐标的曲线。

第一题的matlab源程序：①考虑cos（x）为一个整体，然后乘以中括号里面的全部x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x).*(0.5+3*sin(x)./(1+x.^2)); %y的表达式plot(x,y)%画出图形图如下：②考虑对整体求解cos，先求x乘以括号中的部分x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x.*(0.5+3*sin(x)./(1+x.^2))); %y的表达式plot(x,y) %画出图形图如下：2、产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。

并求该矩阵全体数的平均值和均方差。

第二题的matlab源程序如下：R1=randn(8,6) %产生正态分布随机矩阵R1 =1.0933 -0.7697 1.5442 -0.1924 1.4193 0.21571.1093 0.3714 0.0859 0.8886 0.2916 -1.1658-0.8637 -0.2256 -1.4916 -0.7648 0.1978 -1.14800.0774 1.1174 -0.7423 -1.4023 1.5877 0.1049-1.2141 -1.0891 -1.0616 -1.4224 -0.8045 0.7223-1.1135 0.0326 2.3505 0.4882 0.6966 2.5855-0.0068 0.5525 -0.6156 -0.1774 0.8351 -0.66691.5326 1.1006 0.7481 -0.1961 -0.2437 0.1873aver=(sum(R1(1:end,1:end)))./8 %产生各行的平均值aver =0.0768 0.1363 0.1022 -0.3473 0.4975 0.1044a=std(R1(1:end,1:end)) %产生各行的均方差也就是标准差a =1.0819 0.8093 1.3456 0.8233 0.8079 1.2150aver1=(sum(R1(:)))./48 %全体数的平均值aver1 =0.0950b=std(R1(:)) %全体数的均方差即标准差b =1.01033、设x=rcost+3t,y=rsint+3,分别令r=2,3,4，画出参数t=0~10区间生成的x~y 曲线。

(完整版)matlab基础练习题(带答案)

Matlab 基础练习题常量、变量、表达式1、 MATLAB 中，下面哪些变量名是合法的？（）（A ）_num （B ）num_ （C ）num- （D ）-num 2、在MA TLAB 中，要给出一个复数z 的模，应该使用（）函数。

（A ）mod(z) （B ）abs(z) （C ）double(z) （D ）angle(z) 3、下面属于MATLAB 的预定义特殊变量的是？（）（A ）eps （B ）none （C ）zero （D ）exp4、判断：在MA TLAB 的内存工作区中，存放一个英文字符 'a' 需要占用1个字节，存放一个中文字符‘啊’需要占用2个字节。

（错，都是2个字节）5、判断：MA TLAB 中，i 和j （对）6、判断：MA TLAB 中，pi 代表圆周率，它等于3.14。

（错，后面还有很多位小数）7、在MA TLAB 中，若想计算的51)3.0sin(21+=πy 值，那么应该在MA TLAB 的指令窗中输入的MA TLAB 指令是__y1=2*sin(0.3*pi)/(1+sqrt(5))_。

8、在MA TLAB 中，a = 1，b = i ，则a 占_8__个字节，b 占_16_个字节，c 占________字节。

9、在MA TLAB 中，inf 的含义是__无穷大__，nan 的含义是__非数（结果不定）___。

数组1、在MA TLAB 中，X 是一个一维数值数组，现在要把数组X 中的所有元素按原来次序的逆序排列输出，应该使用下面的（）指令。

（A ）X[end:1] （B ）X[end:-1:1] （C ）X (end:-1:1) （D ）X(end:1) 2、在MA TLAB 中，A 是一个字二维数组，要获取A 的行数和列数，应该使用的MATLAB的命令是（）。

（A ）class(A) （B ）sizeof(A) （C ）size(A) （D ）isa(A)3、在MATLAB 中，用指令x=1:9生成数组x 。

Matlab 作业1

喻晓磊 200731510103 电子科学与技术习题一：编写M文件，计算以下问题：口口口口×口＝口口口口以上9个口代表1～9这9个数字，不得遗漏或重复要求：给出解算思路和M文件代码注意算法的效率解题理念：1，设以上方框中的数字分别是1~9之间的数字a、b、c、d、e、f、g、h、i。

2，我们可以推出，个位数e肯定不是1或者5 ，否则两个四位数的个位必然相等，即d=i；再者，其不可能等于9，由不重复的1~9组成的四位数，最大为9876，最小为1234，故e的最大可能取值为9876/1234=8.003……，即最大取8 。

3，我们看到，e的最小取值为2，那么a肯定不能大于或等于5 ，否则乘法运算后的结果为5位数，所以a 只能取1~4。

4，在此基础上，我们采取“穷举法”，逐个试验，从 a 开始，每一位与前面出现位的数字不相等，然后检测其是否满足算式。

程序代码如下：global aglobal bglobal cglobal dglobal eglobal fglobal gglobal hglobal ifor a=1:4for b=1:9if b~=a;for c=1:9if (c~=b)&&(c~=a);for d=1:9if (d~=b)&&(d~=a)&&(d~=c);for e=2:8 e~=5;if (e~=a)&&(e~=b)&&(e~=c)&&(e~=d);for f=1:9if (f~=a)&&(f~=b)&&(f~=c)&&(f~=d)&&(f~=e);for g=1:9if(g~=a)&&(g~=b)&&(g~=c)&&(g~=d)&&(g~=e)&&(g~=f);for h=1:9if(h~=a)&&(h~=b)&&(h~=c)&&(h~=d)&&(h~=e)&&(h~=f)&&(h~=g);for i=1:9if(i~=a)&&(i~=b)&&(i~=c)&&(i~=d)&&(i~=e)&&(i~=f)&&(i~=g)&&(i~=h);x=1000*a+100*b+10*c+d;y=e*x;z=1000*f+100*g+10*h+i;if y==z;r=xs=et=yend;end;******end;end;得到的结果如下：我们看到，结果有两组：1738 * 4= 69521963 * 4= 7852这两组结果都显示到了MATLAB软件的命令窗（COMMAND WINDOW）中，我们是使用了一个小技巧：将x、e、y的值赋给r、s、t时并没有在句末加分号，所以计算的过程也显示出来了，但是看工作区（work space）中，r、s、t 的值却只对应后面一组，这是因为，当循环进行到算出第二组结果时，便替换掉了第一组的值。

matlab大作业例子

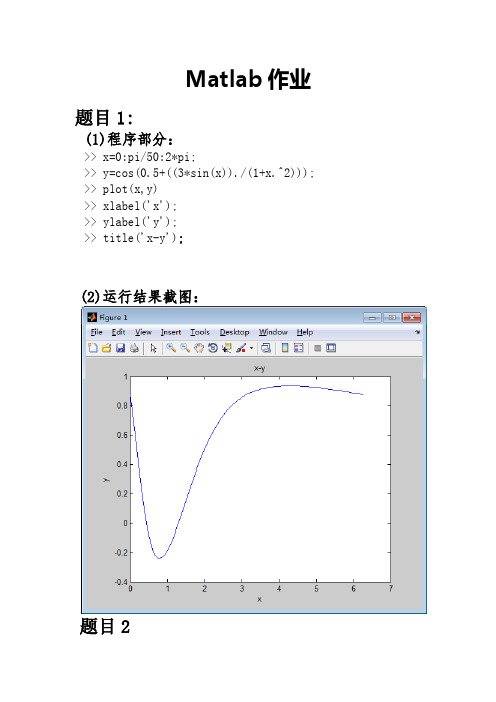
Matlab作业题目1:(1)程序部分：>> x=0:pi/50:2*pi;>> y=cos(0.5+((3*sin(x))./(1+x.^2))); >> plot(x,y)>> xlabel('x');>> ylabel('y');>> title('x-y');(2)运行结果截图：（1）程序部分：>> clear>> clc>> x=0:pi/100:4*pi;>> y1=sin(x);>> y2=cos(x);>> plot(x,y1,'r-',x,y2,'g:') >> hold on>> y3=x(find(abs(y1-y2)<0.001)); >> plot(y3,sin(y3),'*')（2）运行结果截图：（1）程序部分：>> t=(0:2*pi/100:2*pi)'; >> y1=sin(t)*[1,-1]; >> y2=sin(t).*sin(9*t); >> subplot(2,1,1);>> plot(t,[y1,y2]);>> subplot(2,1,2);>> plot(t,[y1,y2]) （2）运行结果截图：题目4（1）程序部分：>> t=0:pi/50:4*pi;>> y=exp(-t/3);>> y0=exp(-t/3).*sin(3*t); >> plot(t,y,'r-',t,y0,'b:') >> xlabel('\bf\it t')>> ylabel('\bf\it y')>> grid on;（2）运行结果截图：题目5（1）程序部分：>> n=0;>> sum=0;>> while sum<2000n=n+1;sum=sum+n;end>> n（2）运行结果截图：题目6（1）程序部分：for j=1:3n=input('n='); sum=0;for i=1:na=1/(i.^2);sum=sum+a;endPI=sqrt(6*sum) end（2）运行结果截图：题目7（1）程序部分：n0=0;y0=0;while 3*y0<5n0=n0+1;y0=y0+1/(2*n0-1);y=y0-1/(2*n0-1);n=n0-1;endn（2）运行结果截图：题目8（1）程序部分：for i=1:7x=input('put x:');if x<0&x~-3y=x^2+x-6;elseif x>=0&x<5&x~=3&x~=2 y=x*x-5*x+6;elsey=x*x-x-1;endend（2）运行结果截图：题目9①switch语句（1）程序部分：>> score=input('请输入成绩'); switch fix(score/10)case {9,10}disp('A');case {8}disp('B');case {7}disp('C');case {6}disp('D');case {0,5}disp('E');otherwisedisp('error');end（2）运行结果截图：如右图②if语句（1）程序部分：score=input('请输入成绩:') n=score/10;if n>=9&n<10disp Aelseif n>=8&n<9disp Belseif n>=7&n<8disp Celseif n>=6&n<7disp Delseif n>=0&n<6disp Eelsedisp errorend（2）运行结果截图：题目10（1）程序部分：t=input('员工的工作时间:')if t<60m=84*t-700;elseif t>120m=84*(t-120)*1.15+84*120;elsem=84*t;endm2）运行结果截图：题目11（1）程序部分：a=round(20*rand(5,6))n=input('请输入n的值:') tryb=a(n,:);catchb=a(5,:);endblasterr（2）运行结果截图：。

MATLAB习题及答案

填空题1. MATLAB于1984年由美国Mathworks公司推出，其后每年更新（两次。

2. MATLAB是一种以（矩阵）运算为基础的交互式程序设计语言。

3. MATLAB具有卓越的数值计算能力和符号计算、文字处理、可视化建模仿真和实时控制等众多功能，其每个变量代表一个（矩阵），每个元素都看作（复数）。

4.通过命令（help）、（lookfor），可以查找所有命令或函数的使用方法。

5.执行语句a=1:2:10，得到的一维数组是（1 3 5 7 9）.6.执行语句b=linspace（1,10,10）后，一维数组b包含（10）个元素，最大值是10）7.函数rem（）的功能是取（余）数。

8.若p=[1 0 0;1 1 0],则p|〜p=（[1 1 1;1 1 1]）.（注：填空时请用本题的p的方式表示结果）9.若p=[1 0 0;1 1 0],则all（p）=（[1 0 0]）.10.矩阵的加减运算，要求相加减的矩阵阶数相同。

若A=[1 2 3 4；2 3 1 8]，则执行语句：[n,m]=size（A），则n=（2 ）,m=（4 ）.11.对于一维矩阵，求其长度的函数是（length（））.12.数组和数组之间的运算，尤其是对于乘除运算和乘方运算，如果采用点方式进行计算，表明是数组的（元素）之间的运算关系。

13.求矩阵运算A*B时，要求在维度上，A的（列）数与B的（行）数相等。

二、判断题1.MATLAB只有一种数据类型，一种标准的输入输出语句，不需编译，可直接运行。

（对2.MATLAB的特殊常量是一些预选定义好的数值变量。

（对3.MATLAB变量名不区分大小写。

（错4.i是特殊常量。

（对5.NAN是非数。

（对6.MATLAB中所有的变量都表示一个矩阵或一个向量。

（对7.MATLAB中变量不需要先定义后使用，会自动根据实际赋值的类型对变量类型进行定义。

（对8.clc命令可以从内存中删除一个、多个和所有变量。

matlab经典编程例题30道

MATLAB是一款功能强大的数学软件，其编程功能也受到越来越多人的关注。

下面介绍的是30个matlab经典编程例题，可以帮助大家熟悉matlab的编程语法，提高matlab 编程技能。

1. 请编写一个程序，计算出两个数的和。

2. 请编写一个程序，计算出两个数的最大值和最小值。

3. 请编写一个程序，计算出一组数据的平均值和标准差。

4. 请编写一个程序，将一个矩阵转置。

5. 请编写一个程序，求出两个矩阵的乘积。

6. 请编写一个程序，求出一个矩阵的逆矩阵。

7. 请编写一个程序，求出一个矩阵的行列式。

8. 请编写一个程序，计算出一元二次方程的解。

9. 请编写一个程序，计算出两个数组的相似度。

10. 请编写一个程序，计算出一个矩阵的特征值和特征向量。

11. 请编写一个程序，求出两个矩阵的秩。

12. 请编写一个程序，求出一个矩阵的特定元素。

13. 请编写一个程序，求出一组数据的最高值和最低值。

14. 请编写一个程序，求出两个数组的交集。

15. 请编写一个程序，求出一个矩阵的行和列之和。

16. 请编写一个程序，使用循环语句计算出100以内所有奇数的和。

17. 请编写一个程序，使用循环语句计算出1到1000以内的和。

18. 请编写一个程序，使用递归函数计算出斐波那契数列的第n项。

19. 请编写一个程序，求出一个多项式的导数。

20. 请编写一个程序，求出一个函数的极值点。

21. 请编写一个程序，求出一个数组的非零元素个数。

22. 请编写一个程序，计算出函数的不定积分。

23. 请编写一个程序，计算出函数的定积分。

24. 请编写一个程序，求出一个矩阵的秩。

25. 请编写一个程序，求出函数的极限值。

26. 请编写一个程序，求出一个矩阵的特征值分解。

27. 请编写一个程序，求出一个矩阵的LU分解。

28. 请编写一个程序，求出一个矩阵的QR分解。

29. 请编写一个程序，求出三次多项式的根。

30. 请编写一个程序，求出一个函数的积分。

matLAB经典例题及答案

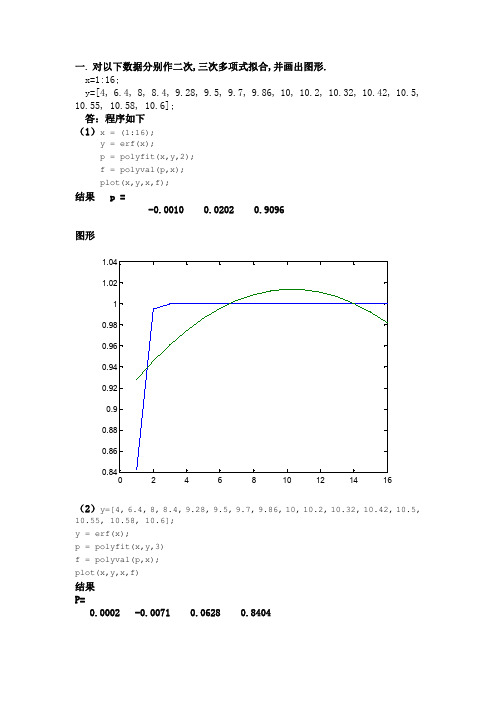
一.对以下数据分别作二次,三次多项式拟合,并画出图形.x=1:16;y=[4,6.4,8,8.4,9.28,9.5,9.7,9.86,10,10.2,10.32,10.42,10.5, 10.55,10.58,10.6];答：程序如下（1）x=(1:16);y=erf(x);p=polyfit(x,y,2);f=polyval(p,x);plot(x,y,x,f);结果p=-0.00100.02020.9096（2）y=[4,6.4,8,8.4,9.28,9.5,9.7,9.86,10,10.2,10.32,10.42,10.5, 10.55,10.58,10.6];y=erf(x);p=polyfit(x,y,3)f=polyval(p,x);plot(x,y,x,f)结果P=0.0002-0.00710.06280.8404二.在[0,4pi]画sin(x),cos(x)(在同一个图象中);其中cos(x)图象用红色小圆圈画.并在函数图上标注“y=sin(x)”,“y=cos(x)”,x轴,y轴,标题为“正弦余弦函数图象”.答：程序如下x=[0:720]*pi/180;plot(x,sin(x),x,cos(x),'ro');x=[2.5;7];y=[0;0];s=['y=sin(x)';'y=cos(x)'];text(x,y,s);xlabel('正弦余弦函数图象'),ylabel('正弦余弦函数图象')图形如下三.选择一个单自由度线性振动系统模型，自定质量、弹簧刚度、阻尼、激振力等一组参数，分别编程（m 文件）计算自由和强迫振动时的响应，并画出振动曲线图。

（要求画出该单自由度线性振动系统模型图）其中质量为m=1000kg,弹性刚度k=48020N/m,阻尼c=1960N.s/m,激振力f(t)=0.阻尼比ζ的程序p=1960/(2*sqrt(48020*1000))求得p=0.1414而p为阻尼比ζ强迫振动时的响应程序g =tf([-101],[48020048020*1.9848020]);bode(g)图形g =tf([001],[0001]);bode(g)振动曲线图程序：函数文件function dx =rigid(t,x)dx =zeros(2,1);dx(1)=x(2);dx(2)=(-48020*x(1)-1960*x(2))/1000;命令文件options =odeset('RelTol',1e-4,'AbsTol',[1e-41e-4]);[T,X]=ode45(@rigid,[012],[11],options);plot(T,X(:,1),'-')其图形如下024681012-6-5-4-3-2-11234单自由度线性强迫振动系统模型图其中质量为m=1000kg,弹性刚度k=48020N/m,阻尼c=1960N.s/m，f(t)=cos(3*pi*t)振动曲线图程序：函数文件function dx=rigid(t,x)dx=zeros(2,1);dx(1)=x(2);dx(2)=(-48020*x(1)-1960*x(2))/1000+cos(3*pi*t);命令文件options=odeset('RelTol',1e-4,'AbsTol',[1e-41e-4]);[T,X]=ode45(@rigid,[020],[11],options);plot(T,X(:,1),'-')力等一组参数，建立Simulink仿真模型框图进行仿真分析。