2018年沪科版八年级数学下册《第19章四边形》测试卷及答案
沪科版八年级数学下册《第十九章四边形》练习题含答案

第十九章四边形1 如图 19- Y- 1,在?ABCD 中,M 是 BC 延伸线上的一点,若∠ A=135° ,则∠ MCD的度数是()图 19-Y- 1A. 45°B. 55°C. 65°D. 75°2 内角和为 540°的多边形是 ( )图 19-Y- 23 如图 19-Y- 3, ?ABCD 的对角线AC , BD 订交于点O,且 AC + BD = 16, CD = 6,则△ ABO 的周长是 ()图 19-Y- 3A.10B. 14C. 20D. 224 如图 19- Y- 4,在△ ABC 中,∠ ACB =90°, AC =8, AB = 10, DE 垂直均分AC 交AB 于点 E,则 DE 的长为 ()图 19-Y- 4A. 6 B. 5 C. 4 D .35 以下判断错误的选项是( )A.两组对边分别相等的四边形是平行四边形B.四个内角都相等的四边形是矩形C.四条边都相等的四边形是菱形D .两条对角线垂直且均分的四边形是正方形6如图 19- Y- 5,在 ?ABCD 中,对角线 AC 与 BD 交于点 O,若增添一个条件,使?ABCD成为菱形,以下给出的条件不正确的选项是()图 19-Y- 5A. AB =AD1B. AC ⊥BDC. AC =BDD .∠ BAC =∠ DAC7 如图 19-Y- 6,在 ?ABCD 中,AB > AD ,按以下步骤作图:以点 A 为圆心,小于 AD1的长为半径画弧,分别交AB,AD于点E,F,再分别以点E,F 为圆心,大于2EF 的长为半径画弧,两弧交于点 G.作射线 AG 交 CD 于点 H,则以下结论中不可以由条件推理得出的是()图 19-Y- 6A. AG 均分∠ DABB. AD =DHC. DH =BCD.CH=DH8如图 19-Y- 7,在?ABCD 中, AB =6, BC= 8,∠ C 的均分线交 AD 于点 E,交 BA的延伸线于点F,则 AE +AF 的值等于 ()图 19-Y- 7A. 2B. 3C. 4D . 69 如图 19-Y-8,在矩形 ABCD 中(AD >AB) ,点 E 是 BC 上一点,且 DE=DA,AF⊥ DE ,垂足为 F.在以下结论中,不必定正确的选项是()图 19-Y- 8A.△ AFD ≌△ DCE1B. AF =2ADC. AB =AFD.BE=AD -DF10如图 19- Y- 9,矩形 ABCD 的对角线 AC 与 BD 订交于点 O, CE∥BD , DE∥ AC ,AD = 2 3, DE= 2,则四边形OCED 的面积为 ()2图 19-Y- 9A.2 3B. 4C.4 3D . 811 如图 19- Y- 10,在 Rt△ ABC 中,E 是斜边 AB 的中点.若 AB = 10,则 CE =________.图 19- Y- 1012如图 19- Y- 11,在 ?ABCD 中,BE ⊥ AB 交对角线 AC 于点 E,若∠ 1= 20°,则∠ 2 的度数为 ________.图 19-Y- 1113 已知矩形的对角线AC 与 BD 订交于点 O,若 AO = 1,那么 BD = ________.图 19- Y- 1214如图 19-Y- 13 所示,在 ?ABCD 中,∠ C=40°,过点 D 作 AD 的垂线,交 AB 于点E,交 CB 的延伸线于点 F,则∠ BEF 的度数为 ________.图 19- Y- 1315如图 19- Y- 14,在矩形 ABCD 中,AB = 3,对角线 AC , BD 订交于点 O, AE 垂直均分 OB 于点 E,则 AD 的长为 ________.图 19- Y- 1416如图 19- Y- 15,菱形 ABCD 的面积为 120 cm2,正方形 AECF 的面积为 50 cm2,则菱形的边长为 ________cm.图 19- Y- 1517.如图 19-Y- 16,在正方形ABCD 中,对角线 AC 与 BD 订交于点O, E 为 BC 上一3点,CE =5, F 为 DE 的中点.若△CEF 的周长为18,则 OF 的长为 ________.图 19- Y- 1618如图 19-Y- 17,已知 BD 是△ ABC 的角均分线,点 E, F 分别在边 AB , BC 上,ED ∥ BC, EF∥ AC. 求证: BE = CF.图 19- Y- 1719如图 19- Y-18,在 Rt△ ABC 中,∠B =90°,点 E 是 AC 的中点,AC = 2AB ,∠BAC 的均分线AD 交 BC 于点 D ,作 AF ∥ BC ,连结 DE 并延伸交AF 于点 F,连结 FC.求证:四边形ADCF 是菱形.图 19- Y- 1820如图 19-Y- 19,AC 为矩形 ABCD 的对角线,将边 AB 沿 AE 折叠,使点 B 落在AC 上的点 M 处,将边 CD 沿 CF 折叠,使点 D 落在 AC 上的点 N 处.(1)求证:四边形 AECF 是平行四边形;(2)若 AB = 6, AC = 10,求四边形 AECF 的面积.4图 19- Y - 19[ 分析 ] 设多边形的边数是 n ,则 (n - 2) ·180°= 540°, 解得 n = 5.应选 C.[分析 ] ∵四边形ABCD 是平行四边形 ,∴ AO = CO ,BO=DO ,DC = AB = 6.∵ AC+ BD =16, ∴ AO + BO = 8,∴△ ABO 的周长是 14.1. A 2. C 3.B54. D [ 分析 ] ∵在 Rt △ ACB 中, ∠ ACB = 90°, AC = 8, AB = 10,∴ BC = 6.又∵ DE 垂直均分 AC 交 AB 于点 E , ∴ DE 是△ ACB 的中位线 , ∴DE =1BC = 3.2 5.D [ 分析 ] A 选项,两组对边分别相等的四边形是平行四边形 ,正确,故本选项错误; B 选项 ,四个内角都相等的四边形是矩形 ,正确,故本选项错误; C 选项 ,四条边都相等的四边形是菱形,正确,故本选项错误;D 选项 ,两条对角线垂直且均分的四边形是正方形,错误 ,应当是菱形 ,故本选项正确.6. C [ 分析 ] A 选项 ,依据菱形的定义可得 ,当 AB = AD 时 ?ABCD 是菱形; B 选项 ,依据对角线相互垂直的平行四边形是菱形即可判断 ,当 AC ⊥BD 时,?ABCD是菱形;C 选项 ,对角线相等的平行四边形是矩形 ,不必定是菱形 ,命题错误;D 选项 ,∠ BAC =∠ DAC 时,∵在 ?ABCD 中,AD ∥ BC ,∴∠ ACB =∠ DAC ,∴∠ BAC =∠ ACB , ∴AB = AC , ∴ ?ABCD 是菱形.7 . D [ 分析 ] 依据作图的方法可得 AG 均分∠ DAB. ∵ AG 均分∠ DAB , ∴∠ DAH = ∠ BAH. ∵ CD ∥AB ,∴∠ DHA =∠ BAH ,∴∠ DAH =∠ DHA ,∴ AD =DH ,BC =DH ,应选 D.8.C [分析 ] ∵四边形 ABCD 是平行四边形 , ∴AB ∥ CD ,AD = BC = 8,CD = AB =6, ∴∠ F =∠ DCF.∵∠ C 的均分线为 CF ,∴∠ FCB =∠ DCF , ∴∠ F =∠ FCB ,∴ BF =BC =8,同理 DE =CD =6,∴ AF = BF - AB = 2,AE = AD - DE =2,∴ AE +AF =4.9. B [分析 ] A 项,由四边形 ABCD 是矩形 , AF ⊥DE 可得∠ C =∠ AFD = 90°, AD ∥ BC , ∴∠ ADF =∠ DEC. 又∵ DE = AD , ∴△ AFD ≌△ DCE(AAS) ,故 A 项正确;B 项,∵∠ ADF 不必定等于 30°,∴在直角三角形 ADF 中,AF 不必定等于 AD 的一半 ,故 B 项错误;C 项,由△ AFD ≌△ DCE ,可得 AF = CD ,由四边形 ABCD 是矩形 ,可得 AB = CD ,∴ AB = AF ,故 C 项正确;D 项,由△ AFD ≌△ DCE ,可得 CE = DF.由四边形 ABCD 是矩形 ,可得 BC = AD. 又∵ BE= BC -EC ,∴ BE = AD - DF ,故 D 项正确.10. A [ 分析 ] 连结 OE ,与 DC 交于点 F.∵四边形ABCD 为矩形 , ∴OA = OC , OB =OD ,且 AC = BD ,即 OA = OB = OC = OD.∵ OD ∥ CE ,OC ∥ DE ,∴四边形 ODEC 为平行四边形.∵ OD =OC , ∴四边形 ODEC 为菱形 , ∴DF = CF , OF = EF , DC ⊥ OE.∵ DE ∥ OA ,且 DE = OA ,∴四边形 ADEO 为平行四边形.∵AD =23,DE =2,∴OE =23,即 OF = EF = 3.在 Rt △ DEF 中,依据勾股定理得 DF = 4- 3= 1,即 DC = 2,则 S 菱形 ODEC = 1OE ·DC2 1=2×23× 2=2 3.11. 512. 110° [分析 ] ∵四边形 ABCD 是平行四边形 , ∴ AB ∥CD ,∴∠ BAE =∠ 1= 20° .∵ BE ⊥AB , ∴∠ ABE =90° ,∴∠ 2=∠ BAE +∠ ABE = 110°.13. 2 [分析 ] 在矩形 ABCD 中,∵角线 AC 与 BD 订交于点 O , AO = 1, ∴ AO = CO6= BO =DO = 1,∴ BD = 2.14.50° [分析 ] ∵四边形 ABCD 是平行四边形 ,∴ DC ∥AB ,∴∠ C =∠ ABF. 又∵∠ C= 40°, ∴∠ ABF = 40° .∵ EF ⊥ AD ,AD ∥ BC , ∴EF ⊥ BF ,∴∠ F = 90° ,∴∠ BEF = 90° - 40°= 50° .15. 3 3 [分析 ] ∵四边形 ABCD 是矩形 ,∴ OB = OD ,OA = OC ,AC = BD ,∴ OA = OB.∵AE 垂直均分 OB , ∴AB = AO , ∴OA = AB = OB = 3, ∴ BD = 2OB = 6, ∴AD = BD 2-AB 2= 62- 32= 3 3.16. 13[分析 ] 由于正方形 AECF 的面积为 50 cm 2,因此 AC = 2× 50= 10(cm).由于菱 形 ABCD 的 面 积 为 120 cm 2, 所 以 BD =2× 120 = 24(cm) , 所 以 菱 形 的 边 长 =10 (10)2+(24) 2= 13(cm).2217. 7[分析 ] ∵ CE = 5,△CEF 的周长为 18,∴ CF + EF = 18- 5=13.∵ F 为 DE 的中点 ,2∴ DF = EF.∵∠ BCD = 90° , ∴ CF = 1DE , ∴ EF = CF = 1DE = 6.5, ∴ DE = 2EF = 13, ∴CD2 2 = DE 2-CE 2= 132- 52= 12.∵四边形 ABCD 是正方形 ,∴BC = CD = 12,O 为 BD 的中点 ,11 7 .∴ OF 是△ BDE 的中位线 , ∴OF = (BC - CE)= (12- 5)= 2 2 218. 证明: ∵ ED ∥ BC , EF ∥AC , ∴四边形 EFCD 是平行四边形 ,∴ DE = CF.∵ BD 均分∠ ABC , ∴∠ EBD =∠ DBC. ∵ DE ∥BC ,∴∠ EDB =∠ DBC , ∴∠ EBD =∠ EDB , ∴ BE =ED ,∴BE = CF. 19. 证明: ∵ AF ∥ CD , ∴∠ AFE =∠ CDE. ∵点 E 是AC 的中点, ∴ AE = CE.在△ AFE 和△ CDE 中,∠ AFE =∠ CDE ,∠ AEF =∠ CED ,AE = CE ,∴△ AEF ≌△ CED(AAS) ,∴ AF = CD. ∵AF ∥CD ,∴四边形 ADCF 是平行四边形.∵∠ B = 90° , ∠ACB =30° , ∴∠ CAB =60° . ∵ AD 均分∠ CAB ,∴∠ DAC =∠ DAB = 30°=∠ ACD , ∴ DA =DC ,∴四边形 ADCF 是菱形.20.解: (1)证明:由折叠可知 AM = AB ,CN = CD ,∠ FNC =∠ D = 90° ,∠ AME =∠ B = 90°,∴∠ ANF = 90° , ∠CME = 90° .∵四边形 ABCD 为矩形 ,7∴AB =CD,AD ∥BC,∴AM =CN ,∠ FAN =∠ ECM ,∴AM -MN = CN- MN ,即 AN=CM.在△ ANF 和△ CME 中,∠FAN =∠ ECM ,AN =CM ,∠ANF =∠ CME ,∴△ ANF ≌△ CME(ASA) ,∴AF = CE.又∵ AF∥ CE,∴四边形 AECF 是平行四边形.(2)∵AB =6,AC =10,∴BC = 102-62= 8,设 CE= x,则 EM= 8- x, CM = 10-6= 4,在 Rt△ CEM 中, (8-x) 2+ 42=x2,解得 x= 5,∴四边形AECF 的面积为EC·AB = 5× 6= 30.8。
八年级数学下册《第十九章 四边形》单元测试卷及答案解析-沪科版

八年级数学下册《第十九章 四边形》单元测试卷及答案解析-沪科版一、单选题1.若一个n 边形内角和为540︒,则n 的值为( )A .5B .6C .7D .82.在ABC 中,点D ,E 分别是AB ,AC 上的点,且DE BC ,点F 是DE 延长线上一点,连接CF .添加下列条件后,不能判断四边形BCFD 是平行四边形的是( )A .BD CFB .DF BC = C .BD CF = D .=B F ∠∠3.菱形的边长为5,它的一条对角线的长为6,则菱形的另一条对角线的长为( )A .8B .6C .5D .44.如图,菱形ABCD 的对角线相交于点O ,AC=5cm ,10cm BD =则菱形的面积为( )A .25cmB .210cmC .225cmD .250cm5.已知一个多边形的内角和是它的外角和的3倍,则这个多边形是( )A .九边形B .八边形C .七边形D .六边形6.如图,在平行四边形ABCD 中120BAD ∠=︒连接BD ,作AE //BD 交CD 延长线于点E ,过点E 作EF BC ⊥交BC 的延长线于点F ,且1CF =,则AB 的长是()A .1B .2C 3D 27.如图,在矩形ABCD 中,AB=3,BC=6,对角线AC 的垂直平分线分别交AD 、AC 于点M ,N ,则AM 的长为( )A .154B .153C .254D .2538.如图,在菱形ABCD 中,E ,F 分别是边CD ,BC 上的动点,连接AE ,EF ,G ,H 分别为AE ,EF 的中点,连接GH .若45B ∠=︒,23BC =则GH 的最小值为()A 3B .22C 6D 69.如图,在边长为5的正方形ABCD 中,点M 为线段CD 上一点,且23CM DM =,点P 是对角线AC 上一动点,过点P 作PE AD ⊥于点E ,PF CD ⊥于点F ,则PM EF +的最小值为( )A 21B .52C 29D .213+10.正多边形通过镶嵌能够密铺成一个无缝隙的平面,下列组合中不能镶嵌成一个平面的是( ) A .正三角形和正方形B .正三角形和正六边形C .正方形和正六边形D .正方形和正八边形二、填空题11.已知一个多边形的每个外角都是45°,则这个多边形的边数为12.如图,在▱ABCD 中,▱B =75°,AC =AD ,则▱DAC 的度数是 °.13.如图,在菱形ABCD 中,过点A 作AE BC ⊥于点E ,交对角线BD 于点F ,点G 为DF 的中点.若90BAG ∠=︒,则DBC ∠= °.14.用两类不同形状的正多边形密铺地面,除了正三角形与正六边形可供选择外,还可以选择 与 来密铺.三、解答题15.在四边形ABCD 中,▱D=60°,▱B 比▱A 大20°,C 是▱A 的2倍,求▱A ,▱B ,▱C 的大小。
(模拟题)沪科版八年级下册数学第19章 四边形含答案

沪科版八年级下册数学第19章四边形含答案一、单选题(共15题,共计45分)1、如图,将矩形沿折叠,使点落在边上的点,点的对应点为点,连接、、与交于点,与交于点,若点为中点,,,则的长为()A. B. C. D.2、如图所示,已知中,,若沿图中虚线减去,则等于()A. B. C. D.3、在菱形ABCD中,记∠ABC=∠α(0°<∠α<90°),菱形的面积记作S,菱形的周长记作C,若AD=2,则()A.C与∠α的大小有关B.当∠α=45°时,S=C.A,B,C,D 四个点可以在同一个圆上D.S随∠α的增大而增大4、如图1是边长分别为的两个正方形,经如图2所示的割补可以得到边长为的正方形,且面积等于割补前的两正方形的面积之和.利用这个方法可以推得或验证勾股定理.现请你通过对图2的观察指出下面对割补过程的理解错误的是()A.割⑤补⑥B.割③补①C.割①补④D.割③补②5、下列判断错误的是()A.两组对角分别相等的四边形是平行四边形B.四个内角都相等的四边形是矩形C.一组对边平行且对角线相等的四边形是矩形D.四条边都相等的四边形是菱形6、用两种正多边形镶嵌,不能与正三角形匹配的正多边形是()A.正方形B.正六边形C.正八边形D.正十二边形7、如图,E,F分别是矩形ABCD边AD,BC上的点,且△ABG,△DCH的面积分别为15和20,则图中阴影部分的面积为()A.15B.20C.35D.408、如图,在▱ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=3,则四边形ABCD的面积为( )A.6B.12C.20D.249、如图,▱ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是()A.10B.14C.20D.2210、所示,有一张一个角为的直角三角形纸片,沿其一条中位线剪开后,不能拼成的四边形是()A.邻边不等的矩形B.等腰梯形C.有一个角是锐角的菱形D.正方形11、已知四边形,有以下四个条件:①;②;③;④.从这四个条件中任选两个,能使四边形成为平行四边形的选法种数共有()。
沪科版八年级数学下册《第十九章四边形》单元测试卷-附答案
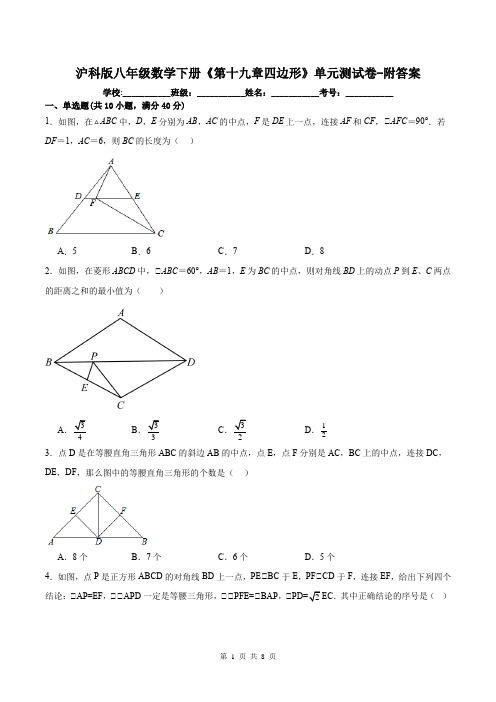
沪科版八年级数学下册《第十九章四边形》单元测试卷-附答案学校:___________班级:___________姓名:___________考号:___________一、单选题(共10小题,满分40分)1.如图,在ABC中,D,E分别为AB,AC的中点,F是DE上一点,连接AF和CF,∠AFC=90°.若DF=1,AC=6,则BC的长度为()A.5B.6C.7D.82.如图,在菱形ABCD中,∠ABC=60°,AB=1,E为BC的中点,则对角线BD上的动点P到E、C两点的距离之和的最小值为()A3B3C3D.123.点D是在等腰直角三角形ABC的斜边AB的中点,点E,点F分别是AC,BC上的中点,连接DC,DE,DF,那么图中的等腰直角三角形的个数是()A.8个B.7个C.6个D.5个4.如图,点P是正方形ABCD的对角线BD上一点,PE∠BC于E,PF∠CD于F,连接EF,给出下列四个结论:∠AP=EF,∠∠APD一定是等腰三角形,∠∠PFE=∠BAP,2.其中正确结论的序号是()A .∠∠∠B .∠∠C .∠∠∠D .∠∠∠5.如图,E 、F 、G 、H 分别是四边形ABCD 四条边的中点,若AC=BD ,那么四边形EFGH 是( )A .梯形B .菱形C .矩形D .正方形6.已知一个n 边形的各内角都等于150︒,则这个n 边形的对角线的总条数为( ).A .9B .54C .12D .607.已知点E ,F ,G ,H 分别在正方形ABCD 的边AB BC CD DA ,,,上,若EG BC ∥,FH CD ∥则四边形EFGH 一定是( )A .矩形B .菱形C .正方形D .对角线互相垂直且相等的四边形8.如图,在ABC 中90BAC ∠=︒,AD 是高,BE 是中线,CF 是角平分线,CF 交AD 于点G ,交BE 于点H ,给出以下结论:∠BE BCE S S =△A △;∠AFG AGF ∠=∠;∠2FAG ACF ∠=∠;∠BH CH =.其中结论正确的有( )A .1个B .2个C .3个D .4个9.在平面直角坐标系中,长方形ABCD 如图所示(6,2),(2,2),(2,3)A B C --,则点D 的坐标为( )A .(6,3)-B .(3,6)-C .(6,3)--D .(3,6)--10.如图,点E 是正方形ABCD 对角线AC 上一点,过点E 作EF BC ∥交AB 于点F ,连接DE ,若13DE =,12BF =则AC 的长为( )A .2B .132C .2D .52二、填空题(共8小题,满分32分)11.如图,在菱形ABCD 中,对角线AC 和BD 交于点O ,30ABD ∠=︒ AB=4,分别以点A 、点C 为圆心,以OA 的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为 .(结果保留π)12.定义:在平面直角坐标系中,把从点P 出发沿横或纵方向到达点Q (至多拐一次弯)的路径长称为P ,Q 的“实际距离”.如图,若()1,1P -,()2,3Q 则P ,Q 的“实际距离”为5,即5PS SQ +=或5PT TQ +=.环保低碳的公共自行车,逐渐成为市民出行喜欢的交通工具.设A ,B ,C 三个小区的坐标分别为()3,1A --和()5,3B -,()1,5C 若点M 表示公共自行车停放点,且满足M 到A ,B ,C 的“实际距离”相等,则点M 的坐标是 .13.如图,有一矩形纸片OABC 放在直角坐标系中,O 为原点,C 在x 轴上,OA =6,OC =10,如图,在OA 上取一点E ,将△EOC 沿EC 折叠,使O 点落在AB 边上的D 点处,则点E 的坐标为 。
沪科版数学八年级下册第19章 四边形 单元测试卷及答案

第19章四边形单元测试卷(满分120分,2018年3月)一、选择题(每题4分,共40分)1.正多边形的一个内角是120°,则这个正多边形的边数为()A.4B.8C.6D.122.菱形具有而一般平行四边形不具有的性质是()A.对边相等B.对角相等C.对角线互相平分D.对角线互相垂直3.在▱ABCD中,AB=3,BC=4,连接AC,BD,当▱ABCD的面积最大时,下列结论正确的有()①AC=5;②∠BAD+∠BCD=180°;③AC⊥BD;④AC=BD.A.①②③B.①②④C.②③④D.①③④4.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是()A.6B.7C.8D.95.菱形的周长是它的高的4倍,则菱形中较大的一个角是()A.100°B.120°C.135°D.150°6.以三角形一条中位线和第三边上的中线为对角线的四边形是()A.平行四边形B.矩形C.菱形D.正方形7.如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线AC的长是()A.20B.15C.10D.58.如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则AE的长为()A.4B.C.D.59.如图,梯形ABCD中,AB∥CD,点E,F,G分别是BD,AC,DC的中点.已知两底之差是6,两腰之和是12,则△EFG的周长是()A.8B.9C.10D.1210.如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC 的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE是菱形;③四边形ABCD的面积为EF·BD;④∠ADE=∠EDO;⑤△DEF是轴对称图形.其中正确的结论有()A.5个B.4个C.3个D.2个二、填空题(每题5分,共20分)11.如图,在矩形ABCD中,E,F,G,H分别是边AB,CD,BC,DA的中点,则四边形EGFH是______________形.12.如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=BC.若AB=10,则EF的长是__________.13.如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF,CF,则下列结论中一定成立的是__________.(把所有正确结论的序号都填在横线上)①∠DCF=∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.14.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是__________.三、解答题(22,23题每题9分,其余每题6分,共60分)15.如图,四边形ABCD是菱形,对角线AC与BD相交于点O,AB=5,OA=4,求BD的长.16.如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.猜想线段CD与线段AE的位置关系和大小关系,并加以证明.17.如图,▱ABCD中,点E,F在直线AC上(点E在点F左侧),BE∥DF.(1)求证:四边形BEDF是平行四边形;(2)若AB⊥AC,AB=4,BC=2,当四边形BEDF为矩形时,求线段AE 的长.18.如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A 按顺时针方向旋转得到的,连接BE,CF,相交于点D.(1)求证:BE=CF;(2)当四边形ACDE为菱形时,求BD的长.19.如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC的外角∠CAM的平分线,CE⊥AN,垂足为点E.(1)求证:四边形ADCE为矩形.(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.20.若a,b,c,d是四边形ABCD的四条边长,且满足a4+b4+c4+d4=4abcd,试判断四边形ABCD的形状,并说明理由.21.已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.(1)若CE=1,求BC的长;(2)求证:AM=DF+ME.22.如图,△ABC中,D是BC边上的一点,E为AD的中点,过A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.23.如图①所示,在正方形ABCD和正方形CGEF中,点B,C,G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM.易证DM=FM,DM⊥FM.(不需写证明过程)(1)如图②,当点B,C,F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明.(2)如图③,当点E,B,C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.参考答案一、1.【答案】C 2.【答案】D3.【答案】B解:根据题意得,当▱ABCD的面积最大时,四边形ABCD为矩形,∴∠BAD=∠ABC=∠BCD=90°,AC=BD.∴AC==5.①正确,②正确,③不正确,④正确.故选B.4.【答案】C解:根据从一个n边形的某个顶点出发,可以引(n-3)条对角线,把n边形分为(n-2)个三角形列出方程n-2=6,解得n=8.5.【答案】C6.【答案】A7.【答案】D8.【答案】C解:设BE=x.∵四边形ABCD是菱形,∴BC=AB=5,∴CE=5-x,根据勾股定理得52-x2=62-(5-x)2,解得x=,∴AE==.9.【答案】B解:由三角形中位线定理得EG=BC,FG=AD,EF是两底之差的一半,所以△EFG的周长=×12+×6=9.10.【答案】B解:①正确,根据三角形的面积公式可得到结论.②根据已知条件利用菱形的判定定理可证得其正确.③正确,根据菱形的面积等于对角线乘积的一半即可求得.④不正确,根据已知可求得∠FDO=∠EDO,∠ADE=∠CDF,而无法求得∠ADE=∠EDO.⑤正确,由已知可证得△DEO≌△DFO,从而可推出此结论正确.二、11.【答案】菱12.【答案】513.【答案】①②④解:在▱ABCD中,AB=CD,AB∥CD,AD∥BC.∵F是AD的中点,AD=2AB,∴DF=DC,∴∠DFC=∠DCF.∵AD∥BC,∴∠DFC=∠BCF,∴∠DCF=∠BCF,∴∠DCF=∠BCD,①正确;延长EF交CD的延长线于点M.∵AB∥CD,∴∠A=∠MDF.在△AEF和△DMF中,∴△AEF≌△DMF,∴EF=FM.∵CE⊥AB,AB∥CD,∴CE⊥CD,∴CF= EM=EF,②正确;∵EF=FM,∴S△CEF=S△CMF.∵CM>BE,∴S△BEC<S△CEM=2S△CEF,③错误;设∠FEC=x,则∠FCE=x,∴∠DCF=90°-x,∠EFC=180°-2x,∴∠DFE=90°-x+180°-2x=27 0°-3x.∵∠AEF=90°-x,∴∠DFE=3∠AEF,④正确.14.【答案】10解:如图,连接DE,交AC于P',连接BP',则P'B+P'E即为PB+PE的最小值.∵四边形ABCD是正方形,∴B,D关于直线AC对称,∴P'B=P'D,∴P'B+P'E=P'D+P'E=DE.∵BE=2,AE=3BE,∴AE=6,∴AD =AB=8,∴DE==10,故PB+PE的最小值是10.三、15.解:∵四边形ABCD是菱形,∴OD=OB,AC⊥BD,∴在Rt△AOB中,OB===3,∴BD=2OB=6.16.解:线段CD与线段AE的位置关系和大小关系是平行且相等.证明:∵CE∥AB,∴∠ADO=∠CEO,∠DAO=∠ECO.又∵OA=OC,∴△ADO≌△CEO,∴AD=CE,∴四边形ADCE是平行四边形,∴CD∥AE,CD=AE.17.(1)证明:连接BD,交AC于点O,∵四边形ABCD是平行四边形,∴OB=OD.∵BE∥DF,∴∠BEO=∠DFO.又∵∠EOB=∠FOD,∴△BEO≌△DFO.∴BE=DF.又BE∥DF,∴四边形BEDF是平行四边形.(2)解:∵AB⊥AC,AB=4,BC=2,∴AC=6,∴OA=3,∴BO==5.又∵四边形BEDF是矩形,∴OE=OB=5,∴点E在OA的延长线上,且AE=2.18.(1)证明:由旋转可知,∠EAF=∠BAC,AF=AC,AE=AB.∴∠EAF+∠BAF=∠BAC+∠BAF,即∠BAE=∠CAF.又∵AB=AC,∴AE=AF.∴△ABE≌△ACF,∴BE=CF.(2)解:∵四边形ACDE是菱形,AB=AC=1,∴AC∥DE,DE=AE=AB=1.又∵∠BAC=45°,∴∠AEB=∠ABE=∠BAC=45°.∵∠AEB+∠BAE+∠ABE=180°,∴∠BAE=90°,∴BE===.∴BD=BE-DE=-1.19.(1)证明:在△ABC中,AB=AC,AD⊥BC,∴∠BAD=∠DAC.∵AN是△ABC的外角∠CAM的平分线,∴∠MAE=∠CAE,∴∠DAE=∠DAC+∠CAE=×180°=90°.又∵AD⊥BC,CE⊥AN,∴∠ADC=∠CEA=90°,∴四边形ADCE为矩形.(2)解:当∠BAC=90°时,四边形ADCE是正方形,证明如下:∵∠BAC=90°,AB=AC,AD⊥BC于D,∴∠ACD=∠DAC=45°,∴DC=AD.由(1)知四边形ADCE是矩形,∴四边形ADCE是正方形.解:(2)题答案不唯一.20.解:四边形ABCD是菱形.理由:因为a4+b4+c4+d4=4abcd,所以a4-2a2b2+b4+c4-2c2d2+d4+2a2b2-4abcd+2c2d2=0,所以(a2-b2)2+(c2-d2)2+2(ab-cd)2=0,所以a2-b2=0且c2-d2=0且ab-cd=0.因为a,b,c,d是四边形ABCD的四条边长,所以a>0,b>0,c>0,d>0,所以a=b=c=d,所以四边形ABCD是菱形.21.(1)解:∵四边形ABCD是菱形,∴CB=CD,AB∥CD,∴∠1=∠ACD.∵∠1=∠2,∴∠2=∠ACD,∴MC =MD.∵ME⊥CD,∴CD=2CE=2,∴BC=CD=2.(2)证明:如图,延长DF交AB的延长线于点G.∵四边形ABCD是菱形,∴∠BCA=∠DCA,BC=CD.∵BC=2CF,CD=2CE,∴CE=CF.∵CM=CM,∴△CEM≌△CFM,∴ME=MF.∵AB∥CD,∴∠2=∠G,∠BCD=∠GBF.∵CF=BF,∴△CDF≌△BGF,∴DF=GF.∵∠1=∠2,∠G=∠2,∴∠1=∠G ,∴AM=GM=MF+GF=DF+ME.分析:利用三角形全等来解决线段的有关问题是常见的思考方法,遇到中点延长一倍,是常见的辅助线作法.22.(1)证明:∵AF∥BC,∴∠AFE=∠ECD.又∵E为AD的中点,∴AE=DE.在△AFE与△DCE中,∵∴△AFE≌△DCE(AAS),∴AF=CD.又∵AF=BD,∴BD=CD.(2)解:当AB=AC时,四边形AFBD是矩形.证法一:由(1)知,D为BC的中点,又∵AB=AC,∴AD⊥BC.∵AF∥BC,∴∠DAF=∠ADB=90°.∵△AFE≌△DCE(已证),∴CE=EF.∴DE为△BCF的中位线,∴DE∥BF.∴∠FBD=∠EDC=90°,∴四边形AFBD是矩形.证法二:∵AF=BD,AF∥BD,∴四边形AFBD是平行四边形.由(1)知,D为BC的中点,又∵AB=AC,∴AD⊥BC(三线合一),即∠BDA=90°.∴▱AFBD是矩形.23.解:(1)DM=FM,DM⊥FM.证明:连接DF,NF.如图.∵四边形ABCD和四边形CGEF都是正方形, ∴AD∥BC,BC∥GE.∴AD∥GE.∴∠DAM=∠NEM.∵M是AE的中点,∴AM=EM.∵∠AMD=∠EMN,∴△MAD≌△MEN.∴DM=NM,AD=EN.∵AD=CD,∴CD=EN.∵CF=EF,∠FCD=∠FEN=90°,∴△DCF≌△NEF.∴DF=NF,∠CFD=∠EFN.∵∠EFN+∠CFN=90°,∴∠CFD+∠CFN=90°,即∠DFN=90°.∴DM=FM,DM⊥FM.(2)DM=FM,DM⊥FM.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第19章四边形测试题一、选择题(本大题共6小题,每小题4分,共24分;在每小题列出的四个选项中,只有一项符合题意)1.已知一个多边形的内角和是540°,则这个多边形是()A.四边形B.五边形C.六边形D.七边形2.若一个正多边形的每个外角都等于45°,则它是()A.正六边形B.正八边形C.正十边形D.正十二边形3.若一个多边形的每一个内角都等于150°,则从此多边形一个顶点出发引出的对角线有()A.7条B.8条C.9条D.10条4.如图2-G-1所示,A,B两点分别位于一个池塘的两端,小聪想用绳子测量A,B 两点间的距离,但绳子不够长.一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为10 m,则A,B间的距离为()图2-G-1A.15 mB.20 mC.25 mD.30 m5.如图2-G-2,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是()图2-G-2A.AB∥DC,AD∥BCB.AB=DC,AD=BCC.AO=CO,BO=DOD.AB∥DC,AD=BC6.如图2-G-3所示,在▱ABCD中,CE⊥AB,E为垂足.若∠A=125°,则∠BCE等于()图2-G-3A.55°B.35°C.30°D.25°二、填空题(本大题共6小题,每小题4分,共24分)7.如果一个多边形的内角和等于外角和的3倍,那么这个多边形的边数n=__________.8.如果一个四边形三个内角度数之比为2∶1∶3,第四个内角为60°,那么这三个内角的度数分别为______________________.9.正八边形一个内角的度数为________.10.如图2-G-4所示,若▱ABCD与▱EBCF关于BC所在的直线对称,∠ABE=90°,则∠F=________.图2-G-411.如图2-G-5,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD的周长等________.图2-G-512.如图2-G-6,点D,E,F分别是△ABC各边的中点,连接DE,EF,DF.若△ABC 的周长为10,则△DEF的周长为________.图2-G-6三、解答题(本大题共5小题,共52分)13.(6分)如果某个多边形的各个内角都相等,且它的每个内角比其外角大100°,那么这个多边形的边数是多少?14.(10分)如图2-G-7所示,△ABC的中线BD,CE相交于点O,F,G分别是BO,CO的中点.求证:四边形DEFG是平行四边形.图2-G-715.(10分)如图2-G-8,在▱ABCD中,点E,F在对角线BD上,且BE=DF.求证:(1)AE=CF;(2)四边形AECF是平行四边形.图2-G-816.(12分)如图2-G-9,在▱ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB ⊥BD.(1)求证:△AED≌△CFB;(2)若∠A=30°,∠DEB=45°,求证:DA=DF.图2-G-917.(14分)(1)如图2-G-10①,在△ABC中,D,E分别为AB,AC的中点.请说明DE与BC的数量关系;(不必说明理由)图2-G-10(2)如图2-G-10②,点O是△ABC所在平面内一动点,连接OB,OC,并将AB,OB,OC,AC的中点D,E,F,G依次连接.如果点D,E,F,G能构成四边形,根据问题(1)的结论,判断四边形DEFG是否为平行四边形,请说明理由;(3)当点O移动到△ABC外时,(2)中的结论是否仍然成立?画出图形,不必说明理由.详答1.B [解析] 本题主要考查n 边形的内角和公式(n -2)·180°,由(n -2)·180°=540°,得n =5.本题也用到方程的解题思想.2.B3.C [解析] 由题意求得该多边形的每一个外角为180°-150°=30°,所以这个多边形的边数为360°÷30°=12,所以从一个顶点出发引出的对角线有12-3=9(条).4.B5.D [解析] A 项,由“AB ∥DC ,AD ∥BC ”可知,四边形ABCD 的两组对边互相平行,所以该四边形是平行四边形.故本选项不符合题意;B 项,由“AB =DC ,AD =BC ”可知,四边形ABCD 的两组对边分别相等,所以该四边形是平行四边形.故本选项不符合题意;C 项,由“AO =CO ,BO =DO ”可知,四边形ABCD 的两条对角线互相平分,所以该四边形是平行四边形.故本选项不符合题意;D 项,由“AB ∥DC ,AD =BC ”可知,四边形ABCD 的一组对边平行,另一组对边相等,据此不能判定该四边形是平行四边形.故本选项符合题意.故选D .6.B [解析] 根据平行四边形的性质得∠B =180°-∠A =55°.在Rt △BCE 中,∠BCE =90°-∠B =35°.故选B.7.8 [解析] 由题意,得(n -2)·180°=360°×3,解得n =8.8.100°,50°,150° [解析] 设这三个内角的度数分别为2x ,x ,3x ,则有2x +x +3x =360°-60°,解得x =50°,则2x =100°,3x =150°. 故答案为100°,50°,150°.9.135° [解析] 正八边形的内角和为(8-2)×180°=1080°,每一个内角的度数为18×1080°=135°.10.45° [解析] 根据轴对称的性质,得∠EBC =∠ABC =45°,因为平行四边形的对角相等,所以∠F =∠EBC =45°.11.20 [解析] ∵四边形ABCD 为平行四边形,∴AE ∥BC ,AD =BC ,AB =CD ,∴∠AEB =∠EBC .∵BE 平分∠ABC ,∴∠ABE =∠EBC ,∴∠ABE =∠AEB ,∴AB =AE ,∴AE +DE =AD =BC =6,∴AE =4,∴AB =CD =4,∴▱ABCD 的周长=4+4+6+6=20.12.5 [解析] ∵D ,E 分别是AB ,BC 的中点,∴DE 是△ABC 的中位线,∴DE =12AC ,同理有EF =12AB ,DF =12BC ,∴△DEF 的周长=12(AC +BC +AB )=12×10=5.13.解:设每个内角的度数为x ,边数为n . 则x -(180°-x )=100°,解得x =140°. ∴(n -2)·180°=140°·n ,解得n =9. 即这个多边形的边数是9.14.证明:∵E ,D 分别是AB ,AC 的中点, ∴DE 是△ABC 的中位线,∴DE ∥BC ,DE =12BC .又∵F ,G 分别是OB ,OC 的中点, ∴FG 是△OBC 的中位线,∴FG ∥BC ,FG =12BC .∴DE ∥FG ,DE =FG ,∴四边形DEFG 是平行四边形.15.证明:(1)∵四边形ABCD 是平行四边形, ∴AB =CD ,AB ∥CD , ∴∠ABE =∠CDF .在△ABE 和△CDF 中,⎩⎨⎧AB =CD ,∠ABE =∠CDF ,BE =DF ,∴△ABE ≌△CDF (SAS ), ∴AE =CF .(2)∵△ABE ≌△CDF , ∴∠AEB =∠CFD , ∴∠AEF =∠CFE , ∴AE ∥CF . ∵AE =CF ,∴四边形AECF 是平行四边形.16.证明:(1)∵四边形ABCD 是平行四边形, ∴AD =CB ,∠A =∠C ,AD ∥CB , ∴∠ADB =∠CBD .∵ED ⊥DB ,FB ⊥BD , ∴∠EDB =∠FBD =90°, ∴∠ADE =∠CBF ,在△AED 和△CFB 中,⎩⎨⎧∠ADE =∠CBF ,AD =CB ,∠A =∠C ,∴△AED ≌△CFB (ASA ). (2)作DH ⊥AB ,垂足为H ,在Rt △ADH 中,∠A =30°,∴AD =2DH . 在Rt △DEB 中,∠DEB =45°, ∴EB =2DH ,∴AD =EB . ∵△AED ≌△CFB , ∴DE =BF .∵∠EDB =∠DBF =90˚, ∴ED ∥BF ,∴四边形EBFD 为平行四边形, ∴FD =EB ,∴DA =DF .17.解:(1)根据三角形的中位线定理得DE =12BC .(2)四边形DEFG 是平行四边形.理由如下:∵D ,G 分别为AB ,AC 的中点, ∴DG 是△ABC 的中位线,∴DG ∥BC 且DG =12BC .∵E ,F 分别为OB ,OC 的中点, ∴EF 是△OBC 的中位线,∴EF ∥BC 且EF =12BC ,∴DG ∥EF 且DG =EF ,∴四边形DEFG 是平行四边形.(3)(2)中的结论仍然成立,如图所示.。
