11.2简谐运动的描述
11-2简谐运动的描述

水平弹簧振子周期公式=竖直弹簧振子周期公式:
M:m:振子质量 K:弹簧劲度系数
***竖直弹簧振子
1.两种判断物体是否做简谐运动的条件:
F-x满足F=-kx的形式
“相同”或“相反”).
例题4:有一个在光滑水平面内的弹簧振子,
第一次用力把弹簧压缩x后释放,第二次把弹 簧压缩2x后释放,则先后两次振动的周期和振 幅之比分别为多少?
T1:T2=1:1
A1:A2=1:2
如图是某质点做简谐振动的振动图象。根据图像中的信息,回答下 面问题。
(1)质点离开平衡位置的最大距离有多大?
一、简谐运动:
物体运动时,如果离开 平衡位置的位移(或角 位移)按余弦函数(或 正弦函数)的规律随时 间变化,这种运动就叫 简谐运动。
x Acos(t )
振动图象:表示在不同时刻偏离平衡位置的位移
右
E E
E
G
E
0
F 相反
B
简谐运动的表达式 x Asin(t )
振动方程中各变量的含义:
1. A 代表物体振动的振幅. 2. 叫做角速度,表示简谐运动的快慢。 =2f
路程=_0._5_m.
练习2: 写出振动方程 X=10sin(2π t)cm.
简谐运动的振幅与位移的区别?
例题2:写出振动方程.
s
s
x=10sin(2π t) cm
例题3:某简谐运动的位移与时间关系为:
x=0.1sin(100πt+π)cm, 由此可知该振动
的振幅是_0_._1___cm,频率是 50 Hz,零时 刻 振 动 物 体 的 速 度 与 规 定 正 方 向 _相___反_ ( 填
简谐运动的描述

11.2 简谐运动的描述【教案目标】(一)知识与技能1、知道振幅、周期和频率的概念,知道全振动的含义。
2、了解初相和相位差的概念,理解相位的物理意义。
3、了解简谐运动位移方程中各量的物理意义,能依据振动方程描绘振动图象。
(二)过程与方法1、在学习振幅、周期和频率的过程中,培养学生的观察能力和解决实际问题的能力。
2、学会从相位的角度分析和比较两个简谐运动。
(三)情感、态度与价值观1、每种运动都要选取能反映其本身特点的物理量来描述,使学生知道不同性质的运动包含各自不同的特殊矛盾。
2、通过对两个简谐运动的超前和滞后的比较,学会用相对的方法来分析问题。
【教案重点】简谐运动的振幅、周期和频率的概念;相位的物理意义。
【教案难点】1、振幅和位移的联系和区别、周期和频率的联系和区别。
2、对全振动概念的理解,对振动的快慢和振动物体运动的快慢的理解。
3、相位的物理意义。
【教案方法】分析类比法、讲解法、实验探索法、多媒体教案。
【教案用具】CAI课件、劲度系数不同的弹簧、质量不同的小球、秒表、铁架台、音叉、橡皮槌;两个相同的单摆、投影片。
【教案过程】(一)引入新课教师:描述匀速直线运动的物理量有位移、时间和速度;描述匀变速直线运动的物理量有时间、速度和加速度;描述匀速圆周运动的物体时,引入了周期、频率、角速度等能反映1 / 7其本身特点的物理量。
上节课我们学习了简谐运动,简谐运动也是一种往复性的运动,所以研究简谐运动时我们也有必要像匀速圆周运动一样引入周期、频率等能反映其本身特点的物理量。
本节课我们就来学习描述简谐运动的几个物理量。
(二)进行新课1.振幅如果我们要乘车,我想大家都愿意坐小汽车,而不坐拖拉机,因为拖拉机比小汽车颠簸得厉害。
演示:在铁架台上悬挂一竖直方向的弹簧振子,分别把振子从平衡位置向下拉不同的距离,让振子振动。
现象:①两种情况下,弹簧振子振动的范围大小不同;②振子振动的强弱不同。
在物理学中,我们用振幅来描述物体的振动强弱。
§11.2 简谐运动的描述

应县一中高二物理问题导学卡(B)编写翟甫礼王勇审稿课时 1 课时序号 2 一、学习目标1.知道振幅、周期和频率的概念,知道全振动的含义。
2.了解初相和相位差的概念,理解相位的物理意义。
3二、导学1.描述简谐运动的物理量⑴振幅①定义:②单位:③物理意义:④振幅和位移的区别振幅是一个(标量或矢量),是指振动物体离开平衡位置的最大距离。
它(有、无)大小,(有、无)方向。
位移是一个(标量或矢量)它(有、无)大小,也(有、无)方向。
振幅(=、>、<)位移..值。
..的最大⑵周期和频率①全振动从O点开始,一次全振动的完整过程为:和振动状态都相同时所经历的过程,叫做一次全振动。
②周期和频率周期:做简谐运动的物体完成所需的时间,叫做振动的周期,单位。
频率:单位时间内完成,叫频率,单位:,1Hz=1 s-1③周期和频率之间的关系:④周期和频率的物理意义:⑤周期(频率)与振幅的关系思考:改变弹簧振子的振幅,弹簧振子的周期或频率改变吗?观察弹簧振子的运动发现,开始拉伸(或压缩)弹簧的程度不同,振动的振幅,但是对同一个振子,振动的频率(或周期)。
可见,简谐运动的频率与振幅(有、无)关。
⑶相位相位是表示物体振动步调的物理量,用相位来描述周期性运动的物体在所处的不同状态如:两个用长度相同的悬线悬挂的小球,把它们拉起同样的角度同时释放,们说它们的相位,如果两小球不同时释放,于前一个的相位.2.谐运动的表达式⑴ 简谐运动的振动方程 x=A sin (ωt +ϕ)公式中的A 代表 ,ω叫做 ,物理意义 它与频率f 之间的关系为: ;公式中的(ωt +ϕ)表示简谐运动的 ,t=0时的相位ϕ叫 简称初相。
⑵ 两个同频率简谐运动的相位差设两个简谐运动的频率相同,则据ω=2πf ,得到它们的圆频率相同,设它们的初相分别为ϕ1和ϕ2,它们的相位差就是=∆ϕ =ϕ2-ϕ1三、导思1.如何表示振动物体运动范围的大小?2.振子在一个周期内通过的位移大小和路程分别是多少?3.谈谈你对相位的理解。
高中物理选修3---4第十一章第二节《简谐运动的描述》

(2)符号A,是标量
(3)振动物体运动范围为振幅的两倍(2A)
(4)物理意义:描述振动强弱的物理量
(5)简谐运动没有能量损耗,所以机械 能守恒定律。系统总的机械能为:
E
Ek
Ep
1 2
kA(2 其中k为一个常数)
课堂小 结
二、全振动: 1.定义:做简谐运动的物体从某一初始状态开 始,再次回到初始状态(即位移、速度、加速 度其中的任意两个物理量完全相同)所经历的 过程。
A
定为4A;
B
(2)半个周期通过的路程必 定为2A;
x/m
(3)四分之一个周期通过的路
程可能等于A,可能小于A,还
可能大于A。
t/s
六、拓展延伸:
3.简谐运动初相位 0 的求解方法:
x/m
注意:
一般情况下,初相位的取值范围- 0
t/s
①函数法:
将位移与时间的函数关系式正确表示出来:
A C O DB
物体的运动存在 周期性。
二、全振动:
A C O DB
1.定义:做简谐运动的物体从某一初始状态开始,再次回到初 始状态(即位移、速度、加速度其中的任意两个物理量完全相 同)所经历的过程。
2.规律:物体完成一次全振动经过的路程为4A。
3.规律:物体完成一次全振动所用时间均相同。
问题:若从振子经过C向右起,经过怎样的运动才叫完成一次 全振动?
x Asin(t 0) ,其中A0,0
②平移法:
将x A sin t的图像在- 范围内平移得到
x A sin(t 0 )的图像,当向左移时,0取正值, 向右移时0取负值,并且0 t
【例题】有两个简谐动:
第11章-2 简谐运动的描述
上一页
返回首页
下一页
振幅与路程的关系 振动中的路程是标量,是随时间不断增大的.一个周期内的路程为 4 倍的 振幅,半个周期内的路程为 2 倍的振幅. (1)若从特殊位置开始计时,如平衡位置、最大位移处,14周期内的路程等于 振幅. (2)若从一般位置开始计时,14周期内的路程与振幅之间没有确定关系,路程 可能大于、等于或小于振幅.
【提示】 猜想:影响弹簧振子周期的因素可能有:振幅、振子的质量、 弹簧的劲度系数等.我们可以设计这样一个实验:弹簧一端固定,弹簧的另一 端连着有孔小球,使小球在光滑的水平杆上滑动.通过改变振幅、振子的质量 和弹簧的劲度系数,测量不同情况下振子的周期,注意在改变一个物理量的时 候其他物理量应保持不变.
上一页
返回首页
下一页
【解析】 O 点为平衡位置,B,C 为两侧最远点,则从 B 起经 O,C,O, B 的路程为振幅的 4 倍,即 A 正确;若从 O 起经 B,O,C,B 的路程为振幅的 5 倍,超过一次全振动,即 B 错误;若从 C 起经 O,B,O,C 的路程为振幅的 4 倍,即 C 正确;因弹簧振子的系统摩擦不考虑,所以它的振幅一定,即 D 错 误,E 正确.
知 识 点 一
学
2 简谐运动的描述
业 分
层
测
评
知
识
点
二
上一页
返回首页
下一页
学习目标 1.理解振幅、周期和频率的物理意义,了解相位、初相、相位差的概念.(重 点) 2.理解周期和频率的关系. 3.掌握用公式描述简谐运动的方法.(难点)
上一页
返回首页
下一页
知识脉络
上一页
11-2 简谐运动的描述

位移
路程
大小和方向随时 随时间增 间做周期性变化 加
(1)振幅等于位移最大值的数值;(2)振子在 联系 一个周期内的路程等于4个振幅;而振子在 一个周期内的位移等于零。
第十一章
第二节
成才之路 ·物理 ·人教版 · 必修3-4
振动物体的位移是第1节中的一个重要物理量,振幅是 本节的一个重要物理量,有人说振幅只不过是振动中位移的 一个特殊值而已,你是否赞同这个观点?
第十一章
第二节
成才之路 ·物理 ·人教版 · 必修3-4
π 有两个振动的振动方程分别是:x1=3sin(100πt+ ),x2 3 π =5sin(100πt+ ),下列说法正确的是( 4 A.它们的振幅相同 B.它们的周期相同 C.它们的相差恒定 D.它们的振动步调一致
答案:BC
第十一章 第二节
成才之路· 物理
人教版 ·选修3-4
路漫漫其修远兮 吾将上下而求索
成才之路 ·物理 ·人教版 · 必修3-4
第十一章
机械振动
第十一章
机械振动
成才之路 ·物理 ·人教版 · 必修3-4
第二节
简谐运动的描述
第十一章
第二节
成才之路 ·物理 ·人教版 · 必修3-4
课堂情景切入 考点题型设计 知识自主梳理 课后强化作业 重点难点突破
第二节
成才之路 ·物理 ·人教版 · 必修3-4
重点难点突破
第十一章
第二节
成才之路 ·物理 ·人教版 · 必修3-4
一、对全振动的理解 正确理解全振动的概念,应注意把握振动的五个特征。 (1)振动特征:一个完整的振动过程。(2)物理量特征:位移 (x)、加速度(a)、速度(v)三者第一次同时与初始状态相同。 (3)时间特征:历时一个周期。(4)路程特征:振幅的4倍。(5) 相位特征:增加2π。
11-2 简谐运动的描述

第2节简谐运动的描述学习目标:1.理解振幅、全振动、周期、频率.2.了解相位、初相位及相位差,知道简谐运动的表达式和式中各物理量的含义.3.能用公式和图象描述简谐运动的特征.一、描述简谐运动的物理量[课本导读]预习教材第5页~第7页“描述简谐运动的物理量”部分,请同学们关注以下问题:1.什么是全振动?什么是振幅?它的物理意义是怎样的?2.什么是周期、频率,它们各自的单位、物理意义是什么?它们之间有什么关系?3.什么是相位?它的物理意义是怎样的?[知识识记]1.振幅是指振动物体离开平衡位置的最大距离,通常用字母A 表示,是标量.2.振子完成一次完整的振动过程称为一次全振动,不论从哪一位置开始计时,弹簧振子完成一次全振动所用的时间总是相同的.3.做简谐运动的物体完成一次全振动所需要的时间,叫做振动的周期,用字母T 表示.其物理意义是表示物体振动的快慢.4.单位时间内完成全振动的次数,叫做振动的频率,用字母f 表示;其单位是赫兹,符号是Hz.5.周期与频率的关系是T =1/f .频率的大小表示振动的快慢.6.用来描述周期性运动在各个时刻所处的不同状态的物理量叫相位,当t =0时的相位称做初相位,用字母φ表示.二、简谐运动的表达式[课本导读]预习教材第7页~第9页“简谐运动的表达式”部分,请同学们关注以下问题:1.简谐运动的表达式是怎样的?2.表达式中各物理量的含义是怎样的?[知识识记]简谐运动的一般表达式为x =A sin(ωt +φ).1.x 表示离开平衡位置的位移,A 表示简谐运动的振幅,表示振动的强弱.2.式中ω叫做“圆频率”,它与周期频率的关系为ω=2πT =2πf .可见ω、T 、f 相当于一个量,描述的都是振动的快慢.简谐运动的表达式也可写成:x =A sin ⎝ ⎛⎭⎪⎫2πT t +φ或x =A sin(2πft +φ).3.式中(ωt+φ)表示相位,描述做周期性运动的物体在各个不同时刻所处的不同状态,是描述不同振动的振动步调的物理量.它是一个随时间变化的量,相当于一个角度,单位为弧度,相位每增加2π,意味着物体完成了一次全振动.4.式中φ表示t=0时简谐运动质点所处的状态,称为初相位或初相.5.相位差:即某一时刻的相位之差.两个具有相同ω的简谐运动,设其初相分别为φ1和φ2,其相位差Δφ=(ωt+φ2)-(ωt+φ1)=φ2-φ1.1.振子从离开平衡位置到第一次回到平衡位置的过程是一次全振动.()[答案]×2.振幅是振子通过的路程.()[答案]×3.振子一次全振动走过的路程为振幅的4倍.()[答案]√4.振子位移相同时,速度和加速度相同.()[答案]×5.振子经过关于平衡位置对称的两点,速度方向一定不同.()[答案]×6.振子先后经过同一位置经过的时间就是一个周期.()[答案]×7.ω、T、f描述的都是振动的快慢.()[答案]√要点一对描述简谐运动的各物理量及其关系的理解——概念辨析型[合作探究]1.弹簧振子经历一次全振动后,其位移、加速度、速度有何特点?弹簧振子的一次全振动经历了多长时间?提示:弹簧振子的位移、加速度、速度第一次同时与初始状态相同;弹簧振子的一次全振动的时间刚好为一个周期.2.始末速度相同的过程是一次全振动吗?简谐运动在一个周期内,振子通过的路程一定等于多少个振幅?振子在半个周期内通过的路程又是多少呢?14个周期呢?提示:不是.一次全振动,物体的始末速度一定相同,始末速度相同的一个过程不一定是一次全振动.一次全振动的路程等于四个振幅,半个周期内振子通过的路程等于两个振幅.若从平衡位置或从最大位移处开始计时,14个周期内振子通过的路程等于一个振幅,从其他位置开始计时,14个周期内振子通过的路程可能大于或小于一个振幅.[知识精要]1.对全振动的理解(1)全振动的定义:振动物体以相同的速度相继通过同一位置所经历的过程,叫做一次全振动.(2)注意把握全振动的四个特征①物理量特征:位移(x)、加速度(a)、速度(v)三者第一次同时与初始状态相同.②时间特征:历时一个周期.③路程特征:振幅的四倍.④相位特征:增加2π.2.对振幅的理解(1)定义:振动物体离开平衡位置的最大距离叫做振动的振幅.在国际单位制中,振幅的单位是米(m).(2)振幅是标量,只有大小,没有方向,是用来表示振动强弱的物理量.(3)同一振动系统,系统的能量仅由振幅决定,振动越强,振幅就越大,振动能量也越多.(4)振幅与位移、路程的区别①振幅是振动物体离开平衡位置的最大距离,是标量;而位移是由平衡位置指向末位置的有向线段,是矢量;路程是运动路径的总长度,是标量.一个周期内的路程为振幅的四倍,半个周期内的路程为振幅的两倍.②当物体做简谐运动时,振幅是定值;位移的大小和方向时刻都在变化;路程则会持续不断地增加.3.对周期和频率的理解(1)周期(T)和频率(f)都是标量,反映了振动的快慢,T=1f,即周期越大,频率越小,振动越慢.(2)振动周期、频率由振动系统决定,与振幅无关.(3)全振动次数N与周期T和振动时间t的关系为N=t T.[典例剖析](对简谐运动的描述)如图所示,将弹簧振子从平衡位置拉下一段距离Δx,释放后振子在A、B间振动,且AB=20 cm,振子首次由A到B的时间为0.1 s,求:(1)振子振动的振幅、周期和频率.(2)振子由A到O的时间.(3)振子在5 s内通过的路程及位移大小.[审题指导](1)AB间距与振幅有何关系?(2)振子首次由A到B的时间与周期有何关系?[尝试解答](1)从题图可知,振子振动的振幅为10 cm,t=0.1 s=T2,所以T=0.2 s.由f=1T得f=5 Hz.(2)根据简谐运动的对称性可知,振子由A到O的时间与振子由O到B的时间相等,均为0.05 s.(3)设弹簧振子的振幅为A,A=10 cm.振子在1个周期内通过的路程为4A,故在t=5 s=25T内通过的路程s=40×25 cm=1000 cm.5 s内振子振动了25个周期,5 s末振子仍处在A点,所以振子偏离平衡位置的位移大小为10 cm.[答案](1)10 cm0.2 s 5 Hz(2)0.05 s(3)1000 cm10 cm如图,弹簧振子在BC间做简谐运动,O为平衡位置,BC间距离是10 cm,B→C运动时间是1 s,求:(1)振子的周期、振幅和频率;(2)振子从O 到C 的时间;(3)从O 位置,经过10 s ,振子走过的距离.[审题指导] (1)BC 间距与振幅有何关系?(2)振子首次由B 到C 的时间与周期有何关系?[尝试解答] (1)由B →C 运动特征可知,振幅A =5 cm ,周期T=2 s ,由f =1T 得频率为0.5 Hz.(2)若是直线从O 至C ,则为T 4=0.5 s ,若是O →B →C ,则为3T 4=1.5 s.(3)由n =t T ,经过10 s ,做了5次全振动,通过的路程为5A =20cm.[答案] (1)2 s 5 cm 0.5 Hz (2)1.5 s (3)20 cm判断全振动的两种思路思路1:物体完成一次全振动时,一定回到了初位置,且以原来相同的速度回到初位置.思路2:全振动中路程与振幅有固定关系,即一次全振动通过的路程是振幅的四倍.要点二对简谐运动表达式的理解——概念理解型[合作探究]两个频率相同的简谐运动,相位差为Δφ=φ2-φ1,若Δφ>0或Δφ<0时,说明两振动满足什么关系?提示:若Δφ>0,表示振动2比振动1超前;若Δφ<0,表示振动2比振动1滞后.[知识精要]做简谐运动的物体位移x随时间t变化的表达式:x=A sin(ωt+φ)1.x:表示振动质点相对于平衡位置的位移.2.A:表示振幅,描述简谐运动振动的强弱.3.ω:圆频率,它与周期、频率的关系为ω=2π/T=2πf.可见ω、T、f相当于一个量,描述的都是振动的快慢.4.ωt+φ:表示相位,描述做周期性运动的物体在各个不同时刻所处的不同状态,是描述不同振动的振动步调的物理量.它是一个随时间变化的量,相当于一个角度,相位每增加2π,意味着物体完成了一次全振动.5.φ:表示t=0时振动质点所处的状态,称为初相位或初相.6.相位差:即某一时刻的相位之差.两个具有相同ω的简谐运动,设其初相分别为φ1和φ2,其相位差Δφ=(ωt +φ2)-(ωt +φ1)=φ2-φ1.[题组训练]1.(简谐运动的表达式)(多选)物体A 做简谐运动的振动位移x A =3sin ⎝ ⎛⎭⎪⎫100t +π2m ,物体B 做简谐运动的振动位移x B =5sin ⎝ ⎛⎭⎪⎫100t +π6m.比较A 、B 的运动( )A .振幅是矢量,A 的振幅是6 m ,B 的振幅是10 mB .周期是标量,A 、B 周期相等为100 sC .A 振动的频率f A 等于B 振动的频率f BD .A 的相位始终超前B 的相位π3[解析] 振幅是标量,A 、B 的振动范围分别是6 m 、10 m ,但振幅分别为3 m 、5 m ,A 错;A 、B 的周期T =2πω=2π100s =6.28×10-2 s ,B 错;因为T A =T B ,故f A =f B ,C 对;Δφ=φA 0-φB 0=π3,D 对. [答案] CD2.(简谐运动的表达式)(多选)某质点做简谐运动,其位移随时间变化的关系式为x =A sin π4t ,则质点( ) A .第1 s 末与第3 s 末的位移相同B .第1 s 末与第3 s 末的速度相同C .第3 s 末至第5 s 末的位移方向都相同D .第3 s 末至第5 s 末的速度方向都相同[解析] 根据x =A sin π4t 可求得该质点振动周期T =8 s ,则该质点振动图象如图所示,图象的斜率为正,表示速度为正,反之为负,由图可以看出第1 s 末和第3 s 末的位移相同,但斜率一正一负,故速度方向相反,选项A 正确、B 错误;第3 s 末和第5 s 末的位移方向相反,但两点的斜率均为负,故速度方向相同,选项C 错误、D 正确.[答案] AD3.(对简谐运动表达式的理解)(多选)某质点做简谐运动,其位移随时间变化的关系式为x =10sin ⎝ ⎛⎭⎪⎫π4t cm ,则下列关于质点运动的说法中正确的是( )A .质点做简谐运动的振幅为10 cmB .质点做简谐运动的周期为4 sC .在t =4 s 时质点的速度最大D .在t =4 s 时质点的位移最大[解析] 由简谐运动的表达式x =10sin ⎝ ⎛⎭⎪⎫π4t cm ,知质点的振幅为10 cm ,2πT =π4,得:T =8 s ,故A 正确,B 错误;将t =4 s 代入x =10 sin ⎝ ⎛⎭⎪⎫π4t cm ,可得位移为零,质点正通过平衡位置,速度最大,故C 正确,D 错误.[答案] AC要点三 简谐运动图象与简谐运动表达式对比分析——重难点突破型[合作探究]到现在为止,我们描述简谐运动有几种方法?它们各自的特点是什么?提示:我们可以用函数表达式和图象描述简谐运动.图象形象、直观;函数表达式精确、抽象,两种方法是从不同的角度描述同一个简谐运动过程.[知识精要]简谐运动两种描述方法的比较1.简谐运动图象即x -t 图象是直观表示质点振动情况的一种手段,直观表示了质点的位移x 随时间t 变化的规律.2.x =A sin(ωt +φ)是用函数表达式的形式反映质点的振动情况. 两者对同一个简谐运动的描述应该是一致的,只是描述的方法不同.我们可以根据振动方程作出振动图象,也可以根据振动图象读出振幅、周期、初相,进而写出位移的函数表达式.[题组训练]1.(简谐运动的表达式与图象)用余弦函数描述一简谐运动,已知振幅为A ,周期为T ,初相φ=-13π,则振动曲线为( )[解析] 根据题意可以写出振动表达式为x =A cos ⎝ ⎛⎭⎪⎫2πT t -π3,故选A.[答案] A2.(简谐运动的图象)一质点做简谐运动,其位移和时间关系如图所示.(1)求t =0.25×10-2 s 时的位移;(2)在t =1.5×10-2 s 到2×10-2 s 的振动过程中,质点的位移、回复力、速度、动能、势能如何变化?(3)在t =0到8.5×10-2 s 时间内,质点的路程、位移各多大?[解析] (1)由题图可知A =2 cm ,T =2×10-2 s ,振动方程为x =A sin ⎝ ⎛⎭⎪⎫ωt -π2=-A cos ωt =-2cos100πt cm. 当t =0.25×10-2s 时,x =-2cos π4 cm =- 2 cm. (2)由图可知,在1.5×10-2~2×10-2 s 的振动过程中,质点的位移变大,回复力变大,速度变小,动能变小,势能变大.(3)从t =0至8.5×10-2 s 时间内为4.25个周期,质点的路程为s =17A =34 cm ,位移为2 cm.[答案] (1)- 2 cm (2)变大 变大 变小 变小 变大(3)34 cm 2 cm3.(简谐运动的表达式与图象)有一弹簧振子在水平方向上的B 、C 之间做简谐运动,已知B 、C 间的距离为20 cm ,振子在2 s 内完成了10次全振动.若从某时刻振子经过平衡位置时开始计时(t =0),经过14周期振子有负向最大位移. (1)求振子的振幅和周期;(2)画出该振子的位移—时间图象;(3)写出振子的位移随时间变化的关系式.[解析] (1)弹簧振子在B 、C 之间做简谐运动,故振幅A =10 cm ,振子在2 s内完成了10次全振动,振子的周期T=tn=0.2 s.(2)振子从平衡位置开始计时,故t=0时刻,位移是0,经14周期振子的位移为负向最大,故如图所示.(3)由函数图象可知振子的位移与时间函数关系式为x=10sin(10πt+π) cm.[答案](1)10 cm0.2 s(2)图见解析(3)x=10sin(10πt+π) cm要点四简谐运动的多解问题——易错型[合作探究]一质点在平衡位置O附近做简谐运动,从它经过平衡位置起开始计时,经t1质点第一次通过M点,再经t2第二次通过M点,则质点振动周期的值为多少?提示:将物理过程模型化,画出具体化的图景如图所示.第一种可能,质点从平衡位置O 向右运动到M 点,那么质点从O 到M 运动时间为t 1,再由M 经最右端A 返回M 经历时间为t 2,如图甲所示.此时周期为4(t 1+t 2/2).另一种可能就是M 点在O 点左方,如图乙所示,质点由O 点经最右方A 点后向左经过O 点到达M 点历时t 1,再由M 点向左经最左端A ′点返回M 点历时t 2.此时周期为43⎝ ⎛⎭⎪⎫t 1+t 22. [知识精要]由于振动的往复性,质点经过某一位置时因速度方向不确定常会导致多解,或由于简谐运动的方向的不确定以及对称性,质点先后经过同一位置的时间不确定,而导致多解.[题组训练]1.(简谐运动的周期性)下列说法中正确的是( )A .若t 1、t 2两时刻振动物体在同一位置,则t 2-t 1=TB .若t 1、t 2两时刻振动物体在同一位置,且运动情况相同,则t 2-t 1=TC .若t 1、t 2两时刻振动物体的振动反向,则t 2-t 1=T 2D .若t 2-t 1=T 2,则在t 1、t 2时刻振动物体的振动反向[解析]该题考查了振动的周期性及其相位的问题.相差一个周期的两时刻,物体在同一位置且运动情况相同;但物体在同一位置,两时刻的时间差不一定是一个周期.即使物体在同一位置,且运动情况相同,它可能是一个周期,也可能是几个周期,故A、B错误.振动情况反向,不一定是相隔半个周期,但相隔半个周期振动一定反向,故C错,D对.[答案]D2.(简谐运动的对称性)一质点在平衡位置O附近做简谐运动,从它经过平衡位置起开始计时,经0.13 s质点第一次通过M点,再经0.1 s第二次通过M点,则质点振动周期的值为多少?[解析]设质点从平衡位置O向右运动到M点,那么质点从O 点到M点运动时间为0.13 s,再由M点经最右端A点返回M点经历时间为0.1 s,如图甲、乙所示.根据以上分析,可以看出从O→M→A′历时0.18 s,根据简谐运动的对称性,可得到T1=4×0.18 s=0.72 s.另一种可能如图乙所示,由O→A→M历时t1=0.13 s,由M→A′历时t2=0.05 s,则34T2=t1+t2,故T2=43(t1+t2)=0.24s,所以周期的可能值为0.72 s和0.24 s.[答案]0.72 s和0.24 s3.(简谐运动的周期性)物体做简谐运动,通过A点时的速度为v,经过1 s后物体第一次以相同速度v通过B点,再经过1 s物体紧接着又通过B点,已知物体在2 s内所走过的总路程为12 cm,则该简谐运动的周期和振幅分别是多大?[解析]物体通过A点和B点时的速度大小相等,A、B两点一定关于平衡位置O点对称.依题意作出物体的振动路径草图如图甲、乙所示,在图甲中物体从A向右运动到B,即图中从1运动到2,时间为1 s,从2运动到3,又经过1 s,从1到3共经历了0.5T,即0.5T =2 s,T=4 s,2A=12 cm,A=6 cm.在图乙中,物体从A先向左运动,当物体第一次以相同的速度通过B点时,即图中从1运动到2时,时间为1 s,从2运动到3,又经过1 s,同样A、B两点关于O点对称,从图中可以看出从1运动到3共经历了1.5T,即1.5T=2 s,T=43s,1.5×4A=12 cm,A=2cm.[答案]T=4 s,A=6 cm或T=43s,A=2 cm课堂归纳小结[知识体系][本节小结]1.全振动以及描述简谐运动的物理量:振幅、周期、频率、角速度以及它们的关系.2.简谐运动的表达式:x=A sin(ωt+φ),明确相位、初相位、相位差.3.简谐运动的表达式和图象之间的关系:两者对同一个简谐运动的描述应该是一致的,只是描述的方法不同(如要点三题组训练1、2).4.简谐运动的周期性和对称性(如要点四题组训练1、2、3).。
《简谐运动的描述》示范教案

11.2、简谐运动的描述示范教案教学目标:1.知道简谐运动的振幅、周期和频率的含义。
2.理解周期和频率的关系。
3.知道振动物体的固有周期和固有频率,并正确理解与振幅无关。
重点难点:振幅、周期和频率的物理意义;理解振动物体的固有周期和固有频率与振幅无关。
教学方法:实验观察、讲授、讨论,计算机辅助教学。
教具:弹簧振子,音叉,教学过程1.新课引入上节课讲了简谐运动的现象和受力情况。
我们知道振子在回复力作用下,总以某一位置为中心做往复运动。
现在我们观察弹簧振子的运动。
将振子拉到平衡位置O的右侧,放手后,振子在O点的两侧做往复运动。
振子的运动是否具有周期性?在圆周运动中,物体的运动由于具有周期性,为了研究其运动规律,我们引入了角速度、周期、转速等物理量。
为了描述简谐运动,也需要引入新的物理量,即振幅、周期和频率。
2.新课讲授实验演示:观察弹簧振子的运动,可知振子总在一定范围内运动。
说明振子离开平衡位置的距离在一定的数值范围内,这就是我们要学的第一个概念——振幅。
(1)、振幅A:振动物体离开平衡位置的最大距离。
我们要注意,振幅是振动物体离开平衡位置的最大距离,而不是最大位移。
这就意味着,振幅是一个数值,指的是最大位移的绝对值。
【板书】2、振动的周期和频率(1)、振动的周期T:做简谐运动的物体完成一次全振动的时间。
振动的频率f:单位时间内完成全振动的次数。
(2)、周期的单位为秒(s)、频率的单位为赫兹(Hz)。
实验演示:下面我们观察两个劲度系数相差较大的弹簧振子,让这两个弹簧振子开始振动,用秒表或者脉搏计时,比较一下这两个振子的周期和频率。
演示实验表明,周期越小的弹簧振子,频率就越大。
【板书】(3)、周期和频率都是表示振动快慢的物理量。
两者的关系为:T=1/f 或f=1/T举例来说,若周期T=0.2s,即完成一次全振动需要0.2s,那么1s内完成全振动的次数,就是1/0.2=5s-1.也就是说,1s钟振动5次,即频率为5Hz.【板书】3、简谐运动的周期或频率与振幅无关实验演示(引导学生注意听):敲一下音叉,声音逐渐减弱,即振幅逐渐减小,但音调不发生变化,即频率不变.【板书】振子的周期(或频率)由振动系统本身的性质决定,称为振子的固有周期或固有频率.例如:一面锣,它只有一种声音,用锤敲锣,发出响亮的锣声, 锣声很快弱下去,但不会变调.摆动着的秋千,虽摆动幅度发生变化,但频率不发生变化.弹簧振子在实际的振动中, 会逐渐停下来,但频率是不变的.这些都说明所有能振动的物体,都有自己的固有周期或固有频率.巩固练习:1.A、B两个完全一样的弹簧振子,把A振子移到A的平衡位置右边10cm,把B振子移到B的平衡位置右边5cm,然后同时放手,那么:A.A、B运动的方向总是相同的.B.A、B运动的方向总是相反的.C.A、B运动的方向有时相同、有时相反.D.无法判断A、B运动的方向的关系.作业1.动手作业:同学们自己制作一个弹簧振子,观察其运动.分别改变振子振动的振幅、弹簧的劲度和振子的质量,其周期和频率是否变化?2.书面作业:把课本10页练习二(1)、(2)题做在练习本上.。
2021-2022学年人教版选修3-4 11.2 简谐运动的描述 教案 Word版含答案

课时11.2简谐运动的描述1.理解振幅、周期和频率的概念,知道全振动的含义。
2.了解初相位和相位差的概念,理解相位的物理意义。
3.了解简谐运动位移方程中各量的物理意义,能依据振动方程描绘振动图象。
4.理解简谐运动图象的物理意义,会依据振动图象推断振幅、周期和频率等。
重点难点:对简谐运动的振幅、周期、频率、全振动等概念的理解,相位的物理意义。
教学建议:本节课以弹簧振子为例,在观看其振动过程中位移变化的周期性、振动快慢的特点时,引入描绘简谐运动的物理量(振幅、周期和频率),再通过单摆试验引出相位的概念,最终对比前一节得出的图象和数学表达式,进一步体会这些物理量的含义。
本节要特殊留意相位的概念。
导入新课:你有宠爱的歌手吗?我们经常在听歌时会评价,歌手韩红的音域宽广,音色洪亮圆润;歌手王心凌的声音甜蜜;歌手李宇春的音色嘶哑,独具共性……但同样的歌曲由大多数一般人唱出来,却经常显得干巴且单调,为什么呢?这些是由音色打算的,而音色又与频率等有关。
1.描述简谐运动的物理量(1)振幅振幅是振动物体离开平衡位置的①最大距离。
振幅的②两倍表示的是振动的物体运动范围的大小。
(2)全振动振子以相同的速度相继通过同一位置所经受的过程称为一次③全振动,这一过程是一个完整的振动过程,振动质点在这一振动过程中通过的路程等于④4倍的振幅。
(3)周期和频率做简谐运动的物体,完成⑤一次全振动的时间,叫作振动的周期;单位时间内完成⑥全振动的次数叫作振动的频率。
在国际单位制中,周期的单位是⑦秒,频率的单位是⑧赫兹。
用T表示周期,用f表示频率,则周期和频率的关系是⑨f=。
(4)相位在物理学中,我们用不同的⑩相位来描述周期性运动在各个时刻所处的不同状态。
2.简谐运动的表达式(1)依据数学学问,xOy坐标系中正弦函数图象的表达式为y=A sin(ωx+φ)。
(2)简谐运动中的位移(x)与时间(t)关系的表达式为x=A sin(ωt+φ),其中A代表简谐运动的振幅,ω叫作简谐运动的“圆频率”,ωt+φ代表相位。
11.2简谐运动的描述

x A sin(t )
-A
t
位移—时间关系
圆频率
2 2f T
初相位
二、简谐振动的表达式
x A sin(t )
相位差:两个具有相同频率的简谐运动 的初相之差.
△ = 2- 1
(1)同相:相位差为零。 (2)反相:相位差为 。
例
弹簧振子做简谐振动,0为平衡位置,以它从0点开始运动
质点在A处,A’处时的位移?
一、描述简谐振动的物理量 2.周期和频率
振子的运动最显著的特点是什么?
A’ O A
往复性-重复性-周期性
(1)全振动:物体往返一次的运动叫做一次全振动。 全振动质点路程:
/ A A/
O O
B
B
A A
4A
无论哪个作为起点,质点完成一次全振动时间总是相同。
一、描述简谐振动的物理量 2.周期和频率
作为计时起点,经过0.3s后第一次到达M点,再经过0.2s
后第二次达达M点,则它第三次到达M点还需要经过的时
间为(
A 1/3 s
)
B 1.4s C 1.6s D 1.8s.
一、描述动的物理量
振幅与位移: 1.振幅:标量;振动物体离开平衡位置的最大位置。 2.位移:矢量;物体相对于平衡位置的位置变化。
振幅与路程:
1.一个周期内,路程一定为4A.
2.半个周期内,路程一定为2A.
T 周期内,路程. 4
A 大于A 小于A
3.
二、简谐振动的表达式振幅xA(偏离平衡位置的位移)
3-4
机械振动
简谐运动的描述
一、描述简谐振动的物理量 1.振幅
(1)定义:振动物体离开平衡位置的最大 距离,叫做振动的振幅,单位是m,符号A。
物理:简谐运动的描述_同步练习5(人教)

作业内容第十一章11.2简谐运动的描述【课后练习】1、关于简谐运动的以下几个说法中,错误的是( )A、质点从平衡位置起第1次到最大位移处所需时间为T/4(T是周期).B、质点走过一个振幅那么长的路程用的时间总是T/4.C、质点在T/4时间内走过的路程恒等于一个振幅的长度.D、质点在T/4时间内走过的路程可以大于、也可以小于一个振幅的长度.2、下列关于振动周期的说法中正确的是:()A、物体完成一次全振动所经过的时间叫周期;B、振动物体连续两次以同方向通过平衡位置时所经过的时间叫做周期;C、振动物体从一个状态出发,第一次回到开始状态所经过的时间叫做周期;D、振动物体从一个位置出发,第一次回到开始的位置所经过的时间叫做周期。
3、一个做简谐运动的弹簧振子,周期为T,振幅为A,设振子第一次从平衡位置运动到x=A/2 处所用的最短时间为t1,第一次从最大位移处运动到x=A/2所用的最短时间为t2,关于t1 t2说法正确的是:()A.t1=t2 B.t1<t2 C.t1>t2 D.无法判断4、如图4所示为一简谐振动的图象,则下列判断正确的是() A。
该质点的振动周期为0.7SB。
该质点的振幅为5cmC。
该质点在0。
1s和0.5s时振动速度最大D.质点在0。
3s和0.7s时的速度为零5、对于图4所示的简谐振动图象,下列判断正确的是()A.在0.2s~0.4s这段时间内,质点运动方向不变,速度在增大B.在0。
2s~0。
4s这段时间内,质点运动方向不变,速度先增大然后减小C。
在0。
3s时,质点沿X轴正方向运动D.在0.6s时,质点的运动方向与位移方向相同6、一个弹簧振子的振动周期是0。
025s,当振子从平衡位置开始向右运动,经过0。
18s时,振子的运动情况是:( )A、正在向右做减速运动;B、正在向右做加速运动;C、正在向左做减速运动;D、正在向左做加速运动.7、如图是一个弹簧振子的振动图象,在这个坐标系中画出另一个弹簧振子的振动图象,它的振幅是第一个振子的0。
简谐运动的描述教案(高三物理)

第十一章 机械振动 11.2简谐运动的描述【教学目标】 1.掌握用振幅、周期和频率来描述简谐运动的方法。
2.理解振幅、周期和频率的物理意义。
3.明确相位、初相和相位差的概念。
4.知道简谐运动的表达式,明确各量表示的物理意义。
重点:振幅、周期和频率的物理意义。
理解振动物件的固有周期和固有频率与振幅无关。
难点:理解振动物体的固有周期和固有频率与振幅无关。
相位的物理意义。
【自主预习】1.振幅:振动物体离开平衡位置的________距离。
振幅的________表示的是做振动的物体运动范围的大小。
①定义:振动物体离开平衡位置的最大距离,叫做振动的振幅,用A 表示,在国际单位制中的单位是米(m)。
②物理意义:振幅是表示振动强弱的物理量,振幅越大,表示振动越强。
2.简谐运动是一种________运动,一个完整的振动过程称为一次________。
3.周期:做简谐运动的物体完成________所需要的时间,用________表示。
频率:单位时间内完成全振动的________,用________表示。
周期与频率的关系是________。
在国际单位制中,周期的单位是________,频率的单位是______________,简称________,符号是________,1 Hz =1________。
物理意义:周期和频率都是表示振动快慢的物理量4.简谐运动的表达式:x =___ _____。
其中ω=________=________。
做简谐运动的物体位移x 随时间t 变化的表达式:x =A sin(ωt +φ)(1)式中x 表示振动质点相对平衡位置的位移。
(2)式中A 表示简谐运动的振幅。
(3) 式中ω是简谐运动的圆频率,他也表示简谐运动的快慢(4)式中φ表示t =0时简谐运动质点所处的位置,称为初相位,或初相;(ωt +φ)代表了做简谐运动的质点在t 时刻处在一个运动周期中的某个状态,所以代表简谐运动的相位。
(5)相位差:即某一时刻的相位之差,两个具有相同圆频率(ω)的简谐运动,设其初相分别为φ1和φ2,当φ2>φ1时,其相位差Δφ=(ωt +φ2)-(ωt +φ1)=φ2-φ1。
11.2简谐运动的描述

11.2简谐运动的描述1.弹簧振子做简谐运动,振动图像如图所示,则下列说法正确的是()A.t1、t2时刻振子的速度大小相等,方向相反B.t1、t2时刻振子的位移大小相等,方向相反C.t2、t3时刻振子的速度大小相等,方向相反D.t2、t4时刻振子的位移大小相等,方向相反2.如图所示,弹簧振子在光滑的水平杆上做简谐运动,往返于a-O-b之间,O是平衡位置。
下列说法中正确的是()A.振子由a向O运动时,所受的弹力方向与加速度方向相反B.振子由O向b运动时,加速度方向与速度方向相反C.振子由O向b运动时,加速度越来越大D.振子由O向a运动时,速度越来越大3.一质点做简谐运动,质点的位移随时间变化的规律如图所示,则从图中可以看出____。
A.质点做简谐运动的周期为4sB.质点做简谐运动的振幅为2cmC.t=3s时,质点的速度为零D.t=3s时,质点沿y轴正向运动E.t=1s时,质点的加速度最大4.如图所示,一个质量为1kgm=,一小球连接在轻质弹簧的一端,弹簧的另一端固定在天花板上,该弹簧的劲度系数100N/mk=,用手把小球向上托起,直到弹簧恢复原长时,由静止释放小球,忽略空气阻力,g取210m/s,小球会在竖直方向上来回振动。
下列说法正确的是()A.小球速度最大时,弹簧处于原长B.小球运动到最低点,弹性势能是1JC.以最低点为重力势能零参考面,小球运动到最高点时重力势能为2JD.小球的最大速度是1m/s5.如图所示,小球在B、C之间做简谐运动,O为BC间的中点,B、C间的距离为10cm,则下列说法正确的是()A.小球的最大位移是10cmB.只有在B、C两点时,小球的振幅是5cm,在O点时,小球的振幅是0C.无论小球在任何位置,它的振幅都是5cmD.从任意时刻起,一个周期内小球经过的路程都是20cm6.如图甲所示,一弹簧振子在A、B之间做简谐运动,O点为振子静止的位置,其振动图像如图乙所示,规定向右的方向为正方向,试根据图像分析以下问题:(1)在t=0时刻,振子所处的位置为___________,正在向___________(选填“左”或“右”)方向运动。
11.2简谐运动的描述

11.2
阅读课本P 阅读课本P5—P6,完成下列问题
1、振幅的定义及其物理意义 2、什么叫做全振动、周期、 什么叫做全振动、周期、 频率? 频率? 3、什么叫相位,初相位,相位差? 什么叫相位,初相位,相位差? 相位的物理意义是什么? 相位的物理意义是什么?
一、描述简谐运动的物理量
1、振幅(符号A) 振幅(符号A)
____
(3) 对于一个给定的振动,振子的位 对于一个给定的振动, 移是时刻变化的,但振幅是不变的. 移是时刻变化的,但振幅是不变的
-A≤X≤A
(4) 振幅等于最大位移的数值 振幅等于最大位移的数值.
问题1 若从振子经过C 问题1:若从振子经过C向 右起, 右起,经过怎样的运动才 叫完成一次振动? 叫完成一次振动?
π
π
科学漫步——月相 科学漫步——月相 1、随着月亮每天在星空 中自西向东移动, 中自西向东移动,在地球 上看,它的形状从圆到缺, 上看,它的形状从圆到缺, 又从缺到圆周期性地变化 着,周期为29.5天,这就 周期为29.5 29.5天 是月亮位相的变化, 是月亮位相的变化,叫做 月相。 月相。 2、随着月亮相对于地球和 太阳的位置变化, 太阳的位置变化,使它被 太阳照亮的一面有时朝向 地球,有时背向地球; 地球,有时背向地球;朝 向地球的月亮部分有时大 一些,有时小一些, 一些,有时小一些,这样 就出现了不同的月相。 就出现了不同的月相。
题1: 一个质点作简谐运动的振动 :
图像如图.从图中可以看出, 图像如图.从图中可以看出,该质点 的振幅A= 0.1 m,周期T=__ s,频 __ ,周期T 0.4 , 的振幅 开始在△ 0 内 率f= __ Hz,从t=0开始在△t=0.5s内 从 开始在 2.5 __ 路程 ___ 路程= 质点的位移0.1m,路程 0.5m .
教法分析11.2 简谐运动的描述

第2节简谐运动的描述
本节思路:
“振幅”、“周期和频率”、“相位”几个术语的物理意义
↓
利用数学知识引入表达式x= A sin (ωt+φ)
↓
分析它们在表达式中各由哪个量来代表
P7相位:“在物理学中,我们用不同的相位来描述周期性运动在各个时刻所处的不同状态。
”这不是定义,没给严格的定义。
目的:描述任何周期性运动都
会涉及相位。
图11.2-3有待改进。
P8简谐运动的表达式
“x= A sin (ωt+φ)”
与数学课本中公式的形式完
全一样!
P9公式中(ωt+φ)代表相位。
P9下面的标示很有用:
P10科学漫步:乐音和音阶
不同唱名的频率有不同的约定:
P11做一做:用计算机观察声音的波形
可以利用计算机的录音功能
P11第2题:
2. 图11.2-5是两个简谐运动的振动图象,它们的相位差是多少?
两种说法。
11-2简谐运动的描述

编写时间年月日/ 执行时间年月日 / 总序第个教案(新课引入)复习引入,在前面我们已经认识了简谐运动,那么首先我们先来回顾如下几个概念。
1、什么是机械运动2、弹簧振子有什么特征3、什么是简谐运动我们已经知道了简谐运动是一种周期性变化的运动,那么我们也可以用振幅、周期、频率和相位等物理量来描述简谐运动。
当然,在分析这些物理量前,我们先认识一个全新的物理概念:全振动——振动物体从某一初始状态开始,再次回到初始状态(即位移、速度均与初态完全相同)所经历的过程。
也就是说,完成一次循环,就是做了一次全振动。
,(新课教学)一、简谐运动的基本物理量1、振幅(A)(1)定义:振动物体离开平衡位置的____最大距离____.(2)物理意义:振幅是表示___振动强弱__的物理量,它是标量,振幅的两倍表示的是做振动的物体____运动范围___的大小.2、振动的周期和频率(1)全振动:振子以相同的____速度___相继通过同一位置所经历的过程.振动质点在一个全振动过程中通过的路程等于__4倍____的振幅.不管以哪里作为开始研究的起点,弹簧振子完成一次全振动的时间总是____相等__的.(2)振动的周期T:做简谐运动的物体完成一次全振动的时间。
振动的频率f:单位时间内完成全振动的次数。
,(3)周期的单位为秒(s )、频率的单位为赫兹(Hz )。
3、周期和频率都是表示振动快慢的物理量。
两者的关系为:T=1/f 或 f=1/T举例来说,若周期T=,即完成一次全振动需要,那么1s 内完成全振动的次数,就是1/=5s-1.也就是说,1s 钟振动5次,即频率为5Hz.4、简谐运动的周期或频率与振幅无关振子的周期(或频率)由振动系统本身的性质决定,称为振子的固有周期或固有频率.T=2π√l/g二、对振动特征量关系的理解1.对全振动的理解正确理解全振动的概念,应注意把握振动的五种特征.(1)振动特征:一个完整的振动过程.(2)物理量特征:位移(x )、加速度(a )、速度(v )三者第一次同时与初始状态相同.(3)时间特征:历时一个周期.·(4)路程特征:振幅的4倍.(5)相位特征:增加2π.2.简谐运动中振幅和几个常见量的关系(1)振幅和振动系统的能量关系对一个确定的振动系统来说,系统能量仅由振幅决定,振幅越大,振动系统能量越大.(2)振幅与位移的关系振动中的位移是矢量,振幅是标量,在数值上,振幅与某一时刻位移的大小可能相等,但在同一简谐运动中振幅是确定的,而位移随时间做周期性的变化.特别提醒:(1)振幅大,振动物体的位移不一定大,但其最大位移一定大.(2)求路程时,首先应明确振动过程经过了几个整数周期,再具体分析最后不到一周期时间内的路程,两部分相加即为总路程.三、对简谐运动表达式的理解做简谐运动的物体位移x 随时间t 变化的表达式:-x =A sin(ωt +φ)1.式中x 表示振动质点相对平衡位置的位移.2.式中A 表示振幅,描述的是振动的强弱.3.式中ω叫做圆频率,它与周期、频率的关系为ω=2πT=2πf .可见ω、T 、f 相当于一个量,描述的都是振动的快慢.6.相位差:即某一时刻的相位之差.两个具有相同ω的简谐运动,设其初相分别为φ1和φ2,其相位差Δφ=(ωt +φ2)-(ωt +φ1)=φ2-φ1.特别提醒:相位差的取值范围一般为-π≤Δφ≤π,当Δφ=0时两运动步调完全相同,称为同相,当Δφ=π(或-π)时,两运动步调相反,称为反相.小结:一、描述简谐运动的物理量 1、振幅:描述振动强弱;2、周期和频率:描述振动快慢;3、相位:描述振动步调. 二、简谐运动的表达式:课后反思:()sinx A tωϕ=+。
第十一章 2简谐运动的描述

【解题探究】(1)从简谐运动的表达式中,可以直接得到哪 些物理量? 提示:从表达式中可直接找出振幅、初相、圆频率。
(2)简谐运动中怎样根据周期T或频率f求ω?
2 1 提示: ,f , 2f。 T T
【标准解答】选C。振幅是标量,A、B的振动范围分别是6 m、
由此得到: B A 。 2 6
答案:
3
3
【总结提升】用简谐运动表达式解答振动问题的方法 应用简谐运动的表达式x=Asin(ωt+φ)解答简谐运动问题时,
首先要明确表达式中各物理量的意义,找到各物理量对应的
数值,根据 2 2f 确定三个描述振动快慢的物理量间的
T
关系,有时还需要通过画出其振动图像来解决有关问题。
三、简谐运动图像与简谐运动表达式 简谐运动两种描述方法的比较: (1)简谐运动图像即x-t图像是直观表示质点振动情况的一种
手段,直观表示了质点的位移x随时间t变化的规律。
(2)x=Asin(ωt+φ)是用函数表达式的形式反映质点的振动
情况。
(3)两者对同一个简谐运动的描述应该是一致的。我们能够做 到两个方面:一是根据振动方程作出振动图像,二是根据振动图 像读出振幅、周期、初相,进而写出位移的函数表达式。
2 3 3 个周期或 次全振动。 4 4 2
提示:简谐运动的位移和时间的关系既可以用正弦函数表示,也
可以用余弦函数表示,只是对应的初相位不同。
一、描述简谐运动的物理量及其关系的理解
1.对全振动的理解: (1)全振动的定义:振动物体以相同的速度相继通过同一位置所 经历的过程,叫做一次全振动。 (2)正确理解全振动的概念,还应注意把握全振动的四个特征。
高二物理3-4新授课11.2简谐运动的描述学案
高二物理选修3-411.2:简谐运动的描述【核心素养定位】1.知道振幅、周期、频率和相位的概念,知道全振动的含义,理解周期和频率的关系。
2.知道简谐运动的表达式及其各量的物理意义。
3.了解初相和相位差的概念,理解相位的物理意义。
4.能依据简谐运动的表达式描绘图象,或根据简谐运动图象写出表达式。
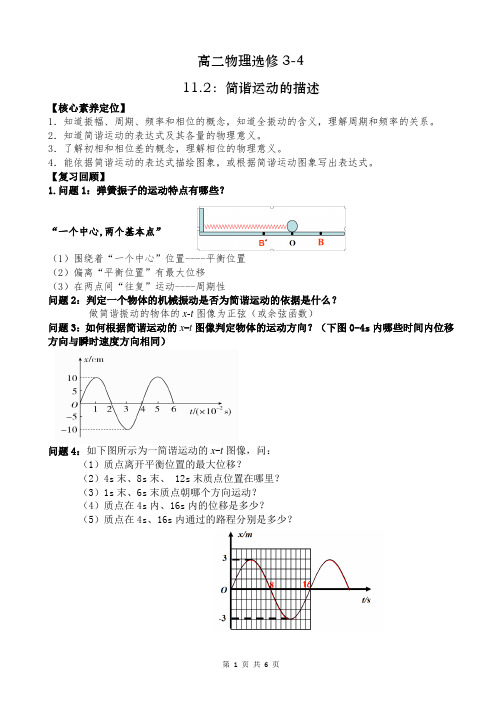
【复习回顾】1.问题1:弹簧振子的运动特点有哪些?“一个中心,两个基本点”(1)围绕着“一个中心”位置----平衡位置(2)偏离“平衡位置”有最大位移(3)在两点间“往复”运动----周期性问题2:判定一个物体的机械振动是否为简谐运动的依据是什么?做简谐振动的物体的x-t图像为正弦(或余弦函数)问题3:如何根据简谐运动的x-t图像判定物体的运动方向?(下图0-4s内哪些时间内位移方向与瞬时速度方向相同)问题4:如下图所示为一简谐运动的x-t图像,问:(1)质点离开平衡位置的最大位移?(2)4s末、8s末、 12s末质点位置在哪里?(3)1s末、6s末质点朝哪个方向运动?(4)质点在4s内、16s内的位移是多少?(5)质点在4s、16s内通过的路程分别是多少?一、描述简谐运动的物理量1.偏离“平衡位置”有最大位移振幅质点离开平衡位置的最大距离叫振幅问题1:该弹簧振子的振幅多大?问题2:该弹簧振子到达A点时候离O点的距离?2.在两点间“往复”运动周期T(频率f)振子进行一次完整的振动(全振动)所经历的时间问题1:O—D—B—D—O是一个周期吗?问题2:若从振子经过C向右起,经过怎样的运动才叫完成一次全振动?3.全振动(1)一次全振动:振子在AA/之间振动,O为平衡位置。
如果从A点开始运动,经O点运动到A/点,再经过O点回到A点,就说它完成了一次全振动,此后振子只是重复这种运动。
①从O→A→O→A/→O也是一次全振动②从B→A→O→A/→O→B也是一次全振动(2)一次全振动的特点:振动路程为振幅的4倍想一想:①半个周期内的位移一定是2A吗?那么四分之一周期内的路程呢?②一个完整的全振动过程,有什么显著的特点?4.在一次全振动过程中,一定是振子连续两次以相同速度通过同一点所经历的过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、固有周期和固有频率
周期和频率都反映振动快慢,那么它们与哪些因素有关呢? 演示
①与振幅无关。
②与弹簧有关,劲度系数(回复系数)越大,周期越小。 m T 2 ③与振子质量有关,质量越大,周期越大。
k
四、相位及简谐运动的表达式
四、相位及简谐运动的表达式
1.相位的作用 用于描述周期运动在各个时刻所处的不同状态 位移 2.简谐运动表达式 x r sin A sin t 初相位
11.2
简谐运动的描述
一、振幅,周期和频率
演示
上面所标的两段A有何特点?代表什么?
一、振幅,周期和频率
1.振幅 ①振动物体离开平衡位置的最大位移叫振幅。 振幅能够反映什么?
②振幅用来反映振动物体振动的强弱(系统蕴涵的能量) ③振幅的单位是m,符号是A。 运动快慢与振动快慢有区别吗? V→运动快慢 ?→振动快慢
一、振幅,周期和频率
2.周期 ①全振动:振动物体以相同速度相继通过同一位置所经 历的过程叫做一次全振动。 ②做简谐运动的物体完成一次全振动所花的时间叫做一 个周期,是用来反映物体振动快慢的物理量。
③周期的单位是s,常用符号是T。
3.频率 ①做简谐运动的物体,在单位时间内完成全振动的次数 叫频率。它也用来反映物体的振动快慢。 ②频率的单位是 赫兹(Hz),常用符号为 f
五、振子的路程和位移
①无论从什么位置开始计时,物体在一个周期内 通过的路程均为4A ②无论从什么位置开始计时,物体在1/2个周期内 通过的路程均为2A一个周期内 通过的路程均为4A。 ②无论从什么位置开始计时,物体在1/2个周期内 通过的路程均为2A。 ③物体在任意1/4周期内通过的路程不一定等于A, 可能大于A,可能小于A,当然也可能等于A。
x0 x
三、固有周期和固有频率
周期和频率都反映振动快慢,那么它们与哪些因素有关呢?
三、固有周期和固有频率
周期和频率都反映振动快慢,那么它们与哪些因素有关呢? 演示
①与振幅无关。
三、固有周期和固有频率
周期和频率都反映振动快慢,那么它们与哪些因素有关呢? 演示
①与振幅无关。
②与弹簧有关,劲度系数(回复系数)越大,周期越小。
A sin(t 0 )
振幅 相位
r ) θ x
相位的单位应该是怎样的? 相位的单位是 弧度(rad)
2 x A sin( t 0 ) T
五、振子的路程和位移
做简谐运动的物体在任意一个周期内通过的路程是多少? ①无论从什么位置开始计时,物体在一个周期内 通过的路程均为4A 做简谐运动的物体在任意1/2个周期内通过的路程是多少? ②无论从什么位置开始计时,物体在1/2个周期内 通过的路程均为2A 做简谐运动的物体在任意1/4个周期内通过的路程是多少?
二、振幅与位移,周期与频率的关系
振幅与位移一样吗? 1.振幅与位移 ①振幅反映振动强弱,位移反映位置变化。
②振幅是标量,位移是矢量
③振幅是偏离平衡位置的最大距离,位移是偏离平衡位置的 距离。位移最大值的大小就是振幅 2.周期与频率 ①都是反映振动快慢的物理量 如何反映?两者有何关系? ②两者互为倒数。即: T=1/f
六、如何判断物体是否做简谐运动
方法 分析回复力的形式是否满足:F=-kx
实践 如图为一竖直悬挂的弹簧振
子,当用手把物体拉低至一 定位置释放后,试分析物体 的运动是否为简谐运动。
六、如何判断物体是否做简谐运动
方法 分析回复力的形式是否满足:F=-kx
实践 如图为一竖直悬挂的弹簧振
子,当用手把物体拉低至一 定位置释放后,试分析物体 的运动是否为简谐运动。
