客观测试题的解题分析与题解(第七章)位移法
位移法例题

第7章 位移法习 题7-1:用位移法计算图示超静定梁,画出弯矩图,杆件EI 为常数。
题7-1图7-2:用位移法计算图示刚架,画出弯矩图,杆件EI 为常数。
题7-2图7-3:用位移法计算图示刚架,画出弯矩图,杆件EI 为常数。
题7-3图7-4:用位移法计算图示超静定梁,画出弯矩图。
q2题7-4图7-5:用位移法计算图示刚架,画出弯矩图,杆件EI 为常数。
题7-5图7-6:用位移法计算图示排架,画出弯矩图。
题7-6图7-7:用典型方程法计算7-2题,画出弯矩图。
7-8:用典型方程法计算7-3题,画出弯矩图。
7-9:用典型方程法计算7-5题,画出弯矩图。
7-10:用典型方程法计算图示桁架,求出方程中的系数和自由项。
题7-10图7-11:用典型方程法计算图示刚架,求出方程中的系数和自由项。
10kN3.510kN4 E题7-11图7-12:用位移法计算图示结构,杆件EI 为常数(只需做到建立好位移法方程即可)。
题7-12图7-13:用位移法计算图示结构,并画出弯矩图。
题7-13图7-14:用位移法计算图示结构,并画出弯矩图。
FF题7-14图7-15:用位移法计算图示刚架,画出弯矩图。
题7-15图7-16:用位移法计算图示结构,并画出弯矩图。
题7-16图7-17:用位移法计算图示结构,并绘弯矩图,所有杆件的EI 均相同。
q题7-17图7-18:确定图示结构用位移法求解的最少未知量个数,并画出基本体系。
题7-18图7-19:利用对称性画出图示结构的半刚架,并在图上标出未知量,除GD 杆外,其它杆件的EI 均为常数。
(c )(b )B7-20:请求出图示刚架位移法方程中的系数和自由项。
题7-20图7-21:利用对称性对图示结构进行简化,画出半刚架,并确定未知量,杆件的 EI 为常数。
题7-21图7-22:对图示结构请用位移法进行计算,只要做到建立好位移法方程即可。
原结构基本体系题7-22图7-23:用位移法计算图示结构,并绘弯矩图。
结构力学课后解答:第7章__位移法
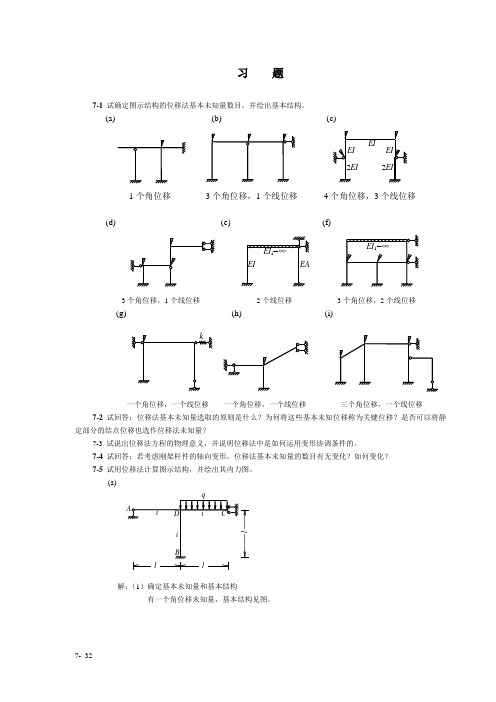
习题7-1 试确定图示结构的位移法基本未知量数目,并绘出基本结构。
(a) (b) (c)1个角位移3个角位移,1个线位移4个角位移,3个线位移(d) (e) (f)3个角位移,1个线位移2个线位移3个角位移,2个线位移(g) (h)(i)一个角位移,一个线位移一个角位移,一个线位移三个角位移,一个线位移7-2 试回答:位移法基本未知量选取的原则是什么?为何将这些基本未知位移称为关键位移?是否可以将静定部分的结点位移也选作位移法未知量?7-3 试说出位移法方程的物理意义,并说明位移法中是如何运用变形协调条件的。
7-4 试回答:若考虑刚架杆件的轴向变形,位移法基本未知量的数目有无变化?如何变化?7-5 试用位移法计算图示结构,并绘出其内力图。
(a)解:(1)确定基本未知量和基本结构有一个角位移未知量,基本结构见图。
l7- 32Z 1M 图(2)位移法典型方程11110p r Z R +=(3)确定系数并解方程iql Z ql iZ ql R i r p 24031831,821212111==-∴-==(4)画M 图M 图(b)解:(1)确定基本未知量1个角位移未知量,各弯矩图如下4m 4m4m7- 341Z =1M 图3EIp M 图(2)位移法典型方程11110p r Z R +=(3)确定系数并解方程1115,352p r EI R ==- 153502EIZ -=114Z EI=(4)画M 图()KN mM ⋅图(c)解:(1)确定基本未知量一个线位移未知量,各种M 图如下6m 6m 9m1M 图243EI 243EI 1243EI p M 图F R(2)位移法典型方程11110p r Z R +=(3)确定系数并解方程1114,243p p r EI R F ==- 140243p EIZ F -=12434Z EI=(4)画M 图94M 图(d)解:(1)确定基本未知量一个线位移未知量,各种M 图如下a 2aa2aaF P7- 3611Z=1111r 252/25EA a 简化图1pR pp M(2)位移法典型方程11110p r Z R +=(3)确定系数并解方程11126/,55p p r EA a R F ==- 126055p EA Z F a -=13a Z EA=(4)画M 图图M(e)解:(1)确定基本未知量两个线位移未知量,各种M 图如下l图1=11211 EA r l r ⎛⇒=⎝⎭1M221EA r l ⎛=⎝⎭图12 0p p p R F R ⇒=-=p M pF(2)位移法典型方程1111221211222200p p r Z r Z R r Z r Z R ++=++= (3)确定系数并解方程11122122121,1,0p p p EA r r r l EA r l R F R ⎛=== ⎝⎭⎛=⎝⎭=-=代入,解得7- 3812p p lZ F EAlZ F EA=⋅=⋅(4)画M 图图M p7-6 试用位移法计算图示结构,并绘出M 图。
位移法的基本原理

位移法的基本原理位移法是物理学中一种常用的求解方法,可以用来分析物体在空间中的运动。
它的基本原理是通过观察物体在一段时间内的位移,来推导出物体的速度和加速度等运动信息。
位移法的基本原理可以通过以下几个步骤来理解和应用:1. 观察物体的位移:位移是指物体在某段时间内从一个位置移动到另一个位置的距离。
在位移法中,我们需要观察物体在一段时间内的位移情况,可以通过测量物体的起始位置和结束位置来计算位移的大小和方向。
2. 计算物体的平均速度:在位移法中,我们可以利用物体的位移和时间来计算物体的平均速度。
平均速度是指物体在某段时间内的位移与时间的比值,可以用公式v=Δx/Δt来表示,其中v表示平均速度,Δx表示位移,Δt表示时间。
通过计算平均速度,我们可以获得物体在某段时间内的平均速度信息。
3. 推导物体的瞬时速度:瞬时速度是指物体在某一时刻的速度。
在位移法中,我们可以利用物体的平均速度和时间间隔的缩小来逼近物体的瞬时速度。
当时间间隔趋近于0时,平均速度就可以无限接近瞬时速度。
因此,我们可以通过计算物体在时间间隔趋近于0时的平均速度来推导物体的瞬时速度。
4. 求解物体的加速度:加速度是指物体在某一时刻的速度变化率。
在位移法中,我们可以通过物体的瞬时速度和时间的变化率来求解物体的加速度。
加速度可以用公式a=Δv/Δt来表示,其中a表示加速度,Δv表示速度的变化量,Δt表示时间的变化量。
通过计算加速度,我们可以获得物体在某一时刻的加速度信息。
5. 应用位移法分析运动问题:通过以上步骤,我们可以利用位移法来分析物体的运动问题。
例如,我们可以根据物体的位移和时间来计算物体的速度;根据物体的速度和时间来计算物体的加速度;根据物体的加速度和时间来计算物体的位移等。
通过位移法,我们可以得到物体在不同时间点的运动信息,从而对物体的运动进行更详细和准确的描述。
位移法是一种基于观察物体位移的方法,通过计算物体的位移、速度和加速度等参数来分析物体的运动。
位移法习题解答

8-2、清华8-2c 试用位移法计算图示结构,并作内力图。
题8-2c (a )方法一:列位移法典型方程解:(1)D 处定向支座与AD 段不平行,视为固定端。
AB 段剪力、弯矩是静定的,弯矩图、剪力图直接可以画出来,DA 杆D 端支座与杆轴线不平行,视为固定端。
结构只有一个转角位移法基本未知量。
基本结构如图(b)。
(2)建立典型方程:11110P k z R ⋅+=(3)画基本结构的P M 、1M 的弯矩图:如图(c) 、(d) 所示。
(4)利用结点的力矩平的平衡求系数:1110;k i =1P R P l =-⋅(5)将系数,自由项代入典型方程得z 1。
110P lz i⋅=(6)利用叠加法求各杆端的最后弯矩,如图(f ):11P M M M z =+⋅30.3()1040.4()20.2()101030.3()10AC AD DA AEP lM i Pl i P l P lM i Pl M i Pl i iP l M i Pl i⋅=+⋅=⋅⋅=+⋅==+⋅=⋅=+⋅=左拉上拉下拉右拉 方法二:转角位移法(c)ACMAB(d)(b)(e)Q ABF Q解:(1)确定结构的基本未知量。
有一个角位移z1,如图所示(b)。
(2)列杆端的转角位移方程:AB段剪力和弯矩静定,DA杆D端支座与杆轴线不平行,视为固定端。
C1111,,3,3,4,2 FAB AB A AE AD DAM Pl M Pl M i z M i z M i z M i z =-=-=⋅=⋅=⋅=⋅(3)根据刚结点的力矩平衡,列位移方程,求未知量z1:111100343010AB AC AD AEPl M M M M M Pl i z i z i z zi =→+++=→-+⋅+⋅+⋅=→=∑(4)将所求位移代回转角位移方程求各杆端力,并作结构的弯矩图,如图(c)所示。
C1111,,330.3,330.3,1010440.4,220.21010FAB ABA AEAD DAM Pl M PlPl PlM i z i Pl M i z i Pli iPl PlM i z i Pl M i z i Pli i=-=-=⋅=⨯==⋅=⨯==⋅=⨯==⋅=⨯=讨论;本题将D处的滑动支座改为与杆轴线平行。
三根杆的位移法例题

三根杆的位移法例题
摘要:
一、位移法简介
1.位移法的定义
2.位移法的基本原理
二、三根杆的位移法例题解析
1.问题描述
2.位移法解题步骤
2.1 确定基本未知量
2.2 建立位移方程
2.3 求解位移方程
2.4 计算杆件内力
3.答案与解析
正文:
位移法是一种求解杆件内力的方法,其基本原理是通过位移来建立内力与位移之间的关系。
接下来,我们将通过一个三根杆的位移法例题来详细解析位移法的解题过程。
题目描述:一个刚性三根杆件结构,其中两根杆固定,另一根杆在两端受力,求解杆件的内力分布。
位移法解题步骤如下:
1.确定基本未知量:首先需要确定一个基本未知量,通常选择一个杆件的
位移作为基本未知量。
2.建立位移方程:根据位移法原理,我们需要建立一个关于位移的方程。
这个方程通常包括两部分:刚度方程和边界条件。
刚度方程反映了杆件的弹性特性,而边界条件则反映了杆件与外部结构的连接关系。
3.求解位移方程:通过求解位移方程,我们可以得到杆件的位移分布。
这一步通常需要使用数值方法,如牛顿法或梯度下降法。
4.计算杆件内力:在得到杆件的位移分布后,我们可以通过力学平衡方程计算出杆件的内力分布。
根据以上步骤,我们可以得出三根杆的位移法例题的解答。
物理高中位移题型总结归纳

物理高中位移题型总结归纳物理是自然科学的一门重要学科,它研究物质的运动规律和能量的转化过程。
在高中物理课程中,位移是一个重要的概念,它描述了物体在一段时间内从起始位置到终止位置的变化情况。
本文将对高中物理位移题型进行总结归纳,以帮助学生更好地理解和应用位移概念。
一、位移的定义和计算方法位移是一个矢量量,它的大小和方向都很重要。
物理中常用的单位是米(m)。
位移可以通过以下公式计算:位移 = 终止位置 - 起始位置如果物体沿着一条直线运动,则位移也在此直线上。
如果物体的运动不是沿着一条直线,则需要考虑向量运算。
二、直线运动中的位移题型1. 匀速直线运动在匀速直线运动中,物体的速度保持不变。
位移的大小等于物体在一段时间内行进的距离,并且与起始位置无关。
2. 变速直线运动在变速直线运动中,物体的速度随时间的变化而变化。
位移需要考虑物体在不同时间段的速度和时间间隔。
可以使用速度-时间图像、加速度-时间图像等分析解题。
三、曲线运动中的位移题型1. 圆周运动在圆周运动中,物体绕着一个固定中心进行旋转运动。
对于物体沿着圆周运动的情况,位移的计算需要考虑物体在圆周上沿弧长行进的距离以及角度与半径的关系。
可以利用弧长公式和角度的关系来计算位移。
2. 抛体运动抛体运动是指物体在重力作用下进行抛射运动。
对于抛体运动,位移的计算需要考虑物体在水平方向和垂直方向上的位移。
可以分别计算水平方向和垂直方向的位移,并根据两个方向的位移计算总的位移。
四、实际应用中的位移题型1. 弹簧振子在弹簧振子中,弹簧的伸缩运动可用位移描述。
位移的计算需要考虑振子的振幅、角频率和时间等因素。
2. 粒子在电磁场中的运动在粒子在电磁场中的运动中,粒子的位移可以由洛伦兹力和外加电场、磁场的关系计算出来。
综上所述,高中物理位移题型需要根据具体情况考虑物体的运动方式和相关因素。
通过掌握位移的定义和计算方法,结合具体题目的要求,进行适当的分析和推导,可以解决各种位移相关的问题。
7.3 位移法解题的基本思路及基本概念

M AB
2i AB Z1
3 Pl 56
M BA
4i AB Z1
3Pl 28
M BC
3iBC
Z1
3Pl 16
3Pl 28
MCB 0
(五)作M图:
3Pl
28
P
A
C
3Pl
B
56
M 图 (kN m) 11Pl 56
7.3 位移法解题的基本思路及基本概念
一、基本思路
位移法通过引入附加约束,把原 超静定结构转化为若干单跨梁的组合 体,从而把复杂结构的计算问题转化 为简单杆件的分析和综合问题。
B
M BC
M BA
为了区别弯矩转向和力的方向, 在Z1方向上带两道竖杠,以表示 它是转角位移。
平衡条件
MB 0
RB 0
即,RB M BC M BA 0
7.3 位移法解题的基本思路及基本概念
一、基本思路
(三)列方程求Z1:
平衡条件
M BA M BC 0
Z1 P
列等截面直杆转角位移方程:
(一)n1:表示刚结点数目:
注意: 1.包含组合结点;
2.不包含与EI=∞杆刚结的结点。
EI
Z1
Z2
EA
n1=2
7.3 位移法解题的基本思路及基本概念
2、位移法基本未知量数目 (二)n2:独立的结点线位移数目:
认为变形前后杆件两端距离保持不变
n2:由不动点原理来确定; 不动点:无线位移的点。
7.3 位移法解题的基本思路及基本概念
二、位移法基本概念: (一)基本结构:
在原结构上增加一些附加约束(刚臂、支座
链杆),以使原结构变成若干单跨超静定梁的组 合体。该组合体称为位移法基本结构。
位移法复习题

位移法复习题位移法复习题位移法是力学中的一种重要方法,用于求解物体在受力作用下的运动情况。
它通过分析物体的位移来推导出物体的速度和加速度等运动参数。
在学习位移法时,我们需要掌握一些基本的概念和方法,并通过练习题来加深理解。
下面,我们将通过一些典型的位移法复习题来巩固知识。
1. 一辆汽车以20 m/s的速度匀速行驶了5秒钟,求汽车的位移。
解析:根据位移的定义,位移等于速度乘以时间。
所以汽车的位移等于20 m/s × 5 s = 100 m。
2. 一个物体以2 m/s²的加速度匀加速运动了10秒钟,求物体的位移。
解析:根据匀加速运动的位移公式,位移等于初速度乘以时间加上加速度乘以时间的平方的一半。
所以物体的位移等于0 m/s × 10 s + 2 m/s² × (10 s)² / 2 = 100 m。
3. 一个自由落体物体从静止开始下落,求物体下落5秒钟后的位移。
解析:自由落体物体的加速度等于重力加速度,即9.8 m/s²。
根据自由落体运动的位移公式,位移等于初速度乘以时间加上加速度乘以时间的平方的一半。
由于物体从静止开始下落,所以初速度为0 m/s。
所以物体的位移等于0 m/s × 5 s + 9.8 m/s² × (5 s)² / 2 = 122.5 m。
4. 一个物体以10 m/s的速度向上抛出,求物体到达最高点时的位移。
解析:当物体到达最高点时,它的速度为0 m/s。
根据物体的运动规律,物体到达最高点时的位移等于它的初速度乘以时间。
所以物体到达最高点时的位移等于10 m/s × (10 m/s / 9.8 m/s²) = 10.2 m。
5. 一个物体以5 m/s的速度向上抛出,求物体落地时的位移。
解析:当物体落地时,它的位移等于它的初速度乘以时间加上加速度乘以时间的平方的一半。
位移法习题答案

位移法习题答案位移法是力学中的一种重要方法,用于求解刚体或弹性体的位移和变形。
它通过建立坐标系和运用力平衡条件,将问题转化为求解位移的数学问题。
本文将通过几个典型的位移法习题,来展示位移法的应用和解题思路。
第一个习题是关于简支梁的弯曲变形。
考虑一个长度为L的简支梁,在梁的中点施加一个集中力F。
我们的目标是求解梁的弯曲变形。
首先,我们需要建立坐标系。
假设梁的左端为原点O,梁的水平方向为x轴正方向,竖直向上为y轴正方向。
选择一个合适的参考点A,将其坐标设为(x, y)。
接下来,我们需要运用力平衡条件。
考虑梁上的一个微小段dx,其长度为dl。
由于梁是简支的,我们可以得到以下平衡方程:∑F_x = 0: -N(x+dx) + N(x) + F = 0∑F_y = 0: T(x+dx) - T(x) - dl*w = 0其中,N(x)和T(x)分别表示梁上某一点处的法向力和切向力,w表示单位长度的梁的重力。
将上述方程进行展开,并忽略高阶微小量,我们可以得到:-dN/dx*dx + F = 0dT/dx*dx - dl*w = 0由于dx是一个无穷小量,我们可以将上述方程进行积分,得到:-N(x) + F*x + C_1 = 0T(x) - dl*w*x + C_2 = 0其中,C_1和C_2是积分常数。
接下来,我们需要确定积分常数C_1和C_2。
考虑梁的边界条件,即在梁的两端点处,梁的位移为零。
根据这个条件,我们可以得到:N(0) = 0: C_1 = 0N(L) = 0: -F*L + C_1 = 0解上述方程组,我们可以得到C_1 = 0和C_2 = dl*w*L。
最后,我们可以得到梁上任意一点的位移表达式:y(x) = ∫(0 to x) [T(x')/dl*w*x' - dl*w*x'] dx'将T(x)和C_2的表达式代入,我们可以得到:y(x) = ∫(0 to x) [(dl*w*x' - dl*w*L)/dl*w*x' - dl*w*x'] dx'= ∫(0 to x) (1 - L/x') dx'对上述积分进行计算,我们可以得到:y(x) = x - L * ln(x)通过上述推导,我们成功地求解了简支梁的弯曲变形问题。
结构力学第7章课后答案全解
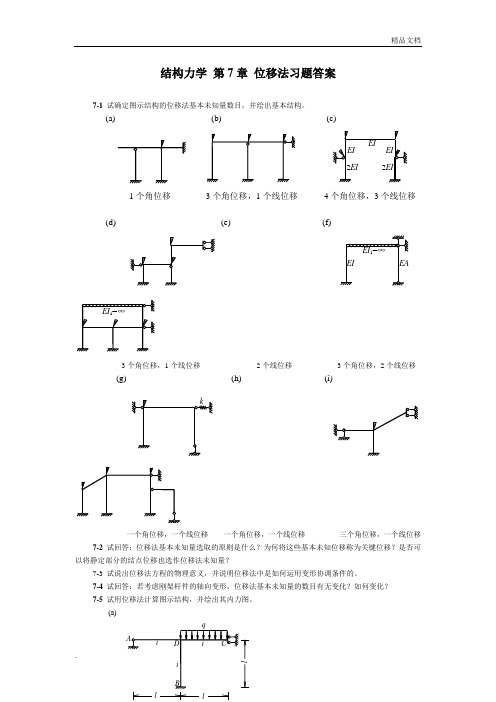
由图可知,得到各系数:
求解得:
(2)求解最终弯矩图
7-11试利用对称性计算图示刚架,并绘出M图。
(a)
解:(1)利用对称性得:
(2)由图可知:
可得:
(3)求最终弯矩图
(b)
解:(1)利用对称性,可得:
(2)由图可知,各系数分别为:
解得:
(3)求最终弯矩图如下
(c)
解:(1)在D下面加一支座,向上作用1个单位位移,由于BD杆会在压力作用下缩短,所以先分析上半部分,如下图。
(a)
解:(1)确定基本未知量和基本结构
有一个角位移未知量,基本结构见图。
(2)位移法典型方程
(3)确定系数并解方程
(4)画M图
(b)
解:(1)确定基本未知量
1个角位移未知量,各弯矩图如下
(2)位移法典型方程
(3)确定系数并解方程
(4)画M图
(c)
解:(1)确定基本未知量
一个线位移未知量,各种M图如下
7-12试计算图示结构在支座位移作用下的弯矩,并绘出M图。
(a)
代入,解得
(4)求最终弯矩图
7-7试分析以下结构内力的特点,并说明原因。若考虑杆件的轴向变形,结构内力有何变化?
(a) (b) (c)
(d) (e) (f)
7-8试计算图示具有牵连位移关系的结构,并绘出M图。
(a)
解:(1)画出 图
由图可得:
由图可知:
(2)列方程及解方程组
解得:
(3)最终弯矩图
(b)
7-2试回答:位移法基本未知量选取的原则是什么?为何将这些基本未知位移称为关键位移?是否可以将静定部分的结点位移也选作位移法未知量?
结构力学位移法

二、基本未知量的确定 1.无侧移结构基本未知量:所有刚结点的转角
2.有侧移结构
例1. B
C 例2. B
C
A
A
只有一个刚结点B,由于忽 略轴向变形,B结点只有
只有一个刚结点B, 由于忽略轴向变形及C 结点的约束形式,B结 点有一个转角和水平位 移
例3.
有两个刚结点B、C,由于忽略轴向
变形,B、C点的竖向位移为零,B、C
(a)
(b) (c)
2)求图(2)中 φA2和φB2 3)叠加得到
变换式上式可得杆端内力的刚度方程(转角位移方程):
由平衡条件得杆端剪力:见图(d)
(d)
1.两端固定单元,在A端发生一个顺时针的转角 。
MAB A
由力法求得
B MBA
2i
4i
M
2.两端固定单元,在B端发生一个顺时针的转角 。
MAB A
,得:
BC杆
4. 解方程,得:
5. 把结点位移回代,得杆端弯矩
6. 画弯矩图
ql2 14
B ql2 C 8
A
ql2
28 M图
例2.
1、基本未知量θB、θC
40 43.5 2406k.N9/m
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
24.5 14.7
AA 4i=I 1 1
BB 3.4
51I62.5 CC
1
94.118I DD
二、形常数和载常数
形常数:由单位杆端位移引起的单跨超静定梁的杆端力 载常数:由荷载引起的固端力
1.由杆端位移求杆端内力(形常数)
MAB
Δ
根据力法可求解:
QAB φA
MAB
φB MBA
位移法

位移法位移法也是计算超静定结构的基本方法。
位移法是以结构的结点位移(结点角位移和结点线位移)作为基本未知量,通过平衡条件建立位移法方程,求出位移后,即可利用位移和内力之间的关系,求出杆件和结构的内力。
在位移法求解超静定问题中,有七大步骤:第一步:分析结构体系(是否为几何不变体系,是否有结点位移),结构体系中的结点位移(结点角位移和结点线位移)就是结构的所求的基本未知量。
第二步:选取基本结构,即在原结构中的基本未知量(结点角位移和结点线位移)处加上约束(刚臂和链杆),均假设顺时针转动。
第三步:列位移法方程:01111=+P R Z r (一个结点位移未知量)当为n 次超静定时,0022112222212111212111=++++=++++=++++nP n nm n n P n n P n n R Z r Z r Z r R Z r Z r Z r R Z r Z r Z r第四步:画P M M 、1图,求nP nm R r 、(画P M M 、1图,通过查表得出,注意形常数及载常数的查法,记住是以顺时针转动为正。
)第五步:求解未知位移n Z 。
第六步:求杆端弯矩:P R Z M M +=11(一结点位移未知量)P n n i i R Z M Z M Z M Z M M ++++++= 2211(n 个结点位移未知量)此步骤的正负号规定容易与力法正负号规定混淆。
在位移法中,杆端弯矩以顺时针转动为正,逆时针转动为负。
第七步:求跨中弯矩(针对于集中力作用在跨中处以及均布荷载作用情况),作M图,Q图(注意:求跨中弯矩时的正负号规定,同力法一样)讨论:针对位移法中正负号规定判断需要注意的问题。
1、什么是杆端弯矩?例如:如图所示超静定梁假如截AB杆研究,就会暴露出三个内力(弯矩,剪力,轴力),现只研究弯矩,如图所示(夸张放大画出来):图中所标的即为杆端弯矩,它的作用是相对于杆端而言的。
2、如何判断正负号及运用正负号画弯矩图?M为正的上图中杆端弯矩的方向是假设出来的,由图可知,杆ABM为负的(逆时针)。
结构力学位移法题目及详细解答

结构力学位移法题目及详细解答位移法中含无穷刚度杆的结构是考研结构力学的一大难点,很多热门院校都喜欢出这类型的题目,下面以两道有复杂牵连位移的含无穷刚度杆位移法题目为例,对三种解法进行讲解,题目取自东南大学真题和烟台大学真题。
1.用位移法绘制图示结构的弯矩图,BC杆 EI=∞,其余各杆 EI 为常数(东南大学2017年真题)。
解:根据局部变形图找出位移牵连关系,B点角位移,B点竖向线位移,C点角位移三者牵连,只有1个独立,有三种方法。
法一:基本体系一:以 B点竖向线位移为基本未知量,难点是无穷刚结点处会引起线位移和角位移,过程如图:M2¯图绘制是一个难点,需要通过无穷刚度杆的局部变形图判断弹性杆的变形,从而指导画出形常数图。
计算过程略,最后弯矩图如图:法二:基本体系二:以 C 点角位移为基本未知量,难点是剪力平衡,过程如下:M2¯图绘制是一个难点,需要通过无穷刚度杆的局部变形图判断弹性杆的变形,从而指导画出形常数图。
法二的典型错误:无穷刚度杆弯矩图不会画。
正确思路:从弹性杆画到无穷刚度杆,通过刚结点平衡条件确定杆端弯矩,杆上没有集中力作用,剪力不变,弯矩图斜率相同。
这里注意,超静定结构在荷载作用下内力值只与刚度相对值有关,与绝对值无关,所以从弹性杆到无穷刚度杆弯矩是不会倍增的。
另外,若有集中力作用于无穷刚度杆上,则按照简支梁叠加即可。
法三:基本体系三:以B点角位移为基本为质量,难点是剪力平衡,过程如下:点评:法三位移一定可以发生,因为线位移和两个角位移有两个独立,一个牵连,刚结点任取一个角位移都可以是独立的,无穷刚度杆上增加刚臂后相当于大地固定端,不能动,刚臂发生相当于固定端发生单位角位移的支座移动。
位移法基本原理及方法

位移法基本原理及方法位移法是一种测量物体或系统位移的方法,在科学、工程和技术领域中具有广泛的应用。
它基于位移的产生和测量,通过记录物体在空间中的位置变化来分析和计算特定的性质和参数。
本文将对位移法的基本原理和方法进行详细介绍。
1.基本原理:位移法基于物体在空间中位置的变化来测量位移,其基本原理是将物体的初始位置与其移动后的位置进行比较,计算出两者之间的差异,从而得到物体的位移量。
位移法的原理主要包括以下几个方面:(1)参考坐标系:位移法中需要确定一个参考坐标系,以便记录物体的初始位置和移动后的位置。
常用的参考坐标系有笛卡尔坐标系、极坐标系和球坐标系等。
(2)位移量的计算:位移量可以通过物体的位置改变来计算,通常使用向量的减法来计算两个位置之间的差异。
根据不同的坐标系和物体的运动方式,位移量的计算方法也有所差异。
(3)位移的性质:位移具有矢量性质,包括大小、方向和位置等信息。
通过位移的性质,可以进一步分析物体的运动状态和变化规律。
2.基本方法:位移法的基本方法根据测量对象的不同可以分为以下几种:(1)直接测量法:直接测量法是通过仪器设备直接读取物体的位置信息来计算位移量。
常见的直接测量仪器有测距仪、全站仪和位移传感器等。
直接测量法适用于需要高精度位移测量的场合,如工程测量、建筑施工和实验室研究等。
(2)间接测量法:间接测量法是通过测量物体的其他性质来推导出位移量。
例如,通过测量物体的速度或加速度,再对其进行积分可以得到位移量。
间接测量法适用于无法直接测量位置的物体或系统,如天体测量、行星运动和汽车运动等。
(3)相对测量法:相对测量法是在已知物体初始位置的基础上,通过测量物体相对于初始位置的位置变化来计算位移量。
常见的相对测量方法有三角测量法、单目视觉测量法和雷达测量法等。
相对测量法适用于需要比较位置变化的场合,如建筑结构变形监测和地震测量等。
(4)绝对测量法:绝对测量法是直接测量物体在绝对坐标系中的位置来计算位移量。
位移法习题与答案

位移法习题与答案位移法是结构力学中常用的一种分析方法,通过计算结构在外力作用下的位移,来求解结构的应力、应变和变形等问题。
在学习位移法时,习题与答案的练习是非常重要的,可以帮助我们加深对位移法的理解和掌握。
下面将给大家介绍一些位移法习题及其答案。
习题一:求解简支梁的弯矩分布已知一根长度为L的简支梁,受到均布载荷q作用,求解弯矩分布。
解答:首先,我们需要根据受力分析确定梁的反力。
对于简支梁,两个支座处的反力相等,且为qL/2。
接下来,我们可以利用位移法求解弯矩分布。
假设梁的弯矩分布为M(x),则根据位移法的基本原理,可以得到以下方程:d2M(x)/dx2 = -q对该方程进行两次积分,得到:M(x) = -q*x^2/2 + C1*x + C2由于梁两端是简支条件,即位移和转角为零,可以得到边界条件:M(0) = 0M(L) = 0代入上述方程,解得C1 = qL/2,C2 = -qL^2/2。
因此,弯矩分布为:M(x) = -q*x^2/2 + qL/2*x - qL^2/2习题二:求解悬臂梁的挠度已知一根长度为L的悬臂梁,受到集中力F作用在悬臂端点,求解梁的挠度。
解答:首先,我们需要根据受力分析确定梁的反力。
对于悬臂梁,端点处的反力只有一个,即为F。
接下来,我们可以利用位移法求解梁的挠度。
假设梁的挠度为δ(x),则根据位移法的基本原理,可以得到以下方程:d2δ(x)/dx2 = -F/(EI)对该方程进行两次积分,得到:δ(x) = -F*x^2/(2EI) + C1*x + C2由于梁端点处的位移为零,可以得到边界条件:δ(0) = 0dδ(x)/dx|_(x=L) = 0代入上述方程,解得C1 = 0,C2 = 0。
因此,梁的挠度为:δ(x) = -F*x^2/(2EI)习题三:求解悬臂梁的最大挠度已知一根长度为L的悬臂梁,受到均布载荷q作用,求解梁的最大挠度。
解答:首先,我们需要根据受力分析确定梁的反力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在线测试题试题库及解答
第七章位移法
一、单项选择题
1、如果位移法基本体系的附加约束中的反力(矩)等于零,则
A、基本体系就与原结构受力一致,变形一致。
B、基本体系就与原结构受力不一致,变形不一致。
C、基本体系就与原结构受力一致,但变形不一致。
D、基本体系就与原结构受力不一致,但变形一致。
标准答案 A
2、超静定结构计算
A、要综合考虑平衡条件和变形协调条件
B、只需考虑平衡条件
C、只需考虑变形协调条件
D、只需考虑物理条件形协调条件
标准答案 A
3、用位移法计算荷载作用下的超静定结构时,采用各杆的相对刚度进行计算,所得到的
A、结点位移是结构的真正位移、内力不是正确的
B、结点位移不是结构的真正位移、内力是正确的
C、结点位移和内力都是正确的
D、结点位移和内力都不正确的
标准答案 B
4、两端固定的等截面超静定梁,已知A端的转角为θA,则杆端弯矩MB为
A、MB=3iθA
B、MB=2iθA
C、MB=iθA
D、MB=-iθ
标准答案 B
5、位移法的基本未知量是
A、支座反力
B、杆端弯矩
C、独立的结点位移
D、多余未知力
标准答案 C
6、两端固定的等截面超静定梁,已知A端的转角为θA,则杆件的内力错误的是
A、MB=2iθA
B、MA=4iθA
C、QAB=-3iθA/l
D、QBA=-6iθA/l
标准答案 C
7、在位移法典型方程r11×Z1+r12×Z2+R1P=0,r21×Z1+r22×Z2+R2P=0中,下列式子正确的是
A、r11 = r22
B、r12 = r21
C、r12×Z2 = r21×Z1
D、R1P= R2P
标准答案 B
8、一端固定一端铰支的等截面超静定梁,已知固定端的转角为θA,则杆端剪力QBA 为
A、QBA=-3iθA/l
B、QBA=-6iθA/l
C、QBA=-12iθA/l
D、QBA=0
标准答案 A
9、A端固定B端铰支的等截面超静定梁,已知固定端的转角为θA,下列结论错误的是
A、MB=0
B、MA=3iθA
C、QBA=0
D、QAB=-3iθA/l
标准答案 C
10、一端固定一端滑动支承的等截面超静定梁,已知固定端的转角为θA,则杆端弯矩MB 为
A、MB=-iθA
B、MB=iθA
C、MB=2iθA
D、MB=0
标准答案 A
11、结构位移法方程中与角位移相应的的主系数等于使位移法基本结构该结点发生单位转动时,
A、产生的各杆端弯矩之和
B、产生的该结点处各杆端弯矩之和
C、产生的各杆远端弯矩之和
D、该结点处各杆端的剪力之和
标准答案 B
12、结构位移法方程中与侧移相应的的主系数等于使位移法基本结构该侧移方向发生单位侧移时,
A、该结点所在的相邻两层各柱的剪力之和
B、产生的各杆近端弯矩之和
C、该结点所在的相邻两层各柱的杆端弯矩之和
D、该结点所在的相邻两层各柱端的转动刚度之和
标准答案 A
13、单跨超静定斜梁在竖向荷载作用下的弯矩=
A、相应的静定梁的弯矩
B、相应的静定水平梁的弯矩
C、相应的超静定水平梁的弯矩
D、相应的超静定竖向梁的弯矩
标准答案 C
14、横梁刚度为无穷大的单跨单层无铰矩形刚架,下列关于位移法基本未知量的论述,正确的是
A、三个基本未知量
B、两个基本未知量
C、两刚结点转角为零,只有一个未知量
D、两刚结点转角不为零,只有一个未知量Δ
标准答案 C
15、横梁刚度为无穷大的单跨单层,平行柱斜梁无铰刚架,下列关于位移法基本未知量的论述,正确的是
A、三个基本未知量
B、两刚结点转角为零,只有一个未知量
C、两个基本未知量
D、两刚结点转角不为零,只有一个未知量Δ
标准答案 B
二、多项选择题
1、A、B两端固定的单跨超静定梁,左端发生顺时针转角β,右端发生逆时针转角β,下列结论正确的是
A、左端弯矩=2iβ
B、右端弯矩=-2iβ
C、左端剪力=0
D、左端弯矩=6iβ
E、右端剪力=0
标准答案 ABCF
2、位移法的基本未知量是
A、多余未知力
B、杆端弯矩
C、结点角位移
D、独立的结点线位移
E、支座反力
标准答案 CD
3、如果位移法基本体系的附加约束中的反力(矩)等于零,则
A、基本体系就与原结构受力一致,变形一致。
B、基本体系就与原结构受力不一致,变形不一致。
C、基本体系就与原结构受力一致,但变形不一致。
D、基本体系就与原结构受力不一致,但变形一致。
E、基本体系就与原结构等价。
标准答案 AE
4、单跨对称结构在反对称荷载作用下,对称轴上的截面
A、沿对称轴方向上的位移为零
B、垂直对称轴方向上的位移为零
C、角位移为零
D、弯矩为零
E、轴力为零
标准答案 ADF
5、两跨对称结构在对称荷载作用下,下列论述正确的是
A、对称轴上的刚结点线位移为零
B、对称轴上的刚结点角位移为零
C、中柱无弯矩
D、中柱无剪力
E、中柱无轴力
标准答案 ABCD
6、单跨对称结构在对称荷载作用下,对称轴上的截面
A、沿对称轴方向上的位移为零
B、垂直对称轴方向上的位移为零
C、角位移为零
D、弯矩为零
E、剪力为零
标准答案 BCE
7、两跨对称结构在反对称荷载作用下,下列论述正确的是
A、对称轴上的刚结点竖向线位移为零
B、对称轴上的刚结点角位移为零
C、中柱无弯矩
D、中柱无剪力
E、中柱无轴力
标准答案 AE
8、用位移法计算荷载作用下的超静定结构时,采用各杆的相对刚度进行计算,所得到的
A、结点位移不是结构的真正位移
B、内力是正确的
C、结点位移是结构的真正位移
D、内力不是正确的
E、结点位移和内力都是正确的
标准答案 AB
9、一端固定一端滑动支承的等截面超静定梁,已知固定端的转角为θA,则杆件的内力为
A、MB=-iθA
B、MB=2iθA
C、MA=iθA
D、MA=3iθA
E、剪力=0
标准答案 ACE
10、A端固定B端铰支的等截面超静定梁,已知固定端A端的转角为θA,则杆件的内力为
A、MB=0
B、MB=2iθA
C、MA=3iθA
D、MA=4iθA
E、左端剪力=-3iθA/l
标准答案 ACE
11、下列哪些位移可以不作为位移法的基本未知量是
A、铰结点处的转角
B、铰支座处的转角
C、滑动支座处的侧移
D、刚结点的转动
E、刚结点的线位移
标准答案 ABC
12、载常数指的是单跨超静定梁在
A、杆端位移作用下产生的杆端弯矩
B、杆端位移作用下产生的杆端剪力
C、跨间荷载作用下产生的杆端剪力
D、单位杆端位移作用下产生的杆端剪力
E、跨间荷载作用下产生的杆端弯矩
标准答案 CE
13、形常数指的是单跨超静定梁在
A、杆端位移作用下产生的杆端弯矩
B、杆端位移作用下产生的杆端剪力
C、单位杆端位移作用下产生的杆端弯矩
D、单位杆端位移作用下产生的杆端剪力
E、跨间荷载作用下产生的杆端弯矩
标准答案 CD
14、求超静定结构的位移时,可将虚拟单位荷载加在
A、任意静定的基本体系上
B、原结构上
C、几何可变体系
D、几何常变体系
E、几何瞬变体系
标准答案 AB
15、下列关于位移法基本体系的论述正确的是
A、位移法基本体系是一组单跨超静定梁
B、位移法基本体系是静定结构
C、一个结构的位移法基本体系是唯一的
D、一个结构位移法基本体系有多种选择
E、位移法基本体系可以是几何不变体系
标准答案 AC
三、判断题
1、一端固定一端滑动支承的等截面超静定梁,已知固定端的转角为θA,则滑动端的侧移ΔB=-θA/2(逆时针转)。
2、位移法典型方程的物理含义是基本体系附加约束中的反力或反力矩等于零,实质上是原结构的平衡条件。
3、A端固定B端铰支的等截面超静定梁,已知θA,则θB=-θA/2(逆时针转)。
4、一端固定一端铰支的等截面超静定梁,已知固定端的转角为θA,则铰支端的转角θB=-θA/2(逆时针转)。
5、位移法可计算超静定结构也可计算静定结构.
6、超静定结构计算总原则是欲求超静定结构先取一个基本体系,然后让基本体系在受力方面和变形方面与原结构完全一样。
7、用位移法计算荷载作用下的超静定结构时,采用各杆的相对刚度进行计算,所得到的结点位移不是结构的真正位移,求出的内力是正确的。
8、位移法基本结构有多种选择。
9、超静定结构计算依据是综合考虑平衡条件和变形协调条件。
10、位移法不能计算静定结构。
11、位移法基本结构是唯一的。
12一端固定一端铰支的等截面超静定梁,已知固定端的转角为θA,则固定端的弯矩MA=3i θA。
13、位移法的基本未知量与超静定次数有关。
14、一端固定一端铰支的等截面超静定梁,已知固定端的转角为θA,则杆件的剪力QAB=-3i θA/l。
15、如果位移法基本体系的附加约束中的反力(矩)等于零,则基本体系就与原结构受力一致,但变形不一致。
