《结构力学习题集》下矩阵位移法习题及答案 2
结构力学课后习题解答:9矩阵位移法习题解答.docx

第9章矩阵位移法习题解答习题9.1是非判断题(1)矩阵位移法既可计算超静定结构,又可以计算静定结构。
()(2)矩阵位移法基本未知量的数目与位移法基本未知量的数目总是相等的。
()(3)单元刚度矩阵都具有对称性和奇异性。
()(4)在矩阵位移法中,整体分析的实质是建立各结点的平衡方程。
()(5)结构刚度矩阵与单元的编号方式有关。
()(6)原荷载与对应的等效结点荷载使结构产生相同的内力和变形。
()【解】(1)正确。
(2)错误。
位移法中某些不独立的杆端位移不计入基本未知量。
(3)错误。
不计结点线位移的连续梁单元的单刚不具奇异性。
(4)正确。
(5)错误。
结点位移分量统一编码会影响结构刚度矩阵,但单元或结点编码则不会。
(6)错误。
二者只产生相同的结点位移。
习题9.2填空题(1)矩阵位移法分析包含三个基本环节,其一是结构的,其二是分析,其三是分析。
(2)已知某单元的定位向量为[3 5 6 7 8 9]七则单元刚度系数炫应叠加到结构刚度矩阵的元素中去。
(3)将非结点荷载转换为等效结点荷载,等效的原则是。
(4)矩阵位移法中,在求解结点位移之前,主要工作是形成矩阵和_________________ 列阵。
(5)用矩阵位移法求得某结构结点2的位移为4=[. V2 ft]T=[0.8 0.3 0.5]T,单元①的始、末端结点码为3、2,单元定位向量为尸>=[0 0 0 3 4 5]T ,设单元与x轴之间的夹角为a =买,则2 尹> =O(6 )用矩阵位移法求得平面刚架某单元在单元坐标系中的杆端力为F e =[7.5 -48 -70.9 -7.5 48 -121.09]T ,则该单元的轴力心=kN。
【解】(1)离散化,单元,整体;(2)灯8;(3)结点位移相等;(4)结构刚度,综合结点荷载;(5)[0 0 0 0.3 -0.8 0.5]。
(6)-7.5o离、空的值以及K ⑴中元素妍、愚、姒的值。
【解】各刚度系数的物理意义如习题解9.3图所示。
结构力学(9.14.1)--矩阵位移法习题2
5kN m
8m 8m
8m
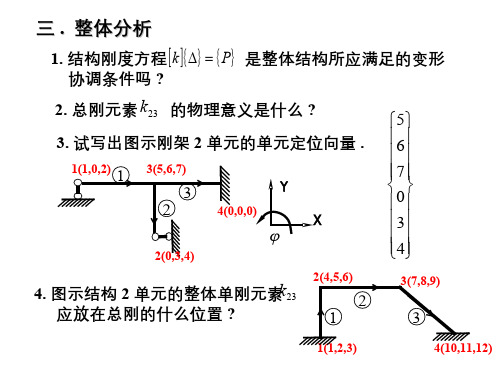
三 . 整体分析
12. 试求图示结构 ( 不计轴变 ) 的荷载列阵 ( 先处理法 ).
1(1,0,2) 2(1,0ቤተ መጻሕፍቲ ባይዱ3) 3(1,0,3)
X1
X2
4(0,0,0)
P
X
1
0
X
2
0
四 . 求杆端力
1. 连续梁在一般荷载作用下 , 单元杆端力由下式计算 . 是否正确 ?
6
48
4
2
1(0,0,0)
12
1 6
k
6
48
4(1,0,3)
3
2(0,0,0)
3
1
2
3
例 . 不计轴变 , 作弯矩图
已知 : 各杆长均为 12m, 线刚度均为 12
P 10kN, q 5kN / m
P 10kN, q 5kN / m
解 : 1 6 1 6
k
1
6
1
48 6
6 1
24
6
6
24
6
48
3(1,0,2)
2
1
1 6 1 6 1 0
k
1
6 1
48 6
6 1
24
2
0
63 1
6 24
EI
EI
EA 2l
2 2
l
l
三 . 整体分析
4(1,0,0)
5(1,0,0)
龙驭球《结构力学》笔记和课后习题(含真题)详解(矩阵位移法)【圣才出品】

第9章 矩阵位移法9.1 复习笔记一、矩阵位移法的基本思路矩阵位移法又称为杆件结构的有限元法。
分析的两个基本步骤:(1)单元分析;(2)整体分析。
单元分析:建立杆端力与杆端位移间的刚度方程,形成单元刚度矩阵。
整体分析:将单元合成整体,按照刚度集成规则形成整体刚度矩阵,建立位移基本方程。
二、单元刚度矩阵(局部坐标系)进行单元分析,推导单元刚度方程和单元刚度矩阵。
单元刚度方程是指由单元杆端位移求单元杆端力的一组方程,可以用“”表示,由位移求力称为“正问题”。
相应的由力求位移称为“反问题”。
正问题的解是唯一的确定的,但是反问题则可能无解,如果有解也非唯一解。
当外部荷载为不平衡力系时,反问题无解;当外荷载为平衡力系时,反问题有解但是因为杆件除本身变形外还可有任意刚体位移,此时反问题的解不唯一。
本书暂不考虑反问题的求解。
1.一般单元图9-1所示为平面刚架中的一个等截面直杆单元.单元的两个端点采用局部编码1和2,由端点1到端点2的方向规定为杆轴的正方向,在图中用箭头标明。
F →∆e图9-1图中采用坐标系,其中轴与杆轴重合。
这坐标系称为单元坐标系或者局部坐标系。
字母、的上面都画了一横,作为局部坐标系的标志。
推导单元刚度方程时,有以下几点需要注意:重新规定正负号规则、讨论杆件单元的一般情况、采用矩阵表示形式。
在局部坐标系中,图9-2所示的位移、力分量方向为正方向。
图9-2杆件性质:长度l ,截面面积A ,截面惯性矩I ,弹性模量E ;杆端位移u 、v 、θ。
根据杆端位移可以推导出下面两组刚度方程:(9-1)x y x x y(9-2)将上述六个刚度方程列成矩阵形式:(9-3)其中就是局部坐标系下单元刚度矩阵,即为(9-4)2.单元刚度矩阵的性质 (1)单元刚度系数的意义e e ek F∆=eK代表单元杆端第j 个位移分量等于1时所引起的第i 个杆端力分量。
(2)是对称矩阵,即。
(3)一般单元的是奇异矩阵,即,因此不存在逆矩阵。
(参考资料)结构力学答案(下册)

2l 2 -3l
-3l 6
l2
⎥ ⎥
-3l ⎥
⎥
⎢⎣3l l 2 -3l 2l2 ⎥⎦
(4)总刚度矩阵
12
3
4
1
2
3
⎡12 6l -12 6l 0 0
⎢⎢6l 4l 2 -6l 2l 2 0 0
⎢⎡k11① k12 ①
kθ
=
⎢k ⎢
① 21
⎢0
k 22 ① + k 22 ② k32 ②
0
0⎤
⎢-12
2m
解:(1)结构标识 y
②3 ③2
①
1x
单元 局部坐标系( i → j ) 杆长
① 1→2
2
② 2→3
2
cosα
0
3 2
sin α
1
1 2
(2)建立结点位移向量,结点力向量
[ ] ∆ = µ2 ν 2 θ2 θ3 T
F = [20 0 - 30 0]T
(3)建立单元刚度矩阵(l=2m)
µ2
⎡12 EI
(3)计算单元刚度矩阵
1
2
⎡12 6l -12 6l ⎤
k①
= ⎢⎡k11①
⎢⎣k
① 21
k12 ① k 22 ①
⎤ ⎥ ⎥⎦
=
2EI l3
⎢⎢6l ⎢−12 ⎢
4l 2 -6l
-6l
2l
2
⎥ ⎥
12 -6l ⎥
⎥
⎢⎣6l 2l 2 -6l 4l 2 ⎥⎦
1
2
⎡6 3l -6 3l ⎤
k ② = ⎢⎡k22② ⎢⎣k32②
③
x
1
2
02 结构力学——矩阵位移法2

2 2 2
M3
θ3 3
结点力平衡 结点位移协调
7 / 55
第十三章 矩阵位移法 第六节 连续梁受力分析
单元集合时应满足位移 协调条件 单元集合时应满足结点 平衡条件
δ = θ1
1 1
δ 21 = δ 12 = θ 2 2 δ 2 = θ3
F1 4ie = F2 2ie
对于复杂结构,传统位移法将非常繁琐且不宜模式化, 为使计算过程纳入一种统一的模式,一般均采用单元集 成法,或称直接刚度法。
•单元集成法:分别考虑每个单元对结点力的贡献 单元集成法: 单元集成法 1 2 总码 2 1 局码 2
1
3
6 / 55
第十三章 矩阵位移法 第六节 连续梁受力分析
4i1δ11 + 2i1δ21
M1 4i1 M 2 = 2i1 M 0 3
2i1 4i1 + 4i2 2i 2
0 θ1 θ {P } = [K ]{∆} 2i 2 2 5 / 55 4i2 θ 3
第十三章 矩阵位移法 第六节 连续梁受力分析
写出单元刚度方程
F1 4ie = F2 2ie
e
2 ie δ 1 4ie δ 2
e
e = 1,2 …,n-1 …,
15 / 55
第十三章 矩阵位移法 第六节 连续梁受力分析
P1 θ1 1 P2 θ2 2 3 4 …… 将离散单元集合时应满 足结点平衡条件 Pnθn n
第十三章 矩阵位移法 第六节 连续梁受力分析
由结点间的平衡条件,计算单元杆端力并叠加 由结点间的平衡条件,计算单元杆端力并叠加(集成)
第8章矩阵位移法例题 结构力学

0
K
(2)
0
对
0 0.0142
称
0 0.060 0.3396
2.8285 0 0
2.8285
0 0.0142
0.060 0
0.0142
0
0.060
0.
1698
0
105
0.060
0.3396
4.列出整体坐标表示的单元刚度矩阵
单元(1)(3)的单元坐标和整体坐标一致,所以
4 0
0 4 0
l
1 ql
1 ql
2
2
p
1 pl 8
1 pl 8
l
l
2
2
1p
1p
2
2
第8章矩阵位移法
例题 2 (1)求各单元在局部坐标系中固端力向量
例题 2
第8章矩阵位移法
(2)将
转换成
单元①
单元②
例题 2
第8章矩阵位移法
(3)利用单元定位向量,将
中元素反号后叠加集成
第8章矩阵位移法
例题 3
图示桁架,已知结点位移列阵
0
0
0.04 0.12
0
0.04 0.12
K
(1)
K
(3)
0
0.48
0 4
0.12 0
0.24 0
105
对 称
0.04 0.12
0.48
单元(2)的单元坐标和整体坐标不一致,必须经过以下变换
第一种方法: 直接代入公式:
2 1 2i 2 BCx l2 Cy
(e)
K
1 2i (B l2 )CxC y
0
0
1
第8章矩阵位移法
矩阵位移法方法课习题

已知图示结构的单元编码及局部坐标如图, 已知图示结构的单元编码及局部坐标如图,局部坐标单元刚 度矩阵相同如( ) 按结点号顺序写出结点位移编, 度矩阵相同如(c)式。求:按结点号顺序写出结点位移编, 并求结构刚度矩阵。 并求结构刚度矩阵。
2 i
①
3
1
−10 0 0 0 0 10 0 −2 2 0.5 0 0.5 0 0.5 0.2 0 −0.5 0.1 e 6 k = ×10 L(c) 0 10 0 0 −10 0 0 −2 −0.5 0 2 −0.5 0 −0.5 0.2 0 0.5 0.1
3kN/m
① ②
4m
用矩阵位移法求解图示结构。标示整体坐标系, 用矩阵位移法求解图示结构。标示整体坐标系,单元局 部坐标系;按结点号顺序编写结点位移编码; 部坐标系;按结点号顺序编写结点位移编码;写出单元 定位向量;求结构结点荷载列阵{F}。 定位向量;求结构结点荷载列阵 。
4 4m 20kN/m 1 2 4m 3 6m 10 kN . m
T
试求杆14的轴力。 试求杆 的轴力。 EA = 1kN 的轴力
1kN 1kN 2 4 6 1m 1 3 1m 1m y 5 M, θ x
已知图示结构的结点位移列阵为
{ ∆} = [ 0
0 0 0.841 − 0.5752 − 0.9964 0 0 − 0.7425]
T
试求杆32的杆端力列阵中 端的剪力 试求杆 的杆端力列阵中1端的剪力。 的杆端力列阵中 端的剪力。
l
y
M, θ x
试求图示结构在所示位移编码情况下的结点荷载列阵
P 1(0,0,0) 2 (0,0,1) q 3 (0,2,3) 4 (0,0,0) l 5 (0,0) l
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第10章 矩阵位移法【圣才出品】

二、单元刚度矩阵(见表 10-1-2) ★★★★★ 表 10-1-2 单元刚度矩阵
2 / 46
圣才电子书
十万种考研考证电子书、题库视频学习平 台
3 / 46
圣才电子书
十万种考研考证电子书、题库视频学习平 台
三、单元刚度矩阵的坐标转换(见表 10-1-3) ★★★★★ 表 10-1-3 单元刚度矩阵的坐标转换
6.结构的总刚度方程的物理意义是什么?总刚度矩阵的形成有何规律?其每一程的物理意义:尚未进行支承条件处理的表示所有结点外力与 结点位移之间的关系的平衡方程。
(2)总刚矩阵的形成规律:把每个单元刚度矩阵的四个子块按其两个下标号码逐一
9 / 46
圣才电子书
十万种考研考证电子书、题库视频学习平
台
4.为何用矩阵位移法分析时,要建立两种坐标系?
答:在利用矩阵位移法分析结构的时候,要进行单元分析和整体分析,单元分析是为
了建立每个单元的单元刚度矩阵,整体分析是为了建立整体结构的刚度方程。在单元分析
的过程中,以各单元的轴线为局部坐标系的 x 轴,以垂直轴线的方向为局部坐标系的 y 轴,
台
送到结构原始刚度矩阵中相应的行和列的位置上去,就可得到结构原始刚度矩阵,即各单
刚子块“对号入座”形成总刚。
(3)每一元素的物理意义:当其所在列对应的结点位移分量等于 1(其余各结点位移
分量均为零)时,所引起的其所在行对应的结点外力分量的数值。例如 Kij 表示第 j 号位置
3.矩阵位移法中,杆端力、杆端位移和结点力、结点位移的正负号是如何规定的? 答:杆端力沿局部坐标系的、的正方向为正,杆端弯矩逆时针为正;杆端位移的正负 号规定同杆端力和弯矩。结点力沿整体坐标系 x、y 的正方向为正,结点力偶逆时针为正; 结点位移的正负号规定同结点力和力偶。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章 矩阵位移法一、就是非题1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。
2、单元刚度矩阵均具有对称性与奇异性。
3、局部坐标系与整体坐标系之间的坐标变换矩阵T 就是正交矩阵。
4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。
5、用 矩 阵 位 移 法 计 算 连 续 梁 时 无 需 对 单 元 刚 度 矩 阵 作 坐 标 变 换。
6、结 构 刚 度 矩 阵 就是 对 称 矩 阵 ,即 有K i j = K j i ,这 可 由 位 移 互 等 定 理 得 到 证 明 。
7、结构刚度方程矩阵形式为:[]{}{}K P ∆=,它就是整个结构所应满足的变形条件。
8、在直接刚度法的先处理法中,定位向量的物理意义就是变形连续条件与位移边界条件。
9、等效结点荷载数值等于汇交于该结点所有固端力的代数与。
10、矩阵位移法中,等效结点荷载的“等效原则”就是指与非结点荷载的结点位移相等。
11、矩阵位移法既能计算超静定结构,也能计算静定结构。
二、选择题1、已知图示刚架各杆EI = 常数,当只考虑弯曲变形,且各杆单元类型相同时,采用先处理法进行结点位移编号,其正确编号就是:(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.21341234123412342、平面杆件结构一般情况下的单元刚度矩阵[]k 66⨯,就其性质而言,就是: A.非对称、奇异矩阵; B.对称、奇异矩阵;C.对称、非奇异矩阵;D.非对称、非奇异矩阵。
3、单元i j 在图示两种坐标系中的刚度矩阵相比:A.完全相同;B.第2、3、5、6行(列)等值异号;C.第2、5行(列)等值异号;D.第3、6行(列)等值异号。
xi4、矩阵位移法中,结构的原始刚度方程就是表示下列两组量值之间的相互关系: A.杆端力与结点位移; B.杆端力与结点力;C.结点力与结点位移;D.结点位移与杆端力 。
5、单 元 刚 度 矩 阵 中 元 素 k ij 的 物 理 意 义 就是 :A.当 且 仅 当 δi =1 时 引 起 的 与 δj 相 应 的 杆 端 力 ;B.当 且 仅 当 δj =1时 引 起 的 与 δi 相 应 的 杆 端 力 ;C.当 δj =1时 引 起 的 δi 相 应 的 杆 端 力 ;D.当 δi =1时 引 起 的 与 δj 相 应 的 杆 端 力。
三、填充题1、图示结构用矩阵位移法计算时(计轴向变形)未知量数目为8个。
2、图 示 刚 架 用 两 种 方 式 进 行 结 点 编 号 ,结 构 刚 度 矩 阵 最 大 带 宽 较 小 的 就是 图 。
35641271234567(a)(b)3、图 示 梁 结 构 刚 度 矩 阵 的 主 元 素 K K 1122== , 。
ll4、图 示 桁 架 结 构 刚 度 矩 阵 有 个 元 素 ,其 数 值 等 于 。
3m3m ABC DEAEAEA5、用 矩 阵 位 移 法 解 图 示 连 续 梁 时 ,结 构 的 综 合 结 点 荷 载 就是l /2ll l /26、已知图示桁架杆件①的单元刚度矩阵为式(a),又已知各结点位移为式(b),则杆件①的轴力(注明拉力或压力)应为N①= 。
l[]k EA l u v u v u v u v Pl EA ①=--⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎧⎨⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎫⎬⎪⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎪=-⎧⎨⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎫⎬⎪⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎪1(a) b)010*********005100230011223344 (四、计算题1、用先处理法写出图示梁的整体刚度矩阵[]K 。
123llli 0123i i2、用先处理法写出图示梁的结构刚度矩阵[]K 。
123ll4lEI EI EI 233、计算图示结构的综合结点荷载列阵{}P 。
l /2l /2l /2l /2ll4、计算图示连续梁对应于自由结点位移的荷载列阵{}P 。
l /2ll /25、已 知 图 示 连 续 梁 结点 位 移 列 阵 {}θ如 下 所示 ,试 用 矩 阵 位 移 法 求 出 杆 件 23 的 杆 端 弯 矩 并 画 出 连 续 梁 的 弯 矩 图 。
设 q = 20kN /m ,23 杆 的 i =⨯⋅10106.kN cm 。
{}θ=--⎧⎨⎪⎪⎩⎪⎪⎫⎬⎪⎪⎭⎪⎪⨯-365714572286104....rad6、已知图示梁结点转角列阵为{}[]∆=056516822-/ /Tql i ql i ,EI =常数。
计算B支座的反力。
1m1m7、试 用 矩 阵 位 移 法 解 图 示 连 续 梁 ,绘 弯 矩 图 。
EI = 已 知 常 数 。
xθ8、试 求 结 构 原 始 刚 度 矩 阵 中 的 子 块 []K 22 ,已 知 单 元 ①的 整 体 坐 标 的 单 元 刚 度矩 阵 为 :[]K ①=-⨯-⨯---⨯-⨯⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥72360072360036003600723600360036001103600210442101107244ll9、用先处理法写出图示结构的结构刚度矩阵[]K 。
E =常数。
ll10、用先处理法计算图示连续梁的结点荷载列阵{}P 。
m4m4m411、计算图示连续梁对应于自由结点位移的荷载列阵{}P 。
m3m3m 4m 412、已 知 图 示 两 端 固 定 梁 跨 中 结 点 C 的 竖 向 位 移 为 ∆CV l EI =-5123() ,转 角 ϕC =0 ,l =5m ,EI =常 数 。
试 求 单 元 ①、② 的 杆 端 力 列 阵。
ll13、用先处理法计算图示结构刚度矩阵的元素133322,,K K K 。
123ll4l5EI2EIEA(0,0,0)(0,0,1)(0,2,3)(0,0,0)(0,2,4)(0,0,0)EI14、用先处理法计算图示刚架结构刚度矩阵的元素153422,,K K K 。
EI ,EA 均为常数。
l15、写出图示结构以子矩阵形式表达的结构原始刚度矩阵的子矩阵[][]K K 2224,。
[][]k k 1112 [][]k k 2122 []k =ii iii单刚分块形式为 :16、用先处理法集成结构刚度矩阵[]K 。
(用子块形式写出)。
5[][]k k1112 [][]k k 2122 []k =ii iii单刚分块形式为 :17、用先处理法写出图示刚架的结构刚度矩阵[]K ,只考虑弯曲变形。
EI EI EIEI=o ol ll18、用先处理法写出图示结构的结构刚度矩阵[]K 。
各杆长度为l ,EA 、EI 为常数。
ABCD19、用先处理法写出以子块表示的图示结构的结构刚度矩阵[]K 。
m 12m20、用先处理法写出图示刚架结构刚度矩阵[]K 。
已知:[][][]k k k ①②③===⨯--------⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥10300003000001230012300301000305030000300000123001230030500301004x21、计算图示结构结点3的等效结点荷载列阵{}P 3E 。
2222、计算图示结构结点2的等效结点荷载列阵{}P 2E 。
l /2l /223、计算图示结构的综合结点荷载列阵元素431,,P P P 。
ll l24、用先处理法计算图示结构的综合结点荷载列阵{}P 。
l/2/225、计算图示结构结点荷载列阵中的元素654,,P P P 。
l/2l /2(0,7,8)326、计算图示结构综合结点荷载列阵中的元素431,,P P P 。
l l l27、计算图示结构综合结点荷载列阵{}P 中的元素9873,,,P P P P 。
lll228、计算图示刚架对应于自由结点位移的综合结点荷载列阵{}P 。
m3m3m29、计算图示刚架对应自由结点位移的综合结点荷载列阵{}P 。
各杆长度为 4m 。
30、计算图示结构结点2的综合结点荷载列阵{}P 2。
l /2l l /2l l31、计算图示刚架考虑弯曲、轴向变形时的综合结点荷载列阵{}P 。
32、若考虑弯曲、轴向变形,用先处理法写出图示结构综合结点荷载列阵{}P 。
l /2l/2ql33、考虑弯曲、轴向变形,计算图示结构综合结点荷载列阵{}P 。
m4m2m2m334、考虑弯曲、轴向变形时,用先处理法计算图示结构综合结点荷载列阵{}P 。
8mm5m635、用先处理法计算图示结构的综合结点荷载列阵{}P 。
/2/2ll36、试 用 矩 阵 位 移 法 解 图 示 结构,绘 弯 矩 图 。
m 1mm1kN m.37、计算下图结构(a)中杆34的杆端力列阵中的第3个元素与第6个元素。
不计杆件的轴向变形。
已知下图结构(a)结点位移列阵为:{}[]T 0.66667 0.2 0.7556- 0 0.3667 0 0.3333 0.2 0.2- 0.1333 0 0.2- 0 0 0=∆。
1m1mll(a) (b)38、计算上图结构(b)单元③的杆端力列阵{}③F,已知各杆,cm 300 ,kN/cm 101.2424=⨯=I E ,cm 202=A cm l 100=,结点2位移列阵{}[][]T T 2rad cm cm 5313.04596.04730.01012222--⨯⨯==-θ∆v u 。
39、考虑杆件的轴向变形,计算图示结构中单元①的杆端力{}F①。
已知:I =(/),124m 4E =⨯3107kN /m 2, m 2A =05.。
结点1的位移列阵{}[]δ16110370022710151485=⨯⨯---...m m rad T。
5m40、计算图示刚架单元①在局部坐标下的杆端力{}F ①。
已知各杆E 、A 、I 、l 均为常数,不考虑杆件的轴向变形,{}[]∆=--ql EIl l 2100002727 0 5 19 0 0T。
lq41、已求得图示结构结点2、3的结点位移为式(a)、(b)并已知单元②的整体坐标的单元刚度矩阵。
计算单元②2端的弯矩。
(长度单位m,力单位kN,角度单位弧度)(b)10 , (a)1040-160-0.2=5-5- ⨯⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧---=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⨯⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧108.1593.0333222φφv u v u[]510205.1105.1050005005.105.15.105.1105.1205.1050005005.105.15.105.1⨯⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-------=②k42、用先处理法写出图示桁架的结构刚度矩阵[]K 。
