《结构力学习题集》-矩阵位移法习题及答案(DOC)
结构力学课后习题解答:9矩阵位移法习题解答.docx

第9章矩阵位移法习题解答习题9.1是非判断题(1)矩阵位移法既可计算超静定结构,又可以计算静定结构。
()(2)矩阵位移法基本未知量的数目与位移法基本未知量的数目总是相等的。
()(3)单元刚度矩阵都具有对称性和奇异性。
()(4)在矩阵位移法中,整体分析的实质是建立各结点的平衡方程。
()(5)结构刚度矩阵与单元的编号方式有关。
()(6)原荷载与对应的等效结点荷载使结构产生相同的内力和变形。
()【解】(1)正确。
(2)错误。
位移法中某些不独立的杆端位移不计入基本未知量。
(3)错误。
不计结点线位移的连续梁单元的单刚不具奇异性。
(4)正确。
(5)错误。
结点位移分量统一编码会影响结构刚度矩阵,但单元或结点编码则不会。
(6)错误。
二者只产生相同的结点位移。
习题9.2填空题(1)矩阵位移法分析包含三个基本环节,其一是结构的,其二是分析,其三是分析。
(2)已知某单元的定位向量为[3 5 6 7 8 9]七则单元刚度系数炫应叠加到结构刚度矩阵的元素中去。
(3)将非结点荷载转换为等效结点荷载,等效的原则是。
(4)矩阵位移法中,在求解结点位移之前,主要工作是形成矩阵和_________________ 列阵。
(5)用矩阵位移法求得某结构结点2的位移为4=[. V2 ft]T=[0.8 0.3 0.5]T,单元①的始、末端结点码为3、2,单元定位向量为尸>=[0 0 0 3 4 5]T ,设单元与x轴之间的夹角为a =买,则2 尹> =O(6 )用矩阵位移法求得平面刚架某单元在单元坐标系中的杆端力为F e =[7.5 -48 -70.9 -7.5 48 -121.09]T ,则该单元的轴力心=kN。
【解】(1)离散化,单元,整体;(2)灯8;(3)结点位移相等;(4)结构刚度,综合结点荷载;(5)[0 0 0 0.3 -0.8 0.5]。
(6)-7.5o离、空的值以及K ⑴中元素妍、愚、姒的值。
【解】各刚度系数的物理意义如习题解9.3图所示。
《结构力学习题集》(含答案)
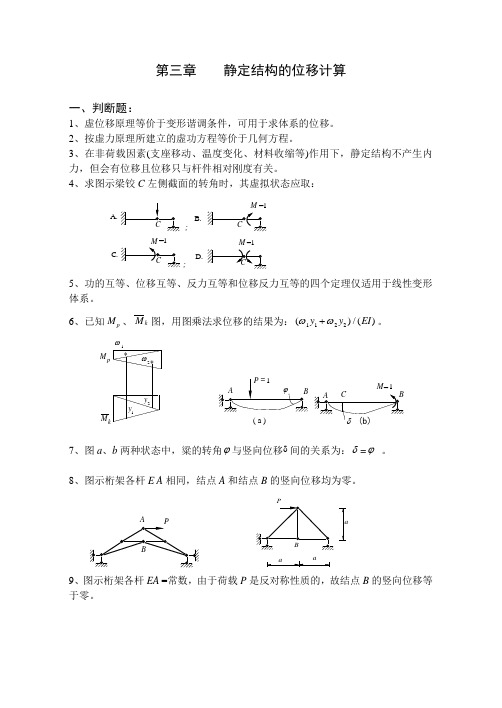
第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.M =15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M 17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l l /3 2 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
q15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI =常数。
l ll/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/2219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I = 常数。
ll21、求图示结构B点的竖向位移,EI = 常数。
自测题9 矩阵位移法答案

整体(结构)坐标系、局部(单元)坐标系
转换:
定位:
名称和意义:各矩阵、列阵(向量)、
第十章矩阵位移法
答案
一、1 O 2 X 3 X4X
二、1 A2 B 3 B4 C5 B
6 C7 D
三、
1、1、2EA/L
2、b
3、
四、
(7分)
五、
(10分)
六、
(7分)
七、
(7分)
八、
( 7分)
九、
(7分)
十、
(4分);
(2分)
(3分)
M图(3分)
本章小结
编码:
整体(结构)编码:
单元码①②③…
结点码ABCD…(1234…)
结点位移(力)码=总码1234…
局部(单元)编码:
杆端码1 2
(局部坐标系)杆端位移(力)码=局部码
(整体坐标系)杆端位移(力)码=局部码
不同结点:固定端、铰支端、自由端、中间铰、
中间滑动
不同结构:刚架、忽略轴向变形矩形刚架、来自、连续梁、桁架、组合结构
单元:
刚架单元 、梁单元 、连续梁单元 、桁架单元
《结构力学习题集》-矩阵位移法习题及答案

第八章 矩阵位移法 – 老八校一、判断题:1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。
2、单元刚度矩阵均具有对称性和奇异性。
3、局部坐标系与整体坐标系之间的坐标变换矩阵T 是正交矩阵。
4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。
5、结构刚度方程矩阵形式为:[]{}{}K P ∆=,它是整个结构所应满足的变形条件。
6、图示结构用矩阵位移法计算时(计轴向变形)未知量数目为8个。
7、在直接刚度法的先处理法中,定位向量的物理意义是变形连续条件和位移边界条件。
8、等效结点荷载数值等于汇交于该结点所有固端力的代数和。
9、矩阵位移法中,等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。
10、矩阵位移法既能计算超静定结构,也能计算静定结构。
11、已知图示刚架各杆EI = 常数,当只考虑弯曲变形,且各杆单元类型相同时,采用先处理法进行结点位移编号,其正确编号是:(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.2134123412341234( )二、计算题:12、用先处理法计算图示结构刚度矩阵的元素133322,,K K K 。
123ll4l5EI2EIEA(0,0,0)(0,0,1)(0,2,3)(0,0,0)(0,2,4)(0,0,0)EI13、用先处理法计算图示刚架结构刚度矩阵的元素153422,,K K K 。
EI ,EA 均为常数。
l14、计算图示结构整体刚度矩阵的元素665544,,K K K 。
E 为常数。
ll1342A , I AA /222A I , 2A15、写出图示结构以子矩阵形式表达的结构原始刚度矩阵的子矩阵[][]K K 2224,。
[][]k k 1112 [][]k k 2122 []k =ii iii单刚分块形式为 :16、已知平面桁架单元在整体坐标系中的单元刚度矩阵,计算图示桁架结构原始刚度矩阵[]K 中的元素,,7877K K EA =常数。
习题课1 矩阵位移法(含答案作业)_518706462

4
5
6
7
8
k
i = 2,3 (1) 54
+ k
i = 2,3 (1) 55
(2) (3) (3) (3) k16 k15 k16 k14 0 (2) (3) (3) (3) k26 k25 k26 k24 0 (2) (3) (3) (3) k36 k34 k35 k36 0
+ k
+
(i ) 33
k
3EIa 2 a 3 + b3
A
3EIab a 3 + b3
B A
3EIab a 3 + b3
3EIb 2 a 3 + b3
B
3EIa a 3 + b3
e θA =1
−3EIa a 3 + b3
3EIb a 3 + b3
e θB =1
−3EIb a 3 + b3
[k ]
e
=
a2 ab
ab b2
e
3EI a 3 + b3
{F }
u2
v2 θ 2 θ 3 ]
−M 0 ]
[0 M 0
0 0 2M 0
T
4
3
3
4
5
0
0
6
2 2 2 2 2 2 k12 k13 k14 k15 k16 k11
2 2 2 2 2 2 k22 k24 k25 k21 k23 k26 2 2 2 2 2 2 k32 k34 k35 k31 k33 k36 2 2 2 2 2 2 k42 k45 k44 k41 k46 k43
y
x
解: T 用位移法求解,未知量为 {∆} = [θ 2 v3 ] 。 1) 杆端弯矩表达式
第8章矩阵位移法例题 结构力学

0
K
(2)
0
对
0 0.0142
称
0 0.060 0.3396
2.8285 0 0
2.8285
0 0.0142
0.060 0
0.0142
0
0.060
0.
1698
0
105
0.060
0.3396
4.列出整体坐标表示的单元刚度矩阵
单元(1)(3)的单元坐标和整体坐标一致,所以
4 0
0 4 0
l
1 ql
1 ql
2
2
p
1 pl 8
1 pl 8
l
l
2
2
1p
1p
2
2
第8章矩阵位移法
例题 2 (1)求各单元在局部坐标系中固端力向量
例题 2
第8章矩阵位移法
(2)将
转换成
单元①
单元②
例题 2
第8章矩阵位移法
(3)利用单元定位向量,将
中元素反号后叠加集成
第8章矩阵位移法
例题 3
图示桁架,已知结点位移列阵
0
0
0.04 0.12
0
0.04 0.12
K
(1)
K
(3)
0
0.48
0 4
0.12 0
0.24 0
105
对 称
0.04 0.12
0.48
单元(2)的单元坐标和整体坐标不一致,必须经过以下变换
第一种方法: 直接代入公式:
2 1 2i 2 BCx l2 Cy
(e)
K
1 2i (B l2 )CxC y
0
0
1
第8章矩阵位移法
结构力学大作业(矩阵位移法)

矩阵位移法编程大作业姓名:学号:一、编程原理本程序的原理是基于结构力学矩阵位移法原理,以结构结点位移作基本未知量,将要分析的结构拆成已知节点力—结点力位移关系的单跨梁集合,通过强令结构发生待定的基本未知位移,在各个单跨梁受力分析结果的基础上通过保证结构平衡建立位移法的线性方程组,从而求得基本未知量。
二、程序说明本程序是计算10个节间距的悬索-拱组合体系主塔顶节点水平位移、主塔底截面弯矩、拱顶节点竖向位移、拱顶截面弯矩和轴力的程序。
首先将各杆件的交汇点作为结点,共有20个结点,51个位移,然后根据不同结构单元分别建立单元刚度矩阵,然后转换为整体坐标系下的刚度矩阵,然后将所有杆件的单元刚度矩阵整合成为总体刚度矩阵,在进行整合时连续运用for函数,最终形成51阶的总体刚度矩阵。
然后通过对荷载的分析确定出荷载矩阵,直接写进程序。
这样就可以把20个结点的51个位移求得,然后再利用各个单元的单元刚度矩阵和所得的位移求得单元杆件的内力。
三、算法流程建立各单位在局部结构离散化编号进行单元分析坐标系下的单位刚度方程确定各单位在总体将单元刚度矩阵集合确定综合结点坐标系下的单元矩阵方程成总体刚度矩阵点荷载矩阵建立方程利用杆件单元刚度矩阵输出结果求解位移和所求位移求内力结束四、源代码L=input('输入单节间L:');EIc=input('主塔的抗弯刚度EIc:');EAc=input('主塔的抗压刚度EAc:');EAb=input('悬索和斜索的抗拉刚度EAb:');EAt=input('吊杆的抗拉刚度EAt:');EIa=input('拱的抗弯刚度EIa:');EAa=input('拱的抗压刚度EAa:');q=input('拱上沿轴向均布荷载集度q:');T1=[0,1,0,0,0,0;-1,0,0,0,0,0;0,0,1,0,0,0;0,0,0,0,1,0;0,0,0,-1,0,0;0,0,0,0,0,1;];%主塔的转换矩阵h=(5*L)/2;KcO=[EAc/h,0,0,-EAc/h,0,0;0,12*EIc/(h*h*h),6*EIc/(h*h),0,-12*EIc/(h*h*h),6*EIc/(h*h);0,6*EIc/(h*h),4*EIc/h,0,-6*EIc/(h*h),2*EIc/h;-EAc/h,0,0,EAc/h,0,0;0,-12*EIc/(h*h*h),-6*EIc/(h*h),0,12*EIc/(h*h*h),-6*EIc/(h*h);0,6*EIc/(h*h),2*EIc/h,0,-6*EIc/(h*h),4*EIc/h;];%主塔的单元刚度矩阵x=atan(2*L/h);T2=[cos(x),sin(x),0,0;-sin(x),cos(x),0,0;0,0,cos(x),sin(x);0,0,-sin(x),cos(x);];y=-atan(2*L/h);T21=[cos(y),sin(y),0,0;-sin(y),cos(y),0,0;0,0,cos(y),sin(y);0,0,-sin(y),cos(y);];%斜索的转换矩阵s1=sqrt(2*L*2*L+h*h);KbO1=(EAb/s1)*[1 0 -1 0;0 0 0 0;-1 0 1 0;0 0 0 0;];%斜索的单元刚度矩阵f2(1)=5*L/2;f2(2)=58*L/25;f2(3)=109*L/50;f(4)=52*L/25;f2(5)=101*L/50;f2 (6)=2*L;f2(7)=101*L/50;f2(8)=52*L/25;f2(9)=109*L/50;f2(10)=58*L/25;f2(1 1)=5*L/2;y=zeros(10,1);for i=1:10y(i)=atan((f2(i+1)-f2(i))/L);endT3=zeros(4,40);for i=1:10T3(1:4,4*i-3:4*i)=[cos(y(i)),sin(y(i)),0,0;-sin(y(i)),cos(y(i)),0,0;0,0,cos(y(i)),sin(y(i));0,0,-sin(y(i)),cos(y(i));];end%悬索的转换矩阵s2=zeros(10,1);for i=1:10s2(i)=sqrt((f2(i+1)-f2(i))^2+L^2);endKbO2=zeros(4,40);KbO2(1:4,4*i-3:4*i)=(EAb/s2(i))*[1 0 -1 0;0 0 0 0;-1 0 1 0;0 0 0 0;];end%悬索的单元刚度矩阵f1(1)=0;f1(2)=9*L/20;f1(3)=4*L/5;f1(4)=21*L/20;f1(5)=6*L/5;f1(6)=5*L/4; f1(7)=6*L/5;f1(8)=21*L/20;f1(9)=4*L/5;f1(10)=9*L/20;f1(11)=0;z=zeros(10,1);for i=1:10z(i)=atan((f1(i+1)-f1(i))/L);endT4=zeros(6,60);for i=1:10T4(6*i-5:6*i,6*i-5:6*i)=[cos(z(i)),sin(z(i)),0,0,0,0;-sin(z(i)),cos(z(i)),0,0,0,0;0,0,1,0,0,0;0,0,0,cos(z(i)),sin(z(i)),0;0,0,0,-sin(z(i)),cos(z(i)),0;0,0,0,0,0,1;];end%拱的转换矩阵s3=zeros(10,1);for i=1:10s3(i)=sqrt((f1(i+1)-f1(i))^2+L^2);endKaO=zeros(6,60);for i=1:10KaO(1:6,6*i-5:6*i)=[EAa/s3(i) 0 0 -EAa/s3(i) 0 0;0 12*EIa/(s3(i)*s3(i)*s3(i)) 6*EIa/(s3(i)*s3(i)) 0-12*EIa/(s3(i)*s3(i)*s3(i)) 6*EIa/(s3(i)*s3(i));0 6*EIa/(s3(i)*s3(i)) 4*EIa/s3(i) 0 -6*EIa/(s3(i)*s3(i)) 2*EIa/s3(i);-EAa/s3(i) 0 0 EAa/s3(i) 0 0;0 -12*EIa/(s3(i)*s3(i)*s3(i)) -6*EIa/(s3(i)*s3(i)) 012*EIa/(s3(i)*s3(i)*s3(i)) -6*EIa/(s3(i)*s3(i));0 6*EIa/(s3(i)*s3(i)) 2*EIa/s3(i) 0 -6*EIa/(s3(i)*s3(i)) 4*EIa/s3(i);]; end%拱的单元刚度矩阵T5=[0 1 0 0;-1 0 0 0;0 0 0 1;0 0 -1 0;];%吊杆的转换矩阵s4=zeros(9,1);s4(i)=f2(i+1)-f1(i+1);endKtO=zeros(4,36);for i=1:9KtO(1:4,4*i-3:4*i)=(EAt/s4(i))*[1 0 -1 0;0 0 0 0;-1 0 1 0;0 0 0 0;];end%吊杆的单元刚度矩阵Kc=T1'*KcO*T1;%总体坐标下主塔的单元刚度矩阵Kb1=T2'*KbO1*T2;Kb11=T21'*KbO1*T21;%总体坐标下斜索的单元刚度矩阵Kb2=zeros(4,40);for i=1:10T3O=T3(1:4,4*i-3:4*i);Kb2(1:4,4*i-3:4*i)=T3O'*KbO2(1:4,4*i-3:4*i)*T3O;end%总体坐标下悬索的单元刚度矩阵Ka=zeros(6,60);for i=1:10T4O=T4(6*i-5:6*i,6*i-5:6*i);Ka(1:6,6*i-5:6*i)=T4O'*KaO(1:6,6*i-5:6*i)*T4O;end%总体坐标下拱的单元刚度矩阵Kt=zeros(4,36);for i=1:9KtOO=KtO(1:4,4*i-3:4*i);Kt(1:4,4*i-3:4*i)=T5'*KtOO*T5;end%总体坐标下吊杆的单元刚度矩阵%定义51阶0矩阵K1=zeros(51,51);K2=zeros(51,51);K3=zeros(51,51);K4=zeros(51,51);K5=zero s(51,51);X=zeros(51,51);Y=zeros(51,51);Z=zeros(51,51);%把主塔整合到整体刚度矩阵中:K1(1:3,1:3)=KcO(4:6,4:6);K1(22:24,22:24)=KcO(4:6,4:6);%把斜索整合到整体刚度矩阵中:K2(1:2,1:2)=Kb1(3:4,3:4);K2(22:23,22:23)=Kb11(1:2,1:2);%把悬索整合到整体刚度矩阵中:K3(1:2,1:2)=KbO2(1:2,1:2);K3(1:2,4:5)=KbO2(1:2,3:4);for i=2:10X(2*i:2*i+3,2*i:2*i+3)=KbO2(1:4,4*i-3:4*i);K3=K3+X;end%把拱整合到整体刚度矩阵中:K4(25:27,25:27)=KaO(4:6,4:6);K4(49:51,49:51)=KaO(1:3,55:57);for i=2:9Y(3*i+19:3*i+24,3*i+19:3*i+24)=KaO(1:6,6*i-5:6*i); K4=K4+Y;end%把吊杆整合到整体刚度矩阵中:for i=1:9Z(2*i+2:2*i+3,2*i+2:2*i+3)=KtO(1:2,1:2);Z(2*i+2:2*i+3,3*i+22:3*i+23)=KtO(1:2,3:4);Z(3*i+22:3*i+23,2*i+2:2*i+3)=KtO(3:4,1:2);Z(3*i+22:3*i+23,3*i+22:3*i+23)=KtO(3:4,3:4);K5=K5+Z;endK=K1+K2+K3+K4+K5;%荷载矩阵:P=zeros(51,1);P(26,1)=-q*L/(2*cos(s3(1)));P(27,1)=q*L*L/(12*cos(s3(1)));P(50,1)=-q*L/(2*cos(s3(10)));P(51,1)=-q*L*L/(12*cos(s3(10)));for i=2:9P0=zeros(51,1);P0(3*i+20,1)=-q*L/(2*cos(s3(i)));P0(3*i+21,1)=-q*L*L/(12*cos(s3(i)));P0(3*i+23,1)=-q*L/(2*cos(s3(i)));P0(3*i+24,1)=q*L*L/(12*cos(s3(i)));P=P+P0;endA=K\P;%结构的位移%主塔底截面的弯矩:Ac(4:6,1)=A(1:3,1);Bc=KcO*Ac;Mc=Bc(3,1);%拱顶截面的弯矩和轴力:Aa=A(34:39,1);KaO17=KaO(1:6,25:30);Ba=KaO17*Aa;Ma=Ba(6,1);Fa=Ba(4,1);%输出结果fprintf('主塔顶结点的水平位移%f\n',A(1,1)); fprintf('主塔底截面的弯矩%f\n',Mc);fprintf('拱顶结点的竖向位移%f\n',A(38,1)); fprintf('拱顶截面的弯矩%f\n',Ma);fprintf('拱顶截面的轴力%f\n',Fa);五、试算算例输入单节间L:1主塔的抗弯刚度EIc:1主塔的抗压刚度EAc:1悬索和斜索的抗拉刚度EAb:1吊杆的抗拉刚度EAt:1拱的抗弯刚度EIa:1拱的抗压刚度EAa:1拱上沿轴向均布荷载集度q:1主塔顶结点的水平位移NaN主塔底截面的弯矩NaN拱顶结点的竖向位移0.016046拱顶截面的弯矩3.791098拱顶截面的轴力0.000000。
9矩阵位移法习题.docx

第9章矩阵位移法习题解答习题9・1是非判断题(1)矩阵位移法既可计算超静定结构,又可以计算静定结构。
(T )(2)矩阵位移法棊木未知量的数冃与位移法棊木未知量的数冃总是相等的。
(|T*) F(3)单元刚度矩阵都具有对称性和奇界性。
(F )(4)在矩阵位移法中,整体分析的实质是建立各结点的平衡方程。
(T )(5)结构刚度短阵与单元的编号方式冇关。
(F )(6)原荷载与对应的等效结点荷载使结构产生相同的内力和变形。
(F )【解】(1)正确。
(2)错误。
位移法中某些不独立的杆端位移不计入基本未知量。
(3)错谋。
不计结点线位移的连续梁单元的单刚不具奇异性。
(4)正确。
(5)错误。
结点位移分量统-•编码会影响结构刚度矩阵,但单元或结点编码则不会。
(6)错误。
二者只产生相同的结点位移。
习题9.2填空题(1) ______________________________________________________________ 矩阵位移法分析包含三个基本环节,其一是结构的___________________________________ ,其二是_________ 分析,-其三是______ 分析。
(2)已知某单元©的定位向量为[3 5 6 7 8 9]丁,则单元刚度系数紜应叠加到结构刚度矩阵的元素—中去。
(3) ________________________________________________________________________ 将非结点荷载转换为等效结点荷载,等效的原则是____________________________________ o(4)矩阵位移法屮,在求解结点位移之前,主要工作是形成_____________________ 矩阵和_______________ 列阵。
(5)用矩阵位移法求得某结构结点2的位移为J2=[w2V2 ft]T=[O.S 0.3 0.5]丁,单元①的始、末端结点码为3、2,单元定位向量为= [0 0 0 3 4 5]T,设单元与兀轴之间的夹角为« = |,则(6 )用短阵位移法求得平面刚架某单元在单元坐标系中的杆端力为戸=[7.5 -48 -70.9 -7.5 48 -121.09]7,则该单元的轴力F* _______________________ k N。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八章 矩阵位移法一、判断题:1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。
2、单元刚度矩阵均具有对称性和奇异性。
3、局部坐标系与整体坐标系之间的坐标变换矩阵T 是正交矩阵。
4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。
5、结构刚度方程矩阵形式为:[]{}{}K P ∆=,它是整个结构所应满足的变形条件。
6、图示结构用矩阵位移法计算时(计轴向变形)未知量数目为8个。
7、在直接刚度法的先处理法中,定位向量的物理意义是变形连续条件和位移边界条件。
8、等效结点荷载数值等于汇交于该结点所有固端力的代数和。
9、矩阵位移法中,等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。
10、矩阵位移法既能计算超静定结构,也能计算静定结构。
11、已知图示刚架各杆EI = 常数,当只考虑弯曲变形,且各杆单元类型相同时,采用先处理法进行结点位移编号,其正确编号是:(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.2134123412341234( )二、计算题:12、用先处理法计算图示结构刚度矩阵的元素133322,,K K K 。
123ll4l5EI2EIEA(0,0,0)(0,0,1)(0,2,3)(0,0,0)(0,2,4)(0,0,0)EI13、用先处理法计算图示刚架结构刚度矩阵的元素153422,,K K K 。
EI ,EA 均为常数。
l14、计算图示结构整体刚度矩阵的元素665544,,K K K 。
E 为常数。
ll1342A , I AA /222A I , 2A15、写出图示结构以子矩阵形式表达的结构原始刚度矩阵的子矩阵[][]K K 2224,。
[][]k k 1112 [][]k k 2122 []k =ii iii单刚分块形式为 :16、已知平面桁架单元在整体坐标系中的单元刚度矩阵,计算图示桁架结构原始刚度矩阵[]K 中的元素,,7877K K EA =常数。
,cos α=C ,sin α=S ,C C A ⋅= S S D S C B ⋅=⋅=,,各杆EA 相同。
l[]k EA l i=A B A BD B D A B D -i i---对称17、计算图示刚架结构刚度矩阵中的元素8811,K K (只考虑弯曲变形)。
设各层高度为h ,各跨长度为l h l 5.0,=,各杆EI 为常数。
18、计算图示结构原始刚度矩阵的元素4544,K K 。
l19、用先处理法写出图示梁的整体刚度矩阵[]K 。
123llli 0123i i20、用先处理法写出图示梁的结构刚度矩阵[]K 。
123ll4lEI EI EI 2321、已知图示结构在整体坐标系中的单元刚度矩阵。
用先处理法集成结构刚度矩阵[]K 。
(用子块形式写出)。
5[][]k k 1112 [][]k k 2122 []k =ii iii单刚分块形式为 :22、用先处理法写出图示结构的结构刚度矩阵[]K 。
E =常数。
ll23、用先处理法写出图示刚架的结构刚度矩阵[]K,只考虑弯曲变形。
EI EI EIEI=o ol ll24、用先处理法写出图示结构的结构刚度矩阵[]K 。
各杆长度为l ,EA 、EI 为常数。
ABCD25、用先处理法写出图示结构的结构刚度矩阵[]K 。
各杆长度为 l 。
A BCD EA EIEI226、用先处理法写出以子块表示的图示结构的结构刚度矩阵[]K 。
m12m27、用先处理法写出图示桁架的结构刚度矩阵[]K 。
已知各杆EA =常数。
[][]kkEA l ①②==--⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥1010*********000,整体坐标系中的单元刚度矩阵:[]k EA l ③=--------⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥241111111111111111l28、用先处理法写出图示刚架结构刚度矩阵[]K 。
已知:[][][]kkk①②③===⨯--------⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥1030000300000123001230030100030503000030000012300123003050030100429、计算图示结构结点3的等效结点荷载列阵{}P 3E 。
m224m43kN/m30、计算图示结构结点2的等效结点荷载列阵{}P 2E 。
l/2l /2q31、计算图示结构结点2的等效结点荷载列阵{}P 2E 。
l /2ll /2l32、计算图示结构的综合结点荷载列阵{}P 。
l /2l /2l /2l /2ll33、计算图示连续梁对应于自由结点位移的荷载列阵{}P 。
l /2l l /234、计算图示连续梁对应于自由结点位移的荷载列阵{}P 。
m3m3m 4m 435、用先处理法计算图示连续梁的结点荷载列阵{}P 。
m4m4m436、计算图示结构的综合结点荷载列阵元素431,,P P P 。
lll37、用先处理法计算图示结构的综合结点荷载列阵{}P 。
l/2/238、计算图示结构结点荷载列阵中的元素654,,P P P 。
l/2l /2(0,7,8)339、计算图示结构综合结点荷载列阵中的元素431,,P P P 。
ll l40、计算图示结构综合结点荷载列阵{}P 中的元素9873,,,P P P P 。
lll241、计算图示刚架对应于自由结点位移的综合结点荷载列阵{}P 。
m3m3m42、计算图示刚架对应自由结点位移的综合结点荷载列阵{}P 。
各杆长度为 4m 。
43、计算图示结构结点2的综合结点荷载列阵{}P 2。
l /2l l /2l l44、计算图示刚架考虑弯曲、轴向变形时的综合结点荷载列阵{}P 。
45、若考虑弯曲、轴向变形,用先处理法写出图示结构综合结点荷载列阵{}P 。
l /2l/2ql46、考虑弯曲、轴向变形,计算图示结构综合结点荷载列阵{}P 。
m4m2m2m347、考虑弯曲、轴向变形时,用先处理法计算图示结构综合结点荷载列阵{}P 。
8mm5m648、用先处理法计算图示结构的综合结点荷载列阵{}P 。
/2/2ll49、用先处理法计算图示桁架的综合结点荷载列阵{}P 。
3m450、计算图示结构的自由结点荷载列阵{}P 。
8m10kN51、计算图示结构中杆12的杆端力列阵中的第6个元素。
已知杆12的杆端位移列阵为{}[]δ120=---- 0 0.3257 0.0305 0.1616 0.1667T。
1m1m=1kNEI=1kN m.252、计算杆14的轴力。
已知图示桁架EA =1kN ,结点位移列阵为:{}[]∆=--01726504007 0 2.5677 0.0415 1.0415 1.3673 1.6092 1.6408 0 1.2084 T..。
1m1m53、计算杆23的杆端力列阵的第2个元素。
已知图示结构结点位移列阵为: {}[]∆=0 0 0 -0.1569 -0.2338 0.4232 0 0 0T。
m 1mm1kN m.54、计算图示结构中杆34的杆端力列阵中的第3个元素和第6个元素。
不计杆件的轴向变形。
已知图示结构结点位移列阵为:{}[]∆=---0 0 0 0.2 0 0.1333 0.2 0.2 0.3333 0 0.3667 0 0.7556 0.2 0.6667T 。
1m1m55、已知图示桁架的结点位移列阵(分别为结点2、4沿x 、y 方向位移)为:{}∆=(/())1EA ×[]342322. 1139.555 137.680 1167.111T ---,设各杆EA 为常数。
计算单元①的内力。
4m20kN56、已知图示桁架杆件①的单元刚度矩阵为式(a),又已知各结点位移为式(b),则杆件①的轴力(注明拉力或压力)应为N ①= 。
l[]k EA l u v u v u v u v Pl EA ①=--⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎧⎨⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎫⎬⎪⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎪=-⎧⎨⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎫⎬⎪⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎪1(a) b)010*********005100230011223344 (57、已求得图示结构结点2、3的结点位移为式(a)、(b)并已知单元②的整体坐标的单元刚度矩阵为式(c)。
计算单元②2端的弯矩。
(长度单位m ,力单位kN ,角度单位弧度)u v u v 22233303159810φφ⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪⨯⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪=---⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪⨯=0.2-160-4010(a) , 10(b) -5-5..[]k ②=-------⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥⨯1501515015050005001502150115015150150500050015011502105............ (c)58、计算单元①的轴力。
已知图示结构结点1、3的结点位移为:[][]u v u v Pl EA 1133 5 1 2 3TT=-⋅/。
1234①②⑤④③59、已知各杆的E A=⨯=-21101042.kN/m, m22,{}[]T∆21009524025689⨯=-..。
计算图示桁架单元①的杆端力列阵。
4m2kN60、计算图示结构单元③的杆端力列阵{}③F,已知各杆,cm300,kN/cm101.2424=⨯=IE,cm202=A cml100=,结点2位移列阵{}[][]T2T2222rad5313.0cm4596.0cm4730.0101--⨯⨯==∆-θvu。
3l l20kN61、考虑杆件的轴向变形,计算图示结构中单元①的杆端力{}F ①。
已知:I =(/),124m 4E =⨯3107kN /m 2, m 2A =05.。
结点1的位移列阵{}[]δ16110370022710151485=⨯⨯---...m m rad T。
5m62、计算图示刚架单元①在局部坐标下的杆端力{}F ①。
已知各杆E 、A 、I 、l 均为常数,{}[]∆=--ql EIl l 2100002727 0 519 0 0T,不考虑杆件的轴向变形。
lq63、已知图示梁结点转角列阵为{}[]∆=056516822 -/ /Tql i ql i ,EI =常数。
计算B支座的反力。
1m1m第八章 矩阵位移法(参考答案)1、(O)2、(X)3、(O)4、(X)5、(X)6、(O)7、(O)8、(X) 9、(O) 10、(O) 11、(A)12、i K l EI i i K l EA k k l i K 4,/,12,/,/361333222====+=13、K EA l EI l K EI l K 223342151260=+==//,/, 14、K EA l K EI l EA l K EI l 4455366336412==+=/,//,/ 15、[][][][][][]K K K K K K 222222222421=++=①②③③,16、K EA l 77241=+⎛⎝ ⎫⎭⎪⎪, K EAl7824=-17、K EI l K EI l 1138828820==/,/18、lEA lEI K +=34412 045=K 2134(1,2,3)(10,11,12)(7,8,9)(4,5,6)(4,5,0)① ② ③(7,8,0)19、[]K i i i i i i i i i =⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥4202224122223333(+) 4(+) 020、[]K i i i i i i i =⎡⎣⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥840012216612 0 对称,i EI l =/21、[][][][][][][][]K K K K K K K K =+++⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥22222112112222①③③③③②④22、[]K i l i l i l i i i i EI l=-⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=366622/// 12 4对称,式中:23、[]⎥⎦⎤⎢⎣⎡=336l EI K24、 25、(0,0,0)统一编码如图:①② ③ (1,0,4)63(0,0,0)1(1,0,2)4(1,0,3)5(0,0,0)2(0,0,0)(0,0,0)(1,2,3)(0,0,0)(1,2,0)单 元 结 点 位 移 编 码 如 图 :③① ②13524[]4 0 4 0 0 46- 0 0 12223⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+=l EI l EI l EIl EI l EI l EA K[]⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛+= 12 6 36 0 0 223l EI l EI l EA l EI l EI K26、、k k k k k k 221112212222①②②②②③++⎡⎣⎢⎢⎤⎦⎥⎥ 27、123①②③ (0,0)(0,0)(0,1)(0,1)(2,3)(2,3)[]K EA l =⨯+-+---⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥24221111221111128、[]K =⨯⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥1061203003240300300429、{}P 3E kN kN kN m =-⋅⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪212230、{}P ql ql ql 2E =--⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪//22231、{}P ql ql 2E =-⎧⎨⎩⎫⎬⎭224/ 32、{}P ql ql ql ql =--⎧⎨⎪⎪⎩⎪⎪⎫⎬⎪⎪⎭⎪⎪2222242524248////33、{}[]P M Pl Pl ql ql =---(/)(//)/88121222 T34、{}[]P =-7 34 0T35、(0,0)(1,2)(0,3)(0,0)① ② ③{}P =--⋅-⋅⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪ kN 5kN m 16kN m 236、P ql P ql P ql 1324224===-,/,37、{}P ql ql ql =-⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪ ///222524238、P ql P ql P ql 45622212==-=/,/,/39、P p l P P ql P M P l ql 1133412812=-=--=-+,,40、2685、P ql P ql P ql P 327891112220==-=-=/,/,/, 41、{}[]P =---6 22 14 5 12 18T42、{}[]P =---4 10 4 0 6 4T43、{}P P P Pl 2 =--⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪///2323444、(0,0,0)(1,4,3)(0,0,0)(1,2,3)1234 {}P =---⋅⎧⎨⎪⎪⎩⎪⎪⎫⎬⎪⎪⎭⎪⎪38170kN kN kN m45、(1,0,2)(3,4,5)(0,6,0,)(0,0,0){}P ql ql ql ql ql =--⎧⎨⎪⎪⎪⎪⎩⎪⎪⎪⎪⎫⎬⎪⎪⎪⎪⎭⎪⎪⎪⎪ 01112238222////46、{}[]P T40 -32 -14=47、{}P =--⋅⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪ kN 10kN 10kN m 1048、{}TPl ql ql P P ⎥⎦⎤⎢⎣⎡+--=812,2,2,0,0249、{}P =⎧⎨⎩⎫⎬⎭8kN 6kN50、{}[]kN P T40,30,20,10--= 51、4319.066-==F S 52、N 1400587=-.kN 53、F 202336=.kN54、F F 3603330333=⋅=-⋅.,.kN m kN m55、{}[]F ①=-85581.kN 85.581kN T 56、3P (压力)57、M 28925②=-.kN58、N P ①=3(压 力 ) 59、{}⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧-=0 kN 5 0 kN 5 ①F60、{}F ③=----⎧⎨⎪⎪⎪⎪⎩⎪⎪⎪⎪⎫⎬⎪⎪⎪⎪⎭⎪⎪⎪⎪ kN kN kN.m kN kN kN.m 19319726651561193197261321..... 61、{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⋅-⋅-=m kN 3873.13kN 8698.13 kN 1006.11 m kN 0385.4kN 1302.10 kN 1006.11 ①F62、{}F ql ql ql ql ①分=⎧⎨⎪⎪⎪⎪⎩⎪⎪⎪⎪⎫⎬⎪⎪⎪⎪⎭⎪⎪⎪⎪ 007902340020800575722....()63、R ql B =↑067857.()。
