结构力学-第9章 矩阵位移法课堂练习
结构力学课后习题解答:9矩阵位移法习题解答.docx

第9章矩阵位移法习题解答习题9.1是非判断题(1)矩阵位移法既可计算超静定结构,又可以计算静定结构。
()(2)矩阵位移法基本未知量的数目与位移法基本未知量的数目总是相等的。
()(3)单元刚度矩阵都具有对称性和奇异性。
()(4)在矩阵位移法中,整体分析的实质是建立各结点的平衡方程。
()(5)结构刚度矩阵与单元的编号方式有关。
()(6)原荷载与对应的等效结点荷载使结构产生相同的内力和变形。
()【解】(1)正确。
(2)错误。
位移法中某些不独立的杆端位移不计入基本未知量。
(3)错误。
不计结点线位移的连续梁单元的单刚不具奇异性。
(4)正确。
(5)错误。
结点位移分量统一编码会影响结构刚度矩阵,但单元或结点编码则不会。
(6)错误。
二者只产生相同的结点位移。
习题9.2填空题(1)矩阵位移法分析包含三个基本环节,其一是结构的,其二是分析,其三是分析。
(2)已知某单元的定位向量为[3 5 6 7 8 9]七则单元刚度系数炫应叠加到结构刚度矩阵的元素中去。
(3)将非结点荷载转换为等效结点荷载,等效的原则是。
(4)矩阵位移法中,在求解结点位移之前,主要工作是形成矩阵和_________________ 列阵。
(5)用矩阵位移法求得某结构结点2的位移为4=[. V2 ft]T=[0.8 0.3 0.5]T,单元①的始、末端结点码为3、2,单元定位向量为尸>=[0 0 0 3 4 5]T ,设单元与x轴之间的夹角为a =买,则2 尹> =O(6 )用矩阵位移法求得平面刚架某单元在单元坐标系中的杆端力为F e =[7.5 -48 -70.9 -7.5 48 -121.09]T ,则该单元的轴力心=kN。
【解】(1)离散化,单元,整体;(2)灯8;(3)结点位移相等;(4)结构刚度,综合结点荷载;(5)[0 0 0 0.3 -0.8 0.5]。
(6)-7.5o离、空的值以及K ⑴中元素妍、愚、姒的值。
【解】各刚度系数的物理意义如习题解9.3图所示。
第九章矩阵位移法习题集

第九章 矩阵位移法 【练习题】9-1 是非题:1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。
2、单元刚度矩阵均具有对称性和奇异性。
3、局部坐标系与整体坐标系之间的坐标变换矩阵T 是正交矩阵。
4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。
5、用 矩 阵 位 移 法 计 算 连 续 梁 时 无 需 对 单 元 刚 度 矩 阵 作 坐 标 变 换。
6、结 构 刚 度 矩 阵 是 对 称 矩 阵 ,即 有K i j = K j i ,这 可 由 位 移 互 等 定 理 得 到 证 明 。
7、结构刚度方程矩阵形式为:[]{}{}K P ∆=,它是整个结构所应满足的变形条件。
8、在直接刚度法的先处理法中,定位向量的物理意义是变形连续条件和位移边界条件。
9、等效结点荷载数值等于汇交于该结点所有固端力的代数和。
10、矩阵位移法中,等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。
11、矩阵位移法既能计算超静定结构,也能计算静定结构。
9-2 选择题:1、已知图示刚架各杆EI = 常数,当只考虑弯曲变形,且各杆单元类型相同时,采用先处理法进行结点位移编号,其正确编号是:(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.21341234123412342、平面杆件结构一般情况下的单元刚度矩阵[]k 66⨯,就其性质而言,是: A .非对称、奇异矩阵; B .对称、奇异矩阵; C .对称、非奇异矩阵; D .非对称、非奇异矩阵。
3、单元i j 在图示两种坐标系中的刚度矩阵相比:A .完全相同;B .第2、3、5、6行(列)等值异号;C .第2、5行(列)等值异号;D .第3、6行(列)等值异号。
jxi4、矩阵位移法中,结构的原始刚度方程是表示下列两组量值之间的相互关系: A .杆端力与结点位移; B .杆端力与结点力; C .结点力与结点位移; D .结点位移与杆端力 。
结构力学(9.14.1)--矩阵位移法习题2
5kN m
8m 8m
8m
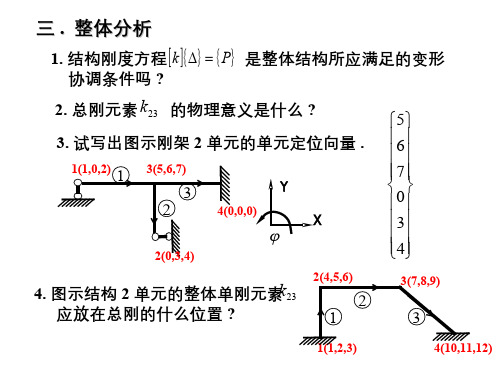
三 . 整体分析
12. 试求图示结构 ( 不计轴变 ) 的荷载列阵 ( 先处理法 ).
1(1,0,2) 2(1,0ቤተ መጻሕፍቲ ባይዱ3) 3(1,0,3)
X1
X2
4(0,0,0)
P
X
1
0
X
2
0
四 . 求杆端力
1. 连续梁在一般荷载作用下 , 单元杆端力由下式计算 . 是否正确 ?
6
48
4
2
1(0,0,0)
12
1 6
k
6
48
4(1,0,3)
3
2(0,0,0)
3
1
2
3
例 . 不计轴变 , 作弯矩图
已知 : 各杆长均为 12m, 线刚度均为 12
P 10kN, q 5kN / m
P 10kN, q 5kN / m
解 : 1 6 1 6
k
1
6
1
48 6
6 1
24
6
6
24
6
48
3(1,0,2)
2
1
1 6 1 6 1 0
k
1
6 1
48 6
6 1
24
2
0
63 1
6 24
EI
EI
EA 2l
2 2
l
l
三 . 整体分析
4(1,0,0)
5(1,0,0)
龙驭球《结构力学》笔记和课后习题(含真题)详解(矩阵位移法)【圣才出品】

第9章 矩阵位移法9.1 复习笔记一、矩阵位移法的基本思路矩阵位移法又称为杆件结构的有限元法。
分析的两个基本步骤:(1)单元分析;(2)整体分析。
单元分析:建立杆端力与杆端位移间的刚度方程,形成单元刚度矩阵。
整体分析:将单元合成整体,按照刚度集成规则形成整体刚度矩阵,建立位移基本方程。
二、单元刚度矩阵(局部坐标系)进行单元分析,推导单元刚度方程和单元刚度矩阵。
单元刚度方程是指由单元杆端位移求单元杆端力的一组方程,可以用“”表示,由位移求力称为“正问题”。
相应的由力求位移称为“反问题”。
正问题的解是唯一的确定的,但是反问题则可能无解,如果有解也非唯一解。
当外部荷载为不平衡力系时,反问题无解;当外荷载为平衡力系时,反问题有解但是因为杆件除本身变形外还可有任意刚体位移,此时反问题的解不唯一。
本书暂不考虑反问题的求解。
1.一般单元图9-1所示为平面刚架中的一个等截面直杆单元.单元的两个端点采用局部编码1和2,由端点1到端点2的方向规定为杆轴的正方向,在图中用箭头标明。
F →∆e图9-1图中采用坐标系,其中轴与杆轴重合。
这坐标系称为单元坐标系或者局部坐标系。
字母、的上面都画了一横,作为局部坐标系的标志。
推导单元刚度方程时,有以下几点需要注意:重新规定正负号规则、讨论杆件单元的一般情况、采用矩阵表示形式。
在局部坐标系中,图9-2所示的位移、力分量方向为正方向。
图9-2杆件性质:长度l ,截面面积A ,截面惯性矩I ,弹性模量E ;杆端位移u 、v 、θ。
根据杆端位移可以推导出下面两组刚度方程:(9-1)x y x x y(9-2)将上述六个刚度方程列成矩阵形式:(9-3)其中就是局部坐标系下单元刚度矩阵,即为(9-4)2.单元刚度矩阵的性质 (1)单元刚度系数的意义e e ek F∆=eK代表单元杆端第j 个位移分量等于1时所引起的第i 个杆端力分量。
(2)是对称矩阵,即。
(3)一般单元的是奇异矩阵,即,因此不存在逆矩阵。
09矩阵位移法(学习版)(1)

1
2
3 6
4
y
5
θ x
O
练习:
3 ④ 2 ① 1
8 ⑨ ⑤ 6 ⑦ ② 4 5 ⑧ 7 ⑩ ⑥
13
12 10 11 ③ 9
(2)结点位移编码 矩阵位移法基本未知量的确定: 矩阵位移法基本未知量的确定不是唯一的,它与 单元如何划分,是否考虑轴向变形以及如何编写程序 有关。 结点位移的统一编码 —— 整体码 用矩阵位移法进行结构分析时,基本未知量是结点 位移,这就需要将结构中全部结点位移分量进行统一编 码。
第九章
矩阵位移法
9.1 概述
1. 概述
结构矩阵分析是采用矩阵方法分析结构力学问题的 一种方法。与传统的力法、位移法相对应,结构矩阵分 析中也有矩阵力法和矩阵位移法,或柔度法与刚度法。 矩阵位移法易于实现计算过程程序化而被广泛应用。 矩阵位移法是以结点位移为基本未知量,借助矩阵 进行分析,并用计算机解决各种杆系结构受力、变形等 计算的方法。
e
e
建立单元的杆端力和杆端 位移之间关系的过程称单元分 析,形成的方程称单元刚度方 程。
e
⎡δ 1 ⎤ ⎡ u i ⎤ ⎢ ⎥ ⎢ ⎥ δ 2 ⎥ ⎢ vi ⎥ ⎢ e ⎡ δ i ⎤ ⎢δ 3 ⎥ ⎢θ i ⎥ e δ =⎢ ⎥ =⎢ ⎥ =⎢ ⎥ ⎣δ j ⎦ ⎢δ 4 ⎥ ⎢u j ⎥ ⎢δ 5 ⎥ ⎢ v j ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎦ ⎦ ⎢ ⎣θ j ⎥ ⎣δ 6 ⎥
2. 单元分析
y y e i x
α
j x
局部坐标系(单元坐标系):进行某一单元的单元分析时所 建立的坐标系。 局部坐标系相对于整体坐标系的方位角用α表示。α的方向 以 x 轴向 x 轴逆时针转动为正。即便在一个结构中,各单元的局 部坐标系也不完全相同。
第9章 矩阵位移法 例题

第9章 矩阵位移法习 题9-1:请给图示结构编号(同时用先处理法和后处理法)及建立坐标。
题9-1图 9-2:求图示连续梁的整体刚度矩阵。
题9-2图9-3:求图示刚架的整体刚度矩阵。
(c )(e )题9-3图9-4:求图示组合结构的整体刚度矩阵。
题9-4图9-5:求图示桁架结构的整体刚度矩阵,所有杆件的EA 均相同。
题9-5图9-6:求图示排架结构的整体刚度矩阵。
题9-6图 9-7:求图示结构的等效结点荷载,请利用结构的对称性。
1kN/m题9-7图9-8:求图示结构的等效结点荷载,请利用结构的对称性。
题9-8图9-9:求图示结构的等效结点荷载。
题9-9图9-10:求出图示结构的荷载列阵。
题9-10图9-11:求出图示结构的荷载列阵,请分别用先处理法和后处理法进行编号。
qq题9-11图9-12:求图示结构的荷载列阵,考虑轴向变形。
题9-12图9-13:求图示结构的荷载列阵。
题9-13图9-14:图示连续梁中间支座发生了下向的移动a ,请求出其整体刚度方程。
题9-14图10kN/mq9-15:请求出图示连续梁的整体刚度方程。
题9-15图9-16:求图示连续梁的整体刚度矩阵。
题9-16图9-17:图示结构温度发生了变化,请求出整体刚度方程。
杆件的EI 、EA 相同。
题9-17图9-18:图示结构温度发生了变化,请求出整体刚度方程。
题9-18图9-19:图示结构发生了支座移动,请画出结构的内力图。
00题9-19图9-20:已知图示梁B 点的B v 、B ϕ和C 点的C ϕ,请求出单元杆端力的列阵。
题9-20图9-21:求题9-3图示刚架的整体刚度矩阵,忽略轴向变形。
9-22:求题9-10图示结构的整体刚度矩阵,用后处理法编号。
9-23:求出梁的整体刚度方程,弹簧的刚度系数为k 。
题9-23图9-24:求出图示结构的整体刚度方程,忽略轴向变形,弹簧刚度系数为k 。
题9-24图L。
结构力学基础矩阵位移法基本概念、计算程序和例题讲解

例形成图示刚架可动结点劲度矩阵,E,I ,A为常数。
解: 1.编号,如图(b) 2.确定单元杆端自由度序号。
3.计算 kmi 4.计算单元转换矩阵
5.形成单元在整体坐标系中的劲度矩阵
6.根据单元杆端自由度序号叠加
二、可动结点劲度矩阵性质
1.对称方阵
反力互等定理
2.非奇异矩阵 考虑了约束条件,排除了刚体位移
7.求杆端力Fmi
8.求支座反力 支座反力由下式
计算,得
9.内力图
例2 求图2-21(a)所示平面刚架的内力,已知各杆 I 0.005m4
A0.05m2,E2106kNmA2B杆、CD杆杆
返回
§9—3 可动结点劲度矩阵
一、形成可动结点劲度矩阵的步骤
步骤: 1.对结构进行结点编号、单元标号、自由度编号: 2.确定单元杆端自由度序号(考虑约束条件); 3.计算单元在局部坐标系中的劲度矩阵kmi 4.计算单元转换矩阵Ti 5.形成单元在整体坐标系中的劲度矩阵ki TiTkmiTi
6.按”对号入座”原则,将ki叠加到 k 中。
结构力学基础 矩阵位移法基本概念、计算程
序和例题讲解
§9-1 矩阵位移法基本概念 §9-2 单元劲度矩阵 §9-3 可动结点劲度矩阵 §9-4 可动结点等效荷载列阵 §9-5 单元杆端力和支座反力 §9-6 例题 §9-7 平面刚架计算程序
§9—1 矩阵位移法的基本概念
一、坐标系和符号规定 图示连续梁:
4.求 K
(1)计算机各单元的方向余弦和杆长:
(2)求 kmi
(3)求ki
单元(1):Cx=0 Cy=1
杆长:l 同理:
(4)求 按照“对号入座“原则,由ki形成k哪
例如: 同理:
矩阵位移法练习题

结构力学自测题(第八单元)矩阵位移法姓名 学号一、是 非 题(将 判 断 结 果 填 入 括 弧 :以 O 表 示 正 确 ,以 X 表 示 错 误 )1、用 矩 阵 位 移 法 计 算 连 续 梁 时 无 需 对 单 元 刚 度 矩 阵作 坐 标 变 换。
()2、结 构 刚 度 矩 阵 是 对 称 矩 阵 ,即 有K ij = K ji ,这 可 由位 移 互 等 定 理 得 到 证 明 。
() 3、图 示 梁 结 构 刚 度 矩 阵 的 元 素 K EI l 11324=/ 。
()EI llEI 212xy M , θ附:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--------l EI l EI l EI l EI lEI l EI l EI l EI l EAl EA l EI lEI l EI l EI l EI l EI l EI l EI lEA l EA 4602606120612000002604606120612000002223232223234、在 任 意 荷 载 作 用 下 ,刚 架 中 任 一 单 元 由 于 杆 端 位移 所 引 起 的 杆 端 力 计 算 公 式 为 :{}[][]{}FT K eee=δ 。
()二、选 择 题 ( 将 选 中 答 案 的 字 母 填 入 括 弧 内 )1、已 知 图 示 刚 架 各杆 EI = 常 数,当 只 考 虑 弯 曲 变 形 ,且各 杆 单 元 类 型 相 同 时 ,采 用 先 处 理 法 进 行 结 点 位 移 编 号 ,其 正 确 编 号 是 :(0,1,2) (0,0,0) (0,0,0) (0,1,3) (0,0,0) (1,2,0) (0,0,0) (0,0,3)(1,0,2)(0,0,0) (0,0,0) (1,0,3) (0,0,0)(0,1,2)(0,0,0) (0,3,4)A.B.C.D.2134 123 4 12 34 1 2 3 4 xyM , θ ( ) 2、平 面 杆 件 结 构 一 般 情 况 下 的 单 元 刚 度 矩 阵 []k 66⨯,就 其 性 质 而 言 ,是 :()A .非 对 称 、奇 异 矩 阵 ;B .对 称 、奇 异 矩 阵 ;C .对 称 、非 奇 异 矩 阵 ;D .非 对 称 、非 奇 异 矩 阵 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结构力学练习题——矩阵位移法
一、是 非 题(将 判 断 结 果 填 入 括 弧 :以 O 表 示 正 确 ,以 X 表 示 错 误 ) 1、用 矩 阵 位 移 法 计 算 连 续 梁 时 无 需 对 单 元 刚 度 矩 阵 作 坐 标 变 换。
)(对 2、结 构 刚 度 矩 阵 是 对 称 矩 阵 ,即 有
K ij = K ji ,这 可 由 位 移 互 等 定 理 得 到 证
明 。
()错 3、图 示 梁 结 构 刚 度 矩 阵 的 元 素 K EI l 113
24=/ 。
(
)错
l
l
附:
⎥⎥⎥⎥⎥
⎥
⎥⎥⎥⎥⎥⎥⎥⎦⎤
⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢
⎢⎢⎢⎣
⎡--------l EI l EI l EI l EI l
EI l EI l EI l EI l EA l EA l EI l
EI l EI l EI l EI l EI l EI l EI l
EA l EA 4602606120612000002604606120612000002
22323222323
二、选 择 题 ( 将 选 中 答 案 的 字 母 填 入 括 弧 内 )
1、已 知 图 示 刚 架 各杆 EI = 常 数,当 只 考 虑 弯 曲 变 形 ,且 各 杆 单 元 类 型 相 同
时 ,采 用 先 处 理 法 进 行 结 点 位 移 编 号 ,其 正 确 编 号 是 :A
(0,1,2) (0,0,0) (0,0,0) (0,1,3) (0,0,0) (1,2,0) (0,0,0) (0,0,3)
(1,0,2)
(0,0,0) (0,0,0) (1,0,3) (0,0,0)
(0,1,2)
(0,0,0) (0,3,4)
A.
B.
C.
D.
2
1
3
4 1
2
3 4 1
2 3
4 1 2 3 4
( )
2、平 面 杆 件 结 构 一 般 情 况 下 的 单 元 刚 度 矩 阵
[]k 66
⨯,就 其 性 质 而 言 ,是 :
(
)B
A .非 对 称 、奇 异 矩 阵 ;
B .对 称 、奇 异 矩 阵 ;
C .对 称 、非 奇 异 矩 阵 ;
D .非 对 称 、非 奇 异 矩 阵 。
3、单 元 i j 在 图 示 两 种 坐 标 系 中 的 刚 度 矩 阵 相 比 :B
A . 完 全 相 同 ;
B . 第 2、3、5、6 行 (列 ) 等 值 异 号 ;
C . 第 2、5 行 (列 )等 值 异 号 ;
D . 第 3、6 行 (列 ) 等 值 异 号 。
(
)
y
x
i
4、矩 阵 位 移 法 中 ,结 构 的 原 始 刚 度 方 程 是 表 示 下 列 两 组 量 值 之 间 的 相 互
关 系 :
(
)C
A .杆 端 力 与 结 点 位 移 ;
B .杆 端 力 与 结 点 力 ;
C .结 点 力 与 结 点 位 移 ;
D .结 点 位 移 与 杆 端 力 。
5、单 元 刚 度 矩 阵 中 元 素 k ij 的 物 理 意 义 是 :B
A .当 且 仅 当 δi =1 时 引 起 的 与 δj 相 应 的 杆 端 力 ;
B .当 且 仅 当 δj =1时 引 起 的 与 δi 相 应 的 杆 端 力 ;
C .当 δj =1时 引 起 的 δi 相 应 的 杆 端 力 ;
D .当 δi =1时 引 起 的 与 δj 相 应 的 杆 端 力。
()
7、用 矩 阵 位 移 法 解 图 示 结 构 时 ,已 求 得 1 端 由 杆 端 位 移 引 起 的 杆 端 力 为
{}[]T F 461--=,则 结 点 1 处 的 竖 向 反 力 Y 1 等 于 :D
A .6-;
B .-10;
C .10 ;
D .14 。
(
)
M 20kN/m
三、填 充 题 ( 将 答 案 写 在 空 格 内)
1、图 示 桁 架 结 构 刚 度 矩 阵 有 1个 元 素 ,其 数 值 等 于2EA/L。
3m
3m A
B
C D
EA
EA
EA
2、图 示 刚 架 用 两 种 方 式 进 行 结 点 编 号 ,结 构 刚 度 矩 阵 最 大 带 宽 较 小 的 是
图
B 。
35
641
2
71
234567
(a)
(b)
3、图 示 梁 结 构 刚 度 矩 阵 的 主 元 素 K K 1122== , 12I 4I 。
l
l
五、图 a 所 示 结 构 (整 体 坐 标 见 图 b ),图 中 圆 括 号 内 数 码 为 结 点 定 位 向 量 (力
和 位 移 均 按 水 平 、竖 直 、转 动 方 向 顺 序 排 列 )。
求 结 构 刚 度 矩 阵 []K 。
(不 考 虑 轴 向 变
形 )
6m
(a)
(b)
六、求 图 示 结 构 的 自 由 结 点 荷
载 列 阵 {}P 。
l
l
七、图 a 所 示 结 构 ,整 体 坐 标 见 图 b ,图 中 圆 括 号 内 数 码 为 结 点 定 位 向 量 (
力 和 位 移 均 按 水 平 、竖 直 、转 动 方 向 顺 序 排 列 )。
求 等 效 结 点 荷 载 列 阵 {}P E 。
( 不 考 虑 轴 向 变 形 )
3m 36
八、已 知 图 示 连 续 梁 结 点 位 移 列 阵 {}θ如 下 所 示 ,试 用 矩 阵 位 移 法 求 出 杆
件 23 的 杆 端 弯 矩 并 画 出 连 续 梁 的 弯 矩 图 。
设 q = 20kN/m ,23 杆 的
i =⨯⋅10106.kN cm 。
{}θ=--⎧⎨⎪⎪⎩⎪⎪⎫⎬⎪⎪⎭⎪⎪⨯-365
714572286104
....rad
6m
3m
3m
九、已 知 图 示 桁 架 的 结 点 位 移 列 阵 为
{}[]∆=--017265
04007 0 2.5677 0.0415 1.0415 1.3673 1.6092 1.6408 0 1.2084 T
..
,EA =1kN 。
试 求 杆 14 的
轴 力 。
1m
1m
矩阵位移法答案
一、 1 O 2 X 3 X
二、 1 A 2 B 3 B 4 C 5 B
6 C
7 D
三、
1、 1 、 2EA/L
2、 b
3、 i EI l
K i K i === , , 1122124 (7分 )
五、
[]K i =--⎡⎣⎢⎢⎢⎤
⎦
⎥⎥⎥ 1 0 1 8 2 0 2 413/ (10分 )
六、
{}[]
T
/ql +m -/ql -P 12202= (7分 )
七、
{}[] 2 3
422142
E T
1P =-- (7分 )
八、
M M 233242885140⎧⎨⎩⎫⎬⎭=-⎧⎨⎩⎫⎬⎭.. 42.88
51.40
90
(kN m).M
( 7分)
九、
N 1400587=-.kN (7分 )。
