西工大计算流体力学试卷(整合)
最新西工大计算流体力学试卷(整合)

试卷1. 简述计算流体力学的特点及其应用领域。
CFD 是以计算机作为模拟手段,运用一定的计算技术寻求流体力学各种复杂问题的离散化数值解。
它的主要特征:(1)数值解而不是解析解;(2)计算技术起关键作用;(3)与计算机的发展紧密相关。
(成本较低,适用范围宽,可靠性差,表达困难)应用领域:航空、航天、气象、船舶、武器装备、 水利、化工、建筑、机械、汽车、海洋、体育、环境、卫 生等2. 等步长网格分布情况下u x∂∂的一阶向前差分、22u x ∂∂的二阶中心差分表达式。
(P89) 一阶向前差分:1,,,()i j i j i j u u u x x x+-∂=+O ∆∂∆() 二阶中心差分:21,,1,2,222()()i j i j i j i j u u u u x x x +--+∂=+O ∆∂∆() 3. 简答题1) 什么是差分方程的相容性?差分方程与微分方程的差别是截断误差R 。
必要时通过缩小空间步长(网格尺寸)h 和时间步长t ,这一误差应可缩小至尽可能小。
当h->0和t->0时,若R->0,则差分方程趋于微分方程,表示这两个方程是一致的。
这时称该差分方程与微分方程是相容的。
2) 什么是差分解的收敛性?当微分方程在离散为差分方程来求解,当步长h 0→时,存在着差分方程的解n y 能够收敛到微分方程的准确解y()n x ,这就是差分方法的收敛性。
收敛性定义:对于任意节点的0n x x nh =+,如果数值解n y 当h 0→(同时n →∞)时趋向于准确解y()n x ,则称该方法是收敛的。
3) 什么是差分解的稳定性?数值计算时,除计算机舍入误差(字长有限)外,初始条件或方程中某些常数项也有可能给的不尽精确。
舍入误差和这些误差在计算过程中可能一步步积累与传递,误差的传递,有时可能变大,有时可能变小。
某一步舍入误差放大或缩小的问题,称为差分解的数值稳定性问题。
稳定性定义:对于存在正常数0h 和对于每个0ε>存在一个正常数δ,使得当初值和右端的扰动满足max ()h x I s x σδ∈+<时, 原方程与扰动方程的解对一切满足估计式max ()()hx I y x y x ε∈-<,则称该格式是稳定的。
西工大-计算流体力学大作业
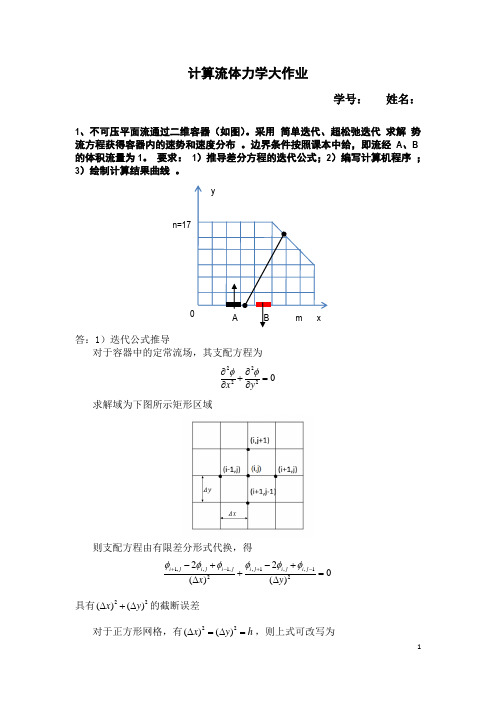
计算流体力学大作业学号: 姓名:1、不可压平面流通过二维容器(如图)。
采用 简单迭代、超松弛迭代 求解 势流方程获得容器内的速势和速度分布 。
边界条件按照课本中给,即流经 A 、B 的体积流量为1。
要求: 1)推导差分方程的迭代公式;2)编写计算机程序 ; 3)绘制计算结果曲线 。
答:1)迭代公式推导对于容器中的定常流场,其支配方程为22220x yφφ∂∂+=∂∂ 求解域为下图所示矩形区域则支配方程由有限差分形式代换,得1,,1,,1,,122220()()i j i j i ji j i j i j x y φφφφφφ+-+--+-++=∆∆具有22()()x y ∆+∆的截断误差对于正方形网格,有22()()x y h ∆=∆=,则上式可改写为n=17,1,1,,1,11()4i j i j i j i j i j φφφφφ+-+-=+++若采用简单迭代公式,即Liebmann 公式,则有(1)()(1)()(1),1,1,,1,11()4n n n n n i j i j i j i j i j φφφφφ++++-+-=+++若采用超松弛迭代,即SOR 公式,则有(1)()()(1)()(1),,1,1,,1,1(1)()4n n n n n n i j i j i j i j i j i j ωφωφφφφφ++++-+-=-++++其中松弛因子12ω<<。
ω最佳值opt ω为opt ω=式中cos(/)cos(/)m n αππ=+,m ,n 分别表示在网格系统中垂直线和水平线的总数。
2)计算机程序本程序采用C 语言编写。
程序源代码如下: #include<stdio.h> #include<math.h> void main() { int m=25,n=17,ilast[17],jlast[25]; int step1,step2; double h=0.25; double psi_j[25][17],psiprv_j,vel_j[25][17],velx_j[25][17],vely_j[25][17]; double psi_c[25][17],psiprv_c,vel_c[25][17],velx_c[25][17],vely_c[25][17]; double Pi,Alpha,Omega,Error; int i,j; for(i=0;i<17;i++) jlast[i]=17; for(i=17;i<m;i++) jlast[i]=17-(i-16); for(j=0;j<9;j++) ilast[j]=25; for(j=9;j<n;j++) ilast[j]=25-(j-8); //数据初始化 for(j=0;j<n;j++) { psi_j[0][j]=1.0; psi_c[0][j]=1.0;}for(i=1;i<m;i++){psi_j[i][jlast[i]-1]=1.0;psi_c[i][jlast[i]-1]=1.0; }for(j=0;j<8;j++){psi_j[m-1][j]=1.0;psi_c[m-1][j]=1.0;}for(i=1;i<m-1;i++){if(i>6 && i<21){psi_j[i][0]=0.0;psi_c[i][0]=0.0;}else{psi_j[i][0]=1.0;psi_c[i][0]=1.0;}}for(i=1;i<m-1;i++){for(j=1;j<jlast[i]-1;j++){psi_j[i][j]=0.5;psi_c[i][j]=0.5;}}//处理右上角数据for(i=0;i<m;i++){for(j=0;j<n;j++){if(j>jlast[i]-1){psi_j[i][j]=0;vel_j[i][j]=3;psi_c[i][j]=0;vel_c[i][j]=3;}}}Pi=4.0*atan(1.0);Alpha=cos(Pi/m)+cos(Pi/n);Omega=(8.0-4*sqrt(4-pow(Alpha,2)))/pow(Alpha,2);//计算速势step1=0;step2=0;//简单迭代while(1){Error=0.0;for(i=1;i<m-1;i++){for(j=1;j<jlast[i]-1;j++){psiprv_j=psi_j[i][j];psi_j[i][j]=(psi_j[i-1][j]+psi_j[i+1][j]+psi_j[i][j-1]+psi_j[i][j+1])/4.0;Error=Error+fabs(psi_j[i][j]-psiprv_j);}}step1++;if(step1>1000)break;if(Error<=0.001)break;}//超松弛迭代while(1){Error=0.0;for(i=1;i<m-1;i++){for(j=1;j<jlast[i]-1;j++){psiprv_c=psi_c[i][j];psi_c[i][j]=(1-Omega)*psi_c[i][j]+Omega*(psi_c[i-1][j]+psi_c[i+1][j]+psi_c[i][j-1]+psi_c[i][j+1])/4.0;Error=Error+fabs(psi_c[i][j]-psiprv_c);}}step2++;if(step2>1000)break;if(Error<=0.001)break;}//计算速度for(i=0;i<m;i++){for(j=0;j<jlast[i];j++){if(j==0){vely_j[i][j]=(-3*psi_j[i][j]+4*psi_j[i][j+1]-psi_j[i][j+2])/2/h;vely_c[i][j]=(-3*psi_c[i][j]+4*psi_c[i][j+1]-psi_c[i][j+2])/2/h;}else if(j==jlast[i]-1){vely_j[i][j]=(psi_j[i][j-2]-4*psi_j[i][j-1]+3*psi_j[i][j])/2/h;vely_c[i][j]=(psi_c[i][j-2]-4*psi_c[i][j-1]+3*psi_c[i][j])/2/h;}else{vely_j[i][j]=(psi_j[i][j+1]-psi_j[i][j-1])/2/h;vely_c[i][j]=(psi_c[i][j+1]-psi_c[i][j-1])/2/h;}}}for(j=0;j<n;j++){for(i=0;i<ilast[j];i++){if(i==0){velx_j[i][j]=(-3*psi_j[i][j]+4*psi_j[i+1][j]-psi_j[i+2][j])/2/h;velx_c[i][j]=(-3*psi_c[i][j]+4*psi_c[i+1][j]-psi_c[i+2][j])/2/h;}else if(i==ilast[j]-1){velx_j[i][j]=(psi_j[i-2][j]-4*psi_j[i-1][j]+3*psi_j[i][j])/2/h;velx_c[i][j]=(psi_c[i-2][j]-4*psi_c[i-1][j]+3*psi_c[i][j])/2/h;}else{velx_j[i][j]=(psi_j[i+1][j]-psi_j[i-1][j])/2/h;velx_c[i][j]=(psi_c[i+1][j]-psi_c[i-1][j])/2/h;}}}for(i=0;i<m;i++){for(j=0;j<jlast[i];j++){vel_j[i][j]=sqrt(pow(velx_j[i][j],2)+pow(vely_j[i][j],2));vel_c[i][j]=sqrt(pow(velx_c[i][j],2)+pow(vely_c[i][j],2));}}//输出结果分布FILE *fp;fp=fopen("f:\\ESL\\YFresult.txt","w");fprintf(fp,"简单迭代结果\n");fprintf(fp,"速度势分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",psi_j[i][j]);}}fprintf(fp,"速度分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",vel_j[i][j]);}}fprintf(fp,"超松弛迭代结果\n");fprintf(fp,"速度势分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",psi_c[i][j]);}}fprintf(fp,"速度分布\n");for(j=n-1;j>=0;j--){for(i=0;i<ilast[j];i++){fprintf(fp,"%-10.6f\n",vel_c[i][j]);}}fclose(fp);//输出tecplot数据FILE *fp1;fp1=fopen("f:\\ESL\\TECPLOT-result.txt","w");fprintf(fp1,"title=erwei grid\n");fprintf(fp1,"variables=x, y, psi_easy, velocity_easy, psi_SOR\n, velocity_SOR\n");fprintf(fp1,"zone t=grid,i=25,j=17,f=point\n");for(j=0;j<n;j++){for(i=0;i<m;i++){fprintf(fp1,"%-10.6f,%-10.6f,%-10.6f,%-10.6f,%-10.6f,%-10.6f\n",i*h,j*h,psi_j[i][j],vel_j[i][j],p si_c[i][j],vel_c[i][j]);}}fclose(fp1);}3)计算结果采用简单迭代,容器内的速势和速度分布速势分布(简单迭代)速度分布(简单迭代)采用超松弛迭代,容器内的速势和速度分布速势分布(SOR ) 速度分布(SOR )2、用点源(汇)分布在对称轴的源汇模拟流体绕过NACA0012旋称体的二维轴对称势流解。
工程流体力学计算题集(含答案)

30.(6分)飞机在10000m 高空(T=223.15K,p=0.264bar)以速度800km/h 飞行,燃烧室的进口扩压通道朝向前方,设空气在扩压通道中可逆压缩,试确定相对于扩压通道的来流马赫数和出口压力。
(空气的比热容为C p =1006J/(kg ·K),等熵指数为k=1.4,空气的气体常数R 为287J/(kg ·K))T 0=T ∞+v C p ∞=+⨯⨯232222315*********21006/.()/()=247.69KM ∞=v a ∞∞=⨯⨯⨯=(/)...80010360014287223150743 P 0=p ∞11221+-⎡⎣⎢⎤⎦⎥∞-k M k k =0.26411412074038214141+-⨯⎡⎣⎢⎤⎦⎥=-.....bar31.(6分)一截面为圆形风道,风量为10000m 3/h ,最大允许平均流速为20m/s ,求:(1)此时风道内径为多少?(2)若设计内径应取50mm 的整倍数,这时设计内径为多少? (3)核算在设计内径时平均风速为多少? 依连续方程(ρ=C )v 1A 1=v 2A 2=q v(1)v 1π412d q v = d 1=100004360020⨯⨯π=0.42m=420mm (2)设计内径应取450mm 为50mm 的9倍,且风速低于允许的20m/s (3) 在设计内径450mm 时,风速为 v q d m s v 2222441000036000451746==⨯⨯=ππ../ 32.(7分)离心式风机可采用如图所示的集流器来测量流量,已知风机入口侧管道直径d=400mm,U 形管读数h=100mmH 2O ,水与空气的密度分别为ρ水=1000kg/m 3,ρ空=1.2kg/m 3,忽略流动的能量损失,求空气的体积流量q v 。
由伯努利方程0+0+0=p gρ+0+v g 22得v=-2p ρ由静力学方程p+ρ水gh=0⇒p=-ρ水gh 代入 得 v=22980701100012ghρρ水=⨯⨯⨯...=40.43m/s q v =v •=⨯⨯=ππ44043404508223d m s .(.)./33.(7分)要为某容器底部设计一个带水封的疏水管,结构如图示:容器内部的压强值,最高时是表压强p e =1500Pa,最低时是真空值p v =1200Pa,要求疏水管最高水位应低于容器底部联接法兰下a=0.1m ,最低水位应在疏水管口上b=0.2m(水密度ρ=1000kg/m 3,重力加速度g=9.8m/s 2)求:(1)疏水管长度L 。
大学生工程流体力学历年试卷及答案(题库集)(考点集)

《工程流体力学》综合复习资料×√一、判断题1、根据牛顿内摩擦定律,当流体流动时,流体内部内摩擦力大小与该处的流速大小成正比。
F2、一个接触液体的平面壁上形心处的水静压强正好等于整个受压壁面上所有各点水静压强的平均值。
T3、流体流动时,只有当流速大小发生改变的情况下才有动量的变化。
F4、在相同条件下,管嘴出流流量系数大于孔口出流流量系数。
T5、稳定(定常)流一定是缓变流动。
×6、水击产生的根本原因是液体具有粘性。
×7、长管是指运算过程中流速水头不能略去的流动管路。
×8、所谓水力光滑管是指内壁面粗糙度很小的管道。
×9、外径为D,内径为d的环形过流有效断面,其水力半径为4dD。
√10、凡是满管流流动,任何断面上的压强均大于大气的压强。
×参考答案一、判断题×√×√××××√×《工程流体力学》复习题及参考答案×√一、是非题。
1.流体静止或相对静止状态的等压面一定是水平面。
(×)2.平面无旋流动既存在流函数又存在势函数。
(×)3.附面层分离只能发生在增压减速区。
(正确)4.等温管流摩阻随管长增加而增加,速度和压力都减少。
(错误)5.相对静止状态的等压面一定也是水平面。
(×)6.平面流只存在流函数,无旋流动存在势函数。
(正确)7.流体的静压是指流体的点静压。
(正确)8.流线和等势线一定正交。
(正确)9.附面层内的流体流动是粘性有旋流动。
()10.亚音速绝热管流摩阻随管长增加而增加,速度增加,压力减小。
()11.相对静止状态的等压面可以是斜面或曲面。
(正确)12.超音速绝热管流摩阻随管长增加而增加,速度减小,压力增加。
(正确)13. 壁面静压力的压力中心总是低于受压壁面的形心。
( )14. 相邻两流线的函数值之差,是此两流线间的单宽流量。
计算流体力学复习题答案

《计算流体力学》复习题1. 用待定系数法,用000 , , x kh x x lh -+三点构造一阶导数值 ()0f x ' 的差分近似,这里k 、l 为已知的正整数。
【解答】所求的差商近似,表达式应为()()()()()000001pk l f x c f x kh c f x c f x lh h h -'=-++++⎡⎤⎣⎦O 通过泰勒展开,可有()()()()()()()()()()()22000003324430011211624k l k l k l k l k l f x c c c f x kc lc f x k c l c hf x h k c l c h f x k c l c h f x -----''''=+++-+++'''''''+-++++比较上式两边,得到确定系数k c -、0c 、l c 的方程组0220111022k l k l k l c c c kc lc k c l c ---⎧++=⎪⎪⎪-+=⎨⎪⎪+=⎪⎩,解得()()0kl lc k k l l k c kl k c l k l -⎧=-⎪+⎪⎪-⎪=⎨⎪⎪=⎪+⎪⎩从而得到差商近似的表达式()()()()()()()000020116l l k kf x f x kh f x f x lh h k k l kl l k l kl h f x ⎡⎤-'=--+++⎢⎥++⎣⎦'''+⋅+由于0k ≠、0l ≠,所以差分近似具有二阶精度。
2. 考虑对流方程0u u t x∂∂∂∂+= , (1)用特征线法构造方程的单侧三点迎风格式; (2)分析这一格式的截断误差; (3)分析这一格式的格式粘性。
【解答】(1)根据迎风原则,应选用 n j u 、1nj u -、2n j u - 构造单侧三点迎风格式。
西工大流体力学试题(卷)与答案解析

一.填空题(共30分,每小题2分)1.均质不可压缩流体的定义为 ρ=c 。
2.在常压下,液体的动力粘度随温度的升高而 降低 。
3.在渐变流过流断面上,动压强分布规律的表达式为P/ρg +z=0 。
5.只要比较总流中两个渐变流断面上单位重量流体的 总机械能 大小,就能判别出流动方向。
6.产生紊流附加切应力的原因是 脉动 。
7.在静止流体中,表面力的方向是沿作用面的 内法线 方向。
8.圆管紊流粗糙区的沿程阻力系数λ与 速度梯度 有关。
9.渐变流流线的特征是 近似为平行直线 。
10.任意空间点上的运动参数都不随时间变化的流动称为 恒定流 。
11.局部水头损失产生的主要原因是 漩涡 。
12.直径为d 的半满管流的水力半径R = d/4 。
13.平面不可压缩流体的流动存在流函数的条件是流速x u 和y u 满足 方程 ∂U x / ∂t + ∂U y / ∂t =0 。
14.弗劳德数Fr 表征惯性力与 重力 之比。
15.在相同的作用水头下,同样口径管嘴的出流量比孔口的出流量 大 。
二.(14分)如图所示,一箱形容器,高 1.5h m =,宽(垂直于纸面)2b m =,箱内充满水,压力表的读数为220/kN m ,用一半径1r m =的园柱封住箱的一角,求作用在园柱面上的静水总压力的大小与方向。
解:2220p ()()()82.05()2p 31(0.50.5)8220 2.044.64p 45.53c x z z hgh hb g hb kN g gvv r H bH g v kN ρρρπ===+=−−→=+⨯+⨯====三.(14分)如图所示,一水平放置的管道在某混凝土建筑物中分叉。
已知主管直径3D m =,主管流量335/Q m s =,分叉管直径2d m =,两分叉管流量均为2Q ,分叉管转角060θ=,1-1断面中点的压强2294/p kN m =,不计水头损失,求水流对支座的作用力。
流体力学试题及答案..(可编辑修改word版)

一、填空题流体力学复习题-----2013 制1、1mmH2O= 9.807 Pa2、描述流体运动的方法有欧拉法和拉格朗日法。
3、流体的主要力学模型是指连续介质、无粘性和不可压缩性。
4、雷诺数是反映流体流动状态的准数,它反映了流体流动时粘性力与惯性力的对比关系。
5、流量Q1 和Q2,阻抗为S1 和S2 的两管路并联,则并联后总管路的流量Q 为Q= Q1 + Q2,总阻抗S 为。
串联后总管路的流量 Q 为 Q= Q1 =Q2,总阻抗 S 为S1+S2 。
6、流体紊流运动的特征是脉动现行,处理方法是时均法。
7、流体在管道中流动时,流动阻力包括沿程阻力和局部阻力。
8、流体微团的基本运动形式有:平移运动、旋转流动和变形运动。
9、马赫数气体动力学中一个重要的无因次数,他反映了惯性力与弹性力的相对比值。
10、稳定流动的流线与迹线重合。
全11、理想流体伯努力方程z + p + u 2= 常数中,其中 + p 称为 z测压管 水头。
r 2g r12、一切平面流动的流场,无论是有旋流动或是无旋流动都存在 流线,因而一切平面流动都存在 流函数 ,但是,只有无旋流动才存在势函数。
13、雷诺数之所以能判别 流态 ,是因为它反映了惯性力 和 粘性力的对比关系。
14、流体的主要力学性质有 粘滞性 、 惯性 、 重力性、表面张力性 和 压缩膨胀性。
15、毕托管是广泛应用于测量 气体和 水流一种仪器。
16、流体的力学模型按粘性是否作用分为理想气体和 粘性气体 。
作用与液上的力包括 质量力, 表面力。
17、力学相似的三个方面包括 几何相似 、 运动相似与 动力相似 。
18、流体的力学模型是连续介质 模型。
19、 理 想 气 体 伯 努 力 方 程 p +- +u 2中 ,(z 1 - z 2)( g ) 2p +(z 1 - z 2)( -g ) 称势 压, u 2p +2压, p +- +u 2称总压(z 1 - z 2)( g ) 220、紊流射流的动力特征是 各横截面上的动量相等。
西工大动力与能源学院研究生入学考试工程流体力学样题

(得 3 分)
气流作用于叶片的力 Fd 的两个分量分别为 − Fix ,− Fiy ,合力及方向倾角分别是
Fd = ( − Fix ) + ( − Fiy ) = ρt (V2 y
2 2 2
⎛ V1 y + V2 y − V1 y ) ⎜ ⎜ 2 ⎝
⎞ 2 ⎟ ⎟ + V2 x ⎠
2
⎛ V1 y + V2 y = ρt (V2 y − V1 y ) ⎜ ⎜ 2 ⎝
1 ( 2a ) 3 Lρg 12 = ( p 0 + ρgh )2aL
=
ρga 2 3( p 0 + ρgh )
ρga 2 (得 5 分) 3( p0 + ρgh ) 其中 hc 表示腔壁曲面的水平投影中心 c 在叶面下的深度,J c 代表此曲面对应的静距。
y0 = −
由于腔壁曲面任意一点上作用的压力均与该点法线方向一致,即对应的半径方向 一致,其延长线一定过轴心,对轴心的力矩为零。所以合力的作用线或其延长线也一 定过轴心,对轴心的力矩为零,据此可得: r r Fx Fy F × r0 = 0 即 = x0 y0 F 4a ∴ x 0 = x y 0 = y 0 ctg (α ) = − (得 3 分) Fy 3π 2.证明: (得 5 分)设等直圆管直径为 d,上下游压差为 ∆p (如下图)。其流动损失水头为压
y
0
y
ab
0
y
bc
a
Fx
h x
b
( Байду номын сангаас0 , y0 )
c
⎡⎛ 1 1 ⎞ ⎛ ⎞⎤ = − ρg ⎢⎜ aLh + πa 2 L ⎟ − ⎜ aLh − πa 2 L ⎟⎥ 4 4 ⎠ ⎝ ⎠⎦ ⎣⎝ 1 = − πρga 2 L 2 其中 p 0 代表液面的气压。
[考研类试卷]流体力学(流体静力学)历年真题试卷汇编4.doc
![[考研类试卷]流体力学(流体静力学)历年真题试卷汇编4.doc](https://img.taocdn.com/s3/m/c1e42d3d443610661ed9ad51f01dc281e53a5688.png)
[考研类试卷]流体⼒学(流体静⼒学)历年真题试卷汇编4.doc[考研类试卷]流体⼒学(流体静⼒学)历年真题试卷汇编4⼀、多项选择题下列各题的备选答案中,⾄少有⼀个是符合题意的,请选出所有符合题意的备选答案。
1 (西南交通⼤学2003—2004学年第1学期期末考试试题A卷)下列关于压⼒体的说法中,正确的有( )。
(A)当压⼒体和液体在曲⾯的同侧时,为实压⼒体,P z⽅向向下(B)当压⼒体和液体在曲⾯的同侧时,为虚压⼒体,P z⽅向向上(C)当压⼒体和液体在曲⾯的异侧时,为实压⼒体,P z⽅向向下(D)当压⼒体和液体在曲⾯的异侧时,为虚压⼒体,P z⽅向向上2 (中国农业⼤学2007⼀2008年度秋季学期期末考试试题)判断题:基准⾯可以任意选取。
(A)正确(B)错误3 (西南交通⼤学2003--2004学年第1学期期末考试试题A卷)判断题:在⼯程流体⼒学中,单位质量⼒是指作⽤在单位重量流体上的质量⼒。
(A)正确(B)错误4 (哈尔滨⼯业⼤学2007年秋季学期期末考试试题)推求流体静平衡微分⽅程。
5 (哈尔滨⼯业⼤学2007年秋季学期期末考试试题)说明静⽌流体对曲⾯壁总作⽤⼒的计算⽅法。
6 (南京⼤学2005—2006学年第2学期期末考试试题)质量⼒和⾯⼒的区别是什么?四、单项选择题下列各题的备选答案中,只有⼀个是符合题意的。
7 (西南交通⼤学2003—2004学年第1学期期末考试试题A卷)平衡流体的等压⾯⽅程为( )。
(A)f x⼀f y⼀f z=0(B)f x+f y+f z=0(C)f x dx⼀f y dy⼀f z dz=0(D)f x dx+f y dy+f z dz=08 (西南交通⼤学2003—2004学年第1学期期末考试试题A卷)静⽌液体作⽤在曲⾯上的静⽔总压⼒的⽔平分⼒P x=p c A x=ρgh c A x,式中的( )。
(A)p c为受压⾯形⼼处的绝对压强(B)p c为压⼒中⼼处的相对压强(C)A x为受压曲⾯的⾯积(D)A x为受压曲⾯在铅垂⾯上的投影⾯积9 (中国⽯油⼤学<华东>2004--2005学年第2学期期末考试试题)作⽤在流体的⼒有两⼤类,⼀类是表⾯⼒,另⼀类是( )。
流体测试题及答案详解

流体测试题及答案详解一、选择题(每题2分,共10分)1. 以下哪项不是流体静力学的基本假设?A. 流体是连续介质B. 流体是不可压缩的C. 流体各向同性D. 流体是完全弹性体答案:D2. 流体的粘性系数在下列哪种情况下会增加?A. 温度升高B. 压力增大C. 流速增加D. 流体密度增加答案:A3. 流体在管道中流动时,流速最大的地方是:A. 管道入口B. 管道出口C. 管道中心D. 管道壁答案:C4. 流体的雷诺数是用来描述流体流动的哪种特性?A. 压缩性B. 粘性C. 惯性D. 表面张力答案:B5. 流体动力学中的伯努利方程适用于以下哪种流体流动?A. 可压缩流体B. 非定常流动C. 粘性流体D. 不可压缩流体答案:D二、填空题(每题2分,共10分)1. 流体的______是流体力学研究的基础假设之一。
答案:连续性2. 流体的粘性可以通过______来测量。
答案:粘度计3. 流体的______是指流体在单位时间内通过某一截面的体积。
答案:流量4. 流体的______是指流体在单位时间内通过某一截面的质量。
答案:质量流率5. 流体的______是指流体内部各点的速度分布。
答案:流速剖面三、简答题(每题5分,共20分)1. 简述流体静力学的基本原理。
答案:流体静力学的基本原理是流体在静止状态下,作用在流体上的力达到平衡状态,即流体内部的压强在各个方向上相等。
2. 什么是流体的粘性?它对流体流动有何影响?答案:流体的粘性是指流体内部分子间的摩擦力,它对流体流动的影响主要表现在流体的阻力和能量损失上。
3. 描述流体的雷诺数是如何影响流体流动的。
答案:流体的雷诺数是描述流体流动特性的一个重要无量纲数,它反映了流体流动的惯性力与粘性力之间的相对关系。
雷诺数较低时,流体流动呈层流状态;雷诺数较高时,流体流动呈湍流状态。
4. 流体的伯努利方程在实际工程中有哪些应用?答案:流体的伯努利方程在实际工程中应用广泛,如在管道设计、喷嘴设计、水轮机设计等领域,用于计算流体在管道或通道中的流速、压力和高度的变化。
流体测试题及答案详解

流体测试题及答案详解一、选择题1. 流体静力学的基本方程是:A. 伯努利方程B. 欧拉方程C. 连续性方程D. 牛顿流体方程答案:D2. 在不可压缩流体中,流体的密度是:A. 恒定的B. 随压力变化C. 随温度变化D. 随流速变化答案:A二、填空题1. 流体力学中的雷诺数是用来描述_________的无量纲数。
答案:流体流动的层流与湍流特性2. 流体的粘性系数通常用_________来表示。
答案:帕斯卡秒(Pa·s)三、简答题1. 简述流体静力学中的压力分布规律。
答案:在流体静力学中,流体内部的压力分布遵循帕斯卡定律,即流体内部的压力在所有方向上都是相等的。
此外,流体的压力还受到重力的影响,因此在静止流体中,压力会随着深度的增加而增加。
四、计算题1. 已知一个容器内装有水,水的深度为10米,求容器底部受到的水压。
答案:首先,我们需要知道水的密度,通常水的密度为1000kg/m³。
然后,使用静水压力公式P = ρgh,其中 P 是压力,ρ 是密度,g 是重力加速度(约9.81 m/s²),h 是水的深度。
将已知数值代入公式,得到 P = 1000 kg/m³ × 9.81 m/s² × 10 m = 98100 Pa。
五、论述题1. 论述流体动力学中的伯努利定理及其应用。
答案:伯努利定理是流体动力学中的一个重要原理,它指出在理想流体的稳定流动中,流体的总能量(包括动能、势能和压力能)在沿流线的任何两点都是相等的。
这个原理可以用来解释许多现象,如飞机的升力、喷气发动机的工作原理以及管道流动中的压力降低等。
在实际应用中,伯努利定理可以帮助设计更有效的流体输送系统,优化能源消耗和提高效率。
六、实验题1. 设计一个实验来验证流体的连续性方程。
答案:实验设计可以包括以下步骤:- 准备一个管道,管道的两端具有不同的横截面积。
- 在管道的一端安装一个流量计,以测量通过管道的流体流量。
西工大861流体力学

题号:861《工程流体力学》考试大纲一、考试内容根据学校教学及该试题涵盖专业的特点,对考试范围作以下要求:1.流体的基本特性:流体的分子特点与力学特性,流体的压缩性、膨胀性、粘性及热传导性的概念,及其物理本质及影响因素。
2.流体静力学:静止流体受力及其计算方法;流体静力学平衡方程及其应用;非惯性坐标系中静止流体平衡方程的应用;静止流体内部压强计算方法;压强测量方法。
3.一维定常流动:迹线、流线、流管的概念;流线方程、迹线方程;一维定常流动的连续方程、动量方程、能量方程和伯努力方程的物理意义及其应用。
4.管道流动:完全发展的管道层流和湍流流动;管道流动损失的分类,产生的原因;流动损失计算方法;串、并联及分支管道流动损失的计算原则和方法。
5.流体多维运动:多维流动中随流导数的概念和计算方法;多维流运动分析及变形量计算;多维流的连续性方程、动量方程和能量方程及其边界条件。
6.不可压平面势流:流函数、势函数概念及其与速度之间的关系;直匀流,点源,点涡,偶极子的流函数和势函数;叠加原理及其应用;圆柱绕流及特点。
7.粘性流动:粘性应力和广义牛顿定律;粘性流体运动方程;边界层概念及其特点;边界层厚度及积分关系式应用;分离现象及物理本质。
8.可压缩平面流动:可压缩流体的压强、温度、密度、马赫数等概念及反映相互关系的气动函数的应用。
9.扰动波在气流中的传播规律;膨胀波和激波的概念和计算。
10.可压缩一维定常流动:可压缩一维管流的方程及计算方法;换热管流计算;收敛喷管和拉瓦尔喷管流动状态及计算。
二、参考书目1.邢宗文主编:《流体力学基础》,西北工业大学出版社,1992。
2.王新月主编:《气体动力学基础》,西北工业大学出版社,2006。
3.王新月主编:《热力学与气体动力学基础》,西北工业大学出版社,2004。
4.张也影主编:《流体力学》(第二版),高等教育出版社,1999。
流体力学试题及参考答案

考试试卷(A B卷)学年第二学期课程名称:流体力学一、判断题(20分)1.物理方程等式两边的量纲或因次一定相等。
(T)2.为了减小压差阻力,就应该设法推迟边界层分离现象的发生。
(T)3.压力体的体积表示一个数学积分,与压力体内是否有气体无关。
(T)4.流体静止时,切应力为零。
(T)5.温度升高液体的表面张力系数增大。
(F)6.液滴内的压强比大气压小。
(F)7.声音传播过程是一个等熵过程。
(T)8.气体的粘性随温度的升高而增大。
(T)9.应用总流伯努利方程解题时,两个断面间一定是缓变流,方程才成立。
(F)10.雷诺数是表征重力与惯性力的比值。
(F)11.不可压缩流体只有在有势力的作用下才能保持平衡。
(T)12.对流程是指海拔11km以上的高空。
(F)13.静止的流体中任意一点的各个方向上的压强值均相等。
(T)14.在拉格朗日法中,流体质点轨迹给定,因此加速度很容易求得。
(T)15.对于定常流动的总流,任意两个截面上的流量都是相等的。
(T)16.紊流水力粗糙管的沿程水头损失系数与雷诺数无关。
(T)17.在研究水击现象时,一定要考虑流体的压缩性。
(T)18.雷诺数是一个无量纲数,它反映流动的粘性力与重力的关系。
(F)19.线当马赫数小于一时,在收缩截面管道中作加速流动。
(T)20.对于冷却流动dq小于0,亚音速流作减速运动,超音速流作加速运动。
(T)二、填空题(10分)1.流动相似指的是两个流动系统所有对应点的对应物理量之比相等,具体地说,就是要满足,几何相似、运动相似和动力相似。
2.自由面上的压强的任何变化,都会等值地传递到液体中的任何一点,这就是由斯卡定律。
3.流动相似的主导因素是动力相似,只有满足了这一点才能保证运动相似。
4.从海平面到11km处是对流层,该层内温度随高度线性地降低。
5.马赫准则要求两种流动的惯性力与由于压缩性引起的弹性力成比例。
6.水头损失可分为两种类型:沿层损失和局部损失。
7.在工程实践中,通常认为,当管流的雷诺数超过 2320 ,流态属于紊流。
西工大875 流体力学期末考试练习题及答案

西工大875 流体力学期末考试练习题一、选择题1.按连续介质的概念,流体质点是指A .流体的分子; B. 流体内的固体颗粒;C . 无大小的几何点;D. 几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
2.作用在流体的质量力包括A. 压力;B. 摩擦力;C. 重力;D. 惯性力。
3.单位质量力的国际单位是:A . N ;B. m/s;C. N/kg;D. m/s2。
4.与牛顿内摩擦定律直接有关系的因素是A. 切应力和压强; B. 切应力和剪切变形速率; C. 切应力和剪切变形。
5.水的粘性随温度升高而A . 增大;B. 减小;C. 不变。
6.气体的粘性随温度的升高而A. 增大;B. 减小;C. 不变。
7.流体的运动粘度υ的国际单位是A. m2/s ;B. N/m2;C. kg/m ;D. N·s/m28.理想流体的特征是A. 粘度是常数;B. 不可压缩;C. 无粘性; D. 符合pV=RT。
9.当水的压强增加1个大气压时,水的密度增大约为A. 200001;B. 100001;C. 40001。
10.水力学中,单位质量力是指作用在A. 单位面积液体上的质量力;B. 单位体积液体上的质量力;C. 单位质量液体上的质量力;D. 单位重量液体上的质量力11.以下关于流体粘性的说法中不正确的是A. 粘性是流体的固有属性;B. 粘性是在运动状态下流体具有抵抗剪切变形速率能力的量度C. 流体的粘性具有传递运动和阻滞运动的双重作用;D. 流体的粘性随温度的升高而增大。
12.已知液体中的流速分布µ-y如图所示,其切应力分布为A.τ=0;B.τ=常数;C. τ=ky (k为常数)。
13.以下关于液体质点和液体微团的正确论述是A. 液体微团比液体质点大;B. 液体微团包括有很多液体的质点;C. 液体质点没有大小,没有质量;D. 液体质点又称液体微团。
14.液体的汽化压强随温度升高而A. 增大;B. 减小;C. 不变;15.一封闭容器盛以水,当其从空中自由下落时(不计空气阻力),其单位质量力为A. 0 ;B. -g ;C. mg ;D. –mg 。
2019-计算流体力学试卷-推荐word版 (12页)

本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==计算流体力学试卷篇一:计算流体力学试题?u?2u1. 等步长网格分布情况下的一阶向前差分、2的二阶中心差分表达式。
(P89) ?x?xui?1,j?ui,j?u()??(?x) i,j?一阶向前差分:?x?xui?1,j?2ui,j?ui?1,j?2u2()???(?x)2i,j二阶中心差分: ?x(?x)22. 简述计算流体力学的特点及其应用领域。
CFD是以计算机作为模拟手段,运用一定的计算技术寻求流体力学各种复杂问题的离散化数值解。
它的主要特征:(1)数值解而不是解析解;(2)计算技术起关键作用;(3)与计算机的发展紧密相关。
(成本较低,适用范围宽,可靠性差,表达困难)应用领域:航空、航天、气象、船舶、武器装备、水利、化工、建筑、机械、汽车、海洋、体育、环境、卫生等3. 简答题1) 什么是差分方程的相容性?差分方程与微分方程的差别是截断误差R。
必要时通过缩小空间步长(网格尺寸)h和时间步长t,这一误差应可缩小至尽可能小。
当h->0和t->0时,若R->0,则差分方程趋于微分方程,表示这两个方程是一致的。
这时称该差分方程与微分方程是相容的。
2) 什么是差分解的收敛性?当微分方程在离散为差分方程来求解,当步长h?0时,存在着差分方程的解yn能够收敛到微分方程的准确解y(xn),这就是差分方法的收敛性。
收敛性定义:对于任意节点的xn?x0?nh,如果数值解yn当h?0(同时n??)时趋向于准确解y(xn),则称该方法是收敛的。
3) 什么是差分解的稳定性?数值计算时,除计算机舍入误差(字长有限)外,初始条件或方程中某些常数项也有可能给的不尽精确。
舍入误差和这些误差在计算过程中可能一步步积累与传递,误差的传递,有时可能变大,有时可能变小。
某一步舍入误差放大或缩小的问题,称为差分解的数值稳定性问题。
流体力学期末试题及答案

流体力学期末试题及答案流体力学是工程学和物理学中的一个重要分支,它研究流体(液体和气体)的运动规律以及流体与固体边界之间的相互作用。
以下是一份流体力学期末试题及其答案,供参考。
# 流体力学期末试题一、选择题(每题2分,共20分)1. 流体力学中,流体的连续性方程描述了什么?A. 流体的密度变化B. 流体的质量守恒C. 流体的动量守恒D. 流体的能量守恒2. 以下哪项不是流体力学中的基本概念?A. 流体B. 粘性C. 压缩性D. 弹性3. 流体的雷诺数Re表示的是:A. 流体的密度B. 流体的动量C. 流体的惯性力与粘性力的比值D. 流体的压强4. 以下哪个不是流体力学中的边界层概念?A. 粘性边界层B. 热边界层C. 速度边界层D. 压力边界层5. 流体力学中的伯努利方程适用于:A. 静止流体B. 可压缩流体C. 不可压缩流体D. 任何流体...二、简答题(每题10分,共30分)1. 简述流体力学中的粘性对流体流动的影响。
2. 描述流体力学中的纳维-斯托克斯方程,并解释其物理意义。
3. 解释什么是流体的湍流,并简述其特点。
三、计算题(每题25分,共50分)1. 假设有一个圆形管道,其直径为0.2米,管道内流动的水的速度为2米/秒。
求管道的雷诺数,并判断流动状态是层流还是湍流。
2. 考虑一个不可压缩流体在水平管道中流动,管道直径为0.3米,管道内流体的密度为1000 kg/m³,粘性系数为0.001 Pa·s。
若管道的摩擦系数f=0.02,求管道的流速和流量。
...四、论述题(共30分)1. 论述流体力学在航空航天工程中的应用,并举例说明。
# 流体力学期末试题答案一、选择题1. 答案:B(流体的质量守恒)2. 答案:D(弹性)3. 答案:C(流体的惯性力与粘性力的比值)4. 答案:D(压力边界层)5. 答案:C(不可压缩流体)...二、简答题1. 粘性是流体内部分子间摩擦力的量度,它影响流体流动的阻力和能量损失。
西北工业大学级《力学》期末考试试卷(西北工业大学级《力学》期末考试标准答案及评分标准可在文

诚信保证
本人知晓我校考场规则和违纪处分条例的有关规定,保证遵守考场规则,诚实做人。
本人签字:
编号:
西北工业大学期末考试试题(卷)
2008~2009学年第一学期
开课学院理学院课程力学学时60
考试日期2009年1月12日考试时间2小时考试形式(闭)(A)卷
班级学号姓名
重要提示:
1.本试卷分为“单选题”、“填空题”和计算题三部分,总分为100分;2.在答题卡上答题,最后把试卷和答题卡一并交回;
3.答题卡分为两张,答题卡(1)为机读卡,答题卡(2)为书写卡;4.机读卡中数字用钢笔填写,涂点用2B铅笔填涂。
填空题答案栏每格填1位数字,小数点单独占1格,左对齐填写,按要求取位,4舍5入进位;5.题中所涉重力加速度g一律取9.8 m/s2计算;
6.草稿纸不再另发,将试题的背面作为草稿纸,
一、单选题(共30分,每小题3分,在答题卡(1)上完成)
1.对于惯性参考系,下列那项叙述是正确的?(a)在惯性参考系物体所受合力为零,则该物体保持静止或匀速运动的状态;(b)在任何惯性参考系所描述的物理现象都是相同的;(c)两不同惯性参考系间的相对运动,不一定是匀速运动。
A.abc皆正确;B.只有ab正确;
C.只有bc正确;D.只有ac正确。
计算流体力学试题(含答案08)

一.简要回答以下问题(20分)1.差分格式的基本特征相容性,稳定性,收敛性,守恒性,有界性,真实性,精确性2.差分格式的稳定性和收敛性的关系对于适定的线性微分方程的初值问题,与之相容的差分方程稳定的充分必要条件是差分格式收敛。
3.显格式和隐格式显格式:离散方程的解可以直接求解隐格式:离散方程的解需要通过求解线性代数方程组的形式来获得隐格式具有较高的稳定性4.列举四种常用的流体力学数值计算模型(方法)边界元法,有限差分法,有限体积法,有限元法,有限分析法,谱方法等5.二阶偏微分方程有那些基本类型,试举例说明 椭圆型方程:02222=∂∂+∂∂yu x u 抛物型方程:022=∂∂+∂∂y u xu 双曲型方程:02222=∂∂-∂∂yu x u 二.写出函数),,(t y x u 在时间t 附近的泰勒展开式(仅对时间项)(保留到3阶)(15分)))(()(),,(61)(),,(21),,(),,(),,(4333222t O t tt y x u t t t y x u t t t y x u t y x u t t y x u ∆+∆∂∂+∆∂∂+∆∂∂+=∆+三.分别写出微分xy x u a ∂∂),(的UDS ,CDS ,FDS ,BDS 差分格式(15分) UDS :xu u a a x u u a a x u a i i i i ∆--+∆-+=∂∂+-1122 CDS :xu u a x u a i i ∆-=∂∂-+211 BDS :xu u a x u a i i ∆-=∂∂-1 FDS :xu u a x u ai i ∆-=∂∂+1四.采用有限体积法离散下列积分方程(假设数值网格为等距网格)(15分)⎰⎰∇⋅Γ=∂∂ds dV t t y x φφn ),,()2()2(1n P n S n N n P n W n E n P n P yx x y y x t φφφφφφφφ-+∆∆Γ+-+∆∆Γ=∆∆∆-+五.给出圆球无粘性绕流的定解条件(15分)⎪⎩⎪⎨⎧-=∂∂=∇xUn n φφ02六.采用有限差分法离散对流扩散方程,并分析其稳定性。
