Applying LDPC Codes to the GPRS

合集下载

GPRS原理、协议、应用

MF009001 GPRS原理ISSUE1.0目录课程说明 (1)课程介绍 (1)课程目标 (1)相关资料 (1)第1章 GPRS概述 (1)1.1 GPRS的产生 (1)1.2 GPRS的发展 (1)1.3 GPRS与HSCSD业务的比较 (2)1.4 CSD与GPRS的比较 (3)1.4.1 电路交换的通信方式 (3)1.4.2 分组交换的通信方式 (4)第2章 GPRS基本功能和业务 (6)2.1 GPRS业务种类 (6)第3章 GPRS基本体系结构和传输机制 (8)3.1 GPRS接入接口和参考点 (8)3.2 网络互通 (8)3.3 逻辑体系结构 (8)3.3.2 主要网络实体 (10)3.3.3 主要网络接口 (12)3.4 高层功能 (14)3.4.1 网络接入控制功能 (14)3.4.2 分组路由和转发功能 (15)3.4.3 移动性管理功能 (17)3.4.4 逻辑链路管理功能 (17)3.4.5 无线资源管理功能 (18)3.4.6 网络管理功能 (18)3.5 功能分配 (19)3.6 GPRS数据传输平面 (20)3.7 GPRS信令平面 (21)3.7.1 MS与SGSN间信令平面 (21)3.7.2 SGSN与HLR间信令平面 (22)3.7.3 SGSN与MSC/VLR间信令平面 (22)3.7.4 SGSN与EIR间信令平面 (23)3.7.5 SGSN与SMS-GMSC、SMS-IWMSC间信令平面 (23)3.7.6 GPRS支持节点间信令平面 (24)3.7.7 GGSN与HLR间信令平面 (24)第4章移动性管理 (25)4.1 MM状态 (25)4.1.1 IDLE状态 (25)4.1.2 STANDBY状态 (25)4.1.3 READY状态 (26)4.2 MM状态功能 (26)4.2.1 MM状态迁移 (26)4.2.2 就绪定时器功能 (27)4.2.3 周期性路由区更新定时器功能 (28)4.2.4 用户可及定时器功能 (28)4.3 SGSN与MSC/VLR的交互 (29)4.3.1 SGSN-MSC/VLR关联的管理 (29)4.3.2组合RA/LA更新 (29)4.3.3 CS寻呼协调及网络操作模式 (30)4.4 MM规程 (31)4.4.1 GPRS附着功能 (31)4.4.2 GPRS分离规程 (33)4.4.3 清除功能 (36)4.5 安全性功能 (36)4.5.1 用户鉴权 (36)4.5.2 用户身份机密性 (37)4.5.3 用户数据和GMM/SM信令机密性 (37)4.5.4 用户身份检查 (38)4.6 位置管理功能 (38)4.6.1 小区更新规程 (39)4.6.2 路由区更新规程 (39)4.6.3组合RA/LA更新规程 (42)4.6.4 周期性路由区更新和位置区更新 (43)4.7 用户数据管理功能 (44)4.7.1 插入用户数据规程 (44)4.7.2 删除用户数据规程 (44)4.8 MS类标处理功能 (45)第5章无线资源管理功能 (46)第6章分组路由与传输功能 (48)6.1 PDP状态和状态转换 (48)6.2 会话管理规程 (49)6.2.1 静态地址与动态地址 (49)6.2.2 PDP上下文的激活规程 (50)6.2.3 PDP上下文的修改 (52)6.2.4 PDP上下文的去激活 (53)6.3 业务流程举例 (54)6.3.1 MS发起分组数据业务 (54)6.3.2 网络发起分组数据业务 (55)第7章用户数据传输 (57)7.1 传输模式 (57)7.1.1 GTP传输模式 (57)7.1.2 LLC传输模式 (57)7.1.3 RLC传输模式 (57)7.2 LLC功能 (57)7.2.1寻址 (58)7.2.2服务 (58)7.2.3功能 (58)7.3 SNDCP功能 (58)7.4 PPP功能 (60)7.5 Gb接口 (60)7.5.1物理层 (60)7.5.2 FR子层 (60)7.5.3 NS子层 (61)7.5.4 BSSGP层 (61)7.6 Abis接口 (62)7.6.1结构A (63)7.6.2结构B (64)7.6.3结构C (64)第8章信息存储 (66)8.1 HLR (66)8.2 SGSN (67)8.3 GGSN (69)8.4 MS (69)8.5 MSC/VLR (70)第9章编号 (71)9.1 IMSI (71)9.2 P-TMSI (72)9.3 NSAPI/TLLI (72)9.3.1 NSAPI (72)9.3.2 临时逻辑链路标志（TLLI） (72)9.4 PDP地址和类型 (73)9.5 TID (73)9.6 路由区识别 (73)9.7 小区标识 (74)9.8 GSN地址 (74)9.9 接入点名字 (74)第10章运营方面的问题 (75)10.1 计费信息 (75)10.2 计费功能 (75)10.2.1 分组型业务计费方式和电路型业务计费方式的区别 (75)10.2.2 计费基本功能 (76)10.2.3 话单类型 (76)10.2.4 话单传送接口 (77)10.3 网络服务质量（QoS） (77)10.3.1 优先级别 (78)10.3.2 延时级别 (78)10.3.3 可靠性级别 (78)10.3.4 峰值吞吐量级别 (78)10.3.5 平均吞吐量级别 (79)10.4 消息过滤功能 (80)10.5 兼容性问题 (80)第11章与GSM其它业务的交互 (81)11.1 与点对点短消息业务关系 (81)11.2 与电路交换业务的关系 (81)11.3 与补充业务的关系 (82)第12章 IP相关的基础知识 (83)12.1 NAT (83)12.2 FIREWALL (83)12.3 GRE (83)12.4 DNS (84)12.5 RADIUS (84)MF009001 GPRS原理ISSUE1.0 课程说明课程说明课程介绍本课程为华为传送网网络级网管T2100的一个整体介绍，主要阐述了网络级网管T2100兴起和发展的客观需求，华为传送网管的一体化解决方案。

美国最新卫星调制解调器产品介绍

Doubletalk Carrier-In-Carrier
DoubleTalk Carrier-in-Carrier, based on patented “Adaptive Cancellation” technology, allows transmit and receive carriers of a duplex link to share the same transponder space. Figure 1 shows the typical full duplex satellite link, where the two carriers are adjacent to each other. Figure 2 shows the typical DoubleTalk Carrier-in-Carrier operation, where the two carriers are overlapping, thus sharing the same spectrum.
• Cellular Backhaul • G.703 Trunking • IP Trunking • Offshore & Maritime
Communommunications onthe-Move
• Satellite News
Gathering
Typical Users
• Mobile Operators • Telecom Operators • Satellite Service
Providers
• Government & Military • Enterprise • Offshore
Common Applications
Features

以太网数据转发约束的高速LDPC码设计

以太网数据转发约束的高速LDPC码设计李霈霈;周志刚;那美丽【摘要】为了灵活支持多种高速以太网接口，将低密度奇偶校验（LDPC）编码运用在以太网数据转发，取消传统数据包解码，提出了LDPC并行编码架构。

在考虑1G到100G以太网物理层编码码字长度约束的基础上，分别设计了针对1G、10G、100G接口中最大通道速率的LDPC（192，120），LDPC（594，462），LDPC（1188，990）码字，实现了信道编码处理的低时延。

仿真结果表明，构造的准循环LDPC码误码性能优，系统的处理时延小（考虑了编码时延和译码时延）。

LDPC编码时延在0.58~1.17μs之间，译码时延在3.20~4.26μs之间，可以满足不同以太网接口的最大通道编译速率。

%This paper presented interface-aware Low Density Parity Check (LDPC) codes in parallel encoding framework to support high-speed Ethernet data transmission and cancel the packets decoding process. Considering constraints of encoded codeword length of 1G to 100G Ethernet physical layer, LDPC(192,120), LDPC(594,462), LDPC(1188,990) codes aiming the maximum channel ratefor 1G, 10G and 100G Ethernet interface were designed to reach low latency in channel coding process. The simulation results claimed that LDPC codes have excellent performance and minimum processing delay in system, taking encoding delay and decoding delay into consideration. The encoding delay of 0.58~1.17 μs and the decoding delay of 3.20~4.26μs could meet the maximum code rate for different channels in Ethernet interfaces.【期刊名称】《电子设计工程》【年(卷),期】2016(024)022【总页数】4页(P1-4)【关键词】以太网接口;数据转发;并行编码架构;编码时延;译码时延【作者】李霈霈;周志刚;那美丽【作者单位】中国科学院上海微系统与信息技术研究所，上海 200050;中国科学院上海微系统与信息技术研究所，上海 200050;中国科学院上海微系统与信息技术研究所，上海 200050【正文语种】中文【中图分类】TN911.22以太网是现有局域网采用的最通用的通信协议标准。

Low-Density Parity-Check (LDPC) Codes

IPN Progress Report42-154August15,2003Low-Density Parity-Check(LDPC)CodesConstructed from ProtographsJ.Thorpe1We introduce a new class of low-density parity-check(LDPC)codes constructed from a template called a protograph.The protograph serves as a blueprint forconstructing LDPC codes of arbitrary size whose performance can be predictedby analyzing the protograph.We apply standard density evolution techniques topredict the performance of large protograph codes.Finally,we use a randomizedsearch algorithm toﬁnd good protographs.I.IntroductionLow-density parity-check(LDPC)codes have emerged as one of the top contenders for near-channel-capacity error correction.Recently,more and more sophisticated classes of LDPC codes have been forwarded by members of the research community,each oﬀering advances in one area or another.An LDPC code is described by its(sparse)parity-check matrix.Such matrices can be eﬃciently represented by a bipartite(Tanner)graph.The standard iterative decoding algorithm,known as belief propagation(BP),passes messages along the edges of this graph.Much research has gone into under-standing the properties required of a Tanner graph to produce an LDPC code that performs well under this decoding algorithm.In this article,we introduce a new class of LDPC codes constructed from a template called a proto-graph.The protograph serves as a blueprint for constructing LDPC codes of arbitrary size whose perfor-mance can be predicted by analyzing the protograph.We apply standard density evolution techniques to predict the performance of large protograph codes.Finally,we use a randomized search algorithm to ﬁnd good protographs.II.Protographs and Protograph CodesA protograph can be any Tanner graph,typically one with a relatively small number of nodes.A protograph G=(V,C,E)consists of a set of variable nodes V,a set of check nodes C,and a set of edges E.Each edge e∈E connects a variable node v e∈V to a check node c e∈C.Parallel edges are permitted,so the mapping e→(v e,c e)∈V×C is not necessarily1:1.1Communications Systems and Research Section.The research described in this publication was carried out by the Jet Propulsion Laboratory,California Institute of Technology,under a contract with the National Aeronautics and Space Administration.As a simple example,we consider the protograph shown in Fig.1.This graph consists of|V|=4 variable nodes and|C|=3check nodes,connected by|E|=8edges.The four variable nodes in the protograph are denoted by“Type1,2,3,4,”and the three check nodes by“Type A,B,C.”By itself,this graph may be recognized as the Tanner graph of an(n=4,k=1)LDPC code(in this case,a repetition code).We can obtain a larger graph by a“copy-and-permute”operation,illustrated in Figs.2and3.In Fig.2,the protograph has been copied three times.Here the three copies are overlaid so that same-type vertices are in close proximity,but the overall graph consists of three disconnected subgraphs.In Fig.3, the endpoints of the three copies of each edge in the protograph have been permuted among the three copies of the corresponding variable and check nodes.After this swapping of endpoints of edges,the three subgraphs are now interconnected.The graph in Fig.3is the Tanner graph of an(n=12,k=3)LDPC code.We call this graph the derived graph,and the corresponding LDPC code a protograph code.Type 1Type 2Type 3Type 4Type A Type B Type CFig. 1. A simple protograph.Type 1Type 1Type 1Type 2Type 2Type 2Type 3Type 3Type 3Type 4Type 4Type 4Type A Type A Type A Type B Type B Type B Type C Type C Type CFig. 2. A protograph copied three times.Type 1Type 1Type 1Type 2Type 2Type 2Type 3Type 3Type 3Type 4Type 4Type 4Type A Type A Type A Type B Type B Type B Type C Type C Type CFig. 3. A derived graph.In general,we can apply the copy-and-permute operation to any protograph to obtain derived graphs of diﬀerent sizes.This operation consists of ﬁrst making T copies of the protograph,and then permuting the endpoints of each edge among the T variable and T check nodes connected to the set of T edges copied from the same edge in the protograph.Formally,we have the following deﬁnitions.Deﬁnition 1.Let G =(V,C,E )be a protograph.Let T be any positive integer and,for each e ∈E ,let πe be an arbitrary permutation of {1,2,···T }.The derived graph is G =(V ,C ,E ),where V =V ×{1,2,···T },C =C ×{1,2,···T },E =E ×{1,2,···T },and an edge (e,t )∈E connects the variable node (v e ,t )∈V to the check node c e ,πe (t ) ∈C .Deﬁnition 2.A protograph code is an LDPC code whose Tanner graph is a derived graph.The usual mapping of Tanner graphs to LDPC codes makes the implicit assumption that each variable node in the graph corresponds to a code symbol that will be transmitted over a channel.However,a useful reﬁnement [1]is to allow the variable node set V to contain untransmitted variables.Under this reﬁnement,each variable node v ∈V may be designated a transmitted node or an untransmitted node.The number of transmitted nodes is denoted n ,and the number of untransmitted nodes is denoted u ;thus n +u =|V |.The number of check nodes is denoted r =|C |.The dimension k of a code with untransmitted variables is k =n +u −r ,and its rate is R =(n +u −r )/n .A variable node (v,t )in G has the same transmitted/untransmitted designation as v .The derived graph contains nT transmitted and uT untransmitted variable nodes,as well as rT check nodes.Thus,any derived graph has the same rate R as its protograph.Untransmitted variables can improve the performance of protograph codes.These variables are de-coded by the decoder in the same way as if the channel had yielded an “erasure.”III.Deterministic NeighborhoodsA property of protograph codes not shared by other classes of irregular codes is that the local neigh-borhood of a node (v,t )in G is completely determined by G .The local neighborhood to depth d consists of all nodes and edges connected to (v,t )by a path of length d or less.This neighborhood is a tree if there is at most one path of length d or less to any other node.In this tree,each node is adjacent to (diﬀerent copies of)the same node types as in the protograph.To illustrate,we expand the neighborhood of a variable v of type 1in Fig.1to depth d =3in Fig.4.Type 4Type B Type C Type A Type B Type BFig. 4. An example of a neighborhood.The local neighborhood tree can be constructed uniquely from the root downward.This leads to the following property of the local neighborhoods of derived graphs.Property 1.If a neighborhood to depth d of a variable node (v,t )in the derived graph G is tree-like,its structure is determined by the adjacencies in the protograph G .Note that v need not be tree-like within depth d in G .We can expect that the performance of belief propagation on derived graphs should be relatively insensitive to the choice of {πe }because of the structure imposed by G .By contrast,in a Tanner graph generated from a given irregular degree proﬁle,the structure of such a neighborhood is random,and the performance of belief propagation may depend more on the particular graph.IV .Analysis of Protograph Code EnsemblesWe have deﬁned an arbitrary protograph code by applying a copy-and-permute operation to a proto-graph G .We now deﬁne an ensemble of protograph codes by specifying a probability distribution over the permutations {πe ,e ∈E }.The ensemble that we shall consider is that obtained by generating πe uniformly over all permutations of length T ,and independently for each e ∈E .For this ensemble,it can be shown that as T →∞,the probability that the neighborhood to ﬁxed depth d of any node (v,t )is tree-like goes to 1,and thus the ensemble meets the criteria for analysis by density evolution.Density evolution (DE)analysis [2]can be carried out on a protograph to determine whether or not decoding will yield arbitrarily small bit-error probability on a large derived graph.In this technique,the messages that are deﬁned in the message-passing algorithm are treated as random variables,and their distributions are computed.For the ensemble of codes constructed from a given protograph G ,and for a given symmetric channel C ,we compute two distributions −→q i e and ←−q i e on the messages passed in either direction along edge e at iteration i .Because of the deterministic neighborhood property,the message distributions −→q i e and ←−q i e computed for an edge e in the protograph G are valid for any corresponding edge (e,t )in the derived graph G as long as the neighborhood to depth 2i is tree-like.Based on the message distributions −→q i e ,←−q i e ,and the channel C ,DE predicts a probability of decodererror P (i )v for variable nodes of type v at iteration i .If message densities evolve such that P (i )v →0as i →∞for all v ,then DE predicts that decoding will be successful,given large enough T .For a channel C θ,whose ﬁdelity increases with the parameter θ,the DE threshold θ∗for protograph G is the inﬁmum of θsuch that DE predicts successful decoding for G and C θ.V .Finding Good Protograph CodesWe devised an algorithm to search for protograph codes that perform well under BP on the additive white Gaussian noise (AWGN)channel.This search uses a randomized iterative algorithm called simu-lated annealing (SA)and is directed by our estimate of how the DE threshold changes as an underlying protograph is perturbed.SA approximately minimizes over a search space S an energy function E :S →R R.It requires a random perturbation function ρ:S →S and a decreasing temperature proﬁle T j .It begins with anarbitrary solution s 0∈S ,and at each iteration j applies the random perturbation ρto generate a new solution s j =ρ(s j ).If E s j <E (s j ),then s j +1=s j .If E s j ≥E (s j ),then s j +1=s j with probability exp − E (s j )−E (s j ) /T j and s j otherwise.The algorithm returns the solution s j at the ﬁnal iteration.In our application,we search over protographs G withﬁxed n,u,and r.Since the code rate R is determined by these parameters,it is constant throughout the optimization space.Thus,we can design good codes for any desired rate by a judicious choice of n,u,and r.We deﬁne three types of perturbations on a protograph G in the search space:removing an edge in G, adding an edge to G,and swapping the endpoints of two edges in G.The random perturbationρchooses one of these types at random,and chooses uniformly randomly among all possibilities for that type.We would ideally like to use the DE threshold as our energy function E.However,it is quite impractical to run full DE at each iteration.Instead,we use the reciprocal-channel approximation introduced in[3],a single-parameter approximation to DE for the AWGN channel.Further,instead of running approximate DE several times per SA iteration(j)to determine the threshold(under approximate DE)accurately, we run approximate DE just once at an operating point above the threshold for the current solution G j. We let our energy function E be the number of decoding iterations(i)required to drive the output error probability below some small constantε.Empirically,we have observed that this quantity varies nearly monotonically with the threshold.VI.Protograph Optimization ResultsFigure5shows an example of a simple rate1/2protograph found by the SA search method.This optimized protograph has n=8transmitted variables,u=1untransmitted variable,r=5checks, and a total of|E|=29edges,including5pairs of parallel edges.The untransmitted variable node has degree9,the transmitted variable nodes have degrees{2,2,2,2,3,3,3,3},and the check nodes have degrees{4,5,6,6,8}.The(approximate)DE threshold on the AWGN channel for long codes constructed from this protograph is E b/N0=0.283dB,which is about0.1dB better than the(exact)DE threshold of0.4090dB found by Richardson and Urbanke[4]for optimized irregular LDPC codes with maximum variable node degree9.The irregular LDPC codes in[4]are connected according to a random ensemble constrained only by the distribution of node degrees,not by the additional structure built into the protograph.We constructed a large(n=8192,k=4096)protograph code by interconnecting T=1024copies of the protograph in Fig.5.The interconnections are determined by29separate permutations of{1,···,1024}, selected using a variation of the progressive edge growth(PEG)algorithm[5]to avoid short loops in the derived graph.The decoding performance of this code is shown in Fig.6and compared to that ofFig. 5. An optimized protograph for a rate 1/2 protograph code.0.50.60.70.80.9 1.01.1 1.2 1.3 1.4 1.5E b /N 0, dB10−610−510−410−310−210−11W O R D -E R R O R R A T E (W E R )B I T -E R R O R R A T E (B E R )Fig. 6. Decoding performance of a large protograph code constructed fromthe protograph in Fig. 5.a multi-edge-type LDPC code that we designed using the principles discussed in [1].The performance of the protograph code is perhaps 0.1dB better than that of the multi-edge-type code in the threshold region,but it suﬀers from the appearance of a true error ﬂoor due to low-weight codewords above a word-error rate of 10−4.Our current criterion for selecting a good protograph minimizes the protograph code’s (asymptotic)threshold but does not penalize code structures that might yield high error ﬂoors.Future work will investigate how to eliminate the error ﬂoor or to trade it oﬀversus a small sacriﬁce in the optimized threshold.References[1]T.Richardson,“Multi-Edge Type LDPC Codes,”presented at the Workshophonoring Prof.Bob McEliece on his 60th birthday (but not included in theproceedings),California Institute of Technology,Pasadena,California,May 24–25,2002.[2]T.J.Richardson and R.L.Urbanke,“The Capacity of Low-Density Parity-CheckCodes under Message-Passing Decoding,”IEEE rm.Theory ,vol.47,pp.599–618,February 2001.[3]S.-Y.Chung,On the Construction of Some Capacity-Approaching CodingSchemes,Ph.D.dissertation,Massachusetts Institute of Technology,Cambridge,Massachusetts,September 2000.[4]T.J.Richardson and R.L.Urbanke,“Design of Capacity-Approaching Irreg-ular Low-Density Parity-Check Codes,”IEEE rm.Theory,vol.47, pp.619–637,February2001.[5]X.-Y.Hu,E.Eleftheriou,and D.-M.Arnold,“Progressive Edge-Growth TannerGraphs,”IEEE Global Telecommunications Conference2001,vol.2,pp.995–1001,November25–29,2001.。

CCSDS标准中LDPC码译码器研究与实现

CCSDS标准中LDPC码译码器研究与实现Research and Implementation of LDPC Codes Decoder in CCSDS Standards薛丽(中国西南电子技术研究所,四川成都610036)Xue Li(Southwest China Electronic Technology Institute,Sichuan Chengdu610036)摘要：目前，准循环LDPC(QC_LDPC)已经广泛应用IEEE802.11、IEEE802.16、DVB-S2、CCSDS、3GPP5G-NR等系列标准。

LDPC码的性能非常优越、复杂度较低、吞吐量高、可以进行并行解码，解码时延小。

该文针对CCSDS131.0-B-2标准中10种码字的LDPC码以码率为单位在FPGA上进行了兼容实现，并给出了进一步实现高速译码和降低硬件资源的方法，为在实际工程实现需要提供了重要参考。

关键词：准循环低密度校验码(QC_LDPC码)；译码器；FPGA实现中图分类号：TN911.22文献标识码：A文章编号：1003-0107(2021)05-0099-06Abstract:Nowadays,Quasi-cyclic low-density parity-check(QC_LDPC)codes has been widely used in IEEE 802.11,IEEE802.16,DVB-S2,CCSDS,3GPP5G-NR series of standards.LDPC code has excellent perfor-mance,low complexity,high throughput,parallel decoding and small decoding delay.This paper aims to compatible implement the10kinds of code in the CCSDS131.0-B-2standard on the FPGA,and gives the method of further realizing high speed decoding and reducing hardware resources,providing important reference to the realization needs of engineering.Key words:Quasi-cyclic low-density parity-check codes;decoder;FGPGA implementationCLC number:TN911.22Document code:A Article ID：1003-0107(2021)05-0099-060引言低密度校验码(LDPC)[1-2]是在1963年由Gallager发明的线性分组码。

改进的LDPC译码方案设计及性能分析

综上所述，本文将ARQ技术应用到中继系统场景中，设计了一种改进的LDPC译码方案，其主要利用信源信息与中继信息间的相关性计算比特翻转概率来获取可靠的外信息，从而实现联合迭代译码，以改善传输系统的误码率性能。
收稿日期：2018-03-20；修订日期：2019-04-25 基金项目：国家自然科学基金项目(61771474)；国家青年科学基金项目(61601464) 作者简介：单宝玲(1992-),女，山东临沂人，硕士研究生，研究方向为信道编码以及网络编码；+通讯作者：李宗艳(1982 -),女，山东临沂人，博士，讲师，研究方向为信道编码以及网络编码。E-mail: lizongyan@
Abstract： To improve the bit error rate performance of information transmission, an improved LDPC decoding scheme was pro posed. The base station estimated received sources information of direct link to obtain a source node factor with an error and sent a retransmission request to the relay through a feedback channel, the relay forwarded adaptively according to the received ARQ information. The base station estimated the bit flip probability based on the correlation between the source information and the relay information, and it was used in the joint iterative decoding process to update the external information. Simulation results show that the improved LDPC decoding scheme can effectively improve the BER performance of information transmission, and theperformanceisimprovedwiththeimprovementofthesource-relaytransmissionlink. Key words： automatic repeat request； LDPC codes； bit-flipping probability； log-likelihood rate； bit error rate

Quasi-Cyclic LDPC Codes for Deep Space and High Data Rate

Quasi-Cyclic Low-Density Parity-Check (QC-LDPC) Codes for Deep Space and High Data RateApplicationsNikoleta Andreadou, Fotini-Niovi Pavlidou Dept. of Electrical & Computer Engineering Aristotle University of ThessalonikiThessaloniki, Greecenandread@auth.gr Stylianos Papaharalabos, P. Takis Mathiopoulos Institute for Space Applications and Remote Sensing National Observatory of AthensAthens, Greecespapaha@space.noa.grAbstract—In this paper we investigate and compare the performance of a selected class of Low-Density Parity-Check (LDPC) codes, i.e. Quasi-Cyclic (QC) LDPC codes, against the currently used turbo codes for deep space and high data rate applications. This is useful in future updates of the channel code option used for such applications by the Consultative Committee for Space Data Systems (CCSDS). A wide range of different code rates is examined and the obtained Bit Error Rate (BER) performance versus the Bit Energy to Noise Spectral Density ratio (E b/N0) is reported. Both low and high code rates are being studied, and specifically the 1/2, 1/3, 1/4 and 1/5 as well as the 2/3, 3/4 and 4/5 code rates are taken under consideration. The role of the iteration rounds in the decoding procedure of LDPC codes is also examined showing that QC-LDPC codes outperform the currently used CCSDS turbo codes. Another advantage of QC-LDPC codes is their simple encoding procedure, which reduces the encoding complexity. Since deep space applications are considered, the signals are transmitted over the Additive White Gaussian Noise (AWGN) channel, with the specific block size of 7136 bits.Keywords—Quasi-Cyclic Low-Density Parity-Check (QC-LDPC) Codes, Turbo Codes, Deep Space Communications.I.I NTRODUCTIONThe evolution in the telecommunications area over the last years has led to an increased interest in using advanced error control coding techniques. Turbo codes, due to their enhanced Bit Error Rate (BER) performance, are considered as a serious candidate for modern communication systems [1]. Another coding scheme is Low-Density Parity-Check (LDPC) codes, which were first introduced by Gallager in 1963 [2]. Although LDPC codes had been neglected for many years, they have become the target of research and investigation over the last decade, after the development of practical decoding implementation technologies. Their main advantage is that their performance can be similar to that reached by turbo codes [3], however LDPC codes can allow parallel decoding This research work was carried out in the context of IST SatNEx-II FP6 Project (IST-027393)architectures, thus achieving higher throughputs as compared to turbo codes [4].LDPC codes are described by their parity check matrix and the way this is constructed. LDPC codes are divided into two categories, namely regular and irregular codes, with the latter ones experiencing a better BER performance in general. In addition, the modification introduced by the construction of the parity check matrix results in random codes [5] and also structured codes [6–8]. The former category describes LDPC codes when their parity check matrix is designed by a random computer-based procedure. On the other hand, the second category implies that this matrix has been constructed based on combinatorial methods. Such examples are the Quasi – Cyclic (QC) LDPC codes. Their main advantage against randomly constructed codes is that they involve easier implementation in terms of the encoding procedure [7]. The main feature of QC-LDPC codes is that their parity check matrix consists of circulant submatrices, which could be either based on on the identity matrix [8, 9] or a smaller random matrix [6]. Permutation vectors could also be used in order to create the circulant submatrices. Their encoding procedure can be accomplished by using a series of shift registers, while the complexity is proportional to the number of parity bits or the total code length [7].In this paper, a thorough study is carried out in terms of achievable BER under different coding schemes, such as turbo codes and LDPC codes, with low code rates as well as high code rates suitable for deep space and high data rate applications. In particular, QC-LDPC codes are employed, in order to reduce encoding complexity. The corresponding performance evaluation results show that QC-LDPC codes outperform the currently used Consultative Committee for Space Data Systems (CCSDS) turbo codes for a given number of iteration rounds. This performance evaluation study is useful in future updates of the channel code option used in deep space communications by the CCSDS [10].The rest of the paper is organized as follows. Section II describes the turbo codes currently used in deep space communications. The next Section III addresses the proposed LDPC code construction, the coding and decoding techniques used for such applications. In Section IV various performance evaluation results by means of computer simulations and appropriate comparisons are depicted, while the conclusions are drawn in Section V.II.T URBO C ODES U SED I N D EEP S PACE A PPLICATIONSFirst, state-of-the-art channel coding techniques have traditionally been used in deep space communications, as the received signal power in such applications is very low, due to the extremely large propagation distances. Thus, the use of powerful error-correcting codes is the enabler key, in order to provide with large coding gains and improve the link budget computations. For this, turbo codes have been used by the CCSDS since 1999 [10]. In particular, turbo codes have demonstrated an additional coding gain of approximately 2 dB with respect to the former channel code solution consisting of a Reed-Solomon (RS) code concatenated with a Convolutional Code (CC) through a bit interleaver [11].Fig. 1 depicts the turbo encoder used by the CCSDS standard. It is a Parallel Concatenated Convolutional Code (PCCC) that makes use of two Recursive Systematic Convolutional (RSC) codes, each one having 16-states and code rate equal to 1/4. The different code rate options in CCSDS standard, i.e. 1/2, 1/3, 1/4 and 1/6, are obtained through appropriate interconnections of the parity bits produced by the two RSC codes, as explicitly shown in Fig. 1. The interleaver permutation, been designed by Berrou, follows a deterministic procedure in order to reduce as much as possible the memory storage requirements. There are four frame length options in CCSDS standard, i.e. 1784, 3568, 7136, and 8920 bits. For trellis termination, an additional output sequence of bits is produced, depending on the code rate, in order to flash the constituent RSC encoders to the zerostate.Fig. 1. Turbo encoder used by CCSDS standard.III. P ROPOSED LDPC C ODING T ECHNIQUEA. Characteristics of LDPC codesLDPC codes belong to the category of linear block codes meaning that a codeword (c ) of n bits is produced by the original uncoded word (u ) of k bits. Their parity check matrix describes this class of codes, which is sparse and the majority of its digits are zero. A codeword c is valid if the subsequent parity check equation is true:H * c T = 0(1)The resultant code rate k /n defines the size of the parity check matrix, which is specified as (n – k ) x n . Uniform and non-uniform row and column weights as regards to the parity check matrix, result in regular and irregular LDPC codes, respectively [12].A typical characteristic of LDPC codes is that they can be described by a bipartite graph. Two groups of nodes, namely the check nodes and bit nodes constitute this bipartite graph. The size of the parity check matrix plays an important role in determining the number of these nodes, meaning that if its sizeis m x n , then the graph will consist of m check nodes and n bit nodes, respectively. One row in the parity check matrix is represented by one check node, whereas each bit node corresponds to one codeword bit [12]. The presence of an ace in each row of the parity check matrix means that the two corresponding nodes are connected to each other in the bipartite graph [13]. For example, if there is an ace in the third column and fifth row of the matrix, then the third bit node will be connected to the fifth check node. Having an irregular code implies that not every bit node is connected to the same number of check nodes. In Fig. 2 an example of a parity check matrix and its equivalent bipartite graph are demonstrated. ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=110010010110111001100100101100101001010011011010001110010011000101101101HFig. 2. A parity check matrix (H) and its corresponding bipartite graph.B. Encoding Procedure of QC-LDPC Codes This class of LDPC codes is characterised by a parity checkmatrix H, which consists of square blocks, as already has been mentioned. The square blocks could either be the zero matrix or circulant permutation matrices. Eq. (2) illustrates apermutation matrix P of size q x q .0100001000011000P ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦K M M M M K (2) Let P i stand for the circulant permutation matrix, which is derived from the identity matrix I after the latter one is shifted to the right by i times (0 ≤ i ≤ q ). The zero matrix is defined as P ∞, whereas the resulting parity check matrix H of size (j·q ) x (k·q ) is denoted in Eq. (3): 1(1)111122(1)2212212(1)k k k k j j j k jk a a a a a a a a a a a a P P PP P P P P H P P P P −−−⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦L L M M M M M L (3) where a il Є {0, 1, …, q – 1, ∞} [8]. Parameters k and j are related to the resultant overall code rate R by: R ≥ 1 – j / k (4)Special care should be taken so that q is set to a prime number and the equation q ≥ k ≥ j is not validated, otherwise the coding system would be inadequate.By selecting the parity check matrix in such a way results inreduced memory needed for storage, since after positioning theaces in the first row of each block matrix P, then the rest acescan easily be located. Depending on how the blocks are defined, we can obtain both regular and irregular QC-LDPC codes. In case of regular codes, the code rate is larger than 1 –j / k , as shown in Eq. (4) [8].In this paper we focus on QC-LDPC codes having a parity check matrix in the form of the following Eq. (5): (2)(2)2(3)2(3)(1)()0(,,)00000j k j k j k j I I I I I I P P P H q j k I P P IP−−−−−−⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦KK K K K L M M M KM K MK K (5)It is noticeable from Eq. (5) that this matrix is in upper triangular form leading to irregular codes. The encoding procedure is also facilitated, while the overall code rate is 1-j/k . C. Decoding Procedure In general an iterative algorithm, the so-called Message Passing Algorithm or Belief Propagation Algorithm, describesaccurately the decoding procedure followed by LDPC codes[14]. This algorithm is better comprehended via the code’s bipartite graph. Although its main structure is similar, several versions have been presented in the open technical literature [14], [15]. According to this algorithm, each bit node sends amessage to the check nodes with which it is connected, duringeach iteration round. This message is an estimation on the exact value of the corresponding codeword bit this node represents. Afterwards, all the messages received at each check node areupdated so that other messages are sent back to the neighbouring bit nodes, meaning that one iteration round is completed. Subsequently, the messages are further processed and the bit nodes send information back to check nodes, so that the algorithm is repeated. The messages exchanged betweenconnected nodes entail extrinsic information only, which is themain feature of the algorithm. As a result, the message sent by a check node to one bit node is based on the information received by the check node from all the other bit nodes except for this particular bit node. The situation is similar when it comes to messages sent from bit nodes to check nodes. At the end of each iteration round and after the bit nodes’ messagesare processed, a codeword is produced. Whether or not the resultant codeword is correct this is checked at the end of eachiteration round. The algorithm stops either after a predefined number of iterations are carried out or in case the correctcodeword is already found during the algorithm’s execution [14]. From this point, it is obvious that the number of iteration rounds plays an important role in the system’s performance. Incase the number of iteration rounds is small, it is likely that the correct codeword is not obtained. On the other hand, a greaternumber of iteration rounds, leads to an increased system’s complexity.The nature of the messages sent by the nodes determines the difference between the algorithm versions. For instance, themessages can be either log-likelihood ratios [15] or not [14]. Inthis paper, the messages sent at each iteration round of the decoding procedure are in the probability domain [14]. It should be also mentioned that irregular codes offer more protection to the information bits, due to the appropriateconstruction of their parity check matrix. In particular, the bit nodes that are connected to a greater number of check nodestend to update their values quicker than the ones that are only connected to a limited number of check nodes. Because of the way encoding is performed, these bit nodes are the ones that contain the useful information, meaning that the information bits are the first ones to be corrected as long as the iterativealgorithm proceeds. IV. P ERFORMANCE E VALUATION R ESULTSIn this section BER performance evaluation results areillustrated by the means of computer simulations. It is assumedBinary Phase Shift Keying (BPSK) modulation and the AWGN channel. In principle, regarding the LDPC codes the lower the code rate used the larger the parity check matrix becomes. Thus, more computer resources are required. In addition, due to the matrix calculations and to the numerous components the systems consists of, the total simulation time has been large. Consequently, there had to be a trade off between the number of transmitted data blocks and the minimum possible BER value the results approach. Moreover, the maximum number of iteration rounds used in the decoding procedure was set to 15, since it was observed that there was no noticeable difference at the resulting decoded words when more iteration rounds were applied.The simulations were run with a block size of 7136 bits. The number of iteration rounds was afterwards set to 5 in order to observe how a single parameter can affect the system’s performance. It should also be noted here that the iterationrounds concerning the turbo decoder were set to 10.Fig. 3. Bit error rate versus Eb/N 0 for QC – LDPC and turbo codes of code rates1/2 and 2/3 respectively.In Fig. 3 the BER performance is shown when QC-LDPC and turbo codes of 1/2 and 2/3 code rate are used. It is noticeable that the two code rates follow the same trend throughout the whole E b /N 0 range. It is also clear that for higher E b /N 0 rates, there is a sharp decrease concerning the BER of LDPC for both code rates. Two different curves are displayed for the LDPC code. In the first one the number of iteration rounds is set to 15, while in the second one it is set to 5. It is obvious that by changing one vital parameter, the system’s performance can be highly altered. A smaller number of iteration rounds means that the system fails to correct all the errors occurring during the signal’s transmission, whereas a larger number of iteration rounds leads to a better system’s performance. However, the main aspect observed from this graph is that LDPC codes outperform turbo codes, while the difference in their performance is significant especially for lower E b / N 0 values. This confirms the theory that LDPC codes are a promising coding technique and can result in a high system’s performance. It is also clear that when fewer iteration rounds are defined in the decoding procedure, the LDPC coding scheme seems to perform close to turbo codes.Both high and low code rates have been examined. Fig. 4 shows the system’s performance when the higher code rates are being employed into the system. In particular, 3/4 and 4/5 code rates are used both for LDPC and turbo codes. On the other hand, the system’s performance regarding the lower code rates, i.e. 1/3, 1/4 and 1/5, is illustrated in Fig. 5 and Fig. 6, respectively. The lower code rates are the ones that give themost interesting results regarding the system’s effectiveness.Fig. 4. Bit error rate versus Eb/N 0 for QC – LDPC codes of code rates 3/4 and4/5 respectively.Fig. 5. Bit error rate versus Eb/N 0 for QC – LDPC and turbo codes of code rates1/3 and 1/4 respectively.Correspondingly to the case of 1/2 and 2/3 code rate, the curves in Figs. 4, 5 and 6 experience the same inclination. Furthermore, it is noticeable that the deep fall in the BER plot occurs for lower E b /N 0 rates in Fig. 3 and higher ones in Fig. 4. This is explicable by the fact that for higher code rates, the bits redundancy is decreased at the expense of the signal’s quality. Thus, at the presence of fewer coded bits the protection offered to the original data bits is of inferior quality. As a result, the 1/5 code rate experiences the best performance, as it can be shown from Fig. 6.Fig. 6. Bit error rate versus Eb/N0 for QC – LDPC and turbo codes of code rate1/5.The most important thing to notice when examining the curves is that LDPC codes clearly outperform turbo codes for all code rates when a large number of iteration rounds are set. It is also apparent that when fewer iteration rounds are present, the system’s performance tends to become similar for LDPC and turbo codes.V.C ONCLUSIONSThe applicability of LDPC codes for future deep space and high data rate communication systems was demonstrated. Several code rates were examined and it was shown that LDPC codes outperform turbo codes, when a large number of iteration rounds was set. The two coding schemes experience a similar performance, when fewer iteration rounds were used. In addition, as opposed to the currently used turbo codes, QC-LDPC codes offer some implementation advantages in both the encoding and decoding side. That is, the use of a series of shift registers for linear time encoding operation and the possibility of a parallel decoding implementation.R EFERENCES[1] C. Berrou, A. Glavieux, and P. Thitimajhima, “Near Shannon limit errorcorrecting coding and decoding: Turbo codes”, IEEE Int. Conf.Commun. (ICC), pp. 1064-1070, Geneva, Switzerland, May, 1993. [2]R. G. Gallager, Low – Density Parity Check Code s. Cambridge, MA:MIT Press, 1963.[3]T. J. Richardson, and R. L. Urbanke, “Efficient Encoding of Low-Density Parity-Check Codes”, IEEE Trans. Information Theory, vol. 47, no. 2, pp. 638-656, Feb. 2001.[4] A. J. Blanksby, and C. J. Howland,: “A 960-mW 1 Gb/s 1024-b, rate 1/2low-density parity-check code decoder', IEEE Journal of Solid-State Circuits, Vol. 37, No. 3, pp. 404-412, 2002.[5]R. M. Tanner, “A recursive approach to low complexity codes”, IEEETrans. Inf. Theory, vol. IT-27, no. 9, pp. 533–547, Sep. 1981.[6]R. Echard, and C.Shih-Chun, “The π-rotation low-density parity checkcodes”, IEEE Globecom 2001, vol. 2, pp. 980–984. 25-29 Nov. 2001. [7]Z. Li, L. Chen, L. Zeng, S.Lin, and W. H. Fong, “Efficient Encoding ofQuasi-Cyclic Low-Density Parity-Check Codes”, IEEE Transactions on Communications, vol. 54, no. 1, Jan. 2006, pp. 71–81.[8]S. Myung, K. Yang, and J. Kim, “Quasi-Cyclic LDPC Codes for FastEncoding”, IEEE Transactions on Information Theory, vol. 51, no. 8, pp.2894 – 2901, Aug. 2005.[9] E. Eleftheriou and S. Olcer, “Low-density parity-check codes formultilevel modulation,” in Proc. IEEE Int. Symp. Information Theory (ISIT2002), Lausanne, Switzerland, Jun./Jul. 2002, p. 442.[10]TM Synchronization and Channel Coding, CCSDS 131.0 B-1, Sep.2003.[11]G. P. Calzolari, F. Chiaraluce, R. Garello, and E. Vassallo, “Turbo CodeApplications on Telemetry and Deep Space Communications”, in Turbo Code Applications: A Journey From a Paper to Realization, Chapter 13, (Ed.) S. Sripmanwat, Springer, 2005.[12]H. Zhong and T. Zhang, “Block-LDPC: A Practical LDPC CodingSystem Design Approach”, IEEE Trans. Circuits and Systems—I: Regular Papers, vol. 52, no. 4, pp. 766-775, Apr. 2005.[13]J. Hou,P. H. Siegel, and L. B. Milstein, “Performance Analysis andCode Optimization of Low Density Parity-Check Codes on Rayleigh Fading Channels”, IEEE J. Select. Areas Commun., vol. 19, no. 5, pp.924-934, May 2001.[14]Robert H. Morelos - Zaragoza, “The Art of Error Correcting Coding,Second Edition”, Wiley 2006.[15]H. Nakagawa, D. Umehara, S. Denno and Y. Morihiro, “A Decoding forLow Density Parity Check Codes over Impulsive Noise Channels”, IEEE ISPLC, pp. 85-89, 2005.。

无短环不规则QC_LDPC码的快速编码及联合译码

无短环不规则QC_LDPC码的快速编码及联合译码刘蕾;孙书龙;常亮;李华旺【摘要】The low density parity check(LDPC)codes and the implementation scheme of the decoding structure were de-signed based on irregular semi-parallel structure. LDPC codes without four cycles have high throughput and low complexity, whose length and rate are variable. This coding structure can extend irregular semi-parallel LDPC codes with different code length. The decoder adopts Sum-Min algorithm to realize decoding. The memory address of middle information nodes applies Gray coding to reduce dynamic power consumption. Based on this structure,encoder and decoder of irregular semi-parallel LDPC codes were designed by using Xilinx Virtex-5 XC5VtX150T-ff1156 FPGA,whose code length is 1 270 bit and code rate is 1 2. The comprehensive results show that the information throughput of this encoder can achieve 2.52 Gb/s and the information throughput rate of the decoder can reach 44 Mb/s in the case of 10 iterations.%基于不规则部分并行结构设计了一种高吞吐量,低复杂度,码长码率可变且去除四环的低密度奇偶校验LDPC码及其译码结构实现方案,该编码结构可针对不同码长的不规则部分并行结构LDPC码进行扩展,译码器采用缩放最小和定点(Sum-Min)算法实现译码,中间信息节点存储器地址采用格雷码编码,降低动态功耗;采用Xilinx公司的Virtex-5 XC5VtX150T-ff1156FPGA芯片设计了一款码长1 270,码率1 2的不规则部分并行LDPC码的编码器和译码器.综合结果表明:该编码器信息吞吐量为2.52 Gb/s,译码器在10次迭代的情况下信息吞吐率达到44 Mb/s.【期刊名称】《现代电子技术》【年(卷),期】2015(038)017【总页数】4页(P34-37)【关键词】低密度奇偶校验码;不规则码;部分并行结构;FPGA【作者】刘蕾;孙书龙;常亮;李华旺【作者单位】中国科学院上海微系统所,上海 200050;中国科学院上海微系统所,上海 200050;上海微小卫星工程中心,上海 200120;上海微小卫星工程中心,上海200120【正文语种】中文【中图分类】TN911.22-34低密度奇偶校验码（Low Desity Parity Check，LDPC）又被称为Gallager码，是Gallager在1960年提出的，LDPC码在AWGN信道下具有非常好的性能，目前最好的仿真结果表明，随机LDPC码在AWGN白噪声下距离Shannon限仅0.004 5 dB。

5G标准中的LDPC码研究及在图像传输中的应用

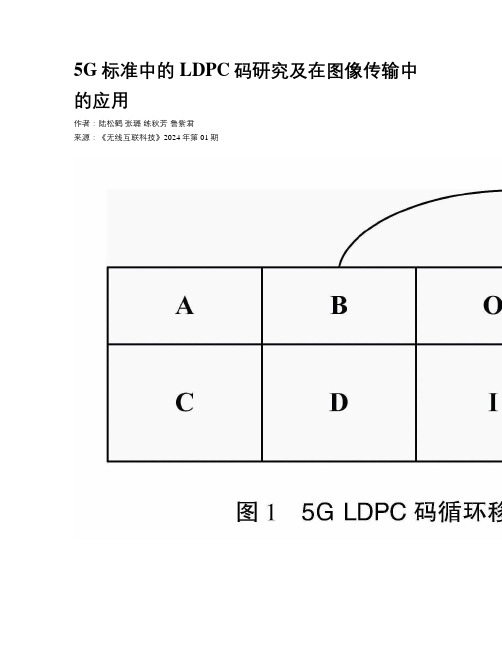
5G标准中的LDPC码研究及在图像传输中的应用作者：陆松鹤张璐练秋芳鲁紫君来源：《无线互联科技》2024年第01期基金项目：泉州市科技计划；项目名称：5G通信中的LDPC码关键技术研究与应用；项目编号：2018C108R。

作者简介：陆松鹤（1983—），男，高级工程师，硕士；研究方向：5G通信及应用。

*通信作者：练秋芳（1998—），女，助理实验师，硕士；研究方向：无线通信及应用。

摘要：在第五代移动通信系统（5G）中，为满足用户随时随地接入网络的需求，在增强移动宽带应用场景中使用低密度奇偶校验（Low-Density Parity-Check，LDPC）码作为数据信道的信道编码方案。

文章探讨了5G标准中的LDPC码在图像传输中的应用。

仿真结果表明：与未经过信道编译码的图像传输系统相比，经过LDPC码编码的系统在相同的信噪比条件下，图像质量有着非常明显的提高，在信噪比为2 dB时已经十分接近原图。

关键词：5G；LDPC码；图像传输；信道编码中图分类号：TN911.22 文献标志码：A0 引言低密度奇偶校验（Low-Density Parity-Check，LDPC）码由Gallager教授提出，可满足5G 标准中低延时和编码灵活性的要求［1］。

然而，LDPC码的译码器存在硬件资源消耗大和收敛速度慢的问题，吴淼等［2］设计了一种全并行分层结构的译码器。

图像通信作为数字通信的一部分，在生活中的应用十分广泛，而如何在信道中，可靠和有效地传输图像信息，一直是图像通信中的研究热点。

本文在此基础上设计图像传输系统来测试5G LDPC码的性能。

1 LDPC码概述1.1 5G标准中LDPC码的特性因为5G通信系统具有较高的复杂度，设计者需从多个维度考量LDPC码的构造。

为了使5G LDPC码更易实现，5G通信系统在eMBB场景中采用二元准循环LDPC码来减少硬件资源的使用率。

基于准循环LDPC码校验矩阵双对角的特性，为方便后文使用循环移位矩阵Hp来介绍校验矩阵。

LDPC码ADMM惩罚译码的早停止方法

收稿日期:2017-12-23 网络出版时间:2018-03-07基金项目:国家自然科学基金资助项目(61471286,61602010);重庆市/信息产业部计算机网络与通信技术重点实验室开放基金资助项目(C Y -C N C L -2017-03);宝鸡市科技计划资助项目(15R K X -1-5-8);宝鸡文理学院校级重点资助项目(Z K 2017001,Z K 12094)作者简介:王彪(1982-),男,西安电子科技大学博士研究生,E -m a i l :w a n g b i a o 401@s i n a .c o m.网络出版地址:h t t p://k n s .c n k i .n e t /k c m s /d e t a i l /61.1076.T N.20180307.1034.004.h t m l d o i :10.3969/j.i s s n .1001-2400.2018.05.008L D P C 码A DMM 惩罚译码的早停止方法王彪1,2,慕建君1,焦晓鹏1,王钟斐2(1.西安电子科技大学计算机学院,陕西西安710071;2.宝鸡文理学院数学与信息科学学院,陕西宝鸡721013)摘要:为了减少低密度校验码译码的平均迭代次数,通过深入分析迭代译码中码字所满足的校验约束个数的变化规律,设计了低密度校验码交替方向乘子法惩罚译码的一种早停止方法.该方法能够在译码的早期阶段检测出错误码字而停止译码,从而节省了不必要的译码迭代.与现有交替方向乘子法惩罚译码的两种停止方法相比较,所提出的早停止方法在低信噪比区域降低了交替方向乘子法惩罚译码的平均迭代次数,而且其译码性能几乎没有损失.关键词:低密度校验码;交替方向乘子法;惩罚译码;早停止中图分类号:T N 911.22 文献标识码:A 文章编号:1001-2400(2018)05-0043-07M e t h o d f o r e a r l y t e r m i n a t i o no fA D MM p e n a l i z e dd e c o d i n gf o rL D P Cc o d e sWA N GB i a o 1,2,MUJ i a n j u n 1,J I A O X i a o p e n g 1,WA N GZ h o n g fe i 2(1.S c h o o lo fC o m p u t e rS c i e n c ea n d T e c h n o l o g y ,X i d i a n U n i v .,X i a n710071,C h i n a ;2.S c h o o lo f M a t h e m a t i c s a n d I n f o r m a t i o nS c i e n c e ,B a o j iU n i v .o fA r t s a n dS c i e n c e s ,B a o ji 721013,C h i n a )A b s t r a c t : I no r d e r t o r e d u c e t h e a v e r a g en u m b e r o f i t e r a t i o n s f o r l o w -d e n s i t yp a r i t y -c h e c k (L D P C )c o d e s d e c o d i n g ,am e t h o d f o r e a r l y t e r m i n a t i o n (E T )o f t h e a l t e r n a t i n g d i r e c t i o nm e t h o do fm u l t i pl i e r s (A D MM )p e n a l i z e dd e c o d i n g i sd e s i g n e df o rL D P Cc o d e sb y m a k i n g at h o r o u g ha n a l y s i so f t h ec h a n ger u l eo f t h e n u m b e r o f s a t i s f i e d p a r i t y -c h e c k c o n s t r a i n t s i n i t e r a t i v ede c o d i n g .T h e p r o p o s e dm e t h o d c a nd e t e c t t h e e r r o r c o d e w o r d sa ta n e a r l y s t a g eo fd e c o d i n g a n dt h e nt h ed e c o d i n g p r o c e s si ss t o p p e d ,w h i c h s a v e st h e u n n e c e s s a r y d e c o d i n g i t e r a t i o n s .C o m p a r e d w i t ht h et w oe x i s t i n g s t o p p i n g me t h o d so fA D MM p e n a l i z e d d e c o d i n g ,t h e p r o p o s e dE T m e t h o d r e d u c e s t h e a v e r a g en u m b e r of i t e r a t i o n s o fA D MM p e n a l i z e dd e c o d i ng a t l o ws i g n a l -t o -n o i s e r a t i o n sw i t han e g l i g i b l e d e c o d i n gp e r f o r m a n c e l o s s .K e y W o r d s : l o w -d e n s i t y p a r i t y -c h e c k c o d e s ;a l t e r n a t i n g d i r e c t i o n m e t h o d o f m u l t i p l i e r s ;p e n a l i z e d d e c o d i n g ;e a r l y te r m i n a t i o n 近年来,具有逼近香农限良好性能的低密度校验(L o w -D e n s i t y P a r i t y -C h e c k ,L D P C )码受到了研究学者的普遍关注[1-2].线性规划(L i n e a rP r o g r a mm i n g,L P )译码是L D P C 码的一种重要译码方法,但其译码复杂度较高[3].文献[4]提出了一种基于交替方向乘子法(A l t e r n a t i n g D i r e c t i o nM e t h o d o fM u l t i pl i e r s ,A D MM )的L P 译码方法,该方法能够降低L D P C 码L P 译码方法的译码复杂度[4].为了进一步降低L D P C 码A D MM 译码的复杂度,许多学者进行了以下几个方面的研究:简化译码过程,主要包括利用割查找算法(C u t S e a r c hA l g o r i t h m ,C S A )来设计低复杂度的欧几里德投影算法[5],提出用单纯形(S i m pl e x )替代校验多2018年10月第45卷第5期西安电子科技大学学报(自然科学版)J O UR N A L O F X I D I A N U N I V E R S I T YO c t .2018V o l .45 N o .5h t t p ://w w w.x d x b .n e t胞体(C h e c kP o l y t o p e )的欧几里德投影算法[6],直接降低欧几里德投影的次数[7],基于查表法提出简化的欧几里德投影算法[8],以及设计不需排序的迭代欧几里德投影算法[9];通过改变消息在变量节点和校验节点间的传递方式,设计高效的消息调度策略[10];利用多核处理器的结构特征优化A D MM 译码算法的软件实现[11];通过在L P 模型目标函数中加入罚函数[12]㊁加权罚函数[13]和改进罚函数[14]来设计A D MM 惩罚译码方法,此类方法不仅可以降低A D MM 译码复杂度,同时能够改善L D P C 码的译码性能.早停止(E a r l y Te r m i n a t i o n ,E T )方法也是一种能够降低L D P C 码译码复杂度的有效方法.当译出正确码字或达到最大迭代次数时,L D P C 码译码器会停止译码[15].如果译码器能够在早期阶段(即不达到最大译码迭代次数时)停止译码,即判断出正确码字或错误码字,那么就可以节省不必要的译码迭代,从而降低译码的平均迭代次数.目前,针对L D P C 码置信传播(B e l i e fP r o p a ga t i o n ,B P )译码方法,基于奇偶校验计算的早停止方法[16]和基于后验对数似然比的早停止方法[17]均能够有效降低L D P C 码的译码复杂度.关于L D P C 码A D MM 惩罚译码算法的研究,学者们目前主要集中在简化欧几里德投影㊁设计合适的调度策略及优化实现方法等方面来降低其译码复杂度,还未深入开展针对该算法的早停止方法研究.现有A D MM 惩罚译码的停止方法只有两种:标准的ε规则[4]和H x T =0的早停止方法[5].标准的ε规则将A D MM 译码中每次迭代的主残差(P r i m a lR e s i d u a l )和对偶残差(D u a lR e s i d u a l )分别与ε(ε>0)比较,若这两个残差值都小于ε,则译码迭代停止;而H x T =0的早停止方法主要依据所有校验方程H x T=0是否满足来确定译码停止.通过计算L D P C 码译码迭代过程中码字所满足的校验约束个数,设计了L D P C 码A D MM 惩罚译码的一种早停止方法,该方法能够在早期阶段判断出错误码字而停止译码.仿真结果表明,所设计的早停止方法能够在低信噪比区域降低L D P C 码A D MM 惩罚译码的平均迭代次数,且其译码性能几乎没有损失.1 基于A D MM 的L P D C 码惩罚译码设L D P C 码C 的校验矩阵为m ˑn 的矩阵H ,其对应的T a n n e r 图中所有变量节点集合I ={1,2, ,n },所有校验节点集合J ={1,2, ,m }.设集合N v (i )表示与变量节点v i 相关联的所有校验节点集合,而集合N c (j )表示与校验节点c j 相关联的所有变量节点集合.令d v i =N v (i ),表示变量节点v i 的度数;d c j=N c (j ),表示校验节点c j 的度数.假设发送端将码字x ={x i ɪ{0,1}|i ɪI }经过加性高斯白噪声(A d d i t i v e W h i t eG a u s s i a nN o i s e ,AWG N )信道发送后,接收端接收到的序列r ={r i |i ɪI },r 对应的对数似然比向量记为γ={γi |i ɪI },其中γi =l o (g P r (r i |0)r (r i |1)),P r (㊃)表示括号内代表的事件发生的概率.通过引入辅助变量z j ɪR dc j (j ɪJ )可以得到LP 译码数学模型为[4]m i n γTx ,s .t .T j x =z j ,z j ɪP d cj, ∀j ɪJ {,(1)其中,校验多胞体P d c j表示所有长度为d c j 且含有偶数个1的二进制向量构成的凸包,d c j ˑn 二进制转换矩阵T j 选出x 中与第j 校验节点所关联的d c j个分量.为了改善L D P C 码A D MM 译码在低信噪比区域的译码性能,文献[12]通过在目标函数中加入罚函数提出了基于A D MM 的惩罚译码方法.于是式(1)中的目标函数变为f (x )=γT x +αði ɪI g (x i),其中α为罚参数,g (x )为罚函数.目前,常用的罚函数主要有l 1罚函数g 1(x )=-x -0.5和l 2罚函数g 2(x )=-(x -0.5)2[12].2 A D MM 惩罚译码的早停止方法2.1 码字所满足校验约束个数分析B P 译码中,若第l 次迭代输出的是正确码字^x(l)={^x (l)iɪ{0,1}|i ɪI },则其对应的校正子44 西安电子科技大学学报(自然科学版) 第45卷h t t p ://w w w.x d x b .n e t(S y n d r o m e )S =[s 1,s 2, ,s m]T =H ^x (l )=0.第l 次迭代时码字所满足的校验约束(S a t i s f i e dP a r i t y -c h e c k C o n s t r a i n t s ,S P C )个数为N (l )s p c ,N (l )s pc 可利用下式来计算[15]:N (l )s pc =m -1T H ^x (l ) ,(2)其中,1T表示长度为m 的全1行向量.图1 (576,288)L D P C 码A D MM 惩罚译码迭代时10个码字所满足的校验约束个数变化规律设A D MM 惩罚译码第l 次迭代时得到的向量为x (l )={x (l)i ɪ[0,1]|i ɪI },执行下面所给硬判决操作,^x (l )i =0 ,当x (l)i<0.5 ,1 ,当x (l )iȡ0.5 {,(3)从而得到向量^x (l )={^x (l )iɪ{0,1}|i ɪI },这时可以类似地利用式(2)来计算码字的S P C 个数N (l)s p c .图1给出了码率为0.5的(576,288)L D P C 码A D MM 惩罚译码迭代时10个码字的S P C 个数N (l)s pc 的变化规律.由图1可以看出,经过不同次数迭代后其中的5个码字能够收敛为正确码字,经过迭代10次后其余5个错误码字的S P C 个数N (l )s pc 仍然在一定范围内震荡而不会收敛到正确码字.根据错误码字的S P C 个数N(l)s pc 的分布特点,若当前迭代时码字的N (l )s p c 以及随后连续几次迭代时码字的N (l )s pc 都在一定范围内上下震荡而其对应曲线不会持续上升,则可判定该码字为错误码字而停止译码.基于这一思路,设计了L D P C 码A D MM 惩罚译码的一种早停止方法.2.2 早停止方法设计基于上一小节码字所满足校验约束个数N (l)s pc 变化规律的分析,通过计算A D MM 惩罚译码迭代过程中码字的S P C 个数N (l)s p c ,设计了L D P C 码A D MM 惩罚译码的一种早停止方法.该方法能够在译码早期阶段检测出错误码字而停止译码,从而节省了不必要的译码迭代次数.译码过程中该早停止方法所涉及的参数有:表示码字的S P C 个数N (l)s p c 变化趋势的计数器N c o u n t e r ㊁检测错误码字的比较阈值T ㊁统计计数器N c o u n t e r 的起始迭代次数I m i n ㊁检测错误码字的起始迭代次数I d e c ㊁计算N c o u n t e r 时连续两次迭代之间码字的N (l)s pc 差值为非正的个数d 以及该停止方法允许的N (l)s pc 差值为非正的个数最大值d m a x (仿真实验结果表明,d m a x 值取2较为合适).所设计的L D P C 码A D MM 惩罚译码的早停止方法可以概括为:第1步计算A D MM 惩罚译码第l 次迭代时经硬判决处理后的向量^x (l )={^x (l )iɪ{0,1}|i ɪI }的S P C 个数N (l)s pc (1ɤl ɤI m a x ,I m a x 表示最大迭代次数).第2步若l ȡI m i n ,则令N c o u n t e r ѳN (Im i n )s pc .第3步若l >I m i n ,则计算连续两次迭代之间向量的N (l )s p c 差值N (l )s p c -N (l -1)s p c ,这时若该差值N (l )s p c -N (l -1)s pc >0,则令N c o u n t e r ѳN c o u n t e r +(N (l )s p c -N (l -1)s pc );否则,保持N c o u n t e r 不变.第4步若l ȡIde c 且N c o u n t e r <T ,则统计译码从第I m i n 次到第l 次迭代的所有差值N (l )s p c -N (l -1)s p c 为非正的个数d .第5步若N (l)s pc =m 或d >d m a x 或l >I m a x ,则停止A D MM 惩罚译码;否则,进行下一次迭代译码.说明第5步中,N (l )s p c =m ,表示当前向量的S P C 个数N (l)s pc 满足正确码字的校验约束个数,则判定该向量为正确码字而停止译码;d >d m a x ,表示差值N (l )s p c -N (l -1)s pc 为非正的个数d 超过该停止方法允许的非正差值个数的最大值d m a x ,这说明按照当前向量的S P C 个数N (l)s pc 的递增趋势可判断当前向量不能在允许范围内迭代到正确码字,从而判定该向量为错误码字而停止译码;l >I m a x ,表示迭代次数超过最大迭代次数而停止译码.2.3 计算复杂度分析在L D P C 码A D MM 惩罚译码第l 次迭代中,标准的ε规则涉及2次比较运算㊁2[m (췍d c -1)+(m -1)]54第5期王彪等:L D P C 码A D MM 惩罚译码的早停止方法h t t p ://w w w.x d x b .n e t次加法运算㊁2(m 췍d c )次乘法运算和2m 次开方运算;关于H x T =0的早停止方法,在对向量x 进行硬判决时涉及n 次比较运算,计算H x T 时涉及m (췍d c -1)次异或运算,判定Hx T =0时涉及m 次比较运算;在最坏计算复杂度情况下,文中早停止方法第1步涉及n 次比较运算㊁m (췍d c -1)次异或运算㊁m -1次加法运算和1次减法运算,第2步涉及1次比较运算,第3步涉及2次比较运算㊁1次减法运算和1次加法运算,第4步涉及l -I m i n +3次比较运算和l -I m i n 次加法运算,第5步涉及3次比较运算.表1给出了3种停止方法中比较运算㊁异或运算㊁加/减法运算㊁乘法运算和开方运算的次数比较.췍d c 表示校验节点度数的平均值.表1 每次迭代中3种停止方法的计算复杂度比较停止方法标准ε规则H x T =0的早停止文中的早停止*比较2m +n n +l -I m i n +9异或m (췍d c -1)m (췍d c -1)加/减法2[m (췍d c -1)+(m -1)]m +l -I m i n +2乘法2(m 췍d c)开方2m表1中, *表示在迭代过程中文中的早停止方法在最坏情况下进行的计算复杂度分析.由此可见,文中所设计的早停止方法的计算复杂度低于标准ε规则的计算复杂度,而该早停止方法在最坏情况下的计算复杂度略高于H x T=0的早停止方法的计算复杂度(假设比较运算和加减法运算的计算复杂度相近).3 仿真实验以I E E E802.16e 标准中码率为0.5的(576,288)L D P C 码C 1和码率为0.75的(1152,288)L D P C 码C 2为例,从译码平均迭代次数和译码性能(误帧率)两个方面,对所设计的LD P C 码A D MM 惩罚译码的早停止方法与现有A D MM 惩罚译码的标准的ε规则及H x T =0的早停止方法进行了比较.仿真实验中,A D MM惩罚译码器采用l 1罚函数进行译码,所涉及的罚参数按照文献[12]中的方法进行优化选择,且最大迭代次数㊁译码容差值(E r r o rT o l e r a n c eV a l u e )和超松弛参数(O v e rR e l a x a t i o nP a r a m e t e r )分别取40㊁10-5和1.9.3.1 参数选择下面给出所设计的L D P C 码A D MM 惩罚译码的早停止方法所涉及的检测错误码字的比较阈值T ㊁统计计数器N c o u n t e r 的起始迭代次数I m i n 及检测错误码字的起始迭代次数I d e c 这3个关键参数的选择方法.图2 T 变化时码C 1的译码平均迭代次数和误帧率比较首先,取I m i n =15和I d e c =20来研究比较阈值T 的变化对译码效果的影响.图2给出了T 依次取260㊁270和280时,码C 1采用所设计早停止方法的译码平均迭代次数和译码性能比较.从图2可以看出,采用3种不同T 值时,在高信噪比区域的译码平均迭代次数大致相同,而在低信噪比区域T =280时,译码的平均迭代次数最低,然而其译码误帧率反而最差.当T =260和T =270时的译码平均迭代次数基本相同,而在低信噪比区域T =270时的误帧率较好.因此,选取T =270作为所设计早停止方法的参数值.64 西安电子科技大学学报(自然科学版) 第45卷h t t p ://w w w.x d x b .n et图3 I m i n 和I d e c 变化时码C 1的译码平均迭代次数和误帧率比较其次,取T =270来研究I m i n 和I d e c 的变化对译码效果的影响.针对3组不同参数值(I m i n =10,I d e c =15),(I m i n =15,I d e c =20)和(I m i n =20,I d e c =25),图3给出了码C 1采用所设计的早停止方法的A D MM 惩罚译码时,译码平均迭代次数和译码性能比较.由图3可以看到,I m i n 和I d e c 的3组不同取值的译码平均迭代次数在高信噪比区域大致相同,而在低信噪比区域有所不同,其中取参数值(I m i n =20,I d e c =25)时译码的平均迭代次数最高,取参数值(I m i n =10,I d e c =15)时译码的平均迭代次数最低;3组不同取值的误帧率在高信噪比区域几乎相同,而在低信噪比区域选取(I m i n =15,I d e c =20)的误帧率较好.因此,选取(I m i n =15,I d e c =20)作为所设计早停止方法的参数值.3.2 平均迭代次数和译码性能比较适当选择所设计早停止方法的参数后,以码C 1和码C 2为例,比较了所设计的L D P C 码A D MM 惩罚译码的早停止方法㊁标准的ε规则以及H x T =0的早停止方法3种停止方法的平均迭代次数和误帧率.针对码C 1所设计的早停止方法取定参数T =270㊁I m i n =15和I d e c =20,图4给出了所设计的早停止方法与标准的ε规则以及H x T =0的早停止方法的译码平均迭代次数和误帧率的比较.从图4看出,译码时利用3种停止方法的误帧率大致相同,而其平均迭代次数则明显不同.在较低信噪比区域H x T=0的早停止方法的平均迭代次数高于标准的ε规则,这是因为较低信噪比区域错误码字通常较多,而H x T=0的早停止方法需要更多的迭代次数才能判定错误码字.而所设计的早停止方法克服了H x T=0的早停止方法的这一缺点,在较低信噪比区域可明显降低L D P C 码译码的平均迭代次数,且译码性能几乎没有损失.图4 码C 1采用3种停止方法的译码平均迭代次数和误帧率比较类似地,对于码C 2所设计早停止方法的参数依次取T =270,I m i n =15和I d e c =20.图5给出了采用3种停止方法的译码平均迭代次数和误帧率的比较.从图5可以看出,与现有两种停止方法相比较,所设计早停止方法在较低信噪比区域降低了译码的平均迭代次数,且译码性能几乎没有损失.74第5期王彪等:L D P C 码A D MM 惩罚译码的早停止方法h t t p ://w w w.x d x b .n et图5 码C 2采用3种停止方法的译码平均迭代次数和误帧率比较4 结束语通过计算迭代译码中码字所满足的校验约束个数,设计了一种能够在L D P C 码A D MM 惩罚译码早期阶段检测出错误码字的早停止方法.针对I E E E802.16e 标准中两个典型L D P C 码的仿真实验结果表明,与现有A D MM 惩罚译码的标准的ε规则和H x T=0的早停止方法相比较,所设计的早停止方法能够在几乎没有损失译码性能的同时可降低L D P C 码低信噪比区域译码的平均迭代次数.因此,该方法适合在噪声较大环境下作为L D P C 码A D MM 惩罚译码的停止方法来提高译码收敛速度.参考文献:[1]C HU N GS Y,F OM E Y G DJ ,R I C HA R D S O N TJ ,e t a l .O nt h eD e s i g no fL o w -d e n s i t y P a r i t y -c h e c kC o d e sw i t h i n 0.0045d Bo f t h eS h a n n o nL i m i t [J ].I E E EC o mm u n i c a t i o n sL e t t e r s ,2001,5(2):58-60.[2]范亚楠,王丽冲,姚秀娟,等.交叠的分层置信度传播L D P C 译码算法[J ].西安电子科技大学学报,2017,44(2):88-94.F A N Y a n a n ,WA N GL i c h o n g ,Y A O X i u j u a n ,e t a l .O v e r l a p p e dL a y e r e dB e l i e f -p r o p a g a t i o nL D P CD e c o d i n g A l g o r i t h m [J ].J o u r n a l o fX i d i a nU n i v e r s i t y,2017,44(2):88-94.[3]F E L D MA NJ ,WA I NWR I G H T M J ,K A R G E R D R.U s i n g L i n e a rP r o g r a mm i n g t oD e c o d eB i n a r y L i n e a rC o d e s [J ].I E E ET r a n s a c t i o n s o n I n f o r m a t i o nT h e o r y,2005,51(3):954-972.[4]B A R MA NS ,L I UX,D R A P E RSC ,e t a l .D e c o m p o s i t i o nM e t h o d s f o r L a r g e S c a l eL PD e c o d i n g [J ].I E E ET r a n s a c t i o n s o n I n f o r m a t i o nT h e o r y,2013,59(12):7870-7886.[5]Z HA N G X,S I E G E L P H.E f f i c i e n tI t e r a t i v e L P D e c o d i n g o fL D P C C o d e s w i t h A l t e r n a t i n g Di r e c t i o n M e t h o do f M u l t i p l i e r s [C ]//P r o c e e d i n g so f t h e2013I E E EI n t e r n a t i o n a lS y m p o s i u m o nI n f o r m a t i o n T h e o r y .P i s c a t a w a y:I E E E ,2013:1501-1505.[6]Z HA N G G,H E U S D E N SR,K L E I J N W B .L a r g e S c a l eL PD e c o d i n g w i t hL o wC o m p l e x i t y [J ].I E E EC o mm u n i c a t i o n s L e t t e r s ,2013,17(11):2152-2155.[7]W E IH Y,J I A O XP ,MUJ J .R e d u c e d -c o m p l e x i t y L i n e a rP r o g r a mm i n g D e c o d i n g B a s e do nA D MMf o rL D P CC o d e s [J ].I E E EC o mm u n i c a t i o n sL e t t e r s ,2015,19(6):909-912.[8]J I A O X P ,MU JJ ,H E Y C ,e ta l .E f f i c i e n tA D MM D e c o d i n g o fL D P C C o d e s U s i n g L o o k u p T a b l e s [J ].I E E E T r a n s a c t i o n s o nC o mm u n i c a t i o n s ,2017,65(4):1425-1436.[9]W E IH Y,B A N I HA S H E M IA H.A n I t e r a t i v eC h e c kP o l y t o p eP r o j e c t i o nA l g o r i t h mf o rA D MM -b a s e dL PD e c o d i n g o f L D P CC o d e s [J ].I E E EC o mm u n i c a t i o n sL e t t e r s ,2018,22(1):29-32.[10]J I A O XP ,MUJ J ,W E IH Y.R e d u c e dC o m p l e x i t y N o d e -w i s eS c h e d u l i n g o fA D MM D e c o d i n g f o rL D P CC o d e s [J ].I E E EC o mm u n i c a t i o n sL e t t e r s ,2017,21(3):472-475.[11]D E B B A B I I ,L EG A LB ,K HO U J A N,e t a l .M u l t i c o r e a n d M a n y c o r e I m pl e m e n t a t i o n so fA D MM -b a s e dD e c o d e r s f o r 84 西安电子科技大学学报(自然科学版) 第45卷h t t p ://w w w.x d x b .n e tL D P CD e c o d i n g [J ].J o u r n a l o f S i g n a l P r o c e s s i n g S ys t e m s ,2017:1-17.[12]L I U X,D R A P E RSC .T h eA D MM P e n a l i z e dD e c o d e r f o rL D P CC o d e s [J ].I E E ET r a n s a c t i o n s o n I n f o r m a t i o nT h e o r y ,2016,62(6):2966-2984.[13]J I A O XP ,W E IH Y,MUJ J ,e t a l .I m p r o v e dA D MM P e n a l i z e dD e c o d e r f o r I r r e g u l a rL o w -d e n s i t y P a r i t y -c h e c kC o d e s [J ].I E E EC o mm u n i c a t i o n sL e t t e r s ,2015,19(6):913-916.[14]WA N GB ,MUJ J ,J I A O XP ,e t a l .I m p r o v e dP e n a l t y F u n c t i o n so fA D MM P e n a l i z e dD e c o d e r f o rL D P CC o d e s [J ].I E E EC o mm u n i c a t i o n sL e t t e r s ,2017,21(2):234-237.[15]A L L E Y N ED,S O D HAJ .O nS t o p p i n g C r i t e r i a f o rL o w -d e n s i t y P a r i t y -c h e c kC o d e s [C ]//P r o c e e d i n g so f t h e20086t h I n t e r n a t i o n a lS y m p o s i u m o n C o mm u n i c a t i o n S y s t e m s ,N e t w o r k sa n d D i g i t a lS i g n a lP r o c e s s i n g .P i s c a t a w a y:I E E E ,2008:633-637.[16]H E R A A,B O N C A L O O,G A V R I L I U C E ,e ta l .A n a l y s i sa n dI m p l e m e n t a t i o no fo nt h eF l y S t o p p i n g Cr i t e r i af o r L a y e r e dQ C L D P C D e c o d e r s [C ]//P r o c e e d i n g so f t h e201522n dI n t e r n a t i o n a lC o n f e r e n c e M i x e d D e s i g no f I n t e g r a t e d C i r c u i t s a n dS y s t e m s .P i s c a t a w a y:I E E E ,2015:287-291.[17]D E C L E R C Q D,S A V I N V,B O N C A L O O,e t a l .A n I m p r e c i s eS t o p p i n g C r i t e r i o nB a s e do n i n -b e t w e e nL a y e r sP a r t i a l S yn d r o m e s [J ].I E E EC o mm u n i c a t i o n sL e t t e r s ,2018,22(1):13-16.(编辑:王瑞)(上接第37页)[8]A Z I Z A.A S o f t -d e c i s i o n F u s i o n A p p r o a c hf o r M u l t i p l e -s e n s o r D i s t r i b u t i o n B i n a r y D e t e c t i o n S y s t e m s [J ].I E E E T r a n s a c t i o n s o nA e r o s p a c e a n dE l e c t r o n i cS ys t e m s ,2011,47(3):2208-2216.[9]L L O Y DS .L e a s t S q u a r e sQ u a n t i z a t i o n i nP C M [J ].I E E ET r a n s a c t i o n s o n I n f o r m a t i o nT h e o r y ,1982,28(2):129-137.[10]Z HO US ,L I U H.S i g n a lF u s i o n -b a s e dT a r g e tD e t e c t i o nA l g o r i t h mf o rS p a t i a lD i v e r s i t y R a d a r [J ].I E T R a d a r ,S o n a r a n dN a v i g a t i o n ,2011,5(3):204-214.[11]K E L L YEJ .A n A d a p t i v eD e t e c t i o n A l g o r i t h m [J ].I E E E T r a n s a c t i o n so n A e r o s p a c ea n dE l e c t r o n i cS y s t e m s ,1986,22(1):115-127.[12]胡勤振,杨芊,苏洪涛,等.分布式M I MO 雷达双门限G L R TC F A R 检测[J ].西安电子科技大学学报,2016,43(4):29-33.HU Q i n z h e n ,Y A N G Q i a n ,S U H o n g t a o ,e t a l .D o u b l e -t h r e s h o l dG L R TC F A R D e t e c t i o n i nD i s t r i b u t e d M I MO R a d a r [J ].J o u r n a l o fX i d i a nU n i v e r s i t y,2016,43(4):29-33.[13]胡勤振,苏洪涛,周生华,等.多基地雷达中双门限C F A R 检测算法[J ].电子与信息学报,2016,28(10):2430-2436.HU Q i n z h e n ,S U H o n g t a o ,Z HO US h e n gh u a ,e t a l .D o u b l eT h r e s h o l dC F A RD e t e c t i o n f o rM u l t i s i t eR a d a r [J ].J o u r n a l o fE l e c t r o n i c s a n d I n f o r m a t i o nT e c h n o l o g y,2016,28(10):2430-2436.[14]C A O D,Z HO USH,L I U H W,e t a l .S i g n a lC e n s o r i n g a n dF u s i n g w i t hS y s t e m -l e v e lC o mm u n i c a t i o nC o n s t r a i n t s i n M u l t i s t a t i cR a d a r :a J -d i v e r g e n c ea n dB h a t t a c h a r y y aD i s t a n c eB a s e dA p p r o a c h [J ].I E T R a d a r ,S o n a ra n d N a v i ga t i o n ,2017,11(12):1802-1814.(编辑:郭华)94第5期王彪等:L D P C 码A D MM 惩罚译码的早停止方法。

低信噪比下LDPC码的性能研究的开题报告

低信噪比下LDPC码的性能研究的开题报告1. 研究背景在通信系统中，由于信道的噪声和干扰等影响，接收端接收到的信号往往会存在一定的误码率。

为了提高通信系统的可靠性和性能，编码技术被广泛应用于通信系统中。

其中，低密度奇偶校验码（Low-Density Parity Check, LDPC）码是一种性能优异的编码技术，被广泛应用于数字通信系统中。

然而，在低信噪比的情况下，LDPC码的译码性能可能会受到较大影响。

因此，本课题拟对低信噪比下LDPC码的性能进行深入的研究，以期提高LDPC 码在低信噪比下的译码性能。

2. 研究目的和意义本研究旨在研究低信噪比下LDPC码的性能，探究其译码性能与信噪比之间的关系，以期提高LDPC码在低信噪比下的译码性能。

具体目的和意义如下：（1）研究LDPC码在低信噪比下的译码性能，探究信噪比对LDPC码译码性能的影响。

（2）分析LDPC码在低信噪比下的优化方法，以提高其译码性能。

（3）验证研究结果，并对LDPC码在低信噪比下的应用进行探讨。

本研究对于提高LDPC码在低信噪比环境下的译码性能具有一定的理论意义和实际应用价值。

同时，研究结果对于提高数字通信系统的可靠性和性能也具有一定的指导意义。

3. 研究内容和方法本研究主要包括以下内容和方法：（1）LDPC码的理论介绍：介绍LDPC码的基本原理、编码和译码过程、码长、码率等基本概念。

（2）低信噪比下LDPC码的性能分析：通过理论分析和仿真实验，探究低信噪比下LDPC码译码性能的变化规律及其影响因素。

（3）LDPC码译码性能优化：对LDPC码在低信噪比下的性能进行优化研究，探究译码性能优化方法和策略。

（4）研究结果验证：通过实验验证研究结果的正确性和可行性。

本研究将采用仿真实验和理论分析相结合的方法，对低信噪比下LDPC码的性能进行深入研究与分析，通过对数字通信系统的实际应用场景进行模拟验证，从而得出相应的研究结论。

4. 参考文献[1] Richardson T J, Urbanke R L. The capacity of low-density parity-check codes under message-passing decoding[J]. Ieee Transactions on Information Theory, 2001, 47(2):599-618.[2] Gallager R G. Low-density parity-check codes[J]. Ieee Transactions on Information Theory, 1963, 8(1):21-28.[3] Song C, Hou X. A comparative study on the performance of LDPC and Turbo codes in wireless communication systems[J]. Frequency Conversion & Signal Processing, 2018, 39(2):76-83.[4] Zhou H, He X. Analysis of LDPC code performance under different code rates and code lengths[J]. Physics Procedia, 2012, 33:1168-1173.[5] Zhang L, Sun L, Li H, et al. Low-SNR performance analysis of LDPC code based on EXIT chart and degree distribution optimization[J]. IEEE Access, 2019,7:36618-36633.。

Accumulating LDPC (low density parity check) decod

专利名称：Accumulating LDPC (low density paritycheck) decoder发明人：Andrew J. Blanksby,Alvin Lai Lin申请号：US12512490申请日：20090730公开号：US08341488B2公开日：20121225专利内容由知识产权出版社提供专利附图：摘要：Accumulating LDPC (Low Density Parity Check) decoder. The accumulatingdecoding architecture described herein is applicable to LDPC codes operating on a parity check matrix, H, consisting of CSI (Cyclic Shifted Identity) sub-matrices (or matrix sub-blocks) or permuted identity sub-matrices (or matrix sub-blocks). In such a structure, the entire LDPC matrix is broken into square sub-matrices such that each sub-matrix consists of either a CSI sub-matrix or a permuted identity sub-matrix, or a null matrix. The iterative decoding process operates by updating of APP (a posteriori probability) or gamma (γ) values and check edge message (λ) values, and this by updating one or more individual rows within a number of sub-matrix rows (or all sub-matrix or sub-block rows) are processed in parallel. The amount of parallelism is specified by the designer and is typically an integer divisor of the sub-matrix (or sub-block) size.申请人：Andrew J. Blanksby,Alvin Lai Lin地址：Neptune NJ US,Londonderry GB国籍：US,GB代理机构：Garlick & Markison代理人：Shayne X. Short更多信息请下载全文后查看。

无线网络中的信道编码综述

运营探讨无线网络中的信道编码综述周宇翔1，周华2南京210044；2.南京信息工程大学在无线网络中，由于没有有线通信信道，信息源和接收端之间的信息共享非常复杂，因此无线信道经常受到许多干扰的影响而导致信宿接收到错误的码字。

为了检测和纠正传输数据中的错误，信道编码技术应运而生。

信道编码能够在传输的数据中找出错误，并且往往有着一定的纠错能力，能够恢复出原始数据。

在噪声较大的无线网络中通常需要优异的编码码字，以保证较好的传输性能。

以此为基础的数据传输通常有两个过程，一个是利用映射或编码的方式将输入数据转换为信道输入序列，另一个是利用反向映射或解码以检索原始传输数据。

信道编码的类型有很多，常用的有线性分组码、卷积码、Turbo码以及LDPC码等。

通过对无线网络中的信道编码进行论述，信道编码；无线网络；线性分组码；卷积码；Turbo码；LDPCOverview of Channel Coding in Wireless NetworksZHOU Yuxiang1, ZHOU Hua. Changwang School of Honors, Nanjing University of Information Science & Technology, Nanjing. School of Electronics and Information Engineering, Nanjing University of Information Science and Technology,图1 码字传输原理在分组码中，信息序列被划分成固定长度的消息分组，每一个消息分组含有k 个信息比特，一共有个不同的消息。

在(n ,k )分组码中，这k 个消息比特按照一定的编码规则被编码成长为n （n ＞k ）的二进制序列c =(c 1,c 1,…,c n-1)，由编码器产生的n -k 个添加到每个输入消息中的比特称为冗余比特。

基于寻找小重量码字算法的LDPC码开集识别

2017年6月Journal on Communications June 2017 第38卷第6期通信学报 V ol.38No.6基于寻找小重量码字算法的LDPC码开集识别于沛东，彭华，巩克现，陈泽亮（解放军信息工程大学信息系统工程学院，河南郑州 450001）摘要：LDPC码的开集识别是信道编码识别领域的一个难点。

首先，对实现开集识别所需接收码向量的数量进行了分析，给出了其理论下界。

然后，根据这一下界，基于寻找小重量码字的算法，提出了一种新的LDPC码开集识别方法。

该方法在接收码向量空间的对偶空间中逐个寻找小重量向量，即待识别的稀疏校验向量，从而重建稀疏校验矩阵。

利用指数分布对迭代次数进行建模，给出了该方法的迭代停止准则及运算量分析。

在无误码条件下，新方法克服了已有方法在适用范围和所需数据量的局限。

在有误码条件下，与已有方法相比，在提高抗误码能力的同时保持较低的运算复杂度，更能满足实际应用的需求。

对于QC-LDPC码，利用其稀疏校验矩阵的准循环特性，可以显著提高识别性能。

关键词：信道编码识别；LDPC码；准循环LDPC码；指数分布中图分类号：TN911.7 文献标识码：ALDPC code reconstruction based on algorithmof finding low weight code-wordsYU Pei-dong, PENG Hua, GONG Ke-xian, CHEN Ze-liang(School of Information Systems Engineering, PLA Information Engineering University, Zhengzhou 450001, China) Abstract: LDPC code reconstruction without a candidate set is one of the tough problems in channel code reconstruction.First, theoretical analysis was provided for the number of received code-vectors needed for the reconstruction, and a low-er bound was derived. Then, according to the lower bound, and based on an algorithm for finding low weight code-words,a new reconstruction method was proposed. It looked for low weight vectors one by one from the dual space of the re-ceived code-vector space and used them to reconstruct the sparse parity-check matrices. Numb er of iterations and the computational complexity of the method were analyzed based on exponential distribution theory. Under noise-free condi-tions, drawbacks of the existing method, including limited applicable range and large quantity of required data, have been overcame. Under noisy conditions, the proposed method has higher robustness against noise and relatively low complex-ity, compared to existing methods. For QC-LDPC codes, the reconstruction performance can be further improved using the quasi-cyclic property of their sparse parity-check matrices.Key words: channel code reconstruction, LDPC code, quasi-cyclic LDPC code, exponential distribution1引言近年来，信道编码识别问题成为一个研究热点。

LDPC的FPGA实现

关键词：原模图 LDPC 码；FPGA；AWGN 信道；磁记录信道
II
Abstract

Abstract
With the rapid development of information and large demand of multimedia, the transmission reliability of information become more and more important. As the core technology of physical layer in digital communication system, the most important role of channel error correcting code is to ensure the reliability of information transmission. Compared with traditional wide range of mobile communication, some of the lower BER requirement of specific applications, such as: magnetic recording system, high-definition digital TV system, the wireless medical human network, etc, it is particularly important to the reliability of information transmission. These applications typically require the BER of 10 −10 , we call it a very-low error rate, and excellent channel error correcting code can provide such a extremely low BER performance. Low density parity check (LDPC) code is one of the best kinds of such codes, it is a block code with very excellent performance. Protograh-LDPC codes is one kind of low density parity check code, compare with the traditional LDPC codes, it has a simpler structure and is easier to extend and hardware implementation. It also has a very excellent performance and meet the requirement of very low bit error rate in some communication systems. In usually studies, people's attention is focused on how to construct better code and find better encoding and decoding algorithms, they are less concern about how to verify that the code is a good code and to evaluate the complexity of the application. Performance validation can be divided into theoretical validation and experimental simulation test. It lack of reliable analysis methods of mathematical for randomly construct LDPC codes, so the experimental simulation test become the most important method of performace validation in such applications. As the method based on Field-Programmable Gate Array(FPGA) hardware emulation platform, because of their fast spped and reconfigurable characteristics, it became a very effective verification method of channel error correct coedes, particularly for such applications

LDPC的BP译码算法

课程名称：现代编码理论任课教师：王琳洪少华论文题目：LDPC码的BP译码算法姓名：曹沙沙赵卜寒学号：************** **************2014 年07月06日目录摘要 .............................................................................................................................. I I Abstract . (III)第一章 LDPC码的概述 (1)1.1 LDPC码的发展史 (1)1.2、LDPC码的表示 (1)1.3 二进制LDPC码的编码方法 (3)1.3.1校验矩阵的生成 (3)1.3.2编码算法 (4)第二章 LDPC码译码算法 (6)2.1 Gallager概率译码基本思路 (6)2.2 BP算法研究 (8)2.3 用对数似然比表示的BP算法 (11)第三章 LDPC的性能分析 (14)3.1 LDPC的仿真模型 (14)3.2 LDPC的译码性能 (15)3.2.1码长对性能的影响 (15)3.2.2迭代次数对译码性能的影响 (16)结论 (18)参考文献 (19)摘要低密度奇偶校验码是Gallager提出的一种线性分组码，其性能可以非常接近香农极限。

它是根据低密度稀疏校验矩阵H和二分图来构造的，本文详细的阐述了二进制，规则的LDPC的BP译码算法，其校验矩阵每一行和每一列的1的个数是相同的，分别为p和q,其Tanner图中比特节点的度和校验节点的度分别对应着一个固定值，通常用（m，n，p，q）表示。

BP译码算法是一种迭代的概率译码算法，本文着重于BP译码算法及其简化运算。

本论文主要介绍了LDPC码的构造、编码和译码基本原理。

阐述了LDPC编译码的过程，并通过MATLAB仿真工具对LDPC码在AWGN信道的误比特率性能进行了仿真，分析了信噪比、码长和迭代次数对误比特率性能的影响。

LDPC的BP译码算法

BP译码算法是一种迭代的概率译码算法，本文着重于BP译码算法及其简化运算。

本论文主要介绍了LDPC码的构造、编码和译码基本原理。

阐述了LDPC编译码的过程，并通过MATLAB仿真工具对LDPC码在AWGN信道的误比特率性能进行了仿真，分析了信噪比、码长和迭代次数对误比特率性能的影响。

ISI信道下LDPC码ADMM译码算法研究

摘要摘要低密度校验码(Low-Density Parity-Check Codes，LDPC码)具有逼近信道容量限的良好性能和较低的译码复杂度，其已经成为学者们研究的热点之一。

而且，低密度校验码被ITU-T G.9960、Wi-Fi、CCSDS、DTMB、CMMB等许多通信标准所采纳。

特别地，2016年的3GPP会议确定LDPC码为5G增强移动带宽场景数据信道的编码方案。

LDPC码的交替方向乘子法(Alternating Direction Method of Multipliers，ADMM)译码算法在无记忆信道下表现出较好的译码性能，而目前有记忆信道下LDPC码ADMM译码算法的研究工作还相对较少。

符号间干扰(Inter Symbol Interference，ISI)信道是数字存储系统的一种常用有记忆信道模型，本文对ISI信道下LDPC码的ADMM译码方法进行了比较深入的研究，主要工作概括如下：1. 概述了LDPC码和线性分组码。

详细分析了ISI信道下基于Turbo均衡的LDPC 码和积译码算法及ISI信道下基于内点法的LDPC码译码算法的性能。

同时对无记忆信道下LDPC码的ADMM译码算法、和积译码算法及其最小和译码算法进行了仿真，并分析了三种典型译码算法下LDPC码的性能。

2. ISI信道下传统的基于Turbo均衡的LDPC码译码利用的是和积译码算法，而LDPC码的ADMM惩罚译码算法在无记忆信道下比和积译码算法具有更好的译码性能。

本文提出了一种ISI信道下LDPC码的基于Turbo均衡思想的ADMM惩罚译码算法。

通过对LDPC码仿真结果的分析可知，与现有的ISI信道下基于Turbo均衡的和积译码算法相比较，所提出的译码算法在高信噪比区域具有更好的性能。

3. ISI信道下LDPC码的译码问题可以看作是一个二次规划问题，通过深入分析交替方向乘子法这一经典的凸优化问题求解方法，提出了一种ISI信道下基于ADMM 的LDPC码惩罚译码算法。

LDPC短码的编译码

252012年第09期，第45卷通信技术 Vol.45，No.09,2012 总第249期 Communications Technology No.249,TotallyLDPC 短码的编译码研究胡应鹏①，王健①，程雯②（①解放军理工大学通信工程学院研究生1队，江苏南京 210007；②西安电子科技大学通信工程学院综合业务网理论及关键技术国家重点实验室,陕西西安 710071）【摘要】这里研究了原模图LDPC 码和BP 译码算法，首先提出了一种基于PEG 算法构造原模图LDPC 码的算法，该码字在码率为1/2，码长256比特的情况下，译码性能超过了PEG 算法，然后针对LDPC 短码不可避免存在四环的特殊性，提出了一种修正四环中变量节点迭代信息的BP 译码改进算法，使得具有四环的LDPC 短码的译码性能得到较大提升。

【关键词】LDPC 短码；原模图；ACE；PEG；BP 译码算法【中图分类号】TN911 【文献标识码】A 【文章编号】1002-0802(2012)09-0025-04Modified Coding/Decoding Algorithm for Short LDPC CodeHU Ying-peng ①， WANG Jian ①， CHENG Wen ②(①Postgraduate Team 1 of ICE, PLAUST, Nanjing Jiangsu 210007, China;②ISN laboratory, School of Telecommunications Engineering, Xidian University, Xi’an Shaanxi 710071, China)【Abstract】This paper discusses the protograph-based LDPC codes and BP decoding algorithm. It gives first the protograph-based LDPC codes algorithm constructed on PEG method, and with code rate of 1/2 and code length of 256 bits, this algorithm outperforms PEG algorithm in decoding; then it proposes a modified BP decoding algorithm to correct variable nodes iteration information in the 4-circles, for LDPC codes inevitablely have 4- circles, thus greatly improving the performance of LDPC codes with 4-circles.【Key words 】short-LDPC codes; protograph; ACE，PEG，BP decoding algorithm0 引言低密度校验码(LDPC)[1]是目前发现的最为逼近Shannon 限的信道编码方案之一。

一类来自有限域 GF（16）子群上的高码率的 LDPC码

一类来自有限域 GF（16）子群上的高码率的 LDPC码胡万宝;胡芳;钟娇娇【摘要】Recently, Sobhani constructed group permutation LDPC codes from permutations associated with elements in a fi-nite group.Based on the work, a class of these high-rate codes for which the Tanner graphs with girth at least 8 associated with their parity-check matrices are presented .Simulation results show their good performance compared with random-like and quasi-cy-clic codes counterparts.%最近，Sobhani等人利用在有限群上的元素置换方法构造群置换LDPC码，本文在此基础上，给出了一类在有限域GF（16）的子群上构造的高码率的LDPC码，其Tanner图围长至少为8。

仿真结果表明，这类码执行性能优于相应类型的随机LDPC码和其代数结构的准循环LDPC码。

【期刊名称】《安庆师范学院学报（自然科学版）》【年(卷),期】2014(000)002【总页数】3页(P1-3)【关键词】低密度奇偶校验码LDPC;有限域;有限群【作者】胡万宝;胡芳;钟娇娇【作者单位】安庆师范学院数学与计算科学学院，安徽安庆 246133;安庆师范学院数学与计算科学学院，安徽安庆 246133;安庆师范学院数学与计算科学学院，安徽安庆 246133【正文语种】中文【中图分类】TN911.21低密度奇偶校验码(LDPC码)首次提出是1962年麻省理工学院Robert Gallager在其博士论文[1]中提出的一种具有稀疏校验矩阵的分组纠错码，该码是由其他学者[2-6]再次发现了它的超强的纠错性能和高效的解码算法，因而极大的吸引了研究者的兴趣。