相似证明题
相似三角形证明题

相似三角形证明题1.如图,在ABC ∆中,C ABC ∠=∠2,BD 平分ABC ∠,试说明:AB·B C = AC·CD2.已知:ΔACB 为等腰直角三角形,∠ACB=900延长BA 至E ,延长AB 至F ,∠ECF=135求证:ΔEAC ∽ΔCBF3.如图,点C 、D 在线段AB 上,且ΔPCD 是等边三角形. (1)当AC ,CD ,DB 满足怎样的关系时,ΔACP ∽ΔPDB ; (2)当ΔPDB ∽ΔACP 时,试求∠APB 的度数.4.如图,4531===∠=∠∠=∠BC DE AB D B ,,, (1)ABC ∆∽ADE ∆吗?说明理由。
(2)求AD 的长。
5.已知:如图,CE 是Rt ΔABC 的斜边AB 上的高,BG ⊥AP. 求证:CE 2=ED ·EP.6.如图,四边形ABCD 是平行四边形,AE ⊥BC 于E ,AF ⊥CD 于F. (1)ΔABE 与ΔADF 相似吗?说明理由. (2)ΔAEF 与ΔABC 相似吗?说说你的理由.7.如图,D 为ΔABC 内一点,E 为ΔABC 外一点,且∠1=∠2,∠3=∠4. (1)ΔABD 与ΔCBE 相似吗?请说明理由. (2)ΔABC 与ΔDBE 相似吗?请说明理由.8.如图:⊿ABC 中,D 是AB 上一点,AD = AC ,BC 边上的中线AE 交CD 于F ,求证: DF CF AC AB ::AB C EDF9.四边形ABCD 中,AC 为AB 、AD 的比例中项,且AC 平分∠DAB ,求证:22CD BC DE BE =10.矩形ABCD 中,a AB =,b BC =,M 是BC 的中点,DE ⊥AM ,E 是垂足, 求证:2242ba ab DE +=11.如图,过平行四边形ABCD 的顶点A 的直线交BD 于P ,交CD 于Q ,并交BC 的延长线于R ,求证:22PBPD PR PQ =A BCR12.如图所示,在平行四边形ABCD 中,过点B 作BE ⊥CD ,垂足为E ,连结AE ,F 为AE 上一点,且∠BFE =∠C(1)求证:△ABF ∽△EAD ;(2)若AB =4,∠BAE =30°, 求AE 的长;(3)在(1)(2)的条件下,若AD =3,求BF 长.(计算结果含根号).13.如图,P 在线段MN 上,如果PM 2= MN ·PN ,,那么,P 是线段MN 的一个黄金分割点。
相似证明题集锦

相似证明题集锦1、如图,已知E 是矩形ABCD 的边CD 上一点,BF AE ⊥于F ,试说明:ABF EAD △∽△.2、如图,CD 是Rt △ABC 的斜边AB 上的高线,∠BAC 的平分线分别交BC ,CD 于点E ,F ,求证:(1)△ACF ∽△ABE ;(2)AC•AE=AF•AB3、如图,E 是四边形ABCD 的对角线BD 上一点,且ADAC AE AB =,∠1=∠2, 求证:∠ABC=∠AED 。
4、如图,AD 是直角△ABC 斜边上的高,DE ⊥DF ,且DE 和DF 分别交AB 、AC 于E 、F .求证: AF:AD=BE:BD .(第1题) (第20题)5、如图,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.求证:(1)∠EAF=∠B;(2)AF2=FE•FB.6、如图,点D,E分别在△ABC的边BC,BA上,四边形CDEF是等腰梯形,EF∥CD.EF与AC交于点G,且∠BDE=∠A.(1)试问:AB•FG=CF•CA成立吗?说明理由;(2)若BD=FC,求证:△ABC是等腰三角形.7、已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.问:点C在什么位置时,分割得到的三角形与Rt△OAB相似(注:在图上画出所有符合要求的线段PC,并求出相应的点C的坐标).8、在正方形ABCD 中,点M 在AB 上,点N 在BC 上,且BM=BN,BP⊥CM,垂足为P,求证:DP⊥NP9、如图,正方形ABCD 的边长为4,E 是BC 边的中点,点P 在射线AD 上,过P 作PF ⊥AE 于F .(1)求证:△PFA ∽△ABE ;(2)当点P 在射线AD 上运动时,设PA=x ,是否存在实数x ,使以P ,F ,E 为顶点的三角形也与△ABE 相似?若存在,请求出x 的值;若不存在,说明理由.10、如图所示,在矩形ABCD 中,AB =12cm ,BC =6cm ,点P 沿AB 边从点A 开始向D A M NB C P点B 以2厘米/秒的速度移动;点Q 沿DA 边从点D 开始向点A 以1厘米/秒的速度移动。
相似证明题集锦

相似证明题集锦1、如图,已知E 是矩形ABCD 的边CD 上一点,BF AE ⊥于F ,试说明:ABF EAD △∽△.2、如图,CD 是Rt △ABC 的斜边AB 上的高线,∠BAC 的平分线分别交BC ,CD 于点E ,F ,求证:(1)△ACF ∽△ABE ;(2)AC•AE=AF•AB3、如图,E 是四边形ABCD 的对角线BD 上一点,且ADAC AE AB =,∠1=∠2, 求证:∠ABC=∠AED 。
4、如图,AD 是直角△ABC 斜边上的高,DE ⊥DF ,且DE 和DF 分别交AB 、AC 于E 、F .求证: AF :AD=BE :BD .(第1题) (第20题)5、如图,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.求证:(1)∠EAF=∠B;(2)AF2=FE•FB.6、如图,点D,E分别在△ABC的边BC,BA上,四边形CDEF是等腰梯形,EF∥CD.EF与AC交于点G,且∠BDE=∠A.(1)试问:AB•FG=CF•CA成立吗?说明理由;(2)若BD=FC,求证:△ABC是等腰三角形.7、已知:Rt△OAB在直角坐标系中的位置如下图,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.问:点C在什么位置时,分割得到的三角形与Rt△OAB相似(注:在图上画出所有符合要求的线段PC,并求出相对应的点C的坐标).8、在正方形ABCD 中,点M 在AB 上,点N 在BC 上,且BM=BN,BP⊥CM,垂足为P,求证:DP⊥NP9、如图,正方形ABCD 的边长为4,E 是BC 边的中点,点P 在射线AD 上,过P 作PF ⊥AE 于F .(1)求证:△PFA ∽△ABE ;(2)当点P 在射线AD 上运动时,设PA=x ,是否存有实数x ,使以P ,F ,E 为顶点的三角形也与△ABE 相似?若存有,请求出x 的值;若不存在,说明理由.10、如图所示,在矩形ABCD 中,AB =12cm ,BC =6cm ,点P 沿AB 边从点A 开始向D A M NB C P点B以2厘米/秒的速度移动;点Q沿DA边从点D开始向点A以1厘米/秒的速度移动。
圆与相似三角形相关的证明题

圆与相似三角形相关的证明题1. 在图中,已知PC=PD,PD切圆O于D,PB交圆O于A,连结AC和BC。
要证明AC·PB=PC·BC。
证明:由于PD是圆O的切线,所以∠PDC=∠ACB。
又因为PC=PD,所以∠PCD=∠PDC。
因此,∠ACB=∠PCD。
又因为∠BCP=∠PBD,所以三角形PBD和PBC相似。
因此,PB·PC=PD2。
由于三角形ACD和BDC相似,所以AC·BD=CD2。
将BD替换为PD+PC,得到AC·(PD+PC)=CD2,即AC·PB=PC·BC。
因此,原命题成立。
2. 在图中,已知AB∥CD,DC延长线交EB延长线于F,EB与圆O相交于F,DF交圆O于G。
要证明AD·ED=BE·DF。
证明:由于AB∥CD,所以∠___∠EAD。
又因为EB是圆O的切线,所以∠___∠EDF。
因此,∠___∠EAD。
又因为AB是圆O的直径,所以∠EAB=90°。
因此,三角形EAB和EDF相似。
因此,AD·ED=BE·DF。
因此,原命题成立。
3. 在图中,___于P,PE⊥AB于E,AC⊥CD,BD⊥CD。
要证明①PE:AC=PB:PA,②PE2=AC·BD。
证明:①由于PE⊥AB,所以∠APE=90°。
又因为AC⊥CD,所以∠ACP=90°。
因此,∠APE=∠ACP。
又因为∠APB=90°,所以三角形APE和APB相似。
因此,PE:AC=PB:PA。
②由于PE⊥AB,所以∠APE=90°。
又因为BD⊥CD,所以∠___°。
因此,四边形AEPD和BEPC是直角四边形。
因此,PE2=AE2-AP2=AC·BD。
因此,原命题成立。
4. 在图中,ABC是内接于圆O的三角形,BD是圆O的直径,AF⊥BD于F,AF延长线与BC交于G。
(相似三角形)证明题

1、如图,△ABC中,三条内角平分线交于D,过D作AD垂线,分别交AB、AC于M、N,请写出图中相似的三角形,并说明其中两对相似的正确性。
2、如图,AD为△ABC的高,DE⊥AB,DF⊥AC,垂足分别为E、F,试判断∠ADF与∠AEF的大小,并说明明理由,…3、如图,在△ABC中,点D、E分别在BC、AB上,且∠CAD=∠ADE=∠B,AC:BC=1:2,设△EBD、△ADC、△ABC的周长分别为m1 、m2、m3,求的值,*4、如图,已知△ABC中,D为BC中点,AD=AC,DE⊥BC,DE与AB交于E,EC与AD相交于点F,(1)△ABC与△FCD相似吗请说明理由;(2)若S =5,BD=10,求DE的长。
:5、AD是△ABC的高,E是BC的中点,EF⊥BC交AC于F,若BD=15,DC=27,AC=45.求AF的长。
\6、已知:如图,在△PAB中,∠APB=120O,M、N是AB上两点,且△PMN是等边三角形。
求证: BM·PA=PN·BP7、已知:如图,D是△ABC的边AC上一点,且CD=2AD,AE⊥BC于E, 若BC=13, △BDC的面积是39, 求AE的长。
?????*8、已知:如图,在△ABC中,AB=15,AC=12,AD是∠BAC的外角平分线且AD交BC的延长线于点D,DE ∥AB交AC的延长线于点E。
《9、已知: 如图,四边形ABCD中,CB⊥BA于B,DA⊥BA于A,BC=2AD,DE⊥CD交AB于E,连结CE,求证:DE2=AE?CE】10、如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.(1)ΔABE与ΔADF相似吗请说明理由.(2)若AB=6,AD=12,BE=8,求DF的长./11、如图:三角形ABC是一快锐角三角形余料,边BC=120mm,高AD =80mm,要把它加工成正方形零件,是正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少ANP12、已知:如图:FGHI 为矩形,AD ⊥BC 于D ,95GH FG ,BC =36cm,AD =12cm 。
初中数学练习题相似与全等的证明

初中数学练习题相似与全等的证明数学是一门逻辑性很强的学科,其中相似与全等也是重要的概念。
下面将通过一些初中数学练习题来进行相似与全等的证明。
题目一:已知三角形ABC中,AB=AC,角B=角C。
E是AB上一点,D是AC上一点,使得BD=CE,连接DE。
证明:△EDC≌△EBD。
解答一:首先,由题目中已知可以得出△ABC是一个等腰三角形,即AB=AC,角B=角C。
又因为BD=CE,连接DE,所以可以得到△BED≌△CED。
然后,根据相等三角形的性质可以知道,△BED和△CED的对应边分别相等,即BE=CE,BD=CD,角B=角C。
根据三角形全等的定义,我们只需再证明DE=DE即可,而这是显然成立的,因此,根据三角形全等的定义,可以得出△EDC≌△EBD。
证毕。
题目二:已知△ABC,其中AB=BC,角A=角C。
D是AC上的一点,使得AD=DC。
证明:△ABD≌△BDC。
解答二:题目中给出了△ABC中的已知条件:AB=BC,角A=角C。
并且有一辅助线段AD=DC,并连接BD。
首先,连接AD与BD,根据题目中给出的条件可以得知△ABD和△BDC的一组边相等,即BD=BD,AD=DC。
其次,根据三角形的全等定理,我们只需证明△ABD和△BDC的另一组边相等即可,即证明AB=BC。
因为△ABC中已知AB=BC,而根据题目给出的条件,角A=角C,所以根据等角的性质可以得到∠B=∠B。
由于∠B是共有的顶点,而且∠B相等,所以可以得出△ABD≌△BDC。
证毕。
通过以上两个题目的证明,我们可以总结得出相似与全等的证明方法。
对于相似的证明,我们可以通过找到相等的角度以及对应的边长比例,根据相似三角形的定义来进行证明。
而对于全等的证明,我们需要找到两组边长完全相等的三角形,或者找到相等的角度以及对应的边长,根据全等三角形的定义来进行证明。
相似与全等是初中数学中非常重要的概念,它们在几何图形的研究中起着重要的作用。
通过掌握相似与全等的证明方法,我们能够更好地理解数学知识,并在解题过程中运用得当。
相似证明题

E A B G F C D
练3.已知:如图,CE是RtΔABC的斜边 AB上的高,BG⊥AP. 求证: CE 2 ED EP
小测 1.过平行四边形ABCD的 一个顶点A作一直线分别 B 交对角线BD、边BC,边 DC的延长线于E、F、G . 求证:EA2 EF EG 2.如图,AB∥CD, AO=OB, DF=FB,DF交AC于E,A 求证:ED 2 EO EC
例2.D为△ABC中AB边上一点, ∠ACD= ∠ ABC. 2 求证: AC AD AB
C
A
D
B
练2.已知:如图,△ABC中,点E在 DEB ABC 中线AD上, . 2 求证:(1) DB DE DA ; (2) DCE DAC .
B D
C
E
A
例3.已知:平行四边形ABCD,E是BA 延长线上一点,CE与AD、BD交于 G、F, 求证: CF 2 GF EF
例1.如图,在正方形ABCD中,F是 BC上一点,EA⊥AF,AE交CD的延 长线于E,连结EF交AD于G.
(1)求证:⊿ABF ≌⊿ADE;
(2)求证:BF· =DG· FC EC;
A B
G E D
F
C
练1.如图,△ABC中,D是AC的中点,E 是BC延长线上一点,过A作AH∥BE,连 结ED并延长交AB于F,交AH于H。 (1)求证:AH=CE (2)如果AB=4AF,EH=8,求DF的长。
A E F G
D O E C
相似三角形六大证明技巧(提高类技巧训练)

相似三角形六大证明技巧(提高类技巧训练)1.如图,在△ABC中,∠B=∠C,点D在AB边上,点E在AC边上,且AD=CE。
求证:△BED∽△CDE。
2.如图,在△ABC中,点D在AB边上,点E在AC边上,且∠XXX∠C。
求证:△BED∽△ABC。
ABF∽△ECF证明:首先根据题目中给出的比例式,可以得到:frac{BF}{AB}=\frac{BE}{BC}$$移项可得:frac{AB-BF}{AB}=\frac{BC-BE}{BC}$$化简可得:frac{AF}{AB}=\frac{CE}{BC}$$由此可知,△ABF与△ECF的两个对应角分别为∠A和∠C,因为它们有一个共同的角∠B,所以根据相似三角形的性质,可知△ABF∽△ECF。
例1】如图,在△ABC中,AD平分∠BAC,AD的垂直平分线交AD于E,交BC的延长线于F,要证明FD2=FB·FC。
证明:连接AF,因为AE=ED,所以∠EAD=∠EDA,即AD是∆AEF的角平分线,所以AF=EF,又因为AF∥BC,所以∆BFC与∆AFE相似,所以FB/AF=FC/FE,即FB·FE=FC·AF,代入AF=EF,得到FB·FC=FD2,即证。
例2】如图,四边形ABCD是平行四边形,点E在边BA 的延长线上,CE交AD于F,要证明AC·BE=CE·AD。
证明:连接BE、CF,因为AB∥CD,所以∠BCE=∠EAD,所以∆BCE与∆EAD相似,所以BE/AD=CE/AC,即AC·BE=CE·AD,即证。
例3】如图,△ACB为等腰直角三角形,AB=AC,∠BAC=90°,∠DAE=45°,要证明AB2=BE·CD。
证明:连接AE、BD,因为AB=AC,所以∠ABC=∠ACB=45°,所以∆ABD与∆AEC相似,所以AB/AC=BD/CE,即AB·CE=BD·AC,又因为AB=AC,所以AB2=BD·AC,代入AB·CE=BD·AC,得到AB2=BE·CD,即证。
专题09 三角形中的相似证明问题(解析版)

专题09 三角形中的相似证明问题1、如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.(1)求证:△BDE∽△EFC.(2)设,①若BC=12,求线段BE的长;②若△EFC的面积是20,求△ABC的面积.(1)证明:∵DE∥AC,∴∠DEB=∠FCE,∵EF∥AB,∴∠DBE=∠FEC,∴△BDE∽△EFC;(2)解:①∵EF∥AB,∴==,∵EC=BC﹣BE=12﹣BE,∴=,解得:BE=4;②∵=,∴=,∵EF∥AB,∴△EFC∽△BAC,∴=()2=()2=,∴S△ABC=S△EFC=×20=45.2、如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=6,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.(1)求线段DE的长;(2)取线段AD的中点M,联结BM,交线段DE于点F,延长线段BM交边AC于点G,求的值.解:(1)∵AD平分∠BAC,∠BAC=60°,∴∠DAC=30°,在Rt△ACD中,∠ACD=90°,∠DAC=30°,AC=6,∴CD=2,在Rt△ACB中,∠ACB=90°,∠BAC=60°,AC=6,∴BC=6,∴BD=BC﹣CD=4,∵DE∥CA,∴,∴DE=4;(2)∵点M是线段AD的中点,∴DM=AM,∵DE∥CA,∴,∴DF=AG,∵DE∥CA,∴,∴,∵BD=4,BC=6,DF=AG,∴.3、如图①,△ABC中,∠ACB=90°,点D从点A出发沿A→C方向匀速运动,速度为1cm/s.点E是AC上位于点D右侧的动点,点M是AB上的动点,在运动过程中始终保持MD=ME,DE=2cm.过M作MN∥AC交BC于N,当点E与点C重合时点D停止运动.设△MDE的面积为S(cm2),点D的运动时间为t(s),S与t的函数关系如图②所示:(1)AC=cm,BC=cm;(2)设四边形MDEN的面积为y,求y的最大值;(3)是否存在t的值,使得以M,E,N为顶点的三角形与△MDE相似?如果存在,求t的值;如果不存在,说明理由.解:(1)由函数图象知,当t=4时,AD=4,点E与点C重合,∵DE=2,∴AC=4+2=6,当t=0时,S=2,点A与点D重合,如图1,过M作MH⊥AC于H,∵DE=2,∴MH=2,∵MD=ME,∴AH=EH=1,∵∠C=90°,∴MH∥BC,∴△AHM∽△ACB,∴=,∴=,∴BC=12故答案为:6,12;(2)如图2,过M作MH⊥AC于H,∵MD=ME,DE=2,∴DH=DE=1,∴AH=t+1,∵tan A==2,∴MH=2t+2,∵MN∥AC,∠ACB=90°,∴∠MNC=90°,∵MH⊥DE,∴∠MNC=∠C=∠MHC=90°,∴四边形MHCN是矩形,∴MN=HC=AC﹣AH=6﹣(t+1)=5﹣t,∴y=S△MDE+S△MNE==﹣t2+6t+7=﹣(t﹣3)2+16,由题意得,0≤t≤4,∴当t=3时,y由最大值是16;(3)假设存在t的值,使得以M,E,N为顶点的三角形与△MDE相似,∵MN∥AC,∴∠MED=∠EMN,①当∠MNE=∠EDN时,△ENM∽△MDE,∴,∴MN=ED,∴5﹣t=2,∴t=3;②当∠MEN=∠EDM时,△NEM∽△MDE,此时,NE=NM=5﹣t,∵∠ACB=90°,∴EC2+NC2=EN2,∴(4﹣t)2+(2t+2)2=(5﹣t)2,解得:t=(负值舍去),∴存在t的值,使得以M,E,N为顶点的三角形与△MDE相似,此时,t=3或.4、如图,在△ABC中,AG⊥BC,垂足为点G,点E为边AC上一点,BE=CE,点D为边BC上一点,GD=GB,连接AD交BE于点F.(1)求证:∠ABE=∠EAF;(2)求证:AE2=EF•EC;(3)若CG=2AG,AD=2AF,BC=5,求AE的长.(1)证明:∵EB=EC,∴∠EBC=∠C,∵AG⊥BD,BG=GD,∴AB=AD,∴∠ABD=∠ADB,∵∠ABD=∠ABE+∠EBC,∠ADB=∠DAC+∠C,∴∠ABE=∠DAC,即∠ABE=∠EAF.(2)证明:∵∠AEF=∠BEA,∠EAF=∠ABE,∴△AEF∽△BEA,∴=,∴AE2=EF•EB,∵EB=EC,∴AE2=EF•EC.(3)解:设BE交AG于J,连接DJ,DE.∵AG垂直平分线段BD,∴JB=JD,∴∠JBD=∠JDG,∵∠JBD=∠C,∴∠JDB=∠C,∴DJ∥AC,∴∠AEF=∠DJF,∵AF=DF,∠AFE=∠DFJ,∴△AFE≌△DFJ(AAS),∴EF=FJ,AE=DJ,∵AF=DF,∴四边形AJDE是平行四边形,∴DE∥AG,∵AG⊥BC,∴ED⊥BC,∵EB=EC,∴BD=DC=,∴BG=DG=,∵tan∠JDG=tan∠C===,∴JG=,∵∠JGD=90°,∴DJ===,∴AE=DJ=.5、已知,在△ABC和△EFC中,∠ABC=∠EFC=90°,点E在△ABC内,且∠CAE+∠CBE=90°(1)如图1,当△ABC和△EFC均为等腰直角三角形时,连接BF,①求证:△CAE∽△CBF;②若BE=2,AE=4,求EF的长;(2)如图2,当△ABC和△EFC均为一般直角三角形时,若=k,BE=1,AE=3,CE=4,求k的值.解:(1)①∵△ABC和△CEF都是等腰直角三角形,∴∠ECF=∠ACB=45°,∴∠BCF=∠ACE,∵△ABC和△CEF都是等腰直角三角形,∴CE=CF,AC=CB,∴=,∴,∴△BCF∽△ACE;②由①知,△BCF∽△ACE,∴∠CBF=∠CAE,=,∴BF=AE=×4=2,∵∠CAE+∠CBE=90°,∴∠CBF+∠CBE=90°,即:∠EBF=90°,根据勾股定理得,EF===2;(2)如图(2),连接BF,在Rt△ABC中,tan∠ACB==k,同理,tan∠ECF=k,∴tan∠ACB=tan∠ECF,∴∠ACB=∠ECF,∴∠BCF=∠ACE,在Rt△ABC中,设BC=m,则AB=km,根据勾股定理得,AC==m;在Rt△CEF中,设CF=n,则EF=nk,同理,CE=n ∴,=,∴,∵∠BCF=∠ACE,∴△BCF∽△ACE,∴∠CBF=∠CAE,∵∠CAE+∠CBE=90°,∴∠CBF+∠CBE=90°,即:∠EBF=90°,∵△BCF∽△ACE,∴,∴BF=AE=,∵CE=4,∴n=4,∴n=,∴EF=,在Rt△EBF中,根据勾股定理得,BE2+BF2=EF2,∴12+()2=()2,∴k=或k=﹣(舍),即:k的值为.6、如图,在▱ABCD中,AB=4,∠B=45°,AC⊥AB,P是BC上一动点,过P作AP的垂线交CD于E,将△PCE折叠得到△PCF,延长FP交AB于H,连结AE,PE交AC于G.(1)求证PH=PF;(2)当BP=3PC时,求AE的长;(3)当AP2=AH•AB时,求AG的长.解:(1)∵四边形ABCD是平行四边形,∴AB∥CD,∴∠B+∠PCE=180°,∵∠B=45°,∴∠PCE=135°,由折叠知,∠PCF=∠PCE=135°,∵AC⊥AB,∴∠ACB=45°,∴∠ACB+∠PCF=180°,∴点F在AC的延长线上,∵∠CEG+∠CGE=90°,∠CGE=∠PGA,∴∠CEG+∠PGA=90°,∵∠PAG+∠PGA=90°,∴∠PEC=∠PAG,∵∠PEC=∠F,∴∠PAF=∠F,∴PA=PF,∵∠CAP+∠PAH=90°,∠F+∠PHA=90°,∴∠PAH=∠PHA,∴PA=PH,∴PF=PH;(2)过点A作AM⊥BC于M,∵AB=AC,AB=4,∴BM=CM=2,AM=2,∵BC=3CP,∴MP=,∴AP=,由折叠知,PE=PF,由(1)知,PA=PF,∴AP=PE,∵∠APE=90°,∴△APE是等腰直角三角形,∴AE=2;(3)∵AP2=AH•AB,∠PAH=∠PAB,∴△APH∽△ABP,∴∠APH=∠B=45°,∴∠PAF=∠F=22.5°,∴∠BPA=∠BAP=67.5°,∴BP=AB=4,∴PC=4﹣4,∵∠EPC=∠FPC=∠ACP﹣∠F=22.5°,∴∠GPC=∠PAC,∵∠APC=∠APC,∴△CPG∽△CAP,∴CP2=CG•CA,∴CG=12﹣8,∴AG=8﹣8.7、如图,在△ABC中,∠B=45°,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,E、F分别在AB、AC上,AD交EF于点H.(1)求证:△AEF∽△ABC;(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求出最大面积;(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线AD匀速向上运动(当矩形的边PQ到达A点时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S 与t的函数关系式,并写出t的取值范围.1)证明:∵四边形EFQP是矩形,∴EF∥QP,∴EF∥BC,∴∠AEH=∠EBQ,∠AFH=∠FCP,∴△AEF∽△ABC.(2)解:∵∠B=45°,∴BD=AD=4,∴CD=BC﹣BD=5﹣4=1.∵EF∥BC,∴△AEH∽△ABD,∴=,∵EF∥BC,∴△AFH∽△ACD,∴=,∴=,即=,∴EH=4HF,已知EF=x,则EH=x.∵∠B=45°,∴EQ=BQ=BD﹣QD=BD﹣EH=4﹣x.S矩形EFPQ=EF•EQ=x•(4﹣x)=﹣x2+4x=﹣(x﹣)2+5,∴当x=时,矩形EFPQ的面积最大,最大面积为5.(3)解:由(2)可知,当矩形EFPQ的面积最大时,矩形的长为,宽为4﹣×=2.在矩形EFPQ沿射线AD的运动过程中:①当0≤t≤2时,如答图①所示.设矩形与AB、AC分别交于点K、N,与AD分别交于点H1,D1.此时DD1=t,H1D1=2,∴HD1=HD﹣DD1=2﹣t,HH1=H1D1﹣HD1=t,AH1=AH﹣HH1=2﹣t,.∵KN∥EF,∴=,即=,得KN=(2﹣t).S=S梯形KNFE+S矩形EFP1Q1=(KN+EF)•HH1+EF•EQ1=[(2﹣t)+]×t+(2﹣t)=﹣t2+5;(II)当2<t≤4时,如答图②所示.设矩形与AB、AC分别交于点K、N,与AD交于点D2.此时DD2=t,AD2=AD﹣DD2=4﹣t,∵KN∥EF,∴=,即=,得KN=5﹣t.S=S△AKN=KN•AD2=(5﹣t)(4﹣t)=t2﹣5t+10.综上所述,S与t的函数关系式为:S=.8、如图,正方形ABCD的对角线AC、BD交于点O,∠CBD的平分线BG交AC于E,交CD于F,且DG⊥BG.(1)求证:BF=2DG;(2)若BE=,求BF的长.(1)证明:延长DG、BC交于点H,∵BG平分∠CBD,∴∠1=∠2,∵DG⊥BG,∴∠BGD=∠BGH=90°,又∵BG=BG,∴△BGD≌△BGH(ASA),∴BD=BH,∴DH=2DG,∵四边形ABCD是正方形,∴BC=DC,∠BCF=∠DCH=90°,又∵∠BGD=90°,∠3=∠4,∴∠2=∠5,∴△BCF≌△DCH(ASA),∴BF=DH,∴BF=2DG;(2)∵四边形ABCD是正方形,∴∠ACB=∠BDC=45°,∴∠BCE=∠BDF,又∵∠1=∠2,∴△BEC∽△BFD,∴,∵BE=,∴BF=.9、如图①,正方形ABCD中,点E是BC的中点,过点B作BG⊥AE于点G,过点C作CF垂直BG的延长线于点H,交AD于点F.(1)求证:△ABE≌△CDF;(2)如图②,连接AH并延长交CD于点M,连接ME.①求证:AE2=AB•AM;②若正方形ABCD的边长为2,求cos∠BAM.(1)证明:如图①中,∵AE⊥BH,CF⊥BH,∴AE∥CF∵ABCD是正方形,∴AD∥BC,∴四边形AECF是平行四边形,∴CE=AF,∴,∴AF=FD,∴BE=DF,∵AB=CD,∠ABE=∠CDF=90°,∴△ABE≌△CDF(SAS).(2)①证明:如图②中连接EH.由(1)得AE∥FC,∵BE=CE,∴BG=HG,∵BG⊥AE,∴AB=AH,∴∠EAB=∠MAE,∵∠EAB=∠FCD,∵∠MAE=∠AHF,∠MHC=∠AHF,∴∠FCD=∠MHC,∴MH=MC,∵,∴EM是CH的垂直平分线,∴EM⊥CF,∴EM⊥AE,∴∠ABE=∠AEM=90°,∴△ABE~△AEM,∴=,∴AE2=AB•AM.②由①得AH=AB=2,MC=MH,设CM=x,则HM=x,∴AD=2,AM=2+x,DM=2﹣x,在Rt△ADM中,则有(x+2)2=4+(2﹣x)2解得:,∴,∴.10、如图,CM、BN是等腰△ABC两腰上的高,CM、BN相交于点O.(1)求证:OB=OC;(2)点P在边CB的延长线上,过P作PE∥AB交CM的延长线于点E,作PF∥AC交NB的延长线于点F.求证:AM•PF+OM•BN=AM•PE.解:(1)∵等腰△ABC中,AB=AC,∴∠ABC=∠ACB,∵CM⊥AB,BN⊥AC,∴∠BMC=∠CNB=90°,∵BC=BC,∠ABC=∠ACB,∠BMC=∠CNB=90°,∴△BCM≌△CBN(AAS),∴∠OBC=∠OCB,∴OB=OC;(2)连接OP,∵PE∥AB,PF∥AC,∴∠PEC=∠BMC=90°,∠PFB=∠CNB=90°,∵S△BOC=S△COP﹣S△BOP,∴OC•BM=OC•PE﹣OB•PF,∵OB=OC,∴PE﹣PF=BM,∵∠BMC=∠ANB=90°,∠BMO=∠NBA,∴△BOM∽△BAN,∴,∴OM•BN=BM•AN=(PE﹣PF)•AN,∵AB=AC,BM=CN,∴AM=AN,∴OM•BN=(PE﹣PF)•AM,∴AM•PF+OM•BN=AM•PE.11、如图,⊙O内两条互相垂直的弦AB,CD(不是直径)相交于点E,连接AD,BD,AC,过点O作OF⊥AC于点F.过点A作的切线PA,交CD的延长线于点P..(1)求证:2OF=BD.(2)若,BD=3,PD=1,求AD的长.证明:(1)如图,连接AO并延长交⊙O于H,连接CH,∵OF⊥AC,∴FC=AF,又∵AO=OH,∴OF∥CH,CH=2OF,∴∠HCA=∠OFA=90°,∴∠AHC+∠CAH=90°,∵AB⊥CD,∴∠ADC+∠BAD=90°,又∵∠ADC=∠AHC,∴∠CAH=∠DAB,∴,∴CH=BD,∴BD=2OF;(2)如图,连接BC,∵,∴∠ADC=∠BCA,∵四边形ACBD是圆内接四边形,∴∠ACB+∠ADB=180°,∵∠ADC+∠ADP=180°,∴∠ADB=∠ADP,∵PA是⊙O切线,∴∠PAH=90°,∴∠PAD+∠DAH=90°,∵∠ACH=90°=∠ACD+∠HCD,∠HCD=∠HAD,∴∠PAD=∠ACD,∵∠ACD=∠ABD,∴∠PAD=∠ABD,∴△ADP∽△BDA,∴,∴AD2=PD•BD=3×1=3,∴AD=.12、(1)证明推断:如图①,在△ABC中,D,E分别是边BC,AB的中点,AD,CE相交于点G,求证:==.(2)类比探究:如图②,在正方形ABCD中,对角线AC、BD交于点O,E为边BC的中点,AE、BD 交于点F,若AB=6,求OF的长;(3)拓展运用:若正方形ABCD变为▱ABCD,如图③,连结DE交AC于点G,若四边形OFEG的面积为,求▱ABCD的面积.(1)证明:如图①,连结ED,∵D,E分别是边BC,AB的中点,∴DE是△ABC的中位线,∴DE∥AC,DE=AC,∴△DEG∽△ACG,∴===2,∴==;(2)解:∵四边形ABCD为正方形,E为边BC的中点,对角线AC、BD交于点O,∴AD∥BC,BE=BC=AD,BO=BD,∴△BEF∽△DAF,∴==,∴BF=DF,∴BF=BD,∵BO=BD,∴OF=OB﹣BF=BD﹣BD=BD,∵正方形ABCD中,AB=6,∴BD=6,∴OF=;(3)解:如图③,连接OE,由(1)知,BF=BD,OF=BD,∴=2,∵△BEF与△OEF的高相同,∴△BEF与△OEF的面积比为=2,同理,△CEG与△OEG的面积比=2,∴S△CEG+S△BEF=2(S△OEG+S△OEF)=2×=1.∴S△BOC=,∴S▱ABCD=4×=6.。
相似三角形证明专题练习

相似的判定证明题1、如图所示,在⊙O 中,CD 过圆心O ,且CD ⊥AB 于D ,弦CF 交AB 于E .求证:CB 2=CF ·CE .2、如图,已知⊙O 的弦CD 垂直于直径AB ,点E 在CD 上,且EC = EB .(1)求证:△CEB ∽△CBD ;(2)求证:CB 2=CE ·CD(3)若CE = 3,CB=5 ,求DE 的长.3、(绥化)如图,点A ,B ,C ,D 为⊙O 上的四个点,AC 平分∠BAD ,AC 交BD 于点E ,CE=4,CD=6,(1)求证:CD 2=CE •CA (2)求:AE 的长为多少?4.已知:如图19,在Rt △ABC 中,∠ABC =90°,以AB 上的 点O 为圆心,OB 的长为半径的圆与AB 交于点E ,与AC 切于点D . (1)求证:BC =CD ; (2)求证:∠ADE =∠ABD ;(3)设AD =2,AE =1,求⊙O 直径的长.5.已知:如图,AB 是半圆O 的直径,CD ⊥AB 于D 点。
(1)求证:CD 2=AD •BD(2)求证:CB 2=BD •BA6、(黔东南州)如图,⊙O 是△ABC 的外接圆,圆心O 在AB 上,过点B 作⊙O 的切线交AC 的延长线于点D .(1)求证:CB 2=AC •CD(2)若AC=8,BC=6,求△BDC 的面积.7. (四川雅安)如图,在△ABC 中,AB=AC ,以AB 为直径作⊙O ,交BC 于点D ,过点D 作DE ⊥AC ,垂足为E .(1)求证:DE 是⊙O 的切线;(2)求证:CD 2=CE •CA8.(2016•呼和浩特)如图,已知AD 是△ABC 的外角∠EAC 的平分线,交BC 的延长线于点D ,延长DA 交△ABC 的外接圆于点F ,连接FB ,FC .(1)求证:∠FBC=∠FCB ;(2)求证:FB 2=FA ·FD(3)若AB 是△ABC 外接圆的直径,FA=2,AD=4,求CD 的长.•ABC DEO。
相似三角形证明题
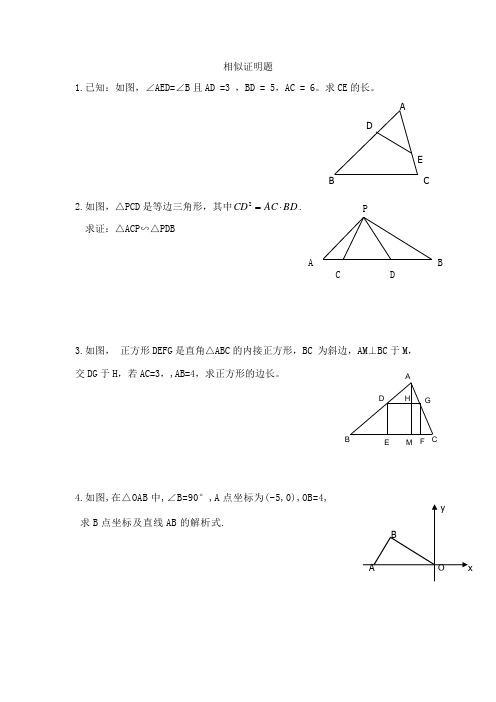
相似证明题1.已知:如图,∠AED=∠B 且AD =3 ,BD = 5,AC = 6。
求CE 的长。
2.如图,△PCD 是等边三角形,其中BD AC CD ⋅=2求证:△ACP∽△PDB3.如图, 正方形DEFG 是直角△ABC 的内接正方形,BC 为斜边,AM ⊥BC 于M ,交DG 于H ,若AC=3,,AB=4,求正方形的边长。
4.如图,在△OAB 中,∠B=90°,A 点坐标为(-5,0),OB=4, 求B 点坐标及直线AB 的解析式.A CF EBDGHMD CBAABCD 5.如图,梯形ABCD 中,AB ∥CD,F 是DC 的中点,BF 的延长线交射线AD 于点G,BG 交AC 于点E.求证: FE GB BE GF ⋅=⋅6.已知:AB⊥DB 于B 点,CD⊥DB 于D 点,AB=6,CD =4,BD =14,则在DB 上是否存在P 点,使以C 、D 、P 为顶点的三角形与以P 、B 、A 为顶点的三角形相似?如果存在,请你求DP 的长;如果不存在,请你说明理由.7.梯形ABCD 中,AD ∥BC ,∠A =90°,∠ADC =150°,对角线BD ⊥DC ,若AD =8,求BC 的长。
8.已知,如图△ABC 中,AB=7,AD=4,∠B=∠ACD ,求AC 的长。
GEF BCDACEAB D CF9.已知:ΔACB 为等腰直角三角形,∠ACB=900 延长BA 至E ,延长AB 至F ,∠ECF=1350求证:ΔEAC ∽ΔCBF10、如图:在大小为4×4的正方形方格中, △ABC 的顶点A 、B 、C 在单位正方形的顶点上,请在图中画一个△A 1B 1C 1 ,使△A 1B 1C 1∽△ABC (相似比不为1),且点A 1 、B 1 、C 1 都在单位正方形的顶点上。
11、已知:如图,平行四边形ABCD 中,E 是CB 延长线上一点,DE 交AB 于F 。
相似三角形证明题

相似三角形证明题1.如图:⊿ABC 中,D 是AB 上一点,AD =AC ,BC 边上的中线AE 交CD 于F ,求证:DF CF AC AB ::=2.四边形ABCD 中,AC 为AB 、AD 的比例中项,且AC 平分∠DAB ,求证:22CD BC DE BE =3.如图,已知菱形ABCD 中,在AD 上任取一点E ,连结CE 并延长与BA 的延长线交于点F ,过E 作EG ∥FB 交FD 于G ,求证:GF =AECA BB4.在Rt ⊿ABC 中,∠ACB =Rt ∠,AD 平分∠CAB ,CE ⊥AB 于E ,交AD 于F ,过F 作FG ∥AB 交CB 于G ,求证:CD =GB5.矩形ABCD 中,a AB =,b BC =,M 是BC 的中点,DE ⊥AM ,E 是垂足,求证:2242b a ab DE +=C6.如图,过平行四边形ABCD 的顶点A 的直线交BD 于P ,交CD 于Q ,并交BC 的延长线于R ,求证:22PB PD PR PQ 7.已知,如图,在平行四边形ABCD 中,E 为AC 三分之一处,即AE =31AC ,DE 的延长线交AB 于F ,求证:AF =FB8.如图所示,在平行四边形ABCD 中,过点B 作BE ⊥CD ,垂足为E ,连结AE ,F 为AE 上一点,且∠BFE =∠C(1)求证:△ABF ∽△EAD ;(2)若AB =4,∠BAE =30°,求AE 的长;(3)在(1)(2)的条件下,若AD =3,求BF 长.(计算结果含根号).R9.如图,P 在线段MN 上,如果PM 2=PM ·PN ,,那么,P 是线段MN 的一个黄金分割点。
现有一等腰ΔABC (如图),AB=AC ,∠ABC=2∠A ,BD 是角平分线。
(1)求证:D 是AC 的黄金分割点。
(2)若AC=1,求AD 的长。
选择题;1.如图是一个正方体包装盒的表面展开图,若在其中的三个正方形A 、B 、C 内分别填上适当的数,使得将这个表面展开图沿虚线折成正方体后,相对面上的两数互为相反数,则填在A 、B 、C 内的三个数依次是()(A )0,-2,1(B )0,1,-2(C )1,0,-2(D )-2,0,12.如图是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是(A )25(B )66(C )91(D )1203.如图:在一块长为a ,宽为b 的长方形的草地上,修两条宽度为h 的小路,则下列结论中成立的是:()A.修路后,留下草地的面积是:bhah ab --B.))((2h b h a h ha hb ab --=+--C.))((2h b h a h ha hb ab --=---D.))((2h b h a h ha hb ab -+=---(1)(2)(3)a bh h。
相似三角形证明计算训练题

相似三角形证明计算训练题一.解答题(共29小题)1.Rt△ABC中,∠C=90°,F为AC边上的一点,AD⊥AB交BF的延长线于点D,且AF =AD,DE⊥AC.(1)求证:∠CBF=∠ABF.(2)求证:CF=AE.(3)如果2CF=3EF,且BD=5,求AB的值.2.如图,已知在四边形ABCD中,E、F分别为AD、DC的中点,AD∥BC,AD:DC=1:,AB=10、BC=6、EF=4.(1)求AD的长;(2)△DEF是什么三角形?请你给出正确的判断,并加以说明;(3)求四边形ABCD的面积.3.如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为F,G.(1)求证:;(2)FD与DG是否垂直?若垂直,请给出证明;若不垂直,请说明理由;(3)当AB=AC时,△FDG为等腰直角三角形吗?并说明理由.4.在△ABC中,中线BE、CF交于点O,M、N分别是BO、CO中点,则四边形MNEF是什么特殊四边形?并说明理由.5.如图,已知△ABC的两边AB、AC的中点分别为M、N.求证:MN∥BC,且MN=BC.6.已知:平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点.求证:(1)BE⊥AC;(2)EG=EF.7.如图,在△ABC中,D、E分别是AB、AC边的中点.求证:DE=BC且DE∥BC.8.如图,已知△ABC中,点F是BC的中点,DE∥BC,则DG和GE有怎样的关系?请你说明理由.9.(1)如图1,在△ABC中,已知OB,OC分别平分∠ABC,∠ACB,BP,CP分别平分∠ABC,∠ACB的外角∠DBC,∠ECB.①若∠A=50°,则∠O=,∠P=;②若∠A=α,则∠O=,∠P=.(用含α的式子表示)(2)如图2,在四边形ABCD中,BP,CP分别平分外角∠EBC,∠FCB,请探究∠P 与∠A,∠D的数量关系,并说明理由;(3)如图3,在六边形ABCDEF中,CP,DP分别平分外角∠GCD,∠HDC,请直接写出∠P与∠A,∠B,∠E,∠F的数量关系.10.已知:如图,在菱形ABCD中,AE⊥BC,AF⊥CD,垂足分别为点E和点F,AE、AF 分别与BD相交于点M、N.(1)求证:EF∥BD;(2)当MN:EF=2:3时,求证:△AMN是等边三角形.11.如图所示,在菱形ABCD中,点E,F分别在CD,BC上,且CE=CF,求证:AE=AF.12.点D是等腰Rt△ABC的直角边BC上一点,AD的中垂线EF分别交AC、AD、AB于E、O、F,且BC=2.①当CD=时,求AE;②当CD=2(﹣1)时,试证明四边形AEDF是菱形.13.如图1,矩形铁片ABCD中,AD=8,AB=4;为了要让铁片能穿过直径为3.8的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔).(1)直接写出矩形铁片ABCD的面积;(2)如图2,M、N、P、Q分别是AD、AB、BC、CD的中点,将矩形铁片的四个角去掉.①证明四边形MNPQ是菱形;②请你通过计算说明四边形铁片MNPQ能穿过圆孔.(3)如图3,过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合),沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片.当BE=DF=1时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由.14.如图1,半圆O为△ABC的外接半圆,AC为直径,D为上的一动点.(1)问添加一个什么条件后,能使得?请说明理由;(2)若AB∥OD,点D所在的位置应满足什么条件?请说明理由;(3)如图2,在(1)和(2)的条件下,四边形AODB是什么特殊的四边形?证明你的结论.15.在矩形ABCD中,DC=,CF⊥BD分别交BD、AD于点E、F,连接BF.(1)求证:△DEC∽△FDC;(2)当F为AD的中点时,求sin∠FBD的值及BC的长度.16.(根据课本习题改编)如图1,在△ABC中,∠C=90°,AC=4,BC=3,四边形DEFG 为△ABC的内接正方形,若设正方形的边长为x,容易算出x的长为.探究与计算:(1)如图2,若三角形内有并排的两个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为;(2)如图3,若三角形内有并排的三个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为;(3)如图4,若三角形内有并排的n个全等的正方形,它们组成的矩形内接于△ABC,请你猜想正方形的边长是多少?并对你的猜想进行证明.17.如图,矩形ABCD中,AB=8,AD=6.动点P从点A出发,沿线段AB(不包括端点A,B)以每秒2个单位长度的速度,匀速向点B运动;动点Q从点B出发,沿线段BC (不包括端点B,C)以每秒1个单位长度的速度,匀速向点C运动.连接DQ并延长交AB的延长线于点E,把DE沿DC翻折交BC延长线于点F,连接EF.点P,Q同时出发,同时停止,设运动时间为t秒.(1)当DP⊥DF时,求t的值;(2)当PQ∥DF时,求t的值;(3)在运动的过程中,△DEF的面积是否变化?如果改变,求出变化的范围;如果不变,求出它的值.18.如图,平面直角坐标系xOy中,矩形OABC如图放置,点B(4,3),E,F分别为OA,BC边上的中点,动点P从点E出发以每秒2个单位速度沿EO方向向点O运动,同时,动点Q从点F出发以每秒1个单位速度沿FB方向向点B运动.当一个点到达终点时,另一个点随之停止.连接EF、PQ,且EF与PQ相交于点M,连接AM.(1)求线段AM的长度;(2)连接BM,求∠BMA的正切值.19.如图所示,矩形ABCD中,BD是对角线,AB=4,AD=3.(1)尺规作图:作∠ADB的平分线DM(保留作图痕迹,不写作法);(2)设DM与AB交于点E,过点E作EF⊥BD于F,求EF的长.20.已知如图,正方形ABCD中,E为DC上一点,连接BE,作CF⊥BE于P交AD于F 点,若恰好使得AP=AB.求证:E为DC中点.21.如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.(1)判断四边形ACED的形状,并说明理由;(2)若BD=8cm,求线段BE的长.22.如图已知四边形ABCD、AEFP,均为正方形.(1)如图1若连接BE、DP猜想BE与DP满足怎样的数量关系和位置关系;(2)如图2若四边形AEFP绕点A按逆时针方向旋转,在旋转过程中,(1)中猜想出的结论是否总成立?若成立请给予证明;若不成立,请说明理由;(3)如图3若四边形AEFP绕点A按逆时针方向继续旋转,在旋转过程中,(1)中猜想出的结论是否总成立?直接写出结论.23.(1)如图1,ABCD是一个正方形花园,要在边AD、DC的E、H处开两个门,且DE =CH,要修建两条小路BE、AF.那么这两条小路长度和位置各有什么关系?并证明你的结论;(2)如图2,在(1)的图形中,如果要在正方形四边E、H、F、G处各开一个门,并用小路EF、HG连接起来,如果EF⊥GH,求的值;(3)把(2)中的正方形改为矩形,如图3,AB=a,AD=b,其它条件不变,求的值.24.正方形ABCD中,E、F分别在边AD,AB上,且AE=BF=AB,EF与AC交于点P.(1)求EF:AE的值;(2)设AB=x,四边形BCPF的面积为y,求y关于x的函数解析式.25.如图,在△ABC中,按如下步骤作图:①以点A为圆心,AB长为半径画弧;②以点C为圆心,CB长为半径画弧,两弧相交于点D;③连接BD,与AC交于点E,连接AD、CD;(1)求证:∠BAE=∠DAE;(2)当AB=BC时,猜想四边形ABCD是什么四边形,并证明你的结论;(3)当AC=8cm,BD=6cm,现将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长是多少?26.已知矩形ABCD中,AB=4,BC=8,E是DC上一点,连AE并延长交BC的延长线于点F,正方形CGHM的顶点G、H、M分别在△ECF的三边上.(1)当点E为DC中点时,求正方形CGHM的边长a1;(2)当时,求正方形CGHM的边长a2;(3)当、、、…、时,正方形CGHM的边长分别记为a1、a2、a3、…、a n,则a n=.(直接写出结果)27.小杰和他的同学组成了“爱琢磨”学习小组,有一次,他们碰到这样一道题:“已知正方形ABCD,点E、F、G、H分别在边AB、BC、CD、DA上,若EG⊥FH,则EG=FH“经过思考,大家给出了以下两个方案:(甲)过点A作AM∥HF交BC于点M,过点B作BN∥EG交CD于点N;(乙)过点A作AM∥HF交BC于点M,作AN∥EG交CD的延长线于点N;小杰和他的同学顺利的解决了该题后,大家琢磨着想改变问题的条件,作更多的探索.…(1)对小杰遇到的问题,请在甲、乙两个方案中任选一个,加以证明(如图1);(2)如果把条件中的“正方形”改为“长方形”,并设AB=2,BC=3(如图2),试探究EG、FH之间有怎样的数量关系,并证明你的结论;(3)如果把条件中的“EG⊥FH”改为“EG与FH的夹角为45°”,并假设正方形ABCD 的边长为1,FH 的长为(如图3),试求EG的长度.28.如图,已知在正方形ABCD中,P为BC上的一点,E是边BC延长线上一点,连接AP 过点P作PF⊥AP,与∠DCE的平分线CF,相交于点F,连接AF,与边CD相交于点G,连接PG.(1)求证:①∠P AB=∠FPC;②AP=FP;(2)试判断PB、DG、PC,这三条线段存在怎样的数量关系,并说明理由.29.如图,在正方形ABCD中,以对角线AC为一边作一等边△ACE,连接ED并延长交AC 于点F.(Ⅰ)求证:EF⊥AC;(Ⅱ)延长AD交CE于点G,试确定线段DG和线段DE的数量关系.第11页(共11页)。
相似证明精选好题
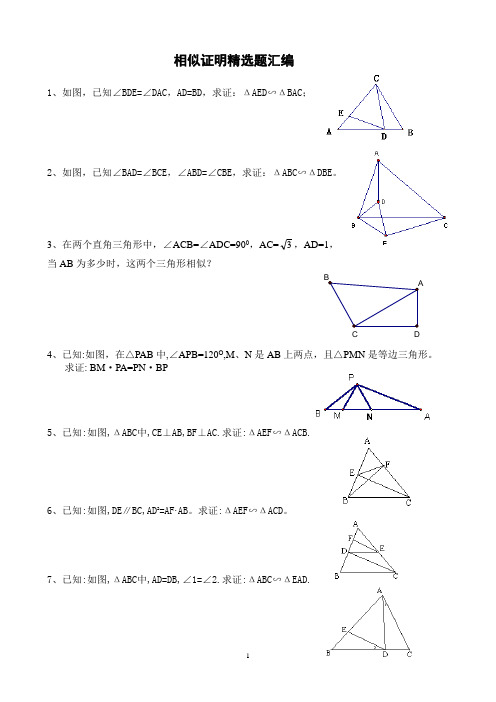
C D相似证明精选题汇编1、如图,已知∠BDE=∠DAC ,AD=BD ,求证:ΔAED ∽ΔBAC ;2、如图,已知∠BAD=∠BCE ,∠ABD=∠CBE ,求证:ΔABC ∽ΔDBE 。
3、在两个直角三角形中,∠ACB=∠ADC=900,AC=3,AD=1,当AB 为多少时,这两个三角形相似?4、已知:如图,在△PAB 中,∠APB=120O ,M 、N 是AB 上两点,且△PMN 是等边三角形。
求证: BM ·PA=PN ·BP5、已知:如图,ΔABC 中,CE ⊥AB,BF ⊥AC.求证:ΔAEF ∽ΔACB.6、已知:如图,DE ∥BC,AD 2=AF ·AB 。
求证:ΔAEF ∽ΔACD 。
7、已知:如图,ΔABC 中,AD=DB,∠1=∠2.求证:ΔABC ∽ΔEAD.8、如图,∠B=900,AB=BE=EF=FC=1。
求证:ΔAEF ∽ΔCEA.9、如图,等腰三角形ABC 中,AB=AC,D 为CB 延长线上一点,E 为BC 延长线上点,且满足AB 2=DB ·CE. (1)求证:△ADB ∽△EAC ;(2)若∠BAC=40°,求∠DAE 的度数10、如下图,在△ABC 中,D 、E 分别为BC 的三等分点,CM 为AB 上的中线,CM分别交AE、AD 于F 、G ,则CF ∶FG ∶GM=5∶3∶211、如图,等腰直角三角形ABC 中,顶点为C ,∠MCN=45°,试说明△BCM ∽△ANC .12、在△ABC 中,BF 交AD 于E.(1)若AE:ED=2:3,BD:DC=3:2,求AF:FC ; (2)若AF:FC=2:7,BD:DC=4:3,求AE:ED.(3)BD:CD=2:3,AE:ED=3:4 求13、在△ABC 中,D 、E 分别为BC 的三等分点,AC 边上的中线BM 交AD 于P ,交AE 于Q ,若BM=10cm ,试求BP 、PQ 、QM 的长.A B C E D14、如图,M 为线段AB 的中点,AE 与BD 交于点C ,∠DME =∠A =∠B =α, 且DM 交AC 于F ,ME 交BC 于G .写出图中三对相似三角形,并证明其中的一对;15、已知:AM :MD=4:1,BD :DC=2:3,则AE :EC=_________。
三角形相似证明训练题

三角形相似证明训练题姓名_______ 学号_______ 总分_______1、如图,P 为△ABC 边AB 上的一点,要使△ACP ∽△ABC,只要添加条件_____________;并说明理由;若△ACP ∽△ABC,你可以得到哪些结论?2、如图,AD ∥BC,AB 、CD 相交于点E ,过点E 作EF ∥AD 交AC 于点F 。
找出一对相似三角形,并说明理由。
FEDCBA3、如图,已知D 是△ABC 的边AB 上任一点,DF ∥AC 交BC 于E .AF 交BC 于M ,且∠B=∠F ,那么△AMC ∽△BDE 吗?请说明理由.4、如图,∠1=∠2,AE =12,AD =15,AC =20,AB =25, 证明:△ADE ∽△ABC 。
5、如图,在梯形ABCD 中,AB ⊥BC ,∠BAD=90°,对角线BD ⊥DC 。
(1)△ABD 与△DCB 相似吗?请说明理由。
(2)如果AD=4,BC=9,求BD 的长。
6、如图,正方形ABCD 中,P 是BC 上一点,且BP=3PC ,Q 是CD 的中点.求证: △ADQ ∽△QCP.A BCP CD BP A Q7、已知:如图,ΔABC 中,∠ABC=2∠C,BD 平分∠ABC.求证:△ABDC ∽△ACB8、矩形ABCD 中,AB =4,BC =6,M 是BC 的中点,DE ⊥AM ,E 是垂足. ①△ABM ∽△AED ; ②求DE的长9、已知:如图,在△ABC 中,AB =AC ,AD ⊥AB ,AD 交BC 于点E ,DC ⊥BC ,与AD 交于点D .求证:AC 2=AE ·AD .10、已知:ΔACB 为等腰直角三角形,∠ACB=900延长BA 至E ,延长AB 至F ,∠ECF=1350求证:ΔEAC ∽ΔCBF11、如图,AE 2=AD ·AB ,且∠1=∠2,试说明△BCE ∽△EBD 。
12、如图为了估算河的宽度,我们可以在河对岸选定一点A ,再在河的这一边选定点B 和点C ,使得AB ⊥BC ,然后选定点E ,使EC ⊥BC ,确定BC 与AE 的交点D ,若测得BD =120米,DC =60米,EC =40米,你能知道小河的宽是多少吗?ABD CE12BC DAE。
相似证明题汇编

相似图形1、下列图形不是形状相同的图形是()A、某人的侧身照片和正面B、用放大镜将一个细小物体图案放大过程中原有图案和放大图案C、像同一张底片冲洗出来的两张大小不同的照片D、一棵树与它倒影在水中的像2、下列图形中不一定是相似图形的是()A、两个等边三角形B、两个等腰直角三角形C、两个长方形D、两个正方形3、下列图形中,不一定相似的是()A 邻边之比相等的两个矩形B 四条边对应成比例的两个四边形C 有一个角相等的菱形D 两条对角线的比相等且夹角相等的两个平行四边形4、下列说法中不一定正确的是()A、相似的图形大小可以相等B、所有等边三角形均相似C、所有正方形均相似D、所有菱形均相似5、下列说法正确的是()A .所有的等腰三角形都相似B.所有的直角三角形都相似C.所有的等腰直角三角形都相似D.有一个角相等的两个等腰三角形都相似6、下列说法中错误的是( )A.所有的等腰三角形都相似B.所有的等边三角形都相似C.有一对锐角相等的两个直角三角形相似D.全等的三角形一定相似7、下列命题中,(1)所有的等腰三角形都相似;(2)所有的等边三角形都相似;(3)所有的等腰直角三角形都相似;(4)所有的直角三角形都相似。
其中真命题的序号是。
8、下列说法“①凡正方形都相似;②凡等腰三角形都相似;③凡等腰直角三角形都相似;④直角三角形斜边上的中线与斜边的比为1∶2;⑤两个相似多边形的面积比为4∶9,则周长的比为16∶81.”中,正确的个数有()个A、1B、2C、3D、4 对应理解1、下列条件能判定△ABC和△A'B'C'相似的有①∠A=47°AB=15,AC=20;∠ B'=47°, A'B'=28,B'C'=21②∠A=47°AB=2,AC=3;∠A'=47°, A'B'=4,B'C'=6③∠C=90°AC=6,AB=10;∠C'=90°, A'C'=16,B'C'=12④∠A=100°,AB=5cm,AC=10cm∠A′=100°,A′B′=8cm,A′C′=12cm;⑤AB=4cm,BC=6cm,AC=8cm,A′B′=12cm,B′C′=18cm,A′C′=24cm,⑥ABCABABCAB'∠=∠''''=且⑦BBCAACBAAB'∠=∠''=''且⑧CACAACBAAB'∠=∠''=''且2、已知ΔABC的三边长分别为2,6,2, ΔA′B′C′的两边长分别是1和3,如果ΔABC与ΔA′B′C′相似,那么ΔA′B′C′的第三边长应该是( )A.2B.22C.26D.333、如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值()A.只有1个 B.可以有2个C.有2个以上但有限 D.有无数个平行型1、如图,已知AB CD EF∥∥,那么下列结论正确的是()A.AD BCDF CE=B.BC DFCE AD=C.CD BCEF BE=D.CD ADEF AF=2、如图,四边形ABCD是平行四边形.O 是对角线AC的中点,过点O的直线EF 分别交AB、DC于点E、F,与CB、AD的延长线分别交于点G、H.写出图中不全等的两个相似三角形(不要求证明);找角类1、△ABC中,∠1=∠2=∠3,试说明△ABC ∽△DEF2、如图,M为线段AB的中点,AE与BD 交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.写出图中三对相似三角形,并证明其中的一对;3、如图,已知在△ABC中,D、E为AC边上的点,AD=AB,∠EBD=∠DBC,求证:AD2=AE·AC4、如图,在中,过点B 作BE ⊥CD,垂足为E,连结AE,F 为AE 上一点,且∠BFE=∠C.(1)求证:△ABF ∽△EAD5、如图,已知△ABC 中CE⊥AB 于E,BF⊥AC 于F,求证:⑴ΔABF ∽ΔACE ;⑵ΔAEF ∽ΔACB 。
相似三角形证明题精选题
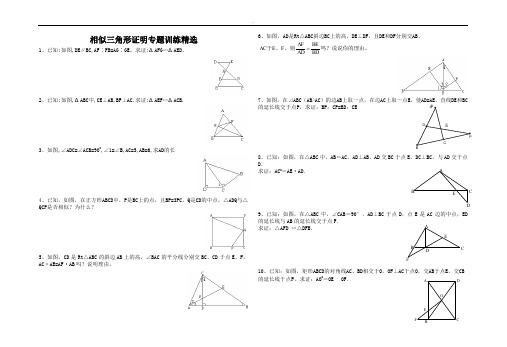
..相似三角形证明专题训练精选1、已知:如图,DE∥BC,AF ∶FB=AG ∶GE 。
求证:ΔAFG ∽ΔAED 。
2、已知:如图,ΔABC 中,CE ⊥AB,BF ⊥AC.求证:ΔAEF ∽ΔACB.3、如图,∠ADC=∠ACB=900,∠1=∠B,AC=5,AB=6,求AD 的长4、已知,如图,在正方形ABCD中,P 是BC 上的点,且BP=3PC ,Q 是CD 的中点,△ADQ 与△QCP 是否相似?为什么?5、如图,CD 是Rt △ABC 的斜边AB 上的高,∠BAC 的平分线分别交BC 、CD 于点E 、F ,AC ·AE=AF ·AB 吗?说明理由。
6、如图,AD 是Rt △ABC 斜边BC 上的高,DE ⊥DF ,且DE 和DF 分别交AB、AC E F AF AD BEBD于、。
则吗?说说你的理由。
7、如图,在⊿ABC (AB>AC )的边AB 上取一点,在边AC 上取一点E ,使AD=AE ,直线DE 和BC的延长线交于点P ,求证:BP :CP=BD :CE8、已知:如图,在△ABC 中,AB =AC ,AD ⊥AB ,AD 交BC 于点E ,DC ⊥BC ,与AD 交于点D .求证:AC 2=AE ·AD .9、已知:如图,在△ABC 中,∠CAB =90°,AD ⊥BC 于点D ,点E 是AC 边的中点,ED 的延长线与AB 的延长线交于点F .求证:△AFD ∽△DFB .10、已知:如图,矩形ABCD 的对角线AC 、BD 相交于O ,OF ⊥AC 于点O ,交AB 于点E ,交CB 的延长线于点F ,求证:AO 2=OE · OF . B C D A EBCD A FEO B CD AE F..11、己知:如图,AB ∥CD,AF=FB,CE=EB. 求证:GC 2=GF ·GD. 12、已知:如图,ΔABC 中,∠ACB=900,F 为AB 的中点,EF ⊥AB.求证:ΔCDF ∽ΔECF.13、已知:如图,DE ∥BC,AD 2=AF ·AB 。
初中平行线相似证明练习题

初中平行线相似证明练习题
本文档将提供一些初中平行线相似证明的练题,帮助学生加深对该知识点的理解与应用。
问题一
已知:四边形ABCD中,AB平行CD,且AD与BC相交于点O。
证明:三角形AOD与三角形BOC相似。
解答一
由已知条件可得,AB平行CD,根据平行线的性质,可以推出∠ACD=∠BDC。
又AD与BC相交于点O,根据垂直角的性质,可以得出
∠AOD=∠COB。
综上所述,根据AAA相似性质,可以得出三角形AOD与三角形BOC相似。
问题二
已知:图中的两条直线AB和CD平行,∠FAD=∠DCB。
证明:三角形ADF与三角形CBD相似。
解答二
由已知条件可得,直线AB平行CD,根据平行线的性质,可以推出∠FAD=∠DCB。
综上所述,根据AA相似性质,可以得出三角形ADF与三角形CBD相似。
问题三
已知:图中的直线AB和CD平行,∠EAD=∠CDB。
证明:三角形AED与三角形BCD相似。
解答三
由已知条件可得,直线AB平行CD,根据平行线的性质,可以推出∠EAD=∠CDB。
综上所述,根据AA相似性质,可以得出三角形AED与三角形BCD相似。
结论
通过以上练题的解答,我们可以得出结论:在平行线的相关知识点中,可利用平行线性质和角的性质,通过简单的证明步骤可以得出平行线相似的结论。
希望以上内容对你的学习有所帮助!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1已知:如图,CE 是Rt ΔABC 的斜边AB 上的高,BG ⊥AP. 求证:CE 2
=ED ·
EP.
2如图:⊿ABC 中,D 是AB 上一点,AD = AC ,BC 边上的中线AE 交CD 于F ,求证:
3如图,已知菱形ABCD 中,在AD 上任取一点E ,连结CE 并延长与BA 的延长线交于点
4在Rt ⊿ABC 中,∠ACB = Rt ∠,AD 平分∠CAB ,CE ⊥AB 于E ,交AD 于F ,过F 作
.
5如图所示,在平行四边形ABCD 中,过点B 作BE ⊥CD ,垂足为E ,连结AE ,F 为AE
C
B
A
上一点,且∠BFE=∠C (1)求证:△ABF∽△EAD;(2)若AB=4,∠BAE=30°,
求AE的长;(3)在(1)(2)的条件下,若AD=3,求BF长.
(计算结果含根号).
C
6已知:△ABC中,AB=3AC,AD是∠BAC的平分线,BE⊥AD交AD延长线于E点。
求证:AD=DE
证明:延长AC、BE交于P,经E作EG‖BC交CP于G。
∵∠BAE=∠PAE,BE
⊥AE. ∠BEA=∠PEA=90°. AE=AE. ∴△ABE≌△APE,AB=AP,BE=EP. ∵GE‖BC,
∴CG=GP, . ∴ . EG‖BC,EG‖DC,∴△ADC∽△AEG. ∴,∴AD=DE。
7已知:△ABC中,AB=AC=5,BC=6,动点D在边AB上,DE⊥AB,点E在边BC 上,又点F在边AC上,且∠DEF=∠B。
(1)求证:△FCE∽△EBD;(2)当点D
在边AB上运动时,是否可能使?如果可能,求出BD的长;如果不可能,请说
明理由
证明:∠DEC=∠B+∠BDE=∠DEF+∠FEC. ∠BDE=90°,∠B=∠DEF。
∴∠FEC=
∠BDE=90°,∵AB=AC. ∴∠B=∠C,△FCE∽△EBD。
(2)△FCE中斜边最大时,CF=CA,即F重合于A,这时E为BC中点,BE=3,CF=5.
∵△FCE∽△EBD. ∴ . ∴不可能使
8三角形ABC中,角C=90,BD平分角ABC交AC于D,求证:BC^2/BD^2=AC/2AD
过A点做BC平行线AE交BD延长线于点E,
八字形,三角形AED相似于三角形BCD CD/AD=BC/AE @
BC/BD=AE/ED 所以BC/AE=BD/ED 等式两边同时加1,1+BC/AE=1+BD/ED 得
(AE+BC)/AE=(ED+BD)/ED=BE/ED
@式两边同时加1得1+CD/AD=1+BC/AE 所以得(AD+CD)/AD=(AE+BC)/AE=AC/AD
整理得AC/AD=BE/ED
BC/BD=AE/ED BC^2/BD^2=AE^2/ED^2 所以就变成求证BE/2ED=AE^2/ED^2 两边
一约分得AE^2/ED=BE/2即2AE^2=BE* ED。
