初中几何证明的经典难题好题

初中数学几何证明经典题(含答案)

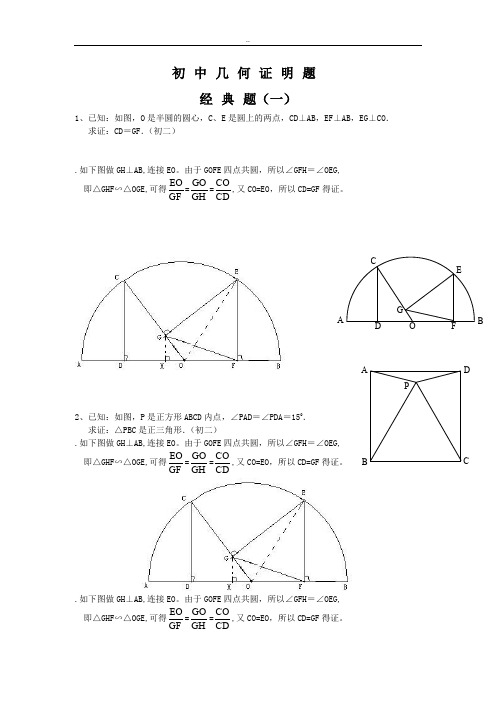
初中几何证明题经典题（一）1、已知：如图，O是半圆的圆心，C、E是圆上的两点，CD⊥AB，EF⊥AB，EG⊥CO．求证：CD＝GF．（初二）.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

2、已知：如图，P是正方形ABCD内点，∠PAD＝∠PDA＝150．求证：△PBC是正三角形．（初二）.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

APCDBAFGCEBOD3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 BF2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC点P 是EF 的中点．求证：点P 到边AB 的距离等于AB的一半．经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、证：AB ＝DC ，BC ＝AD ．（初三）经典1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC 求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA ＝200，求∠BED的度数．经典题（一）1.如下图做GH⊥AB,连接EO。

初中数学-几何证明经典试题(含答案)

初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEFB 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）E经典题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）D经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．APCBACBPDEDCB AA CBPD经典题（一）1.如下图做GH⊥AB,连接EO。

初中几何证明的经典难题

几何证明1.如图，点E是BC中点，CDEAB=∠，求证：CD=BAE∠2. 如图，在ABC∠90AB=，BABAC，AC∆中，︒=CD//，点P是BC上一点，连结AP，过点P做APPE⊥交CD于E.探究PE与PA的数量关系.3. 如图，在ABCBD=，DE交AB=，点D在AB上，点E在AC的延长线上，且CE ∆中，ACBC于点P.探究PE与PD的数量关系.4. 如图，在ABC ∆中，A ECB DBC ∠=∠=∠21，BD 、CE 交于点P .探究BE 与CD 的数量关系.5．如图，在EBC ∆中，BD 平分EBC ∠，延长DE 至点A ，使得ED EA =，且C ABE ∠=∠. 探究AB 与CD 的数量关系.6.如图，在ABC ∆中，︒=∠90C ，BC AC =，P 为AB 的中点，PF PE ⊥分别交AC 、BC 于E 、F .探究PE 、PF 的数量关系.7. 如图，CD CB =，︒=∠+∠180CDE ABC ，DE AB =.探究：AF 与EF 之间的数量关系8.如图，直线1l 、2l 相交于点A ，点B 、点C 分别在直线1l 、2l 上，AC k AB ⋅=，连结BC ，点D 是线段AC 上任意一点（不与A 、C 重合），作α=∠=∠BAC BDE ，与ECF ∠的一边交于点E ，且ABC ECF ∠=∠.⑴如图1，若1=k ，且︒=∠90α时，猜想线段BD 与DE 的数量关系，并加以证明； ⑵如图2，若1≠k ，时，猜想线段BD 与DE 的数量关系，并加以证明.9.如图，在ABC ∆中，AB CD =，BDA BAD ∠=∠，AE 是BD 边的中线.求证：AE AC 2=10.如图，在ABC ∆中，AD 平分BAC ∠，G 为BC 的中点，AD EG //交CA 延长线于E . 求证：EC BF =11.如图，等腰直角ABC ∆与等腰直角BDE ∆，P 为CE 中点，连接PA 、PD .探究PA 、PD 的关系.12.如图，两个正方形ABDE和ACGF，点P为BC的中点，连接PA交EF于点Q.探究AP与EF的关系.13．已知：如图，正方形ABCD和正方形EBGF，点M是线段DF的中点.⑴试说明线段ME与MC的关系.⑵如图，若将上题中正方形EBGF绕点B顺时针旋转α度数（︒α），其他条件不变，上<90述结论还正确吗？若正确，请你证明；若不正确，请说明理由.14.⑴如图1，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上（BCCG>）取线段AE的中点P.探究：线段PD、PF的关系，并加以证明.⑵如图2，将正方形CGEF绕点C旋转任意角度后，其他条件不变. 探究：线段PD、PF的关系，并加以证明.。

初中数学经典几何难题及答案

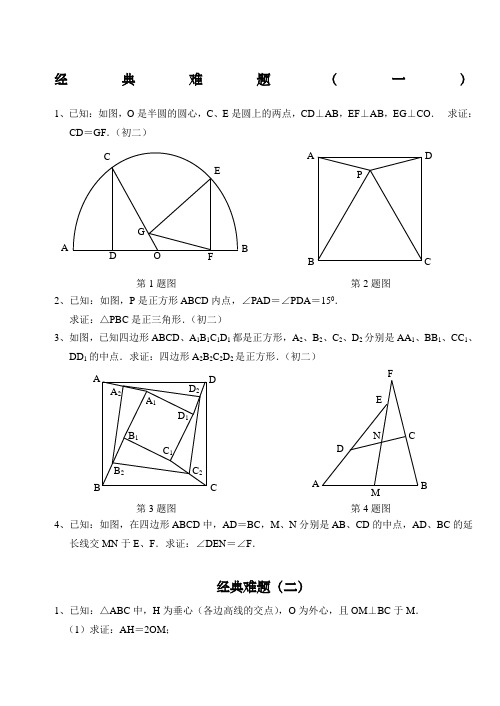
经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）第1题图第2题图2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）第3题图第4题图4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典难题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；ANFE CDM BD 2C 2B 2A 2D 1C 1B 1C BDAA 1APC DBAFGCEB O D（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）第1题图第2题图2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）第3题图第4题图4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．（初二）经典难题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）PCGFBQ ADE· OQPBDEC NM· A·GA O DBECQPNM·AD HEM C BO第1题图第2题图2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）第3题图第4题图4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）经典难题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）第1题图第2题图2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）PADCBAPC BOD BF AECPFE PCBAE DA CBFAFDECBD3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）第3题图第4题图4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．第1题图第2题图2、P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．第3题图第4题图4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300， ∠EBA ＝200，求∠BED 的度数．EDCBAAC BPDAC BPDAPCBFPDE CBACBDA经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF 。

初中数学经典几何难题及答案

经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）第1题图第2题图2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）第3题图第4题图4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典难题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；ANFE CDM BD 2C 2B 2A 2D 1C 1B 1C BDAA 1APC DBAFGCEB O D（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）第1题图第2题图2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）第3题图第4题图4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．（初二）经典难题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）PCGFBQ ADE· OQPBDEC NM· A·GA O DBECQPNM·AD HEM C BO第1题图第2题图2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）第3题图第4题图4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）经典难题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）第1题图第2题图2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）PADCBAPC BOD BF AECPFE PCBAE DA CBFAFDECBD3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）第3题图第4题图4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．第1题图第2题图2、P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．第3题图第4题图4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300， ∠EBA ＝200，求∠BED 的度数．EDCBAAC BPDAC BPDAPCBFPDE CBACBDA经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF 。

初中数学经典几何难题20例及答案

经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）第1题图第2题图2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）第3题图第4题图4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典难题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）ANFE CDMB D 2C 2B 2A 2D 1C 1B 1C BDAA 1APC DBAFGCEB O D第1题图第2题图2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）第3题图第4题图4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．（初二）经典难题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）PCGFBQ ADE· OQPBDEC NM· A·GA O DBECQPNM·AD HEM C BO第1题图第2题图2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）第3题图第4题图4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）经典难题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）第1题图第2题图2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）PADCBAPC BO D BF AECPFE PCBAE DA CBFAFDECBD3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）第3题图第4题图4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．第1题图第2题图2、P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．第3题图第4题图4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300， ∠EBA ＝200，求∠BED 的度数．EDCBAAC BPDAC BPDA PCBFPDE CBACBDA经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF 。

初中数学几何证明经典试题(含答案)

初中几何证明题经典题（一）1、已知：如图，O是半圆的圆心，C、E是圆上的两点，CD⊥AB，EF⊥AB，EG⊥CO．求证：CD＝GF．（初二）.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

2、已知：如图，P是正方形ABCD内点，∠PAD＝∠PDA＝150．求证：△PBC是正三角形．（初二）.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

APCDBAFGCEBOD3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC求证：P A ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，D ．求证：AB ＝DC ，BC ＝AD．（初三）经典1、已知：△ABC 是正三角形，P 是三角形内一点，P A ＝3，PB ＝4，求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．C BD A F PD E CB A APCBACBPDA CBPD4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典题（一）1.如下图做GH⊥AB,连接EO。

初中数学几何证明经典试题(含答案)

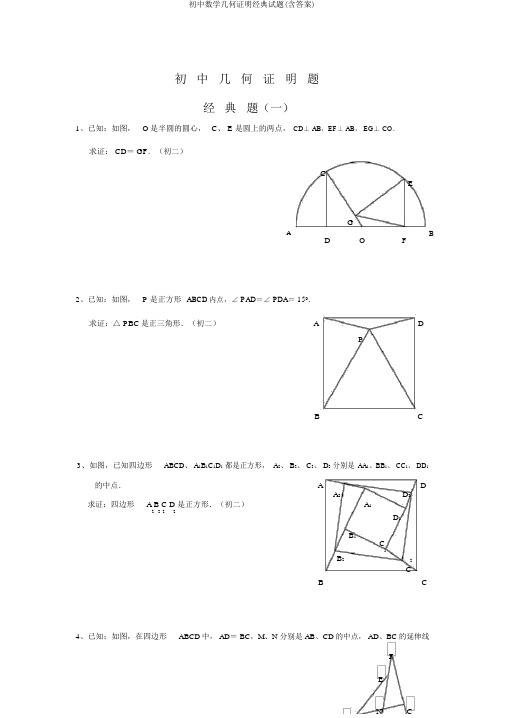
初中几何证明题经典题（一）1、已知：如图，O是半圆的圆心，C、 E 是圆上的两点，CD⊥ AB，EF⊥ AB， EG⊥ CO．求证： CD＝ GF．（初二）CEGA BD O F2、已知：如图，P 是正方形ABCD内点，∠ PAD＝∠ PDA＝ 150．求证：△ PBC是正三角形．（初二）A DPB C3、如图，已知四边形ABCD、 A1B1C1D1都是正方形， A2、 B2、 C2、 D2分别是AA1、BB1、 CC1、 DD1的中点．A DA2D2求证：四边形 A B C D 是正方形．（初二）A12222D1B1C1B22CB C4、已知：如图，在四边形ABCD中， AD＝ BC，M、N 分别是 AB、CD的中点， AD、BC的延伸线FEN C交 MN于 E、 F．求证：∠ DEN＝∠ F．经典题（二）1、已知：△ ABC中， H 为垂心（各边高线的交点）， O为外心，且 OM⊥ BC于M．（ 1）求证： AH＝2OM；A（ 2）若∠ BAC＝ 600，求证： AH＝ AO．（初二）O·H EB M D C2、设 MN是圆 O外向来线，过 O作 OA⊥ MN于 A，自 A引圆的两条直线，交圆于B、C及D、E，直线 EB及 CD分别交 MN于 P、 Q．GE求证： AP＝ AQ．（初二）O·CB DMP A Q N3、假如上题把直线MN由圆外平移至圆内，则由此可得以下命题：设 MN是圆 O的弦，过 MN的中点 A 任作两弦 BC、DE，设 CD、 EB分别交 MN于 P、 Q．求证： AP＝AQ．（初二）CEA M Q·P N·O B D4、如图，分别以△ABC的 AC和 BC为一边，在△ ABC的外侧作正方形ACDE和正方形 CBFG，点 P是 EF的中点．求证：点P 到边 AB的距离等于AB的一半．（初二）DGCEPFA Q B经典题（三）1、如图，四边形ABCD为正方形， DE∥AC， AE＝AC， AE与 CD订交于 F．求证： CE＝CF．（初二）AB2、如图，四边形ABCD为正方形， DE∥AC，且 CE＝ CA，直线 EC交 DA延伸线于求证： AE＝ AF．（初二）DF ECF．F A DB C3、设 P 是正方形ABCD一边 BC上的任一点，PF⊥ AP， CF均分∠ DCE．求证： PA＝ PF．（初二）AE DFBP C E4、如图， PC切圆 O于 C，AC为圆的直径， PEF为圆的割线， AE、AF 与直线 PO订交于 B、D．求证： AB＝ DC， BC＝ AD．（初三）AB O DPEFC经典题（四）A1、已知：△ ABC是正三角形， P 是三角形内一点，PA＝3， PB＝ 4， PC＝ 5．P 求：∠ APB的度数．（初二）B C2、设 P 是平行四边形ABCD内部的一点，且∠PBA＝∠ PDA．求证：∠ PAB＝∠ PCB．（初二）A DPB C3、设 ABCD为圆内接凸四边形，求证：AB· CD＋AD· BC＝AC· BD．（初三）ADB C4、平行四边形ABCD中，设 E、 F 分别是 BC、 AB上的一点， AE 与 CF订交于 P，且AE＝ CF．求证：∠ DPA＝∠ DPC．（初二）A DFPB E C经典难题（五）A1、设 P 是边长为 1 的正△ ABC内任一点， L＝ PA＋ PB＋ PC，PB C求证：≤ L＜2．2、已知： P 是边长为 1 的正方形ABCD内的一点，求PA＋ PB＋ PC的最小值．A DPCB3、 P 为正方形ABCD内的一点，而且PA＝ a， PB＝ 2a， PC＝ 3a，求正方形的边长．A DPCB4、如图，△ ABC中，∠ ABC＝∠ ACB＝ 800， D、 E 分别是 AB、 AC上的点，∠ DCA＝ 300，∠ EBAAE＝ 200，求∠ BED的度数．经典题（一）1.以下列图做 GH⊥ AB,连结 EO。

初中数学几何证明经典题(含答案)

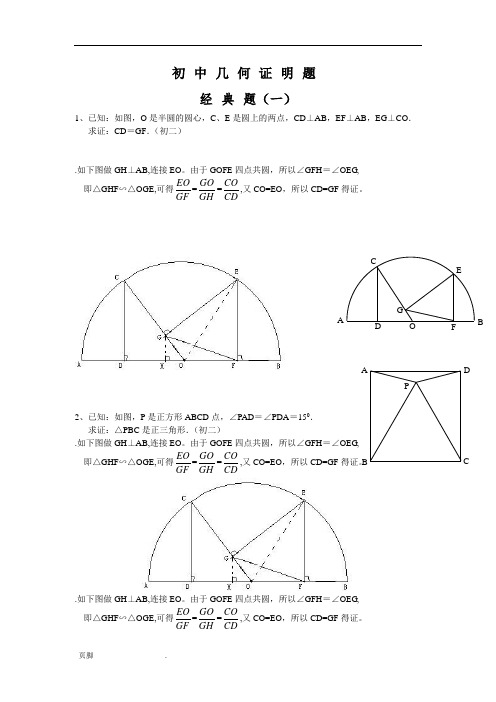
初中几何证明题经典题（一）1、已知：如图，O是半圆的圆心，C、E是圆上的两点，CD⊥AB，EF⊥AB，EG⊥CO．求证：CD＝GF．（初二）.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

2、已知：如图，P是正方形ABCD点，∠PAD＝∠PDA＝150．求证：△PBC是正三角形．（初二）.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

.如下图做GH⊥AB,连接EO。

由于GOFE四点共圆，所以∠GFH＝∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO，所以CD=GF得证。

APCDBAFGCEBOD3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O （1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 AN FE CDMB· A HEOF2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEFB 、D ．求证：AB ＝DC ，BC ＝AD．（初三）经典1、已知：△ABC 是正三角形，P 是三角形一点，PA ＝3，PB ＝4，PC 求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．C BD A F PD E CB A APCBACPDA CBPD4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典题（一）1.如下图做GH⊥AB,连接EO。

初中数学-几何证明经典试题(含答案)

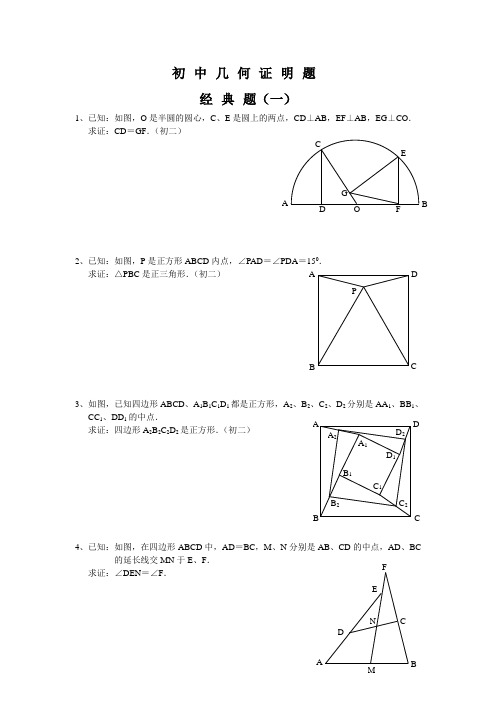
初中几何证明题经典题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF经典题（二）1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典题（三）1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEFB 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）E经典题（四）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB·CD ＋AD·BC ＝AC·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）D经典难题（五）求证：≤L＜2．2、已知：P是边长为1的正方形ABCD内的一点，求PA＋PB＋PC的最小值．3、P为正方形ABCD内的一点，并且PA＝a，PB＝2a，PC＝3a，求正方形的边长．4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．经典题（一）1.如下图做GH⊥AB,连接EO。

(完整版)初中数学经典几何题及答案

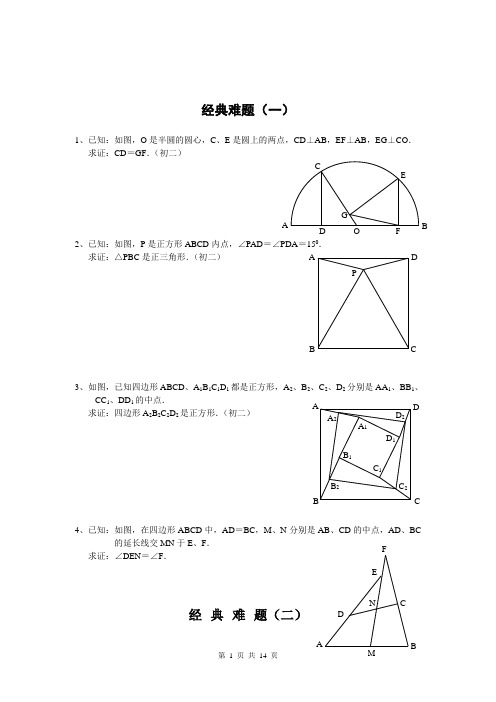
经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．经典难题（二）A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．经典难 1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEFB 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）经典难1、已知：△ABC 是正三角形，P求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）经典难题（五）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．经典难题（一）1.如下图做GH ⊥AB,连接EO 。

初中几何证明的经典难题

初中几何证明的经典难题一．割补法：1.（全等）如图，点E 是BC 中点，CDE BAE ∠=∠，求证：CD AB =（相似）如图，点E 是BC 上一点，EC k BE ⋅=，CDE BAE ∠=∠，猜想AB 、CD 的数量关系.2. （全等）如图，在ABC ∆中，︒=∠90BAC ，AC AB =，BA CD //，点P 是BC 上一点，连结AP ，过点P 做AP PE ⊥交CD 于E .探究PE 与PA 的数量关系.（相似）如图，在ABC ∆中，︒=∠90BAC ，AC k AB ⋅=，BA CD //，点P 是BC 上一点，连结AP ，过点P 做AP PE ⊥交CD 于E .探究PE 与PA 的数量关系.3. （全等）如图，在ABC ∆中，AC AB =，点D 在AB 上，点E（相似）如图，在ABC ∆中，AC k AB ⋅=，点D 在AB 上，点E 在AC 的延长线上，且CE BD =，DE 交BC 于点P .探究PE 与PD 的数量关系.4. （全等）如图，在ABC ∆中，A ECB DBC ∠=∠=∠21，BD 、CE 交于点P . 探究BE 与CD 的数量关系.（相似）如图，在ABC ∆中，A ECB DBC ∠=∠+∠，BD 、CE 交于点P ，PC k PB ⋅=. 探究BE 与CD 的数量关系.5．（全等）如图，在EBC ∆中，BD 平分EBC ∠，延长DE 至点A ，使得ED EA =，且C ABE ∠=∠. 探究AB 与CD 的数量关系.（相似）如图，BD 平分EBC ∠，D '是BD 上一点，且D B k BD '⋅=，连结C D '、DE ，并延长DE 至点A ，使得ED EA =，且C ABE ∠=∠.探究AB 与D C '的数量关系.6.（全等）如图，在ABC ∆中，︒=∠90C ，BC AC =，P 为AB 的中点，PF PE ⊥分别交AC 、BC 于E 、F .探究PE 、PF 的数量关系.（相似）如图，在ABC ∆中，︒=∠90C ，BC AC =，P 为AB 上一点，且PB k AP ⋅=，PF PE ⊥分别交AC 、BC 于E 、F .探究PE 、PF 的数量关系.（相似）如图，在ABC ∆中，BC AC =，P 为AB 上一点，且PB k AP ⋅=，︒=∠+∠180C EPF ，EPF ∠的两边分别交AC 、BC 于E 、F .探究PE 、PF 的数量关系.7. （全等）如图，CD CB =，︒=∠+∠180CDE ABC ，DE AB =. 探究：AF 与EF 之间的数量关系9（相似）如图，CD CB =，︒=∠+∠180CDE ABC ，DE k AB ⋅=. 探究：AF 与EF 之间的数量关系10如图，直线1l 、2l 相交于点A ，点B 、点C 分别在直线1l 、2l 上，AC k AB ⋅=，连结BC ，点D 是线段AC 上任意一点（不与A 、C 重合），作α=∠=∠BAC BDE ，与ECF ∠的一边交于点E ，且ABC ECF ∠=∠.⑴如图1，若1=k ，且︒=∠90α时，猜想线段BD 与DE 的数量关系，并加以证明； ⑵如图2，若1≠k ，时，猜想线段BD 与DE 的数量关系，并加以证明.二．倍长中线法：11. （全等）如图，点E 是BC 中点，CDE BAE ∠=∠，求证：CD AB =12（相似）如图，AD 是ABC ∆的中线，AC k AB ⋅=，点E 是AC 延长线上一点，且BAD AEF ∠=∠，EF 交BA 延长线于点F .探究AE 、AF 的数量关系.13 （全等）如图，在ABC ∆中，AB CD =，BDA BAD ∠=∠，AE 是BD 边的中线.求证：AE AC 2=14（相似）如图，在ABC ∆中，AD k AB ⋅=，BDA BAD ∠=∠，AE 是BD 边的中线，且C EAD ∠=∠. 探究AE 、AC 的数量关系.15. （全等）如图，在ABC ∆中，AD 平分BAC ∠，G 为BC 的中点，AD EG //交CA 延长线于E . 求证：EC BF =17（全等）如图，等腰直角ABC ∆与等腰直角BDE ∆，P 为CE 中点，连接PA 、PD . 探究PA 、PD 的关系.18（相似）如图，ABC ∆与BDE ∆中，︒=∠=∠90BDE CAB ，AB k AC ⋅=，DB k DE ⋅=，P 为CE 中点，连接PA 、PD .探究PA 、PD 的数量关系.19（全等）如图，两个正方形ABDE 和ACGF ，点P 为BC 的中点，连接PA 交EF 于点Q . 探究AP 与EF 的关系.20（相似）⑴如图1，两个矩形ABDE 和ACGF 相似，AB k AE ⋅=，点P 为BC 的中点，连接PA 交EF 于点Q .探究AP 与EF 的关系.⑵如图2，若将“两个矩形ABDE和ACGF相似”改为“两个平行四边形ABDE和ACGF相似”，且α∠EAB.探究AP与EF的关系.=21．已知：如图，正方形ABCD和正方形EBGF，点M是线段DF的中点.⑴试说明线段ME与MC的关系.α），其他条件不变，上述结论还⑵如图，若将上题中正方形EBGF绕点B顺时针旋转α度数（︒<90正确吗？若正确，请你证明；若不正确，请说明理由.22.如图1，正方形ABCD中，对角线AC、BD交于点O.⑴操作：将三角板中的︒90角的顶点与点O重合，使这个角落在ABC∆的内部，两边分别与正方形ABCD的边AB、BC交于F、E.当F、E的位置发生变化时，请你通过测量并回答，每组AF、FE、EC三条线段中，哪一条线段是中始终最长.⑵以AF、FE、EC这三条线段能否组成以FE为斜边的直角三角形？若能，请你证明；若不能，请你说明理由.结论是否仍然成立？请你证明.23⑴如图1，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上（BCCG ）取线段AE的中点P.探究：线段PD、PF的关系，并加以证明.⑵如图2，将正方形CGEF绕点C旋转任意角度后，其他条件不变. 探究：线段PD、PF的关系，并加以证明.。

初中数学经典几何题(难)及答案分析

经典难题（一）1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE 于P 、Q ．求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ．求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·BD ．（初三）4、平行四边形ABCD 中，设E 、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．AP CB ACBPDEDCB A A CBPD1.如下图做GH⊥AB,连接EO。

初中几何经典难题合集(附答案)

初中几何经典难题合集（附答案）1．已知：如图，O是半圆的圆心，C、E是圆上的两点，CD⊥AB，EF⊥AB，EG⊥CO。

求证：CD＝GF。

（初二）证明：如图，作GH⊥AB，连接EO。

因为GOFE四点共圆，所以∠GFH＝∠OEG。

又因为∠GHF＝∠OGE ＝90°，所以△GHF∽△OGE。

可得GF/GE＝GH/OE。

因为CO＝EO，所以GF/GE＝GH/CO，即GF＝GH·GE/CO。

又因为∠CDO＝∠EGO＝90°，∠COD＝∠EOG，所以△CDO∽△EGO。

可得CD/GE＝CO/OE，即CD＝CO·GE/OE。

因为CO＝EO，所以CD＝GF，得证。

已知：如图，在△ABC中，AB = AC，∠BAC = 80°，P为△ABC内一点，∠PBC = 10°，∠PCB = 30°，求∠PAB的度数。

（初二）证明：作∠BAC的平分线AD，交BC于点D。

因为AB = AC，∠BAC = 80°，所以∠ABC = ∠ACB = (180°- ∠BAC) / 2 = (180° - 80°) / 2 = 50°。

因为∠PBC = 10°，∠PCB = 30°，所以∠ABP = ∠ABC - ∠PBC = 50°- 10° = 40°，∠ACP = ∠ACB - ∠PCB = 50° - 30° = 20°。

在△ABC中，根据三角形内角和定理，∠BAC + ∠ABC + ∠ACB = 180°，所以∠BAC = 180° - ∠ABC - ∠ACB = 180° - 50° - 50° = 80°。

因为AD是∠BAC的平分线，所以∠BAD = ∠CAD = ∠BAC / 2 = 80° / 2 = 40°。