《数学史》朱家生版+课后题目参考答案+第五章
数学史朱家生版课后题目参考答案第
1.数学的起源于世界xxxx产生的关系11数本（1）班郭奇2011041047“数学”这个词在我们的生活中可谓是无处不在，他作为人类思维的表达形式，反映了人们的积极进取的意志、缜密周详的推理及对完美境界的追求。
“数学”与我们身边的其他学科也有着密切联系。
例如在天文学方面、医学方面、经济学方面等等。
大到天文地理，小到生活琐事，数学的魅力可谓是发挥的淋漓尽致。
然而关于数学的起源，却有着一个古老而神奇的传说。
相传在非常非常遥远的古代，有一天在黄河的波涛中突然跳出一匹“龙马”来，马背上驮着一幅图，图上画着许多神秘的数学符号，后来，从波澜不惊的河水中又爬出一只“神龟”来，龟背上也驮着一卷书，书中则阐述了数的排列方法。
马背上的图叫“河图”，乌龟背上的书叫做“洛书”，当“河图洛书”出现后，数学也就诞生了。
当然，这个也只不过是个传说罢了。
数学作为最古老的一门学科，他的起源可以上溯到一万多年以前。
但是，公元1000年以前的资料留存下来的极少，迄今所知，只有在古代埃及和巴比伦发现了比较系统的数学文献。
远在一万五千年以前，人类就可以相当逼真的描绘出人和动物的形象，这是萌发图形意识的最早证据。
后来就开始逐渐对圆形和直线型的追求，从而成为数学图形的最早的原型。
在日常的生活实践中又逐渐产生了记数的意识和系统。
人类摸索过许多种记数的方法，例如用石块记数，结绳记数等，最后逐步发展到现在我们所用的数字。
图形意识和记数意识发展到一定阶段，又产生了度量的意识。
从人类社会的发展史来看，人们对数学本质特征的认识也在不断变化和深化着。
欧几里得说过“数学的根源在于普通的常识，最显著的例子是非负整数。
”他的算术来自于普通常识中的非负整数。
而且直到十九世纪中叶，对于数的科学探索还停留在普通的常识。
因此，十九世纪以前，人们普遍认为数学是一门自然学科，经验学科，因为那时的数学与现实之间的联系非常密切。
随着数学研究的不断深入，从十九世纪中叶以后，数学是一门演绎科学的观点逐渐占据主导地位。
大学高等数学第五章 定积分及其应用答案
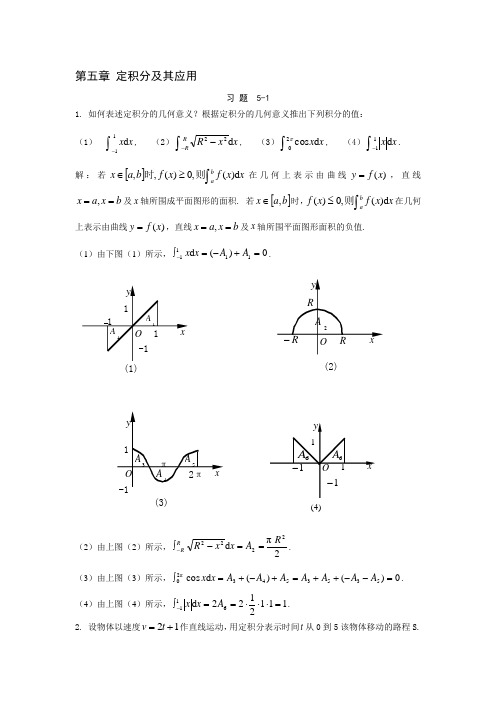
第五章 定积分及其应用习 题 5-11. 如何表述定积分的几何意义？根据定积分的几何意义推出下列积分的值： （1）⎰-x x d 11, （2）⎰--x x R R R d 22, （3）⎰x x d cos 02π, （4）⎰-x x d 11.解：若[]⎰≥∈x x f x f b a x ab d )(,0)(,,则时在几何上表示由曲线)(x f y =，直线b x a x ==,及x 轴所围成平面图形的面积. 若[]b a x ,∈时，⎰≤x x f x f ab d )(,0)(则在几何上表示由曲线)(x f y =，直线b x a x ==,及x 轴所围平面图形面积的负值. （1）由下图（1）所示，0)(d 1111=+-=⎰-A A x x .（2）由上图（2）所示，2πd 2222R A x x R R R==-⎰-.（3）由上图（3）所示，0)()(d cos 5353543π20=--++=+-+=⎰A A AA A A A x x . （4）由上图（4）所示，1112122d 611=⋅⋅⋅==⎰-A x x . 2. 设物体以速度12+=t v 作直线运动，用定积分表示时间t 从0到5该物体移动的路程S.( 2 )( 1 )( 3 )(4)解：=s ⎰+t t d )12(053. 用定积分的定义计算定积分⎰bax c d ,其中c 为一定常数.解：任取分点b x x x x a n =<<<<= 210,把],[b a 分成n 个小区间],[1i i x x -)2,1(n i =，小区间长度记为x ∆i =i x -1-i x )2,1(n i =,在每个小区间[]i i x x ,1-上任取一点i ξ作乘积i i x f ∆⋅)(ξ的和式：∑∑==--=-⋅=∆⋅n i ni i iiia b c x xc x f 111)()()(ξ,记}{max 1i n i x ∆=≤≤λ, 则)()(lim )(lim d 0a b c a b c x f x c ni i i b a-=-=∆⋅=∑⎰=→→λλξ.4. 利用定积分定义计算120d x x ⎰.解：上在]1,0[)(2x x f =连续函数，故可积，因此为方便计算，我们可以对[]0,1 n 等分，分点i i n i nix ξ;1,,2,1,-==取相应小区间的右端点，故 ∑∑∑===∆=∆=∆ni i i ni i i ni i i x x x x f 12121)(ξξ=∑∑===ni ni in n n i 1232111)(=311(1)(21)6n n n n ⋅++ =)12)(11(61nn ++ 当时0→λ（即时∞→n ），由定积分的定义得： 120d x x ⎰=31．5. 利用定积分的估值公式，估计定积分⎰-+-1134)524(x x x d 的值.解：先求524)(34+-=x x x f 在[]1,1-上的最值，由0616)(23=-='x x x f , 得0=x 或83=x . 比较 35093(1)11,(0)5,(),(1)781024f f f f -====的大小，知min max 5093,111024f f ==，由定积分的估值公式，得[])1(1d )524()]1(1[max 1134min --⋅≤+-≤--⋅⎰-f x x x f ,即14315093(425)d 22512x x x -≤-+≤⎰. 6. 利用定积分的性质说明⎰1d xe x与⎰1d 2x e x ，哪个积分值较大？解：在[]0,1区间内：22xx x x e e ≥⇒≥ 由性质定理知道：⎰1d xe x≥⎰1d 2x e x7. 证明：⎰---<<2121212d 22x e ex 。
数学史答案——精选推荐
数学史答案四、简答题1、阿基⽶德在数学上的主要贡献：（1）研究⼤数：《沙粒计算》填满宇宙的沙粒数相当于，他还曾⽤过相当于的⼤数。
（2）⼏何学⽅⾯：发现⼤量⽴体体积公式。
（3）数学⽅法论⽅⾯：他曾⽤“原⼦法”和“穷竭法”计算⾯积和体积；他⾸创⽤“平衡法”证明数学问题（如证明球体积公式）；他还⽤“积分”求和法求⾯积和体积；他通过引⼊特征三⾓形找到求曲线的⼀般⽅法；他把求极值问题归结为求切线问题；他还采⽤类似现在的“插值法”计算螺线长度。
他的这些思想⽅法使他成为微积分的先躯。
后来微积分开创者的许多思想都源于阿基⽶德。
阿基⽶德数学研究的主要特点：①注重联系实际，将数学与⼒学、物理学等实际问题结合；②注重⽅法论，其⽅法中体现了数学思想的深度；③注重论述的精确性、严谨性，成为他那个时代的典范。
2、刘徽的主要数学贡献：（1）算术⽅⾯：①⾸次使⽤⼗进⼩数;②完善齐同术;③其它：刘徽明确提出分数的基本性质：“法实俱长，意亦等也”；他对求最⼤公约数的⽅法进⾏了理论说明；对化带分数为假分数的⽅法进⼀步明确；他还研究了各种⽐例算法。
（2）代数⽅⾯：①⾸次给出正负数定义、记法及性质;②改进解线性⽅程组的“直除法”;③提出解⽅程组的新⽅法;④研究等差数列，并给出求和公式。
（3）⼏何⽅⾯：①提出“割圆术”;②开始⼏何定理的证明;③研究了球体体积;(4)极限思想；（5）创⽴重差术。
3、⽂艺复兴时期欧洲数学的主要进展1.代数⽅程论的发展；2. 符号代数的产⽣；3.三⾓学的确⽴；4.⼏何学的新突破；5. 计算技术的重⼤进步（1）⼗进⼩数的发明（2）对数的发明（3）计算⼯具的产⽣4、举例说明《九章算术》中解线性⽅程组的“直除法”《九章算术》中的“⽅程”，实际是线性⽅程组．例如卷⼋第⼀题：“今有上⽲三秉，中⽲⼆秉，下⽲⼀秉，实三⼗九⽃；上⽲⼆秉，中⽲三秉，下⽲⼀秉，实三⼗四⽃；上⽲⼀秉，中⽲⼆秉，下⽲三秉，实⼆⼗六⽃．问上中下⽲实⼀秉各⼏何？”(⽲即庄稼，秉即捆，实即粮⾷．)依术列筹式如图4．11，它相当于三元⼀次⽅程组其中x，y，z分别为上中下三等⽲每捆打粮⾷的⽃数．按《九章算术》解法，⽤(1)式x的系数3去乘(2)的各项，得6x+9y＋3z＝102．(4)⽤(4)减(1)⼆次，得5y＋z=24．(5)再⽤(3)×3，得3x＋6y+9z＝78．(6)(6)减(1)，得4y＋8z＝39．(7)中把这种⽅法叫“直除法”，即连续相减法．它的原理与现在加减消元法⼀致，只是⽐较烦琐．6．简述卡⽡列⾥不可分量⽅法的基本思想。
数学史知识点及答案讲解
千里之行，始于足下。
数学史知识点及答案讲解数学史知识点及答案讲解数学是一门古老而且重要的学科，它的发展与人类文明的进步密切相关。
下面将介绍数学史的一些知识点及答案的讲解。
1. 古代数学古代数学的发展可以追溯到古埃及、巴比伦和古希腊等文明，其中最著名的数学家是古希腊的欧几里德和阿基米德。
欧几里德的《几何原本》是一部详尽而完整的几何学著作，其中引入了许多重要的几何定理和证明方法。
阿基米德则在几何学和力学方面做出了重要贡献，特别是他的浮力定律和杠杆原理。
2. 中世纪数学中世纪数学的发展受到了基督教教义的限制，因此在这个时期数学的进展相对较慢。
然而，一些重要的数学家如斯内尔和费马还是在这个时期做出了一些突破性的工作。
斯内尔提出了无理数的概念，并证明了它的存在。
费马则发展了一种新的证明方法，称为费马大定理，在证明中使用了分析几何的技巧。
3. 近代数学近代数学的发展可以追溯到17世纪的启蒙时代，这个时期出现了许多重要的数学家和数学理论。
牛顿和莱布尼茨同时独立地发现了微积分学，这是一种用于研究曲线和函数的重要工具。
欧拉则在数学分析和图论方面做出了重要贡献，他是数学史上最多产的数学家之一，发表了大量的著作和论文。
4. 现代数学现代数学的发展可以追溯到19世纪末和20世纪初，这个时期出现了一系列重要的数学理论和概念。
高斯和黎曼对复数和复变函数的研究开创了复分析第1页/共3页锲而不舍，金石可镂。
学的发展。
庞加莱在拓扑学方面做出了重要贡献，提出了庞加莱猜想，并且开创了现代数学的基础。
其他重要的数学家还包括维尔斯特拉斯、魏尔斯特拉斯、哥尼尔和伯努利等。
5. 现代数学的应用现代数学的应用非常广泛，几乎涉及到所有的科学领域。
数学在物理学、工程学、计算机科学、经济学等领域有着重要的应用。
例如，在物理学中，数学被用来建立和解决物理定律和方程，如牛顿的运动定律和麦克斯韦方程。
在计算机科学中，数学被用来研究和设计算法和数据结构。
在经济学中，数学被用来研究和模拟经济系统，如供求关系和市场机制。
高等数学课后习题及参考答案第五章
高等数学课后习题及参考答案（第五章）习题5-11. 利用定积分定义计算由抛物线y =x 2+1, 两直线x =a 、x =b (b >a )及横轴所围成的图形的面积.解 第一步: 在区间[a , b ]内插入n -1个分点i nab a x i -+=(i =1, 2, ⋅ ⋅ ⋅, n -1), 把区间[a , b ]分成n 个长度相等的小区间, 各个小区间的长度为: nab x i -=∆(i =1, 2, ⋅ ⋅ ⋅, n ). 第二步: 在第i 个小区间[x i -1, x i ] (i =1, 2, ⋅ ⋅ ⋅, n )上取右端点i nab a x i i -+==ξ, 作和 nab i n a b a x f S ni i i ni n -⋅+-+=∆=∑∑==]1)[()(211ξ ∑=+-+-+-=n i i na b i n a b a a n a b 12222]1)()(2[ ]6)12)(1()(2)1()(2[)(222n n n n n a b n n n a b a na n a b +++⋅-++⋅-+-= ]16)12)(1()()1)(()[(222+++-++-+-=n n n a b n n a b a a a b . 第三步: 令λ=max{∆x 1, ∆x 2, ⋅ ⋅ ⋅ , ∆x n }nab -=, 取极限得所求面积 ∑⎰=→∆==ni i i ba x f dx x f S 10)(lim )(ξλ]16)12)(1()()1)(()[(lim 222+++-++-+-=∞→n n n a b n n a b a a a b n a b a b a b a b a a a b -+-=+-+-+-=)(31]1)(31)()[(3322.2. 利用定积分定义计算下列积分: (1)xdx ba ⎰(a <b ); (2)dx e x ⎰10.解 (1)取分点为i n a b a x i -+=(i =1, 2, ⋅ ⋅ ⋅, n -1), 则nab x i -=∆(i =1, 2, ⋅ ⋅ ⋅, n ). 在第i 个小区间上取右端点i nab a x i i -+==ξ (i =1, 2, ⋅ ⋅ ⋅, n ). 于是 ∑∑⎰=∞→=∞→-⋅-+=∆=ni n ni i i n ba nab i n a b a x xdx 11)(lim lim ξ )(21]2)1()()([lim )(22222a b n n n a b a b a a b n -=+-+--=∞→. (2)取分点为ni x i =(i =1, 2, ⋅ ⋅ ⋅, n -1), 则n x i 1=∆(i =1, 2, ⋅ ⋅ ⋅, n ). 在第i 个小区间上取右端点nix i i ==ξ (i =1, 2, ⋅ ⋅ ⋅, n ). 于是) (1lim 1lim 21110n n n i i n xe e e nn e dx e +⋅⋅⋅++==∞→=∞→∑⎰1)1(]1[lim1])(1[1lim 11111-=--=--⋅=∞→∞→e e n e e e e e nn n n n n n .3. 利用定积分的几何意义说明下列等式:(1)1210=⎰xdx ; (2)41102π=-⎰dx x ;(3)⎰-=ππ0sin xdx ;(4)⎰⎰=-2022cos 2cos πππxdx xdx .解 (1)⎰102xdx 表示由直线y =2x 、x 轴及直线x =1所围成的面积, 显然面积为1.(2)⎰-1021dx x 表示由曲线21x y -=、x 轴及y 轴所围成的四分之一圆的面积, 即圆x 2+y 2=1的面积的41:41411212ππ=⋅⋅=-⎰dx x .(3)由于y =sin x 为奇函数, 在关于原点的对称区间[-π, π]上与x 轴所夹的面积的代数和为零, 即⎰-=ππ0sin xdx .(4)⎰-22cos ππxdx 表示由曲线y =cos x 与x 轴上]2,2[ππ-一段所围成的图形的面积. 因为cos x为偶函数, 所以此图形关于y 轴对称. 因此图形面积的一半为⎰20cos πxdx , 即⎰⎰=-2022cos 2cos πππxdx xdx .4. 水利工程中要计算拦水闸门所受的水压力, 已知闸门上水的压强p (单位面积上的压力大小)是水深h 的函数, 且有p =9⋅8h (kN/m 2). 若闸门高H =3m , 宽L =2m , 求水面与闸门顶相齐时闸门所受的水压力P .解 建立坐标系如图. 用分点i nHx i =(i =1, 2, ⋅ ⋅ ⋅, n -1)将区间[0, H ]分为n 分个小区间, 各小区间的长为nHx i =∆(i =1, 2, ⋅ ⋅ ⋅, n ). 在第i 个小区间[x i -1, x i ]上, 闸门相应部分所受的水压力近似为 ∆P i =9.8x i l ⋅∆x i . 闸门所受的水压力为22118.42)1(lim8.9lim 8.98.9lim H L n n n H L n Hi n H L x L x P n n i n n i i i n ⋅=+⋅=⋅=∆⋅⋅=∞→=∞→=∞→∑∑. 将L =2, H =3代入上式得P =88.2(千牛).5. 证明定积分性质: (1)⎰⎰=ba b a dx x f k dx x kf )()(; (2)a b dx dx ba b a -==⋅⎰⎰1.证明 (1)⎰∑∑⎰=∆=∆==→=→ba ni i i ni i i ba dx x f k x f k x kf dx x kf )()(lim )(lim )(1010ξξλλ.(2)a b a b x x dx ni i ni i ba -=-=∆=∆⋅=⋅→=→=→∑∑⎰)(lim lim 1lim 101010λλλ.6. 估计下列各积分的值: (1)⎰+412)1(dx x ; (2)⎰+ππ4542)sin 1(dx x ;(3)⎰331arctan xdx x ;(4)⎰-022dx e xx.解 (1)因为当1≤x ≤4时, 2≤x 2+1≤17, 所以 )14(17)1()14(2412-⋅≤+≤-⋅⎰dx x , 即 51)1(6412≤+≤⎰dx x . (2)因为当ππ454≤≤x 时, 1≤1+sin 2x ≤2, 所以 )445(2)sin 1()445(14542ππππππ-⋅≤+≤-⋅⎰dx x ,即 ππππ2)sin 1(4542≤+≤⎰dx x .(3)先求函数f (x )=x arctan x 在区间]3 ,31[上的最大值M 与最小值m .21a r c t a n )(xx x x f ++='. 因为当331≤≤x 时, f '(x )>0, 所以函数f (x )=x arctan x 在区间]3 ,31[上单调增加. 于是3631arctan31)31(π===f m , 33arctan 3)3(π===f M .因此)313(3arctan )313(36331-≤≤-⎰ππxdx x ,即32arctan 9331ππ≤≤⎰xdx x . (4)先求函数xx e x f -=2)(在区间[0, 2]上的最大值M 与最小值m .)12()(2-='-x e x f xx, 驻点为21=x .比较f (0)=1, f (2)=e 2, 41)21(-=e f ,得41-=e m , M =e 2. 于是)02()02(22012-⋅≤≤-⎰--e dx e e xx,即 41022222---≤≤-⎰e dx dx e e xx .7. 设f (x )及g (x )在[a , b ]上连续, 证明: (1)若在[a , b ]上f (x )≥0, 且0)(=⎰ba dx x f , 则在[a ,b ]上f (x )≡0;(2)若在[a , b ]上, f (x )≥0, 且f (x )≢0, 则0)(>⎰ba dx x f ; (3)若在[a ,b ]上, f (x )≤g (x ), 且⎰⎰=ba ba dx x g dx x f )()(, 则在[ab ]上f (x )≡g (x ).证明 (1)假如f (x )≢0, 则必有f (x )>0. 根据f (x )在[a , b ]上的连续性, 在[a , b ]上存在一点x 0, 使f (x 0)>0, 且f (x 0)为f (x )在[a , b ]上的最大值.再由连续性, 存在[c , d ]⊂[a , b ], 且x 0∈[c , d ], 使当x ∈[c , d ]时, 2)()(0x f x f >. 于是0)(2)()()()()()(0>-≥≥++=⎰⎰⎰⎰⎰c d x f dx x f dx x f dx x f dx x f dx x f dc bd d c c a b a . 这与条件0)(=⎰ba dx x f 相矛盾. 因此在[a ,b ]上f (x )≡0.(2)证法一 因为f (x )在[a , b ]上连续, 所以在[a , b ]上存在一点x 0, 使f (x 0)>0, 且f (x 0)为f (x )在[a , b ]上的最大值.再由连续性, 存在[c , d ]⊂[a , b ], 且x 0∈[c , d ], 使当x ∈[c , d ]时, 2)()(0x f x f >. 于是⎰⎰>-≥≥badcc d x f dx x f dx x f 0)(2)()()(0. 证法二 因为f (x )≥0, 所以0)(≥⎰ba dx x f . 假如0)(>⎰ba dx x f 不成立. 则只有0)(=⎰ba dx x f , 根据结论(1), f (x )≡0, 矛盾. 因此0)(>⎰ba dx x f . (3)令F (x )=g (x )-f (x ), 则在[a ,b ]上F (x )≥0且0)()()]()([)(=-=-=⎰⎰⎰⎰ba b a b a b a dx x f dx x g dx x f x g dx x F ,由结论(1), 在[a , b ]上F (x )≡0, 即f (x )≡g (x ).4. 根据定积分的性质及第7题的结论, 说明下列积分哪一个的值较大: (1)⎰102dx x 还是⎰103dx x ？(2)⎰212dx x 还是⎰213dx x ？ (3)⎰21ln xdx 还是⎰212)(ln dx x ？ (4)⎰10xdx 还是⎰+10)1ln(dx x ？ (5)⎰10dx e x 还是⎰+10)1(dx x ？解 (1)因为当0≤x ≤1时, x 2≥x 3, 所以⎰⎰≥103102dx x dx x . 又当0<x <1时, x 2>x 3, 所以⎰⎰>103102dx x dx x . (2)因为当1≤x ≤2时, x 2≤x 3, 所以⎰⎰≤213212dx x dx x . 又因为当1<x ≤2时, x 2<x 3, 所以⎰⎰<213212dx x dx x .(3)因为当1≤x ≤2时, 0≤ln x <1, ln x ≥(ln x )2, 所以⎰⎰≥21221)(ln ln dx x xdx . 又因为当1<x ≤2时, 0<ln x <1, ln x >(ln x )2, 所以⎰⎰>21221)(ln ln dx x xdx . (4)因为当0≤x ≤1时, x ≥ln(1+x ), 所以⎰⎰+≥1010)1ln(dx x xdx . 又因为当0<x ≤1时, x >ln(1+x ), 所以⎰⎰+>1010)1ln(dx x xdx .(5)设f (x )=e x -1-x , 则当0≤x ≤1时f '(x ) =e x -1>0, f (x )=e x -1-x 是单调增加的. 因此当0≤x ≤1时, f (x )≥f (0)=0, 即e x ≥1+x , 所以⎰⎰+≥1010)1(dx x dx e x .又因为当0<x ≤1时, e x >1+x , 所以⎰⎰+>1010)1(dx x dx e x .习题5-21. 试求函数⎰=xtdt y 0sin 当x =0及4π=x 时的导数.解 x tdt dx dy x sin sin 0=='⎰, 当x =0时, y '=sin0=0;当4π=x 时, 224sin =='πy .2. 求由参数表示式⎰=tudu x 0sin , ⎰=tudu y 0cos 所给定的函数y 对x的导数.解 x '(t )=sin t , y '(t )=cos t ,t t x t y dx dy cos )()(=''=. 3. 求由⎰⎰=+xy ttdt dt e 00cos 所决定的隐函数y 对x 的导数dxdy. 解 方程两对x 求导得 0cos =+'x y e y , 于是ye x dx dy cos -=. 4. 当x 为何值时, 函数⎰-=xt dt te x I 02)(有极值？解 2)(x xe x I -=', 令I '(x )=0, 得x =0.因为当x <0时, I '(x )<0; 当x >0时, I '(x )>0, 所以x =0是函数I (x )的极小值点. 5. 计算下列各导数:(1)⎰+2021x dt t dx d ; (2)⎰+32411x x dt tdx d ; (3)⎰x x dtt dxd cos sin 2)cos(π.解 (1)dxdu dt t du d u x dt t dx d u x ⋅+=+⎰⎰02202112令 421221x x x u +=⋅+=.(2)⎰⎰⎰+++=+323204044111111x x x x dt t dx d dt t dx d dt t dx d ⎰⎰+++-=3204041111x x dt t dx d dt t dx d )()(11)()(11343242'⋅++'⋅+-=x x x x 12281312xx x x +++-=. (3)⎰⎰⎰+-=x x x x dt t dx d dt t dx d dt t dx d cos 02sin 02cos sin 2)cos()cos()cos(πππ))(cos cos cos())(sin sin cos(22'+'-=x x x x ππ )cos cos(sin )sin cos(cos 22x x x x ππ⋅-⋅-= )sin cos(sin )sin cos(cos 22x x x x πππ-⋅-⋅-= )sin cos(sin )sin cos(cos 22x x x x ππ⋅+⋅-= )sin cos()cos (sin 2x x x π-=.6. 计算下列各定积分: (1)⎰+-adx x x 02)13(;解a a a x x x dx x x a a+-=+-=+-⎰230230221|)21()13(.(2)⎰+2142)1(dx xx ;解852)11(31)22(31|)3131()1(333321332142=---=-=+---⎰x x dx x x . (3)⎰+94)1(dx x x ;解942394194|)2132()()1(x x dx x x dx x x +=+=+⎰⎰6145)421432()921932(223223=+-+=.(4)⎰+33121x dx ; 解 66331arctan 3arctan arctan 13313312πππ=-=-==+⎰x x dx . (5)⎰--212121x dx ; 解3)6(6)21arcsin(21arcsin arcsin 1212121212πππ=--=--==---⎰x x dx .(6)⎰+ax a dx 3022;解aa a ax a x a dx a a30arctan 13arctan 1arctan 1303022π=-==+⎰.(7)⎰-1024x dx ;解60arcsin 21arcsin 2arcsin 41012π=-==-⎰x x dx .(8)dx x x x ⎰-+++012241133; 解 01301221224|)arctan ()113(1133---+=++=+++⎰⎰x x dx x x dx x x x 41)1arctan()1(3π+=----=.(9)⎰---+211e xdx ; 解1ln 1ln ||1|ln 12121-=-=+=+------⎰e x xdx e e .(10)⎰402tan πθθd ;解4144tan )(tan )1(sec tan 4040242πππθθθθθθπππ-=-=-=-=⎰⎰d d .(11)dx x ⎰π20|sin |; 解⎰⎰⎰-=ππππ2020sin sin |sin |xdx xdx dx xπππ20cos cos x x +-==-cos π +cos0+cos2π-cos π=4. (12)⎰2)(dx x f , 其中⎪⎩⎪⎨⎧>≤+=1 2111)(2x x x x x f . 解38|)61(|)21(21)1()(213102212102=++=++=⎰⎰⎰x x x dx x dx x dx x f . 7. 设k 为正整数. 试证下列各题: (1)⎰-=ππ0cos kxdx ;(2)⎰-=ππ0sin kxdx ;(3)⎰-=πππkxdx 2cos ;(4)⎰-=πππkxdx 2sin .证明 (1)⎰--=-=--==ππππππ000)(sin 1sin 1|sin 1cos k kk k kx k kxdx . (2))(cos 1cos 1cos 1sin ππππππ-+-=-=--⎰k kk k x k k kxdx0cos 1cos 1=+-=ππk kk k .(3)πππππππππ=+=+=+=---⎰⎰22|)2sin 21(21)2cos 1(21cos 2kx k x dx kx kxdx . (4)πππππππππ=+=-=-=---⎰⎰22|)2sin 21(21)2cos 1(21sin 2kx k x dx kx kxdx . 8. 设k 及l 为正整数, 且k ≠l . 试证下列各题: (1)⎰-=ππ0sin cos lxdx kx ;(2)⎰-=ππ0cos cos lxdx kx ;(3)⎰-=ππ0sin sin lxdx kx .证明 (1)⎰⎰----+=ππππdx x l k x l k lxdx kx ])sin()[sin(21sin cos0])cos()(21[])cos()(21[=----++-=--ππππx l k l k x l k l k .(2)⎰⎰---++=ππππdx x l k x l k lxdx kx ])cos()[cos(21cos cos0])sin()(21[])sin()(21[=--+++=--ππππx l k l k x l k l k .(3)⎰⎰----+-=ππππdx x l k x l k lxdx kx ])cos()[cos(21sin sin . 0])sin()(21[])sin()(21[=--+++-=--ππππx l k l k x l k l k .9. 求下列极限: (1)xdt t xx ⎰→020cos lim ; (2)⎰⎰→xt xt x dttedt e 0220022)(lim.解 (1)11cos lim cos lim20020==→→⎰x xdt t x xx . (2)22222200022)(2lim)(limx xt x t x xt xt x xedt e dt e dttedt e '⋅=⎰⎰⎰⎰→→222220202lim2limx xt x x x xt x xedte xeedt e ⎰⎰→→=⋅=2212lim 22lim 2020222=+=+=→→x e x e e x x x x x . 10. 设⎩⎨⎧∈∈=]2 ,1[ ]1 ,0[ )(2x x x x x f . 求⎰=x dt t f x 0)()(ϕ在[0, 2]上的表达式,并讨论ϕ(x )在(0, 2)内的连续性.解 当0≤x ≤1时, 302031)()(x dt t dt t f x xx===⎰⎰ϕ;当1<x ≤2时, 6121212131)()(2211020-=-+=+==⎰⎰⎰x x tdt dt t dt t f x xxϕ.因此 ⎪⎩⎪⎨⎧≤<-≤≤=21 612110 31)(23x x x x x ϕ.因为31)1(=ϕ, 3131lim )(lim 30101==-→-→x x x x ϕ,316121)6121(l i m )(l i m 20101=-=-=+→+→x x x x ϕ,所以ϕ(x )在x =1处连续, 从而在(0, 2)内连续.11. 设⎪⎩⎪⎨⎧><≤≤=ππx x x x x f 或0 00 sin 21)(. 求⎰=x dt t f x 0)()(ϕ在(-∞, +∞)内的表达式.解 当x <0时,00)()(0===⎰⎰xxdt dt t f x ϕ;当0≤x ≤π时,21cos 21|cos 21sin 21)()(000+-=-===⎰⎰x t tdt dt t f x xxxϕ;当x >π时,πππϕ000|cos 210sin 21)()(t dt tdt dt t f x x x-=+==⎰⎰⎰10cos 21cos 21=+-=π.因此 ⎪⎩⎪⎨⎧≥≤≤-<=ππϕx x x x x 10 )cos 1(210 0)(.12. 设f (x )在[a , b ]上连续, 在(a , b )内可导且f '(x )≤0,⎰-=x a dt t f ax x F )(1)(. 证明在(a , b )内有F '(x )≤0.证明 根据积分中值定理, 存在ξ∈[a , x ], 使))(()(a x f dt t f xa -=⎰ξ.于是有)(1)()(1)(2x f ax dt t f a x x F x a -+--='⎰ ))(()(1)(12a x f a x x f a x ----=ξ )]()([1ξf x f ax --=.由 f '(x )≤0可知f (x )在[a , b ]上是单调减少的, 而a ≤ξ≤x , 所以f (x )-f (ξ)≤0. 又在(a , b )内, x -a >0, 所以在(a , b )内)]()([1)(≤--='ξf x f a x x F .习题5-31. 计算下列定积分:(1)⎰+πππ2)3sin(dx x ;解 0212132cos 34cos)3cos()3sin(22=-=+-=+-=+⎰ππππππππx dx x . (2)⎰-+123)511(x dx;解51251110116101)511(2151)511(22122123=⋅+⋅-=+-⋅=+-----⎰x x dx. (3)⎰203cos sin πϕϕϕd ;解⎰⎰-=20323sin cos cos sin ππϕϕϕϕϕd s d410cos 412cos 41cos 4144204=+-=-=πϕπ.(4)⎰-πθθ03)sin 1(d ; 解⎰⎰⎰⎰-+=+=-πππππθθθθθθθθ02002003cos )cos 1(cos sin )sin 1(d d d d34)cos 31(cos 03-=-+=πθθππ.(5)⎰262cos ππudu ;解22262622sin 4121)2cos 1(21cos ππππππππu u du u udu +=+=⎰⎰836)3sin (sin 41)62(21-=-+-=πππππ.(6)dx x ⎰-2022;解dt t tdt t t x dx x ⎰⎰⎰+=⋅=-02022)2cos 1(cos 2cos 2sin 22ππ令 2)2sin 21(2ππ=+=t t .(7)dy y ⎰--22228;解⎰⎰⎰---⋅=-=-44222222cos 2cos 22sin 24228ππxdx x xy dy y dy y 令)2(2)2sin 21(22)2cos 1(224444+=+=+=--⎰πππππy x dx x .(8)⎰-121221dx xx ;解41)cot ()1sin 1(cos sin cos sin 122212122πππππππ-=--=-=⋅=-⎰⎰⎰t t dt t tdt t t t x dx x x 令.(9)⎰-adx x a x 0222; 解⎰⎰⎰=⋅⋅=-2024202202222sin4cos cos sin sin ππtdt a tdt a t a t a t a x dx x a xa令164sin 328)4cos 1(84204204204ππππa t a t a dt t a =-=-=⎰. (10)⎰+31221xxdx ;解⎰⎰⋅⋅=+34223122secsec tan 1tan 1ππtdt t t tx xxdx 令3322sin 1sin cos 34342-=-==⎰ππππt dt tt. (11)⎰--1145xxdx ;解61)315(81)5(81454513133211=--=-=--⎰⎰-u u du u u x x xdx 令. (12)⎰+411xdx ;解)32ln 1(2|)1|ln (2)111(2211121212141+=+-=+-=⋅+=+⎰⎰⎰u u du u udu u u x x dx 令.(13)⎰--14311x dx ;解2ln 21|)1|ln (2)111(2)2(1111121010021143-=-+=-+=-⋅-=---⎰⎰⎰u u du u du u u ux x dx 令.(14)⎰-axa xdx 20223;解)13(3)3(3121320202222222022-=--=---=-⎰⎰a x a x a d x a xa xdx a a a.(15)dt te t ⎰-1022;解2110102221021)2(222-----=-=--=⎰⎰e etd e dt tet t t .(16)⎰+21ln 1e x x dx; 解)13(2ln 12ln ln 11ln 1222111-=+=+=+⎰⎰e e e xx d xxx dx .(17)⎰-++02222x x dx;解 2)1arctan(1arctan )1arctan()1(112202022022π=--=+=++=++---⎰⎰x dx x x x dx .(18)⎰-222cos cos ππxdx x ;解32)sin 32(sin sin )sin 21(2cos cos 2322222=-=-=---⎰⎰ππππππx x x d x xdx x . (19)⎰--23cos cos ππdx x x ;解⎰⎰---=-23cos 1cos cos cos ππππdx x x dx x x34cos 32cos 32sin cos )sin (cos 2023023202=-=+-=--⎰⎰ππππx xxdx x dx x x (20)⎰+π02cos 1dx x .解22cos 2sin 22cos 1000=-==+⎰⎰πππxxdx dx x .2. 利用函数的奇偶性计算下列积分: (1)⎰-ππxdx x sin 4;解 因为x 4sin x 在区间[-π, π]上是奇函数, 所以0sin 4=⎰-ππxdx x . (2)⎰-224cos 4ππθθd ;解⎰⎰⎰+==-202204224)22cos 1(8cos 42cos 4ππππθθθθθd x d d ⎰⎰++=++=20202)4cos 212cos 223(2)2cos 2cos 21(2ππθθd x x d x x23)4sin 412sin 23(20πθπ=++=x x . (3)⎰--2121221)(arcsin dx xx ;解⎰⎰⎰=-=--21221022212122)(arcsin )(arcsin 21)(arcsin 21)(arcsin x d x dx xx dx xx324)(arcsin 3232103π==x .(4)⎰-++55242312sin dx x x xx . 解 因为函数12sin 2423++x x x x 是奇函数, 所以012sin 552423=++⎰-dx x x x x .3. 证明:⎰⎰-=aa adx x dx x 022)(2)(ϕϕ, 其中ϕ(u )为连续函数.证明 因为被积函数ϕ(x 2)是x 的偶函数, 且积分区间[-a , a ]关于原点对称, 所以有⎰⎰-=aa adx x dx x022)(2)(ϕϕ.4. 设f (x )在[-b , b ]上连续, 证明⎰⎰---=bb bb dx x f dx x f )()(. 证明 令x =-t , 则dx =-dt , 当x =-b 时t =b , 当x =b 时t =-b , 于是⎰⎰⎰----=--=b b bb bbdt t f dt t f dx x f )()1)(()(,而 ⎰⎰---=-bb bb dx x f dt t f )()(, 所以⎰⎰---=bb bb dx x f dx x f )()(.5. 设f (x )在[a , b ]上连续., 证明⎰⎰-+=ba ba dx xb a f dx x f )()(. 证明 令x =a +b -t , 则dx =d t , 当x =a 时t =b , 当x =b 时t =a , 于是 ⎰⎰⎰-+=--+=b a ba ab dt t b a f dt t b a f dx x f )()1)(()(, 而 ⎰⎰-+=-+ba badx x b a f dt t b a f )()(,所以⎰⎰-+=ba ba dx xb a f dx x f )()(.6. 证明:⎰⎰>+=+11122)0(11x x x x dxx dx. 证明 令t x 1=, 则dt tdx 21-=, 当x =x 时x t 1=, 当x =1时t =1, 于是⎰⎰⎰+=-⋅+=+11111211)1(111xxdt t dt t tx dx , 而⎰⎰+=+x x dx x dt t 1121121111, 所以 ⎰⎰+=+1112211x xdx x dx.7. 证明:⎰⎰-=-1010)1()1(dx x x dx x xm n n m.证明 令1-x =t , 则⎰⎰⎰⎰-=-=--=-10100110)1()1()1()1(dx x x dt t t dt t t dx x x m n n m n m n m , 即⎰⎰-=-1010)1()1(dx x x dx x x m n n m . 8. 证明: ⎰⎰=ππ020sin 2sinxdx xdx n n.证明 ⎰⎰⎰+=ππππ020sin sin sin xdx xdx xdx nn n,而⎰⎰⎰⎰==---=2020202sin sin ))((sin sinπππππππxdx tdt dt t t x xdx n n nn 令,所以⎰⎰=ππ020sin 2sinxdx xdx n n.9. 设f (x )是以l 为周期的连续函数, 证明⎰+1)(a a dx x f 的值与a 无关.证明 已知f (x +l )=f (x ). ⎰⎰⎰⎰⎰⎰⎰-+=++=+++ala ll la ll a a adx x f dx x f dx x f dx x f dx x f dx x f dx x f 00001)()()()()()()(,而 ⎰⎰⎰⎰=+=++=+a a ala ldx x f dx l x f dt l t f l t x dx x f 000)()()()(令,所以 ⎰⎰=+la adx x f dx x f 01)()(.因此⎰+1)(a adx x f 的值与a 无关.10. 若f (t )是连续函数且为奇函数, 证明⎰xdt t f 0)(是偶函数; 若f (t )是连续函数且为偶函数, 证明⎰xdt t f 0)(是奇函数. 证明 设⎰=xdt t f x F 0)()(.若f (t )是连续函数且为奇函数, 则f (-t )=-f (t ), 从而)()()()1)(()()(0000x F dx x f dx u f du u f u t dt t f x F x x xx ===---==-⎰⎰⎰⎰-令,即⎰=xdt t f x F 0)()(是偶函数.若f (t )是连续函数且为偶函数, 则f (-t )=f (t ), 从而)()()()1)(()()(0000x F dx x f dx u f du u f u t dt t f x F x x x x -=-=-=---==-⎰⎰⎰⎰-令,即⎰=xdt t f x F 0)()(是奇函数.11. 计算下列定积分: (1)⎰-10dx xe x ; 解11011010101021--------=--=+-=-=⎰⎰⎰e e e dx e xe xde dx xe xx x x x .(2)⎰e xdx x 1ln ; 解)1(414121121ln 21ln 21ln 21220212121+=-=⋅-==⎰⎰⎰e x e dx x x x x xdx xdx x ee e e e.(3)⎰ωπω20sin tdt t (ω为常数); 解⎰⎰⎰+-=-=ωπωπωπωπωωωωωωω20202020cos 1cos 1cos 1sin tdt tt t td tdt t 220222sin 12ωπωωωπωπ-=+-=t.(4)⎰32sin ππdx xx;解343432sin ln 4313cot cot cot sin ππππππππππππxxdx xx x xd dx x x++⋅-=+-=-=⎰⎰⎰23ln 21)9341(+-=π.(5)⎰41ln dx x x; 解 ⎰⎰⎰⋅-==4141414112ln 2ln 2ln dx xx x x x xd dx xx )12ln 2(442ln 8122ln 84141-=-=-=⎰x dx x.(6)⎰10arctan xdx x ;解x d x x x x xdx xdx x ⎰⎰⎰+⋅-==1022102102101121arctan 21arctan 21arctan214)41(218)arctan (218)111(21810102-=--=--=+--=⎰πππππx x x d x. (7)⎰02cos πxdx e x ; 解⎰⎰⎰-==022020202sin 2sin sin cos ππππxdx e xe x d e xdx e x x x x⎰⎰⎰-+=-+=+=202202202202cos 42cos 4cos 2cos 2πππππππxdx e e xdx e xe e x d e e x x xx所以)2(51cos 202-=⎰ππe xdx e x ,于是(8)⎰212log xdx x ; 解⎰⎰⎰⋅-==212212221222122ln 121log 21log 21log dx x x x x xdx xdx x2ln 432212ln 212212-=⋅-=x . (9)⎰π02)sin (dx x x ; 解⎰⎰⎰-=-=ππππ02302022sin 4161)2cos 1(21)sin (x d x x dx x x dx x x πππππππ03000332cos 41622sin 412sin 416⎰⎰-=⋅+-=xxd xdx x xx 462sin 81462cos 412cos 416303003ππππππππ-=+-=+-=⎰x xdx x x .(10)⎰edx x 1)sin(ln ; 解法一 ⎰⎰⋅=101sin ln )sin(ln dt e t t x dx x te令.因为⎰⎰⎰-==⋅10101010cos sin sin sin tdt e te tde dt e t t tt t⎰⎰--⋅=-⋅=101010sin cos 1sin cos 1sin tdt e t e e tde e t t t⎰-+⋅-⋅=10sin 11cos 1sin tdt e e e t , 所以 )11cos 1sin (21sin 10+⋅-⋅=⎰e e tdt e t .因此)11cos 1sin (21)sin(ln 1+⋅-⋅=⎰e e dx x e. 解法二⎰⎰⎰-⋅=⋅⋅-⋅=e e eedx x e dx x x x x x dx x 1111)cos(ln 1sin 1)cos(ln )sin(ln )sin(ln ⎰⋅⋅-⋅-⋅=e edx x x x x x e 111)sin(ln )cos(ln 1sin ⎰-+⋅-⋅=edx x e e 0)sin(ln 11cos 1sin , 故)11cos 1sin (21)sin(ln 1+⋅-⋅=⎰e e dx x e . (11)dx x e e⎰1|ln |; 解⎰⎰⎰⎰⎰-++-=+-=eee eee e e dx dx xx x x dx x dx x dx x 1111111111ln ln ln ln |ln |)11(2)1()11(1ee e e e -=---++-=.(12)⎰-102)1(dx xm (m 为自然数); 解⎰⎰+=-2011022cos sin )1(πtdt t x dx xm m 令.根据递推公式⎰⎰--=20220cos 1cos ππxdx n n xdx n n ,⎪⎩⎪⎨⎧⋅⋅⋅⋅⋅--⋅--⋅+⋅⋅⋅⋅⋅⋅--⋅--⋅+=-⎰为偶数为奇数m m m m m m m m m m m m m m dx x m325476 34121 2214365 34121)1(1022π. (13)⎰=π0sin xdx x J m m (m 为自然数). 解 因为⎰⎰⎰⎰-=----=ππππππππ0000sin sin )1)((sin )(sin tdt t tdt dt t t t x xdx x mm m m 令,所以 ⎰⎰⎰⎰=⋅===20200sin sin 22sin 2sin πππππππxdx xdx xdx xdx x J m m mmm (用第8题结果).根据递推公式⎰⎰--=20220sin 1sin ππxdx n n xdx n n , ⎪⎩⎪⎨⎧⋅⋅⋅⋅⋅--⋅--⋅-⋅⋅⋅⋅⋅⋅--⋅--⋅-=为奇数为偶数m m m m m m m m m m m m m m J m 325476 45231 2214365 452312ππ.习题5-71. 判别下列各反常积分的收敛性, 如果收敛, 计算反常积分的值:(1)⎰+∞14xdx; 解 因为3131)31(lim 3131314=+-=-=-+∞→+∞-+∞⎰x x x dx x , 所以反常积分⎰+∞14x dx收敛, 且3114=⎰∞+x dx . (2)⎰+∞1xdx ;解 因为+∞=-==+∞→+∞∞+⎰22lim 211x xxdx x , 所以反常积分⎰+∞1xdx 发散.(3)dx e ax ⎰+∞-0(a >0); 解 因为aa e a e adx e ax x ax ax 11)1(lim 100=+-=-=-+∞→+∞-+∞-⎰, 所以反常积分dx e ax ⎰+∞-0收敛, 且adx e ax 10=⎰+∞-.(4)⎰+∞-0ch tdt e pt (p >1); 解 因为1]1111[21][21ch 2)1()1(0)1()1(0-=+--=+=+∞+--∞++--∞+-⎰⎰p p e pe p dt e e tdt e tp t p t p tp pt ,所以反常积分⎰+∞-0ch tdt e pt 收敛, 且1ch 20-=⎰∞+-p p tdt e pt .(5)⎰+∞-0sin tdt e pt ω(p >0, ω>0); 解⎰⎰+∞-+∞--=0cos 1sin t d e tdt e pt pt ωωω⎰⎰+∞-+∞-+∞--=-⋅+-=020sin 1)(cos 1cos 1t d e pdt pe t te pt pt pt ωωωωωωω⎰+∞-+∞--⋅+-=0202)(sin sin 1dt pe t pte p ptpt ωωωωω⎰+∞--=022sin 1tdt e p pt ωωω,所以 22sin w p tdt e pt +=⎰+∞-ωω.(6)⎰+∞∞-++222x x dx;解 πππ=--=+=++=++⎰⎰+∞∞-+∞∞-+∞∞-)2(2)1arctan()1(12222x x dxx x dx .(7)dx xx ⎰-121;解 这是无界函数的反常积分, x =1是被积函数的瑕点.11)1(lim 112110212=+--=--=--→⎰x x dx x x x . (8)⎰-22)1(x dx;解 这是无界函数的反常积分, x =1是被积函数的瑕点. 因为⎰⎰⎰-+-=-212102202)1()1()1(x dxx dx x dx , 而 +∞=--=-=--→⎰111lim 11)1(110102xx x dx x ,所以反常积分⎰-202)1(x dx发散. (9)⎰-211x xdx ;解 这是无界函数的反常积分, x =1是被积函数的瑕点.21232121]12)1(32[)111(1-+-=-+-=-⎰⎰x x dx x x x xdx322]12)1(32[lim 3831=-+--=+→x x x . (10)⎰-ex x dx 12)(ln 1.解 这是无界函数的反常积分, x =e 是被积函数的瑕点.2)arcsin(ln lim )arcsin(ln ln )(ln 11)(ln 111212π===-=--→⎰⎰x x x d x x x dx ex e ee.2. 当k 为何值时, 反常积分⎰+∞)(ln kx x dx收敛? 当k 为何值时, 这反常积分发散? 又当k 为何值时, 这反常积分取得最小值?解 当k <1时, +∞=-==+∞+-+∞+∞⎰⎰2122)(ln 11ln )(ln 1)(ln k k k x k x d x x x dx ;当k =1时, +∞===+∞+∞+∞⎰⎰222)ln(ln ln ln 1)(ln x x d x x x dxk ; 当k >1时,k k kkk x kx d x x x dx -+∞+-+∞+∞-=-==⎰⎰12122)2(ln 11)(ln 11ln )(ln 1)(ln . 因此当k >1时, 反常积分⎰+∞0)(ln k x x dx 收敛; 当k ≤1时, 反常积分⎰+∞0)(ln k x x dx发散. 当k >1时, 令k kk x x dx k f -∞+-==⎰10)2(ln 11)(ln )(, 则 )2ln ln 11()1(2ln ln )2(ln 2ln ln )2(ln 11)2(ln )1(1)(21112+---=----='---k k k k k f k kk. 令f '(k )=0得唯一驻点2ln ln 11-=k . 因为当2ln ln 111-<<k 时f '(k )<0, 当2ln ln 11->k 时f '(k )>0, 所以2ln ln 11-=k 为极小值点,同时也是最小值点, 即当2ln ln 11-=k 时, 这反常积分取得最小值 3. 利用递推公式计算反常积分⎰+∞-=0dx e x I x n n . 解 因为101000-+∞--+∞-+∞-+∞-=+-=-==⎰⎰⎰n x n x n x n x n n nI dx e x n e x de x dx e x I ,所以 I n = n ⋅(n -1)⋅(n -2)⋅ ⋅ ⋅2⋅I 1. 又因为 1000001=-=+-=-==+∞-+∞-+∞-+∞-+∞-⎰⎰⎰xx xx x e dx e xe xde dx xe I ,所以 I n = n ⋅(n -1)⋅(n -2)⋅ ⋅ ⋅2⋅I 1=n !.总习题五1. 填空:(1)函数f (x )在[a , b ]上(常义)有界是f (x )在[a , b ]上可积的______条件, 而f (x )在[a , b ]上连续是f (x )在[a , b ]上可积______的条件;解 函数f (x )在[a , b ]上(常义)有界是f (x )在[a , b ]上可积的___必要___条件, 而f (x )在[a , b ]上连续是f (x )在[a , b ]上可积___充分___的条件;(2)对[a , +∞)上非负、连续的函数f (x ), 它的变上限积分⎰xa dx x f )(在[a , +∞)上有界是反常积分⎰+∞a dx x f )(收敛的______条件;解 对[a , +∞)上非负、连续的函数f (x ), 它的变上限积分⎰xa dx x f )(在[a , +∞)上有界是反常积分⎰+∞a dx x f )(收敛的___充分___条件;(3)绝对收敛的反常积分⎰+∞a dx x f )(一定______; 解 绝对收敛的反常积分⎰+∞a dx x f )(一定___收敛___;(4)函数f (x )在[a , b ]上有定义且|f (x )|在[a , b ]上可积, 此时积分⎰ba dx x f )(______存在. 解 函数f (x )在[a ,b ]上有定义且|f (x )|在[a , b ]上可积, 此时积分⎰b a dx x f )(___不一定___存在.2. 计算下列极限:(1)∑=∞→+n i n nin 111lim ;解 )122(32)1(32111lim 103101-=+=+=+⎰∑=∞→x dx x n i n n i n . (2)121lim+∞→+⋅⋅⋅++p pp p n nn (p >0);解 11111])( )2()1[(lim 21lim 101101+=+==⋅⋅⋅⋅++=+⋅⋅⋅+++∞→+∞→⎰p x p dx x n n n n n n n p p p p p n p p p p n . (3)nn nn !lnlim ∞→; 解 ]ln 1)ln 2ln 1(ln 1[lim !lnlim n n nn n n n n nn ⋅-+⋅⋅⋅++=∞→∞→nn n n n n 1)]ln (ln )ln 2(ln )ln 1[(ln lim ⋅-+⋅⋅⋅+-+-=∞→⎰=⋅+⋅⋅⋅++=∞→10ln 1)ln 2ln 1(ln lim xdx n n n n n n1)ln ()ln (10101010-=-=-=⎰xx x dx x x .(4)⎰-→xaa x dt t f a x x )(lim, 其中f (x )连续; 解法一 )()(lim )(lima af xf dt t f ax x axa ax ==-→→⎰ξξ (用的是积分中值定理). 解法二 )(1)()(lim )(lim )(lim a af x xf dt t f a x dt t f x dt t f a x x xaa x xa a x x a a x =+=-=-⎰⎰⎰→→→ (用的是洛必达法则). (5)1)(arctan lim 22+⎰+∞→x dtt xx .解4)(arctan 1lim 1)(arctan lim 1)(arctan lim 22222202π=+=+=+∞→+∞→+∞→⎰x x x x x x x dtt x x xx . 3. 下列计算是否正确, 试说明理由:(1)⎰⎰----=-=+-=+111111222)1arctan ()1(1)1(1πx xx d x dx ;解 计算不正确, 因为x 1在[-1, 1]上不连续. (2)因为⎰⎰--++-=++111122111t t dt tx x x dx , 所以⎰-=++11201x x dx .解 计算不正确, 因为t1在[-1, 1]上不连续.(3)01lim 122=+=+⎰⎰-∞→+∞∞-A A A dx x xdx x x . 解 不正确, 因为⎰⎰⎰⎰-+∞→+∞→+∞∞--∞→+≠+++=+A A A b b a a dx xxdx x x dx x x dx x x 2020221lim 1lim 1lim 1. 4. 设p >0, 证明⎰<+<+10111p x dx p p. 证明 p pp p p p px x x x x x x ->+-=+-+=+>11111111. 因为⎰⎰⎰<+<-1010101)1(dx x dxdx x pp,而 110=⎰dx , pp p x x dx x p p+=+-=-+⎰1)1()1(10110, 所以⎰<+<+10111pxdx p p. 5. 设f (x )、g (x )在区间[a , b ]上均连续, 证明: (1)⎰⎰⎰⋅≤ba ba ba dx x g dx x f dx x g x f )()(])()([222;证明 因为[f (x )-λg (x )]2≥0, 所以λ2g 2(x )-2λ f (x )g (x )+f 2(x )≥0, 从而 0)()()(2)(222≥+-⎰⎰⎰ba ba ba dx x f dx x g x f dx x g λλ.上式的左端可视为关于λ的二次三项式, 因为此二次三项式大于等于0, 所以其判别式小于等于0, 即0)()(4])()([4222≤⋅-⎰⎰⎰ba ba ba dx x g dx x f dx x g x f ,亦即 ⎰⎰⎰⋅≤ba ba ba dx x g dx x f dx x g x f )()(])()([222. (2)()()()212212212)()()]()([⎰⎰⎰+≤+b ab a b a dx x g dx x f dx x g x f , 证明⎰⎰⎰⎰++=+ba ba ba ba dx x g x f dx x g dx x f dx x g x f )()(2)()()]()([222。
高等数学参考解答 (5)
5.对所给方程配方可知
可见，是球面方程，球心坐标 半径5
6.（1）椭圆柱面（2）双曲线柱面（3）抛物柱面（4）椭圆柱面
7.椭球
B组
1.选择练习题
(1)空间点 关于 轴的对称点是
A B
C D
(2)在空间直角坐标系中，点 位于
A第5卦限B第4卦限
C第2卦限D第3卦限
(3)在 坐标面上与已知三点 ， 和 等距的点是
解之得
又在(2，1)点有 ， ， ，因此
，
从而函数在(2，1)点处有极小值 。
⑵求偏导，联立求驻点
解之得 ，
在(-3，-2)点有 ， ， ，因此
，
从而函数在(-3，-2)点处有极大值 ；
另一方面，在(-3，2)点有 ， ， ，因此此点处有
从而，驻点 不是极值点.
7.设长方体的长宽高分别为x, y, z，先给出体积函数
2.(1)(-x,y,z)，(x,-y,-z)，(0,0,z)(2)
(3)c(y-b)+b(z-c)=0。
3.（1）过z轴，则平面的方程为
又过点（ ，1， ），则有 ，因此平面方程为
x+3y=0
（2）平行于x轴的平面方程为
又过点A（ ，1， ）和B（3，0，5），从而
得
从而所求平面的方程为
（3）平行于xOy面的平面方程为
3.⑴ ,
⑵ ，
⑶ ，
⑷ ，
⑸ ，
⑹ ，
4.⑴先求一阶偏导数
，
因此
， ，
⑵先求一阶偏导数
，
因此
， ，
⑶先求一阶偏导数
，
因此
， ，
⑷先求一阶偏导数
数学史朱家生习题答案
数学史朱家生习题答案数学史朱家生习题答案数学作为一门古老而又重要的学科，其历史可以追溯到古代文明的起源。
在数学的发展过程中，许多数学家都做出了重要的贡献，其中朱家生是中国数学史上的一位重要人物。
本文将通过回答一些与朱家生相关的习题，来探讨他的数学思想和贡献。
1. 朱家生是谁？他的数学成就有哪些？朱家生（1916-2004）是中国著名的数学家，他在数学教育和研究领域做出了重要的贡献。
他曾任教于北京大学，并担任中国数学会主席。
朱家生的数学成就包括但不限于：在数论和代数几何方面作出了重要的研究，提出了朱家生猜想，并在数学教育改革中起到了重要的推动作用。
2. 朱家生猜想是什么？它为数学界带来了什么影响？朱家生猜想是一个关于数论中的整数分拆问题的猜想。
具体来说，它猜测了任何一个正整数都可以表示为不同奇素数的和。
这个猜想在数论领域引起了广泛的关注，并且至今尚未被证明或者推翻。
朱家生猜想的提出激发了许多数学家对整数分拆问题的研究，推动了相关领域的发展。
3. 朱家生如何影响了数学教育改革？朱家生在中国的数学教育改革中起到了重要的推动作用。
他提倡“数学思维”的培养，强调数学教育应该注重培养学生的创造力和解决问题的能力。
他主张通过培养学生的数学素养来提高整个国家的科学技术水平。
朱家生的观点对中国的数学教育产生了深远的影响，推动了数学教育的改革和发展。
4. 朱家生的数学思想有哪些特点？朱家生的数学思想具有以下几个特点：首先，他注重数学的实际应用。
他认为数学应该与实际问题相结合，通过解决实际问题来推动数学的发展。
其次，他强调数学的创造性思维。
他认为数学不仅仅是一种工具，更是一种思维方式，通过培养学生的创造力和解决问题的能力来推动数学的发展。
最后，他重视数学教育的普及。
他认为数学是一门普及的学科，应该为更多的人所了解和掌握，通过数学的普及来提高整个社会的科学素养。
5. 朱家生对中国数学界的影响是什么？朱家生对中国数学界的影响是深远的。
数学史 答案
1.勾股定理的证明方法来源毕达哥拉斯树是一个基本的几何定理，传统上认为是由古希腊的毕达哥拉斯所证明。
据说毕达哥拉斯证明了这个定理后，即斩了百头牛作庆祝，因此又称“百牛定理”。
在中国，《周髀算经》记载了勾股定理的公式与证明，相传是在商代由商高发现，故又有称之为商高定理；三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释，又给出了另外一个证明[1]。
法国和比利时称为驴桥定理，埃及称为埃及三角形。
我国古代把直角三角形中较短的直角边叫做勾，较长的直角边叫做股，斜边叫做弦。
1.关于勾股定理的证明：（利用相似三角形性质证明）如图，在RtΔABC中，设直角边AC、BC的长度分别为a、b，斜边AB的长为c，过点C作CD⊥AB，垂足是D.在ΔADC和ΔACB中，∵∠ADC = ∠ACB = 90º，∠CAD = ∠BAC，∴ΔADC ∽ΔA CB.∴AD∶AC = AC ∶AB，即.同理可证，ΔCDB ∽ΔACB，从而有.∴，即】（欧几里得证明）做三个边长分别为a、b、c的正方形，把它们拼成如图所示形状，使H、C、B 三点在一条直线上，连结BF、CD. 过C作CL⊥DE，交AB于点M，交DE于点L.∵AF = AC，AB = AD，∠FAB = ∠GAD，∴ΔFAB ≌ΔGAD，∵ΔFAB的面积等于，ΔGAD的面积等于矩形ADLM的面积的一半，∴矩形ADLM的面积=.同理可证，矩形MLEB的面积=.∵正方形ADEB的面积= 矩形ADLM的面积+ 矩形MLEB的面积∴，即.2. 论述数学史对数学教育的意义和作用.数学史进入课程是数学新课程改革的重要理念之一。
在课程变革由结构——功能视角向文化——个人视角转变的过程中，文化融入是师生对课程改革适应性的一个重要因素。
对数学学科而言，数学史是数学文化生成的文库性资源，是最具权威的课程资源，具有明理、哲思与求真三重教育价值。
明理：数学知识从何而来?数学史展示数学知识的起源、形成与发展过程，诠释数学知识的源与流；哲思：数学是一门什么样的科学?数学史明晰数学科学的思想脉络和发展趋势，让学生领悟数学科学的本质，引发学生对数学观问题自觉地进行哲学沉思，有利于学生追求真理和尊崇科学品德的形成；求真：数学科学有什么用?数学史引证数学科学伟大的理性力量，让学生感悟概念思维创生的数学模式对于解析客观物质世界的真理性，提高学生对数学的科学价值、应用价值、文化价值的认识。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1.导致欧洲中世纪黑暗时期出现的主要原因是什么?因为中世纪时期是欧洲最为混乱的时期,也是其经济、政治、文化、军事等全面停滞发展的时期,当时的欧洲居民生活在水深火热之中,所以被称为黑暗时期.1、政治的黑暗、政权的分散：自罗马帝国衰亡后,中欧、西欧被来自东欧的日耳曼民族统治,日耳曼民族又有很多种族,因此相互征伐不断,如法兰克帝国、神圣罗马帝国、英格兰王国、教皇国等等,这些国家相互征伐、动乱不已,而且中世纪时期虽然是欧洲的封建时期,但却不集权、不统一,类似分封制的封建制度导致封建国家缺乏强有力的基础,例如神圣罗马帝国、皇帝仅仅是一个称号而已.而封建地主又对百姓盘剥,加之战乱不断、瘟疫横行,民不聊生.2、宗教的干涉：这一时期的基督教对各国的干扰极强,甚至对政权的建立、稳定都十分重要.宗教严格的控制文化教育、人们的生活：一方面他们严格要求中下层教士及普通百姓,另一方面,上层教士又和封建势力相勾结,腐败没落,压榨百姓和人民,中世纪的宗教裁判所又有极大的权力,可以处死他们所认为的异端分子,由于思想、科学被严格控制,这一时期的欧洲思想、文化、科学鲜有成就.3、经济的没落,由于盘剥严重、科技落后,这一时期的经济几乎没有发展,没有进步就代表了落后；4、瘟疫盛行：宗教的干涉,科技的落后,医学的不发达,导致瘟疫的盛行,540年~590年查士丁尼瘟疫导致东地中海约2500万人死亡；1346年到1350的鼠疫导致欧洲约2500万人死亡,灾难极大地打击的了欧洲的经济、政治甚至人口的发展.简而言之,这一时期的欧洲百姓生活在一种暗无天日,毫无希望的生活里,所以被称为黑暗时期.2、在欧洲中世纪黑暗时期曾经出现过那些知名的数学家，他们在当时那样的背景下各自做了哪些数学工作？答：罗马人博伊西斯（罗马贵族），曾不顾禁令用拉丁文从古希腊著作的片段中编译了一些算术、几何、音乐、天文的初级读物，他把这些内容称为“四大科”，其中的数学著作还被教会学校作为标准课本使用了近千年之久，但博伊西斯本人还是遭受政治迫害被捕入狱并死在狱中。
7世纪，在英格兰的北部出现了一位博学多才的神学家，这就是被称为“英格兰文化之父”的比德。
在数学方面，比德曾写过一些算术著作，研究过历法及指头计算方法。
当时，对耶稣复活期的推算是教会讨论最热烈的课题之一，据说，这位比德大师就是最先求得复活节的人。
培根是英格兰人（贵族），曾在牛津大学和巴黎大学任教，会多种语言，对当时几乎所有的知识感兴趣，号称“万能博士”。
他提倡科学，重视现实，反抗权威（应为不惧权威）。
他认为，数学的思想方法是与生俱来的，并且是与自然规律相一致的。
在他看来，数学是一切科学的基础，科学真理之所以是珍贵的，是因为它们是在数学的形成中被反映出来，即用数量和尺规刻画的。
培根认为：“寻找和发现真理有两条路，也只有两条路，一种方法是通过感觉和特例飞跃到普遍的公理，然后通过这些原则及一劳永逸的真理发现和判断派生的公理。
另一种方法是从感觉和特例收集公理，不断地逐步上升，这样最后达到更普遍的公理。
这后一种方法是真实的，但尚未有人使用过。
”他号召人们面向自然，进行有目的的试验，去了解自然，征服自然。
虽然培根成为了那个时代的牺牲品，但他的呐喊还是在漫漫黑夜中点燃了人们复苏的愿望。
意大利的列昂纳多.斐波那契是欧洲黑暗时期最出色的数学家。
1202年，斐波那契综合阿拉伯和希腊资料著成一部重要著作《算盘书》，这部著作共15章，主要介绍算术与代数，内容非常丰富，包括：印度—阿拉伯数码的读法与写法；整数与分数的计算；平方根与立方根的求法；线性方程组和二次方程的解法等，给出了数学在实物交易、合股、比例法和测量几何中的应用。
这部著作还给出一个有趣的所谓“兔子问题”。
斐波那契还写过一部纯几何著作《实用几何》，书中运用欧几里得等人的方法介绍了直线型的面积、圆的度量、球和圆柱等。
3.导致欧洲文艺复兴的因素有哪些?在欧洲文艺复兴时期主要出现了哪些数学成绩?1、城市是文艺复兴的摇篮中世纪晚期意大利由一些重要的和独立城邦国家组成，拥有欧洲最先进的城市社会（有名的如佛罗伦萨、米兰、威尼斯、热那亚和那不勒斯等）。
城市是财富的聚集地，城市是文明的向导。
意大利的贵族通常生活在城市中心，完全参与城市的公共事务。
贵族从事银行业或商业活动，以致到了14世纪和15世纪贵族与上级资产阶级之间实际上已没有什么明显界限了，例：梅蒂奇家族。
工商业和城市的发展，使资产阶级的力量壮大起来，有些与贵族合流，使得上流社会更喜爱文化，更热爱生活，也要求在文化中加入自己喜欢的精神。
图：当时的木屐，反映着时尚的变化。
图：精美的梳子表明了主人的追求。
图：虽是16世纪的城市景象，也反映了时代的变迁，人们热爱生活。
2、意大利地区与古典文明区有着紧密的联系与西欧任何其他地区相比，该地区对古典过去有着强烈得多的感情联系。
此外，在14和15世纪意大利人尤为热衷于重新利用他们的古代遗产，因为此时意大利正想方设法建立一种独立的文化特性，以与和法国关系十分密切的经院哲学相对立。
不仅教皇机构在14世纪大部分时间里迁到了阿维尼翁（从1309年起），随后自1378 至 1415年旷日持久的大分裂加剧了意大利和法国之间的敌对情绪，而且在14世纪在各个领域都出现了反经院哲学的思想文化潮流，这使得意大利人自然而然地偏爱古典文献资料提供的另一种文化选择。
罗马模式有助于意大利人创造一个取代法国的哥特建筑艺术风格的艺术选择。
3、意大利经济的繁荣，具有投资文化的财富基础在中世纪晚期的意大利，人们之所以异乎寻常地大量投资于文化事业，是因为城市荣誉感的增强和人均财富的集中。
在第一个阶段，最富有的一些城市竞相兴建辉煌的公共纪念性建筑并资助作家，约1250年出现于意大利。
第二阶段也即在15世纪初到中叶，投资文化成了个人的行为。
在15世纪一百年间，随着多数意大利城市国家屈从于王公家族的世袭统治（最初城市是由行会控制的），资助文化事业便为王公贵族所专擅。
如米兰的维斯孔蒂家族和斯福扎家族；佛罗伦萨的梅迪奇家族(图为梅迪奇家族的洛伦佐）；费拉拉的埃斯特家族和罗马教皇等。
4、一些因祸得福的因素在文艺复兴前的200年里，意大利遭受了一系列沉重的打击。
在13世纪，神圣罗马帝国与罗马教廷战火不断，意大利国土遭到严重破坏。
在一场战役中，神圣罗马帝国战败，霍亨斯陶芬王朝在意大利的统治终结。
而教皇无力填补权力的真空，战争同时削弱了他们道德规范和政治力量。
意大利处在分裂状态，但就局部地区来说，却非常有利于思想的自由创造和发挥。
14世纪中叶，欧洲黑死病流行，但瘟疫摧毁的仅仅是人，而非财物，而劫后余生的人们却更懂得了生命的宝贵和人的价值，更懂得享受人生。
代数学在文艺复兴时期取得了重要发展，三、四次方程的解法被发现。
意大利人卡尔达诺在他的著作《大术》中发表了三次方程的求根公式，但这一公式的发现实应归功于另一学者塔塔利亚。
四次方程的解法由卡尔达诺的学生费拉里发现，在《大术》中也有记载。
邦贝利在他的著作中阐述了三次方程不可约的情形，并使用了虚数，还改进了当时流行的代数符号。
符号代数学是由16世纪的法国数学家韦达确立的。
他于1591年出版了《分析方法入门》，对代数学加以系统的整理，第一次自觉地使用字母来表示未知数和已知数。
韦达在他的另一部著作《论方程的识别与订正中，改进了三、四次方程的解法，还建立了二次方程和三次方程方程根与系数之间的关系，现代称之为韦达定理。
三角学在文艺复兴时期也获得了较大的发展。
德国数学家雷格蒙塔努斯的《论各种三角形》是欧洲第一部独立于天文学的三角学著作。
书中对平面三角和球面三角进行了系统的阐述，还有很精密的三角函数表。
哥白尼的学生雷蒂库斯在重新定义三角函数的基础上，制作了更多精密的三角函数表。
法国人笛卡儿于1637年，在创立了坐标系后，成功地创立了解析几何学。
费马建立了求切线、求极大值和极小值以及定积分方法，对微积分做出了重大贡献。
其将不定方程的研究限制在整数范围内，从而开始了数论这门数学分支。
在和帕斯卡在相互通信以及著作中建立了概率论的基本原则——数学期望的概念.4、意大利数学家的三、四次方程解法的主要思想是什么？试通过具体例子说明他们是如何求解三次方程的。
答: 主要思想是透视理论的创立与三角学的产生，如何把三维的现实世界反映到二维的画布上来。
将平面三角与球面三角放在一起处理，给出了球面三角的余弦定理和正弦定理，对于如何解平面与球面三角形做出了较全面的论述。
例 如解三次方程 q px =+3x令33x n m -=，即,)(33331323131323x mn n m n n m n m m x --=-+-= 于是方程变为 .)(3m 31q px x mn n +-=-- 当时，或27mn )(,m 331p p mn q n ===-可以满足方程，故有 ,274m ,2742.2744,2m 3232223222p q n p q n mn m p nm q n mn +=++=++==+-由此得两式相加得 又因为.27422742x ,2742q -,2m ,3323323227423p q q p q q p q n q P q n m p --+++=++=++==-于是从而有5.欧洲数学家为什么要引入对数的概念?试比较纳皮尔和比尔吉引入对数的方法.对数方法是苏格兰的 Merchiston 男爵约翰·纳皮尔1614年在书《Mirifici Logarithmorum Canonis Descriptio 》中首次公开提出的,(Joost B ürgi 独立的发现了对数；但直到 Napier 之后四年才发表).这个方法对科学进步有所贡献,特别是对天文学,使某些繁难的计算成为可能.在计算器和计算机发明之前,它持久的用于测量、航海、和其他实用数学分支中. 约翰·纳皮尔（John Napier,1550～1617）,苏格兰数学家、神学家,对数的发明者. Napier出身贵族,于1550年在苏格兰爱丁堡附近的小镇梅奇斯顿（Merchiston Castle,Edinburgh,Scotland）出生,是Merchiston城堡的第八代地主,未曾有过正式的职业. 年轻时正值欧洲掀起宗教革命,他行旅其间,颇有感触.苏格兰转向新教,他也成了写文章攻击旧教（天主教）的急先锋（主要文章于1593年写成）.其时传出天主教的西班牙要派无敌舰队来攻打,Napier就研究兵器（包括拏炮、装甲马车、潜水艇等）准备与其拚命.虽然Napier的兵器还没制成,英国已把无敌舰队击垮,他还是成了英雄人物. 他一生研究数学,以发明对数运算而著称.那时候天文学家Tycho Brahe（第谷,1546～1601）等人做了很多的观察,需要很多的计算,而且要算几个数的连乘,因此苦不堪言.1594年,他为了寻求一种球面三角计算的简便方法,运用了独特的方法构造出对数方法.这让他在数学史上被重重地记上一笔,然而完成此对数却整整花了他20年的工夫.1614年6月在爱丁堡出版的第一本对数专著《奇妙的对数表的描述》（"Mirifici logarithmorum canonis descriptio"）中阐明了对数原理,后人称为纳皮尔对数：Nap logX.1616年Briggs（亨利·布里格斯,1561 - 1630）去拜访纳皮尔,建议将对数改良一下以十为基底的对数表最为方便,这也就是后来常用的对数了.可惜纳皮尔隔年于1617年春天去世,后来就由Briggs以毕生精力继承纳皮尔的未竟事业,以10为底列出一个很详细的对数表.并且于1619年发表了《奇妙对数规则的结构》,于书中详细阐述了对数计算和造对表的方法.。