高等数学第五章课后习题答案.
长沙理工大学高等数学 练习册 第五章 定积分答案

习题5.1略习题5.2—5.3(A )一 计算下列定积分1.⎰203cos sin πxdx x解:原式2342011cos cos cos 44xd x x ππ=-=-=⎰2.⎰-a dx x a x 0222解:令t a x sin =,则tdt a dx cos = 当0=x 时0=t ,当a x =时2π=t原式⎰⋅⋅=2022cos cos sin πtdt a t a t a()⎰⎰-==2420244c o s 182s i n 4ππdt t a tdt a 42044164sin 41828a t a a πππ=-=3.⎰+31221xxdx解:令θtg x =,则θθd dx 2sec = 当1=x ,3时θ分别为4π,3π原式θθθθππd tg ⎰=3422sec sec()⎰-=342s i n s i n ππθθd3322-=4.⎰--1145xxdx解:令u x =-45,则24145u x -=,udu dx 21-= 当1-=x ,1时,1,3=u 原式()61581132=-=⎰du u 5.⎰+411x dx解:令t x =,tdt dx 2=当1=x 时,1=t ;当4=x 时,2=t 原式⎥⎦⎤⎢⎣⎡+-=+=⎰⎰⎰2121211212t dt dt t tdt ()[]32ln 221ln 22121+=+-=t t6.⎰--14311x dx解:令u x =-1,则21u x -=,udu dx 2-= 当1,43=x 时0,21=u 原式2ln 21111212210021-=-+-=--=⎰⎰du u u du u u7.⎰+21ln 1e xx dx解:原式()⎰⎰++=+=2211ln 1ln 11ln ln 11e e x d xx d x232ln 1221-=+=e x8.⎰-++02222x x dx解:原式()()⎰--+=++=0222111x arctg x dx()24411πππ=+=--=a r c t g a r c t g9.dx x ⎰+π2cos 1解:原式⎰⎰==ππ2cos 2cos 2dx x dx x()⎰⎰-+=πππ220c o s 2c o s 2dx x xdx22s i n s i n 2220=⎥⎦⎤⎢⎣⎡-=πππx x 10.dx x x ⎰-ππsin 4解:∵x x sin 4为奇函数∴⎰-=ππ0sin 4xdx x11.dx x ⎰-224cos 4ππ解:原式()⎰⎰=⋅=222204cos 22cos 24ππdx x xdx()()⎰⎰++=+=2022022cos 2cos 2122cos 12ππdx x x dx x()⎰⎰+++=220204cos 12cos 22πππdx x xdx x⎰+++=202044cos 4122sin 2ππππx xd x πππ234sin 412320=+=x12.⎰-++55242312sin dx x x xx 解:∵12sin 2423++x x xx 为奇函数 ∴012sin 552423=++⎰-dx x x xx13.⎰342sin ππdx x x解:原式⎰-=34ππxdctgx⎰+-=3434ππππc t g x d xx c t g x 34s i nln 9341πππx +⎪⎪⎭⎫ ⎝⎛-= 22ln 23ln 9341-+⎪⎪⎭⎫ ⎝⎛-=π 23ln 219341+⎪⎪⎭⎫ ⎝⎛-=π 14.⎰41ln dx xx解:原式⎰=41ln 2x xd⎥⎦⎤⎢⎣⎡-=⎰4141ln ln 2x d x x x ⎥⎦⎤⎢⎣⎡-=⎰4112ln 42dx x x⎰--=412122ln 8dx x42ln 8-= 15.⎰10xarctgxdx解:原式⎰=10221arctgxdx ⎥⎦⎤⎢⎣⎡+-=⎰1022102121dx x x arctgx x ⎰⎰++-=10210121218x dx dx π101021218a r c t g xx +-=π214-=π16.⎰202cos πxdx e x解:原式⎰=202sin πx d e x⎰⋅-=2022022s i n s i nππdx e x x e x x⎰+=202c o s2ππx d e e x ⎰⋅-+=2022022c o s 2c o s 2πππdx e x x e e x x⎰--=202c o s 42ππx d x e e x故()251cos 202-=⎰ππe xdx e x 17.()dx x x ⎰π2sin 解:原式()⎰⎰-==ππ2222cos 1sin dx xx dx x x ⎰⎰-=ππ02022c o s2121x d x x dx x ⎰-=ππ0232s i n 4161x d x x⎥⎦⎤⎢⎣⎡⋅--=⎰πππ002322s i n 2s i n 416x d x x x x⎰-=ππ032c o s 416x xd 462c o s 2c o s 4163003πππππ-=⎥⎦⎤⎢⎣⎡--=⎰x d x x x 18.()dx x e⎰1ln sin解:原式()()⎰⋅-=eedx xx x x x 111ln cos ln sin()⎰-=edx x e 1ln cos 1sin()()⎥⎦⎤⎢⎣⎡⋅+-=⎰e e dx x x x x x e 111ln sin ln cos 1sin()⎰-+-=edx x e e 1ln sin 11cos 1sin故()()11cos 1sin 2ln sin 1+-=⎰edx x e19.⎰--243cos cos ππdx x x解:原式()⎰--=242cos 1cos ππdx x x()⎰⎰+-=-2004s i n c o s s i n c o s ππx d xx dx x x ()()2230423c o s 32c o s 32ππ⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡=-x x 32344-=20.⎰+4sin 1sin πdx xx解:原式()⎰--=42sin 1sin 1sin πdx xx x ⎰⎪⎭⎫ ⎝⎛-=4022c o s s i n πdx x tg x x ()⎰⎰---=402421s e c c o s c o s ππdx x xx d ()242c o s 14040-+=--=πππx t g x x 21.dx xxx ⎰+π02cos 1sin解:令t x -=2π,则原式⎰-⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--=2222cos 12sin 2πππππdt t t t ⎰-+-+-=2222s i n 1c o s s i n 1c o s2πππdt t t t t t ()4s i n s i n 1c o s 220202πππππ==+=⎰t a r c t g dt t t 22.⎰-+2111lndx xxx 解:原式⎰⎪⎪⎭⎫⎝⎛-+=2102211ln x d x x ()()()⎰--+--⋅+-⋅--+=210222102111111211ln 2dx x x x x x x x x x ⎰-+=210221l n 3l n 81dx x x ⎰⎰-++=210221013ln 81x dxdx21011ln 21213ln 81+-++=x x3ln 8321-=(B)一 解答1.求由0cos 0=+⎰⎰xyt tdt dt e 所决定的隐函数y 对x 的导数dxdy 。
高等数学(第二版)第五章答案

习题5.11.,,,,,().11,,().22ABCD AB AD AC DB MA M AC DB MA AM AC ===+=-=-=-=-+设为一平行四边形试用表示为平行四边形对角线的交点解a b.a b a b a b a b()2.,1().211221().2M AB O OM OA OB OM OA AM OA AB OA OB OAOA OB =+=+=+=+-=+设为线段的中点,为空间中的任意一点证明证 3.,,1().3221()3321(),31(),3M ABC O OM OA OB OC OM OA AM OA AD OA AB AC OA AB AC OM OB BA BC OM OC =++=+=+=+⨯+=++=++=设为三角形的重心为空间中任意一点证明证1().313,().3CA CB OM OA OB OC OM OA OB OC ++=++=++ 4.,1,().41(),211(),(),221().24ABCD M O OM OA OB OC OD OM OA AM OA AB AD OM OB BA AD OM OC BA DA OM OD AB DA OM OA OB OC OD =+++=+=++=++=++=++=+++设平行四边形的对角线交点为为空间中的任意一点证明证1,().4OM OA OB OC OD =+++2222225.?(1)()();(2)();(3)()().(1).:()().(2).:()0, 1.(3),6.==⨯=⨯======0对于任意三个向量与判断下列各式是否成立不成立例如,不成立例如,成立都是与组成的平行六面体的有向体积利用向量证明三角形两边中点的连线平行解a,b c,a b c b c a a b a b a b c c a b a b i c =j.a b c =j,b c a =a i b j,a b a b a,b c .,112211().22DE DA AE BA AC BA AC BC =+=+=+=于第三边并且等于第三边长度之半.证2227.:(1),;(2).(1)()()()()||||0.()cos |||||||||||||AC BD AB BC BC CD AB BC BC CD BC CD AB AC AB AB AD AB AB AB AD a AB ADAB AC AB AC AB AC α=++=+-=-=+++===利用向量证明菱形的对角线互相垂直且平分顶角勾股弦定理证2,||()cos cos .|||||||||||,.a AC AD AB AD AD AB AD AD a AB ADAB AC AB AC a AC βααβαβ+++=====与都是锐角故22222(2)||()()||||2||||.AC AC AC AB BC AB BC AB BC AB BC AB BC ==++=++=+2222222222222222228.()()||||.()()||||cos ||||sin ||||(cos sin )||||.9..||.AB AC ABC ABC ABDC AB AC αααα⨯+=⨯+=+=+=∆=⨯证明恒等式试用向量与表示三角形的面积11的面积=的面积22证解a b a b a b a b a b a b a b a b a b222222222210.,,,()()2().()()()()()()222().=++-=+++-=+++--=-+给定向量记为即现设为任意向量证明证a a a a a a a.a b , :a b a b a b a b a b a b a b a b a b a a +b b +a b +a a +b b a b =a b2222222222211.,,:().:()||(||sin )||sin ||.,αα⨯≤⨯=⨯==≤=对于任意向量证明问等号成立的充分必要条件是什么?等号成立的充分必要条件是正交证22a b a b a b a b a b a ||b a ||b a ||b a b a b .习题5.22 1.(,,),,,,.||,||,2.(1,2,1),(3,0,1),(2,1,2),,,,(3,0,1)(1,2,1)(4,2xy z xy yz O x y z x y z Oxy Oyz d d d d z d x d x A B C AB BA AC BC AB =======-===--=-写出点分别到轴轴轴平面平面以及原点的距离已知三点求的坐标与模.解解,0),||20|(4,2,0)(4,2,0)25,(2,1,2)(1,2,1)(3,1,1),||11,(2,1,2)(3,0,1)(1,1,1),|| 3.3.(3,2,2),(1,3,2),(8,6,2),132(9,6,6)2AB BA AB AC AC BC BC ===-=--=-=-=--=-==--=-==-==---+a b c a b +c =1112(2,6,4)(4,3,1)(11,9,1).4.(2,5,1),(1,2,7),,.2,7).(2,5,)(1,2,7)(21,5,2,7),70,7.5.,(,,)(k k xy k k k k k k k k k A B x y z x ︒︒---+-=-==-+=-+=+-=+-++==-设分别求出沿和方向的单位向量并求常数使与平面平行1设两点的坐标分别为和解a b a b ,a b a b a b 22111222121212,,),,.111()((,,)(,,))(,,).2226.(1,2,3),(5,2,1),(1)23(2)(3)cos ,.(1)2366(2)12.(2)1(3)cosy z A B C OC OA OB x y z x y z x x y yz z =+=+=+++=-=-<>⨯-=-求连线中点的坐标设求解解a b a b a i a b a b =a b =a i = .2222,|||147.||1,||3,||2,|/3,?17|()()||||||2()11942(3),23333,cos ||||322π-<>======+⊥+=+=++=++++==+++⨯+==⨯设求解a b a b |a b a b c a b +c |=a c <a,b >=<b,c >=a b +c |a b +c a b +c a b c a b +b c a c b c b c b c =<b,c >=b c .6π<b,c >=22228.||2,||6,,()()||||4360,1/3.k k k k k k k k ==⊥--=-=-==±设试求常数使解a b a +b a b.a +b a b a b 9.(1,2,1),(1,1,3),(2,5,3)(1)(2)(3)()(4)()(5)().(1)121(5,2,1),113(2)253(3,0,2).01121(3)()11323.(4)()5212532=-=-=-⨯⨯⨯⨯⨯⨯⨯⨯-=---⨯-=-⨯-=-⨯⨯---解a b c a b c j a b c a b c a b c ijka b =i j kc j =ijka b c =a b c =(1,13,21).53(5)113(12,9,7),()121(23,19,15).2531297=---⨯-=-⨯⨯=-=-----i jk i j kb c =a b c10.,(2,1,0)(0,1,2),,.(2,1,0)(0,1,2)(2,0,2),(0,1,2)(2,1,0)(2,2,2).cos ,|ABCD AB AD AC BD AC AB AD BD AD AB AC BD AC BD AC ==-<>=+=+-==-=--=--<>=在平行四边形中求两对角线的夹角解00,,.2||||||||||5,,,.2AC BD BD AC BD AB AD ABCD AC BD ππ==<>===<>=平行四边形为菱形故两对角线的夹角解二|11.(3,4,1),(2,3,0),(3,5,1),.(1,1,1)(1,1,1),(0,1,0),111(1,0,1),01012A B C ABC AB AC AB AC ABC =---=-=⨯==-=已知三点求三角形的面积三角形的面积解i j k12.(3,4,5),(1,2,2)(9,14,16).345(,,)1220,,9141613.|1,||5,3,|.344cos ,,sin ,,|||||sin ,15 4.||||555======-⨯-<>==<>=⨯=<>=⨯⨯=证明向量和是共面的因为故和是共面的.已知|求||证解a b c a b c a b c a =b a b =a b a b a b a b a b a b a b a b14.cos ,cos ,cos ,,(1)cos 0,cos 0,cos 0;(2)cos cos 0,cos 0;(3)cos cos cos .(1)(2)115.||,2x z αβγαβγαβγαβγπαβγ=≠≠==≠==-===设向量的方向余弦在下列各情况下指出的方向特征与轴垂直是沿轴的的向量.(3)与三个轴的夹角相等,都是设的三个方向角满足求的坐标解a a .a .a a a aa 22222222cos 21,(2cos 1) 1.1cos ,2(21)1,4211,2(21)0,0,.2cos 0,,(0,0,213cos ,cos ,.(1,1,0).24416.,(75)(3),(4)(72),co x x x x x x x x x αααααπααππααα+=+-==+-=-+=-=========-⊥+-⊥-设为两非零向量且求22解2cos 2cos .a a =ab ,a b a b a b a b 2222222222s ,.(75)(3)0,7||15||16||||cos ,0,(4)(72)0,7||8||30||||cos ,0.||||1516cos ,7,||||||||830cos ,7.||||716730||1516||83<>-+=-+<--=+-<⎧-+<-⎪⎪⎨⎪-<-⎪⎩---=--解a b a b a b a b a b a b >=a b a b a b a b a b >=b b a b >=a a b b a b >=a a b a ||1,1||157871cos ,.15162830==---<==--b a a b >习题5.31.:(1)5310(2)270(3)50(4)290(5)50(6)0.(1).(2).(3).(4).(5).(6).2.:(1)(1,5,1)(3,2,2);(2)(5,2,8);(3)x z x y z y y z x y x y Oxz x z Oyz y Oxz -+=+-=+=-=--==---指出下列平面位置的特点平行于轴过原点平行于平面过轴平行于轴平面求下列各平面的方程平行于轴且通过点和平行于平面且通过点垂直于平解451(2,7,3)(0,0,0);(4)(5,4,3)(2,1,8).(1)(0,1,0),(2,7,3),010(3,0,2).2733(1)2(1)0,3250.(2) 2.(3)(1,4,5),(2,7,3),145(47,13,1).27347x y z Oyz x z x z y -+=---==-==-------=+-===-=-=-=----面且通过点及垂直于平面且通过点及解i jka b n i j ka b n 1310.(4)(1,0,0),(7,5,5),100(0,5,5)5(0,1,1).755(4)(3)0,70.x y y z y z ++===-==-=---++-=-+=ij ka b n3.(2,4,8),(3,1,5)(6,2,7).(5,3,3)(4,6,1).533(15,17,42),46115(2)17(4)42(8)0,1517422380.4.1,A B C x y z x y z y z a a --=---=-----=--------+-=+-+=++=求通过点及的平面方程设一平面在各坐标轴上的截距都不等于零并相等,且过点(5,-7,4),求此平面的方程.x 5 a 解解a ,b i jkn =741,2,20.5.(2,1,2)(8,7,5),.(6,8,7).6(8)8(7)7(5)0,6871390.a x y z a aA B B AB x y z x y z -++==++-=--=-+-+-=++-=a 已知两点及求过且与线段垂直的平面解n126.(2,0,3)22470,3250.224(0,16,8)8(0,2,1).2(3)0,30.3127.94230.0,420,1,2,20.2408.:380x y z x y z y z y z x x y z By Cz B C B C y z x z l l y z --++=+-+=-==++=++=---+=+=--===--=+-=⎧⎨-+=⎩求过点且与垂直的平面方程求通过轴且与平面垂直的平面方程取求通过直线且与直线解解ijkn =0101240:.60102(6,1,3),110(1,1,1),03111613(2,9,7).0,4,8/3.1112(4)9(8/3)7()0,297320.383129.::1324x y y z z l y x y z x y z x t x y z l l y t z --=⎧⎨--=⎩==--=--=-=--===---++-=-+-+==+++-===+0平行的平面方程用代入的方程得x 求直线与直线解ij ki j ka b =i j k n 000,26383112621116,11,,3243223131413148,,,(8,,3333324(0,6,3)3(0,2,1).2(1)(2)0,240.312t t t t t t t t x y z y z y z ⎧⎪⎨⎪=+⎩+++++-==+=+=+=-=-=-=----==-=-+--=-+=的交点坐标并求通过此两直线的平面方程.求两条直线交点坐标:交点).解i j kn121112210.::.211422(1,1,1)(2,2,0).211(4,5,3).3314(1)5(1)3(1)0,45320.x y z x y zl l x y z x y z -+++-====-------=------+++=--++=求通过两直线和的平面方程两直线平行.平面过点和解 i j kn =1221121211.::.121012,(1,2,1)(0,1,2)21123,5,0,.121210(1)3x y z x y z l l t t l t t x y z -++--====----⎧--+-+⎪====⎨-⎪⎩+-+=证明两直线和是异面直线证首先两直线的方向向量 和 不平行.x=-2y=1+t 矛盾故两直线无公共点.z=2-2t两直线不平行,又无交点,故是异面直线.12.将下列直线方程化为标准方程及参数方程:0000350(2)280;280.(1)211(1,7,5).31210(1)0,6,7.280;67.7567,.75(2)(1)103(3,2,1).012(2)0,x z x y z y z y z x y z y z y z x t y t t z t -+=⎧⎧⎨⎨-+-=-+=⎩⎩=-=----+=⎧===⎨-+-=⎩--==--=⎧⎪=--∞<<+∞⎨⎪=-⎩=-=-=解中令解之得x 标准方程1参数方程:中令z 直i j kn i j kn 005,8.58.3215382,.y x y zx t y t t z t =-=-++===-+⎧⎪=-+-∞<<+∞⎨⎪=⎩接得x 标准方程参数方程:00013.(3,2,5)3790.100(0,5,2),325520.5203790.052(33,6,15)3(11,2,5).317500,0, 3.390.3:11x y z y z y z x y z y z y x x y x ---+===-+=+=⎧⎨--+=⎩==--=----=⎧===-⎨-+=⎩+=-求通过点及x 轴的平面与平面的交线方程解地第一个平面的法向量平面方程直线方程直线的方向向量直线方程i j kn i j ka .25y z=-0000121326014.,403260(0,0,),40260 3.02404015.::.380601020x y z D Oz x y z D x y z Oz z x y z D z D z z D x z x y l l y z z y l -+-=⎧⎨+-+=⎩-+-=⎧⇔⎨+-+=⎩-=⎧⇔⇔==⎨-+=⎩--=--=⎧⎧⎨⎨-+=-+=⎩⎩=-当为何值时直线与轴相交?解直线与轴相交存在在此直线上试求通过直线并与直线平行的平面方程解的方向向量ij ka 2000(6,1,3).31110(1,1,1)(1,1,1).011613(2,3,5).111804,.38:2(4)3()50,2350.3l z x y x y z x y z =-=-=---=--==--===----++=+-=的方向向量平面的法向量在的方程中令得所求平面方程即i j kb ij kn04316.(1,2,3).132(1,2,3):(1)3(2)2(3)0.43.32:1(1)3(432)2(323)0,,215(,,2).222x y z x y z x t y t z t t t t t d --==-------==⎧⎪=-⎨⎪=-⎩-------====求点到直线的距离解过点垂直于直线的平面直线参数方程:代入平面方程得对应交点的参数直线与平面交点为所求距离000017.(2,1,3)2230.(2,1,3)2230:2212,.322(22)2(12)(3)30..9141325,,.999141325(2,1,3)2230,,999x y z x y z x ty t t z t t t t t x y z x y z -+-=-+-==+⎧⎪=--∞<<+∞⎨⎪=+⎩+--++-==-===⎛-+-=求点到平面的距离与投影解过点垂直于平面的直线方程的参数方程代入平面方程点在平面上的投影为.(2,1,3)22302.3x y z ⎫ ⎪⎝⎭-+-==点在平面的距离为0111118..12312311(1,1,0)12311(1,1,0)123(1)2(1)30.12,131(1)2(2)3(13)0,7x y z x y z x y z x y z x y z x t y t z t t t t t -++-====--+--==-+--==---++==⎧⎪=--⎨⎪=+⎩---++==-求两平行直线与的距离解所求的就是点到直线的距离.作法与16题雷同.过点垂直于直线的平面:直线的参数方程代入平面方程111.154(,,).7771119.(2,1,3):3213(2)2(1)(3)0.1312:3(33)2(2d x y zA l A l x y z x t l y tz t t t t --==+-==--+---==-+⎧⎪=+⎨⎪=-⎩-++直线与平面交点所求距离求过点并与直线垂直且相交的直线方程.解过点垂直于直线的平面方程直线的参数方程代入平面方程求交点对应的参数他03)(3)0,.72133(,,).777,2133126246(2,1,3)(,,)(2,1,4).7777777213:.214t t B A B AB x y z ---==-=----=--=-----==-交点连结点 的直线的方向向量所求直线方程022220.36270362140.7(0,0,)2367/227/22)140,391837,(,,).777149186()()() 3.777x y z x y z A x t A y tz t t t +--=+-+=-=⎧⎪=⎨⎪=--⎩--+==----=++=求两平行平面与之间的距离解点在第一张平面上.过垂直于第二张平面的直线的参数方程:求直线与第二张平面的交点:3(3t)+6(6t)-2(所求距离 习题5.42222222222222222222221.23446161602344616160,2344616172(1)23(1)34(2)16162(1)3(1)4(2)50.(1)(1)(2)1,555232x y z x y z x y z x y z x y z x y z x y z x y z x y z ++--++=++--++=++--++=--+--++-+=-+-++-=--+++=⎛⎫ ⎪⎝⎭求椭球面的中心的坐标及三个半轴之长度.解555:(1,1,2),:,,.232-中心坐标半轴22222222222222.,:(1)811241;.(2)491425;.(3)29169;(4)2;(5)2;(6).x y z x y z x y z x y x y z x z xy ++=--=-+-=--=+==说出下列曲面的名称并画出略图椭球面单叶双曲面双叶双曲面.双曲柱面.椭圆抛物面.双曲抛物面.2222222222222222223.:(1)(1)(1)(3);(2)1;(3)1;944916(4);(5).x y z R y z x y z x x y z y z z a b a b-+++-=++=+-==-=+求下列曲面的参数方程1sin cos (1)1sin sin 0,02;3cos x R y R z R ϕθϕθϕπθπϕ=+⎧⎪=-+≤≤≤<⎨⎪=+⎩解sin cos (2)3sin sin 0,02;2cos x y z ϕθϕθϕπθπϕ=⎧⎪=≤≤≤<⎨⎪=⎩习题5.5023********(1),,,(1,1,1);(2),(2,2,4);(3)(0)(,0,).11111,2,3,(1,2,3),,123:(1)2(1)3(1)0P x t y t z t P z x y x P x y R R z x y P R R x y z x y t z t x y z =======+=>=+=---'''======-+-+-=1.求下列曲线在指定点的切线方程和法平面方程:曲面与的交线柱面与平面的交线()切线方程:法平面方程解t 211,2360.224(2),,,1,1,2,(1,1,4).,114:(2)(2)4(4)0,4200.(3)(2,2,0)(2,0,0),(1,1,1),200(0,2,2)2(0,1,1),11101x y z x y z x x y x z x x y z x x y z x y z x y R R R R R x R y z ++-=---'''=========-+-+-=++-====-===---==切线方程:法平面方程切线方程:t ij kn n a ,:0.1Ry z R +-=法平面方程2cos (5)sin 0,02x ar y br r z r θθθπ⎧=⎪=≤<+∞≤≤⎨⎪=⎩2cos 4sin 0,02cos x r y r r z r θθθπθ⎧=⎪=≤<+∞≤≤⎨⎪=⎩()cos 2.sin (0,0,02)(,,)(sin ,cos ,),(cos ,cos ,cos )sin ,cos ,),cos .0x R t y R t R b t z bt z x y z R t R t b R t R t b παβγπ=⎧⎪=>>≤≤⎨⎪=⎩'''=-==-==<求出螺旋线在任意一点处的切线的方向余弦,并证明切线与轴之夹角为常数.常数常数.解t <t,k ><t,k ><,<t,k >=12312311223311223.()(),.()()()()()().()((),(),()),()((),(),()),()()()()()()()(),()()[()()()t t t dt t t t t t dtt a t a t a t t b t b t b t t t a t b t a t b t a t b t d dt t a t b t a t b dt dtαβ==<<''=+===++=+设与是两个可导的向量函数证明设证a a b b a b a b a b a b a b a b 33111122223333112233112233()()()]()()()()()()()()()()()()[()()()()()()][()()()()()()]()()()().t a t b t a t b t a t b t a t b t a t b t a t b t a t b t a t b t a t b t a t b t a t b t a t b t a t b t t t t t +''''''=+++++''''''=+++++''=+a b a b22 4.()(),|()|().(),()()0.()(),()(),()()()()0,2()()0,()()0.t t t C t t t d d t t C t t C t t t t t t dt dtt t αβ=<<='='''==+=='=设是一条光滑曲线切常数证明与切线垂直即证r r r r r r r r r r r r r r r r r r第五章总练习题2222222222,,:(1)||||;(2)|||||;(3)(1)||||||||||||2||||20,(2)|||||||(|||)||||2|=-=--=-⇔=-⇔++=++⇔⇔=-⇔=-⇔++⇔1.设 为两个非零向量指出下列等式成立的充分必要条件与共线正交.a b a +b a b a +b a |b a +b a b .a +b a b a +b a b a b a b a b a b a b =a b a +b a |b a +b a |b a b a b a 解22|||2||||||||||||cos ||||cos 1,(3)()()000,+-⇔=⇔<>=-⇔<>=-⇔-⇔⨯-=⇔⨯-⨯=⇔⨯⇔共线且方向相反与共线共线.b a b a b a b a b a,b a b a,b a b .a +b a b a +b a b b a a b a b =a b2222222.,:(1)()();(2)();(3)()()(1)()().(2).:()0 1.(3).()(),=⨯=⨯=≠=≠=⨯⨯0设为非零向量判断下列等式是否成立不成立.例如:不成立例如成立和都是的有向体积且定向相同a,b,c a b c a b c a b =a b a b c a b c.i i j j i i j i j =i j a b c a b c a,b,c .解3.5342.5)(3)0,(4)(72)0.715160 (1)78300 (2)(1)15(2)8161()0,0.4.,:.,ABC A -+----+=--=⎧-+=⎪⎨-=⎪⎩⨯+⨯-=-=∠设为非零向量,且7与正交,与与7正交,求7利用向量运算证明下列几何命题射影定理考虑直角三角形其中2222222222a,b a b a b a b a b a b a b a b a b a b a b a b a +b a b a b a b 解(22222,,,,.,,0()(),AD AD BD CD AB BD BC AC CD CB AB AD DB AC AD DC AB AC AD DB AD DC AD AD DC DB AD DB DC AD DB DC A ====+=+==++=+++=+为直角是斜边上的高则证222222222(,).()).().D DB DC BD DC BD DC BD DC AB AD BD BD CD BD BD CD BD BD BC AC AD CD BD CD CD CD BD CD CD BC =-==⨯=+=+=+==+=+=+=同向5.,,(1,0,0),(1,1,0),(1,1,1)..(1,0,0),(1,1,0),(1,1,1).(0,1,1),(0,1,0),(0,2,1),(1,0,0)(0,2,1)(1,2,1).A B C ACDBD D A B C AC AB AD AB AC OD OA AD D ======+==+=+=已知三点的坐标分别为若是一平行四边形,求点的坐标点的解(1,2,1).坐标22222222222222212126.,()().()|||sin ,|||(1cos ,)||||||||cos ,().112127.:,:,,121012.121012x y z x y z L L L L ⨯-⨯=<>=-<>=-<>=--++--====--=-=-设为非零向量,证明设有两直线求平行于且与它们等距的平面方程2222a b a b =a b a b a b a |b a b a |b a b a b a b a b a b a b i jkn 证解(5,2,1),(1/2,1/2,1/2),5(1/2)2(1/2)(1/2)0,5210.A x y z x y z ---=-+----=+++=所求平面过点所求平面:-001101018.,||.||||||||.L P L P P P L d d P P AB d P P ⨯==⨯=⨯设直线通过点且其方向向量为证明外一点到的距离可表为平行四边形的面积v v v v v 证112121212121212121212121212121212129.,,.()0.,,()0.10.,,,.min ||Q L Q LL L PP L L PP L L PP PP L L P P L L d Q Q ∈∈⨯=⇔⇔⨯==设两直线分别通过点且它们的方向向量为证明与共面的充分必要条件为与共面共面设两直线分别通过点且它们的方向向量为与之间的距离定义为证明:,v v v v v v v v ,v v 证1211211212121212121211121212112(1),|||()|(2).||(1),8,.||()(2)(||PP L L d PP L L d L L L L PP d PP PP ⨯=⨯=⨯⨯=⨯=⨯当与平行时它们之间的距离可表示为当与为异面直线时,它们之间的距离可表示为当与平行时,它们之间的距离为上任意一点到的距离由第题v v v v v v v v v v v v v 证21212121212121212)|()|()||PP L L PP PP L L ︒︒⨯⨯⨯=⨯是在与的公垂线方向的单位向量上的投影,故其长度||是异面直线与之间的距离.v v v v v v v111122221211111222221211111222011.0:(1),()()0;(2),,()(A x B y C z D L A x B y C z D A x B y C z D A x B y C z D L L A x B y C z D A x B λλλλπλλπλλ+++=⎧⎨+++=⎩+++++++=+++++设直线L的方程为:证明对于任意两个不全为零的常数,方程表示一个通过直线的平面任意给定一个通过直线的平面必存在两个不全为零的实数,使平面的方程为22111222121111122222111122211112222)0.(1)(,,)(,,),,,()()0(,,)(,,)(0,0,0),0(,,)0y C z D A B C A B C A x B y C z D A x B y C z D A B C A B C L A x B y C z D x y z A x B y C z D λλλλλλ++=+++++++=≠+++=⎧⎨+++=2向量与不共线故对于两个不全为零的常数的主系数+是一个平面的方程,并且 上点的坐标 满足证1111122222000000111222111222,()()0.(2),()()()0.(,,).(,,)(,,)(,,),,(,,)(,,),A x B y C z D A x B y C z D L A x x B y y C z z Ax By Cz D x y z L A B C A B C A B C L A B C A B C λλπ⎩+++++++=-+-+-=+++=故满足设平面通过直线其方程为在上三个向量 与均垂直于的方向向量故共面又与都是非零向量故存在两个不全为零的121111222200012201220112201101010220202011221111122222,,(,,)(,,)(,,).()()()()().()()0.A B C A B C A B C D Ax By Cz A A x B B y C C z A x B y C z A x B y C z D D A x B y C z D A x B y C z D λλλλλλλλλλλλλλπλλ==---=---+=-++-++=++++++++=11常数使得+++故表示为121212121221212121212124012.::113380(24)(38)0,3(2)480.,(,3,2)(1,1,1)0,320,20.2,x z L L x y z y z x z y z x y z L λλλλλλλλλλλλλλλλλλλλ--=⎧-=+=-⎨-+=⎩--+-+=++---+=--=+--=-+==试求通过直线且与直线平行的平面方程.根据题的结论所求平面方程有形式由于平面与平行令解11,21,250.x y z =+-=得所求平面方程3 22213.:1,:2260.42(1);(2),.(1)(2,,).420.222()()()02y z S x x y z S S y yS x z x z yx X x Y y z Z z ππππ++=+++=++=-+-+-=已知曲面S的方程为平面的方程为求曲面的平行于的切平面方程在曲面上求到平面距离为最短及最长的点并求最短及最长的距离的法向量解22222213.:1,:2260.42(1);(2),.(1)(,,).(2,,).22/2.2,.212:21,y z S x x y z S S yS x y z S x z xy zz x y z x x x x πππππ++=+++=====++==±已知曲面S的方程为平面的方程为求曲面的平行于的切平面方程在曲面上求到平面距离为最短及最长的点并求最短及最长的距离上的点记为的法向量切平面与平行,则法向量对应坐标成比例:与曲面方程联立解 111111221,1, 1.22()()()0212 2. 2.22(3,0,0).17(,1,1),(,1,1),227(,1,1)(2,1,2)102.||331(,1,1),2y z yx X x Y y z Z z yxX Y zZ X Y Z A P A P P A P A P d P P ππ=±=±-+-+-=++=±±±==-===------====---切平面方程:,利用曲面方程得平面过点点到平面的距离点n n 2225(,1,1),25(,1,1)(2,1,2)22.||3311(,1,1)(,1,1),22210.33A P A P d S ππ=--===---到平面的距离在曲面上到平面距离为最短及最长的点分别是和并求最短及最长的距离分别是和n n222114.,1011.11011,1cos 1sin ,02.x y z z x z y z z z x y z z z x z y z z z z θθθπ-===⎧⎪=-∞<<+∞⎨⎪=⎩-==+⎧=+⎪⎪=+-∞<<+∞≤≤⎨⎪=⎪⎩直线绕轴旋转一周求所得旋转曲面的方程.直线参数方程直线绕轴旋转,对于固定的z,旋转曲面上的点组成一个圆,其半径为故旋转曲面的方程解2222222221(,0),15.01.y z b c z b c x x y z b c⎧-=>⎪⎨⎪=⎩+-=求双曲线绕轴旋转一周所得曲面的方程.解22222222116.2.21,(1) 2.x y z Oxy z yx y y x y ⎧++=⎪⎨=⎪⎩++=++=求曲线在平面上的投影曲线的方程解。
高数上册习题答案5-2

高数上册习题答案5-2高数上册习题答案5-2高等数学是大学数学的一门重要课程,它是理工科学生必修的一门课程。
在高数上册中,第五章是关于极限与连续的内容。
本文将为大家提供高数上册习题答案5-2,帮助大家更好地理解和掌握这一章节的知识。
1. 求极限(a) $\lim\limits_{x \to 0} \dfrac{\sin 2x}{\tan 3x}$解:根据极限的性质,我们可以将$\sin 2x$和$\tan 3x$分别求极限。
$\lim\limits_{x \to 0} \sin 2x = \sin 0 = 0$$\lim\limits_{x \to 0} \tan 3x = \tan 0 = 0$所以,$\lim\limits_{x \to 0} \dfrac{\sin 2x}{\tan 3x} = \dfrac{0}{0}$,这是一个不定式,我们可以尝试使用洛必达法则求解。
令$f(x) = \sin 2x$,$g(x) = \tan 3x$,则原式可以转化为$\lim\limits_{x \to 0} \dfrac{f(x)}{g(x)}$。
根据洛必达法则,我们有$\lim\limits_{x \to 0} \dfrac{f'(x)}{g'(x)} = \lim\limits_{x \to 0} \dfrac{2\cos2x}{3\sec^2 3x} = \dfrac{2}{3}$所以,$\lim\limits_{x \to 0} \dfrac{\sin 2x}{\tan 3x} = \dfrac{2}{3}$。
(b) $\lim\limits_{x \to \infty} \dfrac{x^3 + 3x^2 - 2}{2x^3 - 5x^2 + 4x}$解:根据极限的性质,我们可以将$x^3 + 3x^2 - 2$和$2x^3 - 5x^2 + 4x$分别除以$x^3$。
$\lim\limits_{x \to \infty} \dfrac{x^3 + 3x^2 - 2}{2x^3 - 5x^2 + 4x} =\lim\limits_{x \to \infty} \dfrac{1 + \dfrac{3}{x} - \dfrac{2}{x^3}}{2 - \dfrac{5}{x} + \dfrac{4}{x^2}}$当$x \to \infty$时,$\dfrac{3}{x}$和$\dfrac{2}{x^3}$的值趋近于0,$\dfrac{5}{x}$和$\dfrac{4}{x^2}$的值也趋近于0。
最新中国人民大学出版社(第四版)高等数学一第5章课后习题详解

高等数学一第5章课后习题详解课后习题全解习题5-1★★1.利用定积分的定义计算由抛物线21y x =+,直线x a =,x b =()b a >及横轴所围成的图形的面积知识点:定积分的定义及几何意义 思路:根据求定积分的三步骤做 解:将[],a b 分成n 等分,取(1,2,)i i n ξ=为第i 个小区间1[(),()]i ia b a a b a n n-+-+-的右端点,则,i b a x n λ-=∆=,i b aa i nξ-=+ 显然, 0,n λ→⇔→∞于是根据定积分的几何意义,该图形面积lim ()nbi i ai A ydx y x λξ→===∆∑⎰ 21lim [()1]nn i b a b aa in n→∞=--=++∑ 22221()lim [12]n n i b a b a b a a ai i n n n→∞=---=+++∑222211()lim [(1)2]nnn i i b a b a b a n a a i in n n →∞==---=+++∑∑22232()(1)()1lim{()[1(1)(21)]}26n a b a n n b a b a a n n n n n →∞-+-=-+++++221()11()lim[1()(1)(1)(2)]6n b a b a a a b a n n n→∞-=-++-++++ 222()()[1]3b a b a a ab a -=-++-+33().3b a b a -=+- ★★2.利用定积分的定义计算下列积分:知识点:定积分的定义 思路:根据求定积分的三步骤做(1)baxdx ⎰()a b <.解:易见函数[](),f x x C a b =∈,从而可积,将[],a b 分成n 等分,则,i b ax nλ-=∆=于是0,n λ→⇔→∞;取(1,2,)i i n ξ=为第i 个小区间的右端点,则,0,1,2,,1,ib aa ii n nξ-=+=-所以110lim ()lim ()n n bi i an i i b a b axdx f x a in nλξ--→→∞==--=∆=+∑∑⎰1()lim{[(0121)]}n b ab a na n n n→∞-=-+++++-2(1)()lim[]2n b a n n b a a n →∞--=-+1()lim[(1)]2n b a b a a n→∞-=-+-221()()().22b a b a a b a -=-+=-(2)1ln exdx ⎰解:用分点(0,1,,)i ni x e i n ==划分区间[]1,e :11,1,2,,i i nni i i x x x e e i n --∆=-=-=, 取i ξ是区间右端点,则 ,()ln()ln ,i i nnii i i i x e f e nξξξ=====作和,并取极限得:111ln lim ()lim ()i i nnenn i i n n i i i xdx f x e e nξ-→∞→∞===∆=-∑∑⎰111111lim{[()]}i i i nn n n nn i i i i e e e n n n --→∞==-=-+∑∑11111(1)lim lim (1)i nn n n i n e e e e n n e -→∞→∞=-=-=--∑111(1)lim ()1n n e e n e →∞=--- 记()1xx g x e =-,则当0x →时,()g x 是0型的,由洛必达法则, 有 001lim lim 11x xx x x e e →→==---从而,当n →+∞时,有111lim 11n nne →+∞=--,故1ln (1) 1.exdx e e =+-=⎰★3.利用定积分的几何意义,说明下列等式:(1)121xdx =⎰.知识点:定积分的几何意义思路:定积分的几何意义为被积函数与边界所形成曲边梯形的面积解:等式左边为直线2y x =与x 轴和1x =三条直线所围成的面积,该面积等于11212==等式右边. (2)sin 0xdx ππ-=⎰解: 等式左边为正弦曲线sin y x =与x 轴在x π=及x π=-之间所围成的面积,其左右两边面积互为相反数. 则sin ()0xdx A A ππ-=-+==⎰等式右边★★4.用定积分的几何意义求a⎰(0)b >的值.知识点:定积分的几何意义思路:定积分的几何意义为被积函数与边界所形成曲边梯形的面积 解:=是以2a b +为圆心,2b a-为半径的上半圆,其面积为:2221()()2228b a b a S r πππ--===由定积分的几何意义知:2().8ab a π-=⎰★★★5.试将和式的极限112lim p p pp n n n +→∞+++(0)p >表示成定积分.知识点:定积分的定义思路:根据定积分的定义推导过程可知,求和的极限公式可表示为定积分解: 112112limlim [()()()]p p p p pp p n n n n n n n nn +→∞→∞+++=+++11lim ()n pn i i n n→∞==∑设()p f x x =,则用定义求解1()f x dx ⎰为:①、等分[0,1]为n 个小区间:11[,], 1,2,, i i ii n x n nn-=∆=②、求和:取区间1[,]i i n n -上的右端点为i ξ,即i in ξ=,作和:111()n ni i i i i f x nn ξ==∆=⨯∑∑③、求极限:011111lim()lim ()lim ()nnn p pi i n n i i i i i f x nn n n λξ→→∞→∞===∆=⨯=∑∑∑∴1101121lim lim ()p p p n pp p n n i n i x dx n n n+→∞→∞=+++==∑⎰ ★★★6.有一河,宽为200米,从一岸到正对岸每隔20米测量一次水深,测得数据如下:试用梯形公式求此河横截面面积的近似值.知识点:定积分的几何意义思路:由定积分定义知:求定积分(曲边梯形面积)的第二步:用小矩形面积近似代替小曲边梯形面积,即1()()ii x i i x f x f x dx ξ-∆≈⎰,若用小梯形面积近似代替小曲边梯形面积则为:111[()()]()2i i x i i i x f x f x x f x dx --+∆≈⎰。
高等数学同济大学数学系 第七版上册第五章课后答案

高等数学(同济大学数学系-第七版)上册第五章课后答案高等数学(同济大学数学系第七版)上册第五章:定积分课后习题答案39/ 1.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 2.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 3.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 4.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 5.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 6.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 7.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 8.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 9.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 10.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 11.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 12.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 13.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 14.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 15.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 16.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 17.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 18.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 19.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 20.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 21.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 22.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 23.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 24.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 25.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 26.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 27.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 28.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 29.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 30.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 31.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 32.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 33.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 34.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 35.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 36.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 37.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 38.高等数学(同济大学数学系-第七版)上册第五章课后答案39/ 39.。
完整,《高等数学》候风波第五章不定积分思考题答案参考

第五章不定积分第一节不定积分的概念及性质思考题:1.在不定积分的性质x x f k x x kf d )(d )(中,为何要求0k ?答:因为0k 时,C x x x kf d 0d )((任意常数),而不是0.2.思考下列问题:(1)若C x x x f x sin 2d )(,则)(x f 为何?答:x x x f x f x cos 2ln 2)d )(()(.(2)若)(x f 的一个原函数的x cos ,则()d f x x 为何?答:C x C x f xx f x x x f sin )(d )(,sin )(cos )(.(3)若)(x f 的一个原函数为3x ,问)(x f 为何?答:233)()(x x x f .第二节不定积分的积分方法思考题:1.第一换元法(即凑微分法)与第二换元法的区别是什么?答:第一换元法与第二换元法的区别在于置换的变元不同,前者将被积函数)()]([x x f 中的中间变量)(x 作为新的积分变量,而后者将原积分变量x 替换成函数)(t ,以t 作为新的积分变量.2.应用分部积分公式u v uv v u d d 的关键是什么?对于积分x x g x f d )()(,一般应按什么样的规律设u 和v d ?答:应用分部积分公式的关键是恰当的选择u 和v d ,对于积分x x g x f d )()(,一般应按如下的规律去设u 和v d :(1)由v d 易求得v ;(2)u vd 应比v ud 容易积出.3.分别总结第一换元法、第二换元法的规律.答:一般地,若被积函数中含有22a x 或22x a,则可利用三角函数的平方关系化原积分为三角函数的积分;若被积函数中含有n b ax ,则可令n b ax =t ,将原积分化为有理函数的积分.。
23高数切片讲义第5章课后习题与答案

第五章 二重积分【基础练习题44】1. 根据二重积分的性质,比较下列积分的大小 (1)2d Dx y 与 3d Dx y ,其中积分区域D 是由x 轴、y 轴与直线1x y 所围成; (2)2d Dx y 与 3d Dx y ,其中积分区域D 是由圆周 22212x y 所围成; (3)ln d Dx y 与 2ln d Dx y,其中积分区域D 是三角形闭区域,三个顶点分别为 1,0,1,1,2,0; (4)ln d Dx y 与 2ln d Dx y,其中 ,35,01.D x y x y2.设1D I,222cos()d DI x y ,2223cos()d DI x y, 其中22(,)1D x y x y ,则 ( )(A )123I I I . (B )321I I I . (C )312I I I .(D )213I I I .【基础练习题44解析】1.【解析】(1)在积分区域D 上,01x y ,故有32()()x y x y . 故32d d DDx y x y . (2)由于积分区域D 位于半平面(,)1x y x y 内,故在D 上有23()()x y x y . 从而23d d DDx y x y . (3)由于积分区域D 位于条形区域(,)12x y x y 内,故知区域D 上的点满足0ln()1x y ,从而有2[ln()]ln()x y x y . 因此高等数学切片课后习题23高数切片讲义第3章课后习题与答案2ln d ln d DDx y x y. (4)由于积分区域D 位于半平面(,)e x y x y 内,故在D 上有ln()1x y ,从而2[ln()]ln()x y x y. 因此 2ln d ln d DDx y x y. 2.【答案】A.【解析】当221x y 时,有222220()1x y x y又cos x 在 0,1上为减函数,故有22222cos()cos x y x y且等号仅在部分点成立,由二重积分的比较性质知,321.I I I【基础练习题45】1. 画出积分区域,并计算下列二重积分:(1)D ,其中D 是由两条抛物线y 2y x 所围成的闭区域;(2)2d Dxy,其中D 是由圆周224x y 及y 轴所围成的右半闭区域; (3)e d x y D,其中(,) 1D x y x y ; (4)22()d D xy x ,其中D 是由直线2,y y x 及2y x 所围成的闭区域.2. 改换下列二次积分的积分次序: (1)10d (,)d yy f x y x;(2)2220d (,)d yy y f x y x;(3)10d (,)d y f x y x ; (4)212d (,)d x x f x y y ;(5)11d (,)d xx f x y y;(6)sin 0sin2d (,)d xxx f x y y.【基础练习题45解析】1.【解析】(1)D 可用不等式表示为2x y 01x (如图1).于是,237111424000226d d ()d .3355Dx x x y x y x x x x(2)D 可用不等式表示为0x 22y (如图2).故,22222222164d d d (4)d .215Dxy y y x x y y y图1 图2 (3)如图3,12D D D ,其中12(,)11,10,(,) 11,01.D x y x y x x D x y x y x x因此,12e d e d e d x y x y x yDD D 0111111e d e d e d e d x x x y x y x x x y x y1211211(ee )d (e e )d x x x x1e e . (4):,022yD x y y (如图4),故 2222202()d d ()d yy Dx y x y x y x x32222d 32yy x x y x y232019313d 2486y y y.图3 图4 2.【解析】(1)所给二次积分等于二重积分(,)d Df x y ,其中 (,)0,01D x y x y y .D 可改写为 (,)1,01x y x y x (如图5),于是 原式110d (,)d xx f x y y.(2)所给二次积分等于二重积分(,)d Df x y ,其中 2(,)2 ,D x y yx y02y .又D可表示为(,)42x x y y x(如图6),因此原式42d (,)d x x f x y y.图5 图6 (3)所给二次积分等于二重积分(,)d Df x y ,其中(,)1D x y x y.又D可表示为(,)011x y y x (如图7), 因此原式11d (,)d x f x y y.(4)所给二次积分等于二重积分(,)d Df x y,其中(,)2D x y x y12x . 又D可表示为(,)211x y y x y (如图8),故原式1102d (,)d yy f x y x.图7 图8 (5)111101d (,)d d (,)d d (,)d .xyxx f x y y x f x y y y f x y x【注】原二次积分11d (,)d xx f x y y中对y 的积分上限小于下限,不符合累次积分转化规则,需要线添加负号互换上下限. (6)如图9,将积分区域D 表示为12D D ,其中12(,)arcsin arcsin ,01,(,)2arcsin ,10.D x y y x y y D x y y x y于是,原式1arcsin 00arcsin 12arcsin d (,)d d (,)d yyyy f x y x y f x y x.图9【基础练习题46】1. 把下列积分化为极坐标形式,并计算积分值: (1)222d )d ax x y y; (2)0d a x y;(3)211222d ()d x xx x y y; (4)220d )d ay x y x .2. 选用适当的坐标计算下列各题: (1)22d Dx y,其中D 是由直线2,x y x 及曲线1xy 所围成的闭区域; (2)D,其中D 是由圆周221x y 及坐标轴所围成的第一象限内的闭区域; (3)22()d Dx y ,其中D 是由直线,,,3 (0)y x y x a y a y a a 所围成的闭区域.3. 作适当变换,计算下列二重积分: (1)22sin d d Dx y x y x y ,其中D 是平行四边形闭区域,它的四个顶点是π,0,2π,π,π,2π,0,π;(2)22d d Dx y x y ,其中D 是由两条双曲线1xy 和2xy 与两条直线y x 和4y x 所围成的在第一象限内的闭区域.【基础练习题46解析】1.【解析】(1)积分区域D 如图1所示. 在极坐标系中,(,)02cos ,02D a,于是,2cos 42cos 2220444420d d d 43134cos d 4.4224a a aa a原式(2)如图2,在极坐标系中,(,) 0sec ,04D a.图1 图2 于是,原式3sec 3440d d sec d 3a a340sec tan ln(sec tan )6a31)]6a . (3)积分区域D 如图3所示. 在极坐标系中,抛物线2y x 的方程是22sin cos ,即tan sec ;射线 (0)y x x 的方程是4,故 (,)0tan sec , 04D.图3于是tan sec44401d d tan sec d sec 1.原式(4)积分区域(,)0(,)0, 02D x y x y a a,故42420d d 248aa a原式.2.【解析】(1)D 如图4所示,根据D 的形状,选用直角坐标较宜,1(,) ,12D x y y x x x,故22223122119d d d ()d 4x x Dx x x y x x x y y.图4(2)根据积分区域D 的形状和被积函数的特点,选用极坐标为宜,(,)01,02D,故200d d d d D原式23111000d 221124011)2241201arcsin 22(2)8. (3)D 如图5所示. 选用直角坐标为宜. 又根据D 的边界曲线的情况,宜采用先对x 、后对y 的积分次序. 于是3332222224()d d ()d 2d 14.3a yaa y aaDa xy y x y x ay a y y a图53.【解析】(1)令,u x y v x y ,则,22u v v ux y. 在这变换下,D 的边界x y ,x y ,x y ,3x y 依次与u ,v ,u ,3v对应. 后者构成uOv 平面上D 对应的闭区域D 的边界,于是(,),3D u v u v (如图6).图6又 11(,)12211(,)222x y J u v , 因此2222223341()sin ()d d sin d d 21d sin d 21sin 2.23243D D x y x y x y u v u v u u v v u v v(2)令,yu xy v x,则x y . 在这变换下,D 的边界1xy ,y x , 2,4xy y x 依次与1,1,2,4u v u v 对应,后者构成uOv 平面上与D对应的闭区域D 的边界. 于是(,),4D u v u v (如图7).图7又(,)1111(,)42x y J u v v v v. 因此242222111117d d d d d d ln 2.223DD x y x y u u v u u v v v【基础练习题47】1.设222222322111d ,cos sin d ,e 1d ,xy x y x y x y M x y N x y P则必有( ) (A ) M N P . (B ) N M P . (C ) M N P . (D ) N P M .2. 设区域D 为222x y R ,则22d d Dx x y a .3. 设22(,)1D x y x y ,则2()d d Dx y x y . 4. 已知22,2D x y xy y ,计算二重积分32d d Dx y x y .5. 已知 ,,,1D x y y x y x x,计算二重积分esin d d xDy x y .6. 已知区域D 为圆224x y 在第一象限所围的部分,计算二重积分d d Dxx y x y .7. 求二重积分 22121e d d x y Dy x x y的值,其中D 是由直线,1y x y ,1x 围成的平面区域.8. 设区域22(,)1,0D x y x y x ,计算二重积分221d d 1Dxyx y x y . 【基础练习题47解析】1.【答案】(B ).【解析】因为 3322333x y x x y xy y ,函数3223,3,3,x x y xy y 分别是关于,,,x y x y 的奇函数,又积分区域1x y 关于x 轴、y 轴对称,故31d 0.x y M x y又22cos sin x y 在积分区域221x y 上大于0,且不恒为0;22e1x y 在积分区域221x y 上小于0,由二重积分的比较性质知2222222211cos sin d 0,e1d 0.x y x y x y N x y P故 N M P ,(B )正确.2.【答案】42π4R a .【解析】 【法1】直接利用极坐标计算2422322201d d cos d d 4RDx R x y r r a a a.【法2】由于积分区域D 关于y x 对称知222222222π222220044221d d d d d d 211d d d d 221π2π.244D DD R D x y x y x y x y x y a a a a x y x y r r r a a R R a a3.【答案】π4. 【解析】22()d d d d d d DDDx y x y x x y y x y ,因为积分区域D 关于x 轴对称,被积函数y 为关于y 的奇函数,故d d 0.Dy x y又积分区域D 关于y x 对称,故由轮换对称性知,222222π12001()d d d d d d d d 21πd d .24DDDDx y x y x x y y x y x y x y r r r4.【解析】因为积分区域D 关于y 轴对称,被积函数32x y 为关于x 的奇函数,故32d d 0.Dx y x y 5.【解析】因为积分区域D 关于x 轴对称,被积函数e sin xy 为关于y 的奇函数,故e sin d d 0.x Dy x y 6.【解析】因为积分区域D 关于y x 对称,故由轮换对称性知,21d d d d d d 2111ππd d 2.22242D DD D Dx y x y x y x y x y x y x y x y x y x y S7.【解析】如图,积分区域D 可拆分为12,D D ,其中1D 关于y 轴对称,2D 关于x 轴对称.又2121222211221e d d d d e d d ,x y x D D y D D D y x x y y x y xy x y 积分函数y 为关于y 的奇函数,关于x 的偶函数,而积分函数2212ex y xy 为关于,x y 的奇函数,由对称性知,12210210211e d d d d d d 22d .3y x y y D D y x x y y x y y y x y y8.【解析】因为22222211d d d d d d ,111D D Dxy xyx y x y x y x y x y x y 又积分区域D 关于x 轴对称,由对称性知,22d d 0,1Dxyx y x y 故 π12π202211220022221d d 11d 1πln22πln 1π.12211d d d d 11D Dr r xy x y x y x r y x y r r r。
北大版高等数学课后习题答案 完整版

习题1.1222222222222222222.,,.3,3.3,,313 2.961,9124,31.3,93,3,3.,,.,,,,p p p q p q p q q p p k p k p k k p k k p p k k q q k q p q p a a a b p a pb b b====+=+=++=++======为互素自然数除尽必除尽否则或除将余故类似得除尽与互素矛盾.设是正的素数为互素自然数,则素证 2.证 1.2222222,,.,..,:(1)|||1| 3.\;(2)|3| 2.0,13,22,1,(1,0);01,13,13,(0,1);1,13,3/2,(1,3/2).(1,0)(0,1)p a p a a pk p k pb pk b p b a b x x x x x x x x x x x x x x x X ===+-<-<<-+-<>->--<<+-<<>+-<<=-⋃数除尽故除尽类似得除尽此与为互素自然数矛盾.解下列不等式若则若则若则3.解(1)222(1,3/2).(2)232,15,1||5,1||(1).,(1)||||||;(2)||1,|||| 1.(1)|||()|||||||||,||||||.(2)|||()||||||x x x x x a b a b a b a b a b a a b b a b b a b b a b a b a b a b b a b b ⋃-<-<<<<<<<=⋃-+≥--<<+=++-≤++-=+++≥-=+-≤+-<设为任意实数证明设证明证4.,| 1.(1)|6|0.1;(2)||.60.160.1. 5.9 6.1.(, 6.1)( 5.9,).(2)0,(,)(,);0,;0,(,).11,01,.1, 1.11x x a l x x x x X l X a l a l l x a l X a a n n a b a ++>->+>+<->-<-=-∞-⋃-+∞>=++∞⋃-∞-=≠<=-∞+∞-><<>=>-=-=解下列不等式或或若若若若证明其中为自然数若解(1)证5.:6.1200001)(1)1).(,),(,).1/10.{|}.(,),,{|},10{|}./10,(1)/10,/10(1)/101/10n n n n n n n n n n n b b n a b a b n b a mA A m A a b ABC B A x x b C A x x a B m m C b a m m --+++><-=∈⋂=∅=⋃=⋂≥=⋂≤-∈-≤-Z 设为任意一个开区间证明中必有有理数取自然数 满足考虑有理数集合= 若则中有最小数-=证7.(,),(,).1/10.|}.10n n nn a b a b mn b a A m <-=∈Z ,此与的选取矛盾. 设为任意一个开区间证明中必有无理数取自然数 满足考虑无理数集合 以下仿8题.8.证习题1.26426642642666613.(1,)1).13.(,).13||13,||1,3,11||3,(,).yy xx x xyxx x x x x x xx xx x xy y x=+∞===<>++=-∞+∞+++++≤≤>≤=++=≤∈-∞+∞证明函数内是有界函数.研究函数在内是否有界时,时证解习题1.4221.-(1)0);(2)lim;(3)lim;(4)lim cos cos.1)0,|,,||.,||,|,(2)0x ax a x a x a x ax aa x a e e x ax a x aεδεεεδδεε→→→→→=>===∀>=<<<-<=-<<=∀>直接用说法证明下列各极限等式:要使取则当时故证(222222,|| 1.||||||,|||||2|1|2|,1|2|)||,||.min{,1},||,1|2|1|2|||,lim(3)0,.||(1),01),1x ax a a x a x aax a x a x a x ax a x a a aa x a x a x aa ax a x ax a e e e e eeεεεεδδεεεε→---<-=+-<+≤-+<++-<-<=-<++-<=∀>>-=-<<-<<不妨设要使由于只需(取则当时故设要使即(.1,0ln1,min{,1},0,||,1|2|lim lim lim0,|cos cos|2sin sin2sin sin||,2222,|,|cos cosx aax aax a x a x ax a x a x aeex a x a e ee ae e e e e ex a x a x a x ax a x a x a x aεεεδδεεδεδ-→+→-→<+⎛⎫<-<+=<-<-<⎪+⎝⎭===+-+-∀>-==≤-=-<-取则当时故类似证故要使取则当|时...(4)2|,lim cos cos.2.lim(),(,)(,),().1,0,0|-|,|()|1,|()||()||()|||1||.(1)1(1)lim lim2x ax ax xx af x l a a a a a u f xx a f x lf x f x l l f x l l l Mxxεδδεδδ→→→→<==-⋃+==><<-<=-+≤-+<+=+-=故设证明存在的一个空心邻域使得函数在该邻域内使有界函数对于存在使得当 时从而求下列极限证3.:2002222200000221222lim(1) 1.222sin sin1cos11122(2)lim lim lim1.2222(3)0).22(4)lim.22332(5)lim22xx x xx xxxx x xxx xxxx xax xx xx xx x→→→→→→→→+=+=⎛⎫⎛⎫⎛⎫⎪ ⎪⎪-⎝⎭⎝⎭⎪====⎪⎪⎝⎭==>---=-------2.33-=-20103030300022********(23)(22)2(6)lim 1.(21)2 1.13132(8)lim lim lim 11(1)(1)(1)(1)(1)(2)lim lim (1)(1)x x x x x x x x x x x x x x x x x x x x x x x x x x x x →∞→→→-→-→-→--+==+==-+---⎛⎫-== ⎪+++-++-+⎝⎭+-==+-+214442100(2)31.(1)3244.63(1)1(1)12(10)lim lim lim .1(11)lim x x x nn n xy y x x x x n n ny y y x y n x y y→-→→→→→→→∞--==--+====-+++-+-===-1011001001010010120.(12)lim (0)./,(13)lim(0)0,, .(14)lim lim 1x m m m mnn n x n n mm m n n x nx x a x a x a a b b x b x b b a b m na x a x a a bn m b x b x b m n x --→--→∞→∞→∞==+++≠=+++=⎧+++⎪≠=>⎨+++⎪∞>⎩=+21.11/x =+03323223220312(12)5lim(112)55lim.3(112)(16)0,l x x x xx x x x x x xx x x x x x a →→→→-+=+-+=++-+==++-+>00im lim lim x a x a x a →+→+→+⎛⎫=⎛⎫=00lim lim x a x a →+→+⎛⎫=⎫==000222200000sin 14.lim 1lim 1sin sin (1)limlim lim cos .tan sin sin(2)sin(2)2(2)lim lim lim 100323tan 3sin 2tan 3sin 2(3)lim lim lim sin 5sin 5xx x x x x x x x x x x x e x x x x x x x x x x x x xx x x x x αααββββ→→∞→→→→→→→→→⎛⎫=+= ⎪⎝⎭=====-=-利用及求下列极限:00()1/0321.sin 5555(4)lim lim 2cos sinsin sin 22(5)lim lim cos .2(6)lim 1lim 1lim 1.(7)lim(15)x x x a x a kxxxk kk k x x x yy x x xxx a x a x a a x a x ak k k e x x x y →→+→→----→∞→∞→∞→=-===+--==--⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥+=+=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦-=51/(5)50100100lim(15).111(8)lim 1lim 1lim 1.5.lim ()lim ().lim ():0,0,0|-|().lim (y y x xx x x x ax x a x y e e x x x f x f x f x A x a f x A f x δδ--→+→∞→∞→∞→→-∞→→-∞⎡⎤-=⎢⎥⎣⎦⎡⎤⎛⎫⎛⎫⎛⎫+=++= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=+∞=-∞=+∞>><<>给出及的严格定义对于任意给定的存在使得当时):0,0,().A x f x A =-∞>∆><-∆<-对于任意给定的存在使得当时习题1.5222 21.(2)sin5.(1)0,|.,,|||||,0555()(2)(1)0,|sin5sin5|2|cos||sin|.22xx x axx x x xx a x ax aεδεεεδδεεε-==∀>=<≤<<=<<=+-∀>-=<试用说法证明连续在任意一点连续要使只需取则当时有连续.要使由于证000000555()2|cos||sin|5||,5||,||,225,|||sin5sin5|,sin55()()0,0||()0.(),()/2,0||(x a x ax a x a x ax a x a x x a y f x x f x x x f xf x x f x x xf xεεεδδεδδεδδ+-≤--<-<=-<-<==>>-<>=>-<只需取则当时有故在任意一点连续.2.设在处连续且证明存在使得当时由于在处连续对于存在存在使得当时证000000000000 )()|()/2,()()()/2()/20.3.()(,),|()|(,),?(,),.0,0|||()()|,||()||()|||()()|,||.f x f x f x f x f x f xf x a b f x a bx a b f x x xf x f x f x f x f x f x f xεδδεε-<>-=>∈>>-<-<-≤-<于是设在上连续证明在上也连续并且问其逆命题是否成立任取在连续任给存在使得当时此时故在连续其证0001,,(),()|11,ln(1),1,0,(1)()(2)()arccos, 1.0;lim()lim1(0),lim()(0)x x xxf x f xxax xxf x f xa x xa x xf x f f x fπ→-→→+⎧=≡⎨-⎩+≥⎧<==⎨<+≥⎩⎪⎩=====逆命题是有理数不真例如处处不连续但是|处处连续.是无理数4.适当地选取,使下列函数处处连续:解(1)11112sin2limsin31.(2)lim()lim ln(1)ln2(1),lim()lim arccos(1)ln2,ln2.5.3:(1)lim cos lim cos0 1.(2)lim(3)lim xx x x xx xxxxxaf x x f f x a x a fae eπ→→+→+→-→-→+∞→+∞→→==+====-===-=====利用初等函数的连续性及定理求下列极限sin22sin33.(4)lim arctan arctan1.4xxx xeπ→∞→∞====()()(ln ())()(5)6.lim ()0,lim (),lim)().lim)()lim)x g x b x x x x x x g x f x g x x x x x f x a g x b f x a f x e →→→→→=====>====设证明证0lim [(ln ())()]ln 22.7.,,(1)()cos ([]),,(2)()sgn(sin ),,,,1,(3)()1,1/2, 1.1(4)()x x f x g x b a b e e a f x x x n f x x n n x x f x x x x f x ππ→===-∈=∈⎧≠==⎨=⎩+=Z Z 指出下列函数的间断点及其类型若是可去间断点请修改函数在该点的函数值,使之称为连续函数:间断点第一类间断点.间断点第一类间断点.间断点第一类间断点.,011,sin,12,11,01,2(5)(),12,2,1,2 3.1x x x x x x f x x x x x xπ⎧≤≤⎪=⎨<≤⎪-⎩⎧≤≤⎪-⎪=<≤=⎨⎪⎪<≤-⎩间断点第二类间断点.间断点第一类间断点.0000008.(),(),()()()()()()()()()()(()())()()()()()0,()().y f x y g x x h x f x g x x f x g x x h x f x g x x x g x f x g x f x x x f x g x x f x g x D x ϕϕ===+==+=+-=≡=R R 设在上是连续函数而在上有定义但在一点处间断.问函数及在点是否一定间断?在点一定间断.因为如果它在点连续,将在点连续,矛盾.而在点未必间断.例如解习题1.600001.:()lim (),lim (),,,,()0,()0,[,],,(,),()0.2.01,,sin ,.(x x P x P x P x A B A B P A P B P A B x A B P x y y x x f x εε→+∞→-∞=+∞=-∞<<>∈=<<∈=-R 证明任一奇数次实系数多项式至少有一实根.设是一奇数次实系数多项式,不妨设首项系数是正数,则存在在连续根据连续函数的中间值定理存在使得设证明对于任意一个方程有解且解是唯一的令证证000000000000000212121212121)sin ,(||1)||1||,(||1)||1||,[||1,||1],,[||1,||1],().,()()(sin sin )||0,.3.()(,x x f y y y y f y y y y f y y x y y f x y x x f x f x x x x x x x x x f x a b εεεεε=---=--+<-≤+≥+->≥--+∈--+=>-=---≥--->在连续由中间值定理存在设故解唯一设在1212112212121121121112212221212121212),,(,),0,0,(,)()()().()(),.()(),()()()()()()()(),[,]x x a b m m a b m f x m f x f m m f x f x x f x f x m f x m f x m f x m f x m f x m f x f x f x m m m m m m x x ξξξ∈>>∈+=+==<+++=≤≤=+++连续又设证明存在使得如果取即可设则在上利用连续函数的中间值定理证.4.()[0,1]0()1,[0,1].[0,1]().()(),(0)(0)0,(1)(1)10.,01.,,(0,1),()0,().5.()[0,2],(0)(2).y f x f x x t f t t g t f t t g f g f t t g t f t t y f x f f =≤≤∀∈∈==-=≥=-≤∈====即可设在上连续且证明在存在一点使得如果有一个等号成立取为或如果等号都不成立则由连续函数的中间值定理存在使得即设在上连续且证明证12121212[0,2],||1,()().()(1)(),[0,1].(0)(1)(0),(1)(2)(1)(0)(1)(0).(0)0,(1)(0),0, 1.(0)0,(0),(1),,(0,1)()(1x x x x f x f x g x f x f x x g f f g f f f f g g f f x x g g g g f ξξξ-===+-∈=-=-=-=-====≠∈=+在存在两点与使得且令如果则取如果则异号由连续函数的中间值定理存在使得证12)()0,, 1.f x x ξξξ-===+取第一章总练习题221.:581 2.3|58|1422.|58|6,586586,.3552(2)33,52333,015.5(3)|1||2|1(1)(2),2144,.22|2|,.2,2,4,2;2,3x x x x x x x x x x x x x x x x x y x x x y x y x y x y x y x -≥-≥-≥-≥-≤-≥≤-≤-≤-≤≤≤+≥-+≥-+≥-+≥=+-≤=+≤=->=求解下列不等式()或或设试将表示成的函数当时当时解解解2.解222312312,4,(2).32,41(2), 4.313.1.22,4(1)44,0.1,0.4.:1232(1)2.222221211,.22123222n n y x y y y x y y x x x x x x x x x x n n n n ->=--≤⎧⎪=⎨->⎪⎩<+≥-<++<++>≥-≠+++++=-+==++的全部用数学归纳法证明下列等式当时,2-等式成立设等式对于成立,则解证1231111121211222112312222222124(1)(1)3222,22221..1(1)(2)123(1).(1)1(11)1(1)1,(1)(1)n n n n n n n n n n n n n n n n n n n n n x nx x x nxx x x x x n x x ++++++-+++++=++++++++-+++=-+=-=-+-++++++=≠--++-===--即等式对于也成立故等式对于任意正整数皆成立当时证1,1212.1(1)123(1)(1)(1)n n n nnn n x nx x x nxn x n xx +--++++++++=++-等式成立设等式对于成立,则122122112211221221(1)(1)(1)(1)1(1)(12)(1)(1)1(1)(2)(1)(1)1(1)(2)(1)(1)1(2)(1),(1)1n n n n n n n n n n n n n n n n n n n x nx x n x x n x nx x x n x x n x nx x x x n x n x nx x x x n x n x n x x n ++++++++++-+++-+=--+++-++=--+++-++=--+++-++=--+++=-+即等式对于成立.,.|2|||25.()(1)(4),(1),(2),(2);(2)();(3)0()(4)224211222422(1)(4)1,(1)2,(2)2,(2)0.41224/,2(2)()x x f x xf f f f f x x f x x f f f f x x f x +--=---→→----------==--==-====----≤-=由归纳原理等式对于所有正整数都成立设求的值将表成分段函数当时是否有极限:当时是否有极限?解00022222222;2,20;0,0.(3).lim ()2,lim ()0lim ().(4).lim ()lim (4/)2,lim ()lim 22lim (),lim () 2.6.()[14],()14(1)(0),x x x x x x x x x x x f x f x f x f x x f x f x f x f x x f x x f →-→+→-→--→--→-+→-+→--→-⎧⎪-<≤⎨⎪>⎩==≠=-======--无因为有设即是不超过的最大整数.求003,;2(2)()0?(3)()?391(1)(0)[14]14,1467.[12]12.244(2).lim ()lim[14]14(0).(3).()12,()x y x x f f f x x f x x f f f f x y f f x f x →→+⎛⎫⎪⎝⎭==⎛⎫⎡⎤⎡⎤=-=-=-=-+=-=-=- ⎪⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦=-=-==-的值在处是否连续在连续因为不连续因为解111111.7.,0,,:(1)(1);(2)(1).n n n n n n a b a b n b a b a n b n a b a b a++++=-≤<--<++<--设两常数满足对一切自然数证明1111111()()(1),(1).118.1,2,3,,1,1.:{},{}..111,1,7,111n n n n n n n n n n n n nn n n n n n n b a b a b b a a b b b b n b b a b a b a n a b an a b n n a b a b a b n nn ++--+++--+++=<+++=+--->+-⎛⎫⎛⎫==+=+ ⎪ ⎪⎝⎭⎝⎭<+=++⎛+ ⎝类似有对令证明序列单调上升而序列单调下降,并且令则由题中的不等式证证=11111111111(1)1,111111111(1)11(1)1111111,11111.1111(1)11n n nn n nn nn nn n n n n n n n n n n n n n n n n n n n n n +++++++⎫⎛⎫-+⎪ ⎪+⎛⎫⎭⎝⎭<++ ⎪⎝⎭-+⎛⎫⎛⎫⎛⎫+-+<++ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+-+<+ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫+<+ ⎪ ⎪+⎝⎭⎝⎭⎛⎫+ ⎛⎫⎝⎭++< ⎪+⎝⎭111111121111111111(1)1111(1)11111111111111111.1111111.111n n nn n nn n n n n n n n n n n n n n n n n n nn n n n n +++++++⎛⎫-+⎪ ⎪+⎝⎭-+⎛⎫⎛⎫⎛⎫++<+-+ ⎪ ⎪⎪+++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+<+-+ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+++<+ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫++>+ ⎪++⎝⎭⇔我们证明22111211111(1)11..(1)(1)1111,1,1,11.nn n n n n n n n n n n e e e n n n n ++++>+++++⇔>++⎛⎫⎛⎫⎛⎫⎛⎫→∞+→+→+<<+ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭最后不等式显然成立当时故9.求极限22222222221111lim 1111234111111112341324351111().2233442210.()lim (00, ()lim n n n n n n n n n n n n nxf x a nx ax nxf x nx a →∞→∞→∞⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭++==→→∞=≠+===+作函数)的图形.解解0;1/,0.x x ⎧⎨≠⎩1111.?,()[,]|()|,[,].,(),[,],max{||,||}1,|()|,[,].,|()|,[,],(),[,].12.f x a b M f x M x a b M N f x N x a b M M N f x M x a b M f x M x a b M f x M x a b <∀∈≤≤∀∈=+<∀∈<∀∈-<<∀∈1在关于有界函数的定义下证明函数在区间上为有界函数的充要条件为存在一个正的常数使得设存在常数使得M 取则有反之若存在一个正的常数使得则证12121212:()()[,],()()()()[,].,,|()|,|()|,[,].|()()||()||()|,|()()||()||()|,[,].113.:()cos 0y f x y g x a b f x g x f x g x a b M M f x M g x M x a b f x g x f x g x M M f x g x f x g x M M x a b f x x x xπ==+<<∀∈+≤+<+=<∀∈==证明若函数及在上均为有界函数则及也都是上的有界函数存在证明在的任一证,0().11(,),00,,,(),1()(,)0,()(21/2)cos(21/2)0,21/20().n x f x M n n M f n M n nf x f x n n n x f x δδδδδδπ→->><>=>-=→=++=→∞+→n 邻域内都是无界的但当时不是无穷大量任取一个邻域和取正整数满足和则故在无界.但是x 故当时不是无穷大量证11111000114.lim (1)ln (0).1ln 1,ln ln(1),.lim lim 10.ln(1)ln(1)lim lim ln(1)ln lim(1)ln 1,ln (1)ln ().ln(1)15.()()nn nn n n n n y y y y y n nn n x x x xx y x y n y x n y y y y e y y xn x x n y f x g x →∞→∞→∞→→→-=>-==+==-=++=+=+==-=→→∞+证明令则注意到我们有设及在实轴上有证00002022222220000.:()(),,()lim ()lim ()().1cos 116.lim.22sin 1cos 2sin 1sin 12lim lim lim lim 1422n n n n n x x x y y f x g x x x x f x f x g x g x x x x x y y x x y y →∞→∞→→→→→→===-=⎛⎫-==== ⎪⎝⎭定义且连续证明若与在有理数集合处处相等,则它们在整个实轴上处处相等.任取一个无理数取有理数序列证明证证0011000000001.2ln(1)17.:(1)lim 1;(2)lim .ln(1)(1)lim lim ln(1)ln lim(1)ln 1.(1)11(2)lim lim lim lim ln(1)ln(1)lim1.1x a xa y x y y y y y x a a a x x aa ax x x y y a a y e e e y x y y y e ye e e e e y e e e y x x x y ye e +→→→→→+→→→→→=+-==+=+=+==---====++==证明证0111018.()lim ()0,()lim ()()0.|()|,0||.0,0,0|||()|/.min{,},0||,|()()||()||()|,li x ax ay f x a f x y g x a f x g x g x M x a x a f x M x a f x g x f x g x M Mδεδδεδδδδεε→→====<<-<>><-<<=<-<=<=设在点附近有定义且有极限又设在点附近有定义,且是有界函数.证明设对于任意存在使得当时令则时故证m ()()0.x af xg x →=19.()(,),,()()|()|() () ()(),()(,).y f x c g x f x f x c g x c f x cc f x c g x g x =-∞+∞≤⎧⎪=>⎨⎪-<-⎩-∞+∞设在中连续又设为正的常数定义如下 当当当试画出的略图并证明在上连续0000000000000|()|,0,||lim ()lim ()()().(),0,||()lim ()lim ().(),().0,,0,x x x x x x x x f x c x x g x f x f x g x f x c x x f x c g x c c g x f x c g x c c δδδδεεδ→→→→<>-<===>>-<>=====><>一若则存在当时|f(x)|<c,g(x)=f(x),若则存在当时,g(x)=c,若则对于任意不妨设存在使证()0000121212|||()|.||.(),()(),|()()||()|,(),(),|()-()|0.()()min{(),}max{(),}().max{(),()}(|()()|()())/2.min x x f x c x x f x c g x f x g x g x f x c f x c g x c g x g x g x f x c f x c f x f x f x f x f x f x f x δεδεε-<-<-<≤=-=-<>==<=+--=-++得当时设若则若 则二利用证121212123123123111123{(),()}(|()()|(()())/2.120.()[,],[()()()],3,,[,].[,],().()()(),(),.()min{(),(),()},f x f x f x f x f x f x f x a b f x f x f x x x x a b c a b f c f x f x f x f x c x f x f x f x f x f ηηη=--++=++∈∈======设在上连续又设其中证明存在一点使得若则取即可否则设证31231313000000()min{(),(),()},()(),[,],,[,],().21.()(),()g(),,.0()g()()g()x f x f x f x f x f x f x x c a b f c y f x x g x x x kf x l x x k l l kf x l x x kf x l x x ηη=<<∈==+=+≠+在连续根据连续函数的中间值定理存在一点使得设 在点连续而在点附近有定义但在不连续问是否在连续其中为常数如果在连续;如果在解,l 0,000000||()[[()lg()]()]/.22.Dirichlet ..,()1;,()0;lim (),()11(1)lim 0;(2)lim (arctan )sin 12n n n n x x x x x g x kf x x kf x l x x x x D x x x D x D x D x x x x x →→∞→+∞=+-''→→→→+⎛⎫= ⎪+⎝⎭不连续,因否则将在连续证明函数处处不连续任意取取有理数列则取无理数列则故不存在在不连续.23.求下列极限:证222001/112132100;2tan 5tan 5/5(3)lim lim 5.ln(1)sin [[ln(1)]/]sin /1lim(1).24.()[0,),0().0,(),(),,().{x x y x y n n x x x x x x x x x x x y e y f x f x x a a f a a f a a f a π→→→→+=====++++=+==+∞≤≤≥===设函数在内连续且满足设是一任意数并假定一般地试证明11},lim .lim ,(),().(),{}()0(1,2,),{}n n n n n n n n n n n n a a l a l f x x f l l a f a a a a f a n a →∞→∞++====≤=≥=单调递减且极限存在若则是方程的根即单调递减.又单调递减有下界,证111lim ,lim lim ()(lim )().25.()(,),:(0)1,(1),()()().()((,)).()()().()()n n n n n n n n n x n n a l a l a f a f a f l y E x E E e E x y E x E y E x e x E x x E x E x E nx E x +→∞→∞→∞→∞======-∞+∞==+==∀∈-∞+∞++==故有极限.设则设函数在内有定义且处处连续并且满足下列条件证明用数学归纳法易得于是证11.,()(11)(1).1(0)(())()()(),().().1111,(1)()()()(),().11()()().,n n n n n n nn mmm n n n E n E E e E E n n E n E n e E n E n e E n e n E E n E n E e E E e n n n n m E E m E e e r E n n n -=++====+-=-=--======⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭设是正整数则于对于任意整数对于任意整数即对于所有有理数lim ().,,(),()lim ()lim ().nn n r x x x x n n n r e x x E x E x E x e e e e →∞→∞→∞=→====n 对于无理数取有理数列x 由的连续性的连续性习题2.1201.,.,.()2(0)(1),;(2),?(3)lim ,?x l O x x m x x x l x x m mx mx ∆→=≤≤∆∆∆∆∆∆设一物质细杆的长为其质量在横截面的分布上可以看作均匀的现取杆的左端点为坐标原点杆所在直线为轴设从左端点到细杆上任一点之间那一段的质量为给自变量一个增量求的相应增量求比值问它的物理意义是什么求极限问它的物理意义是什么2222222000(1)2()22(2)22(2).2(2)(2)2(2).(3)lim lim 2(2)4.lim x x x m x x x x x x x x x x x m x x x m x x x x x x x x m mx x x x x x∆→∆→∆→∆=+∆-=+∆+∆-=∆+∆∆∆+∆∆==+∆+∆∆∆∆∆∆=+∆=∆∆是到那段细杆的平均线密度.是细杆在点的线密度.解333032233222000002.,:(1);(2)2,0;(3)sin 5.()(1)lim(33)lim lim (33)3.2()2(2)lim 2lim(2lim x x x x x x y ax y px p y x a x x ax y xx x x x x x x a a x x x x ax xp x x px x x xy p x xx p ∆→∆→∆→∆→∆→∆→==>=+∆-'=∆+∆+∆+∆-==+∆+∆=∆+∆-+∆-'==∆∆+∆=根据定义求下列函数的导函数解0000000)()2lim()()212lim.25(2)52cossin sin 5()sin 522(3)limlim55(2)552cos sin sin5(2)2222lim 5lim cos lim 5522x x x x x x x x x x x x xp x x x x x x x x p p x x x xx x xx x xy xxx x x x x x x ∆→∆→∆→∆→∆→∆→∆→-+∆+∆=∆+∆+∆+∆+==+∆++∆∆+∆-'==∆∆+∆∆∆+∆==∆∆5cos5.2x x =00223.()(,()):(1)2,(0,1); (2)2,(3,11).(1)2ln 2,(0)ln 2,1ln 2(-0),(ln 2) 1.(2)2,(3)6,:116(3).4.2(0)(,)(0,0)x x y f x M x f x y M y x B y y y x y x y x y y x y px p M x y x y ===+''==-==+''==-=-=>>>求下列曲线在指定点处的切线方程切线方程切线方程试求抛物线上任一点处的切线斜率解,0,.2p F x ⎛⎫⎪⎝⎭,并证明:从抛物线的焦点发射光线时其反射线一定平行于轴200022222222,,().22(),.,2222,.222,.p p py px y M PMN Y y X x yy px p y x N X y X x X x x y p p p p FN x FM x y x pxp p p x px x x FN FNM FMN M PQ x PMQ FNM FMN '===-=--=-=-=-⎛⎫⎛⎫=+=-+=-+ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫=++=+=+=∠=∠ ⎪ ⎪⎝⎭⎝⎭∠=∠=∠过点的切线方程:切线与轴交点(,0),故过作平行于轴则证2005.2341,.224,1,6,4112564(1),4 2.:6(1),.444y x x y x y x x y k y x y x y x y x =++=-'=+====⎛⎫-=-=+-=--=-+ ⎪⎝⎭曲线上哪一点的切线与直线平行并求曲线在该点的切线和法线方程切线方程:法线方程解323226.,,;(),,, (1)():(2)();(3)().()lim ()lim,lim ()limr R r R r R r R r g r GMrr R R g r R M G GM r R rg r r g r g r r GMr GMr R g r g r R RGM g r r →-→-→+→+⎧<⎪⎪=⎨⎪≥⎪⎩≠====离地球中心处的重力加速度是的函数其表达式为其中是地球的半径是地球的质量是引力常数.问是否为的连续函数作的草图是否是的可导函数明显地时连续.解,2lim (),()r R GMg r g r r R R→-==在连续.(2)33(3)()2(),()(),().r R g r GM GMg R g R g R g r r R R R-+-≠'''==-≠=时可导.在不可导227.(),:(1,3)(),(0)3,(2) 1.3(),()2.34111113,,3(),()3.2222P x y P x P P a b c P x ax bx c P x ax b b a b b a c a b P x x x ''===++=⎧⎪'=++=+=⎨⎪+=⎩==-=-+==-++求二次函数已知点在曲线上且解3222222222228.:(1)87,24 1.(2)(53)(62),5(62)12(53)903610.(3)(1)(1)tan (1)tan ,(2)tan (1)sec .9(92)(56)5(9)51254(4),56(56)y x x y x y x x y x x x x x y x x x x x y x x x x x x x x x x x x y y x x '=++=+'=+-=-++=+-'=+-=-=+-+++-+++'===++求下列函数的导函数22.(56)122(5)1(1),.11(1)x x y x y x x x ++'==-+≠=---23322222226(6)(1),.1(1)1(21)(1)1(7),.(8)10,1010ln1010(1ln10).sin cos sin (9)cos ,cos sin .(10)sin ,sin cos (s x x x x xx x x x x x x x x y x y x x x x x e e x x x x y y e e ey x y x x x x x xy x x y x x x x x y e x y e x e x e -'=≠=--+++-++-+-'==='==+=+-'=+=-+'==+=in cos ).x x +00000001001100009.:()()()(),()0().()()(1)(2).()()(),()0()()()()()()(()()())()(),(m k k k k k P x P x x x g x g x x P x m x P x k x P x k k P x x x g x g x P x k x x g x x x g x x x kg x x x g x x x h x h x ---=-≠'->=-≠''=-+-'=-+-=-定义若多项式可表为则称是的重根今若已知是的重根,证明是的重根证00)()0,()(1)kg x x P x k '=≠-由定义是的重根.000000010.()(,),()(),().()(0),(0)0.()(0)()(0)()(0)(0)lim limlim (0),(0)0.()()11.(),lim22x x x x f x a a f x f x f x f x f f f x f f x f f x f f f f xx x f x x f x x f x x f x→→→∆→--=''=-----'''==-=-=-+∆--∆'=∆若在中有定义且满足则称为偶函数设是偶函数,且存在试证明设在处可导证明证=000000000000000000000().()()()()()()1lim lim 22()()()()1lim 2()()()()11lim lim [()22x x x x x x f x x f x x f x x f x f x x f x x x x f x x f x f x x f x x x f x x f x f x x f x f x x x ∆→∆→∆→∆→∆→+∆--∆+∆--∆-⎡⎤=-⎢⎥∆∆∆⎣⎦+∆--∆-⎡⎤=+⎢⎥∆-∆⎣⎦+∆--∆-⎡⎤'=+=+⎢⎥∆-∆⎣⎦证002()]().12.,(0/2)()((),()):.f x f x y x t t P t x t y t OP x t t π''==<<=一质点沿曲线运动且已知时刻时质点所在位置满足直线与轴的夹角恰为求时刻时质点的位置速度及加速度.222222422222()()()tan ,()tan ,()()(tan ,tan ),()(sec ,2tan sec ),()(2sec tan ,2sec 4tan sec )2sec (sec ,2tan ).y t x t x t t y t t x t x t t t v t t t t v t t t t t t t t t ===='=''=+=位置解y =x 21/1/1/1/1/000013.,0()10, 00.1111(0)lim lim 1,(0)lim lim 0.1114.()||(),()()0.().()limxx x x x x x x x x xx f x ex x x x e e f f x e xe f x x a x x x a a f x x a f a ϕϕϕ→-→-→+→+-→⎧≠⎪=+⎨⎪=⎩=++''======++=-=≠='=求函数在的左右导数设其中在处连续且证明在不可导-+解证()()()()(),()lim ()().a x a a x x x a x a a a f a x a x aϕϕϕϕ-→---''=-==≠--+-f习题2.2()()()22221.,:111(2)[ln(1)],.[ln(1)](1).111(3)2.22x x xx x xx xx x x x''=-=-='''-=-=-=---'''⎡==⎣'''⎡=+=⎣=下列各题的计算是否正确指出错误并加以改正错错错3322222()221(4)ln|2sin|(14sin)cos,.2sin1ln|2sin|(14sin cos).2sin2.(())()|.() 1.(1)(),(0),(),(sin);(2)(),(sin);(3)u g xx x x xx xx x x xx xf g x f u f x xf x f f x f xd df x f xdx dx=='⎡⎤+=+⎣⎦+'⎡⎤+=+⎣⎦+''==+''''错记现设求求[]()[][]2222223(())(())?.(1)()2,(0)0,()2,(sin)2sin.(2)()()224.(sin)(sin)(sin)2sin cos sin2.(3)(())(()),(())(())().f g x f g xf x x f f x x f x xdf x f x x x x xdxdf x f x x x x xdxf g x f g x f g x f g x g x''''''====''===''==='''''=与是否相同指出两者的关系与不同解()()()222233312232323.2236(1),.111(2)sec,(cos)(cos)(cos)(cos)(sin)tan sec.(3)sin3cos5,3cos35sin5.(4)sin cos3,3sin cos cos33sin sin33sinx xy yx x xy x y x x x x x x x y x x y x xy x x y x x x x x---'==-=----'''===-=--='=+=-'==-=求下列函数的导函数:2(cos cos3sin sin3)3sin cos4.x x x x x x x-=22222222222232222222241sin 2sin cos cos (1sin )(sin )2(5),cos cos sin 2cos 2(1sin )(sin ).cos 1(6)tan tan ,tan sec sec 13tan sec tan tan (sec 1)tan .(7)sin ,s ax ax x x x x x x x y y x x x x x x x xy x x x y x x x x x x x x x y e bx y ae +-+-'==++='=-+=-+=-=-='==5422in cos (sin cos ).(8)cos 5cos sin 11(9)ln tan ,sec 24224tan 2411112tan cos 2sin 24242ax ax bx be bx e a bx b bx y y x x y y x x x x ππππππ+=+'==-=⎛⎫⎛⎫'=+=+ ⎪ ⎪⎛⎫⎝⎭⎝⎭+ ⎪⎝⎭==⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭222cos 42411sec .cos sin()211()()1(10)ln (0,),.22()x x x x x a x a x a x a y a x a y a x a a x a x a x a ππ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭===+-++--'=>≠±==+-+-22222222224.:11(1)arcsin (0),11111(2)arctan (0),.1(3)arccos (||1),2arccos 1111(4)arctan ,.111(5)ar 2xy a y aa a x y a y a a a a a x x a y x x x y x x y y x x x xa y '=>==-'=>==+⎛⎫+ ⎪⎝⎭'=<=-'===-++=求下列函数的导函数csin (0),x a a>22222222(6)ln(0)212(7)arcsin,1ya xy aayxy xx'=+==+=>⎛⎫'=++===≠±+22222222221.2112sgn(1)2.111(8)(0).212211sec2()tan()cos()s22xx x xyx xxxy a bxyxx xab a b a b a b--'===++-⎫=>≥⎪⎪⎭⎛⎫'= ⎪⎝⎭==++-++-2in21.cos(9)(1ln(1ln(1ln(1 /.(10)(11)(12)xa b xy yy yy yy yy y=+=+++=++++ '=+⎡⎤'='=='==y y'==222222222311(13)ln(),1.21(14)(1)(31)(2).ln ln(1)ln(31)ln(2),331211131321211.13132(15),(1).(16)xxxx e x e x x e x y x x a y x x a x a x ay x x x y x x x y y x x x y y x x x y e e y e e e e e ⎛⎫'=++=+= ⎪++++⎝⎭=-+-=-+++-'-=++-+--⎡⎤'=++⎢⎥-+-⎣⎦'=+=+=+11112(0).ln ()ln ln ln ln .aaxa a xaaxa x a a a x a a x a ax a a x y x a a a y a x a a ax a aa aa x a aa x a a a ----=++>'=++=++222225.()1()()84,tan (),24001001()arctan ,()100110t x t t x t t t t t t t t θθθθ===='==+2一雷达的探测器瞄准着一枚安装在发射台上的火箭,它与发射台之间的距离是400m.设t=0时向上垂直地发射火箭,初速度为0,火箭以的匀加速度8m/s 垂直地向上运动;若雷达探测器始终瞄准着火箭.问:自火箭发射后10秒钟时,探测器的仰角的变化速率是多少?解222110,(10)0.1(/).505010101006.,2m t s θπθ'==⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭弧度在图示的装置中飞轮的半径为且以每秒旋转4圈的匀角速度按顺时针方向旋转.问:当飞轮的旋转角为=时,活塞向右移动的速率是多少?20()2cos8(8)()16sin8,811()8,,,()16.2161616m/s.x t t t x t t t t t t x ππππππαπππ='=-'====-活塞向右移动的速率是解习题2.323222(1)(1).1.0,?(1)10100.1(2)2(3)(1cos)2sin ,222.:0,()().()().()()3.()()(0),()()(0).o o o x o o o x x y x x x y x xy x x x x x x x x x x x x xx x x x x x αααααβ=→=++===-=→=====→=→当时下列各函数是的几阶无穷小量阶.阶.阶.已知当时试证明设试证明证00(1)(1)(1)()()()(0).()()()().()()().4.(1)sin ,/4.sin cos ,1,1.444(2)(1)(0).o o o o o o o x x x x x x x x x x xx x x x y x x x y x x x y dy dx y x y ααβαβαβππππα+=→+=+=+=+=⎛⎫⎫⎫''===+=+=+ ⎪⎪⎪⎝⎭⎭⎭=+>':上述结果有时可以写成计算下列函数在指定点处的微分:是常数证122(1),(0),.5.1222(1)1,,.11(1)(1)(2),(1).(1).26.(1),3 3.001,11,(3).222.001x x x x x x y dy dx x dx y y dy x x x x y xe y e xe e x dy e x dx y x x x y y αααα-'=+==-'==-+=-=-++++'==+=+=+=≠-''=-∆=求下列各函数的微分:设计算当由变到时函数的增量和向相应的微分.22解 y =-(x -1)1222113333332220.0010.0011,.2.00127..1.162(1) 2.002.5328.:11(1)(0).0,.33(2)()()(,,).2()2()dy y x y a a xy y y x x a y b c a b c x a y b y ---=-=-==+=⎛⎫''+=>+==- ⎪⎝⎭-+-='-+-=求下列方程所确定的隐函数的导函数为常数0,.x ay y b-'=--。
华理高数答案第5章

华理高数答案第5章第5章(之1)第23次作业教学内容:§5.1定积分的概念5.2定积分的性质1.选择题*(1)用定积分表示的和的极限为()b?an(a).lim?n??ni?1nn??i?1nb?an?i?f?(b?a)?(b).lim?n??nni?1i?1?f?(b?a)??n?(c)林先生?f(?i)?席(席?1,席?)(d)林先生?f(?i)?席(??max1,2,?n席?1,席?)0i?1答复:D*(2)设:ibaF(x)DX,根据定积分的几何意义()(a).i是由曲线y?f(x)及直线x?a,x?b与x轴所围图形的面积,所以i?0.(b).若i?0,则上述图形面积为零,从而图形的"高"f(x)?0.(c).i是曲线y?f(x)及直线x?a,x?b与x轴之间各部分面积的代数和.(d).i是曲线y?f(x)及直线x?a,x?b与x轴所围图形的面积。
答:c*(3)函数f(x)在闭区间a,B上是连续的,f(x)在a,B()上是可积的(a).必要条件(b).充分条件答:b*(4)通过(c)。
充分必要条件(d)。
既不是充分条件,也不是必要条件a,b?上连续曲线y?f(x),直线x?a,x?b(a?b)和x轴围成图形s区?()bbb?f(b)?f(a)?(b?a) (a).f(x)dx (b).f(x)dx (c).f(x)dx(d)..?a?a?a2答:c**(5)设置在a和B部分上f(x)?0,f?(x)?0,f??(x)?0,令s1??af(x)dx,b1?f(b)?f(a)?(b?a),则有()2 (a)s1?s2?s3;(b)s2?s1?s3;(c)s3?s1?s2;(d)s2?s3?s1.s2?f(b)(b?a),s3?答:b63*2.试证不等式:4.202? 辛克斯?二证明:0?sinx?1,x?[0,?sinx2],?12?2??1,1sinx4??2dx??20212dx??2?01dx?2.**3. 尝试估算以下积分值:1dx0。
高等数学(黄立宏)(第三版)习题五课后答案
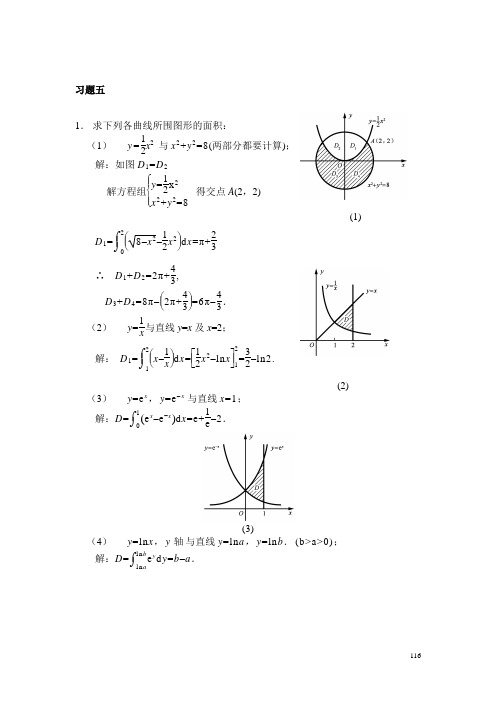
1.求下列各曲线所围图形的面积:
(1)与x2+y2=8(两部分都要计算);
解:如图D1=D2
解方程组得交点A(2,2)
(1)
∴,
.
(2)与直线y=x及x=2;
(16)
对于任意的y∈[0,h],过点(0,y)且垂直于y轴的平面截该立体为一椭圆,且该椭圆的半轴为:,同理可得该椭圆的另一半轴为:.
故该椭圆面积为
从而立体的体积为
.
5.计算底面是半径为R的圆,而垂直于底面一固定直径的所有截面都是等边三角形的立体体积.见图17.
(17)
解:以底面上的固定直径所在直线为x轴,过该直径的中点且垂直于x轴的直线为y轴,建立平面直角坐标系,则底面圆周的方程为:x2+y2=R2.
过区间[R,R]上任意一点x,且垂直于x轴的平面截立体的截面为一等边三角形,若设与x对应的圆周上的点为(x,y),则该等边三角形的边长为2y,故其面积等于
从而该立体的体积为
.
6. 求下列旋转体的体积:
(1)由y=x2与y2=x3围成的平面图形绕x轴旋转;
解:求两曲线交点得(0,0),(1,1)
.(14)
(9)极坐标曲线ρ=asin3φ;
解:
.
(9)
(10)ρ=2acosφ;
解:
.
(10)
2.求下列各曲线所围成图形的公共部分的面积:
(1)r=a(1+cosθ)及r=2acosθ;
解:由图11知,两曲线围成图形的公共部分为半径为a的圆,故D=πa2.
(11)
高等数学第五章习题附答案

利用定积分定义计算由抛物线y=x 2 , 两直线x =a,x =b (b >a )及横轴所围成的图形的面积. 题型:计算题答案:第一步: 在区间[a,b ]内插入n -1个分点i nab a x i -+=(i =1, 2, ⋅ ⋅ ⋅, n -1), 把区间[a, b]分成n 个长度相等的小区间, 各个小区间的长度为: nab x i -=∆(i =1, 2, ⋅ ⋅ ⋅, n ). 第二步: 在第i 个小区间[xi -1, xi] (i =1, 2, ⋅ ⋅ ⋅, n )上取右端点i n a b a x i i -+==ξ, 作和 n ab i n a b a x f S n i i i n i n -⋅+-+=∆=∑∑==]1)[()(211ξ ∑=+-+-+-=n i i n a b i n a b a a n a b 12222]1)()(2[ ]6)12)(1()(2)1()(2[)(222n n n n n a b n n n a b a na n a b +++⋅-++⋅-+-=]16)12)(1()()1)(()[(222+++-++-+-=nn n a b n n a b a a a b . 第三步: 令l =max {∆x 1, ∆x 2, ⋅ ⋅ ⋅ , ∆x n }nab -=, 取极限得所求面积 ∑⎰=→∆==n i i i b a x f dx x f S 10)(lim )(ξl]16)12)(1()()1)(()[(lim 222+++-++-+-=∞→n n n a b n n a b a a a b na b a b a b a b a a a b -+-=+-+-+-=)(31]1)(31)()[(3322.分数:10所属所属知识点:定积分的计算 难度:7利用定积分定义计算下列积分: (1)xdx ba ⎰(a <b);题型:计算题 答案:取分点为i n a b a x i -+=(i =1, 2, ⋅ ⋅ ⋅, n -1), 则nab x i -=∆(i =1, 2, ⋅ ⋅ ⋅, n ). 在第i 个小区间上取右端点i nab a x i i -+==ξ (i =1, 2, ⋅ ⋅ ⋅, n ). 于是 ∑∑⎰=∞→=∞→-⋅-+=∆=ni n n i i i n ba nab i n a b a x xdx 11)(lim lim ξ)(21]2)1()()([lim )(22222a b n n n a b a b a a b n -=+-+--=∞→. 分数:10所属所属知识点:定积分的计算 难度:6利用定积分定义计算下列积分: dx e x ⎰10. 题型:计算题答案:取分点为ni x i =(i =1, 2, ⋅ ⋅ ⋅, n -1), 则nx i 1=∆(i =1, 2, ⋅ ⋅ ⋅, n ). 在第i 个小区间上取右端点ni x i i ==ξ (i =1, 2, ⋅ ⋅ ⋅, n ). 于是) (1lim 1lim 21110n n n n n n i n i n xe e e nn e dx e +⋅⋅⋅++==∞→=∞→∑⎰1)1(]1[lim1])(1[1lim 11111-=--=--⋅=∞→∞→e e n e e e e e nnn n nn n n n .分数:10所属所属知识点:定积分的计算 难度:6利用定积分的几何意义 说明下列等式 1210=⎰xdx ;题型:证明题答案:⎰102xdx 表示由直线y =2x 、x 轴及直线x =1所围成的面积, 显然面积为1. 分数:12所属所属知识点:定积分的计算 难度:5利用定积分的几何意义 说明下列等式41102π=-⎰dx x ;题型:证明题答案:⎰-1021dx x )表示由曲线21x y -=、x 轴及y 轴所围成的四分之一圆的面积, 即圆x2+y2=1的面积的41: 414112102ππ=⋅⋅=-⎰dx x .分数:12所属所属知识点:定积分的计算 难度:5利用定积分的几何意义说明下列等式 ⎰-=ππ0sin xdx ;.题型:证明题答案:由于y =sin x 为奇函数, 在关于原点的对称区间[-π, π]上与x 轴所夹的面积的代数和为零, 即 ⎰-=ππ0sin xdx . 分数:12难度:5利用定积分的几何意义 说明下列等式 ⎰⎰=-2022cos 2cos πππxdx xdx .题型:证明题答案: ⎰-22cos ππxdx 表示由曲线y =cos x 与x 轴上]2,2[ππ-一段所围成的图形的面积.因为cos x 为偶函数, 所以此图形关于y 轴对称. 因此图形面积的一半为⎰20cos πxdx , 即 ⎰⎰=-2022cos 2cos πππxdx xdx .分数:12所属所属知识点:定积分的计算 难度:5水利工程中要计算拦水闸门所受的水压力, 已知闸门上水的压强p (单位面积上的压力大小)是水深h 的函数, 且有p =9×8h (kN/m2). 若闸门高H =3m , 宽L =2m , 求水面与闸门顶相齐时闸门所受的水压力P. 题型:计算题答案:建立坐标系如图. 用分点i nHx i =(i =1, 2, ⋅ ⋅ ⋅, n -1)将区间[0, H ]分为n 分个小区间, 各小区间的长为nHx i =∆(i =1, 2, ⋅ ⋅ ⋅, n ). 在第i 个小区间[x i -1, x i ]上, 闸门相应部分所受的水压力近似为 ∆Pi =9.8x il ×∆x i . 闸门所受的水压力为22118.42)1(lim 8.9lim 8.98.9lim H L nn n H L n Hi n H L x L x P n ni n ni i i n ⋅=+⋅=⋅=∆⋅⋅=∞→=∞→=∞→∑∑.将L =2, H =3代入上式得P =88.2(千牛). 分数:10所属所属知识点:定积分的计算 难度:7证明定积分性质 (1)⎰⎰=b a b a dx x f k dx x kf )()(; (2)a b dx dx ba b a -==⋅⎰⎰1. 题型:证明题 答案:(1)⎰∑∑⎰=∆=∆==→=→ba ni i i n i i i ba dxx f k x f k x kf dx x kf )()(lim )(lim )(1010ξξl l (2)a b a b x x dx n i i ni i ba -=-=∆=∆⋅=⋅→=→=→∑∑⎰)(lim lim 1lim 101010l l l 分数:8难度:5估计下列各积分的值: ⎰+412)1(dx x 1); 题型:计算题答案:因为当1£x £4时, 2£x2+1£17, 所以 )14(17)1()14(2412-⋅£+£-⋅⎰dx x ,即51)1(6412£+£⎰dx x .分数:5所属所属知识点:定积分的计算 难度:6估计下列各积分的值 ⎰+ππ4542)sin 1(dx x题型:计算题 答案:因为当ππ454££x 时, 1£1+sin2x £2, 所以)445(2)sin 1()445(14542ππππππ-⋅£+£-⋅⎰dx x ,即 ππππ2)sin 1(4542£+£⎰dx x .分数:5所属所属知识点:定积分的计算 难度:6估计下列各积分的值 ⎰331arctan xdx x ;题型:计算题答案:先求函数f(x)=x arctan x 在区间]3 ,31[上的最大值M 与最小值m.21arctan )(xx x x f ++='. 因为当331££x 时, f '(x)>0, 所以函数f(x)=x arctan x在区间]3 ,31[上单调增加. 于是 3631arctan31)31(π===f m ,33arctan 3)3(π===f M .因此)313(3arctan )313(36331-££-⎰ππxdx x ,即32arctan 9331ππ££⎰xdx x . 分数:5所属所属知识点:定积分的计算难度:6估计下列各积分的值 ⎰-022dx e xx .题型:计算题答案:先求函数xxe xf -=2)(在区间[0, 2]上的最大值M 与最小值m.)12()(2-='-x e x f xx, 驻点为21=x . 比较f(0)=1, f(2)=e 2, 41)21(-=e f ,得41-=e m , M =e 2. 于是)02()02(220412-⋅££-⎰--e dx e e x x ,即 41022222---££-⎰e dx dx e e xx .分数:5所属所属知识点:定积分的计算 难度:6设f(x)及g(x)在[a, b]上连续, 证明: (1)若在[a, b]上f(x)³0, 且0)(=⎰ba dx x f ,则在[a, b]上f(x)º0; (2)若在[a, b]上, f(x)³0, 且f(x)≢0, 则0)(>⎰ba dx x f ; (3)若在[a, b]上, f(x)£g(x), 且⎰⎰=ba ba dx x g dx x f )()(, 则在[a b]上f(x)ºg(x). 题型:证明题答案:(1)假如f(x)≢0, 则必有f(x)>0. 根据f(x)在[a , b]上的连续性, 在[a , b]上存在一点x0, 使f(x0)>0, 且f(x0)为f(x)在[a , b]上的最大值. 再由连续性,存在[c, d]Ì[a, b], 且x0Î[c, d], 使当x Î[c, d]时,2)()(0x f x f >. 于是0)(2)()()()()()(0>-³³++=⎰⎰⎰⎰⎰c d x f dx x f dx x f dx x f dx x f dx x f dc bd d c c a b a .这与条件0)(=⎰badx x f 相矛盾. 因此在[a, b]上f(x)º0. (2)证法一 因为f(x)在[a, b]上连续, 所以在[a, b]上存在一点x0, 使f(x0)>0, 且f(x0)为f(x)在[a, b]上的最大值. 再由连续性, 存在[c, d]Ì[a, b], 且x0Î[c, d], 使当x Î[c, d]时,2)()(0x f x f >. 于是⎰⎰>-³³badcc d x f dx x f dx x f 0)(2)()()(0. 证法二 因为f(x)³0, 所以0)(³⎰b a dx x f .假如)(>⎰ba dx x f 不成立. 则只有0)(=⎰badx x f ,根据结论(1), f(x)º0, 矛盾. 因此0)(>⎰ba dx x f . (3)令F(x)=g(x)-f(x), 则在[a, b]上F(x)³0且0)()()]()([)(=-=-=⎰⎰⎰⎰ba ba ba ba dx x f dx x g dx x f x g dx x F , 由结论(1), 在[a, b]上F(x)º0, 即f(x)ºg(x).分数:12所属所属知识点:定积分的计算 难度:7根据定积分的性质及第7题的结论, 说明下列积分哪一个的值较大: (1)⎰102dx x 还是⎰103dx x ? (2)⎰212dx x 还是⎰213dx x ? (3)⎰21ln xdx 还是⎰212)(ln dx x ?(4)⎰10xdx 还是⎰+10)1ln(dx x ?(5)⎰10dx e x 还是⎰+10)1(dx x ? 题型:计算题答案:(1)因为当0£x £1时, x2³x3, 所以⎰⎰³103102dx x dx x . 又当0<x <1时, x2>x3, 所以⎰⎰>103102dx x dx x . (2)因为当1£x £2时, x2£x3, 所以⎰⎰£213212dx x dx x . 又因为当1<x £2时, x2<x3, 所以⎰⎰<213212dx x dx x . (3)因为当1£x £2时, 0£ln x <1, ln x ³(ln x)2, 所以⎰⎰³21221)(ln ln dx x xdx . 又因为当1<x £2时, 0<ln x <1, ln x >(ln x)2, 所以⎰⎰>21221)(ln ln dx x xdx . (4)因为当0£x £1时, x ³ln(1+x), 所以⎰⎰+³1010)1ln(dx x xdx . 又因为当0<x £1时, x >ln(1+x), 所以⎰⎰+>1010)1ln(dx x xdx . (5)设f(x)=ex -1-x , 则当0£x £1时f '(x) =ex -1>0, f(x)=ex -1-x 是单调增加的. 因此当0£x £1时, f(x)³f(0)=0, 即ex ³1+x , 所以⎰⎰+³1010)1(dx x dx e x .又因为当0<x £1时, ex >1+x , 所以⎰⎰+>1010)1(dx x dx e x .分数:10所属所属知识点:定积分的计算 难度:6 试求函数⎰=xtdt y 0sin 当x =0及4π=x 时的导数.题型:计算题答案:x tdt dx d y x sin sin 0=='⎰, 当x =0时, y '=sin0=0; 当4π=x 时, 224sin =='πy . 分数:6所属所属知识点:微积分的计算 难度:5求由参数表示式⎰=tudu x 0sin , ⎰=tudu y 0cos 所给定的函数y 对x 的导数.题型:计算题答案:x '(t)=sin t , y '(t)=cos t , t t x t y dx dy cot )()(=''=. 分数:5所属所属知识点:微积分的计算 难度:5 求由⎰⎰=+xyttdt dt e 00cos 所决定的隐函数y 对x 的导数dxdy . 题型:计算题答案:方程两对x 求导得 0cos =+'x y e y, 于是y ex dx dy cos -=. 分数:6所属所属知识点:微积分的计算 难度:5当x 为何值时, 函数⎰-=xt dt te x I 02)(有极值?题型:计算题答案:2)(x xe x I -=', 令I '(x)=0, 得x =0. 因为当x <0时, I '(x)<0; 当x >0时, I '(x)>0, 所以x =0是函数I(x)的极小值点. 分数:6所属所属知识点:微积分的计算 难度:5计算下列各导数: (1)⎰+2021x dt t dx d ; (2)⎰+32411x x dt t dx d ; (3)⎰x xdt t dx d cos sin 2)cos(π.题型:计算题 答案:(1)dxdudt t du d u x dt t dx d u x ⋅+=+⎰⎰02202112令421221x x x u +=⋅+=. (2)⎰⎰⎰+++=+323204044111111x x x x dt t dx d dt t dx d dt t dx d⎰⎰+++-=3204041111x x dt t dx d dt t dx d)()(11)()(11343242'⋅++'⋅+-=x x x x 12281312xx x x +++-=. (3)⎰⎰⎰+-=x x x x dt t dx d dt t dx d dt t dx d cos 02sin 02cos sin 2)cos()cos()cos(πππ))(cos cos cos())(sin sin cos(22'+'-=x x x x ππ分数:15所属所属知识点:微积分的计算 难度:6⎰+-adx x x 02)13(;题型:计算题 答案:a a a x x x dx x x a a+-=+-=+-⎰230230221|)21()13(. 分数:5所属所属知识点:微积分的计算 难度:5⎰+2142)1(dx x x ; 题型:计算题 答案:852)11(31)22(31|)3131()1(333321332142=---=-=+---⎰x x dx x x . 分数:5所属所属知识点:微积分的计算 难度:5⎰+94)1(dx x x ;题型:计算题答案:94223942194|)2132()()1(x x dx x x dx x x +=+=+⎰⎰6145)421432()921932(223223=+-+= 分数:5所属所属知识点:微积分的计算 难度:5⎰+33121x dx ; 题型:计算题答案:66331arctan 3arctan arctan 13313312πππ=-=-==+⎰x x dx .分数:5所属所属知识点:微积分的计算 难度:4⎰--212121x dx ; 题型:计算题 答案:3)6(6)21arcsin(21arcsin arcsin 1212121212πππ=--=--==---⎰x x dx .分数:5所属所属知识点:微积分的计算 难度:4⎰+ax a dx 3022; 题型:计算题 答案:aa a ax a x a dx a a30arctan 13arctan 1arctan 1303022π=-==+⎰.分数:5所属所属知识点:微积分的计算 难度:5⎰-124x dx ; 题型:计算题 答案:60arcsin 21arcsin 2arcsin 41012π=-==-⎰x x dx分数:5所属所属知识点:微积分的计算 难度:5dx x x x ⎰-+++012241133; 题型:计算题 答案:13012201224|)arctan ()113(1133---+=++=+++⎰⎰x x dx x x dx x x x 41)1arctan()1(3π+=----=分数:5所属所属知识点:微积分的计算 . 难度:5⎰---+211e xdx ; 题型:计算题 答案:1ln 1ln ||1|ln 12121-=-=+=+------⎰e x xdx e e .分数:5所属所属知识点:微积分的计算 难度:4⎰42tan πθθd ;题型:计算题 答案:4144tan )(tan )1(sec tan 4040242πππθθθθθθπππ-=-=-=-=⎰⎰d d .分数:5所属所属知识点:微积分的计算 难度:5dx x ⎰π20|sin |;题型:计算题 答案:⎰⎰⎰-=ππππ2020sin sin |sin |xdx xdx dx x πππ20cos cos x x +-==-cos π +cos0+cos2π-cos π=4. 分数:5所属所属知识点:微积分的计算 难度:5⎰2)(dx x f , 其中⎪⎩⎪⎨⎧>£+=1 2111)(2x x x x x f . 题型:计算题 答案:38|)61(|)21(21)1()(213102212102=++=++=⎰⎰⎰x x x dx x dx x dx x f . 分数:5所属所属知识点:微积分的计算 难度:6设k 为正整数. 试证下列各题: (1)⎰-=ππ0cos kxdx ; (2)⎰-=ππ0sin kxdx ;(3)⎰-=πππkxdx 2cos ; (4)⎰-=πππkxdx 2sin .题型:证明题 答案:(1)⎰--=-=--==ππππππ000)(sin 1sin 1|sin 1cos k kk k kx k kxdx . (2))(cos 1cos 1cos 1sin ππππππ-+-=-=--⎰k k k k x k k kxdxcos 1cos 1=+-=ππk kk k . (3)πππππππππ=+=+=+=---⎰⎰22|)2sin 21(21)2cos 1(21cos 2kx k x dx kx kxdx .(4)πππππππππ=+=-=-=---⎰⎰22|)2sin 21(21)2cos 1(21sin 2kx k x dx kx kxdx 分数:20所属所属知识点:微积分的计算设k 及l 为正整数, 且k ¹l . 试证下列各题: (1)⎰-=ππ0sin cos lxdx kx ; (2)⎰-=ππ0cos cos lxdx kx ; (3)⎰-=ππ0sin sin lxdx kx .题型:证明题 答案:(1)⎰⎰----+=ππππdx x l k x l k lxdx kx ])sin()[sin(21sin cos 0])cos()(21[])cos()(21[=----++-=--ππππx l k l k x l k l k . (2)⎰⎰---++=ππππdxx l k x l k lxdx kx ])cos()[cos(21cos cos])sin()(21[])sin()(21[=--+++=--ππππx l k l k x l k l k . (3)⎰⎰----+-=ππππdxx l k x l k lxdx kx ])cos()[cos(21sin sin .])sin()(21[])sin()(21[=--+++-=--ππππx l k l k x l k l k 分数:15所属知识点:微积分的计算 难度:6求下列极限: (1)xdtt xx ⎰→02cos lim ; (2)⎰⎰→xt xt x dttedt e 0220022)(lim.题型:计算题 答案:(1)11cos lim cos lim20020==→→⎰x xdt t x xx . (2)222222022)(2lim)(limx xt x t x xt x t x xedt e dt e dttedt e '⋅=⎰⎰⎰⎰→→22222202lim2limxxt x x x xt x xe dte xeedt e ⎰⎰→→=⋅=2212lim 22lim 2020222=+=+=→→x e x e e x x x x x .所属知识点:变上限积分函数 难度:6设⎩⎨⎧ÎÎ=]2 ,1[ ]1 ,0[ )(2x x x x x f . 求⎰=x dt t f x 0)()(ϕ在[0, 2]上的表达式, 并讨论(x)在(0, 2)内的连续性.题型:计算题 答案:当0£x £1时,302031)()(x dt t dt t f x xx===⎰⎰ϕ; 当1<x £2时,6121212131)()(221102-=-+=+==⎰⎰⎰x x tdt dt t dt t f x xxϕ. 因此⎪⎩⎪⎨⎧£<-££=21 612110 31)(23x x x x x ϕ. 因为31)1(=ϕ, 3131lim )(lim 30101==-→-→x x x x ϕ, 316121)6121(lim )(lim 20101=-=-=+→+→x x x x ϕ, 所以(x)在x =1处连续, 从而在(0, 2)内连续. 分数:10所属所属知识点:微积分的计算 难度:7设⎪⎩⎪⎨⎧><££=ππx x x x x f 或0 00 sin 21)(. 求⎰=x dt t f x 0)()(ϕ在(-∞, +∞)内的表达式.题型:计算题答案:当x <0时, 00)()(0===⎰⎰xxdt dt t f x ϕ; 当0£x £π时,21cos 21|cos 21sin 21)()(00+-=-===⎰⎰x t tdt dt t f x xxxϕ; 当x >π时,πππϕ000|cos 210sin 21)()(t dt tdt dt t f x xx -=+==⎰⎰⎰10cos 21cos 21=+-=π. 因此 ⎪⎩⎪⎨⎧³££-<=ππϕx x x x x 10 )cos 1(210 0)(.分数:12所属所属知识点:微积分的计算 难度:7设f(x)在[a, b]上连续, 在(a, b)内可导且f '(x)£0, ⎰-=x adt t f a x x F )(1)(. 证明在(a, b)内有F '(x)£0. 题型:证明题答案:根据积分中值定理, 存在ξÎ[a, x], 使))(()(a x f dt t f xa-=⎰ξ. 于是有)(1)()(1)(2x f ax dt t f a x x F x a -+--='⎰))(()(1)(12a x f a x x f a x ----=ξ )]()([1ξf x f a x --=. 由f '(x)£0可知f(x)在[a, b]上是单调减少的, 而a £ξ£x , 所以f(x)-f(ξ)£0. 又在(a, b)内, x -a >0, 所以在(a, b)内 0)]()([1)(£--='ξf x f ax x F . 分数:10所属所属知识点:微积分的计算 难度:8试求函数⎰=xtdt y 0sin 当x =0及4π=x 时的导数.题型:计算题 答案:x tdt dx d y x sin sin 0=='⎰, 当x =0时, y '=sin0=0; 当4π=x 时, 224sin =='πy 分数:5所属所属知识点:微积分的计算 难度:4求由参数表示式⎰=tudu x 0sin , ⎰=tudu y 0cos 所给定的函数y 对x 的导数. 题型:计算题答案:x '(t)=sin t , y '(t)=cos t , t t x t y dx dy cot )()(=''=. 分数:5所属所属知识点:微积分的计算 难度:4求由⎰⎰=+xyt tdt dt e 000cos 所决定的隐函数y 对x 的导数dxdy . 题型:计算题答案:方程两对x 求导得 e y y ' +cos x =0, 于是 y exdx dy cos -=. 分数:6所属所属知识点:微积分的计算 难度:5当x 为何值时, 函数⎰-=xt dt te x I 02)(有极值? 题型:计算题答案:2)(x xe x I -=', 令I '(x)=0, 得x =0. 因为当x <0时, I '(x)<0; 当x >0时, I '(x)>0, 所以x =0是函数I(x)的极小值点.分数:6所属所属知识点:微积分的计算 难度:5计算下列各导数: (1)⎰+2021x dt t dxd ;题型:计算题答案:(1)42022021221112x x x u dxdu dt t du d u x dt t dx d u x +=⋅+=⋅+=+⎰⎰令. 分数:5所属所属知识点:微积分的计算 难度:5计算下列各导数: ⎰+32411x x dt tdx d ;题型:计算题 答案:⎰⎰⎰+++=+323204044111111x x x x dt t dx d dt t dx d dt t dx d ⎰⎰+++-=3204041111x x dt t dx d dt t dx d )()(11)()(11343242'⋅++'⋅+-=x x x x 12281312xx xx +++-=.分数:5所属所属知识点:微积分的计算 难度:5计算下列各导数:⎰xx dt t dxd cos sin 2)cos(π题型:计算题 答案:⎰⎰⎰+-=x x x x dt t dxd dt t dx d dt t dx d cos 02sin 02cos sin 2)cos()cos()cos(πππ =-cos(πsin 2x)(sin x)'+ cos(πcos 2x)( cos x)' =-cos x ×cos(πsin 2x)-sin x ×cos(πcos 2x) =-cos x ×cos(πsin2x)- sin x ×cos(π-πsin2x) =-cos x ×cos(πsin2x)+ sin x ×cos(πsin2x) =(sin x -cos x)cos(πsin2x) 分数:5所属所属知识点:微积分的计算 难度:5⎰+-adx x x02)13(;题型:计算题答案: a a a x x x dx x x aa+-=+-=+-⎰230230221|)21()13(分数:5所属所属知识点:微积分的计算 难度:5⎰+2142)1(dx x x ;题型:计算题 答案: 852)11(31)22(31|)3131()1(333321332142=---=-=+---⎰x x dx xx 分数:5所属所属知识点:微积分的计算 难度:5⎰+94)1(dx x x ;题型:计算题 答案: 6145)421432()921932(|)2132()()1(22322394223942194=+-+=+=+=+⎰⎰x x dx x x dx x x 分数:5所属所属知识点:微积分的计算 难度:5⎰+33121x dx ; 题型:计算题 答案: 66331arctan3arctan arctan 13313312πππ=-=-==+⎰xxdx分数:5所属所属知识点:微积分的计算 难度:5⎰--212121xdx ;题型:计算题 答案:3)6(6)21arcsin(21arcsin arcsin 1212121212πππ=--=--==---⎰xx dx分数:5所属所属知识点:微积分的计算 难度:5⎰+axa dx 3022;题型:计算题 答案:aa a a x a x a dxa a30arctan 13arctan 1arctan1303022π=-==+⎰. 分数:5所属所属知识点:微积分的计算 难度:5⎰-124xdx ;题型:计算题 答案:60arcsin 21arcsin 2arcsin41012π=-==-⎰x x dx . 分数:5所属所属知识点:微积分的计算 难度:5dx x x x ⎰-+++012241133;题型:计算题答案:41)1arctan()1(|)arctan ()113(11333013012201224π+=----=+=++=+++---⎰⎰x x dx x x dx x x x . 分数:5所属所属知识点:微积分的计算 难度:5⎰---+211e x dx ;题型:计算题 答案:1ln 1ln ||1|ln 12121-=-=+=+------⎰e x xdx e e . 分数:5所属所属知识点:微积分的计算 难度:5⎰402tanπθθd ;题型:计算题 答案:4144tan )(tan )1(sec tan 40402402πππθθθθθθπππ-=-=-=-=⎰⎰d d .分数:5所属所属知识点:微积分的计算 难度:5dx x ⎰π20|sin |;题型:计算题答案:⎰⎰⎰-=ππππ2020sin sin |sin |xdx xdx dx x =-cos x|π0+cos x|ππ2=-cos π +cos0+cos2π-cos π=4. 分数:5所属所属知识点:微积分的计算 难度:5⎰20)(dx x f , 其中⎪⎩⎪⎨⎧>£+=1 211 1)(2x x x x x f .题型:计算题答案:38|)61(|)21(21)1()(2131022121020=++=++=⎰⎰⎰x x x dx x dx x dx x f . 分数:6所属所属知识点:微积分的计算 难度:5设k 为正整数. 试证下列各题:(1)⎰-=ππ0cos kxdx ; (2)⎰-=ππ0sin kxdx ; (3)⎰-=πππkxdx 2cos ; (4)⎰-=πππkxdx 2sin .题型:证明题答案:(1)⎰--=-=--==ππππππ000)(sin 1sin 1|sin 1cos k kk k kx k kxdx . (2). (3)πππππππππ=+=+=+=---⎰⎰22|)2sin 21(21)2cos 1(21cos 2kx k x dx kx kxdx . (4)πππππππππ=+=-=-=---⎰⎰22|)2sin 21(21)2cos 1(21sin 2kx k x dx kx kxdx . 分数:20所属所属知识点:微积分的计算 难度:6设k 及l 为正整数, 且k ¹l . 试证下列各题: (1)⎰-=ππ0sin cos lxdx kx ; (2)⎰-=ππ0cos cos lxdx kx ; (3)⎰-=ππ0sin sin lxdx kx .题型:证明题 答案:(1)⎰⎰----+=ππππdx x l k x l k lxdx kx ])sin()[sin(21sin cos 0])cos()(21[])cos()(21[=----++-=--ππππx l k l k x l k l k .(2)⎰⎰---++=ππππdx x l k x l k lxdx kx ])cos()[cos(21cos cos0])sin()(21[])sin()(21[=--+++=--ππππx l k l k x l k l k . (3)⎰⎰----+-=ππππdx x l k x l k lxdx kx ])cos()[cos(21sin sin .0])sin()(21[])sin()(21[=--+++-=--ππππx l k l k x l k l k . 分数:15所属所属知识点:微积分的计算 难度:6求下列极限: (1)xdt t x x ⎰→02cos lim ; (2)⎰⎰→xt xt x dttedt e 0220022)(lim.题型:计算题 答案:(1)11cos lim cos lim 2002==→→⎰x xdtt x xx .(2)2222222222002002000022002lim2lim)(2lim)(limx xt x x xxt x x xt xt x xt xt x xedt e xee dt e xedt e dt e dttedt e ⎰⎰⎰⎰⎰⎰→→→→=⋅='⋅=⎰--=+-=-+-=-=ππππππππ0cos 1cos 1)(cos 1cos 1|cos 1sin k k k k k k k k kx k kxdx2212lim22lim2020222=+=+=→→x ex ee x x x x x .分数:10所属所属知识点:微积分的计算 难度:7设⎩⎨⎧ÎÎ=]2 ,1[ ]1 ,0[ )(2x x x x x f . 求⎰=xdt t f x 0)()(ϕ在[0, 2]上的表达式, 并讨论(x)在(0, 2)内的连续性. 题型:计算题答案:当0£x £1时, 302031)()(x dt t dt t f x xx===⎰⎰ϕ; 当1<x £2时,6121212131)()(2211020-=-+=+==⎰⎰⎰x x tdt dt t dt t f x x x ϕ. 因此 ⎪⎩⎪⎨⎧£<-££=21 612110 31)(23x x x x x ϕ. 因为31)1(=ϕ, 3131lim)(lim 30101==-→-→x x x x ϕ, 316121)6121(lim )(lim 20101=-=-=+→+→x x x x ϕ, 所以(x )在x =1处连续, 从而在(0, 2)内连续.分数:10所属所属知识点:微积分的计算 难度:8设⎪⎩⎪⎨⎧><££=ππx x x x x f 或0 00 sin 21)(. 求⎰=xdt t f x 0)()(ϕ在(-∞, +∞)内的表达式. 题型:计算题答案:当x <0时, 00)()(00===⎰⎰xx dt dt t f x ϕ; 当0£x £π时,21cos 21|cos 21sin 21)()(000+-=-===⎰⎰x t tdt dt t f x xx xϕ; 当x >π时,10cos 21cos 21|cos 210sin 21)()(000=+-=-=+==⎰⎰⎰πϕπππt dt tdt dt t f x xx . 因此⎪⎪⎩⎪⎪⎨⎧³££-<=ππϕx x x x x 10 )cos 1(210 0)(.分数:12所属所属知识点:微积分的计算 难度:8设f(x)在[a, b]上连续, 在(a, b)内可导且f '(x)£0, ⎰-=xa dt t f ax x F )(1)(. 证明在(a, b)内有F '(x)£0. 题型:证明题答案:根据积分中值定理, 存在ξÎ[a, x], 使))(()(a x f dt t f xa -=⎰ξ. 于是有))(()(1)(1)(1)()(1)(22a x f a x x f a x x f a x dt t f a x x F xa----=-+--='⎰ξ)]()([1ξf x f ax --=. 由f '(x)£0可知f(x)在[a, b]上是单调减少的, 而a £ξ£x , 所以f(x)-f(ξ)£0. 又在(a, b)内, x -a >0, 所以在(a, b)内0)]()([1)(£--='ξf x f ax x F . 分数:8所属所属知识点:微积分的计算 难度:8⎰+πππ2)3sin(dx x ;题型:计算题答案:0212132cos 34cos)3cos()3sin(22=-=+-=+-=+⎰ππππππππx dx x . 分数:5所属所属知识点:定积分的计算 难度:5⎰-+123)511(x dx;题型:计算题 答案:51251110116101)511(2151)511(22122123=⋅+⋅-=+-⋅=+-----⎰x x dx. 分数:5所属所属知识点:定积分的计算 难度:5⎰203cossin πϕϕϕd ;题型:计算题 答案:⎰⎰-=20323sin cos cos sin ππϕϕϕϕϕd s d410cos 412cos 41cos 4144204=+-=-=πϕπ.分数:5所属所属知识点:定积分的计算 难度:5⎰-πθθ03)sin1(d ;题型:计算题答案:⎰⎰⎰⎰-+=+=-πππππθθθθθθθθ02002003cos )cos 1(cos sin )sin 1(d d d d34)cos 31(cos 03-=-+=πθθππ分数:5所属所属知识点:定积分的计算 难度:5⎰262cosππudu ;题型:计算题 答案:2626262622sin 4121)2cos 1(21cos ππππππππu u du u udu +=+=⎰⎰836)3sin (sin 41)62(21-=-+-=πππππ. 分数:5所属所属知识点:定积分的计算 难度:5dx x ⎰-222;题型:计算题 答案:dt t tdt t t x dx x ⎰⎰⎰+=⋅=-202022)2cos 1(cos 2cos 2sin 22ππ令2)2sin 21(20ππ=+=t t .分数:5所属所属知识点:定积分的计算 难度:5dy y ⎰--22228;题型:计算题 答案:⎰⎰⎰---⋅=-=-44222222cos 2cos 22sin 24228ππxdx x xy dyy dy y 令)2(2)2sin 21(22)2cos 1(224444+=+=+=--⎰πππππy x dx x .分数:5所属所属知识点:定积分的计算 难度:5⎰-121221dx x x ;题型:计算题 答案:41)cot ()1sin 1(cos sin cos sin 12424224212122πππππππ-=--=-=⋅=-⎰⎰⎰t t dt t tdt t t t x dx xx 令.分数:5所属所属知识点:定积分的计算 难度:5⎰+31221xxdx ;题型:计算题 答案:⎰⎰⋅⋅=+34223122secsec tan 1tan 1ππtdt t t tx xxdx 令3322sin 1sin cos 34342-=-==⎰ππππt dt tt. 分数:5所属所属知识点:定积分的计算 难度:6⎰--1145xxdx ;题型:计算题 答案:61)315(81)5(81454513133211=--=-=--⎰⎰-u u du u u x xxdx 令. 分数:5所属所属知识点:定积分的计算 难度:6⎰+411xdx ;题型:计算题 答案:)32ln 1(2|)1|ln (2)111(2211121212141+=+-=+-=⋅+=+⎰⎰⎰u u du u udu u u x xdx 令.分数:5所属所属知识点:定积分的计算 难度:6⎰--14311x dx ;题型:计算题 答案:2ln 21|)1|ln (2)111(2)2(11111210210021143-=-+=-+=-⋅-=---⎰⎰⎰u u du u du u u ux x dx 令.分数:5所属所属知识点:定积分的计算 难度:6⎰-axa xdx 20223;题型:计算题 答案:)13(3)3(3121320202222222022-=--=---=-⎰⎰a x a x a d x a xa xdx a a a.分数:5所属所属知识点:定积分的计算 难度:6dt tet ⎰-1022;题型:计算题 答案:2110102221021)2(222-----=-=--=⎰⎰e e t d edt tet t t .分数:5所属所属知识点:定积分的计算 难度:6⎰+21ln 1e xx dx ;题型:计算题 答案:)13(2ln 12ln ln 11ln 1222111-=+=+=+⎰⎰e e e xx d xxx dx.分数:5所属所属知识点:定积分的计算 难度:6⎰-++02222x x dx;题型:计算题 答案:2)1arctan(1arctan )1arctan()1(1122022222π=--=+=++=++---⎰⎰x dx x x x dx .分数:5所属所属知识点:定积分的计算 难度:6⎰-222cos cos ππxdx x ;题型:计算题答案:32)sin 32(sin sin )sin 21(2cos cos 22322222=-=-=---⎰⎰ππππππx x x d x xdx x . 分数:5所属所属知识点:定积分的计算 难度:6⎰--223cos cos ππdx x x ;题型:计算题 答案:⎰⎰---=-222223cos 1cos cos cos ππππdx x x dx x x34cos 32cos 32sin cos )sin (cos 2023223202=-=+-=--⎰⎰ππππx xxdx x dx x x 分数:5所属所属知识点:定积分的计算 难度:6⎰+π2cos 1dx x .题型:计算题答案:22cos 2sin 22cos 1000=-==+⎰⎰πππx xdx dx x .分数:5所属所属知识点:定积分的计算 难度:5利用函数的奇偶性计算下列积分: (1)⎰-ππxdx x sin 4;(2)⎰-224cos 4ππθθd ;(3)⎰--2121221)(arcsin dx x x ;(4)⎰-++55242312sin dx x x xx . 题型:计算题答案:(1) 因为x 4sin x 在区间[-π, π]上是奇函数, 所以0sin 4=⎰-ππxdx x . (2)⎰⎰⎰+==-202204224)22cos 1(8cos 42cos 4ππππθθθθθd x d d ⎰⎰++=++=20202)4cos 212cos 223(2)2cos 2cos 21(2ππθθd x x d x x23)4sin 412sin 23(2πθπ=++=x x .(3) ⎰⎰⎰=-=--21221022212122)(arcsin )(arcsin 21)(arcsin 21)(arcsin x d x dx xx dx xx324)(arcsin 3232103π==x .因为函数12sin 2423++x x x x 是奇函数, 所以012sin 552423=++⎰-dx x x x x .分数:20所属所属知识点:定积分的计算 难度:6证明: ⎰⎰-=aa adx x dx x 022)(2)(ϕϕ, 其中(u)为连续函数.题型:证明题答案:因为被积函数(x2)是x 的偶函数, 且积分区间[-a, a]关于原点对称, 所以有 ⎰⎰-=aa adx x dx x 022)(2)(ϕϕ. 分数:6所属所属知识点:定积分的计算 难度:5设f(x)在[-b, b]上连续, 证明⎰⎰---=bb bb dx x f dx x f )()(.题型:证明题答案:令x =-t, 则dx =-dt, 当x =-b 时t =b , 当x =b 时t =-b , 于是⎰⎰⎰----=--=b b bb b b dt t f dt t f dx x f )()1)(()(, 而⎰⎰---=-bb b b dx x f dt t f )()(, 所以⎰⎰---=b b bb dx x f dx x f )()(.分数:8所属所属知识点:定积分的计算 难度:6设f(x)在[a, b]上连续., 证明⎰⎰-+=ba ba dx xb a f dx x f )()(.题型:证明题答案:令x =a +b -t , 则dx =dt , 当x =a 时t =b, 当x =b 时t =a , 于是⎰⎰⎰-+=--+=b a b a abdt t b a f dt t b a f dx x f )()1)(()(, 而 ⎰⎰-+=-+ba b a dx x b a f dt t b a f )()(, 所以 ⎰⎰-+=ba ba dx xb a f dx x f )()(. 分数:8所属所属知识点:定积分的计算 难度:7 证明: ⎰⎰>+=+11122)0(11xx x x dx x dx .题型:证明题答案:令tx 1=, 则dt t dx 21-=, 当x =x 时xt 1=, 当x =1时t =1, 于是 ⎰⎰⎰+=-⋅+=+11121122211)1(1111x x xdt t dt t tx dx , 而 ⎰⎰+=+x x dx x dt t 1121121111, 所以⎰⎰+=+1112211x x x dx x dx.分数:10所属所属知识点:定积分的计算 难度:7证明: ⎰⎰-=-1010)1()1(dx x x dx x x m n n m . 题型:证明题答案:令1-x =t , 则⎰⎰⎰⎰-=-=--=-10100110)1()1()1()1(dx x x dt t t dt t t dx x x m n n m n m n m , 即⎰⎰-=-1010)1()1(dx x x dx x xm n n m.分数:8所属所属知识点:定积分的计算 难度:6证明: ⎰⎰=ππ020sin 2sin xdx xdx n n . 题型:证明题 答案:⎰⎰⎰+=ππππ2020sin sin sinxdxxdx xdx n n n, 而 ⎰⎰⎰⎰==---=202022sin sin ))((sin sinπππππππxdxtdt dt t tx xdx n n nn 令,所以⎰⎰=ππ020sin 2sin xdx xdx nn .分数:8所属所属知识点:定积分的计算 难度:8设f(x)是以l 为周期的连续函数, 证明⎰+1)(a a dx x f 的值与a 无关. 题型:证明题 答案:已知f(x +l)=f(x).⎰⎰⎰⎰⎰⎰⎰-+=++=+++ala llla lla a adxx f dx x f dx x f dx x f dx x f dx x f dx x f 00001)()()()()()()(,而⎰⎰⎰⎰=+=++=+a a ala ldx x f dx l x f dt l t f l t x dx x f 000)()()()(令, 所以 ⎰⎰=+l a adx x f dx x f 01)()(. 因此⎰+1)(a a dx x f 的值与a 无关. 分数:10所属所属知识点:定积分的计算 难度:8若f(t)是连续函数且为奇函数, 证明⎰xdt t f 0)(是偶函数; 若f(t)是连续函数且为偶函数, 证明⎰xdt t f 0)(是奇函数. 题型:证明题答案:设⎰=xdt t f x F 0)()(. 若f (t )是连续函数且为奇函数, 则f (-t )=-f (t ), 从而 )()()()1)(()()(0000x F dx x f dx u f du u f ut dtt f x F xx xx===---==-⎰⎰⎰⎰-令, 即⎰=xdt t f x F 0)()(是偶函数. 若f (t )是连续函数且为偶函数, 则f (-t )=f (t ), 从而 )()()()1)(()()(0000x F dx x f dx u f du u f ut dtt f x F xx xx-=-=-=---==-⎰⎰⎰⎰-令, 即⎰=xdt t f x F 0)()(是奇函数.分数:12所属所属知识点:定积分的计算。
《高等数学教程》第五章 定积分 习题参考答案-推荐下载

对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关,1系电过,力管根保线据护敷生高设产中技工资术艺料0不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层,机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试2下卷2,高总而中体且资配可料置保试时障卷,各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并22工且22作尽22下可22都能22可地护以缩1关正小于常故管工障路作高高;中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整,处核或理对者高定对中值某资,些料审异试核常卷与高弯校中扁对资度图料固纸试定,卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置,跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等,料,编试要5写、卷求重电保技要气护术设设装交备备置底4高调、动。中试电作管资高气,线料中课并敷3试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术,技含以来术线及避槽系免、统不管启必架动要等方高多案中项;资方对料式整试,套卷为启突解动然决过停高程机中中。语高因文中此电资,气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技,进术合行,理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对:于于在调差分试动线过保盒程护处中装,高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时,术,作是应为指采调发用试电金人机属员一隔,变板需压进要器行在组隔事在开前发处掌生理握内;图部同纸故一资障线料时槽、,内设需,备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切,验除线报从缆告而敷与采设相用完关高毕技中,术资要资料进料试行,卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
华理高数答案第5章

华理高数答案第5章第5章(之1)第23次作业教学内容:§5.1定积分的概念5.2定积分的性质1.选择题*(1)用定积分表示的和的极限为()b?an(a).lim?n??ni?1nn??i?1nb?an?i?f?(b?a)?(b).lim?n??nni?1i?1?f?(b?a)??n?(c)林先生?f(?i)?席(席?1,席?)(d)林先生?f(?i)?席(??max1,2,?n席?1,席?)0i?1答复:D*(2)设:ibaF(x)DX,根据定积分的几何意义()(a).i是由曲线y?f(x)及直线x?a,x?b与x轴所围图形的面积,所以i?0.(b).若i?0,则上述图形面积为零,从而图形的"高"f(x)?0.(c).i是曲线y?f(x)及直线x?a,x?b与x轴之间各部分面积的代数和.(d).i是曲线y?f(x)及直线x?a,x?b与x轴所围图形的面积。
答:c*(3)函数f(x)在闭区间a,B上是连续的,f(x)在a,B()上是可积的(a).必要条件(b).充分条件答:b*(4)通过(c)。
充分必要条件(d)。
既不是充分条件,也不是必要条件a,b?上连续曲线y?f(x),直线x?a,x?b(a?b)和x轴围成图形s区?()bbb?f(b)?f(a)?(b?a) (a).f(x)dx (b).f(x)dx (c).f(x)dx(d)..?a?a?a2答:c**(5)设置在a和B部分上f(x)?0,f?(x)?0,f??(x)?0,令s1??af(x)dx,b1?f(b)?f(a)?(b?a),则有()2 (a)s1?s2?s3;(b)s2?s1?s3;(c)s3?s1?s2;(d)s2?s3?s1.s2?f(b)(b?a),s3?答:b63*2.试证不等式:4.202? 辛克斯?二证明:0?sinx?1,x?[0,?sinx2],?12?2??1,1sinx4??2dx??20212dx??2?01dx?2.**3. 尝试估算以下积分值:1dx0。
北大版高等数学第五章 向量代数与空间解析几何答案 习题52.

习题5.21.(,,),,,,.||,||,2.(1,2,1),(3,0,1),(2,1,2),,,,(3,0,1)(1,2,1)(4,2xy z xy yz O x y z x y z Oxy Oyz d d d d z d x d x A B C AB BA AC BC AB =======-===--=-写出点分别到轴轴轴平面平面以及原点的距离已知三点求的坐标与模.解解,0),||20|(4,2,0)(4,2,0)25,(2,1,2)(1,2,1)(3,1,1),||11,(2,1,2)(3,0,1)(1,1,1),|| 3.3.(3,2,2),(1,3,2),(8,6,2),132(9,6,6)2AB BA AB AC AC BC BC ===-=--=-=-=--=-==--=-==-==---+a b c a b +c =1112(2,6,4)(4,3,1)(11,9,1).4.(2,5,1),(1,2,7),,.2,7).(2,5,)(1,2,7)(21,5,2,7),70,7.5.,(,,)(k k xy k k k k k k k k k A B x y z x ︒︒---+-=-==-+=-+=+-=+-++==-设分别求出沿和方向的单位向量并求常数使与平面平行1设两点的坐标分别为和解a b a b ,a b a b a b 22111222121212,,),,.111()((,,)(,,))(,,).2226.(1,2,3),(5,2,1),(1)23(2)(3)cos ,.(1)2366(2)12.(2)1(3)cos y zA B C OC OA OB x y z xy z x x y yz z =+=+=+++=-=-<>⨯-=-求连线中点的坐标设求解解a b a b a i a b a b =a b =a i = .2222,|||7.||1,||3,||2,|/3,?17|()()||||||2()11942(3),23333,cos ||||π<>======+⊥+=+=++=++++==+++⨯+==设求解a b a b |a b a b c a b +c |=a c <a,b >=<b,c >=a b +c |a b +c a b +c a b c a b +b c a c b c b c b c =<b,c >=b c .6π<b,c >=22228.||2,||6,,()()||||4360,1/3.k k k k k k k k ==⊥--=-=-==±设试求常数使解a b a +b a b.a +b a b a b 9.(1,2,1),(1,1,3),(2,5,3)(1)(2)(3)()(4)()(5)().(1)121(5,2,1),113(2)253(3,0,2).01121(3)()11323.(4)()5212532=-=-=-⨯⨯⨯⨯⨯⨯⨯⨯-=---⨯-=-⨯-=-⨯⨯---解a b c a b c j a b c a b c a b c ijka b =i j kc j =ijka b c =a b c =(1,13,21).53(5)113(12,9,7),()121(23,19,15).2531297=---⨯-=-⨯⨯=-=-----i jk i j kb c =a b c10.,(2,1,0)(0,1,2),,.(2,1,0)(0,1,2)(2,0,2),(0,1,2)(2,1,0)(2,2,2).cos ,|ABCD AB AD AC BD AC AB AD BD AD AB AC BD AC BD AC ==-<>=+=+-==-=--=--<>=在平行四边形中求两对角线的夹角解00,,.2||||||||||5,,,.2AC BD BD AC BD AB AD ABCD AC BD ππ==<>===<>=平行四边形为菱形故两对角线的夹角解二|11.(3,4,1),(2,3,0),(3,5,1),.(1,1,1)(1,1,1),(0,1,0),111(1,0,1),01012A B C ABC AB AC AB AC ABC =---=-=⨯==-=已知三点求三角形的面积三角形的面积解i j k12.(3,4,5),(1,2,2)(9,14,16).345(,,)1220,,9141613.|1,||5,3,|.344cos ,,sin ,,|||||sin ,15 4.||||555======-⨯-<>==<>=⨯=<>=⨯⨯=证明向量和是共面的因为故和是共面的.已知|求||证解a b c a b c a b c a =b a b =a b a b a b a b a b a b a b a b14.cos ,cos ,cos ,,(1)cos 0,cos 0,cos 0;(2)cos cos 0,cos 0;(3)cos cos cos .(1)(2)115.||,2x z αβγαβγαβγαβγπαβγ=≠≠==≠==-===设向量的方向余弦在下列各情况下指出的方向特征与轴垂直是沿轴的的向量.(3)与三个轴的夹角相等,都是设的三个方向角满足求的坐标解a a .a .a a a aa 22222222cos 21,(2cos 1) 1.1cos ,2(21)1,4211,2(21)0,0,.2cos 0,,(0,0,213cos ,cos ,.(1,1,0).24416.,(75)(3),(4)(72),co x x x x x x x x x αααααπααππααα+=+-==+-=-+=-=========-⊥+-⊥-设为两非零向量且求22解2cos 2cos .a a =ab ,a b a b a b a b 2222222222s ,.(75)(3)0,7||15||16||||cos ,0,(4)(72)0,7||8||30||||cos ,0.||||1516cos ,7,||||||||830cos ,7.||||716730||1516||83<>-+=-+<--=+-<⎧-+<-⎪⎪⎨⎪-<-⎪⎩---=--解a b a b a b a b a b a b >=a b a b a b a b a b >=b b a b >=a a b b a b >=a a b a ||1,1||157871cos ,.15162830==---<==--b a a b >。
《高等数学一》第五章 一元函数积分学 历年试题模拟试题课后习题(含答案解析)

第五章一元函数积分学[单选题]1、设函数f(x)连续,,则=()A、x f (x)B、a f(x)C、-x f(x)D、-a f (x)【从题库收藏夹删除】【正确答案】 C【您的答案】您未答题【答案解析】本题考察积分上限函数应用..[单选题]2、如果是的原函数,则另一个原函数是()A、B、C、sin2xD、cos2x【从题库收藏夹删除】【正确答案】 A【您的答案】您未答题【答案解析】且[单选题]3、已知且,则y= ()A、B、C、D、【从题库收藏夹删除】【正确答案】 B【您的答案】您未答题【答案解析】故故.[单选题]4、微分方程cosydy=sinxdx的通解是()A、sinx+cosy=CB、cosx+siny=CC、cosx-siny=CD、cosy-sinx=C【从题库收藏夹删除】【正确答案】 B【您的答案】您未答题【答案解析】分离变量,两端积分得sin y=-cos x+C,即cos x+sin y=C. [单选题]5、下列广义积分收敛的是().A、B、C、D、【从题库收藏夹删除】【正确答案】 A【您的答案】您未答题【答案解析】[单选题]6、().A、B、C、D、【从题库收藏夹删除】【正确答案】 C【您的答案】您未答题【答案解析】[单选题]7、计算().A、eB、0C、1D、e+1【从题库收藏夹删除】【正确答案】 C【您的答案】您未答题【答案解析】[单选题]8、().A、ln2B、ln4C、0D、1【从题库收藏夹删除】【正确答案】 A【您的答案】您未答题【答案解析】[单选题]9、下列积分中不能直接使用牛顿—莱布尼兹公式的是().A、B、C、D、【从题库收藏夹删除】【正确答案】 B【您的答案】您未答题【答案解析】[单选题]10、设是连续函数,且,则().A、0B、C、1D、2【从题库收藏夹删除】【正确答案】 B【您的答案】您未答题【答案解析】[单选题]11、计算().A、B、C、D、【从题库收藏夹删除】【正确答案】 C【您的答案】您未答题【答案解析】[单选题]12、微分方程的解为(). A、B、C、D、【从题库收藏夹删除】【正确答案】 A【您的答案】您未答题【答案解析】原方程可化为,即,由公式和通解可得:[单选题]13、设,则下列结论中错误的是().A、B、C、D、【从题库收藏夹删除】【正确答案】 A【您的答案】您未答题【答案解析】根据定积分的性质:,且都是任意常数,[单选题]14、().A、-1B、1C、2D、-2【从题库收藏夹删除】【正确答案】 A【您的答案】您未答题【答案解析】[单选题]15、设D是由直线和所围成的平面图形,其面积A =().A、B、0C、D、【从题库收藏夹删除】【正确答案】 A【您的答案】您未答题【答案解析】.[单选题]16、用换元法计算().A、B、C、D、【从题库收藏夹删除】【正确答案】 A【您的答案】您未答题【答案解析】令[单选题]17、若()A、B、C、D、【从题库收藏夹删除】【正确答案】 C【您的答案】您未答题【答案解析】[单选题]18、若().A、B、C、D、【从题库收藏夹删除】【正确答案】 B【您的答案】您未答题【答案解析】?[单选题]19、=().A、0B、1C、2D、5【从题库收藏夹删除】【正确答案】 A【您的答案】您未答题【答案解析】被积函数是奇函数,所以在对称区间上的积分为0. [单选题]20、().A、B、C、D、【从题库收藏夹删除】【正确答案】 B【您的答案】您未答题【答案解析】[单选题]21、().A、B、C、0D、【从题库收藏夹删除】【正确答案】 C【您的答案】您未答题【答案解析】给定函数对关于t的定积分,当x求导,原式相当于常数.. [单选题]22、=().A、B、C、0D、【从题库收藏夹删除】【正确答案】 C【您的答案】您未答题【答案解析】被积函数是奇函数,所以在对称区间上的积分为0.[单选题]23、已知生产某商品x个的边际收益为30-2x,则总收益函数为()A、30-2x2B、30-x2C、30x-2x2D、30x-x2【从题库收藏夹删除】【正确答案】 D【您的答案】您未答题【答案解析】R=当x=0时,R=0,所以C=0,此时R=30x-x2[单选题]24、无穷限积分().A、B、C、-1D、1【从题库收藏夹删除】【正确答案】 A【您的答案】您未答题【答案解析】. [单选题]25、积分的值为()A、0B、4C、10D、20【从题库收藏夹删除】【正确答案】 D【您的答案】您未答题【答案解析】本题用到奇函数在对称区间上的积分为0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 五 章 定 积 分
1.证明定积分性质: (是常数).
证:
2.估计下列积分值:
(1)
解:令,则
得驻点:
由,
得
由性质,得
(2)
解:令,,
所以在上单调增加,,,
即
3.比较下列积分值的大小:
(1)与
解:当时,有,且不恒等于,
,即 。
(2)与
解:当时,有,且不恒等于,,即 。
(3)与
解:令,则,
所以在上单调增加,,
且不恒等于,所以
(4)与
解:令,则,
所以在上单调增加,,
且不恒等于,所以
4.求下列各导数:
(1 (2
解:= 解:=
(3
解:
(4
解:
5.求由参数表示式所给定的函数对的导数。
解:
6.求由所确定的隐函数对的导数。
解:方程两边对求导,得:,所以
7.求下列极限:
(1)
(2)
8.设 ,求在内的表达式。
解:当时,
当时,
当时,
9.计算下列各定积分:
(1)=
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9), 其中
解:
(10),其中 .
解:
10.计算下列定积分:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
11.设在上连续,证明:.
证:令,则
左边右边
12.证明:.
证:令,则
左边=右边
13.设是以为周期的函数,证明的值与无关。
证一:
而
所以的值与无关。
证二:令,则,
所以是与无关的常数。
14.若是连续函数且为奇函数,证明是偶函数。
证:令,则
所以是偶函数。
15.证明:.
证:
即
16.
17.
18.
19.
20.
21.
22.判别下列各广义积分的收敛性,如果收敛,计算广义积分的值:
(1)
解:
即广义积分收敛于.
(2)
解:
发散.
(3)
解:
即广义积分收敛于.
(4)
解:
所以广义积分发散.
注意:本题按以下解法是错误的:
(5)
解:
而
所以
