平行四边形全章综合检测题3

合集下载

2020年人教版初中数学八年级下册第18章《平行四边形》单元综合测试题含答案

平行四边形一．选择题（共10小题）1．如图，A、B两地被池塘隔开，小康通过下列方法测出了A、B间的距离：先在AB外选一他点C，然后测出AC，BC的中点M、N，并测量出MN的长为18m，由此他就知道了A、B间的距离．下列有关他这次探究活动的结论中，错误的是（）A．AB＝36m B．MN∥AB C．MN＝CB D．CM＝AC2．平行四边形两邻角的平分线相交所成的角的大小是（）A．90°B．60°C．45°D．30°3．下列不能判定一个四边形是平行四边形的是（）A．两组对边分别平行的四边形是平行四边形B．两组对边分别相等的四边形是平行四边形C．一组对边平行另一组对边相等的四边形是平行四边形D．对角线互相平分的四边形是平行四边形4．下列说法正确的有（）①对角线互相平分的四边形是平行四边形；②平行四边形的对角互补；③平行线间的线段相等；④两个全等的三角形可以拼成一个平行四边形；⑤平行四边形的四内角之比可以是2：3：2：3．A．1个B．2个C．3个D．4个5．直角三角形中，两直角边分别是12和5，则斜边上的中线长是（）A．34 B．26 C．8.5 D．6.56．如图，在菱形ABCD中，∠BAD＝120°，点A坐标是（﹣2，0），则点B坐标为（）A．（0，2）B．（0，）C．（0，1）D．（0，2）7．下列说法中，错误的是（）A．平行四边形的对角线互相平分B．对角线互相垂直的四边形是菱形C．菱形的对角线互相垂直D．对角线互相平分的四边形是平行四边形8．如图，在△ABC中，∠BAC＝90°，AB＝8，AC＝6，M为BC上的一动点，ME⊥AB于E，MF⊥AC于F，N为EF的中点，则MN的最小值为（）A．4.8 B．2.4 C．2.5 D．2.69．如图，两把完全一样的直尺叠放在一起，重合的部分构成一个四边形，这个四边形一定是（）A．矩形B．菱形C．正方形D．无法判断10．把一张长方形纸片ABCD按如图方式折一下，就一定可以裁出（）纸片ABEF．A．平行四边形B．菱形C．矩形D．正方形二．填空题（共8小题）11．如图，在平行四边形ABCD中，∠BCD和∠ABC的平分线分别交AD于E、F两点，AB＝6，BC＝10，则EF的长度是．12．如图，四边形ABCD的对角线交于点O，从下列条件：①AD∥BC，②AB＝CD，③AO＝CO，④∠ABC ＝∠ADC中选出两个可使四边形ABCD是平行四边形，则你选的两个条件是．（填写一组序号即可）13．如图，将两条宽度都是为2的纸条重叠在一起，使∠ABC＝45°，则四边形ABCD的面积为．14．如图，矩形ABCD中，AB＝20cm，BC＝4cm，点P从A开始沿折线A﹣B﹣C﹣D以4cm/s的速度运动，点Q从C开始沿CD边以1cm/s的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达D时，另一点也随之停止运动，设运动时间为t（s），当t＝时，四边形APQD 也为矩形．15．如图，在平行四边形ABCD中，AB＝8，∠BAD的平分线与BC的延长线交于点E，与DC交于点F，且点F为边DC的中点，DG⊥AE，垂足为G，若DG＝3，则AE的边长为．16．在▱ABCD中，AE平分∠BAD交边BC于E，DF⊥AE，交边BC于F，若AD＝10，EF＝4，则AB＝．17．矩形ABCD与CEFG，如图放置，点B、C、E共线，点C、D、G共线，连接AF，取AF的中点H，连接GH，若BC＝EF＝4，CD＝CE＝2，则GH＝．18．如图，正方形OABC在直角坐标系中，点B（﹣2，2），点D为BC的中点，点E在线段OC上运动，射线ED交AB延长线于点F，设E（0，t），当△AEF是以AE为腰的等腰三角形时，点E的坐标是．三．解答题（共7小题）19．如图，在△ABC中，已知AB＝6，AC＝10，AD平分∠BAC，BD⊥AD于点D，E为BC中点．求DE 的长．20．在▱ABCD中，点E在CD边上，点F在AB边上，连接AE、CF、DF、BE，∠DAE＝∠BCF．（1）如图1，求证：四边形DFBE是平行四边形；（2）如图2，设AE交DF于点G，BE交CF于点H，连接GH，若E是CD边的中点，在不添加任何辅助线的情况下，请直接写出图中以GH为边或对角线的所有平行四边形．21．已知：如图，在矩形ABCD中，点M、N在边AD上，且AM＝DN，求证：BN＝CM．22．如图，在正方形ABCD中，点M是对角线BD上的一点，过点M作ME∥CD交BC于点E，作MF∥BC交CD于点F．求证：AM＝EF．23．已知，如图，∠ABC＝∠ADC＝90°，点E、F分别是AC、BD的中点，AC＝10，BD＝6．（1）求证：EF⊥BD；（2）求EF的长．24．如图，在△ABC中，∠ACB＝90°，CD为AB边上的中线，过点D作DE⊥BC于E，过点C作AB 的平行线与DE的延长线交于点F，连接BF，AE．（1）求证：四边形BDCF为菱形；（2）若四边形BDCF的面积为24，tan∠EAC＝，求CF的长．25．如图，在平行四边形ABCD中，过点D作DE⊥BC交BC于点E，且DE＝AD，F为DC上一点，且AD＝FD，连接AF与DE交于点G．（1）若∠C＝60°，AB＝2，求GF的长；（2）过点A作AH⊥AD，且AH＝CE，求证：AB＝DG+AH．第《18章平行四边形》单元测试题参考答案与试题解析一．选择题（共10小题）1．【分析】根据三角形的中位线定理即可判断；【解答】解：∵CM＝MA，CNB，∴MN∥AB，MN＝AB，∵MN＝18m，∴AB＝36m，故A、B、D正确，故选：C．【点评】本题考查的是三角形的中位线定理在实际生活中的运用，锻炼了学生利用几何知识解答实际问题的能力．2．【分析】根据平行四边形的性质得到∠DAB+∠ABC＝180°，由角平分线可得∠BAO+∠ABO＝90°，根据三角形的内角和定理得∠AOB＝90°，即可得到所选选项．【解答】解：▱ABCD的∠DAB的平分线和∠ABC的平分线交于O，∴∠DAB+∠ABC＝180°，∠DAO＝∠BAO＝∠DAB，∠ABO＝∠CBO＝∠ABC，∴∠BAO+∠ABO＝90°，∴∠AOB＝180°﹣90°＝90°．故选：A．【点评】本题主要考查了平行四边形的性质，角平分线的定义，三角形的内角和定理等知识点，能综合利用性质进行证明是解此题的关键．3．【分析】根据平行四边形的判定：①两组对边分别平行的四边形是平行四边形；②两组对边分别相等的四边形是平行四边形；③两组对角分别相等的四边形是平行四边形；④对角线互相平分的四边形是平行四边形；⑤一组对边平行且相等的四边形是平行四边形，即可选出答案．【解答】解：根据平行四边形的判定定理，A、B、D均符合是平行四边形的条件，C则不能判定是平行四边形．故选：C．【点评】此题主要考查学生对平行四边形的判定的掌握情况．对于判定定理：“一组对边平行且相等的四边形是平行四边形．”应用时要注意必须是“一组”，而“一组对边平行且另一组对边相等”的四边形不一定是平行四边形．4．【分析】根据平行四边形的判定定理以及性质定理即可判断．【解答】解：①正确；②平行四边形的对角相等，命题错误；③平行线间的平行线段相等，命题错误；④正确；⑤正确．故选：C．【点评】本题考查了平行四边形的判定定理以及性质定理，正确理解定理的内容是关键．5．【分析】利用勾股定理列式求出斜边，再根据直角三角形斜边上的中线等于斜边的一半解答．【解答】解：由勾股定理得，斜边＝＝13，所以，斜边上的中线长＝×13＝6.5．故选：D．【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，勾股定理，熟记性质是解题的关键．6．【分析】根据菱形的性质可得∠OAB＝∠BAD＝60°，∠AOB＝90°，解直角△AOB，求出OB，即可得到点B坐标．【解答】解：∵在菱形ABCD中，∠BAD＝120°，点A坐标是（﹣2，0），∴∠OAB＝∠BAD＝60°，∠AOB＝90°，在直角△AOB中，∵OA＝2，∴OB＝OA•tan∠OAB＝2×＝2，∴点B坐标为（0，2）．故选：D．【点评】本题考查了菱形的性质，掌握菱形的两条对角线互相垂直，并且每一条对角线平分一组对角是解题的关键．也考查了锐角三角函数定义，坐标与图形性质．7．【分析】根据平行四边形和菱形的性质对各个选项进行分析从而得到最后答案．【解答】解：根据平行四边形和菱形的性质得到ACD均正确，而B不正确，因为对角线互相垂直的四边形也可能是梯形．故选：B．【点评】主要考查了平行四边形和特殊平行四边形的特性，并利用性质解题．平行四边形基本性质：①平行四边形两组对边分别平行；②平行四边形的两组对边分别相等；③平行四边形的两组对角分别相等；④平行四边形的对角线互相平分．菱形的特性是：四边相等，对角线互相垂直平分．8．【分析】过点A作AM⊥BC于点M′，根据勾股定理求出BC的长，再由三角形的面积公式求出AM′的长．根据题意得出四边形AEMF是矩形，故可得出AM＝EF，MN＝AM，当MN最小时，AM最短，此时M与M′重合，据此可得出结论．【解答】解：过点A作AM⊥BC于点M′，∵在△ABC中，∠BAC＝90°，AB＝8，AC＝6，∴BC＝＝10，∴AM′＝＝．∵ME⊥AB于E，MF⊥AC于F，∴四边形AEMF是矩形，∴AM＝EF，MN＝AM，∴当MN最小时，AM最短，此时点M与M′重合，∴MN＝AM′＝＝2.4．故选：B．【点评】本题考查了矩形的性质的运用，勾股定理的运用，三角形的面积公式的运用，垂线段最短的性质的运用，解答时求出AM的最小值是关键．9．【分析】由条件可知AB∥CD，AD∥BC，再再证明AB＝BC即可解决问题．【解答】解：过点D作DE⊥AB于E，DF⊥BC于F．∵两张长方形纸条的宽度相等，∴DE＝DF．又∵平行四边形ABCD的面积＝AB•DE＝BC•DF，∴AB＝BC，∴平行四边形ABCD为菱形．故选：B．【点评】本题考查了菱形的判定，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．10．【分析】根据折叠定理得：所得的四边形有三个直角，且一组邻边相等，所以可以裁出正方形纸片．【解答】解：由已知，根据折叠原理，对折后可得：∠FAB＝∠B＝∠AFE＝90°，AB＝AF，∴四边形ABEF是正方形，故选：D．【点评】此题考查了正方形的判定和折叠的性质，关键是由折叠原理得到四边形有三个直角，且一组邻边相等．二．填空题（共8小题）11．【分析】根据平行四边形的性质可知∠DEC＝∠ECB，又因为CE平分∠BCD，所以∠DCE＝∠ECB，则∠DEC＝∠DCE，则DE＝DC，同理可证AF＝AB，那么EF就可表示为AF+ED﹣BC＝2AB﹣BC，继而可得出答案．【解答】解：∵平行四边形ABCD，∴∠DEC＝∠ECB，又CE平分∠BCD，∴∠DCE＝∠ECB，∴∠DEC＝∠DCE，∴DE＝DC，同理可证：AF＝AB，∴2AB﹣BC＝AF+ED﹣BC＝EF＝2．故答案为2．【点评】本题主要考查了平行四边形的性质，在平行四边形中，当出现角平分线时，一般可构造等腰三角形，进而利用等腰三角形的性质解题，难度不大，关键是解题技巧的掌握．12．【分析】根据AD∥BC可得∠DAO＝∠OCB，∠ADO＝∠CBO，再证明△AOD≌△COB可得BO＝DO，然后再根据对角线互相平分的四边形是平行四边形可得答案．【解答】解：可选条件①③，∵AD∥BC，∴∠DAO＝∠OCB，∠ADO＝∠CBO，在△AOD和△COB中，，∴△AOD≌△COB（AAS），∴DO＝BO，∴四边形ABCD是平行四边形．故答案为：①③．【点评】此题主要考查了平行四边形的判定，关键是掌握对角线互相平分的四边形是平行四边形．13．【分析】根据折叠的性质易知，重合部分为菱形，然后根据菱形的面积公式计算即可．【解答】解：如图，过点A作AE⊥BC于点E，AF⊥CD于点F．则AE＝AF＝2．∵纸条的对边平行，即AB∥CD，AD∥BC，∴四边形ABCD是平行四边形，∵两张纸条的宽度都是2，∴S四边形ABCD＝BC×2＝CD×2，∴BC＝CD，∴平行四边形ABCD是菱形，即四边形ABCD是菱形．∴四边形ABCD的面积为2×2×＝4．故答案是：4．【点评】本题主要考查菱形的性质和特殊角的三角函数值，通过折叠变换考查学生的逻辑思维能力，解决此类问题，应结合题意，最好实际操作图形的折叠，易于找到图形间的关系．14．【分析】四边形APQD为矩形，也就是AP＝DQ，分别用含t的代数式表示，解即可．【解答】解：根据题意，当AP＝DQ时，四边形APQD为矩形．此时，4t＝20﹣t，解得t＝4（s）．故答案是：4．【点评】本题考查了矩形的判定与性质．此题利用了矩形的对边相等的性质进行解题的．15．【分析】由平行四边形的性质和角平分线证出AD＝DF，由F为DC中点，AB＝CD，求出AD与DF 的长，得出三角形ADF为等腰三角形，根据三线合一得到G为AF中点，在直角三角形ADG中，由AD与DG的长，利用勾股定理求出AG的长，进而求出AF的长，再由AAS证明ADF≌△ECF全等，得出AF＝EF，即可求出AE的长．【解答】解：∵AE为∠DAB的平分线，∴∠DAE＝∠BAE，∵DC∥AB，∴∠BAE＝∠DFA，∴∠DAE＝∠DFA，∴AD＝FD，又F为DC的中点，∴DF＝CF，∴AD＝DF＝DC＝AB＝4，在Rt△ADG中，根据勾股定理得：AG＝，则AF＝2AG＝2，∵平行四边形ABCD中，∴AD∥BC，∴∠DAF＝∠E，∠ADF＝∠ECF，在△ADF和△ECF中，，∴△ADF≌△ECF（AAS），∴AF＝EF，则AE＝2AF＝2×2＝4，故答案为：4【点评】此题考查了平行四边形的性质，全等三角形的判定与性质，勾股定理，等腰三角形的判定与性质；熟练掌握平行四边形的判定与性质，证明三角形全等是解本题的关键．16．【分析】根据平行线的性质得到∠ADF＝∠DFC，根据角平分线的定义得到∠BAE＝∠DAE，推出AB＝BE，根据已知条件推出∠ADF＝∠ADC，得到∠DFC＝∠CDF，推出CF＝CD，于是得到结论．【解答】解：①如图1，在▱ABCD中，∵BC＝AD＝10，BC∥AD，CD＝AB，CD∥AB，∴∠DAE＝∠AEB，∠ADF＝∠DFC，∵AE平分∠BAD交BC于点E，∴∠BAE＝∠DAE，∴∠BAE＝∠AEB，∴AB＝BE，∵DF⊥AE，∴∠DAE+∠ADF＝90°，∵∠BAD+∠ADC＝180°，∴∠ADF＝∠ADC，∴∠ADF＝∠CDF，∵∠ADF＝∠DFC，∴∠DFC＝∠CDF，∴CF＝CD，∴AB＝BE＝CF＝CD∵EF＝4，∴BC＝BE+CF﹣EF＝2AB﹣EF＝2AB﹣4＝10，∴AB＝7；②如图2，在▱ABCD中，∵BC＝AD＝10，BC∥AD，CD＝AB，CD∥AB，∴∠DAE＝∠AEB，∠ADF＝∠DFC，∵AE平分∠BAD交BC于点E，∴∠BAE＝∠DAE，∴∠BAE＝∠AEB，∴AB＝BE，∵DF⊥AE，∴∠DAE+∠ADF＝90°，∵∠BAD+∠ADC＝180°，∴∠ADF＝∠ADC，∴∠ADF＝∠CDF，∵∠ADF＝∠DFC，∴∠DFC＝∠CDF，∴CF＝CD，∴AB＝BE＝CF＝CD∵EF＝4，∴BC＝BE++EF+CF＝2AB+EF＝2AB+4＝10，∴AB＝3；综上所述：AB的长为7或3．故答案为：7或3．【点评】本题考查了等腰三角形的判定和性质，平行线的性质，平行四边形的性质，解答本题的关键是判断出AB＝BE＝CF＝CD．17．【分析】延长GH交AD于点P，先证△APH≌△FGH得AP＝GF＝2，GH＝PH＝PG，再利用勾股定理求得PG＝2，从而得出答案．【解答】解：如图，延长GH交AD于点P，∵四边形ABCD和四边形CEFG都是矩形，∴∠ADC＝∠ADG＝∠CGF＝90°，AD＝BC＝4、GF＝CE＝2，∴AD∥GF，∴∠GFH＝∠PAH，又∵H是AF的中点，∴AH＝FH，在△APH和△FGH中，∵，∴△APH≌△FGH（ASA），∴AP＝GF＝2，PH＝HG＝PG，∵PD＝AD﹣AP＝2，GD＝GC﹣CD＝4﹣2＝2∴GP＝＝2∴GH＝GP＝故答案为：【点评】本题主要考查矩形的性质，解题的关键是掌握全等三角形的判定与性质、矩形的性质、勾股定理等知识点．18．【分析】由ASA证明△DBF≌△DCE，得出BF＝CE＝2﹣t，得出AF＝AB+BF＝4﹣t，即可得出点F的坐标；分两种情况：①当AE＝AF时，根据勾股定理得出AE2＝OA2+OE2，得出方程22+t2＝（4﹣t）2，解方程即可求出t的值；②当AE＝EF时，点E在AF的垂直平分线上，得出OE＝AF，即t＝（4﹣t），解方程即可求出t的值，从而求解．【解答】解：（1）∵四边形OABC是正方形，∴OA＝AB＝BC＝OC＝2，∠AOC＝∠ABC＝∠BCO＝90°，∴∠FBD＝90°，∵D是BC的中点，∴BD＝CD，在△DBF和△DCE中，，∴△DBF≌△DCE（ASA），∴BF＝CE＝2﹣t，∴AF＝AB+BF＝4﹣t，∴D的坐标为（﹣2，4﹣t），当△AEF是以AE为腰的等腰三角形时，分两种情况：①当AE＝AF时，∵AE2＝OA2+OE2，∴22+t2＝（4﹣t）2，解得：t＝1.5；②当AE＝EF时，点E在AF的垂直平分线上，∴OE＝AF，即t＝（4﹣t），解得：t＝．综上所述：当△AEF是以AE为腰的等腰三角形时，点E的坐标是（0，1.5）或（0，）．故答案为：（0，1.5）或（0，）．【点评】考查了正方形的性质、全等三角形的判定与性质、勾股定理、等腰三角形的性质等知识；本题综合性强，有一定难度，需要进行分类讨论才能得出结果．三．解答题（共7小题）19．【分析】延长BD与AC相交于点F，根据等腰三角形的性质可得BD＝DF，再利用三角形的中位线平行于第三边并且等于第三边的一半可得DE＝CF，然后求解即可．【解答】解：如图，延长BD与AC相交于点F，∵AD平分∠BAC，BD⊥AD，∴∠DAB＝∠DAF，AD＝AD，∠ADB＝∠ADF，∴△ADB≌△ADF，∴AF＝AB，BD＝DF，∵AB＝6，AC＝10，∴CF＝AC﹣AF＝AC﹣AB＝10﹣6＝4，∵E为BC中点，∴DE是△BCF的中位线，∴DE＝CF＝×4＝2．【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半，等腰三角形的判定与性质，作辅助线构造出以DE为中位线的三角形是解题的关键．20．【分析】（1）由平行四边形的性质得出AB∥CD，∠ADE＝∠CBF，AD＝BC，由ASA证明△ADE≌△CBF，得出DE＝BF，即可得出四边形DFBE是平行四边形；（2）由中点的定义得出DE＝CE，由平行四边形的判定方法即可得出平行四边形．【解答】（1）证明：∵四边形ABCD是平行四边形，∴AB∥CD，∠ADE＝∠CBF，AD＝BC，在△ADE和△CBF中，，∴△ADE≌△CBF（ASA），∴DE＝BF，又∵DE∥BF，∴四边形DFBE是平行四边形；（2）解：∵E是CD的中点，∴DE＝CE，∴以GH为边的平行四边形有平行四边形GHFA、平行四边形GHBF、平行四边形GHED、平行四边形GHCE；以GH为对角线的平行四边形有GFHE．【点评】本题考查了平行四边形的性质与判定、全等三角形的判定与性质；熟练掌握平行四边形的性质，证明三角形全等得出DE＝BF是解决问题（1）的关键．21．【分析】由矩形的性质可得出BA＝CD、∠A＝∠D，由AM＝DN可得出AN＝DM，进而即可证出△ABN≌△DCM（SAS），根据全等三角形的性质可证出BN＝CM．【解答】证明：∵四边形ABCD为矩形，∴BA＝CD，∠A＝∠D．∵AM＝DN，∴AN＝DM．在△ABN和△DCM中，，∴△ABN≌△DCM（SAS），∴BN＝CM．【点评】本题考查了矩形的性质以及全等三角形的判定与性质，利用全等三角形的判定定理SAS 证出△ABN≌△DCM是解题的关键．22．【分析】延长EM交AD于点P，延长FM交AB于点Q，根据正方形的性质可得出：四边形PMFD、BEMQ为正方形，四边形AQMP、MECF为矩形，进而可得出AQ＝FM，QM＝ME，结合∠AQM＝∠FME＝90°即可证出△AQM≌△FME（SAS），再利用全等三角形的性质可证出AM＝EF．【解答】证明：延长EM交AD于点P，延长FM交AB于点Q，如图所示．∵四边形ABCD为正方形，点M为对角线BD上一点，∴四边形PMFD、BEMQ为正方形，四边形AQMP、MECF为矩形，∴AQ＝PM＝FM，QM＝ME．在△AQM和△FME中，，∴△AQM≌△FME（SAS），∴AM＝EF．【点评】本题考查了全等三角形的判定与性质、正方形的性质以及矩形的性质，利用全等三角形的判定定值SAS证出△AQM≌△FME是解题的关键．23．【分析】（1）根据直角三角形斜边上的中线等于斜边的一半，可求BE＝DE，根据等腰三角形的性质，可得结论；（2）根据题意可得BE＝5，BF＝3，根据勾股定理可求EF的长【解答】证明：（1）连接BE，DE∵∠ABC＝∠ADC＝90°，点E是AC的中点，∴BE＝AC，DE＝AC∴BE＝DE∵点F是BD的中点，BE＝DE∴EF⊥BD（2）∵BE＝AC∴BE＝5∵点F是BD的中点∴BF＝DF＝3在Rt△BEF中，EF＝＝＝4【点评】本题考查了直角三角形斜边上的中线等于斜边的一半，等腰三角形的性质，勾股定理，熟练掌握直角三角形斜边上的中线等于斜边的一半是本题的关键．24．【分析】（1）求出四边形ADFC是平行四边形，推出CF＝AD＝BD，根据平行四边形的判定得出四边形BDCF是平行四边形，求CD＝BD，根据菱形的判定得出即可；（2）设CE＝2x，AC＝3x，求出BC＝4x，DF＝AC＝3x，根据菱形的面积公式求出x，求出EF和CE，根据勾股定理求出CF即可．【解答】（1）证明：DE⊥BC，∠ACB＝90°，∴∠BED＝∠ACB，∴DF∥AC，∵CF∥AB，∴四边形ADFC是平行四边形，∴AD＝CF，∵D为AB的中点，∴AD＝BD，∴BD＝CF，∵BD∥CF，∴四边形BDCF是平行四边形，∵∠ACB＝90°，D为AB的中点，∴DC＝BD，∴四边形BDCF是菱形；（2）解：∵tan∠EAC＝＝，∴设CE＝2x，AC＝3x，∵四边形BDCF是菱形，∴BE＝CE＝2x，∴BC＝4x，∵四边形ADFC是平行四边形，∴DF＝AC＝3x，∵四边形BDCF的面积为24，∴＝24，解得：x＝2（负数舍去），∴CE＝4，DF＝6，∴DE＝EF＝×6＝3，∵DE⊥BC，∴∠CEF＝90°，∴由勾股定理得：CF＝＝＝5．【点评】本题考查了勾股定理，平行四边形的判定和性质，菱形的判定，直角三角形的性质的应用，能熟记菱形的性质和判定定理是解此题的关键．25．【分析】（1）过G作GH⊥CD于H，根据三角形的内角和得到∠CDE＝60°，根据平行四边形的性质得到AD∥BC，AB＝CD＝2，得到∠ADC＝120°，解直角三角形即可得到结论；（2）根据全等三角形的性质得到∠ADH＝∠EDC，∠H＝∠C，DH＝DC，根据平行四边形的性质得到AB＝CD，AB∥CD，推出∠DFA＝∠C，在DH上截取HM＝AH，得到∠HAM＝∠HMA，求得∠DAM ＝∠H，根据全等三角形的性质即可得到结论．．【解答】解：（1）如图1，过G作GH⊥CD于H，∵DE⊥BC，∴∠DEC＝90°，∵∠C＝60°，∴∠CDE＝60°，∵四边形ABCD是平行四边形，∴AD∥BC，AB＝CD＝2，∴∠ADC＝120°，∵AD＝DF，∴∠DAF＝∠DFA＝30°，∴∠GDF＝∠DFG，∴DG＝GF，∵CD＝2，∴DF＝，∴HF＝DF＝，∴GF＝1；（2）∵AH⊥AD，DE⊥BC，∴∠DAH＝∠DEC＝90°，在△ADE与△DEC中，，∴△ADE≌△DEC（SAS），∴∠ADH＝∠EDC，∠H＝∠C，DH＝DC，∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，∴∠DAB＝∠C，∠DFA＝∠BAF，∵AD＝DF，∴∠DAF＝∠DFA，∴∠DFA＝∠C，如图2，在DH上截取HM＝AH，∴∠HAM＝∠HMA，∴∠H＝180°﹣2∠HAM，∵∠MAD＝90°﹣∠HAM，∴∠DAM＝∠H，∴∠MAD＝∠GFD，在△ADM与△FDG中，，∴△ADM≌△FDG（ASA），∴DM＝DG，∵AB＝CD＝DH＝HM+DM，∴AB＝AH+DG．【点评】本题考查了平行四边形的性质，全等三角形的判定和性质，直角三角形的性质，等腰三角形的判定和性质，正确的作出辅助线是解题的关键．。

八年级数学下册《平行四边形》单元测试卷(附答案)

八年级数学下册《平行四边形》单元测试卷（附答案）一．选择题（共10小题，满分40分）1．如图，在▱ABCD中，DE平分∠ADC，AD＝8，BE＝3，则CD＝（）A．4B．5C．6D．72．如图，在平行四边形ABCD中，AC、BD相交于点O，∠ODA＝90°，AC＝10cm，BD＝6cm，则BC的长为（）A．4cm B．5cm C．6cm D．8cm3．下面关于平行四边形的说法中，不正确的是（）A．对角线互相平分的四边形是平行四边形B．有一组对边平行，一组对角相等的四边形是平行四边形C．有一组对边相等，一组对角相等的四边形是平行四边形D．有两组对角相等的四边形是平行四边形4．如图，在▱ABCD中，EF∥AD，HN∥AB，则图中的平行四边形（不包括四边形ABCD）的个数共有（）A．9个B．8个C．6个D．4个5．如图，▱ABCD中，CE平分∠BCD，交AB于点E，AE＝3，BE＝5，DE＝4，则CE的长为（）A．B．C．D．6．如图，在▱ABCD中，对角线AC，BD相交于点O，OE⊥BD交AD于点E，连接BE，若▱ABCD的周长为30，则△ABE的周长为（）A．30B．26C．20D．157．如图，平行四边形ABCD的周长为16，AC、BD相交于点O，OE⊥AC交AD于E，则△DCE的周长为（）A．4B．6C．8D．108．如图，将▱DEBF的对角线EF向两端延长，分别至点A和点C，且使AE＝CF，连接AB，BC，AD，CD．求证：四边形ABCD为平行四边形．以下是证明过程，其顺序已被打乱，①∴四边形ABCD为平行四边形；②∵四边形DEBF为平行四边形，∴OD＝OB，OE＝OF；③连接BD，交AC于点O；④又∵AE＝CF，∴AE+OE＝CF+OF，即OA＝OC．正确的证明步骤是（）A．①②③④B．③④②①C．③②④①D．④③②①9．如图，在▱ABCD中，点M，N分别是AD、BC的中点，点O是CM，DN的交点，直线AB分别与CM，DN的延长线交于点P、Q．若▱ABCD的面积为192，则△POQ的面积为（）A．72B．144C．208D．21610．如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC＝60°，，则下列结论：①∠CAD＝30°②③S平行四边形ABCD＝AB•AC④，正确的个数是（）A．1B．2C．3D．4二．填空题（共8小题，满分32分）11．如图，已知▱ABCD中，AD⊥BD，AC＝10，AD＝4，则BD的长是．12．下列条件能判定四边形ABCD是平行四边形的是．A．AB∥CD，AD∥BC B．AD＝BC，AB＝CDC．AB∥CD，AD＝BC D．∠A＝∠C，∠B＝∠D13．如图，平行四边形ABCD中，对角线AC、BD相交于点O，若AB＝2，BC＝3，∠ABC＝60°，则图中阴影部分的面积是．14．如图，平行四边形ABCD的顶点A，B，C的位置用数对分别表示为（4，6），（1，3），（5，3），则顶点D的位置用数对表示为．15．如图，▱ABCD的对角线相交于点O，且AB＝5，△OCD的周长为23，则▱ABCD的两条对角线长的和．16．如图，在▱ABCD中，AB＝5，BC＝8，∠ABC和∠BCD的角平分线分别交AD于点E、F，若BE＝6，则CF＝．17．如图，在平行四边形ABCD中，BD是对角线，E，F分别是边AD，BC上不与端点重合的两点，连接EF，下列条件中使得四边形BFDE是平行四边形的是．（多选）A．AE＝CFB．EF经过BD的中点C．BE∥DFD．EF⊥AD18．在如图的网格中，以格点A、B、C、D、E、F中的4个点为顶点，你能画出平行四边形的个数为个．三．解答题（共6小题，满分48分）19．如图，在▱ABCD中，AE平分∠BAD交BD于点E，交BC于点M，CF平分∠BCD交BD于点F．（1）求证：AE＝CF；（2）若∠ABC＝70°，求∠AMB的度数．20．在▱ABCD中，对角线AC⊥AB，BE平分∠ABC交AD于点E，交AC于点F．（1）求证：AE＝AB；（2）若AB＝3，BC＝5，求AF的长．21．如图，在平行四边形ABCD中，点F是AD中点，连接CF并延长交BA的延长线于点E．（1）求证：AB＝AE．（2）若BC＝2AE，∠E＝31°，求∠DAB的度数．22．如图，点B、C、E、F在同一直线上，BE＝CF，AC⊥BC于点C，DF⊥EF于点F，AC＝DF．求证：（1）△ABC≌△DEF；（2）四边形ABED是平行四边形．23．如图，在等边△ABC中，D是BC的中点，以AD为边向左侧作等边△ADE，边ED与AB交于点G．（1）求∠CAE的度数；（2）取AB的中点F，连接CF，EF，求证：四边形CDEF是平行四边形．24．在▱ABCD中，点O是对角线BD的中点，点E在边BC上，EO的延长线与边AD交于点F，连接BF、DE如图1．（1）求证：四边形BEDF是平行四边形；（2）若DE＝DC，∠CBD＝45°，过点C作DE的垂线，与DE、BD、BF分别交于点G、H、P如图2．①当CD＝6．CE＝4时，求BE的长；②求证：CD＝CH．参考答案与解析一．选择题（共10小题，满分40分）1．解：在▱ABCD中，AD＝8；∴BC＝AD＝8，AD∥BC；∴CE＝BC﹣BE＝8﹣3＝5，∠ADE＝∠CED；∵DE平分∠ADC；∴∠ADE＝∠CDE；∴∠CDE＝∠CED；∴CD＝CE＝5；故选：B．2．解：∵四边形ABCD是平行四边形，AC＝10cm，BD＝6cm；∴OA＝OC＝AC＝5（cm），OB＝OD＝BD＝3（cm）；∵∠ODA＝90°；∴AD＝＝＝4（cm）；∴BC＝AD＝4（cm）；故选：A．3．解：A、∵对角线互相平分的四边形是平行四边形；∴选项A不符合题意；B、∵有一组对边平行，一组对角相等的四边形是平行四边形；∴选项B不符合题意；C、∵有一组对边相等，一组对角相等的四边形不一定是平行四边形；∴选项C符合题意；D、∵有两组对角相等的四边形是平行四边形；∴选项D不符合题意；故选：C．4．解：设EF与NH交于点O；∵在▱ABCD中，EF∥AD，HN∥AB；∴AD∥EF∥BC，AB∥NH∥CD；则图中的四边BEON、DFOH、DHNC、BEFC、BAHN、AEOH、AEFD、ONCF都是平行四边形，共8个．故选：B．5．解：∵AE＝3，BE＝5；∴AB＝8；∵四边形ABCD是平行四边形；∴CD＝AB＝8，AB∥CD，AD＝BC；∴∠DCE＝∠CEB；∵CE平分∠BCD；∴∠DCE＝∠BCE；∴∠BCE＝∠BEC；∴BC＝BE＝5＝AD；∵AE2+DE2＝9+16＝25，AD2＝25；∴AE2+DE2＝AD2；∴∠AED＝90°；∵DC∥CD；∴∠CDE＝90°；在△DCE中，由勾股定理可得：CE＝＝＝4；故选：A．6．解：∵四边形ABCD是平行四边形；∴AB＝CD，AD＝BC，OB＝OD；又∵OE⊥BD；∴OE是线段BD的中垂线；∴BE＝DE；∴AE+ED＝AE+BE；∵▱ABCD的周长为30；∴AB+AD＝15；∴△ABE的周长＝AB+AE+BE＝AB+AD＝15；故选：D．7．解：∵平行四边形ABCD；∴AD＝BC，AB＝CD，OA＝OC；∵EO⊥AC；∴AE＝EC；∵AB+BC+CD+AD＝16；∴AD+DC＝8；∴△DCE的周长是：CD+DE+CE＝AE+DE+CD＝AD+CD＝8；故选：C．8．解：连接BD，交AC于点O，如图所示：∵四边形DEBF为平行四边形；∴OD＝OB，OE＝OF；又∵AE＝CF；∴AE+OE＝CF+OF；即OA＝OC；∴四边形ABCD为平行四边形；即正确的证明步骤是③②④①；故选：C．9．解：连接MN，如图所示：∵四边形ABCD是平行四边形；∴CD∥AB，AD∥BC，AD＝BC；∴∠CDQ＝∠Q，∠DCB＝∠CBQ；∵点M，N分别是AD、BC的中点；∴DM＝CN，CN＝BN；∴四边形CDMN是平行四边形；在△CDN和△BQN中；；∴△CDN≌△BQN（AAS）；同理可得：△CDM≌△P AM；∴△POQ的面积＝四边形ABCD的面积+△COD的面积，O是CM的中点；∵▱ABCD的面积为192；∴四边形CDMN的面积是96；∴△CDM的面积为四边形CDMN的面积的一半，即48；∴△COD的面积为24；∴△POQ的面积＝四边形ABCD的面积+△COD的面积＝192+24＝216．故选：D．10．解：①∵AE平分∠BAD；∴∠BAE＝∠DAE；∵四边形ABCD是平行四边形；∴AD∥BC，∠ABC＝∠ADC＝60°；∴∠DAE＝∠BEA；∴∠BAE＝∠BEA；∴AB＝BE＝1；∴△ABE是等边三角形；∴AE＝BE＝1；∵BC＝2；∴EC＝1；∴AE＝EC；∴∠EAC＝∠ACE；∵∠AEB＝∠EAC+∠ACE＝60°；∴∠ACE＝30°；∵AD∥BC；∴∠CAD＝∠ACE＝30°；故①正确；②∵BE＝EC，OA＝OC；∴OE＝AB＝，OE∥AB；∴∠EOC＝∠BAC＝60°+30°＝90°；Rt△EOC中，OC＝；∵四边形ABCD是平行四边形；∴∠BCD＝∠BAD＝120°；∴∠ACB＝30°；∴∠ACD＝90°；Rt△OCD中，OD＝；∴BD＝2OD＝；故②正确；③由②知：∠BAC＝90°；∴S平行四边形ABCD＝AB•AC；故③正确；④由②知：OE是△ABC的中位线；∴OE＝AB；∵AB＝BC；∴OE＝BC＝AD；故④正确；故选：D．二．填空题（共8小题，满分32分）11．解：∵四边形ABCD是平行四边形；∴AO＝CO＝AC，DO＝BO；∵AC＝10；∴AO＝5；∵AD⊥DB；∴∠ADB＝90°，AD＝4；∴DO＝＝3；∴BD＝6；故答案为：6．12．解：A．根据AB∥CD，AD∥BC能推出四边形ABCD是平行四边形；B．根据AD＝BC，AB＝CD能推出四边形ABCD是平行四边形；C．根据AB∥CD，AD＝BC能得出四边形是等腰梯形，不能推出四边形ABCD是平行四边形D．根据∠A＝∠C，∠B＝∠D能推出四边形ABCD是平行四边形；故答案为：ABD．13．解：作AM⊥BC于M，如图所示：则∠AMB＝90°；∵∠ABC＝60°；∴∠BAM＝30°；∴BM＝AB＝×2＝1；在Rt△ABM中，AB2＝AM2+BM2；∴AM＝＝＝；∴S平行四边形ABCD＝BC•AM＝3；∵四边形ABCD是平行四边形；∴AD∥BC，BO＝DO；∴∠OBE＝∠ODF；在△BOE和△DOF中；；∴△BOE≌△DOF（ASA）；∴S△BOE＝S△DOF；∴图中阴影部分的面积＝▱ABCD的面积＝；故答案为：．14．解：∵平行四边形ABCD的顶点A，B，C的位置用数对分别表示为（4，6），（1，3），（5，3）；∴点D坐标为（8，6）；故答案为：（8，6）．15．解：∵四边形ABCD是平行四边形；∴AB＝CD＝5；∵△OCD的周长为23；∴OD+OC＝23﹣5＝18；∵BD＝2DO，AC＝2OC；∴平行四边形ABCD的两条对角线的和＝BD+AC＝2（DO+OC）＝36；故答案为：36．16．解：如图，设BE与FC的交点为H，过点A作AM∥FC，交BE与点O；∵四边形ABCD是平行四边形；∴AD∥BC，AB∥CD；∴∠ABC+∠DCB+180°；∵BE平分∠ABC，CF平分∠BCD；∴∠ABE＝∠EBC，∠BCF＝∠DCF；∴∠CBE+∠BCF＝90°；∴∠BHC＝90°；∵AM∥CF；∴∠AOE＝∠BHC＝90°；∵AD∥BC；∴∠AEB＝∠EBC＝∠ABE；∴AB＝AE＝5；又∵∠AOE＝90°；∴BO＝OE＝3；∴AO＝＝＝4；在△ABO和△MBO中；；∴△ABO≌△MBO（ASA）；∴AO＝OM＝4；∴AM＝8；∵AD∥BC，AM∥CF；∴四边形AMCF是平行四边形；∴CF＝AM＝8；故答案为：8．17．解：∵四边形ABCD是平行四边形；∴AD∥BC；∵AE＝CF，AD＝BC；∴DE＝BF；∴四边形BFDE是平行四边形；故A选项符合题意；若EF经过BD的中点O；∵AD∥BC；∴∠EDO＝∠FBO；在△BOF和△DOE中；；∴△BOF≌△DOE（ASA）；∴BF＝DE；∴四边形BFDE是平行四边形；故B选项符合题意；∵DE∥BF，BE∥DF；∴四边形BFDE是平行四边形；故C选项符合题意；由EF⊥AD不能判定四边形BFDE是平行四边形；故D选项不符合题意；故答案为：A，B，C．18．解：如图所示：图中平行四边形有▱ABEC，▱BDEC，▱BEFC共3个．故答案为：3．三．解答题（共6小题，满分48分）19．（1）证明：∵四边形ABCD是平行四边形；∴AB∥CD，AB＝CD，∠BAD＝∠BCD∴∠ABE＝∠CDF；∵AE平分∠BAD，CF平分∠BCD；∴∠BAE＝∠DCF；∴△ABE≌△CDF（ASA）；∴AE＝CF；（2）∵四边形ABCD是平行四边形；∴AD∥BC，∠BAD+∠ABC＝180°；∵∠ABC＝70°；∴∠BAD＝110°；∵AM平分∠BAD，AD∥BC；∴∠AMB＝∠DAM＝55°．20．（1）证明：∵四边形ABCD为平行四边形；∴∠AEB＝∠EBC；∵BE平分∠ABC；∴∠ABE＝∠EBC；∴∠ABE＝∠AEB；∴AE＝AB；（2）解：AC⊥AB，AB＝3，BC＝5；∴AC＝；过F点作FH⊥BC，垂足为H；∵BE平分∠ABC，AC⊥AB；∴AF＝FH；∵S△ABC＝S△ABF+S△BFC；∴AB•AC＝AB•AF+BC•FH；即；∴AF＝．21．（1）证明：∵四边形ABCD是平行四边形；∴AB＝CD，AB∥CD，BC＝AD；∴∠E＝∠DCF；∵点F是AD中点；∴AF＝DF；∵∠EF A＝∠CFD；∴△AFE≌△DFC（AAS）；∴CD＝AE；∴AB＝AE；（2）解：由（1）可得AF＝DF，BC＝AD；∵BC＝2AE；∵∠E＝31°；∴∠AFE＝∠E＝31°；∴∠DAB＝2∠E＝62°．22．证明：（1）∵BE＝CF；∴BE﹣CE＝CF﹣CE；即BC＝EF；又∵AC⊥BC于点C，DF⊥EF于点F；∴∠ACB＝∠DFE＝90°；在△ABC和△DEF中；；∴△ABC≌△DEF（SAS）；（2）由（1）知△ABC≌△DEF；∴AB＝DE，∠ABC＝∠DEF；∴AB∥DE；∴四边形ABED是平行四边形．23．（1）解：∵△ABC是等边三角形，D是BC的中点；∴AD⊥BC，∠BAC＝60°；∴∠DAC＝∠BAC＝30°；∵△AED是等边三角形；∴∠EAD＝60°；∴∠CAE＝∠EAD+∠DAC＝90°；（2）证明：∵F是等边△ABC边AB的中点，D是边BC的中点；∴CF＝AD，CF⊥AB；∵△AED是等边三角形；∴AD＝ED；∴CF＝ED；∵∠BAD＝∠BAC＝30°，∠EAG＝∠EAD＝30°；∴ED⊥AB；∴CF∥ED；∵CF＝ED；∴四边形CDEF是平行四边形．24．（1）证明：∵在平行四边形ABCD中，点O是对角线BD的中点；∴AD∥BC，BO＝DO；∴∠ADB＝∠CBD；在△BOE与△DOF中；；∴△BOE≌△DOF（ASA）；∴DF＝BE且DF∥BE；∴四边形BEDF是平行四边形；（2）①解：如图，过点D作DN⊥EC于点N；∵DE＝DC＝6，DN⊥EC，CE＝4；∴EN＝CN＝2；∴DN＝＝＝4；∵∠DBC＝45°，DN⊥BC；∴∠DBC＝∠BDN＝45°；∴DN＝BN＝4；∴BE＝BN﹣EN＝4；②证明：∵DN⊥EC，CG⊥DE；∴∠CEG+∠ECG＝90°，∠DEN+∠EDN＝90°；∴∠EDN＝∠ECG；∵DE＝DC，DN⊥EC；∴∠EDN＝∠CDN；∵∠DHC＝∠DBC+∠BCH＝45°+∠BCH，∠CDB＝∠BDN+∠CDN＝45°+∠CDN；∴∠CDB＝∠DHC；∴CD＝CH．。

初中数学湘教版八年级下册第2章四边形2.2 平行四边形-章节测试习题(3)

章节测试题1.【答题】如图，在平行四边形ABCD中，EF∥AD，HN∥AB，则图中的平行四边形的个数共有（）A. 12个B. 9个C. 7个D. 5个【答案】B【分析】根据平行四边形的定义即可求解．【解答】根据平行四边形的定义：两组对边分别平行的四边形是平行四边形，则图中的四边AEOH，HOFD，EBNO，ONCF，AEFD，EBCF，ABNH，HNCD，ABCD都是平行四边形，共9个．选B.【点评】此题考查的知识点是平行四边形的判定，本题可根据平行四边形的定义，直接从图中数出平行四边形的个数，但数时应有一定的规律，以避免重复．2.【答题】如图，已知△ABC，分别以A，C为圆心，BC，AB长为半径画弧，两弧在直线BC 上方交于点D，连结AD，CD，则有（）A. ∠ADC与∠BAD相等B. ∠ADC与∠BAD互补C. ∠ADC与∠ABC互补D. ∠ADC与∠ABC互余【答案】B【分析】首先根据已知条件可以证明四边形ABCD是平行四边形，然后利用平行四边形的性质即可作出判定．【解答】解：如图，依题意得AD=BC、CD=AB，∴四边形ABCD是平行四边形，∴∠ADC+∠BAD=180°，∴B正确．选B.【点评】此题主要考查了平行四边形的判定与性质，先根据已知条件判定平行四边形是解题的关键．3.【答题】已知四边形ABCD，有以下四个条件：①AB∥CD；②AB=CD；③BC∥AD；④BC=AD.从这四个条件中任选两个，能使四边形ABCD成为平行四边形的选法种数共有（）A. 6种B. 5种C. 4种D. 3种【答案】C【分析】根据平行四边形的判定方法即可找到所有组合方式：（1）两组对边平行①③；（2）两组对边相等②④；（3）一组对边平行且相等①②或③④，所以有四种组合．【解答】依题意得有四种组合方式：（1）①③，利用两组对边平行的四边形是平行四边形判定；（2）②④，利用两组对边相等的四边形是平行四边形判定；（3）①②或③④，利用一组对边平行且相等的四边形是平行四边形判定．选C.【点评】此题主要考查了平行四边形的判定方法，熟练掌握平行四边形的判定方法是解题的关键．4.【答题】如图，▱ABCD与▱DCFE的周长相等，且∠BAD=60°，∠F=110°，则∠DAE的度数为______°.【答案】25【分析】由，▱ABCD与▱DCFE的周长相等，可得到AD=DE即△ADE是等腰三角形，再由且∠BAD=60°，∠F=110°，即可求出∠DAE的度数.【解答】解：∵▱ABCD与▱DCFE的周长相等，且CD=CD，∴AD=DE，∵∠DAE=∠DEA，∵∠BAD=60°，∠F=110°，∴∠ADC=120°，∠CDE═∠F=110°，∴∠ADE=360°﹣120°﹣110°=130°，∴∠DAE= =25°，故答案为：25°.5.【答题】如图，在周长为10cm的平行四边形ABCD中，AB≠AD，AC、BD相交于点O，OE⊥BD交AD于点E，连接BE，则△ABE的周长为______cm.【答案】5【分析】先判断出EO是BD的中垂线，得出BE=ED，从而可得出△ABE的周长=AB+AD，再由平行四边形的周长为10cm，即可得出答案.【解答】解：∵点O是BD中点，EO⊥BD，∴EO是线段BD的中垂线，∴BE=ED，故可得△ABE的周长=AB+AD，又∵平行四边形的周长为10cm，∴AB+AD=5cm.故答案为：5cm.6.【答题】如图，在平行四边形ABCD中，已知对角线AC和BD相交于点O，△ABO的周长为17，AB=6，那么对角线AC+BD=______.【答案】22【分析】本题考查的是平行四边形的性质.【解答】因为△ABO的周长为17，AB=6，所以OA+OB=11，∵OA=OC，OB=OD，所以AC+BD=22.故答案为22.【点评】本题的关键是平行四边形的对角线互相平分的性质的运用，求出对角线一半的和，从而求出对角线的和.7.【答题】若平行四边形的周长为80cm，两条邻边的比为3：5，则较短的边为______cm.【答案】15【分析】设平行四边形的两条邻边的分别为3x，5x，再由周长为80cm求出x的值，即可得出答案.【解答】解：设平行四边形的两条邻边的分别为3x，5x，∵平行四边形的周长为80cm，∴2（3x+5x）=80cm，解得x=5cm.∴3x=15cm；故答案为：15cm.8.【答题】如图，在▱ABCD中，∠B=60°，∠BCD的平分线交AD点E，若CD=3，四边形ABCE的周长为13，则BC长为______.【答案】5【分析】利用平行四边形的对边相等且互相平行，进而得出DE=CD=3，再求出AE+BC=7，BC﹣AE=3，即可求出BC的长.【解答】解：∵CE平分∠BCD交AD边于点E，∴∠ECD=∠ECB，∵在平行四边形ABCD中，AD∥BC，AB=CD=3，AD=BC，∠D=∠B=60°，∴∠DEC=∠ECB，∴∠DEC=∠DCE，∴DE=CD=3，∴△CDE是等边三角形，∴CE=CD=3，∵四边形ABCE的周长为13，∴AE+BC=13﹣3﹣3=7①，∵AD﹣AE═DE=3，即BC﹣AE=3②，由①②得：BC=5；故答案为：5.9.【答题】在▱ABCD中，对角线AC、BD交于一点O，AB=11cm，△OCD的周长为27cm，则AC+BD=______cm.【答案】32【分析】首先由平行四边形的性质可求出CD的长，由条件△OCD的周长为27，即可求出OD+OC的长，再根据平行四边的对角线互相平分即可求出平行四边形的两条对角线的和.【解答】解：∵四边形ABCD是平行四边形，∴AB=CD=11cm，OA=OC，OB=OD，∵△OCD的周长为27cm，∴OD+OC=27﹣11=16cm，∵BD=2DO，AC=2OC，∴BD+AC=2（OD+OC）=32cm，故答案为：32.10.【答题】若▱ABCD中，∠A=40°，对角∠C=______°.【答案】40【分析】由▱ABCD中，∠A=40°，根据平行四边形的对角相等，即可求得答案.【解答】解：∵▱ABCD中，∠A=40°，∴∠C=∠A=40°.故答案为：40°.【点评】此题考查了平行四边形的性质.注意掌握平行四边形的对角相等定理的应用是解此题的关键.11.【答题】如图，在平行四边形ABCD中，点E在AD上，BD平分∠EBC.若平行四边形ABCD的周长为10，则△AEB的周长为______.【答案】5【分析】证出BE=DE，得出△AEB的周长=AB+AD即可.【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠ADB=∠CBD，∵BD平分∠EBC，∴∠EBD=∠ADB，∴BE=DE，∴△AEB的周长=AB+BE+AE=AB+DE+AE=AB+AD，∵▱ABCD的周长为10，∴AB+AD=5，∴△ABE的周长=AB+AD=5；故答案为：5.12.【答题】如图，在平行四边形ABCD中，E为AD上一点，∠EBC=40°，且BE=BC，CE=CD，则∠A=______°.【答案】110【分析】先根据平行四边形的性质得出∠2=∠3，再根据BE=BC，CE=CD，∠1=∠2，∠3=∠D，进而得出∠1=∠2=∠3=∠D，求出∠D=70°，即可得出∠A的度数.【解答】解：如图所示：∵四边形ABCD是平行四边形，∴AD∥BC，CD=AB，AB∥CD，∴∠2=∠3，∠A+∠D=180°，∵BE=BC，CE=CD，∴BE=BC=10，CE=CD=6，∠1=∠2，∠3=∠D，∵∠EBC=40°，∴∠D=∠1=∠3=70°，∴∠A=180°﹣70°=110°；故答案为：110°.13.【答题】在平行四边形ABCD中，∠BAD的平分线AE交BC于点E，且BE=3，若平行四边形ABCD的周长是16，则EC等于______.【答案】2【分析】由平行四边形的性质和已知条件证出∠BAE=∠BEA，证出AB=BE=3；求出AB+BC=8，得出BC=5，即可得出EC的长.【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，AB=CD，AD=BC，∴∠AEB=∠DAE，∵平行四边形ABCD的周长是16，∴AB+BC=8，∵AE是∠BAD的平分线，∴∠BAE=∠DAE，∴AB=BE=3，∴BC=5，∴EC=BC﹣BE=5﹣3=2；故答案为：2.14.【答题】在平行四边形ABCD中，∠A=70°，则∠C=______度.【答案】70【分析】根据平行四边形的对角相等得出∠A=∠C，代入求出即可.【解答】解：∵四边形ABCD是平行四边形，∴∠A=∠C，∵∠A=70°，∴∠C=70°，故答案为70.15.【答题】如图，在△ABC中，∠ABC=90°，点D在AB边上，将△ACD沿直线CD翻折后，点A落在点E处，如果四边形BCDE是平行四边形，那么∠ADC=______°.【答案】135【分析】延长CD到点F，根据平行四边形的性质可得出BC∥DE，结合∠ABC=90°，即可得出∠ADE=90°，再根据翻折的性质即可得出∠ADF=∠EDF=45°，从而得出∠BDC=45°，由∠ADC、∠BDC互补即可得出结论.【解答】解：延长CD到点F，如图所示.∵四边形BCDE是平行四边形，∴BC∥DE，∵∠ABC=90°，∴∠BDE=90°，∴∠ADE=90°.∵将△ACD沿直线CD翻折后，点A落在点E处，∴∠ADF=∠EDF= ∠ADE=45°，∴∠BDC=∠ADF=45°，∴∠ADC=180°﹣∠BDC=135°.故答案为：135°.【点评】本题考查了平行四边形的性质，解题的关键是求出∠BDC=45°.本题属于基础题，难度不大，解决该题型题目时，根据平行线的性质找出相等的角是关键.16.【答题】在平行四边形ABCD中，对角线AC和BD交于点O，AB=2，AC=6，BD=8，那么△COD的周长为______.【答案】9【分析】△COD的周长=OC+OD+CD，根据平行四边形的对角线互相平分的性质求得OC与OD的长，根据平行四边形的对边相等可得CD=AB=2，进而求得答案.【解答】解：∵四边形ABCD是平行四边形，∴OC=OA= AC=3，OD=OB= BD=4，CD=AB=2，∴△COD的周长=OC+OD+CD=3+4+2=9.故答案为9.17.【答题】如图，已知AD∥BC，CE=5，CF=8，则AD与BC间的距离是______．【答案】5【分析】根据平行线间的距离的定义解答．【解答】解：由图可知，平行线AD与BC间的距离CE，∵CE=5，∴AD与BC间的距离是5．故答案为：5．【点评】本题考查了平行线之间的距离，熟记定义并准确识图是解题的关键．18.【答题】如图，在▱ABCD中，AB=3，BC=5，以点B的圆心，以任意长为半径作弧，分别交BA、BC于点P、Q，再分别以P、Q为圆心，以大于PQ的长为半径作弧，两弧在∠ABC 内交于点M，连接BM并延长交AD于点E，则DE的长为______．【答案】2【分析】根据作图过程可得BE平分∠ABC；再根据角平分线的性质和平行四边形的性质可证明∠AEB=∠CBE，证出AE=AB=3，即可得出DE的长．，【解答】解：根据作图的方法得：BE平分∠ABC，∴∠ABE=∠CBE∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC=5，∴∠AEB=∠CBE，∴∠ABE=∠AEB，∴AE=AB=3，∴DE=AD-AE=5-3=2；故答案为：2．【点评】此题考查了平行四边形的性质、等腰三角形的判定．熟练掌握平行四边形的性质，证出AE=AB是解决问题的关键．19.【答题】如图，在▱ABCD中，BE⊥AB交对角线AC于点E，若∠1=20°，则∠2的度数为______°．【答案】110【分析】首先由在▱ABCD中，∠1=20°，求得∠BAE的度数，然后由BE⊥AB，利用三角形外角的性质，求得∠2的度数．【解答】解：∵四边形ABCD是平行四边形，∴AB∥CD，∴∠BAE=∠1=20°，∵BE⊥AB，∴∠ABE=90°，∴∠2=∠BAE+∠ABE=110°．故答案为：110°．【点评】此题考查了平行四边形的性质以及三角形外角的性质．注意平行四边形的对边互相平行．20.【答题】如图所示，在▱ABCD中，∠C=40°，过点D作AD的垂线，交AB于点E，交CB 的延长线于点F，则∠BEF的度数为______°．【答案】50【分析】由“平行四边形的对边平行”、“两直线平行，同位角相等”以及“直角三角形的两个锐角互余”的性质进行解答．【解答】解：∵四边形ABCD是平行四边形，∴DC∥AB，∴∠C=∠ABF．又∵∠C=40°，∴∠ABF=40°．∵EF⊥BF，∴∠F=90°，∴∠BEF=90°-40°=50°．故答案是：50°．【点评】本题考查了平行四边形的性质．利用平行四边形的对边平行推知DC∥AB是解题的关键．。

平行四边形单元测试卷

平行四边形单元测试卷一、选择题（每题2分，共10分）1. 平行四边形的对边具有什么性质？A. 相等B. 平行C. 垂直D. 以上都不是2. 下列哪个不是平行四边形的性质？A. 对角线互相平分B. 对边相等C. 对角相等D. 内角和为360°3. 平行四边形的面积如何计算？A. 底乘高B. 对角线乘积的一半C. 周长除以4D. 以上都不是4. 如果一个平行四边形的两组对边分别相等，那么这个平行四边形是：A. 矩形B. 菱形C. 梯形D. 不能确定5. 平行四边形的对角线将平行四边形分成：A. 两个三角形B. 两个梯形C. 两个矩形D. 四个小平行四边形二、填空题（每空1分，共10分）1. 平行四边形的对角线_______。

2. 矩形的四个角都是_______。

3. 菱形的对角线_______。

4. 平行四边形的面积公式为_______。

5. 如果一个平行四边形的底为5厘米，高为3厘米，那么它的面积是_______平方厘米。

三、判断题（每题1分，共5分）1. 所有平行四边形都是矩形。

（）2. 菱形的四条边都是相等的。

（）3. 平行四边形的对角线一定垂直。

（）4. 矩形和菱形都是特殊的平行四边形。

（）5. 梯形不是平行四边形。

（）四、简答题（每题5分，共10分）1. 请简述平行四边形和矩形的区别。

2. 请解释为什么平行四边形的对角线互相平分。

五、计算题（每题10分，共20分）1. 一个平行四边形的底是8厘米，高是4厘米，请计算它的面积。

2. 如果一个平行四边形的对角线长度分别为10厘米和12厘米，且它们相交于中点，求这个平行四边形的面积。

六、解答题（每题15分，共15分）1. 一个平行四边形的对角线互相垂直，且长度分别为12厘米和16厘米。

如果这个平行四边形的面积是96平方厘米，请求出它的底和高。

答案：一、选择题：1-5 BACAD二、填空题：1. 互相平分 2. 直角 3. 垂直且互相平分 4. 底×高 5.15三、判断题：1-5 ×√×√×四、简答题：1. 平行四边形的对边平行且相等，而矩形的四个角都是直角，且对角线相等。

初中数学北师大版八年级下册第六章平行四边形3.三角形的中位线-章节测试习题(3)

章节测试题1.【答题】如图，在△ABC中，点D，E分别是边AB，AC的中点，点F是线段DE上的一点．连接AF，BF，∠AFB＝90°，且AB＝8，BC＝14，则EF的长是（）A. 2B. 3C. 4D. 5【答案】B【分析】本题考查三角形的中位线.【解答】∵点D，E分别是边AB，AC的中点，∴DE是△ABC的中位线，∵BC＝14，∴DE BC＝7，∵∠AFB＝90°，AB＝8，∴DF AB＝4，∴EF＝DE﹣DF＝7﹣4＝3，选B．2.【答题】如图，在四边形ABCD中，P是对角线BD的中点，点E、F分别是AB、CD 的中点，AD＝BC，∠EPF＝140°，则∠EFP的度数是（）A. 50°B. 40°C. 30°D. 20°【答案】D【分析】本题考查三角形的中位线.【解答】∵P是BD的中点，E是AB的中点，∴PE是△ABD的中位线，∴PE AD，同理，PF BC，∵AD＝BC，∴PE＝PF，∴∠EFP（180°﹣∠EPF）（180°﹣140°）＝20°，选D．3.【答题】如图，在△ABF中，点C在中位线DE上，且CE CD，连接AC，BC，∠ACB＝90°，若BF＝20，则AB的长为（）A. 10B. 12C. 14D. 16【答案】D【分析】本题考查三角形的中位线.【解答】∵DE是△ABC的中位线，BF＝20，∴DE BF＝10，∵CE CD，∴CD DE＝8，∵∠ACB＝90°，∴AB＝2CD＝16，选D.4.【答题】如图，△ABC中，N是BC边上的中点，AM平分∠BAC，BM⊥AM于点M，若AB＝8，MN＝2．则AC的长为（）A. 10B. 11C. 12D. 13【答案】C【分析】本题考查三角形的中位线.【解答】延长BM交AC于D，如图所示：∵BM⊥AM于点M，∴∠AMB＝∠AMD＝90°，∵AM平分∠BAC，∴∠BAM＝∠DAM，在△BAM和△DAM中，，∴△BAM≌△DAM（ASA）．∴AD＝AB＝8，BM＝MD，∵N是BC边上的中点，∴MN为△BCD的中位线，∴DC＝2MN＝4，∴AC＝AD+DC＝8+4＝12．选C．5.【答题】如图，在△ABC中，∠A＝90°，D是AB的中点，过点D作BC的平行线交AC于点E，作BC的垂线交BC于点F，若AB＝CE，且△DFE的面积为1，则BC的长为（）A. 2B. 5C. 4D. 10【答案】A【分析】本题考查三角形的中位线.【解答】如图，过A作AH⊥BC于H.∵D是AB的中点，∴AD＝BD，∵DE∥BC，∴AE＝CE，∴DE BC，∵DF⊥BC，∴DF∥AH，DF⊥DE，∴BF＝HF，∴DF AH，∵△DFE的面积为1，∴DE•DF＝1，∴DE•DF＝2，∴BC•AH＝2DE•2DF＝4×2＝8，∴AB•AC＝8，∵AB＝CE，∴AB＝AE＝CE AC，∴AB•2AB＝8，∴AB＝2（负值舍去），∴AC＝4，∴BC．选A．6.【答题】如图，∠MAN＝90°，点C在边AM上，AC＝2，点B为边AN上一动点，连接BC，△A'BC与△ABC关于BC所在直线对称，点D，E分别为AC，BC的中点，连接DE并延长交A'B于点F，连接A'E．当△A'EF为直角三角形时，AB的长为______．【答案】或2【分析】本题考查三角形的中位线.【解答】当△A'EF为直角三角形时，存在两种情况：①当∠A'EF＝90°时，如图，∵△A'BC与△ABC关于BC所在直线对称，∴A'C＝AC＝2，∠ACB＝∠A'CB，∵点D，E分别为AC，BC的中点，∴DE是△ABC的中位线，∴DE∥AB，∴∠CDE＝∠MAN＝90°，∴∠CDE＝∠A'EF，∴∠ACB＝∠A'EC，∴∠A'CB＝∠A'EC，∴A'C＝A'E＝2，在Rt△A'CB中，E是斜边BC的中点，∴BC＝2AE'＝4，由勾股定理可得AB2＝BC2﹣AC2，∴AB；②当∠A'FE＝90°时，如图，∵∠ADF＝∠A＝∠DFB＝90°，∴∠ABF＝90°，∵△A'BC与△ABC关于BC所在直线对称，∴∠ABC＝∠CBA'＝45°，∴△ABC为等腰直角三角形，∴AB＝AC＝2．综上，AB的长为或2．故答案为或2．7.【答题】如图，在△ABC中，M，N分别是AB和AC的中点，连接MN，点E是CN的中点，连接ME并延长，交BC的延长线于点D．若BC＝4，则CD的长为______．【答案】2【分析】本题考查三角形的中位线.【解答】∵M，N分别是AB和AC的中点，∴MN是△ABC的中位线，∴MN BC＝2，MN∥BC，∴∠NME＝∠D，∠MNE＝∠DCE，∵点E是CN的中点，∴NE＝CE，∴△MNE≌△DCE（AAS），∴CD＝MN＝2．故答案为2．8.【答题】如图，△ABC的周长为16，D，E，F分别为AB，BC，AC的中点，M，N，P分别为DE，EF，DF的中点，则△MNP的周长为______．如果△ABC，△DEF，△MNP分别为第1个，第2个，第3个三角形，按照上述方法继续作三角形，那么第n个三角形的周长是______．【答案】4；【分析】本题考查三角形的中位线.【解答】∵△ABC的周长为16，D、F、E分别为AB、AC、BC的中点，∴EF、DF、DE为三角形中位线，∴EF AB，DE AC，DF BC，∴EF+DE+DF（AB+AC+BC），即△DEF的周长是△ABC周长的一半，同理，△MNP的周长是△DEF的周长的一半，即△MNP的周长＝△ABC的周长的16＝4，以此类推，第n个小三角形的周长是第一个三角形周长的16＝，故答案为4；．9.【题文】如图，在△ABC中，AB＝AC，点D是边AB的点，DE∥BC交AC于点E，连接BE，点F、G、H分别为BE、DE、BC的中点．（1）求证：FG＝FH；（2）当∠A为多少度时，FG⊥FH？并说明理由．【答案】（1）见解答；（2）当∠A＝90°时，FG⊥FH．理由见解答. 【分析】本题考查三角形的中位线.【解答】（1）证明：∵AB＝AC．∴∠ABC＝∠ACB，∵DE∥BC，∴∠ADE＝∠ABC，∠AED＝∠ACB，∴∠ADE＝∠AED，∴AD＝AE，∴DB＝EC，∵点F、G、H分别为BE、DE、BC的中点，∴FG是△EDB的中位线，FH是△BCE的中位线，∴FG BD，FH CE，∴FG＝FH；（2）解：如图，延长FG交AC于N，∵FG是△EDB的中位线，FH是△BCE的中位线，∴FH∥AC，FN∥AB，∵FG⊥FH，∴∠A＝90°，∴当∠A＝90°时，FG⊥FH．10.【题文】如图，在△ABC中，AE平分∠BAC，BE⊥AE于点E，点F是BC的中点．（1）如图1，BE的延长线与AC边相交于点D，求证：EF（AC﹣AB）；（2）如图2，△ABC中，AB＝9，AC＝5，求线段EF的长．【答案】（1）见解答；（2）2.【分析】本题考查三角形的中位线.【解答】（1）证明：在△AEB和△AED中，，∴△AEB≌△AED（ASA），∴BE＝ED，AD＝AB，∵BE＝ED，BF＝FC，∴EF CD（AC﹣AD）（AC﹣AB）；（2）解：如图，分别延长BE、AC交于点H，在△AEB和△AEH中，，∴△AEB≌△AED（ASA），∴BE＝EH，AH＝AB＝9，∵BE＝EH，BF＝FC，∴EF CH（AH﹣AC）＝2．11.【答题】如图，在中，，分别是，的中点，，是上一点，连接，，．若，则的长度为（）A. B. C. D.【答案】B【分析】本题考查的是三角形中位线定理和直角三角形的性质，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．根据直角三角形的性质求出FE，根据三角形中位线定理计算即可．【解答】，，，；，分别是，的中点，为的中位线，，选B．12.【答题】如图，的周长为，点，都在边上，的平分线垂直于，垂足为，的平分线垂直于，垂足为，若，则的长为（）A. B. C. D.【答案】C【分析】本题考查了三角形的中位线定理，解答本题的关键是判断出△BAE、△CAD是等腰三角形，利用等腰三角形的性质确定PQ是△ADE的中位线．首先判断△BAE、△CAD是等腰三角形，从而得出BA=BE，CA=CD，由△ABC的周长为32，及BC=12，可得DE=8，利用中位线定理可求出PQ．【解答】平分，，.，，，，同理，点是的中点，点是中点（三线合一），是的中位线，，，．选C．13.【答题】如图，在四边形ABCD中，已知AB＝CD，M、N、P分别是AD、BC、BD的中点∠ABD＝20°，∠BDC＝70°，则∠NMP的度数为（）A. 50°B. 25°C. 15°D. 20°【答案】B【分析】本题考查了三角形中位线定理及等腰三角形的判定和性质，解题时要善于根据已知信息，确定应用的知识．根据中位线定理和已知，易证明△PMN是等腰三角形，根据等腰三角形的性质和已知条件即可求出∠PMN的度数．【解答】在四边形ABCD中，∵M、N、P分别是AD、BC、BD的中点，∴PN，PM分别是△CDB与△DAB的中位线，∴PM AB，PN DC，PM∥AB，PN∥DC．∵AB=CD，∴PM=PN，∴△PMN是等腰三角形，∴∠PMN=∠PNM．∵PM∥AB，PN∥DC，∴∠MPD=∠ABD=20°，∠BPN=∠BDC=70°，∴∠MPN=∠MPD+∠NPD=20°+（180﹣70）°=130°，∴∠PMN25°．选B．14.【答题】已知，四边形ABCD中，AB=2，CD=3，M、N分别是AD，BC的中点，则线段MN的取值范围是（）A. 1＜MN＜5B. 1＜MN≤5C. ＜MN＜D. ＜MN≤【答案】D【分析】本题考查了三角形的中位线，解答此题的关键是根据题意作出辅助线，利用三角形的中位线定理和三角形的三边关系求解．当AB∥CD时，MN最短，利用中位线定理可得MN的最长值，作出辅助线，利用三角形中位线及三边关系可得MN的其他取值范围．【解答】连接BD，过M作MG∥AB，连接NG．∵M是边AD的中点，AB=2，MG∥AB，∴MG是△ABD的中位线，BG=GD，MG=AB=×2=1；∵N是BC的中点，BG=GD，CD=3，∴NG是△BCD的中位线，NG=CD=×3=，在△MNG中，由三角形三边关系可知MG-NG＜MN＜MG+NG，即-1＜MN＜+1，∴＜MN＜，当MN=MG+NG，即MN=时，四边形ABCD是梯形，故线段MN长的取值范围是＜MN≤．选D．15.【答题】如图，点、、分别是的边、、的中点，连接、、得，如果的周长是，那么的周长是（）A. B. C. D.【答案】B【分析】本题考查了三角形中位线定理．解题的关键是根据中位线定理得出边之间的数量关系．由于D、E分别是AB、BC中点，则DE是△ABC的中位线，那么DE=AC，同理有EF=AB，DF=BC，于是易求△DEF的周长．【解答】、分别是的边、的中点，，同理，，．选B．16.【答题】如图，中，是的中点，平分，于点，若，，则等于（）A. B. C. D.【答案】C【分析】本题考查的是三角形中位线定理、全等三角形的判定和性质，三角形的中位线平行于第三边，且等于第三边的一半．延长BD交AC于H，证明△ADB≌△ADH，根据全等三角形的性质得到AH=AB=12，BD=DH，求出HC，根据三角形中位线定理计算即可．【解答】延长交于，平分，，，，，是中点，，，选C．17.【答题】如图，在四边形中，，，，分别是，，的中点，若，，则等于（）A. B. C. D.【答案】A【分析】本题考查了三角形中位线定理和等腰三角形的判定与性质．中位线是三角形中的一条重要线段，由于它的性质与线段的中点及平行线紧密相连，因此，它在几何图形的计算及证明中有着广泛的应用．根据三角形中位线定理和等腰三角形等边对等角的性质求解即可.【解答】，，，分别是，，中点，是的中位线，是的中位线，，，，．又，，，，，，．选A．18.【答题】已知△ABC的周长为1，连接其三边中点构成第二个三角形，再连接第二个三角形的中点构成第三个三角形，以此类推，则第2012个三角形的周长为（）A. B. C. D.【答案】C【分析】本题考查相似三角形的性质.【解答】∵连接△ABC三边中点构成第二个三角形，∴新三角形的三边与原三角形的三边的比值为1：2，∴它们相似，且相似比为1：2，同理：第三个三角形与第二个三角形的相似比为1：2，即第三个三角形与第一个三角形的相似比为1：22，以此类推：第2012个三角形与原三角形的相似比为1：22011，∵周长为1，∴第2012个三角形的周长为1：22011．选C．19.【答题】如图，▱ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE＝3cm，则AB的长为（）A. 3cmB. 6cmC. 9cmD. 12cm【答案】B【分析】本题考查三角形的中位线.【解答】∵四边形ABCD是平行四边形，∴OA=OC；又∵点E是BC的中点，∴BE=CE，∴AB=2OE=2×3=6（cm），选B．20.【答题】如图，在中，，分别是，的中点，是线段上一点，连接，，若，，，则的长为______．【答案】18【分析】本题考查是三角形中位线定理、直角三角形的性质，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．根据直角三角形的性质得到DF=8，根据EF=1，得到DE=9，根据三角形中位线定理解答即可．【解答】，点是的中点，，，，、分别是，的中点，，故答案为．。

初中数学第19章平行四边形综合检测题(三)及答案

第19章平行四边形综合检测题(三)一、选择题（每题3分，共30分）1、一块均匀的不等边三角形的铁板，它的重心在（）A.三角形的三条角平分线的交点B.三角形的三条高线的交点C.三角形的三条中线的交点D.三角形的三条边的垂直平分线的交点 2、如图1，如果□ABCD 的对角线AC 、BD 相交于点O ，那么图中的全等三角形共有（）A.1对B.2对C.3对D.4对3、平行四边形的一边长是10cm ，那么这个平行四边形的两条对角线的长可以是（）A.4cm 和6cmB.6cm 和8cmC.8cm 和10cmD.10cm 和12cm4、在四边形ABCD 中，O 是对角线的交点，能判定这个四边形是正方形的条件是( )A.AC ＝BD ，AB ＝CD ，AB ∥CDB.AD //BC ，∠A ＝∠CC.AO ＝BO ＝CO ＝DO ，AC ⊥BDD.AO ＝CO ，BO ＝DO ，AB ＝BC5、如图2，过矩形ABCD 的四个顶点作对角线AC 、BD 的平行线，分别相交于E 、F 、G 、H 四点，则四边形EFGH 为（）A.平行四边形 B 、矩形 C 、菱形 D. 正方形6、如图3，大正方形中有2个小正方形，如果它们的面积分别是S 1、S 2，那么S 1、S 2的大小关系是（）A.S 1 > S 2B.S 1 = S 2C.S 1<S 2D.S 1、S 2 的大小关系不确定 7、矩形一个角的平分线分矩形一边为1cm 和3cm 两部分，则这个矩形的面积为（）A.3cm 2B. 4cm 2C. 12cm 2D. 4cm 2或12cm 28、如图4，菱形花坛 ABCD 的边长为 6m ，∠B ＝60°，其中由两个正六边形组成的图形部分种花，则种花部分的图形的周长（粗线部分）为（） A.123m B.20m C.22m D.24m图3A DCBHEFG图2OABD C图19、如图5，将一个边长分别为4、8的长方形纸片ABCD 折叠，使C 点与A 点重合，则折痕EF 的长是( ) A ．3B ．23C ．5D ．2510、如图6，是由两个正方形组成的长方形花坛ABCD ，小明从顶点A 沿着花坛间小路直到走到长边中点O ，再从中点O 走到正方形OCDF 的中心O 1，再从中心O 1走到正方形O 1GFH 的中心O 2，又从中心O 2走到正方形O 2IHJ 的中心O 3，再从中心O 3走2走到正方形O 3KJP 的中心O 4，一共走了31 2 m ，则长方形花坛ABCD 的周长是（） A.36 m B.48 mC.96 mD.60 m二、填空题（每题3分，共30分）11、如图7, 若将四根木条钉成的矩形木框变形为平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角的值等于＿＿＿.12、如图8，过矩形ABCD 的对角线BD 上一点K 分别作矩形两边的平行线MN 与PQ ，那么图中矩形AMKP 的面积S 1与矩形QCNK 的面积S 2的大小关系是S 1 S 2（填“＞”或“＜”或“＝”）.13、如图9，四边形ABCD 是正方形，P 在CD 上，△ADP 旋转后能够与△ABP ′重合，若AB ＝3，DP ＝1，则PP ′＝＿＿＿.14、已知菱形有一个锐角为60°，一条对角线长为6cm ，则其面积为＿＿＿cm 2.图6图4FEDCBA图5D CBA 图7图9图8 KNM Q CB15、如图10，在梯形ABCD 中,已知AB ∥CD ,点E 为BC 的中点, 设△DEA 的面积为S 1,梯形ABCD 的面积为S 2,则S 1与S 2的关系为＿＿＿.16、如图11，四边形ABCD 的两条对角线AC 、BD 互相垂直，A 1B 1C 1D 1四边形ABCD 的中点四边形.如果AC ＝8，BD ＝10，那么四边形A 1B 1C 1D 1的面积为＿＿＿.17、如图12，□ABCD 中，点E 在边AD 上，以BE 为折痕，将△ABE 向上翻折，点A 正好落在CD 上的点F ，若△FDE 的周长为8，△FCB 的周长为22，则FC 的长为＿＿＿. 18、将一张长方形的纸对折,如图13所示，可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕，那么对折四次可以得到条折痕，如果对折n 次，可以得到条折痕.三、解答题（共40分）19、如图14，等腰梯形ABCD 中,AD ∥BC ,∠DBC =45°,翻折梯形ABCD ,使点B 重合于D ,折痕分别交边AB 、BC 于点F 、E ,若AD =2,BC =8.求BE 的长.……第一次对折第二次对折第三次对折图13图11A 1B 1C 1D 1D ABC D ABCEF图12FE DCBA 图14图10ED CB A20、在一次数学实践探究活动中，小强用两条直线把平行四边形ABCD 分割成四个部分，使含有一组对顶角的两个图形全等；(1)根据小强的分割方法，你认为把平行四边形分割成满足以上全等关系的直线有＿＿＿组；（2）请在图15的三个平行四边形中画出满足小强分割方法的直线；（3）由上述实验操作过程，你发现所画的饿两条直线有什么规律？21、如图16，已知四边形ABCD 是平行四边形，∠BCD 的平分线CF 交边AB 于F ，∠ADC 的平分线DG 交边AB 于G . （1）线段AF 与GB 相等吗？（2）请你在已知条件的基础上再添加一个条件，使得△EFG 为等腰直角三角形,并说明理由.ABCDABCDDCBA图15图1622、如图17，已知□ABCD 中，E 为AD 的中点，CE 的延长线交BA 的延长线于点E .（1）试说明线段CD 与F A 相等的理由；（2）若使∠F ＝∠BCF ，□ABCD 的边长之间还需再添加一个什么条件？请你补上这个条件，并说明你的理由(不要再增添辅助线).23、如图，已知平行四边形ABCD 中，对角线AC BD ，交于点O ，E 是BD 延长线上的点，且ACE △是等边三角形．（1）求证：四边形ABCD 是菱形；（2）若2AED EAD ∠=∠，求证：四边形ABCD 是正方形．ECDBAOABCDE F图1724、已知：如图19，四边形ABCD 是菱形，E 是BD 延长线上一点，F 是DB 延长线上一点，且DE ＝BF .请你以F 为一个端点，和图中已标明字母的某一点连成一条新的线段，猜想并证明它和图中已有的某一条线段相等（只须证明一组线段相等即可）. （1）连结____________；（2）猜想：______=______；（3）证明：25、如图20，已知正方形ABCD 的对角线AC 、BD 相交于点O ，E 是AC 上一点，连结EB ，过点A 作AM ⊥BE ，垂足为M ，AM 交BD 于点F .(1)试说明OE ＝OF ；(2)如图21，若点E 在AC 的延长线上，AM ⊥BE 于点M ，交DB 的延长线于点F ，其它条件不变，则结论“OE ＝OF ”还成立吗?如果成立，请给出说明理由；如果不成立，请说明理由.O C图19DABEF图20EM F CO DBA图21EFOCMDAB参考答案一、1，C ；2，D ；3，D ；4，C ；5，C ；6，A ；7，D ；8，B ；9，D ；10，C .二、11，30°；12，＝；13，14，；15，1212S S =；16，20；17，7；18，15、2n －1.三、21，由题意得△BEF ≌△DFE,∴DE=BE,∵在△BDE 中,DE=BE,∠DBE=45°,∴∠BD E=∠DBE=45°,∴∠DEB=90°,∴DE ⊥BC.∴EC=12(BC -AD)= 12(8-2)=3.∴BE=5；22，（1）无数；（2）只要两条直线都过对角线的交点即可；（3）这两条直线过平行四边形的对称中心（或对角线的交点）； 23，：（1）四边形ABCD 是平行四边形，AO CO ∴=．又ACE △是等边三角形，EO AC ∴⊥，即DB AC ⊥．∴平行四边形ABCD 是菱形；（2）ACE △是等边三角形，60AEC ∴∠=．EO AC ⊥，1302AEO AEC ∴∠=∠=．2AED EAD ∠=∠，15EAD ∴∠=．45ADO EAD AED ∴∠=∠+∠=．四边形ABCD 是菱形，290ADC ADO ∴∠=∠=．∴四边形ABCD 是正方形．24，（1）说明△CED ≌△CEA 即可，（2）BC ＝2AB ，理由略；25，（1）四边形ABCD 是矩形.连结OE .∵四边形ABCD 是平行四边形，∴DO =OB ，∵四边形DEBF 是菱形，∴DE =BE ，∴EO ⊥BD ，∴∠DOE = 90°，即∠DAE = 90°，又四边形ABCD 是平行四边形，∴四边形ABCD 是矩形.（2）解：∵四边形DEBF 是菱形，∴∠FDB =∠EDB ，又由题意知∠EDB =∠EDA ，由（1）知四边形ABCD 是矩形，∴∠ADF =90°即∠FDB +∠EDB +∠ADE =90°，则∠ADB = 60°，∴在Rt △ADB 中，有AD ∶AB =1：3，即3=BCAB；26，（1）连结AF ；（2）猜想AF =AE ；（3）连结AC ，交BD 于O ，因为四边形ABCD 是菱形，所以AC ⊥BD 于O ，DO =BO ，因为DE ＝BF ，所以EO ＝BO 所以AC 垂直平分EF ，所以AF ＝AE ；27，(1)因为四边形ABCD 是正方形，所以∠BOE =∠AOF ＝90°，OB ＝OA ，又因为AM ⊥BE ，所以∠MEA +∠MAE ＝90°=∠AFO +∠MAE ，所以∠MEA ＝∠AFO ，所以Rt △BOE 可以看成是绕点O 旋转90°后与Rt △AOF 重合，所以OE =OF ；(2)OE ＝OF 成立.证明：因为四边形ABCD是正方形，所以∠BOE=∠AOF＝90°，OB＝OA又因为AM BE，所以∠F+∠MBF＝90°＝∠B+∠OBE，又因为∠MBF＝∠OBE，所以∠F＝∠E，所以Rt△BOE可以看成是由Rt△AOF绕点O旋转90°以后得到的，所以OE=OF；。

平行四边形全章测试卷及参考答案

《平行四边形》全章试卷（时间：45分钟满分100分）班级________ 学号__________ 姓名____________ 成绩_____________一、选择题：（每小题5分，共30分）1、已知正方形的边长为4cm ，则其对角线长是………………………………（） A ．8cm B ．16cm C ．32cm D ．42cm2、下列命题中，真命题是…………………………………………………………（）A 、有两边相等的平行四边形是菱形B 、有一个角是直角的四边形是矩形C 、四个角相等的菱形是正方形D 、两条对角线互相垂直且相等的四边形是正方形3、关于四边形ABCD ①两组对边分别平行；②两组对边分别相等；③有一组对边平行且相等；④对角线AC 和BD 相等；以上四个条件中可以判定四边形ABCD 是平行四边形的有（）。

A 、 1个B 、2个C 、3个D 、4个4、若顺次连结四边形ABCD 各边中点所得四边形是矩形，则四边形ABCD 必定是（）A 、菱形B 、对角线相互垂直的四边形C 、正方形D 、对角线相等的四边形5、如图，将一个边长分别为4、8的长方形纸片ABCD 折叠，使C 点与A 点重合，则折痕EF ( )A ．3B ．23C ．5D ．256、如图，矩形ABCD 中，DE ⊥AC 于E ，且∠ADE ：∠EDC=3：2，则∠BDE 的度数为（）A 、36oB 、9oC 、27oD 、18o二、填空题：（每题5分，共40分）7、平行四边形ABCD 中，∠A=500，AB=30cm ，则∠B=____度，DC=____ cm ；8、菱形的两条对角线分别是6cm ，8cm ，则菱形的边长为_____ cm ，面积为______ cm 2；9、若矩形的对角线长为8cm ，两条对角线的一个交角为600，则该矩形的面积为 cm 2；10、如图，点D E F ，，分别是ABC △三边上的中点．若ABC △的面积为12，则DEF △的面积为；11、如图，已知P 是正方形ABCD 对角线BD 上一点，且BP = BC ，则∠ACP 度数是；12、如图，在边长为2 cm 的正方形ABCD 中，点Q 为BC 边的中点，点P 为对角线AC 上一动点，连接P B ，P Q ，则△P BQ 周长的最小值为__________cm(结果不取近似值)。

(常考题)人教版初中数学八年级数学下册第三单元《平行四边形》测试题(答案解析)

一、选择题1．如图，在平行四边形ABCD 中，DE 平分,6,2ADC AD BE ∠==，则平行四边形ABCD 的周长是（）A ．16B ．18C ．20D ．242．图1中甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD ．已知图甲中，45F ∠=︒，15H ∠=︒，图乙中 2MN =，则图2中正方形的对角线AC 长为（）A ．22B ．23C ．231+D ．232+ 3．已知正方形ABCD 中，对角线4AC =，这个正方形的面积是（） A ．8B ．16C ．82D ．1624．如图，M 是ABC 的边BC 的中点AN 平分BAC ∠．且BN AN ⊥，垂足为N 且6AB =，10BC =．2MN =，则ABC 的周长是（）A ．24B ．25C ．26D ．28 5．顺次连接菱形四边中点得到的四边形一定是（）A ．矩形B ．平行四边形C ．菱形D ．正方形6．已知四边形ABCD 是平行四边形，下列结论中不正确的是（） A ．当AB BC =时，四边形ABCD 是菱形 B ．当AC BD ⊥时，四边形ABCD 是菱形C ．当90ABC ∠=时，四边形ABCD 是矩形 D ．当AC BD =时，四边形ABCD 是正方形7．如图1，平行四边形纸片ABCD 的面积为120，20AD =．今沿两对角线将四边形ABCD 剪成甲、乙、丙、丁四个三角形纸片．若将甲、丙合并（AD 、CB 重合）形成一轴对称图形（戊），如图2所示，则图形戊的两对角线长度和为（）A ．26B ．29C ．2243D ．12538．如图，已知ABC ∆的面积为24,点D 在线段AC 上，点F 在线段BC 的延长线上，且4,BC CF =四边形DCFE 是平行四边形，则图中阴影部分的面积为（）A ．6B ．8C ．3D ．49．如图，在123A A A △中，160A ∠=︒，230A ∠=︒，131A A =，3+n A 是1(1,2,3)n n A A n +=⋅⋅⋅的中点，则202120222023A A A △中最短边的长为（）A ．100912B ．101012C ．101112D ．10211210．如图，点P 是矩形ABCD 的对角线上一点，过点P 作//EF BC ，分别交,AB CD 于,E F ，连接,PB PD ，若1,3AE PF ==，则图中阴影部分的面积为（）A ．3B ．6C ．9D ．1211．如图，在Rt ABC 中，90C =∠，30A ∠=，D 是 AC 边的中点，DE AC ⊥于点D ，交AB 于点E ，若83AC =，则DE 的长是（）A ．8B ．6C ．4D ．212．如图，将矩形ABCD 折叠，使点C 和点A 重合，折痕为EF ．若5AF =，3BE =，则EF 的长为（）A ．23B ．17C ．25D ．35二、填空题13．如图，在平行四边形ABCD 中，10,AB BAD =∠的平分线与BC 的延长线交于点E ､与DC 交于点F ，且点F 为边DC 的中点，ADC ∠的平分线交AB 于点M ，交AE 于点N ，连接DE ．若6DM =，则DE 的长为_______．14．如图，在平行四边形ABCD 中，2AD CD =，F 是AD 的中点，CE AB ⊥，垂足E 在线段AB 上．下列结论①DCF ECF ∠=∠；②EF CF =；③3DFE AEF ∠=∠；④2BECCEFSS<中，一定成立的是_________．（请填序号）15．如图，Rt ABC △中，90,5∠=︒=B AB ，D 为AC 的中点， 6.5=BD ，则BC 的长为__________．16．如图，将两个边长为1的小正方形，沿对角线剪开，重新拼成一个大正方形，则大正方形的边长是______．17．如图，AC 是ABCD 的对角线，点E 在AC 上，AD AE BE ==，102D =︒，则BAC ∠的度数是______．18．如图，矩形ABCD 中，10AD =，14AB =，点E 为DC 上一个动点，把ADE 沿AE 折叠，点D 的对应点为D ，若D 落在ABC ∠的平分线上时，DE 的长为_____．19．已知：如图，把长方形纸片ABCD 沿EF 折叠，使D C 、分别落在D C ''、的位置，若65EFB ︒∠=，则AED '∠的度数为_________．20．如图，点E 是平行四边形ABCD 的边BC 上一点，连结AE ，并延长AE 与DC 的延长线交于点F ，若AB AE =，50F ∠=︒，则D ∠=______︒．三、解答题21．如图，BD 为ABC 的角平分线，E 为AB 上一点，BE BC =，连结DE ．（1）求证：BDC BDE ≅△△；（2）若7AB =，2CD =，90︒∠=C ，求ABD △的面积．22．已知：如图，在ABCD 中，4,6,AC BD CA AB ==⊥，求ABCD 的周长和面积．23．如图，点E 在ABCD 内部，//,//AF BE DF CE ．（1）求证：BCE ADF ≅∆；（2）求证：AEDF 1S 2ABCDS =四边形24．如图，在Rt ABC △中，90BAC ∠=︒，中线BD ，CE 相交于点O ，点F ，G 分别为OB ，OC 的中点．（1）求证：//EF DG ，EF DG =；（2）若3AB =，4AC =，求四边形EFGD 的面积．25．正方形ABCD 中，对角线AC 、BD 交于点O ，E 为BD 上一点，延长AE 到点N ，使AE EN =，连接CN 、CE ．（1）求证：CAN △为直角三角形．（2）若45AN =，正方形的边长为6，求BE 的长．26．已知：如图，在ABCD 中，延长DC 至点E ，使得DC CE =，连接AE ，交边BC 于点F ．连接AC ，BE ．（1）求证：四边形ABEC 是平行四边形．（2）若2AFC D ∠=∠，求证：四边形ABEC 是矩形．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】根据角平分线的定义以及两直线平行，内错角相等求出∠CDE=∠CED ，再根据等角对等边的性质可得CE=CD ，然后利用平行四边形对边相等求出CD 、BC 的长度，再求出▱ABCD 的周长．【详解】解：∵DE 平分∠ADC ， ∴∠ADE=∠CDE ，∵四边形ABCD 是平行四边形， ∴AD ∥BC ，BC=AD=6，AB=CD ， ∴∠ADE=∠CED ， ∴∠CDE=∠CED ， ∴CE=CD ， ∵AD=6，BE=2， ∴CE=BC-BE=6-2=4， ∴CD=AB=4，∴▱ABCD 的周长=6+6+4+4=20．故选：C ．【点睛】本题考查了平行四边形对边平行，对边相等的性质，角平分线的定义，等角对等边的性质，熟练掌握平行四边形的性质，证明CE=CD 是解题的关键．2．D解析：D 【分析】连接HF ，过点G 作GIHF 交HF 于点I ，根据甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD ，可得EFH △是等腰直角三角形，则可求得45GFI ，30GHI，根据勾股定理，可得：1GI =，3HI ，则有1FIGI ，31EFHFHIFI，根据正方形的对角线2AC EF =可求出答案．【详解】解：如图示，连接HF ，过点G 作GIHF 交HF 于点I ，∵甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD ． ∴根据题意，根据对称性可得EFH △是等腰直角三角形，则有：90EFH ，45EHFHEF∵45GFE，15EHG，∴45GFI ，30GHI,又∵GI HF ，2MN =，∴根据勾股定理，可得：1GI =，3HI ，则有1FI GI ， ∴31EFHFHIFI，∴正方形的对角线2231232AC EF ，故选：D ．【点睛】本题考查了正方形的性质，勾股定理，直角三角形的性质，熟悉相关性质是解题的关键．3．A解析：A 【分析】根据勾股定理，可得正方形的边长，进而可得正方形的面积．【详解】∵正方形ABCD 中，对角线4AC =， ∴AB 2＋BC 2＝AC 2， ∴2AB 2＝42， ∴AB 2＝8．故选：A ．【点睛】本题主要考查的是正方形的性质，勾股定理，熟练掌握勾股定理是解题的关键．4．C解析：C 【分析】延长BN 交AC 于D ，根据等腰三角形的性质得到AD=AB=6，BN=ND ，根据三角形中位线定理得到DC=2MN=4，计算即可．【详解】解：延长BN 交AC 于D ， ∵AN 平分∠BAC ，BN ⊥AN ，∴AD=AB=6，BN=ND ，又M 是△ABC 的边BC 的中点， ∴DC=2MN=4， ∴AC=AD+DC=10，则△ABC 的周长=AB+AC+BC=6+10+10=26，故选C ．【点睛】本题考查的是三角形中位线定理、等腰三角形的性质，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．5．A解析：A【分析】画出图形，根据菱形的性质得到AC⊥BD，根据三角形中位线定理、矩形的判定定理证明结论．【详解】解：∵四边形ABCD是菱形，∴AC⊥BD，∵E，F，G，H是菱形各边的中点，∴EF∥BD，FG∥AC，∴EF⊥FG，同理：FG⊥HG，GH⊥EH，HE⊥EF，∴四边形EFGH是矩形．故选：A．【点睛】本题考查的是中点四边形，掌握菱形的性质定理、矩形的判定定理以及三角形的中位线定理是解题的关键．6．D解析：D【分析】根据邻边相等的平行四边形是菱形；根据所给条件可以证出邻边相等；根据有一个角是直角的平行四边形是矩形；根据对角线相等的平行四边形是矩形．【详解】解：A、根据邻边相等的平行四边形是菱形可知：四边形ABCD是平行四边形，当=时，它是菱形，故本选项不符合题意；AB BC⊥时，四边形ABCD是菱B、根据对角线互相垂直的平行四边形是菱形知：当AC BD形，故本选项不符合题意；C、根据有一个角是直角的平行四边形是矩形知：当90∠=时，四边形ABCD是ABC矩形，故本选项不符合题意；=时，它是矩形，不是正方D、根据对角线相等的平行四边形是矩形可知：当AC BD形，故本选项符合题意；综上所述，符合题意是D选项；故选：D．【点睛】本题考查了对矩形的判定、菱形的判定，正方形的判定的应用，能正确运用判定定理进行判断是解此题的关键，难度适中．7．A解析：A【分析】由题意可得对角线EF⊥AD，且EF与平行四边形的高相等，进而利用面积与边的关系求出BC边的高即可．【详解】解：如图，连接AD、EF，则可得对角线EF⊥AD，且EF与平行四边形的高相等．∵平行四边形纸片ABCD的面积为120，AD=20，∴BC=AD=20，12EF×AD=12×120，∴EF=6，又AD=20，∴则图形戊中的四边形两对角线之和为20+6=26，故选：A．【点睛】本题考查了平行四边形的性质以及图形的对称问题，熟练掌握平行四边形的性质是解题的关键．8．A解析：A【分析】想办法证明S阴=S△ADE+S△DEC=S△AEC，再由EF∥AC，可得S△AEC=S△ACF解决问题；【详解】解：如图连接AF、EC．∵BC=4CF ，S △ABC =24，∴S △ACF = 14×24=6， ∵四边形CDEF 是平行四边形，∴DE ∥CF ，EF ∥AC ，∴S △DEB =S △DEC ，∴S 阴=S △ADE +S △DEC =S △AEC ，∵EF ∥AC ，∴S △AEC =S △ACF =6，∴S 阴=6．故选：A ．【点睛】本题考查平行四边形的性质、三角形的面积、等高模型等知识，解题的关键是熟练掌握等高模型解决问题，学会用转化的思想思考问题，属于中考常考题型．9．B解析：B【分析】根据已知条件和图形的变化可得前几个图形的最短边的长度，进而可得结论．【详解】解：在△A 1A 2A 3中，∠A 1A 3A 2=90°，∠A 2=30°，A 1A 3=1，A n+3是A n A n+1（n=1、2、3…）的中点，可知：A 4A 5//A 1A 3，A 3A 4=A 2A 4，∴∠A 3A 5A 4=90°，∠A 4A 3A 2=∠A 2=30°，∴△A 1A 2A 3是含30°角的直角三角形，同理可证△A n A n+1A n+2是含30°角的直角三角形．△A 1A 2A 3中最短边的长度为A 1A 3=1=012， △A 3A 4A 5中最短边的长度为A 4A 5=12=112， △A 5A 6A 7中最短边的长度为A 5A 7=21142=， …，所以△A n A n+1A n+2中最短边的长度为1212n -，则△A 2019A 2020A 2021中最短边的长度为120211221122n --==101012．故选：B ．【点睛】本题考查了规律型：图形的变化类，解决本题的关键是观察图形的变化寻找规律．也考查了直角三角形斜边的中线，三角形的中位线，平行线的性质，含30°角的直角三角形的性质，以及等腰三角形的性质等知识．10．A解析：A【分析】先根据矩形的性质证得DFP PBE SS =，然后求解即可．【详解】解：作PM ⊥AD 于M ，交BC 于N ，∴四边形AEPM 、四边形DFPM 、四边形CFPN 和四边形BEPN 都是矩形，∵ADC ABC S S =△△，AMP AEP SS =，PBE PBN S S =，PFD PDM S S =，PFC PCN S S =， ∴S 矩形DFPM =S 矩形BEPN ，∵PM=AE=1，PF=NC=3， ∴131322DFP PBE S S ==⨯⨯=△△， ∴S 阴=33+=322，故选：A ．【点睛】本题主要考查矩形的性质、三角形的面积等知识，证得DFP PBE S S =是解答本题的关键． 11．C解析：C【分析】根据直角三角形的性质得到AB=2BC ，利用勾股定理求出BC ，再根据三角形中位线定理求出DE ．【详解】解：∵在Rt △ABC 中，∠C=90°，∠A=30°，∴AB=2BC ，设BC=x ，则AB=2x ， ∴(22243x x =+，解得：x=8或-8（舍），∴BC=8，∵D 是 AC 边的中点，DE AC ⊥，∴DE=12BC=4，故选C ．【点睛】本题考查了含30°角的直角三角形的性质，三角形的中位线的性质，熟练掌握直角三角形的性质是解题的关键．12．C解析：C【分析】如图，过E 作EM AD ⊥于M ，证明//,AD BC 90B ∠=︒，四边形ABEM 为矩形，再证明5AE AF ==，求解43ME AB AM BE ====，，可得：2MF =，再利用勾股定理可得答案．【详解】解：如图，过E 作EM AD ⊥于M ，矩形ABCD ，53AF BE ==，，//,AD BC ∴ 90B ∠=︒，四边形ABEM 为矩形，,AFE CEF ∴∠=∠由对折可知：,AEF CEF ∠=∠,AFE AEF ∴∠=∠5AE AF ∴==，224AB AE BE ∴=-=，四边形ABEM 为矩形，43ME AB AM BE ∴====，，2MF ∴=，22+2 5.EF ME MF ∴=故选：.C【点睛】本题考查的是轴对称的性质，矩形的判定与性质，等腰三角形的判定，勾股定理的应用，掌握以上知识是解题的关键．二、填空题13．【分析】先判定△ADF≌△ECF即可得到AF=EF依据平行线的性质以及角平分线的定义即可得出AF⊥DM；再根据等腰三角形的性质即可得到DN=MN=3最后依据勾股定理即可得到AN与NE的长进而得出DE解析：【分析】先判定△ADF≌△ECF，即可得到AF=EF，依据平行线的性质以及角平分线的定义，即可得出AF⊥DM；再根据等腰三角形的性质，即可得到DN=MN=3，最后依据勾股定理即可得到AN与NE的长，进而得出DE的长．【详解】解：∵点F为边DC的中点，∴DF=CF=12CD=12AB=5，∵AD∥BC，∴∠ADF=∠ECF，∵∠AFD=∠EFC，∴△ADF≌△ECF（ASA），∴AF=EF，∵CD∥AB，∴∠ADC+∠DAB=180°，又∵AF平分∠BAD，DM平分∠ADC，∴∠ADN+∠DAN=90°，∴AF⊥DM，∵AF平分∠BAD，∴∠BAF=∠DAF，又∵DC∥AB，∴∠BAF=∠DFA，∴∠DAF=∠DFA，∴AD=DF=5，同理可得，AM=AD=5，又∵AN平分∠BAD，∴DN=MN=3，∴Rt△ADN中，4=，∴AF=2AN=8，EF=8，∴NE=AE-AN=12，∴Rt△DEN中，=故答案为：【点睛】本题主要考查了平行四边形的性质以及勾股定理的运用，判定AF ⊥DM ，利用勾股定理进行计算是解决问题的关键．14．②③④【分析】如图延长EF 交CD 的延长线于H 作EN ∥BC 交CD 于NFK ∥AB 交BC 于K 利用平行四边形的性质全等三角形的判定和性质一一判断即可解决问题【详解】解：如图延长EF 交CD 的延长线于H 作EN ∥ 解析：②③④【分析】如图延长EF 交CD 的延长线于H ．作EN ∥BC 交CD 于N ，FK ∥AB 交BC 于K ．利用平行四边形的性质，全等三角形的判定和性质一一判断即可解决问题．【详解】解：如图，延长EF 交CD 的延长线于H ．作EN ∥BC 交CD 于N ，FK ∥AB 交BC 于K ． ∵四边形ABCD 是平行四边形，∴AB ∥CH ，∴∠A=∠FDH ，在△AFE 和△DFH 中，A FDH AFE HFD AF DF ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AFE ≌△DFH ，∴EF=FH ，∵CE ⊥AB ，AB ∥CH ，∴CE ⊥CD ，∴∠ECH=90°，∴CF=EF=FH ，故②正确，∵DF=CD=AF ，∴∠DFC=∠DCF=∠FCB ，∵∠FCB ＞∠ECF ，∴∠DCF ＞∠ECF ，故①错误，∵FK ∥AB ，FD ∥CK ，∴四边形DFKC 是平行四边形，∵AD=2CD ，F 是AD 中点，∴DF=CD ，∴四边形DFKC 是菱形，∴∠DFC=∠KFC ，∵AE ∥FK ，∴∠AEF=∠EFK ，∵FE=FC ，FK ⊥EC ，∴∠EFK=∠KFC ，∴∠DFE=3∠AEF ，故③正确，∵四边形EBCN 是平行四边形，∴S △BEC =S △ENC ，∵S △EHC =2S △EFC ，S △EHC ＞S △ENC ，∴S △BEC ＜2S △CEF ，故④正确，故正确的有②③④．故答案为②③④．【点睛】本题考查平行四边形的性质、全等三角形的判定和性质、直角三角形斜边的中线的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．15．12【分析】根据直角三角形斜边上的中线等于斜边的一半可求出再根据勾股定理求解即可【详解】解：∵D 为的中点∴∴故答案是：12【点睛】考查了勾股定理和直角三角形斜边上的中线熟悉相关性质是解题的关键解析：12．【分析】根据直角三角形斜边上的中线等于斜边的一半，可求出AC ，再根据勾股定理求解即可．【详解】解：∵90B ∠=︒，D 为AC 的中点， 6.5=BD∴22 6.513AC BD ==⨯=， ∴222212135BC AC AB =--，故答案是：12．【点睛】考查了勾股定理和直角三角形斜边上的中线，熟悉相关性质是解题的关键．16．【分析】由题意和图示可知将两个边长为1的正方形沿对角线剪开将所得的四个三角形拼成一个大正方形大正方形的边长恰好是小正方形的对角线的长根据正方形的性质利用勾股定理求出小正方形对角线的长即可【详解】∵如【分析】由题意和图示可知，将两个边长为1的正方形沿对角线剪开，将所得的四个三角形拼成一个大正方形，大正方形的边长恰好是小正方形的对角线的长，根据正方形的性质，利用勾股定理求出小正方形对角线的长即可．【详解】∵如图是两个边长为1的小正方形，∴其对角线的长度==，∴【点睛】本题主要考查正方形的性质和勾股定理，熟练运用和掌握以上两个知识点是解题的关键．17．【分析】由四边形ABCD是平行四边形得到∠ABC=∠D=102°再AD=AE=BE 得出∠EAB=∠EBA∠BEC=∠BCA继而得到∠ACB=2∠BAC再根据∠BAC+∠ACB=3∠BAC=180°-解析：26︒【分析】由四边形ABCD是平行四边形，得到∠ABC=∠D=102°，再AD=AE=BE，得出∠EAB=∠EBA，∠BEC=∠BCA，继而得到∠ACB=2∠BAC，再根据∠BAC+∠ACB=3∠BAC=180°-∠ABC求解即可．【详解】解：∵四边形ABCD是平行四边形，∴AD=BC，∠ABC=∠D=102°，∵AD=AE=BE，∴BC=AE=BE，∴∠EAB=∠EBA，∠BEC=∠BCA，∵∠BEC=∠EAB＋∠EBA=2∠EAB，∴∠ACB=2∠BAC，∴∠BAC+∠ACB=3∠BAC=180°-∠ABC=180°-102°=78°，∴3∠BAC=78°，即∠BAC=26°，故答案为：26°．【点睛】本题考查平行四边形的性质、三角形外角的性质、等腰三角形的性质，解题的关键是综合运用相关知识．18．5或【分析】连接BD′过D′作MN⊥AB交AB于点MCD于点N作D′P⊥BC 交BC于点P先利用勾股定理求出MD′再分两种情况利用勾股定理求出DE【详解】解：如图连接BD′过D′作MN⊥AB交AB于点解析：5或10 3【分析】连接BD′，过D′作MN⊥AB，交AB于点M，CD于点N，作D′P⊥BC交BC于点P，先利用勾股定理求出MD′，再分两种情况利用勾股定理求出DE．【详解】解：如图，连接BD′，过D′作MN⊥AB，交AB于点M，CD于点N，作D′P⊥BC交BC于点P∵点D的对应点D′落在∠ABC的角平分线上，∴MD′=PD′，设MD′=x，则PD′=BM=x，∴AM=AB-BM=14-x，又折叠图形可得AD=AD′=10，∴x2+（14-x）2=100，解得x=6或8，即MD′=6或8．在Rt△END′中，设ED′=a，①当MD′=6时，AM=14-6=8，D′N=10-6=4，EN=8-a，∴a2=42+（8-a）2，解得a=5，即DE=5，②当MD′=8时，AM=14-8=6，D′N=10-8=2，EN=6-a，∴a2=22+（6-a）2，解得103a=，即103DE=.故答案为：5或10 3.【点睛】本题主要考查了折叠问题，解题的关键是明确掌握折叠以后有哪些线段是对应相等的．19．【分析】由长方形纸片可得再求解由折叠的性质求解结合平角的定义可得答案【详解】解：长方形纸片由折叠可得：故答案为：【点睛】本题考查的是矩形与折叠平行线的性质简单题解题的关键是理解折叠的性质解析：50︒【分析】由长方形纸片ABCD ，65EFB ∠=︒可得//,AD BC 再求解,DEF ∠ 由折叠的性质求解,D EF '∠ 结合平角的定义可得答案．【详解】解：长方形纸片ABCD ，65EFB ∠=︒，//,AD BC ∴65DEF EFB ∴∠=∠=︒，由折叠可得：65D EF DEF '∠=∠=︒，180180656550.AED D EF DEF ''∴∠=︒-∠-∠=︒-︒-︒=︒故答案为：50.︒【点睛】本题考查的是矩形与折叠，平行线的性质，简单题，解题的关键是理解折叠的性质． 20．65【分析】利用平行四边形的性质以及平行线的性质得出∠F=∠BAE=50°进而由等腰三角形的性质和三角形内角和定理求得∠B=∠AEB=65°利用平行四边形对角相等得出即可【详解】解：如图所示∵四边形解析：65【分析】利用平行四边形的性质以及平行线的性质得出∠F=∠BAE=50°，进而由等腰三角形的性质和三角形内角和定理求得∠B=∠AEB=65°，利用平行四边形对角相等得出即可．【详解】解：如图所示，∵四边形ABCD 是平行四边形，∴AB ∥DC ，∴∠F=∠BAE=50°，．∵AB=AE ，∴∠B=∠AEB=65°，∴∠D=∠B=65°．故答案是：65．【点睛】此题主要考查了平行四边形的性质，熟练应用平行四边形的性质得出是解题关键．三、解答题21．（1）证明见解析；（2）7【分析】（1）根据角平分线的性质可得DBC DBE ∠=∠，再根据已知条件BE BC =，BD BD =，即可证明；（2）根据（1）中结果，得2DE CD ==，90DEB C ∠=∠=︒，即可求得ABD △的面积．【详解】（1）∵BD 平分ABC ∠，∴DBC DBE ∠=∠，∴在BDC 和BDE 中，BD BD =，DBC DBE ∠=∠，BE BC =，∴BDC ≌BDE ；（2）∵BDC ≌BDE ，∴2DE CD ==，90DEB C ∠=∠=︒， ∴1172722ABD S AB DE =⋅=⨯⨯=△．【点睛】本题考查了角平分线的性质、全等三角形的证明和性质、三角形面积等知识，解题的关键是熟练掌握运用以上知识点．22．25221+，45【分析】依据平行四边形的对角线互相平分，即可得到2AO =，3BO =，再根据勾股定理即可得出AB 与BC 的长，进而得到ABCD 的周长和面积．【详解】解：如图所示，4AC =，6BD =，2AO ∴=，3BO =，又CA AB ⊥， Rt AOB ∴∆中，2222325AB BO AO =-=-=，Rt ABC 中，2222(5)421BC AB AC =+=+=，ABCD ∴的周长2(521)25221=+=+，ABCD 的面积5445AB AC =⨯=⨯=．【点睛】本题主要考查了平行四边形的性质以及勾股定理的运用，解题时注意：平行四边形的对角线互相平分．23．（1）见解析；（2）见解析【分析】（1）先证明CBE DAF ∠=∠，BCE ADF ∠=∠，然后利用ASA 证明：△BCE ≌△ADF ；（2）根据点E 在ABCD 内部，可知：S △BEC +S △AED =12S ▱ABCD ，可得结论．【详解】解：()1四边形ABCD 是平行四边形，,//AD BC AD BC =，180,ABC BAD ∴∠+∠=//,AF BE180,EAB BAF ∴∠+∠=︒,CBE DAF ∴∠=∠同理得,BCE ADF ∠=∠()BCE ADF ASA ∴∆≅∆()2点E 在ABCD 内部， ∴12BEC AED ABCD S S S ∆∆+=，由()1知： ,BCE ADF ∆≅∆BCE ADF S S ∆∆∴= ∴AEDF 1S 2ADF AED BEC AED ABCD S S S S S ∆∆∆∆=+=+=四边形．【点睛】此题主要考查了平行四边形的性质以及全等三角形的判定与性质，熟练利用三角形和平行四边形边的关系得出面积关系是解题关键．24．（1）见解析；（2）2【分析】（1）利用中位线性质可得12ED BC =，//ED BC ．12FG BC =，//FG BC ．可证四边形EFGD 是平行四边形．由平行四边形性质可得EF DG =，//EF DG ．（2）由EFGD 和OG GC =，可推得EO OG CG ==．求13462ABC S =⨯⨯=△由点D 是AC 中点，1322DEC AEC S S ==△△．由三等分可求2231332DEG DEC S S ==⨯=△△．根据平行四边形性质可得四边形DEFG 的面积22DEG S ==△．【详解】（1）证明：∵点E ，D 分别是AB ，AC 的中点， ∴12ED BC =，//ED BC ． ∵点F ，G 分别是OB ，OC 的中点， ∴12FG BC =，//FG BC ． ∴FG ED =，//FG ED ．∴四边形EFGD 是平行四边形．∴EF DG =，//EF DG ；（2）解：∵EFGD ，∴EO OG =．又∵OG GC =，∴EO OG CG ==． ∵3AB =，4AC =， ∵13462ABC S =⨯⨯=△， ∵点D 是AC 中点， ∴1322DEC AEC S S ==△△． ∴2231332DEG DEC S S ==⨯=△△． ∴四边形DEFG 的面积22DEG S ==△．【点睛】本题考查中位线性质，平行四边形的判定与性质，中线的性质，掌握中位线性质，平行四边形的判定与性质，中线的性质，注意中线与中位线的区别以及它们性质是解题关键． 25．（1）见解析；（2）BE =【分析】（1）由四边形ABCD 是正方形，易证得△ABE ≌△CBE ，继而证得AE=CE ，再由AE=CE ，AE=EN ，即可证得∠ACN=90°，则可判定△CAN 为直角三角形；（2）由6，易求得CN 的长，然后由三角形中位线的性质，求得OE 的长，继而求得答案．【详解】解：（1）证明：∵四边形ABCD 是正方形，∴∠ABD=∠CBD=45°，AB=CB ，在△ABE 和△CBE 中，AB CB ABE CBE BE BE ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABE ≌△CBE （SAS ），∴AE=CE ；∵AE=CE ，AE=EN ，∴∠EAC=∠ECA ，CE=EN ，∴∠ECN=∠N ，∵∠EAC+∠ECA+∠ECN+∠N=180°，∴∠ACE+∠ECN=90°，即∠ACN=90°，∴△CAN 为直角三角形；（2）∵正方形的边长为6， ∴AC BD == ∵90,ACN AN ∠=︒= ∴CN ==∵,OA OC AE EN ==，∴12OE CN ==∵12OB BD == ∴BE OB OE =+=【点睛】此题考查了正方形的性质、全等三角形的判定与性质、直角三角形的判定以及勾股定理等知识．注意利用勾股定理求得各线段的长是关键．26．（1）见解析；（2）见解析【分析】（1）根据题意可得到//AB CE ，从而再证明AB CE =即可得出结论；（2）结合（1）的结论可以得到//BC AD ，BCE D ∠=∠，再根据2AFC D ∠=∠推出FEC FCE ∠=∠，从而得到FC FE =即可得出结论．【详解】（1）∵四边形ABCD 是平行四边形，∴//AB CD ，AB CD =，即//AB CE ，∵DC CE =，∴AB CE =，∴四边形ABEC 是平行四边形；（2）∵四边形ABCD 是平行四边形，∴//BC AD ，BCE D ∠=∠，∵四边形ABEC 是平行四边形，又∵AFC FEC BCE ∠=∠+∠，∴当2AFC D ∠=∠时，则有FEC FCE ∠=∠，∴FC FE =，AE BC =，∴四边形ABEC 是矩形．【点睛】本题考查平行四边形的性质与判定，矩形的判定，熟练掌握基本的性质定理以及判定方法是解题关键．。

平行四边形单元测试试卷三套题

新人教版八年级下册第18章平行四边形单元测试试卷（时间90分钟满分100分）班级学号姓名得分一、填空题（共14小题，每题2分，共28分）1．如图，平行四边形ABCD中，E，F分别为AD，BC边上的一点．若再增加一个条件＿＿＿＿＿＿＿＿＿，就可得BE=DF．2．将一矩形纸条，按如图所示折叠，则∠1 = _______度．3．如图，矩形ABCD中，MN∥AD，PQ∥AB，则S1与S2的大小关系是______．第1题第2题第11题4．已知平行四边形ABCD的面积为4，O为两对角线的交点，则△AOB的面积是．5．菱形的一条对角线长为6cm，面积为6cm2，则菱形另一条对角线长为___ ___cm．6．如果梯形的面积为216cm2，且两底长的比为4:5，高为16cm，那么两底长分别为_____．7．如图，在菱形ABCD中，已知AB＝10，AC＝16，那么菱形ABCD的面积为．8．如图，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置，若∠EFB＝65°，则∠AED′＝______．9．如图，若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状，并使其面积为矩形面积的一半，则这个平行四边形的一个最小内角的度数等于______．第7题第8题第9题10．有若干张如图所示的正方形和长方形卡片，如果要拼一个长为（2a + b ），宽为（a + b ）的矩形，则需要A 类卡片张，B 类卡片张，C 类卡片张．11．如图，把矩形ABCD 沿EF 折叠，使点C 落在点A 处，点D 落在点G 处，若∠CFE =60，且DE =1，则边BC 的长为．12．如图，正方形ABCD 的周长为16cm ，顺次连接正方形ABCD 各边的中点，得到四边形EFGH ，则四边形EFGH 的周长等于 cm ，四边形EFGH 的面积等于 cm 2．第10题EABHGFED CBA ABCDEGF13．如图，将一块边长为12的正方形纸片ABCD的顶点A折叠至DC Array边上的点E，使DE=5，折痕为PQ，则PQ的长为_______．14．在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点．观察图中每一个正方形（实线）四条边上的整点的个数，请你猜测由里向外第10个正方形（实线）四条边上的整点个数共有___ __个．第14题二、选择题（共4小题，每题3分，共12分）15．已知平行四边形一边长为10，一条对角线长为6，则它的另一条对角线a 的取值范围为（） A ．4<a<16 B ．14<a<26 C ．12<a<20 D ．以上答案都不正确 16．在菱形ABCD 中，AC 与BD 相交于点O ，则下列说法不正确的是（） A ．AO ⊥BO B ．∠ABD=∠CBD C ．AO=BO D ．AD=CD17．等腰梯形的两底差等于一腰的长，则它的腰与下底的夹角是（）A ．15°B ．30°C ．45°D ．60°18．如图，已知四边形ABCD 中，R 、P 分别是BC 、CD 上的点，E 、F 分别是AP 、RP 的中点，当点P 在CD 上从C 向D 移动而点R 不动时，那么下列结论成立的是（）A ．线段EF 的长逐渐增大B ．线段EF 的长逐渐减小RPD CBAEF 第18题C．线段EF的长不变 D．线段EF的长与点P的位置有关三、解答题（共60分）19．（5分）我们学习了四边形和一些特殊的四边形，右图表示了在某种条件下它们之间的关系．如果①，②两个条件分别是：①两组对边分别平行；②有且只有一组对边平行．那么请你对标上的其他6个数字序号写出相对应的条件．20．（5分）已知：如图，E、F是平行四边行ABCD的对角线AC上的两点，AE=CF．求证：（1）△ADF≌△CBE；（2）EB∥DF．21．（5分）如图，在梯形纸片ABCD中，AD//BC，AD>CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C处，折痕DE交BC于点E，连结C′E．求证：四边形CDC′E是菱形．C′A D22．（6分）如图，在ABC，分别是AD及其延长线上的点，CF BE∥．△中，D是BC边的中点，F E（1）求证：BDE CDF△≌△．（2）请连结BF CE，，试判断四边形BECF是何种特殊四边形，并说明理由．23．（6分）如图，已知平行四边形ABCD中，对角线AC BD△，交于点O，E是BD延长线上的点，且ACE 是等边三角形．（1）求证：四边形ABCD是菱形；（2）若2∠=∠，求证：四边形ABCD是正方形．AED EADEAB24．（6分）如图，四边形ABCD是矩形，E是AB上一点，且DE=AB，过C作CF⊥DE，垂足为F．（1）猜想：AD与CF的大小关系；（2）请证明上面的结论．25．（6分）如图8，在四边形ABCD中，点E是线段AD上的任意一点（E与A D，不重合），G F H，，分别是BE BC CE，，的中点．（1）证明四边形EGFH是平行四边形；（2）在（1）的条件下，若EF BC⊥，且12EF BC=，证明平行四边形EGFH是正方形．BGA EFHDC26．（6分）将平行四边形纸片ABCD按如图方式折叠，使点C与A重合，点D落到D′处，折痕为EF．（1）求证：△ABE≌△AD′F；（2）连接CF，判断四边形AECF是什么特殊四边形？证明你的结论．AB C DE FD′27．（7分）四边形ABCD、DEFG都是正方形，连接AE、CG．（1）求证：AE=CG；（2）观察图形，猜想AE与CG之间的位置关系，并证明你的猜想．28．（8分）已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，（1）求证：四边形ADCE为矩形；（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．N参考答案一、填空题1．答案不唯一，如AE=CF或BE∥DF等 2．52 3．S1＝S2 4．1 5．2 6．12 cm和15cm 7．9613．13 14．408．50° 9．30 10．2，1，3． 11．3 12．二、选择题15．B 16．C 17．D 18．C三、解答题19．③有一个内角为直角；④一组邻边相等；⑤一组邻边相等；⑥有一个内角为直角；⑦两腰相等；⑧一条腰垂直于底边 20．略 21．略 22．（1）略；（2）菱形 23．略 24．（1）AD=CF；（2）略 25．略 26．（1）略；（3）四边形AECF是菱形 27．（1）略；（2）猜想：AE⊥CG，证明略 28．（1）略；（2）AD=1BC等（答案不唯一）2新人教版八年级下册第18章平行四边形单元测试试卷（A卷）（时间90分钟满分100分）班级学号姓名得分一、填空题（共14小题，每题2分，共28分）1．四边形的内角和等于º，外角和等于º．2．正方形的面积为4，则它的边长为，一条对角线长为．3．一个多边形，若它的内角和等于外角和的3倍，则它是边形．4．如果四边形ABCD满足条件，那么这个四边形的对角线AC和BD互相垂直（只需填写一组你认为适当的条件）．5．如果边长分别为4cm和5cm的矩形与一个正方形的面积相等，那么这个正方形的边长为______cm．6．已知菱形两条对角线的长分别为5cm和8cm，则这个菱形的面积是______cm．7．平行四边形ABCD ，加一个条件__________________，它就是菱形．8．等腰梯形的上底是10cm ，下底是14cm ，高是2cm ，则等腰梯形的周长为______cm ． 9．已知菱形的一条对角线长为12，面积为30，则这个菱形的另一条对角线的长为．10．如图，中，AE ⊥BC 于E ，AF ⊥DC 于F ，BC=5，AB=4，AE=3，则AF 的长为． 11．如图，梯形ABCD 中，AD ∥BC ，已知AD=4，BC=8，则EF= ，EF 分梯形所得的两个梯形的面积比S 1 ：S 2为．12．下列矩形中，按虚线剪开后，既能拼出平行四边形和梯形，又能拼出三角形的是图形_______（请填图形下面的代号）．第10题第11题13．如图，小亮从A 点出发，沿直线前进10米后向左转30°，再沿直线前进10米，又向左转30°，……照这样走下去，他第一次回到出发地A 点时，一共走了米．14．如图，依次连接第一个正方形各边的中点得到第二个正方形，再依次连接第二个正方形各边的中点得到第三个正方形，按此方法继续下去，若第一个正方形的边长为1，则第n 个正方形的面积是．二、填空题（共4小题，每题3分，共12分）15．如图， ABCD 中，AE 平分∠DAB ，∠B=100°，则∠DAE30°30°30°A第13题第15题等于（）A．100° B．80° C．60° D．40°16．某校计划修建一座既是中心对称图形又是轴对称图形的花坛，•从学生中征集到设计方案有等腰三角形、正三角形、等腰梯形、菱形等四种图案，你认为符合条件的是（）A．等腰三角形 B．正三角形 C．等腰梯形 D．菱形17．一个多边形的每一个内角都等于140°，那么从这个多边形的一个顶点出发的对角线的条数是（）A．6条 B．7条 C．8条 D．9条18．如图，图中的△BDC′是将矩形ABCD沿对角线BD折叠得到的，第18题图中（包括实线、虚线在内）共有全等三角形（）对．A．1 B．2 C．3 D．4三、解答题（共60分）19．（5分）如图，在□ABCD中，DB=CD，∠C=70°，AE⊥BD于点E．试求∠DAE的度数．20．（5分）已知：如图，在△ABC中，中线BE，CD交于点O，F，G分别是OB，OC的中点．求证：四边形DFGE是平行四边形．21．（5分）在一个平行四边形中若一个角的平分线把一条边分成长是2cm和3cm•的两条线段，求该平行四边形的周长是多少？22．（6分）已知：如图，ABCD中，延长AB到E，延长CD到F，使BE=DF 求证：AC与EF互相平分23．（6分）如图，一块正方形地板由全等的正方形瓷砖铺成，这地板的两条对角线上的瓷砖全是黑色，其余的瓷砖是白色的，如果有101块黑色瓷砖，那么瓷砖的总数是多少？24．（6分）顺次连结等腰梯形四边中点所得的四边形是什么特殊的四边形？画出图形，写出已知，求证并证明．已知：求证：证明：25．（6分）如图，△ABC中，点O是AC边上的一个动点，过点O作直线MN•∥BC，•设MN•交∠BCA 的平分线于点E，交∠BCA的外角平分线于点F．（1）判断OE与OF的大小关系？并说明理由？（2）当点O运动何处时，四边形AECF是矩形？并说出你的理由．26．（6分）如图，若已知△ABC中，D、E分别为AB、AC的中点，则可得DE∥BC，且DE=1BC．•2根据上面的结论：（1）你能否说出顺次连结任意四边形各边中点，可得到一个什么特殊四边形？•并说明理由．（2）如果将（1）中的“任意四边形”改为条件是“平行四边形”或“菱形”或“矩形”或“等腰梯形”，那么它们的结论又分别怎样呢？请说明理由．27．（7分）如图，△ABD、△BCE、△ACF均为等边三角形，请回答下列问题（不要求证明）（1）四边形ADEF是什么四边形？（2）当△ABC满足什么条件时，四边形ADEF是矩形？（3）当△ABC满足什么条件时，以A、D、E、F为顶点的四边形不存在？28．（8分）如图，以△ABC的三边为边在BC的同侧分别作三个等边三角形，•即△ABD•、•△BCE、△ACF，请回答下列问题，并说明理由．（1）四边形ADEF是什么四边形？（2）当△ABC满足什么条件时，四边形ADEF是矩形？（3）当△ABC满足什么条件时，以A、D、E、F为顶点的四边形不存在．参考答案一、填空题1．360 ，360 2．2，22 3．8 4．四边形ABCD 是菱形或四条边都相等或四边形ABCD 是正方形等 5．．20 7．一组邻边相等或对角线互相垂直 8． 9．5 10．41511．6，7512．② 13.120 14．112n -⎛⎫⎪⎝⎭二、选择题15．•D •16．D 17．A 18．D 三、解答题19．∠DAE=20° 20．略 21．14cm 或16cm 22．略 23．2601块 24．略 25．（1）OE=OF ；（2）当点O 运动到AC 的中点时，四边形AECF•是矩形 26．（1）平行四边形；（2）平行四边形，矩形，菱形，正方形 27．（1）平行四边形；（2）满足∠BAC=150º时，四边形ADEF 是矩形；（3）当△ABC 为等边三角形时，以A 、D 、E 、F 为顶点的四边形不存在 28．（1）平行四边形；（2）当∠BAC=150°时是矩形；（3）∠BAC=60°第18章平行四边形单元综合检测（三）一、选择题(每小题4分,共28分)1.已知四边形ABCD是平行四边形,则下列各图中∠1与∠2一定不相等的是( )2.如图,已知菱形ABCD的对角线AC,BD的长分别是6cm,8cm,AE⊥BC于点E,则AE的长是( )A.5cmB.2cmC.cmD.cm3.如图,在平行四边形ABCD中,DE是∠ADC的平分线,F是AB的中点,AB=6,AD=4,则AE∶EF∶BE为( )A.4∶1∶2B.4∶1∶3C.3∶1∶2D.5∶1∶24.(2013·邵阳中考)如图所示,点E是矩形ABCD的边AD延长线上的一点,且AD=DE,连接BE交CD 于点O,连接AO,下列结论不正确的是( )A.△AOB≌△BOCB.△BOC≌△EODC.△AOD≌△EODD.△AOD≌△BOC5.如图,过矩形ABCD的四个顶点作对角线AC,BD的平行线,分别相交于E,F,G,H四点,则四边形EFGH为( )A.平行四边形B.矩形C.菱形D.正方形6.(2013·威海中考)如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC 于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )A.BC=ACB.CF⊥BFC.BD=DFD.AC=BF7.如图,△ABC中,AB=AC,点D,E分别是边AB,AC的中点,点G,F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为( )A.3cmB.4cmC.2cmD.2cm二、填空题(每小题5分,共25分)8.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为.9.(2013·厦门中考)如图,▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是18厘米,则EF= 厘米.10.如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是.11.(2013·牡丹江中考)如图,边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连接AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是.12.(2013·钦州中考)如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是.三、解答题(共47分)13.(10分)(2013·大连中考)如图,在平行四边形ABCD中,点E,F分别在AD,BC上,且AE=CF.求证:BE=DF.14.(12分)(2013·晋江中考)如图,BD是菱形ABCD的对角线,点E,F分别在边CD,DA上,且CE=AF.求证:BE=BF.15.(12分)(2013·铁岭中考)如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形.(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.16.(13分)(2013·济宁中考)如图1,在正方形ABCD中,E,F分别是边AD,DC上的点,且AF⊥BE.(1)求证:AF=BE.(2)如图2,在正方形ABCD中,M,N,P,Q分别是边AB,BC,CD,DA上的点,且MP⊥NQ,判断MP与NQ是否相等?并说明理由.答案解析1.【解析】选C.A项,根据两直线平行内错角相等可得到,故正确;B项,根据对顶角相等可得到,故正确;C项,根据两直线平行内错角相等可得到∠1=∠ACB,∠2为一外角,所以不相等,故不正确;D 项,根据平行四边形对角相等可得到,故正确.2.【解析】选D.由于菱形ABCD的对角线AC,BD的长分别是6cm,8cm,所以菱形边长为=5,所以×6×8=5AE,解得AE=.3.【解析】选A.∵四边形ABCD是平行四边形,∴∠CDE=∠DEA.∵DE是∠ADC的平分线,∴∠CDE=∠ADE,∴∠DEA=∠ADE,∴AE=AD=4.∵F是AB的中点,∴AF=AB=3.∴EF=AE-AF=1,BE=AB-AE=2,。

平行四边形单元测试题及答案

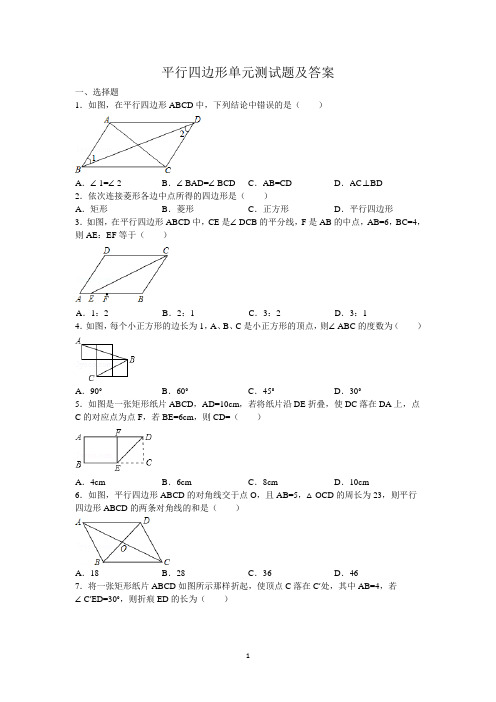
平行四边形单元测试题及答案一、选择题1．如图，在平行四边形ABCD中，下列结论中错误的是（）A．∠1=∠2 B．∠BAD=∠BCD C．A B=CD D．A C⊥BD2．依次连接菱形各边中点所得的四边形是（）A．矩形B．菱形C．正方形D．平行四边形3．如图，在平行四边形ABCD中，CE是∠DCB的平分线，F是AB的中点，AB=6，BC=4，则AE：EF等于（）A．1：2 B．2：1 C．3：2 D．3：14．如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为（）A．90°B．60°C．45°D．30°5．如图是一张矩形纸片ABCD，AD=10cm，若将纸片沿DE折叠，使DC落在DA上，点C的对应点为点F，若BE=6cm，则CD=（）A．4cm B．6cm C．8cm D．10cm6．如图，平行四边形ABCD的对角线交于点O，且AB=5，△OCD的周长为23，则平行四边形ABCD的两条对角线的和是（）A．18 B．28 C．36 D．467．将一张矩形纸片ABCD如图所示那样折起，使顶点C落在C′处，其中AB=4，若∠C′ED=30°，则折痕ED的长为（）A ． 4B ．C ． 8D ．8．如图，在菱形ABCD 中，对角线AC ，BD 分别等于8和6，将BD 沿CB 的方向平移，使D 与A 重合，B 与CB 延长线上的点E 重合，则四边形AECD 的面积等于（）A ． 36B ． 48C ． 72D ． 969．如图，已知四边形ABCD 中，R ，P 分别是BC ，CD 上的点，E ，F 分别是AP ，RP 的中点，当点P 在CD 上从C 向D 移动而点R 不动时，那么下列结论成立的是（）A ．线段EF 的长逐渐增大B ．线段EF 的长逐渐减少C ．线段EF 的长不变D ．线段EF 的长与点P 的位置有关10．如图，甲、乙两人想在正五边形ABCDE 内部找一点P ，使得四边形ABPE 为平行四边形，其作法如下：（甲）连接BD 、CE ，两线段相交于P 点，则P 即为所求（乙）先取CD 的中点M ，再以A 为圆心，AB 长为半径画弧，交AM 于P 点，则P 即为所求．对于甲、乙两人的作法，下列判断何者正确？（）A ．两人皆正确B ．两人皆错误C ．甲正确，乙错误D ．甲错误，乙正确二、填空题11.四边形ABCD 中，如果AB=DC ，当AB________DC 时，四边形ABCD 是平行四边形；当AD________BC 时，四边形ABCD 是平行四边形.12.如图菱形ABCD 的边长是2cm ，E 是AB 的中点，且DE ⊥AB ，则菱形ABCD 的面积为________cm 2.13．如图,▱ABCD 的对角线AC,BD 相交于点O,点E,F 分别是线段AO,BO 的中点.若AC+BD=24第12题第13题厘米,△OAB的周长是18厘米,则EF=厘米.14．在平行四边形ABCD中，∠C＝∠B+∠D,则∠A＝＿＿＿，∠D＝＿＿＿。

北师大版八年级数学下册第6章《平行四边形》章节综合测试含答案

∵AD＝a， ∴a 的取值范围是：2＜a＜10．故答案为：2＜a＜10． 15．【解答】解：∵四边形 ABCD 是平行四边形， ∴∠AEB＝∠EBC，AD＝BC＝5cm， ∵BE 平分∠ABC，
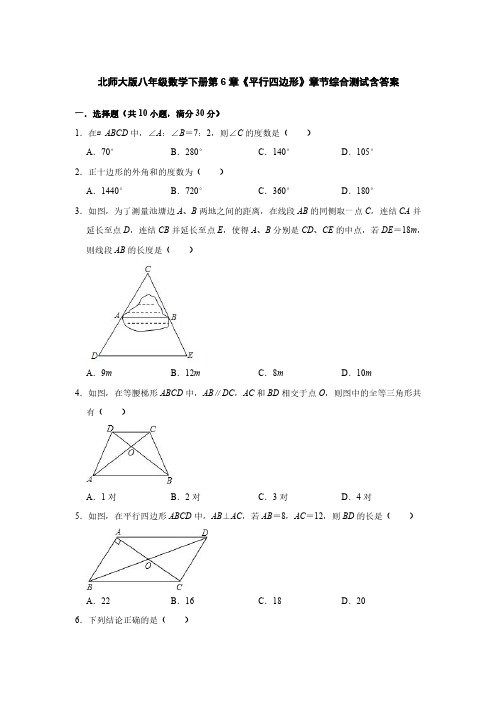
∴∠ABE＝∠EBC， ∴∠ABE＝∠AEB， ∴AB＝AE＝3cm，同理可得：DF＝DC＝3cm， ∴EF＝AE+FD﹣AD＝3+3﹣5＝1（cm）．故答案为：1cm． 16．【解答】解：连接 DE 并延长交 AB 于 H． ∵CD∥AB， ∴∠C＝∠A， ∵E 是 AC 中点， ∴DE＝EH，在△DCE 和△HAE 中，
新多边形的内角和为 720°，则对应的图形是（）
A．
B．
C．
D．
10．平面直角坐标系中一个平行四边形的三个顶点的坐标分别（0，0），（3，0），（1，3），
则第四个顶点的坐标可能是下列坐标：①（4，3）②（﹣2，3）③（﹣1，﹣3）④（2，
﹣3）中的哪几个（）
A．①②③
B．②③④
C．①②④
D．①③④
有（）
A．1 对
B．2 对
C．3 对
D．4 对
5．如图，在平行四边形 ABCD 中，AB⊥AC，若 AB＝8，AC＝12，则 BD 的长是（）
A．22
B．16
6．下列结论正确的是（）
C．18
D．20
A．平行四边形是轴对称图形
B．平行四边形的对角线相等
C．平行四边形的对边平行且相等
D．平行四边形的对角互补，邻角相等
北师大版八年级数学下册第 6 章《平行四边形》章节综合测试含答案
一．选择题（共 10 小题，满分 30 分）
1．在▱ ABCD 中，∠A：∠B＝7：2，则∠C 的度数是（）

北师大版2020九年级数学上册第一章特殊平行四边形单元综合基础过关测试题3(附答案详解)

12．已知正方形①、②在直线上，正方形③如图放置，若正方形①、②的面积分别27和54，则正方形③的边长为______.
13．如图，正方形ABCD的边长为4，点E是CD的中点，AF平分∠BAE交BC于点F，将△ADE绕点A顺时针旋转90°得△ABG，则CF的长为____.
14．E、F，G、H依次为四边形ABCD各边的中点，若四边形ABCD满足______条件，那么四边形EFGH是矩形.（只需填一个你认为合适的条件）
5．B
【解析】
【分析】
由正方形性质可得AB＝AD，∠BAD＝90°，由等边三角形性质可得AE＝AD，∠DAE＝∠AED＝60°，再根据等腰三角形性质和三角形内角和定理即可求得∠BED．
【详解】
解：∵四边形ABCD是正方形
∴AB＝AD，∠BAD＝90°
∵△ADE是等边三角形
∴AE＝AD，∠DAE＝∠AED＝60°
【详解】
过点E作EF⊥AF，交AB的延长线于点F，则∠F=90°，
∵四边形ABCD为正方形，
∴AD=AB，∠A=∠ABC=90°，
∴∠ADP+∠APD=90°，
由旋转可得：PD=PE，∠DPE=90°，
∴∠APD+∠EPF=90°，
∴∠ADP=∠EPF，
在△APD和△FEP中，
∵ ，
∴△APD≌△FEP（AAS），
30．如图，□ABCD中，在对角线BD上取E、F两点，使BE＝DF，连AE，CF，过点E作EN⊥FC交FC于点N，过点F作FM⊥AE交AE于点M；
（1）求证：△ABE≌△CDF；
（2）判断四边形ENFM的形状，并说明理由．
参考答案
1．B
【解析】
【分析】
根据正方形的性质得到∠DAC=∠ACD=45°，由作图知，∠CAP=

平行四边形综合题(共40道)—2023-2024学年八年级数学下册专题训练 (解析版)

z 平行四边形综合题（共40道）!一、单选题1．如图，平行四边形ABCD 的对角线AC,BD 相交于点O,∠ABC =60°，AB =2BC,E 是AB 的中点，连接CE,OE ．下列结论：①∠ACD =30°；②CE 平分∠DCB ；③CD =4OE ；④S △"#$=%&S 四边形'(")．其中结论正确的序号有（）A ．①②B ．②③④C ．①②③D ．①③④ 【答案】C【分析】根据AB =2BC ，点E 是AB 的中点，∠ABC =60°，可知△BCE 是等边三角形，得出∠BEC =∠BCE =60°，AE =BE =CE ，进而得出∠AEC ，根据平行四边形得性质可判断①，再根据平行四边形的性质得∠BCD =120°，即可说明CE 是否平分∠DCB ，然后说明OE 是△ABC 的中位线，可判断CD 和OE 的关系，再根据点O 是AC 的中点，得S △'#$=S △"#$，由点E 是AB 的中点，得S △'"$=S △("$=2S △"#$，进而得S △'("=4S △"#$，然后根据平行四边形的性质得S 四边形'(")=2S △'("，即可判断④，得出答案．【详解】∵AB =2BC ，点E 是AB 的中点， ∴AB =2BE .∵AB =2BC ，∠ABC =60°，∴BC =BE ，∴△BCE 是等边三角形，∴∠BEC =∠BCE =60°，AE =BE =CE ，∴∠AEC =120°，∴∠ACE =∠CAE =30°．∵四边形ABCD 是平行四边形，∴AB ∥CD ，AB =CD =2BC ，∴∠ACD =∠CAE =30°，∠BCD =120°，∴CE 是平分∠DCB ．则①②正确；∵点E 是AB 的中点，点O 是AC 的中点，∴OE 是△ABC 的中位线，∴2OE =BC ，∴CD =4OE ．则③正确；∵点O 是AC 的中点，∴S △'#$=S △"#$．∵点E 是AB 的中点，∴S △'"$=S △("$=2S △"#$，∴S △'("=4S △"#$．由平行四边形的性质得S 四边形'(")=2S △'("， ∴S 四边形'(")=8S △"#$，即S △"#$=18S 四边形'(")．则④不正确．所以正确的有①②③.故选：C.【点睛】本题主要考查了平行四边形的性质，等边三角形的判定和性质，中位线的性质，求三角形的面积等，弄清各三角形的面积之间的关系是解题的关键．2．如图，四边形ABCD 是平行四边形，点E 是边CD 上一点，且BC =EC ，CF ⊥BE 交AB 于点F ，P 是EB 延长线上一点，则下列结论：①BE 平分∠CBF ；②CF 平分∠DCB ；③BC =FB ；④PF =PC ．其中正确结论的有（）A ．①②③B ．①②④C ．②③④D ．①②③④【答案】D【分析】根据等边对等角，平行四边形的性质，平行线的性质即可证明①正确；根据线段垂直平分线的判定即可证明②正确；根据平行线的性质，等角对等边即可证明③正确；根据线段垂直平分线的判定即可证明④正确；即可得出答案．【详解】解：证明：∵BC=EC，∴∠CEB=∠CBE，∵四边形ABCD是平行四边形，∴DC∥AB，∴∠CEB=∠EBF，∴∠CBE=∠EBF，∴BE平分∠CBF，①正确；∵BC=EC，CF⊥BE，∴∠ECF=∠BCF，∴CF平分∠DCB，②正确；∵DC∥AB，∴∠DCF=∠CFB，∵∠ECF=∠BCF，∴∠CFB=∠BCF，∴BF=BC，∴③正确；∵FB=BC，CF⊥BE，∴B点一定在FC的垂直平分线上，即PB垂直平分FC，∴PF=PC，故④正确．故选：D．【点睛】本题考查了平行四边形的性质，平行线的性质，线段垂直平分线的性质，等腰三角形的性质等知识，正确应用等腰三角形的性质是解题关键．3．如图，在▱ABCD中，对角线AC、BD相交于点O，BD=2AD，E、F、G分别是OC、OD、AB的中点，∠ADO；②EG=EF；③GF平分∠AGE；④GF⊥AC，其中正确的有（）下列结论：①∠OBE=%*zA ．1个B ．2个C ．3个D ．4个【答案】D【分析】根据AD ∥BC ，AD =BC 可得OB =BC ，由E 是OC 的中点，即可判断①；由E 是OC 的中点，OB =BC ，可得∠AEB =90°，再由点E 、F 是OC 、OD 的中点，即可判断②；证明四边形BEFG 是平行四边形，可判断③，由GF ∥BE ，即可判断④；【详解】解：在▱ABCD 中，AD ∥BC ，AD =BC ，∴∠ADO =∠OBC ，∵BD =2AD ，∴OB =BC ，∵E 是OC 的中点，∴∠OBE =%*∠OBC =%*∠ADO ，故①正确；∵E 是OC 的中点，OB =BC ，∴∠AEB =90°，∵G 是AB 的中点，∴EG =%*AB ， ∵点E 、F 是OC 、OD 的中点，∴EF =%*CD ，EF ∥CD ，∵AB =CD ，∴EG =EF ，故②正确；∵EF ∥CD ，AB ∥CD ，∴BG ∥GF∵BG =%*AB =%*CD =EF ， ∴四边形BEFG 是平行四边形，∴GF ∥BE ，∴∠AGF=∠ABE，∠FGE=∠BEG，∵BG=GE，∴∠ABE=∠BEG，∴∠AGF=∠FGE，∴GF平分∠AGE，故③正确；∵GF∥BE，∴∠OEB=∠FHO=90°，∴GF⊥AC，故④正确。

【精品】人教版八年级数学下册第十八章平行四边形复习检测题(含答案)【3套】试题

人教版八年级数学下册第十八章平行四边形复习检测题（含答案）一、选择题。

1．下列命题中，错误的是()A．平行四边形的对角线互相平分B．菱形的对角线互相垂直平分C．矩形的对角线相等且互相垂直平分D．角平分线上的点到角两边的距离相等2．在▱ABCD中，已知AB＝(x＋1)cm，BC＝(x－2)cm，CD＝4 cm，则▱ABCD的周长为()A．5 cm B．10 cm C．14 cm D．28 cm3．直角三角形中，两直角边分别是12和5，则斜边上的中线长是()A．34 B．26 C．8.5 D．6.54．如图，在Rt△ABC中，∠A＝30°，BC＝1，点D，E分别是直角边BC，AC的中点，则DE的长为()A．1 B．2 C. 3 D．1＋ 35．正方形的一条对角线长为4，则这个正方形面积是()A．8 B．4 2 C．8 2 D．166.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为（）A．13 B．14 C．15 D．167．如图，四边形ABCD是菱形，AC＝8，DB＝6，DH⊥AB于点H，则DH等于()A.245B.125C ．5D ．48．如图，把矩形纸片ABCD 沿对角线BD 折叠，设重叠部分为△EBD ，则下列说法错误的是( )A ．AB ＝CD B ．∠BAE ＝∠DCEC ．EB ＝ED D ．∠ABE 一定等于30°9．如图，在矩形ABCD 中，E ，F 分别是AD ，BC 中点，连接AF ，BE ，CE ，DF 分别交于点M ，N ，四边形EMFN 是( )A ．正方形B ．菱形C ．矩形D ．无法确定10．将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD ，转动这个四边形，使它形状改变，当∠B ＝90°时，如图1，测得AC ＝2，当∠B ＝60°时，如图2，AC ＝( ) A. 2 B ．2 C. 6 D ．2 2二、填空题11．如图，在菱形ABCD 中，AC ，BD 相交于点O ，若∠BCO ＝55°，则∠ADO ＝____________．12．如图，在▱ABCD中，BE⊥AB交对角线AC于点E，若∠1＝20°，则∠2的度数为____________．13．如图，矩形ABCD沿着对角线BD折叠，使点C落在C′处，BC′交AD于点E，AD ＝8，AB＝4，则DE的长为____________．14．如图，在四边形ABCD中，对角线AC，BD交于点O，OA＝OC，OB＝OD，添加一个条件使四边形ABCD是菱形，那么所添加的条件可以是____________．(写出一个即可)15．如图，正方形ABCO的顶点C，A分别在x轴、y轴上，BC是菱形BDCE的对角线，若∠D＝60°，BC＝2，则点D的坐标是____________．16．如图，正方形ABCD的边长为2，点E为边BC的中点，点P在对角线BD上移动，则PE＋PC的最小值是____________．三、解答题(共52分)17．(10分)如图，点A，F，C，D在同一直线上，点B和点E分别在直线AD的两侧，且AB＝DE，∠A＝∠D，AF＝DC.(1)请写出图中两对全等的三角形；(2)求证：四边形BCEF是平行四边形．18．(10分)如图，AC是▱ABCD的对角线，∠BAC＝∠DAC.(1)求证：AB＝BC；(2)若AB＝2，AC＝23，求▱ABCD的面积．19．(10分)如图，已知，在△ABC中，AB＝AC＝5，BC＝6，AD是BC边上的中线，四边形ADBE是平行四边形．(1)求证：四边形ADBE是矩形；(2)求矩形ADBE的面积．20．(10分)如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE.(1)求证：CE＝CF；(2)若点G在AD上，且∠GCE＝45°，则GE＝BE＋GD成立吗？为什么？21．(12分)已知AC是菱形ABCD的对角线，∠BAC＝60°，点E是直线BC上的一个动点，连接AE，以AE为边作菱形AEFG，并且使∠EAG＝60°，连接CG，当点E在线段BC上时，如图1，易证：AB＝CG＋CE.(1)当点E在线段BC的延长线上时(如图2)，猜想AB，CG，CE之间的关系并证明；(2)当点E在线段CB的延长线上时(如图3)，直接写出AB，CG，CE之间的关系．参考答案一、选择题1.C2.B3.D4.A5.A6.A7.A8.D9.B 10.A 二、填空题。

八年级数学第十八章《平行四边形》全章基础测试题含答案

八年级数学第十八章《平行四边形》全章基础测试题测试1 平行四边形的性质(一)学习要求1．理解平行四边形的概念，掌握平行四边形的性质定理；2．能初步运用平行四边形的性质进行推理和计算，并体会如何利用所学的三角形的知识解决四边形的问题．课堂学习检测一、填空题1．两组对边分别______的四边形叫做平行四边形．它用符号“□”表示，平行四边形ABCD 记作__________。

2．平行四边形的两组对边分别______且______；平行四边形的两组对角分别______；两邻角______；平行四边形的对角线______；平行四边形的面积＝底边长×______．3．在□ABCD中，若∠A－∠B＝40°，则∠A＝______，∠B＝______．4．若平行四边形周长为54cm，两邻边之差为5cm，则这两边的长度分别为______．5．若□ABCD的对角线AC平分∠DAB，则对角线AC与BD的位置关系是______．6．如图，□ABCD中，CE⊥AB，垂足为E，如果∠A＝115°，则∠BCE＝______．6题图7．如图，在□ABCD中，DB＝DC、∠A＝65°，CE⊥BD于E，则∠BCE＝______．7题图8．若在□ABCD中，∠A＝30°，AB＝7cm，AD＝6cm，则S□ABCD＝______．二、选择题9．如图，将□ABCD沿AE翻折，使点B恰好落在AD上的点F处，则下列结论不一定成．．．．立．的是( )．(A)AF＝EF(B)AB＝EF(C)AE＝AF(D)AF＝BE10．如图，下列推理不正确的是( )．(A)∵AB∥CD∴∠ABC＋∠C＝180°(B)∵∠1＝∠2 ∴AD∥BC(C)∵AD∥BC∴∠3＝∠4(D)∵∠A＋∠ADC＝180°∴AB∥CD11．平行四边形两邻边分别为24和16，若两长边间的距离为8，则两短边间的距离为( )．(A)5 (B)6(C)8 (D)12综合、运用、诊断一、解答题12．已知：如图，□ABCD中，DE⊥AC于E，BF⊥AC于F．求证：DE＝BF．13．如图，在□ABCD中，∠ABC的平分线交CD于点E，∠ADE的平分线交AB于点F，试判断AF与CE是否相等，并说明理由．14．已知：如图，E、F分别为□ABCD的对边AB、CD的中点．(1)求证：DE＝FB；(2)若DE、CB的延长线交于G点，求证：CB＝BG．15．已知：如图，□ABCD中，E、F是直线AC上两点，且AE＝CF．求证：(1)BE＝DF；(2)BE∥DF．拓展、探究、思考16．已知：□ABCD中，AB＝5，AD＝2，∠DAB＝120°，若以点A为原点，直线AB为x 轴，如图所示建立直角坐标系，试分别求出B、C、D三点的坐标．17．某市要在一块□ABCD的空地上建造一个四边形花园，要求花园所占面积是□ABCD面积的一半，并且四边形花园的四个顶点作为出入口，要求分别在□ABCD的四条边上，请你设计两种方案：方案(1)：如图1所示，两个出入口E、F已确定，请在图1上画出符合要求的四边形花园，并简要说明画法；图1方案(2)：如图2所示，一个出入口M已确定，请在图2上画出符合要求的梯形花园，并简要说明画法．图2测试2 平行四边形的性质(二)学习要求能综合运用所学的平行四边形的概念和性质解决简单的几何问题．课堂学习检测一、填空题1．平行四边形一条对角线分一个内角为25°和35°，则4个内角分别为______．2．□ABCD中，对角线AC和BD交于O，若AC＝8，BD＝6，则边AB长的取值范围是______．3．平行四边形周长是40cm，则每条对角线长不能超过______cm．4．如图，在□ABCD中，AE、AF分别垂直于BC、CD，垂足为E、F，若∠EAF＝30°，AB＝6，AD＝10，则CD＝______；AB与CD的距离为______；AD与BC的距离为______；∠D＝______．5．□ABCD的周长为60cm，其对角线交于O点，若△AOB的周长比△BOC的周长多10cm，则AB＝______，BC＝______．6．在□ABCD中，AC与BD交于O，若OA＝3x，AC＝4x＋12，则OC的长为______．7．在□ABCD中，CA⊥AB，∠BAD＝120°，若BC＝10cm，则AC＝______，AB＝______．8．在□ABCD中，AE⊥BC于E，若AB＝10cm，BC＝15cm，BE＝6cm，则□ABCD的面积为______．二、选择题9．有下列说法：①平行四边形具有四边形的所有性质；②平行四边形是中心对称图形；③平行四边形的任一条对角线可把平行四边形分成两个全等的三角形；④平行四边形的两条对角线把平行四边形分成4个面积相等的小三角形．其中正确说法的序号是( )．(A)①②④(B)①③④(C)①②③(D)①②③④10．平行四边形一边长12cm，那么它的两条对角线的长度可能是( )．(A)8cm和16cm (B)10cm和16cm (C)8cm和14cm (D)8cm和12cm 11．以不共线的三点A、B、C为顶点的平行四边形共有( )个．(A)1 (B)2 (C)3 (D)无数12．在□ABCD中，点A1、A2、A3、A4和C1、C2、C3、C4分别是AB和CD的五等分点，点B1、B2、和D1、D2分别是BC和DA的三等分点，已知四边形A4B2C4D2的面积为1，则□ABCD的面积为( )(A)2(B)53 (C)35 (D)1513．根据如图所示的(1)，(2)，(3)三个图所表示的规律，依次下去第n 个图中平行四边形的个数是( )……(1) (2) (3)(A)3n (B)3n (n ＋1) (C)6n(D)6n (n ＋1)综合、运用、诊断一、解答题14．已知：如图，在□ABCD 中，从顶点D 向AB 作垂线，垂足为E ，且E 是AB 的中点，已知□ABCD 的周长为8.6cm ，△ABD 的周长为6cm ，求AB 、BC 的长．15．已知：如图，在□ABCD 中，CE ⊥AB 于E ，CF ⊥AD 于F ，∠2＝30°，求∠1、∠3的度数．拓展、探究、思考16．已知：如图，O 为□ABCD 的对角线AC 的串点，过点O 作一条直线分别与AB 、CD 交于点M 、N ，点E 、F 在直线MN 上，且OE ＝OF ．(1)图中共有几对全等三角形?请把它们都写出来；(2)求证：∠MAE＝∠NCF．17．已知：如图，在□ABCD中，点E在AC上，AE＝2EC，点F在AB上，BF＝2AF，若△BEF的面积为2cm2，求□ABCD的面积．测试3 平行四边形的判定(一)学习要求初步掌握平行四边形的判定定理．课堂学习检测一、填空题1．平行四边形的判定方法有：从边的条件有：①两组对边__________的四边形是平行四边形；②两组对边__________的四边形是平行四边形；③一组对边__________的四边形是平行四边形．从对角线的条件有：④两条对角线__________的四边形是平行四边形．从角的条件有：⑤两组对角______的四边形是平行四边形．注意：一组对边平行另一组对边相等的四边形______是平行四边形．(填“一定”或“不一定”)2．四边形ABCD中，若∠A＋∠B＝180°，∠C＋∠D＝180°，则这个四边形______(填“是”、“不是”或“不一定是”)平行四边形．3．一个四边形的边长依次为a、b、c、d，且满足a2＋b2＋c2＋d2＝2ac＋2bd，则这个四边形为______．4．四边形ABCD中，AC、BD为对角线，AC、BD相交于点O，BO＝4，CO＝6，当AO＝______，DO＝______时，这个四边形是平行四边形．5．如图，四边形ABCD中，当∠1＝∠2，且______∥______时，这个四边形是平行四边形．二、选择题6．下列命题中，正确的是( )．(A)两组角相等的四边形是平行四边形(B)一组对边相等，两条对角线相等的四边形是平行四边形(C)一条对角线平分另一条对角线的四边形是平行四边形(D)两组对边分别相等的四边形是平行四边形7．已知：园边形ABCD中，AC与BD交于点O，如果只给出条件“AB∥CD”，那么还不能判定四边形ABCD为平行四边形，给出以下四种说法：①如果再加上条件“BC＝AD”，那么四边形ABCD一定是平行四边形；②如果再加上条件“∠BAD＝∠BCD”，那么四边形ABCD一定是平行四边形；③如果再加上条件“OA＝OC”，那么四边形ABCD一定是平行四边形；④如果再加上条件“∠DBA＝∠CAB”，那么四边形ABCD一定是平行四边形．其中正确的说法是( )．(A)①②(B)①③④(C)②③(D)②③④8．能确定平行四边形的大小和形状的条件是( )．(A)已知平行四边形的两邻边(B)已知平行四边形的相邻两角(C)已知平行四边形的两对角线(D)已知平行四边形的一边、一对角线和周长综合、运用、诊断一、解答题9．如图，在□ABCD中，E、F分别是边AB、CD上的点，已知AE＝CF，M、N是DE和FB的中点，求证：四边形ENFM是平行四边形．10．如图，在□ABCD中，E、F分别是边AD、BC上的点，已知AE＝CF，AF与BE相交于点G，CE与DF相交于点H，求证：四边形EGFH是平行四边形．11．如图，在□ABCD中，E、F分别在边BA、DC的延长线上，已知AE＝CF，P、Q分别是DE和FB的中点，求证：四边形EQFP是平行四边形．12．如图，在□ABCD中，E、F分别在DA、BC的延长线上，已知AE＝CF，F A与BE的延长线相交于点R，EC与DF的延长线相交于点S，求证：四边形RESF是平行四边形．13．已知：如图，四边形ABCD中，AB＝DC，AD＝BC，点E在BC上，点F在AD上，AF＝CE，EF与对角线BD交于点O，求证：O是BD的中点．14．已知：如图，△ABC中，D是AC的中点，E是线段BC延长线上一点，过点A作BE 的平行线与线段ED的延长线交于点F，连结AE、CF．求证：CF∥AE.拓展、探究、思考15．已知：如图，△ABC，D是AB的中点，E是AC上一点，EF∥AB，DF∥BE．(1)猜想DF与AE的关系；(2)证明你的猜想．16．用两个全等的不等边三角形ABC和三角形A′B′C′(如图)，可以拼成几个不同的四边形?其中有几个是平行四边形?请分别画出相应的图形加以说明．测试4 平行四边形的判定(二)学习要求进一步掌握平行四边形的判定方法．课堂学习检测一、填空题1．如图，□ABCD中，CE＝DF，则四边形ABEF是____________．1题图2．如图，□ABCD，EF∥AB，GH∥AD，MN∥AD，图中共有______个平行四边形．2题图3．已知三条线段长分别为10，14，20，以其中两条为对角线，其余一条为边可以画出______个平行四边形．4．已知三条线段长分别为7，15，20，以其中一条为对角线，另两条为邻边，可以画出______个平行四边形．5．已知：如图，四边形AEFD和EBCF都是平行四边形，则四边形ABCD是______．5题图二、选择题6．能判定一个四边形是平行四边形的条件是( )．(A)一组对边平行，另一组对边相等(B)一组对边平行，一组对角互补(C)一组对角相等，一组邻角互补(D)一组对角相等，另一组对角互补7．能判定四边形ABCD是平行四边形的题设是( )．(A)AD＝BC，AB∥CD(B)∠A＝∠B，∠C＝∠D(C)AB＝BC，AD＝DC(D)AB∥CD，CD＝AB8．能判定四边形ABCD是平行四边形的条件是：∠A∶∠B∶∠C∶∠D的值为( )．(A)1∶2∶3∶4 (B)1∶4∶2∶3(C)1∶2∶2∶1 (D)1∶2∶1∶29．如图，E、F分别是□ABCD的边AB、CD的中点，则图中平行四边形的个数共有( )．(A)2个(B)3个(C)4个(D)5个10．□ABCD的对角线的交点在坐标原点，且AD平行于x轴，若A点坐标为(－1，2)，则C点的坐标为( )．(A)(1，－2) (B)(2，－1) (C)(1，－3) (D)(2，－3)11．如图，□ABCD中，对角线AC、BD交于点O，将△AOD平移至△BEC的位置，则图中与OA相等的其他线段有( )．(A)1条(B)2条(C)3条(D)4条综合、运用、诊断一、解答题12．已知：如图，在□ABCD中，点E、F在对角线AC上，且AE＝CF．请你以F为一个端点，和图中已标明字母的某一点连成一条新线段，猜想并证明它和图中已有的某一条线段相等(只需证明一组线段相等即可)．(1)连结______；(2)猜想：______＝______；(3)证明：13．如图，在△ABC中，EF为△ABC的中位线，D为BC边上一点(不与B、C重合)，AD 与EF交于点O，连结EF、DF，要使四边形AEDF为平行四边形，需要添加条件______．(只添加一个条件)证明：14．已知：如图，△ABC中，AB＝AC＝10，D是BC边上的任意一点，分别作DF∥AB交AC 于F ，DE ∥AC 交AB 于E ，求DE ＋DF 的值．15．已知：如图，在等边△ABC 中，D 、F 分别为CB 、BA 上的点，且CD ＝BF ，以AD 为边作等边三角形ADE ．求证：(1)△ACD ≌△CBF ；(2)四边形CDEF 为平行四边形．拓展、探究、思考16．若一次函数y ＝2x －1和反比例函数x k y 2=的图象都经过点(1，1)． (1)求反比例函数的解析式；(2)已知点A 在第三象限，且同时在两个函数的图象上，利用图象求点A 的坐标；(3)利用(2)的结果，若点B 的坐标为(2，0)，且以点A 、O 、B 、P 为顶点的四边形是平行四边形，请你直接写出点P 的坐标．17．如图，点A (m ，m ＋1)，B (m ＋3，m －1)在反比例函数xk y =的图象上．(1)求m，k的值；(2)如果M为x轴上一点，N为y轴上一点，以点A，B，M，N为顶点的四边形是平行四边形，试求直线MN的函数表达式．测试5 平行四边形的性质与判定学习要求能综合运用平行四边形的判定定理和平行四边形的性质定理进行证明和计算．课堂学习检测一、填空题：1．平行四边形长边是短边的2倍，一条对角线与短边垂直，则这个平行四边形各角的度数分别为______．2．从平行四边形的一个锐角顶点作两条高线，如果这两条高线夹角为135°，则这个平行四边形的各内角的度数为______．3．在□ABCD中，BC＝2AB，若E为BC的中点，则∠AED＝______．4．在□ABCD中，如果一边长为8cm，一条对角线为6cm，则另一条对角线x的取值范围是______．5．□ABCD中，对角线AC、BD交于O，且AB＝AC＝2cm，若∠ABC＝60°，则△OAB 的周长为______cm．6．如图，在□ABCD中，M是BC的中点，且AM＝9，BD＝12，AD＝10，则□ABCD的面积是______．7．□ABCD中，对角线AC、BD交于点O，若∠BOC＝120°AD＝7，BD＝10，则□ABCD 的面积为______．8．如图，在□ABCD中，AB＝6，AD＝9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，AF＝5，2BG，则△CEF的周长为______．49．如图，BD为□ABCD的对角线，M、N分别在AD、AB上，且MN∥BD，则S△DMC______ S△BNC．(填“＜”、“＝”或“＞”)综合、运用、诊断一、解答题10．已知：如图，△EFC中，A是EF边上一点，AB∥EC，AD∥FC，若∠EAD＝∠F AB．AB ＝a，AD＝b．(1)求证：△EFC是等腰三角形；(2)求EC＋FC．11．已知：如图，△ABC中，∠ABC＝90°，BD⊥AC于D，AE平分∠BAC，EF∥DC，交BC于F．求证：BE＝FC．12．已知：如图，在□ABCD中，E为AD的中点，CE、BA的延长线交于点F．若BC＝2CD，求证：∠F＝∠BCF．13．如图，已知：在□ABCD中，∠A＝60°，E、F分别是AB、CD的中点，且AB＝2AD．求证：BF∶BD＝3∶3．拓展、探究、思考14．如图1，已知正比例函数和反比例函数的图象都经过点M(－2，－1)，且P(－1，－2)是双曲线上的一点，Q为坐标平面上一动点，P A垂直于x轴，QB垂直于y轴，垂足分别是A、B．图1(1)写出正比例函数和反比例函数的关系式；(2)当点Q在直线MO上运动时，直线MO上是否存在这样的点Q，使得△OBQ与△OAP面积相等?如果存在，请求出点的坐标，如果不存在，请说明理由；(3)如图2，当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的平行四边形OPCQ，求平行四边形OPCQ周长的最小值．图2测试6 三角形的中位线学习要求理解三角形的中位线的概念，掌握三角形的中位线定理．课堂学习检测一、填空题：1．(1)三角形的中位线的定义：连结三角形两边____________叫做三角形的中位线．(2)三角形的中位线定理是三角形的中位线____________第三边，并且等于____________________________________．2．如图，△ABC的周长为64，E、F、G分别为AB、AC、BC的中点，A′、B′、C′分别为EF、EG、GF的中点，△A′B′C′的周长为_________．如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形，按照上述方法继续作三角形，那么第n个三角形的周长是__________________．3．△ABC中，D、E分别为AB、AC的中点，若DE＝4，AD＝3，AE＝2，则△ABC的周长为______．二、解答题4．已知：如图，四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点．求证：四边形EFGH是平行四边形．5．已知：△ABC的中线BD、CE交于点O，F、G分别是OB、OC的中点．求证：四边形DEFG是平行四边形．综合、运用、诊断6．已知：如图，E为□ABCD中DC边的延长线上的一点，且CE＝DC，连结AE分别交BC、BD于点F、G，连结AC交BD于O，连结OF．求证：AB＝2OF．7．已知：如图，在□ABCD中，E是CD的中点，F是AE的中点，FC与BE交于G．求证：GF＝GC．8．已知：如图，在四边形ABCD中，AD＝BC，E、F分别是DC、AB边的中点，FE的延长线分别与AD、BC的延长线交于H、G点．求证：∠AHF＝∠BGF．拓展、探究、思考9．已知：如图，△ABC中，D是BC边的中点，AE平分∠BAC，BE⊥AE于E点，若AB ＝5，AC＝7，求ED．10．如图在△ABC中，D、E分别为AB、AC上的点，且BD＝CE，M、N分别是BE、CD 的中点．过MN的直线交AB于P，交AC于Q，线段AP、AQ相等吗?为什么?测试7 矩形学习要求理解矩形的概念，掌握矩形的性质定理与判定定理．课堂学习检测一、填空题1．(1)矩形的定义：__________________的平行四边形叫做矩形．(2)矩形的性质：矩形是一个特殊的平行四边形，它除了具有四边形和平行四边形所有的性质，还有：矩形的四个角______；矩形的对角线______；矩形是轴对称图形，它的对称轴是____________．(3)矩形的判定：一个角是直角的______是矩形；对角线______的平行四边形是矩形；有______个角是直角的四边形是矩形．2．矩形ABCD中，对角线AC、BD相交于O，∠AOB＝60°，AC＝10cm，则AB＝______cm，BC＝______cm．3．在△ABC中，∠C＝90°，AC＝5，BC＝3，则AB边上的中线CD＝______．4．如图，四边形ABCD是一张矩形纸片，AD＝2AB，若沿过点D的折痕DE将A角翻折，使点A落在BC上的A1处，则∠EA1B＝______°。

平行四边形单元测试综合卷学能测试试卷

平行四边形单元测试综合卷学能测试试卷一、解答题1．如图，平行四边形ABCD 的对角线AC BD 、交于点O ，分别过点C D 、作//,//CF BD DF AC ，连接BF 交AC 于点E ．(1)求证: FCE BOE ≌；(2)当ADC ∠等于多少度时，四边形OCFD 为菱形?请说明理由．2．如图，四边形OABC 中，BC ∥AO ，A （4，0），B （3，4），C （0，4）．点M 从O 出发以每秒2个单位长度的速度向A 运动；点N 从B 同时出发，以每秒1个单位长度的速度向C 运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点N 作NP 垂直x 轴于点P ，连结AC 交NP 于Q ，连结MQ ．（1）当t 为何值时，四边形BNMP 为平行四边形？（2）设四边形BNPA 的面积为y ，求y 与t 之间的函数关系式．（3）是否存在点M ，使得△AQM 为直角三角形？若存在，求出点M 的坐标；若不存在，请说明理由．3．已知四边形ABCD 是正方形，将线段CD 绕点C 逆时针旋转α（090α︒<<︒），得到线段CE ，联结BE 、CE 、DE . 过点B 作BF ⊥DE 交线段DE 的延长线于F ．（1）如图，当BE =CE 时，求旋转角α的度数；（2）当旋转角α的大小发生变化时，BEF ∠的度数是否发生变化?如果变化，请用含α的代数式表示；如果不变，请求出BEF ∠的度数；（3）联结AF ，求证：2DE =．4．如图1，点E 为正方形ABCD 的边AB 上一点，EF EC ⊥，且EF EC =，连接AF ，过点F 作FN 垂直于BA 的延长线于点N ．（1）求EAF ∠的度数；（2）如图2，连接FC 交BD 于M ，交AD 于P ，试证明：2BD BG DG AF DM =+=+．5．如图，锐角ABC ∆，AB AC =，点D 是边BC 上的一点，以AD 为边作ADE ∆，使AE AD =，EAD BAC ∠=∠．（1）过点E 作//EF DC 交AB 于点F ，连接CF （如图①）①请直接写出EAB ∠与DAC ∠的数量关系；②试判断四边形CDEF 的形状，并证明；（2）若60BAC ∠=，过点C 作//CF DE 交AB 于点F ，连接EF （如图②），那么（1）②中的结论是否任然成立？若成立，请给出证明，若不成立，请说明理由．6．已知：在矩形ABCD 中，点F 为AD 中点,点E 为AB 边上一点，连接CE 、EF 、CF ，EF 平分∠AEC ．(1)如图1，求证：CF ⊥EF;(2)如图2，延长CE 、DA 交于点K, 过点F 作FG ∥AB 交CE 于点G 若，点H 为FG 上一点，连接CH,若∠CHG=∠BCE, 求证：CH=FK;(3)如图3, 过点H 作HN ⊥CH 交AB 于点N,若EN=11,FH-GH=1,求GK 长.7．如图，在四边形OABC 是边长为4的正方形点P 为OA 边上任意一点（与点O A 、不重合），连接CP ，过点P 作PM CP ⊥，且PM CP =，过点M 作MN AO ∥，交BO 于点,N 联结BM CN 、，设OP x =.（1）当1x =时，点M 的坐标为（，）（2）设CNMB S y =四形边，求出y 与x 的函数关系式，写出函数的自变量的取值范围.（3）在x 轴正半轴上存在点Q ，使得QMN 是等腰三角形，请直接写出不少于4个符合条件的点Q 的坐标（用x 的式子表示）8．已知E ，F 分别为正方形ABCD 的边BC ，CD 上的点，AF ，DE 相交于点G ，当E ，F 分别为边BC ，CD 的中点时，有：①AF=DE ；②AF ⊥DE 成立．试探究下列问题：（1）如图1，若点E 不是边BC 的中点，F 不是边CD 的中点，且CE=DF ，上述结论①，②是否仍然成立？（请直接回答“成立”或“不成立”），不需要证明）（2）如图2，若点E ，F 分别在CB 的延长线和DC 的延长线上，且CE=DF ，此时，上述结论①，②是否仍然成立？若成立，请写出证明过程，若不成立，请说明理由；（3）如图3，在（2）的基础上，连接AE 和BF ，若点M ，N ，P ，Q 分别为AE ，EF ，FD ，AD 的中点，请判断四边形MNPQ 是“矩形、菱形、正方形”中的哪一种，并证明你的结论．9．阅读下列材料，并解决问题：如图1，在Rt ABC ∆中，90C ∠=︒，8AC =，6BC =，点D 为AC 边上的动点（不与A 、C 重合），以AD ，BD 为边构造ADBE ，求对角线DE 的最小值及此时AD AC的值是多少．在解决这个问题时，小红画出了一个以AD ，BD 为边的ADBE （如图2），设平行四边形对角线的交点为O ，则有AO BO =．于是得出当OD AC ⊥时，OD 最短，此时DE 取最小值，得出DE 的最小值为6．参考小红的做法，解决以下问题：（1）继续完成阅读材料中的问题：当DE 的长度最小时，AD AC=_______；（2）如图3，延长DA 到点F ，使AF DA =．以DF ，DB 为边作FDBE ，求对角线DE 的最小值及此时AD AC的值．10．如图①，在ABC 中，AB AC =，过AB 上一点D 作//DE AC 交BC 于点E ，以E 为顶点，ED 为一边，作DEF A ∠=∠，另一边EF 交AC 于点F ．（1）求证：四边形ADEF 为平行四边形；（2）当点D 为AB 中点时，ADEF 的形状为；（3）延长图①中的DE 到点,G 使,EG DE =连接,,,AE AG FG 得到图②，若,AD AG =判断四边形AEGF 的形状，并说明理由．【参考答案】***试卷处理标记，请不要删除一、解答题1．（1）见解析；（2）当ADC 满足90ADC ∠=︒时，四边形OCFD 为菱形，证明详见解析【分析】（1）证明四边形OCFD 是平行四边形，得出OD=CF ，证出OB=CF ，再证明全等即可（2）证出四边形ABCD 是矩形，由矩形的性质得出OC=OD ，即可得出四边形OCFD 为菱形.【详解】(1)证明:∵//,//CF BD DF AC ，∴四边形OCFD 是平行四边形， OBE CFE ∠=∠，∴OD CF =，∵四边形ABCD 是平行四边形，∴OB OD =，∴OB CF =，在FCE △和BOE △中， OBE CFE BEO FEC OB CF ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()FCE BOE AAS ≌．(2)当ADC 满足90ADC ∠=︒时，四边形OCFD 为菱形.理由如下:∵90ADC ∠=︒，四边形ABCD 是平行四边形，∴四边形ABCD 是矩形∴,,,OA OC OB OD AC BD ===∴OC OD =，∴四边形OCFD 为菱形【点睛】本题考查全等三角形判定与性质，平行四边形和菱形的判定与性质等知识，熟练掌握平行四边形的判定和性质和菱形的判定是解题的关键.2．（1）34；（2）y =4t +2；（3）存在，点M 的坐标为（1，0）或（2，0）．【分析】（1）因为BN ∥MP ，故当BN=MP 时，四边形BNMP 为平行四边形，此时点M 在点P 的左侧，求解即可；（2）y =12（BN +PA ）•OC ，即可求解；（3）①当∠MQA 为直角时，则△MAQ 为等腰直角三角形，则PA =PM ，即可求解；②当∠QMA 为直角时，则NB +OM =BC =3，即可求解．【详解】（1）∵BN ∥MP ，故当BN =MP 时，四边形BNMP 为平行四边形．此时点M 在点P 的左侧时，即0≤t ＜1时，MP =OP ﹣OM =3﹣t ﹣2t =3﹣3t ，BN =t ，即3﹣3t =t ，解得：t =34；（2）由题意得：由点C 的坐标知，OC =4，BN =t ，NC =PO =3﹣t ，PA =4﹣OP =4﹣（3﹣t ）=t +1，则y =12(BN +PA )•OC =12(t +t +1)×4=4t +2；（3）由点A 、C 的坐标知，OA =OC =4，则△COA 为等腰直角三角形，故∠OCA =∠OAC =45°，①当∠MQA 为直角时，∵∠OAC =45°，故△MAQ 为等腰直角三角形，则PA =PM ，而PA =4﹣(3﹣t )=t +1，PM =OP ﹣OM =(3﹣t )﹣2t =3﹣3t ，故t +1=3﹣3t ，解得：t =12，则OM =2t =1，故点M （1，0）；②当∠QMA 为直角时，则点M 、P 重合，则NB +OM =BC =3，即2t +t =3，解得：t =1，故OM =OP =2t =2，故点M （2，0）；综上，点M 的坐标为（1，0）或（2，0）．【点睛】本题是四边形综合题，涉及坐标与图形、平行四边形的性质、等腰直角三角形的判定和性质、图形的面积计算等，复杂度较高，难度较大，其中（3）要分类求解，避免遗漏．3．（1）30°；（2）不变；45°；（3）见解析【分析】（1）利用图形的旋转与正方形的性质得到△BEC 是等边三角形，从而求得α=∠DCE =30°．（2）因为△CED 是等腰三角形，再利用三角形的内角和即可求∠BEF =18045CED CEB ︒-∠-∠=︒.（3）过A 点与C 点添加平行线与垂线，作得四边形AGFH 是平行四边形，求得△ABG ≌△ADH .从而求得矩形AGFH 是正方形，根据正方形的性质证得△AHD ≌△DIC ，从而得出结论．【详解】（1）证明：在正方形ABCD 中, BC =CD .由旋转知，CE =CD ,又∵BE =CE ,∴BE =CE =BC ,∴△BEC 是等边三角形，∴∠BCE =60°.又∵∠BCD =90°,∴α=∠DCE =30°.（2）∠BEF 的度数不发生变化.在△CED 中，CE =CD ,∴∠CED =∠CDE =1809022︒-αα︒-，在△CEB 中,CE =CB ,∠BCE =90α︒-,∴∠CEB =∠CBE =1804522BCE α︒-∠=︒+, ∴∠BEF =18045CED CEB ︒-∠-∠=︒.（3）过点A 作AG ∥DF 与BF 的延长线交于点G ，过点A 作AH ∥GF 与DF 交于点H ，过点C 作CI ⊥DF 于点I易知四边形AGFH 是平行四边形，又∵BF ⊥DF ，∴平行四边形AGFH 是矩形.∵∠BAD =∠BGF =90°，∠BPF =∠APD ，∴∠ABG =∠ADH .又∵∠AGB =∠AHD =90°，AB =AD ，∴△ABG ≌△ADH .∴AG =AH ，∴矩形AGFH 是正方形.∴∠AFH =∠FAH =45°，∴AH =AF∵∠DAH +∠ADH =∠CDI +∠ADH =90°∴∠DAH =∠CDI又∵∠AHD =∠DIC =90°，AD =DC ，∴△AHD ≌△DIC∴AH =DI ，∵DE =2DI ，∴DE =2AH =2AF【点晴】本题考查正方形的性质和判定、图形的旋转、等腰三角形的性质、全等三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．4．（1）∠EAF=135°；（2）证明见解析．【分析】（1）根据正方形的性质，找到证明三角形全等的条件，只要证明△EBC ≌△FNE （AAS ）即可解决问题；（2）过点F 作FG ∥AB 交BD 于点G ．首先证明四边形ABGF 为平行四边形，再证明△FGM ≌△DMC （AAS ）即可解决问题；【详解】（1）解：∵四边形ABCD 是正方形，∴90B N CEF ∠=∠=∠=︒，∴90NEF CEB ∠+∠=，90CEB BCE ∠+∠=，∴NEF ECB ∠=∠，∵EC EF =，∴EBC ∆≌FNE ∆∴FN BE =，EN BC =，∵BC AB =∴EN AB =∴EN AE AB AE -=-∴AN BE =，∴FN AN =，∵FN AB ⊥，∴45NAF ∠=，∴135EAF =∠（2）证明：过点F 作//FG AB 交BD 于点G .由（1）可知135EAF =∠，∵45ABD ∠=︒∴135180EAF ABD ∠=︒+∠=︒，∴//AF BG ，∵//FG AB ，∴四边形ABGF 为平行四边形，∴AF BG =，FG AB =，∵AB CD =，∴FG CD =，∵//AB CD ，∴//FG CD ，∴FGM CDM ∠=∠，∵FMG CMD ∠=∠∴FGM ∆≌CDM ∆∴GM DM =，∴2DG DM =，∴2BD BG DG AF DM =+=+.【点睛】本题考查全等三角形的判定和性质、正方形的性质、平行四边形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．5．（1）①EAB DAC ∠=∠； ② 平行四边形，证明见解析；（2）成立，证明见解析．【分析】（1）①根据EAD BAC ∠=∠，两角有公共角BAD ∠，可证EAB DAC ∠=∠；②连接EB ，证明△EAB ≌△DAC ，可得,ABE ACD EB CD ∠=∠=,再结合平行线的性质和等腰三角形的判定定理可得EF=DC ，由此可根据一组对边平行且相等的四边形是平行四边形证明四边形CDEF 为平行四边形．（2）根据60BAC ∠=︒，可证明△AED 和△ABC 为等边三角形，再根据ED ∥FC 结合等边三角形的性质，得出∠AFC=∠BDA ，求证△ABD ≌△CAF ，得出ED=CF ，进而求证四边形EDCF 是平行四边形．【详解】解：（1）①EAB DAC ∠=∠，理由如下：∵EAD BAC ∠=∠，EAD EAB BAD ∠=∠+∠，BAC BAD DAC ∠=∠+∠, ∴EAB BAD BAD DAC ∠+∠=∠+∠，∴EAB DAC ∠=∠；②证明：如下图，连接EB,在△EAB 和△DAC 中∵AE AD EAB DAC AB AC =⎧⎪∠=∠⎨⎪=⎩∴△EAB ≌△DAC （SAS ）∴,ABE ACD EB CD ∠=∠=,∵AB AC =，∴ABC ACD ∠=∠,∴ABE ABC ∠=∠，∵//EF DC ，∴EFB ABC ∠=∠,∴ABE EFB ∠=∠,∴EB EF =,∴DC EF =∴四边形CDEF 为平行四边形；（2）成立；理由如下：理由如下：∵60BAC ∠=︒，∴=60EAD BAC ∠=∠︒，∵AE=AD ，AB=AC ，∴△AED 和△ABC 为等边三角形，∴∠B=60°，∠ADE=60°，AD=ED,∵ED ∥FC ，∴∠EDB=∠FCB ，∵∠AFC=∠B+∠BCF=60°+∠BCF ，∠BDA=∠ADE+∠EDB=60°+∠EDB ，∴∠AFC=∠BDA ，在△ABD 和△CAF 中，60BDA AFC B BAC AB CA ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△ABD ≌△CAF （AAS ），∴AD=FC ，∵AD=ED ，∴ED=CF ，又∵ED ∥CF ，∴四边形EDCF 是平行四边形．【点睛】本题考查全等三角形的性质和判定，等腰三角形的性质和判定，等边三角形的性质和判定，平行四边形的判定定理，平行线的性质．在做本题时可先以平行四边形的判定定理进行分析，在后两问中已知一组对边平行，所以只需证明这一组对边相等即可，一般证明线段相等就是证明相应的三角形全等．本题中是间接证明全等，在证明线段相等的过程中还应用到等腰三角形的判定定理（第（1）小题的第②问）和等边三角形的性质（第（2）小题），难度较大．6．(1)证明见解析；(2)证明见解析；(3)CN=25.【解析】【分析】(1)如图，延长EF交CD延长线于点Q，先证明CQ=CE，再证明△FQD≌△FEA，根据全等三角形的对应边相等可得EF=FQ，再根据等腰三角形的性质即可得CF⊥EF；(2)分别过点F、H作FM⊥CE ，HP⊥CD，垂足分别为M、P，证明四边形DFHP是矩形，继而证明△HPC≌△FMK，根据全等三角形的性质即可得CH=FK；(3)连接CN，延长HG交CN于点T，设∠DCF=α，则∠GCF=α，先证明得到FG=CG=GE，∠CGT=2α，再由FG是BC的中垂线，可得BG = CG，∠CGT=∠FGK=∠BGT=2α，再证明HN∥BG，得到四边形HGBN是平行四边形，继而证明△HNC≌△KGF，推导可得出HT=CT=TN ，由FH-HG=1，所以设GH=m，则BN=m，FH=m+1，CE=2FG=4m+2，继而根据22222=-=-，可得关于m的方程，解方程求得m的值即可求得答案. BC CN BN CE BE【详解】(1)如图，延长EF交CD延长线于点Q，∵矩形ABCD，AB∥CD，∴∠AEF=∠CQE，∠A=∠QDF，又∵EF 平分∠AEC ，∴∠AEF=∠CEF，∴∠CEF=∠CQE，∴CQ=CE，∵点F是AD中点，∴AF=DF，∴△FQD≌△FEA，∴EF=FQ，又∵CE=CQ，∴CF⊥EF；(2)分别过点F、H作FM⊥CE ，HP⊥CD，垂足分别为M、P，∵CQ=CE ，CF⊥EF，∴∠DCF=∠FCE，又∵FD⊥CD，∴FM=DF，∵FG//AB，∴∠DFH=∠DAC=90°，∴∠DFH=∠FDP=∠DPH=90°，∴四边形DFHP是矩形，∴DF=HP，∴FM= DF=HP，∵∠CHG=∠BCE，AD∥BC，FG∥CD，∴∠K=∠BCE=∠CHG=∠DCH，又∵∠FMK=∠HPC=90°，∴△HPC≌△FMK，∴CH=FK；(3)连接CN，延长HG交CN于点T，设∠DCF=α，则∠GCF=α，∵FG∥CD ，∴∠DCF=∠CFG，∴∠FCG=∠CFG，∴FG=CG，∵CF⊥EF，∴∠FEG+∠FCG=90°，∠CFG+∠GFE=90°，∴∠GFE=∠FEG，∴GF=FE，∴FG=CG=GE，∠CGT=2α，∵FG是BC的中垂线，∴BG = CG，∠CGT=∠FGK=∠BGT=2α，∵∠CHG=∠BCE=90°-2α，∠CHN=90°，∴∠GHN=∠FGK=∠BGT=2α，∴HN∥BG，∴四边形HGBN是平行四边形，∴HG=BN ，HN=BG = CG =FG ，∴△HNC ≌△KGF ，∴GK=CN ，∠HNC=∠FGK=∠NHT=2α，∴HT=CT=TN ，∵FH-HG=1，∴设GH=m ，则BN=m ，FH=m+1，CE=2FG=4m+2，∵GT=1122EN =，∴CN=2HT=11+2m ， ∵22222BC CN BN CE BE =-=-，∴2222(112)(42)(11)m m m m +-=+-+ ∴1176m =-(舍去)，27m =， ∴CN=GK=2HT=25.【点睛】本题考查的是四边形综合题，涉及了等腰三角形的判定与性质，全等三角形的判定与性质，平行四边形的判定与性质，矩形的性质与判定，三角形外角的性质等，综合性较强，难度较大，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.7．（1）点M 的坐标为(51)，；（2）()44y x =-()04x <<；（3）()240Q x +， ()340Q x + ，()40Q x ，()504)Q x x << 【分析】（1）过点M 作ME OA ⊥，由“AAS ”可证COP PEM ∆≅∆，可得4CO PE ==，1OP ME ==，即可求点M 坐标；（2）由（1）可知COP PEM ∆≅∆,设OP=x ，则可得M 点坐标为（4+x ，x ），由直线OB 解析式可得N （x ，x ），即可知MN=4，由一组对边平行而且相等的四边形是平行四边形即可证明四边形BCNM 是平行四边形，进而可求y 与x 的函数关系式；（3）首先画出符合要求的点Q 的图形，共分三种情况，第一种情况：当MN 为底边时，第二种情况：当M 为顶点MN 为腰时，第三种情况：当N 为顶点MN 为腰时，然后根据图形特征结合勾股定理求出各种情况点的坐标即可解答．【详解】解：（1）如图，过点M 作ME OA ⊥，CP PM ⊥90CPO MPE ∴∠+∠=︒，且90CPO PCO ∠+∠=︒PCO MPE ∴∠=∠，且CP PM =，90COP PEM ∠=∠=︒()COP PEM AAS ∴∆≅∆4CO PE ∴==，1OP ME ==5OE ∴=∴点M 坐标为(5,1)故答案为(5,1)（2）由（1）可知COP PEM ∆≅∆4CO PE ∴==，OP ME x ==∴点M 坐标为(4,)x x +四边形OABC 是边长为4的正方形，∴点(4,4)B∴直线BO 的解析式为：y x =//MN AO ，交BO 于点N ，∴点N 坐标为(,)x x4MN BC ∴==，且//BC MN∴四边形BCNM 是平行四边形4(4)y x ∴=- (04)x <<（3）在x 轴正半轴上存在点Q ，使得QMN ∆是等腰三角形，此时点Q 的坐标为：1(2,0)Q x +，22(416Q x x +-，0)，23(416Q x x ++-，240)(16Q x x +-250)(16Q x x -，0)其中(04)x <<，理由：当（2）可知，(04)OP x x =<<，4MN PE ==，//MN x 轴，所以共分为以下几种请：第一种情况：当MN 为底边时，作MN 的垂直平分线，与x 轴的交点为1Q ，如图2所示111222PQ PE MN ===， 12OQ x ∴=+，1(2,0)Q x ∴+第二种情况：如图3所示，当M 为顶点MN 为腰时，以M 为圆心，MN 的长为半径画弧交x 轴于点2Q 、3Q ，连接2MQ 、3MQ ，则234MQ MQ ==，2222Q E MQ ME ∴=-222416OQ OE Q E x x ∴=-=+-，22(416Q x x ∴+-0)，32Q E Q E =，233416OQ OE Q E x x =+=+-23(416Q x x ∴++-0)；第三种情况，当以N 为顶点、MN 为腰时，以N 为圆心，MN 长为半径画圆弧交x 轴正半轴于点4Q ，当022x <<4所示，则2224416PQ NQ NP x =-=-，24416OQ OP PQ x x ∴=+=+-，即24(16Q x x +-，0)．当22x =时，则4ON =，此时Q 点与O 点重合，舍去；当224x <<时，如图5，以N 为圆心，MN 为半径画弧，与x 轴的交点为4Q ，5Q ．4Q 的坐标为：24(16Q x x -0)．2516OQ x x =-25(16Q x x ∴-0)所以，综上所述，1(2,0)Q x +，22(416Q x x +-，0)，23(416Q x x ++-，240)(16Q x x +-250)(16Q x x -，0)使QMN ∆是等腰三角形．【点睛】本题考查四边形综合题，解题的关键是明确题意，画出相应的图象，找出所求问题需要的条件，利用数形结合的思想解答问题．8．（1）成立；（2）成立，理由见试题解析；（3）正方形，证明见试题解析．【解析】试题分析：（1）因为四边形ABCD 为正方形，CE=DF ，可证△ADF ≌△DCE （SAS ），即可得到AF=DE ，∠DAF=∠CDE ，又因为∠ADG+∠EDC=90°，即有AF ⊥DE ；（2）∵四边形ABCD 为正方形，CE=DF ，可证△ADF ≌△DCE （SAS ），即可得到AF=DE ，∠E=∠F，又因为∠ADG+∠EDC=90°，即有AF⊥DE；（3）设MQ，DE分别交AF于点G，O，PQ交DE于点H，因为点M，N，P，Q分别为AE，EF，FD，AD的中点，可得MQ=PN=12DE，PQ=MN=12AF，MQ∥DE，PQ∥AF，然后根据AF=DE，可得四边形MNPQ是菱形，又因为AF⊥DE即可证得四边形MNPQ是正方形．试题解析：（1）上述结论①，②仍然成立，理由是：∵四边形ABCD为正方形，∴AD=DC，∠BCD=∠ADC=90°，在△ADF和△DCE中，∵DF=CE，∠ADC=∠BCD=90°，AD=CD，∴△ADF≌△DCE（SAS），∴AF=DE，∠DAF=∠CDE，∵∠ADG+∠EDC=90°，∴∠ADG+∠DAF=90°，∴∠AGD=90°，即AF⊥DE；（2）上述结论①，②仍然成立，理由是：∵四边形ABCD为正方形，∴AD=DC，∠BCD=∠ADC=90°，在△ADF和△DCE中，∵DF=CE，∠ADC=∠BCD=90°，AD=CD，∴△ADF≌△DCE（SAS），∴AF=DE，∠E=∠F，∵∠ADG+∠EDC=90°，∴∠ADG+∠DAF=90°，∴∠AGD=90°，即AF⊥DE；（3）四边形MNPQ是正方形．理由是：如图，设MQ，DE分别交AF于点G，O，PQ交DE于点H，∵点M，N，P，Q分别为AE，EF，FD，AD的中点，∴MQ=PN=12DE，PQ=MN=12AF，MQ∥DE，PQ∥AF，∴四边形OHQG是平行四边形，∵AF=DE，∴MQ=PQ=PN=MN，∴四边形MNPQ是菱形，∵AF⊥DE，∴∠AOD=90°，∴∠HQG=∠AOD=90°，∴四边形MNPQ是正方形．考点：1．四边形综合题；2．综合题．9．（1）12；（2）13ADAC=．【分析】（1）易证四边形CDEB是矩形，由条件“四边形ADBE是平行四边形可得AD＝EB＝DC，从而得到ADAC的值．（2）由题可知当DE AC⊥时，DE最短，可以证到四边形DCBE是矩形．从而可以得到各边关系从而求出ADAC的值．【详解】解：（1）∵四边形ADBE是平行四边形，∴AD∥BE，AD＝BE．∵DE ⊥AC ，∠ACB ＝90°，∴∠ADE ＝∠C ＝90°．∴DE ∥BC ．∵DC ∥BE ，DE ∥BC ，∠C ＝90°，∴四边形DCBE 是矩形．∴EB ＝DC ．∴AD ＝DC ． ∴AD AC =＝12．故答案为：12．（2）如图，由题可知当DE AC ⊥时，DE 最短．最小值是6．∵四边形FDBE 是平行四边形，∴//DF BE ，DF BE =．∵DE AC ⊥，90C ∠=︒，∴90ADE C ∠=∠=︒．∴//DE BC ．∴四边形CDEB 是平行四边形，又∵90C ∠=︒，∴四边形CDEB 是矩形．∴BE CD =，6DE BC ==．∴DF CD =．∵AF AD =，∴2DC DF AD ==．∴3AC AD DC AD =+=． ∴13AD AC =．【点睛】本题考查了平行线之间的距离、平行线的判定、矩形的判定与性质、平行四边形的性质等知识，具有一定的综合性；本题还考查了阅读能力，体现了自主探究与合作交流相结合的新课程理念，是一道好题．10．（1）证明见解析；（2）菱形；（3）四边形AEGF 是矩形，理由见解析．【分析】（1）根据平行线的性质得到BDE A ∠=∠，根据题意得到DEFBDE ∠=∠，根据平行线的判定定理得到//AD EF ，根据平行四边形的判定定理证明；（2）根据三角形中位线定理得到12DE AC =，得到AD DE =，根据菱形的判定定理证明；（3）根据等腰三角形的性质得到AE EG ⊥，根据有一个角是直角的平行四边形是矩形证明．【详解】（1）证明：//DE AC ，BDE A ∴∠=∠，DEF A ∠=∠，DEF BDE ∴∠=∠，//AD EF ∴，又//DE AC ，∴四边形ADEF 为平行四边形；（2）解：ADEF 的形状为菱形，理由如下：点D 为AB 中点， 12AD AB ∴=， //DE AC ，点D 为AB 中点，12DE AC ∴=， AB AC =，AD DE ∴=，∴平行四边形ADEF 为菱形，故答案为：菱形；（3）四边形AEGF 是矩形，理由如下：由（1）得，四边形ADEF 为平行四边形，//AF DE ∴，AF DE =，EG DE ，//=，∴，AF GEAF DE∴四边形AEGF是平行四边形，=，AD AG，EG DE∴⊥，AE EG∴四边形AEGF是矩形．【点睛】本题考查的是平行四边形、矩形、菱形的判定，掌握它们的判定定理是解题的关键．。

(人教版)沈阳市八年级数学下册第三单元《平行四边形》检测卷(有答案解析)

一、选择题1．如图，ABC 中，//DE BC ，//EF AB ，要判定四边形DBFE 是菱形，可添加的条件是（）A ．BD EF =B ．AD BD =C ．BE AC ⊥D ．BE 平分ABC ∠ 2．如图，正方形ABCD 中，6AB =，点E 在边CD 上，且2CE DE =．将ADE 沿AE 对折至AFE △，延长EF 交边BC 于点G ，连结AG 、CF ．下列结论：①ABG AFG △≌△；②BG GC =；③//AG CF ；④3FGC S =．其中正确结论的个数是（）A ．1B ．2C ．3D ．43．在平面直角坐标系中，长方形OACB 的顶点O 在坐标原点，顶点A 、B 分别在x 轴、y 轴的正半轴上，OA ＝3，OB ＝4，D 为边OB 的中点，若E 为x 轴上的一个动点，当△CDE 的周长最小时，求点E 的坐标（）A ．（一3，0）B ．（3，0）C ．（0，0）D ．（1，0） 4．如图，在平行四边形ABCD 中，100B D ︒∠+∠=，则B 等于（）A ．50°B ．65°C ．100°D ．130°5．如图，已知正方形ABCD 的边长为4，点Р是对角线BD 上一动点（不与D ，B 重合），PF CD ⊥于点F ，PE BC ⊥于点E ，连接AP ，EF ．则下列结论错误的是（）A ．2PD EC =B ．AP EF =，且AP EF ⊥C ．四边形PECF 的周长是8D ．12BD EF AB ≤< 6．已知平行四边形ABCD 的一边长为5，则对角线AC ，BD 的长可取下列数据中的（）A ．2和4B ．3和4C ．4和5D ．5和6 7．下列条件中不能判定一定是平行四边形的有（）A ．一组对角相等，一组邻角互补B ．一组对边平行，另一组对边相等C ．两组对边相等D ．一组对边平行，且另一组对边也平行8．四边形ABCD 中，对角线AC BD 、交于点O ．给出下列四组条件：①AB ∥CD ，AD ∥BC ；②AB CD =，AD BC =；③AO CO =，BO DO =；④AB ∥CD ，AD BC =．其中一定能判定这个四边形是平行四边形的条件共有（）A ．1组；B ．2组；C ．3组；D ．4组． 9．下列命题中，正确的命题是（）A ．菱形的对角线互相平分且相等B ．顺次联结菱形各边的中点所得的四边形是矩形C ．矩形的对角线互相垂直平分D ．顺次连结矩形各边的中点所得的四边形是正方形10．在平面直角坐标系中，点A ，B ，C 的坐标分别为()5,0，()1,3--，()2,5-，当四边形ABCD 是平行四边形时，点D 的坐标为（）A ．()8,2-B ．()7,3-C ．()8,3-D ．()14,0 11．在Rt △ABC 中，∠C =90°，点P 在边AB 上．BC =6， AC =8， ( )A ．若∠ACP=45°，则CP=5B ．若∠ACP=∠B ，则CP=5C ．若∠ACP=45°，则CP=245D ．若∠ACP=∠B ，则CP=24512．矩形不一定具有的性质是（）A ．对角线互相平分B ．是轴对称图形C ．对角线相等D ．对角线互相垂直参考答案二、填空题13．如图所示，在平行四边形ABCD 中2=AD AB ，CE 平分BCD ∠交AD 边于点E ，且4AE =，则AB 的长为______．14．菱形的周长为20cm ，一条对角线长为8cm ，则菱形的面积为______cm 2．15．三角形的三边长分别为21，5，2，则该三角形最长边上的中线长为____． 16．如图，在Rt △ABC 中，∠ACB ＝90°，CD 是斜边AB 上的中线，E 、F 分别为DB 、BC 的中点，若AB ＝8，则EF ＝_____．17．如图，Rt ABC △中，90,5∠=︒=B AB ，D 为AC 的中点， 6.5=BD ，则BC 的长为__________．18．如图，EF 过ABCD 对角线的交点O ，交AD 于E ，交BC 于F ，若ABCD 的周长为19， 2.5OE =，则四边形EFCD 的周长为_____．19．在△ABC 中， AD 是BC 边上的高线，CE 是AB 边上的中线，CD =AE ，且CE <AC ．若AD =6，AB =10，则CE =___________20．如图所示，在ABCD 中，AC 与BD 相交于点O ，若DAC EAC ∠=∠，4AE =，3AO =，则AEC S ∆的面积为____．三、解答题21．如图，BD 为ABC 的角平分线，E 为AB 上一点，BE BC =，连结DE ．（1）求证：BDC BDE ≅△△；（2）若7AB =，2CD =，90︒∠=C ，求ABD △的面积．22．如图，矩形ABCD 中，4AB =，6AD =，E ，F 分别是AD 和AB 上的点，2AE =，F 是AB 的中点，请使用无刻度的直尺，分别按下列要求作图．（1）在图1中，作一个以EF 为直角边的直角三角形；（2）在图2中，作一个以EF 为边的平行四边形．23．已知：如图，在ABCD 中，4,6,AC BD CA AB ==⊥，求ABCD 的周长和面积．24．如图，在▱ABCD 中，AB =12cm ，BC =6cm ，∠A =60°，点P 沿AB 边从点A 开始以2cm/秒的速度向点B 移动，同时点Q 沿DA 边从点D 开始以1cm/秒的速度向点A 移动，用t 表示移动的时间（0≤t ≤6）．（1）当t 为何值时，△PAQ 是等边三角形？（2）当t 为何值时，△PAQ 为直角三角形？25．如图，平行四边形ABCD 中，BD 是它的一条对角线，过A 、C 两点作,AE BD CF BD ⊥⊥，垂足分别为E 、F ，延长AE 、CF 分别交CD 、AB 于M 、N ．（1）求证：四边形CMAN 是平行四边形；（2）已知4,3DE FN ==．求BN 的长．26．如图，在矩形ABCD 中，M ，N 分别是AD ，BC 的中点，P ，Q 分别是BM ，DN 的中点．（1）求证：四边形BNDM是平行四边形．（2）猜想：四边形MPNQ是哪种特殊的平行四边形？并证明你的猜想．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】当BE平分∠ABC时，四边形DBFE是菱形，可知先证明四边形BDEF是平行四边形，再证明BD=DE即可解决问题．【详解】解：当BE平分∠ABC时，四边形DBFE是菱形，理由：∵DE∥BC，∴∠DEB=∠EBC，∵∠EBC=∠EBD，∴∠EBD=∠DEB，∴BD=DE，∵DE∥BC，EF∥AB，∴四边形DBFE是平行四边形，∵BD=DE，∴四边形DBFE是菱形．其余选项均无法判断四边形DBFE是菱形，故选：D．【点睛】本题考查菱形的判定、平行四边形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题．2．C解析：C【分析】由正方形和折叠的性质得出AF＝AB，∠B＝∠AFG＝90°，由HL即可证明Rt △ABG ≌Rt △AFG ，得出①正确；设BG ＝x ，则CG ＝BC−BG ＝6−x ，GE ＝GF ＋EF ＝BG ＋DE ＝x ＋2，由勾股定理求出x ＝3，得出②正确；由等腰三角形的性质和外角关系得出∠AGB ＝∠FCG ，证出平行线，得出③正确；根据三角形的特点及面积公式求出△FGC 的面积,即可求证④．【详解】∵四边形ABCD 是正方形，∴AB ＝AD ＝DC ＝6，∠B ＝D ＝90°，∵CD ＝3DE ，∴DE ＝2，∵△ADE 沿AE 折叠得到△AFE ，∴DE ＝EF ＝2，AD ＝AF ，∠D ＝∠AFE ＝∠AFG ＝90°，∴AF ＝AB ，∵在Rt △ABG 和Rt △AFG 中，AG AG AB AF =⎧⎨=⎩， ∴Rt △ABG ≌Rt △AFG （HL ），∴①正确；∵Rt △ABG ≌Rt △AFG ，∴BG ＝FG ，∠AGB ＝∠AGF ，设BG ＝x ，则CG ＝BC−BG ＝6−x ，GE ＝GF ＋EF ＝BG ＋DE ＝x ＋2，在Rt △ECG 中，由勾股定理得：CG 2＋CE 2＝EG 2，∵CG ＝6−x ，CE ＝4，EG ＝x ＋2∴（6−x ）2＋42＝（x ＋2）2解得：x ＝3，∴BG ＝GF ＝CG ＝3，∴②正确；∵CG ＝GF ，∴∠CFG ＝∠FCG ，∵∠BGF ＝∠CFG ＋∠FCG ，又∵∠BGF ＝∠AGB ＋∠AGF ，∴∠CFG ＋∠FCG ＝∠AGB ＋∠AGF ，∵∠AGB ＝∠AGF ，∠CFG ＝∠FCG ，∴∠AGB ＝∠FCG ，∴AG ∥CF ，∴③正确；∵△CFG 和△CEG 中，分别把FG 和GE 看作底边，则这两个三角形的高相同．∴35CFG CEG SFG S GE ==， ∵S △GCE ＝12×3×4＝6， ∴S △CFG ＝35×6＝185， ∴④不正确；正确的结论有3个，故选：C ．【点睛】本题考查了正方形性质、折叠性质、全等三角形的性质和判定、等腰三角形的性质和判定、平行线的判定等知识点的运用；主要考查学生综合运用性质进行推理论证与计算的能力，有一定难度．3．D解析：D【分析】由于C 、D 是定点，则CD 是定值，如果△CDE 的周长最小，即DE ＋CE 有最小值．为此，作点D 关于x 轴的对称点D′，当点E 在线段CD′上时，△CDE 的周长最小．【详解】如图，作点D 关于x 轴的对称点D′，连接CD′与x 轴交于点E ，连接DE ．若在边OA 上任取点E′与点E 不重合，连接CE′、DE′、D′E′由DE′＋CE′＝D′E′＋CE′＞CD′＝D′E ＋CE ＝DE ＋CE ，∴△CDE 的周长最小．∵OB ＝4，D 为边OB 的中点，∴OD ＝2，∴D （0，2），∵在长方形OACB 中，OA ＝3，OB ＝4，D 为OB 的中点，∴BC ＝3，D′O ＝DO ＝2，D′B ＝6，∵OE ∥BC ，∴Rt △D′OE ∽Rt △D′BC ，∴OE D O BC D B=''，即：623OE =，即：OE ＝1， ∴点E 的坐标为（1，0）故选：D ．【点睛】此题主要考查轴对称−−最短路线问题，解决此类问题，一般都是运用轴对称的性质，将求折线问题转化为求线段问题，其说明最短的依据是：两点之间线段最短．4．A解析：A【分析】根据平行四边形的对角相等求出∠B 即可得解．【详解】解：□ABCD 中，∠B ＝∠D ，∵∠B +∠D ＝100°，∴∠B ＝12×100°＝50°，故选：A ．【点睛】本题考查了平行四边形的性质，主要利用了平行四边形的对角相等是基础题． 5．A解析：A【分析】由三个直角的四边形是矩形，由此判断四边形PECF 是矩形，得到EC PF =，再结合正方形的性质，解得2PD EC =，由此判断A ；过点P 作PN AB ⊥垂足为N ，过P 作//PM EF 交DC 于点M ，连接AM ，由角平分线的性质得到PN PE =，继而结合勾股定理证明AP EF =、证明四边形PEFM 是平行四边形，即可得到EF PM AP ==，设BE x =，结合勾股定理证明222PM A M P A +=，即可判断B ；根据等腰直角三角形的性质计算四边形PECF 的周长即可判断C ；设BE x =，由勾股定理解得EF 的长，再结合04x ≤≤，解得EF 与BD AB 、的数量关系即可判断D ．【详解】解：A. ,PE BC PF CD ⊥⊥90PEC PFC ∴∠=∠=︒90C ∠=︒∴四边形PECF 是矩形EC PF ∴=正方形ABCD 中45PDF ∠=︒ 22PD PF EC ∴==故A 错误；B.过点P 作PN AB ⊥垂足为N ，过P 作//PM EF 交DC 于点M ，连接AM ，BD 平分ABC ∠，PN AB ⊥，PE BC ⊥ PN PE ∴=222222,AP AN PN EF EC PE =+=+且,AN EC PN PE == AP EF ∴=//,//PM EF PE CD∴四边形PEFM 是平行四边形EF PM AP ∴==设BE x =，则,42PE FC MF x DM x ====-，4EC PF x ==- 22(4)AP EF PM x x ===+-222216(42)AD MD AM x +==+-222AP PM AM +=AP PM ∴⊥AP EF ∴⊥故B 正确；C. BPE 为等腰直角三角形PE BE ∴=4PE PF BE EC BC ∴+=+==故四边形PECF 的周长为2()8PE PF +=，故C 正确；D.设BE x =EF ∴=2222(4)28+16=2(2)4x x x x x +-=--+04x ≤≤EF ∴≥12EF BD ∴≥ 4EF <EF AB ∴<12BD EF AB ∴≤< 故D 正确，故选：A ．【点睛】本题考查四边形的综合题，涉及勾股定理、矩形的判定与性质、正方形的判定与性质、平行四边形的判定与性质等知识，是重要考点，难度一般，掌握相关知识是解题关键． 6．D解析：D【分析】由三角形三边关系可得三角形两边之和大于第三边，两边之差小于第三边．【详解】解：由于两条对角线的一半与平行四边形的一边组成一个三角形，所以12（AC-BD ）＜5＜12（AC+BD ），由题中数据可得，AC 和BD 的长可取5和6，故选D ．【点睛】本题考查了平行四边形对角线互相平分及三角形三边关系问题，能够熟练求解此类问题． 7．B解析：B【分析】平行四边形的五种判定方法分别是：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形；（4）两组对角分别相等的四边形是平行四边形；（5）对角线互相平分的四边形是平行四边形．根据平行四边形的判定逐一验证．【详解】A 、能用两组对角相等的四边形是平行四边形判定平行四边形；B 、不能判定平行四边形，如等腰梯形；C 、能用两组对边相等的四边形是平行四边形判定平行四边形；D 、能用两组对边分别平行的四边形是平行四边形判定平行四边形；故选：B ．【点睛】本题考查平行四边形的判定，解题的关键是掌握平行四边形的判定定理．8．C解析：C【分析】根据平行四边形的判定方法对①②③④分别作出判断即可求解．【详解】解：①AB ∥CD ，AD ∥BC ，根据两组对边分别平行的四边形是平行四边形即可得到四边形是平行四边形；②AB CD =，AD BC =，根据两组对边分别相等的四边形是平行四边形即可得到四边形是平行四边形；；③AO CO =，BO DO =，根据对角线互相平分的四边形是平行四边形即可得到四边形是平行四边形；④AB ∥CD ，AD BC =，无法判定四边形是平行四边形．故选：C【点睛】本题考查了平行四边形的判定，熟练掌握平行四边形的定义和判定定理是解题关键． 9．B解析：B【分析】根据菱形的性质、矩形的性质、中点四边形的定义逐一判断即可．【详解】解：A. 菱形的对角线互相平分，但不相等，该命题错误；B. 顺次联结菱形各边的中点所得的四边形是矩形，该命题正确；C. 矩形的对角线互相平分，但是不垂直，该命题错误；D. 顺次连结矩形各边的中点所得的四边形是菱形，该命题错误；故选：B ．【点睛】本题考查特殊四边形的判定和性质，掌握菱形的性质、矩形的性质、中点四边形的定义是解题的关键．10．A解析：A【分析】以AC 为对角线，可得AD ∥BC ，AD=BC ；以AB 为对角线，可得AD ∥BC ，AD=BC ；以AD 为对角线，可得AB ∥CD ，AB=CD ．【详解】解：①以AD 为对角线时，可得AB ∥CD ，AB ＝CD ，∴A 点向左平移6个单位，再向下平移3个单位得B 点，∴C 点向左平移6个单位，再向下平移3个单位得D₁(-4，-8)；②以AC 为对角线时，可得AD ∥BC ，AD=BC ，∴B点向右平移6个单位，再向上平移3个单位得B点，∴C点向右平移6个单位，再向上平移3个单位得D₂(8，-2)；③以AB为对角线时，可得AD∥BC，AD=BC，∴C点向右平移3个单位，再向上平移5个单位得A，∴B点向右平移3个单位，再向上平移5个单位得D₃(2，2)；综上可知，D点的坐标可能为：D₁(-4，-8)、D₂(8，-2)、D₃(2，2)，故选：A．【点睛】本题考查了坐标与图形的性质，利用平行四边形的判定：对边平行且相等的四边形是平行四边形，要分类讨论，以防遗漏．11．D解析：D【分析】四个选项，A、C选项CP为顶角的平分线， B、D选项CP为底边上的高线，根据直角三角形斜边上的中线可得斜边上的中线等于5，利用等面积法可得底边上的高线等于245，易得三角形不是等腰三角形，所以它斜边上的高线、中线和直角的角平分线不是同一条，可得正确的为D选项．【详解】解：∵∠C=90°，点P在边AB上．BC=6，AC=8，∴22228610AB AC BC+=+=，当CP为AB的中线时，152CP AB==，若∠ACP=45°，如图1，则CP为直角∠ACB的平分线，∵BC≠AC，∴CP与中线、高线不重合，不等于5，故A选项错误；若∠ACP=∠B，如图2∵∠ACB=90°,∴∠A+∠B=90°，∴∠A+∠ACP =90°，∴∠APC=90°，即CP为AB的高线，∵BC≠AC，∴CP与中线不重合，不等于5，故B选项错误；当CP为AB的高线时，1122ABCS AC BC AB PC =⋅=⋅△,即11861022PC⨯⨯=⨯⋅，解得245PC=,故D选项正确，C选项错误．故选：D．【点睛】本题考查直角三角形斜边上的中线，等腰三角形三线合一，勾股定理等．能根据等面积法算出斜边上的高线的长度是解题关键．12．D解析：D【分析】根据矩形的性质即可判断．【详解】解：∵矩形的对角线线段，四个角是直角，对角线互相平分，∴选项A、B、C正确，故选：D．【点睛】本题考查矩形的性质，解题的关键是记住矩形的性质．二、填空题13．4【分析】根据平行四边形性质得出AB=DCAD∥BC推出∠DEC=∠BCE求出∠DEC=∠DCE推出DE=DC=AB得出AD=2DE即可求出AB的长【详解】解：∵四边形ABCD是平行四边形∴AB=D解析：4【分析】根据平行四边形性质得出AB=DC，AD∥BC，推出∠DEC=∠BCE，求出∠DEC=∠DCE，推出DE=DC=AB，得出AD=2DE，即可求出AB的长．【详解】解：∵四边形ABCD是平行四边形，∴AB=DC，AD∥BC，∴∠DEC=∠BCE，∵CE平分∠DCB，∴∠DCE=∠BCE，∴∠DEC=∠DCE，∴DE=DC=AB ，∵AD=2AB=2CD ，CD=DE ，∴AD=2DE ，∴AE=DE=4，∴DC=AB=DE=4，故答案为：4．【点睛】本题考查了平行四边形性质，平行线性质，角平分线定义，等腰三角形的性质和判定的应用；熟练掌握平行四边形的性质，证出DE=AE=DC 是解决问题的关键．14．24【分析】画出符合题意的图形利用菱形的对角线互相垂直平分求解另一条对角线的长再利用菱形的面积等于两条对角线的长之积的一半即可得到答案【详解】解：如图菱形的周长为20cm 一条对角线的长为8cm 故答案解析：24【分析】画出符合题意的图形，利用菱形的对角线互相垂直平分，求解另一条对角线的长，再利用菱形的面积等于两条对角线的长之积的一半即可得到答案．【详解】解：如图，菱形ABCD 的周长为20cm ，一条对角线AC 的长为8cm ，5,4,,,AD AB BC CD cm OA OC cm OB OD AC BD ∴=======⊥2222543OD AD AO ∴=-=-=，26,BD OD cm ∴==2116824.22ABCD S AC BD cm ∴==⨯⨯=菱形故答案为：24.【点睛】本题考查的是菱形的性质，菱形的面积，掌握菱形的性质及菱形的面积的计算是解题的关键．15．【分析】利用勾股定理逆定理判断出此三角形是直角三角形再根据直角三角形斜边上的中线等于斜边的一半解答【详解】∵∴此三角形是直角三角形斜边为5∴该三角形最长边上的中线长为：5=故答案为：【点睛】本题考查解析：52【分析】利用勾股定理逆定理判断出此三角形是直角三角形，再根据直角三角形斜边上的中线等于斜边的一半解答．【详解】∵2222255+==，∴此三角形是直角三角形，斜边为5，∴该三角形最长边上的中线长为：12⨯5=52．故答案为：52．【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，勾股定理逆定理的应用，熟记性质并判断出此三角形是直角三角形是解题的关键． 16．2【分析】根据直角三角形的性质求出再根据三角形中位线定理计算即可【详解】解：在中是斜边上的中线分别为的中点是的中位线故答案为：2【点睛】本题考查的是直角三角形的性质三角形中位线定理掌握三角形的中位线解析：2【分析】根据直角三角形的性质求出CD ，再根据三角形中位线定理计算即可．【详解】解：在Rt ABC ∆中，90ACB ∠=︒，CD 是斜边AB 上的中线，8AB =，118422CD AB ∴==⨯=， E 、F 分别为DB 、BC 的中点，EF ∴是BCD ∆的中位线，114222EF CD ∴==⨯=，故答案为：2．【点睛】本题考查的是直角三角形的性质、三角形中位线定理，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．17．12【分析】根据直角三角形斜边上的中线等于斜边的一半可求出再根据勾股定理求解即可【详解】解：∵D 为的中点∴∴故答案是：12【点睛】考查了勾股定理和直角三角形斜边上的中线熟悉相关性质是解题的关键解析：12．【分析】根据直角三角形斜边上的中线等于斜边的一半，可求出AC ，再根据勾股定理求解即可．【详解】解：∵90B ∠=︒，D 为AC 的中点， 6.5=BD∴22 6.513AC BD ==⨯=， ∴12BC =，故答案是：12．【点睛】考查了勾股定理和直角三角形斜边上的中线，熟悉相关性质是解题的关键．18．145【分析】根据平行四边形的性质易证三角形全等进而易得AE=CF 故四边形的周长=AD+CD+EF 根据已知求解即可【详解】解：在平行四边形ABCD 中AD ∥BCAC 与BD 互相平分∴AO=OC ∠DAC=解析：14.5【分析】根据平行四边形的性质易证三角形全等，进而易得AE=CF ，故四边形EFCD 的周长=AD+CD+EF ，根据已知求解即可．【详解】解：在平行四边形ABCD 中，AD ∥BC ，AC 与BD 互相平分∴AO=OC ，∠DAC=∠ACB ，∠AOE=∠COF∴△AOE ≌△COF∴AE=CF ，OF=OE=2.5∴四边形EFCD 的周长=CF+DE+CD+EF=AE+DE+CD+EF=AD+CD+EF =19 2.52+×2 =14.5．故答案为：14.5．【点睛】本题考查了平行四边形的性质以及三角形全等的证明，将所求线段转化为已知线段是解题的关键．19．【分析】先根据勾股定理求得AB 再做△ABD 的中位线EF 可得EF=3BF=DF=4从而可得CF=1再次利用勾股定理即可求得CE 【详解】解：∵AD 是BC 边上的高线AD=6AB=10∴∠D=90°∵CE 是【分析】先根据勾股定理求得AB ，再做△ABD 的中位线EF ，可得EF=3，BF=DF=4，从而可得CF=1，再次利用勾股定理即可求得CE ．【详解】解：∵AD 是BC 边上的高线，AD =6，AB =10，∴∠D=90°，BD 8==，∵CE 是AB 边上的中线，CD =AE ， ∴152CD AE BE AB ====，取BD 的中点F,连接CF ，∴EF 为△ABD 的中位线，∴132EF AD ==,EF//AD ， ∴∠EFB=∠D=90°，在Rt △BEF 中，根据勾股定理，2222534BF BE EF =-=-=,∴DF=BD-BF=8-4=4，∴CF=CD-DF=5-4=1，在Rt △CEF 中，根据勾股定理，22221310CE CF EF +=+=10【点睛】本题考查三角形中位线的定理，勾股定理．能正确作出辅助线，构造直角三角形是解题关键．20．【分析】先证明△AEC 是等腰三角形再证OE ⊥AC 然后用勾股定理求出OE 即可求【详解】解：如图1连接OE ∵四边形ABCD 是平行四边形∴OA=OC=3AD ∥BC ∴∠DAC=∠ACB 又∵∴∠ACB=∠EA解析：37【分析】先证明△AEC 是等腰三角形，再证OE ⊥AC ，然后用勾股定理求出OE ，即可求AEC S ∆．【详解】解：如图1，连接OE ，∵四边形ABCD 是平行四边形，∴OA=OC=3，AD ∥BC ，∴∠DAC=∠ACB ，又∵DAC EAC ∠=∠，∴∠ACB=∠EAC ，∴AE=EC=4，∴△AEC 是等腰三角形，∴OE ⊥AC ，在Rt △AOE 中，由勾股定理得，AO 2+OE 2=AE 2，∴32+OE 2=42，∴7 ∴167372AEC s =⨯= 故答案是：37【点睛】本题综合考查了平行四边形的性质，等腰三角形的判定与性质和勾股定理等相关知识，证明△AEC 是等腰三角形是解本题的关键．三、解答题21．（1）证明见解析；（2）7【分析】（1）根据角平分线的性质可得DBC DBE ∠=∠，再根据已知条件BE BC =，BD BD =，即可证明；（2）根据（1）中结果，得2DE CD ==，90DEB C ∠=∠=︒，即可求得ABD △的面积．【详解】（1）∵BD 平分ABC ∠，∴DBC DBE ∠=∠，∴在BDC 和BDE 中，BD BD =，DBC DBE ∠=∠，BE BC =，∴BDC ≌BDE ；（2）∵BDC ≌BDE ，∴2DE CD ==，90DEB C ∠=∠=︒，∴1172722ABD S AB DE =⋅=⨯⨯=△．【点睛】本题考查了角平分线的性质、全等三角形的证明和性质、三角形面积等知识，解题的关键是熟练掌握运用以上知识点．22．（1）答案见解析；（2）答案见解析．【分析】(1)连接CE ，CF ，先利用勾股定理计算EF ，EC ，CF 的长，再利用勾股定理的逆定理，判定三角形的形状即可；(2)过点E 作BC 的垂线E 1G ，连接1G D ，取CD ，C 1G 的中点即可，过点E 作E 1H ⊥1G D ，垂足为1H ，也可以得到符合题意的平行四边形.【详解】解：（1）在图1中，连接CE ，CF ，则EFC 即为所作；理由如下：∵4AB =，6AD =，2AE =，F 是AB 的中点，∴AF=BF=2，ED=4，∵四边形ABCD 是矩形，∴∠A=∠B=∠D=90°，∴2EF =22AE AF +=8，2EC =22DE DC +=32，2CF =22BC BF +=40，∵2EF +2EC =2CF ，∴EFC 是直角三角形.（2）如图2，四边形EFGH 即为所作．【点睛】本题考查了勾股定理及其逆定理，平行四边形的判定，矩形的性质，正方形的性质，熟练掌握勾股定理及其逆定理，平行四边形的判定定理是解题的关键.23．25221+，45 【分析】依据平行四边形的对角线互相平分，即可得到2AO =，3BO =，再根据勾股定理即可得出AB 与BC 的长，进而得到ABCD 的周长和面积．【详解】解：如图所示，4AC =，6BD =，2AO ∴=，3BO =，又CA AB ⊥， Rt AOB ∴∆中，2222325AB BO AO =-=-=，Rt ABC 中，2222(5)421BC AB AC =+=+=，ABCD ∴的周长2(521)25221=+=+，ABCD 的面积5445AB AC =⨯=⨯=．【点睛】本题主要考查了平行四边形的性质以及勾股定理的运用，解题时注意：平行四边形的对角线互相平分．24．（1）t =2；（2）t =3或65t =．【分析】（1）根据等边三角形的性质，列出关于t 的方程，进而即可求解．（2）根据△PAQ 是直角三角形，分两类讨论，分别列出方程，进而即可求解．【详解】解：（1）由题意得：AP =2t （米），AQ =6-t （米）．∵∠A =60°，∴当△PAQ 是等边三角形时，AQ =AP ，即2t =6-t ，解得：t =2，∴当t =2时，△PAQ 是等边三角形．（2）∵△PAQ 是直角三角形，∴当∠AQP =90°时，有∠APQ =30°，即AP =2AQ ，∴2t =2（6-t ），解得：t =3（秒），当∠APQ =90°时，有∠AQP =30°，即AQ =2AP ，∴6-t =2·2t ，解得65t =（秒）， ∴当t =3或65t =时，△PAQ 是直角三角形．【定睛】本题主要考查等边三角形的性质，直角三角形的定义以及平行四边形的定义，熟练掌握等边三角形的性质，直角三角形的定义，列出方程，是解题的关键．25．（1）见解析；（2）5【分析】（1）只要证明CM ∥AN ，AM ∥CN 即可．（2）先证明△DEM ≌△BFN 得BN ＝DM ，再在Rt △DEM 中，利用勾股定理即可解决问题．【详解】解：（1）证明：∵四边形ABCD 是平行四边形，∴CD ∥AB ，∵AM ⊥BD ，CN ⊥BD ，∴AM ∥CN ，∴CM ∥AN ，AM ∥CN ，∴四边形AMCN 是平行四边形．（2）∵四边形AMCN 是平行四边形，∴CM ＝AN ，∵四边形ABCD 是平行四边形，∴CD ＝AB ，CD ∥AB ，∴DM ＝BN ，∠MDE ＝∠NBF ，在△MDE 和△NBF 中， MDE NBF DEM NFB DM BN ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△MDE ≌△NBF （AAS ），∴ME ＝NF ＝3，在Rt △DME 中，∵∠DEM ＝90°，DE ＝4，ME ＝3，∴DM=5，∴BN ＝DM ＝5．【点睛】本题考查平行四边形的判定和性质、全等三角形的判定和性质、勾股定理等知识，解题的关键是记住平行四边形的判定方法和性质，正确寻找全等三角形解决问题，属于中考常考题型．26．（1）见解析；（2）菱形，理由见解析【分析】（1）因为M，N分别是AD，BC的中点，由矩形的性质可得DM=BN，DM∥BN，利用平行四边形的判定定理可得结论；（2）由四边形DMBN是平行四边形，求出BM=DN，BM∥DN，求出三角形MPNQ是平行四边形，根据直角三角形斜边上中线性质求出MQ=NQ，根据菱形判定推出即可．【详解】解：（1）证明：∵四边形ABCD是矩形，∴AD∥BC，AD=BC，∵M、N分别AD、BC的中点，∴DM=BN，∴四边形DMBN是平行四边形；（2）四边形MPNQ是菱形．∵四边形DMBN是平行四边形，∴BM=DN，BM∥DN，∵P、Q分别BM、DN的中点，∴MP=NQ，MP∥NQ，∴四边形MPNC是平行四边形，连接MN，∵四边形ABCD是矩形，∴AD∥BC，AD=BC，∵M、N分别AD、BC的中点，∴DM=CN，∴四边形DMNC是矩形，∴∠DMN=∠C=90°，∵Q是DN中点，∴MQ=NQ，∴四边形MPNQ是菱形．【点睛】本题考查了平行四边形的性质和判定，菱形的判定，矩形的性质，综合运用各性质定理是解答此题的关键。

(人教版)厦门市八年级数学下册第三单元《平行四边形》检测卷(含答案解析)

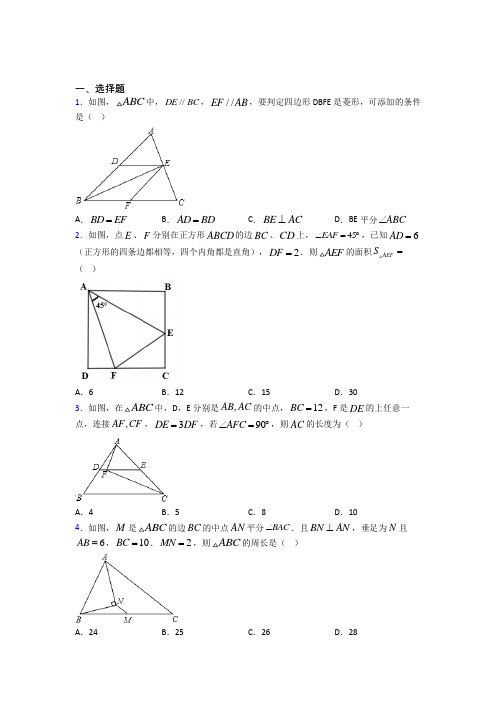
一、选择题1．如图，ABC 中，//DE BC ，//EF AB ，要判定四边形DBFE 是菱形，可添加的条件是（）A ．BD EF =B ．AD BD =C ．BE AC ⊥D ．BE 平分ABC ∠ 2．如图，点E 、F 分别在正方形ABCD 的边BC 、CD 上，45EAF ∠=︒，已知6AD =（正方形的四条边都相等，四个内角都是直角），2DF =．则AEF 的面积AEF S =（）A ．6B ．12C ．15D ．303．如图，在ABC 中，D ，E 分别是,AB AC 的中点，12BC =，F 是DE 的上任意一点，连接,AF CF ，3DE DF =，若90AFC ∠=︒，则AC 的长度为（）A ．4B ．5C ．8D ．104．如图，M 是ABC 的边BC 的中点AN 平分BAC ∠．且BN AN ⊥，垂足为N 且6AB =，10BC =．2MN =，则ABC 的周长是（）A ．24B ．25C ．26D ．285．下列命题是真命题的是（）A ．三角形的三条高线相交于三角形内一点B ．一组对边平行，另一组对边相等的四边形是平行四边形C ．对于所有自然数n ，237n n -+的值都是质数D ．三角形一条边的两个顶点到这条边上的中线所在直线的距离相等6．已知四边形ABCD 中，90A B C ∠=∠=∠=，如果添加一个条件，即可判定该四边形是正方形，那么所添加的这个条件可以是（）A ．90D ∠=；B ．AB CD =；C ．AD BC =； D ．BC CD =． 7．在矩形ABCD 中，对角线AC 、BD 相交于点O ，AE 平分BAD ∠交BC 于点E ，15CAE ∠=︒．连接OE ，则下面的结论：①DOC 是等边三角形；②BOE △是等腰三角形；③2BC AB =；④150∠=︒AOE ；⑤AOE COE S S =，其中正确的结论有（）A ．2个B ．3个C ．4个D ．5个8．在菱形ABCD 中，∠ABC=60゜，AC=4，则BD=( )A 3B ．3C ．3D ．39．菱形的一个内角是60︒，边长是3cm ，则这个菱形的较短的对角线长是（） A ．3cm 2 B 33cm 2 C ．3cm D ．33cm 10．在平面直角坐标系中，点A ，B ，C 的坐标分别为()5,0，()1,3--，()2,5-，当四边形ABCD 是平行四边形时，点D 的坐标为（）A ．()8,2-B ．()7,3-C ．()8,3-D ．()14,0 11．如图，菱形ABCD 的对角线AC 、BD 相交于点O ，过点D 作DH ⊥AB 于点H ，连接OH ，若OA ＝6，S 菱形ABCD ＝48，则OH 的长为（）A ．4B ．8C ．13D ．612．如图所示，已知Rt ABC 中，90B ︒∠=，3AB =，4BC =，D F 、分别为AB AC 、的中点，E 是BC 上动点，则DEF 周长的最小值为（）A ．240+B ．213+C ．13D ．6二、填空题13．如图，平行四边形ABCD 中，CE AD ⊥于点E ，点F 为边AB 的中点，连接EF ，CF ，若12AD CD =，38CEF ∠=︒，则AFE ∠=_____________．14．三角形的三边长分别为21，5，2，则该三角形最长边上的中线长为____． 15．如图，Rt ABC △中，90,5∠=︒=B AB ，D 为AC 的中点， 6.5=BD ，则BC 的长为__________．16．如图，EF 过ABCD 对角线的交点O ，交AD 于E ，交BC 于F ，若ABCD 的周长为19， 2.5OE =，则四边形EFCD 的周长为_____．17．如图，在ABC 中，45BAC ∠=︒，4AB AC ==，点D 是AB 上一动点，以AC 为对角线的所有平行四边形ADCE 中，DE 的最小值是________．18．如图，点E 是矩形ABCD 的边AD 上的一点，且12DE AE =，连接BE 并延长交CD 的延长线于点F ，若4AB =，6BC =，则EDF 的周长为__________．19．如图，在Rt △ABC 中，∠ACB ＝90°，D 是斜边AB 中点，若∠B ＝30°，AC ＝2，则CD ＝_____．20．如图所示，在ABCD 中，AC 与BD 相交于点O ，若DAC EAC ∠=∠，4AE =，3AO =，则AEC S ∆的面积为____．三、解答题21．用总长度为4a 的铁丝可围成一个长方形或正方形，小东同学认为围成一个正方形的面积较大．小东同学的看法对不对？请你用数学知识进行说理．22．如图，四边形ABCD 中，//AD BC ，90A D ∠=∠=︒，点E 是AD 的中点，连接BE ，将ABE △沿BE 折叠后得到GBE ，且点G 在四边形ABCD 内部，延长BG 交DC 于点F ，连接EF ．（1）求证：EGF EDF △△≌；（2）求证：BG CD =；（3）若点F 是CD 的中点，8BC =，求CD 的长．23．已知：如图，在四边形ABCD 中，点G 在边BC 的延长线上，CE 平分BCD ∠、CF 平分GCD ∠，//EF BC 交CD 于点O ．（1）求证：OE OF =；（2）若点O 为CD 的中点，求证：四边形DECF 是矩形．24．如图，点E 在ABCD 内部，//,//AF BE DF CE ．（1）求证：BCE ADF ≅∆；（2）求证：AEDF 1S 2ABCD S =四边形25．如图，在四边形ABCD 中，,E F 分别是,AD BC 的中点，,G H 分别是对角线,BD AC 的中点，依次连接,,,E G F H 连接,EF GH ．（1）求证：四边形EGFH 是平行四边形；（2）当AB CD =时，EF 与GH 有怎样的位置关系？请说明理由；（3）若,20,70AB CD ABD BDC =∠=︒∠=︒，则GEF ∠= ︒．26．如图，在ABCD 中，AE 平分BAD ∠交BD 于点E ，交BC 于点M ，CF 平分BCD ∠交BD 于点F ．（1）若70ABC ∠=︒，求AMB ∠的度数；（2）求证：AE CF =．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】当BE 平分∠ABC 时，四边形DBFE 是菱形，可知先证明四边形BDEF 是平行四边形，再证明BD=DE 即可解决问题．【详解】解：当BE 平分∠ABC 时，四边形DBFE 是菱形，理由：∵DE ∥BC ，∴∠DEB=∠EBC ，∵∠EBC=∠EBD ，∴∠EBD=∠DEB ，∴BD=DE ，∵DE ∥BC ，EF ∥AB ，∴四边形DBFE 是平行四边形，∵BD=DE ，∴四边形DBFE 是菱形．其余选项均无法判断四边形DBFE 是菱形，故选：D ．【点睛】本题考查菱形的判定、平行四边形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题．2．C解析：C【分析】延长CD 到G ，使DG=BE ，连接AG ，易证ADG ABE △≌△所以AE=AG ，BAE=DAG ∠∠ ，证AFG AEG △≌△，所以 GF=EF ，设BE=DG=x ，则EF=FG=x+2，在ECF Rt △中，利用勾股定理得222462x x 解得求出x ，最后求AGF S △问题即可求解．【详解】解：延长CD 到G ，使DG=BE ，连接AG ，在正方形ABCD 中，AB=AD ，90ADB B C ADC ∠=∠=∠=∠=︒ 90ADG B ∴∠=∠=︒，ADG ABE(SAS)∴△≌△，,AG AE BAE DAG ∴=∠=∠，45EAF ∠=︒ ，45DAF BAE ∴∠+∠=︒ ，GAF=45DAG DAF ∴∠∠+∠=︒，GAF=EAF ∴∠∠，又AF=AF ，AFG AEG ∴△≌△(SAS)，EF=FG ∴，设BE=DG=x ，则EC=6-x ，FC=4，EF=FG=x+2，在ECF Rt △中，222=FC CE EF +，()()22246=2x x ∴+-+，解得，x=3， GF=DG DF=2+3=5∴+，AEF AGF 11S =S =GF AD=56=1522∴⨯⨯△△，故选：C ．【点睛】本题考查了正方形的性质，全等三角形的判定和性质，勾股定理，正确构造辅助线，证三角形全等是解决本题的关键.3．C解析：C【分析】根据三角形中位线定理求出DE，根据题意求出EF，根据直角三角形的性质计算即可．【详解】解：∵D、E分别是AB、AC的中点，∴DE是△ABC的中位线，∴DE=1BC=6，2∵DE=3DF，∴EF=4，∵∠AFC=90°，E是AC的中点，∴AC=2EF=8，故选：C．【点睛】本题考查的是三角形中位线定理、直角三角形的性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．4．C解析：C【分析】延长BN交AC于D，根据等腰三角形的性质得到AD=AB=6，BN=ND，根据三角形中位线定理得到DC=2MN=4，计算即可．【详解】解：延长BN交AC于D，∵AN平分∠BAC，BN⊥AN，∴AD=AB=6，BN=ND，又M是△ABC的边BC的中点，∴DC=2MN=4，∴AC=AD+DC=10，则△ABC的周长=AB+AC+BC=6+10+10=26，故选C．【点睛】本题考查的是三角形中位线定理、等腰三角形的性质，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．5．D解析：D【分析】根据钝角三角形的高的交点在三角形外部可对A进行判断；根据平行四边形的判定对B进行判断；取n=6可对C进行判断；根据三角形全等的知识可对D进行判断．【详解】解：A、钝角三角形的三条高线相交于三角形外一点，所以A选项错误；B、一组对边平行，另一组对边也平行的四边形是平行四边形，所以B选项错误；C、当n=6时，n2-3n+7=25，25不是质数，所以C选项错误；D、通过证明三角形全等，可以证明三角形一条边的两个顶点到这条边上的中线所在直线的距离相等，所以D选项准确．故选：D．【点睛】本题考查了命题：判断事物的语句叫命题；正确的命题称为真命题；错误的命题称为假命题．也考查了平行四边形的判定及全等三角形的判定和性质．6．D解析：D【分析】由已知可得该四边形为矩形，再添加条件：一组邻边相等，即可判定为正方形．【详解】解：由∠A=∠B=∠C=90°可判定四边形ABCD为矩形，因此再添加条件：一组邻边相等，即可判定四边形ABCD为正方形，故选：D．【点睛】本题考查正方形的判定．掌握相关判定定理正确推理论证是解题关键．7．B解析：B【分析】判断出△ABE 是等腰直角三角形，根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ACB ＝30°，再判断出△ABO ，△DOC 是等边三角形，可判断①；根据等边三角形的性质求出OB ＝AB ，再求出OB ＝BE ，可判断②，由直角三角形的性质可得BC AB ，可判断③，由等腰三角形性质求出∠BOE ＝75°，再根据∠AOE ＝∠AOB ＋∠BOE ＝135°，可判断④；由面积公式可得AOE COE SS =可判断⑤；即可求解．【详解】解：∵AE 平分∠BAD ，∴∠BAE ＝∠DAE ＝45°，∴∠AEB ＝45°，∴△ABE 是等腰直角三角形，∴AB ＝BE ，∵∠CAE ＝15°，∴∠ACE ＝∠AEB−∠CAE ＝45°−15°＝30°，∴∠BAO ＝90°−30°＝60°，∵矩形ABCD 中：OA ＝OB ＝OC ＝OD ，∴△ABO 是等边三角形，△COD 是等边三角形，故①正确；∴OB ＝AB ，又∵ AB ＝BE ，∴OB ＝BE ，∴△BOE 是等腰三角形，故②正确；在Rt △ABC 中∵∠ACB=30°∴BC，故③错误；∵∠OBE ＝∠ABC−∠ABO ＝90°−60°＝30°＝∠ACB ，∴∠BOE ＝12（180°−30°）＝75°， ∴∠AOE ＝∠AOB ＋∠BOE ＝60°＋75°＝135°，故④错误；∵AO ＝CO ，∴AOE COE S S =，故⑤正确；故选：B ．【点睛】本题考查了矩形的性质，等腰直角三角形的性质，等边三角形的判定与性质，等腰三角形的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记各性质是解题的关键．8．D解析：D【分析】根据菱形的性质可得到直角三角形，利用勾股定理计算即可；【详解】如图，AC 与BD 相较于点O ，∵四边形ABCD 是菱形，4AC =，∴AC BD ⊥，2AO =，又∵∠ABC=60゜，∴30ABO ∠=︒，∴24AB AO ==， ∴224223BO =-= ∴243BD BO ==；故选D ．【点睛】本题主要考查了菱形的性质，结合勾股定理计算是解题的关键．9．C解析：C【分析】根据菱形的四边相等和一个内角是60°，可判断较短对角线与两边组成等边三角形，根据等边三角形的性质可求较短的对角线长．【详解】解：因为菱形的四边相等，当一个内角是60°，则较短对角线与两边组成等边三角形． ∵菱形的边长是3cm ，∴这个菱形的较短的对角线长是3cm ．故选：C ．【点睛】此题考查了菱形四边都相等的性质及等边三角形的判定，解题关键是判断出较短对角线与两边构成等边三角形．10．A解析：A【分析】以AC 为对角线，可得AD ∥BC ，AD=BC ；以AB 为对角线，可得AD ∥BC ，AD=BC ；以AD 为对角线，可得AB ∥CD ，AB=CD ．【详解】解：①以AD 为对角线时，可得AB ∥CD ，AB ＝CD ，∴A点向左平移6个单位，再向下平移3个单位得B点，∴C点向左平移6个单位，再向下平移3个单位得D₁(-4，-8)；②以AC为对角线时，可得AD∥BC，AD=BC，∴B点向右平移6个单位，再向上平移3个单位得B点，∴C点向右平移6个单位，再向上平移3个单位得D₂(8，-2)；③以AB为对角线时，可得AD∥BC，AD=BC，∴C点向右平移3个单位，再向上平移5个单位得A，∴B点向右平移3个单位，再向上平移5个单位得D₃(2，2)；综上可知，D点的坐标可能为：D₁(-4，-8)、D₂(8，-2)、D₃(2，2)，故选：A．【点睛】本题考查了坐标与图形的性质，利用平行四边形的判定：对边平行且相等的四边形是平行四边形，要分类讨论，以防遗漏．11．A解析：A【分析】由菱形的性质得出OA＝OC＝6，OB＝OD，AC⊥BD，则AC＝12，由直角三角形斜边上的中线性质得出OH＝12AB，再由菱形的面积求出BD＝8，即可得出答案．【详解】解：∵四边形ABCD是菱形，∴OA＝OC＝6，OB＝OD，AC⊥BD，∴AC＝12，∵DH⊥AB，∴∠BHD＝90°，∴OH＝12BD，∵菱形ABCD的面积＝12×AC×BD＝12×12×BD＝48，∴BD＝8，∴OH＝12BD＝4；故选：A．【点睛】本题考查了菱形的性质，直角三角形的性质，菱形的面积公式，关键是根据直角三角形斜边上的中线性质求得OH=12 BD．12．B 解析：B 【分析】先根据三角形的中位线定理可求得DF 的长为2，然后作出点F 关于BC 的对称点F′，连接DF′交BC 于点E ，此时DEF 周长的最小，由轴对称图形的性质可知EF=EF′，从而可得到ED+EF=DF′，再证明四边形DBMF 为矩形，得出FF′=3，然后在Rt △DFF′中，由勾股定理可求得DF′的长度，从而可求得三角形DEF 周长的最小值．【详解】解：如图，作点F 关于BC 的对称点F′，连接DF′交BC 于点E ．此时DE+EF 最小∵点D 、F 分别是AB 和AC 的中点，BC=4，3AB =，∴DF=12BC=2，DF//BC ，BD=1.5， ∵点F 与点F′关于BC 对称，∴EF=EF′，FF′⊥BC ，FM= F′M ， ∴DE+EF 最小值为DE+ EF′=DF′，90DFF ∠'=︒，∵DF//BC ，90B ∠=︒，∴90B BDF FMB ∠=∠=∠=︒，∴四边形DBMF 为矩形，∴BD=FM=1.5，∴FF′=3，在Rt △DFF′中，2'2222313DF DF FF +=+='∴△DEF 周长的最小值=DF+DE+EF=13故选：B【点睛】本题主要考查的是轴对称路径最短问题，以及勾股定理，矩形的判定，作出点F 关于BC 的对称点，将DE+EF 转化为DF′的长是解题的关键．二、填空题13．24°【分析】延长CF 交DA 延长线于点G 证△BCF ≌△AGF 得GF=FC 由垂直得△FEC 是等腰三角形可知△BFC 是等腰三角形求出∠GFE 和∠GFA 即可【详解】解：延长CF 交DA 延长线于点G ∵AG ∥B解析：24°【分析】延长CF 交DA 延长线于点G ，证△BCF ≌△AGF ，得GF=FC ，由垂直得△FEC 是等腰三角形，12AD CD =，可知△BFC 是等腰三角形，求出∠GFE 和∠GFA 即可．【详解】解：延长CF 交DA 延长线于点G ，∵AG ∥BC ，∴∠G=∠BCF ，∠GAF=∠B ，∵AF=FB ，∴△AGF ≌△BCF ，∴GF=CF ，AG=BC ，∵CE AD ⊥，∴EF=FG=FC ，∠GEC=90°，∵38CEF ∠=︒，∴∠FEG=∠FGE=52°，∠GFE=76°， ∵12AD CD =， ∴BC=BF=AF ，∵AG=BC ，∴AG=AF ，∠G=∠AFG=52°， AFE ∠=76°-52°=24°．【点睛】本题考查了平行四边形的性质，直角三角形的性质，等腰三角形的性质，全等三角形的性质与判定，解题关键是作出适当的辅助线，构造等腰三角形．14．【分析】利用勾股定理逆定理判断出此三角形是直角三角形再根据直角三角形斜边上的中线等于斜边的一半解答【详解】∵∴此三角形是直角三角形斜边为5∴该三角形最长边上的中线长为：5=故答案为：【点睛】本题考查解析：52【分析】利用勾股定理逆定理判断出此三角形是直角三角形，再根据直角三角形斜边上的中线等于斜边的一半解答．【详解】∵2222255+==，∴此三角形是直角三角形，斜边为5，∴该三角形最长边上的中线长为：12⨯5=52．故答案为：52．【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，勾股定理逆定理的应用，熟记性质并判断出此三角形是直角三角形是解题的关键． 15．12【分析】根据直角三角形斜边上的中线等于斜边的一半可求出再根据勾股定理求解即可【详解】解：∵D 为的中点∴∴故答案是：12【点睛】考查了勾股定理和直角三角形斜边上的中线熟悉相关性质是解题的关键解析：12．【分析】根据直角三角形斜边上的中线等于斜边的一半，可求出AC ，再根据勾股定理求解即可．【详解】解：∵90B ∠=︒，D 为AC 的中点， 6.5=BD∴22 6.513AC BD ==⨯=， ∴12BC =，故答案是：12．【点睛】考查了勾股定理和直角三角形斜边上的中线，熟悉相关性质是解题的关键．16．145【分析】根据平行四边形的性质易证三角形全等进而易得AE=CF 故四边形的周长=AD+CD+EF 根据已知求解即可【详解】解：在平行四边形ABCD 中AD ∥BCAC 与BD 互相平分∴AO=OC ∠DAC=解析：14.5【分析】根据平行四边形的性质易证三角形全等，进而易得AE=CF ，故四边形EFCD 的周长=AD+CD+EF ，根据已知求解即可．【详解】解：在平行四边形ABCD 中，AD ∥BC ，AC 与BD 互相平分∴AO=OC ，∠DAC=∠ACB ，∠AOE=∠COF∴△AOE ≌△COF∴AE=CF，OF=OE=2.5∴四边形EFCD的周长=CF+DE+CD+EF =AE+DE+CD+EF=AD+CD+EF=192.5 2×2=14.5．故答案为：14.5．【点睛】本题考查了平行四边形的性质以及三角形全等的证明，将所求线段转化为已知线段是解题的关键．17．2【分析】平行四边形ADCE的对角线的交点是AC的中点O当OD⊥AB时OD最小即DE最小根据直角三角形勾股定理即可求解【详解】解：如图∵平行四边形ADCE的对角线的交点是AC的中点O又AB=AC=4解析：22【分析】平行四边形ADCE的对角线的交点是AC的中点O，当OD⊥AB时，OD最小，即DE最小，根据直角三角形勾股定理即可求解．【详解】解：如图∵平行四边形ADCE的对角线的交点是AC的中点O，又AB=AC=4∴OC=OA=12AC=2当OD⊥AB时，OD最小，即DE最小．∵OD⊥BA，∠BAC=45°，∴∠AOD=45°∴△ADO为等腰直角三角形在Rt△ADO由勾股定理可知OD=222∴2故答案为：2【点睛】本题考查了勾股定理，平行四边形的性质，即平行四边形对角线互相平分，正确理解DE 最小值的条件是关键．18．【分析】由矩形ABCD 证明求解再证明证明再利用勾股定理求解从而可得答案【详解】解：矩形ABCD 故答案为：【点睛】本题考查的是勾股定理的应用等腰三角形的判定与性质矩形的性质掌握以上知识是解题的关键解析：【分析】由矩形ABCD ，4AB =，6BC =，12DE AE =，证明6,AD BC == 90,A ADC ∠=∠=︒求解4AB AE ==，再证明45FED AEB ∠=∠=︒，证明2DE DF ==，再利用勾股定理求解,EF 从而可得答案．【详解】解：矩形ABCD ，4AB =，6BC =6,AD BC ∴== 90,A ADC ∠=∠=︒ 12DE AE =，,AE DE AD += 42AE DE ∴==，，4AB AE ∴==，45,AEB ∴∠=︒45,FED ∴∠=︒90ADC ∠=︒，90EDF ，∴∠=︒ 45DEF DFE ∴∠=∠=︒，2DE DF ∴==，EF ∴===224DEF C ∴=++=+故答案为：4+【点睛】本题考查的是勾股定理的应用，等腰三角形的判定与性质，矩形的性质，掌握以上知识是解题的关键．19．【分析】先由所对的直角边是斜边的一半求解再利用直角三角形斜边上的中线等于斜边的一半可得答案【详解】解：∠ACB ＝90°∠B ＝30°AC ＝2D 是斜边AB 中点故答案为：【点睛】本题考查的是含的直角三角形解析：2.【分析】先由30所对的直角边是斜边的一半求解,AB 再利用直角三角形斜边上的中线等于斜边的一半可得答案．【详解】解： ∠ACB ＝90°，∠B ＝30°，AC ＝2，24AB AC ∴==，D 是斜边AB 中点， 1 2.2CD AB ∴== 故答案为：2.【点睛】本题考查的是含30的直角三角形的性质，直角三角形斜边上的中线等于斜边的一半，掌握以上知识是解题的关键．20．【分析】先证明△AEC 是等腰三角形再证OE ⊥AC 然后用勾股定理求出OE 即可求【详解】解：如图1连接OE ∵四边形ABCD 是平行四边形∴OA=OC=3AD ∥BC ∴∠DAC=∠ACB 又∵∴∠ACB=∠EA解析：37【分析】先证明△AEC 是等腰三角形，再证OE ⊥AC ，然后用勾股定理求出OE ，即可求AEC S ∆．【详解】解：如图1，连接OE ，∵四边形ABCD 是平行四边形，∴OA=OC=3，AD ∥BC ，∴∠DAC=∠ACB ，又∵DAC EAC ∠=∠，∴∠ACB=∠EAC ，∴AE=EC=4，∴△AEC 是等腰三角形，∴OE ⊥AC ，在Rt △AOE 中，由勾股定理得，AO 2+OE 2=AE 2，∴32+OE 2=42，∴7∴162AEC s =⨯=故答案是：【点睛】本题综合考查了平行四边形的性质，等腰三角形的判定与性质和勾股定理等相关知识，证明△AEC 是等腰三角形是解本题的关键．三、解答题21．对，见解析【分析】设长方形的长为x ，则宽为4222a x a x -=-，由长方形面积公式求得(2)S x a x =-长方形，2S a =正方形，由两者左侧22(2)()0S S a x a x a x -=--=->正方形长方形，即S S >正方形长方形即可．【详解】解：小东同学的看法对，理由如下，设长方形的长为x ，则宽为4222a x a x -=-， 2x a x ≠-，x a ∴≠，长方形面积为：(2)S x a x =-长方形，若铁丝围成正方形，则其边长为a ，2S a =正方形，∴()()2222220S S a x a x a ax x a x -=--=-+=->正方形长方形，即S S >正方形长方形，所以正方形的面积较大．小东同学认为围成一个正方形的面积较大．小东同学的看法对．【点睛】本题考查周长一定，围成的长方形中，正方形面积最大问题，掌握求长方形与正方形面积公式，作差后利用公式因式分解是解题关键．22．（1）见解析；（2）见解析；（3）【分析】（1）根据HL 证明Rt △EGF ≌Rt △EOF 即可；（2）证明四边形ABCD 为矩形，可得BG=CD ；（3）设CD=x ，分别表示出BE 2，EF 2，BF 2，证明∠BEF=90°，利用勾股定理得到方程，解之即可．【详解】解：（1）∵E 是AD 中点，∴AE=DE ，由折叠可知：AE=EG ，∠EGB=∠EGF=∠D=∠A=90°，∴EG=ED ，又EF=EF ，∴Rt △EGF ≌Rt △EOF （HL ）；（2）△ABE 折叠得到△GBE ，∴AB=BG ，∵AD ∥BC ，∠A=∠D=90°，∴∠ABC=90°，∠C=90°，∴四边形ABCD 为矩形，∴AB=DC ，∴BG=CD ；（3）∵点E 是AD 中点，AD=BC=8，∴AE=DE=4，∵点F 是CD 中点，∴设CD=x ，则DF=12x ，则BE 2=BG 2+EG 2，即BE 2=CD 2+AE 2，即BE 2=x 2+42，且EF 2=DE 2+DF 2，即EF 2=42+（12x ）2，且BF 2=BC 2+CF 2，即BF 2=82+（12x ）2， ∵∠AEB=∠GEB ，∠DEF=∠GEF ，∴∠BEF=∠GEB+∠GEF=90°，∴BF 2=BE 2+EF 2，∴82+（12x ）2= x 2+42+42+（12x ）2，解得：x=，即CD=【点睛】本题考查了矩形的判定和性质，勾股定理，折叠的性质，全等三角形的判定和性质，熟记性质，找出三角形全等的条件，合理利用勾股定理得到方程是解题的关键．23．（1）见解析；（2）见解析【分析】（1）由角平分线的定义及平行线的性质可证得DCE FEC ∠=∠，EFC DCF ∠=∠，得OE OC =，OF OC =，即可得出结论；（2）先证得四边形DECF 是平行四边形，再利用角平分线的定义可求得90ECF ∠=︒，则可证得四边形DECF 为矩形．【详解】证明：（1）∵CE 平分BCD ∠、CF 平分GCD ∠∴BCE DCE ∠=∠，DCF GCF ∠=∠∵EF ∥BC ，∴BCE FEC ∠=∠，EFC GCF ∠=∠∴DCE FEC ∠=∠，EFC DCF ∠=∠∴OE OC =，OF OC =，∴OE OF =．（2）∵点O 为CD 的中点，∴OD OC =，又OE OF =，∴四边形DECF 是平行四边形∵CE 平分BCD ∠、CF 平分GCD ∠， ∴12DCE BCD ∠=∠，12DCF DCG ∠=∠ ∴()11=9022DCE DCF BCD DCG BCG ∠+∠=∠+∠∠=︒ ∵DCE DCF ECF ∠+∠=∠， ∴90ECF ∠=︒∵四边形DECF 是平行四边形，∴平行四边形DECF 是矩形．【点睛】本题主要考查了矩形的判定、平行四边形的判定与性质、等腰三角形的判定以及平行线的性质等知识，掌握相关性质定理正确推理论证是解题关键．24．（1）见解析；（2）见解析【分析】（1）先证明CBE DAF ∠=∠，BCE ADF ∠=∠，然后利用ASA 证明：△BCE ≌△ADF ；（2）根据点E 在ABCD 内部，可知：S △BEC +S △AED =12S ▱ABCD ，可得结论．【详解】解：()1四边形ABCD 是平行四边形， ,//AD BC AD BC =，180,ABC BAD ∴∠+∠=//,AF BE180,EAB BAF ∴∠+∠=︒,CBE DAF ∴∠=∠同理得,BCE ADF ∠=∠()BCE ADF ASA ∴∆≅∆()2点E 在ABCD 内部， ∴12BEC AED ABCD S S S ∆∆+=，由()1知： ,BCE ADF ∆≅∆BCE ADF S S ∆∆∴= ∴AEDF 1S 2ADF AED BEC AED ABCD S S S S S ∆∆∆∆=+=+=四边形．【点睛】此题主要考查了平行四边形的性质以及全等三角形的判定与性质，熟练利用三角形和平行四边形边的关系得出面积关系是解题关键．25．（1）见解析；（2）GH EF ⊥，见解析；（3）25︒【分析】（1）利用中位线性质得//EG AB ，且12GE AB =，//HF AB ，且12HF AB =，可推出//EG HF ，且EG HF =，可证四边形EGFH 是平行四边形；（2由G F 、分别是BD BC 、的中点，可得12GF CD =，由（1）知12GE AB =，由AB CD =，可证GE GF =，由（1）知四边形EGFH 是平行四边形，可证四边形EGFH 是菱形即可；（3）先证四边形EGFH 是平行四边形；再证四边形EGFH 是菱形，由EG ∥AB ，GF ∥CD ，可求∠EGD=∠ABD=20°，∠BGF=∠BDC=70°利用平角可求∠DGF=180°-∠BGF=110°，利用两角和求∠EGF=130°利用菱形性质求∠GEH=180°-∠EGF=50º，由FE 平分∠GEH ，∠GEF=25︒即可．【详解】证明：（1）E G 、分别是AD BD 、的中点，//EG AB ∴，且12GE AB =，同理可证：//HF AB ，且12HF AB =， //EG HF ∴，且EG HF =，∴四边形EGFH 是平行四边形；（2）GH EF ⊥，理由：G F 、分别是BD BC 、的中点，12GF CD ∴=，由（1）知12GE AB =，又AB CD =，GE GF ∴=，又四边形EGFH 是平行四边形，∴四边形EGFH 是菱形，GH EF ∴⊥；（3）E G 、分别是AD BD 、的中点，F H 、分别是BC AC 、的中点，//EG AB ∴，//HF AB ，12GE AB =， //EG HF ∴，同理可证//EH GF ，12GF CD =， ∴四边形EGFH 是平行四边形，∵AB CD =，GE GF ∴=，∴四边形EGFH 是菱形，20,70ABD BDC ∠=︒∠=︒，EG ∥AB ，GF ∥CD ，∴∠EGD=∠ABD=20°，∠BGF=∠BDC=70°，∴∠DGF=180°-∠BGF=110°，∴∠EGF=∠EGD+∠DGF=20°+110°=130°，∴∠GEH=180°-∠EGF=50º，∵FE 平分∠GEH ，∴∠GEF=11502522GEH ∠=⨯︒=︒．故答案为：25︒．【点睛】本题考查平行四边形，菱形判断与性质，求菱形内角，掌握平行四边形的判定方法，菱形的判定与性质，会利用菱形的性质求角度是解题关键．26．（1）55°；（2）见解析【分析】（1）根据平行四边形的性质得到//AD BC ，根据平行线的性质得到180ABC BAD ∠+∠=︒，根据角平分线的定义得到1552DAM BAD ∠=∠=︒，于是得到结论；（2）根据平行四边形的性质得到AB CD =，BAD BCD ∠=∠，//AB CD ，求得ABE CDF ∠=∠，根据角平分线的定义及等量代换得到BAE DCF ∠=∠，根据全等三角形的性质即可得到AE CF =．【详解】（1）解：∵四边形ABCD 是平行四边形，∴//AD BC ，∴ 180ABC BAD ∠+∠=︒．∵70ABC ∠=︒，∴110BAD ∠=︒．∵AE 平分BAD ∠， ∴1552DAM BAD ∠=∠=︒． ∵//AD BC ，∴55AMB DAM ∠=∠=︒．（2）证明：∵四边形ABCD 是平行四边形，∴AB CD =，BAD BCD ∠=∠，//AB CD ，∴ ABE CDF ∠=∠．∵AE 平分BAD ∠， ∴12BAE BAD ∠=∠． ∵CF 平分BCD ∠， ∴12DCF BCD ∠=∠． ∵BAD BCD ∠=∠， ∴BAE DCF ∠=∠．又∵AB CD =，ABE CDF ∠=∠，∴ABE CDF △≌△，∴AE CF =．【点睛】本题考查了平行四边形的性质，全等三角形的判定和性质，正确的识别图形是解题的关键．。

人教版八年级下册第18章《平行四边形》章末质量检测题 (附答案解析)

人教版八年级下册第18章《平行四边形》章末质量检测题（满分100分时间80分钟）一．选择题（共10小题，满分30分）1．矩形不一定具有的性质是（）A．对角线互相平分B．对角线互相垂直C．对角线相等D．是轴对称图形2．直角三角形两条直角边长分别是6和8，则斜边上的中线长为（）A．3B．4C．5D．63．下列说法不正确的是（）A．四边都相等的四边形是平行四边形B．两组对角分别相等的四边形是平行四边形C．对角线互相垂直的四边形是平行四边形D．两组对边分别平行的四边形是平行四边形4．如图，菱形ABCD中，∠D＝130°，则∠1＝（）A．30°B．25°C．20°D．15°5．如图，矩形ABCD的对角线交于点O．若∠BAO＝55°，则∠AOD等于（）A．110°B．115°C．120°D．125°6．如图，点O是矩形ABCD的对角线AC的中点，点M是AD的中点．若AB＝3，BC＝4，则四边形ABOM的周长是（）A．7B．8C．9D．107．如图，▱ABCD中，下列说法一定正确的是（）A．AC＝BD B．AC⊥BD C．AO＝CO D．AB＝BC8．如图，在正方形ABCD的外侧作等边△ADE，则∠AEB的度数为（）A．10°B．12.5°C．15°D．20°9．如图，矩形ABCD中，BC＞AB，对角线AC、BD交于O点，且AC＝10，过B点作BE⊥AC于E点，若BE＝4，则AD的长等于（）A．8B．10C．3D．410．如图，在菱形ABCD中，点E为对角线AC上一点，且CE＝CD，连接DE，若AB＝5，AC＝8，则＝（）A．B．C．D．二．填空题（共6小题，满分18分）11．平行四边形ABCD中，∠A比∠B小20°，那么∠C＝．12．如图，在△ABC中，点D、E分別是AB，AC的中点，若BC＝6，则DE＝．13．菱形的两条对角线长分别为2cm和2cm，则该菱形的面积为cm2．14．如图，在▱ABCD中，BE平分∠ABC，BC＝6，DE＝2，则▱ABCD的周长等于．15．在平面直角坐标系中，O为坐标系原点，A（﹣3，0）、B（﹣5，2）、C在坐标平面内，若以O、A、B、C为顶点的四边形是平行四边形，则点C坐标为．16．如图，在正方形ABCD中，AB＝1，点E、F分别在边BC和CD上，AE＝AF，∠EAF＝60°，则CF的长是．三．解答题（共7小题，满分52分）17．如图，D是△ABC的边AB上一点，CE∥AB，DE交AC于点F，若F A＝FC．求证：四边形ADCE是平行四边形；18．如图，在△ABC中，AB＝BC，BD平分∠ABC．四边形ABED是平行四边形，DE交BC于点F，连接CE．求证：四边形BECD是矩形．19．如图，在平行四边形ABCD中，O是AB的中点，连接DO并延长交CB的延长线于点E，连接AE、DB．（1）求证：△AOD≌△BOE；（2）若DC＝DE，判断四边形AEBD的形状，并说明理由．20．如图，在矩形AFCG中，BD垂直平分对角线AC，交CG于点D，交AF于点B，交AC于点O．连接AD、BC．（1）求证：四边形ABCD是菱形；（2）若E为AB的中点，DE⊥AB，求∠BDC的度数；（3）在（2）的条件下，若AB＝2，求矩形AFCG的面积．21．已知，四边形ABCD是菱形，∠B＝60°，∠EAF的两边分别与射线CB，DC相交于点E，F，且∠EAF＝60°．（1）如图1，当点E是线段CB上任意一点时（点E不与B，C重合），求证：BE＝CF；（2）如图2，当点E在线段CB的延长线上，连接AC，在不添加任何辅助线的情况下，直接写出图2中三对相等的线段（菱形ABCD相等的边除外）．22．如图，在平面直角坐标系中，AB∥OC，A（0，12），B（a，c），C（b，0），并且a，b满足b＝++16．一动点P从点A出发，在线段AB上以每秒2个单位长度的速度向点B运动；动点Q从点O出发在线段OC上以每秒1个单位长度的速度向点C运动，点P、Q分别从点A、O同时出发，当点P运动到点B时，点Q随之停止运动．设运动时间为t（秒）（1）求B、C两点的坐标；（2）当t为何值时，四边形PQCB是平行四边形？并求出此时P、Q两点的坐标；（3）当t为何值时，△PQC是以PQ为腰的等腰三角形？并求出P、Q两点的坐标．23．如图，在正方形ABCD中，点E为AB上的点（不与A，B重合），△ADE与△FDE关于DE对称，作射线CF，与DE的延长线相交于点G，连接AG，（1）当∠ADE＝15°时，求∠DGC的度数；（2）若点E在AB上移动，请你判断∠DGC的度数是否发生变化，若不变化，请证明你的结论；若会发生变化，请说明理由；（3）如图2，当点F落在对角线BD上时，点M为DE的中点，连接AM，FM，请你判断四边形AGFM的形状，并证明你的结论．参考答案一．选择题（共10小题，满分30分）1．解：∵矩形的对角线线段，四个角是直角，对角线互相平分，∴选项A、C、D正确，选：B．2．解：∵直角三角形两条直角边长分别是6和8，∴斜边＝＝10，∴斜边上的中线长＝×10＝5．选：C．3．解：A、四边都相等是四边形是菱形，也是平行四边形；该选项不合题意；B、两组对角分别相等的四边形是平行四边形，该选项不合题意；C、对角线互相垂直的四边形不是平行四边形，该选项符合题意；D、两组对边分别平行的四边形是平行四边形，该选项不合题意；选：C．4．解：∵四边形ABCD是菱形，∴DC∥AB，∠DAC＝∠1，∵∠D＝130°，∴∠DAB＝180°﹣130°＝50°，∴∠1＝∠DAB＝25°．选：B．5．解：∵四边形ABCD是矩形，∴OA＝OB．∴∠BAO＝∠ABO＝55°．∴∠AOD＝∠BAO+∠ABO＝55°+55°＝110°．选：A．6．解：∵O是矩形ABCD的对角线AC的中点，M是AD的中点，∴OM＝CD＝AB＝1.5，∵AB＝3，AD＝4，∴AC＝＝5，∵O是矩形ABCD的对角线AC的中点，∴BO＝AC＝2.5，∴四边形ABOM的周长为AB+AM+BO+OM＝3+2+2.5+1.5＝9，选：C．7．解：在▱ABCD中，可得：AO＝OC，选：C．8．解：∵四边形ABCD是正方形，∴∠BAD＝90°，AB＝AD，又∵△ADE是正三角形，∴AE＝AD，∠DAE＝60°，∴△ABE是等腰三角形，∠BAE＝90°+60°＝150°，∴∠ABE＝∠AEB＝15°．选：C．9．解：∵四边形ABCD是矩形，∴∠BAD＝90°，设AD＝BC＝a，AB＝DC＝b，∵AC＝10，BE⊥AC，BE＝4，∴a2+b2＝102，又∵S矩形ABCD＝2S△ABC∴ab＝2××10×4＝40，∵BC＞AB，解得：a＝4，b＝2，即AD＝4，选：D．10．解：连接BD交AC于点O，∵AB＝CD＝AD＝5，∴CD＝CE＝5，∵AC＝8，∴AE＝3，OC＝4，OE＝1，在Rt△CDO中，由勾股定理可知：DO＝3，在Rt△DOE中，由勾股定理可知：DE＝，∴＝，选：B．二．填空题（共6小题，满分18分）11．解：∵四边形ABCD为平行四边形，∴，解得：，∴∠C＝∠A＝80°．答案为：80°．12．解：∵点D、E分別是AB，AC的中点，∴DE＝BC＝×6＝3，答案为：3．13．解：∵菱形的面积＝对角线积的一半∴菱形的面积＝×2×2＝2cm2，答案为：214．解：∵四边形ABCD为平行四边形，∴AE∥BC，AD＝BC，AB＝CD，∴∠AEB＝∠EBC，∵BE平分∠ABC，∴∠ABE＝∠EBC，∴∠ABE＝∠AEB，∴AB＝AE，∴AE+DE＝AD＝BC＝6，∴AE+2＝6，∴AE＝4，∴AB＝CD＝4，∴▱ABCD的周长＝4+4+6+6＝20，答案为：20．15．解：如图所示：∵A（﹣3，0），∴OA＝3，①当四边形OACB是平行四边形时，BC＝OA＝3，∵B（﹣5，2），∴C（﹣2，2），②当四边形OABC′是平行四边形时，BC'＝OA＝3，∵B（﹣5，2），∴C（﹣8，2）；③当四边形OBAC′'是平行四边形时，∵A（﹣3，0），B（﹣5，2），∴C（2，﹣2），答案为：（﹣2，2）或（﹣8，2）或（2，﹣2）．16．解：∵四边形ABCD是正方形，∴∠B＝∠D＝∠BAD＝90°，AB＝BC＝CD＝AD＝1，在Rt△ABE和Rt△ADF中，，∴Rt△ABE≌Rt△ADF（HL），∴∠BAE＝∠DAF，∵∠EAF＝60°，∴∠BAE+∠DAF＝30°，∴∠DAF＝15°，在AD上取一点G，使∠GF A＝∠DAF＝15°，如图所示，∴AG＝FG，∠DGF＝30°，∴DF＝FG＝AG，DG＝DF，设DF＝x，则DG＝x，AG＝FG＝2x，∵AG+DG＝AD，∴2x+x＝1，解得：x＝2﹣，∴DF＝2﹣，∴CF＝CD﹣DF＝1﹣（2﹣）＝﹣1；答案为．三．解答题（共7小题，满分52分）17．证明：∵CE∥AB，∴∠BAC＝∠ECA，在△DAF和△ECF中，∴△DAF≌△ECF（ASA），∴CE＝AD，∴四边形ADCE是平行四边形；18．证明：∵AB＝BC，BD平分∠ABC，∴BD⊥AC，AD＝CD．∵四边形ABED是平行四边形，∴BE∥AD，BE＝AD，∴BE＝CD，∴四边形BECD是平行四边形．∵BD⊥AC，∴∠BDC＝90°，∴▱BECD是矩形．19．证明：（1）∵四边形ABCD是平行四边形，∴AD∥CE．∴∠ADO＝∠BEO．∵O是BC中点，∴AO＝BO．又∠AOD＝∠BOE．∴△AOD≌△BOE（AAS）；（2）四边形AEBD是矩形，理由如下：∵△AOD≌△BOE，∴DO＝EO．又AO＝BO，∴四边形AEBD是平行四边形．∵DC＝DE＝AB，∴四边形AEBD是矩形．20．（1）证明：∵BD垂直平分AC，∴OA＝OC，AD＝CD，AB＝BC，∵四边形AFCG是矩形，∴CG∥AF，∴∠CDO＝∠ABO，∠DCO＝∠BAO，且OA＝OC ∴△COD≌△AOB（AAS），∴CD＝AB，∴AB＝BC＝CD＝DA，∴四边形ABCD是菱形．（2）∵E为AB中点，DE⊥AB，∴DE垂直平分AB，∴AD＝DB，∵AD＝AB，∴△ADB为等边三角形，∴∠DBA＝60°，∵CD∥AB，∴∠BDC＝∠DBA＝60°．（3）∵∠BDC＝60°，CB＝CD，∴△CDB是等边三角形，∴BC＝CD＝BD＝AB＝2，∠DCB＝60°∵CD∥AB∴∠DCB＝∠CBF＝60°，且∠F＝90°，BC＝2∴BF＝1，CF＝∴矩形AFCG的面积＝AF×CF＝3×＝321．（1）证明：∵四边形ABCD是菱形，∠B＝60°，∴AB＝BC＝CD＝AD，∠B＝∠D＝60°，∴△ABC，△ADC是等边三角形，∴∠BAC＝∠DAC＝60°，∵∠BAC＝∠EAF＝60°，∴∠BAE＝∠CAF，在△BAE和△CAF中，，∴△BAE≌△CAF（ASA），∴BE＝CF．（2）解：AE＝AF，BE＝CF，CE＝DF．由（1）知△ABC，△ADC是等边三角形，∴∠BAC＝∠DAC＝∠ACD＝60°，∵∠BAC＝∠EAF＝60°，∠ABE＝∠ACF，∴∠BAE＝∠CAF，∵AB＝AC，∴△BAE≌△CAF（ASA），∴AE＝AF，BE＝CF，∴BE+BC＝CF+CD，即CE＝DF．22．解：（1）∵b＝++16，∴a＝21，b＝16，B（21，12）C（16，0）；（2）由题意得：AP＝2t，QO＝t，则：PB＝21﹣2t，QC＝16﹣t，∵当PB＝QC时，四边形PQCB是平行四边形，∴21﹣2t＝16﹣t，解得：t＝5，∴P（10，12）Q（5，0）；（3）当PQ＝CQ时，过Q作QN⊥AB，由题意得：122+t2＝（16﹣t）2，解得：t＝，P（7，12），Q（，0），当PQ＝PC时，过P作PM⊥x轴，由题意得：QM＝t，CM＝16﹣2t，则t＝16﹣2t，解得：t＝，2t＝，P（，12），Q（，0）．23．解：（1）∵∠ADE＝15°，∴∠FDE＝15°，∠CDF＝60°．∵DC＝AD＝DF，∴∠CFD＝60°．又∠CFD＝∠DGC+∠FDE＝15°+∠DGC，∴∠DGC＝45°；（2）不变，理由如下：∵△ADE与△FDE关于DE对称，∴∠AGD＝∠DGF．设∠ADE＝x，可得∠FDE＝x，∠CDF＝90°﹣2x，∵DC＝AD＝DF，∴∠CFD＝45°+x．又∠CFD＝∠DGC+∠FDE＝x+∠DGC，∴∠DGC＝45°；（3）四边形AGFM是正方形；理由：∵∠DAE＝∠DFE＝90°，点M为DE的中点，∴AM＝FM＝DM＝DE，∴∠ADM＝∠DAM，∠MDF＝∠DFM，∴∠AME＝∠FMF＝2∠ADM＝2∠MDF＝45°，∴∠AMF＝90°，∵∠MGF＝45°，∴FM＝FG，在△ADG与△FDG中，，∴△ADG≌△FDG（SAS），∴AG＝FG，∴AM＝MF＝FG＝AG，∵∠AMF＝90°，∴四边形AGFM是正方形．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

E F
D C
B
A
D
B
A 平行四边形全章综合检测题
一、选择题（每题5分，共30分）
1、正方形具有而菱形不一定具有的性质是（）
A对角线互相平分; B对角线相等; C对角线平分一组对角; D对角线互相垂直
2、能判定四边形ABCD为平行四边形的题设是（）．
A、AB∥CD，AD=BC;
B、∠A=∠B，∠C=∠D;
C、AB=CD，AD=BC;
D、AB=AD，CB=CD
3、如图所示,矩形ABCD中,AB=8,BC=6,E、F是AC的三等分点,则△BEF 的面积是
( )A.8 B.12 C.16 D.24
4、菱形ABCD的对角线长分别为6cm和8cm，则菱形
的面积为（）A.12， B.24 C.36 D.48
5．下列说法不正确的是（）
（A）对角线相等且互相平分的四边形是矩形;（B）对角线互相垂直平分的四边形
是菱形; （C）对角线垂直的菱形是正方形;（D）两条对角线垂直且相等的平行四
边形是正方形;
6、如图1，在平行四边形ABCD中，CE AB
⊥，E
为垂足．如果125
A=
∠，则BCE=
∠（）
Ａ．55 Ｂ．35 Ｃ．25 Ｄ．30
7、如图11，在菱形ABCD中，∠BAD＝80°，AB的垂直平分线交对角线AC于点
E，交AB于点F，F为垂足，连接DE，
则∠CDE＝_____度
8如图1，在平行四边形ABCD中，MN分别是AB、CD的中点，BD分别交AN、CM于
点P、Q，在结论：①DP=PQ=QB ②AP=CQ ③CQ=2MQ ④S△ADP=
1
4
S ABCD中，正
确的个数为（）．
（A）1 （B）2 （C）3 （D）4
9如图,周长为68的矩形ABCD被分成7个完全一样的小矩形,则
矩形ABCD的面积为( )
A.98
B.196
C.280
D.284
10.如图，在平面直角坐标系中，□ABCD的顶点A、B、D的坐标
分别是（0，0），（5，0）（2，3），则顶点C的坐标是（）
A.（3，7）
B.（5，3）
C.（7，3）
D.（8，2）
二、填空题（每题5分，共30分）
11、顺次连结任意四边形各边中点所得到的四边形一定是__ ___
12如图6，ABCD中，过对角线交点O，引一直线交BC于E，交AD于F，若AB=2.4cm，
BC=4cm，OE=1.1cm，则四边形CDFE周长为________．
13、如图2，矩形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD
和BC于点E、F，23
AB BC
==
，，则图中阴影部分的面积为．
14、如图3，若□ABCD与□EBCF关于BC所在直线对称，∠ABE＝90°，则∠F
＝°
N
M
Q
P D
C
B
A
15、如图4，把一张矩形纸片ABCD 沿EF 折叠后，点C D ，分别落在C D ''，的位置上，EC '交AD 于点G ．则△EFG 形状为
16．如图6，AC 是正方形ABCD 的对角线，AE 平分∠BAC ，EF ⊥AC 交AC 于点F ，若BE=2，则CF 长为
17、如图13，已知：平行四边形ABCD 中，BCD ∠的平分线CE 交边AD 于E ，
ABC ∠的平分线BG 交CE 于F ，交AD 于G ．若AB=4cm ，AD=6cm ，则
EG=_______ cm .
18、将矩形纸片ABCD 按如图14所示的方式折叠，得到菱形AECF ．若AB ＝9，则AC 的长为 _________
三、解答题（每题10分，共40分）
19、已知：如图7，E 、F 是平行四边行ABCD 的对角线AC 上的两点，AE=CF 。

求证：∠CDF ＝∠ABE
20、如图8，把正方形ABCD 绕着点A ，按顺时针方向旋转得到正方形AEFG ，边FG 与BC 交于点H ．求证：HC=HF.
21、已知：如图9，在△ABC 中，AB =AC ，AD ⊥BC ，垂足为点D ，AN 是△ABC 外角∠CAM 的平分线，CE ⊥AN ，垂足为点E ，猜想四边形ADCE 的形状，并给予证明.
22、如图10，在梯形纸片ABCD 中，AD//BC ，AD >CD ，将纸片沿过点D 的直线折叠，使点C 落在AD 上的点C 处，折痕DE 交BC 于点E ，连结C′E ．
求证：四边形CDC′E 是菱形．
23.已知：如图，在正方形ABCD 中，AE ⊥BF ，垂足为P ，AE 与CD 交于点E ，•BF•与AD 交于点F ，求证：AE=BF ．
24．如图,在□ABCD 中,AC 的平行线MN 交DA 的延长线于M,交DC 的延长线于N,交AB,BC 于P,Q. 求证：MP=QN
25如图所示，四边形ABCD 是正方形，M 是AB 延长线上一点，直角三角尺的一条直角边经过点D ，且直角顶点E 在AB 边上滑动（点E 不与点A ，B 重合），另一直角边与∠CBM 的平分线BF 相交于点F ．
（1）如图（1）所示，当点E 在AB 边的中点位置时：
①通过测量DE ，EF 的长度，猜想DE 与EF 满足的数量关系是_______． ②连接点E 与AD 边的中点N ，猜想NE 与BF 满足的数量关系是________． ③请证明你的上述两个猜想．
（2）如图（2）所示，当点E 在AB 边上的任意位置时，请你在AD 边上找到一点N ，使得NE=BF ，进而猜想此时DE 与EF 有怎样的数量关系．。