§12.8 气体分子的平均碰撞频率和平均自由程
§12.8气体分子的平均碰撞频率和平均自由程

运动 ( 其他分子静止 )。
则:△t 时间内与该分子碰
撞的分子个数为:
N n d 2ut
vt zt
v z
分子数密度 :n
☻ z 、 与哪些因素相关
Chapter 6. 气体动理论
§6. 5 气体分子的平均碰撞频率和平均自由程 作者:杨茂田
kT 2 d2 p
p
kT 0.63 (Pa) 6.22 106 atm 2 d2
( The end )
瓶胆承受的压力~1.01×104kg/m2!
Chapter 6. 气体动理论
§6. 5 气体分子的平均碰撞频率和平均自由程 作者:杨茂田
P. 13 / 12 .
作业: 答疑时间:周二下午1:30-3:30
例 试计算0℃时,不同压强下空气分子的平均自由程。 解:空气分子的有效直径 d = 3.5×10-10m,则
p (Pa)
(m)
5
1.01 10
6.9 10
8Leabharlann 1.33 1025.2 10 5 5.2 10 3 5.2 10 1
1.33
1.33 10 2 1.33 10 4
Chapter 6. 气体动理论
§6. 5 气体分子的平均碰撞频率和平均自由程 作者:杨茂田
P. 1 / 12 .
§ 12-8 气体分子的平均碰撞 频率和平均自由程
Chapter 6. 气体动理论
§6. 5 气体分子的平均碰撞频率和平均自由程 作者:杨茂田
P. 2 / 12 .
☻为什么
打开香水瓶后,我们并不能立即闻到香水的 香味,为什么?
分子碰撞频率和平均自由度

(二) λ Z 间的关系
v ----气体分子运动的平均速度,即每秒走过的平均距离.
Z -故(-1-)-,气气λ体体或分分Z子子平平与气均均体自每所由秒出程碰的:撞状态次有数λ关.=,如Zv气体单位体积内分子
数n大,分子碰撞的机会多.
(2) λ 或 Z 与气体种类(或性质)有关,分子直径大,碰撞机会多.
过程看作弹性碰撞过程,两这直径只是分 子有效直径,并非分子真正大小.
r0
r
f斥
d
Z = πd 2un
u = 2v 平均相对速率 , v 平均速率.
所以: Z = 2πd 2nv
看出λ 与宏观平均速率 v 无关.
与宏观λ 量(p,V,T)的关系:
λ= v =
Q p=nkT
n = p /kT
Z
∴ λ = kT 2π d 2 p
1
2π d 2 n
a
• 讨论:(1)气体温度一定p增大, λ 减小数量级概念,
v (3) 大,其它条件一定,碰撞机会多.
简略推导: 1) 气体分子为弹性小球,直径d.
2) 假设一定量气体中只有一个分子在运动,其它分子不动,平
均速率为 v ,而此分子运动相对其它分子的相对速率为u ,分
子a运动,轨迹为直线,和分子球心距离等于或小于分子直径 的那些分子与a碰撞.
则a分子在单位时间内和其它分子碰撞的次数为:
地球海平面 p=1大气压=
帕,
T=237K
此时 1.01=31×0-710米5
{ 地面上空(100公里处) p=0.133帕,
=1米λ
地面上空(300公里处) p=
帕
=10米λ
《物理学教学课件》7-5碰撞频率和平均自由程

在气体分子运动论中,平均自由程表示气体分子在连续两次碰撞之间所经过的平均距离。 通过研究平均自由程,可以深入理解气体分子的扩散和输运过程。
热力学第二定律
热传导
在热力学第二定律中,热传导是热量自发地从高温物体传递到低温物体的过程。 通过研究气体分子碰撞频率和平均自由程,可以深入理解热传导的微观机制和 热能传递的规律。
应用
在计算气体分子的平均速度、扩散系 数等物理量时,需要用到平均自由程 。
平均自由程的影响因素
分子间的相互作用力
分子间的相互作用力决定了碰撞 频率,进而影响平均自由程的大 小。
分子质量
较轻的分子具有较长的平均自由 程,因为它们受到的空气阻力较 小。
气体温度
气体温度越高,分子热运动越剧 烈,碰撞频率越高,平均自由程 越短。
、压力等实验条件的关系。
实验结果与数据分析
实验结果
通过实验,获得气体分子的碰撞 频率和平均自由程数据。
数据分析
分析碰撞频率和平均自由程与温度、 压力等实验条件的关系,得出气体 分子运动和相互作用的规律。
结果讨论
根据实验结果,讨论碰撞频率和平 均自由程在气体分子扩散、传递过 程中的作用,以及在实际应用中的 意义。
粘性流动
粘性流动是气体在流动过程中由于分子间的内摩擦力而产生的阻力。通过研究气 体分子碰撞频率和平均自由程,可以进一步了解粘性流动的微观机制和气体流动 的规律。
Part
05
实验研究
实验目的与原理
实验目的
通过实验研究,掌握碰撞频率和平均自由程的概念,理解气体分子碰撞和扩散的基本原理。
实验原理
气体分子在容器内不断进行碰撞,其碰撞频率与气体分子的密度、温度和分子间的相互作用力有关。分子在两次 碰撞之间的平均距离称为平均自由程。通过测量容器内气体分子的碰撞频率和平均自由程,可以深入了解气体分 子运动和相互作用的规律。
理想气体的分子平均碰撞频率碰撞次数的期望

理想气体的分子平均碰撞频率碰撞次数的期望理想气体是指分子之间弱相互作用力,分子体积可以忽略不计的气体。
理想气体的分子运动是无规则的,分子之间会发生碰撞,这些碰撞是理解气体性质和研究气体行为的基础。
本文将探讨理想气体中分子的平均碰撞频率以及碰撞次数的期望。
1. 分子平均碰撞频率的概念及计算方法理想气体中分子的平均碰撞频率是指单位时间内发生的分子碰撞的次数。
设气体中共有N个分子,每个分子半径为r,平均速率为v。
在t时间内,一个分子能与其他分子产生碰撞的有效碰撞距离为2r。
因此,单位时间内一个分子能与其他分子产生的有效碰撞次数为:n = v / (πr^2)在整个气体中,每个分子都可以看作是等概率地与其他分子发生碰撞。
因此,总的平均碰撞频率为:z = n * N = (Nv) / (πr^2)2. 分子碰撞次数的期望及计算方法一个分子在单位时间内与其他分子发生的有效碰撞次数可以看作是一个随机事件,我们可以用概率的方法来研究这个问题。
设一个分子在t时间内与其他分子发生的有效碰撞次数为X,则X是一个服从二项分布的随机变量。
在小时间段(dt)内,一个分子能够与其他分子发生碰撞的概率为:P(dt) = n * dt = v * dt / (πr^2)根据二项分布的性质,一个分子在t时间内与其他分子发生k次有效碰撞的概率为:P(X=k) = C(N-1, k) * [P(dt)]^k * [1- P(dt)]^(N-1-k)根据期望的定义,我们可以计算分子在t时间内与其他分子发生有效碰撞的次数的期望值:E(X) = ∑k=0到N-1(k * P(X=k))通常情况下,当气体的分子数目很大时,可以使用泊松分布来近似描述二项分布,这样计算起来更加简单。
泊松分布的期望值等于其参数λ。
3. 碰撞频率和碰撞次数期望的物理意义及应用理解和计算分子平均碰撞频率以及碰撞次数的期望对研究理想气体的性质和行为非常重要。
通过对碰撞频率和碰撞次数的分析,我们可以得到以下几个方面的理解和应用:3.1. 热导率:分子之间的碰撞也将导致能量的传递。
气体分子的平均碰撞频率和平均自由程.ppt

p kT 0.63 (Pa) 6.22106 atm 2 d2
瓶胆承受的压力~1.01×104kg/m2!
( The end )
Chapter 6. 气体动理论 §6. 5 气作体者分:子杨的茂平田均碰撞频率和平均自由程
P. 13 / 12 .
作业:
12-25,12-28
答疑时间:周二下午1:30-3:30
1.5cm 1.5102m kT
2 d2 p p kT 0.63 (Pa) 6.22106 atm
2 d2
1.5cm
Chapter 6. 气体动理论 §6. 5 气作体者分:子杨的茂平田均碰撞频率和平均自由程
P. 12 / 12 .
1. 平均碰撞频率: z 2 n d2v
2. 平均自由程: kT 2 d2 p
▲平均碰撞频率:分子在单位时间内的平均碰撞次数。
常用 z 表示。
则,在 △t 时间内,有:
vt zt
v z
☻ z、与哪些因素相关
Chapter 6. 气体动理论 §6. 5 气作体者分:子杨的茂平田均碰撞频率和平均自由程
P. 5 / 12 .
二、平均碰撞频率与平均自由程
设分子的有效直径为d,某分子以 u 相对于其他分子
解:空气分子的有效直径 d = 3.5×10-10m,则
p (Pa)
(m)
1.01105 1.33 102
6.9 108 5.2 105
kT 2 d2 p
常温常压下: 约108 ~ 107 (m)
Chapter 6. 气体动理论 §6. 5 气作体者分:子杨的茂平田均碰撞频率和平均
1
2 d2 n
而: p nkT
z
分子的平均碰撞频率和平均自由程

第21讲 分子的平均碰撞频率和平均自由程 习题课教学要求理解气体分子的平均碰撞次数及平均自由程。
重点与难点重点:分子的平均碰撞次数及平均自由程。
难点:分子的平均碰撞次数及平均自由程。
7.7 分子的平均碰撞频率和平均自由程气体分子无规则热运动,频繁碰撞。
每个分子在两次碰撞之间自由行进多长的路径和用多长时间完全是偶然的、不确定的(如图7-10)。
但对大量分子,从统计的角度看,每个分子在单位时间内与其它分子平均碰撞多少次和平均自由行进多少路径却是有规律的。
7.7.1 平均碰撞频率z平均碰撞频率z 就是对于处于平衡状态下的大量气体分子组成的系统,一个分子单位时间内与其它分子的平均碰撞次数。
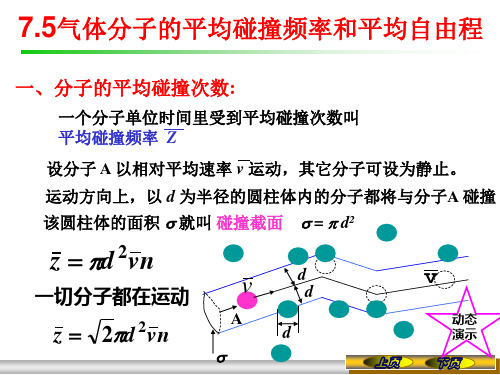
根据简化的气体分子模型,同种气体分子中每个分子都是直径为d 的刚性球,设想跟踪一个气体分子A ,为简化计算起见,首先假定其它分子不动,A 分子以平均相对速率u 接近其它分子,那么1秒内有哪些分子能与A 分子相碰呢?在A 分子运动过程中,它的质心轨迹是一条折线abce , 凡是其它分子的质心离开此折线的距离小于或等于分子有效直径d 的,都将与A 分子相碰(图7-11)。
如果以1秒内A 分子质心运动轨迹为轴,以分子有效直径d 为半径作一圆柱体(该圆柱体体积为2πd u )。
质心在该圆柱体内的分子都将与A 分子相碰。
设n 为分子数密度,则该圆柱体内的分子数为2πn d u ,亦即1秒内A 分子与其它分图7-10气体分子的碰撞e子发生碰撞的平均次数。
所以平均碰撞频率2πZ n d u =式中,,2πd σ=称为分子的碰撞截面。
考虑所有分子同时以平均速率υ运动,分子间平均相对运动速率为υ2=u , 故2Z d n υ=(7-23)上式表明,分子热运动平均碰撞频率与分子数密度n 、分子平均速率υ成正比,也与分子碰撞截面σ或分子有效直径d 的平方成正比。
7.7.2 平均自由程 λ平均自由程 λ 就是在平衡状态下,一个分子在连续两次碰撞之间所经过的路程的平均值。
热学气体分子平均自由程

气体分子的碰撞截面
碰撞截面
截面对平均自由程的影响
气体分子间的碰撞截面决定了分子间 的相互作用和碰撞概率。
碰撞截面越大,分子间的碰撞概率越 高,平均自由程越短。
截面大小
不同气体分子间的碰撞截面大小不同, 与分子间的距离和相互作用力有关。
气体分子的能量损失
能量损失
01
气体分子在碰撞过程中会损失能量,导致平均自由程的变化。
特性
与气体分子的速度、气体分子的分布、气体分子的碰撞频率等因素有关。
平均自由程与气体分子碰撞频率的关系
碰撞频率
气体分子在单位时间内所发生的碰撞 次数。
关系
平均自由程与气体分子碰撞频率成反 比,碰撞频率越高,平均自由程越小。
平均自由程在热学中的重要性
热传导
平均自由程是影响气体热传导的重要因素之一,通过 改变平均自由程可以调节气体的热传导性能。
总结词
在高温高压条件下,气体分子间的相互 作用力减弱,分子间的碰撞频率降低, 因此平均自由程较大。
VS
详细描述
在高温高压条件下,气体分子间的平均距 离增大,分子间的碰撞频率减少,导致气 体分子的平均自由程增大。这种情况下, 气体分子的运动受到的相互碰撞的限制较 小,运动路径较长。
04 气体分子平均自由程的影 响因素
探索气体分子平均自由程在极端条件下的行为
研究高温、高压、高密度等极端 条件下气体分子平均自由程的变 化规律,揭示其与温度、压力、
密度的关系。
探讨极端条件下气体分子与障碍 物的相互作用,以及气体分子间 的相互作用,以理解其行为特性。
研究极端条件下气体分子输运性 质的变化,为相关领域的应用提
供理论支持。
感谢您的观看
气体分子的平均自由程

一. 分子的平均碰撞频率
一个分子单位时间内
和其它分子碰撞的平 均次数,称为分子的 平均碰撞频率。
假设 · 每个分子都可以看成直径为d 的弹性小球,分子间的碰撞 为完全弹性碰撞。大量分子中,只有被考察的特定分子A 以平均速率 运动,其它分子都看作静止不动。
单位时间内与分子 A · 发生碰撞的分子数为 平均碰撞频率为 ·
例 估算氢气分子在标准状态下的平均碰撞频率
解 在标准状态下,有
对氢气分子取
,则
常温常压下,一个分子在一秒内平均要碰撞几十亿次,可 见气体分子之间的碰撞是多么的频繁!
-2 -3 例 真空管的线度为 10 m ,其中真空度为 1.33× 10 Pa 。 设空气分子的有效直径为 3×10-10 m 。
考虑到所有分子实际上都在运动,则有 ·
用宏观量 p 、T 表示的平均碰撞频率为
二. 分子的平均自由程
分子在连续两次碰撞之间自由运动的平均路程,称为分子 的平均自由程 。
用宏观量 p 、T 表示的分子平均自由程为
பைடு நூலகம்
说明 在标准状态下,各种气体分子的平均碰撞频率的数量级
约为 109 s-1,平均自由程的数量级约为10-7 ~ 10-8 m 。
求 27℃ 时单位体积内的空气分子数、平均自由程、平均碰撞 次数 。 解 由气体的状态方程, 有
在这种情况下气体分子相互之间很少发生碰撞,只是不 断地来回碰撞真空管的壁,因此气体分子的平均自由程 就应该是容器的线度。 即
作业 8.19
《大学物理》75 气体分子的平均碰撞频率和平均自由程.
448 9 1 Z 5.1 10 s 8 8.71 10
上页 下页
v
=
v
Z
=
1
2 d2 n
=
kT
2 d2 P
上页
下页
2
一切分子都在运动
v
A d
v
动态 演示
z 2d v n
2
上页
下页
二、平均自由程
一个分子连续两次碰撞之间经历的平均自由路 程叫平均自由程 单位时间内分子经历的 平均距离 v , 平均碰撞 Z 次
=
v Z v Z
因为
P=nkT
=
=
1
2 d2 n
=
kT
2 d2 P
上页 下页
10-10m。已知空气的平均分子量为29。
解: 已知 T 273 K , P 1.0atm 1.013 105 Pa ,
d 3.10 10 10 m
上页 下页
kT 2d 2 P
23
1.38 10 273 8 8.71 10 m 10 5 1.41 3.14 ( 3.5 10 ) 1.01 10
在标准状态下,几种气体分子的平均自由程
气体 氢
7
氮
氧
7
空气
7
(m ) 1.123 10
0.599 10
0.647 10
7.00 10
8
d ( m ) 2.30 10 10 3.10 10 10 2.98 1010 3.10 1010
气体分子的平均碰撞频率和平均自由程

气体动理论
第9讲 气体分子的平均碰撞频率 和平均自由程
一、分子的平均碰撞频率
平均碰撞频率和平均自由程
平衡态宏观性质的维持 非平衡态向平衡态过渡
依靠分子间的频繁碰撞实现
刚性球 模型
不可以像讨论压强那样 将分子看成质点
不需像讨论内能那样考 虑分子内部结构
分子的有效直径 d 约为10-10 m
无引力刚 性球模型
=
1.013×105 1.38×10−23 × 273
=
2.69 ×1025 m−3
λ = 1 = 2.14 ×10−7 m 2π d 2n
z = v = 7.95×109 s−1
λ
(约80亿次)
平均碰撞频率和平均自由程
d d
假定: 分子是直径为d 的弹性小球
分子A以平均相对速率 u 运动, 其他分子静止 由麦克斯韦速率分布可证 u = 2 v
球心轨迹为轴, d 为半径作折圆柱体
平均碰撞频率和平均自由程
d d
球心在圆柱体内的分子将与A碰撞
单位时间内有 πd 2u n 个分子与A发生碰撞
平均碰撞频率: z = 2π d 2nv
• 当温度一定时,平均自由程与压强成反比,压强越小,平 均自由程越长.
平均碰撞频率和平均自由程
例. 求氢在标准状态下一秒内分子的平均碰撞次数. (已知 分子直径d = 2×10-10m )
解:
v=
8RT =
Mπ
8×8.31× 273
2 ×10−3π
= 1.70 ×103 m ⋅ s−1
n
=
P kT
二、平均自由程平均碰撞频率平均自由程平均自由程( λ ): 分子在连续两次和其它分子发生碰撞
平均碰撞频率和自由程

dN (r ,v ) Ce /kT dvxdvydvz dxdydz
2
§12.10 平均碰撞频率和平均自由程
一. 分子的平均碰撞频率 Z
一个分子单位时间内 和其它分子碰撞的平 均次数,称为分子的 平均碰撞频率。
·假设
每个分子都可以看成直径为 d 的弹性小球,分子间的碰 撞为完全弹性碰撞。大量分子中,只有被考察的特定分
可以推知:有 N 个分子时,分子的总微观态数 2N ,总宏
观态数( N+1 ) ,每一种微观态概率 (1/2N )
10
20个分子的位置分布
宏观状态
一种宏观状态对应的微观状态数
左20
右0
1
左18
右2
190
左15
右5
15504
左11 左10
右9 右10
167960 184756
左9
右11
167960
左5
25
二. 熵 熵增原理
1. 熵
孤立系统 状态(1)
能否自动进行? 判据是什么?
状态(2)
微观态数少的宏观态
微观态数多的宏观态
为了定量的表示系统状态的这种性质,从而定量说明自发 过程进行的方向,而引入熵的概念。
14
玻尔兹曼(Ludwig Edward Boltzmann, 1844-1906)
奥地利物理学家和哲学家,热力学和统计物理学的奠基人之一
一. 热力学第二定律的统计意义
1. 气体分子位置的分布规律
3个分子的分配方式
a b c
气体的自由膨胀
左半边 abc ab bc ac a b c 0
右半边 0 c a b bc ac ab abc
第三讲 平均碰撞频率与平均自由程

5.试以气体为例,用分子热运动观点对内摩擦、 热传导、扩散现象做出微观定性解释。
答案
—— 热学 ——
真实气体 范德瓦斯方程
作业
P149:1.26
预习 第二章 1、2、3、4节
—— 热学 ——
气体分子的平均自由程
1、粘滞现象
河流中水流的流速分布:
河岸
河流 u
河岸
f
u2
下层对上层的阻力
u1
f
上层对下层的作用力
—— 热学 ——
真实气体 范德瓦斯方程
各层气流的流速不同 相邻两层气流之间产生阻碍气体流动的阻力 ——称为粘性力。(这种现象称为内摩擦现象)
du -----速度梯度 dy
平均碰撞频率
z
平均自由程
平均速率
—— 热学 ——
λυ z
气体分子的平均自由程
(实际上其它分子也在运动)
平均相对速率 u 2υ 分子有效直径:d
—— 热学 ——
气体分子的平均自由程
d
u u
d
A
d
引入: 碰撞截面
d 2
结论: z 2σnυ
1
kT
λ
2σn 2πd 2 p
注:实际平均自由程可能与容器线度有关。
迁移现象产生的原因: 流速、温度、密度不均匀
无外界干预时,系统要从非平衡态自发地向平衡态 过渡。亦称输运过程。 讨论气体在非平衡态下的三种特殊过程。 即:三种迁移现象:
粘 滞 现 象 ——分子动量迁移; 热 传 导 现 象——分子能量迁移; 扩 散 现 象 ——分子密度迁移;
—— 热学 ——
气体平均自由程计算公式

气体平均自由程计算公式以气体平均自由程计算公式为标题,我们来探讨一下这个公式的含义和应用。
在研究气体分子运动时,平均自由程是一个重要的物理量。
它表示了气体分子在碰撞之间所能飞行的平均距离。
通过计算平均自由程,我们可以了解气体分子的运动规律,以及气体的输运性质。
那么,如何计算气体的平均自由程呢?在理想气体模型中,平均自由程的计算公式为:λ = (1 / (sqrt(2) * π * d^2 * n)),其中,λ表示平均自由程,d表示气体分子的直径,n表示气体分子的数密度。
这个公式的推导过程比较复杂,我们不详细展开。
但是,通过这个公式,我们可以得出一些有趣的结论。
平均自由程与气体分子的直径成反比。
这意味着,气体分子越大,其平均自由程就越小。
因为大分子的直径相对较大,分子之间的碰撞更加频繁,所以平均自由程就相对较短。
平均自由程与气体分子的数密度成反比。
数密度越大,分子之间的距离就越近,碰撞的概率就越高,所以平均自由程就越短。
通过平均自由程的计算,我们还可以推导出气体的输运性质。
例如,气体的导热性和电导率与平均自由程有关。
当气体的平均自由程很长时,分子之间的碰撞较少,热量和电流可以更迅速地传递,所以导热性和电导率就较高。
相反,当平均自由程较短时,热量和电流的传递速度就会减慢,导热性和电导率就会降低。
平均自由程还与气体的粘滞性有关。
粘滞性是指气体分子在流动中的阻力。
当气体的平均自由程较短时,分子之间的碰撞频率较高,气体的粘滞性就会增加。
而当平均自由程较长时,分子之间的碰撞较少,气体的粘滞性就会减小。
通过计算平均自由程,我们可以更好地理解气体的性质和行为。
这对于工程应用和科学研究都具有重要意义。
例如,在研究气体的输运过程中,我们可以通过计算平均自由程来估算气体的扩散速率和传质速度,从而指导工艺设计和环境保护。
平均自由程是一个重要的物理量,用于描述气体分子的运动规律和气体的输运性质。
通过计算平均自由程,我们可以更好地理解气体的特性,为工程应用和科学研究提供指导。
分子动理论气体分子的运动和碰撞

分子动理论气体分子的运动和碰撞分子动理论:气体分子的运动和碰撞气体是由大量分子组成的一种物质状态,其微观粒子——分子,不断地进行着无规则的运动和碰撞。
这种运动和碰撞的规律可以通过分子动理论来解释。
一、分子运动的特点根据分子动理论,气体分子的运动具有以下特点:1. 分子无规则运动:气体分子在空间中做着无规则的直线运动,速度和方向都随机变化。
2. 高速运动:气体分子具有较高的平均速度,其速度大小与温度有关,温度越高,分子平均速度越大。
3. 自由碰撞:气体分子之间存在弹性碰撞,碰撞后速度可以改变,但总动能保持不变。
分子之间的碰撞不受外力影响,只由分子本身的热运动引起。
4. 分子间距较大:相对于分子的体积而言,分子之间的间距很大,故气体呈现较低的密度。
二、平均自由程和平均自由时间根据分子动理论,分子在运动过程中会与其他分子发生碰撞,碰撞的概率与气体的浓度有关。
因此,分子的运动过程可以用平均自由程和平均自由时间来描述。
1. 平均自由程:指分子在连续运动过程中平均走过的距离,与分子的直径和气体的密度有关。
一般情况下,气体分子的平均自由程很短,远小于容器的尺寸。
2. 平均自由时间:指分子在到达下一个碰撞点所需要的平均时间,与气体分子的平均速度和碰撞概率有关。
气体分子的平均自由时间很短,约为纳秒级别。
三、气体分子的碰撞理论气体分子的碰撞是导致气体性质的重要因素之一,根据分子动理论,可以得出以下结论:1. 碰撞速度的关系:在相同温度下,气体分子速度越快,碰撞的力量越大。
这是因为分子速度的增加会增大碰撞的撞击力。
2. 分子碰撞的频率:气体分子碰撞的频率与气体的浓度和温度有关。
浓度越高、温度越高,分子碰撞的频率越高。
3. 碰撞和平均自由程的关系:碰撞的频率和平均自由程成反比。
平均自由程越小,分子之间的碰撞越频繁。
4. 碰撞的弹性:气体分子之间的碰撞是完全弹性碰撞,即碰撞前后的总动能保持不变。
四、分子动理论的应用分子动理论广泛应用于物理、化学等领域,为解释和预测许多气体性质和现象提供了理论依据。
理想气体的分子平均自由程分子间碰撞的距离

理想气体的分子平均自由程分子间碰撞的距离理想气体分子平均自由程指的是气体分子在单位时间内所能自由行进的平均距离。
它是描述气体分子自由运动状态的重要参数,也是研究气体物理性质和动力学过程的基础。
1. 理想气体的特征理想气体是一种理论模型,虽然与真实气体有所差别,但在一定条件下能较好地描述气体的行为。
理想气体分子间无相互作用力,体积可以忽略,分子运动符合牛顿力学,分子之间的碰撞是弹性碰撞。
2. 分子平均自由程的定义分子平均自由程(mean free path)是指理想气体分子在运动过程中,平均而言所能行进的距离。
分子平均自由程与气体分子的性质、压力和温度密切相关。
3. 分子平均自由程的计算分子平均自由程的计算可以利用气体动理论及运动学原理。
根据气体分子的平均速率、总碰撞频率和化学势梯度,可以推导出分子平均自由程的表达式。
4. 气体分子的平均速率根据气体动理论,气体分子的平均速率与温度成正比。
气体温度的提高会使分子的平均速率增加,因此分子在单位时间内所行进的平均距离也会相应增大。
5. 总碰撞频率分子平均自由程与总碰撞频率成反比。
碰撞频率取决于气体分子的浓度和平均速率。
当气体分子的浓度增加或分子的平均速率减小时,总碰撞频率增大,分子平均自由程减小。
6. 分子平均自由程的应用分子平均自由程对于描述气体扩散、热传导、电导等现象具有重要的意义。
在实际应用中,可以通过改变气体的温度、压力和浓度等参数,来调控分子平均自由程,实现对相关物理过程的控制和优化。
7. 影响分子平均自由程的因素除了温度、压力和浓度等因素外,分子平均自由程还受到气体分子的碰撞横截面、分子的大小和形状等因素的影响。
不同气体的分子平均自由程也会有所不同。
8. 分子间碰撞的距离分子间碰撞的距离即为分子平均自由程。
在弹性碰撞的过程中,分子在运动过程中相互接近,发生碰撞,然后各自改变方向继续运动。
分子间碰撞的距离与碰撞横截面和总碰撞频率有关。
结论:理想气体的分子平均自由程是描述气体分子运动状态的重要参数,它与气体的温度、压力、浓度、分子大小等因素密切相关。
高二物理竞赛课件平均碰撞频率平均自由程

平均碰撞频率 平均自由程
【问题】摔碎一个汽油瓶,为什么先听到声音,后 闻到气味?
平均碰撞频率 平均自由程
一.碰撞简化模型
1. 气体分子是直径为d的刚球
(有效直径)
2.假设某分子a以平均相对
d
速率u运动 u 2v
二.平均碰撞频率mean collision frequency
20 oC 时,水为 1.01 10-3 Pa·s 空气为 1.82 10-5 Pa·s
微观上,这种粘滞力是动量传递的结果
z
z0
1 6
v
n
1 6
v
n
u(z0+ )
x
u(z0 - )
下层 平均自由程 l 的区域, 单位时间通过 dS 面积,向 上层输运动量的平均 x 分量
1 6
vnmu
(z0 - )dS
BE 过饱和蒸汽 遇凝结核心 - 液化 云室 人工降雨
CF 过热液体 遇汽化核心 - 汽化
气泡室
1.定义:单位时间内分子的平均碰撞次数 Z 。
平均碰撞频率 平均自由程
2.Z的计算 ①柱体中的分子数
N n d 2ut
② 平均碰撞频率
Z n d 2 u
Z 2nd 2 v
平均碰撞频率 平均自由程
三.平均自由程 mean free path 1.定义: 分子在连续两次碰撞之间所通过的 自由路程的平均值2.计算vZ来自Z2nd 2 v
1
2 d 2n
3.与P、T的关系
P nkT kT
2 d 2P
平均碰撞频率 平均自由程
Z 2nd 2 v
kT
2 d 2 p
1
2 d 2n
分子的平均自由程

分子的平均自由程什么是分子的平均自由程?分子的平均自由程指的是分子在气体中自由运动的平均路径长度。
在气体状态下,分子会不断地进行碰撞和运动。
由于分子之间存在相互作用力的存在,分子在运动过程中会受到其他分子的碰撞,从而改变自己的运动方向和速度。
分子的平均自由程代表了分子在两次碰撞之间所运动的平均距离。
影响分子平均自由程的因素分子的平均自由程受到多种因素的影响,主要包括:1.气体的密度:气体的密度越高,分子之间的碰撞频率就越高,分子平均自由程就越短。
相反,气体的密度越低,分子之间的碰撞频率就越低,分子平均自由程就越长。
2.气体分子的大小:气体分子的大小直接影响了分子之间碰撞的概率。
分子的碰撞概率与其有效碰撞截面积成正比。
分子的平均自由程与其有效碰撞截面积成反比。
因此,分子越大,其有效碰撞截面积越大,平均自由程就越短。
3.气体的温度:温度对分子平均自由程的影响较为复杂。
在相同的密度条件下,温度升高会导致分子速度的增加,碰撞的频率增加,分子平均自由程减小。
但是在不同的气体中,温度对分子平均自由程的影响并不相同。
4.气体分子间相互作用力:气体分子之间的相互作用力会对分子平均自由程产生影响。
分子之间的吸引力会减小分子之间的运动速度,增加碰撞概率,从而缩短分子平均自由程。
分子平均自由程的计算方法分子平均自由程可以通过以下公式计算得到:其中,λ是分子平均自由程,d是气体分子的直径,n是气体分子的密度。
分子平均自由程的实际应用分子的平均自由程在科学研究和工程应用中有着广泛的应用。
以下是一些常见的实际应用场景:1.气体传导-热传导:在研究热传导过程中,了解气体分子的平均自由程对预测热传导性能非常重要。
通过计算得到的分子平均自由程,可以帮助研究者确定气体中能量传递的距离,从而优化热传导器件的设计。
2.气体分离:气体分子的平均自由程在气体分离领域也有重要应用。
例如在空气净化中,利用分子平均自由程的大小差异,可以通过选择合适的孔径大小来实现对不同气体分子的筛选分离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P. 2 / 12 .
☻为什么
由 v = 8RT / (π M) 可知,常温下气体分子的平 可知, 均速率 v ~ 102 m / s,但打开香水瓶后,我们并不能 但打开香水瓶后, 立即闻到香水的香味,为什么? 立即闻到香水的香味,为什么? 1cm3的空气约有 亿亿个 的空气约有27亿亿 亿亿个 气体分子,香水分子碰撞极其 气体分子, 频繁,如何衡量这种碰撞的频 频繁, 繁程度? 繁程度?
p (Pa)
λ (m )
5
1.01×10
6.9×10
−8
1.33×102
5.2×10−5
λ=
kT 2π d2 ⋅ p
常温常压下: 常温常压下: 约10−8 ~ 10−7 (m λ )
Chapter 12. 气体动理论 作者:杨茂田 12. 12 §12. 作者: . 8 气体分子的平均碰撞频率和平均自由程
−1
1.33×10−4
52
Chapter 12. 气体动理论 作者:杨茂田 12. 12 §12. 作者: . 8 气体分子的平均碰撞频率和平均自由程
P. 11 / 12 .
例 热水瓶瓶胆厚度为1.5cm,开水 t = 100 ℃ ,考虑到 热水瓶瓶胆厚度为1.5cm, 保温性能,抽真空后,胆内压强应为多少? 保温性能,抽真空后,胆内压强应为多少? × , 解:空气分子的有效直径 d = 3.5×10-10m,T = 373K 考虑到保温性能,应取: 考虑到保温性能,应取:
Chapter 12. 气体动理论 作者:杨茂田 12. 12 §12. 作者: . 8 气体分子的平均碰撞频率和平均自由程
P. 1 / 12 .
§ 12-8 气体分子的平均碰撞 频率和平均自由程
Chapter 12. 气体动理论 作者:杨茂田 12. 12 §12. 作者: . 8 气体分子的平均碰撞频率和平均自由程
v∆t ∆ λ= z∆t ∆
λ =v
z
☻ z、λ 与哪些因素相关
Chapter 12. 气体动理论 作者:杨茂田 12. 12 §12. 作者: . 8 气体分子的平均碰撞频率和平均自由程
P. 5 / 12 .
二、平均碰撞频率与平均自由程
设分子的有效直径为d,某分子以 u 相对于其他分子 分子的有效直径为 , 有效直径 运动 ( 其他分子静止 )。 则:△t 时间内与该分子碰 撞的分子个数为: 撞的分子个数为:
分子数密度 :n
Chapter 12. 气体动理论 作者:杨茂田 12. 12 §12. 作者: . 8 气体分子的平均碰撞频率和平均自由程
P. 9 / 12 .
例 试计算0℃时,不同压强下空气分子的平均自由程。 试计算0 不同压强下空气分子的平均自由程。 解:空气分子的有效直径 d = 3.5×10-10m,则 × ,
P. 12 / 12 .
1. 平均碰撞频率: z = 2 nπ d2v 平均碰撞频率: 2. 平均自由程: λ = 平均自由程:
kT 2 2π d ⋅ p
p=
kT ≈ 0.63 (Pa) ≈ 6.22×10−6 atm 2π d2 ⋅ λ
( The end )
瓶胆承受的压力~1.01×104kg/m2! 瓶胆承受的压力~
P. 10 / 12 .
例 试计算0℃时,不同压强下空气分子的平均自由程。 试计算0 不同压强下空气分子的平均自由程。 解:空气分子的有效直径 d = 3.5×10-10m,则 × ,
p (Pa)
λ (m )
5
1.01×10
6.9××10−5
1.33
1.33×10
−2
5.2×10−3 5.2×10
2
可知:z ∝ n, d2 , v 可知:
则,平均自由程为: 平均自由程为:
λ = v=
z
而: p = nkT
1 2 π d2 ⋅ n
z = ∆N = nπ d2u ∆t
理论修正: u = 2 v 理论修正:
分子数密度 :n
Chapter 12. 气体动理论 作者:杨茂田 12. 12 §12. 作者: . 8 气体分子的平均碰撞频率和平均自由程
λ = 1.5cm = 1.5×10−2 m
λ=
p=
kT 2π d2 ⋅ p
kT ≈ 0.63 (Pa) ≈ 6.22×10−6 atm 2π d2 ⋅ λ
1.5cm
瓶胆承受的压力~1.01×104kg/m2! 瓶胆承受的压力~
Chapter 12. 气体动理论 作者:杨茂田 12. 12 §12. 作者: . 8 气体分子的平均碰撞频率和平均自由程
Chapter 12. 气体动理论 作者:杨茂田 12. 12 §12. 作者: . 8 气体分子的平均碰撞频率和平均自由程
P. 4 / 12 .
一、定义
▲平均自由程: 平均自由程:分子在连续两次碰撞间所经过的平均
路程。常用 路程。 常用
表示。 λ 表示。
分子在单位时间内的平均碰撞次数。 分子在单位时间内的平均碰撞次数。 ▲平均碰撞频率: 平均碰撞频率: 表示。 z 表示。 则,在 △t 时间内,有: 时间内,
P. 8 / 12 .
∴ z = 2 nπ d v ~ 109 (s-1 )
2
可知:z ∝ n, d2 , v 可知:
则,平均自由程为: 平均自由程为:
λ = v=
z
而: p = nkT
1 2 π d2 ⋅ n
λ=
kT 2π d2 ⋅ p
常温常压下: 常温常压下: 约10−8 ~ 10−7 (m λ )
∆ ∆N = nπ d2u∆t
z = ∆N = nπ d2u ∆t
理论修正: u = 2 v 理论修正:
分子数密度 :n
Chapter 12. 气体动理论 作者:杨茂田 12. 12 §12. 作者: . 8 气体分子的平均碰撞频率和平均自由程
P. 7 / 12 .
∴ z = 2 nπ d v ~ 109 (s-1 )
Chapter 12. 气体动理论 作者:杨茂田 12. 12 §12. 作者: . 8 气体分子的平均碰撞频率和平均自由程
P. 3 / 12 .
☻你知道吗
一段时间后,热水瓶中的水温变低了。 一段时间后,热水瓶中的水温变低了。从能量的 角度考虑, 角度考虑,热水瓶中的能量是通过什么方式传到外 界的? 界的? 瓶胆中仍有稀薄的空气。空气分 瓶胆中仍有稀薄的空气。 子的频繁碰撞会将能量从一个地方 传到另一个地方。考虑到保温性能, 传到另一个地方。考虑到保温性能, 对瓶胆的厚度有何要求? 对瓶胆的厚度有何要求?
∆ ∆N = nπ d2u∆t
v∆t ∆ λ= z∆t ∆
λ =v
z
分子数密度 :n
☻ z、λ 与哪些因素相关
Chapter 12. 气体动理论 作者:杨茂田 12. 12 §12. 作者: . 8 气体分子的平均碰撞频率和平均自由程
P. 6 / 12 .
二、平均碰撞频率与平均自由程
设分子的有效直径为d,某分子以 u 相对于其他分子 分子的有效直径为 , 有效直径 运动 ( 其他分子静止 )。 则:△t 时间内与该分子碰 撞的分子个数为: 撞的分子个数为:
