170班数学《二元一次方程组》练习题

合集下载

二元一次方程组练习题100道

二元一次方程组练习题100道二元一次方程组练题100道（卷一）（范围：代数：二元一次方程组）一、判断1.判断以下方程组是否是方程组y5=26的解：x-3y=1x+2y=3改写：判断以下方程组是否是方程组y=5/26的解：x-3y=1x+2y=32.判断以下方程组是否是方程3x-2y=13的一个解：y=1-x3x+2y=5改写：判断以下方程组是否是方程3x-2y=13的一个解：y=1-x3x+2y=53.由两个二元一次方程组成方程组一定是二元一次方程组。

改写：错误，没有必要改写。

4.判断以下方程组是否可以转化为（2y-3)x+6y=-27x+8：2y-3x=45x+3y=2改写：判断以下方程组是否可以转化为（2y-3)x+6y=-27x+8：2y-3x=45x+3y=25.若(a^2-1)x^2+(a-1)x+(2a-3)y=0是二元一次方程，则a的值为±1.改写：若(a^2-1)x^2+(a-1)x+(2a-3)y=0是二元一次方程，则a的值为±1.6.若x+y=0，且|x|=2，则y的值为2.改写：若x+y=0，且|x|=2，则y的值为-2.7.判断以下方程组是否有唯一的解，若有，则m的值为m≠-5：mx+my=m-3x4x+10y=8改写：判断以下方程组是否有唯一的解，若有，则m的值为m≠-5：mx+my=m-3x4x+10y=88.判断以下方程组是否有无数多个解：x+y=23x+y=6改写：判断以下方程组是否有无数多个解：x+y=23x+y=69.判断以下方程是否有5组整数解：x+y=5x|<5.|y|<5改写：判断以下方程是否有5组整数解：x+y=55<x<5.-5<y<510.判断以下方程组是否是方程x+5y=3的解，反过来方程x+5y=3的解：3x-y=1x+5y=3改写：判断以下方程组是否是方程x+5y=3的解，反过来方程x+5y=3的解：3x-y=1x+5y=311.若|a+5|=5，a+b=1，则a的值为-2.改写：若|a+5|=5，a+b=1，则a的值为-2.12.在方程4x-3y=7里，如果用x的代数式表示y，则x=7+3y/4.改写：在方程4x-3y=7里，如果用x的代数式表示y，则x=7+3y/4.二、选择：13.任何一个二元一次方程都有无数多个解。

七年级数学解二元一次方程组计算题30道(含答案)

七年级数学解二元一次方程组计算题30道（含答案）1. 解方程组：(1){x +2y =13x −2y =11(2){x −y =33x −8y =142. 解方程组：{2(x−y)3−x+y 4=−112,3(x +y)−2(2x −y)=3.3. 解方程组(1){y =2x −43x +y =1 (2){x−16−2−y 3=12(x −1)=13−(y +2)(3){x +2y +z =82x −y −z =−33x +y −2z =−14. 关于x ，y 的方程组{x +y =5k x −y =9k的解满足2x +3y =6，试求k 的值．5. 解方程组(Ⅰ){y =2x −53x +4y =2(Ⅱ){3(x −1)=y +5y−13=x+556. 解方程组：{2x+13+4y−32=2,3(2x +1)−2(4y −3)=5.7. 解二元一次方程组：{2x +y =2,8x +3y =9.8. 解方程组：{2x −3y =−53x +2y =12．9. 解方程组：{3(x +y)−4(x −y)=4x+y 2+x−y 6=110. 解下列二元一次方程组：(1){2x −5y =72x +3y =−1(2){2x −y =53x +4y =211. 关于x ，y 的方程组{3x −y =54ax +5by =−22与{2x +3y =−4ax −by =8有相同的解，求a +b 的值．12. 解方程组：(1){x +2y =9,3x −2y =−1;(2){x 4+y 3=3,3x −2(y −1)=11.13. 解方程和方程组：(1){x +y =14x +y =10(2)2−20x+10020=5x−20514. (1)解方程：32[2(x −23)+43]=1(2)解方程组：{2x −y =2①4y +x =−1②15. 用加减法解下面的方程组：(1){2x +3y =7,x −3y =8;(2){3x −y =2,9x +8y =17.16. 解二元一次方程组{3x −2y =−1,x +3y =7;17. 解方程组：{x 3+y 5=1,3(x +y)+2(x −3y)=15.18. 解二元一次方程组{3(x +y )−4(x −y )=4,x+y 2+x−y 6=1⋅19. 解二元一次方程组{3(x +y )−5(x −y )=16,2(x +y )+(x −y )=15;20. 解方程组：{x −3y =42x +3y =−1．21. 用代入法解方程组：(1){x −3y =−2,2x +y =3;(2){3x +4y =11,5x −y =3.5(x +y)−3(x −y)=−30.23. 用加减法解{2x +3y =03x −y =11．24. 解方程组{2x +4y =74x +9y =18．25. 解方程组：{x +y =13x +y =526. 解二元一次方程组：{2x+y 3−2y =0,①2(2x +y)−5=7y.②27. 解方程组：{4(x −y −1)=3(1−y)−228. 已知关于x ，y 的二元一次方程组{x +2y =k −12x +y =k +1，若方程组的解互为相反数，求k 的值．29. 解方程组：{3x +12y =8, ①2x −12y =2. ②30. 解方程组：{4x −y =5x 2+y 3=231.解方程：{x −y =52(x −1)=y −11.【答案】解：(1){x +2y =1①3x −2y =11②， ①+②，得：4x =12，解得：x =3，将x =3代入①，得：3+2y =1，解得：y =−1，所以方程组的解为{x =3y =−1；(2){x −y =3①3x −8y =14②， ①×3−②，得：5y =−5，解得：y =−1，将y =−1代入①，得：x +1=3，解得：x =2，所以方程组的解为{x =2y =−1．【解析】(1)利用加减消元法求解可得；(2)利用加减消元法求解可得．此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．2.【答案】解：整理原方程组得{5x −11y =−1, ①5y −x =3, ②由 ②得x =5y −3， ③将 ③代入 ①得25y −15−11y =−1，即14y =14，解得y =1，将y =1代入 ③得x =2，∴原方程组的解为{x =2,y =1.【分析】本题主要考查了二元一次方程组，关键是熟练掌握代入消元法解方程组的解法步骤.先整理方程组为最简形式，然后利用代入消元法先求出y 的值，再代入求出x 的值，从而得到方程组的解即可．3.【答案】解：(1){y =2x −4①3x +y =1②, 把①代入②得3x +2x −4=1，x =1，把x =1代入①得y =−2，所以方程组的解为{x =1y =−2； (2)原方程可变形为{x +2y =11①2x +y =13②, ①×2−②得3y =9，y =3，把y =3代入①得x =5，所以方程组的解为{x =5y =3； (3){x +2y +z =8①2x −y −z =−3②3x +y −2z =−1③,①+②得3x +y =5④，②×2−③得x −3y =−5⑤，④−⑤×3得10y =20，y =2，把y =2代入④得x =1，把y =2，x =1代入①得z =3，所以方程组的解为{x =1y =2z =3．【解析】本题考查了解二元一次方程组和解三元一次方程组．(1)利用代入消元法求解即可；(2)利用加减消元法求解即可；(3)利用加减消元法求解即可．4.【答案】解：{x +y =5k ①x −y =9k ②， ①+②得：x =7k ，①−②得：y =−2k ，代入方程得：14k −6k =6，∴k =34．即k 的值是34．【解析】本题主要考查对等式的性质，解一元一次方程，解二元一次方程组，二元一次方程的解等知识点的理解和掌握，能求出关于k 的方程是解此题的关键．把k 当作已知数，求出方程组的解，把x y 的值代入方程即可求出k ．5.【答案】解：(1){y =2x −5①3x +4y =2②, 把①代入②得，3x +4(2x −5)=2，解得，x =2，把x =2代入①得：y =−1．所以原方程组的解为{x =2y =−1； (2)化简得{3x −y =8①3x −5y =−20②, ①−②得，4y =28，解得y =7，把y =7代入①得，3x −7=8，解得x =5．所以原方程组的解为{x =5y =7．【解析】本题考查的是加减消元法和代入消元法解二元一次方程组，关键是把二元一次方程组转化成一元一次方程，通过做此题培养了学生的计算能力．(1)把①代入②出一个关于x 的方程，求出x ，把x 的值代入①求出y 即可；(2)先化简方程组，再①−②得出关于y 的方程，求出y ，把y 的值代入①求出x 即可．6.【答案】解：令2x+13=m ，4y−32=n ，将原方程组化为{m +n =2,①9m −4n =5.②, ①×4+②，得13m =13，解得m =1，把m =1代入①，得n =1，即2x+13=1，4y−32=1，解得x =1，y =54．【解析】本题主要考查二元一次方程组的解及其解法中的加减消元法，掌握好二元一次方程组的解法是解题的关键.令2x+13=m ，4y−32=n ，得{m +n =2,①9m −4n =5.②，然后①×4+②得m =1，再将m 的值代入①可得n 的值，从而经过计算可得答案．7.【答案】解：{2x +y =2 ①8x +3y =9 ②，法1：②−①×3，得 2x =3，解得：x =32，把x =32代入①，得 y =−1，∴原方程组的解为{x =32y =−1；法2：由②得：2x +3(2x +y)=9，把①代入上式，解得：x =32，把x =32代入①，得 y =−1，∴原方程组的解为{x =32y =−1．【解析】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．方程组利用加减消元法与代入消元法求出解即可．8.【答案】解：{2x −3y =−5 ①3x +2y =12 ②， ①×2+②×3得：13x =26，x =2并代入②得：y =3．∴原方程组的解是{x =2y =3．【解析】本题两个未知数的系数的最小公倍数都是6，但y 的系数的符号相反，为了少出差错可考虑用加减消元法先消去y ，然后求解．当所给方程组的两个未知数的系数的最小公倍数大小差不多时，应考虑先消去符号相反的未知数．9.【答案】解：化简原方程组，得{−x +7y =4 ①2x +y =3 ②，由①得：x =7y −4③，将③代入②，得2(7y −4)+y =3，解得：y =1115，将y =1115代入③，得x =1715，则方程组的解为{x =1715y =1115．【解析】方程组整理后，利用代入消元法求出解即可．此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．10.【答案】解：(1){2x −5y =7①2x +3y =−1②, ①−②得，−8y =8，解得y =−1，把y =−1代入②得，2x −3=−1，解得x =1．所以原方程组的解为{x =1y =−1．(2){2x −y =5①3x +4y =2②, ①×4+②得，11x =22，解得，x =2，把x =2代入①得，4−y =5，解得y =−1．所以原方程组的解为{x =2y =−1．【解析】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．(1)此方程组利用加减消元法求出解即可；(2)方程组利用加减消元法求出解即可．11.【答案】解：根据题意可联立{3x −y =5①2x +3y =−4②， ①×3+②，得11x =11，解得x =1．把x =1代入①，得y =−2．∴方程组的解为{x =1y =−2；根据题意，得{4a −10b =−22a +2b =8即{2a −5b =−11①a +2b =8②， ②×2−①，得9b =27，解得b =3．把b =3代入②，得a =2．则a +b =3+2=5．【解析】根据题意可联立已知方程组，求出x 和y 的值，再将x 和y 的值代入含a 和b 的方程中组成关于a 和b 的方程组，求出a 和b 的值，进而得解．本题考查了二元一次方程组的解，解决本题的关键是掌握二元一次方程组的解法．12.【答案】解：(1){x +2y =9 ①,3x −2y =−1 ②, ①+ ②得4x =8，解得x =2，将x =2代入 ①，得2+2y =9，解得y =72，∴方程组的解为{x =2,y =72.(2)方程组整理得{3x +4y =36 ①3x −2y =9 ②, ①− ②得6y =27，解得y =92，将y =92代入 ②，得3x −9=9，解得x =6，∴方程组的解为{x =6y =92【解析】略13.【答案】解：(1){x +y =1①4x +y =10②②−①得，3x =9，解得，x =3，把x =3代入①得，3+y =1，解得，y =−2，所以方程组的解为：{x =3y =−2(2) 2−20x +10020=5x −2052−(x +5)=x −42−x −5=x −4−2x=−1x=12【解析】本题主要考查了解二元一次方程组和解一元一次方程．(1)利用加减消元法，②−①得 x =3，把x =3代入①得出y =−2，即可求出原方程组的解；(2)先化简原方程，然后根据解一元一次方程的步骤解答即可．14.【答案】解：(1)去括号，得：3(x −23)+2=1整理可得：3x =1未知数系数化为1：x =13(2) 由①得：y =2x −2③将③代入②，得4(2x −2)+x =−1解得：x =79将x =79代入③，得y =−49所以，原方程组的解为{x =79y =−49【解析】本题考查的是解一元一次方程、解二元一次方程组，属基础题。

初一数学二元一次方程组练习题(含答案)

初一数学练习题：二元一次方程组（答案附后）一．选择题（共17小题）1．下列是二元一次方程的是（）A ．x ﹣yB ．x +y ﹣m ＝0C ．2x +3＝0 D ．x ﹣2y ＝12．下列方程中是二元一次方程的有（） ①5n−m ＝12；②32y =16z +1；③2a+n=1；④mn ＝7；⑤x +y ＝6zA ．1个B ．2个C ．3个D ．4个3．若x|2m ﹣3|+（m ﹣2）y ＝8是关于x 、y 的二元一次方程，则m 的值是（）A ．1B ．任何数C ．2D ．1或24．有下列方程：①xy ＝2；②3x ＝4y ；③x +1y=2；④y 2＝4x ；⑤x2=3y ﹣1；⑥x +y ﹣z ＝1．其中二元一次方程有（） A ．1个B ．2个C ．3个D ．4个5．下列各式中，是关于x ，y 的二元一次方程的是（） A ．2x ﹣y B ．xy +x ﹣2＝0 C ．2x −y =0D ．x ﹣3y ＝﹣156．方程（m ﹣1009）x |m |﹣1008+（n +3）y |n |﹣2＝2018是关于x 、y 的二元一次方程，则（）A ．m ＝±1009；n ＝±3B ．m ＝1009，n ＝3C ．m ＝﹣1009，n ＝﹣3D ．m ＝﹣1009，n ＝37．把二元一次方程2x ﹣7y ＝8，“用含有一个未知数的代数式来表示另一个未知数”，其中变形不正确的是（） A ．x =7y+82B ．x =4+72y C ．y =27x −87D ．y =−27x +88．下列是二元一次方程2x +y ＝8的解的是（） A ．{x =1y =5B ．{x =2y =3C ．{x =2y =4D ．{x =4y =29．二元一次方程2x ﹣y ＝1有无数多个解，下列四组值中是该方程的解的是（） A ．{x =0y =−0.5B ．{x =4y =7C ．{x =1y =−1D ．{x =−5y =−310．已知{x =ay =−2是关于x ，y 的方程3x ﹣ay ＝5的一个解，则a 的值为（） A ．1 B ．2C ．3D ．411．若方程（a +3）x +3y |a |﹣2＝1是关于x ，y 的二元一次方程，则a 的值为（） A ．﹣3 B ．±2 C ．±3 D ．312．下列各组数不是方程2x +y ＝20的解的是（） A ．{x =−10，y =0 B ．{x =1，y =18 C ．{x =−1，y =22 D ．{x =0，y =2013．下列方程中是二元一次方程的是（） A ．x 2+y ＝0 B ．x+y 3−2y ＝0 C ．x =2y +1D ．xy ＝314．已知{x =2，y =1是二元一次方程ax +2y ＝4的一个解，则下列数对也是这个方程的解的是（） A ．{x =−2，y =3B ．{x =1，y =2C ．{x =−1，y =2D ．{x =2，y =−115．方程x +2y ＝4的正整数解有（）组．A ．1B ．2C ．3D ．416．若{x =2y =−1是关于x 、y 的二元一次方程ax +by ﹣5＝0的一组解，则2a ﹣b ﹣2的值为（）A ．﹣3B ．3C ．﹣7D ．717．已知二元一次方程12x ﹣3y ＝4的一组解为{x =ay =b ，则a ﹣6b +3的值为（）A ．11B ．7C ．5D ．无法确定二．填空题（共4小题）18．若方程x |m |﹣2+（m +3）y 2m ﹣n ＝6是关于x ，y 的二元一次方程，则m +n ＝．19．已知二元一次方程x 4+y 2=1，用含x 的代数式表示y 为y ＝；用含y 的代数式表示x 为x＝．20．若（a﹣2）x a2−3+3y b﹣2＝2是关于x，y的二元一次方程，则a﹣b＝．21．已知关于x，y的二元一次方程（2m﹣1）x+（m+1）y﹣m+2＝0，无论实数m取何值，此二元一次方程都有一个相同的解，则这个相同的解是．三．解答题（共3小题）22根据题意列二元一次方程组：（1）两批货物，第一批360吨，用5节火车皮和12辆汽车正好装完；第二批500吨，用7节火车皮和16辆汽车正好装完．每节火车皮和每辆汽车平均各装货物多少吨？（2）某校课外小组的学生准备外出活动；若每组7人，则余下3人；若每组8人，则有一组只有3人；求这个课外小组分成几组？共有多少人？23．一个两位数，两个数位上的数字之和是11，如果把这个两位数加63，那么和的数的个位上的数与十位上的数恰好分别是原两位数的十位和个位，求原两位数。

二元一次方程组50题

．，
①×2+②得：13x=91，即 x=7，将 x=7 代入①得：35﹣2y=36，即 y=﹣ ，
则方程组的解为
二元一次方程组计算 50 题
．
30．解方程组：
解答：
解：原方程组可化为
，
①﹣②得，3y=﹣6，解得 y=﹣2，把 y=﹣2 代入①得，3x+4=4，解得 x=0．
故原方程组的解为
则方程组的解为．
25．解方程组：
．
解答：
解：
，
②×2﹣①得：5b=10，即 b=2，将 b=2 代入②得：a=5，
则方程组的解为．
二元一次方程组计算 50 题
26．解方程组：
．
解答：
解：
，
①+②得：6x=24，即 x=4，将 x=4 代入②得：y=﹣3，
则方程组的解为．
27．解方程组：
．
解答：
6．解方程组：
．
解答：
解：
，
①×3﹣②×2 得：13y=14，即 y= ，将 y= 代入①得：x= ，
则方程组的解为．
7．解方程组：
解答：解：
①×2﹣②，得 3x=3， x=1．代入②，得 1+6y=7， y=1．
所以原方程组的解为．
8．解方程组：
．
解答：解：
二元一次方程组计算 50 题
所以，方程组的解是．
10．解方程组：
．
解答：
解：
，
①×4﹣②得：13y=13，即 y=1，把 y=1 代入①得：x=﹣6，
则方程组的解为．
11．解方程组：
．
解答：
解：
，

二元一次方程组练习题(含答案)

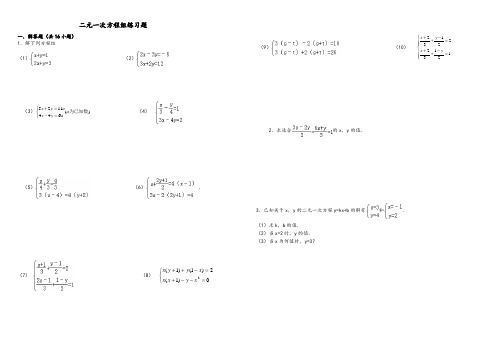
二元一次方程组练习题一．解答题（共16小题） 1．解下列方程组（1）（2）（3）)(6441125为已知数a a y x a y x ⎩⎨⎧=-=+ （4）（5）（6）．（7）（8）⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x（9）（10） ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x2．求适合的x ，y 的值．3．已知关于x ，y 的二元一次方程y=kx+b 的解有和．（1）求k ，b 的值．（2）当x=2时，y 的值．（3）当x 为何值时，y=3？1．解下列方程组（1）（2）；（3）；（4）（5）．（6）（7）（8）（9）（10）；2．在解方程组时，由于粗心，甲看错了方程组中的a，而得解为，乙看错了方程组中的b，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解.二元一次方程组解法练习题精选参考答案与试题解析一．解答题（共16小题）1．求适合的x，y的值．考点：解二元一次方程组．分析：先把两方程变形（去分母），得到一组新的方程，然后在用加减消元法消去未知数x，求出y的值，继而求出x的值．解答：解：由题意得：，由（1）×2得：3x ﹣2y=2（3），由（2）×3得：6x+y=3（4），（3）×2得：6x﹣4y=4（5），（5）﹣（4）得：y=﹣，把y的值代入（3）得：x=，∴．点评：本题考查了二元一次方程组的解法，主要运用了加减消元法和代入法．2．解下列方程组（1）（2）（3）（4）．考点：解二元一次方程组．分析：（1）（2）用代入消元法或加减消元法均可；（3）（4）应先去分母、去括号化简方程组，再进一步采用适宜的方法求解．解答：解：（1）①﹣②得，﹣x=﹣2，解得x=2，把x=2代入①得，2+y=1，解得y=﹣1．故原方程组的解为．（2）①×3﹣②×2得，﹣13y=﹣39，解得，y=3，把y=3代入①得，2x﹣3×3=﹣5，解得x=2．故原方程组的解为．（3）原方程组可化为，①+②得，6x=36，x=6，①﹣②得，8y=﹣4，y=﹣．所以原方程组的解为．（4）原方程组可化为：，①×2+②得，x=，把x=代入②得，3×﹣4y=6，y=﹣．所以原方程组的解为．点评：利用消元法解方程组，要根据未知数的系数特点选择代入法还是加减法：①相同未知数的系数相同或互为相反数时，宜用加减法；②其中一个未知数的系数为1时，宜用代入法．3．解方程组：考解二元一次方程组．点：专题：计算题．分析：先化简方程组，再进一步根据方程组的特点选用相应的方法：用加减法．解答：解：原方程组可化为， ①×4﹣②×3，得 7x=42，解得x=6．把x=6代入①，得y=4．所以方程组的解为．点评：；二元一次方程组无论多复杂，解二元一次方程组的基本思想都是消元．消元的方法有代入法和加减法．4．解方程组：考点：解二元一次方程组．专题：计算题．分析：把原方程组化简后，观察形式，选用合适的解法，此题用加减法求解比较简单．解答：解：（1）原方程组化为，①+②得：6x=18， ∴x=3．代入①得：y=．所以原方程组的解为．点评：要注意：两个二元一次方程中同一未知数的系数相反或相等时，把这两个方程的两边相加或相减，就能消去这个未知数，得到一个一元一次方程，这种方法叫做加减消元法．本题适合用此法．5．解方程组：考点：解二元一次方程组．专题：计算题；换元法．分析：本题用加减消元法即可或运用换元法求解．解答：解：，①﹣②，得s+t=4， ①+②，得s ﹣t=6，即，解得．所以方程组的解为．点评：此题较简单，要熟练解方程组的基本方法：代入消元法和加减消元法．6．已知关于x ，y 的二元一次方程y=kx+b 的解有和．（1）求k ，b 的值．（2）当x=2时，y 的值．（3）当x 为何值时，y=3？考点：解二元一次方程组．专题：计算题．分析：（1）将两组x ，y 的值代入方程得出关于k 、b 的二元一次方程组，再运用加减消元法求出k 、b 的值．（2）将（1）中的k 、b 代入，再把x=2代入化简即可得出y 的值．（3）将（1）中的k 、b 和y=3代入方程化简即可得出x 的值．解答：解：（1）依题意得：①﹣②得：2=4k ，所以k=，所以b=．（2）由y=x+，把x=2代入，得y=．（3）由y=x+把y=3代入，得x=1．点评：本题考查的是二元一次方程的代入消元法和加减消元法，通过已知条件的代入，可得出要求的数．7．解方程组：（1）；（2）．考点：解二元一次方程组．分析：根据各方程组的特点选用相应的方法：（1）先去分母再用加减法，（2）先去括号，再转化为整式方程解答．解答：解：（1）原方程组可化为，①×2﹣②得：y=﹣1，将y=﹣1代入①得：x=1．∴方程组的解为；（2）原方程可化为，即，①×2+②得：17x=51，x=3，将x=3代入x ﹣4y=3中得：y=0．∴方程组的解为．点评：这类题目的解题关键是理解解方程组的基本思想是消元，掌握消元的方法有：加减消元法和代入消元法．根据未知数系数的特点，选择合适的方法．8．解方程组：考点：解二元一次方程组．专题：计算题．分析：本题应把方程组化简后，观察方程的形式，选用合适的方法求解．解答：解：原方程组可化为，①+②，得10x=30，x=3，代入①，得15+3y=15，y=0．则原方程组的解为．点评：解答此题应根据各方程组的特点，有括号的去括号，有分母的去分母，然后再用代入法或加减消元法解方程组．9．解方程组：考点：解二元一次方程组．专题：计算题．分析：本题为了计算方便，可先把（2）去分母，然后运用加减消元法解本题．解答：解：原方程变形为：，两个方程相加，得4x=12，x=3．把x=3代入第一个方程，得4y=11，y=．解之得．点评：本题考查的是二元一次方程组的解法，方程中含有分母的要先化去分母，再对方程进行化简、消元，即可解出此类题目．10．解下列方程组：（1）（2）考点：解二元一次方程组．专题：计算题．分析：此题根据观察可知：（1）运用代入法，把①代入②，可得出x，y的值；（2）先将方程组化为整系数方程组，再利用加减消元法求解．解答：解：（1），由①，得x=4+y③，代入②，得4（4+y）+2y=﹣1，所以y=﹣，把y=﹣代入③，得x=4﹣=．所以原方程组的解为．（2）原方程组整理为，③×2﹣④×3，得y=﹣24，把y=﹣24代入④，得x=60，所以原方程组的解为．点评：此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过题目的训练达到对知识的强化和运用．11．解方程组：（1）（2）考点：解二元一次方程组．专题：计算题；换元法．分析：方程组（1）需要先化简，再根据方程组的特点选择解法；方程组（2）采用换元法较简单，设x+y=a，x﹣y=b，然后解新方程组即可求解．解答：解：（1）原方程组可化简为，解得．（2）设x+y=a，x﹣y=b，∴原方程组可化为，解得，∴∴原方程组的解为．点评：此题考查了学生的计算能力，解题时要细心．12．解二元一次方程组：（1）；（2）．考点：解二元一次方程组．专题：计算题．分析：（1）运用加减消元的方法，可求出x、y的值；（2）先将方程组化简，然后运用加减消元的方法可求出x、y的值．解答：解：（1）将①×2﹣②，得15x=30，x=2，把x=2代入第一个方程，得y=1．则方程组的解是；（2）此方程组通过化简可得：，①﹣②得：y=7，把y=7代入第一个方程，得x=5．则方程组的解是．点评：此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过题目的训练达到对知识的强化和运用．13．在解方程组时，由于粗心，甲看错了方程组中的a，而得解为，乙看错了方程组中的b ，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．考点：解二元一次方程组．专题：计算题．分析：（1）把甲乙求得方程组的解分别代入原方程组即可；（2）把甲乙所求的解分别代入方程②和①，求出正确的a 、b，然后用适当的方法解方程组．解答：解：（1）把代入方程组，得，解得：．把代入方程组，得，解得：．∴甲把a看成﹣5；乙把b看成6；（2）∵正确的a是﹣2，b是8，∴方程组为，解得：x=15，y=8．则原方程组的解是．点评：此题难度较大，需同学们仔细阅读，弄清题意再解答．14．考点：解二元一次方程组．分析：先将原方程组中的两个方程分别去掉分母，然后用加减消元法求解即可．解答：解：由原方程组，得，由（1）+（2），并解得x=（3），把（3）代入（1），解得y=∴原方程组的解为．点评：用加减法解二元一次方程组的一般步骤：1．方程组的两个方程中，如果同一个未知数的系数既不互为相反数又不相等，就用适当的数去乘方程的两边，使一个未知数的系数互为相反数或相等；2．把两个方程的两边分别相加或相减，消去一个未知数，得到一个一元一次方程；3．解这个一元一次方程；4．将求出的未知数的值代入原方程组的任意一个方程中，求出另一个未知数，从而得到方程组的解．15．解下列方程组：（1）；（2）．考点：解二元一次方程组．分析：将两个方程先化简，再选择正确的方法进行消元．解答：解：（1）化简整理为，①×3，得3x+3y=1500③，②﹣③，得x=350．把x=350代入①，得350+y=500，∴y=150．故原方程组的解为．（2）化简整理为，①×5，得10x+15y=75③，②×2，得10x﹣14y=46④，③﹣④，得29y=29，∴y=1．把y=1代入①，得2x+3×1=15，∴x=6．故原方程组的解为．点评：方程组中的方程不是最简方程的，最好先化成最简方程，再选择合适的方法解方程．16．解下列方程组：（1）（2）考点：解二元一次方程组．分析：观察方程组中各方程的特点，用相应的方法求解．解答：解：（1）①×2﹣②得：x=1，将x=1代入①得：2+y=4，y=2．∴原方程组的解为；（2）原方程组可化为，①×2﹣②得：﹣y=﹣3，y=3．将y=3代入①得：x=﹣2．∴原方程组的解为．点评：解此类题目要注意观察方程组中各方程的特点，采用加减法或代入法求解．。

二元一次方程组练习题(含答案)word

二元一次方程组练习题一．解答题（共16小题） 1．解下列方程组（1）（2）（3）)(6441125为已知数a a y x a y x ⎩⎨⎧=-=+ （4）（5）（6）．（7）（8）⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x（9）（10） ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x 2．求适合的x ，y 的值．3．已知关于x ，y 的二元一次方程y=kx+b 的解有和．（1）求k ，b 的值．（2）当x=2时，y 的值．（3）当x 为何值时，y=3？1．解下列方程组（1）（2）；（3）；（4）（5）．（6）（7）（8）（9）（10）； 2．在解方程组时，由于粗心，甲看错了方程组中的a ，而得解为，乙看错了方程组中的b ，而得解为．（1）甲把a 看成了什么，乙把b 看成了什么？（2）求出原方程组的正确解.二元一次方程组解法练习题精选参考答案与试题解析一．解答题（共16小题）1．求适合的x ，y 的值．考点：解二元一次方程组．分析：先把两方程变形（去分母），得到一组新的方程，然后在用加减消元法消去未知数x ，求出y 的值，继而求出x 的值．解答：解：由题意得：，由（1）×2得：3x ﹣2y=2（3），由（2）×3得：6x+y=3（4），（3）×2得：6x ﹣4y=4（5），（5）﹣（4）得：y=﹣，把y 的值代入（3）得：x=，∴．点评：本题考查了二元一次方程组的解法，主要运用了加减消元法和代入法．2．解下列方程组（1）（2）（3）（4）．考点：解二元一次方程组．分析：（1）（2）用代入消元法或加减消元法均可；（3）（4）应先去分母、去括号化简方程组，再进一步采用适宜的方法求解．解答：解：（1）①﹣②得，﹣x=﹣2，解得x=2，把x=2代入①得，2+y=1，解得y=﹣1．故原方程组的解为．（2）①×3﹣②×2得，﹣13y=﹣39，解得，y=3，把y=3代入①得，2x﹣3×3=﹣5，解得x=2．故原方程组的解为．（3）原方程组可化为，①+②得，6x=36，x=6，①﹣②得，8y=﹣4，y=﹣．所以原方程组的解为．（4）原方程组可化为：，①×2+②得，x=，把x=代入②得，3×﹣4y=6，y=﹣．所以原方程组的解为．点评：利用消元法解方程组，要根据未知数的系数特点选择代入法还是加减法：①相同未知数的系数相同或互为相反数时，宜用加减法；②其中一个未知数的系数为1时，宜用代入法．3．解方程组：考点：解二元一次方程组．专题：计算题．分析：先化简方程组，再进一步根据方程组的特点选用相应的方法：用加减法．解答：解：原方程组可化为，①×4﹣②×3，得7x=42，解得x=6．把x=6代入①，得y=4．所以方程组的解为．点评：；二元一次方程组无论多复杂，解二元一次方程组的基本思想都是消元．消元的方法有代入法和加减法．4．解方程组：考点：解二元一次方程组．专题：计算题．分析：把原方程组化简后，观察形式，选用合适的解法，此题用加减法求解比较简单．解答：解：（1）原方程组化为，①+②得：6x=18，∴x=3．代入①得：y=．所以原方程组的解为．点评：要注意：两个二元一次方程中同一未知数的系数相反或相等时，把这两个方程的两边相加或相减，就能消去这个未知数，得到一个一元一次方程，这种方法叫做加减消元法．本题适合用此法．5．解方程组：考点：解二元一次方程组．专题：计算题；换元法．分析：本题用加减消元法即可或运用换元法求解．解答：解：，①﹣②，得s+t=4，①+②，得s﹣t=6，即，解得．所以方程组的解为．点评：此题较简单，要熟练解方程组的基本方法：代入消元法和加减消元法．6．已知关于x，y的二元一次方程y=kx+b 的解有和．（1）求k，b的值．（2）当x=2时，y的值．（3）当x为何值时，y=3？考点：解二元一次方程组．专题：计算题．分析：（1）将两组x，y的值代入方程得出关于k、b 的二元一次方程组，再运用加减消元法求出k、b的值．（2）将（1）中的k、b代入，再把x=2代入化简即可得出y的值．（3）将（1）中的k、b和y=3代入方程化简即可得出x的值．解答：解：（1）依题意得：①﹣②得：2=4k，所以k=，所以b=．（2）由y=x+，把x=2代入，得y=．（3）由y=x+把y=3代入，得x=1．点评：本题考查的是二元一次方程的代入消元法和加减消元法，通过已知条件的代入，可得出要求的数．7．解方程组：（1）；（2）．考点：解二元一次方程组．分析：根据各方程组的特点选用相应的方法：（1）先去分母再用加减法，（2）先去括号，再转化为整式方程解答．解答：解：（1）原方程组可化为，①×2﹣②得：y=﹣1，将y=﹣1代入①得：x=1．∴方程组的解为；（2）原方程可化为，即，①×2+②得：17x=51，x=3，将x=3代入x﹣4y=3中得：y=0．∴方程组的解为．点评：这类题目的解题关键是理解解方程组的基本思想是消元，掌握消元的方法有：加减消元法和代入消元法．根据未知数系数的特点，选择合适的方法．8．解方程组：考点：解二元一次方程组．专题：计算题．分析：本题应把方程组化简后，观察方程的形式，选用合适的方法求解．解答：解：原方程组可化为，①+②，得10x=30，x=3，代入①，得15+3y=15，y=0．则原方程组的解为．点评：解答此题应根据各方程组的特点，有括号的去括号，有分母的去分母，然后再用代入法或加减消元法解方程组．9．解方程组：考点：解二元一次方程组．专题：计算题．分析：本题为了计算方便，可先把（2）去分母，然后运用加减消元法解本题．解答：解：原方程变形为：，两个方程相加，得4x=12，x=3．把x=3代入第一个方程，得4y=11，y=．解之得．点评：本题考查的是二元一次方程组的解法，方程中含有分母的要先化去分母，再对方程进行化简、消元，即可解出此类题目．10．解下列方程组：（1）（2）考点：解二元一次方程组．专题：计算题．分析：此题根据观察可知：（1）运用代入法，把①代入②，可得出x，y的值；（2）先将方程组化为整系数方程组，再利用加减消元法求解．解答：解：（1），由①，得x=4+y③，代入②，得4（4+y）+2y=﹣1，所以y=﹣，把y=﹣代入③，得x=4﹣=．所以原方程组的解为．（2）原方程组整理为，③×2﹣④×3，得y=﹣24，把y=﹣24代入④，得x=60，所以原方程组的解为．点评：此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过题目的训练达到对知识的强化和运用．11．解方程组：（1）（2）考点：解二元一次方程组．专题：计算题；换元法．分析：方程组（1）需要先化简，再根据方程组的特点选择解法；方程组（2）采用换元法较简单，设x+y=a，x﹣y=b，然后解新方程组即可求解．解答：解：（1）原方程组可化简为，解得．（2）设x+y=a，x﹣y=b，∴原方程组可化为，解得，∴∴原方程组的解为．点评：此题考查了学生的计算能力，解题时要细心．12．解二元一次方程组：（1）；（2）．考点：解二元一次方程组．专题：计算题．分析：（1）运用加减消元的方法，可求出x、y的值；（2）先将方程组化简，然后运用加减消元的方法可求出x、y的值．解答：解：（1）将①×2﹣②，得15x=30，x=2，把x=2代入第一个方程，得y=1．则方程组的解是；（2）此方程组通过化简可得：，①﹣②得：y=7，把y=7代入第一个方程，得x=5．则方程组的解是．点评：此题考查的是对二元一次方程组的解法的运用和理解，学生可以通过题目的训练达到对知识的强化和运用．13．在解方程组时，由于粗心，甲看错了方程组中的a ，而得解为，乙看错了方程组中的b ，而得解为．（1）甲把a看成了什么，乙把b看成了什么？（2）求出原方程组的正确解．考点：解二元一次方程组．专题：计算题．分析：（1）把甲乙求得方程组的解分别代入原方程组即可；（2）把甲乙所求的解分别代入方程②和①，求出正确的a、b，然后用适当的方法解方程组．解答：解：（1）把代入方程组，得，解得：．把代入方程组，得，解得：．∴甲把a看成﹣5；乙把b看成6；（2）∵正确的a是﹣2，b是8，∴方程组为，解得：x=15，y=8．则原方程组的解是．点评：此题难度较大，需同学们仔细阅读，弄清题意再解答．14．考点：解二元一次方程组．分析：先将原方程组中的两个方程分别去掉分母，然后用加减消元法求解即可．解答：解：由原方程组，得，由（1）+（2），并解得x=（3），把（3）代入（1），解得y=∴原方程组的解为．点评：用加减法解二元一次方程组的一般步骤：1．方程组的两个方程中，如果同一个未知数的系数既不互为相反数又不相等，就用适当的数去乘方程的两边，使一个未知数的系数互为相反数或相等；2．把两个方程的两边分别相加或相减，消去一个未知数，得到一个一元一次方程；3．解这个一元一次方程；4．将求出的未知数的值代入原方程组的任意一个方程中，求出另一个未知数，从而得到方程组的解．15．解下列方程组：（1）；（2）．考点：解二元一次方程组．分析：将两个方程先化简，再选择正确的方法进行消元．解答：解：（1）化简整理为，①×3，得3x+3y=1500③，②﹣③，得x=350．把x=350代入①，得350+y=500，∴y=150．故原方程组的解为．（2）化简整理为，①×5，得10x+15y=75③，②×2，得10x﹣14y=46④，③﹣④，得29y=29，∴y=1．把y=1代入①，得2x+3×1=15，∴x=6．故原方程组的解为．点评：方程组中的方程不是最简方程的，最好先化成最简方程，再选择合适的方法解方程．16．解下列方程组：（1）（2）考点：解二元一次方程组．分析：观察方程组中各方程的特点，用相应的方法求解．解答：解：（1）①×2﹣②得：x=1，将x=1代入①得：2+y=4，y=2．∴原方程组的解为；（2）原方程组可化为，①×2﹣②得：﹣y=﹣3，y=3．将y=3代入①得：x=﹣2．∴原方程组的解为．点评：解此类题目要注意观察方程组中各方程的特点，采用加减法或代入法求解．。

二元一次方程组习题及答案100道

二元一次方程组习题及答案100道二元一次方程组习题及答案100道1.2x+9y=813x+y=342.9x+4y=358x+3y=303.7x+2y=527x+4y=624.4x+6y=549x+2y=875.2x+y=72x+5y=196.x+2y=213x+5y=567.5x+7y=525x+2y=228.5x+5y=657x+7y=203x+4y=21 10.5x+7y=41 5x+8y=44 11.7x+5y=54 3x+4y=38 12.x+8y=154x+y=29 13.3x+6y=24 9x+5y=46 14.9x+2y=62 4x+3y=36 15.9x+4y=46 7x+4y=42 16.9x+7y=135 4x+y=41 17.3x+8y=51 x+6y=27 18.9x+3y=99 4x+7y=95 19.9x+2y=38 3x+6y=18 20.5x+5y=45 7x+9y=69 21.8x+2y=2822.x+6y=143x+3y=2723.7x+4y=672x+8y=2624.5x+4y=527x+6y=744x+6y=1626.6x+6y=486x+3y=4227.8x+2y=167x+y=1128.4x+9y=778x+6y=9429.6x+8y=687x+6y=6630.2x+2y=227x+2y=471) 66x+17y=3967 25x+y=1200答案：x=48 y=47 (2) 18x+23y=2303 74x-y=1998 答案：x=27 y=79(3) 44x+90y=7796 44x+y=3476答案：x=79 y=48 (4) 76x-66y=4082 30x-y=2940 答案：x=98 y=51 (5) 67x+54y=8546 71x-y=5680 答案：x=80 y=59 (6) 42x-95y=-1410 21x-y=1575 答案：x=75 y=48 (7) 47x-40y=85334x-y=2006答案：x=59 y=48 (8) 19x-32y=-1786 75x+y=4950 答案：x=66 y=95 (9) 97x+24y=7202 58x-y=2900 答案：x=50 y=98 (10) 42x+85y=6362 63x-y=1638 答案：x=26 y=62 (11) 85x-92y=-251827x-y=486答案：x=18 y=44 (12) 79x+40y=2419 56x-y=1176 答案：x=21 y=19 (13) 80x-87y=2156 22x-y=880 答案：x=40 y=12 (14) 32x+62y=5134 57x+y=2850 答案：x=50 y=57 (15) 83x-49y=82答案：x=37 y=61 (16) 91x+70y=5845 95x-y=4275 答案：x=45 y=25 (17) 29x+44y=5281 88x-y=3608 答案：x=41 y=93 (18) 25x-95y=-4355 40x-y=2000 答案：x=50 y=59 (19) 54x+68y=3284 78x+y=1404 答案：x=18 y=34 (20) 70x+13y=3520 52x+y=2132 答案：x=41 y=50 (21) 48x-54y=-3186 24x+y=1080 答案：x=45 y=99 (22) 36x+77y=7619 47x-y=799答案：x=17 y=91 (23) 13x-42y=-2717 31x-y=1333 答案：x=43 y=78 (24) 28x+28y=3332 52x-y=4628 答案：x=89 y=30 (25) 62x-98y=-2564 46x-y=2024 答案：x=44 y=54 (26) 79x-76y=-4388 26x-y=832 答案：x=32 y=91 (27) 63x-40y=-821 42x-y=546答案：x=13 y=41(28) 69x-96y=-1209 42x+y=3822答案：x=91 y=78 (29) 85x+67y=7338 11x+y=308 答案：x=28 y=74 (30) 78x+74y=12928 14x+y=1218 答案：x=87 y=83 (31) 39x+42y=5331 59x-y=5841 答案：x=99 y=35 (32) 29x+18y=1916 58x+y=2320 答案：x=40 y=42 (33) 40x+31y=6043 45x-y=3555 答案：x=79 y=93 (34) 47x+50y=8598 45x+y=3780 答案：x=84 y=93 (35) 45x-30y=-1455 29x-y=725 答案：x=25 y=86 (36) 11x-43y=-136147x+y=799答案：x=17 y=36 (37) 33x+59y=3254 94x+y=1034 答案：x=11 y=49 (38) 89x-74y=-2735 68x+y=1020 答案：x=15 y=55 (39) 94x+71y=7517 78x+y=3822 答案：x=49 y=41 (40) 28x-62y=-4934 46x+y=552 答案：x=12 y=85 (41) 75x+43y=8472 17x-y=1394 答案：x=82 y=54 (42) 41x-38y=-1180 29x+y=1450答案：x=75 y=14 (44) 95x-56y=-401 90x+y=1530 答案：x=17 y=36 (45) 93x-52y=-852 29x+y=464答案：x=16 y=45 (46) 93x+12y=8823 54x+y=4914 答案：x=91 y=30 (47) 21x-63y=84 20x+y=1880答案：x=94 y=30 (48) 48x+93y=9756 38x-y=950答案：x=25 y=92 (49) 99x-67y=4011 75x-y=5475 答案：x=73 y=48 (50) 83x+64y=9291 90x-y=3690 答案：x=41 y=92 (51) 17x+62y=3216 75x-y=7350 答案：x=98 y=25 (52) 77x+67y=2739 14x-y=364答案：x=26 y=11(53) 20x-68y=-4596 14x-y=924答案：x=66 y=87 (54) 23x+87y=4110 83x-y=5727 答案：x=69 y=29 (55) 22x-38y=804 86x+y=6708答案：x=78 y=24 (56) 20x-45y=-3520 56x+y=728 答案：x=13 y=84 (57) 46x+37y=7085 61x-y=4636 答案：x=76 y=97 (58) 17x+61y=4088 71x+y=5609 答案：x=79 y=45 (59) 51x-61y=-1907 89x-y=2314 答案：x=26 y=53 (60) 69x-98y=-2404 21x+y=1386 答案：x=66 y=71 (61) 15x-41y=75474x-y=6956答案：x=94 y=16 (62) 78x-55y=656 89x+y=5518答案：x=62 y=76 (63) 29x+21y=1633 31x-y=713答案：x=23 y=46 (64) 58x-28y=2724 35x+y=3080 答案：x=88 y=85 (65) 28x-63y=-2254 88x-y=2024 答案：x=23 y=46 (66) 43x+50y=7064 85x+y=8330 答案：x=98 y=57 (67) 58x-77y=1170 38x-y=2280 答案：x=60 y=30 (68) 92x+83y=11586 43x+y=3010 答案：x=70 y=62 (69) 99x+82y=6055 52x-y=1716 答案：x=33 y=34 (70) 15x+26y=1729 94x+y=8554答案：x=41 y=29 (72) 94x+66y=10524 84x-y=7812 答案：x=93 y=27 (73) 65x-79y=-5815 89x+y=2314 答案：x=26 y=95 (74) 96x+54y=6216 63x-y=1953 答案：x=31 y=60 (75) 60x-44y=-352 33x-y=1452 答案：x=44 y=68 (76) 79x-45y=510 14x-y=840答案：x=60 y=94 (77) 29x-35y=-218 59x-y=4897 答案：x=83 y=75(78) 33x-24y=1905 30x+y=2670答案：x=89 y=43 (79) 61x+94y=11800 93x+y=5952 答案：x=64 y=84 (80) 61x+90y=5001 48x+y=2448 答案：x=51 y=21 (81) 93x-19y=286x-y=1548答案：x=18 y=88 (82) 19x-96y=-5910 30x-y=2340 答案：x=78 y=77 (83) 80x+74y=8088 96x-y=8640 答案：x=90 y=12 (84) 53x-94y=1946 45x+y=2610 答案：x=58 y=12 (85) 93x+12y=9117 28x-y=2492 答案：x=89 y=70 (86) 66x-71y=-167399x-y=7821答案：x=79 y=97 (87) 43x-52y=-1742 76x+y=1976 答案：x=26 y=55 (88) 70x+35y=8295 40x+y=2920 答案：x=73 y=91 (89) 43x+82y=4757 11x+y=231 答案：x=21 y=47 (90) 12x-19y=236 95x-y=7885答案：x=83 y=40 (91) 51x+99y=8031 71x-y=2911 答案：x=41 y=60 (92) 37x+74y=4403 69x-y=6003 答案：x=87 y=16 (93) 46x+34y=4820 71x-y=5183 答案：x=73 y=43 (94) 47x+98y=5861 55x-y=4565 答案：x=83 y=20(95) 30x-17y=23928x+y=1064答案：x=38 y=53(96) 55x-12y=411279x-y=7268答案：x=92 y=79(97) 27x-24y=-45067x-y=3886答案：x=58 y=84(98) 97x+23y=811914x+y=966答案：x=69 y=62(99) 84x+53y=1127570x+y=6790答案：x=97 y=59(100) 51x-97y=29719x-y=1520答案：x=80 y=39教育之通病是教用脑的人不用手，不教用手的人用脑，所以一无所能。

七年级数学二元一次方程组经典练习题及答案

二元一次方程组练习题100道（卷一）（范围：代数：二元一次方程组）一、判断1、⎪⎩⎪⎨⎧-==312y x 是方程组⎪⎪⎩⎪⎪⎨⎧=-=-910326523y x y x 的解 …………（） 2、方程组⎩⎨⎧=+-=5231y x xy 的解是方程3x -2y =13的一个解（）3、由两个二元一次方程组成方程组一定是二元一次方程组（）4、方程组⎪⎪⎩⎪⎪⎨⎧=-++=+++25323473523y x y x ，可以转化为⎩⎨⎧-=--=+27651223y x y x （）5、若(a 2-1)x 2+(a -1)x +(2a -3)y =0是二元一次方程，则a 的值为±1（）6、若x +y =0，且|x |=2，则y 的值为2 …………（）7、方程组⎩⎨⎧=+-=+81043y x xm my mx 有唯一的解，那么m 的值为m ≠-5 …………（）8、方程组⎪⎩⎪⎨⎧=+=+623131y x y x 有无数多个解 …………（） 9、x +y =5且x ，y 的绝对值都小于5的整数解共有5组 …………（） 10、方程组⎩⎨⎧=+=-3513y x y x 的解是方程x +5y =3的解，反过来方程x +5y =3的解也是方程组⎩⎨⎧=+=-3513y x y x 的解 ………（）11、若|a +5|=5，a +b =1则32-的值为b a ………（）12、在方程4x -3y =7里，如果用x 的代数式表示y ，则437yx +=（）二、选择：13、任何一个二元一次方程都有（）（A ）一个解；（B ）两个解；（C ）三个解；（D ）无数多个解；14、一个两位数，它的个位数字与十位数字之和为6，那么符合条件的两位数的个数有（）（A ）5个（B ）6个（C ）7个（D ）8个 15、如果⎩⎨⎧=+=-423y x ay x 的解都是正数，那么a 的取值范围是（）（A ）a <2；（B ）34->a ；（C ）342<<-a ；（D ）34-<a ； 16、关于x 、y 的方程组⎩⎨⎧=-=+m y x my x 932的解是方程3x +2y =34的一组解，那么m 的值是（）（A ）2；（B ）-1；（C ）1；（D ）-2；17、在下列方程中，只有一个解的是（）（A ）⎩⎨⎧=+=+0331y x y x（B ）⎩⎨⎧-=+=+2330y x y x（C ）⎩⎨⎧=-=+4331y x y x（D ）⎩⎨⎧=+=+3331y x y x18、与已知二元一次方程5x -y =2组成的方程组有无数多个解的方程是（）（A ）15x -3y =6 （B ）4x -y =7 （C ）10x +2y =4 （D ）20x -4y =319、下列方程组中，是二元一次方程组的是（）（A ）⎪⎩⎪⎨⎧=+=+9114y x y x （B ）⎩⎨⎧=+=+75z y y x（C ）⎩⎨⎧=-=6231y x x（D ）⎩⎨⎧=-=-1y x xyy x20、已知方程组⎩⎨⎧-=+=-135b y ax y x 有无数多个解，则a 、b 的值等于（）（A ）a =-3,b =-14（B ）a =3,b =-7 （C ）a =-1,b =9（D ）a =-3,b =14 21、若5x -6y =0，且xy ≠0，则y x yx 3545--的值等于（）（A ）32（B ）23 （C ）1 （D ）-122、若x 、y 均为非负数，则方程6x =-7y 的解的情况是（）（A ）无解（B ）有唯一一个解（C ）有无数多个解（D ）不能确定23、若|3x +y +5|+|2x -2y -2|=0，则2x 2-3xy 的值是（）（A ）14 （B ）-4 （C ）-12 （D ）12 24、已知⎩⎨⎧-==24y x 与⎩⎨⎧-=-=52y x 都是方程y =kx +b 的解，则k 与b 的值为（）（A ）21=k ，b =-4 （B ）21-=k ，b =4 （C ）21=k ，b =4（D ）21-=k ，b =-4三、填空：25、在方程3x +4y =16中，当x =3时，y =________，当y =-2时，x =_______ 若x 、y 都是正整数，那么这个方程的解为___________； 26、方程2x +3y =10中，当3x -6=0时，y =_________；27、如果0.4x -0.5y =1.2，那么用含有y 的代数式表示的代数式是_____________； 28、若⎩⎨⎧-==11y x 是方程组⎩⎨⎧-=-=+1242a y x b y ax 的解，则⎩⎨⎧==______________b a ； 29、方程|a |+|b |=2的自然数解是_____________； 30、如果x =1，y =2满足方程141=+y ax ，那么a =____________； 31、已知方程组⎩⎨⎧-=+=+m y x ay x 26432有无数多解，则a =______，m =______；32、若方程x -2y +3z =0，且当x =1时，y =2，则z =______；33、若4x +3y +5=0，则3(8y -x )-5(x +6y -2)的值等于_________；34、若x +y =a ，x -y =1同时成立，且x 、y 都是正整数，则a 的值为________； 35、从方程组)0(030334≠⎩⎨⎧=+-=--xyz z y x z y x 中可以知道，x :z =_______；y :z =________；36、已知a -3b =2a +b -15=1，则代数式a 2-4ab +b 2+3的值为__________；四、解方程组37、⎪⎪⎩⎪⎪⎨⎧=-=-1332343n m nm ； 38、)(6441125为已知数a a y x a y x ⎩⎨⎧=-=+；39、⎪⎪⎩⎪⎪⎨⎧=++=+125432y x yx y x ； 40、⎪⎩⎪⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x ； 41、⎪⎪⎩⎪⎪⎨⎧++=++=+=+6253)23(22)32(32523233y x y x yx y x ； 42、⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x ；43、⎪⎩⎪⎨⎧=-+-=-+=-+3113y x z x z y z y x ； 44、⎪⎩⎪⎨⎧=+=+=+101216x z z y y x ；45、⎪⎩⎪⎨⎧=-+=+-=-+35351343z y x z y x z y x ； 46、⎪⎩⎪⎨⎧=+-==30325:3:7:4:z y x z x y x ；五、解答题：47x 的系数，解得⎪⎪⎩⎪⎪⎨⎧==475847107y x ；乙看错了方程②中的y 的系数，解得⎪⎪⎩⎪⎪⎨⎧==19177681y x ，若两人的计算都准确无误，请写出这个方程组，并求出此方程组的解；48、使x +4y =|a |成立的x 、y 的值，满足(2x +y -1)2+|3y -x |=0，又|a |+a =0，求a 的值；49、代数式ax 2+bx +c 中，当x =1时的值是0，在x =2时的值是3，在x =3时的值是28，试求出这个代数式；50、要使下列三个方程组成的方程组有解，求常数a 的值。

二元一次方程组练习题(含答案).doc

二元一次方程组练习题(含答案)二元一次方程组练习题一、选择题：1．下列方程中，是二元一次方程的是（）A．3x－2y=4z B．6xy+9=0 C．1x+4y=6 D．4x=24y-2．下列方程组中，是二元一次方程组的是（）A．228 423119 (23754624)x yx y a b xB C Dx y b c y x x y+= +=-=⎧⎧=⎧⎧⎨⎨⎨⎨+=-==-=⎩⎩⎩⎩3．二元一次方程5a－11b=21 （）A．有且只有一解B．有无数解C．无解D．有且只有两解4．方程y=1－x与3x+2y=5的公共解是（）A．3333...2422 x x x xB C Dy y y y==-==-⎧⎧⎧⎧⎨⎨⎨⎨===-=-⎩⎩⎩⎩5．若│x－2│+（3y+2）2=0，则的值是（）A．－1 B．－2 C．－3 D．3 26．方程组43235x y kx y-=⎧⎨+=⎩的解与x与y的值相等，则k等于（）7．下列各式，属于二元一次方程的个数有（）①xy+2x－y=7；②4x+1=x－y；③1x+y=5；④x=y；⑤x2－y2=2⑥6x－2y ⑦x+y+z=1 ⑧y（y－1）=2y2－y2+xA．1 B．2 C．3 D．48．某年级学生共有246人，其中男生人数y比女生人数x的2倍少2人，•则下面所列的方程组中符合题意的有（）A．246246216246... 22222222 x y x y x y x yB C Dy x x y y x y x+=+=+=+=⎧⎧⎧⎧⎨⎨⎨⎨=-=+=+=+⎩⎩⎩⎩二、填空题9．已知方程2x+3y－4=0，用含x的代数式表示y为：y=_______；用含y的代数式表示x为：x=________．10．在二元一次方程－12x+3y=2中，当x=4时，y=_______；当y=－1时，x=______．11．若x3m－3－2y n－1=5是二元一次方程，则m=_____，n=______．12．已知2,3xy=-⎧⎨=⎩是方程x－ky=1的解，那么k=_______．13．已知│x－1│+（2y+1）2=0，且2x－ky=4，则k=_____．14．二元一次方程x+y=5的正整数解有______________．15．以57xy=⎧⎨=⎩为解的一个二元一次方程是_________．16．已知2316x mx yy x ny=-=⎧⎧⎨⎨=--=⎩⎩是方程组的解，则m=_______，n=______．三、解答题17．当y=－3时，二元一次方程3x+5y=－3和3y－2ax=a+2（关于x，y的方程）•有相同的解，求a的值．18．如果（a－2）x+（b+1）y=13是关于x，y的二元一次方程，则a，b满足什么条件？19．二元一次方程组437(1)3x ykx k y+=⎧⎨+-=⎩的解x，y的值相等，求k．20．已知x，y是有理数，且（│x│－1）2+（2y+1）2=0，则x－y的值是多少？21．已知方程12x+3y=5，请你写出一个二元一次方程，•使它与已知方程所组成的方程组的解为41xy=⎧⎨=⎩．22．根据题意列出方程组：（1）明明到邮局买0.8元与2元的邮票共13枚，共花去20元钱，•问明明两种邮票各买了多少枚？（2）将若干只鸡放入若干笼中，若每个笼中放4只，则有一鸡无笼可放；•若每个笼里放5只，则有一笼无鸡可放，问有多少只鸡，多少个笼？23．方程组2528x yx y+=⎧⎨-=⎩的解是否满足2x－y=8？满足2x－y=8的一对x，y的值是否是方程组2528x yx y+=⎧⎨-=⎩的解？24．（开放题）是否存在整数m，使关于x的方程2x+9=2－（m－2）x在整数范围内有解，你能找到几个m的值？你能求出相应的x的解吗？一、选择题1．D 解析：掌握判断二元一次方程的三个必需条件：①含有两个未知数；②含有未知数的项的次数是1；③等式两边都是整式．2．A 解析：二元一次方程组的三个必需条件：①含有两个未知数，②每个含未知数的项次数为1；③每个方程都是整式方程．3．B 解析：不加限制条件时，一个二元一次方程有无数个解．4．C 解析：用排除法，逐个代入验证．5．C 解析：利用非负数的性质．6．B7．C 解析：根据二元一次方程的定义来判定，•含有两个未知数且未知数的次数不超过1次的整式方程叫二元一次方程，注意⑧整理后是二元一次方程．8．B二、填空题9．424332x y--10．43－1011．43，2 解析：令3m－3=1，n－1=1，∴m=43，n=2．12．－1 解析：把2,3xy=-⎧⎨=⎩代入方程x－ky=1中，得－2－3k=1，∴k=－1．13．4 解析：由已知得x－1=0，2y+1=0，∴x=1，y=－12，把112xy=⎧⎪⎨=-⎪⎩代入方程2x－ky=4中，2+12k=4，∴k=1．14．解：12344321 x x x xy y y y====⎧⎧⎧⎧⎨⎨⎨⎨====⎩⎩⎩⎩解析：∵x+y=5，∴y=5－x，又∵x，y均为正整数，∴x为小于5的正整数．当x=1时，y=4；当x=2时，y=3；当x=3，y=2；当x=4时，y=1．∴x+y=5的正整数解为12344321 x x x xy y y y====⎧⎧⎧⎧⎨⎨⎨⎨====⎩⎩⎩⎩15．x+y=12 解析：以x与y的数量关系组建方程，如2x+y=17，2x－y=3等，此题答案不唯一．16．1 4 解析：将2316x mx y y x ny =-=⎧⎧⎨⎨=--=⎩⎩代入方程组中进行求解．三、解答题 17．解：∵y=－3时，3x+5y=－3，∴3x+5×（－3）=－3，∴x=4，∵方程3x+5y=•－•3•和3x －2ax=a+2有相同的解，∴3×（－3）－2a ×4=a+2，∴a=－119． 18．解：∵（a －2）x+（b+1）y=13是关于x ，y 的二元一次方程，∴a －2≠0，b+1≠0，•∴a ≠2，b ≠－1解析：此题中，若要满足含有两个未知数，需使未知数的系数不为0．（•若系数为0，则该项就是0）19．解：由题意可知x=y ，∴4x+3y=7可化为4x+3x=7，∴x=1，y=1．将x=1，y=•1•代入kx+（k －1）y=3中得k+k －1=3，∴k=2 解析：由两个未知数的特殊关系，可将一个未知数用含另一个未知数的代数式代替，化“二元”为“一元”，从而求得两未知数的值．20．解：由（│x │－1）2+（2y+1）2=0，可得│x │－1=0且2y+1=0，∴x=±1，y=－12．当x=1，y=－12时，x －y=1+12=32；当x=－1，y=－12时，x －y=－1+12=－12．解析：任何有理数的平方都是非负数，且题中两非负数之和为0，则这两非负数（│x │－1）2与（2y+1）2都等于0，从而得到│x │－1=0，2y+1=0．21．解：经验算41x y =⎧⎨=⎩是方程12x+3y=5的解，再写一个方程，如x －y=3． 22．（1）解：设0．8元的邮票买了x 枚，2元的邮票买了y 枚，根据题意得130.8220x y x y +=⎧⎨+=⎩．（2）解：设有x 只鸡，y 个笼，根据题意得415(1)y x y x+=⎧⎨-=⎩． 23．解：满足，不一定．解析：∵2528x yx y+=⎧⎨-=⎩的解既是方程x+y=25的解，也满足2x－y=8，•∴方程组的解一定满足其中的任一个方程，但方程2x－y=8的解有无数组，如x=10，y=12，不满足方程组25 28x yx y+=⎧⎨-=⎩．24．解：存在，四组．∵原方程可变形为－mx=7，∴当m=1时，x=－7；m=－1时，x=7；m=•7时，x=－1；m=－7时x=1．。

二元一次方程组计算题专项训练

二元一次方程组计算题专项训练一、用代入法解下列方程组（1）⎩⎨⎧=+=-5253y x y x （2）⎩⎨⎧=--=523x y x y二、用加减法解下列方程组（1）⎩⎨⎧-=+-=-53412911y x y x （2）⎩⎨⎧=+=-524753y x y x 三、用适当的方法解下列方程组： 1、⎩⎨⎧=+=+16156653y x y x 2、{3x y 304x 3y 17－－＝＋＝（3）⎪⎩⎪⎨⎧=-=+2.03.05.0523151y x y x 4、x 2y+2=02y+22x536⎧⎪⎨⎪⎩－－－＝7⎪⎩⎪⎨⎧=+=+=+634323x z z y y x 8234x y y z z x +=⎧⎪+=⎨⎪+=⎩四、解答题1、如果1032162312=--+--b a b a y x 是一个二元一次方程，那么数a =？b =？2、已知⎩⎨⎧-==24y x 与⎩⎨⎧-=-=52y x 都是方程y =kx +b 的解，则k 与b 的值为多少？3、若方程组322,543x y k x y k +=⎧⎨+=+⎩的解之和为x+y=-5，求k 的值，并解此方程组．4、已知方程组4234ax by x y -=⎧⎨+=⎩与2432ax by x y +=⎧⎨-=⎩的解相同，那么a=?b=? 5、关于x 、y 的方程组⎩⎨⎧=-=+m y x m y x 932的解是方程3x +2y =17的一组解，那么m 的值是多少？ 6、一个星期天，小明和小文同解一个二元一次方程组{ax+by=16bx+ay=1　①　②小明把方程①抄错，求得的解为{x=1y=3－，小文把方程②抄错，求得的解为{x=3y=2，求原方程组的解。